Category: Class 6

Balbharti Maharashtra State Board Class 6 Science Solutions Chapter 11 Work and Energy Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Science Solutions Chapter 11 Work and Energy

Class 6 Science Chapter 11 Work and Energy Textbook Questions and Answers

1. Fill in each blank with the appropriate term from the brackets.

Question a.
A bucketful of water is to be drawn from a well ………. will be done when a ………… is applied to do this, because there will be an ……………. of water.
(displacement, workforce)
Answer:
work, force, displacement

Question b.
If a ball is dropped on the sloping roof of a house, it acquires ……………. and falls on the ground. That is transformation of ………… energy into ……….. energy takes place.
(kinetic, potential, motion)
Answer:
motion, kinetic, potential

Question c.
You might have seen some beautiful fireworks during Diwali. It is an example of transformation of ……….. energy into ………………. energy.
(light, atom, chemical, solar)
Answer:
chemical, light

Question d.
The solar cooker is an application of the ………… energy of the sun, while solar cells, solar lamps are applications of the ………….. energy of the sun.
(light, chemical, heat)
Answer:
heat, light

Question e.
One labourer carried four pans of road metal through a distance of 100 metres. If he carries two pans of road metal through a 200 metre distance …………. work will be done.
(equal, more, less)
Answer:
equal

Question f.
The capacity that an object has for doing work is called ………… .
(energy, displacement, force)
Answer:
energy

2. Match the pairs.

Question a.

Column ‘A’	Column ‘B’
1. Rolling object	a. Heat energy
2. Food	b. Atomic energy
3. Stretched bow	c. Kinetic energy
4. Sunlight	d. Potential energy
5. Uranium	e. Chemical energy

Answer:

Column ‘A’	Column ‘B’
1. Rolling object	c. Kinetic energy
2. Food	e. Chemical energy
3. Stretched bow	d. Potential energy
4. Sunlight	a. Heat energy
5. Uranium	b. Atomic energy

3. Can you tell?

Question a.
When can we say that displacement has taken place?
Answer:
When the position of an object changes, we say that the object is displaced.

Question b.
What are the various forms of energy?
Answer:
Various forms of energy are: mechanical energy, heat energy, light energy, sound energy, chemical energy and electrical energy.

Question c.
Describe the natural chain of transformation of energy.
Answer:

1. In the course of water cycle, water evaporates due to the heat of the sun.
2. This water vapour forms clouds that give rain.
3. Rainwater flows into rivers and is stored in reservoirs or dams.
4. This stored water at a height has potential energy.
5. As the water falls down, this is transformed into kinetic energy.
6. When the water falls on the turbine, its kinetic energy is transferred to turbine.
7. The turbine rotates producing electrical energy.

Question d.
What should be taken into account for measuring work?
Answer:
For measuring work both force and displacement must be taken into account.

Question e.
Why should we save energy?
Answer:
Due to increasing population and increasing use of energy resources, there is a danger that limited reserves of coal, petrol, etc. will get exhausted. Hence, we should save energy for future generation.

Question f.
What is ‘green energy’?
Answer:
The energy resources which do not produce smoke and carbon gases such as carbon dioxide or carbon monoxide are called ‘green energy resources’. Energy from them is called green energy.

Question g.
What are the non-conventional energy resources?
Answer:
The resources that:

1. have not been used traditionally.
2. are inexhaustible and continuous.
3. That can be used in various forms again and again are called non-conventional energy resources.
4. e.g.: solar energy, wind energy, tidal energy, hydal power.

Question h.
Which forms of energy from the sun is used in solar energy devices?
Answer:

1. Heat energy from the sun is used in solar cookers, solar water heaters, solar driers.
2. Light energy from the sun is used in solar cells, solar panels.
3. Solar electric plants have the capacity to produce electricity on large scale.

Question i.
Why should we maximize the use of non- ntional energy sources?
Answer:

1. Due to increase in population there is increasing use of conventional sources like petrol, coal, etc. Their reserves are limited and they may get exhausted.
2. Hence, it will be better to use non- conventional sources of energy to save conventional resources for future.

4. Who is the odd-one-out?

Class 6 Science Chapter 11 Work And Energy Question 1.
Diesel, crude oil, natural gas, wind.
Answer:
wind

Work And Energy Class 6 Maharashtra Board Question 2.
A running car, hauling a log, a book kept on a table, picking up the school bag.
Answer:
A book kept on table.

Work And Energy Class 6 Question 3.
Sunlight, wind, wave, petrol.
Answer:
Petrol.

11 Work And Energy Class 6 Question 4.
Leaving the fan on in a vacant room, leaving the TV on while working, using A.C during winter, putting off the light when going out.
Answer:
putting off the light when going out.

5. Find out the types of energy from the following puzzle.

Question a.
Find out the types of energy from the following puzzle.

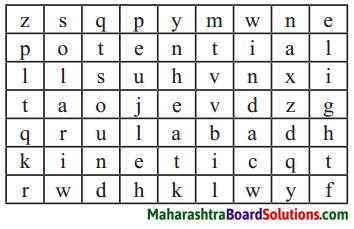
Answer:
Potential, Kinetic, Solar, Wind, Sound, Light, Heat

Activity:

Work And Energy Exercise Class 6 Question 1.
How can you save energy at home and in school? Discuss this with your friends and list all such measures. Put them into practice.

Work And Energy Class 6 Questions Answers Question 2.
Find out about energy saving devices available in the market.

Class 6 Science Chapter 11 Work and Energy Important Questions and Answers

Fill in the blanks with suitable words.

Work And Energy Class 6 Exercise Question 1.
Falling water possesses ………………… energy.
(potential, kinetic, chemical)
Answer:
kinetic

Work And Energy Class 6 Questions And Answers Question 2.
Heat is measured in unit called ……………….. .
(kilometres, kilogram, calorie)
Answer:
calorie

Class 6 Science Chapter 11 Question 3.
Plant stores the food in the form of ……………….. energy.
(mechanical, light, chemical)
Answer:
chemical

11. Work And Energy Class 6 Question 4.
We should use ……………….. energy resources with care.
(conventional, non-conventional, both)
Answer:
conventional

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
1. Solar energy	a. Waves
2. Tidal energy	b. Home cooking
3. Natural gas	c. Car
4. Petrol	d. Solar water heater

Answer:

Column ‘A’	Column ‘B’
1. Solar energy	d. Solar water heater
2. Tidal energy	a. Waves
3. Natural gas	b. Home cooking
4. Petrol	c. Car

Can you tell?

6th Science Work And Energy Question 1.
Water in dams or reservoirs shows potential energy.
Answer:
Rainwater flows into river and is stored in reservoirs on dams. These are at height and therefore, their water has potential energy.

Class 6 Science Chapter 11 Question Answer Question 2.
The sun is the most important source of all energy.
Answer:
All forms of energy are utilizing indirectly solar energy in all transformation of energy. Therefore, the sun is the most important source of all energy.

Question 3.
What is tidal energy?
Answer:
A wall is constructed at a narrow region of a creek. Due to waves generated by high and low tides, the turbine of the generator fitted in the wall starts rotating and electricity is generated.

Use your brain power!

Question 1.
Why do you get hungry after physical exercise?
Answer:

1. When we do physical exercise we use the energy stored in the body.
2. To replenish this energy, we have to eat. Hence we feel hungry.

Question 2.
From where does our body get energy.
Answer:
Our body gets energy from the food we eat.

Question 3.
Why do we get tired?
Answer:
When we do any work, we use the energy. If this energy level becomes very low, then we feel tired.

Question 4.
What is the unit of work and energy?
Answer:
The unit of work and energy in SI (System International) is ‘Joule’.

Question 5.
If no displacement occurs on applying a force, what does it indicate?
Answer:
If no displacement occurs, then no work is said to be performed.

Can you tell?

Question 1.
In the game of marbles, from where does one marble get energy to set another marble in motion?
Answer:
When we apply physical force to the fast marble, it gains some force and when it strikes the second marble, energy in the form of force is transferred to the second marble and this force sets the second marble in motion.

Question 2.
While playing carrom from where does the striker gets the energy to make the pieces move?
Answer:
When we strike the striker, the force exerted by our muscles is transferred to the striker. When the striker strikes the coin, this energy is transferred to the coin which may help to pocket the coin.

Question 3.
What will happen as result of the action in the picture?

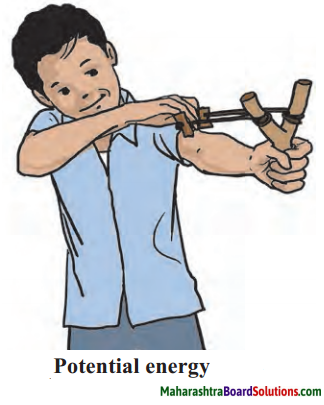
Question i.
The rubber band is released after streaching it.
Answer:
It comes back to its orriginal position.

Question ii.
A stone is held in the rubber of a catapult, the rubber is stretched and released.
Answer:
Stone gets thrown to a distance and rubber band cones back to its original position.

Let’s try this.

Question 1.
If we hold a convex lens over a sheet of paper in sunlight such that there is tiny spot of light on the paper for a while. What happens? Why?
Answer:

1. If a convex lens is held over a paper in sunlight such that there is a tiny spot of light on the paper for a while the paper bums.
2. This is due to the heat energy of the sun concentrated at a point due to the convex lens.

Question 2.
How does a picture appear on the screen of a TV?
Answer:
When a TV is switched on, the electrical energy is converted into light and sound energy. Hence, a picture appears on TV.

Question 3.
In which form is energy stored in plant food?
Answer:
Energy stored in plant food is in the form of chemical energy.

Question 4.
How is energy obtained from cooking gas?
Answer:
Energy obtained from cooking gas is heat energy which is obtained by conversion of chemical energy.

Question 5.
Why is Energy not visible to us?
Answer:
Energy is the capacity to do work. Energy is converted from one form to another in the form of work being done. Hence it is not visible to us.

How are we different from each other?

Question 1.
Potential energy and Kinetic energy
Answer:

Potential energy	Kinetic energy
1. Energy stored in an object due to its position is called potential energy.	1. Energy possessed by a body due to its motion is called kinetic energy.
2. No work is performed.	2. Work is performed.

Question 2.
Work and energy
Answer:

Work	Energy
1. When an object is displaced by applying force on it, work is said to be done.	1. Energy is the capacity to do work.
2. Work is done as a result of using energy.	2. Energy is the cause for work to be done.

Question 3.
Conventional and Non-conventional energy sources
Answer:

Conventional source of energy	Non-Conventional source of energy
1. Man has been using these energy resources for centuries.	1. These resources have not been used traditionally.

Classify as directed:

Question 1.
Into kinetic and potential energy
Waterfalls, water in a reservoir, a stretched spring, a boy running in a race.
Answer:

• Potential – water in a reservoir, a stretched spring.
• Kinetic – waterfalls, a boy running in a race.

Question 2.
Into conventional and non-conventional energy sources.
Tidal energy, diesel, cooking gas, coal, hydropower, solar energy.
Answer:

• Conventional energy sources – diesel, cooking gas, coal.
• Non-conventional energy sources – tidal energy, hydropower, solar energy.

Question 3.
Into different forms of energy

1. rubber band is released
2. cooking food
3. switching on fan
4. a battery
5. radio
6. TV

Answer:

1. Mechanical energy
2. Heat energy
3. Mechanical energy, electrical energy
4. Chemical energy
5. Sound energy
6. Light and sound energy

Define:

Question 1.
Work
Answer:
When an object is displaced by applying a force on it, work is said to be done.

Question 2.
Energy
Answer:
Energy is the capacity to do work.

Question 3.
Chemical energy
Answer:
The energy obtained through chemical action is called chemical energy.

Question 4.
Potential energy
Answer:
The energy which is stored in an object due to a specific state or position of that object is called potential energy.

Question 5.
Kinetic energy
Answer:
The energy obtained by the virtue of its motion is called kinetic energy.

Question 6.
Solar energy
Answer:
The enormous and continuous energy obtained from the sun is called solar energy. Solar energy is at the root of all energy available on earth.

Question 7.
Conventional energy resources: (non-renewable energy sources)
Answer:
The energy sources which man has been using for centuries and that cannot be replenished are called conventional energy sources.

Question 8.
Renewable energy sources: (non – conventional energy sources)
Answer:
The resources that have not been used traditionally and that are inexhaustible, continuous and can be used in various forms again and again are called renewable energy sources.

Explain – why?

Question 1.
Energy is not visible to us.
Answer:
There is energy in every substance in the universe. It is present in non-living as well as living things. But still we can only feel the energy when some work is done, e.g. When wind blows, we can feel the coolness in air. When we switch on the light in a dark room, we can see things due to light energy.

Question 2.
Save energy, (use alternative energy sources)
Answer:

1. Due to increasing population, there is increasing usage of energy resources.
2. There is a danger that limited reserves of conventional resources like diesel, crude oil, may get exhausted.
3. We should save energy so that future availability is ensured.
4. It will be better to use alternative and supplementary energy sources.

Question 3.
Methods of saving energy.
Answer:

1. Saving energy is as good as generating energy.
2. There are several ways of saving energy such as putting off lamps when not needed.
3. Making maximum use of sunlight.
4. Saving energy and energy resources is absolutely necessary. Otherwise, we will have to face the serious calamity like global warming.

Question 4.
State the energy conversions in following cases.

1. Solar water heater
2. Solar cell
3. Fission of uranium, thorium
4. Switch on mixer
5. Switch on lamp
6. Switch on TV
7. Switch on radio
8. Ram plays tabla
9. Ravi plays shehnai
10. You switch on the torch
11. Your mother lights the gas stove to cook
12. Dinesh is bursting crackers during Diwali

Answer:

1. Solar energy to heat energy
2. Solar energy to electrical energy
3. Atomic energy to heat energy and then to electrical energy
4. Electrical energy to mechanical energy
5. Electrical energy to light energy
6. Electrical energy to light energy and sound energy
7. Electrical energy to sound energy,
8. Mechanical energy to sound energy
9. Wind energy to sound energy
10. Chemical energy to light energy
11. Chemical energy to heat energy
12. Chemical energy to heat, light and sound energy

Observe the figure below and answer the question given.

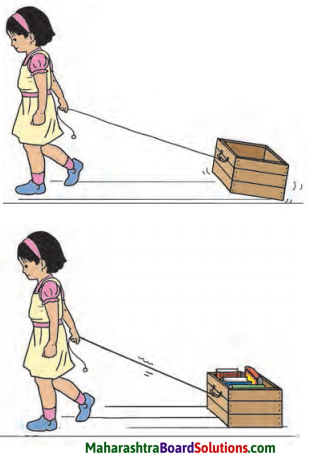
Question i.
In the above activity, which are the different forces acting on the box?
Answer:
In the above activity, muscular force, frictional force and gravitational force act on the box.

Question ii.
Is displacement possible without force?
Answer:
No, force has to be applied in order to displace the box.

Question iii.
If force is applied to both the boxes is same, which box will be displaced more?
Answer:
If force applied to both the boxes is same, then empty box will be displaced more than box with books.

Question iv.
If me e books are added to box, and same force is applied, will the displacement be more or less?
Answer:
If the same force is applied for a heavier load then the displacement will be less.

Question v.a.
If a force is applied with both the hands on a wall, will there be a displacement?
Answer:
Whatever be the amount of force applied, the wall will not be displaced.

Question b.
If no displacement occurs on applying as force, what does it indicate?
Answer:
If no displacement occurs, then no work is said to be performed.

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 13 मोठी आई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 13 मोठी आई

Marathi Sulabhbharti Class 6 Solutions Chapter 13 मोठी आई Textbook Questions and Answers

1. एका वाक्यात उत्तर लिहा.

प्रश्न अ.
घर बांधण्यासाठी कोणकोणत्या वस्तू लागतात?
उत्तर:
दगड, माती, विटा, चुना व लाकूड इत्यादी या वस्तू घर बांधण्यासाठी लागतात.

प्रश्न आ.
जमिनीच्या पोटात कोणकोणती खनिजे सापडतात?
उत्तर:
चांदी, रूपे, पितळ, तांबे, कथील, दगडी कोळसा, लोखंड इ. खनिजे जमिनीच्या पोटात सापडतात.

प्रश्न इ.
कारखान्यात धातूपासून कोणकोणत्या वस्तू तयार होतात?
उत्तर:
लोखंडी खुा, पलंग, सुया, टाचण्या, चाकू, कात्र्या, गुंड्या, काचेचे सामान, मोटारी, आगगाड्या, विमाने इत्यादी वस्तू कारखान्यात धातूपासून तयार होतात.

प्रश्न ई.
चुना कशासन तयार करतात?
उत्तर:
चुनखडीच्या खडकापासून चुना तयार करतात.

प्रश्न उ.
लेखिकेच्या मते मातृभूमीबद्दल प्रेमभाव का बाळगावा?
उत्तर:
माणसांना प्रत्येक गोष्ट या भूमीनेच दिली आहे, म्हणून लेखिकेच्या मते मातृभूमीबद्दल प्रेमभाव बाळगायला हवा.

2. तुम्ही खात असलेल्या अन्नपदार्थांतील कोणकोणत्या वस्तू जमिनीकडून आपणांस मिळतात, यांची यादी बनवा.

प्रश्न 1.
तुम्ही खात असलेल्या अन्नपदार्थांतील कोणकोणत्या वस्तू जमिनीकडून आपणांस मिळतात, यांची यादी बनवा.
उत्तर:

1. धान्य – ज्वारी, बाजरी, नाचणी, गहू, मळा, तांदूळ इ.
2. कडधान्य – मूग, मटकी, चवळी, वाटाणा, हरभरा, वाल, तूर, उडीद इ.
3. पालेभाज्या – मेथी, शेपू, तांदळी, चाकवत, पालक, माठ इ.
4. फळभाज्या – वांगी, कोबी, फ्लॉवर, दुधीभोपळा, दोडका, कारले, टोमॅटो, गवार, शेवगा, भेंडी, घेवडा, राजमा इ.
5. कंदमुळे – कांदा, गाजर, बीट, मुळा, रताळे, भुईमुगाच्या शेंगा इ.
6. फळे – केळी, चिकू, पेरू, आंबा, फणस, अननस, द्राक्षे, सफरचंद, जांभळे, कवठ, बोरे, पपई, काजू, बदाम, अक्रोड इ.

3. आपण मातृभूमीबद्दल प्रेमभाव का बाळगायला हवा ते तुमच्या शब्दांत लिहा.

प्रश्न 1.
आपण मातृभूमीबद्दल प्रेमभाव का बाळगायला हवा ते तुमच्या शब्दांत लिहा.
उत्तर:
मातृभूमी म्हणजेच जमीन, काळी आई आपणास अन्न-वस्त्र देते, दाग-दागिने देते, घरदार देते, धनधान्य देते, भांडीकुंडी देते, पाटी-पेन्सिल देते. त्या भूमीतले अन्न खाऊनच आपण मोठे झालो, शहाणे झालो. माणसांना प्रत्येक गोष्ट दिली ती या भूमीनेच. माती आहे म्हणूनच आपण जिवंत आहोत. म्हणून अशा या दातृत्वपूर्ण मातृभूमीबद्दल प्रेमभाव बाळगायला हवा.

4. ‘मोठी आई’ साठी पाठात वापरले गेलेले शब्द शोधून लिहा.

प्रश्न 1.
‘मोठी आई’ साठी पाठात वापरले गेलेले शब्द शोधून लिहा.
उत्तर:

1. भूमी
2. जमीन
3. भूमाता
4. धरणीमाता
5. मातृभूमी
6. मायभूमी

5. पाटीपेन्सिल’ सारखे जोडशब्द पाठातून शोधून लिहा.

प्रश्न 1.
पाटीपेन्सिल’ सारखे जोडशब्द पाठातून शोधून लिहा.
उत्तरः

1. सोनेरूपे
2. दागदागिने
3. दगडमाती
4. दूधदही
5. गाई-म्हशी
6. अन्न-वस्त्र
7. चहासाखर
8. धरणीमाता
9. मायभूमी
10. प्रेमभाव

6. खालील शब्दांचे समनार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे समनार्थी शब्द लिहा.
उत्तर:
(अ) मातृभूमी – धरित्री, धरती, पृथ्वी
(आ) आई – माता, माय, जननी

7. हे शब्दा असेच लिहा.

प्रश्न 1.
हे शब्दा असेच लिहा.
उत्तर:

8. खालील पदार्थ कशापासून बनतात ते लिहा.

प्रश्न 1.
खालील पदार्थ कशापासून बनतात ते लिहा.
उदा. साखर – ऊस
उत्तर:
(अ) फुटाणे – चणे
(आ) मनुके – द्राक्षे
(इ) भाकरी – ज्वारी, बाजरी, तांदूळ, नाचणी
(ई) चपाती – गहू
(उ) वेफर्स – बटाटे
(ऊ) सॉस – टोमॅटो
(ए) सरबत – कोकम, लिंबू इ.
(ऐ) चिक्की – गुळ, शेंगदाणे, तीळ.

9. खालील शब्दांचे अनेकवचन लिहा.

(अ) तुळई – तुळया
(आ) बिजागरी – बिजागऱ्या
(इ) झाड – झाडे
(ई) दागिना – दागिने
(उ) कवठ – कवठे

10. खालील तक्ता भरा.

प्रश्न 1.
खालील तक्ता भरा.

उत्तर:

मनुष्याचे खादय	घरबांधणीला उपयुक्त वस्तू	विविध खनिजे	प्राण्यांचे खादय
धान्य, कडधान्य	लाकूड	लोखंड	पाला, पाचोळा
भाज्या	लोखंड	सोने	गवत
फळे	माती	चांदी	मांस
मांस, मटण	चुना	पितळ	कडबा

11. शेतात पीक यावे म्हणून शेतकरी कोणकोणती कामे करतो ते खालील वेबमध्ये लिहा.

प्रश्न 1.
शेतात पीक यावे म्हणून शेतकरी कोणकोणती कामे करतो ते खालील वेबमध्ये लिहा.
उत्तरः

12. खालील तक्ता पूर्ण करा.

प्रश्न 1.
खालील तक्ता पूर्ण करा.

उत्तर:

लोखंडी वस्तू	काचेच्या वस्तू	लाकडी वस्तू	मातीच्या वस्तू
1. खुर्ध्या	ग्लास	खुर्ध्या	घागर
2. पलंग	बाटली	टेबल	माठ
3. सुया	मूर्त्या	पलंग	रांजण
4. टाचण्या	फुलदाणी	कपाट	हंडी
5. चाकू	आरसा	खेळणी	खेळणी
6. कात्र्या	बरणी	बैलगाडी	भांडी
7. गाड्या	बांगड्या	नांगर	कुंड्या
8. मोटारी	बशी	कुळव	घरे
9. आगगाड्या	दिवे	पाट	फुलदाण्या
10. विमाने	घड्याळ	दरवाजे	बरणी

13. जमिनीच्या खाली येणारी पिके व जमिनीच्या वर येणारी पिके यांची माहिती करून घ्या. त्यांची यादी तयार करा.

प्रश्न 1.
जमिनीच्या खाली येणारी पिके व जमिनीच्या वर येणारी पिके यांची माहिती करून घ्या. त्यांची यादी तयार करा.
उत्तरः

14. खालील वस्तूंपासून तुमच्या घरी कोणकोणते पदार्थ तयार केले जातात. याविषयी आपापसांत गप्पा मारा.

प्रश्न 1.
खालील वस्तूंपासून तुमच्या घरी कोणकोणते पदार्थ तयार केले जातात. याविषयी आपापसांत गप्पा मारा.

उत्तरः

15. मोठ्या आईपासून प्राप्त होणाऱ्या गोष्टी लिहून आकृती पूर्ण करा.

प्रश्न 1.
मोठ्या आईपासून प्राप्त होणाऱ्या गोष्टी लिहून आकृती पूर्ण करा.

उपक्रम: आई, मातृभूमी या विषयावरील कवितांचा संग्रह करून त्या कवितांचे वर्गात वाचन करा.
प्रकल्प: शिक्षक किंवा पालकांच्या मदतीने जवळच्या शेताला भेट दया. शेतात येणाऱ्या विविध पिकांचे निरीक्षण करून शेतातील अन्नधान्याबद्दल माहिती मिळवा.
उत्तरः

16. खालील वाक्यांत (?, !, ‘-‘, “-“, . , ,) ही विरामचिन्हे घालून वाक्ये पुन्हा लिहा.

प्रश्न अ.
आवडले का तुला पुस्तक आई म्हणाली.
उत्तर:
“आवडले का तुला पुस्तक?” आई म्हणाली.

प्रश्न आ.
तो प्रामाणिक आहे बाबांनी सांगितले.
उत्तर:
तो ‘प्रामाणिक’ आहे बाबांनी सांगितले.

प्रश्न इ.
गणू म्हणाला अगं आई उदया सुट्टी आहे असे दिनूने सांगितले म्हणून मी शाळेत गेलो नाही
उत्तरः
गणू म्हणाला, “अगं आई, उदया सुट्टी आहे, असे दिनूने सांगितले. म्हणून मी शाळेत गेलो नाही.”

प्रश्न ई.
अहाहा किती छान चित्र आहे.
उत्तर:
अहाहा! किती छान चित्र आहे!

प्रश्न उ.
तुला लाडू आवडतो भका.
उत्तर:
तुला लाडू आवडतो का?

प्रश्न ऊ.
माझे काका मुंबईला राहतात
उत्तरः
माझे काका ‘मुंबईला’ राहतात.

प्रश्न ए.
मधू राजा रझिया व मारिया गप्पा मारत बसले
उत्तर:
मधू, राजा, रझिया व मारिया गप्पा मारत बसले.

Class 6 Marathi Chapter 13 मोठी आई Additional Important Questions and Answers

रिकाम्या जागी योग्य शब्द भरून वाक्य पूर्ण करून लिहा.

प्रश्न 1.
आपली आई आपल्यावर किती …………… करते.
उत्तर:
माया

प्रश्न 2.
तिचे नाव भूमी ! ……………!
उत्तर:
जमीन

प्रश्न 3.
माती आहे म्हणूनच आपण …….. आहोत.
उत्तर:
जिवंत

प्रश्न 4.
जेवणाच्या ताटातला प्रत्येक ………….. मोठ्या आईने दिला.
उत्तर:
जिन्नस

प्रश्न 5.
दाराच्या कड्या, तुळया व बिजागऱ्या आहेत.
उत्तर:
लोखंडी

प्रश्न 6.
त्या मोठ्या आईचे केवढे …..मानले पाहिजेत!
उत्तर:
उपकार

प्रश्न 7.
त्या भूमीतले …………….. खाऊनच आपण मोठे झालो.
उत्तर:
अन्न

प्रश्न 8.
माणसांना प्रत्येक गोष्ट दिली ती या …………………
उत्तर:
भूमीनेच

प्रश्न 9.
त्या मायभूमीबद्दल आपण मनात नेहमी ………………….. बाळगावयास नको का?
उत्तर:
प्रेमभाव

प्रश्न 10.
पली मोठी ………………… म्हणजेच आपली मायभूमी!
उत्तर:
आई

खालील प्रश्नांची एक ते दोन वाक्यात उत्तर लिहा.

प्रश्न 1.
आपल्या आईहूनही एक मोठी आई आहे ती कोण?
उत्तर:
आपल्या आईहूनही एक मोठी आई आहे, तिचे नाव ‘भूमी! जमीन’!

प्रश्न 2.
जमिनीत काय आहे?
उत्तर:
जमिनीत माती आहे.

प्रश्न 3.
आपण आज जिवंत कोणामुळे आहोत?
उत्तर:
माती आहे म्हणून आज आपण जिवंत आहोत.

प्रश्न 4.
जेवणाच्या ताटातला प्रत्येक जिन्नस आपणास कोणी दिला?
उत्तर:
जेवणाच्या ताटातला प्रत्येक जिन्नस आपणास मोठ्या आईने दिला.

प्रश्न 5.
गहू, तांदूळ व जोंधळे कोठे तयार होतात?
उत्तर:
गहू, तांदूळ व जोंधळे आपणास शेतातूनच म्हणजेच मातीतून मिळतात.

प्रश्न 6.
कापूस कोठून मिळतो?
उत्तर:
कापूस कपाशीच्या झाडापासून मिळतो.

प्रश्न 7.
रेशीम कोठून मिळते?
उत्तर:
रेशीम रेशमाच्या किड्यापासून मिळते.

प्रश्न 8.
रेशमाचे किडे कोणत्या झाडावर जगतात?
उत्तर:
रेशमाचे किडे तुतीच्या झाडावर जगतात.

प्रश्न 9.
प्रत्येक गिरणी व प्रत्येक कारखाना कशामुळे चालतो?
उत्तर:
प्रत्येक गिरणी व प्रत्येक कारखाना लोखंड व कोळसा यामुळे चालतो.

प्रश्न 10.
विटा कशापासून बनवल्या जातात?
उत्तर:
विटा लाल मातीपासून बनवल्या जातात.

प्रश्न 11.
लाकूड कोठून आणतात?
उत्तर:
मोठमोठ्या रानांतील वाळलेली प्रचंड झाडे तोडून लाकूड आणतात.

प्रश्न 12.
गाई-म्हशींपासून आपण काय मिळवतो?
उत्तर:
दूध, दही, तूप आपण गाई-म्हशींपासून मिळवतो.

प्रश्न 13.
गाई-म्हशी कशावर जगतात?
उत्तर:
गवत व कडबा यांवर गाई-म्हशी जगतात.

व्याकरण व भाषाभ्यास.

प्रश्न 1.
एक- अनेक लिहा.

1. गोष्ट
2. छान
3. जिन्नस
4. घर
5. भूमी
6. फूल
7. औषध
8. झाड
9. कापूस
10. रूपे
11. दागिने
12. उत्तर
13. दार
14. प्रचंड

उत्तर:

1. कथा, कहाणी
2. सुंदर
3. नग, वस्तू
4. सदन
5. जमीन
6. पुष्प, सुमन
7. दवा
8. वृक्ष, तरू
9. कपासी
10. चांदी
11. अलंकार
12. जवाब
13. दरवाजा
14. मोठा

प्रश्न 2.
एक – अनेक लिहा.
उत्तर:

प्रश्न 3.
पाठात आलेले जोडशब्द शोधून लिहा.
उत्तरः

1. जिन्नस
2. प्रचंड
3. प्रत्येक
4. खुर्ध्या
5. काव्या
6. गुंड्या
7. तुळ्या
8. गोष्ट
9. उत्पन्न
10. वस्त्र
11. कड्या
12. म्हशी
13. अन्न
14. पेन्सिल
15. टाचण्या
16. साऱ्या
17. धनधान्य
18. पाटीपेन्सिल

प्रश्न 13.
खालील वस्तूंपासून तुमच्या घरी कोणकोणते पदार्थ करतात ते वेब मध्ये लिहा.
उत्तरः

लेखन विभाग

प्रश्न अ.
जमिनीच्या वर येणारी पिके यांची यादी खालील वेबमध्ये लिहा.
उत्तरः

मोठी आई Summary in Marathi

काव्य परिचय:

आपल्या आईपेक्षाही आपणास अजून एक मोठी आई असते. ती म्हणजे ‘भूमी ! जमीन!’ याच आईचा मोठेपणा या पाठात लेखिकेने गायला आहे. आज आपण सर्व व आपणास जन्म देणारी आई ही सुद्धा याच आईची लेकरे आहेत. तिनेच आपणास या सर्व वस्तू पुरवल्या आहेत. ती नसती तर आपले अस्तित्वच या भूतलावर नसते आणि म्हणून त्या भूमीविषयी कृतज्ञतेची भावना आपण सतत मनात जपली पाहिजे हाच संदेश या पाठातून लेखिकेने दिला आहे.

शब्दार्थ:

1. आई – माता,जननी (mother)
2. माया – प्रेम, ममता (love)
3. पोटोशी – गरोदर (pregnant)
4. गोष्ट – कथा (story)
5. स्वरूप – रूप (charm, beauty)
6. जिन्नस – वस्तू (an article)
7. भूमी – जमीन, धरित्री, धरती (Land, earth)
8. जोंधळा – ज्वारी (jowar)
9. पाटी – (slate)
10. ऊस – (sugarcane)
11. तुतीचे झाड – (murberry tree)
12. सापडणे – मिळणे (to be found)
13. लोखंड – लोह (iron)
14. गिरणी – मिल (a mill)
15. खांब – स्तंभ (a pillar)
16. दार – दरवाजा (a door)
17. खिडकी – झरोका (window)
18. तुळई – घराच्या मध्यावरील लाकूड
19. बिजागरी – सांधपट्टी (hinger)
20. कडबा – कणसे कापून घेऊन उरलेला गुरांना खाण्याचा भाग, वैरण (fodder)
21. दागिने – अलंकार (jewellery)
22. मायभूमी – पृथ्वी (motherland)
23. भांडीकुंडी – छोटी मोठी भांडी (vessles and pots)

वाक्प्रचार व अर्थ:

1. माया करणे – प्रेम करणे.
2. लक्षात येणे – कळणे, समजणे, ध्यानात येणे.
3. प्रेमभाव बाळगणे – मनात प्रेम बाळगणे.

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 7 उद्यानात भेटलेला विद्यार्थी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 7 उद्यानात भेटलेला विद्यार्थी

Marathi Sulabhbharti Class 6 Solutions Chapter 7 उद्यानात भेटलेला विद्यार्थी Textbook Questions and Answers

1. एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
चर्नी रोड उद्यानात केळूस्कर गुरुजी कशासाठी येत ?
उत्तर:
चर्नी रोड उद्यानात केळूस्कर गुरुजी बाकावर बसून पुस्तक वाचण्यासाठी येत.

प्रश्न आ.
उद्यानात गुरुजींचे कोणाकडे लक्ष गेले?
उत्तर:
उद्यानात गुरुजींचे लक्ष थोड्या अंतरावर बसून पुस्तक वाचणाऱ्या विद्यार्थ्याकडे गेले.

प्रश्न इ.
गुरुजींना उद्यानात वाचन करत बसलेल्या विदयार्थ्यांची विचारपूस करावी असे का वाटले ?
उत्तर:
गुरुजींना उद्यानात एक विद्यार्थी सलग तीन दिवस वाचन करत बसलेला दिसला. तो इतर मुलांसारखी मस्ती करताना दिसत नसे, म्हणून गुरुजींना त्याची विचारपूस करावी असे वाटले.

प्रश्न ई.
केळूस्कर गुरुजींची व डॉ. आंबेडकरांची गट्टी का जमली?
उत्तर:
केळूस्कर गुरुजी व डॉ. आंबेडकर यांची रोज उद्यानात भेट होऊ लागली. गुरुजी त्यांना चांगल्या लेखकांची पुस्तके वाचायला देऊ लागले, त्यामुळे दोघांची गट्टी जमली.

प्रश्न उ.
डॉ. आंबेडकरांनी कोणता नावलौकिक मिळवला?
उत्तर:
डॉ. आंबेडकरांनी मिळालेल्या उच्च शिक्षणाच्या संधीचे सोने करून, उच्चविद्याविभूषित होऊन, जगातील एक विद्वान म्हणून नावलौकिक मिळवला.

2. खालील वाक्ये कोण, कोणास व का म्हणाले ते लिहा.

प्रश्न अ.
“बाळ, तुझं नाव काय?”
उत्तर:
भीमराव रोज उदयानात पुस्तक वाचत असलेला पाहून गुरुजी भीमरावला म्हणाले.

प्रश्न आ.
“चांगली पुस्तके वाचली पाहिजेत.”
उत्तर:
भीमरावला अवांतर वाचनाची आवड असलेली पाहून गुरुजी भीमरावला म्हणाले.

प्रश्न इ.
“मला ती पुस्तके वाचायला आवडतील!”
उत्तर:
काही लेखकांची पुस्तके वाचायला देईन, असे गुरुजींनी सांगितल्यावर भीमराव गुरुजींना म्हणाले.

3. असे का घडले? ते लिहा.

प्रश्न अ.
केळूस्कर गुरुजींच्या मनात उदयानात वाचत बसलेल्या विदयार्थ्याबाबत कुतूहल निर्माण झाले.
उत्तर:
उदयानात वाचत बसलेला विदयार्थी इतर मुलांसारखी मस्ती करताना दिसत नव्हता तर सतत तीन दिवस गुरुजी त्याला वाचन करताना पाहत होते. म्हणूनच त्यांच्या मनात या मुलाबद्दल कुतूहल निर्माण झाले.

प्रश्न आ.
भीमराव उदयानात वाचत बसायचे.
उत्तर:
भीमरावांना शाळेतील पुस्तकांशिवाय अवांतर पुस्तके वाचण्याची आवड होती म्हणून शाळा सुटल्यानंतर उदयानात काही वेळ पुस्तक वाचत बसायचे.

प्रश्न इ.
गुरुजी व भीमराव यांच्यात गट्टी जमली.
उत्तर:
गुरुजी नेहमी भीमरावाला पुस्तके वाचायला देत. भीमरावच्या वाचनामुळे गुरुजी व भीमराव यांच्यात गट्टी जमली.

प्रश्न ई.
गुरुजींनी भीमरावच्या डोक्यावरून हात फिरवला.
उत्तर:
भीमरावला वाचन कसे करावे हे गुरुजींनी समजाविले. काही लेखकांची पुस्तके वाचायला देईन असे जेव्हा गुरुजी म्हणाले तेव्हा भीमरावने वाचनाची तयारी दर्शवली. तेव्हा मायेने गुरुजींनी भीमरावच्या डोक्यावरून हात फिरवला.

प्रश्न उ.
गुरुजींनी भीमरावच्या उच्च शिक्षणासाठी शिफारस केली.
उत्तर:
केळूस्कर गुरुजींनी भीमरावची तल्लख बुद्धिमत्ताओळखून महाविदयालयीन आणि उच्च शिक्षणासाठी अमेरिकेत पाठवण्यासाठी सयाजीराव गायकवाड महाराजांकडे शिफारस केली.

4. पाठातील खालील घटना योग्य क्रमाने लिहा. 

प्रश्न 1.
पाठातील खालील घटना योग्य क्रमाने लिहा.
(अ) गुरुजी व भीमराव यांच्यात गट्टी जमली.
(आ) गुरुजींनी विद्यार्थ्याकडे फारसे लक्ष दिले नाही.
(इ) त्या विदयार्थ्यानेदेखील गुरुजींकडे बघितले.
(ई) डॉ. आंबेडकरांनी स्वतंत्र भारताची राज्यघटना लिहिली.
(उ) गुरुजींनी भीमरावाला वाचन कसे करावे याविषयी माहिती दिली.
(ऊ) गुरुजी मुलाजवळ आले.
उत्तरः
(अ) गुरुजींनी विदयार्थ्याकडे फारसे लक्ष दिले नाही.
(आ) त्या विद्यार्थ्यानेदेखील गुरुजींकडे बघितले.
(इ) गुरुजींनी भीमरावाला वाचन कसे करावे याविषयी माहिती दिली.
(ई) गुरुजी व भीमराव यांच्यात गट्टी जमली
(उ) डॉ. आंबेडकरांनी स्वतंत्र भारताची राज्यघटना लिहिली.

5. खालील शब्दांत लपलेले शब्द शोधा व लिहा.
उदा., वाचनाला – वाचन, नाच, नाला, लावा, चना.
(अ) तुझ्याजवळ
(आ) दिवसापासून
(इ) मार्गदर्शन
(ई) आवडतील

प्रश्न 1.
खालील शब्दांत लपलेले शब्द शोधा व लिहा.
उदा., वाचनाला – वाचन, नाच, नाला, लावा, चना.
उत्तरः

1. वाचनाला – वाचला, नाच, नाला, लावा, चना
2. दिवसापासून – दिवसा, सून, पान, वसा, दिन, पाव, सासू
3. मार्गदर्शन – मार्ग, दर्श, दमा, दर्शन, मान
4. आवडतील – वड, आड, आव, आतील, लव
5. महाविदयालयीन – मन, हाल, महाल, नदया, मल, विमल

6. खालील शब्दांचे वचन बदला.

प्रश्न 1.
खालील शब्दांचे वचन बदला.
(अ) लेखक
(आ) पुस्तक
(इ) शाळा
(ई) भेट
(उ) शिफारस
(ऊ) शब्द
उत्तरः
(अ) लेखक
(आ) पुस्तके
(इ) शाळा
(ई) भेटी
(उ) शिफारसी
(ऊ) शब्द

7. आंतरजालावरून खालील मुद्द्यांच्या आधारे डॉ. आंबेडकर यांची माहिती मिळवा व लिहा.
(अ) पूर्ण नाव
(आ) जन्म स्थळ
(इ) जन्म दिनांक
(ई) आई – वडिलांचे नाव
(उ) शिक्षण
(ऊ) लिहिलेली पुस्तके
(ए) कार्य

प्रश्न 1.
आंतराजालावरून खालील मुद्द्यांच्या आधारे डॉ. आंबेडकर यांची माहिती मिळवा व लिहा.
उत्तर:
डॉ. बाबासाहेब आंबेडकर यांचे पूर्ण नाव भीमराव रामजी आंबेडकर. रत्नागिरी जिल्ह्यात आंबवडे गावात दिनांक 14 एप्रिल 1891 साली त्यांचा जन्म झाला. त्यांच्या आईचे नाव भीमाबाई व वडिलांचे नाव रामजी होते. त्यांनी एम.ए., पी.एच.डी. पर्यंत शिक्षण घेतलेच पण डी.एस.सी, एल.एल.डी., डी.लि.ट, बॅरिस्टर एंट लॉ. या पदव्याही प्राप्त केल्या. भगवान बुद्ध आणि धम्म, धर्मांतर कां? जातिप्रथेचे विध्वंसन, पुणे करार, शुद्र पूर्वी कोण होते, बुद्ध की कार्ल मार्क्स अशी अनेक पुस्तके त्यांनी लिहिली.

हिंदू स्त्रियांची उन्नती आणि अवनती हे स्त्रीविषयक माहितीपर व माझी आत्मकथा हे व्यक्तिचित्रण ही त्यांनी लिहिले आहे. त्यांनी महाडच्या तळ्यातील पाणी अस्पृश्यांना खुले करून दिले. नाशिकच्या काळाराम मंदिरात अस्पृश्यांना प्रवेश मिळवून दिला. ‘शिका, संघटीत व्हा व संघर्ष करा’ हा मुलमंत्र त्यांनी दलितांना दिला. त्यांना मरणोत्तर भारतरत्न’ हा किताब भारत सरकारने बहाल केला.

8. खालील शब्द शिक्षकांच्या मदतीने समजून घ्या.
(अ) शब्द – सुशब्द, अपशब्द.
(आ) स्पष्ट – सुस्पष्ट, अस्पष्ट.
(इ) बुद्धी – सुबुद्धी, बुद्धिमत्ता, बुद्धिमान, निर्बुद्ध, दुर्बुद्धी

9. खालील शब्द असेच लिहा.

उपक्रम: वेगवेगळ्या वृत्तपत्रांत डॉ. बाबासाहेब आंबेडकर यांच्या कार्याविषयी आलेल्या माहितीची कात्रणे गोळा करा व वहीत चिकटवा. त्याचे वाचन करा.

सांगा पाहू.

प्रश्न 1.
कधी हातावर, कधी भिंतीवर जाऊन मी बसतो, तीन हात माझे सतत फिरवत मी असतो, वेळ वाया घालव नका असा नेहमी उपदेश करतो
उत्तर:
घड्याळ

प्रश्न 2.
शिस्तीचे धडे, उत्तम गडे, कणकण शोधते, कधीच न रडे
उत्तर:
मुंगी

Marathi Sulabhbharti Class 6 Solutions Chapter 7 उद्यानात भेटलेला विद्यार्थी Important Additional Questions and Answers

चूक की बरोबर ते लिहा.

प्रश्न 1.
चूक की बरोबर ते लिहा.

1. चर्नी रोड उद्यानात सायंकाळच्या वेळी अनेक नागरिक फिरायला यायचे.
2. गुरुजी सोबत आणलेले वर्तमानपत्र वाचत.
3. भीमरावाला अवांतर पुस्तके वाचनाची आवड होती.
4. इतर मुलांसारखा भीमरावही मस्ती करीत होता.
5. गुरुजींनी भीमरावला वाचन कसे करावे याविषयी माहिती दिली.

उत्तर:

1. बरोबर
2. चूक
3. बरोबर
4. चूक
5. बरोबर

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
चर्नीरोड उद्यानात सायंकाळी कोण कोण येत?
उत्तर:
चर्नीरोड उदयानात सायंकाळी अनेक नागरिक फिरायला येत. तसेच विल्सन हायस्कूलचे मुख्याध्यापक आणि विदयाव्यासंगी लेखक केळूस्कर गुरुजी व भीमराव येत असत.

प्रश्न 2.
भीमरावांनी स्वत:बद्दलची कोणती माहिती गुरुजींना सांगितली?
उत्तर:
भीमराव एलफिन्स्टन हायस्कूल, भायखळा येथे शिकत आहेत. शाळेतील पुस्तकांशिवाय अवांतर पुस्तके वाचण्याची त्यांना आवड आहे व शाळा सुटल्यानंतर ते चर्नी रोड उदयानात काही वेळ पुस्तक वाचत बसतात ही माहिती भीमरावांनी गुरुजींना सांगितली.

प्रश्न 3.
भीमरावांनी संधीचे सोने कसे केले?
उत्तर:
आपल्या तल्लख बुद्धिमत्तेने, वाचनाने व कष्टाने ते जगातील एक विद्वान म्हणून नावलौकिक प्राप्त करणारे उच्च विदयाविभूषित डॉ. बाबासाहेब आंबेडकर झाले. त्यांनी स्वतंत्र भारताची राज्यघटना लिहिली. अशाप्रकारे भीमरावांनी संधीचे सोने केले.

व्याकरण व भाषाभ्यास

प्रश्न 1.
खालील शब्दांचे वचन बदला.

1. संधी
2. महाविदयालय
3. विद्वान
4. विदयार्थी

उत्तर:

1. संधी
2. महाविदयालये
3. विद्वान
4. विदयार्थी

खालील वाक्यांत योग्य ठिकाणी विरामचिन्हे घालून वाक्य पुन्हा लिहा.

प्रश्न 1.
बाळ तुझं नाव काय.
उत्तर:
“बाळ तुझं नाव काय?”

प्रश्न 2.
वा छान नाव आहे तुझं.
उत्तर:
“वा! छान नाव आहे तुझं!”

प्रश्न 3.
जरुर दया गुरुजी मला ती पुस्तके वाचायला आवडतील.
उत्तर:
“जरुर दया गुरुजी! मला ती पुस्तके वाचायला आवडतील!”

प्रश्न 4.
खालील शब्दांचे लिंग बदला.

1. मुख्याध्यापक
2. विदयार्थी
3. बालक
4. माता
5. महाराजा
6. विद्वान
7. शिक्षक
8. लेखक
9. मित्र

उत्तर:

1. मुख्याध्यापिका
2. विद्यार्थिनी
3. बालिका
4. पिता
5. महाराणी
6. विदूषी
7. शिक्षिका
8. लेखिका
9. मैत्रिण

खालील वाक्प्रचारांचे अर्थ सांगून वाक्यात उपयोग करा.

प्रश्न 1.
कुतूहल निर्माण होणे – जिज्ञासा निर्माण होणे.
उत्तर:
शास्त्रीय प्रयोगामुळे विदयार्थ्यांच्या मनात कुतूहल निर्माण झाले.

प्रश्न 2.
संधीचे सोने करणे – वेळेचा सदुपयोग करणे
उत्तर:
अपार कष्टाने डॉ. रघुनाथ माशेलकरांनी संधीचे सोने केले.

प्रश्न 3.
नावलौकिक मिळवणे – प्रसिद्धी मिळवणे
उत्तर:
गायनामुळे लता मंगेशकरने नावलौकिक मिळवला.

लेखन विभाग:

सांगा पाहू.

प्रश्न 1.
भिंतीवर चढतो, खाली पडतो प्रयत्नांची पराकाष्ठा करतो. जाळे विणतो, हार न मानतो.
उत्तर:
कोळी

उद्यानात भेटलेला विद्यार्थी Summary in Marathi

पाठ परिचयः

प्रस्तुत पाठात बालपणी डॉ. भीमराव आंबेडकरांना वाचनाची किती आवड होती व त्यांचा हा वाचननाद केळूस्कर गुरुजींनी कसा ओळखला याचे वर्णन केले आहे. पुढे त्यांच्या मार्गदर्शनाने व शिफारसीने भीमराव उच्च शिक्षण घेऊ शकले व उच्च विद्याविभूषित होऊन स्वतंत्र भारताची राज्यघटना लिहू शकले, ‘वाचाल तर वाचाल’ हे किती सार्थ आहे हे या पाठातून कळते.

शब्दर्थ:

1. उदयान – बाग (garden)
2. सायंकाळ – संध्याकाळ (evening)
3. नागरिक – रहिवासी (citizen)
4. विदयाव्यासंगी- अभ्यासाची आवड असणारे (studious)
5. बाक – बसण्याची जागा (bench)
6. कुतूहल – जिज्ञासा (curiosity)
7. आपुलकीने – आपलेपणाने (affectionately)
8. आदर – सन्मान (respect)
9. आतुरता – उत्सुकता (excitement, eagerness)
10. विस्तृत – अफाट, मोठे (vast)
11. अभेदय – तोडता न येणारी (imperitrable)
12. तल्लख – तीक्ष्ण (sharp)
13. गट्टी – मैत्री, दोस्ती (friendship)
14. शिफारस – नाव सुचविणे (recommendation)
15. नावलौकिक – प्रसिद्धी (fame, popularity)
16. राज्यघटना – संविधान (constitution)

वाक्प्रचार व अर्थ:

1. कुतूहल निर्माण होणे – जिज्ञासा निर्माण होणे
2. संधीचे सोने करणे – वेळेचा सदुपयोग करणे
3. नावलौकिक मिळवणे – प्रसिद्धी मिळवणे

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 4 माहिती घेऊया Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 4 माहिती घेऊया

Marathi Sulabhbharti Class 6 Solutions Chapter 4 माहिती घेऊया Textbook Questions and Answers

1. भारतीय संशोधकांची नावे व त्यांनी लावलेले शोध यांची माहिती घेऊन तक्ता तयार करा. वर्गात लावा.

प्रश्न 1.
भारतीय संशोधकांची नावे व त्यांनी लावलेले शोध यांची माहिती घेऊन तक्ता तयार करा. वर्गात लावा.
उत्तर:

भारतीय संशोधक	लावलेले शोध
1. ए. पी. जे. अब्दुल कलाम	अग्नी, पृथ्वी, क्षेपणास्त्र स्वदेशी पद्धतीने बनवले
2. जयंत विष्णू नारळीकर	ब्रहमांड उत्पत्ती शोध – बिग बँग थियरी
3. विक्रम साराभाई	आण्विक उर्जा, इलेक्ट्रॉनिक्स
4. डॉ. जगदीशचंद्र बोस	रेडीयो, सूक्ष्म तरंगांचे प्रकाशिकीवर कार्य
5. डॉ. होमी जहांगीर भाभा	परमाणू उर्जा

2. कोणकोणत्या गोष्टींमध्ये संशोधन व्हावे असे तुम्हांला वाटते? विचार करा व लिहा.

प्रश्न 1.
कोणकोणत्या गोष्टींमध्ये संशोधन व्हावे असे तुम्हांला वाटते? विचार करा व लिहा.
उत्तर:

1. कॅन्सरच्या सर्व पातळ्यांवर
2. अवयव प्रत्यारोपण
3. थर्माकोल विघटन
4. इलेक्ट्रॉनिक्स कचऱ्याची विल्हेवाट

3. खालील वाक्याचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा., भिंत कोसळली – भिंती कोसळल्या.

उप्रकम: आंतरजालाचा उपयोग करून डॉ. वसंत गोवारीकर यांची माहिती मिळवा. कोलाज तयार करा.
प्रकल्प: वर्तमानपत्रात शास्त्रज्ञ, संशोधक यांच्याविषयी येणाऱ्या माहितीची कात्रणे काढून चिकटवही बनवा.

प्रश्न 1.
खालील वाक्याचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा., भिंत कोसळली – भिंती कोसळल्या.

उत्तर:

1. मला कविता आठवली.	आम्हाला कविता आठवल्या.
2. त्याने खुर्ची ठेवली.	त्यांनी खुर्ध्या ठेवल्या.
3. मधू आंबा खा.	मधू आंबे खा.

Marathi Sulabhbharti Class 6 Solutions Chapter 4 माहिती घेऊया Important Additional Questions and Answers

योग्य पर्याय निवडून उत्तरे लिहा.

1. डॉ. वसंत गोवारीकरांचा जन्म …………… (25 मार्च, 1933, 25 मार्च 1923)
2. त्यांनी पत्र पाठविले …………… (विक्रम साराभाईंना, हेन्री फोर्डला)
3. डॉ. वसंत गोवारीकरांनी नवीन पद्धत शोधून काढली. ……………(मान्सूनच्या अंदाजाची, उर्जेची)

उत्तर:

1. 25 मार्च 1933
2. हेन्री फोर्डला
3. मान्सूनच्या अंदाजाची

एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
डॉ. वसंत गोवारीकरांचे पदवीपर्यंतचे शिक्षण कुठे झाले?
उत्तर:
डॉ. वसंत गोवारीकरांचे पदवीपर्यंतचे शिक्षण कोल्हापूरला झाले.

प्रश्न 2.
डॉ. वसंत गोवारीकरांनी कोणते तंत्र विकसित केले?
उत्तर:
डॉ. वसंत गोवारीकरांनी अग्निबाणाच्या मोटारीकरिता घन इंधन बनवण्याचे तंत्र विकसित केले.

प्रश्न 3.
देशभर कोणती चिंता असते?
उत्तर:
पाऊस केव्हा पडेल? किती पडेल? याची देशभर चिंता असते.

प्रश्न 4.
पत्राचे इंग्रजी भाषांतर करण्यासाठी गोवारीकरांनी कोणाची मदत घेतली?
उत्तर:
पत्राचे इंग्रजी भाषांतर करण्यासाठी गोवारीकरांनी मित्राची मदत घेतली.

प्रश्न 5.
गोवारीकरांचा कोणत्या दोन गुणांची चुणूक लहानपणीच दिसून आली?
उत्तर:
त्यांच्या कुशाग्र बुद्धिमत्तेची आणि दृढ संकल्पाची चुणूक लहानपणीच दिसून आली.

प्रश्न 6.
पदवीपर्यंतच्या शिक्षणानंतर गोवारीकर उच्च शिक्षणासाठी कुठे गेले?
उत्तर:
पदवीपर्यंतच्या शिक्षणानंतर गोवारीकर उच्च शिक्षणासाठी इंग्लंडला गेले.

प्रश्न 7.
कोणत्या विदयापीठात त्यांनी ‘रासायनिक अभियांत्रिकी’ विषयात संशोधन केले?
उत्तर:
बर्मिंगहॅम विद्यापीठात त्यांनी ‘रासायनिक अभियांत्रिकी’ विषयात संशोधन केले.

प्रश्न 8.
संशोधक म्हणून त्यांनी कोठे काम केले?
उत्तर:
इंग्लंडच्या उर्जा संशोधन केंद्रात संशोधक म्हणून काम केले.

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
भारताच्या विज्ञान क्षेत्रातील डॉ. गोवारीकरांनी केलेली
कामगिरी लिहा.
उत्तर:
विक्रम साराभाईंच्या आग्रहामुळे 1967 साली ते भारताच्या अवकाश संशोधन केंद्रात रुजू झाले. ‘घन पदार्थातील उर्जा’ या विषयाच्या संशोधनासाठी त्यांच्या पुढाकाराने नवा प्रकल्प सुरू करण्यात आला. अग्निबाणाच्या मोटारीकरिता घन इंधन बनवण्याचे तंत्र त्यांनी विकसित केले. मान्सूनच्या अंदाजाची नवी पद्धत शोधून काढली.

प्रश्न 2.
शाळेत असताना त्यांना कोणती कल्पना सुचली? त्याची कशी दखल घेतली गेली?
उत्तर:
शाळेत असताना आपण मोटार बनवावी असे त्यांना वाटले. तेराव्या वर्षी त्यांनी अमेरिकेतील हेन्री फोर्डला पत्र लिहून आपली इच्छा कळवली. हेनरी फोर्डला मराठीतील पत्र कळणार नाही म्हणून मित्राच्या मदतीने पत्राचे इंग्रजी भाषांतर केले. हेन्री फोर्डने डॉ. गोवारीकरांच्या पत्राची दखल घेऊन उत्तरही पाठवले. सोबत काही पुस्तके पाठविली.

व्याकरण व भाषाभ्यास:

प्रश्न 1.
खालील वाक्यांचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा. भिंत कोसळली – भिंती कोसळल्या
उत्तर:

1. मीराला पिशवी सापडली.	मीराला पिशव्या सापडल्या.
2. रामने पुस्तक वाचले.	रामने पुस्तके वाचली.

प्रश्न 2.
लिंग बदला.

1. मित्र
2. आजोबा
3. भाऊ
4. मुलगा
5. मामा
6. लेखक
7. कवी
8. समाजसेवक
9. बाई
10. नट

उत्तर:

1. मैत्रिण
2. आजी
3. बहिण
4. मुलगी
5. मामी
6. लेखिका
7. कवयित्री
8. समाजसेविका
9. माणूस
10. नटी

प्रश्न 3.
विरूद्धार्थी शब्द लिहा.

1. दूर
2. नवी
3. मित्र
4. कुशाग्र
5. दृढ
6. मोठी
7. विकसित
8. घन

उत्तर:

1. जवळ
2. जुनी
3. शत्रू
4. मंद
5. डळमळीत
6. छोटी, लहान
7. अविकसित
8. द्रव

प्रश्न 4
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:

1. विकसित करणे – शेतकऱ्यांनी संत्रांचा वापर करून शेती विकसित केली.
2. रुजू होणे – बरेच दिवसांच्या सुट्टीनंतर रमेश कामावर रुजू झाला.

लेखन विभाग:

प्रश्न 1.
आंतरजालाचा उपयोग करून डॉ. वसंत गोवारीकर यांची माहिती मिळवा.
उत्तर:
डॉ. वसंत रणछोड गोवारीकर यांचा जन्म 25 मार्च 1933 रोजी झाला. एक भारतीय शास्त्रज्ञ म्हणून त्यांचा नावलौकिक आहे. इंडियन स्पेस रिसर्च ऑर्गनायझेशन मध्ये ते मुख्य पदावर विराजमान होते. अंतराळ, हवामान, लोकसंख्या विषयांवरचे त्यांचे योगदान महत्त्वपूर्ण आहे. पद्मश्री व पद्मभूषण या पुरस्करांनी त्यांना सन्मानित केले गेले. 2 जानेवारी 2015 रोजी ते अनंतात विलीन झाले.

माहिती घेऊया Summary in Marathi

पाठ परिचयः

पद्मश्री व पद्मभूषण पुरस्कार प्राप्त असलेले श्री. वसंत गोवारीकर एक भारतीय संशोधक होते. अवकाश संशोधनाच्या मुख्य पदावर कार्यरत असलेले वसंत गोवारीकर 1991 – 1993 च्या काळात पंतप्रधानांचे सल्लागारही होते. अंतराळ संशोधन, हवामान, लोकसंख्या या विविध विषयांवरचे त्यांचे योगदान अमूल्य आहे. प्रस्तुत पाठात त्यांच्याविषयी अधिक माहिती जाणून घेता येईल.

शब्दर्थ:

1. देश – राष्ट्र (nation)
2. चिंता – काळजी (worry)
3. शोधणे – हुडकून काढणे (to invent)
4. कल्पना – युक्ती (idea)
5. भाषांतर – एका भाषेतून दुसऱ्या भाषेत लिहिणे. (translation)
6. थेट – सरळ (direct)
7. कुशाग्र – तीक्ष्ण (sharp)
8. संकल्प – figale (resolution)
9. संशोधन – नवीन शोध (invention)
10. प्रकल्प – योजना (project)
11. क्षेत्र – विभाग (field, area)
12. कामगिरी – कार्यवाही (execution of work)
13. इंधन – जळाऊ पदार्थ (fuel)
14. विकसित करणे – वाढविणे (to develop)
15. घन – कठीण (solid)
16. चुणूक – झलक (a faint indication)

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 9 वह देश कौन-सा है? Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 9 वह देश कौन-सा है?

Hindi Sulabhbharti Class 6 Solutions Chapter 9 वह देश कौन-सा है? Textbook Questions and Answers

चित्रकथाः

चित्र के आधार पर काल संबंधी वाक्य बनाओ और समझोः

Answer:
(१) रामू ने लड्डू खाया।
(२) रामू लड्डू खा रहा है।
(३) रामू लड्डू खाएगा।

जरा सोचो ….. बताओ:

‘यदि हिमालय की बर्फ पिघलना बंद हो जाए तो…’ (कहानी लेखन)
Answer:
यदि हिमालय की बर्फ पिघलना बंद हो जाए तो हमारे देश में जल-संकट उत्पन्न हो जाएगा। हिमालय पर जमी बर्फ ईश्वर द्वारा संचित जल का भंडार है, जो धीरे-धीरे पिघलती है। वहीं जल नीचे आते – आते नदियों का रूप धारण कर लेती है। इस प्रकार पूरे वर्ष जल की आपूर्ति वहाँ से होती रहती है। यदि यह बंद हो जाए तो नदियाँ सूख जाएँगी। नदियों के बिना जीना एकदम कठिन हो जाएगा।

खोजबीनः

‘परमवीर चक्र’ पुरस्कार प्राप्त सैनिकों की सूची बनाओ। (परियोजना-कार्य)
Answer:
(१) मेजर सोमनाथ शर्मा
(२) लांस नायक करम सिंह
(३) सेकेंड लेफ्टिनेंट राम राघोबा राने
(४) नायक जादुनाथ सिंह
(५) कंपनी हवलदार मेजर प्रभु सिंह
(६) कैप्टन गुरु बचन सिंह
(७) मेजर धनसिंह थापा
(८) सुबेदार जोगिन्दर सिंह
(९) मेजर शैल्तान सिंह
(१०) कंपनी हवलदार मेजर अब्दुल हमीद आदि

सुनो तो जराः

देशभक्ति पर आधारित कविता सुनो और सुनाओ। (कविता-लेखन)
Answer:
भारत कितना प्यारा है!
यहीं हिमालय – सा पहाड़ है, यहीं गंग की धारा है। यमुना लहराती है सुंदर, भारत कितना प्यारा है।
फल-फूलों से भरी भूमि है, खेतों में हरियाली है। आमों की डाली पर बैठी,
गाती कोयल काली है। बच्चों ! माँ ने पाल-पोसकर तुमको बड़ा बनाया है। लेकिन यह मत भूलो तुमने अन्न कहाँ का खाया है।
तुमने पानी पिया कहाँ का, खेले मिट्टी में किसकी। चले हवा में किसकी बोलो, बच्चे, प्यारे भारत की।

बताओ तो सही:

अपने परिवेश में शांति किस प्रकार स्थापित की जा सकती है? (अनुच्छेद लेखन)
Answer:
अपने परिवेश में जब सब लोग मिल जुलकर प्रेम से रहने लगेंगे, तो शांति स्थापित की जा सकती है। इसके लिए सभी को याद रखना होगा कि हम सब एक देश के निवासी हैं। सभी लोग आपस में भाई – बहन हैं। पूरा विश्व ही हमारा परिवार है। इस प्रकार की भावना यदि सब में जागृत हो जाए, तो पूरे विश्व में शांति स्थापित की जा सकती है।

वाचन जगत से:

वैज्ञानिक की जीवनी पढ़ो और उसके आविष्कार लिखोः
Answer:
डॉ. ए. पी. जे. अब्दुल कलाम हमारे भारत के पूर्व राष्ट्रपति डॉ. अब्दुल पकीर जैनुलाबदीन अब्दुल कलाम का जन्म १४ अक्टूबर, सन् १९३१ ई. को रामेश्वरम में हुआ था। उनके पिता का नाम पकौर जैनुलाबदीन था। बी. एससी. करने के बाद इन्होंने मद्रास इंस्टीट्यूट ऑफ टेक्नोलॉजी, चेन्नई में एरोनाटिकल इंजीनियरिंग में प्रवेश ले लिया। सन् १९६३ ई. में वे विक्रम साराभाई स्पेस सेंटर में आ गए। इनके द्वारा तैयार किए गए प्रमुख प्रक्षेपास्त्र निम्नलिखित हैं – पृथ्वी, आकाश, त्रिशूल, नाग, अग्नि आदि। २५ नवंबर, १९९७ को उन्हें देश का सर्वोच्च सम्मान भारत रत्न से सम्मानित किया गया। दिनांक २५ जुलाई, २००२ ई. को वे भारत के राष्ट्रपति बने।

कलम से:

क्रमानुसार भारत के राष्ट्रपति, प्रधानमंत्री के नाम लिखो। (परियोजन-कार्य)
Answer:
भारत के राष्ट्रपति:

(१) डॉ. राजेंद्र प्रसाद
(२) डॉ. राधाकृष्णन
(३) डॉ. ज़ाकिर हुसैन
(४) वी. वी. गिरी
(५) डॉ. फकरुद्दीन अहमद
(६) नीलम संजीवा रेड्डी
(७) ज्ञानी जैल सिंह
(८) आर वेंकटरमन
(९) डॉ. शंकर दयाल शर्मा
(१०) के. आर. नारायणन
(११) डॉ. ए.पी.जे. अब्दुल कलाम
(१२) प्रतिभा देवी सिंह पाटिल
(१३) प्रणव मुखर्जी

भारत के प्रधानमंत्री:

(१) जवाहरलाल नेहरू १९६४
(२) गुलज़ारीलाल नंदा १९६४, १९६६
(३) लालबहादुर शास्त्री १९६४ – १९६६
(४) इंदिरा गांधी १९६६-७७, १९८०-८४
(५) मोरार जी देसाई १९७७-७९
(६) चरण सिंह १९७९-८०
(७) राजीव गांधी १९८४ – ८९
(८) वी. पी. सिंह १९८९ – ९०
(९) चंद्रशेखर १९९० – ९१
(१०) पी. वी. नरसिंहाराव १९९१ – ९६
(११) अटल बिहारी बाजपेई १९९६, १९९८ – २००४
(१२) एच डी देवेगौड़ा १९९६ – ९७
(१३) इंद्रकुमार गुजराल १९९७ – ९८
(१४) मनमोहन सिंह २००४ – २०१४
(१५) नरेंद्र मोदी २०१४ से

इस कविता के आधार पर भारत की विविधता एवं विशेषताएँ सात – आठ वाक्यों में लिखो। (अनुच्छेद लेखन)
Answer:
भारत विविधताओं से भरा देश है। एक तरफ हिमालय की बफीर्ली वादियाँ हैं, तो दूसरी तरफ रेगिस्तान। एक तरफ नदियों का अमृत जल धरती को हरा-भरा बना रहा है, तो दूसरी तरफ समुद्र। कहीं पहाड़, कहीं मैदान तो कहीं घनघोर जंगल हैं। धरती के अंदर कहीं कोयला, तो कहीं हीरा पन्ना आदि बहुमूल्य रल भरे पड़े हैं। अनेक बोलियाँ एवं भाषाएँ हैं। तीज-त्योहार भी अलग-अलग हैं। खान-पान, रहन-सहन अलग होते हुए भी हम सब एक हैं। यही भारत की विशेषता हैं।

सदैव ध्यान में रखोः

ऐतिहासिक वस्तुओं का संरक्षण हम किस तरह से करते है?
Answer:
ऐतिहासिक वस्तुओं का संरक्षण करना हमारा कर्तव्य है। ऐसी वस्तुओं से हमें अतीत के बारे में जानकारी मिलती है। अतीत में पूर्वजों जो ने गल्तियाँ कौं, उनसे बचने की प्रेरणा मिलती है। साथ ही हमें हमारी गौरवशाली परंपराओं पर गर्व होता है।

विचार मंथन:

‘स्वतंत्रता मेरा जन्मसिद्ध अधिकार है।'(संस्मरण लेखन)
Answer:
आजादी सभी को प्रिय है। ईश्वर ने सभी प्राणियों को जीने का अधिकार दिया है। अत: सभी को स्वतंत्र रहने का अधिकार है। दुर्भाग्य से हमारा देश परतंत्र रहा और ऐसे गुलामी के समय लोकमान्य बाल गंगाधर तिलक ने यह नारा लोगों को दिया। लोगों ने इस बात को समझा और गुलामी की जंजीरों को तोड़ दिया। अब सब स्वतंत्र हैं और सभी को यह अधिकार जन्म से प्राप्त है।

स्वयं अध्ययनः

नीचे दिए गए राष्ट्रीय प्रतीकों के चित्र देखो और उनके नाम लिखो:

Answer:
(१) राष्ट्रीय ध्वज तिरंगा
(२) राष्ट्रीय पशु बाघ
(३) राष्ट्रीय पक्षी मोर
(४) राष्ट्रीय फल आम
(५) राष्ट्रीय फूल कमल
(६) राष्ट्रीय खेल हॉकी

स्वयं अध्ययन:

चित्रों का वाचन करके अपने शब्दों में कहानी लिखो और उचित शीर्षक बताओ? (कहानी लेखन)
Answer:
राष्ट्रीय पशु बाघ किसी गाँव में एक चित्रकार रहता था। उसका नाम कृष्ण कांत था। वह एक दिन प्राकृतिक दृश्य का चित्र बनाने के लिए नदी के किनारे पहुँचा। नदी की दूसरी ओर पहाड़ियाँ थीं। कृष्ण कांत को यह स्थान बहुत सुंदर लगा। वे उस स्थान का चित्र बनाने लगे। चित्र बनाते-बनाते वे एकदम लीन हो गए थे। तभी वहाँ एक बाघ आकर बैठ गया। चित्रकार अपनी धुन में मग्न थे। उन्होंने बाघ का भी चित्र बनाना शुरू कर दिया। थोड़ी देर बाद बाघ नदी की तरफ जाने लगा। चित्रकार कृष्ण कांत का चित्र अभी अधूरा था। वे नाव में बैठकर बाघ की ओर चल दिए। बाघ जब सामने आया, उन्होंने अपनी कलाकृति को पूरा किया और अपने गाँव की ओर चल दिए। शिक्षा – हमें अपना कार्य तन्मयता के साथ मन लगाकर करना चाहिए।

हमें जानो:

मार्ग पर चलते हुए तुमने कुछ यातायात संकेत देखे होंगे। इन सांकेतिक चिह्नों का क्या अर्थ है, लिखो:

Answer:
(१) रुको।
(२) घूमना मना है। (यू टर्न मना है)
(३) एक तरफ का मार्ग प्रतिबंधित है।
(४) एकल मार्ग।
(५) प्रवेश निषेध।
(६) हार्न बजाना मना है।
(७) भारी वाहन प्रवेश वर्जित।
(८) आगे विद्यालय है।

Hindi Sulabhbharti Class 6 Solutions Chapter 9 वह देश कौन-सा है? Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्द में लिखिए:

Question 1.
भारत किसकी गोद में बसा है?
Answer:
प्रकृति।

Question 2.
भारत का चरण कौन धो रहा है?
Answer:
रत्नेश।

Question 3.
भारत का मुकुट किसे कहा गया है?
Answer:
हिमालय।

Question 4.
भारत में सुधा की धारा कौन बहा रही हैं?
Answer:
नदियाँ।

Question 5.
मैदान, गिरि और वनों में क्या लहराती हैं?
Answer:
हरियालियाँ।

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
भारत कैसी प्रकृति की गोद में बसा है?
Answer:
भारत मनमोहिनी प्रकृति की गोद में बसा है।

Question 2.
भारत के सब अंगों में क्या सजे हैं?
Answer:
भारत के सब अंगों में रसीले फल, कंद, अनाज और मेवे सजे हैं।

Question 3.
भारत की धरती कैसी है?
Answer:
भारत की धरती अनंत धन-धान्य से भरी पड़ी है।

Question 4.
संसार का शिरोमणि किसे कहा गया है?
Answer:
संसार का शिरोमणि भारत को कहा गया है।

Question 5.
भारत के लोग कैसे हैं?
Answer:
भारतवासी नवक्रांति के पुजारी, सेवक और सपूत हैं।

रिक्त स्थानों की पूर्ति कीजिए:

Question 1.
मनमोहिनी प्रकृति की जो ……………… में बसा है।
Answer:
गोद

Question 2.
सींचा हुआ ……………… वह देश कौन-सा है?
Answer:
सलोना

Question 3.
……………… हँस रहे हैं, वह देश कौन-सा है?
Answer:
दिन-रात

Question 4.
जिसके ……………… धन से धरती भरी पड़ी है।
Answer:
अनंत

Question 5.
भारत सिवाय दूजा वह ………………?
Answer:
देश कौन-सा है

उचित जोड़ियाँ मिलाइए:

Answer:
१ – १
२ – घ
३ – क
४ – च
५ – ख
६ – ग

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. मनमोहिनी
2. प्रकृति
3. गोद
4. रत्नेश
5. सुधा
6. प्रसून
7. सलोना
8. दुलारा
9. सेवक
10. धरती

Answer:

1. मनोहारिणी
2. निसर्ग
3. अंक
4. समुद्र
5. अमृत
6. फूल
7. सुंदर
8. प्यारा
9. दास
10. वसुंधरा

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. नदी
2. धारा
3. रसीला
4. मेवा
5. हरियाली

Answer:

1. नदियाँ
2. धाराएँ
3. रसीले
4. मेवे
5. हरियालियाँ

‘खेलना’ इस क्रिया के सकर्मक, अकर्मक, संयुक्त, सहायक और प्रेरणार्थक दोनों रूपों का वाक्यों में प्रयोग करो और लिखोः
Answer:
सकर्मक . लड़की क्रिकेट खेल रही है। अकर्मक – लड़की खेलती है। संयुक्त – रमेश क्रिकेट खेलने लगा है। सहायक – रमेश ने क्रिकेट खेल लिया। प्रथम प्रेरणार्थक – शिक्षक वरुण को क्रिकेट खिलाता
द्वितीय प्रेरणार्थक- शिक्षक छात्रों को कोच से क्रिकेट खिलवाता है।

निम्नलिखित शब्द युग्मों से विशेषण शब्द छाँटिए:

1. मनमोहिनी प्रकृति
2. रसीले फल
3. सुंदर प्रसून
4. अनंत धन

Answer:

1. मनमोहिनी
2. रसीले
3. सुंदर
4. अनंत

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 1 उपयोग हमारे Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 1 उपयोग हमारे

Hindi Sulabhbharti Class 6 Solutions Chapter 1 उपयोग हमारे Textbook Questions and Answers

चित्रो का परिचय: चित्र का निरीक्षण करो और बताओ।

डाकघर:

विद्यार्थियों से चित्रों का निरीक्षण कराकर उनको प्रश्न पूछने के लिए कहें । बड़ों की सहायता से उन्हें डाकघर में जाकर टिकट खरीदने तथा बैंक में बाल-बचत खाता खुलवाने और परिचित डाकिए, बैंक कर्मचारी, नर्स, हवलदार से बातचीत करने की सूचना दें।

Answer:
प्रस्तुत चित्र डाकघर का है। डाकघर भारत-सरकार का सबसे पुराना व बड़ा उपक्रम है। चित्र में डाकघर के अलग-अलग हिस्सों में होने वाले काम के बारे में बताया गया है। लोग अपना पत्र और मनी ऑर्डर भेजने के लिए कतार में खड़े हैं। पोस्टमैन पत्रों पर कुछ लिख रहे हैं। एक व्यक्ति बचत खाता-काउन्टर पर डाक कर्मचारी से कुछ पूछताछ कर रहा है। दूसरा व्यक्ति मनी ऑर्डर-काउन्टर पर बैठी डाक-कर्मचारी से कुछ जानकारी प्राप्त कर रहा है। डाकघर में सूचना-फलक लगा हुआ है। डाकघर के अन्य कर्मचारी भी अपने काम में व्यस्त हैं। हम आपकी आवश्यकता समझते हैं।’ इस सुविचार के माध्यम से ग्राहकों में अपनेपन का भाव पैदा करने का प्रयास किया गया है। छोटे बच्चे अपने माता-पिता के साथ डाकघर में आए हैं और सभी चीज़ों का निरीक्षण कर रहे हैं। गमले के पास कूड़ेदान रखा गया है। ‘बचत आपकी, प्रगति देश की।’ इस सुंदर पंक्ति द्वारा लोगों में देश की प्रगति की भावना भी जागृत करने का प्रयत्न किया गया है। प्रगति के आज के दौर में हमारी सरकार डाकघरों का महत्त्व बरकरार रखने के लिए बैंकों की तर्ज पर उनका पुनर्गठन कर रही है।

बैंक:

उपरोक्त स्थानों की कार्य प्रक्रिया संबंधी जानकारी देकर चर्चा करें । प्रत्यक्ष जाकर विद्यार्थियों को वहाँ की सूचना पढ़ने के लिए कहें । उनसे अपने गाँव/शहर के महत्त्वपूर्ण स्थानों के दूरध्वनि क्रमांकों की सूची बनवाएँ और सहायता लेने की सूचना दें।

Answer:
प्रस्तुत चित्र बैंक का है। प्रतिदिन के कार्य का चित्रण इसमें किया गया है। छोटे बच्चे अपने माता-पिता के साथ बैंक में आए हैं। बैंक में आए कई ग्राहक अपना कार्य कर रहे हैं। एक महिला पूछताछ-काउन्टर पर बैठे बैंक कर्मचारी से कुछ बातचीत कर रही है। दूसरी महिला बचत खाता काउन्टर पर अपना कार्य करने के लिए खड़ी है। कुछ ग्राहक कैशिअर के पास से अपने रुपये लेने के लिए कतार में खड़े हैं। एक महिला कैशिअर काउन्टर पर रुपये जमा कर रही है। कुछ ग्राहक अपने कार्य की प्रतीक्षा में बैठे हैं। एक ग्राहक शाखा प्रबंधक (मैनेजर) के कक्ष में बैठकर कुछ वार्तालाप कर रहा है। बंदूकधारी सुरक्षा कर्मचारी बैंक की सुरक्षा के लिए खड़ा है। अन्य ग्राहक अपने काम में व्यस्त दिखाई दे रहे हैं। बैंक की ओर से ग्राहकों को सूचना देने के लिए सूचना फलक लगा हुआ है।

Hindi Sulabhbharti Class 6 Solutions Chapter 1 उपयोग हमारे Additional Important Questions and Answers

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(प्रगति, सूचना, टिकट, कूड़ेदान)

Question 1.
डाकघर में लोगों और कर्मचारियों को सूचित करने के लिए ………………… फलक लगाया जाता है।
Answer:
सूचना

Question 2.
हमें कचरा ……………….. में फेंकना चाहिए।
Answer:
कूड़ेदान

Question 3.
हमारे बचत करने से देश की …………………. होगी।
Answer:
प्रगति

Question 4.
पत्र पर ……………… लगाकर हम उसे डाकघर में देते है।
Answer:
टिकट प्रश्न

निम्नलिखित वाक्य सही हैं या गलत लिखिए:

Question 1.
डाकघर में हम पैसे जमा कर सकते हैं।
Answer:
सही

Question 2.
हमें कचरा गमले में फेंकना चाहिए।
Answer:
गलत

Question 3.
बच्चे डाकघर में खेल रहे हैं।
Answer:
गलत

Question 4.
मेज पर पत्र बिखरे पड़े हैं।
Answer:
सही

Question 5.
बचत खाता काउंटर पर महिला कर्मचारी बैठी है।
Answer:
गलत

निम्नलिखित चित्रों के साथ सही जोड़ियाँ मिलाइए:

Answer:
१ – घ
२ – ग
३ – ड़
४ – क
५ – ख

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
डाकघर में हम क्यों जाते हैं?
Answer:
हम डाकघर में पत्र डालने, लाने अथवा मनी ऑर्डर तथा रजिस्ट्री करने जाते हैं।

Question 2.
डाकघर के चित्र में कितने विभाग दिखाये गए हैं और कौन से?
Answer:
डाकघर के चित्र में तीन विभाग दिखाये गए है।

• बचत खाता
• मनी ऑर्डर
• रजिस्ट्री/टिकट

Question 3.
डाकघर के फलक पर कौन-सा सुंदर वाक्य लिखा है?
Answer:
डाकघर के फलक पर ‘बचत आपकी, प्रगति देश की’ यह सुंदर वाक्य लिखा है।

Question 4.
छोटे बच्चे किसके साथ डाकघर में आए है?
Answer:
छोटे बच्चे अपने माता – पिता के साथ डाकघर में आए है।

Question 5.
‘हम आपकी आवश्यकता समझते हैं।’ इस वाक्य से आप क्या समझते हैं?
Answer:
इस वाक्य से हम यह समझते है कि आपका समय और आपका कार्य हमारे लिए महत्त्वपूर्ण है।

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(ग्राहक, पूछताछ, बंदूक, बचत, छड़ी)

Question 1.
महिला . …………… कर रही है।
Answer:
पूछताछ

Question 2.
दूसरी महिला ……………… खाता काउन्टर के पास खड़ी है।
Answer:
बचत

Question 3.
सुरक्षा कर्मचारी के पास ……………… है।
Answer:
बंदूक

Question 4.
मैनेजर ……………….. से बातचीत कर रहा है।
Answer:
ग्राहक

Question 5.
बूढ़े ग्राहक के हाथ में ………………….
Answer:
छड़ी

निम्नलिखित बाक्य सही हैं या गलत लिखिए:

Question 1.
बैंक में कैशिअर पैसे का लेन-देन एवं हिसाब का काम देखता है।
Answer:
सही

Question 2.
बैंक में हमें पत्र मिलता है।
Answer:
गलत

Question 3.
मैनेजर का काम लोगों की रक्षा करना होता है।
Answer:
गलत

Question 4.
आज-कल बैंक का अधिकतर काम संगणक पर होता है।
Answer:
सही

Question 5.
बैंक से हमें कर्ज मिलता है।
Answer:
सही

निम्नलिखित बैंक व पोस्ट से संबंधित शब्दों को अलग अलग करके लिखिए:

(पूछताछ, बचत खाता, कैशिअर, डाकिया, मैनेजर, डाक अधिकारी, रजिस्ट्री, चालू खाता, पत्र, धनादेश, मनी ऑर्डर)
Answer:
पोस्ट ऑफिस:

• डाकिया
• बचत खाता
• डाक अधिकारी
• रजिस्ट्री
• पत्र
• मनी ऑर्डर

बैंक:

• बचत खाता
• कैशिअर
• चालू खाता
• धनादेश
• पूछताछ

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
बैंक में खजांची क्या कार्य करते हैं?
Answer:
बैंक में खजांची रुपये लेन-देन का एवं उसका हिसाब रखने का कार्य करते हैं।

Question 2.
बैंक में पूछताछ-कक्ष क्यों होता है?
Answer:
बैंक में आने वाले ग्राहकों की समस्याओं का निवारण करने के लिए बैंक में पूछताछ-कक्ष होता है।

Question 3.
बैंक में सुरक्षा कर्मचारी क्यों तैनात किए जाते हैं?
Answer:
बैंक में आने-जाने वाले ग्राहकों एवं बैंक के मालमत्ते की रक्षा करने के लिए बैंक में सुरक्षा कर्मचारी तैनात किए जाते हैं।

Question 4.
बैंकों की आवश्यकता क्यों होती है?
उत्तर :
हमारी धन-संपत्ति को सुरक्षित रखने के लिए हमें बैंकों की आवश्यकता होती है।

Question 5.
बैंक के मुख्य अधिकारी को क्या कहते हैं?
Answer:
बैंक के मुख्य अधिकारी को शाखा प्रबंधक कहते हैं।

Question 6.
साधारण या आम जनता बैंक में किस प्रकार का खाता खोलती है?
Answer:
साधारण या आम जनता बैंक में बचत खाता खोलती है।

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 8 टीटू और चिंकी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 8 टीटू और चिंकी

Hindi Sulabhbharti Class 6 Solutions Chapter 8 टीटू और चिंकी Textbook Questions and Answers

मैं कौनः

चित्रों के आधार पर वाक्य बनाओ। (काल्पनिक लेखन)

Answer:
पहले चित्र – के आधार पर दो चिड़ियाँ आसमान में उड़ रही हैं। आसमान में बादल छाए हैं। नीचे सुंदर फूल खिले हैं। चित्र में एक छोटा घर भी दिखाई दे रहा है।
दूसरा चित्र – दूसरे चित्र में एक पेड़ दिखाई पड़ रहा है। पेड़ के ऊपर एक चिड़िया उड़ रही है। पीछे पहाड़ दिख रहा है। पेड़ के पास कुछ फूल खिले हैं।
तीसरा चित्र – तीसरे चित्र में पहाड़ के पीछे उगता सूर्य दिख रहा है। चित्र में एक घिसकनी (फिसलपट्टी) है। बच्चे उस पर फिसलकर खेल रहे हैं।

खोजबीनः

विलुप्त होते हुए प्राणियों तथा पक्षियों की जानकारी प्राप्त करके सूची बनाओ। (परियोजना-कार्य)
Answer:

विचार मंथन:

जीवदया ही धर्म है। (अनुच्छेद लेखन)
Answer:
दया धर्म का मूल है। जीव मात्र पर दया करना सबसे बड़ा धर्म है। गाँधी जी के प्रिय भजन में भी इसका उल्लेख है। वैष्णव जन तो तेने कहिए, जे पीर पराई जाने रे। गीता में भगवान श्री कृष्ण ने कहा है – ‘समोहम सर्व भूतेषु।’ अर्थात मैं सभी सभी प्राणियों में समत्व भाव रखता हूँ। अत: सभी जीवों पर दया करना ही सभी प्राणियों पर दया करना है।

सुनो तो जरा:

विभिन्न पशु पक्षियों की बोलियों की नकल सुनाओ:
Answer:

• गाया – मां …….मां ………
• कुत्ता – भों…… भो…….
• बिल्ली – म्याऊँ……. म्याऊँ..
• बकरी – में…… में……..
• घोड़ा – हिं… हि… हिं…
• कोयल – कू… कू… कू…
• कौआ – काँव… काँव…
• चिड़िया – चिं चि चि ….

बताओ तो सही:

अपने साथ घटित कोई मज़ेदार घटना बताओ? (कहानी लेखन)
Answer:
एक दिन मेरे विद्यालय में अन्तर विद्यालयीय क्रिकेट मैच था। मेरा विद्यालय फाइनल में पहुँच चुका था। फाइनल मैच से पहले ही मेरे एक मित्र को अभ्यास करते समय चोट लग गई और मुझे फाइनल मैच में खेलने का अवसर मिल गया। मैं ओपनिंग में गया और आखिर तक टिका रहा और मेरा विद्यालय मैच जीत गया। मुझे बहुत मज़ा आया।

वाचन जगत से:

उपन्यास सम्राट प्रेम-चंद की कोई एक कहानी पढ़ो। उसका विषय बताओ?
Answer:
मैंने प्रेमचंद की एक कहानी पढ़ी, जिसका नाम था – बड़े भाई साहब। इसमें बड़े भाई साहब और उनका छोटा भाई छात्रावास में रहते हैं। दोनों में दो साल का अंतर रहता है। बड़े भाई खूब पढ़ते हैं और छोटा भाई खूब खेलता-कूदता है। फिर भी बड़े भाई नौवी में दो बार फेल हो जाते हैं और छोटा भाई उनकी कक्षा में उनकी बराबरी पर आ जाता है।

मेरी कलम से:

‘बाघ बचाओ परियोजना’ के बारे में जानकारी प्राप्त कर लिखो। (निबंध लेखन)
Answer:
सिंह, बाघ और चीता एक ही प्रजाति के जीव माने जाते हैं। इनकी नस्ल अब समाप्ति की तरफ बढ़ रही है। वर्तमान में १४११बाघ बचे हैं. इसलिए आजकल ‘बाघ बचाओ का नारा’ अनेक बार सामने आ रहा है। बाघ संविधान द्वारा संरक्षित क्षेत्रों में ही पाए जाते हैं। समाचार माध्यमों के अनुसार अनेक शिकारी अवैध रूप से वहाँ प्रवेश कर उनका शिकार करते हैं। दरअसल यह संकट वनों के सिकुड़ते दायरे की वजह से पैदा हुआ है।

जरा सोचो…. लिखो:

‘यदि प्राणी नहीं होते तो……’ (काल्पनिक लेखन)
Answer:
यदि प्राणी नहीं होते तो प्रकृति असंतुलित हो जाती। ईश्वर ने प्रकृति को संतुलित रखने के लिए विभिन्न प्राणियों को बनाया है। उनका भोजन भी इसी को ध्यान में रखते हुए निर्धारित किया है। यह धरती घास और पेड़-पौधों से संतुलित रहे, इसके लिए कुछ प्राणियों को शाकाहारी बनाया और यह धरती प्राणियों से संतुलित रहे, इसलिए कुछ को मांसाहारी बनाया। मनुष्य सभी प्राणियों में समझदार और शक्तिशाली है। उसने अपने निहित स्वार्थ के लिए ईश्वर की इस व्यवस्था में गड़बड़ी पैदा करना शुरू कर दिया है। यह अनुचित है। यहाँ सभी प्राणियों की उपयोगिता है।

स्वबं अध्ययनः

‘डिस्कवरी चैनल’ पर दिखाए जाने वाले किसी अनोखे जीव की जानकारी प्राप्त करो।
Answer:
‘डायनासोर’ जिसका अर्थ यूनानी भाषा में बड़ी छिपकली होता है। लगभग १६ करोड़ वर्ष तक पृथ्वी के सबसे प्रमुख स्थलीय कशेरूकी जीव थे। हिंदी में डायनासोर शब्द का अनुवाद भीमसरट है, जिसका संस्कृत में अर्थ भयानक छिपकली है। इन पशुओं के विविध समूह थे। जीवाश्म विज्ञानियों ने डायनासोर के अब तक ५०० विभिन्न वंशों और १००० से अधिक प्रजातियों की पहचान की है और इनके अवशेष पृथ्वी के हर महाद्वीप पर पाए जाते हैं। कुछ डायनासोर शाकाहारी तो कुछ मांसाहारी थे। कुछ द्विपाद तो कुछ चौपाए थे। कुछ आवश्यकतानुसार द्विपाद या चतुर्पाद के रूप में अपने शरीर की मुद्रा को परिवर्तित कर लेते थे।

अध्ययन कौशल:

चित्रों को पहचानकर जलचर, नभचर, थलचर और उभयचर प्राणियों में वर्गीकरण करो।

Answer:

• जलचरः मछली, मगरमच्छ, सौंप, ऑक्टोपस
• थलचरः गिलहरी, शेर, ऊँट, चूहा
• नभचर: चिड़िया, तोता, उल्लू
• उभयचर: मेंढक, भैंस, हाथी, दरयाई घोड़ा

Hindi Sulabhbharti Class 6 Solutions Chapter 8 टीटू और चिंकी Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्द में लिखिए:

Question 1.
गिलहरी का नाम क्या था?
Answer:
टीटू।

Question 2.
टीटू की पड़ोसिन कौन थी?
Answer:
चिकी।

Question 3.
साँप कहाँ रहता था।
Answer:
बिल में।

Question 4.
साँप बिल से निकलकर कहाँ चढ़ने लगा?
उत्तरः
पेड़ पर।

Question 5.
टीटू और चिंकी के बच्चों ने किसकी ताकत को देख लिया था?
Answer:
एकता की।

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए:

Question 1.
चिंकी का घोंसला कहाँ था?
Answer:
चिंकी का घोंसला पेड़ की शाखाओं पर था।

Question 2.
चिंकी जब दाना चुगने जाती, तब सभी बच्चो का ध्यान कौन रखता था?
Answer:
चिंकी जब दाना चुगने जाती, तब सभी बच्चों का ध्यान टीटू रखती थी।

Question 3.
अंत में पेड़ छोड़ने का मन में विचार किसने बना लिया?
Answer:
अंत में पेड़ छोड़ने का मन में विचार टीटू और चिकी ने बना लिया।

Question 4.
टीटू के बच्चों का क्या कहना था?
Answer:
टीटू के बच्चों का कहना था कि पेड़ उनका है।

Question 5.
साँप का पेड़ पर चढ़ना मुश्किल क्यों होने लगा?
Answer:
साँप का पेड़ पर चढ़ना मुश्किल होने लगा, क्योंकि जहाँ – जहाँ चिंकी ने चोंच मारी, वहाँ-वहाँ पेड़ से गाढ़ा चिपचिपा दूध बहने लगा।

कोष्ठक से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(भाड़, मिलजुलकर, खोखल, गिलहरी, बसेरा).

Question 1.
हमें …………….. रहना चाहिए।
Answer:
मिलजुलकर

Question 2.
हमारा जन्म इसी ……………… में हुआ।
Answer:
खोखल

Question 3.
इसकी टहनियों पर हमारा ……………… है।
Answer:
बसेरा

Question 4.
टीटू ……………… यह सुन बड़ी परेशान हुई।
Answer:
गिलहरी

Question 5.
अकेला चना ……………… नहीं फोड़ सकता।
Answer:
भाड़

निम्नलिखित वाक्यों के सामने सही / अथवा गलत का निशान लगाइए:

Question 1.
टीटू के बच्चे का नाम मिंटू था।
Answer:
सही

Question 2.
चिंकी खोखल में रहती थी।
Answer:
गलत

Question 3.
रिंकी की माँ चिंकी थी।
Answer:
सही

Question 4.
डर के मारे चिंकी नाचने लगी।
Answer:
गलत

Question 5.
टीटू गिलहरी बिल में छिप तमाशा देख रही थी।
Answer:
गलत

किसने, किससे कहा?

Question 1.
“तुम कैसे कह सकते हो कि यह पेड़ तुम्हारा है?”
Answer:
रिंकी ने मिंटू से कहा।

Question 2.
“शाखाएँ हमारी तो फल भी हमारे।”
Answer:
टीटू के बच्चों ने रिंकी से का।

Question 3.
“सावधान टीटू बहन, साँप ऊपर आ रहा है।”
Answer:
चिंकी ने टीटू से कहा।

Question 4.
“हम तुम्हें टहनियों तक नहीं आने देंगे और न ही इसके फल खाने देंगे।”
Answer:
चिंकी के बच्चों ने टीटू के बच्चों से कहा।

Question 5.
“चिंकी चिड़िया को यह पेड़ छोड़ना होगा।”
Answer:
टीटू के बच्चों ने चिंकी के बच्चों से कहा।

व्याकरण और भाषाभ्यास:

विरामचिह्न रहित अनुच्छेद में विरामचिह्न लगाओ

काबुलीवाले ने पूछा बिटिया अब कौन सी चूड़ियाँ चाहिए मैंने अपनी गुड़िया दिखाकर कहा मेरी गुड़िया के लिए अच्छी सी चूड़ियाँ दे दो जैसे लाल नीली पीली
Answer:
काबुलीवाले ने पूछा- बिटिया ! अब कौन-सी चूड़ियाँ चाहिए? मैंने अपनी गुड़िया दिखाकर कहा, “मेरी गुड़िया के लिए अच्छी-सी चूड़ियाँ दे दो। जैसे-लाल, नीली, पीली।”

उचित जोड़ियाँ मिलाइए:

Answer:
1. – ;
2. – “ ”
3. – –
4. – ,
5. – ।
6 – ?

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. शाखा
2. चिड़िया
3. घोंसला
4. बच्चा
5. हवा
6. अंडा
7. माता
8. साँस
9. चोंच
10. मुश्किल

Answer:

1. शाखाएँ
2. चिड़ियाँ
3. घोंसले
4. बच्चे
5. हवाएँ
6. अंडे
7. माताएँ
8. साँसें
9. चोंचें
10. मुश्किलें

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. टहनियाँ
2. नीड़
3. आसमान
4. साँप
5. बसेरा

Answer:

1. शाखाएँ
2. घोंसला
3. आकाश
4. सर्प
5. घर

निम्नलिखित शब्दों के विलोम शब्द लिखिए:

1. डर
2. सुबह
3. जन्म
4. बच्चे
5. सावधान
6. अँधेरा
7. सुरक्षित
8. मुश्किल
9. नरम
10. धर्म

Answer:

1. निडर
2. शाम
3. मृत्यु
4. बूढ़े
5. असावधान
6. उजाला
7. असुरक्षित
8. आसान
9. कठोर
10. अधर्म

निम्नलिखित शब्दों के लिंग बदलिए:

1. साँप
2. पड़ोसी
3. बहन
4. माता

Answer:

1. साँपिन
2. पड़ोसिन
3. भाई
4. पिता

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 6 स्वास्थ्य संपदा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 6 स्वास्थ्य संपदा

Hindi Sulabhbharti Class 6 Solutions Chapter 6 स्वास्थ्य संपदा Textbook Questions and Answers

कार्य हमारा

चित्र देखकर क्रियायुक्त शब्दों से वाक्य बनाओ।

Answer:

1. लता सेब खाती है।
2. बच्चे हँस रहे थे।
3. गुड़िया अलमारी से गिर गई है।
4. माँ अपने बच्चे को सुला रही है।
5. रमेश अपनी बहन को खाना खिला रहा है।
6. मैं अपने-आप खाना खा लेता हूँ।
7. माँ अपनी बिटिया को खाना खिलाती है।

जरा सोचो…..लिखो:

यदि भोजन से नमक गायब हो जाए तो….
Answer:
यदि भोजन से नमक गायब हो जाए तो भोजन स्वादिष्ट नहीं लगेगा। हर चीज फीकी लगेगी। फीका भोजन करना मुश्किल होगा और हमारा पेट नहीं भरेगा। पेटभर खाना न खाने से हमें कमजोरी आ जाएगी। हम ढंग से कोई काम नहीं कर सकेंगे। नमक के बिना हमारे शरीर को आयोडीन नहीं मिलेगा, जिससे शरीर का विकास रुक जाएगा।

मैंने समझा:

__________
___________
Answer:
इस पाठ में गांधी जी यह समझाना चाहते हैं कि हमें अपना शरीर स्वस्थ रखना चाहिए। हमें पर्याप्त मात्रा में दूध, मक्खन, फल, हरी सब्जियाँ, गेहूँ की रोटी आदि पौष्टिक पदार्थ अपने भोजन में लेने चाहिए। हमें शुद्ध हवा में रहते हुए प्राणायाम व व्यायाम भी करना चाहिए।

खोजबीन:

खादी का कपड़ा कैसे बनाया जाता है इसकी जानकारी प्राप्त करके लिखो।
Answer:
चरखे पर रूई से सूत काता जाता है। फिर उस सूत से जुलाहा हथकरघे पर कपड़ा बुनता है। इसके पश्चात इस कपड़े को रंगा जाता है। हाथ से बुना कपड़ा कुछ मोटा होता है। इसी कपड़े को खादी कहते हैं।

अध्ययन कौशल:

पढ़ाई का नियोजन करते हुए अपनी दिनचर्या लिखो।
Answer:
मेरा स्कूल सुबह साढ़े सात बजे से दोपहर दो बजे तक रहता है। मैं ढाई बजे घर आ जाता हूँ। खाना खाने और थोड़ा आराम करने के बाद मैं अपने स्कूल का गृहकार्य करने बैठ जाता हूँ। फिर गृहकार्य पूरा कर मैं खेलने चला जाता हूँ, क्योंकि मेरी उम्र के सभी बच्चे उसी समय अपनी पढ़ाई आदि खत्म करके खेलने आते हैं। दो घंटा खेलने के बाद मैं घर आता हूँ। खाना खाते समय मैं टीवी पर समाचार और डिस्कवरी जैसे ज्ञानवर्धक चैनल देखता हूँ। फिर स्कूल बैग तैयार करके दस बजे मैं सोने चला जाता हूँ। इस तरह यह मेरी दिनचर्या सुबह से रात तक की है।

बताओ तो सही।

संतुलित आहार पर पाँच वाक्य बोलो।
Answer:

1. पर्याप्त मात्रा में पौष्टिक तत्त्वों से भरे आहार को संतुलित आहार’ कहते हैं।
2. मजबूत एवं स्वस्थ शरीर के लिए संतुलित आहार लेना चाहिए।
3. संतुलित आहार हमारे कार्य करने की शक्ति एवं गति को बढ़ाता है।
4. इससे हमारे शरीर का संपूर्ण रूप से शारीरिक एवं मानसिक विकास होता है।
5. संतुलित आहार हमारे शरीर की रोग-प्रतिरोधक क्षमता बढ़ाता है।

मेरी कलम से:

अपने मित्र को शुभकामना/बधाई पत्र लिखो।
Answer:

एक वाक्य में उत्तर लिखो।

Question 1.
जैतून के तेल की जगह मक्खन क्यों लिया जाना चाहिए?
Answer:
मक्खन में जो विटामिन होते हैं वह जैतून के तेल में नहीं होते, इसलिए जैतून के तेल की जगह मक्खन लिया जाना चाहिए।

Question 2.
रक्षक का धर्म कौन-सा है?
Answer:
रक्षा करना रक्षक का धर्म है।

Question 3.
किन-किन सब्जियों की गिनती अच्छी, हरी सब्जियों में होती है?
Answer:
लौकी, फूलगोभी, पत्तागोभी, बिना बीज की सेम, बैंगन आदि की गिनती अच्छी और हरी सब्जियों में होती है।

Question 4.
फेफड़ों के लिए क्या अति आवश्यक है?
Answer:
चौबीसों घंटे शुद्ध-से-शुद्ध हवा फेफड़ों के लिए अति आवश्यक है।

सदैव ध्यान में रखो:

नवयुवकों की शक्ति देशहित में लगनी चाहिए।
Answer:
मनुष्य के अंदर उसके पूरे जीवन में सबसे अधिक ऊर्जा युवावस्था में होती है। इस उम्र में वह अधिक-से-अधिक मुश्किल कार्य कर सकता है। मनुष्य का कर्तव्य होता है कि वह अपने परिवार और समाज के साथ-साथ देश के विकास के लिए भी कार्य करे। अत: नवयुवक या युवावर्ग को अपनी शक्ति देशहित में लगानी चाहिए, जिससे देश ज्यादा-से-ज्यादा सफलता प्राप्त कर सके।

विचार मंथन:

स्वस्थ शरीर, स्वस्थ मन। योगासन है, उत्तम साधन।
Answer:
स्वास्थ्य सबसे बड़ा धन है। अच्छे स्वास्थ्य के बिना सब कुछ व्यर्थ है। कहते हैं कि स्वस्थ शरीर में स्वस्थ मन वास करता है, इसलिए हमें हमेशा अपने स्वास्थ्य पर ध्यान देना चाहिए। इसके लिए अच्छे खान-पान के साथ-साथ शारीरिक व्यायाम भी अनिवार्य है। हमें सुबह जल्दी उठना चाहिए और रात को भी समय पर सो जाना चाहिए। सुबह उठकर खुली हवा में सैर करना लाभदायक होता है। साथ ही हमें योगासन भी अवश्य करना चाहिए। योगासन में शारीरिक क्रियाओं के अलावा श्वासोच्छवास पर ध्यान केंद्रित किया जाता है। इस तरह शारीरिक और मानसिक शक्तियों का विकास होता है। अत: स्वस्थ तन-मन के लिए योगासन एक उत्तम साधन है।

भाषा की ओर:

निम्न विशेषण शब्द का अपने वाक्य में प्रयोग करके उनका प्रकार लिखो।

Answer:

1. पाँच
   प्रकार: पाँच – संख्यावाचक विशेषण
   वाक्य: मैं रोज सुबह पाँच बजे सोकर उठता हूँ।
2. यही
   प्रकार: यही – सार्वनामिक विशेषण
   वाक्य: यही लड़का कल स्कूल नहीं आया था।
3. कुछ
   प्रकार: कुछ – परिमाणवाचक विशेषण
   वाक्य: कुछ फल लेते आना।
4. मीठी
   प्रकार: मीठी – गुणवाचक विशेषण
   वाक्य: रीना मीठी दही खाती है।

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 7 नदी कंधे पर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 7 नदी कंधे पर

Hindi Sulabhbharti Class 6 Solutions Chapter 7 नदी कंधे पर Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए:

Question 1.
बालक किसको कंधे पर लाना चाहता है?
Answer:
नदी को।

Question 2.
बालक किसके साथ नहाना चाहता है?
Answer:
मित्रों के साथ।

Question 3.
वह नदी का परिचय किससे कराना चाहता है?
Answer:
भद्रजनों से।

निम्नलिखित प्रश्नों के उत्तर लिखिए:

Question 1.
बालक नदी के उस पार खड़े-खड़े क्या करना चाहता
Answer:
बालक नदी के उस पार खड़े-खड़े ‘मम्मी-मम्मी’ चिल्लाना चाहता है।

Question 2.
शाम ढलने पर बालक क्या करता?
Answer:
शाम ढलने पर बालक नदी को उठाकर अपने कंधे पर रखवाता और जहाँ से उसे लाया था, वहीं रख आता।

Question 3.
वह मित्रों के साथ किस प्रकार नहाना चाहता है?
Answer:
वह मित्रों के साथ कूद-कूदकर और उछल-उछलकर नहाना चाहता है।

Question 4.
बालक नदी को कहाँ बहाना चाहता है?
Answer:
बालक नदी को अपने घर के ठीक सामने बहाना चाहता है।

Question 5.
बालक सबको किसलिए आमंत्रित करता?
Answer:
बालक सबको नदी में नहाने के लिए आमंत्रित करता।

कविता में आए हुए लयात्मक शब्दों को ढूँढकर लिखिए:

उदाहरण: बहाते – बहाते

1. मस्ताते
2. रखवाते
3. करवाते

Answer:

1. चिल्लाते
2. रख आते
3. इतराते

रिक्त स्थानों की पूर्ति कीजिए:

Question 1.
अगर हमारे ……………… में होता।
Answer:
बस

Question 2.
……………… उठाकर घर ले आते।
Answer:
नदी

Question 3.
अपने घर के ठीक ………….
Answer:
सामने

Question 4.
उसको हम ……………… बहाते।
Answer:
हर रोज़

Question 5.
……………… उछल-उछलकर।
Answer:
कूद-कूदकर

Question 6.
अपने मित्रों के साथ ………………।
Answer:
चहाते

उचित जोड़ियाँ मिलाइए:

Answer:
१ – घ
२ – ग
३ – क
४ – ड
५ – ख

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. नदी
2. कंधा
3. बहाता

Answer:

1. नदियाँ
2. कंधे
3. बहाते

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. घर
2. नदी
3. आमंत्रित
4. शाम
5. मम्मी
6. मित्र
7. झटपट
8. इतराते

Answer:

1. गृह
2. सरिता
3. निमंत्रित
4. संध्या
5. माता
6. सखा
7. जल्दी-जल्दी
8. इठलाते

निम्नलिखित शब्दों के विपरीतार्थक शब्द लिखिए:

1. खड़े-खड़े
2. यहीं
3. उपस्थित
4. झटपट
5. सामने
6. भद्र

Answer:

1. बैठे-बैठे
2. वहीं
3. अनुपस्थित
4. धीरे-धीरे
5. पीछे
6. अभद्र

निम्नलिखित शब्दों में अनुस्वार ‘ या अनुनासिक लगाकर शब्द लिखिए:

1. मित्रो
2. कधे
3. जहा
4. आमत्रित
5. जनो

Answer:

1. मित्रों
2. कंधे
3. जहाँ
4. आमंत्रित
5. जनों

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 9 वह देश कौन-सा है? Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions स्वयं अध्ययन २

Hindi Sulabhbharti Class 6 Solutions स्वयं अध्ययन २ Textbook Questions and Answers

चित्रवाचन करके अपने शब्दों में कहानी लिखो और उचित शीर्षक बताओ:

विद्यार्थियों से ऊपर दिए गए चित्रों का क्रमानुसार निरीक्षण कराएँ । चित्र में कौन-कौन-सी घटनाएं घटी होंगी, उन्हें सोचने के लिए कहें । उन्हें अन्य चित्रों एवं घटनाओं के आधार पर कहानी लिखने के लिए प्रेरित करें और उचित शीर्षक देने के लिए कहें।
Answer:
छात्र स्वयं करें