Category: Class 6

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 5 (अ) क्या तुम जान ते हो?, (ब) पहेलियाँ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 5 (अ) क्या तुम जान ते हो?, (ब) पहेलियाँ

Hindi Sulabhbharti Class 6 Solutions Chapter 5 (अ) क्या तुम जान ते हो?, (ब) पहेलियाँ Textbook Questions and Answers

(अ) क्या तुम जानते हो?

Question 1.
भारत में सबसे अधिक जनसंख्या वाला शहर कौन-सा है?
Answer:
मुंबई

Question 2.
विश्व का प्रथम विश्वविदयालय कौन-सा है?
Answer:
तक्षशिला विश्वविद्यालय

Question 3.
अंतरराष्ट्रीय महिला दिवस कब मनाया जाता है?
Answer:
८ मार्च

Question 4.
विश्व का सबसे बड़ा जीव कौन-सा है?
Answer:
ब्लू व्हेल

Question 5.
किस ग्रह को “भोर का तारा” कहते हैं?
Answer:
शुक्र ग्रह

Question 6.
भारत का राष्ट्रीय मानक समय किस शहर में माना जाता है?
Answer:
मिर्जापुर, उत्तर प्रदेश

Question 7.
भूभाग की दृष्टि से भारत का सबसे बड़ा और सबसे छोटा राज्य कौन-सा है?
Answer:
सबसे बड़ा राज्य – राजस्थान सबसे छोटा राज्य – गोवा

Question 8.
भारत का संविधान बनाने में कितना समय लगा?
Answer:
२ वर्ष ११ माह १८ दिन

Question 9.
भारत में कितने राज्य और कितने केंद्रशासित प्रदेश हैं?
Answer:
राज्य – २९ केंद्रशासित प्रदेश -७

Question 10.
विश्व में सबसे ऊँचाई पर कौन-सी सड़क है?
Answer:
खरदुंग ला (लद्दाख, भारत)

(ब) पहेलियाँ:

Question 1.
जल में, थल में रहता,
वर्षाऋतु का गायक।
कहो कौन टर्र-टर्र करता,
इधर-उधर फुदक-फुदक।
Answer:
मेंढक

Question 2.
मिट्टी धूप हवा से भोजन,
वह प्रतिदिन ही लेता है।
कहो कौन, जो प्राणवायु संग,
छाया भी हमको देता है।
Answer:
पेड़

Question 3.
अर्धचक्र और सतरंगी,
नभ में बादल का संगी।
कहो कौन, जो शांत मनोहर,
रंग एक है, जिसमें नारंगी।
Answer:
इंद्रधनुष

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 9 सोई मेरी छौना रे! Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 9 सोई मेरी छौना रे!

Hindi Sulabhbharti Class 6 Solutions Chapter 9 सोई मेरी छौना रे! Textbook Questions and Answers

लेखन विभाग

जरा सोचो ….. बताओ:

यदि सच में हमारे मामा का घर चाँद पर होता तो ..(काल्पनिक लेखन)
Answer:
यदि सच में हमारे मामा का घर चाँद पर होता तो हम छुट्टियों में वहाँ घूमने जाया करते। छुट्टी भर वहीं चाँद पर घूमते। वहाँ के दृश्य फोटो में खींच कर लाते। वहाँ से धरती का भी फोटो खींचते और यहाँ आकर सबको फोटो दिखाते और वहाँ के बारे में सबको बताते।

खोजबीन:

विभिन्न क्षेत्रों की प्रथम भारतीय महिलाओं की सचित्र जानकारी कॉपी में चिपकाओ। (परियोजना-कार्य)
Answer:

स्वयं अध्ययन:

अपने परिवार के प्रिय व्यक्ति के लिए चार काव्य पंक्तियाँ लिखो। (कविता-लेखन)
Answer:
मेरी माँ प्यारी माँ, भोली माँ कितनी अच्छी सुबह सबेरे उठ जाती सैर सपाटे हमें कराती पूरी-हलवा टिफिन में भरकर रोज़ हमें स्कूल ले जाती जब भी करता मैं शैतानी माँ हो जाती मेरी उदास कान पकड़ जब मैं माफ़ी माँगता गले लगाती मेरी माँ।

भाषा की ओर:

हिंदी-मराठी के समोच्चारित शब्दों की अर्थ भिन्नता बताओ और लिखो।

Answer:
(१) उद्या/आने वाला कल
(२) बरोबर/ठीक है
(३) उघड़/खोलना
(४) माँ/आना
(५) थर/स्तर

सुनो तो जराः

नीतिपरक दोहे सुनो और आनंदपूर्वक सुनाओ:
Answer:
रहिमन धागा प्रेम का, मत तोड़ो चटकाय। टूटे से फिर ना मिले, मिले गाँठ परि जाय।
रहिमन देखि बड़ेन को, लघु न दीजिए डारि। जहाँ काम आवे सुई, कहा करे तरवारि।।

बताओ तो सही:

माँ को एक दिन की छुट्टी दी जाए तो क्या होगा? (काल्पनिक लेखन)
Answer:
माँ को एक दिन की छुट्टी दी जाए तो सुबह-सुबह सब देर तक सोते रहेंगे। सोकर उठने पर चाय और नाश्ता तैयार नहीं मिलेगा। खुद उठकर चाय और नाश्ता बनाना पड़ेगा। अपने कपड़ों को इधर-उधर से ढूँढना पड़ेगा। दोपहर का भोजन समय पर नहीं मिलेगा। कुल मिलाकर पूरा घर अस्त-व्यस्त नज़र आएगा और सभी लोग हैरान-परेशान होते रहेंगे।

वाचन जगत से:

सुभद्राकुमारी चौहान की कविता पढ़ो और समूह में गाओ:
Answer:
देखो कोयल काली है पर
मीठी है इसकी बोली।
इसने ही तो कूक-कूककर,
कानों में मिसरी घोली।
कोयल-कोयल! सच बतलाओ,
क्या संदेशा लाई हो?
बहुत दिनों के बाद आज फिर,
इस डाली पर आई हो।

मेरी कलम से:

‘नियत’ विषय पर भाषण तैयार करो। (भाषण – लेखन)
Answer:
मंचपर उपस्थित मान्यवर, मैं आपके समक्ष ‘नियत’ विषय पर अपने विचार व्यक्त करने जा रहा हूँ। ‘नियत’ शब्द का अर्थ है आदमी की सोच। जिसकी ‘नियत’ बुरी होती है, वह हमेशा दूसरों के बारे में खराब, अभद्र, बुरा सोचता रहता है। वह कभी भी धोखा दे सकता है। ऐसे व्यक्ति का विश्वास नहीं किया जा सकता, क्योंकि वह सामने तो अच्छा-अच्छा बोलता है, किंतु जैसे ही पीठ पीछे जाता है, वह काम बिगाड़ने में लग जाता है। इसलिए ऐसे व्यक्ति से दूर रहना ही अच्छा होता है।

कविता की पंक्तियाँ पूरी करो:

Answer:
चाँद सितारे जाग रहे,
नाच रही है चाँदनिया।
फूल खिले हैं चाँदी के,
फूली मेरी आँगनिया।

Answer:
मेरा सुख अनहोना रे,
सोई मेरी छौना रे!
गीत सुनाऊँ सोए तू,
तू सोए औ गाऊँ मैं।

सदैव ध्यान में रखोः

‘जीवन में माँ का स्थान क्या है’ इस विषयपर अपनी किताब में १० से १५ पंक्तियाँ लिखिए:
Answer:
बच्चे का जब जन्म होता है, तब सबसे पहले वह अपनी माँ को देखता है। माँ की गोद ही उसकी सारी दुनिया होती है, इसलिए बच्चे अपनी माँ के बहुत करीब होते हैं। माता ही संतान की पहली गुरु होती है। बच्चे को चलना, उठना, बोलना सब उसकी माँ ही सिखाती है। सब दुख-दर्द सहकर भी माँ अपनी संतान की भलाई में लगी रहती है। संतान की बेहतरी के लिए वह अपना सब कुछ त्याग देती है, इसलिए जीवन में माँ का स्थान असाधारण होता है।

विचार मंथनः

‘जननी – जन्मभूमिश्च स्वर्गादपि गरीयसी।
Answer:
माता और मातृभूमि स्वर्ग से भी श्रेष्ठ होती हैं। इसलिए अपनी मातृ और मातृभूमि के प्रति हमेशा आदर और भक्ति भाव रखना चाहिए। कहा गया है कि तीनों लोकों का स्वामी भी बिना माँ के भिखारी ही होता है।

अध्ययन कौशल:

अपने परिवार का वंश – वक्ष तैयार करो और रिश्ते नातों के नाम लिखो:
Answer:

जोड़ो हमें:

दिए गए पेड़ के पत्तों पर दिए गए वर्षों से संयुक्ताक्षरयुक्त शब्द बनाओ:
(आथे होकर, पाई हटाकर, हल लगाकर, ‘र’ के प्रकार)

Answer:
(क) डॉक्टर
(ग) लकड़बग्घा
(थ) पथ्य
(व) व्यय
(द) गिद्ध
(प) प्याज
(ट) पट्टा
(ह) ह्रस्व
(त) कुत्ता
(ड) डॉक्टर
(ष) मनुष्य
(ड) पाठ्यपुस्तक
(घ) घर
(ठ) फ्लेमिंगो
(ट) टटू
(फ) चम्पा

Hindi Sulabhbharti Class 6 Solutions Chapter 9 सोई मेरी छौना रे! Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्दों में लिखिए:

Question 1.
कैसा झूला झूल रहा है?
Answer:
सोने का।

Question 2.
फूल किसके खिले हैं?
Answer:
चाँदी के।

Question 3.
कौन नाच रही है?
Answer:
चाँदनिया।

Question 4.
मेरा सुख कैसा है?
Answer:
अनहोना।

Question 5.
माँ बच्चे को कैसे मनाना चाहती है?
Answer:
हँस-हँस।

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए:

Question 1.
माँ मीठे सपनों में क्या सुनकर खोई है?
Answer:
माँ मीठे सपनों में परियों की लोरी सुन-सुनकर खोई है।

Question 2.
कौन-कौन जाग रहे हैं?
Answer:
चाँद और सितारे जाग रहे हैं।

Question 3.
माँ की आँगनिया किन फूलों से फूली है?
Answer:
माँ की आँगनिया चाँदी के फूलों से फूली है।

Question 4.
नन्हा बालक क्या-क्या करता है?
Answer:
नन्हा बालक जागता है, खेलता है और रूठता है।

Question 5.
माँ नन्हें बच्चे को कहाँ सैर करवाना चाहती है?
Answer:
माँ नन्हें बच्चे को खिलौनों की दुनिया की सैर करवाना चाहती है।

उचित जोड़ियाँ मिलाइए:

Answer:
१ – घ
२ – छ
३ – ड़
४ – च
५ – ग
६ – ख
७ – क

निमलिखित शब्दों के बहुवचन-रूप लिखिए:

1. झूला
2. सितारा
3. आँगन
4. लोरी
5. खिलौना
6. परी
7. चाँदनी

Answer:

1. झूले
2. सितारे
3. आँगन
4. लोरियाँ
5. खिलौने
6. परियाँ
7. चाँदनियाँ

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. डोरी
2. फूल
3. सोना
4. चाँदी
5. दुनिया

Answer:

1. रस्सी
2. कुसुम
3. स्वर्ण
4. रजत
5. संसार

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 8 जन्मदिन Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 8 जन्मदिन

Hindi Sulabhbharti Class 6 Solutions Chapter 8 जन्मदिन Textbook Questions and Answers

लेखन विभाग

मैं कौन हूँ?:

सूचना, निर्देश, आदेश, अनुरोध, बिनती के बाक्य विरामचिह्न सहित पढ़ो और समझोः

Question 1.
बगीचे के फल-फूल तोड़ना मना है।
Answer:
सूचना

Question 2.
जैसे-फल, सब्जी लेकर घर आओ।
Answer:
निर्देश

Question 3.
‘चंदामामा’ बालपत्रिका पढ़ो।
Answer:
आदेश

Question 4.
अपनी कृपा दृष्टि बनाए रखें।
Answer:
अनुरोध

Question 5.
बच्चों ने कहा, “कृपया हमें अंतरिक्ष के बारे में बताएँ।”
Answer:
विनती

विचार मंथन:

सौर ऊर्जा, अक्षय ऊर्जा के बारेमें बताओ।
Answer:
सौर ऊर्जा अर्थात सूर्य से निकलने वाली ऊर्जा अक्षय है।
सूर्य में अनंत ऊर्जा है और वह समाप्त होने वाली नहीं है।
अन्य ऊर्जा का भंडार सीमित है, परंतु सौर ऊर्जा असीमित है।
अत: आज आवश्यकता इस बात की है कि हम अधिकसे-अधिक सौर ऊर्जा का उपयोग करें।

जरा सोचो …. बताओ:

यदि पानी की टोंटी बोलने लगे …(काल्पनिक लेखन)
Answer:
यदि पानी की टोंटी बोलने लगे तो बहुत हद तक पानी की बचत होने लगेगी। अक्सर लोग पानी की टोंटी खुली छोड़ देते हैं। यही नहीं, मुँह धोते समय भी टोंटी खुली होती है और ब्रश करते रहते हैं।

खोजबीन

विभिन्न क्षेत्रों की प्रथम भारतीय महिलाओं’ की सचित्र जानकारी कॉपी में चिपकाओ।

स्वयं अध्ययनः

मातृभाषा के दस शब्द एवं दो वाक्यों का हिंदी अनुवाद करो:
Answer:
(१) मुलगी – लड़की
(२) मुलगा – लड़की
(३) घड्याळ – घड़ी
(४) झाड़ – पेड़
(५) आंबा – आम
(६) फणस – कटहल
(७) ससा – खरगोश
(८) ढग – बादल
(९) खटारा – बैलगाड़ी
(१०) गवत – घास

(अ) वर्गात स्वच्छता राखा
कक्षा में स्वच्छता रखो।
(ब) अभ्यास करताना शांतता राखा.
पढ़ाई करते समय शांति रखो।

सुनो तो जरा:

ध्वनिफीति सी.डी पर कोई लोकगीत सुनोः(आत्मकथा लेखन)
Answer:
विद्यार्थी अपने घर पर लोकगीत सुनेंगे।

बताओ तो सही:

तुम अपनी छोटी बहन छोटे भाई के लिए क्या करते हो?
Answer:
मैं अपनी छोटी बहन/छोटे भाई की पढ़ाई में मदद करता हूँ। विद्यालय से मिले गृहकार्य करवाता हूँ। उसके साथ खेलता हूँ। चित्रकला एवं अन्य कार्यों में उसकी मदद करता हूँ।

भाषा की ओर:

शब्दयुग्मों की जोड़ियाँ मिलाओ।

Answer:
अड़ोस – पड़ोस
बारी – बारी
अच्छा – बुरा
नहाना – वहाना
हँसी – खुशी

वाचन जगत से:

डॉ. ए. पी. जे. अब्दुल कलाम की आत्मकथा का अंश पड़कर उनके बारे में लिखिए:
Answer:
पाँच वर्ष की अवस्था में रामेश्वरम के प्राथमिक स्कूल में कलाम की शिक्षा का प्रारंभ हुआ। उनकी प्रतिभा को देखकर उनके शिक्षक उनपर स्नेह रखने लगे। एक बार बुखार आ जाने के कारण कलाम स्कूल नहीं पहुँचे, यह देखकर उनके शिक्षक मुत्थुरा जी काफी चिंतित हो गए। स्कूल समाप्त होने के बाद वे उनके घर जा पहुँचे। उन्होंने कलाम के स्कूल न आने का कारण पूछा और कहा कि यदि उन्हें किसी प्रकार की सहायता की आवश्यकता हो तो नि:संकोच कह सकते हैं।

दो-तीन वाक्य में उत्तर लिखो:

Question 1.
बबलू की आदत से कौन परेशान थे?
Answer:
बबलू की आदत से उसके माता-पिता दोनों परेशान थे।

Question 2.
शीला मौसी ने बिजली की कटौती का क्या कारण बताया?
Answer:
शीला मौसी ने बिजली की कटौती का यह कारण बताया कि गरमी बढ़ जाने से बाहर तमाम जगहों पर बिजली का भार बढ़ गया है। आज कॉलोनी के इस ब्लॉक में कटौती हुई
है। फिर बारी-बारी दूसरे ब्लॉकों में कटौती होगी।

Question 3.
प्यास के कारण बबलू की स्थिति कैसी बनी थी?
Answer:
प्यास के कारण बबलू बेचैन हो उठा। वह पानी-पानी चिल्लाने लगा। प्यास से उसका गला सूखा जा रहा था। खाने का एक कौर भी गले से नीचे नहीं उतर रहा था।

Question 4.
बबलू ने किस बात को कभी नहीं जाना?
Answer:
बबलू ने इस बात को कभी नहीं जाना कि शीला मौसी के यहाँ जन्मदिन की पार्टी में जो कुछ हुआ, वह एक नाटक था।

मेरी कलम से:

अपने नाना जी/दादा जी को अपने मन की बात लिखकर भेजो। (पत्र लेखन)
Answer:
छात्रावास
मुंबई। पूज्य नाना जी/ दादा जी सादर प्रणाम।

मैं यहाँ सकुशल हूँ। आशा है आप सब भी सकुशल होंगे। आज हमारे विद्यालय का वार्षिक परीक्षा परिणाम घोषित हुआ। आपको यह जानकर हार्दिक प्रसन्नता होगी कि मैंने अपनी कक्षा में प्रथम स्थान प्राप्त किया है। यह सब आपके आशीर्वाद एवं कुशल मार्गदर्शन के कारण ही संभव हो पाया है।
माता जी और पिता जी को प्रणाम तथा अमीषा को प्यारभरा आशीर्वाद।

आपका आज्ञाकारी
पोता/नाती

सदैव ध्यान में रखोः

प्राकृतिक संपदाओं की बचत करना आवश्यक है। (अनुच्छेद – लेखन)
Answer:
प्रकृति की सर्वश्रेष्ठ रचना मनुष्य है। मनुष्य के जीवन को सुखमय बनाने के लिए प्राकृतिक संपदाएँ भरी पड़ी हैं। किंतु आज हम उन संपदाओं का दुरुपयोग कर रहे हैं। यही नहीं, प्रकृति को ही प्रदूषित कर रहे हैं। अत: अपने जीवन को बचाना है तो हमें प्राकृतिक संपदाओं की बचत करना आवश्यक है।

अध्ययन कौशल:

निम्नांकित चित्रों के नाम बताओ और जानकारी लिखोः

Answer:
(१) पेड़ – पेड़ हमारे सच्चे मित्र हैं। पेड़ों से हमें फल-फूल, लकड़ी, दवाएँ आदि मिलती हैं। पेड़ से हमें ऑक्सीजन भी प्राप्त होती है। अत: अधिक-से अधिक पेड़ लगाने चाहिए।

(२) कुआँ – कुएँ ग्रामीण क्षेत्रों में बहुत काम आते हैं। खेती के कार्य में एवं पीने के लिए भी इससे जल प्राप्त होता है। इससे भूजल स्तर में वृद्धि होती है।

(३) झरना – पहाड़ों से एकत्रित होकर पानी मैदानी भाग में गिरता है, तो उससे झरने का निर्माण होता है। इससे प्राप्त जल का उपयोग कृषि कार्य एवं अन्य कार्यों में किया जाता है।

(४) बादल – बादल को आकाश में देखते ही किसान खुश हो जाते हैं। बादल जब बरसते हैं, तो किसान खेती के कार्य में लग जाते हैं। अच्छी वर्षा किसानों और देश के लिए समृद्धि का सूचक है।

(५) नदी – नदी के जल से देश के अधिकांश भागों में सिंचाई की जाती है। नदियों का जल पीने के काम में आता है। नदियों का धार्मिक महत्त्व भी है। नदियों में स्नान करना पुण्यकारक माना जाता है।

Hindi Sulabhbharti Class 6 Solutions Chapter 8 जन्मदिन Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्द में लिखिएः

Question 1.
सूरज क्या बरसाने लगा?
Answer:
आग।

Question 2.
बबलू को बाथरूम में घुसे कितना घंटा हो चुका था?
Answer:
आधा।

Question 3.
बबलू को शीला मौसी के घर क्या देखकर आश्चर्य हुआ?
Answer:
सन्नाटा।

Question 4.
बबलू किससे बेचैन था?
Answer:
प्यास।

Question 5.
शीला मौसी के घर जो कुछ हुआ, वह क्या था?
Answer:
नाटक।

कोष्ठक में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(भोजन, बिजली, भरोसा, तीखे, मोमबत्तियों, जन्मदिन, उपाय, कॉलनी)

Question 1.
धीरे धीरे उसके तेवर ………………. हो चले।
Answer:
तीखे

Question 2.
उन्हें कोई ……………… नहीं सूझ रहा था।
Answer:
उपाय

Question 3.
मेज पर ……………… लगा हुआ था।
Answer:
भोजन

Question 4.
केवल दो-एक ……………… का धीमा प्रकाश फैला हुआ था।
Answer:
मोमबत्तियों

Question 5.
………….. के इस ब्लॉक में कटौती हुई है।
Answer:
कॉलनी

Question 6.
हम पूजा का ……………… तो हँसी – खुशी से मनाएंगे।
Answer:
जन्मदिन

Question 7.
अचानक ……………… आ गई।
Answer:
बिजली

Question 8.
शीला मौसी ने भी कुछ करने का …………… दिया था।
Answer:
भरोसा

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए:

Question 1.
बबलू की घमा-चौकड़ी कहाँ मची हुई थी?
Answer:
बबलू की धमा-चौकड़ी शावर के नीचे मची हुई थी।

Question 2.
उस दिन किसका जन्मदिन था?
Answer:
उस दिन शीला मौसी की बेटी पूजा का जन्मदिन था।

Question 3.
चलने से पहले शीला मौसी और माँ ने क्या किया?
Answer:
चलने से पहले शीला मौसी और माँ एक-दूसरे को देखकर कुछ मुसकुराई।

Question 4.
घर पहुँचने पर माँ को क्या दिखाई पड़ा?
Answer:
घर पहुँचने पर माँ को बबलू किसी सोच में डूबा दिखाई पड़ा।

किसने, किससे कहाः

Question 1.
“बबलू, क्यों इस तरह पानी बरबाद कर रहे हो?”
Answer:
माँ ने बबलू से का।

Question 2.
“आज कॉलोनी के इस ब्लॉक में कटौती हुई है।”
Answer:
शीला मौसी ने सभी मेहमानों से कहा।

Question 3.
“अरे बच्चो, मैं तो भूल ही गया था कि बड़ेवाले पानी के कूलर में पानी भरा हुआ है।”
Answer:
अंकल ने बच्चों से कहा।

Question 4.
“माँ, अब पानी की एक बूंद भी बरबाद नहीं होगी।”
Answer:
बबलू ने माँ से कहा

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. आग
2. पानी
3. नहाना
4. बिजली
5. उपाय
6. बेटी
7. प्रकाश
8. कामयाब
9. नाटक

Answer:

1. अग्नि
2. जल
3. सान
4. विद्युत
5. तरकीब
6. पुत्री
7. उजाला
8. सफल
9. दिखावा

निम्नलिखित शब्दों के विलोम शब्द लिखिए:

1. गरमी
2. तीखे
3. नीचे
4. सीमित
5. धीमा
6. खुशी
7. दोस्त

Answer:

1. ठंढी
2. मौठे
3. ऊपर
4. असीमित
5. तेज़
6. दुखी
7. दुश्मन

निम्नलिखित शब्दों के लिंग बदलिए:

1. मौसी
2. बेटी

Answer:

1. मौसा
2. बेटा

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. कमरा
2. तीखा
3. गुब्बारा
4. मिठाई
5. मोमबत्ती
6. बच्चा
7. आँख
8. पंखा

Answer:

1. कमरे
2. तीखे
3. गुब्बारे
4. मिठाइयाँ
5. मोमबत्तियाँ
6. बच्चे
7. आँखें
8. पंखे

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 16 मुक्या प्राण्यांची कैफियत Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 16 मुक्या प्राण्यांची कैफियत

Marathi Sulabhbharti Class 6 Solutions Chapter 16 मुक्या प्राण्यांची कैफियत Textbook Questions and Answers

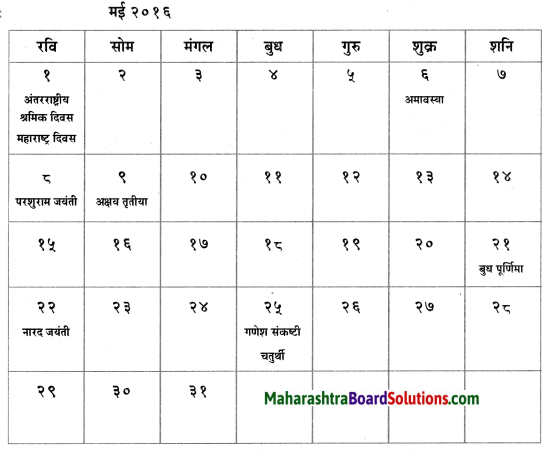
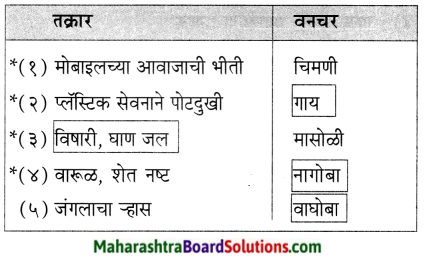
1. तक्रार व वनचर यांच्या माध्यामातून जोड्या पूर्ण करा.

प्रश्न 1.
तक्रार व वनचर यांच्या माध्यामातून जोड्या पूर्ण करा.

उत्तर:

2. दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
या पाठात कोणाकोणात संवाद झालेला आहे?
उत्तर:
या पाठात गाय, चिमणी, मासोळी, नागोबा, सर्व प्राणी व माणूस यांच्यात संवाद झालेला आहे.

प्रश्न आ.
चिमणीला कोणता त्रास होतो?
उत्तर:
मोबाईलच्या आवाजाने चिमणीची छाती धडधडून तिचा जीव व्याकूळ होतो. तिला काही सुचत नाही.

प्रश्न इ.
गाईचे डोळे का पाणावले?
उत्तर:
माणसाने टाकलेले प्लॅस्टिक घासाबरोबर गाईच्या पोटात जाऊन तिचे पोट दुखू लागले व तिचे डोळे पाणावले.

प्रश्न ई.
मासोळीने आपली कोणती समस्या मांडली आहे?
उत्तर:
सांडपाणी व रसायने टाकून माणसाने पाणी विषारी करून टाकले आहे. ते पाणी घाण असल्याने पिण्यासारखे नाही. म्हणून जलचर तडफडत आहेत. ही समस्या मांडली आहे.

प्रश्न उ.
नागोबाची तक्रार कोणती आहे?
उत्तर:
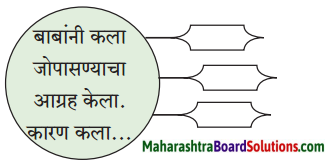
गवत, शेती नष्ट झाल्याने वारूळेही राहिली नाहीत. मानवाने पर्यावरणाचा -हास केला आहे. नागोबांना पकडून नागपंचमीला दूध, लाया दिले जाते. हे त्याचे अन्न नाही. अंधश्रद्धेपोटी माणूस नागांच्या जीवावर उठला आहे. ही तक्रार आहे.

3. घोटभर, मैलभर, तासभर, कणभर, चमचाभर हे शब्द वापरून वाक्ये लिहा.

प्रश्न 1.
घोटभर, मैलभर, तासभर, कणभर, चमचाभर हे शब्द वापरून वाक्ये लिहा.

उत्तर:

1. घोटभर – उन्हाळ्यात घोटभर पाणी मिळाले तरी समाधान वाटते.
2. मैलभर – मैलभर अंतर चालून गेल्यावर एक देऊळ लागले.
3. तासभर – झाकीरने तासभर तबला वाजविला.
4. कणभर – कणभरही अन्न वाया जाऊ देऊ नये.
5. चमचाभर- चमचाभर औषध तापाला घालविते.
6. टिचभर – मुंबईत टिचभर ही जागा शिल्लक नाही.
7. रात्रभर – यात्रेकरू रात्रभर डोंगर चढत होते.

4. कोण ते सांगा. (वनचर, भूचर, जलचर, उभयचर)

प्रश्न 1.
कोण ते सांगा. (वनचर, भूचर, जलचर, उभयचर)
उत्तर:
पाण्यात राहणारे – जलचर
जमिनीवर राहणारे – भूचर
जंगलात राहणारे – वनचर
जमीन व पाणी या दोन्ही ठिकाणी राहणारे – उभयचर

5. खालील शब्दांचे समानार्थी शब्द पाठातून शोधून लिहा.

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द पाठातून शोधून लिहा.

1. किनारा
2. शेवट
3. जल
4. आठवण
5. मासा
6. नातेवाईक
7. व्याकूळ
8. आचरण

उत्तर:

1. काठ
2. गडप
3. जळ
4. स्मरण
5. मासोळी
6. सोयरे
7. कासावीस
8. वर्तन

6. खालील शब्दांचे अर्थ शिक्षकांच्या मदतीने समजून घ्या.

प्रश्न 1.
खालील शब्दांचे अर्थ शिक्षकांच्या मदतीने समजून घ्या.
सगेसोयरे, पाहुणे, नातेवाईक, भाऊबंद

7. खालील शब्दांचे लिंग बदला.

प्रश्न 1.
खालील शब्दांचे लिंग बदला.
उत्तर:

1. चिमणी – चिमण्या
2. नाग – नाग
3. वाघ – वाघ

8. खालील वाक्यांत कंसातील योग्य वाक्प्रचार घाला. (उदास दिसणे, कासावीस होणे, डोळे पाणावणे, डोळे उघडणे)

प्रश्न अ.
सह्याद्री डोंगर चढताना आमचा जीव पाणी पिण्यासाठी ……………….. होत होता.
उत्तर:
सह्याद्री डोंगर चढताना आमचा जीव पाणी पिण्यासाठी कासावीस होत होता.

प्रश्न आ.
आवडते पेन हरवल्याने संजय आज …………………… होता.
उत्तर:
आवडते पेन हरवल्याने संजय आज उदास होता.

प्रश्न इ.
पाणी टंचाई भासू लागताच पाणी बचतीबाबत सर्वांचे ………………. उघडले.
उत्तर:
पाणी टंचाई भासू लागताच पाणी बचतीबाबत सर्वांचे डोळे उघडले.

प्रश्न ई.
रस्त्यावर घडलेला अपघात बघून सर्वांचे …………………. .
उत्तर:
रस्त्यावर घडलेला अपघात बघून सर्वांचे डोळे पाणावले.

9. धडधड, तगमग यासारखे आणखी शब्द लिहा.

प्रश्न 1.
धडधड, तगमग यासारखे आणखी शब्द लिहा.
उत्तर:
सरसर, झरझर, गडगड, झगमग, धगधग

प्रश्न 2.
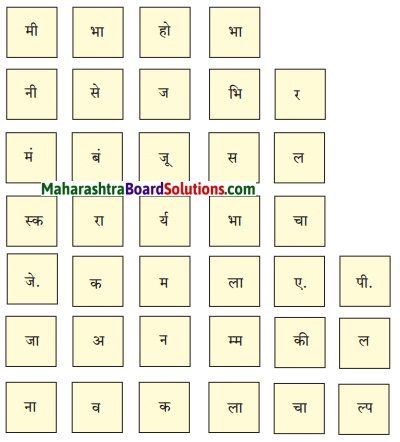
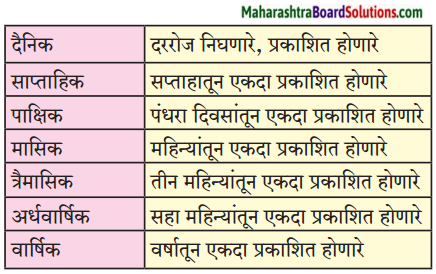
खालील चौकटीत काही प्राणी व काही पक्ष्यांची नावे लपलेली आहेत. ते शोधा व त्यांची नावे लिहा.

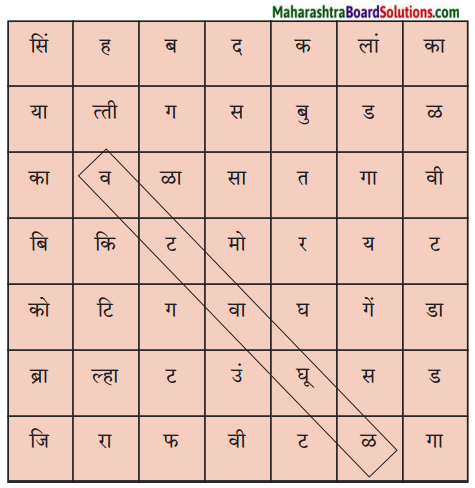
उदा. वटवाघूळ
उत्तरः

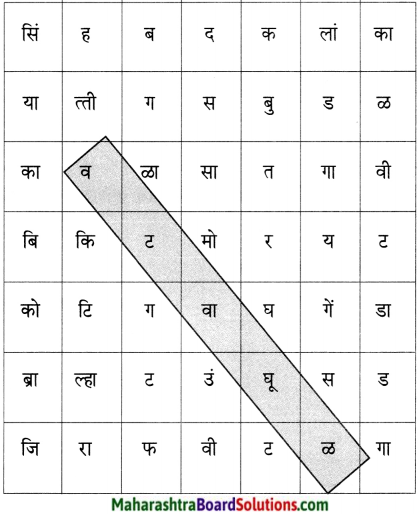
प्रश्न 2.
दवाखान्याचा ठिकाणी असलेल्या सुचनांच्या पाट्या तयार करा.

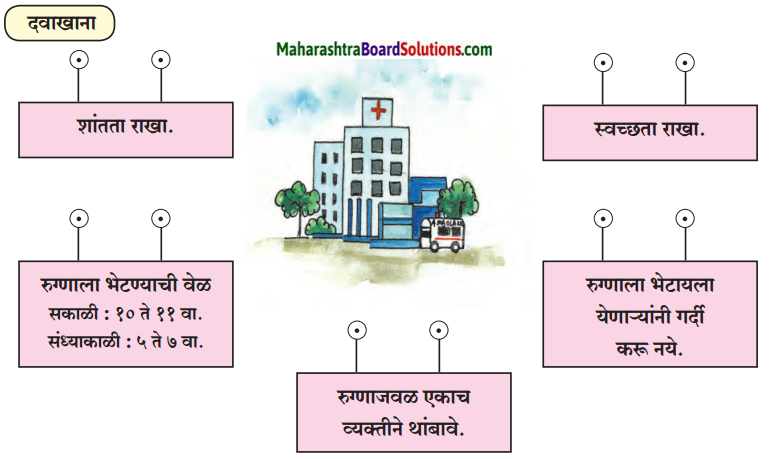
उत्तरः

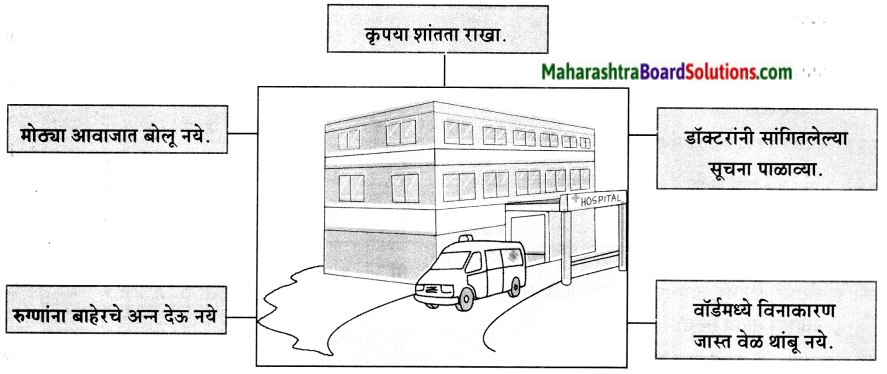
प्रश्न 3.
शाळेच्या परिसरात स्वच्छताविषयक कोणत्या पाट्या लावाल.

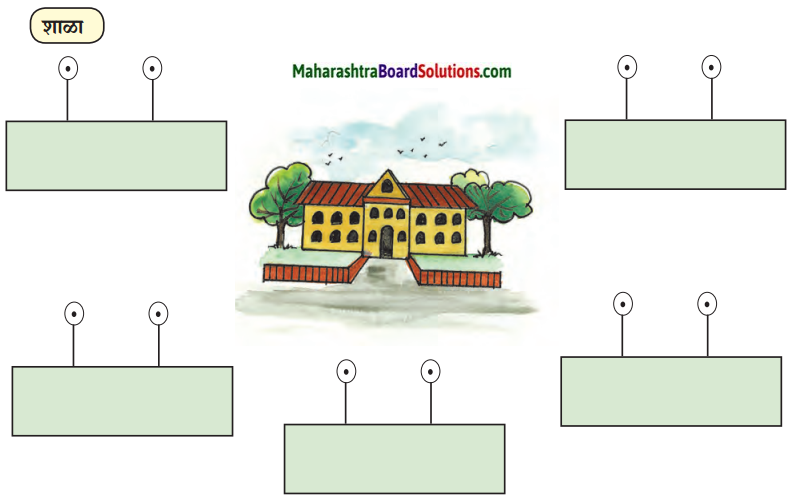
उत्तरः

प्रश्न 4.
‘पर्यावरण संरक्षण’ याविषयी पाठाच्या शेवटी माणसाने केलेली प्रतिज्ञा तुमच्या शब्दात लिहा.

उत्तरः

प्रश्न 5.
वाचा. समजून घ्या.
उत्तरः

आपण समजून घेऊया.

प्रश्न 1.
खालील वाक्यांतील अधोरेखित शब्द पाहा.

1. ही माझी छत्री आहे.
2. तू कोणाचा मुलगा आहेस?
3. मी कालच गावाहून आलो.
4. जी वेगाने पळेल, ती जिंकेल.

प्रश्न 2.
अधोरेखित केलेले शब्द ‘एकाक्षरी’ शब्द आहेत. एकाक्षरी शब्दांना दयायची वेलांटी किंवा उ-कार नेहमी | दीर्घ लिहितात. या नियमाला फक्त ‘नि’ हा शब्द अपवाद आहे. खालील शब्दांपासून वाक्ये बनवा.

1.  ती –
2. पी –
3. मी –
4. ही –

प्रश्न 3.
खालील शब्द वाचा. शब्दांतील शेवटच्या अक्षराला दिलेली वेलांटी, उ-कार समजून घ्या.
चिमणी, विळी, मिरची, कढई, चटई, सफाई, खिडकी, मागू, चिकू, पेरू, नाचू, वस्तू, गाऊ, शिंगरू, कांगारू, ताई, समई, पाहुणी, पाणी. मराठी भाषेत शब्दांतील शेवटच्या अक्षराला दयायची वेलांटी किंवा उ-कार नेहमी दीर्घ लिहितात. या नियमाला ‘आणि’, ‘परंतु’ हे शब्द अपवाद आहेत.

Class 6 Marathi Chapter 16 मुक्या प्राण्यांची कैफियत Additional Important Questions and Answers

दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
माणसाने सगेसोयरे कोणाला म्हटले आहे?
उत्तर:
माणसाने कीटक, पक्षी, जलचर, वनचर यांना सगेसोयरे म्हटले आहे.

प्रश्न 2.
माणसाने प्राण्यांपाशी काय कबूल केले?
उत्तर:
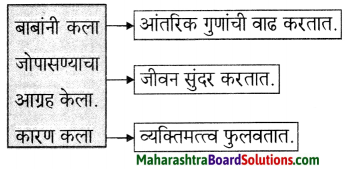
पर्यावरणाचा केलेला हास माणसाच्या लक्षात आला. सर्व प्राणी तक्रार करू लागले. माणसाने तेव्हा यापुढे आम्ही आमचे वर्तन बदलू व पर्वत, जल, वातावरणात प्रदूषण करणार नाही असे सांगून वृक्षारोपण करू, वनीकरण करू असे ही आश्वासन दिले.

प्रश्न 3.
मानवाने केलेल्या प्रदूषणाचा कोणता दुष्परिणाम होईल, असे सर्व प्राण्यांनी सांगितले?
उत्तर:
प्राणी तक्रार करू लागले. मानवाने हवेचे, पाण्याचे, भूमीचे प्रदूषण केले. त्यामुळे वनचर आता तुझे सोयरे नाहीत. धरती माता दूषण देईल. मग माणूस दूध, अन्न पाण्यावाचून तडफडेल, असे सर्व प्राण्यांनी मानवाने केलेल्या प्रदूषणाचे दुष्परिणाम सांगितले.

व्याकरण व भाषाभ्यास

प्रश्न 1.
खालील शब्दांचे लिंग बदला.

1. मोर
2. सिंह
3. गाय
4. मांजर
5. राघू
6. कासव
7. हरिण

उत्तर:

1. लांडोर
2. सिंहिण
3. बैल
4. बोका
5. मैना
6. कासविण
7. हरिणी

प्रश्न 2.
खालील शब्दांचे लिंग बदला.

1. गाय
2. मासा
3. जंगल
4. पक्षी
5. माणूस

उत्तर:

1. गाई
2. मासे
3. जंगले
4. पक्षी
5. माणसे

हे लक्षात ठेवा:

एकाक्षरी शब्दांना दयायची वेलांटी किंवा उ-कार नेहमी दीर्घ लिहितात. अपवाद – ‘नि’.

प्रश्न 1.
खालील शब्दांपासून वाक्ये बनवा.
उत्तर:

1. ती – ती खूप हुशार आहे.
2. पी – तू पाणी पी.
3. मी – मी अभ्यास करतो.
4. ही – ही साडी छान आहे.

शब्दातील शेवटच्या अक्षराला दयायची वेलांटी किंवा उ-कार नेहमी दीर्घ लिहितात.

अपवाद – आणि, परंतु उदा. चिमणी, कढई, वस्तू, विक्री इ.

प्रश्न 2.
खालील शब्दांपासून वाक्ये बनवा.
उत्तर:
मिरची – पोपट मिरची खातो.
सफाई – दिवाळीत घरातील सफाई करतात.
चिकू – मला चिकू आवडतात.
गाऊ – आम्ही गाणे गाऊ.

प्रश्न 3.
कोण ते सांगा. (वनचर, भूचर, जलचर, उभयचर)
उत्तर:
पाण्यात राहणारे – जलचर
जमिनीवर राहणारे – भूचर
जंगलात राहणारे – वनचर
जमीन व पाणी या दोन्ही ठिकाणी राहणारे – उभयचर

प्रश्न 4.
खालील शब्दांचे विरूद्धार्थी शब्द पाठातून शोधून लिहा.

1. प्रसन्न
2. कठोर
3. वेडा
4. बिनविषारी
5. स्वच्छ
6. श्रद्धा

उत्तर:

1. उदास
2. नाजूक
3. शहाणा
4. विषारी
5. घाण
6. अंधश्रद्धा

मुक्या प्राण्यांची कैफियत Summary in Marathi

पाठपरिचयः

सदर पाठात पशू-पक्षी, जलचरांना मानवाकडून, त्याच्या अविचाराने होणारा त्रास वर्णन केला आहे. जलचर, भूचर त्रस्त आहेत. याचे दुष्परिणाम सर्व प्राणी मानवास जेव्हा सांगतात तेव्हा डोळे उघडतात. ‘पर्यावरण रक्षण’ कसे करावे हे यातून शिकता येते.

शब्दार्थ:

1. कैफियत – तक्रार (complaint)
2. वन – अरण्य, जंगल (forest)
3. भीती – भय (fear)
4. नाजक – कोमल (delicate)
5. ढीग – रास (heap)
6. पोटशूळ – पोट दुखणे (stomach ache)
7. शहाणा – विवेकी (wise)
8. जल – पाणी (water)
9. विषारी – विषमिश्रीत (poisonous)
10. वारूळ – मुंग्यांचे घर (ant hill)
11. अंधश्रद्धा – चुकीच्या संकल्पना (superstition)
12. हास – नष्ट (destruction)
13. सोयरे – नातेवाईक (relatives)
14. स्मरण – आठवण (remembrance)
15. जागृत – सावध, जागरूक (to be aware of, vigilant)
16. पर्यावरण – वातावरण (enviornment)
17. वर्तन – आचरण (behaviour)
18. वनीकरण – वन, जंगले वसविणे (forestation)
19. वनचर – वनात फिरणारे प्राणी (wild animals)
20. नच – नाही (no, not)
21. वातावरण – आजूबाजूचा परिसर (atmosphere)
22. प्रदूषण – दूषित करणे (pollution)
23. हिरवेगार – गर्द हिरवे (greenish)

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati पुनरावर्तन २ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions पुनरावर्तन २

Hindi Sulabhbharti Class 6 Solutions पुनरावर्तन २ Textbook Questions and Answers

Question 1.
शाक (पत्तोंवाली) और सब्जियों के पाँच – पाँच नाम सुनो और सुनाओ:
Answer:
शाक (पत्तोंवाली) के नाम:

(१) पालक
(२) सोवा
(३) मेथी
(४) बथुआ
(५) चौलाई

सब्ज़ियों के नाम:

(१) भिंडी
(२) बैंगन
(३) लौकी
(४) कुम्हड़ा
(५) बोड़ी

Question 2.
एक महीने की दिनदर्शिका बनाओ और विशेष दिन बताओ:
Answer:

Question 3.
१ से १०० तक की संख्याओं का मुखर वाचन करोः
Answer:

1. १ एक
2. – २ दो
3. – ३ तीन
4. – ४ चार
5. – ५ पांच
6. – ६ छह
7. – ७ सात
8. – ८ आठ
9. – ९ नौ
10. – १० दस
11. – ११ ग्यारह
12. – १२ बारह
13. – १३ तेरह
14. – १४ चौदह
15. – १५ पंद्रह
16. – १६ सोलह
17. – १७ सत्रह
18. – १८ अठारह
19. – १९ उन्नीस
20. – २० बीस
21. – २१ इकीस
22. – २२ बाईस
23. – २३ तेइस
24. – २४ चौबीस
25. – २५ पच्चीस
26. – २६ छब्बीस
27. – २७ सताइस
28. – २८ अट्ठाइस
29. – २९ उनतीस
30. – ३० तीस
31. – ३१ इकतीस
32. – ३२ बतीस
33. – ३३ तैंतीस
34. – ३४ चौंतीस
35. – ३५ पैंतीस
36. – ३६ छतीस
37. – ३७ सैंतीस
38. – ३८ अड़तीस
39. – ३९ उनतालीस
40. – ४० चालीस
41. – ४१ इकतालीस
42. – ४२ बयालीस
43. – ४३ तैतालीस
44. – ४४ चवालीस
45. – ४५ पैंतालीस
46. – ४६ छयालिस
47. – ४७ सैंतालीस
48. – ४८ अड़तालीस
49. – ४९ उनचास
50. – ५० पचास
51. – ५१ इक्यावन
52. – ५२ बावन
53. – ५३ तिरपन
54. – ५४ चौवन
55. – ५५ पचपन
56. – ५६ छप्पन
57. – ५७ सतावन
58. – ५८ अठावन
59. – ५९ उनसठ
60. – ६० साठ
61. – ६१ इकसठ
62. – ६२ बासठ
63. – ६३ तिरसठ
64. – ६४ चौंसठ
65. – ६५ पैंसठ
66. – ६६ छियासठ
67. – ६७ सड़सठ
68. – ६८ अड़सठ
69. – ६९ उनहतर
70. – ७० सत्तर
71. – ७१ इकहतर
72. – ७२ बहतर
73. – ७३ तिहतर
74. – ७४ चौहतर
75. – ७५ पचहतर
76. – ७६ छिहतर
77. – ७७ सतहतर
78. – ७८ अठहतर
79. – ७९ उन्नासी
80. – ८० अस्सी
81. – ८१ इक्यासी
82. – ८२ बयासी
83. – ८३ तिरासी
84. – ८४ चौरासी
85. – ८५ पचासी
86. – ८६ छियासी
87. – ८७ सतासी
88. – ८८ अट्ठासी
89. – ८९ नवासी
90. – ९० नब्बे
91. – ९१ इक्यानवे
92. – ९२ बानवे
93. – ९३ तिरानवे
94. – ९४ चौरानवे
95. – ९५ पचानवे
96. – ९६ छियानवे
97. – ९७ सतानवे
98. – ९८ अट्ठानवे
99. – ९९ निन्यानवे
100. – १०० एक सौ

Question 4.
अपना परिचय देते हुए अपने परिवार के बारे में दस बाक्य लिखो:
Answer:
मेरा नाम ………… है।
मेरे पिता जी का नाम श्री …………. है।
मैं कक्षा छठी में पढ़ता हूँ।
मेरे विद्यालय का नाम ………… है।
मेरे पिताजी एक ………… हैं।
मेरी माँ ………… हैं।
मेरा परिवार संयुक्त है।
मेरे परिवार में मेरे दादा, दादी, चाचा और चाची साथ रहते है।
मुझे मेरा परिवार बहुत अच्छा लगता है।

Question 5.
अक्षर समूह में से वैज्ञानिकों के उचित नाम बताओ और लिखो।

Answer:
(१) होमी भाभा
(२) नीरज भिसे
(३) मंजू बंसल
(४) भास्कराचार्य
(५) ए. पी. जे. कलाम
(६) जानकी अम्मल
(७) कल्पना चावला

Hindi Sulabhbharti Class 6 Solutions पुनरावर्तन २ Additional Important Questions and Answers

Question 1.
अपने बारे में भाई / बहन से सुनो।
Answer:
विद्यार्थियों द्वारा स्वयं किया जाए।

Question 2.
इस वर्ष तुम कौन – सा विशेष कार्य करोगे, बताओ?
Answer:
इस वर्ष मैं ग्रीष्मावकाश में तैराकी सीलूँगा और संगीत एवं कैसियो की पढ़ाई करूँगा। संगीत में मेरी रुचि है, अत: मैं शास्त्रीय संगीत सीखने की कोशिश करूँगा।

Question 3.
सप्ताह में एक दिन कहानियाँ पढ़ो।
Answer:
विद्यार्थियों द्वारा स्वयं किया जाए।

Question 4.
पढ़ी हुई सामग्री की विश्लेषणात्मक प्रस्तुति करो।
Answer:
विद्यार्थियों द्वारा स्वयं किया जाए।

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 10 बाबांचं पत्र Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 10 बाबांचं पत्र

Marathi Sulabhbharti Class 6 Solutions Chapter 10 बाबांचं पत्र Textbook Questions and Answers

1. एका शब्दात उत्तरे लिहा.

प्रश्न 1.
(अ) कठीण गेलेला पेपर
(आ) वैष्णवीला पत्र लिहणारे
(इ) परीक्षेतील गुणांपेक्षा महत्त्वाचे गुण
(ई) वैष्णवीसाठी बाबा आणणार असलेला खाऊ
उत्तर:
(अ) कठीण गेलेला पेपर – गणित
(आ) वैष्णवीला पत्र लिहणारे – बाबा
(इ) परीक्षेतील गुणांपेक्षा महत्त्वाचे गुण – आंतरिक गुण
(ई) वैष्णवीसाठी बाबा आणणार असलेला खाऊ – पुस्तके

2. एका वाक्यात उत्तरे लिहा.

प्रश्न अ.
आईने दूरध्वनीवरून बाबांना कोणता निरोप दिला?
उत्तर:
‘सहामाही परीक्षेत गणिताचा पेपर खूपच कठीण गेल्यामुळे वैष्णवी फार निराश झाली आहे’ हा निरोप आईने बाबांना दूरध्वनीवरून दिला.

प्रश्न आ.
बाबांनी दूरध्वनीवरून बोलणे का पसंत केले नाही?
उत्तर:
बाबांना वैष्णवीशी हितगुज करावेसे वाटले, म्हणून बाबांनी दूरध्वनीवरून बोलणे पसंत केले नाही.

प्रश्न इ.
गणित विषय वैष्णवीचा लाडका होण्यासाठी बाबांनी कोणते उपाय सुचवले आहेत?
उत्तर:
गणित विषय वैष्णवीचा लाडका होण्यासाठी बाबांनी वैष्णवीला सांगितले की, गणिताचा पेपर कठीण गेला, म्हणून गणितानंतर असलेल्या विषयांचे पेपर अवघडच जाणार असे होत नाही ना! मग त्याच त्या गोष्टीचा विचार करत बसल्याने उरलेल्या पेपरवरही त्याचा विपरीत परिणाम होतो. ‘अगं, एखादया विषयात गुण कमी पडले, तर याचा अर्थ आपण आयुष्यात अपयशी झालो असे नाही.

तुला सांगतो, गणिताशी तू मैत्री कर. मग बघ गंमत या विषयाची. तुला मुळीच भीती वाटणार नाही. गणितातील संकल्पना, संबोध, क्रिया तू नीट समजून घे. उदाहरणे सोडवण्याचा चांगला सराव कर. हा विषय लवकरच तुझा लाडका होईल.’ हा उपाय सुचवला.

3. खालील शब्दांचे समानार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

उत्तर:

4. खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

उत्तर:

5.

प्रश्न अ.

उत्तर:

प्रश्न आ.

उत्तर:

6. सध्याच्या युगात पत्र पाठवण्याची कोणकोणती साधने उपलब्ध आहेत त्यांची यादी करा. 

प्रश्न 1.
सध्याच्या युगात पत्र पाठवण्याची कोणकोणती साधने उपलब्ध आहेत त्यांची यादी करा.
उत्तर:

1. पत्रपेटी
2. टपालगाडी
3. कुरिअर
4. ईमेल
5. विमान

7. दिवाळीच्या सुट्टीत तुम्ही काय काय गंमत करणार त्याची यादी बनवा.

प्रश्न 1.
दिवाळीच्या सुट्टीत तुम्ही काय काय गंमत करणार त्याची यादी बनवा.
उत्तरः

1. प्रथम मी नवीन कपडे विकत घेणार,
2. बाबांना सोबत घेऊन फटाके विकत घेणार.
3. आई बरोबर मामाच्या गावी जाणार.
4. आई व आजी यांना फराळ बनवण्यात मदत करणार.
5. मित्रांबरोबर मोकळ्या अंगणात फटाके वाजवणार.
6. शिक्षकांनी दिलेला गृहपाठ वेळेवर पूर्ण करेन.
7. मित्रांसोबत घराच्या अंगणात मातीचा किल्ला तयार करणार.
8. किल्ल्यावर शिवाजी महाराज व इतर शिपाई यांची मांडणी करणार.

8. तुमच्या मित्राला/मैत्रिणीला पोहण्याच्या स्पर्धेत राज्यातून प्रथम क्रमांक प्राप्त झाला. त्याचे तिचे अभिनंदन करणारा संदेश खालील चौकटीत लिहा.

प्रश्न 1.
तुमच्या मित्राला/मैत्रिणीला पोहण्याच्या स्पर्धेत राज्यातून प्रथम क्रमांक प्राप्त झाला. त्याचे तिचे अभिनंदन करणारा संदेश खालील चौकटीत लिहा.
उत्तर:
प्रिय सुप्रिया, अभिनंदन ! अभिनंदन !! अभिनंदन!!!
तुझा पोहण्याच्या स्पर्धेत राज्यातून प्रथम क्रमांक आला हे ऐकून खूप अभिमान वाटला.
असेच यश तुझ्या वाट्याला पुढे पुढे येवो, हिच ईश्वर चरणी प्रार्थना….

9. अपयश ही यशाची पहिली पायरी आहे.’ यासारखी दोन वाक्ये खालील चौकटीत लिहा. 

प्रश्न 1.
अपयश ही यशाची पहिली पायरी आहे.’ यासारखी दोन वाक्ये खालील चौकटीत लिहा.
उत्तर:
1. सुख आणि दुःख यांना सारखेच सामोरे जावे,
2. संकटांना जो धैर्याने तोंड देतो, तोच जीवनात विजयी होतो.

प्रकल्प: साने गुरुजी यांचे ‘सुंदर पत्रे’ हे पुस्तक मिळवा. वाचा. त्यातील तुम्हांला आवडलेली पत्रे सुरेख अक्षरांत लिहा.

प्रश्न 2.
खालील वाक्यांतील रिकाम्या जागी कंसातील योग्य विशेषणे लिहा.
(टवटवीत, उंच, नवा, शंभर)
(अ) हिमालय ………… पर्वत आहे.
(आ) कंपास घ्यायला आईने मला ……………. रुपये दिले.
(इ) बागेत ………….. फुले आहेत.
(ई) ताईने मला …………..’ सदरा दिला.
उत्तर:
(अ) उंच
(आ) शंभर
(इ) टवटवीत
(ई) नवा

आपण समजून घेऊया.

प्रश्न 3.
खालील तक्ता वाचा. समजून घ्या.

उत्तर:

वाक्ये	क्रियापदे	काळ
1. सुनीताने बोरे खाल्ली.	खाल्ली	भूतकाळ
2. मी क्रिकेटची मॅच पाहीन.	पाहीन	भविष्यकाळ
3. सुधीर पत्र लिहीत आहे.	आहे	वर्तमानकाळ
4. वनिता गोड गाणे गाते.	गाते	वर्तमानकाळ
5. आईने कादंबरी वाचली.	वाचली	भूतकाळ

क्रियापदाच्या रूपावरून वाक्यांतील काळ ओळखता येतो.
काळाचे मुख्य तीन प्रकार आहेत.

1. वर्तमानकाळ
2. भूतकाळ
3. भविष्यकाळ

Marathi Sulabhbharti Class 6 Solutions Chapter 10 बाबांचं पत्र Important Additional Questions and Answers

खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
बाबांनी वैष्णवीला कोणत्या विषयाशी मैत्री करायला सांगितले आहे?
उत्तर:
बाबांनी वैष्णवीला गणित विषयाशी मैत्री करायला सांगितले आहे.

प्रश्न 2.
परीक्षेतील गुण किंवा श्रेणी पेक्षा अजून कोणती गोष्ट महत्त्वाची आहे?
उत्तर:
परीक्षेतील गुण किंवा श्रेणी पेक्षा आपल्या आंतरिक गुणांची वाढ करणे हे अधिक महत्त्वाचे आहे.

प्रश्न 3.
स्वत:मधील गुणांची वाढ करण्याकरिता प्रत्येकाने काय केले पाहिजे?
उत्तर:
स्वत:मधील गुणांची वाढ करण्याकरिता प्रत्येकाने एखादी तरी कला जोपासली पाहिजे.

प्रश्न 4.
दिवाळीच्या सुट्टीत बाबा कुठे येणार आहेत?
उत्तर:
दिवाळीच्या सुट्टीत बाबा गावी येणार आहेत.

प्रश्न 5.
गावी येताना बाबा वैष्णवीसाठी काय आणणार आहेत?
उत्तर:
गावी येताना बाबा वैष्णवीसाठी खाऊ आणणार आहेत.

प्रश्न 6.
बाबा गावी येताना वैष्णवीसाठी कोणती पुस्तके आणणार आहेत?
उत्तर:
बाबा गावी येताना वैष्णवीसाठी गोष्टीची पुस्तके आणणार आहेत.

बाबांचं पत्र Summary in Marathi

पाठपरिचय:

हे एक वडिलांनी आपल्या मुलीला लिहिलेले सांत्वनपर पत्र आहे. आपल्या मुलीला गणिताचा पेपर अवघड गेल्यामुळे आलेली | निराशा वडीलांनी अतिशय सहजतेने कशी दूर करण्याचा प्रयत्न केला, त्याचे हे पत्र म्हणजे एक सुंदर उदाहरण आहे.

शब्दार्थ:

1. प्रिय – प्रेमळ (dear)
2. शुभ – मंगलदायक, पवित्र (holy)
3. पुरता – पुरेसा (enough)
4. गुरफटणे – गुंतून राहणे (involve, entangled)
5. निराश – नाराज (disappointed)
6. हितगुज करणे – मनातील गोष्ट सांगणे (to chat)
7. विपरीत – वाईट (bad)
8. संबोध – मूळ संकल्पना (concept)
9. सराव – कृती (practice)
10. लाडका – आवडीचा (favourite)
11. आंतरिक – आतील गुण (internal qualities)
12. उत्तम – अधिक चांगले (very good)
13. नृत्य – नाच (dance)
14. जोपासणे – सांभाळणे (to keep safe, to look after)
15. पुरेपूर – पूर्णपणे (completely)
16. खात्री – विस्वास (belief, trust)
17. भेटीअंती – भेट झाल्यानंतर (after meeting)

वाक्प्रचार व अर्थ:

1. निराश होणे – नाराज होणे.
2. हितगुज करणे – मनातील गोष्ट सांगणे.
3. विपरीत परिणाम होणे – वाईट परिणाम होणे.
4. संधी मिळणे – वाव मिळणे.
5. खात्री असणे – विश्वास असणे.

Balbharti Maharashtra State Board Class 6 English Solutions Chapter 2.3 A Wall Magazine for your Class! Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 English Solutions Chapter 2.3 A Wall Magazine for your Class!

Class 6 English Chapter 2.3 A Wall Magazine for your Class! Textbook Questions and Answers

Question 1.
Prepare a notice asking students to contribute towards the school magazine.
Answer:
PVR Public School, Mumbai
Notice
Class Wall Magazine

29th June, 2016

Students of Standard VI are invited to contribute towards the Wall Magazine to be put up in your class. You could get different articles from old newspapers or periodicals. You could also write short stories, poems, jokes, riddles and much more. All materials brought should be handed over to your class representatives. Hurry!! Come up with different ideas and make a unique Wall Magazine in your class.

Question 2.
Ways to plan a Wall Magazine.
Answer:

1. Create a theme – e.g., craft ideas, I need help, recipes, etc.
2. Gather material from students.
3. See which matter would fit the theme.
4. Use creativity in preparing the title.
5. Decide how to arrange the content.
6. Make the wall magazine colourful.
7. Avoid spelling mistakes.
8. Pictures and articles should be put in the right places.

Question 3.
Importance of Team Work
Answer:
A Wall Magazine teaches students how to cordially work in groups, bringing out the best in everyone. It inculcates values such as sharing, tolerance, acceptance, etc.

1. Brings about efficiency
2. Better understanding
3. Unique ideas
4. Brings out the best in each student
5. Makes work easier
6. Makes work fun

Question 4.
List of topics that can be included on a Wall
Answer:

1. Stories
2. Poems
3. Puzzles
4. Riddles
5. Craft ideas
6. Informative articles
7. Jokes I need help
8. Board games
9. Book reviews
10. Quizzes
11. Study tips
12. Health tips
13. Fashion tips
14. Beauty tips
15. Gardening tips
16. Recipes
17. Solve my problem
18. Science comer
19. Photography comer
20. Baby talk

You can add more to the list.

A Wall Magazine for your Class! Summary in English

Introduction:

A wall magazine is a must for every class. It encourages and motivates students to shed their inhibitions and contribute their share of talent towards the magazine. It is a wonderful way to encourage students to read, write and find articles to be put up on the wall magazine. The topics could range from stories, poems, puzzles, riddles, quizzes, games, study tips, health tips, gardening tips, fashion designing, science and recipes. This would be an activity where most students would love to participate.

Balbharti Maharashtra State Board Class 6 English Solutions Chapter 3.7 At the Science Fair Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 English Solutions Chapter 3.7 At the Science Fair

Class 6 English Chapter 3.7 At the Science Fair Textbook Questions and Answers

1. Answer the following questions:

Question a.
What two basic rules were followed in the Science Fair?
Answer:
The two basic rules to be followed in the Science Fair were:

1. Everything should be handled by students
2. The entertainment booths and refreshment stalls had to have a scientific base.

Question b.
How early did the preparations for the Science Fair begin?
Answer:
The preparations for the Science Fair began a couple of months in advance.

Question c.
How was the committee formed?
Answer:
A committee of parents and teachers was set up to look after all the work of the fair. Some students representative were also taken on the committee to give them a firsthand experience of managing big programmes.

Question d.
What themes did the committee identify?
Answer:
The themes identified by the committee were – Plant, Animals, Properties of Substances, Energy, Science in our Everyday Life, Latest News from the World of Science and Food and Nutrition.

Question e.
How did the students prepare for their stalls/ presentations?
Answer:
Stalls were allotted to many groups of children. Each group selected a topic/idea from the chosen themes. The young scientists began collecting a lot of information about their topic using their science text book, their school library and the internet. They shared and discussed this information in their groups and decided the exact activity for their stall deciding whether they would build and display a model, give a demonstration, present their project through posters or simply exhibit a collection.

Question f.
What did Mr Gizare appreciate the most?
Answer:
Mr Gizare appreciated the fact that in most of the stalls, visitors could try out the various science experiments and models.

Question g.
What did the Clean Brigade do?
Answer:
The Clean Brigade members made rounds of the Fair spreading the message of cleanliness and they had vowed to keep the school premises spick and span during the Fair.

2. Make charts to show the important points to remember while making –

Question a.
A graphic presentation
Answer:
Graphic Presentation:

• Write to the point so that a visitor may read a chart or poster at a glance.
• Make use of bullet points or bulleted lists.
• Use pictures and diagrams and label them.
• Use pictograms, graphs, pie-charts etc. to show numerical data.
• Plan all your posters, charts properly before you start making them.
• Make a rough ‘mini-copy’ before you begin work on the big, final poster or chart.
• Don’t forget to check your spellings, sentences or other errors in the ‘mini-copy’ itself.
• Use different colours to highlight important features, but use them judiciously.
• If you have used any text, pictures, diagrams, etc. from elsewhere, acknowledge the source.

Question b.
An oral presentation
Answer:

Do’s	Don’ts
a. Keep the oral presentation short and to the point	a. Don’t cross the allotted time
b. Be confident	b. Don’t fidget
c. Rehearse the speech well	c. Don’t use ‘umms’ and ‘errs’
d. Relate to the topics exhibited directly	d. Don’t talk irrelevant things
e. Be ready to answer relevant questions	e. Don’t give irrelevant answers
f. Use visuals or graphics	f. Don’t leave the walls of the stalls empty
g. Point to the relevant graphic or visual while speaking	g. Don’t speak without pointing to visuals or graphics
h. Wear clean and tidy clothes	h. Don’t dress up to show off
i. Be polite and pleasant when you talk to visitors	i. Don’t be rude or fast while talking to visitors
j. Say out if you don’t know an answer	j. Don’t talk everything else other than the answer
k. Smile, it makes others feel nice	k. Don’t keep a grumpy face

3. Relate the themes of the fair to your science text book by writing the relevant chapter numbers under each theme.

Question 1.
Relate the themes of the fair to your science text book by writing the relevant chapter numbers under each theme.
Answer:
To be done by students.

4. Find in your science textbook, the topics of the stalls handled by the students of VI A (Write the page number).

Question 1.
Find in your science textbook, the topics of the stalls handled by the students of VI A (Write the page number).
Answer:
To be done by students.

5. What themes would you like to add to the themes given in this passage?

Question 1.
What themes would you like to add to the themes given in this passage?
Answer:

1. Why does honey crystallize?
2. How to make a lemon battery?
3. Build your own telescope.

6. Imagine you are visiting the Science Fair. What other stalls (apart from the ones mentioned here) are you likely to find there? Try to list at least five more stalls.

Question 1.
Imagine you are visiting the Science Fair. What other stalls (apart from the ones mentioned here) are you likely to find there? Try to list at least five more stalls.
Answer:

1. Use of empty aerated bottles as life belts to save from drowning.
2. Manually rotating a wheel to generate electric energy.
3. Replantation of a tree instead of cutting it down.

7. Using your imagination, and information from other sources, describe anyone stall in detail.

Question 1.
Using your imagination, and information from other sources, describe anyone stall in detail.
Answer:
I visited a stall at the Science Fair. The theme of the stall was ‘Energy’, The experiments shown were to produce electricity at home and the method was very simple, but the part of the experiment was that it was so simple that anyone could try it out themselves at the stall.

• The prize winning project was how to make lemon Battery.
• The aim of the experiment was to make Lemon Battery.

The material used were 2 lemons, Copper wires, 2 large paper chips, 2 coins, a digital clock, scissors and a knife.
Besides the Lemon Battery Projects, there were other projects which focussed on the use of Kinetic Energy, Uses of Potential Energy, Electrostatic Energy, Sound, Food adulteration, Mechanical Energy and Fun with Magnets. Also Charts were put up best with bold writing.

8. Choose a ‘question’ through your own observation. Try to follow the scientific method to find the answer to that question. Take the help of your teacher/parents to set up the experiment.

Question 1.
Choose a ‘question’ through your own observation. Try to follow the scientific method to find the answer to that question. Take the help of your teacher/parents to set up the experiment.
Answer:

9. Visit a library: Find and read the biography of your favourite scientist.

Question 1.
Visit a library: Find and read the biography of your favourite scientist.

At the Science Fair Summary in English

Introduction:

Science Fair is an opportunity for students to apply the scientific method to conduct independent research. The result is presented in a schoolwide science fair, where the student’s efforts are displayed, where students are questioned too. Students are helped by teachers and parents. They have to follow guidelines and be thoroughly prepared to answer any questions put across by visitors, regarding their topic.

Glossary:

1. basic (adj) – necessary
2. volunteered (v) – to do or offer to do something
3. allotted (v) – to distribute, to assign
4. themes (n) – an idea
5. graphic (adj) (n) – a drawing or a picture
6. inaugurated (adj) – marking the beginning of a venture
7. adulteration (n) – mixing other matter of inferior quality with food or drink which is to be sold

Balbharti Maharashtra State Board Class 6 English Solutions Chapter 3.6 The Merchant of Venice Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 English Solutions Chapter 3.6 The Merchant of Venice

Class 6 English Chapter 3.6 The Merchant of Venice Textbook Questions and Answers

1. Say whether the following statements are true or false.

Question a.
The merchant ships brought spices and other treasures from India and other countries to Italy.
Answer:
True

Question b.
Antonio had gone on a long voyage.
Answer:
False

Question c.
Bassanio was very rich.
Answer:
False

Question d.
Portia had many brothers and sisters.
Answer:
False

Question e.
Portia’s suitors chose the gold and silver caskets.
Answer:
True

Question f.
Bassanio borrowed money from Shylock in Antonio’s name.
Answer:
True

Question g.
Shylock was not at all generous.
Answer:
True

Question h.
Shy lock demanded a pound of Antonio’s flesh.
Answer:
True

Question i.
Portia saved Antonia in the court of law.
Answer:
True

Question j.
Antonio’s ships were lost at sea.
Answer:
False

2. Write a few lines about each character.

Question 1.
Antonio:
Answer:
Antonio was a rich merchant who lived in the prosperous city of Venice in Italy. He sent his ships to faraway countries bringing back spices and other treasures, thus making a lot of profit. He was a kind man with many friends. His best friend was Bassanio, for whom he was even ready to stake his life.

Question 2.
Bassanio:
Answer:
Bassanio was a young and handsome nobleman with no money. He wanted to marry Portia. He had to go to Belmont to try his luck to marry Portia. He won Portia’s hand in marriage.

Question 3.
Portia:
Answer:
Portia was a beautiful and intelligent woman. She was the only daughter of a very wealthy man. Her father had died leaving her a large estate. Her father had written a will on how Portia’s husband had to be selected. Portia happily married Bassanio in accordance with her father’s will.

Question 4.
Shylock:
Answer:
Shylock was a Jewish moneylender. He had a lot of money. He was not a generous person. Money was all that he cared for. He did not like Antonio and wanted to harm him. He got a chance to do so when Antonio went to him to borrow money for Bassanio. He readily gave the money but with a strange condition which was very cruel and inhuman.

3. Write the following in short:

Question 1.
The story of the three caskets
Answer:
Portia’s father, a very wealthy man died leaving her a large estate. Her father had prepared a will in which he had written how her husband should be selected. He had to choose between three caskets – one of gold, one of silver and . one of lead. Each had something written on it and a message inside the box. The one who took the right casket which was the lead casket won Portia’s hand in marriage.

Question 2.
What the young lawyer pleaded?
Answer:
Antonio was taken to court by Shylock to demand and fulfill his strange and cruel condition. If the condition was fulfilled, Antonio would lose his life. A lawyer entered the court to fight Antonio’s case. The lawyer requested Shylock to show mercy though the law was on his side.

The lawyer pleaded that mercy is a quality of God. He further said that when a person shows mercy to someone, both are blessed. He said that mercy was more valuable than a king’s crown. All the pleadings of the young lawyer did not have any effect on Shylock who stuck to his inhuman condition of wanting a pound of Antonio’s flesh.

Question 3.
The events at the court
Answer:
When Antonio was taken to court by Shylock to get his inhuman demand fulfilled, the Duke who liked Antonio felt sorry for him. Portia asked Bassanio to pay Shylock double the amount which Shylock refused. Everyone in the court considered Shylock’s demand to be inhuman.

The Duke asked Shylock to show mercy but Shylock refused. A young lawyer entered the court to fight Antonio’s case. This was the turning point. The lawyer fought for Antonio very cleverly and helped him get out of the inhuman condition.

4. Write the conditions that Portia put down to warn Shylock.

Question 1.
Write the conditions that Portia put down to warn Shylock.
Answer:
The young lawyer fighting Antonio’s case asked Shylock to show mercy. Shylock was adamant and stuck to the bond saying that all he wanted was a pound of Antonio’s flesh. The lawyer then cleverly allowed Shylock to take Antonio’s pound of flesh. The lawyer warned the Jew that while doing so, he should not shed even one drop of Antonio’s blood. He also warned Shylock that he should cut exactly one pound of flesh – nothing less and nothing more, according to the bond.

5. Find four words ending with ‘-ous’ from the story. Can you add three more words ending with ‘-ous’ to this list?

Question 1.
Find four words ending with ‘-ous’ from the story. Can you add three more words ending with ‘-ous’ to this list?
Answer:

1. prosperous
2. generous
3. monstrous
4. jealous

6. Read the following words. Write the words that are combined to make these words. Add ten more to the list on your own.

Question 1.
Read the following words. Write the words that are combined to make these words.

1. faraway
2. nobleman
3. whoever
4. moneylender
5. sometimes

Add ten more words to the list on your own. Each of the component words must be meaningful.
Answer:

1. faraway – far, away
2. nobleman – noble, man
3. whoever – who, ever
4. moneylender – money, lender
5. sometimes – some, times

7. Read the following chains of words:

Question 1.
Read the following chains of words:
Answer:

1. fortune – fortunate – fortunately – unfortunately
2. know knowing – knowingly – unknowingly
3. amaze – amazing – amazingly
4. possible – impossible – impossibly

8. A letter or group of letters added to the front of a word to change its meaning and make a new word is called a prefix.
Examples: fortunately – unfortunately, agree – disagree, possible – impossible, human – inhuman, legal – illegal
Add proper prefixes to the following words to make new words:

1. kind
2. intelligent
3. advantage
4. happy
5. allow
6. safe

Answer:

1. kind – unkind
2. intelligent – unintelligent
3. advantage – disadvantage
4. happy – unhappy
5. allow – disallow
6. safe -unsafe

9. Find at least three sentences in the story which have modal verbs.

Question 1.
Portia’s husband should be selected.
Answer:
should-modal

Question 2.
Whoever chooses me, must give and hazard all he has.
Answer:
must-modal

Question 3.
Shylock would cut off a pound of Antonio’s flesh.
Answer:
would-modal

Question 3.
He was very happy that Antonio would not be able to pay the money.
Answer:
would – modal

Question 4.
But what could he do?
Answer:
could – modal

10. Visit a library. Read other tales by Shakespeare, for example, Julius Caesar, As You Like It, Macbeth and The Tempest.

11. Hold a mock trial for any one of the following offences. There should be a complainant, a defendant, and lawyers to argue that case on behalf of them. The whole class can vote to pass the judgement. On what occasions will you plead for justice? What punishment will you suggest? When will you plead for mercy?
a. A very poor and honest servant has broken a vase while cleaning it. The vase was valuable and the employer liked it very much.
b. A poor man stole some ornaments from a rich girl.
c. A young man was injured in a road accident due to another man’s careless driving.

Class 6 English Chapter 3.6 The Merchant of Venice Additional Important Questions and Answers

Answer the following questions in one or two sentences.

Question 1.
Where did Antonio live?
Answer:
Antonio lived in Venice, a prosperous city in Italy.

Question 2.
What did the ships of adventurous merchants bring back?
Answer:
The ships of adventurous merchants brought back spices and other treasures from India and other countries.

Question 3.
What made the merchants rich?
Answer:
The merchants sold the merchandise brought back from other countries in Europe and made a lot of profit, thus making them rich.

Question 4.
Who was Bassanio?
Answer:
Bassanio was a young and handsome nobleman, who had no money.

Question 5.
What had the suitors of Portia to choose between?
Answer:
Portia’s suitors had to choose between three caskets – one of gold, one of silver and one of lead.

Question 6.
What was written on the gold casket?
Answer:
‘Whoever chooses me shall gain what men desire’ was written on the gold casket.

Question 7.
What was written on the silver casket?
Answer:
‘Whoever chooses me shall get as much as he deserves’, was written on the silver casket.

Question 8.
What was written on the casket of lead?
Answer:
‘Whoever chooses me must give and hazard all he has’, was written on the casket of lead.

Question 9.
Who chose the gold casket?
Answer:
The Prince of Morocco chose the gold casket.

Question 10.
What was the message on the gold casket?
Answer:
The message on the gold casket was, ‘All that glitters is not gold’.

Question 11.
Who was Shylock?
Answer:
Shylock was a Jewish moneylender.

Question 12.
Why did Shylock dislike Antonio?
Answer:
Shylock disliked Antonio because he sometimes lent money to people without charging any interest on it.

Question 13.
What was the strange condition Shylock put to Antonio?
Answer:
The strange condition Shylock put to Antonio was that if Antonio failed to return the money he borrowed from Shylock within three months, he would cut a pound of Antonio’s flesh.

Question 14.
What news made Shylock happy? Why?
Answer:
The news that Antonio had lost his ships made Shylock happy. He was very happy because he was sure that Antonio would not be able to repay the money he had borrowed from Shylock.

Question 15.
Why was Antonio unable to avoid Shylock’s strange condition?
Answer:
Antonio was unable to avoid Shylock’s strange condition because Antonio had written a bond to that effect.

Question 16.
What did Portia tell Bassanio to do to save Antonio?
Answer:
Portia told Bassanio to pay Shylock twice the amount to save Antonio.

Question 17.
Why did Shylock want revenge?
Answer:
Shylock wanted revenge because he felt that Antonio and the others had treated him badly before.

Question 18.
What was mercy more valuable than?
Answer:
Mercy was more valuable than a king’s crown.

Question 19.
What did the lawyer warn Shylock while cutting off Antonio’s flesh?
Answer:
The lawyer warned Shylock that while cutting off the flesh, Shylock should not shed even one drop of Antonio’s blood. The lawyer also told Shylock that he should cut exactly one pound of flesh – nothing less and nothing more.

Question 20.
How was Antonio’s life saved?
Answer:
When Shylock realised that he could not do what the young lawyer had asked him to do, he accepted defeat and thus Antonio’s life was saved.

Question 21.
Why do you think Portia’s father prepared such a will?
Answer:
Portia was the only daughter of a wealthy man. Her father had died leaving Portia all his fortune and estate. He knew that Portia being alone could be cheated and would lose her wealth and property. So in order that Portia would get a good husband, Portia’s father made his will in this manner.

Reading Skills, Vocabulary and Grammar.

Question 1.
Write 3 sentences about Antonio.
Answer:
Antonia was a rich merchant of Venice, a prosperous city in Italy. He sent his ships to faraway countries bringing back spices and other treasures, thus making a lot of profit. He was a kind man with many friends. Bassanio was his best friend for whom he was ready even to stake his life.

Question 2.
When were sea voyages dangerous?
Answer:
Sea voyages were dangerous about five hundred years ago.

Question 3.
What was Antonio waiting for? Why?
Answer:
Antonio was waiting for his ships to return with merchandise. He was waiting for the ships because he had put almost all his money in the ships.

Question 4.
Antonio was a kind man. (Change into a negative sentence)
Answer:
Antonio was not an unkind man. OR Antonio was not a cruel man.

Question 5.
Give the antonyms of:
Answer:
a. dangerous × harmless, safe
b. kind × unkind

Question 6.
What are the qualities you would like in your best friend?
Answer:
A friend is one who is kind and good natured. He/She must be approachable so that I can tell him/ her my problems without being judgmental about me. I must feel free to confide all my happy as well as sad moments with him/ her. A best friend is one who makes you laugh a little louder, smile a little brighter and live a little better. These are the qualities I would like in my best friend.

Language Study.

Question 1.
Find four words ending with ‘-ous’ from the story. Add some more of your own words ending with ‘-ous’ to this list.
Answer:

1. dangerous
2. advantageous
3. wondrous
4. treacherous
5. mountainous

Question 2.
Read the following words. Write the words that are combined to make these words. Add ten more to the list on your own.
Answer:

1. cupboard – cup, board
2. careless – care, less
3. painless – pain, less
4. comfortable – comfort, able
5. handsome – hand, some
6. forward – for, ward
7. photograph – photo, graph
8. strawberry – straw, berry
9. pineapple – pine, apple
10. anywhere – any, where

Question 3.
Read the following chains of words:
Answer:
1. taste – tasty – tasteful – tastefully
2. fashion – fashionable – unfashionable – fashionably – unfashionably

Do as directed:

Question 1.
Bassanio was a young and handsome nobleman. (Name the word class of the underlined word)
Answer:
young – adjective

Question 2.
He had no money. (Add a question tag)
Answer:
He had no money, hadn’t he?

Question 3.
They made a lot of profit. (Identify the kind of sentence)
Answer:
Assertive/Declarative – Affirmative

Question 4.
Antonio was waiting for his ships.
a. Pick out the verb and state its tense.
b. Pick out the auxiliary (helping) verb from the sentence
Answer:
a. was waiting – past continuous tense
b. was – auxiliary verb

The Merchant of Venice Summary in English

‘The Merchant of Venice’ written by William Shakespeare is a comical play. The story of the play revolves around Antonio, the rich merchant of Venice, his best friend Bassanio who wanted to marry Portia, the beautiful and intelligent daughter of a wealthy man but had no money to reach Belmont where Portia lived. Shylock, the Jewish moneylender who wanted a pound of Antonio’s flesh in exchange of the money he lent to Bassanio. In the court, Portia disguises as a man and fights Antonio’s case which ends on a happy note.

Introduction:

The play highlights the fact that love is more important than money and mercy is preferable to revenge and love lasts forever.

Glossary:

1. prosperous (ad)) – to be successful
2. adventurous (ad)) – willing to incur risks
3. merchandise (n) – commodities offered for sale
4. will (n) – a legal document stating one’s intent concerning the disposal of one’s property after death
5. casket (n) – a little box, e.g., for jewelry
6. hazard (v) – to risk something or put it in danger
7. generous (adj) – willing to give and share
8. adamant (adj) – firm, determined
9. inhuman (adj) – something relating to cruelty, uncivilized
10. tragic (adj) – causing great sadness or suffering

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 12 चंद्रावरची शाळा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 12 चंद्रावरची शाळा(कविता)

Marathi Sulabhbharti Class 6 Solutions Chapter 12 चंद्रावरची शाळा Textbook Questions and Answers

1. एका वाक्यात उत्तर लिहा.

प्रश्न अ.
चंद्रावरती शाळा कोणत्या शतकात भरेल ?
उत्तर:
चंद्रावरती शाळा एकविसाव्या शतकात भरेल.

प्रश्न आ.
चंद्रावरच्या शाळेत जाताना कशाचे ओझे नसेल?
उत्तर:
चंद्रावरच्या शाळेत जाताना दप्तराचे ओझे नसेल.

प्रश्न इ.
चंद्रावरच्या शाळेत कशाची कटकट राहणार नाही ?
उत्तर:
चंद्रावरच्या शाळेत भाजी पोळीच्या डब्याची कटकट राहणार नाही.

प्रश्न ई.
चंद्रावरच्या शाळेत अभ्यास कसा करावा लागेल?
उत्तर:
चंद्रावरच्या शाळेत फक्त बटणे दाबायचाच अभ्यास करावा लागेल.

2. दोन-तीन वाक्यात उत्तरे लिहा.

प्रश्न अ.
चंद्रावरच्या शाळेत पास केव्हा केले जाते?
उत्तर:
चंद्रावरच्या शाळेत खडू व फळा नाही. दप्तराचे ओझे मुलांच्या पाठीवर नाही. बटणे दाबायची एवढाच फक्त तिथे अभ्यास असतो. बटणे दाबून अभ्यास केला की तिथेच पास केले जाते.

प्रश्न आ.
चंद्रावरच्या शाळेत चांदण्यांशीच का खेळावे लागणार आहे?
उत्तर:
शाळेत गेल्यावर जसे खेळाचे साहित्य असते, खेळण्यासाठी मैदान असते. त्याप्रमाणे चंद्रावर कोणत्याही प्रकारचे खेळाचे साहित्य नसणार. तेथे फक्त चांदण्याच काय त्या खेळण्यासाठी उपलब्ध असणार म्हणून चंद्रावरच्या शाळेत मुलांना चांदण्यांशीच खेळावे लागणार आहे.

3. योग्य कारण शोधून उत्तर लिहा.

प्रश्न 1.
चंद्रावरच्या शाळेत जाताना ऑक्सिजनचा सिलिंडर न्यावा लागेल कारण ………………….
(अ) दप्तराऐवजी सिलिंडर न्यावा हा नियम असल्यामुळे.
(आ) चंद्रावरती प्राणवायूचे प्रमाण कमी असल्यामुळे.
(इ) सिलिंडर नेला तर शाळेत येऊ देतात म्हणून.
उत्तर:
(आ) चंद्रावरती प्राणवायूचे प्रमाण कमी असल्यामुळे.

प्रश्न 2.
चंद्रावर एक उडी मारताच तरंगत राहतात कारण ……………………
(अ) शिक्षक अशीच पी.टी. शिकवतात.
(आ) विदयार्थ्याचे वजन कमी असते म्हणून तरंगतात.
(इ) चंद्रावर गेल्यावर गुरुत्वाकर्षण कमी होते म्हणून तरंगतात.
उत्तर:
(इ) चंद्रावर गेल्यावर गुरुत्वाकर्षण कमी होते म्हणून तरंगतात.

4. शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधा व लिहा.

प्रश्न 1.
शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधा व लिहा. उदा., भरेल – नसेल
उत्तर:

1. शाळा – फळा
2. मुले – खुले
3. कटकट – पटपट
4. पहाल – राल
5. अभ्यास – पास

5. ‘पटपट’ यासारखे शब्द लिहा.

प्रश्न 1.
‘पटपट’ यासारखे शब्द लिहा.
उत्तर:

1. कटकट
2. धडधड
3. चटचट
4. बडबड
5. वटवट
6. खटपट
7. चटपट
8. कळकळ
9. तळमळ
10. चळवळ इ.

6. कवितेत आलेले इंग्रजी शब्द शोधून यादी करा.

प्रश्न 1.
कवितेत आलेले इंग्रजी शब्द शोधून यादी करा.
उत्तर:

1. ऑक्सिजन
2. सिलिंडर
3. पी. टी
4. बटण
5. पास

7. तुम्ही डब्यात रोज कोणकोणते पदार्थ नेता? त्याची नावे लिहा.

प्रश्न 1.
तुम्ही डब्यात रोज कोणकोणते पदार्थ नेता? त्याची नावे लिहा.
उत्तर:

1. पोळी – भाजी
2. पाव – भाजी
3. बिस्किटे
4. केचप – पाव
5. कांदेपोहे
6. उपमा
7. पराठे
8. वाटाण्याची उसळ
9. चण्याची उसळ
10. वडापाव इ.

8. कोणते पदार्थ डब्यात आणायचे नाहीत असे शिक्षक तुम्हाला वारंवार सांगतात? का ते लिहा.

प्रश्न 1.
कोणते पदार्थ डब्यात आणायचे नाहीत असे शिक्षक तुम्हाला वारंवार सांगतात? का ते लिहा.
उत्तर:
तिखट, चमचमीत पदार्थ खाऊ नका, असे शिक्षक नेहमी सांगत असतात. कारण तिखट व चमचमीत पदार्थ खाल्ले की, आपली प्रकृती बिघडते. अपचन होणे, ढेकर येणे यासारखे आजार होतात. मग शाळेत आपली अनुपस्थिती होते. आपण शाळेत गैरहजर राहतो. मग त्याचा परिणाम अभ्यासावर होतो. तेव्हा आपण शाळेत वडापाव, समोसे वगैरे सारखे पदार्थ आणू नयेत असे शिक्षक नेहमी सांगत असतात.

9. चंद्रावरच्या शाळेत तुम्ही शिकत आहात. तुम्हाला ‘पृथ्वीचे वर्णन करायला सांगितले आहे. कल्पना करा व लिहा.

प्रश्न 1.
उपक्रम: चंद्रावरच्या शाळेचे चित्र तुमच्या कल्पनेने काढून रंगवा.
प्रकल्प: चंद्रावरच्या पाच कविता मिळवा व संग्रह करा.
उत्तर:
चंद्रावरच्या शाळेत कोणत्याही सुख-सुविधा नसणार आहेत. त्या सर्व पृथ्वीवरील शाळेतच असतात. या सर्व सुविधा
पृथ्वीवरच्या शाळेत असणे याचे कारण पृथ्वीवरचा अजब, सुंदर, रमणीय व विलोभनीय परिसर होय. पृथ्वीवरचा निसर्ग आहेच असा! तिथे वाहणारी थंड, शीतल हवा आहे, पाणी आहे. मोकळा सूर्यप्रकाश आहे. त्यामुळे चंद्रापेक्षा पृथ्वीवर सजीव सृष्टीला अतिशय पोषक असेच वातावरण असल्यामुळे पृथ्वी कशी नव्या नवरीने हिरवा शालू नेसून सजून यावी अशीच वाटते. त्यामुळे मला चंद्रावरच्या शाळेपेक्षा पृथ्वीवरच्या शाळेतच शिकायला खूप आवडेल.

प्रश्न 2.
खालील वाक्ये वाचा.

प्रश्न अ.
गणेश आईला म्हणाला मी कधीही चुकीचे वागणार नाही.
उत्तर:
गणेश आईला म्हणाला, “मी कधीही चुकीचे वागणार नाही.”

प्रश्न आ.
ताई दादाला म्हणाली मला उदया शाळेला सोडशील का? बोलणाऱ्याच्या तोंडचे शब्द दाखवण्याकरता ” – ” असे दुहेरी अवतरणचिन्ह वापरले जाते.
उत्तर:
ताई दादाला म्हणाली, “मला उदया शाळेला सोडशील का?”

Class 6 Marathi Chapter 12 चंद्रावरची शाळा Additional Important Questions and Answers

खाली दिलेल्या कवितेच्या ओळी पूर्ण करा.

प्रश्न 1.
एकविसाव्या शतकात भरेल …………………
………………… खडू आणि फळा
उत्तर:
चंद्रावरती शाळा, चंद्रावरच्या शाळेत नसेल

प्रश्न 2.
पी.टी. चा तास
……………….. तसेच तरंगत रहाल.
उत्तर:
कसा होतो ते पहाल, एक उडी मारताच

प्रश्न 3.
अशी असेल भारी ………………….
……………………. चांदण्यांशीच खेळा.
उत्तर:
चंद्रावरची शाळा, चंद्रावरच्या शाळेत फक्त

खालील प्रश्नांची एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
चंद्रावरच्या शाळेत कोणत्या गोष्टी नसणार आहेत?
उत्तर:
चंद्रावरच्या शाळेत ‘खडू’ आणि ‘फळा’ या दोन गोष्टी नसणार आहेत.

प्रश्न 2.
चंद्रावरती मुले कशातून शाळेत जाणार आहेत?
उत्तर:
चंद्रावरती मुले छोट्या छोट्या यानांतून शाळेत जाणार आहेत.

प्रश्न 3.
शाळेचे दार कधी खुले होईल?
उत्तर:
बटण दाबताच शाळेचे दार खुले होईल.

प्रश्न 4.
पी.टी.च्या तासाला काय होईल?
उत्तर:
पी.टीच्या तासाला एक उडी मारताच मुले तशीच तरंगत राहतील.

प्रश्न 5.
चंद्रावरच्या शाळेत फक्त कोणासोबत खेळता येईल?
उत्तर:
चंद्रावरच्या शाळेत फक्त चांदण्यांशीच खेळता येईल.

प्रश्न 6.
‘चंद्रावरची शाळा’ या कवितेच्या कवयित्रीचे नाव काय आहे?
उत्तर:
‘चंद्रावरची शाळा’ या कवितेच्या कवयित्रीचे नाव ‘चारूता पेंढरकर’ आहे.

खालील प्रश्नांची दोन-तीन वाक्यात उत्तरे लिहा.

प्रश्न 1.
चंद्रावरच्या शाळेत कोणकोणत्या गोष्टी नसणार आहेत?
उत्तर:
चंद्रावरच्या शाळेत खडू आणि फळा नसणार आहे. तेथील शाळेच्या दारांना कडी व कुलूप नसणार आहे. मुलांच्या पाठीवर दप्तराचे ओझे नसणार आहे. भाजी-पोळीच्या डब्याची कटकट तेथे नसणार आहे. तेथे तासन् तास बसून करण्याचा अभ्यास नसणार आहे. तेथील शाळेत कोणत्याच प्रकारची
खेळाची साधनं नसणार आहेत.

व्याकरण व भाषाभ्यास.

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. शतक
2. शाळा
3. फळा
4. बटण
5. दार.
6. ओझे
7. पोळी
8. कटकट
9. अभ्यास
10. पास
11. भारी
12. चंद्र

उत्तरः

1. शंभर
2. विद्यालय
3. श्यामपटल
4. कळ
5. दरवाजा
6. भार
7. चपाती
8. त्रास
9. सराव
10. उत्तीर्ण
11. चांगली
12. शशी

खालील वाक्यांत दुहेरी अवतरण चिन्हांचा वापर करून लिहा.

प्रश्न 1.
मला माहीत नाही बाळ आई म्हणायची.
उत्तर:
“मला माहीत नाही बाळ.” आई म्हणायची.

चंद्रावरची शाळा Summary in Marathi

काव्यपरिचयः

एकविसावे शतक हे विज्ञानाचे शतक म्हणून ओळखले जाते. या शतकात विज्ञानाने खूप प्रगती केली व माणूस चंद्रावरती जाऊन पोहोचला. शाळेतील मुलांनासुद्धा चंद्राविषयी माहिती मिळाली. परंतु चंद्रावरच्या शाळेत कोणत्या गोष्टी नसतील याचे सुंदर वर्णन या कवितेत कवयित्रीने केले आहे. व चंद्रावरची व पृथ्वीवरच्या शाळेची तुलना केली आहे.

शब्दार्थ:

1. चंद्र – चांदोबा (moon)
2. शतक – शंभर (hundred)
3. छोट्या – लहान (small)
4. खुलणे – उघडणे (open)
5. दप्तर – (school bag)
6. ओझे – वजन, भार (weight)
7. न्यावा – नेणे (to carry)
8. यान – अवकाशातून प्रवास करणारे सुसज्ज वाहन (spacecraft)
9. गोळी – (tablet)
10. पटपट – झटपट (hurry)
11. पी.टी. – शारीरिक शिक्षण (physical training)
12. पाहणे – बघणे (to see)
13. तरंगणे – अधांतरी राहणे (to float)
14. भारी – चांगली (good)
15. चांदण्या – चमकणारे छोटे तारे (stars)