Category: Class 10

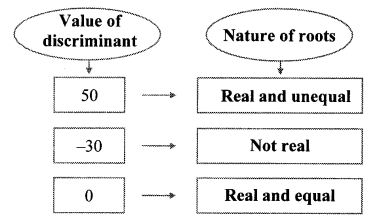
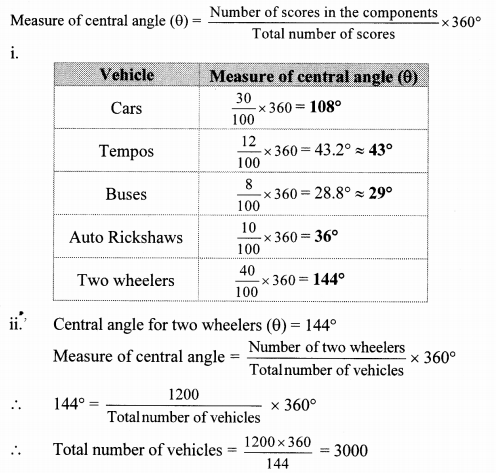
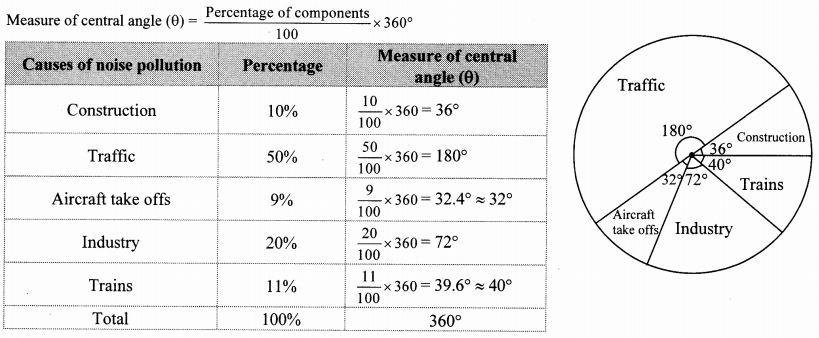
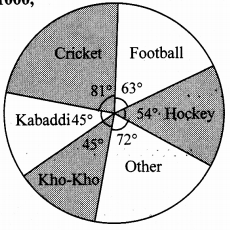
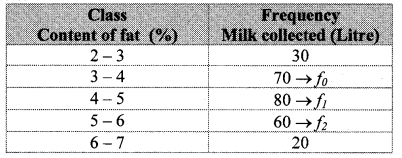
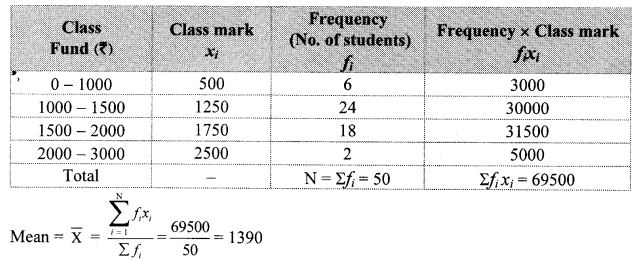
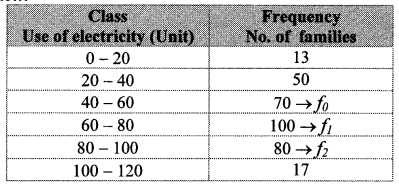
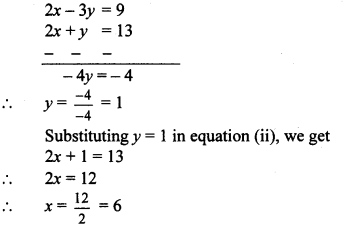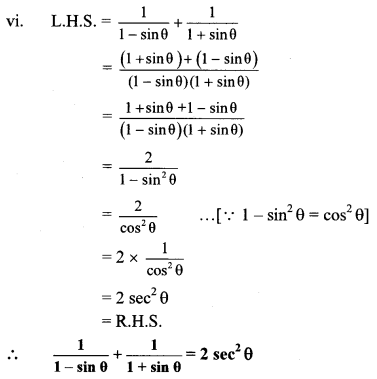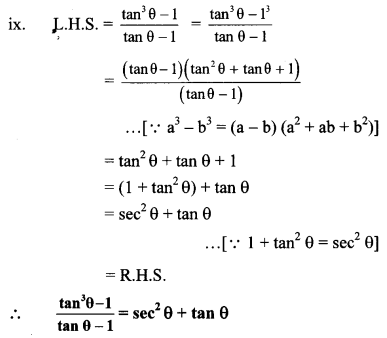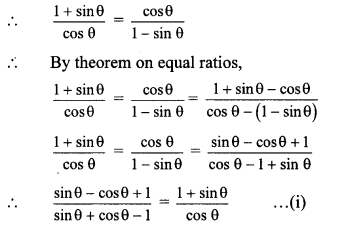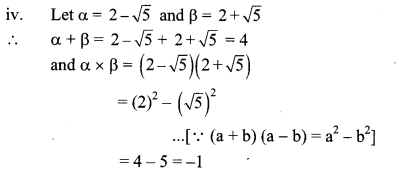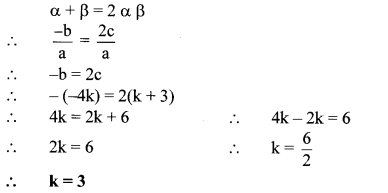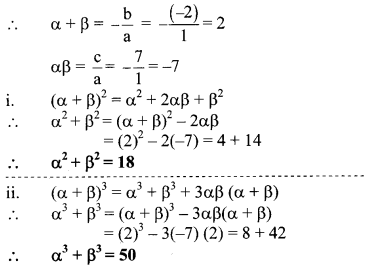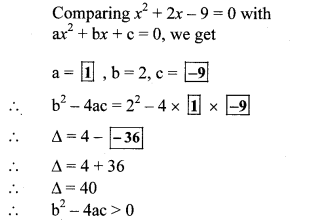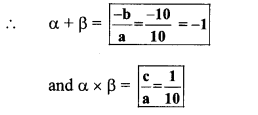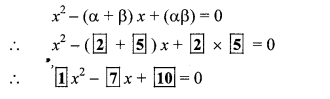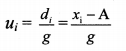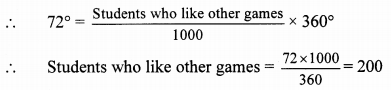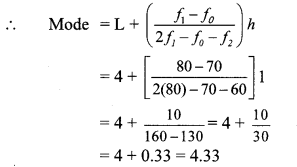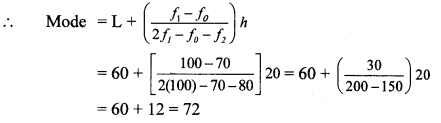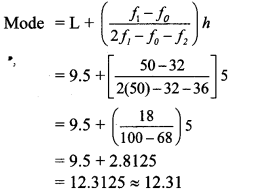10th Standard Maths 1 Practice Set 1.2 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Practice Set 1.2 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

10th Maths 2 Practice Set 1.2 Question 1.
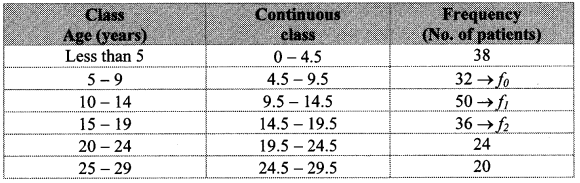
Complete the following table to draw graph of the equations.
i. x + y = 3
ii. x – y = 4
Answer:
i. x + y = 3

ii. x – y = 4

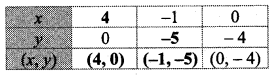
Linear Equations In Two Variables Practice Set 1.2  Question 2.
Solve the following simultaneous equations graphically.
i. x + y = 6 ; x – y = 4
ii. x + y = 5 ; x – y = 3
iii. x + y = 0 ; 2x – y = 9
iv. 3x – y = 2 ; 2x – y = 3
v. 3x – 4y = -7 ; 5x – 2y = 0
vi. 2x – 3y = 4 ; 3y – x = 4
Solution:
i. The given simultaneous equations are
x + y = 6                                                                                                        x – y = 4
∴ y = 6 – x                                                                                                     ∴ y = x – 4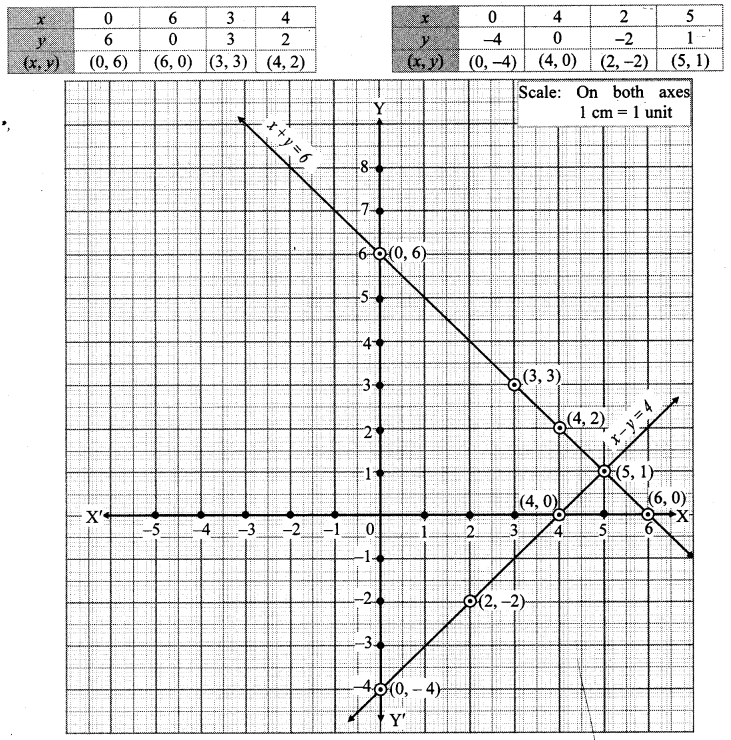
The two lines intersect at point (5, 1).
∴ x = 5 and y = 1 is the solution of the simultaneous equations x + y = 6 and x – y = 4.

ii. The given simultaneous equations are


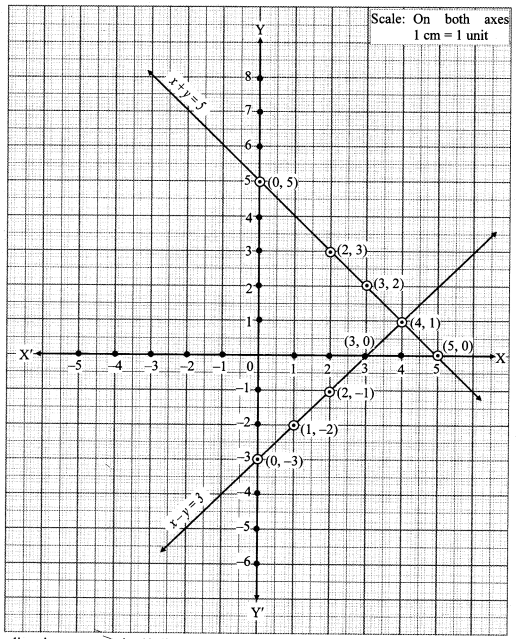
The two lines intersect at point (4, 1).
∴ x = 4 and y = 1 is the solution of the simultaneous equations x+y = 5 and x – y = 3.

iii. The given simultaneous equations are


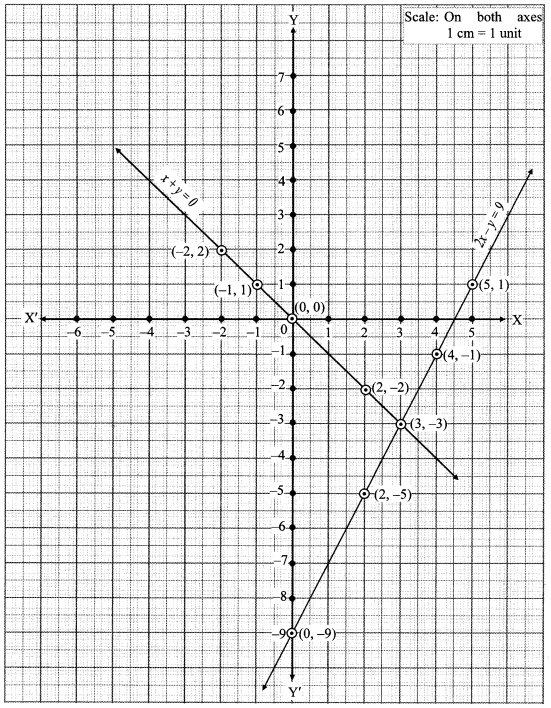
The two lines intersect at point (3, -3).
∴ x = 3 and y = -3 is the solution of the simultaneous equations x + y = 0 and 2x – y = 9.

iv. The given simultaneous equations are


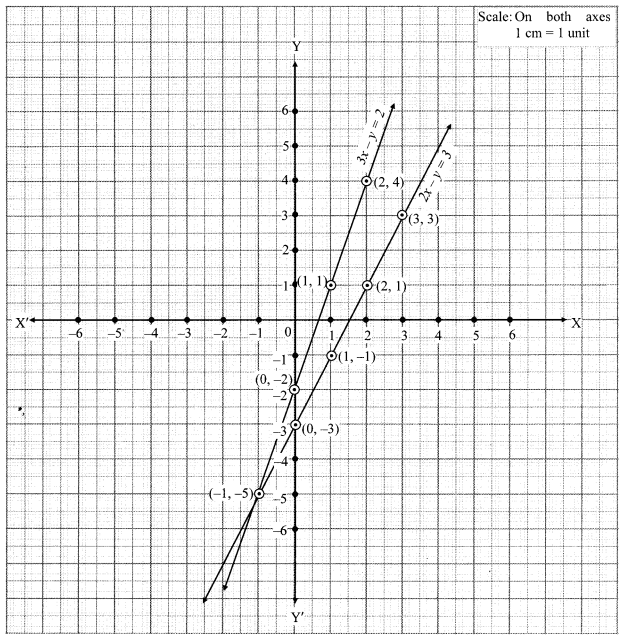
The two lines intersect at point (-1, -5).
∴ x = -1 and y = -5 is the solution of the simultaneous equations 3x- y = 2 and 2x- y = 3.

v. The given simultaneous equations are


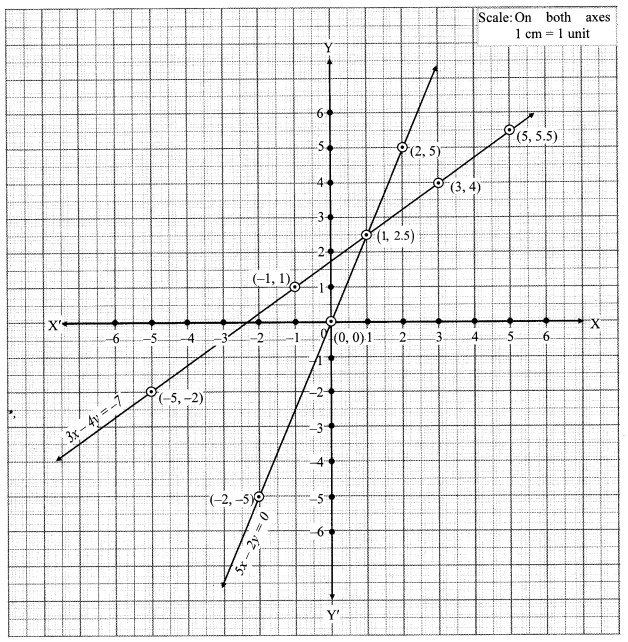
The two lines intersect at point (1, 2.5).
∴ x = 1 and y = 2.5 is the solution of the simultaneous equations 3x – 4y = -7 and 5x – 2y = 0.

vi. The given simultaneous equations are


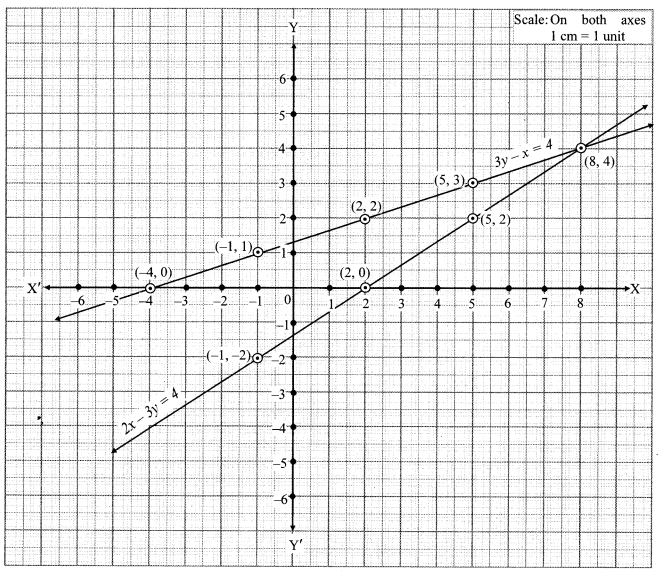
The two lines intersect at point (8, 4).
∴ x = 8 and y = 4 is the solution of the simultaneous equations 2x – 3y = 4 and 3y – x = 4.

10th Math Part 2 Practice Set 1.2  Question 1.
Solve the following simultaneous equations by graphical method. Complete the following tables to get ordered pairs.

i. Plot the above ordered pairs on the same co-ordinate plane.
ii. Draw graphs of the equations.
iii. Note the co-ordinates of the point of intersection of the two graphs. Write solution of these equations. (Textbook pg. no. 8)
Solution:

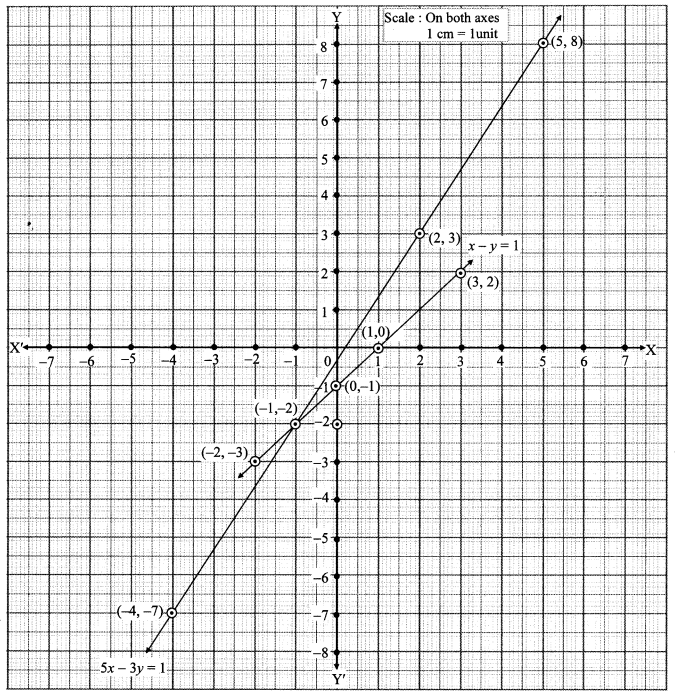
The two lines intersect at point (-1, -2).
∴ (x , y) = (-1, -2) is the solution of the given simultaneous equations.

Mathematics Part 1 Standard 9 Practice Set 1.2 Answer  Question 1.
Solve the above equations by method of elimination. Check your solution with the solution obtained by graphical method. (Textbook pg. no. 8)
Solution:
The given simultaneous equations are
x – y = 1 …(i)
5x – 3y = 1 …(ii)
Multiplying equation (i) by 3, we get
3x – 3y = 3 …(iii)
Subtracting equation (iii) from (ii), we get

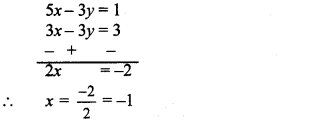
Substituting x = -1 in equation (i), we get
-1 -y= 1
∴ -y = 1 + 1
∴ -y = 2
∴ y = -2
∴ (x,y) = (-1, -2) is the solution of the given simultaneous equations.
∴ The solution obtained by elimination method and by graphical method is the same.

1.2 Maths Class 10 Question 2.
The following table contains the values of x and y co-ordinates for ordered pairs to draw the graph of 5x – 3y = 1.

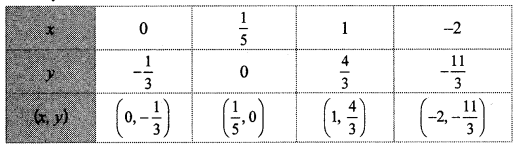
i. Is it easy to plot these points?
ii. Which precaution is to be taken to find ordered pairs so that plotting of points becomes easy? (Textbook pg. no. 8)
Solution:
i. No

The above numbers are non-terminating and recurring decimals.
∴ It is not easy to plot the given points.

ii. While finding ordered pairs, numbers should be selected in such a way that the co-ordinates obtained will be integers.

Linear Equations ¡n Two Variables Class 10 Maths Question 3.
To solve simultaneous equations x + 2y = 4; 3x + 6y = 12 graphically, following are the ordered pairs.

Plotting the above ordered pairs, graph is drawn. Observe it and find answers of the following questions.

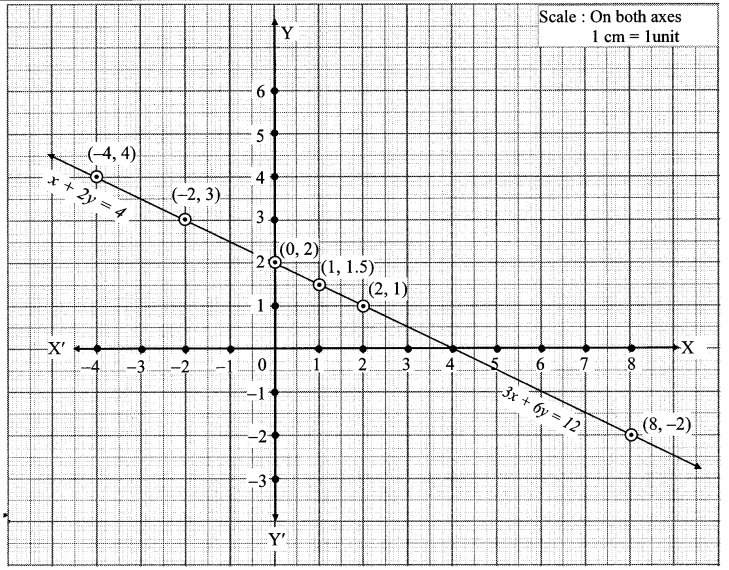
i. Are the graphs of both the equations different or same?
ii. What are the solutions of the two equations x + 2y = 4 and 3x + 6y = 12? How many solutions are possible?
iii. What are the relations between coefficients of x, coefficients of y and constant terms in both the equations?
iv. What conclusion can you draw when two equations are given but the graph is only one line? (Textbook pg. no. 9)
Solution:
i. The graphs of both the equations are same.
ii. The solutions of the given equations are (-2, 3), (0, 2), (1, 1.5), etc.
∴ Infinite solutions are possible.
iii. Ratio of coefficients of x = \(\frac { 1 }{ 3 } \)
Ratio of coefficients of y = \(\frac { 2 }{ 6 } \) = \(\frac { 1 }{ 3 } \)
Ratio of constant terms = \(\frac { 4 }{ 12 } \) = \(\frac { 1 }{ 3 } \)
∴ Ratios of coefficients of x = ratio of coefficients of y = ratio of the constant terms
iv. When two equations are given but the graph is only one line, the equations will have infinite solutions.

Class 10 Maths Part 1 Practice Set 1.2 Question 4.
Draw graphs of x- 2y = 4, 2x – 4y = 12 on the same co-ordinate plane. Observe it. Think of the relation between the coefficients of x, coefficients ofy and the constant terms and draw the inference. (Textbook pg. no. 10)
Solution:

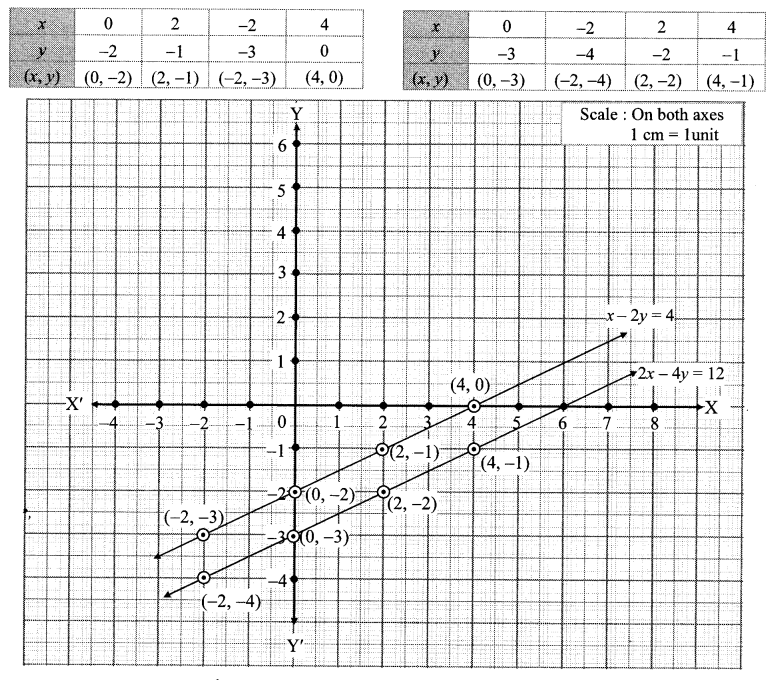
ii. Ratio of coefficients of x =\(\frac { 1 }{ 2 } \)
Ratio of coefficients of y = \(\frac { -2 }{ -4 } \) = \(\frac { 1 }{ 2 } \)
Ratio of constant terms = \(\frac { 4 }{ 12 } \) = \(\frac { 1 }{ 3 } \)
∴ Ratio of coefficients of x = ratio of coefficients of y ratio of constant terms
iii. If ratio of coefficients of x = ratio of coefficients of y ≠ ratio of constant terms, then the graphs of the two equations will be parallel to each other.

Condition of consistency in Equations:

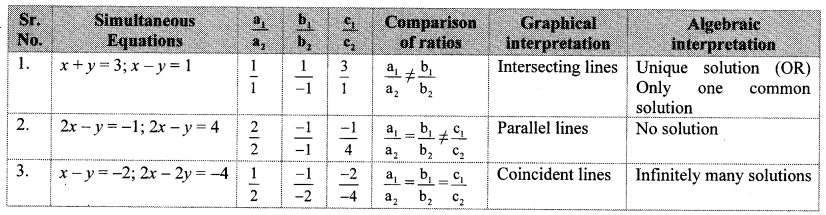
Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 1.1 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Practice Set 1.1 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Question 1.
Complete the following activity to solve the simultaneous equations.
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Solution:
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Add equations (i) and (ii).

Question 2.
Solve the following simultaneous equations.
i. 3a + 5b = 26; a + 5b = 22
ii. x + 7y = 10; 3x – 2y = 7
iii. 2x – 3y = 9; 2x + y = 13
iv. 5m – 3n = 19; m – 6n = -7
v. 5x + 2y = -3;x + 5y = 4
vi. \(\frac { 1 }{ 3 } \) x+ y = \(\frac { 10 }{ 3 } \) ; 2x + \(\frac { 1 }{ 4 } \) y = \(\frac { 11 }{ 4 } \)
vii. 99x + 101y = 499 ; 101x + 99y = 501
viii. 49x – 57y = 172; 57x – 49y = 252
Solution:
i. 3a + 5b = 26 …(i)
a + 5b = 22 …(ii)
Subtracting equation (ii) from (i), we get

Substituting a = 2 in equation (ii), we get
2 + 5b = 22
∴ 5b = 22 – 2
∴ 5b = 20
∴ b = \(\frac { 20 }{ 5 } \) =4
∴ (a, b) = (2, 4) is the solution of the given simultaneous equations.

ii. x + 7y = 10
∴ x = 10 – 7y …(i)
3x – 2y = 7 …1(ii)
Substituting x = 10 – ly in equation (ii), we get
3 (10 – 7y) – 2y = 7
∴ 30 – 21y – 2y = 7
∴ -23y = 7 – 30
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \)
Substituting y = 1 in equation (i), we get
x = 10 – 7 (1)
= 10 – 7 = 3
∴ (x, y) = (3, 1) is the solution of the given simultaneous equations.

iii. 2x – 3y = 9 …(i)
2x + y = 13 …(ii)
Subtracting equation (ii) from (i), we get

∴ (x, y) = (6, 1) is the solution of the given simultaneous equations.

iv. 5m – 3n = 19 …(i)
m – 6n = -7
∴ m = 6n – 7 …(ii)
Substituting m = 6n – 7 in equation (i), we get
5(6n – 7) – 3n = 19
∴ 30n – 35 – 3n = 19
∴ 27n = 19 + 35
∴ 27n = 54
∴ n = \(\frac { 54 }{ 27 } \) = 2
Substituting n = 2 in equation (ii), we get
m = 6(2) – 7
= 12 – 7 = 5
∴ (m, n) = (5, 2) is the solution of the given simultaneous equations.

v. 5x + 2y = -3 …(i)
x + 5y = 4
∴ x = 4 – 5y …(ii)
Substituting x = 4 – 5y in equation (i), we get
5(4 – 5y) + 2y = -3
∴ 20 – 25y + 2y = -3
∴ -23y = -3 – 20
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \) = 1
Substituting y = 1 in equation (ii), we get
x = 4 – 5(1)
= 4 – 5 = -1
∴ (x, y) = (-1, 1) is the solution of the given simultaneous equations.

Substituting y = 3 in equation (i), we get
x = 10 – 3(3)
= 10 – 9 = 1
∴ (x, y) = (1, 3) is the solution of the given simultaneous equations.

vii. 99x + 101 y = 499 …(i)
101 x + 99y = 501 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 3 in equation (iii), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.

viii. 49x – 57y = 172 …(i)
57x – 49y = 252 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 7 in equation (iv), we get
7 + y = 10
∴ y = 10 – 7 = 3
∴ (x, y) = (7, 3) is the solution of the given simultaneous equations.

Complete the following table. (Textbook pg. no. 1)

Question 1.
Solve: 3x+ 2y = 29; 5x – y = 18 (Textbook pg. no. 3)
Solution:
3x + 2y = 29 …(i)
and 5x- y = 18 …(ii)
Let’s solve the equations by eliminating ‘y’.
Fill suitably the boxes below.
Multiplying equation (ii) by 2, we get

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

10th Standard Maths 2 Problem Set 6 Chapter 6 Trigonometry Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 6 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

Class 10 Maths Part 2 Problem Set 6 Chapter 6 Trigonometry Questions With Answers Maharashtra Board

Question 1.
Choose the correct alternative answer for the following questions.

i. sin θ.cosec θ = ?
(A) 1
(B) 0
(C) \(\frac { 1 }{ 2 } \)
(D) \(\sqrt { 2 }\)
Answer:
(A)

ii. cosec 45° = ?
(A) \(\frac{1}{\sqrt{2}}\)
(B) \(\sqrt { 2 }\)
(C) \(\frac{\sqrt{3}}{2}\)
(D) \(\frac{1}{\sqrt{3}}\)
Answer:
(B)

iii. 1 + tan² θ = ?
(A) cot² θ
(B) cosec² θ
(C) sec² θ
(D) tan² θ
Answer:
(C)

iv. When we see at a higher level, from the horizontal line, angle formed is ______
(A) angle of elevation.
(B) angle of depression.
(C) 0
(D) straight angle.
Answer:
(A)

Question 2.
If sin θ = \(\frac { 11 }{ 61 } \), find the value of cos θ using trigonometric identity.
Solution:
sin θ = \(\frac { 11 }{ 61 } \) … [Given]
We know that,
sin² θ + cos² θ = 1


…[Taking square root of both sides]

Question 3.
If tan θ = 2, find the values of other trigonometric ratios.
Solution:
tan θ = 2 …[Given]
We know that,
1 + tan² θ = sec⁷ θ
∴ 1 + (2)⁷ = sec⁷ θ
∴ 1 + 4 = sec⁷ θ
∴ sec⁷ θ = 5
∴ sec θ = \(\sqrt { 5 }\) …[Taking square root of both sides]

Question 4.
If sec θ = \(\frac { 13 }{ 12 } \), find the values of other trigonometric ratios.
Solution:
sec θ = \(\frac { 13 }{ 12 } \) … [Given]
We know that,
1 + tan² θ = sec² θ


∴ sin θ = \(\frac { 5 }{ 13 } \), cos θ = \(\frac { 12 }{ 13 } \), tan θ = \(\frac { 5 }{ 12 } \), cot θ = \(\frac { 12 }{ 5 } \), cosec θ = \(\frac { 13 }{ 5 } \)

Question 5.
Prove the following:
i. sec θ (1 – sin θ) (sec θ + tan θ) = 1
ii. (sec θ + tan θ) (1 – sin θ) = cos θ
iii. sec² θ + cosec² θ = sec² θ × cosec² θ
iv. cot² θ – tan² θ = cosec² θ – sec² θ
v. tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
vi. \(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = 2 sec2 θ
vii. sec⁶ x – tan⁶ x = 1 + 3 sec² x × tan² x

Proof:
i. L.H.S. = sec θ (1 – sin θ) (sec θ + tan θ)

∴ sec θ (1 – sin θ) (sec θ + tan θ) = 1

ii. L.H.S. = (sec θ + tan θ) (1 – sin θ)

∴ (sec θ + tan θ) (1 – sin θ) = cos θ

iii. L.H.S. = sec² θ + cosec² θ

∴ sec² θ + cosec² θ = sec² θ × cosec² θ

iv. L.H.S. = cot² θ – tan² θ
= (cosec² θ – 1) – (sec² θ – 1)
[∵ tan² θ = sec² θ – 1,
cot² θ = cosec² θ – 1]
= cosec² θ – 1 – sec² θ + 1
cosec² θ – sec² θ
= R.H.S.
∴ cot² θ – tan² θ = cosec² θ – sec² θ

v. L.H.S. = tan⁴ θ + tan² θ
= tan² θ (tan² θ + 1)
= tan² θ. sec² θ
…[∵ 1 + tan² θ = sec² θ]
= (sec² θ – 1) sec² θ
…[∵ tan² θ = sec² θ – 1]
= sec⁴ θ – sec² θ
= R.H.S.
∴ tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

vii. L.H.S. = sec⁶ x – tan⁶ x
= (sec² x)³ – tan⁶ x
= (1 + tan² x)³ – tan⁶ x …[∵ 1 + tan² θ = sec² θ]
= 1 + 3tan² x + 3(tan² x)² + (tan² x)³ – tan⁶ x …[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 1 + 3 tan² x (1 + tan² x) + tan⁶ x – tan⁶ x
= 1 + 3 tan² x sec² x …[∵ 1 + tan² θ = sec² θ]
= R.H.S.
∴ sec³x – tan⁶x = 1 + 3sec²x.tan²x


x. We know that,
sin² θ + cos² θ = 1
∴ 1 – sin² θ = cos² θ
∴ (1 – sin θ) (1 + sin θ) = cos θ. cos θ

Question 6.
A boy standing at a distance of 48 metres from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
Solution:
Let AB represent the height of the building and point C represent the position of the boy.
Angle of elevation = ∠ACB = 30°
BC = 48 m

In right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC } \) … [By definition]

∴ The height of the building is 16\(\sqrt { 3 }\) m.

Question 7.
From the top of the lighthouse, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the lighthouse is 100 metres, then find how far the ship is from the lighthouse.
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.

Angle of depression ∠PAC 30°
AB = 100m.
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 30°
AB = 100m
In right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC } \) …[By definition]
∴ \(\frac{1}{\sqrt{3}}=\frac{100}{\mathrm{BC}}\)
∴ BC = 100\(\sqrt { 3 }\)m
∴ The ship is 1oo\(\sqrt { 3 }\)m far from the lighthouse.

Question 8.
Two buildings are in front of each other on a road of width 15 metres. From the top of the first building, having a height of 12 metre, the angle of elevation of the top of the second building is 30°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.

Draw seg AM ⊥ seg CD
Angle of elevation = ∠CAM = 30°
AB = 12m
BD = 15m
In ꠸ ABDM,
∠B = ∠D = 90°
∠M 90° …[segAM ⊥ segCD]
∠A 90° …[Remaining angle of ꠸ABDM]
꠸ABDM is a rectangle …[Each angle is 90°]

∴ The height of the second building is 20.65 m.

Question 9.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2 m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Solution:
Let AB represent the length of the ladder and AE represent the height of the platform.

Draw seg AC ⊥ seg BD.
Angle of elevation = ∠BAC = 70°
AB = 20 m
AE = 2m
In right angled ∆ABC,
sin 70° = \(\frac { BC }{ AB } \) …..[By definition]
∴ 0.94 = \(\frac { BC }{ 20 } \)
∴ BC = 0.94 × 20
= 18.80 m
In ꠸ACDE,
∠E = ∠D = 90°
∠C = 90° … [seg AC ⊥ seg BD]
∴ ∠A = 90° … [Remaining angle of ꠸ACDE]
∴ ꠸ACDE is a rectangle. … [Each angle is 90°]
∴ CD = AE = 2 m … [Opposite sides of a rectangle]
Now, BD = BC + CD … [B – C – D]
= 18.80 + 2
= 20.80 m
∴ The maximum height from the ground upto which the ladder can reach is 20.80 metres.

Question 10.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing, (sin 20° = 0.342)
Solution:
Let AC represent the initial height and point A represent the initial position of the plane.
Let point B represent the position where plane lands.
Angle of depression = ∠EAB = 20°

Now, seg AE || seg BC
∴ ∠ABC = ∠EAB … [Alternate angles]
∴ ∠ABC = 20°
Speed of the plane = 200 km/hr
= 200 × \(\frac { 1000 }{ 3600 } \) m/sec
= \(\frac { 500 }{ 9 } \) m/sec
∴ Distance travelled in 54 sec = speed × time
= \(\frac { 500 }{ 9 } \) × 54
= 3000 m
∴ AB = 3000 m
In right angled ∆ABC,
sin 20° = \(\frac { AC }{ AB } \) ….[By definition]
∴ 0.342 = \(\frac { AC }{ 3000 } \)
∴ AC = 0.342 × 3000
= 1026 m
∴ The plane was at a height of 1026 m when it started landing.

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 3.2 Chapter 3 Arithmetic Progression Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 3.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.

Class 10 Maths Part 1 Practice Set 3.2 Chapter 3 Arithmetic Progression Questions With Answers Maharashtra Board

Question 1.
Write the correct number in the given boxes from the following A.P.

Solution:

Question 2.
Decide whether following sequence is an A.P., if so find the 20^th term of the progression.
-12, -5, 2, 9,16, 23,30,…
Solution:
i. The given sequence is
-12, -5,2, 9, 16, 23,30,…
Here, t₁ = -1₂, t₂ = -5, t₃ = 2, t₄ = 9
∴ t₂ – t₁ – 5 – (-12) – 5 + 12 = 7
t₃ – t₂ = 2 – (-5) = 2 + 5 = 7
∴ t₄ – t₃ – 9 – 2 = 7
∴ t₂ – t₁ = t₃ – t₂ = … = 7 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P.

ii. t_n = a + (n – 1)d
∴ t₂₀ = -12 + (20 – 1)7 …[∵a = -12, d = 7]
= -12 + 19 × 7
= -12 + 133
∴ t₂₀ = 121
∴ 20^th term of the given A.P. is 121.

Question 3.
Given Arithmetic Progression is 12, 16, 20, 24, … Find the 24^th term of this progression.
Solution:
The given A.P. is 12, 16, 20, 24,…
Here, a = 12, d = 16 – 12 = 4 Since,
t_n = a + (n – 1)d
∴ t₂₄ = 12 + (24 – 1)4
= 12 + 23 × 4
= 12 + 92
∴ t₂₄ = 104
∴ 24th term of the given A.P. is 104.

Question 4.
Find the 19th term of the following A.P. 7,13,19,25…..
Solution:
The given A.P. is 7, 13, 19, 25,…
Here, a = 7, d = 13 – 7 = 6
Since, t_n = a + (n – 1)d
∴ t₁₉ = 7 + (19 – 1)6
= 7 + 18 × 6
= 7 + 108
∴ t₁₉ = 115
∴ 19^th term of the given A.P. is 115.

Question 5.
Find the 27^th term of the following A.P. 9,4,-1,-6,-11,…
Solution:
The given A.P. is 9, 4, -1, -6, -11,…
Here, a = 9, d = 4- 9 = -5
Since, t_n = a + (n – 1)d
∴ t₂₇ = 9 + (27 – 1)(-5)
= 9 + 26 × (-5)
= 9 – 130
∴ t₂₇ = -121
∴ 27^th term of the given A.P. is -121.

Question 6.
Find how many three digit natural numbers are divisible by 5.
Solution:
The three digit natural numbers divisible by
5 are 100, 105, 110, …,995
The above sequence is an A.P.
∴ a = 100, d = 105 – 100 = 5
Let the number of terms in the A.P. be n.
Then, t_n = 995
Since, t_n = a + (n – 1)d
∴ 995 = 100 +(n – 1)5
∴ 995 – 100 = (n – 1)5
∴ 895 = (n – 1)5
∴ n – 1 = \(\frac { 895 }{ 5 } \)
∴ n – 1 = 179
∴ n = 179 + 1 = 180
∴ There are 180 three digit natural numbers which are divisible by 5.

Question 7.
The 11th term and the 21st term of an A.P. are 16 and 29 respectively, then find the 41st term of that A.P.
Solution:
Bor an A.P., let a be the first term and d be the common difference,
t₁₁ = 16, t₂₁ = 29 …[Given]
t_n = a + (n – 1)d
∴ t₁₁, = a + (11 – 1)d
∴ 16 = a + 10d
i.e. a + 10d = 16 …(i)
Also, t₂₁ = a + (21 – 1)d
∴ 29 = a + 20d
i.e. a + 20d = 29 …(ii)
Subtracting equation (i) from (ii), we get a

Question 8.
8. 11, 8, 5, 2, … In this A.P. which term is number-151?
Solution:
The given A.P. is 11, 8, 5, 2,…
Here, a = 11, d = 8 – 11 = -3
Let the n^th term of the given A.P. be -151.
Then, t_n = – 151
Since, t_n = a + (n – 1)d
∴ -151= 11 + (n – 1)(-3)
∴ -151 – 11 =(n – 1)(-3)
∴ -162 = (n – 1)(-3)
∴ n – 1 = \(\frac { -162 }{ -3 } \)
∴ n – 1 = 54
∴ n = 54 + 1 = 55
∴ 55th term of the given A.P. is -151.

Question 9.
In the natural numbers from 10 to 250, how many are divisible by 4?
Solution:
The natural numbers from 10 to 250 divisible
by 4 are 12, 16, 20, …,248
The above sequence is an A.P.
∴ a = 12, d = 16 – 12 = 4
Let the number of terms in the A.P. be n.
Then, t_n = 248
Since, t_n = a + (n – 1)d
∴ 248 = 12 + (n – 1)4
∴ 248 – 12 = (n – 1)4
∴ 236 = (n – 1)4
∴ n – 1 = \(\frac { 236 }{ 4 } \)
∴ n – 1 = 59
∴ n = 59 + 1 = 60
∴ There are 60 natural numbers from 10 to 250 which are divisible by 4.

Question 10.
In an A.P. 17^th term is 7 more than its 10th term. Find the common difference.
Solution:
For an A.P., let a be the first term and d be the common difference.
According to the given condition,
t₁₇ = t₁₀ + 7
∴ a + (17 – 1)d = a + (10 – 1)d + 7 …[∵ t_n = a + (n – 1)d]
∴ a + 16d = a + 9d + 7
∴ a + 16d – a – 9d = 7
∴ 7d = 7
∴ d = \(\frac { 7 }{ 7 } \) = 1
∴ The common difference is 1.

Question 1.
Kabir’s mother keeps a record of his height on each birthday. When he was one year old, his height was 70 cm, at 2 years he was 80 cm tall and 3 years he was 90 cm tall. His aunt Meera was studying in the 10th class. She said, “it seems like Kabir’s height grows in Arithmetic Progression”. Assuming this, she calculated how tall Kabir will be at the age of 15 years when he is in 10th! She was shocked to find it. You too assume that Kabir grows in A.P. and find out his height at the age of 15 years. (Textbook pg. no. 63)
Solution:
Height of Kabir when he was 1 year old = 70 cm Height of Kabir when he was 2 years old = 80 cm
Height of Kabir when he was 3 years old = 90 cm The heights of Kabir form an A.P.
Here, a = 70, d = 80 – 70 = 10
We have to find height of Kabir at the age of 15years i.e. t₁₅.
Now, tn = a + (n – 1)d
∴ t₁₅ = 70 + (15 – 1)10
= 70 + 14 × 10 = 70 + 140
∴ t₁₅ = 210
∴ The height of Kabir at the age of 15 years will be 210 cm.

Question 2.
Is 5, 8, 11, 14, …. an A.P.? If so then what will be the 100^th term? Check whether 92 is in this A.P.? Is number 61 in this A.P.? (Textbook pg. no, 62)
Solution:
i. The given sequence is
5, 8,11,14,…
Here, t₁ = 5, t₂ = 8, t₃ = 11, t₄ = 14
∴ t₂ – t₁ = 8 – 5 = 3
t₃ – t₂ = 11 – 8 = 3
t₄ – t₃ = 14 – 11 = 3
∴ t₂ – t₁ = t₃ – t₂ = t₄ – t₃ = 3 = d = constant
The difference between two consecutive terms is constant
∴ The given sequence is an A.P.

ii. t_n = a + (n – 1)d
∴ t₁₀₀ = 5 + (100 – 1)3 …[∵ a = 5, d = 3]
= 5 + 99 × 3
= 5 + 297
∴ t₁₀₀ = 302
∴ 100^th term of the given A.P. is 302.

iii. To check whether 92 is in given A.P., let t_n = 92
∴ t_n = a + (n – 1)d
∴ 92 = 5 + (n – 1)3
∴ 92 = 5 + 3n – 3
∴ 92 = 2 + 3n
∴ 90 = 3n
∴ n = \(\frac { 90 }{ 3 } \) = 30
∴ 92 is the 30th term of given A.P.

iv. To check whether 61 is in given A.P., let t_n = 61
61 = 5 + (n – 1)3
∴ 61 = 5 + 3n – 3
∴ 61 = 2 + 3n
∴ 61 – 2 = 3n
∴ 59 = 3n
∴ n = \(\frac { 59 }{ 3 } \)
But, n is natural number 59
∴ n ≠ \(\frac { 59 }{ 3 } \)
∴ 61 is not in given A.P.

Maharashtra State Board Class 10 Maths Solutions Part 1

• Arithmetic Progression Practice Set 3.1 Class 10 Maths Solutions
• Arithmetic Progression Practice Set 3.2 Class 10 Maths Solutions
• Arithmetic Progression Practice Set 3.3 Class 10 Maths Solutions
• Arithmetic Progression Practice Set 3.4 Class 10 Maths Solutions
• Arithmetic Progression Problem Set 3 Class 10 Maths Solutions
• Financial Planning Practice Set 4.1 Class 10 Maths Solutions
• Financial Planning Practice Set 4.2 Class 10 Maths Solutions
• Financial Planning Practice Set 4.3 Class 10 Maths Solutions
• Financial Planning Practice Set 4.4 Class 10 Maths Solutions
• Financial Planning Problem Set 4A Class 10 Maths Solutions
• Financial Planning Problem Set 4B Class 10 Maths Solutions

Must Read:

TCS Pivot Point Calculator

10th Standard Maths 1 Practice Set 2.5 Chapter 2 Quadratic Equations Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.5 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.

Class 10 Maths Part 1 Practice Set 2.5 Chapter 2 Quadratic Equations Questions With Answers Maharashtra Board

Question 1.
Fill in the gaps and complete.

Answer:

Question 2.
Find the value of discriminant.
i. x² + 7x – 1 = 0
ii. 2y² – 5y + 10 = 0
iii. √2 x² + 4x + 2√2 = 0
Solution:
i. x² +7 x – 1 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 7, c = -1
∴ b²– 4ac = (7)² – 4 × 1 × (-1)
= 49 + 4
∴ b² – 4ac = 53

ii. 2y² – 5y + 10 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 2, b = -5, c = 10
∴ b² – 4ac = (-5)2 -4 × 2 × 10
= 25 – 80
∴ b² – 4ac = -55

iii. √2 x² + 4x + 2√2 = 0
Comparing the above equation with
ax + bx + c = 0, we get
a = √2,b = 4, c = 2√2
∴ b² – 4ac = (4)2 – 4 × √2 × 2√2
= 16 – 16
∴ b² – 4ac =0

Question 3.
Determine the nature of roots of the following quadratic equations.
i. x² – 4x + 4 = 0
ii. 2y² – 7y + 2 = 0
iii. m² + 2m + 9 = 0
Solution:
i. x² – 4x + 4= 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1,b = -4, c = 4
∴ ∆ = b² – 4ac
= (- 4)² – 4 × 1 × 4
= 16 – 16
∴ ∆ = 0
∴ Roots of the given quadratic equation are real and equal.

ii. 2y² – 7y + 2 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 2, b = -7, c = 2
∴ ∆ = b² – 4ac
= (- 7)² – 4 × 2 × 2
= 49 – 16
∴ ∆ = 33
∴ ∆ > 0
∴ Roots of the given quadratic equation are real and unequal.

iii. m² + 2m + 9 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 1,b = 2, c = 9
∴ ∆ = b² – 4ac
= (2)² – 4 × 1 × 9
= 4 – 36
∴ ∆ = -32
∴ ∆ < 0
∴ Roots of the given quadratic equation are not real.

Question 4.
Form the quadratic equation from the roots given below.
i. 0 and 4
ii. 3 and -10
iii. \(\frac { 1 }{ 2 } \) , \(\frac { 1 }{ 2 } \)
iv. 2 – √5, 2 + √5
Solution:
i. Let a = 0 and β = 4
∴ α + β = 0 + 4 = 4
and α × β = 0 × 4 = 0
∴ The required quadratic equation is
x² – (α + β) x + αβ = 0
∴ x² – 4x + 0 = 0
∴ x² – 4x = 0

ii. Let α = 3 and β = -10
∴ α + β = 3 – 10 = -7
and α × β = 3 × -10 = -30
∴ The required quadratic equation is
x² – (α + β)x + αβ = 0
∴ x² – (-7) x + (-30) = 0

∴ The required quadratic equation is
x² – (α + β)x + αβ = 0
∴ x² – 4x – 1 = 0

Question 5.
Sum of the roots of a quadratic equation is double their product. Find k if equation is x² – 4kx + k + 3 = 0.
Solution:
x² – 4kx + k + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = – 4k, c = k + 3
Let α and β be the roots of the given quadratic equation.
Then, α + β  = \(\frac { -b }{ a } \) and αβ = \(\frac { c }{ a } \)
According to the given condition,

Question 6.
α, β are roots of y² – 2y – 7 = 0 find,
i. α² + β²
ii. α³ + β³
Solution:
y² – 2y – 7 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = -2, c = -7

Question 7.
The roots of each of the following quadratic equations are real and equal, find k.
i. 3y² + ky + 12 = 0
ii. kx (x-2) + 6 = 0
Solution:
i. 3y² + kg + 12 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 3, b = k, c = 12
∴ ∆ = b² – 4ac
= (k)² – 4 × 3 × 12
= k² – 144 = k² – (12)²
∴ ∆ = (k + 12) (k – 12) …[∵ a² – b² = (a + b) (a – b)]
Since, the roots are real and equal.
∴ ∆ = 0
∴ (k + 12) (k – 12) = 0
∴ k + 12 = 0 or k – 12 = 0
∴ k = -12 or k = 12

ii. kx (x – 2) + 6 = 0
∴ kx² – 2kx + 6 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = k, b = -2k, c = 6
∴ ∆ = b² – 4ac
= (-2k)² – 4 × k × 6
= 4k² – 24k
∴ ∆ = 4k (k – 6)
Since, the roots are real and equal.
∴ ∆ = 0
∴ 4k (k – 6) = 0
∴ k(k – 6) = 0
∴ k = 0 or k – 6 = 0
But, if k = 0 then quadratic coefficient becomes zero.
∴ k ≠ 0
∴ k = 6

Question 1.
Fill in the blanks. (Textbook pg. no. 44)
Solution:

Question 2.
Determine nature of roots of the quadratic equation: x² + 2x – 9 = 0 (Textbook pg. no. 45)
Solution:

∴ The roots of the given equation are real and unequal.

Question 3.
Fill in the empty boxes properly. (Textbook pg. no. 46)
Solution:
10x² + 10x + 1 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 10, b = 10, c = 1

Question 4.
Write the quadratic equation if addition of the roots is 10 and product of the roots is 9. (Textbook pg, no. 48)
Answer:

Question 5.
What will be the quadratic equation if α = 2, β = 5. (Textbook pg. no, 48)
Solution:

Must Read:

AUROPHARMA Pivot Point Calculator

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

10th Standard Maths 1 Problem Set 6.1 Chapter 6 Statistics Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 6 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 6 Statistics.

Class 10 Maths Part 1 Problem Set 6.1 Chapter 6 Statistics Questions With Answers Maharashtra Board

10th Geometry Problem Set 6 Question 1.
Find the correct answer from the alternatives given.

i. The persons of O – blood group are 40%. The classification of persons based on blood groups is to be shown by a pie diagram. What should be the measures of angle for the persons of O – blood group?
(A) 114°
(B) 140°
(C) 104°
(D) 144°
Answer:
Measure of the central angle = \(\frac { 40 }{ 100 } \) × 360° = 144°
(D)

ii. Different expenditures incurred on the construction of a building were shown by a pie diagram. The expenditure of ₹ 45,000 on cement was shown by a sector of central angle of 75°. What was the total expenditure of the construction?
(A) 2,16,000
(B) 3,60,000
(C) 4,50,000
(D) 7,50,000
Answer:
Measure of the central angle = \(\frac{\text { Expenditure of cement }}{\text { Total expenditure }} \times 360^{\circ}\)

(A)

iii. Cumulative frequencies in a grouped frequency table are useful to find.
(A) Mean
(B) Median
(C) Mode
(D) All of these
Answer:
(B)

iv. The formula to find mean from a grouped frequency table is \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\sum f_{i} u_{i}}{\sum f_{i}} \times g\)
in the formula u_i = _________.

Answer:

(C)

v.

The median of the distances covered per litre shown in the above data is in the group
(A) 12 – 14
(B) 14 – 16
(C) 16 – 18
(D) 18 – 20
Answer:
(C)

vi.

The above data is to be shown by a frequency polygon. The coordinates of the points to show number of students in the class 4 – 6 are.
(A) (4, 8)
(B) (3,5)
(C) (5,8)
(D) (8,4)
Answer:
Class mark = 5
Frequency = 8
∴ Co-ordinates of the point = (5, 8)
(C)

Statistics Problem Set 6 Question 2.
The following table shows the income of farmers in a grape season. Find the mean of their income.

Solution:

∴ The mean of the income of the farmers is ₹ 52,500.

Statistics Problem Set Question 3.
The loans sanctioned by a bank for construction of farm ponds are shown in the following table. Find the mean of the loans.

Solution:

∴ The mean of the loans given by the bank is ₹ 65,400.

Question 4.
The weekly wages of 120 workers in a factory are shown in the following frequency distribution table. Find the mean of the weekly wages.

Solution:

∴ The mean of the weekly wages of the workers is ₹ 4250.

Problem Set 6 Algebra Class 9 Question 5.
The following frequency distribution table shows the amount of aid given to 50 flood affected families. Find the mean of the amount of aid.

Solution:

∴ The mean of the amount of aid given to families is ₹ 72,400.
[Note: The above problems are solved using direct method. Students can solve these problems by using other method.]

Problem Set 6 Algebra Class 10 Question 6.
The distances covered by 250 public transport buses in a day is shown in the following frequency distribution table. Find the median of the distances.

Solution:

Cumulative frequency which is just greater than (or equal) to 125 is 180.
∴ The median class is 220 – 230.
Now, L = 220, f = 80, cf = 100, h = 10

∴ The median of the distances is 223.13 km (approx.).

Algebra 10th Class Problem Set 6 Question 7.
The prices of different articles and demand for them is shown in the following frequency distribution table. Find the median of the prices.

Solution:

Cumulative frequency which is just greater than (or equal) to 200 is 240.
∴ The median class is 20 – 40.
Now,L = 20, f = 100,cf = 140, h = 20

∴ The median of the prices of different articles is ₹ 32.

10th Algebra Problem Set 6 Question 8.
The following frequency table shows the demand for a sweet and the number of customers. Find the mode of demand of sweet.

Solution:


∴ The mode of the demand of sweet is 397.06 grams.

Question 9.
Draw a histogram for the following frequency distribution.

Solution:

Question 10.
In a handloom factory different workers take different periods of time to weave a saree. The number of workers and their required periods are given below. Present the information by a frequency polygon.

Solution:

Problem Set 6 Question 11.
The time required for students to do a science experiment and the number of students is shown in the following grouped frequency distribution table. Show the information by a histogram and also by a frequency polygon.

Solution:

Question 12.
Draw a frequency polygon for the following grouped frequency distribution table.

Solution:

Question 13.
The following table shows the average rainfall in 150 towns. Show the information by a frequency polygon.

Solution:

Question 14.
Observe the given pie diagram. It shows the percentages of number of vehicles passing a signal in a town between 8 am and 10 am.
i. Find the central angle for each type of vehicle.
ii. If the number of two-wheelers is 1200, find the number of all vehicles.

Solution:

∴ The total number of vehicles is 3000.

Problem Set 6 Geometry Class 10 Question 15.
The following table shows causes of noise pollution. Show it by a pie diagram.

Solution:

Question 16.
A survey of students was made to know which game they like. The data obtained in the survey is
presented in the given pie diagram. If the total number of students are 1000,
i. how many students like cricket?
ii. how many students like football?
iii. how many students prefer other games?

Solution:

∴ 225 students like cricket.

ii. Central angle for football (θ) = 63°

∴ 175 students like football.

iii. Central angle for other games (θ) = 72°

∴ 200 students like other games.

Question 17.
Medical check up of 180 women was conducted in a health centre in a village. 50 of them were short of hemoglobin, 10 suffered from cataract and 25 had respiratory disorders. The remaining women were healthy. Show the information by a pie diagram.
Solution:
Total number of women = 180

Question 18.
On an environment day, students in a school planted 120 trees under plantation project. The information regarding the project is shown in the following table. Show it by a pie diagram.

Solution:
Total number of trees planted = 120

Maharashtra Board Class 10 Maths Solutions

• Probability Practice Set 5.1 Class 10 Maths Solutions
• Probability Practice Set 5.2 Class 10 Maths Solutions
• Probability Practice Set 5.3 Class 10 Maths Solutions
• Probability Practice Set 5.4 Class 10 Maths Solutions
• Probability Problem Set 5 Class 10 Maths Solutions
• Statistics Practice Set 6.1 Class 10 Maths Solutions
• Statistics Practice Set 6.2 Class 10 Maths Solutions
• Statistics Practice Set 6.3 Class 10 Maths Solutions
• Statistics Practice Set 6.4 Class 10 Maths Solutions
• Statistics Practice Set 6.5 Class 10 Maths Solutions
• Statistics Practice Set 6.6 Class 10 Maths Solutions
• Statistics Problem Set 6 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 6.6 Chapter 6 Statistics Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.6 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 6 Statistics.

Class 10 Maths Part 1 Practice Set 6.6 Chapter 6 Statistics Questions With Answers Maharashtra Board

Question 1.
The age group and number of persons, who donated blood in a blood donation camp is given below.
Draw a pie diagram from it.

Solution:
Total number of persons = 80 + 60 + 35 + 25 = 200

Question 2.
The marks obtained by a student in different subjects are shown. Draw a pie diagram showing the information.

Solution:
Total marks obtained = 50 + 70 + 80 + 90 + 60 + 50 = 400

Question 3.
In a tree plantation programme, the number of trees planted by students of different classes is given in the following table. Draw a pie diagram showing the information.

Solution:
Total number of trees planted = 40 + 50 + 75 + 50 + 70 + 75 = 360

Question 4.
The following table shows the percentages of demands for different fruits registered with a fruit vendor. Show the information by a pie diagram.

Solution:
Total percentage = 30 + 15 + 25 + 20 + 10 = 100%

Question 5.
The pie diagram in the given figure shows the proportions of different workers in a town. Answer the following questions with its help.
i. If the total workers is 10,000, how many of them are in the field of construction?
ii. How many workers are working in the administration?
iii. What is the percentage of workers in production?

Solution:

∴ There are 2000 workers working in the field of construction.

∴ There are 1000 workers working in the administration.

∴ 25% of workers are working in the production field.

Question 6.
The annual investments of a family are shown in the given pie diagram. Answer the following questions based on it.
i. If the investment in shares is ? 2000, find the total investment.
ii. How much amount is deposited in bank?
iii. How much more money is invested in immovable property than in mutual fund?
iv. How much amount is invested in post?

Solution:

The total investment is ₹ 12000.

ii. Central angle for deposit in bank (θ) = 90°

∴ The amount deposited in bank is ₹ 3000.

iii. Difference in central angle for immovable property and mutual fund (θ) = 120° – 60° = 60°

∴ ₹ 2000 more is invested in immovable property than in mutual fund.

iv. Central angle for post (θ) = 30°

∴ The amount invested in post is ₹ 1000.

• Probability Practice Set 5.1 Class 10 Maths Solutions
• Probability Practice Set 5.2 Class 10 Maths Solutions
• Probability Practice Set 5.3 Class 10 Maths Solutions
• Probability Practice Set 5.4 Class 10 Maths Solutions
• Probability Problem Set 5 Class 10 Maths Solutions
• Statistics Practice Set 6.1 Class 10 Maths Solutions
• Statistics Practice Set 6.2 Class 10 Maths Solutions
• Statistics Practice Set 6.3 Class 10 Maths Solutions
• Statistics Practice Set 6.4 Class 10 Maths Solutions
• Statistics Practice Set 6.5 Class 10 Maths Solutions
• Statistics Practice Set 6.6 Class 10 Maths Solutions
• Statistics Problem Set 6 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 6.5 Chapter 6 Statistics Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.5 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 6 Statistics.

Class 10 Maths Part 1 Practice Set 6.5 Chapter 6 Statistics Questions With Answers Maharashtra Board

Question 1.
Observe the following frequency polygon and write the answers of the questions below it.
i. Which class has the maximum number of students?
ii. Write the classes having zero frequency.
iii. What is the class mark of the class, having frequency of 50 students?
iv. Write the lower and upper class limits of the class whose class mark is 85.
v. How many students are in the class 80 – 90?

Solution:
i. The class 60 – 70 has the maximum number of students.
ii. The classes 20 – 30 and 90 – 100 have frequency zero.
iii. The class mark of the class having 50 students is 55.
iv. The lower and upper class limits of the class having class mark 85 are 80 and 90 respectively.
v. There are 15 students in the class 80 – 90.

Question 2.
Show the following data by a frequency polygon.

Solution:

Question 3.
The following table shows the classification of percentages of marks of students and the number of students. Draw a frequency polygon from the table.

Solution:

• Probability Practice Set 5.1 Class 10 Maths Solutions
• Probability Practice Set 5.2 Class 10 Maths Solutions
• Probability Practice Set 5.3 Class 10 Maths Solutions
• Probability Practice Set 5.4 Class 10 Maths Solutions
• Probability Problem Set 5 Class 10 Maths Solutions
• Statistics Practice Set 6.1 Class 10 Maths Solutions
• Statistics Practice Set 6.2 Class 10 Maths Solutions
• Statistics Practice Set 6.3 Class 10 Maths Solutions
• Statistics Practice Set 6.4 Class 10 Maths Solutions
• Statistics Practice Set 6.5 Class 10 Maths Solutions
• Statistics Practice Set 6.6 Class 10 Maths Solutions
• Statistics Problem Set 6 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 6.4 Chapter 6 Statistics Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.4 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 6 Statistics.

Class 10 Maths Part 1 Practice Set 6.4 Chapter 6 Statistics Questions With Answers Maharashtra Board

Question 1.
Draw a histogram of the following data.

Solution:

Question 2.
The table below shows the yield of jowar per acre. Show the data by histogram.

Solution:

Question 3.
In the following table, the investment made by 210 families is shown. Present it in the form of a histogram.

Solution:

Question 4.
Time allotted for the preparation of an examination by some students is shown in the table. Draw a histogram to show the information.

Solution:

• Probability Practice Set 5.1 Class 10 Maths Solutions
• Probability Practice Set 5.2 Class 10 Maths Solutions
• Probability Practice Set 5.3 Class 10 Maths Solutions
• Probability Practice Set 5.4 Class 10 Maths Solutions
• Probability Problem Set 5 Class 10 Maths Solutions
• Statistics Practice Set 6.1 Class 10 Maths Solutions
• Statistics Practice Set 6.2 Class 10 Maths Solutions
• Statistics Practice Set 6.3 Class 10 Maths Solutions
• Statistics Practice Set 6.4 Class 10 Maths Solutions
• Statistics Practice Set 6.5 Class 10 Maths Solutions
• Statistics Practice Set 6.6 Class 10 Maths Solutions
• Statistics Problem Set 6 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 6.3 Chapter 6 Statistics Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 6 Statistics.

Class 10 Maths Part 1 Practice Set 6.3 Chapter 6 Statistics Questions With Answers Maharashtra Board

Question 1.
The following table shows the information regarding the milk collected from farmers on a milk collection centre and the content of fat in the milk, measured by a lactometer. Find the mode of fat content.

Solution:

Here, the maximum frequency is 80.
∴ The modal class is 4 – 5.
L = lower class limit of the modal class = 4
h = class interval of the modal class = 1
f₁ = frequency of the modal class = 80
f₀ = frequency of the class preceding the modal class = 70
f₂ = frequency of the class succeeding the modal class = 60

∴ The mode of the fat content is 4.33%.

Question 2.
Electricity used by some families is shown in the following table. Find the mode of use of electricity.

Solution:

Here, the maximum frequency is 100.
∴ The modal class is 60 – 80.
L = lower class limit of the modal class = 60
h = class interval of the modal class = 20
f₁ = frequency of the modal class = 100
f₀ = frequency of the class preceding the modal class = 70
f₂ = frequency of the class succeeding the modal class = 80

∴ The mode of use of electricity is 72 units.

Question 3.
Grouped frequency distribution of supply of milk to hotels and the number of hotels is given in the following table. Find the mode of the supply of milk.

Solution:

Here, the maximum frequency is 35.
∴ The modal class is 9 – 11.
L = lower class limit of the modal class = 9
h = class interval of the modal class = 2
f₁ = frequency of the modal class = 35
f₀ = frequency of the class preceding the modal class = 20
f₂ = frequency of the class succeeding the modal class = 18

∴ The mode of the supply of milk is 9.94 litres (approx.).

Question 4.
The following frequency distribution table gives the ages of 200 patients treated in a hospital in a week. Find the mode of ages of the patients.

Solution:

Here, the maximum frequency is 50.
The modal class is 9.5 – 14.5.
L = lower class limit of the modal class = 9.5
h = class interval of the modal class = 5
f₁ = frequency of the modal class = 50
f₀ = frequency of the class preceding the modal class = 32
f₂ = frequency of the class succeeding the modal class = 36

∴ The mode of the ages of the patients is 12.31 years (approx.).

• Probability Practice Set 5.1 Class 10 Maths Solutions
• Probability Practice Set 5.2 Class 10 Maths Solutions
• Probability Practice Set 5.3 Class 10 Maths Solutions
• Probability Practice Set 5.4 Class 10 Maths Solutions
• Probability Problem Set 5 Class 10 Maths Solutions
• Statistics Practice Set 6.1 Class 10 Maths Solutions
• Statistics Practice Set 6.2 Class 10 Maths Solutions
• Statistics Practice Set 6.3 Class 10 Maths Solutions
• Statistics Practice Set 6.4 Class 10 Maths Solutions
• Statistics Practice Set 6.5 Class 10 Maths Solutions
• Statistics Practice Set 6.6 Class 10 Maths Solutions
• Statistics Problem Set 6 Class 10 Maths Solutions