Some Basic Concepts of Chemistry Class 11 Exercise Question Answers Solutions Maharashtra Board
Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 1 Some Basic Concepts of Chemistry Textbook Exercise Questions and Answers.
Class 11 Chemistry Chapter 1 Exercise Solutions Maharashtra Board
Chemistry Class 11 Chapter 1 Exercise Solutions
1. Choose the most correct option.
Question A.
A sample of pure water, whatever the source always contains …………. by mass of oxygen and 11.1 % by mass of hydrogen.
a. 88.9
b. 18
c. 80
d. 16
Answer:
a. 88.9
Question B.
Which of the following compounds can NOT demonstrate the law of multiple proportions?
a. NO, NO2
b. CO, CO2
c. H2O, H2O2
d. Na2S, NaF
Answer:
d. Na2S, NaF
Question C.
Which of the following temperature will read the same value on celsius and Fahrenheit scales.
a. – 40°
b. + 40°
c. – 80°
d. – 20°
Answer:
a. – 40°
Question D.
SI unit of the quantity electric current is
a. Volt
b. Ampere
c. Candela
d. Newton
Answer:
b. Ampere
![]()
Question E.
In the reaction N2 + 3H2 → 2NH3, the ratio by volume of N2, H2 and NH3 is 1 : 3 : 2 This illustrates the law of
a. definite proportion
b. reciprocal proportion
c. multiple proportion
d. gaseous volumes
Answer:
d. gaseous volumes
Question F.
Which of the following has maximum number of molecules ?
a. 7 g N2
b. 2 g H2
c. 8 g O2
d. 20 g NO2
Answer:
b. 2 g H2
Question G.
How many g of H2O are present in 0.25 mol of it ?
a. 4.5
b. 18
c. 0.25
d. 5.4
Answer:
a. 4.5
Question H.
The number of molecules in 22.4 cm3 of nitrogen gas at STP is
a. 6.022 × 1020
b. 6.022 × 1023
c. 22.4 × 1020
d. 22.4 × 1023
Answer:
a. 6.022 × 1020
![]()
Question I.
Which of the following has the largest number of atoms ?
a. 1g Au(s)
b. 1g Na(s)
c. 1g Li(s)
d. 1g Cl2(g)
Answer:
c. 1g Li(s)
2. Answer the following questions.
Question A.
State and explain Avogadro’s law.
Answer:
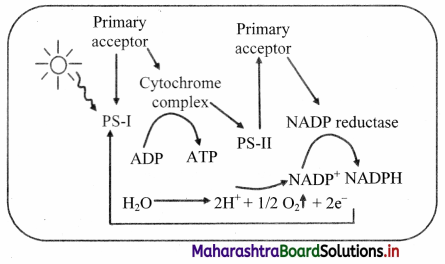
i. In the year 1811, Avogadro made a distinction between atoms and molecules and thereby proposed Avogadro’s law.
ii. Avogadro proposed that, “Equal volumes of all gases at the same temperature and pressure contain equal number of molecules”.
e.g. Hydrogen gas combines with oxygen gas to produce water vapour as follows:

According to Avogadro’s law, if 1 volume contains n molecules, then 2n molecules of hydrogen combine with n molecules of oxygen to give 2n molecules of water, i.e., 2 molecules of hydrogen gas combine with 1 molecule of oxygen to give 2 molecules of water vapour as represented below:
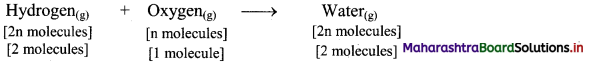
Question B.
Point out the difference between 12 g of carbon and 12 u of carbon.
Answer:
12 g of carbon is the molar mass of carbon while 12 u of carbon is the mass of one carbon atom.
Question C.
How many grams does an atom of hydrogen weigh ?
Answer:
The mass of a hydrogen atom is 1.6736 × 10-24 g.
Question D.
Calculate the molecular mass of the following in u.
a. NH3
b. CH3COOH
c. C2H5OH
Answer:
i. Molecular mass of NH3 = (1 × Average atomic mass of N) + (3 × Average atomic mass of H)
= (1 × 14.0 u) +(3 × 1.0 u)
= 17 u
ii. Molecular mass of CH3COOH = (2 × Average atomic mass of C) + (4 × Average atomic mass of H) + (2 × Average atomic mass of O)
= (2 × 12.0 u) + (4 × 1.0 u) + (2 × 16.0 u)
= 60 u
iii. Molecular mass of C2H5OH = (2 × Average atomic mass of C) + (6 × Average atomic mass of H) + (1 × Average atomic mass of O)
= (2 × 12.0 u) + (6 × 1.0 u) + (1 × 16.0 u)
= 46 u
Ans: i. The molecular mass of NH3 = 17 u
ii. The molecular mass of CH3COOH = 60 u
iii. The molecular mass of C2H5OH = 46 u
![]()
Question E.
How many particles are present in 1 mole of a substance ?
Answer:
The number of particles in one mole is 6.0221367 × 1023.
Question F.
What is the SI unit of amount of a substance ?
Answer:
The SI unit for the amount of a substance is mole (mol).
Question G.
What is meant by molar volume of a gas ?
Answer:
The volume occupied by one mole of a gas at standard temperature (0 °C) and pressure (1 atm) (STP) is called as molar volume of a gas. The molar volume of a gas at STP is 22.4 dm3.
Question H.
State and explain the law of conservation of mass.
Answer:
Law of conservation of mass:
- The law of conservation of mass states that, “Mass can neither be created nor destroyed” during chemical combination of matter.
- Antoine Lavoisier who is often referred to as the father of modem chemistry performed careful experimental studies for various combustion reactions, namely burning of phosphorus and mercury in the presence of air.
- Both his experiments resulted in increased weight of products.
- After several experiments, in burning of phosphorus, he found that the weight gained by the phosphoms was exactly the same as the weight lost by the air. Hence, total mass of reactants = total mass of products.
- When hydrogen gas bums and combines with oxygen to form water, the mass of the water formed is equal to the mass of the hydrogen and oxygen consumed. Thus, this is in accordance with the law of conservation of mass.
Question I.
State the law of multiple proportions.
Answer:
The law states that, “When two elements A and B form more than one compounds, the masses of element B that combine with a given mass of A are always in the ratio of small whole numbers”.
![]()
3. Give one example of each
Question A.
Homogeneous mixture
Answer:
Homogeneous mixture: Solution (An aqueous solution of sugar)
Question B.
Heterogeneous mixture
Answer:
Heterogeneous mixture: Suspension (of sand in water)
Question C.
Element
Answer:
Element: Gold
Question D.
Compound
Answer:
Compound: Distilled water.
![]()
4. Solve problems :
Question A.
What is the ratio of molecules in 1 mole of NH3 and 1 mole of HNO3.
Answer:
One mole of any substance contains particles equal to 6.022 × 1023.
1 mole of NH3 = 6.022 × 1023 molecules of NH3
I mole of HNO3 = 6.022 × 1023 molecules of HNO3
∴ Ratio = \(\frac{6.022 \times 10^{23}}{6.022 \times 10^{23}}\) = 1 : 1
Ans: The ratio of molecules is = 1 : 1.
Question B.
Calculate number of moles of hydrogen in 0.448 litre of hydrogen gas at STP.
Answer:
Given: Volume of hydrogen at STP = 0.448 L
To find: Number of moles of hydrogen
![]()
Molar volume of a gas = 22.4 dm3 mol-1 = 22.4 L at STP

Ans: Number of moles of hydrogen = 0.02 mol
Question C.
The mass of an atom of hydrogen is 1.008 u. What is the mass of 18 atoms of hydrogen.
Answer:
Mass of 1 atom of hydrogen = 1.008 u
∴ Mass of 18 atoms of hydrogen = 18 × 1.008 u = 18.144 u
Ans: The mass of 18 atoms of hydrogen = 18.144 u
Question D.
Calculate the number of atom in each of the following (Given : Atomic mass of I = 127 u).
a. 254 u of iodine (I)
b. 254 g of iodine (I)
Answer:
a. 254 u of iodine (I) = x atoms
Atomic mass of iodine (I) = 127 u
∴ Mass of one iodine atom = 127 u
∴ x = \(\frac{254 \mathrm{u}}{127 \mathrm{u}}\) = 2 atoms
b. 254 g of iodine (I)
Atomic mass of iodine = 127 u
∴ Molar mass of iodine = 127 g mol-1
Now,
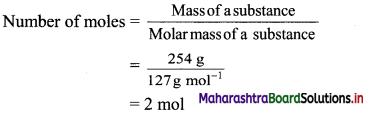
Now,
Number of atoms = Number of moles × Avogadro’s constant
= 2 mol × 6.022 × 1023 atoms/mol
= 12.044 × 1023 atoms
= 1.2044 × 1024 atoms
Ans. i.Number of iodine atoms in 254 u = 2 atoms
ii. Number of iodine atoms in 254 g = 1.2044 × 1024 atoms
![]()
Question E.
A student used a carbon pencil to write his homework. The mass of this was found to be 5 mg. With the help of this calculate.
a. The number of moles of carbon in his homework writing.
b. The number of carbon atoms in 12 mg of his homework writting.
Answer:
a. 5 mg carbon = 5 × 10-3 g carbon
Atomic mass of carbon = 12 u
∴ Molar mass of carbon 12 g mol-1
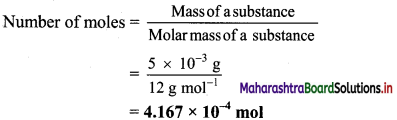
b. 12 mg carbon = 12 × 10-3 g carbon
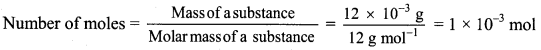
Number of atoms = Number of moles × Avogadro’s constant
Number of atoms of carbon = 1 × 10-3 mol × 6.022 × 1023 atoms/mol
= 6.022 × 1020 atoms
Ans: Number of moles of carbon in his homework writing = 4.167 × 10-4 mol
Number of atoms of carbon in 12 mg homework writing = 6.022 × 1020 atoms
Question F.
Arjun purchased 250 g of glucose (C6H12O6) for Rs 40. Find the cost of glucose per mole.
Answer:
Given: Mass of urea = 250 g, cost for 250 g glucose = Rs 40, molecular formula of glucose = C6H12O6
To find: Cost per mole of glucose
Calculation: Molecular formula of glucose is (C6H12O6).
Molecular mass of glucose
= (6 × Average atomic mass of C) + (12 × Average atomic mass of H) + (6 × Average atomic mass of O)
= (6 × 12 u) + (12 × 1 u) + (6 × 16 u)
=180 u
∴ Molar mass of glucose = 180 g mol-1
![]()
Now,
\(\frac {250}{180}\) mol of glucose cost = Rs 40
1 mol glucose cost = x
∴ x = \(\frac{40 \times 180}{250}\) = Rs 28.8/mol of glucose
Ans. The cost of glucose per mole is Rs 28.8.
[ Calculation using log table:
\(\frac{40 \times 180}{250}\)
= Antilog10 [log10(40) + log10(180) + log10(250)]
= Antilog10 [1.6021 + 2.2553 – 2.3979]
= Antilog10 [1.4595] = 28.80 ]
Question G.
The natural isotopic abundance of 10B is 19.60% and 11B is 80.40 %. The exact isotopic masses are 10.13 and 11.009 respectively. Calculate the average atomic mass of boron.
Answer:
Average atomic mass of Boron(B)
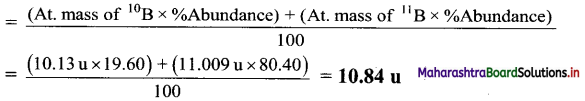
Ans. Average atomic mass of boron = 10.84 u
Question H.
Convert the following degree Celsius temperature to degree Fahrenheit.
a. 40 °C
b. 30 °C
Answer:
a. Given: Temperature in degree Celsius =40°C
To find: Temperature in degree Fahrenheit
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 40 °C in the formula,
°F = \(\frac {9}{5}\) (°C)+32
= \(\frac {9}{5}\) (40) + 32
= 72 + 32
= 104 °F
b. Given: Temperature in degree Celsius = 30 °C
To find: Temperature in degree Fahrenheit
Formula: °F = \(\frac {9}{5}\) (°C) + 32
Calculation: Substituting 30 °C in the formula,
°F = \(\frac {9}{5}\)(°C) + 32
= \(\frac {9}{5}\)(30) + 32
= 54 + 32
= 86 °F
Ans: i. The temperature 40 °C corresponds to 104 °F.
ii. The temperature 30 °C corresponds to 86 °F.
![]()
Question I.
Calculate the number of moles and molecules of acetic acid present in 22 g of it.
Answer:
Given: Mass of acetic acid = 22 g
To find: The number of moles and molecules of acetic acid
Formulae: Number of moles = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
ii. Number of molecules = Number of moles × Avogadro’s constant
Calculator: Mass of acetic acid = 22 g
Molecular mass of acetic acid, CH3COOH
= (2 × Average atomic mass of C) + (4 × Average atomic mass of H) + (2 × Average atomic mass of O)
= (2 × 12 u) + (4 × 1 u) + (2 × 16 u) = 60 u
∴ Molar mass of acetic acid = 60 g mol-1
![]()
Now,
Number of molecules of acetic acid = Number of moles × Avogadro’s constant
= 0.367 mol × 6.022 × 1023 molecules/mol
= 2.210 × 1023 molecules
Ans: Number of moles = 0.367 mol
Number of molecules of acetic acid = 2.210 × 1023 molecules
Question J.
24 g of carbon reacts with some oxygen to make 88 grams of carbon dioxide. Find out how much oxygen must have been used.
Answer:
Given: Mass of carbon (reactant) = 24 g, mass of carbon dioxide (product) = 88 g
To find: Mass of oxygen (reactant)
Calculation: 12 g of carbon combine with 32 g oxygen to form 44 g of carbon dioxide as follows:
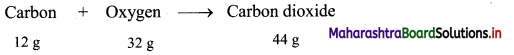
Hence, (2 × 12 = 24 g) of carbon will combine with (2 × 32 = 64 g) of oxygen to give (2 × 44 = 88 g) carbon dioxide.
Ans: Mass of oxygen used = 64 g
Question K.
Calculate number of atoms is each of the following. (Average atomic mass : N = 14 u, S = 32 u)
a. 0.4 mole of nitrogen
b. 1.6 g of sulfur
Answer:
a. 0.4 mole of nitrogen (N)
Number of atoms of N = Number of moles × Avogadro’s constant
= 0.4 mol × 6.022 × 1023 atoms/mol
= 2.4088 × 1023 atoms of N
b. 1.6 g of Sulphur (S)
Molar mass of sulphur = 32 g mol-1
![]()
Number of atoms of S = Number of moles × Avogadro’s constant
= 0.05 mol × 6.022 × 1023 atoms/mol
= 0.3011 × 1023 atoms
= 3.011 × 1022 atoms of S
Ans: a. Number of nitrogen atoms in 0.4 mole = 2.4088 × 1023 atoms of N
b. Number of sulphur atoms in 1.6 g = 3.011 × 1022 atoms of S
Question L.
2.0 g of a metal burnt in oxygen gave 3.2 g of its oxide. 1.42 g of the same metal heated in steam gave 2.27 of its oxide. Which law is verified by these data ?
Answer:
Here, metal oxide is obtained by two different methods; reactions of metal with oxygen and reaction of metal with water vapour (steam).
In first reaction (reaction with oxygen),
The mass of oxygen in metal oxide = 3.2 – 2.0 = 1.2 g
% of oxygen = \(\frac{1.2}{3.2}\) × 100 = 37.5%
% of metal = \(\frac{2.0}{3.2}\) × 100 = 62.5%
In second reaction (reaction with steam),
The mass of oxygen in metal oxide = 2.27 – 1.42 = 0.85 g
% of oxygen = \(\frac{0.85}{2.27}\) × 100 = 37.44 ≈ 37.5%
% of metal = \(\frac{1.42}{2.27}\) × 100 = 62.56 ≈ 62.5%
Therefore, irrespective of the source, the given compound contains same elements in the same proportion. The law of definite proportions states that “A given compound always contains exactly the same proportion of elements by weight”. Hence, the law of definite proportions is verified by these data.
Ans: The law of definite proportions is verified by given data.
![]()
Question M.
In two moles of acetaldehyde (CH3CHO) calculate the following
a. Number of moles of carbon
b. Number of moles of hydrogen
c. Number of moles of oxygen
d. Number of molecules of acetaldehyde
Answer:
Molecular formula of acetaldehyde: C2H4O
Moles of acetaldehyde = 2 mol
a. Number of moles of carbon atoms = Moles of acetaldehyde × Number of carbon atoms
= 2 × 2
= 4 moles of carbon atoms
b. Number of moles of hydrogen atoms = Moles of acetaldehyde × Number of hydrogen atoms
= 2 × 4
= 8 moles of hydrogen atoms
c. Number of moles of oxygen atoms = Moles of acetaldehyde × Number of oxygen atoms
= 2 × 1
= 2 moles of oxygen atoms
d. Number of molecules of acetaldehyde = Moles of acetaldehyde × Avogadro number
= 2 mol × 6.022 × 1023 molecules/mol
= 12.044 × 1023 molecules of acetaldehyde
Ans: i. Number of moles of carbon, hydrogen and oxygen are 4, 8, 2 respectively,
ii. Number of molecules of acetaldehyde = 12.044 × 1023
Question N.
Calculate the number of moles of magnesium oxide, MgO in
i. 80 g and
ii. 10 g of the compound.
(Average atomic masses of Mg = 24 and O = 16)
Answer:
Given: i. Mass of MgO = 80 g
ii. Mass of MgO = 10 g
To find: Number of moles of MgO
Formulae: Number of moles (n) = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
Calculation: i. Molecular mass of MgO = (1 × Average atomic mass of Mg) + (1 × Average atomic mass of O)
= (1 × 24u) + (1 × 16 u)
= 40 u
∴ Molar mass of MgO = 40 g mol-1
Mass of MgO = 80 g
Number of moles (n) = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{80 \mathrm{~g}}{40 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 2 mol
ii. Mass of MgO = 10 g, Molar mass of MgO = 40 g mol-1
Number of moles (n) = \(\frac{\text { Mass of a substance }}{\text { Molar mass of a substance }}\)
= \(\frac{10 \mathrm{~g}}{40 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 0.25 mol
Ans: i. The number of moles in 80 g of magnesium oxide, MgO = 2 mol
ii. The number of moles in 10 g of magnesium oxide, MgO = 0.25 mol
Question O.
What is volume of carbon dioxide, CO2 occupying by i. 5 moles and ii. 0.5 mole of CO2 gas measured at STP.
Answer:
Given: i. Number of moles of CO2 = 5 mol
ii. Number of moles of CO2 = 0.5 mol
To find: Volume at STP
Formula: Number of moies of a gas (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
Calculation: Molar volume of a gas 22.4 dm3 mol-1 at STP.
Number of moles of a gas (n) = \(\frac{\text { Volume of a gas at STP }}{\text { Molar volume of a gas }}\)
∴ i. Volume of the gas at STP = Number of moles of a gas (n) × Molar volume of a gas
= 5mol × 22.4 dm3 mol-1 = 112 dm3
ii. Volume of the gas at STP Number of moles of a gas (n) × Molar volume of a gas
= 0.5 mol × 22.4 dm3 mol-1 = 11.2 dm3
Ans: i. Volume of 5 mol of CO2 = 112 dm3
ii. Volume of 0.5 mol of CO2 = 11.2 dm3
Question P.
Calculate the mass of potassium chlorate required to liberate 6.72 dm3 of oxygen at STP. Molar mass of KClO3 is 122.5 g mol-1.
Answer:
The molecular formula of potassium chlorate is KClO3.
Required chemical equation:
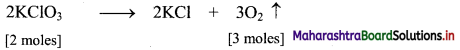
2 moles of KClO3 = 2 × 122.5 = 245 g
3 moles of O2 at STP occupy = (3 × 22.4 dm3) = 67.2 dm3
Thus, 245 g of potassium chlorate will liberate 67.2 dm3 of oxygen gas.
Let ‘x’ gram of KClO3 liberate 6.72 dm3 of oxygen gas at S.T.P.
∴ x = \(\frac{245 \times 6.72}{67.2}\) = 24.5 g
Ans: Mass of potassium chlorate required = 24.5 g
![]()
Question Q.
Calculate the number of atoms of hydrogen present in 5.6 g of urea, (NH2)2CO. Also calculate the number of atoms of N, C and O.
Answer:
Given: Mass of urea = 5.6 g
To find: The number of atoms of hydrogen, nitrogen, carbon and oxygen
Calculation: Molecular formula of urea: (NH2)2CO
Molar mass of urea = 60 g mol-1
![]()
∴ Moles of urea = 0.0933 mol
Number of atoms = Number of moles × Avogadro’s constant
Now, 1 molecule of urea has total 8 atoms, out of which 4 atoms are of H, 2 atoms are of N, 1 of C and 1 of O.
∴ Number of H atoms in 5.6 g of urea = (4 × 0.0933) mol × 6.022 × 1023 atoms/mol
= 2.247 × 1023 atoms of hydrogen
∴ Number of N atoms in 5.6 g of urea = (2 × 0.0933) mol × 6.022 × 1023 atoms/mol
= 1.124 × 1023 atoms of nitrogen
∴ Number of C atoms in 5.6 g of urea = (1 × 0.0933) mol × 6.022 × 1023 atoms/mol
= 0.562 × 1023 atoms of carbon
∴ Number of O atoms in 5.6 g of urea = (1 × 0.0933) mol × 6.022 × 1023 atoms/mol
= 0.562 × 1023 atoms of oxygen
Ans: 5.6 g of urea contain 2.247 × 1023 atoms of H, 1.124 × 1023 atoms of N, 0.562 × 1023 atoms of C and 0.562 × 1023 atoms of O.
Question R.
Calculate the mass of sulfur dioxide produced by burning 16 g of sulfur in excess of oxygen in contact process. (Average atomic mass : S = 32 u, O = 16 u)
Answer:
Given: Mass of sulphur (reactant) = 16 g
To find: Mass of sulphur dioxide (product)
Calculation: 32 g of sulphur combine with 32 g oxygen to form 64 g of sulphur dioxide as follows:
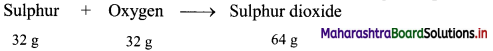
Hence, (0.5 × 32 = 16 g) of sulphur will combine with (0.5 × 32 = 16 g) of oxygen to give (0.5 × 64 = 32 g) sulphur dioxide.
Ans: Mass of sulphur dioxide produced = 32 g
5. Explain
Question A.
The need of the term average atomic mass.
Answer:
- Several naturally occurring elements exist as a mixture of two or more isotopes.
- Isotopes have different atomic masses.
- The atomic mass of such an element is the average of atomic masses of its isotopes.
- For this purpose, the atomic masses of isotopes and their relative percentage abundances are considered.
Hence, the term average atomic mass is needed to express atomic mass of elements containing mixture of two or more isotopes.
Question B.
Molar mass.
Answer:
i. The mass of one mole of a substance (element/compound) in grams is called its molar mass.
ii. The molar mass of any element in grams is numerically equal to atomic mass of that element in u.
e.g.
| Element | Atomic mass (u) | Molar mass (g mol-1) |
| H | 1.0 | 1 0 |
| C | 12.0 | 12.0 |
| O | 16.0 | 16.0 |
iii. Similarly, molar mass of polyatomic molecule, in grams is numerically equal to its molecular mass or formula mass in u.
e.g.
| Polyatomic substance | Molecular/formula mass (u) | Molar mass (g mol-1) |
| O2 | 32.0 | 32.0 |
| H2O | 18.0 | 18.0 |
| NaCl | 58.5 | 58.5 |
Question C.
Mole concept.
Answer:
- Even a small amount of any substance contains very large number of atoms or molecules. Therefore, a quantitative adjective ‘mole’ is used to express the large number of sub-microscopic entities like atoms, molecules, ions, electrons, etc. present in a substance.
- Thus, one mole is the amount of a substance that contains as many entities or particles as there are atoms in exactly 12 g (or 0.012 kg) of the carbon -12 isotope.
- One mole is the amount of substance which contains 6.0221367 × 1023 particles/entities.
![]()
Question D.
Formula mass with an example.
Answer:
- The formula mass of a substance is the sum of atomic masses of the atoms present in the formula.
- In substances such as sodium chloride, positive (sodium), and negative (chloride) entities are arranged in a three-dimensional structure in a way that one sodium (Na+) ion is surrounded by six chlorides (Cl–) ions, all at the same distance from it and vice versa. Thus, sodium chloride does not contain discrete molecules as the constituent units.
- Therefore, NaCl is just the formula that is used to represent sodium chloride though it is not a molecule.
- In such compounds, the formula (i.e., NaCl) is used to calculate the formula mass instead of molecular mass.
e.g. Formula mass of sodium chloride = atomic mass of sodium + atomic mass of chlorine
= 23.0 u + 35.5 u = 58.5 u
Question E.
Molar volume of gas.
Answer:
i. It is more convenient to measure the volume rather than mass of the gas.
ii. It is found from Avogadro law that one mole of any gas occupies a volume of 22.4 dm3 at standard temperature (0 °C) and pressure (1 atm) (STP).
iii. The volume of 22.4 dm3 at STP is known as molar volume of a gas.
iv. The relationship between number of moles and molar volume can be expressed as follows:

[Note: IUPAC has recently changed the standard pressure to 1 bar. Under these new STP conditions the molar volume of a gas is 22.71 L mol-1]
Question F.
Types of matter (on the basis of chemical composition).
Answer:
Matter on the basis of chemical composition can be classified as follows:
i. Pure substances: They always have a definite chemical composition. They always have the same properties regardless of their origin.
e.g. Pure metal, distilled water, etc.
They are of two types:
a. Elements: They are pure substances, which cannot be broken down into simpler substances by ordinary chemical changes.
Elements are further classified into three types:
1. Metals:
- They have a lustre (a shiny appearance).
- They conduct heat and electricity.
- They can be drawn into wire (ductile).
- They can be hammered into thin sheets (malleable).
- e.g. Gold, silver, copper, iron. Mercury is a liquid metal at room temperature.
2. Nonmetals:
- They have no lustre, (except diamond, iodine)
- They are poor conductors of heat and electricity, (except graphite)
- They cannot be hammered into sheets or drawn into wire, because they are brittle. e.g. Iodine
3. Metalloids: Some elements have properties that are intermediate between metals and nonmetals and are called metalloids or semimetals.
e.g. Arsenic, silicon and germanium.
b. Compounds: They are the pure substances which are made up of two or more elements in fixed proportion.
e.g. Water, ammonia, methane, etc.
ii. Mixtures: They have no definite chemical composition and hence no definite properties. They can be separated by physical methods.
e.g. Paint (mixture of oils, pigment, additive), concrete (a mixture of sand, cement, water), etc.
Mixtures are of two types:
- Homogeneous mixture: In homogeneous mixture, constituents remain uniformly mixed throughout its bulk.
e.g. Solution, in which solute and solvent molecules are uniformly mixed throughout its bulk. - Heterogeneous mixture: In heterogeneous mixture, constituents are not uniformly mixed throughout its bulk.
e.g. Suspension, which contains insoluble solid in a liquid.
![]()
11th Chemistry Digest Chapter 1 Some Basic Concepts of Chemistry Intext Questions and Answers
Can you tell? (Textbook Page No. 1)
Question 1.
Which are mixtures and pure substances from the following?
i. Sea water
ii. Gasoline
iii. Skin
iv. A rusty nail
v. A page of textbook
vi. Diamond
Answer:
| No. | Material | Pure substance or mixture |
| i. | Seawater | Mixture |
| ii. | Gasoline | Mixture |
| iii. | Skin | Mixture |
| iv. | A rusty nail | Mixture |
| V. | A page of textbook | Mixture |
| vi. | Diamond | Pure substance |
Can you tell? (Textbook Page No. 2)
Question 1.
Classify the following as element and compound.
i. Mercuric oxide
ii. Helium gas
iii. Water
iv. Table salt
v. Iodine
vi. Mercury
vii. Oxygen
viii. Nitrogen
Answer:
| No. | Material | Element or compound |
| i. | Mercuric oxide | Compound |
| ii. | Helium gas | Element |
| iii. | Water | Compound |
| iv. | Table salt | Compound |
| V. | Iodine | Element |
| vi. | Mercury | Element |
| vii. | Oxygen | Element |
| viii. | Nitrogen | Element |
Can you tell? (Textbook Page No. 6)
Question 1.
If 10 volumes of dihydrogen gas react with 5 volumes of dioxygen gas, how many volumes of water vapour would be produced?
Answer:
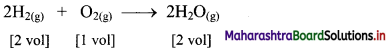
If 10 volumes of dihydrogen gas react with 5 volumes of dioxygen gas, then 10 volumes of water vapour would be produced.
![]()
Can you recall? (Textbook Page No. 6)
Question 1.
What is an atom and molecule? What is the order of magnitude of mass of one atom? What are isotopes?
Answer:
- The smallest indivisible particle of an element is called an atom.
- A molecule is an aggregate of two or more atoms of definite composition which are held together by chemical bonds.
- Every atom of an element has definite mass. The order of magnitude of mass of one atom is 10-27 kg.
- Isotopes are the atoms of the same element having same atomic number but different mass number.
Try this (Textbook Page No. 8)
Question 1.
Find the formula mass of CaSO4, if atomic mass of Ca = 40.1 u, S =32.1 u and O = 16.0 u.
Solution:
Formula mass of CaSO4
= Average atomic mass of Ca + Average atomic mass of S + Average atomic mass of four O
= (40.1) + 32.1 + (4 × 16.0) = 136.2 u
Ans: Formula mass of CaSO4 = 136.2 u
Can you recall? (Textbook Page No. 8)
Question 1.
i. One dozen means how many items?
ii. One gross means how many items?
Answer:
i. One dozen means 12 items.
ii. One gross means 144 items.
Try this (Textbook Page No. 10)
Question 1.
Calculate the volume in dm3 occupied by 60.0 g of ethane at STP.
Solution:
Given: Mass of ethane at STP = 60.0 g
To find: Volume of ethane
Formulae:

Calculation: Molar volume of a gas = 22.4 dm3 mol-1 at STP
Molecular mass of ethane = 30 g mol-1

∴ Volume of the gas at STP = Number of moles of a gas (n) × Molar volume of a gas
= 2 mol × 22.4 dm3 mol-1 = 44.8 dm3
Ans: Volume of ethane = 44.8 dm3
Activity :
Activity 1.
Collect information from various scientists and prepare charts of their contributions to chemistry.
Answer:
| Scientists | Contributions | |
| Joseph Louis Gay-Lussac (1778 – 1850) (French chemist and physicist) | i. | Formulated the gas law. |
| ii. | Collected samples of air at different heights and recorded temperatures and moisture contents. | |
| iii. | Discovered that the composition of the atmosphere does not change with increasing altitude. | |
| Amedeo Avogadro (1776 – 1856) (Italian scholar) | i. | Published article in French journal on determining the relative masses of elementary particles of bodies and proportions by which they enter combinations. |
| ii. | Published a research paper titled “New considerations on the theory of proportions and on the determination of the masses of atoms.” |
Maharashtra State Board Class 11 Chemistry Textbook Solutions
- Some Basic Concepts of Chemistry Class 11 Chemistry Textbook Solutions
- Introduction to Analytical Chemistry Class 11 Chemistry Textbook Solutions
- Basic Analytical Techniques Class 11 Chemistry Textbook Solutions
- Structure of Atom Class 11 Chemistry Textbook Solutions
- Chemical Bonding Class 11 Chemistry Textbook Solutions
- Redox Reactions Class 11 Chemistry Textbook Solutions
- Modern Periodic Table Class 11 Chemistry Textbook Solutions
- Elements of Group 1 and 2 Class 11 Chemistry Textbook Solutions
- Elements of Group 13, 14 and 15 Class 11 Chemistry Textbook Solutions





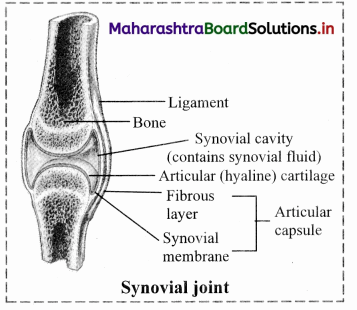
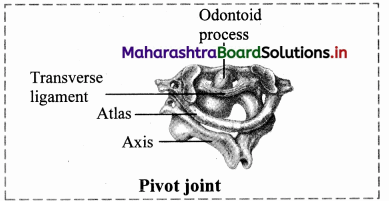
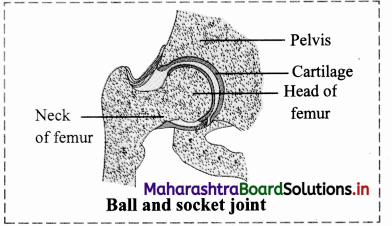
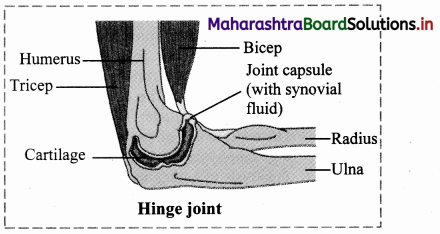
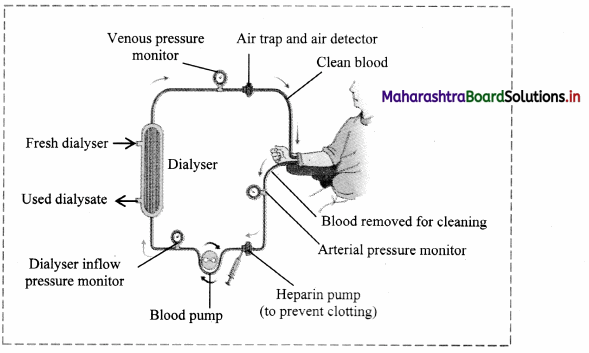



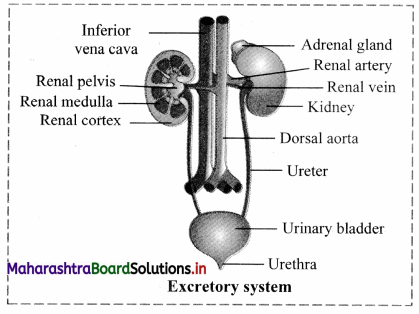
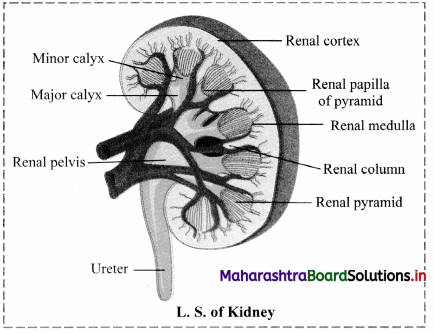



 Answer:
Answer:

 Answer:
Answer:
 Answer:
Answer: