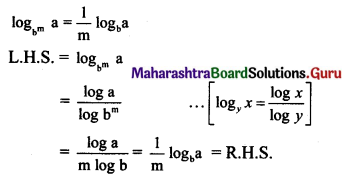
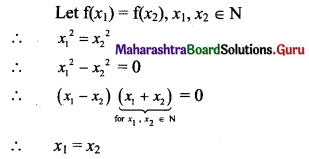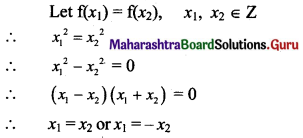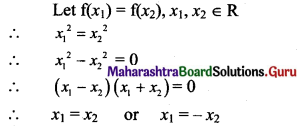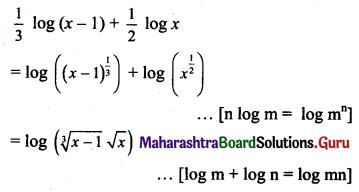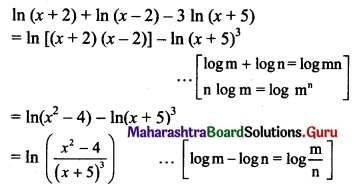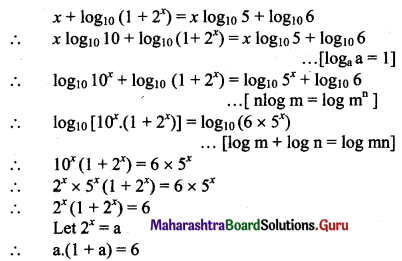Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Ex 7.7 Questions and Answers.
11th Maths Part 2 Limits Exercise 7.7 Questions And Answers Maharashtra Board
I. Evaluate the following:
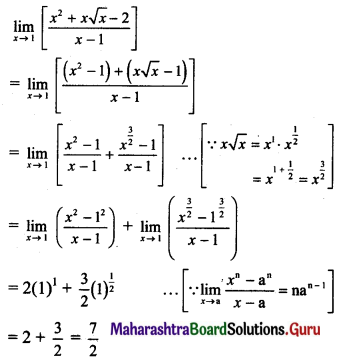
Question 1.
\(\lim _{x \rightarrow \infty}\left[\frac{a x^{3}+b x^{2}+c x+d}{e x^{3}+f x^{2}+g x+h}\right]\)
Solution:
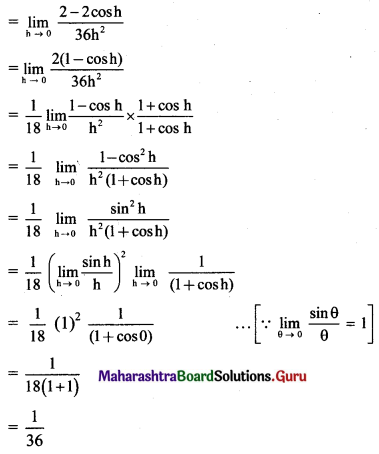
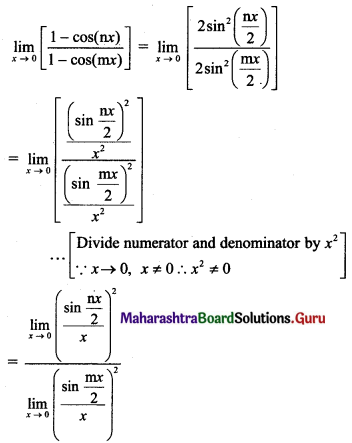
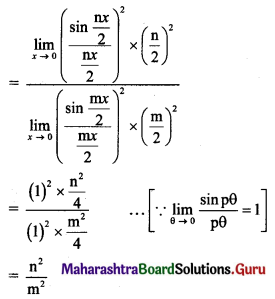
Question 2.
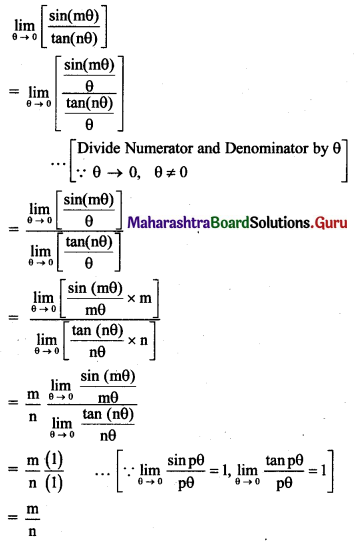
\(\lim _{x \rightarrow \infty}\left[\frac{x^{3}+3 x+2}{(x+4)(x-6)(x-3)}\right]\)
Solution:

![]()
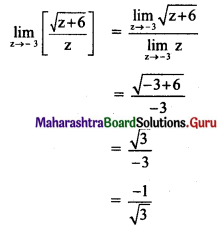
Question 3.
\(\lim _{x \rightarrow \infty}\left[\frac{7 x^{2}+5 x-3}{8 x^{2}-2 x+7}\right]\)
Solution:
II. Evaluate the following:
Question 1.
\(\lim _{x \rightarrow \infty}\left[\frac{7 x^{2}+2 x-3}{\sqrt{x^{4}+x+2}}\right]\)
Solution:

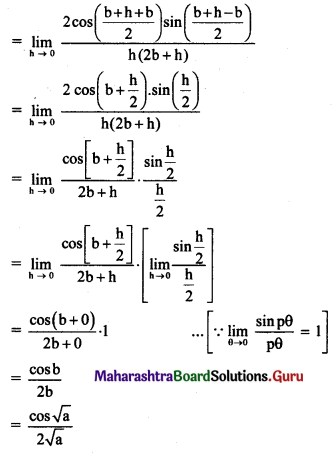
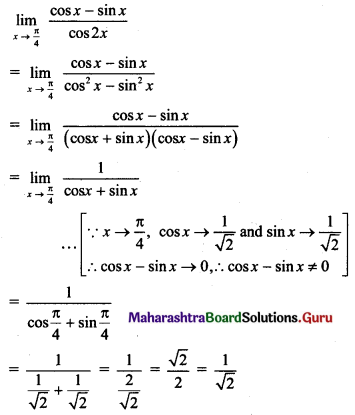
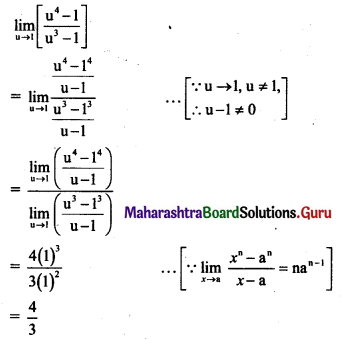
Question 2.
\(\lim _{x \rightarrow \infty}\left[\sqrt{x^{2}+4 x+16}-\sqrt{x^{2}+16}\right]\)
Solution:

![]()
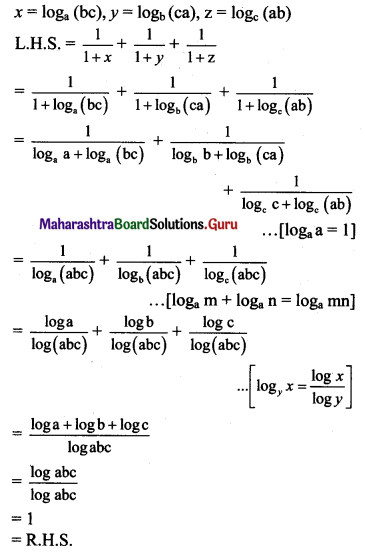
Question 3.
\(\lim _{x \rightarrow \infty}\left[\sqrt{x^{4}+4 x^{2}}-x^{2}\right]\)
Solution:

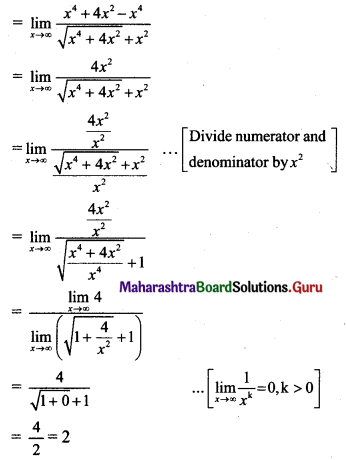
III. Evaluate the following:
Question 1.
\(\lim _{x \rightarrow \infty}\left[\frac{\left(3 x^{2}+4\right)\left(4 x^{2}-6\right)\left(5 x^{2}+2\right)}{4 x^{6}+2 x^{4}-1}\right]\)
Solution:


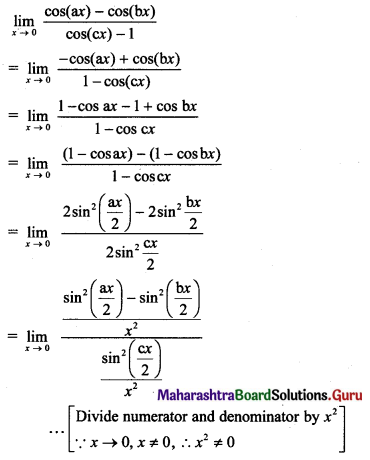
Question 2.
\(\lim _{x \rightarrow \infty}\left[\frac{(3 x-4)^{3}(4 x+3)^{4}}{(3 x+2)^{7}}\right]\)
Solution:

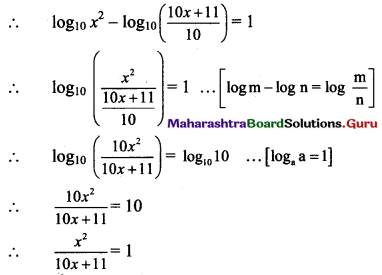
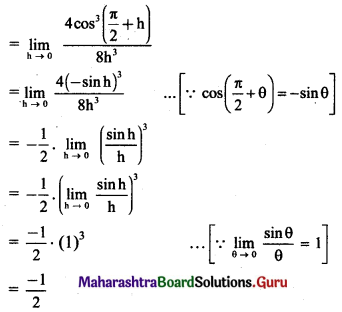
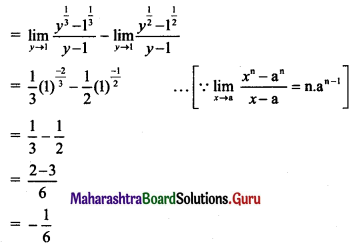
Question 3.
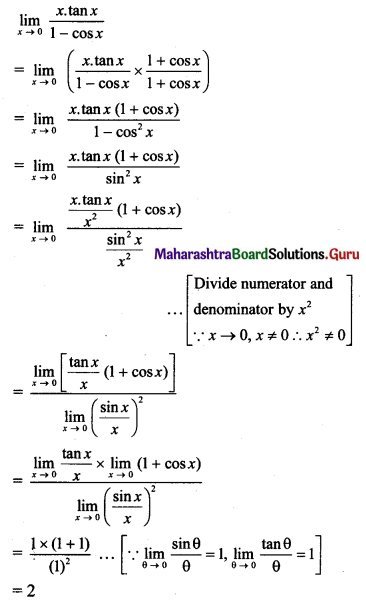
\(\lim _{x \rightarrow \infty}[\sqrt{x}(\sqrt{x+1}-\sqrt{x})]\)
Solution:

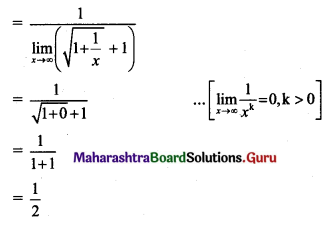
![]()
Question 4.
\(\lim _{x \rightarrow \infty}\left[\frac{(2 x-1)^{20}(3 x-1)^{30}}{(2 x+1)^{50}}\right]\)
Solution:

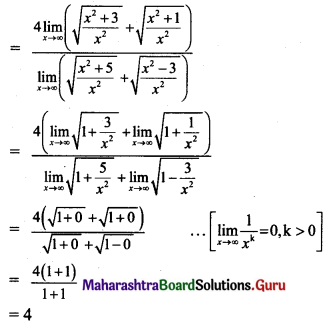
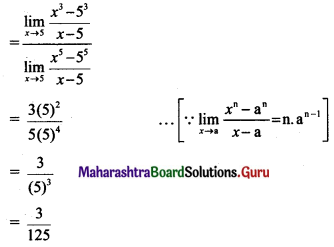
Question 5.
\(\lim _{x \rightarrow \infty}\left[\frac{\sqrt{x^{2}+5}-\sqrt{x^{2}-3}}{\sqrt{x^{2}+3}-\sqrt{x^{2}+1}}\right]\)
Solution:
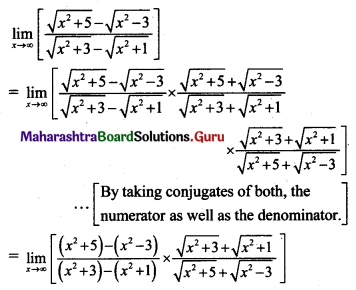
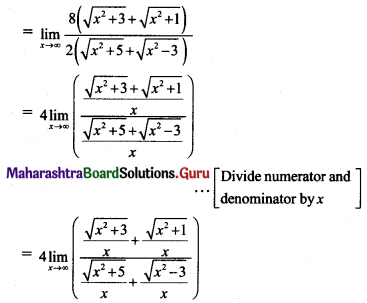
State Board Class 11 Maths Solutions
- Limits Ex 7.1 Class 11 Maths Solutions
- Limits Ex 7.2 Class 11 Maths Solutions
- Limits Ex 7.3 Class 11 Maths Solutions
- Limits Ex 7.4 Class 11 Maths Solutions
- Limits Ex 7.5 Class 11 Maths Solutions
- Limits Ex 7.6 Class 11 Maths Solutions
- Limits Ex 7.7 Class 11 Maths Solutions
- Limits Miscellaneous Exercise 7 Class 11 Maths Solutions


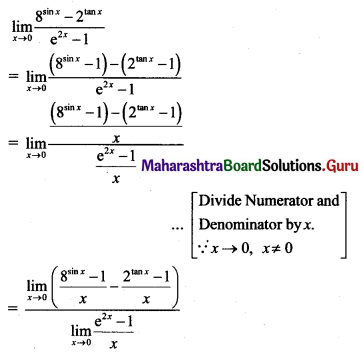
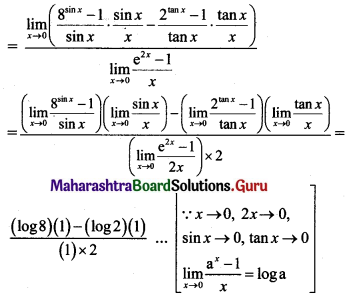
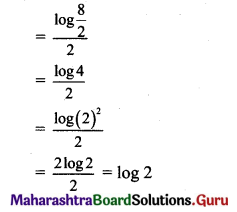

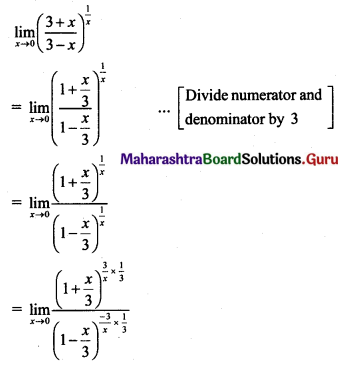







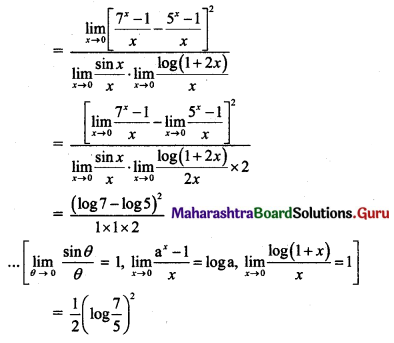

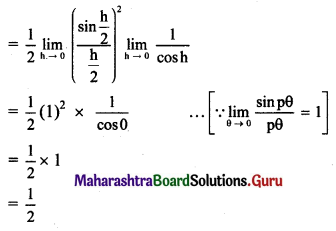
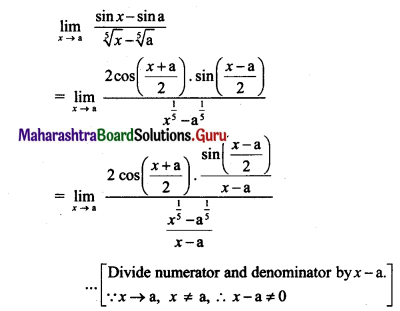
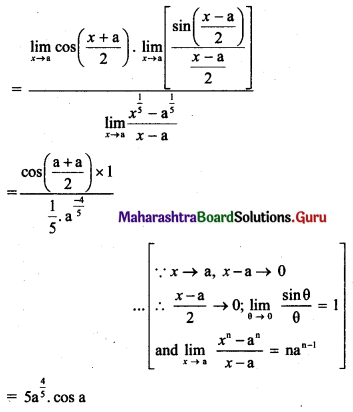
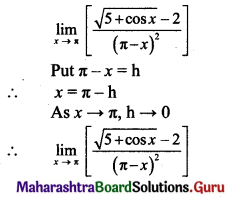



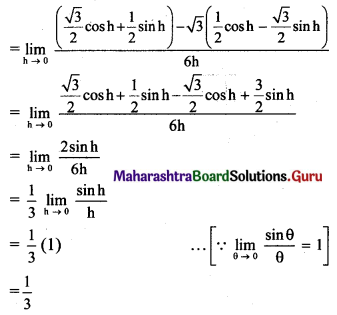



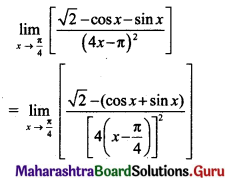



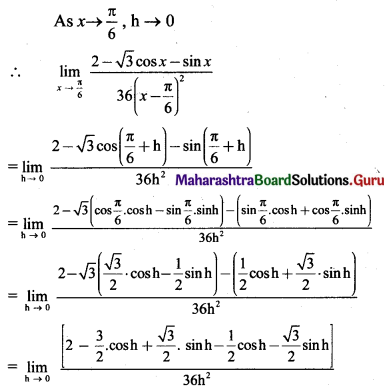
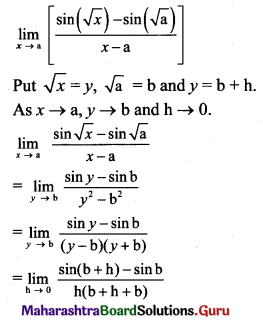

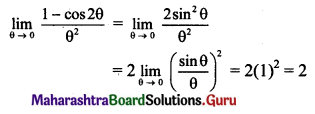
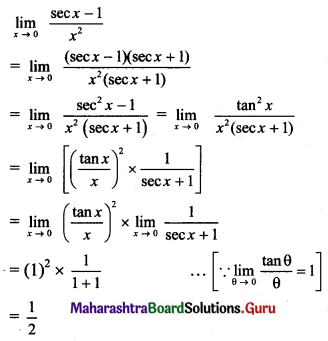



































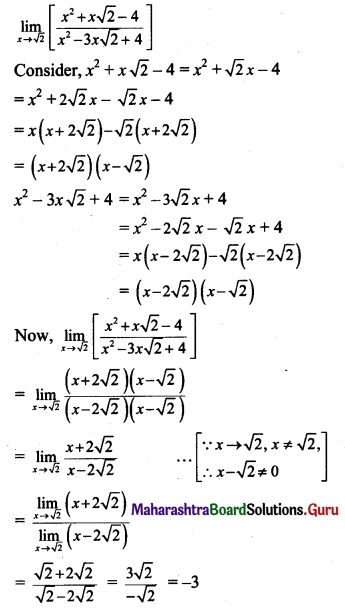

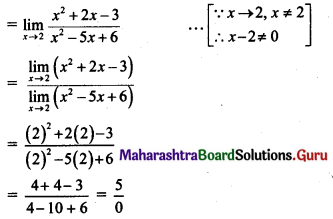











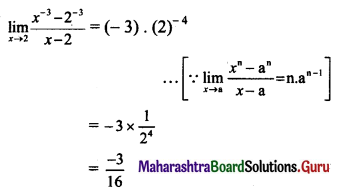








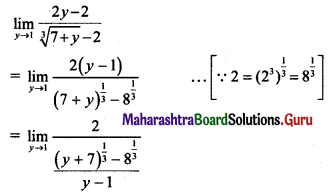






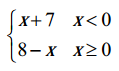
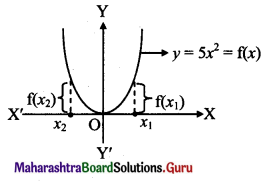
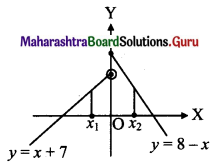
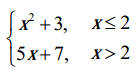 , then find
, then find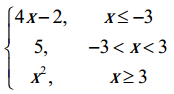 , then find
, then find