Category: Class 11

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 6 Functions Ex 6.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 6 Functions Ex 6.2

Question 1.
If f(x) = 3x + 5, g(x) = 6x – 1, then find
(i) (f + g) (x)
(ii) (f – g) (2)
(iii) (fg) (3)
(iv) (f/g) (x) and its domain
Solution:
f(x) = 3x + 5, g (x) = 6x – 1
(i) (f + g) (x) = f (x) + g (x)
= 3x + 5 + 6x – 1
= 9x + 4

(ii) (f – g) (2) = f(2) – g(2)
= [3(2) + 5] – [6(2) – 1]
= 6 + 5 – 12 + 1
= 0

(iii) (fg) (3) = f (3) g(3)
= [3(3) + 5] [6(3) – 1]
= (14) (17)
= 238

(iv) \(\left(\frac{\mathrm{f}}{\mathrm{g}}\right)(x)=\frac{\mathrm{f}(x)}{\mathrm{g}(x)}=\frac{3 x+5}{6 x-1}, x \neq \frac{1}{6}\)
Domain = R – {\(\frac{1}{6}\)}

Question 2.
Let f: (2, 4, 5} → {2, 3, 6} and g: {2, 3, 6} → {2, 4} be given by f = {(2, 3), (4, 6), (5, 2)} and g = {(2, 4), (3, 4), (6, 2)}. Write down gof.
Solution:
f = {(2, 3), (4, 6), (5, 2)}
∴ f(2) = 3, f(4) = 6, f(5) = 2
g ={(2, 4), (3, 4), (6, 2)}
∴ g(2) = 4, g(3) = 4, g(6) = 2
gof: {2, 4, 5} → {2, 4}
(gof) (2) = g(f(2)) = g(3) = 4
(gof) (4) = g(f(4)) = g(6) = 2
(gof) (5) = g(f(5)) = g(2) = 4
∴ gof = {(2, 4), (4, 2), (5, 4)}

Question 3.
If f(x) = 2x² + 3, g(x) = 5x – 2, then find
(i) fog
(ii) gof
(iii) fof
(iv) gog
Solution:
f(x) = 2x² + 3, g(x) = 5x – 2
(i) (fog) (x) = f(g(x))
= f(5x – 2)
= 2(5x – 2)² + 3
= 2(25x² – 20x + 4) + 3
= 50x² – 40x + 11

(ii) (gof) (x) = g(f(x))
= g(2x² + 3)
= 5(2x + 3) – 2
= 10x² + 13

(iii) (fof) (x) = f(f(x))
= f(2x² + 3)
= 2(2x² + 3)² + 3
= 2(4x⁴ + 12x² + 9) + 3
= 8x⁴ + 24x² + 21

(iv) (gog) (x) = g(g(x))
= g(5x – 2)
= 5(5x – 2) – 2
= 25x – 12

Question 4.
Verify that f and g are inverse functions of each other, where
(i) f(x) = \(\frac{x-7}{4}\), g(x) = 4x + 7
(ii) f(x) = x³ + 4, g(x) = \(\sqrt[3]{x-4}\)
(iii) f(x) = \(\frac{x+3}{x-2}\), g(x) = \(\frac{2 x+3}{x-1}\)
Solution:
(i) f(x) = \(\frac{x-7}{4}\)
Replacing x by g(x), we get
f[g(x)] = \(\frac{g(x)-7}{4}=\frac{4 x+7-7}{4}\) = x
g(x) = 4x + 7
Replacing x by f(x), we get
g[f(x)] = 4f(x) + 7 = 4(\(\frac{x-7}{4}\)) + 7 = x
Here, f[g(x)] = x and g[f(x)] = x.
∴ f and g are inverse functions of each other.

(ii) f(x) = x³ + 4
Replacing x by g(x), we get
f[g(x)] = [g(x)]³ + 4
= \((\sqrt[3]{x-4})^{3}+4\)
= x – 4 + 4
= x
g(x) = \(\sqrt[3]{x-4}\)
Replacing x by f(x), we get
g[f(x)] = \(\sqrt[3]{f(x)-4}=\sqrt[3]{x^{3}+4-4}=\sqrt[3]{x^{3}}\) = x
Here, f[g(x)] = x and g[f(x)] = x
∴ f and g are inverse functions of each other.

(iii) f(x) = \(\frac{x+3}{x-2}\)
Replacing x by g(x), we get

Here, f[g(x)] = x and g[f(x)] = x.
∴ f and g are inverse functions of each other.

Question 5.
Check if the following functions have an inverse function. If yes, find the inverse function.
(i) f(x) = 5x²
(ii) f(x) = 8
(iii) f(x) = \(\frac{6 x-7}{3}\)
(iv) f(x) = \(\sqrt{4 x+5}\)
(v) f(x) = 9x³ + 8
(vi) f(x) =
Solution:
(i) f(x) = 5x² = y (say)

For two values (x₁ and x₂) of x, values of the function are equal.
∴ f is not one-one.
∴ f does not have an inverse.

(ii) f(x) = 8 = y (say)
For every value of x, the value of the function f is the same.
∴ f is not one-one i.e. (many-one) function.
∴ f does not have the inverse.

(iii) f(x) = \(\frac{6 x-7}{3}\)
Let f(x₁) = f(x₂)
∴ \(\frac{6 x_{1}-7}{3}=\frac{6 x_{2}-7}{3}\)
∴ x₁ = x₂
∴ f is a one-one function.
f(x) = \(\frac{6 x-7}{3}\) = y (say)
∴ x = \(\frac{3y+7}{6}\)
∴ For every y, we can get x
∴ f is an onto function.
∴ x = \(\frac{3y+7}{6}\) = f^-1 (y)
Replacing y by x, we get
f-1 (x) = \(\frac{3x+7}{6}\)

(iv) f(x) = \(\sqrt{4 x+5}, x \geq \frac{-5}{4}\)
Let f(x₁) = f(x₂)
∴ \(\sqrt{4 x_{1}+5}=\sqrt{4 x_{2}+5}\)
∴ x₁ = x₂
∴ f is a one-one function.
f(x) = \(\sqrt{4 x+5}\) = y, (say) y ≥ 0
Squaring on both sides, we get
y² = 4x + 5
∴ x = \(\frac{y^{2}-5}{4}\)
∴ For every y we can get x.
∴ f is an onto function.
∴ x = \(\frac{y^{2}-5}{4}\) = f^-1 (y)
Replacing y by x, we get
f^-1 (x) = \(\frac{x^{2}-5}{4}\)

(v) f(x) 9x³ + 8
Let f(x₁) = f(x₂)
∴ \(9 x_{1}^{3}+8=9 x_{2}^{3}+8\)
∴ x₁ = x₂
∴ f is a one-one function.
∴ f(x) = 9x³ + 8 = y, (say)
∴ x = \(\sqrt[3]{\frac{y-8}{9}}\)
∴ For every y we can get x.
∴ f is an onto function.
∴ x = \(\sqrt[3]{\frac{y-8}{9}}\) = f^-1 (y)
Replacing y by x, we get
f^-1 (x) = \(\sqrt[3]{\frac{x-8}{9}}\)

(vi) f(x) = x + 7, x < 0
= 8 – x, x ≥ 0

We observe from the graph that for two values of x, say x₁, x₂ the values of the function are equal.
i.e. f(x₁) = f(x₂)
∴ f is not one-one (i.e. many-one) function.
∴ f does not have inverse.

Question 6.
If f(x) = , then find
(i) f(3)
(ii) f(2)
(iii) f(0)
Solution:
f(x) = x² + 3, x ≤ 2
= 5x + 7, x > 2
(i) f(3) = 5(3) + 7
= 15 + 7
= 22

(ii) f(2) = 2² + 3
= 4 + 3
= 7

(iii) f(0) = 0² + 3 = 3

Question 7.
If f(x) = , then find
(i) f(-4)
(ii) f(-3)
(iii) f(1)
(iv) f(5)
Solution:
f(x) = 4x – 2, x ≤ -3
= 5, -3 < x < 3
= x², x ≥ 3
(i) f(-4) = 4(-4) – 2
= -16 – 2
= -18

(ii) f(-3) = 4(-3) – 2
= -12 – 2
= -14

(iii) f(1) = 5

(iv) f(5) = 5² = 25

Question 8.
If f(x) = 2 |x| + 3x, then find
(i) f(2)
(ii) f(-5)
Solution:
f(x) = 2 |x| + 3x
(i) f(2) = 2|2| + 3(2)
= 2 (2) + 6 ….. [∵ |x| = x, x > 0]
= 10

(ii) f(-5) = 2 |-5| + 3(-5)
= 2(5) – 15 …..[∵ |x| = -x, x < 0]
= 10 – 15
= -5

Question 9.
If f(x) = 4[x] – 3, where [x] is greatest integer function of x, then find
(i) f(7.2)
(ii) f(0.5)
(iii) \(f\left(-\frac{5}{2}\right)\)
(iv) f(2π), where π = 3.14
Solution:
f(x) = 4[x] – 3
(i) f(7.2) = 4 [7.2] – 3
= 4(7) – 3 ………[∵ 7 ≤ 7.2 < 8, [7.2] = 7]
= 25

(ii) f(0.5) = 4[0.5] – 3
= 4(0) – 3 ………[∵ 0 ≤ 0.5 < 1, [0.5] = 0]
= -3

(iii) \(f\left(-\frac{5}{2}\right)\) = f(-2.5)
= 4[-2.5] – 3
= 4(-3) – 3 …….[∵-3 ≤ -2.5 ≤ -2, [-2.5] = -3]
= -15

(iv) f(2π) = 4[2π] – 3
= 4[6.28] – 3 …..[∵ π = 3.14]
= 4(6) – 3 …….[∵ 6 ≤ 6.28 < 7, [6.28] = 6]
= 21

Question 10.
If f(x) = 2{x} + 5x, where {x} is fractional part function of x, then find
(i) f(-1)
(ii) f(\(\frac{1}{4}\))
(iii) f(-1.2)
(iv) f(-6)
Solution:
f(x) = 2{x} + 5x
(i) {-1} = -1 – [-1] = -1 + 1 = 0
∴ f(-1) = 2 {-1} + 5(-1)
= 2(0) – 5
= -5

(ii) {\(\frac{1}{4}\)} = \(\frac{1}{4}\) – [latex]\frac{1}{4}[/latex] = \(\frac{1}{4}\) – 0 = \(\frac{1}{4}\)
f(\(\frac{1}{4}\)) = 2{\(\frac{1}{4}\)} + 5(\(\frac{1}{4}\))
= 2(\(\frac{1}{4}\)) + \(\frac{5}{4}\)
= \(\frac{7}{4}\)
= 1.75

(iii) {-1.2} = -1.2 – [-1.2] = -1.2 + 2 = 0.8
f(-1.2) = 2{-1.2} + 5(-1.2)
= 2(0.8) + (-6)
= -4.4

(iv) {-6} = -6 – [-6] = -6 + 6 = 0
f(-6) = 2{-6} + 5(-6)
= 2(0) – 30
= -30

Question 11.
Solve the following for x, where |x| is modulus function, [x] is the greatest integer function, {x} is a fractional part function.
(i) |x + 4| ≥ 5
(ii) |x – 4| + |x – 2| = 3
(iii) x² + 7|x| + 12 = 0
(iv) |x| ≤ 3
(v) 2|x| = 5
(vi) [x + [x + [x]]] = 9
(vii) {x} > 4
(viii) {x} = o
(ix) {x} = 0.5
(x) 2{x} = x + [x]
Solution:
(i) |x + 4| ≥ 5
The solution of |x| ≥ a is x ≤ -a or x ≥ a
∴ |x + 4| ≥ 5 gives
∴ x + 4 ≤ -5 or x + 4 ≥ 5
∴ x ≤ -5 – 4 or x ≥ 5 – 4
∴ x ≤ -9 or x ≥ 1
∴ The solution set = (-∞, – 9] ∪ [1, ∞)

(ii) |x – 4| + |x – 2| = 3 …..(i)
Case I: x < 2
Equation (i) reduces to
4 – x + 2 – x = 3 …….[x < 2 < 4, x – 4 < 0, x – 2 < 0]
∴ 6 – 3 = 2x
∴ x = \(\frac{3}{2}\)

Case II: 2 ≤ x < 4
Equation (i) reduces to
4 – x + x – 2 = 3
∴ 2 = 3 (absurd)
There is no solution in [2, 4)

Case III: x ≥ 4
Equation (i) reduces to
x – 4 + x – 2 = 3
∴ 2x = 6 + 3 = 9
∴ x = \(\frac{9}{2}\)
∴ x = \(\frac{3}{2}\), \(\frac{9}{2}\) are solutions.
The solution set = {\(\frac{3}{2}\), \(\frac{9}{2}\)}

(iii) x² + 7|x| + 12 = 0
∴ (|x|)² + 7|x| + 12 = 0
∴ (|x| + 3) (|x| + 4) = 0
∴ There is no x that satisfies the equation.
The solution set = { } or Φ

(iv) |x| ≤ 3 The solution set of |x| ≤ a is -a ≤ x ≤ a
∴ The required solution is -3 ≤ x ≤ 3
∴ The solution set is [-3, 3]

(v) 2|x| = 5
∴ |x| = \(\frac{5}{2}\)
∴ x = ±\(\frac{5}{2}\)

(vi) [x + [x + [x]]] = 9
∴ [x + [x] + [x] ] = 9 …….[[x + n] = [x] + n, if n is an integer]
∴ [x + 2[x]] = 9
∴ [x] + 2[x] = 9 …..[[2[x] is an integer]]
∴ [x] = 3
∴ x ∈ [3, 4)

(vii) {x} > 4
This is a meaningless statement as 0 ≤ {x} < 1
∴ The solution set = { } or Φ

(viii) {x} = 0
∴ x is an integer
∴ The solution set is Z.

(ix) {x} = 0.5
∴ x = ….., -2.5, -1.5, -0.5, 0.5, 1.5, …..
∴ The solution set = {x : x = n + 0.5, n ∈ Z}

(x) 2{x} = x + [x]
= [x] + {x} + [x] ……[x = [x] + {x}]
∴ {x} = 2[x]
R.H.S. is an integer
∴ L.H.S. is an integer
∴ {x} = 0
∴ [x] = 0
∴ x = 0

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 6 Functions Ex 6.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 6 Functions Ex 6.1

Question 1.
Check if the following relations are functions.
(a)

Solution:
Yes.
Reason: Every element of set A has been assigned a unique element in set B.

(b)

Solution:
No.
Reason: An element of set A has been assigned more than one element from set B.

(c)

Solution:
No.
Reason:
Not every element of set A has been assigned an image from set B.

Question 2.
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {-1, 0, 1, 2, 3}? Justify.
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)}
(ii) {(1, 2), (2, -1), (3, 1), (4, 3)}
(iii) {(1, 3), (4, 1), (2, 2)}
(iv) {(1, 1), (2, 1), (3, 1), (4, 1)}
Solution:
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)} does not represent a function.
Reason: (2, -1), (2, 2), show that element 2 ∈ A has been assigned two images -1 and 2 from set B.

(ii) {(1, 2), (2, -1), (3, 1), (4, 3)} represents a function.
Reason: Every element of set A has been assigned a unique image in set B.

(iii) {(1, 3), (4, 1), (2, 2)} does not represent a function.
Reason:
3 ∈ A does not have an image in set B.

(iv) {(1, 1), (2, 1), (3, 1), (4, 1)} represents a function
Reason: Every element of set A has been assigned a unique image in set B.

Question 3.
Check if the relation given by the equation represents y as function of x.
(i) 2x + 3y = 12
(ii) x + y² = 9
(iii) x² – y = 25
(iv) 2y + 10 = 0
(v) 3x – 6 = 21
Solution:
(i) 2x + 3y = 12
∴ y = \(\frac{12-2 x}{3}\)
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(ii) x + y² = 9
∴ y² = 9 – x
∴ y = ±\(\sqrt{9-x}\)
∴ For one value of x, there are two values of y.
∴ y is not a function of x.

(iii) x² – y = 25
∴ y = x² – 25
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(iv) 2y + 10 = 0
∴ y = -5
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(v) 3x – 6 = 21
∴ x = 9
∴ x = 9 represents a point on the X-axis.
There is no y involved in the equation.
So the given equation does not represent a function.

Question 4.
If f(m) = m² – 3m + 1, find
(i) f(0)
(ii) f(-3)
(iii) f(\(\frac{1}{2}\))
(iv) f(x + 1)
(v) f(-x)
(vi) \(\left(\frac{\mathbf{f}(2+h)-f(2)}{h}\right)\), h ≠ 0.
Solution:
f(m) = m² – 3m + 1
(i) f(0) = 0² – 3(0) + 1 = 1

(ii) f (-3) = (-3)² – 3(-3) + 1
= 9 + 9 + 1
= 19

(iii) f(\(\frac{1}{2}\)) = \(\left(\frac{1}{2}\right)^{2}-3\left(\frac{1}{2}\right)+1\)
= \(\frac{1}{4}-\frac{3}{2}+1\)
= \(\frac{1-6+4}{4}\)
= \(-\frac{1}{4}\)

(iv) f(x + 1) = (x + 1)² – 3(x + 1) + 1
= x² + 2x + 1 – 3x – 3 + 1
= x² – x – 1

(v) f(-x) = (-x)2 – 3(-x) + 1 = x2 + 3x + 1

(vi) \(\left(\frac{\mathbf{f}(2+h)-f(2)}{h}\right)\)
= \(\frac{(2+h)^{2}-3(2+h)+1-\left(2^{2}-3(2)+1\right)}{h}\)
= \(\frac{\mathrm{h}^{2}+\mathrm{h}}{\mathrm{h}}\)
= h + 1

Question 5.
Find x, if g(x) = 0 where
(i) g(x) = \(\frac{5 x-6}{7}\)
(ii) g(x) = \(\frac{18-2 x^{2}}{7}\)
(iii) g(x) = 6x² + x – 2
(iv) g(x) = x³ – 2x² – 5x + 6
Solution:
(i) g(x) = \(\frac{5 x-6}{7}\)
g(x) = 0
∴ \(\frac{5 x-6}{7}\) = 0
∴ x = \(\frac{6}{5}\)

(ii) g(x) = \(\frac{18-2 x^{2}}{7}\)
g(x) = 0
\(\frac{18-2 x^{2}}{7}\) = 0
∴ 18 – 2x² = 0
∴ x² = 9
∴ x = ±3

(iii) g(x) = 6x² + x – 2
g(x) = 0
∴ 6x² + x – 2 = 0
∴ (2x – 1) (3x + 2) = 0
∴ 2x – 1 = 0 or 3x + 2 = 0
∴ x = \(\frac{1}{2}\) or x = \(\frac{-2}{3}\)

(iv) g(x) = x³ – 2x² – 5x + 6
= ( x- 1) (x² – x – 6)
= (x – 1) (x + 2) (x – 3)
g(x) = 0
∴ (x – 1) (x + 2) (x – 3) = 0
∴ x – 1 = 0 or x + 2 = 0 or x – 3 = 0
∴ x = 1, -2, 3

Question 6.
Find x, if f(x) = g(x) where
(i) f(x) = x⁴ + 2x², g(x) = 11x²
(ii) f(x) = √x – 3, g(x) = 5 – x
Solution:
(i) f(x) = x⁴ + 2x², g(x) = 11x²
f(x) = g(x)
∴ x⁴ + 2x² = 11x²
∴ x⁴ – 9x² = 0
∴ x² (x² – 9) = 0
∴ x² = 0 or x² – 9 = 0
∴ x = 0 or x² = 9
∴ x = 0, ±3

(ii) f(x) = √x – 3, g(x) = 5 – x
f(x) = g(x)
∴ √x – 3 = 5 – x
∴ √x = 5 – x + 3
∴ √x = 8 – x
on squaring, we get
x = 64 + x² – 16x
∴ x² – 17x + 64 = 0
∴ x = \(\frac{17 \pm \sqrt{(-17)^{2}-4(64)}}{2}\)
∴ x = \(\frac{17 \pm \sqrt{289-256}}{2}\)
∴ x = \(\frac{17 \pm \sqrt{33}}{2}\)

Question 7.
If f(x) = \(\frac{a-x}{b-x}\), f(2) is undefined, and f(3) = 5, find a and b.
Solution:
f(x) = \(\frac{a-x}{b-x}\)
Given that,
f(2) is undefined
b – 2 = 0
∴ b = 2 …..(i)
f(3) = 5
∴ \(\frac{a-3}{b-3}\) = 5
∴ \(\frac{a-3}{2-3}\) = 5 ….. [From (i)]
∴ a – 3 = -5
∴ a = -2
∴ a = -2, b = 2

Question 8.
Find the domain and range of the following functions.
(i) f(x) = 7x² + 4x – 1
Solution:
f(x) = 7x² + 4x – 1
f is defined for all x.
∴ Domain of f = R (i.e., the set of real numbers)

∴ Range of f = [\(-\frac{11}{7}\), ∞)

(ii) g(x) = \(\frac{x+4}{x-2}\)
Solution:
g(x) = \(\frac{x+4}{x-2}\)
Function g is defined everywhere except at x = 2.
∴ Domain of g = R – {2}
Let y = g(x) = \(\frac{x+4}{x-2}\)
∴ (x – 2) y = x + 4
∴ x(y – 1) = 4 + 2y
∴ For every y, we can find x, except for y = 1.
∴ y = 1 ∉ range of function g
∴ Range of g = R – {1}

(iii) h(x) = \(\frac{\sqrt{x+5}}{5+x}\)
Solution:
h(x) = \(\frac{\sqrt{x+5}}{5+x}=\frac{1}{\sqrt{x+5}}\), x ≠ -5
For x = -5, function h is not defined.
∴ x + 5 > 0 for function h to be well defined.
∴ x > -5
∴ Domain of h = (-5, ∞)
Let y = \(\frac{1}{\sqrt{x+5}}\)
∴ y > 0
Range of h = (0, ∞) or R+

(iv) f(x) = \(\sqrt[3]{x+1}\)
Solution:
f(x) = \(\sqrt[3]{x+1}\)
f is defined for all real x and the values of f(x) ∈ R
∴ Domain of f = R, Range of f = R

(v) f(x) = \(\sqrt{(x-2)(5-x)}\)
Solution:
f(x) = \(\sqrt{(x-2)(5-x)}\)
For f to be defined,
(x – 2)(5 – x) ≥ 0
∴ (x – 2)(x – 5) ≤ 0
∴ 2 ≤ x ≤ 5 ……[∵ The solution of (x – a) (x – b) ≤ 0 is a ≤ x ≤ b, for a < b]
∴ Domain of f = [2, 5]
(x – 2) (5 – x) = -x² + 7x – 10
= \(-\left(x-\frac{7}{2}\right)^{2}+\frac{49}{4}-10\)
= \(\frac{9}{4}-\left(x-\frac{7}{2}\right)^{2} \leq \frac{9}{4}\)
∴ \(\sqrt{(x-2)(5-x)} \leq \sqrt{\frac{9}{4}} \leq \frac{3}{2}\)
Range of f = [0, \(\frac{3}{2}\)]

(vi) f(x) = \(\sqrt{\frac{x-3}{7-x}}\)
Solution:
f(x) = \(\sqrt{\frac{x-3}{7-x}}\)
For f to be defined,
\(\sqrt{\frac{x-3}{7-x}}\) ≥ 0, 7 – x ≠ 0
∴ \(\sqrt{\frac{x-3}{7-x}}\) ≤ 0 and x ≠ 7
∴ 3 ≤ x < 7
Let a < b, \(\frac{x-a}{x-b}\) ≤ 0 ⇒ a ≤ x < b
∴ Domain of f = [3, 7)
f(x) ≥ 0 … [∵ The value of square root function is non-negative]
∴ Range of f = [0, ∞)

(vii) f(x) = \(\sqrt{16-x^{2}}\)
Solution:
f(x) = \(\sqrt{16-x^{2}}\)
For f to be defined,
16 – x² ≥ 0
∴ x² ≤ 16
∴ -4 ≤ x ≤ 4
∴ Domain of f = [-4, 4]
Clearly, f(x) ≥ 0 and the value of f(x) would be maximum when the quantity subtracted from 16 is minimum i.e. x = 0
∴ Maximum value of f(x) = √16 = 4
∴ Range of f = [0, 4]

Question 9.
Express the area A of a square as a function of its
(a) side s
(b) perimeter P
Solution:
(a) area (A) = s²
(b) perimeter (P) = 4s
∴ s = \(\frac{\mathrm{P}}{4}\)
Area (A) = s² = \(\left(\frac{\mathrm{P}}{4}\right)^{2}\)
∴ A = \(\frac{\mathrm{P}^{2}}{16}\)

Question 10.
Express the area A of a circle as a function of its
(i) radius r
(ii) diameter d
(iii) circumference C
Solution:
(i) Area (A) = πr²

(ii) Diameter (d) = 2r
∴ r = \(\frac{\mathrm{d}}{2}\)
∴ Area (A) = πr² = \(\frac{\pi \mathrm{d}^{2}}{4}\)

(iii) Circumference (C) = 2πr
∴ r = \(\frac{C}{2 \pi}\)
Area (A) = πr² = \(\pi\left(\frac{\mathrm{C}}{2 \pi}\right)^{2}\)
∴ A = \(\frac{C^{2}}{4 \pi}\)

Question 11.
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also, find its domain.
Solution:

Length of the box = 30 – 2x
Breadth of the box = 30 – 2x
Height of the box = x
Volume = (30 – 2x)² x, x < 15, x ≠ 15, x > 0
= 4x(15 – x)², x ≠ 15, x > 0
Domain (0, 15)

Question 12.
Let f be a subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z? Justify?
Solution:
f = {(ab, a + b): a, b ∈ Z}
Let a = 1, b = 1. Then, ab = 1, a + b = 2
∴ (1, 2) ∈ f
Let a = -1, b = -1. Then, ab = 1, a + b = -2
∴ (1, -2) ∈ f
Since (1, 2) ∈ f and (1, -2) ∈ f,
f is not a function as element 1 does not have a unique image.

Question 13.
Check the injectivity and surjectivity of the following functions.
(i) f : N → N given by f(x) = x²
Solution:
f: N → N given by f(x) = x²

∴ f is injective.
For every y = x² ∈ N, there does not exist x ∈ N.
Example: 7 ∈ N (codomain) for which there is no x in domain N such that x² = 7
∴ f is not surjective.

(ii) f : Z → Z given by f(x) = x²
Solution:
f: Z → Z given by f(x) = x2

∴ f is not injective.
(Example: f(-2) = 4 = f(2). So, -2, 2 have the same image. So, f is not injective.)
Since x² ≥ 0,
f(x) ≥ 0
Therefore all negative integers of codomain are not images under f.
∴ f is not surjective.

(iii) f : R → R given by f(x) = x²
Solution:
f : R → R given by f(x) = x²

∴ f is not injective.
f(x) = x² ≥ 0
Therefore all negative integers of codomain are not images under f.
∴ f is not surjective.

(iv) f : N → N given by f(x) = x³
Solution:
f: N → N given by f(x) = x³

∴ f is injective.
Numbers from codomain which are not cubes of natural numbers are not images under f.
∴ f is not surjective.

(v) f : R → R given by f(x) = x³
Solution:
f: R → R given by f(x) = x³

∴ For every y ∈ R, there is some x ∈ R.
∴ f is surjective.

Question 14.
Show that if f : A → B and g : B → C are one-one, then gof is also one-one.
Solution:
f is a one-one function.
Let f(x₁) = f(x₂)
Then, x₁ = x₂ for all x₁, x₂ …..(i)
g is a one-one function.
Let g(y₁) = g(y₂)
Then, y₁ = y₂ for all y₁, y₂ …..(ii)
Let (gof) (x₁) = (gof) (x₂)
∴ g(f(x₁)) = g(f(x₂))
∴ g(y₁) = g(y₂),
where y₁ = f(x₁), y₂ = f(x₂) ∈ B
∴ y₁ = y₂ …..[From (ii)]
i.e., f(x₁) = f(x₂)
∴ x₁ = x₂ ….[From (i)]
∴ gof is one-one.

Question 15.
Show that if f : A → B and g : B → C are onto, then gof is also onto.
Solution:
Since g is surjective (onto),
there exists y ∈ B for every z ∈ C such that
g(y) = z …….(i)
Since f is surjective,
there exists x ∈ A for every y ∈ B such that
f(x) = y …….(ii)
(gof) x = g(f(x))
= g(y) ……[From (ii)]
= z …..[From(i)]
i.e., for every z ∈ C, there is x in A such that (gof) x = z
∴ gof is surjective (onto).

Question 16.
If f(x) = 3(4^x+1), find f(-3).
Solution:
f(x) = 3(4^x+1)
∴ f(-3) = 3(4^-3+1)
= 3(4^-2)
= \(\frac{3}{16}\)

Question 17.
Express the following exponential equations in logarithmic form:
(i) 2⁵ = 32
(ii) 54⁰ = 1
(iii) 23¹ = 23
(iv) \(9^{\frac{3}{2}}\) = 27
(v) 3^-4 = \(\frac{1}{81}\)
(vi) 10^-2 = 0.01
(vii) e² = 7.3890
(viii) \(e^{\frac{1}{2}}\) = 1.6487
(ix) e^-x = 6
Solution:

Question 18.
Express the following logarithmic equations in exponential form:
(i) log₂ 64 = 6
(ii) \(\log _{5} \frac{1}{25}\) = -2
(iii) log₁₀ 0.001 = -3
(iv) \(\log _{\frac{1}{2}}\)(8) = -3
(v) ln 1 = 0
(vi) ln e = 1
(vii) ln \(\frac{1}{2}\) = -0.693
Solution:
(i) log₂ 64 = 6
∴ 64 = 2⁶, i.e., 2⁶ = 64

Question 19.
Find the domain of
(i) f(x) = ln (x – 5)
(ii) f(x) = log10 (x² – 5x + 6)
Solution:
(i) f(x) = ln (x – 5)
f is defined, when x – 5 > 0
∴ x > 5
∴ Domain of f = (5, ∞)

(ii) f(x) = log₁₀ (x² – 5x + 6)
x² – 5x + 6 = (x – 2) (x – 3)
f is defined, when (x – 2) (x – 3) > 0
∴ x < 2 or x > 3
Solution of (x – a) (x – b) > 0 is x < a or x > b where a < b
∴ Domain of f = (-∞, 2) ∪ (3, ∞)

Question 20.
Write the following expressions as sum or difference of logarithms:
(a) \(\log \left(\frac{p q}{r s}\right)\)
Solution:

(b) \(\log (\sqrt{x} \sqrt[3]{y})\)
Solution:

(c) \(\ln \left(\frac{a^{3}(a-2)^{2}}{\sqrt{b^{2}+5}}\right)\)
Solution:

(d) \(\ln \left[\frac{\sqrt[3]{x-2}(2 x+1)^{4}}{(x+4) \sqrt{2 x+4}}\right]^{2}\)
Solution:

Question 21.
Write the following expressions as a single logarithm.
(i) 5 log x + 7 log y – log z
Solution:

(ii) \(\frac{1}{3}\) log(x – 1) + \(\frac{1}{2}\) log(x)
Solution:

(iii) ln (x + 2) + ln (x – 2) – 3 ln (x + 5)
Solution:

Question 22.
Given that log 2 = a and log 3 = b, write log √96 terms of a and b.
Solution:
log 2 = a and log 3 = b
log √96 = \(\frac{1}{2}\) log (96)
= \(\frac{1}{2}\) log (2⁵ x 3)
= \(\frac{1}{2}\) (log 2⁵ + log 3) …..[∵ log mn = log m + log n]
= \(\frac{1}{2}\) (5 log 2 + log 3) ……[∵ log mⁿ = n log m]
= \(\frac{5 a+b}{2}\)

Question 23.
Prove that:
(a) \(b^{\log _{b} a}=a\)
Solution:
We have to prove that \(b^{\log _{b} a}=a\)
i.e., to prove that (logb a) (log_b b) = log_b a
(Taking log on both sides with base b)
L.H.S. = (log_b a) (log_b b)
= log_b a …..[∵ log_b b = 1]
= R.H.S.

(b) \(\log _{b^{m}} a=\frac{1}{m} \log _{b} a\)
Solution:

(c) \(a^{\log _{c} b}=b^{\log _{c} a}\)
Solution:

Question 24.
If f(x) = ax² – bx + 6 and f(2) = 3 and f(4) = 30, find a and b.
Solulion:
f(x) = ax² – bx + 6
f(2) = 3
∴ a(2)² – b(2) + 6 = 3
∴ 4a – 2b + 6 = 3
∴ 4a – 2b + 3 = 0 …..(i)
f(4) = 30
∴ a(4)² – b(4) + 6 = 30
∴ 16a – 4b + 6 = 30
∴ 16a – 4b – 24 = 0 …..(ii)
By (ii) – 2 × (i), we get
8a – 30 = 0
∴ a = \(\frac{30}{8}=\frac{15}{4}\)
Substiting a = \(\frac{15}{4}\) in (i), we get
4(\(\frac{15}{4}\)) – 2b + 3 = 0
∴ 2b = 18
∴ b = 9
∴ a = \(\frac{15}{4}\), b = 9

Question 25.
Solve for x:
(i) log 2 + log (x + 3) – log (3x – 5) = log 3
Solution:
log 2 + log (x + 3) – log (3x – 5) = log 3
∴ log 2(x + 3) – log(3x – 5) = log 3 …..[∵ log m + log n = log mn]
∴ log \(\frac{2(x+3)}{3 x-5}\) = log 3 …..[∵ log m – log n = log \(\frac{m}{n}\)]
∴ \(\frac{2(x+3)}{3 x-5}\) = 3
∴ 2x + 6 = 9x – 15
∴ 7x = 21
∴ x = 3

Check:
If x = 3 satisfies the given condition, then our answer is correct.
L.H.S. = log 2 + log (x + 3) – log (3x – 5)
= log 2 + log (3 + 3) – log (9 – 5)
= log 2 + log 6 – log 4
= log (2 × 6) – log 4
= log \(\frac{12}{4}\)
= log 3
= R.H.S.
Thus, our answer is correct.

(ii) 2log₁₀ x = 1 + \(\log _{10}\left(x+\frac{11}{10}\right)\)
Solution:


∴ x² = 10x + 11
∴ x² – 10x – 11 = 0
∴ (x – 11)(x + 1) = 0
∴ x = 11 or x = -1
But log of a negative numbers does not exist
∴ x ≠ -1
∴ x = 11

(iii) log₂ x + log₄ x + log₁₆ x = \(\frac{21}{4}\)
Solution:

(iv) x + log₁₀ (1 + 2^x) = x log₁₀ 5 + log₁₀ 6
Solution:

∴ a + a² = 6
∴ a² + a – 6 = 0
∴ (a + 3)(a – 2) = 0
∴ a + 3 = 0 or a – 2 = 0
∴ a = -3 or a = 2
Since 2x = -3 is not possible,
2x = 2 = 21
∴ x = 1

Question 26.
If log \(\left(\frac{x+y}{3}\right)\) = \(\frac{1}{2}\) log x + \(\frac{1}{2}\) log y, show that \(\frac{x}{y}+\frac{y}{x}\) = 7.
Solution:

Question 27.
If log\(\left(\frac{x-y}{4}\right)\) = log√x + log√y, show that (x + y)² = 20xy.
Solution:

Question 28.
If x = log_abc, y = log_b ca, z = log_c ab, then prove that \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\) = 1.
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Miscellaneous Exercise 5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Sets and Relations Miscellaneous Exercise 5

(I) Select the correct answer from the given alternative.

Question 1.
For the set A = {a, b, c, d, e} the correct statement is
(A) {a, b} ∈ A
(B) {a} ∈ A
(C) a ∈ A
(D) a ∉ A
Answer:
(C) a ∈ A

Question 2.
If aN = {ax : x ∈ N}, then set 6N ∩ 8N =
(A) 8N
(B) 48N
(C) 12N
(D) 24N
Answer:
(D) 24N
Hint:
6N = {6x : x ∈ N} = {6, 12, 18, 24, 30, ……}
8N = {8x : x ∈ N} = {8, 16, 24, 32, ……}
∴ 6N ∩ 8N = {24, 48, 72, …..}
= {24x : x ∈ N}
= 24N

Question 3.
If set A is empty set then n[P[P[P(A)]]] is
(A) 6
(B) 16
(C) 2
(D) 4
Answer:
(D) 4
Hint:
A = Φ
∴ n(A) = 0
∴ n[P(A)] = 2^n(A) = 2⁰ = 1
∴ n[P[P(A)]] = 2^n[P(A)] = 2¹ = 2
∴ n[P[P[P(A)]]] = 2^n[P[P(A)]] = 2² = 4

Question 4.
In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both car and bus. Then, persons travelling by car or bus are
(A) 80%
(B) 40%
(C) 60%
(D) 70%
Answer:
(C) 60%
Hint:
Let C = Population travels by car
B = Population travels by bus
n(C) = 20%, n(B) = 50%, n(C ∩ B) = 10%
n(C ∪ B) = n(C) + n(B) – n(C ∩ B)
= 20% + 50% – 10%
= 60%

Question 5.
If the two sets A and B are having 43 elements in common, then the number of elements common to each of the sets A × B and B × A is
(A) 43²
(B) 2⁴³
(C) 43⁴³
(D) 2⁸⁶
Answer:
(A) 43²

Question 6.
Let R be a relation on the set N be defied by {(x, y) / x, y ∈ N, 2x + y = 41} Then R is
(A) Reflexive
(B) Symmetric
(C) Transitive
(D) None of these
Answer:
(D) None of these

Question 7.
The relation “>” in the set of N (Natural number) is
(A) Symmetric
(B) Reflexive
(C) Transitive
(D) Equivalent relation
Answer:
(C) Transitive
Hint:
For any a ∈ N, a ≯ a
∴ (a, a) ∉ R
∴ > is not reflexive.
For any a, b ∈ N, if a > b, then b ≯ a.
∴ > is not symmetric.
For any a, b, c ∈ N,
if a > b and b > c, then a > c
∴ > is transitive.

Question 8.
A relation between A and B is
(A) only A × B
(B) An Universal set of A × B
(C) An equivalent set of A × B
(D) A subset of A × B
Answer:
(D) A subset of A × B

Question 9.
If (x, y) ∈ N × N, then xy = x² is a relation that is
(A) Symmetric
(B) Reflexive
(C) Transitive
(D) Equivalence
Answer:
(D) Equivalence
Hint:
Let x ∈ R, then xx = x²
∴ x is related to x.
∴ Given relation is reflexive.
Letx = 0 and y = 2,
then xy = 0 × 2 = 0 = x²
∴ x is related to y.
Consider, yx = 2 × 0 = 0 ≠ y²
∴ y is not related to x.
∴ Given relation is not symmetric.
Let x be related to y and y be related to z.
∴ xy = x² and yz = y²
∴ x = \(\frac{x^{2}}{y}\) and z = \(\frac{y^{2}}{y}\) = y …..[if y ≠ 0]
Consider, xz = \(\frac{x^{2}}{y}\) × y = x²
∴ x is related to z.
∴ Given relation is transitive.

Question 10.
If A = {a, b, c}, The total no. of distinct relations in A × A is
(A) 3
(B) 9
(C) 8
(D) 29
Answer:
(D) 29

(II) Answer the following.

Question 1.
Write down the following sets in set builder form:
(i) {10, 20, 30, 40, 50}
(ii) {a, e, i, o, u}
(iii) {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
Solution:
(i) Let A = {10, 20, 30, 40, 50}
∴ A = {x/x = 10n, n ∈ N and n ≤ 5}

(ii) Let B = {a, e, i, o, u}
∴ B = {x/x is a vowel of English alphabets}

(iii) Let C = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
∴ C = {x/x is a day of a week}

Question 2.
If U = {x/x ∈ N, 1 ≤ x ≤ 12}, A = {1,4, 7,10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}. Write down the sets.
(i) A ∪ B
(ii) B ∩ C
(iii) A – B
(iv) B ∩ C’
(v) A ∪ B ∪ C
(vi) A ∩ (B ∪ C)
Solution:
U = {x/x ∈ N, 1 ≤ x ≤ 12} = {1, 2, 3, …., 12}
A = {1, 4, 7, 10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}
(i) A ∪ B = {1, 2, 4, 6, 7, 10, 11}

(ii) B ∩ C = {}

(iii) A – B = {1, 10}

(iv) C’ = {1, 2, 4, 6, 7, 10, 11}
∴ B ∩ C’ = {2, 4, 6, 7, 11}

(v) A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

(vi) B ∪ C = {2, 3, 4, 5, 6, 7, 8, 9, 11, 12}
∴ A ∩ (B ∪ C) = {4, 7}

Question 3.
In a survey of 425 students in a school, it was found that 115 drink apple juice, 160 drink orange juice, and 80 drink both apple as well as orange juice. How many drinks neither apple juice nor orange juice?
Solution:
Let A = set of students who drink apple juice
B = set of students who drink orange juice
X = set of all students
∴ n(X) = 425, n(A) = 115, n(B) = 160, n(A ∩ B) = 80

No. of students who neither drink apple juice nor orange juice = n(A’ ∩ B’) = n(A ∪ B)’
= n(X) – n(A ∪ B)
= 425 – [n(A) + n(B) – n(A ∩ B)]
= 425 – (115 + 160 – 80)
= 230

Question 4.
In a school, there are 20 teachers who teach Mathematics or Physics. Of these, 12 teach Mathematics and 4 teach both Physics and Mathematics. How many teachers teach Physics?
Solution:
Let A = set of teachers who teach Mathematics
B = set of teachers who teach Physics
∴ n(A ∪ B) = 20, n(A) = 12, n(A ∩ B) = 4

Since n(A ∪ B) = n(A) + n(B) – n(A ∩ B),
20 = 12 + n(B) – 4
∴ n(B) = 12
∴ Number of teachers who teach physics = 12

Question 5.
(i) If A = {1, 2, 3} and B = {2, 4}, state the elements of A × A, A × B, B × A, B × B, (A × B) ∩ (B × A).
(ii) If A = {-1, 1}, find A × A × A.
Solution:
(i) A = {1, 2, 3} and B = {2, 4}
A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
A × B = {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}
B × A = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
B × B = {(2, 2), (2, 4), (4, 2), (4, 4)}
∴ (A × B) ∩ (B × A) = {(2, 2)}

(ii) A = {-1, 1}
∴ A × A × A = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}

Question 6.
If A = {1, 2, 3}, B = {4, 5, 6}, check if the following are relations from A to B. Also, write its domain and range.
(i) R₁ = {(1, 4), (1, 5), (1, 6)}
(ii) R₂ = {(1, 5), (2, 4), (3, 6)}
(iii) R₃ = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
(iv) R₄ = {(4, 2), (2, 6), (5, 1), (2, 4)}
Solution:
A = {1, 2, 3}, B = {4, 5, 6}
∴ A × B = {(1, 4), (1, 5), (1, 6), (2,4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) R₁ = {(1, 4), (1, 5), (1, 6)}
Since R₁ ⊆ A × B,
R₁ is a relation from A to B.
Domain (R₁) = Set of first components of R₁ = {1}
Range (R₁) = Set of second components of R₁ = {4, 5, 6}

(ii) R₂ = {(1, 5),(2, 4),(3, 6)}
Since R₂ ⊆ A × B,
R₂ is a relation from A to B.
Domain (R₂) = Set of first components of R₂ = {1, 2, 3}
Range (R₂) = Set of second components of R₂ = {4, 5, 6}

(iii) R₃ = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
Since R₃ ⊆ A × B,
R₃ is a relation from A to B.
Domain (R₃) = Set of first components of R₃ = {1, 2, 3}
Range (R₃) = Set of second components of R₃ = {4, 5, 6}

(iv) R₄ = {(4, 2), (2, 6), (5, 1), (2, 4)}
Since (4, 2) ∈ R₄, but (4, 2) ∉ A × B,
R₄ ⊄ A × B
∴ R₄ is not a relation from A to B.

Question 7.
Determine the domain and range of the following relations.
(i) R = {(a, b) / a ∈ N, a < 5, b = 4}
(ii) R = {(a, b) / b = |a – 1|, a ∈ Z, |a| < 3}
Solution:
(i) R = {(a, b) / a ∈ N, a < 5, b = 4}
∴ Domain (R) = {a / a ∈ N, a < 5} = {1, 2, 3, 4}
Range (R) = {b / b = 4} = {4}

(ii) R = {(a, b) / b = |a – 1|, a ∈ Z, |a| < 3}
Since a ∈ Z and |a| < 3,
a < 3 and a > -3
∴ -3 < a < 3
∴ a = -2, -1, 0, 1, 2
b = |a – 1|
When a = -2, b = 3
When a = -1, b = 2
When a = 0, b = 1
When a = 1, b = 0
When a = 2, b = 1
Domain (R) = {-2, -1, 0, 1, 2}
Range (R) = {0, 1, 2, 3}

Question 8.
Find R : A → A when A = {1, 2, 3, 4} such that
(i) R = {(a, b) / a – b = 10}
(ii) R = {(a, b) / |a – b| ≥ 0}
Solution:
R : A → A, A = {1, 2, 3,4}
(i) R = {(a, b)/a – b = 10} = { }

(ii) R = {(a, b) / |a – b| ≥ 0}
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}
A × A = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}
∴ R = A × A

Question 9.
R : {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}. Check if R is
(i) reflexive
(ii) symmetric
(iii) transitive
Solution:
R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}
(i) Here, (x, x) ∈ R, for x ∈ {1, 2, 3}
∴ R is reflexive.

(ii) Here, (1, 2) ∈ R, but (2, 1) ∉ R.
∴ R is not symmetric.

(iii) Here, (1, 2), (2, 3) ∈ R,
But (1, 3) ∉ R.
∴ R is not transitive.

Question 10.
Check if R : Z → Z, R = {(a, b) | 2 divides a – b} is an equivalence relation.
Solution:
(i) Since 2 divides a – a,
(a, a) ∈ R
∴ R is reflexive. .

(ii) Let (a, b) ∈ R
Then 2 divides a – b
∴ 2 divides b – a
∴ (b, a) ∈ R
∴ R is symmetric.

(iii) Let (a, b) ∈ R, (b, c) ∈ R
Then a – b = 2m, b – c = 2n,
∴ a – c = 2(m + n), where m, n are integers.
∴ 2 divides a – c
∴ (a, c) ∈ R
∴ R is transitive.
Thus, R is an equivalence relation.

Question 11.
Show that the relation R in the set A = {1, 2, 3, 4, 5} Given by R = {(a, b) / |a – b| is even} is an equivalence relation.
Solution:
(i) Since |a – a| is even,
∴ (a, a) ∈ R
∴ R is reflexive.

(ii) Let (a, b) ∈ R
Then |a – b| is even
∴ |b – a| is even
∴ (b, a) ∈ R
∴ R is symmetric.

(iii) Let (a, b), (b, c) ∈ R
Then a – b = ±2m, b – c = ±2n
∴ a – c = ±2(m + n), where m, n are integers.
∴ (a, c) ∈ R
∴ R is transitive
Thus, R is an equivalence relation.

Question 12.
Show that the following are equivalence relations:
(i) R in A is set of all books given by R = {(x, y) / x and y have same number of pages}
(ii) R in A = {x ∈ Z | 0 ≤ x ≤ 12} given by R = {(a, b) / |a – b| is a multiple of 4}
(iii) R in A = (x ∈ N/x ≤ 10} given by R = {(a, b) | a = b}
Solution:
(i) a. Clearly (x, x) ∈ R
∴ R is reflexive.

b. If (x, y) ∈ R then (y, x) ∈ R.
∴ R is symmetric.

c. Let (x, y) ∈ R, (y, x) ∈ R.
Then x, y, and z are 3 books having the same number of pages.
∴ (x, z) ∈ R as x, z has the same number of pages.
∴ R is transitive.
Thus, R is an equivalence relation.

(ii) a. Since |a – a| is a multiple of 4,
(a, a) ∈ R
∴ R is reflexive.

b. Let (a, b) ∈ R
Then a – b = ±4m,
∴ b – a = ±4m, where m is an integer
∴ (b, a) ∈ R
∴ R is symmetric.

c. Let (a, b), (b, c) ∈ R
a – b = ± 4m, b – c = ± 4n,
∴ a – c = ±4(m + n), where m, n are integers
∴ (a, c) ∈ R
∴ R is transitive
Thus, R is an equivalence relation.

(iii) a. Since a = a
∴ (a, a) ∈ R
∴ R is reflexive.

b. Let (a, b) ∈ R Then a = b
∴ b = a
∴ (b, a) ∈ R
∴ R is symmetric.

c. Let (a, b), (b, c) ∈ R
Then, a = b, b = c
∴ a = c
∴ (a, c) ∈ R
∴ R is transitive.
Thus, R is an equivalence relation.

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Ex 5.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Sets and Relations Ex 5.2

Question 1.
If (x – 1, y + 4) = (1, 2), find the values of x and y.
Solution:
(x – 1, y + 4) = (1, 2)
By the definition of equality of ordered pairs, we have
x – 1 = 1 and y + 4 = 2
∴ x = 2 and y = -2

Question 2.
If \(\left(x+\frac{1}{3}, \frac{y}{3}-1\right)=\left(\frac{1}{2}, \frac{3}{2}\right)\), find x and y.
Solution:
\(\left(x+\frac{1}{3}, \frac{y}{3}-1\right)=\left(\frac{1}{2}, \frac{3}{2}\right)\)
By the definition of equality of ordered pairs, we have
x + \(\frac{1}{3}\) = \(\frac{1}{2}\) and \(\frac{y}{3}\) – 1 = \(\frac{3}{2}\)
∴ x = \(\frac{1}{2}\) – \(\frac{1}{3}\) and \(\frac{y}{3}\) = \(\frac{3}{2}\) + 1
∴ x = \(\frac{1}{6}\) and y = \(\frac{15}{2}\)

Question 3.
If A = {a, b, c}, B = {x, y}, find A × B, B × A, A × A, B × B.
Solution:
A = (a, b, c}, B = {x, y}
A × B = {(a, x), (a, y), (b, x), (b, y), (c, x), (c, y)}
B × A = {(x, a), (x, b), (x, c), (y, a), (y, b), (y, c)}
A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}
B × B = {(x, x), (x, y), (y, x), (y, y)}

Question 4.
If P = {1, 2, 3} and Q = {1, 4}, find sets P × Q and Q × P.
Solution:
P = {1, 2, 3}, Q = {1, 4}
∴ P × Q = {(1, 1), (1, 4), (2, 1), (2, 4), (3, 1), (3, 4)}
and Q × P = {(1, 1), (1, 2), (1, 3), (4, 1), (4, 2), (4, 3)}

Question 5.
Let A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}. Verify,
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × (B ∪ C) = (A × B) ∪ (A × C)
Solution:
A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}
(i) B ∩ C = {5, 6}
A × (B ∩ C) = = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∩ (A × C) = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) B ∪ C = {4, 5, 6}
A × (B ∪ C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3,4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∪ (A × C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
∴ A × (B ∪ C) = (A × B) ∪ (A × C)

Question 6.
Express {(x, y) / x² + y² = 100, where x, y ∈ W} as a set of ordered pairs.
Solution:
{(x, y) / x² + y² = 100, where x, y ∈ W}
We have, x² + y² = 100
When x = 0 and y = 10,
x² + y² = 0² + 10² = 100
When x = 6 and y = 8,
x² + y² = 6² + 8² = 100
When x = 8 and y = 6,
x² + y² = 8² + 6² = 100
When x = 10 and y = 0,
x² + y² = 10² + 0² = 100
∴ Set of ordered pairs = {(0, 10), (6, 8), (8, 6), (10, 0)}

Question 7.
Let A = {6, 8} and B = {1, 3, 5}. Show that R₁ = {(a, b) / a ∈ A, b ∈ B, a – b is an even number} is a null relation, R₂ = {(a, b) / a ∈ A, b ∈ B, a + b is an odd number} is a universal relation.
Solution:
A = {6, 8}, B = {1, 3, 5}
R₁ = {(a, b)/ a ∈ A, b ∈ B, a – b is an even number}
a ∈ A
∴ a = 6, 8
b ∈ B
∴ b = 1, 3, 5
When a = 6 and b = 1, a – b = 5, which is odd
When a = 6 and b = 3, a – b = 3, which is odd
When a = 6 and b = 5, a – b = 1, which is odd
When a = 8 and b = 1, a – b = 7, which is odd
When a = 8 and b = 3, a – b = 5, which is odd
When a = 8 and b = 5, a – b = 3, which is odd
Thus, no set of values of a and b gives a – b as even.
∴ R₁ has a null relation from A to B.
A × B = {(6, 1), (6, 3), (6, 5), (8, 1), (8, 3), (8, 5)}
When a = 6 and b = 1, a + b = 7, which is odd
When a = 6 and b = 3, a + b = 9, which is odd
When a = 6 and b = 5, a + b = 11, which is odd
When a = 8 and b = 1, a + b = 9, which is odd
When a = 8 and b = 3, a + b = 11, which is odd
When a = 8 and b = 5, a + b = 13, which is odd
∴ R₂ = {(6, 1), (6, 3), (6, 5), (8, 1), (8, 3), (8, 5)}
Here, R₂ = A × B
∴ R₂ has a universal relation from A to B.

Question 8.
Write the relation in the Roster form. State its domain and range.
(i) R₁ = {(a, a²) / a is a prime number less than 15}
(ii) R₂ = {(a, \(\frac{1}{a}\)) / 0 < a ≤ 5, a ∈ N}
(iii) R₃ = {(x, y / y = 3x, y ∈ {3, 6, 9, 12}, x ∈ {1, 2, 3}}
(iv) R₄ = {(x, y) / y > x + 1, x = 1, 2 and y = 2, 4, 6}
(v) R₅ = {(x, y) / x + y = 3, x, y ∈ {0, 1, 2, 3}}
(vi) R₆ = {(a, b) / a ∈ N, a < 6 and b = 4}
(vii) R₇ = {(a, b) / a, b ∈ N, a + b = 6}
(viii) R₈ = {(a, b)/ b = a + 2, a ∈ Z, 0 < a < 5}
Solution:
(i) R₁ = {(a, a²) / a is a prime number less than 15}
∴ a = 2, 3, 5, 7, 11, 13
∴ a² = 4, 9, 25, 49, 121, 169
∴ R₁ = {(2, 4), (3, 9), (5, 25), (7, 49), (11, 121), (13, 169)}
∴ Domain (R₁) = {a/a is a prime number less than 15}
= {2, 3, 5, 7, 11, 13}
Range (R₁) = {a²/a is a prime number less than 15}
= {4, 9, 25, 49, 121, 169}

(iii) R₃ = {(x, y) / y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
Here y = 3x
When x = 1, y = 3(1) = 3
When x = 2, y = 3(2) = 6
When x = 3, y = 3(3) = 9
∴ R₃ = {(1, 3), (2, 6), (3, 9)}
∴ Domain (R₃) ={1, 2, 3}
∴ Range (R₃) = {3, 6, 9}

(iv) R₄ = {(x, y) / y > x + 1, x = 1, 2 and y = 2, 4, 6}
Here, y > x + 1
When x = 1 and y = 2, 2 ≯  1 + 1
When x = 1 and y = 4, 4 > 1 + 1
When x = 1 and y = 6, 6 > 1 + 1
When x = 2 and y = 2, 2 ≯  2 + 1
When x = 2 and y = 4, 4 > 2 + 1
When x = 2 and y = 6, 6 > 2 + 1
∴ R₄ = {(1, 4), (1, 6), (2, 4), (2, 6)}
Domain (R₄) = {1, 2}
Range (R₄) = {4, 6}

(v) R₅ = {{x, y) / x + y = 3, x, y ∈ (0, 1, 2, 3)}
Here, x + y = 3
When x = 0, y = 3
When x = 1, y = 2
When x = 2, y = 1
When x = 3, y = 0
∴ R₅ = {(0, 3), (1, 2), (2, 1), (3, 0)}
Domain (R₅) = {0, 1, 2, 3}
Range (R₅) = {3, 2, 1, 0}

(vi) R₆ = {(a, b)/ a ∈ N, a < 6 and b = 4}
a ∈ N and a < 6
∴ a = 1, 2, 3, 4, 5 and b = 4
R₆ = {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4)}
Domain (R₆) = {1, 2, 3, 4, 5}
Range (R₆) = {4}

(vii) R₇ = {(a, b) / a, b ∈ N, a + b = 6}
Here, a + b = 6
When a = 1, b = 5
When a = 2, b = 4
When a = 3, b = 3
When a = 4, b = 2
When a = 5, b = 1
∴ R₇ = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
Domain (R₇) = {1, 2, 3, 4, 5}
Range (R₇) = {5, 4, 3, 2, 1}

(viii) R₈ = {(a, b) / b = a + 2, a ∈ Z, 0 < a < 5}
Here, b = a + 2
When a = 1, b = 3
When a = 2, b = 4
When a = 3, b = 5
When a = 4, b = 6
∴ R₈ = {(1, 3), (2, 4), (3, 5), (4, 6)}
Domain (R₈) = {1, 2, 3, 4}
Range (R₈) = {3, 4, 5, 6}

Question 9.
Identify which of the following relations are reflexive, symmetric, and transitive.

Solution:

(i) Given, R = {(a, b): a, b ∈ Z, a – b is an integer}
Let a ∈ Z, then a – a ∈ Z
∴ (a, a) ∈ R
∴ R is reflexive.
Let (a, b) ∈ R
∴ a – b ∈ Z
∴ -(a – b) ∈ Z, i.e., b – a ∈ Z
∴ (b, a) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ a – b ∈ Z and b – c ∈ Z
∴ (a – b) + (b – c) ∈ Z
∴ a – c ∈ Z
∴ (a, c) ∈ R
∴ R is transitive.

(ii) Given, R = {(a, b) : a, b ∈ N, a + b is even}
Let a ∈ N, then a + a = 2a, which is even.
∴ (a, a) ∈ R
∴ R is reflexive.
Let (a, b) ∈ R
∴ a + b is even
∴ b + a is even
∴ (b, a) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ a + b and b + c is even
Let a + b = 2x and b + c = 2y for x, y ∈ N
∴ (a + b) + (b + c) = 2x + 2y
∴ a + 2b + c = 2(x + y)
∴ a + c = 2(x + y) – 2b = 2(x + y – b)
∴ a + c is even ……..[∵ x, y, b ∈ N, x + y – b ∈ N]
∴ (a, c) ∈ R
∴ R is transitive.

(iii) Given, R = {(a, b) : a, b ∈ N, a divides b}
Let a ∈ N, then a divides a.
∴ (a, a) ∈ R
∴ R is reflexive.
Let a = 2 and b = 8, then 2 divides 8
∴ (a, b) ∈ R
But 8 does not divide 2.
∴ (b, a) ∉ R
∴ R is not symmetric.
Let (a, b) and (b, c) ∈ R
∴ a divides b and b divides c.
Let b = ax and c = by for x, y ∈ N.
∴ c = (ax) y = a(xy)
i.e., a divides c.
∴ (a, c) ∈ R
∴ R is transitive.

(iv) Given, R = {(a, b) : a, b ∈ N, a² – 4ab + 3b² = 0}
Let a ∈ N, then a² – 4aa + 3a² = a² – 4a² + 3a² = 0
∴ (a, a) ∈ R
∴ R is reflexive.
Let a = 3 and b = 1,
then a² – 4ab + 3b² = 9 – 12 + 3 = 0
∴ (a, b) ∈ R
Consider, b² – 4ba + 3a² = 1 – 12 + 9 = -2 ≠ 0
∴ (b, a) ∉ R
∴ R is not symmetric.
Let a = 3, b = 1 and c = \(\frac{1}{3}\),
then a² – 4ab + 3b² = 9 – 12 + 3 = 0 and
b² – 4bc + 3c² = 1 – \(\frac{4}{3}\) + \(\frac{1}{3}\) = 1 – 1 = 0
∴ we get (a, b) and (b, c) ∈ R.
Consider, a² – 4ac + 3c² = 9 – 4 + \(\frac{1}{3}\) = \(\frac{16}{3}\) ≠ 0
∴ (a, c) ∉ R
∴ R is not transitive.

(v) Given, R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls}
Let a ∈ G, then ‘a’ cannot be a sister of herself.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let (a, b) ∈ R
∴ ‘a’ is a sister of ‘b’.
∴ ‘b’ is a sister of ‘a’.
∴ (b, c) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ ‘a’ is a sister of ‘b’ and ‘b’ is a sister of ‘c’
∴ ‘a’ is a sister of ‘c’.
∴ (a, c) ∈ R
∴ R is transitive.

(vi) Given, R = {(a, b) : Line a is perpendicular to line b in a plane}
Let a be any line in the plane, then a cannot be perpendicular to itself.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let (a, b) ∈ R
∴ a is perpendicular to b.
∴ b is perpendicular to a.
∴ (b, a) ∈ R.
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R.
∴ a is perpendicular to b and b is perpendicular to c.
∴ a is parallel to c.
∴ (a, c) ∉ R
∴ R is not transitive.

(vii) Given, R = {(a, b) : a, b ∈ R, a < b}
Let a ∈ R, then a ≮ a.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let a = 1 and b = 2, then 1 < 2
∴ (a, b) ∈ R
But 2 ≮ 1
∴ (b, a) ∉ R
∴ R is not symmetric.
Let (a, b) and (b, c) ∈ R
∴ a < b and b < c
∴ a < c
∴ (a, c) ∈ R
∴ R is transitive.

(viii) Given, R = {(a, b) : a, b ∈ R, a ≤ b³}
Let a = -3, then a³ = -27.
Here, a ≮ a
∴ (a, a) ∉ R
∴ R is not reflexive.
Let a = 2 and b = 9, then b³ = 729
Here, a < b³
∴ (a, b) ∈ R
Consider, a3 = 8
Here, b ≮ a³
∴ (b, a) ∉ R
∴ R is not symmetric.
Let a = 10, b = 3, c = 2,
then b³ = 27 and c³ = 8
Here, a < b³ and b < c³.
∴ (a, b) and (b, c) ∈ R
But a ≮ c³
∴ (a, c) ∉ R.
∴ R is not transitive.

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Ex 5.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Sets and Relations Ex 5.1

Question 1.
Describe the following sets in Roster form:
(i) A = {x/x is a letter of the word ‘MOVEMENT’}
(ii) B = {x/x is an integer, –\(\frac{3}{2}\) < x < \(\frac{9}{2}\)>
(iii) C = {x/x = 2n + 1, n ∈ N}
Solution:
(i) A = {M, O, V, E, N, T}
(ii) B = {-1, 0, 1, 2, 3, 4}
(iii) C = {3, 5, 7, 9, … }

Question 2.
Describe the following sets in Set-Builder form:
(i) {0}
(ii) {0, ±1, ±2, ±3}
(iii) \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
(iv) {0, -1, 2, -3, 4, -5, 6,…}
Solution:
(i) Let A = {0}
0 is a whole number but it is not a natural number.
∴ A = {x / x ∈ W, x ∉ N}

(ii) Let B = {0, ±1, ±2, ±3}
B is the set of elements which belongs to Z from -3 to 3.
∴ B = {x /x ∈ Z, -3 ≤ x ≤ 3}

(iii) Let C = \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
∴ C = {x / x = \(\frac{n}{n^{2}+1}\), n ∈ N, n ≤ 7}

(iv) Let D = {0, -1, 2, -3, 4, -5, 6, …}
∴ D = {x/x = (-1)n-1 × (n – 1), n ∈ N}

Question 3.
If A = {x / 6x² + x – 15 = 0}, B = {x / 2x² – 5x – 3 = 0}, C = {x / 2x² – x – 3 = 0}, then find
(i) (A ∪ B ∪ C)
(ii) (A ∩ B ∩ C)
Solution:
A = [x/6x² + x – 15 = 0)
6x² + x – 15 = 0
6x² + 10x – 9x – 15 = 0
2x(3x + 5) – 3(3x + 5) = 0
(3x + 5) (2x – 3) = 0
3x + 5 = 0 or 2x – 3 = 0
x = \(\frac{-5}{3}\) or x = \(\frac{3}{2}\)
A = {\(\frac{-5}{3}\), \(\frac{3}{2}\)}

B = {x/2x² – 5x – 3 = 0}
2x² – 5x – 3 = 0
2x² – 6x + x – 3 = 0
2x(x – 3) + 1(x – 3) = 0
(x – 3)(2x + 1) = 0
x – 3 = 0 or 2x + 1 = 0
x = 3 or x = \(\frac{-1}{2}\)
B = (\(\frac{-1}{2}\), 3)

C = {x/2x² – x – 3 = 0}
2x² – x – 3 = 0
2x² – 3x + 2x – 3 = 0
x(2x – 3) + 1(2x – 3) = 0
(2x – 3) (x + 1) = 0
2x – 3 = 0 or x + 1 = 0
x = \(\frac{3}{2}\) or x = -1
C = {-1, \(\frac{3}{2}\)}

(i) A ∪ B ∪ C = \(\left\{-\frac{5}{3}, \frac{3}{2}\right\} \cup\left\{\frac{-1}{2}, 3\right\} \cup\left\{-1, \frac{3}{2}\right\}\) = \(\left\{\frac{-5}{3},-1, \frac{-1}{2}, \frac{3}{2}, 3\right\}\)

(ii) A ∩ B ∩ C = { }

Question 4.
If A, B, C are the sets for the letters in the words ‘college’, ‘marriage’ and ‘luggage’ respectively, then verify that [A – (B ∪ C)] = [(A – B) ∩ (A – C)].
Solution:
A = {c, o, l, g, e}
B = {m, a, r, i, g, e}
C = {l, u, g, a, e}
B ∪ C = {m, a, r, i, g, e, l, u}
A – (B ∪ C) = {c, o}
A – B = {c, o, l}
A – C = {c, o}
∴ [(A – B) ∩ (A – C)] = {c, o} = A – (B ∪ C)
∴ [A -( B ∪ C)] = [(A – B) ∩ (A – C)]

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then verify the following:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) (A ∪ B)’ = A’ ∩ B’
(iv) (A ∩ B)’ = A’ ∪ B’
(v) A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = (A ∩ B) ∪ (A’ ∩ B)
(vii) (A ∪ B) = (A – B) ∪ (A ∩ B) ∪ (B – A)
(viii) A ∩ (B ∆ C) = (A ∩ B) ∆ (A ∩ C)
(ix) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
(x) n(B) = n (A’ ∩ B) + n (A ∩ B)
Solution:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8},
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(i) B ∩ C = {4, 5, 6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5, 6} …..(i)
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
∴ (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6} …….(ii)
From (i) and (ii), we get
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

(ii) B ∪ C = {3, 4, 5, 6, 7, 8}
∴ A ∩ (B ∪ C) = {3, 4} ………(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) ∪ (A∩ C) = {3, 4} ……..(ii)
From (i) and (ii), we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(iii) A ∪ B = {1, 2, 3, 4, 5, 6}
∴ (A ∪ B)’ = {7, 8, 9, 10} ………(i)
A’ = {5, 6, 7, 8, 9, 10},
B’ = {1, 2, 7, 8, 9,10}
∴ A’ ∩ B’ = {7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∪ B)’ = A’ ∩ B’

(iv) A ∩ B = {3, 4}
(A ∩ B)’= {1, 2, 5, 6, 7, 8, 9, 10} …….(i)
A’ = {5, 6, 7, 8, 9, 10}
B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∪ B’ = {1, 2, 5, 6, 7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∩ B)’ = A’ ∪ B’

(v) A = {1, 2, 3, 4} ……(i)
A ∩ B = {3, 4}
B’ = {1, 2, 7, 8, 9, 10}
A ∩ B’ = {1, 2}
∴ (A ∩ B) ∪ (A ∩ B’) = {1, 2, 3, 4} …..(ii)
From (i) and (ii), we get
A = (A ∩ B) ∪ (A ∩ B’)

(vi) B = {3, 4, 5, 6} …..(i)
A ∩ B = {3, 4}
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ (A ∩ B) ∪ (A’ ∩ B) = {3, 4, 5, 6} …..(ii)
From (i) and (ii), we get
B = (A ∩ B) ∪ (A’ ∩ B)

(vii) A ∪ B = {1, 2, 3, 4, 5, 6} …….(i)
A – B = {1, 2}
A ∩ B = {3, 4}
B – A = {5, 6}
∴ (A – B) ∪ (A ∩ B) ∪ (B – A) = {1, 2, 3, 4, 5, 6} ……(ii)
From (i) and (ii), we get
A ∪ B = (A – B) ∪ (A ∩ B) ∪ (B – A)

(viii) B – C = {3}
C – B = {7, 8}
B Δ C = (B – C) ∪ (C – B) = {3, 7, 8}
∴ A ∩ (B Δ C) = {3} ……(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) Δ (A ∩ C) = [(A ∩ B) – (A ∩ C)] ∪ [(A ∩ C) – (A ∩ B)] = {3} …..(ii)
From (i) and (ii), we get
A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)

(ix) A = {1, 2, 3, 4}, B = {3, 4, 5, 6}
A ∩ B = {3, 4}, A ∪ B = {1, 2, 3, 4, 5, 6}
∴ n(A) = 4, n(B) = 4,
n(A ∩ B) = 2, n(A ∪ B) = 6 ……(i)
∴ n(A) + n(B) – n(A ∩ B) = 4 + 4 – 2
∴ n(A) + n(B) – n(A ∩ B) = 6 …..(ii)
From (i) and (ii), we get
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

(x) B = {3, 4, 5, 6}
∴ n(B) = 4 …..(i)
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ n(A’ ∩ B) = 2
A ∩ B = {3, 4}
∴ n(A ∩ B) = 2
∴ n(A’ ∩ B) + n(A ∩ B) = 2 + 2 = 4 …..(ii)
From (i) and (ii), we get
n(B) = n(A’ ∩ B) + n (A ∩ B)

Question 6.
If A and B are subsets of the universal set X and n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5, find
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A’ ∩ B)
(iv) n(A ∩ B’)
Solution:
n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5
(i) n(A ∪ B) = n(X) – [n(A ∪ B)’]
= n(X) – n(A’ ∩ B’)
= 50 – 5
= 45

(ii) n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 35 + 20 – 45
= 10

(iii) n(A’ ∩ B) = n(B) – n(A ∩ B)
= 20 – 10
= 10

(iv) n(A ∩ B’) = n(A) – n(A ∩ B)
= 35 – 10
= 25

Question 7.
In a class of 200 students who appeared in certain examinations, 35 students faded in CET, 40 in NEET and 40 in JEE, 20 faded in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE and 5 faded in ad three examinations. Find how many students
(i) did not fail in any examination.
(ii) faded in NEET or JEE entrance.
Solution:
Let A = set of students who failed in CET
B = set of students who failed in NEET
C = set of students who failed in JEE
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40, n(A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5

(i) n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
= 35 + 40 + 40 – 20 – 17 – 15 + 5
= 68
∴ No. of students who did not fail in any exam = n(X) – n(A ∪ B ∪ C)
= 200 – 68
= 132

(ii) No. of students who failed in NEET or JEE entrance = n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63

Question 8.
From amongst 2000 Uterate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read
(i) at least one of the newspapers.
(ii) neither Marathi nor English newspaper.
(iii) only one of the newspapers.
Solution:
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000,
n(M) = \(\frac{70}{100}\) × 2000 = 1400
n(E) = \(\frac{50}{100}\) × 2000 = 1000
n(M ∩ E) = \(\frac{32.5}{100}\) × 2000 = 650
(i) n(M ∪ E) = n(M) + n(E) – n(M ∩ E)
= 1400 + 1000 – 650
= 1750

No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.

(ii) No. of individuals who read neither Marathi nor English newspaper = n(M’ ∩ E’)
= n(M ∪ E)’
= n(X) – n(M ∪ E)
= 2000 – 1750
= 250

(iii) No. of individuals who read only one of the newspapers = n(M ∩ E’) + n(M’ ∩ E)
= n(M ∪ E) – n(M ∩ E)
= 1750 – 650
= 1100

Question 9.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take both tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes atleast one beverage, find the total number of students in the hostel.
Solution:
Let T = set of students who take tea
C = set of students who take coffee
M = set of students who take milk
∴ n(T) = 25, n(C) = 20, n(M) = 15, n(T ∩ C) = 10, n(M ∩ C) = 8, n(T ∩ M) = 0, n(T ∩ M ∩ C) = 0

∴ Total number of students in the hostel = n(T ∪ C ∪ M)
= n(T) + n(C) + n(M) – n(T ∩ C) – n(M ∩ C) – n(T ∩ M) + n(T ∩ M ∩ C)
= 25 + 20 + 15 – 10 – 8 – 0 + 0
= 42

Question 10.
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to
(i) Chemical A but not Chemical B
(ii) Chemical B but not Chemical A
(iii) Chemical A or Chemical B
Solution:
Let A = set of persons exposed to chemical A
B = set of persons exposed to chemical B
X = set of all persons
∴ n(X) = 260, n(A) = 150, n(B) = 74, n(A ∩ B) = 36

(i) No. of persons exposed to chemical A but not to chemical B = n(A ∩ B’)
= n(A) – n(A ∩ B)
= 150 – 36
= 114

(ii) No. of persons exposed to chemical B but not to chemical A = n(A’ ∩ B)
= n(B) – n(A ∩ B)
= 74 – 36
= 38

(iii) No. of persons exposed to chemical A or chemical B = n(A ∪ B)
= n(A) + n(B) – n(A ∩ B)
= 150 + 74 – 36
= 188

Question 11.
Write down the power set of A = {1, 2, 3}.
Solution:
A = {1, 2, 3}
The power set of A is given by
P(A) = {{Φ}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}}

Question 12.
Write the following intervals in Set-Builder form:
(i) (-3, 0)
(ii) [6, 12]
(iii) (6, ∞)
(iv) (-∞, 5]
(v) (2, 5]
(vi) [-3, 4)
Solution:
(i) (-3, 0) = {x / x ∈ R, -3 < x < 0}

(ii) [6, 12] = {x / x ∈ R, 6 ≤ x ≤ 12}

(iii) (6, ∞) = {x / x ∈ R, x > 6}

(iv) (-∞, 5] = {x / x ∈ R, x ≤ 5}

(v) (2, 5] = {x / x ∈ R, 2 < x ≤ 5}

(vi) [-3, 4) = {x / x ∈ R, -3 ≤ x < 4}

Question 13.
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals were awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Solution:
Let A = Set of students who received medals in volleyball
B = Set of students who received medals in football
C = Set of students who received medals in basketball
n(A) = 38, n(B) = 15, n(C) = 20, n(A ∪ B ∪ C) = 58, n(A ∩ B ∩ C) = 3
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
58 = 38 + 15 + 20 – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + 3
∴ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 ……(i)
Number of players who got exactly two medals = p + q + r
Here, s = n(A ∩ B ∩ C) = 3

n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 …..[From (i)]
∴ p + s + s + r + q + s = 18
∴ p + q + r + 3s = 18
∴ p + q + r + 3(3) = 18
∴ p + q + r = 18 – 9 = 9
∴ Number of players who received exactly two medals = 9.

Question 14.
Solve the following inequalities and write the solution set using interval notation.
(i) -9 < 2x + 7 ≤ 19
(ii) x² – x > 20
(iii) \(\frac{2 x}{x-4}\) ≤ 5
(iv) 6x² + 1 ≤ 5x
Solution:
(i) -9 < 2x + 7 ≤ 19
∴ -16 < 2x ≤ 12
∴ -8< x ≤ 6
∴ x ∈ (-8, 6]

(ii) x² – x > 20
∴ x² – x – 20 > 0
∴ x² – 5x + 4x – 20 > 0
∴ (x – 5) (x + 4) > 0
∴ either x – 5 > 0 and x + 4 > 0 or x – 5 < 0 and x + 4 < 0

Case I: x – 5 > 0 and x + 4 > 0
∴ x > 5 and x > -4
∴ x > 5 ….(i)

Case II:
x – 5 < 0 and x + 4 < 0
∴ x < 5 and x < -4
∴ x < -4 …..(ii)
From (i) and (ii), we get
x ∈ (-∞, – 4) ∪ (5, ∞)

(iii) \(\frac{2 x}{x-4}\) ≤ 5
∴ \(\frac{2 x}{x-4}\) – 5 ≤ 0
∴ \(\frac{2 x-5 x+20}{x-4}\) ≤ 0
∴ \(\frac{20-3 x}{x-4}\) ≤ 0
When \(\frac{a}{b}\) ≤ 0,
a ≥ 0 and b < 0 or a ≤ 0 and b > 0
∴ either 20 – 3x ≥ 0 and x – 4 < 0 or 20 – 3x ≤ 0 and x – 4 > 0
Case I:
20 – 3x ≥ 0 and x – 4 < 0
∴ x ≤ \(\frac{20}{3}\) and x < 4
∴ x < 4 ……(I)

Case II: 20 – 3x ≤ 0 and x – 4 > 0
∴ x ≥ \(\frac{20}{3}\) and x > 4
∴ x ≥ \(\frac{20}{3}\) ……(ii)
From (i) and (ii), we get
x ∈ (-∞, 4) ∪ [\(\frac{20}{3}\), ∞)

(iv) 6x² + 1 ≤ 5x
6x² – 5x + 1 ≤ 0
6x² – 3x – 2x + 1 ≤ 0
(3x – 1) (2x – 1) ≤ 0
either 3x – 1 ≤ 0 and 2x – 1 ≥ 0 or 3x – 1 ≥ 0 and 2x – 1 ≤ 0
Case I:
3x – 1 ≤ 0 and 2x – 1 ≥ 0
∴ x ≤ \(\frac{1}{3}\) and x ≥ \(\frac{1}{2}\), which is not possible.

Case II:
3x – 1 ≥ 0 and 2x – 1 ≤ 0
∴ x ≥ \(\frac{1}{3}\) and x ≤ \(\frac{1}{2}\)
∴ x ∈ [\(\frac{1}{3}\), \(\frac{1}{2}\)]

Question 15.
If A = (-7, 3], B = [2, 6] and C = [4, 9], then find
(i) A ∪ B
(ii) B ∪ C
(iii) A ∪ C
(iv) A ∩ B
(v) B ∩ C
(vi) A ∩ C
(vii) A’ ∩ B
(viii) B’ ∩ C’
(ix) B – C
(x) A – B
Solution:
A = (-7, 3], B = [2, 6], C = [4, 9]
(i) A ∪ B = (-7, 6]

(ii) B ∪ C = [2, 9]

(iii) A ∪ C = (-7, 3] ∪ [4, 9]

(iv) A ∩ B = [2, 3]

(v) B ∩ C = [4, 6]

(vi) A ∩ C = { }

(vii) A’ = (-∞, – 7] ∪ (3, ∞)
∴ A’ ∩ B = (3, 6]

(viii) B’ = (-∞, 2) ∪ (6, ∞)
C’ = (-∞, 4) ∪ (9, ∞)
∴ B’ ∩ C’ = (-∞, 2) ∪ (9, ∞)

(ix) B – C = [2, 4)

(x) A – B = (-7, 2)

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4

(I) Select the correct answers from the given alternatives.

Question 1.
The total number of terms in the expression of (x + y)¹⁰⁰ + (x – y)¹⁰⁰ after simplification is:
(A) 50
(B) 51
(C) 100
(D) 202
Answer:
(B) 51
Hint:

Question 2.
The middle term in the expansion of (1 + x)²ⁿ will be:
(A) (n – 1)^th
(B) n^th
(C) (n + 1)^th
(D) (n + 2)^th
Answer:
(C) (n + 1)^th
Hint:
(1 + x)²ⁿ has (2n + 1) terms.
∴ (n + 1 )^th term is the middle term.

Question 3.
In the expansion of (x² – 2x)¹⁰, the coefficient of x¹⁶ is
(A) -1680
(B) 1680
(C) 3360
(D) 6720
Answer:
(C) 3360
Hint:
(x² – 2x)¹⁰ = x¹⁰ (x – 2)¹⁰
To get the coefficient of x¹⁶ in (x² – 2x)¹⁰,
we need to check coefficient of x⁶ in (x – 2)¹⁰
∴ Required coefficient = ¹⁰C₆ (-2)⁴
= 210 × 16
= 3360

Question 4.
The term not containing x in expansion of \((1-x)^{2}\left(x+\frac{1}{x}\right)^{10}\) is
(A) ¹¹C₅
(B) ¹⁰C₅
(C) ¹⁰C₄
(D) ¹⁰C₇
Answer:
(A) ¹¹C₅
Hint:

Question 5.
The number of terms in expansion of (4y + x)⁸ – (4y – x)⁸ is
(A) 4
(B) 5
(C) 8
(D) 9
Answer:
(A) 4
Hint:

Question 6.
The value of ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + …. + ¹⁴C₁₁ is
(A) 2¹⁴ – 1
(B) 2¹⁴ – 14
(C) 2¹²
(D) 2¹³ – 14
Answer:
(D) 2¹³ – 14
Hint:

Question 7.
The value of ¹¹C₂ + ¹¹C₄ + ¹¹C₆ + ¹¹C₈ is equal to
(A) 2¹⁰ – 1
(B) 2¹⁰ – 11
(C) 2¹⁰ + 12
(D) 2¹⁰ – 12
Answer:
(D) 2¹⁰ – 12
Hint:

Question 8.
In the expansion of (3x + 2)⁴, the coefficient of the middle term is
(A) 36
(B) 54
(C) 81
(D) 216
Answer:
(D) 216
Hint:
(3x + 2)⁴ has 5 terms.
∴ (3x + 2)⁴ has 3rd term as the middle term.
The coefficient of the middle term

= 6 × 9 × 4
= 216

Question 9.
The coefficient of the 8th term in the expansion of (1 + x)¹⁰ is:
(A) 7
(B) 120
(C) ¹⁰C₈
(D) 210
Answer:
(B) 120
Hint:
r = 7
t₈ = ¹⁰C₇ x⁷ = ¹⁰C₃ x⁷
∴ Coefficient of 8th term = ¹⁰C₃ = 120

Question 10.
If the coefficients of x² and x³ in the expansion of (3 + ax)⁹ are the same, then the value of a is
(A) \(-\frac{7}{9}\)
(B) \(-\frac{9}{7}\)
(C) \(\frac{7}{9}\)
(D) \(\frac{9}{7}\)
Answer:
(D) \(\frac{9}{7}\)
Hint:

(II) Answer the following.

Question 1.
Prove by the method of induction, for all n ∈ N.
(i) 8 + 17 + 26 + ….. + (9n – 1) = \(\frac{n}{2}\) (9n + 7)
Solution:
Let P(n) ≡ 8 + 17 + 26 +…..+(9n – 1) = \(\frac{n}{2}\) (9n + 7), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 8
R.H.S. = \(\frac{1}{2}\) [9(1) + 7] = 8
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 8 + 17 + 26 +…..+ (9k – 1) = \(\frac{k}{2}\) (9k + 7) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., 8 + 17 + 26 + …… + [9(k + 1) – 1]

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 8 + 17 + 26 +…..+ (9n – 1) = \(\frac{n}{2}\) (9n + 7) for all n ∈ N.

(ii) 1² + 4² + 7² + …… + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1)
Solution:
Let P(n) = 1² + 4² + 7² + ….. + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S.= 1² = 1
R.H.S.= \(\frac{1}{2}\) [6(1)² – 3(1) – 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 4² + 7² +…..+ (3k – 2)² = \(\frac{k}{2}\) (6k² – 3k – 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 4² + 7² + … + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1) for all n ∈ N.

(iii) 2 + 3.2 + 4.2² + …… + (n + 1) 2^n-1 = n . 2ⁿ
Solution:
Let P(n) ≡ 2 + 3.2 + 4.2² +…..+ (n + 1) 2^n-1 = n.2ⁿ, for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(2¹) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 3.2 + 4.2² + ….. + (k + 1) 2^k-1 = k.2^k …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 3.2 + 4.2² +….+ (k + 2) 2^k = (k + 1) 2^k+1

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 3.2 + 4.2² +……+ (n + 1) 2^n-1 = n.2ⁿ for all n ∈ N.

(iv) \(\frac{1}{3.4 .5}+\frac{2}{4.5 .6}+\frac{3}{5.6 .7}+\ldots+\frac{n}{(n+2)(n+3)(n+4)}\) = \(\frac{n(n+1)}{6(n+3)(n+4)}\)
Solution:

Question 2.
Given that t_n+1 = 5t_n – 8, t₁ = 3, prove by method of induction that t_n = 5^n-1 + 2.
Solution:
Let the statement P(n) has L.H.S. a recurrence relation t_n+1 = 5t_n – 8, t₁ = 3
and R.H.S. a general statement t_n = 5^n-1 + 2.
Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 5^1-1 + 2 = 1 + 2 = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Put n = 2
L.H.S = t₂ = 5t₁ – 8 = 5(3) – 8 = 7
R.H.S. = t₂ = 5^2-1 + 2 = 5 + 2 = 7
∴ L.H.S. = R.H.S.
∴ P(n) is tme for n = 2.

Step II:
Let us assume that P(n) is true for n = k.
∴ t_k+1 = 5t_k – 8 and t_k = 5^k-1 + 2

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
t_k+1 = 5^k+1-1 + 2 = 5^k + 2
t_k+1 = 5t_k – 8 and t_k = 5^k-1 + 2 ……[From Step II]
∴ t_k+1 = 5(5^k-1 + 2) – 8 = 5^k + 2
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ t_n = 5^n-1 + 2, for all n ∈ N.

Question 3.
Prove by method of induction
\(\left(\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right)^{n}=\left(\begin{array}{cc}
2 n+1 & -4 n \\
n & -2 n+1
\end{array}\right)\), ∀ n ∈ N.
Solution:


Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\left(\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right)^{n}=\left(\begin{array}{cc}
2 n+1 & -4 n \\
n & -2 n+1
\end{array}\right)\), ∀ n ∈ N.

Question 4.
Expand (3x² + 2y)⁵
Solution:
Here, a = 3x², b = 2y, n = 5.
Using binomial theorem,

Question 5.
Expand \(\left(\frac{2 x}{3}-\frac{3}{2 x}\right)^{4}\)
Solution:

Question 6.
Find third term in the expansion of \(\left(9 x^{2}-\frac{y^{3}}{6}\right)^{4}\)
Solution:

Question 7.
Find tenth term in the expansion of \(\left(2 x^{2}+\frac{1}{x}\right)^{12}\)
Solution:

Question 8.
Find the middle term(s) in the expansion of
(i) \(\left(\frac{2 a}{3}-\frac{3}{2 a}\right)^{6}\)
Solution:
Here, a = \(\frac{2 a}{3}\), b = \(\frac{-3}{2 a}\), n = 6.
Now, n is even.
∴ \(\frac{\mathrm{n}+2}{2}=\frac{6+2}{2}=4\)
∴ Middle term is t4, for which r = 3.

∴ The Middle term is -20.

(ii) \(\left(x-\frac{1}{2 y}\right)^{10}\)
Solution:
Here, a = x, b = \(-\frac{1}{2 y}\), n = 10.
Now, n is even.
∴ \(\frac{\mathrm{n}+2}{2}=\frac{10+2}{2}=6\)
∴ Middle term is t6, for which r = 5

(iii) (x² + 2y²)⁷
Solution:
Here, a = x², b = 2y², n = 7.
Now, n is odd.
∴ \(\frac{\mathrm{n}+1}{2}=\frac{7+1}{2}=4, \frac{\mathrm{n}+3}{2}=\frac{7+3}{2}=5\)
∴ Middle terms are t₄ and t₅, for which r = 3 and r = 4 respectively.

∴ Middle terms are 280x⁸y⁶ and 560x⁶y⁸.

(iv) \(\left(\frac{3 x^{2}}{2}-\frac{1}{3 x}\right)^{9}\)
Solution:

Question 9.
Find the coefficients of
(i) x⁶ in the expantion of \(\left(3 x^{2}-\frac{1}{3 x}\right)^{9}\)
Solution:

(ii) x⁶⁰ in the expansion of \(\left(\frac{1}{x^{2}}+x^{4}\right)^{18}\)
Solution:

Question 10.
Find the constant term in the expansion of
(i) \(\left(\frac{4 x^{2}}{3}+\frac{3}{2 x}\right)^{9}\)
Solution:

(ii) \(\left(2 x^{2}-\frac{1}{x}\right)^{12}\)
Solution:

Question 11.
Prove by method of induction
(i) log_a xⁿ = n log_a x, x > 0, n ∈ N
Solution:

(ii) 15^2n-1 + 1 is divisible by 16, for all n ∈ N.
Solution:
15^2n-1 + 1 is divisible by 16, if and only if (15^2n-1 + 1) is is a multiple of 16.
Let P(n) ≡ 15^2n-1 + 1 = 16m, where m ∈ N.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 15^2n-1 + 1 is divisible by 16, for all n ∈ N.

(iii) 5²ⁿ – 2²ⁿ is divisible by 3, for all n ∈ N.
Solution:

Question 12.
If the coefficient of x¹⁶ in the expansion of (x² + ax)¹⁰ is 3360, find a.
Solution:

Question 13.
If the middle term in the expansion of \(\left(x+\frac{b}{x}\right)^{6}\) is 160, find b.
Solution:

∴ 160 = \(\frac{6 \times 5 \times 4 \times 3 !}{3 \times 2 \times 1 \times 3 !} \times b^{3}\)
∴ 160 = 20b³
∴ 8 = b³
∴ b = 2

Question 14.
If the coefficients of x² and x³ in theexpansion of (3 + kx)⁹ are equal, find k.
Solution:

Question 15.
If the constant term in the expansion of \(\left(x^{3}+\frac{\mathrm{k}}{x^{8}}\right)^{11}\) is 1320, find k.
Solution:

Question 16.
Show that there is no term containing x⁶ in the expansion of \(\left(x^{2}-\frac{3}{x}\right)^{11}\).
Solution:

Question 17.
Show that there is no constant term in the expansion of \(\left(2 x-\frac{x^{2}}{4}\right)^{9}\)
Solution:

Question 18.
State, first four terms in the expansion of \(\left(1-\frac{2 x}{3}\right)^{-1 / 2}\)
Solution:

Question 19.
State, first four terms in the expansion of \((1-x)^{-1 / 4}\).
Solution:

Question 20.
State, first three terms in the expansion of \((5+4 x)^{-1 / 2}\)
Solution:

Question 21.
Using the binomial theorem, find the value of \(\sqrt[3]{995}\) upto four places of decimals.
Solution:

Question 22.
Find approximate value of \(\frac{1}{4.08}\) upto four places of decimals.
Solution:

Question 23.
Find the term independent of x in the expansion of (1 – x²) \(\left(x+\frac{2}{x}\right)^{6}\).
Solution:

Question 24.
(a + bx) (1 – x)⁶ = 3 – 20x + cx² + …, then find a, b, c.
Solution:

Question 25.
The 3rd term of (1 + x)ⁿ is 36x². Find 5th term.
Solution:

Question 26.
Suppose (1 + kx)ⁿ = 1 – 12x + 60x² – …… find k and n.
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.5

Question 1.
Find Sn of the following arithmetico-geometric sequences.
(i) 2, 4x, 6x², 8x³, 10x⁴, ……
Solution:
2, 4x, 6x², 8x³, 10x⁴, ……
Here, 2, 4, 6, 8, 10,… are in A.P.
∴ a = 2, d = 2
∴ nth term = a + (n – 1)d
= 2 + (n – 1)(2)
= 2n

(ii) 1, 4x, 7x², 10x³, 13x⁴, ……
Solution:
1, 4x, 7x², 10x³, 13x⁴, ……
Here, 1, 4, 7, 10, 13,… are in A.P.
a = 1, d = 3
∴ nth term = a + (n – 1)d
= 1 + (n – 1)(3)
= 3n – 2
Also, 1, x, x², x³,… are in G.P.
∴ a = 1, r = x,
nth term = ar^n-1 = x^n-1
nth term of arithmetico-geometric sequence is

(iii) 1, 2 × 3, 3 × 9, 4 × 27, 5 × 81, ……
Solution:
1, 2 × 3, 3 × 9, 4 × 27, 5 × 81, …..
Here, 1, 2, 3, 4, 5, … are in A.P.
∴ a = 1, d = 1
∴ nth term = a + (n – 1)d
= 1 + (n – 1)1
= n

(iv) 3, 12, 36, 96, 240, ……
Solution:
3, 12, 36, 96, 240, ……
i.e., 1 × 3, 2 × 6, 3 × 12, 4 × 24, 5 × 48, …….
Here, 1, 2, 3, 4, 5, ….. are in A.P.
∴ nth term = n
Also, 3, 6, 12, 24, 48, ….. are in G.P.
∴ a = 3, r = 2
∴ nth term = ar^n-1 = 3 . (2^n-1)
∴ nth term of arithmetico-geometric sequence is

Question 2.
Find the sum to infinity of the following arithmetico-geometric sequence.
(i) \(1, \frac{2}{4}, \frac{3}{16}, \frac{4}{64}, \ldots\)
Solution:

(ii) \(3, \frac{6}{5}, \frac{9}{25}, \frac{12}{125}, \frac{15}{625}, \ldots\)
Solution:

∴ \(\frac{4}{5} S=\frac{15}{4}\)
∴ S = \(\frac{75}{16}\)

(iii) \(1, \frac{-4}{3}, \frac{7}{9}, \frac{-10}{27} \ldots\)
Solution:

Balbharti Maharashtra State Board Bookkeeping and Accountancy 11th Solutions Chapter 6 Bank Reconciliation Statement Textbook Exercise Questions and Answers.

Maharashtra State Board Bookkeeping and Accountancy 11th Solutions Chapter 6 Bank Reconciliation Statement

1. Answer in one sentence.

Question 1.
Who prepares a bank Pass Book?
Answer:
The Bank passbook is prepared by the bank.

Question 2.
What is a pay-in-slip?
Answer:
Pay-in-slip is the slip that is filled when the bank account holder deposits a cheque or cash into his bank account.

Question 3.
What is a bank overdraft?
Answer:
The amount withdrawn by the account holder from his current account in excess of the balance standing in that account up to, specified limit is known as bank overdraft.

Question 4.
What is a withdrawal slip?
Answer:
It is a document/form, which is used by the savings account holder for withdrawing cash from his bank account.

Question 5.
Who sends the bank statement?
Answer:
A bank statement is sent by the Bank manager to the account holder informing about debit or credit given by the bank.

Question 6.
What does a debit balance in Cash Book represent?
Answer:
The debit balance of the cash Book indicates a positive Bank balance as per Cash Book.

Question 7.
Who prepares the Bank Reconciliation Statement?
Answer:
A Businessman, trader, or accountant prepares Bank Reconciliation Statement at the end of every month.

Question 8.
What does the debit balance in Pass Book represent?
Answer:
The debit balance of Passbook represents Overdraft as per passbook.

Question 9.
On which side is interest on bank deposit recorded in Pass Book?
Answer:
Interest on bank deposits is recorded on the credit side of the passbook.

Question 10.
Why is Bank Reconciliation Statement prepared?
Answer:
A bank reconciliation statement is prepared to disclose the causes of the difference between the balances shown by the cash book and passbook.

2. Give one word/term/phrase which can substitute each of the following statements:

Question 1.
The account on which overdraft facility is allowed by the bank.
Answer:
Current Account

Question 2.
Extract of ledger account of the account holder in the books of the bank.
Answer:
Pass Book

Question 3.
Alphanumeric code that facilitates electronic funds transfer in India.
Answer:
IFSC (Indian Financial System Code)

Question 4.
Statement showing the causes of disagreement between the balance of Cash Book and Pass Book.
Answer:
Bank Reconciliation Statement

Question 5.
Debit balance in Pass Book.
Answer:
Overdraft as per Pass Book

Question 6.
A form which is filled for depositing cash or cheque into bank.
Answer:
Pay-in-slip

Question 7.
The left-hand side of Pay-in-slip.
Answer:
Counterfoil

Question 8.
Credit balance in Cash Book.
Answer:
Overdraft as per Cash Book

Question 9.
A book maintained by traders to record banking transactions.
Answer:
Cash Book

Question 10.
Excess of bank deposits over withdrawals by a businessman in bank current account.
Answer:
Bank Balance (favourable balance)

3. Do you agree or disagree with the following statements:

Question 1.
The bank column of Cash Book represents the bank account.
Answer:
Agree

Question 2.
A bank statement enables the account holder to prepare Bank Reconciliation Statement.
Answer:
Agree

Question 3.
Cheques issued for payment but not presented to bank appear in Cash Book only.
Answer:
Agree

Question 4.
Bank Reconciliation Statement is prepared only during the year-end.
Answer:
Disagree

Question 5.
Bank Reconciliation Statement is similar to the bank statement.
Answer:
Disagree

Question 6.
Bank balance as per Cash Book is always equal to bank balance as per Pass Book.
Answer:
Disagree

Question 7.
Bank advice is sent by the businessman to the bank.
Answer:
Disagree

Question 8.
Pay-in-slip is used for depositing cheques into banks.
Answer:
Agree

Question 9.
The difference in Cash Book Balance and Pass Book balance may arise due to errors committed while recording.
Answer:
Agree

Question 10.
Payment and receipt of cash through internet banking generate an automatic proof.
Answer:
Agree

4. Select the most appropriate alternative from those given and rewrite the following statements:

Question 1.
Overdraft means ____________ balance of Cash Book.
(a) closing
(b) debit
(c) opening
(d) credit
Answer:
(d) credit

Question 2.
When a cheque is deposited and collected by bank Pass Book is ____________
(a) dishonoured
(b) debited
(c) credited
(d) written
Answer:
(c) credited

Question 3.
A ____________ is a summary of financial transactions that take place over a period of time on a bank account.
(a) withdrawal slip
(b) bank advice
(c) bank statement
(d) Pay-in-slip
Answer:
(c) bank statement

Question 4.
Debiting an entry in Cash Book ____________ cash balance.
(a) increases
(b) decreases
(c) nullifies
(d) none of the above
Answer:
(a) increases

Question 5.
Bank Reconciliation Statement is prepared by ____________
(a) student
(b) businessman
(c) bank
(d) none of the above
Answer:
(b) businessman

Question 6.
Bank balance as per Pass Book means ____________ balance of Pass Book.
(a) credit
(b) opening
(c) debit
(d) closing
Answer:
(a) credit

Question 7.
Bank gives overdraft facility to ____________ account holder.
(a) savings
(b) recurring
(c) current
(d) fixed
Answer:
(c) current

Question 8.
Debit balance as per Cash Book is also known as ____________ balance.
(a) favourable
(b) overdraft
(c) abnormal
(d) unfavourable
Answer:
(a) favourable

Question 9.
When extracts of Cash Book and Pass Book are given for uncommon periods, only ____________ items are considered for preparation of Bank Reconciliation Statement.
(a) uncommon
(b) normal
(c) favourable
(d) common
Answer:
(d) common

Question 10.
When extract of Cash Book and Pass Book is given for common period, only ____________ items are considered
for preparation of Bank Reconciliation Statement.
(a) uncommon
(b) common
(c) favourable
(d) unfavourable
Answer:
(a) uncommon

5. Complete the following statements:

Question 1.
Payments credited in Cash Book are ____________ in Pass Book.
Answer:
Debited

Question 2.
While preparing Bank Reconciliation Statement only ____________ column of Cash Book is considered.
Answer:
Bank

Question 3.
Cheques issued to creditors appear first in ____________ book.
Answer:
Cash

Question 4.
A statement showing the reasons for the difference in Cash Book Balance and Pass Book balance is known as ____________
Answer:
Bank Reconciliation Statement

Question 5.
Overcast on receipt side of Pass Book means ____________ in Pass Book balance.
Answer:
Increase

Question 6.
Online transfer made to our creditors appear on the ____________ side of Cash Book.
Answer:
Payment/Credit

Question 7.
Interest on overdraft charged by bank is ____________ in Pass Book.
Answer:
Debited

Question 8.
Normally the Cash Book shows debit balance and Pass Book shows ____________ balance.
Answer:
Credit

Question 9.
The form filled for withdrawing cash from bank is known as ____________
Answer:
Withdrawal Slip

Question 10.
A businessman can update his records on receiving ____________
Answer:
Bank Advice

6. State whether the following statements are True or False with reasons:

Question 1.
Cheques deposited into the bank but not yet cleared appears in the Pass Book only.
Answer:
This statement is False.
Cheques deposited into the bank but not yet cleared appears in the cash book only. Bank records entry in the passbook only after the cheque is cleared. So there is no entry for this transaction in the Pass Book.

Question 2.
Direct deposit made by debtors into a businessman’s bank account is recorded on the credit side of Pass Book.
Answer:
This statement is True.
The credit side of the passbook means deposits made in the bank account. When direct deposits are made by debtors into a businessman’s bank account. It increases the bank balance and it is recorded on the credit side of Pass Book.

Question 3.
A businessman can prepare a Bank Reconciliation statement only with Cash Book Balance.
Answer:
This statement is False.
The businessman can prepare a Bank Reconciliation statement with the help of a cash book, bank column, and passbook. It is a comparison between the two to correct the differences. Both i.e. cash book and pass book/Bank statement are required to prepare a Bank Reconciliation statement.

Question 4.
When overdraft as per Cash Book is given, bank charges debited in Pass Book only are to be added.
Answer:
This statement is True.
Bank overdraft as per cash book means negative bank balance. The businessman has to pay the Bank. Bank charges are expenses for the business and this increases the amount payable to the bank so bank charges debited in the passbook only are to be added in the cash book.

Question 5.
Bank Statement is sent by Bank to the businessman.
Answer:
This statement is True.
A bank statement is a statement issued by the bank to the current account holder informing about the bank transactions during a particular period of time. Generally, it is issued every i.e. month. It gives details information about bank deposits and withdrawals etc.

7. Draft the following specimen with imaginary Name, Account Number, Amount.

Question 1.
Bank Statement
Answer:
Specimen of Bank Statement is given below:

Question 2.
Pay-in-slip
Answer:
(a) Specimen of pay-in-slip is given below: Front side

(b) Reverse (Back-side) of Pay-in-slip:

Question 3.
Withdrawal slip
Answer:
Specimen form of a withdrawal slip is given below:

Question 4.
Bank Advice
Answer:
Specimen of bank advice is given below:

Question 5.
Pass Book
Answer:
Specimen form of the Bank passbook is given below:
Bank Pass Book

8. Correct and rewrite the following statements.

Question 1.
The form filled for depositing cash or cheque into the bank is known as Pass Book.
Answer:
The form filled for depositing cash or cheque into the bank is known as Pay in slip.

Question 2.
Bank Reconciliation Statement is prepared by Bank.
Answer:
Bank Reconciliation Statement is prepared by Businessman.

Question 3.
Debit balance as per Pass Book is known as favourable balance.
Answer:
Debit balance as per Pass Book is known as unfavorable balance.

Question 4.
When a cheque is deposited into Bank it is credited to Cashbook.
Answer:
When a cheque is deposited into Bank it is debited in Cash Book.

Question 5.
When extracts are given for the common period only common items are to be considered.
Answer:
When extracts are given for the common period only uncommon items are to be considered.

9. Complete the following table.

Question 1.

Answer:

Practical Problems

Question 1.
Following is the extract of the Cash Book (Bank Column only) and passbook. Prepare Bank Reconciliation Statement as of 31st Oct. 2018.
In the books of ____________

In the books of Bank

Solution:
Bank Reconciliation Statement as of 31st October 2018.

Working Notes:
When extract of Cashbook and passbook are given for the same period i.e. for the month of April 2018, we have to consider only uncommon entries for adding and deducting from Bank Reconciliation Statement. This is shown in the following working notes.
In order to find out items to be added and items to be deducted in the Bank Reconciliation Statement, we have to prepare Cash Book and passbook on the basis of accounting information given in the problem:
Cash Book

Bank Pass Book

Explanation:
1. First record the opening balance in the appropriate book i.e. either in Cashbook or passbook.
2. Bank balance of ₹ 9,800 as per Cashbook is recorded on the debit side of Cashbook in a box.
3. In this problem, the entries which are passed on the debit side of the Cashbook and passbook are to be added in the Bank Reconciliation Statement and the entries passed on the credit side of the Cashbook and passbook are to be deducted in the Bank Reconciliation Statement. This is because the opening balance appears on the debit side of the Cash Book.

Question 2.
From the following extract of Cash Book and Pass Book prepare Bank Reconciliation Statement as of 31st March 2019.
In the books of ____________

In the books of Bank
Bank Pass Book

Solution:
Bank Reconciliation Statement as of 31st March 2019

Working Notes:
When extract of Cashbook and passbook are given for the same period i.e. for the month of April 2011, we have to consider only uncommon entries for adding and deducting from Bank Reconciliation Statement. This is shown in the following working notes.
In order to find out items to be added and items to be deducted in the Bank Reconciliation Statement, we have to prepare Cash Book and passbook on the basis of accounting information given in the problem:
Cash Book

Bank Pass Book

Question 3.
On 31st August 2018 bank passbook of Mr. Ravi showed a credit balance of ₹ 33,600, but Cash Book showed a different balance. On comparing the two books following differences were noticed:
1. Cheques paid into the bank but not credited before 31st Aug 2018 amounted to ₹ 24,500.
2. Direct deposit by the customer through NEFT ₹ 33,000 recorded in the passbook only.
3. Cheques issued on 28th Aug 2018 were presented for payment on 5th Sep. 2018 amounted to ₹ 38,800.
4. A bill receivable for ₹ 15,000 discounted with the bank was dishonored on 30th Aug 2018. Intimation of the same was received only on 3rd Sep 2018.
5. Passbook credit side was overcast ₹ 2,000.
6. Bank debited ₹ 400 for bank charges in the passbook, which was not recorded in Cash Book.
Prepare Bank Reconciliation Statement as of 31st August 2018.
Solution:
Bank Reconciliation Statement as of 31st August 2018.

Working Notes:
In order to find out items to be added and items to be deducted in the Bank Reconciliation Statement, we have to prepare Cash Book and passbook on the basic information given in the problem:
Cash Book (With Bank Column)

Bank Pass Book

Explanation:
1. First record the opening balance in the appropriate book and at the appropriate side i.e. either in Cashbook or passbook.

2. In the above problem Bank balance of ₹ 33,600 as per the passbook is recorded on the credit side of the passbook in a box.

3. In this problem, the entries which are passed on the credit side of the Cashbook and passbook are to be added in the Bank Reconciliation Statement and the entries passed on the debit side of the Cash Book and passbook are to be deducted in the Bank Reconciliation Statement. This is because the opening balance appears on the credit side of the passbook.

4. Pass the entry of the given transactions in the book in which entry is not passed due to one or another reason, e.g. cheque of ₹ 24,300 is deposited but not collected. In this case, entry is not passed in the passbook, as the cheque is not collected by the bank. Now draft the entry for the given transaction on the credit side of the passbook. This is because, after the collection of cheques, the bank balance is increased. In the same way for remaining transactions pass the entry in that book where entry is not passed corresponding.

Question 4.
From the following details prepare Bank Reconciliation Statement as of 31st Dec. 2018.
1. Bank overdraft as per Cash Book on 31st Dec. 2018 was ₹ 48,450.
2. Bank charges for SMS alerts ₹ 370 were debited in passbook but not recorded in Cash Book.
3. Interest in overdraft ₹ 2,870 did not appear in Cash Book.
4. A bill for ₹ 12,000 discounted with bank appears in Cash Book at the full amount but the bank has deducted ₹ 200 discounting charges.
5. Cheques issued but not presented for payment before 31st Dec. 2018 amounted to ₹ 32,300.
6. Cheques amounting to ₹ 24,000 were deposited into the bank but only a cheque of ₹ 8,000 was collected by the bank before 31st Dec. 2018.
7. Paid stationary bill ₹ 11,300 by debit card. It was not recorded in Cash Book.
Solution:
Bank Reconciliation Statement as of 31st December 2018.

Working Notes:
Cash Book (With Bank Column)

Bank Pass Book

Question 5.
From the following particulars prepare Rank Reconciliation Statement as of 30th June 2019.
1. Credit balance as per pass book ₹ 20,000.
2. A cheque for ₹ 3,500 was issued and paid by the bank, recorded in Pass Book as ₹ 5,300.
3. Cheque deposited ₹ 9,700 collected by the bank was not recorded in Cash Book.
4. Payment side of the Cash Book was undercast by ₹ 100.
5. Electricity bill paid by bank ₹ 6,200 was recorded twice in Pass Book.
Solution:
Bank Reconciliation Statement as of 30th June 2019.

Working Notes:
Cash Rook (With Rank Column)

Bank Pass Book

Question 6.
Prepare Bank Reconciliation Statement from the following information as of 31st March 2019.
1. Balance as per Cash Book ₹ 10,000.
2. Cheque of ₹ 2,000 issued but not presented to Bank for payment.
3. Our debtor directly deposited ₹ 3,500 to our Bank account by NEFT, not recorded in the Cash Book.
4. Bank paid electricity bill on our behalf ₹ 450 and charged Bank charges ₹ 100.
5. Paid ₹ 1,500 to ABC & company, our supplier by business debit card but recorded in Cash Book as ₹ 150.
6. Bank credited interest on Investment ₹ 500.
7. Cheque of ₹ 885 issued and presented to Bank but wrongly entered in the Pass Book as ₹ 865.
Solution:
Bank Reconciliation Statement as on 31st March 2019

Working Notes:
Cash Book (With Bank Column)

Bank Pass Book

Question 7.
On 31st January 2018 Bank balance as per Cash Book was ₹ 40,000 but Pass Book was showing some other balances following were the causes of the difference.
1. Cheques were issued for ₹ 1,00,000 in January 2018 but cheques of ₹ 50,000 were only presented to the Bank for payment before January 31st, 2018
2. Cheques were sent to the Bank for collection of ₹ 2,00,000 out of which cheques of ₹ 80,000 were only credited by the Bank in January 2018.
3. Following entries were shown in the passbook in January 2018, but no corresponding entries were made in the Cash Book.
(i) Payment of ₹ 6,400 by Bank for Electricity Bill by ECS.
(ii) Interest credited by Bank ₹ 12,000
(iii) Bank debited commission ₹ 1,000 and Bank charges for ₹ 600.
(iv) Direct deposit made by customer ₹ 1,000 by NEFT to our account.
Prepare Bank Reconciliation Statement as of 31st January 2018.
Solution:
Bank Reconciliation Statement as of 31st January 2018

Working Notes:
Cash Book (With Bank Column)

Bank Pass Book

Question 8.
In January 2018, the Pass Book of Mr. Girish Kumbhar showed a bank balance of ₹ 14,000. A comparison of the Cash Book with the Pass Book revealed the following.
1. Cheque deposited but not credited by Bank ₹ 10,000
2. Dividend on shares collected by Bank but not recorded in the Cash Book ₹ 1,000
3. Bank paid Insurance premium as per standing instruction by ECS ₹ 500, no corresponding entry was passed in the Cash Book.
4. Bank debited Commission ₹ 75.
5. A debit of ₹ 900 in respect of cheque dishonored appears in Pass Book only.
6. Cheque of ₹ 1,500 deposited into Bank wrongly recorded twice in the Cash Book.
7. Total cheques of ₹ 20,000 were issued during the month of January 2018, but cheques of ₹ 8,000 only were presented for payment in January 2018.
Prepare Bank Reconciliation Statement as of 31st January 2018.
Solution:
Bank Reconciliation Statement as of 31st March 2019

Working Notes:
Cash Book (With Bank Column)

Pass Book

Question 9.
Form the following details provided by Prasharit enterprises, prepare a Bank Reconciliation Statement as of 31st March 2018.
1. Overdraft as per Cash Book ₹ 28,000
2. Cheque issued of ₹ 2,000 and presented to Bank returned dishonored but the effect of dishonored is not recorded in the Cash Book.
3. Bank debited Bank charges ₹ 150.
4. Bank transferred ₹ 2,500 to the savings account of the proprietor but not recorded in the Cash Book.
5. Cheque issued to the supplier but not presented to Bank before 21st March 2018, ₹ 1,600
6. Cheques of ₹ 3,000 and ₹ 2,000 were deposited into Bank but cheques of ₹ 3,000 were only credited by Bank before 31st March 2018.
7. Out customer directly deposited ₹ 1,500 in our Bank account but wrongly recorded it in the cash column of the Cash Book.
8. Bank debited interest on overdraft ₹ 750.
Solution:
Bank Reconciliation Statement as of 31st March 2018.

Working Notes:
Cash Book (Bank column)

Pass Book

Question 10.
Prepare Bank Reconciliation Statement as of 31st Dec. 2018
1. Debit balance as per pass book ₹ 16,000
2. Customer directly deposited in our Bank account by NEFT ₹ 8,000.
3. Cheques deposited into Bank but not credited by Bank ₹ 10,500.
4. Pass Book shows a debit entry for Bank commission ₹ 300, not recorded in Cash Book.
5. A Bill of Exchange of ₹ 3,500 was discounted with the Bank in December 2018, returned dishonored in January 2019.
6. As per standing instructions Bank paid the Telephone bill of ₹ 650, not recorded in the Cash Book.
7. Cheque of ₹ 975 deposited into the Bank but wrongly recorded on ₹ 795 in Cash Book.
Solution:
Bank Reconciliation Statement as of 31st December 2018.

Working Notes:
Cash Book (with Bank column)

Bank Pass Book

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.2

Question 1.
First, 6 faced die which is numbered 1 to 6 is thrown, then a 5 faced die which is numbered 1 to 5 is thrown. What is the probability that sum of the numbers on the upper faces of the dice is divisible by 2 or 3?
Solution:
When a 6 faced die and a 5 faced die are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4,4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
∴ n(S) = 30
Let event A: The sum of the numbers on the upper faces of the dice is divisible by 2.
A = {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4)}
∴ n(A) = 15
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{15}{30}\)
Let event B: Sum of the numbers on the upper faces of the dice is divisible by 3.
B = {(1, 2), (1, 5), (2, 1), (2, 4), (3, 3), (4, 2), (4, 5), (5, 1), (5, 4), (6, 3)}
∴ n(B) = 10
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{10}{30}\)
Now,
A ∩ B = {(1, 5), (2,4), (3, 3), (4, 2), (5, 1)}
∴ n(A ∩ B) = 5
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{5}{30}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{15}{30}+\frac{10}{30}-\frac{5}{30}\)
= \(\frac{20}{30}\)
= \(\frac{2}{3}\)

Question 2.
A card is drawn from a pack of 52 cards. What is the probability that,
(i) card is either red or black?
(ii) card is either black or a face card?
Solution:
One card can be drawn from the pack of 52 cards in \({ }^{52} \mathrm{C}_{1}\) = 52 ways.
∴ n(S) = 52
The pack of 52 cards consists of 26 red and 26 black cards.
(i) Let event A: A red card is drawn.
∴ Red card can be drawn in \({ }^{26} \mathrm{C}_{1}\) = 26ways
∴ n(A) = 26
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{26}{52}\)
Let event B: A black card is drawn.
∴ Black card can be drawn in \({ }^{26} \mathrm{C}_{1}\) = 26 ways.
∴ n(B) = 26
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{26}{52}\)
Since A and B are mutually exclusive events,
P(A ∩ B) = 0
∴ Required probability
P(A ∪ B) = P(A) + P(B)
= \(\frac{26}{52}+\frac{26}{52}\)
= 1

(ii) Let event A: A black card is drawn.
∴ Black card can be drawn in \({ }^{26} \mathrm{C}_{1}\) = 26 ways.
n(A) = 26
n(A) 26 n(S) ~ 52
Let event B: A face card is drawn.
There are 12 face cards in the pack of 52 cards.
∴ 1 face card can be drawn in \({ }^{12} \mathrm{C}_{1}\) = 12 ways.
∴ n(B) = 12
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{12}{52}\)
There are 6 black face cards.
∴ n(A ∩ B) = 6
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{6}{52}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{26}{52}+\frac{12}{52}-\frac{6}{52}\)
= \(\frac{32}{52}\)
= \(\frac{8}{13}\)

Question 3.
A girl is preparing for National Level Entrance exam and State Level Entrance exam for professional courses. The chances of her cracking National Level exam is 0.42 and that of State Level exam is 0.54. The probability that she clears both the exams is 0.11. Find the probability that
(i) she cracks at least one of the two exams.
(ii) she cracks only one of the two.
(iii) she cracks none.
Solution:
Let event A: The girl cracks the National Level exam.
∴ P(A) = 0.42
Let event B: The girl cracks the State Level exam.
∴ P(B) = 0.54
Also, P(A ∩ B) = 0.11
(i) P(the girl cracks at least one of the two exams)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.42 + 0.54 – 0.11
= 0.85

(ii) P(the girl cracks only one of the two exams)
= P(A) – P(B) – 2P(A ∩ B)
= 0.42 + 0.54 – 2(0.11)
= 0.74

(iii) P(the girl cracks none of the exams)
= P(A’ ∩ B’)
= P(A ∪ B)’
= 1 – P(A ∪ B)
= 1 – 0.85
= 0.15

Question 4.
A bag contains 75 tickets numbered from 1 to 75. One ticket is drawn at random. Find the probability that,
(i) number on the ticket is a perfect square or divisible by 4.
(ii) number on the ticket is a prime number or greater than 40.
Solution:
Out of the 75 tickets, one ticket can be drawn in \({ }^{75} \mathrm{C}_{1}\) = 75 ways.
∴ n(S) = 75
(i) Let event A: The number on the ticket is a perfect square.
∴ A = {1, 4, 9, 16, 25, 36, 49, 64}
∴ n(A) = 8
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{8}{75}\)
Let event B: The number on the ticket is divisible by 4.
∴ B = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72}
∴ n(B) = 18
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{18}{75}\)
Now, A ∩ B = {4, 16, 36, 64}
∴ n(A ∩ B) = 4
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{4}{75}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{8}{75}+\frac{18}{75}-\frac{4}{75}\)
= \(\frac{22}{75}\)

(ii) Let event A: The number on the ticket is a prime number.
∴ A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73}
∴ n(A) = 21
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{21}{75}\)
Let event B: The number is greater than 40.
∴ B = {41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75}
∴ n(B) = 35
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{35}{75}\)
Now,
A ∩ B = {41, 43, 47, 53, 59, 61, 67, 71, 73}
∴ n(A ∩ B) = 9
∴ n(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{9}{75}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{21}{75}+\frac{35}{75}-\frac{9}{75}\)
= \(\frac{47}{75}\)

Question 5.
The probability that a student will pass in French is 0.64, will pass in Sociology is 0.45 and will pass in both is 0.40. What is the probability that the student will pass in at least one of the two subjects?
Solution:
Let event A: The student will pass in French.
∴ P(A) = 0.64
Let event B: The student will pass in Sociology.
∴ P(B) = 0.45
Also, P(A ∩ B) = 0.40
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.64 + 0.45 – 0.40
= 0.69

Question 6.
Two fair dice are thrown. Find the probability that the number on the upper face of the first die is 3 or sum of the numbers on their upper faces is 6.
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let event A: The number on the upper face of the first die is 3.
∴ A = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)}
∴ n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}\)
Let event B: Sum of the numbers on their upper faces is 6.
∴ B = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
∴ n(B) = 5
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{5}{36}\)
Now, A ∩ B = {(3, 3)}
∴ n(A ∩ B) = 1
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{1}{36}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{36}+\frac{5}{36}-\frac{1}{36}\)
= \(\frac{10}{36}\)
= \(\frac{5}{18}\)

Question 7.
For two events A and B of a sample space S, if P(A) = \(\frac{3}{8}\), P(B) = \(\frac{1}{2}\) and P(A ∪ B) = \(\frac{5}{8}\). Find the value of the following.
(a) P(A ∩ B)
(b) P(A’ ∩ B’)
(c) P(A’ ∪ B’)
Solution:
Here, P(A) = \(\frac{3}{8}\), P(B) = \(\frac{1}{2}\), P(A ∪ B) = \(\frac{5}{8}\)
(a) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{3}{8}+\frac{1}{2}-\frac{5}{8}\)
= \(\frac{1}{4}\)

(b) P(A’ ∩ B’) = P(A ∪ B)’
= 1 – P(A ∪ B)
= 1 – \(\frac{5}{8}\)
= \(\frac{3}{8}\)

(c) P(A’ ∪ B’) = P(A ∩ B)’
= 1 – P(A ∩ B)
= 1 – \(\frac{1}{4}\)
= \(\frac{3}{4}\)

Question 8.
For two events A and B of a sample space S, if P(A ∪ B) = \(\frac{5}{6}\), P(A ∩ B) = \(\frac{1}{3}\) and P(B’) = \(\frac{1}{3}\), then find P(A).
Solution:
Here, P(A ∪ B) = \(\frac{5}{6}\), P(A ∩ B) = \(\frac{1}{3}\), P(B’) = \(\frac{1}{3}\)
P(B) = 1 – P(B’)
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
Since P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
\(\frac{5}{6}\) = P(A) + \(\frac{2}{3}-\frac{1}{3}\)
∴ \(\frac{5}{6}\) = P(A) + \(\frac{1}{3}\)
∴ P(A) = \(\frac{5}{6}-\frac{1}{3}\) = \(\frac{1}{2}\)

Question 9.
A bag contains 5 red, 4 blue and an unknown number m of green balls. If the probability of getting both the balls green, when two balls are selected at random is \(\frac{1}{7}\), find m.
Solution:
Total number of balls in the bag = 5 + 4 + m = 9 + m
Two balls are selected from (9 + m) balls in \({ }^{9+m} \mathrm{C}_{2}\) ways.
∴ n(S) = \({ }^{9+m} \mathrm{C}_{2}\)
Let event A: The two balls selected are green.
∴ 2 balls can be selected from m balls in \({ }^{\mathrm{m}} \mathrm{C}_{2}\) ways.
∴ n(A) = \({ }^{\mathrm{m}} \mathrm{C}_{2}\)

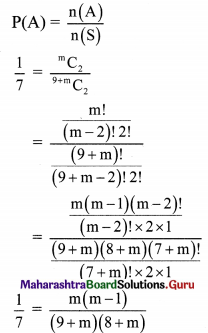
(9 + m)(8 + m) = 7m(m – 1)
72 + 9m + 8m + m2 = 7m2 – 7m
6m2 – 24m – 72 = 0
m2 – 4m – 12 = 0
(m – 6)(m + 2) = 0
m = 6 or m = -2
Since number of balls cannot be negative, m ≠ -2
∴ m = 6

Question 10.
From a group of 4 men, 4 women and 3 children, 4 persons are selected at random. Find the probability that,
(i) no child is selected.
(ii) exactly 2 men are selected.
Solution:
The group consists of 4 men, 4 women and 3 children, i.e., 4 + 4 + 3 = 11 persons.
4 persons are to be selected from this group.
∴ 4 persons can be selected from 11 persons in \({ }^{11} \mathrm{C}_{4}\) ways.
∴ n(S) = \({ }^{11} \mathrm{C}_{4}\)
(i) Let event A: No child is selected.
∴ 4 persons can be selected from 4 men and 4 women, i.e., from 8 persons in \({ }^{8} \mathrm{C}_{4}\) ways.
∴ n(A) = \({ }^{8} \mathrm{C}_{4}\)

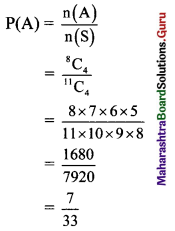
(ii) Let event B: Exactly 2 men are selected.
∴ 2 men are selected from 4 men in \({ }^{4} \mathrm{C}_{2}\) ways, and remaining 2 persons are selected from 7 persons (i.e., 4 women and 3 children) in \({ }^{7} \mathrm{C}_{2}\) ways.

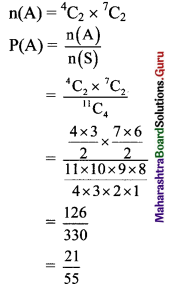
Question 11.
A number is drawn at random from the numbers 1 to 50. Find the probability that it is divisible by 2 or 3 or 10.
Solution:
One number can be drawn at random from the numbers 1 to 50 in \({ }^{50} \mathrm{C}_{1}\) = 50 ways.
∴ n(S) = 50
Let event A: The number drawn is divisible by 2.
∴ A = {2, 4, 6, 8, 10, …, 48, 50}
∴ n(A) = 25
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{25}{50}\)
Let event B: The number drawn is divisible by 3.
B = {3, 6, 9, 12, …, 48}
∴ n(B) = 16
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{16}{50}\)
Let event C: The number drawn is divisible by 10.
C = {10, 20, 30, 40, 50}
∴ n(C) = 5
∴ P(C) = \(\frac{n(C)}{n(S)}=\frac{5}{50}\)
Now, A ∩ B = {6, 12, 18, 24, 30, 36, 42, 48}
∴ n(A ∩ B) = 8
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{8}{50}\)
B ∩ C = {30}
∴ n(B ∩ C) = 1
∴ P(B ∩ C) = \(\frac{\mathrm{n}(\mathrm{B} \cap \mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{1}{50}\)
A ∩ C = {10, 20, 30, 40, 50}
∴ n(A ∩ C) = 5
∴ P(A ∩ C) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{5}{50}\)
A ∩ B ∩ C = {30}
∴ n(A ∩ B ∩ C) = 1
∴ P(A ∩ B ∩C) = \(\frac{n(A \cap B \cap C)}{n(S)}=\frac{1}{50}\)
∴ P(the number is divisible by 2 or 3 or 10)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
= \(\frac{25}{50}+\frac{16}{50}+\frac{5}{50}-\frac{8}{50}-\frac{1}{50}-\frac{5}{50}+\frac{1}{50}\)
= \(\frac{33}{50}\)

దుర్గా సప్తశతీ ప్రధానిక రహస్యం

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2

Question 1.
Expand:
(i) (√3 + √2)⁴
Solution:
Here, a = √3, b = √2 and n = 4.
Using binomial theorem,

∴ (√3 + √2)⁴ = 1(9) (1) + 4(3√3) (√2) + 6(3)(2) + 4(√3) (2√2) + 1(1)(4)
= 9 + 12√6 + 36 + 8√6 + 4
= 49 + 20√6

(ii) (√5 – √2)⁵
Solution:
Here, a = √5, b = √2 and n = 5.
Using binomial theorem,

Question 2.
Expand:
(i) (2x² + 3)⁴
Solution:
Here, a = 2x², b = 3 and n = 4.
Using binomial theorem,

(ii) \(\left(2 x-\frac{1}{x}\right)^{6}\)
Solution:
Here, a = 2x, b = \(\frac{1}{x}\) and n = 6.
Using binomial theorem,

Question 3.
Find the value of
(i) (√3 + 1)⁴ – (√3 – 1)⁴
Solution:

(ii) (2 + √5)⁵ + (2 – √5)⁵
Solution:


Adding (i) and (ii), we get
∴ (2 + √5 )⁵ + (2 – √5)⁵ = (32 + 80√5 + 400 + 200√5 + 250 + 25√5) + (32 – 80√5 + 400 – 200√5+ 250 – 25√5 )
= 64 + 800 + 500
= 1364

Question 4.
Prove that:
(i) (√3 + √2)⁶ + (√3 – √2)⁶ = 970
Solution:

(ii) (√5 + 1)⁵ – (√5 – 1)⁵ = 352
Solution:

Question 5.
Using binomial theorem, find the value of
(i) (102)⁴
Solution:

(ii) (1.1)⁵
Solution:

Question 6.
Using binomial theorem, find the value of
(i) (9.9)³
Solution:

(ii) (0.9)⁴
Solution:

Question 7.
Without expanding, find the value of
(i) (x + 1)⁴ – 4(x + 1)³ (x – 1) + 6(x + 1)² (x – 1)² – 4(x + 1) (x – 1)³ + (x – 1)⁴
Solution:

(ii) (2x – 1)⁴ + 4(2x – 1)³ (3 – 2x) + 6(2x – 1)² (3 – 2x)² + 4(2x – 1)¹ (3 – 2x)³ + (3 – 2x)⁴
Solution:

Question 8.
Find the value of (1.02)⁶, correct upto four places of decimals.
Solution:

Question 9.
Find the value of (1.01)⁵, correct upto three places of decimals.
Solution:

Question 10.
Find the value of (0.9)⁶, correct upto four places of decimals.
Solution: