Category: Class 12

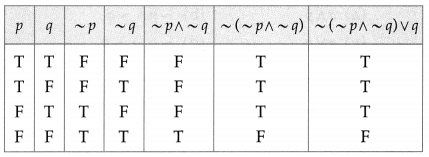
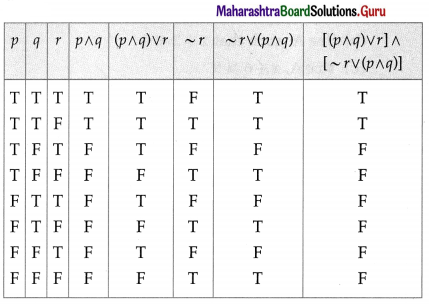
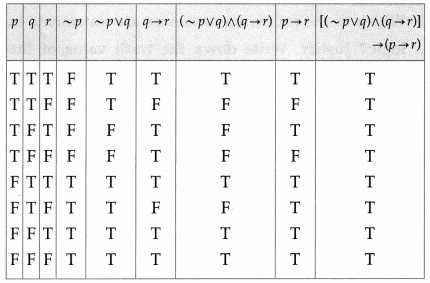
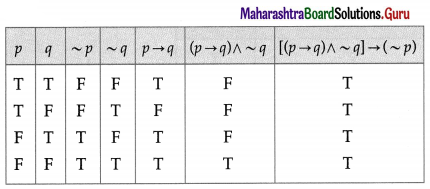
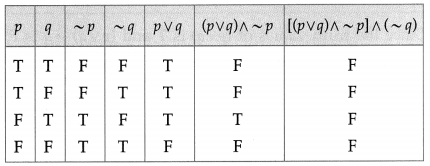
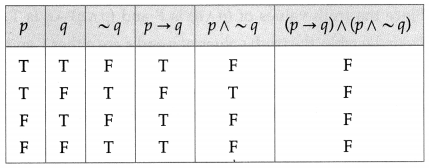
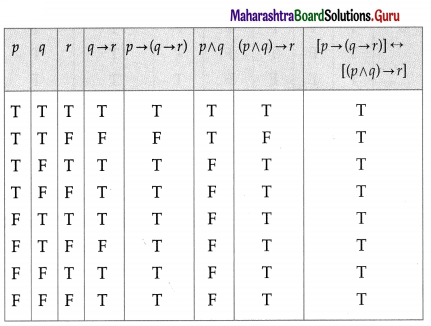
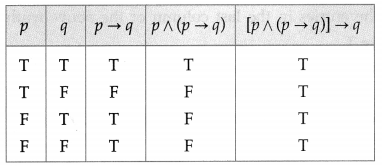
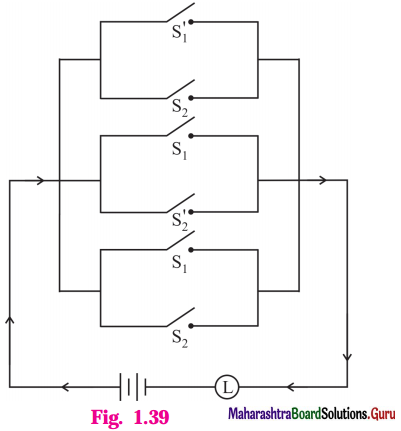
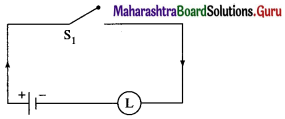
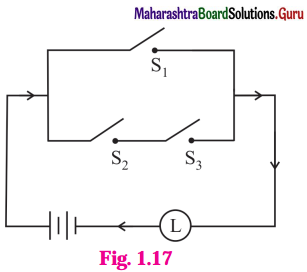
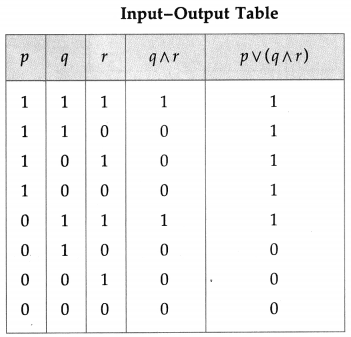
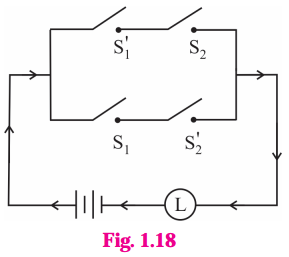
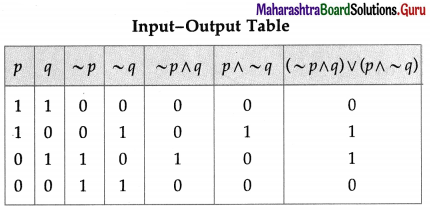
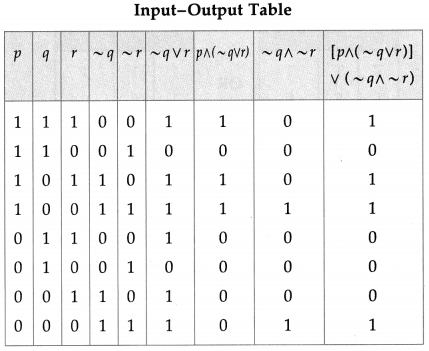
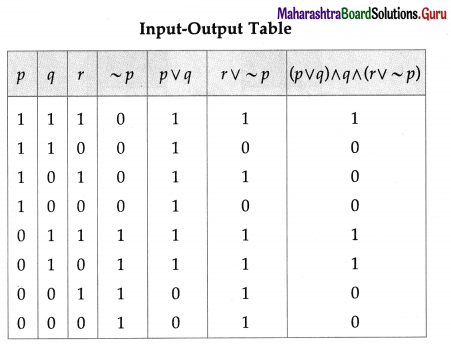
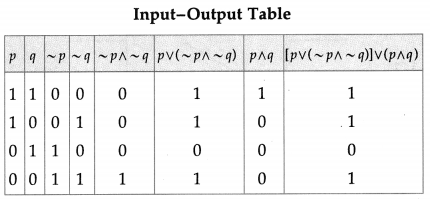
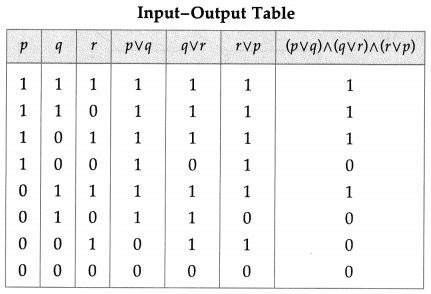
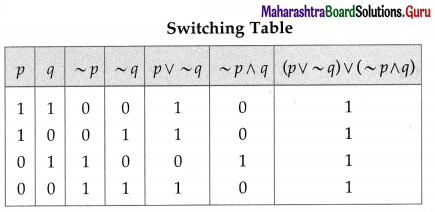
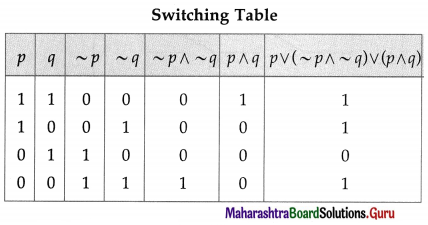
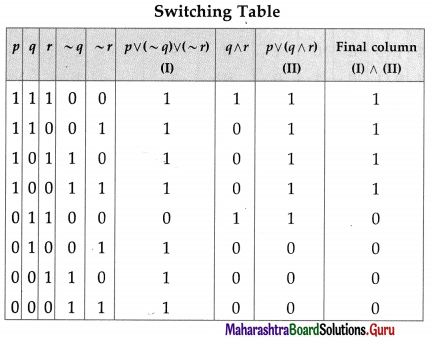
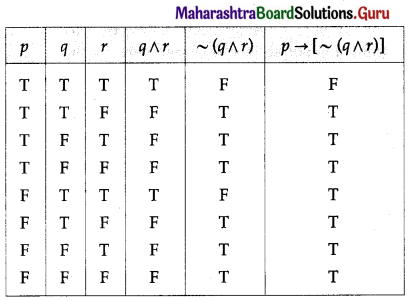
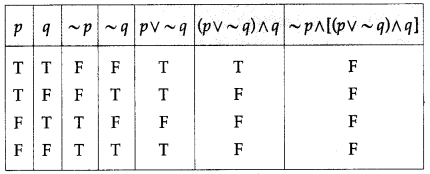
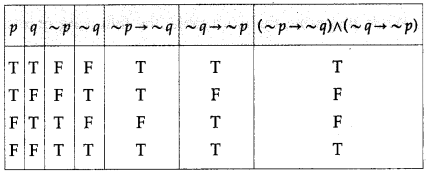
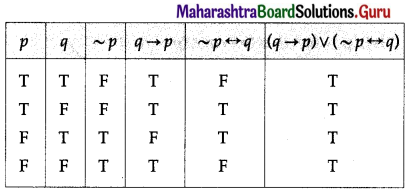
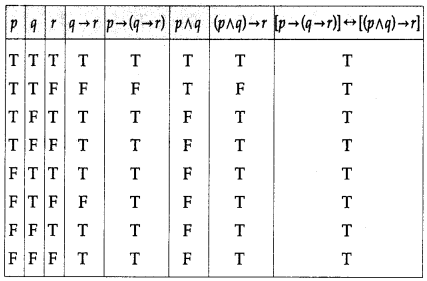
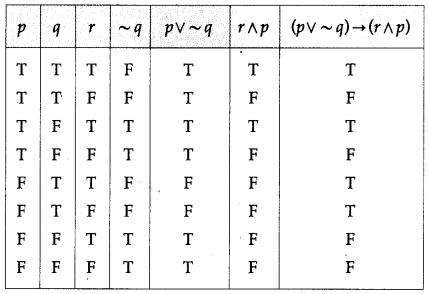
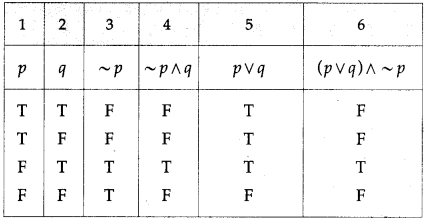
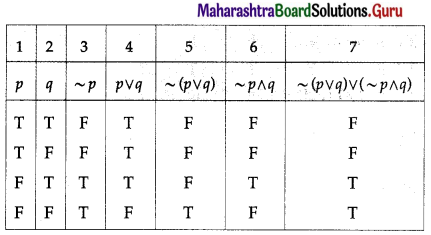
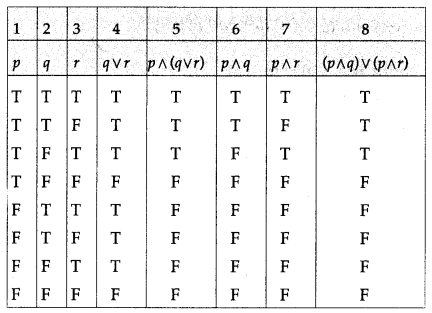
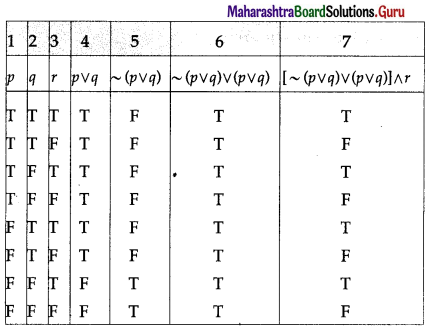
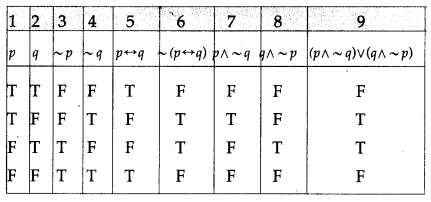
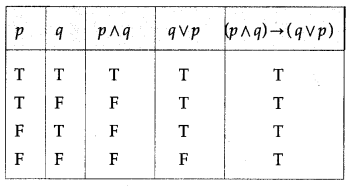
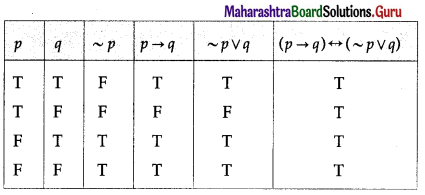
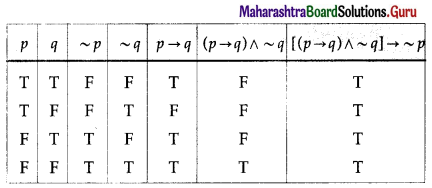
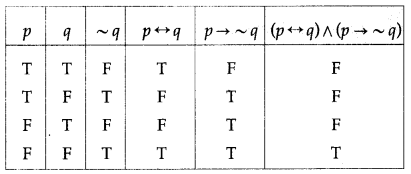
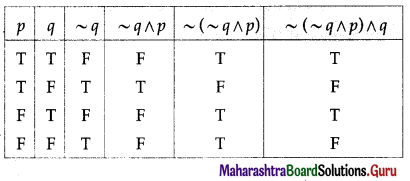
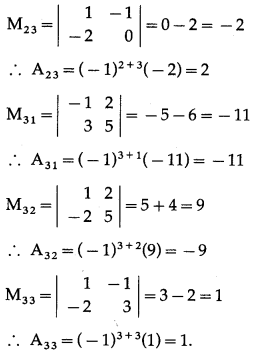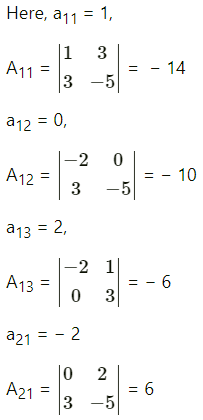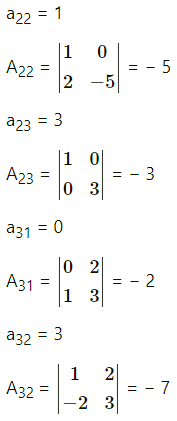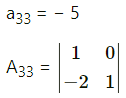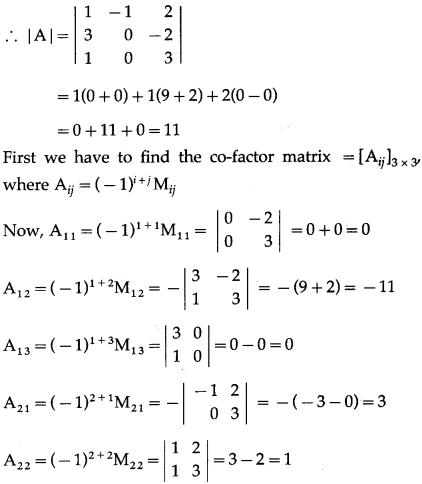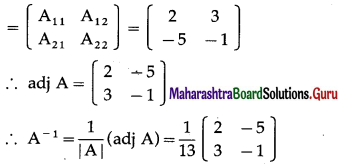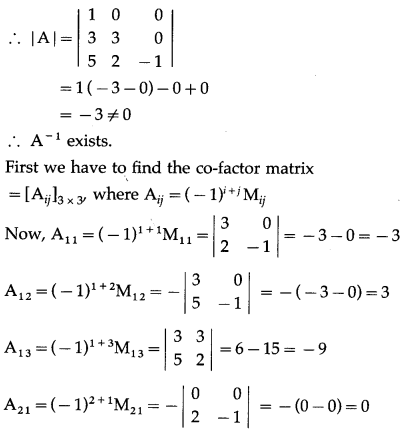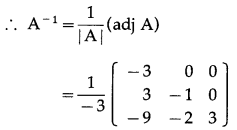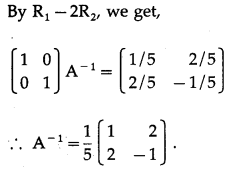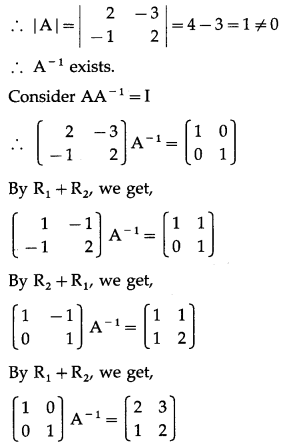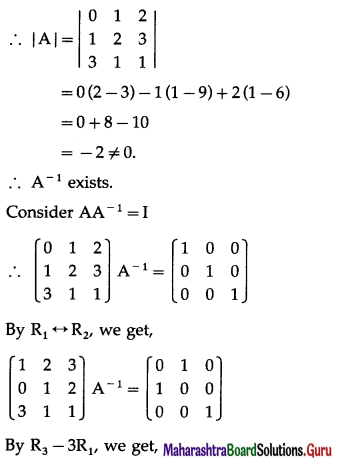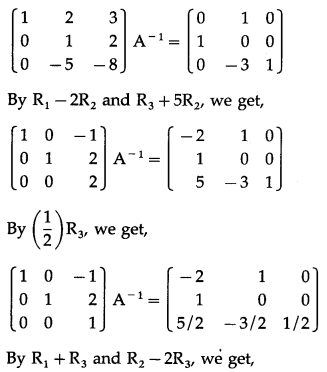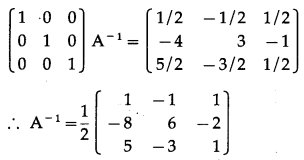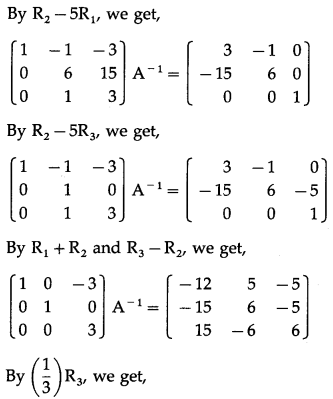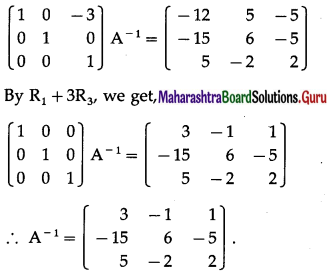Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.3 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.3 Questions And Answers Maharashtra Board

Question 1.
Solve the following equations by the inversion method.
(i) x + 2y = 2, 2x + 3y = 3
Solution:
The given equations can be written in the matrix form as :
\(\left[\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)
This is of the form AX = B, where

∴ A^-1 = \(\left[\begin{array}{rr}
-3 & 2 \\
2 & -1
\end{array}\right]\)
Now, premultiply AX = B by A^-1, we get,
A^-1(AX) = A^-1B
∴ (A^-1A)X = A^-1B
∴ IX = A^-1B
∴ X = \(=\left[\begin{array}{rr}
-3 & 2 \\
2 & -1
\end{array}\right]\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)
∴ \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(=\left[\begin{array}{r}
-6+6 \\
4-3
\end{array}\right]\) = \(=\left[\begin{array}{l}
0 \\
1
\end{array}\right]\)
By equality of matrices,
x = 0, y = 1 is the required solution.

(ii) x + y = 4, 2x – y = 5
Solution:
x + y = 4, 2x – y = 5
The given equations can be written in the matrix form as:
\(\left[\begin{array}{cc}
1 & 1 \\
2 & -1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
4 \\
5
\end{array}\right]\)
This is of the form AX = B ⇒ X ⇒ A^-1B
A = \(\left[\begin{array}{cc}
1 & 1 \\
2 & -1
\end{array}\right]\)
|A| = -1 – 2 = -3 ≠ 0

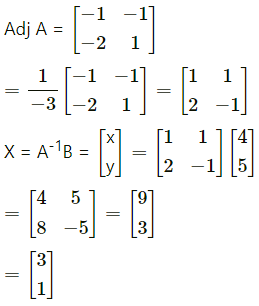
By equality of matrices.
x = 3, y = 1

(iii) 2x + 6y = 8, x + 3y = 5
Solution:
The given equations can be written in the matrix form as :
\(\left[\begin{array}{ll}
2 & 6 \\
1 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
8 \\
5
\end{array}\right]\)
This is of the form AX = B, where
A = \(\left[\begin{array}{ll}
2 & 6 \\
1 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
8 \\
5
\end{array}\right]\)
Let us find A^-1.
|A| = \(\left|\begin{array}{ll}
2 & 6 \\
1 & 3
\end{array}\right|\) = 6 – 6 = 0
∴ A^-1 does not exist.
Hence, x and y do not exist.

Question 2.
Solve the following equations by reduction method.
(i) 2x + y = 5, 3x + 5y = -3
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
2x + y = 5 …(1)
7y = -21 …(2)
From (2), y = -3
Substituting y = -3 in (1), we get,
2x – 3 = 5
∴ 2x = 8 ∴ x = 4
Hence, x = 4, y = -3 is the required solution.

(ii) x + 3y = 2, 3x + 5y = 4.
Solution:
The given equations can be written in the matrix form as :
\(\left[\begin{array}{ll}
1 & 3 \\
3 & 5
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
4
\end{array}\right]\)
By R₂ – 3R₁, we get
\(\left[\begin{array}{rr}
1 & 3 \\
0 & -4
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left(\begin{array}{r}
2 \\
-2
\end{array}\right)\)
∴ \(\left[\begin{array}{l}
x+3 \\
0-4 y
\end{array}\right]\) = \(\left[\begin{array}{r}
2 \\
-2
\end{array}\right]\)
By equality of matrices,
x + 3y = 2 …(1)
-4y = -2
From (2), y = \(\frac{1}{2}\)
Substituting y = \(\frac{1}{2}\) in (1), we get,
x + \(\frac{3}{2}\) = 2
∴ x = 2 – \(\frac{3}{2}=\frac{1}{2}\)
Hence, x = \(\frac{1}{2}\), y = \(\frac{1}{2}\) is the required solution.

(iii) 3x – y = 1, 4x + y = 6
Solution:
The given equations can be written in the matrix form as :

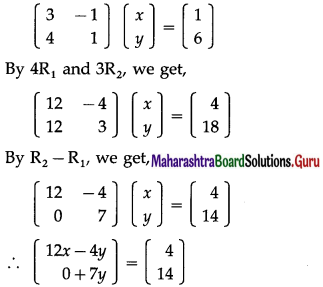
By equality of matrices,
12x – 4y = 4 … (1)
7y = 14 … (2)
From (2), y = 2
Substituting y = 2 in (1), we get,
12x – 8 = 4
∴ 12x = 12 ∴ x = 1
Hence, x = 1, y = 2 is the required solution.

(iv) 5x + 2y = 4, 7x + 3y = 5
Solution:
5x + 2y = 4 ………..(1)
7x + 3y = 5 …………(2)
Multiplying Eq. (1) with 7 and Eq. (2) with 5

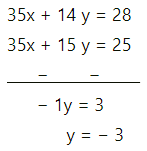
Put y = -3 into Eq. (1)
5x + 2y = 4
5x + 2(-3) = 4
5x – 6 = 4
5x = 4 + 6
5x = 10
x = \(\frac{10}{5}\)
x = 2
Hence, x = 2, y = -3 is the required solution.

Question 3.
The cost of 4 pencils, 3 pens and 2 erasers is ₹ 60. The cost of 2 pencils, 4 pens and 6 erasers is ₹ 90, whereas the cost of 6 pencils, 2 pens and 3 erasers is ₹ 70. Find the cost of each item by using matrices.
Solution:
Let the cost of 1 pencil, 1 pen and 1 eraser be ₹ x, ₹ y and ₹ z respectively.
Then, from the given conditions,
4x + 3y + 2z = 60
2x + 4y + 6z = 90, i.e., x + 2y + 3z = 45
6x + 2y + 3z = 70
These equations can be written in the matrix form as :

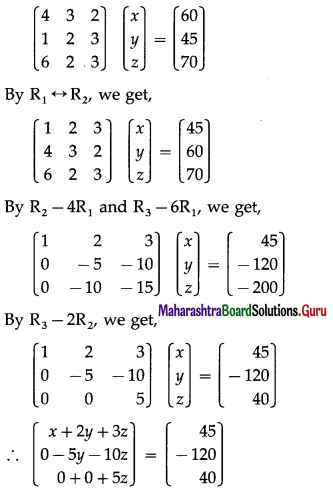
By equality of matrices,
x + 2y + 3z = 45 …….(1)
– 5y – 10z = – 120 …….(2)
5z = 40
From (3), z = 8
Substituting z = 8 in (2), we get,
– 5y – 80 = -120
∴ – 5y = -40 ∴ y = 8
Substituting y = 8, z = 8 in (1), we get,
x + 16 + 24 = 45
∴ x + 40 = 45 ∴ x = 5
∴ x = 5, y = 8, z = 8
Hence, the cost is ₹ 5 for a pencil, ₹ 8 for a pen and ₹ 8 for an eraser.

Question 4.
If three numbers are added, their sum is 2. If 2 times the second number is subtracted from the sum of first and third numbers, we get 8 and if three times the first number is added to the sum of second and third numbers, we get 4. Find the numbers using matrices.
Solution:
Let the three numbers be x, y and z. According to the given conditions,
x + y + z = 2
x + z – 2y = 8, i.e., x – 2y + 2 = 8
and y + z + 3x = 4, i.e., 3x + y + z = 4
Hence, the system of linear equations is
x + y + z = 2
x – 2y + z = 8
3x + y + z = 4
These equations can be written in the matrix form as :

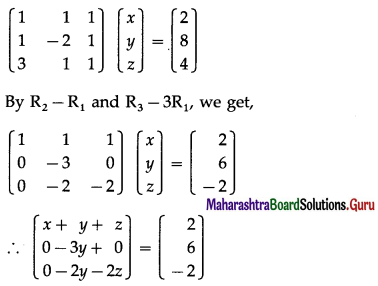
By equality of matrices,
x + y + z = 2 ……(1)
-3y = 6 ……(2)
– 2y – 2z = -2 ……..(3)
From (2), y = -2
Substituting y = -2 in (3), we get,
-2(-2) – 2z = -2
∴ -2z = -6 ∴ z = 3
Substituting y = -2, z = 3 in (1), we get,
x – 2 + 3 = 2 ∴ x = 1
Hence, the required numbers are 1, -2 and 3.

Question 5.
The total cost of 3 T.V. sets and 2 V.C.R.s is ₹ 35000. The shop-keeper wants profit of ₹ 1000 per television and ₹ 500 per V.C.R. He can sell 2 T. V. sets and 1 V.C.R. and get the total revenue as ₹ 21,500. Find the cost price and the selling price of a T.V. sets and a V.C.R.
Solution:
Let the cost of each T.V. set be ₹ x and each V.C.R. be ₹ y. Then the total cost of 3 T.V. sets and 2 V.C.R.’s is ₹ (3x + 2y) which is given to be ₹ 35,000.
∴ 3x + 2y = 35000
The shopkeeper wants profit of ₹ 1000 per T.V. set and of ₹ 500 per V.C.R.
∴ the selling price of each T.V. set is ₹ (x + 1000) and of each V.C.R. is ₹ (y + 500).
∴ selling price of 2 T.V. set and 1 V.C.R. is
₹ [2(x + 1000) + (y + 500)] which is given to be ₹ 21,500.
∴ 2(x + 1000) + (y + 500) = 21500
∴ 2x + 2000 + y + 500 = 21500
∴ 2x + y = 19000
Hence, the system of linear equations is
3x + 2y = 35000
2x + y = 19000
These equations can be written in the matrix form as :

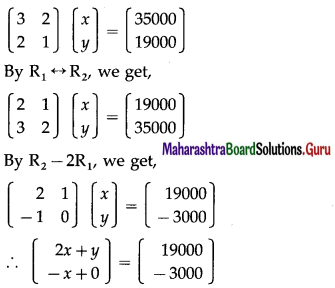
By equality of matrices,
2x + y = 19000 ……….(1)
-x = -3000 ……….(2)
From (2), x = 3000
Substituting x = 3000 in (1), we get,
2(3000) + y = 19000
∴ y = 13000
∴ the cost price of one T.V. set is ₹ 3000 and of one V.C.R. is ₹ 13000 and the selling price of one T.V. set is ₹ 4000 and of one V.C.R. is ₹ 13500.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.2 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.2 Questions And Answers Maharashtra Board

Question 1.
Find the co-factors of the elements of the following matrices
(i) \(\left[\begin{array}{cc}
-1 & 2 \\
-3 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
-1 & 2 \\
-3 & 4
\end{array}\right]\)
Here, a₁₁ = -11, M₁₁ = 4
∴ A₁₁ = (-1)¹⁺¹(4) = 4
a₁₂ = 2, M₁₂ = -3
∴ A₁₂ = (-1)¹⁺²(- 3) = 3
a₂₁ = – 3, M₂₁ = -2
∴ A₂₁ = (- 1)²⁺¹(2) = -2
a₂₂ = 4, M₂₂ = -1
∴ A₂₂ = (-1)²⁺²(-1) = -1.

(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
The co-factor of a_ij is given by A_ij = (-1)^i+jM_ij

Question 2.
Find the matrix of co-factors for the following matrices
(i) \(\left[\begin{array}{rr}
1 & 3 \\
4 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rr}
1 & 3 \\
4 & -1
\end{array}\right]\)
Here, a₁₁ = 1, M₁₁ = -1
∴ A₁₁ = (-1)¹⁺¹(-1) = -1
a₁₂ = 3, M₁₂ = 4
∴ A₁₂ = (-1)¹⁺²(4) = -4
a₂₁ = 4, M₂₁ = 3
∴ A₂₁ = (-1)²⁺¹(3) = -3
a₂₂ = -1, M₂₂ = 1
∴ A₂₂ = (-1)²⁺¹(1) = 1
∴ the co-factor matrix = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\)
= \(\left(\begin{array}{rr}
-1 & -4 \\
-3 & 1
\end{array}\right)\)

(ii) \(\left[\begin{array}{rrr}
1 & 0 & 2 \\
-2 & 1 & 3 \\
0 & 3 & -5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rrr}
1 & 0 & 2 \\
-2 & 1 & 3 \\
0 & 3 & -5
\end{array}\right]\)



A₁₁ = -14, A₁₂ = -10, A₁₃ = -6,
A₂₁ = 6, A₂₂ = -5, A₂₃ = -3,
A₃₁ = -2, A₃₂ = -7, A₃₃ = 1.
∴ the co-factor matrix
= \(\left[\begin{array}{lll}
A_{11} & A_{12} & A_{13} \\
A_{21} & A_{22} & A_{23} \\
A_{31} & A_{32} & A_{33}
\end{array}\right]\) = \(\left[\begin{array}{rrr}
-14 & -10 & -6 \\
6 & -5 & -3 \\
-2 & -7 & 1
\end{array}\right]\)

Question 3.
Find the adjoint of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
Here, a₁₁ = 2, M₁₁= 5
∴ A₁₁ = (-1)¹⁺¹(5) = 5
a₁₂ = -3, M₁₂ = 3
∴ A₁₂ = (-1)¹⁺²(3) = -3
a₂₁ = 3, M₂₁ = -3
∴ A A₂₁ = (-1)²⁺¹(-3) = 3
a₂₂ = 5, M₂₂ = 2
∴ A₂₂ = (-1)²⁺¹ = 2
∴ the co-factor matrix = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\)
= \(\left[\begin{array}{rr}
5 & -3 \\
3 & 2
\end{array}\right]\)
∴ adj A = \(\left(\begin{array}{rr}
5 & 3 \\
-3 & 2
\end{array}\right)\)

(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:


A₁₁ = -3, A₁₂ = -12, A₁₃ = 6,
A₂₁ = -1, A₂₂ = 3, A₂₃ = 2,
A₃₁ = -11, A₃₂ = -9, A₃₃ = 1
∴ the co-factor matrix = \(\left[\begin{array}{lll}
\mathrm{A}_{11} & \mathrm{~A}_{12} & \mathrm{~A}_{15} \\
\mathrm{~A}_{21} & \mathrm{~A}_{22} & \mathrm{~A}_{23} \\
\mathrm{~A}_{31} & \mathrm{~A}_{32} & \mathrm{~A}_{33}
\end{array}\right]\)
= \(\left[\begin{array}{rrr}
-3 & -12 & 6 \\
-1 & 3 & 2 \\
-11 & -9 & 1
\end{array}\right]\)
∴ adj A = \(\left[\begin{array}{rrr}
-3 & -1 & -11 \\
-12 & 3 & -9 \\
6 & 2 & 1
\end{array}\right]\)

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\), verify that A (adj A) = (adj A) A = | A | ∙ I
Solution:
A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)




From (1), (2) and (3), we get,
A(adj A) = (adj A)A = |A|∙I.
Note: This relation is valid for any non-singular matrix A.

Question 5.
Find the inverse of the following matrices by the adjoint method
(i) \(\left[\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right|\) = -2 + 15 = 13 ≠ 0
∴ A^-1 exists.
First we have to find the co-factor matrix
= [A_ij]_2×2, where A_ij = (-1)^i+jM_ij
Now, A₁₁ = (-1)¹⁺¹M₁₁ = 2
A₁₂ = (-1)¹⁺²M₁₂ = -(-3) = 3
A₂₁ = (-1)²⁺¹M₂₁ = -5
A₂₂ = (-1)²⁺²M₂₂ = -1
Hence, the co-factor matrix

(ii) \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
|A| = \(\) = 6 + 8 = 14 ≠ 0
∴ A^-1 exist
First we have to find the co-factor matrix
= [A_ij] _2×2 where A_ij = (-1)^i+jM_ij
Now, A₁₁ = (-1)¹⁺¹M₁₁ = 3
A₁₂ = (-1)¹⁺²M = -4
A₂₁ = (-2)²⁺¹M₂₁ = (-2) = 2
A₂₂ = (-1)²⁺²M₂₂ = 2
Hence the co-factor matrix
= \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\) = \(\left[\begin{array}{cc}
3 & -4 \\
2 & 2
\end{array}\right]\)
∴ adj A = \(\left[\begin{array}{cc}
3 & 2 \\
-4 & 2
\end{array}\right]\)
∴ A^-1 = \(\frac{1}{|\mathrm{~A}|}\) (adj A) = \(\frac{1}{14}\left(\begin{array}{cc}
3 & 2 \\
-4 & 2
\end{array}\right)\)

(iii) \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)



∴ A^-1 = \(\frac{1}{3}\left[\begin{array}{rrr}
3 & 0 & 0 \\
-3 & 1 & 0 \\
9 & 2 & -3
\end{array}\right]\)

(iv) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
∴ |A| = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
= 1(10 – 0) – 0 + 0
= 1(10) – 0 + 0
= 10 ≠ 0
∴ A^-1 exists.
First we have to find the co-factor matrix


∴ A^-1 = \(\frac{1}{|\mathrm{~A}|}\) (adj A)
= \(\frac{1}{10}\left(\begin{array}{rrr}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right)\)
∴ A^-1 = \(\frac{1}{10}\left(\begin{array}{rrr}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right)\)

Question 6.
Find the inverse of the following matrices
(i) \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\)

∴ A^-1 = \(\left(\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right)\)

(iii) \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)

(iv) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.1 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.1 Questions And Answers Maharashtra Board

Question 1.
Apply the given elementary transformation on each of the following matrices.
A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 3
\end{array}\right]\), R₁ ↔ R₂
Solution:
A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 3
\end{array}\right]\)
By R₁ ↔ R₂, we get,
A ~ \(\left[\begin{array}{rr}
-1 & 3 \\
1 & 0
\end{array}\right]\)

Question 2.
B = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 5 & 4
\end{array}\right]\), R₁ → R₁ → R₂
Solution:
B = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 5 & 4
\end{array}\right]\),
R₁ → R₁ → R₂ gives,
B ~ \(\left[\begin{array}{rrr}
-1 & -6 & -1 \\
2 & 5 & 4
\end{array}\right]\)

Question 3.
A = \(\left[\begin{array}{ll}
5 & 4 \\
1 & 3
\end{array}\right]\), C₁ ↔ C₂; B = \(\left[\begin{array}{ll}
3 & 1 \\
4 & 5
\end{array}\right]\), R₁ ↔ R₂. What do you observe?
Solution:
A = \(\left[\begin{array}{ll}
5 & 4 \\
1 & 3
\end{array}\right]\)
By C₁ ↔ C₂, we get,
A ~ \(\left[\begin{array}{ll}
4 & 5 \\
3 & 1
\end{array}\right]\) …(1)
B = \(\left[\begin{array}{ll}
3 & 1 \\
4 & 5
\end{array}\right]\)
By R₁ ↔ R₂, we get,
B ~ \(\left[\begin{array}{ll}
4 & 5 \\
3 & 1
\end{array}\right]\) …(2)
From (1) and (2), we observe that the new matrices are equal.

Question 4.
A = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & 1 & 3
\end{array}\right]\), 2C₂
B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 4 & 5
\end{array}\right]\), -3R₁
Find the addition of the two new matrices.
Solution:
A = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & 1 & 3
\end{array}\right]\)
By 2C₂, we get,
A ~ \(\left[\begin{array}{rrr}
1 & 4 & -1 \\
0 & 2 & 3
\end{array}\right]\)
B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 4 & 5
\end{array}\right]\)
By -3R₁, we get,
B ~ \(\left[\begin{array}{rrr}
-3 & 0 & -6 \\
2 & 4 & 5
\end{array}\right]\)
Now, addition of the two new matrices

Question 5.
A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\), 3R₃ and then C₃ + 2C₂.
Solution:
A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\)
By 3R₃, we get
A ~ \(\left[\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
9 & 9 & 3
\end{array}\right]\)
By C₃ + 2C₂, we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 3+2(-1) \\
2 & 1 & 0+2(1) \\
9 & 9 & 3+2(9)
\end{array}\right)\)
∴ A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
9 & 9 & 21
\end{array}\right)\)

Question 6.
A = \(\left(\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right)\), C₃ + 2C₂ and then 3R₃. What do you conclude from Ex. 5 and Ex. 6 ?
Solution:
A = \(\left(\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right)\)
By C₃ + 2C₂, we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 3+2(-1) \\
2 & 1 & 0+2(1) \\
3 & 3 & 1+2(3)
\end{array}\right)\)
∴ A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
3 & 3 & 7
\end{array}\right)\)
By 3R₃, we get
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
9 & 9 & 21
\end{array}\right)\)
We conclude from Ex. 5 and Ex. 6 that the matrix remains same by interchanging the order of the elementary transformations. Hence, the transformations are commutative.

Question 7.
Use suitable transformation on \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) into an upper triangular matrix.
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
By R₂ – 3R₁, we get,
A ~ \(\left[\begin{array}{rr}
1 & 2 \\
0 & -2
\end{array}\right]\)
This is an upper triangular matrix.

Question 8.
Convert \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\) into an identity matrix by suitable row transformations.
Solution:
Let A = \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\)
By R₂ – 2R₁, we get,
A ~ \(\left[\begin{array}{rr}
1 & -1 \\
0 & 5
\end{array}\right]\)
By \(\left(\frac{1}{5}\right)\)R₂, we get,
A ~ \(\left[\begin{array}{rr}
1 & -1 \\
0 & 1
\end{array}\right]\)
By R₁ + R₂, we get,
A ~ \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
This is an identity matrix.

Question 9.
Transform \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\) into an upper triangular matrix by suitable row transformations.
Solution:
Let A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\)
By R₂ – 2R₁ and R₃ – 3R₁, we get
A ~ \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
0 & 3 & -1 \\
0 & 5 & -2
\end{array}\right]\)
By R₃ – \(\left(\frac{5}{3}\right)\)R₂, we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 2 \\
0 & 3 & -1 \\
0 & 0 & -\frac{1}{3}
\end{array}\right)\)
This is an upper triangular matrix.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Miscellaneous Exercise 1 Questions and Answers.

12th Maths Part 1 Mathematical Logic Miscellaneous Exercise 1 Questions And Answers Maharashtra Board

Question 1.
Select and write the correct answer from the given alternatives in each of the following questions :
i) If p ∧ q is false and p ∨ q is true, the ________ is not true.
(A) p ∨ q
(B) p ↔ q
(C) ~p ∨ ~q
(D) q ∨ ~p
Solution:
(b) p ↔ q.

(ii) (p ∧ q) → r is logically equivalent to ________.
(A) p → (q → r)
(B) (p ∧ q) → ~r
(C) (~p ∨ ~q) → ~r
(D) (p ∨ q) → r
Solution:
(a) p → (q → r) [Hint: Use truth table.]

(iii) Inverse of statement pattern (p ∨ q) → (p ∧ q) is ________.
(A) (p ∧ q) → (p ∨ q)
(B) ~(p ∨ q) → (p ∧ q)
(C) (~p ∧ ~q) → (~p ∨ ~q)
(D) (~p ∨ ~q) → (~p ∧ ~q)
Solution:
(c) (~p ∧ ~q) → (~p ∨ ~ q)

(iv) If p ∧ q is F, p → q is F then the truth values of p and q are ________.
(A) T, T
(B) T, F
(C) F, T
(D) F, F
Solution:
(b) T, F

(v) The negation of inverse of ~p → q is ________.
(A) q ∧ p
(B) ~p ∧ ~q
(C) p ∧ q
(D) ~q → ~p
Solution:
(a) q ∧ p

(vi) The negation of p ∧ (q → r) is ________.
(A) ~p ∧ (~q → ~r)
(B) p ∨ (~q ∨ r)
(C) ~p ∧ (~q → ~r)
(D) ~p ∨ (~q ∧ ~r)
Solution:
(d) ~p ∨ (q ∧ ~r)

(vii) If A = {1, 2, 3, 4, 5} then which of the following is not true?
(A) Ǝ x ∈ A such that x + 3 = 8
(B) Ǝ x ∈ A such that x + 2 < 9
(C) Ɐ x ∈ A, x + 6 ≥ 9
(D) Ǝ x ∈ A such that x + 6 < 10
Solution:
(c) Ǝ x ∈ A, x + 6 ≥ 9.

Question 2.
Which of the following sentences are statements in logic? Justify. Write down the truth
value of the statements :
(i) 4! = 24.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(ii) π is an irrational number.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(iii) India is a country and Himalayas is a river.
Solution:
It is a statement which is false, hence its truth value is ‘F’. ….[T ∧ F ≡ F]

(iv) Please get me a glass of water.
Solution:
It is an imperative sentence, hence it is not a statement.

(v) cos²θ – sin²θ = cos2θ for all θ ∈ R.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(vi) If x is a whole number the x + 6 = 0.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

Question 3.
Write the truth values of the following statements :
(i) \(\sqrt {5}\) is an irrational but \(3\sqrt {5}\) is a complex number.
Solution:
Let p : \(\sqrt {5}\) is an irrational.
q : \(3\sqrt {5}\) is a complex number.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(ii) Ɐ n ∈ N, n² + n is even number while n² – n is an odd number.
Solution:
Let p : Ɐ n ∈ N, n² + n is an even number.
q : Ɐ n ∈ N, n² – n is an odd number.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F].

(iii) Ǝ n ∈ N such that n + 5 > 10.
Solution:
Ǝ n ∈ N, such that n + 5 > 10 is a true statement, hence its truth value is T.
(All n ≥ 6, where n ∈ N, satisfy n + 5 > 10).

(iv) The square of any even number is odd or the cube of any odd number is odd.
Solution:
Let p : The square of any even number is odd.
q : The cube of any odd number is odd.
Then the symbolic form of the given statement is p ∨ q.
The truth values of p and q are F and T respectively.
∴ the truth value of p ∨ q is T. … [F ∨ T ≡ T].

(v) In ∆ ABC if all sides are equal then its all angles are equal.
Solution:
Let p : ABC is a triangle and all its sides are equal.
q : Its all angles are equal.
Then the symbolic form of the given statement is p → q
If the truth value of p is T, then the truth value of q is T.
∴ the truth value of p → q is T. … [T → T ≡ T].

(vi) Ɐ n ∈ N, n + 6 > 8.
Solution:
Ɐ n ∈ N, 11 + 6 > 8 is a false statement, hence its truth value is F.
{n = 1 ∈ N, n = 2 ∈ N do not satisfy n + 6 > 8).

Question 4.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of each of the following statement :
(i) Ǝ x ∈ A such that x + 8 = 15.
Solution:
True

(ii) Ɐ x ∈ A, x + 5 < 12.
Solution:
False

(iii) Ǝ x ∈ A, such that x + 7 ≥ 11.
Solution:
True

(iv) Ɐ x ∈ A, 3x ≤ 25.
Solution:
False

Question 5.
Write the negations of the following :
(i) Ɐ n ∈ A, n + 7 > 6.
Solution:
The negation of the given statements are :
Ǝ n ∈ A, such that n + 7 ≤ 6.
OR Ǝ n ∈ A, such that n + 7 ≯ 6.

(ii) Ǝ x ∈ A, such that x + 9 ≤ 15.
Solution:
Ɐ x ∈ A, x + 9 > 15.

(iii) Some triangles are equilateral triangle.
Solution:
All triangles are not equilateral triangles.

Question 6.
Construct the truth table for each of the following :
(i) p → (q → p)
Solution:

(ii) (~p ∨ ~q) ↔ [~(p ∧ q)]
Solution:

(iii) ~(~p ∧ ~q) ∨ q
Solution:

(iv) [(p ∧ q) ∨ r] ∧ [~r ∨ (p ∧ q)]
Solution:

(v) [(~p ∨ q) ∧ (q → r)] → (p → r)
Solution:

Question 7.
Determine whether the following statement patterns are tautologies contradictions or contingencies :
(i) [(p → q) ∧ ~q)] → ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q)] → ~p is a tautology.

(ii) [(p ∨ q) ∧ ~p] ∧ ~q
Solution:

All the entries in the last column of the above truth table are F.
∴ [(p ∨ q) ∧ ~p] ∧ ~q is a contradiction.

(iii) (p → q) ∧ (p ∧ ~q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p → q) ∧ (p ∧ ~q) is a contradiction.

(iv) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:

All the entries in the last column of the above truth table are T.
∴ [p → (q → r)] ↔ [(p ∧ q) → r] is a tautology.

(v) [(p ∧ (p → q)] → q
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p ∧ (p → q)] → q is a tautology.

(vi) (p ∧ q) ∨ (~p ∧ q) ∨ (p ∨ ~q) ∨ (~p ∧ ~q)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p ∧ q) ∨ (~p ∧ q) ∨ (p ∨ ~q) ∨ (~p ∧ ~q) is a tautology.

(vii) [(p ∨ ~q) ∨ (~p ∧ q)] ∧ r
Solution:

The entries in the last column are neither T nor all F.
∴ [(p ∨ ~q) ∨ (~p ∧ q)] ∧ r is a contingency.

(viii) (p → q) ∨ (q → p)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p → q) ∨ (q → p) is a tautology.

Question 8.
Determine the truth values ofp and q in the following cases :
(i) (p ∨ q) is T and (p ∧ q) is T
Solution:

Since p ∨ q and p ∧ q both are T, from the table the truth values of both p and q are T.

(ii) (p ∨ q) is T and (p ∨ q) → q is F
Solution:

Since the truth values of (p ∨ q) is T and (p ∨ q) → q is F, from the table, the truth values of p and q are T and F respectively.

(iii) (p ∧ q) is F and (p ∧ q) → q is T
Solution:

Since the truth values of (p ∧ q) is F and (p ∧ q) → q is T, from the table, the truth values of p and q are either T and F respectively or F and T respectively or both F.

Question 9.
Using truth tables prove the following logical equivalences :
(i) p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Solution:

The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q).

(ii) (p ∧ q) → r ≡ p → (q → r)
Solution:

The entries in the columns 5 and 7 are identical.
∴ (p ∧ q) → r ≡ p → (q → r).

Question 10.
Using rules in logic, prove the following :
(i) p ↔ q ≡ ~ (p ∧ ~q) ∧ ~(q ∧ ~p)
Solution:
By the rules of negation of biconditional,
~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
∴ ~ [(p ∧ ~ q) ∨ (q ∧ ~p)] ≡ p ↔ q
∴ ~(p ∧ ~q) ∧ ~(q ∧ ~p) ≡ p ↔ q … (Negation of disjunction)
≡ p ↔ q ≡ ~(p ∧ ~ q) ∧ ~ (q ∧ ~p).

(ii) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:
(p ∨ q) ∧ ~ p
≡ (p ∧ ~p) ∨ (q ∧ ~p) … (Distributive Law)
≡ F ∨ (q ∧ ~p) … (Complement Law)
≡ q ∧ ~ p … (Identity Law)
≡ ~p ∧ q …(Commutative Law)
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.

(iii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:
~ (p ∨ q) ∨ (~p ∧ q)
≡ (~p ∧ ~q) ∨ (~p ∧ q) … (Negation of disjunction)
≡ ~p ∧ (~q ∨ q) … (Distributive Law)
≡ ~ p ∧ T … (Complement Law)
≡ ~ p … (Identity Law)
∴ ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p.

Question 11.
Using the rules in logic, write the negations of the following :
(i) (p ∨ q) ∧ (q ∨ ~r)
Solution:
The negation of (p ∨ q) ∧ (q ∨ ~ r) is
~ [(p ∨ q) ∧ (q ∨ ~r)]
≡ ~ (p ∨ q) ∨ ~ (q ∨ ~r) … (Negation of conjunction)
≡ (~p ∧ ~q) ∨ [~q ∧ ~(~r)] … (Negation of disjunction)
≡ {~ p ∧ ~q) ∨ (~q ∧ r) … (Negation of negation)
≡ (~q ∧ ~p) ∨ (~q ∧ r) … (Commutative law)
≡ (~ q) ∧ (~ p ∨ r) … (Distributive Law)

(ii) p ∧ (q ∨ r)
Solution:
The negation of p ∧ (q ∨ r) is
~ [p ∧ (q ∨ r)]
≡ ~ p ∨ ~(q ∨ r) … (Negation of conjunction)
≡ ~p ∨ (~q ∧ ~r) … (Negation of disjunction)

(iii) (p → q) ∧ r
Solution:
The negation of (p → q) ∧ r is
~ [(p → q) ∧ r]
≡ ~ (p → q) ∨ (~ r) … (Negation of conjunction)
≡ (p ∧ ~q) ∨ (~ r) … (Negation of implication)

(iv) (~p ∧ q) ∨ (p ∧ ~q)
Solution:
The negation of (~ p ∧ q) ∨ (p ∧ ~ q) is
~ [(~p ∧ q) ∨ (p ∧ ~q)]
≡ ~(~p ∧ q) ∧ ~ (p ∧ ~q) … (Negation of disjunction)
≡ [~(~p) ∨ ~q] ∧ [~p ∨ ~(q)] … (Negation of conjunction)
≡ (p ∨ ~ q) ∧ (~ p ∨ q) … (Negation of negation)

Question 12.
Express the following circuits in the symbolic form. Prepare the switching table :
(i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q: the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is :
(p ∧ q) ∨ (~p) ∨ (p ∧ ~q).

(ii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed.
Then the symbolic form of the given statement is : (p ∨ q) ∧ (p ∨ r).

Question 13.
Simplify the following so that the new circuit has minimum number of switches. Also, draw the simplified circuit.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p: the switch S₁‘ is closed or the switch S₁ is open
~ q: the switch S₂‘ is closed or the switch S₂ is open.
Then the given circuit in symbolic form is :
(p ∧ ~q) ∨ (~p ∧ q) ∨ (~p ∧ ~q)
Using the laws of logic, we have,
(p ∧ ~q) ∨ (~p ∧ q) ∨ (~p ∧ ~ q)
= (p ∧ ~q) ∨ [(~p ∧ q) ∨ (~p ∧ ~q) …(By Complement Law)
= (p ∧ ~q) ∨ [~p ∧ (q ∨ ~q)} (By Distributive Law)
= (p ∧ ~q) ∨ (~p ∧ T) …(By Complement Law)
= (p ∧ ~q) ∨ ~ p …(By Identity Law)
= (p ∨ ~p) ∧ (~q ∨ ~p) …(By Distributive Law)
= ~q ∨ ~p …(By Identity Law)
= ~p ∨ ~p …(By Commutative Law)
Hence, the simplified circuit for the given circuit is :

(ii)

Solution:
(ii) Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
s : the switch S₄ is closed
t : the switch S₅ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open
~ s : the switch S₄‘ is closed or the switch S₄ is open
~ t : the switch S₅‘ is closed or the switch S₅ is open.
Then the given circuit in symbolic form is
[(p ∧ q) ∨ ~r ∨ ~s ∨ ~t] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)]
Using the laws of logic, we have,
[(p ∧ q) ∨ ~r ∨ ~s ∨ ~ t] ∧ [(p A q) ∨ (r ∧ s ∧ t)]
= [(p∧ q) ∨ ~(r ∧ s ∧ t)] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)] … (By De Morgan’s Law)
= (p ∧ q) ∨ [ ~(r ∧ s ∧ t) ∧ (r ∧ s ∧ t)] … (By Distributive Law)
= (p ∧ q) ∨ F … (By Complement Law)
= p ∧ q … (By Identity Law)
Hence, the alternative simplified circuit is :

Question 14.
Check whether the following switching circuits are logically equivalent – Justify.
(A)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
(A) The symbolic form of the given switching circuits are
p ∧ (q ∨ r) and (p ∧ q) ∨ (p ∧ r) respectively.
By Distributive Law, p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Hence, the given switching circuits are logically equivalent.

(B)

Solution:
The symbolic form of the given switching circuits are
(p ∨ q) ∧ (p ∨ r) and p ∨ (q ∧ r)
By Distributive Law,
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Hence, the given switching circuits are logically equivalent.

Question 15.
Give alternative arrangement of the switching following circuit, has minimum switches.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed, or the switch S₁ is open
~q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form Of the given circuit is :
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r)
Using the laws of logic, we have,
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r)
≡ (p ∧ ~p ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) y (p ∧ ~q ∧ r) …(By Commutative Law)
≡ (F ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Complement Law)
≡ F ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ [(~p ∨ p) ∧ (q ∧ r)] ∨ (p ∧ ~q ∧ r) … (By Distributive Law)
≡ [T ∧ (q ∧ r)] ∨ (p ∧ ~q ∧ r) = (q ∧ r) ∨ (p ∧ ~q ∧ r) …(By Complement Law)
≡ (q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ [q ∨ (p ∧ ~q)] ∧ r … (By Distributive Law)
≡ [q ∨ p) ∧ ((q ∨ ~q)] ∧ r … (By Distributive Law)
≡ [(q ∨ p) ∧ T] ∧ r …(By Complement Law)
≡ (q ∨ p) ∧ r … (By Identity Law)
≡ (p ∨ q) ∧ r …(By Commutative Law)
∴ the alternative arrangement of the new circuit with minimum switches is :

Question 16.
Simplify the following so that the new circuit circuit.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given switching circuit is :
(~p ∨ q) ∨ (p ∨ ~q) ∨ (p ∨ q)
Using the laws of logic, we have,
(~p ∨ q) ∨ (p ∨ ~q) ∨ (p ∨ q)
≡ (~p ∨ q ∨ p ∨ ~q) ∨ (p ∨ q)
≡ [(~p ∨ p) ∨ (q ∨ ~q)] ∨ (p ∨ q) … (By Commutative Law)
≡ (T ∨ T) ∨ (p ∨ q) … (By Complement Law)
≡ T ∨ (p ∨ q) … (By Identity Law)
≡ T … (By Identity Law)
∴ the current always flows whether the switches are open or closed. So, it is not necessary to use any switch in the circuit.
∴ the simplified form of given circuit is :

Question 17.
Represent the following switching circuit in symbolic form and construct its switching table. Write your conclusion from the switching table.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open.
Then, the symbolic form of the given switching circuit is : [p ∨ (~ q) ∨ (~ r)] ∧ [p ∨ (q ∧ r)]

From the table, the’ final column’ and the column of p are identical. Hence, the given circuit is equivalent to the simple circuit with only one switch S₁.
the simplified form of the given circuit is :

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.5 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.5 Questions And Answers Maharashtra Board

Question 1.
Express the following circuits in the symbolic form of logic and writ the input-output table.
(i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed or the switch S₁is open
~q : the switch S₂‘ is closed or the switch S₂ is open
~r : the switch S₃‘ is closed or the switch S₃ is open
l : the lamp L is on
(i) The symbolic form of the given circuit is : p ∨ (q ∧ r) = l
l is generally dropped and it can be expressed as : p ∨ (q ∧ r).

(ii)

Solution:
The symbolic form of the given circuit is : (~ p ∧ q) ∨ (p ∧ ~ q).

(iii)

Solution:
The symbolic form of the given circuit is : [p ∧ (~q ∨ r)] ∨ (~q ∧ ~ r).

(iv)

Solution:
The symbolic form of the given circuit is : (p ∨ q) ∧ q ∧ (r ∨ ~p).

(v)

Solution:
The symbolic form of the given circuit is : [p ∨ (~p ∧ ~q)] ∨ (p ∧ q).

(vi)

Solution:
The symbolic form of the given circuit is : (p ∨ q) ∧ (q ∨ r) ∧ (r ∨ p)

Question 2.
Construct the switching circuit of the following :
(i) (~p∧ q) ∨ (p∧ ~r)
Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open.
Then the switching circuits corresponding to the given statement patterns are :

(ii) (p∧ q) ∨ [~p ∧ (~q ∨ p ∨ r)]
Solution:

(iii) [(p ∧ r) ∨ (~q ∧ ~r)] ∧ (~p ∧ ~r)
Solution:

(iv) (p ∧ ~q ∧ r) ∨ [p ∧ (~q ∨ ~r)]
Solution:

(v) p ∨ (~p ) ∨ (~q) ∨ (p ∧ q)
Solution:

(vi) (p ∧ q) ∨ (~p) ∨ (p ∧ ~q)
Solution:

Question 3.
Give an alternative equivalent simple circuits for the following circuits :
(i)

Solution:
(i) Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch Si is open Then the symbolic form of the given circuit is :
p ∧ (~p ∨ q).
Using the laws of logic, we have,
p ∧ (~p ∨ q)
= (p ∧ ~ p) ∨ (p ∧ q) …(By Distributive Law)
= F ∨ (p ∧ q) … (By Complement Law)
= p ∧ q… (By Identity Law)
Hence, the alternative equivalent simple circuit is :

(ii)

Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~q : the switch S₂‘ is closed or the switch S₂ is open
~r : the switch S₃‘ is closed or the switch S₃ is open.
Then the symbolic form of the given circuit is :
[p ∧ (q ∨ r)] ∨ (~r ∧ ~q ∧ p).
Using the laws of logic, we have
[p ∧ (q ∨ r)] ∨ (~r ∧ ~q ∧ p)
≡ [p ∧ (q ∨ r)] ∨ [ ~(r ∨ q) ∧ p] …. (By De Morgan’s Law)
≡ [p ∧ (q ∨ r)] ∨ [p ∧ ~(q ∨ r)] … (By Commutative Law)
≡ p ∧ [(q ∨ r) ∨ ~(q ∨ r)) … (By Distributive Law)
≡ p ∧ T … (By Complement Law)
≡ p … (By Identity Law)
Hence, the alternative equivalent simple circuit is :

Question 4.
Write the symbolic form of the following switching circuits construct its switching table and interpret it.
i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is :
(p ∨ ~q) ∨ (~p ∧ q)

Since the final column contains all’ 1′, the lamp will always glow irrespective of the status of switches.

ii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~p : the switch S₁ is closed or the switch S₁ is open.
~q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is : p ∨ (~p ∧ ~q) ∨ (p ∧ q)

Since the final column contains ‘0’ when p is 0 and q is ‘1’, otherwise it contains ‘1′.
Hence, the lamp will not glow when S₁ is OFF and S₂ is ON, otherwise the lamp will glow.

iii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~q : the switch S₂‘ is closed or the switch S₂ is open
~r: the switch S₃‘ is closed or the switch S₃ is open.
Then the symbolic form of the given circuit is : [p ∨ (~q) ∨ r)] ∧ [p ∨ (q ∧ r)]

From the switching table, the ‘final column’ and the column of p are identical. Hence, the lamp will glow which S₁ is ‘ON’.

Question 5.
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(i) p ∨ (q ∧ ~ q)
Solution:
Using the laws of logic, we have, p ∨ (q ∧ ~q)
≡ p ∨ F … (By Complement Law)
≡ p … (By Identity Law)
Hence, the simple logical expression of the given expression is p.
Let p : the switch S₁ is closed
Then the corresponding switching circuit is :

(ii) (~p ∧ q) ∨ (~p ∧ ~q) ∨ (p ∧ ~q)]
Solution:
Using the laws of logic, we have,
(~p ∧ q) ∨ (~p ∨ ~q) ∨ (p ∧ ~q)
≡ [~p ∧ (q ∨ ~q)] ∨ (p ∧ ~ q)… (By Distributive Law)
≡ (~p ∧ T) ∨ (p ∧ ~q) … (By Complement Law)
≡ ~p ∨ (p ∧ ~q) … (By Identity Law)
≡ (~p ∨ p) ∧ (~p ∧~q) … (By Distributive Law)
≡ T ∧ (~p ∧ ~q) … (By Complement Law)
≡ ~p ∨ ~q … (By Identity Law)
Hence, the simple logical expression of the given expression is ~ p ∨ ~q.
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open,
Then the corresponding switching circuit is :

(iii) [p (∨ (~q) ∨ ~r)] ∧ (p ∨ (q ∧ r)
Solution:
Using the laws of logic, we have,
[p ∨ (~ (q) ∨ (~r)] ∧ [p ∨ (q ∧ r)]
= [p ∨ { ~(q ∧ r)}] ∧ [p ∨ (q ∧ r)] … (By De Morgan’s Law)
= p ∨ [~(q ∧ r) ∧ (q ∧ r) ] … (By Distributive Law)
= p ∨ F … (By Complement Law)
= p … (By Identity Law)
Hence, the simple logical expression of the given expression is p.
Let p : the switch S₁ is closed
Then the corresponding switching circuit is :

(iv) (p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) ∨ (p ∧ q ∧ r)
Question is Modified
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r)∨ (p ∧ q ∧ r)
Solution:
Using the laws of logic, we have,
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r)
= (p ∧ ~p ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Commutative Law)
= (F ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Complement Law)
= F ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Identity Law)
= (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Identity Law)
= (~ p ∨ p) ∧ (q ∧ r) … (By Distributive Law)
= T ∧ (q ∧ r) … (By Complement Law)
= q ∧ r … (By Identity Law)
Hence, the simple logical expression of the given expression is q ∧ r.
Let q : the switch S₂ is closed
r : the switch S₃ is closed.
Then the corresponding switching circuit is :

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.4 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.4 Questions And Answers Maharashtra Board

Question 1.
Using rules of negation write the negations of the following with justification.
(i) ~q → p
Solution:
The negation of ~q → p is
~(~q → p) ≡ ~ q ∧ ~p…. (Negation of implication)

(ii) p ∧ ~q
Solution:
The negation of p ∧ ~q is
~(p ∧ ~q) ≡ ~p ∨ ~(~q) … (Negation of conjunction)
≡ ~ p ∨ q … (Negation of negation)

(iii) p ∨ ~q
Solution:
The negation of p ∨ ~ p is
~ (p ∨ ~(q) ≡ ~p ∧ ~(~(q) … (Negation of disjunction)
≡ ~ p ∧ q … (Negation of negation)

(iv) (p ∨ ~q) ∧ r
Solution:
The negation of (p ∨ ~ q) ∧ r is
~[(p ∨ ~q) ∧ r] ≡ ~(p ∨ ~q) ∨ ~r … (Negation of conjunction)
≡ [ ~p ∧ ~(~q)] ∨ ~ r… (Negation of disjunction)
≡ (~ p ∧ q) ∧ ~ r … (Negation of negation)

(v) p → (p ∨ ~q)
Solution:
The negation of p → (p ∨ ~q) is
~ [p → (p ∨ ~q)] ≡ p ∧ ~ (p ∧ ~p) … (Negation of implication)
≡ p ∧ [ ~ p ∧ ~ (~(q)] … (Negation of disjunction)
≡ p ∧ (~ p ∧ q) (Negation of negation)

(vi) ~(p ∧ q) ∨ (p ∨ ~q)
Solution:
The negation of ~(p ∧ q) ∨ (p ∨ ~q) is
~[~(p ∧ q) ∨ (p ∨ ~q)] ≡ ~[~(p ∧ q)] ∧ ~(p ∨ ~q) … (Negation of disjunction)
≡ ~[~(p ∧ q)] ∧ [ p ∧ ~(~q)] … (Negation of disjunction)
≡ (p ∧ q) ∧ (~ p ∧ q) … (Negation of negation)

(vii) (p ∨ ~q) → (p ∧ ~q)
Solution:
The negation of (p ∨ ~q) → (p ∧ ~q) is
~[(p ∨ ~q) → (p ∧ ~q)]
≡ (p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of implication)
≡ (p ∨ ~q) ∧ [ ~p ∨ ~(~q)] … (Negation of conjunction)
≡ (p ∨ ~q) ∧ (~p ∨ q) … (Negation of negation)

(viii) (~ p ∨ ~q) ∨ (p ∧ ~q)
Solution:
The negation of (~ p ∨ ~q) ∨ (p ∧ ~ q) is
~ [(~p ∨ ~q) ∨ (p ∧ ~ q)]
≡ ~(~p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of disjunction)
≡ [~(~p) ∧ ~(~q)] ∧ [~p ∨ ~(~q)] … (Negation of disjunction and conjunction)
≡ (p ∧ q) ∧ (~p ∨ q) … (Negation of negation)

Question 2.
Rewrite the following statements without using if .. then.
(i) If a man is a judge then he is honest.
Solution:
Since p → ≡ ~p ∨ q, the given statements can be written as :
A man is not a judge or he is honest.

(ii) It 2 is a rational number then \(\sqrt {2}\) is irrational number.
Solution:
2 is not a rational number or \(\sqrt {2}\) is irrational number.

(iii) It f(2) = 0 then f(x) is divisible by (x – 2).
Solution:
f(2) ≠ 0 or f(x) is divisible by (x – 2).

Question 3.
Without using truth table prove that :
(i) p ↔ q ≡ (p∧ q) ∨ (~ p ∧ ~q)
Solution:
LHS = p ↔ q
≡ (p ↔ q) ∧ (q ↔ p) … (Biconditional Law)
≡ (~p ∨ q) ∧ (~q ∨ p) … (Conditional Law)
≡ [~p ∧ (~q ∨ p)] ∨ [q ∧ (~q ∨ p)] … (Distributive Law)
≡ [(~p ∧ ~q) ∨ (~p ∧ p)] ∨ [(q ∧ ~q) ∨ (q ∧ p)] … (Distributive Law)
≡ [(~p ∧ ~q) ∨ F] ∨ [F ∨ (q ∧ p)] … (ComplementLaw)
≡ (~ p ∧ ~ q) ∨ (q ∧ p) … (Identity Law)
≡ (~ p ∧ ~ q) ∨ (p ∧ q) … (Commutative Law)
≡ (p ∧ q) ∨ (~p ∧ ~q) … (Commutative Law)
≡ RHS.

(ii) (p ∨ q) ∧ (p ∨ ~q) ≡ p
Solution:
LHS = (p ∨ q) ∧ (p ∨ ~q)
≡ p ∨ (q ∧ ~q) … (Distributive Law)
≡ p ∨ F … (Complement Law)
≡ p … (Identity Law)
≡ RHS.

(iii) (p ∧ q) ∨ (~ p ∧ q) ∨ (p ∧ ~q) ≡ p ∨ q
Solution:
LHS = (p ∧ q) v (~p ∧ q) ∨ (p ∧ ~q)
≡ [(p ∨ ~p) ∧ q] ∨ (p ∧ ~q) … (Distributive Law)
≡ (T ∧ q) ∨ (p ∧ ~q) … (Complement Law)
≡ q ∨ (p ∧ ~q) … (Identity Law)
≡ (q ∨ p) ∧ (q ∨ ~q) … (Distributive Law)
≡ (q ∨ p) ∧ T .. (Complement Law)
≡ q ∨ p … (Identity Law)
≡ p ∨ q … (Commutative Law)
≡ RHS.

(iv) ~[(p ∨ ~q) → (p ∧ ~q)] ≡ (p ∨ ~q) ∧ (~p ∨ q)
Solution:
LHS = ~[(p ∨ ~q) → (p ∧ ~q)]
≡ (p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of implication)
≡ (p ∨ ~q) ∧ [~p ∨ ~(~q)] … (Negation of conjunction)
≡ (p ∨ ~ q) ∧ (~p ∨ q)… (Negation of negation)
≡ RHS.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.3 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.3 Questions And Answers Maharashtra Board

Question 1.
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of each of the following.
(i) Ǝ x ∈ A such that x – 8 = 1
Solution:
Clearly x = 9 ∈ A satisfies x – 8 = 1. So the given statement is true, hence its truth value is T.

(ii) Ɐ x ∈ A, x² + x is an even number
Solution:
For each x ∈ A, x² + x is an even number. So the given statement is true, hence its truth value is T.

(iii) Ǝ x ∈ A such that x² < 0
Solution:
There is no x ∈ A which satisfies x² < 0. So the given statement is false, hence its truth value is F.

(iv) Ɐ x ∈ A, x is an even number
Solution:
x = 3 ∈ A, x = 5 ∈ A, x = 7 ∈ A, x = 9 ∈ A, x = 11 ∈ A do not satisfy x is an even number. So the given statement is false, hence its truth value is F.

(v) Ǝ x ∈ A such that 3x + 8 > 40
Solution:
Clearly x = 11 ∈ A and x = 12 ∈ A satisfies 3x + 8 > 40. So the given statement is true, hence its truth value is T.

(vi) Ɐ x ∈ A, 2x + 9 > 14
Solution:
For each x ∈ A, 2x + 9 > 14. So the given statement is true, hence its truth value is T.

Question 2.
Write the duals of each of the following.
(i) p ∨ (q ∧ r)
Solution:
The duals of the given statement patterns are :
p ∧ (q ∨ r)

(ii) p ∧ (q ∧ r)
Solution:
p ∨ (q ∨ r)

(iii) (p ∨ q) ∧ (r ∨ s)
Solution:
(p ∧ q) ∨ (r ∧ s)

(iv) p ∧ ~q
Solution:
p ∨ ~q

(v) (~p ∨ q) ∧ (~r ∧ s)
Solution:
(~p ∧ q) ∨ (~r ∨ s)

(vi) ~p ∧ (~q ∧ (p ∨ q) ∧ ~r)
Solution:
~p ∨ (~q ∨ (p ∧ q) ∨ ~r)

(vii) [~(p ∨ q)] ∧ [p ∨ ~(q ∧ ~s)]
Solution:
[ ~(p ∧ q)] ∨ [p ∧ ~(q ∨ ~s)]

(viii) c ∨ {p ∧ (q ∨ r)}
Solution:
t ∧ {p ∧ (q Ar)}

(ix) ~p ∨ (q ∧ r) ∧ t
Solution:
~p ∧ (q ∨ r) ∨ c

(x) (p ∨ q) ∨ c
Solution:
(p ∧ q) ∧ t

Question 3.
Write the negations of the following.
(i) x + 8 > 11 or y – 3 = 6
Solution:
Let p : x + 8 > 11, q : y — 3 = 6.
Then the symbolic form of the given statement is p ∨ q.
Since ~(p ∨ q) ≡ ~p ∧ ~q, the negation of given statement is :
‘x + 8 > 11 and y – 3 ≠ 6’ OR
‘x + 8 ≮ 11 and y – 3 ≠ 6’

(ii) 11 < 15 and 25 > 20
Solution:
Let p: 11 < 15, q : 25 > 20.
Then the symbolic form of the given statement is p ∧ q.
Since ~(p ∧ q) ≡ ~p ∨ ~q, the negation of given statement is :
’11 ≮ 15 or 25 > 20.’ OR
’11 ≯ 15 or 25 ≮ 20.’

(iii) Qudrilateral is a square if and only if it is a rhombus.
Solution:
Let p : Quadrilateral is a square.
q : It is a rhombus.
Then the symbolic form of the given statement is p ↔ q.
Since ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p), the negation of given statement is :
‘ Quadrilateral is a square but it is not a rhombus or quadrilateral is a rhombus but it is not a square.’

(iv) It is cold and raining.
Solution:
Let p : It is cold.
q : It is raining.
Then the symbolic form of the given statement is p ∧ q.
Since ~(p ∧ q) ≡ ~p ∨ ~q, the negation of the given statement is :
‘It is not cold or not raining.’

(v) If it is raining then we will go and play football.
Solution:
Let p : It is raining.
q : We will go.
r : We play football.
Then the symbolic form of the given statement is p → (q ∧ r).
Since ~[p → (q ∧ r)] ≡ p ∧ ~(q ∧ r) ≡ p ∧ (q ∨ ~r), the negation of the given statement is :
‘It is raining and we will not go or not play football.’

(vi) \(\sqrt {2}\) is a rational number.
Solution:
Let p : \(\sqrt {2}\) is a rational number.
The negation of the given statement is
‘ ~p : \(\sqrt {2}\) is not a rational number.’

(vii) All natural numbers are whole numers.
Solution:
The negation of the given statement is :
‘Some natural numbers are not whole numbers.’

(viii) Ɐ n ∈ N, n² + n + 2 is divisible by 4.
Solution:
The negation of the given statement is :
‘Ǝ n ∈ N, such that n² + n + 2 is not divisible by 4.’

(ix) Ǝ x ∈ N such that x – 17 < 20
Solution:
The negation of the given statement is :
‘Ɐ x ∈ N, x – 17 ≯ 20.’

Question 4.
Write converse, inverse and contrapositive of the following statements.
(i) If x < y then x² < y² (x, y ∈ R)
Solution:
Let p : x < y, q : x² < y².
Then the symbolic form of the given statement is p → q.
Converse : q → p is the converse of p → q.
i.e. If x² < y², then x < y.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If x ≯ y, then x² ≯ y². OR
If x ≮ y, then x² ≮ y².
Contrapositive : ~q → p is the contrapositive of
p → q i.e. If x² ≯ y², then x ≯ y. OR
If x² ≮ y², then x ≮ y.

(ii) A family becomes literate if the woman in it is literate.
Solution:
Let p : The woman in the family is literate.
q : A family become literate.
Then the symbolic form of the given statement is p → q
Converse : q → p is the converse of p → q.
i.e. If a family become literate, then the woman in it is literate.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If the woman in the family is not literate, then the family does not become literate.
Contrapositive : ~q → ~p is the contrapositive of p → q. i e. If a family does not become literate, then the woman in it is not literate.

(iii) If surface area decreases then pressure increases.
Solution:
Let p : The surface area decreases.
q : The pressure increases.
Then the symbolic form of the given statement is p → q.
Converse : q → p is the converse of p→ q.
i.e. If the pressure increases, then the surface area decreases.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If the surface area does not decrease, then the pressure does not increase.
Contrapositive : ~q → ~p is the contrapositive of p → q.
i.e. If the pressure does not increase, then the surface area does not decrease.

(iv) If voltage increases then current decreases.
Solution:
Let p : Voltage increases.
q : Current decreases.
Then the symbolic form of the given statement is p → q.
Converse : q →p is the converse of p → q.
i.e. If current decreases, then voltage increases.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If voltage does not increase, then-current does not decrease.
Contrapositive : ~q → ~p, is the contrapositive of p → q.
i.e. If current does not decrease, then voltage does not increase.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.2 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.2 Questions And Answers Maharashtra Board

Question 1.
Construct the truth table for each of the following statement patterns:
(i) [(p → q) ∧ q] → p
Solution :
Here are two statements and three connectives.
∴ there are 2 × 2 = 4 rows and 2 + 3 = 5 columns in the truth table.

(ii) (p ∧ ~q) ↔ (p → q)
Solution:

(iii) (p ∧ q) ↔ (q ∨ r)
Solution:

(iv) p → [~(q ∧ r)]
Solution:

(v) ~p ∧ [(p ∨ ~q ) ∧ q]
Solution:

(vi) (~p → ~q) ∧ (~q → ~p)
Solution:

(vii) (q → p) ∨ (~p ↔ q)
Solution:

(viii) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:

(ix) p → [~(q ∧ r)]
Solution:

(x) (p ∨ ~q) → (r ∧ p)
Solution:

Question 2.
Using truth tables prove the following logical equivalences.
(i) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:

The entries in the columns 4 and 6 are identical.
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.

(ii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:

The entries in the columns 3 and 7 are identical.
∴ ~(p ∨ q) ∧ (~p ∧ q) = ~p.

(iii) p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)]
Solution:

The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)].

(iv) p → (q → p) ≡ ~p → (p → q)
Solution:

The entries in the columns 4 and 7 are identical.
∴ p → (q → p) ≡ ~p → (p → q).

(v) (p ∨ q ) → r ≡ (p → r) ∧ (q → r)
Solution:

The entries in the columns 5 and 8 are identical.
∴ (p ∨ q ) → r ≡ (p → r) ∧ (q → r).

(vi) p → (q ∧ r) ≡ (p → q) ∧ (p → r)
Solution:

The entries in the columns 5 and 8 are identical.
∴ p → (q ∧ r) ≡ (p → q) ∧ (p → r).

(vii) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Solution:

The entries in the columns 5 and 8 are identical.
∴ p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r).

(viii) [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
Solution:

The entries in the columns 3 and 7 are identical.
∴ [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r.

(ix) ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
Solution:

The entries in the columns 6 and 9 are identical.
∴ ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p).

Question 3.
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
(i) (p ∧ q) → (q ∨ p)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p ∧ q) → (q ∨ p) is a tautology.

(ii) (p → q) ↔ (~p ∨ q)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p → q) ↔ (~p ∨ q) p is a tautology.

(iii) [~(~p ∧ ~q)] ∨ q
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [~(~p ∧ ~q)] ∨ q is a contingency.

(iv) [(p → q) ∧ q)] → p
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [(p → q) ∧ q)] → p is a contingency

(v) [(p → q) ∧ ~q] → ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q] → ~p is a tautology.

(vi) (p ↔ q) ∧ (p → ~q)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (p ↔ q) ∧ (p → ~q) is a contingency.

(vii) ~(~q ∧ p) ∧ q
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ ~(~q ∧ p) ∧ q is a contingency.

(viii) (p ∧ ~q) ↔ (p → q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p ∧ ~q) ↔ (p → q) is a contradiction.

(ix) (~p → q) ∧ (p ∧ r)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (~p → q) ∧ (p ∧ r) is a contingency.

(x) [p → (~q ∨ r)] ↔ ~[p → (q → r)]
Solution:

All the entries in the last column of the above truth table are F.
∴ [p → (~q ∨ r)] ↔ ~[p → (q → r)] is a contradiction

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.1 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.1 Questions And Answers Maharashtra Board

Question 1.
State which of the following sentences are statements. Justify your answer. In case of the statement, write down the truth value :
(i) 5 + 4 = 13.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

(ii) x – 3 = 14.
Solution:
It is an open sentence, hence it is not a statement.

(iii) Close the door.
Solution:
It is an imperative sentence, hence it is not a statement.

(iv) Zero is a complex number.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(v) Please get me breakfast.
Solution:
It is an imperative sentence, hence it is not a statement.

(vi) Congruent triangles are also similar.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(vii) x² = x.
Solution:
It is an open sentence, hence it is not a statement,

(viii) A quadratic equation cannot have more than two roots.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(ix) Do you like Mathematics ?
Solution:
It is an interrogative sentence, hence it is not a statement.

(x) The sun sets in the west.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xi) All real numbers are whole numbers.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

(xii) Can you speak in Marathi ?
Solution:
It is an interrogative sentence, hence it is not a statement.

(xiii) x² – 6x – 7 = 0, when x = 7.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xiv) The sum of cuberoots of unity is zero.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xv) It rains heavily.
Solution :
It is an open sentence, hence it is not a statement.

Question 2.
Write the following compound statements symbolically:
(i) Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Solution:
Let p : Nagpur is in Maharashtra.
q : Chennai is in Tamil Nadu.
Then the symbolic form of the given statement is P∧q.

(ii) Triangle is equilateral or isosceles,
Solution:
Let p : Triangle is equilateral.
q : Triangle is isosceles.
Then the symbolic form of the given statement is P∨q.

(iii) The angle is right angle if and only if it is of measure 90°.
Solution:
Let p : The angle is right angle.
q : It is of measure 90°.
Then the symbolic form of the given statement is p↔q

(iv) Angle is neither acute nor obtuse.
Solution:
Let p : Angle is acute.
q : Angle is obtuse.
Then the symbolic form of the given statement is
~p ∧ ~q.

(v) If ∆ ABC is right angled at B, then m∠A + m∠C = 90°.
Solution:
Let p : ∆ ABC is right angled at B.
q : m∠A + m∠C = 90°.
Then the symbolic form of the given statement is p → q

(vi) Hima Das wins gold medal if and only if she runs fast.
Solution:
Let p : Hima Das wins gold medal
q : She runs fast.
Then the symbolic form of the given statement is p ↔ q.

(vii) x is not irrational number but it is a square of an integer.
Solution:
Let p : x is not irrational number
q : It is a square of an integer
Then the symbolic form of the given statement is p ∧ q
Note : If p : x is irrational number, then the symbolic form of the given statement is ~p ∧ q.

Question 3.
Write the truth values of the following :
(i) 4 is odd or 1 is prime.
Solution:
Let p : 4 is odd.
q : 1 is prime.
Then the symbolic form of the given statement is p∨q.
The truth values of both p and q are F.
∴ the truth value of p v q is F. … [F ∨ F = F]

(ii) 64 is a perfect square and 46 is a prime number.
Solution:
Let p : 64 is a perfect square.
q : 46 is a prime number.
Then the symbolic form of the given statement is p∧q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(iii) 5 is a prime number and 7 divides 94.
Solution:
Let p : 5 is a prime number.
q : 7 divides 94.
Then the symbolic form of the given statement is p∧q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(iv) It is not true that 5 – 3i is a real number.
Solution:
Let p : 5 – 3i is a real number.
Then the symbolic form of the given statement is ~ p.
The truth values of p is F.
∴ the truth values of ~ p is T. … [~ F ≡ T]

(v) If 3 × 5 = 8, then 3 + 5 = 15.
Solution:
Let p : 3 × 5 = 8.
q : 3 + 5 = 15.
Then the symbolic form of the given statement is p → q.
The truth values of both p and q are F.
∴ the truth value of p → q is T. … [F → F ≡ T]

(vi) Milk is white if and only if sky is blue.
Solution:
Let p : Milk is white.
q : Sky is blue
Then the symbolic form of the given statement is p ↔ q.
The truth values of both p and q are T.
∴ the truth value of p ↔ q is T. … [T ↔ T ≡ T]

(vii) 24 is a composite number or 17 is a prime number.
Solution :
Let p : 24 is a composite number.
q : 17 is a prime number.
Then the symbolic form of the given statement is p ∨ q.
The truth values of both p and q are T.
∴ the truth value of p ∨ q is T. … [T ∨ T ≡ T]

Question 4.
If the statements p, q are true statements and r, s are false statements, then determine the truth values of the following:
(i) p ∨ (q ∧ r)
Solution:
Truth values of p and q are T and truth values of r and s are F.
p ∨ (q ∧ r) ≡ T ∨ (T ∧ F)
≡ T ∧ F ≡ T
Hence the truth value of the given statement is true.

(ii) (p → q) ∨ (r → s)
Solution:
(p → q) ∨ (r → s) ≡ (T → T) ∨ (F → F)
≡ T ∨ T ≡ T
Hence the truth value of the given statement is true.

(iii) (q ∧ r) ∨ (~p ∧ s)
Solution:
(q ∧ r) ∨ (~p ∧ s) ≡ (T ∧ F) ∨ (~T ∧ F)
≡ F ∨ (F ∧ F)
≡ F ∨ F ≡ F
Hence the truth value of the given statement is false.

(iv) (p → q) ∧ (~ r)
Solution:
(p → q) ∧ (~ r) ≡ (T → T) ∧ (~ F)
≡ T ∧ T ≡ T
Hence the truth value of the given statement is true.

(v) (~r ↔ p) → (~q)
Solution:
(~r ↔ p) → (~q) ≡ (~F ↔ T) → (~T)
≡ (T ↔ T) → F
≡ T → F ≡ F
Hence the truth value of the given statement is false.

(vi) [~p ∧ (~q ∧ r) ∨ (q ∧ r) ∨ (p ∧ r)]
Solution:
[~p ∧ (~q ∧ r)∨(q ∧ r)∨(p ∧ r)]
≡ [~T ∧ (~T ∧ F)] ∨ [(T ∧ F) V (T ∧ F)]
≡ [F ∧ (F ∧ F)] ∨ [F V F]
≡ (F ∧ F) ∨ F
≡ F ∨ F ≡ F
Hence the truth value of the given statement is false.

(vii) [(~ p ∧ q) ∧ (~ r)] ∨ [(q → p) → (~ s ∨ r)]
Solution:
[(~ p ∧ q) ∧ (~ r)] ∨ [(q → p) → (~ s ∨ r)]
≡ [(~T ∧ T) ∧ (~F)] ∨ [(T → T) → (~F ∨ F)]
≡ [(F ∧ T) ∧ T] ∨ [T → (T ∨ F)]
≡ (F ∧ T) ∨ (T → T)
≡ F ∨ T ≡ T
Hence the truth value of the given statement is true.

(viii) ~ [(~p ∧ r) ∨ (s → ~q)] ↔ (p ∧ r)
Solution :
~ [(~p ∧ r) ∨ (s → ~q)] ↔ (p ∧ r)
≡ ~ [(~T ∧ F) ∨ (F → ~T)] ↔ (T ∧ F)
≡ ~ [(F ∧ F) ∨ (F → F)] ↔ F
≡ ~ (F ∨ T) ↔ F
≡ ~T ↔ F
≡ F ↔ F ≡ T
Hence the truth value of the given statement is true.

Question 5.
Write the negations of the following :
(i) Tirupati is in Andhra Pradesh.
Solution:
The negations of the given statements are :
Tirupati is not in Andhra Pradesh.

(ii) 3 is not a root of the equation x² + 3x – 18 = 0.
Solution:
3 is a root of the equation x² + 3x – 18 = 0.

(iii) \(\sqrt {2}\) is a rational number.
Solution:
\(\sqrt {2}\) is not a rational number.

(iv) Polygon ABCDE is a pentagon.
Solution:
Polygon ABCDE is not a pentagon.

(v) 7 + 3 > 5.
Solution :
7 + 3 > 5.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Mathematical Logic Ex 1.1 Class 12 Maths Solutions
• Mathematical Logic Ex 1.2 Class 12 Maths Solutions
• Mathematical Logic Ex 1.3 Class 12 Maths Solutions
• Mathematical Logic Ex 1.4 Class 12 Maths Solutions
• Mathematical Logic Ex 1.5 Class 12 Maths Solutions
• Mathematical Logic Miscellaneous Exercise 1 Class 12 Maths Solutions
• Matrices Ex 2.1 Class 12 Maths Solutions
• Matrices Ex 2.2 Class 12 Maths Solutions
• Matrices Ex 2.3 Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2A Class 12 Maths Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Maths Solutions

Class 12 English Chapter 4.4 History of Novel Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 4.4 The Sign of Four Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 4.4 Brainstorming Question Answer

12th English Digest Chapter 4.4 The Sign of Four Textbook Questions and Answers

CHARACTER:

(A1)

Question (i)
Read the extract again and complete the web by highlighting the qualities of the following characters:


Answer:

Question (ii)
Describe the character of Mary Morstan from Dr. Watson’s point of view.
Answer:
From Dr. Watson’s point of view: When I first saw Mary, she was dressed simply but tastefully. I could see that she was a person of limited means. Her expression was sweet and pleasant, and I could make out that her nature was refined and sensitive. My calculations told me that she was about 27 years old. She was agitated by the mystery surrounding her life. I found her attractive, though her face did not have regular features or a beautiful complexion. Her eyes showed that she was a sympathetic person. I was much impressed by her and attracted to her.

Question (iii)
Sherlock Holmes is the leading character in the extract. Explain.
Answer:
It is Sherlock Holmes who is the detective and the leading character. Mary Morstan had come to ask his advice about a problem that she was facing. Holmes was the one who took the lead and found out about Major Sholto; it was Holmes who analysed the handwriting in the letter that Mary had received. Holmes was sharp, accurate, intelligent and methodical. He had an excellent record of solving cases, and his deductions were always correct. Watson was merely his friend who helped him and kept a record of his cases.

Question (iv)
Dr. Watson, the narrator, is one of the major characters in the novel. Illustrate.
Answer:
Dr. Watson is the narrator. He was present when the case was brought to Holmes by Mary Morstan. He is generally always with Holmes, helping him to solve cases. He accompanied Holmes whenever necessary.

He also kept a record of all the cases that Holmes was a part of. In this extract, he is present when Mary recounts her case, and he accompanies Holmes and Mary to meet the writer of the anonymous letter. (He marries Mary in the end.)

Question (v)
Holmes is always one step ahead of Dr. Watson in solving cases. Elucidate.
Answer:
Where Watson is emotional, simple and trustful, Holmes is sharp, objective and methodical. Holmes is also analytical and notices the little details which give him clues to solving a case. Watson does not, and hence is often on the wrong track. Holmes is the real detective, while Watson is merely his companion. Holmes is always ahead of Watson and solves cases which Watson is not even near to cracking.

PLOT:

(A2)

Question (i)
Arrange the sentences in correct sequence as per their occurrence in the extract.
Answer:

(ii) Discuss the importance of the following statements from the light of the extract.

Question (a)
The trio-Holmes, Dr. Watson and Mary decide to visit Lyceum Theatre.
Answer:
Mary had received an anonymous letter asking her to be outside the Lyceum Theatre on a particular night at seven o’clock. The letter said that it would be to Mary’s advantage if she came. The letter also mentioned that she could bring two friends with her. However, she did not have any friends who could accompany her, and so she asked Holmes and Watson if they could do so. They agreed. Hence, Holmes, Dr. Watson and Mary decide to visit Lyceum Theatre. This was the first step to solving the case.

Question (b)
Mary received pearls every year on the same day.
Answer:
Major Sholto, Mary’s father’s friend, had cheated Mary’s father of his share in the Agra treasure. When he died, Major Sholto informed his son Thaddeus of this. Though Thaddeus did not have the treasure, he tried to rectify the matter to a certain extent by sending Mary a rare and expensive pearl every year, on the same day as he sent the first one.

Question (c)
Holmes carefully examined the paper given by Mary.
Answer:
Mary had found a curious paper in her father’s desk which no one could understand. Holmes deduced from the colour of the paper that it was an important document. He felt it was related in some way to the mystery on hand. Hence, he examined it carefully to get some clues which would help to solve the mystery.

SETTING:

(A3)

Question (i)
Cite various references (lines) from the extract that tell us about the time and period of the events:
Answer:

Question (ii)
Explain by citting references from the extract the ways the series of actions moves from London to India.
Answer:
The extract begins when Mary Morstan meets Sherlock Holmes at his house in London. They then meet Thaddeus Sholto in a rundown neighbourhood of London. Thaddeus reveals that his father Major Sholto had mistakenly killed Captain Morstan in London. They then go to Bartholomew Sholto’s house to get the treasure; however, Bartholomew is found dead.

Holmes follows Jonathan Small and Tonga, who have escaped by a steam launch, over the river Thames in London. When Small is captured, he tells them about the time he spent in India, where he was an accomplice in stealing the Agra treasure. Thus, the narration goes to India. Major Sholto and Captain Morstan were also at one time stationed in India.

Question (iii)
The extract begins when Mary Morstan meets Sherlock Holmes at his house. After that Holmes, Dr.Watson and Mary visit some places in London. Explain in detail the various places mentioned in the extract.
Answer:
Holmes, Dr.Watson and Mary were taken down the Strand, which was crowded, badly lit and humid. All kinds of people-sad, happy, old and young could be seen moving about in the dim light. Watson found it eerie and ghostlike, and he felt nervous and depressed. They then reached the Lyceum Theatre, where the crowds were pouring in.

A continuous stream of horse carriages could be seen, with stylish people getting out of them. Near the Lyceum Theatre they were met by a coachman who took them in his coach through Rochester Row and Vincent Square onto Vauxhall Bridge Road. They were on the Surrey side, on the bridge from where they got glimpses of the river Thames with lamps shining on the silent water.

The cab then took them through a maze of streets. Holmes could identify Wordsworth Road, Priory Road, Lark Hall Lane, Stockwell Place, Robert Street and Cold Harbor Lane. They were all rundown places. The cab took them further to a rather grim and shady neighbourhood with dull brick houses and cheap and showy public houses at the corner.

Holmes mentions that this was not a very fashionable or rich neighbourhood. This was followed by rows of two-storied villas each with a small front garden, and then again there were never-ending lines of new brick buildings, which were an extension of the city. The houses in the area were all dark and appeared uninhabited.

At last the cab drew up at the third house in a new terrace, which was also dark except for a light in the kitchen. However, when they knocked the door was opened instantly, and an Oriental figure of a servant clad in a yellow turban, white loose-fitting clothes, and a yellow sash stood there. It was strange to find an Oriental figure framed in the doorway of a cheap suburban house.

Question (iv)
Basically the setting of the extract is in London but it has some references of India, too. Explain how the settings of the extract contribute to the theme of the novel.
Answer:
The setting of the extract is in London, where Mary meets Holmes and Watson to explain her problem. She talks about her father being an officer in an Indian regiment. When he returned to England on leave, he called Mary to meet him at a London hotel, but disappeared mysteriously before she could do so. His only friend in London was a Major Sholto. Holmes finds that Major Sholto was also from the 34th Bombay Infantry.

Mary shows Holmes a piece of paper belonging to her father. The paper was of Indian origin, and three of the names written on it were also Indian. Holmes, Watson and Mary go to meet the anonymous letter writer at a rundown suburban house in London. Later they chase Jonathan Small and Tonga, who were trying to escape by boat on the river Thames. When Jonathan Small was captured, he spoke of being an accomplice in stealing the Agra treasure.

He was sent to the Andaman Islands, where Major Sholto and Captain Morstan were prison guards. At the end of the extract, the door of the anonymous letter writer’s house was opened by an Indian servant. His master used an Indian name to call him. Thus, we have a mingling of incidents both in London as well as in India, where the case had its roots.

Question (v)
Describe in brief the importance of the following places in the extract.
(a) London
(b) Lyceum Theatre
(c) Edinburgh
(d) Agra
(e) Andaman Islands
Answer:
(a) London: The case starts here with Mary Morstan meeting Holmes at his place in London. They go to meet Thaddeus Sholto in London. They also chase Jonathan Small and Tonga in London. Tonga is killed and Small captured. Small then narrates the entire story.

(b) Lyceum Theatre: This is the place near which the writer of the anonymous letter told Mary Morstan to reach if she wished to get justice.

(c) Edinburgh: Mary spent her childhood till she was seventeen at a boarding school in Edinburgh.

(d) Agra: When Jonathan Small was standing guard one night at the Agra fortress, he was overpowered by two Sikh troopers, who forced him to waylay a servant of a Rajah and steal a valuable fortune in pearls and jewels. This was called the ‘Agra treasure’.

(e) Andaman Islands: Jonathan Small was arrested and imprisoned on the Andaman Islands for the robbery of the Agra treasure. After 20 years, Small made a deal with John Sholto and Arthur Morstan, who were the prison guards. Sholto would recover the treasure and in return send a boat to pick up Small and the Sikhs. Sholto double-crossed both Morstan and Small and stole the treasure for himself. Small vowed vengeance and four years later escaped from the Andaman Islands with an islander named Tonga after they both killed a prison guard.

Question (vi)
Complete:
Name the places/cities in India and England which are mentioned/have appeared in the extract. Describe their importance.
Answer:

THEME:

(A4)

Question (i)
Write in brief the theme of the extract.
Answer:
The theme of the extract revolves round the mystery of the disappearance of Mary Morstan’s father, the receipt of expensive pearls by Mary and the mysterious letter received by her. It also involves the journey of Holmes, Watson and Mary Morstan to a strange house to meet the writer of the mysterious letter. The theme of the novel revolves around the Agra treasure.

Question (ii)
Write 4-5 sentences about the meeting of Miss Morstan with Holmes.
Answer:
Miss Morstan met Holmes and Watson at their house in Baker Street. She then discussed with them the mysterious disappearance of her father a few years earlier, the receipt of an expensive pearl every year for the past six years, and the receipt of a mysterious letter that morning asking her to meet the writer of the letter. Miss Morstan was intensely agitated and confused and did not know what to do. She showed Holmes the pearls, the boxes in which they had come and the letter. Then they planned to follow the instructions and meet the writer of the letter.

Question (iii)
Write the central idea of the given extract of the novel, “The Sign of Four”.
Answer:
The central idea is the meeting of Mary Morstan with Holmes and Watson, and her explanation of her problems. It is also about the short trip made by the three to meet I the writer of the mysterious letter. This is Watson’s first meeting with Miss Morstan and his attraction towards her.

Question (iv)
Complete the following giving reasons:
Answer:
(a) Miss Morstan plans to meet Sherlock Holmes to ask his advice about the disappearance of her father, the receipt of expensive pearls and the mysterious letter received by her.

(b) Miss Morstan gives the reference of Mrs. Cecil Forrester because Mrs. Cecil Forrester was her employer, whom Holmes had once helped to solve a domestic complication. Mrs. Forrester had been impressed by his kindness and skill.

(c) It’s a singular case because Miss Morstan’s father had come back to England and contacted her, and had seemed happy. After fixing a meeting ; with her at his hotel, he had suddenly ; disappeared and was never seen again, Even his only friend in town, Major Sholto, had not known either of his ; arrival or disappearance.

(d) Holmes needed some references to find out details about Major Sholto, who was the only friend Mary’s father had in England, and who had said that he did not know about his arrival in England.

(e) Miss Morstan received a pearl every year, when she replied to an advertisement asking for her address, adding that it would be to her advantage.

(f) The coachman confirmed that neither of Miss Morstan’s companion was a police officer because this was the condition made by the writer of the mysterious letter, whom they were going to meet.

LANGUAGE:

(A5)

(i) Elaborate the following lines in the light of the novel/extract, “The Sign of Four”:

Question (a)
“You really are an automaton – a calculating machine”.
Answer:
These words are said by Watson to Holmes when Mary Morstan had left after discussing her case. Watson is attracted to her and full of admiration for her. When he voices his admiration, Holmes says that he had not noticed if she is attractive or not. Watson is indignant and calls him a calculating machine.

Question (b)
“The letter speaks of giving her justice.”
Discuss.
Answer:
These are the words of Holmes to Watson, when they are discussing the letter that Mary Morstan has received from an unknown person. He wondered what was the ‘justice’ that the letter spoke of, and who had done ’ something wrong to Mary that she now needed justice.

Question (c)
“Our quest does not appear to take us to very fashionable regions.”
Answer:
These words are said by Holmes to Watson and Mary Morstan, when they are being driven by the coachman to some strange place. They were going through narrow streets in an unfriendly and grim neighbourhood, which had dull brick rows of houses and cheap and showy public houses at the comer. Holmes mentions that this was not a very fashionable or rich neighbourhood.

Question (ii)
Following are some dialogues of the major characters in the extract. Find out who the speaker is, his/her tone, style, significance, etc. of the dialogue.
Answer:

Yuvakbharati English 12th Textbook Answers Solutions Section 4 (Genre-Drama)

• History of Novel Class 11 English Solutions
• To Sir, with Love Class 11 English Solutions
• Around the World in Eighty Days Class 11 English Solutions
• The Sign of Four Class 11 English Solutions