Maharashtra Board 11th Commerce Maths Solutions Chapter 2 Measures of Dispersion Ex 2.1

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 2 Measures of Dispersion Ex 2.1 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 2 Measures of Dispersion Ex 2.1

Question 1.
Find range of the following data:
575, 609, 335, 280, 729, 544, 852, 427, 967, 250
Solution:
Here, largest value (L) = 967, smallest value (S) = 250
∴ Range = L – S
= 967 – 250
= 717

Question 2.
The following data gives the number of typing mistakes done by Radha during a week. Find the range of the data.

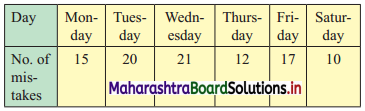
Solution:
Here, largest value (L) = 21, smallest value (S) = 10
∴ Range = L – S
= 21 – 10
= 11

Question 3.
Find range for the following data:

Solution:
Here, upper limit of the highest class (L) = 72, lower limit of the lowest class (S) = 62
∴ Range = L – S
= 72 – 62
= 10

Question 4.
Find the Q. D. for the following data.
3, 16, 8, 15, 19, 11, 5, 17, 9, 5, 3.
Solution:
The given data can be arranged in ascending order as follows:
3, 3, 5, 5, 8, 9, 11, 15, 16, 17, 19
Here, n = 11
Q₁ = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{11+1}{4}\right)^{\text {th }}\) observation
= value of 3rd observation
∴ Q₁ = 5
Q₃ = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{11+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 3)th observation
= value of 9th observation
= 16
∴ Q.D.= \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
= \(\frac{16-5}{2}\)
= \(\frac{11}{2}\)
= 5.5

Question 5.
Given below are the prices of shares of a company for the last 10 days. Find Q.D.:
172, 164, 188, 214, 190, 237, 200, 195, 208, 230.
Solution:
The given data can be arranged in ascending order as follows:
164, 172, 188, 190, 195, 200, 208, 214, 230, 237
Here, n = 10
Q₁ = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{10+1}{4}\right)^{\text {th }}\) observation
= value of (2.75)th observation
= value of 2nd observation + 0.75(value of 3rd observation – value of 2nd observation)
= 172 + 0.75(188 – 172)
= 172 + 0.75(16)
= 172 + 12
= 184
∴ Q₃ = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{10+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 2.75)th observation
= value of (8.25)th observation
= value of 8th observation + 0.25(value of 9th observation – value of 8th observation)
= 214 + 0.25(230 – 214)
= 214 + 0.25(16)
= 214 + 4
= 218
∴ Q.D. = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
= \(\frac{218-184}{2}\)
= \(\frac{34}{2}\)
= 17

Question 6.
Calculate Q.D. for the following data.

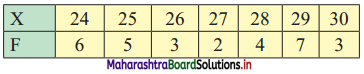
Solution:
Since the given data is arranged in ascending order, we construct less than cumulative frequency table as follows:

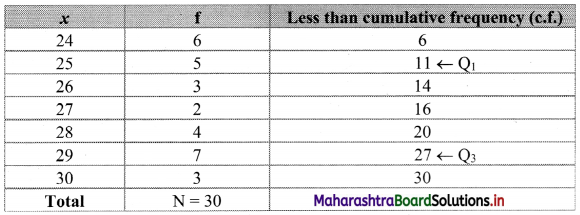
Here, n = 30
Q₁ = value of \(\left(\frac{\mathrm{n}+1}{4}\right)^{\mathrm{th}}\) observation
= value of \(\left(\frac{30+1}{4}\right)^{\text {th }}\) observation
= value of (7.75)th observation
Cumulative frequency which is just greater than (or equal to) 7.75 is 11.
∴ Q₁ = 25
Q₃ = value of \(\left[3\left(\frac{\mathrm{n}+1}{4}\right)\right]^{\mathrm{th}}\) observation
= value of \(\left[3\left(\frac{30+1}{4}\right)\right]^{\text {th }}\) observation
= value of (3 × 7.75)th observation
= value of (23.25)th observation
Cumulative frequency which is just greater than (or equal to) 23.25 is 27.
∴ Q₃ = 29
∴ Q.D. = \(\frac{Q_{3}-Q_{1}}{2}\)
= \(\frac{29-25}{2}\)
∴ Q.D. = 2

Question 7.
Following data gives the age distribution of 240 employees of a firm. Calculate Q.D. of the distribution.

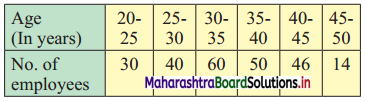
Solution:
We construct the less than cumulative frequency table as follows:

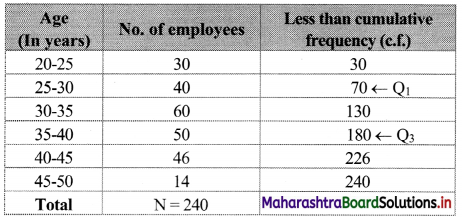
Here, N = 240
Q₁ class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{N}{4}=\frac{240}{4}\) = 60
Cumulative frequency which is just greater than (or equal to) 60 is 70.
∴ Q₁ lies in the class 25 – 30.
∴ L = 25, c.f. = 30, f = 40, h = 5

Cumulative frequency which is just greater than (or equal to) 180 is 180.
∴ Q₃ lies in the class 35-40.
∴ L = 35, c.f. = 130, f = 50, h = 5

Question 8.
Following data gives the weight of boxes. Calculate Q.D. for the data.

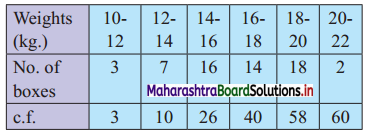
Solution:

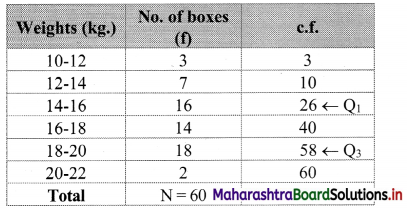
Here, N = 60
Q₁ class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{\mathrm{N}}{4}=\frac{60}{4}\) = 15
Cumulative frequency which is just greater than (or equal to) 15 is 26.
∴ Q₁ lies in the class 14 – 16.
∴ L = 14, c.f. = 10, f = 16, h = 2

Cumulative frequency which is just greater than (or equal to) 45 is 58.
∴ Q₃ lies in the class 18 – 20.
∴ L = 18, c.f. = 40, f = 18, h = 2