Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Miscellaneous Exercise 1 Questions and Answers.
11th Maths Part 2 Complex Numbers Miscellaneous Exercise 1 Questions And Answers Maharashtra Board
(I) Select the correct answer from the given alternatives.
Question 1.
If n is an odd positive integer, then the value of 1 + (i)2n + (i)4n + (i)6n is:
(A) -4i
(B) 0
(C) 4i
(D) 4
Answer:
(B) 0
Hint:
1 + (i2)n + (i4)n + (i2)3n
= 1 – 1 + 1 – 1 …..(n odd positive integer)
= 0
![]()
Question 2.
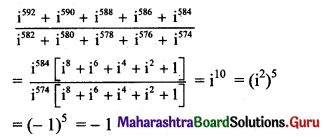
The value of \(\frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}\) is equal to:
(A) -2
(B) 1
(C) 0
(D) -1
Answer:
(D) -1
Hint:
Question 3.
√-3 √-6 is equal to
(A) -3√2
(B) 3√2
(C) 3√2 i
(D) -3√2 i
Answer:
(A) -3√2
Hint:
√-3 √-6
= (√3 i) (√6 i)
= 3√2 (-1)
= -3√2
Question 4.
If ω is a complex cube root of unity, then the value of ω99 + ω100 + ω101 is:
(A) -1
(B) 1
(C) 0
(D) 3
Answer:
(C) 0
Hint:
ω99 + ω100 + ω101
= ω99 (1 + ω + ω2)
= ω99 (0)
= 0
![]()
Question 5.
If z = r(cos θ + i sin θ), then the value of \(\frac{z}{\bar{z}}+\frac{\bar{z}}{z}\) is
(A) cos 2θ
(B) 2cos 2θ
(C) 2cos θ
(D) 2sin θ
Answer:
(B) 2cos 2θ
Hint:

Question 6.
If ω(≠1) is a cube root of unity and (1 + ω)7 = A + Bω, then A and B are respectively the numbers
(A) 0, 1
(B) 1, 1
(C) 1, 0
(D) -1, 1
Answer:
(B) 1, 1
Hint:
(1 + ω)7
= (-ω2)7
= -ω14
= -ω2(ω3)4
= -ω2
= 1 + ω
A = 1, B = 1
Question 7.
The modulus and argument of (1 + i√3)8 are respectively
(A) 2 and \(\frac{2 \pi}{3}\)
(B) 256 and \(\frac{8 \pi}{3}\)
(C) 256 and \(\frac{2 \pi}{3}\)
(D) 64 and \(\frac{4 \pi}{3}\)
Answer:
(C) 256 and \(\frac{2 \pi}{3}\)
Hint:

Question 8.
If arg (z) = θ, then arg \(\overline{(\mathrm{z})}\) =
(A) -θ
(B) θ
(C) π – θ
(D) π + θ
Answer:
(A) -θ
Hint:
Let z = \(\mathrm{re}^{\mathrm{i} \theta}\), then \(\overline{\mathrm{z}}=\mathrm{r} \mathrm{e}^{-\mathrm{i} \theta}\)
∴ arg \(\overline{\mathbf{z}}\) = -θ.
![]()
Question 9.
If -1 + √3 i = \(\mathrm{re}^{\mathrm{i} \theta}\), then θ =
(A) –\(\frac{2 \pi}{3}\)
(B) \(\frac{\pi}{3}\)
(C) –\(\frac{\pi}{3}\)
(D) \(\frac{2 \pi}{3}\)
Answer:
(D) \(\frac{2 \pi}{3}\)
Hint:

Question 10.
If z = x + iy and |z – zi| = 1, then
(A) z lies on X-axis
(B) z lies on Y-axis
(C) z lies on a rectangle
(D) z lies on a circle
Answer:
(D) z lies on a circle
Hint:
|z – zi | = |z| |1 – i| = 1
∴ |z| = \(\frac{1}{\sqrt{2}}\)
∴ x2 + y2 = \(\frac{1}{2}\)
(II) Answer the following:
Question 1.
Simplify the following and express in the form a + ib.
(i) 3 + √-64
Solution:
3 + √-64
= 3 + √64 √-1
= 3 + 8i
(ii) (2i3)2
Solution:
(2i3)2
= 4i6
= 4(i2)3
= 4(-1)3
= -4 …..[∵ i2 = -1]
= -4 + 0i
![]()
(iii) (2 + 3i) (1 – 4i)
Solution:
(2 + 3i)(1 – 4i)
= 2 – 8i + 3i – 12i2
= 2 – 5i – 12(-1) …..[∵ i2 = -1]
= 14 – 5i
(iv) \(\frac{5}{2}\)i(-4 – 3i)
Solution:

(v) (1 + 3i)2 (3 + i)
Solution:
(1 + 3i)2 (3 + i)
= (1 + 6i + 9i2)(3 + i)
= (1 + 6i – 9)(3 + i) ……[∵ i2 = -1]
= (-8 + 6i)(3 + i)
= -24 – 8i + 18i + 6i2
= -24 + 10i + 6(-1)
= -24 + 10i – 6
= -30 + 10i
(vi) \(\frac{4+3 i}{1-i}\)
Solution:
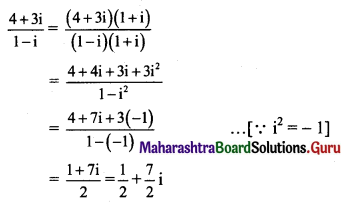
(vii) \(\left(1+\frac{2}{i}\right)\left(3+\frac{4}{i}\right)(5+i)^{-1}\)
Solution:

(viii) \(\frac{\sqrt{5}+\sqrt{3 i}}{\sqrt{5}-\sqrt{3} i}\)
Solution:

(ix) \(\frac{3 i^{5}+2 i^{7}+i^{9}}{i^{6}+2 i^{8}+3 i^{18}}\)
Solution:
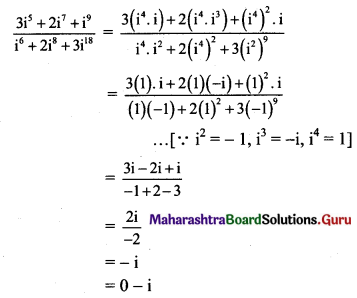
(x) \(\frac{5+7 i}{4+3 i}+\frac{5+7 i}{4-3 i}\)
Solution:

Question 2.
Solve the following equations for x, y ∈ R
(i) (4 – 5i)x + (2 + 3i)y = 10 – 7i
Solution:
(4 – 5i)x + (2 + 3i)y = 10 – 7i
(4x + 2y) + (3y – 5x) i = 10 – 7i
Equating real and imaginary parts, we get
4x + 2y= 10 i.e., 2x + y = 5 ……(i)
and 3y – 5x = -7 ……(ii)
Equation (i) × 3 – equation (ii) gives
11x = 22
∴ x = 2
Putting x = 2 in (i), we get
2(2) + y = 5
∴ y = 1
∴ x = 2 and y = 1
![]()
(ii) \(\frac{x+i y}{2+3 i}\) = 7 – i
Solution:
\(\frac{x+i y}{2+3 i}\) = 7 – i
x + iy = (7 – i)(2 + 3i)
x + iy = 14 + 21i – 2i – 3i2
x + iy = 14 + 19i – 3(-1)
x + iy = 17 + 19i
Equating real and imaginary parts, we get
∴ x = 17 and y = 19
(iii) (x + iy) (5 + 6i) = 2 + 3i
Solution:
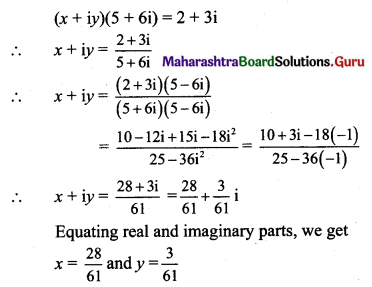
(iv) 2x + i9 y(2 + i) = x i7 + 10 i16
Solution:
2x + i9 y(2 + i) = x i7 + 10 i16
2x + (i4)2 . i . y(2 + i) = x(i2)3 . i + 10 . (i4)4
2x + (1)2 . iy(2 + i) = x(-1)3 . i + 10(1)4 ……..[∵ i2 = -1, i4 = 1]
2x + 2yi + y i2 = -xi + 10
2x + 2yi – y + xi = 10
(2x – y) + (x + 2y)i = 10 + 0 . i
Equating real and imaginary parts, we get
2x – y = 10 ……(i)
and x + 2y = 0 ……..(ii)
Equation (i) × 2 + equation (ii) gives, we get
5x = 20
∴ x = 4
Putting x = 4 in (i), we get
2(4) – y = 10
y = 8 – 10
∴ y = -2
∴ x = 4 and y = -2
Question 3.
Evaluate
(i) (1 – i + i2)-15
Solution:

(ii) i131 + i49
Solution:
i131 + i49
= (i4)32 . i3 + (i4)12 . i
= (1)32 (-i) + (1)12 . i
= -i + i
= 0
![]()
Question 4.
Find the value of
(i) x3 + 2x2 – 3x + 21, if x = 1 + 2i
Solution:

(ii) x4 + 9x3 + 35x2 – x + 164, if x = -5 + 4i
Solution:

Question 5.
Find the square roots of
(i) -16 + 30i
Solution:
Let \(\sqrt{-16+30 \mathrm{i}}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
-16 + 30i = a2 + b2 i2 + 2abi
-16 + 30i = (a2 – b2) + 2abi …..[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = -16 and 2ab = 30
a2 – b2 = -16 and b = \(\frac{15}{a}\)

(ii) 15 – 8i
Solution:
Let \(\sqrt{15-8 i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
15 – 8i = a2 + b2 i2 + 2abi
15 – 8i = (a2 – b2) + 2abi …..[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 15 and 2ab = -8
a2 – b2 = 15 and b = \(\frac{-4}{a}\)

When a = 4, b = \(\frac{-4}{4}\) = -1
When a = -4, b = \(\frac{-4}{-4}\) = 1
∴ \(\sqrt{15-8 i}\) = ±(4 – i)
(iii) 2 + 2√3 i
Solution:
Let \(\sqrt{2+2 \sqrt{3}}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
2 + 2√3 i = a2 + b2 i2 + 2abi
2 + 2√3 i = a2 – b2 + 2abi …..[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 2 and 2ab = 2√3
a2 – b2 = 2 and b = \(\frac{\sqrt{3}}{a}\)

(iv) 18i
Solution:
Let √18i = a + bi, where a, b ∈ R.
Squaring on both sides, we get
18i = a2 + b2 i2 + 2abi
0 + 18i = a2 – b2 + 2abi …..[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 0 and 2ab = 18
a2 – b2 = 0 and b = \(\frac{9}{a}\)
\(a^{2}-\left(\frac{9}{a}\right)^{2}=0\)
\(a^{2}-\frac{81}{a^{2}}=0\)
a4 – 81 = 0
(a2 – 9) (a2 + 9) = 0
a2 = 9 or a2 = -9
But a ∈ R
∴ a2 ≠ -9
∴ a2 = 9
∴ a = ± 3
When a = 3, b = \(\frac{9}{3}\) = 3
When a = -3, b = \(\frac{9}{-3}\) = -3
∴ √18i = ±(3 + 3i) = ±3(1 + i)
![]()
(v) 3 – 4i
Solution:
Let \(\sqrt{3-4 i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
3 – 4i = a2 + b2 i2 + 2abi
3 – 4i = a2 – b2 + 2abi ……[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 3 and 2ab = -4
a2 – b2 = 3 and b = \(\frac{-2}{a}\)

(vi) 6 + 8i
Solution:
Let \(\sqrt{6+8 i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
6 + 8i = a2 + b2 i2 + 2abi
6 + 8i = a2 – b2 + 2abi ……[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 6 and 2ab = 8


Question 6.
Find the modulus and argument of each complex number and express it in the polar form.
(i) 8 + 15i
Solution:
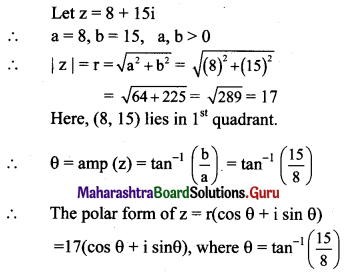
(ii) 6 – i
Solution:

(iii) \(\frac{1+\sqrt{3} \mathbf{i}}{2}\)
Solution:
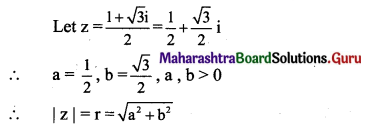

![]()
(iv) \(\frac{-1-\mathbf{i}}{\sqrt{2}}\)
Solution:

(v) 2i
Solution:

(vi) -3i
Solution:
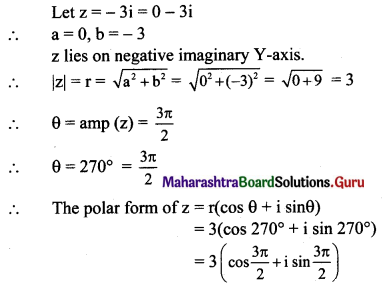
(vii) \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}} \mathbf{i}\)
Solution:

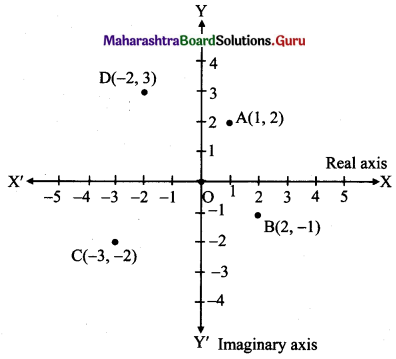
Question 7.
Represent 1 + 21, 2 – i, -3 – 2i, -2 + 3i by points in Argand’s diagram.
Solution:
The complex numbers 1 + 2i, 2 – i, -3 – 2i, -2 + 3i will be represented by the points A(1, 2), B(2, -1), C(-3, -2), D(-2, 3) respectively as shown below:
Question 8.
Show that z = \(\frac{5}{(1-i)(2-i)(3-i)}\) is purely imaginary number.
Solution:

Question 9.
Find the real numbers x and y such that \(\frac{x}{1+2 i}+\frac{y}{3+2 i}=\frac{5+6 i}{-1+8 i}\)
Solution:
\(\frac{x}{1+2 i}+\frac{y}{3+2 i}=\frac{5+6 i}{-1+8 i}\)

(3x + y) + 2(x + y)i = 5 + 6i
Equating real and imaginary parts, we get
3x + y = 5 ……(i)
and 2(x + y) = 6
i.e., x + y = 3 …….(ii)
Subtracting (ii) from (i), we get
2x = 2
∴ x = 1
Putting x = 1 in (ii), we get
1 + y = 3
∴ y = 2
∴ x = 1, y = 2
![]()
Question 10.
Show that \(\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)^{10}+\left(\frac{1}{\sqrt{2}}-\frac{i}{\sqrt{2}}\right)^{10}=0\)
Solution:

Question 11.
Show that \(\left(\frac{1+i}{\sqrt{2}}\right)^{8}+\left(\frac{1-i}{\sqrt{2}}\right)^{8}=2\)
Solution:
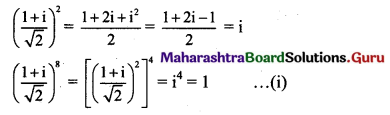
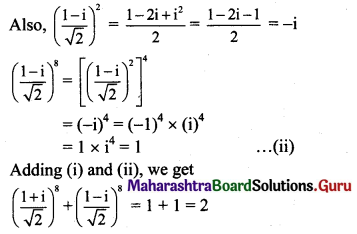
Question 12.
Convert the complex numbers in polar form and also in exponential form.
(i) z = \(\frac{2+6 \sqrt{3} i}{5+\sqrt{3} i}\)
Solution:


(ii) z = -6 + √2 i
Solution:
z = -6 + √2 i
∴ a = -6, b = √2
i.e. a < 0, b > 0

(iii) \(\frac{-3}{2}+\frac{3 \sqrt{3} i}{2}\)
Solution:


Question 13.
If x + iy = \(\frac{a+i b}{a-i b}\), prove that x2 + y2 = 1.
Solution:

![]()
Question 14.
Show that z = \(\left(\frac{-1+\sqrt{-3}}{2}\right)^{3}\) is a rational number.
Solution:

Question 15.
Show that \(\frac{1-2 i}{3-4 i}+\frac{1+2 i}{3+4 i}\) is real.
Solution:
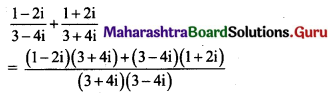

Question 16.
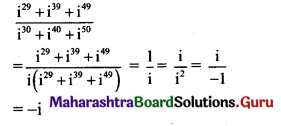
Simplify
(i) \(\frac{\mathrm{i}^{29}+\mathrm{i}^{39}+\mathrm{i}^{49}}{\mathrm{i}^{30}+\mathrm{i}^{40}+\mathrm{i}^{50}}\)
Solution:
(ii) \(\left(\mathrm{i}^{65}+\frac{1}{\mathrm{i}^{145}}\right)\)
Solution:
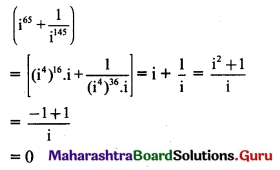
(iii) \(\frac{\mathrm{i}^{238}+\mathrm{i}^{236}+\mathrm{i}^{234}+\mathrm{i}^{232}+\mathrm{i}^{230}}{\mathrm{i}^{228}+\mathrm{i}^{226}+\mathrm{i}^{224}+\mathrm{i}^{222}+\mathrm{i}^{220}}\)
Solution:

Question 17.
Simplify \(\left[\frac{1}{1-2 i}+\frac{3}{1+i}\right]\left[\frac{3+4 i}{2-4 i}\right]\)
Solution:
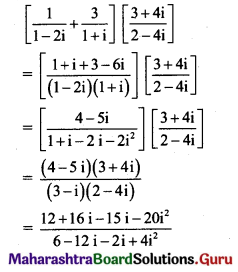

![]()
Question 18.
If α and β are complex cube roots of unity, prove that (1 – α) (1 – β) (1 – α2) (1 – β2) = 9.
Solution:
α and β are the complex cube roots of unity.

Question 19.
If ω is a complex cube root of unity, prove that (1 – ω + ω2)6 + (1 + ω – ω2)6 = 128.
Solution:
ω is the complex cube root of unity.
∴ ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2
∴ L.H.S. = (1 – ω + ω2)6 + (1 + ω – ω2)6
= [(1 + ω2) – ω]6 + [(1 + ω) – ω2]6
= (-ω – ω))6 + (-ω2 – ω2)6
= (-2ω)6 + (-2ω2)6
= 64ω6 + 64ω12
= 64(ω3)2 + 64(ω3)4
= 64(1)2 + 64(1)4
= 128
= R.H.S.
![]()
Question 20.
If ω is the cube root of unity, then find the value of \(\left(\frac{-1+\mathbf{i} \sqrt{3}}{2}\right)^{18}+\left(\frac{-1-\mathbf{i} \sqrt{3}}{2}\right)^{18}\)
Solution:
If ω is the complex cube root of unity, then
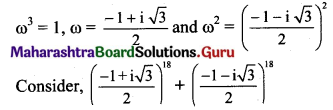
Given Expression = ω18 + (ω2)18
= ω18 + ω36
= (ω3)6 + (ω3)12
= (1)6 + (1)12
= 2
Maths Solutions for Class 11 State Board