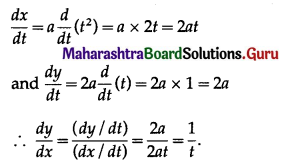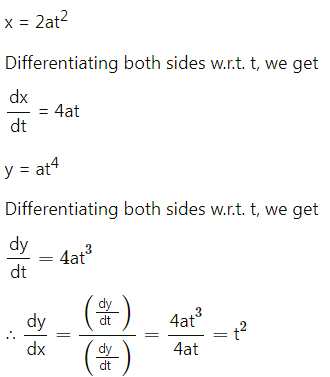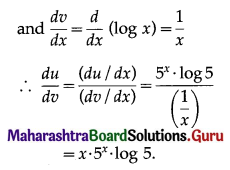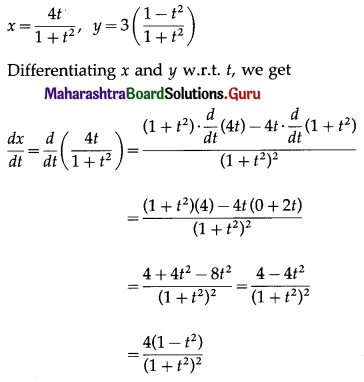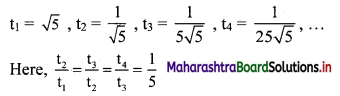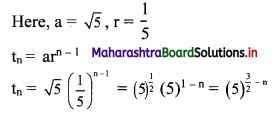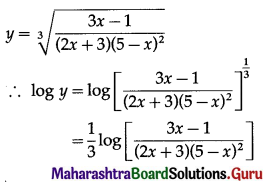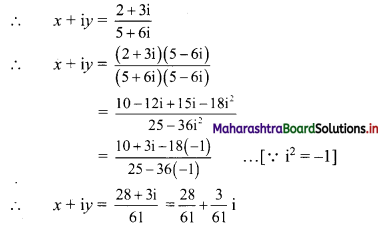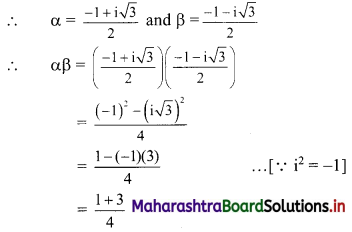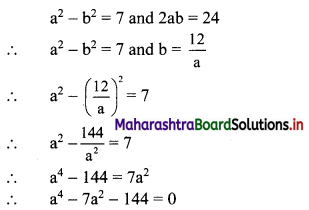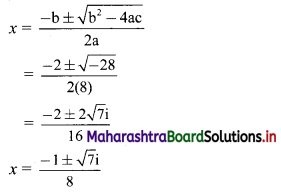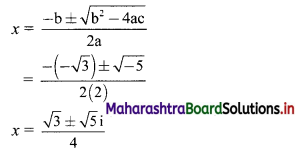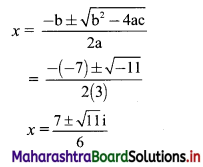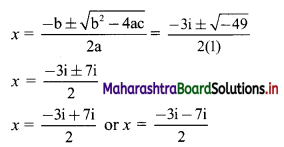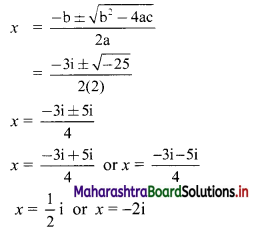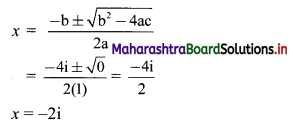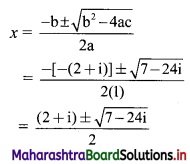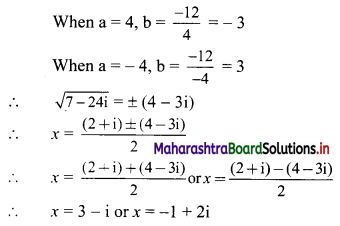Bhagya

Sequences and Series Class 11 Commerce Maths 1 Chapter 4 Exercise 4.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.2 Questions and Answers.

Std 11 Maths 1 Exercise 4.2 Solutions Commerce Maths

Question 1.
For the following G.P.’s, find S_n.
(i) 3, 6, 12, 24, …..
(ii) \(\mathbf{p}, \mathbf{q}, \frac{\mathbf{q}^{2}}{\mathbf{p}}, \frac{\mathbf{q}^{3}}{\mathbf{p}^{2}}, \ldots\)
Solution:

Question 2.
For a G.P., if
(i) a = 2, r = \(-\frac{2}{3}\), find S₆.
(ii) S₅ = 1023, r = 4, find a.
Solution:

Question 3.
For a G. P., if
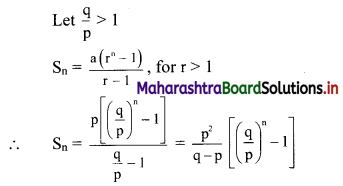
(i) a = 2, r = 3, S_n = 242, find n.
(ii) sum of the first 3 terms is 125 and the sum of the next 3 terms is 27, find the value of r.
Solution:
(i) a = 2, r = 3, S_n = 242
Sn = \(a\left(\frac{r^{n}-1}{r-1}\right)\), for r > 1

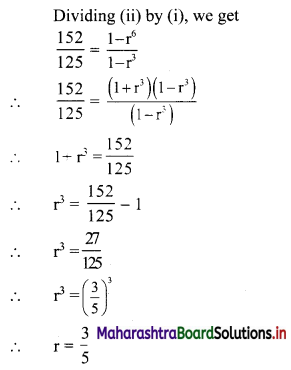
Question 4.
For a G. P.,
(i) if t₃ = 20, t₆ = 160, find S₇.
(ii) if t₄ = 16, t₉ = 512, find S₁₀.
Solution:
(i) t₃ = 20, t₆ = 160
t_n = ar^n-1
∴ t₃ = ar^3-1 = ar²
∴ ar² = 20
∴ a = \(\frac{20}{\mathrm{r}^{2}}\) ……(i)

Question 5.
Find the sum to n terms:
(i) 3 + 33 + 333 + 3333 + ……
(ii) 8 + 88 + 888 + 8888 + ……..
Solution:
(i) S_n = 3 + 33 + 333 +….. upto n terms
= 3(1 + 11 + 111 +….. upto n terms)
= \(\frac{3}{9}\)(9 + 99 + 999 + … upto n terms)
= \(\frac{3}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{3}{9}\)[(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P.
with a = 10, r = \(\frac{100}{10}\) = 10

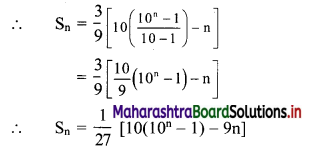
(ii) S_n = 8 + 88 + 888 + … upto n terms
= 8(1 + 11 + 111 + … upto n terms)
= \(\frac{8}{9}\) (9 + 99 + 999 + … upto n terms)
= \(\frac{8}{9}\) [(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{8}{9}\) [(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10

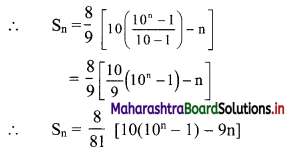
Question 6.
Find the sum to n terms:
(i) 0.4 + 0.44 + 0.444 + ……
(ii) 0.7 + 0.77 + 0.777 + …..
Solution:
(i) S_n = 0.4 + 0.44 + 0.444 + ….. upto n terms
= 4(0.1 + 0.11 + 0.111 + …. upto n terms)
= \(\frac{4}{9}\) (0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{4}{9}\) [(i – 0.1) + (1 – 0.01) + (1 – 0.001) … upto n terms]
= \(\frac{4}{9}\) [(1 + 1 + 1 + …n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P.
with a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1
∴ S_n = \(\frac{4}{9}\left\{\mathrm{n}-0.1\left[\frac{1-(0.1)^{\mathrm{n}}}{1-0.1}\right]\right\}\)

(ii) S_n = 0.7 + 0.77 + 0.777 + … upto n terms
= 7(0.1 + 0.11 + 0.111 + … upto n terms)
= \(\frac{7}{9}\) (0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{7}{9}\) [(1 – 0.1) + (1 – 0.01) + (1 – 0.001) +… upto n terms]
= \(\frac{7}{9}\) [(1 + 1 + 1 +… n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P.
with a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

Question 7.
Find the nth terms of the sequences:
(i) 0.5, 0.55, 0.555,…..
(ii) 0.2, 0.22, 0.222,…..
Solution:
(i) Let t₁ = 0.5, t₂ = 0.55, t₃ = 0.555 and so on.
t₁ = 0.5
t₂ = 0.55 = 0.5 + 0.05
t₃ = 0.555 = 0.5 + 0.05 + 0.005
∴ t_n = 0.5 + 0.05 + 0.005 + … upto n terms
But 0.5, 0.05, 0.005, … upto n terms are in G.P. with a = 0.5 and r = 0.1
∴ t_n = the sum of first n terms of the G.P.

(ii) Let t₁ = 0.2, t₂ = 0.22, t₃ = 0.222 and so on
t₁ = 0.2
t₂ = 0.22 = 0.2 + 0.02
t₃ = 0.222 = 0.2 + 0.02 + 0.002
∴ t_n = 0.2 + 0.02 + 0.002 + … upto n terms
But 0.2, 0.02, 0.002, … upto n terms are in G.P. with a = 0.2 and r = 0.1
∴ t_n = the sum of first n terms of the G.P.

Question 8.
For a sequence, if S_n = 2(3^n-1), find the nth term, hence showing that the sequence is a G.P.
Solution:

Question 9.
If S, P, R are the sum, product and sum of the reciprocals of n terms of a G.P. respectively, then verify that \(\left(\frac{\mathbf{S}}{\mathbf{R}}\right)^{\mathbf{n}}\) = P².
Solution:
Let a be the 1st term and r be the common ratio of the G.P.
∴ the G.P. is a, ar, ar², ar³, …, ar^n-1

Question 10.
If S_n, S_2n, S_3n are the sum of n, 2n, 3n terms of a G.P. respectively, then verify that S_n (S_3n – S_2n) = (S_2n – S_n)².
Solution:
Let a and r be the 1st term and common ratio of the G.P. respectively.

Maharashtra State Board 11th Commerce Maths

• Sequences and Series Ex 4.1 11th Commerce Maths
• Sequences and Series Ex 4.2 11th Commerce Maths
• Sequences and Series Ex 4.3 11th Commerce Maths
• Sequences and Series Ex 4.4 11th Commerce Maths
• Sequences and Series Ex 4.5 11th Commerce Maths
• Sequences and Series Miscellaneous Exercise 4 11th Commerce Maths

Differentiation Class 12 Commerce Maths 1 Chapter 3 Exercise 3.5 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.5 Questions and Answers.

Std 12 Maths 1 Exercise 3.5 Solutions Commerce Maths

1. Find \(\frac{d y}{d x}\) if:

Question 1.
x = at², y = 2at
Solution:
x = at², y = 2at
Differentiating x and y w.r.t. t, we get

Question 2.
x = 2at², y = at⁴
Solution:

Question 3.
x = e^3t, y = e^(4t+5)
Solution:
x = e^3t, y = e^(4t+5)
Differentiating x and y w.r.t. t, we get

2. Find \(\frac{d y}{d x}\) if:

Question 1.
x = \(\left(u+\frac{1}{u}\right)^{2}\), y = \((2)^{\left(u+\frac{1}{u}\right)}\)
Solution:
x = \(\left(u+\frac{1}{u}\right)^{2}\), y = \((2)^{\left(u+\frac{1}{u}\right)}\) ……(1)
Differentiating x and y w.r.t. u, we get,

Question 2.
x = \(\sqrt{1+u^{2}}\), y = log(1 + u²)
Solution:
x = \(\sqrt{1+u^{2}}\), y = log(1 + u²) ……(1)
Differentiating x and y w.r.t. u, we get,

Question 3.
Differentiate 5^x with respect to log x.
Solution:
Let u = 5^x and v = log x
Then we want to find \(\frac{d u}{d v}\)
Differentiating u and v w.r.t. x, we get
\(\frac{d u}{d x}=\frac{d}{d x}\left(5^{x}\right)=5^{x} \cdot \log 5\)

3. Solve the following:

Question 1.
If x = \(a\left(1-\frac{1}{t}\right)\), y = \(a\left(1+\frac{1}{t}\right)\), then show that \(\frac{d y}{d x}\) = -1
Solution:

Question 2.
If x = \(\frac{4 t}{1+t^{2}}\), y = \(3\left(\frac{1-t^{2}}{1+t^{2}}\right)\), then show that \(\frac{d y}{d x}=-\frac{9 x}{4 y}\)
Solution:

Question 3.
If x = t . log t, y = t^t, then show that \(\frac{d y}{d x}\) – y = 0.
Solution:
x = t log t
Differentiating w.r.t. t, we get

Std 12 Commerce Statistics Part 1 Digest Pdf 

• Differentiation Ex 3.1 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.2 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.3 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.4 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.5 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.6 Class 12 Commerce Maths Textbook Solutions
• Differentiation Miscellaneous Exercise 3 Class 12 Commerce Maths Textbook Solutions

Sequences and Series Class 11 Commerce Maths 1 Chapter 4 Exercise 4.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.1 Questions and Answers.

Std 11 Maths 1 Exercise 4.1 Solutions Commerce Maths

Question 1.
Verify whether the following sequences are G.P. If so, write tn.
(i) 2, 6, 18, 54, ……
(ii) 1, -5, 25, -125, …….
(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \ldots\)
(iv) 3, 4, 5, 6, ……
(v) 7, 14, 21, 28, …..
Solution:
(i) 2, 6, 18, 54, …….
t₁ = 2, t₂ = 6, t₃ = 18, t₄ = 54, …..
Here, \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}=\frac{t_{4}}{t_{3}}=3\)
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
Here, a = 2, r = 3
t_n= ar^n-1
∴ t_n = 2(3^n-1)

(ii) 1, -5, 25, -125, ……
t₁ = 1, t₂ = -5, t₃ = 25, t₄ = -125, …..
Here, \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}=\frac{t_{4}}{t_{3}}=-5\)
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
Here, a = 1, r = -5
t_n = ar^n-1
∴ t_n = (-5)^n-1

(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \ldots\)

Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.

(iv) 3, 4, 5, 6,……
t₁ = 3, t₂ = 4, t₃ = 5, t₄ = 6, …..
Here, \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}}=\frac{4}{3}, \frac{\mathrm{t}_{3}}{\mathrm{t}_{2}}=\frac{5}{4}, \frac{\mathrm{t}_{4}}{\mathrm{t}_{3}}=\frac{6}{5}\)
Since, \(\frac{t_{2}}{t_{1}} \neq \frac{t_{3}}{t_{2}} \neq \frac{t_{4}}{t_{3}}\)
∴ the given sequence is not a geometric progression.

(v) 7, 14, 21, 28, …..
t₁ = 7, t₂ = 14, t₃ = 21, t₄ = 28, …..
Here, \(\frac{t_{2}}{t_{1}}=2, \frac{t_{3}}{t_{2}}=\frac{3}{2}, \frac{t_{4}}{t_{3}}=\frac{4}{3}\)
Since, \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}} \neq \frac{\mathrm{t}_{3}}{\mathrm{t}_{2}} \neq \frac{\mathrm{t}_{4}}{\mathrm{t}_{3}}\)
∴ the given sequence is not a geometric progression.

Question 2.
For the G.P.,
(i) if r = \(\frac{1}{3}\), a = 9, find t₇.
(ii) if a = \(\frac{7}{243}\), r = \(\frac{1}{3}\), find t₃.
(iii) if a = 7, r = -3, find t₆.
(iv) if a = \(\frac{2}{3}\), t₆ = 162, find r.
Solution:

Question 3.
Which term of the G. P. 5, 25, 125, 625, ….. is 510?
Solution:

Question 4.
For what values of x, \(\frac{4}{3}\), x, \(\frac{4}{27}\) are in G. P.?
Solution:

Question 5.
If for a sequence, \(t_{n}=\frac{5^{n-3}}{2^{n-3}}\), show that the sequence is a G. P. Find its first term and the common ratio.
Solution:
The sequence (tn) is a G.P., if \(\frac{t_{n}}{t_{n-1}}\) = constant, for all n ∈ N

∴ the sequence is a G. P. with common ratio \(\frac{5}{2}\)
First term, t₁ = \(\frac{5^{\mathrm{l}-3}}{2^{1-3}}=\frac{2^{2}}{5^{2}}=\frac{4}{25}\)

Question 6.
Find three numbers in G. P. such that their sum is 21 and sum of their squares is 189.
Solution:
Let the three numbers in G. P. be \(\frac{a}{\mathrm{r}}\), a, ar.
According to the first condition,



∴ the three numbers are 12, 6, 3 or 3, 6, 12.
Check:
First condition:
12, 6, 3 are in G.P. with r = \(\frac{1}{2}\)
12 + 6 + 3 = 21
Second condition:
12² + 6² + 3² = 144 + 36 + 9 = 189
Thus, both the conditions are satisfied.

Question 7.
Find four numbers in G. P. such that sum of the middle two numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\).
According to the second condition,
\(\frac{\mathrm{a}}{\mathrm{r}^{3}}\left(\frac{\mathrm{a}}{\mathrm{r}}\right)(\mathrm{ar})\left(\mathrm{ar}^{3}\right)=1\)
∴ a⁴ = 1
∴ a = 1
According to the first condition,

Question 8.
Find five numbers in G. P. such that their product is 1024 and the fifth term is square of the third term.
Solution:
Let the five numbers in G. P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the given conditions,

When a = 4, r = -2
\(\frac{a}{r^{2}}\) = 1, \(\frac{a}{r}\) = -2, a = 4, ar = -8, ar² = 16
∴ the five numbers in G.P. are 1, 2, 4, 8, 16 or 1, -2, 4, -8, 16.

Question 9.
The fifth term of a G. P. is x, eighth term of the G. P. is y and eleventh term of the G. P. is z. Verify whether y² = xz.
Solution:

Question 10.
If p, q, r, s are in G. P., show that p + q, q + r, r + s are also in G.P.
Solution:
p, q, r, s are in G.P.

∴ p + q, q + r, r + s are in G.P.

Maharashtra State Board 11th Commerce Maths

• Sequences and Series Ex 4.1 11th Commerce Maths
• Sequences and Series Ex 4.2 11th Commerce Maths
• Sequences and Series Ex 4.3 11th Commerce Maths
• Sequences and Series Ex 4.4 11th Commerce Maths
• Sequences and Series Ex 4.5 11th Commerce Maths
• Sequences and Series Miscellaneous Exercise 4 11th Commerce Maths

Differentiation Class 12 Commerce Maths 1 Chapter 3 Exercise 3.4 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.4 Questions and Answers.

Std 12 Maths 1 Exercise 3.4 Solutions Commerce Maths

1. Find \(\frac{d y}{d x}\) if:

Question 1.
√x + √y = √a
Solution:
√x + √y = √a
Differentiating both sides w.r.t. x, we get

Question 2.
x³ + y³ + 4x³y = 0
Solution:
x³ + y³ + 4x³y = 0
Differentiating both sides w.r.t. x, we get

Question 3.
x³ + x²y + xy² + y³ = 81
Solution:
x³ + x²y + xy² + y³ = 81
Differentiating both sides w.r.t. x, we get

2. Find \(\frac{d y}{d x}\) if:

Question 1.
y.e^x + x.e^y = 1
Solution:
y.e^x + x.e^y = 1
Differentiating both sides w.r.t. x, we get

Question 2.
x^y = e^(x-y)
Solution:
x^y = e^(x-y)
∴ log x^y = log e^(x-y)
∴ y log x = (x – y) log e
∴ y log x = x – y …..[∵ log e = 1]
∴ y + y log x = x
∴ y(1 + log x) = x
∴ y = \(\frac{x}{1+\log x}\)

Question 3.
xy = log(xy)
Solution:
xy = log (xy)
∴ xy = log x + log y
Differentiating both sides w.r.t. x, we get

3. Solve the following:

Question 1.
If x⁵ . y⁷ = (x + y)¹², then show that \(\frac{d y}{d x}=\frac{y}{x}\)
Solution:
x⁵ . y⁷ = (x + y)¹²
∴ log(x⁵ . y⁷) = log(x + y)¹²
∴ log x⁵ + log y⁷ = log(x + y)¹²
∴ 5 log x + 7 log y = 12 log (x + y)
Differentiating both sides w.r.t. x, we get

Question 2.
If log(x + y) = log(xy) + a, then show that \(\frac{d y}{d x}=\frac{-y^{2}}{x^{2}}\)
Solution:
log (x + y) = log (xy) + a
∴ log(x + y) = log x + log y + a
Differentiating both sides w.r.t. x, we get

Question 3.
If e^x + e^y = e^(x+y), then show that \(\frac{d y}{d x}=-e^{y-x}\).
Solution:
e^x + e^y = e^(x+y) ……….(1)
Differentiating both sides w.r.t. x, we get

Std 12 Commerce Statistics Part 1 Digest Pdf 

• Differentiation Ex 3.1 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.2 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.3 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.4 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.5 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.6 Class 12 Commerce Maths Textbook Solutions
• Differentiation Miscellaneous Exercise 3 Class 12 Commerce Maths Textbook Solutions

Differentiation Class 12 Commerce Maths 1 Chapter 3 Exercise 3.3 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.3 Questions and Answers.

Std 12 Maths 1 Exercise 3.3 Solutions Commerce Maths

1. Find \(\frac{d y}{d x}\) if:

Question 1.
y = \(x^{x^{2 x}}\)
Solution:

Question 2.
y = \(x^{e^{x}}\)
Solution:

Question 3.
y = \(e^{x^{x}}\)
Solution:

2. Find \(\frac{d y}{d x}\) if:

Question 1.
y = \(\left(1+\frac{1}{x}\right)^{x}\)
Solution:

Question 2.
y = (2x + 5)^x
Solution:

Question 3.
y = \(\sqrt[3]{\frac{(3 x-1)}{(2 x+3)(5-x)^{2}}}\)
Solution:

3. Find \(\frac{d y}{d x}\) if:

Question 1.
y = (log x)^x + x^{log x}
Solution:

Question 2.
y = x^x + a^x
Solution:

Question 3.
y = \(10^{x^{x}}+10^{x^{10}}+10^{10^{x}}\)
Solution:

Std 12 Commerce Statistics Part 1 Digest Pdf 

• Differentiation Ex 3.1 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.2 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.3 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.4 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.5 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.6 Class 12 Commerce Maths Textbook Solutions
• Differentiation Miscellaneous Exercise 3 Class 12 Commerce Maths Textbook Solutions

Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Miscellaneous Exercise 3 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Miscellaneous Exercise 3 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 3 Solutions Commerce Maths

Question 1.
Find the value of \(\frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}\)
Solution:

Question 2.
Find the value of √-3 × √-6.
Solution:
√-3 × √-6 = √3 × √-1 + √6 × √-1
= √3i × √6i
= √18i²
= -3√2 ……[∵ i² = -1]

Question 3.
Simplify the following and express in the form a + ib.
(i) 3 + √-64
(ii) (2i³)²
(iii) (2 + 3i) (1 – 4i)
(iv) \(\frac{5}{2}\) i(-4 – 3i)
(v) (1 + 3i)2 (3 + i)
(vi) \(\frac{4+3 i}{1-i}\)
(vii) \(\left(1+\frac{2}{i}\right)\left(3+\frac{4}{i}\right)(5+i)^{-1}\)
(viii) \(\frac{\sqrt{5}+\sqrt{3} i}{\sqrt{5}-\sqrt{3} i}\)
(ix) \(\frac{3 i^{5}+2 i^{7}+i^{9}}{i^{6}+2 i^{8}+3 i^{18}}\)
(x) \(\frac{5+7 i}{4+3 i}+\frac{5+7 i}{4-3 i}\)
Solution:
(i) 3 + √-64
= 3 + √64 . √-1
= 3 + 8i

(ii) (2i³)²
= 4i⁶
= 4(i²)³
= 4(-1)³ …..[∵ i² = -1]
= -4
= -4 + 0i

(iii) (2 + 3i)(1 – 4i) = 2 – 8i + 3i – 12i²
= 2 – 5i – 12(-1) ……[∵ i² = -1]
= 14 – 5i

(iv) \(\frac{5}{2}\) i(-4 – 3i)
= \(\frac{5}{2}\) (-4i – 3i²)
= \(\frac{5}{2}\) [-4i – 3(-1)] ……[∵ i² = -1]
= \(\frac{5}{2}\) (3 – 4i)
= \(\frac{15}{2}\) – 10i

(v) (1 + 3i)² (3 + i)
= (1 + 6i + 9i²) (3 + i)
= (1 + 6i – 9)(3 + i) ……[∵ i² = -1]
= (-8 + 6i)(3 + i)
= -24 – 8i + 18i + 6i²
= -24 + 10i + 6(-1)
= -24 + 10i – 6
= -30 + 10i

Question 4.
Solve the following equations for x, y ∈ R:
(i) (4 – 5i) x + (2 + 3i) y = 10 – 7i
(ii) (1 – 3i) x + (2 + 5i) y = 1 + i
(iii) \(\frac{x+i y}{2+3 i}\) = 7 – i
(iv) (x + iy) (5 + 6i) = 2 + 3i
(v) 2x + i⁹ y (2 + i) = x i⁷ + 10 i¹⁶
Solution:
(i) (4 – 5i) x + (2 + 3i)y = 10 – 7i
∴ (4x + 2y) + (3y – 5x) i = 10 – 7i
Equating real and imaginary parts, we get
4x + 2y = 10
i.e., 2x + y = 5 …….(i)
and 3y – 5x = -7 ……..(ii)
Equation (i) × 3 – equation (ii) gives
11x = 22
∴ x = 2
Putting x = 2 in (i), we get
2(2) + y = 5
∴ y = 1
∴ x = 2 and y = 1

(ii) (1 – 3i) x + (2 + 5i) y = 7 + i
∴ (x + 2y) + (-3x + 5y)i = 7 + i
Equating real and imaginary parts, we get
x + 2y = 7 ……..(i)
and -3x + 5y = 1 ……..(ii)
Equation (i) × 3 + equation (ii) gives
11y = 22
∴ y = 2
Putting y = 2 in (i), we get
x + 2(2) = 7
∴ x = 3
∴ x = 3 and y = 2

(iii) \(\frac{x+i y}{2+3 i}\) = 7 – i
∴ x + iy = (7 – i)(2 + 3i)
∴ x + iy = 14 + 21i – 2i – 3i²
∴ x + iy = 14 + 19i – 3(-1) …..[∵ i² = -1]
∴ x + iy = 17 + 19i
Equating real and imaginary parts, we get
x = 17 and y = 19

(iv) (x + iy)(5 + 6i) = 2 + 3i

Equating real and imaginary parts, we get
x = \(\frac{28}{61}\) and y = \(\frac{3}{61}\)

(v) 2x + i⁹ y (2 + i) = x i⁷ + 10 i¹⁶
∴ 2x + (i⁴)² . i . y (2 + i) = x (i²)³ . i + 10 . (i⁴)⁴
∴ 2x + (1)² . iy (2 + i) = x (-1)³ . i + 10 (1)⁴ ……[∵ i² = -1, i⁴ = 1]
∴ 2x + 2yi + yi² = -xi + 10
∴ 2x + 2yi – y + xi = 10
∴ (2x – y) + (x + 2y)i = 10 + 0.i
Equating real and imaginary parts, we get
2x – y = 10 ……(i)
and x + 2y = 0 ……..(ii)
Equation (i) × 2 + equation (ii) gives
5x = 20
∴ x = 4
Putting x = 4 in (i), we get
2(4) – y = 10
∴ y = 8 – 10
∴ y = -2
∴ x = 4 and y = -2

Question 5.
Find the value of:
(i) x³ + 2x² – 3x + 21, if x = 1 + 2i
(ii) x³ – 5x² + 4x + 8, if x = \(\frac{10}{3-i}\)
(iii) x³ – 3x² + 19x – 20, if x = 1 – 4i
Solution:
(i) x = 1 + 2i
∴ x – 1 = 2i
∴ (x – 1)² = 4i²
∴ x² – 2x + 1 = -4 ……[∵ i² = -1]
∴ x² – 2x + 5 = 0 ……(i)

∴ x³ + 2x² – 3x + 21
= (x² – 2x + 5)(x + 4) + 1
= 0.(x + 4) + 1 ……[From (i)]
= 0 + 1
= 1
∴ x³ + 2x² – 3x + 21 = 1

(ii) x = \(\frac{10}{3-i}\)

x³ – 5x² + 4x + 8
= (x² – 6x + 10)(x + 1) – 2
= 0 . (x + 1) – 2 ……[From (i)]
= 0 – 2
∴ x³ – 5x² + 4x + 8 = -2

(iii) x = 1 – 4i
∴ x – 1 = -4i
∴ (x – 1)² = 16i²
∴ x² – 2x + 1 = -16 ……[∵ i² = -1]
∴ x² – 2x + 17 = 0 ……(i)

∴ x³ – 3x² + 19x – 20
= (x² – 2x + 17) (x – 1) – 3
= 0 . (x – 1) – 3 ….[From (i)]
= 0 – 3
= -3
∴ x³ – 3x² + 19x – 20 = -3

Question 6.
Find the square roots of:
(i) -16 + 30i
(ii) 15 – 8i
(iii) 2 + 2√3i
(iv) 18i
(v) 3 – 4i
(vi) 6 + 8i
Solution:
(i) Let \(\sqrt{-16+30 \mathrm{i}}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
-16 + 30i = a² + b²i² + 2abi
∴ -16 + 30i = (a² – b²) + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = -16 and 2ab = 30
∴ a² – b² = -16 and b = \(\frac{15}{a}\)
∴ a² – \(\left(\frac{15}{a}\right)^{2}\) = -16
∴ a² – \(\frac{225}{a^{2}}\) = -16
∴ a⁴ – 225 = – 16a²
∴ a⁴ + 16a² – 225 = 0
∴ (a² + 25)(a² – 9) = 0
∴ a² = -25 or a² = 9
But a ∈ R, a² ≠ -25
∴ a² = 9
∴ a = ±3
When a = 3, b = \(\frac{15}{3}\) = 5
When a = -3, b = \(\frac{15}{-3}\) = -5
∴ \(\sqrt{-16+30 \mathrm{i}}\) = ±(3 + 5i)

(ii) Let \(\sqrt{15-8 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
15 – 8i = a² + b²i² + 2abi
∴ 15 – 8i = (a² – b²) + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 15 and 2ab = -8
∴ a² – b² = 15 and b = \(\frac{-4}{a}\)
∴ a² – (\(\left(\frac{-4}{a}\right)^{2}\)) = 15
∴ a² – \(\frac{16}{a^{2}}\) = 15
∴ a⁴ – 16 = 15a²
∴ a⁴ – 15a² – 16 = 0
∴ (a² – 16)(a² + 1) = 0
∴ a² = 16 or a² = -1
But a ∈ R, a² ≠ -1
∴ a² = 16
∴ a = ±4
When a = 4, b = \(\frac{-4}{4}\) = -1
When a = -4, b = \(\frac{-4}{-4}\) = 1
\(\sqrt{15-8 i}\) = ±(4 – i)

(iii) Let \(\sqrt{2+2 \sqrt{3} i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
2 – 2√3i = a² + b²i² + 2abi
∴ 2 – 2√3i = a² – b² + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 2 and 2ab = 2√3
∴ a² – b² = 2 and b = \(\frac{\sqrt{3}}{\mathrm{a}}\)
∴ a² – \(\left(\frac{\sqrt{3}}{a}\right)^{2}\) = 2
∴ a² – \(\frac{3}{a^{2}}\) = 2
∴ a⁴ – 3 = 2a²
∴ a⁴ – 2a² – 3 = 0
∴ (a² – 3)(a² + 1) = 0
∴ a² = 3 or a² = -1
But a ∈ R, a² ≠ -1
∴ a² = 3
∴ a = ±√3
When a = √3 , b = \(\frac{\sqrt{3}}{\sqrt{3}}\) = 1
When a = -√3 , b = \(\frac{\sqrt{3}}{-\sqrt{3}}\) = -1
∴ \(\sqrt{2+2 \sqrt{3} i}\) = ±(√3 + i)

(iv) Let \(\sqrt{18 \mathrm{i}}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
18i = a² + b²i² + 2abi
∴ 0 + 18i = a² – b² + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 0 and 2ab = 18
∴ a² – b² = 0 and b = \(\frac{9}{\mathrm{a}}\)
∴ a² – \(\left(\frac{9}{a}\right)^{2}\) = 0
∴ a² – \(\frac{81}{a^{2}}\) = 0
∴ a⁴ – 81 = 0
∴ (a² – 9) (a² + 9) = 0
∴ a² = 9 or a² = -9
But a ∈ R, a² ≠ -9
∴ a² = 9
∴ a = ±3
When a = 3, b = \(\frac{9}{3}\) = 3
When a = 3, b = \(\frac{9}{-3}\) = -3
∴ \(\sqrt{18 \mathrm{i}}\) = ±3(1 + i)

(v) Let \(\sqrt{3-4 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
3 – 4i = a² + b²i² + 2abi
∴ 3 – 4i = a² – b² + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 3 and 2ab = -4
∴ a² – b² = 3 and b = \(\frac{-2}{a}\)
∴ a² – \(\left(-\frac{2}{a}\right)^{2}\) = 3
∴ a² – \(\frac{4}{a^{2}}\) = 3
∴ a⁴ – 4 = 3a²
∴ a⁴ – 3a² – 4 = 0
∴ (a² – 4)(a² + 1) = 0
∴ a² = 4 or a² = -1
But, a ∈ R, a² ≠ -1
∴ a² = 4
∴ a = ±2
When a = 2, b = \(\frac{-2}{2}\) = -1
When a = -2, b = \(\frac{-2}{-2}\) = 1
∴ \(\sqrt{3-4 i}\) = ±(2 – i)

(vi) Let \(\sqrt{6+8 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
6 + 8i = a² + b²i² + 2abi
∴ 6 + 8i = a² – b² + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 6 and 2ab = 8
∴ a² – b² = 6 and b = \(\frac{4}{\mathrm{a}}\)
∴ a² – \(\left(\frac{4}{a}\right)^{2}\) = 6
∴ a² – \(\frac{16}{a^{2}}\) = 6
∴ a⁴ – 16 = 6a²
∴ a⁴ – 6a² – 16 = 0
∴ (a² – 8)(a² + 2) = 0
∴ a² = 8 or a² = -2
But a ∈ R, a² ≠ -2
∴ a² = 8
∴ a = ±2√2
When a = 2√2, b = \(\frac{4}{2 \sqrt{2}}\) = √2
When a = -2√2, b = \(\frac{4}{-2 \sqrt{2}}\) = -√2
∴ \(\sqrt{6+8 i}\) = ±(2√2 + √2i) = ±√2(2 + i)

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Differentiation Class 12 Commerce Maths 1 Chapter 3 Exercise 3.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.2 Questions and Answers.

Std 12 Maths 1 Exercise 3.2 Solutions Commerce Maths

1. Find the rate of change of demand (x) of a commodity with respect to price (y) if:

Question 1.
y = 12 + 10x + 25x²
Solution:
Given y = 12 + 10x + 25x²

Hence, the rate of change of demand (x) with respect to price (y) \(=\frac{d x}{d y}=\frac{1}{10+50 x}\)

Question 2.
y = 18x + log(x – 4)
Solution:
Given y = 18x + log (x – 4)

Hence, the rate of change of demand (x) with respect to price (y) \(=\frac{d x}{d y}=\frac{x-4}{18 x-71}\)

Question 3.
y = 25x + log(1 + x²)
Solution:
Given y = 25x + log(1 + x²)

Hence, the rate of change of demand (x) with respect to price (y) \(\frac{d x}{d y}=\frac{1+x^{2}}{25 x^{2}+2 x+25}\)

2. Find the marginal demand of a commodity where demand is x and price is y.

Question 1.
y = xe^-x + 7
Solution:

Question 2.
y = \(\frac{x+2}{x^{2}+1}\)
Solution:

Question 3.
y = \(\frac{5 x+9}{2 x-10}\)
Solution:

Std 12 Commerce Statistics Part 1 Digest Pdf 

• Differentiation Ex 3.1 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.2 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.3 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.4 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.5 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.6 Class 12 Commerce Maths Textbook Solutions
• Differentiation Miscellaneous Exercise 3 Class 12 Commerce Maths Textbook Solutions

Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Exercise 3.3 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Ex 3.3 Questions and Answers.

Std 11 Maths 1 Exercise 3.3 Solutions Commerce Maths

Question 1.
If ω is a complex cube root of unity, show that
(i) (2 – ω)(2 – ω²) = 7
(ii) (2 + ω + ω²)³ – (1 – 3ω + ω²)³ = 65
(iii) \(\frac{\left(\mathbf{a}+\mathbf{b} \omega+\mathbf{c} \omega^{2}\right)}{\mathbf{c}+\mathbf{a} \omega+\mathbf{b} \omega^{2}}\) = ω²
Solution:
ω is the complex cube root of unity.
∴ ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
(i) L.H.S. = (2 – ω)(2 – ω²)
= 4 – 2ω² – 2ω + ω³
= 4 – 2(ω² + ω) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
= R.H.S.

(ii) L.H.S. = (2 + ω + ω²)³ – (1 – 3ω + ω²)³
= [2 + (ω + ω²)]³ – [-3ω + (1 + ω²)]³
= (2 – 1)³ – (-3ω – ω)³
= 13 – (-4ω)³
= 1 + 64ω³
= 1 + 64(1)
= 65
= R.H.S.

(iii) L.H.S. =\(\frac{\left(\mathbf{a}+\mathbf{b} \omega+\mathbf{c} \omega^{2}\right)}{\mathbf{c}+\mathbf{a} \omega+\mathbf{b} \omega^{2}}\)
= \(\frac{a \omega^{3}+b \omega^{4}+c \omega^{2}}{c+a \omega+b \omega^{2}}\) ……[∵ ω³ = 1, ω⁴ = ω]
= \(\frac{\omega^{2}\left(c+a \omega+b \omega^{2}\right)}{c+a \omega+b \omega^{2}}\)
= ω²
= R.H.S.

Question 2.
If ω is a complex cube root of unity, find the value of
(i) ω + \(\frac{1}{\omega}\)
(ii) ω² + ω³ + ω⁴
(iii) (1 + ω²)³
(iv) (1 – ω – ω²)³ + (1 – ω + ω²)³
(v) (1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸)
Solution:
ω is the complex cube root of unity.
∴ ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
(i) ω + \(\frac{1}{\omega}\)
= \(\frac{\omega^{2}+1}{\omega}\)
= \(\frac{-\omega}{\omega}\)
= -1

(ii) ω² + ω³ + ω⁴
= ω² (1 + ω + ω²)
= ω² (0)
= 0

(iii) (1 + ω²)³
= (-ω)³
= -ω³
= -1

(iv) (1 – ω – ω²)³ + (1 – ω + ω²)³
= [1 – (ω + ω²)]³ + [(1 + ω²) – ω]³
= [1 – (-1)]³ + (-ω – ω)³
= 2³ + (-2ω)³
= 8 – 8ω³
= 8 – 8(1)
= 0

(v) (1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸)
= (1 + ω)(1 + ω²)(1 + ω)(1 + ω²) …..[∵ ω³ = 1, ω⁴ = ω]
= (-ω²)(-ω)(-ω²)(-ω)
= ω⁶
= (ω³)²
= (1)²
= 1

Question 3.
If α and β are the complex cube roots of unity, show that α² + β² + αβ = 0.
Solution:
α and β are the complex cube roots of unity.

∴ α – β = -1
L.H.S. = α² + β² + αβ
= α² + 2αβ + β² + αβ – 2αβ ……[Adding and subtracting 2αβ]
= (α² + 2αβ + β²) – αβ
= (α + β)² – αβ
= (-1)² – 1
= 1 – 1
= 0
= R.H.S.

Question 4.
If x = a + b, y = αa + βb and z = aβ + bα, where α and β are the complex cube roots of unity, show that xyz = a³ + b³.
Solution:
x = a + b, y = αa + βb, z = aβ + bα
α and β are the complex cube roots of unity.

Question 5.
If ω is a complex cube root of unity, then prove the following:
(i) (ω² + ω – 1)³ = -8
(ii) (a + b) + (aω + bω²) + (aω² + bω) = 0
Solution:
ω is the complex cube root of unity.
∴ ω³ = 1 and 1 + ω + ω² = 0
Also, 1 + ω² = -ω, 1 + ω = -ω² and ω + ω² = -1
(i) L.H.S. = (ω² + ω – 1)³
= (-1 – 1)³
= (-2)³
= -8
= R.H.S.

(ii) L.H.S. = (a + b) + (aω + bω²) + (aω² + bω)
= (a + aω + aω²) + (b + bω + bω²)
= a(1 + ω + ω²) + b(1 + ω + ω²)
= a(0) + b(0)
= 0
= R.H.S.

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Exercise 3.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Ex 3.2 Questions and Answers.

Std 11 Maths 1 Exercise 3.2 Solutions Commerce Maths

Question 1.
Find the square root of the following complex numbers:
(i) -8 – 6i
Solution:
Let \(\sqrt{-8-6 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
-8 – 6i = (a + bi)²
-8 – 6i = a² + b²i² + 2abi
-8 – 6i = (a² – b²) + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get

(ii) 7 + 24i
Solution:
Let \(\sqrt{7+24 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
7 + 24i = (a + bi)²
7 + 24i = a² + b²i² + 2abi
7 + 24i = (a² – b²) + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get

(iii) 1 + 4√3i
Solution:
Let \(\sqrt{1+4 \sqrt{3} i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
1 + 4√3i = (a + bi)²
1 + 4√3i = a² + b²i² + 2abi
1 +4√3i = (a² – b²) + 2abi ……[∵ i² = -1]
Equating real and imaginary parts, we get

(iv) 3 + 2√10i
Solution:
Let \(\sqrt{3+2 \sqrt{10}} i\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
3 + 2√10i = (a + bi)²
3 + 2√10i = a² + b²i² + 2abi
3 + 2√10i = (a² – b²) + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get
a² – b² = 3 and 2ab = 2√10
a² – b² = 3 and b = \(\frac{\sqrt{10}}{a}\)

(v) 2(1 – √3i)
Solution:
Let \(\sqrt{2(1-\sqrt{3} i)}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
2(1 – √3i) = (a + bi)²
2(1 – √3i) = a² + b²i² + 2abi
2 – 2√3i = (a² – b²) + 2abi …..[∵ i² = -1]
Equating real and imaginary parts, we get

Question 2.
Solve the following quadratic equations.
(i) 8x² + 2x + 1 = 0
Solution:
Given equation is 8x² + 2x + 1 = 0
Comparing with ax² + bx + c = 0, we get
a = 8, b = 2, c = 1
Discriminant = b² – 4ac
= (2)² – 4 × 8 × 1
= 4 – 32
= -28 < 0
So, the given equation has complex roots.
These roots are given by

∴ the roots of the given equation are \(\frac{-1+\sqrt{7} \mathrm{i}}{8}\) and \(\frac{-1-\sqrt{7} \mathrm{i}}{8}\)

(ii) 2x² – √3x + 1 = 0
Solution:
Given equation is 2x² – √3x + 1 = 0
Comparing with ax² + bx + c = 0, we get
a = 2, b = -√3, c = 1
Discriminant = b² – 4ac
= (-√3)² – 4 × 2 × 1
= 3 – 8
= -5 < 0
So, the given equation has complex roots.
These roots are given by

∴ the roots of the given equation are \(\frac{\sqrt{3}+\sqrt{5} i}{4}\) and \(\frac{\sqrt{3}-\sqrt{5} i}{4}\)

(iii) 3x² – 7x + 5 = 0
Solution:
Given equation is 3x² – 7x + 5 = 0
Comparing with ax² + bx + c = 0, we get
a = 3, b = -7, c = 5
Discriminant = b² – 4ac
= (-7)² – 4 × 3 × 5
= 49 – 60
= -11 < 0
So, the given equation has complex roots.
These roots are given by

∴ the roots of the given equation are \(\frac{7+\sqrt{11} i}{6}\) and \(\frac{7-\sqrt{11} i}{6}\)

(iv) x² – 4x + 13 = 0
Solution:
Given equation is x² – 4x + 13 = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = -4, c = 13
Discriminant = b² – 4ac
= (-4)² – 4 × 1 × 13
= 16 – 52
= -36 < 0
So, the given equation has complex roots.
These roots are given by

∴ the roots of the given equation are 2 + 3i and 2 – 3i.

Question 3.
Solve the following quadratic equations.
(i) x² + 3ix + 10 = 0
Solution:
Given equation is x² + 3ix + 10 = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = 3i, c = 10
Discriminant = b² – 4ac
= (3i)² – 4 × 1 × 10
= 9i² – 40
= -9 – 40 …..[∵ i² = -1]
= -49
So, the given equation has complex roots.
These roots are given by

∴ x = 2i or x = -5i
∴ the roots of the given equation are 2i and -5i.
Check:
If x = 2i and x = -5i satisfy the given equation, then our answer is correct.
L.H.S. = x² + 3ix + 10
= (2i)² + 3i(2i) + 10i
= 4i² + 6i² + 10
= 10i² + 10
= -10 + 10 ……[∵ i² = -1]
= 0
= R.H.S.
L.H.S. = x² + 3ix + 10
= (-5i)² + 3i(-5i) + 10
= 25i² – 15i² + 10
= 10i² + 10
= -10 + 10 …..[∵ i² = -1]
= 0
= R.H.S.
Thus, our answer is correct.

(ii) 2x² + 3ix + 2 = 0
Solution:
Given equation is 2x² + 3ix + 2 = 0
Comparing with ax² + bx + c = 0, we get
a = 2, b = 3i, c = 2
Discriminant = b² – 4ac
= (3i)² – 4 × 2 × 2
= 9i² – 16
= -9 – 16
= -25 < 0
So, the given equation has complex roots.
These roots are given by

∴ the roots of the given equation are \(\frac{1}{2}\)i and -2i.

(iii) x² + 4ix – 4 = 0
Solution:
Given equation is x² + 4ix – 4 = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = 4i, c = -4
Discriminant = b² – 4ac
= (4i)² – 4 × 1 × -4
= 16i² + 16
= -16 + 16 …..[∵ i² = -1]
= 0
So, the given equation has equal roots.
These roots are given by

∴ the roots of the given equation are -2i and -2i.

(iv) ix² – 4x – 4i = 0
Solution:
ix² – 4x – 4i = 0
Multiplying throughout by i, we get
i²x² – 4ix – 4i² = 0
∴ -x² – 4ix + 4 = 0 ……[∵ i² = -1]
∴ x² + 4ix – 4 = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = 4i, c = -4
Discriminant = b² – 4ac
= (4i)² – 4 × 1 × -4
= 16i² + 16
= -16 + 16 …..[∵ i² = -1]
= 0
So, the given equation has equal roots.
These roots are given by

∴ the roots of the given equation are -2i and -2i.

Question 4.
Solve the following quadratic equations.
(i) x² – (2 + i) x – (1 – 7i) = 0
Solution:
Given equation is x² – (2 + i)x – (1 – 7i) = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = -(2 + i), c = -(1 – 7i)
Discriminant = b² – 4ac
= [-(2 + i)]² – 4 × 1 × -(1 – 7i)
= 4 + 4i + i² + 4 – 28i
= 4 + 4i – 1 + 4 – 28i …….[∵ i² = -1]
= 7 – 24i
So, the given equation has complex roots.
These roots are given by

(ii) x² – (3√2 + 2i) x + 6√2i = 0
Solution:
Given equation is x² – (3√2 + 2i) x + 6√2i = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = -(3√2 + 2i), c = 6√2i
Discriminant = b² – 4ac
= [-(3√2 + 2i)]² – 4 × 1 × 6√2i
= 18 + 12√2i + 4i² – 24√2i
= 18 – 12√2i – 4 …..[∵ i² = -1]
= 14 – 12√2i
So, the given equation has complex roots.
These roots are given by

(iii) x² – (5 – i) x + (18 + i) = 0
Solution:
Given equation is x² – (5 – i)x + (18 + i) = 0
Comparing with ax² + bx + c = 0, we get
a = 1, b = -(5 – i), c = 18 + i
Discriminant = b² – 4ac
= [-(5 – i)]² – 4 × 1 × (18 + i)
= 25 – 10i + i² – 72 – 4i
= 25 – 10i – 1 – 72 – 4i …..[∵ i² = -1]
= -48 – 14i
So, the given equation has complex roots.
These roots are given by

(iv) (2 + i) x² – (5 – i) x + 2(1 – i) = 0
Solution:
Given equation is
(2 + i) x² – (5 – i) x + 2(1 – i) = 0
Comparing with ax² + bx + c = 0, we get
a = 2 + i, b = -(5 – i), c = 2(1 – i)
Discriminant = b² – 4ac
= [-(5 – i)]² – 4 × (2 + i) × 2(1 – i)
= 25 – 10i + i² – 8(2 + i)(1 – i)
= 25 – 10i + i² – 8(2 – 2i + i – i²)
= 25 – 10i – 1 – 8(2 – i + 1) …..[∵ i² = -1]
= 25 – 10i – 1 – 16 + 8i – 8
= -2i
So, the given equation has complex roots.
These roots are given by

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Exercise 3.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Ex 3.1 Questions and Answers.

Std 11 Maths 1 Exercise 3.1 Solutions Commerce Maths

Question 1.
Write the conjugates of the following complex numbers:
(i) 3 + i
(ii) 3 – i
(iii) -√5 – √7i
(iv) -√-5
(v) 5i
(vi) √5 – i
(vii) √2 + √3i
Solution:
(i) Conjugate of (3 + i) is (3 – i)
(ii) Conjugate of (3 – i) is (3 + i)
(iii) Conjugate of (-√5 – √7i) is (-√5 + √7i)
(iv) -√-5 = -√5 × √-1 = -√5i
Conjugate of -√-5 is √5i
(v) Conjugate of 5i is -5i
(vi) Conjugate of √5 – i is √5 + i
(vii) Conjugate of √2 + √3i is √2 – √3i

Question 2.
Express the following in the form of a + ib, a, b ∈ R, i = √-1. State the values of a and b:
(i) (1 + 2i)(-2 + i)
(ii) \(\frac{\mathrm{i}(4+3 \mathrm{i})}{(1-\mathrm{i})}\)
(iii) \(\frac{(2+i)}{(3-i)(1+2 i)}\)
(iv) \(\frac{3+2 i}{2-5 i}+\frac{3-2 i}{2+5 i}\)
(v) \(\frac{2+\sqrt{-3}}{4+\sqrt{-3}}\)
(vi) (2 + 3i)(2 – 3i)
(vii) \(\frac{4 i^{8}-3 i^{9}+3}{3 i^{11}-4 i^{10}-2}\)
Solution:

Question 3.
Show that (-1 + √3i)³ is a real number.
Solution:
(-1 + √3i)³
= (-1)³ + 3(-1)² (√3i) + 3(-1)(√3i)² +(√3i)³ [∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= -1 + 3√3i – 3(3i²) + 3√3 i³
= -1 + 3√3i – 3(-3) – 3√3i [∵ i² = -1, i³ = -1]
= -1 + 9
= 8, which is a real number.

Question 4.
Evaluate the following:
(i) i³⁵
(ii) i⁸⁸⁸
(iii) i⁹³
(iv) i¹¹⁶
(v) i⁴⁰³
(vi) \(\frac{1}{i^{58}}\)
(vii) i³⁰ + i⁴⁰ + i⁵⁰ + i⁶⁰
Solution:
We know that, i² = -1, i³ = -i, i⁴ = 1
(i) i³⁵ = (i⁴)⁸ (i²) i = (1)⁸ (-1) i = -i
(ii) i⁸⁸⁸ = (i⁴)²²² = (1)²²² = 1
(iii) i⁹³ = (i⁴)²³ . i = (1)²³ . i = i
(iv) i¹¹⁶ = (i⁴)²⁹ = (1)²⁹ = 1
(v) i⁴⁰³ = (i⁴)¹⁰⁰ (i²) i = (1)¹⁰⁰ (-1) i = -i
(vi) \(\frac{1}{i^{88}}=\frac{1}{\left(i^{4}\right)^{14} \cdot i^{2}}=\frac{1}{(1)^{14}(-1)}=-1\)
(vii) i³⁰ + i⁴⁰ + i⁵⁰ + i⁶⁰
= (i⁴)⁷ i² + (i⁴)¹⁰ + (i⁴)¹² i² + (i⁴)¹⁵
= (1)⁷ (-1) + (1)¹⁰ + (1)¹² (-1) + (1)¹⁵
= -1 + 1 – 1 + 1
= 0

Question 5.
Show that 1 + i¹⁰ + i²⁰ + i³⁰ is a real number.
Solution:
1 + i¹⁰ + i²⁰ + i³⁰
= 1 + (i⁴)² . i² + (i⁴)⁵ + (i⁴)⁷ . i²
= 1 + (1)² (-1) + (1)⁵ + (1)⁷ (-1) [∵ i⁴ = 1, i² = -1]
= 1 – 1 + 1 – 1
= 0, which is a real number.

Question 6.
Find the value of
(i) i⁴⁹ + i⁶⁸ + i⁸⁹ + i¹¹⁰
(ii) i + i² + i³ + i⁴
Solution:
(i) i⁴⁹ + i⁶⁸ + i⁸⁹ + i¹¹⁰
= (i⁴)¹² . i + (i⁴)¹⁷ + (i⁴)²² . i + (i⁴)²⁷ . i²
= (1)¹² . i + (1)¹⁷ + (1)²² . i + (1)²⁷(-1) ……[∵ i⁴ = 1, i² = -1]
= i + 1 + i – 1
= 2i

(ii) i + i² + i³ + i⁴
= i + i² + i² . i + i⁴
= i – 1 – i + 1 [∵ i² = -1, i⁴ = 1]
= 0

Question 7.
Find the value of 1 + i² + i⁴ + i⁶ + i⁸ + …… + i²⁰.
Solution:
1 + i² + i⁴ + i⁶ + i⁸ + ….. + i²⁰
= 1 + (i² + i⁴) + (i⁶ + i⁸) + (i¹⁰ + i¹²) + (i¹⁴ + i¹⁶) + (i¹⁸ + i²⁰)
= 1 + [i² + (i²)²] + [(i²)³ + (i²)⁴] + [(i²)⁵ + (i²)⁶] + [(i²)⁷ + (i²)⁸] + [(i²)⁹ + (i²)¹⁰]
= 1 + [-1 + (- 1)²] + [(-1)³ + (-1)⁴] + [(-1)⁵ + (-1)⁶] + [(-1)⁷ + (-1)⁸] + [(-1)⁹ + (-1)¹⁰] [∵ i² = -1]
= 1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1)
= 1 + 0 + 0 + 0 + 0 + 0
= 1

Question 8.
Find the values of x and y which satisfy the following equations (x, y ∈ R):
(i) (x + 2y) + (2x – 3y)i + 4i = 5
(ii) \(\frac{x+1}{1+\mathrm{i}}+\frac{y-1}{1-\mathrm{i}}=\mathrm{i}\)
Solution:
(i) (x + 2y) + (2x – 3y)i + 4i = 5
∴ (x + 2y) + (2x – 3y)i = 5 – 4i
Equating real and imaginary parts, we get
x + 2y = 5 ……..(i)
and 2x – 3y = -4 ………(ii)
Equation (i) × 2 – equation (ii) gives
7y = 14
∴ y = 2
Putting y- 2 in (i), we get
x + 2(2) = 5
∴ x + 4 = 5
∴ x = 1
∴ x = 1 and y = 2
Check:
If x = 1 and y = 2 satisfy the given condition, then our answer is correct.
L.H.S. = (x + 2y) + (2x – 3y)i + 4i
= (1 + 4) + (2 – 6)i + 4i
= 5 – 4i + 4i
= 5
= R.H.S.
Thus, our answer is correct.

(ii) \(\frac{x+1}{1+\mathrm{i}}+\frac{y-1}{1-\mathrm{i}}=\mathrm{i}\)

(x + y) + (y – x – 2)i = 2i
(x + y) + (y – x – 2)i = 0 + 2i
Equating real and imaginary parts, we get
x + y = 0 and y – x – 2 = 2
∴ x + y = 0 ……(i)
and -x + y = 4 ……..(ii)
Adding (i) and (ii), we get
2y = 4
∴ y = 2
Putting y = 2 in (i), we get
x + 2 = 0
∴ x = -2
∴ x = -2 and y = 2

Question 9.
Find the value of:
(i) x³ – x² + x + 46, if x = 2 + 3i
(ii) 2x³ – 11x² + 44x + 27, if x = \(\frac{25}{3-4 i}\)
Solution:
(i) x = 2 + 3i
∴ x – 2 = 3i
∴ (x – 2)² = 9i²
∴ x² – 4x + 4 = 9(-1) …..[∵ i² = -1]
∴ x² – 4x + 13 = 0 ……(i)

∴ x³ – x² + x + 46 = (x² – 4x + 13)(x + 3) + 7
= 0(x + 3) + 7 ……[From (i)]
= 7

(ii) x = \(\frac{25}{3-4 i}\)

∴ x = 3 + 4i
∴ x – 3 = 4i
∴ (x – 3)² = 16i²
∴ x² – 6x + 9 = 16(-1) …….[∵ i² = -1]
∴ x² – 6x + 25 = 0 …….(i)

∴ 2x³ – 11x² + 44x + 27
= (x² – 6x + 25) (2x + 1) + 2
= 0 . (2x + 1) + 2 ……[From (i)]
= 0 + 2
= 2

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths