Bhagya

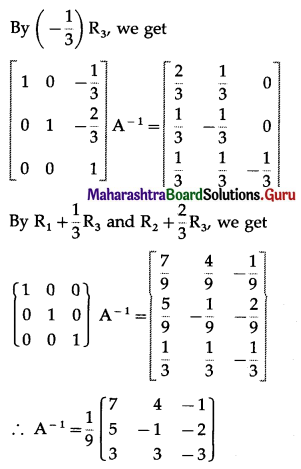
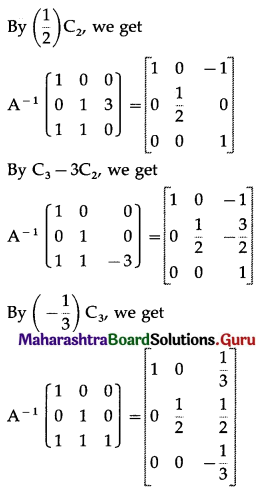
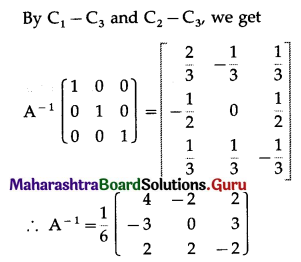
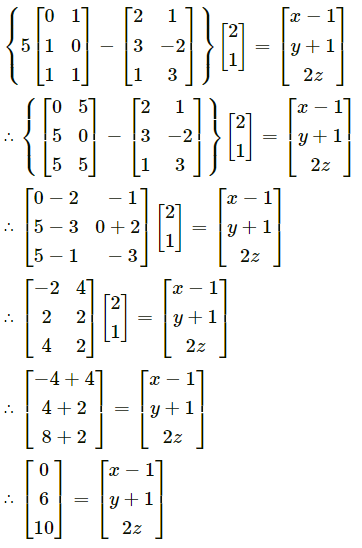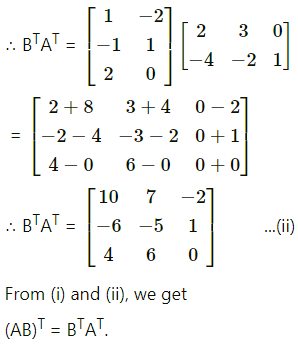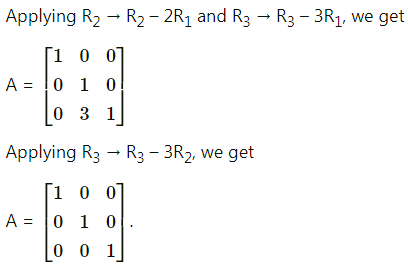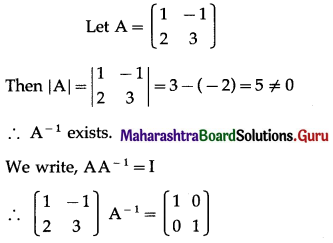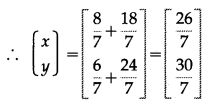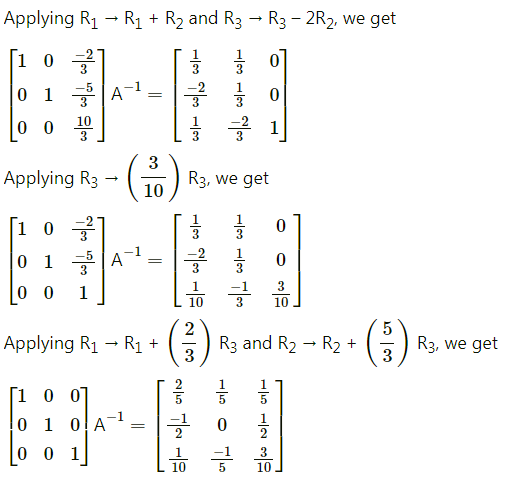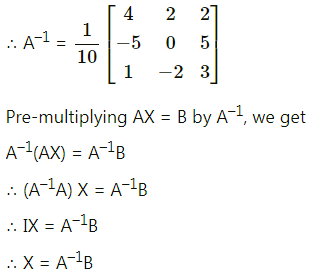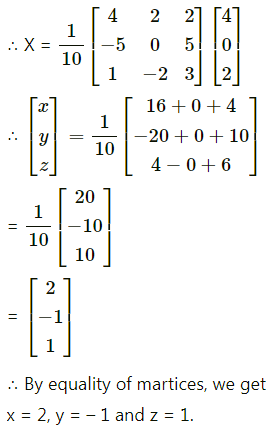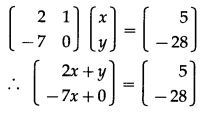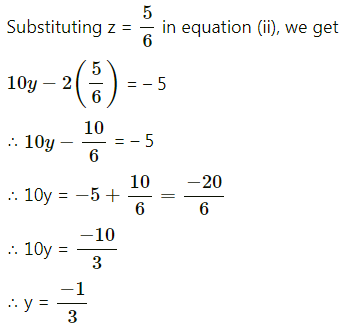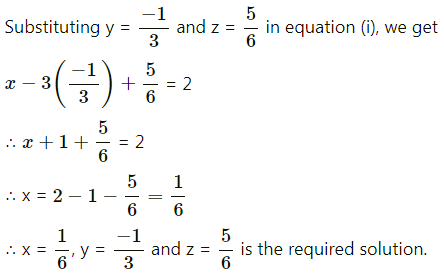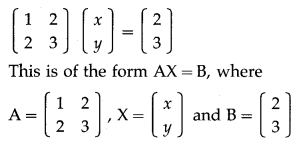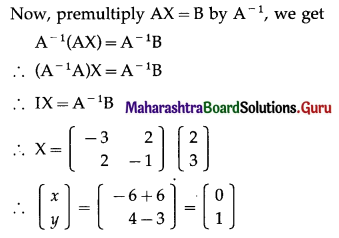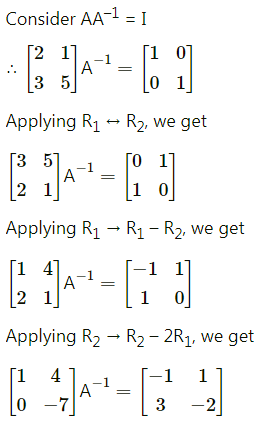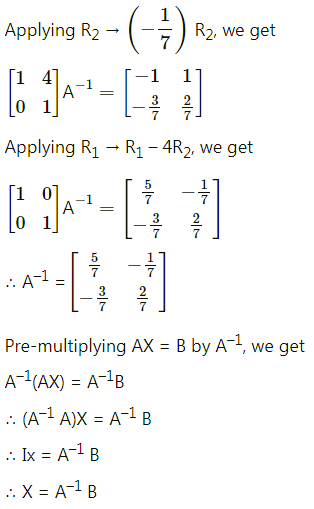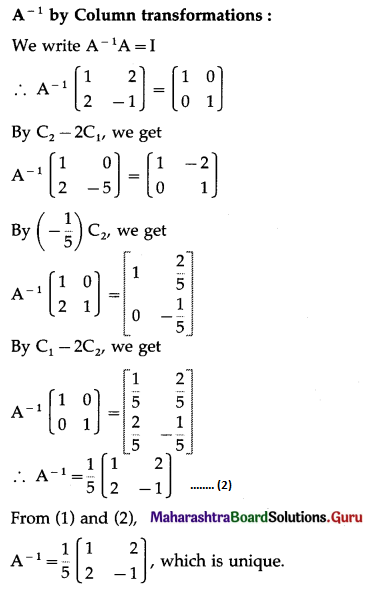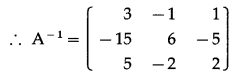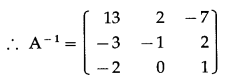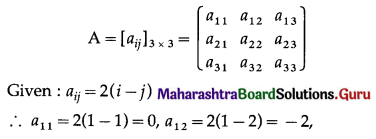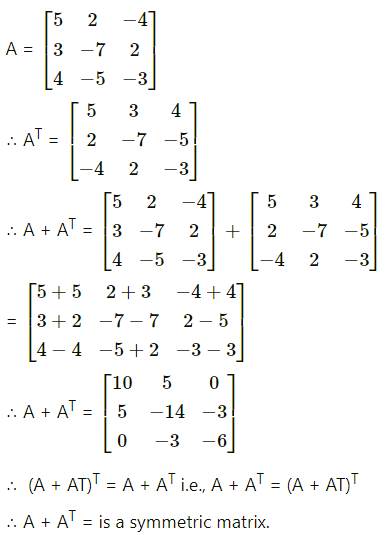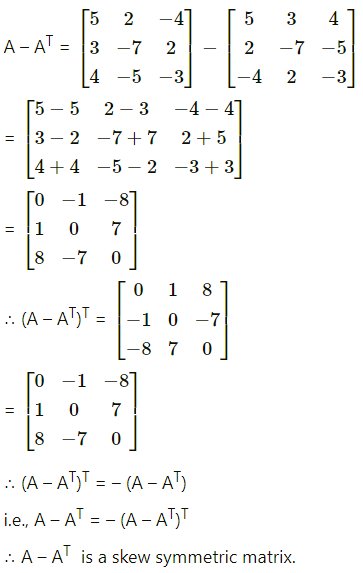Differentiation Class 12 Commerce Maths 1 Chapter 3 Exercise 3.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.1 Questions and Answers.

Std 12 Maths 1 Exercise 3.1 Solutions Commerce Maths

1. Find \(\frac{d y}{d x}\) if,

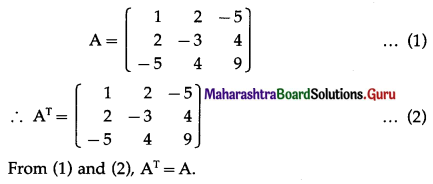
Question 1.
y = \(\sqrt{x+\frac{1}{x}}\)
Solution:

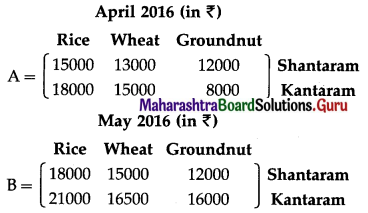
Question 2.
y = \(\sqrt[3]{a^{2}+x^{2}}\)
Solution:

Question 3.
y = (5x³ – 4x² – 8x)⁹
Solution:

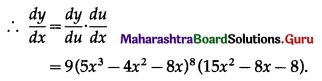
2. Find \(\frac{d y}{d x}\) if:

Question 1.
y = log(log x)
Solution:
Given y = log(log x)
Let u = log x
Then y = log u

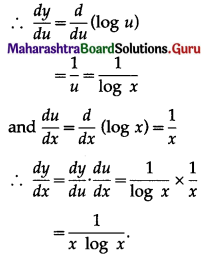
Question 2.
y = log(10x⁴ + 5x³ – 3x² + 2)
Solution:
Given y = log(10x⁴ + 5x³ – 3x² + 2)
Let u = 10x⁴ + 5x³ – 3x² + 2
Then y = log u

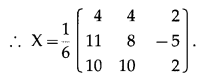
Question 3.
y = log(ax² + bx + c)
Solution:
Given y = log(ax² + bx + c)
Let u = ax² + bx + c
Then y = log u

3. Find \(\frac{d y}{d x}\) if:

Question 1.
y = \(e^{5 x^{2}-2 x+4}\)
Solution:

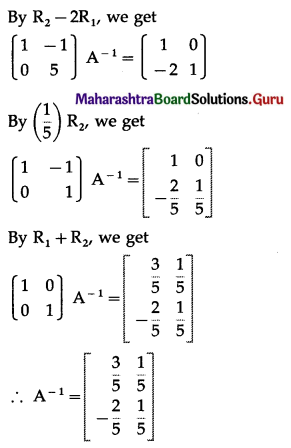
Question 2.
y = \(a^{(1+\log x)}\)
Solution:

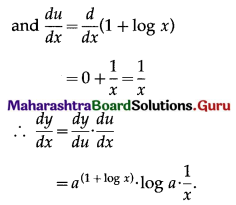
Question 3.
y = \(5^{(x+\log x)}\)
Solution:

Std 12 Commerce Statistics Part 1 Digest Pdf 

• Differentiation Ex 3.1 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.2 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.3 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.4 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.5 Class 12 Commerce Maths Textbook Solutions
• Differentiation Ex 3.6 Class 12 Commerce Maths Textbook Solutions
• Differentiation Miscellaneous Exercise 3 Class 12 Commerce Maths Textbook Solutions

Functions Class 11 Commerce Maths 1 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 2 Functions Miscellaneous Exercise 2 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 2 Solutions Commerce Maths

Question 1.
Which of the following relations are functions? If it is a function determine its domain and range.
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}
(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2), (9, 3), (9, -3), (16, 4), (16, -4)}
(iii) {(1, 1), (3, 1), (5, 2)}
Solution:
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}

Every element of set A has been assigned a unique element in set B.
∴ Given relation is a function.
Domain = {2, 4, 6, 8, 10, 12, 14},
Range = {1, 2, 3, 4, 5, 6, 7}

(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2), (9, 3), (9, -3), (16, 4), (16, -4)}
∴ (1, 1), (1, -1) ∈ the relation
∴ Given relation is not a function.
As element 1 of the domain has not been assigned a unique element of co-domain.

(iii) {(1, 1), (3, 1), (5, 2)}

Every element of set A has been assigned a unique element in set B.
∴ Given relation is a function.
Domain = {1, 3, 5}, Range = {1, 2}

Question 2.
A function f: R → R defined by f(x) = \(\frac{3 x}{5}\) + 2, x ∈ R. Show that f is one-one and onto. Hence, find f^-1.
Solution:
f: R → R defined by f(x) = \(\frac{3 x}{5}\) + 2
First we have to prove that f is one-one function for that we have to prove if
f(x₁) = f(x₂) then x₁ = x₂
Here f(x) = \(\frac{3 x}{5}\) + 2
Let f(x₁) = f(x₂)
∴ \(\frac{3 x_{1}}{5}+2=\frac{3 x_{2}}{5}+2\)
∴ \(\frac{3 x_{1}}{5}=\frac{3 x_{2}}{5}\)
∴ x₁ = x₂
∴ f is a one-one function.
Now, we have to prove that f is an onto function.
Let y ∈ R be such that
y = f(x)
∴ y = \(\frac{3 x}{5}\) + 2
∴ y – 2 = \(\frac{3 x}{5}\)
∴ x = \(\frac{5(y-2)}{3}\) ∈ R
∴ for any y ∈ co-domain R, there exist an element x = \(\frac{5(y-2)}{3}\) ∈ domain R such that f(x) = y
∴ f is an onto function.
∴ f is one-one onto function.
∴ f^-1 exists.
∴ \(\mathrm{f}^{-1}(y)=\frac{5(y-2)}{3}\)
∴ \(f^{-1}(x)=\frac{5(x-2)}{3}\)

Question 3.
A function f is defined as follows:
f(x) = 4x + 5, for -4 ≤ x < 0. Find the values of f(-1), f(-2), f(0), if they exist.
Solution:
f(x) = 4x + 5, -4 ≤ x < 0
f(-1) = 4(-1) + 5 = -4 + 5 = 1
f(-2) = 4(-2) + 5 = -8 + 5 = -3
x = 0 ∉ domain of f
∴ f(0) does not exist.

Question 4.
A function f is defined as follows:
f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3.
Solution:
f(x) = 5 – x
f(x) = 3
∴ 5 – x = 3
∴ x = 5 – 3 = 2

Question 5.
If f(x) = 3x² – 5x + 7, find f(x – 1).
Solution:
f(x) = 3x² – 5x + 7
∴ f(x – 1) = 3(x – 1)² – 5(x – 1) + 7
= 3(x² – 2x + 1) – 5(x – 1) + 7
= 3x² – 6x + 3 – 5x + 5 + 7
= 3x² – 11x + 15

Question 6.
If f(x) = 3x + a and f(1) = 7, find a and f(4).
Solution:
f(x) = 3x + a,
f(1) = 7
∴ 3(1) + a = 7
∴ a = 7 – 3 = 4
∴ f(x) = 3x + 4
∴ f(4) = 3(4) + 4
= 12 + 4
= 16

Question 7.
If f(x) = ax² + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Solution:
f(x) = ax² + bx + 2
f(1) = 3
∴ a(1)² + b(1) + 2 = 3
∴ a + b = 1 …….(i)
f(4) = 42
∴ a(4)² + b(4) + 2 = 42
∴ 16a + 4b = 40
Dividing by 4, we get
4a + b = 10 ……….(ii)
Solving (i) and (ii), we get
a = 3, b = -2

Question 8.
If f(x) = \(\frac{2 x-1}{5 x-2}, x \neq \frac{2}{5}\), verify whether (fof)(x) = x
Solution:
(fof)(x) = f(f(x))

Question 9.
If f(x) = \(\frac{x+3}{4 x-5}\), g(x) = \(\frac{3+5 x}{4 x-1}\), then verify that (fog)(x) = x.
Solution:

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Functions Class 11 Commerce Maths 1 Chapter 2 Exercise 2.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 2 Functions Ex 2.1 Questions and Answers.

Std 11 Maths 1 Exercise 2.1 Solutions Commerce Maths

Question 1.
Check if the following relations are functions.


Solution:
(a) Yes
Reason: Every element of set A has been assigned a unique element in set B.

(b) No
Reason: An element of set A has been assigned more than one element from set B.

(c) No
Reason: Not every element of set A has been assigned an image from set B.

Question 2.
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {-1, 0, 1, 2, 3}? Justify.
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)}
(ii) {(1, 2), (2, -1), (3, 1), (4, 3)}
(iii) {(1, 3), (4, 1), (2, 2)}
(iv) {(1, 1), (2, 1), (3, 1), (4, 1)}
Solution:
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)} does not represent a function.
Reason: (2, -1) and (2, 2) show that element 2 ∈ A has been assigned two images -1 and 2 from set B.

(ii) {(1, 2), (2, -1), (3, 1), (4, 3)} represents a function.
Reason: Every element of set A has a unique image in set B.

(iii) {(1, 3), (4, 1), (2, 2)} does not represent a function.
Reason: 3 ∈ A does not have an image in set B.

(iv) {(1, 1), (2, 1), (3, 1), (4, 1)} represents a function
Reason: Every element of set A has been assigned a unique image in set B.

Question 3.
If f(m) = m² – 3m + 1, find
(i) f(0)
(ii) f(-3)
(iii) f(\(\frac{1}{2}\))
(iv) f(x + 1)
(v) f(-x)
Solution:
f(m) = m² – 3m + 1
(i) f(0) = 0² – 3(0) + 1 = 1

(ii) f(-3) = (-3)² – 3(-3) + 1
= 9 + 9 + 1
= 19

(iii) \(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{2}-3\left(\frac{1}{2}\right)+1\)
= \(\frac{1}{4}-\frac{3}{2}+1\)
= \(\frac{1-6+4}{4}\)
= \(-\frac{1}{4}\)

(iv) f(x + 1) = (x + 1)² – 3(x + 1) + 1
= x² + 2x + 1 – 3x – 3 + 1
= x² – x – 1

(v) f(-x) = (-x)² – 3(-x) + 1 = x² + 3x + 1

Question 4.
Find x, if g(x) = 0 where
(i) g(x) = \(\frac{5 x-6}{7}\)
(ii) g(x) = \(\frac{18-2 x^{2}}{7}\)
(iii) g(x) = 6x² + x – 2
Solution:
(i) g(x) = \(\frac{5 x-6}{7}\)
g(x) = 0
∴ \(\frac{5 x-6}{7}\) = 0
∴ 5x – 6 = 0
∴ x = \(\frac{6}{5}\)

(ii) g(x) = \(\frac{18-2 x^{2}}{7}\)
g(x) = 0
∴ \(\frac{18-2 x^{2}}{7}\) = 0
∴ 18 – 2x² = 0
∴ x² = 9
∴ x = ±3

(iii) g(x) = 6x² + x – 2
g(x) = 0
∴ 6x² + x – 2 = 0
∴ 6x² + 4x – 3x – 2 = 0
∴ 2x(3x + 2) – 1(3x + 2) = 0
∴ (2x – 1)(3x + 2) = 0
∴ 2x – 1 = 0 or 3x + 2 = 0
∴ x = \(\frac{1}{2}\) or x = \(\frac{-2}{3}\)

Question 5.
Find x, if f(x) = g(x) where f(x) = x⁴ + 2x², g(x) = 11x².
Solution:
f(x) = x⁴ + 2x², g(x) = 11x²
f(x) = g(x)
∴ x⁴ + 2x² = 11x²
∴ x⁴ – 9x² = 0
∴ x²(x² – 9) = 0
∴ x² = 0 or x² – 9 = 0
∴ x = 0 or x² = 9
∴ x = 0 or x = ±3

Question 6.
If f(x) = \(\begin{cases}x^{2}+3, & x \leq 2 \\ 5 x+7, & x>2\end{cases}\), then find
(i) f(3)
(ii) f(2)
(iii) f(0)
Solution:
f(x) = x² + 3, x ≤ 2
= 5x + 7, x > 2
(i) f(3) = 5(3) + 7 = 15 + 7 = 22
(ii) f(2) = 2² + 3 = 4 + 3 = 7
(iii) f(0) = 0² + 3 = 3

Question 7.
If f(x) = \(\left\{\begin{array}{cl}
4 x-2, & x \leq-3 \\
5, & -3<x<3 \\
x^{2}, & x \geq 3
\end{array}\right.\), then fmd
(i) f(-4)
(ii) f(-3)
(iii) f(1)
(iv) f(5)
Solution:
f(x) = 4x – 2, x ≤ -3
= 5, -3 < x < 3
= x², x ≥ 3
(i) f(-4) = 4(-4) – 2 = -16 – 2 = -18
(ii) f(-3) = 4(-3) – 2 = -12 – 2 = -14
(iii) f(1) = 5
(iv) f(5) = 5² = 25

Question 8.
If f(x) = 3x + 5, g(x) = 6x – 1, then find
(i) (f + g)(x)
(ii) (f – g)(2)
(iii) (fg)(3)
(iv) \(\left(\frac{\mathbf{f}}{\mathbf{g}}\right)(x)\) and its domain
Solution:
f(x) = 3x + 5, g(x) = 6x – 1
(i) (f + g)(x) = f(x) + g(x)
= 3x + 5 + 6x – 1
= 9x + 4

(ii) (f – g) (2) = f(2) – g(2)
= [3(2) + 5] – [6(2) – 1]
= 6 + 5 – 12 + 1
= 0

(iii) (fg)(3) = f(3) g(3)
= [3(3) + 5] [6(3) – 1]
= (14) (17)
= 238

(iv) \(\left(\frac{\mathrm{f}}{\mathrm{g}}\right) x=\frac{\mathrm{f}(x)}{\mathrm{g}(x)}=\frac{3 x+5}{6 x-1}, x \neq \frac{1}{6}\)
Domain = R – {\(\frac{1}{6}\)}

Question 9.
If f(x) = 2x² + 3, g(x) = 5x – 2, then find
(i) fog
(ii) gof
(iii) fof
(iv) gog
Solution:
f(x) = 2x² + 3, g(x) = 5x – 2
(i) (fog)(x) = f(g(x))
= f(5x – 2)
= 2(5x – 2)² + 3
= 2(25x² – 20x + 4) + 3
= 50x² – 40x + 8 + 3
= 50x² – 40x + 11

(ii) (gof)(x) = g(f(x))
= g(2x² + 3)
= 5(2x² + 3) – 2
= 10x² + 15 – 2
= 10x² + 13

(iii) (fof)(x) = f(f(x))
= f(2x² + 3)
= 2(2x² + 3)² + 3
= 2(4x⁴ + 12x² + 9) + 3
= 8x⁴ + 24x² + 18 + 3
= 8x⁴ + 24x² + 21

(iv) (gog)(x) = g(g(x))
= g(5x – 2)
= 5(5x – 2) – 2
= 25x – 10 – 2
= 25x – 12

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Sets and Relations Class 11 Commerce Maths 1 Chapter 1 Miscellaneous Exercise 1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Sets and Relations Miscellaneous Exercise 1 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 1 Solutions Commerce Maths

Question 1.
Write the following sets in set builder form:
(i) {10, 20, 30, 40, 50}
(ii) {a, e, i, o, u}
(iii) {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
Solution:
(i) Let A = {10, 20, 30, 40, 50}
∴ A = {x / x = 10n, n ∈ N and n ≤ 5}

(ii) Let B = {a, e, i, o, u}
∴ B = {x / x is a vowel of English alphabets}

(iii) Let C = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
∴ C = {x / x represents days of a week}

Question 2.
If U = {x / x ∈ N, 1 ≤ x ≤ 12}, A = {1, 4, 7, 10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}.
Write the sets
(i) A ∪ B
(ii) B ∩ C
(iii) A – B
(iv) B – C
(v) A ∪ B ∪ C
(vi) A ∩ (B ∪ C)
Solution:
U = {x / x ∈ N, 1 ≤ x ≤ 12} = {1, 2, 3, …., 12}
A = {1, 4, 7, 10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}
(i) A ∪ B = {1, 2, 4, 6, 7, 10, 11}

(ii) B ∩ C = { }

(iii) A – B = {1, 10}

(iv) B – C = {2, 4, 6, 7, 11}

(v) A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

(vi) B ∪ C = {2, 3, 4, 5, 6, 7, 8, 9, 11, 12}
∴ A ∩ (B ∪ C) = {4, 7}

Question 3.
In a survey of 425 students in a school, it was found that 115 drink apple juice, 160 drink orange juice, and 80 drink both apple as well as orange juice. How many drinks neither apple juice nor orange juice?
Solution:
Let A = set of students who drink apple juice
B = set of students who drink orange juice
X = set of all students
∴ n(X) = 425, n(A) = 115, n(B) = 160, n(A ∩ B) = 80

No. of students who neither drink apple juice nor orange juice
n(A’ ∩ B’) = n(A ∪ B)’
= n(X) – n(A ∪ B)
= 425 – [n(A) + n(B) – n(A ∩ B)]
= 425 – (115 + 160 – 80)
= 230

Question 4.
In a school, there are 20 teachers who teach Mathematics or Physics. of these, 12 teach Mathematics and 4 teach both Physics and Mathematics. How many teachers teach Physics?
Solution:
Let A = set of teachers who teach Mathematics
B = set of teachers who teach Physics
n(A ∪ B) = 20, n(A) = 12, n(A ∩ B) = 4

Since, n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 20 = 12 + n(B) – 4
∴ n(B) = 12
∴ Number of teachers who teach physics = 12

Question 5.
(i) If A = {1, 2, 3} and B = {2, 4}, state the elements of A × A, A × B, B × A, B × B, (A × B) ∩ (B × A).
(ii) If A = {-1, 1}, find A × A × A.
Solution:
(i) A = {1, 2, 3} and B = {2, 4}
A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
A × B = {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}
B × A = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
B × B = {(2, 2), (2, 4), (4, 2), (4, 4)}
(A × B) ∩ (B × A) = {(2, 2)}

(ii) A = {-1, 1}
∴ A × A × A = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1),(1, 1, 1)}

Question 6.
If A = {1, 2, 3}, B = {4, 5, 6}, which of the following are relations from A to B.
(i) R₁ = {(1, 4), (1, 5), (1, 6)}
(ii) R₂ = {(1, 5), (2, 4), (3, 6)}
(iii) R₃ = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
(iv) R₄ = {(4, 2), (2, 6), (5, 1), (2, 4)}
Solution:
A = {1, 2, 3}, B = {4, 5, 6}
∴ A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) R₁ = {(1, 4), (1, 5), (1, 6)}
Since, R₁ ⊆ A × B
∴ R₁ is a relation from A to B.

(ii) R₂ = {(1, 5), (2, 4), (3, 6)}
Since, R₂ ⊆ A × B
∴ R₂ is a relation from A to B.

(iii) R₃ = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
Since, R₃ ⊆ A × B
∴ R₃ is a relation from A to B.

(iv) R₄ = {(4,2), (2, 6), (5,1), (2, 4)}
Since, (4, 2) ∈ R₄, but (4, 2) ∉ A × B
∴ R₄ ⊄ A × B
∴ R₄ is not a relation from A to B.

Question 7.
Determine the domain and range of the following relation.
R = {(a, b) / a ∈ N, a < 5, b = 4}
Solution:
R = {(a, b) / a ∈ N, a < 5, b = 4}
∴ Domain (R) = {a / a ∈ N, a < 5} = {1, 2, 3, 4}
Range (R) = {b / b = 4} = {4}

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Sets and Relations Class 11 Commerce Maths 1 Chapter 1 Exercise 1.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Sets and Relations Ex 1.2 Questions and Answers.

Std 11 Maths 1 Exercise 1.2 Solutions Commerce Maths

Question 1.
If (x – 1, y + 4) = (1, 2), find the values of x and y.
Solution:
(x – 1, y + 4) = (1, 2)
By the definition of equality of ordered pairs, we have
x – 1 = 1 and y + 4 = 2
∴ x = 2 and y = -2

Question 2.
If \(\left(x+\frac{1}{3}, \frac{y}{3}-1\right)=\left(\frac{1}{3}, \frac{3}{2}\right)\), find x and y.
Solution:
\(\left(x+\frac{1}{3}, \frac{y}{3}-1\right)=\left(\frac{1}{3}, \frac{3}{2}\right)\)
By the definition of equality of ordered pairs, we have
\(x+\frac{1}{3}=\frac{1}{3}\) and \(\frac{y}{3}-1=\frac{3}{2}\)
\(x=\frac{1}{3}-\frac{1}{3}\) and \(\frac{y}{3}=\frac{3}{2}+1=\frac{5}{2}\)
x = 0 and y = \(\frac{15}{2}\)

Question 3.
If A = {a, b, c}, B = {x, y}, find A × B, B × A, A × A, B × B.
Solution:
A = {a, b, c}, B = {x, y}
A × B = {(a, x), (a, y), (b, x), (b, y), (c, x), (c, y)}
B × A = {(x, a), (x, b), (x, c), (y, a), (y, b), (y, c)}
A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}
B × B = {(x, x), (x, y), (y, x), (y, y)}

Question 4.
If P = {1, 2, 3} and Q = {6, 4}, find the sets P × Q and Q × P.
Solution:
P = {1, 2, 3}, Q = {6, 4}
P × Q = {(1, 6), (1, 4), (2, 6), (2, 4), (3, 6), (3, 4)}
Q × P = {(6, 1), (6, 2), (6, 3), (4, 1), (4, 2), (4, 3)}

Question 5.
Let A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}. Find
(i) A × (B ∩ C)
(ii) (A × B) ∩ (A × C)
(iii) A × (B ∪ C)
(iv) (A × B) ∪ (A × C)
Solution:
A= {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}
(i) B ∩ C = {5, 6}
∴ A × (B ∩ C) = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}

(ii) A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∩ (A × C) = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}

(iii) B ∪ C = {4, 5, 6}
∴ A × (B ∪ C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}

(iv) A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∪ (A × C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}

Question 6.
Express {(x, y) / x² + y² = 100, where x, y ∈ W} as a set of ordered pairs.
Solution:
{(x, y) / x² + y² = 100, where x, y ∈ W}
We have, x² + y² = 100
When x = 0 and y = 10,
x² + y² = 0² + 10² = 100
When x = 6 andy = 8,
x² + y² = 6² + 8² = 100
When x = 8 and y = 6,
x² + y² = 8² + 6² = 100
When x = 10 and y = 0,
x² + y² = 10² + 0² = 100
∴ Set of ordered pairs = {(0, 10), (6, 8), (8, 6), (10, 0)}

Question 7.
Write the domain and range of the following relations.
(i) {(a, b) / a ∈ N, a < 6 and b = 4}
(ii) {(a, b) / a, b ∈ N, a + b = 12}
(iii) {(2, 4), (2, 5), (2, 6), (2, 7)}
Solution:
(i) Let R₁ = {(a, b)/ a ∈ N, a < 6 and b = 4}
Set of values of ‘a’ are domain and set of values of ‘b’ are range.
a ∈ N and a < 6
∴ a = 1, 2, 3, 4, 5 and b = 4
Domain (R₁) = {1, 2, 3, 4, 5}
Range (R₁) = {4}

(ii) Let R₂ = {(a, b)/a, b ∈ N and a + b = 12}
Now, a, b ∈ N and a + b = 12
When a = 1, b = 11
When a = 2, b = 10
When a = 3, b = 9
When a = 4, b = 8
When a = 5, b = 7
When a = 6, b = 6
When a = 7, b = 5
When a = 8, b = 4
When a = 9, b = 3
When a = 10, b = 2
When a = 11, b = 1
∴ Domain (R₂) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
Range (R₂) = {11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1}

(iii) Let R₃ = {(2, 4), (2, 5), (2, 6), (2, 7)}
Domain (R₃) = {2}
Range (R₃) = {4, 5, 6, 7}

Question 8.
Let A = {6, 8} and B = {1, 3, 5}.
Let R = {(a, b) / a ∈ A, b ∈ B, a – b is an even number}.
Show that R is an empty relation from A to B.
Solution:
A= {6, 8}, B = {1, 3, 5}
R = {(a, b)/ a ∈ A, b ∈ B, a – b is an even number}
a ∈ A
∴ a = 6, 8
b ∈ B
∴ b = 1, 3, 5
When a = 6 and b = 1, a – b = 5 which is odd
When a = 6 and b = 3, a – b = 3 which is odd
When a = 6 and b = 5, a – b = 1 which is odd
When a = 8 and b = 1, a – b = 7 which is odd
When a = 8 and b = 3, a – b = 5 which is odd
When a = 8 and b = 5, a – b = 3 which is odd
Thus, no set of values of a and b gives a – b even.
∴ R is an empty relation from A to B.

Question 9.
Write the relation in the Roster form and hence find its domain and range.
(i) R₁ = {(a, a²) / a is a prime number less than 15}
(ii) R₂ = {(a, \(\frac{1}{a}\)) / 0 < a ≤ 5, a ∈ N}
Solution:
(i) R₁ = {(a, a²) / a is a prime number less than 15}
∴ a = 2, 3, 5, 7, 11, 13
∴ a2 = 4, 9, 25, 49, 121, 169
∴ R₁ = {(2, 4), (3, 9), (5, 25), (7, 49), (11, 121), (13, 169)}
∴ Domain (R₁) = {a/a is a prime number less than 15} = {2, 3, 5, 7, 11, 13}
Range (R₁) = {a²/a is a prime number less than 15} = {4, 9, 25, 49, 121, 169}

Question 10.
R = {(a, b) / b = a + 1, a ∈ Z, 0 < a < 5}. Find the range of R.
Solution:
R = {(a, b) / b = a + 1, a ∈ Z, 0 < a < 5}
∴ a = 1, 2, 3, 4
∴ b = 2, 3, 4, 5
∴ Range (R) = {2, 3, 4, 5}

Question 11.
Find the following relations as sets of ordered pairs.
(i) {(x, y) / y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
(ii) {(x,y) / y > x + 1, x ∈ {1, 2} and y ∈ {2, 4, 6}}
(iii) {(x, y) / x + y = 3, x, y ∈ {0, 1, 2, 3}}
Solution:
(i) {(x, y) / y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
Here y = 3x
When x = 1, y = 3(1) = 3
When x = 2, y = 3(2) = 6
When x = 3, y = 3(3) = 9
∴ Ordered pairs are {(1, 3), (2, 6), (3, 9)}

(ii) {(x, y) / y > x + 1, x ∈ {1, 2} and y ∈ {2, 4, 6}}
Here, y > x + 1
When x = 1 and y = 2, 2 ≯ 1 + 1
When x = 1 and y = 4, 4 > 1 + 1
When x = 1 and y = 6, 6 > 1 + 1
When x = 2 and y = 2, 2 ≯ 2 + 1
When x = 2 and y = 4, 4 > 2 + 1
When x = 2 and y = 6, 6 > 2 + 1
∴ Ordered pairs are {(1, 4), (1, 6), (2, 4), (2, 6)}

(iii) {(x, y) / x + y = 3, x, y ∈ {0, 1, 2, 3}}
Here, x + y = 3
When x = 0, y = 3
When x = 1, y = 2
When x = 2, y = 1
When x = 3, y = 0
∴ Ordered pairs are {(0, 3), (1, 2), (2, 1), (3, 0)}

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Sets and Relations Class 11 Commerce Maths 1 Chapter 1 Exercise 1.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Sets and Relations Ex 1.1 Questions and Answers.

Std 11 Maths 1 Exercise 1.1 Solutions Commerce Maths

Question 1.
Describe the following sets in Roster form:
(i) {x / x is a letter of the word ‘MARRIAGE’}
(ii) {x / x is an integer, –\(\frac{1}{2}\) < x < \(\frac{9}{2}\)}
(iii) {x / x = 2n, n ∈ N}
Solution:
(i) Let A = {x / x is a letter of the word ‘MARRIAGE’}
∴ A = {M, A, R, I, G, E}

(ii) Let B = {x / x is an integer, –\(\frac{1}{2}\) < x < \(\frac{9}{2}\)}
∴ B = {0, 1, 2, 3, 4}

(iii) Let C = {x / x = 2n, n ∈ N}
∴ C = {2, 4, 6, 8, ….}

Question 2.
Describe the following sets in Set-Builder form:
(i) {0}
(ii) {0, ±1, ±2, ±3}
(iii) \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
Solution:
(i) Let A = {0}
0 is a whole number but it is not a natural number.
∴ A = {x / x ∈ W, x ∉ N}

(ii) Let B = {0, ±1, ±2, ±3}
B is the set of elements which belongs to Z from -3 to 3.
∴ B = {x / x ∈ Z, -3 ≤ x ≤ 3}

(iii) Let C = \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
∴ C = {x / x = \(\frac{n}{n^{2}+1}\), n ∈ N, n ≤ 7}

Question 3.
If A = {x / 6x² + x – 15 = 0}, B = {x / 2x² – 5x – 3 = 0}, C = {x / 2x² – x – 3 = 0}, then find (i) (A ∪ B ∪ C) (ii) (A ∩ B ∩ C)
Solution:
A = {x / 6x² + x – 15 = o}
∴ 6x² + x – 15 = 0
∴ 6x² + 10x – 9x – 15 = 0
∴ 2x(3x + 5) – 3(3x + 5) = 0
∴ (3x + 5) (2x – 3) = 0
∴ 3x + 5 = 0 or 2x – 3 = 0
∴ x = \(\frac{-5}{3}\) or x = \(\frac{3}{2}\)
∴ A = \(\left\{\frac{-5}{3}, \frac{3}{2}\right\}\)

B = {x / 2x² – 5x – 3 = 0}
∴ 2x² – 5x – 3 = 0
∴ 2x² – 6x + x – 3 = 0
∴ 2x(x – 3) + 1(x – 3) = 0
∴ (x – 3)(2x + 1) = 0
∴ x – 3 = 0 or 2x + 1 = 0
∴ x = 3 or x = \(\frac{-1}{2}\)
∴ B = {\(\frac{-1}{2}\), 3}

C = {x / 2x² – x – 3 = 0}
∴ 2x² – x – 3 = 0
∴ 2x² – 3x + 2x – 3 = 0
∴ x(2x – 3) + 1(2x – 3) = 0
∴ (2x – 3) (x + 1) = 0
∴ 2x – 3 = 0 or x + 1 = 0
∴ x = \(\frac{3}{2}\) or x = -1
∴ C = {-1, \(\frac{3}{2}\)}

(i) A ∪ B ∪ C = \(\left\{-\frac{5}{3}, \frac{3}{2}\right\} \cup\left\{\frac{-1}{2}, 3\right\} \cup\left\{-1, \frac{3}{2}\right\}\) = \(\left\{\frac{-5}{3},-1, \frac{-1}{2}, \frac{3}{2}, 3\right\}\)

(ii) A ∩ B ∩ C = { }

Question 4.
If A, B, C are the sets for the letters in the words ‘college’, ‘marriage’ and ‘luggage’ respectively, then verify that [A – (B ∪ C)] = [(A – B) ∩ (A – C)].
Solution:
A = {c, o, l, g, e}
B = {m, a, r, i, g, e}
C = {l, u, g, a, e}
B ∪ C = {m, a, r, i, g, e, l, u}
A – (B ∪ C) = {c, o}
A – B = {c, o, l}
A – C = {c, o}
∴ [(A – B) ∩ (A – C)] = {c, o} = A – (B ∪ C)
∴ [A – (B ∪ C)] = [(A – B) ∩ (A – C)]

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then verify the following:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) (A ∪ B)’ = A’ ∩ B’
(iv) (A ∩ B)’ = A’ ∪ B’
(v) A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = (A ∩ B) ∪ (A’ ∩ B)
(vii) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Solution:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8}, X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(i) B ∩ C = {4, 5, 6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5, 6} ……(i)
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
∴ (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6} ……(ii)
From (i) and (ii), we get
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

(ii) B ∪ C = {3, 4, 5, 6, 7, 8}
∴ A ∩ (B ∪ C) = {3, 4} …..(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) ∪ (A ∩ C) = {3, 4} …..(ii)
From (i) and (ii), we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(iii) A ∪ B = {1, 2, 3, 4, 5, 6}
∴ (A ∪ B)’ = {7, 8, 9, 10} …….(i)
A’ = {5, 6, 7, 8, 9, 10}, B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∩ B’ = {7, 8, 9, 10} ……(ii)
From (i) and (ii), we get
(A ∪ B)’ = A’ ∩ B’

(iv) A ∩ B = {3, 4}
∴ (A ∩ B)’ = {1, 2, 5, 6, 7, 8, 9, 10} ……(i)
A’ = {5, 6, 7, 8, 9, 10}
B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∪ B’ = {1, 2, 5, 6, 7, 8, 9, 10} ……(ii)
From (i) and (ii), we get
(A ∩ B)’ = A’ ∪ B’

(v) A = {1, 2, 3, 4} …..(i)
A ∩ B = {3, 4}
B’ = {1, 2, 7, 8, 9, 10}
A ∩ B’ = {1, 2}
∴ (A ∩ B) ∪ (A ∩ B’) = {1, 2, 3, 4} ……(ii)
From (i) and (ii), we get
A = (A ∩ B) ∪ (A ∩ B’)

(vi) B = {3, 4, 5, 6} …..(i)
A ∩ B = {3, 4}
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ (A ∩ B) ∪ (A’ ∩ B) = {3, 4, 5, 6} …..(ii)
From (i) and (ii), we get
B = (A ∩ B) ∪ (A’ ∩ B)

(vii) A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
A ∩ B = {3, 4}, A ∪ B = {1, 2, 3, 4, 5, 6}
∴ n(A) = 4, n(B) = 4,
n(A ∩ B) = 2,
n(A ∪ B) = 6 …..(i)
∴ n(A) + n(B) – n(A ∩ B) = 4 + 4 – 2
∴ n(A) + n(B) – n(A ∩ B) = 6 …..(ii)
From (i) and (ii), we get
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Question 6.
If A and B are subsets of the universal set X and n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5, find
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A’ ∩ B)
(iv) n(A ∩ B’)
Solution:
n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5
(i) n(A ∪ B) = n(X) – [n(A ∪ B)’]
= n(X) – n(A’ ∩ B’)
= 50 – 5
= 45

(ii) n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 35 + 20 – 45
= 10

(iii) n(A’ ∩ B) = n(B) – n(A ∩ B)
= 20 – 10
= 10

(iv) n(A ∩ B’) = n(A) – n(A ∩ B)
= 35 – 10
= 25

Question 7.
Out of 200 students, 35 students failed in MHT-CET, 40 in AIEEE and 40 in IIT entrance, 20 failed in MHT-CET and AIEEE, 17 in AIEEE and IIT entrance, 15 in MHT-CET and IIT entrance, and 5 failed in all three examinations. Find how many students
(i) did not fail in any examination.
(ii) failed in AIEEE or IIT entrance.
Solution:
Let A = set of students who failed in MHT-CET
B = set of students who failed in AIEEE
C = set of students who failed in IIT entrance
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40,
n(A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5

(i) n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
= 35 + 40 + 40 – 20 – 17 – 15 + 5
= 68
∴ No. of students who did not fail in any exam = n(X) – n(A ∪ B ∪ C)
= 200 – 68
= 132

(ii) No. of students who failed in AIEEE or IIT entrance = n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63

Question 8.
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read
(i) at least one of the newspapers.
(ii) neither Marathi nor English newspaper.
(iii) only one of the newspapers.
Solution:
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000,
n(M) = \(\frac{70}{100}\) × 2000 = 1400
n(E) = \(\frac{50}{100}\) × 2000 = 1000
n(M ∩ E) = \(\frac{32.5}{2}\) × 2000 = 650
n(M ∪ E) = n(M) + n(E) – n(M ∩ E)
= 1400 + 1000 – 650
= 1750

(i) No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.
(ii) No. of individuals who read neither Marathi nor English newspaper = n(M’ ∩ E’)
= n(M ∪ E)’
= n(X) – n(M ∪ E)
= 2000 – 1750
= 250
(iii) No. of individuals who read only one of the newspapers = n(M ∩ E’) + n(M’ ∩ E)
= n(M ∪ E) – n(M ∩ E)
= 1750 – 650
= 1100

Question 9.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take both tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes atleast one beverage, find the number of students in the hostel.
Solution:
Let T = set of students who take tea
C = set of students who take coffee
M = set of students who take milk
∴ n(T) = 25, n(C) = 20, n(M) = 15,
n(T ∩ C) = 10, n(M ∩ C) = 8, n(T ∩ M) = 0, n(T ∩ M ∩ C) = 0

∴ Number of students in the hostel = n(T ∪ C ∪ M)
= n(T) + n(C) + n(M) – n(T ∩ C) – n(M ∩ C) – n(T ∩ M) + n(T ∩ M ∩ C)
= 25 + 20 + 15 – 10 – 8 – 0 + 0
= 42

Question 10.
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to
(i) Chemical A but not Chemical B
(ii) Chemical B but not Chemical A
(iii) Chemical A or Chemical B.
Solution:
Let A = set of persons exposed to chemical A
B = set of persons exposed to chemical B
X = set of all persons
∴ n(X) = 260, n(A) = 150, n(B) = 74, n(A ∩ B) = 36

(i) No. of persons exposed to chemical A but not to chemical B = n(A ∩ B’)
= n(A) – n(A ∩ B)
= 150 – 36
= 114

(ii) No. of persons exposed to chemical B but not to chemical A = n(A’ ∩ B)
= n(B) – n(A ∩ B)
= 74 – 36
= 38

(iii) No. of persons exposed to chemical A or chemical B = n(A ∪ B)
= n(A) + n(B) – n(A ∩ B)
= 150 + 74 – 36
= 188

Question 11.
If A = {1, 2, 3}, write the set of all possible subsets of A.
Solution:
A = {1, 2, 3}
∴ { }, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3} and {1, 2, 3} are all the possible subsets of A.

Question 12.
Write the following intervals in set-builder form:
(i) (-3, 0)
(ii) [6, 12]
(iii) (6, 12)
(iv) (-23, 5)
Solution:
(i) (-3, 0) = {x / x ∈ R, -3 < x < 0}
(ii) [6, 12] = {x / x ∈ R, 6 ≤ x ≤ 12}
(iii) (6, 12) = {x / x ∈ R, 6 < x < 12}
(iv) (-23, 5) = {x / x ∈ R, -23 < x < 5}

Maharashtra State Board 11th Commerce Maths

• Sets and Relations Ex 1.1 11th Commerce Maths
• Sets and Relations Ex 1.2 11th Commerce Maths
• Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
• Functions Ex 2.1 11th Commerce Maths
• Functions Miscellaneous Exercise 2 11th Commerce Maths
• Complex Numbers Ex 3.1 11th Commerce Maths
• Complex Numbers Ex 3.2 11th Commerce Maths
• Complex Numbers Ex 3.3 11th Commerce Maths
• Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths

Matrices Class 12 Commerce Maths 1 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 2 Solutions Commerce Maths

(I) Choose the correct alternative.

Question 1.
If AX = B, where A = \(\left[\begin{array}{cc}
-1 & 2 \\
2 & -1
\end{array}\right]\), B = \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\) then X = ___________
(a) \(\left[\begin{array}{l}
\frac{3}{5} \\
\frac{3}{7}
\end{array}\right]\)
(b) \(\left[\begin{array}{l}
\frac{7}{3} \\
\frac{5}{3}
\end{array}\right]\)
(c) \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\)
(d) \(\left[\begin{array}{l}
1 \\
2
\end{array}\right]\)
Answer:
(c) \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\)

Question 2.
The matrix \(\left[\begin{array}{lll}
8 & 0 & 0 \\
0 & 8 & 0 \\
0 & 0 & 8
\end{array}\right]\) is ___________
(a) identity matrix
(b) scalar matrix
(c) null matrix
(d) diagonal matrix
Answer:
(b) scalar matrix

Question 3.
The matrix \(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\) is ___________
(a) identity matrix
(b) diagonal matrix
(c) scalar matix
(d) null matrix
Answer:
(d) null matrix

Question 4.
If A = \(\left[\begin{array}{lll}
a & 0 & 0 \\
0 & a & 0 \\
0 & 0 & a
\end{array}\right]\), then |adj A| = ___________
(a) a¹²
(b) a⁹
(c) a⁶
(d) a^-3
Answer:
(c) a6
Hint:
adj A = \(\left[\begin{array}{ccc}
a^{2} & 0 & 0 \\
0 & a^{2} & 0 \\
0 & 0 & a^{2}
\end{array}\right]\)
∴ |adj A| = a²(a⁴ – 0) = a⁶

Question 5.
Adjoint of \(\left[\begin{array}{ll}
2 & -3 \\
4 & -6
\end{array}\right]\) is ___________
(a) \(\left[\begin{array}{ll}
-6 & 3 \\
-4 & 2
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
6 & 3 \\
-4 & 2
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-6 & 3 \\
4 & -2
\end{array}\right]\)
Answer:
(a) \(\left[\begin{array}{ll}
-6 & 3 \\
-4 & 2
\end{array}\right]\)

Question 6.
If A = diag. [d₁, d₂, d₃, …, d_n], where d₁ ≠ 0, for i = 1, 2, 3, …….., n, then A^-1 = ___________
(a) diag [1/d₁, 1/d₂, 1/d₃, …, 1/d_n]
(b) D
(c) I
(d) O
Answer:
(a) diag [1/d₁, 1/d₂, 1/d₃, …, 1/d_n]

Question 7.
If A² + mA + nI = O and n ≠ 0, |A| ≠ 0, then A^-1 = ___________
(a) \(\frac{-1}{m}\)(A + nI)
(b) \(\frac{-1}{n}\)(A + mI)
(c) \(\frac{-1}{m}\)(I + mA)
(d) (A + mnI)
Answer:
(b) \(\frac{-1}{n}\)(A + mI)
Hint:
A² + mA + nI = 0
∴ (A² + mA + nI) . A^-1 = 0 . A^-1
∴ A(AA^-1) + m(AA^-1) + nIA^-1 = 0
∴ AI + mI + nA^-1 = 0
∴ nA^-1 = -A – mI
∴ A^-1 = \(\frac{-1}{n}\)(A + mI)

Question 8.
If a 3 × 3 matrix B has its inverse equal to B, then B² = ___________
(a) \(\left[\begin{array}{lll}
0 & 1 & 1 \\
0 & 1 & 0 \\
1 & 0 & 1
\end{array}\right]\)
(b) \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 0 & 1
\end{array}\right]\)
(c) \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]\)
(d) \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Answer:
(d) \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Hint:
B^-1 = B
∴ B² = B.B^-1 = I

Question 9.
If A = \(\left[\begin{array}{cc}
\alpha & 4 \\
4 & \alpha
\end{array}\right]\) and |A³| = 729 then α = ___________
(a) ±3
(b) ±4
(c ) ±5
(d) ±6
Answer:
(c ) ±5
Hint:
|A|= \(\left|\begin{array}{ll}
\alpha & 4 \\
4 & \alpha
\end{array}\right|\) = α² – 16
∴ |A³| = |A|³ = (α² – 16)³ = 729
∴ α² – 16 = 9
∴ α² = 25
∴ α = ±5

Question 10.
If A and B square matrices of order n × n such that A² – B² = (A – B)(A + B), then which of the following will be always true?
(a) AB = BA
(b) either A or B is a zero matrix
(c) either of A and B is an identity matrix
(d) A = B
Answer:
(a) AB = BA
Hint:
A² – B² = (A – B)(A + B)
∴ A² – B² = A² + AB – BA – B²
∴ 0 = AB – BA
∴ AB = BA

Question 11.
If A = \(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\) then A^-1 = ___________
(a) \(\left[\begin{array}{rr}
3 & -5 \\
1 & 2
\end{array}\right]\)
(b) \(\left[\begin{array}{rr}
3 & -5 \\
-1 & 2
\end{array}\right]\)
(c) \(\left[\begin{array}{rr}
3 & 5 \\
-1 & 2
\end{array}\right]\)
(d) \(\left[\begin{array}{ll}
3 & -5 \\
1 & -2
\end{array}\right]\)
Answer:
(b) \(\left[\begin{array}{rr}
3 & -5 \\
-1 & 2
\end{array}\right]\)

Question 12.
If A is a 2 × 2 matrix such that A(adj A) = \(\left[\begin{array}{ll}
5 & 0 \\
0 & 5
\end{array}\right]\), then |A| = ___________
(a) 0
(b) 5
(c) 10
(d) 25
Answer:
(b) 5
Hint:
A(adj A) = |A|.I

Question 13.
If A is a non-singular matrix, then det(A^-1) = ___________
(a) 1
(b) 0
(c) det(A)
(d) 1/det(A)
Answer:
(d) 1/det(A)
Hint:
AA^-1 = I
∴ |A|.|A^-1| = 1
∴ |A^-1| = \(\frac{1}{|\mathrm{~A}|}\)

Question 14.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
-3 & -1
\end{array}\right]\), B = \(\left[\begin{array}{rr}
-1 & 0 \\
1 & 5
\end{array}\right]\) then AB = ___________
(a) \(\left[\begin{array}{rr}
1 & -10 \\
1 & 20
\end{array}\right]\)
(b) \(\left[\begin{array}{rr}
1 & 10 \\
-1 & 20
\end{array}\right]\)
(c) \(\left[\begin{array}{ll}
1 & 10 \\
1 & 20
\end{array}\right]\)
(d) \(\left[\begin{array}{rr}
1 & 10 \\
-1 & -20
\end{array}\right]\)
Answer:
(c) \(\left[\begin{array}{ll}
1 & 10 \\
1 & 20
\end{array}\right]\)

Question 15.
If x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6, then (y, z) = ___________
(a) (-1, 0)
(b) (1, 0)
(c) (1, -1)
(d) (-1, 1)
Answer:
(b) (1, 0)

(II) Fill in the blanks:

Question 1.
A = \(\left[\begin{array}{l}
3 \\
1
\end{array}\right]\) is ___________ matrix.
Answer:
column

Question 2.
Order of matrix \(\left[\begin{array}{lll}
2 & 1 & 1 \\
5 & 1 & 8
\end{array}\right]\) is ___________
Answer:
2 × 3

Question 3.
If A = \(\left[\begin{array}{ll}
4 & x \\
6 & 3
\end{array}\right]\) is a singular matrix, then x is ___________
Answer:
2

Question 4.
Matrix B = \(\left[\begin{array}{ccc}
0 & 3 & 1 \\
-3 & 0 & -4 \\
p & 4 & 0
\end{array}\right]\) is a skew-symmetric, then value of p is ___________
Answer:
-1

Question 5.
If A = [a_ij]_2×3 and B = [b_ij]_m×1, and AB is defined, then m = ___________
Answer:
3

Question 6.
If A = \(\left[\begin{array}{cc}
3 & -5 \\
2 & 5
\end{array}\right]\), then cofactor of a₁₂ is ___________
Answer:
-2

Question 7.
If A = [a_ij]_m×m is non-singular matrix, then A^-1 = \(\frac{1}{\ldots \ldots}\) adj (A).
Answer:
|A|

Question 8.
(A^T)^T = ___________
Answer:
A

Question 9.
If A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 1
\end{array}\right]\) and A^-1 = \(\left[\begin{array}{cc}
1 & -1 \\
x & 2
\end{array}\right]\), then x = ___________
Answer:
-1

Question 10.
If a₁x+ b₁y = c₁ and a₂x + b₂y = c₂, then matrix form is \(\left[\begin{array}{cc}
\cdots & \ldots \\
\cdots & \ldots
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
\ldots \\
\cdots
\end{array}\right]\)
Answer:
\(\left[\begin{array}{ll}
a_{1} & b_{1} \\
a_{2} & b_{2}
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
c_{1} \\
c_{2}
\end{array}\right]\)

(III) State whether each of the following is True or False:

Question 1.
Single element matrix is row as well as a column matrix.
Answer:
True

Question 2.
Every scalar matrix is unit matrix.
Answer:
False

Question 3.
A = \(\left[\begin{array}{ll}
4 & 5 \\
6 & 1
\end{array}\right]\) is non-singular matrix.
Answer:
True

Question 4.
If A is symmetric, then A = -A^T.
Answer:
False

Question 5.
If AB and BA both exist, then AB = BA.
Answer:
False

Question 6.
If A and B are square matrices of same order, then (A + B)² = A² + 2AB + B².
Answer:
False

Question 7.
If A and B are conformable for the product AB, then (AB)^T = A^TB^T.
Answer:
False

Question 8.
Singleton matrix is only row matrix.
Answer:
False

Question 9.
A = \(\left[\begin{array}{cc}
2 & 1 \\
10 & 5
\end{array}\right]\) is invertible matrix.
Answer:
False

Question 10.
A(adj A) = |A| I, where I is the unit matrix.
Answer:
True.

(IV) Solve the following:

Question 1.
Find k, if \(\left[\begin{array}{ll}
7 & 3 \\
5 & k
\end{array}\right]\) is a singular matrix.
Solution:
Let A = \(\left[\begin{array}{ll}
7 & 3 \\
5 & k
\end{array}\right]\)
Since, A is singular matrix, |A| = 0
∴ \(\left|\begin{array}{ll}
7 & 3 \\
5 & k
\end{array}\right|\) = 0
∴ 7k – 15 = 0
∴ k = \(\frac{15}{7}\)

Question 2.
Find x, y, z if \(\left[\begin{array}{lll}
2 & x & 5 \\
3 & 1 & z \\
y & 5 & 8
\end{array}\right]\) is a symmetric matrix.
Solution:

By equality of matrices,
x = 3, y = 5 and z = 5.

Question 3.
If A = \(\left[\begin{array}{ll}
1 & 5 \\
7 & 8 \\
9 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 4 \\
1 & 5 \\
-8 & 6
\end{array}\right]\), C = \(\left[\begin{array}{cc}
-2 & 3 \\
1 & -5 \\
7 & 8
\end{array}\right]\) then show that (A + B) + C = A + (B + C).
Solution:


From (1) and (2),
(A + B) + C = A + (B + C).

Question 4.
If A = \(\left[\begin{array}{ll}
2 & 5 \\
3 & 7
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 7 \\
-3 & 0
\end{array}\right]\), find the matrix A – 4B + 7I, where I is the unit matrix of order 2.
Solution:

Question 5.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & -2 \\
-1 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-3 & 4 & 1 \\
2 & -1 & -3
\end{array}\right]\) verify
(i) (A + 2B^T)^T = A^T + 2B
(ii) (3A – 5B^T)^T = 3A^T – 5B
Solution:

Question 6.
If A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 6 \\
1 & 2 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
-3 & 2 & -1 \\
-2 & 1 & 0
\end{array}\right]\) thenshow that AB and BA are both singular matrices.
Solution:


∴ BA is also a singular matrix.
Hence, AB and BA are both singular matrices.

Question 7.
If A = \(\left[\begin{array}{ll}
3 & 1 \\
1 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
5 & -2
\end{array}\right]\), verify |AB| = |A| |B|.
Solution:

Question 8.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
-1 & 2
\end{array}\right]\), then show that A² – 4A + 3I = 0.
Solution:

Question 9.
If A = \(\left[\begin{array}{cc}
-3 & 2 \\
2 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & a \\
b & 0
\end{array}\right]\) and (A + B)(A – B) = A² – B², find a and b.
Solution:
(A + B)(A – B) = A² – B²
∴ A² – AB + BA – B² = A² – B²
∴ -AB + BA = 0
∴ AB = BA


By equality of matrices,
-3 + 2b = -3 + 2a ……..(1)
-3a = 2 + 4a ……..(2)
2 + 4b = -3b ……..(3)
2a = 2b ……..(4)
From (2), 7a = -2
∴ a = \(\frac{-2}{7}\)
From (3), 7b = -2
∴ b = \(\frac{-2}{7}\)
These values of a and b also satisfy equations (1) and (4).
Hence, a = \(\frac{-2}{7}\) and b = \(\frac{-2}{7}\)

Question 10.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 3
\end{array}\right]\), then find A³.
Solution:

Question 11.
Find x, y, z if \(\left\{5\left[\begin{array}{ll}
0 & 1 \\
1 & 0 \\
1 & 1
\end{array}\right]-\left[\begin{array}{cc}
2 & 1 \\
3 & -2 \\
1 & 3
\end{array}\right]\right\}\left[\begin{array}{l}
2 \\
1
\end{array}\right]=\left[\begin{array}{c}
x-1 \\
y+1 \\
2 z
\end{array}\right]\)
Solution:

∴ By equality of matrices, we get
x – 1 = 0 ∴ x = 1
y + 1 = 6 ∴ y = 5
2z = 10 ∴ z = 5

Question 12.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
3 & -2 \\
0 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 1 & 0
\end{array}\right]\) then showthat(AB)^T = B^TA^T.
Solution:

Question 13.
If A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\), then reduce it to unit matrix by row tranformation.
Solution:

Question 14.
Two farmers Shantaram and Kantaram cultivate three crops rice, wheat, and groundnut. The sale (in ₹) of these crops by both the farmers for the month of April and May 2016 is given below:

Find (i) the total sale in rupees for two months of each farmer for each crop.
(ii) the increase in sales from April to May for every crop of each farmer.
Solution:
The given information can be written in matrix form as:

(i) The total sale in ₹ for two months of each farmer for each crop can be obtained by the addition A + B.
Now, A + B

∴ total sale in ₹ for two months of each farmer for each crop is given by

Hence, the total sale for Shantaram are ₹ 33000 for Rice, ₹ 28000 for Wheat, ₹ 24000 for Groundnut, and for Kantaram are ₹ 39000 for Rice, ₹ 31500 for Wheat, ₹ 24000 for Groundnut.
(ii) The increase in sales from April to May for every crop of each farmer can be obtained by the subtraction of A from B.
Now, B – A

Hence, the increase in sales from April to May of Shantam is ₹ 3000 in Rice, ₹ 2000 in Wheat, nothing in Groundnut and of Kantaram are ₹ 3000 in Rice, ₹ 1500 in Wheat, ₹ 8000 in Groundnut.

Question 15.
Check whether following matrices are invertible or not:
(i) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\)
= 1 – 0
= 1 ≠ 0
∴ A is a non-singular matrix.
Hence, A^-1 exists.

(ii) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right|\)
= 1 – 1
= 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(iii) \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right|\)
= 3(5 – 0) – 4(5 – 0) + 3(4 – 1)
= 15 – 20 + 9
= 4 ≠ 0
∴ A is a non-singular matrix.
Hence, A^-1 exists.

(iv) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 5 \\
2 & 4 & 6
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 5 \\
2 & 4 & 6
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 5 \\
2 & 4 & 6
\end{array}\right|\)
= 1(24 – 20) – 2(12 – 10) + 3(8 – 8)
= 4 – 4 + 0
= 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

Question 16.
Find inverse of the following matrices (if they exist) by elementary transformation:
(i) \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{ccc}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
Solution:

(iv) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:

Question 17.
Find the inverse of \(\left[\begin{array}{lll}
3 & 1 & 5 \\
2 & 7 & 8 \\
1 & 2 & 5
\end{array}\right]\) by adjoint method.
Solution:

Question 18.
Solve the following equations by method of inversion:
(i) 4x – 3y – 2 = 0, 3x – 4y + 6 = 0
Solution:
The given equations are
4x – 3y = 2
3x – 4y = -6
These equations can be written in matrix form as:




By equality of matrices,
x = \(\frac{26}{7}\), y = \(\frac{30}{7}\) is the required solution.

(ii) x + y – z = 2, x – 2y + z = 3 and 2x – y – 3z = -1
Solution:
The given equations can be written in matrix form as:




By equality of matrices,
x = 3, y = 1, z = 2 is the required solution.

(iii) x – y + z = 4, 2x + y – 3z = 0 and x + y + z = 2
Solution:

Question 19.
Solve the following equations by method of reduction:
(i) 2x + y = 5, 3x – 5y = -3
Solution:
The given equation can be written in matrix form as:
\(\left[\begin{array}{ll}
2 & 1 \\
3 & 5
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{r}
5 \\
-3
\end{array}\right]\)
By R₂ – 5R₁, we get

By equality of matrices,
2x + y = 5 …….(1)
-7x = -28 ……(2)
From (2), x = 4
Substituting x = 4 in (1), we get
2(4) + y = 5
∴ y = -3
Hence, x = 4 and y = -3 is the required solution.

(ii) x + 2y + z = 3, 3x – y + 2z = 1 and 2x – 3y + 3z = 2
Solution:
The given equations can be written in matrix form as:

By equality of matrices,
x + 2y + z = 3 …….(1)
-7y – z = -8 …….(2)
2z = 4 …….(3)
From (3), z = 2
Substituting z = 2 in (2), we get
-7y – 2 = -8
∴ -7y = -6
∴ y = \(\frac{6}{7}\)
Substituting y = \(\frac{6}{7}\), z = 2 in (1), we get
x + 2(\(\frac{6}{7}\)) + 2 = 3
x = 3 – 2 – \(\frac{12}{7}\) = \(\frac{-5}{7}\)
Hence, x = \(\frac{-5}{7}\), y = \(\frac{6}{7}\) and z = 2 is the required solution.

(iii) x – 3y + z = 2, 3x + y + z = 1 and 5x + y + 3z = 3.
Solution:

Question 20.
The sum of three numbers is 6. If we multiply the third number by 3 and add it to the second number, we get 11. By adding first and third numbers we get a number that is double the second number. Use this information and find a system of linear equations. Find the three numbers using matrices.
Solution:
Let the three numbers be x, y, and z.
According to the given condition,
x + y + z = 6
3z + y = 11, i.e. y + 3z = 11
and x + z = 2y, i.e. x – 2y + z = 0
Hence, the system of linear equations is
x + y + z = 6
y + 3z = 11
x – 2y + z = 0
These equations can be written in matrix form as:

By equality of matrices,
x + y + z = 6 …….(1)
y + 3z = 11 ………(2)
-3y = -6 ………(3)
From (3), y = 2
Substituting y = 2 in (2), we get
2 + 3z = 11
∴ 3z = 9
∴ z = 3
Substituting y = 2, z = 3 in (1), we get
x + 2 + 3 = 6
∴ x = 1
∴ x = 1, y = 2, z = 3
Hence, the required numbers are 1, 2 and 3.

12th Commerce Maths Book Pdf 

• Matrices Ex 2.1 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.2 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.3 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.4 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.5 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.6 Class 12 Commerce Maths Textbook Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Commerce Maths Textbook Solutions

Matrices Class 12 Commerce Maths 1 Chapter 2 Exercise 2.6 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.6 Questions and Answers.

Std 12 Maths 1 Exercise 2.6 Solutions Commerce Maths

Question 1.
Solve the following equations by the method of inversion:
(i) x + 2y = 2, 2x + 3y = 3
Solution:
The given equations can be written in the matrix form as:



By equality of matrices,
x = 0, y = 1 is the required solution.

(ii) 2x + y = 5, 3x + 5y = -3
Solution:

(iii) 2x – y + z = 1, x + 2y + 3z = 8 and 3x + y – 4z = 1
Solution:
The given equations can be written in the matrix form as:






By equality of matrices,
x = 1, y = 2, z = 1 is the required solution.

(iv) x + y + z = 1, x – y + z = 2 and x + y – z = 3
Solution:

Question 2.
Express the following equations in matrix form and solve them by method of reduction:
(i) x + 3y = 2, 3x + 5y = 4.
Solution:
The given equations can be written in the matrix form as:


Hence, x = \(\frac{1}{2}\), y = \(\frac{1}{2}\) is the required solution.

(ii) 3x – y = 1, 4x + y = 6.
Solution:
The given equations can be written in the matrix form as:

By equality of matrices,
12x – 4y = 4 …..(1)
7y = 14 …..(2)
From (2), y = 2
Substituting y = 2 in (1), we get
12x – 8 = 4
∴ 12x = 12
∴ x = 1
Hence, x = 1, y = 2 is the required solution.

(iii) x + 2y + z = 8, 2x + 3y – z = 11 and 3x – y – 2z = 5.
Solution:
The given equations can be written in the matrix form as:


By equality of matrices,
x + 2y + z = 8 ……(1)
-y – 3z = -5 …….(2)
16z = 16 ……….(3)
From (3), z = 1
Substituting z = 1 in (2), we get
-y – 3= -5
∴ y = 2
Substituting y = 2, z = 1 in (1), we get
x + 4 + 1 = 8
∴ x = 3
Hence, x = 3, y = 2, z = 1 is the required solution.

(iv) x + y + z = 1, 2x + 3y + 2z = 2 and x + y + 2z = 4.
Solution:
The given equations can be written in the matrix form as:

By equality of matrices,
x + y + z = 1 ……(1)
y = 0
z = 3
Substituting y = 0, z = 3 in (1), we get
x + 0 + 3 = 1
∴ x = -2
Hence, x = -2, y = 0, z = 3 is the required solution.

Question 3.
The total cost of 3 T.V. and 2 V.C.R. is ₹ 35000. The shopkeeper wants a profit of ₹ 1000 per T.V. and ₹ 500 per V.C.R. He sells 2 T.V. and 1 V.C.R. and he gets total revenue of ₹ 21500. Find the cost and selling price of T.V. and V.C.R.
Solution:
Let the cost of each T.V. be ₹ x and each V.C.R. be ₹ y.
Then the total cost of 3 T.V. and 2 V.C.R. is ₹ (3x + 2y) which is given to be ₹ 35000.
∴ 3x + 2y = 35000
The shopkeeper wants a profit of ₹ 1000 per T.V. and ₹ 500 per V.C.R.
The selling price of each T.V. is ₹ (x + 1000) and of each V.C.R. is ₹ (y + 500).
∴ selling price of 2 T.V. and 1 V.C.R is
₹ [2(x + 1000) + (y + 500)] which is given to be ₹ 21500.
∴ 2(x + 1000) + (y + 500) = 21500
∴ 2x + 2000 + y + 500 = 21500
∴ 2x + y = 19000
Hence, the system of linear equations is
3x + 2y = 35000
2x + y = 19000
The equations can be written in matrix form as:

By equality of matrices,
-x = -3000 …….(1)
2x + y = 19000 ……….(2)
From (1), x = 3000
Substituting x = 3000 in (2), we get
2(3000) + y = 19000
∴ y = 19000 – 6000 = 13000
Hence, the cost price of one T.V. is ₹ 3000 and of one V.C.R. is ₹ 13000 and the selling price of one T.V. is ₹ 4000 and of one V.C.R. is ₹ 13500.

Question 4.
The sum of the cost of one Economics book, one Cooperation book, and one Account book is ₹ 420. The total cost of an Economic book, 2 Cooperation books, and an Account book is ₹ 480. Also, the total cost of an Economic book, 3 Cooperation books, and 2 Account books is ₹ 600. Find the cost of each book.
Solution:
Let the cost of 1 Economic book, 1 Cooperation book and 1 Account book be ₹ x, ₹ y and ₹ z respectively.
Then, from the given information
x + y + z = 420
x + 2y + z = 480
x + 3y + 2z = 600
These equations can be written in matrix form as:

By equality of matrices,
x + y + z = 420 …….(1)
y = 60
2y + z = 180 ………(2)
Substituting y = 60 in (2), we get
2(60) + z = 180
∴ z = 180 – 120 = 60
Substituting y = 60, z = 60 in (1), we get
x + 60 + 60 = 420
∴ x = 420 – 120 = 300
Hence, the cost of each Economic book is ₹ 300, each Cooperation book is ₹ 60 and each Account book is ₹ 60.

12th Commerce Maths Book Pdf 

• Matrices Ex 2.1 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.2 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.3 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.4 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.5 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.6 Class 12 Commerce Maths Textbook Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Commerce Maths Textbook Solutions

Matrices Class 12 Commerce Maths 1 Chapter 2 Exercise 2.5 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.5 Questions and Answers.

Std 12 Maths 1 Exercise 2.5 Solutions Commerce Maths

Question 1.
Apply the given elementary transformation on each of the following matrices:
(i) \(\left[\begin{array}{cc}
3 & -4 \\
2 & 2
\end{array}\right]\), R₁ ↔ R₂
(ii) \(\left[\begin{array}{cc}
2 & 4 \\
1 & -5
\end{array}\right]\), C₁ ↔ C₂
(iii) \(\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & 1 \\
-1 & 1 & 3
\end{array}\right]\) 3R₂ and C₂ → C₂ – 4C₁
Solution:

Question 2.
Transform \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\) into an upper triangularmatrix by suitable row transformations.
Solution:

Question 3.
Find the cofactor matrix of the following matrices:
(i) \(\left[\begin{array}{cc}
1 & 2 \\
5 & -8
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
5 & 8 & 7 \\
-1 & -2 & 1 \\
-2 & 1 & 1
\end{array}\right]\)
Solution:

Question 4.
Find the adjoint of the following matrices:
(i) \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:

Question 5.
Find the inverses of the following matrices by the adjoint mathod:
(i) \(\left[\begin{array}{rr}
3 & -1 \\
2 & -1
\end{array}\right]\)
(ii) \(\left[\begin{array}{cc}
2 & -2 \\
4 & 5
\end{array}\right]\)
(iii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution:

Question 6.
Find the inverses of the following matrices by the transformation method:
(i) \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:

Question 7.
Find the inverse of A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by elementary column transformations.
Solution:

Question 8.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by the elementary row transformations.
Solution:

Question 9.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\), then find matrix X such that XA = B.
Solution:

Question 10.
Find matrix X, if AX = B, where A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\)
Solution:

12th Commerce Maths Book Pdf 

• Matrices Ex 2.1 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.2 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.3 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.4 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.5 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.6 Class 12 Commerce Maths Textbook Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Commerce Maths Textbook Solutions

Matrices Class 12 Commerce Maths 1 Chapter 2 Exercise 2.4 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.4 Questions and Answers.

Std 12 Maths 1 Exercise 2.4 Solutions Commerce Maths

Question 1.
Find A^T, if
(i) A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
2 & -6 & 1 \\
-4 & 0 & 5
\end{array}\right]\)
Solution:

Question 2.
If A = [a_ij]_3×3 where a_ij = 2(i – j). Find A and A^T. State whether A and A^T both are symmetric or skew-symmetric matrices.
Solution:


Hence, A and A^T are both skew-symmetric matrices.

Question 3.
If A = \(\left[\begin{array}{cc}
5 & -3 \\
4 & -3 \\
-2 & 1
\end{array}\right]\), prove that (A^T)^T = A.
Solution:

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\), prove that A^T = A.
Solution:

Question 5.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 1 \\
4 & -1 \\
-3 & 3
\end{array}\right]\), C = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 4 \\
-2 & 3
\end{array}\right]\), then show that
(i) (A + B)^T = A^T + B^T
(ii) (A – C)^T = A^T – C^T
Solution:

Question 6.
If A = \(\left[\begin{array}{cc}
5 & 4 \\
-2 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-1 & 3 \\
4 & -1
\end{array}\right]\), then find C^T, such that 3A – 2B + C = I, where I is the unit matrix of order 2.
Solution:

Question 7.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 0 \\
0 & 4 & -2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
0 & -2 & 3 \\
2 & 1 & -4
\end{array}\right]\), then find
(i) A^T + 4B^T
(ii) 5A^T – 5B^T
Solution:

Question 8.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
2 & 1 & -4 \\
3 & 5 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
0 & 2 & 3 \\
-1 & -1 & 0
\end{array}\right]\), verify that (A + 2B + 3C)^T = A^T + 2B^T + 3C^T
Solution:

Question 9.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
-3 & 2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-3 & 2 \\
-1 & 3
\end{array}\right]\), prove that (A + B^T)^T = A^T + B.
Solution:

From (1) and (2),
(A + B^T)^T = A^T + B.

Question 10.
Prove that A + A^T is symmetric and A – A^T is a skew-symmetric matrix, where
(i) A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 2 & 1 \\
-2 & -3 & 2
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
5 & 2 & -4 \\
3 & -7 & 2 \\
4 & -5 & -3
\end{array}\right]\)
Solution:

Question 11.
Express each of the following matrix as the sum of a symmetric and a skew-symmetric matrix:
(i) \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
Solution:

Question 12.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
3 & -2 \\
4 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
0 & 3 & -4 \\
2 & -1 & 1
\end{array}\right]\), verify that
(i) (AB)^T = B^TA^T
(ii) (BA)^T = A^TB^T
Solution:

12th Commerce Maths Book Pdf 

• Matrices Ex 2.1 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.2 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.3 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.4 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.5 Class 12 Commerce Maths Textbook Solutions
• Matrices Ex 2.6 Class 12 Commerce Maths Textbook Solutions
• Matrices Miscellaneous Exercise 2 Class 12 Commerce Maths Textbook Solutions