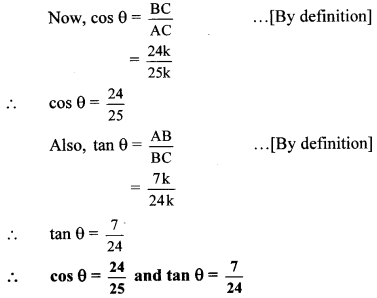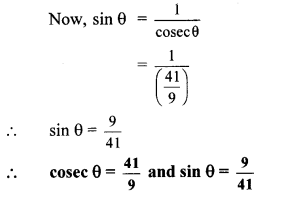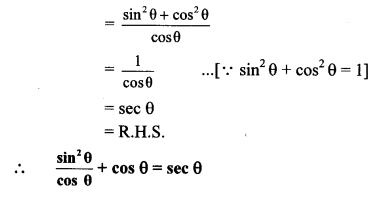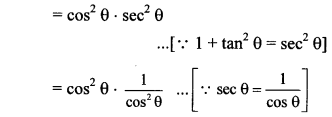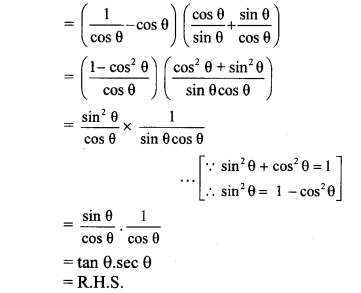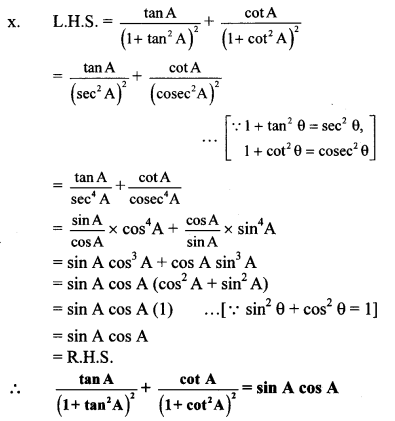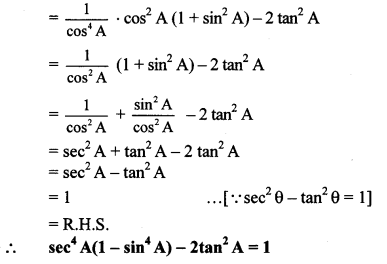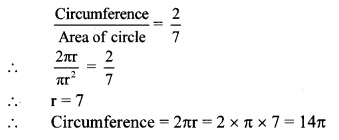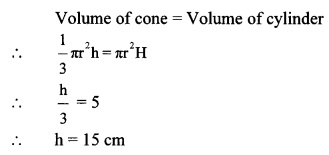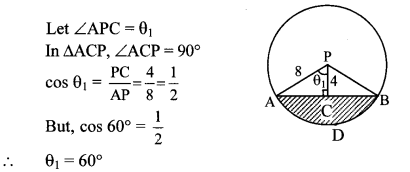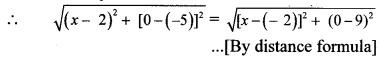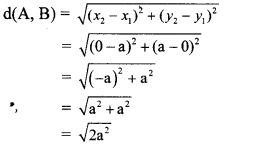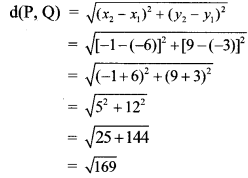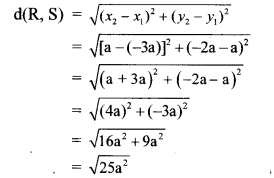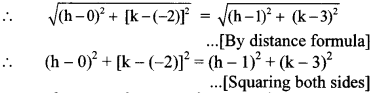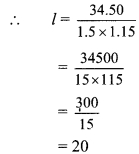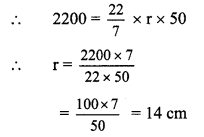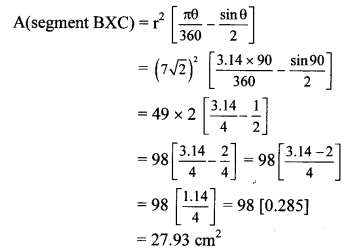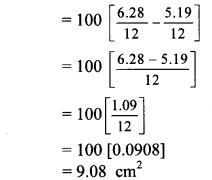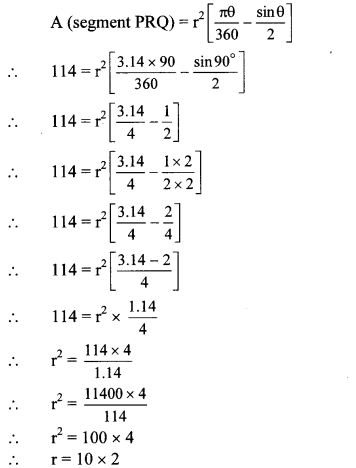Prasanna

Std 9 Science Chapter 12 Study of Sound Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 12 Study of Sound Notes, Textbook Exercise Important Questions and Answers.

Class 9 Science Chapter 12 Study of Sound Question Answer Maharashtra Board

Class 9 Science Chapter 12 Study of Sound Textbook Questions and Answers

1. Fill in the blanks and explain.

a. Sound does not travel through ……………………….……….. .
b The velocity of sound in steel is ……………………….………… than the velocity of sand in water.
c. The incidence of ……………………….………… in daily life shows that the velocity of sound is less than the velocity of light.
d. To discover a sunken ship or objects deep inside the sea, ……………………….………… technology is used.

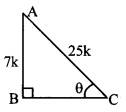
2. Explain giving scientific reasons.

a. The roof of a movie theatre and a conference hall is curved.
Answer:

• Sound waves get reflected from the walls and roof of a room multiple times. This causes a single sound to be heard not once but continuously. This is called reverberation.
• Due to reverberation, some auditoriums or some particular seats in an auditorium have inferior sound reception. This can be compensated with curtains.
• Ceilings of these halls are made curved so that sound after reflecting from the ceiling, reaches all parts of the hall and the quality of sound improves.

b. The intensity of reverberation is higher in a closed and empty house.
Answer:

• Reverberation occurs due to multiple reflections of sound.
• The furniture in the house acts as a sound-absorbing material.
• So if the house is closed and empty, a reflection of sound will be maximum and hence, intensity of reverberation is higher.

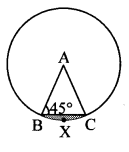
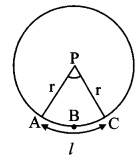
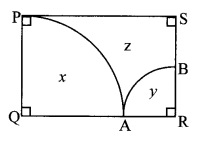
c. We cannot hear the echo produced in a classroom.
Answer:

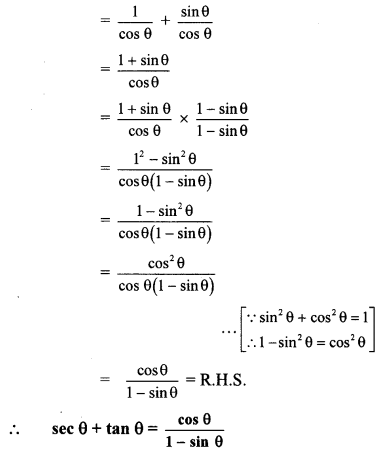
• For distinct echoes, the minimum distance of the reflecting surface from the source of sound must be 17.2 m.
• Benches in the classroom are sound absorbing materials which prevent echo of sound.
• Because of these two reasons echo is not heard in a classroom.

3. Answer the following questions in your own words.

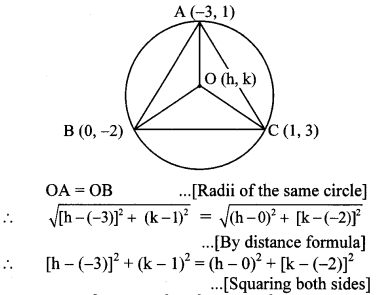
a. What is an echo? What factors are important to get a distinct echo?
Answer:

• An echo is the repetition of the original sound because of reflection by some surface.
• At 22°C, the velocity of sound in air is 344 m/s.
• Our brain retains a sound for 0.1 seconds Thus, for us to be able to hear a distinct echo, the sound should take more than 0.1 seconds after starting from the source to get reflected and. come back to us.
• We know that,
  Distance = speed x time
  = 344 m/s x 0.1 s
  = 34.4 m
• Thus, to be able to hear a distinct echo, the reflecting surface should be at a minimum distance of half of the above, i.e. 17.2 m.
• As the velocity of sound depends on the temperature of air, this distance depends on the temperature.

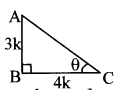
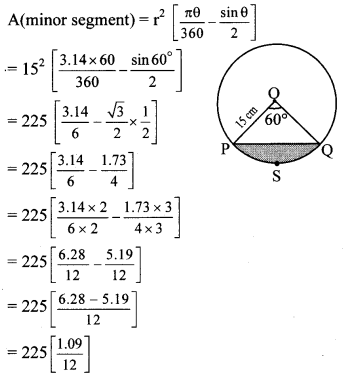
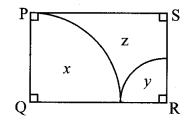
b. Study the construction of the Golghumat at Vijapur and discuss the reasons for the multiple echoes produced there.
Answer:

• Goighumat with a height of 51 metres and diameter of 37 metres with 3 metres thick walls is spread over approximately 1700 square metres.
• This meets the conditions for echo i.e. : 17.2 metres minimum.
• The dome of the golghumat is curved and hence, sound reflects multiple times before reaching the observer.
• This is the reason for multiple echoes being produced.

c. What should be the dimensions and the shape of classrooms so that no echo can be produced there?
Answer:

1. Dimensions: The distance between opposite walls in a classroom must be less than 17.2 m so that the reflected sound returns to the observer within 0.1 s.
2. Shape: The classrooms should have curved ceilings and walls so that the reflected sound is directed towards the observer instantly within 0.1 s

4. Where and why are sound-absorbing materials used?
Answer:
The sound absorbing materials are used in :

• School, cinema hall, concert hall, houses or places where quality of sound is important.
• In the absence of sound absorbing material the sound will undergo multiple reflection causing reverberation of sound.

5. Solve the following examples.

a. The speed of sound in air at O °C is 332 m/s. If it increases at the rate of 0.6 m/s per degree, what will be the temperature when the velocity has increased to 344 m/s?
Answer:
Given:
Initial speed of sound at 0°C 332 m/s.
Final speed of sound -344 m/s.
Rate of increase per degree rise in temp. = 0.6m/s
To find:
Temperature when speed is 344m/s
Formulae:
Increase in temperature

Temperature when the speed of sound is 344 m/sis 20°C

b. Nita heard the sound of lightning after 4 seconds of seeing it. What was the distance of the lightning from her? (The velocity of sound in air is 340 m/s?)
Answer:
Given : Speed of sound (v) = 340 m/s
Time taken (f) = 4 sec
To find : Distance (s) = ?

The lightning has struck at a distance of 1360 m from the observer.

c. Sunil is standing between two walls. The wall closest to him is at a distance of 360 m. If he shouts, he hears the first echo after 4 s and another after another 2 seconds.
1. What is the velocity of sound in air?
2. What is the distance between the two walls? (Ans: 330 m/s; 1650 m)
Answer:
Given:
Distance of the closer wall (S₁) = 660 m
Time of echo from closer wall = 4 sec
∴ Time taken (t₁) = 4/2 sec = 2 sec
Time of echo from distant wall = 6 sec
∴ Time taken (t₂) = 6/2 sec = 3 sec
To find :
Velocity of sound in air (y) =?
Distance between two walls (S₁ + S₂) = ?

The velocity of sound in air is 330 mIs and the distance between two walls is 1650 m.

d. Hydrogen gas is filled in two identical bottles, A and B, at the same temperature. The mass of hydrogen in the two bottles is 12 gm and 48 gm respectively. In which bottle will sound travel faster? How may times as fast as the other? (Ans: In A; Twice)
Answer:
In A; Thrice

e. Helium gas is filled in two identical bottles A and B. The mass of the gas in the two bottles is 10 gm and 40 gm respectively. If the speed of sound is the same in both bottles, what conclusions will you draw? (Ans: Temperature of B is 4 times the temperature of A.)
Given:
Mass of Helium in bottle A = (mA) = 10gm
Mass of Helium in bottle B = (mB) = 40gm


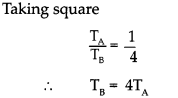
The temperature of B is 4 times the temperature of A

Class 9 Science Chapter 12 Study of Sound Intext Questions and Answers

Study Of Sound Class 9 Notes Maharashtra Board Question 1.
How does the velocity of sound depend on its frequency?
Answer:
The velocity of sound is directly proportional to its frequency
ν = υ λ
when ν = velocity
υ = frequency
λ = wavelength

9th Class Science Chapter 12 Study Of Sound Exercise Question 2.
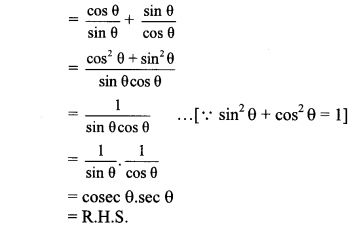
The molecular weight of oxygen gas (O₂) is 32 while that of hydrogen gas (H₂) is 2. Prove that under the same physical conditions, the velocity of sound in hydrogen is four times that in oxygen.
Answer:
Given:
Molecular wt of Oxygen (M_o) =32
Molecular wt of hydrogen (M_H) = 2
To Find:
V_H = 4 v_o


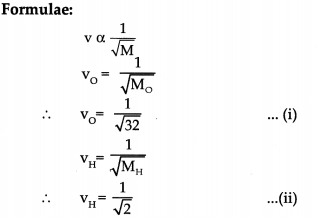
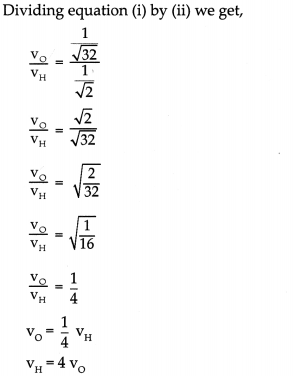
Hence, proved that velocity of sound in hydrogen is four times that in oxygen.

Answer the following:

Study Of Sound Class 9 Maharashtra Board  Question 1.
How will you reduce reverberation in public halls or buildings?
Answer:
(i) Reverberation in public halls or buildings will be reduced by using sound absorbing materials like curtains on wall, carpets on the floor.
(ii) By keeping the windows open, as sound will not get reflected.

12 Study Of Sound 9th Class Exercise  Question 2.
How is ultrasound used in medical science?
Answer:

• Sonography: Sonography technology uses ultrasonic sound waves to generate images of internal organs of the human body.
• Echocardiography: Echocardiography is a test that uses ultrasonic sound waves to produce live images of your heart.

9th Science Chapter 12 Study Of Sound Exercise Question 3.
To hear the echo distinctly, will the distance from the source of sound to the reflecting surface be same at all temperatures? Explain your answer.
Answer:

• No,the distance from the source of sound to the reflecting surface will not be the same at all temperatures.
• Velocity of sound is directly proportional to the square root of temperature.
• One of the conditions of echo is that the time interval between the original and reflected sound should be more than 0.1 sec.
• So if the temperature increases, the velocity of sound increases and the reflected sound reaches in less than 0.1 sec.
• So for echo to be heard the distance between the observer and the reflecting surface has to increase.

9th Science Chapter 12 Study Of Sound Question 4.
When is the reflection of sound harmful?
Answer:

• Reflected sound of high intensity called as noise is disturbing and harmful to the ears.
• When sound reverberates i.e it undergoes multiple reflections, poor quality of sound is produced.

9th Class Science Chapter 12 Study Of Sound Question Answer Question 5.
What kind of waves are created when a stone is dropped in water ?
Answer:

• When a stone is dropped in water, the particles of water oscillate up and down.
• These oscillations are perpendicular to the direction of propagation of the wave, such waves are called transverse waves.

Answer the following question:

12 Study Of Sound 9th Class Question 1.
Observe the graph/ diagram and discuss your observation.
Answer:

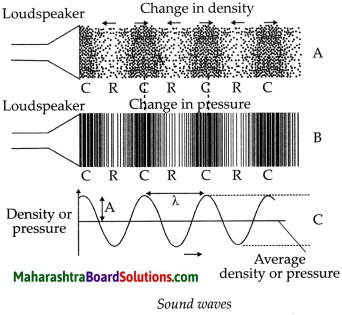
1. Fig. A shows changes in density. The region where particles are crowded is called compression and where they are far apart are rarefaction.
2. Fig. B show change in pressure. The lines represent layers of air. The regions when lines are crowded are high pressure regions while when they are far apart are of low pressure.
3. Fig. C shows changes in density or pressure. The crest represents high pressure region while trough represents low pressure region.

Answer the following question:

Study Of Sound Class 9 Question Answer Question 1.
How are the frequencies of notes sa, re, ga, ma, pa, dha, ni related to each other?
Answer:
The frequencies of notes sa, re, ga, ma, pa, dha, ni are related in the ratio.

i.e if first Sa is 240Hz then the next Sa will be 240 x 2 = 480Hz

Class 9 Science Chapter 12 Study Of Sound Exercise Question 2.
What is the main difference between the frequencies of the voice of a man and that of a woman?
Answer:

• Voice of a woman is high pitch i.e shorter wavelength and higher frequency
• Voice of man is low pitch i.e larger wavelength and smaller frequency.

Question 3.
Try this;

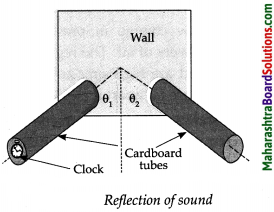
(a) In the above activity, what will happen if you lift one of the tubes to some height?
Answer:
If one of the tubes is lifted, angle of incidence will not be equal to angle of reflection, hence, the sound will not be clearly audible.

(b) Measure the angle of incidence 01 and the angle of reflection 02. Try to see if they are related in any way.
Answer:
Angle of incidence is same as the angle of reflection.

Class 9 Science Chapter 12 Study of Sound Additional Important Questions and Answers

Can you recall?

12.Study Of Sound Question 1.
How is the direction of the oscillation of the particles of the medium related to the direction of propagation if the sound wave?
Answer:

• Sound travels as a longitudinal wave.
• In a longitudinal wave, the particle of the medium oscillate parallel to the direction of propagation of the wave.

Choose and write the correct option:

Class 9 Science Chapter 12 Study Of Sound Question 1.
The unit of frequency is ……………………………… .
(a) Hertz
(b) m/s²
(c) Decibels
(d) m/s
Answer:
(a) Hertz

Study Of Sound Class 9 Exercise Question 2.
The normal hearing range for humans is ……………………………… .
(a) 0 Hz to 20 Hz
(b) greater than 20,000 Hz
(c) 20 Hz to 20,000 Hz
(d) none of these
Answer:
(c) 20 Hz to 20,000 Hz

Class 9th Science Chapter 12 Study Of Sound Question Answer  Question 3.
Sound will not travel through ……………………………… .
(a) Vacuum
(b) Liquid
(c) Solid
(d) Gases
Answer:
(a) vacuum

Class 9 Science Chapter 12 Study Of Sound Question Answer Question 4.
SI unit of ………………………………. is Hertz (Hz).
(a) Wavelength
(b) Frequency
(c) Speed of wave
(d) Velocity
Answer:
(b) frequency

Reflection Of Sound Class 9 Question 5.
The velocity of sound is inversely proportional to the ……………………………… .
(a) Pressure
(b) Square root of temperature
(c) Square root of density
(d) Humidity
Answer:
(c) square root of density

Question 6.
Sound waves with frequency greater than 20 kHz are called ……………………………… .
(a) Infrasound
(b) Ultrasound
(c) Sonic
(d) Damped sound
Answer:
(b) ultrasound

Question 7.
The loudness of a sound depends upon ……………………………… .
(a) Amplitude
(b) Speed
(c) Density
(d) Wavelength
Answer:
(a) Amplitude

Question 8.
……………………………… are used in sonography.
(a) High frequency ultrasound
(b) Stationary waves
(c) High frequency infrasound
(d) High frequency micro waves
Answer:
(a) High frequency ultrasound

Question 9.
The ……………………………… receives the vibrations coming from the membrane and converts them into electrical signals which are sent to the brain through the nerve.
(a) Cochlea
(b) Tympanic cavity
(c) Stapes
(d) Pinna
Answer:
(a) Cochlea

Find the odd one out:

Question 1.
Bats, rats, cats, dolphins
Answer:
Cats: cannot produce ultrasonic sound.

Question 2.
Clothes, paper, curtains, mirror
Answer:
Mirror: is a good reflector of sound, while others are poor reflectors.

Question 3.
Submarines, icebergs, internal organ, sunken ships.
Answer:
Internal organ: sonography is used , while for others sonar system is used.

Question 4.
Temperature, density, molecular weight, pressure
Answer:
Pressure: for a fixed temperature, the speed of sound does not depend on the pressure of the gas, all other factors affect speed of sound.

Answer in one sentence:

Question 1.
How can one produce sound?
Answer:
Vibration set up in an object produces sound (or) sound is produced when an object is disturbed and starts vibrating.

Question 2.
What is velocity of sound wave ?
Answer:
The distance covered by a point on the wave in unit time is the velocity of the sound wave.

Question 3.
What is the minimum distance of the reflecting surface to hear an echo ?
Answer:
To be able to hear a distinct echo, the reflecting surface should be at a minimum distance of 17.2 m.

Match the columns:

Question 1.

Answer:
(1-b- iii),
(2– a- i),
(3 – d – v),
(4 – e – ii),
(5 -c- iv)

Question 2.

Answer:
(1 -b – ii),
(2 -c – i),
(3-d – iv),
(4 – a – iii)

Name the following:

Question 1.
A form of energy which produces sensation of hearing in our ears.
Answer:
Sound energy

Question 2.
Repetitions of sound due to reflection .
Answer:
Echo

Question 3.
The audible range of sound for human being.
Answer:
20 Hz to 20,000 Hz

Question 4.
A method to obtain images of internal organs of the human body.
Answer:
Sonography

Question 5.
The matter or substance through which sound gets transmitted.
Answer:
Solid, liquid, gases

Question 6.
Three major parts of the ear.
Answer:
External ear, the middle ear and the inner ear.

Question 7.
Any two examples in which infrasound is produced.
Answer:
Pendulum, earthquake.

Question 8.
Name the living beings that can produce ultrasound.
Answer:
Bats, dolphins, mice.

Give scientific reasons:

Question 1.
Bats can navigate in dark.
Answer:

• The ultrasonic sound produced by bats, gets reflected on hitting an obstacle.
• This reflected sound is received by their ears and they can locate the obstacle and estimate its distance even in the dark.
• Hence, bats can navigate in dark.

Question 2.
A SONAR system is installed in a ship.
Answer:

• A SONAR system determines the depth of the sea.
• It locates underwater hills, valleys, icebergs, submarines and sunken ships. It also locates the positions of other ships or submarines.
• Hence a SONAR system is installed in a ship.

Question 3.
Sound travels faster in iron than in air.
Answer:

• Sound requires a material medium for its propagation and travels in the form of a longitudinal wave.
• The denser the medium, faster is the propagation of sound.
• Hence, sound travels faster in iron than in air.

Solve the following:

Type – A

Formula:
\(\text { (i) Velocity }=\frac{\text { distance }}{\text { time }}\)

Question 1.
Ultrasonic waves are transmitted downwards into the sea with the help of a SONAR. The reflected sound is received after 4 s. What is the depth of the sea at that place? (Velocity of sound in seawater = 1550 m/s)
Answer:
Given:
Time to hear echo = 4 sec
Time taken by sound waves to reach the bottom 4 of sea (t) = 4/2 sec = 2 sec
Velocity of sound in sea water (v) = 1550 m/s
To find:
Depth of sea(s) = ?

The depth of the sea at that place is 3100 m.

Question 2.
A person standing near a hill fires a gun and hears the echo after 1 second. If speed of sound in air is 340 m/s. Find the distance between the hill and the person.
Answer:
Given:
Time to hear echo = 1 sec 1
Time taken (t) = 1/2 sec
Velocity of sound (v) = 340 m/s
To find:
Distance (s) = ?

Distance between the person and hill is 170 m.

Numerical For Practice

Question 3.
If you hear the thunder 20 seconds after you see the flash of lightning, how far from you has the lightning occurred? (Speed of sound in air = 340 m/s)
Answer:
6800m

Question 4.
Aboy observes smoke from a cannon 3 seconds before he hears the bang. If the cannon is 1020 m from the observer, find the velocity of sound.
Answer:
340 rn/s

Question 5.
A soldier standing between the two buildings fires a gun. He heard the echo of the sounds from the first building after 2 seconds and echo from the second building after 3 seconds. Find the distance between two buildings. (Speed of sound in air = 340 m/s)
Answer:
850m

Type – B

Question 1.
Sound waves of wavelength 1 cm have a velocity of 340 mIs in air. What is their frequency? Can this sound be heard by the human ear?
Answer:
Given:
wave length (λ) = 1cm = 1/100
Velocity of sound (v) = 340 m/s
To fInd :
frequency (u) = ?
Formulae:
ν = υ λ
Solution:

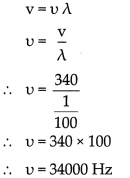
The frequency of the sound waves is 34000 Hz. The frequency is higher than 20000 Hz and therefore, this sound cannot be heard by the human ear.

Question 2.
How long will it take for a sound wave of 25 cm wavelength and 1.5 kHz frequency, to travel a distance of 1.5 km?
Answer:
Given:
frequency (u) = 1.5 kHz = 1500 Hz

\(\begin{array}{l}
=\frac{1500}{375} \\
=4 \mathrm{sec}
\end{array}\)
The sound wave takes 4 sec to travel the distance of 1.5 km.

Question 3.
Calculate distance travelled by a sound wave having frequency 1000 Hz and wavelength 0.25 m, if it travels for 5 seconds in a certain medium.
Answer:
Given:
frequency (u) = 1000 Hz
wavelength (λ) = 0.25 m
time (t) = 5 seconds
To find :
Distance (d) =?
Formulae:
ν = υ λ
Solution:

The distance travelled by the sound wave is 1250 m.

Question 4.
The audible range of sound is 20 Hz to 20000 Hz. At 22°C in air speed of sound is 344 mIs. Express the range of sound in terms of wavelength by calculating the respective values.
Answer:
Given:
frequency (u₁) 20 Hz
frequency ( u₂) = 20,000 Hz
velocity (v) = 344 rn/s
To find :
Wavelengths λ₁ and λ₂ = ?
Formulae:
ν = υ λ
Solution:


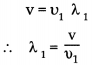
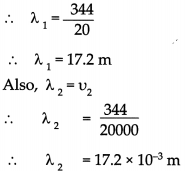
Audible range of wavelength of sound is from 17.2 x 10^-3 m to 17.2 m.

Numerical For Practice

Question 5.
A sound wave has frequency 320 Hz and wavelength 0.25 m. How much distance will it travel in 10 second?
Answer:
The distance travelled is 800 m.

Type – C

Question 1.
Hydrogen gas is filled in two identical bottles, A and B, at the same temperature. The mass of hydrogen in the two bottles is 12 gm and 48 gin respectively. In which bottle will sound travel faster? How many timés as fast as the other?
Answer:
Given:
Mass of hydrogen in bottle A (m_A) = 12gm
Mass of hydrogen in bottle B(m_B) = 48gm
To find:
In which bottle sound travels faster.
Formulae:


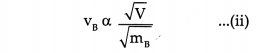
Since both bottles are identical hence, the volume is the same, i.e. v
Dividing (j) and (ii),

(i) Vivacity of sound will be more in bottle A.
(ii) Velocity of sound in bottle A (V_A) is twice of that in bottle B (v_B)

Numerical For Practice

Question 2.
Argon gas is filled in two identical bottles X and Y. The mass of the gas in the two bottles is 5 gm and 25gm respectively. If the speed of sound is the same in both bottles, what conclusions will you draw?
Answer:
(Temperature of Y is 5 times the temperature of X.)

Type – D

Numerical For Practice

Question 1.
Velocity of sound in air at 0°C is 332nVs. It increases by 0.6ni/s for each °Celsius rise in temperature. At what temperature of ait the velocity will be 359m1s?
Answer:
45°C

Question 2.
Velocity of sound In air at 0°C is 332m/s It increases by 0.6mIs for each degree Celsius rise In temperature. What will be the velocity of sound at 60°C?
Answer:
368 rn/s

Define the following:

Question 1.
Wave length (λ)
Answer:
The distance between two consecutive compressions (or crests) or two consecutive rarefactions (or troughs) is called the wavelength.

Question 2.
Amplitude (A)
Answer:
The maximum value of pressure or density is called amplitude.

Question 3.
Frequency (υ)
Answer:
The frequency of a sound wave is defined as the number of complete oscillations of density (or pressure of the medium) per second.

Question 4.
Time Period (T)
Answer:
The time taken for one complete oscillation of pressure or density at a point in the medium is called the time period.

Question 5.
Echo
Answer:
An echo is the repetition of the original sound because of reflection by some surface.

Question 6.
Transverse waves
Answer:
Oscillations of the particles of the medium vibrate at right angles to the direction of propagation of the wave are called transverse waves.

Question 7.
longitudinal waves
Answer:
The particles of the medium oscillate about their central or mean position in a direction parallel to the propagation of wave is called as longitudinal waves.

Question 8.
Velocity of wave
Answer:
The distance covered by a point on the wave (for example the point of highest density or lowest density) in unit time is the velocity of the sound wave.’

Distinguish between:

Question 1.
Infrasound and Ultrasound
Answer:

Question 2.
Transverse waves and Longitudinal waves
Answer:

Question 3.
Consider two cases
(A) whistle of train (B) roar of a lion

(I) In which case the sound is high pitch?
Answer:
Whistle of a train is high pitch as compared to roar of a lion, as the frequency is higher.

(II) What is the real cause of sound production? Explain with examples.
Answer:

• Vibrations in the object are responsible to produce a sound.
• Vibration is a rapid to and fro motion of an object.
• Sometimes the vibrations may be strong enough to be seen by eyes, e.g. string vibrations in string instruments, vibration on mobile phone, blowing air in the cap of your pen by holding it near the lips.

(III) Three sounds 5 Hz, 500 Hz and 50,000 Hz are produced by different sources.
(a) Which sound will be heard by humans?
(b) Which sounds may be produced by bats?
(c) Which sounds may be produced by elephants?
Answer:
(a) 500 Hz – Humans can hear sounds in the range of 20 Hz-20,000 Hz
(b) 50,000 Hz – Bats produce ultrasonic sounds above 20,000 Hz
(c) 5 Hz – Elephants can produce infrasonic sounds below 20 Hz

Question 6.
Suppose you and your friend are on the moon. Will you be able to hear any sound
Answer:
Sound waves need a material medium for their propagation. Since there is no atmosphere on the moon, we cannot hear any sound on the moon.

Answer in detail:

Question 1.
What are the factors on which velocity of sound in gaseous medium depend?
Answer:
The velocity of sound in a gaseous medium depends on the physical conditions i.e. the temperature, density of the gas and its molecular weight.

1. Temperature (T): The velocity of sound is directly proportional to the square root of the temperature of the medium. This means that increasing the temperature four times doubles the velocity.
   \(\text { v } \alpha \sqrt{\mathrm{T}}\)
2. Density(p): The velocity of sound is inversely proportional to the square root of density. Thus, increasing the density four times, reduces the velocity to half its value.
   \(\mathrm{v} \alpha \frac{1}{\sqrt{\rho}}\)
3. Molecular weight (M): The velocity sound is inversely proportional to the square root of molecular weight of the gas. Thus, increasing the molecular weight four times, reduces the velocity to haff its value.
   \(\mathrm{v} \alpha \frac{1}{\sqrt{\mathrm{M}}}\)

Question 2.
What are the uses of ultrasonic sound?
Answer:
Uses of ultrasonic sound are as follows:

• For communication between ships at sea.
• To join plastic surfaces together.
• To sterilize liquids like milk by killing the bacteria in it so that the milk keeps for a longer duration.
• Echocardiography which studies heartbeats, is based on ultrasonic waves (Sonography technology).
• To obtain images of internal organs in a human body.
•  In industry to clean intricate parts of machines where hands cannot reach.
• To locate the cracks and faults in metal blocks.

Question 3.
Explain with the help of a neat labelled diagram the working of human ear.
Answer:

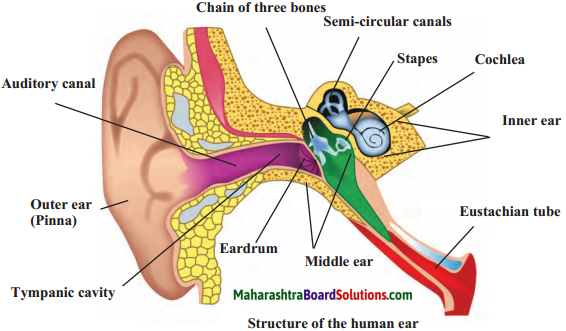
• The ear is an important organ of the human body.
• When sound waves fall on the eardrum, it vibrates and these vibrations are converted into electrical signals which travel to the brain through nerves.
• The ear can be divided into three parts:
  (a) Outer ear
  (b) Middle ear
  (c) Inner ear.

(a) Outer ear or Pinna
The outer ear collects the sound waves and passes them through a tube to a cavity in the middle ear. Its peculiar funnel like shape helps to collect and pass sounds into the middle ear.

(b) Middle ear
There’ is a thin membrane in the cavity of the middle ear called the eardrum. When a compression in a sound wave reaches the eardrum, the pressure outside it increases and it gets pushed inwards. The opposite happens when a rarefaction reaches there. The pressure outside decreases and the membrane gets pulled outwards. Thus, sound waves cause vibrations of the membrane.

(c) Inner ear
The auditory nerve connects the inner ear to the brain. The inner ear has a structure resembling the shell of a snail. It is called the cochlea. The cochlea receives the vibrations coming from the membrane and converts them into electrical signals which are sent to the brain through the nerve. The brain analyses these signals.

Question 4.
Write a short note on SONAR
Answer:

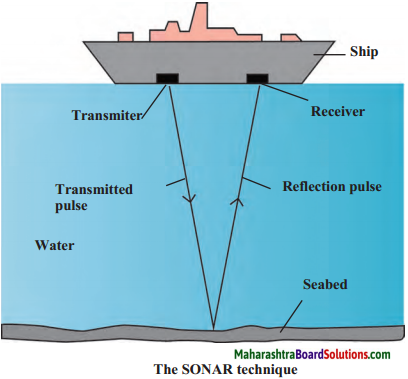
(i) SONAR is the short form for Sound Navigation and Ranging. It is used to determine the direction, distance and speed of an underwater object with the help of ultrasonic sound waves. SONAR has a transmitter and a receiver, which are fitted on ships or boats.

(ii) The transmitter produces and transmits ultrasonic sound waves. These waves travel through water, strike underwater objects and get reflected by them. The reflected waves are received by the receiver on the ship.

(iii) The receiver converts the ultrasonic sound into electrical signals and these signals are properly interpreted. The time difference between transmission and reception is noted. This time and the velocity of sound in water give the distance from the ship, of the object which reflects the waves.

(iv) SONAR is used to determine the depth of the sea. SONAR is also used to search underwater hills, valleys, submarines, icebergs, sunken ships etc.

Question 5.
Write a short note on Sonography. How is it misused?
Answer:

• Sonography technology uses ultrasonic sound waves to generate images of internal organs of the human body.
• This is useful in finding out the cause of swelling, infection, pain, condition of the heart, the state of the heart after a heart attack as well as the growth of foetus inside the womb of a pregnant woman.
• This technique makes use of a probe and a gel.
• The gel is used to make proper contact between the skin and the probe so that the full capacity of the ultrasound can be utilized.
• High-frequency ultrasound is transmitted inside the body with the help of the probe.
• The sound reflected from the internal organ is again collected by the probe and fed to a computer which generates the images of the internal organ.
• As this method is painless, it is increasingly used in medical practice for correct diagnosis.
• This technique is used by many people to find out gender of an unborn baby and this often leads to the incidence of female foeticide.

Balbharati Maharashtra State Board 9th Std Science Textbook Solutions 

• Information Communication Technology (ICT) Class 9 Science Textbook Solutions
• Reflection of Light Class 9 Science Textbook Solutions
• Study of Sound Class 9 Science Textbook Solutions
• Carbon: An Important Element Class 9 Science Textbook Solutions
• Substances in Common Use Class 9 Science Textbook Solutions
• Life Processes in Living Organisms Class 9 Science Textbook Solutions
• Heredity and Variation Class 9 Science Textbook Solutions
• Introduction to Biotechnology Class 9 Science Textbook Solutions
• Observing Space: Telescopes Class 9 Science Textbook Solutions

Std 9 Science Chapter 10 Information Communication Technology (ICT) Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 10 Information Communication Technology (ICT) Notes, Textbook Exercise Important Questions and Answers. BALRAMCHIN Pivot Point Calculator

Class 9 Science Chapter 10 Information Communication Technology (ICT) Question Answer Maharashtra Board

Class 9 Science Chapter 10 Information Communication Technology (ICT) Textbook Questions and Answers

1. Fill in the blanks to complete the statements. Justify the statements.

a. While working with a computer we can read the information stored in its memory and perform other actions in ………………………. memory.
b. While presenting pictures and videos about the works of scientists, we can use ……………………… .
c. To draw graphs based on the quantitative information obtained in an experiment, one uses ……………………… .
d. The first generation computers used to shut down because of ……………………… .
e. A computer will not work unless ………………………. is supplied to it.

2. Answer the following questions.

a. Explain the role and importance of information communication in science and technology.
Answer:

• ICT plays a key role in creating, displaying, collecting, processing and communicating information in the field of science and technology.
• Following is the importance of ICT in science and technology:
  (a) Access to wide range of information
  (b) Storing of Data
  (c) Processing of Data
  (d) Securing work files
  (e) Proper representation of data

b. Which application software in the computer system did you find useful while studying science, and how?
Answer:

• Microsoft word: To write down the information collected and making a document for further evaluation.
• Microsoft excel : To draw graph based on the obtained numerical information from the experiment.
• Internet explorer: To search for information in finding out the solution or solving the queries by reading the available information.

c. How does a computer work?
Answer:

d. What precautions should be taken while using various types of software on the computer?
Answer:

• Antivirus must be installed.
• Software should be legal and from a trusted place.
• Application should be scanned before using.
• Pirated Software should not be used
• Provide all necessary data to obtain the best possible results.

e. Which are the various devices used in information communication? How are they used in the context of science?
Answer:

• Various devices used in information communication are: Computers, Laptops, Mobiles, Radios, Television, etc.
• Computers, Laptops and Mobiles: Help in accessing, collecting, processing, communicating, sharing and storing of information. It helps in determining the appropriate conclusions in all fields, including the field of science.
• Television: Help in getting information about the new and innovative technology.

3. Using a spreadsheet, draw graphs between distance and time, using the information about the movements of Amar, Akbar and Anthony given in the table on page 4, in the lesson on Laws of Motion. What precautions will you take while drawing the graph?

Answer:
Precautions to be taken while drawing a graph:

• The data should be kept in tabular form.
• Whenever there is ‘drag and fill’ option used, ‘smart tag’ option should be used after ‘drag data’ to fill data as required.
• Entered data should be formatted in the manner required.
• Various types of graphs can be created by using the same data, so appropriate graph should be selected.
• Chart titles and axes titles should be updated as per the data.

4. Explain the differences between the different generations of computers. How did science contribute to these developments?
Answer:
Generation: 1st
Time Period: 1946 – 1956
Development: Vacuum Tubes Characteristics:

• Huge in size
• Expensive
• Lot of electricity consumption
• Heat generation

Generation: 2nd
Time Period: 1956 – 1963
Development: Transistors
Characteristics:

• Frequent shutdowns
• Superior to 1st Generation
• Small in size and fast
• Cheaper as compared to 1st Generation
• Less consumption of electricity

Generation: 3rd
Time Period: 1963 -1971
Development: IC
Characteristics:

• Keyboards and monitors
• OS
• Smaller and still cheaper

Generation: 4th
Time Period: 1971 – 2010
Development: Microprocessor Characteristics:

• Use of Internet
• GUI
• Introduction of portable devices like mobiles, laptops, etc.

Generation: 5th
Time Period: 2010 – Till Date
Development: Artificial Intelligence (AI) Characteristics:

• Voice recognition
• Sensors
• Nano technology

1st Generation computers occupied the entire room, but due to advancement in science and technology, today’s computer fits into our pockets.

Initially computers needed a specific language to interact but today we use voice recognition for the same.

In these ways, science has contributed in making the computers faster, smaller, cheaper and much more useful.

5. What devices will you use to share with others the knowledge that you have?
Answer:
Devices like radios, televisions, pendrives, computers, laptops, mobiles, landlines, hard drives, CDs, memory cards help us in sharing our knowledge with others.

6. Using information communication technology, prepare powerpoint presentations on at least three topics in your textbook. Make a flowchart of the steps you used while making these presentations.
Answer:
Steps for preparation of PowerPoint presentations:

7. Which technical difficulties did you face while using the computer? What did you do to overcome them?
Answer:

• Lagging: Due to lot of applications running at the same time, the computer starts lagging and becomes slow. Closing a few applications helped solve the problem of lagging.
• Viruses and Bugs: Cybercrimes are rising daily, even from single mail the computer can be attacked by viruses. Installing a valid antivirus helps solve the problem of viruses and bugs.
• Breach of Privacy: Confidential information being accessed by anyone is the breach of privacy. Putting privacy setting in place helps solve the problem.
• Physical Damage: Hardware over a period of time might get physically damaged. Taking precautions while using will help to solve the problem.

Class 9 Science Chapter 10 Information Communication Technology (ICT) Intext Questions and Answers

Question 1.
Make a list of various hardware and software items of a computer,
Answer:
Hardware: Mouse, Keyboard, Pendrive, Monitor and other parts of computer.
Software: Operating Systems, Application Programs, Antivirus, etc.

Answer the following questions:

Question 2.
Which devices do we directly or indirectly use for collecting, sharing, processing and communicating information?
Answer:

• Computers
• Laptops
• Mobiles
• Memory Cards
• Pendrives
• Landlines
• Hard disks etc.

Question 3.
How is information communication technology important for dealing with explosion of information?
Answer:

• Information explosion means a situation whère information is available in abundance, in other words, too much information.
• Devices like computers, laptops help us in easier accessment of information that we need from all the data.

Class 9 Science Chapter 10 Information Communication Technology (ICT) Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
…………………….. includes communication devices and the use of those devices as well as the services provided with their help.
(a) Operating System
(b) Office
(c) Computers
(d) Information Communication Technology
Answer:
(d) Information Communication Technology

Question 2.
Computers have gone through …………………….. generations.
(a) 5
(b) 7
(c) 10
(d) 8
Answer:
(a) 5

Question 3.
First generation of Computers were considered to be present in the period of ……………………. .
(a) 2000 – 2001
(b) 1901 – 2001
(c) 1946 -1959,
(d) 1996 – 2001
Answer:
(c) 1946-1959

Question 4.
Full form of RAM is ……………………. .
(a) Roaming Application Memory
(b) Random Accessible Media
(c) Random Access Memory
(d) None of the above
Answer:
(c) Random Access Memory

Question 5.
Full form of ROM is ……………………. .
(a) Roaming Only Memory
(b) Random Output Media
(c) Read Only Memory
(d) None of the above
Answer:
(c) Read Only Memory

Question 6.
…………………….. is raw information.
(a) Program
(b) Memory
(c) Data
(d) Operating System
Answer:
(c) Data

Question 7.
…………………….. are used for sharing information.
(a) Telephones
(b) Hard disks
(c) RAM
(d) ROM
Answer:
(a) Telephones

Question 8.
Hard disks are used for …………………….. information.
(a) storing
(b) communicating
(c) sharing
(d) all of the above
Answer:
(a) storing

Question 9.
Computers are used for …………………….. information.
(a) storing
(b) managing
(c) sharing
(d) all of the above
Answer:
(d) All of the above

Question 10.
RAM and ROM are 2 types of …………………….. memory.
(a) external
(b) internal
(c) physical
(d) garbage
Answer:
(b) internal

Question 11.
The information stored in ROM is only …………………….., changes cannot be made.
(a) external memory
(b) readable
(c) accessible
(d) physical
Answer:
(b) readable

Question 12.
…………………….. is a group of commands to be given to the computer.
(a) Program
(b) Memory
(c) Data
(d) Operating System
Answer:
(a) Program

Question 13.
…………………….. communicates between the computer and the person working on it.
(a) Program
(b) Memory
(c) Data
(d) Operating System
Answer:
(d) Operating System

Match the columns:

Answer:
(1 – b),
(2 – d),
(3 – e),
(4 – a),
(5 – c)

State whether the following statements are true or false and if false, correct the false statements:

(1) RAM and ROM are the types of external memory.
(2) ICT includes communication devices and the use of those devices as well as services provided with their help.
(3) A computer cannot be used without its operating system.
(4) Microsoft Excel is used to make PowerPoint.
(5) Software refers to the set of commands given to the computer.
Answer:
(1) False. RAM and ROM are the types of internal memory.
(2) True
(3) True
(4) False. Microsoft Excel is used to make spreadsheets.
(5) True

Answer the following in one sentence:

Question 1.
Name the computer which was made between 1946 -1959.
Answer:
The ENIAC computer was made in the period of 1946-1959.

Question 2.
Give one example of Input Unit.
Answer:
Keyboard.

Question 3.
Name the 3 major parts of the processing units.
Answer:

• Memory unit
• Control unit
• ALU unit

Question 4.
What precautions need to the taken care while entering formula into the excel?
Answer:
While using a formula, the ‘=’ sign should be typed first. Similarly, no space should be inserted while typing any formula.

Question 5.
What is Internet Explorer?
Answer:
This is a kind of Search Engine. It helps to find the information we want from all the information available on the internet.

Question 6.
What is a PDF?
Answer:
A PDF or Portable Document Format file can be used to view the file to print it or to handle files.

Question 7.
What is C-DAC?
Answer:
C-D AC, is a well-known Centre for Development of Advanced Computing, situated in Pune.

Write the Full forms of the following abbreviation:

Question 1.
ICT
Answer:
Information Communication Technology

Question 2.
OS
Answer:
Operating System

Question 3.
RAM
Answer:
Random Access Memory

Question 4.
ROM
Answer:
Read Only Memory

Question 5.
CPU
Answer:
Central Processing Unit

Question 6.
DOS
Answer:
Disk Operating System

Question 7.
PDF
Answer:
Portable Document Format

Question 8.
ALU
Answer:
Arithmetic Logical Unit

Question 9.
GUI
Answer:
Graphical User Interface

Question 10.
C-DAC
Answer:
Centre for Development of Advanced Computing

Question 11.
ISCII
Answer:
Indian Script Code for Information Interchange

Define the following:

Question 1.
Memory
Answer:
Memory is the place for storing data obtained from the input and also the generated solution or answer by the computer.

Question 2.
RAM
Answer:
RAM is created from electronic components and can function only as long as it is supplied with electricity.

Question 3.
ROM
Answer:
Information stored in ROM can only be read and changes cannot be made to the information originally stored here.

Question 4.
Operating System
Answer:
It is a program which provides a means of communication between the computer and the person working on it. It is called the DOS (Disk Operating System).

Question 5.
Program
Answer:
A program is a group of commands to be given to a computer.

Question 6.
Data and Information
Answer:
Data is information in its raw (unprocessed) form.

Question 7.
Hardware
Answer:
Hardware consists of all the electronic and mechanical parts used in computers.

Question 8.
Software:
Answer:
Software refers to the commands given to the computer, information supplied to it (input) and the results obtained from the computer after analysis (output).

Give scientific reasons:

Question 1.
Computer cannot function without its operating system.
Answer:

• Operating system is like a link between the computer and the person working on it.
• Operating system manages all the activities performed by the computer.
• Without the operating system, the user won’t be able to input any data or run any program. Thus, a computer cannot run without an operating system.

Question 2.
ROM is a Read Only Memory.
Answer:

• ROM also known as Read Only Memory is a part of internal memory of a computer where the information stored can only be read.
• ROM helps store data permanently for a long period of time and the information stored cannot be deleted.
• Thus, data in a ROM can only be read and cannot be altered or modified and hence, it is called as Read Only Memory.

Complete the table:
Answer:

Answer the following questions:

Question 1.
What precautions will you take when entering data?
Answer:

1. As far as possible, the data should be kept in tabular form. Different types of data should be entered in different cells. Data should be entered neatly and in one ‘flow’. Unnecessary space and special characters should not be used.
2. Many times we ‘drag and fill’ data. At such times, the ‘smart tag’ can be used after ‘drag data’ to fill any data in any manner as required.
3. Once the data has been entered, it can be formatted in different ways. Similarly, we can perform different types of calculations, using different formulae.
4. While using a formula, the ‘=’ sign should be typed first. Similarly, no space should be inserted while typing any formula.

Answer in detail:

Question 1.
Write in short about the opportunities in the field of ICT.
Answer:
(i) Software Field: This is an important field. Having accepted the challenge of creating software, many companies have entered this field. The opportunities in the software field can be classified as follows – application program development, software package development, operating systems and utility development, special purpose scientific applications.

(ii) Hardware Field: Today, there are several companies in our country too, which make computers. They sell computers that they have themselves made. Others sell computers brought from outside as well as repair them and take maintenance contracts to keep computers in big companies working efficiently without a break. Plenty of jobs are available here. There are job opportunities in hardware designing, hardware production, hardware assembly and testing, hardware maintenance, servicing and repairs, etc.

(iii) Marketing: There are many establishments which make and sell computers and related accessories. They need good sales personnel who are experienced in the working of computers as well as skilled in marketing.

(iv) Training: The training of new entrants for various jobs is a vast field. It is very important to have dedicated teachers who are competent in the field of computers.

Question 2.
Write in short about the industries conducting research in the field of computers.
Answer:

• C-DAC, the well-known Centre for Development of Advanced Computing, situated in Pune, is the leading institute in India that conducts research in the field of computers.
• The first Indian supercomputer was made with help from this institute. Valuable guidance for making this computer (the Param computer) was received from the senior scientist Vijay Bhatkar. Param means the supreme.
• This computer can perform one billion calculations per second. It is used in many fields like space research, movements in the interior of the earth, research in oil deposits, medicine, meteorology, engineering, military etc.
• C-DAC has also participated in developing the ISCII code for writing different language scripts. (Indian Script Code for Information Interchange).

Question 3.
Use Microsoft Word to create a document and write equations.
Answer:

• Click on the Microsoft word 2010 icon on the desktop.
• Select the ‘New option in the ‘File’ tab, and then select the ‘Blank document’ option.
• Type your material on the blank page on the screen using the keyboard. Use the language, font size, bold, etc. options in the Home tab to make the typed material attractive.
• To type equations in the text, select the ‘Equation’ option in the ‘Insert’ tab.
  
• Select the proper equation and type it using mathematical symbols.
  

Balbharati Maharashtra State Board 9th Std Science Textbook Solutions 

• Information Communication Technology (ICT) Class 9 Science Textbook Solutions
• Reflection of Light Class 9 Science Textbook Solutions
• Study of Sound Class 9 Science Textbook Solutions
• Carbon: An Important Element Class 9 Science Textbook Solutions
• Substances in Common Use Class 9 Science Textbook Solutions
• Life Processes in Living Organisms Class 9 Science Textbook Solutions
• Heredity and Variation Class 9 Science Textbook Solutions
• Introduction to Biotechnology Class 9 Science Textbook Solutions
• Observing Space: Telescopes Class 9 Science Textbook Solutions

10th Standard Maths 2 Practice Set 6.1 Chapter 6 Trigonometry Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

Class 10 Maths Part 2 Practice Set 6.1 Chapter 6 Trigonometry Questions With Answers Maharashtra Board

Question 1.
If sin θ = \(\frac { 7 }{ 25 } \), find the values of cos θ and tan θ.
Solution:
sin θ = \(\frac { 7 }{ 25 } \) … [Given]
We know that,
sin² θ + cos² θ = 1

…[Taking square root of both sides] Now, tan θ = \(\frac{\sin \theta}{\cos \theta}\)

Alternate Method:
sin θ = \(\frac { 7 }{ 25 } \) …(i) [Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
sin θ = \(\frac { AB }{ AC } \) … (ii) [By definition]
∴ \(\frac { AB }{ AC } \) = \(\frac { 7 }{ 25 } \) … [From (i) and (ii)]

LetAB = 7k and AC = 25k
In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (7k)² + BC² = (25k)²
∴ 49k² + BC² = 625k²
∴ BC² = 625k² – 49k²
∴ BC² = 576k²
∴ BC = 24k …[Taking square root of both sides]

Question 2.
If tan θ = \(\frac { 3 }{ 4 } \), find the values of sec θ and cos θ.
Solution:

Alternate Method:
tan θ = \(\frac { 3 }{ 4 } \) …(i)[Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
tan θ = \(\frac { AB }{ BC } \) … (ii) [By definition]
∴ \(\frac { AB }{ BC } \) = \(\frac { 3 }{ 4 } \) … [From (i) and (ii)]

Let AB = 3k and BC 4k
In ∆ABC,∠B = 90°
∴ AB² + BC² = AC² …[Pythagoras theorem]
∴ (3k)² + (4k)² = AC²
∴ 9k² + 16k² = AC²
∴ AC² = 25k²
∴ AC = 5k …[Taking square root of both sides]

Question 3.
If cot θ = \(\frac { 40 }{ 9 } \), find the values of cosec θ and sin θ
Solution:

..[Taking square root of both sides]

Alternate Method:
cot θ = \(\frac { 40 }{ 9 } \) ….(i) [Given]
Consider ∆ABC, where ∠ABC = 90° and
∠ACB = θ
cot θ = \(\frac { BC }{ AB } \) …(ii) [By defnition]
∴ \(\frac { BC }{ AB } \) = \(\frac { 40 }{ 9 } \) ….. [From (i) and (ii)]
Let BC = 40k and AB = 9k

In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (9k)² + (40k)² = AC²
∴ 81k² + 1600k² = AC²
∴ AC² = 1681k²
∴ AC = 41k … [Taking square root of both sides]

Question 4.
If 5 sec θ – 12 cosec θ = θ, find the values of sec θ, cos θ and sin θ.
Solution:
5 sec θ – 12 cosec θ = 0 …[Given]
∴ 5 sec θ = 12 cosec θ

Question 5.
If tan θ = 1, then find the value of

Solution:
tan θ = 1 … [Given]
We know that, tan 45° = 1
∴ tan θ = tan 45°
∴ θ = 45°

Question 6.
Prove that:
i. \(\frac{\sin ^{2} \theta}{\cos \theta}+\cos \theta=\sec \theta\)
ii. cos² θ (1+ tan² θ) = 1
iii. \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sec \theta-\tan \theta\)
iv. (sec θ – cos θ) (cot θ + tan θ) tan θ. sec θ
v. cot θ + tan θ cosec θ. sec θ
vi. \(\frac{1}{\sec \theta-\tan \theta}=\sec \theta+\tan \theta\)
vii. sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ
viii. \(\sec \theta+\tan \theta=\frac{\cos \theta}{1-\sin \theta}\)

Proof:
i. L.H.S. = \(\frac{\sin ^{2} \theta}{\cos \theta}+\cos \theta\)

ii. L.H.S. = cos² θ(1 + tan² θ)
= cos² θ sec² θ …[∵ 1 + tan² θ = sec² θ]

= 1
= R.H.S.
∴ cos² θ (1 + tan² θ) = 1

iv. L.H.S. = (sec θ – cos θ) (cot θ + tan θ)

∴ (sec θ – cos θ) (cot θ + tan θ) = tan θ. sec θ

v. L.H.S. = cot θ + tan θ

∴ cot θ + tan θ = cosec θ.sec θ

vii. L.H.S. = sin⁴ θ – cos⁴ θ
= (sin² θ)² – (cos² θ)²
= (sin² θ + cos² θ) (sin² θ – cos² θ)
= (1) (sin² θ – cos² θ) ….[∵ sin² θ + cos² θ = 1]
= sin² θ – cos² θ
= (1 – cos² θ) – cos² θ …[θ sin² θ = 1 – cos² θ]
= 1 – 2 cos² θ
= R.H.S.
∴ sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ

viii. L.H.S. = sec θ + tan θ

xi. L.H.S. = sec⁴ A (1 – sin⁴ A) – 2 tan² A
= sec⁴ A [1² – (sin² A)²] – 2 tan² A
= sec⁴ A (1 – sin²A) (1 + sin² A) – 2 tan² A
= sec⁴ A cos²A (1 + sin² A) – 2 tan²A
[ ∵ sin² θ + cos² θ = 1 ,∵ 1 – sin² θ = cos² θ]

Maharashtra Board Class 10 Maths Chapter 6 Trigonometry Intext Questions and Activities

Question 1.
Fill in the blanks with reference to the figure given below. (Textbook pg. no. 124)

Solution:

Question 2.
Complete the relations in ratios given below. (Textbook pg, no. 124)

Solution:
i. \(\frac{\sin \theta}{\cos \theta}\) = [tan θ]
ii. sin θ = cos (90 – θ)
iii. cos θ = (90 – θ)
iv. tan θ × tan (90 – θ) = 1

Question 3.
Complete the equation. (Textbook pg. no, 124)
sin² θ + cos² θ = [______]
Solution:
sin² θ + cos² θ = [1]

Question 4.
Write the values of the following trigonometric ratios. (Textbook pg. no. 124)

Solution:

Maharashtra Board Class 10 Maths Solutions

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions

10th Standard Maths 2 Problem Set 7 Chapter 7 Mensuration Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 7 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Class 10 Maths Part 2 Problem Set 7 Chapter 7 Mensuration Questions With Answers Maharashtra Board

Problem Set 7 Question 1. Choose the correct alternative answer for each of the following questions.

i. The ratio of circumference and area of a circle is 2 : 7. Find its circumference.
(A) 14 π
(B) \(\frac{7}{\pi}\)
(C) 7π
(D) \(\frac{14}{\pi}\)
Answer:

(A)

ii. If measure of an arc of a circle is 160° and its length is 44 cm, find the circumference of the circle.
(A) 66 cm
(B) 44 cm
(C) 160 cm
(D) 99 cm
Answer:

(D)

iii. Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
(A) 44 cm
(B) 25 cm
(C) 36 cm
(D) 56 cm
Answer:

(B)

iv. Find the curved surface area of a cone of radius 7 cm and height 24 cm.
(A) 440 cm²
(B) 550 cm²
(C) 330 cm²
(D) 110 cm²
Answer:

(B)

v. The curved surface area of a cylinder is 440 cm² and its radius is 5 cm. Find its height.
(A) \(\frac{44}{\pi}\) cm
(B) 22π cm
(C) 44π cm
(D) \(\frac{22}{\pi}\)
Answer:

(A)

vi. A cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5 cm, find the height of the cone.
(A) 15 cm
(B) 10 cm
(C) 18 cm
(D) 5 cm
Answer:

(A)

vii. Find the volume of a cube of side 0.01 cm.
(A) 1 cm
(B) 0.001 cm³
(C) 0.0001 cm³
(D) 0.000001 cm³
Answer:
Volume of cube = (side)³
= (0.01)³ = 0.000001 cm³
(D)

viii. Find the side of a cube of volume 1 m³
(A) 1 cm
(B) 10 cm
(C) 100 cm
(D) 1000 cm
Answer:
Volume of cube = (side)³
∴ 1 = (side)³
∴ Side = 1 m
= 100 cm
(C)

Problem Set 7 Geometry Class 10 Question 2. A washing tub in the shape of a frustum of a cone has height 21 cm. The radii of the circular top and bottom are 20 cm and 15 cm respectively. What is the capacity of the tub? = (π = \(\frac { 22 }{ 7 } \))
Given: For the frustum shaped tub,
height (h) = 21 cm,
radii (r₁) = 20 cm, and (r₂) = 15 cm
To find: Capacity (volume) of the tub.
Solution:
Volume of frustum = \(\frac { 1 }{ 3 } \) πh (r₁² + r₂² + r₁ × r₂)

∴ The capacity of the tub is 20.35 litres.

10th Geometry Problem Set 7 Question 3. Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm and 30 cm respectively. How many balls were melted to make the tube?
Given: For the cylindrical tube,
height (h) = 90 cm,
outer radius (R) = 30 cm,
thickness = 2 cm
For the plastic spherical ball,
radius (r₁) = 1 cm
To find: Number of balls melted.
Solution:

Inner radius of tube (r)
= outer radius – thickness of tube
= 30 – 2
= 28 cm
Volume of plastic required for the tube = Outer volume of tube – Inner volume of hollow tube
= πR²h – πr²h
= πh(R² – r²)
= π × 90 (30² – 28²)
= π × 90 (30 + 28) (30 – 28) …[∵ a² – b² = (a + b)(a – b)]
= 90 × 58 × 2π cm³

∴ 7830 plastic balls were melted to make the tube.

Problem Set 7 Geometry Question 4.
A metal parallelopiped of measures 16 cm × 11cm × 10cm was melted to make coins. How many coins were made if the thickness and diameter of each coin was 2 mm and 2 cm respectively?
Given: For the parallelopiped.,
length (l) = 16 cm, breadth (b) = 11 cm,
height (h) = 10 cm
For the cylindrical coin,
thickness (H) = 2 mm,
diameter (D) 2 cm
To find: Number of coins made.
Solution:
Volume of parallelopiped = l × b × h
= 16 × 11 × 10
= 1760 cm³
Thickness of coin (H) = 2 mm
= 0.2 cm …[∵ 1 cm = 10 mm]
Diameter of coin (D) = 2 cm

∴ 2800 coins were made by melting the parallelopiped.

Mensuration Problem Question 5.  The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of ₹ 10 per sq.m.
Given: For the cylindrical roller,
diameter (d) =120 cm,
length = height (h) = 84 cm
To find: Expenditure of levelling the ground.
Solution:
Diameter of roller (d) = 120 cm

Now, area of ground levelled in one rotation = curved surface area of roller
= 3.168 m²
∴ Area of ground levelled in 200 rotations
= 3.168 × 200 =
633.6 m²
Rate of levelling = ₹ 10 per m²
∴ Expenditure of levelling the ground
= 633.6 × 10 = ₹ 6336
∴ The expenditure of levelling the ground is ₹ 6336.

Question 6.
The diameter and thickness of a hollow metal sphere are 12 cm and 0.01 m respectively. The density of the metal is 8.88 gm per cm3. Find the outer surface area and mass of the sphere, [π = 3.14]
Given: For the hollow sphere,
diameter (D) =12 cm, thickness = 0.01 m
density of the metal = 8.88 gm per cm³
To find: i. Outer surface area of the sphere
ii. Mass of the sphere.

Solution:
Diameter of the sphere (D)
= 12 cm
∴ Radius of sphere (R)
= \(\frac { d }{ 2 } \) = \(\frac { 12 }{ 2 } \) = 6 cm
∴ Surface area of sphere = 4πR²
= 4 × 3.14 × 6²
= 452.16 cm²
Thickness of sphere = 0.01 m
= 0.01 × 100 cm …[∵ 1 m = 100 cm]
= 1 cm
∴ Inner radius of the sphere (r)
= Outer radius – thickness of sphere
= 6 – 1 = 5 cm
∴ Volume of hollow sphere
= Volume of outer sphere – Volume of inner sphere

∴ The outer surface area and the mass of the sphere are 452.16 cm² and 3383.19 gm respectively.

Question 7.
A cylindrical bucket of diameter 28 cm and height 20 cm was full of sand. When the sand in the bucket was poured on the ground, the sand got converted into a shape of a cone. If the height of the cone was 14 cm, what was the base area of the cone?
Given: For the cylindrical bucket,
diameter (d) = 28 cm, height (h) = 20 cm
For the conical heap of sand,
height (H) = 14 cm
To find: Base area of the cone (πR²).
Solution:
Diameter of the bucket (d) = 28 cm


The base area of the cone is 2640 cm².

Question 8.
The radius of a metallic sphere is 9 cm. It was melted to make a wire of diameter 4 mm. Find the length of the wire.
Given: For metallic sphere,
radius (R) = 9 cm
For the cylindrical wire,
diameter (d) = 4 mm
To find: Length of wire (h).
Solution:

∴ The length of the wire is 243 m.

Question 9.
The area of a sector of a circle of 6 cm radius is 157t sq.cm. Find the measure of the arc and length of the arc corresponding to the sector.
Given: Radius (r) = 6 cm,
area of sector = 15 π cm²
To find: i. Measure of the arc (θ),
ii. Length of the arc (l)
Solution:

∴ The measure of the arc and the length of the arc are 150° and 5π cm respectively.

Question 10.
In the adjoining figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.

(π = 3.14, \(\sqrt { 3 }\) = 1.73)
Given: Radius (r) = PA = 8 cm,
PC = 4 cm
To find: Area of shaded region.
Solution:

Similarly, we can show that, ∠BPC = 60°
∠APB = ∠APC + ∠BPC …[Angle sum property]
∴ θ = 60° + 60° = 120°


Area of shaded region = A(P-ADB) – A(∆APB)
= 66.98 – 27.68
= 39.30 cm²
∴ The area of the shaded region is 39.30 cm².

Question 11.
In the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.

Solution:
Side of square ABCD
= radius of sector C-BXD = [20] cm
Area of square = (side)² = 20² = 400 cm² ….(i)
Area of shaded region inside the square = Area of square ABCD – Area of sector C-BXD

Radius of bigger sector
= Length of diagonal of square ABCD
= \(\sqrt { 2 }\) × side
= 20 \(\sqrt { 2 }\) cm
Area of the shaded regions outside the square
= Area of sector A-PCQ – Area of square ABCD
= A(A – PCQ) – A(꠸ABCD)

Alternate method:

□ABCD is a square. … [Given]
Side of □ABCD = radius of sector (C-BXD)
= 20 cm
Radius of sector (A-PCQ) = Diagonal
= \(\sqrt { 2 }\) × side
= \(\sqrt { 2 }\) × 20
= 20 \(\sqrt { 2 }\) cm

Now, Area of shaded region
= A(A-PCQ) – A(C-BXD)
= 628 – 314
= 314 cm²
∴ The area of the shaded region is 314 cm².

Question 12.
In the adjoining figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles.

Solution:
Let the radius of the bigger circle be R and that of smaller circle be r.
OA, OB, OC and OD are the radii of the bigger circle.
∴ OA = OB = OC = OD = R
PQ = PA = r
OQ + BQ = OB … [B – Q – O]
OQ = OB – BQ = R – 9
OE + DE = OD ….[D – E – O]
OE = OD – DE = [R – 5]
As the chords QA and EF of the circle with centre P intersect in the interior of the circle, so by the property of internal division of two chords of a circle,
OQ × OA = OE × OF
∴ (R – 9) × R = (R – 5) × (R – 5) …[∵ OE = OF]
∴ R² – 9R = R² – 10R + 25
∴ -9R + 10R = 25
∴ R = [25units]
AQ = AB – BQ = 2r ….[B-Q-A]
∴ 2r = 50 – 9 = 41
∴ r = \(\frac { 41 }{ 2 } \) = 20.5 units

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions

10th Standard Maths 2 Problem Set 5 Chapter 5 Co-ordinate Geometry Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 5 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

Class 10 Maths Part 2 Problem Set 5 Chapter 5 Co-ordinate Geometry Questions With Answers Maharashtra Board

Question 1.
Fill in the blanks using correct alternatives.

i. Seg AB is parallel to Y-axis and co-ordinates of point A are (1, 3), then co-ordinates of point B can be _______.
(A) (3,1)
(B) (5,3)
(C) (3,0)
(D) (1,-3)
Answer: (D)
Since, seg AB || Y-axis.
∴ x co-ordinate of all points on seg AB
will be the same,
x co-ordinate of A (1, 3) = 1
x co-ordinate of B (1, – 3) = 1
∴ Option (D) is correct.

ii. Out of the following, point lies to the right of the origin on X-axis.
(A) (-2,0)
(B) (0,2)
(C) (2,3)
(D) (2,0)
Answer: (D)

iii. Distance of point (-3, 4) from the origin is _________.
(A) 7
(B) 1
(C) 5
(D) -5
Answer: (C)
Distance of (-3, 4) from origin
\(\begin{array}{l}{=\sqrt{(-3)^{2}+(4)^{2}}} \\ {=\sqrt{9+16}} \\ {=\sqrt{25}=5}\end{array}\)

iv. A line makes an angle of 30° with the positive direction of X-axis. So the slope of the line is ________.
(A) \(\frac { 1 }{ 2 } \)
(B) \(\frac{\sqrt{3}}{2}\)
(C) \(\frac{1}{\sqrt{3}}\)
(D) \(\sqrt { 3 }\)
Answer: (C)

Question 2.
Determine whether the given points are collinear.
i. A (0, 2), B (1, -0.5), C (2, -3)
ii. P(1,2), Q(2,\(\frac { 8 }{ 5 } \)),R(3,\(\frac { 6 }{ 5 } \))
iii L (1, 2), M (5, 3), N (8, 6)
Solution:

∴ slope of line AB = slope of line BC
∴ line AB || line BC
Also, point B is common to both the lines.
∴ Both lines are the same.
∴ Points A, B and C are collinear.

∴ slope of line PQ = slope of line QR
∴ line PQ || line QR
Also, point Q is common to both the lines.
∴ Both lines are the same.
∴ Points P, Q and R are collinear.

∴ slope of line LM ≠ slope of line MN
∴ Points L, M and N are not collinear.
[Note: Students can solve the above problems by using distance formula.]

Question 3.
Find the co-ordinates of the midpoint of the line segment joining P (0,6) and Q (12,20).
Solution:
P(x₁,y₁) = P (0, 6), Q(x₂, y₂) = Q (12, 20)
Here, x₁ = 0, y₁ = 6, x₂ = 12, y₂ = 20
∴ Co-ordinates of the midpoint of seg PQ

∴ The co-ordinates of the midpoint of seg PQ are (6,13).

Question 4.
Find the ratio in which the line segment joining the points A (3, 8) and B (-9, 3) is divided by the Y-axis.
Solution:
Let C be a point on Y-axis which divides seg AB in the ratio m : n.
Point C lies on the Y-axis
∴ its x co-ordinate is 0.
Let C = (0, y)
Here A (x₁,y₁) = A(3, 8)
B (x₂, y₂) = B (-9, 3)
∴ By section formula,


∴ Y-axis divides the seg AB in the ratio 1 : 3.

Question 5.
Find the point on X-axis which is equidistant from P (2, -5) and Q (-2,9).
Solution:
Let point R be on the X-axis which is equidistant from points P and Q.
Point R lies on X-axis.
∴ its y co-ordinate is 0.
Let R = (x, 0)
R is equidistant from points P and Q.
∴ PR = QR

∴ (x – 2)² + [0 – (-5)]² = [x – (- 2)]² + (0 – 9)² …[Squaring both sides]
∴ (x – 2)² + (5)² = (x + 2)² + (-9)²
∴ 4 – 4x + x² + 25 = 4 + 4x + x² + 81
∴ – 8x = 56
∴ x = -7
∴ The point on X-axis which is equidistant from points P and Q is (-7,0).

Question 6.
Find the distances between the following points.
i. A (a, 0), B (0, a)
ii. P (-6, -3), Q (-1, 9)
iii. R (-3a, a), S (a, -2a)
Solution:
i. Let A (x₁, y₁) and B (x₂, y₂) be the given points.
∴ x₁ = a, y₁ = 0, x₂ = 0, y₂ = a
By distance formula,

∴ d(A, B) = a\(\sqrt { 2 }\) units

ii. Let P (x₁, y₁) and Q (x₂, y₂) be the given points.
∴ x₁ = -6, y₁ = -3, x₂ = -1, y₂ = 9
By distance formula,

∴ d(P, Q) = 13 units

iii. Let R (x₁, y₁) and S (x₂, y₂) be the given points.
∴ x₁ = -3a, y₁ = a, x₂ = a, y₂ = -2a
By distance formula,

∴ d(R, S) = 5a units

Question 7.
Find the co-ordinates of the circumcentre of a triangle whose vertices are (-3,1), (0, -2) and (1,3).
Solution:
Let A (-3, 1), B (0, -2) and C (1, 3) be the vertices of the triangle.
Suppose O (h, k) is the circumcentre of ∆ABC.

∴ (h + 3)² + (k – 1)² = h² + (k + 2)²
∴ h² + 6h + 9 + k² – 2k + 1 = h² + k² + 4k + 4
∴ 6h – 2k + 10 = 4k + 4
∴ 6h – 2k – 4k = 4 – 10
∴ 6h – 6k = – 6
∴ h – k = -1 ,..(i)[Dividing both sides by 6]
OB = OC …[Radii of the same circle]

∴ h² + (k + 2)² = (h – 1)² + (k – 3)²
∴ h² + k² + 4k + 4 = h² – 2h + 1 + k² – 6k + 9
∴ 4k + 4 = -2h + 1 – 6k + 9
∴ 2h+ 10k = 6
∴ h + 5k = 3 …(ii)
Subtracting equation (ii) from (i), we get

∴ The co-ordinates of the circumcentre of the triangle are (\(\frac { -1 }{ 3 } \),\(\frac { 2 }{ 3 } \))

Question 8.
In the following examples, can the segment joining the given points form a triangle? If triangle is formed, state the type of the triangle considering sides of the triangle.
i. L (6, 4), M (-5, -3), N (-6, 8)
ii. P (-2, -6), Q (-4, -2), R (-5, 0)
iii. A(\(\sqrt { 2 }\),\(\sqrt { 2 }\)),B(-\(\sqrt { 2 }\),-\(\sqrt { 2 }\)),C(\(\sqrt { 6 }\),\(\sqrt { 6 }\))
Solution:
i. By distance formula,

∴ d(M, N) + d (L, N) > d (L, M)
∴ Points L, M, N are non collinear points.
We can construct a triangle through 3 non collinear points.
∴ The segment joining the given points form a triangle.
Since MN ≠ LN ≠ LM
∴ ∆LMN is a scalene triangle.
∴ The segments joining the points L, M and N will form a scalene triangle.

ii. By distance formula,


∴ d(P, Q) + d(Q, R) = d (P, R) …[From (iii)]
∴ Points P, Q, R are collinear points.
We cannot construct a triangle through 3 collinear points.
∴ The segments joining the points P, Q and R will not form a triangle.

iii. By distance formula,

∴ d(A, B) + d(B, C) + d(A, C) … [From (iii)]
∴ Points A, B, C are non collinear points.
We can construct a triangle through 3 non collinear points.
∴ The segment joining the given points form a triangle.
Since, AB = BC = AC
∴ ∆ABC is an equilateral triangle.
∴ The segments joining the points A, B and C will form an equilateral triangle.

Question 9.
Find k, if the line passing through points P (-12, -3) and Q (4, k) has slope \(\frac { 1 }{ 2 } \).
Solution:
P(x₁,y₁) = P(-12,-3),
Q(X₂,T₂) = Q(4, k)
Here, x₁ = -12, x₂ = 4, y₁ = -3, y₂ = k

But, slope of line PQ (m) is \(\frac { 1 }{ 2 } \) ….[Given]
∴ \(\frac { 1 }{ 2 } \) = \(\frac { k+3 }{ 16 } \)
∴ \(\frac { 16 }{ 2 } \) = k + 3
∴ 8 = k + 3
∴ k = 5
The value of k is 5.

Question 10.
Show that the line joining the points A (4,8) and B (5, 5) is parallel to the line joining the points C (2, 4) and D (1 ,7).
Proof:

∴ Slope of line AB = Slope of line CD
Parallel lines have equal slope.
∴ line AB || line CD

Question 11.
Show that points P (1, -2), Q (5, 2), R (3, -1), S (-1, -5) are the vertices of a parallelogram.
Proof:
By distance formula,

In ꠸PQRS,
PQ = RS … [From (i) and (iii)]
QR = PS … [From (ii) and (iv)]
∴ ꠸ PQRS is a parallelogram.
[A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent]
∴ Points P, Q, R and S are the vertices of a parallelogram.

Question 12.
Show that the ꠸PQRS formed by P (2, 1), Q (-1, 3), R (-5, -3) and S (-2, -5) is a rectangle.
Proof:
By distance formula,


In ꠸PQRS,
PQ = RS …[From (i) and (iii)]
QR = PS …[From (ii) and (iv)]
꠸PQRS is a parallelogram.
[A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent]

In parallelogram PQRS,
PR = QS … [From (v) and (vi)]
∴ ꠸PQRS is a rectangle.
[A parallelogram is a rectangle if its diagonals are equal]

Question 13.
Find the lengths of the medians of a triangle whose vertices are A (-1, 1), B (5, -3) and C (3,5).
Solution:

Suppose AD, BE and CF are the medians.
∴ Points D, E and F are the midpoints of sides BC, AC and AB respectively.
∴ By midpoint formula,


∴ The lengths of the medians of the triangle 5 units, 2\(\sqrt { 13 }\) units and \(\sqrt { 37 }\) units.

Question 14.
Find the co-ordinates of centroid of the triangle if points D (-7, 6), E (8, 5) and F (2, -2) are the mid points of the sides of that triangle.
Solution:

Suppose A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of the triangle.
D (-7, 6), E (8, 5) and F (2, -2) are the midpoints of sides BC, AC and AB respectively.
Let G be the centroid of ∆ABC.
D is the midpoint of seg BC.
By midpoint formula,

E is the midpoint of seg AC.
By midpoint formula,

Adding (i), (iii) and (v),
x₂ + x₃ + x₁ + x₃ + x₁ + x₂ = -14 + 16 + 4
∴ 2x₁ + 2x₂ + 2x₃ = 6
∴ x₁ + x₂ + x₃ = 3 …(vii)
Adding (ii), (iv) and (vi),
y₂ + y₃ + y₁ + y₃ + y₁ +y₂ = 12 + 10 – 4
∴ 2y₁ + 2y₂ + 2y₃ = 18
∴ y₁ + y₂ + y₃ = 9 …(viii)
G is the centroid of ∆ABC.
By centroid formula,

∴ The co-ordinates of the centroid of the triangle are (1,3).

Question 15.
Show that A (4, -1), B (6, 0), C (7, -2) and D (5, -3) are vertices of a square.
Proof:
By distance formula,


∴ □ABCD is a square.
[A rhombus is a square if its diagonals are equal]

Question 16.
Find the co-ordinates of circumcentre and radius of circumcircle of AABC if A (7, 1), B (3,5) and C (2,0) are given.
Solution:
Suppose, O (h, k) is the circumcentre of ∆ABC


∴ h² – 6h + 9 + k² – 10k + 25 = h² – 4h + 4 + k²
∴ 2h + 10k = 30
∴ h + 5k = 15 … (ii)[Dividing both sides by 2]
Multiplying equation (i) by 5, we get
25h + 5k = 115 …(iii)
Subtracting equation (ii) from (iii), we get

Substituting the value of h in equation (i), we get

∴ The co-ordinates of the circumcentre of the triangle are (\(\frac { 25 }{ 6 } \),\(\frac { 13 }{ 6 } \)) and radius of circumcircle is \(\frac{13 \sqrt{2}}{6}\) units.

Question 17.
Given A (4, -3), B (8, 5). Find the co-ordinates of the point that divides segment AB in the ratio 3:1.
Solution:
Suppose point C divides seg AB in the ratio 3:1.
Here; A(x₁, y₁) = A (4, -3)
B (x₂, y₂) = B (8, 5)
By section formula,

∴ The co-ordinates of point dividing seg AB in ratio 3 : 1 are (7, 3).

Question 18.
Find the type of the quadrilateral if points A (-4, -2), B (-3, -7), C (3, -2) and D (2, 3) are joined serially.
Solution:

Slope of AB = slope of CD
∴ line AB || line CD
slope of BC = slope of AD
∴ line BC || line AD
Both the pairs of opposite sides of ∆ABCD are parallel.
∴ ꠸ ABCD is a parallelogram.
∴ The quadrilateral formed by joining the points A, B, C and D is a parallelogram.

Question 19.
The line segment AB is divided into five congruent parts at P, Q, R and S such that A-P-Q-R-S-B. If point Q (12, 14) and S (4, 18) are given, find the co-ordinates of A, P, R, B.
Solution:

Points P, Q, R and S divide seg AB in five congruent parts.
Let A (x₁, y₁), B (x₂, y₂), P (x₃, y₃) and
R (x₄, y₄) be the given points.
Point R is the midpoint of seg QS.
By midpoint formula,
x co-ordinate of R = \(\frac { 12+4 }{ 2 } \) = \(\frac { 16 }{ 2 } \) = 8
y co-ordinate of R = \(\frac { 14+18 }{ 2 } \) = \(\frac { 32 }{ 2 } \) = 16
∴ co-ordinates of R are (8, 16).
Point Q is the midpoint of seg PR.
By midpoint formula,

∴ 28 = y₃ + 16
∴ y₃ = 12
∴ P(x₃,y₃) = (16, 12)
∴ co-ordinates of P are (16, 12).
Point P is the midpoint of seg AQ.
By midpoint formula,

∴ co-ordinates of A are (20, 10).
Point S is the midpoint of seg RB.
By midpoint formula,

∴ 36 = y₂ + 16
∴ y₂ = 20
∴ B(x₂, y₂) = (0, 20)
∴ co-ordinates of B are (0, 20).
∴ The co-ordinates of points A, P, R and B are (20, 10), (16, 12), (8, 16) and (0, 20) respectively.

Question 20.
Find the co-ordinates of the centre of the circle passing through the points P (6, -6), Q (3, -7) and R (3,3).
Solution:
Suppose O (h, k) is the centre of the circle passing through the points P, Q and R.

∴ (h – 6)² + (k + 6)² = (h – 3)² + (k + 7)²
∴ h² – 12h + 36 + k² + 12k + 36
= h² – 6h + 9 + k² + 14k + 49
∴ 6h + 2k = 14
∴ 3h + k = 7 …(i)[Dividing both sides by 2]
OP = OR …[Radii of the same circle]

∴ (h – 6)² + (k + 6)² = (h – 3)² + (k – 3)²
∴ h² – 12h + 36 + k² + 12k + 36
= h² – 6h + 9 + k² – 6k + 9
∴ 6h – 18k = 54
∴ 3h – 9k = 27 …(ii)[Dividing both sides by 2]
Subtracting equation (ii) from (i), we get

Substituting the value of k in equation (i), we get
3h – 2 = 7
∴ 3h = 9
∴ h = \(\frac { 9 }{ 3 } \) = 3
∴ The co-ordinates of the centre of the circle are (3, -2).

Question 21.
Find the possible pairs of co-ordinates of the fourth vertex D of the parallelogram, if three of its vertices are A (5, 6), B (1, -2) and C (3, -2).
Solution:

Let the points A (5, 6), B (1, -2) and C (3, -2) be the three vertices of a parallelogram.
The fourth vertex can be point D or point Di or point D₂ as shown in the figure.
Let D(x₁,y₁), D, (x₂, y₂) and D₂ (x₃,y₃).
Consider the parallelogram ACBD.
The diagonals of a parallelogram bisect each other.
∴ midpoint of DC = midpoint of AB


Co-ordinates of point D(x₁, y₁) are (3, 6).
Consider the parallelogram ABD₁C.
The diagonals of a parallelogram bisect each other.
∴ midpoint of AD₁ = midpoint of BC

∴ Co-ordinates of D₁(x₂,y₂) are (-1,-10).
Consider the parallelogram ABCD₂.
The diagonals of a parallelogram bisect each other.
∴ midpoint of BD₂ = midpoint of AC

∴ co-ordinates of point D₂ (x₃, y₃) are (7, 6).
∴ The possible pairs of co-ordinates of the fourth vertex D of the parallelogram are (3, 6), (-1,-10) and (7,6).

Question 22.
Find the slope of the diagonals of a quadrilateral with vertices A (1, 7), B (6,3), C (0, -3) and D (-3,3).
Solution:
Suppose ABCD is the given quadrilateral.

∴ The slopes of the diagonals of the quadrilateral are 10 and 0.

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions

10th Standard Maths 2 Practice Set 1.3 Chapter 1 Similarity Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 1 Similarity.

Class 10 Maths Part 2 Practice Set 1.3 Chapter 1 Similarity Questions With Answers Maharashtra Board

Practice Set 1.3 Question 1.
In the adjoining figure, ∠ABC = 75°, ∠EDC = 75°. State which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Solution:
In ∆ABC and ∆EDC,
∠ABC ≅ ∠EDC [Each angle is of measure 75°]
∠ACB ≅ ∠ECD [Common angle]
∴ ∆ABC ~ ∆EDC [AA test of similarity]
One to one correspondence is
ABC ↔ EDC

Similarity Class 10 Practice Set 1.3 Question 2.
Are the triangles in the adjoining figure similar? If yes, by which test?

Solution:
In ∆PQR and ∆LMN,
\(\frac { PQ }{ LM } \) = \(\frac { 6 }{ 3 } \) = \(\frac { 2 }{ 1 } \) (i)
\(\frac { QR }{ MN } \) = \(\frac { 8 }{ 4 } \) = \(\frac { 2 }{ 1 } \) (ii)
\(\frac { PR }{ LN } \) = \(\frac { 10 }{ 5 } \) = \(\frac { 2 }{ 1 } \) (iii)
∴ \(\frac { PQ }{ LM } \) = \(\frac { QR }{ MN } \) = \(\frac { PR }{ LN } \) [From (i), (ii) and (iii)]
∴ ∆PQR – ∆LMN [SSS test of similarity]

Similarity Practice Set 1.3 Question 3.
As shown in the adjoining figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m, then how long will be the shadow of the bigger pole at the same time?

Solution:
Here, AC and PR represents the bigger and smaller poles, and BC and QR represents their shadows respectively.
Now, ∆ACB – ∆PRQ [ ∵ Vertical poles and their shadows form similar figures]
∴ \(\frac { CB }{ RQ } \) = \(\frac { AC }{ PR } \) [Corresponding sides of similar triangles]
∴ \(\frac { x }{ 6 } \) = \(\frac { 8 }{ 4 } \)
∴ \(x=\frac{8 \times 6}{4}\)
∴ x = 12 m
∴ The shadow of the bigger pole will be 12 metres long at that time.

Practice Set 1.3 Geometry 10th Maharashtra Board Question 4.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC, B – P – C, A – Q – C, then prove that ∆CPA – ∆CQB. If AP = 7, BQ = 8, BC = 12, then find AC.

Solution:
In ∆CPA and ∆CQB,
∠CPA ≅ ∠CQB [Each angle is of measure 90°]
∠ACP ≅ ∠BCQ [Common angle]
∴ ∆CPA ~ ∆CQB [AA test of similarity]
∴\(\frac { AC }{ BC } \) = \(\frac { AP }{ BQ } \) [Corresponding sides of similar triangles]
∴ \(\frac { AC }{ 12 } \) = \(\frac { 7 }{ 8 } \)
∴ AC = \(x=\frac{12 \times 7}{8}\)
∴ AC = 10.5 Units

10th Geometry Practice Set 1.3 Question 5.
Given: In trapezium PQRS, side PQ || side SR, AR = 5 AP, AS = 5 AQ, then prove that SR = 5 PQ.

Solution:
side PQ || side SR [Given]
and seg SQ is their transversal.
∴ ∠QSR = ∠SQP [Altemate angles]
∴ ∠ASR = ∠AQP (i) [Q – A – S]
In ∆ASR and ∆AQP,
∠ASR = ∠AQP [From (i)]
∠SAR ≅ ∠QAP [Vertically opposite angles]
∆ASR ~ ∆AQP [AA test of similarity]
∴ \(\frac { AS }{ AQ } \) = \(\frac { SR }{ PQ } \) (ii) [Corresponding sides of similar triangles]
But, AS = 5 AQ [Given]
∴ \(\frac { AS }{ AQ } \) = \(\frac { 5 }{ 1 } \) (iii)
∴ \(\frac { SR }{ PQ } \) = \(\frac { 5 }{ 1 } \) [From (ii) and (iii)]
∴ SR = 5 PQ

Practice Set 1.3 Geometry 10th Question 6.
Id trapezium ABCD (adjoining figure), side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15, then find OD.

Solution:
side AB || side DC [Given]
and seg BD is their transversal.
∴ ∠DBA ≅ ∠BDC [Alternate angles]
∴ ∠OBA ≅ ∠ODC (i) [D – O – B]
In ∆OBA and ∆ODC
∠OBA ≅ ∠ODC [From (i)]
∠BOA ≅ ∠DOC [Vertically opposite angles]
∴ ∆OBA ~ ∆ODC [AA test of similarity]
∴ \(\frac { OB }{ OD } \) = \(\frac { AB }{ DC } \) [Corresponding sides of similar triangles]
∴ \(\frac { 15 }{ OD } \) = \(\frac { 20 }{ 6 } \)
∴ OD = \(x=\frac{15 \times 6}{20}\)
∴ OD = 4.5 units

Class 10 Geometry Practice Set 1.3 Question 7.
꠸ ABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

Solution:
Proof:
꠸ ABCD is a parallelogram. [Given]
∴ side AB || side CD [Opposite sides of a parallelogram]
∴ side AT || side CD [A – B – T]
and seg DT is their transversal.
∴ ∠ATD ≅ ∠CDT [Alternate angles]
∴ ∠BTE ≅ ∠CDE (i) [A – B – T, T – E – D]
In ∆BTE and ∆CDE,
∠BTE ≅ ∠CDE [From (i)]
∠BET ≅ ∠CED [Vertically opposite angles]
∴ ∆BTE ~ ∆CDE. [AA test of similarity]
∴ \(\frac { TE }{ DE } \) = \(\frac { BE }{ CE } \) [Corresponding sides of similar triangles]
∴ DE × BE = CE × TE

Geometry Practice Set 1.3 Question 8.
In the adjoining figure, seg AC and seg BD intersect each other in point P and \(\frac { AP }{ CP } \) = \(\frac { BP }{ DP } \) Prove that, ∆ABP ~ ∆CDP

Solution:
Proof:
In ∆ABP and ∆CDP,
\(\frac { AP }{ CP } \) = \(\frac { BP }{ DP } \) [Given]
∠APB ≅ ∠CPD [Vertically opposite angles]
∴ ∆ABP ~ ∆CDP [SAS test of similarity]

Math 2 Practice Set 1.3 Question 9.
In the adjoining figure, in ∆ABC, point D is on side BC such that, ∠BAC = ∠ADC. Prove that, CA² = CB × CD,

Solution:
Proof:
In ∆BAC and ∆ADC,
∠BAC ≅ ∠ADC [Given]
∠BCA ≅ ∠ACD [Common angle]
∴ ∆BAC ~ ∆ADC [AA test of similarity]
∴ \(\frac { CA }{ CD } \) = \(\frac { CB }{ CA } \) [Corresponding sides of similar triangles]
∴ CA × CA = CB × CD
∴ CA² = CB × CD

Question 1.
In the adjoining figure, BP ⊥ AC, CQ ⊥ AB, A – P – C, A – Q – B, then prove that ∆APB and ∆AQC are similar. (Textbook pg. no. 20)

Solution:

2. SAS test for similarity of triangles:
For a given correspondence, if two pairs of corresponding sides are in the same proportion and the angle between them is congruent, then the two triangles are similar.

In the given figure, if \(\frac { AB }{ PQ } \) = \(\frac { BC }{ QR } \), and ∠B ≅∠Q, then ∆ABC ~ ∆PQR

3. SSS test for similarity of triangles:
For a given correspondence, if three sides of one triangle are in proportion with the corresponding three sides of the another triangle, then the two triangles are similar.

In the given figure, if \(\frac { AB }{ PQ } \) = \(\frac { BC }{ QR } \) = \(\frac { AC }{ PR } \), then ∆ABC ~ ∆PQR

Properties of similar triangles:

1. Reflexivity: ∆ABC ~ ∆ABC
2. Symmetry : If ∆ABC ~ ∆DEF, then ∆DEF ~ ∆ABC.
3. Transitivity: If ∆ABC ~ ∆DEF and ∆DEF ~ ∆GHI, then ∆ABC ~ ∆GHI.

Maharashtra State Board Class 10 Maths Solutions Part 2

• Similarity Practice Set 1.1 Class 10 Maths Solutions
• Similarity Practice Set 1.2 Class 10 Maths Solutions
•  Similarity Practice Set 1.3 Class 10 Maths Solutions
• Similarity Practice Set 1.4 Class 10 Maths Solutions
• Similarity Problem Set 1 Class 10 Maths Solutions
• Pythagoras Theorem Practice Set 2.1 Class 10 Maths Solutions
• Pythagoras Theorem Practice Set 2.2 Class 10 Maths Solutions
• Pythagoras Theorem Problem Set 2 Class 10 Maths Solutions

9th Standard Maths 2 Practice Set 9.1 Chapter 9 Surface Area and Volume Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

Class 9 Maths Part 2 Practice Set 9.1 Chapter 9 Surface Area and Volume Questions With Answers Maharashtra Board

Question 1.
Length, breadth and height of a cuboid shape box of medicine is 20 cm, 12 cm and 10 cm respectively. Find the surface area of vertical faces and total surface area of this box.
Given: For cuboid shape box of medicine,
length (l) = 20 cm, breadth (b) = 12 cm and height (h) = 10 cm.
To find: Surface area of vertical faces and total surface area of the box
Solution:
i. Surface area of vertical faces of the box
= 2(l + b) x h
= 2(20+ 12) x 10
= 2 x 32 x 10
= 640 sq.cm.

ii. Total surface area of the box
= 2 (lb + bh + lh)
= 2(20 x 12+ 12 x 10 + 20 x 10)
= 2(240 + 120 + 200)
= 2 x 560
= 1120 sq.cm.
∴ The surface area of vertical faces and total surface area of the box are 640 sq.cm, and 1120 sq.cm, respectively.

Question 2.
Total surface area of a box of cuboid shape is 500 sq.unit. Its breadth and height is 6 unit and 5 unit respectively. What is the length of that box?
Given: For cuboid shape box,
breadth (b) = 6 unit, height (h) = 5 unit Total surface area = 500 sq. unit.
To find: Length of the box (l)
Solution:
Total surface area of the box = 2 (lb + bh + lh)
∴ 500 = 2 (6l + 6 x 5 + 5l)
∴ \(\frac { 500 }{ 2 }\) = (11l + 30)
∴ 250= 11l + 30
∴ 250 – 30= 11l
∴ 220 = 11l
∴ 220 = l
∴ \(\frac { 220 }{ 11 }\) = l
∴ l = 20 units
∴ The length of the box is 20 units.

Question 3.
Side of a cube is 4.5 cm. Find the surface area of all vertical faces and total surface area of the cube.
Given: Side of cube (l) = 4.5 cm
To find: Surface area of all vertical faces and the total surface area of the cube
Solution:
i. Area of vertical faces of cube = 4l²
= 4 (4.5)² = 4 x 20.25 = 81 sq.cm.
ii. Total surface area of the cube = 6l²
= 6 (4.5)²
= 6 x 20.25
= 121.5 sq.cm.
∴ The surface area of all vertical faces and the total surface area of the cube are 81 sq.cm, and 121.5 sq.cm, respectively.

Question 4.
Total surface area of a cube is 5400 sq. cm. Find the surface area of all vertical faces of the cube.
Given: Total surface area of cube = 5400 sq.cm.
To find: Surface area of all vertical faces of the cube
Solution:
i. Total surface area of cube = 6l²
∴ 5400 = 6l²
∴ \(\frac { 5400 }{ 6 }\) = l²
∴ l² = 900
ii. Area of vertical faces of cube = 4l²
= 4 x 900 = 3600 sq.cm.
∴ The surface area of all vertical faces of the cube is 3600 sq.cm.

Question 5.
Volume of a cuboid is 34.50 cubic metre. Breadth and height of the cuboid is 1.5 m and 1.15 m respectively. Find its length.
Given: Breadth (b) = 1.5 m, height (h) = 1.15 m
Volume of cuboid = 34.50 cubic metre
To find: Length of the cuboid (l)
Solution:
Volume of cuboid = l x b x h
∴ 34.50 = l x b x h
∴ 34.50 = l x 1.5 x 1.15

= 20
∴ The length of the cuboid is 20 m.

Question 6.
What will be the volume of a cube having length of edge 7.5 cm ?
Given: Length of edge of cube (l) = 7.5 cm
To find: Volume of a cube
Solution:
Volume of a cube = l²
= (7.5)³
= 421.875 ≈ 421.88 cubic cm
∴The volume of the cube is 421.88 cubic cm.

Question 7.
Radius of base of a cylinder is 20 cm and its height is 13 cm, find its curved surface area and total surface area, (π = 3.14)
Given: Radius (r) = 20 cm, height (h) = 13 cm
To find: Curved surface area and
the total surface area of the cylinder
Solution:
i. Curved surface area of cylinder = 2πrh
= 2 x 3.14 x 20 x 13
= 1632.8 sq.cm

ii. Total surface area of cylinder = 2πr(r + h)
= 2 x 3.14 x 20(20 + 13)
= 2 x 3.14 x 20 x 33 = 4144.8 sq.cm
∴ The curved surface area and the total surface area of the cylinder are 1632.8 sq.cm and 4144.8 sq.cm respectively.

Question 8.
Curved surface area of a cylinder is 1980 cm² and radius of its base is 15 cm. Find the height of the cylinder. (π = \(\frac { 22 }{ 7 }\))
Given: Curved surface area of cylinder = 1980 sq.cm., radius (r) = 15 cm
To find: Height of the cylinder (h)
Solution:
Curved surface area of cylinder = 2πrh
∴ 1980 = 2 x \(\frac { 22 }{ 7 }\) x 15 x h
∴ \(h=\frac{1980 \times 7}{2 \times 22 \times 15}\)
∴ h = 21 cm
∴ The height of the cylinder is 21 cm.

Maharashtra Board Class 9 Maths Solutions

• Surface Area and Volume Practice Set 9.1 Class 9 Maths Solutions
• Surface Area and Volume Practice Set 9.2 Class 9 Maths Solutions
• Surface Area and Volume Practice Set 9.3 Class 9 Maths Solutions
• Surface Area and Volume Practice Set 9 Class 9 Maths Solutions

9th Standard Maths 2 Practice Set 9.2 Chapter 9 Surface Area and Volume Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

Class 9 Maths Part 2 Practice Set 9.2 Chapter 9 Surface Area and Volume Questions With Answers Maharashtra Board

Question 1.
Perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Given: Height (h) = 12 cm, length (l) = 13 cm
To find: Radius of the base of the cone (r)
Solution:
l² = r² + h²
∴ 13² = r² + 12²
∴ 169 = r² + 144
∴169 – 144 = r²
∴ r² = 25
∴ r = √25 … [Taking square root on both sides]
= 5 cm
∴ The radius of base of the cone is 5 cm.

Question 2.
Find the volume of a cone, if its total surface area is 7128 sq.cm and radius of base is 28 cm. ( π = \(\frac { 22 }{ 7 }\))
Given: Radius (r) = 28 cm,
Total surface area of cone = 7128 sq.cm
To find: Volume of the cone
Solution:
i. Total surface area of cone = πr (l + r)
∴ 7128= y x 28 x (l + 28)
∴ 7128 = 22 x 4 x(l +28)
∴ l + 28 = \(\frac { 7128 }{ 22\times 4 }\)
∴ l + 28 = 81
∴ l = 81 – 28
∴ l = 53cm

ii. Now, l² = r² + h²
∴ 53² = 28²+ h²
∴ 2809 = 784 + h²
∴ 2809 – 784 = h²
∴ h² = 2025
∴ h = \(\sqrt { 2025 }\) …… [Taking square root on both sides]
= 45 cm

= 22 x 4 x 28 x 15
= 36960 cubic.cm
∴ The volume of the cone is 36960 cubic.cm.

Question 3.
Curved surface area of a cone is 251.2 cm² and radius of its base is 8 cm. Find its slant height and perpendicular height, (π = 3.14)
Given: Radius (r) = 8 cm, curved surface area
of cone = 251.2 cm²
To find: Slant height (l) and the perpendicular height (h) of the cone
Solution:
i. Curved surface area of cone = πrl
∴ 251.2 = 3.14 x 8 x l

∴ l= 10 cm

ii. Now, l² = r² + h²
∴ 10² = 8² + h²
∴ 100 = 64 + h²
∴ 100 – 64 = h²
∴ h² = 36
∴ h = √36 … [Taking square root on both sides]
= 6 cm
∴ The slant height and the perpendicular height of the cone are 10 cm and 6 cm respectively.

Question 4.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is ₹ 10 per sq.m?
Given: Radius (r) = 6 m, length (l) = 8 m
To find: Total cost of making the cone
Solution:
i. To find the total cost of making the cone of tin sheet, first we need to find the total surface area of the cone.
Total surface area of the cone = πr (l + r)
= \(\frac { 22 }{ 7 }\) x 6 x (8 + 6)
= \(\frac { 22 }{ 7 }\) x 6 x 14
= 22 x 6 x 2 = 264 sq.m

ii. Rate of making the cone = ₹ 10 per sq.m
∴ Total cost = Total surface area x Rate of making the cone
= 264 x 10
= ₹ 2640
∴ A The total cost of making the cone of tin sheet is ₹ 2640.

Question 5.
Volume of a cone is 6280 cubic cm and base radius of the cone is 20 cm. Find its perpendicular height, (π = 3.14)
Given: Radius (r) = 20 cm,
Volume of cone = 6280 cubic cm
To find: Perpendicular height (h) of the cone
Solution:

∴ The perpendicular height of the cone is 15 cm.

Question 6.
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height (π = 3.14).
Given: Length (l) =10 cm, curved surface area of the cone = 188.4 sq.cm
To find: Perpendicular height (h) of the cone
Solution:
i. Curved surface area of the cone = πrl
∴ 188.4 = 3.14 x r x 10

ii. Now, l² = r² + h²
∴ 10² = 6² + h²
∴ 100 = 36 + h²
∴ 100 – 36 = h²
∴ h² = 64
∴ h = \(\sqrt { 64 }\) … [Taking square root on both sides]
= 8 cm
∴ The perpendicular height of the cone is 8 cm.

Question 7.
Volume of a cone is 1232 cm³ and its height is 24 cm. Find the surface area of the cone. (π = \(\frac { 22 }{ 7 }\))
Given: Height (h) = 24 cm,
Volume of cone = 1232 cm³
To find: Surface area of the cone
Solution:

∴ r² = 49
∴ r = \(\sqrt { 49 }\) … [Taking square root on both sides]
= 7 cm

ii. Now, l² = r² + h²
∴ l² = 7² + 24²
= 49 + 576 = 625
∴ l = \(\sqrt { 625 }\) … [Taking square root on both sides]
= 25

iii. Curved surface area of cone = πrl
= \(\frac { 22 }{ 7 }\) x 7 x 25
= 22 x 25
= 550 sq.cm
∴The surface area of the cone is 550 sq.cm.

Question 8.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. (π = \(\frac { 22 }{ 7 }\))
Given: Length (l) = 50 cm, curved surface area of cone = 2200 sq.cm
To find: Total surface area of the cone
Solution:
i. Curved surface area of cone = πrl

ii. Total surface area of cone = πr (l + r)
= \(\frac { 22 }{ 7 }\) x 14 x (50 + 14)
= \(\frac { 22 }{ 7 }\) x 14 x 64
= 22 x 2 x 64
= 2816 sq.cm
∴ The total surface area of the cone is 2816 sq.cm.

Question 9.
There are 25 persons in a tent which is conical in shape. Every person needs an area of 4 sq.m, of the ground inside the tent. If height of the tent is 18 m, find the volume of the tent.
Given: For the tent,
height (h) = 18m,
number of people in the tent = 25,
area required for each person = 4 sq.m
To find: Volume of the tent
Solution:
i. Every person needs an area of 4 sq.m, of the ground inside the tent.
Surface area of the base of the tent = number of people in the tent × area required for each person
= 25 × 4
= 100 sq.m

ii. Surface area of the base of the tent = πr²
∴ 100 = πr²
∴ πr² = 100

iii. Volume of the tent= \(\frac { 1 }{ 3 }\) πr²h
= \(\frac { 1 }{ 3 }\) x 100 x 18 …….[∵ πr² = 100]
= 100 x 6
= 600 cubic metre
∴ The volume of the tent is 600 cubic metre.

Question 10.
In a field, dry fodder for the cattle is heaped in a conical shape. The height of the cone is 2.1 m and diameter of base is 7.2 m. Find the volume of the heap of the fodder. If it is to be covered by polythene in rainy se&son then how much minimum polythene
sheet is needed? (π = \(\frac { 22 }{ 7 }\) and \(\sqrt { 17.37 }\) = 4.17 ]
Given: Height of the heap (h) = 2.1 m.
diameter of the base (d) = 7.2 m
∴Radius of the base (r) = \(\frac { d }{ 2 }\) = \(\frac { 7.2 }{ 2 }\) = 3.6 m
To find: Volume of the heap of the fodder and polythene sheet required
Solution:
i. Volume of the heap of fodder = \(\frac { 1 }{ 3 }\)πr²h
= \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x (3.6)² x 2.1
= \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x 3.6 x 3.6 x 2.1
= 1 x 22 x 1.2 x 3.6 x 0.3
= 28.51 cubic metre

ii. Now, l² = r² + h²
= (3.6)² + (2.1)²
= 12.96 + 4.41
∴ l² =17.37
∴ l² = \(\sqrt { 17.37 }\) .. .[Taking square root on both sides]
= 4.17 m

iii. Area of the polythene sheet needed to cover the heap of the fodder = Curved surface area of the conical heap
= πrl
= \(\frac { 22 }{ 7 }\) x 3.6 x 4.17
= 47.18 sq.m
∴ The volume of the heap of the fodder is 28.51 cubic metre and a polythene sheet of 47.18 sq.m will be required to cover it.

Maharashtra Board Class 9 Maths Solutions

Maharashtra Board Class 9 Maths Solutions

• Surface Area and Volume Practice Set 9.1 Class 9 Maths Solutions
• Surface Area and Volume Practice Set 9.2 Class 9 Maths Solutions
• Surface Area and Volume Practice Set 9.3 Class 9 Maths Solutions
• Surface Area and Volume Practice Set 9 Class 9 Maths Solutions

10th Standard Maths 2 Practice Set 7.4 Chapter 7 Mensuration Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.4 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Class 10 Maths Part 2 Practice Set 7.4 Chapter 7 Mensuration Questions With Answers Maharashtra Board

Practice Set 7.4 Geometry Class 10 Question 1. In the adjoining figure, A is the centre of the circle. ∠ABC = 45° and AC = 7\(\sqrt { 2 }\) cm. Find the area of segment BXC, (π = 3.14)

Solution:
In ∆ABC,
AC = AB … [Radii of same circle]
∴ ∠ABC = ∠ACB …[Isosceles triangle theorem]
∴ ∠ABC = ∠ACB = 45°
In ∆ABC,
∠ABC + ∠ACB + ∠BAC = 180° … [Sum of the measures of angles of a triangle is 180° ]
∴ 45° + 45° + ∠BAC = 180°
∴ 90° + ∠BAC = 180°
∴ ∠BAC = 90°
Let ∠BAC = θ = 90°

∴ The area of segment BXC is 27.93 cm².

10th Class Geometry Practice Set 7.4 Question 2. In the adjoining figure, O is the centre of the circle.
m(arc PQR) = 60°, OP = 10 cm. Find the area of the shaded region.
(π = 3.14, \(\sqrt { 3 }\) = 1.73)

Given: m(arc PQR) = 60°, radius (r) = OP = 10 cm
To find: Area of shaded region.
Solution:
∠POR = m (arc PQR) …[Measure of central angle]
∴ ∠POR = θ = 60°


∴ The area of the shaded region is 9.08 cm².

7.4 Class 10 Question 3. In the adjoining figure, if A is the centre of the circle, ∠PAR = 30°, AP = 7.5, find the area of the segment PQR. (π = 3.14)

Given: Central angle (θ) = ∠PAR = 30°,
radius (r) = AP = 7.5
To find: Area of segment PQR.
Solution:
Let ∠PAR = θ = 30°

∴ The area of segment PQR is 0.65625 sq. units.

Chapter 7 Maths Class 10 Question 4. In the adjoining figure, if O is the centre of the circle, PQ is a chord, ∠POQ = 90°, area of shaded region is 114 cm2, find the radius of the circle, (π = 3.14)

Given: Central angle (θ) = ∠POQ= 90°,
A (segment PRQ) = 114 cm²
To find: Radius (r).
Solution:

…[Taking square root of both sides]
∴ r = 20 cm
∴ The radius of the circle is 20 cm.

Mensuration Questions for Class 10 Question 5. A chord PQ of a circle with radius 15 cm subtends an angle of 60° with the centre of the circle. Find the area of the minor as well as the major segment. (π = 3.14, \(\sqrt { 3 }\) = 1.73)
Given: Radius (r) =15 cm, central angle (θ) = 60°
To find: Areas of major and minor segments.
Solution:
Let chord PQ subtend ∠POQ = 60° at centre.
∴ θ = 60°

= 225 [0.0908]
= 20.43 cm²
∴ area of minor segment = 20.43 cm²
Area of circle = πr²
= 3.14 × 15 × 15
= 3.14 × 225
= 706.5 cm²
Area of major segment
= Area of circle – area of minor segment
= 706.5 – 20.43
= 686.07 cm²
Area of major segment 686.07 cm²
∴ The area of minor segment Is 20.43 cm² and the area of major segment is 686.07 cm².

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions

10th Standard Maths 2 Practice Set 7.3 Chapter 7 Mensuration Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Class 10 Maths Part 2 Practice Set 7.3 Chapter 7 Mensuration Questions With Answers Maharashtra Board

Practice Set 7.3 Geometry Class 10 Question 1.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given : Radius (r) = 10 cm,
Measure of the arc (θ) = 54°
To find : Area of the sector.
Solution:
Area of sector = \(\frac{\theta}{360} \times \pi r^{2}\)
= \(\frac { 54 }{ 360 } \) × 3.14 × (10)²
= \(\frac { 3 }{ 20 } \) × 3.14 × 100
= 3 × 3.14 × 5
= 15 × 3.14
= 47.1 cm²
∴ The area of the sector is 47.1 cm².

Mensuration Practice Set 7.3 Question 2.
Measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14)
Given: Radius (r) = 18 cm,
Measure of the arc (θ) = 80°
To find: Length of the arc.
Solution:
Length of arc = \(\frac{\theta}{360} \times 2 \pi r\) × 2πr
= \(\frac { 8 }{ 360 } \) × 2 × 3.14 × 18
= \(\frac { 2 }{ 9 } \) × 2 × 3.14 × 18
= 2 × 2 × 3.14 × 2 = 25.12 cm
∴ The length of the arc is 25.12 cm.

Practice Set 7.3 Geometry Question 3.
Radius of a sector of a circle is 3.5 cm and length of its arc is 2.2 cm. Find the area of the sector.
Solution:
Given: Radius (r) = 3.5 cm,
length of arc (l) = 2.2 cm
To find: Area of the sector.
Solution:
Area of sector = \(\frac{l \times \mathrm{r}}{2}\)
= \(\frac{2.2 \times 3.5}{2}\)
= 1.1 × 3.5 = 3.85 cm²
∴ The area of the sector is 3.85 cm².

Question 4.
Radius of a circle is 10 cm. Area of a sector of the circle is 100 cm². Find the area of its corresponding major sector, (π = 3.14)
Given: Radius (r) = 10 cm,
area of minor sector =100 cm²
To find: Area of maj or sector.
Solution:
Area of circle = πr²
= 3.14 × (10)²
= 3.14 × 100 = 314 cm²
Now, area of major sector
= area of circle – area of minor sector
= 314 – 100
= 214 cm²
∴ The area of the corresponding major sector is 214 cm².

Question 5.
Area of a sector of a circle of radius 15 cm is 30 cm². Find the length of the arc of the sector.
Given: Radius (r) =15 cm,
area of sector = 30 cm²
To find: Length of the arc (l).
Solution:

∴ The length of the arc is 4 cm.

Practice Set 7.3 Question 6.
In the adjoining figure, radius of the circle is 7 cm and m (arc MBN) = 60°, find
i. Area of the circle.
ii. A(O-MBN).
iii. A(O-MCN).

Given: radius (r) = 7 cm,
m(arc MBN) = θ = 60°
Solution:
i. Area of circle = πr²
= \(\frac { 22 }{ 7 } \) × (7)²
= 22 × 7
= 154 cm²
∴ The area of the circle is 154 cm²

ii. Central angle (θ) = ∠MON = 60°
Area of sector = \(\frac{\theta}{360} \times \pi r^{2}\)
∴ A(O – MBN) = \(\frac { 60 }{ 360 } \) × \(\frac { 22 }{ 7 } \) × (7)²
\(\frac { 1 }{ 6 } \) × 22 × 7
= 25.67 cm²
= 25.7 cm²
∴ A(O-MBN) = 25.7 cm²

iii. Area of major sector = area of circle – area of minor sector
∴ A(O-MCN) = Area of circle – A(O-MBN)
= 154 – 25.7
∴ A(O-MCN) = 128.3 cm²

Question 7.
In the adjoining figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm. Find A(P-ABC).
Given: Radius (r) = 3.4 cm,
perimeter of sector 12.8 cm
To find: A(P-ABC)

Solution:
Perimeter of sector
= Iength of arc ABC + AP + CP

∴ 12.8 = l + 3.4 + 3.4
∴ 12.8 = l + 6.8
∴ l = 12.8 – 6.8 = 6cm

∴ A(P-ABC) = 10.2 cm²

7.3 Class 10 Question 8.
In the adjoining figure, O is the centre of the sector. ∠ROQ = ∠MON = 60°. OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and (π = \(\frac { 22 }{ 7 } \))

Given: ∠ROQ = ∠MON = 60°,
radius (r) = OR = 7 cm, radius (R) = OM = 21 cm
To find: Lengths of arc RXQ and arc MYN.
Solution:
i. Length of arc RXQ = \(\frac{\theta}{360} \times 2 \pi r\)
= \(\frac { 60 }{ 2 } \) × 2 × \(\frac { 22 }{ 7 } \) × 7
= \(\frac { 1 }{ 6 } \) × 2 × 22
= 7.33 cm
ii. Length of arc MYN = \(\frac{\theta}{360} \times 2 \pi R\)
= \(\frac { 60 }{ 2 } \) × 2 × \(\frac { 22 }{ 7 } \) × 21
= \(\frac { 1 }{ 6 } \) × 2 × 22 × 3
= 22 cm
∴ The lengths of arc RXQ and arc MYN are 7.33 cm and 22 cm respectively.

Question 9.
In the adjoining figure, if A(P-ABC) = 154 cm², radius of the circle is 14 cm, find
i. ∠APC,
ii. l(arc ABC).

Given: A(P – ABC) = 154 cm²,
radius (r) = 14 cm
Solution:
i. Let ∠APC = θ

Std 10 Geometry Mensuration Question 10.
Radius of a sector of a circle is 7 cm. If measure of arc of the sector is
i. 30°
ii. 210°
iii. three right angles, find the area of the sector in each case.
Given: Radius (r) = 7 cm
To find: Area of the sector.
Solution:
i. Measure of the arc (θ) = 30°

∴ Area of the sector is 12.83 cm².
ii. Measure of the arc (θ) = 210°

∴ Area of the sector is 89.83 cm².
iii. Measure of the arc (θ) = 3 right angle
= 3 × 90° = 270°

∴ Area of the sector is 115.50 cm².

Mensuration Practice Question 11.
The area of a minor sector of a circle is 3.85 cm² and the measure of its central angle is 36°. Find the radius of the circle.
Given: Area of minor sector = 3.85 cm²,
central angle (θ) = 36°
To find: Radius of the circle (r).
Solution:
Area of minor sector = \(\frac{\theta}{360} \times \pi r^{2}\)

∴ The radius of the circle ¡s 3.5 cm.

10th Geometry Practice Set 7.3 Question 12.
In the given figure, ꠸PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y and z.

Given: In rectangle PQRS,
PQ = 14 cm, QR = 21 cm
To find: Areas of the parts x, y and z.
Solution:

∠Q = ∠R = θ = 90° …[Angles of a rectangle]

For the sector (Q – PA),
PQ = QA …[Radii of the same circle]
∴ QA = 14 cm
Now, QR = QA + AR … [Q – A – R]
∴ 21 = 14 + AR
∴ AR = 7 cm

Area of rectangle = length × breadth
area of ꠸PQRS = PQ × QR
= 14 × 21
= 294 cm²
Area of part z = area of ꠸PQRS
– area of part x – area of part y
= 294 – 154 – 38.5
= 101.5 cm²
∴ The area of part x is 154 cm², the area of part y is 38,5 cm² and the area of part z is 101.5 cm².

Question 13.
∆ALMN is an equilat triangle. LM = 14 cm. As shown in figure, three sectors are drawn with vertices as centres and radius 7 cm. Find,

i. A (∆ LMN).
ii. Area of any one of the sectors.
iii. Total area of all the three sectors.
iv. Area of the shaded region. (\(\sqrt { 3 }\) = 1.732 )
Given: In equilateral triangle LMN, LM =14 cm,
radius of sectors (r) = 7 cm
Solution:
i. ∆LMN is an equilateral triangle.

ii. Central angle (θ) = 60° …[Angle of an equilateral triangle]

∴ Area of one sector = 25.67 cm²
iii. Total area of all three sectors
= 3 × Area of one sector
= 3 × 25.67
= 77.01 cm²
∴ Total area of all three sectors = 77.01 cm²
iv. Area of shaded region
= A(∆LMN) – total area of all three sectors
= 84.87 – 77.01
= 7.86 cm²
∴ Area of shaded region = 7.86 cm

Maharashtra Board Class 10 Maths Chapter 7 Mensuration Intext Questions and Activities

Mensuration Practice Set 7.3 Question 1.
Complete the following table with the help of given figure. (Textbook pg. no. 149)


Solution:

Question 2.
Observe the figures below. Radii of all circles are equal. Observe the areas of the shaded regions and complete the following table. (Textbook pg. no. 150)

Solution:

Thus, if measure of an arc of a circle is θ, then
Area of sector (A) = \(\frac{\theta}{360}\) × Area of circle
∴ Area of sector (A) = \(\frac{\theta}{360}\) × πr²

Mensuration In Maths Question 3.
In the following figures, radii of all circles are equal. Observe the length of arc in each figure and complete the table. (Textbook pg. no. 151)

Solution:

Thus, if the measure of an arc of a circle is 0, then
Length of arc (l) = \(\frac{\theta}{360}\) × circumference of circle
∴ Length of arc (l) = \(\frac{\theta}{360}\) × 2πr

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions