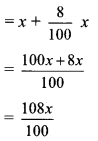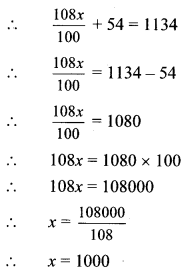Prasanna

Compound Interest Class 8 Maths Chapter 14 Practice Set 14.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 14.1 8th Std Maths Answers Solutions Chapter 14 Compound Interest.

Std 8 Maths Practice Set 14.1 Chapter 14 Solutions Answers

Practice Set 14.1 Class 8 Question 1.
Find the amount and the compound interest.

Solution:
i. Here P = Rs 2000, R = 5 p.c.p.a. and N = 2 years

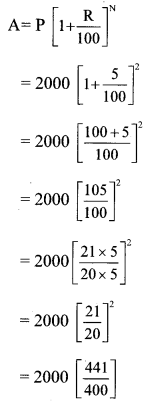
= 5 × 441
∴ A = Rs 2205
I = Amount (A) – Principal (P)
= 2205 – 2000
= Rs 205
∴ The amount is Rs 2205 and the compound interest is Rs 205.

ii. Here, P = Rs 5000, R = 8 p.c.p.a. and N = 3 years

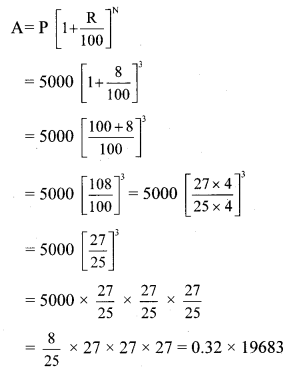
∴ A = Rs 6298.56
I = Amount (A) – Principal (P)
= 6298.56 – 5000
= Rs 1298.56
∴ The amount is Rs 6298.56 and the compound interest is Rs 1298.56.

iii. Here, P = Rs 4000, R = 7.5 p.c.p.a. and N = 2 years

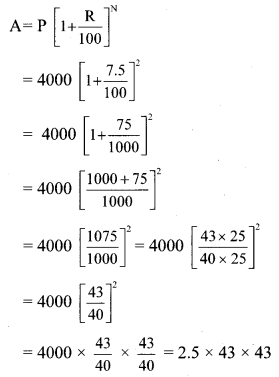
∴A = Rs 4622.50
I = Amount (A) – Principal (P)
= 4622.50 – 4000
= Rs 622.50
∴The amount is Rs 4622.50 and the compound interest is Rs 622.50.

Compound Interest Practice Set 14.1 Question 2.
Sameerrao has taken a loan of Rs 12500 at the rate of 12 p.c.p.a. for 3 years. If the interest is compounded annually then how many rupees should he pay to clear his loan?
Solution:
Here, P = Rs 12,500, R = 12 p.c.p.a. and
N = 3 years

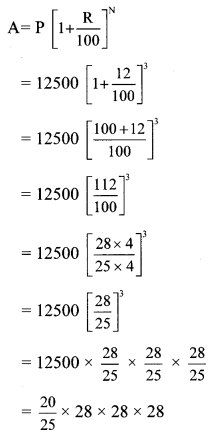
= 0.8 × 28 × 28 × 28
= Rs 17,561.60
Sameerrao should pay Rs 17,561.60 to clear his loan.

8th Standard Maths Practice Set 14.1 Question 3.
To start a business Shalaka has taken a loan of Rs 8000 at a rate of \(10\frac { 1 }{ 2 }\) p.c.p.a. After two years how much compound interest will she have to pay?
Solution:
Here, P = Rs 8000, N = 2 years and


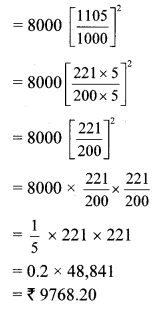
I = Amount (A) – Principal (P)
= 9768.20 – 8000
= Rs 1768.20
∴ After two years Shalaka will have to pay Rs 1768.20 as compound interest.

Maharashtra Board Class 8 Maths Solutions

• Equations in One Variable Practice Set 12.1 Class 8 Maths Solutions
• Equations in One Variable Practice Set 12.2 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.1 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.2 Class 8 Maths Solutions
• Compound Interest Practice Set 14.1 Class 8 Maths Solutions
• Compound Interest Practice Set 14.2 Class 8 Maths Solutions

Direct Proportion and Inverse Proportion Class 7 Maths Chapter 9 Practice Set 37 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 37 Answers Solutions Chapter 9 Direct Proportion and Inverse Proportion.

Std 7 Maths Practice Set 37 Solutions Answers

Question 1.
If 7 kg onions cost Rs 140, how much must we pay for 12 kg onions?
Solution:
Let the cost of 12 kg onions be Rs x.
The quantity of onions and their cost are in direct proportion.
∴ \(\frac{7}{140}=\frac{12}{x}\)
∴ 7x = 12 × 140 ….(Multiplying both sides by 140x)
∴ x = \(\frac { 12\times 140 }{ 7 }\)
= 240
We must pay Rs 240 for 12 kg onions.

Question 2.
If Rs 600 buy 15 bunches of feed, how many will Rs 1280 buy?
Solution:
Let the bunches of feed bought for Rs 1280 be x.
The quantity of feed bought and their cost are in direct proportion.
∴ \(\frac{600}{15}=\frac{1280}{x}\)
∴ 600x = 1280 × 15 …. (Multiplying both sides by 15x)
∴ \(x=\frac{1280 \times 15}{600}=32\)
∴ 32 bunches of feed can be bought for Rs 1280.

Question 3.
For 9 cows, 13 kg 500 g of food supplement are required every day. In the same proportion, how much will be needed for 12 cows?
Solution:
Let the food supplement required for 12 cows be x kg.
The quantity of food supplement required and the number of cows are in direct proportion.
∴ \(\frac{13 \mathrm{kg} 500 \mathrm{gram}}{9}=\frac{x \mathrm{kg}}{12}\)
∴ \(\frac{13.5}{9}=\frac{x}{12}\) ….(13 kg 500 gram = 13.5 kg)
∴ 13.5 × 12 = 9x ….(Multiplying both sides by 9 x 12)
∴ \(\frac{13.5 \times 12}{9}=x\)
∴ x = 18
∴ The food supplement required for 12 cows is 18 kg.

Question 4.
The cost of 12 quintals of soyabean is Rs 36,000. How much will 8 quintals cost?
Solution:
Let the cost of 8 quintals of soyabean be Rs x.
The quantity of soyabeans and their cost are in direct proportion.
∴ \(\frac{12}{36000}=\frac{8}{x}\)
∴ 12x = 8 × 36000 ….(Multiplying both sides by 36000x)
∴ \(x=\frac{8 \times 36000}{12}=24000\)
∴ The cost of 8 quintals of soyabean is Rs 24000.

Question 5.
Two mobiles cost Rs 16,000. How much money will be required to buy 13 such mobiles ?
Solution:
Let the cost of 13 mobiles be Rs x.
The quantity of mobiles and their cost are in direct proportion.
∴ \(\frac{2}{16000}=\frac{13}{x}\)
∴ 2x = 13 × 16000 ….(Multiplying both sides by 16000x)
∴ \(x=\frac{13 \times 16000}{2}=104000\)
∴ Rs 104000 will be required to buy 13 mobiles.

Class 7 Maths Solution Maharashtra Board

• Direct Proportion and Inverse Proportion Practice Set 37 Class 7 Maths Solution
• Direct Proportion and Inverse Proportion Practice Set 38 Class 7 Maths Solution
• Direct Proportion and Inverse Proportion Practice Set 39 Class 7 Maths Solution
• Banks and Simple Interest Practice Set 40 Class 7 Maths Solution
• Banks and Simple Interest Practice Set 41 Class 7 Maths Solution
• Circle Practice Set 42 Class 7 Maths Solution
• Circle Practice Set 43 Class 7 Maths Solution
• Perimeter and Area Practice Set 44 Class 7 Maths Solution
• Perimeter and Area Practice Set 45 Class 7 Maths Solution
• Perimeter and Area Practice Set 46 Class 7 Maths Solution
• Perimeter and Area Practice Set 47 Class 7 Maths Solution

Congruence of Triangles Class 8 Maths Chapter 13 Practice Set 13.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 13.1 8th Std Maths Answers Solutions Chapter 13 Congruence of Triangles.

Std 8 Maths Practice Set 13.1 Chapter 13 Solutions Answers

Congruence of Triangles Practice Set 13.1 Question 1.
In each pair of triangles in the following figures, parts bearing identical marks are congruent. State the test and correspondence of vertices by which triangles in each pair are congruent.
i.

ii.

iii.

iv.

v.

Solution:
i.

The two triangles are congruent by SAS test in the correspondence XWZ ↔ YWZ.

ii.

The two triangles are congruent by hypotenuse-side test in the correspondence KJI ↔ LJI.

iii.

The two triangles are congruent by SSS test in the correspondence HEG ↔ FGE.

iv.
The two triangles are congruent by ASA test is the correspondence SMA ↔ OPT.

v.

The two triangles are congruent by ASA test or SAS test or SAA test in the correspondence MTN ↔ STN.

Maharashtra Board Class 8 Maths Chapter 13 Congruence of Triangles Practice Set 13.1 Intext Questions and Activities

Practice Set 13.1 Question 1.
Write answers to the following questions referring to the given figure.

1. Which is the angle opposite to the side DE?
2. Which is the side opposite to ∠E?
3. Which angle is included by side DE and side DF?
4. Which side is included by ∠E and ∠F?
5. State the angles adjacent to side DE. (Textbook pg, no. 81)

Solution:

1. ∠DFE i.e. ∠F is the angle opposite to side DE.
2. Side DF is the side opposite to ∠E.
3. ∠EDF i.e. ∠D is included by side DE and side DF.
4. Side EF is included by ∠E and ∠F.
5. ∠DEF and ∠EDF i.e. ∠E and ∠D are adjacent to side DE.

Congruence of Triangles Class 8th Practice Set 13.1 Question 2.
In the given figure, parts of triangles indicated by identical marks are congruent.
a. Identify the one-to-one correspondence of vertices in which the two triangles are congruent and write the congruence.
b. State with reason, whether the statement, ∆XYZ ≅ ∆STU is right or wrong. (Textbook pg. no. 82)

Solution:
a. From the figure,
S ↔ X, T ↔ Z, U ↔ Y i.e.,
STU ↔ XZY, or SUT ↔ XYZ, or
TUS ↔ ZYX, or TSU ↔ ZXY, or
UTS ↔ YZX, or UST ↔ YXZ

∴ ∆STU ≅ ∆XZY, or ∆SUT ≅ ∆XYZ, or
∆TUS ≅ ∆ZYX, or ∆TSU ≅ ∆ZXY, or
∆UTS ≅ ∆YZX, or ∆UST ≅ ∆YXZ

b. If ∆XYZ ≅ ∆STU, then
∠Y ≅ ∠T, ∠Z ≅ ∠U,
seg XY ≅ seg ST, seg XZ ≅ seg SU
∴ But, all the above statements are wrong. The statement AXYZ ≅ ASTU is wrong.

Maharashtra Board Class 8 Maths Solutions

• Equations in One Variable Practice Set 12.1 Class 8 Maths Solutions
• Equations in One Variable Practice Set 12.2 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.1 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.2 Class 8 Maths Solutions
• Compound Interest Practice Set 14.1 Class 8 Maths Solutions
• Compound Interest Practice Set 14.2 Class 8 Maths Solutions

Equations in One Variable Class 8 Maths Chapter 12 Practice Set 12.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.2 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Std 8 Maths Practice Set 12.2 Chapter 12 Solutions Answers

Equation In One Variable Practice Set 12.2 Question 1.
Mother is 25 years older than her son. Find son’s age, if after 8 years ratio of son’s age to mother’s age will be \(\frac { 4 }{ 9 }\).
Solution:
Let the son’s present age be x years.
∴ Mother’s present age = (x + 25) years
After 8 years,
Son’s age = (x + 8) years
Mother’s age = (x + 25 + 8) = (x + 33) years
Since, the ratio of the son’s age to mother’s age after 8 years is \(\frac { 4 }{ 9 }\).
∴ \(\frac{x+8}{x+33}=\frac{4}{9}\)
∴ 9 (x + 8) = 4 (x + 33)
∴ 9x + 72 = 4x + 132
∴ 9x – 4x = 132 – 72
∴ 5x = 60
∴ x = \(\frac { 60 }{ 5 }\)
∴ x = 12
∴ Son’s present age is 12 years.

8th Std Maths Practice Set 12.2 Question 2.
The denominator of a fraction is greater than its numerator by 12. If the numerator is decreased by 2 and the denominator is increased by 7, the new fraction is equivalent to \(\frac { 1 }{ 2 }\) . Find the fraction.
Solution:
Let the numerator of the fraction be x.
The denominator of a fraction is greater than its numerator by 12.
∴ Denominator of the fraction = (x + 12)
∴ The required fraction = \(\frac { x }{ x+12 }\)
For the new fraction,
numerator is decreased by 2.
∴ The new numerator = (x – 2)
Also, denominator is increased by 7.
∴ The new denominator = (x + 12) + 7
= (x + 19)
Since, the new fraction is equivalent to \(\frac { 1 }{ 2 }\).
∴ \(\frac{x-2}{x+19}=\frac{1}{2}\)
∴ 2(x – 2) = 1(x + 19)
∴ 2x – 4 = x + 19
∴ 2x – x = 19 + 4
∴ x = 23
∴ The required fraction = \(\frac{x}{x+12}=\frac{23}{23+12}=\frac{23}{35}\)
∴ The required fraction is \(\frac { 23 }{ 35 }\)

Practice Set 12.2 Class 8 Question 3.
The ratio of the weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Let the weight of zinc in the brass utensil be x gm.
Since, the ratio of the weights of copper to zinc in brass is 13:7.

∴ Weight of copper in the brass utensil = \(\left(\frac{13}{7} x\right)\) gm
The weight of the brass utensil = 700 gm
∴ \(\frac { 13 }{ 7 }x+x=700\)
∴ \(\frac { 13 }{ 7 }x\) x × 7 + x × 7 = 700 × 7
∴ 13x + 7x = 4900
∴ 20x = 4900
∴ \(x=\frac { 4900 }{ 20 }\)
∴ x = 245
∴ The weight of zinc in the brass utensil is 245 gm.

Practice Set 12.2 8th Class Question 4.
Find three consecutive whole numbers whose sum is more than 45 but less than 54.
Solution:
Let the three consecutive whole numbers be (x – 1), x and (x + 1).
∴ Sum of the three numbers
= (x – 1) + x + (x + 1)
= 3x
Given that, the sum of the three numbers is greater than 45 and less than 54.
When the sum of the three numbers is 45,
3x = 45
∴ x = \(\frac { 45 }{ 3 }\)
∴ x = 15
When the sum of the three numbers is 54,
∴ 3x = 54
∴ x = \(\frac { 54 }{ 3 }\)
∴ x = 18
∴ the value of x is greater than 15 and less than 18.
∴ the value of x is either 16 or 17

Case I:
If the value of x is 16, then the three consecutive whole numbers are
(16 – 1), 16,(16 + 1)i.e., 15, 16, 17

Case II:
If the value of x is 17, then the three consecutive whole numbers are (17 – 1), 17, (17 + 1) i.e., 16, 17, 18.
∴ The three consecutive whole numbers are 15, 16, 17 or 16, 17, 18.

Practice Set 12.2 8th Standard Question 5.
In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let the digit at unit’s place be x.
The digit at the ten’s place is twice the digit at unit’s place.
∴ The digit at ten’s place = 2x

Since, the sum of the original number and the new number is 66.
∴ 21x + 12x = 66
∴ 33x = 66
∴ x = \(\frac { 66 }{ 33 }\)
∴ x = 2
∴ Original number = 21x = 21 × 2 = 42
∴ the original number is 42.

8th Standard Maths Practice Set 12.2 Question 6.
Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let the number of tickets sold of Rs 100 be x.
The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100.
∴ Number of tickets sold of Rs 200 = (x + 20)
∴ Total amount received by the theatre through the sale of tickets = 100 × x + 200 × (x + 20)
= 100x + 200x + 4000
= 300x + 4000
Since, the total amount received by the theatre through the sale of tickets = Rs 37000
∴ 300x + 4000 = 37000
∴ 300x = 37000 – 4000
∴ 300x = 33000
∴ \(x=\frac { 33000 }{ 300 }\)
∴ x = 110
∴ 110 tickets of Rs 100 were sold.

8th Maths Practice Set 12.2 Question 7.
Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let the three consecutive natural numbers be (x – 1), x and (x + 1).
Here, the smallest number is (x – 1) and the greatest number is (x + 1).
Since, five times the smallest number is 9 more than four times the greatest number.
∴ 5 × (x – 1) = [4 × (x + 1)] + 9
∴ 5x – 5 = 4x + 4 + 9
∴ 5x – 5 = 4x + 13
∴ 5x – 4x = 13 + 5
∴ x = 18 .
∴ the three numbers are (18 – 1), 18, (18 + 1)
i. e., 17, 18, 19
∴ The three consecutive natural numbers are 17,18 and 19.

Raju Sold A Bicycle to Amit at 8 Question 8.
Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let the cost price at which Raju purchased the bicycle be Rs x.
Since, Raju sold the bicycle at 8% profit to Amit.
∴ Selling price of bicycle for Raju = x + 8% of x

Since, Amit spent Rs 54 on repairing the bicycle and then sold it to Nikhil for Rs 1134, at no loss and no profit.
∴ Selling price of bicycle + repairing cost = Rs 1134

∴ The cost price of the bicycle at which Raju purchased it is Rs 1000.

Class 8 Maths Practice Set 12.2 Question 9.
A cricket player scored 180 runs in the first match and 257 runs in the second match. Find the number of runs he should score in the third match so that the average of runs in the three matches be 230.
Solution:
Let the number of runs required by the cricket player to score in the third match be x.
Number of runs scored by the player in first match = 180
Number of runs scored in second match = 257
∴ Total runs scored by the player = 180 + 257 + x = 437 + x
Average of runs in the three matches = \(\frac { 437+x }{ 3 }\)
Since, the average of runs should be 230.
\(\frac { 437+x }{ 3 }=230\)
∴ 437 + x = 230 × 3
∴ 437 + x = 690
∴ x = 690 – 437
∴ x = 253
∴ The cricket player should score 253 runs in the third match.

8th Class Math Practice Set 12.2 Question 10.
Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let Viru’s present age be x years.
Sudhir’s present age is 5 more than three times the age of Viru.
∴ Sudhir’s present age = (3x + 5) years
Anil’s age is half the age of Sudhir.
∴ Anil’s present age = \(\left(\frac{3 x+5}{2}\right)\) years
Since, the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6.

∴ 2 × (24x + 30) = 45x + 75
∴ 48x + 60 = 45x + 75
∴ 48x – 45x = 75 – 60
∴ 3x = 15
∴ x = \(\frac { 15 }{ 3 }\)
∴ x = 5
∴ Viru’s present age is 5 years.

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.2 Intext Questions and Activities

8th Math Practice Set 12.2 Question 1.
Write correct numbers in the boxes given. (Textbook pg. no. 78)
length is 3 times the breadth

Perimeter of the rectangle = 40
2(__x + __x) = 40
2 × __ x = 40
__ x = 40
x = __
∴ Breadth of rectangle = __ cm and Length of rectangle = __ cm
Solution:
length is 3 times the breadth

Perimeter of the rectangle = 40
∴ 2(3x + 1x) = 40
∴ 2 × 4x = 40
∴ 8x = 40
∴ x = 5
∴ Breadth of rectangle = 5 cm and Length of rectangle = 15 cm

Maharashtra Board Class 8 Maths Solutions

• Equations in One Variable Practice Set 12.1 Class 8 Maths Solutions
• Equations in One Variable Practice Set 12.2 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.1 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.2 Class 8 Maths Solutions
• Compound Interest Practice Set 14.1 Class 8 Maths Solutions
• Compound Interest Practice Set 14.2 Class 8 Maths Solutions

Equations in One Variable Class 8 Maths Chapter 12 Practice Set 12.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.1 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Std 8 Maths Practice Set 12.1 Chapter 12 Solutions Answers

Equation in One Variable Practice Set 12.1 Question 1. Each equation is followed by the values of the variable. Decide whether these values are the solutions of that equation.
i. x – 4 = 3, x = – 1, 7, – 7
ii. 9m = 81, m = 3, 9, -3
iii. 2a + 4 = 0, a = 2, – 2, 1
iv. 3 – y = 4, y = – 1, 1, 2
Solution:
i. x – 4 = 3 ….(i)
Substituting x = – 1 in L.H.S. of equation (i),
L.H.S. = (-1) – 4
= – 5
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 1 is not the solution of the given equation.

Substituting x = 7 in L.H.S. of equation (i),
L.H.S. = (7) – 4
= 3
R.H.S. = 3
∴ L.H.S. = R.H.S.
∴ x = 7 is the solution of the given equation.

Substituting x = – 7 in L.H.S. of equation (i),
L.H.S. = (- 7) – 4
= -11
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 7 is not the solution of the given equation.

ii. 9m = 81 …(i)
Substituting m = 3 in L.H.S. of equation (i),
L.H.S. = 9 × (3)
= 27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = 3 is not the solution of the given equation.

Substituting m = 9 in L.H.S. of equation (i),
L.H.S. = 9 × (9)
= 81
R.H.S. = 81
∴L.H.S. = R.H.S.
∴m = 9 is the solution of the given equation.

Substituting m = – 3 in L.H.S. of equation (i),
L.H.S. = 9 × (- 3)
= -27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = – 3 is not the solution of the given equation.

iii. 2a + 4 = 0 …..(i)
Substituting a = 2 in L.H.S. of equation (i),
L.H.S. = 2 (2) + 4
= 4 + 4
= 8
R.H.S. = 0
∴L.H.S. ≠ R.H.S.
∴a = 2 is not the solution of the given equation.

Substituting a = – 2 in L.H.S. of equation (i),
L.H.S. = 2 (-2)+ 4
= -4 + 4
= 0
R.H.S. = 0
∴L.H.S. = R.H.S.
∴a = – 2 is the solution of the given equation.

Substituting a = 1 in L.H.S. of equation (i),
L.H.S. = 2(1)+ 4
= 2 + 4
= 6
R.H.S. = 0
∴ L.H.S. ≠ R.H.S.
∴a = 1 is not the solution of the given equation.

iv. 3 – y = 4 …(i)
Substituting y = -1 in L.H.S. of equation (i),
L.H.S. = 3 – (- 1)
= 3 + 1
= 4
R.H.S. = 4
∴L.H.S. = R.H.S.
∴y = – 1 is the solution of the given equation.

Substituting y = 1 in L.H.S. of equation (i),
L.H.S. = 3-(1)
= 2
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 1 is not the solution of the given equation.

Substituting y = 2 in L.H.S. of equation (i),
L.H.S. = 3-(2)
= 1
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 2 is not the solution of the given equation.

Practice Set 12.1 Question 2.
Solve the following equations:
i. 17p – 2 = 49
ii. 2m + 7 = 9
iii. 3x + 12 = 2x – 4
iv. 5 (x – 3) = 3 (x + 2)
v. \(\frac { 9x }{ 8 }+1=10\)
vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)
vii. 13x – 5 = \(\frac { 3 }{ 2 }\)
viii. 3 (y + 8) = 10 (y – 4) + 8
ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
x. \(\frac{y-4}{3}+3 y=4\)
xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
Solution:
i. 17p – 2 = 49
∴ 17p – 2 + 2 = 49 + 2
…[Adding 2 on both the sides]
∴ 17p = 51
∴ \(\frac{17 p}{17}=\frac{51}{17}\) …[Dividing both the sides by 17]
p = 3

ii. 2m + 7 = 9
∴ 2m + 7 – 7 = 9 – 7
…[Subtracting 7 from both the sides]
∴ 2m = 2
∴ \(\frac{2 m}{2}=\frac{2}{2}\) [Dividing both the sides by 2]
∴ m = 1

iii. 3x + 12 = 2x – 4
∴ 3x + 12 – 12 = 2x – 4 – 12
…[Subtracting 12 from both the sides]
∴ 3x = 2x – 16
∴ 3x – 2x = 2x – 16 – 2x
…[Subtracting 2x from both the sides]
∴ x = – 16

iv. 5 (x – 3) = 3 (x + 2)
∴ 5x – 15 = 3x + 6
∴ 5x – 15 + 15 = 3x + 6 + 15
…[Adding 15 on both the sides]
∴ 5x = 3x + 21
∴ 5x – 3x = 3x + 21 – 3x
…[Subtracting 3x from both the sides]
∴ 2x = 21
∴ \(\frac{2 x}{2}=\frac{21}{2}\) …[Dividing both the sides by 2]
∴ \(x=\frac{21}{2}\)

v. \(\frac { 9x }{ 8 }+1=10\)

vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)

vii. 13x – 5 = \(\frac { 3 }{ 2 }\)

viii. 3 (y + 8) = 10 (y – 4) + 8
∴ 3y + 24 = 10y – 40 + 8
∴ 3y + 24 = 10y – 32
∴ 3y + 24 – 24 = 10y – 32 – 24
…[Subtracting 24 from both the sides]
∴ 3y = 10y – 56
∴ 3y – 10y = 10y – 56
…[Subtracting 10y from both the sides]
∴ – 7y = – 56
∴ \(\frac{-7 y}{-7}=\frac{-56}{-7}\)…[Dividing both the sides by – 7]
∴ y = 8

ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
∴\(\frac{x-9}{x-5} \times 7(x-5)=\frac{5}{7} \times 7(x-5)\)
…[Multiplying both the sides by 7 (x – 5)]
∴7 (x – 9) = 5 (x – 5)
∴7x – 63 = 5x – 25
∴7x – 63 + 63 = 5x – 25 + 63
…[Adding 63 on both the sides]
∴7x = 5x + 38
∴7x – 5x = 5x + 38 – 5x
…[Subtracting 5x from both the sides]
∴ 2x = 38
∴\(\frac{2 x}{2}=\frac{38}{2}\) …[Dividing both the sides by 2]
∴x = 19

x. \(\frac{y-4}{3}+3 y=4\)
∴\(\frac{y-4}{3} \times 3+3 y \times 3=4 \times 3\)
…[Multiplying both the sides by 3]
∴y – 4 + 9y = 12
∴10y – 4 = 12
∴10y – 4 + 4=12 + 4
…[Adding 4 on both the sides]
∴10y = 16
∴\(\frac{10 y}{10}=\frac{16}{10}\)…[Dividing both the sides by 10]
∴y = \(\frac { 8 }{ 5 }\)

xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
∴\(\frac{b+(b+1)+(b+2)}{4} \times 4=21 \times 4\)
…[Multiplying both the sides by 4]
∴b + b + 1 + b + 2 = 84
∴3b + 3 = 84
∴3b + 3 – 3 = 84 – 3
…[ Subtracting 3 from both the sides]
∴3b = 81
∴\(\frac{3 b}{3}=\frac{81}{3}[/latex …[Dividing both the sides by 3]
∴b = 27

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.1 Intext Questions and Activities

Std 8 Maths Practice Set 12.1 Question 1.
Fill in the boxes to solve the following equations. (Textbook pg. no. 75)
i. x + 4 = 9
∴x + 4 – __ = 9 – __
… [Subtracting 4 from both the sides]
∴ x = __

ii. x – 2 = 7
∴x – 2 + __ = 7 + __
… [Adding 2 on both the sides]
∴x = __

iii. [latex]\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × __ = 4 ×__
∴x = __

iv. 4x = 24
∴ __ = __
∴x = __
Solution:
i. x + 4 = 9
∴x + 4 – 4 = 9 – 4
… [Subtracting 4 from both the sides]
∴ x = 5

ii. x – 2 = 7
∴x – 2 + 2 = 7 + 2
… [Adding 2 on both the sides]
∴x = 9

iii. \(\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × 3 = 4 × 3
… [Multiplying both the sides by 3]
∴x = 12

iv. 4x = 24
∴ \(\frac{4 x}{[4]}=\frac{24}{[4]}\)
… [Dividing both the sides by 4]
∴x = 6

Maharashtra Board Class 8 Maths Solutions

• Equations in One Variable Practice Set 12.1 Class 8 Maths Solutions
• Equations in One Variable Practice Set 12.2 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.1 Class 8 Maths Solutions
• Congruence of Triangles Practice Set 13.2 Class 8 Maths Solutions
• Compound Interest Practice Set 14.1 Class 8 Maths Solutions
• Compound Interest Practice Set 14.2 Class 8 Maths Solutions

Algebraic Expressions and Operations on them Class 7 Maths Chapter 8 Practice Set 35 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 35 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Std 7 Maths Practice Set 35 Solutions Answers

Question 1.
Multiply:
i. 16xy × 18xy
ii. 23xy² × 4yz²
iii. (12a + 17b) × 4c
iv. (4x + 5y) × (9x + 7y)
Solution:
i. 16xy × 18xy
= 16 × 18 × xy × xy
= 288x²y²

ii. 23xy² × 4yz²
= 23 × 4 × xy² × yz²
= 92xy³z²

iii. (12a + 17b) × 4c = 12a × 4c + 17b × 4c
= 48ac + 68bc

iv. (4x + 5y) × (9x + 7y)
= 4x × (9x + 7y) + 5y × (9x + 7y)
= (4x × 9x) + (4x × 7y) + (5y × 9x) + (5y × 7y)
= 36x² + 28xy + 45xy + 35y²
= 36x² + 73xy + 35y²

Question 2.
A rectangle is (8x + 5) cm long and (5x + 3) cm broad. Find its area. Solution:
Length of the rectangle = (8x + 5) cm
Breadth of the rectangle = (5x + 3) cm
∴ Area of the rectangle = length × breadth
= (8x + 5) × (5x + 3)
= 8x × (5x + 3) + 5 × (5x + 3)
= (8x × 5x) + (8x × 3) + (5 × 5x) + (5 × 3)
= 40x² + 24x + 25x + 15
= 40x² + 49x + 15
∴ The area of the rectangle is (40x² + 49x + 15) sq. cm.

Class 7 Maths Solution Maharashtra Board

• Indices Practice Set 26 Class 7 Maths Solution
• Indices Practice Set 27 Class 7 Maths Solution
• Indices Practice Set 28 Class 7 Maths Solution
• Indices Practice Set 29 Class 7 Maths Solution
• Indices Practice Set 30 Class 7 Maths Solution
• Joint Bar Graph Practice Set 31 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 32 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 33 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 34 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 35 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 36 Class 7 Maths Solution

Algebraic Expressions and Operations on them Class 7 Maths Chapter 8 Practice Set 36 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 36 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Std 7 Maths Practice Set 36 Solutions Answers

Question 1.
Simplify (3x – 11y) – (17x + 13y) and choose the right answer.
(A) 7x – 12y
(B) -14x – 54y
(C) -3(5x + 4y)
(D) -2(7x + 12y)
Solution:
(D) -2(7x + 12y)

Hints:
(3x – 11y) – (17x + 13y) = 3x – 11y – 17x – 13y
= – 14x – 24y
= – 2 × 7x – 2 × 12y
= – 2(7x + 12y)

Question 2.
The product of (23x²y³z) and (-15x³yz²) is __
(A) -34x⁵y⁴z³
(B) 34x²y³z⁵
(C) 145x³y²z
(D) 170x³y²z³
Solution:
(A) -34x⁵y⁴z³

Question 3.
Solve the following equations:
i. \(4 x+\frac{1}{2}=\frac{9}{2}\)
ii. 10 = 2y + 5
iii. 5m – 4 = 1
iv. 6x – 1 = 3x + 8
v. 2(x – 4) = 4x + 2
vi. 5(x + 1) = 74
Solution:
i. \(4 x+\frac{1}{2}=\frac{9}{2}\)

ii. 10 = 2y + 5

iii. 5m – 4 = 1

iv. 6x – 1 = 3x + 8

v. 2(x – 4) = 4x + 2

vi. 5(x + 1) = 74

Question 4.
Rakesh’s age is less than Sania’s age by 5 years. The sum of their ages is 27 years. How old are they?
Solution:
Let the age of Rakesh be x years.
∴ Sania’s age = (x + 5) years.
According to the given condition,
x + (x + 5) = 27
∴ 2x + 5 = 27
∴ 2x = 27 – 5
∴ 2x = 22
∴ \(x=\frac { 22 }{ 2 }=11\)
Sania’s age = x + 5 = 11 + 5 = 16 years
∴ The ages of Rakesh and Sania are 11 years and 16 years respectively.

Question 5.
When planting a forest, the number of jambhul trees planted was greater than the number of ashoka trees by 60. If there are altogether 200 trees of these two types, how many jambhul trees were planted?
Solution:
Let the number of jambhul trees planted be x.
∴ Number of ashoka trees = x – 60
According to the given condition, x + x – 60 = 200
∴ 2x = 200 + 60
∴ 2x = 260
∴ \(x=\frac { 260 }{ 2 }=130\)
∴ 130 jambhul trees were planted.

Question 6.
Shubhangi has twice as many 20-rupee notes as she has 50-rupee notes. Altogether, she has 2700 rupees. How many 50-rupee notes does she have?
Solution:
Let the number of 50-rupee notes with shubhangi be x.
∴ Number of 20-rupee notes = 2x
∴ Total amount with Shubhangi = Number of 50-rupee notes × 50 + Number of 20-rupee notes × 20
= x × 50 + 2x × 20
= 50x + 40x
= 90x
According to the given condition,
90x = 2700
∴ \(x=\frac { 2700 }{ 90 }=30\)
∴ Shubhangi has 30 notes of 50 rupees.

Question 7.
virat made twice as many runs as Rohit. The total of their scores is 2 less than a double century. How many runs did each of them make?
Solution:
Let the runs made by Rohit be x.
∴ Runs made by Virat = 2x
According to the given condition,
x + 2x = 200 – 2
∴ 3x = 198
∴ \(x=\frac { 198 }{ 3 }=66\)
∴ Runs made by Virat = 2x = 2 × 66 = 132
∴ The runs made by Virat and Rohit are 132 and 66 respectively.

Maharashtra Board Class 7 Maths Chapter 8 Algebraic Expressions and Operations on them Practice Set 36 Intext Questions and Activities

Question 1.
Solve the following equations. (Textbook pg. no. 59)
i. x + 7 = 4
ii. 4p = 12
iii. m – 5 = 4
iv. \(\frac { t }{ 3 }=6\)
Solution:
i. x + 7 = 4
∴ x + 7 – 7 = 4 – 7 ….(Subtracting 7 from both sides)
∴ x + 0 = -3
∴ x = -3

ii. 4p = 12
∴ \(\frac{4 p}{4}=\frac{12}{4}\) ….(Dividing both sides by 4)
∴ p = 3

iii. m – 5 = 4
∴ m – 5 + 5 = 4 + 5
…. (Adding 5 to both sides)
∴ m + 0 = 9
∴ m = 9

iv. \(\frac { t }{ 3 }=6\)
∴ \(\frac { t }{ 3 }\) × 3 = 6 × 3 …. (Multiplying both sides by 3)
∴ t = 18

Class 7 Maths Solution Maharashtra Board

• Indices Practice Set 26 Class 7 Maths Solution
• Indices Practice Set 27 Class 7 Maths Solution
• Indices Practice Set 28 Class 7 Maths Solution
• Indices Practice Set 29 Class 7 Maths Solution
• Indices Practice Set 30 Class 7 Maths Solution
• Joint Bar Graph Practice Set 31 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 32 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 33 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 34 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 35 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 36 Class 7 Maths Solution

Algebraic Expressions and Operations on them Class 7 Maths Chapter 8 Practice Set 34 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 34 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Std 7 Maths Practice Set 34 Solutions Answers

Question 1.
Subtract the second expression from the first.
i. (4xy – 9z); (3xy – 16z)
ii. (5x + 4y + 7z); (x + 2y + 3z)
iii. (14x² + 8xy + 3y²); (26x² – 8xy – 17y²)
iv. (6x² + 7xy + 16y²); (16x² – 17xy)
v. (4x + 16z); (19y – 14z + 16x)
Solution:
i. (4xy – 9z) – (3xy – 16z)
= 4xy – 9z – 3xy + 16z
= (4xy – 3xy) + (16z – 9z)
= xy + 7z

ii. (5x + 4y + 7z) – (x + 2y + 3z)
= 5x + 4y + 7z – x – 2y – 3z
= (5x – x) + (4y – 2y) + (7z – 3z)
= 4x + 2y + 4z

iii. (14x² + 8xy + 3y²) – (26x² – 8xy – 17y²)
= 14x² + 8xy + 3y² – 26x² + 8xy + 17y²
= (14x² – 26x²) + (8xy + 8xy) + (3y² + 17y²)
= -12x² + 16xy + 20y²

iv. (6x² + 7xy + 16y²) – (16x² – 17xy)
= 6x² + 7xy + 16y² – 16x² + 17xy
= (6x² – 16x²) + (7xy + 17xy) + 16y²
= -10x² + 24xy + 16y²

v. (4x + 16z) – (19y— 14z + 16x)
= 4x + 16z – 19y + 14z – 16x
= (4x – 16x) – 19y + (16z + 14z)
= -12x – 19y + 30z

Class 7 Maths Solution Maharashtra Board

• Indices Practice Set 26 Class 7 Maths Solution
• Indices Practice Set 27 Class 7 Maths Solution
• Indices Practice Set 28 Class 7 Maths Solution
• Indices Practice Set 29 Class 7 Maths Solution
• Indices Practice Set 30 Class 7 Maths Solution
• Joint Bar Graph Practice Set 31 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 32 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 33 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 34 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 35 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 36 Class 7 Maths Solution

Algebraic Expressions and Operations on them Class 7 Maths Chapter 8 Practice Set 32 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 32  Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Std 7 Maths Practice Set 32 Solutions Answers

Question 1.
Classify the following algebraic expressions as monomials, binomials, trinomials or polynomials.
i. 7x
ii. 5y – 7z
iii. 3x³ – 5x² – 11
iv. 1 – 8a – 7a² – 7a³
v. 5m – 3
vi. a
vii. 4
viii. 3y² – 7y + 5
Solution:
i. Monomial
ii. Binomial
iii. Trinomial
iv. Polynomial
v. Binomial
vi. Monomial
vii. Monomial
viii. Trinomial

Class 7 Maths Solution Maharashtra Board

• Indices Practice Set 26 Class 7 Maths Solution
• Indices Practice Set 27 Class 7 Maths Solution
• Indices Practice Set 28 Class 7 Maths Solution
• Indices Practice Set 29 Class 7 Maths Solution
• Indices Practice Set 30 Class 7 Maths Solution
• Joint Bar Graph Practice Set 31 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 32 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 33 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 34 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 35 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 36 Class 7 Maths Solution

Algebraic Expressions and Operations on them Class 7 Maths Chapter 8 Practice Set 33 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 33 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Std 7 Maths Practice Set 33 Solutions Answers

Question 1.
Add:
i. 9p + 16q; 13p + 2q
ii. 2a + 6b + 8c; 16a + 13c + 18b
iii. 13x² – 12y²; 6x² – 8y²
iv. 17a²b² + 16c; 28c – 28a²b²
v. 3y² – 10y + 16; 2y – 7
vi. – 3y² + 10y – 16; 7y² + 8
Solution:
i. (9p + 16q) + (13p + 2q)
= (9p + 13p) + (16q + 2q)
= 22p + 18q

ii. (2a + 6b + 8c) + (16a + 13c + 18b)
= (2a + 16a) + (6b + 18b) + (8c + 13c)
= 18a + 24b + 21c

iii. (13x² – 12y²) + (6x² – 8y²)
= (13x² + 6x²) + [(-12y²) + (-8y²)]
= 19x² + (-20y²)
= 19x² – 20y²

iv. (17a²b² + 16c) + (28c – 28a²b²)
= [17a²b² + (-28a²b²)] + (16c + 28c)
= -11a²b² + 44c

v. (3y² – 10y + 16) + (2y – 7)
= 3y² + (-10y + 2y) + (16 – 7)
= 3y² – 8y + 9

vi. (-3y² + 10y – 16) + (7y² + 8)
= (-3y² + 7y²) + (10y) + (-16 + 8)
= 4y² + 10y – 8

Maharashtra Board Class 7 Maths Chapter 8 Algebraic Expressions and Operations on them Practice Set 33 Intext Questions and Activities

Question 1.
Answer the following questions. (Textbook pg. no. 57)

1. 3x + 4y = How many?
2. 3 guavas + 4 mangoes = 7 guavas.
3. 7m – 2n = 5m.

Solution:

1. 3x and 4y are unlike terms. Hence, they cannot be added, further to get a single term.
2. No. Guava and mango are different fruits. Hence, 3 guavas + 4 mangoes & 7 guavas.
3. No. 7m and 2n are unlike terms. Hence, 7m – 2n ≠ 5m.

Class 7 Maths Solution Maharashtra Board

• Indices Practice Set 26 Class 7 Maths Solution
• Indices Practice Set 27 Class 7 Maths Solution
• Indices Practice Set 28 Class 7 Maths Solution
• Indices Practice Set 29 Class 7 Maths Solution
• Indices Practice Set 30 Class 7 Maths Solution
• Joint Bar Graph Practice Set 31 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 32 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 33 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 34 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 35 Class 7 Maths Solution
• Algebraic Expressions and Operations on them Practice Set 36 Class 7 Maths Solution