Prasanna

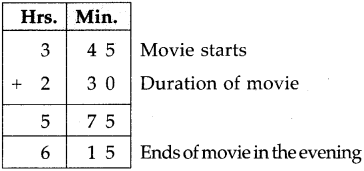
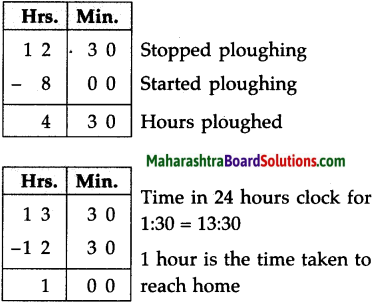
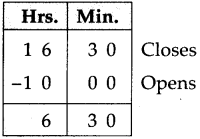
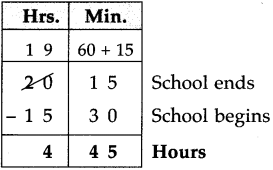
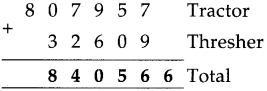
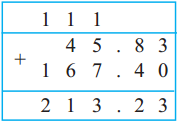
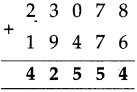
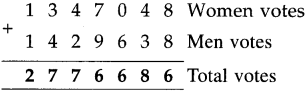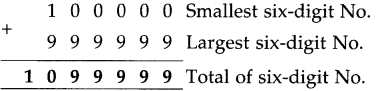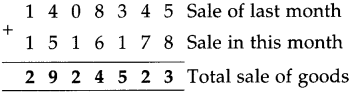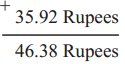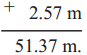Multiples and Factors Class 5 Problem Set 35 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 35 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 8 Multiples and Factors

Determine whether the pairs of numbers given below are co-prime numbers.
(1) 22, 24
Answer:
Common factors of 22 and 24 are 1 and 2. (Not only 1 common factor) So, 22, 24 are not co-prime numbers.

(2) 14, 21
Answer:
Common factors of 14 and 21 are 1 and 7. So, this pair is not co-prime numbers.

(3) 10, 33
Answer:
Common factors of 10 and 33 is only 1. So, 10 and 33 are co-prime numbers.

(4) 11, 30
Answer:
Common factors of 11 and 30 is only 1. So, 11 and 30 are co-prime numbers.

(5) 5, 7
Answer:
Common factor of 5 and 7 is only 1. So, 5 and 7 are co-prime numbers.

(6) 15, 16
Answer:
Common factors of 15 and 16 is only 1. So, 15 and 16 are co-prime numbers.

(7) 50, 52
Answer:
Common factors of 50 and 52 are 1 and 2. So, 50 and 52 are not co-prime numbers.

(8) 17, 18
Answer:
Common factors of 17 and 18 is only 1. So, 17 and 18 are co-prime numbers.

Activity 1 :

• Write numbers from 1 to 60.
• Draw a blue circle around multiples of 2.
• Draw a red circle around multiples of 4.
• Do all numbers with a blue circle also have a red circle around them?
• Do all the numbers with a red circle have a blue circle around them?
• Are all multiples of 2 also multiples of 4?
• Are all multiples of 4 also multiples of 2?

Activity 2 :

• Write numbers from 1 to 60.
• Draw a triangle around multiples of 2.
• Draw a circle around multiples of 3.
• Now find numbers divisible by 6. Can you find a property that they share?

Eratosthenes’ method of finding prime numbers
Eratosthenes was a mathematician who lived in Greece about 250 BC. He discovered a method to find prime numbers. It is called Eratosthenes’ Sieve. Let us see how to find prime numbers between 1 and 100 with this method.

• 1 is neither a prime nor a composite number. Put a square [ ] around it
• 2 is a prime number, so put a circle around it.
• Next, strike out all the multiples of 2. This tells us that of these 100 numbers more than half of numbers are not prime numbers.
• The first number after 2 not yet struck off is 3. So, 3 is a prime number.
• Draw a circle around 3. Strike out all the multiples of 3.
• The next number after 3 not struck off yet is 5. So, 5 is a prime number.
• Draw a circle around 5. Put a line through all the multiples of 5.
• The next number after 5 without a line through it is 7. So, 7 is a prime number.
• Draw a circle around 7. Put a line through all the multiples of 7.

In this way, every number between 1 and 100 will have either a circle or a line through it. The circled numbers are prime numbers. The numbers with a line through them are composite numbers.

One more method to find prime numbers

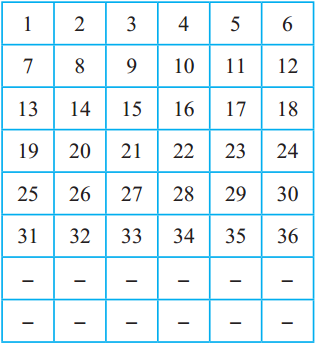
See how numbers from 1 to 36 have been arranged in six columns in the table alongside.

Continue in the same way and write numbers up to 102 in these six columns.

You will see that, in the columns for 2, 3, 4, and 6, all the numbers are composite numbers except for the prime numbers 2 and 3. This means that all the remaining prime numbers will be in the columns for 1 and 5. Now isn’t it easier to find them? So, go ahead, find the prime numbers!

Something more

• Prime numbers with a difference of two are called twin prime numbers. Some twin prime number pairs are 3 and 5, 5 and 7, 29 and 31 and 71 and 73. 5347421 and 5347423 are also a pair of twin prime numbers.
• There are eight pairs of twin prime numbers between 1 and 100. Find them.
• Euclid the mathematician lived in Greece about 300 BC. He proved that if prime numbers, 2, 3, 5, 7, ……., are written in serial order, the list will never end, meaning that the number of prime numbers is infinite.

Multiples and Factors Problem Set 35 Additional Important Questions and Answers

Determine whether the pairs of numbers given below are co-prime numbers.

(1) (12,18)
Answer:
Common factors of 12 and 18 are 1, 2, 3, 6. Hence 12 and 18 are not co-prime numbers.

(2) (26, 39)
Answer:
Common factors of 26 and 39 are 1 and 13. Hence, 26 and 39 are not co-prime numbers.

(3) (23, 29)
Answer:
Common factor of 23 and 29 is only 1. Hence, 23 and 29 are co-prime numbers.

(4) (28, 32)
Answer:
Common factors of 28 and 32 are 1, 2, 4 (not only 1). Hence, 28, 32 are not co-prime numbers.

Maharashtra Board Class 5 Maths Solutions

• Multiples and Factors Problem Set 32 Class 5 Maths Solutions
• Multiples and Factors Problem Set 33 Class 5 Maths Solutions
• Multiples and Factors Problem Set 34 Class 5 Maths Solutions
• Multiples and Factors Problem Set 35 Class 5 Maths Solutions

Measuring Time Class 5 Problem Set 45 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 10 Measuring Time Problem Set 45 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 10 Measuring Time

Question 1.
Add the following :
(1) 2 hours 30 minutes + 4 hours 55 minutes
Solution:

85 minutes = 1 hr 25 min

(2) 3 hours 50 minutes + 4 hours 20 minutes
Solution:

70 minutes = 1 hr 10 min.

(3) 3 hours 45 minutes + 1 hour 35 minutes
Solution:

80 minutes = 1 hr 20 min

(4) 4 hours 15 minutes + 2 hours 50 minutes
Solution:

65 minutes = 1 hr 05 min

Question 2.
Subtract the following :
(1) 3 hours 10 minutes – 2 hours 40 minutes

(2) 5 hours 20 minutes – 2 hours 35 minutes
Solution:

(3) 4 hours 25 minutes – 1 hour 55 minutes

(4) 6 hours 15 minutes – 2 hours 45 minutes

Question 3.
A government office opens at 7 in the morning and closes at 3 in the afternoon. How long is this office open?
Solution:

∴ Office remain open for 8 hours

Question 4.
A movie starts at 45 minutes past 3 in the afternoon and finishes two and a half hours later. At what time does the movie end?
Solution:

∴ Movie ends at 6:15 in the evening

Question 5.
Sakharam was ploughing the field from 8 in the morning. At 12:30 in the afternoon, he stopped and started for home. He reached home at 1:30. How long was he ploughing the field? How long did it take him to reach home from the field?
Solution:

∴ He ploughed for 4:30 hrs. He took 1 hour to reach home.

Question 6.
Rambhau started the water pump at ten-thirty at night and put it off the same night at a quarter to twelve. How long was the water pump on?
Solution:
Quater to 12 is 11:45 pm

∴ pump was on for 1 hour 15 minutes

Question 7.
Geeta taught in the classroom for 2 hours and 25 minutes in the morning and 1 hour and 45 minutes in the afternoon. How long was she teaching in all?
Solution:

∴ Total teaching of Geeta was for 4 hrs 10 min.

Question 8.
If a bank is open for business from 10 in the morning to 4:30 in the evening, how long is it open?
Solution:
Here, in 24 hours clock, 4:30 in the evening = 16:30

∴ Bank opens for 6 hrs 30 min.

Question 9.
If a shop is open from 9:30 am to 10 pm, how long is it open?
Solution:
Here, 10 pm in 24 hours clock is 22:00

∴ Shop opens for 12 hours 30 minutes

Question 10.
If the Maharashtra Express leaving from Kolhapur at 15:30 arrives at Gondia the next day at 20:15, how long is the journey from Kolhapur to Gondia?
Solution:
15:30 to next 15:30 is 24 hours

24 hours + 4 hr. 45 min. = 28 hr. 45 min.
∴ jurney from Koihapur to Gondiya is 28 hours and 45 minutes.

Measuring Time Problem Set 45 Additional Important Questions and Answers

Question 1.
Add the following.

(1) 5 hours 25 minutes + 2 hours 35 minutes
Solution:

60 minutes = 1 hr

(2) 6 hours 55 minutes + 2 hours 15 minutes
Solution:

70 minutes = 1 hr. 10 min

Question 2.
Subtract the following.

(1) 7 hours 30 minutes – 4 hours 50 minutes
Solution:

(2) 2 hours 35 minutes – 1 hour 40 minutes
Solution:

Question 3.
Solve the following:

(1) Supriya left for a picnic at 7:15 am. She came back at 6:45 pm. How long was she out for the picnic?
Here 6:45 pm = 18:45 (In 24 hours clock)
Solution:

∴ Total time of picnic is 11:30 hrs.

(2) In Dave’s school, the tree planting ceremony started at 10:00 in the morning and got over at 13:45. How long did the ceremony go on?
Solution:

∴ Ceremony of planting tree go on for 3 hrs 45 min

Question 4.
Write the time shown in each clock in the box given below it.

Answer:
35 minutes past 3

Answer:
Five minutes to 5

Answer:
Quarter to 2

Answer:
Half past eight

Question 5.
Draw the hands of the clock to show the time given in the box.

Answer:
Quater past 6

Answer:
50 minutes past 1

Answer:
Half past 3

Answer:
5 minutes to 5

Question 6.
The time below is given by the 12 hour clock. Write the same by the 24 hour clock.
(1) 45 minutes past 8 in the morning.
(2) 30 minutes past 2 in the evening.
(3) 50 minutes past 7 in the evening.
(4) 15 minutes past 11 in the evening.
(5) 25 minutes past after midnight.
(6) 25 minutes past 12 in afternoon.
Answer:
(1) 8:45
(2) 114:30
(3) 19:50
(4) 23:15
(5) 00:25
(6) 12:25

Question 7.
Match the following.

Answer:
(1 – c),
(2 – a),
(3 – e),
(4 – b),
(5 – d)

Question 8.
Add the following.
(1) 3 hours 40 minutes + 2 hours 55 minutes
(2) 5 hours 25 minutes + 4 hours 35 minutes
(3) 6 hours 45 minutes + 1 hour 30 minutes
(4) 7 hours 50 minutes + 2 hours 30 minutes
(5) 9 hours 10 minutes + 3 hours 20 minutes
(6) 15 hours 45 minutes + 20 hours 15 minutes
Answer:
(1) 6 hrs 35 min
(2) 10 hrs
(3) 8 hrs 15 min
(4) 10 hrs 20 min
(5) 12 hrs 30 min
(6) 36 hours

Question 9.
Subtract the following.
(1) 4 hours 20 minutes – 1 hour 30 minutes
(2) 3 hours 25 minutes – 1 hour 45 minutes
(3) 5 hours 10 minutes – 2 hours 40 minutes
(4) 2 hours 15 minutes – 50 minutes
(5) 9 hours 10 minutes – 6 hours 10 minutes
(6) 17 hours 30 minutes – 5 hours 25 minutes
Answer:
(1) 2 hours 50 minutes
(2) 1 hour 40 minutes
(3) 2 hours 30 minutes
(4) 1 hour 25 minutes
(5) 3 hours
(6) 12 hours 05 minutes

Question 10.
Solve the following word problems.
(1) A play started at 9:50 at night and finished at 11:45 the same night. What was the duration of the play?
(2) Ramu went out at 10:45 in the morning and came back home at 7 pm. How long he was out of the home?
(3) Local train started from the Virar station at 8:35 am and reached at Churchgate at 10:30 am. Find the journey time taken by the train.
(4) Anita started her homework at 5:45 pm and completed the work at 7:30 pm. How much time is taken by Anita for the homework?
(5) One day test started at 9:15 am and the test ends at 4-.10 in the evening. How much time was taken for this test?
(6) Seema travelled for 2 hours and 20 minutes by train and 1 hour 30 niinutes by bus. What the total time of her journey?
(7) A train that starts from Mumbai at 17:50 reaches Nira at 2:10. How long does the Mumbai – Nira journey take?
Answer:
(1) 1 hour 55 minutes
(2) 8 hrs 15 min
(3) 1 hr 55 min
(4) 1 hr 45 min
(5) 6 hrs 55 min
(6) 3 hrs 50 min
(7) 8 hrs 20 min

Maharashtra Board Class 5 Maths Solutions

• Measuring Time Problem Set 43 Class 5 Maths Solutions
• Measuring Time Problem Set 44 Class 5 Maths Solutions
• Measuring Time Problem Set 45 Class 5 Maths Solutions

Multiples and Factors Class 5 Problem Set 34 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 34 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 8 Multiples and Factors

Question 1.
Write all the prime numbers between 1 and 20.
Answer:
2, 3, 5, 7, 11, 13, 17, 19.

Question 2.
Write all the composite numbers between 21 and 50.
Answer:
Composite numbers between 21 and 50 are 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49.

Question 3.
Circle the prime numbers in the list given below. 22, 37, 43, 48, 53, 60, 91, 57, 59, 77, 79, 97, 100
Answer:

Question 4.
Which of the prime numbers are even numbers?
Answer:
Only even prime number is 2. (the Rest of the even numbers are composites.)

Co-prime numbers

Dada : Tell me all the factors of 12 and 18.

Anju : I’ll tell the factors of 12: 1, 2, 3, 4, 6, 12.

Manju : I’ll give the factors of 18: 1, 2, 3, 6, 9, 18.

Dada : Now find the common factors of 12 and 18.

Anju : Common factors ?

Dada : 1, 2, 3 and 6 are in both groups, which means that they are common factors. Now tell me the factors of 10 and 21.

Sanju : Factors of 10 : 1, 2, 5, 10.

Manju : Factors of 21: 1, 3, 7, 21.

Dada : Which of the factors in these two groups are common?

Sanju : 1 is the only common factor.

Dada : Numbers which have only 1 as a common factor are called co-prime numbers, so 10 and 21 are co-prime numbers. The common factors of 12 and 18 are 1, 2, 3 and 6; which means that the common factors are more than one. Therefore, 12 and 18 are not co-prime numbers. Now tell me whether 8 and 10 are co-prime numbers.

Manju : The factors of 8 are 1, 2, 4 and 8 and the factors of 10 are 1, 2, 5 and 10. These numbers have two factors, 1 and 2, in common, so 8 and 10 are not co-prime numbers.

Multiples and Factors Problem Set 32 Additional Important Questions and Answers

Question 1.
21 to 50
Answer:
23, 29, 31, 37, 41, 43, 47

Question 2.
Which of the number is neither prime nor composite?
Answer:
1

Question 13.
Between nearest which two prime numbers the prime number 43 lies?
Answer:
43 lies between prime numbers 41 and 47.

Question 14.
Which of the prime numbers are odd numbers?
Answer:
All prime numbers are odd except 2.

Maharashtra Board Class 5 Maths Solutions

• Multiples and Factors Problem Set 32 Class 5 Maths Solutions
• Multiples and Factors Problem Set 33 Class 5 Maths Solutions
• Multiples and Factors Problem Set 34 Class 5 Maths Solutions
• Multiples and Factors Problem Set 35 Class 5 Maths Solutions

Preparation for Algebra Class 5 Problem Set 55 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 16 Preparation for Algebra Problem Set 55 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 16 Preparation for Algebra

Question 1.
Say whether right or wrong.

(1) (23 + 4) = (4 + 23)
Answer:
27 = 27 is right

(2) (9 + 4) > 12
Answer:
13 > 12 is right

(3) (9 + 4) < 12
Answer:
13 < 12 is wrong

(4) 138 > 138
Answer:
Wrong

(5) 138 < 138
Answer:
Wrong

(6) 138 = 138
Answer:
right

(7) (4 × 7) = 30 – 2
Answer:
28 = 28 is right

(8) \(\frac{25}{5}\) > 5
Answer:
5 > 5 is wrong.

(9) (5 × 8) = (8 × 5)
Answer:
40 = 40 is right

(10) (16 + 0) = 0
Answer:
16 + 0
= 16
16 = 0 is wrong

(11) (16 + 0) = 16
Answer:
16 = 16 is right.

(12) (9 + 4) = 12
Answer:
13 = 12 is wrong.

Question 2.
Fill in the blanks with the right symbol from <, > or =.

(1) (45 ÷ 9) [ ] (9 – 4)
Answer:
45 ÷ 9 = 5,
9 – 4 = 5 5
= 5
so, (45 + 9) = (9 – 4)

(2) (6 + 1) [ ] (3 × 2)
Answer:
6 + 1 = 7,
3 x 2 = 6
7 > 6
so, (6 + 1) > (3 x 2)

(3) (12 × 2) [ ] (25 + 10)
Answer:
12 x 2 = 24,
25 + 10 = 35
24 < 35
so, (12 x 2) < (25 + 10)

Question 3.
Fill in the blanks in the expressions with the proper numbers.

(1) (1 × 7) = ( [ ] × 1)
Answer:
1 x 7 = 7,
7 x 1 = 7
so, (1 x 7) = ( 7 x 1)

(2) (5 × 4) > (7 × [ ] )
Answer:
5 x 4 = 20, 7 x ………… must be less than 20.
7 x 2 = 14
so, (5 x 4) > ( 7 x 2)

(3) (48 ÷ 3) < ( [ ] × 5)
Answer:
48 – 3 = 16,
5 x 4 = 20
5 x 3 = 15
16 > 15 and 16 < 20 so, (48 + 3) <(4 x 5)

(4) (0 + 1) > (5 × [ ] )
Answer:
0 + 1 = 1,
5 x 1 = 5
5 x 0 = 0
1 < 5 and 1 > 0 so, (0 + 1) > (5 x Q)

(5) (35 ÷ 7) = ( [ ] + [ ] )
Answer:
35 ÷ 7 = 5,
3 + 2 = 5 so, (35 + 7) = (3 + 2)

(6) (6 – [ ] ) < (2 + 3)
Answer:
6 – < 2 + 3 = 5
5 > 6 – 2
so, (6 – 2) < (2 + 3)

Using letters
Symbols are frequently used in mathematical writing. The use of symbols makes the writing very short. For example, using symbols, ‘Division of 75 by 15 gives us 5’ can be written in short as ‘75 ÷ 15 = 5’. It is also easier to grasp.

Letters can be used like symbols to make our writing short and simple.

While adding, subtracting or carrying out other operations on numbers, you must have discovered many properties of the operations.

For example, what properties do you see in sums like (9 + 4), (4 + 9)?

The sum of any two numbers and the sum obtained by reversing the order of the two numbers is the same.

Now see how much easier and faster it is to write this property using letters.

• Let us use a and b to represent any two numbers. Their sum will be ‘a + b’.

Changing the order of those numbers will make the addition ‘b + a’. Therefore, the rule will be : ‘For all values of a and b, (a + b) = (b + a).’

Let us see two more examples.

• Multiplying any number by 1 gives the number itself. In short, a × 1 = a.
• Given two unequal numbers, the division of the first by the second is not the same as the division of the second by the first.

In short, if a and b are two different numbers, then (a ÷b) ≠ (b ÷a).

Take the value of a as 8 and b as 4 and verify the property yourself.

Preparation for Algebra Problem Set 54 Additional Important Questions and Answers

Say whether right or wrong.

(1) (15 ÷ 3) =5
Answer:
5 = 5 is right.

(2) (2 x 1) = 1
Answer:
2 = 1 is wrong.

(3) (16 ÷ 8) = (2 x 2)
Answer:
2 = 4 is wrong.

(4) (13 – 7) = 6
Answer:
6 = 6 is right.

(5) (1 x 0) = 1
Answer:
1 = 1 is wrong.

(6) (1 + 0) = 1
Answer:
1 = 1 is right.

Fill in the blanks with the right symbol from <, >, or =.

(1) (12 + 6) (10 X 2)
Answer:
12 + 6 = 18,
10 x 2 = 20
18 < 20
so, (12 + 6) < (10 x 2)

(2) (4 X 5) (10 X 2)
Answer:
4 x 5 = 20,
10 x 2 = 20
20 = 20
so, (4 x 5) = (10 x 2)

(3) (7 + 3) ………….. (3 X 3)
Answer:
7 + 3 = 10,
3 x 3 = 9
10 > 9
so, (7+ 3) > (3 x 3)

Fill in the blanks in the expressions with the proper numbers.

(1) (8 + ………….. ) = (8 x 1)
Answer:
8 + ……………. = 8,
8 x 1 = 8
8 + 0 = 8
so, (8 + 0) = (8 x 1)

(2) (5 x 6) > (14 x ……….. )
Answer:
5 x 6 = 30,
14 x 1 = 14
14 x 2 = 28
14 x 3 = 42
30 >28
so, (5 x 6) >(14 x 2)

(3) (6 X 7) < ( x 5)
Ans.
6 x 7 = 42,
9 x 5 = 45
42 < 45, 50, 55
so, (6 x 7) < (9 x 5)

Maharashtra Board Class 5 Maths Solutions

• Three Dimensional Objects and Nets Problem Set 51  Class 5 Maths Solutions
• Pictographs Problem Set 52 Class 5 Maths Solutions
• Patterns Problem Set 53 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 54 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 55 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 56 Class 5 Maths Solutions

Addition and Subtraction Class 5 Problem Set 9 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 3 Addition and Subtraction Problem Set 9 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 3 Addition and Subtraction

Solve the following problems.

Question 1.
In a certain election, 13,47,048 women and 14,29,638 men cast their votes. How many votes were polled altogether?
Solution:
1 3 4 7 0 4 8 Women votes
+
1 4 2 9 6 3 8 Men votes
2 7 7 6 6 8 6 Total votes

Answer:
Altogether 27,76,686 votes were polled.

Question 2.
What will be the sum of the smallest and the largest six-digit numbers?
Solution:
1 0 0 0 0 0 Smallest six-digit No.
+
9 9 9 9 9 9 Largest six-digit No.
1 0 9 9 9 9 9 Total of six-digit No.

Answer:
Altogether 10,99,999 six-digit numbers.

Question 3.
If Surekhatai bought a tractor for ₹ 8,07,957 and a thresher for ₹ 32,609, how much money did she spend altogether?
Solution:
8 0 7 9 5 7 Tractor
+
3 2 6 0 9 Thresher
8 4 0 5 6 6 Total

Answer:
Surekhatai spend ₹ 8,40,566 altogether.

Question 4.
A textile mill produced 17,24,938 metres of cloth last year and 23,47,056 metres this year. What was the total production for the two years?
Solution:
1724938 m. prod, last year
+
2347056 m. prod, this year
4071994 m. prod, in 2 years

Answer:
40,71,994 metres was the total production for the two years.

Question 5.
If the Government gave ₹ 34,62,950 worth of computers and ₹ 3,26,578 worth of TV sets to the schools, what is the total amount it spent on this equipment?
Solution:
3 4 6 2 9 5 0 ₹ Computers
3 2 6 5 7 8 ₹ TV sets
3 7 8 9 5 2 8 Total ₹

Answer:
Total amount spent on equipments is ₹ 37,89,528

Subtraction : Revision

Study the following example.

Last year, 38,796 students took a certain exam. This year the number was 47,528. How many more students took the exam this year?

8,732 more students took the exam this year.

Addition and Subtraction Problem Set 9 Additional Important Questions and Answers

Question 1.
Solve the following problems.

(1) Goods of ₹ 14,08,345 was sold on last month and goods of ₹ 15,16,178 sold this month. What is the total sale of goods in these two months?
Solution:
1 4 0 8 3 4 5 Sale of last month
+
1 5 1 6 1 7 8 Sale in this month
2 9 2 4 5 2 3 Total sale of goods

Answer:
Total sale of good is ₹ 29,24,523

(2) Sundar purchased the flat of ₹ 28,15,000 and a Car of ₹ 12,05,500. What is the total amount spent by him?
Solution:
2 8 1 5 0 0 0 Cost of flat
1 2 0 5 5 0 0 Cost of Car
4 0 2 0 5 0 0 Total cost

Answer:
Total cost of ₹ 40,20,500

Maharashtra Board Class 5 Maths Solutions

• Addition and Subtraction Problem Set 7 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 8 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 9 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 10 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 11 Class 5 Maths Solutions 
• Addition and Subtraction Problem Set 12 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 13 Class 5 Maths Solutions

Number Work Class 5 Problem Set 3 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 2 Number Work Problem Set 3 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 2 Number Work

Question 1.
Read the numbers and write them in words.
(1) 7,65,234
(2) 4,73,225
(3) 3,27,001
(4) 8,75,375
(5) 1,50,437
(6) 2,03,174
(7) 6,47,851
(8) 9,00,999
(9) 5,75,010
(10) 4,03,005
Answer:
(1) Seven lakh, sisxty-five thousand, two hundred and thirty-four.
(2) Four lakh, seventy-three thousand, two hundred and twenty-five.
(3) Three lakh, twenty-seven thousand and one
(4) Eight lakh seventy-five thousand three hundred and seventy-five
(5) One lakh fifty thousand four hundred and thirty seven
(6) Two lakh three thousand one hundred and seventy-four
(7) Six lakh forty seven thousand eight hundred and fifty-one
(8) Nine lakh nine hundred and ninety-nine
(9) Five lakh seventy-five thousand and ten
(10) Four lakh three thousand and five.

Question 2.
Read the numbers and write them in figures.
(1) One lakh thirty-five thousand eight hundred and fifty-five
(2) Seven lakh twenty-seven thousand
(3) Four lakh twenty-five thousand three hundred
(4) Nine lakh nine thousand ninety-nine
(5) Seven lakh forty-nine thousand three hundred and sixty-two
(6) Eight lakh one sixty tow
Answer:
(1) 1,35,008
(2) 7,27,1 55
(3) 4,25,003
(4) 9,09,099
(5) 7,49,003
(6) 8,00,162

Question 3.
Make five six-digit numbers, each time using any of the digits 0 to 9 only once.
Answer:

• 4,09,138
• 3,17,045
• 1,20,645
• 9,72,860
• 6,54,302

Introducing seven-digit numbers
Teacher : Now we shall learn about seven-digit numbers. Suppose 10 farmers borrow ₹ 1,00,000 each from a Co-operative Bank. Then, how much is the total loan given by the bank to them?

Ajit : We must find out what is ten times 1,00,000. That is, we multiply 1,00,000 by 10. That means we write one zero after the number to be multiplied.

Ajay : 1,00,000 × 10 = 10,00,000

Teacher : This becomes a seven-digit number. We read it as ‘Ten lakh’. We must make one more place for the 10 lakhs to the left of the lakhs place. In western countries, the term million is used. One million is equal to ten lakhs.

Thus, ten lakh = 10,00,000.

Just as we read ten thousands and thousands together, we read ten lakhs and lakhs together. So, we read 18,35,614 as ‘eighteen lakh, thirty-five thousand, six hundred and fourteen.

Study the seven-digit numbers given below in figures and in words.

• 31,25,745 : thirty-one lakh, twenty-five thousand, seven hundred and forty-five
• 91,00,006 : ninety-one lakh and six
• 63,00,988 : sixty-three lakh, nine hundred and eighty-eight
• 88,00,400 : eighty-eight lakh, four hundred
• seventy-two lakh and ninety-five : 72,00,095
• seventy lakh, two thousand, three hundred : 70,02,300

Roman Numerals Problem Set 2 Additional Important Questions and Answers

Question 1.
Read the numbers and write them in words:

(1) 4,00,527
Answer:
Four lakh five hundred and twenty-seven.

(2) 7,34,016
Answer:
Seven lakh thirty-four thousand and sixteen.

Question 2.
Read the numbers and write them in figures.
(1) Nine lakh three thousand and twenty-three.
(2) One lakh one thousand one hundred and one.
Answer:
(1) 9,03,023
(2) 1,01,101

Class 5 Maths Solution Maharashtra Board

• Roman Numerals Problem Set 1 Class 5 Maths Solutions
• Number Work Problem Set 2 Class 5 Maths Solutions
• Number Work Problem Set 3 Class 5 Maths Solutions
• Number Work Problem Set 4 Class 5 Maths Solutions
• Number Work Problem Set 5 Class 5 Maths Solutions
• Number Work Problem Set 6 Class 5 Maths Solutions

Decimal Fractions Class 5 Problem Set 40 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 40 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 9 Decimal Fractions

Write the following fractions as decimal fractions.

(1) Two and a half
Answer:
2 \(\frac{1}{2}\) = 2.5 = 2.50

(2) Two and a quarter
Answer:
2 \(\frac{1}{4}\) = 2.25

(3) Two and three quarters
Answer:
2 \(\frac{3}{4}\) = 2.75

(4) Ten and a half
Answer:
10 \(\frac{1}{2}\) = 10.5 = 10.50

(5) Fourteen and three quarters
Answer:
14 \(\frac{3}{4}\) = 14.75

(6) Sixteen and a quarter
Answer:
16 \(\frac{1}{4}\) = 16.25

(7) Twenty-eight and a half
Answer:
28 \(\frac{1}{2}\) = 28.50 = 28.5

Adding decimal fractions

Sir : If the cost of one pencil is two and a half rupees and the cost of a pen is four and half rupees, what is the total cost?

Sumit : Two and a half rupees means two rupees and one half rupee. Similarly, four and a half rupees means four rupees and one-half rupee. 4 rupees and 2 rupees make 6 rupees and two half rupees make one rupee, so both objects together cost 6 + 1 = 7 rupees.

Sir : Correct ! Now, see how this is done using decimals.
The sum of the 0’s in the hundredths place is 0.
0.5 + 0.5 is the same as
\(\frac{5}{10}+\frac{5}{10}=\frac{5+5}{10}=\frac{10}{10}=\frac{1}{1}=1\)

This 1 is carried over to the units place. There is nothing in the tenths place, so we put a zero there. In the units place, 2 + 4 = 6 plus the carried over 1 makes 7.

So 2.50 rupees and 4.50 rupees add up to 7 rupees.

We use the decimal system to write whole numbers. We extend the same method to write fractions; therefore, we can add in the same way as we add whole numbers.

I will now show some more additions. Watch carefully.

Sumit : There is no carried over number in the first sum, but there are carried over numbers in the second and third sums.

Rekha : While adding whole numbers, we add units first. Similarly, here, tenths are added first. In the second example, the sum of the tenths place is 13. 13 tenths are 10 tenths + 3 tenths = 1 unit + 3 tenths.

Sumit : That is why, in the sum, 3 stayed in the tenths place and 1 was carried over to the units place. 6 + 5 plus 1 carried over makes 12.

Sir : Your observations are absolutely correct. We write digits one below the other according to their place values while adding whole numbers. We do the same thing here. Remember that while writing down an addition problem and the total, the decimal points should always be written one below the other.

Study the following additions. (Note that: 10 tenths = 1 unit. 10 hundredths = 1 tenth)

Example (1) Add : 7.09 + 54.93
First, add the digits in the 100ths place. 9 + 3 = 12.

The 1 from the sum 12 in the hundredths place is carried over to the tenths place and 2 is written in the hundredths place. Adding 1 + 9 gives 10 tenths or 1 unit. This 1 is carried over to the units place. 0 is left in the tenths place. Then, the addition is completed in the usual way.

Example (2) Add : 45.83 + 167.4
4 5 . 8 3 We arrange the numbers so that the places and
+
1 6 7. 4 decimal points come one below the other.

\(\frac{4}{10}=\frac{4 \times 10}{10 \times 10}=\frac{40}{100}\) Therefore, to make the denominators of the fractions equal, 167.4 is written as 167.40 and then the fractions are added.

As usual, the digits with the smallest place values are added first and then those with bigger place values are added serially.

Example (3) 10.46 Rupees

Example (4) 48.80 m

Example (5) 7.5 cm

Decimal Fractions Problem Set 40 Additional Important Questions and Answers

(1) Thirty and a quarter
Answer:
30 \(\frac{1}{4}\) = 30.25

(2) Thirty and a half
Answer:
30 \(\frac{1}{2}\) = 30.50 = 30.5

(3) Thirty and three quarters
Answer:
30 \(\frac{3}{4}\) = 30.75

Maharashtra Board Class 5 Maths Solutions

• Decimal Fractions Problem Set 36 Class 5 Maths Solutions
• Decimal Fractions Problem Set 37 Class 5 Maths Solutions
• Decimal Fractions Problem Set 38 Class 5 Maths Solutions
• Decimal Fractions Problem Set 39 Class 5 Maths Solutions
• Decimal Fractions Problem Set 40 Class 5 Maths Solutions
• Decimal Fractions Problem Set 41 Class 5 Maths Solutions
• Decimal Fractions Problem Set 42 Class 5 Maths Solutions

Addition and Subtraction Class 5 Problem Set 13 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 3 Addition and Subtraction Problem Set 13 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 3 Addition and Subtraction

Solve the following mixed word problems:

Question 1.
The Forest Department planted 23,078 trees of khair, 19,476 of behada besides trees of several other kinds. If the Department planted 50,000 trees altogether, how many trees were neither of khair nor of behada?
Solution:
2 3 0 7 8 Trees of khair
+
1 9 4 7 6 Trees of behada
4 2 5 5 4 Trees of khair and behada

5 0 0 0 0 Total trees planted
–
4 2 5 5 4 Khair and behada trees planted
7 4 4 6 Other kind of trees planted

Answer:
7,446 trees planted other than khair and behada trees.

Question 2.
A city has a population of 37,04,926. If this includes 11,24,069 men and 10,96,478 women, what is the number of children in the city?
Solution:
1 1 2 4 0 6 9 Men
+
1 0 9 6 4 7 8 Women
2 2 2 0 5 4 7 Total of men and women

3 7 0 4 9 2 6 Total population
–
2 2 2 0 5 4 7 Men and women
1 4 8 4 3 7 9 No. of children

Answer:
Number of children in the city is 14,84,379.

Question 3.
The management of a certain factory had 25,40,600 rupees in the labour welfare fund. From this fund, 12,37,865 rupees were used for medical expenses, 8,42,317 rupees were spent on the education of the workers’ children and the remaining was put aside for a canteen. How much money was put aside for the canteen?
Solution:
₹ 1 2 3 7 8 6 5 Medical expenses
₹ 8 4 2 3 1 7 Education for workers children
₹ 2080182 Spent for medical and education.
₹ 2 5 4 0 6 0 0 Labour welfare fund
₹ 2 0 8 0 1 8 2 Medical & education
₹ 4 6 0 4 1 8 Kept a side for canteen


Answer:
₹ 4,60,418 put aside for the canteen,

Question 4.
For a three-day cricket match, 13,608 tickets were sold on the first day and 8,955 on the second day. If, altogether, 36,563 tickets were sold in three days, how many were sold on the third day?
Solution:
1 3 6 0 8 Tickets sold on 1st day
+
8 9 5 5 Ticket sold on 2nd day
2 2 5 6 3 Tickets sold on 1st and 2nd day
3 6 5 6 3 Tickets sold in 3 days
–
2 2 5 6 3 Tickets sold in 2 days
1 4 0 0 0 Tickets sold on 3rd day


Answer:
₹ 14,000 tickets sold on the third day.

Addition and Subtraction Problem Set 13 Additional Important Questions and Answers

Solve the following mixed word problems:

Question 1.
A man had ₹ 1,65,346 in the bank. He deposited ₹ 2,47,190 in the bank, then he gave a cheque of ₹ 3,18,649 to Ashutosh. How much’is the balance in the bank now?
Solution:
₹ 1 6 5 3 4 6 Had in the bank
+
₹ 2 4 7 1 9 0 Deposited in the bank
₹ 4 1 2 5 3 6 Total balance
₹ 4 1 2 5 3 6 Total
–
₹ 3 1 8 6 4 9 Gave to Ashutosh
₹ 9 3 8 8 7 Balance in the bank

Answer:
Balance in the bank ₹ 93,887.

Question 2.
Vighanesh had ₹ 36,28,500 from this amount he gave ₹ 15,04,930 to his wife and ₹ 10,13,825to his son. How much amount left with him?
Solution:
₹ 3 6 2 8 5 0 0 Vighanesh had
–
₹ 1 5 0 4 9 3 0 given to wife
₹ 2 1 2 3 5 7 0 Total

₹ 2 1 2 3 5 7 0 Balance
–
₹ 1 0 1 3 8 2 5 Gave to son
₹ 1 1 0 9 7 4 5 Left with him

Answer:
₹ 11,09,745 left with Vighanesh.

Question 2.
Add the following:

(1) 3 0 5 8 3
+
1 2 3 2 9
_____________
_____________
Answer:
42912

(2) 4 5 3 7 8
+
4 4 6 2 2
_____________
_____________
Answer:
90000

(3) 7 5 0 3 8
+
1 7 4 1 8
_____________
_____________
Answer:
92456

(4) 2 2 1 0 5
+
3 9 6 5 1
_____________
_____________
Answer:
61756

Question 3.
Add the following:
(1) 63,348 + 74,35,631
(2) 9,65,247 + 3,28,925
(3) 7,61,856 + 1,45,437
(4) 33,23,057 + 35,28,436
(5) 3,451 + 62,507 + 3,40,678
(6) 48 + 38,41,705 + 98,314
(7) 25,38,781 + 328 + 16,508
(8) 29,145 + 40,37,615 + 8,70,469
Answer:
(1) 74,98,979
(2) 12,94,172
(3) 9,07,293
(4) 68,51,493
(5) 4,06,636
(6) 39,40,065
(7) 25,55,617
(8) 49,37,229

Question 4.
Match the equal numbers in three columns

Answer:
(1) b – iv
(2) d – iii
(3) a – ii
(4) c – i

Question 5.
Subtract the following:

(1) 7 6 3 8 5
–
5 7 6 3 7
____________
____________
Answer:
18,748

(2) 5 6 0 4 7
–
3 2 3 7 8
____________
____________
Answer:
23,669

(3) 8 2 3 5 6
–
4 1 5 6 3 9
____________
____________
Answer:
36,927

(4) 4 5 4 2 9
–
3 5 9 6 8
____________
____________
Answer:
04,788

(5) 7 4 3 5 0 8
–
4 1 5 6 3 9
____________
____________
Answer:
3,27,869

(6) 2 4 8 1 3 6 7
–
1 7 8 4 2 7 8
____________
____________
Answer:
6,97,089

(7) 5 9 3 1 6 6 5
–
4 3 6 5 7 4 9
____________
____________
Answer:
19,79,109

(8) 8 0 5 1 4 3 6
–
4 3 6 5 7 4 9
____________
____________
Answer:
36,85,687

Question 6.
Solve the following examples :
(1) (a) 64,83,217 – 23,94,128 + 16,84,579
(b) 36,94,523 + 28,17,689 – 50,49,876
(c) 83,47,215 – 38,58,386 – 25,74,978
(d) 3,72,190 + 2,18,310 – 1,56,900
(e) 36,00,800 – 27,91,978 – 3,01,005
(f) 51,51,515 – 5,55,555 + 6,66,006
Answer:
(a) 57,73,668
(b) 14,62,336
(c) 19,13,851
(d) 4,33,600
(e) 5,07,817
(f) 52,61,966

Maharashtra Board Class 5 Maths Solutions

• Addition and Subtraction Problem Set 7 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 8 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 9 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 10 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 11 Class 5 Maths Solutions 
• Addition and Subtraction Problem Set 12 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 13 Class 5 Maths Solutions

Quadrilaterals Class 6 Maths Chapter 16 Practice Set 37 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 16 Quadrilaterals Class 6 Practice Set 37 Answers Solutions.

Std 6 Maths Practice Set 37 Solutions Answers

Question 1.
Observe the figures below and find out their names:

Solution:
i. Pentagon (5 sides)
ii. Hexagon (6 sides)
iii. Heptagon (7 sides)
iv. Octagon (8 sides)

Maharashtra Board Class 6 Maths Chapter 16 Quadrilaterals Practice Set 37 Intext Questions and Activities

Question 1.
Observe the figures given below and say which of them are quadrilaterals. (Textbook pg. no. 81)

Solution:
Is a quadrilateral: (i)

Question 2.
Draw a quadrilateral. Draw one diagonal of this quadrilateral and divided it into two triangles. Measures all the angles in the figure. Is the sum of the measures of the four angles of the quadrilateral equal to the sum of the measures of the six angles of the two triangles? Verity that this is so with other quadrilaterals. (Textbook pg. no. 84)
Solution:

m∠PQR = 104°
m∠QRP = 26°
m∠RPQ = 50°
m∠PRS = 34°
m∠RSP = 106°
m∠SPR = 40°
∴ Sum of the measures of the angles of quadrilateral = m∠PQR + m∠QRP + m∠RPQ + m∠PRS + m∠RSP + m∠SPR
= 104° + 26° + 50° + 34° + 106° + 40°
= 360°
Also, we observe that
Sum of the measures of the angles of quadrilateral = Sum of the measures of angles of the two triangles (PQR and PRS)
= (104°+ 26°+ 50°)+ (34° + 106° + 40°)
= 180° + 180°
= 360°
[Note: Students should drew different quadrilaterals and verify the property.]

Question 3.
For the pentagon shown in the figure below, answer the following: (Textbook pg. no. 84)

1. Write the names of the five vertices of the pentagon.
2. Name the sides of the pentagon.
3. Name the angles of the pentagon.
4. See if you can sometimes find players on a field forming a pentagon.

Solution:

1. The vertices of the pentagon are points A, B, C, D and E.
2. The sides of the pentagon are segments AB, BC, CD, DE and EA.
3. The angles of the pentagon are ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB.
4. The players shown in the above figure form a pentagon. The players are standing on the vertices of

Question 4.
Cut out a paper in the shape of a quadrilateral. Make folds in it that join the vertices of opposite angles. What can these folds be called? (Textbook pg. no. 83)

Solution:
The folds are called diagonals of the quadrilateral.

Question 5.
Take two triangular pieces of paper such that . one side of one triangle is equal to one side of the other. Let us suppose that in ∆ABC and ∆PQR, sides AC and PQ are the equal sides. Join the triangles so that their equal sides lie B side by side. What figure do we get? (Textbook pg. no. 83)

Solution:
If we place the triangles together such that the equal sides overlap, the two triangles form a quadrilateral.

6th Std Maths Digest Pdf Download

• Triangles and their Properties Practice Set 36 Class 6 Maths Solution
• Quadrilaterals Practice Set 37 Class 6 Maths Solution
• Quadrilaterals Practice Set 38 Class 6 Maths Solution
• Geometrical Constructions Practice Set 39 Class 6 Maths Solution
• Geometrical Constructions Practice Set 40 Class 6 Maths Solution
• Three Dimensional Shapes Practice Set 41 Class 6 Maths Solution

Angles Class 6 Maths Chapter 2 Practice Set 3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 2 Angles Class 6 Practice Set 3 Answers Solutions.

Std 6 Maths Practice Set 3 Solutions Answers

Question 1.
Use the proper geometrical instruments to construct the following angles. Use the compass and the ruler to bisect them:

1. 50°
2. 115°
3. 80°
4. 90°

Solution:

Maharashtra Board Class 6 Maths Chapter 2 Angles Practice Set 3 Intext Questions and Activities

Question 1.
Construct an angle bisector to obtain an angle of 30°. (Textbook pg. no. 11)
Solution: .
In order to get a bisected angle of a given measure, the student has to draw the angle having twice the measurement of required bisected angle.

For getting measurement of 30° (for the bisected angle), one has to make an angle of 60° (i.e. 30° × 2).

Step 1:
Draw ∠ABC of 60°.

Step 2:
Cut arcs on the rays BA and BC. Name these points as D and E respectively.

Step 3:
Place the compass point on point D and draw an arc inside the angle.
Without changing the distance of the compass, place the compass point on point E and cut the previous arc. Name the point of intersection as O

Step 4:
Draw ray BO.
Ray BO is the angle bisector of ∠ABC.
i.e. m∠ABO = m∠CBO = 30°

Question 2.
Construct an angle bisector to draw an angle of 45°. (Textbook pg. no. 11)
Solution:
For getting measurement of 45° (for the bisected angle), one has to make an angle of 90° (i.e. 45° × 2).
Step 1:
Draw ∠PQR of 90°.

Step 2:
Cut arcs on the rays QP and QR.
Name these points as M and N respectively.

Step 3:
Place the compass point on point M and draw an arc inside the angle.
Without changing the distance of the compass, place the compass point on point N and cut the

Step 4:
Draw ray QO.
Ray QO is the angle bisector of ∠PQR.
i.e. m∠PQO = m∠RQO = 45°

Question 3.
Ask three or more children to stand in a straight line. Take two long ropes. Let the child in the middle hold one end of each rope. With the help of the ropes, make the children on either side stand along a straight line. Tell them to move so as to form an acute angle, a right angle, an obtuse angle, a straight angle, a reflex angle and a full or complete angle in turn. Keeping the rope stretched will help to ensure that the children form straight lines. (Textbook pg. no. 6)
Solution:

Question 4.
Look at the pictures below and identify the different types of angles. (Textbook pg. no. 8)

Solution:
i. Complete angle
ii. Reflex and Acute angle
iii. Acute and Obtuse angle

6th Std Maths Digest Pdf Download

• Basic Concepts in Geometry Practice Set 1 Class 6 Maths Solution
• Angles Practice Set 2 Class 6 Maths Solution
• Angles Practice Set 3 Class 6 Maths Solution
• Integers Practice Set 4 Class 6 Maths Solution
• Integers Practice Set 5 Class 6 Maths Solution
• Integers Practice Set 6 Class 6 Maths Solution
• Integers Practice Set 7 Class 6 Maths Solution
• Integers Practice Set 8 Class 6 Maths Solution