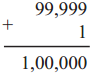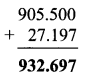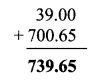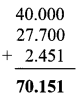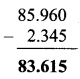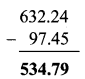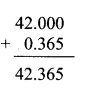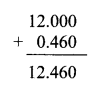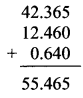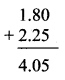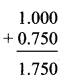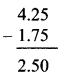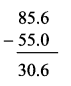Decimal Fractions Class 6 Maths Chapter 5 Practice Set 15 Solutions Maharashtra Board
Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 15 Answers Solutions.
Std 6 Maths Practice Set 15 Solutions Answers
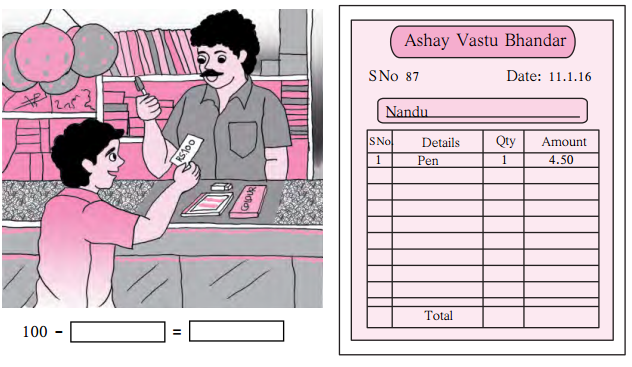
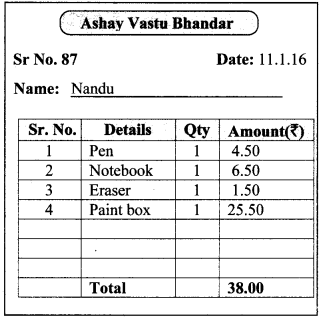
Question 1.
Write the proper number in the empty boxes.

Solution:

Question 2.
Convert the common fractions into decimal fractions:
i. \(\frac { 3 }{ 4 }\)
ii. \(\frac { 4 }{ 5 }\)
iii. \(\frac { 9 }{ 8 }\)
iv. \(\frac { 17 }{ 20 }\)
v. \(\frac { 36 }{ 40 }\)
vi. \(\frac { 7 }{ 25 }\)
vii. \(\frac { 19 }{ 200 }\)
Solution:
i. \(\frac { 3 }{ 4 }\)
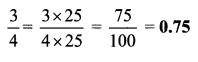
ii. \(\frac { 4 }{ 5 }\)
iii. \(\frac { 9 }{ 8 }\)
iv. \(\frac { 17 }{ 20 }\)
v. \(\frac { 36 }{ 40 }\)
vi. \(\frac { 7 }{ 25 }\)
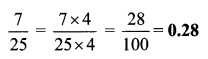
vii. \(\frac { 19 }{ 200 }\)
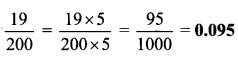
Question 3.
Convert the decimal fractions into common fractions:
i. 27.5
ii. 0.007
iii. 90.8
iv. 39.15
v. 3.12
vi. 70.400
Solution:
i. 27.5
= \(\frac { 275 }{ 10 }\)
ii. 0.007
= \(\frac { 7 }{ 1000 }\)
iii. 90.8
= \(\frac { 908 }{ 10 }\)
iv. 39.15
= \(\frac { 3915 }{ 100 }\)
v. 3.12
= \(\frac { 312 }{ 100 }\)
vi. 70.400
= 70.4
= \(\frac { 704 }{ 10 }\)
6th Std Maths Digest Pdf Download
- Operations on Fractions Practice Set 9 Class 6 Maths Solution
- Operations on Fractions Practice Set 10 Class 6 Maths Solution
- Operations on Fractions Practice Set 11 Class 6 Maths Solution
- Operations on Fractions Practice Set 12 Class 6 Maths Solution
- Operations on Fractions Practice Set 13 Class 6 Maths Solution
- Decimal Fractions Practice Set 14 Class 6 Maths Solution
- Decimal Fractions Practice Set 15 Class 6 Maths Solution
- Decimal Fractions Practice Set 16 Class 6 Maths Solution
- Decimal Fractions Practice Set 17 Class 6 Maths Solution