Category: Class 10

Class 10 English Chapter 2.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.2 The Boy who Broke The Bank Notes, Textbook Exercise Important Questions and Answers.

The Boy Who Broke The Bank Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.2 The Boy who Broke The Bank Textbook Questions and Answers

Warming up!

Chit-chat:

Question 1.
‘A lie can run round the world before truth has got its boots on.’ The above quotation expresses how fast rumours spread:
Talk with your group about some recent rumour, when people believed at first and suffered for it, later.
Answer:
There was a rumour recently in my locality, about a travel company that it was promising people a world tour at just ₹ 50,000. It had begun from a man’s misinterpretation of a newspaper advertisement, which stated that the company was offering a discount of ₹ 50,000. In no time, people were ready to book the tour for themselves.

They started contacting the company, in a rush, so that they didn’t miss the wonderful offer. On hearing the rumour, a conman thought of playing a trick. He claimed to be an employee of the company and started collecting money from people as advance. He even presented a fake Identity Card of himself, made fake bookings for the people and even gave them fake receipts for the payment they had made.

He took as many bookings as he could in a week and asked people to visit the company’s office in a week’s time to discuss further details. After a week, when people started showing up at the company’s office, they found out that the man never worked there and that the whole thing was a scam. More than 15 families fell victims to this scam and vowed never to believe in any such rumours again.

Question 2.
Discuss, how one can decide whether some news is a fact or fake.
Answer:
Points :
Find if it is reliable – believable – if it has any rational explanation – if it stands to your reason – or consider it fake and untrue – common sense can lead us to facts.

Question 3.
Who, do you think, are responsible for spreading fake news ?
Points :
Fake news are spread by some loafers or idle people or some mischief-makers – some spread false newsfor passing time – some justfor enjoying fun – some for taking revenge and harassing some targeted persons.

Question 4.
Do you believe in all the news you come across?
Points :
No – can use common sense – reasoning and its reliability.

Question 5.
Give one example of a rumour which seemed to be a fact in the beginning later it was proved false,
Answer:
SSC exams have been postponed for uncertain period. This news was not published by SSC Board.

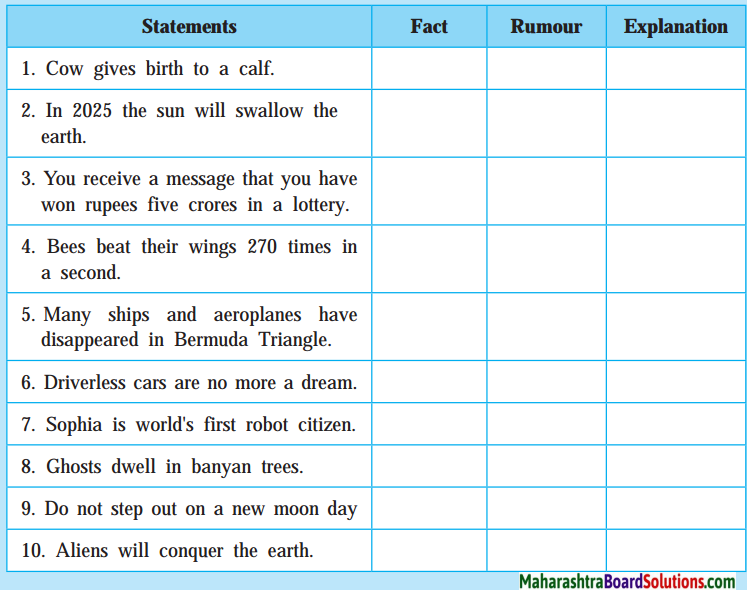
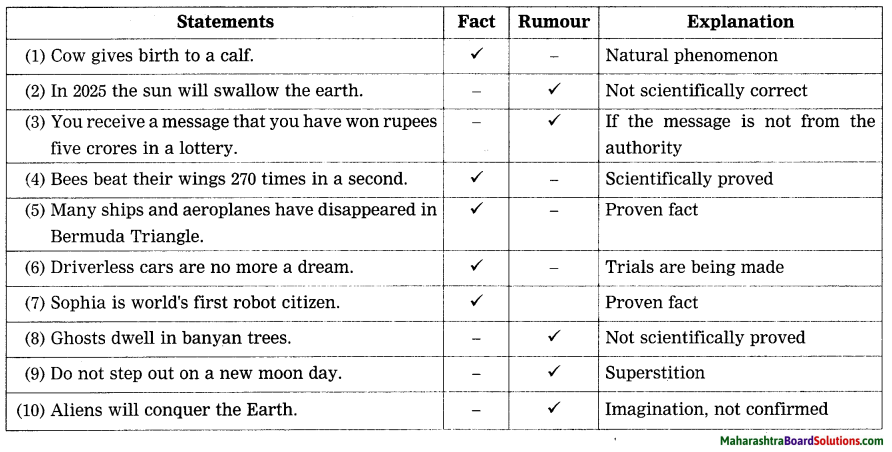
2. Read the following statements. Describe whether they are facts or rumours. Justify your decision.

Question 1.
Read the following statements. Describe whether they are facts or rumours. Justify your decision.

Answer:

English Workshop:

1. Who am I? (Identify the character from the extract.)

Question 1.
Who am I? (Identify the character from the extract.)
(a) I am the washerman’s son. Who am I? Sitaram
(b) I am the owner of the bank, who am I? ……………..
(c) I am the sweeper, who am I? ………………
(d) I am the friend of Mrs. Srivastava, who am I? ……………..
(e) I am the hair dresser. Who am I?
(f) I have a crooked leg, who am I?
Answer:
(a) I am the washerman’s son. Who am I? – Sitaram
(b) I am the owner of the bank, who am I? – Seth Govind Ram
(c) I am the sweeper, who am I? – Nathu
(d) I am the friend of Mrs. Srivastava, who am I? – Mrs. Bhushan
(e) I am the hair dresser. Who am I? – Deep Chand
(f) I have a crooked leg, who am I? – The beggar Ganpat.

2. Make a list of customers of Pipalnagar Bank, from the extract.

Question 1.
Make a list of customers of Pipalnagar Bank, from the extract.
Answer:

1. Betel-seller
2. Tailor
3. Free vendor
4. Jeweller
5. Beggar
6. Deep Chand, the barber
7. Elderly Gentleman
8. Ganpat, the beggar

3. Match the following and write the complete meaningful sentences.

Question 1.
Match the following and write the complete meaningful sentences.

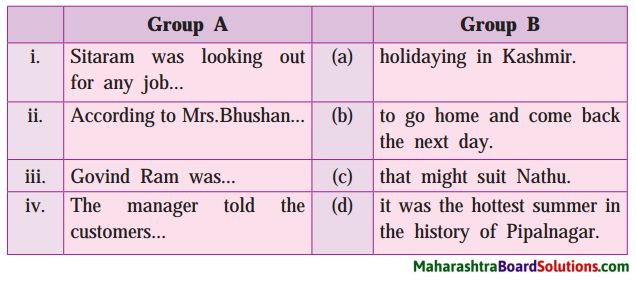
Answer:

4. Write who said to whom.

Question a.
“Don’t raise such dust!”
Answer:
Sitaram, the washerman’s son said this to Nathu, the sweeper.

Question b.
“Who would have thought the bank would collapse !“
Answer:
Nathu said this to himself.

Question c.
“Where did you disappear?”
Answer:
Mrs. Bhushan said this to her husband.

Question d.
“The bird has flown!”
Answer:
The elderly gentleman said to Deep Chand, the barber.

5. Why was the Manager of the Bank in a dilemma? Write down in 5 to 6 lines in your notebook.

Question 1.
Why was the Manager of the Bank in a dilemma? Write down in 5 to 6 lines in your notebook.
Answer:

1. The news of the collapse of the bank spread through Pipalnagar like wildfire and people rushed to the bank to withdraw their money.
2. By noon, the bank had exhausted all its ready cash.
3. This put the manager of the bank in a dilemma because emergency funds could only be obtained from another bank that was thirty miles away and he wasn’t sure that he would be able to convince the crowd to wait that long.
4. He was also worried because he had no way of contacting the owner of the bank, Seth Govind Ram, on his houseboat in Kashmir.

6. Cross out the odd man.

Question 1.
(a) sweeper, hooligan, beggar, declare, locker
(b) hurriedly, carelessly, salary, definitely, suddenly
(c) imminent, latest, pavement, awful, shocking
(d) morning, scattering, raising, collecting, shouting
Answer:
(a) sweeper, hooligan, beggar, declare, locker – declare
(b) hurriedly, carelessly, salary, definitely, suddenly – salary
(c) imminent, latest, pavement, awful, shocking – pavement
(d) morning, scattering, raising, collecting, shouting – morning

7. Find the describing words for the following from the text.

Question 1.
Find the describing words for the following from the text.

• …….. tour
• …….. shop
• …….. window
• …….. leg

Answer:

• customary tour
• photography shop
• plate glass window
• crooked leg

8. Complete the following table.

Question 1.
Complete the following table.

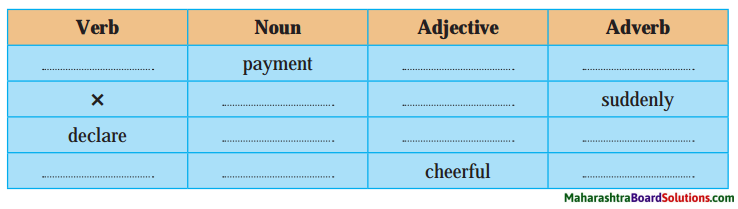
Answer:

9. Write in your own words a few sentences about each of the following :
(a) Nathu
(b) Mrs. Shrivastava
(c) Seth Govind Ram
(d) Sitaram

Question a.
Nathu
Answer:
Nathu: Nathu was a sweeper working with the Pipalnagar Bank, owned by Seth Govind Ram. He was annoyed because the Bank had not paid his salary though they were the last days of the month. He was sweeping hurriedly and carelessly because he was not happy with the owner. He was thinking of leaving that job.

Question b.
Mrs. Shrivastava
Answer:
Mrs Srivastava was Sitaram’s customer and was the lady of the house he visited. She gave some instructions to the ayah and the cook and then went the Pipalnagar market place, to make her usual tour of the cloth market. At one end of the bazaar she met her friend Mrs Bhushan. They both complained of the hot summer and they talked about a sample of cloth. Then Mrs Srivastava told Mrs Bhushan that Seth Govind Ram’s bank could not pay their sweeper for over a month. She seems to be very talkative lady and was the root cause of the rumour about Pipalnagar Bank.

Question c.
Seth Govind Ram
Answer:
Seth Govind Ram was the owner of the Pipalnagar Bank. A rumour was spread that the bank was about to go bankrupt. There was chaos among the people of Pipalnagar. Seth was holidaying in Kashmir and the manager of the Bank was in dilemma as he was unable to contact Seth Govind Ram who was on his houseboat in Kashmir. There were rumours about Seth’s absence in Pipalnagar.

Question d.
Sitaram
Answer:
Sitaram: Sitaram was a washerman’s son. He used to deliver freshly pressed clothes to every home. He plodded barefoot along the road to deliver a big bundle of clothes on his head. He was a helpful person. He was glad that he would be of service to both, a customer and his friend, Nathu.

10. Expand the theme in a write-up of about 20 lines.

Question a.
‘Rumours are spread by fools and accepted by greater fools’.
Answer:
‘Rumours are spread by fools and accepted by greater fools’ It is a common tendency of idle people or mischief-makers to spread rumours. These rumour-mongers themselves are fools. They spread some nasty, false news. They themselves do not know the truth or fact in the news. Many a times they have not heard or seen anything but repeat some story/news to people without believing it themselves.

A rumour is any talk, report or hearsay of doubtful nature or unverified statement or assertion. If we track such a rumour, we will find that it either is a falsehood, gossip or an exaggeration of the truth. So we can say that those who start spreading such rumours are fools. Every rumour suggests something more than it conveys and gives people uncomfortable sense of suspicion, mystery and sometimes dreadful traumas.

Some rumours are harmless though, they are spread by fools who intend to get joy and fun in doing so. Any kind of rumour does not stop at one place it goes from one person to another and one place to another. But greater fools are those who satisfy their natural tendency to believe what they want to believe and that also without going to the root of the news. People accept these rumours, add something to each and tell others and they go on nastier and nastier.

So responsibility, who accept the rumours, is greater. Not only gullible, ignorant people fall prey to rumours but also some educated, knowledgeable persons believe them because at that moment they do not use their reason and common sense or rational explanation and then suffer themselves. These people are greater fools because they never care to examine if that particular rumour is reliable, true or if it can stand to their reason.

Before you accept any such rumour be sure it is a fact, nothing untrue and unreliable in it. Or you will have to face unpleasant memories and experiences. So keep away from rumours.

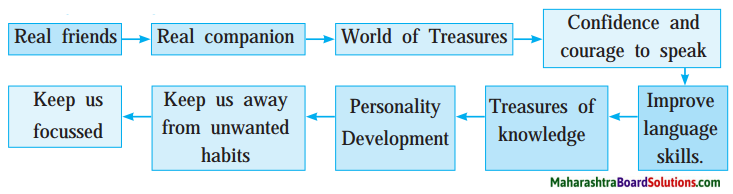
Question b.
‘Books are our real friends’
Answer:
Books are our real friends Books are our never-failing friends. They have their own value. As we need food for our body so we need books for our mind. They are our closest friends who give us precious wealth of knowledge and experience. They deal with various subjects in the world and on every aspect of our life. They are the world of treasures.

The books entertain us, advise us and give comfort and contentment to our soul and most importantly they impart wisdom that helps us throughout our life. They help you in your sufferings, depression and soothe your soul. They give you company when you are alone.

They are your real companions. Making friendship with books itself is a blessing. They take us to the journey into the beautiful world and help you to achieve your success like your true best friends. Good books also teach you the qualities that last long in your life. They give you confidence and courage to speak, to improve your language skills and develop your personality.

They accompany you in painful struggles, difficulties and bad days. They also help you to avoid your mistakes, flaws, teaching you wise conduct and wise tolerance towards others.

The books influence you forever and make you a gentle and knowledgeable person.
So, borrow books, buy books, preserve them and make friends with them as your true, real friends!

11. Project: Collect the names of books written by Ruskin Bond.

Question 1.
Collect the names of books written by Ruskin Bond.
Answer:
The names of books written by Ruskin Bond.
The Room of the Roof, Blue Umbrella, The Night Train at Deoli, Rusty, the Boy from the Hills, Road to Musoorie, Tales and Legends from India, Our Trees still Grow in Dehra, The India I love, Maharani, The Flight of Pigeons, Dust of the Mountain, The Book of Simple Living, The Kitemakers, All Roads Lead to Ganga, A Season of Ghosts, Vagrants in the Valley, etc.

Language Study:

1. I know of a sweeper boy who’s looking for work.
Observe the underlined part of the sentence. It tells us more about the sweeper boy. An adjective clause begins with words such as how, that, what, whatever, who, which, where, why etc.
Now, complete the sentences given below using your own adjective clauses.

• I know of a school boy …………………………….. .
• I know the joke …………………………….. .
• I know of a doctor ……………………………… .
• I know of a place ………………………………. .
• I know the reason …………………………….. .

Question 1.
Complete the sentences given below using your own adjective clauses :

• I know of a school boy …………………………….. .
• I know the joke …………………………….. .
• I know of a doctor ……………………………… .
• I know of a place ………………………………. .
• I know the reason …………………………….. .

Answer:

• I know of a school boy who is expert in horse riding.
• I know the joke that will split your sides with laughter.
• I know of a doctor who is hard of hearing.
• I know of a place where people crave for . bull-fights.
• I know the reason why the girl is always gloomy in the class.

2. Rewrite the following sentences joining them with ‘when’, where’, ‘which’, ‘why’.

Question a.
Sitaram had a bundle of freshly pressed clothes. He balanced it on his head.
Answer:
Sitaram had a bundle of freshly pressed clothes which he balanced on his head.

Question b.
A large shady tamarind tree grew at one end of the bazaar. Mrs. Srivastava found her friend Mrs. Bhushan there.
Answer:
Mrs Srivastava found her friend Mrs Bhushan where a large shady tamarind tree grew at one end of the bazaar.

Question c.
The Pipalnagar Bank has stopped paying employees. It is about to collapse.
Answer:
Pipalnagar bank which is about to collapse, has stopped paying his employees.

Question d.
He had finished his work. He sat down on the highest step.
Answer:
He sat down on the highest step when he had finished his work.

My English Coursebook 10th Digest Chapter 2.2 The Boy who Broke The Bank Additional Important Questions and Answers

Read the following passage and do the activities:

Simple Factual Activities:

Question 1.
Who am I? (Identify the character)
Answer:
I am the place where you can deposit and withdraw money. – Bank

Question 2.
Complete the sentences using the information from the passage:
(Answers are directly given and underlined.)
Answer:

1. Sitaram was looking out for any job that might suit Nathu.
2. The lady of the house was in need of a sweeper.
3. Sitaram talked to Mrs Srivastava about Nathu.

Question 3.
Who said to whom:

Question a.
‘Well, I wish you luck.’
Answer:
Sitaram said to Nathu.

Question b.
“But you go from one shop to another.”
Answer:
Mr Bhushan said this to his wife.

Question c.
“We want it now!”
Answer:
Some of the crowd said to the manager.

Question 4.
Complete the sentences using the information from the passage:
(Answers are directly given and underlined.)
Answer:

1. Mr Srivastava was talking to Kamal Kishore the owner of the photography shop.
2. Sitaram was glad that he had been of service to both a customer and his friend.
3. According to Mrs Bhushan, it was the hottest summer in the history of Pipalnagar.
4. Mr Bhushan said to his wife, “You go from one shop to another, like a bee in a flower garden.”

Question 5.
Who am I? (Identify the characters).
Answer:

1. I am the owner of the photography shop. – Kamal Kishore
2. I am the friend of Mrs Srivastava – Mrs Bhushan

Question 6.
Who am I? (Identify the characters)
Answer:
I sell betels. – betel seller

Question 7.
Who said to whom?

Question a.
‘The Pipalnagar Bank is about to collapse.’
Answer:
Kamal Kishore said this to Deep Chand.

Question 8.
Complete the following sentences using the information from the passage:
(Answers are directly given and underlined.)
Answer:

1. Govind Ram was holidaying in Kashmir.
2. The rumour about collapse of the Pipalnagar Bank spread through the bazaar with the rapidity of forest fire.
3. The photography shop was just next to the barber shop.
4. The elderly gentleman ran out of the barber’s shop and made a beeline for his office and chequebook.
5. The elderly gentleman called a bird to Seth Govind Ram.

Question 9.
Complete the following sentences with the information given in the passage:
(Answers are directly given and underlined.)
Answer:

1. The man with crooked leg was old Ganpat, the beggar.
2. Someone said that the Seth had hanged himself from the tamarind tree.
3. Ganpat ran to the Bank speedily to withdraw his one thousand rupees from the bank.
4. The crash of the Pipalnagar Bank set everyone talking and speculating and rushing about in a frenzy.

Question 10.
State whether the following statements are Rumours or Facts:
Answer:

1. The manager told the customers to go home and come back next day. – Fact
2. Nathu was disgusted to see the broken glass and stones cluttering the steps. – Fact
3. Seth Govind Ram was hiding in a safe deposit locker. – Rumour
4. The bank was going out of business. – Rumour

Question 11.
Who are the persons referred to in the following sentences:
1. He was the last person to know about the Pipalnagar Bank going bankrupt.
2. He was happy that he did not have a bank account in Pipalnagar Bank.
Answer:
1. Nathu, the sweeper
2. Sitaram, the washerman’s son.

Complex Factual Activities:

Question 1.
Arrange the following sentences as per their sequence occurred in the passage:
1. Nathu complained about his irregular pay.
2. Nathu used the small broom hurriedly.
3. Sitaram called out to Nathu.
4. Nathu grumbled as he swept the steps of the bank.
Answer:
4. Nathu grumbled as he swept the steps of the bank.
2. Nathu used the small broom hurriedly.
3. Sitaram called out to Nathu.
1. Nathu complained about his irregular pay.

Question 2.
Complete the web about Nathu’s annoyance.
(Answer is directly given.)
Answer:

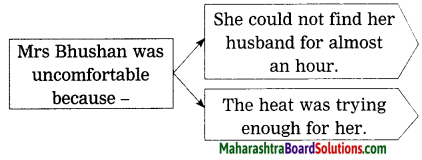
Question 3.
Complete the following web:
(Answer is directly given.)
Answer:

Question 4.
Complete the flow chart:
(Answers are directly given)
Answer:

Question 5.
How did the news spread everywhere?
Answer:
The news of the Bank’s collapse spread through the bazaar with the rapidity of fire. From Mr. Bhushan to Mr Kishore, Mr Kishore to the barber Deep Chand and the elderly gentleman and from there to the general merchant’s it travelled to the shop, circulated amongst the customers, then spread in various directions, to the betel-seller, the tailor, the free vendor, the jeweller, the beggar sitting on the pavement. It played havoc everywhere in Pipalnagar.

Question 6.
Complete the following sentences that tell you about Ganpat, the beggar:
(Answers are directly given and underlined.)
Answer:

1. Ganpat was an old beggar who had a crooked leg.
2. He had been squatting on the pavement for years.
3. He never used to walk.
4. When he learnt the collapse of the Bank, he leapt to his feet and ran at top speed in the direction of the Bank to withdraw his thousand rupees.

Question 7.
What was the effect of the rumour on the people of Pipalnagar?
Answer:
Men stood in groups at street corners and started discussing about the situation. Everyone was talking and speculating and rushing about in a frenzy. Some congratulated themselves for already taking out their money or never having put their money in the Bank. Some speculated that Seth Govind Ram’s excessive indulgence was the reason of crash.

Question 8.
What were the four rumours about Seth Govind Ram?
Answer:
The four rumours about Seth Govind Ram were as follows

1. The Seth had fled the State.
2. He had fled the country.
3. He was hiding in Pipalnagar.
4. He had hanged himself from the tamarind tree.

Question 9.
Complete the web: (Answer is directly given.)
Answer:

Activities based on Vocabulary:

Question 1.
Match the describing words with the nouns:

Answer:

Question 2.
Find the describing words for the following from the passage:

1. rupees
2. home
3. week

Answer:

1. extra two rupees
2. fourth home
3. another week.

Question 3.
Find describing words for the following from the passage:
meal
tamarind tree
Answer:
midday meal
large shady tamarind tree

Question 4.
Complete the following table.
(Answer is directly given.)
Answer:

Question 5.
Find the words from the passage that mean the following:

1. usual
2. raised to higher position
3. stable
4. without enough money to pay what you owe

Answer:

1. customary
2. hoisted
3. stationary
4. bankrupt

Question 6.
Make a list of customers of the Bank.:
Answer:
List of the customers: general merchant, customers of shops, betel-seller, the tailor, the free vendor, the jeweller, the beggar and many others.

Question 7.
Match the words in column ‘A’ with their meanings in Column ‘B’:

Answer:

Question 8.
Match the words in Column ‘A’ with their meanings in Column ‘B’:

Answer:

Question 9.
Find the describing words for the following from the passage:

1. fund
2. manager
3. speed

Answer:

1. emergency fund
2. harassed manager
3. top speed

Question 10.
Write one word for the following:

1. a person who deliberately causes trouble to people.
2. a person who washes clothes for other people.
3. a person who behaves extremely noisy and violent way in public.
4. a person who is in charge of the business of an organisation.

Answer:

1. a mischief-maker
2. a washerman
3. a hooligan
4. a manager

Question 11.
Find and write the infinitives with ‘to’ from the passage:
Answer:

1. to return
2. to placate
3. to go
4. to sweep
5. to take up
6. to be paid
7. to claim
8. to await
9. to get.

Question 12.
Underline the odd man:
(Answers are directly given.)
Answer:

1. washerman, mischief-maker, sweeper, counter, hooligan
2. hurtled, cried, declared, gathered, joined
3. their, our, his, they, your
4. sound, locker, new, door, broom, bicycle

Activities based on Contextual Grammar:

Question 1.
He called out to Nathu.
(Rewrite the sentence in Past Continuous Tense.)
Answer:
He was calling out to Nathu.

Question 2.
Mrs Srivastava said, “Tell him to come and see me tomorrow.” (Change into indirect speech.)
Answer:
Mrs Srivastava told (asked) him to tell him: to come and see her the next day.

Question 3.
He swept the steps.
(Begin your sentence with ‘The steps …)
Answer:
The steps were swept by him.

Question 4.
Sitaram was on his delivery round.
(Choose the correct question tag)
(a) was he?
(b) didn’t he?
(c) wasn’t he?
Answer:
Sitaram was on his delivery round, wasn’t he?

Question 5.
Mrs Bhushan went in search of her husband. He was sitting in front of Kamal Kishore’s photography shop.
(Rewrite the sentence joining it with ‘who)
Answer:
Mrs Bhushan went in search of her husband who was sitting in front of Kamal Kishore’s photography shop.

Question 6.
That summer was the hottest in the history of Pipalnagar.
(Change the sentence into Positive Degree.)
Answer:
No other summer in the history of Pipalnagar was so hot as that.

Question 7.
‘Shocking!’ (Rewrite it as an assertive sentence.)
Answer:
It was really very shocking.

Question 8.
Rewrite the following sentences joining with when/where/which/why:

Question a.
He sped across the road to the general:
merchant’s store. There was a telephone there.
Answer:
He sped across the road to the general merchant’s store where there was a telephone.

Question 9.
Mr Kishore said, “Deep Chand, have you heard the latest?” (Change into indirect speech.)
Answer:
Mr Kishore asked Deep Chand if he had heard the latest.

Question 10.
The Seth was holidaying in Kashmir. (Frame a wh-question to get the underlined word as answer.)
Answer:
Where was the Seth holidaying?

Question 11.
I must know the reason. You are late.
(Join the sentence with the word ‘why’.)
Answer:
I must know why you are late.

Question 12.
He was hiding in Pipalnagar.
(Rewrite the sentence using Simple Present Tense.)
Answer:
He hides in Pipalnagar.

Question 13.
He wasn’t sure he could persuade the crowd.
(Add a question tag.)
Answer:
He wasn’t sure he could persuade the crowd, was he?

Personal Response:

Question 1.
What qualities do you find in Sitaram?
Answer:
Sitaram was a hardworking young boy. He ‘ was always ready to help others and sympathetic towards suffering people. He felt happy to serve his customer and his friend.

Question 2.
What makes you angry? What do you do then?
OR
How do you show your annoyance?
Answer:
Somebody’s bad behaviour or arrogance makes me angry. When I get annoyed I do not react with harsh words or any violent action. I try to keep myself cool and try to bring to his/her notice, the wrong he/she is doing with me. I shall take time: and prove him/her wrong.

Question 3.
Do you think, Mr Bhushan was right to compare his wife with a bee in a flower garden? Give your reason.
Answer:
Yes, I think Mr Bhushan was absolutely right to compare his wife with a bee in flower garden. We know that bees buzz from flower to flower in gardens for collecting honey. He knew that his wife similarly used to visit many shops for selecting her clothes or only to have a look at them.

Question 4.
Why, do you think, did the elderly gentleman rush to his office for a chequebook?
Answer:
The elderly gentleman had heard the rumour about Seth Govind Ram’s Bank. He thought that the Seth had gone broke and so he must have fled to another town. I think the gentleman ran for his chequebook because he wanted to withdraw all his money from the bank before it was declared bankrupt.

Question 5.
Have you ever heard a rumour that harmed people? Elaborate it.
Answer:
Yes, I have not only heard but also have experienced such a rumour that has harmed people. We had been to a theatre to watch a movie. It was the first show of the movie. In the middle of the show a person shouted ‘Fire! Fire!’. People in the theatre left their seats in fright and ran helter- skelter to the exits for safety. Many fell and were trampled underfoot in the rush. It was an awful scene. Truth came to light that the miscreant was an agent of a producer who wanted the movie to fail.

Question 6.
How are rumours spread? Are the rumours harmful? Why?/Why not?
Answer:
The rumour-mongers talk to some people about a news, which is not true. They talk to others and it goes from one person to another and spreads like forest fire. They generally don’t think if the news is reliable or rational or false. Some rumours are harmful and some are harmless. The rumours that are spread intentionally to harm the sentiments of people are harmful. These rumours depress, disturb and cause harassment to people. The rumours that are spread just for fun are harmless but they fool people.

Do as directed:

Question 1.
Nathu raised his hands in a gesture of horror. He cried. (Join the sentences beginning with the word ‘Raising’.)
Answer:
Raising his hand in a gesture of horror Nathu cried.

Question 2.
He was determined to get his pay.
(Change the sentence into exclamatory sentence.)
Answer:
How determined he was to get his pay!

Question 3.
Give us our money.
(Change the sentence in Passive Voice.)
Answer:
Let our money be given to us.

Question 4.
So, they gathered outside.
(Write the sentence in Present Continuous Tense.)
Answer:
So, they are gathering outside.

Question 5.
Complete the words by using the correct letters:

1. r o _ n d
2. t h i _ k
3. p l _ t e
4. s t _ r e

Answer:

1. r o u n d
2. t h i n k
3. p l a t e
4. s t o r e

Question 6.
Put the words in alphabetical order:

1. shook, beggar, thousand, jeweller.
2. soon, street, seldom, speculate.

Answer:

1. beggar, jeweller, shook, thousand.
2. seldom, soon, speculate, street.

Question 7.
Punctuate the following sentences:
1. fetch the Seth, we know hes hiding in a safe deposit locker
2. Do you know my dear that Seth govind Rams bank cant even pay its employees
Answer:
1. “Fetch the Seth, we know he’s hiding in a safe deposit locker!”
2. “Do you know, my dear, that Seth Govind Ram’s bank cant even pay its employees?”

Question 8.
Write related words as shown in the example:
(Answer is directly given and underlined.)
Answer:

Question 9.
Complete these word-chain of verbs:
tell → ………. → …………. → ………. → …………..
Answer:
tell → learn → need → dare → eat.

Do as directed:

1. Attempt any one:

Question a.
Make a meaningful sentence of your own using the phrase: to take up
Answer:
Recently he has taken up a new project in hand.
OR
Question b.
Add a clause to the following sentence to expand it meaningfully:
This is the answer – ………………..
Answer:
This is the answer that I was longing for.

2. Attempt anyone:

Question a.
Add a prefix or suffix to make new words:
1. possible
2. certain
Answer:
1. impossible
2. uncertain
OR
Question b.
Make a meaningful sentence using any one of the following words:
1. possible
2. certain
Answer:
1. It is not possible to do this work in such a short time.
2. The young boy was certain about his future career.

My English Coursebook 10th Digest Pdf Unit 2 

• You Start Dying Slowly … 10th English Solutions
• The Boy who Broke The Bank 10th English Solutions
• The Twins 10th English Solutions
• An Epitome of Courage 10th English Solutions
• Book Review – Swami and Friends 10th English Solutions
• World Heritage 10th English Solutions

Class 10 English Chapter 2.6 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.6 Science and Spirituality Notes, Textbook Exercise Important Questions and Answers.

Science and Spirituality Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 2.6 Warming Up Questions and Answers

Question 1.
Get into pairs/groups and match the columns:

Answer:

Question 2.
Given below are some incomplete Quotes. Complete them choosing from the words SCIENCE /RELIGION /SPIRITUAL and make them meaningful:

• ………………………….. without religion is lame; without science is blind. ………………………….. has outrun our power, we have guided missiles, but misguided man.
• On a ………………………….. journey, we all have the same destination.
• ………………………….. is meant to awaken man’s love for his Source – God!
• ………………………….. provides a means of with the Creator of Heaven and Earth, in the language of your heart and soul.
• ………………………….. is a beautiful gift to humanity; we should not distort it.

Answer:

• Science, Religion
• Science, Spiritual
• Spiritual
• Religion
• Religion
• Science

Question 3.
What’s the difference between science and technology? Discuss in pairs and tell your answer to the class.
Answer:
We generally assume that science and technology mean almost the same thing. HowSver, there is a difference. The goal of science is the pursuit of knowledge for its own sake while the goal of technology is to turn the scientific knowledge into industrial and commercial use. Simply put, technology is the practical application of science,

Question 4.
Do you think that science and faith are both important in our lives? Why? Discuss in your group and give a small presentation in front of the class.
Answer:
Yes, both science and faith are important in our lives. There is no contradiction between the two. Both genuinely seek the truth. Science explores the truth about the material and physical world. Faith introspects on the spiritual aspects including the Self and the Creator. Science helps us understand the physical structure of the universe, while faith deals with human values and morals. Both complement each other. In the words of Einstein, ‘Science without religion is lame; religion without science is blind.’

Question 5.
We need science

Answer:

Question 6.
Refer to a dictionary to find out the meanings of the following words.

• Spirit- a person’s mind or feelings or soul.
• Spiritual
• Spirituality
• Spiritualism
• Spiritualist

Answer:

• Spiritual – relating to or affecting the human spirit or soul, as opposed to material or physical things
• Spirituality – the quality of being concerned with the human spirit, or soul, as opposed to material or physical things
• Spiritualism – a system of belief or religious practice based on supposed communication with the spirits of the dead, especially through mediums
• Spiritualist – an advocate of the doctrine that the spirit exists as distinct from matter, or that spirit is the only reality

Science and Spirituality Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
(A) Read ‘Part I’ and match the words in Column ‘A’ with associating words given in Column ‘B’.

(i) …………………………..
(ii) …………………………..
(iii) …………………………..
(iv) …………………………..
(v) …………………………..
Answer:

(B) Read ‘Part II’. Go through the given statements and say whether you agree or disagree to each of them.
(a) The Space Research set up facility was planned at Allapi, Kerala – …………………………..
(b) The person who could help and can be contacted was the Bishop – …………………………..
(c) It was quite easy to relocate so many people and destroy religious institutions for space-research centre – …………………………..
(d) Dr. Kalam joined ISRO in 1970 – …………………………..
(e) Science and spirituality seeks prosperity of the human life – …………………………..
Answer:
(a) Disagree
(b) Agree
(c) centre Disagree
(d) Disagree
(e) Agree

(C) Go through ‘Part III’ and complete the following statements.
(a) The essence of a happy life and a peaceful society lies in one sentence – …………………………..
(b) To keep this planet liveable and the human race thriving, we have to …………………………..
(c) Mahaswamiji’s greatest contribution is the …………………………..
(d) We can remove the  our souls by …………………………..
(e) The narrator, Srijan, realised that through Dr. Kalam’s words of wisdom …………………………..
(f) Mahaswamiji possesses powers that kept him so strong were ………………………….. or
Answer:
(a) The essence of a happy life and a peaceful society lies in one sentence – ‘What can I give’.
(b) To keep this planet liveable and the human race thriving, we have to replace this attitude of ‘what can I take’ with the goodness of
(c) Mahaswamiji’s greatest contribution was the establishment of a free residential education system for more than nine thousand children in the ashram.
(d) We can remove the impurities obscuring our souls by living pure and ethical lives and by serving humanity.
(e) The narrator, Srijan, realized that through Dr Kalam’s words of wisdom he was getting to learn from countless great minds.
(f) The narrator (Srijan) said this to Dr Kalam ‘ while discussing the Mahaswamiji’s 102nd birthday i celebrations.

2. Choose the correct alternative for the given statements.
(A) Dr. Kalam’s father was an …………………………. .
(a) teacher
(b) scientist
(c) farmer
(d) imam.
Answer:
(d) imam.

(B) Dr. Kalam’s friends discussed on …………………………. .
(a) science and technology
(b) discoveries and inventions.
(c) science and spirituality
(d) community’s problems and solutions.
Answer:
(c) science and spirituality

(C) According to Dr. Kalam, the need that is felt more than ever is ………………………….. .
(a) a laboratory to conduct experiments.
(b) a new technology to find results.
(c) a dialogue among cultures, religions and civilizations.
(d) a dialogue between people of different professions.
Answer:
(c) a dialogue among cultures, religions and civilizations.

(D) Dr. Kalam’s father was a symbol of ………………………….. .
(a) trust and faith.
(b) simplicity and divinity
(c) teacher and disciple.
(d) father and friend.
Answer:
(b) simplicity and divinity

(E) Spirituality takes care of ………………………….. .
(a) education, teaching and learning.
(b) science, technology and sci-fi.
(c) confusion, misery or failure.
(d) crime, illiteracy and child labour.
Answer:
(c) confusion, misery or failure.

(F) How can academic brilliance diminish?
(a) by disturbance and frustration.
(b) by going off track
(c) by a coating of dust.
(d) by losing focus and seriousness.
Answer:
(d) by losing focus and seriousness

(G) What was most astonishing about 102 year old Swamiji?
(a) He was a great speaker and orator.
(b) He was a great scientist.
(c) He was a great admirer of technology.
(d) He looked as steady and alert as any other youngster.
Answer:
(d) He looked as steady and alert as any other youngster.

(H) What Dr. Kalam gathered while swimming in silence at the shores of Mahapragyaji?
(a) beautiful sea shores
(b) tree lined beaches
(c) sands of conscience
(d) beautiful sun-set.
Answer:
(c) sands of conscience

Question 3.
Among the three parts, there are people who touched and influenced the life of Dr. A. P. J. Kalam in one or the other ways. Complete the web chart by writing the names of such people.
Answer:
Kalam In one way or the other were:

Question 4.
Write the significance of the following years, as given in the text.
1960 ……………………………
1970 ……………………………
1980 ……………………………
2009 ……………………………
2012 ……………………………
Answer:
1960 → Is significant as Dr Kalamoined ISRO that year.
1970 → Dr Kalam made his first unsuccessful launch.
1980 → Dr Kalam made his first successful launch.
2009 → The writer graduated from IIMA and met Dr Kalam
2012 → The writer was discussing with Dr Kalam the number of Ph.D’s he (Dr Kalam) had received.

Question 5.
Who said to whom and when?
(a) “Can we give up God’s abode for such a great scientific mission ?”
…………………………………………………………………..
Answer:
Reverend Father Pereira said this to „the people in the Church, one Sunday. On the previous day, Dr Sarabhai and Dr Kalam had approached him to request the people to give up the church land for the building of a space research centre.

(b) “And then God will shine through us.”
…………………………………………………………………..
Answer:
Professor Satish Dhawan to Dr Kalam when ‘ they were talking about academic brilliance.

(c) “I wonder what power Mahaswamiji possesses, that keeps him so strong.”
…………………………………………………………………..
Answer:
Reverend Father Pereira said this to „the people in the Church, one Sunday. On the previous day, Dr Sarabhai and Dr Kalam had approached him to request the people to give up the church land for the building of a space research centre.

Question 6.
Answer the following in your own words, and write in your notebook.
(a) What makes Dr Kalam a humble personality?
Answer:
Even though Dr Kalam was indisputably a great scientist, he had deep faith and espoused the cause of the betterment of humanity. This shows that he was indeed a humble personality.

(b) How were different virtues inculcated in Dr Kalam?
Answer:
Dr Kalam inculcated the virtue of humility from his father who was a boatman. He learnt from his father how simplicity and divinity could go together.

(c) How did the Reverend relate and compare the work that he and Dr Sarabhai did for people?
Answer:
The Reverend said that Dr Sarabhai was a scientist. We benefit from the devices that science has developed in many ways – in our homes and in the fields of medicine and technology. A priest prays for the peace and well-being of his people. Thus both science and spirituality seek the Almighty’s blessing for the prosperity of the human mind and body. In short, both are doing the sameob.

(d) What was so remarkable about Dr Sri Sri Shivakumar Mahaswamiji?
Answer:
The remarkable aspect about Dr Sri Shivakumara Mahaswamiji was that he had dedicated his life to the service of humanity.

(e) Why is there an urgent need to replace ‘What can I take’ with ‘What can I give?
Answer:
There is an urgent need to replace ‘What can I take’ with ‘What can I give’ for the very survival of humanity. Unless we realize the gravity of the message, this planet will become a hub of environmental degradation, social evils, inequity and corruption. If we do not take up the challenge, our planet will not be liveable and the human race will not prosper.

Question 7.
In your notebook, write a short paragraph on each of the following covering up their profession and personality traits with examples.
(a) Rev. Peter Bernard Pereira
(b) Dr Sri Shivakumar Mahaswamiji
(c) Dr A. P. J. Abdul Kalam
Answer:
(a) His interactions with the great scientist Professor Vikram Sarabhai and the Reverend Peter Bernard Pereira shaped Dr Kalam’s thoughts on religion.
(b) The 102nd birthday celebrations of His Holiness Dr Sri Sri Shivakumara Mahaswamiji.
(c) Dr A P Abdul Kalam was the past President of India. By the way, he was a great scientist, orator and a humanitarian.

8. Write in your own simple words what the following expressions convey in the context they occur in the text.
(a) Faith and fact can, together, create a better planet.
…………………………………………………………………..
Answer:
If people have belief in a greater power! as well as understand the truth of things that exist around them, this world will become a better place for all of us to live in harmony.

(b) Dr Kalam’s own life was nourished by multiple faiths.
…………………………………………………………………..
Answer:
This means that the life of Dr Kalam improved in quality because of the discussion he had with people of different faiths, such as the head priest of a temple who was a Vedic scholar, and a Christian priest.

(c) But there was a major roadblock.
…………………………………………………………………..
Answer:
This expression conveys the fact that something was being planned, but there were serious issues that hindered its progress.

(d) Only when the dust is removed, does the mirror shine and the reflection becomes clear.
…………………………………………………………………..
Answer:
This expression is a comparison between the mind and the mirror. The brilliance of both can be diminished by many factors that act like coatings of dust. However, when that coating is removed, both shine and radiate brilliance.

(e) Through his (Kalam’s) words of wisdom, I was getting to learn from countless great minds.
…………………………………………………………………..
Answer:
This expression first of all conveys the information that Dr Kalam himself was a very well- read person who had acquired his knowledge from innumerable great minds of the past. Further, it conveys that the speaker (Narrator; Srijan) himself received an education from Dr Kalam by association with him.

(f) He gathered the sands of conscience to be our guide, our best friend.
…………………………………………………………………..
Answer:
These words convey the idea that Dr Kalam realized that our own conscience is our guide and! best friend.

(g) ‘What can I take?’ is the thought which is responsible for all the wrong, seen around us.
…………………………………………………………………..
Answer:
These words convey the idea that when people think only in terms of what they can get S from others, it leads to every possible illegal or bad behaviour.

9. (A) From the lesson, pick out one word for each of the following.
(a) increase the speed …………………………
(b) point of view …………………………
(c) nearness in space …………………………
(d) a place of residence …………………………
(e) eager to know everything …………………………
(f) echoed loudly …………………………
(g) giving away much to the needy …………………………
(h) without making a difference …………………………
Answer:
(a) accelerate
(b) perspective
(c) proximity
(d) abode
(e) inquIsitive
(f) reverberated
(g) munificence
(h) indiscriminately

(B) Arrange the following words in the alphabetical order.

• inventions,
• indisputable,
• interactions,
• inequity,
• institutions,
• inquisitive,
• indiscriminately

Answer:

• indiscrimInately,
• Indisputable,
• inequity,
• Inquisitive,
• institutions,
• Interactions,
• Inventions.

(C) Find from the lesson the noun forms of –
1. combine …………………………
2. solve …………………………
3. simple …………………………
4. divine …………………………
5. advance …………………………
6. tranquil …………………………
7. liveable …………………………
8. strong …………………………
Answer:
1. combination
2. solution
3. simplicity
4. divinity
5. advancement
6. tranquillity
7. life
8. strength

Question 10.
Match the word connectors with reference to part I, II, III respectively. Make sentences of each of these connectors.

Answer:
(1) Some government officials came to our village to inspect the sanitary conditions.
(2) Gandhiji’s efforts were for the betterment of humanity.
(3) The hermit was revered for living a pure and ethical life.
(4) We formed a core team to look into the community’s problems.
(5) We need religious discipline in order to develop a clear conscience.
(6) The most astonishing aspect of this great king’s personality is his humility.
(7) The district required more skilled manpower for technological advancement.
(8) The teacher had a frank dialogue with the youth about his drug problem.
(9) He left his good secureob in order to dedicate himself to social service.
(10) In order to make progress, people should avoid conservative faith curbs.
(11) To be a good detective, ond must basically be an inquisitive person.
(12) All through his school and college days he displayed academic brilliance.
(13) Plastics are major contributors to environmental degradation.
(14) There was pin-drop silence when the sad news was announced.
(15) The owner was provided alternate accommodation until his flat was renovated.
(16) Lai Bahadur Shastri was a remarkable person.
(17) Our inner beliefs should be the silent motivation to do good to others.
(18) The communal kitchen is a great boon to famished bodies.
(19) At the first attempt it was an unsuccessful launch.
(20) ISRO is a space research centre in Bengaluru.

Question 11.
Simple sentence : subject + verb + object/complement/adverbial: Analysing a simple sentence is done by separating the subject and the predicate. The predicate is further analysed into –
(1) verb + object as in ‘A doctor treats patients’./ ‘He greeted the teacher.’
(2) verb + complement as in ‘They are very tired.’ / ‘I have a cold.’
(3) verb + adverbial as in (He walks slowly. / Raj arrived late. / The thief is hiding there.)

Say whether the predicates in the following sentences have an object/a complement/an adverbial.
(1) There was silence. …………………………
(2) Alexander Bell invented the telephone. …………………………
(3) They have a holiday. …………………………
(4) The dancer danced gracefully. …………………………
(5) The milkman comes daily. …………………………
(6) The hostess served tea. …………………………
(7) The kite soared upwards. …………………………
Answer:
(1) Complement
(2) Object
(3) Complement
(4) Adverbial
(5) Adverbial
(6) Object
(7) Adverbial

Question 12.
(A) Punctuate the following sentences to make them meaningful.
(1) dinesh took a bus that stopped at nanded railway station after crossing somvar peth
(2) dr a p j abdul kalam was the past president of india by the way he was a great scientist orator and a humanitarian
(3) nouns are of different types common proper abstract concrete material
(4) what a lot of noise you all make said the teacher cant you keep quiet for a while
(5) wow how lovely that cake looks they said we cant wait to eat it
Answer”
(1) Dinesh took a bus that stopped at Nanded railway station after crossing Somvar Peth.
(2) Dr A P J Abdul Kalam was the past President of India. By the way, he was a great scientist, orator and a humanitarian.
(3) Nouns are of different types: common, proper, abstract, concrete, material.
(4) “What a lot of noise you all make!” said the teacher, “Can’t you keep quiet for a while?”
(5) “Wow! How lovely that cake looks!” they said, “We can’t wait to eat it.”

(B) Copy the first paragraph on page 92 in your notebook, carefully. Encircle all the punctuation marks with a colored pencil/pen.
“Dear children …………………. ‘amen’.

Question 13.
Project :
Read Dr. A.P.J. Abdul Kalam’s very renowned books ‘Wings of Fire’; and ‘Ignited Minds’, to find the following :
(a) Subject of the book
(b) Special features of the book
(c) Teachings/learnings/moral/message from the book
(d) Your own opinion/idea/comment on the book
Answer:
Dr A. P.. Kalam was the son of an imam, a simple fisherman. He was born in Rameswaram on 15 October 1931. He went on to become the 11th President of India from 2002 to 2007. He was widely acclaimed as the ‘People’s President’. He was particularly fond of children and youth and made himself approachable to them at all times.

He was a student of Physics and aerospace engineering. He was a scientist and science administrator mainly at the Defence Research and Development Organisation (DRDO) and Indian Space Research Organisation (ISRO) for nearly four decades. He was intimately involved in India’s civilian space programme and military missile development efforts.

He is famous as the Missile Man of India for his work on the development of ballistic missile and launch vehicle technology. He also played a pivotal organisational, technical, and political role in India’s Pokhran-II nuclear tests in 1998, the first since the initial nuclear test by India in 1974.

He was the recipient of several prestigious awards, including the Bharat Ratna in 1997, India’s highest civilian honour.

Amongst his writings, the most famous are ‘Transcendence: My Spiritual Experiences with Pramukh Swamiji’, and ‘India 2020’.

While delivering a lecture at the Indian Institute of Management, Shillong, Kalam collapsed and died from an apparent cardiac arrest on 27uly 2015, aged 83. Thousands including national-level dignitaries attended the funeral ceremony held in his hometown of Rameswaram, where he was buried with full state honours.

Question 14.
(A) Draft a speech that you would give at your School Assembly convincing junior students that the secret of true happiness lies in Giving and Sharing more than in Receiving and Taking.

Write it with the appropriate steps in your notebook.
Answer:
Friends,
It is through experience I .have learned that ‘AS’ you give, so you live’.

There was a time in my life when I only wanted things. I was happy only when I received gifts. My main goal in life was to take as many things from others as I could.

But then one day, on the way to market, I saw a beggar boy running along the road. In his hand he held a loaf of bread. He ran to his mother, who was lying on the sidewalk. He sat next to her and started feeding her. It touched me deeply that this boy who must have been hungry himself, found greateroy in feeding his famished mother.

From that day onwards I started giving things to others. If I had two pens and someone wanted one, I would give it to him or her. I asked my mother to give my old clothes to a poor child from a nearby slum. For my birthday celebrations, instead of having a party, I went along with my mother to the temple and fed a line of beggars.

Giving things to others brings me greatoy and happiness. Receiving something gives temporary satisfaction. But reaching out to others and seeing them smile, sharing things with others and making it worthwhile – these are far more precious than any other personal possessions.

Thank you.

(B) Divide your class in two groups and have a Debate on the topic ‘Science and Spirituality can go hand in hand’.
Answer:
For (view):
Both science and spirituality study aspects of our world. Both require mental discipline. Both require belief in certain axioms and truths. Hence both are valid. Science is the body. Spirituality is the mind. Science explores the creations of God. Spirituality delves into the nature of God. Both are two sides of the same coin. Both complement each other.

It is inevitable therefore that science and spirituality go hand in hand.

Against (counterview):

Science requires factual knowledge. It is a component of millions of physical laws. Spirituality is a free bird that soars on the wings- of personal belief. It does not require proof. Only faith. How then can they be considered to be on the same plane? One is concrete; the other abstract. In order to draw upon spirituality, one may conjure up any image in the mind and be satisfied. Science seeks explanation in logical reasoning based upon unlimited past experiences and developed into a truth by considering experiment after experiment.

The two are poles apart and cannot go hand in hand.

Question 15.
State whether the statements are True or False:
Answer:
(a) It is necessary for science and faith to function true to their roles.
(b) Kalam’s status as a great scientist is in dispute.
(c) Both fact and faith are required for a better world.
(d) There is never any conflict between believers in science and believers in religion.
Answer:
(a) True
(b) False
(c) True
(d) False

Question 16.
Why do science and faith have to go hand in hand?
Answer:
Science and faith must go hand in hand for the sake of human good. Science provides focus on human activities while faith gives one a perspective, which is essential for success.

Question 17.
From the passage pick out one word for each of the following:
(a) keeps something within limits
(b) unable to be challenged or doubted
Answer:
(a) curbs
(b) indisputable

Question 18.
Write the noun forms of:
(a) create
(b) coexist
(c) discover
(d) conceive
(e) accelerate.
Answer:
(a) create – creation
(b) coexist – coexistence
(c) discover – discovery
(d) conceive – conception
(e) accelerate – acceleration.

Question 19.
Faith provides perspective. (Rewrite beginning with ‘Perspective’.)
Answer:
Perspective is provided by faith.

Question 21.
Fill in the blanks with suitable prepositions: (The answers are given directly and underlined.)
Answer:
Conflict often arises between people who believe in science and people who believe in religion,

Question 22.
Which, according to you, is more important for our planet to survive – science or religion? Give your reasons in brief.
Answer:
According to me, both are important – science \ as well as religion. Science provides us with facts that tell us about our planet. Religion educates us about the proper attitude towards all things created on earth. We need both for our planet to survive. Both go hand in hand.

Question 23.
Complete the following map:
Answer:

Question 24.
Complete the following based on the passage: (The answers are given directly and underlined.)
Answer:
People who touched and influenced Dr A. P.. Kalam in one way or the other were:

Question 25.
Complete the following.
Answer:

Question 26.
Give evidence from the passage to show that Dr Kalam’s father combined the virtues of ‘simplicity’ and ‘divinity’.
Answer:
Dr Kalam’s father was a boatman. This was the basis for his simplicity. He was also an imam in a mosque and believed strongly in leading a spiritual life. This was the basis of his divinity.

Question 27.
Write from the passage four words that are connected with or related to religions.
Answer:
imam, mosque, Hindu, Christian (priest, temple, Vedic, reverend father, church, divinity, spiritual, spirituality)

Question 28.
Match the words in column ‘A’ with their meanings in column ‘B’:

Answer:

Question 29.
Write the noun forms of:
(a) solve
(b) frank
(c) believe.
Answer:
(a) Solve – solution
(b) frank – frankness
(c) believe – belief.

Question 30.
(1) Write whether the predicates in the following sentences have an object/a complement/an adverbial:
(a) His father was a boatman.
(b) Father Bodal had built the first church.
Answer:
(a) complement
(b) object

Question 31.
Pick out the auxiliaries and state the mood:
(a) All three of them used to sit and discuss the community’s problems.
(b) Simplicity and divinity could go together.
Answer:
(a) used to – past habit
(b) could – possibility.

Question 32.
Even though his father was a boatman, Dr Kalam went on to become the President of India. (Rewrite using ‘yet’.)
Answer:
Dr Kalam’s father was a boatman, yet” he went on to become the President of India.

Question 33.
Complete the following based on the passage:
Answer:
People who touched and influenced Dr A. P.. Kalam in one way or the other were:

Question 34.
What is the significance of the year 1960 as given in the passage?
Answer:
1960 is significant as Dr Kalamoined ISRO that year.

Question 35.
Complete the following.
Answer:

Question 36.
Write from the passage words that sound the same as:
(a) grate
(b) dew
(c) wood
(d) hear
(e) two
(f) sew.
Answer:
(a) grate – great
(b) dew – due
(c) wood – would
(d) hear – here
(e) two – to
(f) sew – so.

Question 37.
Pick out from the following words that, do not begin with the prefix ‘re-’ religion, reverend, religious, research, relocate, region
Answer:
religion, reverend, religious, region

Question 38.
Match the phrases with one word from the passage:

Answer:

Question 39.
Professor Sarabhai and his team had selected a site in Thumba, Kerala. (Pick out the subject of the sentence.)
Answer:
Professor Sarabhai and his team

Question 40.
It was here that he learnt about the true meaning of religious service.
Answer:
Where did he learn about the true meaning of religious service?

Question 41.
It would be impossible to relocate so many people. (Rewrite using ‘not’.)
Answer:
It would not be possible to relocate so many people.

Question 42.
What do you learn from this passage?
Answer:
From this passage, I learn that people belonging to different religions can come together and reach a common understanding to resolve major and sensitive issues. Religious harmony is the theme of this passage.

Question 43.
Complete the following:
(a) Reverend Father Pereira helped to solve the problem of acquiring the site.
(b) Father Pereira described the Church in three ways: (i) his abode (ii) his children’s abode (iii) God’s abode.
Answer:
(a) Reverend Father Pereira
(b) (i) abode
(ii) his children’s
(iii) God’s.

Question 44.
Go through the given statements and say whether you Agree or Disagree with each of them:
Answer:
(a) Science and spirituality seek the prosperity of human life. –
(b) Reverend Pereira absolutely refused to consider Dr Kalam’s request. –
(c) Alternate accommodation was offered only to the fishermen. – Disagree
(d) Everyone present in the church agreed to Reverend Pereira’s plea –
Answer:
(a) Agree
(b) Disagree
(c) Disagree
(d) Agree

Question 45.
Who said to whom and when? ‘Can we give up God’s abode for such a great scientific mission?’
Answer:
Reverend Father Pereira said this to „the people in the Church, one Sunday. On the previous day, Dr Sarabhai and Dr Kalam had approached him to request the people to give up the church land for the building of a space research centre.

Question 46.
Complete the following with the reference to the passage:
(1) We benefit from the devices that science has developed to light up our homes.
(2) We can talk to a large gathering and be heard using a microphone.
(3) Medical science allows doctors to diagnose and treat patients.
(4) Science and technology enhance the overall comfort and quality of human life.
Answer:
(1) to light up our homes.
(2) using a microphone.
(3) diagnose and treat patients.
(4) comfort and quality of human life.

Question 47.
Write one word for:
(a) one who follows a teacher or a leader
(b) eager to know everything
(c) a place of residence
(d) echoed loudly
Answer:
(a) discIple
(b) inquisitive
(c) abode
(d) reverberated

Question 48.
Write from the passage two words that have almost the same meaning as ‘prosperity’:
Answer:
comfort, well-being

Question 49.
Write from the passage two words that indicate noise.
Answer:
reverberated, deafening.

Question 50.
How is it possible? (Rewrite as an assertive sentence.)
Answer:
It is not possible.

Question 51.
I am able to talk to you using this mic. (Rewrite using ‘can’.)
Answer:
I can talk to you using this mic.

Question 52.
The whole church reverberated with the deafening noise of a collective ‘amen’. (Pick out the prepositions.)
Answer:
with, of

Question 53.
Add question tags:
(a) Vikram and I are doing the sameob.
(b) I am able to talk to you using this mic.
Answer:
(a) Vikram and I are doing the sameob, aren’t we?
(b) I am able to talk to you using this mie, aren’t I’

Question 54.
How did the people respond to the appeal made by Reverend Pereira? Would you give the ( same response?
Answer:
The people got up and the whole church reverberated with the deafening noise of a collective ‘amen’. Yes, if I had been part of the gathering, I too would haveoined in with a loud positive response, Considering the importance of the space research centre, I would have been willing to suffer the agony i of relocation.

Question 55.
Complete the following:
(a) We can lead a pure life by serving humanity.
(b) The philosophy of Dr Kalam had an impact on the narrator.
Answer:
(a) serving humanity.
(b) Dr Kalam

Question 56.
Who had directly influenced Dr Kalam’s beliefs?
(a) Professor Satish Dhawan
(b) Srijan
(c) God
(d) countless great minds
Answer:
(a) Professor Satish Dhawan

Question 57.
Who said the following to whom and when? “And then God will shine through us.”
Answer:
Professor Satish Dhawan to Dr Kalam when ‘ they were talking about academic brilliance.

Question 58.
Match the words in column ‘A’ with their opposites in column ‘B’: ‘

Answer:

Question 59.
Choose from the following words/phrases that more or less indicate the meaning of the word ‘wisdom’:
humanity, brilliance, ethical lives, academically accomplished, great minds
Answer:
brilliance, academically accomplished, great minds

Question 60.
Write the noun forms of:
(a) responded
(b) accomplished
(c) different
(d) clear t
(e) pure
Answer:
(a) responded – response
(b) accomplished – accomplishment
(c) different – difference
(d) clear – clarity
(e) pure – purity.

Question 61.
Academic brilliance is no different from the brilliance of a mirror. (Rewrite without ‘no’.)
Answer:
Academic brilliance is similar to the brilliance of a mirror.

Question 62.
God will shine through us. (Add a question tag.)
Answer:
God will shine through us, won’t He?

Question 63.
He had advised me to use my degree and gold medal to transform society. (Pick out the infinitives.)
Answer:
to use, to transform

Question 64.
Name the following based on the passage. The person who touched and influenced the life of Dr APJ Abdul Kalam. –
Answer:
Dr Sri Sri Shivakumara Mahaswamiji.

Question 65.
Find evidence from the passage that indicates that Swamiji:
(a) was dedicated
(b) has inner strength
(c) contributed to the good of the society
(d) was younger than the young generation
Answer:
(a) Who has dedicated his life to the service of humanity.
(b) Swamiji stood on his feet without any support!
(c) his greatest contribution is the establishment of a free residential education. Swamiji feeds thousands of children.
(d) He looked as steady and alert as any other youngster present there.

Question 66.
Complete the following.
Answer:

Question 67.
Write a short paragraph on Dr Sri Shivakumara Mahaswamiji covering his profession and mentioning his personality traits with examples.
Answer:
Dr Sri Sri Shivakumara Mahaswamiji was a remarkable person. He had dedicated his life to the service of humanity and had established a free residential education system for more than nine thousand children. At the age of 102 he could stand without support, give a wise discourse for half an hour and then go on to feed thousands of children. He looked as steady and alert as any other youngster present there and displayed tremendous amount of inner strength.

Question 68.
Write the opposites of the following words using prefixes (un-, in-, etc.):
(a) invited
(b) remarkable
(c) humanity
(d) wise.
Answer:
(a) invited – uninvited
(b) remarkable – unremarkable
(c) humanity – inhumanity
(d) wise – unwise.

Question 69.
Guess the meanings of:
(i) genetics
(ii) googled?
Answer:
(i) genetics – heredity and the variation of inherited characteristics.
(ii) googled – found out information about the subject on the Google website

Question 70.
Find out the noun forms of the following from the passage:
(a) celebrated ……
(b) contribute …..
(c) educate …
(d) strong ….
Answer:
(a) celebrated – celebration
(b) contribute – contribution
(c) educate – education
(d) strong – strength

Question 71.
This display of inner strength touched Dr Kalam deeply. (Rewrite beginning ‘Dr Kalam
Answer:
Dr Kalam was deeply touched by this display of inner strength.

Question 72.
How many of these four would be able to stand tall for half an hour? (Rewrite as an assertive sentence.)
Answer:
Not many of these four would be able to stand tall for half an hour.

Question 73.
I had googled the subject beforehand. (Identify the tense of the sentence.)
Answer:
Past perfect tense

Question 74.
We were discussing this unusual birthday party. (Add a question tag.)
Answer:
We were discussing this unusual birthday party, weren’t we?

Question 75.
What measures will you take to keep yourself physically and mentally fit?
Answer:
To keep myself physically fit, I will take good care of my diet and eat only healthy foods. I will exercise regularly. To keep myself mentally fit, I will try to have a positive attitude towards life, be cheerful and happy and help others.

Question 76.
Fill in the blanks:
(a) Dr Kalam observed great …………………… in Swami Sivananda.
(b) Dr Kalam’s father believed in the value of …………………. .
(c) Mahaswamiji gives education to famished ……………………, food to famished ………………….. .
(d) The essence of a happy life and a peaceful society lies in one sentence – ……………………. .
Answer:
(a) tranquillity
(b) giving back
(c) minds, bodies
(d) ‘What can i give’

Question 77.
Complete the following based on the passage:
Answer:
The people who touched and influenced Dr APJ Kalam in one way or the other were:

Question 78.
Complete the following table:

Answer:
(a) Goodness of action
(b) Pure and ethical life
(c) Selflessness in service
(d) Tranquillity
(e) Simplicity, giving back
(f) Munificence

Question 79.
Rearrange the letters to form sensible words:
(a) y e s f i l l e t =
(b) s c e n e c o i n c =
Answer:
(a) y e s f i l l e t = lifestyle
(b) s c e n e c o i n c = conscience

Question 80.
From the lesson write one word for:
Answer:
(a) giving away much to the needy munificence
(b) the basic idea of something essence

Question 81.
Complete the following choosing from the words/phrases given below: [moral sense of right and wrong, purity, characteristic spirit of a culture, principle or belief, simplicity, peace, generosity, spirituality]
(a) A tenet is a principle or belief.
(b) Conscience is a moral sense of right and wrong.
(c) Ethos is the characteristic spirit of a culture.
(d) Tranquillity is peace.
Answer:
(a) Principle or belief.
(b) Moral sense of right and wrong.
(c) Characteristic spirit of a culture.
(d) Peace.

Question 82.
Write the noun forms of:
(a) pure
(b) settle
(c) final.
Answer:
(a) pure – purity
(b) settle – settlement
(c) final – finality.

Question 83.
Activities based on Contextual Grammar:
(1) In giving so much, he becomes strong. (Rewrite using ‘because’.)
Answer:
He becomes strong because he gives so much.

Question 84.
His munificence fuels his strength. (Rewrite beginning with ‘His strength …’.)
Answer:
His strength is fuelled by his munificence.

Question 86.
What was the secret of Mahaswamiji’s fitness even at the age of 102 years?
Answer:
Mahaswamiji was a remarkable man. He lived with the belief of giving selflessly to famished minds and bodies. By giving, he himself became stronger. His spirit of generosity increased his strength and kept him standing tall and active in life.

Question 87.
Fill in the blanks:
(1) Dr Kalam’s message made an impact on the writer because of its gravity and the challenge it posed became his silent motivation.
(2) The truth of humanity lies in the answer to the question ‘What can I give?’
Answer:
(1) gravity, challenge
(2) truth, humanity

Question 88.
What makes society corrupt and unfair?
Answer:
Society becomes corrupt and unfair when humans think they can take indiscriminately from the environment and destroy it or when they think only of what they can take from other humans.

Question 89.
Complete the following with word from the passage:
Answer:

Question 90.
Pick out the adverbs: circumspectiy, indiscriminately, inequity, gravity.
Answer:
circumspectly, indiscriminately

Question 91.
Write what the underlined auxiliaries indicate:
(a) What can I give?
(b) We have to replace this attitude …
Answer:
(a) can – ability, possibility
(b) have to – obligation, compulsion.

Question 92.
The gravity of the message struck me. (Rewrite in the passive voice.)
Answer:
I was struck by the gravity of the message.

Question 93.
What answers do you get when you ask yourself the question ‘What can I give’?
Answer:
When I ask myself the question ‘What can I give’, I get the answer that I can ‘give’ my talents, my proper moral attitudes, my efforts in the service of others, financial help according to my means …!

Question 94.
Punctuate the following sentences to make them meaningful: (Note: 1 sentence will be asked in the activity sheet.)
(1) Spot the errors and rewrite the sentence correctly: We discussing the number of Ph.D’s Dr Kalam received.
(2) Arrange the following words in alphabetical order: inventions, indisputable, interactions, inequity, institutions, inquisitive, indiscriminately.
(3) Identify the type of sentence: Within a year he wants to build scientific facilities near the sea coast.
(4) Rearrange the letters to form two sensible words:
(1) i c e g e n t s
(2) f u n m i n c e i c e
(5) Make a meaningful sentence using the phrase: to come full circle.
(6) Pick out an infinitive and use it in your own sentence: I am able to talk to you using this mic.
(7) Write two smaller words hidden in the given word: perspective
(8) Complete the following word chain with words from the lesson: church, _ _ _ _ _e,
Answer:
(1) We weref discussing the number of Ph.D’s Dr Kalam had received.
(2) indiscriminately, indisputable, inequity, inquisitive, institutions, interactions, inventions
(3) Assertive Sentence
(4) (1) genetics (2) munificence
(6) It is firstanuary, the year has come full circle.
(6) Infinitive: to talk Sentence: The headmaster wants to talk to you about the annual function.!
(7) perspective: price, respect (spice, spite)
(8) church, house, equator, religious, scientist, team, mic, culture

Question 95.
(1) Write a word that sounds the same as ‘there’ and make a sentence.
(2) Prepare a word register of eight words for the word ‘house’.
(3) Rewrite beginning with the underlined part. His team had selected a site in Thumba.
Answer:
(1) Homophone: there – their! Sentence: They wanted admission for their child,
(2) House: apartment, residence, abode, dwelling, home, habitation, domicile, lodging, settlement
(3) A site in Thumba had been selected (by his team).

Question 96.
(1) Underline the modal auxiliary and state its function: They must have come full circle.
(2) Use the word ‘benefit’ as a noun as well as a verb in sentences.
Answer:!
(1) They must have come full circle. Function: past certainty.
(2) (a) Science confers many benefits on mankind, (noun)
(b) The bonus will benefit our family in many ways, (verb)

English Kumarbharati 10th Digest PDF

• Animals 10th English Textbook Solutions
• Three Questions 10th English Textbook Solutions
• Connecting the Dots 10th English Textbook Solutions
• The Pulley 10th English Textbook Solutions
• Let’s March 10th English Textbook Solutions
• Science and Spirituality 10th English Textbook Solutions

Class 10 English Chapter 3.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.5 Unbeatable Super Mom-Mary Kom Notes, Textbook Exercise Important Questions and Answers.

Unbeatable Super Mom-Mary Kom Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 3.5 Warming Up Questions and Answers

Unbeatable Super Mom Mary Kom English Workshop Question 1.
Discuss and find out the jobs which were done only by men in the past but nowadays women too have started doing them.
……………………………………………………………………….
……………………………………………………………………….
……………………………………………………………………….
……………………………………………………………………….
……………………………………………………………………….
Answer:
HR Manager, Finance Manager, Accountant, Auditor. Budget Analyst, Underwriter, Tax Examiner, Real Estate Agent, Media person, Psychotherapists, Advertising Manager, Event Manager, Social and Community Service Manager, Officer in the Civil Services, Officer in the Armed Forces, Commercial Airline, Pilot, Veterinarian, an Autorickshaw driver.

Unbeatable Super Mom Mary Kom Question 2.
Complete the following web of India’s winning medals in Olympics.

Answer:

Unbeatable Super Mom-Mary Kom Question Answer Question 3.
The text is about a famous female boxer, Mary Kom, who has brought laurels to our country by winning many national and international boxing championships. Make a list of famous men and women boxers across the world. You can take help of internet or your school library to get this information to complete the table.

Name of boxer	Gender	Country
1.  Mary Kom 2. 3. 4. 5. 6. 7. 8. 9.	Female	India

Answer:

Unbeatable Super Mom-Mary Kom Class 10 English Workshop Questions and Answers Maharashtra Board

4.4 Unbeatable Super Mom – Mary Kom Question 1.
Choose the correct alternative and underline it.
(a) What is included in the text?
(i) story
(ii) speech
(iii) interview
(iv) poem
Answer:
(iii) interview

(b) Which State does Mary Kom belong to?
(i) Maharashtra
(ii) Tamil Nadu
(iii) Kerala
(iv) Manipur
Answer:
(iv) Manipur

(c) Who inspired Mary Kom and other youngsters in Manipur to choose boxing as a career?
(i) Dingko Singh
(ii) Charles Atkinson
(iii) Mangte Tonpa Kom
(iv) Adams
Answer:
(i) Dingko Singh

(d) What does Mary Kom prefer being called?
(i) Super mom
(ii) Super boxer
(iii) Super woman
(iv) Super being
Answer:
(i) Super Mom

Question 2.
Go through the text again and find out the name of cities and their importance in Mary Kom’s life. One is given for you.
(a) Kangthei – Mary Kom’s birth place
(b) …………………….. – ……………………..
(c) …………………….. – ……………………..
(d) …………………….. – ……………………..
Answer:
Kangthei – Mary Kom’s birthplace.
Manipur – home state of Dingko Singh and Mary Korn
Bangkok – city that hosted the Asian games of 1998’
United States – Country that hosted the first AlBA Women’s World Boxing. Championship

10th English Workshop 4.4 Question 3.
Go through the text again and complete the following sentences.
1. Mary Kom helped her parents with …………………………. .
2. The success of Dingko Singh inspired …………………………. .
3. Mary Kom made her debut at …………………………. .
4. We can get more gold medals if …………………………. .
5. Mary Kom was able to increase her weight by …………………………. .
6. Mary Kom is good at …………………………. .
7. Mary Kom loves to be …………………………. .
8. Mary Kom apologised the nation for …………………………. .
9. Kom’s parents were Her father was …………………………. .
10. Kom was the first woman boxer to …………………………. .
Answer:
(1) farm-related chores.
(2) many, youngsters in Manipur to try boxing.
(3) the first AIBA Women’s World Boxing Championship in the United States.
(4) more and more people take up sports as a full-time career.
(5) eating the right kind of healthy food rather than bad saturated fats.
(7) Mary Kom loves to be a mom, acknowledging that it is the best thing that has ever happened to her. cooking and other household work too.
(10) qualify and win a bronze medal in the 51 kg flyweight category of Boxing.

Unbeatable Super Mom Mary Kom 10th Std Question 4.
You will find some Acronyms (short forms) in the text. Go to the library or search the internet to find their full forms. Discuss with your partner. One is given for you.
(a) OGQ – Olympic Gold Quest
(b) IBN –
(c) MTV –
(d) YPA –
(e) AIBA –
(f) CNN
Answer:
(a) OGQ – Olympic Gold Quest
(b) IBN – Indian Broadcasting Network
(c) MTV – Music Television
(d) YPA – Yellow Pages Advertising
(e) AIBA – Association Internationale de Boxe Amateur (International Boxing Association)
(f) CNN – Cable News Network

Unbeatable Super Mom Mary Kom English Workshop Pdf Question 5.
Fill in the fact file of Mary Kom.
(a) Full name :
(b) Native of :
(c) Early life and interests :
(d) Special sports taken up :
(e) Inspired by :
(f) Coach :
(g) Early achievements :
(h) International achievements :
(i) Her passion :
(j) Future plans :
Answer:
(1) Gerund: cooking Sentence: Though I do not like cooking, I have to do it.
(2) I ate the right kind of food and gained weight.
(3) (a) fly + weight (b) sports + men
(4) “What do you prefer being called – Super Mom or Super Boxer?”
(5) (a) focussing (b) sparring
(б) I receive letters and picture souvenirs from my penpals all the year round.
(7) Imperative Sentence
(8) whenever, where, which, who
(g) Early achievements:

• Manipur State Women’s Boxing Championship
• Regional championship in West Bengal

(h) International achievements:

• 2001: International debut at the first AIBA Women’s World Boxing Championship in United States – won the silver medal in the 48 kg category.
• 2012: Bronze medal at the Olympics, flyweight (51 kg category)
• five times World Amateur Boxing Champion

(i) Her passion: cooking
(j) Future plans: coaching Indian women

10th Class English Workshop 4.4 Question 6.
Glance through the text and find the special qualities of Mary Kom. Complete the web by putting different qualities of Mary Kom in the boxes.
Answer:

Unbeatable Super Mom Mary Kom Question Answer Question 7.
‘Super Mom’ refers to an excellent mother. Give three reasons why ‘super’ has been added to the word ‘mom’ as in the title.
1. ……………………………….
2. ……………………………….
3. ……………………………….
Answer:
(1) The word ‘Super’ is used to describe a person who aims for the highest standards of excellence. As a boxer Mary Kom aimed for the highest standards. As a result, she achieved success at the Olympics.

(2) When asked if she preferred the title ‘Super Mom’ to ‘Super Boxer’, she opted for the former. It was heroy to be a mother. In her words, it was the best thing that ever happened to her.

(3) This title gives us an idea of the priorities in Mary Korn’s life. Motherhood is her first preference. Hence the writer uses this word in the title.

Unbeatable Super Mum Mary Kom Question 8.
Answer the following questions in your own words.
(a) What makes the writer call Mary Kom ‘a legend’?
Answer:
The writer calls Mary Kom a legend not only because of her exceptional achievements as a woman boxer but also because of her truthful admission and apology to the nation about not being able to win the Gold at the Olympics.

(b) What prime quality did Mary Kom display during her first attempt in Olympic games? What was her bad luck?
Answer:
During her first attempt in the Olympic games, Mary Kom displayed the prime quality of underplaying the faults of others and taking on the blame for her losses upon herself. It was her bad luck that theudges did not press the buttons in her favour during her semi-final against Adams.

(c) What does Mary Kom suggest, for India to win more Olympic Gold Medals?
Answer:
Mary Kom suggests that more and more people should take up sports as a full-time career, so that India might win more Olympic Gold Medals

4.4 Unbeatable Super Mom-Mary Kom Question 9.
Rearrange the facts below in their proper order, as per the text.
(a) Mary Kom made her first appearance at international level.
(b) She sparred with male boxers in Pune.
(c) Mary Kom won the Manipur State’s Women’s Boxing Championship.
(d) She won a bronze medal in the 2012 Olympics.
(e) Mary Kom decided to take up boxing.
Answer:
(e) Mary Kom decided to take up boxing.
(c) Mary Kom won the Manipur State Women’s Boxing Championship.
(b) She sparred with male boxers in Pune.
(a) Mary Kom made her first appearance at the international level.
(d) She won a bronze medal in the 2012 Olympics.

Unbeatable Super Mom Mary Kom English Question 10.
Mary Kom prepared rigorously to win many championships. Read the text again and make a list of various things done by Kom regarding her preparations.

• Variety of preparations
• Diet
• Focus

Answer:

Unbeatable Super Mom Mary Kom Question Answer Question 11.
Make sentences of your own using the following words.
(a) debut : ……………………………….
(b) elation : ……………………………….
(c) sponsor : ……………………………….
(d) reinforced : ……………………………….
(e) humble surroundings : ……………………………….
Answer:
(a) debut – He wanted his daughter to make a debut as a dancer at the prestigious Manipuri Folk Festival.
(b) We received the news of our victory with great elation.
(c) sponsor: The college students wanted a sponsor for their fashion show.
(d) reinforced – His reputation as a brave soldier was reinforced by the many stories told about him by his comrades who fought alongside him.
(e) humble surroundings: Abraham Lincoln grew up in humble surroundings.

4.4 Unbeatable Super Mom – Mary Kom Question 12.
Find antonyms of the following words from the text.
(a) Arrogant x …………………
(b) Finally x …………………
(c) Depressed x …………………
(d) Disqualify x …………………
(e) Diffident x …………………
(f) Float x …………………
Answer:
(a) arrogant X humble
(b) finally X initially
(c) depressed x exhilarated
(d) disqualify X qualify
(e) diffident X confident
(f) float x sink

Question 13.
Underline the subordinate clauses and state their kind.
(a) Enough has been said about this great warrior, who conqured the world. (Subordinate ………………… clause)
(b) The male boxers kindly practised with me whenever I required them. …………………
(c) I think that more people should take up sports as a full – time career …………………
(d) Do you think nutrition is a neglected area in Indian sports? …………………
(e) That’s the best thing, that has happened to me. …………………
(f) India managed just 6 medals in 2012 Olympics even though we are a nation of 1.3 billion people. …………………
Answer:
(a) Enough has been said about this great warrior who conquered the world. – Subordinate Adjective Clause
(b) The male boxers kindly practised with me whenever I required them – Adverb Clause of Time
(c) More and more people should take up sports as a career – Obligation
(b) nutrition is a neglected area in Indian sports? – Noun Clause.
(e) That’s the best thing that has happened to me. Subordinate Adjective Clause
(f) even though we are a nation of 1.3 billion people. – Adverb Clause of Concession.

Question 14.
(A) Pick out from the lesson the Verb forms of :
(a) qualification …………………
(b) negligence …………………
(c) company …………………
(d) decisions …………………
(e) practice …………………
(f) birth …………………
Answer:
(a) qualify
(b) neglect
(c) accompany.
(d) decisively
(e) practise
(f) born

(B) Pick out the Noun forms of :
(a) represent …………………
(b) change …………………
(c) prepare …………………
(d) achieve …………………
(e) aware …………………
(f) succeed …………………
Answer:
(a) representative
(b) change
(c) preparation
(d) achievement
(e) awareness
(f) success

(C) Pick out the Adjective forms of :
(a) favour …………………
(b) proportion …………………
(c) finance …………………
(d) nutrition …………………
(e) female …………………
(f) addition …………………
Answer:
(a) favourite
(b) proportionate
(c) financial
(d) nutritional
(e)  female, feminine
(f) additional

Question 15.
Imagine that you are the Captain of your team. A famous cricketer is going to visit your school. You are assigned the task to conduct an interview of that famous cricketer. Frame a set of 10 questions that you will ask the cricketer. Take help of the points given below.
(a) Early life
(b) Interest in this field
(c) Inspiration
(d) Coaching and guidance
(e) Achievements/ Records
(f) Future plans
(g) Advice to youngsters
Answer:
Questions of the Interviewer:
Sir, welcome to our school. May I ask you a few questions? Thank you.
(1) Could you tell us something about your early life?
(2) Which field of sports were you interested in your early life?
(3) Who was your inspiration?
(4) Who was your coach and your guide during your early years of training?
(5) Which aspect of cricket. do you prefer batting, bowling or fielding?
(6)ust for the record, could you list your achievements and records?
(7) Surely you must have some future plans, What are they?
(8) What difficulties did .you face when you started your career?
(9) Who do you think is a model cricketer today?
(10) What is your advice to youngsters?

Question 16.
Write a short paragraph describing the life and work of Mary Kom. Take help of the points given below. You can take help of the fact file that you have prepared earlier (Activity 5).
(a) Early life
(b) Training
(c) Achievements
(d) Future Plans
Answer:
Mary Korn’s full name is Chungneijang Mary Kom Mangte. She hails from a village in Manipur. Her father was an ex-wrestler. Right from an early age, Mary Kom was interested in athletics and boxing. Finally she took up boxing, despite objections from her father. He was worried that boxing would mar her face and that would make it difficult for him to arrange a suitable marriage for her. She trained under Charles Atkinson and sparred with some of the finest male boxers in Pune.

Mary Kom has a list of National and International achievements. She won the Manipur State Women’s Boxing Championship. Then she won the Regional championship for boxing in West Bengal. She made her International debut in 2001 at the first AIBA Women’s World Boxing Championship in the United States. There she won the silver medal in the 48 kg category.

In 2012, she won the bronze medal at the Olympics in the flyweight (51kg category). She has been five times World Amateur Boxing Champion. She plans to take up coaching for women boxers with potential.

Question 17.
‘What men can do, women can do better.’
Divide your class in 2 groups. Let one group offer points ‘For the topic’ and the other, ‘Against the topic.’ Note down the points in your note books and expand the points in two separate write- ups, as views and counterviews. Suggest suitable titles for each.
Answer:
View: Men cannot compare to women Women have inherent qualities, not possessed by men, that enable them to do things better than men do. There was a time when certain professions or careers were considered the sole domain of men. In recent years, women have pooh-poohed the very idea.

Women have more patience and endurance than men. Hence when entrusted with any task, they stick it out and see it through. They are painstaking and focus on every detail. They are able to see the overall picture, unlike men who work for short-term benefits and instant solutions.

Women tend to communicate more effectively them men, focussing on how to create a solution that works for the group, talking through issues, and utilize non-verbal cues such as tone, emotion, and empathy whereas men tend to be more task-oriented, less communicative, and more isolated. Men have a more difficult time understanding emotions that are not explicitly verbalized, while women tend to intuit emotions and emotional cues.

Men tend to have a ‘fight or flight’ response to stress situations while women seem to approach these situations with a ‘tend or befriend’ strategy.

Hence women do very well as PR Managers, HR Managers, Psychologists, Psychiatrists, Counsellors, etc., – which were previously considered exclusive male-dominated fields of work.

Counterview: Men are the superior species With no disrespect or offence intended, when it comes to theob-front, men are superior to women. They have the discipline, the psychological assurance and presence and most important, the time to sit overtime and meet targets.

Women tend to be straightforward, outspoken and curt in their dealings with clients. Men are more polite, patient and considerate, especially with irate customers. This is because they are more hormonally stable and balanced than women. They tend to view things from a long-term viewpoint and are focused on the goals of the establishment they work for.

Men tend to process better in the left hemisphere of the brain while women tend to process equally well between the two hemispheres. This difference explains why men are generally stronger with left- brain activities and approach problem-solving from a task-oriented perspective.

Question 18.
Two famous proverbs – ‘Actions speak louder than words’ and ‘Fortune favours the brave’ are best suited to the personality of Mary Kom. Form two groups in the class. Each group should write a paragraph on one proverb with reference to the life and achievements of Mary Kom.
Answer:
(1) Actions Speak Louder Than Words

Mary Korn’s life and personality exemplify the proverb ‘Actions speak louder than words’.

Right from an early age she was interested in athletics and boxing. Her father, a former wrestler, was against her entering the field of boxing for fear of disfigurement, but Mary Kom went ahead, trained rigorously, left her home-state and pursued her goal.

There are many who express desires and ambitions, but limit themselves to highfalutin talks. Mary Kom made her dreams a reality and went on to win a medal at the Olympics for India. Her wo^ds always echoed humility. She avoided blaming others for her losses, but took the responsibility upon herself.

Mary Korn’s life has been aourney of high-voltage action, despite the fact that she is by nature a shy, soft-spoken girl.

(2) Fortune Favours The Brave
It is not easy for a girl to enter and participate in a male-dominated field such as boxing. Mary Kom hailed from Manipur, which is a conservative state to say the least.

Mary Kom, however, was brave enough to challenge gender-bias, opposition from her father and the tough rigours of sparring with professional male boxers at Pune.

Her daring and courage were rewarded with awards and national recognition. But the icing on the cake was when she went on to win international events, finally culminating in winning the bronze medal at the 2012 Olympic event.

Lady luck had smiled on her for her persistence, her continual efforts and her unswerving focus on her goals. Indeed, Mary Kom has proyed by her life and her achievements that if one has the spirit of challenging odds, one will surely reap rich dividends.

Question 19.
Name the following:
(1) According to the writer, the great warrior who conquered the world: ……………………
(2) The State in which Mary Kom was born: ……………………
(3) The kind of farms in which Mary Korn’s parents were working as tenant farmers: ……………………
(4) The sportsman who inspired many youngsters in Manipur: ……………………
Answer:
(1) Mary Mangte Kom
(2) Manipur
(3) hum fields
(4) Dingko Singh

Question 20.
Complete the following sentences.
(a) Korn’s parents were …………………… who worked in …………………
(b) Mary Kom apologized to the nation …………………..
Answer:
(a) tenant farmers, hum fields.
(b) for not being able to win gold.

Question 21.
Complete the following:
Answer:

Question 22.
What was Mary Kom’s exceptional achievement?
Answer:
Mary Kom’s exceptional achievement was that In the 2012 Olympics, she became the first Indian woman boxer to qualify and win a bronze medal in the 51 kg flyweight category of Boxing.

Question 23.
What has added to Mary’s greatness as a boxing champion?
Answer:
As a boxing champion Mary’s greatness is reinforced by the way she’ apologised to the whole nation for not being able to win the gold.

Question 24.
Find antonyms of the following words from the passage:
(a) urban
(b) failure
(c) defeat
(d) weakened
(e) wealthy
Answer:
(a) urban X rural
(b) failure X success
(c) defeat X victory
(d) weakened X reinforced
(e) wealthy X poor

Question 27.
She is a legend for sure and an idol for all sportswomen to look up to. (use ‘not only…. but also’)
Answer:
She is not only a legend for sure but also an idol for all sportswomen to look up to.

Question 28.
In the 2012 Olympics, Mary become the first Indian woman boxer to qualify and win a bronze medal. (Rewrite using ‘as well as’)
Answer:
In the 2012 Olympics, Mary became the first Indian woman boxer to qualify as well as win a bronze medal.

Question 29.
What qualities do you think are required to become a good sports person?
Answer:
A good sportsperson should be hard working and persevering. He/She should be humble enough to accept defeat and amibtious enough to pursue success. He/She must have pride in his/her country and team. Above all, he/she must have the all-important sportsman spirit.

Question 30.
Choose the correct alternative for each question and underline it: (The answers are given directly and underlined.)
(a) What is the name of the interviewer?
(i) Sportskeeda
(ii) Taruka Srivastava
(iii) Charles Atkinson
(iv) Adams
Answer:
(ii) Taruka Srivastava

(b) Where did Mary Kom train?
(1) Manipur
(ii) the US
(iii) at home
(iv) Pune
Answer:
(iv) Pune

Question 31.
Say whether the following are True or False: (The answers are givemdirectly and underlined.)
Answer:
(a) Adams was Mary Kom’s friend.
(b) Charles Atkinson was Mary Kom’s coach.
(c) Theudges for Mary Kom’s semi-finals at the Olympics were fair.
(d) Charles Atkinson went along with Mary Kom for the Olympic finals.
Answer:
(a) False
(b) True
(c) False
(d) False

Question 32.
What failed to pressurize Mary Kom during the Olympics?
Answer:
During the Olympics, the fact that she was the only female representative from India in boxing failed to pressurize Mary Kom.

Question 33.
How could Mary Kom manage without her coach at the Olympics?
Answer:
Mary Kom could manage because they had already done their homework and she was well- prepared.

Question 34.
Find antonyms of the following words from the passage:
(a) gain
Answer:
(a) gain x loss

Question 35.
Write one word for each of the following: (The answers are given directly.)
Answer:
(a) a person employed to report for a newspaper ……………………
(b) a person who wins a medal at an event ……………………
(c) a person who takes an interview of a celebrity ……………………
(d) a person whose interview is taken ……………………
Answer:
(a) correspondent
(b) medallist
(c) interviewer
(d) interviewee

Question 36.
Find the noun forms of the following words:
(a) decide
Answer:
(a) decide – decision

Question 37.
Find the adjective forms of the following words:
(a) confidence
(b) tactics
Answer:
(a) confidence – confident
(b) tactics – tactical

Question 38.
Rewrite as an exclamatory sentence:
I am really happy.
Answer:
How happy I am!

Question 39.
Rewrite using ‘but’: Although she carried power, she wasn’t very tactical.
Answer:
She carried power but she wasn’t very tactical.

Question 40.
Fill in the blanks:
(a) Mary Kom had to gain ………… in order to fight in the 51 kg event
(b) In 2012, India won ………. medals in the Olympics.
(c) Mary Kom usually participated in the ………….. event.
(d) Mary Kom had decided to participate in the ………… event at the Olympics.
Answer:
(a) 3kg
(b) 6
(c) 48kg
(d) 51kg

Question 41.
What can help Indian sportsmen win more Olympic Medals?
Answer:
Mary Kom feels that if more corporates sponsored players, the players would not have any financial pressure and could focus on their games. This would help Indian sportsmen win more Olympic Medals.

Question 42.
Make sentences of your own using the following words:
(a) sponsor: The college students wanted a ………….. for their fashion show.
(b) a key factor: Heavy rain was …………… to our canceling the family picnic.
Answer:
(a) sponsor
(b) a key factor

Question 43.
Find the verb forms of:
(a) focus
(b) requirement
(c) weight
(d) health
Answer:
(a) focus – focus
(b) requirement – requIre
(c) weight – weigh
(d) health – healthy

Question 44.
What, according to you, are essential requirements for sportspersons in general?
Answer:
I think that sportspersons in general should spend all their time and energy practising and mastering the sport they are engaged in. They should also exercise daily in order to keep fit. The most important, however, is regulating the diet so as to ingest the best nutrition required by the body.

Question 45.
(1) Choose the correct alternative for each question and underline it:

(a) What is the full form of OGQ?
(i) Olympic Group Queries
(ii) Olympic Gold Quest
(iii) Overseas Guest Qualifications
(iv) Olympic Golf Qualifications
Answer:
(ii) Olympic Gold Quest

Question 46.
Is Mary Kom more proud of being a boxer or a mother?
Answer:
Mary Kom is more proud of being a mother.

Question 47.
What did OGQ do for Mary Kom?
Answer:
OGQ helped Mary Kom out whenever she needed something.. By taking care of everything, it helped her focus on her boxing and kept her stress- free.

Question 48.
(1) Find antonyms from the passage for the following words:
(a) few
(b) modern
(c) worst
(d) indifferent
Answer:
(a) few x several
(b) modern x traditional
(c) worst x best
(d) indifferent x interested

Question 49.
Write the adjective forms of the following words:
(a) care
(b) tradition
(c) importance
(d) difficulty.
Answer:
(a) care – careful, careless
(b) tradition – traditional
(c) importance – important
(d) difficulty – difficult

Question 50.
The future is very bright. (Rewrite as an exclamatory sentence.)
Answer:
How bright the future is!

Question 51.
Underline the determiners: You have broken several stereotypes about the women in India.
Answer:
You have broken several stereotypes about the women in India.

Question 52.
(1) Pick out the gerund and make a sentence : I am good at cooking.
(2) Spot the errors and rewrite the correct sentence : I eaten the right kind of food and gains weight.
(3) Write the root words that form the following compound words : (а) flyweight (b) sportsmen
(4) Punctuate the sentence : what do you prefer being called super mom or super boxer
(5) Form present participles using the given words : (a) focus (b) spar
(6) Make a meaningful sentence using the phrase : ‘all the year round’.
(7) Identify the kind of sentence :ust let their mother box.
(8) Arrange the following words in alphabetical order : where, who, whenever, which
Answer:
(1) Gerund : cooking Sentence : Though I do not like cooking, I have to do it.
(2) I ate the right kind of food and gained weight.
(3) (a) fly + weight (b) sports + men
(4) “What do you prefer being called – Super Mom or Super Boxer?”
(5) (a) focussing (b) sparring
(б) I receive letters and picture souvenirs from my penpals all the year round.
(7) Imperative Sentence
(8) whenever, where, which, who

Question 53.
(a) Rewrite using the simple future tense : I had to focus on what to eat.
(b) Rewrite beginning with the underlined part: OGQ played an important role in my success.
(c) Write a word register for the word ‘nutrition’.
(d) Write sentences to show the different meanings of the word ‘pretty’.
Answer:
(a) I will have to focus on what to eat.
(b) An important role was played by OGQ in my success.
(c) nutrition: diet, nourishment, wholesome, balanced, food, edibles, foodstuff, menu, sustenance.
(d) (1) The little child had a pretty face, (pleasing or attractive to the eye)
(2) It has been pretty hot this summer, (quite, but not extremely)

Question 54.
Change to the comparative degree: That’s the best thing that has happened to me.
Answer:
That’s better than any other thing that has happened to me.

English Kumarbharati 10th Digest PDF

• Night of the Scorpion 10th English Textbook Solutions
• The Night I Met Einstein 10th English Textbook Solutions
• Stephen Hawking 10th English Textbook Solutions
• The Will to Win 10th English Textbook Solutions
• Unbeatable Super Mom-Mary Kom 10th English Textbook Solutions
• The Concert 10th English Textbook Solutions

Class 10 English Chapter 2.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.2 Three Questions Notes, Textbook Exercise Important Questions and Answers.

Three Questions Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 2.2 Warming Up Questions and Answers

Question 1.
Expressions in English classified under different heads. Pair up with your partner, guess and match the columns. (Use a dictionary.)

Answer:

Question 2.
Read the polite requests/suggestions and complete the gaps in the responses. Make sure they are polite and not repeated.
→ Could you lend me your dictionary?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, here it is.
Refuse (2) I’m sorry, I can’t. I am using it now.

→ Can you please pass the salad?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Sure!
Accept (2) Here you are.

→ May I know the exact time?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Right now It is exactly ten to six.
Accept (2) It’s 10 minutes past 5.

→ Shall we plan a class-picnic?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, let’s!
Refuse (2) Not now; I’m going to my native place for a month.

→ Do you need help?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, please.
Refuse (2) It’s all right, thank you. I can manage.

→ Is it alright if I use your laptop?
Accept (1) ………………..
Refuse (2) ………………..
Answer:
Accept (1) Yes, I can spare It for an hour.
Refuse (2) Well… could you wait some time? I have some things I need to complete.

Question 3.
Let’s see if you remember a nursery rhyme you must have sung, as a kid :
Fill in the missing words: ………………..
‘The ……………….. time to be happy is
The to be happy is here.
And the way to be ……………….., is to ……………….. someone
happy And have a little ……………….. right here!’
(happy, make, heaven, now, place)
(You can listen to this song on the internet.)
Answer:
(happy, make, heaven, now, place)
The time to be happy is now.
The place to be happy is here.
And the way to be happy is to make someone happy. And have a little heaven right here!

Three Questions Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
Read the story and answer whether the following statements are true or false.
(a) The people convinced the King to make a proclamation. ……………………………..
(b) The hermit spoke usually to everyone. ……………………………..
(c) The King received all answers from the hermit. ……………………………..
(d) The person the King saved and helped was his enemy. ……………………………..
(e) To do good to people is the purpose of our life. ……………………………..
Answer:
(a) True
(b) False
(c) False
(d) True
(e) True

Question 2.
Match the titles with the contents of the proper paragraph.

Answer:

Question 3.
The character traits of the king and hermit are mixed up. Sort them out in the right box.

Answer:
KiNG
impatient. eager to succeed, helpful

HERMIT
feeble, enlightened, patient, convincing, wise

Question 4.
Complete the Tree diagrams associated with the happenings in the story.

Answer:

Question 5.
Write down in your notebook two points for each of the following. How do you know . . .
(a) the learned advisers who came to the court confused the king.
(b) the king was humble.
(c) the king’s enemy was repentant.
(d) the hermit was truly wise.
Answer:
We come to know that the king was humble by the fact that he did not mind doing ordinary work such as digging. He did not use his authority as king to force the hermit to answer his questions. Instead he requested the hermit politely and was ready to go away if the hermit refused to answer his questions.

Question 6.
Choose the correct answer and fill in the blanks.
(a) “Varied” (Paragraph-3) means ……………………
(i) different
(ii) unnecessary
(iii) unequal
(iv) unimportant.
Answer:
(a) different

(b) Many learned people came to the court and gave ……………………
(i) The same answers
(ii) correct answers
(iii) different answers
(iv) wrong answers.
Answer:
(iii) different answers

(c) The synonym of ‘convinced’ is ……………………
(i) persuaded
(ii) happy
(iii) unhappy
(iv) angry.
Answer:
(i) persuaded

(d) The King wanted to know the …………………… time to begin everything.
(i) right
(ii) exact
(iii) proper
(iv) good.
Answer:
(i) right

(e) ‘‘I pray you to answer my question.’’ Here ‘pray’ means ……………………
(i) plead to God
(ii) request
(iii) order
(iv) suggest.
Answer:
(ii) request

(f) Choose an adverb that collocates with “breathed ……………………
(i) hurriedly
(ii) heavily
(iii) hardly
(iv) calmly.
Answer:
(i) heavily

Question 7.
Answer the following questions.
(a) The learned people were sometimes divided in their opinions, different persons giving quite different answers; at other times, none of them gave an answer. They all suggested ways to look for an answer. Point out one example of each.
Answer:
To know the right time for every action: Draw up in advance a table of days, months and years and live strictly according to it. The people the king most needed: Councillors The most important occupation: Science.

(b) Though the hermit did not say anything to the king for some time, he did not ignore the king or treat him rudely in any way. Do you agree? What evidence of his politeness can you point out? What shows that he listened and responded to the king’s words?
Answer:
I agree that though the hermit did not say anything to the king for some time, he did not ignore the king or treat him rudely in any way. His politeness is evident by the fact that he greeted the king. By spitting on his hand before he resumed digging, the hermit indicated that the work he was doing was more important and that the king would have to wait.

(c) The hermit ‘spoke only to common people’; so the king ‘put on simple clothes’. Do you think the king hoped to be mistaken for a common man, or was he just showing that he was a humble person? What shows that the hermit knew him to be the king?
Answer:
The king put on* simple clothes because he did not want the hermit to refuse to answer his questions. The king was aware that the hermit was wise and would know that he was the king and not mistake him for a common person. Out of humility and respect, the king dressed up like a commoner. We know that-the hermit knew that he was the king by the way he returned the king’s greeting.

(d) Did the king behave as an ordinary person, rather than as a ruler, at the hermit’s hut? What shows it? Did he also act as a good, kind person? When did he do so?
Answer:
Like any other ordinary person, the king tended to the wounded man. He even washed the wound and bandaged it many times. When required, he brought and gave the man water to drink. The king went out of his way to be good and kind to the man. All this happened after the wounded man came running, wounded, to the hermit’s hut.

(e) Do you think the hermit knew, beforehand, not only about the king’s arrival but about the ambush by his enemy? Think a little about this and say what you really feel.
Answer:
I think the hermit somehow knew everything before the king arrived. He must have known about the plan of the king’s enemy and so was able to deal with it purposefully when the king arrived. News about the ambush must definitely have come to his ears. Otherwise he would not have been able to answer the king’s questions in such a real and practical way. He was a hermit, a wise man, and nothing of importance would have escaped his consideration.

Question 8.
Consider this list of the different things that happened and rearrange them in the order of time, that is, what happened first, what happened next and so on. Read the related paragraph again if you are uncertain.

(a) The bearded man resolved to kill the king.
(b) The king went alone to see the hermit.
(c) The king executed the bearded man’s brother.
(d) The king spent the night at the hermit’s hut.
(e) The bearded man laid an ambush to kill the king.
(f) The king’s bodyguards recognised and wounded the bearded man.
(g) The bearded man came out of the ambush.
Answer:
(b) The king executed the bearded man’s brother.
(a) The bearded man resolved to kill the king.
(c) The bearded man laid an ambush to kill the king.
(e) The bearded man came out of the ambush.
(d) The king’s bodyguards recognised and wounded the bearded man.
(f) The king spent the night at the hermit’s hut.
(g) The king went alone to see the hermit.

Question 9.
Read the story in your own language, summarize the following aspects of the story in 4 to 5 lines each in your own language. Write it in your notebook.
(a) King’s problem: ……………………
Answer:
The King’s problem was that he wanted someone from his kingdom to give him the answers to three questions.
(1) What was the right time to begin everything?
(2) Who are the right people to listen to?
(3) What was the most important thing to do?

(b) Attempts made to find a solution: ……………………
(c) Climax: ……………………
(d) Solution: ……………………
(e) Message: ……………………
Answer:
The King wanted the answers to three questions. In order to find a solution, he had a proclamation made in his kingdom. He also announced a great reward to anyone who would give him the answers to his questions.

Question 10.
(A) The following compound words from the story are spelt in a jumbled order. Rearrange the letters to make them meaningful.
(1) a r e e t u k d n = ……………………
(2) y o n n a e = ……………………
(3) s t a p s i e m = ……………………
(4) h e e d a r f o n b = ……………………
(5) n e v h i g r e t y = ……………………
(6) h e i l n e w a m = ……………………
(7) d a d e b e r = ……………………
Answer:
(1) a r e e t u k d n = undertake
(2) y o n n a e = anyone
(3) s t a p s i e m = pastimes
(4) h e e d a r f o n b = beforehand
(5) n e v h i g r e t y = everything
(6) h e i l n e w a m = meanwhile
(7) d a d e b e r = bearded

(B) From the story, find the collocations of the following.
(1) …………………… important.
(2) …………………… intently
(3) frail and ……………………
(4) widely ……………………
(5) …………………… time
(6) …………………… blood
(7) simple ……………………
(8) closed ……………………
(9) …………………… asleep
(10) …………………… peace
(11) took ……………………..
Answer:
(1) most important
(2) gazing intently
(3) frail and weak
(4) widely renowned
(5) right time
(6) warm blood
(7) simple clothes
(8) closed eyes
(9) fell asleep.
(10) made peace
(11) took leave

Question 11.
Say whether the Verbs underlined in the sentences are finite (limited by the number or person of the subject) or non-finite (not governed by the subject, number or person).
(1) He decides to go to a hermit.
(2) I have come to you, wise hermit.
(3) He gave the reward to none.
(4) The hermit was digging the ground.
(5) I pray you to answer my questions.
(6) ‘‘ Forgive me.’’
(7) The sun began to sink.
Answer:
(1) decides – finite; to go – non-finite.
(2) have come – finite; to ask, to answer-non- finite.
(3) gave – finite; This sentence has no non-finite verb.
(4) was – finite; digging – non-finite.
(5) pray – finite: to answer – non-finite
(6) forgive – finIte
(7) began – finite; to sink – non-finite.

Question 12.
Narrate an experience of your own that has helped you to realise that ‘Patience is bitter, but its fruit is sweet.’ Write it in your notebook, in about 20 lines.
Answer:
Patience is bitter, but its fruit is sweet!

It was Rousseau who said, ‘Patience is bitter, but its fruit is sweet.’

I realized the truth of this statement when I was in Std. X. It was an important year for me. My school was far from my home. So were my classes. I had to spend a lot of time walking in order to reach either school or classes. This meant a lot of waste of precious time that I could use very well for study.

I was an only child and my father had passed away four years ago. My mother would tell me, ‘Have patience. Things will work out.’ But I really could not understand her.

The rainy months passed by with me trudging anxiously to school or to the classes. If I was lucky, someone would give me a lift, dy studies were suffering.

I was lagging behind in keeping up with homework and revision.

Then one day the postman delivered a letter. Mother read it in excitement.

‘You know what? There’s a good news. Your uncle from the US is coming to visit us. He is your dad’s brother. The last time he saw you was when you were j a baby.’

‘Oh,’ I said, wondering how that could be good for us. On the contrary, I would have to take my uncle visiting and that would take up more of the time I required for earnest study.

The day arrived. My uncle came over. A jolly fellow, full of stories and fun and small delightful gifts. In the afternoon I took his leave saying I had to go to school and then classes.

‘How are you going?’ he asked.
I put my head down and said, ‘Walking’.
‘Come, I’ll take you by autorickshaw,’ he said. And so we went.
‘It’s quite a distance,’ my uncle commented. I nodded silently.
In the evening when I came home, I could not believe my eyes.
There, resting against the wall was the most beautiful bicycle I had ever seen.
Mother and my uncle came out to greet me.
‘This is yours, boy. No more walking long distances for you!’
Tears welled up in my eyes and I ran and hugged my uncle.
‘Thank you so much,’ I said.
Indeed, my patience had been rewarded with sweet fruit!

Question 13.
After reading this story, develop a dialogue with 2 of your classmates about the characters in the story. Besides the tactful introduction to the conversation and write 8 to 10 sets of dialogues.
Answer:
My self: Hey, did you like the story, ‘Three Questions’?

Student 1: Yes, I was particularly impressed with the king. He was very humble. He was eager to know more about life.

My self: Yes, he did not claim that he knew everything just because he was king.

Student 2: I liked the hermit. He was quite a cool character.

My self: He was very wise. He knew beforehand that the king would come to him. He also knew the solution to the king’s problem, even before the incidents occurred.

Student 1: Yes. And the surprising thing is that the king indirectly got the answers to his questions from a long-forgotten enemy.

My self: The story is very cleverly written, woven around these three characters. One seeks answers to questions. One knows the answers to the questions. One is the medium through which the answers are given.

Student 2: If the king’s bodyguards had not attacked the man, he would not have come to the hermit’s hut and met the king.

My self: If the man had not been wounded and the king had not bandaged his wounds and saved his life, the man would not have forgiven him for a cruel wrongdoing in the past.

Student 1: Yes, Leo Tolstoy wanted to give us the message of forgiveness and doing good even to our enemies. Through the three characters in the story and their interactions, the writer brought out his message very well.

My sfelf : Indeed, a well-written story, and one from which we learn such a lot!

Question 14.
From the library or Internet, read the story ‘How much land does a man need?’ by Leo Tolstoy and write a review of the same, covering the following points.
Background of the story
Characters
Plot/Theme
Climax
Message/Moral
Answer:
The climax of the story is that the person whom the king had wronged by executing his brother years ago, finally forgave him. This is because the king had saved his life.

(a) rose got up from a sitting or kneeling position a flower
(b) sink drop downwards go down below the surface of a liquid
(c) bed a garden plot a piece of furniture for resting
(d) rest to cease work in order to relax or sleep the remaining part

By saving the life of the wounded man, who was in fact the king’s enemy, the king passes on to us the message that the most important thing in life is to do good to others, because it is for that purpose alone we were sent into this life.

Question 15.
What final suggestion did the last group of learned men offer regarding the best time?
Answer:
The last group of learned men said that it was impossible for one man to decide correctly the right time for every action and that the king should, instead, have a council of wise people, who would help him to fix the proper time for everything.

Question 16.
Choose the correct question tag from the alternatives and write the complete answer:
He would give a great reward,…
(a) would he?
(b) won’t he?
(c) wouldn’t he?
(d) will he?
Answer:
He would give a great reward, wouldn’t he?

Question 17.
Pick out the finite and non-finite verbs from the sentences:
(1) He always knew the right time to begin everything.
(2) He was right in thinking this way.
Answer:
(1) knew – finite; to begin – non-finite
(2) was – finite; thinking – non-finite.

Question 18.
They all gave different answers. (Rewrite using the opposite of ‘different’.)
Answer:
None of them gave similar answers.

Question 19.
He was convinced that he was right. (Pick out the clauses and name them.)
Answer:
He was convinced – Main clause.
that he was right – Subordinate Noun clause.

Question 20.
What is the right time, according to you?
Answer:
According to me, the right time is the present. Yesterday cannot be undone. Tomorrow cannot be predicted. Therefore, the only right time is today, i.e. the present.

Question 21.
The learned advisers who came to the court confused the king. How do you know?
Answer:
By giving the king’ different answers, the learned advisers who came to the court confused the king. None of the answers given by the advisers was complete or comprehensive. From their answers it is quite clear to me that each one of them dwelt on part of the truth and not the whole truth.

Question 22.
Read the following passage and do the activities:
(1) Arrange these incidents in proper sequence:
(a) The king asked the hermit the three questions.
(b) The king saw that the hermit was digging the ground.
*(c) The king went alone to see the hermit.
(d) The hermit greeted the king.
Answer:
(c) The king went alone to see the hermit.
(b) The king saw that the hermit was digging the ground.
(d) The hermit greeted the king.
(a) The king asked the liermit the three questions.

Question 23.
State whether the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(a) The hermit was well known. True
(b) The hermit spoke usually to everyone. False
(c) The hermit dug the ground easily False
(d) The hermit was strong. False

Question 24.
Why did the king go to the hermit in disguise?
Answer:
The hermit spoke only to common people. The king knew this. So he wanted to present himself as a common man and elicit answers for his questions. That is why he went to the hermit in disguise.

Question 25.
Write from the passage synonyms for:
(a) famous
(b) weak.
Answer:
(a) renowned
(b) frail.

Question 26.
The following compound words from the passage are spelt in jumbled order. Rearrange the letters to make them meaningful.
Answer:
(i) d ubgyroad = bodyguard
(ii) frawera = warfare

Question 27.
The king was convinced by none of these answers. (Rewrite beginning with ‘None of these answers …’.)
Answer:
None of these answers convinced the king.

Question 28.
State whether the following statements are True or False:
Answer:
(a) The king got irritated with the hermit. False
(b) The hermit answered all the questions of the king. False
(c) It was evening when the king met the hermit. True
(d) The hermit was full of energy. False

Question 29.
Who said to whom?
(a) Let me take the spade and work a while for you.
(b) Now rest a while and let me work a bit.
Answer:
(a) The king said this to the hermit.
(b) The hermit said this to the king.

Question 30.
How did the hermit respond to the king’s questions?
Answer:
The hermit listened to the king but said nothing. He just spat on his hand and continued digging. Later, when the king felt sorry for him, the hermit handed the king the spade to take over. When the king asked his question again, instead of giving an answer, the hermit rose and stretched out his hand for the spade.

Question 31.
In what state was the bearded man when he arrived?
Answer:
The bearded man was wounded. He fainted. He had a large wound in his stomach. The bleeding j would not stop and the wound had to be bandaged and re-bandaged. The bandage was soaked with blood. The bearded man was indeed in a very serious condition when he arrived.

Question 32.
Choose adverbs/adjectives that collocate with these words:
(1) moaning:
(a) profusely
(b) heavily
(c) feebly
(d) sadly.
Answer:
(i) moaning feebly

(ii) blood:
(a) profuse
(b) warm
(c) fresh
(d) bandaged.
Answer:
warm

Question 33.
Complete the following table with meanings from the brackets:
(Meanings: go down below the surface of a liquid, to cease work in order to relax or sleep, a piece of furniture for resting, a garden plot, got up from a sitting or kneeling position, drop downwards, the remaining part, a flower) (The answers are given directly in the table.)
Answer:
Words Meaning in the text Other meaning
(a) rose got up from a sitting or kneeling position a flower
(b) sink drop downwards go down below the surface of a liquid
(c) bed a garden plot a piece of furniture for resting
(d) rest to cease work in order to relax or sleep the remaining part

Question 34.
Pick out the finite and non-finite verbs from the sentences:
(a) The king continued to dig.
Answer:
(a) continued – finite; to dig – non-finite.

Question 35.
‘Here comes someone running,’ said the hermit. (Rewrite in indirect speech.)
Answer:
The hermit said that there came someone running.

Question 36.
He fainted and fell to the ground. (Rewrite using a present participle in place of the underlined word.)
Answer:
Fainting, he fell to the ground.

Question 37.
The blood would not stop flowing. (Rewrite without ‘not’.)
Answer:
The blood flowed continuously.

Question 38.
Say whether the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(a) The person the king saved and helped was his enemy. True
(b) The hermit helped the king. True
(c) When he awoke, the king immediately realized where he was. False
(d) The king had gone out for a walk. False

Question 39.
Why had the wounded man asked for the king’s pardon?
Answer:
The wounded man had resolved to kill the king. In try ng to do so. he was wounded and the king saved his life. Hence the wounded man asked for the king’s pardon.

Question 40.
Write two points for the following:
The king’s enemy was repentant. How do you know?
Answer:
The king’s enemy tells him that since the king had saved his life, if he (the king) wished it, he would serve him all his life. This shows that he was repentant.

Question 41.
Match the words with their opposites:
Answer:
Answer:
(a) familiar X strange
(b) forget X remember.
(c) firm X weak
(d) everything x nothing.

Question 42.
Forgive me,’ said the beard€d man. (Rewrite In indirect speech.)
Answer:
The bearded man asked him (the king) to forgive him.

Question 43.
What qualities of the king do you notice in this passage?
Answer:
Even though he was king, he did not hesitate to carry the wounded man into the hut. He was humble enough to sleep in a hut next to a wounded man. All this shows, that the king was not proud of his royal position. He was, at heart, kind, considerate and humane.

Question 44.
State whether the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(1) The hermit pitied the king’s weakness. False
(2) The king received all answers from the hermit. True
(3) The present is the only time when we have power. True
(4) To do good to people is the purpose of our life. True

Question 45.
How did the hermit finally point out the answers to the king’s questions?
Answer:
The hermit finally pointed out the answers to the king’s questions by referring to incidents that the king actually experienced when he visited the hermit. With the help of each incident, the- hermit explained to the king what the most important time was,’ who the most important person was and what the most important action was.

Question 46.
Summarize the following aspect in 4 to 5 lines each in your own words:
(a) The solution.
Answer:
The king finally got the answers to his questions. The most important time was when the king was digging the beds and when he was attending to the wounded man. Otherwise he would not have met the man and the man would have died. The most important action was bandaging the man’s wounds. If the man had died, he would not have made peace with the king. The most important man was the hermit, who made it possible for the king to find the answers to his questions.

Question 47.
Match the following:
‘A’ ‘B’
(1) one who heals – (a) sower
(2) one who lives alone in a forest – (b) physician
(3) one who plants seeds – (c) enemy
(4) one who is actively opposed to you – (d) hermit
Answer:
(1) one who heals – physician
(2) one who lives alone in a forest – hermit
(3) one who plants seeds – sower
(4) one who is actively opposed to you – enemy

Question 48.
He was the most important man. (Rewrite as a question.)
Answer:
Wasn’t he the most important man?

Question 49.
There is only one time that is important. (Rewrite using ‘no’.)
Answer:
There is no other time that is important.

Question 50.
For that purpose alone were you sent into this world. (Rewrite beginning with the subject ‘you’.)
Answer:
You were sent into this world for that purpose alone.

Question 51.
What qualities of the king stand out as he forgave his enemy?
Answer:
As the king forgave his enemy, we see him as a very humane person, as a person who believes in peace and forgiveness and one who shows mercy to even those who would wish to harm him.

Question 52.
(1) Pick out the infinitives in the given sentence and make your own sentence: He would give a reward to anyone who would teach him how he might know the most important thing to do.
(2) Write two compound words from the lesson.
(3) Punctuate the sentence: ive nothing to forgive you for said the king
(4) Make a meaningful sentence using the phrase: to feel sorry for (someone)
(5) Find out two hidden words in the given word: approaching
(6) Spot the error and rewrite the correct sentence: The king convinced none of these answers.
(7) Write the present participle forms of the given verbs: let, beg (run)
(8) Write these words in alphabetical order: beforehand, bearded, breathed, bodyguard.
Answer:
(1) Infinitive: to do Sentence: We were asked to do a simple activity before the session began.
(2) undertake, warfare
(3) T ve nothing to forgive you for,” said the king.
(4) Feeling sorry for the poor man, I gave him some food to eat.
(5) approach, aching
(6) The king was convinced by none of these answers.
(7) letting, begging (running)
(8) bearded, beforehand, bodyguard, breathed.

Question 53.
(1) Rewrite using indirect narration: “O wise one! Could you give me the answer to my three questions?” the king said to the hermit.
(2) Complete the following word chain with words from the lesson:
we . . . . . → . . . . . → . . . . . → . . . . .
(3) Rewrite beginning with the underlined part: The hermit again gave no answer.
(4) Make sentences of your own to show the difference of meaning between the words: ‘pray’ and ‘prey’.
Answer:
(1) Addressing the hermit as the ‘wise one’, the king asked him if he could give him the answer to his three questions.
(2) weak → king → ground → different.
(3) Again no answer was given by the hermit.
(4) (a) Every night the little boy would kneel by his bedside and pray.

(b) The vulture is a bird of prey.
(B) Do as directed (Challenging Activities):
(1) Change to the positive degree: What you did for him was your most important business.
(2) Use the given word as a noun and as a verb: wish
Answer:
(1) No other business of yours was as important as what you did for him.
(2) Word: wish
Sentences: (a) Make a wish and it will come true. (noun)
(b) You may leave if you wish, (verb)

English Kumarbharati 10th Digest PDF

• Animals 10th English Textbook Solutions
• Three Questions 10th English Textbook Solutions
• Connecting the Dots 10th English Textbook Solutions
• The Pulley 10th English Textbook Solutions
• Let’s March 10th English Textbook Solutions
• Science and Spirituality 10th English Textbook Solutions

Class 10 English Chapter 1.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.2 An Encounter of a Special Kind Notes, Textbook Exercise Important Questions and Answers.

An Encounter of a Special Kind Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.2 An Encounter of a Special Kind Textbook Questions and Answers

Warming up!
Chit-chat

Question 1.
What do you see in the picture?
Answer:
I see a small girl carrying a puppy in a large round tub, in neck-deep water of the river.

Question 2.
What do you think the girl is trying to do? Why?
Answer:
The girl, I believe, is trying to rescue the puppy from drowning in the river because anyhow she wanted to save the puppy.

Question 3.
If you were in the place of that girl, what would you do?
Answer:
I would also have tried to rescue the puppy, if that was within my reach.

Question 4.
Do you think, she was successful in her action?
Answer:
Yes, the girl has rescued the puppy from drowning in the river. So, I think she was successful in saving the puppy.

Match the appropriate headings with the images.

Question 1.

1. Our luxurious bungalows. [ ]
2. My Favourite pastime. [ ]
3. What a commotion! [ ]
4. Engrossed in my book. [ ]

Answer:

1. Our Luxurious Bungalows [C]
2. My Favourite Pastime. [A]
3. What a Commotion! [D]
4. Engrossed in my book. [B]

English Workshop:

1. State whether you agree or disagree with the following statements. Justify your choice with proper reasons.

Question 1.
(a) The compound where the writer was living, was rich in nature’s bounty.
(b) Holidays provide us an opportunity to read various magazines and storybooks.
(c) The narrator made a mistake by saving the baby langur.
(d) Animals cannot convey emotions.
(e) The narrator was fifty-five years old when this incident occured.
Answer:
(a) The compound where the writer was living was rich in nature’s bounty. – Agree
(b) Holidays provide the children an opportunity to read various magazines and storybooks. – Agree
(c) The incident occurred during summer vacation. – Disagree
(d) Magazines and storybooks were published specially for adults in the festive season. – Disagree
(e) Writer’s father was a medical professional. – Agree

2. Match the phrases given in Group ‘A’ with their meanings in Group ‘B’.

Question 1.

Answer:

3. Write In your own words

Question a.
Why did the narrator Ignore the barking of dogs?
(i) …………………………………………………………………………………
(ii) …………………………………………………………………………………
Answer:
(i) The narrator thought that the pack of dogs, as usual, must have trapped an unfortunate pig.
(ii) So he ignored the barking of dogs.

Question b.
Why did motherelangur make no effort to grab her baby from the coop?
(i) …………………………………………………………………………………
(ii) …………………………………………………………………………………
Answer:
(i) Mother langur did not make any effort to grab her baby.
(ii) It was because she was completely sure that the writer was not doing any harm to her baby and whatever he was doing was for the good of the baby.

4. Read the text carefully and arrange the occurance of happenings in the text in a sequential order.

Question 1.
Read the text carefully and arrange the occurance of happenings in the text in a sequential order.

Answer:

5. Discuss the following and write about it in your own words in 5-6 lines.

Question a.
What would you do, if you find an injured bird while returning from your school?
Answer:
If I find an injured animal, I will pick it up tenderly and bring it to my home carefully. I will put some drops of water in his mouth to make it fresh. I will examine its injury and apply antiseptic ointment to its injured part and bandage it without hurting it. When it is a little bit comfortable, I will provide it water and food. Then I shall keep it in small basket with cotton spread in it. I will see to it that it is safe in the place. I will take its care till it has enough strength or till it is fully recovered from the injury.

Question b.
What opinion do you form about the narrator, from the story?
Answer:
The writer of this story is a very sensitive, sympathetic and loving person. His qualities of humanity and courage are admirable and incredible. His thoughts about human-animal relations are great. He believes that communication between man and animal depends not only on food but also on trust, compassion and mutual understanding.

6. Complete the following and write a paragraph on each of the given activities.

Question 1.
Complete the following and write a paragraph on each of the given activities.
Answer:

Paragraph: Mother-child Relationship
The relationship between Mother and child is very close and inseparable. Mother’s love for a child is eternal. It is selfless. Her love and affection for her children are boundless and invaluable. She looks after them, nurses them and strives hard for her children’s upbringing and keeping them healthy.

She teaches them their family culture and moral values. The child also loves its mother immensely. Mother guides, inspires and encourages her children throughout their life. How wonderful and pleasant relationship is this!

Paragraph: How I will help an injured Animal
If I find an injured animal, I will pick it up tenderly and bring it to my home carefully. I will put some drops of water in his mouth to make it fresh. I will examine its injury and apply antiseptic ointment to its injured part and bandage it without hurting it. When it is a little bit comfortable, I will provide it water and food.

Then I shall keep it in small basket with cotton spread in it. I will see to it that it is safe in the place. I will take its care till it has enough strength or till it is fully recovered from the injury.

7. Work in pairs and make as many words as you can, using letters in the word. ‘ENCOUNTER’.

Question 1.
Make smaller words (minimum 3 letters each) using the letters in the word ‘Encounter’ :
(Note : In the activity sheet you will be asked to write only four words)

Answer:

8. Translate the following proverbs in good English : 

Question 1.
जनसेवा हीच खरी ईश्वरसेवा.
Answer:
Service to man is service to God.

Question 2.
पेरावे तसे उगवते.
Answer:
As you sow, so shall you reap.

9. Write a paragraph and give an appropriate title to it. Use the following points.

Question 1.
Write a paragraph and give an appropriate title to it. Use the following points.

Man’s Best Friends – Birds and Animals
Answer:
The relations between birds, animals and man are complementing each other. In absence of this relationship our environment is disturbed and we risk our whole balance of ecology in our area. That is why, man must treat the birds and animals with great love and affection. They are our best friends. They are loyal to man and serve us in many ways. We must preserve our eternal relationship kindly, honestly and compassionately. So it is our duty to protect them; take care of their security without hurting them.

It is our duty to maintain this relationship because they cannot speak. They try to explain their feelings without words. Their eyes and actions speak. Try to understand them with love, affection and help them in their needs. Man needs the company of birds and animals. Love the wildlife and avoid loneliness. Protect them!

10. (A) Complete the remaining blocks determining the types of news.

Question a.

Answer:

(B) Read the following headline and write a news report. Follow the steps as given.

Question 1.
Read the following headline and write a news report. Follow the steps as given.
Headline → ‘Tiger attacks 8-year old at Rajiv Gandhi National Park.’
Answer:
Tiger attacks 8-year old at Rajiv Gandhi National Park.
Goregon July 4: Recently tiger attacks on humans have become frequent in the nearby areas of Rajiv Gandhi National Park. A tragic death of 8 year old child attacked by a tiger, has shocked the people in the slum area near the Rajiv Gandhi National Park. It is learnt that early in the morning the child entered alone in the wildlife reserve for defecation.

The tiger crouching behind a fence of bushes attacked the young child and killed him. Slum dwellers gathered around to rescue him could not save him. The slum-dwellers are demanding that the Forest Department should arrange for rigorous patrols to restrict such incidents of human-animal conflicts and construct a boundary wall between the human- habitats and the Park.

(C) Read the following Headlines and write the dateline, intro and a short continuing paragraph.

Question 1.
Read the following Headlines and write the dateline, intro and a short continuing paragraph.

Answer:
Career Counselling with Achievers Wednesday, 15th August, Kripa Sindhu High School, Nagpur. Kripa Sindhu High School had organised the ‘Career Counselling Camp’ for the students of Standard X, on 15th August 2019 at 5 pm. Some renowned persons who had achieved name and fame in different professions were invited to share their own experiences about their career and their success. There were professionals from different fields-medicine, sports, arts, acting, engineering, I etc.

Each one of them explained how and why they dreamed of and pursued their own career and how they secured their achievement in their field. They advised students that great heights can be achieved by constant efforts, even when they have to face nerve-wrecking challenges in their life and have to fight against all overwhelming odds. Audiences were moved when they learnt about the heart-rending stories of some professionals who are now on the top of the world.

The students realized the importance of the career counselling event. It was a great treat for the students who had come there for vocational guidance.

Answer:
Note: Students should write this news report in their notebooks based on following points to emphasize the need of separate Tourism University.
Points: Tourism-a flourishing industry- many employments aya liable – trained candidates required – importance of tourism – can impart education in hospitality, booking, accommodation, selection of tour destinations, etc.-good prospects-responsibility of smooth pleasure tours – a good decision to establish Tourism University.

Language Study:

1. Present Participle: The form of a verb, ending in ‘ing’, which is used in forming continuous tenses. For example, He is sitting here. Present participle can also be used as an adjective. For example, He uses a walking stick.
Now, find out the ‘ing’ forms from the story and classify them into the following table.

Question 1.
find out the ‘ing’ forms from the story and classify them into the following table.

Answer:

2. Spot the error and correct the following sentences.

Question 1.
(a) My grandparents laid down for an afternoon nap.
(b) A stranger were knocking at our door.
(c) My sister and I shares a study room.
(d) One of my friend, is leaving school.
(e) A flock of birds were flying overhead.
Answer:
(a) My grandparents lay down for an afternoon nap.
(b) A stranger was knocking at our door.
(c) My sister and I share a study room.
(d) One of my friends, is leaving the school.
(e) A flock of birds is flying overhead.

3. Rewrite the sentences as per instructions given along with.

Question a.
I took the baby langur to our backyard. ………………………….
(Rewrite the sentence in the Past Perfect Tense)
Answer:
I had taken the baby langur to our backyard.

Question b.
She simply sat there quietly ………………………….
(Rewrite the sentence in the Present Continuous Tense)
Answer:
She is simply sitting there quietly.

Question c.
The mother langur looked straight into my eyes. ………………………….
(Rewrite the sentence in the Simple Present Tense)
Answer:
The mother langur looks straight into my eyes.

Question d.
She surveyed the area for the vicious male langur. ………………………….
(Rewrite the sentence in the Simple Future Tense)
Answer:
She will survey the area for the vicious male langur.

My English Coursebook 10th Digest Chapter 1.2 An Encounter of a Special Kind Additional Important Questions and Answers

Complex Factual Activities :

Question 1.
Complete the web describing the campus where writer’s family lived:
(Answer is directly given and underlined.)
Answer:

Question 2.
How did the family relax after lunch?
Answer:
After eating sufficient and wholesome lunch the writer’s parents and his sisters lay down for an afternoon nap. The author settled down with a storybook. The sound of their snoring in sleep was such that it occasionally broke the silence of the writer’s house.

Question 3.
What wicked custom is practised by animals who live in groups?
Answer:
According to the wicked custom in the animal clan who live in groups, a dominant, powerful male does not allow another male or adult to survive within its group. Mostly the leader of the group kills male babies or adults.

Question 4.
Complete the web with the help of the information given in the passage :
(Answer is directly given and underlined.)
Answer:

Question 5.
What did the writer do to restrain the big langur from killing the baby langur?
Answer:
When the writer realised that the big langur was about to kill the baby langur, he gathered a big, strong stick in one hand and threw a piece of stone at the attacking langur. The big langur did not take notice of his attack; so he started throwing more ! stones at it. In this way, the writer restrained the big langur from killing the baby langur.

Question 6.
Complete the following web and describe the condition of wounded baby langur :
(Answer is directly given and underlined.)
Answer:

Question 7.
Complete the following web with the information from the passage :
(Answer is directly given.)
Answer:

Question 8.
Arrange the following events as per their sequence:
(Board’s Model Activity Sheet)
1. Writer’s father provided first aid to clean the wounds.
2. After a few shaky attempts, the baby langur sat up.
3. The writer turned away from the coop.
4. The writer took the baby langur to their backyard.
Answer:
4. The writer took the baby langur to their backyard.
1. Writer’s father provided first aid to clean the wounds.
2. After a few shaky attempts, the baby langur sat up.
3. The writer turned away from the coop.

Question 9.
Complete the following :
(Answers are directly given and underlined.)
Answer:

1. Mother langur simply sat quitely because she was convinced that no harm was being done to her child.
2. The baby langur started to sob and cry because he sensed the presence of his mother.
3. The baby found comfort and peace in caring arms of his mother.
4. (Mother langur gave a thorough inspection of baby langur’s body because she wanted to check his injuries.

Question 10.
Complete the web:
Answer:

Activities based on Vocabulary:

Question 1.
Match the words in Column ‘A’ with their meanings in Column ‘B’ :

Answer:

Question 2.
Match the phrases in Column ‘A’ with their meanings in Column ‘B’:

Answer:

Question 3
Write from the passage the antonyms of the following :

1. mercifully
2. submissive
3. recognize
4. greater

Answer:

1. mercifully × mercilessly
2. submissive × aggressive
3. recognize × ignore
4. greater × lesser

Question 4.
Find present participles and past participles used as adjectives :
Answer:
1. Present Participles: sloping roof, twinkling eyes.
2. Past Participles: unexpected attack, unknown quarter, muffled cry, peeled banana.

Question 5.
Match the words in column ‘A’ with their meanings in column ‘B’ :

Answer:

Question 6.
Match the synonyms :
(Board’s Model Activity Sheet)

Answer:

Question 7.
Write opposites of the following from the passage :

1. steady
2. known
3. expected
4. firm.

Answer:

1. steady × unsteady
2. known × unknown
3. expected × unexpected
4. firm × shaky

Question 8.
Write the meaning of the following words from the options given in the brackets :
(breast, comfort, weird, evil)

1. uncanny
2. vicious
3. bosom
4. solace

Answer:

1. uncanny – weird
2. vicious – evil
3. bosom – breast
4. solace – comfort

Activities based on Contextual Grammar :

Rewrite the sentences as per tenses mentioned in the brackets :

Question 1.
My father was a medical professional.
(Past Perfect Tense.)
Answer:
My father had been a medical professional.

Question 2.
The holidays provided an opportunity for me to read various magazines and storybooks.
(Simple Present Tense.)
Answer:
The holidays provide me an opportunity to read various magazines and storybooks.

Question 3.
I heard a group of street dogs barking.
(Present Continuous Tense.)
Answer:
I am hearing a group of street dogs barking.

Question 4.
The big male langur was holding a baby langur in his hands.
(Past Perfect Continuous Tense.)
Answer:
The big male langur had been holding a baby langur in his hands.

Question 5.
They were witnessing my rescue operation. (Simple Past Tense.)
Answer:
They witnessed my rescue operation.

Question 6.
He was in a state of shock. (Past Perfect Tense.)
Answer:
He had been in a state of shock.

Question 7.
The baby sensed the presence of his mother.
(Present Perfect Tense.)
Answer:
The baby has sensed the presence of his mother.

Personal Response:

Question 1.
Do you have a reading hobby? How do you ! pursue it?
Answer:
Yes, I do have a reading hobby. I read a lot. I read anything and everything that comes in my sight. I keep on reading storybooks, novels, ‘ biographies, magazines, newspapers, etc. Whenever I find time I love and enjoy reading especially during long vacation.
Note: Students may give their own appropriate answer in all

Question 2.
Do you think that the custom of baby killing by dominant male in animal clan is good? Explain.
Answer:
No, I don’t think so. It’s a bad custom in any animal clan. It is the duty of dominant males to protect them and bring them up kindly and lovingly. They should not deprive them of their basic right to live.

Question 3.
Have you ever saved a puppy/dog or any other animal from naughty children who were throwing stones at him? Write about your
experience.
Answer:
Yes, I have saved a dog who was in such a situation. Though the stones thrown by the urchins did not hit the dog very much, he was frightened to death and was running helter skelter. I gathered a long stick and shouted at them. Then I hit one of the boys with the stick and they ran away. The dog had gratitude in his eyes for me.

Question 4.
What is your mother’s state of mind during your illness?
Answer:
My mother is always worried about my smallest illness. Deep anxiety overpowers her. She is restless and uneasy all the time. She keeps herself awake at night worrying about my ill-health. She is always by my bedside providing me food and medicine on time. She remains in a state of anxiety until I get well.

Question 5.
What did the mother langur seem to convey to the narrator?
Answer:
The mother langur seemed to convey the narrator that she was very grateful to him for saving her child. She was expressing her big thanks to him through her silent eyes. Her eyes showered silent gratitude for the narrator for his kindness and compassion. The narrator could understand her feelings, sentiments and the way of thanking him through her eloquent eyes.

Read the following passage and do the activities :

Simple Factual Activities :

Question 1.
Say whether the following statements are True or False :
Answer:

1. A big male langur did not intend to kill the baby langur. – False
2. The writer started throwing more stones at the big langur. – True
3. The mother langur was watching her baby being killed. – True
4. According to the custom of animal clan, a dominant male protects another male baby or adult. – False

Question 2.
Complete the following sentences using the information given in the passage :
(Answers are directly given and underlined.)
Answer:

1. The langur baby was listless and appeared to be dead.
2. The writer’s parents and sisters had come out on the veranda and were witnessing his rescue operation.
3. The baby langur’s eyes welled up with tears.
4. The unexpected attack forced the langur to drop the baby from the sloping roof over the veranda.

Question 3.
Complete the following sentences :
(Answers are directly given and underlined.)
Answer:

1. The writer offered the baby langur a peeled banana.
2. The baby langur was in state of shock.
3. Splashes of cold water made the baby stir.
4. The mother langur was sitting on their kitchen roof.

Question 4.
Say whether the following statements are True or False :
Answer:

1. The baby langur sensed the presence of his mother. – True
2. The mother langur was sitting on the floor of the coop. – False
3. The writer cuddled the baby langur tightly in his bosom. – False
4. The writer’s attention was fixed on the revival of the baby langur. – True

Question 5.
Complete the following sentences :
(Answers are directly given and underlined.)
Answer:

1. The mother langur was sitting on their kitchen roof.
2. The mother sat still with the baby in her lap for a few minutes.

Question 6.
State whether you Agree or Disagree with the following statements :
Answer:

1. The narrator made a mistake by saving the baby langur. – Disagree
2. Animals cannot convey emotions. – Disagree
3. The narrator was fifty-five years old when this incident occurred. – Disagree
4. Even today, the narrator cannot forget that look in the mother langur’s eyes. – Agree

Choose correct reasons from the given options :

Question 1.
The writer ignored the commotion of street dogs.
(a) Thinking about the dogs’ involvement in some food items.
(b) Thinking about the dogs’ involvement in some stranger.
(c) Thinking about the dogs’ involvement in some thieves.
(d) Thinking about the dogs’ involvement in some unfortunate pig.
Answer:
(d) Thinking about the dogs’ involvement in some unfortunate pig.

Question 2.
The langur did not take notice of the writer’s assault.
(a) Because he was very busy.
(b) Because he was eating the baby langur.
(c) Because he was very infuriated.
(d) Because he ignored the writer’s presence.
Answer:
(c) Because he was very infuriated.

Do as directed :

Question 1.
I started throwing more stones.
(Begin with – ‘More stones were ….)
Answer:
More stones were being thrown by me.

Question 2.
It hardly took notice of my assault.
(Make this as a negative sentence.)
Answer:
It did not take notice of my assault.

Question 3.
My parents and sisters had come out on to the veranda. (Add a question tag.)
Answer:
My parents and sisters had come out on the veranda, hadn’t they?

Question 4.
He took the baby langur to our backyard. (Frame a Wh-question to get the underlined word as an answer.)
Answer:
Where did he take the baby langur?

Question 5.
The baby remained motionless.
(Make negative without changing the meaning.)
(Board’s Model Activity Sheet)
Answer:
The baby did not move. OR The baby did no movements.

Question 6.
She simply sat there quietly.
(Choose correct question tag.)
(Board’s Model Activity Sheet)
(i) doesn’t she?
(ii) didn’t she?
(iii) wasn’t she?
(iv) don’t she?
Answer:
She simply sat there, didn’t she?

Question 7.
I turned away from the coop and looked up. (Begin the sentence with – Turning … and rewrite it.)
Answer:
Turning away from the coop, I looked up.

Question 8.
She gave the baby a thorough body inspection. (Change the sentence into passive voice. Begin with – The baby …)
Answer:
The baby was given a thorough body inspection by her.

Question 9.
I cannot forget that look in her eyes.
(Add a question tag.)
Answer:
I cannot forget that look in her eyes, can I?

Question 10.
I was overwhelmed by the emotion.
(Write the sentence in Active voice. Begin with – The emotion ….)
Answer:
The emotion overwhelmed me.

Activities based on Language Study

Do as directed :

Question 1.
Complete the words by using correct letter:

1. fa_her
2. ha_sh
3. adu_t
4. tr_st

Answer:

1. father
2. harsh
3. adult
4. trust

Question 2.
Put the following words in alphabetical order :

1. baby, unsteady, mother, almost.
2. suddenly, splash, shock, started.

Answer:

1. almost, baby, mother, unsteady.
2. shock, splash, started, suddenly.

Question 3.
Punctuate the following sentences :

1. Mohan said to rajan, i shall never come with you
2. shall we reach pune on time he asked

Answer:

1. Mohan said to Rajan, “I shall never come with you.”
2. “Shall we reach Pune on time?” he asked.

Question 4.
Write related words as shown in the example :
(Answer is directly given and underlined.)
Answer:

Question 5.
Complete the word-chain of adjectives. Add four words each beginning with the last letter of the previous word :
dominant → ……….. → ……….. → ……….. → ………..
Answer:
dominant → tall → loyal → long → good

Question 6.
Attempt anyone :
a. Make a meaningful sentence by using the phrase ‘to catch hold of’
Answer:
Ramesh caught hold of his friend’s arm and stopped him from leaving the place.
OR
b. Add a clause to the following sentence to expand it meaningfully :
The person, who
Answer:
The person, who is sitting on the stage, is a great social worker of this area.

Question 7.
Attempt anyone :
a. Add a prefix or suffix to make new words.
1. communicate
2. inspect
Answer:
1. communication
2. inspection
OR
b. Make a meaningful sentence using any one of the following words :
1. communicate
2. inspect
Answer:
1. She communicated her feelings through her eyes.
2. Let the office inspect the papers.

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer 10th English Solutions
• An Encounter of a Special Kind 10th English Solutions
• Basketful of Moonlight 10th English Solutions
• Be SMART…! 10th English Solutions
• His First Flight 10th English Solutions

Class 10 English Chapter 2.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.1 Animals Notes, Textbook Exercise Important Questions and Answers.

Animals Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 2.1 Warming Up Questions and Answers

Question 1.
Get into pairs and attempt the following :
“The more I learn about people, the more I like my dog.”- Mark Twain. – Discuss with your partner what Mark Twain means from the above quote.

Write in your own words
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
Answer:
‘The more I learn about people, the more I like my dog. – Mark Twain.

Ely the above quote, Mark Twain means that his dog has certain qualities which he finds lacking in human beings. Each day, as he comes across different people and learns more about human nature, the feeling grows within him that humans possess many disagreeable qualities that do not help in improving relationships. As a result, he begins to love his dog more than human beings.

Question 2.
Put the following attributes/abilities given below in the proper circles.
(a) self-control
(b) communicates
(c) love and care
(d) cooks
(e) good manners
(f) has 3600 vision
(g) shows gratitude
(h) lives for more than 150 years
(i) swims
(j) learns computing
(k) worships god
(l) sleeps in standing position
(m) stands up immediately after birth
(n) brings up children
(o) belongs to various species

Answer:

Question 3.
At times, especially when you are frustrated, you wish you were an animal/ a bird/ a fish/ a butterfly and not a human being.

Say which of the above you would choose to transform to and give 3 or 4 reasons for your choice.
I wish I could be a ………………………………………..
…………………………………………………………………….
…………………………………………………………………….
Answer:
When I am frustrated, I wish I could be a bird, so I could fly away from the cause of frustration. At such times, I would like to be far from the noise and crowd on earth and sail in silence across the sky. I would prefer to concentrate on my own thoughts and regain my peace, and the best place for that would be the vast open sky. Flapping my wings would keep me active and busy and help me forget about my worries.

Question 4.
We come across many animals in our vicinity. We have also read about different animals in books. Make a list of all animals that fall under various categories. One is given for you.

Answer:

Animals Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
(A) Match the words given in table A with their meanings in table B.

Answer:

(B) Find adjectives from the poem which refer to positive and negative thinking

Answer:

Question 2.
Complete the following.
(a) The poet wishes he could ……………………………….
(b) Animals do not complain about ……………………………….
(c) Animals do not merely discuss ……………………………….
(d) Animals are not crazy about ……………………………….
Answer:
(a) The poet wishes he could turn and live with animals.
(b) Animals do not complain about their condition.
(c) Animals do not merely discuss their duty to God.
(d) Animals are not crazy about owning things.

Question 3.
State whether the following statements are true or false.
(a) Animals are self-reliant. ……………………………….
(b) Animals quarrel for their possessions. ……………………………….
(c) Animals do not worship other animals. ……………………………….
(d) Humans have given up many good qualities. ……………………………….
(e) Animals suffer humiliation. ……………………………….
(f) The poet has retained all his natural virtues. ……………………………….
Answer:
(a) True
(b) False
(c) True
(d) True
(e) False
(f) False

Question 4.
With the help of the poem find the differences between animals and human beings.

Answer:

Question 5.
Read the text again, and complete the web, highlighting the good values/habits which we can learn from animals.

Answer:

Question 6.
Find outlines from the poem that are examples of the following Figures of Speech.

Answer:

Question 7.
Identify the Figures of Speech in the following lines.
(a) I stand and look at them long and long.
………………………………………………………………..

(b) They do not sweat and whine about their condition.
………………………………………………………………..

(c) They do not make me sick discussing their duty to God.
………………………………………………………………..

(d) …… not one is demented with the mania of owning things.
………………………………………………………………..

(e) They bring me tokens of myself.
………………………………………………………………..

(f) No one is respectable or unhappy over the whole earth.
………………………………………………………………..
Answer:
(a) Repetition
(b) Tautology
(c) Alliteration
(d) Hyperbole
(e) Paradox
(f) Hyperbole

Question 8.
Read the poem again and write an appreciation of the poem in a paragraph format with the help of given points. (Refer to page no. 5)
Answer:
Point Format
(for understanding)
The title of the poem : Animals’
The poet : Walt Whitman
Rhyme scheme : free verse (no rhyme scheme)
Figures of speech : Repetition, Alliteration. Tautology, Hyperbole, etc.
The theme/central idea : Animals are better than humans.

Paragraph Format
The poem ‘Animals’ has been penned by Walt Whitman.

The poet has broken away from the conventional use of a rhyme scheme and has written the poem in free verse.

The chief figure of speech used in the poem is Repetition. Lines such as ‘They do not sweat …’. ‘They do not lie awake …’. ‘They do not make me sick …’ make a strong impact, expressing the qualities that humans should possess, but do not. The other figures of speech are Alliteration, Tautology, Hyperbole, etc.

The central idea of the poem is that animals today are better than humans

Question 9.
Divide the class into two groups. One group should offer points in favor of (views) and the other against (counterviews) the topic ‘Life of an animal is better than that of a human being.’

Later use the points to express your own views/counterviews in paragraph format in your notebook.
Answer:
Point Format

Question 10.
What craze do animals never display?
Answer:
Animals never display the craze of owning things.

Question 11.
What could have happened to the tokens of the poet’s self?
Answer:
The tokens of the poet’s self might have been lost from the time man resorted to manipulating nature and considered himself apart from it.

Question 12.
What does the poet mean by ‘They bring me tokens of myself?
Answer:
By ‘They bring me tokens of myself the poet means that animals possess and express visible signs of qualities such as innocence and simplicity that he himself (i.e. all human beings) must have possessed.

Question 13.
Give one example of a Rhetorical Question from the poem. Explain.
Answer:
Did I pass that way huge times ago and negligently drop them?
The poet uses a question to assert that we human beings unmindfully discarded the good qualities that we possessed somewhere along the line.

English Kumarbharati 10th Digest PDF

• Animals 10th English Textbook Solutions
• Three Questions 10th English Textbook Solutions
• Connecting the Dots 10th English Textbook Solutions
• The Pulley 10th English Textbook Solutions
• Let’s March 10th English Textbook Solutions
• Science and Spirituality 10th English Textbook Solutions

Class 10 English Chapter 1.6 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.6 The Alchemy of Nature Notes, Textbook Exercise Important Questions and Answers.

The Alchemy of Nature Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 1.6 Warming Up Questions and Answers

Alchemy Of Nature Class 10 Question 1.
Rearrange the good qualities in each set, so that the first letter of each of the words should make a meaningful word. Join the sets and get a message.

Set 1: U nderstanding/A daptable/Tolerant/N eat/Encouraging Resourceful.
– The word is ……………………………………………………
Set 2: Selfless/Inspiring
– The word is ……………………………………………………
Set 3: Youthful/Modest
– The word is ……………………………………………………
Set 4: Affectionate/Compassionate/Empathetic/Earnest/Honest/Reliable/Trustworthy
– The word is ……………………………………………………
– The message is …………………………………………………… …………………………………………………… ……………………………………………………
Answer:
NATURE
IS
MY
TEACHER
The message Is: NATURE IS MY TEACHER.

Alchemy Of Nature Class 10 Questions And Answers Question 2.
Various aspects of Nature have special features that make them differ from one another.
For example, Birds :- appearance, shape, colour, size, food habits, habitat, sound etc.
Write such special features of each of the following.
Land …………………………………………………… …………………………………………………… ……………………………………………………
Water …………………………………………………… …………………………………………………… ……………………………………………………
Trees …………………………………………………… …………………………………………………… ……………………………………………………
Animals …………………………………………………… …………………………………………………… ……………………………………………………
Insects …………………………………………………… …………………………………………………… ……………………………………………………
Answer:
Land: geographical features, soil colour, terrain, fertility, chemical composition, crops grown.

Water: width and length of various water bodies, chemical composition (sweet water, salt water), colours (according to sand beds), rocks, coral reefs, variety of sea creatures.

Trees: height and shape of leaves, changing (or unchanging) colour during seasons, fruits, flowers, medicinal products, types of soil, climate and habitat required for their existence.

AnImals: shapes, sizes, colours, different habitats, kinds: wild or domestic, place in the food chain.

Insects: shapes, sizes, colours, number of legs, different habitats, soundš, carriers of dIseases.

The Alchemy Of Nature Question Answer Question 3.
Make a list of living creatures in the alphabetical order. You can write more than one beginning with the same letter.
A …………………………………………………… B ……………………………………………………
C …………………………………………………… D ……………………………………………………
E …………………………………………………… F ……………………………………………………
G …………………………………………………… H ……………………………………………………
I …………………………………………………… J ……………………………………………………
K …………………………………………………… L ……………………………………………………
M …………………………………………………… N ……………………………………………………
O …………………………………………………… P ……………………………………………………
Q …………………………………………………… R ……………………………………………………
S …………………………………………………… T ……………………………………………………
U …………………………………………………… V ……………………………………………………
W …………………………………………………… Y ……………………………………………………
Z ……………………………………………………
Answer:
A -alligator, antelope, ant, etc., B ……………. Z.

The Alchemy of Nature Class 10 English Workshop Questions and Answers Maharashtra Board

The Alchemy Of Nature Questions And Answers Question 1.
What things in nature teach us the following :
(a) Nothing is impossible to achieve ……………………………………………………
(b) Problems are not permanent ……………………………………………………
(c) Be humble and adjust ……………………………………………………
(d) Make the best use of time and opportunity ……………………………………………………
(e) Be persistent ……………………………………………………
(f) Many hands make work light ……………………………………………………
(g) Delicate structures are not a sign of weakness ……………………………………………………
Answer:
(a) Nothing is impossible to achieve: ants small bits of grass peeping from cracks In the concrete
(b) Problems are not permanent: trees that are bare in winter
(c) Be humble and adjust: water
(d) Make the best use of time and opportunity: flowers
(e) Be persistent: ants waler
(f) Many bands make light work: ants
(g) Delicate structures are not a sign of weakness: picr_webs

The Alchemy Of Nature English Workshop Question 2.
Read the questions from the lesson. What do they imply?
(a) Are you listening? …………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………

(b) What if we too lived our lives, however short, to its fullest? ……………………………………………………
………………………………………………………………………………………………………………………………………………………………

(c) What if we too are consistent, organised, focused . . . ? ……………………………………………………
………………………………………………………………………………………………………………………………………………………………
Answer:
(a) It implies that one must listen.
(b) It Implies that we too should live our lives to… the fullest, however short they may be.
(c) It Implies that we too could do wonders If we were consistent, organised focussed

Question 3.
Go through the lesson again and complete the flow-chart that highlights the life of a ‘hibiscus’ flower.

Answer:

Alchemy Of Nature Class 10 English Workshop Question 4.
Fill in the web.

Answer:

English Workshop 10th The Alchemy Of Nature Question 5.
The writer explains the contrasting features of ‘water’ and ‘rock’ in the lesson. Write all the features of both water and rock in the given table.

Water	Rock
1.	1.
2.	2.
3.	3.
4.	4.

Answer:

Alchemy Of Nature Class 10 Solutions Question 6.
The writer has very positively described the different things in nature. Discuss with your partner the special features of each one of them. Add on the list.

Answer:

Part of nature	Special feature	Value learnt
1. rainbow	cheerfulness; acceptance.	Even when there are problems in the surroundings, we must be cheerful and spread colour and happiness.
2. caterpillar	patience; acceptance.	There is a bright and beautiful future ahead.
3. hibiscus flower	optimism; cheerfulness	However short life may be, we must live it to the fullest.
4. rocks	obedience to nature; adjustment; humility	Obey the commands of nature; adjust to the situation; be humble
5. bits of grass	optimism; perseverance.	However impossible things may look, there is an opening.
6. bare tree	optimism, faith; conviction	However difficult things are in the present, it will not remain so forever. With conviction we should remind ourselves that this too will pass.
7. water	perseverance; determination; humility.	(i) Even colossal problems can be surmounted if we persist. (ii) Learn to adapt to others without any hint of ego.

Alchemy Of Nature Questions And Answers Question 7.
Think and answer in your own words.
(a) How should you deal with difficulties and problems?
Answer:
When coming across problems In lilt. I turn towards nature for inspiration. I try to understand how the different elements in nature deal with their difficulties and try to solve my own problems in the same way.

(b) ‘An oyster turns a grain of sand into a pearl.’ What can we learn from this example?
Answer:
We learn that there Is a mysterious power or magic In nature that can change things dramatically.

(c) How does nature succeed in its ‘Alchemy’? What can it turn a small person into?
Answer:
Nature succeeds in Its ‘Alchemy’ by changing things in a mysterious way. It can turn a small person Into anything he/she wishes one touches nature and becomes gold oneself.

(d) Which two aspects of nature teach us to accept change and adjust according to the situation?
Answer:
With gentle humility, water changes its form according to the dictates of the sun and the wind. The bare trees wait patiently during the winter months for the arrival of spring, when they get Wesh green leaves. These two aspccts of nature teach us to accept change and adjust according to the situation.

(e) Why does the writer begin by quoting the lines from William Blake’s poem (Auguries of Innocence)?
Answer:
These lines show that it we pause to relleci, there Is much beauty In nature and plenty that we cari learn from it. The write-up expands on the sanie idea, thus reflecting the philosophy of the quoted lines from William Blake.

Question 8.
(A) Pick out from the lesson 10 examples of each.
Concrete Nouns (that you can touch or see)
For example, sand
(1) …………………………………………
(2) …………………………………………
(3) …………………………………………
(4) …………………………………………
(5) …………………………………………
(6) …………………………………………
(7) …………………………………………
(8) …………………………………………
(9) …………………………………………
(10) …………………………………………
Answer:
(1) bird,
(2) ant,
(3) oyster.
(4) pearl.
(5) caterpillar,
(6) butterfly
(7) flower,
(8) ocean,
(9) rock,
(10) water.

Abstract Nouns (that which you cannot touch or see)
For example, infinity
(1) …………………………………………
(2) …………………………………………
(3) …………………………………………
(4) …………………………………………
(5) …………………………………………
(6) …………………………………………
(7) …………………………………………
(8) …………………………………………
(9) …………………………………………
(10) …………………………………………
Answer:
(1) majesty.
(2) conviction.
(3) perseverance,
(4) passion
(5) infinity.
(6) Imagination,
(7) joy,
(8) significance,
(9) experience,
(10) difference.

(B) Underline the verbs in the sentences below and say whether they are Transitive (needing an Object) or Intransitive (need not have an Object).
(1) One can witness and experience the beauty of Heaven.
(2) It leaves me in complete awe.
(3) Nature soothes and nurtures.
(4) It withers completely.
(5) The flower comes to life only for a day.
(6) A rainbow colours the entire sky.
(7) It smiles and dances.
Answer:
(1) One can witness and experience the beauty of Heaven. (T)
(2) It leaves mc In complete awe. (T)
(3) Nature soothes and nurtures. (I)
(4) It withers completely. (I)
(5) The flower comes to life one for a day. (I)
(6) A rainbow colours the entire sky. (T)
(7) It smiles and dances. (I)

Question 9.
(A) Compose about 8 to 10 sets of imaginary dialogues between a bird, a tree and its fruit regarding the effects of environmental changes. Write it in your notebook.
Answer:
Conversation between a bird, a tree and its fruit:
Conversation 1:
Bird: Hi there, tree! How are you doing?
Tree: Not too well. I can’t breathe. There’s too much of dust and smoke here.
Bird: What, here too? I’ve come here to escape just that!
Fruit: Wrong place, birdie. Look at me do I look healthy? I’m not growing. Too many insecticides have been sprayed on me.
Bird: Oh, oh. Maybe I should leave this place too.

Conversation 2:
Tree: Oh, no! Something is happening! My roots are getting loose!
Bird: That’s called erosion. Soil erosion.
Tree: What happens next?
Bird: The next time it rains heavily-boom! Down you will go! And away I will fly.
Tree: Can’t someone help me?
Fruit: What about me?

(B) Prepare a Fact file of any of the following plants/trees, using the points given.
[coconut / neem / basil / cactus / apple]

• Name of Plant/Tree …………………………………………
• Scientific name …………………………………………
• Region and climate …………………………………………
• Features …………………………………………
• Growth …………………………………………
• Size, shape and colour …………………………………………
• Uses …………………………………………
• Any special feature …………………………………………

Answer:
Profile of the Coconut Tree and Fruit
(1) Names: English name – Coconut Sanskrit name – Narikela Hindi name – Nariyal.
(2) Scientific name: cocos nucifera belongs to the family ‘Palmae’ or the palm family (also known as Arecaceae).
(3) Region and Climate: Tropical and sub-tropical coastal regions, especially near sea beaches.
(4) Features:

• Fruit: has a thick fibrous coir over the hard shell inside the kernel colourless liquid;
• leaves: feather-shaped and split into lots of leaflets.

(5) Growth – Size and shape: Coconut trees can: grow from 15 to 30 metres in height in plantations. Coconut fruits are oval in shape. The trunk of the coconut tree is ringed with scars where old leaves have fallen. The top of the trunk is crowned with a rosette of leaves. The leaves can grow up to 7 feet long and can have 250 leaflets.
(6) Uses:

• Coir and leaves: matting, thatching and weaving.
• Hard outer shell about 10 to 15 inches in length used to make articles such as spoons, eating utensils, charcoal, etc.
• Inside of the shell: lined with a white edible layer called the meat used for cooking, or extraction of oil which is used in making soaps or cosmetics also to make chemical, industrial and medicinal products contains coconut water which is very nutritious.
• Husk and leaves: used as material to make a variety of products for furnishing and decorating,

(7) Any special feature: Known in India as ‘kalpavriksha’ or the ‘tree of heaven’ because of its many uses the term coconut is derived from the 16th century Portuguese and Spanish, meaning ‘grinning face’, from the three small holes on the coconut shell that resemble human facial features.

Question 10.
‘Impossible’ itself says ‘I M possible’. Do you agree? Justify your answer by citing something that you have experienced or heard from someone.
Answer:
Yes, I agree. It is possible to do the most , difficult of things providing we have the will and conviction to do so. The example that comes to my mind as justification is that of Sudha Chandran, the j dancer. Though her leg was amputated below the knee, with great grit and determination she restarted dancing, and went on to become a famous dancer ! and actress. This shows that one can do things which seem to be impossible.

Question 11.
You have an environment protection week celebration in your school. You have invited an environmentalist. Your friend interviews him/her about how to save the environment. Frame suitable Interview Questions.
Answer:
Jai interviews Mr. Ali, an environmentalist:
Jai: Good morning, Sir. Welcome to our school. I would like to ask you a few questions for a write-up in our school magazine. My first question: What is your opinion about the concept of having am ‘environment protection week’ celebration?

Mr. Ali: I think it’s a wonderful idea, though I would not call it a ‘celebration’.

Jai: Why is that, sir?

Mr. Ali: Well, you have a celebration when you are happy about something. In our town, the protection of the environment is so poor that I, as an environmentalist, am not at all happy about it.

Jai: Can you give us some tips to protect the environment?

Mr. Ali: Certainly, my boy. First of all, we should grow more trees wherever possible. It should be made mandatory for every factory, office, residential building, etc. to plant trees before starting construction.

Jai: What about the menace of plastic, sir?

Mr. Ali: We cannot eliminate plastic completely however, the thickness of plastic bags and the methods of disposal should be made clear to all. Air, water and noise pollution must be dealt with too.

Jai: Please expand on that, sir.

Mr. Ali: Well, industrial and vehicular pollution must be controlled water bodies must be kept clean. Those who break rules must be penalized. Loudspeakers must be banned during the night hours. Oh, there are lots of things to be done, lots of things.

Jai: Thank you sir, for giving some of your precious time for this interview.

Question 12.
Write a News Report on the ‘Environment Day’ celebrated in your school.
Answer:
Environment Day Celebrations
Nagpur, June 7: ‘World Environment Day’ was celebrated in New Era School with great fanfare on June 5. The main purpose of the celebration was j to spread awareness about the need to protect the: environment and the ways to do it.

The day was flagged off by a tree plantation drive in the locality. Three hundred quick-growing trees, which do not need much water on a daily basis, were planted near the school wall and in the surrounding area. An eminent environmentalist, Mr. A.T. Ali, spoke on the ways to protect the environment. He also judged the ‘Posters and Photographs’ exhibition “and gave away prizes for the best entries. Environmentally- friendly articles, like disposable plates and cups made from bamboo and banana stem, bags made from leaf waste, etc. were on sale. Students gave power-point ) presentations on the threats to the environment. Last i but not least, was the spirited debate on the topic ‘Man: The worst enemy of the Environment’.

All in all, the day was a great success, and has certainly made a difference to the way we view our environment.

– Josh Matthew
New Era School.

Question 13.
Just For Laughs! Enjoy!
Divide the class into two groups. On 12 to 15 slips of paper, Group A writes 12 to 15 conditional clauses beginning with ‘If’.
(For example, If I work very hard, ………………………………………………)
Group B writes 12 to 15 main clauses.)
(For example, I would/shall have a pizza.)
Now, one student from Group ‘A’ reads the first conditional clause (possibility) and one student from Group ‘B’ reads the first main clause. It forms crazy sentences, just for laughter and fun. ENJOY!

Question 14.
Pick out the statements that are false and write them correctly:
(1) On the beach. the author found rocks carved and sculpted by the wInd.
(2) The hibiscus flower smiles with the sun and dances with the wind.
(3) Rocks take the shape that (he water commands.
(4) Our problems are big and so are we.
Answer:
Statements (1) and (4) are false. The corrected statements are:
(1) On the beach, the author found rocks carved and sculpted by the water.
(4) Our problems are very big, and we are very small.

Question 15.
ExplaIn how the hibiscus flower makes the most of Its short life span.
Answer:
The hibiscus flower smiles with the sun and dances with the wind. The flower comes to life only for a day yet It makes the most of the day by living its short life in full splendour, with big, bright and tender blooms.

Question 16.
Complete the flowchart that highlights the life of a hibiscus flower:
Answer:
The life of a hibiscus flower

Question 17.
Guess the meaning of the ‘splendour’.
Answer:
Splendour – great beauty which attracts admiration and attention.

Question 18.
Choose the correct ‘not only … but also …….’ form of the sentence:
Natures soothes and nurtures.
(a) Not only nature soothes but nurtures also.
(b) Nature soothes not only but also nurtures.
(c) Nature soothes but also nurtures not only.
(d) Nature not only soothes but also nurtures.
Answer:
(d) Nature not only soothes but also nurtures.

Question 19.
By evening It falls and becomes one with the earth again. (Rewrite using the ‘-tng form of the underlined word.)
Answer:
By evening it falls, becoming one with the earth agaIn.

Question 20.
Who Is stronger – water or rocks? Justify your answer.
Answer:
I think water is stronger. It wears down tue hard rock by its gentle patience, persistence and perseverance

Question 21.
State whether the ¿ilowlng statements are True or False: (The answers are given directly and underlined.)
Answer:
(i) The spider’s webs are delicate as well as weak. ‘ False
(Ii) The teamwork and perseverance of ants were Impressive. True

Question 22.
What teaches us that hard times do not last forever? How?
Answer:
The following things teach us that hard times do not last forever:
(i) bits of grass peeping through small cracks in a concrete pavement and
(ii) the green leaves on a tree In spring The grass had been nearly destroyed by the concrete but had come to life again. The tree had been bare all through the cold winter months, before regaining Its former green majesty.

Question 23.
Choose the sentence In the Past Perfect Tense from the sentences given below:
(a) The ants had organised themselves around the fly.
(b) The ants organized themselves around the fly.
(c) The ants hat’e organized themselves around the Jly.
Answer:
(a) The ants had organised themselves around the fly.

Question 24.
A rainbow colours the entire sky. (Begin the sentence with The entire sky …‘)
Answer:
The entire sky is coloured by a rainbow.

Question 25.
However Impossible things may look, there Is always an opening. (Rewrite beginning with ‘Even if..’.)
Answer:
Even if things, look Impossible. there is always an openIng.

Question 26.
Spider webs are delicate, yet very strong. (Rewrite beginning with ‘Although ….)
Answer:
Although spider webs arc delicate, they are very strong.

Question 27.
(1) PIck out an Infinitive from the lesson and use It In your own sentence.
(2) Punctuate what If we too had lived our lives however short to its fullest
(3) Find out two hidden words from the given word: approaches
(4) Make a meaningful sentence by using the given phrase: set In
(5) Spot the error and rewrite the correct sentence: When I do. It leave me In complete awe.
(6) IdentIfy the type of sentence: However dimcult things are right now, it will not remain so forever.
(7) WrIte the following words In alphabetical order: perseverance, withers, majesty, ‘oysters.
(8) Pick ont the verb from the following that can form both the present and past participle by doubling the last letter, and write the forms: hit. admtt. turn, feed
Answer:
(1) I went to the beach because I wanted to see the ship.
(2) What if we too had lived our lives, however short, to Its fullest?
(3) approaches — approach, perch (cheap, peach, preach)
(4) Many people try to avoid being In Mumbal when the summer sets in.
(5) When I do, It leaves me In complete awe,
(6) Assertive sentence (negative)
(7) majesty, oysters, perseverance, withers
(8) admit — admitting, admitted

Question 28.
Write 4 words related to things in nature.
Answer:
(1) (i) We must plant more trees to attract rain.
(ii) The new plant started production last year.
(2) We had gone to a rocky beach.
(3) We are soothed and nurtured by nature.
(4) Nature: sand, flower, tree, sun, ocean, rock. water, grass

Question 29.
(1) Use the following word as a verb and a noun in two separate sentences: touch
(2) Analyse the sentence: We saw small bits of grass peeping through the small cracks in a concrete pavement.
Answer:
(1) (i) “Can you touch the sky. Papa7 asked the little girl. (verb)
(ii) The old lady would wake UI) at the slightest touch. (noun)
(2) Simple Sentence.

English Kumarbharati 10th Digest PDF 

• Where the mind is Without fear 10th English Textbook Solutions
• The Thief’s Story 10th English Textbook Solutions
• On Wings of Courage 10th English Textbook Solutions
• All the World’s a Stage 10th English Textbook Solutions
• Joan of Arc 10th English Textbook Solutions
• The Alchemy of Nature 10th English Textbook Solutions

Class 10 English Chapter 3.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.4 The Will to Win Notes, Textbook Exercise Important Questions and Answers.

The Will to Win Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 3.4 Warming Up Questions and Answers

The Will To Win Poem Appreciation Question 1.
Get into pairs, discuss and tick the most appropriate answer :
(a) You may have lost the match; but
(i) It is important that you start fighting with your opponent.
(ii) It is important to have the will to win.
(iii) It is important that you blame the organizers for the rough ground.
Answer:
(ii) It is important to have the will to win.

(b) Success is always measured by :
(i) Ability to pounce upon at the opponent and fight with full force.
(ii) Match-fixing before the match begins.
(iii) Ability to bounce back after a fall.
Answer:
(c) The ability to bounce back after a fall.

(c) For attaining success; we need to :
(i) Sleep day in and day out and dream about success.
(ii) Scheme out things to make the opponent fall.
(iii) Work hard day and night for it.
Answer:
(c) Work hard day and night for it.

Appreciation Of Poem The Will To Win Question 2.
How can we achieve success in life? Complete the boxes by filling the essential qualities required for achieving success.

Answer:

Appreciation Of The Poem The Will To Win Question 3.
Discuss and write 5 proverbs/quotations related to the importance of having a strong will-power.
(a) ………………………………..
(b) ………………………………..
(c) ………………………………..
(d) ………………………………..
(e) ………………………………..
Answer:
(a) Where there’s a will, there’s a way.
(b) If at first you don’t succeed, try, try again.
(c) The truest wisdom is a resolute determination. -Napoleon Bonaparte
(d) Nothing is impossible. -Napoleon Bonaparte
(e) Determination is the key to success.

The Will To Win Question 4.
Complete the following table.
Make a list of great personalities of present and past who have achieved success in different walks of life. You can take help of your school library or search on the internet.

Answer:

The Will to Win Class 10 English Workshop Questions and Answers Maharashtra Board

The Will To Win Appreciation Question 1.
(A) In order to achieve success the poet wants us to
(a) ………………………………..
(b) ………………………………..
(c) ………………………………..
Answer:
(a) go out and fight for it
(b) work day and night for it
(c) give up time, peace and sleep for ft.

(B) Write as many phrases as you can using ‘enough’ and use them in your sentences.
Example : good enough
Answer:
(1) hard enough : If you work hard enough, you will be rewarded.
(2) bold enough : He was not bold enough to realise his ambitions.
(3) fast enough : He was not fast enough to understand the joke at his expense.
(4) strong enough : The little bird was still not strong enough to fly away on its own.
(5) reasonable enough : The price seemed reasonable enough; yet I hesitated to buy It.

(C) What does the word ‘Scheme’ mean here ? Choose the correct alternative from the following.
(a) Housing colony
(b) Goal in life
(c) Rhyme pattern
(d) Plan of action
Answer:
(d) plan of action

(D) Do you think the line ‘Give up your time and your peace and your sleep for it’ means that one should be ‘desperate’ or restless’ to achieve one’s goal. Explain your opinion, in your notebook.
Answer:
No. If you are ‘desperate’, you might take unnecessary risks to achieve your goal. If you are ‘restless’, you will have no peace of mind. What the poet means by losing ‘time’. ‘peace’ and sleep’ means spending many hours working hard to gain one’s objectives and to continually keep on thinking about it until it is achicvcd.

(E) Following lines are given to you. Find their appropriate meanings after discussing with your partner.
(a) To go out and fight for it.
(b) If you gladly sweat for, fret for and plan for it.
(c) Lose all your terror of opposition for it.
(d) With all your capacity, strength and sagacity.
Answer:
(a) to try one’s best and struggle hard in order to achieve something.
(d) making full use of all your capabilities, power and wisdom.
(c) sweat for it, fret for and plan for it and lose all your terror of the opposition for it
(d) to try one’s best and struggle hard in order to achieve something.

(F) Read the poem again and complete the web showing all those things that can turn one away from ones efforts towards a goal.

Answer:

(G) Find the lines from the poem which mean-
(a) become crazy for the goal
(b) toil hard happily
(c) get rid of all fears
(d) make efforts continuously
(e) extremely poor condition
Answer:
(a) if you are mad enough for it
(b) gladly sweat
(c) work day and night
(d) If neither cold poverty, famish or gaunt,

Question 2.
The poet has mentioned some hurdles in the poem that keep us away from achieving our goal in our life. Discuss with your partner and make a list of all the hurdles mentioned in the poem.

• sickness

Answer:

• or sickness or pain

Appreciation Of The Will To Win Question 3.
The poem explicitly describes some strengths and weaknesses with the help of some words and phrases. The poet wants us to possess all the strengths and keep away from all the weaknesses. Make a list of all the words and phrases showing Strengths in table A and Weaknesses in table B. One is done for you.

A Strengths	B Weaknesses
Work day and night	Sickness

Answer:

A Will To Win Question 4.
Listen to the poem carefully and state whether the following statements are true or false. Correct the false statements.
(a) If you want a thing you should not give up your sleep.
(b) You should be afraid of your opposition.
(c) Cold or poverty cannot keep you away from achieving your goal.
(d) You can achieve your goal with the help of God.
(e) Life will not seem useless and worthless without achieving your goal.
Answer:
(a) False
(b) False
(c) True
(d) True
(e) False

The Will To Win Poem Question 5.
Form pairs and complete the web with suitable responses. Tell the class what all things the poet wants us to do to win.

Answer:

The Will To Win Speech Question 6.
Match the phrases in table A with lines of the poem given in table B.

Answer:

Will To Win Question 7.
Every stanza begins with word ‘if’. How does it add to the effectiveness of the poem?
Answer:
Without the word ‘if’, the poem would remain as a simple statement of rules for success. By beginning each stanza with the word ‘if’, first of all, the poet implies that every human being has the choice of wanting to be successful in life. This is a more effective way of expression. Also by using the word ‘if’, he puts forward the conditions that will determine success in any sphere.

Will To Win Poem Appreciation Question 8.
(A) In poetry, when words/ideas are arranged in an ascending order of importance, the figure of speech used is called ‘Climax’.
For example, Man should work for his family, his country, but most of all for God.
Pick out two examples of ‘Climax’ from the poem.
Answer:
(a) to go out and fight for it, work day and night for it, give up your time and your peace and your sleep for it
(b) … sweat for it, fret for and plan for it and lose all your terror of the opposition for it …

(B) When some words, in the line of the poem, express the same idea in different ways, the figure of speech used is ‘Tautology’.
For example, . . . happy and joyful.
. . . motionless and still.
Pick out two examples of ‘Tautology’ from the poem.
Answer:
… neither cold poverty, famish
The words ‘poverty’ and ‘famish’ imply almost the same human physical condition.

(C) Pick out one example of the following Figures of Speech.
(1) Antithesis : ………………………
(2) Alliteration : ………………………
(3) Repetition : ………………………
Answer:
(1) Work day and night for it.
(2) … of body and brain
(3) … or sickness or pain

Will To Win Poem Question 9.
Work in group and prepare and present a speech on ‘How to Achieve Success.’
Answer:
How to Achieve Success
Friends,
I, Ajai Chitnis, do not hold with those who say, ‘Success is only for the privileged few!’ In my opinion, any and everyone can achieve success. All that is required is belief in one’s potential and a few rules of thumb in order to be a winner.

First of all you must have a goal. In order to reach that goal, you must have the necessary education and skills. For this you have to study or train. Then you have to look for opportunities. Life presents choices. You have to make the right choice. Having made the right choice, you must work hard to edge towards your goal. Only after much labour, sacrifice, determination and effort will you finally achieve success. This is my opinion on ‘How to achieve success’.

Thank you.

Question 10.
Read the poem again and write an appreciation of the poem ‘The Will to Win’ in a paragraph format.
Answer:
Point Format (for understanding)
The title of the poem : ‘The Will To Win’
The poet : Berton Braley
Rhyme scheme : No specific rhyme scheme, rhymes are used randomly
Figures of speech : Repetition, Climax, Tautology, Antithesis, etc.
The central ideatheme : What we should do and what we should avoid in order to achieve success.

Paragraph Format
Berton Braley has written this inspirational poem, ‘The Will To Win’.

The poem has no specific rhyme scheme, but rhymes are used randomly all throughout. The most common type is lines ending with the word ‘it’; e.g., ‘for it’, ‘of it’, ‘of it’; ‘without it’, ‘about it’; ‘beget it’, ‘get it’; ‘sweat for if, ‘fret for if and so on. Other examples are ‘capacity’, ‘sagacity’, ‘tenacity’: ‘pain’, ‘brain’.

The main figure of speech used is Repetition, as seen in the abundance of ‘for if phrases used throughout the poem. The other figures of speech are Climax, Tautology, Antithesis, etc.

The poet gives us a formula for sure success. He tells us what we should do and what we should avoid doing in order to achieve success.

It is an inspirational poem. It motivates one to set targets and achieve goals.

Question 11.
Project :
Make a list of Berton Braley’s collection of selected poems. You can take help of your teacher, library or search on internet. Recite Braley’s any one poem in front of the class.

Question 11.
State whether the following statements are True of False. Correct the false statements : 
(a) If you want a thing, you should not give up your sleep.
Corrected statement : If you want a thing, you should willingly give up your sleep.

(b) You should be afraid of your opposition.
Corrected statement : You should not fear the opposition.

(c) Life will not seem useless and worthless without achieving your goal.
Corrected statement : Life will seem utterly useless and worthless without achieving the goal.
Answer:
(a) False
(b) False
(c) False

Question 12.
Find the appropriate meanings of the following lines :
(b) makes you quite mad enough
(c) lose all the terror of God or man for it
Answer:
(b) impels you to do crazy things like taking risks
(c) get rid of all your fears of God or man or opposition.

Question 13.
Match the phrases in table A with lines from the extract given in table :

Answer:

Question 14.
Give an example of each of the following from the extract :
(a) Tautology.
Answer:
Life seems useless and worthless without it. The words ‘useless’ and ‘worthless’ have almost the same meaning.

(b) get rid of all fears
Answer:
lose all your terror

Question 15.
State whether the following statements are True or False. Correct the false statements :
(a) Cold or poverty cannot keep you away from achieving your goal.
(b) You can achieve your goal with the help of God.
Answer:
(a) True
(b) True

Question 16.
Find the lines from the extract which mean :
(a) make winning possible by using forceful action
Answer:
(a) besiege and beget it

English Kumarbharati 10th Digest PDF

• Night of the Scorpion 10th English Textbook Solutions
• The Night I Met Einstein 10th English Textbook Solutions
• Stephen Hawking 10th English Textbook Solutions
• The Will to Win 10th English Textbook Solutions
• Unbeatable Super Mom-Mary Kom 10th English Textbook Solutions
• The Concert 10th English Textbook Solutions

Class 10 English Chapter 2.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.4 An Epitome of Courage Notes, Textbook Exercise Important Questions and Answers.

An Epitome of Courage Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.4 An Epitome of Courage Textbook Questions and Answers

Warming up!

Chit-chat:

A Strange Truth – ‘Handicapped are those who refuse to take up challenges, even with all their senses and physiology in perfect condition.’

Question 1.
Understand and discuss the above truth.
Answer:
(वरील सत्याविषयी समजून घ्या व चर्चा करा.)

Question 2.
How can you encourage such people to change and become confident? Discuss at least 4 to 5 ways you can do the above.
Answer:
1. The discussion should be related to the people who are not really disabled mentally or physically. This truth is about the people who are mentally and physically perfect but avoid, hesitate or neglect doing something challenging. By some reasons, they are not ready to change their attitude or fixed ideas. They don’t wish to change their mindset and stick to their passive and inactive attitude.

2. Think and try to understand the reasons behind their lethargy, inactiveness or indifference and try to encourage them and give them confidence.

3. Ways to encourage them and give confidence :

• Know his mindset, know his/her handicaps and obstacles he faced.
• Talk to him/her in friendly manner about his good qualities.
• Give examples of successful persons who have faced the challenges.
• Advice him/her to be brave, courageous and active.
• Help him/her in the fields where he/she lacks (confidence, courage, boldness, openness, etc.)

1. There are pleasant and polite ways of referring to people with physical and mental disabilities. Fill in the table below:

Question 1.
There are pleasant and polite ways of referring to people with physical and mental disabilities. Fill in the table below:

Answer:

2. Read the beginning and complete the story in your own words:
Sumit, the son oç a shoe maker, was a highly intelligent student in a municipal school. His Maths teacher Called him 1Einstein’, for he was brilliant in Maths.
He loved Maths. umit wanted to study further after C, however he suffered
from Polio and …..
Now, continue the story with a favourable/positive ending.
………………………………………………………………………………………………………
………………………………………………………………………………………………………
………………………………………………………………………………………………………

English Workshop:

1. Match the following. 

Question 1.
Match the following.

Answer:

2. Complete the following web-chart containing the qualities of Dr. Stephen Hawking.

Question 1.
Complete the following web-chart containing the qualities of Dr. Stephen Hawking.

Answer:

3. Arrange the following statements according to the occurance in the life history of Dr Stephen Hawking.

Question 1.
Arrange the following statements according to the occurance in the life history of Dr Stephen Hawking.
(a) At the age of 17, Stephen noticed that he fell down a couple of times for no reason.
(b) He became a fellow of the Royal Society and a member of the US National Academy of Science.
(c) He believes that in the next millenium, science will discover the core secrets of the universe.
(d) Stephen was born on 8th January, 1942 and then grew up like an average child and a normal teenager.
(e) The disease worked its way into Stephen’s body and left him disabled.
(f) Stephen decided to continue his doctoral research work with renewed vigor.
(g) Stephen was diagnosed with a rare disease – ALS or LOU.
(h) Though confined to a wheelchair he worked on computer and expressed his thoughts.
Answer:
(a) Stephen was born on 8th January, 1942 and then grew up like an average child and a normal teenager.
(b) At the age of 17, Stephen noticed that he fell down a couple of times for no reason.
(c) Stephen was diagnosed with a rare disease- ALS or LOU.
(d) Stephen decided to continue his doctoral research work with renewed vigour.
(e) The disease worked its way into Stephen’s body and left him disabled.
(f) Though confined to a wheelchair he worked on computer and expressed his thoughts.
(g) He became a fellow of the Royal Society and a member of the US National Academy of Science.
(h) He believes that in the next millennium, science will discover the core secrets of the universe.

4. Homographs – Pairs of words that are spelled and pronounced the same, but have different meanings, in different contexts.
For example

• watch – observe
• watch – device that shows time

Question 1.
Use the following words in two different contexts.
Answer:
(a) couple – couple
1. The bowler managed to take a couple of wickets.
2. The elderly couple was taking a walk in the park.

(b) mind – mind
1. There were many thoughts in his mind, before he left his house.
2. Do you mind, if I put on the fan?

(c) space – space
1. We shall make some space for our new table.
2. Man is thinking of building a space station on the moon.

(d) sound – sound
1. The loud sound at midnight startled everyone.
2. His idea of celebrating birthday in a different way sounds quite interesting.

(e) left – left
1. Go straight and then turn left to reach the station.
2. As soon as he completed his Ph.D., he left for USA.

5. Use the following words/phrases in your own sentences.

Question 1.
Use the following words/phrases in your own sentences.
(a) quirk of fate
(b) confined to
(c) exaggeration
(d) an epitome of
(e) millennium.
Answer:
(a) By the quirk of fate, all the members of the happy family died in an accident.
(b) My neighbour is confined to bed for a long time with paralysis.
(c) He told me the strange news without any . exaggeration.
(d) The champion cricketer is an epitome of modesty
(e) I believe that man will go to stay on other planets before the next millennium.

6. Expand the given themes. Make use of this support/hints:

Question 1.

Answer:
Question a.
Falling ill during the Final Exam.
Answer:
If I fall ill during my final exam, I’ll feel worried in the beginning. But soon I’ll collect myself and will face the problem boldly. Determinedly I’ll continue to appear for the remaining exam papers because there will be no reason getting into a panic about the final exam. I already have completed my study and revised it well before the exam.
My parents, I am sure, will be there to nurse me well and look after my health, medicines and my fast recovery. My friends also will help me in my

studies. They will comfort me and give me confidence. If I feel a little better, I myself will continue my studies for the final exam. So everything will fall into place.

Question b.
Helping a Disabled Person.
Answer:
If I meet a disabled person who needs help, I’ll treat him kindly. I shall sympathetically enquire about his difficulties and his requirements. I shall, with the help of my friends, try to provide him with the things he needs. If his needs are beyond our reach, we shall contact the persons or the organizations who could support him and fulfill his needs and requirements. We shall continue our efforts till he meets all his essential needs and equipment.

Question c.
Helping a Friend in Trouble.
Answer:
If any of my friends is in trouble, I will immediately visit him and find out the nature of his trouble. I shall try to pacify him if he is really very much affected. I shall console him if his trouble is because of emotional or financial problems. My friends and I will promise him to share his problem if he speaks it up clearly and freely. A trouble shared is a trouble halved. We shall advise him to be patient and tolerate the situation bravely and courageously. We shall try to help and support our friend in every possible way.

Question d.
Meeting a Great Person like Dr. Stephen Hawking.
Answer:
Before meeting such a great person like Dr. Stephen Hawking, I will have to preplan my visit and get permission for the visit from him. I must be ready with the information about his life history, his characteristics, his education, his achievements and his display of exemplary courage in the face of overwhelming odds.

It is difficult to face and get to talk to such an awe-inspiring person. But I know how to handle myself in this situation. I will talk to him boldly and respectfully. I will overcome my fear of meeting such a great man. I will tell him how I am impressed and inspired by his work and achievements. I will get the greatest joy of my life in meeting such a great personality.

7. You happen to meet a successful person who is a disabled. Write an imaginary dialogue between you and him/her. You can take support of the hints provided.

Question 1.
You happen to meet a successful person who is a disabled. Write an imaginary dialogue between you and him/her. You can take support of the hints provided.
(a) introductionlwelcome/greetings
(b) congratulating/honouring
(c) cause/reason for the disability
(d) decisionlplan/organisationlimplementation
(e) idols in life
(f) parents/friends – support if any
(g) success stories/accomplishments
(h) conclusion/final message if any
Answer:
Answer:
An Imaginary Dialogue between Sumit, a disabled and you:

• Myself: Hello, Sir, nice to meet you. I have read that you have received ‘The Sangeet Samrat’ Award of our city. Congratulations!
• Sumit: Yes, you are right, and thank you for your good wishes.
• Myself: You are confined to the wheelchair and both your legs are amputated. What made you disabled?
• Sumit: At the age of five I was crippled by Polio, The disease worked its way into my legs and they had to be amputated. I was confined to this wheelchair since then.
• Myself: I wonder how you could achieve such a great feat. Didn’t you feel depressed?
• Sumit: That is a long story. Music was in my blood. My father was a great classical singer. I used to listen to him since my childhood. He was my first Guru.
• Myself: With all your sufferings and this disability, what made you live a normal life and who inspired you?

Sumit: God is great! And courage is a wonderful thing! I was optimistic, so I faced the calamity without losing heart. Fortunately one of our teachers in our special school inspired me. He told me the story of Wilma Rudolf whose legs were crippled by Polio. Even then she wanted to become the fastest runner in the world and she did it! She practised with determination.

She failed in many races got up started again. The day came when she reached Rome for participating in the 1960 Olympics. In women’s running races (events), she won gold medals in 100 metres running, 200 metres running and 400 metres relay race, defeating all the participants. She became the fastest runner in the then world. The story inspired me and I started my riyaz undauntedly for hours together and here I am today.

• Myself: Were there any obstacles?
• Sumit: Yes, there were. I faced them boldly and moved ahead. People began to admire my songs and music. Now people respect me as rich and famous, but a humble music director.
• Myself: Could you please tell me about the most memorable day in your career as a music composer?
• Sumit: Yes, It is unforgettable that I received my ‘Sangeet Samrat Award’ from Godlike Guru Pandit Hridaynath Mangeshkar.
• Myself: What are your plans for future?
• Sumit: I will continue my service to music and please my fans.
• Myself: What is your advice to the younger generation?
• Sumit: Come what may. Work hard determinently. Win over your physical or mental calamities courageously. Don’t give up and try your best to get success in life.
• Myself: Thank you for giving your precious time and talk.
• Sumit: It’s my pleasure!

Language Study:

1. Complete the following Word Chain of adjectives.

Question 1.
Complete the following Word Chain of adjectives
(a) cruel →____→ ____ → ____ → ____.
(b) medicine →____ → ____ → ____ → ____.
(c) grow →____ →____ → ____ → ____.
(d) physics →______ → ______→ ______ → ______.
Answer:
(a) cruel → lazy → yearlong → genuine → enthusiastic.
(b) medicine → energy → yardstick → keyboard → diary.
(c) grow → withstand → develop → practice → entertain.
(d) physics → secretary → yawn → nature → eligible

2. (A) Convert the following to Exclamatory sentences of the same meaning.

Question 1.
Convert the following to Exclamatory sentences of the same meaning.
(a) Dr Hawking is a very humble man.
(b) He was very clumsy.
(c) He was very simple and intelligent.
(d) Courage is a truly wonderful thing.

Answer:
(a) How humble a man Dr. Hawking is!
(b) How clumsy was he!
(c) How simple and intelligent was he!
(d) How truly wonderful a thing courage is!

(B) Convert the following to Interrogative (Question) form.

Question 1.
Convert the following to Interrogative (Question) form.

1. The prognosis was bad.
2. Stephen decided to continue his research.
3. There are many people who display exemplary courage.
4. His mind would soar up into space like light.

Answer:

1. Wasn’t the prognosis bad?
2. Didn’t Stephen decide to continue his research?
3. Aren’t there many people who display exemplary courage?
4. Wouldn’t his mind soar up into space, like light?

My English Coursebook 10th Digest Chapter 2.4 An Epitome of Courage Additional Important Questions and Answers

Read the following passage and do the activities:

Simple Factual Activities:

Question 1.
Complete the following sentences with the help of the information from the passage:
(Answers are directly given and underlined.)
Answer:

1. Dr. Stephen Hawking was born on the eighth day of January 1942 in Oxford.
2. Courage is the quality which makes people not to lose heart when faced with a great calamity.
3. Dr. Stephen Hawking was a living legend of Cosmology.
4. He wanted to study mathematics but the Oxford University did not have mathematics course then, so he opted to study physics instead.
5. Stephen Hawking’s parents failed to know ! about Stephen that one day their little boy ; will be acclaimed as one of the greatest scientist of this century.
6. Stephen Hawkings was sent to the University of Oxford to study Mathematics.

Question 2.
State whether the following sentences are True or False:
Answer:

1. Dr. Stephen Hawking was born on the eighth day of February 1942. – False
2. Dr. Stephen Hawking was a living legend of Biology. – False
3. Courage makes people not lose heart when faced with a great calamity. – True
4. Dr. Stephen Hawking was born before the death of Galileo. – False

Question 3.
Say whether the following statements are True or False:
Answer:

1. At the age of 17 Dr. Stephen Hawking was suffering from an extremely rare disease. – True
2. Stephen’s teachers liked his handwriting very much. – False
3. He got his Ph.D. studying the concept of ‘Black Holes’. – True
4. At the dismal stage Dr. Hawking enjoyed his life the most. – True

Question 4.
Complete the following sentences with the help of the information given in the passage:
(Answers are directly given and underlined.)
Answer:

1. Dr. Hawking is a very humble man, though he is considered Einstein’s equal in intelligence.
2. Dr. Hawking expressed his thoughts with the help of his finger and with a computer.
3. He was bestowed with numerous honorary doctorates and awards.
4. Dr. Hawking’s ‘A Brief History of Time’ is one of the best selling books of our time.

Complex Factual Activities

Question 1.
What do you know about Dr Stephen Hawking from this passage?
Answer:
Dr Stephen Hawking was born in Oxford on the 8th of January 1942. Nobody could imagine that the little boy would be one of the greatest scientists of this century. He faced a great calamity with great courage and became living legend of Cosmology. His body was bound to a wheelchair but his mind was working and that made him one of the greatest scientists of this century.

As a child he had a lot of love for music and mathematics. His father wanted him to study medicine but he was bent on studying mathematics. The Oxford University did not have a course in mathematics, so he opted to study physics.

Question 2.
Complete the web:
(Answers are directly given and underlined.)
Answer:

Question 3.
Complete the following web showing the effects of the disease ALS or LOU on Dr Hawking:
(Answers are directly given and underlined.)
Answer:

Question 4.
What did Dr. Stephen achieve even after the disease disabled him?
Answer:
Even after the disease disabled Stephen he continued his doctoral research work with renewed vigour. He studied the concept of “Black Holes” and got his Ph.D. in the subject. The study sparked his imagination with bright ideas. He made many epoch-making statements that shook established theories. To explain the concept of ‘Big Bang’ better, Stephen invented what is known as “Lie Algebra”.

Question 5.
What does the writer say about the books authored by Dr. Hawking?
Answer:
The writer says about Dr. Hawking’s books that he wrote many books dealing with his terrific ideas keeping a common man in mind. His writing is full of wit and humour. His style is so lucid that non-scientists can also understand his writing. His book ‘A Brief History of Time’ is one of the best selling books of our time.

Question 6.
Which of Dr. Hawking’s achievements are mentioned in this passage?
Answer:
Dr. Hawking is an authority on profound subjects of science. Numerous honorary doctorates and awards have been bestowed upon him. He is a Fellow of the Royal Society and a member of the US National Academy of Sciences. He has authored many books dealing with his awesome ideas. His book ‘A Brief History of Time’ is one of best selling books of our times.

Activities based on Vocabulary:

Question 1.
Classify the following words into verbs, adjectives and nouns:
whole, know, little, predict, calamity, legend, mind, physics, great, imagine, wonderful, cruel, courage, faced, grew, heart, fate, course.
Answer:

1. Verbs – know, predict, imagine, faced, grew
   
2. Adjectives – little, wonderful, cruel, whole, great
3. Nouns – calamity, legend, mind, physics, courage, heart, fate, course

Question 2.
Find the similar meaning word/phrase for the following from the passage
Answer:

1. a period of hundred years – century
2. a very fine example of something – epitome
3. acclaimed – hailed
4. unexpected change of destiny – quirk of fate

Question 3.
Match the words in Column ‘A’ with their meanings in Column ‘B’:

Answer:

Question 4.
Write the adjectives for the following nouns from the passage:

1. ideas
2. style
3. courage
4. secrets.

Answer:

1. awesome ideas
2. lucid style
3. exemplary courage
4. core secrets

Question 5.
Match the words in Column ‘A’ with their meanings in Column ‘B’:

Answer:

Activities based on Contextual Grammar:

Question 1.
Make the following sentences exclamatory:

i. Courage is truly a wonderful thing.
Answer:
What a wonderful thing courage is!

ii. He was very clumsy.
Answer:
How clumsy he was!

Question 2.
Change the following sentence into positive and comparative degree:
Dr Hawking is one of the greatest scientists of this century.
Answer:
i. Positive degree: Very few (Not many) scientists of this century are as great as Dr. Hawking.
ii. Comparative degree: Dr. Hawking is greater than most other scientists of this century.

Question 3.
He is one of the greatest scientists of this century. (Choose the correct question tag from the given alternatives.)
(a) aren’t he?
(b) is he?
(c) wasn’t he?
(d) isn’t he?
Answer:
He is one of the greatest scientists of this century; isn’t he?

Question 4.
He made many epoch-making statements. (Rewrite the sentence using Present Continuous Tense.)
Answer:
He is making many epoch-making statements.

Question 5.
This disease came as a bolt from the blue. (Rewrite the sentence using Past Perfect Tense.)
Answer:
This disease had come as a bolt from the blue.

Personal Responses:

Question 1.
Do you think, that courage is a wonderful thing? Why do you think so?
Answer:
Yes, I do think that courage is a wonderful I think because it can work miracles in one’s life. A person with great courage stimulates an ordinary or even a disabled person to achieve the impossible, I know a small boy who rescued his younger sister from a tiger’s fierce attack. A courageous person is brave enough to do whatever he/she feels to be right and good in his or her opinion.

Question 2.
What, do you think, are the miseries of a person who is confined to wheelchair?
Answer:
I think, the person who is confined to a wheelchair has to face many restrictions, difficulties and inconveniences. He is mentally and physically depressed all the time. He is deprived of living comfortable happy life. He neither has control over his limbs nor on his mind.

Question 3.
How do you know that Dr. Hawking is a perfect example of optimism and hope?
Answer:
He fully believed in his courage, his intelligence and his authority on profound subjects of science. He did not lose his hopes, even when he was suffering from the dreaded ALS disease. He believed that his life was not different from other people. He tried his best and lived a normal life like other people. He did not think about his sufferings or regret the things that prevented him from doing the things he hoped. His optimism helped him to fulfill his hopes and goals.

Do as directed:

Question 1.
His writing is full of wit and humour.
(Rewrite the sentence using Past Perfect Tense.)
Answer:
His writing had been full of wit and humour.

Question 2.
He is a fellow of the Royal society and a member of the US National Academy of Science.
(Use not only – but also)
Answer:
He is not only a fellow of the Royal society but also a member.

Activities based on Language Study

Do as directed:

Question 1.
Complete the words by using the correct letter:

1. d e _ t h
2. s t _ g e
3. b o o _ s
4. b _ a v e

Answer:

1. d e a t h
2. s t a g e
3. b o o k s
4. b r a v e

Question 2.
Put the following words in alphabetical order:

1. profound, prognosis, planet, possible
2. undaunted, confined, awesome, explain

Answer:

1. planet, possible, profound, prognosis
2. awesome, confined, explain, undaunted

Question 3.
Punctuate the following sentences:

1. he said to her we must have to come out of this calamity
2. shall we reach meeras house on time i asked.

Answer:

1. He said to her, “We must have to come out of this calamity.”
2. “Shall we reach Meera’s house on time?” I asked.

Question 4.
Make four words (minimum 3 letters each) using the letters in the word meanwhile:
Answer:
mean, while, meal, mile

Question 5.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Do as directed:

1. Attempt anyone:

b. Add a clause to the following sentence to expand it meaningfully.
Nobody thought that
Answer:
Nobody thought that he would become such a great sportsman.

2. Attempt anyone:

a. Add a prefix or suffix to make new words:
1. known
2. lucky
Answer:
1. unknown
2. unlucky

OR

b. Make a meaningful sentence using any one of the following words:
1. known
2. lucky
Answer:
1. Satyendra Nath Bose was one of the known scientists of India.
2. Our school team was lucky to win the Kabaddi match at the last moment.

My English Coursebook 10th Digest Pdf Unit 2 

• You Start Dying Slowly … 10th English Solutions
• The Boy who Broke The Bank 10th English Solutions
• The Twins 10th English Solutions
• An Epitome of Courage 10th English Solutions
• Book Review – Swami and Friends 10th English Solutions
• World Heritage 10th English Solutions

Class 10 English Chapter 4.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.4 The Height of the Ridiculous Notes, Textbook Exercise Important Questions and Answers.

The Height of the Ridiculous Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 4.4 Warming Up Questions and Answers

The Height Of The Ridiculous Appreciation Question 1.
The teacher writes incomplete sentences on the board. He/She asks the students to complete them in their notebooks.
(a) Today, I am happy because ……………………………… .
(b) Today after the class, I wish ……………………………… .
(c) Tomorrow, I feel that ……………………………… .
(d) I want to laugh because ……………………………… .
(e) Today, the class seems to be cheerful about ……………………………… .
Answer:
(a) my grandparents are coming for a holiday.
(b) to eat an ice cream.
(c) I will go for a movie.
(d) I am very happy.
(e) the forthcoming football match.

The Height Of The Ridiculous Question 2.
The teacher writes an incomplete sentence and asks the students to complete it in a funny way.
Answer:
(1) Mother gave me cheese but the cat ate it.
(2) I went to the market and bought an elephant.

Appreciation Of Poem The Height Of Ridiculous Question 3.
Give the words related to:

Syllable
A syllable is a unit of spoken language made up of a single uninterrupted sound formed by a vowel and consonants. For example, single syllable : ant, two syllables – water, three syllables : Inferno.
Answer:

The Height Of The Ridiculous Theme Question 4.
Pick out the word from the given box and write it in the correct columns below.

Here the focus is not on the spellings but the pronunciation of the words.

Words with one syllable	Words with two syllables

Answer:

The Height Of The Ridiculous Notes Question 5.
Count the syllables and circle the appropriate number in the box.

Answer:

The Height Of The Ridiculous Question 6.
Write the names of any five of your friends and mention the number of syllables in each name.

Name	Number of syllables

Answer:

The Height of the Ridiculous Class 10 English Workshop Questions and Answers Maharashtra Board

The Height Of The Ridiculous Question 1.
Find out expressions from the poem that indicate funny moments.
For example, I laughed as I would die.
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
Answer:
(1) was all upon the grin
(2) the grin grew broad
(3) and shot from ear to ear
(4) He read the third; a chuckling noise
(5) The fourth; he broke into a roar
(6) The fifth; his waistband split;
(7) The sixth; he burst five buttons off;
(8) And tumbled in a fit.

Appreciation Of The Poem The Height Of Ridiculous Question 2.
Order of sequence : Arrange the following reactions in their proper order, as per the poem.
(a) His waistband split
(b) The grin grew broad.
(c) Sleepless eye.
(d) Was all upon the grin.
(e) He broke into a roar.
(f) He burst five buttons off.
Answer:
(d) Was all upon the grin
(b) The grin grew bro^d
(e) He broke into a roar
(a) His waistband split
(f) He burst five buttons
(c) Sleepless eye

Height Of Ridiculous Appreciation Question 3.
Form pairs and find out the various rhyming words in the poem and two of your own. Complete the following table.

Answer:

The Height Of Ridiculous Appreciation Question 4.
Match the lines with the Figures of Speech.

Answer:

Appreciation Of The Poem The Height Of The Ridiculous Question 5.
Copy any two stanzas of the poem in the lines below. Using a coloured pen underline the stressed syllables in each line and put a stress-mark ( ) over each.
Answer:
I wrote some lines once on a time
In wondrous merry mood,
And thought, as usual, men would say
They were exceeding good.

The Height Of The Ridiculous Question 6.
Complete the lines of the poem by choosing proper pairs of rhyming words and make it meaningful.
– We returned home late, one ………………………. ,
In the window, there glowed a ………………………. .
Burglars !! was our very first ………………………. ;
For defence, sticks ‘n stones we ………………………. .
”Let’s grab the loot and ………………………. ,”
was uttered soft, by ………………………..
The door we softly ……………………….,
And then we were truly ………………………..
Oops! Before, outside, we’d ……………………….,
The television had been left ………………………..
(run, shocked, gone, night, sought, on, someone, thought, light, unlocked)
Answer:
We returned home late, one night,
In the window there glowed a light.
Burglars! Was our very first thought,
For defence, sticks ‘n stones we sought.
“Let’s grab the loot and run.”
Was uttered soft, by someone.
The door we softly unlocked.
And then we were truly shocked.
Oops! Before outside we’d gone,
The television had been left on!

The Height Of Ridiculous Poem Appreciation Question 7.
Form goups in your class and together compose a short humorous poem. Use jokes, experiences, etc. and convert it to a poetic form. Write and decorate it on chart-paper and put it up in your class, in turns.

Appreciation Of The Height Of The Ridiculous Question 8.
Go through the poem and write an appreciation of the poem in a paragraph format.
Answer:
Point Format
(for understanding)
The title of the poem: ‘The Height of the Ridiculous’
The poet: Oliver Wendell Holmes
Rhyme scheme: abcb.
Figures of speech: Transferred Epithet, Hyperbole, Onomatopoeia, Tautology, Alliteration, etc.
Theme/Central idea: A funny poem to simply entertain the audience; written for Enjoyment.

Paragraph Format
The poem ‘The Height of the Ridiculous’ is written by Oliver Wendell Holmes.

The rhyme scheme of the poem is abcb. There are many figures of speech, like Hyperbole, Tautology, Onomatopoeia, Alliteration, etc. but the one that stands out is Transferred Epithet. In the line ‘Ten days and nights, with sleepless eye’, the adjective ‘sleepless’ should be for the man and not for the eye.

The poem is a humorous one written for enjoyment, with plenty of funny expressions. The main purpose of the poet is to simply entertain the reader.

Appreciation Of Poem The Height Of The Ridiculous Question 9.
Project :
Reading a poem.
Arrange the poetry reading competition. Select the poem of your choice.

• Read the poem silently.
• Repeat the reading of the poem.
• Focus on the pauses, stresses, intonation etc.
• Pay attention to the proper pronunciations.

Poem Appreciation Of The Height Of Ridiculous Question 10.
Choose the correct alternatives: (The answers are given directly and underlined.)
(1) The poet was in a very …………….. mood when he wrote the lines.
(a) tired
(b) happy
(c) bored
(d) wondering
Answer:
(b) happy

(2) The poet was generally a ……………… man.
(a) humorous
(b) wonderful
(c) serious
(d) good
Answer:
(c) serious

Question 11.
Explain:
(a) the contrast between the poet and his servant.
Answer:
The poet was a thin and slender man while his servant was strong and muscular.

(b) the poet’s reaction when he read the lines.
Answer:
The poet laughed heartily when he read the lines. He laughed so hard he thought he would die.

Question 12.
Find out the expression from the extract that indicates funny moments:
Answer:
‘I laughed as I would die’.

Question 13.
Match the lines with the figures of speech:
Lines – Figures of Speech
(a) A sober man am I – (c) Tautology
(b) To mind a slender man like me – (d) Inversion
Answer:
(a) A sober man am I – Inversion
(b) To mind a slender man like me – Alliteration

Question 14.
Complete the following:
(1) There was a grin on the servant’s face when …………………………
(2) The chuckling noise was heard when ……………………..
(3) When he read the fifth line ………………….
(4) The grin grew from ear to ear when the servant ………………….
Answer:
(1) he read the first line.
(2) the servant read the third line.
(3) his waistband split.
(4) read the second line.

Question 15.
Describe the outcome of this experience on the poet.
Answer:
After this experience, the poet has never dared to write any more funny poems.

Question 16.
Which line suggests that the servant was totally out of control?
Answer:
The line ‘And tumbled into a fit’ suggests that the servant was totally out of control.

English Kumarbharati 10th Digest PDF

• A Thing of Beauty is a Joy For Ever 10th English Textbook Solutions
• The Luncheon 10th English Textbook Solutions
• World Heritage 10th English Textbook Solutions
• The Height of the Ridiculous 10th English Textbook Solutions
• The Old Man and The Sea Book Review 10th English Textbook Solutions
• The Gift of the Magi 10th English Textbook Solutions