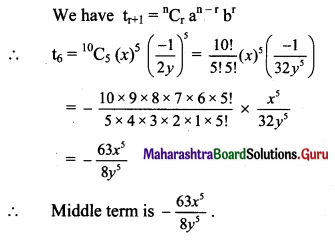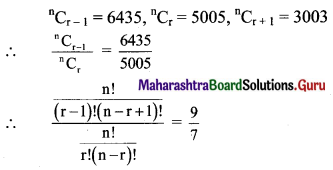Category: Class 11

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Ex 5.2 Questions and Answers.

11th Maths Part 2 Sets and Relations Exercise 5.2 Questions And Answers Maharashtra Board

Question 1.
If (x – 1, y + 4) = (1, 2), find the values of x and y.
Solution:
(x – 1, y + 4) = (1, 2)
By the definition of equality of ordered pairs, we have
x – 1 = 1 and y + 4 = 2
∴ x = 2 and y = -2

Question 2.
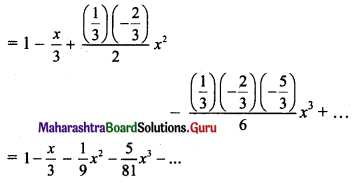
If \(\left(x+\frac{1}{3}, \frac{y}{3}-1\right)=\left(\frac{1}{2}, \frac{3}{2}\right)\), find x and y.
Solution:
\(\left(x+\frac{1}{3}, \frac{y}{3}-1\right)=\left(\frac{1}{2}, \frac{3}{2}\right)\)
By the definition of equality of ordered pairs, we have
x + \(\frac{1}{3}\) = \(\frac{1}{2}\) and \(\frac{y}{3}\) – 1 = \(\frac{3}{2}\)
∴ x = \(\frac{1}{2}\) – \(\frac{1}{3}\) and \(\frac{y}{3}\) = \(\frac{3}{2}\) + 1
∴ x = \(\frac{1}{6}\) and y = \(\frac{15}{2}\)

Question 3.
If A = {a, b, c}, B = {x, y}, find A × B, B × A, A × A, B × B.
Solution:
A = (a, b, c}, B = {x, y}
A × B = {(a, x), (a, y), (b, x), (b, y), (c, x), (c, y)}
B × A = {(x, a), (x, b), (x, c), (y, a), (y, b), (y, c)}
A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}
B × B = {(x, x), (x, y), (y, x), (y, y)}

Question 4.
If P = {1, 2, 3} and Q = {1, 4}, find sets P × Q and Q × P.
Solution:
P = {1, 2, 3}, Q = {1, 4}
∴ P × Q = {(1, 1), (1, 4), (2, 1), (2, 4), (3, 1), (3, 4)}
and Q × P = {(1, 1), (1, 2), (1, 3), (4, 1), (4, 2), (4, 3)}

Question 5.
Let A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}. Verify,
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × (B ∪ C) = (A × B) ∪ (A × C)
Solution:
A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}
(i) B ∩ C = {5, 6}
A × (B ∩ C) = = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∩ (A × C) = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) B ∪ C = {4, 5, 6}
A × (B ∪ C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3,4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∪ (A × C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
∴ A × (B ∪ C) = (A × B) ∪ (A × C)

Question 6.
Express {(x, y) / x² + y² = 100, where x, y ∈ W} as a set of ordered pairs.
Solution:
{(x, y) / x² + y² = 100, where x, y ∈ W}
We have, x² + y² = 100
When x = 0 and y = 10,
x² + y² = 0² + 10² = 100
When x = 6 and y = 8,
x² + y² = 6² + 8² = 100
When x = 8 and y = 6,
x² + y² = 8² + 6² = 100
When x = 10 and y = 0,
x² + y² = 10² + 0² = 100
∴ Set of ordered pairs = {(0, 10), (6, 8), (8, 6), (10, 0)}

Question 7.
Let A = {6, 8} and B = {1, 3, 5}. Show that R₁ = {(a, b) / a ∈ A, b ∈ B, a – b is an even number} is a null relation, R₂ = {(a, b) / a ∈ A, b ∈ B, a + b is an odd number} is a universal relation.
Solution:
A = {6, 8}, B = {1, 3, 5}
R₁ = {(a, b)/ a ∈ A, b ∈ B, a – b is an even number}
a ∈ A
∴ a = 6, 8
b ∈ B
∴ b = 1, 3, 5
When a = 6 and b = 1, a – b = 5, which is odd
When a = 6 and b = 3, a – b = 3, which is odd
When a = 6 and b = 5, a – b = 1, which is odd
When a = 8 and b = 1, a – b = 7, which is odd
When a = 8 and b = 3, a – b = 5, which is odd
When a = 8 and b = 5, a – b = 3, which is odd
Thus, no set of values of a and b gives a – b as even.
∴ R₁ has a null relation from A to B.
A × B = {(6, 1), (6, 3), (6, 5), (8, 1), (8, 3), (8, 5)}
When a = 6 and b = 1, a + b = 7, which is odd
When a = 6 and b = 3, a + b = 9, which is odd
When a = 6 and b = 5, a + b = 11, which is odd
When a = 8 and b = 1, a + b = 9, which is odd
When a = 8 and b = 3, a + b = 11, which is odd
When a = 8 and b = 5, a + b = 13, which is odd
∴ R₂ = {(6, 1), (6, 3), (6, 5), (8, 1), (8, 3), (8, 5)}
Here, R₂ = A × B
∴ R₂ has a universal relation from A to B.

Question 8.
Write the relation in the Roster form. State its domain and range.
(i) R₁ = {(a, a²) / a is a prime number less than 15}
(ii) R₂ = {(a, \(\frac{1}{a}\)) / 0 < a ≤ 5, a ∈ N}
(iii) R₃ = {(x, y / y = 3x, y ∈ {3, 6, 9, 12}, x ∈ {1, 2, 3}}
(iv) R₄ = {(x, y) / y > x + 1, x = 1, 2 and y = 2, 4, 6}
(v) R₅ = {(x, y) / x + y = 3, x, y ∈ {0, 1, 2, 3}}
(vi) R₆ = {(a, b) / a ∈ N, a < 6 and b = 4}
(vii) R₇ = {(a, b) / a, b ∈ N, a + b = 6}
(viii) R₈ = {(a, b)/ b = a + 2, a ∈ Z, 0 < a < 5}
Solution:
(i) R₁ = {(a, a²) / a is a prime number less than 15}
∴ a = 2, 3, 5, 7, 11, 13
∴ a² = 4, 9, 25, 49, 121, 169
∴ R₁ = {(2, 4), (3, 9), (5, 25), (7, 49), (11, 121), (13, 169)}
∴ Domain (R₁) = {a/a is a prime number less than 15}
= {2, 3, 5, 7, 11, 13}
Range (R₁) = {a²/a is a prime number less than 15}
= {4, 9, 25, 49, 121, 169}

(iii) R₃ = {(x, y) / y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
Here y = 3x
When x = 1, y = 3(1) = 3
When x = 2, y = 3(2) = 6
When x = 3, y = 3(3) = 9
∴ R₃ = {(1, 3), (2, 6), (3, 9)}
∴ Domain (R₃) ={1, 2, 3}
∴ Range (R₃) = {3, 6, 9}

(iv) R₄ = {(x, y) / y > x + 1, x = 1, 2 and y = 2, 4, 6}
Here, y > x + 1
When x = 1 and y = 2, 2 ≯  1 + 1
When x = 1 and y = 4, 4 > 1 + 1
When x = 1 and y = 6, 6 > 1 + 1
When x = 2 and y = 2, 2 ≯  2 + 1
When x = 2 and y = 4, 4 > 2 + 1
When x = 2 and y = 6, 6 > 2 + 1
∴ R₄ = {(1, 4), (1, 6), (2, 4), (2, 6)}
Domain (R₄) = {1, 2}
Range (R₄) = {4, 6}

(v) R₅ = {{x, y) / x + y = 3, x, y ∈ (0, 1, 2, 3)}
Here, x + y = 3
When x = 0, y = 3
When x = 1, y = 2
When x = 2, y = 1
When x = 3, y = 0
∴ R₅ = {(0, 3), (1, 2), (2, 1), (3, 0)}
Domain (R₅) = {0, 1, 2, 3}
Range (R₅) = {3, 2, 1, 0}

(vi) R₆ = {(a, b)/ a ∈ N, a < 6 and b = 4}
a ∈ N and a < 6
∴ a = 1, 2, 3, 4, 5 and b = 4
R₆ = {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4)}
Domain (R₆) = {1, 2, 3, 4, 5}
Range (R₆) = {4}

(vii) R₇ = {(a, b) / a, b ∈ N, a + b = 6}
Here, a + b = 6
When a = 1, b = 5
When a = 2, b = 4
When a = 3, b = 3
When a = 4, b = 2
When a = 5, b = 1
∴ R₇ = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
Domain (R₇) = {1, 2, 3, 4, 5}
Range (R₇) = {5, 4, 3, 2, 1}

(viii) R₈ = {(a, b) / b = a + 2, a ∈ Z, 0 < a < 5}
Here, b = a + 2
When a = 1, b = 3
When a = 2, b = 4
When a = 3, b = 5
When a = 4, b = 6
∴ R₈ = {(1, 3), (2, 4), (3, 5), (4, 6)}
Domain (R₈) = {1, 2, 3, 4}
Range (R₈) = {3, 4, 5, 6}

Question 9.
Identify which of the following relations are reflexive, symmetric, and transitive.

Solution:

(i) Given, R = {(a, b): a, b ∈ Z, a – b is an integer}
Let a ∈ Z, then a – a ∈ Z
∴ (a, a) ∈ R
∴ R is reflexive.
Let (a, b) ∈ R
∴ a – b ∈ Z
∴ -(a – b) ∈ Z, i.e., b – a ∈ Z
∴ (b, a) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ a – b ∈ Z and b – c ∈ Z
∴ (a – b) + (b – c) ∈ Z
∴ a – c ∈ Z
∴ (a, c) ∈ R
∴ R is transitive.

(ii) Given, R = {(a, b) : a, b ∈ N, a + b is even}
Let a ∈ N, then a + a = 2a, which is even.
∴ (a, a) ∈ R
∴ R is reflexive.
Let (a, b) ∈ R
∴ a + b is even
∴ b + a is even
∴ (b, a) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ a + b and b + c is even
Let a + b = 2x and b + c = 2y for x, y ∈ N
∴ (a + b) + (b + c) = 2x + 2y
∴ a + 2b + c = 2(x + y)
∴ a + c = 2(x + y) – 2b = 2(x + y – b)
∴ a + c is even ……..[∵ x, y, b ∈ N, x + y – b ∈ N]
∴ (a, c) ∈ R
∴ R is transitive.

(iii) Given, R = {(a, b) : a, b ∈ N, a divides b}
Let a ∈ N, then a divides a.
∴ (a, a) ∈ R
∴ R is reflexive.
Let a = 2 and b = 8, then 2 divides 8
∴ (a, b) ∈ R
But 8 does not divide 2.
∴ (b, a) ∉ R
∴ R is not symmetric.
Let (a, b) and (b, c) ∈ R
∴ a divides b and b divides c.
Let b = ax and c = by for x, y ∈ N.
∴ c = (ax) y = a(xy)
i.e., a divides c.
∴ (a, c) ∈ R
∴ R is transitive.

(iv) Given, R = {(a, b) : a, b ∈ N, a² – 4ab + 3b² = 0}
Let a ∈ N, then a² – 4aa + 3a² = a² – 4a² + 3a² = 0
∴ (a, a) ∈ R
∴ R is reflexive.
Let a = 3 and b = 1,
then a² – 4ab + 3b² = 9 – 12 + 3 = 0
∴ (a, b) ∈ R
Consider, b² – 4ba + 3a² = 1 – 12 + 9 = -2 ≠ 0
∴ (b, a) ∉ R
∴ R is not symmetric.
Let a = 3, b = 1 and c = \(\frac{1}{3}\),
then a² – 4ab + 3b² = 9 – 12 + 3 = 0 and
b² – 4bc + 3c² = 1 – \(\frac{4}{3}\) + \(\frac{1}{3}\) = 1 – 1 = 0
∴ we get (a, b) and (b, c) ∈ R.
Consider, a² – 4ac + 3c² = 9 – 4 + \(\frac{1}{3}\) = \(\frac{16}{3}\) ≠ 0
∴ (a, c) ∉ R
∴ R is not transitive.

(v) Given, R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls}
Let a ∈ G, then ‘a’ cannot be a sister of herself.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let (a, b) ∈ R
∴ ‘a’ is a sister of ‘b’.
∴ ‘b’ is a sister of ‘a’.
∴ (b, c) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ ‘a’ is a sister of ‘b’ and ‘b’ is a sister of ‘c’
∴ ‘a’ is a sister of ‘c’.
∴ (a, c) ∈ R
∴ R is transitive.

(vi) Given, R = {(a, b) : Line a is perpendicular to line b in a plane}
Let a be any line in the plane, then a cannot be perpendicular to itself.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let (a, b) ∈ R
∴ a is perpendicular to b.
∴ b is perpendicular to a.
∴ (b, a) ∈ R.
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R.
∴ a is perpendicular to b and b is perpendicular to c.
∴ a is parallel to c.
∴ (a, c) ∉ R
∴ R is not transitive.

(vii) Given, R = {(a, b) : a, b ∈ R, a < b}
Let a ∈ R, then a ≮ a.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let a = 1 and b = 2, then 1 < 2
∴ (a, b) ∈ R
But 2 ≮ 1
∴ (b, a) ∉ R
∴ R is not symmetric.
Let (a, b) and (b, c) ∈ R
∴ a < b and b < c
∴ a < c
∴ (a, c) ∈ R
∴ R is transitive.

(viii) Given, R = {(a, b) : a, b ∈ R, a ≤ b³}
Let a = -3, then a³ = -27.
Here, a ≮ a
∴ (a, a) ∉ R
∴ R is not reflexive.
Let a = 2 and b = 9, then b³ = 729
Here, a < b³
∴ (a, b) ∈ R
Consider, a3 = 8
Here, b ≮ a³
∴ (b, a) ∉ R
∴ R is not symmetric.
Let a = 10, b = 3, c = 2,
then b³ = 27 and c³ = 8
Here, a < b³ and b < c³.
∴ (a, b) and (b, c) ∈ R
But a ≮ c³
∴ (a, c) ∉ R.
∴ R is not transitive.

State Board 11th Maths Book Answers 

• Sets and Relations Ex 5.1 Class 11 Maths Solutions
• Sets and Relations Ex 5.2 Class 11 Maths Solutions
• Sets and Relations Miscellaneous Exercise 5 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Ex 5.1 Questions and Answers.

11th Maths Part 2 Sets and Relations Exercise 5.1 Questions And Answers Maharashtra Board

Question 1.
Describe the following sets in Roster form:
(i) A = {x/x is a letter of the word ‘MOVEMENT’}
(ii) B = {x/x is an integer, –\(\frac{3}{2}\) < x < \(\frac{9}{2}\)>
(iii) C = {x/x = 2n + 1, n ∈ N}
Solution:
(i) A = {M, O, V, E, N, T}
(ii) B = {-1, 0, 1, 2, 3, 4}
(iii) C = {3, 5, 7, 9, … }

Question 2.
Describe the following sets in Set-Builder form:
(i) {0}
(ii) {0, ±1, ±2, ±3}
(iii) \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
(iv) {0, -1, 2, -3, 4, -5, 6,…}
Solution:
(i) Let A = {0}
0 is a whole number but it is not a natural number.
∴ A = {x / x ∈ W, x ∉ N}

(ii) Let B = {0, ±1, ±2, ±3}
B is the set of elements which belongs to Z from -3 to 3.
∴ B = {x /x ∈ Z, -3 ≤ x ≤ 3}

(iii) Let C = \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
∴ C = {x / x = \(\frac{n}{n^{2}+1}\), n ∈ N, n ≤ 7}

(iv) Let D = {0, -1, 2, -3, 4, -5, 6, …}
∴ D = {x/x = (-1)n-1 × (n – 1), n ∈ N}

Question 3.
If A = {x / 6x² + x – 15 = 0}, B = {x / 2x² – 5x – 3 = 0}, C = {x / 2x² – x – 3 = 0}, then find
(i) (A ∪ B ∪ C)
(ii) (A ∩ B ∩ C)
Solution:
A = [x/6x² + x – 15 = 0)
6x² + x – 15 = 0
6x² + 10x – 9x – 15 = 0
2x(3x + 5) – 3(3x + 5) = 0
(3x + 5) (2x – 3) = 0
3x + 5 = 0 or 2x – 3 = 0
x = \(\frac{-5}{3}\) or x = \(\frac{3}{2}\)
A = {\(\frac{-5}{3}\), \(\frac{3}{2}\)}

B = {x/2x² – 5x – 3 = 0}
2x² – 5x – 3 = 0
2x² – 6x + x – 3 = 0
2x(x – 3) + 1(x – 3) = 0
(x – 3)(2x + 1) = 0
x – 3 = 0 or 2x + 1 = 0
x = 3 or x = \(\frac{-1}{2}\)
B = (\(\frac{-1}{2}\), 3)

C = {x/2x² – x – 3 = 0}
2x² – x – 3 = 0
2x² – 3x + 2x – 3 = 0
x(2x – 3) + 1(2x – 3) = 0
(2x – 3) (x + 1) = 0
2x – 3 = 0 or x + 1 = 0
x = \(\frac{3}{2}\) or x = -1
C = {-1, \(\frac{3}{2}\)}

(i) A ∪ B ∪ C = \(\left\{-\frac{5}{3}, \frac{3}{2}\right\} \cup\left\{\frac{-1}{2}, 3\right\} \cup\left\{-1, \frac{3}{2}\right\}\) = \(\left\{\frac{-5}{3},-1, \frac{-1}{2}, \frac{3}{2}, 3\right\}\)

(ii) A ∩ B ∩ C = { }

Question 4.
If A, B, C are the sets for the letters in the words ‘college’, ‘marriage’ and ‘luggage’ respectively, then verify that [A – (B ∪ C)] = [(A – B) ∩ (A – C)].
Solution:
A = {c, o, l, g, e}
B = {m, a, r, i, g, e}
C = {l, u, g, a, e}
B ∪ C = {m, a, r, i, g, e, l, u}
A – (B ∪ C) = {c, o}
A – B = {c, o, l}
A – C = {c, o}
∴ [(A – B) ∩ (A – C)] = {c, o} = A – (B ∪ C)
∴ [A -( B ∪ C)] = [(A – B) ∩ (A – C)]

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then verify the following:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) (A ∪ B)’ = A’ ∩ B’
(iv) (A ∩ B)’ = A’ ∪ B’
(v) A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = (A ∩ B) ∪ (A’ ∩ B)
(vii) (A ∪ B) = (A – B) ∪ (A ∩ B) ∪ (B – A)
(viii) A ∩ (B ∆ C) = (A ∩ B) ∆ (A ∩ C)
(ix) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
(x) n(B) = n (A’ ∩ B) + n (A ∩ B)
Solution:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8},
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(i) B ∩ C = {4, 5, 6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5, 6} …..(i)
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
∴ (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6} …….(ii)
From (i) and (ii), we get
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

(ii) B ∪ C = {3, 4, 5, 6, 7, 8}
∴ A ∩ (B ∪ C) = {3, 4} ………(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) ∪ (A∩ C) = {3, 4} ……..(ii)
From (i) and (ii), we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(iii) A ∪ B = {1, 2, 3, 4, 5, 6}
∴ (A ∪ B)’ = {7, 8, 9, 10} ………(i)
A’ = {5, 6, 7, 8, 9, 10},
B’ = {1, 2, 7, 8, 9,10}
∴ A’ ∩ B’ = {7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∪ B)’ = A’ ∩ B’

(iv) A ∩ B = {3, 4}
(A ∩ B)’= {1, 2, 5, 6, 7, 8, 9, 10} …….(i)
A’ = {5, 6, 7, 8, 9, 10}
B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∪ B’ = {1, 2, 5, 6, 7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∩ B)’ = A’ ∪ B’

(v) A = {1, 2, 3, 4} ……(i)
A ∩ B = {3, 4}
B’ = {1, 2, 7, 8, 9, 10}
A ∩ B’ = {1, 2}
∴ (A ∩ B) ∪ (A ∩ B’) = {1, 2, 3, 4} …..(ii)
From (i) and (ii), we get
A = (A ∩ B) ∪ (A ∩ B’)

(vi) B = {3, 4, 5, 6} …..(i)
A ∩ B = {3, 4}
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ (A ∩ B) ∪ (A’ ∩ B) = {3, 4, 5, 6} …..(ii)
From (i) and (ii), we get
B = (A ∩ B) ∪ (A’ ∩ B)

(vii) A ∪ B = {1, 2, 3, 4, 5, 6} …….(i)
A – B = {1, 2}
A ∩ B = {3, 4}
B – A = {5, 6}
∴ (A – B) ∪ (A ∩ B) ∪ (B – A) = {1, 2, 3, 4, 5, 6} ……(ii)
From (i) and (ii), we get
A ∪ B = (A – B) ∪ (A ∩ B) ∪ (B – A)

(viii) B – C = {3}
C – B = {7, 8}
B Δ C = (B – C) ∪ (C – B) = {3, 7, 8}
∴ A ∩ (B Δ C) = {3} ……(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) Δ (A ∩ C) = [(A ∩ B) – (A ∩ C)] ∪ [(A ∩ C) – (A ∩ B)] = {3} …..(ii)
From (i) and (ii), we get
A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)

(ix) A = {1, 2, 3, 4}, B = {3, 4, 5, 6}
A ∩ B = {3, 4}, A ∪ B = {1, 2, 3, 4, 5, 6}
∴ n(A) = 4, n(B) = 4,
n(A ∩ B) = 2, n(A ∪ B) = 6 ……(i)
∴ n(A) + n(B) – n(A ∩ B) = 4 + 4 – 2
∴ n(A) + n(B) – n(A ∩ B) = 6 …..(ii)
From (i) and (ii), we get
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

(x) B = {3, 4, 5, 6}
∴ n(B) = 4 …..(i)
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ n(A’ ∩ B) = 2
A ∩ B = {3, 4}
∴ n(A ∩ B) = 2
∴ n(A’ ∩ B) + n(A ∩ B) = 2 + 2 = 4 …..(ii)
From (i) and (ii), we get
n(B) = n(A’ ∩ B) + n (A ∩ B)

Question 6.
If A and B are subsets of the universal set X and n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5, find
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A’ ∩ B)
(iv) n(A ∩ B’)
Solution:
n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5
(i) n(A ∪ B) = n(X) – [n(A ∪ B)’]
= n(X) – n(A’ ∩ B’)
= 50 – 5
= 45

(ii) n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 35 + 20 – 45
= 10

(iii) n(A’ ∩ B) = n(B) – n(A ∩ B)
= 20 – 10
= 10

(iv) n(A ∩ B’) = n(A) – n(A ∩ B)
= 35 – 10
= 25

Question 7.
In a class of 200 students who appeared in certain examinations, 35 students faded in CET, 40 in NEET and 40 in JEE, 20 faded in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE and 5 faded in ad three examinations. Find how many students
(i) did not fail in any examination.
(ii) faded in NEET or JEE entrance.
Solution:
Let A = set of students who failed in CET
B = set of students who failed in NEET
C = set of students who failed in JEE
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40, n(A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5

(i) n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
= 35 + 40 + 40 – 20 – 17 – 15 + 5
= 68
∴ No. of students who did not fail in any exam = n(X) – n(A ∪ B ∪ C)
= 200 – 68
= 132

(ii) No. of students who failed in NEET or JEE entrance = n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63

Question 8.
From amongst 2000 Uterate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read
(i) at least one of the newspapers.
(ii) neither Marathi nor English newspaper.
(iii) only one of the newspapers.
Solution:
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000,
n(M) = \(\frac{70}{100}\) × 2000 = 1400
n(E) = \(\frac{50}{100}\) × 2000 = 1000
n(M ∩ E) = \(\frac{32.5}{100}\) × 2000 = 650
(i) n(M ∪ E) = n(M) + n(E) – n(M ∩ E)
= 1400 + 1000 – 650
= 1750

No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.

(ii) No. of individuals who read neither Marathi nor English newspaper = n(M’ ∩ E’)
= n(M ∪ E)’
= n(X) – n(M ∪ E)
= 2000 – 1750
= 250

(iii) No. of individuals who read only one of the newspapers = n(M ∩ E’) + n(M’ ∩ E)
= n(M ∪ E) – n(M ∩ E)
= 1750 – 650
= 1100

Question 9.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take both tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes atleast one beverage, find the total number of students in the hostel.
Solution:
Let T = set of students who take tea
C = set of students who take coffee
M = set of students who take milk
∴ n(T) = 25, n(C) = 20, n(M) = 15, n(T ∩ C) = 10, n(M ∩ C) = 8, n(T ∩ M) = 0, n(T ∩ M ∩ C) = 0

∴ Total number of students in the hostel = n(T ∪ C ∪ M)
= n(T) + n(C) + n(M) – n(T ∩ C) – n(M ∩ C) – n(T ∩ M) + n(T ∩ M ∩ C)
= 25 + 20 + 15 – 10 – 8 – 0 + 0
= 42

Question 10.
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to
(i) Chemical A but not Chemical B
(ii) Chemical B but not Chemical A
(iii) Chemical A or Chemical B
Solution:
Let A = set of persons exposed to chemical A
B = set of persons exposed to chemical B
X = set of all persons
∴ n(X) = 260, n(A) = 150, n(B) = 74, n(A ∩ B) = 36

(i) No. of persons exposed to chemical A but not to chemical B = n(A ∩ B’)
= n(A) – n(A ∩ B)
= 150 – 36
= 114

(ii) No. of persons exposed to chemical B but not to chemical A = n(A’ ∩ B)
= n(B) – n(A ∩ B)
= 74 – 36
= 38

(iii) No. of persons exposed to chemical A or chemical B = n(A ∪ B)
= n(A) + n(B) – n(A ∩ B)
= 150 + 74 – 36
= 188

Question 11.
Write down the power set of A = {1, 2, 3}.
Solution:
A = {1, 2, 3}
The power set of A is given by
P(A) = {{Φ}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}}

Question 12.
Write the following intervals in Set-Builder form:
(i) (-3, 0)
(ii) [6, 12]
(iii) (6, ∞)
(iv) (-∞, 5]
(v) (2, 5]
(vi) [-3, 4)
Solution:
(i) (-3, 0) = {x / x ∈ R, -3 < x < 0}

(ii) [6, 12] = {x / x ∈ R, 6 ≤ x ≤ 12}

(iii) (6, ∞) = {x / x ∈ R, x > 6}

(iv) (-∞, 5] = {x / x ∈ R, x ≤ 5}

(v) (2, 5] = {x / x ∈ R, 2 < x ≤ 5}

(vi) [-3, 4) = {x / x ∈ R, -3 ≤ x < 4}

Question 13.
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals were awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Solution:
Let A = Set of students who received medals in volleyball
B = Set of students who received medals in football
C = Set of students who received medals in basketball
n(A) = 38, n(B) = 15, n(C) = 20, n(A ∪ B ∪ C) = 58, n(A ∩ B ∩ C) = 3
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
58 = 38 + 15 + 20 – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + 3
∴ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 ……(i)
Number of players who got exactly two medals = p + q + r
Here, s = n(A ∩ B ∩ C) = 3

n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 …..[From (i)]
∴ p + s + s + r + q + s = 18
∴ p + q + r + 3s = 18
∴ p + q + r + 3(3) = 18
∴ p + q + r = 18 – 9 = 9
∴ Number of players who received exactly two medals = 9.

Question 14.
Solve the following inequalities and write the solution set using interval notation.
(i) -9 < 2x + 7 ≤ 19
(ii) x² – x > 20
(iii) \(\frac{2 x}{x-4}\) ≤ 5
(iv) 6x² + 1 ≤ 5x
Solution:
(i) -9 < 2x + 7 ≤ 19
∴ -16 < 2x ≤ 12
∴ -8< x ≤ 6
∴ x ∈ (-8, 6]

(ii) x² – x > 20
∴ x² – x – 20 > 0
∴ x² – 5x + 4x – 20 > 0
∴ (x – 5) (x + 4) > 0
∴ either x – 5 > 0 and x + 4 > 0 or x – 5 < 0 and x + 4 < 0

Case I: x – 5 > 0 and x + 4 > 0
∴ x > 5 and x > -4
∴ x > 5 ….(i)

Case II:
x – 5 < 0 and x + 4 < 0
∴ x < 5 and x < -4
∴ x < -4 …..(ii)
From (i) and (ii), we get
x ∈ (-∞, – 4) ∪ (5, ∞)

(iii) \(\frac{2 x}{x-4}\) ≤ 5
∴ \(\frac{2 x}{x-4}\) – 5 ≤ 0
∴ \(\frac{2 x-5 x+20}{x-4}\) ≤ 0
∴ \(\frac{20-3 x}{x-4}\) ≤ 0
When \(\frac{a}{b}\) ≤ 0,
a ≥ 0 and b < 0 or a ≤ 0 and b > 0
∴ either 20 – 3x ≥ 0 and x – 4 < 0 or 20 – 3x ≤ 0 and x – 4 > 0
Case I:
20 – 3x ≥ 0 and x – 4 < 0
∴ x ≤ \(\frac{20}{3}\) and x < 4
∴ x < 4 ……(I)

Case II: 20 – 3x ≤ 0 and x – 4 > 0
∴ x ≥ \(\frac{20}{3}\) and x > 4
∴ x ≥ \(\frac{20}{3}\) ……(ii)
From (i) and (ii), we get
x ∈ (-∞, 4) ∪ [\(\frac{20}{3}\), ∞)

(iv) 6x² + 1 ≤ 5x
6x² – 5x + 1 ≤ 0
6x² – 3x – 2x + 1 ≤ 0
(3x – 1) (2x – 1) ≤ 0
either 3x – 1 ≤ 0 and 2x – 1 ≥ 0 or 3x – 1 ≥ 0 and 2x – 1 ≤ 0
Case I:
3x – 1 ≤ 0 and 2x – 1 ≥ 0
∴ x ≤ \(\frac{1}{3}\) and x ≥ \(\frac{1}{2}\), which is not possible.

Case II:
3x – 1 ≥ 0 and 2x – 1 ≤ 0
∴ x ≥ \(\frac{1}{3}\) and x ≤ \(\frac{1}{2}\)
∴ x ∈ [\(\frac{1}{3}\), \(\frac{1}{2}\)]

Question 15.
If A = (-7, 3], B = [2, 6] and C = [4, 9], then find
(i) A ∪ B
(ii) B ∪ C
(iii) A ∪ C
(iv) A ∩ B
(v) B ∩ C
(vi) A ∩ C
(vii) A’ ∩ B
(viii) B’ ∩ C’
(ix) B – C
(x) A – B
Solution:
A = (-7, 3], B = [2, 6], C = [4, 9]
(i) A ∪ B = (-7, 6]

(ii) B ∪ C = [2, 9]

(iii) A ∪ C = (-7, 3] ∪ [4, 9]

(iv) A ∩ B = [2, 3]

(v) B ∩ C = [4, 6]

(vi) A ∩ C = { }

(vii) A’ = (-∞, – 7] ∪ (3, ∞)
∴ A’ ∩ B = (3, 6]

(viii) B’ = (-∞, 2) ∪ (6, ∞)
C’ = (-∞, 4) ∪ (9, ∞)
∴ B’ ∩ C’ = (-∞, 2) ∪ (9, ∞)

(ix) B – C = [2, 4)

(x) A – B = (-7, 2)

State Board 11th Maths Book Answers 

• Sets and Relations Ex 5.1 Class 11 Maths Solutions
• Sets and Relations Ex 5.2 Class 11 Maths Solutions
• Sets and Relations Miscellaneous Exercise 5 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Questions and Answers.

11th Maths Part 2 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Questions And Answers Maharashtra Board

(I) Select the correct answers from the given alternatives.

Question 1.
The total number of terms in the expression of (x + y)¹⁰⁰ + (x – y)¹⁰⁰ after simplification is:
(A) 50
(B) 51
(C) 100
(D) 202
Answer:
(B) 51
Hint:

Question 2.
The middle term in the expansion of (1 + x)²ⁿ will be:
(A) (n – 1)^th
(B) n^th
(C) (n + 1)^th
(D) (n + 2)^th
Answer:
(C) (n + 1)^th
Hint:
(1 + x)²ⁿ has (2n + 1) terms.
∴ (n + 1 )^th term is the middle term.

Question 3.
In the expansion of (x² – 2x)¹⁰, the coefficient of x¹⁶ is
(A) -1680
(B) 1680
(C) 3360
(D) 6720
Answer:
(C) 3360
Hint:
(x² – 2x)¹⁰ = x¹⁰ (x – 2)¹⁰
To get the coefficient of x¹⁶ in (x² – 2x)¹⁰,
we need to check coefficient of x⁶ in (x – 2)¹⁰
∴ Required coefficient = ¹⁰C₆ (-2)⁴
= 210 × 16
= 3360

Question 4.
The term not containing x in expansion of \((1-x)^{2}\left(x+\frac{1}{x}\right)^{10}\) is
(A) ¹¹C₅
(B) ¹⁰C₅
(C) ¹⁰C₄
(D) ¹⁰C₇
Answer:
(A) ¹¹C₅
Hint:

Question 5.
The number of terms in expansion of (4y + x)⁸ – (4y – x)⁸ is
(A) 4
(B) 5
(C) 8
(D) 9
Answer:
(A) 4
Hint:

Question 6.
The value of ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + …. + ¹⁴C₁₁ is
(A) 2¹⁴ – 1
(B) 2¹⁴ – 14
(C) 2¹²
(D) 2¹³ – 14
Answer:
(D) 2¹³ – 14
Hint:

Question 7.
The value of ¹¹C₂ + ¹¹C₄ + ¹¹C₆ + ¹¹C₈ is equal to
(A) 2¹⁰ – 1
(B) 2¹⁰ – 11
(C) 2¹⁰ + 12
(D) 2¹⁰ – 12
Answer:
(D) 2¹⁰ – 12
Hint:

Question 8.
In the expansion of (3x + 2)⁴, the coefficient of the middle term is
(A) 36
(B) 54
(C) 81
(D) 216
Answer:
(D) 216
Hint:
(3x + 2)⁴ has 5 terms.
∴ (3x + 2)⁴ has 3rd term as the middle term.
The coefficient of the middle term

= 6 × 9 × 4
= 216

Question 9.
The coefficient of the 8th term in the expansion of (1 + x)¹⁰ is:
(A) 7
(B) 120
(C) ¹⁰C₈
(D) 210
Answer:
(B) 120
Hint:
r = 7
t₈ = ¹⁰C₇ x⁷ = ¹⁰C₃ x⁷
∴ Coefficient of 8th term = ¹⁰C₃ = 120

Question 10.
If the coefficients of x² and x³ in the expansion of (3 + ax)⁹ are the same, then the value of a is
(A) \(-\frac{7}{9}\)
(B) \(-\frac{9}{7}\)
(C) \(\frac{7}{9}\)
(D) \(\frac{9}{7}\)
Answer:
(D) \(\frac{9}{7}\)
Hint:

(II) Answer the following.

Question 1.
Prove by the method of induction, for all n ∈ N.
(i) 8 + 17 + 26 + ….. + (9n – 1) = \(\frac{n}{2}\) (9n + 7)
Solution:
Let P(n) ≡ 8 + 17 + 26 +…..+(9n – 1) = \(\frac{n}{2}\) (9n + 7), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 8
R.H.S. = \(\frac{1}{2}\) [9(1) + 7] = 8
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 8 + 17 + 26 +…..+ (9k – 1) = \(\frac{k}{2}\) (9k + 7) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., 8 + 17 + 26 + …… + [9(k + 1) – 1]

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 8 + 17 + 26 +…..+ (9n – 1) = \(\frac{n}{2}\) (9n + 7) for all n ∈ N.

(ii) 1² + 4² + 7² + …… + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1)
Solution:
Let P(n) = 1² + 4² + 7² + ….. + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S.= 1² = 1
R.H.S.= \(\frac{1}{2}\) [6(1)² – 3(1) – 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 4² + 7² +…..+ (3k – 2)² = \(\frac{k}{2}\) (6k² – 3k – 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 4² + 7² + … + (3n – 2)² = \(\frac{n}{2}\) (6n² – 3n – 1) for all n ∈ N.

(iii) 2 + 3.2 + 4.2² + …… + (n + 1) 2^n-1 = n . 2ⁿ
Solution:
Let P(n) ≡ 2 + 3.2 + 4.2² +…..+ (n + 1) 2^n-1 = n.2ⁿ, for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(2¹) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 3.2 + 4.2² + ….. + (k + 1) 2^k-1 = k.2^k …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 3.2 + 4.2² +….+ (k + 2) 2^k = (k + 1) 2^k+1

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 3.2 + 4.2² +……+ (n + 1) 2^n-1 = n.2ⁿ for all n ∈ N.

(iv) \(\frac{1}{3.4 .5}+\frac{2}{4.5 .6}+\frac{3}{5.6 .7}+\ldots+\frac{n}{(n+2)(n+3)(n+4)}\) = \(\frac{n(n+1)}{6(n+3)(n+4)}\)
Solution:

Question 2.
Given that t_n+1 = 5t_n – 8, t₁ = 3, prove by method of induction that t_n = 5^n-1 + 2.
Solution:
Let the statement P(n) has L.H.S. a recurrence relation t_n+1 = 5t_n – 8, t₁ = 3
and R.H.S. a general statement t_n = 5^n-1 + 2.
Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 5^1-1 + 2 = 1 + 2 = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Put n = 2
L.H.S = t₂ = 5t₁ – 8 = 5(3) – 8 = 7
R.H.S. = t₂ = 5^2-1 + 2 = 5 + 2 = 7
∴ L.H.S. = R.H.S.
∴ P(n) is tme for n = 2.

Step II:
Let us assume that P(n) is true for n = k.
∴ t_k+1 = 5t_k – 8 and t_k = 5^k-1 + 2

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
t_k+1 = 5^k+1-1 + 2 = 5^k + 2
t_k+1 = 5t_k – 8 and t_k = 5^k-1 + 2 ……[From Step II]
∴ t_k+1 = 5(5^k-1 + 2) – 8 = 5^k + 2
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ t_n = 5^n-1 + 2, for all n ∈ N.

Question 3.
Prove by method of induction
\(\left(\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right)^{n}=\left(\begin{array}{cc}
2 n+1 & -4 n \\
n & -2 n+1
\end{array}\right)\), ∀ n ∈ N.
Solution:


Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\left(\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right)^{n}=\left(\begin{array}{cc}
2 n+1 & -4 n \\
n & -2 n+1
\end{array}\right)\), ∀ n ∈ N.

Question 4.
Expand (3x² + 2y)⁵
Solution:
Here, a = 3x², b = 2y, n = 5.
Using binomial theorem,

Question 5.
Expand \(\left(\frac{2 x}{3}-\frac{3}{2 x}\right)^{4}\)
Solution:

Question 6.
Find third term in the expansion of \(\left(9 x^{2}-\frac{y^{3}}{6}\right)^{4}\)
Solution:

Question 7.
Find tenth term in the expansion of \(\left(2 x^{2}+\frac{1}{x}\right)^{12}\)
Solution:

Question 8.
Find the middle term(s) in the expansion of
(i) \(\left(\frac{2 a}{3}-\frac{3}{2 a}\right)^{6}\)
Solution:
Here, a = \(\frac{2 a}{3}\), b = \(\frac{-3}{2 a}\), n = 6.
Now, n is even.
∴ \(\frac{\mathrm{n}+2}{2}=\frac{6+2}{2}=4\)
∴ Middle term is t4, for which r = 3.

∴ The Middle term is -20.

(ii) \(\left(x-\frac{1}{2 y}\right)^{10}\)
Solution:
Here, a = x, b = \(-\frac{1}{2 y}\), n = 10.
Now, n is even.
∴ \(\frac{\mathrm{n}+2}{2}=\frac{10+2}{2}=6\)
∴ Middle term is t6, for which r = 5

(iii) (x² + 2y²)⁷
Solution:
Here, a = x², b = 2y², n = 7.
Now, n is odd.
∴ \(\frac{\mathrm{n}+1}{2}=\frac{7+1}{2}=4, \frac{\mathrm{n}+3}{2}=\frac{7+3}{2}=5\)
∴ Middle terms are t₄ and t₅, for which r = 3 and r = 4 respectively.

∴ Middle terms are 280x⁸y⁶ and 560x⁶y⁸.

(iv) \(\left(\frac{3 x^{2}}{2}-\frac{1}{3 x}\right)^{9}\)
Solution:

Question 9.
Find the coefficients of
(i) x⁶ in the expantion of \(\left(3 x^{2}-\frac{1}{3 x}\right)^{9}\)
Solution:

(ii) x⁶⁰ in the expansion of \(\left(\frac{1}{x^{2}}+x^{4}\right)^{18}\)
Solution:

Question 10.
Find the constant term in the expansion of
(i) \(\left(\frac{4 x^{2}}{3}+\frac{3}{2 x}\right)^{9}\)
Solution:

(ii) \(\left(2 x^{2}-\frac{1}{x}\right)^{12}\)
Solution:

Question 11.
Prove by method of induction
(i) log_a xⁿ = n log_a x, x > 0, n ∈ N
Solution:

(ii) 15^2n-1 + 1 is divisible by 16, for all n ∈ N.
Solution:
15^2n-1 + 1 is divisible by 16, if and only if (15^2n-1 + 1) is is a multiple of 16.
Let P(n) ≡ 15^2n-1 + 1 = 16m, where m ∈ N.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 15^2n-1 + 1 is divisible by 16, for all n ∈ N.

(iii) 5²ⁿ – 2²ⁿ is divisible by 3, for all n ∈ N.
Solution:

Question 12.
If the coefficient of x¹⁶ in the expansion of (x² + ax)¹⁰ is 3360, find a.
Solution:

Question 13.
If the middle term in the expansion of \(\left(x+\frac{b}{x}\right)^{6}\) is 160, find b.
Solution:

∴ 160 = \(\frac{6 \times 5 \times 4 \times 3 !}{3 \times 2 \times 1 \times 3 !} \times b^{3}\)
∴ 160 = 20b³
∴ 8 = b³
∴ b = 2

Question 14.
If the coefficients of x² and x³ in theexpansion of (3 + kx)⁹ are equal, find k.
Solution:

Question 15.
If the constant term in the expansion of \(\left(x^{3}+\frac{\mathrm{k}}{x^{8}}\right)^{11}\) is 1320, find k.
Solution:

Question 16.
Show that there is no term containing x⁶ in the expansion of \(\left(x^{2}-\frac{3}{x}\right)^{11}\).
Solution:

Question 17.
Show that there is no constant term in the expansion of \(\left(2 x-\frac{x^{2}}{4}\right)^{9}\)
Solution:

Question 18.
State, first four terms in the expansion of \(\left(1-\frac{2 x}{3}\right)^{-1 / 2}\)
Solution:

Question 19.
State, first four terms in the expansion of \((1-x)^{-1 / 4}\).
Solution:

Question 20.
State, first three terms in the expansion of \((5+4 x)^{-1 / 2}\)
Solution:

Question 21.
Using the binomial theorem, find the value of \(\sqrt[3]{995}\) upto four places of decimals.
Solution:

Question 22.
Find approximate value of \(\frac{1}{4.08}\) upto four places of decimals.
Solution:

Question 23.
Find the term independent of x in the expansion of (1 – x²) \(\left(x+\frac{2}{x}\right)^{6}\).
Solution:

Question 24.
(a + bx) (1 – x)⁶ = 3 – 20x + cx² + …, then find a, b, c.
Solution:

Question 25.
The 3rd term of (1 + x)ⁿ is 36x². Find 5th term.
Solution:

Question 26.
Suppose (1 + kx)ⁿ = 1 – 12x + 60x² – …… find k and n.
Solution:

Maths Solutions for Class 11 State Board

• Methods of Induction and Binomial Theorem Ex 4.1 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.2 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.3 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.4 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.5 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.5 Questions and Answers.

11th Maths Part 2 Methods of Induction and Binomial Theorem Exercise 4.5 Questions And Answers Maharashtra Board

Question 1.
Show that C₀ + C₁ + C₂ + ….. + C₈ = 256
Solution:
Since C₀ + C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ
Putting n = 8, we get
C₀ + C₁ + C₂ + ….. + C₈ = 2⁸
∴ C₀ + C₁ + C₂ + ….. + C₈ = 256

Question 2.
Show that C₀ + C₁ + C₂ + …… + C₉ = 512
Solution:
Since C₀ + C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ
Putting n = 9, we get
C₀ + C₁ + C₂ + ….. + C₉ = 2⁹
∴ C₀ + C₁ + C₂ + …… + C₉ = 512

Question 3.
Show that C₁ + C₂ + C₃ + ….. + C₇ = 127
Solution:
Since C₀ + C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ
Putting n = 7, we get
C₀ + C₁ + C₂ + ….. + C₇ = 2⁷
∴ C₀ + C₁ + C₂ +….. + C₇ = 128
But, C₀ = 1
∴ 1 + C₁ + C₂ + ….. + C₇ = 128
∴ C₁ + C₂ + ….. + C₇ = 128 – 1 = 127

Question 4.
Show that C₁ + C₂ + C₃ + ….. + C₆ = 63
Solution:
Since C₀ + C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ
Putting n = 6, we get
C₀ + C₁ + C₂ + ….. + C₆ = 2⁶
∴ C₀ + C₁ + C₂ + …… + C₆ = 64
But, C₀ = 1
∴ 1 + C₁ + C₂ + ….. + C₆ = 64
∴ C₁ + C₂ + ….. + C₆ = 64 – 1 = 63

Question 5.
Show that C₀ + C₂ + C₄ + C₆ + C₈ = C₁ + C₃ + C₅ + C₇ = 128
Solution:
Since C₀ + C₁ + C₂ + C₃ + …… + C_n = 2ⁿ
Putting n = 8, we get
C₀ + C₁ + C₂ + C₃ + …… + C₈ = 2⁸
But, sum of even coefficients = sum of odd coefficients
∴ C₀ + C₂ + C₄ + C₆ + C₈ = C₁ + C₃ + C₅ + C₇
Let C₀ + C₂ + C₄ + C₆ + C₈ = C₁ + C₃ + C₅ + C₇ = k
Now, C₀ + C₁ + C₂ + C₃ + C₄ + C₅ + C₆ + C₇ + C₈ = 256
∴ (C₀ + C₂ + C₄ + C₆ + C₈) + (C₁ + C₃ + C₅ + C₇) = 256
∴ k + k = 256
∴ 2k = 256
∴ k = 128
∴ C₀ + C₂ + C₄ + C₆ + C₈ = C₁ + C₃ + C₅ + C₇ = 128

Question 6.
Show that C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ – 1
Solution:
Since C₀ + C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ
But, C₀ = 1
∴ 1 + C₁ + C₂ + C₃ + …… + C_n = 2ⁿ
∴ C₁ + C₂ + C₃ + ….. + C_n = 2ⁿ – 1

Question 7.
Show that C₀ + 2C₁ + 3C₂ + 4C₃ + ….. + (n + 1)C_n = (n + 2) 2^n-1
Solution:

Maths Solutions for Class 11 State Board

• Methods of Induction and Binomial Theorem Ex 4.1 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.2 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.3 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.4 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.5 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.4 Questions and Answers.

11th Maths Part 2 Methods of Induction and Binomial Theorem Exercise 4.4 Questions And Answers Maharashtra Board

Question 1.
State, by writing the first four terms, the expansion of the following, where |x| < 1.
(i) (1 + x)^-4
Solution:

(ii) (1 – x)^1/3
Solution:

(iii) (1 – x²)^-3
Solution:

(iv) (1 + x)^-1/5
Solution:

(v) (1 + x²)^-1
Solution:

Question 2.
State by writing first four terms, the expansion of the following, where |b| < |a|.
(i) (a – b)^-3
Solution:
(a – b)^-3 = \(\left[a\left(1-\frac{b}{a}\right)\right]^{-3}\)

(ii) (a + b)^-4
Solution:

(iii) (a + b)^1/4
Solution:

(iv) (a – b)^-1/4
Solution:
(a – b)^-1/4 = \(\left[a\left(1-\frac{b}{a}\right)\right]^{\frac{-1}{4}}\)

(v) (a + b)^-1/3
Solution:

Question 3.
Simplify the first three terms in the expansion of the following:
(i) (1 + 2x)^-4
Solution:

(ii) (1 + 3x)^-1/2
Solution:

(iii) (2 – 3x)^1/3
Solution:

(iv) (5 + 4x)^-1/2
Solution:

(v) (5 – 3x)^-1/3
Solution:

Question 4.
Use the binomial theorem to evaluate the following upto four places of decimals.
(i) √99
Solution:

= 10 [1 – 0.005 – 0.0000125 – ……]
= 10(0.9949875)
= 9.94987 5
= 9.9499

(ii) \(\sqrt[3]{126}\)
Solution:

(iii) \(\sqrt[4]{16.08}\)
Solution:

(iv) (1.02)^-5
Solution:

(v) (0.98)^-3
Solution:

Maths Solutions for Class 11 State Board

• Methods of Induction and Binomial Theorem Ex 4.1 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.2 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.3 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.4 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.5 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3 Questions and Answers.

11th Maths Part 2 Methods of Induction and Binomial Theorem Exercise 4.3 Questions And Answers Maharashtra Board

Question 1.
In the following expansions, find the indicated term.
(i) \(\left(2 x^{2}+\frac{3}{2 x}\right)^{8}\), 3rd term
Solution:

(ii) \(\left(x^{2}-\frac{4}{x^{3}}\right)^{11}\), 5th term
Solution:

(iii) \(\left(\frac{4 x}{5}-\frac{5}{2 x}\right)^{9}\), 7th term
Solution:

(iv) In \(\left(\frac{1}{3}+a^{2}\right)^{12}\), 9th term
Solution:

(v) In \(\left(3 a+\frac{4}{a}\right)^{13}\), 10th term
Solution:

Question 2.
In the following expansions, find the indicated coefficients.
(i) x³ in \(\left(x^{2}+\frac{3 \sqrt{2}}{x}\right)^{9}\)
Solution:

(ii) x⁸ in \(\left(2 x^{5}-\frac{5}{x^{3}}\right)^{8}\)
Solution:

(iii) x⁹ in \(\left(\frac{1}{x}+x^{2}\right)^{18}\)
Solution:

(iv) x^-3 in \(\left(x-\frac{1}{2 x}\right)^{5}\)
Solution:

(v) x^-20 in \(\left(x^{3}-\frac{1}{2 x^{2}}\right)^{15}\)
Solution:

Question 3.
Find the constant term (term independent of x) in the expansion of
(i) \(\left(2 x+\frac{1}{3 x^{2}}\right)^{9}\)
Solution:

(ii) \(\left(x-\frac{2}{x^{2}}\right)^{15}\)
Solution:

(iii) \(\left(\sqrt{x}-\frac{3}{x^{2}}\right)^{10}\)
Solution:

(iv) \(\left(x^{2}-\frac{1}{x}\right)^{9}\)
Solution:

(v) \(\left(2 x^{2}-\frac{5}{x}\right)^{9}\)
Solution:

Question 4.
Find the middle terms in the expansion of
(i) \(\left(\frac{x}{y}+\frac{y}{x}\right)^{12}\)
Solution:

(ii) \(\left(x^{2}+\frac{1}{x}\right)^{7}\)
Solution:

(iii) \(\left(x^{2}-\frac{2}{x}\right)^{8}\)
Solution:

(iv) \(\left(\frac{x}{a}-\frac{a}{x}\right)^{10}\)
Solution:

(v) \(\left(x^{4}-\frac{1}{x^{3}}\right)^{11}\)
Solution:

Question 5.
In the expansion of (k + x)⁸, the coefficient of x⁵ is 10 times the coefficient of x⁶. Find the value of k.
Solution:

Question 6.
Find the term containing x⁶ in the expansion of (2 – x) (3x + 1)⁹.
Solution:

Question 7.
The coefficient of x² in the expansion of (1 + 2x)^m is 112. Find m.
Solution:
The coefficient of x² in (1 + 2x)^m = ^mC₂ (2²)
Given that the coefficient of x² = 112
∴ ^mC₂ (4) = 112
∴ ^mC₂ = 28
∴ \(\frac{\mathrm{m} !}{2 !(\mathrm{m}-2) !}=28\)
∴ \(\frac{m(m-1)(m-2) !}{2 \times(m-2) !}=28\)
∴ m(m – 1) = 56
∴ m² – m – 56 = 0
∴ (m – 8) (m + 7) = 0
As m cannot be negative.
∴ m = 8

Maths Solutions for Class 11 State Board

• Methods of Induction and Binomial Theorem Ex 4.1 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.2 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.3 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.4 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.5 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2 Questions and Answers.

11th Maths Part 2 Methods of Induction and Binomial Theorem Exercise 4.2 Questions And Answers Maharashtra Board

Question 1.
Expand:
(i) (√3 + √2)⁴
Solution:
Here, a = √3, b = √2 and n = 4.
Using binomial theorem,

∴ (√3 + √2)⁴ = 1(9) (1) + 4(3√3) (√2) + 6(3)(2) + 4(√3) (2√2) + 1(1)(4)
= 9 + 12√6 + 36 + 8√6 + 4
= 49 + 20√6

(ii) (√5 – √2)⁵
Solution:
Here, a = √5, b = √2 and n = 5.
Using binomial theorem,

Question 2.
Expand:
(i) (2x² + 3)⁴
Solution:
Here, a = 2x², b = 3 and n = 4.
Using binomial theorem,

(ii) \(\left(2 x-\frac{1}{x}\right)^{6}\)
Solution:
Here, a = 2x, b = \(\frac{1}{x}\) and n = 6.
Using binomial theorem,

Question 3.
Find the value of
(i) (√3 + 1)⁴ – (√3 – 1)⁴
Solution:

(ii) (2 + √5)⁵ + (2 – √5)⁵
Solution:


Adding (i) and (ii), we get
∴ (2 + √5 )⁵ + (2 – √5)⁵ = (32 + 80√5 + 400 + 200√5 + 250 + 25√5) + (32 – 80√5 + 400 – 200√5+ 250 – 25√5 )
= 64 + 800 + 500
= 1364

Question 4.
Prove that:
(i) (√3 + √2)⁶ + (√3 – √2)⁶ = 970
Solution:

(ii) (√5 + 1)⁵ – (√5 – 1)⁵ = 352
Solution:

Question 5.
Using binomial theorem, find the value of
(i) (102)⁴
Solution:

(ii) (1.1)⁵
Solution:

Question 6.
Using binomial theorem, find the value of
(i) (9.9)³
Solution:

(ii) (0.9)⁴
Solution:

Question 7.
Without expanding, find the value of
(i) (x + 1)⁴ – 4(x + 1)³ (x – 1) + 6(x + 1)² (x – 1)² – 4(x + 1) (x – 1)³ + (x – 1)⁴
Solution:

(ii) (2x – 1)⁴ + 4(2x – 1)³ (3 – 2x) + 6(2x – 1)² (3 – 2x)² + 4(2x – 1)¹ (3 – 2x)³ + (3 – 2x)⁴
Solution:

Question 8.
Find the value of (1.02)⁶, correct upto four places of decimals.
Solution:

Question 9.
Find the value of (1.01)⁵, correct upto three places of decimals.
Solution:

Question 10.
Find the value of (0.9)⁶, correct upto four places of decimals.
Solution:

Maths Solutions for Class 11 State Board

• Methods of Induction and Binomial Theorem Ex 4.1 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.2 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.3 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.4 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.5 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1 Questions and Answers.

11th Maths Part 2 Methods of Induction and Binomial Theorem Exercise 4.1 Questions And Answers Maharashtra Board

Prove by the method of induction, for all n ∈ N.

Question 1.
2 + 4 + 6 + …… + 2n = n(n + 1)
Solution:
Let P(n) = 2 + 4 + 6 + …… + 2n = n(n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(1 + 1) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 4 + 6 + ….. + 2k = k(k + 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 4 + 6 + …… + 2(k + 1) = (k + 1) (k + 2)
L.H.S. = 2 + 4 + 6 + …+ 2(k + 1)
= 2 + 4 + 6+ ….. + 2k + 2(k + 1)
= k(k + 1) + 2(k + 1) …..[From (i)]
= (k + 1).(k + 2)
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 4 + 6 + …… + 2n = n(n + 1) for all n ∈ N.

Question 2.
3 + 7 + 11 + ……… to n terms = n(2n + 1)
Solution:
Let P(n) = 3 + 7 + 11 + ……… to n terms = n(2n +1), for all n ∈ N.
But 3, 7, 11, …. are in A.P.
∴ a = 3 and d = 4
Let t_n be the nth term.
∴ t_n = a + (n – 1)d = 3 + (n – 1)4 = 4n – 1
∴ P(n) = 3 + 7 + 11 + ……. + (4n – 1) = n(2n + 1)

Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 1[2(1)+ 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 3 + 7 + 11 + ….. + (4k – 1) = k(2k + 1) …..(i)

Sept III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
3 + 7 + 11 + …+ [4(k + 1) – 1] = (k + 1)(2k + 3)
L.H.S. = 3 + 7 + 11 + …… + [4(k + 1) – 1]
= 3 + 7 + 11 + ….. + (4k – 1) + [4(k+ 1) – 1]
= k(2k + 1) + (4k + 4 – 1) …..[From (i)]
= 2k² + k + 4k + 3
= 2k² + 2k + 3k + 3
= 2k(k + 1) + 3(k + 1)
= (k + 1) (2k + 3)
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 3 + 7 + 11 + ….. to n terms = n(2n + 1) for all n ∈ N.

Question 3.
1² + 2² + 3² +…..+ n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Solution:
Let P(n) = 1² + 2² + 3² +…..+ n² = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 1² = 1
RHS = \(\frac{1(1+1)[2(1)+1]}{6}=\frac{6}{6}\) = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 2² + 3² +…+ k² = \(\frac{k(k+1)(2 k+1)}{6}\) …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 2² + 3² + …+ n² = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N.

Question 4.
1² + 3² + 5² + ….. + (2n – 1)² = \(\frac{n}{3}\) (2n – 1)(2n + 1)
Solution:
Let P(n) = 1² + 3² + 5²+…..+ (2n – 1)² = \(\frac{n}{3}\) (2n – 1)(2n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 1² = 1
R.H.S. = \(\frac{1}{3}\) [2(1) – 1][2(1) + 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1² + 3² + 5² +….+(2k – 1)² = \(\frac{k}{3}\) (2k – 1)(2k + 1) …….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1² + 3² + 5² + …+ (2n – 1)² = \(\frac{n}{3}\) (2n – 1)(2n + 1) for all n ∈ N.

Question 5.
1³ + 3³ + 5³ + ….. to n terms = n² (2n² – 1)
Solution:
Let P(n) = 1³ + 3³ + 5³ + …. to n terms = n² (2n² – 1), for all n ∈ N.
But 1, 3, 5, are in A.P.
∴ a = 1, d = 2
Let tn be the nth term.
t_n = a + (n – 1) d = 1 + (n – 1) 2 = 2n – 1
∴ P(n) = 1³ + 3³ + 5³ +…..+ (2n – 1)³ = n² (2n² – 1)

Step I:
Put n = 1
L.H.S. = 1³ = 1
R.H.S. = 1² [2(1)² – 1] = 1
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1³ + 3³ + 5³ +…+ (2k – 1)³ = k² (2k² – 1) …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1³ + 3³ + 5³ + … to n terms = n² (2n² – 1) for all n ∈ N.

Question 6.
1.2 + 2.3 + 3.4 +… + n(n + 1) = \(\frac{n}{3}\) (n + 1)(n + 2)
Solution:
Let P(n) = 1.2 + 2.3 + 3.4 +….+n(n + 1) = \(\frac{n(n+1)(n+2)}{3}\), for all n ∈ N.

Step I:
Put n = 1
L.H.S. = 1.2 = 2
R.H.S. = \(\frac{1}{3}\) (1 + 1)(1 + 2) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1.2 + 2.3 + 3.4 + ….. + k(k + 1) = \(\frac{k}{3}\) (k + 1)(k + 2) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.2 + 2.3 + 3.4 + … + n(n + 1) = \(\frac{n}{3}\) (n + 1)(n + 2), for all n ∈ N.

Question 7.
1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n² + 6n – 1)
Solution:
Let P(n) = 1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n² + 6n -1), for all n ∈ N.
But first factor in each term, i.e., 1, 3, 5,… are in A.P. with a = 1 and d = 2.
∴ nth term = a + (n – 1)d = 1 + (n – 1) 2 = (2n – 1)
Also, second factor in each term,
i.e., 3, 5, 7, … are in A.P. with a = 3 and d = 2.
∴ nth term = a + (n – 1) d = 3 + (n – 1) 2 = (2n + 1)
∴ nth term, t_n = (2n – 1) (2n + 1)
∴ P(n) ≡ 1.3 + 3.5 + 5.7 + …. + (2n – 1) (2n + 1) = \(\frac{n}{3}\) (4n² + 6n – 1)

Step I:
Put n = 1
L.H.S. = 1.3 = 3
R.H.S. = \(\frac{1}{3}\) [4(1)² + 6(1) – 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is trae for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 1.3 + 3.5 + 5.7 +….+ (2k – 1)(2k + 1) = \(\frac{k}{3}\) (4k² + 6k – 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.3 + 3.5 + 5.7 +… to n terms = \(\frac{n}{3}\) (4n² + 6n – 1) for all n ∈ N.

Question 8.
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
Solution:
Let P(n) ≡ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\), for all n ∈ N.

Step I:
Put n = 1
L.H.S. = \(\frac{1}{1.3}=\frac{1}{3}\)
R.H.S. = \(\frac{1}{2(1)+1}=\frac{1}{3}\)
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 k-1)(2 k+1)}=\frac{k}{2 k+1}\) …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\), for all n ∈ N.

Question 9.
\(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\)
Solution:
Let P(n) ≡ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\), for all n ∈ N.
But first factor in each term of the denominator,
i.e., 3, 5, 7, ….. are in A.P. with a = 3 and d = 2.
∴ nth term = a + (n – 1)d = 3 + (n – 1) 2 = (2n + 1)
Also, second factor in each term of the denominator,
i.e., 5, 7, 9, … are in A.P. with a = 5 and d = 2.
∴ nth term = a + (n – 1) d = 5 + (n – 1) 2 = (2n + 3)
∴ nth term, t_n = \(\frac{1}{(2 n+1)(2 n+3)}\)
P(n) ≡ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 n+1)(2 n+3)}\) = \(\frac{n}{3(2 n+3)}\)

Step I:
Put n = 1
L.H.S. = \(\frac{1}{3.5}=\frac{1}{15}\)
R.H.S. = \(\frac{1}{3[2(1)+3]}=\frac{1}{3(2+3)}=\frac{1}{15}\)
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 k+1)(2 k+3)}\) = \(\frac{k}{3(2 k+3)}\) ….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that


∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \text { to } n \text { terms }=\frac{n}{3(2 n+3)}\), for all n ∈ N.

Question 10.
(2³ⁿ – 1) is divisible by 7.
Solution:
(2³ⁿ – 1) is divisible by 7 if and only if (2³ⁿ – 1) is a multiple of 7.
Let P(n) ≡ (2³ⁿ – 1) = 7m, where m ∈ N.

Step I:
Put n = 1
∴ 2³ⁿ – 1 = 2³⁽¹⁾ – 1 = 2³ – 1 = 8 – 1 = 7
∴ (2³ⁿ – 1) is a multiple of 7.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
i.e., 2^3k – 1 is a multiple of 7.
∴ 2^3k – 1 = 7a, where a ∈ N
∴ 2^3k = 7a + 1 ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2^3(k+1) – 1 = 7b, where b ∈ N.
∴ P(k + 1) = 2^3(k+1) – 1
= 2^3k+3 – 1
= 2^3k . (2³) – 1
= (7a + 1)8 – 1 …..[From (i)]
= 56a + 8 – 1
= 56a + 7
= 7(8a + 1)
7b, where b = (8a + 1) ∈ N
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (2⁴ⁿ – 1) is divisible by 7, for all n ∈ N.

Question 11.
(2⁴ⁿ – 1) is divisible by 15.
Solution:
(2⁴ⁿ – 1) is divisible by 15 if and only if (2⁴ⁿ – 1) is a multiple of 15.
Let P(n) ≡ (2⁴ⁿ – 1) = 15m, where m ∈ N.

Step I:
Put n = 1
∴ 2⁴⁽¹⁾ – 1 = 16 – 1 = 15
∴ (2⁴ⁿ – 1) is a multiple of 15.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2^4k – 1 = 15a, where a ∈ N
∴ 2^4k = 15a + 1 …..(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
∴ 2^4(k+1) – 1 = 15b, where b ∈ N
∴ P(k + 1) = 2^4(k+1) – 1 = 2^4k+4 – 1
= 2^4k . 2⁴ – 1
= 16 . (2^4k) – 1
= 16(15a + 1) – 1 …..[From (i)]
= 240a + 16 – 1
= 240a + 15
= 15(16a + 1)
= 15b, where b = (16a + 1) ∈ N
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (2⁴ⁿ – 1) is divisible by 15, for all n ∈ N.

Question 12.
3ⁿ – 2n – 1 is divisible by 4.
Solution:
(3ⁿ – 2n – 1) is divisible by 4 if and only if (3ⁿ – 2n – 1) is a multiple of 4.
Let P(n) ≡ (3ⁿ – 2n – 1) = 4m, where m ∈ N.

Step I:
Put n = 1
∴ (3ⁿ – 2n – 1) = 3⁽¹⁾ – 2(1) – 1 = 0 = 4(0)
∴ (3ⁿ – 2n – 1) is a multiple of 4.
∴ P(n) is tme for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 3^k – 2k – 1 = 4a, where a ∈ N
∴ 3^k = 4a + 2k + 1 ….(i)

Step III:
We have to prove that P(n) is tme for n = k + 1,
i.e., to prove that
3^(k+1) – 2(k + 1) – 1 = 4b, where b ∈ N
P(k + 1) = 3^k+1 – 2(k + 1) – 1
= 3^k . 3 – 2k – 2 – 1
= (4a + 2k + 1) . 3 – 2k – 3 …….[From (i)]
= 12a + 6k + 3 – 2k – 3
= 12a + 4k
= 4(3a + k)
= 4b, where b = (3a + k) ∈ N
∴ P(n) is tme for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is tme for all n ∈ N.
∴ 3ⁿ – 2n – 1 is divisible by 4, for all n ∈ N.

Question 13.
5 + 5² + 5³ + ….. + 5ⁿ = \(\frac{5}{4}\) (5ⁿ – 1)
Solution:
Let P(n) ≡ 5 + 52 + 53 +…..+ 5n = \(\frac{5}{4}\) (5n – 1), for all n ∈ N.

Step I:
Put n = 1
L.H.S. = 5
R.H.S. = \(\frac{5}{4}\) (5¹ – 1) = 5
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 5 + 5² + 5³ + ….. + 5^k = \(\frac{5}{4}\) (5^k – 1) …….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 5 + 5² + 5³ + … + 5ⁿ = \(\frac{5}{4}\) (5ⁿ – 1), for all n ∈ N.

Question 14.
(cos θ + i sin θ)ⁿ = cos (nθ) + i sin (nθ)
Solution:
Let P(n) ≡ (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ, for all n ∈ N.
Step I:
Put n = 1
L.H.S. = (cos θ + i sin θ)¹ = cos θ + i sin θ
R.H.S. = cos[(1)θ] + i sin[(1)θ] = cos θ + i sin θ
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ (cos θ + i sin θ)^k = cos kθ + i sin kθ …….(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
(cos θ + i sin θ)^k+1 = cos (k + 1)θ + i sin (k + 1)θ
L.H.S. = (cos θ + i sin θ)^k+1
= (cos θ + i sin θ)^k . (cos θ + i sin θ)
= (cos kθ + i sin kθ) . (cos θ + i sin θ) ……[From (i)]
= cos kθ cos θ + i sin θ cos kθ + i sin kθ cosθ – sin kθ sin θ ……[∵ i² = -1]
= (cos kθ cos θ – sin k θ sin θ) + i(sin kθ cos θ + cos kθ sin θ)
= cos(kθ + θ) + i sin(kθ + θ)
= cos(k + 1) θ + i sin (k + 1) θ
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (cos θ + i sin θ)ⁿ = cos (nθ) + i sin (nθ), for all n ∈ N.

Question 15.
Given that t_n+1 = 5 t_n+4, t₁ = 4, prove by method of induction that t_n = 5ⁿ – 1.
Solution:
Let the statement P(n) has L.H.S. a recurrence relation t_n+1 = 5 t_n+4, t₁ = 4 and R.H.S. a general statement t_n = 5ⁿ – 1.
Step I:
Put n = 1
L.H.S. = 4
R.H.S. = 5¹ – 1 = 4
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Put n = 2
L.H.S. = t₂ = 5t₁ + 4 = 24
R.H.S. = t₂ = 5² – 1 = 24
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 2.

Step II:
Let us assume that P(n) is true for n = k.
∴ t_k+1 = 5 t_k+4 and t_k = 5^k – 1

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that t_k+1 = 5^k+1 – 1
Since t_k+1 = 5 t_k+4 and t_k = 5^k – 1 …..[From Step II]
t_k+1 = 5 (5^k – 1) + 4 = 5^k+1 – 1
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ t_n = 5ⁿ – 1, for all n ∈ N.

Question 16.
Prove by method of induction
\(\left(\begin{array}{ll}
1 & 2 \\
0 & 1
\end{array}\right)^{n}=\left(\begin{array}{cc}
1 & 2 n \\
0 & 1
\end{array}\right) \forall n \in N\)
Solution:

Maths Solutions for Class 11 State Board

• Methods of Induction and Binomial Theorem Ex 4.1 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.2 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.3 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.4 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Ex 4.5 Class 11 Maths Solutions
• Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 3 Permutations and Combination Ex 3.6 Questions and Answers.

11th Maths Part 2 Permutations and Combination Exercise 3.6 Questions And Answers Maharashtra Board

Question 1.
Find the value of
(a) ¹⁵C₄
Solution:

(b) ⁸⁰C₂
Solution:

(c) ¹⁵C₄ + ¹⁵C₅
Solution:

(d) ²⁰C₁₆ – ¹⁹C₁₆
Solution:

Question 2.
Find n if
(a) ⁶P₂ = n(⁶C₂)
Solution:

(b) ²ⁿC₃ : ⁿC₂ = 52 : 3
Solution:

(c) ⁿC_n-3 = 84
Solution:

Question 3.
Find r if ¹⁴C_2r : ¹⁰C_2r-4 = 143 : 10.
Solution:

∴ 2r(2r – 1) (2r – 2) (2r – 3) = 14 × 12 × 10
∴ 2r(2r – 1) (2r – 2) (2r – 3) = 8 × 7 × 6 × 5
Comparing on both sides, we get
∴ r = 4

Question 4.
Find n and r if,
(a) ⁿP_r = 720 and ⁿC_n-r = 120
Solution:

(b) ⁿC_r-1 : ⁿC_r : ⁿC_r+1 = 20 : 35 : 42
Solution:

Question 5.
If ⁿP_r = 1814400 and ⁿC_r = 45, find ⁿ⁺⁴C_r+3.
Solution:

Question 6.
If ⁿC_r-1 = 6435, ⁿC_r = 5005, ⁿC_r+1 = 3003, find ^rC₅.
Solution:

Question 7.
Find the number of ways of drawing 9 balls from a bag that has 6 red balls, 8 green balls, and 7 blue balls so that 3 balls of every colour are drawn.
Solution:
9 balls are to be selected from 6 red, 8 green, 7 blue balls such that the selection consists of 3 balls of each colour.
∴ 3 red balls can be selected from 6 red balls in ⁶C₃ ways.
3 reen balls can be selected from 8 green balls in ⁸C₃ ways.
3 blue balls can be selected from 7 blue balls in ⁷C₃ ways.
∴ Number of ways selection can be done if the selection consists of 3 balls of each colour

Question 8.
Find the number of ways of selecting a team of 3 boys and 2 girls from 6 boys and 4 girls.
Solution:
There are 6 boys and 4 girls.
A team of 3 boys and 2 girls is to be selected.
∴ 3 boys can be selected from 6 boys in ⁶C₃ ways.
2 girls can be selected from 4 girls in ⁴C₂ ways.
∴ Number of ways the team can be selected

Question 9.
After a meeting, every participant shakes hands with every other participants. If the number of handshakes is 66, find the number of participants in the meeting.
Solution:
Let there be n participants present in the meeting.
A handshake occurs between 2 persons.
∴ Number of handshakes = ⁿC₂
Given 66 handshakes were exchanged.
66 = ⁿC₂
66 = \(\frac{\mathrm{n} !}{2 !(\mathrm{n}-2) !}\)
66 × 2 = \(\frac{n(n-1)(n-2) !}{(n-2) !}\)
132 = n (n – 1)
n(n – 1) = 12 × 11
Comparing on both sides, we get n = 12
∴ 12 participants were present at the meeting.

Question 10.
If 20 points are marked on a circle, how many chords can be drawn?
Solution:
To draw a chord we need to join two points on the circle.
There are 20 points on a circle.
∴ Total number of chords possible from these points

Question 11.
Find the number of diagonals of an n-sided polygon. In particular, find the number of diagonals when
(i) n = 10
(ii) n = 15
(iii) n = 12
(iv) n = 8
Solution:
In n-sided polygon, there are ‘n’ points and ‘n’ sides.
∴ Through ‘n’ points we can draw ⁿC₂ lines including sides.
∴ Number of diagonals in n sided polygon = ⁿC₂ – n (n = number of sides)

Question 12.
There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.
Solution:
There are 20 lines such that no two of them are parallel and no three of them are concurrent.
Since no two lines are parallel, they intersect at a point.
∴ Number of points of intersection if no two lines are parallel and no three lines are concurrent = ²⁰C₂
= \(\frac{20 !}{2 ! 18 !}\)
= \(\frac{20 \times 19 \times 18 !}{2 \times 1 \times 18 !}\)
= 190

Question 13.
Ten points are plotted on a plane. Find the number of straight lines obtained by joining these points if (a) no three points are collinear (b) four points are collinear
Solution:
There are 10 points on a plane.
(a) When no three of them are collinear.
A line is obtained by joining 2 points.
∴ Number of lines passing through these points = ¹⁰C₂
= \(\frac{10 !}{2 ! 8 !}\)
= \(\frac{10 \times 9 \times 8 !}{2 \times 1 \times 8 !}\)
= 5 × 9
= 45

(b) When 4 of them are collinear.
If no three points are collinear, we get a total of ¹⁰C₂ = 45 lines by joining them. …..[From (i)]
Since 4 points are collinear, only one line passes through these points instead of ⁴C₂ lines.
∴ ⁴C₂ – 1 extra lines are included in 45 lines.
Number of lines passing through these points
= 45 – (⁴C₂ – 1)
= 45 – \(\frac{4 !}{2 ! 2 !}\) + 1
= 45 – \(\frac{4 \times 3 \times 2 !}{2 \times 2 !}\) + 1
= 45 – 6 + 1
= 40

Question 14.
Find the number of triangles formed by joining 12 points if
(a) no three points are collinear
(b) four points are collinear
Solution:
There are 12 points on the plane.
(a) When no three of them are collinear.
A triangle can be drawn by joining any three non-collinear points.
∴ Number of triangles that can be obtained from these points = ¹²C₃
= \(\frac{12 !}{3 ! 9 !}\)
= \(\frac{12 \times 11 \times 10 \times 9 !}{3 \times 2 \times 1 \times 9 !}\)
= 220

(b) When 4 of these points are collinear.
If no three points are collinear, total we get ¹²C₃ = 220 triangles by joining them. ……[From (i)]
Since 4 points are collinear, no triangle can be formed by joining these four points.
∴ ⁴C₃ extra triangles are included in 220 triangles.
∴ Number of triangles that can be obtained from these points = ¹²C₃ – ⁴C₃
= 220 – \(\frac{4 !}{3 ! \times 1 !}\)
= 220 – \(\frac{4 \times 3 !}{3 !}\)
= 220 – 4
= 216

Question 15.
A word has 8 consonants and 3 vowels. How many distinct words can be formed if 4 consonants and 2 vowels are chosen?
Solution:
There are 8 consonants and 3 vowels.
From 8 consonants, 4 can be selected in ⁸C₄
= \(\frac{8 !}{4 ! 4 !}\)
= \(\frac{8 \times 7 \times 6 \times 5 \times 4 !}{4 \times 3 \times 2 \times 1 \times 4 !}\)
= 70 ways.
From 3 vowels, 2 can be selected in ³C₂
= \(\frac{3 !}{2 ! 1 !}\)
= \(\frac{3 \times 2 !}{2 !}\)
= 3 ways.
Now, to form a word, these 6 ietters (i.e., 4 consonants and 2 vowels) can be arranged in ⁶P₆ = 6! ways.
∴ Total number of words that can be formed = 70 × 3 × 6!
= 70 × 3 × 720
= 151200
∴ 151200 words of 4 consonants and 2 vowels can be formed.

Question 16.
Find n if,
(i) ⁿC₈ = ⁿC₁₂
Solution:
ⁿC₈ = ⁿC₁₂
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ 8 = 12 or 8 = n – 12
But 8 = 12 is not possible
∴ 8 = n – 12
∴ n = 20

(ii) ²³C_3n = ²³C_2n+3
Solution:
²³C_3n = ²³C_2n+3
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ 3n = 2n + 3 or 3n = 23 – 2n – 3
∴ n = 3 or n = 4

(iii) ²¹C_6n = \({ }^{21} \mathrm{C}_{\left(\mathrm{n}^{2}+5\right)}\)
Solution:
²¹C_6n = \({ }^{21} \mathrm{C}_{\left(\mathrm{n}^{2}+5\right)}\)
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ 6n = n² + 5 or 6n = 21 – (n² + 5)
∴ n² – 6n + 5 = 0 or 6n = 21 – n² – 5
∴ n² – 6n + 5 = 0 or n² + 6n – 16 = 0
If n² – 6n + 5 = 0, then (n – 1)(n – 5) = 0
∴ n = 1 or n = 5
If n = 5 then
n² + 5 = 30 > 21
∴ n ≠ 5
∴ n = 1
If n² + 6n – 16 = 0, then (n + 8)(n – 2) = 0
n = -8 or n = 2
n ≠ -8
∴ n = 2
∴ n = 1 or n = 2

Check:
n = 2
∴ n² + 5 = 2² + 5 = 9
²¹C_6n = ²¹C₁₂
and \({ }^{21} \mathrm{C}_{\left(\mathrm{n}^{2}+5\right)}\) = ²¹C₉
∴ ⁿC_r = ⁿC_n-r
∴ ²¹C₁₂ = ²¹C₉
∴ n = 2 is a right answer.

(iv) ²ⁿC_r-1 = ²ⁿC_r+1
Solution:
²ⁿC_r-1 = ²ⁿC_r+1
If ⁿC_x = ⁿC_y, then either x = y or x = n – y
∴ r – 1 = r + 1 or r – 1 = 2n – (r + 1)
But r – 1 = r + 1 is not possible
∴ r – 1 = 2n – (r + 1)
∴ r + r = 2n
∴ r = n

Check:
²ⁿC_r-1 = ²ⁿC_n-1
and ²ⁿC_r+1 = ²ⁿC_n+1
using ⁿC_r = ⁿC_n-r, we have
²ⁿC_n+1 = ²ⁿC_2n-(n+1) = ²ⁿC_n-1
∴ ²ⁿC_r-1 = ²ⁿC_r+1

(v) ⁿC_n-2 = 15
Solution:
ⁿC_n-2 = 15
∴ ⁿC₂ = 15 …..[∵ ⁿC_r = ⁿC_n-r]
∴ \(\frac{n !}{(n-2) ! 2 !}=15\)
∴ \(\frac{n(n-1)(n-2) !}{(n-2) ! \times 2 \times 1}=15\)
∴ n(n – 1) = 30
∴ n(n – 1) = 6 × 5
Equating both sides, we get
∴ n = 6

Question 17.
Find x if ⁿP_r = x ⁿC_r.
Solution:

Question 18.
Find r if ¹¹C₄ + ¹¹C₅ + ¹²C₆ + ¹³C₇ = ¹⁴C_r.
Solution:

Question 19.
Find the value of \(\sum_{r=1}^{4}{ }^{(21-r)} \mathrm{C}_{4}\).
Solution:

Question 20.
Find the differences between the greatest values in the following:
(a) ¹⁴C_r and ¹²C_r
Solution:
Greatest value of ¹⁴C_r.
Here, n = 14, which is even.
Greatest value of nCr occurs at r = \(\frac{n}{2}\) if n is even.
∴ r = \(\frac{n}{2}\)
∴ r = \(\frac{14}{2}\) = 7

∴ Difference between the greatest values of ¹⁴C_r and ¹²C_r = ¹⁴C_r – ¹²C_r
= 3432 – 924
= 2508

(b) ¹³C_r and ⁸C_r
Solution:
Greatest value of ¹³C_r.
Here n = 13, which is odd.
Greatest value of nCr occurs at r = \(\frac{n-1}{2}\) if n is odd.
∴ r = \(\frac{\mathrm{n}-1}{2}\)
∴ r = \(\frac{13-1}{2}\) = 6

∴ Difference between the greatest values of ¹³C_r and ⁸C_r = ¹³C_r – ⁸C_r
= 1716 – 70
= 1646

(c) ¹⁵C_r and ¹¹C_r
Solution:
Greatest value of ¹⁵C_r.
Here n = 15, which is odd.
Greatest value of nCr occurs at r = \(\frac{n-1}{2}\) if n is odd.
∴ r = \(\frac{n-1}{2}\)
∴ r = \(\frac{15-1}{2}\) = 7

∴ Difference between the greatest values of ¹⁵C_r and ¹¹C_r = ¹⁵C_r – ¹¹C_r
= 6435 – 462
= 5973

Question 21.
In how many ways can a boy invite his 5 friends to a party so that at least three join the party?
Solution:
Boy can invite = (3 or 4 or 5 friends)
Consider the following table:

∴ Number of ways a boy can invite his friends to a party so that three or more of join the party = 10 + 5 + 1 = 16

Question 22.
A group consists of 9 men and 6 women. A team of 6 is to be selected. How many of possible selections will have at least 3 women?
Solution:
There are 9 men and 6 women.
A team of 6 persons is to be formed such that it consist of at least 3 women.
Consider the following table:

∴ No. of ways this can be done = 1680 + 540 + 54 + 1 = 2275
∴ 2275 teams can be formed if team consists of at least 3 women.

Question 23.
A committee of 10 persons is to be formed from a group of 10 women and 8 men. How many possible committees will have at least 5 women? How many possible committees will have men in majority?
Solution:
(i) A committee of 10 persons is to be formed from 10 women and 8 men such that the committee contains at least 5 women.
Consider the following table:

∴ Number of committees with at least 5 women
= 14112 + 14700 + 6720 + 1260 + 81
= 36873

(ii) Number of committees with men in majority = Total number of committees – (Number of committees with women in majority + women and men equal in number)
= ¹⁸C₁₀ – 36873
= ¹⁸C₈ – 36873
= 43758 – 36873
= 6885

Question 24.
A question paper has two sections. Section I has 5 questions and section II has 6 questions. A student must answer at least two questions from each section among 6 questions he answers. How many different choices does the student have in choosing questions?
Solution:
There are 11 questions, out of which 5 questions are from section I and 6 questions are from section II.
The student has to select 6 questions taking at least 2 questions from each section.
Consider the following table:

∴ Number of choices = 150 + 200 + 75 = 425
∴ In 425 ways students can select 6 questions, taking at least 2 questions from each section.

Question 25.
There are 3 wicketkeepers and 5 bowlers among 22 cricket players. A team of 11 player is to be selected so that there is exactly one wicketkeeper and at least 4 bowlers in the team. How many different teams can be formed?
Solution:
There are 22 cricket players, of which 3 are wicketkeepers and 5 are bowlers.
A team of 11 players is to be chosen such that exactly one wicket keeper and at least 4 bowlers are to be included in the team.
Consider the following table:

∴ Number of ways a team of 11 players can be selected
= 45045 + 6006
= 51051

Question 26.
Five students are selected from 11. How many ways can these students be selected if
(a) two specified students are selected?
(b) two specified students are not selected?
Solution:
5 students are to be selected from 11 students.
(a) When 2 specified students are included,
then remaining 3 students can be selected from (11 – 2) = 9 students.
∴ Number of ways of selecting 3 students from 9 students = ⁹C₃
= \(\frac{9 !}{3 ! \times 6 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 !}{3 \times 2 \times 1 \times 6 !}\)
= 84
∴ Selection of students is done in 84 ways when 2 specified students are included.

(b) When 2 specified students are not included, then 5 students can be selected from the remaining (11 – 2) = 9 students.
∴ Number of ways of selecting 5 students from 9 students = ⁹C₅
= \(\frac{9 !}{5 ! 4 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 \times 5 !}{5 ! \times 4 \times 3 \times 2 \times 1}\)
= 126
∴ Selection of students is done in 126 ways when 2 specified students are not included.

Maths Solutions for Class 11 State Board

• Permutations and Combination Ex 3.1 Class 11 Maths Solutions
• Permutations and Combination Ex 3.2 Class 11 Maths Solutions
• Permutations and Combination Ex 3.3 Class 11 Maths Solutions
• Permutations and Combination Ex 3.4 Class 11 Maths Solutions
• Permutations and Combination Ex 3.5 Class 11 Maths Solutions
• Permutations and Combination Ex 3.6 Class 11 Maths Solutions
• Permutations and Combination Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 3 Permutations and Combination Ex 3.5 Questions and Answers.

11th Maths Part 2 Permutations and Combination Exercise 3.5 Questions And Answers Maharashtra Board

Question 1.
In how many different ways can 8 friends sit around a table?
Solution:
We know that ‘n’ persons can sit around a table in (n – 1)! ways.
∴ 8 friends can sit around a table in 7!
= 7 × 6 × 5 × 4 × 3 × 2 × 1
= 5040 ways.

Question 2.
A party has 20 participants. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host?
Solution:
A party has 20 participants.
All of them and the host (i.e., 21 persons) can be seated at a circular table in (21 – 1)! = 20! ways.
When two particular participants are seated on either side of the host.
The host takes the chair in 1 way.
These 2 persons can sit on either side of the host in 2! ways.
Once the host occupies his chair, it is not circular permutation more.
The remaining 18 people occupy their chairs in 18! ways.
∴ A total number of arrangements possible if two particular participants are seated on either side of the host = 2! × 18! = 2 × 18!

Question 3.
Delegates from 24 countries participate in a round table discussion. Find the number of seating arrangements where two specified delegates are (a) always together. (b) never together.
Solution:
(a) Delegates of 24 countries are to participate in a round table discussion such that two specified delegates are always together.
Let us consider these 2 delegates as one unit. They can be arranged among themselves in 2! ways.
Also, these two delegates are to be seated with 22 other delegates (i.e. total of 23) which can be done in (23 – 1)! = 22! ways.
∴ Required number of arrangements = 2! × 22!

(b) When 2 specified delegates are never together then, other 22 delegates can be participate in a round table discussion in (22 – 1)! = 21! ways.
∴ There are 22 places of which any 2 places can be filled by those 2 delegates so that they are never together.
∴ Two specified delegates can be arranged in ²²P₂ ways.
∴ Required number of arrangements = ²²P₂ × 21!
= \(\frac{22 !}{(22-2) !} \times 21 !\)
= \(\frac{22 !}{20 !}\) × 21!
= 22 × 21 × 21!
= 21 × 22 × 21!
= 21 × 22!

Question 4.
Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours.
Solution:
There are 15 people to sit around a table.
∴ They can be arranged in(15 – 1)! = 14! ways.
But, they should not have the same neighbour in any two arrangements.
Around the table, arrangements (i.e., clockwise and anticlockwise) coincide.

∴ Required number of arrangements = \(\frac{14 !}{2}\)

Question 5.
A committee of 10 members sits around a table. Find the number of arrangements that have the President and the Vice-president together.
Solution:
A committee of 10 members sits around a table.
But, President and Vice-president sit together.
Let us consider President and Vice-president as one unit.
They can be arranged among themselves in 2! ways.
Now, this unit with the other 8 members of the committee is to be arranged around a table, which can be done in (9 – 1)! = 8! ways.
∴ Required number of arrangements = 8! × 2! = 2 × 8!

Question 6.
Five men, two women, and a child sit around a table. Find the number of arrangements where the child is seated (a) between the two women. (b) between two men.
Solution:
5 men, 2 women, and a child sit around a table.
(a) When the child is seated between two women.
5 men, 2 women, and a child are to be seated around a round table such that the child is seated between two women.
∴ the two women can be seated on either side of the child in 2! ways.
Let us consider these 3 (two women and a child) as one unit.
Now, this one unit is to be arranged with the remaining 5 men,
i.e., a total of 6 units are to be arranged around a round table, which can be done in (6 – 1)! = 5! ways.
∴ Required number of arrangements = 5! × 2!
= 120 × 2
= 240

(b) Two men can be selected from 5 men in
⁵C₂ = \(\frac{5 !}{2 !(5-2) !}=\frac{5 \times 4 \times 3 !}{2 \times 3 !}\) = 10 ways.
Also, these two men can sit on either side of the child in 2! ways.
Let us take two men and a child as one unit.
Now, this one unit is to be arranged with the remaining 3 men and 2 women,
i.e., a total of 6 units (3 + 2 + 1) are to be arranged around a round table, which can be done in (6 – 1)! = 5! ways.
∴ Required number of arrangements = 10 × 2! × 5!
= 10 × 2 × 120
= 2400

Question 7.
Eight men and six women sit around a table. How many sitting arrangements will have no two women together?
Solution:
8 men can be seated around a table in (8 – 1)! = 7! ways.
No two women should sit together.
There are 8 gaps created by 8 men’s seats.
∴ Women can be seated in 8 gaps in ⁸P₆ ways.
∴ Required number of arrangements = 7! × ⁸P₆

Question 8.
Find the number of seating arrangements for 3 men and 3 women to sit around a table so that exactly two women are together.
Solution:
2 women (who wish to sit together) can be selected from 3 in
³C₂ = \(\frac{3 !}{2 !(3-2) !}=\frac{3 \times 2 !}{2 ! \times 1 !}\) = 3 ways.
Also, these two women can sit together in 2! ways.
Let us take two women as one unit.
Now, this one unit is to be arranged with the remaining 3 men and 1 woman,
i.e., a total of 5 units are to be arranged around a round table, which can be done in (5 – 1)! = 4! ways.
∴ Required number of arrangements = 3 × 2! × 4!
= 3 × 2 × 24
= 144

Question 9.
Four objects in a set of ten objects are alike. Find the number of ways of arranging them in a circular order.
Solution:
Ten things can be arranged in a circular order of which 4 are alike in \(\frac{9 !}{4 !}\) ways.
∴ Required number of arrangements = \(\frac{9 !}{4 !}\)

Question 10.
Fifteen persons sit around a table. Find the number of arrangements that have two specified persons not sitting side by side.
Solution:
Since 2 particular persons can’t be sitting side by side,
the other 13 persons can be arranged around the table in (13 – 1)! = 12! ways.
The two persons who are not sitting side by side may take 13 positions created by 3 persons in ¹³P₂ ways.
∴ Required number of arrangements = 12! × ¹³P₂
= 12! × 13 × 12
= 13 × 12! × 12
= 12 × 13!

Maths Solutions for Class 11 State Board

• Permutations and Combination Ex 3.1 Class 11 Maths Solutions
• Permutations and Combination Ex 3.2 Class 11 Maths Solutions
• Permutations and Combination Ex 3.3 Class 11 Maths Solutions
• Permutations and Combination Ex 3.4 Class 11 Maths Solutions
• Permutations and Combination Ex 3.5 Class 11 Maths Solutions
• Permutations and Combination Ex 3.6 Class 11 Maths Solutions
• Permutations and Combination Miscellaneous Exercise 3 Class 11 Maths Solutions