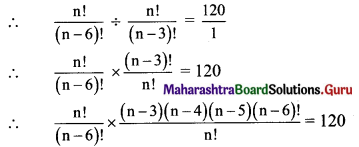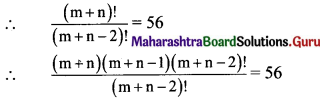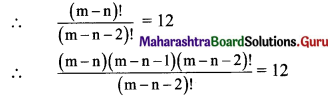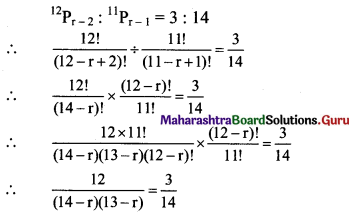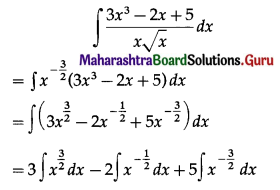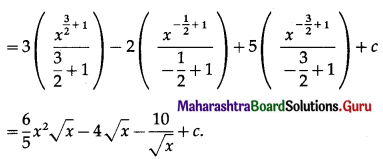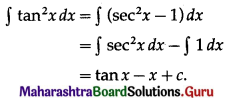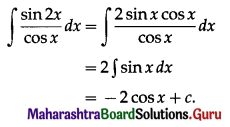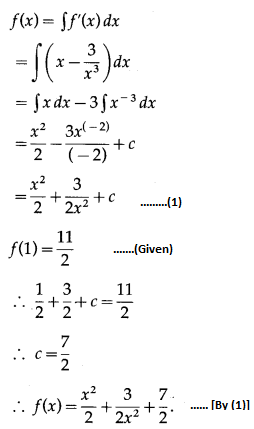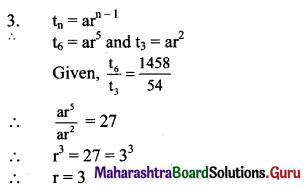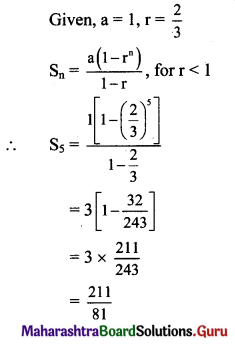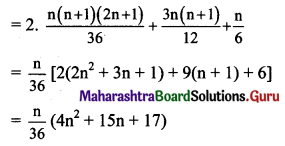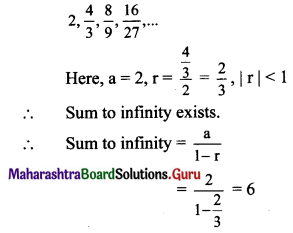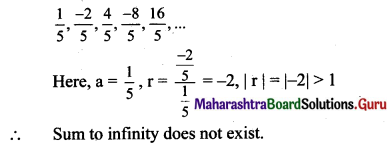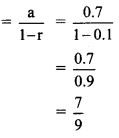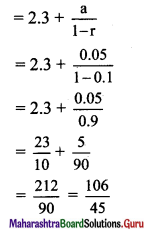Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 3 Permutations and Combination Ex 3.4 Questions and Answers.
11th Maths Part 2 Permutations and Combination Exercise 3.4 Questions And Answers Maharashtra Board
Question 1.
Find the number of permutations of letters in each of the following words.
(i) DIVYA
(ii) SHANTARAM
(iii) REPRESENT
(iv) COMBINE
(v) BAL BHARATI
Solution:
(i) There are 5 distinct letters in the word DIVYA.
∴ Number of permutations of the letters of the word DIVYA = 5! = 120
(ii) There are 9 letters in the word SHANTARAM in which ‘A’ is repeated 3 times.
∴ Number of permutations of the letters of the word SHANTARAM = \(\frac{9 !}{3 !}\)
= 9 × 8 × 7 × 6 × 5 × 4
= 60480
(iii) There are 9 letters in the word REPRESENT in which ‘E’ is repeated 3 times and ‘R’ is repeated 2 times.
∴ Number of permutations of the letters of the word REPRESENT = \(\frac{9 !}{3 ! 2 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4}{2}\)
= 30240
(iv) There are 7 distinct letters in the word COMBINE.
∴ Number of permutations of the letters of the word COMBINE = 7! = 5040
(v) There are 10 letters in the word BALBHARATI in which ‘B’ is repeated 2 times and ‘A’ is repeated 3 times.
∴ Number of permutations of the letters of the word BALBHARATI = \(\frac{10 !}{2 ! 3 !}\)
= \(\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 3 \times 2}\)
= 302400
![]()
Question 2.
You have 2 identical books on English, 3 identical books on Hindi, and 4 identical books on Mathematics. Find the number of distinct ways of arranging them on a shelf.
Solution:
There are total 9 books to be arranged on a shelf.
Out of these 9 books, 2 books on English, 3 books on Hindi and 4 books on mathematics are identical.
∴ Total number of arrangements possible = \(\frac{9 !}{2 ! 3 ! 4 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 !}{2 \times 3 \times 2 \times 4 !}\)
= 9 × 4 × 7 × 5
= 1260
Question 3.
A coin is tossed 8 times. In how many ways can we obtain (a) 4 heads and 4 tails? (b) at least 6 heads?
Solution:
A coin is tossed 8 times. All heads are identical and all tails are identical.
(a) 4 heads and 4 tails are to be obtained.
∴ Number of ways it can be obtained = \(\frac{8 !}{4 ! 4 !}\)
= \(\frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2}\)
= 70
(b) At least 6 heads are to be obtained.
∴ Outcome can be (6 heads and 2 tails) or (7 heads and 1 tail) or (8 heads)
∴ Number of ways it can be obtained = \(\frac{8 !}{6 ! 2 !}+\frac{8 !}{7 ! 1 !}+\frac{8 !}{8 !}\)
= \(\frac{8 \times 7}{2}\) + 8 + 1
= 28 + 8 + 1
= 37
Question 4.
A bag has 5 red, 4 blue, and 4 green marbles. If all are drawn one by one and their colours are recorded, how many different arrangements can be found?
Solution:
There is a total of 13 marbles in a bag.
Out of these 5 are Red, 4 Blue, and 4 are Green marbles.
All balls of the same colour are taken to be identical.
∴ Required number of arrangements = \(\frac{13 !}{5 ! 4 ! 4 !}\)
![]()
Question 5.
Find the number of ways of arranging letters of the word MATHEMATICAL. How many of these arrangements have all vowels together?
Solution:
There are 12 letters in the word MATHEMATICAL in which ‘M’ is repeated 2 times, ‘A’ repeated 3 times and ‘T’ repeated 2 times.
∴ Required number of arrangements = \(\frac{12 !}{2 ! 3 ! 2 !}\)
When all the vowels,
i.e., ‘A’, ‘A’, ‘A’, ‘E’, ‘I’ are to be kept together.
Let us consider them as one unit.
Number of arrangements of these vowels among themselves = \(\frac{5 !}{3 !}\) ways.
This unit is to be arranged with 7 other letters in which ‘M’ and ‘T’ repeated 2 times each.
∴ Number of such arrangements = \(\frac{8 !}{2 ! 2 !}\)
∴ Required number of arrangements = \(\frac{8 ! \times 5 !}{2 ! 2 ! 3 !}\)
Question 6.
Find the number of different arrangements of letters in the word MAHARASHTRA. How many of these arrangements have (a) letters R and H never together? (b) all vowels together?
Solution:
There are 11 letters in the word MAHARASHTRA in which ‘A’ is repeated 4 times, ‘H’ repeated 2 times, and ‘R’ repeated 2 times.
∴ Total number of words can be formed = \(\frac{11 !}{4 ! 2 ! 2 !}\)
(a) When letters R and H are never together.
Other than 2R, 2H there are 4A, 1S, 1T, 1M.
These letters can be arranged in \(\frac{7 !}{4 !}\) ways = 210.
These seven letters create 8 gaps in which 2R, 2H are to be arranged.
Number of ways to do = \(\frac{{ }^{8} \mathrm{P}_{4}}{2 ! 2 !}\) = 420
Required number of arrangements = 210 × 420 = 88200.
(b) When all vowels are together.
There are 4 vowels in the word MAHARASHTRA, i.e., A, A, A, A.
Let us consider these 4 vowels as one unit, which can be arranged among themselves in \(\frac{4 !}{4 !}\) = 1 way.
This unit is to be arranged with 7 other letters in which ‘H’ is repeated 2 times, ‘R’ is repeated 2 times.
∴ Total number of arrangements = \(\frac{8 !}{2 ! 2 !}\)
Question 7.
How many different words are formed if the letter R is used thrice and letters S and T are used twice each?
Solution:
To find the number of different words when ‘R’ is taken thrice, ‘S’ is taken twice and ‘T’ is taken twice.
∴ Total number of letters available = 7, of which ‘S’ and ‘T’ repeat 2 times each, ‘R’ repeats 3 times.
∴ Required number of words = \(\frac{7 !}{2 ! 2 ! 3 !}\)
= \(\frac{7 \times 6 \times 5 \times 4 \times 3 !}{2 \times 1 \times 2 \times 1 \times 3 !}\)
= 7 × 6 × 5
= 210
![]()
Question 8.
Find the number of arrangements of letters in the word MUMBAI so that the letter B is always next to A.
Solution:
There are 6 letters in the word MUMBAI.
These letters are to be arranged in such a way that ‘B’ is always next to ‘A’.
Let us consider AB as one unit.
This unit with the other 4 letters in which ‘M’ repeats twice is to be arranged.
∴ Required number of arrangements = \(\frac{5 !}{2 !}\)
= \(\frac{5 \times 4 \times 3 \times 2 !}{2 !}\)
= 60
Question 9.
Find the number of arrangements of letters in the word CONSTITUTION that begin and end with N.
Solution:
There are 12 letters in the word CONSTITUTION, in which ‘O’, ‘N’, ‘I’ repeat two times each, ‘T’ repeats 3 times.
When the arrangement starts and ends with ‘N’,
other 10 letters can be arranged between two N,
in which ‘O’ and ‘I’ repeat twice each and ‘T’ repeats 3 times.
∴ Required number of arrangements = \(\frac{10 !}{2 ! 2 ! 3 !}\)
Question 10.
Find the number of different ways of arranging letters in the word ARRANGE. How many of these arrangements do not have the two R’s and two A’s together?
Solution:
There are 7 letters in the word ARRANGE in which ‘A’ and ‘R’ repeat 2 times each.
∴ Number of ways to arrange the letters of word ARRANGE = \(\frac{7 !}{2 ! 2 !}\) = 1260
Consider the words in which 2A are together and 2R are together.
Let us consider 2A as one unit and 2R as one unit.
These two units with remaining 3 letters can be arranged in = \(\frac{5 !}{2 ! 2 !}\) = 30 ways.
Number of arrangements in which neither 2A together nor 2R are together = 1260 – 30 = 1230
Question 11.
How many distinct 5 digit numbers can be formed using the digits 3, 2, 3, 2, 4, 5.
Solution:
5 digit numbers are to be formed from 2, 3, 2, 3, 4, 5.
Case I: Numbers formed from 2, 2, 3, 4, 5 OR 2, 3, 3, 4, 5
Number of such numbers = \(\frac{5 !}{2 !}+\frac{5 !}{2 !}\) = 5! = 120
Case II: Numbers are formed from 2, 2, 3, 3 and any one of 4 or 5
Number of such numbers = \(\frac{5 !}{2 ! 2 !}+\frac{5 !}{2 ! 2 !}\) = 60
Required number of numbers = 120 + 60 = 180
![]()
Question 12.
Find the number of distinct numbers formed using the digits 3, 4, 5, 6, 7, 8, 9, so that odd positions are occupied by odd digits.
Solution:
A number is to be formed with digits 3, 4, 5, 6, 7, 8, 9 such that odd digits always occupy the odd places.
There are 4 odd digits, i.e. 3, 5, 7, 9.
∴ They can be arranged at 4 odd places among themselves in 4! = 24 ways.
There are 3 even digits, i.e. 4, 6, 8.
∴ They can be arranged at 3 even places among themselves in 3! = 6 ways.
∴ Required number of numbers formed = 24 × 6 = 144
Question 13.
How many different 6-digit numbers can be formed using digits in the number 659942? How many of them are divisible by 4?
Solution:
A 6-digit number is to be formed using digits of 659942, in which 9 repeats twice.
∴ Required number of numbers formed = \(\frac{6 !}{2 !}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\)
= 360
A 6-digit number is to be formed using the same digits that are divisible by 4.
For a number to be divisible by 4, the last two digits should be divisible by 4,
i.e. 24, 52, 56, 64, 92 or 96.
Case I: When the last two digits are 24, 52, 56 or 64.
As the digit 9 repeats twice in the remaining four numbers, the number of arrangements = \(\frac{4 !}{2 !}\) = 12
∴ 6-digit numbers that are divisible by 4 so formed are 12 + 12 + 12 + 12 = 48.
Case II: When the last two digits are 92 or 96.
As each of the remaining four numbers are distinct, the number of arrangements = 4! = 24
∴ 6-digit numbers that are divisible by 4 so formed are 24 + 24 = 48.
∴ Required number of numbers framed = 48 + 48 = 96
Question 14.
Find the number of distinct words formed from letters in the word INDIAN. How many of them have the two N’s together?
Solution:
There are 6 letters in the word INDIAN in which I and N are repeated twice.
Number of different words that can be formed using the letters of the word INDIAN = \(\frac{6 !}{2 ! 2 !}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 \times 2 !}\)
= 180
When two N’s are together.
Let us consider the two N’s as one unit.
They can be arranged with 4 other letters in \(\frac{5 !}{2 !}\)
= \(\frac{5 \times 4 \times 3 \times 2 !}{2 !}\)
= 60 ways.
∴ 2 N can be arranged in \(\frac{2 !}{2 !}\) = 1 way.
∴ Required number of words = 60 × 1 = 60
![]()
Question 15.
Find the number of different ways of arranging letters in the word PLATOON if (a) the two O’s are never together. (b) consonants and vowels occupy alternate positions.
Solution:
There are 7 letters in the words PLATOON in which ‘O’ repeat 2 times.
(a) When the two O’s are never together.
Let us arrange the other 5 letters first, which can be done in 5! = 120 ways.
The letters P, L, A, T, N create 6 gaps, in which O’s are arranged.
Two O’s can take their places in 6P2 ways.
But ‘O’ repeats 2 times.
∴ Two O’s can be arranged in \(\frac{{ }^{6} \mathrm{P}_{2}}{2 !}\)
= \(\frac{\frac{6 !}{(6-2) !}}{2 !}\)
= \(\frac{6 \times 5 \times 4 !}{4 ! \times 2 \times 1}\)
= 3 × 5
= 15 ways
∴ Required number of arrangements = 120 × 15 = 1800
(b) When consonants and vowels occupy alternate positions.
There are 4 consonants and 3 vowels in the word PLATOON.
∴ At odd places, consonants occur and at even places, vowels occur.
4 consonants can be arranged among themselves in 4! ways.
3 vowels in which O occurs twice and A occurs once.
∴ They can be arranged in \(\frac{3 !}{2 !}\) ways.
Now, vowels and consonants should occupy alternate positions.
∴ Required number of arrangements = 4! × \(\frac{3 !}{2 !}\)
= 4 × 3 × 2 × \(\frac{3 \times 2 !}{2 !}\)
= 72
Maths Solutions for Class 11 State Board
- Permutations and Combination Ex 3.1 Class 11 Maths Solutions
- Permutations and Combination Ex 3.2 Class 11 Maths Solutions
- Permutations and Combination Ex 3.3 Class 11 Maths Solutions
- Permutations and Combination Ex 3.4 Class 11 Maths Solutions
- Permutations and Combination Ex 3.5 Class 11 Maths Solutions
- Permutations and Combination Ex 3.6 Class 11 Maths Solutions
- Permutations and Combination Miscellaneous Exercise 3 Class 11 Maths Solutions