Category: Class 12

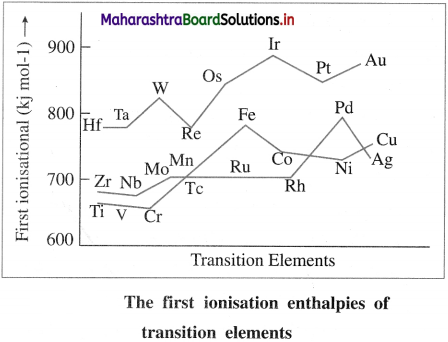
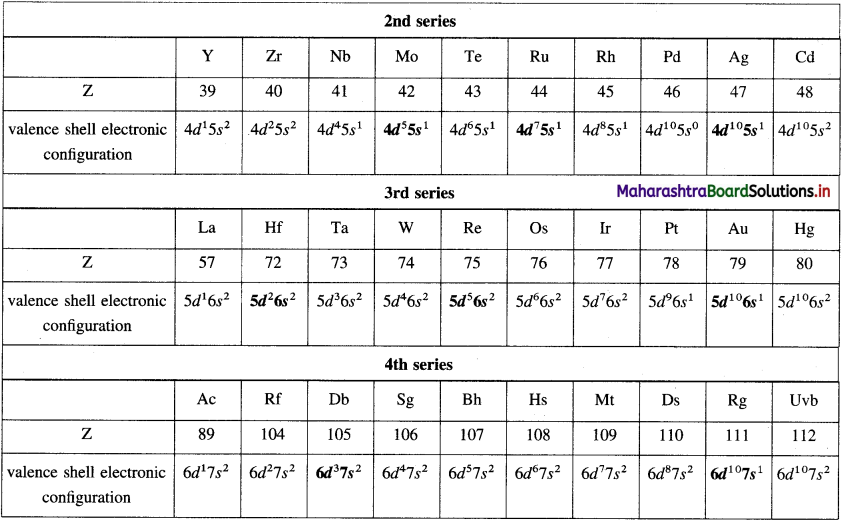
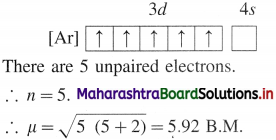
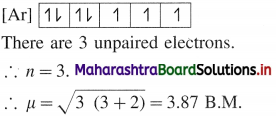
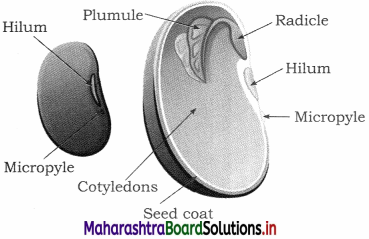
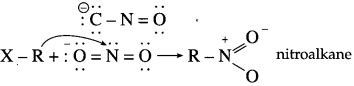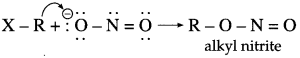Alcohols, Phenols and Ethers Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 11 Alcohols, Phenols and Ethers Textbook Exercise Questions and Answers.

Class 12 Chemistry Chapter 11 Exercise Solutions Maharashtra Board

Chemistry Class 12 Chapter 11 Exercise Solutions

1. Choose the correct option.

Question i.
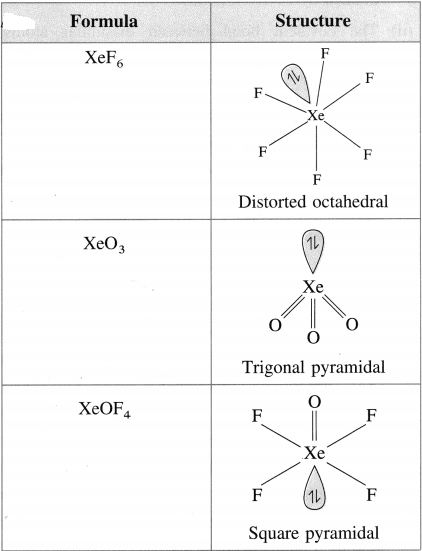
Which of the following represents the increasing order of boiling points of (1), (2), and (3)?
(1) CH₃ – CH₂ – CH₂ – CH₂ – OH
(2) (CH₃)₂ CH – O – CH₃
(3) (CH₃)₃COH
A. (1) < (2) < (3)
B. (2) < (1) < (3)
C. (3) < (2) < (1)
D. (2) < (3) < (1)
Answer:
(a) (1) < (2) < (3)

Question ii.
Which is the best reagent for carrying out following conversion ?

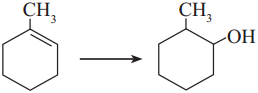
A. LiAlH₄
B. Conc. H₂SO₄, H₂O
C. H₂/Pd
D. B₂H₆, H₂O₂ – NaOH
Answer:
B. Conc. H₂SO₄, H₂O

Question iii.
Which of the following reaction will give ionic organic product on reaction ?
A. CH₃ – CH₂ – OH + Na
B. CH₃ – CH₂ – OH + SOCl₂
C. CH₃ – CH₂ – OH + PCl₅
D. CH₃ – CH₂ – OH + H₂SO₄
Answer:
C. CH₃ – CH₂ – OH + PCl₅

Question iv.
Which is the most resistant alcohol towards oxidation reaction among the follwoing ?

Answer:
(c)

Question v.
Resorcinol on distillation with zinc dust gives
A. Cyclohexane
B. Benzene
C. Toluene
D. Benzene-1, 3-diol
Answer:
(b) Benzene

Question vi.
Anisole on heating with concerntrated HI gives
A. Iodobenzene
B. Phenol + Methanol
C. Phenol + Iodomethane
D. Iodobenzene + methanol
Answer:
B. Phenol + Methanol

Question vii.
Which of the following is the least acidic compound ?

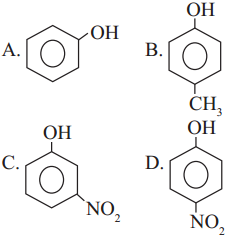
Answer:
(b)

Question viii.
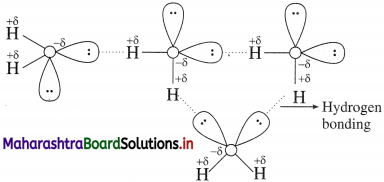
The compound incapable of hydrogen bonding with water is ……

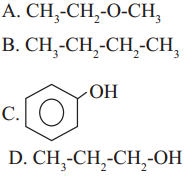
Answer:
(b)

Question ix.
Ethers are kept in air tight brown bottles because
A. Ethers absorb moisture
B. Ethers evaporate readily
C. Ethers oxidise to explosive peroxide
D. Ethers are inert
Answer:
C. Ethers oxidise to explosive peroxide

Question x.
Ethers reacts with cold and concentrated H₂SO₄ to form
A. oxonium salt
B. alkene
C. alkoxides
D. alcohols
Answer:
A. oxonium salt

2. Answer in one sentence/ word.

Question i.
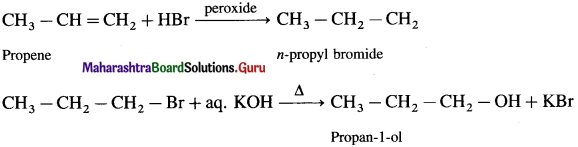
Hydroboration-oxidation of propene gives…..
Answer:
n-propyl alcohol (CH₃ – CH₂ – CH₂ – OH)

Question ii.
Write the IUPAC name of alcohol having molecular formula C₄H₁₀O which is resistant towards oxidation.
Answer:

Question iii.
Write the structure of optically active alcohol having molecular formula C₄H₁₀O
Answer:

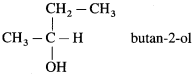
Question iv.
Write name of the electrophile used in Kolbe’s Reaction.
Answer:
Electrophile : Carbon dioxide (O = C = O)

3. Answer in brief.

Question i.
Why phenol is more acidic than ethyl alcohol ?
Answer:
(1) In ethyl alcohol, the -OH group is attached to sp³ – hybridised carbon while in phenols, it is attached to sp² – hybridised carbon.

(2) Due to higher electronegativity of sp² – hybridised carbon, electron density on oxygen decreases. This increases the polarity of O-H bond and results in more ionization of phenol than that of alcohols.

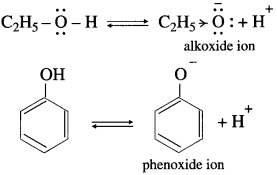
(3) Electron donating inductive effect (+1 effect) of the alkyl group destabilizes alkoxide ion. As a result alcohol does not ionize much in water, therefore alcohol is neutral compound in aqueous medium.

(4) In alkoxide ion, the negative charge is localized on oxygen, while in phenoxide ion the negative charge is delocalized. The delocalization of the negative charge (structure I to V) makes phenoxide ion more stable than that of phenol.

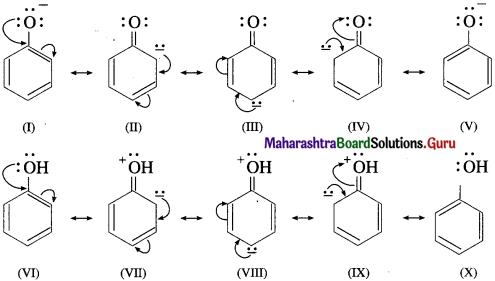
The delocalization of charge in phenol (structures VI to X), the resonating structures have charge separation (where oxygen atom of OH group to be positive and delocalization of negative charge over the ortho and para positions of aromatic ring) due to which phenol molecule is less stable than phenoxide ion. This favours ionization of phenol. Thus phenols are more acidic than ethyl alcohol.

Question ii.
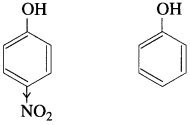
Why p-nitrophenol is a stronger acid than phenol ?
Answer:
(1) In p-nitrophenol, nitro group (NO₂) is an electron withdrawing group present at para position which enhances the acidic strength (-1 effect). The O-H bond is under strain and release of proton (H⁺) becomes easy. Further p-nitrophenoxide ion is more stabilised due to resonance.

(2) Since the absence of electron withdrawing group (like – NO₂) in phenol at ortho and para position, the acidic strength of phenol is less than that of p-nitrophenol.

Question iii.
Write two points of difference between properties of phenol and ethyl alcohol.
Answer:

Question iv.
Give the reagents and conditions necessary to prepare phenol from
a. Chlorobenzene
b. Benzene sulfonic acid.
Answer:
(1) From chlorobenzene : Reagents required : NaOH and dil. HC1 Temperature : 623 K, Pressure : 150 atm
(2) From Benzene sulphonic acid : Reagents required : aq NaOH, caustic soda, dil. HC1 Temperature : 573 K

Question v.
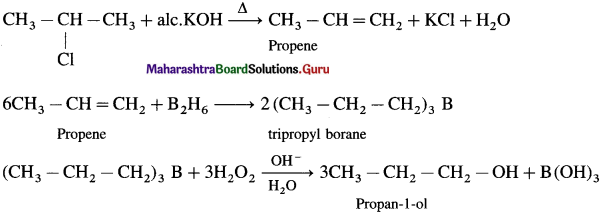
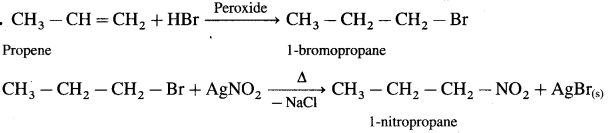
Give the equations of the reactions for the preparation of phenol from isopropyl benzene.
Answer:
Preparation of phenol from cumene (isopropylbenzene) : This is the commercial method of preparation of phenol. When a stream of air is passed through cumene (isopropylbenzene) suspended in aqueous Na₂CO₃ solution in the presence of cobalt naphthenate catalyst, isopropyl benzene hydroperoxide or cumene hydroperoxide is formed. Isopropylbenzene hydroperoxide on warming with dil. H₂SO₄ gives phenol and acetone. Acetone is an important by-product of the reaction and is separated by distillation. The reaction is called auto oxidation.

Question vi.
Give a simple chemical test to distinguish between ethanol and ethyl bromide.
Answer:
When ethyl bromide is heated with aq NaOH; ethyl alcohol is formed whereas ethanol does not react with aq NaOH

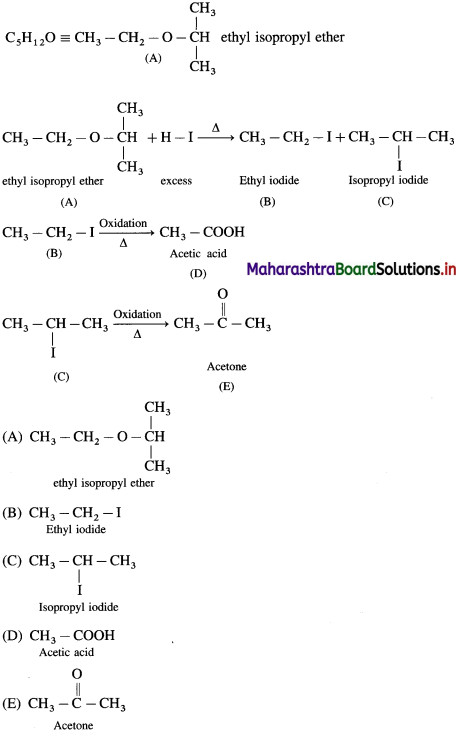
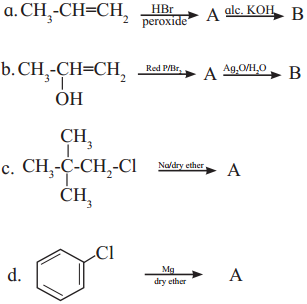
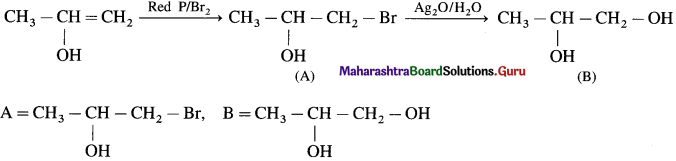
4. An ether (A), C₅H₁₂O, when heated with excess of hot HI produce two alkyl halides which on hydrolysis form compound (B)and (C), oxidation of (B) gave and acid (D), whereas oxidation of (C) gave a ketone (E). Deduce the structural formula of (A), (B), (C), (D) and (E).
Answer:

5. Write structural formulae for

a. 3-Methoxyhexane
b. Methyl vinyl ether
c. 1-Ethylcyclohexanol
d. Pentane-1,4-diol
e. Cyclohex-2-en-1-ol
Answer:

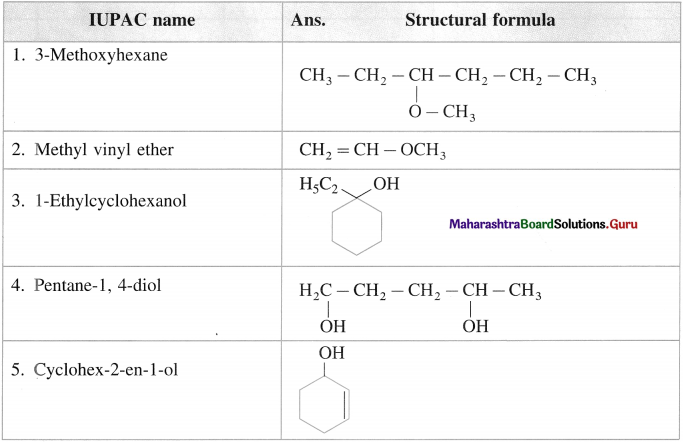
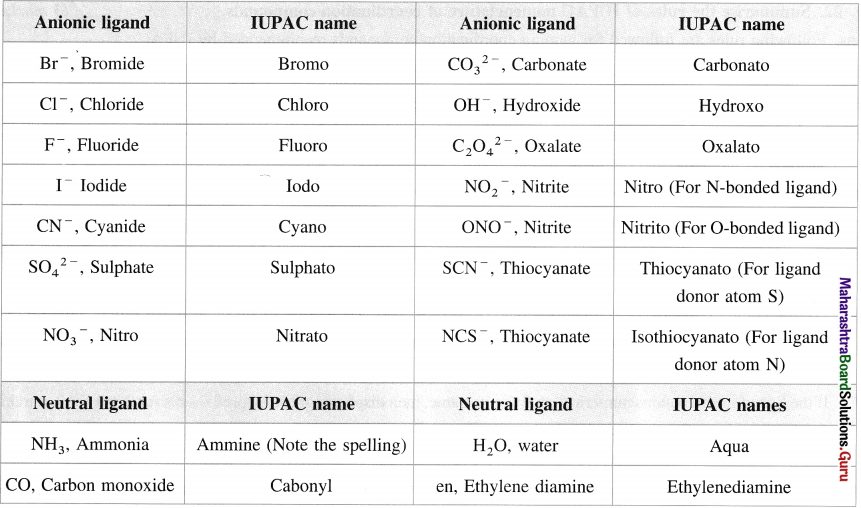
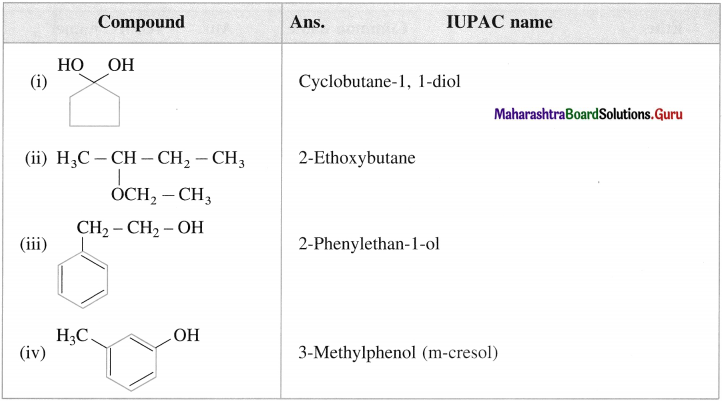
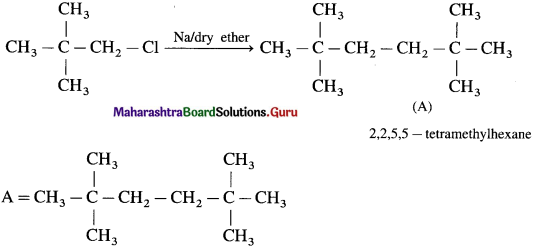
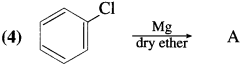
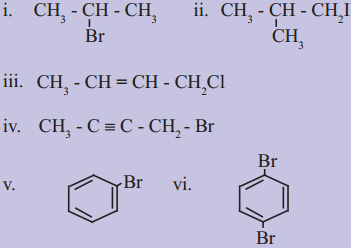
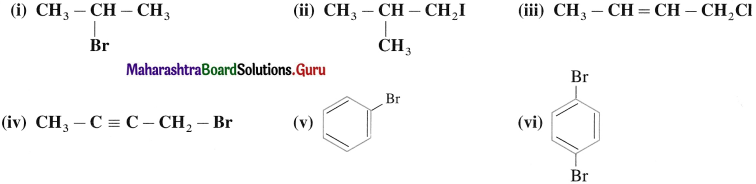
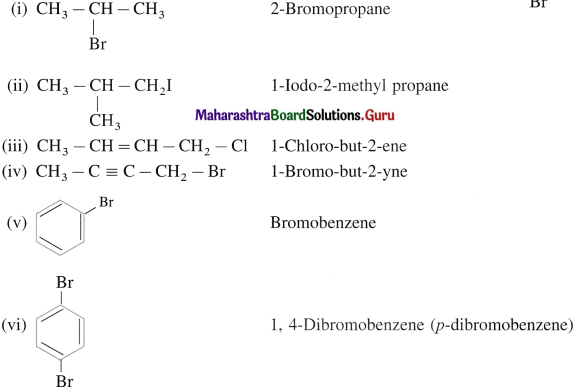
6. Write IUPAC names of the following

Answer:

Activity :
• Collect information about production of ethanol as byproduct in sugar industry and its importance in fuel economy.
• Collect information about phenols used as antiseptics and polyphenols having antioxidant activity.

12th Chemistry Digest Chapter 11 Alcohols, Phenols and Ethers Intext Questions and Answers

Use your brain power! (Textbook Page No 235)

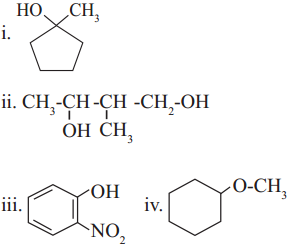
Question 1.
Classify the following alcohols as l0/2°/3° and allylic/benzylic

Answer:
(1) Ally lie alcohol (primary)
(2) Allylic alcohol (secondary)
(3) Allylic alcohol (tertiary)
(4) Benzylic alcohol (primary)
(5) Benzylic alcohol (secondary)

Use your brain power ….. (Textbook Page No 236)

Question 1.
Name t-butyl alcohol using carbinol system of nomenclature.
Answer:
Trimethyl carbinol.

Problem 11.1 (Textbook Page No 238)

Question 1.
Draw structures of following compounds:
(i) 2,5-DiethIphenoI
(ii) Prop-2-en-I-oI
(iii) 2-methoxypropane
(iv) Phenylmethanol
Solution :

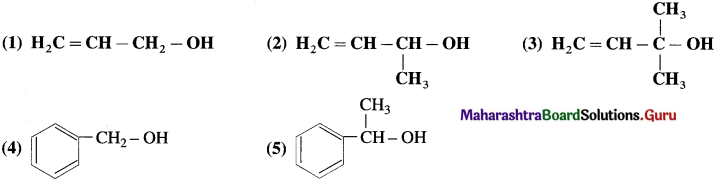
Try this ….. (Textbook Page No 238)

Write IUPAC names ol (he following compounds.

Do you know (Textbook Page No 238)

Question 1.
The mechanism of hydration of ethylcnc to ethyl alcohol.
Answer:
The mechanism of hydration of ethylene involves three steps:

Step 1: Ethylene gets protonated to form carbocation by electrophilic attack of H₃O (Formation of carbocation intermediate).

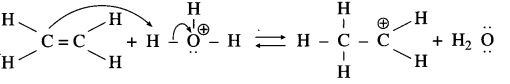
Step 2 : Nucleophilic attack of water on carbocation

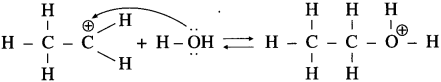
Step 3 : Deprotonation to form an alcohol

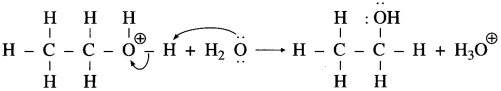
Problem 11.2 : (Textbook Page No 239)

Question 1.
Predict the products for the following reaction.

Solution:
The substrate (A) contains an isolated and an aldehyde group. H₂/Ni can reduce both these functional groups while LiAlH₄ can reduce only – CHO of the two, Hence

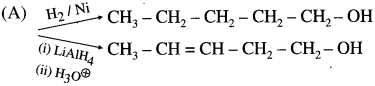
Try this ….. (Textbook page 240)

Question 1.
Arrange O – H, C – H and N – H bonds in increasing order of their bond polarity.
Answer:
Increasing order of polarity :C – H, N – H, O – H

Problem 11.3 : (Textbook Page No 241)

Question 1.
The boiling point of n-butyl alcohol, isobutyl alcohol, sec-butyl alcohol and tert-butyl alcohol are 118 °C, 108 °C. 99 °C and 82 °C respectively. Explain.
Solution:
As branching increases, intermolecular van der Waal’s force become weaker and the boiling point decreases. Therefore, n-butyl alcohol has highest boiling point 118 °C and tert-butyl alcohol has lowest boiling point 83 °C. Isobutyl alcohol is a primary alcohol and hence its boiling point is higher than that of sec-butyl alcohol.

Problem 11.4 : (Textbook Page No 242)

The solubility of o-nitrophenol and p-nitrophenol is 0.2 g and 1.7 g/100 g of H₂O respectively. Explain the difference.
Solution :

p-Nitrophenol has strong intermolecular hydrogen bonding with solvent water. On the other hand, o-nitrophenol has strong intramolecular hydrogen bonding and therefore the intermolecular attraction towards solvent water is weak. The stronger the intermolecular attraction between solute and solvent higher is the solubility. Hence p-nitrophenol has higher solubility in water than that of o-nitrophenol.

Problem 11.5 : (Textbook Page No 243 & 244)

Question 1.
Arrange the following compounds in decreasing order of acid strength and justify.
(1) CH₃ – CH₂ – OH
(2) (CH₃)₃ C – OH
(3) C₆H₅ – OH
(4) p-NO₂ – C₆H₄ – OH
Solution :
Compounds (3) and (4) are phenols and therefore are more acidic than the alcohols (1) and (2). The acidic strengths of compounds depend upon stabilization of the corresponding conjugate bases. Hence let us compare electronic effects in the conjugate bases of these compounds :

The conjugate base of the alcohol (1) is destabilized by + 1 effect of one alkyl group, whereas conjugate base of the alcohol (2) is destabilized by +1 effect of three alkyl groups. Hence (2) is weaker acid than (1)

Phenols : The conjugate base of p-nitrophenol (4) is better resonance stabilized due to six resonance structures compared to the five resonance structure of conjugate base of phenol (3). The resonance structure VI has – ve charge on only electronegative oxygens. Hence the phenol (4) is stronger acid than (3). Thus the decreasing order of acid strength is (4), (3), (1), (2).

Use your brain power (Textbook Page No 244)

Question 1.
What are the electronic effects exerted by – OCH₃ and – Cl? Predict the acid strength of

Answer:
The electronic effects exerted by – Cl and – O CH₃ are as follows :
(1) Cl being more electronegative atom it pulls the bonding electrons towards itself. This is known as negative inductive effect (- I).

(2) – OCH₃ is less electronegative group which repels the bonding electrons away from it. This is known as positive inductive effect ( + I).

(3) The relative to parent phenol, is more acidic than .

Problem 11.6 : (Textbook Page No 245)

Question 1.
Mechanism of acid catalyzed dehydration of ethanol to give ethene.
Answer:
The mechanism of dehydration of ethanol involves the following order :
Step 1 : Formation of protonated alcohols : Initially ethyl alcohol gets protonated to form ethyl oxonium ion.

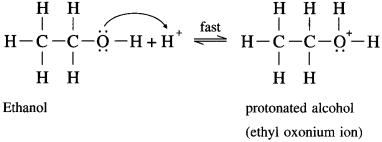
Step 2 : Formation of carbocation : It is the slowest step and hence, the rate determining step of the reaction.

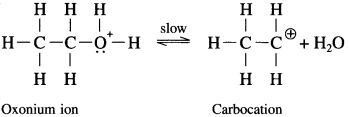
Steps 3: Formation of ethene: Removal of a proton (H⁺) from carbocation.

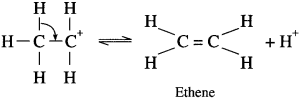
The acidused in step I is released in step 3, the equilibrium is shifted to the right, ethene is removed as it is formed.

Problem 11.6 : (Textbook Page No 245)

Question 1.
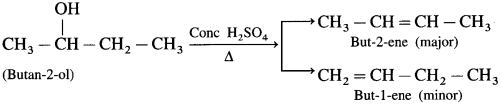
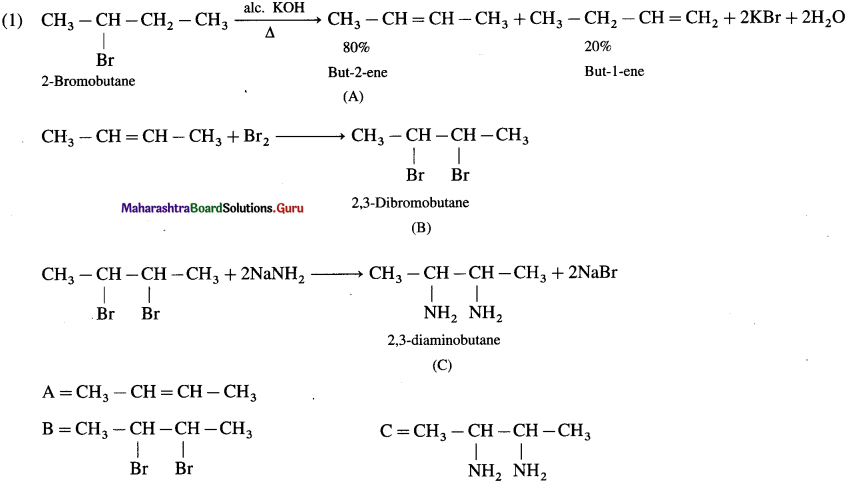
Write the reaction showing major and minor products formed on heating butan-2-ol with concentrrated sulphuric acid.
Solution :
In the reaction described butan-2-ol undergoes dehydration to give but-2-ene (major) and but-l-ene (minor) in accordance with Saytzeff rule.

Problem 11.7 : (Textbook Page No 246)

Question 1.
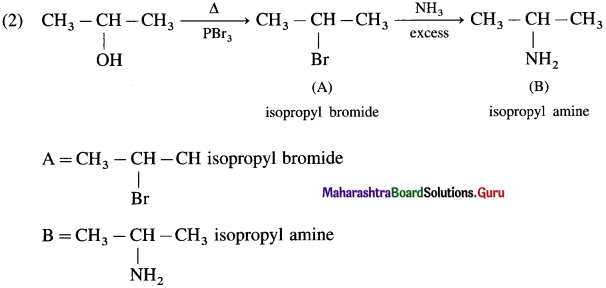
Write and explain reactions to convert propan-l-ol into propan-2-ol.
Solution :
The dehydration of propane-l-ol to propene is the first step. Markownikoff hydration of propene is the second step to get the product propan-2-ol. This is brought about by reaction with concemtrated H₂SO₄ followed by hydrolysis.

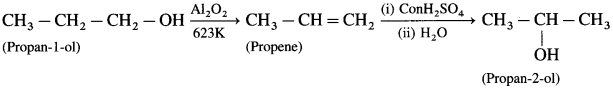
Problem 11.8 : (Textbook Page No 246)

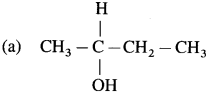
Question 1.
An organic compound gives hydrogen on reaction with sodium metal. It forms an aldehyde having molecular formula C₂H₄O on oxidation with pyridinium chlorochromate. Name the compounds and give equations of these reactions.
Solution :
The given molecular formula C₂H₄O of aldehyde is written as CH₃ – CHO. Hence the formula of alcohol from which this is obtained by oxidation must be CH₃ – CH₂ – OH. The two reactions can, therefore, be represented as follows :

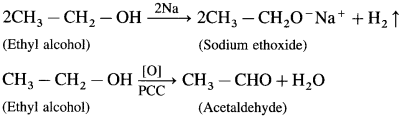
(Do you know? Textbook Page No 248)

Question 90.
Write the mechanism of dehydration of alcohol to give ether.
Answer:
Dehydration of alcohols to form ether is SN₂ reaction. The mechanism of dehydration of ethanol involves the following steps.

Step 1 (Protonation) : Initially ethyl alcohol gets protonated in the presence of acid to form ethyl oxonium ion.

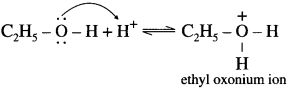
Step 2 (SN² mechanism) : Protonated alcohol species undergoes a backside attack by second molecule of alcohol is a slow step.

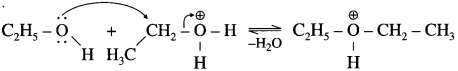
Step 3 (Deprotonation) : Formation of diethyl ether by elimination of proton

Problem 11.9 : (Textbook Page No 249)

Question 1.
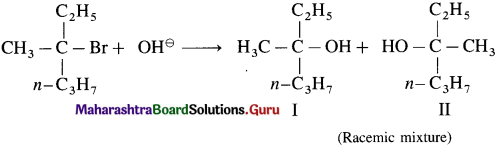
Ethyl isopropyl ether does not form on reaction of sodium ethoxide and isopropyl chloride.

(i) What would be the main product of this reaction?
(ii) Write another reaction suitable for the preparation of ethyl isopropyl ether.
Solution :
(i) Isopropyl chloride is a secondary chloride. On treating with sodium ethoxide it gives elimination reaction to form propene as the main product.

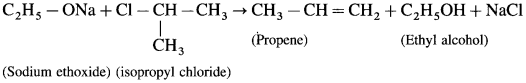
(ii) Ethyl isopropyl ether can be prepared as follows using ethyl chloride (1⁰ chloride) as substrate.

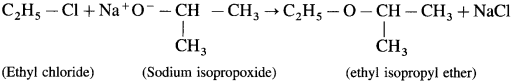
Do you know? (Textbook Page No 250)

Question 1.
The mechanism of the reaction of HI with methoxy ethane.
Answer:
The reaction mechanism takes place as follows :
Step 1 : Protonation of ether Initially the ether molecule (methoxy ethane) protonated by cone. HI to form oxonium ion.

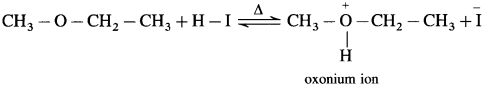
Step 2 : Iodide is a good nucleophile. It attacks the least substituted carbon of the oxonium ion formed in step 1 and displaces an alcohol molecule by SN² mechanism.

For example :
• Use of excess HI converts the alcohol into alkyl iodide.
• In the case of ether having one tertiary alkyl group the reaction with hot HI follows the SN1 mechanism, and tertiary iodide is formed rather than tertiary alcohol.

Step 1 :

Step 2 :

Maharashtra State Board 12th Std Chemistry Textbook Solutions

• Coordination Compounds Class 12 Chemistry Textbook Solutions
• Halogen Derivatives Class 12 Chemistry Textbook Solutions
• Alcohols, Phenols and Ethers Class 12 Chemistry Textbook Solutions
• Aldehydes, Ketones and Carboxylic Acids Class 12 Chemistry Textbook Solutions
• Amines Class 12 Chemistry Textbook Solutions
• Biomolecules Class 12 Chemistry Textbook Solutions
• Introduction to Polymer Chemistry Class 12 Chemistry Textbook Solutions
• Green Chemistry and Nanochemistry Class 12 Chemistry Textbook Solutions

Halogen Derivatives Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 10 Halogen Derivatives Textbook Exercise Questions and Answers.

Class 12 Chemistry Chapter 10 Exercise Solutions Maharashtra Board

Chemistry Class 12 Chapter 10 Exercise Solutions

1. Choose the most correct option.

Question i.
The correct order of increasing reactivity of C-X bond towards nucleophile in the following compounds is

a. I < II < III < IV
b. II < I < III < IV
c. III < IV < II < I
d. IV < III < I < II
Answer:
(d) IV < III < I < II

Question ii.

The major product of the above reaction is,

Answer:
(c)

Question iii.
Which of the following is likely to undergo racemization during alkaline hydrolysis?

Answer:
(a) Only I

Question iv.
The best method for preparation of alkyl fluorides is
a. Finkelstein reaction
b. Swartz reaction
c. Free radical fluorination
d. Sandmeyer’s reaction
Answer:
b. Swartz reaction

Question v.
Identify the chiral molecule from the following.
a. 1-Bromobutane
b. 1,1- Dibromobutane
c. 2,3- Dibromobutane
d. 2-Bromobutane
Answer:
(d) 2-Bromobutane

Question vi.
An alkyl chloride on Wurtz reaction gives 2,2,5,5-tetramethylhexane. The same alkyl chloride on reduction with zinc-copper couple in alchol give hydrocarbon with molecular formula C₅H₁₂. What is the structure of alkyl chloride

Answer:
(a)

Question vii.
Butanenitrile may be prepared by heating
a. propanol with KCN
b. butanol with KCN
c. n-butyl chloride with KCN
d. n-propyl chloride with KCN
Answer:
(d) n-propyl chloride with KCN

Question viii.
Choose the compound from the following that will react fastest by S_N1 mechanism.
a. 1-iodobutane
b. 1-iodopropane
c. 2-iodo-2 methylbutane
d. 2-iodo-3-methylbutane
Answer:
(c) 2-iodo-2 methylbutane

Question ix.

The product ‘B’ in the above reaction sequence is,

Answer:
(d)

Question x.
Which of the following is used as source of dichlorocarbene
a. tetrachloromethane
b. chloroform
c. iodoform
d. DDT
Answer:
(b) chloroform

2. Do as directed.

Question i.
Write IUPAC name of the following compounds

Answer:

Question ii.
Write structure and IUPAC name of the major product in each of the following reaction.


Answer:
Structure and IUPAC name

Question iii.
Identify chiral molecule/s from the following.

Answer:
Chiral molecule

Question iv.
Which one compound from the following pairs would undergo S_N2 faster from the?

Answer:
(1) Sincey is a primary halide it undergoes S_N2 reaction faster than .
(2) Since iodine is a better leaving group than chloride, 1-iodo propane (CH₃CH₂CH₂I) undergoes S_N2 reaction faster than l-chloropropane (CH₃CH₂CH₂CI).

Question v.
Complete the following reactions giving major product.

Answer:

Answer:

Answer:

Answer:

Question vi.
Name the reagent used to bring about the following conversions.
a. Bromoethane to ethoxyethane
b. 1-Chloropropane to 1 nitropropane
c. Ethyl bromide to ethyl isocyanide
d. Chlorobenzene to biphenyl
Answer:

Question vii.
Arrange the following in the increase order of boiling points
a. 1-Bromopropane
b. 2- Bromopropane
c. 1- Bromobutane
d. 1-Bromo-2-methylpropane
Answer:
l-Bromo-2-methylpropane, 2-Bromopropane, 1-Bromopropane, 1-Bromo butane

Question viii.
Match the pairs.

Answer:

3. Give reasons

Question i.
Haloarenes are less reactive than haloalkanes.
Answer:
Haloarenes (Aryl halides) are less reactive than (alkyl halides) haloalkanes due to the following reasons :

(1) Resonance effect : In haloarenes, the electron pairs on halogen atom are in conjugation with 7r-electrons of the benzene ring. The delocalization of these electrons C-Cl bond acquires partial double bond character.

Due to partial double bond character of C-Cl bond in aryl halides, the bond cleavage in haloarene is difficult and are less reactive. On the other hand, in alkyl halides, carbon is attached to chlorine by a single bond and it can be easily broken.

(2) Aryl halides are stabilized by resonance but alkyl halides are not. Hence, the energy of activation for the displacement of halogen from aryl halides is much greater than that of alkyl halides.

(3) Different hybridization state of carbon atom in C-X bond :
(i) In alkyl halides, the carbon of C-X bond is sp³-hybridized with less 5-character and greater bond length of 178 pm, which requires less energy to break the C-X bond.

(ii) In aryl halides, the carbon of C-X bond is sp³-hybridized with more 5-character and shorter bond length which requires more energy to break C-X bond. Therefore, aryl halides are less reactive than alkyl halides.

(iii) Polarity of the C-X bond : In aryl halide C-X bond is less polar than in alkyl halides. Because sp³-hybrid carbon of C-X bond has less tendency to release electrons to the halogen than a sp³-hybrid carbon in alkyl halides. Thus halogen atom in aryl halides cannot be easily displaced by nucleophile.

(2) Aryl halides are extremely less reactive towards nucleophilic substitution reactions.
Answer:
Aryl halides are extremely less reactive towards nucleophilic substitution reaction due to the following reasons : (1) Resonance effect : In haloarenes, the electron pairs on halogen atom are in conjugation with 7r-electrons of the benzene ring. The delocalization of these electrons C-Cl bond acquires partial double bond character.

Due to partial double bond character of C-Cl bond in aryl halides, the bond cleavage in haloarene is difficult and are less reactive towards nucleophilic substitution.

(2) Sp² hybrid state of C : Different hybridization state of carbon atom in C-X bond : In aryl halides, the carbon of C-X bond is sp²-hybridized with more 5-character and shorter bond length of 169 pm which requires more energy to break C-X bond. It is difficult to break a shorter bond than a longer bond, in alkyl chloride (bond length 178 pm) therefore, aryl halides are less reactive towards nucleophilic substitution reaction.

(3) Instability of phenyl cation : In aryl halides, the phenyl cation formed due to self ionisation will not be stabilized by resonance which rules out possibility of S_N1 mechanism. Also backside attack of nucleophile is blocked by the aromatic ring which rules out S_N2 mechanism. Thus cations are not formed and hence aryl halides do not undergo nucleophilic substitution reaction easily.

(4) As any halides are electron rich molecules due to the presence of re-bond, they repel electron rich nucleophilic, attack. Hence, aryl halides are less reactive towards nucleophilic substitution reactions. However, the presence of electron withdrawing groups at o/p position activates the halogen of aryl halides towards substitution.

(3) Aryl halides undergo electrophilic substitution reactions slowly.
Answer:
Aryl halides undergo electrophilic substitution reactions slowly and it can be explained as follows :

(1) Inductive effect : The strongly electronegative halogen atom withdraws the electrons from carbon, atom of the ring, hence aryl halides show reactivity towards electrophilic attack.

(2) Resonance effect : The resonating structures of aryl halides show increase in electron density at ortho and para position, hence it is o, p directing.

The inductive effect and resonance effect compete with each other. The inductive effect is stronger than resonance effect. The reactivity of aryl halides is controlled by stronger inductive effect and o, p orientation is controlled by weaker resonating effect.

The attack of electrophile (Y) on haloarenes at ortho and para positions are more stable due to formation of chloronium ion. The chloronium ion formed is comparatively more stable than other hybrid structures of carbonium ion.

(4) Reactions involving Grignard reagent must be carried out under anhydrous condition.
Answer:
(1) Grignard reagent (R Mg X) is an organometallic compound. The carbon-magnesium bond is highly polar and magnesium halogen bond is in ionic in nature. Grignard reagent is highly reactive.

(2) The reactions of Grignard reagent are carried out in dry conditions because traces of moisture may spoil the reaction and Grignard reagent reacts with water to produce alkane. Hence, reactions involving Grignard reagent must be carried out under anhydrous condition.

(5) Alkyl halides are generally not prepared by free radical halogenation of alkane.
Answer:
(1) Free radical halogenation of alkane gives a mixture of all different possible Monohaloalkanes as well as polyhalogen alkanes.
(2) In this method, by changing the quantity of halogen the desired product can be made to predominate over the other
products. Hence, alkyl halides are generally not prepared by free radical halogenation of alkane.

Question ii.
Alkyl halides though polar are immiscible with water.
Answer:
(1) In alkyl halide, the halogen atom is more electronegative than carbon atom, the C – X bond is polar.
(2) Though alkyl halide is polar, it is insoluble in water because alkyl halide is not able to form hydrogen bonds with water. Attraction between alkyl halide molecule is stronger than attraction between alkyl halide and water.

(2) C-F bond in CH₃F is the strongest bond and C-I bond in CH₃I is the weakest bond. Explain.
Answer:
(1) Methyl fluoride (CH₃F) is highly polar molecule and has the shortest C-F bond length (139 pm) and the strongest C-F bond due to greater overlap of orbitals of the same principal quantum number i.e., overlap of 2sp³ orbital of carbon with 2pz orbital of fluorine.
(2) Methyl iodide (CH₃I) is much less polar and has the longest (C-I) bond length (214 pm) and the weakest C-I bond due to poor overlap of 2sp³ orbital carbon with 5pz orbital of iodine i.e., 2sp³ orbital of carbon cannot penetrate into larger p-orbitals.

(3) The boiling point of alkyl iodide is higher than that of alkyl fluoride.
Answer:
For a given alkyl group, the boiling point increases with increasing atomic mass of the halogen, because magnitude of van der Waals force increases with increase in size and mass of halogen. Therefore, boiling point of alkyl iodide is higher than that of alkyl fluoride.

(4) The boiling point of isopropyl bromide is lower than that of it-propyl bromide.
Answer:
For isomeric alkyl halides (isopropyl bromide and n-propyl bromide), the boiling point decreases as the branching increases, surface area decreases on branching and van der Waals forces decrease, therefore, the boiling point of isopropyl bromide is lower than that of n-propyl bromide.

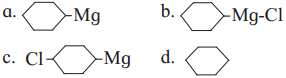
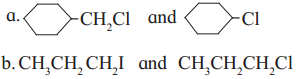
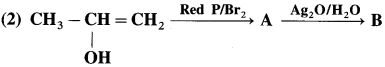
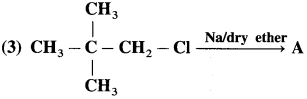
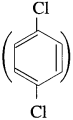(5) p-Dichlorobenzene has mp. higher than those of o-and rn-isomers.
Answer:
p-Dichlorobenzene has higher melting point than those of o-and m-isomers. This is because of its symmetrical structure which can easily fits in crystal lattice. As a result intermolecular forces of attraction are stronger and therefore greater energy is required to overcome its lattice energy.

Question iii.
Reactions involving Grignard reagent must be carried out under anhydrous conditions.

Question iv.
Alkyl halides are generally not prepared by free radical halogenation of alkanes.
Answer:
(1) Direct fluorination of alkanes is highly exothermic, explosive and invariably leads to polyfluorination and decomposition of the alkanes. It is difficult to control the reaction.
(2) Direct iodination of alkanes is highly reversible and difficult to carry out.
(3) In direct chlorination and bromination, the reaction is not selective. It can lead to different isomeric monohalogenated alkanes (alkyl halides) as well as polyhalogenated alkanes.
Hence, halogenation of alkanes is not a good method of preparation of alkyl halides.

4. Distinguish between – S_N1 and S_N2 mechanism of substitution reaction ?
Answer:

5. Explain – Optical isomerism in 2-chlorobutane.
Answer:
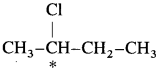(1) 2-Chlorobutane contains an asymmetric. carbon atom (the starred carbon atom) which is attached to four different groups, i.e., ethyl (-CH₂ – CH₃), methyl (CH₃), chloro (Cl) and hydrogen (H) groups.

(2) Two different arrangements of these groups around the carbon atom are possible as shown in the figure. Hence, it exists as a pair of enanti¬omers. The two enantiomers are mirror images of each other and are not superimposable.

(3) One of the enantiomers will rotate the plane of plane-polarized light to the left hand side and is called the laevorotatory isomer (/-isomer). The other enantiomer will rotate the plane of plane-polarized light to the right hand side and is called the dextrorotatory isomer (d-isomer).

(4) Equimolar mixture of the d- and the 1-isomers is optically inactive and is called the racemic mixture or the racemate (dl-mixture). The optical inactivity of the racemic mixture is due to external compensation.

6. Convert the following.

Question i.
Propene to propan-1-ol
Answer:

Question ii.
Benzyl alcohol to benzyl cyanide
Answer:

Question iii.
Ethanol to propane nitrile
Answer:

Question iv.
But-1-ene to n-butyl iodide
Answer:

Question v.
2-Chloropropane to propan-1-ol
Answer:

Question vi.
tert-Butyl bromide to isobutyl bromide
Answer:

Question vii.
Aniline to chlorobenzene
Answer:

Question viii.
Propene to 1-nitropropane
Answer:

7. Answer the following

Question i.
HCl is added to a hydrocarbon ‘A’ (C₄H₈) to give a compound ‘B’ which on hydrolysis with aqueous alkali forms tertiary alcohol ‘C’ (C₄H10O). Identify ‘A’ , ‘B’ and ‘C’.
Answer:

Question ii.
Complete the following reaction sequences by writing the structural formulae of the organic compounds ‘A’, ‘B’ and ‘C’.

Answer:

Question iii.
Observe the following and answer the questions given below.

a. Name the type of halogen derivative
b. Comment on the bond length of C-X bond in it
c. Can react by S_N1 mechanism? Justify your answer.
Answer:
a. Vinyl halide
b. C – X bond length shorter in vinyl halide than alkyl halide. Vinyl halide has partial double bond character due to resonance.

In vinyl halide, carbon is sp hybridised. The bond is shorter and stronger and the molecule is more stable.

c. Yes, It reacts by S_N1 mechanism. S_N1 mechanism involves formation of carbocation intermediate. The vinylic carbocation intermediate formed is resonance stabilized, hence S_N1 mechanism is favoured.

Activity :
1. Collect detailed information about Freons and their uses.
2. Collect information about DDT as a persistent pesticide.
Reference books
i. Organic chemistry by Morrison, Boyd, Bhattacharjee, 7^th edition, Pearson
ii. Organic chemistry by Finar, Vol 1, 6^th edition, Pearson

12th Chemistry Digest Chapter 9 Halogen Derivatives Intext Questions and Answers

Use your brain power….. (Textbook page 212)

Question 1.
Write IUPAC names of the following:

Answer:

Question 10.1 : (Textbook page 213)

How will you obtain 1.bromo.1-methylcyclohexane from alkene? Write possible structures of alkene and the reaction involved.

Answer:

Use your brain power ….. (Textbook page 213)

Question 1.
Rewrite the following reaction by filling the blanks:

Answer:

Question 10.2 : (Textbook page 216)

Arrange the following compounds in order of increasing boiling points : bromoform, chloromethane, dibromomethane, bromomethane.
Answer:
The comparative boiling points of halogen derivatives are mainly related with van der Waals forces of attraction which depend upon the molecular size. In the present case all the compounds contain only one carbon. Thus the molecular size depends upon the size of halogen and number of halogen atoms present.

Thus increasing order of boiling point is, CH₃CI < CH₃Br < CH₂Br₂ < CHBr₃

Try this ….. (Textbook page 2016)

Question 1.
(1) Make a three-dimensional model of 2-chlorobutane.
(2) Make another model which is a mirror image of the first model.
(3) Try to superimpose the two models on each other.
(4) Do they superimpose on each other exactly ?
(5) Comment on whether the two models are identical or not.
Answer:
(1) (2) and (3)

(4) Two models are non-superimposable mir ror images of each other called enantiomers.

(5) Two enantiomers are identical. Theyhave the same physical properties (such as melting points, boiling points, densities refractive index). They also have identical chemical properties. The magnitude of their optical rotation is equal but the sign of optical rotation is opposite.

Try this ….. (Textbook page 219)

Question 1.
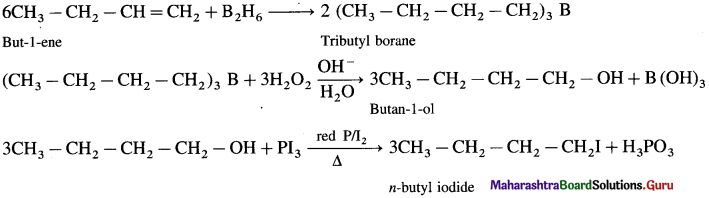
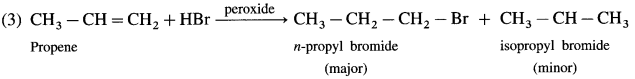
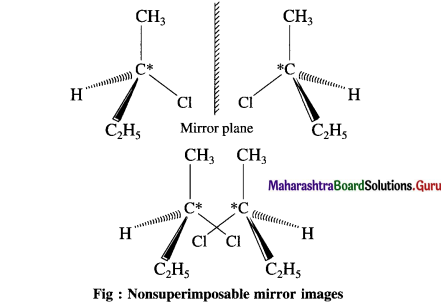
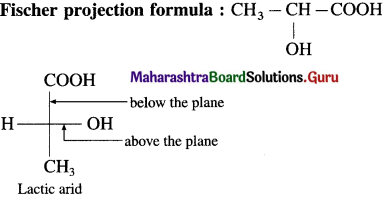
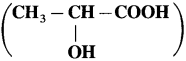1. Draw structares of enantiomers of lactic acid using Fischer projection formulae.
2. Draw structures of enantiomers of 2-bromobutane using wedge formula.
Answer:
(1)

(2) Wedge formula : 2-brornobutane

Can you tell? (Textbook page 220)

Question 1.
Alkyl halides, when treated with alcoholic solution of silver nitrite, give nitroalkanes whereas with sodium nitrite they give alkyl nitrites. Explain.
Answer:
Nitrite ion is an ambident nucleophile, which can attack through ‘O’ or ‘N’.

Both nitrogen and oxygen are capable of donating electron pair. C – N bond, being stronger than N – O bond, attack occurs through C atom from alkyl halide forming nitroalkane.

However, sodium nitrite (NaNO₂) is an ionic compound and oxygen is free to donate pair of electrons. Hence, attack occurs through oxygen resulting in the formation of alkyl nitrite.

Use your brain power! (Textbook page 222)

Question 1.
Draw the Fischer projection formulae of two products obtained when compound (A) reacts with OHe by S_N1 mechanis.

Answer:

Question 2.
Draw the Fischer projection formula of the product formed when compound (B) reacts with OHΘ by S_N2 mechanism.

Answer:

Question 10.4 : (Textbook page 223)

Allylic and benzylic halides show high reactivity towards the S_N1 mechanism than other primary alkyl halides. Explain.
Answer:
In allylic and benzylic halide, the carbocation formed undergoes stabilization through the resonance. Hence, allylic and benzylic halides show high reactivity towards the S_N1 reaction. The resonating structures are

Resonance stabilization of allylic carbocation

Resonance stabilization of benzylic carbocation

Question 10.5 : (Textbook page 224)

Which of the following two compounds would react faster by SN2 mechanism and Why?

Answer :
In S_N2 mechanism, a pentacoordinate T.S. is involved. The order of reactivity of alkyl halides towards S_N2 mechanism is.
Primary > Secondary > Tertiary, (due to increasing crowding in T.S. from primary to tertiary halides.
1- Chlorobutane being primary halide will react faster by S_N2 mechanism, than the secondary halide 2- chlorobutane.)

Can you tell? (Textbook page 227)

Question 1.
Conversion of chlorobenzene to phenol by aqueous sodium hydroxide requires a high temperature of about 623K and high pressure. Explain.

Answer:
Due to the partial double bond character in chlorobenzene, the bond cleavage in chlorobenzene is difficult and is less reactive. Hence, during the conversion of chlorobenzene to phenol by a question NaOH requires high temperature & high pressure.

Maharashtra State Board 12th Std Chemistry Textbook Solutions

• Coordination Compounds Class 12 Chemistry Textbook Solutions
• Halogen Derivatives Class 12 Chemistry Textbook Solutions
• Alcohols, Phenols and Ethers Class 12 Chemistry Textbook Solutions
• Aldehydes, Ketones and Carboxylic Acids Class 12 Chemistry Textbook Solutions
• Amines Class 12 Chemistry Textbook Solutions
• Biomolecules Class 12 Chemistry Textbook Solutions
• Introduction to Polymer Chemistry Class 12 Chemistry Textbook Solutions
• Green Chemistry and Nanochemistry Class 12 Chemistry Textbook Solutions

Coordination Compounds Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 9 Coordination Compounds Textbook Exercise Questions and Answers.

Class 12 Chemistry Chapter 9 Exercise Solutions Maharashtra Board

Chemistry Class 12 Chapter 9 Exercise Solutions

1. Choose the most correct option.

Question i.
The oxidation state of cobalt ion in the complex [Co(NH₃)₅Br]SO₄ is ……………………….
a. + 2
b. + 3
c. + 1
d. + 4
Answer:
(b) + 3

Question ii.
IUPAC name of the complex [Pt(en)₂(SCN)₂]²⁺ is ………………………
a. bis (ethylenediamine dithiocyanatoplatinum (IV) ion
b. bis (ethylenediamine) dithiocyantoplatinate (IV) ion
c. dicyanatobis (ethylenediamine) platinate IV ion
d. bis (ethylenediammine)dithiocynato platinate (IV) ion
Answer:
(a) bis(ethylenediamine dithiocyanatoplatinum (IV) ion

Question iii.
Formula for the compound sodium hexacynoferrate (III) is
a. [NaFe(CN)₆]
b. Na₂[Fe(CN)₆]
c. Na[Fe(CN)₆]
d. Na₃[Fe(CN)₆]
Answer:
(d) Na₃[Fe(CN)₆]

Question iv.
Which of the following complexes exist as cis and trans isomers?
1. [Cr(NH₂)₂Cl₄]^⊕
2. [Co(NH₃)₅Br]^2⊕
3. [PtCl₂Br₂]^2⊕ (square planar)
4. [FeCl₂(NCS)₂]^2⊕ (tetrahedral)
a. 1 and 3
b. 2 and 3
c. 1 and 3
d. 4 only
Answer:
(a) 1 and 3

Question v.
Which of the following complexes are chiral?
1. [Co(en)₂Cl₂]^⊕
2. [Pt(en)Cl₂]
3. [Cr(C₂O₄)₃]^3⊕
4. [Co(NH₃)4CI₂]^⊕
a. 1 and 3
b. 2 and 3
c. 1 and 4
d. 2 and 4
Answer:
(a) 1 and 3

Question vi.
On the basis of CFT predict the number of unpaired electrons in [CrF₆]^3⊕.
a. 1
b. 2
c. 3
d. 4
Answer:
(c) 3

Question vii.
When an excess of AgNO₃ is added to the complex one mole of AgCl is precipitated. The formula of the complex is ……………..
a. [CoCl2(NH₃)₄]Cl
b. [CoCl(NH₃)₄] Cl₂
c. [CoCl₃(NH₃)₃]
d. [Co(NH₃)₄]Cl₃
Answer:
(a) [COCI₃(NH₃)₄]CI

Question viii.
The sum of coordination number and oxidation number of M in [M(en)₂C₂O₄]Cl is
a. 6
b. 7
c. 9
d. 8
Answer:
(c) 9

2. Answer the following in one or two sentences.

Question i.
Write the formula for tetraammineplatinum (II) chloride.
Answer:
Formula of tetraamineplatinum(II) chloride : [Pt(NH₃)₄]CI₂

Table 9.1 : IUPAC names of anionic and neutral ligands

Table 9.2: IUPAC names of anionic complexes

Table 9.3 : IUPAC names of some complexes

Question ii.
Predict whether the [Cr(en)₂(H₂O)₂]³⁺ complex is chiral. Write structure of its enantiomer.
Answer:
(i) Complex is chiral.
(ii) The following are its enantiomers

Question iv.
Name the Lewis acids and bases in the complex [PtCl₂(NH₃)₂].
Answer:
Lewis acid : Pt²⁺
Lewis bases : Cl^– and NF₃

Question v.
What is the shape of a complex in which the coordination number of central metal ion is 4?
Answer:
A complex with the coordination number of central metal ion equal to 4 may be tetrahedral or square planar.

Question vi.
Is the complex [CoF₆] cationic or anionic if the oxidation state of cobalt ion is +3?
Answer:
In the complex, Co carries + 3 charge while 6F^– carry – 6 charge. Hence the net charge on the complex is – 3.
Therefore it is an anionic complex.

Question vii.
Consider the complexes [Cu(NH₃)₄][PtCl₄] and [Pt(NH₃)₄] [CuCl₄]. What type of isomerism these two complexes exhibit?
Answer:
Since in these two given complexes, there is an exchange of ligands between cationic and anionic constituents, they exhibit coordination isomerism.

Question viii.
Mention two applications of coordination compounds.
Answer:
(1) In biology : Several biologically important natural compounds are metal complexes which play an important role in number of processes occurring in plants and animals.

For example, chlorophyll in plants is a complex of Mg²⁺ ions, haemoglobin in blood is a complex of iron, vitamin B₁₂ is a complex of cobalt.

(2) In medicine : The complexes are used on a large scale in medicine. Many medicines in the complex form are more stable, more effective and can be assimilated easily.

For example, platinum complex [Pt(NH₃)₂CI₂] known as cisplatin is effectively used in cancer treatment. EDTA is used to treat poisoning by heavy metals like lead.

(3) To estimate hardness of water :

• The hardness of water is due to the presence Mg²⁺ and Ca²⁺ ion in water.
• The strong field ligand EDTA forms stable complexes with Mg²⁺ and Ca²⁺. Hence these ions can be removed by adding EDTA to hard water.

Similarly these ions can be selectively estimated due to the difference in their stability constants.

(4) Electroplating : This involves deposition of a metal on the other metal. For smooth plating, it is necessary to supply continuously the metal ions in small amounts.
For this purpose, a solution of a coordination compound is used which dissociates to a very less extent. For example, for uniform and thin plating of silver and gold, the complexes K[Ag(CN)₂] and K[Au(CN)₂] are used.

3. Answer in brief.

Question i.
What are bidentate ligands? Give one example.
Answer:
Bidentate ligand : This ligand has two donor atoms in the molecule or ion. For example, ethylenediamine, H₂N – (CH₂)₂ – NH₂.

Question ii.
What is the coordination number and oxidation state of metal ion in the complex [Pt(NH₃)Cl₅]²?
Answer:
Coordination number = 6
Oxidation state of Pt = +4.

Question iii.
What is the difference between a double salt and a complex? Give an example.
Answer:

Question iv.
Classify the following complexes as homoleptic and heteroleptic
[Cu(NH₃)₄]SO₄, [Cu(en)₂(H₂O)Cl]^3⊕, [Fe(H₂O)₅(NCS)]^2⊕, tetraammine zinc (II) nitrate.
Answer:
Homoleptic complex :
(a) [Cu(NH₃)₄]SO₄
(d) Tetraaminezinc (II) nitrate : [Zn(NH₃)₄](NO₃)₂

Heteroleptic Complex :
(b) [Cu(en)₂(H₂O)CI]²⁺
(c) [Fe(H₂O)₅(NCS)]²⁺

Question v.
Write formulae of the following complexes
a. Potassium ammine-tri chloroplatinate (II)
b. Dicyanoaurate (I) ion
Answer:
(a) Potassium amminetrichloroplatinate(II) K[Pt(NH₃)CI₃]
(b) Dicyanoaurate (I) ion [AU(CN)₂]^–

Question vi.
What are ionization isomers? Give an example.
Answer:
Ionisation isomers : The coordination compounds having same molecular composition but differ in the compositions of coordination (or inner) sphere and outer sphere and produce different ions on ionisation in the solution are called ionisation isomers. For example, Pentaamminesulphatocobalt (III) bromide [Co(NH₃)₅SO₄] Br, Pentaamminebromocobalt(III) sulphate [Co(NH₃)₅Br] SO₄.

Question vii.
What are the high-spin and low-spin complexes?
Answer:
(1) High spin complex (HS) :

• The complex which has greater iwmher of unpaired electrons and hence a higher value of resultant spin and magnetic moment is called high spin (or spin free) or IlS complex.
• It is formed with weak field ligands and the complexes have lower values for crystal field splitting energy (CFSE). Δ₀
• The paramagnetism of HS complex is larger.

(2) Low spin complex (LS) :

• The complex which has the Icasi number of unpaired electrons or all electrons paired and hence the lowest
  (or no) resultant spin or magnetic moment is called low spin (or spin paired) or LS complex.
• It is formed with strong tickl ligands and the complexes have higher values of crystal field splitting energy (Δ₀).
• Low spin complex is diamagnetic or has low paramagnetism.

Table 9.5 : d-orbitai diagrams fir high spin and low spin complexes

(Only the electronic configurations c4 to d1 render the high spin and low spin complexes)

Question viii.
[CoCl₄]^2⊕ is a tetrahedral complex. Draw its box orbital diagram. State which orbitals participate in hybridization.
Answer:
₂₇Co [Ar] 3d⁷4s²
Oxidation state of Co = +2 Co²⁺ [Ar] 3d⁷ 4s°
Since CI^– is a weak ligand, there is no pairing of electrons. Since C.N. is 4, there is sp³ hybridisation.

Question ix.
What are strong field and weak field ligands? Give one example of each.
Answer:
The ligands are then classified as (a) strong field and (b) weak field ligands. Strong field ligands are those in which donor atoms are C,N or P. Thus CN^–, NC^–, CO, HN₃, EDTA, en (ethylenediammine) are considered to be strong ligands. They cause larger splitting of d orbitals and pairing of electrons is favoured. These ligands tend to form low spin complexes. Weak field ligands are those in which donor atoms are halogens, oxygen or sulphur.

For example, F^–, CI^–, Br^–, I^–, SCN^–, C₂O₄^2-. In case of these ligands the A0 parameter is smaller compared to the energy required for the pairing of electrons, which is called as electron pairing energy. The ligands then can be arranged in order of their increasing field strength as
I^– < Br^– < CI^– < S^2- < F^– < OH^– < C₂O₄^2- < H₂O < NCS^– < EDTA < NH₃ < en < CN^– < CO.

Question x.
With the help of a crystal field energy-level diagram explain why the complex [Cr(en)₃]^3⊕ is coloured?
Answer:

Since (en) is a strong field ligand there is pairing of electrons. The electrons occupy the t_2g orbitals of lower energy. It has one unpaired electron. Due to d-d transition, it is coloured.

4. Answer the following questions.

Question i.
Give valence bond description for the hybrid orbitals are used by the metal? State the number of unpaired electrons.
Answer:
Since CI^– is a weak ligand, there is no pairing of electrons.
Number of unpaired electrons = 2
Type of hybridisation = sp³

Geometry of complex ion = Tetrahedral
The complex ion is paramagnetic.

Question ii.
Draw a qualitatively energy-level diagram showing d-orbital splitting in the octahedral environment. Predict the number of unpaired electrons in the complex [Fe(CN)₆]^4⊕. Is the complex diamagnetic or paramagnetic? Is it coloured? Explain.
Answer:
(A) r-orbital splitting in the octahedral environment :

(B) [Fe (CN)₆]^4- is an octahedral complex.
(C) Since CN^– is a strong ligand, there is pairing of electrons and the complex is diamagnetic.
(D) The complex exists as lemon yellow crystals.
(In the complex all electrons in t_2g are paired and requires high radiation energy for excitation.)

Question iii.
Draw isomers in each of the following
a. [Pt(NH₃)₂ClNO₂]
b. [Ru(NH₃)4Cl₂]
c. [Cr(en₂)Br₂]^⊕
Answer:
(a) [Pt(NH₃)₂CINO₂]

(b) [RU(NH₃)₄CI₂]

(c) [Cr(en₂)Br₂]⁺

Question iv.
Draw geometric isomers and enantiomers of the following complexes.
a. [Pt(en)₃]^4⊕
b. [Pt(en)₂ClBr]^2⊕
Answer:
The complex [Pt(en)₃]⁴⁺ has two optical isomers.

Question v.
What are ligands? What are their types? Give one example of each type.
Answer:
Ligands : The neutral molecules or negatively charged anions (or rarely positive ions) which are bonded by coordinate bonds to the central metal atom or metal ion in a coordination compound are called ligands or donor groups. For example in [Cu(CN)₄]^2-, four CN^– ions are ligands coordinated to central metal ion Cu²⁺. Ligands can be classified on the basis of number of electron donor atoms in the ligand i.e. denticity.

(1) Monodentate or unidentate ligand : A ligand molecule or an ion which has only one donor atom with a lone pair of electrons forming only one coordinate bond with metal atom or ion in the complex is called monodentate or unidentate ligand. For example NH₃, Cl^–, OH^–, H₂O, etc.

(2) Polydentate or multidentate ligand : A ligand molecule or an ion which has two or more donor atoms with the lone pairs of electrons forming two or more coordinate bonds with the central metal atom or ion in the complex is called polydentate or multidentate ligand. For example, ethylene diamine, H₂N – (CH₂)₂ – NH₂.
According to the number of donor atoms they are classified as follows :

• Bidentate ligand : This ligand has two donor atoms in the molecule or ion. For example, ethylenediamine, H₂N – (CH₂)₂ – NH₂.
• Tridentate ligand : This ligand molecule has three donor atoms or three sites of attachment.
  E.g. Diethelene triamine, H₂N – CH₂ – CH₂ – NH – CH₂ – CH₂ – NH₂. This has three N donor atoms.
• Tetradentate (or quadridentate) ligand : This ligand molecule has four donor atoms.
  Eg. Triethylene tetraamine which has four N donor atoms.
• Hexdentate ligand : This ligand molecule has six donor atoms. E.g. Ethylenediamine tetracetato.

(3) Ambidentate ligand : A ligand molecule or an ion which has two or more donor atoms, however in the formation of a complex, only one donor atom is attached to the metal atom or an ion is called ambidentate ligand. For example, NO^–₂ which has two donor atoms N and O forming a coordinate bond, M ← ONO (nitrito) or M ← NO₂ (nitro).

(4) Bridging ligand : A monodentate ligand having more than one lone pairs of electrons, hence can attach to two or more metal atoms or ions and hence acts as a bridge between different metal atoms is called bridging ligand. For example : OH^–, F^–, SO₄^-2, etc.

Question vi.
What are cationic, anionic and neutral complexes? Give one example of each.
Answer:
(1) Cationic sphere complexes : A positively charged coordination sphere or a coordination compound having a positively charged coordination sphere is called cationic sphere complex.

For example : [Zn(NH₃)₄]²⁺ and [Co(NH₃)₅CI] SO₄ are cationic complexes. The latter has coordination sphere [Co(NH₃)₅CI]²⁺, the anion SO₄²⁺ makes it electrically neutral.

(2) Anionic sphere complexes : A negatively charged coordination sphere or a coordination compound having negatively charged coordination sphere is called anionic sphere complex. For example, [Ni(CN)₄]²⁺ and K₃[Fe(CN)₆] have anionic coordination sphere; [Fe(CN)₆]^3- and three K+ ions make the latter electrically neutral.

(3) Neutral sphere complexes : A neutral coordination complex does not possess cationic or anionic sphere.

[Pt(NH₃)₂CI₂] or [Ni(CO)₄] are neither cation nor anion but are neutral sphere complexes.

Question vii.
How stability of the coordination compounds can be explained in terms of equilibrium constants?
Answer:
Stability of the coordination compounds : The stability of coordination compounds can be explained on the basis of their stability constants. The stability of coordination compounds depends on metal-ligand interactions. In the complex, metal serves as electron-pair acceptor (Lewis acid) while the ligand as Lewis base (since it is electron
donor). The metal-ligand interaction can be realized as the Lewis acid-Lewis base interaction. Stronger the interaction greater is stability of the complex.

Consider the equilibrium for the metal-ligand interaction :
M^a+ + nL^x- ⇌ [ML_n]^a+(-nx)
where a, x, [a + ( – nx)] denote the charge on the metal, ligand and the complex, respectively. Now, the equilibrium constant K is given by

Stability of the complex can be explained in terms of K. Higher the value of K larger is the thermodynamic stability of the complex hence K is called stability constant, and denoted by Kstah. The equilibria for the complex formation with the corresponding K values are given below.

Ag⁺ + 2CN^– ⇌ [Ag(CN)2]^– K = 5.5 x 10¹⁸
Cu²⁺ + 4CN^– ⇌ [CU(CN)4]^2- K = 2.0 x 10²⁷
Co³⁺ + 6NH₃ ⇌ [CO(NH3)6]³⁺ K = 5.0 x 10³³

From the above data, the stability of the complexes is [Co(NH₃)₆]³⁺ > [Cu(CN)₄]^2- > [Ag(CN)₂]^–.

Question viii.
Name the factors governing the equilibrium constants of the coordination compounds.
Answer:
The equilibrium constant of the complex depends on the following factors :

(a) Charge to size ratio of the metal ion : Higher the ratio greater is the stability. For the divalent metal ion complexes their stability shows the trend : Cu²⁺ > Ni²⁺ > Co²⁺ > Fe²⁺ > Mn²⁺ > Cd²⁺. The above stability order is called the Irving-William order. In the above list both Cu and Cd have the charge + 2, however, the ionic radius of Cu2 + is 69 pm and that of Cd2 + is 97 pm. The charge to size ratio of Cu²⁺ is greater than that of Cd²⁺. Therefore the Cu²⁺ forms stable complexes than Cd²⁺.

(b) Nature of the ligand : A second factor that governs stability of the complexes is related to how easily the ligand can donate its lone pair of electrons to the central metal ion that is, the basicity of the ligand. The ligands those are stronger bases tend to form more stable complexes.

Activity :
1. The reaction of chromium metal with H 2SO4 in the absence of air gives blue solution of chromium ion.
Cr(s) + 2H^⊕(aq) → Cr^2⊕(aq) + H₂(s)
Cr^2⊕ forms octahedral complex with H₂O ligands.
a. Write formula of the complex
b. Describe bonding in the complex using CFT and VBT.
Draw crystal field splitting and valence bond orbital diagrams.

2. Reaction of complex [Co(NH₃)₃(NO₂)₃ with HCl gives a complex [Co(NH₃)₃H₂OCl₂]^⊕ in which two chloride ligands are trans to one another.
a. Draw possible stereoisomers of starting material
b. Assuming that NH₃ groups remain in place, which of two starting isomers would give the observed product?

12th Chemistry Digest Chapter 9 Coordination Compounds Intext Questions and Answers

Use your brain power ……. (Textbook page 192)

Question 1.
Draw Lewis structures of the following ligands and identify the donor atom in them :
NH₃, H₂O.
Answer:

Try this ………. (Textbook page 193)

Question 1.
Can you write ionisation of [Ni (NH₃)₆] CI₂?
Answer:
[Ni (NH₃)₆] CI₂ → [Ni(NH₃)₆]²⁺ + 2CI^–

Question 2.
Identify coordination sphere and counter ions.
Answer:
Coordination sphere : [Ni(NH₃)₆]²⁺
Counter ions : CI^–

Can you tell ? (Textbook page 193)

Question 1.
A complex is made of Co (III) and consists of four NH₃ molecules and two CI^– ions as ligands. What is the charge number and formula of complexion?
Answer:
The complex ion has formula, [Co(NH₃)₄CI₂]⁺.
The charge number is + 1.

Use vour brain power ……………… (Textbook page 193)

Question 1.
Coordination number used in coordination of compounds is somewhat different than that used in solid state. Explain.
Answer:

• In a coordination compound the coordination number is the number of donor atoms of ligands directly attached to metal atom or ion.
• In a solid state, the number of closest constituent atoms or ions in contact with a particular atom in the crystal lattice is called coordination number.
• In a coordination compound, coordination number depends upon nature of metal atom or ion, and its electronic configuration.
• In a solid state, the coordination number depends upon the crystalline structure of the unit cell.

Can you tell? ………………. (Textbook page 194)

Question 1.
What is the coordination number of
(a) Co in [CoCl₂(en)₂]⁺ = 6
(b) Ir in [Ir(C₂O₄)₂Cl₂]³⁺ and
(c) Pt in [Pt(NO₂)₂(NH₃)₂] ?
Answer:
(a) Coordination number of Co in [CoCl₂(en)₂]⁺ = 6
(b) Coordination number of Ir in [Ir(C₂O₄)₂Cl₂]³⁺ = 6
(c) Coordination number of Pt in [Pt(NO₂)₂(NH₃)₂] = 4

Use your brain power ……… (Textbook page 195)

Question 1.
Classify the complexes as homoleptic and heteroleptic:
(a) [Co (NH₃)₅CI]SO₄,
(b) [CO(ONO)(NH₃)₅]CI₂,
(c) [CoCl(NH₃)(en)₂]²⁺ and
(d) [Cu(C2O₄)₃]^3-
Answer:
Homoleptic Complexes : (d) [Cu(C₂O₄)₃]^3-
Heteroleptic Complexes : (a) [CO(NH₃)₅CI]SO₄
(b) [CO(ONO)(NH₃)₅]CI₂,
(C) [CoCl(NH₃)(en)₂]²⁺

Use your brain power ……… (Textbook page 195)

Question 1.
Classify the complexes as cationic, anionic or Cr(H₂O)₂(C₂O₄)_2^3-, PtCI₂(en)₂ and Cr(CO)₆.
Answer:
Cationic complexes : [CO(NH₃)₆]CI₂
Anionic complexes : Na4[Fe(CN)₆], [Cr(H₂O)₂ (C₂O₄)2]^3-
Neutral complexes : Cr(CO)₆, Pt CI₂(en)₂

Try this ……. (Textbook page 197)

Question 1.
Write the representation of the following :
(i) Tricarbonatocobaltate(III) ion.
(ii) Sodium hexacyanoferrate(III).
(iii) Potassium hexacyafioferrate(II).
(iv) Aquachlorobis(ethylenediamine)cobalt(III).
(v) Tetraaquadichlorochromium(III) chloride.
(vi) Diamminedichloroplatinum(II).
Answer:
(i) [Co(C0₃)₃]^3-
(ii) Na₃[Fe(CN)₆]
(iii) K₄[Fe(CN)₆]
(iv) Co(en)₂(H₂O)(Cl)
(v) [Cr(H₂O)₄CI₂]CI
(vi) Pt(NH₃)₂CI₂

Try this …… (Textbook page 196)

Question 1.
Find out the EAN of
(a) [Zn(NH₃)₄]²⁺
(b) [Fe(CN)₆]⁴⁺
Answer:
(a) For the complex ion, [Zn(NH₃)₄]²⁺ :
Atomic number of Zn = Z = 30
Charge on metal ion = + 2
∴ Number of electrons lost by Zn atom = X = 2 Total number of electrons donated by 4NH^₂3
ligands = Y = 2 x 4 = 8
EAN = Z – X + Y
= 30 – 2 + 8
= 36

(Note : This is atomic number of the nearest inert element 3₆Kr.)

(b) For the complex ion, [Fe(CN)J^4- :
For Fe, Z = 26 (Atomic number)
X = 2 (Due to + 2 charge on Fe)
Y = 12 (Due to 6 CN^– ligands)
∴ EAN = Z – X + Y
= 26 – 2 + 12
= 36

Use your brain power …… (Textbook page 197)

Question 1.
Do the following complexes follow the EAN rule
(a) Cr(CO)₄,
(b) Ni(CO)₄,
(c) Mn(CO)₅,
(d) Fe(CO)₅?
Answer:
(a) Cr(CO)₄ : EAN = Z – X + Y
(b) Ni(C0)4 : EAN = Z – X + Y
= 24 – 0 + 8
= 28 – 0 + 8
= 32
= 36
(c) Mn(CO)₅ : EAN = Z – X + Y
= 25 – 0 + 10
= 35

(d) Fe(CO)5 : EAN = Z – X + Y
= 26 – 0 + 10
= 36

Conclusion :
(a) Cr(CO)₄ and (c) Mn(CO)₅ do not follow EAN Rule.

Try this ….. (Textbook page 199)

Question 1.
Draw structures of ci,c and trans isomers of [Fe(NH₃)₂(CN)₄]
Answer:

Remember ….. (Textbook page 199)

Our hands are non-superimposable mirror images. When you hold your left hand up to a mirror the image looks like right hand.

Try this ….. (Textbook page 199)

Question 1.
Draw enantiomers of [Cr(OX)₂]³ where OX = C₂O4 :
Answer:

Question 2.
Draw (A) enantiomers and (B) cis and trans isomers of [Cr(H₂O)₂(OX)₂] :
Answer:
(A) Enantiomers :

(B) as and trans isomers :

Can you tell ? ….. (Textbook page 200)

Question 1.
Can you write IUPAC names of isomers (I) [Co(NH₃)₅SO₄]Br and (II) [Co(NH₃)₅Br]SO₄?
Answer:

Question 2.
Write linkage isomers of [Fe(H₂O)₅SCN]⁺. Write their IUPAC names.
Answer:

Use your brain power …..(Textbook page 201)

Question 1.
The stability constant K of the [Ag(CN)₂]^– is 5.5 x 10 while that for the corresponding [Ag(NH₃)₂]⁺ is 1.6 x 10⁷. Explain why [Ag(CN)₂]^2- is more stable.
Answer:
Stability constant of [Ag(CN)₂]^2- is larger than that of [Ag(NH₃)₂]⁺ and hence [Ag(CN)₂]^2- is more stable. Also, CN is a stronger ligand than NH₃.

Remember …… (Textbook Page 202)

Question 1.
Complete the missing entries.

(Note : The missing entries are underlined.)

Table 9.3: Type of hybridisation and geometry of a complex

Try this ….. (Textbook page 204)

Question 1.
Based on the VBT predict structure and magnetic behaviour of the [Ni(NH₃)₆]
Answer:
₂₈Ni [Ar] 3d⁸ 4s²
Ni³⁺ [Ar] 3d⁷ 4s°
Hybridisation : sp³d²
Geometry : Octahedral
Magnetic property : Paramagnetic

Try this …… (Textbook page 202)

Question 1.
Give VBT description of bonding in each of following complexes. Predict their magnetic behaviour.
(a) [ZnCI₄]²⁺
(b) [CO(H₂O)₆]^2- (high spin)
(c) [Pt(CN)₄]^2- (square planar)
(d) [CoCI₄]^2- (tetrahedral)
(e) [Cr(NH₃)₆]³⁺

Try this ……. (Textbook page 206)

Question 1.
Sketch qualitatively crystal field d orbital energy level diagrams for each of the following complexes :
(a) [Ni(en)₃]²⁺ (b) [Mn(CN)₆]^3- (c) [Fe(H₂O)₆]²⁺
Predict whether each of the complexes is diamagnetic or paramagnetic.
Answer:
(a) The complex ion, [Ni(en)₃]²⁺ is octahedral.
₂₈Ni [Ar] 3d⁸ 4s²
Ni²⁺ [Ar] 3d⁸ 4s°.

Since en is a strong ligand there is pairing of electrons.
Number of unpaired electrons = n = 2 in t_2g, orbitals
Magnetic moment = \(\mu=\sqrt{n(n+2)}\)
\(=\sqrt{2(2+2)}=2.83 \mathrm{~B} . \mathrm{M} .\)

The complex ion is paramagnetic.

(b) The complex ion [Mn(CN)₆]^3- is octahedral.
₂₅Mn [Ar] 3d⁵ 4s²
Mn³⁺ [Ar] 3d⁴ 4s°

Since CN^– is a strong ligand there is pairing of electrons.
Number of unpaired electrons = n = 2 in t_2g, orbitals
Magnetic moment = \(\mu=\sqrt{n(n+2)}\)
\(=\sqrt{2(2+2)}=2.83 \mathrm{~B} . \mathrm{M}\).

The complex ion is paramagnetic.

(c) The complex ion [Fe(H₂O)₆]²⁺ is octahedral.
₂₆Fe [Ar] 3d⁶ 4s²
Fe²⁺ [Ar] 3d⁶ 45°

Since H₂O is a weak ligand, there is no pairing of electrons.
Number of unpaired electrons = n = 4 in t_2g and e_g orbitals.
Magnetic moment
\(\begin{aligned}
=\mu &=\sqrt{n(n+2)} \\
&=\sqrt{4(4+2)} \\
&=4.90 \mathrm{~B} . \mathrm{M} .
\end{aligned}\)
The complex ion is paramagnetic.

Maharashtra State Board 12th Std Chemistry Textbook Solutions

• Coordination Compounds Class 12 Chemistry Textbook Solutions
• Halogen Derivatives Class 12 Chemistry Textbook Solutions
• Alcohols, Phenols and Ethers Class 12 Chemistry Textbook Solutions
• Aldehydes, Ketones and Carboxylic Acids Class 12 Chemistry Textbook Solutions
• Amines Class 12 Chemistry Textbook Solutions
• Biomolecules Class 12 Chemistry Textbook Solutions
• Introduction to Polymer Chemistry Class 12 Chemistry Textbook Solutions
• Green Chemistry and Nanochemistry Class 12 Chemistry Textbook Solutions

Transition and Inner Transition Elements Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 8 Transition and Inner Transition Elements Textbook Exercise Questions and Answers.

Class 12 Chemistry Chapter 8 Exercise Solutions Maharashtra Board

Chemistry Class 12 Chapter 8 Exercise Solutions

1. Choose the most correct option.

Question i.
Which one of the following is diamagnetic
a. Cr^3⊕
b. Fe^3⊕
c. Cu^2⊕
d. Sc^3⊕
Answer:
d. Sc^3⊕

Question ii.
Most stable oxidation state of Titanium is
a. +2
b. +3
c. +4
d. +5
Answer:
c. +4

Question iii.
Components of Nichrome alloy are
a. Ni, Cr, Fe
b. Ni, Cr, Fe, C
c. Ni, Cr
d. Cu, Fe
Answer:
(c) Ni, Cr

Question iv.
Most stable oxidation state of Ruthenium is
a. +2
b. +4
c. +8
d. +6
Answer:
(b) +4

Question v.
Stable oxidation states for chromium are
a. +2, +3
b. +3, +4
c. +4, +5
d. +3, +6
Answer:
d. +3, +6

Question vi.
Electronic configuration of Cu and Cu⁺¹
a. 3d¹⁰, 4s⁰; 3d⁹, 4s⁰
b. 3d⁹, 4s¹; 3d⁹4s⁰
c. 3d¹⁰, 4s¹; 3d¹⁰, 4s⁰
d. 3d⁸, 4s¹; 3d¹⁰, 4s⁰
Answer:
c. 3d¹⁰, 4s¹; 3d¹⁰, 4s°

Question vii.
Which of the following have d0s0 configuration
a. Sc^3⊕
b. Ti^4⊕
c. V^5⊕
d. all of the above
Answer:
d. All of the above

Question viii.
Magnetic moment of a metal complex is 5.9 B.M. Number of unpaired electrons in the complex is
a. 2
b. 3
c. 4
d. 5
Answer:
d. 5

Question ix.
In which of the following series all the elements are radioactive in nature
a. Lanthanoids
b. Actinoids
c. d-block elements
d. s-block elements
Answer:
b. Actinides

Question x.
Which of the following sets of ions contain only paramagnetic ions
a. Sm^3⊕, Ho^3⊕, Lu^3⊕
b. La^3⊕, Ce^3⊕, Sm^3⊕
c. La^3⊕, Eu^3⊕, Gd^3⊕
d. Ce^3⊕, Eu^3⊕, Yb^3⊕
Answer:
d. Ce^3⊕, Eu^3⊕, Yb^3⊕

Question xi.
Which actinoid, other than uranium, occur in a significant amount naturally?
a. Thorium
b. Actinium
c. Protactinium
d. Plutonium
Answer:
a. Thorium

Question xii.
The flux added during extraction of Iron from hematite are its?
a. Silica
b. Calcium carbonate
c. Sodium carbonate
d. Alumina
Answer:
b. Calcium carbonate

2. Answer the following

Question i.
What is the oxidation state of Manganese in
\(\text { (i) } \mathrm{MnO}_{4}^{2-}(\mathrm{ii}) \mathrm{MnO}_{4}^{-} \text {? }\)
Answer:
Oxidation state of Manganese in
\((i) \mathrm{MnO}_{4}^{2-} is +6
(ii) \mathrm{MnO}_{4}^{-}is +7\)

*Question ii.
Give uses of KMnO₄

Question iii.
Why salts of Sc^3⊕, Ti^4⊕, V^5⊕ are colorless?
Answer:
(i) Sc³⁺ salts are colourless :

• The electronic configuration of ₂₁Sc [Ar| 3d¹ 4s² and Sc³⁺ [Ar] d°.
• Since there are no unpaired electrons in 3d subshell, d → d transition is not possible.
• Therefore, Sc³⁺ ions do not absorb the radiations in the visible region. Hence salts of Sc³⁺ are colourless (or white).

(ii) Ti⁴⁺ salts are colourless :

• The electronic configuration of ₂₂Ti [Ar] 3d²4s² and Ti⁴⁺ : [Ar] d°
• Since there are no unpaired electrons in 3d subshell, d-*d transition is not possible.
• Therefore, Ti³⁺ ions do not absorb the radiation in visible region. Hence salts of Ti³⁺ are colourless.

(iii) Vs⁵⁺ salts are eolourless :

• The electronic configuration of ₂₃V : [Ar] 3d³4s² and V⁵⁺ : [Ar] 3d°
• Since there are no unpaired electrons in 3d-subshell, d – d transition is not possible.
• Therefore, V⁵⁺ ions do not absorb the radiations in the visible region. Hence, V⁵⁺ salts are colourless, a

Question iv.
Which steps are involved in the manufacture of potassium dichromate from chromite ore?
Answer:
Steps in the manufacture of potassium dichromate from chromite ore are :

• Concentration of chromite ore.
• Conversion of chromite ore into sodium chromate (Na₂CrO₄).
• Conversion of Na₂CrO₄ into sodium dichromate (Na₂Cr₂O₇).
• Conversion of Na₂Cr₂O₇ into K₂Cr₂O₇.

Question v.
Balance the following equation
(i) KMnO₄ + H₂C₂O4 + H₂SO₄ → MnSO₄ + K₂SO₄ + H₂O + O₂
(ii) K₂Cr₂O₇ + KI + H₂SO₄ → K₂SO₄ + Cr₂(SO₄)₃ + 7H₂O + 3I₂
Answer:
(i) 2KMnO₄ + 3H₂SO₄ + 5H₂C₂O₄ → K₂SO₄ + 2MnSO₄ + 8H₂O + 10CO₂
(ii) Acidified potassium dichromate oxidises potassium iodide (KI) to iodine (I2). Potassium dichromate is reduced to chromic sulphate. Liberated iodine turns the solution brown K₂Cr₂O₇ + 6KI + 7H₂SO₄ → 4K₂SO₄ + Cr₂(SO₄)₃ + 7H₂O + 3I₂ [Oxidation state of iodine increases from – 1 to zero]

Question vi.
What are the stable oxidation states of plutonium, cerium, manganese, Europium?
Answer:
Stable oxidation states :
Plutonium + 3 to + 7
Cerium + 3, + 4
Manganese + 2, + 4, + 6, + 7
Europium +2, +3

Question vii.
Write the electronic configuration of chromium and copper.
Answer:
Chromium (₂₄Cr) has electronic configuration,
₂₄Cr (Expected) : Is² 2s² 2p⁶ 3s² 3p⁶ 3d⁴ 4s²
(Observed) : Is² 2s² 2p⁶ 3s² 3p⁶ 3d⁵ 4s¹

Explanation :

• The energy difference between 3d- and 45-orbitals is very low.
• d-orbitals being degenerate, they acquire more stability when they are half-filled (3d⁵).
• Therefore, there arises a transfer of one electron from 45-orbital to 3d-orbital in Cr giving more stable half-filled orbital. Hence, the configuration of Cr is [Ar] 3d⁵ 4s¹ and not [Ar] 3d⁴ 4s².

Copper (₂₉CU) has electronic configuration,
₂₉Cu (Expected) : Is² 2s³ 2p⁶ 3s³ 3p⁶ 3d⁹ 4s²
(Observed) : Is² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹

Explanation :

• The energy difference between 3d- and 45-orbitals is very low.
• d-orbitals being degenerate, they acquire more stability when they are completely filled.
• Therefore, there arises a transfer of one electron from 45-orbital to 3d-orbital in Cu giving completely filled more stable d-orbital.

Hence, the configuration of Cu is [Ar] 3d¹⁰ 4s¹ and not [Ar] 3d⁹ 4s².

Question viii.
Why nobelium is the only actinoid with +2 oxidation state?
Answer:

• Nobelium has the electronic configuration ₁₀₂NO : [Rn] 5f¹⁴6d°7s²
• No²⁺ : [Rn] 5f¹⁴6d°
• Since the 4f subshell is completely filled and 6d° empty, + 2 oxidation state is the stable oxidation state.
• Other actinoids in + 2 oxidation state are not as stable due to incomplete 4f subshell.

Question ix.
Explain with the help of balanced chemical equation, why the solution of Ce(IV) is prepared in acidic medium.
Answer:
Ce⁴⁺ undergoes hydrolysis as, Ce⁴⁺+ 2H₂O → Ce(OH)₄ + 4H⁺.
Due to the presence of H⁺ in the solution, the solution is acidic.

Question x.
What is meant by ‘shielding of electrons’ in an atom?
Answer:
The inner shell electrons in an atom screen or shield the outermost electron from the nuclear attraction. This effect is called the shielding effect.

The magnitude of the shielding effect depends upon the number of inner electrons.

Question xi.
The atomic number of an element is 90. Is this element diamagnetic or paramagnetic?
Answer:
The 90th element thorium has an electronic configuration, [Rn] 6d²7s². Since it has 2 unpaired electrons it is paramagnetic.

3. Answer the following

Question i.
Explain the trends in atomic radii of d-block elements
Answer:

1. The atomic or ionic radii of 3-d series transition elements are smaller than those of representative elements, with the same oxidation states.
2. For the same oxidation state, there is an increase in nuclear charge and a gradual decrease in ionic radii of 3d-series elements is observed. Thus ionic radii of ions with oxidation state + 2 decreases with increase in atomic number.
3. There is slight increase is observed in Zn²⁺ ions. With the higher oxidation states, effective nuclear charge increases. Therefore ionic radii decrease with increase in oxidation state of the same element. For example, Fe²⁺ ion has ionic radius 77 pm whereas Fe³⁺ has 65 pm.

Question ii.
Name different zones in the Blast furnace. Write the reactions taking place in them.
Answer:
(i) Zone of combustion : The hot air oxidises coke to CO which is an exothermic reaction, due to which the temperature of furnace rises.
C + ^1/2 O₂ → CO ΔH= – 220kJ
Some part of CO dissociates to give finely divided carbon and O₂.
2CO → 2C + O₂
The hot gases with CO rise up in the furnace and heats the charge coming down. CO acts as a fuel as well as a reducing agent.

(ii) Zone of reduction : At about 900 °C, CO reduces Fe₂O₃ to spongy (or porous) iron.
Fe₂O₃ + 3CO → 2Fe + 3CO₂
Carbon also reduces partially Fe₂0₃ to Fe.
Fe₂O₃ + 3C → 2Fe + 3CO

(iii) Zone of slag formation : At 1200 K limestone, CaCO₃ in the charge, decomposes and forms a basic flux CaO which further reacts at 1500 K with gangue (SiO₂, Al₂O₃) and forms a slag of CaSiO₃ and Ca₃AlO₃.
CaCO₃ + CaO + CO₂.
CaO + SiO₂ → CaSiO₃
12CaO + 2Al₂O₃ → 4Ca₃AlO₃ + 3O₂

The slag is removed from the bottom of the furnace through an outlet.

(iv) Zone of fusion : The impurities in ore like MnO₂ and Ca₃(PO₄)₂ are reduced to Mn and P while SiO₂ is reduced in Si. The spongy iron moving down in the furnace melts in the fusion zone and dissolves the impurities like C, Si, Mn, phosphorus and sulphure. The molten iron collects at the bottom of furnace. The lighter slag floats on the molten iron and prevents its oxidation.

The molten iron is removed and cooled in moulds. It is called pig iron or cast iron. It contains about 4% carbon.

Question iii.
What are the differences between cast iron, wrought iron and steel?
Answer:

Question iv.
Iron exhibits +2 and +3 oxidation states. Write their electronic configuration. Which will be more stable? Why?
Answer:
The electronic configuration of Fe^{2 +} and Fe³⁺ :
Fe²⁺ : Is² 2s² 2p⁶ 3s² 3p⁶ 3d⁶
Fe³⁺ : Is² 2s² 2p⁶ 3s² 3p⁶ 3d⁵

Due to loss of two electrons from the 4.v-orbital and one electron from the 3d-orbital, iron attains 3⁺ oxidation state. Since in Fe³⁺, the 3d-orbital is half-filled, it gets extra stability, hence Fe³⁺ is more stable than Fe²⁺.

Question v.
Give the similarities and differences in elements of 3d, 4d and 5d series.
Answer:
Similarity :

• They are placed between .s-block and p-block of the periodic table.
• All elements are metals showing metallic characters.
• Some are paramagnetic.
• Most of them give coloured compounds.
• They have catalytic properties.
• They form complexes.
• They have variable oxidation states.

Differences :

• In 4d and 5d series lanthanide and actinoid contraction is observed. In 3d series atomic size changes are less marked.
• 4d and 5d elements have high coordination numbers compared to 3d elements.
• 4d and 5d series have similar properties whereas 3d series have different properties.

Question vi.
Explain trends in ionisation enthalpies of d-block elements.
Answer:

1. The ionisation enthalpies of transition elements are quite high and lie between those of 5-block and p-block elements. This is because the nuclear charge and atomic radii of transition elements lie between those of 5-block and p-block elements.
   
2. As atomic number of transition elements increases along the period and along the group, first ionisation enthalpy increases even though the increase is not regular.
3. If IE_1; IE₂ and IE₃ are the first, second and third ionisation enthalpies of the transition elements, then IE₁ < IE₂ < IE₃.
4. In the transition elements, the added last differentiating electron enters into (n – 1) d-orbital and shields the valence electrons from the nuclear attraction. This gives rise to the screening effect of (n – 1) d-electrons.
5. Due to this screening effect of (n – 1) d electrons, the ionisation enthalpy increases slowly and the increase is not very regular.

Question vii.
What is meant by diamagnetic and paramagnetic metal? Give one example of diamagnetic and paramagnetic transition metal and lanthanoid metal.
Answer:

1. Paramagnetic substances : When a magnetic field is applied, substances which are attracted towards the applied magnetic field are called paramagnetic substances. Example : Ni²⁺, Pr⁴⁺
2. Diamagnetic substances : When a magnetic field is applied, substances which are repelled by the magnetic fields are called diamagnetic substances. Example : Zn²⁺, La³⁺
3. Ferromagnetic substances : When a magnetic field is applied, substances which are attracted very strongly are called ferromagnetic substances. These substances can be magnetised. For example, Fe, Co, Ni are ferromagnetic.

Question viii.
Why the ground-state electronic configurations of gadolinium and lawrencium are different than expected?

Question ix.
Write steps involved in the metallurgical process
Answer:
The various steps and principles involved in the extraction of pure metals from their ores are as follows.:

• Concentration of ores in which impurities (gangue) are removed.
• Conversion of ores into oxides or other reducible compounds of metals.
• Reduction of ores to obtain crude metals.
• Refining of metals giving pure metals.

Question x.
Cerium and Terbium behaves as good oxidising agents in +4 oxidation state. Explain.
Answer:

• The most stable oxidation state of lanthanoids is +3.
• Hence, Ce⁴⁺ (cerium) and Tb⁴⁺ (terbium) tend to get + 3 oxidation state which is more stable.
• Since they get reduced by accepting electron, they are good oxidising agents in + 4 oxidation state.

Question xi.
Europium and Ytterbium behave as good reducing agents in +2 oxidation state explain.
Answer:

• The most stable oxidation state of lanthanoids is + 3.
• Hence, Eu²⁺ and Yb²⁺ tend to get + 3 oxidation states by losing one electron.
• Since they get oxidised, they are good reducing agents in + 2 oxidation state.

Activity :
Make groups and each group prepare a PowerPoint presentation on the properties and applications of one element. You can use your imagination to create some innovative ways of presenting data.

You can use pictures, images, flow charts, etc. to make the presentation easier to understand. Don’t forget to cite the reference(s) from where data for the presentation is collected (including figures and charts). Have fun!

12th Chemistry Digest Chapter 8 Transition and Inner Transition Elements Intext Questions and Answers

Do you know? (Textbook Page No 165)

Question 1.
In which block of the modern periodic table are the transition and inner transition elements placed?
Answer:
The transition elements are placed in d-block and inner transition elements are placed in f-block of the modern periodic table.

Use your brain power! (Textbook Page No 167)

Question 1.
Fill in the blanks with correct outer electronic configurations.
Answer:
Answers are given in bold.

Try this….. (Textbook Page No 168)

Question 1.
Write the electronic configuration of Cr and Cu.
Answer:
₂₄Cr : [Ar] 3d⁵4s¹ ₃₀Cu : [Ar] 3d¹⁰4s¹

Can you tell? (Textbook Page No 168)

Question 1.
Which of the first transition series element shows the maximum number of oxidation states and why?
Answer:

• ₂₅Mn shows the maximum number of oxidation states, + 2 to +7.
• ₂₅Mn : [Ar] 3d⁵4s³
• Mn has incompletely filled J-subshell.
• Due to small difference in energy between 3d and 4s -orbitals, Mn can lose (or share) electrons from both the orbitals.
• Hence Mn shows oxidation states from + 2 to +7.

Question 2.
Which elements in the 4d and 5d-series will show maximum number of oxidation states?
Answer:
In 4d-series maximum number of oxidation states are for Ruthenium Ru ( + 2, +3, + 4„ +6, +7, + 8). In 5d-series, maximum number of oxidation states are for Osmium, Os ( + 2 to + 8).

Try this ….. (Textbook Page No 168)

Question 1.
Write the electronic configuration of Mn⁶⁺, Mn⁴⁺, Fe⁴⁺, Co⁵⁺, Ni²⁺.
Answer:

Try this ….. (Textbook Page No 171)

Question 1.
Pick up the paramagnetic species from the following : Cu¹⁺, Fe³⁺, Ni²⁺, Zn²⁺, Cd²⁺, Pd²⁺.
Answer:
The following ions are paramagnetic : Fe³⁺, Ni²⁺, Pd²⁺

Try this ….. (Textbook Page No 171)

Question 1.
What will be the magnetic moment of transition metal having 3 unpaired electrons?
(a) equal to 1.73 B.M.?
(b) less than 1.73 BM.
(c) more than 1.73 B.M.?
Answer:
By spin-only formula, \(\mu=\sqrt{n(n+2)}\) where n is number of unpaired electrons.
\(\mu=\sqrt{3(3+2)}=\sqrt{3(5)}=3.87 \mathrm{~B} . \mathrm{M}\)
Thus the value is more than 1.73 B.M.

Use your brain power! (Textbook Page No 171)

Question 1.
A metal ion from the first transition series has two unpaired electrons. Calculate the magnetic moment.
Answer:
\(\)\begin{aligned}
\mu &=\sqrt{n(n+2)} \\
&=\sqrt{2(2+2)} \\
&=\sqrt{8} \\
&=2.84 \text { B.M. }
\end{aligned}\(\)

Problem (Textbook Page No 172)

Question 1.
Calculate the spin-only magnetic moment of divalent cation of a transition metal with atomic number 25.
Answer:
For element with atomic number 25. electronic configuration of its divalent cation will be : [Ar] 3d⁵.

Try this….. (Textbook Page No 172)

Question 1.
Calculate the spin-only magnetic moment of a divalent cation of element Slaving atomic number 27.
Answer:
Electronic configuration of divalent ion of an element with atomic number 27 : [Ar] 3d⁷;

Can you tell? (Textbook Page No 172)

Question 1.
Compounds of s and p-block elements are almost white. What could be the absorbed radiation? (uv or visible)?
Answer:
The white colour of a compound indicates the absorption of uv radiation.

Can you tell? (Textbook Page No 181)

Question 1.
Why f-block elements are called inner transition metals?
Answer:
f-block elements are called inner transition elements since f-orbital lies much inside the f-orbital in relation to the transition metals, These elements have 1 to 14 electrons in their f-orbital.

Question 2.
Are there an similarities between transition and inner transition metals?
Answer:
There are some properties similarity between transition and inner transition metals.

• They are placed between s and p-block elements.
• They are metals with filling of inner suhshells in their electronic configuration.
• They show variable oxidation slates.
•  They show magnetism.
• They form coloured compounds.
• They have catalytic property.

Problem (Textbook Page No 184)

Question 1.
Which of the following will have highest fourth ionisation enthalpy, La⁴⁺, Gd⁴⁺, Lu⁴⁺.
Answer:
La : 4f°5d¹6s²
Gd : 4f¹5d¹6s²
Lu : 4f¹⁴5d¹6s²
Lu will have the highest fourth ionisation enthalpy since Lu³⁺ has the most stable configuration of 4f¹⁴.

Use your brain power! (Textbook Page No 185)

Question 1.
Do you think that lanthanoid complex would show magnetism?
Answer:
Lanthanoid complexes may show magnetism.

Question 2.
Can you calculate the spin only magnetic moment of lanthanoid complexes using the same formula that you used for transition metal complexes?
Answer:
You cannot calculate magnetic moment of lanthanoid complexes using spin only formula as you have to consider orbital momentum also.

Question 3.
Calculate the spin only magnetic moment of La³⁺. Compare the value with that given in the table.
Answer:
La³⁺ ion has no unpaired electron.

La³⁺ ion has zero value of magnetic moment same as given in the table.

Maharashtra State Board 12th Std Chemistry Textbook Solutions

• Solid State Class 12 Chemistry Textbook Solutions
• Solutions Class 12 Chemistry Textbook Solutions
• Ionic Equilibria Class 12 Chemistry Textbook Solutions
• Chemical Thermodynamics Class 12 Chemistry Textbook Solutions
• Electrochemistry Class 12 Chemistry Textbook Solutions
• Chemical Kinetics Class 12 Chemistry Textbook Solutions
• Elements of Groups 16, 17 and 18 Class 12 Chemistry Textbook Solutions
• Transition and Inner Transition Elements Class 12 Chemistry Textbook Solutions

Elements of Groups 16, 17 and 18 Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 7 Elements of Groups 16, 17 and 18 Textbook Exercise Questions and Answers.

Class 12 Chemistry Chapter 7 Exercise Solutions Maharashtra Board

Chemistry Class 12 Chapter 7 Exercise Solutions

1. Select appropriate answers for the following.

Question i.
Which of the following has the highest electron gain enthalpy?
A. Fluorine
B. Chlorine
C. Bromine
D. Iodine
Answer:
B. Chlorine

Question ii.
Hydrides of group 16 are weakly acidic. The correct order of acidity is
A. H₂O > H₂S > H₂Se > H₂Te
B. H₂Te > H₂O > H₂S > H₂Se
C. H₂Te > H₂Se > H₂S > H₂O
D. H₂Te > H₂Se > H₂O > H₂S
Answer:
C. H₂Te > H₂Se > H₂S > H₂O

Question iii.
Which of the following element does not show oxidation state of +4 ?
A. O
B. S
C. Se
D. Te
Answer:
A. O

Question iv.
HI acid when heated with conc. H₂SO₄ forms
A. HIO₃
B. KIO₃
C. I₂
D. KI
Answer:
C. I₂

Question v.
Ozone layer is depleted by
A. NO
B. NO₂
C. NO₃
D. N₂O₅
Answer:
A. NO

Question vi.
Which of the following occurs in liquid state at room temperature?
A. HIO₃
B. HBr
C. HCl
D. HF
Answer:
D. HF

Question vii.
In pyrosulfurous acid oxidation state of sulfur is
A. Only +2
B. Only +4
C. +2 and +6
D. Only +6
Answer:
B. Only + 4

Question viii.
Stability of interhalogen compounds follows the order
A. BrF > IBr > ICl > ClF > BrCl
B. IBr > BeF > ICl > ClF > BrCl
C. ClF > ICl > IBr > BrCl > BrF
D. ICl > ClF > BrCl > IBr > BrF
Answer:
C. ClF > ICl > IBr > BrCl > BrF

Question ix.
BrCl reacts with water to form
A. HBr
B. Br₂ + Cl₂
C. HOBr
D. HOBr + HCl
Answer:
D. HOBr + HCl

Question x.
Chlorine reacts with excess of fluorine to form.
A. ClF
B. ClF₃
C. ClF₂
D. Cl₂F₃
Answer:
B. ClF₃

Question xi.
In interhalogen compounds, which of the following halogens is never the central atom.
A. I
B. Cl
C. Br
D. F
Answer:
D. F

Question xii.
Which of the following has one lone pair of electrons?
A. IF₃
B. ICl
C. IF₅
D. ClF₃
Answer:
C. IF₅

Question xiii.
In which of the following pairs, molecules are paired with their correct shapes?
A. [I₃] : bent
B. BrF₅ : trigonal bipyramid
C. ClF₃ : trigonal planar
D. [BrF₄] : square planar
Answer:
A. [I₃] : bent

Question xiv.
Among the known interhalogen compounds, the maximum number of atoms is
A. 3
B. 6
C. 7
D. 8
Answer:
D. 8

2. Answer the following.

Question i.
Write the order of the thermal stability of the hydrides of group 16 elements.
Answer:
The thermal stability of the hydrides of group 16 elements decreases in the order of H₂O > H₂S > H₂Se > H₂Te.

Question ii.
What is the oxidation state of Te in TeO₂?
Answer:
The oxidation state of Te in TeO₂ is + 4.

Question iii.
Name two gases which deplete ozone layer.
Answer:
Nitrogen oxide (NO) released from exhaust systems of car or supersonic jet aeroplanes and chlorofluorocarbons (Freons) used in aerosol sprays and refrigerators deplete ozone layer.

Question iv.
Give two uses of ClO₂
Answer:
(i) ClO₂ is used as a bleaching agent for paper pulp and textiles.
(ii) It is also used in water treatment.

Question v.
What is the action of bromine on magnesium metal?
Answer:
Bromine reacts instantly with magnesium metal to give magnesium bromide.

Question vi.
Write the names of allotropic forms of selenium.
Answer:
Selenium has two allotropic forms as follows :
(i) Red (non-metallic) form
(ii) Grey (metallic) form

Question vii.
What is the oxidation state of S in H₂SO₄.
Answer:
The oxidation state of S in H₂SO₄ is + 6.

Question viii.
The pKa values of HCl is -7.0 and that of HI is -10.0. Which is the stronger acid?
Answer:
For HCl, pK_a = -7.0, hence its dissoClation constant is, K_a = 1 x 10^-7.
For HI pK_a = – 10.0, hence its dissoClation constant is K_a = 1 x 10^-7. Hence HCl dissoClates more than HI.
Therefore HCl is a stronger acid than HI.

Question ix.
Give one example showing reducing property of ozone.
Answer:
Ozone decomposes to liberate nascent oxygen, hence it is a powerful oxidising agent. O_3(g) → O_2(g) + O

For example :
(i) It oxidises lead sulphide (PbS) to lead sulphate (PbSO₄).
pbS_(s) + 4O_3(g) → PbSO_(s) + 4O_2(g)
(ii) Potassium iodide, KI is oxidised to iodine, I₂ in the solution.
2KI_(aq) + H₂O₍₁₎ + O_3(g) → 2KOH_(aq) + I_2(s) + O_2(g)

Question x.
Write the reaction of conc. H₂SO₄ with sugar.
Answer:
Concentrated sulphuric acid when added to sugar, it is dehydrated giving carbon.

The carbon that is left behind is called sugar charcoal and the process is called char.

Question xi.
Give two uses of chlorine.
Answer:
Chlorine is used for :

• for sterilization of drinking water.
• bleaching wood pulp required for the manufacture of paper and rayon, cotton and textiles are also bleached using chlorine.
• in the manufacture of organic compounds like CHCl₃, CCl₄, DDT, dyes and drugs.
• in the extraction of metals like gold and platinum.
• in the manufacture of refrigerant like Freon (i.e., CCl₂F₂).
• in the manufacture of several poisonous gases like mustard gas (Cl-C₂H₄-S-C₂H₄-Cl), phosgene (COCl₂) used in warfare.
• in the manufacture of tear gas (CCl₃NO₂).

Question xii.
Complete the following.
1. ICl₃ + H₂O …….. + …….. + ICl
2. I₂ + KClO₃ ……. + KIO₂
3. BrCl + H₂O ……. + HCl
4. Cl₂ + ClF₃ ……..
5. H₂C = CH₂ + ICl …….
6. XeF₄ + SiO₂ ……. + SiF₄
7. XeF₆ + 6H₂O …….. + HF
8. XeOF₄ + H₂O ……. + HF
Answer:
1. 2ICI₃ + 3H₂O → 5HCl + HlO₃ + ICl
2. I₂ + KCIO₃ → ICl + KIO₃
3. BrCl + H₂O → HOBr + HCl
4. Cl₂ + C1F₃ → 3ClF
5. CH₂ = CH₂ + ICl → CH₂I – CH₂Cl
6. 2XeF₆ + SiO₂ → 2XeOF₄ + SiF₄
7. XeF₆ + 3H₂O → XeO₃ + 6HF
8. XeOF₄ + H₂O→  XeO₂F₂ + 2HF

Question xiii.
Match the following
A – B
XeOF₂ – Xenon trioxydifluoride
XeO₂F₂ – Xenon monooxydifluoride
XeO₃F₂ – Xenon dioxytetrafluoride
XeO₂F₄ – Xenon dioxydifluoride
Answer:
XeOF₂ – Xenon monooxydifluoride
XeO₂F₂ – Xenon dioxydifluoride
XeO₃F₂ – Xenon trioxydifluoride
XeO₂F₄ – Xenon dioxytetrafluoride

Question xiv.
What is the oxidation state of xenon in the following compounds?
XeOF₄, XeO₃, XeF₅, XeF₄, XeF₂.
Answer:

3. Answer the following.

Question i.
The first ionisation enthalpies of S, Cl and Ar are 1000, 1256 and 1520 kJ/mol^-1, respectively. Explain the observed trend.
Answer:
(i) The atomic number increases as, ₁₆S < ₁₇Cl < ₁₈Ar₁.
(ii) Due to decrease in atomic size and increase in effective nuclear charge, Cl binds valence electrons strongly.
(iii) Hence ionisation enthalpy of Cl (1256 kJ mol^-1) is higher than that of S(1000 kJ mol^-1)
(iv) Ar has electronic configuration 3s²3p⁶. Since all electrons are paired and the octet is complete, it has the highest ionisation enthalpy, (1520 kJ mol^-1)

Question ii.
“Acidic character of hydrides of group 16 elements increases from H₂O to H₂Te” Explain.
Answer:
(i) The thermal stability of the hydrides of group 16 elements decreases from H₂O to H₂Te. This is because the bond dissociation enthalpy of the H-E bond decreases down the group.
(ii) Thus, the acidic character increases from H₂O to H₂Te.

Question iii.
How is dioxygen prepared in laboratory from KClO₃?
Answer:
By heating chlorates, nitrates and permanganates.
Potassium chlorate in the presence of manganese dioxide on heating decomposes to form potassium chloride and oxygen.

Question iv.
What happens when
a. Lead sulfide reacts with ozone (O₃).
b. Nitric oxide reacts with ozone.
Answer:
(i) It oxidises lead sulphide (PbS) to lead sulphate (PbSO₄) changing the oxidation state of S from – 2 to +6.
PbS_(s) + 4O_3(g) → PbSO_(s) + 4O_2(g)

(ii) Ozone oxidises nitrogen oxide to nitrogen dioxide.
NO_(g) + O_3(g) → NO_2(g) + O_2(g)

Question v.
Give two chemical reactions to explain oxidizing property of concentrated H₂SO₄.
Answer:
Hot and concentrated H₂SO₄ acts as an oxidising agent, since it gives nascent oxygen on heating.

Question vi.
Discuss the structure of sulfur dioxide.
Answer:
(i) SO₂ molecule has a bent V shaped structure with S-O-S bond angle 119.5° and bond dissoClation enthalpy is 297 kJ mol^-1.
(ii) Sulphur in SO₂ is sp² hybridised forming three hybrid orbitals. Due to lone pair electrons, bond angle is reduced from 120° to 119.5°.
(iii) In SO₂, each oxygen atom is bonded to sulphur by σ and a π bond.
(iv) a bond between S and O are formed by sp²-p overlapping.
(v) One of π bonds is formed by pπ – pπ overlapping while other n bond is formed by pπ – dπ overlap.
(vi) Due to resonance both the bonds are identical having observed bond length 143 pm due to resonance,

Question vii.
Fluorine shows only -1 oxidation state while other halogens show -1, +1, +3, +5 and +7 oxidation states. Explain.
Answer:

• Halogens have outer electronic configuration ns² np⁵.
• Halogens have tendency to gain or share one electron to attain the stable configuration of nearest inert element with configuration ns²np⁶.
• Hence they are monovalent and show oxidation state – 1.
• Since fluorine does not have vacant d-orbital, it shows only one oxidation state of – 1 while all other halogens show variable oxidation states from – 1 to +7.
• These oxidation states are, – 1, +1, + 3, +5 and + 7. Cl and Br also show oxidation states + 4 and + 6 in their oxides and oxyaClds.

Question viii.
What is the action of chlorine on the following
a. Fe
b. Excess of NH₃
Answer:
(a) Chlorine reacts with Fe to give ferric chloride.
2Fe + 3Cl₂ → 2FeCl₃

(b) Chlorine reacts with the excess of ammonia to form ammonium chloride, NH₄Cl and nitrogen.

Question ix.
How is hydrogen chloride prepared from sodium chloride?
Answer:

1. In the laboratory, hydrogen chloride, HCl is prepared by heating a mixture of NaCl and concentrated H₂SO₄.
   
2. Hydrogen chloride gas, is dried by passing it through a dehydrating agent like concentrated H₂SO₄ and then collected by upward displacement of air.

Question x.
Draw structures of XeF₆, XeO₃, XeOF₄, XeF₂.
Answer:

Question xi.
What are interhalogen compounds? Give two examples.
Answer:
Interhalogen compounds : Compounds formed by the combination of atoms of two different halogens are called interhalogen compounds. In an interhalogen compound, of the two halogen atoms, one atom is more electropositive than the other. The interhalogen compound is regarded as the halide of the more electropositive halogen.
For example ClF, BrF₃, ICl

Question xii.
What is the action of hydrochloric acid on the following?
a. NH₃
b. Na₂CO₃
Answer:
a. Hydrochloric acid reacts with ammonia to give white fumes of ammonium chloride.
NH₃ + HCl → NH₄Cl

b. Hydrochloric acid reacts with sodium carbonate to give sodium chloride, water with the liberation of carbon dioxide gas.
Na₂CO₃ + 2HCl → 2NaCl + H₂O + CO₂

Question xiii.
Give two uses of HCl.
Answer:
Hydrogen chloride (OR hydrochloric acid) is used :

• in the manufacture of chlorine and ammonium chloride,
• to manufacture glucose from com, starch
• to manufacture dye
• in mediClne and galvanising
• as an important reagent in the laboratory
• to extract glue from bones and for the purification of bone black.
• for dissolving metals, Fe + 2HCl_(aq) → FeCl₂ + H_2(g)

Question xiv.
Write the names and structural formulae of oxoacids of chlorine.
Answer:

Question xv.
What happens when
a. Cl₂ reacts with F₂ in equal volume at 437 K.
b. Br₂ reacts with excess of F₂.
Answer:
(a) Cl₂ reacts with F₂ in equal volumes at 437 K to give chlorine monofluoride ClF.

(b) Br₂ reacts with excess of F₂ to give bromine trifluoride BF₃.

Question xvi.
How are xenon fluorides XeF₂, XeF₄ and XeF₆ obtained ? Give suitable reactions.
Answer:
Xenon fluorides are generally prepared by the direct reaction of xenon and fluorine in different ratios and under appropriate experimental conditions, such as temperature, in the presence of an electric discharge and by a photochemical reaction.
(i) Preparation of XeF₂ :

(ii) Preparation of XeF₄ :

(iii) Preparation of XeF₆ :

Question xvii.
How are XeO₃ and XeOF₄ prepared?
Answer:
Preparation of XeO₃ : Xenon trioxide (XeO₃) is prepared by the hydrolysis of XeF₄ or XeF₆.

• By hydrolysis of XeF₄ :
  3XeF₄ + 6H₂0 → 2Xe + XeO₃ + 12 HF + \(1 \frac{1}{2} \mathrm{O}_{2}\)
• By hydrolysis of XeF₆ :
  XeF₆ + 3H₂O → XeO₃ + 6HF
• Preparation of XeOF₄ :
  Xenon oxytetrafluoride (XeOF₄) is prepared by the partial hydrolysis of XeF₆.
  XeF₆ + H₂O → XeOF₄ + 2HF

Question xviii.
Give two uses of neon and argon.
Answer:
Uses of neon (Ne) :

• Neon is used in the production of neon discharge lamps and signs by filling Ne in glass discharge tubes.
• Neon signs are visible from a long distance and also have high penetrating power in mist or fog.
• A mixture of neon and helium is used in voltage stabilizers and current rectifiers.
• Neon is also used in the production of lasers and fluorescent tubes.

Uses of argon (Ar) :

• Argon is used to fill fluorescent tubes and radio valves.
• It is used to provide inert atmosphere for welding and production of steel.
• It is used along with neon in neon sign lamps to obtain different colours.
• A mixture of 85% Ar and 15% N2 is used in electric bulbs to enhance the life of the filament.

Question xix.
Describe the structure of Ozone. Give two uses of ozone.
Answer:
(A)

• Ozone has molecular formula O₃.
• The lewis dot and dash structures for O₃ are :
  
• Infrared and electron diffraction spectra show that O₃ molecule is angular with 0-0-0 bond angle 117°.
• Both 0-0 bonds are identical having bond length 128 pm which is intermediate between single and double bonds.
• This is explained by considering resonating structures and resonance hybrid.
  

(B) Uses of Ozone :

• Ozone sterilises drinking water by oxidising germs and bacteria present in it.
• It is used as a bleaching agent for ivory, oils, starch, wax and delicate fabrics like silk.
• Ozone is used to purify the air in crowded places like Clnema halls, railways, tunnels, etc.
• In industry, ozone is used in the manufacture of synthetic camphor, potassium permanganate, etc.

Question xx.
Explain the trend in following atomic properties of group 16 elements.
i. Atomic radii
ii. Ionisation enthalpy
iii. Electronegativity.
Answer:
(1) Atomic and ionic radii :

1. As compared to group 15 elements, the atomic and ionic radii of group 16 elements are smaller due to higher nuclear charge.
2. The atomic and ionic radii increase down the group from oxygen to polonium. This is due to the addition of a new shell at each successive elements on moving down the group. The atomic radii increases in the order O < S < Se < Te < Po

(2) Ionisation enthalpy :

• The ionisation enthalpy of group 16 elements has quite high values.
• Ionisation enthalpy decreases down the group from oxygen to polonium. This is due to the increase in atomic volume down the group.
• The first ionisation enthalpy of the lighter elements of group 16 (O, S, Se) have lower values than those of group 15 elements in the corresponding periods. This is due to difference in their electronic configurations.

Group 15 : (valence shell) ns² np_x¹ np_y¹ np_z¹
Group 16 : (valence shell) ns² np_x² np_y¹ np_z¹

Group 15 elements have extra stability of half-filled and more symmetrical orbitals, while group 16 elements acquire extra stability by losing one of paired electrons from npx- orbital forming half-filled p-orbitals.

Hence group 16 elements have lower first ionisation enthalpy than group 15 elements.

(3) Electronegativity :

• The electronegativity values of group 16 elements have higher values than corresponding group 15 elements in the same periods.
• Oxygen is the second most electronegative elements after fluorine. (O = 3.5, F = 4)
• On moving down the group electronegativity decreases from oxygen to polonium.
• On moving down the group atomic size increases, hence nuclear attraction decreases, therefore electro-negativity decreases.

4. Answer the following.

Question i.
Distinguish between rhombic sulfur and monoclinic sulfur.
Answer:

Question ii.
Give two reactions showing oxidizing property of concentrated H₂SO₄.
Answer:
Hot and concentrated H₂SO₄ acts as an oxidising agent, since it gives nascent oxygen on heating.

Question iii.
How is SO₂ prepared in the laboratory from sodium sulfite? Give two physical properties of SO₂.
Answer:
(A) Laboratory method (From sulphite) :

• Sodium sulphite on treating with dilute H₂SO₄ forms SO₂.
  Na₂SO₃ + H₂SO_4(aq) → Na₂SO₄ + H₂O₍₁₎ + SO_2(g)
• Sodium sulphite, Na₂SO₃ on reaction with dilute hydrochloric acid solution forms SO₂.
  Na₂SO_3(aq) + 2HCl_(aq) → 2NaCl_9aq0 + H₂O₍₁₎ + SO_2(g)

(B) Physical properties of SO₂

• It is a colourless gas with a pungent smell.
• It is highly soluble in water and forms sulphurous acid, H₂SO₃ SO_2(g) + H₂O₍₁₎ → H₂SO_3(aq)
• It is poisonous in nature.
• At room temperature, it liquefies at 2 atmospheres. It has boiling point 263K.

Question iv.
Describe the manufacturing of H₂SO₄ by contact process.
Answer:
Contact process of the manufacture of sulphuric acid involves following steps :

(1) Preparation of SO₂ : Sulphur or pyrite ores like iron pyrites, FeS₂ on burning in excess of air, form SO₂.

(2) Oxidation of SO₂ to SO₃ : SO₂ is oxidised to SO₃ in the presence of a heterogeneous catalyst V₂O₅ and atmospheric oxygen. This oxidation reaction is reversible.

To avoid the poisoning of a costly catalyst, it is necessary to make SO₂ free from the impurities like dust, moisture, As₂O₃ poison, etc.

The forward reaction is exothermic and favoured by increase in pressure. The reaction is carried out at high pressure (2 bar) and 720 K temperature. The reacting gases, SO₂ and O₂ are taken in the ratio 2:3.

(3) Dissolution of SO₃ : SO₃ obtained from catalytic converter is absorbed in 98%. H₂SO₄ to obtain H₂S₂O₇, oleum or fuming sulphuric acid.


Flow diagram for the manufacture of sulphuric acid

Question 7.1 (Textbook Page No 141)

12th Chemistry Digest Chapter 7 Elements of Groups 16, 17 and 18 Intext Questions and Answers

Question 1.
Elements of group 16 generally show lower values of first ionisation enthalpy compared to the elements of corresponding period of group 15. Why?
Answer:
Group 15 elements have extra stable, half filled p-orbitals with electronic configuration (ns²np³). Therefore more amount of energy is required to remove an electron compared to that of the partially filled orbitals (ns²np⁴) of group 16 elements of the corresponding period.

Question 7.2 (Textbook Page No 141)

Question 1.
The values of first ionisation enthalpy of S and Cl are 1000 and 1256 kJ mol^-1, respectively. Explain the observed trend.
Answer :
The elements S and Cl belong to second period of the periodic table.
Across a period effective nuclear charge increases and atomic size decreases with increase in atomic number. Therefore the energy required for the removal of electron from the valence shell (I.E.) increases in the order S < Cl.

Question 7.4 (Textbook Page No 141)

Question 1.
Fluorine has less negative electron gain affinity than chlorine. Why?
Answer :
The size of fluorine atom is smaller than chlorine atom. As a result, there are strong inter electronic repulsions in the relatively small 2p orbitals of fluorine and therefore, the incoming electron does not experience much attraction. Thus fluorine has less negative electron gain affinity than chlorine.

Try this… (Textbook Page No 140)

Question 1.
Explain the trend in the following properties of group 17 elements.

(1) Atomic size,
(2) Ionisation enthalpy,
(3) Electronegativity,
(4) Electron gain enthalpy.
Answer:
(1) Atomic size :

• Atomic and ionic radii increase down the group as atomic number increases due to the addition of new electronic valence shell to each succeeding element.
• The atomic radii increase in the order F < Cl < Br < 1
• Halogens possess the smallest atomic and ionic radii in their respective periods since the effective nuclear charge experienced by valence electrons in halogen atoms is the highest.

(2) Ionisation enthalpy :

• The ionisation enthalpies of halogens are very high due to their small size and large nuclear attraction.
• The ionisation ethalpies decrease down the group since the atomic size increases.
• The ionisation enthalpy decreases in the order F > Cl > Br > I.
• Among halogens fluorine has the highest ionisation enthalpy due to its smallest size.

(3) Electronegativity :

• Halogens have the highest values for electronegativity due to their small atomic radii and high effective nuclear charge.
• Each halogen is the most electronegative element of its period.
• Fluorine has the highest electronegativity as compared to any element in the periodic table.
• The electronegativity decreases as,
  F > Cl > Br > I
  4.0 3.2 3.0 2.7 (electronegativity)

(4) Electron gain enthalpy (Δ_egH) :

• The halogens have the highest negative values for electron gain enthalpy.
• Electron gain enthalpies of halogens are negative indicating release of energy.
• Halogens liberate maximum heat by gain of electron as compared to other elements.
• Since halogens have outer valence electronic configuration, ns² np⁵, they have strong tendency to accept an electron to complete an octet and acquire electronic configuration of the nearest inert elements.
• In case of fluorine due to small size of 2 p-orbitals and high electron density, F has less negative electron gain enthalpy than Cl.
  F_(g) + e^– → F^–_(g) Δ_egH = – 333 klmol^-1
  Cl_(g) + e^– → Cl^–_(g) Δ_egH = – 349 kJ mol^-1
• The variation in electron gain enthalpy is in the order of, Cl > F > Br > I.

Question 2.
Oxygen has less negative electron gain enthalpy than sulphur. Why?
Answer:

• Oxygen has a smaller atomic size than sulphur.
• It is more electronegative than sulphur.
• It has a larger electron density.
• Due to high electron density, oxygen does not accept the incoming electron easily and therefore has less electron gain enthalpy than sulphur.

Question 7.3 (Textbook Page No 141)

Question 1.
Why is there a large difference between the melting and boiling points of oxygen and sulphur?
Answer :
Oxygen exists as diatomic molecule (O₂) whereas sulphur exists as polyatomic molecule (S₈). The van der Waals forces of attraction between O₂ molecules are relatively weak owing to their much smaller size. The large van der Waals attractive forces in the S₈ molecules are due to large molecular size. Therefore oxygen has low m.p. and b.p. as compared to sulphur.

Question 7.5 (Textbook Page No 141)

Question 1.
Bond dissoClation enthalpy of F₂ (158.8 kj mol^-1) is lower than that of Cl₂ (242.6 kj mol^-1) Why?
Answer :
Fluorine has small atomic size than chlorine. The lone pairs on each F atom in F₂ molecule are so close together that they strongly repel each other, and make the F – F bond weak. Thus, it requires less amount of energy to break the F – F bond. In Cl₂ molecule the lone pairs on each Cl atom are at a larger distance and the repulsion is less.

Thus Cl – Cl bond is comparatively stronger. Therefore bond dissoClation enthalpy of F₂ is lower than that of Cl₂.

Question 7.6 (Textbook Page No 142)

Question 1.
Noble gases have very low melting and boiling points. Why?
Answer :
Noble gases are monoatomic, the only type of interatomic interactions which exist between them are weak van der Waals forces. Therefore, they can be liquefied at very low temperatures and have very low melting or boiling points.

Can you tell? (Textbook Page No 142)

Question 1.
The first member of the a group usually differs in properties from the rest of the members of the group. Why?
Answer:
The first member of a group usually differs in properties from the rest of the members of the group for the following reasons :

• Its small size
• High electronegativity
• Absence of vacant d-orbitals in its valence shell.

Use your brain power! (Textbook Page No 142)

Question 1.
Oxygen forms only OF₂ with fluorine while sulphur forms SF₆. Explain. Why?
Answer:

• Oxygen combines with the most electronegative element fluorine to form OF₂ and exhibits positive oxidation state (+ 2). Since, oxygen does not have vacant J-orbitals it cannot exhibit higher oxidation states.
• Sulphur has vacant d-orbitals and hence can exhibit + 6 oxidation state to form SF₆.

Question 2.
Which of the following possesses hydrogen bonding? H₂S, H₂O, H₂Se, H₂Te
Answer:

• Oxygen being more electronegative, is capable of forming hydrogen bonding in the compound H₂O.
• The other elements S, Se and Te of Group 16, being less electronegative do not form hydrogen bonds.
• Thus, hydrogen bonding is not present in the other hydrides H₂S, H₂Se and H₂Te.

Question 3.
Show hydrogen bonding in the above molecule with the help of a diagram.
Answer:

Try this….. (Textbook Page No 143)

Question 1.
Complete the following tables :

Answer:

Can you tell? (Textbook Page No 146)

Question 1.
What is allotropy?
Answer:
The property of some elements to exist in two or more different forms in the same physical state is called allotropy.

Question 2.
What is the difference between allotropy and polymorphism?
Answer:

• Allotropy is the existence of an element in more than one physical form. It means that under different conditions of temperature and pressure an element can exist in more than one physical forms.
• Coal, graphite and diamond etc., are different allotropic forms of carbon.
• Polymorphism is the existence of a substance in more than one crystalline form.
• It means that under different conditions of temperature and pressure, a substance can form more than one type of crystal. For example, mercuric iodide exists in the orthorhombic and trigonal form.

Question 7.7 (Textbook Page No 146)

Which form of sulphur shows paramagnetic behaviour?
Answer :
In the vapour state, sulphur partly exists as S₂ molecule, which has two unpaired electrons in the antibonding π^* orbitals like O₂. Hence it exhibits paramagnetism.

Try this….. (Textbook Page No 149)

Question 1.
Why water in a fish pot needs to be changed from time to time?
Answer:
A fish pot is an artificial ecosystem and the fish in it are selective and maintained in a restricted environment.

In a fish pot, the unwanted food and waste generated by the fish mix with the water and remain untreated due to lack of decomposers.

Accumulation of waste material will decrease the levels of dissolved oxygen in the water pot.

Hence, it is necessary to change the water from time to time.

Question 7.8 (Textbook Page No 149)

Dioxygen is paramagnetic in spite of having an even number of electrons. Explain.
Answer :
Dioxygen is a covalently bonded molecule.
The paramagnetic behaviour of O₂ can be explained with the help of molecular orbital theory.
Electronic configuration O₂
KK σ(2s)² σ(2s)² σ^*(2p_z)² π(2p_x)² π(2p_x)² π(2p_y)² π^*(2p_x)¹ π^*(2p_y)¹. Presence of two unpaired electrons in antibonding orbitals explains paramagnetic nature of dioxygen.

Question 7.9 (Textbook Page No 150)

High concentration of ozone can be dangerously explosive. Explain.
Answer :
Thermal stability : Ozone is thermodynamically unstable than oxygen and decomposes into O₂. The decomposition is exothermic and results in the liberation of heat (ΔH is – ve) and an increase in entropy (ΔS is positive). This results in large negative Gibbs energy change (ΔG). Therefore high concentration of ozone can be dangerously explosive. Eq O₃ → O₂ + O

Try this…… (Textbook Page No 151)

(a) Ozone is used as a bleaching agent. Explain.
Answer:

• Ozone due to its oxidising property can act as a bleaching agent. O_3(g) → O_2(g) + O
• It bleaches coloured matter. coloured matter + O → colourless matter
• Ozone bleaches in the absence of moisture, so it is also known as dry bleach.
• Ozone can bleach ivory and delicate fabrics like silk.

(b) Why does ozone act as a powerful oxidising agent?
Answer:
Ozone decomposes to liberate nascent oxygen, hence it is a powerful oxidising agent. O_3(g) → O_2(g) + O
For example :

• It oxidises lead sulphide (PbS) to lead sulphate (PbSO₄).
  pbS_(s) + 4O_3(g) → PbSO_(s) + 4O_2(g)
• Potassium iodide, KI is oxidised to iodine, I₂ in the solution.
  2KI_(aq) + H₂O₍₁₎ + O_3(g) → 2KOH_(aq) + I_2(s) + O_2(g)

Question 7.10 : (Textbook Page No 154)

What is the action of concentrated H₂SO₄ on (a) HBr (b) HI
Answer :
Concentrated sulphuric acid oxidises hydrobromic acid to bromine.

2HBr + H₂SO₄ → Br₂ + SO₂ + 2H₂O
It oxidises hydroiodic acid to iodine.
2HI + H₂SO₄ → I₂ + SO₂ + 2H₂O

Try this….. (Textbook Page No 156)

Question 1.
Give the reasons for the bleaching action of chlorine.
Answer:

• Chlorine acts as a powerful bleaching agent due to its oxidising nature.
• In moist conditions or in the presence of water it forms unstable hypochlorous acid, HOCl which decomposes giving nascent oxygen which oxidises the vegetable colouring matter of green leaves, flowers, litmus, indigo, etc.
  Cl₂ + H₂O → HCl + HOCl
  HOCl → HCl + [O]
  Vegetable coloured matter + [O] → colourless matter.

Question 2.
Name two gases used in war.
Answer:
Phosgene : COCl₂
Mustard gas: Cl – CH₂ – CH₂ – S – CH₂ – CH₂ – Cl

Use your brain power! (Textbook Page No 157)

Question 1.
Chlorine and fluorine combine to form interhalogen compounds. The halide ion will be of chlorine or fluorine?
Answer:
Among the- two halogens, chlorine is more electropositive than fluorine (Electronegativity values: F = 4.0, Cl = 3.2)

The interhalogen compound is regarded as the halide of the more electropositive halogen. Hence, the interhalogen compound is the fluoride of chlorine, i.e. chlorine monofluoride, CiF.

Question 2.
Why does fluorine combine with other halogens to form maximum number of fluorides?
Answer:
Since fluorine is the most electronegative element and has the smallest atomic radius compared to other halogen fluorine forms maximum number of fluorides.

Use your brain power! (Textbook Page No 158)

Question 1.
What will be the names of the following compounds: ICl, BrF?
Answer:
ICl : Iodine monochloride
BrF : Bromine monofluoride

Question 2.
Which halogen (X) will have maximum number of other halogen (X ) attached?
Answer:
The halogen Iodine (I) will have the maximum number of other halogens attached.

Question 3.
Which halogen has tendency to form more interhalogen compounds?
Answer:
The halogen fluorine (F) has the maximum tendency to form more interhalogen compounds as it has a small size and more electronegativity.

Question 4.
Which will be more reactive?
(a) ClF₃ or ClF,
(b) BrF₅ or BrF
Answer:
ClF₃ is more reactive than ClF, while BrF₅ is more reactive than BrF. Both ClF₃ and BrF₅ are unstable compared to ClF and BrF respectively due to steric hindrance hence are more reactive.

Question 5.
Complete the table :

Answer:

Use your brain power! (Textbook Page No 159)

Question 1.
In the special reaction for ICl, identify the oxidant and the reductant? Denote oxidation states of the species.
Answer:

Potassium chlorate, KClO₃ is the oxidising agent or oxidant and iodine is the reducing agent or reductant.

Use your brain power! (Textbook Page No 162)

Question 1.
What are missing entries?

Answer:

Maharashtra State Board 12th Std Chemistry Textbook Solutions

• Solid State Class 12 Chemistry Textbook Solutions
• Solutions Class 12 Chemistry Textbook Solutions
• Ionic Equilibria Class 12 Chemistry Textbook Solutions
• Chemical Thermodynamics Class 12 Chemistry Textbook Solutions
• Electrochemistry Class 12 Chemistry Textbook Solutions
• Chemical Kinetics Class 12 Chemistry Textbook Solutions
• Elements of Groups 16, 17 and 18 Class 12 Chemistry Textbook Solutions
• Transition and Inner Transition Elements Class 12 Chemistry Textbook Solutions

Reproduction in Lower and Higher Plants Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 1 Reproduction in Lower and Higher Plants Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 1 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 1 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Insect pollinated flowers usually possess ………………
(a) sticky pollen with a rough surface
(b) large quantities of pollens
(c) dry pollen with a smooth surface
(d) light-colored pollens
Answer:
(a) sticky pollen with a rough surface

Question 2.
In ovule, meiosis occurs in ………………
(a) Integument
(b) Nucellus
(c) Megaspore
(d) Megaspore mother cell
Answer:
(d) Megaspore mother cell

Question 3.
The ploidy level is NOT the same in ………………
(a) Integuments and nucellus
(b) Root tip and shoot tip
(c) Secondary nucleus and endosperm
(d) Antipodals and synergids
Answer:
(c) Secondary nucleus and endosperm

Question 4.
Which of the following types require pollination but result is genetically similar to autogamy?
(a) Geitonogamy
(b) Xenogamy
(c) Apogamy
(d) Cleistogamy
Answer:
(a) Geitonogamy

Question 5.
If diploid chromosome number in a flowering plant is 12, then which one of the following will have 6 chromosomes?
(a) Endosperm
(b) Leaf cells
(c) Cotyledons
(d) Synergids
Answer:
(d) Synergids

Question 6.
In angiosperms, endosperm is formed by/ due to ………………
(a) free nuclear divisions of megaspore
(b) polar nuclei
(c) polar nuclei and male gamete
(d) synergids and male gametes
Answer:
(c) polar nuclei and male gamete

Question 7.
Point out the odd one.
(a) Nucellus
(b) Embryo sac
(c) Micropyle
(d) Pollen grain
Answer:
(d) Pollen grain

2. Very Short Answer Questions

Question 1.
The part of gynoecium that determines the compatible nature of pollen grain.
Answer:
Stigmatic surface.

Question 2.
How many haploid cells are present in a mature embryo sac?
Answer:
6 cells, 2 synergids, 1 egg cell, 3 antipodals.

Question 3.
Even though each pollen grain has 2 male gametes why at least 20 pollen grains are required to fertilize 20 ovules in a particular carpel?
Answer:
Angiosperms have phenomenon of double fertilization in which both the male gametes are utilized, one for fusion with egg cell to form zygote and other for fusion with secondary nucleus to form endosperm.

Question 4.
Megasporogenesis
Answer:
It is the process of formation of haploid megaspores from diploid megaspore mother cell.

Question 5.
What is hydrophily?
Answer:
Transfer of pollen grains in pollination process through agency of water is known as hydrophily.

Question 6.
The layer which supplies nourishment to the developing pollen grains.
Answer:
Tapetum

Question 7.
Parthenocarpy
Answer:
The condition in which fruit is developed without the process of fertilization is called parthenocarpy.

Question 8.
Are pollination and fertilization necessary in apomixis?
Answer:
Apomixis is formation of embryos without formation of gametes hence there is no need of pollination and fertilization.

Question 9.
The part of pistil which develops into fruit and seed.
Answer:
Ovary develops into fruit and ovules into seed.

Question 10.
What is the function of filiform apparatus ?
Answer:
Filiform apparatus guides the pollen tube towards egg cell.

3. Short Answer Questions

Question 1.
How polyembryony can be commercially exploited?
Answer:

1. Polyembryony is the development of more than one embryo inside the seed.
2. When such polyembryonic seed germinate we get multiple seedlings from it.
3. This condition increases the chances of survival of new plants.
4. Nucellar embryos are genetically identical to parent plants hence we get uniform plants.
5. In horticulture we can utilize these as rootstock for grafting, hence they have significant role in fruit breeding programmes e.g. Citrus, Mango.

Question 2.
Pollination and seeds formation are very crucial for the fruit formation, Justify.
Answer:

1. After fertilization, ovary is transformed into fruit, where ovary wall becomes fruit wall, i.e pericarp.
2. Mature ovules are transformed into seeds after fertilization.
3. Fertilization is a process where male gametes unites with female gamete to form zygote which develops into embryo.
4. In pollination process pollen grains carrying non-motile male gamete are transferred on stigma.
5. Seeds have embryo which germinate into new plant hence the goal of reproduction to create offspring for next generation is achieved. Hence these are the crucial events for fruit formation.

Question 3.
Incompatibility is a natural barrier in the fusion of gametes. How will you explain this statement?
Answer:

1. Self incompatibility or self-sterility is a genetic mechanism that prevents germination of pollen on stigma of same flower. This favours cross pollination. E.g. Tobacco.
2. In pollen-pistil interaction, when pollen grain is deposited on stigma, pistil has the ability to recognize and allow germination of right type of pollen.
3. Special type of proteins on stigmatic surface determine compatibility or incompatibility.
4. A physiological mechanism operates to ensure successful germination of compatible pollen.
5. Compatible pollen absorbs water and nutrients from stigmatic surface that are absent in pollen and then pollen tube emerges which grow-s through style.

Question 4.
Describe three devices by which cross pollination is encouraged in Angiosperms by avoiding self-pollination?
Answer:

1. Unisexuality, dichogamy, prepotency, heteromorphy and herkogamy are the outbreeding devices.
2. Unisexuality : The plants bear either male or female flowers. Due to unisexual nature, self-pollination is avoided. Plants are either dioecious, e.g. Papaya or monoecious, e.g. maize.
3. Heteromorphy : In same plants different types of flowers are produced. In these flowers, stigmas and anthers are situated at different levels. There is heterostyly and heteroanthy. This prevents self-pollination e.g. Primrose.
4. Herkogamy : In bisexual flowers we may come across mechanical device to prevent self-pollination. Natural physical barrier avoids contact of pollens with stigma. E.g. Calotropis where pollinia are situated below the stigma.

4. Long Answer Questions

Question 1.
Describe the process of double fertilization.
Answer:
Double fertilization:
(1) Out of the two male gametes produced by the male gametophyte in angiosperms, one unites with the female gamete and the other with the secondary nucleus. Since both the male gametes take part in fertilization and fertilization occurs twice, it is called double fertilization.

(2) During double fertilization, the pollen tube on reaching the ovule enters the embryo sac through micropyle and bursts in one of the synergids. Owing to this, the two male gametes contained in the pollen tube, are set free.

(3) Out of the two male gametes, one unites with the egg or female gamete and the other unites with the secondary nucleus of the embryo sac, forming a triploid or triple fusion nucleus, called the primary endosperm nucleus. The process involving the fusion of one of the male gametes with the egg nucleus, resulting in the formation of a diploid zygote is called syngamy.

(4) The reproductive process in which non-motile male nuclei are carried to the egg cell through a pollen tube is called siphonogamy.

(5) After fertilization, zygote develops into an embryo. Certain changes take place in the ovule leading to the development of a seed.

Question 2.
Explain the stages involved in the maturation of microspore into male gametophyte.
OR
Describe the development of male gametophyte before pollination in angiosperms.
OR
Sketch and label male gametophyte in angiosperm.
Answer:

1. Microspore or pollen grain is first cell of male gametophyte.
2. The protoplast of pollen grain divides mitotically to form two unequal cells – a small thin walled generative cell and a large naked vegetative or tube cell.
3. The generative cell possesses thin cytoplasm and a nucleus. It separates and floats in the cytoplasm of vegetative cell.
4. The vegetative, possesses thick cytoplasm, irregular shaped nucleus and the reserved food.
5. In majority of the angiosperms, the pollen grains are liberated at two-celled stage after the dehiscence of the anther.
6. The generative cell of the pollen grain divides by mitosis to form two male non-motile gametes.

Question 3.
Explain the development of dicot embryo.
Answer:
Development of embryo (dicot) in angio- sperm:

The oospore undergoes a transverse division to form a large basal cell towards the micropyle and a small apical or terminal cell towards the chalaza of the embryo sac. This two celled structure is called proembryo. The basal cell or suspensor initial undergoes repeated transverse divisions to form a multicellular structure called suspensor. The suspensor pushes the embryo towards the endosperm to draw its nutrition.

1. The development of embryo from a zygote is called embryogenesis.
2. The fusion of male gamete and an egg cell during fertilization results in the formation of a diploid zygote. The zygote develops a wall around it and is converted into oospore.
3. The apical cell or embryonal initial of the proembryo undergoes a transverse division followed by two vertical divisions at right angles to form an octant stage.
4. From octant, the lower four cells form hypocotyl and radicle while four cells of upper side form plumule with two cotyledons.
5. The lowermost cell of suspensor is hypophysis and by its further division forms part of radicle and root cap.
6. The cells from upper side of octant divide repeatedly to form heart shaped which elongated further to form two lateral cotyledons.
7. Enlargement of hypocotyl and cotyledon results into curved embryo which appears horse shoe shaped.

Question 4.
Draw a diagram of the L.S of anatropous ovule and list the components of embryo sac and mention their fate after fertilization.
Answer:
Components of Embryo sac.

1. Mature embryo sac is 7-celled and 8 nucleate.
2. Egg apparatus at micropylar end – with 2 synergids and egg cell.
3. Central cell with secondary nucleus formed by 2 polar nuclei
4. Antipodal cells at chalazal end – 3 cells.
5. Pollen tube enters the synergids, Synergids guide the growth of pollen tube towards egg.
6. Male gamete fuses with female gamete, i.e. syngamy to form zygote which develops into embryo.
7. One male gamete fuses with secondarynucleus to form primary endosperm nucleus (PEN) which forms endosperm, nutritive tissue for embryo.

5. Fill in the Blanks

Question 1.
The ……………… collects the pollen grains.
Answer:
biotic agents

Question 2.
The male whorl, called the ……………… produces ………………
Answer:
androecium, pollen grains

Question 3.
The pollen grains represent the ………………
Answer:
male

Question 4.
The ……………… contains the egg or ovum.
Answer:
embryo sac

Question 5.
…………….. takes place when one male gamete and the egg fuse together. The fertilized egg grows vs into seed from which the new plants can grow.
Answer:
Fertilization

Question 6.
The ……………… is the base of the flower to which other floral parts are attached.
Answer:
thalamus

Question 7.
……………… is the transfer of pollen grains from anther of the flower to the stigma of the same or a different flower.
Answer:
Pollination

Question 8.
Once the pollen reaches the stigma, pollen tube traverses down the ……………… to the ovary where fertilization occurs.
Answer:
style

Question 9.
The ……………… are coloured to attract the insects that carry the pollen. Some flowers also produce ……………… or ……………… that attracts insects.
Answer:
petals, fragrance, nectar

Question 10.
The whorl ……………… is green that protects the flower until it opens.
Answer:
Calyx.

6. Label the Parts of seed.

Answer:

7. Match the following

(a) A-v, B-i, C-ii, D-iv
(b) A-iii, B-iv, C-i, D-v
(c) A-iv, B-i, C-v D-ii
(d) A-iv, B-v C-iii, D-ii
Answer:
(c) A-iv, B-i, C-v D-ii

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Biodiversity, Conservation and Environmental Issues Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 15 Biodiversity, Conservation and Environmental Issues Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 15 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 15 Exercise Solutions

1. Multiple choice questions

Question 1.
Observe the graph and select the correct option.

(a) Line A represents, S = CA²
(b) Line B represents, log C = log A + Z log S
(c) Line A represents, S = CA^Z
(d) Line B represents, log S = log Z + C log A
Answer:
(c) Line A represents, S = CA^Z

Question 2.
Select odd one out on the basis of Ex situ conservation.
(a) Zoological park
(b) Tissue culture
(c) Sacred groves
(d) Cryopreservation
Answer:
(a) Zoological park

Question 3.
Which of the following factors will favour species diversity?
(a) Invasive species
(b) Glaciation
(c) Forest canopy
(d) Co-extinction
Answer:
(a) Invasive species

Question 4.
The term “terror of Bengal’ is used for
(a) algal bloom
(b) water hyacinth
(c) increased BOD
(d) eutrophication
Answer:
(b) water hyacinth

Question 5.
CFC are air polluting agents which are produced by
(a) Diesel trucks
(b) Jet planes
(c) Rice fields
(d) Industries
Answer:
(b) Jet planes

2. Very short answer type questions.

Question 1.
Give two examples of biodegradable materials released from sugar industry.
Answer:

1. Molasses
2. Bagasse.

Question 2.
Name any two modern techniques of protection of endangered species.
OR
Two modern methods of ex-situ conservation of species
Answer:

1. Tissue culture
2. In vitro fertilization of eggs
3. Cryopreservation.

Question 3.
Where was ozone hole discovered?
Answer:
Ozone hole was discovered in Antarctica.

Question 4.
Give one example of natural pollutant.
Answer:
Volcanic ash is a natural pollutant.

Question 5.
What do you understand by EW category of living being?
Answer:
A species which becomes extinct in the wild (EW) is called EW category, their members are seen only in captivity or as a naturalized population outside its historic range due to massive habitat loss.

3. Short answer type questions.

Question 1.
Dandiya raas is not allowed after 10.00 pm. Why?
Answer:
Dandiya rass involves blaring loudspeakers which cause noise pollution. It is undesired loud sound which could be hazardous for ears and general health. In India, the Air (Prevention and Control of Pollution) Act 1981, Amendment 1987, includes noise as an air pollutant. As per law noise after 10 pm is not allowed as many people may be resting. Therefore, Dandiya Raas is not allowed after 10 pm.

Question 2.
Tropical regions exhibit species richness as compared to polar regions. Justify.
Answer:

1. Tropical regions are bestowed by thicker vegetation and ample food due to available sunlight and humidity.
2. Polar regions are covered over with snow, with almost no vegetation.
3. Only handful species of animals can survive here due to their adaptations.
4. Species richness always shows latitudinal gradient for many plants and animal species. It is high at lower latitudes and there is a steady decline towards the poles. Therefore, tropical regions show more species richness.

Question 3.
How does genetic diversity affect sustenance of a species?
Answer:

1. Genetic diversity develops the capability of the species to adapt to the varying changes in the environment.
2. The large variation of the different gene sets allows an individual or the whole population to have the capacity to endure environmental stress in any form.
3. Some individuals have, a better capacity to endure the increasing pollution in the environment whereas some do not have it.
4. Those that do not have show infertility or even death from the same conditions.
5. Those who are able to endure and adapt to this change survive and live in a better way.
6. This is called natural selection which leads to a loss of genetic diversity in particular habitats.
7. Thus, due to genetic diversity can affect sustenance of some species.

Question 4.
Greenhouse effect is boon or bane? Give your opinion.
Answer:
(1) The natural greenhouse effect is good, it is a boon but human enhanced greenhouse effect is a bane.

(2) In the absence of an atmosphere, Earth’s surface temperature would be about -18 °C, or 0 °F, which is too cold for sustaining life.

(3) Earth is habitable because of the natural greenhouse effect. Heating of Earth’s atmosphere due to the presence of greenhouse gases such as water vapour, carbon dioxide (CO₂), methane (CH₄) and oxides of nitrogen (NO₂).

(4) Greenhouse gases have just the right molecular structure to absorb infrared radiation that the Earth emits. It re-emits most of that infrared energy in all directions, warming the atmosphere to its comfortable average temperature of 15 °C (60 °F). So, the greenhouse effect was a boon in olden days before industrialization and invention of automobiles.

(5) However, due to human impact, the proportion of greenhouse gases has increased tremendously causing global warming. Thus, now greenhouse effect has become a bane.

Question 5.
State the effects of CO in human body.
OR
How does CO cause giddiness and exhaustion?
Answer:
Effects of Carbon monoxide:

1. Carbon monoxide is tasteless, colourless and odourless gas, therefore its presence goes unnoticed.
2. It can inhibit the blood’s ability to carry oxygen to body tissues.
3. Supply of oxygen to vital organs such as.the heart and brain is affected due to presence of CO.
4. When CO is inhaled, it combines with the oxygen carrying haemoglobin of the blood to form carboxyhaemoglobin. Once combined with the haemoglobin, that haemoglobin is no longer available for transporting oxygen.
5. The symptoms of CO poisoning are headache, nausea, giddiness, etc.

Question 6.
Name two types of particulate pollutants found in air. Add a note on ill effects of the same on human health.
OR
Describe any 2 particulate and gaseous pollutants.
Answer:
I. Types of gaseous pollutants include CO₂, CO, SO₂, NO, NO₂, etc.
(1) Carbon dioxide : It is a greenhouse gas. It is produced in excess due to human activities such as burning of fossil fuels. It is also rising due to increasing deforestation. The natural cycle of Carbon dioxide is disturbed due to human interference. Otherwise, the process of photosynthesis can balance CO₂ : O₂ ratio of the air. Aeroplane traffic such as a jet plane also emits lots of CO₂.

(2) Carbon monoxide (CO) : CO is produced due to incomplete combustion of fuels. It is a toxic gas. Vehicular exhausts produce lot of CO.

II. Types of particulate pollutants are mist, dust, fume and smoke particles, smog, pesticides, heavy metals and radioactive elements, etc.
(1) Dust are fine particles which enter the respiratory passage and can cause damage to delicate tissues in the lungs. Various processes such as construction work, demolition of buildings and traffic can cause dust pollution. There are natural causes of release of dust too, through wind or volcanic eruption.

(2) Smoke and smog are worst type of particulate air pollutants which can cause many respiratory problems like emphysema or asthma.

4. Long answer type questions.

Question 1.
Montreal Protocol is an essential step. Why is it so?
Answer:

1. Montreal Protocol was an international treaty signed at Montreal in Canada in 1987.
2. Later many more efforts have been made and protocols have laid down definite roadmaps separately for developing and developed countries.
3. All these efforts were for reducing emission of CFCs and other ozone depleting chemicals.
4. All nations realized that ozone depletion can cause penetration of harmful UV radiations to the earth’s surface. This is very hazardous, for flora, fauna and for mainly human beings. Therefore, urgent action was needed to combat this effect.
5. Montreal Protocol was a very positive move because after 1987, there have been much better condition of ozone layer.

Question 2.
Name any 2 personalities who have contributed to control deforestation in our country. Elaborate on importance of their work.
Answer:
Two personalities who have contributed to control deforestation in our country are:
Saalumara Thimmakka from Karnataka and Moirangthem Loiya from Manipur.
1. Saalumara Thimmakka :

• Saalumara Thimmakka is the best example of peoples’ participation in reforestation.
• She is an Indian environmentalist from Karnataka. She has taken up work of planting and tending to 385 banyan trees along a 4 km stretch of highway between Hulikal and Kudur. Other 800 trees are also planted by her.
• She is honoured with the National Citizens Award of India and Padma Shri in 2019.

2. Moirangthem Loiya :

• Moirangthem Loiya is from Manipur who has restored Punshilok forest. For last 17 years he is planting trees after leaving his job.
• He brought the lost glory back for the 300 acres forest land. He planted a variety of trees like, bamboo, oak Ficus, teak, jackfruit and Magnolia.
• This forest now has over 250 varieties of plants including 25 varieties of bamboo along with many animals making the forest rich in biodiversity.

Question 3.
How BS emission standards changed over time? Why is it essential?
Answer:

1. BS emission standards changed over the time due to changing city life and more vehicular traffic on the road, especially in the megacities.
2. Since capital city of Delhi was declared as worst polluted city as far as its air quality is concerned, various measures were taken by the Government of India. There was new fuel policy declared, in which Bharat stage emission standards (BS) were set.
3. These norms were set to reduce sulphur and aromatic content of petrol and diesel. Also the vehicular engines were upgraded.
4. Bharat stage emission standards (BS) are standards which are equivalent to Euro norms and have evolved on similar lines as Bharat Stage II (BS II) to BS VI from 2001 to 2017.
5. Since population of Delhi was to be saved, in 2001, Bharat stage II emission norms were set for CNG and LPG vehicles.
6. This helped in reduced emission of sulphur which was controlled at 50 ppm in diesel and 150 ppm in petrol. Also aromatic hydrocarbons were reduced at 42% in concerned fuel according to norms.
7. Because, in spite of all the efforts, Delhi was declared as worst air-polluted city in the world in 2016, therefore, Government of India directly adapted BS VI in the year 2018, skipping BS V These efforts decreased the levels of CO₂ and SO₂ in Delhi.

Question 4.
During large public gatherings like Pandharpur vari, mobile toilets are deployed by the government. Explain how this organic waste is disposed.
Answer:

1. The toilets deployed at Pandharpur at the time of vari are of the Ecosan type.
2. Ecosan toilet is a closed system without water and it is an alternative to leach pit toilets.
3. When the pit of an Ecosan toilet fills up after some time, then it is closed and sealed for about 8-9 months.
4. In this time the faeces get completely composted to organic manure. In this way the organic waste can be disposed.
5. It is a practical, efficient and cost-effective solution for human waste disposal.
6. Also, open-air defecation is prohibited which can cause health problems. Therefore, during large public gatherings like Pandharpur vari mobile toilets like Ecosan are deployed by the government.

Question 5.
How Indian culture and traditions helped in bio-diversity conservation? Give importance of conservation in terms of utilitarian reasons.
Answer:
In Indian culture and traditions in different religions, biodiversity is protected and conserved. Few examples of worship of animals and plants can be given here.

1. Nagpanchami festival is towards the respect of snakes. They are worshipped on that day and the local people are aware of their role in ecosystem of control of rat population.
2. Vatapournima festival is worshipping a banyan tree.
3. Various other festivals teach the value of plants and animals surrounding us. Even the cattle are worshipped on a particular day as a tradition.
4. Jain religion strongly advocates protection of all animals through vegetarianism.

Conservation in terms of utilitarian reasons:
The conservation of biodiversity can be done in utilitarian way or for ethical reasons. Utilitarian reasons are further classified into narrowly utilitarian and broadly utilitarian reasons:

I. Narrowly utilitarian reasons:

1. Humans always reap material benefits from biodiversity in the form of resources for basic needs such as food, clothes, shelter.
2. Industrial products like resins, tannins, perfume base, etc. are also obtained through biodiversity resources.
3. For making ornaments or artefacts for aesthetic purpose, again biodiversity is sacrificed.
4. Many medicines are also obtained through biodiversity resources which shares 25% of global medicine market.
5. Around 25000 species are used for traditional medicines by tribal population worldwide.
6. Bioprospecting which is a systematic search for development of new sources of chemical compounds, genes, microorganisms, macroorganisms, and other valuable products from nature which is of economically important species is also due to biodiversity.

II. Broadly utilitarian reasons:

1. Production of oxygen done by all green plants helps human beings to thrive. Amazon forest alone gives 25% of the oxygen to the entire world.
2. Insects carry out pollination and seed dispersal.
3. If insects do not carry out pollination and seed dispersal, man would go hungry without crops and fruits.
4. Biodiversity also is useful in recreation of human beings.

III. Taking all these aspects in consideration, conservation of biodiversity becomes essential. Therefore, to protect and conserve our rich biodiversity on the planet, we have to remember all the utilitarian reasons.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions

Ecosystems and Energy Flow Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 14 Ecosystems and Energy Flow Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 14 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 14 Exercise Solutions

1. Multiple choice questions

Question 1.
Which one of the following has the largest population in a food chain?
(a) Producers
(b) Primary consumers
(c) Secondary consumers
(d) Decomposers
Answer:
(a) Producers

Question 2.
The second trophic level in a lake is ……………………
(a) Phytoplankton
(b) Zooplankton
(c) Benthos
(d) Fishes
Answer:
(b) Zooplankton

Question 3.
Secondary consumers are …………………….
(a) Herbivores
(b) Producers
(c) Carnivores
(d) Autotrophs
Answer:
(c) Carnivores

Question 4.
What is the % of photosynthetically active radiation in the incident solar radiation?
(a) 100%
(b) 50%
(c) 1-5%
(d) 2-10%
Answer:
(b) 50%

Question 5.
Give the term used to express a community in its final stage of succession?
(a) End community
(b) Final community
(c) Climax community
(d) Dark community
Answer:
(c) Climax community

Question 6.
After landslide which of the following type of succession occurs?
(a) Primary
(b) Secondary
(c) Tertiary
(d) Climax
Answer:
(a) Primary

Question 7.
Which of the following is most often a limiting factor of the primary productivity in any ecosystem?
(a) Carbon
(b) Nitrogen
(c) Phosphorus
(d) Sulphur
Answer:
(c) Phosphorus

2. Very short answer question.

Question 1.
Give an example of ecosystem which shows inverted pyramid of numbers.
Answer:
Number of insects dependent on a single tree, is an example of ecosystem having inverted pyramid of numbers.

Question 2.
Give an example of ecosystem which shows inverted pyramid of biomass.
Answer:
Oceanic ecosystem has inverted pyramid of biomass.

Question 3.
Which mineral acts as limiting factor for productivity in an aquatic ecosystem?
Answer:
Phosphorus acts as limiting factor for productivity in an aquatic ecosystem.

Question 4.
Name the reservoir and sink of carbon in carbon cycle.
Answer:
Atmosphere is the reservoir of carbon cycle, while fossil fuels embedded in ocean and oceanic waters are the sink of carbon in carbon cycle.

3. Short answer questions.

Question 1.
Upright and inverted pyramid of biomass.
Answer:

Question 2.
Food chain and Food web.
Answer:

4. Long answer questions

Question 1.
Define ecological pyramids and describe with examples, pyramids of number and biomass.
Answer:
1. Ecological Pyramids : Ecological Pyramids are the representation of relationships between different components of ecosystem at successive trophic levels.

2. Pyramid of numbers:

• Pyramid of numbers is the diagrammatic representation which shows the relationship between producers, herbivores and carnivores at successive trophic levels in terms of their numbers.
• As we go up the trophic levels, the interdependent organisms keep on reducing in their numbers.
• For example, the number of grasses are more than the number of herbivores which eat them. The number of herbivores such as rabbits would be lesser than grass but greater than the carnivores that are dependent upon the population of rabbits.
• Thus, the producers would be more than primary consumers and primary consumers would be more than secondary consumers. The top level consumers would be least in their numbers. This pyramid shows upright nature.

3. Pyramid of biomass:
(1) Pyramid of biomass are constructed by taking into consideration the different biomass in every successive trophic level.
(2) Pyramid of biomass in seas in inverted as the biomass of fishes is more than the biomass of phytoplankton.

Question 2.
What is primary productivity? Give brief description of factors that affect primary productivity.
Answer:
(1) Primary Productivity : The rate of generation of biomass in an ecosystem which is expressed in units of mass per unit surface (or volume) per unit time, for instance grams per square metre per day (g/m²/day) is called primary productivity.

(2) Primary productivity is described as gross primary productivity (GPP) and net primary productivity (NPP).

(3) The rate of production of organic matter during photosynthesis is called gross primary productivity of an ecosystem. Of this the amount of energy lost through respiration of plants is called respiratory losses.

(4) Gross primary productivity minus respiratory losses gives the net primary productivity (NPP).

(5) Net primary productivity is the available biomass for the consumption to heterotrophs (herbivores, carnivores and decomposers).

(6) Factors affecting primary productivity: Gross primary productivity (GPP) depends on the following factors:

• Plant species inhabiting a particular area.
• Variety of environmental factors such as temperature, sunlight, salinity, oxygen and carbon dioxide content, etc.
• Availability of nutrients and
• Photosynthetic capacity of plants.

Question 3.
Define decomposition and describe the processes and products of decomposition.
Answer:

1. Decomposition is the process carried out by the decomposer organisms.
2. Most of the bacteria, actinomycetes and fungi are decomposers. They convert the dead and decaying organic matter into simpler compounds. These simpler inorganic substances return back to the environment.
3. Decomposition takes place through detritus food chain. It starts from the dead organic matter. Detritus eating organisms called detritivores like earthworm, etc. breakdown the detritus into smaller fragments. Therefore, this first step of decomposition is called fragmentation.
4. Water soluble inorganic nutrients seep into the soil after fragmentation. These nutrients get precipitated as salts. Therefore, this second step of decomposition is called leaching.
5. The third step of decomposition is called catabolism. In this step, fungal and bacterial enzymes degrade the detritus into simple inorganic substances.
6. The partially decomposed organic matter is called humus which is formed by the process of humification. Humus is a dark coloured amorphous substance which is the reservoir of nutrients.
7. Humus too undergoes decomposition by bacterial action at a very slow rate and ultimately releases inorganic matter. This process is therefore called mineralization.
8. Decomposition requires oxygen in greater amount. The rate of decomposition is dependent upon the temperature and the humidity of the environment.

Question 4.
Write important features of a sedimentary cycle in an ecosystem.
Answer:

1. Reservoir of sedimentary cycles is earth’s crust.
2. The nutrients such as phosphorus which show sedimentary cycle, moves through hydrosphere, lithosphere and biosphere.
3. There is no respiratory release of nutrients into the atmosphere which show sedimentary cycle.
4. Natural reservoir of such nutrients are usually in the form of rocks. The rocks upon weathering release such nutrients into circulation.
5. Sedimentary cycles are very slow in their reactions.

Question 5.
Describe carbon cycle and add a note on the impact of human activities on carbon cycle.
Answer:
I. Carbon cycle:
(1) The entire carbon cycle has following basic processes viz. Photosynthesis, Respiration, Decomposition, Sedimentation and Combustion.

(2) Carbon is an important element as it forms 49% of the dry weight of all organisms. 71% of global carbon is present in the oceans. Therefore, ocean is the major reservoir of carbon. Carbon is also present in all fossil fuels. This is long term storage places or sinks for carbon which is in the form of coal, natural gas, etc.

(3) Respiration and photosynthesis are the two events that keep the carbon in cyclic circulation. During respiration, oxygen is used for combustion of carbohydrates as a result of which carbon dioxide and water are formed with the release of energy. The process of photosynthesis utilizes carbon dioxide and water vapour liberating oxygen and producing carbohydrates at the same time.

(4) Solar energy is stored in the carbon-carbon bonds of carbohydrates during photosynthesis whereas respiration releases the same stored energy.

(5) The main reservoirs for carbon dioxide are in the oceans and in rocks. Carbon dioxide is highly soluble in water and forms mild carbonic acid upon dissolving. This dissolved carbon dioxide precipitate as a solid rock or limestone which is calcium carbonate. This reaction in the seas is aided by corals and algae which in turn builds the coral reefs made up of limestone.

(6) Carbon moves through food chains. Autotrophic green plants on land and in water take up carbon dioxide and manufacture carbohydrates by the process of photosynthesis. The carbon stored in plants has three different fates, viz. liberation into atmosphere, consumption by animals upon feeding, storage in the plant till the plant dies.

(7) Animals get their carbon requirement through their food. When autotrophs are consumed, the heterotrophs obtain carbon. Carbon in animals also has three fates, viz. release back into the atmosphere in the process of respiration, release of stored carbon from the body by the action of decomposers or conversion into fossil fuels if buried intact.

(8) Fossil fuels such as coal, oil, natural gas, etc. can be mined and burned for energy purposes. This burning releases carbon dioxide back into the atmosphere.

(9) Carbon from limestone can also be released if pushed to the surfaces and slowly weathered away. Subducting and volcanic eruptions can also release the stored carbon from sediments.

II. Impact of human activities on carbon cycle:
(1) Excessive burning of fossils fuels for power plants, industrial processes and vehicular traffic, adds excessive carbon dioxide into atmosphere. When fossil fuels burn to run factories, power plants, motor vehicles, most of the carbon quickly enters the atmosphere as carbon dioxide gas.

(2) Each year, 5.5 billion tonnes of carbon is released through combustion of fossil fuels. Of this massive amount, 3.3 billion tonnes stays in the atmosphere.

(3) Rapid deforestation also increases carbon dioxide. Since plants absorb carbon dioxide for their photosynthesis, they always reduce the concentration of CO₂. But deforestation upsets this balance.

(4) Massive burning of fossil fuel for energy and transport, have significantly increased the rate of release of carbon dioxide into the atmosphere which is causing global warming and resultant climate change.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions

Organisms and Populations Class 13 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 13 Organisms and Populations Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 13 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 13 Exercise Solutions

1. Multiple choice questions

Question 1.
Which factor of an ecosystem includes plants, animals, and microorganisms?
(a) Biotic factor
(b) Abiotic factor
(c) Direct factor
(d) Indirect factor
Answer:
(a) Biotic factor

Question 2.
An assemblage of individuals of different species living in the same habitat and having functional interactions is ……………….
(a) Biotic community
(b) Ecological niche
(c) Population
(d) Ecosystem
Answer:
(a) Biotic community

Question 3.
Association between sea anemone and Hermit crab in gastropod shell is that of ………………..
(a) Mutualism
(b) Commensalism
(c) Parasitism
(d) Amensalism
Answer:
(b) Commensalism

Question 4.
Select the statement which explains best parasitism.
(a) One species is benefited.
(b) Both the species are benefited.
(c) One species is benefited, other is not affected.
(d) One species is benefited, other is harmed.
Answer:
(d) One species is benefited, other is harmed.

Question 5.
Growth of bacteria in a newly inoculated agar plate shows ………………….
(a) exponential growth
(b) logistic growth
(c) Verhulst-Pearl logistic growth
(d) zero growth
Answer:
(c) Verhulst-Pearl logistic growth

2. Very short answer questions.

Question 1.
Define the following terms
a. Commensalism
Answer:
The interaction between two species in which one species gets benefits and the other is neither harmed nor benefited is called commensalism.

b. Parasitism
Answer:
The interaction between two species in which one parasitic species derives benefit from the other host species by harming it is called parasitism.

c. Camouflage
Answer:
Camouflage is the disguising colouration or behaviour to merge with the surrounding so that prey or predator can remain hidden.

Question 2.
Give one example for each
a. Mutualism
b. Interspecific competition
Answer:
a. Lichen is composed of alga (cyanobacteria) and fungus. They cannot survive independently. Their association is mutualistic alga synthesises food by photosynthesis and fungus does the absorption of moisture.

b. Leopard and lion competing for a same prey. Sheep and cow competing for grazing in the same land.

Question 3.
Name the type of association:
a. Clown fish and sea anemone
b. Crow feeding the hatchling of Koel
c. Humming birds and host flowering plants
Answer:
a. Commensalism
b. Brood parasitism
c. Mutualism

Question 4.
What is the ecological process behind the biological control method of managing with pest insects?
Answer:

1. Pest insects act as prey to predator birds or frogs.
2. The biological control method consists of releasing the predators in the farms so that they can control the pest population in the natural way.
3. This also eliminates the use of chemical pesticides.
4. Frogs are natural predators of locust, therefore the population of this hazardous insect is controlled by frogs and the produce from agricultural farm can be saved.

Protocooperation:

1. Protocooperation is a type of population interaction where two species interact with each other.
2. Both are benefited but they have no need to interact with each other.
3. They can survive and grow even in the absence of other species.
4. Therefore this interaction is purely for the gain that they receive in such type of interaction.
5. The interaction that occurs can be between different kingdoms.

3. Short answer questions.

Question 1.
How is the dormancy of seeds different from hibernation in animals?
Answer:
In dormancy seed is not showing any metabolic activities. It can come back to life if and only if it gets suitable moisture and sunlight. Hibernation is suspended state, in which metabolic reactions do take place but at a very reduced pace. Animal arouses on its own after the winter sleep is over. This arousal is spontaneous and depends upon the ambient temperature. Dormant seed does not show such change unless it is planted or thrown in to moist place.

Question 2.
If a marine fish is placed in a fresh water aquarium, will it be able to survive? Give reason.
Answer:
Marine fish has its own osmoregulation which is different from the osmoregulation seen in fresh water fish. In marine water, the ambient salinity is more than the concentration of ions in the body. But in fresh water reverse is the case. Therefore, marine fish has different machinery to cope up with high saline environment. Therefore, it cannot survive in fresh water as its osmoregulation is not possible in less saline waters.

Question 3.
How is the dormancy of seeds different from hibernation in animals?
Answer:
In dormancy seed is not showing any metabolic activities. It can come back to life if and only if it gets suitable moisture and sunlight. Hibernation is suspended state, in which metabolic reactions do take place but at a very reduced pace. Animal arouses on its own after the winter sleep is over. This arousal is spontaneous and depends upon the ambient temperature. Dormant seed does not show such change unless it is planted or thrown into moist place.

Question 4.
An orchid plant is growing on the branch of mango tree. How do you describe this interaction between the orchid and the mango tree?
Answer:

1. Orchid is an epiphyte. It gets the support from the mango tree. But it does not cause any harm to the mango tree.
2. Mango tree does not derive any benefit from this association. Therefore, this interaction is of type of commensalism.

Question 5.
Distinguish between the following:
a. Hibernation and Aestivation
Answer:

b. Ectotherms and Endotherms
Answer:

c. Parasitism and Mutualism
Answer:

Question 6.
Write a short note on
a. Adaptations of desert animals
Answer:

1. Animals which are well-adapted to live in deserts are called xerocoles. These animals show adaptations for water conservation or heat tolerance.
2. These animals show low basal metabolic rate. They obtain moisture from succulent plants and rarely drink water. E.g Gazella and Oryx.
3. Desert animals like camel produce concentrated urine and dry dung.
4. Many other hot desert animals are nocturnal, seeking out shade during the day or dwelling underground in burrows.
5. Smaller animals from desert, emerge from their burrows at night.
6. Mammals living in cold deserts have developed greater insulation through warmer body fur and insulating layers of fat beneath the skin.
7. Few adaptations to desert life are unable to cool themselves by sweating so they shelter during the heat of the day. Many desert reptiles are ambush predators and often bury themselves in the sand, waiting for prey to come within range.
8. Other animals have bodies designed to save water. Scorpions and wolf spiders have a thick outer covering which reduces moisture loss. The kidneys of desert animals concentrate urine, so that they excrete less water.

b. Adaptations of plants to water scarcity
Or
Adaptations in desert plants.
Answer:

1. Thick cuticle on their leaf surfaces
2. Stomata of desert plants is sunken that is it is in deep pits to minimize loss of water through transpiration.
3. Desert plants also have a special photosynthetic pathway (CAM -Crassulacean acid metabolism) that enables their stomata to remain closed during daytime.
4. Some desert plants like Opuntia, have their leaves reduced or they are modified to spines. Loss of leaf surface helps in prevention of transpiration.
5. Photosynthetic function is taken over by the flattened stems called as phylloclade.

c. Behavioural adaptations in animals
Answer:

1. Behavioural responses to cope with variations in their environment are shown by few animals.
2. Desert lizards manage to keep their body temperature fairly constant by behavioural adaptations. They bask in the sun and absorb heat, when their body temperature drops below the comfort zone, but move into shade, when the ambient temperature starts increasing. Even snakes also show basking during winter months.
3. Since they are ectothermic, this kind of behaviour saves them from extreme temperatures.
4. Many smaller animals show burrowing behaviour to adapt to the temperature extremes.
5. Some species burrow into the sand to hide and escape from the heat.
6. Migrations shown by the birds and mammals are also behavioural responses for adapting to severe winter temperatures.

Question 7.
Define Population and Community.
Answer:
Population:
Group of organisms belonging to same species that can potentially interbreed with each other and live together in a well-defined geographical area by sharing or competing for similar resources, is called population.

Community:
Several populations of different species in a particular area makes a community.

4. Long answer questions.

Question 1.
With the help of suitable diagram, describe the logistic population growth curve.
Answer:

1. Naturally all populations of any species always have limited resources to permit exponential growth. Due to this there is always competition between individuals for limited resources. The most fit organisms succeed by survival and reproduction.
2. A given habitat has enough resources to support a maximum possible number, but beyond a particular limit the further growth is impossible.
3. This limit is called nature’s carrying capacity (K) for that species in that habitat.
4. A population growing in a habitat with limited resources show following phases in a sequential manner, (a) A lag phase (b) Phase of acceleration (c) Phase of deceleration (d) An asymptote, when the population density reaches the carrying capacity.
5. A plot of N in relation to time (t) results in a sigmoid curve. This type of population growth is called Verhulst-Pearl Logistic Growth.
6. Since resources for growth for most animal populations are finite and become limiting sooner or later, the logistic growth model is considered as a more realistic one.
7. Logistic growth thus always shows sigmoid curve.

Question 2.
Enlist and explain the important characteristics of a population.
Answer:
Important characteristics of a population are as follows:
1. Natality:

1. Natality is the birth rate of a population. Due to increased natality the population density rises.
2. Natality is a crude birth rate or specific birth rate.
3. Crude birth rate : Number of births per 1000 population/year gives crude birth rate. Crude birth rate is helpful in calculating population size.
4. Specific birth rate : Crude birth rate is relative to a specific criterion such as age. E.g. If in a pond, there were 200 carp fish and their population rises to 800. Then, taking the current population to 1000, the birth rate becomes 800/200 = 4 offspring per carp per year. This is specific birth rate.
5. Absolute Natality : The number of births under ideal conditions when there is no competition and the resources such as food and water are abundant, then it give absolute natality.
6. Realized Natality : The number of births under different environmental pressures give realized natality. Absolute natality will be always more than realized natality.

2. Mortality:

1. Mortality is the death rate of a population. It gives a measure of the number of deaths in a particular population, in proportion to the size of that population, per unit of time.
2. Mortality rate is typically expressed in deaths per 1,000 individuals per year.
   A mortality rate of 9.5 (out of 1,000) in a population of 1,000 would mean 9.5 deaths per year in that entire population or 0.95% out of the total.
3. Absolute Mortality : The number of deaths under ideal conditions when there is no competition, and all the resources such as food and water are abundant, then it gives absolute mortality.
4. Realized Mortality : The number of deaths under environmental pressures come into play gives realized mortality.
5. It must be remembered that absolute mortality will always be less than realized mortality.

3. Density:
The density of a population in a given habitat during a given period fluctuates due to changes in four basic processes, viz.

1. Natality i.e. birth rate (The number of births during a given period in the population that are added to the initial density).
2. Mortality i.e. death rate (The number of deaths in the population during a given period).
3. Immigration i.e. number of individuals of the same species that have come into the habitat from elsewhere during the time period under consideration.
4. Emigration i.e. the number of individuals of the population who left the habitat and gone elsewhere during the time period under consideration.
5. Natality and immigration increase in population density whereas mortality and emigration decrease it.

4. Sex ratio : Ratio of the number of individuals of one sex (male) to that of the other sex (female) is called sex ratio. In nature male, female ratio is always 1 : 1. This 1 : 1 ratio is called evolutionary stable strategy of ESS for each population.

5. Age distribution and age pyramid : This parameter is important for human population. Each population is composed of individuals of different ages. The age distribution is plotted for the population, the resulting structure is called an age pyramid. For making the age pyramid, the entire population is divided into three age groups as Pre-Reproductive (age 0-14 years), Reproductive (age 15-44 years) and Post-reproductive (age 45 -85+ years).

6. Growth : Growth of a population causes rise in its density. The size and density are dynamic parameters as they keep on changing with time, and various factors including food, predation pressure and adverse weather. From the density, one comes to know if the population is flourishing or declining.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions

Biotechnology Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 12 Biotechnology Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 12 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 12 Exercise Solutions

1. Multiple choice questions

Question 1.
MU The bacterium which causes a plant disease called crown gall is ………………..
(a) Helicobacter pylori
(b) Agrobacterium tumifaciens
(c) Thermophilus aquaticus
(d) Bacillus thuringienesis
Answer:
(b) Agrobacterium tumtfaciens

Question 2.
The enzyme nuclease hydrolyses ……………….. of polynucleotide chain of DNA.
(a) hydrogen bonds
(b) phosphodiester bonds
(c) glycosidic bonds
(d) peptide bonds
Answer:
(b) phosphodiester bonds

Question 3.
In vitro amplification of DNA or RNA segment is known as ………………..
(a) chromatography
(b) southern blotting
(c) polymerase chain reaction
(d) gel electrophoresis
Answer:
(c) polymerase chain reaction

Question 4.
Which of the following is the correct recognition sequence of restriction enzyme hind III.
(a) 5′ —A-A-G-C-T-T— 3′
3′ —T-T-C-G-A-A—5′
(b) 5′ — G-A-A-T-T-C—3′
3′ — C-T-T-A-A-G—5′
(c) 5′ — C-G-A-T-T-C—3′
3′ — G-C-T-A-A-G—5′
(d) 5′ — G-G-C-C—3′
3′ — C-C-G-G—5′
Answer:
(a) 5’ —A-A-G-C-T-T—3’
3’ —T-T-C-G-A-A—5’

Question 5.
Recombinant protein ……………….. is used to dissolve blood clots present in the body.
(a) insulin
(b) tissue plasminogen activator
(c) relaxin
(d) erythropoietin
Answer:
(b) tissue plasminogen activator

Question 6.
Recognition sequence of restriction enzymes are generally ……………….. nucleotide long.
(a) 2 to 4
(b) 4 to 8
(c) 8 to 10
(d) 14 to 18
Answer:
(b) 4 to 8

2. Very short answer questions

Question 1.
Name the vector which is used in production of human insulin through recombinant DNA technology.
Answer:
PBR 322

Question 2.
Which cells from Langerhans of pancreas do produce a peptide hormone insulin?
Answer:
cells of islets of Langerhans of a peptide hormone insulin.

Question 3.
Give the role of Ca⁺⁺ ions in the transfer of recombinant vector into bacterial host cell.
Answer:
Ca⁺⁺ ions promotes binding of plasmid DNA to lipo polysaccharides on bacterial cell surface. Then plasmid can enter the cell on heat shock.

Question 4.
Expand the following acronyms which are used in the held of biotechnology:

1. YAC
2. RE
3. dNTP
4. PCR
5. GMO
6. MAC
7. CCMB.

Answer:

1. YAC : Yeast Artificial chromosome
2. RE : Restriction Endonuclease
3. dNTP : Deoxyribonucleoside triphosphates
4. PCR : Polymerase Chain Reaction
5. GMO : Genetically Modified Organisms
6. MAC : Mammalian Artificial Chromosome
7. CCMB : Centre for Cellular and Molecular Biology

Question 5.
Fill in the blanks and complete the chart.

Answer:

3. Short answer type questions.

Question 1.
Explain the properties of a good or ideal cloning vector for r-DNA technology.
Answer:
Desired characteristics of ideal cloning vector are as follows:

1. Vector should be able to replicate independenly (through ori gene), so that as vector replicates, multiple copies of the DNA insert are also produced.
2. It should be able to easily transferred into host cells.
3. It should have suitable control elements like promoter, operator, ribosomal binding sites, etc.
4. It should have marker genes for antibiotic resistance and restriction enzyme recognition sites within them.

Question 2.
A PCR machine can rise temperature up to 100 °C but after that it is not able to lower the temperature below 70 °C automatically. Which step of PCR will be hampered first in this faulty machine? Explain why?
Answer:

1. If the faulty machine is not able to lower the temperature below 70 °C, then the primer annealing step will be hampered first.
2. Each primer has a specific annealing temperature, depending upon its A, T, G, C content.
3. For most of the primers annealing temperature is about 40-60 °C.
4. Hence, if temperature is more than primers annealing temperature, it will be able to pair with its complementary sequence in ssDNA.

Question 3.
In the process of r-DNA technology, if two separate restriction enzymes are used to cut vector and donor DNA then which problem will arise in the formation of r-DNA or chimeric DNA? Explain.
Answer:
In the process of r-DNA technology, if two separate restriction enzymes are used to cut vector and donor DNA, then it will result in fragments with different sticky ends which will not be complementary to each other.

Question 4.

Answer:

4. Long answer type questions.

Question 1.
(i) Define and explain the terms Bioethics.
Answer:

1. Bioethics is the study of moral vision, decision and policies of human behaviour in relation to biological phenomena or events.
2. Bioethics deals with wide range of reactions on new developments like cloning, transgenic, gene therapy, eugenics, r-DNA technology, in vitro fertilization, sperm bank, gene therapy, euthanasia, death, maintaining those who are in comatose state, prenatal genetic selection, etc.
3. Bioethics also includes the discussion on subjects like what should and should not be done in using recombinant DNA techniques.

Ethical aspects pertaining to the use of biotechnology are:

1. Use of animals cause great sufferings to them.
2. Violation of integration of species caused due to transgenosis.
3. Transfer of human genes into animals and vice versa.
4. Indiscriminate use of biotechnology pose risk to the environment, health and biodiversity.
5. The effects of GMO on non-target organisms, insect resistance crops, gene flow, the loss of diversity.
6. Modification process disrupting the natural process of biological entities.

(ii) Define and explain the term Biopiracy.
Answer:

1. Biopiracy is defined as ‘theft of various natural products and then selling them by getting patent without giving any benefits or compensation back to the host country’.
2. It is unauthorized misappropriation of any biological resource and traditional knowledge.
3. It is bio-patenting of bio-resource or traditional knowledge of another nation without proper permission of the concerned nation or unlawful exploitation and use of bioresources without giving compensation.

Following are the examples of biopiracy:
(a) Patenting of Neem (Azadirachta indica):

1. Pirating India’s traditional knowledge about the properties and uses of neem, the USDA and an American MNC W.R. Grace sought a patent from the European Patent Office (EPO) on the “method for controlling on plants by the aid of hydrophobic extracted neem oil,” in the early 90s.
2. The patenting of the fungicidal properties of Neem, was an example of biopiracy.

(b) Patenting of Basmati:

1. Texmati is a trade name of “Basmati rice line and grains” for which Texas based American company Rice Tec Inc was awarded a patent by the US Patent and Trademark Office (USPTO) in 1997.
2. This is a case of biopiracy as Basmati is a long-grained, aromatic variety of rice indigenous to the Indian subcontinent.
3. Very broad claims about “Inventing” the said rice was the basis of patent application.
4. The UPSTO has rejected all the claims due to people movement against Rice Tec in March 2001.

(c) Haldi (Turmeric) Biopiracy:

1. A patent claim about the healing properties of Haldi was made by two American researchers of Indian origin of the University of Mississippi Medical Center, to the US Patent and Trademark Office.
2. They were granted a patent in March 1995.
3. This is an example of biopiracy because healing properties of Haldi is not a new discovery, but it is a traditional knowledge in ayurvedas for centuries.
4. The Council of Scientific and Industrial Research (CSIR) applied to the US Patent Office for a reexamination and they realized the mistake and cancelled the patent.

(iii) Define and explain the term Biopatent.
Answer:

1. Biopatent is a biological patent awarded for strains of microorganisms, cell lines, genetically modified strains, DNA sequences, biotechnological processes, product processes, product and product applications.
2. It allows the patent holder to exclude others from making, using, selling or importing protected invention for a limited period of time.
3. Duration of biopatentis five years from the date of the grant or seven years from the date of filing the patent application, whichever is less.
4. Awarding biopatents provides encouragement to innovations and promote development of scientific culture in society. It also emphasizes the role of biology in shaping human society.
5. First biopatent was awarded for genetically engineered bacterium ‘Pseudomonas’ used for clearing oils spills.
6. Patent jointly issued by Delta and Pineland company and US department of agriculture having title ‘control of plant gene expression’, is based on a gene that produces a protein toxic to plant and thus prevents seed germination.

This patent was not granted by Indian government. Such a patent is considered morally unacceptable and fundamentally unequitable. Such patents would pose a threat to global food security as financially powerful corporations would acquire monopoly over biotechnological process.

Question 2.
Explain the steps in process of r-DNA technology with suitable diagrams.
Answer:

The steps involved in gene cloning are as follows:
(1) Isolation of DNA (gene) from the donor organism:

• To obtain the desired gene to be cloned, the cells of the donor organism are sheared with the blender and treated with suitable detergent. Genetic material is then isolated and purified.
• Isolated purified DNA is then cleaved using restriction Endonucleases.
• Restriction fragment containing desired gene is isolated and selected for cloning. This is now called foreign DNA or passanger DNA.
• A desired gene can also be obtained directly from genomic library or c-DNA library.

(2) Insertion of desired foreign gene into a cloning vector (vehicle DNA):

• The foreign DNA or passanger DNA is inserted into a cloning vector (vehicle DNA) like bacterial plasmids and the bacteriophages like lamda phage and M13. The most commonly used plasmid is pBR 322.
• Plasmids are isolated from the bacteria and are cleaved by using same RE which is used in the isolation of the desired gene from the donor.
• Enzyme DNA ligase is used to join foreign DNA and the plasmid DNA.
• Plasmid DNA containing foreign DNA is called recombinant DNA (r-DNA) or chimeric DNA.

(3) Transfer of r-DNA into suitable competent host or cloning organism:

• The r-DNA is introduced into a competent host cell, which is mostly a bacterium.
• Host cell takes up naked r-DNA by process of ‘transformation’ and incorporates it into its own chromosomal DNA which finally expresses the trait controlled by passenger DNA.
• The transfer of r-DNA into a bacterial cell is assisted by divalent Ca⁺⁺.
• The cloning organisms are E.coli and Agrobacterium tumifaciens.
• The competent host cells which have taken up r-DNA are called transformed cells.
• By using techniques like electroporation, microinjection, lipofection, shot gun, ultrasonification, biolistic method, etc. Foreign DNA can also be transferred directly into the naked cell or protoplast of the competent host cell, without using vector.
• In plant biotechnology the transformation is through Ti plasmids of A. tumifaciens.

(4) Selection of the transformed host cell:

• For isolation of recombinant cell from non-recombinant cell, marker gene of plasmid vector is employed.
• For example, pBR322 plasmid vector contains different marker genes like ampicillin resistant gene and tetracycline resistant gene. When pstl RE is used, it knocks out ampicillin resistant gene from the plasmid, so that the recombinant cells become sensitive to ampicillin.

(5) Multiplication of transformed host cell:

• The transformed host cells are introduced into fresh culture media where they divide.
• The recombinant DNA carried by them also multiplies.

(6) Expression of gene to obtain desired product. Then desired products like enzymes, antibiotiocs etc. separated and purified through down stream processing using bioreactors.

Question 3.
Explain the gene therapy. Give two types of it.
Answer:
Gene therapy is the treatment of genetic disorders by replacing, altering or supplementing a gene that is absent or abnormal and whose absence or abnormality is responsible for the disease.
Types of gene therapy:
(a) Germ line gene therapy:

1. In this germ cells are modified genetically to correct a genetic defect.
2. Normal gene is introduced into germ cells like sperms, eggs, early embryos.
3. It allows transmission of the modified genetic information to the next generation.
4. Although it is highly effective in treatment of the genetic disorders, its use is not preferred in human beings because of various technical and ethical reasons.

(b) Somatic cell gene therapy:

1. In this somatic cells are modified genetically to correct a genetic defect.
2. Healthy genes are introduced in somatic cells like bone marrow cells, hepatic cells, fibroblasts endothelium and pulmonary epithelial cells, central nervous system, endocrine cells and smooth muscle cells of blood vessel walls.
3. Modification of somatic cells only affects the person being treated and the modified chromosomes cannot be passed on the future generations.
4. Somatic cell gene therapy is the only feasible option and the clinical trials have already employed for the treatment of disorders like cancer, rheumatoid arthritis, SCID, Gaucher’s disease, familial hypercholesterolemia, haemophilia, phenylketonuria, cystic fibrosis, sickle-cell anaemia, Duchenne muscular dystrophy, emphysema, thalassemia, etc.

Question 4.
How are the transgenic mice used in cancer research?
Answer:

1. Transgenic mice are used in various research areas of cancer research.
2. Transgenic mice containing a particular oncogene (cancer causing gene) develop specific cancer.
3. They are used to study the relationship between oncogenes and cancer development, cancer treatment and prevention of malignancy.
4. The transgenic mouse model for the investigation of the breast cancer was developed in the laboratory of Philip Leder in Harvard (USA).
5. Transgenic mice containing oncogenes myc and ras were analyzed to find out role of these genes in the development of breast cancer.

Question 5.
Give the steps in PCR or polymerase chain reaction with suitable diagrams.
Answer:

(1) The DNA segment and excess of two primer molecules, four types of dNTPs, the thermostable DNA polymerase are mixed together in ‘eppendorf tube’.

(2) One PCR cycle is of 3-4 minutes duration and it involves following steps:

• Denaturation : The reaction mixture is heated at 90-98°C. Due to this hydrogen bonds in the DNA break and two strands of DNA separate. This is called denaturation.
• Annealing of primer : When the reaction mixture is cooled to 40-60°C, the primer pairs with its complementary sequences in ssDNA. This is called annealing.
• Extension of primer : In this step, the temperature is increased to 70-75°C. At this temperature thermostable Taq DNA polymerase adds nucleotides to 3’end of primer using single-stranded DNA as template. This is called primer extension. Duration of this step is about two minutes.

(3) In an automatic thermal cycler, the above three steps are automatically repeated 20-30 times.
(4) Thus, at the end of ‘n’ cycles 2n copies of DNA segments, get synthesized.

Question 6.
What is a vaccine? Give advantages of oral vaccines or edible vaccines.
Answer:

1. A vaccine is a biological preparation that provides active acquired immunity against a certain disease.
2. Vaccine is often made from a weakened or killed form of the microorganism, its toxins or one of its surface protein antigens.
3. Edible vaccine is an edible plant part engineered to produce an immunogenic protein, which when consumed gets recognized by immune system.
4. Immunogenic protein of certain pathogens are active when’administered orally.
5. When animals or mainly humans consume these plant parts, they get vaccinated against certain pathogen.
6. Oral or edible vaccines have low cost, they are easy to administer and store.

Question 7.
Enlist different types of restriction enzymes commonly used in r-DNA technology? Write on their role.
Answer:

1. Different restriction enzymes commonly used in r-DNA technology are Alu I, Bam HI, Eco RI, Hind II, Hind III, Pst I, Sal I, Taq I, Mbo II, Hpa I, Bgl I, Not I, Kpn I, etc.
2. They are the molecular scissors which recognize and cut the phosphodiester back bone of DNA on both strands, at highly specific sequences.
3. The sites recognized by them are called recognition sequences or recognition sites.
4. Different restriction enzymes found in different organisms recognize different nucleotide sequences and therefore cut DNA at different sites.
5. Restriction cutting may result in DNA fragments with blunt ends or cohesive or sticky ends or staggered ends (having short, single stranded projections).
6. Restriction endonucleases like Bam HI and EcoRI produce fragments with sticky ends.
7. Restriction endonucleases like Alu I, Hind III produce fragments with blunt ends.
8. Type I restriction endonucleases fuction simultaneously as endonuclease and methylase e.g. EcoK.
9. Type II restriction endonucleases have separate cleaving and methylation activities. They are more stable and are used in r-DNA technology e.g. EcoRI, Bgll. They cut DNA at specific sites within the palindrome.
10. Type III restriction endonucleases cut DNA at specific non-palindromic sequences e.g. Hpal, MboII.
11. In bacterial cells, REs destroy various viral DNAs that might enter the cell, thus restricting the potential growth of the virus.

Question 8.
Enlist and write in brief about the different biological tools required in r-DNA technology.
Answer:
The biological tools used in r-DNA technology are various enzymes, cloning vectors and competent hosts.
(1) Enzymes:

• Enzymes like lysozymes, nucleases (exonucleases and endonucleases), DNA ligase, reverse transcriptase, DNA polymerase, alkaline phosphatases, etc. are used in r-DNA technology.
• The restriction endonucleases are used as biological or molecular scissors. They are able to cut a DNA molecule at a specific recognition site.

(2) Vectors:

• Vectors are DNA molecules which carry foreign DNA segment and replicate inside the host cell.
• Vectors may be plasmids, bacteriophages (M13, lambda virus), cosmid, phagemids, BAC (bacterial artificial chromosome), YAC (yeast artificial chromosome), transposons, baculoviruses and mammalian artificial chromosomes (MACs).
• Most commonly used vectors are plasmid vectors (pBR 322, pUC, Ti plasmid) and bacteriophages (lamda phage, M13 phage).

(3) Competent host cells:

1. They are bacteria like Bacillus haemophilus, Helicobacter pyroliand E. coli.
2. Mostly E. coli is used for the transformation with recombinant DNA.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions