Category: Class 8

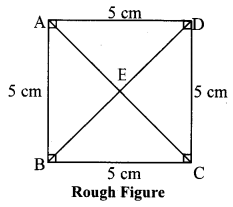
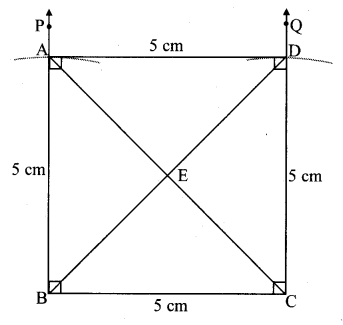
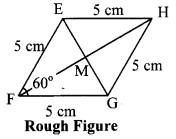
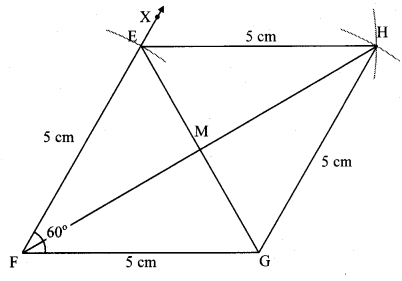
Quadrilateral: Constructions and Types Class 8 Maths Chapter 8 Practice Set 8.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.1 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Std 8 Maths Practice Set 8.1 Chapter 8 Solutions Answers

Construct the following quadrilaterals of given measures.

Question 1.
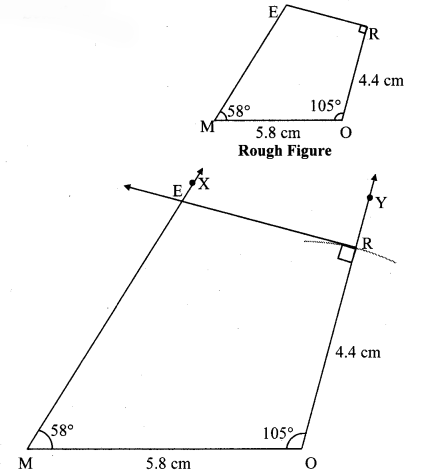
In ∆MORE, l(MO) = 5.8 cm, l(OR) = 4.4 cm, m∠M = 58°, m∠O = 105°, m∠R = 90°.
Solution:

Question 2.
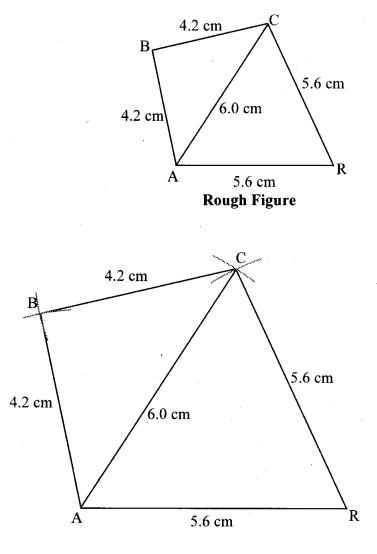
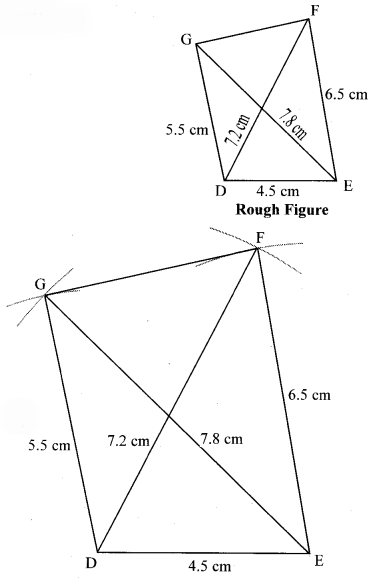
Construct ∆DEFG such that l(DE) = 4.5 cm, l(EF) = 6.5 cm, l(DG) = 5.5 cm, l(DF) = 7.2 cm, l(EG) = 7.8 cm.
Solution:

Question 3.
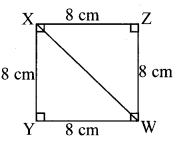
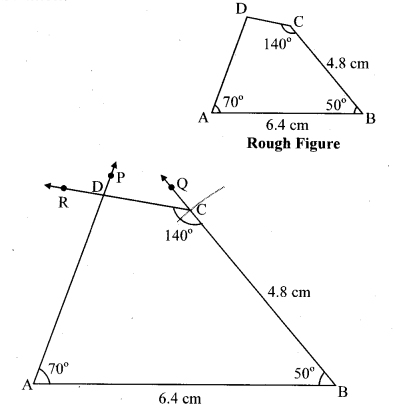
In ∆ABCD, l(AB) = 6.4 cm, l(BC) = 4.8 cm, m∠A = 70°, m∠B = 50°, m∠C = 140°.
Solution:

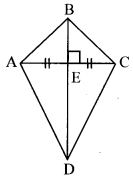
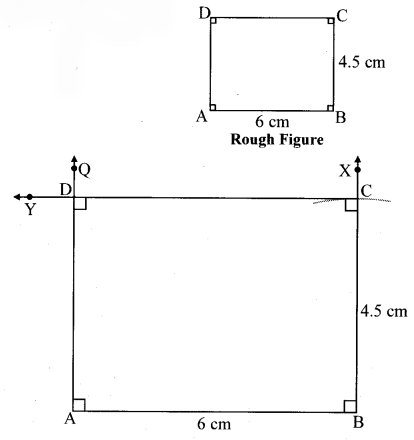
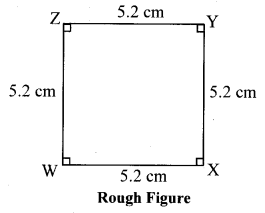
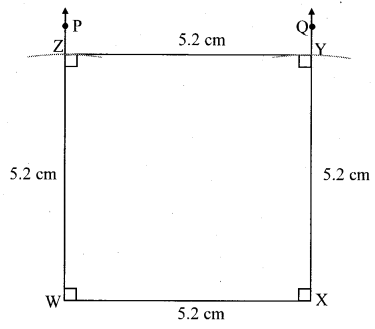
Question 4.
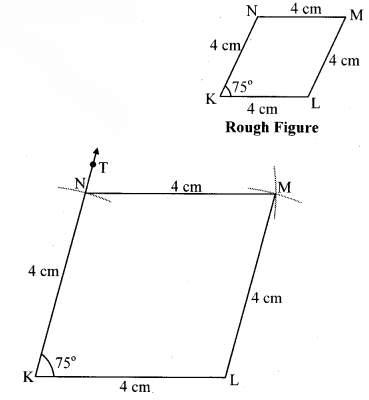
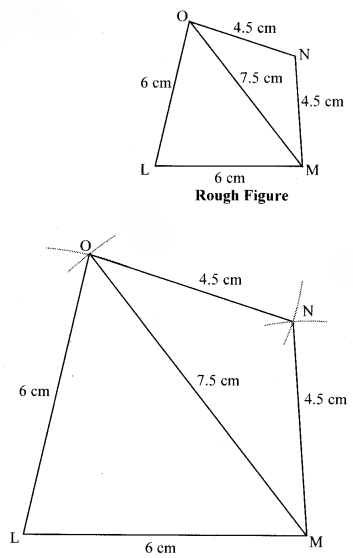
Construct ₹LMNO such that
l(LM) = l(LO) = 6 cm,
l(ON) = l(NM) = 4.5 cm, l(OM) = 7.5 cm.
Solution:

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.1 Intext Questions and Activities

Question 1.
Construction of a triangle:
Construct the triangles with given measures. (Textbook pg. no. 41)
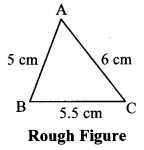
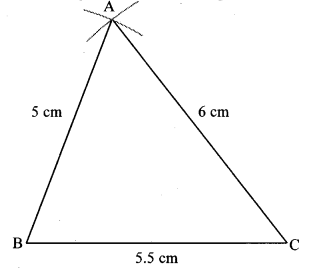
i. ∆ABC: l(AB) = 5 cm, l(BC) = 5.5, l(AC) = 6 cm.
Solution:

Steps of construction:
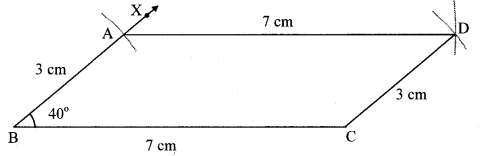
Step 1 : As shown in the rough figure, draw seg BC of length 5.5 cm as the base.
Step 2 : By taking a distance of 5 cm on the compass and placing the metal tip of the compass on point B, draw an arc on one side of BC.
Step 3 : By taking a distance 6 cm on the compass and placing the metal tip of the t compass on point C and draw an arc ’ such that it intersects the previous arc. Name the point as A.
Step 4 : Draw segments AB and AC to get the triangle. ∆ABC is the required triangle.

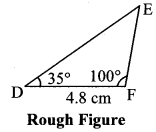
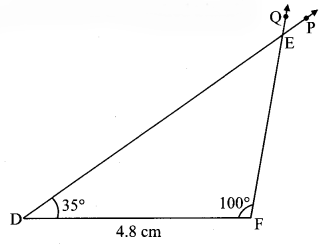
ii. ∆DEF: m∠D = 35°, m∠F = 100°, l(DF) = 4.8 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg DF of length 4.8 cm as the base.
Step 2 : Placing the centre of the protractor at point D, mark point P such that m∠PDF = 35°.
Step 3 : Placing the centre of the protractor at point F, mark point Q such that m∠QFD = 100°.
Step 4 : Draw ray DP and ray FQ. Name their point of intersection as E.
∆DEF is required triangle.

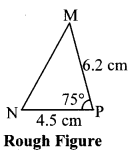
iii. ∆MNP: l(MP) = 6.2 cm, l(NP) = 4.5 cm, m∠P = 75°.
Solution:

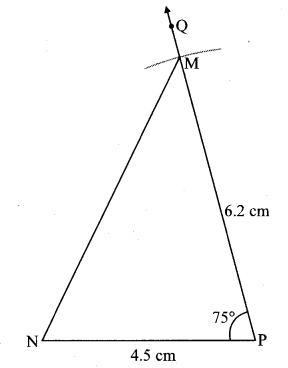
Steps of construction:
Step 1 : As shown in the rough figure, draw seg PN of length 4.5 cm as the base.
Step 2 : Placing the centre of the protractor at point P, mark point Q such that m∠QPN = 75°.
Step 3 : By taking a distance of 6.2 cm on the compass and placing the metal tip at point P, draw an arc on ray PQ. Name the point as M.
Step 4 : Draw seg MN to get the triangle. ∆MNP is the required triangle.

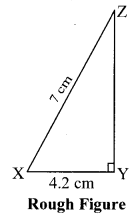
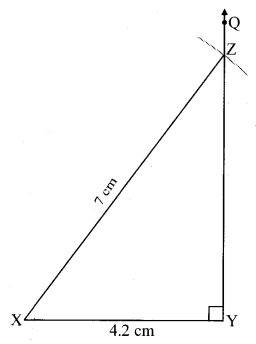
iv. ∆XYZ: m∠Y = 90°, l(XY) = 4.2 cm, l(XZ) = 7 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg XY of 4.2 cm as the base.
Step 2 : Placing the centre of the protractor at point Y, mark point Q such that m∠QYX = 90°.
Step 3 : By taking a distance of 7 cm on the compass and placing the metal tip on point X, draw an arc on ray YQ. Name the point as Z.
Step 4 : Draw seg XZ to get the triangle. ∆XYZ is the required triangle.

Maharashtra Board Class 8 Maths Solutions

• Variation Practice Set 7.1 Class 8 Maths Solutions
• Variation Practice Set 7.2 Class 8 Maths Solutions
• Variation Practice Set 7.3 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.1 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.2 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.3 Class 8 Maths Solutions

Quadrilateral: Constructions and Types Class 8 Maths Chapter 8 Practice Set 8.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.3 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Std 8 Maths Practice Set 8.3 Chapter 8 Solutions Answers

Question 1.
Measures of opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of its each angle.
Solution:
Let ₹PQRS be the parallelogram.
m∠Q = (3x – 2)° and m∠S = (50 – x)°

m∠Q = m∠S
…..(i)
[Opposite angles of a parallelogram are congruent]
∴ 3x – 2 = 50 – x
∴ 3x + x = 50 + 2
∴ 4x = 52
∴ x = \(\frac { 52 }{ 4 }\)
∴ x = 13
Now, m∠Q = (3x – 2)°
= (3 x 13 – 2)° = (39 – 2)° = 37°
∴ m∠S = m∠Q = 37° …[From(i)]
m∠P + m∠Q = 180°
….[Adjacent angles of a parallelogram are supplementary]
∴ m∠P + 37° = 180°
∴ m∠P = 180° – 37° = 143°
∴ m∠R = m∠P = 143°
…..[Opposite angles of a parallelogram are congruent]
∴ The measures of the angles of the parallelogram are 37°, 143°, 37° and 143°.

Question 2.
Referring the given figure of a parallelogram, write the answers of questions given below.
i. If l(WZ) = 4.5 cm, then l(XY) = ?
ii. If l(YZ) = 8.2 cm, then l(XW) = ?
iii. If l(OX) = 2.5 cm, then l(OZ) = ?
iv. If l(WO) = 3.3 cm, then l(WY) = ?
v. If m∠WZY = 120°, then m∠WXY = ? and m∠XWZ = ?

Solution:
i. l(WZ) = 4.5 cm … [Given]
l(X Y) = l(WZ) ….[Opposite sides of a parallelogram are congrument ]
∴ l(X Y) = 4.5cm

ii. l(YZ) = 8.2 cm …[Given]
l(XW) = l(YZ)
…[Opposite sides of a parallelogram are congruent]
∴ l(XW) = 8.2cm … [Given]

iii. l(OX) = 2.5 cm …[Given]
l(OZ) = l(OX)
….[Diagonals of a parallelogram bisect each other]
∴ l(OZ) = 2.5cm

iv. l(WO) = 3.3 cm … [Given]
l(WO) = \(\frac { 1 }{ 2 }\) l(WY)
….[Diagonals of a parallelogram bisect each other]
∴ 3.3 = \(\frac { 1 }{ 2 }\) l(WY)
∴ 3.3 x 2 = l(WY)
∴ l(WY) = 6.6cm

v. m∠WZY =120° … [Given]
m∠WXY = m∠WZY
…..[Opposite angles of a parallelogram are congrument]
∴ m∠WXY = 120° …(i)
m∠XWZ + m∠WXY = 180°
….[Adjacent angles of a parallelogram are supplementary]
∴ m∠XWZ + 120° = 180° … [From (i)]
∴ m∠XWZ = 180°- 120°
∴ m∠XWZ = 60°

Question 3.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40°, l(AB) = 3 cm
Solution:

Opposite sides of a parallelogram are congruent.
∴ l(AB) = l(CD) = 3cm
l(BC) = l(AD) = 7 cm

Question 4.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write with reason, what type of a quadrilateral it is.
Solution:
Let ₹PQRS be the quadrilateral.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4.
Let the common multiple be x.
∴m∠P = x°, m∠Q = 2x°, m∠R = 3x° and m∠S = 4x°
In ₹PQRS,
m∠P + m∠Q + m∠R + m∠S = 360°
…[Sum of the measures of the angles of a quadrilateral is 360°]
∴x° + 2x° + 3x° + 4x° = 360°
∴10 x° = 360°
∴x° = \(\frac { 360 }{ 10 }\)
∴x° = 36°
∴m∠P = x° = 36°

m∠Q = 2x° = 2 × 36° = 72°
m∠R = 3x° = 3 × 36° = 108° and
m∠S = 4x° = 4 × 36° = 144°
∴The measures of the angles of the quadrilateral are 36°, 72°, 108°, 144°.
Here, m∠P + m∠S = 36° + 144° = 180°
Since, interior angles are supplementary,
∴side PQ || side SR
m∠P + m∠Q = 36° + 72° = 108° ≠ 180°
∴side PS is not parallel to side QR.
Since, one pair of opposite sides of the given quadrilateral is parallel.
∴The given quadrilateral is a trapezium.

Question 5.
Construct ₹BARC such that
l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Solution:

Question 6.
Construct ₹PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ₹PQRS is a parallelogram, which of the given information is unnecessary?
Solution:

1. Since, the opposite sides of a parallelogram are congruent.
   ∴ Either l(PQ) or l(SR) is required.
2. To construct a parallelogram lengths of adjacent sides and measure of one angle is required.
   ∴ Either l(PQ) and m∠Q or l(SR) and m∠R is the unnecessary information given in the question.

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.3 Intext Questions and Activities

Question 1.
Draw a parallelogram PQRS. Take two rulers of different widths, place one ruler horizontally and draw lines along its edges. Now place the other ruler in slant position over the lines drawn and draw lines along its edges. We get a parallelogram. Draw the diagonals of it and name the point of intersection as T.

1. Measure the opposite angles of the parallelogram.
2. Measure the lengths of opposite sides.
3. Measure the lengths of diagonals.
4. Measure the lengths of parts of the diagonals made by point T. (Textbook pg. no. 47)

Solution:
[Students should attempt the above activities on their own.]

Question 2.
In the given figure of ₹ABCD, verify with a divider that seg AB ≅ seg CB and seg AD ≅ seg CD. Similarly measure ∠BAD and ∠BCD and verify that they are congruent. (Textbook pg. no. 48)

Solution:
[Students should attempt the above activities on their own.]

Maharashtra Board Class 8 Maths Solutions

• Variation Practice Set 7.1 Class 8 Maths Solutions
• Variation Practice Set 7.2 Class 8 Maths Solutions
• Variation Practice Set 7.3 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.1 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.2 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.3 Class 8 Maths Solutions

Quadrilateral: Constructions and Types Class 8 Maths Chapter 8 Practice Set 8.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.2 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Std 8 Maths Practice Set 8.2 Chapter 8 Solutions Answers

Question 1.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l(BC) = 4.5 cm.
Solution:

Question 2.
Draw a square WXYZ with side 5.2 cm.
Solution:

Question 3.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
Solution:

Question 4.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
Solution:

Let ₹ABCD be the rectangle.
l(BC) = 24cm, l(AC) = 26cm
In ∆ABC,
m∠ABC = 90° …[Angle of a rectangle]
∴[l(AC)]² = [l(AB)]2 + [l(BC)]²
…[Pythagoras theorem]
∴ (26 )² = [l(AB)]² + (24)²
∴(26)² – (24)² = [l(AB)]²
∴(26 + 24) (26 – 24) = [l(AB)]²
…[∵ a² – b² = (a + b)(a – b)]
∴50 x 2 = [l(AB)]²
∴100 = [l(AB)]²
i.e. [l(AB)]² = 100
∴l(AB) = √100
…[Taking square root of both sides]
∴l(AB) =10 cm
∴The length of the other side is 10 cm.

Question 5.
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
Solution:
In rhombus ABCD,

l(AC) = 16 cm and l(BD) = 12 cm.
Let the diagonals of rhombus ABCD intersect at point O.
l(AO) = \(\frac { 1 }{ 2 }\) l(AC)
…[Diagonals of a rhombus bisect each other]
∴l(AO) = \(\frac { 1 }{ 2 }\) × 16
∴l(AO) = 8 cm
Also, l(DO) = \(\frac { 1 }{ 2 }\) l(BD)
…[Diagonals of a rhombus bisect each other]
∴l(DO) = \(\frac { 1 }{ 2 }\) × 12
∴l(DO) = 6 cm
In ∆DOA,
m∠DOA = 90°
..[Diagonals of a rhombus are perpendicular to each other]
[l(AD)]² = [l(AO)]² + [l(DO)]²
…[Pythagoras theorem]

= (8)² + (6)²
= 64 + 36
∴[l(AD)]² = 100
∴l(AD) = √100
… [Taking square root of both sides]
∴l(AD) = 10 cm
∴l(AB) = l(BC) = l(CD) = l(AD) = 10 cm
…[Sides of a rhombus are congruent]
Perimeter of rhombus ABCD
= l(AB) + l(BC) + l(CD) + l(AD)
= 10+10+10+10
= 40 cm
∴The side and perimeter of the rhombus are 10 cm and 40 cm respectively.

Question 6.
Find the length of diagonal of a square with side 8 cm.
Solution:
Let ₹XYWZ be the square of side 8cm.

seg XW is a diagonal.
In ∆ XYW,
m∠XYW = 90°
… [Angle of a square]
∴ [l(XW)]² = [l(XY)]² + [l(YW)]²
…[Pythagoras theorem]
= (8)² + (8)²
= 64 + 64
∴ [l(XW)]² = 128
∴ l(XW) = √128
…[Taking square root of both sides]
= √64 × 2
= 8 √2 cm
∴ The length of the diagonal of the square is 8 √2 cm.

Question 7.
Measure of one angle of a rhombus is 50°, find the measures of remaining three angles.
Solution:
Let ₹ABCD be the rhombus.

m∠A = 50°
m∠C = m∠A
….[Opposite angles of a rhombus are congruent]
∴ m∠C = 50°
Also, m∠D = m∠B …(i)
….[Opposite angles of a rhombus are congruent]
In ₹ABCD,
m∠A + m∠B + m∠C + m∠D = 360°
….[Sum of the measures of the angles of a quadrilateral is 360°]
∴ 50° + m∠B + 50° + m∠D = 360°
∴ m∠B + m∠D + 100° = 360°
∴ m∠B + m∠D = 360° – 100°
∴ m∠B + m∠B = 260° …[From (i)]
∴ 2m∠B = 260°
∴ m∠B = \(\frac { 260 }{ 2 }\)
∴ m∠B = 130°
∴ m∠D = m∠B = 130° …[From (i)]
∴ The measures of the remaining angles of the rhombus are 130°, 50° and 130°.

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.2 Intext Questions and Activities

Question 1.
Construct a rectangle PQRS by taking two convenient adjacent sides. Name the point of intersection of diagonals as T. Using divider and ruler, measure the following lengths.
i. lengths of opposite sides, seg QR and seg PS.
ii. lengths of seg PQ and seg SR.
iii. lengths of diagonals PR and QS.
iv. lengths of seg PT and seg TR, which are parts of the diagonal PR.
v. lengths of seg QT and seg TS, which are parts of the diagonal QS.
Observe the measures. Discuss about the measures obtained by your classmates. (Textbook pg. no. 44)
Solution:
Draw a rectangle PQRS such that, l(PQ) = 3 cm and l(QR) = 4 cm.

Steps of construction:
i. As shown in the rough figure, draw seg QR of length 4 cm.
ii. Placing the centre of the protractor at point Q, draw ray QW making an angle of 90° with seg QR.
iii. By taking a distance of 3 cm on the compass and placing it at point Q, draw an arc on ray QW. Name the point as P.
iv. Draw ray PV and ray RU making an angle of 90° with seg PQ and seg QR respectively.
v. Name the point of intersection of ray PV and ray RU as S.
₹PQRS is the required rectangle.

From the figure,
i. l(QR) = l(PS) = 4 cm
ii. l(PQ) = l(SR) = 3 cm
iii. l(PR) = l(QS) = 5 cm
iv. l(PT) = l(TR) = 2.5 cm
v. l(QT) = l(TS) = 2.5 cm

From the above measures, we can say that for any rectangle,
i. Opposite sides are congruent.
ii. Diagonals are congruent.
iii. Diagonals bisect each other.

Question 2.
Draw a square by taking convenient length of side. Name the point of intersection of its diagonals as E. Using the apparatus in a compass box, measure the following lengths.
i. lengths of diagonal AC and diagonal BD.
ii. lengths of two parts of each diagonal made by point E.
iii. all the angles made at the point E.
iv. parts of each angle of the square made by each diagonal, (e.g. ∠ADB and ∠CDB).
Observe the measures. Also observe the measures obtained by your classmates and discuss about them. (Textbook pg. no. 44)
Solution:
Draw a square ABCD such that its side is 5cm

Steps of construction:
i. As shown in the rough figure, draw seg BC of length 5 cm.
ii. Placing the centre of the protractor at point B, draw ray BP making an angle of 90° with seg BC.
iii. By taking a distance of 5 cm on the compass and placing it at point B, draw an arc on ray BP. Name the point as A.
iv. Placing the centre of the protractor at point C, draw ray CQ making an angle of 90° with seg BC.
v. By taking a distance of 5 cm on the compass and placing it at point C, draw an arc on ray CQ. Name the point as D.
vi. Draw seg AD.
₹ABCD is the required square.

From the figure,
i. l(AC) = l(BD) ≅ 7cm
ii. l(AE) = l(EC) ≅ 3.5cm,
l(BE) = l(ED) ≅ 3.5cm
iii. m∠AED = m∠BEC = m∠CED = m∠BEA = 90°
iv. Angles made by diagonal AC:
m∠BAC = m∠DAC = 45°
m∠BCA = m∠DCA = 45°
Angles made by diagonal BD:
m∠ABD = m∠CBD = 45°
m∠ADB = m∠CDB = 45°

From the above measures, we can say that for any square,
i. Diagonals are congruent.
ii. Diagonals bisect each other.
iii. Diagonals are perpendicular to each other.
iv. Diagonals bisect the opposite angles.

Question 3.
Draw a rhombus EFGH by taking convenient length of side and convenient measure of an angle.
Draw its diagonals and name their point of Intersection as M.
i. Measure the opposite angles of the quadrilateral and angles at the point M.
ii. Measure the two parts of every angle made by the diagonal.
iii. Measure the lengths of both diagonals. Measure the two parts of diagonals made by point M.
Observe the measures. Also observe the measures obtained by your classmates and discuss about them. (Textbook pg. no. 45)
Solution:
Draw a rhombus EFGH such that its side is 5 cm and m∠F = 60°.

Steps of construction:
i. As shown in the rough figure, draw seg FG of length 5 cm.
ii. Placing the centre of the protractor at point F, draw ray FX making an angle 60° with seg FG.
iii. By taking a distance of 5 cm on the compass and placing it at point F, draw an arc on ray FX. Name the point as E.
iv. By taking a distance of 5 cm on the compass and placing it at point E and point G, draw arcs. Name the point of intersection of arcs as H. ₹EFGH is the required rhombus.

From the figure,
i. Opposite angles:
m∠EFG = m∠GHE = 60°,
m∠FEH = m∠HGF = 120°
Angles at the point M:
m∠EMF = m∠FMG = m∠GMH = m∠HME = 90°

ii. Angles made by diagonal FH:
m∠EFH = m∠GFH = 30° m∠EHF = m∠GHF = 30°
Angles made by diagonal EG:
m∠FEG = m∠HEG = 60° m∠FGE = m∠HGE = 60°

iii. l(FH) ≈ 8.6 cm
l(EG) = 5 cm
l(FM) = l(HM) ≈ 4.3 cm
l(EM) = l(GM) ≈ 2.5 cm

From the above measures, we can say that for any rhombus,
i. Opposite angles are congruent.
ii. Diagonals bisect the opposite angles.
iii. Diagonals bisect each other and they are perpendicular to each other.

Maharashtra Board Class 8 Maths Solutions

• Variation Practice Set 7.1 Class 8 Maths Solutions
• Variation Practice Set 7.2 Class 8 Maths Solutions
• Variation Practice Set 7.3 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.1 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.2 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.3 Class 8 Maths Solutions

Variation Class 8 Maths Chapter 7 Practice Set 7.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 7.3 8th Std Maths Answers Solutions Chapter 7 Variation.

Std 8 Maths Practice Set 7.3 Chapter 7 Solutions Answers

Question 1.
Which of the following statements are of inverse variation?
i. Number of workers on a job and time taken by them to complete the job.
ii. Number of pipes of same size to fill a tank and the time taken by them to fill the tank.
iii. Petrol filled in the tank of a vehicle and its cost.
iv. Area of circle and its radius.
Solution:
i. Let, x represent number of workers on a job, and y represent time taken by workers to complete the job.
As the number of workers increases, the time required to complete the job decreases.
∴ \(x \propto \frac{1}{y}\)

ii. Let, n represent number of pipes of same size to fill a tank and t represent time taken by the pipes to fill the tank.
As the number of pipes increases, the time required to fill the tank decreases.
∴ \(\mathrm{n} \propto \frac{1}{\mathrm{t}}\)

iii. Let, p represent the quantity of petrol filled in a tank and c represent the cost of the petrol.
As the quantity of petrol in the tank increases, its cost increases.
∴ p ∝ c

iv. Let, A represent the area of the circle and r represent its radius.
As the area of circle increases, its radius increases.
∴ A ∝ r
∴ Statements (i) and (ii) are examples of inverse variation.

Question 2.
If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
Solution:
Let, n represent the number of workers building the wall and t represent the time required.
Since, the number of workers varies inversely with the time required to build the wall.
∴ \(\mathrm{n} \propto \frac{1}{\mathrm{t}}\)
∴ \(\mathrm{n}=\mathrm{k} \times \frac{1}{\mathrm{t}}\)
where k is the constant of variation
∴ n × t = k …(i)
15 workers can build a wall in 48 hours,
i.e., when n = 15, t = 48
∴ Substituting n = 15 and t = 48 in (i), we get
n × t = k
∴ 15 × 48 = k
∴ k = 720
Substituting k = 720 in (i), we get
n × t = k
∴ n × t = 720 …(ii)
This is the equation of variation.
Now, we have to find number of workers required to do the same work in 30 hours.
i.e., when t = 30, n = ?
∴ Substituting t = 30 in (ii), we get
n × t = 720
∴ n × 30 = 720
∴ n = \(\frac { 720 }{ 30 }\)
∴ n = 24
∴ 24 workers will be required to build the wall in 30 hours.

Question 3.
120 bags of half litre milk can be filled by a machine within 3 minutes find the time to fill such 1800 bags?
Solution:
Let b represent the number of bags of half litre milk and t represent the time required to fill the bags.
Since, the number of bags and time required to fill the bags varies directly.
∴ b ∝ t
∴ b = kt …(i)
where k is the constant of variation.
Since, 120 bags can be filled in 3 minutes
i.e., when b = 120, t = 3
∴ Substituting b = 120 and t = 3 in (i), we get
b = kt
∴ 120 = k × 3
∴ k = \(\frac { 120 }{ 3 }\)
∴ k = 40
Substituting k = 40 in (i), we get
b = kt
∴ b = 40 t …(ii)
This is the equation of variation.
Now, we have to find time required to fill 1800 bags
∴ Substituting b = 1800 in (ii), we get
b = 40 t
∴ 1800 = 40 t
∴ t = \(\frac { 1800 }{ 40 }\)
∴ t = 45
∴ 1800 bags of half litre milk can be filled by the machine in 45 minutes.

Question 4.
A car with speed 60 km/hr takes 8 hours to travel some distance. What should be the increase in the speed if the same distance is
to be covered in \(7\frac { 1 }{ 2 }\) hours?
Solution:
Let v represent the speed of car in km/hr and t represent the time required.
Since, speed of a car varies inversely as the time required to cover a distance.
∴ \(v \propto \frac{1}{t}\)
∴ \(\mathbf{v}=\mathbf{k} \times \frac{1}{\mathbf{t}}\)
where, k is the constant of variation.
∴ v × t = k …(i)
Since, a car with speed 60 km/hr takes 8 hours to travel some distance.
i.e., when v = 60, t = 8
∴ Substituting v = 60 and t = 8 in (i), we get
v × t = k
∴ 60 × 8 = t
∴ k = 480
Substituting k = 480 in (i), we get
v × t = k
∴ v × t = 480 …(ii)
This is the equation of variation.
Now, we have to find speed of car if the same distance is to be covered in \(7\frac { 1 }{ 2 }\) hours.
i.e., when t = \(7\frac { 1 }{ 2 }\) = 7.5 , v = ?
∴ Substituting, t = 7.5 in (ii), we get
v × t = 480
∴ v × 7.5 = 480
\(v=\frac{480}{7.5}=\frac{4800}{75}\)
∴ v = 64
The speed of vehicle should be 64 km/hr to cover the same distance in 7.5 hours.
∴ The increase in speed = 64 – 60
= 4km/hr
∴ The increase in speed of the car is 4 km/hr.

Maharashtra Board Class 8 Maths Solutions

• Variation Practice Set 7.1 Class 8 Maths Solutions
• Variation Practice Set 7.2 Class 8 Maths Solutions
• Variation Practice Set 7.3 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.1 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.2 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.3 Class 8 Maths Solutions

Variation Class 8 Maths Chapter 7 Practice Set 7.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 7.2 8th Std Maths Answers Solutions Chapter 7 Variation.

Std 8 Maths Practice Set 7.2 Chapter 7 Solutions Answers

Question 1.
The information about number of workers and number of days to complete a work is given in the following table. Complete the table.

Solution:
Let, n represent the number of workers and d represent the number of days required to complete a work.
Since, number of workers and number of days to complete a work are in inverse poportion.
∴ \(\mathbf{n} \propto \frac{1}{\mathrm{d}}\)
∴ \(\mathrm{n}=\mathrm{k} \times \frac{1}{\mathrm{d}}\)
where k is the constant of variation.
∴ n × d = k …(i)

i. When n = 30, d = 6
∴ Substituting n = 30 and d = 6 in (i), we get
n × d = k
∴ 30 × 6 = k
∴ k = 180
Substituting k = 180 in (i), we get
∴ n × d = k
∴ n × d = 180 …(ii)
This is the equation of variation

ii. When d = 12, n = 7
∴ Substituting d = 12 in (ii), we get
n × d = 180
∴ n × 12 = 180
∴ n = \(\frac { 180 }{ 12 }\)
∴ n = 15

iii. When n = 10, d = ?
∴ Substituting n = 10 in (ii), we get
n × d = 180
10 × d = 180
∴ d = \(\frac { 180 }{ 10 }\)
∴ d = 18

iv. When d = 36, n = ?
∴ Substituting d = 36 in (ii), we get
n × d = 180
∴ n × 36 = 180
∴ n = \(\frac { 180 }{ 36 }\)
∴ n = 5

Question 2.
Find constant of variation and write equation of variation for every example given below:
i. \(p \propto \frac{1}{q}\) ; if p = 15 then q = 4.
ii. \(z \propto \frac{1}{w}\) ; when z = 2.5 then w = 24.
iii. \(s \propto \frac{1}{t^{2}}\) ; if s = 4 then t = 5.
iv. \(x \propto \frac{1}{\sqrt{y}}\) ; if x = 15 then y = 9.
Solution:
i. \(p \propto \frac{1}{q}\) …[Given]
∴ p = k × \(\frac { 1 }{ q }\)
where, k is the constant of variation.
∴ p × q = k …(i)
When p = 15, q = 4
∴ Substituting p = 15 and q = 4 in (i), we get
p × q = k
∴ 15 × 4 = k
∴ k = 60
Substituting k = 60 in (i), we get
p × q = k
∴ p × q = 60
This is the equation of variation.
∴ The constant of variation is 60 and the equation of variation is pq = 60.

ii. \(z \propto \frac{1}{w}\) …[Given]
∴ z = k × \(\frac { 1 }{ w }\)
where, k is the constant of variation,
∴ z × w = k …(i)
When z = 2.5, w = 24
∴ Substituting z = 2.5 and w = 24 in (i), we get
z × w = k
∴ 2.5 × 24 = k
∴ k = 60
Substituting k = 60 in (i), we get
z × w = k
∴ z × w = 60
This is the equation of variation.
∴ The constant of variation is 60 and the equation of variation is zw = 60.

iii. \(s \propto \frac{1}{t^{2}}\) …[Given]
∴ \(s=k \times \frac{1}{t^{2}}\)
where, k is the constant of variation,
∴ s × t² = k …(i)
When s = 4, t = 5
∴ Substituting, s = 4 and t = 5 in (i), we get
s × t² = k
∴ 4 × (5)² = k
∴ k = 4 × 25
∴ k = 100
Substituting k = 100 in (i), we get
s × t² = k
∴ s × t² = 100
This is the equation of variation.
∴ The constant of variation is 100 and the equation of variation is st² = 100.

iv. \(x \propto \frac{1}{\sqrt{y}}\) …[Given]
∴ \(x=\mathrm{k} \times \frac{1}{\sqrt{y}}\)
where, k is the constant of variation,
∴ x × √y = k …(i)
When x = 15, y = 9
∴ Substituting x = 15 and y = 9 in (i), we get
x × √y = k
∴ 15 × √9 = k
∴ k = 15 × 3
∴ k = 45
Substituting k = 45 in (i), we get
x × √y = k
∴ x × √y = 45 .
This is the equation of variation.
∴ The constant of variation is k = 45 and the equation of variation is x√y = 45.

Question 3.
The boxes are to be filled with apples in a heap. If 24 apples are put in a box then 27 boxes are needed. If 36 apples are filled in a box how many boxes will be needed?
Solution:
Let x represent the number of apples in each box and y represent the total number of boxes required.
The number of apples in each box are varying inversely with the total number of boxes.
∴ \(x \infty \frac{1}{y}\)
∴ \(x=k \times \frac{1}{y}\)
where, k is the constant of variation,
∴ x × y = k …(i)
If 24 apples are put in a box then 27 boxes are needed.
i.e., when x = 24, y = 27
∴ Substituting x = 24 and y = 27 in (i), we get
x × y = k
∴ 24 × 27 = k
∴ k = 648
Substituting k = 648 in (i), we get
x × y = k
∴ x × y = 648 …(ii)
This is the equation of variation.
Now, we have to find number of boxes needed
when, 36 apples are filled in each box.
i.e., when x = 36,y = ?
∴ Substituting x = 36 in (ii), we get
x × y = 648
∴ 36 × y = 648
∴ y = \(\frac { 648 }{ 36 }\)
∴ y = 18
∴ If 36 apples are filled in a box then 18 boxes are required.

Question 4.
Write the following statements using symbol of variation.

1. The wavelength of sound (l) and its frequency (f) are in inverse variation.
2. The intensity (I) of light varies inversely with the square of the distance (d) of a screen from the lamp.

Solution:

1. \(l \propto \frac{1}{\mathrm{f}}\)
2. \(\mathrm{I} \propto \frac{1}{\mathrm{d}^{2}}\)

Question 5.
\(x \propto \frac{1}{\sqrt{y}}\) and when x = 40 then y = 16. If x = 10, find y.
Solution:
\(x \propto \frac{1}{\sqrt{y}}\)
∴ \(x=\mathrm{k} \times \frac{1}{\sqrt{y}}\)
where, k is the constant of variation.
∴ x × √y = k …(i)
When x = 40, y = 16
∴ Substituting x = 40 andy = 16 in (i), we get
x × √y = k
∴ 40 × √16 = k
∴ k = 40 × 4
∴ k = 160
Substituting k = 160 in (i), we get
x × √y = k
∴ x × √y = 160 …(ii)
This is the equation of variation.
When x = 10,y = ?
∴ Substituting, x = 10 in (ii), we get
x × √y = 160
∴ 10 × √y = 160
∴ √y = \(\frac { 160 }{ 10 }\)
∴ √y = 16
∴ y = 256 … [Squaring both sides]

Question 6.
x varies inversely as y, when x = 15 then y = 10, if x = 20, then y = ?
Solution:
Given that,
\(x \propto \frac{1}{\sqrt{y}}\)
∴ \(x=\mathrm{k} \times \frac{1}{\sqrt{y}}\)
where, k is the constant of variation.
∴ x × y = k …(i)
When x = 15, y = 10
∴ Substituting, x = 15 and y = 10 in (i), we get
x × y = k
∴ 15 × 10 = k
∴ k = 150
Substituting, k = 150 in (i), we get
x × y = k
∴ x × y = 150 …(ii)
This is the equation of variation.
When x = 20, y = ?
∴ substituting x = 20 in (ii), we get
x × y = 150
∴ 20 × y = 150
∴ y = \(\frac { 150 }{ 20 }\)
∴ y = 7.5

Maharashtra Board Class 8 Maths Solutions

• Variation Practice Set 7.1 Class 8 Maths Solutions
• Variation Practice Set 7.2 Class 8 Maths Solutions
• Variation Practice Set 7.3 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.1 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.2 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.3 Class 8 Maths Solutions

Variation Class 8 Maths Chapter 7 Practice Set 7.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 7.1 8th Std Maths Answers Solutions Chapter 7 Variation.

Std 8 Maths Practice Set 7.1 Chapter 7 Solutions Answers

Question 1.
Write the following statements using the symbol of variation.

1. Circumference (c) of a circle is directly proportional to its radius (r).
2. Consumption of petrol (l) in a car and distance traveled by that car (d) are in direct variation.

Solution:

1. c ∝ r
2. l ∝ d

Question 2.
Complete the following table considering that the cost of apples and their number are in direct variation.

Solution:
The cost of apples (y) and their number (x) are in direct variation.
∴y ∝ x
∴y = kx …(i)
where k is the constant of variation

i. When, x = 1, y = 8
∴ Substituting, x = 1 and y = 8 in (i), we get y = kx
∴ 8 = k × 1
∴ k = 8
Substituting k = 8 in (i), we get
y = kx
∴ y = 8x …(ii)
This the equation of variation

ii. When,y = 56, x = ?
∴ Substituting y = 56 in (ii), we get
y = 8x
∴ 56 = 8x
∴ x = \(\frac { 56 }{ 8 }\)
∴ x = 7

iii. When, x = 12, y = ?
∴ Substituting x = 12 in (ii), we get
y = 8x
∴ y = 8 × 12
∴ y = 96

iv. When, y = 160, x = ?
∴ Substituting y = 160 in (ii), we get
y = 8x
∴ 160 = 8x
∴ x = \(\frac { 160 }{ 8 }\)
∴ x = 20

Question 3.
If m ∝ n and when m = 154, n = 7. Find the value of m, when n = 14.
Solution:
Given that,
m ∝ n
∴ m = kn …(i)
where k is constant of variation.
When m = 154, n = 7
∴ Substituting m = 154 and n = 7 in (i), we get
m = kn
∴ 154 = k × 7
∴ \(k=\frac { 154 }{ 7 }\)
∴ k = 22
Substituting k = 22 in (i), we get
m = kn
∴ m = 22n …(ii)
This is the equation of variation.
When n = 14, m = ?
∴ Substituting n = 14 in (ii), we get
m = 22n
∴ m = 22 × 14
∴ m = 308

Question 4.
If n varies directly as m, complete the following table.

Solution:
Given, n varies directly as m
∴ n ∝ m
∴ n = km …(i)
where, k is the constant of variation

i. When m = 3, n = 12
∴ Substituting m = 3 and n = 12 in (i), we get
n = km
∴ 12 = k × 3
∴ \(k=\frac { 12 }{ 3 }\)
∴ k = 4
Substituting, k = 4 in (i), we get
n = km
∴ n = 4m …(ii)
This is the equation of variation.

ii. When m = 6.5, n = ?
∴ Substituting, m = 6.5 in (ii), we get
n = 4m
∴ n = 4 × 6.5
∴ n = 26

iii. When n = 28, m = ?
∴ Substituting, n = 28 in (ii), we get
n = 4m
∴ 28 = 4m
∴ 28 = 4m
∴ \(m=\frac { 28 }{ 4 }\)
∴ m = 7

iv. When m = 1.25, n = ?
∴ Substituting m = 1.25 in (ii), we get
n = 4m
∴ n = 4 × 1.25
∴ n = 5

Question 5.
y varies directly as square root of x. When x = 16, y = 24. Find the constant of variation and equation of variation.
Solution:
Given, y varies directly as square root of x.
∴ y ∝ √4x
∴ y = k √x …(i)
where, k is the constant of variation.
When x = 16 ,y = 24.
∴ Substituting, x = 16 and y = 24 in (i), we get
y = k√x
∴24 = k√16
∴24 = 4k
∴ \(k=\frac { 24 }{ 4 }\)
∴ k = 6
Substituting k = 6 in (i), we get
y = k√x
∴ y = 6√x
This is the equation of variation
∴ The constant of variation is 6 and the equation of variation is y = 6√x .

Question 6.
The total remuneration paid to laborers, employed to harvest soybean is in direct variation with the number of laborers. If remuneration of 4 laborers is Rs 1000, find the remuneration of 17 laborers.
Solution:
Let, m represent total remuneration paid to laborers and n represent number of laborers employed to harvest soybean.
Since, the total remuneration paid to laborers, is in direct variation with the number of laborers.
∴ m ∝ n
∴ m = kn …(i)
where, k = constant of variation
Remuneration of 4 laborers is Rs 1000.
i. e., when n = 4, m = Rs 1000
∴ Substituting, n = 4 and m = 1000 in (i), we get m = kn
∴ 1000 = k × 4
∴ \(k=\frac { 1000 }{ 4 }\)
∴ k = 250
Substituting, k = 250 in (i), we get
m = kn
∴ m = 250 n …(ii)
This is the equation of variation
Now, we have to find remuneration of 17 laborers.
i. e., when n = 17, m = ?
∴ Substituting n = 17 in (ii), we get
m = 250 n
∴ m = 250 × 17
∴ m = 4250
∴ The remuneration of 17 laborers is Rs 4250.

Maharashtra Board Class 8 Maths Chapter 7 Variation Practice Set 7.1 Intext Questions and Activities

Question 1.
If the rate of notebooks is Rs 240 per dozen, what is the cost of 3 notebooks?
Also find the cost of 9 notebooks, 24 notebooks and 50 notebooks and complete the following table. (Textbook pg. no. 35)

Solution:
As the number of notebooks increases their cost also increases.
∴ Number of notebooks and cost of notebooks are in direct proportion.

i.

∴ y = 3 × 20
∴ y = 60

ii.

∴ y = 9 × 20
∴ y = 180

iii.

∴ y = 24 × 20
∴ y = 480

iv.

∴ y = 50 × 20
∴ y = 1000

Maharashtra Board Class 8 Maths Solutions

• Variation Practice Set 7.1 Class 8 Maths Solutions
• Variation Practice Set 7.2 Class 8 Maths Solutions
• Variation Practice Set 7.3 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.1 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.2 Class 8 Maths Solutions
• Quadrilateral: Constructions and Types Practice Set 8.3 Class 8 Maths Solutions

Factorisation of Algebraic Expressions Class 8 Maths Chapter 6 Practice Set 6.4 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.4 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Std 8 Maths Practice Set 6.4 Chapter 6 Solutions Answers

Question 1.
Simplify:
i. \(\frac{m^{2}-n^{2}}{(m+n)^{2}} \times \frac{m^{2}+m n+n^{2}}{m^{3}-n^{3}}\)
ii. \(\frac{a^{2}+10 a+21}{a^{2}+6 a-7} \times \frac{a^{2}-1}{a+3}\)
iii. \(\frac{8 x^{3}-27 y^{3}}{4 x^{2}-9 y^{2}}\)
iv. \(\frac{x^{2}-5 x-24}{(x+3)(x+8)} \times \frac{x^{2}-64}{(x-8)^{2}}\)
v. \(\frac{3 x^{2}-x-2}{x^{2}-7 x+12} \div \frac{3 x^{2}-7 x-6}{x^{2}-4}\)
vi. \(\frac{4 x^{2}-11 x+6}{16 x^{2}-9}\)
vii. \(\frac{a^{3}-27}{5 a^{2}-16 a+3} \div \frac{a^{2}+3 a+9}{25 a^{2}-1}\)
viii. \(\frac{1-2 x+x^{2}}{1-x^{3}} \times \frac{1+x+x^{2}}{1+x}\)
Solution:
i. \(\frac{m^{2}-n^{2}}{(m+n)^{2}} \times \frac{m^{2}+m n+n^{2}}{m^{3}-n^{3}}\)

ii. \(\frac{a^{2}+10 a+21}{a^{2}+6 a-7} \times \frac{a^{2}-1}{a+3}\)

iii. \(\frac{8 x^{3}-27 y^{3}}{4 x^{2}-9 y^{2}}\)

iv. \(\frac{x^{2}-5 x-24}{(x+3)(x+8)} \times \frac{x^{2}-64}{(x-8)^{2}}\)

v. \(\frac{3 x^{2}-x-2}{x^{2}-7 x+12} \div \frac{3 x^{2}-7 x-6}{x^{2}-4}\)

vi. \(\frac{4 x^{2}-11 x+6}{16 x^{2}-9}\)

vii. \(\frac{a^{3}-27}{5 a^{2}-16 a+3} \div \frac{a^{2}+3 a+9}{25 a^{2}-1}\)

viii. \(\frac{1-2 x+x^{2}}{1-x^{3}} \times \frac{1+x+x^{2}}{1+x}\)

Maharashtra Board Class 8 Maths Solutions

• Factorisation of Algebraic Expressions Practice Set 6.1 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.2 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.3 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.4 Class 8 Maths Solutions

Factorisation of Algebraic Expressions Class 8 Maths Chapter 6 Practice Set 6.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.3 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Std 8 Maths Practice Set 6.3 Chapter 6 Solutions Answers

Question 1.
Factorize
i. y³ – 27
ii. x³ – 64y³
iii. 27m³ – 216n³
iv. 125y³ – 1
v. \(8 p^{3}-\frac{27}{p^{3}}\)
vi. 343a³ – 512b³
vii. 64x³ – 729y³
viii. \(16 a^{3}-\frac{128}{b^{3}}\)
Solution:
i. y³ – 27
= y³ – (3)³
Here, a = y and b = 3
∴ y³ – 27 = (y – 3)[y² + y(3) + (3)2]
…[∵ a³ – b³ = (a – b) (a² + ab + b²)]
= (y – 3)(y² + 3y + 9)

ii. x³ – 64y³
= x³ – (4y)³
Here, a = x and b = 4y
∴ x³ – 64y³ = (x – 4y)[x² + x(4y) + (4y)²]
…[∵ a³ – b³ = (a – b)(a² + ab + b²)]
= (x – 4y)(x² + 4xy + 16y²)

iii. 27m³ – 216n³
= 27 (m³ – 8n³)
… [Taking out the common factor 27]
= 27 [m³ – (2n)³]
Here, a = m and b = 2n
∴ 27m³ – 216n³
= 27 {(m – 2n) [m² + m(2n) + (2n)²]}
….[∵ a³ – b³ = (a – b) (a² + ab + b²)]
= 27 (m – 2n)(m² + 2mn + 4n²)

iv. 125y³ – 1
= (5y)³ – 1³
Here, a = 5y and b = 1
∴ 125y³ – 1 = (5y – 1) [(5y)² + (5y)(1) + (1)²]
…[∵ a³ – b³ = (a – b)(a² + ab + b²)]
= (5y – 1) (25y² + 5y + 1)

v. \(8 p^{3}-\frac{27}{p^{3}}\)

vi. 343a³ – 512b³
= (7a)³ – (8b)³
Here, A = 7a and B = 8b
∴ 343a³ – 512b³
= (7a – 8b) [(7a)² + (7a)(8b) + (8b)²]
…[∵ A³ – B³ = (A – B)(A² + AB + B²)]
= (7a – 8b) (49a² + 56ab + 64b²)

vii. 64x³ – 729y³
= (4x)³ – (9y)³
Here, a = 4x and b = 9y
∴ 64x³ – 729y³
= (4x – 9y) [(4x)² + (4x) (9y) + (9y)²]
…[∵ a³ – b³ = (a – b)(a² + ab + b²)]
= (4x – 9y) (16x² + 36xy + 81y²)

viii. \(16 a^{3}-\frac{128}{b^{3}}\)

Question 2.
Simplify:
i. (x + y)³ – (x – y)³
ii. (3a + 5b)³ – (3a – 5b)³
iii. (a + b)³ – a³ – b³
iv. p³ – (p + 1)³
v. (3xy – 2ab)³ – (3xy + 2ab)³
Solution:
i. (x + y)³ – (x – y)³
Here, a = x + y and b = x – y
(x + y)³ – (x – y)³
= [(x + y) – (x – y)] [(x + y)² + (x + y) (x – y) + (x – y)]
…[a³ – b³ = (a – b)(a² + ab + b²)]
= (x + y – x + y) [(x² + 2xy + y²) + (x² – y²) + (x² – 2xy + y²)]
= 2y(x² + x² + x² + 2xy – 2xy + y² – y² + y²)
= 2y (3x² + y²)
= 6x²y + 2y³

ii. (3a + 5b)³ – (3a – 5b)³
Here, A = 3a + 5b and B = 3a – 5b
= [(3a + 5b) – (3a – 5b)] [(3a + 5b)² + (3a + 5b) (3a – 5b) + (3a – 5b)²]
…[∵ A³ – B³ = (A – B)(A² + AB + B²)]
= (3a + 5b – 3a + 5b) [(9a² + 30ab + 25b²) + (9a² – 25b²) + (9a² – 30ab + 25b²)]
= 10b (9a² + 9a² + 9a² + 30ab – 30ab + 25b² – 25b² + 25b²)
= 10b (27a² + 25b²)
= 270a²b + 250b³

iii. (a + b)³ – a³ – b³
= a³ + 3a²b + 3ab² + b³ – a³ – b³
= 3a²b + 3ab²

iv. p³ – (p + 1)³
= p³ – (p³ + 3p² + 3p + 1) …[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= p³ – p³ – 3p² – 3p – 1
= – 3p² – 3p – 1

v. (3xy – 2ab)³ – (3xy + 2ab)³
Here, A = 3xy – 2ab and B = 3xy + 2ab
∴ (3xy – 2ab)³ – (3xy + 2ab)³
= [(3xy – 2ab) – (3xy + 2ab)] [(3xy – 2ab)² + (3xy – 2ab) (3xy + 2ab) + (3xy + 2ab)²]
…[∵ A³ – B³ = (A – B) (A² + AB + B²)]
= (3xy – 2ab – 3xy – 2ab) [(9x²y² – 12xyab + 4a²b²) + (9x²y² – 4a²b²) + (9x²y² + 12xyab + 4a²b²)]
= (- 4ab) (9x²y² + 9x²y² + 9x²y² – 12xyab + 12xyab + 4a²b² – 4a²b² + 4a²b²)
= (- 4ab) (27 xy² + 4a²b²)
= -108x²y²ab – 16a³b³

Maharashtra Board Class 8 Maths Solutions

• Factorisation of Algebraic Expressions Practice Set 6.1 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.2 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.3 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.4 Class 8 Maths Solutions

Factorisation of Algebraic Expressions Class 8 Maths Chapter 6 Practice Set 6.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.2 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Std 8 Maths Practice Set 6.2 Chapter 6 Solutions Answers

Question 1.
Factorise:
i. x³ + 64y³
ii. 125p³ + q³
iii. 125k³ + 27m³
iv. 2l³ + 432m³
v. 24a³ + 81b³
vi. \(y^{3}+\frac{1}{8 y^{3}}\)
vii. \(\mathrm{a}^{3}+\frac{8}{\mathrm{a}^{3}}\)
viii. \(1+\frac{\mathrm{q}^{3}}{125}\)
Solution:
i. x³ + 64y³
= x³ + (4y)³
Here, a = x and b = 4y
∴ x³ + 64y³ = (x + 4y) [x² – x(4y) + (4y)²]
….[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= (x + 4y)(x² – 4xy + 16y²)

ii. 125p³ + q³
= (5p)³ + q³
Here, a = 5p and b = q
∴ 125p³ + q³ = (5p + q)[(5p)² – (5p)(q) + q²]
…[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= (5p + q)(25p² – 5pq + q²)

iii. 125k³ + 27m³
= (5k)³ + (3m)³
Here, a = 5k and b = 3m
∴ 125k³ + 27m³
= (5k + 3m) [(5k)² – (5k)(3m) + (3m)²]
…[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= (5k + 3m)(25k² – 15km + 9m²)

iv. 2l³ + 432m³
= 2 (l³ + 216m³)
… [Taking out the common factor 2]
= 2[l³ + (6m)³]
Here, a = l and b = 6m
2l³ + 432m³ = 2 {(l + 6m)[l² – l(6m) + (6m)²]}
…[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= 2(l + 6m)(l² – 6lm + 36m²)

v. 24a³ + 81b³
…[Taking out the common factor 3]
= 3 [(2a)³ + (3b)³]
Here, A = 2a and B = 3b
∴ 24a³ + 81b³
= 3 {(2a + 3b) [(2a)² – (2a)(3b) + (3b)²]}
…[∵ A³ + B³ = (A + B) (A² – AB + B²)]
= 3(2a + 3b)(4a² – 6ab + 9b²)

vi. \(y^{3}+\frac{1}{8 y^{3}}\)

vii. \(\mathrm{a}^{3}+\frac{8}{\mathrm{a}^{3}}\)

viii. \(1+\frac{\mathrm{q}^{3}}{125}\)

Maharashtra Board Class 8 Maths Solutions

• Factorisation of Algebraic Expressions Practice Set 6.1 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.2 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.3 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.4 Class 8 Maths Solutions

Factorisation of Algebraic Expressions Class 8 Maths Chapter 6 Practice Set 6.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.1 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Std 8 Maths Practice Set 6.1 Chapter 6 Solutions Answers

Question 1.
Factorize:
i. x² + 9x + 18
ii. x² – 10x + 9
iii. y² + 24y + 144
iv. 5y² + 5y – 10
v. p² – 2p – 35
vi. p² – 7p – 44
vii. m² – 23m + 120
viii. m² – 25m + 100
ix. 3x² + 14x + 15
x. 2x² + x – 45
xi. 20x² – 26x + 8
xii. 44x² – x – 3
Solution:
i. x² + 9x + 18
= x² + 6x + 3x + 18
= x (x + 6) + 3(x + 6)
= (x + 6) (x + 3)

ii. x² – 10x + 9
= x² – 9x – x + 9
= x (x – 9) – 1(x – 9)
= (x – 9)(x – 1)

iii. y² + 24y + 144
= y² + 12y + 12y + 144
= y(y + 12) + 12(y + 12)
= (y + 12)(y + 12)

iv. 5y² + 5y – 10
= 5(y² + y – 2)
… [Taking out the common factor 5]
= 5(y² + 2y – y – 2)
= 5[y(y + 2) – 1(y + 2)]
= 5 (p + 2)(y- 1)

v. p² – 2p – 35
= p² – 7p + 5p – 35
= p(p – 7) + 5(p – 7)
= (p – 7)(p + 5)

vi. p² – 7p – 44
= p² – 11p + 4p – 44
= p(p – 11) + 4(p – 11)
= (p – 11)(p + 4)

vii. m² – 23m + 120
= m² – 15m – 8m + 120
= m (m – 15) – 8 (m – 15)
= (m – 15) (m – 8)

viii. m² – 25m + 100
= m² – 20m – 5m + 100
= m(m – 20) – 5(m – 20)
= (m – 20) (m – 5)

ix. 3x² + 14x + 15 3 × 15 = 45
= 3x² + 9x + 5x + 15
= 3x(x + 3) + 5(x + 3)
= (x + 3) (3x + 5)

x. 2x² + x – 45 2 × (- 45) = -90
= 2x² + 10x – 9x – 45
= 2x(x + 5) – 9 (x + 5)
= (x + 5) (2x – 9)

xi. 20x² – 26x + 8
= 2(10x² – 13x + 4) 10 × 4 = 40
… [Taking out the common factor 2]
= 2(10x² – 8x – 5x + 4)
= 2[2x(5x – 4) – 1(5x – 4)]
= 2 (5x – 4) (2x – 1)

xii. 44x² – x – 3 44 × (-3) = -132
= 44x² – 12x + 11x – 3
= 4x(11x – 3) + 1(11x – 3)
= (11x – 3) (4x + 1)

Maharashtra Board Class 8 Maths Solutions

• Factorisation of Algebraic Expressions Practice Set 6.1 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.2 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.3 Class 8 Maths Solutions
• Factorisation of Algebraic Expressions Practice Set 6.4 Class 8 Maths Solutions