Prasanna

10th Standard Maths 2 Practice Set 2.1 Chapter 2 Pythagoras Theorem Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 2 Pythagoras Theorem.

Class 10 Maths Part 2 Practice Set 2.1 Chapter 2 Pythagoras Theorem Questions With Answers Maharashtra Board

Question 1.
Identify, with reason, which of the following are Pythagorean triplets.
i. (3,5,4)
ii. (4,9,12)
iii. (5,12,13)
iv. (24,70,74)
v. (10,24,27)
vi. (11,60,61)
Solution:
i. Here, 5² = 25
3² + 4² = 9 + 16 = 25
∴ 5² = 3² + 4²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (3,5,4) is a Pythagorean triplet.

ii. Here, 12² = 144
4² + 9²= 16 + 81 =97
∴ 12² ≠ 4² + 92
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (4,9,12) is not a Pythagorean triplet.

iii. Here, 13² = 169
5² + 12² = 25 + 144 = 169
∴ 13² = 5² + 12²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (5,12,13) is a Pythagorean triplet.

iv. Here, 74² = 5476
24² + 70² = 576 + 4900 = 5476
∴ 74² = 24² + 70²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (24, 70,74) is a Pythagorean triplet.

v. Here, 27² = 729
10² + 24² = 100 + 576 = 676
∴ 27² ≠ 10² + 24²
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (10,24,27) is not a Pythagorean triplet.

vi. Here, 61² = 3721
11² + 60² = 121 + 3600 = 3721
∴ 61² = 11² + 60²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (11,60,61) is a Pythagorean triplet.

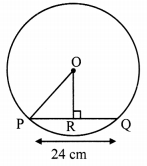
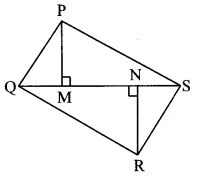
Question 2.
In the adjoining figure, ∠MNP = 90°, seg NQ ⊥ seg MP,MQ = 9, QP = 4, find NQ.

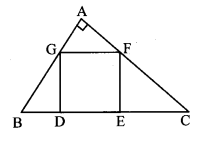
Solution:
In ∆MNP, ∠MNP = 90° and [Given]
seg NQ ⊥ seg MP
NQ² = MQ × QP [Theorem of geometric mean]
∴ NQ = \(\sqrt { MQ\times QP }\) [Taking square root of both sides]
= \(\sqrt { 9\times 4 } \)
= 3 × 2
∴NQ = 6 units

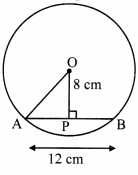
Question 3.
In the adjoining figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q – M – R, PM = 10, QM = 8, find QR.

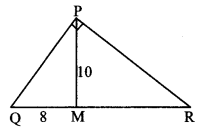
Solution:
In ∆PQR, ∠QPR = 90° and [Given]
seg PM ⊥ seg QR
∴ PM² = OM × MR [Theorem of geometric mean]
∴ 10² = 8 × MR
∴ MR = \(\frac { 100 }{ 8 } \)
= 12.5
Now, QR = QM + MR [Q – M – R]
= 8 + 12.5
∴ QR = 20.5 units

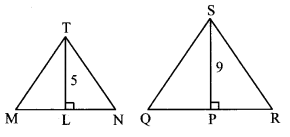
Question 4.
See adjoining figure. Find RP and PS using the information given in ∆PSR.

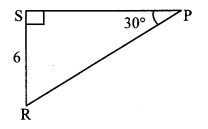
Solution:
In ∆PSR, ∠S = 90°, ∠P = 30° [Given]
∴ ∠R = 60° [Remaining angle of a triangle]
∴ ∆PSR is a 30° – 60° – 90° triangle.
RS = \(\frac { 1 }{ 2 } \) RP [Side opposite to 30°]
∴6 = \(\frac { 1 }{ 2 } \) RP
∴ RP = 6 × 2 = 12 units
Also, PS = \(\frac{\sqrt{3}}{2}\) RP [Side opposite to 60°]
= \(\frac{\sqrt{3}}{2}\) × 12
= \(6 \sqrt{3}\) units
∴ RP = 12 units, PS = 6 \(\sqrt { 3 }\) units

Question 5.
For finding AB and BC with the help of information given in the adjoining figure, complete the following activity.

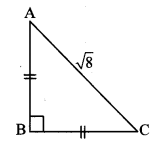
Solution:
AB = BC [Given]
∴ ∠BAC = ∠BCA [Isosceles triangle theorem]
Let ∠BAC = ∠BCA = x (i)
In ∆ABC, ∠A + ∠B + ∠C = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x + 90° + x = 180° [From (i)]
∴ 2x = 90°
∴ x = \(\frac { 90° }{ 2 } \) [From (i)]
∴ x = 45°

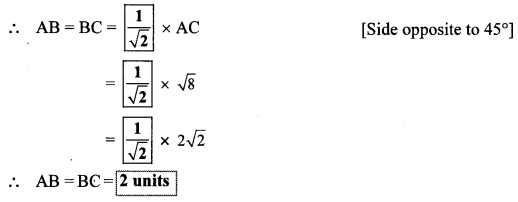
Question 6.
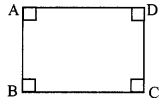
Find the side and perimeter of a square whose diagonal is 10 cm.

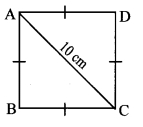
Solution:
Let ꠸ABCD be the given square.
l(diagonal AC) = 10 cm
Let the side of the square be ‘x’ cm.
In ∆ABC,
∠B = 90° [Angle of a square]
∴ AC² = AB² + BC² [Pythagoras theorem]
∴ 10² = x² + x²
∴ 100 = 2x²
∴ x² = \(\frac { 100 }{ 2 } \)
∴x² = 50
∴ x = \(\sqrt { 50 }\) [Taking square root of both sides]
= \(=\sqrt{25 \times 2}=5 \sqrt{2}\)
∴side of square is 5\(\sqrt { 2 }\) cm.
= 4 × 5 \(\sqrt { 2 }\)
∴ Perimeter of square = 20 \(\sqrt { 2 }\) cm

Question 7.
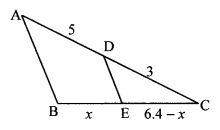
In the adjoining figure, ∠DFE = 90°, FG ⊥ ED. If GD = 8, FG = 12, find
i. EG
ii. FD, and
iii. EF

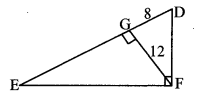
Solution:
i. In ∆DEF, ∠DFE = 90° and FG ⊥ ED [Given]
∴ FG² = GD × EG [Theorem of geometric mean]
∴ 122 = 8 × EG .
∴ EG = \(\frac { 144 }{ 8 } \)
∴ EG = 18 units

ii. In ∆FGD, ∠FGD = 90° [Given]
∴ FD² = FG² + GD² [Pythagoras theorem]
= 122 + 82 = 144 + 64
= 208
∴ FD = \(\sqrt { 208 }\) [Taking square root of both sides]
∴ FD = 4 \(\sqrt { 13 }\) units

iii. In ∆EGF, ∠EGF = 90° [Given]
∴ EF² = EG² + FG² [Pythagoras theorem]
= 182 + 122 = 324 + 144
= 468
∴ EF = \(\sqrt { 468 }\) [Taking square root of both sides]
∴ EF = 6 \(\sqrt { 13 }\) units

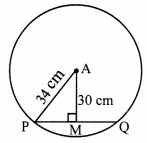
Question 8.
Find the diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.

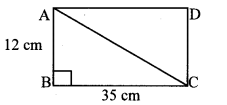
Solution:
Let ꠸ABCD be the given rectangle.
AB = 12 cm, BC 35 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
∴ AC² = AB² + BC² [Pythagoras theorem]
= 122 + 352
= 144 + 1225
= 1369
∴ AC = \(\sqrt { 1369 }\) [Taking square root of both sides]
= 37 cm
∴ The diagonal of the rectangle is 37 cm.

Question 9.
In the adjoining figure, M is the midpoint of QR. ∠PRQ = 90°.
Prove that, PQ² = 4 PM² – 3 PR².

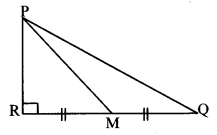
Solution:
Proof:
In ∆PQR, ∠PRQ = 90° [Given]
PQ² = PR² + QR² (i) [Pythagoras theorem]
RM = \(\frac { 1 }{ 2 } \) QR [M is the midpoint of QR]
∴ 2RM = QR (ii)
∴ PQ² = PR² + (2RM)² [From (i) and (ii)]
∴ PQ² = PR² + 4RM² (iii)
Now, in ∆PRM, ∠PRM = 90° [Given]
∴ PM² = PR² + RM² [Pythagoras theorem]
∴ RM² = PM² – PR² (iv)
∴ PQ² = PR² + 4 (PM² – PR²) [From (iii) and (iv)]
∴ PQ² = PR² + 4 PM² – 4 PR²
∴ PQ² = 4 PM² – 3 PR²

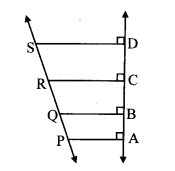
Question 10.
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Solution:
Let AC and CE represent the ladder of length 5.8 m, and A and E represent windows of the buildings on the opposite sides of the street. BD is the width of the street.

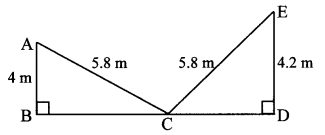
AB = 4 m and ED = 4.2 m
In ∆ABC, ∠B = 90° [Given]
AC² = AB² + BC² [Pythagoras theorem]
∴ 5.8² = 4² + BC²
∴ 5.8² – 4² = BC²
∴ (5.8 – 4) (5.8 + 4) = BC²
∴ 1.8 × 9.8 = BC²

CE² = CD² + DE² [Pythagoras theorem]
∴ 5.8² = CD² + 4.22
∴ 5.8² – 4.2² = CD²
∴ (5.8 – 4.2) (5.8 + 4.2) = CD²
∴ 1.6 × 10 = CD²
∴ CD² = 16
∴ CD = 4m (ii) [Taking square root of both sides]
Now, BD = BC + CD [B – C – D]
= 4.2 + 4 [From (i) and (ii)]
= 8.2 m
∴ The width of the street is 8.2 metres.

Question 1.
Verify that (3,4,5), (5,12,13), (8,15,17), (24,25,7) are Pythagorean triplets. (Textbook pg. no. 30)
Solution:
i. Here, 5² = 25
3² + 4² = 9 + 16 = 25
∴ 5² = 3² + 4²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 3,4,5 is a Pythagorean triplet.

ii. Here, 13² = 169
5² + 12² = 25 + 144 = 169
∴ 13² = 5² + 12²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 5,12,13 is a Pythagorean triplet.

iii. Here, 17² = 289
8² + 15² = 64 + 225 = 289
∴ 17² = 8² + 15²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 8,15,17 is a Pythagorean triplet.

iv. Here, 25² = 625
7² + 24² = 49 + 576 = 625
∴ 25² = 7² + 24²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 24,25, 7 is a Pythagorean triplet.

Question 2.
Assign different values to a and b and obtain 5 Pythagorean triplets. (Textbook pg. no. 31)
Solution:
i. Let a = 2, b = 1
a² + b² = 2² + 1² = 4 + 1 = 5
a² – b² = 2² – 1² = 4 – 1 = 3
2ab = 2 × 2 × 1 = 4
∴ (5, 3, 4) is a Pythagorean triplet.

ii. Let a = 4,b = 3
a² + b² = 4² + 3² = 16 + 9 = 25
a² – b² = 4² – 3² = 16 – 9 = 7
2ab = 2 × 4 × 3 = 24
∴ (25, 7, 24) is a Pythagorean triplet.

iii. Let a = 5, b = 2
a² + b² = 5² + 2² = 25 + 4 = 29
a² – b² = 5² – 2² = 25 – 4 = 21
2ab = 2 × 5 × 2 = 20
∴ (29, 21, 20) is a Pythagorean triplet.

iv. Let a = 4,b = 1
a² + b² = 4² + 1² = 16 + 1 = 17
a² – b² = 42 – 12 = 16 – 1 = 15
2ab = 2 × 4 × 1 = 8
∴ (17, 15, 8) is a Pythagorean triplet.

v. Let a = 9, b = 7
a² + b² = 92 + 72 = 81 + 49 = 130
a² – b² = 92 – 72 = 81 – 49 = 32
2ab = 2 × 9 × 7 = 126
∴ (130,32,126) is a Pythagorean triplet.

Note: Numbers in Pythagorean triplet can be written in any order.

Maharashtra State Board Class 10 Maths Solutions Part 2

• Similarity Practice Set 1.1 Class 10 Maths Solutions
• Similarity Practice Set 1.2 Class 10 Maths Solutions
•  Similarity Practice Set 1.3 Class 10 Maths Solutions
• Similarity Practice Set 1.4 Class 10 Maths Solutions
• Similarity Problem Set 1 Class 10 Maths Solutions
• Pythagoras Theorem Practice Set 2.1 Class 10 Maths Solutions
• Pythagoras Theorem Practice Set 2.2 Class 10 Maths Solutions
• Pythagoras Theorem Problem Set 2 Class 10 Maths Solutions

9th Standard Maths 2 Practice Set 6.1 Chapter 6 Circle Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 6 Circle.

Class 9 Maths Part 2 Practice Set 6.1 Chapter 6 Circle Questions With Answers Maharashtra Board

Question 1.
Distance of chord AB from the centre of a circle is 8 cm. Length of the chord AB is 12 cm. Find the diameter of a circle.
Given: In a circle with centre O,
OA is radius and AB is its chord,
seg OP ⊥ chord AB, A-P-B
AB = 12 cm, OP =8 cm
To Find: Diameter of the circle
Solution:

i. AP = \(\frac { 1 }{ 2 }\) AB [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
∴ AP = \(\frac { 1 }{ 2 }\) x 12 = 6 cm ….(i)

ii. In ∆OPA, ∠OPA = 90°
∴ OA² = OP² + AP² [Pythagoras theorem]
= 8² + 6² [From (i)]
= 64 + 36
∴ OA² = 100
∴ OA = \(\sqrt { 100 }\) [Taking square root on both sides]
= 10 cm

iii. Radius (r) = 10 cm
∴ Diameter = 2r = 2 x 10 = 20 cm
∴ The diameter of the circle is 20 cm.

Question 2.
Diameter of a circle is 26 cm and length of a chord of the circle is 24 cm. Find the distance of the chord from the centre.
Solution:

Given: In a circle with centre O,
PO is radius and PQ is its chord,
seg OR ⊥ chord PQ, P-R-Q
PQ = 24 cm, diameter (d) = 26 cm
To Find: Distance of the chord from the centre (OR)
Solution:
Radius (OP) = \(\frac { d }{ 2 }\) = \(\frac { 26 }{ 2 }\) = 13 cm ……(i)
∴ PR = \(\frac { 1 }{ 2 }\) PQ [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
= \(\frac { 1 }{ 2 }\) x 24 = 12 cm …..(ii)

ii. In ∆ORP, ∠ORP = 90°
∴ OP²= OR² + PR² [Pythagoras theorem]
∴ 13² = OR² + 12² [From (i) and (ii)]
∴ 169 = OR² + 144
∴ OR² = 169 – 144
∴ OR² = 25
∴ OR = √25 = 5 cm [Taking square root on both sides]
∴ The distance of the chord from the centre of the circle is 5 cm.

Question 3.
Radius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord.
Given: in a circle with centre A,
PA is radius and PQ is chord,
seg AM ⊥ chord PQ, P-M-Q
AP = 34 cm, AM = 30 cm
To Find: Length of the chord (PQ)
Solution:

I. In ∆AMP, ∠AMP = 90°
∴ AP² = AM² + PM² [Pythagoras theorem]
34² = 30² + PM²
∴ PM² = 34² – 30²
∴ PM² (34 – 30)(34 + 30) [a² – b² = (a – b)(a + b)]
= 4 x 64
∴ PM = \(\sqrt { 4\times64 }\) ………(i) [Taking square root on both sides]
= 2 x 8 = 16cm

ii. Now, PM = \(\frac { 1 }{ 2 }\)(PQ) [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
16 = \(\frac { 1 }{ 2 }\)(PQ) [From (i)]
∴ PQ = 16 x 2
= 32cm
∴ The length of the chord of the circle is 32cm.

Question 4.
Radius of a circle with centre O is 41 units. Length of a chord PQ is 80 units, find the distance of the chord from the centre of the circle.
Given: In a circle with centre O,
OP is radius and PQ is its chord,
seg OM ⊥ chord PQ, P-M-Q
OP = 41 units, PQ = 80 units,
To Find: Distance of the chord from the centre of the circle(OM)
Solution:

i. \(\frac { 1 }{ 2 }\)PM = (PQ) [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
= \(\frac { 1 }{ 2 }\)(80) = 40 Units ….(i)

ii. In ∆OMP, ∠OMP = 90°
∴ OP² = OM² + PM² [Pythagoras theorem]
∴ 41² = OM² + 40² [From (i)]
∴ OM² = 41² – 40²
= (41 -40) (41 +40) [a² – b² = (a – b) (a + b)]
= (1)(81)
∴ OM² = 81 OM = √81 = 9 units [Taking square root on both sides] [From (i)]
∴ The distance of the chord from the centre of the circle is 9 units.

Question 5.
In the adjoining figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q. Show that AP = BQ.

Given: Two concentric circles having centre O.
To prove: AP = BQ
Construction: Draw seg OM ⊥ chord AB, A-M-B
Solution:
Proof:
For smaller circle,
seg OM ⊥ chord PQ [Construction, A-P-M, M-Q-B]
∴ PM = MQ …..(i) [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
For bigger circle,
seg OM ⊥ chord AB [Construction]
∴ AM = MB [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ AP + PM = MQ + QB [A-P-M, M-Q-B]
∴ AP + MQ = MQ + QB [From (i)]
∴ AP = BQ

Question 6.
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
Solution:

Given: O is the centre of the circle.
seg PQ is the diameter.
Diameter PQ bisects the chords AB and CD in points M and N respectively.
To prove: chord AB || chord CD.
Proof:
Diameter PQ bisects the chord AB in point M [Given]
∴ seg AM ≅ seg BM
∴ seg OM ⊥ chord AB [Segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord, P-M-O, O-N-Q]
∴ ∠OMA = 90° …..(i)
Also, diameter PQ bisects the chord CD in point N [Given]
∴ seg CN ≅ seg DN
seg ON ⊥ chord CD [Segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord, P-M-O, O-N-Q]
∴ ∠ONC = 90° …..(ii)
Now, ∠OMA + ∠ONC = 90° + 90° [From (i) and (ii)]
= 180°
But, ∠OMA and ∠ONC form a pair of interior angles on lines AB and CD when seg MN is their transversal.
∴ chord AB || chord CD [Interior angles test]

Maharashtra Board Class 9 Maths Solutions

• Circle Practice Set 6.1 Class 9 Maths Solutions
• Circle Practice Set 6.2 Class 9 Maths Solutions
• Circle Practice Set 6.3 Class 9 Maths Solutions
• Circle Problem Set 6 Class 9 Maths Solutions

9th Standard Maths 2 Practice Set 5.4 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Class 9 Maths Part 2 Practice Set 5.4 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board

Question 1.
In □IJKL, side IJ || side KL, ∠I = 108° and ∠K = 53°, then find the measures of ∠J and ∠L.
Solution:

i. ∠I = 108° [Given]
side IJ || side KL and side IL is their transveral. [Given]
∴ ∠I + ∠L = 180° [Interior angles]
∴ 108° + ∠L = 180°
∴ ∠L = 180° – 108° = 72°

ii. ∠K = 53° [Given]
side IJ || side KL and side JK is their transveral. [Given]
∴ ∠J + ∠K = 180° [Interior angles]
∴ ∠J + 53° = 180°
∴ ∠J= 180°- 53° = 127°
∴ ∠L = 72°, ∠J = 127°

Question 2.
In □ABCD, side BC || side AD, side AB ≅ side DC. If ∠A = 72°, then find the measures of ∠B and ∠D.
Construction: Draw seg BP ⊥ side AD, A – P – D, seg CQ ⊥ side AD, A – Q – D.
Solution:

i. ∠A = 72° [Given]
In □ABCD, side BC || side AD and side AB is their transversal. [Given]
∴ ∠A + ∠B = 180° [Interior angles]
∴ 72° +∠B = 180°
∴ ∠B = 180° – 72° = 108°

ii. In ∆BPA and ∆CQD,
∠BPA ≅ ∠CQD [Each angle is of measure 90°]
Hypotenuse AB ≅ Hypotenuse DC [Given]
seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]
∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]
∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]
∴ ∠A = ∠D
∴ ∠D = 72°
∴ ∠B = 108°, ∠D = 72°

Question 3.
In □ABCD, side BC < side AD, side BC || side AD and if side BA ≅ side CD, then prove that ∠ABC = ∠DCB.

Given: side BC < side AD, side BC || side AD, side BA = side CD
To prove: ∠ABC ≅ ∠DCB
Construction: Draw seg BP ⊥ side AD, A – P – D
seg CQ ⊥ side AD, A – Q – D
Solution:
Proof:
In ∆BPA and ∆CQD,
∠BPA ≅ ∠CQB [Each angle is of measure 90°]
Hypotenuse BA ≅ Hypotenuse CD [Given]
seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]
∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]
∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]
∴ ∠A = ∠D ….(i)
Now, side BC || side AD and side AB is their transversal. [Given]
∴ ∠A + ∠B = 180°…..(ii) [Interior angles]
Also, side BC || side AD and side CD is their transversal. [Given]
∴ ∠C + ∠D = 180° …..(iii) [Interior angles]
∴ ∠A + ∠B = ∠C + ∠D [From (ii) and (iii)]
∴ ∠A + ∠B = ∠C + ∠A [From (i)]
∴ ∠B = ∠C
∴ ∠ABC ≅ ∠DCB

Maharashtra Board Class 9 Maths Solutions

• Quadrilaterals Practice Set 5.1 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.2 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.3 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.4 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.5 Class 9 Maths Solutions
• Quadrilaterals Problem Set 5 Class 9 Maths Solutions

9th Standard Maths 2 Practice Set 5.3 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Class 9 Maths Part 2 Practice Set 5.3 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board

Question 1.
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm, then find BO and if ∠CAD = 35°, then find ∠ACB.
Solution:

i. AC = 8 cm …(i) [Given]
□ABCD is a rectangle [Given]
∴ BD = AC [Diagonals of a rectangle are congruent]
∴ BD = 8 cm [From (i)]
BO = \(\frac { 1 }{ 2 }\) BD [Diagonals of a rectangle bisect each other]
∴ BO = \(\frac { 1 }{ 2 }\) x 8
∴ BO = 4 cm

ii. side AD || side BC and seg AC is their transversal. [Opposite sides of a rectangle are parallel]
∴ ∠ACB = ∠CAD [Alternate angles]
∠ACB = 35° [ ∵∠CAD = 35°]
∴ BO = 4 cm, ∠ACB = 35°

Question 2.
In a rhombus PQRS, if PQ = 7.5 cm, then find QR. If ∠QPS 75°, then find the measures of ∠PQR and ∠SRQ.
Solution:

i. PQ = 7.5 cm [Given]
□PQRS is a rhombus. [Given]
∴ QR = PQ [Sides of a rhombus are congruent]
∴ QR = 7.5 cm

ii. ∠QPS = 75° [Given]
∠QPS + ∠PQR = 180° [Adjacent angles of a rhombus are supplementary]
∴ 75° + ∠PQR = 180°
∴ ∠PQR = 180° – 75°
∴ ∠PQR =105°

iii. ∠SRQ = ∠QPS [Opposite angles of a rhombus]
∴ ∠SRQ = 75°
∴ QR = 7.5 cm, ∠PQR = 105°,
∠SRQ = 75°

Question 3.
Diagonals of a square IJKL intersects at point M. Find the measures of ∠IMJ, ∠JIK and ∠LJK.
Solution:

□IJKL is a square. [Given]
∴ seg IK ⊥ seg JL [Diagonals of a square are perpendicular to each other]
∠ IMJ=90°
∠ JIL 90° ……. (i) [Angle of a square]

ii. ∠JIK = \(\frac { 1 }{ 2 }\)∠JIL [Diagonals of a square bisect the opposite angles]
∠JIK = \(\frac { 1 }{ 2 }\) (90°) [From (i)
∴ ∠JIK = 45°
∠IJK = 90° (ii) [Angle of a square]

iii. ∠LJK = \(\frac { 1 }{ 2 }\)∠IJK [Diagonals of a square bisect the opposite angles]
∠LJK = \(\frac { 1 }{ 2 }\) (90°) [From (ii)]
∴ ∠LJK = 45°
∴ ∠LJK = 90°, ∠JIK = 45°, ∠LJK=45°

Question 4.
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its Perimeter.
Solution:

i. Let □ABCD be the rhombus.
AC = 20 cm, BD = 21 cm

ii. In ∆AOB, ∠AOB = 90° [Diagonals of a rhombus are prependicular to each other]
∴ AB² = AO² + BO² [Pythagoras theorem]

iii. Perimeter of □ABCD
= 4 x AB = 4 x 14.5 = 58 cm
∴ The side and perimeter of the rhombus are 14.5 cm and 58 cm respectively.

Question 5.
State with reasons whether the following statements are ‘true’ or ‘false’.
i. Every parallelogram is a rhombus.
ii. Every rhombus is a rectangle,
iii. Every rectangle is a parallelogram.
iv. Every square is a rectangle,
v. Every square is a rhombus.
vi. Every parallelogram is a rectangle.
Answer:
i. False.
All the sides of a rhombus are congruent, while the opposite sides of a parallelogram are congruent.
ii. False.
All the angles of a rectangle are congruent, while the opposite angles of a rhombus are congruent.
iii. True.
The opposite sides of a parallelogram are parallel and congruent. Also, its opposite angles are congruent.
The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.
iv. True.
The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.
All the sides of a square are parallel and congruent. Also, all its angles are congruent.
v. True.
All the sides of a rhombus are congruent. Also, its diagonals are perpendicular bisectors of each other.
All the sides of a square are congruent. Also, its diagonals are perpendicular bisectors of each other.
vi. False.
All the angles of a rectangle are congruent, while the opposite angles of a parallelogram are congruent.

Maharashtra Board Class 9 Maths Solutions

• Quadrilaterals Practice Set 5.1 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.2 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.3 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.4 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.5 Class 9 Maths Solutions
• Quadrilaterals Problem Set 5 Class 9 Maths Solutions

9th Standard Maths 2 Practice Set 5.1 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Class 9 Maths Part 2 Practice Set 5.1 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board

Question 1.
Diagonals of a parallelogram WXYZ intersect each other at point O. If ∠XYZ∠ = 135°, then measure of ∠XWZ and ∠YZW? If l(OY) = 5 cm, then l(WY) = ?
Solution:

i. ∠XYZ = 135°
□WXYZ is a parallelogram.
∠XWZ = ∠XYZ
∴ ∠XWZ = 135° …..(i)

ii. ∠YZW + ∠XYZ = 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠YZW + 135°= 180° [From (i)]
∴ ∠YZW = 180°- 135°
∴ ∠YZW = 45°

iii. l(OY) = 5 cm [Given]
l(OY) = \(\frac { 1 }{ 2 }\) l(WY) [Diagonals of a parallelogram bisect each other]
∴ l(WY) = 2 x l(OY)
= 2 x 5
∴ l(WY) = 10 cm
∴∠XWZ = 135°, ∠YZW = 45°, l(WY) = 10 cm

Question 2.
In a parallelogram ABCD, if ∠A = (3x + 12)°, ∠B = (2x – 32)°, then liptl the value of x and the measures of ∠C and ∠D.
Solution:

□ABCD is a parallelogram. [Given]
∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary],
∴ (3x + 12)° + (2x-32)° = 180°
∴ 3x + 12 + 2x – 32 = 180
∴ 5x – 20 = 180
∴ 5x= 180 + 20
∴ 5x = 200
∴ x = \(\frac { 200 }{ 5 }\)
∴ x = 40

ii. ∠A = (3x + 12)°
= [3(40) + 12]°
=(120 +12)°= 132°
∠B = (2x – 32)°
= [2(40) – 32]°
= (80 – 32)° = 48°
∴ ∠C = ∠A = 132°
∠D = ∠B = 48° [Opposite angles of a parallelogram]
∴ The value of x is 40, and the measures of ∠C and ∠D are 132° and 48° respectively.

Question 3.
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
Solution:

i. Let □ABCD be the parallelogram and the length of AD be x cm.
One side is greater than the other by 25 cm.
∴ AB = x + 25 cm
AD = BC = x cm
AB = DC = (x + 25) cm [Opposite angles of a parallelogram]

ii. Perimeter of □ABCD = 150 cm [Given]
∴ AB + BC + DC + AD = 150
∴ (x + 25) +x + (x + 25) + x – 150
∴ 4x + 50 = 150
∴ 4x = 150 – 50
∴ 4x = 100
∴ x = \(\frac { 100 }{ 4 }\)
∴ x = 25

iii. AD = BC = x = 25 cm
AB = DC = x + 25 = 25 + 25 = 50 cm
∴ The lengths of the sides of the parallelogram are 25 cm, 50 cm, 25 cm and 50 cm.

Question 4.
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
Solution:

i. Let □ABCD be the parallelogram.
The ratio of measures of two adjacent angles of a parallelogram is 1 : 2.
Let the common multiple be x.
∴ ∠A = x° and ∠B = 2x°
∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
∴ x + 2x = 180
∴ 3x = 180
∴ x = \(\frac { 180 }{ 3 }\)
∴ x = 60

ii. ∠A = x° = 60°
∠B = 2x° = 2 x 60° = 120°
∠A = ∠C = 60°
∠B = ∠D= 120° [Opposite angles of a parallelogram]
∴ The measures of the angles of the parallelogram are 60°, 120°, 60° and 120°.

Question 5.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO show that □ABCD is a rhombus.

Given: AO = 5, BO = 12 and AB = 13.
To prove: □ABCD is a rhombus.
Solition:
Proof:
AO = 5, BO = 12, AB = 13 [Given]
AO² + BO² = 5² + 12²
= 25 + 144
∴ AO² + BO² = 169 …..(i)
AB² = 13² = 169 ….(ii)
∴ AB² = AO² + BO² [From (i) and (ii)]
∴ ∆AOB is a right-angled triangle. [Converse of Pythagoras theorem]
∴ ∠AOB = 90°
∴ seg AC ⊥ seg BD …..(iii) [A-O-C]
∴ In parallelogram ABCD,
∴ seg AC ⊥ seg BD [From (iii)]
∴ □ABCD is a rhombus. [A parallelogram is a rhombus perpendicular to each other]

Question 6.
In the adjoining figure, □PQRS and □ABCR are two parallelograms. If ∠P = 110°, then find the measures of all the angles of □ABCR.
Solution:

□PQRS is a parallelogram. [Given]
∴ ∠R = ∠P [Opposite angles of a parallelogram]
∴ ∠R = 110° …..(iii)
□ABCR is a parallelogram. [Given]
∴ ∠A + ∠R= 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠A+ 110°= 180° [From (i)]
∴ ∠A= 180°- 110°
∴ ∠A = 70°
∴ ∠C = ∠A = 70°
∴ ∠B = ∠R= 110° [Opposite angles of a parallelogram]
∴ ∠A = 70°, ∠B = 110°,
∴ ∠C = 70°, ∠R = 110°

Question 7.
In the adjoining figure, □ABCD is a parallelogram. Point E is on the ray AB such that BE = AB, then prove that line ED bisects seg BC at point F.

Given: □ABCD is a parallelogram.
BE = AB
To prove: Line ED bisects seg BC at point F i.e. FC = FB
Solution:
Proof:
□ABCD is a parallelogram. [Given]
∴ seg AB ≅ seg DC …….(i) [Opposite angles of a parallelogram]
seg AB ≅ seg BE ……..(ii) [Given]
seg DC ≅ seg BE ……..(iii) [From (i) and (ii)]
side DC || side AB [Opposite sides of a parallelogram]
i.e. side DC || seg AE and seg DE is their transversal. [A-B-E]
∴ ∠CDE ≅ ∠AED
∴ ∠CDF ≅ ∠BEF …..(iv) [D-F-E, A-B-E]
In ∆DFC and ∆EFB,
seg DC = seg EB [From (iii)]
∠CDF ≅ ∠BEF [From (iv)]
∠DFC ≅ ∠EFB [Vertically opposite angles]
∴ ∆DFC ≅ ∆EFB [SAA test]
∴ FC ≅ FB [c.s.c.t]
∴ Line ED bisects seg BC at point F.

Maharashtra Board Class 9 Maths Chapter 5 Quadrilaterals Practice Set 5.1 Intext Questions and Activities

Question 1.
Write the following pairs considering □ABCD. (Textbook pg. no 57)

Pairs of adjacent sides:
i. AB, AD
ii. AD, DC
iii. DC, BC
iv. BC, AB

Pairs of adjacent angles:
i. ∠A, ∠B
ii. ∠C, ∠D
iii. ∠B, ∠C
iv. ∠D, ∠A

Pairs of opposite sides:
i. AB, DC
ii. AD, BC

Pairs of opposite angles:
i. ∠A, ∠C
ii. ∠B, ∠D

Question 2.
Complete the following tree diagram. (Textbook pg. no 57)

Question 3.
In the above theorem, to prove ∠DAB ≅ ∠BCD, is any change in the construction needed? If so, how will you write the proof making the change? (Textbook pg. no. 60)

Solution:
Yes
Construction: Draw diagonal BD.
Proof:
side AB || side CD and diagonal BD is their transversal. [Given]
∴ ∠ABD ≅ ∠CDB ……..(i) [Alternate angles]
side BC || side AD and diagonal BD is their transversal. [Given]
∴ ∠ADB ≅ ∠CBD ……..(ii) [Alternate angles]
In ∆DAB and ∆BCD,
∠ABD ≅ ∠CDB [From (i)]
seg BD ≅ seg DB [Common side]
∴ ∠ADB ≅ ∠CBD [From (ii)]
∴ ∆DAB ≅ ∆BCD [ASA test]
∴ ∠DAB ≅ ∠BCD [c.a.c.t.]
Note: ∠DAB s ∠BCD can be proved using the same construction as in the above theorem.
∠BAC ≅ ∠DCA …..(i)
∠DAC ≅ ∠BCA ……(ii)
∴ ∠BAC + ∠DAC ≅ ∠DCA + ∠BCA [Adding (i) and (ii)]
∴ ∠DAB ≅ ∠BCD [Angle addition property]

Maharashtra Board Class 9 Maths Solutions

• Quadrilaterals Practice Set 5.1 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.2 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.3 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.4 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.5 Class 9 Maths Solutions
• Quadrilaterals Problem Set 5 Class 9 Maths Solutions

9th Standard Maths 2 Practice Set 5.2 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

Class 9 Maths Part 2 Practice Set 5.2 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board

Question 1.
In the adjoining figure, □ABCD is a parallelogram, P and Q are midpoints of sides AB and DC respectively, then prove □APCQ is a parallelogram.

Given: □ABCD is a parallelogram. P and Q are the midpoints of sides AB and DC respectively.
To prove: □APCQ is a parallelogram.
Solution:
Proof:
AP = \(\frac { 1 }{ 2 }\) AB …..(i) [P is the midpoint of side AB]
QC = \(\frac { 1 }{ 2 }\) DC ….(ii) [Q is the midpoint of side CD]
□ABCD is a parallelogram. [Given]
∴ AB = DC [Opposite sides of a parallelogram]
∴ \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) DC [Multiplying both sides by \(\frac { 1 }{ 2 }\)]
∴ AP = QC ….(iii) [From (i) and (ii)]
Also, AB || DC [Opposite angles of a parallelogram]
i.e. AP || QC ….(iv) [A – P – B, D – Q – C]
From (iii) and (iv),
□APCQ is a parallelogram. [A quadrilateral is a parallelogram if its opposite sides is parallel and congruent]

Question 2.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.

Given:
□ABCD is a rectangle.
To prove: Rectangle ABCD is a parallelogram.
Solution:
Proof:
□ABCD is a rectangle.
∴ ∠A ≅ ∠C = 90° [Given]
∠B ≅ ∠D = 90° [Angles of a rectangle]
∴ Rectangle ABCD is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]

Question 3.
In the adjoining figure, G is the point of concurrence of medians of ADEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that □GEHF is a parallelogram.

Given: Point G (centroid) is the point of concurrence of the medians of ADEF.
DG = GH
To prove: □GEHF is a parallelogram.
Solution:
Proof:

Let ray DH intersect seg EF at point I such that E-I-F.
∴ seg DI is the median of ∆DEF.
∴ El = FI ……(i)
Point G is the centroid of ∆DEF.
∴ \(\frac { DG }{ GI }\) = \(\frac { 2 }{ 1 }\) [Centroid divides each median in the ratio 2:1]
∴ DG = 2(GI)
∴ GH = 2(GI) [DG = GH]
∴ GI + HI = 2(GI) [G-I-H]
∴ HI = 2(GI) – GI
∴ HI = GI ….(ii)
From (i) and (ii),
□GEHF is a parallelogram [A quadrilateral is a parallelogram, if its diagonals bisect each other]

Question 4.
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.

Given: □ABCD is a parallelogram.
Rays AS, BQ, CQ and DS bisect ∠A, ∠B, ∠C and ∠D respectively.
To prove: □PQRS is a rectangle.
Solution:
Proof:
∠BAS = ∠DAS = x° …(i) [ray AS bisects ∠A]
∠ABQ = ∠CBQ =y° ….(ii) [ray BQ bisects ∠B]
∠BCQ = ∠DCQ = u° …..(iii) [ray CQ bisects ∠C]
∠ADS = ∠CDS = v° ….(iv) [ray DS bisects ∠D]
□ABCD is a parallelogram. [Given]
∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠BAS + ∠DAS + ∠ABQ + ∠CBQ = 180° [Angle addition property]
∴ x°+x°+ v° + v° = 180 [From (i) and (ii)]
∴ 2x° + 2v° =180
∴ x + y = 90° ……(v) [Dividing both sides by 2]
Also, ∠A + ∠D= 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠BAS + ∠DAS + ADS + ∠CDS = 180° [Angle addition property]
∴ x° + x° + v° + v° = 180°
∴ 2x° + 2v° = 180°
∴ x° + v° = 90° …..(vi) [Dividing both sides by 2]
In ∆ARB,
∠RAB + ∠RBA + ∠ARB = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x° + y° + ∠SRQ = 180° [A – S – R, B – Q – R]
∴ 90° + ∠SRQ = 180° [From (v)]
∴ ∠SRQ = 180°- 90° = 90° …..(vi)
Similarly, we can prove
∠SPQ = 90° …(viii)
In ∆ASD,
∠ASD + ∠SAD + ∠SDA = 180° [Sum of the measures of angles a triangle is 180°]
∴ ∠ASD + x° + v° = 180° [From (vi)]
∴ ∠ASD + 90° = 180°
∴∠ASD = 180°- 90° = 90°
∴ ∠PSR = ∠ASD [Vertically opposite angles]
∴ ∠PSR = 90° …..(ix)
Similarly we can prove
∠PQR = 90° ..(x)
∴ In □PQRS,
∠SRQ = ∠SPQ = ∠PSR = ∠PQR = 90° [From (vii), (viii), (ix), (x)]
∴ □PQRS is a rectangle. [Each angle is of measure 90°]

Question 5.
In the adjoining figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS, then prove that □PQRS is a parallelogram.

Given: □ABCD is a parallelogram.
AP = BQ = CR = DS
To prove: □PQRS is a parallelogram.
Solution:
Proof:
□ABCD is a parallelogram. [Given]
∴ ∠B = ∠D ….(i) [Opposite angles of a parallelogram]
Also, AB = CD [Opposite sides of a parallelogram]
∴ AP + BP = DR + CR [A-P-B, D-R-C]
∴ AP + BP = DR + AP [AP = CR]
∴ BP = DR ….(ii)
In APBQ and ARDS,
seg BP ≅ seg DR [From (ii)]
∠PBQ ≅ ∠RDS [From (i)]
seg BQ ≅ seg DS [Given]
∴ ∆PBQ ≅ ∆RDS [SAS test]
∴ seg PQ ≅ seg RS …..(iii) [c.s.c.t]
Similarly, we can prove that
∆PAS ≅ ∆RCQ
∴ seg PS ≅ seg RQ ….(iv) [c.s.c.t]
From (iii) and (iv),
□PQRS is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]

Maharashtra Board Class 9 Maths Chapter 5 Quadrilaterals Practice Set 5.2 Intext Questions and Activities

Question 1.
Points D and E are the midpoints of side AB and side AC of ∆ABC respectively. Point F is on ray ED such that ED = DF. Prove that □AFBE is a parallelogram. For this example write ‘given’ and ‘to prove’ and complete the proof. (Text book pg. no. 66)

Given: D and E are the midpoints of side AB and side AC respectively.
ED = DF
To prove: □AFBE is a parallelogram.
Solution:
Proof:
seg AB and seg EF are the diagonals of □AFBE.
seg AD ≅ seg DB [Given]
seg DE ≅ seg DF [Given]
∴ Diagonals of □AFBE bisect each other.
∴ □AFBE is a parallelogram. [ By test of parallelogram]

Maharashtra Board Class 9 Maths Solutions

• Quadrilaterals Practice Set 5.1 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.2 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.3 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.4 Class 9 Maths Solutions
• Quadrilaterals Practice Set 5.5 Class 9 Maths Solutions
• Quadrilaterals Problem Set 5 Class 9 Maths Solutions

9th Standard Maths 2 Problem Set 4 Chapter 4 Constructions of Triangles Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

Class 9 Maths Part 2 Problem Set 4 Chapter 4 Constructions of Triangles Questions With Answers Maharashtra Board

Question 1.
Construct ∆XYZ, such that XY + XZ = 10.3 cm, YZ = 4.9 cm, ∠XYZ = 45°.
Solution:

As shown in the rough figure draw segYZ = 4.9cm
Draw a ray YT making an angle of 45° with YZ
Take a point W on ray YT, such that YW= 10.3 cm
Now,YX + XW = YW [Y-X-W]
∴ YX + XW=10.3cm …..(i)
Also, XY + X∠10.3cm ……(ii) [Given]
∴ YX + XW = XY + XZ [From (i) and (ii)]
∴ XW = XZ
∴ Point X is on the perpendicular bisector of seg WZ
∴ The point of intersection of ray YT and perpendicular bisector of seg WZ is point X.

Steps of construction:
i. Draw seg YZ of length 4.9 cm.
ii. Draw ray YT, such that ∠ZYT = 75°.
iii. Mark point W on ray YT such that l(YW) = 10.3 cm.
iv. Join points W and Z.
v. Draw perpendicular bisector of seg WZ intersecting ray YT. Name the point as X.
vi. Join the points X and Z.
Hence, ∆XYZ is the required triangle.

Question 2.
Construct ∆ABC, in which ∠B = 70°, ∠C = 60°, AB + BC + AC = 11.2 cm.
Solution:

i. As shown in the figure, take point D and E on line BC, such that
BD = AB and CE = AC ……(i)
BD + BC + CE = DE [D-B-C, B-C-E]
∴ AB + BC + AC = DE …..(ii)
Also,
AB + BC + AC= 11.2 cm ….(iii) [Given]
∴ DE = 11.2 cm [From (ii) and (iii)]

ii. In ∆ADB
AB = BD [From (i)]
∴ ∠BAD = ∠BDA = x° ….(iv) [Isosceles triangle theorem]
In ∆ABD, ∠ABC is the exterior angle.
∴ ∠BAD + ∠BDA = ∠ABC [Remote interior angles theorem]
x + x = 70° [From (iv)]
∴ 2x = 70° x = 35°
∴ ∠ADB = 35°
∴ ∠D = 35°
Similarly, ∠E = 30°

iii. Now, in ∆ADE
∠D = 35°, ∠E = 30° and DE = 11.2 cm
Elence, ∆ADE can be drawn.

iv. Since, AB = BD
∴ Point B lies on perpendicular bisector of seg AD.
Also AC = CE
∴ Point C lies on perpendicular bisector of seg AE.
∴ Points B and C can be located by drawing the perpendicular bisector of AD and AE respectively.
∴ ∆ABC can be drawn.

Steps of construction:
i. Draw seg DE of length 11.2 cm.
ii. From point D draw ray making angle of 35°.
iii. From point E draw ray making angle of 30°.
iv. Name the point of intersection of two rays as A.
v. Draw the perpendicular bisector of seg DA and seg EA intersecting seg DE in B and C respectively.
vi. Join AB and AC.
Hence, ∆ABC is the required triangle.

Question 3.
The perimeter of a triangle is 14.4 cm and the ratio of lengths of its side is 2 : 3 : 4. Construct the triangle.
Solution:

Let the common multiple be x
∴ In ∆ABC,
AB = 2x cm, AC = 3x cm, BC = 4x cm
Perimeter of triangle = 14.4 cm
∴ AB + BC + AC= 14.4
∴ 9x = 14.4
∴ x = \(\frac { 14.4 }{ 9 }\)
∴ x = 1.6
∴ AB = 2x = 2x 1.6 = 3.2 cm
∴ AC = 3x = 3 x 1.6 = 4.8 cm
∴ BC = 4x = 4 x 1.6 = 6.4 cm

Question 4.
Construct ∆PQR, in which PQ – PR = 2.4 cm, QR = 6.4 cm and ∠PQR = 55°.
Solution:

Here, PQ – PR = 2.4 cm
∴ PQ > PR
As shown in the rough figure draw seg QR = 6.4 cm
Draw a ray QT making on angle of 55° with QR
Take a point S on ray QT, such that QS = 2.4 cm.
Now, PQ – PS = QS [Q-S-P]
∴ PQ – PS = 2.4 cm …(i)
Also, PQ – PR = 2.4 cm ….(ii) [Given]
∴ PQ – PS = PQ – PR [From (i) and (ii)]
∴ PS = PR
∴ Point P is on the perpendicular bisector of seg RS
∴ Point P is the intersection of ray QT and the perpendicular bisector of seg RS

Steps of construction:
i. Draw seg QR of length 6.4 cm.
ii. Draw ray QT, such that ∠RQT = 55°.
iii. Take point S on ray QT such that l(QS) = 2.4 cm.
iv. Join the points S and R.
v. Draw perpendicular bisector of seg SR intersecting ray QT.
Name that point as P.
vi. Join the points P and R.
Hence, ∆PQR is the required triangle.

Maharashtra Board Class 9 Maths Solutions

• Constructions of Triangles Practice Set 4.1 Class 9 Maths Solutions
• Constructions of Triangles Practice Set 4.2 Class 9 Maths Solutions
• Constructions of Triangles Practice Set 4.3 Class 9 Maths Solutions
• Constructions of Triangles Problem Set 4 Class 9 Maths Solutions

10th Standard Maths 2 Problem Set 1 Chapter 1 Similarity Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Statistics.

Class 10 Maths Part 2 Problem Set 1 Chapter 1 Similarity Questions With Answers Maharashtra Board

Question 1.
Select the appropriate alternative.
i. In ∆ABC and ∆PQR, in a one to one correspondence \(\frac { AB }{ QR } \) = \(\frac { BC }{ PR } \) = \(\frac { CA }{ PQ } \), then

(A) ∆PQR – ∆ABC
(B) ∆PQR – ∆CAB
(C) ∆CBA – ∆PQR
(D) ∆BCA – ∆PQR
Answer:
(B)

ii. If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E, then which of the following statements is false?

(A) \(\frac { EF }{ PR } \) = \(\frac { DF }{ PQ } \)
(B) \(\frac { DE }{ PQ } \) = \(\frac { EF }{ RP } \)
(C) \(\frac { DE }{ QR } \) = \(\frac { DF }{ PQ } \)
(D) \(\frac { EF }{ RP } \) = \(\frac { DE }{ QR } \)
Answer:
∆DEF ~ ∆QRP … [AA test of similarity]
∴ \(\frac { DE }{ QR } \) = \(\frac { EF }{ RP } \) = \(\frac { DF }{ PQ } \) …[Corresponding sides of similar triangles]
(B)

iii. In ∆ABC and ∆DEF, ∠B = ∠E, ∠F = ∠C and AB = 3 DE, then which of the statements regarding the two triangles is true?

(A) The triangles are not congruent and not similar.
(B) The triangles are similar but not congruent.
(C) The triangles are congruent and similar.
(D) None of the statements above is true.
Answer:
(B)

iv. ∆ABC and ∆DEF are equilateral triangles, A(∆ABC) : A(∆DEF) = 1 : 2. If AB = 4, then what is length of DE?

(A) 2√2
(B) 4
(C) 8
(D) 4√2
Answer:
Refer Q. 6 Practice Set 1.4
(D)

v. In the adjoining figure, seg XY || seg BC, then which of the following statements is true?

(A) \(\frac { AB }{ AC } \) = \(\frac { AX }{ AY } \)
(B) \(\frac { AX }{ XB } \) = \(\frac { AY }{ AC } \)
(C) \(\frac { AX }{ YC } \) = \(\frac { AY }{ XB } \)
(D) \(\frac { AB }{ YC } \) = \(\frac { AC }{ XB } \)
Answer:
∆ABC ~ ∆AXY … [AA test of similarity]
∴ \(\frac { AB }{ AX } \) = \(\frac { AC }{ AY } \) …[Corresponding sides of similar triangles]
∴ \(\frac { AB }{ AC } \) = \(\frac { AX }{ AY } \) …[Altemendo]
(A)

Question 2.
In ∆ABC, B-D-C and BD = 7, BC = 20, then find following ratios.

Solution:

Draw AE ⊥ BC, B – E – C.
BC = BD + DC [B – D – C]
∴ 20 = 7 + DC
∴ DC = 20 – 7 = 13

i. ∆ABD and ∆ADC have same height AE.
\(\frac{\mathrm{A}(\Delta \mathrm{ABD})}{\mathrm{A}(\Delta \mathrm{ADC})}=\frac{\mathrm{BD}}{\mathrm{DC}}\) [Triangles having equal height]
∴ \(\frac{A(\Delta A B D)}{A(\Delta A D C)}=\frac{7}{13}\)

ii. ∆ABD and ∆ABC have same height AE.
\(\frac{\mathrm{A}(\Delta \mathrm{ABD})}{\mathrm{A}(\Delta \mathrm{ABC})}=\frac{\mathrm{BD}}{\mathrm{BC}}\) [Triangles having equal height]
∴ \(\frac{A(\Delta A B D)}{A(\Delta A B C)}=\frac{7}{20}\)

iii. ∆ADC and ∆ABC have same height AE.
\(\frac{A(\Delta A D C)}{A(\Delta A B C)}=\frac{D C}{B C}\) [Triangles having equal height]
∴ \(\frac{A(\Delta A D C)}{A(\Delta A B C)}=\frac{13}{20}\)

Question 3.
Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm, then what is the corresponding base of the bigger triangle?
Solution:
Let A₁ and A₂ be the areas of two triangles. Let b₁ and b₂ be their corresponding bases.
A₁ : A₂ = 2 : 3

∴ The corresponding base of the bigger triangle is 9 cm.

Question 4.
In the adjoining figure, ∠ABC = ∠DCB = 90°, AB = 6, DC = 8, then \(\frac{\mathbf{A}(\Delta \mathbf{A} \mathbf{B} \mathbf{C})}{\mathbf{A}(\mathbf{\Delta D C B})}=?\)

Solution:
∆ABC and ∆DCB have same base BC.

Question 5.
In the adjoining figure, PM = 10 cm, A(∆PQS) = 100 sq. cm,
A(∆QRS) = 110 sq. cm, then find NR.

Solution:

∴ NR = 11 cm

Question 6.
∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio \(\frac{A(\Delta M N T)}{A(\Delta Q R S)}\)

Solution:
∆MNT- ∆QRS [Given]
∴ ∠M ≅ ∠Q (i) [Corresponding angles of similar triangles]
In ∆MLT and ∆QPS,
∠M ≅ ∠Q [From (i)]
∠MLT ≅ ∠QPS [Each angle is of measure 90°]
∴ ∆MLT ~ ∆QPS [AA test of similarity]

Question 7.
In the adjoining figure, A – D – C and B – E – C. seg DE || side AB. If AD = 5, DC = 3, BC = 6.4, then find BE.

Solution:
In ∆ABC,
seg DE || side AB [Given]
∴ \(\frac { DC }{ AD } \) = \(\frac { EC }{ BE } \) [Basic proportionality theorem]
∴ \(\frac { 3 }{ 4 } \) = \(\frac { 6.4-x }{ x } \)
∴ 3x = 5 (6.4 – x)
∴ 3x = 32 – 5x
∴ 8x = 32
∴ x = \(\frac { 32 }{ 8 } \) =4
∴ BE = 4 units

Question 8.
In the adjoining figure, seg PA, seg QB, seg RC and seg SD are perpendicular to line AD. AB = 60, BC = 70, CD = 80, PS = 280, then find PQ, QR and RS.

Solution:
seg PA, seg QB, seg RC and seg SD are perpendicular to line AD. [Given]
∴ seg PA || seg QB || seg RC || seg SD (i) [Lines perpendicular to the same line are parallel to each other]
Let the value of PQ be x and that of QR be y.
PS = PQ + QS [P – Q – S]
∴ 280 – x + QS
∴ QS = 280 – x (ii)
Now, seg PA || seg QB || seg SD [From (i)]
∴ \(\frac { AB }{ BD } \) = \(\frac { PQ }{ QS } \) [Property of three parallel lines and their transversals]
∴\(\frac { AB }{ BC+CD } \) = \(\frac { PQ }{ QS } \) [B – C – D]
∴ \(\frac { 60 }{ 70+80 } \) = \(\frac { x }{ 280-x } \)
∴ \(\frac { 60 }{ 150 } \) = \(\frac { x }{ 280-x } \)
∴ \(\frac { 2 }{ 5 } \) = \(\frac { x }{ 280-x } \)
∴ 5x = 2 (280 – x)
∴ 5x = 560 – 2x
∴ 7x = 560
∴ x = \(\frac { 560 }{ 7 } \) = 80
∴ PQ = 80 units
QS = 280 – x [From (ii)]
= 280 – 80
= 200 units
But, QS = QR + RS [Q – R – S]
∴ 200 = y + RS
∴ RS = 200 – y (ii)
Now, seg QB || seg RC || seg SD [From (i)]
∴\(\frac { BC }{ CD } \) = \(\frac { QR }{ RS } \) [Property of three parallel lines and their transversals]
∴ \(\frac { 70 }{ 80 } \) = \(\frac { y }{ 200-y } \)
∴ \(\frac { 7 }{ 8 } \) = \(\frac { y }{ 200-y } \)
∴ 8y = 7(200 – y)
∴ 8y = 1400 – 7y
∴ 15y = 1400
∴ y = \(\frac { 1400 }{ 15 } \) = \(\frac { 280 }{ 3 } \)
∴ QR = \(\frac { 280 }{ 3 } \) units
RS = 200 – 7 [From (iii)]
= 200 – \(\frac { 280 }{ 3 } \)
= \(\frac{200 \times 3-280}{3}\)
= \(\frac { 600-280 }{ 3 } \)
∴ RS = \(\frac { 320 }{ 3 } \) units

Question 9.
In ∆PQR, seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR
Complete the proof by filling in the boxes.

Solution:
Proof:
In ∆PMQ, ray MX is bisector of ∠PMQ.

Question 10.
In the adjoining figure, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y.
AB = 5, AC = 4, BC = 6, then find \(\frac { AX }{ XY } \).

Solution:
Let the value of BY be x.
BC = BY + YC [B – Y – C]
∴ 6 = x + YC
∴ YC = 6 – x
in ∆BAY, ray BX bisects ∠B. [Given]
∴ \(\frac { AB }{ BY } \) = \(\frac { AX }{ XY } \) (i) [Property of angle bisector of a triangle]
Also, in ∆CAY, ray CX bisects ∠C. [Given]

Question 11.
In ꠸ABCD, seg AD || seg BC. Diagonal AC and diagonal BD intersect each other in point P. Then show that \(\frac { AP }{ PD } \) = \(\frac { PC }{ BP } \)

Solution:
proof:
seg AD || seg BC and BD is their transversal. [Given]
∴ ∠DBC ≅ ∠BDA [Alternate angles]
∴ ∠PBC ≅ ∠PDA (i) [D – P – B]
In ∆PBC and ∆PDA,
∠PBC ≅ ∠PDA [From (i)]
∠BPC ≅ ∠DPA [Vertically opposite angles]
∴ ∆PBC ~ ∆PDA [AA test of similarity]
∴ \(\frac { BP }{ PD } \) = \(\frac { PC }{ AP } \) [Corresponding sides of similar triangles]
∴ \(\frac { AP }{ PD } \) = \(\frac { PC }{ BP } \) [By altemendo]

Question 12.
In the adjoining figure, XY || seg AC. If 2 AX = 3 BX and XY = 9, complete the activity to find the value of AC.

Solution:
2 AX = 3 BX [Given]

Question 13.
In the adjoining figure, the vertices of square DEFG are on the sides of ∆ABC. If ∠A = 90°, then prove that DE² = BD × EC.
(Hint: Show that ∆GBD is similar to ∆ CFE. Use GD = FE = DE.)

Solution:
proof:
꠸DEFG is a square.
∴ DE = EF = GF = GD (i) [Sides of a square]
∠GDE = ∠DEF = 90° [Angles of a square]
∴ seg GD ⊥ side BC, seg FE ⊥ side BC (ii)
In ∆BAC and ∆BDG,
∠BAC ≅ ∠BDG [From (ii), each angle is of measure 90°]
∠ABC ≅ ∠DBG [Common angle]
∴ ∆BAC – ∆BDG (iii) [AA test of similarity]
In ∆BAC and ∆FEC,
∠BAC ≅ ∠FEC [From (ii), each angle is measure 90°]
∠ACB ≅ ∠ECF [Common angle]
∴ ∆BAC – ∆FEC (iv) [AA test of similarity]
∴ ∆BDG – ∆FEC [From (iii) and (iv)]
∴ \(\frac { BD }{ EF } \) = \(\frac { GD }{ EC } \) (v) [Corresponding sides of similar triangles]
∴ \(\frac { BD }{ DE } \) = \(\frac { DE }{ EC } \) [From (i) and (v)]
∴ DE² = BD × EC

Maharashtra State Board Class 10 Maths Solutions Part 2

• Similarity Practice Set 1.1 Class 10 Maths Solutions
• Similarity Practice Set 1.2 Class 10 Maths Solutions
•  Similarity Practice Set 1.3 Class 10 Maths Solutions
• Similarity Practice Set 1.4 Class 10 Maths Solutions
• Similarity Problem Set 1 Class 10 Maths Solutions
• Pythagoras Theorem Practice Set 2.1 Class 10 Maths Solutions
• Pythagoras Theorem Practice Set 2.2 Class 10 Maths Solutions
• Pythagoras Theorem Problem Set 2 Class 10 Maths Solutions

9th Standard Maths 2 Practice Set 4.3 Chapter 4 Constructions of Triangles Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

Class 9 Maths Part 2 Practice Set 4.3 Chapter 4 Constructions of Triangles Questions With Answers Maharashtra Board

Question 1.
Construct ∆PQR, in which ∠Q = 70°, ∠R = 80° and PQ + QR + PR = 9.5 cm.
Solution:

i. As shown in the figure, take point T and S on line QR, such that
QT = PQ and RS = PR ….(i)
QT + QR + RS = TS [T-Q-R, Q-R-S]
∴ PQ + QR + PR = TS …..(ii) [From (i)]
Also,
PQ + QR + PR = 9.5 cm ….(iii) [Given]
∴ TS = 9.5 cm

ii. In ∆PQT
PQ = QT [From (i)]
∴ ∠QPT = ∠QTP = x° ….(iv) [Isosceles triangle theorem]
In ∆PQT, ∠PQR is the exterior angle.
∴ ∠QPT + ∠QTP = ∠PQR [Remote interior angles theorem]
∴ x + x = 70° [From (iv)]
∴ 2x = 70° x = 35°
∴ ∠PTQ = 35°
∴ ∠T = 35°
Similarly, ∠S = 40°

iii. Now, in ∆PTS
∠T = 35°, ∠S = 40° and TS = 9.5 cm Hence, ∆PTS can be drawn.

iv. Since, PQ = TQ,
∴ Point Q lies on perpendicular bisector of seg PT.
Also, RP = RS
∴ Point R lies on perpendicular bisector of seg PS.
Points Q and R can be located by drawing the perpendicular bisector of PT and PS respectively.
∴ ∆PQR can be drawn.

Steps of construction:
i. Draw seg TS of length 9.5 cm.
ii. From point T draw ray making angle of 35°.
iii. From point S draw ray making angle of 40°.
iv. Name the point of intersection of two rays as P.
v. Draw the perpendicular bisector of seg PT and seg PS intersecting seg TS in Q and R respectively.
vi. Join PQ and PR.
Hence, ∆PQR is the required triangle.

Question 2.
Construct ∆XYZ, in which ∠Y = 58°, ∠X = 46° and perimeter of triangle is 10.5 cm.
Solution:

i. As shown in the figure, take point W and V on line YX, such that
YW = ZY and XV = ZX ……(i)
YW + YX + XV = WV [W-Y-X, Y-X-V]
∠Y + YX + ∠X = WV ……(ii) [From (i)]
Also,
∠Y + YX + ∠X = 10.5 cm …..(iii) [Given]
∴ WV = 10.5 cm [From (ii) and (iii)]

ii. In ∆ZWY
∠Y = YM [From (i)]
∴ ∠YZW = ∠YWZ = x° …..(iv) [Isosceles triangle theorem]
In ∆ZYW, ∠ZYX is the exterior angle.
∴ ∠YZW + ∠YWZ = ∠ZYX [Remote interior angles theorem]
∴ x + x = 58° [From (iv)]
∴ 2x = 58°
∴ x = 29°
∴ ∠ZWY = 29°
∴ ∠W = 29°
∴ Similarly, ∠V = 23°

iii. Now, in ∆ZWV
∠W = 29°, ∠V = 23° and
WV= 10.5 cm
Hence, ∆ZWV can be drawn.

iv. Since, ZY = YW
∴ Point Y lies on perpendicular bisector of seg ZW.
Also, ZX = XV
∴ Point X lies on perpendicular bisector of seg ZV.
∴ Points Y and X can be located by drawing the perpendicular bisector of ZW and ZV respectively.
∴ ∆XYZ can be drawn.

Steps of construction:
i. Draw seg WV of length 10.5 cm.
ii. From point W draw ray making angle of 29°.
iii. From point V draw ray making angle of 23°.
iv. Name the point of intersection of two rays as Z.
v. Draw the perpendicular bisector of seg WZ and seg VZ intersecting seg WV in Y and X respectively.
vi. Join XY and XX.
Hence, ∆XYX is the required triangle

Question 3.
Construct ∆LMN, in which ∠M = 60°, ∠N = 80° and LM + MN + NL = 11 cm.
Solution:

i. As shown in the figure, take point S and T on line MN, such that
MS = LM and NT = LN …..(i)
MS + MN + NT = ST [S-M-N, M-N-T]
∴ LM + MN + LN = ST …..(ii)
Also,
LM + MN + LN = 11 cm ….(iii)
∴ ST = 11 cm [From (ii) and (iii)]

ii. In ∆LSM
LM = MS
∴ ∠MLS = ∠MSL = x° …..(iv) [isosceles triangle theorem]
In ∆LMS, ∠LMN is the exterior angle.
∴ ∠MLS + ∠MSL = ∠LMN [Remote interior angles theorem]
∴ x + x = 60° [From (iv)]
∴ 2x = 60°
∴ x = 30°
∴ ∠LSM = 30°
∴ ∠S = 30°
Similarly, ∠T = 40°

iii. Now, in ∆LST
∠S = 30°, ∠T = 40° and ST = 11 cm
Hence, ALST can be drawn.

iv. Since, LM = MS
∴ Point M lies on perpendicular bisector of seg LS.
Also LN = NT
∴ Point N lies on perpendicular bisector of seg LT.
∴ Points M and N can be located by drawing the perpendicular bisector of LS and LT respectively.
∴ ∆LMN can be drawn.

Steps of construction:
i. Draw seg ST of length 11 cm.
ii. From point S draw ray making angle of 30°.
iii. From point T draw ray making angle of 40°.
iv. Name the point of intersection of two rays as L.
v. Draw the perpendicular bisector of seg LS and seg LT intersecting seg ST in M and N respectively.
vi. Join LM and LN.
Hence, ∆LMN is the required triangle.

Maharashtra Board Class 9 Maths Solutions

• Constructions of Triangles Practice Set 4.1 Class 9 Maths Solutions
• Constructions of Triangles Practice Set 4.2 Class 9 Maths Solutions
• Constructions of Triangles Practice Set 4.3 Class 9 Maths Solutions
• Constructions of Triangles Problem Set 4 Class 9 Maths Solutions

9th Standard Maths 2 Practice Set 4.2 Chapter 4 Constructions of Triangles Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

Class 9 Maths Part 2 Practice Set 4.2 Chapter 4 Constructions of Triangles Questions With Answers Maharashtra Board

Question 1.
Construct ∆XYZ, such that YZ = 7.4 cm, ∠XYZ = 45° and XY – XZ = 2.7 cm.
Solution:

Here, XY – XZ = 2.7 cm
∴ XY > XZ
As shown in the rough figure draw seg YZ = 7.4 cm
Draw a ray YP making an angle of 45° with YZ
Take a point W on ray YP, such that
YW = 2.7 cm.
Now, XY – XW = YW [Y-W-X]
∴ XY – XW = 2.7 cm ….(i)
Also, XY – XZ = 2.7 cm ….(ii) [Given]
∴ XY – XW = XY – XZ [From (i) and (ii)]
∴ XW = XZ
∴ Point X is on the perpendicular bisector of seg ZW
∴ Point X is the intersection of ray YP and the perpendicular bisector seg ZW

Steps of construction:
i. Draw seg YZ of length 7.4 cm.
ii. Draw ray YP, such that ∠ZYP = 45°.
iii. Mark point W on ray YP such that l(YW) = 2.7 cm.
iv. Join points W and Z.
v. Join the points X and Z.
Hence, ∆XYZ is the required triangle.

Question 2.
Construct ∆PQR, such that QR = 6.5 cm, ∠PQR = 60° and PQ – PR = 2.5 cm.
Solution:

Here, PQ – PR = 2.5 cm
∴ PQ > PR
As shown in the rough figure draw seg QR = 6.5 cm
Draw a ray QT making on angle of 60° with QR
Take a point S on ray QT, such that QS = 2.5 cm.
Now, PQ – PS = QS [Q-S-T]
∴ PQ – PS = 2.5 cm ……(i) [Given]
Also, PQ – PR = 2.5 cm …..(ii) [From (i) and (ii)]
∴ PQ – PS = PQ – PR
∴ PS = PR
∴ Point P is on the perpendicular bisector of seg RS
∴ Point P is the intersection of ray QT and the perpendicular bisector of seg RS

Steps of construction:
i. Draw seg QR of length 6.5 cm.
ii. Draw ray QT, such that ∠RQT = 600.
iii. Mark point S on ray QT such that l(QS) = 2.5 cm.
iv. Join points S and R.
v. Draw perpendicular bisector of seg SR intersecting ray QT. Name the point as P.
vi. Join the points P and R.
Hence, ∆PQR is the required triangle.

Question 3.
Construct ∆ABC, such that BC = 6 cm, ∠ABC = 100° and AC – AB = 2.5 cm.

Solution:
Here, AC – AB = 2.5 cm
∴ AC > AB
As shown in the rough figure draw seg BC = 6 cm
Draw a ray BT making an angle of 100° with BC.
Take a point D on opposite ray of BT, :
such that BD 2.5 cm.
Now, AD – AB = BD [A-B-D]
∴ AD – AB = 2.5cm …..(i)
Also, AC – AB = 2.5 cm …..(ii) [Given]
∴ AD – AB = AC – AB [From (i) and (ii)]
∴ AD = AC
∴ Point A is on the perpendicular bisector of seg DC
∴ Point A is the intersection of ray BT and the perpendicular bisector of seg DC

Steps of construction:
i. Draw seg BC of length 6 cm.
ii. Draw ray BT, such that ∠CBT = 100°.
iii. Take point D on opposite ray of BT such that l(BD) = 2.5 cm.
iv. Join the points D and C.
v. Draw the perpendicular bisector of seg DC intersecting ray BT. Name the point as A.
vi. Join the points A and C.
Hence, ∆ABC is the required triangle.

Maharashtra Board Class 9 Maths Solutions

• Constructions of Triangles Practice Set 4.1 Class 9 Maths Solutions
• Constructions of Triangles Practice Set 4.2 Class 9 Maths Solutions
• Constructions of Triangles Practice Set 4.3 Class 9 Maths Solutions
• Constructions of Triangles Problem Set 4 Class 9 Maths Solutions