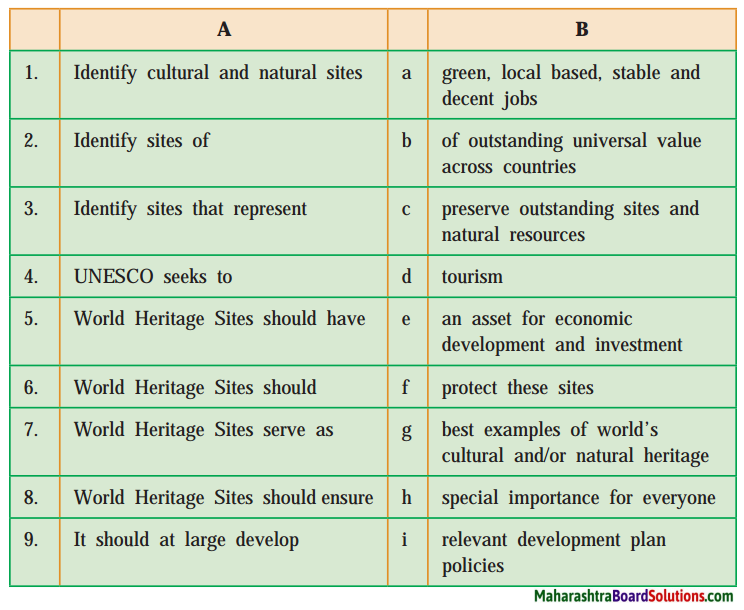
Class 10 English Chapter 1.2 Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.2 The Thief’s Story Notes, Textbook Exercise Important Questions and Answers.
The Thief’s Story Poem 10th Std Question Answer
Maharashtra Board Class 10 English Solutions Unit 1.2 Warming Up Questions and Answers
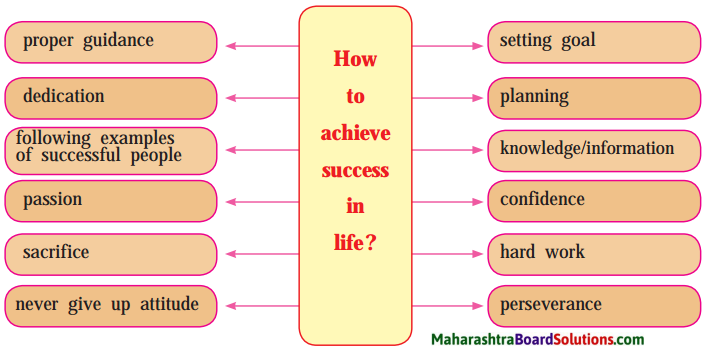
The Thief’s Story Class 10 Questions and Answers Maharashtra Board Question 1.
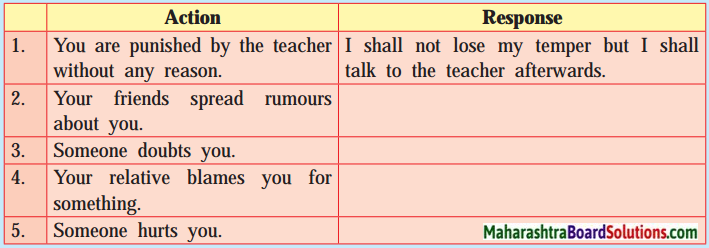
Read the following incident.
Lokesh had always been a class-topper in tests and examinations. However, invariably, he used foul means during exams to gain those high marks.
Once, on the day of History examination, Lokesh realized that his classmate and friend Farhan came all prepared for Maths instead of History. Farhan had become desperate. So Lokesh offered to let him copy from his answer-sheet, since Farhan sat just behind him.
Farhan refused. He said, ‘‘It’s all right even if I get a zero, but I can call it my own zero. I do not want to score a single mark, unearned. Cheating in exams is for cowards. Not me!’’
These words were a turning point in Lokesh’s life. He gave up cheating for ever. He worked hard for what he desired and never, ever used false measures to acquire anything.
![]()
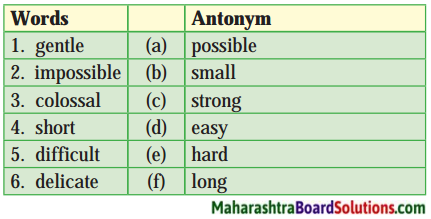
(a) In the given story, which words/phrases can be replaced by the following ones?
(i) became aware …………………………
(ii) always …………………………
(iii) very upset and helpless …………………………
(iv) cheating …………………………
(v) without working for it …………………………
(vi) a sudden change …………………………
(vii) gain/achieve …………………………
Answer:
(i) became aware – realized
(ii) always – invariably
(iii) very upset and helpless – desperate
(iv) cheating – foul means
(v) without working for it – unearned
(vi) a sudden change – a turning point
(vii) gain/achieve – acquire
(b) Summarize the incident in 6 to 8 lines making Lokesh, the narrator :
Begin with : ‘I was always a class topper.
………………………………………………………………………………
………………………………………………………………………………
………………………………………………………………………………
………………………………………………………………………………
………………………………………………………………………………
………………………………………………………………………………
Answer:
I was always a class topper in tests and examinations. However, I have to accept that I invariably used false means to gain those high marks. Once, on the day of the History examination, Farhan became desperate as he had come prepared for Maths instead of History. I offered to let him copy from my answer sheet, but Farhan refused, saying that he did not want to score a single unearned mark, and that cheating was for cowards. This was the turning point in my life, and from that day I gave up cheating and learnt to work hard for whatever I wanted.
The Thief’s Story Class 10 English Workshop Questions and Answers Maharashtra Board
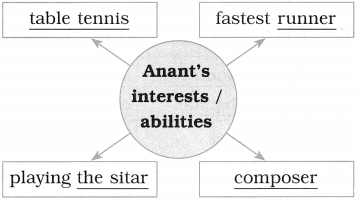
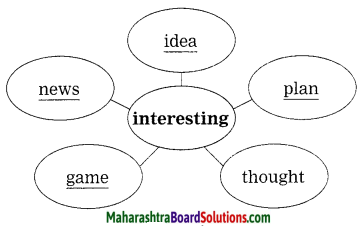
Question 1.
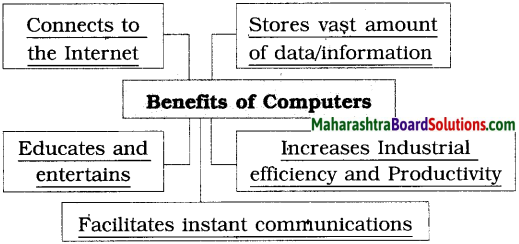
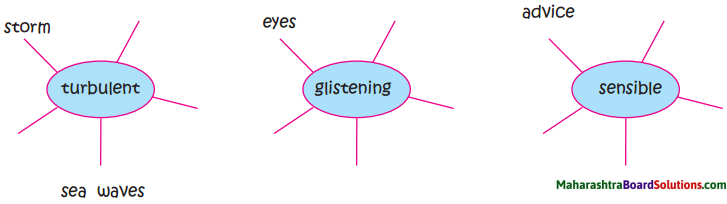
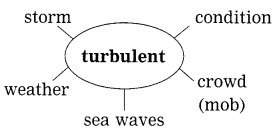
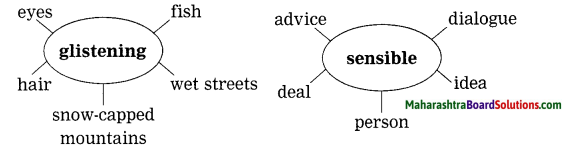
Complete the web diagram.

Answer:
![]()
The Thief’s Story English Workshop Question 2.
Insert the appropriate word/phrase given below, in the sentences that follow. ( flattery, appealing, by fits and starts, dashed to, undetected, spirits rose )
(a) I …………………………… the school gate when I heard the school-bell ring.
Answer:
I dashed to the school gate when I heard the school-bell ring.
(b) After the death of my pet dog, my …………………………… when dad got me a new pup.
Answer:
After the death of my pet dog, my spirits rose when dad got me a new pup.
(c) Do not stoop to …………………………… just to gain something from someone.
Answer:
Do not stoop to flattery just to gain: something from someone.
(d) The artist completes his paintings …………………………… .
Answer:
The artist completes his paintings by fits and starts.
(e) The crime went …………………………… for 11 years.
Answer:
The crime went undetected for 11 years.
(f) When the baby saw its mother it gave an …………………………… smile.
Answer:
When the baby saw its mother, it gave an appealing smile.
The Thief’s Story Question And Answers Pdf SSC Question 3.
(a) Find from the text the collocation for the following.
(i) ……………………… dog
(ii) ……………………… man
(iii) ticket ………………………
(iv) ……………………… slowly
(v) ……………………… drizzle
(vi) ……………………… sentences
(vii) ……………………… spirits.
Answer:
(i) stray dog
(ii) greedy man
(iii) ticket office
(iv) walked slowly
(v) light drizzle
(vi) whole sentences
(vii) spirits rose
![]()
(b) Complete the compound words from the story.
(i) oil ………………………
(ii) fifty ………………………
(iii) easy ………………………
(iv) tower ………………………
(v) moon ………………………
Answer:
(i) oil rich
(ii) fifty rupee
(iii) easy going
(iv) clock tower
(v) moon light.
(c) Pick out from the story 3 or 4 examples of Code-mixing (Indian words used in English).
Answer:
Examples of code-mixing are:
- bazaar,
- maidan,
- pajamas.
The Thief Story Class 10 Question 4.
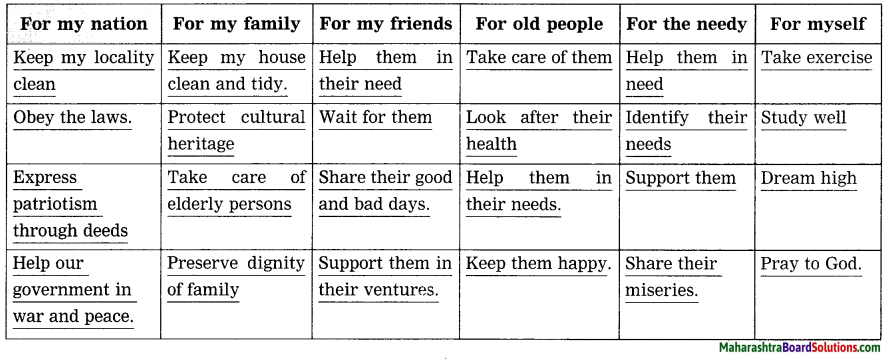
Read the story carefully and complete the table.
| Total no. of characters | Names | Age | Physical appearance | Earned money by | Qualities |
Answer:
| Total no. of characters | Names | Ages | Physical appearance | Earned money by | Qualities |
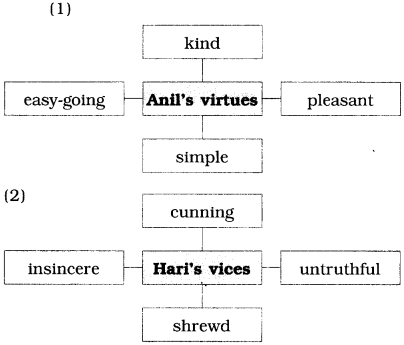
| 2 | Anil | 25 | tall, lean, with a clear, unlined face | writing for magazines; writing books | kind, simple, easy-going, pleasant, forgiving, tactful |
| Hari | 15 | thin, with many scars on the face | stealing and cheating people | cunning, shrewd, insincere, untruthful, ambitious, grateful |
The Thief Story Class 10 Solutions Question 5.
Complete the given sentences.
(a) Anil kept Hari as a cook because ………………………..
(b) Hari was grateful ………………………..
(c) Hari continued making money ………………………..
(d) Anil didn’t hand Hari over to the police ………………………..
(e) The moral of the story is ………………………..
Answer:
(a) Anil kept Hari as a cook because he wanted someone to cook for him. He perhaps also felt sorry for Hari.
(b) Hari was grateful because Anil was teaching him to read, write and add numbers, and all this would be useful to him in his life.
(c) Hari continued making money by cheating Anil while buying the day’s supplies.
(d) Anil was probably too kind-hearted to hand Hari over to the police. He might also have thought that he could try to make an honest man of Hari. If he had handed Hari over to the police, Hari would’ probably have been very bitter and angry, and would have continued in his dishonest ways.
(e) The moral of the story is that if we are good, people are good to us in return. Even thieves respect goodness and kindness.
![]()
Question 6.
Think and write in your own words, in your notebook.
(a) Why did Anil employ Hari as a cook, although he could not afford to pay him?
Answer:
Anil wanted someone to cook for him. He felt that perhaps Hari could cook for him, and in i return he could feed him, as he could not afford to pay him. Anil was also kind-hearted and probably felt / sorry for Hari.
(b) What did Hari learn from Anil in the beginning?
Answer:
In the beginning, Anil taught Hari to cook and write his name.
(c) Why didn’t Anil hand over Hari to the police? What effect would it have had on Hari?
Answer:
Anil was probably too kind-hearted to hand Hari over to the police. He might also have thought that he could try to make an honest man of Hari. If he had handed Hari over to the police, Hari would’ probably have been very bitter and angry, and would have continued in his dishonest ways. Not handing him over to the police had a positive effect on Hari, and may have changed the way he lived his life.
(d) Do you feel Anil’s way of handling a thief like Hari was effective? Justify your answer.
Answer:
Yes, Anil’s way of handling a thief like Hari was effective. Anil knew that Hari was not a hardened seasoned thief. He had realized that Hari really wished to learn to write whole sentences, get an education and become a big man. So by forgiving him and giving him the motivation to learn, he changed Hari. Handing him over to the police would have branded Hari a thief for life and the sudden reform might never have been possible.
(e) What tact had Anil used to change Hari’s dishonest ways?
Answer:
Anil had ignored Hari’s attempts at robbing him. He had then encouraged Hari by saying that they would start writing sentences, for he knew that I this was what Hari wished for wholeheartedly. Anilprovided motivation for Hari to change his ways.
(f) ‘And the smile came by itself without any effort.’ Say why. When do people give fake smiles?
Answer:
People give fake smiles when they are not happy with the situation they are in, or they realize that the other person is trying to cheat them or they want to get something.
![]()
Question 7.
Write a character sketch of ‘Hari Singh’ with the help of the following points, using the paragraph format.
Hari Singh’ s background ……………………….
His dishonesty ……………………….
His aspirations ……………………….
His courage to change himself. ……………………….
Answer:
Hari Singh was fifteen years old, but already an experienced and fairly successful thief. He used to change his name frequently so as to hoodwink his former employers and the police. He even cheated Anil when he went to buy the daily supply of groceries. However, he wished to get an education so that he could become a big and respected man, who would be able to achieve a lot.
He stole a large sum of money from Anil, but regretted it when he realized that in doing so he had lost his only chance of getting an education. He was courageous enough to return the money, even though he knew that he might be caught in the process. However, his desire to change himself is so great that it motivates him and gives him courage to return to Anil.
Question 8.
Frame ‘Wh’ questions to get the answers underlined below. (Change the first-person pronouns to the second person where necessary.)
(a) I hurried back to the room.
(b) I had made a study of men’s faces.
(c) I drew them out, without a sound.
(d) The poor man showed acceptance.
(e) I made tea in the morning.
Answer:
(a) Where did you hurry back to?
(b) What had you made?
(c) How did you draw them out?
(d) Who showed acceptance?
(e) When did you make tea?
![]()
Question 9.
Imagine that Anil catches Hari red-handed when Hari is stealing the money from under the mattress. Compose a short dialogue between the two, which reflects Anil’s shock and Hari’s repeated apologies.
Answer:
Anil: Who’s that? Hari? What are you doing?
Hari: Um..nothing; I was just seeing if your money was safe.
Anil: You mean you were trying to steal my money. You are dressed; you were planning to rob me and run away! Yes, that’s it!
Hari: I’m sorry, Anil, I’m sorry.
Anil: How can you steal from the hand that feeds you? I thought you would have improved! Don’t you want to read and write properly? Do maths?
Hari: I did not think about it. I’m sorry, really sorry.
Anil: Alright, I’ll overlook this, providing you promise I me never to steal again, from me or from anyone else.
Hari: Yes, yes, I promise. Will you really forgive me and continue to teach me?
Anil: Yes. I hope you keep your word,
Hari: Thank you. I’ll keep my word. I promise. Sorry once again.
Question 10.
Choose the correct alternatives from the given options and rewrite the sentences:
(The answers are given directly and underlined.) (appealing, casually, flattery, well-oiled)
Answer:
- I followed casually.
- Anil talked about the well-oiled wrestlers.
- I gave him my most appealing smile.
- A little flattery helps in making friends.
Question 11.
The narrator changed his name every month.
Answer:
The narrator was a thief. He changed his name every month to fool the police and his former employers.
Question 12.
Find similar meanings from the passage for the following:
(1) endearing
(2) miscalculated
(3) humbly
(4) awful
Answer:
(1) appealing
(2) misjudged
(3) modestly
(4) terrible.
![]()
Question 13.
I can’t pay you. (Rewrite making it affirmative.)
Answer:
I am unable to pay you.
Question 14.
“I want to work for you,” I said.
(Change into indirect speech.)
Answer:
I said that I wanted to work for him.
Question 15.
‘We should learn from our own mistakes.’ Explain.
Answer:
First of all, we should accept and understand that we have made a mistake. Then we should analyse and find out what went wrong. Everyone makes l mistakes, but we should learn our lesson from them,Only then will we be able to progress and become good human beings. However, learning from the mistakes of others is probably a better option.
Question 16.
Write whether the following sentences are True or False: (The answers are given directly and: underlined.)
Answer:
(1) In the beginning, Anil taught Hari to cook and write his name. – True
(2) Anil writes for magazines for a living. – True
(3) Hari liked working for Anil. – True
(4) Anil kept a small bundle of notes in a cupboard. – False
Question 17.
Describe the favors Anil did for the narrator.
Answer:
Anil took Hari to his room and told him that he could sleep on the balcony. Even though the meal that Hari cooked that night was terrible, Anil allowed him to live with him. He later taught Hari to cook and write his name. He also ignored the fact that Hari made a little money by cheating him while buying the day’s supplies.
![]()
Question 18.
What proves that the narrator still practiced deceit?
Answer:
The narrator cheated his employer Anil while buying the day’s supplies. This proves that he still practiced deceit.
Question 19.
Anil gave it to a stray dog and told me to be off.
Answer:
gave, told – simple past tense.
Question 20.
It seems he wrote for magazines – a queer way to make a living.
Answer:
seems – simple present tense; wrote – simple past tense.
Question 21.
Add a question tag:
Anil kept worrying about his next cheque.
Answer:
Anil kept worrying about his next cheque, didn’t he?
Question 22.
Anil knew he was being robbed yet he did not say anything. What would you have done in Anil’s place?
Answer:
Cheating and robbing small amounts can lead to bigger thefts. If I were Anil, the moment I knew that I was being robbed, I would have warned him. If he cheated again, I would certainly have told him to be off.
Question 23.
Explain how Hari justified his intention of < stealing the money.
Answer:
Hari thought that he was out of practice and that it was time that he stole some big amount. He also felt that it was alright to take the money for Anil ! did not pay him a salary. Hari tried to justify his act s by convincing himself that Anil, otherwise, would.havewasted that money on his friends.
Question 24.
Write the adjective forms of the following words:
(1) opportunity
(2) pleasure
(3) sleep
(4) situation
Answer:
(1) opportune
(2) pleasant
(3) sleepy/sleepless
(4) situational
![]()
Question 25.
Cross the odd man out: (The answer words are crossed out directly and explanation is given in brackets under each group.)
Answer:
- blanket, magazine, maintain, mattress.
(maintain is a verb; the others are nouns) - rob, take, search.
(time is a noun; the others are verbs) - queer, small, greedy, plettspre.
(pleasure is a noun; the others are adjectives) - quickly, mostly, rfipqty, peacefully
(money is a noun; the others are adverbs)
Question 26.
He was the most trusting person I had ever met. (Rewrite using ‘never’.)
Answer:
I had never met a more trusting person than he is.
Question 27.
I had not done anything in my line of work. (Rewrite without ‘not’)
Answer:
I had yet to do something in my line of work.
Question 28.
Rewrite the following sentences by adding the correct tail tag from those given in the brackets: (does he?, didn’t he?, isn’t it?, wasn’t he?, doesn’t he?, is it?)
(1) Anil was sleeping peacefully.
(2) He doesn’t even notice he’s been robbed.
(3) It’s difficult to rob a careless man.
Answer:
(1) Anil was sleeping peacefully, wasn’t he?
(2) He doesn’t even notice he’s been robbed, does
(3) It’s difficult to rob a careless man, isn’t it?
Question 29.
What could have caused the scars on Hari’sface?
Answer:
Hari was a thief. He probably had got into fights while robbing people. He could also have been inbad company and got into fights with his companions, and someone might have injured him with a knife or any other sharp object. This could have led to scars on his face.
![]()
Question 30.
What will you do if you are robbed by ! someone you know very well? !
Answer:
If I am robbed by someone I know very well, I will firstly thrash out the matter with the thief frankly. I will then cut off my friendship with him/her and take care to keep my belongings under lock and key. I will also keep a close watch on his/her actions,
Question 31.
Choose the correct alternatives from the given options:
Answer:
(1) The Lucknow Express had picked up/not picked up speed. not picked up
(2) Hari wanted to/did not want to stay at a hotel. did not want to
(3) On discovering the theft, Anil would feel sad for the loss of his money/the loss of trust. the loss of trust
(4) Hari had never bought/always bought a ticket in his life. never bought
Question 32.
Hari believed that friends were more trouble than help.
Answer:
Hari was a thief. In his line of work, friends would probably try to borrow from him or give away his whereabouts to the police. Or perhaps they would create trouble for him to save themselves. Hence he felt that friends were more trouble.
Question 33.
When I reached the station I did not stop at the ticket office.
Answer:
(a) Compound sentence: 1 reached the station but (I) did not stop at the ticket office.
(b) Simple sentence: I did not stop at the ticket office on reaching the station/After reaching the station, I did not stop at the ticket office.
Question 34.
When the train had gone, I found myself standing alone on the deserted platform.
Answer:
(a) Compound sentence: The train had gone and I found myself standing alone on the deserted platform.
(b) Simple sentence: The train having gone, I found myself standing alone on the deserted platform.
Question 35.
What is face-reading? Can you read faces?
Answer:
Face-reading is observing the expressions and emotions on thc faces of people and Interpreting them correctly. I am observant and read faces quite well. I am trying to improve this ability.
Question 36.
Fill in the blanks with the correct options from the brackets: (The answers are given directly and underlined.)
Answer:
(1) Han felt very nervous when he returned to the room that night. (nervous/excited)
(2) Han slipped the notes under the edge of the mattress. (bed / mattress)
(3) Hail’s heart sank when he thought that his theft had been discovered. (undetected /discovered)
(4) Anil was asleep when Hart returned to the room. (awake/asleep)
![]()
Question 37.
Rearrange the sentences in the order of occurrence:
(1) He crept to the head of the bed.
(2) He slipped the notes under the mattress.
(3) He opened the door quietly.
(4) He went back to the room.
Answer:
(4) He went back to the room.
(3) He opened the door quietly.
(1) He crept to the head of the bed.
(2) He slipped the notes under the mattress.
Question 38.
Describe Hari’s regrets as he pondered over his theft.
Answer:
As he pondered over his theft, Hari regretted ! that henceforth he could not cook Anil’s meals, runto the bazaar or learn to write whole sentences any S more. He regretted that he would not become a big! man, clever and respected.
Question 39.
Does Anil realize that he has been robbed?
Answer:
Yes, Anil realises that he has been robbed.
Question 40.
‘And the smile came by itself without any effort.’ Say why.
OR
Explain why Hari gave a genuine appeal! smile.
Answer:
Hari regretted what he had done. He went; back to Anil in order to get an education. He realised that Anil knew about the theft. He was relieved and happy that Anil had decided to ignore what had happened and to teach him to write whole sentences.
Anil’s response brought forth a change of heart in – Hari. So, instead of his usual affected smile, a genuine appealing smile came upon Hari’s face.
Question 41.
What tact had Anil used to change Hari’s dishonest ways?
Question 42.
Rewrite using the modal auxiliary ‘might’.
He would probably have given me two or three rupees to go to the cinema.
Answer:
He might have given me two or three rupees to go to the cinema.
Question 43.
Whole sentences, I knew, could one day bring me more than a few hundred rupees.
Answer:
Whole sentences, I knew, might one day bring me more than a few hundred rupees.
Question 44.
Why didn’t Anil hand Hari over to the police? What effect would it have on Hari?
Answer:
Anil was probably too kind-hearted to hand Hari over to the police. He might also have thought that he could try to make an honest man of Hari. If he had handed Hari over to the police, Hari would’ probably have been very bitter and angry, and would have continued in his dishonest ways. Not handing him over to the police had a positive effect on Hari, and may have changed the way he lived his life.
![]()
Question 45.
Do you feel Anil’s way of handling a thief like Hari was effective? Justify your answer.
Answer:
Yes, Anil’s way of handling a thief like Hari was effective. Anil knew that Hari was not a hardened seasoned thief. He had realized that Hari really wished to learn to write whole sentences, get an education and become a big man. So by forgiving him and giving him the motivation to learn, he changed Hari. Handing him over to the police would have branded Hari a thief for life and the sudden reform might never have been possible.
Question 46.
Punctuate: I asked can you feed me
Answer:
- There was a touch of sadness in the face of the beautiful woman.
- My hand found the edge of the mattress.
- publisher – publish, brush, (blush, plush, slurp).
- I wanted to get a good book from the library.
- Interrogative sentence.
- present participle-robbing; past participle- robbed.
- I asked, “Can you feed me?”
Question 47.
Do as directed (Medium Level Activities):
(1) Use the following word and its homophone in two separate sentences: knew
(2) I took a new name every month. (Change the voice beginning A new …)
(3) Anil talked about the well-oiled wrestlers. (Rewrite using the past progressive tense of the verb.)
(4) “Well,” I said modestly, “I do wrestle a bit.” (Rewrite in reported speech.)
Answer:
(1) (i) The boy knew the poem very well,
(ii) The jacket was new and expensive.
(2) A new name was taken by me every month.
(3) Anil was talking about the well-oiled wrestlers.
(4) I modestly said that I did wrestle a bit.
Question 48.
Do as directed (Challenging Activities):
(1) Use the following word as a verb and a noun in two separate sentences: cook
(2) Analyse the sentence:
I was still a thief when I met Anil.
Answer:
(1) (i) We cook fresh meals daily at home. (verb)
(ii) The new cook resigned from his job after just two days, (noun)
(2) Complex Sentence:
I was still a thief – Main Clause ; when
I met Anil – adverb clause of time.
![]()
Question 49.
Prepare a short character sketch of Anil.
Answer:
Anil was a kind, simple and easy-going young man. He was tall and lean in stature and interested in sports like wrestling. He was not very rich, and could not afford to employ Hari as a cook. He had the patience and goodness to not only teach Hari to cook but also to read, write and add numbers. Though he knew that Hari was making a profit out of the grocery purchase, he ignored this fact.
Anil was a writer who wrote for magazines and made money in fits and starts. He was a very trusting person. Even when he earned a large amount of money, he kept the money under his mattress and not under lock and key. He was generous and paid Hari when he got some money, even though he knew that Hari had tried to steal the money from him. He was forgiving, for he forgave Hari the theft and continued to be good to him.
English Kumarbharati 10th Digest PDF
- Where the mind is Without fear 10th English Textbook Solutions
- The Thief’s Story 10th English Textbook Solutions
- On Wings of Courage 10th English Textbook Solutions
- All the World’s a Stage 10th English Textbook Solutions
- Joan of Arc 10th English Textbook Solutions
- The Alchemy of Nature 10th English Textbook Solutions