Category: Class 11

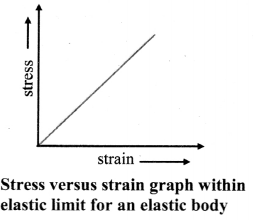
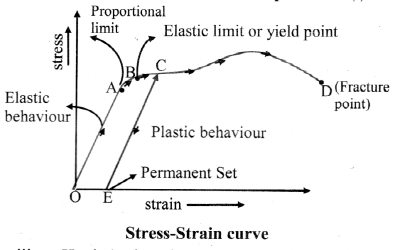
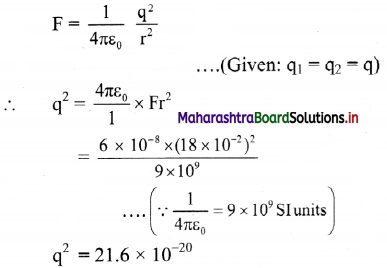Cell Division Class 11 Exercise Question Answers Solutions Maharashtra Board

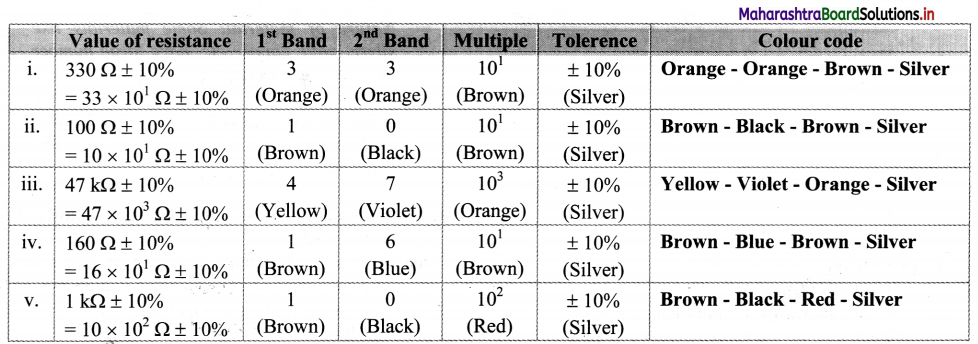
Balbharti Maharashtra State Board 11th Biology Textbook Solutions Chapter 7 Cell Division Textbook Exercise Questions and Answers.

Class 11 Biology Chapter 7 Exercise Solutions Maharashtra Board

Biology Class 11 Chapter 7 Exercise Solutions

1. Choose the correct option

Question (A)
The connecting link between Meiosis – I and Meiosis – II is …………
(a) interphase – I
(b) interphase – II
(c) interkinesis – III
(d) anaphase – IV
Answer:
(c) interkinesis – III

Question (B)
Synapsis is pairing of ………………. .
(a) any two chromosomes
(b) non – homologous chromosomes
(c) sister chromatids
(d) homologous chromosomes
Answer:
(d) homologous chromosomes

Question (C)
Spindle apparatus is formed during which stage of mitosis?
(a) Prophase
(b) Metaphase
(c) Anaphase
(d) Telophase
Answer:
(b) S-phase

Question (D)
Chromosome number of a cell is almost doubled up during _______ .
(a) G₁ – phase
(b) S – phase
(c) G₂-phase
(d) G₀-phase
[Note: Due to DNA replication the DNA content of cell doubles during S-phase. But the number of chromosomes remain the same.]
Answer:
(b) S – phase

Question (E)
How many meiotic divisions are necessary for formation of 80 sperms?
(a) 80
(b) 40
(c) 20
(d) 10
Answer:
(c) 20

Question (F)
How many chromatids are present in anaphase – I of meiosis – I of a diploid cell having 20 chromosomes?
(a) 4
(b) 6
(c) 20
(d) 40
Answer:
(d) 40

Question (G)
In which of the following phase of mitosis chromosomes are arranged at equatorial plane?
(a) Prophase
(b) Metaphase
(c) Anaphase
(d) Telophase
Answer:
(b) Metaphase

Question (H)
Find incorrect statement.
(a) Condensation of chromatin material occurs in prophase.
(b) Daughter chromatids are formed in anaphase.
(c) Daughter nuclei are formed at metaphase.
(d) Nuclear membrane reappears in telophase.
Answer:
(c) Daughter nuclei are formed at metaphase.

Question (I)
Histone proteins are synthesized during
(a) G₁ phase
(b) S – phase
(c) G₂ – phase
(d) Interphase
Answer:
(b) S – phase

2. Answer the following questions

Question (A)
While observing a slide, student observed many cells with nuclei. But some of the nuclei were bigger as compared to others but their nuclear membrane was not so clear. Teacher inferred it as one of the phase in the cell division. Which phase may be inferred by teacher?
Answer:
Prophase.

Question (B)
Students prepared a slide of onion root tip. There were many cells seen under microscope. There was a cell seen under microscope. There was a cell with two groups of chromosomes at opposite ends of the cell. This cell is in which phase of mitosis?
Answer:
Anaphase.

Question (C)
Students were shown some slides of cancerous cells. Teacher made a comment as if there would have been a control at one of its cell cycle phase, there wouldn’t have been a condition like this. Which phase the teacher was referring to?
Answer:
The phase teacher was referring would be G_i phase.

Question (D)
Some Mendelian crossing experimental results were shown to the students. Teacher informed that there are two genes located on the same chromosome. He enquired if they will be ever separated from each other?
Answer:

1. Genes are located on chromosomes at specific distance and position.
2. The greater this distance, the greater the chance that a crossover can occur between the genes and the greater the chances of recombination.
3. The chances of recombination are less between the genes that are placed closed to each other on the chromosome.
4. Therefore, due to recombination the two genes located on the same chromosome have possibility of separating from each other.

Question (E)
Students were observing a film on Paramoecium. It underwent a process of reproduction. Teacher said it is due to cell division. But students objected and said that there was no disappearance of nuclear membrane and no spindle formation, how can it be cell division? Can you clarify?
Answer:

1. Paramoecium is a unicellular organism. The division in Paramoecium occurs by amitosis.
2. It is the simplest mode of cell division.
3. In amitosis, nucleus elongates and a constriction appears. This constriction deepens and divides the nucleus in two daughter nuclei followed by the division of cytoplasm.

Question (F)
Is the meiosis responsible for evolution? Justify your answer.
Answer:

1. Meiosis ensures that organisms produced by sexual reproduction contain correct number of chromosomes.
2. Meiosis exhibits genetic variation by the process of recombination.
3. Variations increase further after union of gametes during fertilization creating offspring with unique characteristics. Thus, it creates diversity of life and is responsible for evolution.

Question (G)
Why mitosis and meiosis – II are called as homotypic division?
Answer:
1. In mitosis, the chromosome number and genetic material of daughter cells remain same as that of the parent cell.
2. In meiosis – II, two haploid cells formed during first meiotic division divide further into four haploid cells. This division is identical to mitosis. The daughter cells formed in second meiotic division are similar to their parent cells with respect to the chromosome number formed in meiosis -1. Hence mitosis and meiosis – II are called homotypic division.

Question (H)
Write the significance of mitosis.
Answer:

1. As mitosis is equational division, the chromosome number is maintained constant.
2. It ensures equal distribution of the nuclear and the cytoplasmic content between the daughter cells, both quantitatively and qualitatively. Therefore, the process of mitosis also maintains the nucleo-cytoplasmic ratio.
3. The DNA is also equally distributed.
4. It helps in growth and development of organisms.
5. Old and worn-out cells are replaced through mitosis.
6. It helps in the asexual reproduction of organisms and vegetative propagation in plants.

Question (I)
Enlist the different stages of prophase – I.
Answer:
1. Prophase -I:
It is the most complicated and longest phase of meiotic division.
It is further divided into five sub-phases viz. leptotene, zygotene, pachytene, diplotene and diakinesis.

a. Leptotene:
The volume of the nucleus increases.
The chromosomes become long distinct and coiled.
They orient themselves in a specific fonn known as bouquet stage. This is characterized with the ends of chromosomes converged towards the side of nucleus where the centrosome lies. j Lep
The centriole duplicates into two and migrates to opposite poles. [Note: Centrioles divide during Gj phase of interphase.]

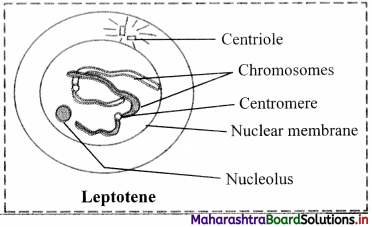
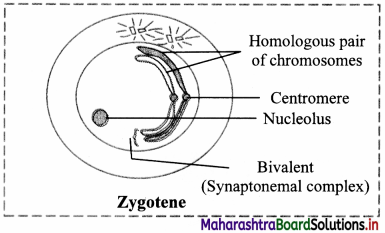
b. Zygotene:
Pairing of non-sister chromatids of homologous chromosomes takes place by formation of synaptonemal complex. This pairing is called synapsis.
Each pair consists of a maternal chromosome and a paternal chromosome. Chromosomal pairs are called bivalents or tetrads.

c. Pachytene:
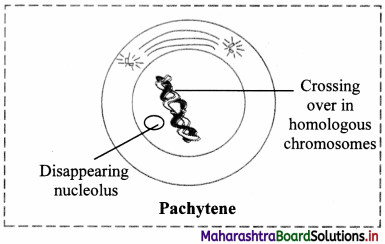
Each individual chromosome begins to split longitudinally into two similar chromatids. Therefore, each bivalent now appears as a tetrad consisting of four chromatids.
The homologous chromosomes begin to separate but they do not separate completely and remain attached to one or more points. These points are called chiasmata (Appear like a cross-X).
Chromatids break at these points and broken segments are exchanged between non-sister chromatids of homologous chromosomes resulting in recombination.

d. Diplotene:
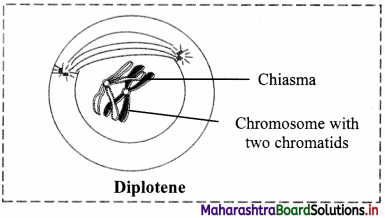
The chiasma becomes clearly visible in diplotene due to beginning of repulsion between synapsed homologous chromosomes. This is known as desynapsis. Synaptonemal complex also starts to disappear.

e. Diakinesis:
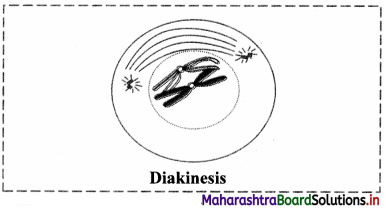
The chiasmata begin to move along the length of chromosomes from the centromere towards the ends of chromosomes. The displacement of chiasmata is termed as terminalization.
The terminal chiasmata exist till the metaphase.
The nucleolus and nuclear membrane completely disappear and spindle fibres begin to appear.

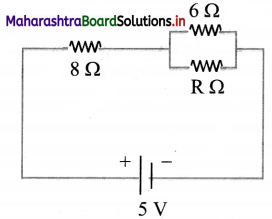
3. Draw labelled diagrams and write explanation

Question (A)
With the help of suitable diagram, describe the cell cycle.
Answer:
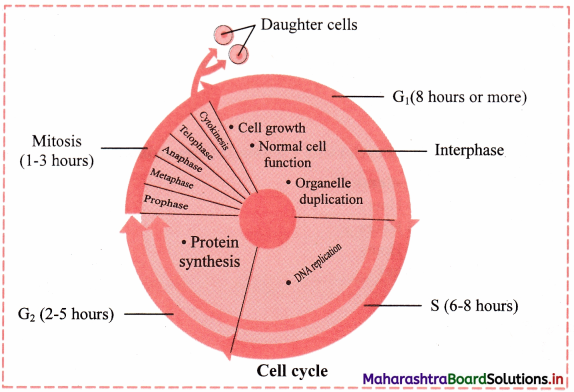
1. Series of events occurring in the life of a cell is called cell cycle. Interphase and M – phase are the two phases of cell cycle.
2. Interphase: It is the stage between two successive cell divisions. It is the longest phase of a cell cycle during which the cell is highly active and prepares itself for cell division.
The interphase is subdivided into three sub-phases as G₁ – phase, S-phase and G₂-phase.
a. G₁ – phase (First gap period/First Gap Phase):
It begins immediately after cell division.
RNA (mRNA, rRNA and tRNA) synthesis, protein synthesis and synthesis of membranes take place during this phase.
b. S – phase (Synthesis phase):
In this phase DNA is synthesized (replicated), so that amount of DNA per cell doubles.
Synthesis of histone proteins takes place in this phase.
c. G₂ – phase (Second growth phase/Second Gap Phase):
Metabolic activities essential for cell division occur during this phase.
Various proteins which are necessary for the cell division are also synthesized in this phase.
Apart from this, RNA synthesis also occurs during this phase.
In animal cells, a daughter pair of centrioles appears near the pre-existing pair.

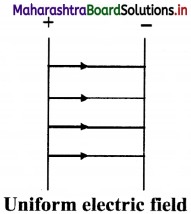
Question (B)
Distinguish between mitosis and meiosis.
Answer:

Question (C)
Draw labelled diagrams and write explanation Draw the diagram of metaphase.
Answer:
Metaphase:
a. Chromosomes are completely condensed and appear short.
b. Centromere and sister chromatids become very prominent.
c. All the chromosomes are arranged at equatorial plane of cell. This is called metaphase plate.
d. Mitotic spindle is fully formed in this phase.
e. Centromere of each chromosome divides horizontally into two, each being associated with a chromatid. [Note: The centromeres divide at the beginning of anaphase so that the two chromatids of each chromosome become separated from each other.
Source: Cell Division, Donald B. McMillan, Richard J. Harris, in An Atlas of Comparative Vertebrate Histology, 2018.]

Question 4.
Match the following column – A with column – B

Answer:

Question 5.
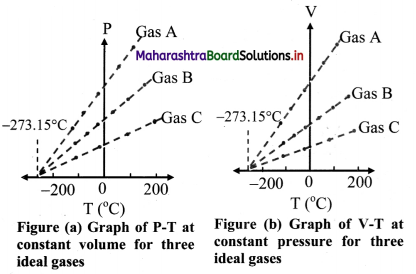
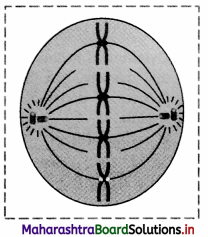
Is the given figure correct? Why?

Answer:
1. The given figure is incorrect as the spindle fibres are not attached to centromere of the chromosomes.
2. During metaphase, chromosomes are attached to spindle fibres with the help of centromeres.

Question 6.
If an onion has 16 chromosomes in its leaf cell, how many chromosomes will be there in its root cell and pollen grain.
Answer:
1. The chromosomes in root cell will be 16 as root cell is a diploid cell.
2. The chromosomes in pollen grain will be 8 as pollen grain is a haploid cell.

7. Identify the following phases of mitosis and label the ‘A’ and ‘B’ given in diagrams.

Question (i)

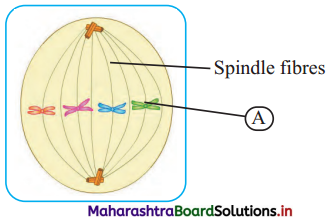
Answer:
The diagram shown is of Metaphase.
A: Chromosomes arranged on metaphase plate

Question (ii)

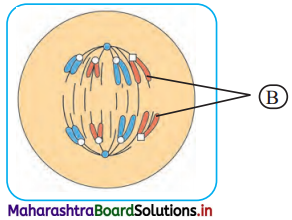
Answer:
The diagram shown is of Anaphase.
B: Chromatids moving to opposite poles.

Practical / Project:

Question 1.
Fix the onion root tips at different durations of the day starting from 6am up to 9am at the intervals of half an hour. Prepare the slide of each fixed root tip and analyse the relation between time and phase of mitosis.
Answer:
Mitotic division is an equational division in which one parent cell give rise to two daughter cells with equal number of chromosomes in daughter cells and mother cell. It has four sub phases: prophase, metaphase, anaphase, telophase.

Mitosis is affected by temperature and time. Mitotic index is high in morning so the mitosis is observed clearly in the morning. (Mitotic index is defined as the ratio between the number of cells in a population undergoing mitosis to the total number of cells in a population. )
[Note: Students catt use above information for reference and perform this activity on their own.]

11th Biology Digest Chapter 7 Cell Division Intext Questions and Answers

Can you recall? (Textbook Page No. 76)

How do your wounds heal?
Answer:
a. A wound is an injury to living tissue.
b. Healing of wound take place by mitosis.
c. Repetitive mitotic divisions near the site of injury results in healing of wound.

Can you tell? (Textbook Page No. 79)

What is cell cycle?
Answer:

1. Sequential events occurring in the life of a cell is called cell cycle.
2. Interphase and M – phase are the two phases of cell cycle.
3. Cell undergoes growth or rest during interphase and divides during M – phase.

Discuss with teacher (Textbook Page No. 76)

Some cells do not have gap phase in their cell cycle whereas some cells spend maximum part of their life in gap phase. Search for such cells. Some cells are said to be in G₀ phase. What is this G₀ phase?
Answer:

1. G₀ is the phase of the cell cycle in eukaryotes in which many cell types stop dividing. It is also called a quiescent stage.
2. If cells are deprived of appropriate growth factors, they stop at the Gi checkpoint of the cell cycle. Their growth and division are arrested and they remain in G₀ phase.
3. Mature neurons and muscle cells remain in G₀ phase.

Question 5.
Can you tell? (Textbook Page No. 79)
Answer:
1. Series of events occurring in the life of a cell is called cell cycle. Interphase and M – phase are the two phases of cell cycle.
2. Interphase: It is the stage between two successive cell divisions. It is the longest phase of a cell cycle during which the cell is highly active and prepares itself for cell division.
The interphase is subdivided into three sub-phases as G₁ – phase, S-phase and G₂-phase.
a. G₁ – phase (First gap period/First Gap Phase):
It begins immediately after cell division.
RNA (mRNA, rRNA and tRNA) synthesis, protein synthesis and synthesis of membranes take place during this phase.
b. S – phase (Synthesis phase):
In this phase DNA is synthesized (replicated), so that amount of DNA per cell doubles.
Synthesis of histone proteins takes place in this phase.
c. G₂ – phase (Second growth phase/Second Gap Phase):

1. Metabolic activities essential for cell division occur during this phase.
2. Various proteins which are necessary for the cell division are also synthesized in this phase.
3. Apart from this, RNA synthesis also occurs during this phase.
4. In animal cells, a daughter pair of centrioles appears near the pre-existing pair.

Internet my friend (Textbook Page No. 77)

What is Karyogram or Karyotype?
Answer:
1. A karyotype is a representation of condensed chromosomes arranged in pairs.
2. Analysis of the karyotype of a particular individual indicates whether the individual has a normal set of chromosomes or whether there are abnormalities in number or appearance of individual chromosomes.

Can you tell? (Textbook Page No. 79)

Which are the steps of mitosis?
Answer:
Steps in mitosis are Karyokinesis and Cytokinesis. Karyokinesis includes four stages – Prophase, Metaphase, Anaphase and Telophase.

Internet my friend (Textbook Page No. 79)

How the life span of a cell is decided?
Answer:

1. Life span of different cells vary greatly.
2. Life span of a cell is decided by its growth rate, metabolic activities and cell size.
3. The life span of a cell can be analysed in laboratory by applying carbon-14 technique to DNA.
4. This method is commonly used in archaeology and paleontology to find the age of fossils. Same can be applied to determine the life span of a cell.

Do yourself (Textbook Page No. 80)

Write down the explanation of prophase I in your own words.
Answer:
1. Prophase -I:
It is the most complicated and longest phas0e of meiotic division.
It is further divided into five sub-phases viz. leptotene, zygotene, pachytene, diplotene and diakinesis.

a. Leptotene:

1. The volume of the nucleus increases.
2. The chromosomes become long distinct and coiled.
3. They orient themselves in a specific fonn known as bouquet stage. This is characterized with the ends of chromosomes converged towards the side of nucleus where the centrosome lies.
4. The centriole duplicates into two and migrates to opposite poles. [Note: Centrioles divide during G_j phase of interphase.]

b. Zygotene:

1. Pairing of non-sister chromatids of homologous chromosomes takes place by formation of synaptonemal complex. This pairing is called synapsis.
2. Each pair consists of a maternal chromosome and a paternal chromosome. Chromosomal pairs are called bivalents or tetrads.

c. Pachytene:

1. Each individual chromosome begins to split longitudinally into two similar chromatids. Therefore, each bivalent now appears as a tetrad consisting of four chromatids.
2. The homologous chromosomes begin to separate but they do not separate completely and remain attached to one or more points.
3. These points are called chiasmata (Appear like a cross-X).
4. Chromatids break at these points and broken segments are exchanged between non-sister chromatids of homologous chromosomes resulting in recombination.

d. Diplotene:
The chiasma becomes clearly visible in diplotene due to beginning of repulsion between synapsed homologous chromosomes. This is known as desynapsis. Synaptonemal complex also starts to disappear.

e. Diakinesis:

1. The chiasmata begin to move along the length of chromosomes from the centromere towards the ends of chromosomes. The displacement of chiasmata is termed as terminalization.
2. The terminal chiasmata exist till the metaphase.
3. The nucleolus and nuclear membrane completely disappear and spindle fibres begin to appear.

Curiosity Box: (Textbook Page No. 81)

(i) What is exact structure of synaptonemal complex?
Answer:
Synaptonemal complexes are zipper like structures assembled between homologous chromosomes during the prophase of first meiotic division.
[Source: ncbi.nlm. nih.gov/pubmed/8743892]

(ii) What is structure of chiasma?
Answer:
Chiasma is a X-shaped point of attachment between two non-sister chromatids of a homologous chromosomes.

(iii) Which type of proteins are involved in formation of spindle fibres?
Answer:
Spindle fibres are formed from microtubules with many accessory proteins.

(iv) Why and how spindle fibres elongate and some contract?
Answer:
a. Spindle fibres elongate for assembly of chromosomes at equatorial plane of the cell during metaphase and spindle fibres contract for pulling chromosomes towards opposite poles during anaphase.
b. The spindle fibres elongate (polymerize) by incorporating subunits of the protein tubulin and contract

(v) What is the role of centrioles in formation of spindle apparatus?
Answer:
Centriole plays an important role in cell division. Centrioles help organize microtubule assembly and forms spindle apparatus that separate the chromosomes during cell division.

Curiosity box (Textbook Page No. 81)

What would have happened in absence of meiosis?
Answer:

1.  Gametes are produced by the process of meiosis which are essential for sexual reproduction.
2. Diploid organisms have two set of chromosomes (one paternal and one maternal).
3. For a diploid organism to undergo sexual reproduction it needs to create gametes that contain only one set of chromosomes so the number of chromosomes remains same in the next generation.
4. In absence of meiosis, the chromosome number of parents and their offsprings will differ in every generation; hence no species will hold its characters.
5. Also, there will be no crossing over of homologous chromosomes. Thus, there will be no variations with respect to the changing environment in progeny to maintain their existence, which may lead to extinction of species.

Can you tell? (Textbook Page No. 82)

(i) What is the difference between mitosis and meiosis?
Answer:

(ii) What is difference between meiosis – I and meiosis – II?
Answer:

(iii) Elaborate the process of recombination.
Answer:
a. Recombination is exchange of genetic material between paternal and maternal chromosomes during gamete formation.
b. The points where crossing over takes place is known as chiasmata.
c. Chromatids acquire new combinations of alleles by physically exchanging segments in crossing-over.
d. The exchange of genetic material between homologous chromosomes involves accurate breakage and joining of DNA molecules through a complex mechanism.
e. It is catalyzed by enzymes.

Do Yourself (Textbook Page No. 82)

Prepare a concept map on cell division in following box.
Answer:
Refer Quick Review

Internet My Friend (Textbook Page No. 82)

Different types of proteins like cyclins, maturation promoting factor (MPF), cyclosomes, enzymes like cyclin dependent kinases (CDK) play important role in control of cell cycle. Collect more information about these proteins and enzymes from internet, prepare a power-point presentation and present it in the class.
Answer:

1. The regulation of the cell cycle involves an internal control system consisting of proteins called cyclins and enzymes called cyclin-dependent kinases.
2. A Cdk is a protein kinase. When the kinase of the Cdk is activated upon binding to a cyclin, it phosphorylates target proteins in the cell, regulating their activities.
3. Those proteins play important roles in initiating or regulating significant events of the cell cycle, such as DNA replication, mitosis, and cytokinesis.
4. Maturation Promoting Factor (MPF) triggers the cell’s passage into the mitotic phase.
   [Note: Students are expected to perform the above activity by their own with the help of information provided in the answer.]

Maharashtra State Board Class 11 Biology Textbook Solutions

• Living World Class 11 Biology Textbook Solutions
• Systematics of Living Organisms Class 11 Biology Textbook Solutions
• Kingdom Plantae Class 11 Biology Textbook Solutions
• Kingdom Animalia Class 11 Biology Textbook Solutions
• Cell Structure and Organization Class 11 Biology Textbook Solutions
• Biomolecules Class 11 Biology Textbook Solutions
• Cell Division Class 11 Biology Textbook Solutions

Semiconductors Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 14 Semiconductors Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 14 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 14 Exercise Solutions

1. Choose the correct option.

Question 1.
Electric conduction through a semiconductor is due to:
(A) Electrons
(B) holes
(C) none of these
(D) both electrons and holes
Answer:
(D) both electrons and holes

Question 2.
The energy levels of holes are:
(A) in the valence band
(B) in the conduction band
(C) in the band gap but close to valence band
(D) in the band gap but close to conduction band
Answer:
(C) in the band gap but close to valence band

Question 3.
Current through a reverse biased p-n junction, increases abruptly at:
(A) Breakdown voltage
(B) 0.0 V
(C) 0.3V
(D) 0.7V
Answer:
(A) Breakdown voltage

Question 4.
A reverse biased diode, is equivalent to:
(A) an off switch
(B) an on switch
(C) a low resistance
(D) none of the above
Answer:
(A) an off switch

Question 5.
The potential barrier in p-n diode is due to:
(A) depletion of positive charges near the junction
(B) accumulation of positive charges near the junction
(C) depletion of negative charges near the junction,
(D) accumulation of positive and negative charges near the junction
Answer:
(D) accumulation of positive and negative charges near the junction

2. Answer the following questions.

Question 1.
What is the importance of energy gap in a semiconductor?
Answer:

1. The gap between the bottom of the conduction band and the top of the valence band is called the energy gap or the band gap.
2. This band gap is present only in semiconductors and insulators.
3. Magnitude of the band gap plays a very important role in the electronic properties of a solid.
4. Band gap in semiconductors is of the order of 1 eV.
5. If electrons in valence band of a semiconductor are provided with energy more than band gap energy (in the form of thermal energy or electrical energy), then the electrons get excited and occupy energy levels in conduction band. These electrons can easily take part in conduction.

Question 2.
Which element would you use as an impurity to make germanium an n-type semiconductor?
Answer:
Germanium can be made an n-type semiconductor by doping it with pentavalent impurity, like phosphorus (P), arsenic (As) or antimony (Sb).

Question 3.
What causes a larger current through a p-n junction diode when forward biased?
Answer:
In case of forward bias the width of the depletion region decreases and the p-n junction offers a low resistance path allowing a high current to flow across the junction.

Question 4.
On which factors does the electrical conductivity of a pure semiconductor depend at a given temperature?
Answer:
For pure semiconductor, the number density of free electrons and number density of holes is equal. Thus, at a given temperature, the conductivity of pure semiconductor depends on the number density of charge carriers in the semiconductor.

Question 5.
Why is the conductivity of a n-type semiconductor greater than that of p-type semiconductor even when both of these have same level of doping?
Answer:

1. In a p-type semiconductor, holes are majority charge carriers.
2. When a p-type semiconductor is connected to terminals of a battery, holes, which are not actual charges, behave like a positive charge and get attracted towards the negative terminal of the battery.
3. During transportation of hole, there is an indirect movement of electrons.
4. The drift speed of these electrons is less than that in the n-type semiconductors. Mobility of the holes is also less than that of the electrons.
5. As, electrical conductivity depends on the mobility of charge carriers, the conductivity of a n-type semiconductor is greater than that of p-type semiconductor even when both of these have same level of doping.

3. Answer in detail.

Question 1.
Explain how solids are classified on the basis of band theory of solids.
Answer:
i. The solids can be classified into conductors, insulators and semiconductors depending on the distribution of electron energies in each atom.

ii. As an outcome of the small distances between atoms, the resulting interaction amongst electrons and the Pauli’s exclusion principle, energy bands are formed in the solids.

iii. In metals, conduction band and valence band overlap. However, in a semiconductor or an insulator, there is gap between the bottom of the conduction band and the top of the valence band. This is called the energy gap or the band gap.

iv. For metals, the valence band and the conduction band overlap and there is no band gap as shown in figure (b). Therefore, electrons can easily gain electrical energy when an external electric field is applied and are easily available for conduction.

v. In case of semiconductors, the band gap is fairly small, of the order of 1 eV or less as shown in figure (c). Hence, with application of external electric field, electrons get excited and occupy energy levels in conduction band. These can take part in conduction easily.

vi. Insulators, on the contrary, have a wide gap between valence band and conduction band of the order of 5 eV (for diamond) as shown in figure (d). Therefore, electrons find it very difficult to gain sufficient energy to occupy energy levels in conduction band.

vii. Thus, an energy band gap plays an important role in classifying solids into conductors, insulators and semiconductors based on band theory of solids.

Question 2.
Distinguish between intrinsic semiconductors and extrinsic semiconductors
Answer:

Question 3.
Explain the importance of the depletion region in a p-n junction diode.
Answer:
i. The region across the p-n junction where there are no charges is called the depletion layer or the depletion region.

ii. During diffusion of charge carriers across the junction, electrons migrate from the n-side to the p-side of the junction. At the same time, holes are transported from p-side to n-side of the junction.

iii. As a result, in the p-type region near the junction there are negatively charged acceptor ions, and in the n-type region near the junction there are positively charged donor ions.

iv. The potential barrier thus developed, prevents continuous flow of charges across the junction. A state of electrostatic equilibrium is thus reached across the junction.

v. Free charge carriers cannot be present in a region where there is a potential barrier. This creates the depletion region.

vi. In absence of depletion region, all the majority charge carriers from n-region (i.e., electron) will get transferred to the p-region and will get combined with the holes present in that region. This will result in the decreased efficiency of p-n junction.

vii. Hence, formation of depletion layer across the junction is important to limit the number of majority carriers crossing the junction.

Question 4.
Explain the I-V characteristic of a forward biased junction diode.
Answer:

1. Figure given below shows the I-V characteristic of a forward biased diode.
2. When connected in forward bias mode, initially, the current through diode is very low and then there is a sudden rise in the current.
3. The point at which current rises sharply is shown as the ‘knee’ point on the I-V characteristic curve.
4. The corresponding voltage is called the knee voltage. It is about 0.7 V for silicon and 0.3 V for germanium.
5. A diode effectively becomes a short circuit above this knee point and can conduct a very large current.
6. To limit current flowing through the diode, resistors are used in series with the diode.
7. If the current through a diode exceeds the specified value, the diode can heat up due to the Joule’s heating and this may result in its physical damage.

Question 5.
Discuss the effect of external voltage on the width of depletion region of a p-n junction.
Answer:

1. A p-n junction can be connected to an external voltage supply in two possible ways.
2. A p-n junction is said to be connected in a forward bias when the p-region connected to the positive terminal and the n-region is connected to the negative terminal of an external voltage source.
3. In forward bias connection, the external voltage effectively opposes the built-in potential of the junction. The width of depletion region is thus reduced.
4. The second possibility of connecting p-n junction is in reverse biased electric circuit.
5. In reverse bias connection, the p-region is connected to the negative terminal and the n-region is connected to the positive terminal of the external voltage source. This external voltage effectively adds to the built-in potential of the junction. The width of potential barrier is thus increased

11th Physics Digest Chapter 14 Semiconductors Intext Questions and Answers

Internet my friend (Textbookpage no. 256)

i. https://www.electronics-tutorials.ws/diode
ii. https://www.hitachi-hightech.com
iii. https://nptel.ac.in/courses
iv. https://physics.info/semiconductors
v. http://hyperphysics.phy- astr.gsu.edu/hbase/Solids/semcn.html

[Students are expected to visit above mentioned links and collect more information regarding semiconductors.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Electromagnetic Waves and Communication System Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 13 Electromagnetic Waves and Communication System Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 13 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 13 Exercise Solutions

1. Choose the correct option.

Question 1.
The EM wave emitted by the Sun and responsible for heating the Earth’s atmosphere due to the greenhouse effect is
(A) Infra-red radiation
(B) X-ray
(C) Microwave
(D) Visible light
Answer:
(A) Infra-red radiation

Question 2.
Earth’s atmosphere is richest in
(A) UV
(B) IR
(C) X-ray
(D) Microwaves
Answer:
(B) IR

Question 3.
How does the frequency of a beam of ultraviolet light change when it travels from air into glass?
(A) depends on the values of p and e
(B) increases
(C) decreases
(D) remains same
Answer:
(D) remains same

Question 4.
The direction of EM wave is given by
(A) \(\bar{E}\) × \(\bar{B}\)
(B) \(\bar{E}\).\(\bar{B}\)
(C) along \(\bar{E}\)
(D) along \(\bar{B}\)
Answer:
(A) \(\bar{E}\) × \(\bar{B}\)

Question 5.
The maximum distance upto which TV transmission from a TV tower of height h can be received is proportional to
(A) h½
(B) h
(C) h^3/2
(D) h²
Answer:
(A) h½

Question 6.
The waves used by artificial satellites for communication purposes are
(A) Microwave
(B) AM radio waves
(C) FM radio waves
(D) X-rays
Answer:
(A) Microwave

Question 7.
If a TV telecast is to cover a radius of 640 km, what should be the height of transmitting antenna?
(A) 32000 m
(B) 53000 m
(C) 42000 m
(D) 55000 m
Answer:
(A) 32000 m

2. Answer briefly.

Question 1.
State two characteristics of an EM wave.
Answer:
i. The electric and magnetic fields, \(\vec{E}\) and \(\vec{B}\) are always perpendicular to each other and also to the direction of propagation of the EM wave. Thus, the EM waves are transverse waves.

ii. The cross product (\(\vec{E}\) × \(\vec{B}\)) gives the direction in which the EM wave travels. (\(\vec{E}\) × \(\vec{B}\)) also gives the energy carried by EM wave.

Question 2.
Why are microwaves used in radar?
Answer:
Microwaves are used in radar systems for identifying the location of distant objects like ships, aeroplanes etc.

Question 3.
What are EM waves?
Answer:
Waves that are caused by the acceleration of charged particles and consist of electric and magnetic fields vibrating sinusoidally at right angles to each other and to the direction of propagation are called EM waves or EM radiation.

Question 4.
How are EM waves produced?
Answer:

1. According to quantum theory, an electron, while orbiting around the nucleus in a stable orbit does not emit EM radiation even though it undergoes acceleration.
2. It will emit an EM radiation only when it falls from an orbit of higher energy to one of lower energy.
3. EM waves (such as X-rays) are produced when fast moving electrons hit a target of high atomic number (such as molybdenum, copper, etc.).
4. An electric charge at rest has an electric field in the region around it but has no magnetic field.
5. When the charge moves, it produces both electric and magnetic fields.
6. If the charge moves with a constant velocity, the magnetic field will not change with time and hence, it cannot produce an EM wave.
7. But if the charge is accelerated, both the magnetic and electric fields change with space and time and an EM wave is produced.
8. Thus, an oscillating charge emits an EM wave which has the same frequency as that of the oscillation of the charge.

Question 5.
Can we produce a pure electric or magnetic wave in space? Why?
Answer:
No.
In vacuum, an electric field cannot directly induce another electric field so a “pure” electric field wave cannot exist and same can be said for a “pure” magnetic wave.

Question 6.
Does an ordinary electric lamp emit EM waves?
Answer:
Yes, ordinary electric lamp emits EM waves.

Question 7.
Why light waves travel in vacuum whereas sound wave cannot?
Answer:
Light waves are electromagnetic waves which can travel in vacuum whereas sound waves travel due to the vibration of particles of medium. Without any particles present (like in a vacuum) no vibrations can be produced. Hence, the sound wave cannot travel through the vacuum.

Question 8.
What are ultraviolet rays? Give two uses.
Answer:
Production:

1. Ultraviolet rays can be produced by the mercury vapour lamp, electric spark and carbon arc lamp.
2. They can also be obtained by striking electrical discharge in hydrogen and xenon gas tubes.
3. The Sun is the most important natural source of ultraviolet rays, most of which are absorbed by the ozone layer in the Earth’s atmosphere.

Uses:

1. Ultraviolet rays destroy germs and bacteria and hence they are used for sterilizing surgical instruments and for purification of water.
2. Used in burglar alarms and security systems.
3. Used to distinguish real and fake gems.

Question 9.
What are radio waves? Give its two uses.
Answer:

1. Radio waves are produced by accelerated motion of charges in a conducting wire. The frequency of waves produced by the circuit depends upon the magnitudes of the inductance and the capacitance.
2. Thus, by choosing suitable values of the inductance and the capacitance, radio waves of desired frequency can be produced.

Uses:

1. Radio waves are used for wireless communication purpose.
2. They are used for radio broadcasting and transmission of TV signals.
3. Cellular phones use radio waves to transmit voice communication in the ultra high frequency (UHF) band.

Question 10.
Name the most harmful radiation entering the Earth’s atmosphere from the outer space.
Answer:
Ultraviolet radiation.

Question 11.
Give reasons for the following:
i. Long distance radio broadcast uses short wave bands.
ii. Satellites are used for long distance TV transmission.
Answer:
i. Long distance radio broadcast uses short wave bands because electromagnetic waves only in the frequency range of short wave bands only are reflected by the ionosphere.

ii. a. It is necessary to use satellites for long distance TV transmissions because television signals are of high frequencies and high energies. Thus, these signals are not reflected by the ionosphere.
b. Hence, satellites are helpful in long distance TV transmission.

Question 12.
Name the three basic units of any communication system.
Answer:
Three basic (essential) elements of every communication system are transmitter, communication channel and receiver.

Question 13.
What is a carrier wave?
Answer:
The high frequency waves on which the signals to be transmitted are superimposed are called carrier waves.

Question 14.
Why high frequency carrier waves are used for transmission of audio signals?
Answer:
An audio signal has low frequency (<20 kHz) and low frequency signals cannot be transmitted over large distances. Because of this, a high frequency carrier waves are used for transmission.

Question 15.
What is modulation?
Answer:
The signals in communication system (e.g. music, speech etc.) are low frequency signals and cannot be transmitted over large distances. In order to transmit the signal to large distances, it is superimposed on a high frequency wave (called carrier wave). This process is called modulation.

Question 16.
What is meant by amplitude modulation?
Answer:
When the amplitude of carrier wave is varied in accordance with the modulating signal, the process is called amplitude modulation.

Question 17.
What is meant by noise?
Answer:

1. A random unwanted signal is called noise.
2. The source generating the noise may be located inside or outside the system.
3. Efforts should be made to minimize the noise level in a communication system.

Question 18.
What is meant by bandwidth?
Answer:
The bandwidth of an electronic circuit is the range of frequencies over which it operates efficiently.

Question 19.
What is demodulation?
Answer:
The process of regaining signal from a modulated wave is called demodulation. This is the reverse process of modulation.

Question 20.
What type of modulation is required for television broadcast?
Answer:
Amplitude modulation is required for television broadcast.

Question 21.
How does the effective power radiated by an antenna vary with wavelength?
Answer:

1. To transmit a signal, an antenna or an aerial is needed.
2. Power radiated from a linear antenna of length l is, P ∝ (\(\frac {l}{λ}\))²
   where, λ is the wavelength of the signal.

Question 22.
Why should broadcasting programs use different frequencies?
Answer:
If broadcasting programs run on same frequency, then the information carried by these waves will get mixed up with each other. Hence, different broadcasting programs should run on different frequencies.

Question 23.
Explain the necessity of a carrier wave in communication.
Answer:

1. Without a carrier wave, the input signals could be carried by very low frequency electromagnetic waves but it will need quite a bit of amplification in order to transmit those very low frequencies.
2. The input signals themselves do not have much power and need a fairly large antenna in order to transmit the information.
3. Hence, it is necessary to impose the input signal on carrier wave as it requires less power in order to transmit the information.

Question 24.
Why does amplitude modulation give noisy reception?
Answer:
i. In amplitude modulation, carrier is varied in accordance with the message signal.

ii. The higher the amplitude, the greater is magnitude of the signal. So even if due to any reason, the magnitude of the signal changes, it will lead to variation in the amplitude of the signal. So its easy for noise to disturb the amplitude modulated signal.

Question 25.
Explain why is modulation needed.
Answer:
Modulation helps in avoiding mixing up of signals from different transmitters as different carrier wave frequencies can be allotted to different transmitters. Without the use of these waves, the audio signals, if transmitted directly by different transmitters, would get mixed up.

3. Solve the numerical problem.

Question 1.
Calculate the frequency in MHz of a radio wave of wavelength 250 m. Remember that the speed of all EM waves in vacuum is 3.0 × 10⁸ m/s.
Answer:
Given: λ = 250 m, c = 3 × 10⁸ m/s
To find: Frequency (v)
Formula: c = v⁸
Calculation: From formula,
v = \(\frac {c}{λ}\) = \(\frac {3×10^8}{250}\) = 1.2 × 10⁶ Hz
= 1.2 MHz

Question 2.
Calculate the wavelength in nm of an X-ray wave of frequency 2.0 × 10¹⁸ Hz.
Solution:
Given: c = 3 × 10⁸, v = 2 × 10¹⁸ Hz
To find: Wavelength (λ)
Formula: c = vλ
Calculation. From formula,
λ = \(\frac {c}{v}\) = \(\frac {3×10^8}{2×10^{18}}\) = 1.5 × 10^-10
= 0.15 nm

Question 3.
The speed of light is 3 × 10⁸ m/s. Calculate the frequency of red light of wavelength of 6.5 × 10^-7 m.
Answer:
Given: c = 3 × 10⁸ m/s, λ = 6.5 × 10^-7 m
To find: Frequency (v)
Formula: c = vλ
Calculation: From formula,
v = \(\frac {c}{λ}\) = \(\frac {3×10^8}{6.5×10^{-7}}\) = 4.6 × 10¹⁴ Hz

Question 4.
Calculate the wavelength of a microwave of frequency 8.0 GHz.
Answer:
Given: v = 8 GHz = 8 × 10⁹ Hz,
c = 3 × 10⁸ m/s
To find: Wavelength (λ)
Formula: c = vλ
Calculation: From formula,
λ = \(\frac {c}{λ}\) = \(\frac {3×10^8}{8×10^9}\) = 3.75 × 10^-2
= 3.75 cm

Question 5.
In a EM wave the electric field oscillates sinusoidally at a frequency of 2 × 10¹⁰ What is the wavelength of the wave?
Answer:
Given: v = 2 × 10¹⁰ Hz, c = 3 × 10⁸ m
To find: Wavelength (λ)
Formula: c = vλ
Calculation: From formula,
λ = \(\frac {c}{λ}\) = \(\frac {3×10^8}{2×10^{10}}\) = 1.5 × 10^-2

Question 6.
The amplitude of the magnetic field part of a harmonic EM wave in vacuum is B0 = 5 X 10-7 T. What is the amplitude of the electric field part of the wave?
Answer:
Given: B₀ = 5 × 10^-7 T, c = 3 × 10⁸
To find: Amplitude of electric field (E₀)
Formula: c = \(\frac {E_0}{B_0}\)
Calculation /From formula,
E₀ = c × B₀
= 3 × 10⁸ × 5 × 10^-7
= 150 V/m

Question 7.
A TV tower has a height of 200 m. How much population is covered by TV transmission if the average population density around the tower is 1000/km²? (Radius of the Earth = 6.4 × 10⁶ m)
Answer:
Given: h = 200 m,
Population density (n)
= 1000/km² = 1000 × 10^-6/m² = 10^-3/m²
R = 6.4 ×10⁶ m
To find: Population covered
Formulae: i. A = πd² = π(\(\sqrt{2Rh}\))² = 2πRh
ii. Population covered = nA
Calculation /From formula (i),
A = 2πRh
= 2 × 3.142 × 6.4 × 10⁶ × 200
≈ 8 × 10⁹ m²
From formula (ii),
Population covered = nA
= 10^-3 × 8 × 10⁹
= 8 × 10⁶

Question 8.
Height of a TV tower is 600 m at a given place. Calculate its coverage range if the radius of the Earth is 6400 km. What should be the height to get the double coverage area?
Answer:
Given: h = 600 m, R = 6.4 × 10⁶ m
To find: Range (d)
Height to get the double coverage (h’)
Formula: d = \(\sqrt{2hR}\)
Calculation: From formula,
d = \(\sqrt{2×600×6.4×10^6}\) = 87.6 × 10³ = 87.6 km
Now, for A’ = 2A
π(d’)² = 2 (πd²)
∴ (d’)² = 2d²
From formula,
h’ = \(\frac{(d’)^2}{2R}\)
= \(\frac{2d^2}{2R}\)
= 2 × h ……….. (∵ h = \(\frac{d^2}{2R}\))
= 2 × 600
=1200 m

Question 9.
A transmitting antenna at the top of a tower has a height 32 m and that of the receiving antenna is 50 m. What is the maximum distance between them for satisfactory communication in line of sight mode? Given radius of Earth is 6.4 × 10⁶ m.
Answer:
Given: h_t = 32 m, h_r = 50 m, R = 6.4 × 10⁶ m
To find: Maximum distance or range (d)
Formula: d = \(\sqrt{2Rh}\)
Calculation: From formula,
d_t = \(\sqrt{2Rh_t}\) = \(\sqrt{2×6.4×10^6×32}\)
= 20.238 × 10³ m
= 20.238 km
d_r = \(\sqrt{2Rh_t}\)
= \(\sqrt{2×6.4×10^6×50}\)
= 25.298 × 10³ m
= 25.298 km
Now, d = d_t + d_r
= 20.238 + 25.298
= 45.536 km

11th Physics Digest Chapter 13 Electromagnetic Waves and Communication System Intext Questions and Answers

Can you recall? (Textbookpage no. 229)

Question 1.
i. What is a wave?
Answer:
Wave is an oscillatory disturbance which travels through a medium without change in its form.

ii. What is the difference between longitudinal and transverse waves?
Answer:
a. Transverse wave: A wave in which particles of the medium vibrate in a direction perpendicular to the direction of propagation of wave is called transverse wave.
b. Longitudinal wave: A wave in which particles of the medium vibrate in a direction parallel to the direction of propagation of wave is called longitudinal wave.

iii. What are electric and magnetic fields and what are their sources?
Answer:
a. Electric field is the force experienced by a test charge in presence of the given charge at the given distance from it.
b. A magnetic field is produced around a magnet or around a current carrying conductor.

iv. By which mechanism heat is lost by hot bodies?
Answer:
Hot bodies lose the heat in the form of radiation.

Question 2.
What are Lenz’s law, Ampere’s law and Faraday’s law?
Answer:
Lenz’s law:
Whereas, Lenz’s law states that, the direction of the induced emf is such that the change is opposed.

Ampere’s law:
Ampere’s law describes the relation between the induced magnetic field associated with a loop and the current flowing through the loop.

Faraday’s law:
Faraday’s law states that, time varying magnetic field induces an electromotive force (emf) and an electric field.

Internet my friend. (Tpxtboakpage no. 240)

https//www.iiap.res.in/centers/iao
[Students are expected to visit the above mentioned website and collect more information about different EM wave propagations used by astronomical observatories.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Magnetism Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 12 Magnetism Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 12 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 12 Exercise Solutions

1. Choose the correct option.

Question 1.
Let r be the distance of a point on the axis of a bar magnet from its center. The magnetic field at r is always proportional to
(A) \(\frac {1}{r^2}\)
(B) \(\frac {1}{r^3}\)
(C) \(\frac {1}{r}\)
(D) Not necessarily \(\frac {1}{r^3}\) at all points
Answer:
(B) \(\frac {1}{r^3}\)

Question 2.
Magnetic meridian is the plane
(A) perpendicular to the magnetic axis of Earth
(B) perpendicular to geographic axis of Earth
(C) passing through the magnetic axis of Earth
(D) passing through the geographic axis
Answer:
(C) passing through the magnetic axis of Earth

Question 3.
The horizontal and vertical component of magnetic field of Earth are same at some place on the surface of Earth. The magnetic dip angle at this place will be
(A) 30°
(B) 45°
(C) 0°
(D) 90°
Answer:
(B) 45°

Question 4.
Inside a bar magnet, the magnetic field lines
(A) are not present
(B) are parallel to the cross sectional area of the magnet
(C) are in the direction from N pole to S pole
(D) are in the direction from S pole to N pole
Answer:
(D) are in the direction from S pole to N pole

Question 5.
A place where the vertical components of Earth’s magnetic field is zero has the angle of dip equal to
(A) 0°
(B) 45°
(C) 60°
(D) 90°
Answer:
(A) 0°

Question 6.
A place where the horizontal component of Earth’s magnetic field is zero lies at
(A) geographic equator
(B) geomagnetic equator
(C) one of the geographic poles
(D) one of the geomagnetic poles
Answer:
(D) one of the geomagnetic poles

Question 7.
A magnetic needle kept nonparallel to the magnetic field in a nonuniform magnetic field experiences
(A) a force but not a torque
(B) a torque but not a force
(C) both a force and a torque
(D) neither force nor a torque
Answer:
(C) both a force and a torque

2. Answer the following questions in brief.

Question 1.
What happens if a bar magnet is cut into two pieces transverse to its length/ along its length?
Answer:
i. When a magnet is cut into two pieces, then each piece behaves like an independent magnet.

ii. When a bar magnet is cut transverse to its length, the two pieces generated will behave as independent magnets of reduced magnetic length. However, the pole strength of all the four poles formed will be same as that of the original bar magnet. Thus, the new dipole moment of the smaller magnets will be,

iii. When the bar magnet is cut along its length, the two pieces generated will behave like an independent magnet with reduced pole strength. However, the magnetic length of both the new magnets will be same as that of the original bar magnet. Thus, the new dipole moment of the smaller magnets will be,

Question 2.
What could be the equation for Gauss’ law of magnetism, if a monopole of pole strength p is enclosed by a surface?
Answer:
i. According to Gauss’ law of electrostatics, the net electric flux through any Gaussian surface is proportional to net charge enclosed in it. The equation is given as,
ø_E = ∫\(\vec{E}\) . \(\vec{dS}\) = \(\frac {q}{ε_0}\)

ii. Similarly, if a monopole of a magnet of pole strength p exists, the Gauss’ law of magnetism in S.I. units will be given as,
ø_E = ∫\(\vec{B}\) . \(\vec{dS}\) = µ₀P

3. Answer the following questions in detail.

Question 1.
Explain the Gauss’ law for magnetic fields.
Answer:
i. Analogous to the Gauss’ law for electric field, the Gauss’ law for magnetism states that, the net magnetic flux (ø_B) through a closed Gaussian surface is zero. ø_B = ∫\(\vec{B}\) . \(\vec{dS}\) = 0

ii. Consider a bar magnet, a current carrying solenoid and an electric dipole. The magnetic field lines of these three are as shown in figures.

iii. The areas (P) and (Q) are the cross – sections of three dimensional closed Gaussian surfaces. The Gaussian surface (P) does not include poles while the Gaussian surface (Q) includes N-pole of bar magnet, solenoid and the positive charge in case of electric dipole.

iv. The number of lines of force entering the surface (P) is equal to the number of lines of force leaving the surface. This can be observed in all the three cases.

v. However, Gaussian surface (Q) of bar magnet, enclose north pole. As, even thin slice of a bar magnet will have both north and south poles associated with it, the number of lines of Force entering surface (Q) are equal to the number of lines of force leaving the surface.

vi. For an electric dipole, the field lines begin from positive charge and end on negative charge. For a closed surface (Q), there is a net outward flux since it does include a net (positive) charge.

vii. Thus, according to the Gauss’ law of electrostatics ø_E = ∫\(\vec{E}\) . \(\vec{dS}\) = \(\frac {q}{ε_0}\), where q is the positive charge enclosed.

viii. The situation is entirely different from magnetic lines of force. Gauss’ law of magnetism can be written as ø_B = ∫\(\vec{B}\) . \(\vec{dS}\) = 0
From this, one can conclude that for electrostatics, an isolated electric charge exists but an isolated magnetic pole does not exist.

Question 2.
What is a geographic meridian? How does the declination vary with latitude? Where is it minimum?
Answer:
A plane perpendicular to the surface of the Earth (vertical plane) and passing through geographic axis is geographic meridian.

i. Angle between the geographic and the magnetic meridian at a place is called magnetic declination (a).
ii. Magnetic declination varies with location and over time. As one moves away from the true north the declination changes depending on the latitude as well as longitude of the place. By convention, declination is positive when magnetic north is east of true north, and negative when it is to the west. The declination is small in India. It is 0° 58′ west at Mumbai and 0° 41′ east at Delhi.

Question 3.
Define the angle of dip. What happens to angle of dip as we move towards magnetic pole from magnetic equator?
Answer:
Angle made by the direction of resultant magnetic field with the horizontal at a place is inclination or angle of dip (ø) at the place.
At the magnetic pole value of ø = 90° and it goes on decreasing when we move towards equator such that at equator value of (ø) = 0°.

4. Solve the following problems.

Question 1.
A magnetic pole of bar magnet with pole strength of 100 Am is 20 cm away from the centre of a bar magnet. Bar magnet has pole strength of 200 Am and has a length 5 cm. If the magnetic pole is on the axis of the bar magnet, find the force on the magnetic pole.
Answer:
Given that, (q_m)₁ = 200 Am
and (2l) = 5 cm = 5 × 10^-2 m
∴ m = 200 × 5 × 10^-2 = 10 Am²
For a bar magnet, magnetic dipole moment is,
m = q_m (21)
For a point on the axis of a bar magnet at distance, r = 20 cm = 0.2 m,
B_a = \(\frac{\mu_{0}}{4 \pi} \times \frac{2 m}{r^{3}}\)
= 10^-7 × \(\frac{2 \times 10}{(0.2)^{3}}\)
= 0.25 × 10^-3
= 2.5 × 10^-4 Wb/m²
The force acting on the pole will be given by,
F = q_m B_a = 100 × 2.5 × 10^-4
= 2.5 × 10^-2 N

Question 2.
A magnet makes an angle of 45° with the horizontal in a plane making an angle of 30° with the magnetic meridian. Find the true value of the dip angle at the place.
Answer:
Let true value of dip be ø. When the magnet is kept 45° aligned with declination 30°, the horizontal component of Earth’s magnetic field.
B’_H = B_H cos 30° Whereas, vertical component remains unchanged.
∴ For apparent dip of 45°,
tan 45° = \(\frac{\mathrm{B}_{\mathrm{V}}^{\prime}}{\mathrm{B}_{\mathrm{H}}^{\prime}}=\frac{\mathrm{B}_{\mathrm{V}}}{\mathrm{B}_{\mathrm{H}} \cos 30^{\circ}}=\frac{\mathrm{B}_{\mathrm{v}}}{\mathrm{B}_{\mathrm{H}}} \times \frac{1}{\cos 30^{\circ}}\)
But, real value of dip is,
tan ø = \(\frac {B_V}{B_H}\)
∴ tan 45° = \(\frac {tan ø}{cos 30°}\)
∴ tan ø = tan 45° × cos 30°
= 1 × \(\frac {√3}{2}\)
∴ ø = tan^-1 (0.866)

Question 3.
Two small and similar bar magnets have magnetic dipole moment of 1.0 Am² each. They are kept in a plane in such a way that their axes are perpendicular to each other. A line drawn through the axis of one magnet passes through the centre of other magnet. If the distance between their centres is 2 m, find the magnitude of magnetic field at the midpoint of the line joining their centres.
Answer:
Let P be the midpoint of the line joining the centres of two bar magnets. As shown in figure, P is at the axis of one bar magnet and at the equator of another bar magnet. Thus, the magnetic field on the axis of the first bar magnet at distance of 1 m from the centre will be,

B_a = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{r^{3}}\)
= 10^-7 × \(\frac {2×1.0}{(1)^3}\)
= 2 × 10^-7 Wb/m²
Magnetic field on the equator of second bar magnet will be,
B_eq = \(\frac{\mu_{0}}{4 \pi} \frac{m}{r^{3}}\)
= 10^-7 × \(\frac {1.0}{(1)^3}\)
= 1 × 10^-7 Wb/m²
The net magnetic field at P,
B_net = \(\sqrt {B_a^2+B_{eq}^2}\)
= \(\sqrt {(2×10^{-7})^2+(1×10^{-7})^2}\)
= \(\sqrt {(10^{-7})^2×(4+1)}\)
= √5 × 10^-7 Wb/m²

Question 4.
A circular magnet is made with its north pole at the centre, separated from the surrounding circular south pole by an air gap. Draw the magnetic field lines in the gap. Draw a diagram to illustrate the magnetic lines of force between the south poles of two such magnets.
Answer:
i. For a circular magnet:

Question 5.
Two bar magnets are placed on a horizontal surface. Draw magnetic lines around them. Mark the position of any neutral points (points where there is no resultant magnetic field) on your diagram.
Answer:
The magnetic lines of force between two magnets will depend on their relative positions. Considering the magnets to be placed one besides the other as shown in figure, the magnetic lines of force will be as shown.

11th Physics Digest Chapter 12 Magnetism Intext Questions and Answers

Can you recall? (Textbook page no. 221)

Question 1.
What are the magnetic lines of force?
Answer:
The magnetic field around a magnet is shown by lines going from one end of the magnet to the other. These lines are named as magnetic lines of force.

Question 2.
What are the rules concerning the lines of force?
Answer:
i. Magnetic lines of force originate from the north pole and end at the south pole.
ii. The magnetic lines of force of a magnet or a solenoid form closed loops. This is in contrast to the case of an electric dipole, where the electric lines of force originate from the positive charge and end on the negative charge.
iii. The direction of the net magnetic field \(\vec {B}\) at a point is given by the tangent to the magnetic line of force at that point.
iv. The number of lines of force crossing per unit area decides the magnitude of magnetic field \(\vec {B}\)
v. The magnetic lines of force do not intersect. This is because had they intersected, the direction of magnetic field would not be unique at that point.

Question 3.
What is a bar magnet?
Answer:
Bar magnet is a magnet in the shape of bar having two poles of equal and opposite pole strengths separated by certain distance (2l).

Question 4.
If you freely hang a bar magnet horizontally, in which direction will it become stable?
Answer:
A bar magnet suspended freely in air always aligns itself along geographic N-S direction.

Try this (Textbook page no. 221)

You can take a bar magnet and a small compass needle. Place the bar magnet at a fixed position on a paper and place the needle at various positions. Noting the orientation of the needle, the magnetic field direction at various locations can be traced.
Answer:
When a small compass needle is kept at any position near a bar magnet, the needle always aligns itself in the direction parallel to the direction of magnetic lines of force.

Hence, by placing it at different positions, A, B, C, D,… as shown in the figure, the direction of magnetic lines of force can be traced. The direction of magnetic field will be a tangent at that point.

Internet my friend: (Text book page no. 227)

https://www.ngdc.noaa.gov
[Students are expected to visit above mentioned link and collect more information about Geomagnetism.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Electric Current Through Conductors Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 11 Electric Current Through Conductors Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 11 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 11 Exercise Solutions

1. Choose the correct Alternative.

Question 1.
You are given four bulbs of 25 W, 40 W, 60 W, and 100 W of power, all operating at 230 V. Which of them has the lowest resistance?
(A) 25 W
(B) 40 W
(C) 60 W
(D) 100 W
Answer:
(D) 100 W

Question 2.
Which of the following is an ohmic conductor?
(A) transistor
(B) vacuum tube
(C) electrolyte
(D) nichrome wire
Answer:
(D) nichrome wire

Question 3.
A rheostat is used
(A) to bring on a known change of resistance in the circuit to alter the current.
(B) to continuously change the resistance in any arbitrary manner and there by alter the current.
(C) to make and break the circuit at any instant.
(D) neither to alter the resistance nor the current.
Answer:
(B) to continuously change the resistance in any arbitrary manner and there by alter the current.

Question 4.
The wire of length L and resistance R is stretched so that its radius of cross-section is halved. What is its new resistance?
(A) 5R
(B) 8R
(C) 4R
(D) 16R
Answer:
(D) 16R

Question 5.
Masses of three pieces of wires made of the same metal are in the ratio 1 : 3 : 5 and their lengths are in the ratio 5 : 3 : 1. The ratios of their resistances are
(A) 1 : 3 : 5
(B) 5 : 3 : 1
(C) 1 : 15 : 125
(D) 125 : 15 : 1
Answer:
(D) 125 : 15 : 1

Question 6.
The internal resistance of a cell of emf 2 V is 0.1 Ω, it is connected to a resistance of 0.9 Ω. The voltage across the cell will be
(A) 0.5 V
(B) 1.8 V
(C) 1.95 V
(D) 3V
Answer:
(B) 1.8 V

Question 7.
100 cells each of emf 5 V and internal resistance 1 Ω are to be arranged so as to produce maximum current in a 25 Ω resistance. Each row contains equal number of cells. The number of rows should be
(A) 2
(B) 4
(C) 5
(D) 100
Answer:
(A) 2

Question 8.
Five dry cells each of voltage 1.5 V are connected as shown in diagram

What is the overall voltage with this arrangement?
(A) 0 V
(B) 4.5 V
(C) 6.0 V
(D) 7.5 V
Answer:
(B) 4.5 V

2. Give reasons / short answers

Question 1.
In given circuit diagram two resistors are connected to a 5V supply.

i. Calculate potential difference across the 8Q resistor.
ii. A third resistor is now connected in parallel with 6 Ω resistor. Will the potential difference across the 8 Ω resistor be larger, smaller or same as before? Explain the reason for your answer.
Answer:
Total current flowing through the circuit,
I = \(\frac {V}{R_s}\)
= \(\frac {5}{8+6}\)
= \(\frac {5}{14}\) = 0.36 A
∴ Potential difference across 8 f2 (Vi) = 0.36 × 8
= 2.88 V

ii. Potential difference across 8 Ω resistor will be larger.
Reason: As per question, the new circuit diagram will be

When any resistor is connected parallel to 6 Ω resistance. Then the resistance across that branch (6 Ω and R Ω) will become less than 6 Ω. i.e., equivalent resistance of the entire circuit will decrease and hence current will increase. Since, V = IR, the potential difference across 8 Ω resistor will be larger.

Question 2.
Prove that the current density of a metallic conductor is directly proportional to the drift speed of electrons.
Answer:
i. Consider a part of conducting wire with its free electrons having the drift speed vd in the direction opposite to the electric field \(\vec{E}\).

ii. All the electrons move with the same drift speed vd and the current I is the same throughout the cross section (A) of the wire.

iii. Let L be the length of the wire and n be the number of free electrons per unit volume of the wire. Then the total number of free electrons in the length L of the conducting wire is nAL.

iv. The total charge in the length L is,
q = nALe ………….. (1)
where, e is the charge of electron.

v. Equation (1) is total charge that moves through any cross section of the wire in a certain time interval t.
∴ t = \(\frac {L}{v_d}\) ………….. (2)

vi. Current is given by,
I = \(\frac {q}{t}\) = \(\frac {nALe}{L/v_d}\) ……………. [From Equations (1) and (2)]
= n Av_de
Hence
v_d = \(\frac {1}{nAe}\)
= \(\frac {J}{ne}\) …………. (∵ J = \(\frac {1}{A}\))
Hence for constant ‘ne’, current density of a metallic conductor is directly proportional to the drift speed of electrons, J ∝ v_d.

3. Answer the following questions.

Question 1.
Distinguish between ohmic and non ohmic substances; explain with the help of example.
Answer:

Question 2.
DC current flows in a metal piece of non uniform cross-section. Which of these quantities remains constant along the conductor: current, current density or drift speed?
Answer:
Drift velocity and current density will change as it depends upon area of cross-section whereas current will remain constant.

4. Solve the following problems.

Question 1.
What is the resistance of one of the rails of a railway track 20 km long at 20°C? The cross-section area of rail is 25 cm² and the rail is made of steel having resistivity at 20°C as 6 × 10^-8 Ω m.
Answer:
Given: l = 20 km = 20 × 10³ m,
A = 25 cm² = 25 × 10^-4 m²,
ρ = 6 × 10^-8 Ω m
To find: Resistance of rail (R)
Formula: ρ = \(\frac {RA}{l}\)
Calculation: From formula.
R = ρ\(\frac {l}{A}\)
∴ R = \(\frac {6×10^{-8}×20×10^3}{A}\) = \(\frac {6×4}{5}\) × 10^-1
= 0.48 Ω

Question 2.
A battery after a long use has an emf 24 V and an internal resistance 380 Ω. Calculate the maximum current drawn from the battery. Can this battery drive starting motor of car?
Answer:
E = 24 V, r = 380 Ω
i. Maximum current (I_max)
ii. Can battery start the motor?
Formula: I_max = \(\frac {E}{r}\)
Calculation:
From formula,
I_max = \(\frac {24}{380}\) = 0,063 A
As, the value of current is very small compared to required current to run a starting motor of a car, this battery cannot be used to drive the motor.

Question 3.
A battery of emf 12 V and internal resistance 3 O is connected to a resistor. If the current in the circuit is 0.5 A,
i. Calculate resistance of resistor.
ii. Calculate terminal voltage of the battery when the circuit is closed.
Answer:
Given: E = 12 V, r = 3 Ω, I = 0.5 A
To find:
i. Resistance (R)
ii. Terminal voltage (V)
Formulae:
i. E = I (r + R)
ii. V = IR
Calculation: From formula (i),
E = Ir + IR
∴ R = \(\frac {E-Ir}{l}\)
= \(\frac {12-0.5×3}{0.5}\)
= 21 Ω
From formula (ii),
V = 0.5 × 21
= 10.5 V

Question 4.
The magnitude of current density in a copper wire is 500 A/cm². If the number of free electrons per cm³ of copper is 8.47 × 10²², calculate the drift velocity of the electrons through the copper wire (charge on an e = 1.6 × 10^-19 C)
Answer:
Given: J = 500 A/cm² = 500 × 10⁴ A/m²,
n = 8.47 × 10²² electrons/cm³
= 8.47 × 10²⁸ electrons/m³
e = 1.6 × 10^-19 C
To Find: Drift velocity (v_d)
Formula: v_d = \(\frac {J}{ne}\)
Calculation:
From formula,
v_d = \(\frac {500×10^4}{8.47×10^{28}×1.6×10^{-19}}\)
= \(\frac {500}{8.47×1.6}\) × 10^-5
= {antilog [log 500 – log 8.47 – log 1.6]} × 10^-5
= {antilog [2.6990 – 0.9279 -0.2041]} × 10^-5
= {antilog [1.5670]} × 10^-5
= 3.690 × 10¹ × 10^-5
= 3.69 × 10^-4 m/s

Question 5.
Three resistors 10 Ω, 20 Ω and 30 Ω are connected in series combination.
i. Find equivalent resistance of series combination.
ii. When this series combination is connected to 12 V supply, by neglecting the value of internal resistance, obtain potential difference across each resistor.
Answer:
Given: R₁ = 10 Ω, R₂ = 20 Ω,
R₃ = 30 Ω, V = 12 V
To Find: i. Series equivalent resistance(R_s)
ii. Potential difference across each resistor (V₁, V₂, V₃)
Formula: i. R_s = R₁ + R₂ + R₃
ii. V = IR
Calculation:
From formula (i),
R_s = 10 + 20 + 30 = 60 Ω
From formula (ii),
I = \(\frac {V}{R}\) = \(\frac {12}{60}\) = 0.2 A
∴ Potential difference across R₁,
V₁ = I × R₁ = 0.2 × 10 = 2 V
∴ Potential difference across R₂,
V₂ = 0.2 × 20 = 4 V
∴ Potential difference across R₃,
V₃ = 0.2 × 30 = 6 V

Question 6.
Two resistors 1 Ω and 2 Ω are connected in parallel combination.
i. Find equivalent resistance of parallel combination.
ii. When this parallel combination is connected to 9 V supply, by neglecting internal resistance, calculate current through each resistor.
Answer:
R₁ = 1 kΩ = 10³ Ω,
R₂ = 2 kΩ = 2 × 10³ Ω, V = 9 V
To find:
i. Parallel equivalent resistance (R_p)
ii. Current through 1 kΩ and 2 kΩ (I₁ and I₂)
Formula:
i. \(\frac {1}{R_p}\) = \(\frac {1}{R_1}\) + \(\frac {1}{R_2}\)
ii. V = IR
Calculation: From formula (i),
\(\frac {1}{R_p}\) = \(\frac {1}{10^3}\) + \(\frac {1}{2×10^3}\)
= \(\frac {3}{2×10^3}\)
∴ R^p = \(\frac {2×10^3}{3}\) = 0.66 kΩ
From formula (ii),
I₁ = \(\frac {V}{R_1}\) + \(\frac {9}{10^3}\)
= 9 × 10^-3 A
= 3 mA
I₂ = \(\frac {V}{R_2}\) + \(\frac {9}{2×10^3}\)
= 4.5 × 10^-3 A
= 4.5 mA

Question 7.
A silver wire has a resistance of 4.2 Ω at 27°C and resistance 5.4 Ω at 100°C. Determine the temperature coefficient of resistance.
Answer:
Given: R₁ =4.2 Ω, R₂ = 5.4 Ω,
T, = 27° C, T2= 100 °C
To find: Temperature coefficient of resistance (α)
Formula: α = \(\frac {R_2-R_1}{R_1(T_2-T_1)}\)
Calculation:
From Formula
α = \(\frac {5.4-4.2}{4.2(100-27)}\) = 3.91 × 10^-3/°C

Question 8.
A 6 m long wire has diameter 0.5 mm. Its resistance is 50 Ω. Find the resistivity and conductivity.
Answer:
Given: l = 6 m, D = 0.5 mm,
r = 0.25 mm = 0.25 × 10^-3 m, R = 50 Ω
To find:
i. Resistivity (ρ)
ii. Conductivity (σ)
Formulae:
i. ρ = \(\frac {RA}{l}\) = \(\frac {Rπr^2}{l}\)
ii. σ = \(\frac {1}{ρ}\)
Calculation:
From formula (i),
ρ = \(\frac {50×3.142×(0.25×10^{-3})^2}{6}\)
= {antilog [log 50 + log 3.142 + 21og 0.25 -log 6]} × 10^-6
= {antilog [ 1.6990 + 0.4972 + 2(1.3979) -0.7782]} × 10^-6
= {antilog [2.1962 + 2 .7958 – 0.7782]} × 10^-6
= {antilog [0.9920 – 0.7782]} × 10^-6
= {antilog [0.2138]} × 10^-6
= 1.636 × 10^-6 Ω/m
From formula (ii),
σ = \(\frac {1}{1.636×10^{-6}}\)
= 0.6157 × 10⁶
….(Using reciprocal from log table)
= 6.157 × 10⁵ m/Ω

Question 9.
Find the value of resistances for the following colour code.
i. Blue Green Red Gold
ii. Brown Black Red Silver
iii. Red Red Orange Gold
iv. Orange White Red Gold
v. Yellow Violet Brown Silver
Answer:
i. Given: Blue – Green – Red – Gold
To find: Value of resistance
Formula: Value of resistance
= (xy × 10^z ± T%)Ω
Calculation:

From formula,
Value of resistance = (65 × 10² ± 5%) Ω
Value of resistance = 6.5 kΩ ± 5%

ii. Given: Brown – Black – Red – Silver
To find: Value of resistance
Formula: Value of resistance
= (xy × 10^z + T%) Ω
Calculation:

From formula,
Value of resistance = (10 × 10² ± 10%) Ω
Value of resistance = 1.0 kΩ ± 10%

iii. Given: Red – Red – Orange – Gold
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10^z ± T%)
Calculation:

From formula,
Value of resistance = (22 × 10³ ± 5%)Ω
Value of resistance = 22 kΩ ± 5%
[Note: The answer given above is presented considering correct order of magnitude.]

iv. Given: Orange – White – Red – Gold
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10^z ± T%)
Calculation:

From formula,
Value of resistance = (39 × 10² ± 5%) Ω
Value of resistance = 3.9 kΩ ± 5%

v. Given: Yellow-Violet-Brown-Silver
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10^z ± T%)
Calculation:

From formula,
Value of resistance = (47 × 10 ± 10%) Ω
Value of resistance = 470 Ω ± 10%
[Note: The answer given above is presented considering correct order of magnitude.]

Question 10.
Find the colour code for the following value of resistor having tolerance ± 10%.
i. 330 Ω
ii. 100 Ω
iii. 47 kΩ
iv. 160 Ω
v. 1 kΩ
Answer:

Question 11.
A current of 4 A flows through an automobile headlight. How many electrons flow through the headlight in a time of 2 hrs?
Answer:
Given: I = 4 A, t = 2 hrs = 2 × 60 × 60 s
To find: Number of electrons (N)
Formula: I = \(\frac {q}{t}\) = \(\frac {Ne}{t}\)
Calculation: As we know, e = 1.6 × 10^-19 C
From formula,
N = \(\frac {It}{e}\) = \(\frac {4×2×60×60}{1.6×10^{-19}}\) = 18 × 10^-23

Question 12.
The heating element connected to 230 V draws a current of 5 A. Determine the amount of heat dissipated in 1 hour (J = 4.2 J/cal).
Answer:
Given: V = 230 V, I = 5 A,
At = 1 hour = 60 × 60 sec
To find: Heat dissipated (H)
Formula: H = ∆U = I∆tV
Calculation: From formula,
H = 5 × 60 × 60 × 230
= 4.14 × 10⁶ J
Heat dissipated in calorie,
H = \(\frac {4.14×10^6}{4.2}\) = 985.7 × 10³ cal
= 985.7 kcal

11th Physics Digest Chapter 11 Electric Current Through Conductors Intext Questions and Answers

Can you recall? (Textbookpage no. 207)

An electric current in a metallic conductor such as a wire is due to the flow of electrons, the negatively charged particles in the wire. What is the role of the valence electrons which are the outermost electrons of an atom?
Answer:
i. The valence electrons become de-localized when a large number of atoms come together in a metal.
ii. These electrons become conduction electrons or free electrons constituting an electric current when a potential difference is applied across the conductor.

Internet my friend (Textbook page no. 218)

https://www.britannica.com/science/supercond activity physics

[Students are expected to visit the above-mentioned website and Collect more information about superconductivity.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Electrostatics Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 10 Electrostatics Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 10 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 10 Exercise Solutions

1. Choose the correct option.

Question 1.
A positively charged glass rod is brought close to a metallic rod isolated from the ground. The charge on the side of the metallic rod away from the glass rod will be
(A) same as that on the glass rod and equal in quantity
(B) opposite to that on the glass of and equal in quantity
(C) same as that on the glass rod but lesser in quantity
(D) same as that on the glass rod but more in quantity
Answer:
(A) same as that on the glass rod and equal in quantity

Question 2.
An electron is placed between two parallel plates connected to a battery. If the battery is switched on, the electron will
(A) be attracted to the +ve plate
(B) be attracted to the -ve plate
(C) remain stationary
(D) will move parallel to the plates
Answer:
(A) be attracted to the +ve plate

Question 3.
A charge of + 7 µC is placed at the centre of two concentric spheres with radius 2.0 cm and 4.0 cm respectively. The ratio of the flux through them will be
(A) 1 : 4
(B) 1 : 2
(C) 1 : 1
(D) 1 : 16
Answer:
(C) 1 : 1

Question 4.
Two charges of 1.0 C each are placed one meter apart in free space. The force between them will be
(A) 1.0 N
(B) 9 × 10⁹ N
(C) 9 × 10^-9 N
(D) 10 N
Answer:
(B) 9 × 10⁹ N

Question 5.
Two point charges of +5 µC are so placed that they experience a force of 80 × 10^-3 N. They are then moved apart, so that the force is now 2.0 × 10^-3 N. The distance between them is now
(A) 1/4 the previous distance
(B) double the previous distance
(C) four times the previous distance
(D) half the previous distance
Answer:
(B) double the previous distance

Question 6.
A metallic sphere A isolated from ground is charged to +50 µC. This sphere is brought in contact with other isolated metallic sphere B of half the radius of sphere A. The charge on the two sphere will be now in the ratio
(A) 1 : 2
(B) 2 : 1
(C) 4 : 1
(D) 1 : 1
Answer:
(D) 1 : 1

Question 7.
Which of the following produces uniform electric field?
(A) point charge
(B) linear charge
(C) two parallel plates
(D) charge distributed an circular any
Answer:
(C) two parallel plates

Question 8.
Two point charges of A = +5.0 µC and B = -5.0 µC are separated by 5.0 cm. A point charge C = 1.0 µC is placed at 3.0 cm away from the centre on the perpendicular bisector of the line joining the two point charges. The charge at C will experience a force directed towards
(A) point A
(B) point B
(C) a direction parallel to line AB
(D) a direction along the perpendicular bisector
Answer:
(C) a direction parallel to line AB

2. Answer the following questions.

Question 1.
What is the magnitude of charge on an electron?
Answer:
The magnitude of charge on an electron is 1.6 × 10^-19 C

Question 2.
State the law of conservation of charge.
Answer:
In any given physical process, charge may get transferred from one part of the system to another, but the total charge in the system remains constant”
OR
For an isolated system, total charge cannot be created nor destroyed.

Question 3.
Define a unit charge.
Answer:
Unit charge (one coulomb) is the amount of charge which, when placed at a distance of one metre from another charge of the same magnitude in vacuum, experiences a force of 9.0 × 10⁹ N.

Question 4.
Two parallel plates have a potential difference of 10V between them. If the plates are 0.5 mm apart, what will be the strength of electric charge.
Answer:
V=10V
d = 0.5 mm = 0.5 × 10^-3 m
To find: The strength of electric field (E)
Formula: E = \(\frac {V}{d}\)
Calculation: From formula,
E = \(\frac {10}{0.5×10^{-3}}\)
20 × 10³ V/m

Question 5.
What is uniform electric field?
Answer:
A uniform electric field is a field whose magnitude and direction are same at all points. For example, field between two parallel plates as shown in the diagram.

Question 6.
If two lines of force intersect of one point. What does it mean?
Answer:
If two lines of force intersect of one point, it would mean that electric field has two directions at a single point.

Question 7.
State the units of linear charge density.
Answer:
SI unit of λ is (C / m).

Question 8.
What is the unit of dipole moment?
Answer:
i. Strength of a dipole is measured in terms of a quantity called the dipole moment.

ii. Let q be the magnitude of each charge and 2\(\vec{l}\) be the distance from negative charge to positive charge. Then, the product q(2\(\vec{l}\)) is called the dipole moment \(\vec{p}\).

iii. Dipole moment is defined as \(\vec{p}\) = q(2\(\vec{l}\))

iv. A dipole moment is a vector whose magnitude is q (2\(\vec{l}\)) and the direction is from the negative to the positive charge.

v. The unit of dipole moment is coulomb-metre (C m) or debye (D).

Question 9.
What is relative permittivity?
Answer:
i. Relative permittivity or dielectric constant is the ratio of absolute permittivity of a medium to the permittivity of free space.
It is denoted as K or ε_r.
i.e., K or ε_r = \(\frac {ε}{ε_0}\)

ii. It is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.
i.e., K or ε_r = \(\frac {F_{vacuum}}{F_{medium}}\)

iii. It is also called as specific inductive capacity or dielectric constant.

3. Solve numerical examples.

Question 1.
Two small spheres 18 cm apart have equal negative charges and repel each other with the force of 6 × 10^-8 N. Find the total charge on both spheres.
Solution:
Given: F = 6 × 10^-8 N, r = 18 cm = 18 × 10^-2 m
To find: Total charge (q₁ + q₂)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,

Taking square roots from log table,
∴ q = -4.648 × 10^-10 C
….(∵ the charges are negative)
Total charge = q₁ + q₂ = 2q
= 2 × (-4.648) × 10^-10
= -9.296 × 10^-10 C

Question 2.
A charge + q exerts a force of magnitude – 0.2 N on another charge -2q. If they are separated by 25.0 cm, determine the value of q.
Answer:
Given: q₁ = + q, q₂ = -2q, F = -0.2 N
r = 25 cm = 25 × 10^-2 m
To find: Charge (q)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,

[Note: The answer given above is calculated in accordance with textual method considering the given data]

Question 3.
Four charges of +6 × 10^-8 C each are placed at the corners of a square whose sides are 3 cm each. Calculate the resultant force on each charge and show in direction on a diagram drawn to scale.
Answer:
Given: q_A = q_B = q_C = q_D = 6 × 10^-8 C, a = 3 cm

∴ Resultant force on ‘A’
= F_AD cos 45 + F_AB cos 45 + F_AC
= (3.6 × 10^-2 × \(\frac {1}{√2}\)) + (3.6 × 10^-2 × \(\frac {1}{√2}\)) + 1.8 × 10^-2
= 6.89 × 10^-2 N directed along \(\vec{F_{AC}}\)

Question 4.
The electric field in a region is given by \(\vec{E}\) = 5.0 \(\hat{k}\) N/C Calculate the electric flux through a square of side 10.0 cm in the following cases
i. The square is along the XY plane
ii. The square is along XZ plane
iii. The normal to the square makes an angle of 45° with the Z axis.
Answer:
Given: \(\vec{E}\) = 5.0 \(\hat{k}\) N/C, |E| = 5 N/C
l = 10 cm = 10 × 10^-2 m = 10^-1 m
A = l² – 10^-2m²
To find: Electric flux in three cases.
(ø₁) (ø₂) (ø₃)
Formula: (ø₁) = EA cos θ
Calculation:
Case I: When square is along the XY plane,
∴ θ = 0
ø₁ = 5 × 10^-2 cos 0
= 5 × 10^-2 V m

Case II: When square is along XZ plane,
∴ θ = 90°
ø₁ = 5 × 10^-2 cos 90° = 0 V m

Case III: When normal to the square makes an angle of 45° with the Z axis.
∴ 0 = 45°
∴ ø₃ = 5 × 10^-2 × cos 45°
= 3.5 × 10^-2 V m

Question 5.
Three equal charges of 10 × 10^-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm and 25 cm respectively. Find the force exerted on the charge located at the 90° angle.
Answer:
Given: q_A = q_B = q_C = 10 × 10^-8

Force on B due to A,

Question 6.
A potential difference of 5000 volt is applied between two parallel plates 5 cm apart. A small oil drop having a charge of 9.6 x 10-19 C falls between the plates. Find (i) electric field intensity between the plates and (ii) the force on the oil drop.
Answer:
Given: V = 5000 volt, d = 5 cm = 5 × 10^-2 m
q = 9.6 × 10^-19 C
To find:
i. Electric field intensity (E)
ii. Force (F)
Formula:
i. E = \(\frac {V}{d}\) \(\frac {q}{r}\)
ii. E = \(\frac {F}{q}\)
Calculation: From formula (i),
E = \(\frac {F}{q}\) = 10⁵ N/C
From formula (ii)
F = E x q
= 10⁵ × 9.6 × 10^-19
= 9.6 × 10^-14 N

Question 7.
Calculate the electric field due to a charge of -8.0 × 10^-8 C at a distance of 5.0 cm from it.
Answer:
Given: q = – 8 × 10^-8 C, r = 5 cm = 5 × 10^-2 m
To Find: Electric field (E)
Formula: E = \(\frac {1}{4πε_0}\) \(\frac {q}{r^2}\)
Calculation: From formula,
E = 9 × 10⁹ × \(\frac {(-8×10^{-8})}{(5×10^{-2})^2}\)
= -2.88 × 10⁵ N/C

11th Physics Digest Chapter 10 Electrostatics Intext Questions and Answers

Can you recall? (Textbookpage no. 188)

Question 1.
Have you experienced a shock while getting up from a plastic chair and shaking hand with your friend?
Answer:
Yes, sometimes a shock while getting up from a plastic chair and shaking hand with friend is experienced.

Question 2.
Ever heard a crackling sound while taking out your sweater in winter?
Answer:
Yes, sometimes while removing our sweater in winter, some crackling sound is heard and the sweater appears to stick to body.

Question 3.
Have you seen the lightning striking during pre-monsoon weather?
Answer:
Yes, sometimes lightning striking during pre-pre-monsoon weather seen.

Can you tell? (Textbook page no. 189)

i. When a petrol or a diesel tanker is emptied in a tank, it is grounded.
ii. A thick chain hangs from a petrol or a diesel tanker and it is in contact with ground when the tanker is moving.
Answer:
i. When a petrol or a diesel tanker is emptied in a tank, it is grounded so that it has an electrically conductive connection from the petrol or diesel tank to ground (Earth) to allow leakage of static and electrical charges.

ii. Metallic bodies of cars, trucks or any other big vehicles get charged because of friction between them and the air rushing past them. Hence, a thick chain is hanged from a petrol or a diesel tanker to make a contact with ground so that charge produced can leak to the ground through chain.

Can you tell? (Textbook page no. 194)

Three charges, q each, are placed at the vertices of an equilateral triangle. What will be the resultant force on charge q placed at the centroid of the triangle?
Answer:

Since AD. BE and CF meets at O, as centroid of an equilateral triangle.
∴ OA = OB = OC
∴ Let, r = OA = OB = OC
Force acting on point O due to charge on point A,
\(\overrightarrow{\mathrm{F}}_{\mathrm{OA}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}_{i}^{2}} \hat{\mathrm{r}}_{\mathrm{AO}}\)
Force acting on point O due to charge on point B,
\(\overrightarrow{\mathrm{F}}_{O \mathrm{~B}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}_{\mathrm{BO}}\)
Force acting on point O due to charge on point C,
\(\overrightarrow{\mathrm{F}}_{\mathrm{OC}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}} \mathrm{co}\)
∴ Resultant force acting on point O,
F = \(\vec{F}\)_OA + \(\vec{F}\)_OB + \(\vec{F}\)_OC
On resolving \(\vec{F}\)_OB and \(\vec{F}\)_OC, we get –\(\vec{F}\)_OA
i.e., \(\vec{F}\)_OB + \(\vec{F}\)_OC = –\(\vec{F}\)_OA
∴ \(\vec{F}\) = \(\vec{F}\)_OA – \(\vec{F}\)_OA = 0
Hence, the resultant force on the charge placed at the centroid of the equilateral triangle is zero.

Can you tell? (Textbook page no. 197)

Why a small voltage can produce a reasonably large electric field?
Answer:

1. Electric field produced depends upon voltage as well as separation distance.
2. Electric field varies linearly with voltage and inversely with distance.
3. Hence, even if voltage is small, it can produce a reasonable large electric field when the gap between the electrode is reduced significantly.

Can you tell? (Textbook page no. 198)

Lines of force are imaginary; can they have any practical use?
Answer:
Yes, electric lines of force help us to visualise the nature of electric field in a region.

Can you tell? (Textbook page no. 204)

The surface charge density of Earth is σ = -1.33 nC/m². That is about 8.3 × 10⁹ electrons per square metre. If that is the case why don’t we feel it?
Answer:
The Earth along with its atmosphere acts as a neutral system. The atmosphere (ionosphere in particular) has nearly equal and opposite charge.

As a result, there exists a mechanism to replenish electric charges in the form of continual thunderstorms and lightning that occurs in different parts of the globe. This makes average charge on surface of the Earth as zero at any given time instant. Hence, we do not feel it.

Internet my friend (Textbook page no. 205)

i. https://www.physicsclassroom.com/class
ii. https://courses.lumenleaming.com/physics/
iii. https://www,khanacademy.org/science
iv. https://www.toppr.com/guides/physics/
[Students are expected to visit the above mentioned websites and collect more information about electrostatics.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Optics Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 9 Optics Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 9 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 9 Exercise Solutions

1. Multiple Choise Questions

Question 1.
As per the recent understanding, light consists of
(A) rays
(B) waves
(C) corpuscles
(D) photons obeying the rules of waves
Answer:
(D) photons obeying the rules of waves

Question 2.
Consider the optically denser lenses P, Q, R, and S drawn below. According to the Cartesian sign convention which of these have a positive focal length?

(A) Only P
(B) Only P and Q
(C) Only P and R
(D) Only Q and S
Answer:
(B) Only P and Q

Question 3.
Two plane mirrors are inclined at angle 40° between them. Number of images seen of a tiny object kept between them is
(A) Only 8
(B) Only 9
(C) 8 or 9
(D) 9 or 10
Answer:
(C) 8 or 9

Question 4.
A concave mirror of curvature 40 cm, used for shaving purpose produces image of double size as that of the object. Object distance must be
(A) 10 cm only
(B) 20 cm only
(C) 30 cm only
(D) 10 cm or 30 cm
Answer:
(D) 10 cm or 30 cm

Question 5.
Which of the following aberrations will NOT occur for spherical mirrors?
(A) Chromatic aberration
(B) Coma
(C) Distortion
(D) Spherical aberration
Answer:
(A) Chromatic aberration

Question 6.
There are different fish, monkeys and water of the habitable planet of the star Proxima b. A fish swimming underwater feels that there is a monkey at 2.5 m on the top of a tree. The same monkey feels that the fish is 1.6 m below the water surface. Interestingly, height of the tree and the depth at which the fish is swimming are exactly same. Refractive index of that water must be
(A) 6/5
(B) 5/4
(C) 4/3
(D) 7/5
Answer:
(B) 5/4

Question 7.
Consider following phenomena/applications: P) Mirage, Q) rainbow, R) Optical fibre and S) glittering of a diamond. Total internal reflection is involved in
(A) Only R and S
(B) Only R
(C) Only P, R and S
(D) all the four
Answer:
(A) Only R and S

Question 8.
A student uses spectacles of number -2 for seeing distant objects. Commonly used lenses for her/his spectacles are
(A) bi-concave
(B) piano concave
(C) concavo-convex
(D) convexo-concave
Answer:
(A) bi-concave

Question 9.
A spherical marble, of refractive index 1.5 and curvature 1.5 cm, contains a tiny air bubble at its centre. Where will it appear when seen from outside?
(A) 1 cm inside
(B) at the centre
(C) 5/3 cm inside
(D) 2 cm inside
Answer:
(B) at the centre

Question 10.
Select the WRONG statement.
(A) Smaller angle of prism is recommended for greater angular dispersion.
(B) Right angled isosceles glass prism is commonly used for total internal reflection.
(C) Angle of deviation is practically constant for thin prisms.
(D) For emergent ray to be possible from the second refracting surface, certain minimum angle of incidence is necessary from the first surface.
Answer:
(A) Smaller angle of prism is recommended for greater angular dispersion.

Question 11.
Angles of deviation for extreme colours are given for different prisms. Select the one having maximum dispersive power of its material.
(A) 7°, 10°
(B) 8°, 11°
(C) 12°, 16°
(D) 10°, 14°
Answer:
(A) 7°, 10°

Question 12.
Which of the following is not involved in formation of a rainbow?
(A) refraction
(B) angular dispersion
(C) angular deviation
(D) total internal reflection
Answer:
(D) total internal reflection

Question 13.
Consider following statements regarding a simple microscope:
(P) It allows us to keep the object within the least distance of distinct vision.
(Q) Image appears to be biggest if the object is at the focus.
(R) It is simply a convex lens.
(A) Only (P) is correct
(B) Only (P) and (Q) are correct
(C) Only (Q) and (R) are correct
(D) Only (P) and (R) are correct
Answer:
(D) Only (P) and (R) are correct

2. Answer the following questions.

Question 1.
As per recent development, what is the nature of light? Wave optics and particle nature of light are used to explain which phenomena of light respectively?
Answer:

1. As per recent development, it is now an established fact that light possesses dual nature. Light consists of energy carrier photons. These photons follow the rules of electromagnetic waves.
2. Wave optics explains the phenomena of light such as, interference, diffraction, polarisation, Doppler effect etc.
3. Particle nature of light can be used to explain phenomena like photoelectric effect, emission of spectral lines, Compton effect etc.

Question 2.
Which phenomena can be satisfactorily explained using ray optics?
Answer:
Ray optics or geometrical optics: Ray optics can be used for understanding phenomena like reflection, refraction, double refraction, total internal reflection, etc.

Question 3.
What is focal power of a spherical mirror or a lens? What may be the reason for using P = \(\frac {1}{f}\) its expression?
Answer:

1. Converging or diverging ability of a lens or of a mirror is defined as its focal power.
2. This implies, more the power of any spherical mirror or a lens, the more is its ability to converge or diverge the light that passes through it.
3. In case of convex lens or concave mirror, more the convergence, shorter is the focal length as shown in the figure.
4. Similarly, in case of concave lens or convex mirror, more the divergence, shorter is the focal length.
5. This explains that the focal power of any spherical lens or mirror is inversely proportional to the focal length.
6. Hence, the expression of focal power is given by the formula, P = \(\frac {1}{f}\).

Question 4.
At which positions of the objects do spherical mirrors produce (i) diminished image (ii) magnified image?
Answer:
i. Amongst the two types of spherical mirrors, convex mirror always produces a diminished image at all positions of the object.

ii. Concave mirror produces diminished image when object is placed:

• Beyond radius of curvature (i.e., u > 2f)
• At infinity (i.e., u = ∞)

iii. Concave mirror produces magnified image when object is placed:

• between centre of curvature and focus (i.e., 2f > u > f)
• between focus and pole of the mirror (i.e., u < f)

Question 5.
State the restrictions for having images produced by spherical mirrors to be appreciably clear.
Answer:
i. In order to obtain clear images, the formulae for image formation by mirrors or lens follow the given assumptions:

• Objects and images are situated close to the principal axis.
• Rays diverging from the objects are confined to a cone of very small angle.
• If there is a parallel beam of rays, it is paraxial, i.e., parallel and close to the principal axis.

ii. In case of spherical mirrors (excluding small aperture spherical mirrors), rays farther from the principle axis do not remain parallel to the principle axis. Thus, the third assumption is not followed and the focus gradually shifts towards the pole.

iii. The relation (f = \(\frac {R}{2}\)) giving a single point focus is not followed and the image does not get converged at a single point resulting into a distorted or defective image.

iv. This defect arises due to the spherical shape of the reflecting surface.

Question 6.
Explain spherical aberration for spherical mirrors. How can it be minimized? Can it be eliminated by some curved mirrors?
Answer:

1. In case of spherical mirrors (excluding small aperture spherical mirror), The rays coming from a distant object farther from principal axis do not remain parallel to the axis. Thus, the focus gradually shifts towards the pole.
2. The assumption for clear image formation namely, ‘If there is a parallel beam of rays, it is paraxial, i.e., parallel and close to the principal axis’, is not followed in this case.
3. The relation f (f = \(\frac {R}{2}\)) giving a single point focus is not followed and the image does not get converged at a single point resulting into a distorted or defective image.
4. This phenomenon is known as spherical aberration.
5. It occurs due to spherical shape of the reflecting surface, hence known as spherical aberration.
6. The rays near the edge of the mirror converge at focal point F_M Whereas, the rays near the principal axis converge at point F_P. The distance between F_M and F_P is measured as the longitudinal spherical aberration.
7. In spherical aberration, single point image is not possible at any point on the screen and the image formed is always a circle.
8. At a particular location of the screen (across AB in figure), the diameter of this circle is minimum. This is called the circle of least confusion. Radius of this circle is transverse spherical aberration.

Remedies for Spherical Aberration:

1. Spherical aberration can be minimized by reducing the aperture of the mirror.
2. Spherical aberration in curved mirrors can be completely eliminated by using a parabolic mirror.

Question 7.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
Answer:
i. Absolute refractive index of a medium is defined as the ratio of speed of light in vacuum to that in the given medium.

ii. A stick or pencil kept obliquely in a glass containing water appears broken as its part in water appears to be raised.

iii. As the speed of light is different in two media, the rays of light coming from water undergo refraction at the boundary separating two media.

iv. Consider speed of light to be v in water and c in air. (Speed of light in air ~ speed of light in vacuum)
∴ refractive index of water = \(\frac {n_w}{n_s}\) = \(\frac {n_w}{n_{vacuum}}\) = \(\frac {c}{v}\)

v. Relative refractive index of a medium 2 is the refractive index of medium 2 with respect to medium 1 and it is defined as the ratio of speed of light v₁ in medium 1 to its speed v₁ in medium 2.
∴ Relative refractive index of medium 2,
¹n₂ = \(\frac {v_1}{v_2}\)

vi. Consider a beaker filled with water of absolute refractive index n₁ kept on a transparent glass slab of absolute refractive index n₂.

vii. Thus, the refractive index of water with respect to that of glass will be,
ⁿw₂ = \(\frac {n_2}{n_1}\) = \(\frac {c/v_2}{c/v_1}\) = \(\frac {v_1}{v_2}\)

Question 8.
Explain ‘mirage’ as an illustration of refraction.
Answer:
i. On a hot clear Sunny day, along a level road, there appears a pond of water ahead of the road. Flowever, if we physically reach the spot, there is nothing but the dry road and water pond again appears some distance ahead. This illusion is called mirage.

ii. Mirage results from the refraction of light through a non-uniform medium.

iii. On a hot day the air in contact with the road is hottest and as we go up, it gets gradually cooler. The refractive index of air thus decreases with height. Hot air tends to be less optically dense than cooler air which results into a non-uniform medium.

iv. Light travels in a straight line through a uniform medium but refracts when traveling through a non-uniform medium.

v. Thus, the ray of light coming from the top of an object get refracted while travelling downwards into less optically dense air and become more and more horizontal as shown in Figure.

vi. As it almost touches the road, it bends (refracts) upward. Then onwards, upward bending continues due to denser air.

vii. As a result, for an observer, it appears to be coming from below thereby giving an illusion of reflection from an (imaginary) water surface.

Question 9.
Under what conditions is total internal reflection possible? Explain it with a suitable example. Define critical angle of incidence and obtain an expression for it.
Answer:
Conditions for total internal reflection:
i. The light ray must travel from denser medium to rarer medium.

ii. The angle of incidence in the denser medium must be greater than critical angle for the given pair of media.

Total internal reflection in optical fibre:
iii. Consider an optical fibre made up of core of refractive index n₁ and cladding of refractive index n₂ such that, n₁ > n₂.

iv. When a ray of light is incident from a core (denser medium), the refracted ray is bent away from the normal.

v. At a particular angle of incidence i_c in the denser medium, the corresponding angle of refraction in the rarer medium is 90°.

vi. For angles of incidence greater than ic, the angle of refraction become larger than 90° and the ray does not enter into rarer medium at all but is reflected totally into the denser medium as shown in figure.

critical angle of incidence and obtain an expression:
i. Critical angle for a pair of refracting media can be defined as that angle of incidence in the denser medium for which the angle of refraction in the rarer medium is 90°.

ii. Let n be the relative refractive index of denser medium with respect to the rarer.

iii. Then, according to Snell’s law,
n = \(\frac {n_{denser}}{n_{rarer}}\) = \(\frac {sin r}{sin i_c}\) = \(\frac {sin 90°}{sin i_c}\)
∴ sin (i_c) = \(\frac {1}{n}\)

Question 10.
Describe construction and working of an optical fibre. What are the advantages of optical fibre communication over electronic communication?
Answer:

Construction:

1. An optical fibre consists of an extremely thin, transparent and flexible core surrounded by an optically rarer flexible cover called cladding.
2. For protection, the whole system is coated by a buffer and a jacket.
3. Entire thickness of the fibre is less than half a mm.
4. Many such fibres can be packed together in an outer cover.

Working:

1. Working of optical fibre is based on the principle of total internal reflection.
2. An optical signal (a ray of light) entering the core suffers multiple total internal reflections before emerging out after a several kilometres.
3. The optical signal travels with the highest possible speed in the material.
4. The emerged optical signal has extremely low loss in signal strength.

Advantages of optical fibre communication over electronic communication:

1. Broad bandwidth (frequency range): For TV signals, a single optical fibre can carry over 90000 independent signals (channels).
2. Immune to EM interference: Optical fibre being electrically non-conductive, does not pick up nearby EM signals.
3. Low attenuation loss: loss being lower than 0.2 dB/km, a single long cable can be used for several kilometres.
4. Electrical insulator: Optical fibres being electrical insulators, ground loops of metal wires or lightning do not cause any harm.
5. Theft prevention: Optical fibres do not use copper or other expensive material which are prone to be robbed.
6. Security of information: Internal damage is most unlikely to occur, keeping the information secure.

Question 11.
Why are prism binoculars preferred over traditional binoculars? Describe its working in brief.
Answer:

1. Traditional binoculars use only two cylinders. Distance between the two cylinders can’t be greater than that between the two eyes. This creates a limitation of field of view.
2. A prism binocular has two right angled glass prisms which apply the principle of total internal reflection.
3. The incident light rays are reflected internally twice giving the viewer a wider field of view. For this reason, prism binoculars are preferred over traditional binoculars.

Working:

1. The prism binoculars consist of 4 isosceles, right angled prisms of material having critical angle less than 45°.
2. The prism binoculars have a wider input range compared to traditional binoculars.
3. The light rays incident on the prism binoculars, first get total internally reflected by the isosceles, right angled prisms 1 and 4.
4. These reflected rays undergo another total internal reflection by prisms 2 and 3 to form the final image.

Question 12.
A spherical surface separates two transparent media. Derive an expression that relates object and image distances with the radius of curvature for a point object. Clearly state the assumptions, if any.
Answer:
i. Consider a spherical surface YPY’ of radius curvature R, separating two transparent media of refractive indices n₁ and n₂ respectively with ni₁ < n₂.

ii. P is the pole and X’PX is the principal axis. A point object O is at a distance u from the pole, in the medium of refractive index n₁.

iii. In order to minimize spherical aberration, we consider two paraxial rays.

iv. The ray OP along the principal axis travels undeviated along PX. Another ray OA strikes the surface at A.

v. As n₁ < n₂, the ray deviates towards the normal (CAN), travels along AZ and real image of point object O is formed at I.

vi. Let α, β and γ be the angles subtended by incident ray, normal and refracted ray with the principal axis.
∴ i = (α + β) and r = (β – γ)

vii. As, the rays are paraxial, all the angles can be considered to be very small.
i.e., sin i ≈ i and sin r ≈ r
Angles α, β and γ can also be expressed as,

viii. According to Snell’s law,
n₁ sin (i) = n₂ sin (r)
For small angles, Snell’s law can be written
as, n₁i = n₂r
∴ n₁ (α + β) = n₂ (β – γ)
∴ (n₂ – n₁)β = n₁α + n₂γ
Substituting values of α, β and γ, we get,
(n₂ – n₁) \(\frac {arc PA}{R}\) = n₁(\(\frac {arc PA}{-u}\)) + n₂(\(\frac {arc PA}{v}\))
∴ \(\frac {(n_2-n_1)}{R}\) = \(\frac {n_2}{v}\) – \(\frac {n_1}{u}\)

Assumptions: To derive an expression that relates object and image distances with the radius of curvature for a point object, the two rays considered are assumed to be paraxial thus making the angles subtended by incident ray, normal and refracted ray with the principal axis very small.

Question 13.
Derive lens makers’ equation. Why is it called so? Under which conditions focal length f and radii of curvature R are numerically equal for a lens?
Answer:
i. Consider a lens of radii of curvature Ri and R2 kept in a medium such that refractive index of material of the lens with respect to the medium is denoted as n.

ii. Assuming the lens to be thin, P is the common pole for both the surfaces. O is a point object on the principal axis at a distance u from P.

iii. The refracting surface facing the object is considered as first refracting surface with radii R₁.

iv. In the absence of second refracting surface, the paraxial ray OA deviates towards normal and would intersect axis at I₁. PI₁ = V₁ is the image distance for intermediate image I₁.

Before reaching I₁, the incident rays (AB and OP) strike the second refracting surface. In this case, image I₁ acts as a virtual object for second surface.

vii. For second refracting surface,
n₂ = 1, n₁ = n, R = R₂, u = v₁ and PI = v
∴ \(\frac{(1-\mathrm{n})}{\mathrm{R}_{2}}=\frac{1}{\mathrm{v}}-\frac{\mathrm{n}}{\mathrm{v}_{1}}-\frac{(\mathrm{n}-1)}{\mathrm{R}_{2}}=\frac{1}{\mathrm{v}}-\frac{\mathrm{n}}{\mathrm{v}_{1}}\) ………… (2)

viii. Adding equations (1) and (2),
(n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)=\frac{1}{v}-\frac{1}{u}\)
For object at infinity, image is formed at focus, i.e., for u = ∞, v = f. Substituting this in above equation,
\(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) …………. (3)
This equation in known as the lens makers’ formula.

ix. Since the equation can be used to calculate the radii of curvature for the lens, it is called the lens makers’ equation.

x. The numeric value of focal length f and radius of curvature R is same under following two conditions:
Case I:
For a thin, symmetric and double convex lens made of glass (n = 1.5), R₁ is positive and R₂ is negative but, |R₁| = |R₂|.
In this case,
\(\frac{1}{\mathrm{f}}=(1.5-1)\left(\frac{1}{\mathrm{R}}-\frac{1}{-\mathrm{R}}\right)=0.5\left(\frac{2}{\mathrm{R}}\right)=\frac{1}{\mathrm{R}}\)
∴ f = R

Case II:
Similarly, for a thin, symmetric and double concave lens made of glass (n = 1.5), R₁ is negative and R₂ is positive but, |R₁| = |R₂|.
In this case,
\(\frac{1}{\mathrm{f}}=(1.5-1)\left(\frac{1}{-\mathrm{R}}-\frac{1}{\mathrm{R}}\right)=0.5\left(-\frac{2}{\mathrm{R}}\right)=-\frac{1}{\mathrm{R}}\)
∴ f = -R or |f| = |R|

3. Answer the following questions in detail.

Question 1.
What are different types of dispersions of light? Why do they occur?
Answer:
i. There are two types of dispersions:
a. Angular dispersion
b. Lateral dispersion

ii. The refractive index of material depends on the frequency of incident light. Hence, for different colours, refractive index of material is different.

iii. For an obliquely incident ray, the angles of refraction are different for each colour and they separate as they travel along different directions resulting into angular dispersion.

iv. When a polychromatic beam of light is obliquely incident upon a plane parallel transparent slab, emergent beam consists of all component colours separated out.

v. In this case, these colours are parallel to each other and are also parallel to their initial direction resulting into lateral dispersion

Question 2
Define angular dispersion for a prism. Obtain its expression for a thin prism. Relate it with the refractive indices of the material of the prism for corresponding colours.
Answer:
i. If a polychromatic beam is incident upon a prism, the emergent beam consists of all the individual colours angularly separated. This phenomenon is known as angular dispersion for a prism.

ii. For any two component colours, angular dispersion is given by,
δ₂₁ = δ₂ – δ₁

iii. For white light, we consider two extreme colours viz., red and violet.
∴ δ_VR = δ_V – δ_R

iv. For thin prism,
δ = A(n – 1)
δ₂₁ = δ₂ – δ₁
= A(n₂ – 1) – A(n₁ – 1) = A(n₂ – n₁)
where n₁ and n₂ are refractive indices for the two colours.

v. For white light,
δ_VR = δ_V – δ_R
= A(n_V – 1) – A(n_R – 1) = A(n_V – n_R).

Question 3.
Explain and define dispersive power of a transparent material. Obtain its expressions in terms of angles of deviation and refractive indices.
Answer:
Ability of an optical material to disperse constituent colours is its dispersive power.

It is measured for any two colours as the ratio of angular dispersion to the mean deviation for those two colours. Thus, for the extreme colours of white light, dispersive power is given by,
\(\omega=\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)} \approx \frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\delta_{\mathrm{Y}}}=\frac{\mathrm{A}\left(\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}\right)}{\mathrm{A}\left(\mathrm{n}_{\mathrm{Y}}-1\right)}=\frac{\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}}{\mathrm{n}_{\mathrm{Y}}-1}\)

Question 4.
(i) State the conditions under which a rainbow can be seen.
Answer:
A rainbow can be observed when there is a light shower with relatively large raindrop occurring during morning or evening time with enough sunlight around.

(ii) Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
Answer:
i. A ray AB incident from Sun (white light) strikes the upper portion of a water drop at an incident angle i.

ii. On entering into water, it deviates and disperses into constituent colours. The figure shows the extreme colours (violet and red).

iii. Refracted rays BV and BR strike the opposite inner surface of water drop and suffer internal reflection.

iv. These reflected rays finally emerge from V’ and R’ and can be seen by an observer on the ground.

v. For the observer they appear to be coming from opposite side of the Sun.

vi. Minimum deviation rays of red and violet colour are inclined to the ground level at θ_R = 42.8° ≈ 43° and θ_V = 40.8 ≈ 41° respectively. As a result, in the rainbow, the red is above and violet is below.

(iii) Explain the formation of a secondary rainbow. For which angular range with the horizontal is it visible?
Answer:
i. A ray AB incident from Sun (white light) strikes the lower portion of a water drop at an incident angle i.

ii. On entering into water, it deviates and disperses into constituent colours. The figure shows the extreme colours (violet and red).

iii. Refracted rays BV and BR finally emerge the drop from V’ and R’ after suffering two internal reflections and can be seen by an observer on the ground.

iv. Minimum deviation rays of red and violet colour are inclined to the ground level at θ_R ≈ 51° and θ_V ≈ 53° respectively. As a result, in the rainbow, the violet is above and red is below.

(iv) Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
Answer:
Yes, it is possible to see primary and secondary rainbows simultaneously. This can occur when the centres of both the rainbows coincide.

Question 5.
(i) Explain chromatic aberration for spherical lenses. State a method to minimize or eliminate it.
Answer:
Lenses are prepared by using a transparent material medium having different refractive index for different colours. Hence angular dispersion is present.
If the lens is thick, this will result into notably different foci corresponding to each colour for a polychromatic beam, like a white light. This defect is called chromatic aberration.
As violet light has maximum deviation, it is focussed closest to the pole.

Reducing/eliminating chromatic aberration:

1. Eliminating chromatic aberrations for all colours is impossible. Hence, it is minimised by eliminating aberrations for extreme colours.
2. This is achieved by using either a convex and a concave lens in contact or two thin convex lenses with proper separation. Such a combination is called achromatic combination.

(ii) What is achromatism? Derive a condition to achieve achromatism for a lens combination. State the conditions for it to be converging.
Answer:
i. To eliminate chromatic aberrations for extreme colours from a lens, either a convex and a concave lens in contact or two thin convex lenses with proper separation are used.

ii. This combination is called achromatic combination. The process of using this combination is termed as achromatism of a lens.

iii. Let ω₁ and ω₂ be the dispersive powers of materials of the two component lenses used in contact for an achromatic combination.

iv. Let V, R and Y denote the focal lengths for violet, red and yellow colours respectively.

v. For lens 1, let
K₁ = (\(\frac {1}{R_1}\)–\(\frac {1}{R_2}\))₁ and K₂ = (\(\frac {1}{R_1}\)–\(\frac {1}{R_2}\))₂

vi. For the combination to be achromatic, the resultant focal length of the combination must be the same for both the colours,

This is the condition for achromatism of a combination of lenses.

Condition for converging:
For this combination to be converging, fY must be positive.
Using equation (3), for f_Y to be positive, (f_Y)₁ < (f_Y)₂ ⇒ ω₁ < ω₂

Question 6.
Describe spherical aberration for spherical lenses. What are different ways to minimize or eliminate it?
Answer:
i. All the formulae used for image formation by lenses are based on some assumption. However, in reality these assumptions are not always true.

ii. A single point focus in case of lenses is possible only for small aperture spherical lenses and for paraxial rays.

iii. The rays coming from a distant object farther from principal axis no longer remain parallel to the axis. Thus, the focus gradually shifts towards pole.

iv. This defect arises due to spherical shape of the refracting surface, hence known as spherical aberration. It results into a blurred image with unclear boundaries.

v. As shown in figure, the rays near the edge of the lens converge at focal point F_M. Whereas, the rays near the principal axis converge at point F_P. The distance between F_M and F_P is measured as the longitudinal spherical aberration.

vi. In absence of this aberration, a single point image can be obtained on a screen. In the presence of spherical aberration, the image is always a circle.

vii. At a particular location of the screen (across AB in figure), the diameter of this circle is minimum. This is called the circle of least confusion. Radius of this circle is transverse spherical aberration.

Methods to eliminate/reduce spherical aberration in lenses:
i. Cheapest method to reduce the spherical aberration is to use a planoconvex or planoconcave lens with curved side facing the incident rays.

ii. Certain ratio of radii of curvature for a given refractive index almost eliminates the spherical aberration. For n = 1.5, the ratio is
\(\frac {R_1}{R_2}\) = \(\frac {1}{6}\) and for n = 2, \(\frac {R_1}{R_2}\) = \(\frac {1}{5}\)

iii. Use of two thin converging lenses separated by distance equal to difference between their focal lengths with lens of larger focal length facing the incident rays considerably reduces spherical aberration.

iv. Spherical aberration of a convex lens is positive (for real image), while that of a concave lens is negative. Thus, a suitable combination of them can completely eliminate spherical aberration.

Question 7.
Define and describe magnifying power of an optical instrument. How does it differ from linear or lateral magnification?
Answer:
i. Angular magnification or magnifying power of an optical instrument is defined as the ratio of the visual angle made by the image formed by that optical instrument (β) to the visual angle subtended by the object when kept at the least distance of distinct vision (α).

ii. The linear magnification is the ratio of the size of the image to the size of the object.

iii. When the distances of the object and image formed are very large as compared to the focal lengths of the instruments used, the magnification becomes infinite. Whereas, the magnifying power being the ratio of angle subtended by the object and image, gives the finite value.

iv. For example, in case of a compound microscope,
M_min = \(\frac {D}{f}\) = \(\frac {25}{5}\) = 5 and M_max = 1 + \(\frac {D}{f}\) = 6
Hence image appears to be only 5 to 6 times bigger for a lens of focal length 5 cm.
For M_min = \(\frac {D}{f}\) = 5, V = ∞
∴ Lateral magnification (m) = \(\frac {v}{u}\) = ∞
Thus, the image size is infinite times that of the object, but appears only 5 times bigger.

Question 8.
Derive an expression for magnifying power of a simple microscope. Obtain its minimum and maximum values in terms of its focal length.
Answer:
i. Figure (a) shows visual angle a made by an object, when kept at the least distance of distinct vision (D = 25 cm). Without an optical instrument this is the greatest possible visual angle as we cannot get the object closer than this.

ii. Figure (b) shows a convex lens forming erect, virtual and magnified image of the same object, when placed within the focus.

iii. The visual angle p of the object and the image in this case are the same. However, this time the viewer is looking at the image which is not closer than D. Hence the same object is now at a distance smaller than D.

iv. Angular magnification or magnifying power, in this case, is given by
M = \(\frac {Visual angle of theimage}{Visual angle of the object at D}\) = \(\frac {β}{α}\)
For small angles,
M = \(\frac {β}{α}\) ≈ \(\frac {tan(β)}{tan(α)}\) = \(\frac {BA/PA}{BA/D}\) = \(\frac {D}{u}\)

v. For maximum magnifying power, the image should be at D. For thin lens, considering thin lens formula.

Question 9.
Derive the expressions for the magnifying power and the length of a compound microscope using two convex lenses.
Answer:
i. The final image formed in compound microscope (A” B”) as shown in figure, makes a visual angle β at the eye.
Visual angle made by the object from distance D is α.

From figure,
tan β = \(\frac {A”B”}{v_c}\) = \(\frac {A’B’}{u_c}\)
and tan α = \(\frac {AB}{D}\)

Question 10.
What is a terrestrial telescope and an astronomical telescope?
Answer:

1. Telescopes used to see the objects on the Earth, like mountains, trees, players playing a match in a stadium, etc. are called terrestrial telescopes.
2. In such case, the final image must be erect. Eye lens used for this purpose must be concave and such a telescope is popularly called a binocular.
3. Most of the binoculars use three convex lenses with proper separation. The image formed by second lens is inverted with respect to object. The third lens again inverts this image and makes final image erect with respect to the object.
4. An astronomical telescope is the telescope used to see the objects like planets, stars, galaxies, etc. In this case there is no necessity of erect image. Such telescopes use convex lens as eye lens.

Question 11.
Obtain the expressions for magnifying power and the length of an astronomical telescope under normal adjustments.
Answer:
i. For telescopes, a is the visual angle of the object from its own position, which is practically at infinity.

ii. Visual angle of the final image is p and its position can be adjusted to be at D. However, under normal adjustments, the final image is also at infinity making a greater visual angle than that of the object.

iii. The parallax at the cross wires can be avoided by using the telescopes in normal adjustments.

iv. Objective of focal length f₀ focusses the parallel incident beam at a distance f₀ from the objective giving an inverted image AB.

v. For normal adjustment, the intermediate image AB forms at the focus of the eye lens. Rays refracted beyond the eye lens form a parallel beam inclined at an angle β with the principal axis.

vi. Angular magnification or magnifying power for telescope is given by,
M = \(\frac {β}{α}\) ≈ \(\frac {tan(β)}{tan(α)}\) = \(\frac {BA/P_cB}{BA/P_0B}\) = \(\frac {f_0}{f_e}\)

vii. Length of the telescope for normal adjustment is, L = f₀ + f_e.

Question 12.
What are the limitations in increasing the magnifying powers of (i) simple microscope (ii) compound microscope (iii) astronomical telescope?
Answer:
i. In case of simple microscope
\(\mathrm{M}_{\max }=\frac{\mathrm{D}}{\mathrm{u}}=1+\frac{\mathrm{D}}{\mathrm{f}}\)
Thus, the limitation in increasing the magnifying power is determined by the value of focal length and the closeness with which the lens can be held near the eye.

ii. In case of compound microscope,
M = \(\mathrm{m}_{0} \times \mathrm{M}_{\mathrm{e}}=\frac{\mathrm{v}_{0}}{\mathrm{u}_{\mathrm{o}}} \times \frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}\)
Thus, in order to increase m₀, we need to decrease u₀. Thereby, the object comes closer and closer to the focus of the objective. This increases v₀ and hence length of the microscope. Therefore, mQ can be increased only within the limitation of length of the microscope.

iii. In case of telescopes,
M = \(\frac {f_0}{f_e}\)
Where f₀ = focal length of the objective
f_e = focal length of the eye-piece
Length of the telescope for normal adjustment is, L = f₀ + f_e.
Thus, magnifying power of telescope can be increased only within the limitations of length of the telescope.

4. Solve the following numerical examples

Question 1.
A monochromatic ray of light strikes the water (n = 4/3) surface in a cylindrical vessel at angle of incidence 53°. Depth of water is 36 cm. After striking the water surface, how long will the light take to reach the bottom of the vessel? [Angles of the most popular Pythagorean triangle of sides in the ratio 3 : 4 : 5 are nearly 37°, 53° and 90°]
Answer:
From figure, ray PO = incident ray
ray OA = refracted ray
QOB = Normal to the water surface.
Given that,
∠POQ = angle of incidence (θ₁) = 53°
Seg OB = 36 cm and n_water = \(\frac {4}{3}\)
From Snell’s law,
n₁ sin θ₁ = n₂ sin θ₂
∴ n_water = \(\frac {sinθ_1}{sinθ_2}\)
Or sin θ₂ = \(\frac {sinθ_1}{n_{water}}\) = \(\frac {sin(53°)×3}{4}\)
∴ θ₂ ~ 37°
ΔOBA forms a Pythagorean triangle with angles 53°, 37° and 90°.
Thus, sides of ΔOBA will be in ratio 3 : 4 : 5 Such that OA forms the hypotenuse. From figure, we can infer that,
Seg OB = 4x = 36 cm
∴ x = 9
∴ seg OA = 5x = 45 cm and
seg AB = 3x = 27 cm.
This means the light has to travel 45 cm to reach the bottom of the vessel.
The speed of the light in water is given by,
v = \(\frac {c}{n}\)
∴ v = \(\frac {3×10^8}{4/3}\) = \(\frac {9}{4}\) × 10⁸ m/s
∴ Time taken by light to reach the bottom of vessel is,
t = \(\frac {s}{v}\) = \(\frac {45×10^{-2}}{\frac {9}{4} × 10^8}\) = 20 × 10^-10 = 2 ns or 0.002 µs

Question 2.
Estimate the number of images produced if a tiny object is kept in between two plane mirrors inclined at 35°, 36°, 40° and 45°.
Answer:
i. For θ₁ =35°
n₁ = \(\frac {360}{θ_1}\) = \(\frac {360}{35}\) = 10.28
As ni is non-integer, N₁ = integral part of n₁ = 10

ii. For θ₂ = 36°
n₂ = \(\frac {360}{36}\) = 10
As n₂ is even integer, N₂ = (n₂ – 1) = 9

iii. For θ₃ = 40°
n₃ = \(\frac {360}{36}\) = 9
As n₃ is odd integer.
Number of images seen (N₃) = n₃ – 1 = 8
(if the object is placed at the angle bisector) or Number of images seen (N₃) = n₃ = 9
(if the object is placed off the angle bisector)

iv. For θ₄ = 45°
n₄ = \(\frac {360}{45}\) = 8
As n₄ is even integer,
N₄ = n₄ – 1 = 7

Question 3.
A rectangular sheet of length 30 cm and breadth 3 cm is kept on the principal axis of a concave mirror of focal length 30 cm. Draw the image formed by the mirror on the same diagram, as far as possible on scale.

Answer:

[Note: The question has been modified and the ray digram is inserted in question in order to find the correct position of the image.]

Question 4.
A car uses a convex mirror of curvature 1.2 m as its rear-view mirror. A minibus of cross section 2.2 m × 2.2 m is 6.6 m away from the mirror. Estimate the image size.
Answer:
For a convex mirror,
f = +\(\frac {R}{2}\) = \(\frac {1.2}{2}\) = +0.6m
Given that, a minibus, approximately of a shape of square is at distance 6.6 m from mirror.
i.e., u = -6.6 m

∴ h₂ = 0.183 m
i.e., h₂ 0.2 m

Question 5.
A glass slab of thickness 2.5 cm having refractive index 5/3 is kept on an ink spot. A transparent beaker of very thin bottom, containing water of refractive index 4/3 up to 8 cm, is kept on the glass block. Calculate apparent depth of the ink spot when seen from the outside air.
Answer:
When observed from the outside air, the light coming from ink spot gets refracted twice; once through glass and once through water.
∴ When observed from water,

∴ Apparent depth = 2 cm
Now when observed from outside air, the total real depth of ink spot can be taken as (8 + 2) cm = 10 cm.
∴ \(\frac {n_w}{n_{air}}\) = \(\frac {Real depth}{Apparent depth}\)
∴ Apparent depth = \(\frac {10}{4/3}\)
= \(\frac {10×3}{4}\) = 7.5 cm

Question 64.
A convex lens held some distance above a 6 cm long pencil produces its image of SOME size. On shifting the lens by a distance equal to its focal length, it again produces the image of the SAME size as earlier. Determine the image size.
Answer:
For a convex lens, it is given that the image size remains unchanged after shifting the lens through distance equal to its focal length. From given conditions, it can be inferred that the object distance should be u = –\(\frac {f}{2}\)
Also, h₁ = 6 cm, v₁ = v₂
From formula for thin lenses,

Question 7.
Figure below shows the section ABCD of a transparent slab. There is a tiny green LED light source at the bottom left corner B. A certain ray of light from B suffers total internal reflection at nearest point P on the surface AD and strikes the surface CD at point Question Determine refractive index of the material of the slab and distance DQ. At Q, the ray PQ will suffer partial or total internal reflection?

Answer:

As, the light ray undergo total internal reflection at P, the ray BP may be incident at critical angle.
For a Pythagorean triangle with sides in ratio 3 : 4 : 5 the angle opposite to side 3 units is 37° and that opposite to 4 units is 53°.
Thus, from figure, we can say, in ΔBAP
∠ABP = 53°
∠BPN = i_c = 53°
∴ n_glass = \(\frac {1}{sin_c}\) = \(\frac {1}{sin(53°)}\) ≈ \(\frac {1}{0.8}\) = \(\frac {5}{4}\)
∴ Refractive index (n) of the slab is \(\frac {5}{4}\)
From symmetry, ∆PDQ is also a Pythagorean triangle with sides in ratio QD : PD : PQ = 3 : 4 : 5.
PD = 2 cm ⇒ QD = 1.5 cm.
As critical angle is i_c = 53° and angle of incidence at Q, ∠PQN = 37° is less than critical angle, there will be partial internal reflection at Question

Question 8.
A point object is kept 10 cm away from a double convex lens of refractive index 1.5 and radii of curvature 10 cm and 8 cm. Determine location of the final image considering paraxial rays only.
Answer:
Given that, R₁ = 10 cm, R₂ = -8 cm,
u = -10 cm and n = 1.5
From lens maker’s equation,

Question 9.
A monochromatic ray of light is incident at 37° on an equilateral prism of refractive index 3/2. Determine angle of emergence and angle of deviation. If angle of prism is adjustable, what should its value be for emergent ray to be just possible for the same angle of incidence.
Answer:
By Snell’s law, in case of prism,

For equilateral prism, A = 60°
Also, A= r₁ + r₂
∴ r₂ = A – r₁ = 60° – 23°39′ = 36°21′
Applying snell’s law on the second surface of

= sin^-1 (0.889)
= 62°44′
≈ 63°
For any prism,
i + e = A + δ
∴ δ = (i + e) – A
= (37 + 63) – 60
= 40°
For an emergent ray to just emerge, the angle r’₂ acts as a critical angle.
∴ r’₂ = sin^-1 (\(\frac {1}{n}\))
= sin^-1 (\(\frac {2}{3}\))
= 41°48′
As, A = r’₁ + r’₂ and i to be kept the same.
⇒ A’ = r’₁ + r’₂‘
= 23°39′ + 41°48′
= 65°27’

Question 10.
From the given data set, determine angular dispersion by the prism and dispersive power of its material for extreme colours. n_R = 1.62 nv = 1.66, δ_R = 3.1°
Answer:
Given: n_R = 1.62, n_V = 1.66, δ_R = 3.1°
To find:
i. Angular dispersion (δ_vr)
ii. Dispersive power (ω_VR)
Formula:
i. δ = A (n – 1)
ii. δ_VR = δ_V – δ_R
(iii) ω = \(\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)}\)
Calculation: From formula (i),
δ_R = A(n_R – 1)
∴ A = \(\frac{\delta_{R}}{\left(n_{R}-1\right)}=\frac{3.1}{(1.62-1)}=\frac{3.1}{0.62}\)
= 5
δV = A(n_v – 1) = 5 × (1.66 – 1) = 3.3C
From formula (ii),
δ_VR = 3.3 – 3.1 = 0.2°
From formula (iii),
ω_VR = \(\frac{3.3-3.1}{\left(\frac{3.3+3.1}{2}\right)}=\frac{0.2}{6.4} \times 2=\frac{0.2}{3.2}=\frac{1}{16}\)
= 0.0625

Question 11.
Refractive index of a flint glass varies from 1.60 to 1.66 for visible range. Radii of curvature of a thin convex lens are 10 cm and 15 cm. Calculate the chromatic aberration between extreme colours.
Answer:
Given the refractive indices for extreme colours. As, n_R < n_V
n_R = 1.60 and n_V = 1.66
For convex lens,
R₁ = 10 cm and R₁₀ = -15 cm

= 0.11
∴ f_V = 11 cm
∴ Longitudinal chromatic aberration
= f_V – f_R = 11 – 10 = 1 cm

Question 12.
A person uses spectacles of ‘number’ 2.00 for reading. Determine the range of magnifying power (angular magnification) possible. It is a concave convex lens (n = 1.5) having curvature of one of its surfaces to be 10 cm. Estimate that of the other.
Answer:
For a single concavo-convex lens, the magnifying power will be same as that for simple microscope As, the number represents the power of the lens,
P = \(\frac {1}{f}\) = 2 ⇒ f = 0.5 m.
∴ Range of magnifying power of a lens will be,
M_min = \(\frac {D}{f}\) = \(\frac {0.25}{0.5}\) = 0.5
and M_min = 1 + \(\frac {D}{f}\) = 1 + 0.5 = 1.5
Given that, n = 1.5, |R₁| = 10 cm
f = 0.5 m = 50 cm
From lens maker’s equation,

Question 13.
Focal power of the eye lens of a compound microscope is 6 dioptre. The microscope is to be used for maximum magnifying power (angular magnification) of at least 12.5. The packing instructions demand that length of the microscope should be 25 cm. Determine minimum focal power of the objective. How much will its radius of curvature be if it is a biconvex lens of n = 1.5.
Answer:
Focal power of the eye lens,
P_e = \(\frac {1}{f_e}\) = 6D
∴ f_e = \(\frac {1}{6}\) = 0.1667 m = 16.67 cm
Now, as the magnifying power is maximum,
v_e = 25 cm,
Also (M_e)_max = 1 + \(\frac {D}{f_e}\) = 1 + \(\frac {25}{16.67}\) ≈ 2.5
Given that,
M = m₀ × M_e = 12.5
∴ m₀ × 2.5 = 12.5
∴ m₀ = \(\frac {v_0}{u_0}\) = 5 ……….. (1)
From thin lens formula,

Length of a compound microscope,
L = |v₀| +|u₀|
∴ 25 = |v₀| + 10
∴ |v₀|= 15 cm
∴ |u₀| = \(\frac {v_0}{5}\) = 3 cm …………… (from 1)
From lens formula for objective,
\(\frac {1}{f_0}\) = \(\frac {1}{v_0}\) – \(\frac {1}{u_0}\)
= \(\frac {1}{15}\) – \(\frac {1}{-3}\)
= \(\frac {2}{5}\)
∴ f₀ = 2.5 cm = 0.025 m
Thus, focal power of objective,
P = \(\frac {1}{f_0(m)}\)
= \(\frac {1}{0.025}\) = 40 D
Using lens maker’s equation for a biconvex lens,
\(\frac{1}{f_{o}}=(n-1)\left(\frac{1}{R}-\frac{1}{-R}\right)\)
∴ \(\frac{1}{2.5}=(1.5-1)\left(\frac{2}{R}\right)=\frac{1}{R}\)
∴ R = 2.5 cm

11th Physics Digest Chapter 9 Optics Intext Questions and Answers

Can you recall? (Textbook rage no 159)

What are laws of reflection and refraction?
Answer:
Laws of reflection:
a. Reflected ray lies in the plane formed by incident ray and the normal drawn at the point of incidence and the two rays are on either side of the normal.
b. Angles of incidence and reflection are equal (i = r).

Laws of refraction:
a. Refracted ray lies in the plane formed by incident ray and the normal drawn at the point of incidence; and the two rays are on either side of the normal.

b. Angle of incidence (θ₁) and angle of refraction (θ₂) are related by Snell’s law, given by, n₁ sin θ₁ = n₂ sin θ₂ where, n₁, n₂ = refractive indices of medium 1 and medium 2 respectively.

Can you recall? (Textbook page no. 159)

Question 1.
What is refractive index?
Answer:
The ratio of velocity of light in vacuum to the velocity’ of light in a medium is called the refractive index of the medium.

Question 2.
What is total internal reflection?
Answer:
For angles of incidence larger than the critical angle, the angle of refraction is larger than 90°. Thus, all the incident light gets reflected back into the denser medium. This is called total internal reflection.

Question 3.
How does a rainbow form?
Answer:

1. The rainbow appears in the sky after a rainfall.
2. Water droplets present in the atmosphere act as small prism.
3. When sunlight enters these water droplets it gets refracted and dispersed.
4. This dispersed light gets totally reflected inside the droplet and again is refracted while coming out of the droplet.
5. As a combined effect of all these phenomena, the seven coloured rainbow is observed.

Question 4.
What is dispersion of light?
Answer:
Splitting of a white light into its constituent colours is known as dispersion of light.

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Sound Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 8 Sound Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 8 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 8 Exercise Solutions

1. Choose the correct alternatives

Question 1.
A sound carried by the air from a sitar to a listener is a wave of the following type.
(A) Longitudinal stationary
(B)Transverse progressive
(C) Transverse stationery
(D) Longitudinal progressive
Answer:
(D) Longitudinal progressive

Question 2.
When sound waves travel from air to water, which of these remains constant?
(A) Velocity
(B) Frequency
(C) Wavelength
(D) All of above
Answer:
(B) Frequency

Question 3.
The Laplace’s correction in the expression for velocity of sound given by Newton is needed because sound waves
(A) are longitudinal
(B) propagate isothermally
(C) propagate adiabatically
(D) are of long wavelength
Answer:
(C) propagate adiabatically

Question 4.
Speed of sound is maximum in
(A) air
(B) water
(C) vacuum
(D) solid
Answer:
(D) solid

Question 5.
The walls of the hall built for music concerns should
(A) amplify sound
(B) Reflect sound
(C) transmit sound
(D) Absorb sound
Answer:
(D) Absorb sound

2. Answer briefly.

Question 1.
Wave motion is doubly periodic. Explain.
Answer:
i. A wave particle repeats its motion after a definite interval of time at every location, making it periodic in time.
ii. Similarly, at any given instant, the form of a wave repeats itself at equal distances making it periodic in space.
iii. Thus, wave motion is a doubly periodic phenomenon, i.e., periodic in time as well as periodic in space.

Question 2.
What is Doppler effect?
Answer:
The apparent change in the frequency of sound heard by a listener, due to relative motion between the source of sound and the listener is called Doppler effect in sound.

Question 3.
Describe a transverse wave.
Answer:
Transverse wave:
A wave in which particles of the medium vibrate in a direction perpendicular to the direction of propagation of the wave is called transverse wave.
Example: Ripples on the surface of water, light waves.

Characteristics of transverse waves:

1. All the particles of medium in the path of wave vibrate in a direction perpendicular to the direction of propagation of wave with same period and amplitude.
2. When transverse wave passes through the medium, the medium is divided into alternate crests i.e., regions of positive displacements and troughs i.e., regions of negative displacement, that are periodic in time.
3. A crest and an adjacent trough form one cycle of a transverse wave. The distance between any two successive crests or troughs is called wavelength ‘λ’ of the wave.
4. Crests and troughs advance in the medium and are responsible for transfer of energy.
5. Transverse waves can travel only through solids and not through liquids and gases. Electromagnetic waves are transverse waves, but they do not require material medium for propagation.
6. When transverse waves advance through a medium, there is no change of pressure and density at any point of the medium, but the shape changes periodically.
7. Transverse wave can be polarised.
8. Medium conveying a transverse wave must possess elasticity of shape, i.e., modulus of rigidity.

Question 4.
Define a longitudinal wave.
Answer:
A wave in which particles of medium vibrate in a direction parallel to the direction of propagation of the wave is called longitudinal wave. Example: Sound waves.

Question 5.
State Newton’s formula for velocity of sound.
Answer:
Newton’s formula for velocity of sound:
i. Sound wave travels through a medium in the form of compression and rarefaction. At compression, the density of medium is greater while at rarefaction density is smaller. This is possible only in elastic medium.

ii. Thus, the velocity of sound depends upon density and elasticity of medium. It is given by
v = \(\sqrt{\frac {E}{ρ}}\) ….(1)
Where, E is the modulus of elasticity of medium and ρ is density of medium.

Assumptions:
1. Newton assumed that during propagation of sound wave in air, average temperature of the medium remains constant. Hence, propagation of sound wave in air is an isothermal process and isothermal elasticity should be considered.

2. The volume elasticity of air determined under isothermal change is called isothermal bulk modulus.

Calculations:
1. For a gas or air, the isothermal elasticity E is equal to the atmospheric pressure P.
Substituting this value in equation (1), the velocity of sound in air or a gas is given by
v = \(\sqrt{\frac {P}{ρ}}\) ….(∵ E = P)
This is the Newton’s formula for velocity of sound in air.

2. But atmospheric pressure is given by,
P = hdg
∴ v = \(\sqrt{\frac {hdg}{ρ}\) ….(2)

3. At N.T.P., h = 0.76 m of mercury, density of mercury d = 13600 kg/m³ and acceleration due to gravity, g = 9.8 m/s², density of air ρ = 1.293 kg/m³

4. From equation (2) we have velocity of sound,
v = \(\sqrt{\frac {0.76×13600×9.8}{1.293}}\) = 279.9 m/s at N.T.P

Question 6.
What is the effect of pressure on velocity of sound?
Answer:
Effect of pressure:
i. Let v be the velocity of sound in air when the pressure is P and density is ρ.

ii. Using Laplace’s formula, we can write,
v = \(\sqrt{\frac {γP}{ρ}}\) ….(1)

iii. If V be the volume of a gas having mass M then, ρ = \(\frac {M}{V}\)

iv. Substituting ρ in equation (1), we get,
v = \(\sqrt{\frac {γPV}{M}}\) ….(2)

v. But according to Boyle’s law,
PV = constant (at constant temperature)
Also, M and γ are constant.
∴ v = constant

vi. Hence, the velocity of sound does not depend upon the change in pressure, as long as the temperature remains constant.

vii. For a gaseous medium, PV= nRT.
Substituting in equation (2), we get,
v = \(\sqrt{\frac {γnRT}{M}}\)

viii. Thus, even for a gaseous medium obeying ideal gas equation, the velocity of sound does not depend upon the change in pressure, as long as the temperature remains constant.

Question 7.
What is the effect of humidity of air on velocity of sound?
Answer:
Effect of humidity:
i. Let v_m and v_d be the velocities of sound in moist air and dry air respectively.

ii. Humid air contains a large proportion of water vapour. Density of water vapour at 0 °C is 0.81 kg/m³ while that of dry air at 0°C is 1.29 kg/m³. So, the density ρ_m of moist air is less than the density ρ_d of dry air i.e., ρ_m < ρ_d.

iii. Thus \(\frac {v_m}{v_d}\) > 1
∴ v_m > v_d

iv. Hence, sound travels faster in moist air than in dry air. It means that velocity of sound increases with increase in moistness (humidity) of air.

Question 8.
What do you mean by an echo?
Answer:
An echo is the repetition of the original sound because of reflection from some rigid surface at a distance from the source of sound.

Question 9.
State any two applications of acoustics.
Answer:
Application of acoustics in nature:
i. Bats apply the principle of acoustics to locate objects. They emit short ultrasonic pulses of frequency 30 kHz to 150 kHz. The resulting echoes give them information about location of the obstacle. This helps the bats to fly in even in total darkness of caves.

ii. Dolphins navigate underwater with the help of an analogous system. They emit subsonic frequencies which can be about 100 Hz. They can sense an object about 1.4 m or larger.

Medical applications of acoustics:
i. High pressure and high amplitude shock waves are used to split kidney stones into smaller pieces without invasive surgery. A reflector or acoustic lens is used to focus a produced shock wave so that as much of its energy as possible converges on the stone. The resulting stresses in the stone causes the stone to break into small pieces which can then be removed easily.

ii. Ultrasonic imaging uses reflection of ultrasonic waves from regions in the interior of body. It is used for prenatal (before the birth) examination, detection of anomalous conditions like tumour etc. and the study of heart valve action.

iii. Ultrasound at a very high-power level, destroys selective pathological tissues which is helpful in treatment of arthritis and certain type of cancer.

Underwater applications of acoustics:
i. SONAR (Sound Navigational Ranging) is a technique for locating objects underwater by transmitting a pulse of ultrasonic sound and detecting the reflected pulse.
ii. The time delay between transmission of a pulse and the reception of reflected pulse indicates the depth of the object.
iii. Motion and position of submerged objects like submarine can be measured with the help of this system.

Applications of acoustics in environmental and geological studies:
i. Acoustic principle has important application to environmental problems like noise control. The quiet mass transit vehicle is designed by studying the generation and propagation of sound in the motor’s wheels and supporting structures.

Reflected and refracted elastic waves passing through the Earth’s interior can be measured by applying the principles of acoustics. This is useful in studying the properties of the Earth.

Principles of acoustics are applied to detect local anomalies like oil deposits etc. making it useful for geological studies.

Question 10.
Define amplitude and wavelength of a wave.
Answer:
i. Amplitude (A): The largest displacement of a particle of a medium through which the wave is propagating, from its rest position, is called amplitude of that wave.
SI unit: (m)

ii. Wavelength (λ): The distance between two successive particles which are in the same state of vibration is called wavelength of the wave.
SI unit: (m)

Question 11.
Draw a wave and indicate points which are (i) in phase (ii) out of phase (iii) have a phase difference of π/2.
Answer:

i. In phase point: A and F; B and H; C and I; D and J
ii. Out of phase points: A and B, B and D, FI and J, E and F,
iii. Point having phase difference of π/2: A and B; B and C; D; D and F; F and H; H and I; J and I

Question 12.
Define the relation between velocity, wavelength and frequency of wave.
Answer:
i. A wave covers a distance equal to the wavelength (λ) during one period (T).
Therefore, the magnitude of the velocity (v) is given by,
Magnitude of velocity = \(\frac {Distance covered}{Corresponding time}\)

ii. v = \(\frac {22}{7}\) i.e., v = λ × (\(\frac {1}{T}\)) …………….. (1)

iii. But reciprocal of the period is equal to the frequency (n) of the waves.
∴ \(\frac {1}{T}\) = n …………… (2)

iv. From equations (1) and (2), we get
v = nλ
i.e., wave velocity = frequency × wavelength.

Question 13.
State and explain principle of superposition of waves.
Answer:
Principle:
As waves don’t repulse each other, they overlap in the same region of the space without affecting each other. When two waves overlap, their displacements add vectorially.

Explanation:
i. Consider two waves travelling through a medium arriving at a point simultaneously.

ii. Let each wave produce its own displacement at that point independent of the others. This displacement can be given as,
y₁ = displacement due to first wave.
y₂ = displacement due to second wave.

iii. Then according to superposition of waves, the resultant displacement at that point is equal to the vector sum of the displacements due to all the waves.
∴\(\vec{y}\) = \(\vec{y_1}\) + \(\vec{y_2}\)

Question 14.
State the expression for apparent frequency when source of sound and listener are
i) moving towards each other
ii) moving away from each other
Answer:
i. Let,
n = actual frequency of the source.
n₀ = apparent frequency of the source,
v = velocity of sound in air.
v_s = velocity of the source.
v_l = velocity of the listener.

ii. Apparent frequency heard by the listener is given by,
n = n₀(\(\frac {v±v_L}{v±v_s}\))
Where upper signs (+ ve in numerator and -ve in denominator) indicate that source and observer move towards each other. Lower signs (-ve in numerator and +ve in denominator) indicate that source and listener move away from each other.

iii. If source and listener are moving towards each other, then apparent frequency is given by,
n = n₀(\(\frac {v+v_L}{v-v_s}\)) i.e., apparent frequency increases.

iv. If source and listener are moving away from each other, then apparent frequency is given by,
n = n₀(\(\frac {v-v_L}{v+v_s}\)) i.e., apparent frequency decreases.

Question 15.
State the expression for apparent frequency when source is stationary and listener is
1) moving towards the source
2) moving away from the source
Answer:
Let,
n = actual frequency of the source.
n₀ = apparent frequency of the source,
v = velocity of sound in air.
v_s = velocity of the source.
v_l = velocity of the listener.

i. If listener is moving towards source then apparent frequency is given by,
n = n₀(\(\frac {v+v_L}{v}\)) i.e., apparent frequency increases.

ii. If listener is receding away from source then apparent frequency is given by,
n = n₀(\(\frac {v-v_L}{v}\)) i.e., apparent frequency decreases.

Question 16.
State the expression for apparent frequency when listener is stationary and source is.

(i) moving towards the listener
(ii) moving away from the listener
Answer:
Let,
n = actual frequency of the source.
n₀ = apparent frequency of the source,
v = velocity of sound in air.
v_s = velocity of the source.
v_l = velocity of the listener.

i. If source is moving towards observer then apparent frequency is given by,
n = n₀(\(\frac {v}{v-v_s}\)) i.e., apparent frequency increases.

ii. If source is receding away from observer then apparent frequency is given by,
n = n₀(\(\frac {v}{v+v_s}\)) i.e., apparent frequency decreases.

Question 17.
Explain what is meant by phase of a wave.
Answer:

i. The state of oscillation of a particle is called the phase of the particle.

ii. The displacement, direction of velocity and oscillation number of the particle describe the phase of the particle at a place.

iii. Particles r and t (q and u or v and s) have same displacements but the directions of their velocities are opposite.

iv. Particles having same magnitude of displacements and same direction of velocity are said to be in phase during their respective oscillations. Example: particles v and p.

v. Separation between two particles which are in phase is wavelength (λ).

vi. The two successive particles differ by ‘1’ in their oscillation number i.e., if particle v is at its n^th oscillation, particle p will be at its (n + 1)^th oscillation as the wave is travelling along + X direction.

vii. In the given graph, if the disturbance (energy) has just reached the particle w, the phase angle corresponding to particle is 0°. At this instant, particle v has completed quarter oscillation and reached its positive maximum (sin θ = +1). The phase angle θ of this particle v is \(\frac {π^c}{2}\) = 90° at this instant.

viii. Phase angles of particles u and q are π^c (180°) and 2rcc (360°) respectively.

ix. Particle p has completed one oscillation and is at its positive maximum during its second oscillation.
∴ phase angle = 2π^c + \(\frac {π^c}{2}\)
= \(\frac {5π^c}{2}\)

x. v and p are the successive particles in the same state (same displacement and same direction of velocity) during their respective oscillations. Phase angle between these two differs by 2π^c.

Question 18.
Define progressive wave. State any four properties.
Answer:
i. Waves in which a disturbance created at one place travels to distant points and keeps travelling unless stopped by an external force are known as travelling or progressive waves.
Properties of progressive waves are:
Amplitude, wavelength, period, double periodicity, frequency and velocity.

Question 19.
Distinguish between traverse waves and longitudinal waves.
Answer:

Question 20.
Explain Newtons formula for velocity of sound. What is its limitation?
Answer:
Newton’s formula for velocity of sound:
i. Sound wave travels through a medium in the form of compression and rarefaction. At compression, the density of medium is greater while at rarefaction density is smaller. This is possible only in elastic medium.

ii. Thus, the velocity of sound depends upon density and elasticity of medium. It is given by
v = \(\sqrt{\frac {E}{ρ}}\) ….(1)
Where, E is the modulus of elasticity of medium and ρ is density of medium.

Assumptions:
1. Newton assumed that during propagation of sound wave in air, average temperature of the medium remains constant. Hence, propagation of sound wave in air is an isothermal process and isothermal elasticity should be considered.

2. The volume elasticity of air determined under isothermal change is called isothermal bulk modulus.

Calculations:
1. For a gas or air, the isothermal elasticity E is equal to the atmospheric pressure P.
Substituting this value in equation (1), the velocity of sound in air or a gas is given by
v = \(\sqrt{\frac {P}{ρ}}\) ….(∵ E = P)
This is the Newton’s formula for velocity of sound in air.

2. But atmospheric pressure is given by,
P = hdg
∴ v = \(\sqrt{\frac {hdg}{ρ}}\) ….(2)

3. At N.T.P., h = 0.76 m of mercury, density of mercury d = 13600 kg/m³ and acceleration due to gravity, g = 9.8 m/s², density of air ρ = 1.293 kg/m³

4. From equation (2) we have velocity of sound,
v = \(\sqrt{\frac {0.76×13600×9.8}{1.293}}\) = 279.9 m/s at N.T.P

Limitations:
1. Experimentally, it is found that the velocity of sound in air at N. T. P is 332 m/s. Thus, there is considerable difference between the value predicted by Newton’s formula and the experimental value.

2. Experimental value is 16% greater than the value given by the formula. Newton failed to provide a satisfactory explanation for the difference.

3. Solve the following problems.

Question 1.
A certain sound wave in air has a speed 340 m/s and wavelength 1.7 m for this wave, calculate
(i) the frequency
(ii) the period.
Answer:
Given: v = 340 m/s, λ = 1.7 m
To find: frequency (n), period (T)
Formulae:
i. n = \(\frac {v}{λ}\)
ii. T = \(\frac {1}{n}\)
Calculation: From formula, (i)
n = \(\frac {340}{1.7}\)
∴ n = 200 Hz
From formula, (ii)
T = \(\frac {1}{n}\) = \(\frac {1}{2×10^2}\)
= 5 × 10^-3
…….. (using reciprocal Table)
∴ T = 0.005 s

Question 2.
A tuning fork of frequency 170 Hz produces sound waves of wavelength 2m. Calculate speed of sound.
Answer:
Given: n = 170 Hz, λ = 2 m
To find: velocity of sound (v)
Formula: v = nλ
Calculation: From formula,
v = 170 × 2
∴ v = 340 m/s

Question 3.
An echo-sounder in a fishing boat receives an echo from a shoal of fish 0.45s after it was sent. If the speed of sound in water is 1500 m/s, how deep is the shoal?
Answer:
Given: t = 0.45 s, v = 1500 m/s,
To Find: depth (d)
Formula: speed (v) = \(\frac {distance}{time}\)
Calculation:
For an echo distance travelled by the sound wave = 2 × (distance between echo sounder and shoal) (d)
v = \(\frac {2 × d}{t}\)
∴ d = \(\frac {1500 × 0.45}{2}\) = 337.5 m

Question 4.
A girl stands 170 m away from a high wall and claps her hands at a steady rateso that each clap coincides with the echo of the one before.
a) If she makes 60 claps in 1 minute, what value should be the speed of sound in air?
b) Now, she moves to another location and finds that she should now make 45 claps in 1 minute to coincide with successive echoes. Calculate her distance for the new position from the wall.
Answer:
i. When the girl makes 60 claps in 1 minute, the value of speed of is 340 m/s.

ii. The girl is at a distance of 226.67 m from the wall when she produces 45 claps per minute.
[Note: The answer given above is calculated in accordance with textual method considering the given data]

Question 5.
Sound wave A has period 0.015 s, sound wave B has period 0.025. Which sound has greater frequency?
Answer:
Given: T_A = 0.015 s, T_B = 0.025 s
To find: greater frequency (n)
Formula: n = \(\frac {1}{T}\)
Calculation: From formula,
n_A = \(\frac {1}{T_A}\) = \(\frac {1}{0.025}\) = \(\frac {1}{2.5 ×10^{-2}}\)
∴ n_A = 66.67
…. (using reciprocal table)
n_B = \(\frac {1}{T_B}\) = \(\frac {1}{0.025}\) = \(\frac {1}{2.5 ×10^{-2}}\)
∴ n_B = 40 Hz
…. (using reciprocal table)
∴ n_A > n_B

Question 6.
At what temperature will the speed of sound in air be 1.75 times its speed at N.T.P?
Answer:
Given:
v_air = 1.75 V_S.T.P = \(\frac {7}{4}\) v_S.T.P
T_S.T.P = 273 K
To find: temperature T_air
Formula: v ∝ √T
Calculation: From formula,

Question 7.
A man standing between 2 parallel eliffs fires a gun. He hearns two echos one after 3 seconds and other after 5 seconds. The separation between the two cliffs is 1360 m, what is the speed of sound?
Answer:
distance (s) = 1360 m,
time for first echo = 3 s,
time for second echo = 5 s
To Find : speed of sound (v)
Formula : speed = \(\frac {distence}{time}\)
Calculation:
Time for first echo = 3 s
∴ time taken by sound to travel given distance t₁
= \(\frac {3}{2}\) = 1.5 s
Time for second echo = 5 s
∴ time taken by sound to travel given distance t₂
= \(\frac {5}{2}\) = 2.5 s
∴Total time taken by sound to travel given distance, T = 1.5 + 2.5 = 4 s
From formula,
v = \(\frac {1360}{4}\)
∴v = 340 m/s

Question 8.
If the velocity of sound in air at a given place on two different days of a given week are in the ratio of 1 : 1.1. Assuming the temperatures on the two days to be same what quantitative conclusion can your draw about the condition on the two days?
Answer:
Let v₁ and v₂ be the velocity of sound on day 1 and day 2 respectively.
\(\frac {v_1}{v_2}\) = \(\frac {1}{1.1}\)
We know, v ∝ \(\frac {1}{√ρ}\)
Let ρ₁ and ρ₂ be the density of air on day 1 and day 2 respectively.
∴ \(\sqrt{\frac {ρ_2}{ρ_1}}\) = \(\frac {1}{1.1}\)
∴ \(\frac {ρ_2}{ρ_1}\) = (\(\frac {1}{1.1}\))²
∴ ρ₁ = 1.1² ρ₂ = 1.21 ρ²
From above equation, we can conclude,
ρ₁ > ρ₂
∴ v₂ > v₁ i.e., the velocity of sound is greater on the second day than on the first day.
We know, speed of sound in moist air (v_m) is greater than speed of sound in dry air (v_d).
∴ We can conclude, air is moist on second day and dry on the first day.

Question 9.
A police car travels towards a stationary observer at a speed of 15 m/s. The siren on the car emits a sound of frequency 250 Hz. Calculate the recorded frequency. The speed of sound is 340 m/s.
Answer:
Given: v_s = 15 m/s, n0 = 250 Hz, v = 340 m/s
To find: Frequency (n)
Formula: n = n₀(\(\frac {v}{v-v_s}\))
Calculation: As the source approaches listener, apparent frequency is given by,
n = 250 (\(\frac {340}{340-15}\)) = \(\frac {3400}{13}\)
∴ n = 261.54 Hz

Question 10.
The sound emitted from the siren of an ambulance has frequency of 1500 Hz. The speed of sound is 340 m/s. Calculate the difference in frequencies heard by a stationary observer if the ambulance initially travels towards and then away from the observer at a speed of 30 m/s.
Answer:
Given: v_s = 30 m/s, n₀ = 1500 Hz, v = 340 m/s
To find: Difference in apparent frequencies (n_A – n’_A)
Formulae:
i. When the ambulance moves towards he stationary observer then n_A = n₀(\(\frac {v}{v-v_s}\))

ii. When the ambulance moves away from the stationary observer then, n’_A = n₀(\(\frac {v}{v+v_s}\))

Calculation:
From formula (i), icon’ 340
n_A = 1500(\(\frac {340}{340-30}\))
∴ n_A = 1645 Hz
From (ii)
n’_A = 1500(\(\frac {340}{340+30}\))
∴ n_A = 1378 Hz
Difference between n_A and n’_A
= n_A – n’_A = 1645 – 1378 = 267 Hz

11th Physics Digest Chapter 8 Sound Intext Questions and Answers

Can you recall? (Textbook page no. 142)

i. What type of wave is a sound wave?
ii. Can sound travel in vacuum?
iii. What are reverberation and echo?
iv. What is meant by pitch of a sound?
Answer:
i. Sound wave is a longitudinal wave.

ii. Sound cannot travel in vacuum.

iii. a. Reverberation is the phenomenon in which sound waves are reflected multiple times causing a single sound to be heard more than once.
b. An echo is the repetition of the original sound because of reflection by some surface.

iv. The characteristic of sound which is determined by the value of frequency is called as the pitch of the sound.

Activity (Textbook page no. 144)

i. Using axes of displacement and distance, sketch two waves A and B such that A has twice the wavelength and half the amplitude of B.
ii. Determine the wavelength and amplitude of each of the two waves P and Q shown in figure below.

Answer:

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

11th Physics Chapter 7 Exercise Thermal Properties of Matter Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 7 Thermal Properties of Matter Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 7 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 7 Exercise Solutions

1. Choose the correct option.

Question 1.
The range of temperature in a clinical thermometer, which measures the temperature of the human body, is
(A) 70 ºC to 100 ºC
(B) 34 ºC to 42 ºC
(C) 0 ºF to 100 ºF
(D) 34 ºF to 80 ºF
Answer:
(B) 34 ºC to 42 ºC

Question 2.
A glass bottle completely filled with water is kept in the freezer. Why does it crack?
(A) Bottle gets contracted
(B) Bottle is expanded
(C) Water expands on freezing
(D) Water contracts on freezing
Answer:
(C) Water expands on freezing

Question 3.
If two temperatures differ by 25 °C on Celsius scale, the difference in temperature on Fahrenheit scale is
(A) 65°
(B) 45°
(C) 38°
(D) 25°
Answer:
(B) 45°

Question 4.
If α, β and γ are coefficients of linear, area l and volume expansion of a solid then
(A) α: β:γ 1:3:2
(B) α:β:γ 1:2:3
(C) α:β:γ 2:3:1
(D) α:β:γ 3:1:2
Answer:
(B) α:β:γ 1:2:3

Question 5.
Consider the following statements-
(I) The coefficient of linear expansion has dimension K^-1
(II) The coefficient of volume expansion has dimension K^-1
(A) I and II are both correct
(B) I is correct but II is wrong
(C) II is correct but I is wrong
(D) I and II are both wrong
Answer:
(A) I and II are both correct

Question 6.
Water falls from a height of 200 m. What is the difference in temperature between the water at the top and bottom of a water fall given that specific heat of water is 4200 J kg^-1 °C^-1?
(A) 0.96 °C
(B) 1.02 °C
(C) 0.46 °C
(D) 1.16 °C
Answer:
(C) 0.46 °C

2. Answer the following questions.

Question 1.
Clearly state the difference between heat and temperature?
Answer:

Question 2.
How a thermometer is calibrated?
Answer:

1. For the calibration of a thermometer, a standard temperature interval is selected between two easily reproducible fixed temperatures.
2. The fact that substances change state from solid to liquid to gas at fixed temperatures is used to define reference temperature called fixed point.
3. The two fixed temperatures selected for this purpose are the melting point of ice or freezing point of water and the boiling point of water.
4. This standard temperature interval is divided into sub-intervals by utilizing some physical property that changes with temperature.
5. Each sub-interval is called as a degree of temperature. Thus, an empirical scale for temperature is set up.

Question 3.
What are different scales of temperature? What is the relation between them?
Answer:

1. Celsius scale:
   • The ice point (melting point of pure ice) is marked as O °C (lower point) and steam point (boiling point of water) is marked as 100 °C (higher point).
   • Both are taken at one atmospheric pressure.
   • The interval between these points is divided into two equal parts. Each of these parts is called as one degree celsius and it is ‘written as 1 °C.
2. Fahrenheit scale:
   • The ice point (melting point of pure ice) is marked as 32 °F and steam point (boiling point of water) is marked as 212 °F.
   • The interval between these two reference points is divided into 180 equal parts. Each part is called as degree fahrenheit and is written as 1 °F.
3. Kelvin scale:
   • The temperature scale that has its zero at -273.15 °C and temperature intervals are same as that on the Celsius scale is called as kelvin scale or absolute scale.
   • The absolute temperature, T and celsius temperature, T_C are related as, T = T_C + 273.15
     eg.: when T_C = 27 °C,
     T = 27+273.15 K = 300.15 K

Relation between different scales of temperature:
\(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}=\frac{\mathrm{T}_{\mathrm{C}}-0}{100}=\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\)
where,
T_F = temperature in fahrenheit scale,
T_C = temperature in celsius scale,
T_K = temperature in kelvin scale,
[Note: At zero of the kelvin scale, every substance in nature has the least possible activity.]

Question 4.
What is absolute zero?
Answer:

1. When the graph of pressure (P) against temperature T (°C) at constant volume for three ideal gases A, B and C is plotted, in each case, P -T graph is straight line indicating direct proportion between them. The slopes of these graphs are different.
2. The individual straight lines intersect the pressure axis at different values of pressure at O °C. but each line intersects the temperature axis at the same point, i.e., at absolute temperature (-273.15 °C).
3. Similarly graph at constant pressure for three different ideal gases A, B and C extrapolate to the same temperature intercept -273.15 °C i.e., absolute zero temperature.
4. It is seen that all the lines for different gases Cut the temperature axis at the same point at -273.15 °C.
5. This point is termed as the absolute zero of temperature.
6. It is not possible to attain a temperature lower than this value. Even to achieve absolute zero temperature is not possible in practice.
   [Note: The point of zero pressure or zero volume does not depend on am specific gas.]

Question 5.
Derive the relation between three coefficients of thermal expansion.
Answer:
Consider a square plate of side l₀ at 0 °C and h at T °C.

1. l_T = l₀ (1 + αT)
   If area of plate at 0 °C is A₀, A₀ = \(l_{0}^{2}\)
   If area of plate at T °C is A_T,
   A_T = \(l_{\mathrm{T}}^{2}=l_{0}^{2}\) (1 + αT)²
   or A_T = A₀ (1 + αT)² …………… (1)
   Also,
   A_T = A₀(1 + βT)² …………… (2)
   ……………. [∵ β = \(\frac{\mathrm{A}_{\mathrm{T}}-\mathrm{A}_{0}}{\mathrm{~A}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)]
2. Using Equations (1) and (2),
   A₀ (1 + αT)² = A₀(1 + βT)
   ∴ 1 + 2αT + α²T² = 1 + βT
3. Since the values of a are very small, the term α²T² is very small and may be neglected,
   ∴ β = 2a
4. The result is general because any solid can be regarded as a collection of small squares.

Relation between coefficient of linear expansion (α) and coefficient of cubical expansion (γ).

1. Consider a cube of side l₀ at 0 °C and l_T at T °C.
   ∴ l_T = l₀(1 + αT)
   If volume of the cube at 0 °C is V₀, V₀ = \(l_{0}^{3}\)
   If volume of the cube at T °C is
   V_T, V_T = \(l_{\mathrm{T}}^{3}=l_{0}^{3}\) (1 + αT)³
   V_T = V₀ (1 + αT)³ ………. (1)
   Also,
   V_T = V₀(1 + γT) …………. (2)
   …………. [∵ γ = \(\frac{\mathrm{V}_{\mathrm{T}}-\mathrm{V}_{0}}{\mathrm{~V}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)]
2. Using Equations (1) and (2),
   V₀(1 + αT)³ = V₀(1 + γT)
   ∴ 1 + 3αT + 3α²T² + α³T³ = 1 + γT
3. Since the values of a are very small, the terms with higher powers of a may be neglected,
   ∴ γ = 3α
4. The result is general because any solid can be regarded as a collection of small cubes.

Relation between α, β and γ is given by,
α = \(\frac{\beta}{2}=\frac{\gamma}{3}\)
where, α = coefficient of linear expansion.
β = coefficient of superficial expansion,
γ = coefficient of cubical expansion.

Question 6.
State applications of thermal expansion.
Answer:
Applications of thermal expansion:

• The steel wheel is heated to expand. This expanded wheel can easily fit over axle. The wheel is then cooled quickly. Upon cooling, wheel contracts and fits tightly upon the axle.
• An electric light bulb gets hot quickly when in use. The wire leads to the filament are sealed into the glass. 1f the glass of the bulbs has significantly different thermal expansivity from the wire leads, the glass and the wire would separate, breaking down the vacuum. To prevent this, wires are made of platinum or some suitable alloy with the same expansivity as ordinary glass.

Question 7.
Why do we generally consider two specific heats for a gas?
Answer:

• A slight change in temperature causes considerable change in pressure as well as volume of the gas.
• Therefore, two principal specific heats are defined for a gas viz., specific heat capacity at constant volume (S_V) and specific heat capacity at constant pressure (S_p).

Question 8.
Are freezing point and melting point same with respect to change of state ? Comment.
Answer:
Though freezing point and melting point mark same temperature (0°C or 32° F), state of change is different for the two points. At freezing point liquid gets converted into solid, whereas at melting point solid gets converted into its liquid state.

Question 9.
Define
(i) Sublimation
(ii) Triple point.
Answer:

1. The change from solid state to vapour stale without passing through the liquid state is called sublimation and the substance is said to sublime.
   Examples: Dry ice (solid CO₂) and iodine.
2. The triple point of water is that point where water in a solid, liquid and gas state co-exists in equilibrium and this occurs only at a unique temperature and a pressure.

Question 10.
Explain the term ‘steady state’.
Answer:

1. When one end of a metal rod is heated, the heat flows by conduction from hot end to the cold end.
   
2. As a result, the temperature of every section of the rod starts increasing.
3. Under this condition, the rod is said to be in a variable temperature state.
4. After some time, the temperature at each section of the rod becomes steady i.e., does not change.
5. Temperature of each cross-section of the rod now becomes constant though not the same. This is called steady state condition.

Question 11.
Define coefficient of thermal conductivity. Derive its expression.
Answer:
Coefficient of thermal conductivity of a material is defined as the quantity of heat that flows in one second between the opposite faces of a cube of side 1 m, the faces being kept at a temperature difference of 1°C (or 1 K).

Expression for coefficient of thermal conductivity:

1. Under steady state condition, the quantity of heat ‘Q’ that flows from the hot face at temperature T₁ to the cold face at temperature T₂ of a cube with side x and area of cross-section A is
   • directly proportional to the cross-sectional area A of the face. i.e.. Q ∝ A
   • directly proportional to the temperature difference between the two faces i.e., Q ∝ (T₁ – T₂)
   • directly proportional to time t (in seconds) for which heat flows i.e.. Q ∝ t
   • inversely proportional to the perpendicular distance x between hot and cold faces i.e., Q ∝ 1/x
2. Combining the above four factors, we have the quantity of heat
   Q ∝ \(\frac{\mathrm{A}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right) \mathrm{t}}{\mathrm{x}}\)
   ∴ Q = \(\)
   where k is a constant of proportionality and is called coefficient of thermal conductivity. Its value depends upon the nature of the material.

Question 12.
Give any four applications of thermal conductivity in every day life.
Answer:
Answer: Applications of thermal conductivity:

1. • Thick walls are used in the construction of cold storage rooms.
   • Brick being a bad conductor of heat is used to reduce the flow of heat from the surroundings to the rooms.
   • Better heat insulation is obtained by using hollow bricks.
   • Air being a poorer conductor than a brick, it further avoids the conduction of heat from outside.
2. Street vendors keep ice blocks packed in saw dust to prevent them from melting rapidly.
3. The handle of a cooking utensil is made of a bad conductor of heat, such as ebonite, to protect our hand from the hot utensil.
4. Two bedsheets used together to cover the body help retain body heat better than a single bedsheet of double the thickness. Trapped air being a bad conductor of heat, the layer of air between the two sheets reduces thermal conduction better than a sheet of double the thickness. Similarly, a blanket coupled with a bedsheet is a cheaper alternative to using two blankets.

Question 13.
Explain the term thermal resistance. State its SI unit and dimensions.
Answer:

1. Consider expression for conduction rate,
   P_cond = kA \(\frac{\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\mathrm{x}}\)
   ⇒ \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}=\frac{\mathrm{x}}{\mathrm{kA}}\) ……………. (1)
2. Ratio \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}\) is called as thermal resistance (R_T) of material.

The SI unit of thermal resistance is °C s/kcal or °C s/J and its dimensional formula is [L^-2M^-1T³K¹].

Question 14.
How heat transfer occurs through radiation in absence of a medium?
Answer:

1. All objects possess thermal energy due to their temperature T(T > 0 K).
2. The rapidly moving molecules of a hot body emit EM waves travelling with the velocity of light. These are called thermal radiations.
3. These carry energy with them and transfer it to the low-speed molecules of a cold body on which they fall.
4. This results in an increase in the molecular motion of the cold body and its temperature rises.
5. Thus transfer of heat by radiation is a two fold process-the conversion of thermal energy into waves and reconversion of waves into thermal energy by the body on which they fall.

Question 15.
State Newton’s law of cooling and explain how it can be experimentally verified.
Answer:
The rate of loss of heat dT/dt of the both’ is directly proportional to the difference of temperature (T – T₀) of the body and the surroundings provided the difference in temperatures is small.

Mathematically, Newton’s law of cooling can be expressed as:
\(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ (T – T₀)
∴ \(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ C(T – T₀)
where, C is constant of proportionality. Experimental verification of Newton’s law of cooling:

1. Fill a calorimeter upto \(\frac{2}{3}\) of its capacity with a boiling water. Cover it with lid with a hole for passing the thermometer.
2. Insert the thermometer through the hole and adjust it so that the bulb of the thermometer is fully immersed in hot water.
3. Keep calorimeter vessel in constant temperature enclosure or just in open air since room temperature will not change much during the experiment.
4. Note down the temperature (T) on the thermometer at every one minute interval until the temperature of water decreases by about 25 °C.
5. Plot a graph of temperature (T) on Y-axis against time (t) on X-axis. This graph is called cooling curve as shown in figure (a).
   
6. Draw tangents to the curve at suitable points on the curve. The slope of each tangent is \(\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathrm{T}}{\Delta \mathrm{t}}\) and gives the rate of fall of temperature at that temperature (T).
7. Now the graph of \(\left|\frac{\mathrm{dT}}{\mathrm{dt}}\right|\) on Y-axis against (T – T₀) on X-axis is plotted with (0, 0) origin. The graph is straight line and passes through origin as shown in figure (b), which verities Newton’s law of cooling.
   
   (b) Graphical verification of Newton’s law of cooling

Question 16.
What is thermal stress? Give an example of disadvantages of thermal stress in practical use?
Answer:

1. Consider a metallic rod of length l₀ fixed between two rigid supports at T °C.
   If the temperature of rod is increased by ∆T, length of rod would become,
   l = l₀(1 + α∆T)
   Where, α is the coefficient of linear expansion of material of the rod.
   But the supports prevent expansion of rod. As a result, rod exerts stress on the supports. Such stress is termed as thermal stress.
2. Disadvantage: Thermal stress can lead to fracture or deformation in substance under certain conditions.
3. Railway tracks are made up of metals which expand upon heating. If no gap is kept between tracks, in hot weather, expansion of metal tracks may exert thermal stress on track. This may lead to bending of tracks which would be dangerous. Hence, railway track is not a continuous piece but is made up of segments separated by gaps.

Question 17.
Which materials can be used as thermal insulators and why?
Answer:

1. Substances such as glass, wood, rubber, plastic, etc. can be used as thermal insulators.
2. These substances do not have free electrons to conduct heat freely throughout the body. Hence, they arc poor conductors of heat.

3. Solve the following problems.

Question 1.
A glass flask has volume 1 × 10^-4 m³. It is filled with a liquid at 30 ºC. If the temperature of the system is raised to 100 ºC, how much of the liquid will overflow. (Coefficient of volume expansion of glass is 1.2 × 10^-5 (ºC)^-1 while that of the liquid is 75 × 10^-5 ºC^-1)
Solution:
Given: V₁ = 1 × 10^-4 m³ = 10^-4 m³, T₁ = 30°C,
T₂ = 100 °C
To find: Volume of liquid that overflows
Formula: γ = \(\frac{V_{2}-V_{1}}{V_{1}\left(T_{2}-T_{1}\right)}\)
Calculation: From formula,
Increase is volume = V₂ – V₁
= γV₁(T₂ – T₁)
increase in volume of beaker
= γ_glass × V₁ (T₂ – T₁)
= 1.2 × 10^-5 × 10^-4 × (100 – 30)
= 1.2 × 70 × 10^-9
= 4 × 10^-9 m³
∴ Increase in volume of beaker
= 84 × 10^-9 m³
Increase in volume of liquid
= γ_liquid × V₁ (T₂ – T₁)
= 75 × 10^-5 × 10 × (100 – 30)
= 75 × 70 × 10
= 5250 × 10^-9 m³
∴ Increase in volume of liquid = 5250 × 10^-9 m³
∴ Volume of liquid which overflows
= (5250 – 84) × 10^-9 m³
= 5166 × 10^-9 m³
= 0.5166 × 10^-7 m³
Volume of liquid that overflows is 0.5166 × 10^-7 m³.
[Note: The answer given above is presented considering standard conventions of writing number with its correct order of magnitude.]

Question 2.
Which will require more energy, heating a 2.0 kg block of lead by 30 K or heating a 4.0 kg block of copper by 5 K? (s_lead = 128 J kg^-1 K^-1, s_copper = 387 J kg^-1 K^-1)
Solution:
Given: m_lead = 2 kg, ∆T_lead = 30 K,
s_lead = 128 J/kg K,
m_Cu =4 kg, ∆T_Cu = 5 K,
s_Cu = 387 J/kg K
To find: Substance requiring more heat energy.
Formula: Q = ms ∆T
Calculation: From formula,
For lead, Q_lead = 2 × 128 × 30 = 7680J
For Copper, Q_Cu = 4 × 387 × 5 = 7740 J
Q_Cu > Q_lead, copper will require more heat energy.
Copper will require more heat energy.

Question 3.
Specific latent heat of vaporization of water is 2.26 × 10⁶ J/kg. Calculate the energy needed to change 5.0 g of water into steam at 100 ºC.
Solution:
Given: L_vap = 2.26 × 10⁶ J/kg
m = 5g = 5 × 10^-3 kg
In this case, no temperature change takes place only change of state occurs.
To find: Heat required to convert water into steam.
Formula: Heat required = mL_vap
Calculation: From formula,
Heat required = 5 × 10^-3 × 2.26 × 10⁶
= 11300J
= 1.13 × 10⁴ J
Heat required to convert water into steam is 1.13 × 10⁴ J
[Note: The answer given above is presented considering standard conventions of writing number with its correct order of magnitude.]

Question 4.
A metal sphere cools at the rate of 0.05 ºC/s when its temperature is 70ºC and at the rate of 0.025 ºC/s when its temperature is 50 ºC. Determine the temperature of the surroundings and find the rate of cooling when the temperature of the metal sphere is 40 ºC.
Solution:

∴ 2(50 – T₀) = 70 – T₀
∴ T₀ = 30 πC
Substituting value of T₀.
0.05 = C (70 – 30)
∴ C = \(\frac{0.05}{40}\) = 0.00125/s.
For T₃ = 40 °C
\(\left(\frac{\mathrm{d} \mathrm{T}}{\mathrm{dt}}\right)_{3}\) = C(T₃ – T₀)
= 0.00125 (40 – 30)
= 0.00125 × 10
= 0.0125°C/s.
i) Temperature of surrounding is 30 °C.
ii) Rate of cooling at 40 °C is 0.0125 °C/s.

Question 5.
The volume of a gas varied linearly with absolute temperature if its pressure is held constant. Suppose the gas does not liquefy even at very low temperatures, at what temperature the volume of the gas will be ideally zero?
Answer:
At temperature of -273.15 °C, the volume of the gas will be ideally zero.

Question 6.
In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 ºC. If maximum temperature in the region is 45 ºC and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10^-5 K^-1 for the material of the rail section?
Solution:
Given. T₁ = 27 °C, T₂ = 45 °C,
L₁ = 10m.
α = 1.2 × 10^-5 K^-1
To find: Gap that should be left (L₂ – L₁)
Formula: L₂ – L₁ = L₁ α(T₂ – T₁)
Calculation: From formula,
L₂ – L₁ = 10 × 1.2 × 10^-5 × (45 – 27)
= 2.16 × 10^-3 m
= 2.16 mm
The gap that should be left between rail sections is 2.16 mm.

Question 7.
A blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the wooden rim and the iron ring are 1.5 m and 1.47 m respectively at room temperature of 27 ºC. To what temperature the iron ring should be heated so that it can fit the rim of the wheel (α_iron = 1.2 × 10^-5 K^-1).
Solution:
Given: d_w = 1.5 m, d = 1.47 m, T₁ = 27 °C.
α_i = 1.2 × 10^-5/ K
To find: Temperature (T₂)
Formula. α = \(\frac{\mathrm{d}_{\mathrm{w}}-\mathrm{d}_{\mathrm{i}}}{\mathrm{d}_{\mathrm{i}}\left(\mathrm{T}_{2}-\mathrm{T}_{1}\right)}\)
Calculation: From formula,
T₂ = \(\frac{\mathrm{d}_{\mathrm{w}}-\mathrm{d}_{\mathrm{i}}}{\mathrm{d}_{\mathrm{i}} \alpha}\) + T₁
= \(\frac{1.5-1.47}{1.47 \times 1.2 \times 10^{-5}}\) + 27
= 1700.7 + 27
= 1727.7 °C
Iron ring should be heated to temperature of 1727.7 °C.

Question 8.
In a random temperature scale X, water boils at 200 °X and freezes at 20 °X. Find the boiling point of a liquid in this scale if it boils at 62 °C.
Solution:
Here thermometric property P is temperature at some random scale X.
Using equation,
T = \(\frac{100\left(P_{T}-P_{1}\right)}{\left(P_{2}-P_{1}\right)}\)
For P₁ = 20 °X,
P₂ = 200 °X,
T = 62°C
∴ 62 = \(\frac{100\left(\mathrm{P}_{\mathrm{T}}-20\right)}{(200-20)}\)
∴ P_T = \(\frac{62 \times(200-20)}{100}\) + 20 = 111.6 + 20
= 131.6 °X
The boiling point of a liquid in this scale is 131.6 °X.

Question 9.
A gas at 900°C is cooled until both its pressure and volume are halved. Calculate its final temperature.
Solution:
Given: T₁ = 900 °C = 900 + 273.15 = 1173.15 K
V₂ = \(\frac{\mathrm{V}_{1}}{2}\), P₂ = \(\frac{\mathrm{P}_{1}}{2}\)
To find: Final temperature (T₂)
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{\mathrm{I}}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: From formula.
\(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{1173.15}=\frac{\mathrm{P}_{1} \mathrm{~V}_{\mathrm{l}}}{4 \mathrm{~T}_{2}}\)
∴ T₂ = \(\frac{1173.15}{4}\) = 293.29 K
Final temperature of gas is 293.29 K.

Question 10.
An aluminium rod and iron rod show 1.5 m difference in their lengths when heated at all temperature. What are their lengths at 0 °C if coefficient of linear expansion for aluminium is 24.5 × 10^-6 /°C and for iron is 11.9 × 10^-6 /°C
Solution:
Given: (L_T)_i – (L_T)_al = 1.5 m, T₀ = 0 °C
α_al = 24.5 × 10^-6/°C
α_i = 11.9 × 10^-6 /°C
To find: Lengths of aluminium and iron rod (L₀)_al and (L₀)_i
Formula: L_T = L₀[(1 + α(T – T₀)]
Calculation: For T₀ = 0 °C
From formula,
L_T = L₀(1 + αT)
For aluminium,
(L₀)_al = (L₀)_al(1 + α_alT) ……………. (1)
For iron,
(L_T)_i = (L₀)_i (1 + α_iT) ………….. (2)
Subtracting equation (2) by (1),
(L_T)_i – (L_T)_al = [(L₀)_i + (L₀)_i α_iT] – [(L₀)_al + (L₀)_alα_alT]
= (L₀)_i – (L₀)_al + [(L₀)_i α_i – (L₀)_al α_al]T
∴ 1.5 = 1.5 + [(L₀)_i α_i – (L₀)_al α_al)]T
⇒ [(L₀)_iα_i – (L₀)_alα_al] T = 0
∴ (L₀)_alα_al = (L₀)_iα_i

Length of aluminium rod at 0 °C is 1.417 m and that of iron rod is 2.917 m.

Question 11.
What is the specific heat of a metal if 50 cal of heat is needed to raise 6 kg of the metal from 20°C to 62 °C ?
Solution:
Given: Q = 50 cal, m =6 kg,
∆T = 62 – 20 = 42 °C
To find: Specific heat (s)
Formula: Q = ms ∆T
Calculation: From formula,
s = \(\frac{\mathrm{Q}}{\mathrm{m} \Delta \mathrm{T}}=\frac{50}{6 \times 42}\) = 0.198 cal/kg °C
Specific heat of metal is copper 0.198 cal/kg °C.

Question 12.
The rate of flow of heat through a copper rod with temperature difference 30 °C is 1500 cal/s. Find the thermal resistance of copper rod.
Solution:
Given: ∆T = 30 °C, P_cond = 1500 cal/s
To find: Thermal resistance (R_T)
Formula: R_T = \(\frac{\Delta \mathrm{T}}{\mathrm{P}_{\text {cond }}}\)
Calculation: From formula,
R_T = \(\frac{30}{1500}\)
= 0.02 °C s/cal.
Thermal resistance of copper rod is 0.02 °C s/cal.

Question 13.
An electric kettle takes 20 minutes to heat a certain quantity of water from 0°C to its boiling point. It requires 90 minutes to turn all the water at 100°C into steam. Find the latent heat of vaporisation. (Specific heat of water = 1cal/g°C)
Solution:
Let heat supplied by kettle in 20 minutes be Q₁ and that in 90 min. be Q₂.
Using heat temperature of water is raised from O °C to 100 °C.
If mass of water in the kettle is ‘m’ then.
Q₁ = ms_water∆T m × 1 × (100 – 0)
= 100 m ………….. (i)
…………. (∵ S_water = 1 cal/g °C)
Similarly using heat Q₂ water is converted from liquid to gas,
∴ Q₂ = mL_vap ……………. (ii)
Given that heat Q₁, Q₂ are supplied to water in 20 min. (t₁) and 90 min (t₂) respectively.
Kettle being same its conduction rate (P_cond) is same.
Using P_cond = \(\frac{\mathrm{Q}_{1}}{\mathrm{t}_{1}}=\frac{\mathrm{Q}_{2}}{\mathrm{t}_{2}}\) …………… (iii)
From (i), (ii) and (iii),
\(\frac{100 \mathrm{~m}}{20}=\frac{\mathrm{mL}_{\text {vap }}}{90}\),
∴ L_vap = 5 × 90 = 450 cal/g
Latent heat of vaporisation for water is 450 cal/g.

Question 14.
Find the temperature difference between two sides of a steel plate 4 cm thick, when heat is transmitted through the plate at the rate of 400 k cal per minute per square metre at steady state. Thermal conductivity of steel is 0.026 kcal/m s K.
Solution:

Temperature difference between two sides is 10.26 K.
[Note: Above answer is expressed in K (‘kelvin considering that thermal conductivity is expressed in units of kcal / ms K, and not as kcal / m s °C. As 1 °C equivalent to 1 K. conceptually temperature difference of 10.26 K will correspond to 10.26 t]

Question 15.
A metal sphere cools from 80 °C to 60 °C in 6 min. How much time with it take to cool from 60 °C to 40 °C if the room temperature is 30°C?
Solution:
Given: T₁ = 80 °C, T₂ = 60 °C, T₃ = 40 °C, T₀ = 30 °C, (dt)₁ = 6 min.
To find: Time taken in cooling (dt)₂

Time taken in cooling is 10 min.

11th Physics Digest Chapter 7 Thermal Properties of Matter Intext Questions and Answers

Can you tell? (Textbook Page No. 125)

Question 1.
i) Why the metal wires for electrical transmission lines sag?
ii) Why a railway track is not a continuous piece but is made up of segments separated by gaps?
iii) How a steel wheel is mounted on an axle to fit exactly?
Answer:

1. In hot weather, metal wires get heated due to increased temperature of surrounding. As a result, they expand increasing the slack between transmission line structure, causing them to sag.
2. Railway tracks are made up of metals which expand upon heating. If no gap is kept between tracks, in hot weather, expansion of metal tracks may exert thermal stress on track. This may lead to bending of tracks which would be dangerous. Hence, railway track is not a continuous piece but is made up of segments separated by gaps.
3. The steel wheel is heated to expand. This expanded wheel can easily fit over axle. The wheel is then cooled quickly. Upon cooling, wheel contracts and fits tightly upon the axle.

Intext question. (Textbook Page No 124)

Question 1.
Can you now tell why the balloon bursts sometimes when you try to fill air in it?
Answer:

1. When balloon is blown, air that is blown inside makes the balloon expand.
2. A given size of balloon can expand upto certain limit.
3. Once that limit is reached and air is still blown inside the balloon, balloon cannot expand further.
4. As a result, air causes additional pressure on inner surface of balloon.
5. Since, pressure inside balloon is now greater than pressure outside balloon, balloon bursts equalizing the two pressures.

Can you tell? (Textbook Page No. 125)

Question 1.
Why lakes freeze first at the surface?
Answer:

1. In cold climate, temperature of water in ponds and lakes starts falling.
2. On getting colder, water contracts. As a result, density of water increases and it goes down. To replace it, warmer water from below rises up. This process continues till temperature of water at the bottom of pond becomes 4 °C.
3. Water, due to its anomalous behaviour possesses maximum density at 4 °C.
4. If the temperature lowers further, ice is formed at the surface of pond with water below it.
5. Ice being poor conductor of heat blocks the further heat exchange between atmosphere and water in the pond and maintains water below surface in liquid state.

Activity (Textbook Page No. 129)

Question 1.
To understand the process of change of state:
Take some cubes of ice in a beaker. Note the temperature of ice (0 °C). Start heating it slowly on a constant heat source. Note the temperature after every minute. Continuously stir the mixture of water and ice. Observe the change in temperature. Continue heating even after the whole of ice gets converted into water. Observe the change in temperature as before till vapours start coming out. Plot the graph of temperature (along Y-axis) versus time (along X-axis). Obtain a graph of temperature versus time.
Answer:
[Students are expected to attempt the activity on their own.]

Can you tell? (Textbook Page No. 130)

Question 1.
What is observed after point D in graph? Can steam be hotter than 100 °C?
Answer:
Beyond point D, thermometer again shows rise in temperature. This means, steam can be hotter than 100 °C and is termed as superheated steam.

Question 2.
Why steam at 100 °C causes more harm to our skin than water at 100 °C?
Answer:

1. Though steam and boiling water have same temperature, the heat contained in steam is more than that in boiling water.
2. Steam is formed when boiling water absorbs specific latent heat of vaporisation i.e.. 22.6 × 10⁵ J/kg.
3. As a result, when steam comes in contact with the skin of a person, it gives off additional 22.6 × 10⁵ joule per kilogram causing severe (more serious) burns.
   Hence, burns caused from steam are more serious than those caused from boiling water at same temperature.

Activity (Textbook Page No. 130)

Activity to understand the dependence of boiling point on pressure:
Take a round bottom flask, more than half filled with water. Keep it over a burner and fix a thermometer and steam outlet through the cork of the flask as shown in figure. As water in the flask gets heated, note that first the air, which was dissolved in the water comes out as small bubbles. Later bubbles of steam form at the bottom but as they rise to the cooler water near the top, they condense and disappear. Finally, as the temperature of the entire mass of the water reaches 100 oc, bubbles of steam reach the surface and boiling is said to occur. The steam in the flask may not be visible hut as it comes out of the flask, It condenses as tiny droplets of water giving a foggy appearance.

If now the steam outlet is closed for a few seconds to increase the pressure in the flask, you will notice that boiling stops. More heat would be required to raise the temperature (depending on the increase in pressure) before boiling starts again. Thus, boiling point increases with increase in pressure. Let us now remove the burner. Allow water to cool to about 80°C. Remove the thermometers and steam outlet. Close the flask with a air tight cork. Keep the flask turned upside down on a stand. Pour icecold water on the flask. Water vapours in the flask condense reducing the pressure on the water surface inside the flask. Water begins to boil again, now at a lower temperature. Thus boiling point decreases with decrease in pressure and increases with increase in pressure.
Answer:
[Students are expected to attempt the activity an their own.]

Can you tell? (Textbook Page No. 131)

Question 1.
i) Why is cooking difficult at high altitude?
ii) Why is cooking faster in pressure cooker?
Answer:

1. • At high altitude density of air is low which causes reduction in atmospheric pressure.
   • As pressure is less, boiling point of water lowers.
   • Water, at high altitude, starts boiling below 100 OC.
   • As food is cooked mostly through the water boiling, cooking of food becomes difficult.
2. • Pressure cooker operates by expelling air within the cooker and trapping steam produced from the liquid. (mostly water) boiling inside.
   • Due to high internal pressure, boiling point of liquid increases and liquid boils at temperature higher than its boiling point.
   • The increased boiling point allows more absorption of heat by liquid and steam formed is superheated.
   • As a result, food gets cooked quickly.

Internet my friend (Textbook Page No. 139)

i) https ://hyperphysics. phy-astr.gsu.edul/base/hframe.html
ii) https://youtu.be/7ZKHc5J6R5Q
iii) https://physics. info/expansion
Answer:
[Students are expected to visit the above mentioned webs it es and collect more information about the thermal properties of matter.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Mechanical Properties of Solids Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 6 Mechanical Properties of Solids Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 6 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 6 Exercise Solutions

1. Choose the correct answer:

Question 1.
Change in dimensions is known as …………..
(A) deformation
(B) formation
(C) contraction
(D) strain.
Answer:
(A) deformation

Question 2.
The point on stress-strain curve at which strain begins to increase even without increase in stress is called…………
(A) elastic point
(B) yield point
(C) breaking point
(D) neck point
Answer:
(B) yield point

Question 3.
Strain energy of a stretched wire is 18 × 10^-3 J and strain energy per unit volume of the same wire and same cross section is 6 × 10^-3 J/m³. Its volume will be………….
(A) 3cm³
(B) 3 m³
(C) 6 m³
(D) 6 cm³
Answer:
(B) 3 m³

Question 4.
……………. is the property of a material which enables it to resist plastic deformation.
(A) elasticity
(B) plasticity
(C) hardness
(D) ductility
Answer:
(C) hardness

Question 5.
The ability of a material to resist fracturing when a force is applied to it, is called……………
(A) toughness
(B) hardness
(C) elasticity
(D) plasticity.
Answer:
(A) toughness

2. Answer in one sentence:

Question 1.
Define elasticity.
Answer:
If a body regains its original shape and size after removal of the deforming force, it is called an elastic body and the property is called elasticity.

Question 2.
What do you mean by deformation?
Answer:
The change in shape or size or both of u body due to an external force is called deformation.

Question 3.
State the SI unit and dimensions of stress.
Answer:

1. SI unit: N m^-2 or pascal (Pa)
2. Dimensions: [L^-1M¹T^-2]

Question 4.
Define strain.
Answer:
Strain:

1. Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
   Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\)
2. Types of strain:
   • Longitudinal strain,
   • Volume strain,
   • Shearing strain.

Question 5.
What is Young’s modulus of a rigid body?
Answer:
Young’s modulus (Y): It is the modulus of elasticity related to change in length of an object like a metal wire, rod, beam, etc., due to the applied deforming force.

Question 6.
Why bridges are unsafe after a very long use?
Answer:
A bridge during its use undergoes recurring stress depending upon the movement of vehicles on it. When bridge is used for long time, it loses its elastic strength and ultimately may collapse. Hence, the bridges are declared unsafe after long use.

Question 7.
How should be a force applied on a body to produce shearing stress?
Answer:
A tangential force which is parallel to the top and the bottom surface of the body should be applied to produce shearing stress.

Question 8.
State the conditions under which Hooke’s law holds good.
Answer:
Hooke’s Taw holds good only when a wire/body is loaded within its elastic limit.

Question 9.
Define Poisson’s ratio.
Answer:
Within elastic limit, the ratio of lateral strain to the linear strain is called the Poisson‘s ratio.

Question 10.
What is an elastomer?
Answer:
A material that can be elastically stretched to a larger value of strain is called an elastomer.

Question 11.
What do you mean by elastic hysteresis?
Answer:

1. In case of some materials like vulcanized rubber, when the stress applied on a body decreases to zero, the strain does not return to zero immediately. The strain lags behind the stress. This lagging of strain behind the stress is called elastic hysteresis.
2. Below figure shows the stress-strain curve for increasing and decreasing load. It encloses a loop. Area of loop gives the energy dissipated during deformation of a material.
   

Question 12.
State the names of the hardest material and the softest material.
Answer:
Hardest material: Diamond
Softest material: Aluminium
[Note: Material with highest strength is steel whereas material with lowest strength is plasticine clay.]

Question 13.
Define friction.
Answer:
The property which resists the relative motion between two surfaces in contact is called friction.

Question 14.
Why force of static friction is known as ‘self-adjusting force?
Answer:
The force of static friction varies in accordance with applied force. Hence, it is called as self adjusting force.

Question 15.
Name two factors on which the coefficient of friction depends.
Answer:
Coefficient of friction depends upon:

1. the materials of the surfaces in contact.
2. the nature of the surfaces.

3. Answer in short:

Question 1.
Distinguish between elasticity and plasticity.
Answer:

Question 2.
State any four methods to reduce friction.
Answer:
Friction can be reduced by using polished surfaces, using lubricants, using grease and using ball bearings.

Question 3.
What is rolling friction? How does it arise?
Answer:

1. Friction between two bodies in contact when one body is rolling over the other, is called rolling friction.
2. Rolling friction arises as the point of contact of the body with the surface keep changing continuously.

Question 4.
Explain how lubricants help in reducing friction?
Answer:

1. The friction between lubricant to surface is much less than the friction between two same surfaces. Hence using lubricants reduces the friction between the two surfaces.
2. When lubricant is applied to machine parts, it fills the depression present on the surface in contact. Thus, less friction is occurred between machine parts.
3. Application of lubricants also reduces wear and tear of machine parts which in turn reduces friction.
4. Advantage: Reduction in function reduces dissipation of energy in machines due to which efficiency of machines increases.

Question 5.
State the laws of static friction.
Answer:
Laws of static friction:

1. First law: The limiting force of static friction (F_L) is directly proportional to the normal reaction (N) between the two surfaces in contact.
   F_L ∝ N
   ∴ F_L = µ_s N
   where, µ_s = constant called coefficient of static friction.
2. Second law: The limiting force of friction is
   independent of the apparent area between the surfaces in contact, so long as the normal reaction remains the same.
3. Third law: The limiting force of friction depends upon materials in contact and the nature of their surfaces.

Question 6.
State the laws of kinetic friction.
Answer:
Laws of kinetic friction:

1. First law: The force of kinetic friction (Fk) is directly proportional to the normal reaction (N) between two surfaces in contact.
   F_k ∝ N
   ∴ F_k = µ_kN
   where, µ_k = constant called coefficient of kinetic friction.
2. Second law: Force of kinetic friction is independent of shape and apparent area of the surfaces in contact.
3. Third law: Force of kinetic friction depends upon the nature and material of the surfaces in contact.
4. Fourth law: The magnitude of the force of kinetic friction is independent of the relative velocity between the object and the surface provided that the relative velocity is neither too large nor too small.

Question 7.
State advantages of friction.
Answer:
Advantages of friction:

1. We can walk due to friction between ground and feet.
2. We can hold object in hand due to static friction.
3. Brakes of vehicles work due to friction; hence we can reduce speed or stop vehicles.
4. Climbing on a tree is possible due to friction.

Question 8.
State disadvantages of friction.
Answer:
Disadvantages of friction:

1. Friction opposes motion.
2. Friction produces heat in different parts of machines. It also produces noise.
3. Automobile engines consume more fuel due to friction.

Question 9.
What do you mean by a brittle substance? Give any two examples.
Answer:

1. Substances which breaks within the elastic limit are called brittle substances.
2. Examples: Glass, ceramics.

4. Long answer type questions:

Question 1.
Distinguish between Young’s modulus, bulk modulus and modulus of rigidity.
Answer:

Question 2.
Define stress and strain. What are their different types?
Answer:
i) Stress:

1. The internal restoring force per unit area of a both is called stress.
   Stress = \(\frac{\text { deforming force }}{\text { area }}=\frac{|\vec{F}|}{\mathrm{A}}\)
   where \(\vec{F}\) is internal restoring force or external applied deforming force.
2. Types of stress:
   • Longitudinal stress,
   • Volume stress,
   • Shearing stress.

ii. Strain:

1. Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
   Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\)
2. Types of strain:
   • Longitudinal strain,
   • Volume strain,
   • Shearing strain.

Question 3.
What is Young’s modulus? Describe an experiment to find out Young’s modulus of material in the form of a long straight wire.
Answer:
Definition: Young ‘s modulus is the ratio of longitudinal stress to longitudinal strain.
It is denoted by Y.
Unit: N/m² or Pa in SI system.
Dimensions: [L^-1M¹T^-2]

Experimental description to find Young’s modulus:

i. Consider a metal wire suspended from a rigid support. A load is attached to the free end of the wire. Due to this, deforming force gets applied to the free end of wire in downward direction and it produces a change in length.
Let,
L = original length of wire,
Mg = weight suspended to wire,
l = extension or elongation,
(L + l) = new length of wire.
r = radius of the cross section of wire

ii. In its equilibrium position,

Question 4.
Derive an expression for strain energy per unit volume of the material of a wire.
Answer:
Expression for strain energy per unit volume;

i. Consider a wire of original length L and cross sectional area A stretched by a force F acting along its length. The wire gets stretched and elongation l is produced in it

ii. If the wire is perfectly elastic then,
Longitudinal stress = \(\frac{F}{A}\)
Longitudinal strain = \(\frac{l}{L}\)

iii. The magnitude of stretching force increases from zero to F during elongation of wire.
Let ‘f’ be the restoring force and ‘x’ be its corresponding extension at certain instant during the process of extension.
∴ f = \(\frac{\text { YAx }}{\mathrm{L}}\) ……………. (2)

iv. Let ‘dW’ be the work done for the further small extension ‘dx’.
Work = force × displacement
∴ dW = fdx
∴ dW= \(\frac{\text { YAx }}{L}\) dx …………..(3) [From (2)]

v. The total amount of work done in stretching the wire from x = 0 to x = l can be found out by integrating equation (3).

∴ Work done in stretching a wire,
W = \(\frac{1}{2}\) × load × extension

vi. Work done by stretching force is equal to strain energy gained by the wire.
∴ Strain energy = \(\frac{1}{2}\) × load × extension

vii. Work done per unit volume

∴ Strain energy per unit volume = \(\frac{1}{2}\) × stress × strain

viii. Other forms:

Question 5.
What is friction? Define coefficient of static friction and coefficient of kinetic friction. Give the necessary formula for each.
Answer:

1. The property which resists the relative motion between two surfaces in contact is called friction.
2. The coefficient of static friction is defined as the ratio of limiting force of friction to the normal reaction.
   Formula: \(\mu_{\mathrm{S}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}\)
3. The coefficient of kinetic friction is defined as the ratio of force of kinetic friction to the normal reaction between the two surfaces in contact.
   Formula: \(\mu_{\mathrm{k}}=\frac{\mathrm{F}_{\mathrm{K}}}{\mathrm{N}}\)

Question 6.
State Hooke’s law. Draw a labelled graph of tensile stress against tensile strain for a metal wire up to the breaking point. In this graph show the region in which Hooke’s law is obeyed.
Answer:
i) Statement: Within elastic limit, stress is directly proportional to strain.
Explanation;

1. According to Hooke’s law,
   Stress ∝ Strain
   
   This constant of proportionality is called modulus of elasticity.
2. Modulus of elasticity of a material is the slope of stress-strain curve in elastic deformation region and depends on the nature of the material.
3. The graph of strain (on X-axis) and stress (on Y-axis) within elastic limit is shown in the figure.

ii)

iii) Hooke’s law is completely obeyed in the region OA.

5. Answer the following

Question 1.
Calculate the coefficient of static friction for an object of mass 50 kg placed on horizontal table pulled by attaching a spring balance. The force is increased gradually it is observed that the object just moves when spring balance shows 50N.
[Answer: µs = 0.102]
Solution:
Given: m = 50 kg, F_L = 50 N, g = 9.8 m/s²
To find: Coefficient of static friction (µ_s)
Formula: µ_s = \(\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{mg}}\)
µ_s = \(\frac{50}{50 \times 9.8}\) = 0.102
Answer:
The coefficient of static friction is 0.102.

Question 2.
A block of mass 37 kg rests on a rough horizontal plane having coefficient of static friction 0.3. Find out the least force required to just move the block horizontally.
[Answer: F= 108.8N]
Solution:
Given: m = 37 kg, µ_s = 0.3, g = 9.8 m /s²
To find: Limiting force (F_L)
Formula: F_L = µ_SN = µ_S mg
Calculation: From formula,
F_L = 0.3 × 37 × 9.8 = 108.8 N
Answer:
The force required to move the block is 108.8 N.

Question 3.
A body of mass 37 kg rests on a rough horizontal surface. The minimum horizontal force required to just start the motion is 68.5 N. In order to keep the body moving with constant velocity, a force of 43 N is needed. What is the value of
a) coefficient of static friction? and
b) coefficient of kinetic friction?
Asw:
a) µ_s = 0.188
b) µ_k = 0.118]
Solution:
Given:
F_L = 68.5 N, F_k = 43 N,
m = 37 kg, g = 9.8 m/s²

To find:

i. Coefficient of static friction (µ_s)
ii. Coefficient of kinetic friction (µ_k)

Formulae:

i. µ_s = \(\frac{F_{L}}{N}\) = \(\frac{F_{L}}{m g}\)
ii. µ_k = \(\frac{F_{k}}{N}\) = \(\frac{\mathrm{F}_{\mathrm{k}}}{\mathrm{mg}}\)

Calculation:
From formula (i),
∴ µ_s = \(\frac{F_{S}}{N}=\frac{68.5}{37 \times 9.8}\) = 0.1889
From formula (ii),
∴ µ_k = \(\frac{F_{k}}{N}=\frac{43}{37 \times 9.8}\) = 0.1186
Answer:

1. The coefficient of static friction is 0.1889.
2. The coefficient of kinetic friction is 0.1186.

[Note: Answers calculated above are in accordance with textual methods of calculation.]

Question 4.
A wire gets stretched by 4mm due to a certain load. If the same load is applied to a wire of same material with half the length and double the diameter of the first wire. What will be the change in its length?
Solution:
Given. l₁ = 4mm = 4 × 10^-3 m
L₂ = \(\frac{\mathrm{L}_{1}}{2}\), D₂ = 2D, r₂ = 2r₁
To find: Change in length (l₂)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,

= 0.5 × 10^-3 m
= 0.5 mm
The new change in length of the wire is 0.5 mm.

Question 5.
Calculate the work done in stretching a steel wire of length 2m and cross sectional area 0.0225mm² when a load of 100 N is slowly applied to its free end. [Young’s modulus of steel= 2 × 10¹¹ N/m²]
Solution:
Given. L = 2m, F = 100 N,
A = 0.0225 mm² = 2.25 × 10^-8 m²,
Y = 2 × 10^-11 N/m²,
To find: Work (W)
Formula: W = \(\frac{1}{2}\) × F × l
Claculation:

= antilog [log 10 – log 4.5]
= antilog [1.0000 – 0.6532 ]
= antilog [0.3468]
∴ W = 2.222 J
Answer:
The work done in stretching the steel wire is 2.222 J.

Question 6.
A solid metal sphere of volume 0.31m³ is dropped in an ocean where water pressure is 2 × 10⁷ N/m². Calculate change in volume of the sphere if bulk modulus of the metal is 6.1 × 10¹⁰ N/m²
Solution:
Given: V= 0.31 m³, dP = 2 × 10⁷ N/m²,
K = 6.1 × 10¹⁰ N/m²
To find: Change in volume (dV)
Formula: K = V × \(\frac{\mathrm{dP}}{\mathrm{dV}}\)
Calculation: From formula,
dV = \(\frac{\mathrm{V} \times \mathrm{dP}}{\mathrm{K}}\)
∴ dV = \(\frac{0.31 \times 2 \times 10^{7}}{6.1 \times 10^{10}}\) ≈ 10^-4 m³
The change in volume of the sphere is 10^-4 m³.

Question 7.
A wire of mild steel has initial length 1.5 m and diameter 0.60 mm is extended by 6.3 mm when a certain force is applied to it. If Young’s modulus of mild steel is 2.1 × 10¹¹ N/m², calculate the force applied.
Solution:
Given:
L = 1.5m, d = 0.60 mm,
r = \(\frac{d}{2}\) = 0.30 mm = 3 × 10^-4 m,
Y = 2.1 × 10¹¹ N/m²,
l = 6.3 mm = 6.3 × 10^-3 m
To find: Force (F)
Calculation:
From formula,

= 2.1 × 3.142 × 6 × 6.3
= antilog [log 2.1 + log 3.142 + log 6 + log 6.3]
= antilog [0.3222 + 0.4972 + 0.7782 + 0.7993]
= antilog [2.3969]
= 2.494 × 10²
≈ 250 N
The force applied on wire is 250 N.

Question 8.
A composite wire is prepared by joining a tungsten wire and steel wire end to end. Both the wires are of the same length and the same area of cross section. If this composite wire is suspended to a rigid support and a force is applied to its free end, it gets extended by 3.25mm. Calculate the increase in length of tungsten wire and steel wire separately.
[Given: Y_steel = 2 × 10¹¹ Pa, Y_Tungsten = 4.11 × 10¹¹ Pa]
Solution:
Given: l_s + l_T = 3.25 mm,
Y_T = 4.11 × 10¹¹ Pa
Y_s = 2 × 10¹¹ Pa
To find: Extension in tungsten wire (l_T)
Extension in steel wire (l_s)

But l_s + l_T = 3.25
l_s + 0.487 l_s = 3.25
l_s(1 + 0.487) = 3.25
l_s = 2.186 mm
∴ l_T = 3.25 – 2.186
= 1.064 mm
The extension in tungsten wire is 1.064 mm and the extension in steel wire is 2.186 mm.

[Note: Values of Young’s modulus of tungsten and steel considered above are standard values. Using them, calculation is carried out ¡n accordance with textual method.]

Question 9.
A steel wire having cross sectional area 1.2 mm² is stretched by a force of 120 N. If a lateral strain of 1.455 mm is produced in the wire, calculate the Poisson’s ratio.
Solution:
Given: A = 1.2 mm² = 1.2 × 10^-6 m²,
F = 120 N, Y_steel = 2 × 10¹¹ N/m²,
Lateral strain = 1.455 × 10^-4
To find: Poisson’s ratio (σ)

The Poisson’s ratio of steel is 0.291.
[Note: Lateral strain being ratio of two same physical quantities, is unitless. hence, value given in question ¡s modified to 1.455 × 10^-4 to reach the answer given in textbook.]

Question 10.
A telephone wire 125m long and 1mm in radius is stretched to a length 125.25m when a force of 800N is applied. What is the value of Young’s modulus for material of wire?
Solution:
Given: L = 125m,
r = 1 mm= 1 × 10^-3 m
l = 125.25 – 125 = 0.25 m,
F = 800N
To find: Young’s modulus (Y)
Formula: Y \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,
Y = \(\frac{800 \times 125}{3.142 \times 10^{-6} \times 0.25}\)
= {antilog [log 800 + log 125 – log 3.142 – log 0.25 ]} × 10⁶
= {antilog [2.9031 + 2.0969 – 0.4972 – \(\overline{1}\) .3979]} × 10⁶
= {antilog[5.1049]} × 10⁶
= 1.274 × 10⁵
= 1.274 × 10¹¹ N/m²
The Young’s modulus of telephone wire is 1.274 × 10¹¹ N/m².

Question 11.
A rubber band originally 30cm long is stretched to a length of 32cm by certain load. What is the strain produced?
Solution:
Given: L = 30 cm = 30 × 10 ^-2 m,
∆l = 32 cm – 30 cm = 2cm = 2 × 10 ^-2 m
To find. Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2 \times 10^{-2}}{30 \times 10^{-2}}\) = 6.667 × 10 ^-2
The strain produced in the wire is 6.667 × 10 ^-2.

Question 12.
What is the stress in a wire which is 50m long and 0.01cm² in cross section, if the wire bears a load of 100kg?
Solution:
Given: M = 100 kg, L 50 m, A = 0.01 × 10^-4 m
To find: Stress
Formula: Stress = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{\mathrm{Mg}}{\mathrm{A}}\)
Calculation: From formula,
Stress = \(\frac{100 \times 9.8}{0.01 \times 10^{-4}}\) = 9.8 × 10⁸ N/m²
The stress in the wire is 9.8 × 10⁸ N/m².

Question 13.
What is the strain in a cable of original length 50m whose length increases by 2.5cm when a load is lifted?
Solution:
Given: L = 50m, ∆l = 2.5cm = 2.5 × 10 ^-2 m
To find: Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2.5 \times 10^{-2}}{50}\) = 5 × 10^-4
The Strain produced in wire is 5 × 10^-4 .

11th Physics Digest Chapter 6 Mechanical Properties of Solids Intext Questions and Answers

Can you recall? (Textbook Page No. 100)

Question 1.

1. Can you name a few objects which change their shape and size on application of a force and regain their original shape and size when the force is removed?
2. Can you name objects which do not regain their original shape and size when the external force is removed?

Answer:

1. Objects such as rubber, metals, quartz, etc. change their shape and size on application of a force (within specific limit) and regain their original shape and size when the force is removed.
2. Objects such as putty, clay, thick mud. etc. do not regain their original shape and size when the external force is removed.

Can you tell? (Textbook Page No. 107)

Question 1.
Why does a rubber band become loose after repeated use?
Answer:

1. After repeated use of rubber band, its stress-strain curve does not remain linear.
2. In such case, since rubber crosses its elastic limit, there is a permanent set formed on the rubber due to which it becomes loose.

Can you tell? (Textbook Page No.111)

Question 1.
i. It is difficult to run fast on sand.
ii. It is easy to roll than pull a barrel along a road.
iii. An inflated tyre rolls easily than a flat tyre.
iv. Friction is a necessary evil.
Answer:
i.

1. The intermolecular space between crystals of sand is very large as compared to that in a rigid surface.
2. Thus, there are number of depressions at the points of contact of feet and sand surface.
3. Projections and depressions between sand and feet are not completely interlocked.
4. Thus, action and reaction force become unbalanced. The horizontal component of force helps to move forward and vertical component of the force resist to move.
   Hence, it becomes difficult to run fast on sand.

ii.

1. When a barrel is pulled along a road, the friction between the tyres and road is kinetic friction, but when its rolls along the road it undergoes rolling friction.
2. The force of kinetic friction is greater than force of rolling friction.
   Hence, it is easy to roll than pull a barrel along a road.

iii.

1. When the tyre is inflated, the pressure inside the tyre is reducing the normal force between tyre and the ground, and thus reducing the friction between the tyre and the road.
2. When the tyre gets deflated, it gets deformed during rolling, the supplied energy is used up in changing the shape and not overcoming the friction, and thus due to deformation, friction increases.
   Hence, an inflated tyre rolls easily than a flat tyre.

iv.

1. Friction helps us to walk, hold objects in hand, lift objects and without friction we cannot walk, we cannot grip or hold objects with our hands,
2. Friction is responsible for wear and tear of various part of machines, it produces heat in different parts of machine and also produces noise but it also helps in ball bearing or connecting screws.
   Hence, friction is said to be a necessary evil because it is useful as well as harmful.

Internet my friend (Textbook Page No. 111)

Question 1.
i. https ://opentextbc. ca/physicstestbook2/ chapter/friction/
ii. https://www.livescience.com/
iii. https://www.khanacademy.org/science/physics
iv. https://courses.lumenleaming.com/physics/ chapter/5-3-elasticity-stress-and-strain/
v. https://www.toppr.com/guides/physics/
Answer:
[Students are expected to visit the above mentioned websites and collect more information about mechanical properties of solid.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions