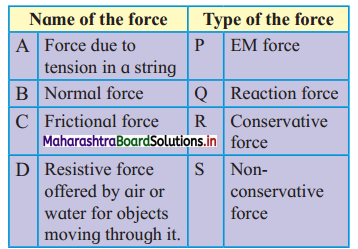
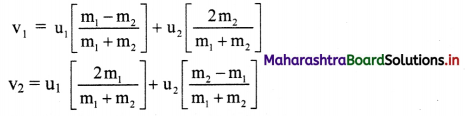
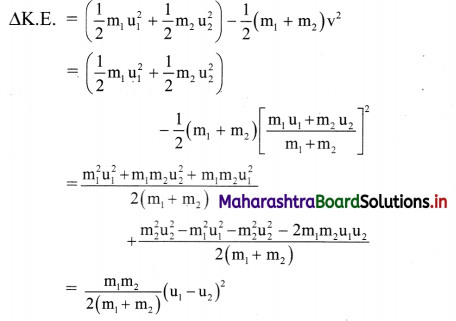
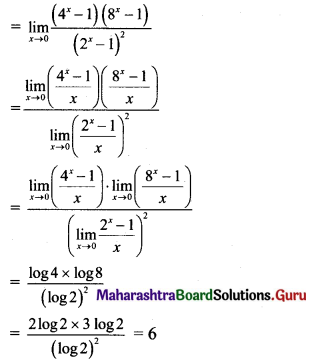
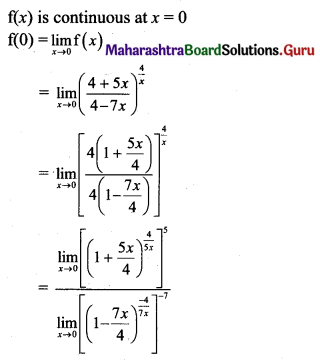
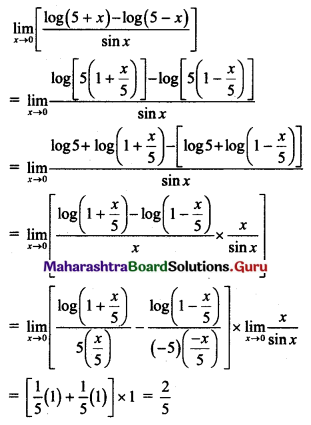
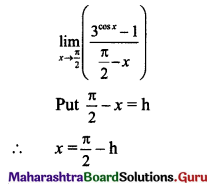
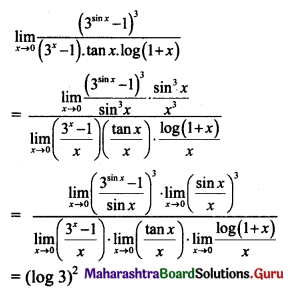
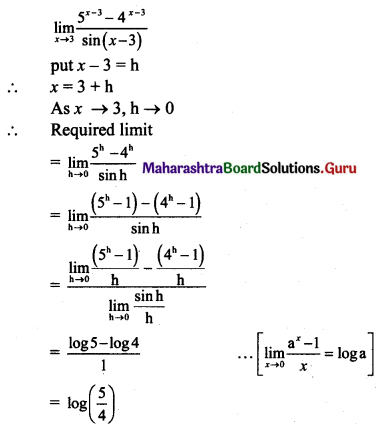
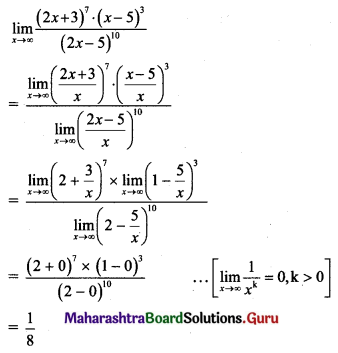
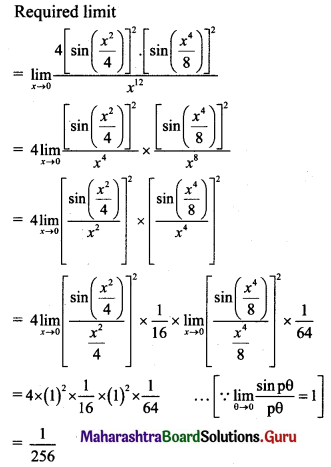
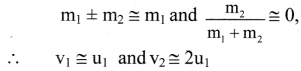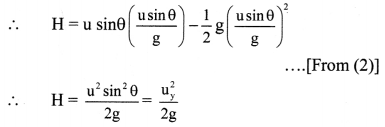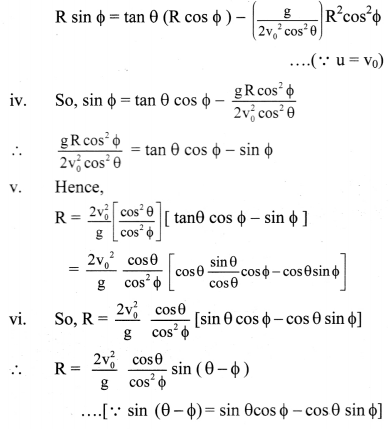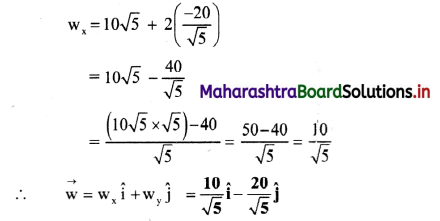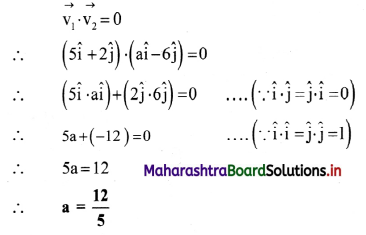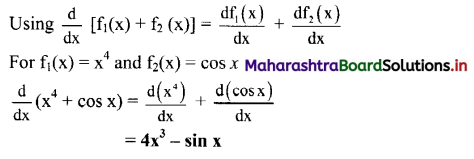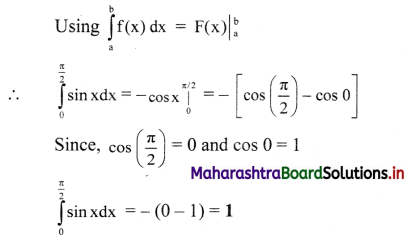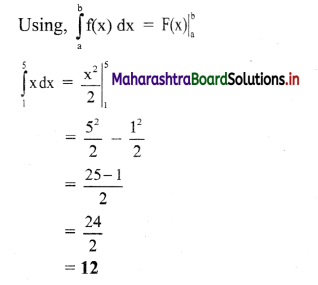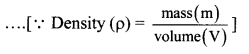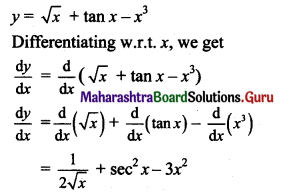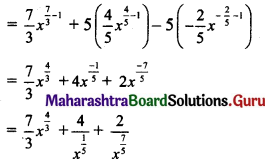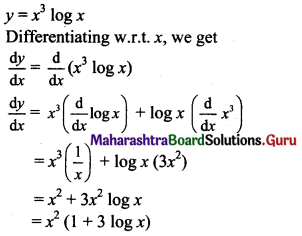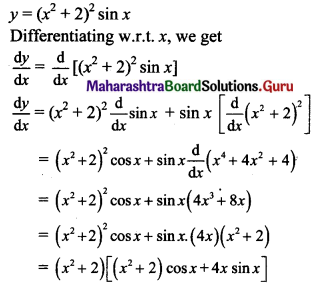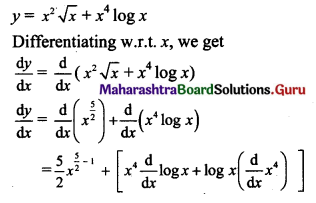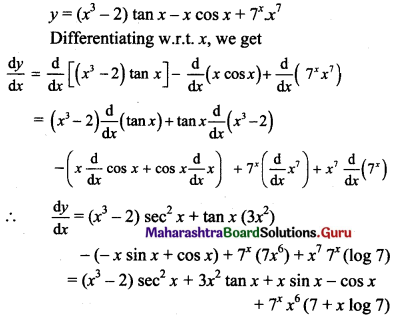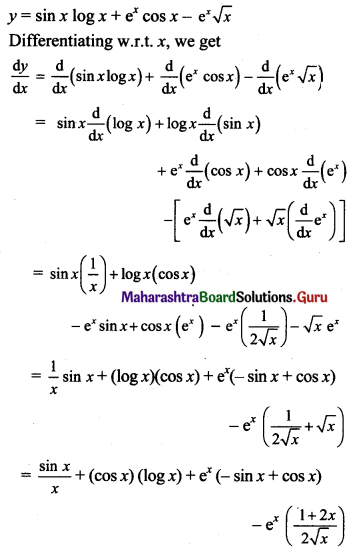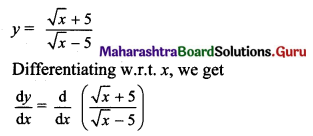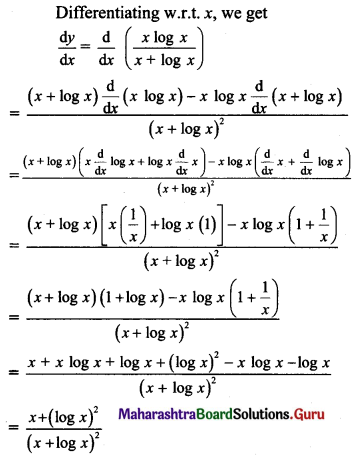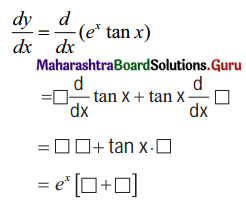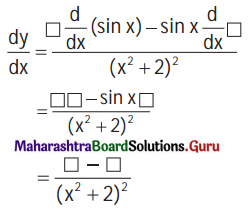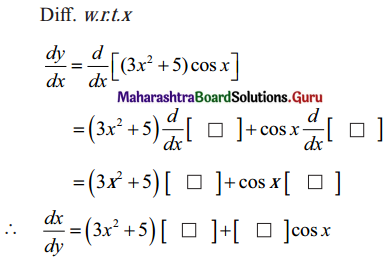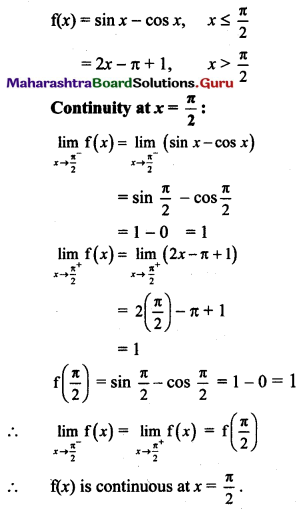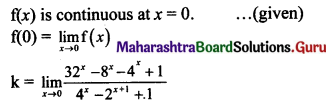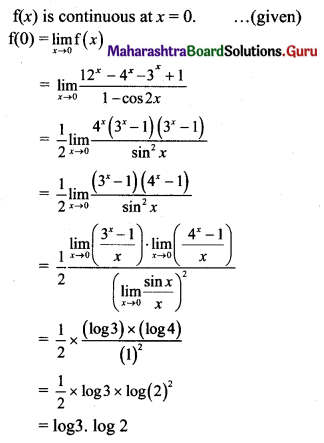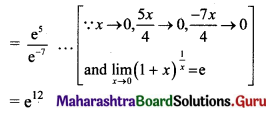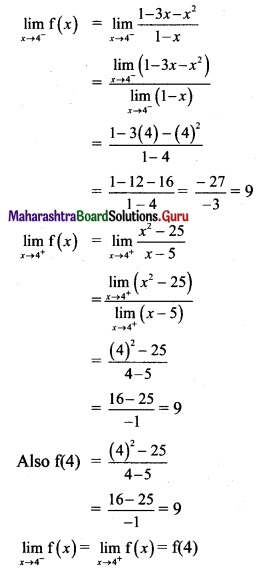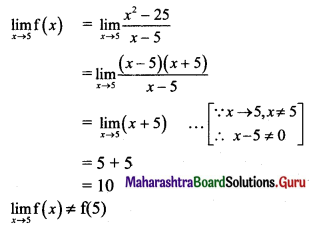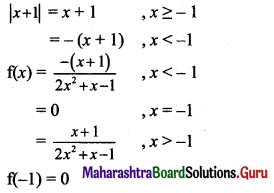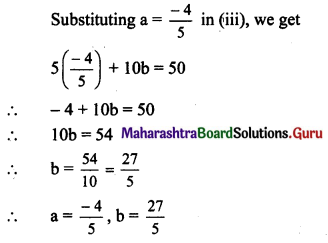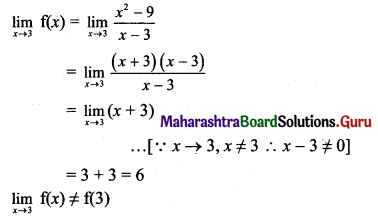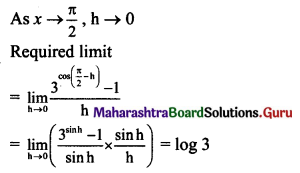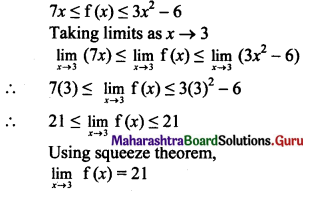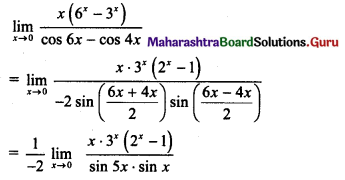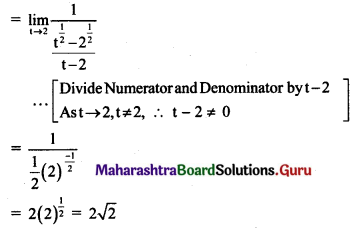Gravitation Class 11 Exercise Question Answers Solutions Maharashtra Board
Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 5 Gravitation Textbook Exercise Questions and Answers.
Class 11 Physics Chapter 5 Exercise Solutions Maharashtra Board
Physics Class 11 Chapter 5 Exercise Solutions
1. Choose the correct option.
Question 1.
The value of acceleration due to gravity is maximum at
(A) the equator of the Earth
(B) the centre of the Earth.
(C) the pole of the Earth.
(D) slightly above the surface of the Earth.
Answer:
(C) the pole of the Earth.
Question 2.
The weight of a particle at the centre of the Earth is _________
(A) infinite.
(B) zero.
(C) same as that at other places.
(D) greater than at the poles.
Answer:
(B) zero.
![]()
Question 3.
The gravitational potential due to the Earth is minimum at
(A) the centre of the Earth.
(B) the surface of the Earth.
(C) a points inside the Earth but not at its centre.
(D) infinite distance.
Answer:
(A) the centre of the Earth.
Question 4.
The binding energy of a satellite revolving around planet in a circular orbit is 3 × 109 J. Its kinetic energy is _________
(A) 6 × 109 J
(B) -3 × 109 J
(C) -6 × 10+9 J
(D) 3 × 10+9J
Answer:
(D) 3 × 10+9J
2. Answer the following questions.
Question 1.
State Kepler’s law equal of area.
Answer:
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
Question 2.
State Kepler’s law of period.
Answer:
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
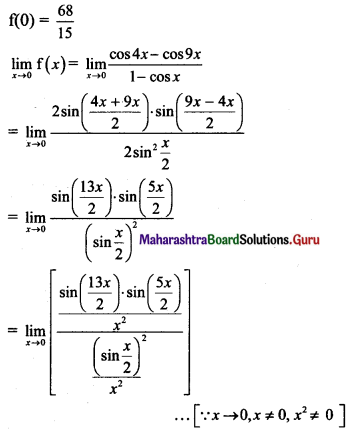
Question 3.
What are the dimensions of the universal gravitational constant?
Answer:
The dimensions of universal gravitational constant are: [L3M-1T-2].
Question 4.
Define binding energy of a satellite.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Question 5.
What do you mean by geostationary satellite?
Answer:
Some satellites that revolve around the Earth in equatorial plane have same sense of rotation as that of the Earth. The also have the same period of rotation as that of the Earth i.e.. 24 hours. Due to this, these satellites appear stationary from the Earth’s surface and are known as geostationary satellites.
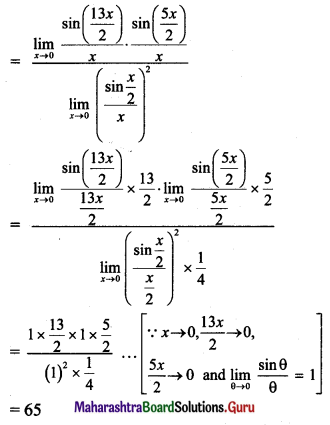
Question 6.
State Newton’s law of gravitation.
Answer:
Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
![]()
Question 7.
Define escape velocity of a satellite.
Answer:
The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (ve) of the body.
Question 8.
What is the variation in acceleration due to gravity with altitude?
Answer:
Variation in acceleration due to gravity due to altitude is given by, gh = g\(\left(\frac{R}{R+h}\right)^{2}\)
where,
gh = acceleration due to gravity of an object placed at h altitude
g = acceleration due to gravity on surface of the Earth
R = radius of the Earth
h = attitude height of the object from the surface of the Earth.
Hence, acceleration due to gravity decreases with increase in altitude.
Question 9.
On which factors does the escape speed of a body from the surface of Earth depend?
Answer:
The escape speed depends only on the mass and radius of the planet.
[Note: Escape velocity does not depend upon the mass of the body]
Question 10.
As we go from one planet to another planet, how will the mass and weight of a body change?
Answer:
- As we go from one planet to another, mass of a body remains unaffected.
- However, due to change in mass and radius of planet, acceleration due to gravity acting on the body changes as, g ∝ \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\).
Hence, weight of the body also changes as, W ∝ \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\)
Question 11.
What is periodic time of a geostationary satellite?
Answer:
The periodic time of a geostationary satellite is same as that of the Earth i.e., one day or 24 hours.
Question 12.
State Newton’s law of gravitation and express it in vector form.
Answer:
- Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. - In vector form, it can be expressed as,
\(\overrightarrow{\mathrm{F}}_{21}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\left(-\hat{\mathrm{r}}_{21}\right)\)
where, \(\hat{\mathbf{r}}_{21}\) is the unit vector from m1 to m2.
The force \(\overrightarrow{\mathrm{F}}_{21}\) is directed from m2 to m1.
Question 13.
What do you mean by gravitational constant? State its SI units.
Answer:
- From Newton’s law of gravitation,
F = G \(\frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
where, G = constant called universal gravitational constant Its value is 667 X 10-11 N m2/kg2. - G = \(\frac{\mathrm{Fr}^{2}}{\mathrm{~m}_{1} \mathrm{~m}_{2}}\)
If m1 = m2 = 1 kg, r = 1 m thenF = G.
Hence, the universal gravitational constant is the force of gravitation between two particles of unit mass separated by unit distance. - Unit: N m2/kg2 in SI system.
![]()
Question 14.
Why is a minimum two stage rocket necessary for launching of a satellite?
Answer:
- For the projection of an artificial satellite, it is necessary for the satellite to have a certain velocity.
- In a single stage rocket, when the fuel in first stage of rocket is ignited on the surface of the Earth, it raises the satellite vertically.
- The velocity of projection of satellite normal to the surface of the Earth is the vertical velocity.
- If this vertical velocity is less than the escape velocity (ve), the satellite returns to the Earth’s surface. While, if the vertical velocity is greater than or equal to the escape velocity, the satellite will escape from Earth’s gravitational influence and go to infinity.
- Hence, minimum two stage rocket, one to raise the satellite to desired height and another to provide required hori7ontal velocity, is necessary for launching of a satellite.
Question 15.
State the conditions for various possible orbits of a satellite depending upon the horizontal speed of projection
Answer:
The path of the satellite depends upon the value of horizontal speed of projection vh relative to critical velocity vc and escape velocity ve.
Case (I) vh < vc:
The orbit of satellite is an ellipse with point of projection as apogee and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere. it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth.
Case (II) vh = vc:
The satellite moves in a stable circular orbit around the Earth.
Case (III) vc < vh < ve:
The satellite moves in an elliptical orbit round the Earth with the point of projection as perigee.
Case (IV) vh = ve
The satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity.
Case (V) vh > ve:
The satellite escapes from gravitational influence of Earth traversing a hyperbolic path.
3. Answer the following questions in detail.
Question 1.
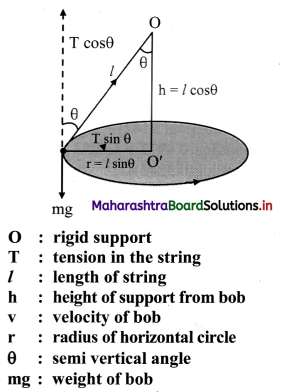
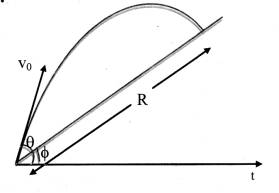
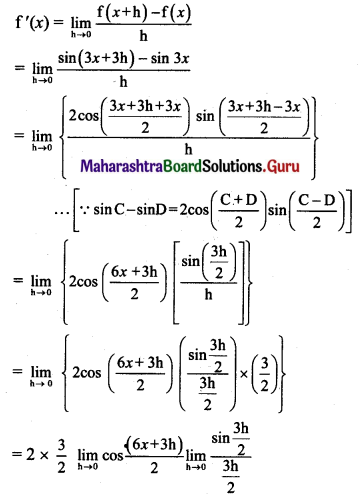
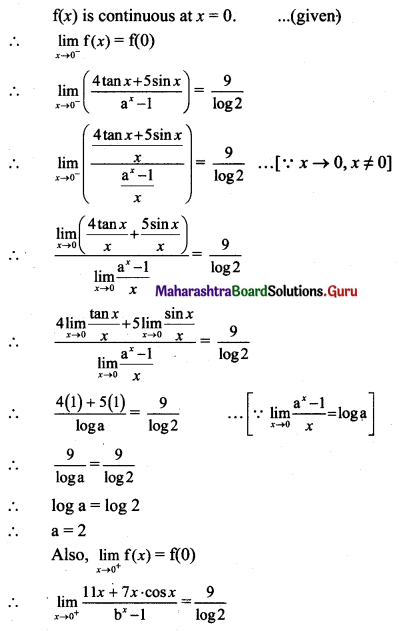
Derive an expression for critical velocity of a satellite.
Answer:
Expression for critical velocity:
- Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius.
- If the satellite is moving in a circular orbit of radius (R + h) = r, its speed must be equal to the magnitude of critical velocity vc.
- The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the satellite on the Earth.
∴ Centripetal force = Gravitational force
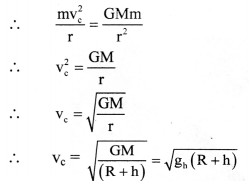
This is the expression for critical speed at the orbit of radius (R + h). - The critical speed of a satellite is independent of the mass of the satellite. It depends upon the mass of the Earth and the height at which the satellite is revolving or gravitational acceleration at that altitude.
![]()
Question 2.
State any four applications of a communication satellite.
Answer:
Applications of communication satellite:
- For the transmission of television and radiowave signals over large areas of Earth’s surface.
- For broadcasting telecommunication.
- For military purposes.
- For navigation surveillance.
Question 3.
Show that acceleration due to gravity at height h above the Earth’s surface is gh = g(\(\frac{R}{R+h}\))2
Answer:
Variation of g due to altitude:
- Let,
R = radius of the Earth,
M = mass of the Earth.
g = acceleration due to gravity at the surface of the Earth. - Consider a body of mass m on the surface of the Earth. The acceleration due to gravity on the Earth’s surface is given by,
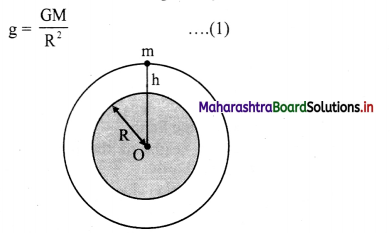
- The body is taken at height h above the surface of the Earth as shown in figure. The acceleration due to gravity now changes to,
gh = \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}\) …………. (2) - Dividing equation (2) by equation (1), we get,
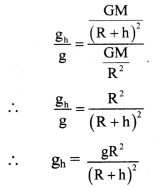
We can rewrite,

This expression can be used to calculate the value of g at height h above the surface of the Earth as long as h<< R.
Question 4.
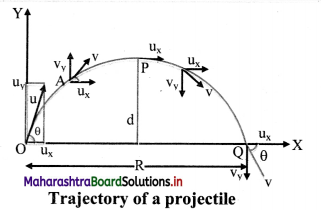
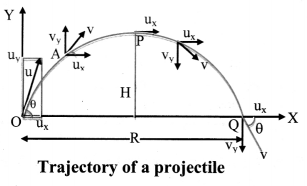
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Answer:
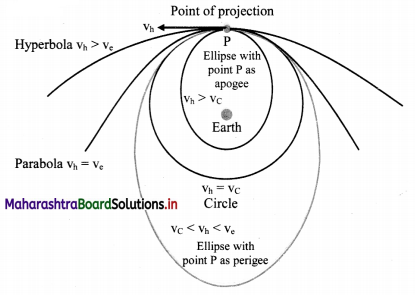
vh = horizontal speed of projection
v c = critical velocity
ve = escape velocity
Question 5.
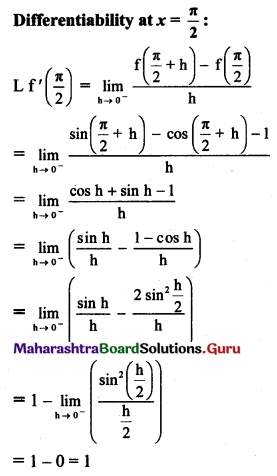
Derive an expression for binding energy of a body at rest on the Earth’s surface.
Answer:
- Let,
M = mass of the Earth
m = mass of the satellite
R = radius of the Earth. - Since the satellite is at rest on the Earth, v = 0
∴ Kinetic energy of satellite.
K.E = \(\frac{1}{2}\) mv2 = 0 - Gravitational potential at the Earth’s surface
= – \(\frac{\mathrm{GM}}{\mathrm{R}}\)
∴ Potential energy of satellite = Gravitational potential × mass of satellite
= –\(\frac{\mathrm{GMm}}{\mathrm{R}}\) - Total energy of sitellite = T.E = P.E + K.E
∴ T.E. = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\) + 0 = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\) - Negative sign in the energy indicates that the satellite is bound to the Earth, due to gravitational force of attraction.
- For the satellite to be free form Earth’s gravitational influence, its total energy should become positive. That energy is the binding energy of the satellite at rest on the surface of the Earth.
∴ B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
![]()
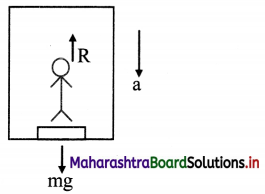
Question 6.
Why do astronauts in an orbiting satellite have a feeling of weightlessness?
Answer:
- For an astronaut, in a satellite, the net force towards the centre of the Earth will always be, F = mg – N.
where, N is the normal reaction. - In the case of a revolving satellite, the satellite is performing a circular motion. The acceleration for this motion is centripetal, which is provided by the gravitational acceleration g at the location of the satellite.
- In this case, the downward acceleration, ad = g, or the satellite (along with the astronaut) is in the state of free fall.
- Thus, the net force acting on astronaut will be, F = mg – mad i.e., the apparent weight will be zero, giving the feeling of total weightlessness.
Question 7.
Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Answer:
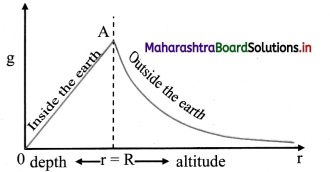
Question 8.
At which place on the Earth’s surface is the gravitational acceleration maximum? Why?
Answer:
- Gravitational acceleration on the surface of the Earth depends on latitude of the place as well as rotation and shape of the Earth.
- At poles, latitude θ = 90°.
∴ g’ = g
i.e., there is no reduction in acceleration due to gravity at poles. - Also, shape of the Earth is actually an ellipsoid, bulged at equator. The polar radius of the Earth is 6356 km which minimum. As g ∝ \(\frac{1}{\mathrm{R}^{2}}\), acceleration due to gravity is maximum at poles i.e., 9.8322 m/s2.
Question 9.
At which place on the Earth surface the gravitational acceleration minimum? Why?
Answer:
- Gravitational acceleration on the surface of the Earth depends on latitude of the place as well as rotation and shape of the Earth.
- At equator, latitude θ = 0°.
∴ g’ = g – Rω2
i.e., the acceleration due to gravity ¡s reduced by amount Rω2(≈ 0.034 m/s2) at equator. - Also, shape of the Earth is actually an ellipsoid, bulged at equator. The equatorial radius of the Earth is 6378 km, which is maximum. As g ∝ \(\frac{1}{\mathrm{R}^{2}}\) acceleration due to gravity is minimum on equator i.e., 9.7804 m/s2.
![]()
Question 10.
Define the binding energy of a satellite. Obtain an expression for binding energy of a satellite revolving around the Earth at certain attitude.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Expression for binding energy of satellite revolving in circular orbit round the Earth:
- Consider a satellite of mass m revolving at height h above the surface of the Earth in a circular orbit. It possesses potential energy as well as kinetic energy.
- Let M be the mass of the Earth, R be the Radius of the Earth, vc be critical velocity of satellite, r = (R + h) be thc radius of the orbit.
- Kinetic energy of satellite = \(\frac{1}{2} \mathrm{mv}_{\mathrm{c}}^{2}=\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\)
- The gravitational potential at a distance r from the centre of the Earth is –\(\frac{\mathrm{GM}}{\mathrm{r}}\)
∴ Potential energy of satellite = Gravitational potential × mass of satellite
= –\(\frac{\mathrm{GMm}}{\mathrm{r}}\) - The total energy of satellite is given as T.E. = KF. + P.E.
= \(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}-\frac{\mathrm{GMm}}{\mathrm{r}}=-\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\) - Total energy of a circularly orbiting satellite is negative. Negative sign indicates that the satellite is bound to the Earth, due to gravitational force of attraction. For the satellite to be free from the Earth’s gravitational influence its total energy should become zero or positive.
- Hence the minimum energy to be supplied to unbind the satellite is +\(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\). This is the binding energy of a satellite.
Question 11.
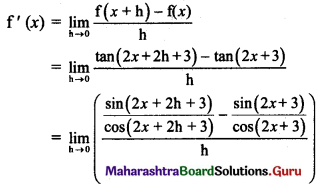
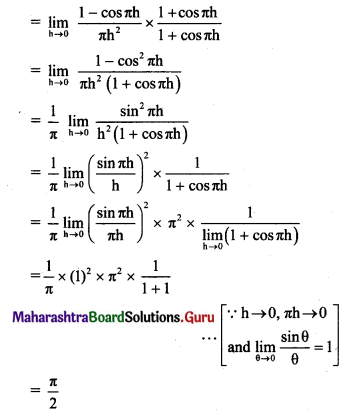
Obtain the formula for acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
Answer:
- The Earth can be considered to be a sphere made of large number of concentric uniform spherical shells.
- When an object is on the surface of the Earth it experiences the gravitational force as if the entire mass of the Earth is concentrated at its centre.
- The acceleration due to gravity on the surface of the Earth is, g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
- Assuming that the density of the Earth is uniform, mass of the Earth is given by
M = volume x density = \(\frac{4}{3}\) πR3ρ
∴ g = \(\frac{\mathrm{G} \times \frac{4}{3} \pi \mathrm{R}^{3} \rho}{\mathrm{R}^{2}}\) = \(\frac{4}{3}\) πRρG ………….. (1) - Consider a body at a point P at the depth d below the surface of the Earth as shown in figure.
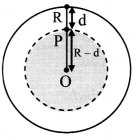
Here the force on a body at P due to outer spherical shell shown by shaded region, cancel out due to symmetry.
The net force on P is only due to the inner sphere of radius OP = R – d. - Acceleration due to gravity because of this sphere is,

This equation gives acceleration due to gravity at depth d below the Earth’s surface.
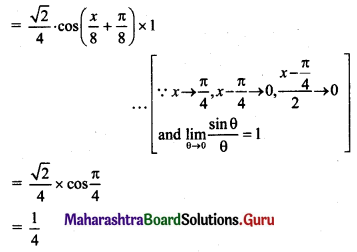
Question 12.
State Kepler’s three laws of planetary motion.
Answer:
- All planets move in elliptical orbits around the Sun with the Sun at one of the foci of the ellipse.
- The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
- The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
![]()
Question 13.
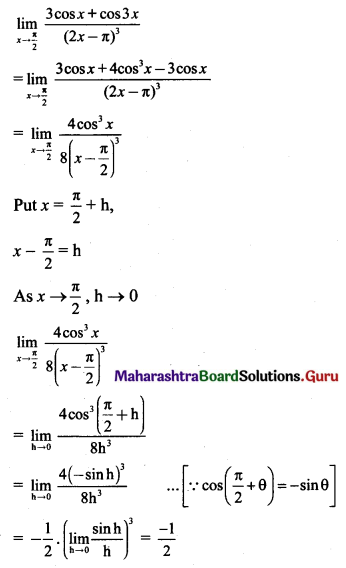
State the formula for acceleration due to gravity at depth ‘d’ and altitude ‘h’ Hence show that their ratio is equal to \(\left(\frac{R-d}{R-2 h}\right)\) by assuming that the altitude is very small as compared to the radius of the Earth.
Answer:
- For an object at depth d, acceleration due to gravity of the Earth is given by,
gd = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) ………………. (1) - Also, the acceleration due to gravity at smaller altitude h is given by,
gh = g(1 – \(\frac{2 \mathrm{~h}}{\mathrm{R}}\)) ……………. (2) - Hence, dividing equation (1) by equation (2),
we get,
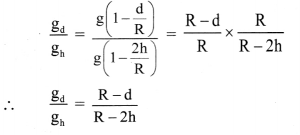
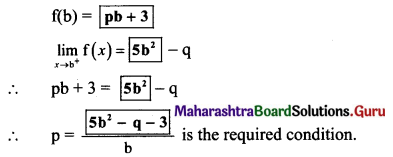
Question 14.
What is critical velocity? Obtain an expression for critical velocity of an orbiting satellite. On what factors does it depend?
Answer:
The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbIt round the Earth is called the critical velocity or orbital velocity (vc).
Expression for critical velocity:
- Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius.
- If the satellite is moving in a circular orbit of radius (R + h) = r, its speed must be equal to the magnitude of critical velocity vc.
- The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the satellite on the Earth.
∴ Centripetal force = Gravitational force

This is the expression for critical speed at the orbit of radius (R + h). - The critical speed of a satellite is independent of the mass of the satellite. It depends upon the mass of the Earth and the height at which the satellite is revolving or gravitational acceleration at that altitude.
Question 15.
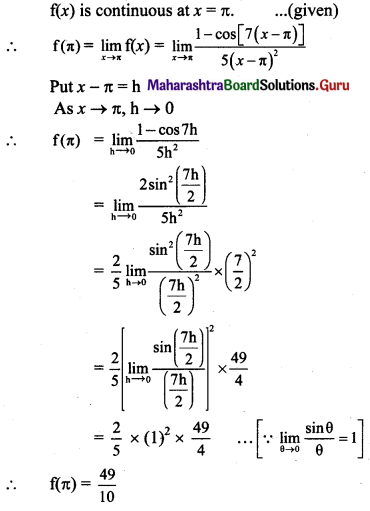
Define escape speed. Derive an expression for the escape speed of an object from the surface of the earth.
Answer:
- The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (ve) of the body.
- As the gravitational force due to Earth becomes zero at infinite distance, the object has to reach infinite distance in order to escape.
- Let us consider the kinetic and potential energies of an object thrown vertically upwards with escape velocity ve.
- On the surface of the Earth,
K.E.= \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}\)
P.E. = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Total energy = P.E. + K.E.
∴ T.E. = \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}\) ………………. (1) - The kinetic energy of the object will go on decreasing with time as it is pulled back by Earth’s gravitational force. It will become zero when it reaches infinity. Thus, at infinite distance from the Earth,
K.E. = 0
Also,
P.E. = –\(\frac{\mathrm{GMm}}{\infty}\) = 0
∴ Total energy = P.E. + K.E. = 0 - As energy is conserved
\(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}=0\) ……[From(1)]
or, ve = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)
![]()
Question 16.
Describe how an artificial satellite using two stage rocket is launched in an orbit around the Earth.
Answer:
- Launching of a satellite in an orbit around the Earth cannot take place by use of single stage rocket. It requires minimum two stage rocket.
- With the help of first stage of rocket, satellite can be taken to a desired height above the surface of the Earth.
- Then the launcher is rotated in horizontal direction i.e.. through 900 using remote control and the first stage of the rocket is detached.
- With the help of second stage of rocket, a specific horizontal velocity (vh) is given to satellite so that it can revolve in a circular path around the Earth.
- The satellite follows different paths depending upon the horizontal velocity provided to it.
4. Solve the following problems.
Question 1.
At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given radius of Earth is 6400 km.
Solution:
Given: gd = 90% of g i.e., \(\frac{\mathrm{g}_{\mathrm{d}}}{\mathrm{g}}\) = 0.9,
R = 6400km = 6.4 × 106 m
To find: Distance below the Earth’s surface (d)

At distance 640 km below the surface of the Earth, value of acceleration due to gravity decreases by 10%.
Question 2.
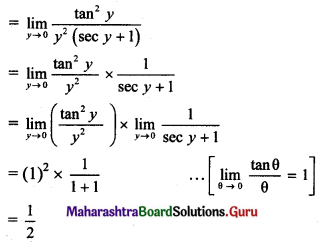
If the Earth were made of wood, the mass of wooden Earth would have been 10% as much as it is now (without change in its diameter). Calculate escape speed from the surface of this Earth.
Solution:

As, we know that the escape speed from surface of the Earth is 11.2 km/s, Substituting value of ve = 11.2 km/s
Vew = 11.2 × \(\frac{1}{\sqrt{10}}=\frac{11.2}{3.162}\)
= 11.2 × \(\frac{1}{3.162}\)
…………… [Taking square root value]
= antilog {log(1 1.2) – Log(3.162)}
= antilog {1.0492 – 0.5000}
= antilog {0.5492} = 3.542
∴ Vew = 3.54km/s
The escape velocity from the surface of wooden Earth is 3.54 km/s.
![]()
Question 3.
Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth.
Given:- G = 6.67 × 10-11 Nm2/kg2
R = 6400 km
M = 6 × 1024 kg
Solution:
Given:- m = 2000 kg, h = 3600 km = 3.6 × 106 m,
G = 6.67 × 10-11 Nm2/kg2
R = 6400 km
M = 6 × 1024 kg
To find: i) Kninetic energy (K.E.)
ii) Potential Energy (P.E.)
iii) Total Energy (T.E.)
iv) Binding Energy (B.E.)

From formula (ii),
P.E. = -2 × 40.02 × 109
= -80.04 × 109 J
From formula (iii),
T.E. = (40.02 × 109) + (-80.02 × 109)
= -40.02 × 109 J
From formula (iv),
B.E.= -(-40.02 × 109)
= 40.02 × 109 J
Kinetic energy of the satellite is 40.02 × 109 J, potential energy is -80.04 × 109 J, total energy is -40.02 × 109 J and binding energy is 40.02 × 109 J.
[Note: Total energy of orbiting satellite is negative.]
Question 4.
Two satellites A and B are revolving around a planet. Their periods of revolution are 1 hour and 8 hours respectively. The radius of orbit of satellite B is 4 × 104 km. find radius of orbit of satellite A .
Solution:
Given: TA = 1 hour, TB = 8 hour,
rB = 4 × 104 km
To find: Radius of orbit of satellite A (rA)

Radius of orbit of satellite A will be 1 × 104 km.
Question 5.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Solution:
Given: MS = 1.99 × 1030 kg
ME = 5.98 × 1024 kg, R = 1.5 × 1011 m.
To find: Gravitational force between the Sun and the Earth (F)
Formula: F = \(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
Calculation:As, we know, G = 6.67 × 10-11 N m2/kg2
From formula,

= antilog {(log(6.67) + log( 1.99) + log(5.98) – log(2.25)} × 1021
= antilog {(0.8241) + (0.2989) + (0.7767) – (0.3522)} × 1021
= antilog {1.5475} × 1021
= 35.28 × 1021
= 3.5 × 1022 N
The gravitational force between the Sun and the Earth is 3.5 × 1022 N.
![]()
Question 6.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
Solution:
Given: h = 300 km = 0.3 × 106 m,
M = 5.98 × 1024 kg,
R = 6400km = 6.4 × 106 m
G = 6.67 × 10-11 Nm2/kg2
To find: Acceleration due to gravity at height (gh)
Formula: gh = \(\frac{G M}{(R+h)^{2}}\)
Calculation: From formula,
gh = \(\frac{6.67 \times 10^{-11} \times 5.98 \times 10^{24}}{\left[\left(6.4 \times 10^{6}\right)+\left(0.3 \times 10^{6}\right)\right]^{2}}\)
= \(\frac{6.67 \times 5.98 \times 10^{13}}{(6.7)^{2} \times 10^{12}}\)
6.67 X 10” x 5.98 X iO
= antilog {log(6.67) + log(5.98) – 2log(6.7)} × 10
= antilog{0.8241 + 0.7767 – 2(0.8261)} × 10
= antilog {1.6008 – 1.6522} × 10
= antilog {\(\overline{1}\) .9486} × 10
= 0.8884 × 10 = 8.884 m/s2
Acceleration due to gravity at 300 km will be 8.884 m/s2.
Question 7.
Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface. ME = 5.98 × 1024 kg, R = 6.4 × 106 m.
Solution:
Given: h = 1000 km = 1 × 106 m,
ME = 5.98 × 1024 kg, R = 6.4 × 106 m,
G = 6.67 × 10-11 N m2/kg2
To find: Speed of satellite (vc)

Speed of the satellite at height 1000 km is 7.34 × 103 m/s.
Question 8.
Calculate the value of acceleration due to gravity on the surface of Mars if the radius of Mars = 3.4 × 103 km and its mass is 6.4 × 1023 kg.
Solution:
Given:
M = 6.4 × 1023 kg
R = 3.4 × 103 = 3.4 × 106 m,
To find: Acceleration due to gravity on the surface of the Mars (gM)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: As, G = 6.67 × 10-11 N m2/kg2
From formula,
gM = \(\frac{6.67 \times 10^{-11} \times 6.4 \times 10^{23}}{\left(3.4 \times 10^{6}\right)^{2}}=\frac{6.67 \times 6.4}{3.4 \times 3.4}\)
= antilog {log(6.67) + log(6.4) – log(3.4) – log(3.4)}
= antilog {(0.8241) + (0.8062) – (0.5315) – (0.53 15)}
= antilog {0.5673}
= 3.693 m/s2
Acceleration due to gravity on the surface of Mars is 3.693 m/s2.
Question 9.
A planet has mass 6.4 × 1024 kg and radius 3.4 × 106 m. Calculate energy required to remove on object of mass 800 kg from the surface of the planet to infinity.
Solution:
Given: M = 6.4 × 1024 kg, R = 3.4 × 106 m, m = 800 kg
To find: Energy required to remove the object from surface of planet to infinity = B.E.
Formula: B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Calculation: We know that,
G = 6.67 × 10-11 N m2/kg2
From formula,
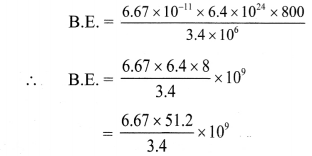
= antilog{log(6.67) + log(51.2) – log(3.4)} × 109
= antilog{0.8241 + 1.7093 – 0.5315} × 109
= antilog {2.0019} × 109
= 1.004 × 102 × 109
= 1.004 × 1011 J
Energy required to remove the object from the surface of the planet is 1.004 × 1011 J.
[Note: Answer calculated above ¡s in accordance with retual methods of calculation.]
![]()
Question 10.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 1024 kg, Radius of the Earth = 6400 km and the acceleration due to gravity on the surface = 9.8 m/s2
Solution:
Given: M = 6 × 1024 kg,
R = 6400km = 6.4 × 106 m,
g = 9.8 m/s2
To find: Gravitational constant (G)
Formula. g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,
G = \(\frac{\mathrm{gR}^{2}}{\mathrm{M}}\)
G = \(\frac{9.8 \times\left(6.4 \times 10^{6}\right)^{2}}{6 \times 10^{24}}=\frac{401.4 \times 10^{12}}{6 \times 10^{24}}\)
∴ G = 6.69 × 10-11 N m2/kg2
The value of gravitational constant is 6.69 × 10-11 N m2/kg2.
Question 11.
A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 1/7 times the mass of the Earth and radius twice that of the Earth’s radius.
Solution:
Given: WE = 5.6 kg-wt.,
\(\frac{\mathrm{M}_{\mathrm{p}}}{\mathrm{M}_{\mathrm{E}}}=\frac{1}{7}, \frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{E}}}\) = 2
To find: Weight of the body on the surface of planet (Wp)
Formula: W = mg = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\)
Calculation: From formula,
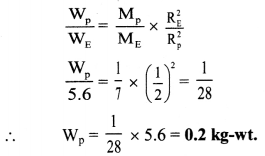
Weight of the body on the surface of a planet will be 0.2 kg-wt.
[Note: The answer given above is calculated in accordance with textual method considering the given data].
Question 12.
What is the gravitational potential due to the Earth at a point which is at a height of 2RE above the surface of the Earth, Mass of the Earth is 6 × 1024 kg, radius of the Earth = 6400 km and G = 6.67 × 10-11 Nm2 kg-2.
Solution:
Given: M = 6 × 1024 kg,
RE = 6400km = 6.4 × 106 m,
G = 6.67 × 10-11 Nm2/kg2,
h = 2RE
To find: Gravitational potential (V)
Formula: V = – \(\frac{\mathrm{GM}}{\mathrm{r}}\)
Calculation: From formula,
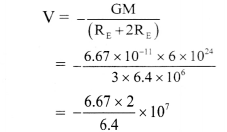
= -2.08 × 107 J kg-1
Negative sign indicates the attractive nature of gravitational potential.
Gravitational potential due to Earth will be 2.08 × 107 J kg-1 towards the centre of the Earth.
[Note: According lo definition of gravitational potential its SI unit is J/kg.]
11th Physics Digest Chapter 5 Gravitation Intext Questions and Answers
Can you recall? (Textbook Page No. 78)
Question 1.
i) What are Kepler’s laws?
ii)What is the shape of the orbits of planets?
Answer:
- The Kepler’s laws are:
- Kepler’s first law: The orbit of a planet is an ellipse with the Sun at one of the foci.
- Kepler’s second law: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
- Kepler’s third law: The square of orbital period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
- The orbits of the planet are elliptical in shape.
![]()
Question 2.
When released from certain height why do objects tend to fall vertically downwards?
Answer:
When released from certain height, objects tend to fall vertically downwards because of the gravitational force exerted by the Earth.
Maharashtra State Board Class 11 Physics Textbook Solutions
- Units and Measurements Class 11 Physics Textbook Solutions
- Mathematical Methods Class 11 Physics Textbook Solutions
- Motion in a Plane Class 11 Physics Textbook Solutions
- Laws of Motion Class 11 Physics Textbook Solutions
- Gravitation Class 11 Physics Textbook Solutions
- Mechanical Properties of Solids Class 11 Physics Textbook Solutions
- Thermal Properties of Matter Class 11 Physics Textbook Solutions
- Sound Class 11 Physics Textbook Solutions
- Optics Class 11 Physics Textbook Solutions
- Electrostatics Class 11 Physics Textbook Solutions
- Electric Current Through Conductors Class 11 Physics Textbook Solutions
- Magnetism Class 11 Physics Textbook Solutions
- Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
- Semiconductors Class 11 Physics Textbook Solutions