Category: Class 11

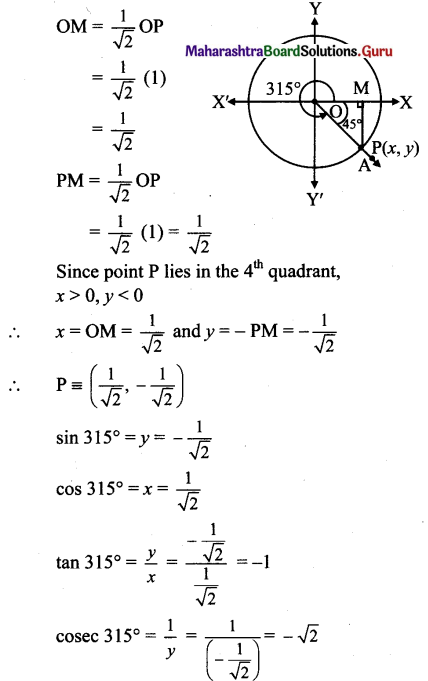
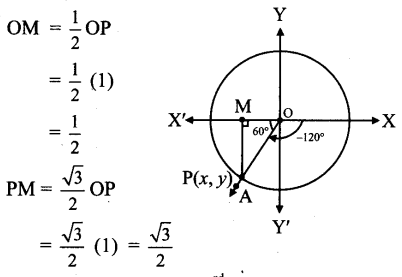
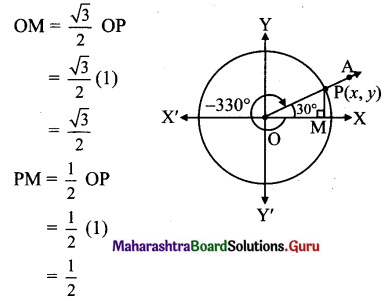
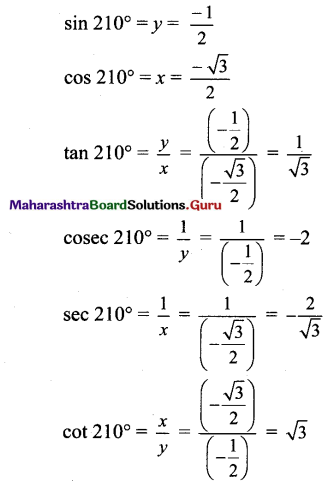
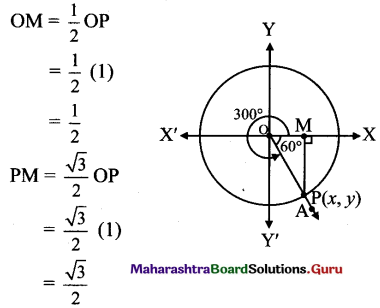
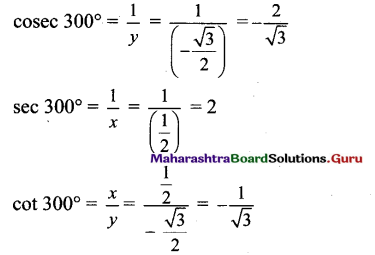
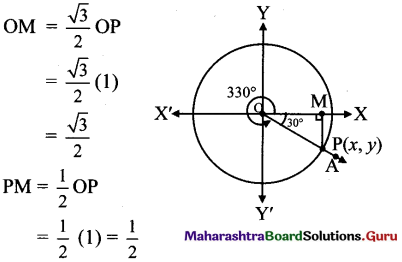
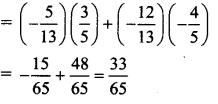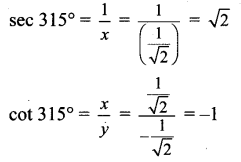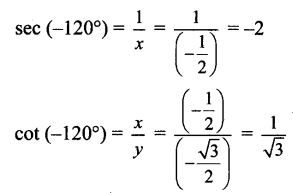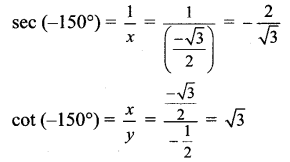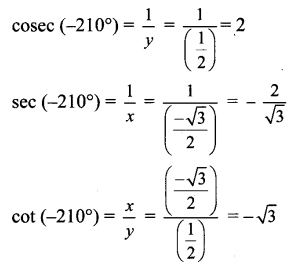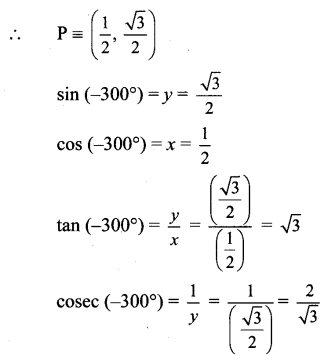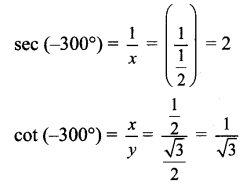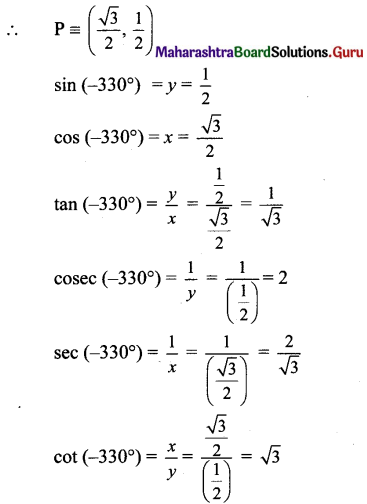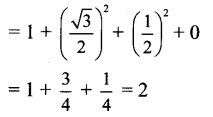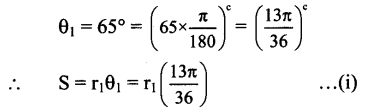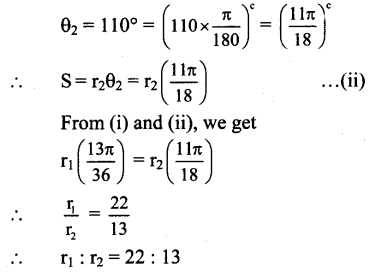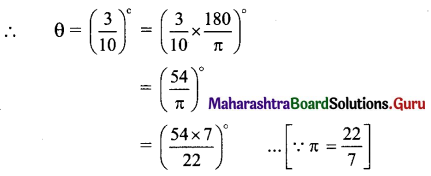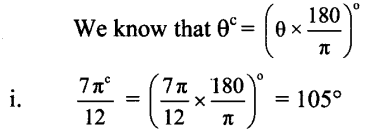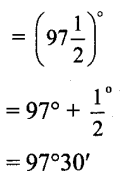Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.3 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.3 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
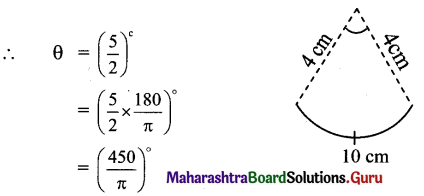
i. sin \(\frac{\pi}{8}\)
ii. \(\frac{\pi}{8}\)
Solution:
We know that sin² θ = \(\frac{1-\cos 2 \theta}{2}[/atex]
Substituting θ = [latex]\frac{\pi}{8}\), we get

ii. We know that, cos² θ = \(\frac{1+\cos 2 \theta}{2}\)
Substituting θ = \(\frac{\pi}{8}\), we get

Question 2.
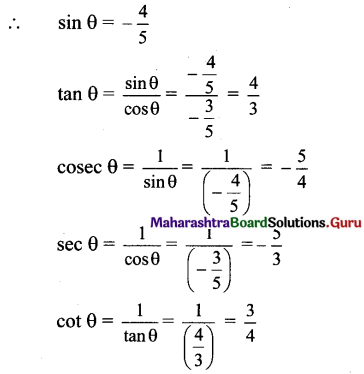
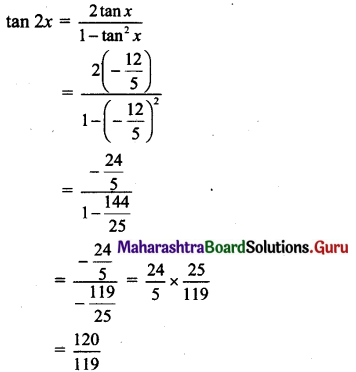
Find sin 2x, cos 2x, tan 2x if sec x = \(-\frac{13}{5}\), \(\frac{\pi}{2}\) < x < π
Solution:
sec x = \(-\frac{13}{5}\), \(\frac{\pi}{2}\) < x < π
We know that
Sect² x = 1 + tan²x
tan²x = \(\frac{169}{25}-1=\frac{144}{25}\)
tan x = \(\pm \frac{12}{5}\)
Since \(\frac{\pi}{2}\) < x < π
x lies in the 2nd quadrant.
tan x < 0

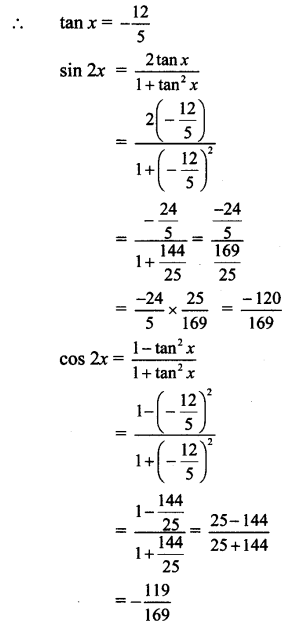
Question 3.
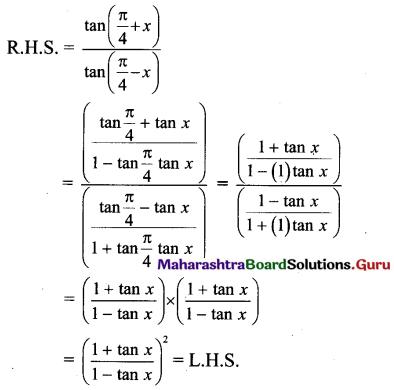
i. \(\) = tan² θ
Solution:
L. H. S. = \(\frac{1-\cos 2 \theta}{1+\cos 2 \theta}\)
= \(\frac{2 \sin ^{2} \theta}{2 \cos ^{2} \theta}\)
= 2tan² θ
= R.H.S.

ii. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
Solution:
L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cosx)cosx
= sin 3x sin x + sin2 x + cos 3x cos x – cos² x
= (cos 3x cos x + sin 3x sin x)
— (cos²x — sin²x)
= cos (3x – x) – cos 2x
= cos 2x – cos 2x
= 0
= R.H.S.

iii. (cos x + cos y )² + (sin x + sin y)² = 4cos² \(\left(\frac{x-y}{2}\right)\)
Solution:
L.H.S. = (cos x + cos y)² + (sin x + sin y)²
= cos²x + cos²y + 2cos x.cos y + sin² x + sin²y + 2sin x.siny
= (cos²x + sin²x) + (cos²y + sin²y) + 2(cos x.cos y + si x.sin y)
= 1 + 1 +2cos(x – y)
= 2 + 2 cos (x – y)
= 2[1 + cos(x – y)]
= 2[2cos² [(\(\left(\frac{x-y}{2}\right)\))] … [∵ 1 + cos θ = 2 cos² \(\frac{\theta}{2}\)]
= 4 cos² (\(\frac{x-y}{2}\))
= R.H.S.
[ Note: The question has been modified]

iv. (cos x – cos y)² + (sin x – sin y)² = 4sin² \(\left(\frac{x-y}{2}\right)\)
Solution:

L.H.S. = (cos x – cos y)² + (sin x – sin y)²
= cos²x + cos²y + 2cos x.cos y + sin² x + sin²y + 2sin x.siny
= (cos²x + sin²x) + (cos²y + sin²y) – 2(cos x.cos y + sin x.sin y)
= 1 + 1 – 2cos(x – y)
= 2 – 2 cos (x – y)
= 2[1 – cos(x – y)]
= 2[2sin² [(\(\left(\frac{x-y}{2}\right)\))] … [∵ 1 – cos θ = 2 sin² \(\frac{\theta}{2}\)]
= 4 sin² (\(\frac{x-y}{2}\))
= R.H.S.

v. tan x + cot x = 2 cosec 2x
Solution:
L.H.S. = tan x + cot x

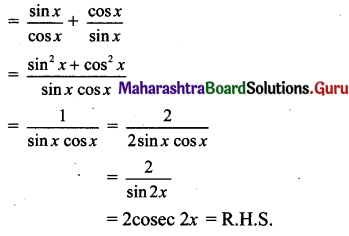
vi. \(\frac{\cos x+\sin x}{\cos x-\sin x}-\frac{\cos x-\sin x}{\cos x+\sin x}\) = 2 tan 2x
Solution:

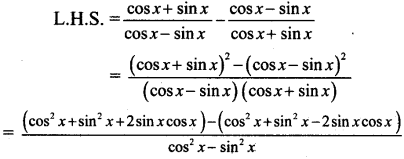
vii. \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 8 x}}}\) = 2 cos x
Solution:

= 2 cos x
= R.H.S.
[Note : The question has been modified.]

viii. 16 sin θ cos θ cos 2θ cos 4θ cos 8θ = sin 16θ
Solution:
L.H.S. = 16 sin θ cos θ cos 2θ cos 4θ cos 8θ
= 8(2sinθ cosθ) cos2θ cos 4θ cos 8θ
= 8sin 2θ cos 2θ cos 4θ cos 8θ
= 4(2sin 2θ cos 2θ) cos 4θ cos 8θ
= 4sin 4θ cos 4θ cos 8θ
= 2(2sin 4θ cos 4θ) cos 8θ
= 2sin 8θ cos 8θ
= sin 16θ
= R.H.S.

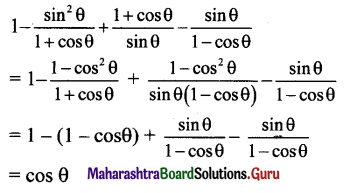
ix. \( = 2 cot 2x
Solution:

x. [latex]\frac{\cos x}{1+\sin x}=\frac{\cot \left(\frac{x}{2}\right)-1}{\cot \left(\frac{x}{2}\right)+1}\)
Solution:

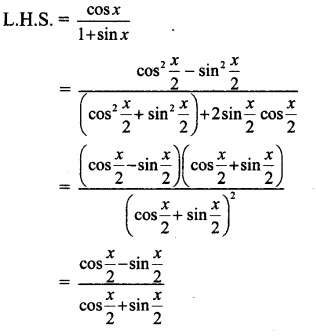
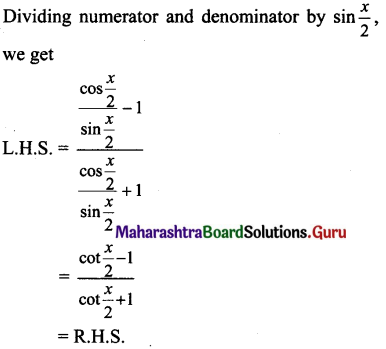
xi. \(\frac{\tan \left(\frac{\theta}{2}\right)+\cot \left(\frac{\theta}{2}\right)}{\cot \left(\frac{\theta}{2}\right)-\tan \left(\frac{\theta}{2}\right)}=\sec \theta\)
Solution:

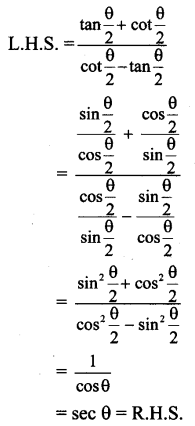
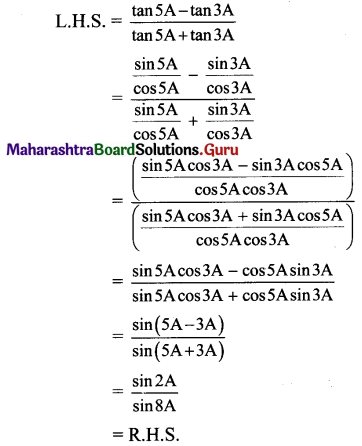
xii. \(\frac{1}{\tan 3 \mathbf{A}-\tan A}-\frac{1}{\cot 3 A-\cot A}\) = cot 2A
Solution:

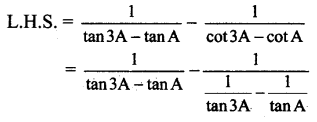
xiii. cos 7° cos 14° cos 28° cos 56° \(\frac{\sin 68^{\circ}}{16 \cos 83^{\circ}}\)
Solution:
L.H.S. = cos 7° cos 14° cos 28° cos 56°
= \(\frac{1}{2 \sin 7^{\circ}}\)(2sin 7°cos 7°)cos 14°cos 28°cos 56°
= \(\frac{1}{2 \sin 7^{\circ}}\) (sin 14° cos 14° cos 28° cos 56°)
…[∵ 2sinθ cosθ = sin 2θ]
= [\frac{1}{2\left(2 \sin 7^{\circ}\right)}latex][/latex] (2sin 14° cos 14°) cos 28° cos 56°
= \(\frac{1}{4 \sin 7^{\circ}}\)(sin 28° cos 28° cos 56°)
= \(\frac{1}{2\left(4 \sin 7^{\circ}\right)}\)(2 sin 28° cos 28°) cos 56°
= \(\frac{1}{8 \sin 7^{\circ}}\) (sin 56° cos 56°)
= \(\frac{1}{8 \sin 7^{\circ}}\) (2 sin 56° cos 56°)
= \(\frac{1}{16 \sin 7^{\circ}}\)(sin 112°)
= \(\frac{\sin \left(180^{\circ}-68^{\circ}\right)}{16 \sin \left(90^{\circ}-83^{\circ}\right)}\)
= \(\frac{\sin 68^{\circ}}{16 \cos 83^{\circ}}\)
= R.H.S.

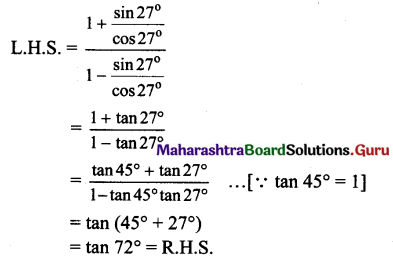
xiv. = \(\frac{\sin ^{2}\left(-160^{\circ}\right)}{\sin ^{2} 70^{\circ}}+\frac{\sin \left(180^{\circ}-\theta\right)}{\sin \theta}\) = sec² 20°
Solution:

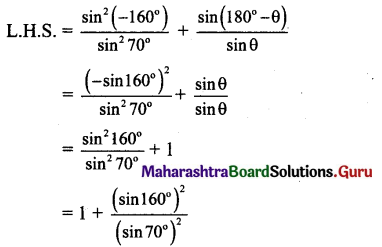
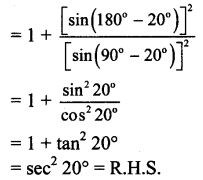
xv. \(\frac{2 \cos 4 x+1}{2 \cos x+1}\) = (2 cos x – 1)(2 cos 2x – 1)
Solution:

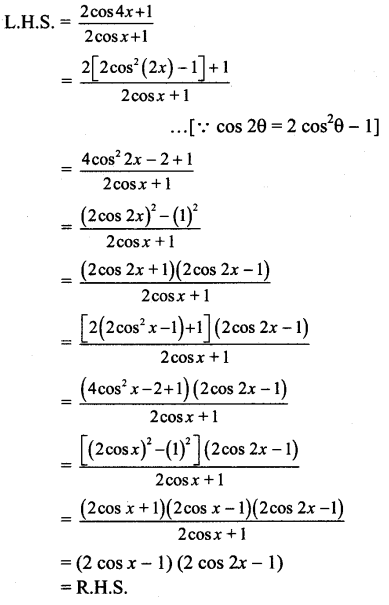
xvi. = cos² x + cos² (x + 120°) + cos²(x – 120°) = \(\frac{3}{2}\)
Solution:
L.H.S = cos² x + cos² (x + 120°) + cos²(x – 120°) =

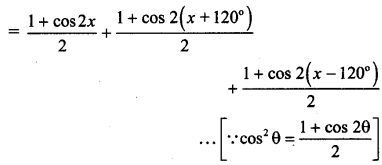
\(\frac{3}{2}+\frac{1}{2}\) [cos 2x + cos(2x + 240°) + cos(2x 240°)]
= \(\frac{3}{2}+\frac{1}{2}\)(cos 2x + cos 2x cos 240°— sin 2x sin 240° + cos 2x cos 240° + sin 2x sin 240°)
= \(\frac{3}{2}+\frac{1}{2}\)(cos 2x + 2 cos 2x cos 240°)
= \(\frac{3}{2}+\frac{1}{2}\) [cos 2x + 2 cos 2x cos( 180° + 60°)]
= \(\frac{3}{2}+\frac{1}{2}\) [cos 2x + 2cos 2x(-cos 600)]
= \(\frac{3}{2}+\frac{1}{2}\) [cos 2x —2 cos 2x(\(\frac{1}{2}\))]
= \(\frac{3}{2}+\frac{1}{2}\) ( cos 2x – cos 2x)
= \(\frac{3}{2}+\frac{1}{2}\) (0)
= \(\frac{3}{2}\) = R.H.S.

xvii. 2 cosec 2x + cosec x = sec cot \(\frac{x}{2}\)
Solution:

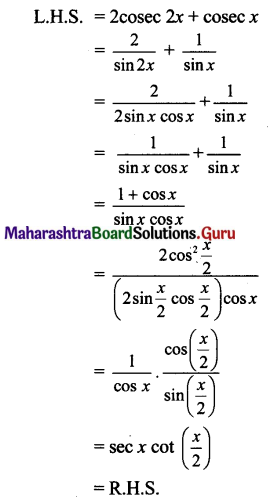
xviii. 4 cos x cos (\(\frac{\pi}{3}\) + x) cos (\(\frac{\pi}{3}\) – x) = cos 3x
\(\)
Solution:

= cos³x — 3cos x.sin²x
= cos³ x — 3cos x (1— cos² x)
= cos³x — 3cos x + 3 cos³x
=4 cos³x — 3cos x
= cos 3x = R.H.S.
INote: The question has been modijìed.I

xix. sin x tan \(\frac{x}{2}\) + 2cos x = \(\frac{2}{1+\tan ^{2}\left(\frac{x}{2}\right)}\)
Solution:
L.H.S. = sin x tan (x/2)+ 2cos x
= \(\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\) + 2cos x
= \(\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\) + 2 cos x
= 2sin² x/2 + 2cosx
= 1 – cosx + 2cosx
= 1 + cos x
=2cos² x/2
= \(\frac{2}{\sec ^{2} \frac{x}{2}}=\frac{2}{1+\tan ^{2} \frac{x}{2}}\) =R.H.S.

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.2 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.2 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
i. sin 690°
ii. sin 495°
iii. cos 315°
iv. cos 600°
v. tan 225°
vi. tan (- 690°)
vii. sec 240°
viii. sec (- 855°)
ix. cosec 780°
x. cot (-1110°)
Solution:
i. sin 690° = sin (720° -30°)
Solution:
i. sin 690° = sin (720° -30°)
= sin (2 x 360° – 30°)
= – sin 30°
= \(\frac{-1}{2}\)

ii. sin 495° = sin (360° + 135°)
= sin (135°)
= sin (90° + 45°)
= cos 45°
= \(\frac{1}{\sqrt{2}}\)

iii. cos 315° = cos (270° + 45°)
sin 45° = \(\frac{1}{\sqrt{2}}\)

iv. cos 600° = cos (360° + 240°)
= cos 240°
= cos (180° + 60°)
= – cos 60°
= \(-\frac{1}{2}\)

v. tan 225° = tan (180° + 45°)
= tan 45°
= 1 .

vi. tan (- 690°) = – tan 690°
= – tan (720° – 30°)
= – tan (2 x 360° – 30°)
= – (- tan 30°)
= tan 30°
= \(\frac{1}{\sqrt{3}}\)

vii. sec 240° = sec (180° + 60°)
= – sec 60°
= – 2

viii. sec (-855°) = sec (855°)
= sec (720°+135°)
= sec (2 x360°+ 135°) = sec 135°
= sec (90° + 45°)
= – cosec 45°
= –\(\sqrt{2}\)

ix. cosec 780° = cosec (720° + 60°)
= cosec (2 x 360° + 60°)
= cosec 60°
= \(\frac{2}{\sqrt{3}}\)

x. cot (-1110°) =-cot (1110°)
= -cot (1080°+ 30°)
= – cot (3 x 360° + 30° )
= – cot 30°
= – \(\sqrt{3}\)

Question 2.
Prove the following:
i. \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}=\cot ^{2} x\)
ii. \(\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]\)
iii. sec 840° cot (- 945°) + sin 600° tan (- 690°) = 3/2
iv. \(\frac{{cosec}\left(90^{\circ}-x\right) \sin \left(180^{\circ}-x\right) \cot \left(360^{\circ}-x\right)}{\sec \left(180^{\circ}+x\right) \tan \left(90^{\circ}+x\right) \sin (-x)}=1\)
v. \(\frac{\sin ^{3}(\pi+x) \sec ^{2}(\pi-x) \tan (2 \pi-x)}{\cos ^{2}\left(\frac{\pi}{2}+x\right) \sin (\pi-x) {cosec}^{2}(-x)}=\tan ^{3} x\)
vi. cos θ + sin (270° + θ) – sin (270° – θ) + cos (180° + θ) = 0
Solution:
i.

ii. L.H.S.
= cos ( \(\frac{3 \pi}{2}\) + x) cos (2π + x) . [cot ( – x) + (2π + x)]
= (sin x)(cos x) (tan x + cot x)
= sin x cos x ( \(\left(\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right)\))
= sin x cos x \(\left(\frac{\sin ^{2} x+\cos ^{2} x}{\sin x \cos x}\right)\)
= sin x cos x \(\left(\frac{1}{\sin x \cos x}\right)\)
= 1 = R.H.S

iii. sec 840° = sec (720° + 120°)
= sec (2 x 360° + 120°)
= sec (120°)
= sec (90° + 30°)
= – cosec 30°
= -2

cot(-945°) = -cot 945°
= -cot (720° + 225°)
= -cot (2 x 360° +225°)
= -cot (225°)
= -cot (180° + 459)
= -cot 45°
= -1

sin 600° = sin (360° + 240°)
= sin (240°)
= sin (180° +60°)
= – sin 60° = –\(\frac{\sqrt{3}}{2}\)

tan (-690°) = – tan 690°
= – tan (360° +330°)
= -tan (330°)
=- tan (360° – 30°)
=-(-tan 30°)
= tan 30°0 = \(\frac{1}{\sqrt{3}}\)

L.H.S. = sec 840° cot (-945°) + sin 600° tan (-690°)
= (-2)(-1) + \(\left(-\frac{\sqrt{3}}{2}\right)\left(\frac{1}{\sqrt{3}}\right)\)
= 2 – \(\frac{1}{2}=\frac{3}{2}\)
= R. H. S.

iv.

= 1
= R.H.S

v.

vi. L.H.S. = cos θ + sin (270° + θ) – sin (270° – θ) + cos (180° + θ)
= cos θ + (- cos θ)-(- cos θ) – cos θ
= cos θ – cos θ + cos θ – cos θ
= 0
= R.H.S.

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.1 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.1 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
i. sin 150°
ü. cos 75°
iii. tan 105°
iv. cot 225°
Solution:
i. sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
\(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
[Note: Answer given in the textbook is \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\) However, as per our calculation it is \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

ii. cos 75° = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°

iii. tan 105° = tan (60° +45°)

iv. cot 225°

Question 2.
Perove the following:
i. \(\cos \left(\frac{\pi}{2}-x\right) \cos \left(\frac{\pi}{2}-y\right) -\sin \left(\frac{\pi}{2}-x\right) \sin \left(\frac{\pi}{2}-y\right)=-\cos (x+y)\)
Solution:
L.H.S

= -(cos x cos y – sin x sin y)
= – cos (x+y)
= R.H.S

ii. \(\tan \left(\frac{\pi}{4}+\theta\right)=\frac{1+\tan \theta}{1-\tan \theta}\)
L.H.S =\(\tan \left(\frac{\pi}{4}+\theta\right)\)

R.H.S.
[Note : The question has been modified.]

iii. \(\left(\frac{1+\tan x}{1-\tan x}\right)^{2}=\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}\)
Solution:

iv. sin [(n+1)A] . sin [(n+2)A] + cos [(n+1)A] . cos [(n+2)A] = cos A
Solution:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let(n+2)Aaand(n+l)Ab …(i)
∴ L.H.S. = cos a. cos b + sin a. sin b
= cos (a — b)
= cos [(n + 2)A — (n + I )A]
…[From (i)]
cos[(n+2 – n – 1)A]
= cos A
= R.H.S.

v. \(\sqrt{2} \cos \left(\frac{\pi}{4}-\mathrm{A}\right)=\cos \mathrm{A}+\sin \mathrm{A}\)
Solution:

vi. \(\frac{\cos (x-y)}{\cos (x+y)}=\frac{\cot x \cot y+1}{\cot x \cot y-1}\)
Solution:

vii. cos (x + y). cos (x – y) = cos²y – sin²x
Solution:
L.H.S. = cos(x + y). cos(x – y)
= (cos x cos y – sin x sin y). (cos x cos y + sin x sin y)
= cos² x cos²y – sin²x sin²y
…[∵ (a – b) (a + b) = a² – b²]
= (1 – sin²x) cos²y – sin²x (1 – cos²y)
…[∵ sin²e + cos²0 = 1]
= cos²y – cos²y sin²x – sin²x + sin²x cos²y
= cos²y – sin²x
=R.H.S.

viii.\(\frac{\tan 5 A-\tan 3 A}{\tan 5 A+\tan 3 A}=\frac{\sin 2 A}{\sin 8 A}\)
Solution:

ix. tan 8θ – tan 5θ – tan 3θ = tan 8θ tan 5θ tan 3θ
Solution:
Since, 8θ = 5θ + 3θ
∴ tan 8θ = tan (5θ + 3θ)
∴ tan 8θ = \(\frac{\tan 5 \theta+\tan 3 \theta}{1-\tan 5 \theta \tan 3 \theta}\)
∴ tan 8θ (1 – tan 5θ.tan 3θ) = tan 5θ + tan 3θ
∴ tan 8θ – tan8θ.tan5θ.tan3θ = tan5θ + tan 3θ
∴ tan 8θ – tan 5θ – tan 3θ = tan 8θ.tan 5θ.tan 3θ

x. tan 50° = tan 40° + 2tan 10°
Solution:
Since, 50° = 10° +40°
∴ tan 50° = tan (10° + 40°)
∴ \(\frac{\tan 10^{\circ}+\tan 40^{\circ}}{1-\tan 10^{\circ} \tan 40^{\circ}}\)
∴ tan 50° (1 – tan 10° tan 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan 50° = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan (90° – 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° cot 40°
= tan 10° + tan 40° …[∵ tan (90° – θ) = cot θ]
∴ tan 50° – tan 10° tan 40°. \(\frac{1}{\tan 40^{\circ}}\) = tan 10° + tan 40°
∴ tan 50° – tan 10°. 1 = tan 10° + tan 40°
∴ tan 50° = tan 40° + 2 tan 10°

xi. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\) = tan 72°
Solution:
\(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\)
Dividing numerator and cos 27°, we get denominator by cos 27°, we get

= tan (45° + 27°)
= tan 72° = R.H.S

xii. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}=\tan 72^{\circ}\)
Solution:
Since 45° = 10° + 35°,
tan 45° = tan (10° +35°)
∴ \(\frac{\tan 10^{\circ}+\tan 35^{\circ}}{1-\tan 10^{\circ} \tan 35^{\circ}}\)
∴ 1 – tan 10° tan 35o = tan 10° + tan 35°
∴ tan 10° + tan 35° + tan 10° tan 35° = 1

xiii. tan 10° + tan 35° + tan 10°. tan 35° = 1
Solution:

xiv. \(\frac{\cos 15^{\circ}-\sin 15^{\circ}}{\cos 15^{\circ}+\sin 15^{\circ}}=\frac{1}{\sqrt{3}}\)
Solution:
Dividing numerator and cos 15°, we get

= tan (45° + 15°)
= tan 30° = \(\frac{1}{\sqrt{3}}\) = R.H.S

Question 3.
If sin A = \(-\frac{5}{13}\),π < A < \(\frac{3 \pi}{2}\) and cos B = \(\frac{3}{5}, \frac{3 \pi}{2}\) < B < 2π, find
i. sin (A+B)
ii. cos (A-B)
iii. tan (A + B)
Solution:
Given, sin A = \(-\frac{5}{13}\)
We know that,
cos² A = 1 – sin²A = \(1-\left(-\frac{5}{13}\right)^{2}=1-\frac{25}{169}=\frac{144}{169}\)
∴ cos A = \(\pm \frac{12}{13}\)
Since, π < A < \(\frac{3 \pi}{2}\)
∴ ‘A’ lies in the 3rd quadrant.
∴ cos A<0
cos A = \(\frac{-12}{13}\)
Also,cos B = \(\frac{3}{5}\)
∴ sin²B = 1 – cos²B = \(1-\left(\frac{3}{5}\right)^{2}=1-\frac{9}{25}=\frac{16}{25}\)
∴ sin B = \(\pm \frac{4}{5}\)
Since, \(\frac{3 \pi}{2}\) < B < 2π
∴ ‘B’ lies in the 4th quadrant.
∴ sin B<0
Sin B = \(\frac{-4}{5}\)

i. sin (A + B) = sin A cos B+cos A sin B

ii. cos (A -B) = cos A cos B + sin A sin B

iii.

Question 4.
If tan A = \(\frac{5}{6}\) , tan B = \(\frac{1}{11}\) prove that A + B = \(\frac{\pi}{4}\)
Solution:
Given tan A = \(\frac{5}{6}\), tan B = \(\frac{1}{11}\)

∴ tan (A + B) = tan \(\frac{\pi}{4}\)
∴ A + B = \(\frac{\pi}{4}\) Class 11 Maths Solutions

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 2 Trigonometry – I Miscellaneous Exercise 2 Questions and Answers.

11th Maths Part 1 Trigonometry – I Miscellaneous Exercise 2 Questions And Answers Maharashtra Board

I. Select the correct option from the given alternatives.

Question 1.
The value of the expression
cos1°. cos2°. cos3° … cos 179° =
(A) -1
(B) 0
(C) \(\frac{1}{\sqrt{2}}\)
(D) 1
Answer:
(B) 0

Explanation:
cos 1° cos 2° cos 3° … cos 179°
= cos 1° cos 2° cos 3° … cos 90°… cos 179°
= 0 …[∵ cos 90° = 0]

Question 2.
\(\frac{\tan \mathrm{A}}{1+\sec \mathrm{A}}+\frac{1+\sec \mathrm{A}}{\tan \mathrm{A}}\) is equal to
(A) 2cosec A
(B) 2 sec A
(C) 2 sin A
(D) 2 cos A
Answer:
(A) 2cosec A

Explanation:

Question 3.
If α is a root of 25cos² θ + 5cos θ – 12 = 0, \(\frac{\pi}{2}\) < α < π, then sin 2α is equal to
(A) \(-\frac{24}{25}\)
(B) \(-\frac{13}{18}\)
(C) \(\frac{13}{18}\)
(D) \(\frac{24}{25}\)
Answer:
(A) \(-\frac{24}{25}\)

Explanation:

25 cos² θ + 5 cos θ – 12 = 0
∴ (5cos θ + 4) (5 cos θ – 3) = 0
∴ cos θ = \(-\frac{4}{5}\) or cos θ = \(\frac{3}{5}\)
Since \(\frac{\pi}{2}\) < α < π,
cos α < 0
∴ cos α = \(-\frac{4}{5}\)
sin² α = 1 – cos² α = 1 – \(\frac{16}{25}=\frac{9}{25}\)
∴ sin α = \(\pm \frac{3}{5}\)
Since \(\frac{\pi}{2}\) < α < π sin α > 0
∴ sin α = 3/5
sin 2 α = 2 sin α cos α
= \(2\left(\frac{3}{5}\right)\left(\frac{-4}{5}\right)=-\frac{24}{25}\)

Question 4.
If θ = 60°, then \(\frac{1+\tan ^{2} \theta}{2 \tan \theta}\) is equal to
(A) \(\frac{\sqrt{3}}{2}\)
(B) \(\frac{2}{\sqrt{3}}\)
(C) \(\frac{1}{\sqrt{3}}\)
(D) \(\sqrt{3}\)
Answer:
(B) \(\frac{2}{\sqrt{3}}\)

Explanation:

Question 5.
If sec θ = m and tan θ = n, then \(\frac{1}{m}\left\{(m+n)+\frac{1}{(m+n)}\right\}\) is equal to
(A) 2
(B) mn
(C) 2m
(D) 2n
Answer:
(A) 2
Explanation:

Question 6.
If cosec θ + cot θ = \(\frac{5}{2}\), then the value of tan θ is
(A) \(\frac{14}{25}\)
(B) \(\frac{20}{21}\)
(C) \(\frac{21}{20}\)
(D) \(\frac{15}{16}\)
Answer:
(B) \(\frac{20}{21}\)

Explanation:
cosec θ + cot θ = \(\frac{5}{2}\) …………….(i)
cosec² θ – cot² θ = 1
∴ (cosec θ + cot θ) (cosec θ – cot θ) = 1
∴ \(\frac{5}{2}\) (cosec θ – cot θ) = 1
∴ cosec θ – cot θ = \(\frac{2}{5}\) …(ii)
Subtracting (ii) from (i), we get
2 cot θ = \(\frac{5}{2}-\frac{2}{5}=\frac{21}{10}\)
∴ cot θ = \(\frac{21}{20}\)
∴ tan θ = \(\frac{20}{21}\)

Question 7.
\(1-\frac{\sin ^{2} \theta}{1+\cos \theta}+\frac{1+\cos \theta}{\sin \theta}-\frac{\sin \theta}{1-\cos \theta}\) equals
(A) 0
(B) 1
(C) sin θ
(D) cos θ
Answer:
(D) cos θ

Explanation:

Question 8.
If cosec θ – cot θ = q, then the value of cot θ is
(A) \(\frac{2 q}{1+q^{2}}\)
(B) \(\frac{2 q}{1-q^{2}}\)
(C) \(\frac{1-\mathrm{q}^{2}}{2 \mathrm{q}}\)
(D) \(\frac{1+q^{2}}{2 q}\)
Answer:
(C) \(\frac{1-\mathrm{q}^{2}}{2 \mathrm{q}}\)

Explanation:

cosec θ – cot θ = q ……(i)
cosec² θ – cot² θ = 1
∴ (cosec θ + cot θ) (cosec θ – cot θ) = 1
∴ (cosec θ + cot θ)q = 1
∴ cosec θ + cot θ = 1/q …….(ii)
Subtracting (i) from (ii), we get
2cot θ = \(\frac{1}{\mathrm{q}}-\mathrm{q}\)
∴ cot θ = \(\frac{1-q^{2}}{2 q}\)

Question 9.
The cotangent of the angles \(\frac{\pi}{3}, \frac{\pi}{4}\) and \(\frac{\pi}{6}\) are in
(A) A.P.
(B) G.P.
(C) H.P.
(D) Not in progression
Answer:
(B) G.P.

Explanation:

Question 10.
The value of tan 1°.tan 2° tan 3° equal to
(A) -1
(B) 1
(C) \(\frac{\pi}{2}\)
(D) 2
Answer:
(B) 1

Explanation:

tan1° tan2° tan3° … tan89°
= (tan 1° tan 89°) (tan 2° tan 88°)
…(tan 44° tan 46°) tan 45°
= (tan 1 ° cot 1 °) (tan 2° cot 2°)
…(tan 44° cot 44°) . tan 45°
…tan(∵ 90° – θ) = cot θ]
= 1 x 1 x 1 x … x 1 x tan 45° =1

II. Answer the following:

Question 1.
Find the trigonometric functions of:
90°, 120°, 225°, 240°, 270°, 315°, -120°, -150°, -180°, -210°, -300°, -330°
Solution:
Angle of measure 90° :
Let m∠XOA = 90°
Its terminal arm (ray OA)
intersects the standard, unit circle at P(0, 1).

∴ x = 0 and y = 1
sin 90° = y = 1
cos 90° = x = 0
tan 90° = \(\frac{y}{x}=\frac{1}{0}\), which is not defined
cosec 90° = \(\frac{1}{y}=\frac{1}{1}\) = 1
sec 90° = \(\frac{1}{x}=\frac{1}{0}\), which is not defined
cot 90° = \(\frac{x}{y}=\frac{0}{1}\) = 0

Angle of measure 120° :
Let m∠XOA =120°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1

Since point P lies in the 2nd quadrant, x < 0, y > 0

[Note: Answer given in the textbook of tan 120° is \(\frac{-1}{\sqrt{3}}\) and cot 120° is \(-\sqrt{3}\). However, as per our \(-\sqrt{3}\) calculation the answer of tan 120° is \(-\sqrt{3}\) and cot 120° is \(-\frac{1}{\sqrt{3}}\)

Angle of measure 225° :
Let m∠XOA = 225°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 45° – 45° – 90° triangle.
OP = 1

Since point P lies in the 3rd quadrant, x < 0, y < 0

Angle of measure 240° :
Let m∠XOA = 240°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 30° – 60° – 90° triangle.
OP = 1

Since point P lies in the 3rd quadrant, x < 0, y < 0

Angle of measure 270° :
Let m∠XOA = 270°
Its terminal arm (ray OA) intersects the standard unit circle at P(0, – 1).
x = 0 andy = – 1
sin 270° = y = -1
cos 270° = x = 0
tan 270° = \(\frac{y}{x}\)

Angle of measure 315° :
Let m∠XOA = 315°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 45° – 45° – 90° triangle.
OP = 1


[Note: Answer given in the textbook of cot 315° is 1. However, as per our calculation it is -1.]

Angle of measure (-120°):
Let m∠XOA = – 120°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,

Since point P lies in the 3rd quadrant, x < 0, y < 0

Angle of measure (-150°) :
Let m∠XOA = – 150°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1

Angle of measure (-180°):
Let m∠XOA = – 180°
Its terminal arm (ray OA) intersects the standard unit circle at P(- 1, 0).
∴ x = – 1 andy = 0
sin (-180°) = y = 0
cos (-180°) = x
= -1

Angle of measure (- 210°):
Let m∠XOA = -210°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1

Angle of measure (- 300°):
Let m∠XOA = – 300° Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 30° – 60° – 90° triangle.
OP = 1

Since point P lies in the 1st quadrant, x>0,y>0
x = OM = \(\frac{1}{2}\) and
y = PM = \(\frac{\sqrt{3}}{2}\)

Angle of measure (- 330°):
Let m∠XOA = – 330°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1

Since point P lies in the 1st quadrant, x > 0, y > 0
∴ x = OM = \(\frac{\sqrt{3}}{2}\) and y = PM = \(\frac{1}{2}\)

Question 2.
State the signs of:
i. cosec 520°
ii. cot 1899°
iii. sin 986°
Solution:
i. 520° =360° + 160°
∴ 520° and 160° are co-terminal angles.
Since 90° < 160° < 180°,
160° lies in the 2nd quadrant.
∴ 520° lies in the 2nd quadrant,
∴ cosec 520° is positive.

ii. 1899° = 5 x 360° + 99°
∴ 1899° and 99° are co-terminal angles.
Since 90° < 99° < 180°,
99° lies in the 2nd quadrant.
∴ 1899° lies in the 2nd quadrant.
∴ cot 1899° is negative.

iii. 986° = 2x 360° + 266°
∴ 986° and 266° are co-terminal angles.
Since 180° < 266° < 270°,
266° lies in the 3rd quadrant.
∴ 986° lies in the 3rd quadrant.
∴ sin 986° is negative.

Question 3.
State the quadrant in which 6 lies if
i. tan θ < 0 and sec θ > 0
ii. sin θ < 0 and cos θ < 0
iii. sin θ > 0 and tan θ < 0
Solution:
i. tan θ < 0 tan θ is negative in 2nd and 4th quadrants, sec θ > 0
sec θ is positive in 1st and 4th quadrants.
∴ θ lies in the 4th quadrant.

ii. sin θ < 0
sin θ is negative in 3rd and 4th quadrants, cos θ < 0
cos θ is negative in 2nd and 3rd quadrants.
.’. θ lies in the 3rd quadrant.

iii. sin θ > 0
sin θ is positive in 1st and 2nd quadrants, tan θ < 0
tan θ is negative in 2nd and 4th quadrants.
∴ θ lies in the 2nd quadrant.

Question 4.
Which is greater?
sin (1856°) or sin (2006°)
Solution:
1856° = 5 x 360° + 56°
∴ 1856° and 56° are co-terminal angles.
Since 0° < 56° < 90°, 56° lies in the 1st quadrant.
∴ 1856° lies in the 1st quadrant,
∴ sin 1856° >0 …(i)
2006° = 5 x 360° + 206°
∴ 2006° and 206° are co-terminal angles.
Since 180° < 206° < 270°,
206° lies in the 3rd quadrant.
∴ 2006° lies in the 3rd quadrant,
∴ sin 2006° <0 …(ii)
From (i) and (ii),
sin 1856° is greater.

Question 5.
Which of the following is positive?
sin(-310°) or sin(310°)
Solution:
Since 270° <310° <360°,
310° lies in the 4th quadrant.
∴ sin (310°) < 0
-310° = -360°+ 50°
∴ 50° and – 310° are co-terminal angles.
Since 0° < 50° < 90°, 50° lies in the 1st quadrant.
∴ – 310° lies in the 1st quadrant.
∴ sin (- 310°) > 0
∴ sin (- 310°) is positive.

Question 6.
Show that 1 – 2sin θ cos θ ≥ 0 for all θ ∈ R.
Solution:
1 – 2 sin θ cos θ
= sin² θ + cos² θ – 2sin θ cos θ
= (sin θ – cos θ)² ≥ 0 for all θ ∈ R

Question 7.
Show that tan² θ + cot² θ ≥ 2 for all θ ∈ R.
Solution:

Question 8.
If sin θ = \(\frac{x^{2}-y^{2}}{x^{2}+y^{2}}\), then find the values of cos θ, tan θ in terms of x and y.
Solution:
Given, sin θ = \(\frac{x^{2}-y^{2}}{x^{2}+y^{2}}\)
we know that
cos²θ = 1 – sin² θ

[Note: Answer given in the textbook of cos θ = \(\frac{2 x y}{x^{2}+y^{2}}\) and tan θ = \(. However, as per our calculation the answer of cos θ = ± [latex]\frac{2 x y}{x^{2}+y^{2}}\) and tan θ = ± \(\frac{x^{2}-y^{2}}{2 x y}\). ]

Question 9.
If sec θ = \(\sqrt{2}\) and \(\frac{3 \pi}{2}\) < θ < 2π, then evaluate \(\frac{1+\tan \theta+{cosec} \theta}{1+\cot \theta-{cosec} \theta}\)
Solution:
Given sec θ = \(\sqrt{2}\)
We know that,
tan² θ = sec² θ – 1
= (\(\sqrt{2}\)) – 1
= 2 – 1 = 1
∴ tan θ = ±1
Since \(\frac{3 \pi}{2}\) < θ < 2π
θ lies in the 4th quadrant.
∴ tan θ < 0
∴ tan θ = -1

Question 10.
Prove the following:

i. sin²A cos² B + cos²A sin²B + cos²A cos²B + sin²A sin²B = 1
Solution:
L.H.S. = sin²A cos² B + cos²A sin²B + cos²A cos²B + sin²A sin²B
= sin²A (cos² B + sin² B) + cos² A (sin² B + cos² B)
= sin²A(1) + cos²A(1)
= 1 = R.H.S.

ii. \(\frac{(1+\cot \theta+\tan \theta)(\sin \theta-\cos \theta)}{\sec ^{3} \theta-{cosec}^{3} \theta}=\sin ^{2} \theta \cos ^{2} \theta\)
Solution:

iii. L.H.S. = \(\left(\tan \theta+\frac{1}{\cos \theta}\right)^{2}+\left(\tan \theta-\frac{1}{\cos \theta}\right)^{2}=2\left(\frac{1+\sin ^{2} \theta}{1-\sin ^{2} \theta}\right)\)
Solution:
L.H.S. = \(\left(\tan \theta+\frac{1}{\cos \theta}\right)^{2}+\left(\tan \theta-\frac{1}{\cos \theta}\right)^{2}\)
= (tanθ + secθ)² + (tanθ – secθ)²
= tan² θ + 2 tan θ sec θ + sec² θ
+ tan² θ – 2 tan θ sec θ +.sec² θ
= 2(tan² θ + sec² θ)

iv. 2.sec² θ – sec⁴ θ – 2.cosec² θ + cosec⁴ θ = cot⁴ θ – tan⁴ θ
Solution:
LHS.
= 2.sec² θ – sec⁴ θ – 2.cosec² θ + cosec⁴ θ =  = 2 sec² θ – (sec² θ)² – 2cosec² θ + (cosec² θ)²
= 2(1+ tan² θ) – (1+ tan² θ)² – 2(1+ cot² θ)
+ (1+ cot² θ)²
= 2 + 2tan² θ – (1 + 2tan² θ + tan⁴ θ)
– 2 – 2cot² θ + 1 + 2cot² θ + cot⁴ θ
= 2 + 2.tan² θ – 1 – 2 tan² θ – tan⁴ θ – 2
– 2 cot² θ + 1 + 2 cot² θ + cot⁴ θ
= cot⁴ θ – tan⁴ θ = R.H.S.

v. sin⁴ θ + cos⁴ θ = sin⁴ θ + cos⁴ θ
Solution:
L.H.S. = sin⁴ θ + cos⁴ θ
= (sin² θ)² + (cos² θ)² = (sin² θ + cos² θ)² – 2sin² θ cos² θ
… [ v a² + b² = (a + b)² – 2ab]
= 1 – 2sin² θ cos² θ
= R.H.S.

vi. 2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ) + 1 = 0
L.H.S =
2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ) + 1=0
= sin⁶ θ + cos⁶ θ
= (sin² θ)³ + (cos² θ)³ = (sin² θ + cos² θ)³
– 3 sin² θ cos² θ (sin2 0 + cos2 0)
…[••• a³ + b³ = (a + b)³ – 3ab(a + b)]
= (1)³ – 3 sin² θ cos² θ(1)
= 1-3 sin² θ cos² θ sin⁴ θ + cos⁴ θ
= (sin² θ)² + (cos² θ)² = (sin² θ + cos² θ)² – 2 sin² θ cos² θ
…[Y a² + b² = (a + b)² – 2ab]
= 1-2 sin² θ cos² θ
L.H.S.= 2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ) + 1
= 2(1-3 sin² θ cos² θ) -3(1 – 2 sin² θ cos² θ) + 1
= 2-6 sin² θ cos² θ – 3 + 6 sin² θ cos² θ + 1 = c
= R.H.S.

vii. cos⁴ θ – sin⁴ θ + 1 = 2cos²θ
L.H.S. = cos⁴ θ – sin⁴ θ + 1
= (cos² θ)² – (sin² θ)² + 1 = (cos²θ + sin²θ) c(os² θ – sin²θ) +1
= (1) (cos²θ – sin²θ) + 1 = cos² θ + (1 – sin²θ)
= cos² θ + cos²θ = 2cos²θ = R.H.S.

viii. sin⁴θ + 2sin²θ cos²θ = 1 – cos⁴θ
L.H.S. = sin⁴θ + 2sin²θ cos²θ = sin²θ(sin²θ + 2cos²θ)
= (sin²θ) (sin²θ + cos²θ + cos²θ) = (1 – cos²θ) (1 + cos²θ)
= 1 – cos⁴θ = R.H.S.

ix. \(\frac{\sin ^{3} \theta+\cos ^{3} \theta}{\sin \theta+\cos \theta}+\frac{\sin ^{3} \theta-\cos ^{3} \theta}{\sin \theta-\cos \theta}=2\)
Solution:

= (sin² θ + cos² θ – sin θ cos θ) + (sin² θ + cos² θ + sinθ cosθ)
= 2 (sin² θ + cos² θ)
= 2(1)
= 2 = R.H.S.

x. tan² θ – sin² θ = sin⁴ θ sec² θ
Solution:
L.H.S. = tan² θ – sin² θ
= \(\frac{\sin ^{2} \theta}{\cos ^{2} \theta}\) – sin²θ
= sin² θ (\(\frac{1}{\cos ^{2} \theta}-1 \))
= \(\frac{\sin ^{2} \theta\left(1-\cos ^{2} \theta\right)}{\cos ^{2} \theta}\)
= (sin² θ) (sin² θ)sec² θ
= sin⁴ θ sec² θ
= R.H.S

xi. (sinθ + cosecθ)² + (cos θ + see θ)² = tan² θ + cot² θ + 7
Solution:
L.H.S. = (sinθ + cosecθ)² + (cos θ + see θ)²
= sin ² θ + cosec² θ + 2sinθ cosec θ
+ cos² θ + sec² θ + 2sec0 cos0
= (sin² θ + cos² θ) + cosec² θ + 2 + sec² θ + 2
= 1 + (1 + cot² θ) + 2 + (1 + tan² θ) + 2 = tan² θ + cot² θ + 7
= R.H.S.

xii. sin⁸θ – cos⁸θ = (sin² θ – cos² θ) (1 – 2sin² θ cos² θ)
Solution:
L.H.S. = sin⁸θ – cos⁸θ
= (sin⁴θ)² – (cos⁴θ)²
= (sin⁴θ – cos⁴θ) (sin⁴θ + cos⁴θ)
= [(sin² θ)² – (cos² θ)² ]
. [(sin² θ)² + (cos² θ)² ]
= (sin² θ + cos² θ) (sin² θ – cos² θ). [(sin² θ + cos² θ)² – 2sin² θ.cos² θ] …[Y a² + b² = (a + b)² – 2ab]
= (1) (sin² θ – cos² θ) (1² – 2sin² θ cos² θ)
= (sin² θ – cos² θ) (1 – 2sin² θ cos² θ)
= R.H.S.

xiii. sin⁶A + cos⁶A = 1 – 3 sin²A + 3sin⁴A
Soluiton:
L.H.S. = sin⁶A + cos⁶A
= (sin² A)³ + (cos² A)³
= (sin² A + cos² A)³
– 3sin²A cos²A(sin² A + cos² A)
…[ a³ + b³ = (a + b)³ – 3ab(a + b)]
= 1³ – 3sin²A cos²A (1)
= 1 – 3sin²A cos²A
= 1 – 3 sin²A (1 – sin²A)
= 1 – 3 sin²A + 3sin⁴A
= R.H.S.

xiv. (1 + tanA tanB)² + (tanA – tanB)² = sec ²A sec²B
Solution:
L.H.S. = (1 + tanA tanB)² + (tanA – tanB)²
= 1 + 2tanA tanB + tan²A tan² + tan² A- 2tanA tanB + tan²B
= 1 + tan²A + tan² B + tan²A tan²B
= 1(1+ tan²A) + tan² B(1 + tan²A)
= (1 + tan²A) (1 + tan²B)
= sec²A sec²B = R.H.S.

xv. \(\frac{1+\cot \theta+{cosec} \theta}{1-\cot \theta+{cosec} \theta}=\frac{{cosec} \theta+\cot \theta-1}{\cot \theta-{cosec} \theta+1}\)
Solution:
We know that cosec²θ – cot² θ = 1
∴ (cosec θ – cot θ) (cosec θ + cot θ) = 1

xvi. \(\frac{\tan \theta+\sec \theta-1}{\tan \theta+\sec \theta+1}=\frac{\tan \theta}{\sec \theta+1}\)
Solution:
We know that
tan²θ = sec² θ – 1
∴ tan θ. tanθ = (sec θ + 1)(sec θ – 1)

xvii. \(\frac{{cosec} \theta+\cot \theta-1}{{cosec} \theta+\cot \theta+1}=\frac{1-\sin \theta}{\cos \theta}\)
Solution:
We know that,
cot² θ = cosec² θ – 1
∴ cot θ . cot θ = (cosec θ + 1)(cosec θ – 1)

Alternate Method:

xviii. \(\frac{{cosec} \theta+\cot \theta+1}{\cot \theta+{cosec} \theta-1}=\frac{\cot \theta}{{cosec} \theta-1}\)
solution:
We know that,
cot² θ = cosec² θ – 1
∴ cot θ.cot θ = (cosec θ + 1) (cosec θ – 1)

Maharashtra State Board 11th Maths Book Solutions 

• Trigonometry – I Ex 2.1 Class 11 Maths Solutions
• Trigonometry – I Ex 2.2 Class 11 Maths Solutions
• Trigonometry – I Miscellaneous Exercise 2 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 2 Trigonometry – I Ex 2.2 Questions and Answers.

11th Maths Part 1 Trigonometry – I Exercise 2.2 Questions And Answers Maharashtra Board

Question 1.
If 2sin A = 1 = \(\sqrt{2}\) cos B and \(\frac{\pi}{2}\) < A < π, \(\frac{3 \pi}{2}\)
Solution:
Given, 2sin A = 1
∴ sin A = 1/2
we know that,
cos² A = 1 – sin² A = 1 – \(\left(\frac{1}{2}\right)^{2}=1-\frac{1}{4}=\frac{3}{4}\)
∴ cos A = \(\pm \frac{\sqrt{3}}{2}\)
Since \(\frac{\pi}{2}\) < A < π
A lies in the 2nd quadrant.

We know that,
Sin² B = 1 – cos² B = 1 – \(\left(\frac{1}{\sqrt{2}}\right)^{2}\)\(\frac{1}{2}=\frac{1}{2}\)
∴ sin B = \(\pm \frac{1}{\sqrt{2}}\)
Since \(\frac{3 \pi}{2}\) < B < 2π
B lies in the 4th quadrant,

Question 2.
If \(\) and A, B are angles in the second quadran, then prove that 4cosA + 3 cos B = -5
Solution:
Given, \(\frac{\sin \mathrm{A}}{3}=\frac{\sin \mathrm{B}}{4}=\frac{1}{5}\)
∴ sin A = \(\frac{3}{5}\) and sin B = \(\frac{4}{5}\)
We know that,
cos² A = 1 – sin² = 1 – \(\left(\frac{3}{5}\right)^{2}\) = 1 – \(\frac{9}{25}=\frac{16}{25}\)
∴ Cos A = ± \([{4}{5}\)
Since A lies in the second quadrant,
cos A < 0
∴ Cos A = –\(\frac{4}{5}\)
Sin B = 4/5
We know that,
cos²B = 1 – sin²B = 1 – \(\left(\frac{4}{5}\right)^{2}=1-\frac{16}{25}=\frac{9}{25}\)
∴ Cos B = ±\(\frac{4}{5}\)
Since B lies in the second quadrant, cos B < 0

Question 3.
If tan θ = \(\frac{1}{2}\), evaluate \(\frac{2 \sin \theta+3 \cos \theta}{4 \cos \theta+3 \sin \theta}\)
Solution:

Question 4.
Eliminate 0 from the following:
i. x = 3sec θ, y = 4tan θ
ii. x = 6cosec θ,y = 8cot θ
iii. x = 4cos θ – 5sin θ, y = 4sin θ + 5cos θ
iv. x = 5 + 6 cosec θ,y = 3 + 8 cot θ
v. x = 3 – 4tan θ,3y = 5 + 3sec θ
Solution:
i. x = 3sec θ, y = 4tan θ
∴ sec θ = \(\frac{x}{3}\) and tan θ= \(\frac{y}{4}\)
We know that,
sec²θ – tan²θ = 1

∴ 16x² – 9y² = 144

ii. x = 6cosec θ and y = 8cot θ
.’. cosec θ = \(\) and cot θ = \(\)
We know that,
cosec² θ – cot² θ =

16x² – 9y² = 576

iii. x = 4cos θ – 5 sin θ … (i)
y = 4sin θ + 5cos θ .. .(ii)
Squaring (i) and (ii) and adding, we get
x² + y² = (4cos θ – 5sin θ)² + (4sin θ + 5cos θ)²
= 16cos²θ – 40 sinθ cosθ + 25 sin²θ + 16 sin² θ + 40sin θ cos θ + 25 cos² θ
= 16(sin² θ + cos² θ) + 25(sin² θ + cos² θ)
= 16(1) + 25(1)
= 41

iv. x = 5 + 6cosec θ andy = 3 + 8cot θ
∴ x – 5 = 6cosec θ and y – 3 = 8cot θ
∴ cosec θ = \(\frac{x-5}{6}\) and cot θ = \(\frac{y-3}{8}\)
We know that,
cosec² θ – cot² θ = 1
∴ \(\left(\frac{x-5}{6}\right)^{2}-\left(\frac{y-3}{8}\right)^{2}\) = 1

v. 2x = 3 – 4tan θ and 3y = 5 + 3sec θ
∴ 2x – 3 = -4tan θ and 3y – 5 = 3sec θ
∴ tan θ = \(\frac{3-2 x}{4}\) and sec θ = \(\frac{3 y-5}{3}\)θ
We know that, sec² θ – tan² θ = 1
∴ \(\left(\frac{3 y-5}{3}\right)^{2}-\left(\frac{3-2 x}{4}\right)^{2}\) = 1
∴ \(\left(\frac{3 y-5}{3}\right)^{2}-\left(\frac{2 x-3}{4}\right)^{2}\) = 1

Question 5.
If 2sin² θ + 3sin θ = 0, find the permissible values of cosθ.
Solution:
2sin² θ + 3sin θ = 0
∴ sin θ (2sin θ + 3) = 0
∴ sin θ = 0 or sin θ = \(\frac{-3}{2}\)
Since – 1 ≤ sin θ ≤ 1,
sin θ = 0
\(\sqrt{1-\cos ^{2} \theta}\) = 0 …[ ∵ sin² θ = 1- cos² θ]
∴ 1 – cos² θ = 0
∴ cos² θ = 1
∴ cos θ = ±1 …[∵ – 1 ≤ cos θ ≤ 1]

Question 6.
If 2cos² θ – 11 cos θ + 5 = 0, then find the possible values of cos θ.
Solution:
2cos²θ – 11 cos θ + 5 = 0
∴ 2cos² θ – 10 cos θ – cos θ + 5 = 0
∴ 2cos θ(cos θ – 5) – 1 (cos θ – 5) = 0
∴ (cos θ – 5) (2cos θ – 1) = 0
cos θ – 5 = 0 or 2cos θ – 1 = 0
∴ cos θ = 5 or cos θ = 1/2
Since, -1 ≤ cos θ ≤ 1
∴ cos θ = 1/2

Question 7.
Find the acute angle θ such 2cos² θ = 3sin θ.
Solution:
2cos²0 = 3sin θ
∴ 2(1 – sin² θ) = 3sin θ
∴ 2 – 2sin² θ = 3sin θ
∴ 2sin² θ + 3sin 9-2 = θ
∴ 2sin² θ + 4sin θ – sin θ – 2 = θ
∴ 2sin θ(sin θ + 2) -1 (sin θ + 2) = θ
∴ (sin θ + 2) (2sin θ – 1) = 0
∴ sin θ + 2 = 0 or 2sin θ – 1 = 0
∴ sin θ = -2 or sin θ = 1/2
Since, -1 ≤ sin θ ≤ 1
∴ Sin θ = 1/2
∴ θ = 30° …[ ∵ sin 30 = 1/2]

Question 8.
Find the acute angle 0 such that 5tan2 0 + 3 = 9sec 0.
Solution:
5tan² θ + 3 = 9sec θ
∴ 5(sec² θ – 1) + 3 = 9sec θ
∴ 5sec² θ – 5 + 3 = 9sec θ
∴ 5sec² θ – 9sec θ – 2 = 0
∴ 5sec² θ – 10 sec θ + sec θ – 2 = 0
∴ 5sec θ(sec θ – 2) + 1(sec θ – 2) = 0
∴ (sec θ – 2) (5sec θ + 1) = 0
∴ sec θ – 2 = 0 or 5sec θ + 1 = 0
∴ sec θ = 2 or sec θ = -1/5
Since sec θ ≥ 1 or sec θ ≤ -1,
sec θ = 2
∴ θ = 60° … [ ∵ sec 60° = 2]

Question 9.
Find sin θ such that 3cos θ + 4sin θ = 4.
Solution:
3cos θ + 4sin θ = 4
∴ 3cos θ = 4(1 – sin θ)
Squaring both the sides, we get .
9cos²θ = 16(1 – sin θ)²
∴ 9(1 – sin² θ) = 16(1 + sin² θ – 2sin θ)
∴ 9 – 9sin² θ = 16 + 16sin² θ – 32sin θ
∴ 25sin² θ – 32sin θ + 7 = 0
∴ 25sin² θ – 25sin θ – 7sin θ + 7 = 0
25sin θ (sin θ – 1) – 7 (sin θ – 1) = 0
∴ (sin θ – 1) (25sin θ – 7) = 0
∴ sin θ – 1 = 0 or 25 sin θ – 7 = 0
∴ sin θ = 1 or sin θ = \(\frac{7}{25}\)
Since, -1 ≤ sin θ ≤ 1
∴ sin θ = 1 or \(\frac{7}{25}\)
[Note: Answer given in the textbook is 1. However, as per our calculation it is 1 or \(\frac{7}{25}\).]

Question 10.
If cosec θ + cot θ = 5, then evaluate sec θ.
Solution:
cosec θ + cot θ = 5
∴ \(\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}=5\)
∴ \(\frac{1+\cos \theta}{\sin \theta}=5\)
∴ 1 + cos θ = 5.sin θ
Squaring both the sides, we get
1 + 2 cos θ + cos² θ = 25 sin² θ
∴ cos² θ + 2 cos θ + 1 = 25 (1 – cos² θ)
∴ cos² θ + 2 cos θ + 1 = 25 – 25 cos² θ
∴ 26 cos² θ + 2 cos θ – 24 = 0
∴ 26 cos² θ + 26 cos θ – 24 cos θ – 24 = 0
∴ 26 cos θ (cos θ + 1) – 24 (cos θ + 1) = 0
∴ (cos θ + 1) (26 cos θ – 24) = 0
∴ cos θ + 1 = θ or 26 cos θ – 24 = 0
∴ cos θ = -1 or cos θ = \(\frac{24}{26}=\frac{12}{13}\)
When cos θ = -1, sin θ = 0
∴ cot θ and cosec x are not defined,
∴ cos θ ≠ -1
∴ cos θ = \(\frac{12}{13}\)
∴ sec θ = \(\frac{1}{\cos \theta}=\frac{13}{12}\)
[Note: Answer given in the textbook is -1 or \(\frac{13}{12}\).
However, as per our calculation it is only \(\frac{13}{12}\).]

Question 11.
If cot θ = \(\frac{3}{4}\) and π < θ < \(\frac{3 \pi}{2}\), then find the value of 4 cosec θ + 5 cos θ.
Solution:
We know that,
cosec²θ = 1 + cot² θ = \(\left(\frac{3}{4}\right)^{2}\) = 1 + \(\frac{9}{16}\)
∴ cosec² θ = \(\frac{25}{16}\)
∴ cosec θ = \(\pm \frac{5}{4}\)
Since π < θ < \(\frac{3 \pi}{2}\)
θ lies in the third quadrant.
∴ cosec θ < 0
∴ cosec θ = –\(\frac{5}{4}\)
cot θ = \(\frac{3}{4}\)
tan θ = \(\frac{1}{\cot \theta}=\frac{4}{3}\)
We know that,
sec² θ = 1 + tan² θ = 1 + \(\left(\frac{4}{3}\right)^{2}\)
= 1 + \(\frac{16}{9}=\frac{25}{9}\)
∴ sec θ = ±\(\frac{5}{3}\)
Since θ lies in the third quadrant,
sec θ < 0
∴ sec θ = –\(\frac{5}{3}\)
cos θ = \(\frac{1}{\sec \theta}=\frac{-3}{5}\)
∴ 4cosec θ + 5cos θ
= \(4\left(-\frac{5}{4}\right)+5\left(-\frac{3}{5}\right)\)
= -5 – 3 = -8
[Note: The question has been modified.]

Question 12.
Find the Cartesian co-ordinates of points whose polar co-ordinates are:
i. (3, 90°) ii. (1, 180°)
Solution:
i. (r, θ) = (3, 90°)
Using x = r cos θ and y = r sin θ, where (x, y) are the required cartesian co-ordinates, we get
x = 3cos 90° and y = 3sin 90°
∴ x = 3(0) = 0 and y = 3(1) = 3
∴ the required cartesian co-ordinates are (0, 3).

ii. (r, θ) = (1, 180°)
Using x = r cos θ and y = r sin θ, where (x, y) are the required cartesian co-ordinates, we get
x = 1(cos 180°) and y = 1(sin 180°)
∴ x = -1 and y = 0
∴ the required cartesian co-ordinates are (-1, 0).

Question 13.
Find the polar co-ordinates of points whose Cartesian co-ordinates are:
1. (5, 5) ii. (1, \(\sqrt{3}\))
ii. (-1, -1) iv. (-\(\sqrt{3}\), 1)
Solution:
i. (x, y) = (5, 5)
∴ r = \(\sqrt{x^{2}+y^{2}}\) = \(\sqrt{25+25}\)
\(=\sqrt{50}=5 \sqrt{2}\)
tan θ = \(\frac{y}{x}=\frac{5}{5}\) = 1
Since the given point lies in the 1st quadrant,
θ = 45° …[∵ tan 45° = 1]
∴ the required polar co-ordinates are (\(5 \sqrt{2}\), 45°).

ii. (x, y) = ( 1, \(\sqrt{3}\))
∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{1+3}=\sqrt{4}=2\)
tan θ = \(\frac{y}{x}=\frac{\sqrt{3}}{1}=\sqrt{3}\)
Since the given point lies in the 1st quadrant,
θ = 60° …[∵ tan 60° = \(\sqrt{3}\)]
∴ the required polar co-ordinates are (2, 60°).

iii. (x, y) = (-1, -1)
∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{1+1}=\sqrt{2}\)
tan θ = \(\frac{y}{x}=\frac{-1}{-1}=1\)
∴ tan θ = tan \(\frac{\pi}{4}\)
Since the given point lies in the 3rd quadrant,
tan θ = tan \(\left(\pi+\frac{\pi}{4}\right)\) …[∵ tan (n + x) = tanx]
∴ tan θ = tan \(\left(\frac{5 \pi}{4}\right)\)
∴ θ = \(\frac{5 \pi}{4}\) = 225°
∴ the required polar co-ordinates are (\(\sqrt{2}\), 225°).

iv. (x, y) = (-\(\sqrt{3}\) , 1)
∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{3+1}=\sqrt{4}=2\)
tan θ = \(\frac{y}{x}=\frac{1}{-\sqrt{3}}\) = -tan \(\frac{\pi}{6}\)
Since the given point lies in the 2nd quadrant,
tan θ = tan \(\left(\pi-\frac{\pi}{6}\right)\) …[∵ tan (π – x) = – tanx]
∴ tan θ = tan \(\left(\frac{5 \pi}{6}\right)\)
∴ θ = \(\frac{5 \pi}{6}\) = 150°
∴ the required polar co-ordinates are (2, 150°)

Question 14.
Find the values of:
i. sin\(\frac{19 \pi^{e}}{3}\)
ii. cos 1140°
iii. cot \(\frac{25 \pi^{e}}{3}\)
Solution:
i. We know that sine function is periodic with period 2π.
sin \(\frac{19 \pi}{3}\) = sin \(\left(6 \pi+\frac{\pi}{3}\right)\) = sin \(\frac{\pi}{3}=\frac{\sqrt{3}}{2}\)

ii. We know that cosine function is periodic with period 2π.
cos 1140° = cos (3 × 360° + 60°)
= cos 60° = \(\frac {1}{2}\)

iii. We know that cotangent function is periodic with period π.
cot \(\frac{25 \pi}{3}\) = cot \(\left(8 \pi+\frac{\pi}{3}\right)\) = cot \(\frac{\pi}{3}\) = \(\frac{1}{\sqrt{3}}\)
dhana work.txt
Displaying dhana work.txt.

Maharashtra State Board 11th Maths Book Solutions 

• Trigonometry – I Ex 2.1 Class 11 Maths Solutions
• Trigonometry – I Ex 2.2 Class 11 Maths Solutions
• Trigonometry – I Miscellaneous Exercise 2 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 2 Trigonometry – I Ex 2.1 Questions and Answers.

11th Maths Part 1 Trigonometry – I Exercise 2.1 Questions And Answers Maharashtra Board

Question 1.
Find the trigonometric functions of 0°, 30°, 45°, 60°, 150°, 180°, 210°, 300°, 330°, – 30°, – 45°, – 60°, – 90°, – 120°, – 225°, – 240°, – 270°, – 315°
Solution:
Angle of measure 0°:

Let m∠XOA = 0° = 0^c
Its terminal arm (ray OA) intersects the standard
unit circle in P(1, 0).
Hence,x = 1 and y = 0
sin 0° = y = 0,
cos 0° = x = 1,
tan 0° = \(\frac{y}{x}=\frac{0}{1}\) = 0
cot 0° = \(\frac{x}{y}=\frac{1}{0}\) which is not defined
sec 0° = \(\frac{1}{x}=\frac{1}{1}\) = 1
cot 0° = \(\frac{1}{y}=\frac{1}{0}\) which is not defined,

Angle of measure 30°:
Let m∠XOA = 30°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y)
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1

Since point P lies in 1st quadrant, x > 0, y > 0
∴ x = OM = \(\frac{\sqrt{3}}{2}\) and y = PM = \(\frac{1}{2}\)

Angle of measure 45°:
Let m∠XOA = 45°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,

Since point P lies in the 1st quadrant, x > 0, y > 0
∴ x = OM = \(\frac{1}{\sqrt{2}}\) and
y = PM = \(\frac{1}{\sqrt{2}}\)
∴ P = (\(\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{2}}\))

Angle of measure 60°:
Let m∠XOA = 60°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,

Angle of measure 150°:
Let m∠XOA = 150°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,

Since point P lies in the 2nd quadrant, x < 0, y > 0

Angle of measure 180°:
Let m∠XOA = 180°
Its terminal arm (ray OA) intersects the standard unit circle at P(-1, 0).
∴ x = – 1 and y = 0
sin 180° =y = 0
cos 180° = x = -1

tan 180° = \(\frac{y}{x}\)
= \(\frac{0}{-1}\) = 0
Cosec 180° = \(\frac{1}{y}\)
= \(\frac{1}{0}\)
which is not defined.
sec 180°= \(\frac{1}{x}=\frac{1}{-1}\) = -1
cot 180° = \(\frac{x}{y}=\frac{-1}{0}\) , which is not defined.

Angle of measure 210°:
Let m∠XOA = 210°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,

Since point P lies in the 3rd quadrant, x < 0,y < 0
∴ x = -OM = \(\frac{-\sqrt{3}}{2}\) and y = -PM = \(\frac{-1}{2}\)
∴ P ≡( \(\frac{-\sqrt{3}}{2}, \frac{-1}{2}\) )

Angle of measure 300°:
Let m∠XOA = 300°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,

Since point P lies in the 1st quadrant, x > 0,y > 0
x = OM = \(\frac{1}{2}\) = and y = -PM = \(\frac{-\sqrt{3}}{2}\)
sin 300° = y = \(\frac{-\sqrt{3}}{2}\)
cos 300° = x = \(\frac{1}{2}\)
tan 300° = \(\frac{y}{x}=\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}=-\sqrt{3}\)

Angle of measure 330°:
Let m∠XOA = 330°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,

Since point P lies in the 4th quadrant, x > 0, y < 0

Angle of measure 30°
Let m∠XOA = -30°
Its terminal arm (ray OA) intersects the standard unit circle at P(x,y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60 — 90° triangle.
op = 1,

Since point P lies in the 4th quadrant x > 0, y < 0

Angle of measure 45°:
Let m∠XOA = 45°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,

Since point P lies in the 4th quadrant x > 0, y < 0

[Note : Answer given in the textbook of sin (45°) = – 1/2. However, as per our calculation it is \(-\frac{1}{\sqrt{2}}\) ]

Angle of measure (-60°):
Let m∠XOA = -60°
Its terminal arm (ray OA) intersects the standard
unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,

Since point P lies in the 4’ quadrant,
x > 0, y < 0
x = OM =\(\frac{1}{2}\) and y = -PM = \(-\frac{\sqrt{3}}{2}\)

Angle of measure (-90°):
Let m∠XOA = -90°
It terminal arm (ray OA) intersects the standard unit circle at P(0, -1)
∴ x = 0 and y = -1
sin (-90°) = y = -1
cos (-90°) = s = 0

Angle of measure (-120°):
Let m∠XOA = – 120°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,

Since point P lies in the 3rd quadrant, x < 0, y < 0

Angle of measure (- 225°):
Let m∠XOA = – 225°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,

Since point P lies in the 2nd quadrant, x < 0, y > 0

Angle of measure 2400):
Let m∠XOA = 240°
Its terminal arm (ray OA) intersects the standard
unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30°  – 60° –  900 triangle.

Since point P lies in the 2nd quadrant, x<0, y>0

Angle of measure (- 270°):
Let m∠XOA = – 270°
Its terminal arm (ray OA)
intersects the standard unit,
circle at P(0, 1).
∴ x = 0 and y = 1
sin (- 270°) = y = 1
cos (- 270°) = x = 0
tan(-270°)= \(\frac{y}{x}=\frac{1}{0}\)
which is not defined.

Angle of measure ( 315°):
Let m∠XOA 315°
Its terminal arm (ray OA) intersects the standard unit circle at P(x,y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,

Question 2.
State the signs of:
i. tan 380°
ii. cot 230°
iii 468°
Solution:
1. 380° = 360° + 20°
∴ 380° and 20° are co-terminal angles.
Since 0° < 20° <90°0,
20° lies in the l quadrant.
∴ 380° lies in the 1st quadrant,
∴ tan 380° is positive.

ii. Since, 180° <230° <270°
∴ 230° lies in the 3rd quadrant.
∴ cot 230° is positive.

iii. 468° = 360°+108°
∴ 468° and 108° are co-terminal angles.
Since 90° < 108° < 180°,
108° lies in the 2nd quadrant.
∴ 468° lies in the 2nd quadrant.
∴ sec 468° is negative.

Question 3.
State the signs of cos 4^c and cos 4°. Which of these two functions is greater?
Solution:
Since 0° < 4° < 90°, 4° lies in the first quadrant. ∴ cos4° >0 …(i)
Since 1^c = 57° nearly,
180° < 4^c < 270°
∴ 4^c lies in the third quadrant.
∴ cos 4^c < 0 ………(ii)
From (i) and (ii),
cos 4° is greater.

Question 4.
State the quadrant in which 6 lies if
i. sin θ < 0 and tan θ > 0
ii. cos θ < 0 and tan θ > 0
Solution:
i. sin θ < 0 sin θ is negative in 3rd and 4th quadrants, tan 0 > 0
tan θ is positive in 1st and 3rd quadrants.
∴ θ lies in the 3rd quadrant.

ii. cos θ < 0 cos θ is negative in 2nd and 3rd quadrants, tan 0 > 0
tan θ is positive in 1st and 3rd quadrants.
∴ θ lies in the 3rd quadrant.

Question 5.
Evaluate each of the following:
i. sin 30° + cos 45° + tan 180°
ii. cosec 45° + cot 45° + tan 0°
iii. sin 30° x cos 45° x lies tan 360°
Solution:
i. We know that,
sin30° = 1/2, cos 45° = \(\frac{1}{\sqrt{2}}\) =, tan 180° = 0
sin30° + cos 45° +tan 180°
= \(\frac{1}{2}+\frac{1}{\sqrt{2}}+0=\frac{\sqrt{2}+1}{2}\)

ii. We know that,
cosec 45° = \(\sqrt{2}\) , cot 45° = 1, tan 0° = 0
cosec 45° + cot 45° + tan 0°
= \(\sqrt{2}\) + 1 + 0 = \(\sqrt{2}\) + 1

iii. We know that,
sin 30° = \(\frac{1}{2}\), cos 45° = \(\frac{1}{\sqrt{2}}\) =, tan 360° = 0
sin 30° x cos 45° x tan 360°
= \(\left(\frac{1}{2}\right)\left(\frac{1}{\sqrt{2}}\right)\) = 0

Question 6.
Find all trigonometric functions of angle in standard position whose terminal arm passes through point (3, – 4).
Solution:
Let θ be the measure of the angle in standard position whose terminal arm passes through P(3, -4).
∴ x = 3 and y = -4
r = OP

Question 7.
If cos θ = \(\frac{12}{13}, 0<\theta<\frac{\pi}{2}\) find the value of \(\frac{\sin ^{2} \theta-\cos ^{2} \theta}{2 \sin \theta \cos \theta}, \frac{1}{\tan ^{2} \theta}\)
Solution:
cos θ = \(\frac{12}{13}\)
We know that,
sin² θ = 1 – cos²θ

∴ sin θ = ± \(\frac{5}{13}\)
Since 0 < θ < \(\frac{\pi}{2}\) , θ lies in the 1st quadrant, ∴ sin θ > 0

Question 8.
Using tables evaluate the following:
i. 4 cot 45° – sec2 60° + sin 30°
ii.\(\cos ^{2} 0+\cos ^{2} \frac{\pi}{6}+\cos ^{2} \frac{\pi}{3}+\cos ^{2} \frac{\pi}{2}\)
Solution:
i. We know that,
cot 45° = 1, sec 60° = 2, sin 30° = 1/2
4 cot 45° – sec² 60° + sin 30°
= 4(1) – (2)² + \(\frac{1}{2}\)
= 4 – 4 + \(\frac{1}{2}=\frac{1}{2}\)

ii. We know that,

Question 9.
Find the other trigonometric functions if
i. cot θ = \(-\frac{3}{5}\), and 180 < θ < 270
ii. Sec A = \(-\frac{25}{7}\) and A lies in the second quadrant.
iii cot x = \(\frac{3}{4}\), x lies in the third quadrant.
iv. tan x = \(\frac{-5}{12}\) x lies in the fourth quadrant.
Solution:
i. cot θ = \(-\frac{3}{5}\)
we know that,
sin²θ = 1 – cos²θ
= 1 – \(\left(-\frac{3}{5}\right)^{2}\)
= 1 – \(\frac{9}{25}=\frac{16}{25}\)
∴ sin θ = ± \(\frac{4}{5}\)
Since 180° < 0 < 270°,
θ lies in the 3rd quadrant.
∴ sin θ < 0

Since A lies in the 2nd quadrant,
tan A < 0

iii. Given, cot x = \(\frac{3}{4}\)
We know that,
cosec² x = 1 + cot² x
= 1 + \(\left(\frac{3}{4}\right)^{2}=1+\frac{9}{16}=\frac{25}{16}\)
∴ cosec x = ± \(\frac{5}{4}\)
Since x lies in the 3rd quadrant, cosec x < 0

iv. Given, tan x = \(-\frac{5}{12}\)
sec² x = 1 + tan²
= 1 + \(\left(-\frac{5}{12}\right)^{2}\)
= 1 + \(\frac{25}{144}=\frac{169}{144}\)
∴ sec x = ± \(\frac{13}{12}\)
Since x lies in the 4th quadrant,
sec x > 0

Maharashtra State Board 11th Maths Book Solutions 

• Trigonometry – I Ex 2.1 Class 11 Maths Solutions
• Trigonometry – I Ex 2.2 Class 11 Maths Solutions
• Trigonometry – I Miscellaneous Exercise 2 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 1 Angle and its Measurement Miscellaneous Exercise 1 Questions and Answers.

11th Maths Part 1 Angle and its Measurement Miscellaneous Exercise 1 Questions And Answers Maharashtra Board

I. Select the correct option from the given alternatives.

Question 1.
\(\left(\frac{22 \pi}{15}\right)^{c}x\) is equal to
(A) 246°
(B) 264°
(C) 224°
(D) 426°
Answer:
(B) 264°

Question 2.
156° is equal to

Answer:
(B)

Question 3.
A horse is tied to a post by a rope. If the horse moves along a circular path, always keeping the rope tight and describes 88 metres when it traces the angle of 12° at the centre, then the length of the rope is
(A) 70 m
(B) 55 m
(C) 40 m
(D) 35 m
Answer:
(A) 70 m

Question 4.
A pendulum 14 cm long oscillates through an angle of 12°, then the angle of the path described by its extremities is


Answer:
(D)

Question 5.
Angle between hands of a clock when it shows the time 9 :45 is
(A) (7.5)°
(B) (12.5)°
(C) (17.5)°
(D) (22.5)°
Answer:
(D) (22.5)°

Question 6.
20 metres of wire is available for fencing off a flower-bed in the form of a circular sector of radius 5 metres, then .the maximum area (in sq. m.) of the flower-bed is
(A) 15
(B) 20
(C) 25
(D) 30
Answer:
(C) 25
r + r + rθ = 20m
2r + rθ = 20

Question 7.
If the angles of a triangle are in the ratio 1:2:3, then the smallest angle in radian is
(A) \(\frac{\pi}{3}\)
(B) \(\frac{\pi}{6}\)
(C) \(\frac{\pi}{2}\)
(D) \(\frac{\pi}{9}\)
Answer:
(B) \(\frac{\pi}{6}\)

Question 8.
A semicircle is divided into two sectors whose angles are in the ratio 4:5. Find the ratio of their areas?
(A) 5:1
(B) 4:5
(C) 5:4
(D) 3:4
Answer:
(B) 4:5

Question 9.
Find the measure of the angle between hour- hand and the minute hand of a clock at twenty minutes past two.
(A) 50°
(B) 60°
(C) 54°
(D) 65°
Answer:
(A) 50°

Question 10.
The central angle of a sector of circle of area 9π sq.cm is 60°, the perimeter of the sector is
(A) π
(B) 3 + π
(C) 6 + π
(D) 6
Answer:
(C) 6 + π

II. Answer the following.

Question 1.
Find the number of sides of a regular polygon, if each of its interior angles is \(\frac{3 \pi^{c}}{4}\).
Solution:
Each interior angle of a regular polygon
= \(\frac{3 \pi}{4}=\left(\frac{3 \pi}{4} \times \frac{180}{\pi}\right)^{\circ}\) = 135°
Interior angle + Exterior angle = 180°
∴ Exterior angle = 180° – 135° = 45°
Let the number of sides of the regular polygon be n.
But in a regular polygon, exterior angle = \(\frac{360^{\circ}}{\text { no.of sides }}\)
∴ 45° = \(\frac{360^{\circ}}{\mathrm{n}}\)
∴ n = \(\frac{360^{\circ}}{45^{\circ}}\) = 8
∴ Number of sides of a regular polygon = 8.

Question 2.
Two circles each of radius 7 cm, intersect each other. The distance between their centres is 7√2 cm. Find the area common to both the circles.
Solution:
Let O and O₁ be the centres of two circles intersecting each other at A and B.
Then OA = OB = O₁A = O₁B = 7 cm
and OO₁ = 7√2 cm
OO₁² = 98 ………………(i)
Since OA² + O₁A² = 7²
= 98
= OO₁² …..[ from (i)]
m∠OAO₁ = 90°
□ OAO₁B is a square.
m∠AOB = m∠AO₁B = 90°

A(□ OAO₁B) = (side)² = (7)² = 49 sq.cm
∴ Required area = area of shaded portion = A(sector OAB) + A(sector O₁AB)) – A(□ OAO₁B)

Question 3.
∆PQR is an equilateral triangle with side 18 cm. A circle is drawn on segment QR as diameter. Find the length of the arc of this circle within the triangle.
Solution:
Let ‘O’ be the centre of the circle drawn on QR as a diameter.
Let the circle intersect seg PQ and seg PR at points M and N respectively.
Since l(OQ) = l(OM),
m∠OM Q = m∠OQM = 60°
m∠MOQ = 60°
Similarly, m∠NOR = 60°
Given, QR =18 cm.
r = 9 cm

θ = 60° = (60 x \(\frac{\pi}{180}\))^c
= \(\left(\frac{\pi}{3}\right)^{c}\)
∴ l(arc MN) = S = rθ = 9 x \(\frac{\pi}{3}\) = 3π cm.

Question 4.
Find the radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm.
Solution:
Let S be the length of the arc and r be the radius of the circle.
θ = 60° = \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
S = 37.4 cm
Since S = rθ,

Question 5.
A wire of length 10 cm is bent so as to form an arc of a circle of radius 4 cm. What is the angle subtended at the centre in degrees?
Solution:
S = 10 cm and r = 4 cm
Since S = rθ,
10 = 4 x θ

Question 6.
If two arcs of the same length in two circles subtend angles 65° and 110° at the centre. Find the ratio of their radii.
Solution:
Let r₁ and r₂ be the radii of the two circles and let their arcs of same length S subtend angles of 65° and 110° at their centres.
Angle subtended at the centre of the first circle,

Angle subtended at the centre of the second circle,

Question 7.
The area of a circle is 81TH sq.cm. Find the length of the arc subtending an angle of 300° at the centre and also the area of corresponding sector.
Solution:
Area of circle = πr²
But area is given to be 81 n sq.cm
∴ πr² = 81π
∴ r2 = 81
∴ r = 9 cm
θ = 300° = \(=\left(300 \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(\frac{5 \pi}{3}\right)^{\mathrm{c}}\)
Since S = rθ
S = 9 x \(\frac{5 \pi}{3}\) = 15π cm
Area of sector = \(\frac{1}{2}\) x r x S
= \(\frac{1}{2}\) x 9 x 15π = \(\frac{135 \pi}{2}\) sq.cm

Question 8.
Show that minute-hand of a clock gains 5° 30′ on the hour-hand in one minute.
Solution:
Angle made by hour-hand in one minute
\(=\frac{360^{\circ}}{12 \times 60}=\left(\frac{1}{2}\right)^{\circ}\)
Angle made by minute-hand in one minute = \(\frac{360^{\circ}}{60}\) = 6°
∴ Gain by minute-hand on the hour-hand in one minute
= \(6^{\circ}-\left(\frac{1}{2}\right)^{\circ}=\left(5 \frac{1}{2}\right)^{\circ}\) = 5°30′
[Note: The question has been modified.]

Question 9.
A train is running on a circular track of radius 1 km at the rate of 36 km per hour. Find the angle to the nearest minute, through which it will turn in 30 seconds.
Solution:
r = 1km = 1000m
l(Arc covered by train in 30 seconds)
= 30 x \(\frac{36000}{60 \times 60}\)m
∴ S = 300 m
Since S = rθ,
300 = 1000 x θ

= (17.18)°
= 17° +(0.18)°
= 17° + (0.18 x 60)’ = 17° + (10.8)’
∴ θ = 17°11′(approx.)

Question 10.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Solution:

Let ‘O’ be the centre of the circle and AB be the chord of the circle.
Here, d = 40 cm
∴ r = \(\frac{40}{2}\) = 20 cm
Since OA = OB = AB,
∆OAB is an equilateral triangle.
The angle subtended at the centre by the minor
arc AOB is θ = 60° = \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
= l(minor arc of chord AB) = rθ = 20 x \(\frac{\pi}{3}\)
= \(\frac{20 \pi}{3}\) cm

Question 11.
The angles of a quadrilateral are in A.P. and the greatest angle is double the least. Find angles of the quadrilateral in radians.
Solution:
Let the measures of the angles of the quadrilateral in degrees be a – 3d, a – d, a + d, a + 3d, where a > d > 0
∴ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 360°
… [Sum of the angles of a quadrilateral is 360°]
∴ 4a = 360°
∴ a = 90°
According to the given condition, the greatest angle is double the least,
∴ a + 3d = 2.(a – 3d)
∴ 90° + 3d = 2.(90° – 3d)
∴ 90° + 3d = 180° – 6d 9d = 90°
∴ d = 10°
∴ The measures of the angles in degrees are
a – 3d = 90° – 3(10°) = 90° – 30° = 60°,
a – d = 90° – 10° = 80°,
a + d = 90°+ 10°= 100°,
a + 3d = 90° + 3(10°) = 90° + 30° = 120°

Maharashtra State Board Class 11 Maths Solutions 

• Angle and its Measurement Ex 1.1 Class 11 Maths Solutions
• Angle and its Measurement Ex 1.2 Class 11 Maths Solutions
• Angle and its Measurement Miscellaneous Exercise 1 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 1 Angle and its Measurement Ex 1.2 Questions and Answers.

11th Maths Part 1 Angle and its Measurement Exercise 1.2 Questions And Answers Maharashtra Board

Question 1.
Find the length of an arc of a circle which subtends an angle of 108° at the centre, if the radius of the circle is 15 cm.
Solution:
Here, r = 15cm and
θ = 108° = \(\left(108 \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(\frac{3 \pi}{5}\right)^{\mathrm{c}}\)
Since S = r.θ
S = 15 x \(\frac{3 \pi}{5}\)
= 9π cm.

Question 2.
The radius of a circle is 9 cm. Find the length of an arc of this circle which cuts off a chord of length equal to length of radius.
Solution:
Here, r = 9cm
Let the arc AB cut off a chord equal to the radius of the circle.
Since OA = OB = AB,
ΔOAB is an equilateral triangle.
m∠AOB = 60°
θ = 60°
= \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
Since S = r.θ,
S = 9 x \(\frac{\pi}{3}\) = 3π cm.

Question 3.
Find the angle in degree subtended at the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm.
Solution:
Here, r = 25 cm and S = 15 cm
Since S = r.θ,
15 = 25 x θ

∴ The required angle in degree is \(\left(\frac{108}{\pi}\right)^{0}\) or (34.40)°(approx.).

Question 4.
A pendulum of length 14 cm oscillates through an angle of 18°. Find the length of its path.
Solution:

Question 5.
Two arcs of the same length subtend angles of 60° and 75° at the centres of the two circles. What is the ratio of radii of two circles?
Solution:
Let r₁, and r₂ be the radii of the two circles and let their arcs of same length S subtend angles of 60° and 75° at their centres.
Angle subtended at the centre of the first circle,
θ₁ = 60° = \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
∴ S = r₁θ₁ = r₁(\(\left(\frac{\pi}{3}\right)\))
Angle subtended at the centre of the second circle,

Question 6.
The area of the circle is 2571 sq.cm. Find the length of its arc subtending an angle of 144° at the centre. Also find the area of the corresponding sector.
Solution:
Area of circle = πr²
But area is given to be 25 π sq.cm
∴ 25π = πr²
∴ r² = 25
∴ r = 5 cm
θ = 144° = \(=\left(144 \times \frac{\pi}{180}\right)^{c}=\left(\frac{4 \pi}{5}\right)^{\mathrm{c}}\)
Since s = rθ
S = 5(\(\frac{4 \pi}{5}\)) = 4π
Also, A(sector) = \(\frac{1}{2}\) x r x S = \(\frac{1}{2}\) x 5 x 4π
= 10π sq. cm

Question 7.
OAB is a sector of the circle having centre at O and radius 12 cm. If m∠AOB = 45°, find the difference between the area of sector OAB and ΔAOB.
Solution:
Here, r = 12 cm
\(\theta=45^{\circ}=\left(45 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{4}\right)^{c}\)

Draw AM ⊥ OB
In ΔOAM,

[Note: The question has been modified.]

Question 8.
OPQ is the sector of a circle having centre at O and radius 15 cm. If m∠POQ = 30°, find the area enclosed by arc PQ and chord PQ.
Solution:
Here, r = 15 cm
m∠POQ = 30°
\(\left(30 \times \frac{\pi}{180}\right)^{c}[/larex]

∴ θ = [latex]\left(\frac{\pi}{6}\right)^{c}\)
Draw QM ⊥ OP
In ΔOQM,
sin 30° = \(\frac{\text { QM }}{15}\)
QM= 15 x \(\frac{1}{2}=\frac{15}{2}\)
Shaded portion indicates the area enclosed by arc PQ and chord PQ.
∴ A(shaded portion)
= A(sector OPQ) – A(ΔOPQ)

Question 9.
The perimeter of a sector of the circle of area 25π sq.cm is 20 cm. Find the area of sector.
Solution:
Area of circle = πr²
But area is given to be 25π sq.cm.
∴ 25π = πr²
∴ r² = 25
∴ r = 5 cm
Perimeter of sector = 2r + S
But perimeter is given to be 20 cm.
∴ 20 = 2(5) + S
∴ 20 = 10 + S
∴ S = 10 cm
Area of sector = \(\frac{1}{2}\) x r x S
= \(\frac{1}{2}\) x 5 x 10
= 25sq.cm.

Question 10.
The perimeter of a sector of the circle of area 64 7i sq.cm is 56 cm. Find the area of the sector.
Solution:
Area of circle = πr²
But area is given to be 25π sq.cm.
∴ 64π = πr²
∴ r² = 64
∴ r = 8 cm
Perimeter of sector = 2r + S
But perimeter is given to be 20 cm.
∴ 56 = 2(5) + S
∴ 56 = 16 + S
∴ S = 40 cm
Area of sector = \(\frac{1}{2}\) x r x S
= \(\frac{1}{2}\) x 8 x 40
= 160sq.cm.

Maharashtra State Board Class 11 Maths Solutions 

• Angle and its Measurement Ex 1.1 Class 11 Maths Solutions
• Angle and its Measurement Ex 1.2 Class 11 Maths Solutions
• Angle and its Measurement Miscellaneous Exercise 1 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 1 Angle and its Measurement Ex 1.1 Questions and Answers.

11th Maths Part 1 Angle and its Measurement Exercise 1.1 Questions And Answers Maharashtra Board

Question 1.
(A) Determine which of the following pairs of angles are co-terminal.
i. 210°, 150°
ii. 360°, -30°
iii. -180°, 540°
iv. -405°, 675°
v. 860°, 580°
vi. 900°, -900°
Solution:
210°,- 150°
210°-(- 150°) = 210°+ 150°
= 360°
= 1 (360°),
which is a multiple of 360°.
∴ The given pair of angles is co-terminal.

ii. 360°, – 30°
360° – (- 30°) = 360° + 30°
= 390°,
which is not a multiple of 360°.
∴ The given pair of angles is not co-terminal.

iii. -180°, 540°
540° -(-180°) = 540°+ 180°
= 720°
= 2(360°),
which is a multiple of 360°.
.’. The given pair of angles is co-terminal.

iv. – 405°, 675°
675° – (- 405°) = 675° + 405°
= 1080°
= 3(360°),
which is a multiple of 360°.
.’. The given pair of angles is co-terminal.

v. 860°, 580°
860° – 580° = 280°
which is not a multiple of 360, °.
∴ The given pair of angles is not co-terminal.

vi. 900°, 900°
900° – (-900°) = 900° + 900°
= 1800°
= 5(360°)
which is a multiple of 360°
∴ The given pair of angles is co-terminal.

Question 1.
(B) Draw the angles of the following measures and determine their quadrants.
i. -140°
ii. 250°
iii. 420°
iv. 750°
v. 945°
vi. 1120°
vii. – 80°
viii. – 330°
ix. – 500°
x. – 820°
Solution:

From the figure, the given angle terminates in quadrant III.

ii.

From the figure, the given angle terminates in quadrant III.

iii.

From the figure, the given angle terminates in quadrant I.

iv.

From the figure, the given angle terminates in quadrant I.

v.

From the figure, the given angle terminates in quadrant III.

vi.

From the figure, the given angle terminates in quadrant I.

vii.

From the figure, the given angle terminates in quadrant IV.

viii.

From the figure, the given angle terminates in quadrant I.

ix.

From the figure, the given angle terminates in quadrant III.
[Note: Answer given in the textbook is ‘Angle lies in quadrant II’. However, we found that it lies in quadrant III.]

x.

From the figure, the given angle terminates in quadrant III.

Question 2.
Convert the following angles into radians,
i. 85°
ii. 250°
iii. -132°
iv. 65°30′
v. 75°30′
vi. 40°48′
Solution:
we know that = \(\theta^{\circ}=\left(\theta \times \frac{\pi}{180}\right)^{c}\)
i. 85° = \(\left(85 \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(\frac{17 \pi}{36}\right)^{\mathrm{c}}\)
ii. 250° = \(\left(250 \times \frac{\pi}{180}\right)^{c}=\left(\frac{25 \pi}{18}\right)^{c}\)
iii. 132° = \(\left(-132 \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(-\frac{11 \pi}{15}\right)^{\mathrm{c}}\)
[Note : Answer given in the textbook is \(\frac{11 \pi}{15}\) However, as per our calculation it is \(\left(\frac{-11 \pi}{15}\right)^{c}\) ]

iv. 65° 30′ = 65° + 30′
= 65° + \(\left(\frac{30}{60}\right)^{\circ}\) … [1′ = (1/60)°]
= 65° + (1/2)°

v. 75° 30′ = 75° + 30′

vi. 40°48′ = 40° + 48′

Question 3.
Convert the following angles in degrees.
i. \(\frac{7 \pi^{c}}{12}\)
ii. \(\frac{-5 \pi^{c}}{3}\)
iii. 5^c
iv. \(\frac{11 \pi^{c}}{18}\)
v. \(\left(\frac{-1}{4}\right)^{c}\)
Solution:

Question 4.
Express the following angles in degrees, minutes and seconds.
i. (183.7)°
ii. (245.33)°
iii. \(\left(\frac{1}{5}\right)^{c}\)
Solution:
We know that 1° = 60′ and 1′ = 60″
i. (183.7)° = 183° +(0.7)°
= 183° + (0.7 x 60)’
= 183°+ 42′
= 183° 42′

ii. (245.33)° = 245° + (0.33)°
= 245° + (0.33 x 60)’
= 245° + (19.8)’
= 245° + 19’+ (0.8)’
= 245° 19’+ (0.8 x 60)”
= 245° 19’+ 48″
= 245° 19′ 48″

iii. We know that θ^c = (θ x \(\frac{180}{\pi}\))°

= (11.46)°
= 11° +(0.46)°
= 11° + (0.46×60)’
= 11°+ (27.6)’
= 11°+ 27’+ (0.6)’
= 11° + 27′ + (0.6×60)”
= 11°27′ + 36″
= 11°27’36” (approx.)

Question 5.
In △ABC, if m∠A = \(\frac{7 \pi^{\mathrm{c}}}{36}\), m∠B = 120°, find m∠C in degree and radian.
Solution:
We know that θ ^c = (θ x \(\left(\theta \times \frac{180}{\pi}\right)^{\circ}\) ) °
In △ABC,
m∠A = \(\frac{7 \pi^{\mathrm{c}}}{36}=\left(\frac{7 \pi}{36} \times \frac{180}{\pi}\right)^{\circ}\) = 35°
m∠B = 120°
∴ m∠A + m∠B + m∠C = 180°
… [Sum of the angles of a triangle is 180°]
∴ 35° + 120° + m∠C = 180° m∠C = 180° – 35° – 120°
∴ m∠C = 25°

Question 6.
Two angles of a triangle are \(\frac{5 \pi}{9}^{\mathrm{c}}\) and \(\frac{5 \pi}{18}^{\mathrm{c}}\) Find the degree and radian measures of third angle.
Solution:
We know that θ^c = [θ x \( ]°
The measures of two angles of a triangle are [latex]\frac{5 \pi^{\mathrm{c}}}{9}, \frac{5 \pi^{\mathrm{c}}}{18},\)
i.e., \(\left(\frac{5 \pi}{9} \times \frac{180}{\pi}\right)^{\circ},\left(\frac{5 \pi}{18} \times \frac{180}{\pi}\right)^{0}\)
i.e., 100°, 50°
Let the measure of third angle of the triangle be x°.
∴ 100°+50°+x° = 180°
…[Sum of the angles of a triangle is 180°]
∴ x° = 180°- 100° – 50°
∴ x° = 30°

∴ The degree and radian measures of the third angle are 30° and \(\left(\frac{\pi}{6}\right)^{\mathrm{c}}\) respectively.

Question 7.
In a right angled triangle, the acute angles are in the ratio 4:5. Find the angles of the triangle in degrees and radians.
Solution:
Since the triangle is aright angled triangle, one of the angles is 90°.
In the right angled triangle, the acute angles are in the ratio 4:5.
Let the measures of the acute angles of the triangle in degrees be 4k and 5k, where k is a constant.
∴ 4k + 5k+ 90°= 180°
… [Sum of the angles of a triangle is 180°]
∴ 9k = 180° – 90°
∴ 9k = 90°
∴ k = 10°
∴ The measures of the angles in degrees are
4k = 4 x 10° = 40°,
5k = 5 x 10° = 50°
and 90°.
we known that θ° = ( θ x \(\frac{\pi}{180}\)) ^c
∴ The measure of the angles in radius are

Question 8.
The sum of two angles is 5π^c and their difference is 60°. Find their measures in degrees.
Solution:
Let the measures of the two angles in degrees be x and y.
Sum of two angles is 5π^c
x + y = 5π^c
x + y = (5π x \( \frac{180}{\pi}\) ) …[ θ^c = \(\left(\theta \times \frac{180}{\pi}\right)^{\circ}\) ]
∴ x + y = 900° ………..(i)
∴ Difference of two angles is 60°.
x – y = 60° ….(ii)
Adding (i) and (ii), we get
2x = 960°
∴ x = 480°
Substituting the value of x in (i), we get
480° + y = 900°
∴ y = 900° — 480° = 420°
∴ The measures of the two angles in degrees are 480° and 420°.

Question 9.
The measures of the angles of a triangle are in the ratio 3:7:8. Find their measures in degrees and radians.
Solution:
The measures of the angles of the triangle are in the ratio 3:7:8.
Let the measures of the angles of the triangle in degrees be 3k, 7k and 8k, where k is a constant.
∴ 3k + 7k + 8k = 180°
… [Sum of the angles of a triangle is 180°]
∴ 18k =180°
∴ k = 10°
∴ The measures of the angles in degrees are
3k = 3 x 10° = 30°,
7k = 7 x 10° = 70° and
8k = 8 x 10° = 80°.

Question 10.
The measures of the angles of a triangle are in A.P. and the greatest is 5 times the smallest (least). Find the angles in degrees and radians.
Solution:
Let the measures of the angles of the triangle in degrees be a – d, a, a + d, where a > d> 0.
∴ a – d + a + a + d = 180°
…[Sum of the angles of a triangle is 180°]
∴ 3a = 180°
∴ a = 60° …(i)
According to the given condition, greatest angle is 5 times the smallest angle.
∴ a + d = 5 (a – d)
∴ a + d = 5a – 5d
∴ 6d = 4a
∴ 3d = 2a
∴ 3d = 2(60°) …[From (i)]
∴ d = \(\frac{120^{\circ}}{3}\) = 40°
∴ The measures of the angles in degrees are
a – d = 60° – 40° = 20°
a = 60° and
a + d = 60° + 40° = 100°

Question 11.
In a cyclic quadrilateral two adjacent angles are 40 and \(\frac{\pi^{c}}{3}\). Find the angles of the quadralateral in degrees.
Solution:
Let ABCD be the cyclic quadrilateral such that
∠A = 40° and

∴  ∠A + ∠C = 180°
∴ 40° + ∠C = 180°
∴ ∠C= 180°- 40°= 140°
Also, ∠B + ∠D = 180°
… [Opposite angles of a cyclic quadrilateral are supplementary]
∴ 60° + ∠D =180°
∴ ∠D = 180°- 60° = 120°
∴ The angles of the quadrilateral in degrees are 40°, 60°, 140° and 120°.

Question 12.
One angle of a quadrilateral has measure \(\frac{2 \pi^{c}}{5}\) and the measures of other three angles are in the ratio 2:3:4. Find their measures in degrees and radians.
Solution:
We know that θ^c = \(\left(\theta \times \frac{180}{\pi}\right)^{\circ}\))
One angle of the quadrilateral has measure\(\frac{2 \pi^{c}}{5}=\left(\frac{2 \pi}{5} \times \frac{180}{\pi}\right)^{\circ}=72^{\circ}\)
Measures of other three angles are in the ratio 2:3:4.
Let the measures of the other three angles of the quadrilateral in degrees be 2k, 3k, 4k, where k is a constant.
∴ 72° + 2k + 3k + 4k = 360°
…[Sum of the angles of a quadrilateral is 360°]
∴ 9k = 288°
k = 32°
∴ The measures of the angles in degrees are
2k = 2 x 32° = 64°
3k = 3 x 32° = 96°
4k = 4 x 32°= 128°
We know that θ° = (θ x \(\frac{\pi}{180}\))^c
∴ The measures of the angles in radians are

Question 13.
Find the degree and radian measures of exterior and interior angles of a regular
i. pentagon
ii. hexagon
iii. septagon
iv. octagon
Solution:
i. Pentagon:
Number of sides = 5
Number of exterior angles = 5
Sum of exterior angles = 360°

Interior angle + Exterior angle = 180°
∴ Each interior angle = 180° — 72° = 108°
= \(

ii. Hexagon:
Number of sides = 6
Number of exterior angles = 6
Sum of exterior angles = 360°

Interior angle + Exterior angle = 180°
∴ Each interior angle = 180° – 60° = 120°
= (120 x [latex]\frac{\pi}{180}\))^c = ( \(\frac{2 \pi}{3}[latex])^c

iii. Septagon:
Number of sides = 7
Number of exterior angles = 7
Sum of exterior angles = 360°
∴ Each exterior angle = [latex]\frac{360^{\circ}}{\text { no. of sides }}=\frac{360^{\circ}}{7}\)
= (51.43)°
= \(\left(\frac{360}{7} \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(\frac{2 \pi}{7}\right)^{\mathrm{c}}\)
Interior angle + Exterior angle = 180°
∴ Each interior angle = 180° – ( \(\frac{360}{7}\))°

iv. Octagon:
Number of sides = 8
Number of exterior angles = 8
Sum of exterior angles = 360°
∴ Each exterior angle = \(\frac{360^{\circ}}{\text { no. of sides }}=\frac{360^{\circ}}{8}\)
= 45°
= \(\left(45 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{4}\right)^{c}\)
Interior angle + Exterior angle = 180°
Each interior angle = 180° – 45° = 135°
= \(\left(135 \times \frac{\pi}{180}\right)^{c}=\left(\frac{3 \pi}{4}\right)^{c}\)

Question 14.
Find the angle between hour-hand and minute-hand in a clock at
i. ten past eleven
ii. twenty past seven
iii. thirty five past one
iv. quarter to six
v. 2:20
vi. 10:10
Solution:
i. At 11:10, the minute-hand is at mark 2 and hour-hand has crossed \(\left(\frac{1}{6}\right)^{\text {th }}\) of the angle between 11 and 12.

Angle between two consecutive marks = \(\frac{360^{\circ}}{12}\) = 30°
Angle traced by hour-hand in 10 minutes
= \(\frac{1}{6}\) (30°) = 5°
Angle between marks 11 and 2 = 3 x 30° = 90°
∴ Angle between two hands of the clock at ten past eleven = 90° – 5° = 85°

ii. At 7 : 20 the minute -hand is at mark 4 and hour -hand has crossed \(\left(\frac{1}{3}\right)^{ }\)rd of angle between 7 and 8.

Angle between two consecutive marks
= 360°/12 = 30°
Angle traced by hour-hand in 20 minutes
= \(\frac{1}{3}\)(30°)= 10°
Angle between marks 4 and 7 = 3 x 30° = 90°
Angle between two hands of the clock at twenty past seven = 90° – 10° = 100°

iii. At 1 : 35 the minute -hand is at mark 7 and hour -hand has crossed \(\left(\frac{7}{12}\right)^{ }\)th of angle between 1 and 2.

Angle between two consecutive marks
= 360°/12 = 30°
Angle traced by hour-hand in 35 minutes
= \(\frac{7}{12}\left(30^{\circ}\right)=\left(\frac{35}{2}\right)^{\circ}=\left(17 \frac{1}{2}\right)^{\circ}\frac{1}{3}\)
Angle between marks 1 and 7 = 6 x 30° = 180°
Angle between two hands of the clock at thirty five past one = 180° – \(\left(17 \frac{1}{2}\right)^{\circ}=\left(162 \frac{1}{2}\right)^{\circ}\)
= 162° + \(\frac{1}{2}\) = 162°30′

iv. At 5:45, the minute-hand is at mark 9 and hour- hand has crossed ( \(frac{3}{4}\) )th of the angle between 5 and 6.

Angle between two consecutive marks
= 360°/12 = 30°
Angle traced by hour-hand in 45 minutes
\(\frac{3}{4}\left(30^{\circ}\right)=(22.5)^{\circ}=\left(22 \frac{1}{2}\right)^{\circ}\)
Angle between marks 5 and 9
= 4 x 30° = 120°
∴ Angle between two hands of the clock at quarter to six = \(120^{\circ}-\left(22 \frac{1}{2}\right)^{0}\)

v. At 2 : 20, the minute-hand is at mark 4 hour hand has crossed \(\frac{1}{3}\)rd of the angle between 2 and 3.

Angle between two consecutive marks = 360°/12 = 30°
Angle traced by hour-hand in 20 minutes
= \(frac{1}{3}\)(30°)= 10°
Angle between marks 2 and 4 = 2 x 30° = 60°
∴ Angle between two hands of the clock at 2 :20 = 60° – 10° = 50°

vi. At 10:10, the minute-hand is at mark 2 and hour-hand has crossed\frac{1}{6}[/latex] th between 10 and 11.

Angle between two consecutive marks
360°/12 = 30°
Angle traced by hour-hand in 10 minutes
= \(\frac{1}{6}\) (30°) = 5°
Angle between marks 10 and 2= 4 x 30° = 120°
… Angle between two hands of the clock at 10:10
= 120° – 5°= 115°

Maharashtra State Board Class 11 Maths Solutions 

• Angle and its Measurement Ex 1.1 Class 11 Maths Solutions
• Angle and its Measurement Ex 1.2 Class 11 Maths Solutions
• Angle and its Measurement Miscellaneous Exercise 1 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Miscellaneous Exercise 9 Questions and Answers.

11th Maths Part 1 Probability Miscellaneous Exercise 9 Questions And Answers Maharashtra Board

(I) Select the correct answer from the given four alternatives.

Question 1.
There are 5 girls and 2 boys, then the probability that no two boys are sitting together for a photograph is
(A) \(\frac{1}{21}\)
(B) \(\frac{4}{7}\)
(C) \(\frac{2}{7}\)
(D) \(\frac{5}{7}\)
Answer:
(D) \(\frac{5}{7}\)
Hint:
There are 5 girls and 2 boys.
They can be arranged among themselves in \({ }^{7} \mathrm{P}_{7}\) = 7! ways.
∴ Girls can be arranged among themselves in \({ }^{5} \mathrm{P}_{5}\) = 5! ways.
No two boys should sit together.
Let girls be denoted by the letter G.
– G – G – G – G – G –
There are 6 places, marked by ‘-’ where boys can sit.
∴ Boys can be arranged in
\({ }^{6} \mathrm{P}_{2}=\frac{6 !}{(6-2) !}\)
= \(\frac{6 \times 5 \times 4 !}{4 !}\)
= 30 ways.
∴ Required probability = \(\frac{5 ! \times 30}{7 !}=\frac{5 ! \times 30}{7 \times 6 \times 5 !}=\frac{5}{7}\)

Question 2.
In a jar, there are 5 black marbles and 3 green marbles. Two marbles are picked randomly one after the other without replacement. What is the possibility that both the marbles are black?
(A) \(\frac{5}{14}\)
(B) \(\frac{5}{8}\)
(C) \(\frac{5}{7}\)
(D) \(\frac{5}{16}\)
Answer:
(A) \(\frac{5}{14}\)

Question 3.
Two dice are thrown simultaneously. Then the probability of getting two numbers whose product is even is
(A) \(\frac{3}{4}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{5}{7}\)
(D) \(\frac{1}{2}\)
Answer:
(A) \(\frac{3}{4}\)
Hint:
Two dice are thrown.
∴ n(S) = 36
Getting two numbers whose product is even, i.e., one of the two numbers must be even.
Let event A: Getting even number on first dice,
event B: Getting even number on second dice.
n(A) = 18, n(B) = 18, n(A ∩ B) = 9
Required probability = P(A ∩ B)
= \(\frac{n(A)+n(B)-n(A \cap B)}{n(S)}\)
= \(\frac{18+18-9}{36}\)
= \(\frac{3}{4}\)

Question 4.
In a set of 30 shirts, 17 are white and the rest are black. 4 white and 5 black shirts are tagged as ‘PARTY WEAR’. If a shirt is chosen at random from this set, the possibility of choosing a black shirt or a ‘PARTY WEAR’ shirt is
(A) \(\frac{11}{15}\)
(B) \(\frac{13}{30}\)
(C) \(\frac{9}{13}\)
(D) \(\frac{17}{30}\)
Answer:
(D) \(\frac{17}{30}\)
Hint:
17 white + 13 black = 30 shirts
4 white and 5 black are ‘PARTY WEAR’
A: Choosing a black shirt
∴ P(A) = \(\frac{{ }^{13} C_{1}}{{ }^{30} C_{1}}=\frac{13}{30}\)
B: Choosing a ‘PARTY WEAR’ shirt.
∴ P(B) = \(\frac{{ }^{9} \mathrm{C}_{1}}{{ }^{30} \mathrm{C}_{1}}=\frac{9}{30}\)
There are 5 black ‘PARTY WEAR’ shirts.
∴ P(A ∩ B) = \(\frac{{ }^{5} \mathrm{C}_{1}}{{ }^{30} \mathrm{C}_{1}}=\frac{5}{30}\)
∴ Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{13}{30}\) + \(\frac{9}{30}\) – \(\frac{5}{30}\)
= \(\frac{17}{30}\)

Question 5.
There are 2 shelves. One shelf has 5 Physics and 3 Biology books and the other has 4 Physics and 2 Biology books. The probability of drawing a Physics book is
(A) \(\frac{9}{14}\)
(B) \(\frac{31}{48}\)
(C) \(\frac{9}{38}\)
(D) \(\frac{1}{2}\)
Answer:
(B) \(\frac{31}{48}\)
Hint:
Let event S₁: First shelve is selected,
event S₂: Second shelve is selected,
event P: Drawing a physics book.
∴ P(S₁) = \(\frac{1}{2}\) and P(S₂) = \(\frac{1}{2}\)
First shelve has 5 physics and 3 biology books, i.e., total 8 books.
∴ P(P/S₁) = \(\frac{{ }^{5} C_{1}}{{ }^{8} C_{1}}=\frac{5}{8}\)
Similarly, P(P/S₂) = \(\frac{{ }^{4} C_{1}}{{ }^{6} C_{1}}=\frac{4}{6}=\frac{2}{3}\)
∴ P(P) = P(S₁) . P(P/S₁) + P(S₂) . P(P/S₂)
= \(\frac{1}{2} \times \frac{5}{8}+\frac{1}{2} \times \frac{2}{3}\)
= \(\frac{31}{48}\)

Question 6.
Two friends A and B apply for a job in the same company. The chances of A getting selected is 2/5 and that of B is 4/7. The probability that both of them get selected is
(A) \(\frac{34}{35}\)
(B) \(\frac{1}{35}\)
(C) \(\frac{8}{35}\)
(D) \(\frac{27}{35}\)
Answer:
(C) \(\frac{8}{35}\)

Question 7.
The probability that a student knows the correct answer to a multiple-choice question is \(\frac{2}{3}\). If the student does not know the answer, then the student guesses the answer. The probability of the guessed answer being correct is \(\frac{1}{4}\). Given that the student has answered the question correctly, the probability that the student knows the correct answer is
(A) \(\frac{5}{6}\)
(B) \(\frac{6}{7}\)
(C) \(\frac{7}{8}\)
(D) \(\frac{8}{9}\)
Answer:
(D) \(\frac{8}{9}\)
Hint:
Let event A: Student knows the correct answer,
event A’: Student guesses the answer,
event B: Answer is correct.
∴ P(A) = \(\frac{2}{3}\), P(A’) = \(\frac{1}{3}\), P(B/A’) = \(\frac{1}{4}\)
Clearly, P(B/A) = 1
Required probability = P(A/B)
= \(\frac{\mathrm{P}(\mathrm{A}) \cdot \mathrm{P}(\mathrm{B} / \mathrm{A})}{\mathrm{P}(\mathrm{A}) \cdot \mathrm{P}(\mathrm{B} / \mathrm{A})+\mathrm{P}\left(\mathrm{A}^{\prime}\right) \mathrm{P}\left(\mathrm{B} / \mathrm{A}^{\prime}\right)}\)
= \(\frac{\frac{2}{3} \times 1}{\frac{2}{3} \times 1+\frac{1}{3} \times \frac{1}{4}}\)
= \(\frac{8}{9}\)

Question 8.
The bag I contain 3 red and 4 black balls while Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. The probability that it was drawn from Bag II is
(A) \(\frac{33}{68}\)
(B) \(\frac{35}{69}\)
(C) \(\frac{34}{67}\)
(D) \(\frac{35}{68}\)
Answer:
(D) \(\frac{35}{68}\)

Question 9.
A fair die is tossed twice. What are the odds in favour of getting 4, 5, or 6 on the first toss and 1, 2, 3, or 4 on the second toss?
(A) 1 : 3
(B) 3 : 1
(C) 1 : 2
(D) 2 : 1
Answer:
(C) 1 : 2
Hint:
A fair dice is tossed twice.
∴ n(S) = 36
A: Getting 4, 5, or 6 on the first toss and Getting 1, 2, 3, or 4 on the second toss.
∴ A = {(4, 1), (4, 2), (4, 3), (4, 4), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4)}
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{12}{36}=\frac{1}{3}\)
∴ Required answer = P(A) : P(A’) = 1 : 2

Question 10.
The odds against an event are 5 : 3 and the odds in favour of another independent event are 7 : 5. The probability that at least one of the two events will occur is
(A) \(\frac{52}{96}\)
(B) \(\frac{71}{96}\)
(C) \(\frac{69}{96}\)
(D) \(\frac{13}{96}\)
Answer:
(B) \(\frac{71}{96}\)

(II) Solve the following.

Question 1.
The letters of the word ‘EQUATION’ are arranged in a row. Find the probability that
(i) all the vowels are together
(ii) arrangement starts with a vowel and ends with a consonant.
Solution:
The letters of the word EQUATION can be arranged in 8! ways.
∴ n(S) = 8!
There are 5 vowels and 3 consonants.
(i) A: all vowels are together we need to arrange (E, U, A, I, O), Q, T, N
Let us consider all vowels as one unit.
So, there are 4 units, which can be arranged in 4! ways.
Also, 5 vowels can be arranged among themselves in 5! ways.
∴ n(A) = 4! × 5!
Required probability = P(A)
= \(\frac{n(A)}{n(S)}\)
= \(\frac{4 ! \times 5 !}{8 !}\)
= \(\frac{1}{14}\)

(ii) B: arrangement start with a vowel and ends with a consonant.
First and last places can be filled in 5 and 3 ways respectively.
Remaining 6 letters are arranged in 6! Ways.
∴ n(B) = 5 × 3 × 6!
Required probability = P(B)
= \(\frac{n(B)}{n(S)}\)
= \(\frac{5 \times 3 \times 6 !}{8 !}\)
= \(\frac{15}{56}\)

Question 2.
There are 6 positive and 8 negative numbers. Four numbers are chosen at random, without replacement, and multiplied. Find the probability that the product is a positive number.
Solution:
Let event A: Four positive numbers are chosen,
event B: Four negative numbers are chosen,
event C: Two positive and two negative numbers are chosen.
Since four numbers are chosen without replacement,
n(A) = 6 × 5 × 4 × 3 = 360
n(B) = 8 × 7 × 6 × 5 = 1680
In event C, four numbers are to be chosen without replacement such that two numbers are positive and two numbers ate negative. This can be done in following ways:
+ + – – OR + – + – OR + – – + OR – + – + OR – – + + OR – + + –
∴ n(C) = 6 × 5 × 8 × 7 + 6 × 8 × 5 × 7 + 6 × 8 × 7 × 5 + 8 × 6 × 7 × 5 + 6 × 5 × 8 × 7 + 8 × 6 × 5 × 7
= 6 × (8 × 7 × 6 × 5)
=10080
Here, total number of numbers = 14
∴ n(S) = 14 × 13 × 12 × 11 = 24024
Since A, B, C are mutually exclusive events,
Required probability = P(A) + P(B) + P(C)

Question 3.
Ten cards numbered 1 to 10 are placed in a box, mixed up thoroughly, and then one card is drawn randomly. If it is known that the number on the drawn card is more than 3, what is the probability that it is an even number?
Solution:
S = {1, 2,…., 10}
∴ n(S) = 10
A: Number is more than 3.
A = {4, 5, 6, 7, 8, 9, 10}
∴ n(A) = 7
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{7}{10}\)
B: Number is even.
B = {2, 4, 6, 8, 10}
∴ A ∩ B = {4, 6, 8, 10}
∴ n(A ∩ B) = 4
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{4}{10}\)
Required probability = P(B/A)
= \(\frac{P(A \cap B)}{P(A)}\)
= \(\frac{\left(\frac{4}{10}\right)}{\left(\frac{7}{10}\right)}\)
= \(\frac{4}{7}\)

Question 4.
If A, B and C are independent events, P(A ∩ B) = \(\frac{1}{2}\), P(B ∩ C) = \(\frac{1}{3}\), P(C ∩ A) = \(\frac{1}{6}\), then find P(A), P(B) and P(C).
Solution:
Since A and B are independent events,
P(A ∩ B) = P(A) . P(B)
∴ P(A) . P(B) = \(\frac{1}{2}\) ……(i)
B and C are independent events.
∴ P(B ∩ C) = P(B) . P(C)
∴ P(B) . P(C) = \(\frac{1}{3}\) ……(ii)
A and C are independent events.
∴ P(A ∩ C) = P(A) . P(C)
∴ P(A) . P(C) = \(\frac{1}{6}\) ……(iii)
Dividing (i) by (ii), we get
\(\frac{\mathrm{P}(\mathrm{A}) \mathrm{P}(\mathrm{B})}{\mathrm{P}(\mathrm{B}) \mathrm{P}(\mathrm{C})}=\frac{\frac{1}{2}}{\frac{1}{3}}\)
P(A) = \(\frac{3}{2}\) P(C) ……(iv)
Substituting equation (iv) in (iii), we get
\(\frac{3}{2}\) P(C) . P(C) = \(\frac{1}{6}\)
[P(C)]² = \(\frac{1}{9}\)
∴ P(C) = \(\frac{1}{3}\)
Substituting P(C) = \(\frac{1}{3}\) in equation (ii), we get P(B) = 1
Substituting P(B) = 1 in equation (i), we get P(A) = \(\frac{1}{2}\)

Question 5.
If the letters of the word ‘REGULATIONS’ be arranged at random, what is the probability that there will be exactly 4 letters between R and E?
Solution:
There are 11 letters in the word ‘REGULATIONS’ which can be arranged among themselves in 11! ways.
∴ n(S) = 11!
Let event A: There will be exactly 4 letters between R and E.
R, E can occur at (1, 6), (2, 7), ….,(6, 11) positions. So, there are 6 possibilities.
Also, R and E can interchange their positions.
So, R, E can be arranged in 2 × 6 = 12 ways.
Remaining 9 letters can be arranged in 9! ways.
∴ n(A) = 12 × 9!
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{12 \times 9 !}{11 !}=\frac{12 \times 9 !}{11 \times 10 \times 9 !}=\frac{6}{55}\)

Question 6.
In how many ways can the letters of the word ARRANGEMENTS be arranged?
(i) Find the chance that an arrangement chosen at random begins with the letters EE.
(ii) Find the probability that the consonants are together.
Solution:
The word ‘ARRANGEMENTS’ has 12 letters in which 2A, 2E, 2N, 2R, G, M, T, S are there.
n(S) = Total number of arrangements = \(\frac{12 !}{2 ! 2 ! 2 ! 2 !}=\frac{12 !}{(2 !)^{4}}\)
(i) A: Arrangement chosen at random begins with the letters EE.
If the first and second places are filled with EE, there are 10 letters left in which 2A, 2N, 2R, G, M, T, S are there.
∴ n(A) = \(\frac{10 !}{2 ! 2 ! 2 !}=\frac{10 !}{(2 !)^{3}}\)

(ii) B: Consonants (G, M, T, S, 2N, 2R) are together.
2A, 2E, and the group containing consonants form total 5 units. Which can be arranged in \(\frac{5 !}{2 ! 2 !}\) ways.
Also, 8 consonants can be arranged among themselves in \(\frac{8 !}{2 ! 2 !}\) ways.

Question 7.
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘STATISTICS’. Find the probability that the selected letters are the same.
Solution:
Word ASSISTANT has 2A, I, N, 3S, 2T, and word STATISTICS has A, C, 2I, 3S, 3T.
C and N are uncommon letters.
In the words ASSISTANT, there are 9 letters out of which 2 letters are ‘A’, and in the word STATISTICS, there are 10 letters, out of which 1 letter is A.
∴ Probability of choosing A from both the letters = \(\frac{{ }^{2} C_{1}}{{ }^{9} C_{1}} \times \frac{{ }^{1} C_{1}}{{ }^{10} C_{1}}=\frac{2}{9} \times \frac{1}{10}=\frac{1}{45}\)
Similarly,
Probability of choosing I from both the letters = \(\frac{{ }^{1} \mathrm{C}_{1}}{{ }^{9} \mathrm{C}_{1}} \times \frac{{ }^{2} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}=\frac{1}{9} \times \frac{2}{10}=\frac{1}{45}\)
Probability of choosing S from both the letters = \(\frac{{ }^{3} \mathrm{C}_{1}}{{ }^{9} \mathrm{C}_{1}} \times \frac{{ }^{3} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{1}}=\frac{3}{9} \times \frac{3}{10}=\frac{1}{10}\)
Probability of choosing T from both the letters = \(\frac{{ }^{2} C_{1}}{{ }^{9} C_{1}} \times \frac{{ }^{3} C_{1}}{{ }^{10} C_{1}}=\frac{2}{9} \times \frac{3}{10}=\frac{1}{15}\)
Required probability = \(\frac{1}{45}+\frac{1}{45}+\frac{1}{10}+\frac{1}{15}\) = \(\frac{19}{90}\)

Question 8.
A die is loaded in such a way that the probability of the face with j dots turning up is proportional to j for j = 1, 2,….., 6. What is the probability, in one roil of the die, that an odd number of dots will turn up?
Solution:
According to the given condition, the probability of the face with 1, 2, 3, 4, 5, 6 dots turning up is proportional to 1, 2, 3, 4, 5, 6.
Let k be the common ration of proportionality.
∴ The probabilities of the faces with 1, 2, 3, 4, 5, 6 dots turning up are 1k , 2k, 3k, 4k, 5k, 6k respectively.
Since sum of the probabilities = 1,
k(1 + 2+ ….. + 6) = 1
k(\(\frac{6 \times 7}{2}\)) = 1
k = \(\frac{1}{21}\)
Required probability = P(1) + P(3) + P(5)
= \(\frac{1}{21}+\frac{3}{21}+\frac{5}{21}\)
= \(\frac{9}{21}\)
= \(\frac{3}{7}\)

Question 9.
An urn contains 5 red balls and 2 green balls. A ball is drawn. If it’s green, a red ball is added to the urn, and if it’s red, a green ball is added to the urn. (The original ball is not returned to the urn). Then a second ball is drawn. What is the probability that the second ball is red?
Solution:
A: Event of drawing a red ball and placing a green ball in the urn
B: Event of drawing a green ball and placing a red ball
C: Event of drawing a red ball in the second draw
P(A) = \(\frac{5}{7}\)
P(B) = \(\frac{2}{7}\)
P(C/A) = \(\frac{4}{7}\)
P(C/B) = \(\frac{6}{7}\)
Required probability
P(C) = P(A) P(C/A) + P(B) P(C/B)
= \(\frac{5}{7} \times \frac{4}{7}+\frac{2}{7} \times \frac{6}{7}\)
= \(\frac{32}{49}\)

Question 10.
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5, find the probability that the problem will be solved.
Solution:
The odds against A solving the problems are 4 : 3.
Let P(A’) = P(A does not solve the problem) = \(\frac{4}{4+3}=\frac{4}{7}\)
So, the probability that A solves the problem = P(A) = 1 – P(A’)
= 1 – \(\frac{4}{7}\)
= \(\frac{3}{7}\)
Similarly, let P(B) = P(B solves the problem)
Since odds in favour of B solving the problem are 7 : 5.
∴ P(B) = \(\frac{7}{7+5}=\frac{7}{12}\)
Required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Since A and B are independent events.
∴ P(A ∩ B) = P(A) . P(B)
∴ Required probability = P(A) + P(B) – P(A) . P(B)
= \(\frac{3}{7}+\frac{7}{12}-\frac{3}{7} \times \frac{7}{12}\)
= \(\frac{16}{21}\)

Question 11.
If P(A) = P(A/B) = \(\frac{1}{5}\), P(B/A) = \(\frac{1}{3}\), then find
(i) P(A’/B)
(ii) P(B’/A’)
Solution:
Since P(A) = P(A/B) = \(\frac{1}{5}\)
P(A) = \(\frac{1}{5}\)
and \(\frac{P(A \cap B)}{P(B)}=\frac{1}{5}\)
∴ P(A) = \(\frac{1}{5}\) ……(i)
P(B) = 5 P(A ∩ B) ……..(ii)
Since P(B/A) = \(\frac{1}{3}\)
\(\frac{P(A \cap B)}{P(A)}=\frac{1}{3}\)
∴ P(A) = 3 P(A ∩ B) ………(iii)

Question 12.
Let A and B be independent events with P(A) = \(\frac{1}{4}\) and P(A ∪ B) = 2P(B) – P(A). Find
(i) P(B)
(ii) P(A/B)
(iii) P(B’/A)
Solution:
A and B are independent events. .
∴ P(A ∩ B) = P(A) × P(B)
(i) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ P(A ∪ B) = P(A) + P(B) – P(A) × P(B)
∴ 2P(B) – P(A) = P(A) + P(B) – P(A) × P(B) ……[∵ P(A ∪ B) = 2P(B) – P(A)]
∴ 2P(B) – \(\frac{1}{4}\) = \(\frac{1}{4}\) + P(B) – \(\frac{1}{4}\) × P(B)
∴ 2P(B) – P(B) + \(\frac{1}{4}\) P(B) = \(\frac{1}{4}\) + \(\frac{1}{4}\)

Question 13.
Find the probability that a year selected will have 53 Wednesdays.
Solution:
A leap year comes after 3 years.
∴ The probability of a year being a leap year = \(\frac{1}{4}\)
∴ Probability of a year being a non-leap year = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
In a non-leap year, there are 52 weeks and one extra day, whereas a leap year has 52 weeks and 2 extra days.
∴ 53rd Wednesday’s chance in a non-leap year = \(\frac{1}{7}\)
Two extra days of a leap year can be
(Mon, Tue), (Tue, Wed), (Wed, Thu), (Thu, Fri), (Fri, Sat), (Sat, Sun), (Sun, Mon)
∴ There are 2 possibilities of 53rd Wednesday in a leap year.
∴ 53rd Wednesday’s chance in a leap year = \(\frac{2}{7}\)
Required probability = P(a non-leap year and Wednesday) + P(a leap year and Wednesday)
= \(\frac{3}{4} \times \frac{1}{7}+\frac{1}{4} \times \frac{2}{7}\)
= \(\frac{5}{28}\)

Question 14.
The chances of P, Q and R, getting selected as principal of a college are \(\frac{2}{5}\), \(\frac{2}{5}\), \(\frac{1}{5}\) respectively. Their chances of introducing IT in the college are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\) respectively. Find the probability that
(a) IT is introduced in the college after one of them is selected as a principal.
(b) IT is introduced by Q.
Solution:
Let event P: P become principal,
event Q: Q become principal,
event R: R become principal,
event E: Subject IT is introduced.
Given, P(P) = \(\frac{2}{5}\)
P(Q) = \(\frac{2}{5}\)
P(R) = \(\frac{1}{5}\)
P(E/P) = \(\frac{1}{2}\)
P(E/Q) = \(\frac{1}{3}\)
P(E/R) = \(\frac{1}{4}\)
(a) Required probability
P(E) = P(P) P(E/P) + P(Q) P(E/Q) + P(R) P(E/R)
= \(\frac{2}{5} \times \frac{1}{2}+\frac{2}{5} \times \frac{1}{3}+\frac{1}{5} \times \frac{1}{4}\)
= \(\frac{1}{5}+\frac{2}{15}+\frac{1}{20}\)
= \(\frac{12+8+3}{60}\)
= \(\frac{23}{60}\)

(b) Required probability = P(Q/E)
By Bayes’ theorem,
P(Q/E) = \(\frac{P(Q) P(E / Q)}{P(E)}\)
= \(\frac{\frac{2}{5} \times \frac{1}{3}}{\frac{23}{60}}\)
= \(\frac{8}{23}\)

Question 15.
Suppose that five good fuses and two defective ones have been mixed up. To find the defective fuses, we test them one-by-one, at random and without replacement What is the probability that we are lucky and find both of the defective fuses in the first two tests?
Solution:
Number of fuses = 5 + 2 = 7
Testing two fuses one-by-one at random, without replacement from 7 can be done in \({ }^{7} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{1}\) ways.
∴ n(S) = \({ }^{7} \mathrm{C}_{1} \times{ }^{6} \mathrm{C}_{1}\) = 7 × 6 = 42
Let event A: Getting defective fuses in the first two tests without replacement.
There are two defective fuses.
∴ n(A) = \({ }^{2} \mathrm{C}_{1} \times{ }^{1} \mathrm{C}_{1}\) = 2 × 1 = 2
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{42}=\frac{1}{21}\)

Question 16.
For three events A, B and C, we know that A and C are independent, B and C are independent, A and B are disjoint, P(A ∪ C) = \(\frac{2}{3}\), P(B ∪ C) = \(\frac{3}{4}\), P(A ∪ B ∪ C) = \(\frac{11}{12}\). Find P(A), P(B) and P(C).
Solution:
Let P(A) = x, P(B) = y, P(C) = z
Since A, B are disjoint,
A ∩ B = Φ and A ∩ B ∩ C = Φ
∴ P(A ∩ B) = 0, P(A ∩ B ∩ C) = 0 ……(i)
Since A and C are independent,
P(A ∩ C) = P(A) P(C) = xz
Since B and C are independent,
P(B ∩ C) = P(B) P(C) = yz
P(A ∪ C) = P(A) + P(C) – P(A ∩ C)
∴ \(\frac{2}{3}\) = x + z – xz ……..(ii)
P(B ∪ C) = P(B) + P(C) – P(B ∩ C)
∴ \(\frac{3}{4}\) = y + z – yz ………(iii)
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
\(\frac{11}{12}\) = x + y + z – 0 – yz – zx + 0 …… [From(i)]
= (x + z – xz) + (y + z – yz) – z
= \(\frac{2}{3}+\frac{3}{4}\) – z ……. [From (ii) and (iii)]

Question 17.
The ratio of boys to girls in a college is 3 : 2 and 3 girls out of 500 and 2 boys out of 50 of that college are good singers. A good singer is chosen. What is the probability that the chosen singer is a girl?
Solution:
Let event S: The student is a good singer,
event B: The student is a boy,
event G: The student is a girl.
Since the ratio of boys to girls is 3 : 2 and 3 girls out of 500 and 2 boys out of 50 are good singers.

Question 18.
A and B throw a die alternatively till one of them gets a 3 and wins the game. Find the respective probabilities of winning. (Assuming A begins the game).
Solution:
Since P(getting 3) = \(\frac{1}{6}\),
P(not getting 3) = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
In 1st throw if A gets 3, A wins
∴ P(A win) = \(\frac{1}{6}\)
In 2nd throw by B (i.e., A does not get 3),
∴ P(B wins) = \(\frac{5}{6} \times \frac{1}{6}\)
In 3rd throw by A, P(A wins) = \(\frac{5}{6} \times \frac{5}{6} \times \frac{1}{6}\)
(3rd throw by A shows that B has lost in 2nd throw) and so on.

Question 19.
Consider independent trials consisting of rolling a pair of fair dice, over and over. What is the probability that a sum of 5 appears before a sum of 7?
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let event A: The sum is 5 in a trial.
A = {(2, 3), (3, 2), (1, 4), (4, 1)}
∴ P(A) = \(\frac{4}{36}=\frac{1}{9}\)
Let event B: The sum is 7 in a trial.
B = {(2, 5), (5, 2), (3, 4), (4, 3), (1, 6), (6, 1)}
∴ P(B) = \(\frac{6}{36}=\frac{1}{6}\)
Let event C: Neither sum is 5 nor 7.
P(C) = 1 – P(A) – P(B)
= 1 – \(\frac{1}{9}\) – \(\frac{1}{6}\)
= \(\frac{26}{36}\)
Let the sum of 5 appear in the nth trial for the first time and the sum of 7 has not occurred in the first (n – 1) trials.

Question 20.
A machine produces parts that are either good (90%), slightly defective (2%), or obviously defective (8%). Produced parts get passed through an automatic inspection machine, which is able to detect any part that is obviously defective and discard it. What is the probability that the quality of the parts that make it through the inspection machine and get shipped?
Solution:
Let event G: The event that machine produces a good part,
event S: The event that machine produces a slightly defective part,
event D: The event that machine produces an obviously defective part.

Question 21.
Given three identical boxes, I, II, and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in box III, there is one gold and one silver coin. A person chooses a box at random and takes out a coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold?
Solution:
Let event B₁: Select box I having two gold coins.
event B₂: Selecting box II having two silver coins,
event B₃: Selecting box III having one silver and one gold coin,
event G: Coin is gold.

To find the probability that the other can in the box is also gold. Which is possible only when it is drawn from the box I.
∴ Required probability = P(B₁/G)
By Bayes’ theorem,

Question 22.
In a factory which manufactures bulbs, machines A, B, and C manufacture respectively 25%, 35% and 40% of the bulbs. Of their outputs, 5, 4, and 2 percent are respectively defective bulbs. A bulb is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by machine B?
Solution:
Let event A: Bulb manufactured by machine A
event B: Bulb manufactured by machine B
event C: Bulb manufactured by machine C
event D: Bulb defective
∴ P(A) = \(\frac{25}{100}\)
P(B) = \(\frac{35}{100}\)
P(C) = \(\frac{40}{100}\)
Machines A, B and C manufacture respectively 25%, 35% and 40% of the bulbs.
Of their outputs, 5, 4, and 2 percent are respectively defective bulbs.

Required probability = P(B/D)
By Bayes’ theorem,

Question 23.
A family has two children. One of them is chosen at random and found that the child is a girl. Find the probability that
(i) both the children are girls.
(ii) both the children are girls given that at least one of them is a girl.
Solution:
A family has two children.
∴ Sample space S = {BB, BG, GB, GG}
(i) A: First child is a girl.
∴ A = {GB, GG}
∴ P(A) = \(\frac{2}{4}=\frac{1}{2}\)
B: Second child is a girl.
∴ B = {BG, GG}
∴ A ∩ B = {GG}
∴ P(A ∩ B) = \(\frac{1}{4}\)
Required probability
P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{2}\)

(ii) A: At least one of the children is a girl.
∴ A = {GG, GB, BG}
∴ P(A) = \(\frac{3}{4}\)
B: both children are girls.
B = {GG}
∴ P(B) = \(\frac{1}{4}\)
Also, A ∩ B = B

11th Maths Book Solutions State Board 

• Probability Ex 9.1 Class 11 Maths Solutions
• Probability Ex 9.2 Class 11 Maths Solutions
• Probability Ex 9.3 Class 11 Maths Solutions
• Probability Ex 9.4 Class 11 Maths Solutions
• Probability Ex 9.5 Class 11 Maths Solutions
• Probability Miscellaneous Exercise 9 Class 11 Maths Solutions