Category: Class 12

Std 12 History Chapter 7 Question Answer Decolonisation to Political Integration of India Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 7 Decolonisation to Political Integration of India Textbook Exercise Questions and Answers.

Class 12 History Chapter 7 Decolonisation to Political Integration of India Question Answer Maharashtra Board

History Class 12 Chapter 7 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
In 1946, under the leadership of the movement of ____________ ‘Civil Disobedience’ was launched in
Goa.
(a) Dr. Ram Manohar Lohia
(b) Dr. T.B. Kunha
(c) Dr. P.P. Shirodkar
(d) Dr. Ram Hegde
Answer:
(a) Dr. Ram Manohar Lohia

Question 2.
Hyderabad’s struggle of freedom was led skillfully by ____________
(a) King Hari Singh
(b) Swami Ramanand Tirth
(c) Pandit Mahadevshastri Joshi
(d) Keshavrao Jedhe
Answer:
(b) Swami Ramanand Tirth

Question 3.
The princely states in India were merged in India mainly through the efforts of ____________
(a) Jayantrao Tilak
(b) Sardar Vallabhbhai Patel
(c) Pandit Jawaharlal Nehru
(d) Dr. T.B. Kunha
Answer:
(b) Sardar Vallabhbhai Patel

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
The merger of the princely state of Kashmir – King Hari Singh (Instrument of Accession)

2. Write the names of historical places/persons/events.

Question 1.
The President of Goa Congress Committee –
Answer:
Dr. T.B. Kunha

Question 2.
The princely states that did not merge in India immediately after its independence –
Answer:
Junagadh, Hyderabad, Kashmir, Dadra and Haveli, Goa and Puducherry

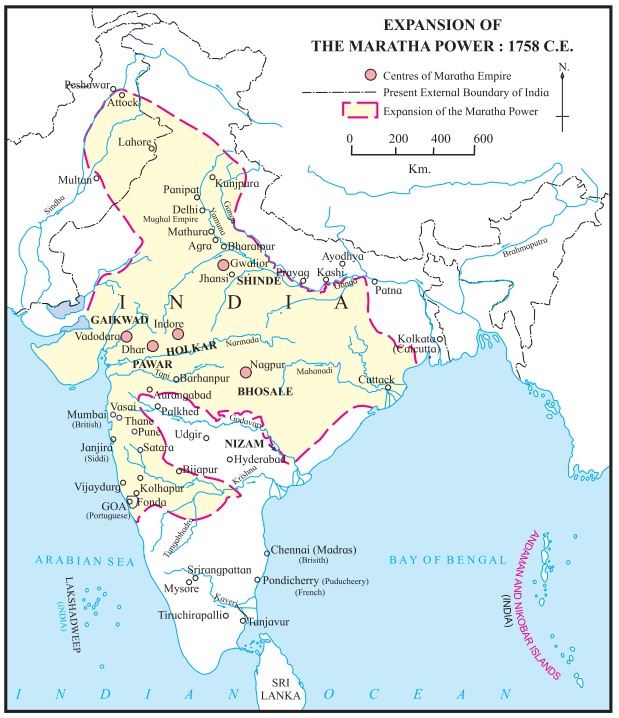
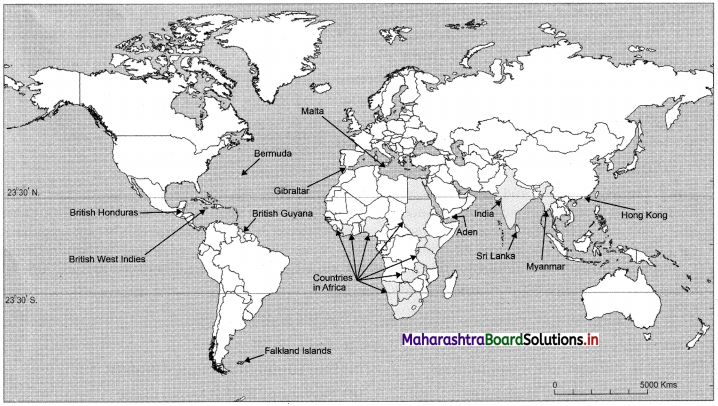
3. Observe the map on textbook page 61 and answer the questions based on it.

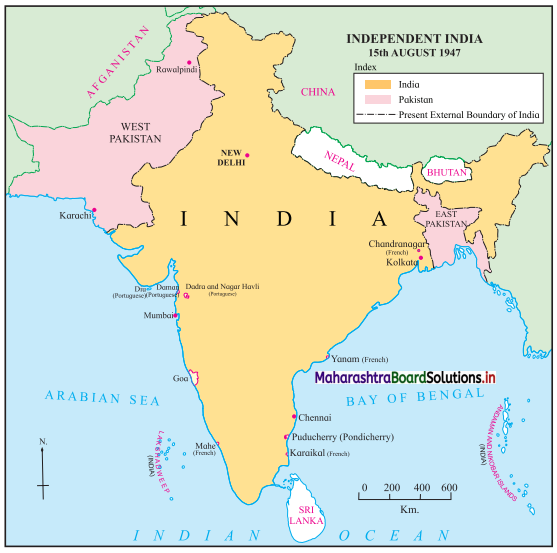
Question 1.
Name the countries located at the northwest border of India.
Answer:
Pakistan and Afghanistan.

Question 2.
Which places in India were the centers of Portuguese rule?
Answer:
Goa, Dadra and Nagar haveli, Diu and Daman.

Question 3.
Which place on the eastern coast of India were the centers of French rule?
Answer:
Puducherry, Yanam and Karaikal.

Question 4.
Which nation is located at the southern tip of India?
Answer:
Sri Lanka

4. Complete the following concept map.

Question 1.

Answer:

5. Explain the following statements with reasons.

Question 1.
Ultimately the princely state of Hyderabad was merged in India.
Answer:

• Hyderabad was under Nizam rule, it was the largest amongst princely states along with Telugu, Kannada, and Marathi regional sections.
• The various organisation was formed to fight against Nizam’s policies for his people.
• Swami Ramanand Tirth alongside loyal workers were leading this organisation to gain freedom from the Nizam.
• Hyderabad State Congress passed a resolution that Hyderabad will merge in India and this was not liked by Nizam, he was willing to join Pakistan.
• The people of Hyderabad wanted to merge in India.
• Kasim Razvi formed a ‘Razakar’ organisation against people.
• In the end, the Indian Government launched a police campaign against Nizam, under the name ‘Operation Polo’.
• In 1948 Nizam surrendered and Hyderabad merged in India.

Question 2.
Puducherry was declared as a Union territory.
Answer:

• Puducherry was under the French colony. India was under the impression that the British and Portuguese will send a message to the French to leave India, however, this did not happen.
• Puducherry, Mahe, Yanam, and Chandranagar in West Bengal were under French control.
• The people of Puducherry got united under Subbayya, a communist politician and leader.
• The government noticed it as serious and strongly demanded that French governments should return all the regions held by them.
• In 1948, a bilateral agreement was signed by both governments. In 1949, Chandranagar was merged.
• In 1954, all French colonies were merged in India. In 1962, the French Parliament approved the bilateral agreement and in 1963, Puducherry became the ‘Union Territory’ of India.

6. State your opinion.

Question 1.
Andhra, Karnataka, Maharashtra Councils (Parishad) were found in the princely state of Hyderabad.
Answer:

• Hyderabad was the largest amongst princely states in India. It comprised Telugu, Kannada, and Marathi regional sections. It was ruled by Nizam.
• Nizam of Hyderabad had put many restrictions on the Civil and Political rights of his subjects to a great extent.
• To fight against such restrictions in the state, people had formed organizations like ‘Andhra Parishad’ in Telangana, ‘Maharashtra Parishad’ in Marathwada, and ‘Karnataka Parishad’ in Karnataka.

Question 2.
The Portuguese rule in Goa remained untouched till 1961.
Answer:

• Goa was under Portuguese control. There prevailed a general notion among Indians that the departure of the British from India would send a signal to the Portuguese and the French to leave India on their own.
• However, this did not happen and many freedom fighters like Dr. Ram Manohar Lohia, Dr. Kunha, and many more have contributed to the struggle against the Portuguese.
• At last, the Indian govt has sent the army, under Operation Vijay, to make Goa free from Portuguese control and became a part of India on 19th December 1961.

Class 12 History Chapter 7 Decolonisation to Political Integration of India Intext Questions and Answers

Try to do this (Textbook Page No. 58)

Try to collect information about the newspapers published during ‘Hyderabad Freedom Struggle’ with the help of the internet.
Answer:
Students should do it on their own.

Try to do this (Textbook Page No. 60)

Collect information about the fort of Panaji and make a poster about the fort.
Answer:
Students should do it on their own.

Project (Textbook Page No. 62)

Collect information about the ‘Gorta Massacre’ a very important instance in the struggle for liberating Hyderabad. To get more information about it visit the following website: www.bhausahebumate.com
Answer:
(i) As we know Qasim Razvi, had founded the Razakar organization (Nizam’s private military) to help Nizam to suppress the voice of people against Nizam of Hyderabad. Gorta was the name of a village (Karnataka) and people were massacred by Razakars of Hyderabad in 1948. Gorta Village is also known as Jaliyanwala Bag of Karanataka, it was a mass killing on May 9th and 10th 1948. Though a plaque kept in front of the village gives fight date May 5th, and it continued for two weeks. It is said that around 200 people were killed by Razakars and property destruction was worth ₹ 70 lakhs.

(ii) A folk song called ‘Bhulai pada’ sung by village women in bitter memory of the massacre. There is demand from village people in front of the Government for the construction of the memorial at Gorta. Local people and local political parties had collected ₹ 27 lakh for a 35-foot memorial and laid the foundation on September 17th, 2014.

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Std 12 History Chapter 6 Question Answer Indian Struggle against Colonialism Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 6 Indian Struggle against Colonialism Textbook Exercise Questions and Answers.

Class 12 History Chapter 6 Indian Struggle against Colonialism Question Answer Maharashtra Board

History Class 12 Chapter 6 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
The region of __________ had become a stronghold of Hansaji Naik.
(a) Satara
(b) Nanded
(c) Pune
(d) Nagpur
Answer:
(b) Nanded

Question 2.
The British plant owners in Bihar were pressing the local farmers to grow only __________
(a) indigo
(b) tea
(c) coffee
(d) sugarcane
Answer:
(a) indigo

Question 3.
The first session of the Indian National Congress was presided by __________
(a) Dwarkanath Tagore
(b) Vyomeshchandra Banerjee
(c) Dadabhai Nauroji
(d) Surendranath Banerjee
Answer:
(b) Vyomeshchandra Banerjee

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
Kunwar Singh – Patna

2. Write the names of historical places/persons/events.

Question 1.
The region of the regime of the parallel government established in 1942 –
Answer:
Satara District

Question 2.
The islands were conquered by Azad Hind Sena from the British in 1943 –
Answer:
Andaman and Nicobar Islands

3. Write short notes.

Question 1.
The Extremists.
Answer:

• The Indian National Congress split into two groups-The Moderates and The Extremists at the Surat session of the Congress in 1907.
• The ‘Extremists’ wing of thinkers insisted that independence should be a natural priority. An independent nation could provide the right set-up for social reformation.
• Lokmanya Tilak who was the leader of the Extremists said that the home taken over by others should be recovered first, then only we can reform it.
• He also felt that the British Government will not yield to applications, requests, and speeches.
• The Extremists did not agree with the Moderators’ policy of avoiding the resolutions of ‘Swadeshi’ and ‘Boycott’ and wanted to stop these attempts of the Moderators.
• The three leaders of the Extremists group were Lala Lajpat Rai, Bal Gangadhar Tilak, and Bipin Chandra Pal. (Lal-Bal-Pal).

Question 2.
Azad Hind Sena.
Answer:

• The Azad Hind Sena was built by Rasbihari Bose by recruiting Indian soldiers and later on was reorganized under the leadership of Subhash Chandra Bose.
• These were the Indian soldiers of the British army who were taken captive by the Japanese army.

Question 3.
Prati Sarkar.
Answer:

• Prati Sarkar or Parallel Government was established by Krantisinha Nana Patil, a revolutionist in the Satara district of Maharashtra.
• He, with the help of his associates, put an end to the British regime in the Satara district and established ‘People’s Government’.
• This government took over the administrative task of collecting revenue, maintaining law and order, solving court cases, and punishing criminals.

4. Answer the following questions in detail.

Question 1.
Lieutenant Outram was successful in crushing the revolt by the Bhils by the end of 1822.
Answer:

• A revolt of the Bhils in which thousands of Bhils participated was crushed by Lt. Outram.
• However, he also stayed among the Bhils and won their confidence. He tried to bring them into the mainstream of urban life.
• He adopted measures like the declaration of amnesty, land grants, agricultural loans and reprieve from the past crimes, and recruitment in the army to weaken the opposition from the Bhils.

Question 2.
Ravindranath gave up his title (Sir.)
Answer:

• On 13th April 1919, the day of Baisakhi thousands of people had gathered for a meeting at Jallianwala Bagh in Amritsar for celebrating the festival.
• Many of them were not aware of the ban put by the government on public gatherings.
• Genera Dyer opened fire on these people without any prior warning.
• About four hundred innocent people were killed and thousands were injured in this incident. It is known as the ‘Jallianwala Bagh Massacre’.
• It created a wave of rage all through India.
• Rabindranath Tagore criticized this act and gave up his title (Sir).

5. State your opinion.

Question 1.
The rise of colonialism was the result of the spreading of European trade.
Answer:

• The Europeans reached all over the world for several reasons such as the urge for adventures, to earn a name to discover unknown lands, to search for gold mines, etc.
• Later, trade and commerce increased to such a great extent for which there was economic, social, and political supremacy among them.
• The Europeans found potential markets in continents like Asia, America, and Africa where they established their colonies. And the first to do so were the Portuguese.

Question 2.
According to Swatantryaveer Savarkar, the Independence War of 1857 was the First War of Independence.
Answer:

• The revolt of 1857 was a unified and national uprising against the British authority.
• The Indian war of Independence as described in his book ‘1857-The First War of Independence was considered to be the first war where the entire nation irrespective of caste, creed, race, and religion had come together and staged an armed protest against the British to gain independence from their colonial rule.

Class 12 History Chapter 6 Indian Struggle against Colonialism Intext Questions and Answers

Try this. (Textbook Page No. 43)

Collect more information about ‘Kayamdhara’, ‘Ryotwari’, ‘Mahalwari’ land revenue systems and discuss it in the class. Also, discuss the present land system of ‘Anewari’.
Answer:
(A) Kayamdhara or Jamindari:

• This system was introduced by Lord Cornwallis in 1793.
• It was introduced in the provinces of Bengal, Bihar, Orissa, and Varanasi.
• Zamindars were recognized as the owners of the lands.
• Zamindars were given the right to collect rent from the peasants.

(B) Ryotwari:

• The Ryotwari system was a land revenue system in British India introduced by Thomas Munro in 1820 based on a system administered by Captain Alexander Read in the Baramahal district.
• This was practiced in Madras and Bombay areas as well as Assam and Coorg provinces.
• In this system, the peasants or cultivators were regarded as the owners of the land.
• Ryot means peasant cultivator.

(C) Mahalwari system:

• The government of Lord William Bentinck Governor-General of India (1828-1835) introduced the Mahalwari system of land revenue in 1833.
• This system was introduced in N W Frontier, Agra, Gangetic Valley, Central Provinces, Punjab, etc.
• Had elements of both the Zamindari and the Ryotwari systems.
• This system divided the lands into Mahals. Sometimes the Mahals constituted one or more villages.
• The tax was assessed on the Mahal.
• Each individual farmer gave his share.
• Revenue was collected by the village headman or village leaders (Lambardar).

(D) Anewari System:

• Paisewari (originally known as Anewari) is a system of survey used by the government to decide whether a village is drought-hit or not
• Prior to the harvest, the Tehsildar along with farmers and representatives of the agricultural department takes stock of the crop and compares it with the yield of the last ten years
• If the value is less than 50 paise, the village is declared drought-hit, and drought mitigating measures are put in place.

Try to do this: (Textbook Page No. 46)

Vishnubhat Godse from Vasai was in Jhansi in 1857. Get the book, ‘Maza Pravas’ authored by him as the eyewitness of the happenings and read it.
Answer:

• ‘Maza Pravas’ translates into English as “My Travels: The story of 1857 Mutiny” is a Marathi travelogue written by Vishnubhat Godse, who traveled on foot from Varsai, a village near Pen (present-day Maharashtra) to the Central and Northern parts of India during 1857-1858 and witnessed several incidents of what he calls “The Mutiny of 1857” also known as the Indian Rebellion of 1857.
• During his travel, he witnessed the events at Mhow, worked for the Rani of Jhansi for a few months, visited Ayodhya, eventually returned penniless to his village.
• Apart from his encounters with the mutiny he also visited most of the Hindu holy places.

Try to do this: (Textbook Page No. 55)

Collect information and pictures about revolutionaries and freedom fighters from your area and make a presentation.
Answer:
Students should do this activity by themselves

Projects (Textbook Page No. 56)

(a) The Rising Ballad of Mangal Panday
(b) The Legend of Bhagat Singh
(c) Khele Hum Jee Janse
These are some Hindi films. Watch them and verify the historical truth of the incidences shown in it.
Answer:
Students do it by themselves

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Std 12 History Chapter 5 Question Answer India: Social and Religious Reforms Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 5 India: Social and Religious Reforms Textbook Exercise Questions and Answers.

Class 12 History Chapter 5 India: Social and Religious Reforms Question Answer Maharashtra Board

History Class 12 Chapter 5 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
Raja Ram Mohan Roy wrote an English letter against the ___________
(a) caste system
(b) child marriage
(c) practice of sati
(d) segregation of women (Purdah system)
Answer:
(c) practice of sati

Question 2.
‘Arya Samaj’ was founded by ___________
(a) Swami Vivekanand
(b) Mahatma Jotirao Phule
(c) Swami Dayanand Saraswati
(d) Ramaswamy Naikar
Answer:
(c) Swami Dayanand Saraswati

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
Paramhamsa Sabha – Dadoba Pandurang Tarkhadkar

2. Write the names of historical places/persons/events.

Question 1.
The title conferred on Raja Ram Mohan Roy by the Mughal Badshah-
Answer:
Raja

Question 2.
The one who founded ‘Mohammadan Anglo-Oriental College’-
Answer:
Sir Sayyad Ahmad Khan

Question 3.
The one who participated in ‘Vykom Satyagraha’-
Answer:
Ramaswamy Naikar

Question 4.
The one who made the law of free and compulsory primary education in Kolhapur Princely State-
Answer:
Rajarshi Shahu Maharaj

3. Write short notes.

Question 1.
Prarthana Samaj.
Answer:
Prarthana Samaj:

• Had its origins in Paramhamsa Sabha.
• Founded by Dadoba Pandurang Tarkhadkar.
• Founding members like Dr. Atmaram Pandurang, Justice M. G. Ranade, Dr. R. G. Bhandarkar opposed idol worship and emphasized monotheism.
• Opened schools for girls, orphanages, and night schools for workers.
• Focussed on gender equality, wiping outcaste discriminations, and appreciating the values of mundane life.

Question 2.
Satyashodhak Samaj.
Answer:
Satyashodhak Samaj:

• Founded in 1873 by Mahatma Jotirao Phule in Pune.
• Cracked a whip on the social customs and practices which pushed the Indian masses into a miserable state.
• Showed a new path to artisans, workers, and other downtrodden people.
• Characteristics of Satyashodhak Samaj included monotheism, rejection of the authority of Vedas and Puranas, acceptance of rationality, opposition to the dominance of priests and idol worship, etc.
• Mahatma Phule and his wife Savitribai Phule started a school for girls.
• His work was continued by Gopalbaba Walangkar who criticized untouchability in his book ‘Vital Vidhwamsan’.
• Shivram Janba drew attention to the problems of deprived women like Murali, Jagatini, and Devdasi.

4. Answer the following questions in detail.

Question 1.
What were the social reforms on which Raja Ram Mohan Roy put a great emphasis?
Answer:
Contribution of Raja Ram Mohan Roy:

• Raja Ram Mohan Roy was born in Bengal.
• Translated Sanskrit Upanishads into Bengali.
• He was a witness to his brother’s wife immolating herself on her husband’s funeral pyre and this incident made him raise his voice against this evil social custom which according to him is not mentioned in any of the religious scriptures as a prescribed social obligation.
• It was due to the efforts of Raja Ram Mohan Roy that a law was passed by the Governor-General of Bengal Lord William Bentinck abolishing Sati in 1829.
• He was also opposed to child marriage and purdah, opened an English medium school, launched the first periodical in Bengali, and also another publication in Persian.
• He started ‘Atmiya Sabha’, a philosophical discussion circle,’ Brahmo Samaj in 1828.
• He spoke in support of the anti-colonial movements in Spanish colonies in South America.
• Ram Mohan Roy laid the foundation of modernity in India.
• Organizations like Manavdharma Sabha, Paramahamsa Sabha, and Dnyanprasar Sabha were inspired by his work.

Question 2.
Write about the contributions of the Ramkrishna Mission.
Answer:
Ramkrishna Mission:

• Swami Vivekananda founded the Ramkrishna Mission in 1897.
• Focussed on serving needy people, working for people affected by famine, health care for the sick people, education for women, etc.
• It also gave a message to the Indian youth to get up to awaken and keep moving until the goal is achieved.

Question 3.
Write about the contributions of Sir Sayyad Ahmad Khan.
Answer:
Sir Sayyad Ahmad Khan:

• Was born in 1817 in Delhi.
• Fluent in Urdu, Persian, Arabic, and English.
• Established ‘Scientific Society’ for Muslims.
• After returning from England he founded the Mohammadan Anglo-Oriental College in 1875 which later developed into ‘Aligarh Muslim University.
• Started a periodical entitled ‘Mohammadan Social Reformer’.
• Worked for the propagation of modern education, science, and technology.

Question 4.
Describe the contribution of Ramaswamy Naikar.
Answer:
Ramaswamy Naikar:

• Born in ‘Erode’ in Tamil Nadu in 1879.
• He became a follower of Mahatma Gandhi’s philosophy and worked for propagating the use of ‘Swadeshi’.
• He participated in the Vykom Satyagraha in Travancore against untouchability.
• Started the ‘Swabhiman Andolan’ in Tamil Nadu.
• Fought against the varna system and child marriage.
• He was addressed as ‘Periyar’ or Great Soul because of his magnanimous work.
• Was a great speaker and author.
• Took a radical position on issues like women’s rights and family planning.

Class 12 History Chapter 5 India: Social and Religious Reforms Intext Questions and Answers

Let us find out. (Textbook Page No. 36)

Collect information about ‘Singh Sabha’ that was founded in Amritsar.
Answer:
The Singh Sabha Movement was a Sikh movement that began in Punjab in the 1870s in reaction to the proselytizing activities of Christians, Hindu reform movements (Brahmo Samaj, Arya Samaj), and Muslims (Aligarh movement and Ahmadiyah). The movement was founded in an era when the Sikh Empire had been dissolved and annexed by the British, the Khalsa had lost its prestige, and mainstream Sikhs were rapidly converting to other religions.

The movement’s aims were to propagate the true Sikh religion and restore Sikhism to its pristine glory; to write and distribute historical and religious books of Sikhs, and to propagate Gurmukhi Punjabi through magazines and media. The movement sought to reform Sikhism and bring back into the Sikh fold the apostates who had converted to other religions; as well as to interest the influential British officials in furthering the Sikh community. At the time of its founding, the Singh Sabha policy was to avoid criticism of other religions and political matters.

Try to do this (Textbook Page No. 36)

Collect information with the help of the internet and teachers about these people: Pandit Ishwar Chandra Vidyasagar, Vishnushastri Pandit, Veereshlingam Pantalu, and Maharshi Dhondo Keshav Karve.
Answer:
(A) Pandit Ishwar Chandra Vidyasagar:

• Pandit Vidyasagar was born on 26th September 1820 in the Midnapore district of Bengal Presidency (now in West Bengal).
• A Sanskrit scholar, he joined Fort William College as the Head Pandit in the Sanskrit department in 1846.
• In 1846, he left Fort William and joined Sanskrit College as ‘Assistant Secretary’.
• In 1851, he became the principal of Sanskrit College.
• In 1854, Vidyasagar started his campaign for widow remarriage.
• Due to his efforts, the ‘Widow Remarriage Act was passed in 1856.
• He was keen to advocate for education for women.
• He exercised his power and lobbied hard for the opening of schools for girls.
• He gave more importance to educational reforms than social reforms.
• He emphasized teaching through Mother’s tongue.
• He has enriched Bengali Education System by writing many good textbooks for students.
• Vidyasagar died in 1891 at the age of 70.

(B) Vishnushastri Pandit:

• Vishnushastri Pandit was born in a Chitpavan Brahmin family to Sanskrit scholar Krishnashastri Chiplunkar.
• Worked as a school teacher in government schools during the years 1872-1879.
• Co-founded the newspapers Kesari (Marathi) and Mahratta (English) along with Lokmanya Tilak and Gopal Ganesh Agarkar.
• Also co-founded The New English School in Pune.
• Began his career as a writer
• In 1874, he started the monthly ‘Nibandmala’ for which he is principally remembered.
• Translated the following works in Marathi-
  • Rasselas by Samuel Johnson
  • Kadambari by Banabhatta
  • The Arabian Nights

(C) Veereshlingam Pantalu:

• Rao Bahadur Kandukuri Veereshlingam Pantalu was considered the ’Father of Renaissance movement in Telugu’.
• Born on 16th April 1848 at Rajamundry, Andhra Pradesh.
• Social reformer and writer at Madras Presidency under British rule.
• After completing his matriculation in 1869, he started working as a school teacher in a village.
• A scholar of three languages namely Telugu, Sanskrit, and English.
• He is most revered for his contribution to the reformation of Telugu society.
• Wrote extensively on the emancipation of women, advocated widow remarriage, and denounced child marriages.
• Set up schools for the education of girls and women.
• In 1887, he started a Brahmo Mandir at Rajamundry.
• In 1893, the government of India conferred the title ‘RaoBahadur’ on him
• He passed away on 27th May 1919 aged 71.

(D) Maharshi Dhondu Keshav Karve:

• Born on 18th April 1858 at Sheravali, India, Dhondu Keshav Karve, or Maharshi Karve he was popularly known as a social reformer in India.
• Was a Professor, Activist, Writer, and Social Worker.
• Noted for supporting the education of women and for organizing associations for the marriage of Hindu widows.
• In 1893, he established the Widow Marriage Association.
• He set an example by marrying a widow after his first wife had died in 1891.
• Established an educational institution in 1896, Hindu Widows Home in Poona.
• He started Shreemati Nathibai Damodar Thackersey Women’s University in 1916.
• On his 100th birthday, he was conferred India’s highest honour the ‘Bharat Ratna’.
• He died in Pune on November 9, 1962, aged 104.

Project (Textbook Page No. 39)

Collect information about the efforts for women’s education in Maharashtra with the help of the internet.
Answer:
Students can use the following points as reference:

• Trace women’s education down the ages.
• Education in Maharashtra from 1818-1903.
• Pioneer of Women’s education in India-Savitribai Phule.
• Female literacy in Maharashtra today.
• Schemes for women by the Government of Maharashtra.

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Std 12 History Chapter 4 Question Answer Colonialism and the Marathas Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 4 Colonialism and the Marathas Textbook Exercise Questions and Answers.

Class 12 History Chapter 4 Colonialism and the Marathas Question Answer Maharashtra Board

History Class 12 Chapter 4 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
Marathas defeated the Portuguese during the siege of __________
(a) Vengurla
(b) Phonda
(c) Surat
(d) Rajapur
Answer:
(b) Phonda

Question 2.
The political relations between Chhatrapati Shivaji Maharaj and the British began due to the __________ episode.
(a) Kudal campaign
(b) Afzal Khan
(c) Fazal Khan
(d) coronation
Answer:
(b) Afzal Khan

Question 3.
The younger brother of Bajirao Peshwa I defeated the __________ at Vasai.
(a) British
(b) French
(c) Dutch
(d) Portuguese
Answer:
(d) Portuguese

Question 4.
The ‘Third Battle of Panipat’ was fought between Marathas and the __________
(a) British
(b) Abdali
(c) Ahmed Khan Bangash
(d) Najib Khan
Answer:
(b) Abdali

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
(c) Francois Martin – Governor General of Pondicherry

2A. Write the names of historical places/persons/events.

Question 1.
The first Europeans to arrive in India-
Answer:
Portuguese

Question 2.
The place where the Portuguese stored their ammunition-
Answer:
Panvel

Question 3.
They honoured Chhatrapati Shivaji Maharaj with tributes for ensuring the safety of their factories and issuing trade permits-
Answer:
The Dutch

Question 4.
The British agent at Jaitapur-
Answer:
Velaji

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
Chhatrapati Shivaji Maharaj levied octroi on the salt trade to __________
(a) oppose the Portuguese
(b) stop the British trade of salt
(c) raise funds for Swarajya
(d) oppose the colonialists
Answer:
(b) stop the British trade of salt

3. State your opinion.

Question 1.
Chhatrapati Shivaji Maharaj built a naval force.
Answer:
Chhatrapati Shivaji Maharaj had foreseen the ulterior motives of the foreigners and their ways of infiltration. He built strategies to arrest their advances in India. He took immediate measures by creating a strong naval force. He levied octroi on British trade salt as a measure to protect the local salt trade. Thus, Chhatrapati Shivaji Maharaj adopted a strong policy against the European colonizers.

Question 2.
Maratha’s policies were anti-colonial.
Answer:
Chhatrapati Shivaji Maharaj had foreseen the ulterior motives of the Europeans and their ways of infiltration. So, he built strategies to arrest their advances in India. Chhatrapati Shivaji Maharaj adopted a very strong policy against the European colonisers by levying octroi on the British salt trade etc. The Marathas were the only Indian rulers to adopt a policy of resistance against the European colonisers.

4. Answer the following questions in detail.

Question 1.
Write about Chhatrapati Shivaji Maharaj’s policies regarding the European traders as seen in his Adnyapatra.
Answer:
The strategy of Chhatrapati Shivaji Maharaj against the Europeans is clearly seen in Adnyapatra.
The following were his policies:

• They should be kept at bay maintaining only business relations.
• Not allotting them any space near the entrance of a creek or a sea fort.
• Their establishments should not be a nuisance.
• They should not be allowed to flaunt their military strength.
• Not allow them to construct any permanent buildings.
• They must accept these conditions otherwise they are of no use.
• He also said that a fine should be collected if any foreign traders were found in the enemy land during expeditions.
• After they pay the fine, they should be sent back to their factory or the place from where they had arrived.
• They should not be treated in the same manner as the enemy is treated.

Question 2.
Explain Chhatrapati Shivaji Maharaj’s resolute policy of safeguarding Maratha sovereignty.
Answer:
Chhatrapati Shivaji Maharaj took several steps to safeguard the Maratha empire.

• Chhatrapati Shivaji Maharaj created a strong naval force and constructed forts for e.g., Hillforts, Sea forts, and Land forts.
• Henry Oxenden, a British agent who was present at the coronation of Chhatrapati Shivaji Maharaj sought permission to open a factory at Rajapur.
• He also levied 2.5% octroi on British goods.
• An agreement was signed between the British and the Marathas on 12th June 1674.
• According to this agreement, the Marathas issued permission to open factories at Rajapur, Dabhol, Chaul, and Kalyan. He also prohibited the usage of British coinage.
• He also refuted some of the conditions put by the British such as the British goods found afloat from the wrecked ships should be returned to them and the Marathas should enter a treaty with the Siddis of Janjira.
• This clearly reveals his resolute policy of safeguarding Maratha’s sovereignty.

Question 3.
Why did the strongest Maratha rule come to an end?
Answer:
There were several reasons for the downfall of the Maratha empire:
(i) Internal weakness of the Maratha Empire: The empire of the Marathas was not well knit. It was a confederacy of the Maratha chiefs who were in conflict with one another. The nominal unity of the Marathas remained only up to the period of the rule of Madhav Rao I.

(ii) Lack of Political Foresight: The Marathas lacked wisdom and farsightedness. They failed to achieve the political unity of India and therefore failed to utilise the resources of the country either for the benefit of the people or for meeting the challenge of a foreign foe.

(iii) Incapable Leadership: All capable Maratha chiefs died by the end of the eighteenth century. After that the leadership of the Marathas was taken over by Bajirao II, Daulatrao Scindia, Yashwant Rao Holkar, and Nana Phadnavis. The Marathas thus lacked leadership.

(iv) Military weakness of the Marathas: The Marathas were militarily weak compared to the English as they had left their traditional method of guerrilla warfare and adopted European methods which they failed to perfect.

(v) Diplomacy of the English: The English were more diplomatic than the Marathas. The quarrels among the Marathas provided a good opportunity for the English to take advantage. Besides, the English had their eyes on the politics of the entire India.

5. Observe the map on textbook page 29 and answer the questions based on it.

Question 1.
Where were the Dutch colonies on the west coast of India?
Answer:
On the west coast of India, there were warehouses at Vengurla in Konkan and at Photo Novo (Parangi Pettai) and Tegna Pattam (Devanapattinam) in Karnataka.

Question 2.
Where did the French establish their colonies on the east coast of India?
Answer:
The French had their colony in Pondicherry (Puducherry) on the east coast.

Question 3.
Whose warehouses were at Agra and Allahabad?
Answer:
This warehouse is not mentioned on the map. This area was ruled by the Mughals.

Project (Textbook Page No. 33)

Question 1.
Collect information about the colonies established by the European colonialists in various countries with the help of internet.
Answer:
The European colonialists had their colonies in the following countries.
(A) Africa:

• Belgium – Belgian Congo, Lado Enclave, Rwanda, and Burundi
• Britain – Sudan, Basutoland, Balleland, British East Africa (Kenya), British Somaliland, British Togoland
• Gold Coast, South Africa, Namibia, Zimbabwe, Swaziland, Uganda, Zambia, Botswana, Nigeria, Ghana, etc.
• France – Gambia, Comoros, French Algeria, French Congo, French Guinea, Ivory Coast, French Madagascar, etc.
• Dutch – Dutch East Indies, Curacao, The Dutch Slave Coast, the Dutch Gold Coast, Surinam.
• Germany – German East Africa, German Southwest Africa, German West Africa.
• Portugal – Angola, Cape Verde, Guinea-Bissau, Mozambique.

(B) Asia:

• Britain – Colony Aden, British Borneo, Burma, Ceylon, Cyprus, India, Iraq, Malay, North Borneo, Palestine, etc.
• France – Cochin, China, Annam, Laos, and Cambodia.
• Dutch – Dutch East Indies, Malacca, Taiwan, Tonkin/Annam, Maluku Islands.
• Portugal – Goa, Malacca and Southeast Asia, China and Japan, Spice Islands, South Asia, Persian Gulf, and the Red Sea.

(C) North America:

• Britain – Massachusetts, New Hampshire, Rhode Island, Connecticut, New York,
• Pennsylvania, Delaware, New Jersey, Maryland, Virginia, North Carolina, South Carolina, and Georgia.
• France – New France (including Canada and Louisiana), French West Indies and
• French Guiana.
• Dutch – New Netherland was the first Dutch colony in North America.

(D) South America:

• Spain – Argentina, Bolivia, Chile, Colombia, Costa Rica, Cuba, Dominican Republic.

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Std 12 History Chapter 3 Question Answer India and European Colonialism Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 3 India and European Colonialism Textbook Exercise Questions and Answers.

Class 12 History Chapter 3 India and European Colonialism Question Answer Maharashtra Board

History Class 12 Chapter 3 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
Vasco da Gama was a seafarer from ___________
(a) Poland
(b) England
(c) France
(d) Portugal
Answer:
(d) Portugal

Question 2.
The license was given by England to the East India Company to trade with eastern countries by ___________
(a) Sir George Oxenden
(b) Princess Braganza
(c) Queen Elizabeth
(d) Homer
Answer:
(c) Queen Elizabeth

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
(a) Arcebispo – Archbishop

2. Complete the concept map.

Question 1.

Answer:

3. Explain the following statements with reasons.

Question 1.
The Indian rulers had to obtain Cartaz.
Answer:
Cartaz: The Cartaz was a license issued by the Portuguese to the Indian rulers for sailing on the Indian Ocean when they established firm control of the Indian Ocean. It usually carried details like the name of the vessel (ship), the name of the captain of the ship, port of departure and arrival, the list of weaponry on the ship loaded for the purpose of self-defense, etc.

Question 2.
Indian rulers found it difficult to fight the Portuguese.
Answer:
The Portuguese established a strong navy. They used to launch sudden attacks on their enemy’s territory from the sea and wreck it completely. The Indian rulers could not match the Portuguese in their war tactics. Later when they established their firm control on the Indian Ocean it became necessary for the Indians to get a license from them for sailing on the Indian Ocean.

4. Answer the following questions in detail.

Question 1.
Which are the places where the Portuguese established their colonies?
Answer:
By 1608, the Portuguese had established their colonies on the western coast of India at Diu, Daman, Chaul, Goa (including Sashti and Bardish), Honnavar, Gangoli, Basrur, Mangalore, Kannur, Kodungallur, Kochi, and Kollam. Similarly, on the eastern coast, they had trader colonies at Nagapattinam, Mylapore or Sao Tome/San Thom, and Hugli in Bengal. This stretch of the Portuguese empire had its capital at Goa.

Question 2.
What were the rights given to United East India Company by the Dutch government?
Answer:
The Dutch government issued a license to the company to conduct trading with the eastern countries. The same license permitted them to appoint staff, establish factories, build forts, engage in battles against the eastern countries, and also sign treaties with them. Accordingly, the company appointed a Governor-General to take care of Indian affairs.

Class 12 History Chapter 3 India and European Colonialism Intext Questions and Answers

Try to do this (Textbook Page No. 19)

Collect information of the church in Kerala, named after Vasco da Gama, with the help of the internet.
Answer:
St. Francis Church:

• Built-in 1503 as one of the oldest European churches in India.
• Originally known as St. Bartholomew.
• Constructed of wood and stone.
• First Portuguese church in India.
• Founded by Pedro Alvarez De Cabral.
• Built-in Persian architecture style.
• The Portuguese built a fort and within the fort, they built a church.
• History has it that Vasco da Gama died during his third visit to India and was buried here in 1524.
• After 14 years his body was moved to Lisbon.

Try to do this (Textbook Page No. 21)

Make a list of the ship-building facilities in pre-independence and post-independence India and collect information about the development of the shipbuilding industry.
Answer:
Students can use the following points as references.

• India’s maritime history began during the 3rd millennium B.C.E.
• When Indus valley had trade contact with Mesopotamia.
• Strabo mentions Rome and Greece had maritime trade relations with India.
• The Portuguese were the first Europeans to reach India by sea and traded in spices etc. followed by the Dutch.
• The shipbuilding activities of Chhatrapati Shivaji Maharaj are particularly noteworthy. Chhatrapati Shivaji Maharaj built a strong naval force.
• In the modern period, the British East India Company shipped substantial quantities of spices.
• Ship Building was a well-established craft.
• Some of the well-known shipyards in India today are Sembmarine Kakinada Ltd (SKL) India, Goa Shipyard Limited (GSL) India, Western India Shipyard Ltd.

Try to do this (Textbook Page No. 21)

The currency of various countries is known by specific names. Prepare a list of countries and their currencies.
Answer:

Project (Textbook Page No. 23)

Compile the names of Governors of British East India Company from 1600 to 1857. C.E.
Answer:
The Regulating Act of 1773 created the office with the title of Governor-General of Presidency of Fort William or Governor-General of Bengal. He was appointed by the Court of Directors of the East India Company.

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Std 12 History Chapter 2 Question Answer European Colonialism Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 2 European Colonialism Textbook Exercise Questions and Answers.

Class 12 History Chapter 2 European Colonialism Question Answer Maharashtra Board

History Class 12 Chapter 2 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
‘Declaration of Independence was drafted by __________
(a) George Washington
(b) Thomas Jefferson
(c) Lord Amherst
(d) Lord Cornwallis
Answer:
(b) Thomas Jefferson

Question 2.
The second Anglo-Burmese war was fought during the times of __________
(a) Lord Amherst
(b) Lord Dufferin
(c) Lord Dalhousie
(d) Ashley Eden
Answer:
(c) Lord Dalhousie

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
Ivory Coast – French colony

2A. Write the names of historical places/persons/events.

Question 1.
The region from Florida to California on the southern coast of America was under the control of-
Answer:
Spain

Question 2.
The sea voyages for exploration were encouraged in the reign of-
Answer:
Queen Elizabeth I

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The British wanted to gain control over Myanmar because __________
(a) they wanted to expand their empire
(b) it was very important to control the natural resources and the market in Myanmar
(c) they wanted to be at the forefront of the colonial competition amongst the European nations
(d) they wanted to teach a lesson to King Thibaw of Myanmar
Answer:
(b) it was very important to control the natural resources and the market in Myanmar

3. Complete the following concept map.

Question 1.

Answer:

4. Write short notes.

Question 1.
Nature of Colonialism.
Answer:

• Colonialism is the act of a developed nation occupying the land of a less developed, distant nation and establishing its rule on the occupied country. Europeans travelled all over the world with various intentions such as the urge for adventures, to earn a name, to discover unknown lands, to search for gold mines, etc.
• The Europeans established colonies wherever they went and in doing so there was a competition to gain economic, social, and political supremacy among the nations. Extreme nationalism, feeling of racial superiority, industrialization, aggressive approach, etc., are the factors that led to the growth of colonialism.
• Thus, Europeans went to America, Australia, and New Zealand. The Europeans also colonised Asia. However, the climate of Asia did not favour them. Favourable or unfavourable, Europeans disposed of the indigenous people in their own lands.
• The Europeans saw these colonies as potential marketplaces to sell their surplus goods which were accumulated as a result of mass production. The Europeans also needed additional sources that would provide ample raw material.
• In the latter half of the 19th century, England built a flourishing trade as a result of the industrial revolution.

Question 2.
American War of Independence.
Answer:
The colonies got into several battles with the British army even after gaining independence. The colonies finally at Saratoga got a decisive victory over the British army. This victory proved to be a turning point for the colonies as the French agreed to support them in their conflict against the British. Eventually, Spain also joined the conflicts in their struggle for independence.

On 7th October 1780, George Washington defeated the British army. On 19th October, British General Lord Cornwallis surrendered and America became independent. The American revolt for independence is also known as the ‘American Revolution’. America proved to the world that the subjects have a right to fight their rulers who deny them their natural rights.

5. Explain the following statements with reasons.

Question 1.
The industrial revolution gave momentum to colonialism.
Answer:
Colonialism was a result of the industrial revolution. Production increased enormously because of the new machines. However, the rate of local consumption was much less compared to the surplus rate of production. Hence, the immediate need of the Europeans was to find new markets for selling their products. It was also necessary that these markets be dependable and easy to dominate.

Question 2.
European nations established colonies in America.
Answer:
The stronger European nations dominated the weaker countries by establishing colonies there and pushed them to subjection. The lands of the original inhabitants in America were seized by the Europeans and were also massacred. The original inhabitants were forced into slavery. The Europeans discovered gold mines and the Spanish colonizers brought African slaves to work in sugarcane and tobacco fields. Farming and mining earned them enormous wealth. Essential raw materials were exported to Spain and the finished goods used to be imported for sale in the local markets for the colonies. The trade of gold and silver also earned huge profits for the king. Witnessing Spain’s prosperity England, Holland and France also began to establish colonies in America.

Class 12 History Chapter 2 European Colonialism Intext Questions and Answers

Try to do this. (Textbook Page No. 11)

Locate the following regions under British domination on the map: Gibraltar, Malta in the Mediterranean Sea; British Guyana, British Honduras, British West Indies, Bermuda and Falkland islands in the Western Hemisphere; Aden, Sri Lanka, Myanmar, Hongkong, India; also, the countries in Africa.
Answer:

Project (Textbook Page No. 18)

Question 1.
Collect information about the biodiversity and sources of minerals in the African continent.
Answer:
1. Meaning of Biodiversity:
Biodiversity consists of two words ‘Biological’ and ‘Diversity’. It refers to all the variety of life that can be found on earth (plants, animals, fungi, and microorganisms) as well as to the communities that they form and the habitats in which they live.

2. Biodiversity in Africa:

• Rich in biodiversity.
• Africa supports the earth’s largest assemblages of large mammals which roam freely in many countries.
• Africa is home to a rich and diverse animal, plant, and marine biodiversity that provide critical ecosystem services.

3. Minerals in Africa:
Africa is rich in mineral reserves and ranks first or second in quantity of world reserves of bauxite, cobalt, industrial diamond, phosphorite, platinum, etc.

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Std 12 History Chapter 1 Question Answer Renaissance in Europe and Development of Science Maharashtra Board

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 1 Renaissance in Europe and Development of Science Textbook Exercise Questions and Answers.

Class 12 History Chapter 1 Renaissance in Europe and Development of Science Question Answer Maharashtra Board

History Class 12 Chapter 1 Question Answer Maharashtra Board

1A. Choose the correct alternative and rewrite the statement.

Question 1.
In 1440 ________ started the printing press.
(a) James Watt
(b) Gutenberg
(c) Aristotle
(d) Homer
Answer:
(b) Gutenberg

Question 2.
In 1609 _______ made a modified telescope.
(a) John Kay
(b) Copernicus
(c) Galileo
(d) Kepler
Answer:
(c) Galileo

Question 3.
_________ was the first explorer to circumnavigate the African continent.
(a) Henry the Navigator
(b) Marco Polo
(c) Bartholomew Dias
(d) Columbus
Answer:
(c) Bartholomew Dias

B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Answer:
Samuel Crompton – Spinning Mule

2. Write the names of historical places/persons/events.

Question 1.
Father of the empirical science —
Answer:
Galileo

Question 2.
Scientists who told the world that the centre of our planetary system is the ‘Sun’ and not the ‘Earth’ —
Answer:
Nicolaus Copernicus

Question 3.
The treatise was written by Varahmihir —
Answer:
Brihatsamhita

3. Complete the following concept map.

Question 1.

Answer:

4. Write short notes.

Question 1.
European Crusades.
Answer:

1. The two cities of Jerusalem and Bethlehem considered holy by the Jews, Christians, and Muslims were under Islamic rule in the 11th century.
2. Christians of Europe wanted to regain hold over these cities and fought several wars known as ‘Crusaders’.
3. The common people in Europe were highly inspired to be part of such religious wars.
4. When the Pope announced that the sins of those who took part in such wars would be forgiven and would immediately go to Heaven, there was spontaneous participation by the common people in the crusaders.
5. Besides social and political circumstances, the Roman emperors were also trying to bring Syria and Asia Minor under their control.
6. Moreover, the rich merchants in Genova and Venice in Italy were looking for Central Asian markets to establish their trade.
7. The first crusade started in 1096 C.E.
8. A second call for the crusade was given by Pope Eugenius III who sought help from the French King Louis VII and the German King Conrad III.
9. The crusaders were ultimately defeated by the Turks and in 1187 C.E. Saladin, the Sultan of Egypt defeated the crusaders by conquering Jerusalem.
10. However, the crusaders failed for several reasons such as the attitude of the Pope and the European rulers common people losing faith, the rift between the Pope and the European kings, etc.

Question 2.
Metallurgy in Europe.
Answer:

1. England had a number of iron mines.
2. Therefore, it was necessary to advance the technique of smelting iron to acquire purified iron from it.
3. The fuel for iron furnaces was replaced from wood to coal.
4. Special machines were made to keep the furnaces at a set temperature and to maintain their aeration.
5. In 1865, the process of producing steel from molten iron was invented and the nature of the iron industry underwent a major transformation.
6. At about the same time, a method was adopted to pour the molten metal into casts for making iron bars (e.g. rails).

5. Explain the following statements with reasons.

Question 1.
The European Renaissance is supposed to have reached its zenith in the 15th-16th centuries.
Answer:

1. The European Renaissance began in the 14th century C.E.
2. It reached its zenith in the 15th and 16th centuries.
3. These three centuries laid the foundations of a culture based on rationalism and science.
4. This age gave a new direction to human intellect genius and way of life.
5. People started writing poetry, drama, and fiction.
6. Novel experiments were conducted in the field of science.
7. In the pre-renaissance period, the thought about the existence of the universe revolved around ‘God’.
8. In short, in this period new inventions, machinery, art, drama, literature, and geographical discoveries have taken place.

Question 2.
The ‘Industrial Revolution first began in England.
Answer:
‘Industrial Revolution’ indicates the transition from manual production to mechanized production.

1. In England, the atmosphere was suitable for the industrial revolution.
2. Large amounts of iron ore and coal were available.
3. The humid climate of England was suitable for producing yarn.
4. These conditions proved to be favourable for the textile industry in England.
5. England had also established a large number of colonies by then so England could obtain raw material at cheap rates from these colonies.
6. England could also export the processed goods and sell it in their colonies with large profit margins using their navy.
7. The availability of cheap labour made it possible for them to maintain an optimum level of costs.
8. These factors prepared the ground for the industrial revolution in England thus giving a boost to its economy. Because of the above reasons Industrial revolution first began in England.

6. State your opinion.

Question 1.
The European natural scientists of the 17th century laid the foundations of modern science.
Answer:
The scientists of the 17th century emphasized the following things:

• To prove that scientific principles established by empirical experiments are true despite time and space.
• To convert the emergent scientific rules into scientific formulae.
• To create new scientific parlance and so on.
  These efforts helped the progress of science.

Question 2.
The economy based on surplus production supported economic nationalism and also imperialism.
Answer:

• Economic nationalism began the vicious circle of continuously capturing new marketplaces, searching for sources of a cheap supply of raw material, maintaining an unbroken chain supply of raw material), to attract more and more investors, to safeguard their investments. This resulted in limitless exploitation of the colonies.
• Extreme nationalism, industrialization, concepts of racial superiority, aggressive colonial policies further supported the growth of imperialism.
• The result was the immense expanse of the empires like England, France, Belgium, Germany, etc.

7. Answer the following questions in detail.

Question 1.
Explain the causes and effects of European crusades.
Answer:
Causes of European crusades:

• The two cities of Jerusalem and Bethlehem considered holy by the Jews, Christians, and Muslims were under Islamic rule in the 11th century.
• Christians of Europe wanted to regain hold over these cities and fought several wars known as ‘Crusaders’.
• The common people in Europe were highly inspired to be part of such religious wars.
• When the Pope announced that the sins of those who took part in such wars would be forgiven and would immediately go to Heaven, there was spontaneous participation by the common people in the crusaders.
• Besides social and political circumstances, the Roman emperors were also trying to bring Syria and Asia Minor under their control.
• Moreover, the rich merchants in Genova and Venice in Italy were looking for Central Asian markets to establish their trade.
• The first crusade started in 1096 C.E.
• A second call for the crusade was given by Pope Eugenius III who sought help from the French King Louis VII and the German King Conrad III.
• The crusaders were ultimately defeated by the Turks and in 1187 C.E. Saladin, the Sultan of Egypt defeated the crusaders by conquering Jerusalem.
• However, the crusaders failed for several reasons such as the attitude of the Pope and the European rulers common people losing faith, the rift between the Pope and the European kings, etc.

The crusades had far-reaching effects:

• According to some historians, the crusades led to the end of feudalism in Europe.
• The faith in the Pope began to decline.
• The contact with the regions in Central Asia led to the increased trade and new venues were opened for cities in Italy and Germany.
• It led to the rise of a new class of traders.
• European warfare went through many changes for e.g. they acquired expertise in building forts, managing the forts as military outposts, building bridges, etc.
• The European kings levied new taxes which were added to the royal treasury.
• The Europeans were introduced to newer types of plants, fruits, perfumes, etc.
• The Europeans came in contact with the Arabs and adopted many Arabic words in Alchemy, Music, and Commerce.

Question 2.
Give detailed information on the development of science and scientific inventions during the renaissance period.
Answer:
The scientists of the 17th century emphasized the following things:

• To prove that scientific principles established by empirical experiments are true despite time and space.
• To convert the emergent scientific rules into scientific formulae.
• To create new scientific parlance and so on.
• These efforts helped the progress of science.
• The compass, the barometer, telescope, and the thermometer were invented during this period.
• Microscopes were invented to observe various types of micro-organisms.
• Robert Boyle, an alchemist discovered that that the absolute pressure and the volume of a gas are inversely proportional.
• The research in physics was more focused on heat and sound.
• In zoology, a methodology known as ‘Taxonomy’ was developed to classify animals.
• Benjamin Franklin’s research was on lightning and electricity. He coined many technical terms which are used in science even today.

Class 12 History Chapter 1 Renaissance in Europe and Development of Science Intext Questions and Answers

Try to do this. (Textbook Page No. 3)

Collect information about how the early European universities worked.
Answer:

• Early European universities were the University of Bologna in 1088 or the University of Paris (1150-1170).
• the University of Bologna is considered the ‘mother of universities’.
• European universities concentrated on science and research
• Original Medieval universities arose from the Roman Catholic Church schools
• Purposes included training of professionals, scientific investigation, and teaching critical thinking and research.
• During Renaissance, the humanist ideas were slowly accepted
• Universities began preparing the student for a civilized life
• The curriculum included liberal arts such as Trivium (grammar, rhetoric, logic) and Quadrivium (arithmetic, geometry, astronomy, music)

Find it out. (Textbook Page No. 8)

Make a list of the European countries where the Industrial Revolution spread in its first stage.
Answer:
The industrial revolution first began in Britain in the late 1770s and first spread to Belgium followed by France and the German states and in North America.

Project (Textbook Page No. 9)

Collect detailed information about the voyages of Bartholomew Dias and Vasco-da- Gama and read it aloud in the class.
Answer:
(A) Bartholomew Dias:

• Bartholomew Dias was a Portuguese explorer.
• He was the first European to sail around the southern tip of Africa which the Portuguese would name as the ‘Cape of Good Hope.
• Dias and his crew departed from Lisbon, Portugal in August 1487 with three ships.
• Dias’s expedition sailed along the African coast following the route of Diogo Cao who had earlier sailed along the African coast in the 1480s.
• Near the southern tip of Africa Dias’s 3 ships sailed into a dangerous storm that pushed them away from the African coast. They sailed around the tip of Africa in January 1488 without seeing the land.
• After 30 days without seeing land, he entered what he named Aguada de Sao Bras (Bay of Saint Blaise) in February 1488.
• Dias wanted to continue to India but he was forced to turn back when his crew refused to go further and the rest of the officers favored going back home.
• It was on his return journey that he actually discovered the Cape of Good Hope in May 1488.
• Dias returned to Lisbon in December 1488 after an absence of 16 months and 17 days.

(B) Vasco da Gama:

• Vasco da Gama was a Portuguese explorer and the first European to reach India by sea.
• His initial voyage to India was the first to link Europe and Asia by an ocean route, connecting the Atlantic and Indian Oceans and therefore the West and the Orient.
• This discovery is considered to be a milestone in world history.
• Vasco da Gama’s discovery of the sea route to India opened the way for an age of imperialism in Asia.
• Vasco da Gama landed in Calicut, India on May 20, 1498.
• This boosted the economy of the Portuguese Empire.
• Vasco da Gama led the two of the India Armadas, the first and the fourth.
• In 1524, Vasco da Gama was appointed as Governor of India, with the title of Viceroy, and was ennobled as Count of Vidigueria in 1519.

Maharashtra State Board 12th Std History Textbook Solutions

• Renaissance in Europe and Development of Science Class 12 History Textbook Solutions
• European Colonialism Class 12 History Textbook Solutions
• India and European Colonialism Class 12 History Textbook Solutions
• Colonialism and the Marathas Class 12 History Textbook Solutions
• India: Social and Religious Reforms Class 12 History Textbook Solutions
• Indian Struggle against Colonialism Class 12 History Textbook Solutions
• Decolonisation to Political Integration of India Class 12 History Textbook Solutions
• World Wars and India Class 12 History Textbook Solutions
• World: Decolonisation Class 12 History Textbook Solutions
• Cold War Class 12 History Textbook Solutions
• India Transformed Part 1 Class 12 History Textbook Solutions
• India Transformed Part 2 Class 12 History Textbook Solutions

Balbharti Maharashtra State Board 12th Commerce Book Keeping & Accountancy Solutions Chapter 5 Reconstitution of Partnership (Death of Partner) Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Book Keeping & Accountancy Solutions Chapter 5 Reconstitution of Partnership (Death of Partner)

1. Objective questions:

A. Select the most appropriate answer from the alternative given below and rewrite the sentences.

Question 1.
Benefit Ratio is the ratio in which _______________
(a) The old partner gain on the admission of a new partner
(b) The Goodwill of a new partner on admission is credited to old partners
(c) The continuing partners’ benefits on retirement or death of a partner
(d) All partners are benefitted.
Answer:
(c) The continuing partner’s benefits on retirement or death of a partner

Question 2.
The ratio by which existing partners are benefitted _______________
(a) gain ratio
(b) sacrifice ratio
(c) profit ratio
(d) capital ratio
Answer:
(a) gain ratio

Question 3.
Profit and Loss Suspense Account is shown in the new Balance Sheet on _______________ side.
(a) debit
(b) credit
(c) asset
(d) liabilities
Answer:
(c) asset

Question 4.
Death is a compulsory _______________
(a) Dissolution
(b) Admission
(c) Retirement
(d) Winding up
Answer:
(c) Retirement

Question 5.
The balance on the Capital Account of a partners, on his death is transferred to _______________ Account.
(a) Relatives
(b) Legal Heir’s Loan/Executors Loan
(c) Partners’ Capital
(d) Partners’ Loan
Answer:
(b) Legal Heir’s Loan/Executors Loan.

B. Write a word, term, phrase, which can substitute each of the following statements.

Question 1.
Excess of credit side over the debit side of Profit and Loss Adjustment Account.
Answer:
Profit

Question 2.
A person who represents the deceased partner on the death of the partner.
Answer:
Legal Heir’s or Executor

Question 3.
Accumulated past profit kept in the form of reserve.
Answer:
Reserve fund or General reserve

Question 4.
The partner who died.
Answer:
Deceased partner

Question 5.
The proportion in which the continuing partners benefit due to the death of a partner.
Answer:
Gain/Benefit ratio

C. State whether the following statements are True or False with reasons.

Question 1.
A deceased partner is not entitled to the Goodwill of the firm.
Answer:
This statement is False.
A deceased partner’s contribution was there in the development of business and goodwill is the value of the business in terms of money. Hence, a deceased partner is entitled to receive goodwill from the firm.

Question 2.
A deceased partner is entitled to his share of General Reserve.
Answer:
This statement is True.
General reserve is created out of past undistributed profit. Past profit is earned due to the efforts and hard work of all the partners including the partner who is now dead. Hence a deceased partner has right on it and therefore a deceased partner is entitled to receive his share of General reserve.

Question 3.
If goodwill is written off, a Deceased Partner’s Capital Account is debited.
Answer:
This statement is False.
When the benefits of goodwill are given to the deceased partner, his capital account is credited and when such goodwill is written off, capital accounts of remaining partners are debited.

Question 4.
After the death of a partner, the entire amount due to the deceased partner is paid to the legal representative of the deceased partner.
Answer:
This statement is True.
After the death of a partner, the entire amount due to the deceased partner is paid to the legal representative of the deceased partner as he is the only person who has the legal right to that amount.

Question 5.
For recording the profit or loss up to the death, the Profit and Loss Appropriation Account is operated.
Answer:
This statement is False.
For recording the profit or loss up to the death, the Profit and Loss suspense Account is created and operated. This is because final accounts cannot be prepared on the date of death of a partner. Till that period a separate account called Profit and Loss Suspense A/c is prepared.

D. Fill in the blanks and rewrite the following sentence.

Question 1.
Deceased Partners’ Executors Account is shown on the _______________ side of the Balance Sheet.
Answer:
Liabilities

Question 2.
On the death of a partner, a ratio in which the continuing partners get more share of profits in future is called as _______________ Ratio.
Answer:
Gain

Question 3.
Deceased partners share of profit up to the death is shown on _______________ side of Balance Sheet.
Answer:
Assets

Question 4.
Benefit Ratio = New Ratio – _______________
Answer:
Old Ratio

Question 5.
When Goodwill is raised at its full value and it is written off _______________ Account is to be credited.
Answer:
Goodwill

E. Answer in one sentence only.

Question 1.
What is Gain Ratio?
Answer:
The profit-sharing ratio which is acquired by the surviving or continuing partners on account of the death of any partner is called gain ratio or benefit ratio.

Question 2.
In which ratio general reserve is distributed on the death of a partner?
Answer:
General reserve is distributed on the death of a partner in their old profit sharing ratio.

Question 3.
To whom do you distribute general reserve on the death of a partner?
Answer:
On the death of a partner general reserve is distributed among all partners in their old profit and loss ratio.

Question 4.
How the death of a partner is a compulsory retirement?
Answer:
After the death of a partner, the business is not able to get any kind of services from the deceased partner and so we can say that the death of a partner is like a compulsory retirement.

Question 5.
To which account profit is to be transferred up to the date of his death?
Answer:
Profit of the deceased partner, up to the date of his death, is transferred to his Legal Heir’s/Executor’s Account.

Practical Problems

Question 1.
Rajesh, Rakesh, and Mahesh were equal Partners on 31st March 2019. Their Balance Sheet was as follows 31st March 2019.
Balance Sheet as of 31st March 2019

Mr. Rajesh died on 30th June 2019 and the following adjustment was agreed as:
1. Furniture was to be adjusted to its market price of ₹ 3,40,000.
2. Land and Building were to be depreciated by 10%.
3. Provide R.D.D. @ 5% on debtors.
4. The profit up to the date of death of Mr. Rajesh is to be calculated on the basis of last year’s profit which was ₹ 1,80,000.
Prepare:
1. Profit and Loss Adjustment A/c
2. Partners’ Capital Account
3. Balance Sheet of the continuing firm.
Solution:
In the books of the Partnership Firm


Balance Sheet as of 1st July 2019

Working Note:
The profit of the firm of last year was ₹ 1,80,000.
Proportionate profit up to the date of death for Rajesh is as follows
= 1,80,000 × \(\frac{3}{12} \times \frac{1}{3}\) (Period) (P & L ratio)
= ₹ 15,000 (Profit and Loss Suspense A/c)

Question 2.
Rahul, Rohit, and Ramesh are in a business sharing profits and losses in the ratio of 3 : 2 : 1 respectively. Their Balance Sheet as of 31st March, 2017 was as follows:
Balance Sheet as of 31st March 2017

On 1st October 2017, Ramesh died and the Partnership deed provided that
1. R.D.D. was maintained at 5% on Debtors.
2. Plant and Machinery and Investment were valued at ₹ 80,000 and ₹ 4,10,000 respectively.
3. Of the creditors an item of ₹ 6,000 was no longer a liability and hence was properly adjusted.
4. Profit for 2017-18 was estimated at ₹ 1,20,000 and Ramesh’s share in it up to the date of his death was given to him.
5. Goodwill of the firm was valued at two times the average profit of the last five years, which were
2012-13 – ₹ 1,80,000
2013-14 – ₹ 2,00,000
2014-15 – ₹ 2,50,000
2015-16 – ₹ 1,50,000
2016-17 – ₹ 1,20,000
Ramesh’s share in it was to be given to him.
6. Salary ₹ 5,000 p.m. was payable to him.
7. Interest on capital at 5% i.e. was payable and on Drawings ₹ 2,000 were charged.
8. Drawings made by Ramesh up to September 2017 were ₹ 5,000 p.m.
Prepare Ramesh’s Capital A/c showing the amount payable to his executors.
Give working of Profit and Goodwill.
Ramesh Capital Balance ₹ 3,41,000
Solution:
In the books of the Partnership Firm

Working Notes:
1. Calculation of share of Goodwill:
(a) Average profit = \(\frac{Total Profit}{No. of years}\)
= \(\frac{1,80,000+2,00,000+2,50,000+1,50,000+1,20,000}{5}\)
= \(\frac{9,00,000}{5}\)
= ₹ 1,80,000

(b) Goodwill = Average profit × No. of years
= 1,80.000 × 2
= ₹ 3,60,000

(c) Share of Goodwill to Ramesh = Goodwill of the firm × Ramesh’s share
= 3,60,000 × \(\frac{1}{6}\)
= ₹ 60,000

2. Calculation of share of profit due to Ramesh:
Share of profit = Last year profit × Share of profit × Period
= 1,20,000 × \(\frac{1}{6} \times \frac{6}{12}\)
= ₹ 10,000 (Profit and Loss Suspense A/c)

3. Interest on Capital is calculated for six months.
∴ Interest = 2,40,000 × \(\frac{6}{12} \times \frac{5}{100}\) = ₹ 6,000

4.

Question 3.
Ram, Madhav, and Keshav are partners sharing profit and losses in the ratio 5 : 3 : 2 respectively. Their Balance Sheet as of 31st March, 2018 was as follows:
Balance Sheet as of 31st March 2018

Keshav died on 31st July 2018 and the following adjustments were agreed by as per the partnership deed.
1. Creditors have increased by ₹ 10,000.
2. Goodwill is to be calculated at 2 years purchase of average profits of 5 years.
3. The profits of the preceding 5 years was
2013-14 – ₹ 90,000
2014-15 – ₹ 1,00,000
2015-16 – ₹ 60,000
2016-17 – ₹ 50,000
2017-18 – ₹ 50,000 (Loss)
Keshav’s share in it was to be given to him.
4. Loose Tools and livestock were valued at ₹ 80,000 and ₹ 1,20,000 respectively.
5. R.D.D. was maintained at ₹ 10,000.
6. Commission ₹ 2,000 p.m. was payable to Keshav. Profit for 2018-19 was estimated at ₹ 45,000 and Keshav’s share in it up to the date of his death was given to him.
Prepare Revaluation A/c, Keshav’s Capital A/c showing the amount payable to his executors.
Solution:
In the books of the Partnership Firm

Working Notes:
1. Calculation of share of Goodwill:
(a) Average profit = \(\frac{\text { Total profit }}{\text { No. of years }}\)
= \(\frac{90,000+1,00,000+60,000+50,000-50,000}{5}\)
= \(\frac{2,50,000}{5}\)
= ₹ 50,000

(b) Goodwill = Average profit × No. of years
= 50,000 × 2
= ₹ 1,00,000

(c) Share of Goodwill to Keshav = Goodwill of the firm × Keshav’s share
= 1,00,000 × \(\frac{2}{10}\)
= ₹ 20,000

2. Calculation of share of profit due to Keshav
Share of profit = Last year profit × Share of Keshav × Period
= 45,000 × \(\frac{2}{10} \times \frac{4}{12}\)
= ₹ 3,000 (Profit and Loss Suspense Account)

Question 4.
Virendra, Devendra, and Narendra were partners sharing profit and losses in the ratio of 3 : 2 : 1. Their Balance Sheet as of 31st March 2019 was as follows.
Balance Sheet as of 31st March 2019

Mr. Virendra died on 31st August 2019 and the partnership deed provided that the event of the death of Mr. Virendra his executors be entitled to be paid out.
1. The capital to his credit at the date of death.
2. His proportion of Reserve at the date of last Balance Sheet.
3. His proportion of Profits to date of death is based on the average profits of the last four years.
4. His share of Goodwill should be calculated at two years purchase of the profits of the last four years for the year ended 31st March were as follows:
2016 – ₹ 40,000
2017 – ₹ 60,000
2018 – ₹ 70,000
2019 – ₹ 30,000
5. Mr. Virendra has drawn ₹ 3,000 p.m. to date of death, There is no increase and decrease in the value of assets and liabilities.
Prepare Mr. Virendra Executors A/c.
Solution:
In the books of the Partnership Firm

Working Notes:
1. Calculation of share of profit:
(a) Average Profit = \(\frac{\text { Total profit }}{\text { No. of years }}\)
= \(\frac{40,000+60,000+70,000+30,000}{4}\)
= \(\frac{2,00,000}{4}\)
= ₹ 50,000

(b) Goodwill = Average profit × No. of years
= 50,000 × 2
= ₹ 1,00,000

(c) Share of Goodwill to Virendra = Goodwill of the firm × Virendra’s share
= 1,00,000 × \(\frac{3}{6}\)
= ₹ 50,000

2. Share of profit due to Virendra
Share of profit = Last year profit × Share of Virendra × Period
= 50,000 × \(\frac{3}{6} \times \frac{5}{12}\)
= ₹ 10,417 (Profit and Loss Suspense A/c)

Question 5.
The Balance Sheet of Sohan, Rohan, and Mohan who were sharing profits and losses in the ratio of 3 : 2 : 1 is as follows:
Balance Sheet as of 31st March 2019

Mr. Rohan died on 1st October 2019 and the following adjustments were made:
1. Goodwill of the firm is valued at ₹ 30,000.
2. Land and Building and Machinery were found to be undervalued by 20%.
3. Investments are valued at ₹ 60,000.
4. Stock to be undervalued by ₹ 5,000 and a provision of 10% as debtors were required.
5. Patents were valueless.
6. Mr. Rohan was entitled to share in profits up to the date of death and it was decided that he may be allowed to retain his drawings as his share of profit. Rohan’s drawings till the date of death were ₹ 25,000.
Prepare Partners’ Capital Accounts.
Solution:
In the books of the Partnership firm

Working Notes:
1.

2. Firm’s goodwill = ₹ 30,000.
DistrIbute among partners in their profit and loss ratio 3 : 2 : 1.

3. Revised value of Land & Building = \(\frac{\text { Book value }}{(100-20)} \times 100\)
= \(\frac{40,000}{80} \times 100\)
= ₹ 50,000.
∴ Increase In the value of Land & Building = Revised value – Book value
= 50,000 – 40,000
= ₹ 10,000.

4. Revised value of Machinery = \(\frac{\text { Book value }}{(100-20)} \times 100\)
= \(\frac{80,000}{80} \times 100\)
= ₹ 1 ,00,000.
∴ Increase in the value of Machinery = 1,00,000 – 80,000 = ₹ 20,000.

5. Patents were valueless means it is a loss for the business.

6. Rohan’s share In profit is ₹ 25,000 and his drawings are ₹ 25,000. Rohan is allowed to retain his drawings as his share of profit. Means write ₹ 25,000 as drawings on the debit side and write ₹ 25,000 as Profit and Loss Suspense A/c on the Credit side of Partners’ Capital A/c.

Std 12 Economics Chapter 10 Question Answer Foreign Trade of India Maharashtra Board

Balbharti Maharashtra State Board Class 12 Economics Solutions Chapter 10 Foreign Trade of India Textbook Exercise Questions and Answers.

Class 12 Economics Chapter 10 Foreign Trade of India Question Answer Maharashtra Board

Economics Class 12 Chapter 10 Question Answer Maharashtra Board

1. Choose the correct option:

Question 1.
Types of foreign trade
a) Import trade
b) Export trade
c) Entrepot trade
d) Internal trade
Options:
1) a and b
2) a, b and c
3) a, b, c and d
4) None of these
Answer:
2) a, b and c

Question 2.
Export trends of India’s foreign trade includes
a) Engineering goods
b) Gems and Jewellery
c) Textiles and ready-made garments
d) Gold
Options:
1) a and c
2) a, b and c
3) b, c and d
4) None of these
Answer:
2) a, b and c

Question 3.
Role of foreign trade is
a) To earn foreign exchange
b) To encourage investment
c) Lead to division of labour
d) Bring change in composition of exports
Options:
1) a and b
2) a, b and c
3) b and d
4) None of these
Answer:
2) a, b and c

2. Identify and explain the concepts from the given illustrations:

Question 1.
India purchased petroleum from Iran.
Answer:
Concept: Import trade
Explanation: Import trade means purchase of goods and services by one country from another country.

Question 2.
Maharashtra purchased wheat from Punjab.
Answer:
Concept: Internal/Home/Domestic trade Explanation : Internal trade is also known as home trade or domestic trade. This trade is within the country. It is between two or more states of the country.

Question 3.
England imported cotton from India, made readymade garments from it and sold them to Malaysia.
Answer:
Concept: Entrepot trade
Explanation : It means purchase of goods and services from one country and selling the same to another country.

Question 4.
Japan sells smart phones to Myanmar.
Answer:
Concept: Export trade
Explanation : It means sell of goods and services by one country to another country.

3. Distinguish between the following:

Question 1.
Internal trade and International trade.
Answer:

Question 2.
Trends in imports and Trends in exports of foreign trade.
Answer:

Question 3.
Balance of payments and Balance of trade.
Answer:

4. Answer the following:

Question 1.
Explain the concept of foreign trade and its types.
Answer:

Foreign trade is the exchange of goods and c services between two or more countries, Foreign trade is the trade across the j boundaries of a country.

There are three important types of foreign trade.

• Import trade : It is a buying of goods and services from other country by home country. Excessive import can have a negative impact on home country. E.g. India buying petroleum from Iraq, Kuwait, etc.
• Export trade : It is selling of goods and services by home country to another country.
  Excessive export can have a positive impact on the home country. E.g. India exporting tea and spices to USA, China, etc.
• Entrepot trade : It means buying of goods and services from one country and selling them to another country. E.g. England importing cotton from India, making readymade garments from it and selling them to Malaysia.

Question 2.
Explain any four features of composition of Indias foreign trade.
Answer:
There are many changes in India’s foreign trade from last seven decades (70 years)

• Gross National Income : India’s foreign trade has great significance for its GNP. It increased upto 48.8% in the year 2016-17.
• Change in composition of exports : After independence there was change in the composition of India’s export trade from primary products to manufactured goods.
• Change in composition of imports :
  After independence there was change in the composition of India’s import trade from consumer goods to capital goods.
• Development of new ports : India’s foreign trade is handled mainly by Mumbai, Calcutta and Chennai ports. India has developed more new ports at Kandla, Cochin, Vishakhapatnam.
• Oceanic trade : Most of India’s foreign trade is by sea. About 68% of India’s trade is by sea.

Question 3.
Explain the trend in India’s imports.
Answer:
India is importing various goods from other countries. Following are the major imported goods of India :

• Petroleum : It has largest share in India’s import. In the year 2016-17, it has 22.6% share in India’s total import.
• Gold: After petroleum, the second most imported item is gold. In the year 2011, ) India’s import of gold was $53.9 billion and in the year 2018-19 it declined upto $32.8 billion.
• Fertilizers: The share of fertilizers in import expenditure declined from 4.1% in 1990-91 to only 1.3% in 2016-17.
• Iron and Steel: In the year 2016-17, the share of iron and steel in India’s total import was 2.1%.

5. State with reasons whether you agree or disagree with the following statements:

Question 1.
During British nile, indigenous handicrafts suffered a severe blow.
Answer:
Yes, I do agree with this statement.

• During the British rule India was exporting raw materials to England and was importing final goods from England.
• Indian handicraft was unable to face competition with imported goods from England.
• An imported goods were cheaper as compared to handicraft goods.
• The demand for machine made cheap commodity had raised in Indian market.
• That’s why Indian handicraft industries suffered during the British rule.

Question 2.
Trade is an engine of growth for an economy.
Answer:
Yes, I agree with this statement.

• Trade permits a more efficient allocation of national resources.
• Foreign trade provide foreign exchange which can be used to import modern machinery and technology from advanced countries.
• Foreign trade encourages producers to produce more goods for export.
• It leads to an increase in total investment in an economy.
• Thus, we can say, trade is an engine to growth for an economy.

Question 3.
Foreign trade leads to division of labour and specialization at world level.
Answer:
Yes, I agree with this statement.

• Some countries have abundant natural resources.
• These countries should export raw material and import finished goods from countries which are advanced in skilled man power
• Under specialisation specific work is given to the workers within a production process.
• Specialisation can increase the productivity of a firm or economy.
• Eg. Incase of car manufacturing company, some workers will design the cars, some workers will work on different section of assembly line, some workers will work on j testing cars, some workers will work on marketing of cars.

6. Observe the following table and answer the questions geven below it.

Direction of Indias imports

Questions:

Question 1.
Which organisation has the least share in the direction of India’s imports in 2015-16?
Answer:
Eastern Europe has the least share in the direction of India’s import.

Question 2.
Which orgamsation has maximum share in India’s direction of imports in 1990-91?
Answer:
OECD [Organisation for Economic Co-operation and Development has maximum share in India’s direction of imports in 1990-91.

Question 3.
Expand the abbreviations of OECD and OPEC
Answer:
OECD : Organisation for Economic Co-operation and Development.
OPEC : Organisation of Petroleum Exporting Countries.

Question 4.
State your opinion regarding the direction of India’s imports from 1990-91 to 2015-16.
Answer:
In the year 1990-91, OECD (54.0%) and in the year 2015-16, Developing nations (43.2%) has the highest share in the direction of India’s imports. India should encourage industries those are producing import substitute goods,which will help to reduce import from developing nations and help to save foreign exchange.

Question 5.
How much is the percentage of increase in the imports of developing nations in 2015-16 as
compared to 1990-9 1?
Answer:
There is 24.6% increase in the imports of developing nations.

7. Answer in detail :

Question 1.
Explain the meaning and role of foreign trade.
Answer:
Trade means buying and selling of goods and services. Foreign trade means when goods and services are exchanged between two or more countries.
According to Wasserman and Hultman “International trade consists of transaction between residents of different countries”.
Role of foreign trade :

• Brings reputation and helps earn goodwill : Exporting country can earn reputation and goodwill in the international market. Eg. Japan in electronic goods- Panasonic, Canon, Sony, Hitachi. Germany in Automobile – BMW, Audi, Mercedes- Benz, Volkswagen, Porsche. USA in food- McDonalds, KFC, USA in computers – Dell HP, IBM.
• Division of labour and specialisation: It helps to increase the productivity of a firm or economy. Under specialisation specific work is given to the workers within a production process. Eg. Some workers will design cars, some workers will work on assembly lines, some workers will work on testing cars, some workers will work on marketing of cars.
• To earn foreign exchange: Foreign trade is playing very important role in earning foreign exchange. This foreign exchange can be used to import advanced technology and machinery from developed countries.
• Encourages investment : Foreign trade leads to an increase in total investment in an economy. The rise in investment help to produce more goods and services for export.
• Availability of multiple choices : Due to availability of imported goods, it helps to improve standard of living of the people in the country.
• Stability in price level : Foreign trade helps to control the changes in price level by keeping demand and supply position stable,
• Helpful during natural calamities : Foreign trade enables a country to import food grains and medicines from other countries to help the affected people.
• Optimum allocation and utlization of resources : Due to foreign trade those goods are produced which have demand in international market. There is maximum allocation and utlisation of resources to produce more goods and services for export.
• Promotes world peace : Foreign trade is bringing countries closer which leads to better understanding, co-operation and integration.

Question 2.
Explain the recent trends in India’s exports.
Answer:
Export means selling of goods and services by home country to another country. Excessive export can have a positive impact on the home country.

(i) Engineering Goods : Engineering goods includes transport equipment, automobiles and auto components, machinery and instruments. India’s top export item is engineering goods accounting for 22.5% in India’s total export in 2014-15 and this share has increased upto 25% in the year 2017-18. India is exporting engineering goods to Sri Lanka, UAE and USA.

(ii) Petroleum Products : India’s refining capacity increased significantly since 2001-02 due to which India turned a net exporter of petroleum refinery products. In the year 2013-14 the share of petroleum products in total export was 20.1% and in the year 2016-17 it declined upto 11.7%.

(iii) Chemicals and chemical products:
It includes drugs (Medicines) and pharmaceuticals. This is one sector where India is highly competitive on both quality and pricing factor. India became global hub for pharma production. India is exporting its chemicals and chemical products to USA, China and Germany. The share of this item was 10.4% in 2014-15.

(iv) Gems and Jewellery: Gems and Jewellery plays an important role in earning the foreign exchange for India. In the year 2014¬15 the share of Gems and Jewellery was 13.3% in India’s total export and it declined upto 5.32% in the year 2018-19.

(v) Textiles and readymade garments :
India’s readymade garments have huge demand in the international market. India is exporting textiles to USA, China and Bangladesh. India is exporting readymade garments to USA, UAE and UK. In the year 2014-15 India’s export of textile and garments was 11.3% of total export of India and it has declined upto 6.3% in the year 2016-17.

Intext Questions

Try this : (Text Book Page No. 94)

Name the goods exported to and imported from India to China and Japan in recent years
Answer:

Find out: (Text Book Page No. 95)

Find the recent share of India’s foreign trade in Gross National Income.
Answer:
India’s foreign trade accounts for 48.8% of her Gross National Income.

Find out: (Text Book Page No. 97)

List the countries coming under OPEC and OECD.
Answer:
The countries coming under OPEC (Organisation of Petroleum Exporting Countries) are :
(a) Algeria, (b) Angola, (c) Congo, (d) Equatorial Guinea, (e) Gabon, (f) Iran, (g) Iraq, (h) Kuwait, (i) Libya, (j) Nigeria, (k) Saudi Arabia (1) United Arab Emirates, 0 Venezuela.

Maharashtra State Board 12th Std Economics Textbook Solutions

• Introduction to Micro and Macro Economics Class 12 Economics Textbook Solutions
• Utility Analysis Class 12 Economics Textbook Solutions
• Demand Analysis Class 12 Economics Textbook Solutions
• Elasticity of Demand Class 12 Economics Textbook Solutions
• Supply Analysis Class 12 Economics Textbook Solutions
• Forms of Market Class 12 Economics Textbook Solutions
• Index Numbers Class 12 Economics Textbook Solutions
• National Income Class 12 Economics Textbook Solutions
• Public Finance in India Class 12 Economics Textbook Solutions
• Money Market and Capital Market in India Class 12 Economics Textbook Solutions
• Foreign Trade of India Class 12 Economics Textbook Solutions

Std 12 Economics Chapter 9 Question Answer Money Market and Capital Market in India Maharashtra Board

Balbharti Maharashtra State Board Class 12 Economics Solutions Chapter 9 Money Market and Capital Market in India Textbook Exercise Questions and Answers.

Class 12 Economics Chapter 9 Money Market and Capital Market in India Question Answer Maharashtra Board

Economics Class 12 Chapter 9 Question Answer Maharashtra Board

1. Complete the following statements:

Question 1.
Development financial institutions were established to …………………
a) provide short term funds.
b) develop industry, agriculture and other key sectors.
c) regulate the money market.
d) regulate the capital market.
Answer:
b) develop industry, agriculture and other key sectors.

Question 2.
Money market faces shortage of funds due to
a) inadequate savings.
b) growing demand for cash.
c) presence of unorganized sector.
d) financial mismanagement.
Answer:
a) inadequate savings.

Question 3.
Individual investors have lost confidence in the
capital market due to
a) lack of financial instruments.
b) high transaction costs.
c) low returns.
d) financial scams.
Answer:
d) financial scams.

Question 4.
Commercial banks act as intermediaries in the financial system to
a) make profits
b) accelerate the country’s economic growth.
c) mobilise the savings and allocating them to various sectors of the economy.
d) control the credit.
Answer:
c) mobilise the savings and allocating them to various sectors of the economy.

2. Complete the correlation:

1) Money market : Short term funds :: …………….. : Long term funds
2) …………….. : Central Bank:: SBI : Commercial Bank
3) Co-operative banks : Organized sector :: Indigenous bankers : ……………..
4) Primary market : …………….. :: Secondary market : Old issues
Answers:

1. Capital market
2. RBI
3. Unorganised sector
4. New issue

3. Find the odd word:

Question 1.
Types of Bank Accounts:
Answer:
Saving A/c, D-mat A/c, Recurring A/c, Current A/c.

Question 2.
Unregulated Financial Intermediates:
Answer:
Mutual fund, Nidhi, Chit fund, Loan Companies.

Question 3.
Financial Assets:
Answer:
Bonds, Land, Government Securities,
Derivatives.

Question 4.
Quantitative Tools:
Answer:
Bank Rate, Open Market Operation, Foreign Exchange Rate, Variable Reserve Ratio.

4. Assertion and Reasoning:

Question 1.
Assertion (A) : Money market economizes use of cash
Reasoning (R) : Money market deals with financial instruments that are close substitutes of money
Options: 1) (A) is True, but (R) is False
2) (A) is False, but (R) is True
3) Both (A) and (R) are True and (R) is the correct explanation of (A)
4) Both (A) and (R) are True and (R) is not the correct explanation of (A)
Answer:
3) Both (A) and (R) are True and (R) is the correct explanation of (A)

Question 2.
Assertion (A) : Regional stock exchanges have witnessed a sharp decline in the volume of trade.
Reasoning (R) : Investors prefer to trade in securities listed in premier stock exchanges like BSE, NSE etc.
Options:
1) (A) is True, but (R) is False
2) (A) is False, but (R) is True
3) Both (A) and (R) are True and (R) is the correct explanation of (A)
4) Both (A) and (R) are True and (R) is not the correct explanation of (A)
Answer:
3) Both (A) and (R) are True and (R) is the correct explanation of (A)

Question 3.
Assertion (A) : The unorganized sector of the money market lacks transparency.
Reasoning (R) : Activities of the unorganized sector are largely confined to rural areas.
Options:
1) (A) is True, but (R) is False
2) (A) is False, but (R) is True
3) Both (A) and (R) are True and (R) is the correct explanation of (A)
4) Both (A) and (R) are True and (R) is not the correct explanation of (A)
Answer:
4) Both (A) and (R) are True and (R) is not the correct explanation of (A)

Question 4.
Assertion (A) : Foreign exchange management and control is undertaken by commercial banks.
Reasoning (R) : RBI has to maintain the official rate of exchange of rupee and ensure its stability.
Options:
1) (A) is True, but (R) is False
2) (A) is False, but (R) is True
3) Both (A) and (R) are True and (R) is the correct explanation of (A)
4) Both (A) and (R) are True and (R) is not the correct explanation of (A)
Answer:
3) Both (A) and (R) are True and (R) is the correct explanation of (A)

5. Identify and explain the concepts from the given illustrations:

Question 1.
Raghu’s father regularly invests his money in stocks and bonds.
Answer:
Concept: Financial Market
Explanation : Financial Market refers to a market where financial assets such as bonds, stocks, derivatives, government securities foreign currency, etc. are sold and purchased.

Question 2.
Sara makes a monthly contribution to a fund jointly created by her friends. The collected fund is then given to a chosen member through lucky draw.
Answer:
Concept: Chit fund
Explanation : Under chit fund, members make regular contribution to the fund, bids or draws are made on the basis of a criteria mutually agreed upon by members.

Question 3.
Tina deposited a lurnpsurn amount of 50,000 in the bank for a period of one year.
Answer:
Concept: Fixed deposit
Explanation : Fixed deposit refers to a lumpsum amount deposited by a customer for a specified period of time. Compared to all other deposits, fixed deposits carry a high rate of interest.

Question 4.
ABC bank provides d-mat facility, safe deposit lockers, internet banking facilities to its customers.
Answer:
Concept: Ancillary function of Commercial Bank
Explanation : Ancillary services are those services of commercial banks which are provided beside the primary services of bank. Ancillary services are transfer of j funds collection of money, making periodical payments on behalf of the customer, merchant banking, foreign exchange, safe deposits lockers, D-mat facility, internet banking.

6. Distinguish between:

Question 1.
Money market and Capital market.
Answer:

Question 2.
Demand deposit and Time deposit.
Answer:

Question 3.
Organized sector and Unorganized sector of money market.
Answer:

7. Answer the following:

Question 1.
Explain the problems faced by the money market in India.
Answer:
Following are the problems of money market in India:
(a) Shortages of Funds : Generally, there is shortage of funds in Indian Money Market on account of various factors like inadequate banking facilities, low savings, lack of banking habits, existence of parallel economy,- etc. have also been responsible for the paucity of funds in the money market.

(b) Existence of Unorganised Money Market : This is one of the major defects of Indian Money Market. It does distinguish between short term and long term finance, and also between the purposes of finance. Since it is outside the control and supervision of RBI. It limits the RBI’s control over money market.

(c) Delays in technological up-gradation: Use of advanced technology is a pre requisite for the development and smooth functioning of financial markets. Delays in up-gradation of technology hampers the working of the money market.

(d) Absence of Well Organized Banking Sector : Branch expansion was very slow before bank nationalization in 1969. Even now the banks are largely concentrated in large towns and small cities. There is lack of movement of funds. Indian banking system is not yet a well organized sector.

(e) No Uniformity in the rates of interest:
There exists too many rates of interest in the Indian Money Market such as the borrowing rate of government, deposits and lending rates of co-operatives and commercial banks, lending rates of financial institutions, etc. This is due to lack of mobility of funds from one section of the money market to another.

(f) Seasonal fluctuations : The seasonal stringency of money and high rate of interest during the busy season (November to June) is striking feature of Indian Money market. There are wide fluctuation in the interest rates from one season to another. Money Market add money into the money market during the busy season and withdraw funds during the slack seasons.

Question 2.
Explain the functions of commercial bank.
Answer:
(A) Meaning A bank is a dealer in credit. Any institution that accepts deposits from public who have more cash than it needs immediately and gives loans to those who are need is called as a bank. Commercial bank performs all these functions for earning profit. Commercial banks play an important role in mobilizing savings and allocating ) them to various sectors of the economy. It includes both scheduled commercial banks l and non scheduled commercial banks.

(B) Definition of Commercial Bank :
Banking Regulation Act 1949 “”Banking means the accepting for the purpose of lending or investment of deposits of money from public repayable on demand or otherwise and withdrawable by cheque, demand draft, order or otherwise.
The above definition clearly indicates the essential function of a bank is mainly dealing in money and credit.

(C) Functions of a Commercial Bank :
Commercial Bank performs a variety of functions to satisfy the needs of the various S sectors of the economy.

The functions of Commercial Banks are as follows:

(I) Accepting Deposits:
The most significant and traditional function of commercial bank is accepting ? deposits from public. A commercial bank acts as the custodian of public deposits. This l function is very important because it helps in the mobilisation of funds from households to businessman for production purposes, Commercial banks act as intermediary by accepting deposits and paying interest on them and giving loans and charging interest) from borrowers at a high rate. The difference j between the two is the profit of the bank. Commercial bank accepts the following types of deposits :

(A) Demand Deposits
(B) Time Deposits

(A) Demand Deposits : The deposits which ; are withdrawable on demand, are known as demand deposits. They are of two types (1) Current Account Deposits (2) Saving) Account Deposits

(1) Current Account Deposits : Current j account deposits are usually held by businessmen, industrial enterprises, public bodies for business transactions. Money deposited in current account can be withdrawn in part or full at any time and any number of times by the depositors without any prior notice. Overdraft facilities and agency service are provided by the bank to the current account holders. Very low or no interest is paid on these accounts as the banks cannot utilise these short term deposits. Banks may charge certain amount of service charges on account holders.

(2) Saving Account Deposits : Saving account deposits are opened by salaried class or people with fixed income for holding their short term savings. Money deposited in these accounts retain high degree of liquidity. At the same time it earns nominal interest. It is a kind of demand deposits which is generally kept by people for sake of safety.

(B) Time Deposits : These are deposits, which are repayable after a certain period of time. They are of two types – (1) Recurring Deposits (2) Fixed Deposits

(1) Recurring Deposits : These are deposits under which people deposit a fixed amount at regular interval for specified period of time. These deposits encourage savings and carry high rate of interest.
(2) Fixed Deposits : Fixed deposits are time deposits or term deposits, which attract fund for a specific period. It is a time bound deposit as the amount deposited cannot be withdrawn before the maturity of the period. However, loans can be taken from the bank against the security of this deposit, within that period. These deposits earn a higher rate of interest.

(II) Advancing / Granting Loans :
The second major function of a commercial bank is to make loans and advances out of the money, which comes to it from the public by way of deposits. Direct loans and advances are given to all types of persons particularly to businessmen and investors against personal security, gold, silver and other assets. The profit earning capacity of commercial banks depends on this function of lending. Generally banks grant loans and advances to the borrowers in the following forms :
(1) Loans (2) Cash Credit (3) Overdraft facility (4) Discounting of bills.

(III) Ancillary Functions :
Commercial Banks also provide variety of ancillary services like – transfer of funds, j collection of money, making periodical ( payments on behalf of the customer, merchant banking, foreign exchange, safe deposit lockers, D-mat facility, internet banking, mobile banking, ATM facility, purchase and sale of securities, etc.

(IV) Credit Creation :
It is an important function of commercial banks. Commercial banks are the creators  of credit.
Commercial Bank collects deposits from public which is called as primary deposits. After deducting required reserves, bank lends money to the borrower which is called j as secondary deposits or derivative deposits. This procedure is followed by entire banking [ system in a country leading to creation of credit.
Thus, every loan creates deposits and every deposits creates loans.

Question 3.
Explain the role of capital market in India.
Answer:
Role of Capital Market:

1. Mobilizes long term savings : Capital market helps to mobilize long term savings from various section of the population through the sale of securities.
2. Provides equity capital : Capital market provides equity capital or share capital to entrepreneurs which will be used by entrepreneurs to purchase business assets and also to fund the business operations.
3. Operational efficiency : Capital market helps to achieve operational efficiency by lowering the transaction costs, simplifying transaction procedures, lowering settlement timings in purchase and sale of stocks.
4. Quick valuation : Capital market helps to determine a fair and quick value of both equity (shares) and debt (bonds, debentures) instruments.
5. Integration : Capital market brings integration among real and financial sectors, equity and debt instruments, government and private sector, domestic and external funds, etc.

Question 4.
Explain the problems of capital market in India.
Answer:
Following are the problems of capital market in India :

• Scams : It is observed that different types of financial scams in the stock exchange have affected the confidence of individual investors in the securities market. Scams involve manipulation of larger amount of money, which results in public distrust and loss of confidence among the individual investors.
• Inadequate debt instruments : There is less trading in debt securities due to narrow investor base, high cost of issue, lack of accessibility to small and medium enterprises.
• Lack of informational efficiency : Indian stock markets lacks informational efficiency as compared to advanced countries.
• Decline in volume of trade : There is sharp decline in the volume of trade in regional stock exchanges. This is due to investors preferring trading in securities listed in premier stock exchanges like BSE and NSE.

8. Answer in detail:

Question 1.
Explain the role of money market in India.
Answer:
(A) Meaning:
Money market is a market for lending and borrowing short term funds.
It is a market for near money.
It deals in short term instruments like trade bills, government securities, promissory notes, etc.

Money market centres are located at Mumbai, Delhi and Kolkata. Money market consists of organised as well as unorganised j sector.

Role of Money Market in India :

(a) Portfolio Management : Money market deals with different types of financial instruments which are designed to suit the risk and return preferences of the investors. This enables the investors to hold a portfolio of different financial assets which in turn, j helps in minimizing risk and maximizing returns.

(b) Implementation of monetary policy :
Various monetary policies are implemented by the Central Bank, with an aim to manage the quantity of money, to meet the requirements of different sectors of the economy and to increase the pace of economic growth. Money market ensures successful implementation of these monetary policies. It also guides the central bank in developing an appropriate interest policy.

(c) Growth of Commerce, Industry and Trade : Money market facilitates discounting bills of exchange to local and international traders who are in urgent need of short-term funds. It also provides working capital for agriculture and small scale industries.

(d) Financial requirements of the Government : Money market helps the Government to fulfil its short term financial requirements on the basis of Treasury Bills.

Economizes the use of cash : Money market deals with various financial instruments that are close substitutes of money and not actual money. Thus, it economizes the use of cash.

Equilibrating mechanism : Money
market helps to establish equilibrium between the demand for and supply of short term funds by allocating rationally the available resources and thus mobilizing the savings of public into fruitful investment channels.

Liquidity Management : Money Market, through the monetary authorities facilitates better management of liquidity and money in the economy. This, in turn, leads to economic stability and development of the country.

Short-term requirements of borrowers :
Money market provides short-term financial needs of the borrowers at reasonable prices.

Question 2.
Explain the functions of RBI.
Answer:
(A) Introduction: Central Bank is the apex or the supreme monetary banking authority and occupies an important position in the monetary and banking structure of the country.
The guiding principle of a Central Bank is to act only in public interest and for the welfare of the country without regards to profit as primary consideration.
In India, The Reserve Bank of India is the Central Bank. It was established as shareholder’s bank on 1st April, 1935. It was nationalized on 1st January, 1949.

(B) Definitions :
(1) According to M. H. de Kock –
“A Central Bank is one which constitutes the apex of the monetary and banking structure of the country. ”

“(2) According to Prof. W. A. Shaw –
“Central Bank is a bank which controls credit.”

(C) Functions of Central Bank :
(1) Issue of Currency Notes : The Central i Bank has been authorised to print and issue ; currency notes. The RBI enjoys the monopoly of note issue of all denominations except one rupee note. The one rupee note and coins are issued by the Ministry of Finance of the government of India but their distribution is undertaken by RBI.

(2) Banker to the Government: The Central Bank acts as (A) a banker, (B) advisor, and (C) agent to the government. It performs all these functions which commercial banks do for their customers.
As a banker to the government, central bank transacts the business of Central and State governments. It accepts money and makes payments on behalf of these governments.
As an advisor, central bank advises the government on various economic issues and policies.
As an agent, central bank acts as a representative of central bank and attends l the international meetings of IMF and World Bank.
In short, it is a friend, philosopher and guide to the government.

(3) Bankers’ Bank : It supervises, co-ordinates j and controls the operations and activities of the commercial banks. As their bank it undertakes the following functions:
(a) acts as custodian of cash reserve.
(b) acts a lender of the last resort.
(c) provides clearing house function.

(4) Controller of Credit or Money Supply : Central Bank regulates the volume of credit and money supply in the country. The main objective behind this is to maintain price and ; economic stability in the country.
There are various methods which Central Bank uses to control the supply of credit in : the economy. They are –

• Quantitative Measures control the quantity or volume of credit created by the commercial banks. They are bank rate, open market operation and cash reserve ratio.
• Qualitative Measures or Selective Measures deal with the purpose and direction of credit. They are – varying margin requirements, regulation of credit, moral suasion and direct action.

(5) Custodian of Foreign Exchange Reserve of the Country: The Central Bank is also a custodian of country’s gold and major foreign currencies like US dollar, Euro the British Pound, etc. obtained by government from international trade.
The central bank also maintains international liquidity.

(6) Developmental and Promotional Functions : In developing countries like India, a very important function of Central Bank is to promote economic development.

• To promote banking habits among the poor people.
• To provide agriculture finance through NABARD and to promote rural and agricultural development.
• To provide industrial finance through IDBI, SFC and IFCI and boost the growth of industrial sector.
• To provide export – import finance through EXIM bank.
• To encourage small savings through Unit Trust of India.

(7) Data Collection and Publicity : The Central Bank also collects and publishes information relating to agriculture, industrial and financial sectors of the economy, exports and imports, banking, trends in money and capital market, etc.
Its main publications include – Report on Currency and Finance, RBI Bulletin, RBI Journals and various research papers.

Intext Questions

Try this (Textbook Page 81)

Identify the type of finance into – Personal finance, Corporate finance or Public finance.
Answer:

Find out (Textbook Page 83)

Find out names of the Central Banks of the following countries.

(1) USA
(2) Canada
(3) Russia
(4) Germany
(5) China
(6) UK (United Kingdom)
(7) Sweden
(8) France
(9) Japan
(10) Australia
Answer:
(1) USA : Federal Reserve System ;
(2) Canada : Bank of Canada
(3) Russia : Central Bank of Russia
(4) Germany : Deutsche Bundes bank
(5) China : People’s Bank of China
(6) UK (United Kingdom) : Bank of England
(7) Sweden : Sveriges Riksbank
(8) France : Banque de France
(9) Japan : Bank of Japan
(10) Australia : Reserve Bank of Australia

Try this (Textbook Page 85)

Pair the logos given with their respective banks as given in the bracket below :
(State Bank of India, HSBC Bank, Union Bank of India, Axis Bank, Standard Chartered Bank, HDFC Bank)
Answer:

Try this (Textbook Page 85)

Collect information of Co-operative banks in your region at different levels.
Answer:
[Students should do this activity by themselves]

Find out (Textbook Page 90):

List the regional stock exchanges in India.
Answer:

• Regional Stock Exchanges in India :
• Bombay Stock Exchange (BSE)
• National Stock Exchange (NSE)
• Calcutta Stock Exchange (CSE) Metropolitan Stock Exchange (MSE)
• India International Exchange (India INX)
• NSE IFSC Ltd.

Maharashtra State Board 12th Std Economics Textbook Solutions

• Introduction to Micro and Macro Economics Class 12 Economics Textbook Solutions
• Utility Analysis Class 12 Economics Textbook Solutions
• Demand Analysis Class 12 Economics Textbook Solutions
• Elasticity of Demand Class 12 Economics Textbook Solutions
• Supply Analysis Class 12 Economics Textbook Solutions
• Forms of Market Class 12 Economics Textbook Solutions
• Index Numbers Class 12 Economics Textbook Solutions
• National Income Class 12 Economics Textbook Solutions
• Public Finance in India Class 12 Economics Textbook Solutions
• Money Market and Capital Market in India Class 12 Economics Textbook Solutions
• Foreign Trade of India Class 12 Economics Textbook Solutions