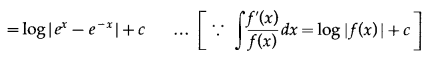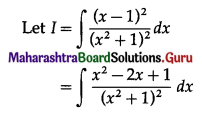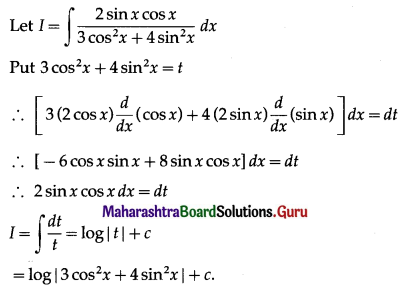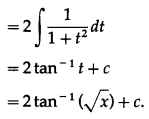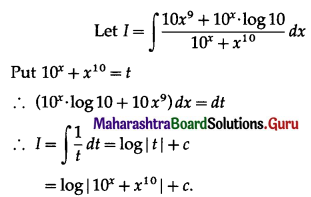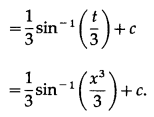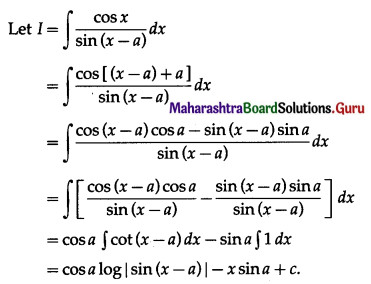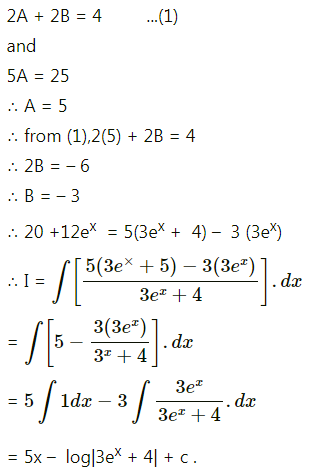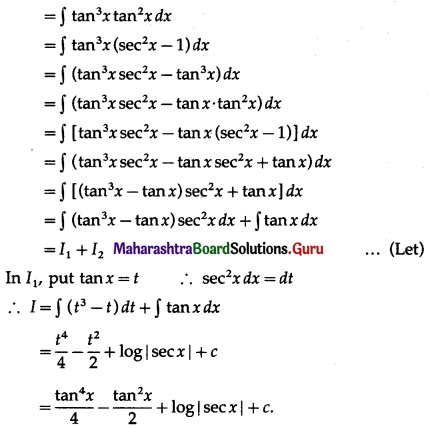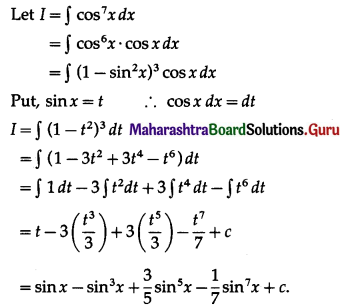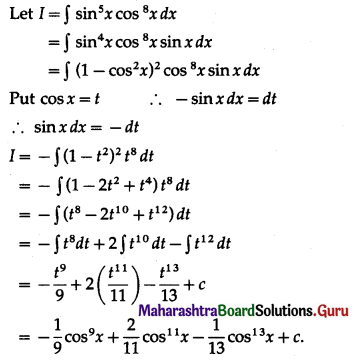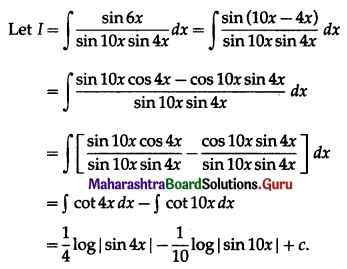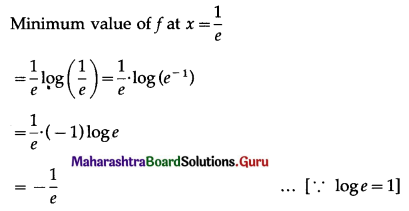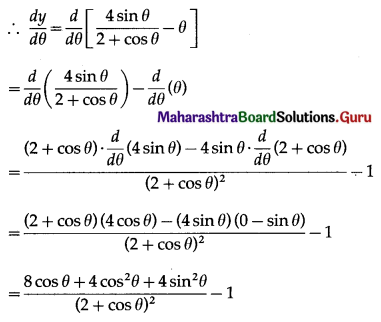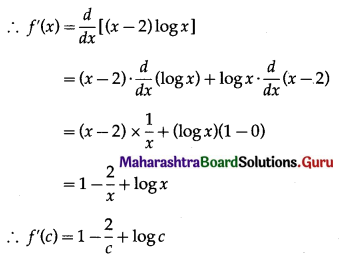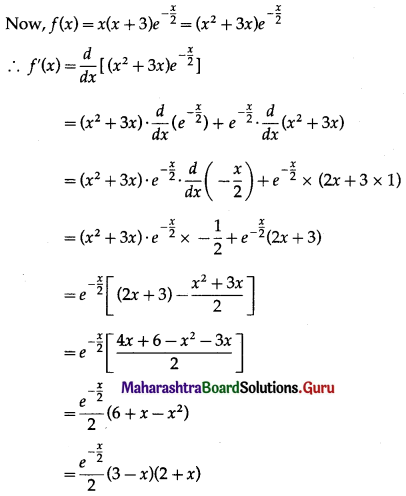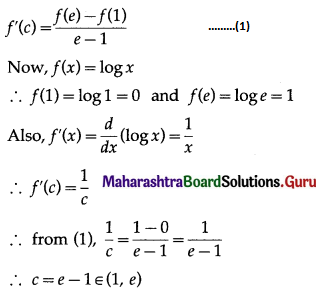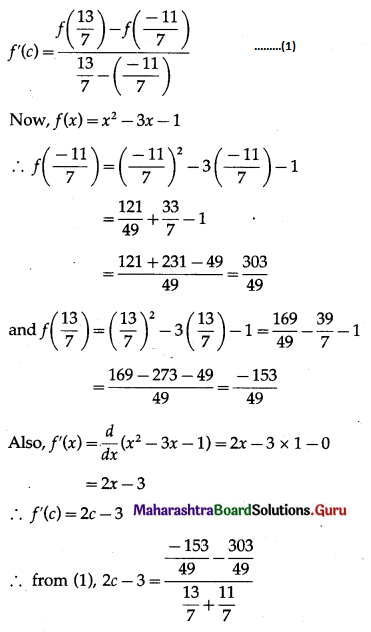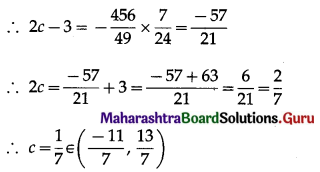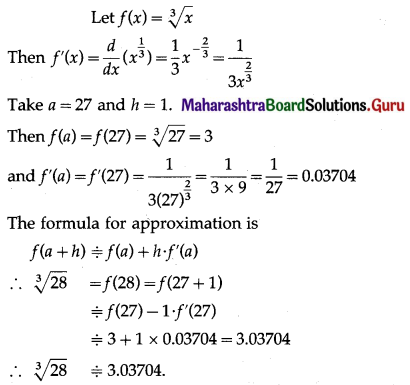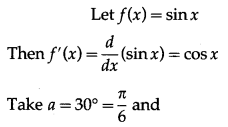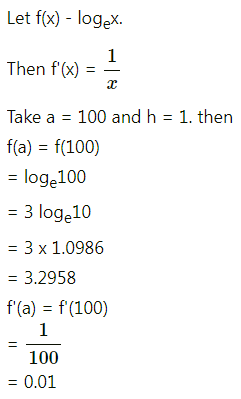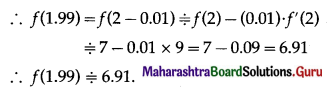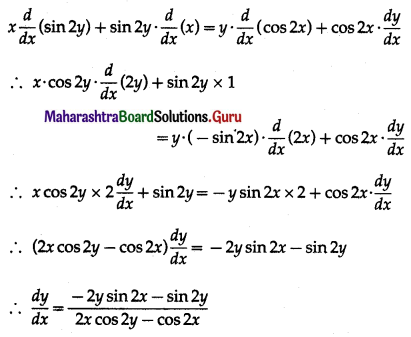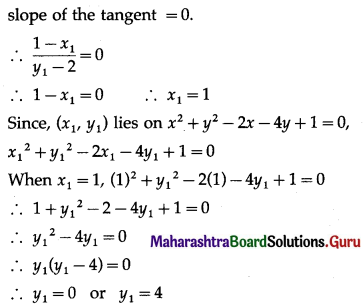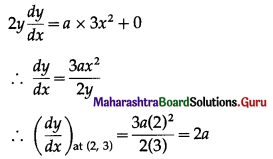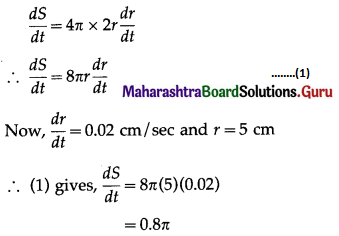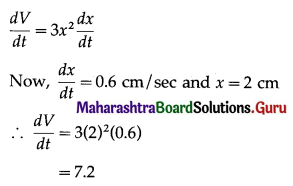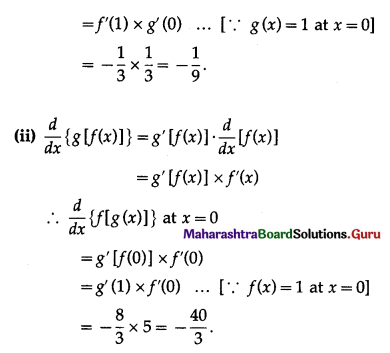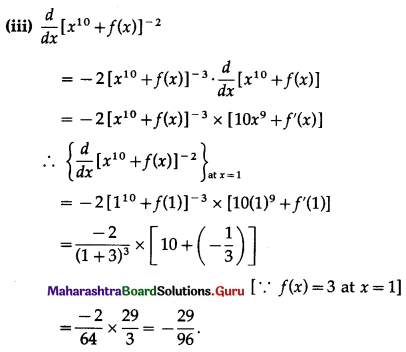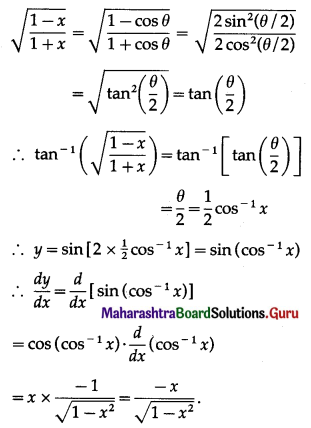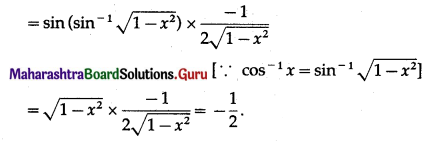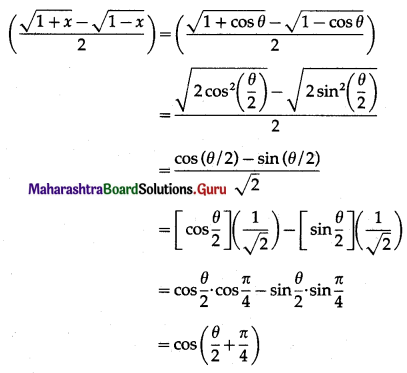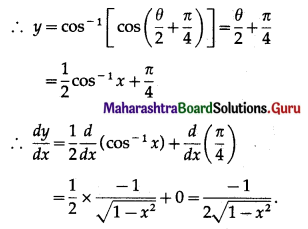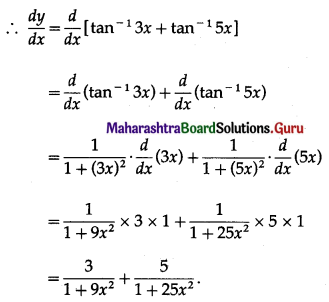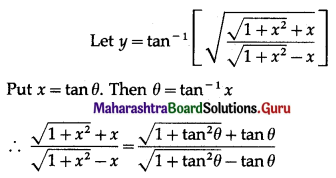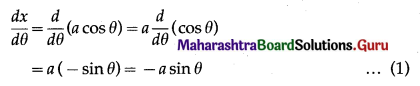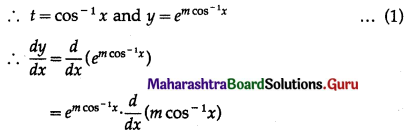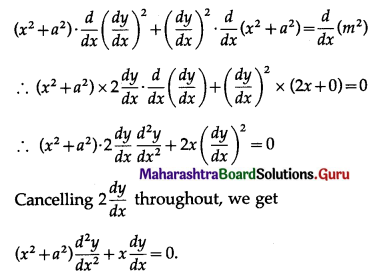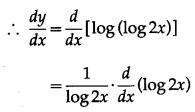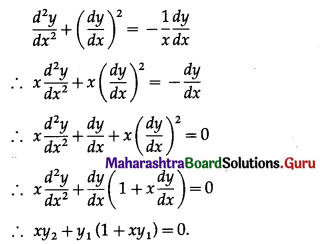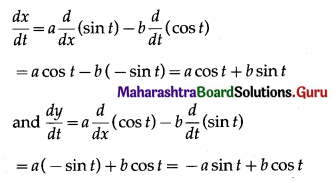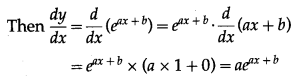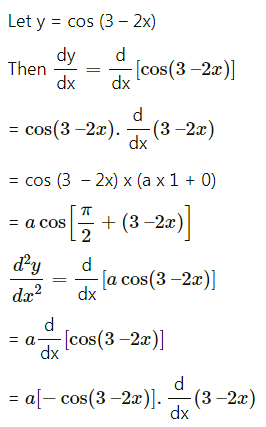Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.2(B) Questions and Answers.
12th Maths Part 2 Indefinite Integration Exercise 3.2(B) Questions And Answers Maharashtra Board
I. Evaluate the following:
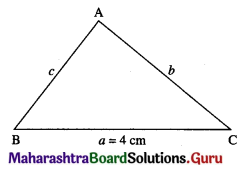
Question 1.
\(\int \frac{1}{4 x^{2}-3} \cdot d x\)
Solution:

Question 2.
\(\int \frac{1}{25-9 x^{2}} \cdot d x\)
Solution:

![]()
Question 3.
\(\int \frac{1}{7+2 x^{2}} \cdot d x\)
Solution:

Question 4.
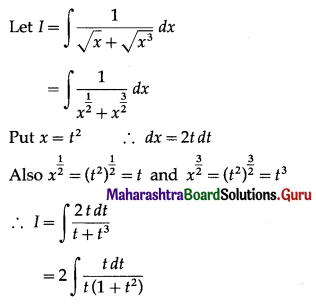
\(\int \frac{1}{\sqrt{3 x^{2}+8}} \cdot d x\)
Solution:


Question 5.
\(\int \frac{1}{\sqrt{11-4 x^{2}}} \cdot d x\)
Solution:

Question 6.
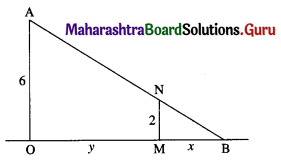
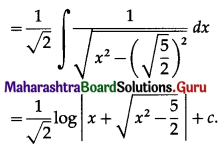
\(\int \frac{1}{\sqrt{2 x^{2}-5}} \cdot d x\)
Solution:
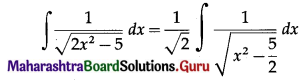
![]()
Question 7.
\(\int \sqrt{\frac{9+x}{9-x}} \cdot d x\)
Solution:

Question 8.
\(\int \sqrt{\frac{2+x}{2-x}} \cdot d x\)
Solution:
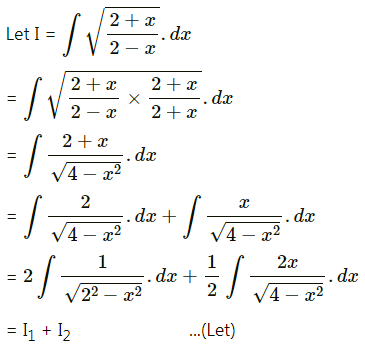
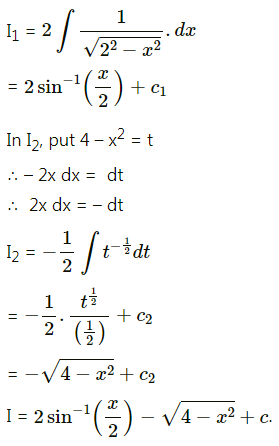
Question 9.
\(\int \sqrt{\frac{10+x}{10-x}} \cdot d x\)
Solution:
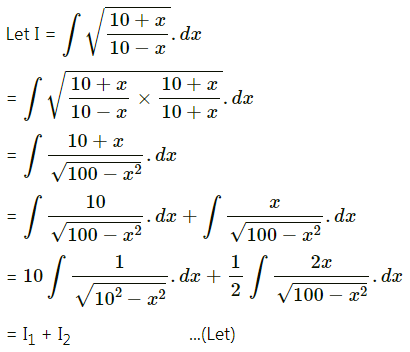
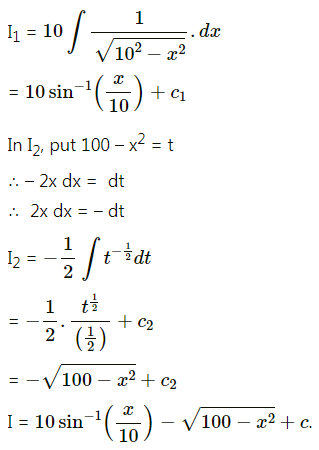
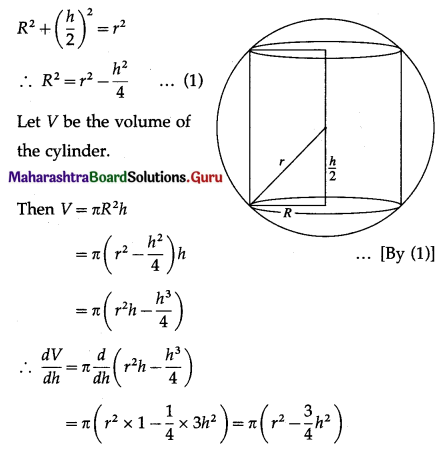
Question 10.
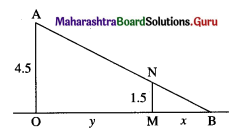
\(\int \frac{1}{x^{2}+8 x+12} \cdot d x\)
Solution:

![]()
Question 11.
\(\int \frac{1}{1+x-x^{2}} \cdot d x\)
Solution:

Question 12.
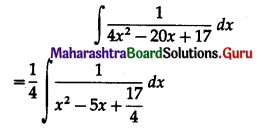
\(\int \frac{1}{4 x^{2}-20 x+17} \cdot d x\)
Solution:

Question 13.
\(\int \frac{1}{5-4 x-3 x^{2}} \cdot d x\)
Solution:


Question 14.
\(\int \frac{1}{\sqrt{3 x^{2}+5 x+7}} \cdot d x\)
Solution:
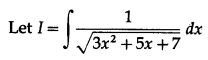

Question 15.
\(\int \frac{1}{\sqrt{x^{2}+8 x-20}} \cdot d x\)
Solution:

Question 16.
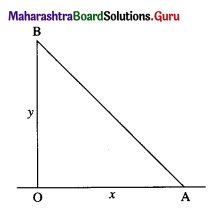
\(\int \frac{1}{\sqrt{8-3 x+2 x^{2}}} \cdot d x\)
Solution:
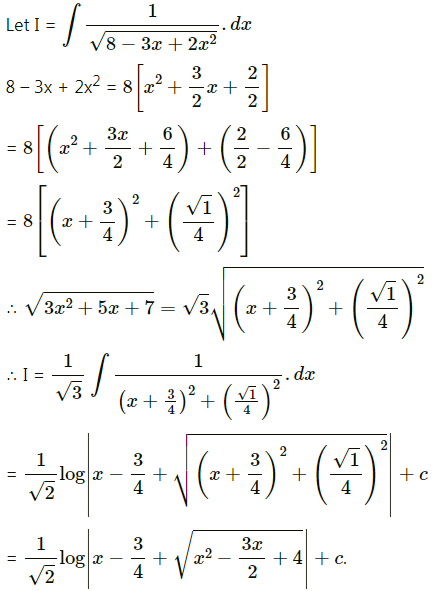
![]()
Question 17.
\(\int \frac{1}{\sqrt{(x-3)(x+2)}} \cdot d x\)
Solution:


Question 18.
\(\int \frac{1}{4+3 \cos ^{2} x} \cdot d x\)
Solution:

Question 19.
\(\int \frac{1}{\cos 2 x+3 \sin ^{2} x} \cdot d x\)
Solution:
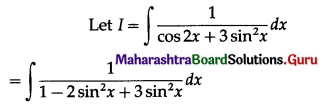

Question 20.
\(\int \frac{\sin x}{\sin 3 x} \cdot d x\)
Solution:

II. Integrate the following functions w. r. t. x:
Question 1.
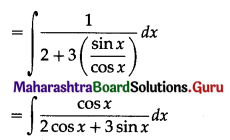
\(\int \frac{1}{3+2 \sin x} \cdot d x\)
Solution:


![]()
Question 2.
\(\int \frac{1}{4-5 \cos x} \cdot d x\)
Solution:
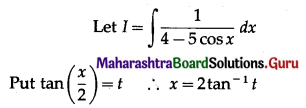

Question 3.
\(\int \frac{1}{2+\cos x-\sin x} \cdot d x\)
Solution:

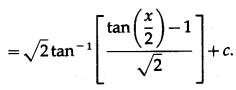
Question 4.
\(\int \frac{1}{3+2 \sin x-\cos x} \cdot d x\)
Solution:

Question 5.
\(\int \frac{1}{3-2 \cos 2 x} \cdot d x\)
Solution:


![]()
Question 6.
\(\int \frac{1}{2 \sin 2 x-3} \cdot d x\)
Solution:


Question 7.
\(\int \frac{1}{3+2 \sin 2 x+4 \cos 2 x} \cdot d x\)
Solution:
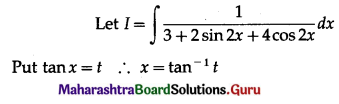

Question 8.
\(\int \frac{1}{\cos x-\sin x} \cdot d x\)
Solution:

![]()
Question 9.
\(\int \frac{1}{\cos x-\sqrt{3} \sin x} \cdot d x\)
Solution:
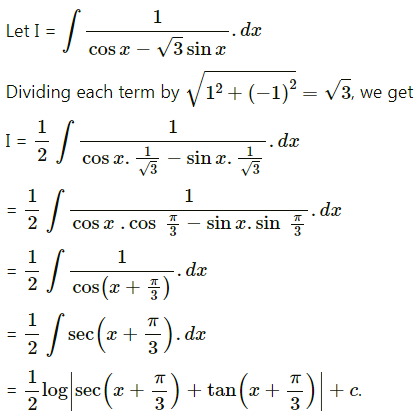
12th Maharashtra State Board Maths Solutions Pdf Part 2
- Indefinite Integration Ex 3.1 Class 12 Maths Solutions
- Indefinite Integration Ex 3.2(A) Class 12 Maths Solutions
- Indefinite Integration Ex 3.2(B) Class 12 Maths Solutions
- Indefinite Integration Ex 3.2(C) Class 12 Maths Solutions
- Indefinite Integration Ex 3.3 Class 12 Maths Solutions
- Indefinite Integration Ex 3.4 Class 12 Maths Solutions
- Indefinite Integration Miscellaneous Exercise 3 Class 12 Maths Solutions