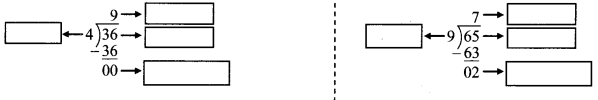Category: Class 6

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 4 जोकर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 4 जोकर

Hindi Sulabhbharti Class 6 Solutions Chapter 4 जोकर Textbook Questions and Answers

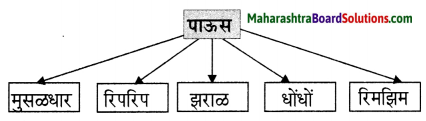
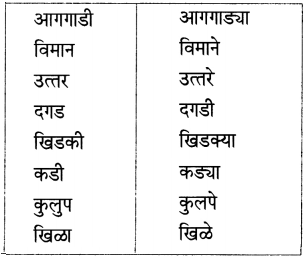
किन्हीं पाँच मुहावरों / कहावतों के सांकेतिक चित्र बनाओ: जैसे

मैंने समझा:
Answer:
प्रस्तुत पाठ में मैंने सीखा कि अपनी बातों को प्रभावी ढंग से कम-से-कम शब्दों में व्यक्त करने के लिए मुहावरों और कहावतों का प्रयोग किया जाता है।

खोजबीन:

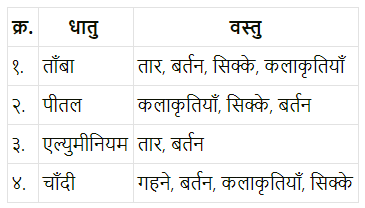
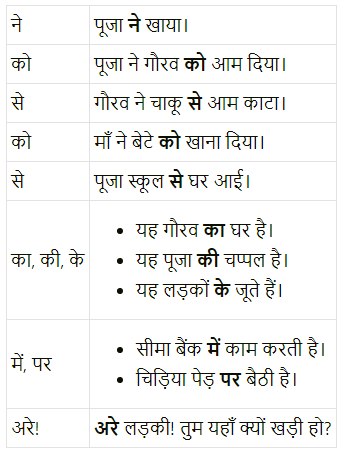
निम्नलिखित शब्द को लेकर चार मुहावरे लिखो।

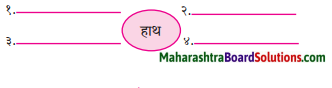
Answer:
हाथ
१. हाथ का मैल होना
२. हाथ तंग होना
३. हाथ धोना
४. हाथ पर हाथ धरे बैठना

स्वयं अध्ययन:

अब पछताए होत क्या, जब चिड़िया चुग गई खेत’ पर आधारित कोई कहानी सुनाओ।
Answer:
चींटी और टिड्डा दोनों पड़ोसी थे। चींटी बहुत मेहनती थी। वह दिनभर मेहनत करती थी। वह अपने भविष्य के लिए भी अनाज इकट्ठा करती रहती थी। वहीं टिड्डा सिर्फ पेट भरने तक का भोजन जुटाकर दिनभर खेलता-कूदता, नाचता-गाता था। कुछ दिनों बाद बरसात का मौसम आया। टिड्डे को । कहीं भी भोजन नहीं मिल पा रहा था, जबकि चींटी आराम से घर में बैठकर बरसात का आनंद ले रही थी। चींटी को देखकर टिड्डे को यह भी समझ में आ गया कि उसने पूरे साल आराम करके गलती की, लेकिन ‘अब पछताए होत क्या, जब चिड़िया चुग गई खेत।’

जरा सोचो ………. बताओ:

यदि साइकिल तुमसे बोलने लगी तो ……
Answer:
यदि साइकिल मुझसे बोलने लगी तो मुझे बहुत खुशी होगी। मैं उससे अपने मन की सारी बातें कहता और वह भी मुझे अपनी सारी बातें बताती।। हम दोनों आपस में बहुत बातें करते। मैं उसे अपनी सबसे अच्छी दोस्त बना लेता और वह बिना मेहनत किए मुझे मेरी मनचाही जगह पर ले जाती। यदि साइकिल मुझसे बोलने लगी, तो मैं उसके सारे दुख-दर्द भी पूगा। सब उस पर सवार होते हैं, उसपर सामान रखते हैं, तो उसे कैसा महसूस होता है? मैं उसकी नजर से दिखने वाली दुनिया के बारे में जानना चाहूँगा। साइकिल जिन-जिन स्थानों का भ्रमण कर चुकी होगी, उन सभी स्थानों के बारे में भी जानकारी लूँगा। यदि साइकिल मुझसे बोलने लगी, तो मैं उसके इतिहास के बारे में जानना चाहूँगा। उसका जन्म कब, कैसे और कहाँ हुआ? इन सबकी जानकारी लूँगा। उससे पूछंगा कि वह पहले किस तरह दिखती थी? उसे पहले यह दुनिया कैसी लगती थी और अब कैसी लगती है? उसकी हालत में कैसे बदलाव आया? साइकिल से ढेर सारी बातें करके उसे अपनेपन का विश्वास दिलाऊँगा तथा उसकी हालत को बेहतर-सेबेहतर बनाने का प्रयत्न करूँगा।

विचार मंथन:

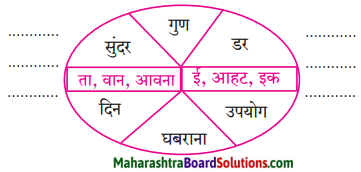
गागर में सागर भरना
Answer:
‘गागर में सागर भरना’ यह एक मुहावरा है। इस मुहावरे का अर्थ है – कम शब्दों में बहुत कुछ कहना। इस मुहावरे को एक उदाहरण द्वारा समझते हैं – कबीरदास ने अपने दोहों के जरिए गागर में सागर भर दिया।

सदैव ध्यान में रखो:

हमें सदैव प्रसन्न रहना चाहिए।
Answer:
हास्य का मतलब होता है हँसना। हँसना स्वास्थ्य के लिए बहुत लाभदायक है। हँसने से रक्त संचार बढ़ता है। हँसने से चेहरे की माँसपेशियों का भी व्यायाम होता है। इससे दिमाग भी स्वस्थ रहता है। यूँ कहा जा सकता है कि हँसना स्वास्थ्य के लिए बहुत गुणकारी है, इसलिए हमें हँसते रहना चाहिए।

समझो हमें:

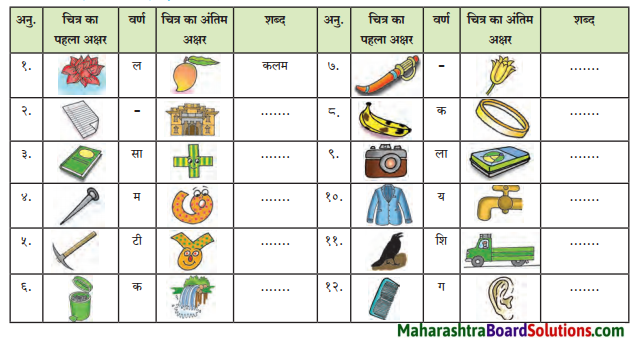
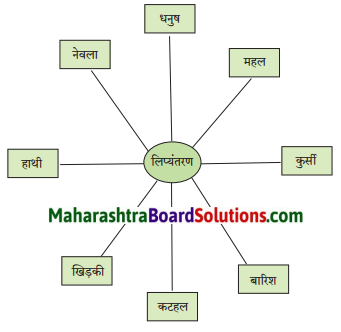
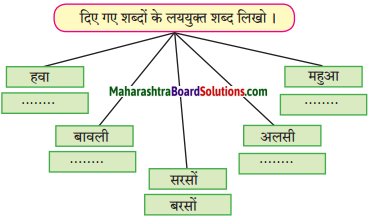
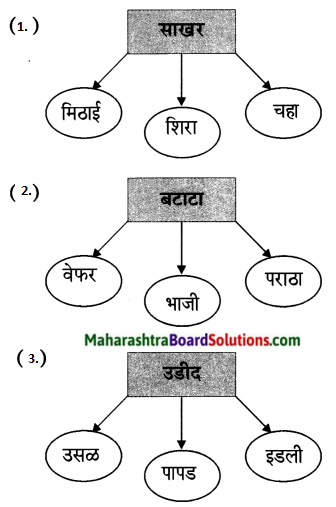
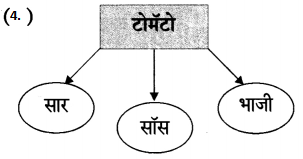
चित्र की सहायता से बारहखड़ी के शब्द बनाकर लिखो।

HCF-LCM Class 6 Maths Chapter 9 Practice Set 23 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 23 Answers Solutions.

Std 6 Maths Practice Set 23 Solutions Answers

Question 1.
Write all the factors of the given numbers and list their common factors:
i. 12, 16
ii. 21, 24
iii. 25, 30
iv. 24, 25
v. 56, 72
Solution:
i. Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 16 = 1, 2, 4, 8, 16
∴ Common factors of 12 and 16 = 1, 2, 4

ii. Factors of 21 = 1, 3, 7, 21
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
∴ Common factors of 21 and 24 = 1, 3

iii. Factors of 25 = 1, 5, 25
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
∴ Common factors of 25 and 30 = 1, 5

iv. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 25 = 1,5, 25
∴ Common factor of 24 and 25 = 1

v. Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
Factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
∴ Common factors of 56 and 72 = 1, 2, 4, 8

Maharashtra Board Class 6 Maths Chapter 9 HCF-LCM Practice Set 23 Intext Questions and Activities

Question 1.
In the empty boxes, write the proper words: dividend, divisor, quotient, remainder. (Textbook pg. no. 46)

Solution:

When we divide 36 by 4, the remainder is zero. Therefore, 4 is a factor of 36 and 36 is a multiple of 4. But, when we divide 65 by 9, the remainder is not zero. Therefore, 9 is not a factor of 65. Also, 65 is not a multiple of 9.

Question 2.
Write all the factors of the numbers 36 and 48. Also, list their common factors. (Textbook pg. no. 46)
Solution:
36 = 1 × 36
= 2 × 18
= 3 × 12
= 4 × 9
= 6 × 6

48 = 1 × 48
= 2 × 24
= 3 × 16
= 4 × 12
= 6 × 8

∴ Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Common factors of 36 and 48: [1] ,[2], [3], [4], [6], [12]

6th Std Maths Digest Pdf Download

• Bar Graphs Practice Set 18 Class 6 Maths Solution
• Bar Graphs Practice Set 19 Class 6 Maths Solution
• Symmetry Practice Set 20 Class 6 Maths Solution
• Symmetry Practice Set 21 Class 6 Maths Solution
• Divisibility Practice Set 22 Class 6 Maths Solution
• HCF-LCM Practice Set 23 Class 6 Maths Solution
• HCF-LCM Practice Set 24 Class 6 Maths Solution
• HCF-LCM Practice Set 25 Class 6 Maths Solution

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 3 पाऊस आला! पाऊस आला! Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 3 पाऊस आला! पाऊस आला! (कविता)

Marathi Sulabhbharti Class 6 Solutions Chapter 3 पाऊस आला! पाऊस आला! Textbook Questions and Answers

1. खालील प्रश्नांची एक दोन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
विजा केव्हा चमकल्या?
उत्तर:
विजा ऐन दुपारी चमकल्या.

प्रश्न आ.
सुटलेला वारा कसा होता?
उत्तर:
सुटलेला वारा भणाणवारा होता.

प्रश्न इ.
पाऊस आल्यामुळे आजोबांनी काय केले?
उत्तर:
पाऊस आल्यामुळे आजोबांनी छत्री शिवली.

प्रश्न ई.
आलेल्या पावसामुळे बाबांनी चडफड का केली?
उत्तर:
बाबांना आधीच उशीर झाला होता व त्यातच पाऊस पडला म्हणून बाबांनी चडफड केली.

प्रश्न उ.
पावसामुळे आईचे कोणते नुकसान झाले?
उत्तर:
पावसामुळे आईचे पापड भिजले.

2.

प्रश्न अ.
शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधा व लिहा. उदा., वारा-गारा
उत्तर:
(अ) कुत्री – छत्री
(आ) गिल्ला – किल्ला
(इ) पापड – चडफड
(ई) पळा – घोटाळा
(उ) कुट्टी – सुट्टी

प्रश्न आ.
कडकड, चडफड, तडफड यांसारखे आणखी शब्द तयार करा.
उत्तर:

1. धडधड
2. गडगड
3. बडबड
4. खडखड
5. रडरड
6. गडबड
7. पडझड

3. खालील शब्दांचे वचन बदला.

प्रश्न 1.
खालील शब्दांचे वचन बदला.
उत्तर:
(अ) माणूस – माणसे
(आ) गाय – गाई
(इ) दप्तर – दप्तरे
(ई) पाणी – पाणी
(उ) वह्या – वही
(ऊ) पत्र – पत्रे

4. अचानक आलेल्या पावसामुळे तुमची कधी फजिती झाली आहे का? तो प्रसंग वर्गात सांगा. 

प्रश्न अ.
अचानक आलेल्या पावसामुळे तुमची कधी फजिती झाली आहे का? तो प्रसंग वर्गात सांगा.
उत्तर:
एकदा ताई आणि मी बाजारात गेलो होतो. अचानक पाऊस आला. छत्र्या नव्हत्या. आम्ही झाडाखाली उभे राहीलो पण पूर्ण भिजलो होतो. रस्त्यात पाणी तुंबले होते. रिक्षा बंद झाल्या होत्या. दोघे कसेबसे घरी पोहोचलो. आईने पापड, मिरच्या वाळवण ठेवले होते. तेही भिजले. बाबांना घरी यायला खूप उशीर झाला. बाहेर वाळत घातलेले कपडेही भिजले. पावसामुळे खूप धावपळ झाली.

5. अचानक आलेल्या पावसामुळे दिवाळीत तुम्ही केलेल्या तयारीचे कोणकोणते नुकसान होते ते चार-पाच वाक्यात लिहा.

प्रश्न अ.
अचानक आलेल्या पावसामुळे दिवाळीत तुम्ही केलेल्या तयारीचे कोणकोणते नुकसान होते ते चार-पाच वाक्यात लिहा.
उत्तर:
दिवाळीत आम्ही सर्व मुलांनी मिळून किल्ला बांधला होता. त्यावर शिपाई, रखवालदार ठेवले होते. मातीच्याच प्रतिमा असल्याने त्या तुटून गेल्या. किल्ला ढासळला. ताईने दारात काढलेली रांगोळी पुसली गेली. आमचे फटाकेही भिजले.

6. सुरुवातीला एक वाक्य दिले आहे. तुमच्या मनाने पुढील वाक्ये लिहा. 

प्रश्न अ.
रिमझिम पाऊस पडत होता.
उत्तर:

1. पाणी झुळझुळ वाहत होते.
2. खारूताई झाडावर सरसर चढली.
3. गांधीजी झरझर चालत जात.
4. आजीचे हात थरथर कापत होते.

प्रश्न आ.
रिक्षा खडखड करत थांबली.
उत्तर:

1. मुले भरभर चालत होती.
2. पंख्याची घरघर सुरू होती.
3. हृदय धडधड करीत होते.
4. पंखांची फडफड थांबली.

7. ‘वारा’ या शब्दाशी संबंधित आलेले शब्द वाचा. त्यांचा वाक्यात उपयोग करा. उदा. भणाणणारा वारा सुटला होता.

प्रश्न अ.
‘वारा’ या शब्दाशी संबंधित आलेले शब्द वाचा. त्यांचा वाक्यात उपयोग करा. उदा. भणाणणारा वारा सुटला होता.
उत्तरः

1. मंदमंद – पहाटे मंदमंद वारा सुटला होता.
2. गिरक्या – मैदानात वाऱ्याच्या गिरक्या येत होत्या.
3. जोरदार – जोरदार मोसमी वारे सुटले होते.
4. थंडगार – हिमालयाचा वारा थंडगार होता.
5. झोंबणारा – हिवाळ्यात नदीकाठचा वारा झोंबणारा होता.

8. पापड कशाकशापासून बनवले जातात याची माहिती आईला विचारून लिहा. 

प्रश्न अ.
पापड कशाकशापासून बनवले जातात याची माहिती आईला विचारून लिहा.
उत्तर:
पापड विविध प्रकारचे असतात. उडदाची डाळ, मिरे यांपासून उडदाचे पापड बनतात. तांदळापासून तांदळाचे पापड बनतात. काही पापड पोयांपासून तर काही नाचणीपासून बनतात. साबूदाण्यापासून व बटाट्यापासूनही उपवासाचे पापड बनतात.

9. उन्हाळ्यांमध्ये वाळवून साठवण्याचे कोणकोणते पदार्थ आई करते ते लिहा. 

प्रश्न अ.
उन्हाळ्यांमध्ये वाळवून साठवण्याचे कोणकोणते पदार्थ आई करते ते लिहा.
उत्तर:
उन्हाळ्यात वाळवून साठवण्याचे पदार्थ – पापड, कुर्डया, सांडगे, शेवया, मिरच्या, आंबापोळी, फणसपोळी, उपवासाच्या चकल्या, उपवासाचे पापड, आमचूर, बोरकूट इ.

10. पावसाळा सुरु होताच तुम्ही पावसातून बचाव करण्यासाठी कोणकोणती पूर्वतयारी करता?
उदा. छत्री खरेदी करणे.

प्रश्न अ.
पावसाळा सुरु होताच तुम्ही पावसातून बचाव करण्यासाठी कोणकोणती पूर्वतयारी करता?
उदा. छत्री खरेदी करणे.
उत्तर:
1. रेनकोट, चपला खरेदी करणे.

2. घराची डागडुजी करणे, दुरुस्ती करणे.
3. वाहने गंजू नये त्यासाठी उपाय करणे.

Marathi Sulabhbharti Class 6 Solutions Chapter 3 पाऊस आला! पाऊस आला! Important Additional Questions and Answers

रिकाम्या जागी कवितेतील योग्य शब्द लिहा.
प्रश्न 1.

1. ……………….. भणाण वारा.
2. दिवाळीतला ………………..
3. आजोबांनी ………………..
4. बाबा गेले ………………..
5. ……………….. पापड
6. हसत म्हणाल्या ………………..
7. ‘………………..’, शाळेला सुट्टी!

उत्तर:

1. कडाड कडकड
2. खचला किल्ला
3. शिवली छत्री
4. करीत चडफड
5. आईचेही भिजले
6. मॅडम कुट्टी
7. चला पळा.

प्रश्न 2.
एका शब्दांत उत्तरे लिहा.

1. ऐन दुपारी चमकल्या
2. जिकडे तिकडे
3. भुंकत सुटली सगळी
4. मुलांनी केला एकच

उत्तर:

1. विजा
2. गारा
3. कुत्री
4. गिल्ला

खालील प्रश्नांची एक दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
मॅडम हसत काय म्हणाल्या?
उत्तर:
मॅडम म्हणाल्या, ‘चला पळा, शाळेला सुट्टी!’

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
ऐन दुपारी काय झाले?
उत्तर:
ऐन दुपारी विजा कडाड कडकड चमकल्या. भणाण वारा सुटला. जिकडे तिकडे गारा पडू लागल्या व पाऊस
पडू लागला.

प्रश्न 2.
पावसामुळे काय काय झाले?
उत्तर:
ऐन दुपारी पाऊस पडला. दिवाळीतला किल्ला खचला. सगळी कुत्री भुंकत सुटली. आजोबांनी छत्री शिवली. बाबांना आधीच उशीर झाला होता, त्यातच पावसाने घोटाळा केला. ते चडफड करीतच गेले. आईचे पापड भिजले.

प्रश्न 3.
शाळेतील मुलांनी गिल्ला का केला?
उत्तर:
अचानक दुपारी पाऊस पडू लागला. सर्व मुलांना मजा वाटली. त्यातच मॅडमनी शाळेला सुट्टी दिली. त्या आनंदात मुलांनी गिल्ला केला.

व्याकरण व भाषाभ्यास:

प्रश्न 1.
खालील शब्दांचे वचन बदला.

1. छत्री
2. कुत्री
3. वीज
4. किल्ला

उत्तर:

1. छत्र्या
2. कुत्रा
3. विजा
4. किल्ले

जोड्या जुळवा.

प्रश्न 1.

उत्तर:

शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधा व लिहा.
उदा. वारा – गारा

प्रश्न 1.
1. जिकडे
2. आला
उत्तर:
1. तिकडे
2. केला

प्रश्न 2.
‘पाऊस’ या शब्दाशी संबंधित आलेले शब्द वाचा. त्यांचा वाक्यात उपयोग करा.

उत्तर:

1. मुसळधार – मुसळधार पावसाने पूर आला.
2. रिपरिप – दिवसभर रिपरिप पाऊस होता.
3. झराळ – झराळ पावसात आम्ही ओलेचिंब झालो.
4. धोंधों – धोंधों पावसाने गावाचे नुकसान झाले.
5. रिमझिम – मुलांना रिमझिम पावसात भिजायला आवडते.

प्रश्न 3.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. खचणे
2. चडफड
3. गिल्ला
4. ऐन दुपारी
5. भिजणे

उत्तर:

1. ढासळणे
2. राग
3. गोंगाट, गोंधळ
4. भर दुपारी
5. ओले होणे

प्रश्न 4.
खालील शब्दांचे विरूद्धार्थी अर्थाचे शब्द लिहा.

1. भिजणे
2. आला
3. शिवणे
4. खचणे
5. उशीर

उत्तर:

1. वाळणे
2. गेला
3. उसवणे
4. उभारणे
5. लवकर

पाऊस आला! पाऊस आला! Summary in Marathi

काव्य परिचय:

प्रस्तुत कवितेत पडणाऱ्या गारा, पावसामुळे आई बाबांची उडालेली तारांबळ, शाळेला मिळालेल्या सुट्टीचा आनंद वर्णन केला आहे.

शब्दर्थ:

1. ऐन दुपारी – भर दुपारी (in the afternoon)
2. खचला – ढासळला (collapse)
3. किल्ला – दुर्ग (fort)
4. जिकडेतिकडे – सर्वत्र (everywhere)
5. गारा – पावसाच्या पाण्याचे बर्फासारखे खडे (hailstones)
6. भुंकणे – कुत्र्याचा आवाज (to bark)
7. चडफड – आतल्या आत राग करणे (to get angry, restlessness)
8. गिल्ला – आवाज, गोंगाट (noise, shouting)
9. कुत्रा – श्वान (dog)
10. शिवणे – (to stitch)
11. घोटाळा – गडबड, गोंधळ (disorder, chaws)

Balbharti Maharashtra State Board Class 6 History Solutions Chapter 4 The Vedic Civilization Notes, Textbook Exercise Important Questions and Answers.

Maharashtra Board Class 6 History Solutions Chapter 4 The Vedic Civilization

Class 6 History Chapter 4 The Vedic Civilization Textbook Questions and Answers

1. Name the following with reference to the lesson:

The Vedic Civilization Class 6 Question 1.
Women scholars in Vedic literature:
Answer:
Lopamudra, Gargi, Maitreyi.

The Vedic Civilization Class 6 Questions And Answers Question 2.
Means of entertainment in the Vedic period:
Answer:
Singing, playing musical instruments, dance, board games, chariot race and hunting.

The Vedic Civilization Class 6 Questions And Answers Maharashtra Board Question 3.
The four ashrams:
Answer:
Brahmacharyashrama, Grihasthashrama, Vanaprasthashrama, Sanyasashrama

2. Right or wrong?

Class 6 History Chapter 4 Question 1.
Rigveda – Mantras uttered during yajna.
Answer:
Wrong.

Vedic Age Question And Answer Class 6 Question 2.
Samaveda – Guidance on singing a mantra during yajna rites.
Answer:
Right.

Vedic Civilization Class 6 Question 3.
Atharvaveda – The Veda derived its name from Atharva rishi.
Answer:
Right.

3. Answer in one word each:

Class 6 History Chapter 4 Questions And Answers Question 1.
The language of Vedic literature:
Answer:
Sanskrit.

Chapter 4 Class 6 History Question 2.
The meaning of vid:
Answer:
To know.

Class 6 History Chapter 4 Notes Question 3.
The head of a family:
Answer:
Grihapati.

History Class 6 Chapter 4 Question 4.
The head of shrenis:
Answer:
Shreshthi

4. Name the following:

Question 1.
The musical instruments you know:
Answer:
Guitar, drums, piano (Keyboard).

Question 2.
Two modern ornaments of women:
Answer:
Earing, necklace.

Question 3.
Today’s means of entertainment:
Answer:
Movies, computer games, T.V.

5. Answer in short:

Question 1.
What foods were included in the diet of the Vedic people?
Answer:
(a) The diet of the people mainly consisted of cereals like wheat, barley and rice. From this they made different preparations like java, godhoom, vihi, etc.
(b) They also relished milk, yoghurt, ghee, butter, honey, black gram, lentil, sesame and meat.

Question 2.
Why were the cows priced highly?
Answer:
(a) Cows were used as means of exchange. They were highly priced.
(b) For the same reason people took great care that their cows should not be stolen.

Question 3.
What was a man expected to do in sanyasashrama ?
Answer:
The fourth stage was the sanyasharam. At this stage a man was expected to renounce all relations, lead a life in order to understand the meaning of human life and not stay in one place.

6. Write notes on:

Question 1.
The religious ideas during the vedic period.
Answer:
(a) In the religious ideas of the vedic period, forces of nature such as the sun, wind, rain, lightening, storms and rivers were given the form of deities.
(b) Yajna is the act of offering havi into fire. The Vedic people put offering (havi) into the yajna fire to please the deities.

Question 2.
Houses in the Vedic period.
Answer:
The houses during the vedic period were earthen or wattle and daub constituents. Wattle means woven lattice of wooden strips which is daubed with clay mixed with cow dung. A house was called griha or shala.

Question 3.
Political system in the Vedic period.
Answer:
(a) The main duties of a king were to protect the people, collect taxes and run the administration efficiently.
(b) In order to run the administration smoothly, the king appointed various officers like the purohit (priest), the senapati and bhagdugh.
(c) There were four institutions who guided the king – sabha, samiti, vidath and jana.

Activity:

• Interview some artisans in your locality and write about them.
• List the new words in the lesson and find their meaning.

Class 6 History Chapter 4 The Vedic Civilization Additional Important Questions and Answers

Name the following with reference to the lesson:

Question 1.
Houses during the Vedic period:
Answer:
Griha or Shala.

Question 2.
The four varnas:
Answer:
Brahmin, Kshatriya, Vaishya and Shudra,

Question 3.
Four institutions who guided the king:
Answer:
Sabha, samiti, vidath and jana.

Right or Wrong?

Question 1.
Brahmanas – Guidance on using vedic mantra in yajna rituals.
Answer:
Right.

Question 2.
Institution who guided the king – Purohit, senapati, bhagdugh.
Answer:
Wrong.

Answer in one word each:

Question 1.
The head of vish:
Answer:
Vishpati.

Question 2.
The head of jana:
Answer:
Nripa.

Complete the sentences by choosing the correct option:

Question 1.
The civilization that is based on vedic literature is known as _________ civilization.
(a) vedic
(b)purans
(c) samhitas
Answer:
(a) vedic

Question 2.
The Vedas are considered to be our _________ literature.
(a) modem
(b) earliest
(c) medieval
Answer:
(b) earliest

Question 3.
The _______ were composed by many sages or rishis.
(a) Brahmana
(b) Aryanakas
(c) Vedas
Answer:
(c) Vedas

Question 4.
Vedic literature is written in _________.
(a) English
(b) Hindi
(c) Sanskrit
Answer:
(c) Sanskrit

Question 5.
The Rigveda is considered to be the _______ text.
(a) first
(b) second
(c) third
Answer:
(a) first

Question 6.
The Vedas have been preserved through the ________ tradition.
(a) ancient
(b) oral
(c) printed
Answer:
(b) oral

Question 7.
The vedas are also called as ________.
(a) Shruti
(b) Mayuri
(c)Yagna
Answer:
(a) Shruti

Question 8.
Each verse of the Veda is known as a ______.
(a) Shruti
(b) Maya
(c) Richa
Answer:
(c) Richa

Question 9.
The Rigveda consists of many ________ composed to praise different deities.
(a) richas
(b) suktas
(c) shruti
Answer:
(b) suktas

Question 10.
Yajurveda provides guidance about how and when the different ______ must be chanted during the yajna rites.
(a) mantras
(b) yajnas
(c) vedas
Answer:
(a) mantras

Question 11.
The samaveda has contributed in a major way in laying the foundation of Indian _______.
(a) society
(b) music
(c) lifestyle
Answer:
(b) music

Question 12.
The Atharvaveda is named after Atharva ________.
(a) Rishi
(b) mantra
(c) veda
Answer:
(a) Rishi

Question 13.
Atharvaveda includes______ to adversities and diseases.
(a) medicine
(b) ways
(c) solutions
Answer:
(c) solutions

Question 14.
The Atharvaveda provides _________ to the king about how he should administer his kingdom.
(a) solution
(b) guidance
(c) tradition
Answer:
(b) guidance

Question 15.
The _______ discuss such serious and profound issues.
(a) Vedas
(b) Aranyakas
(c) Upanishads
Answer:
(c) Upanishads

Question 16.
_________ family system was prevalent in Vedic peroid
(a) Joint
(b) matriarchal
(c) patriarchal
Answer:
(a) Joint

Question 17.
The grihapati was the of the family.
(a) heart
(b) head
(c) hands
Answer:
(b) head

Question 18.
The family system was ______
(a) ancient
(b) matriarchal
(c) patriarchal
Answer:
(c) patriarchal

Question 19.
A ________ was called griha or shala.
(a) house
(b) shed
(c) school
Answer:
(a) house

Question 20.
People in the Vedic period used cotton and woollen ________.
(a) headgear
(b) shawls
(c) garments
Answer:
(c) garments

Question 21.
In the Vedic period, animal skins were also used as ________ the Vedic period.
(a) Agriculture
(b) Clothings
(c) Trade
Answer:
(b) Clothings

Question 22.
_________ was the main occupation during determined on the basis of
(a) Agriculture
(b) birth
(c) death
Answer:
(a) Agriculture

Question 23.
The horse was valued because of its ______.
(a) chariot
(b) speed
(c) beauty
Answer:
(b) speed

Question 24.
The Vedic people were skilled in taming the _______ and harnessing them to the chariots.
(a) cows
(b) bulls
(c) horses
Answer:
(c) horses

Question 25.
The head of the guild was known as ________.
(a) Grihapati
(b) Shreshthi
(c) Raja
Answer:
(b) Shreshthi

Question 26.
A varna was determined by the ________ of the people.
(a) occupation
(b) neighbours
(c) skill
Answer:
(a) occupation

Question 27.
In the later period, the varnas came to be determined on the basis of ________.
(a) bags
(b) birth
(c) shoes
Answer:
(b) birth

Question 28.
The caste system led to ________ in the society.
(a) justice
(b) equality
(c) inequality
Answer:
(c) inequality

Question 29.
The Vedic people put _______ into the yajna fire to please the deities.
(a) offerings
(b) money
(c) water
Answer:
(a) offerings

Question 30.
In the Vedic period, each village had a head known as _______.
(a) grihapati
(b) gramini
(c) nripa
Answer:
(b) gramini

Question 31.
A group of villages formed a vish, whose head was called ________.
(a) grihapati
(b) purohit
(c) vishpati
Answer:
(c) vishpati

Question 32.
The head of the jana was known as nripa or _______.
(a) raja
(b) janapad
(c) senapati
Answer:
(a) raja

Question 33.
The ______ consisted of senior citizens of the state.
(a) samiti
(b) sabha
(c) vidath
Answer:
(b) sabha

Question 34.
After a period of time, the religious stream based on the vedas, smritis, puranas and local traditions came to be known as
(а) Buddhism
(b) Jainism
(c) Hinduism
Answer:
(c) Hinduism

Answer the following in one sentence:

Question 1.
What is vedic civilization?
Answer:
The civilization that is based on vedic literature is known as vedic civilization.

Question 2.
Who composed the vedas?
Answer:
The vedas were composed by many sages or rishis.

Question 3.
In which language is the vedic literature written?
Answer:
Vedic literature is written in Sanskrit.

Question 4.
Name the veda that is considered to be the first text.
Answer:
The Rigveda is considered to be the first text.

Question 5.
Name the four vedas.
Answer:
The four vedas are – Rigveda, Yajurveda, Samaveda and Atharvaveda.

Question 6.
What does Rigveda consist of?
Answer:
The Rigveda consists of many suktas composed to praise different deities.

Question 7.
What does Yajurveda provide?
Answer:
Yajurveda provides guidance about how and when the different mantras must be chanted during yajna rites.

Question 8.
What does Samaveda provide?
Answer:
The Samaveda provides guidance on singing Rigvedic verses to a set rhythm and tune at the time of yajna rites.

Question 9.
After whom is the Atharvaveda named?
Answer:
The Atharvaveda is name after Atharva rishi.

Question 10.
Which texts were written after the Samhitas?
Answer:
The Brahmana texts, Aranyakas and Upanishads were written after the composition of the Samhitas.

Question 11.
What does Aranyakas consists of?
Answer:
Aranyakas consists of the reflections or thoughts expressed after meditating with deep concentration in forests or wilderness.

Question 12.
Which family system was prevalent in the vedic period?
Answer:
Joint family system was prevalent in the vedic period.

Question 13.
Name some women scholars during the vedic period.
Answer:
Women scholars such as Lopamudra, Gargi and Maitreyi are mentioned in the vedic literature.

Question 14.
What did the diet of the people mainly consist of?
Answer:
The diet of the people mainly consists of cereals like wheat, barley and rice.

Question 15.
What was the main occupation during the vedic period?
Answer:
Agriculture was the main occupation during the vedic period.

Question 16.
Name the varnas.
Answer:
The four varnas are Brahmin, Kshatriya, Vaishya and Shudra.

Question 17.
Which four institutions guided the king?
Answer:
The four institutions that guided the king are sabha, samiti, vidath and jana.

Question 18.
What is Hinduism?
Answer:
After a period of time, the religious stream based on the vedas, smritis, puranas and local traditions came to be known as Hinduism.

Answer in short:

Question 1.
What does Atharvaveda consists of?
Answer:

• Atharvaveda consists of solution to adversities and diseases.
• It provides information about medicinal herbs.
• It provides guidance to a king about the way he should administer his kingdom.

Question 2.
Describe the dress of the people during the vedic period.
Answer:
People in the vedic period used cotton and woollen garments, they also used clothes made from the barks of trees. Animal skins were also used as clothing.

Write notes on:

Question 1.
Describe four stages or four ashramas.
Answer:
The four ashramas are brahmacharyashmma, grihasthashrama, vanaprasthashrama, sanyasashrama.

1. The first ashrama was the brahmacharyashrama or the period of staying with the Guru to learn from him.
2. The next stage was grihasthashrama, during this period a man would carry out his duties towards his family and society with the help of his wife.
3. The third stage was vanaprasthashrama when a man was expected to detach himself from the household, retire to a solitary place and lead a very simple life.
4. The fourth stage was the sanyasashrama, the convention was to renounce all relations, lead life in order to understand the meaning of human life and not to stay in one place.

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 4 साेना और लोहा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 4 साेना और लोहा

Hindi Sulabhbharti Class 6 Solutions Chapter 4 साेना और लोहा Textbook Questions and Answers

अध्ययन कौशल:

विभिन्न धातुओं के नाम और उनसे बनने वाली वस्तुएँ लिखो।
Answer:

विचार मंथन:

आराम हराम है
Answer:
‘आराम हराम है।’ यह नारा देश के पहले प्रधानमंत्री पं. जवाहरलाल नेहरू ने दिया था। नेहरू जी ने यह नारा उस समय दिया था, जब देश स्वतंत्र हुआ था। आलस करना या अत्यधिक आराम करना हमारे लिए नुकसानदेह हो सकता है। परीक्षा का समय हो, तो डटकर पढ़ाई करनी चाहिए। किसी प्रकार की प्रतियोगिता हो, तो उसकी तैयारी करनी चाहिए। सोचो यदि हम परीक्षा की तैयारी करने के बजाय आराम करते हैं, तो परीक्षा में असफल भी हो सकते हैं। हम छोटे से जीव चींटी से भी परिश्रम की सीख ले सकते हैं। वह दिन-रात मेहनत कर अपना भोजन इकट्ठा करती है और बरसात के वक्त आराम से अपनी मेहनत का लाभ उठाती है।

भाषा की ओर:

निम्नलिखित शब्दों में प्रत्यय लगाकर लिखो।

Answer:

1. सुंदरता
2. गुणवान
3. डरावना
4. उपयोगी
5. घबराहट
6. दैनिक

सुनो तो जरा |

बस/रेल स्थानक की सूचनाएँ ध्यानपूर्वक सुनकर सुनाओ।
Answer:
१. बस स्थानक की सूचना:

स्थान: माथेरान एस टी बस स्टैंड।
यात्रीगण कृपया ध्यान दें। माथेरान से मुंबई जाने वाली दो बसों के समय में परिवर्तन किया गया है। सुबह ९ बजकर ३० मिनट पर रवाना होने वाली बस अब १० बजकर ११ मिनट पर रवाना होगी तथा सुबह ११ बजे रवाना होने वाली बस दोपहर १२ बजे रवाना होगी। यात्रियों को होने वाली | असुविधा के लिए हमें खेद है। धन्यवाद!

२. रेल स्थानक की सूचना:

स्थान: दादर रेलवे कार्यालय।
नमस्कार! हम दादर के केंद्रीय कार्यालय से बोल रहे हैं। ट्रैक नंबर दो पर मरम्मत-कार्य चालू होने के कारण आज दोपहर चार बजे तक सी. एस. टी. से माटुंगा की दिशा में जाने वाली सभी डाउन गिाड़याँ ट्रैक नंबर एक से चलाई जाएँगी। यात्रियों को होने वाली असुविधा के लिए हमें खेद है। धन्यवाद!

बताओ तो सही।

थर्मामीटर में किस धातु का प्रयोग होता है, बताओ।
Answer:
पारा

मेरी कलम से

अंकुरित अनाजों की सूची बनाओ और उपयोग लिखो।
Answer:

सदैव ध्यान में रखो।

प्रत्येक का अपना-अपना महत्त्व होता है।
Answer:
प्रत्येक वस्तु का अपना-अपना महत्त्व होता है। कोई भी छोटा अथवा बड़ा नहीं होता। बड़ी चीज जितनी उपयोगी है, छोटी चीज भी उतने ही काम की है। बड़ी-बड़ी मशीनों के कल-पूजों को जोड़नेवाले नट-बोल्ट छोटे-छोटे ही होते हैं। सोना अगर कीमती धातु है, तो लोहा मजबूत और रोजाना काम आने वाली धातु है।

जरा सोचो ….. चर्चा करो

यदि खनिज तेल का खजाना समाप्त हो जाए तो…
Answer:
यदि खनिज तेल का खजाना समाप्त हो जाए, तो यातायात व्यवस्था ठप हो जाएगी। खनिज तेल से पेट्रोल, डीजल, मिट्टी का तेल, कुकिंग गैस, वैसलीन आदि बनते हैं। खनिज तेल के समाप्त होने से सड़कों पर गिाड़याँ नहीं दौड़ पाएँगी। हम यात्रा नहीं कर पाएँगे। रोज-रोज पैदल चलना कठिन काम होगा। ट्रक न चलने से घरों, दूकानों, बाजारों तक सामान नहीं पहुँच पाएगा। हम भूखे-प्यासे रह जाएँगे। एलपीजी गैस जिससे खाना बनाया जाता है, उसके बिना घरों में खाना नहीं बन पाएगा। खनिज तेल कई दवाइयों के निर्माण में काम आते हैं। इनके बिना दवाइयाँ भी नहीं बन पाएँगी। इस तरह खनिज तेल समाप्त हो जाने पर पूरी दुनिया का काम-काज रुक जाएगा।

अध्याय

सही या गलत बताओ।

सोना और लोहा प्रश्न उत्तर Question 1.
युद्ध में लोहे के अस्त्र – शस्त्र काम देते हैं।
Answer:
सही

Sona Aur Loha Question Answer Question 2.
रोटियाँ भी सोने के तवे पर सेंकी जाती हैं। ङ्के
Answer:
गलत

Class 6th Hindi Sona Aur Loha Question 3.
श्रम में ही जीवन की सफलता है।
Answer:
सही

Sona Aur Loha 6 Standard Question 4.
जो काम करेंगे, उन्हीं का अब सम्मान नहीं होगा।
Answer:
गलत

Sona Aur Loha Hindi Question 5.
आराम हराम है।
Answer:
सही

सोना और लोहा हिंदी पाठ Question 6.
हमें घमंड करना चाहिए।
Answer:
गलत

खोजबीन:

रुपयों (नोट) पर लिखी कीमत कितनी और किन भाषाओं में अंकित है, बताओ।
Answer:

स्वयं अध्ययन:

सदगुणों को आत्मसात करने के लिए क्या करोगे, इसपर आपस में चर्चा करो।
Answer:

व्याकरण

निम्नलिखित शब्दों का रोमन लिपि में लिप्यंतरण करो।

Answer:
i. Dhanush
ii. Mahal
iii. Kursi
iv. Barish
v. Katahal
vi. Khidki
vii. Hathi
viii. Nevala

निम्नलिखित कारकों का अपने वाक्यों में प्रयोग करो।

Answer:

Hindi Sulabhbharti Class 6 Solutions Chapter 4 साेना और लोहा Additional Important Questions and Answers

निम्नलिखित शब्दों में से सही शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(रक्षा, मूल्य, सेवा, आराम, लद)

6th Standard Hindi Lesson Sona Aur Loha  Question 1.
राजाओं के दिन ……………… गए।
Answer:
लद

Sona Or Loha 6 Standard Question 2.
तेरी ……………… का भार मुझ पर है।
Answer:
रक्षा

Question 3.
मैं तो ……………… से रहना चाहता हूँ।
Answer:
आराम

Question 4.
रुपयों में किसी वस्तु का ……………… लगाना व्यर्थ
Answer:
मूल्य

Question 5.
गरीबों की ……………… करने में मुझे सुख मिलता है।
Answer:
सेवा

निम्नलिखित बाक्य सही हैं या गलत लिखिए:

Question 1.
युद्ध में लोहे के अस्त्र – शस्त्र काम देते हैं।
Answer:
सही

Question 2.
रोटियाँ भी सोने के तवे पर सेंकी जाती हैं।
Answer:
गलत

Question 3.
श्रम में ही जीवन की सफलता है।
Answer:
सही

Question 4.
जो काम करेंगे, उन्हीं का अब सम्मान नहीं होगा।
Answer:
गलत

Question 5.
आराम हराम है।
Answer:
सही

Question 6.
हमें घमंड करना चाहिए।
Answer:
गलत

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्द में लिखिए:

Question 1.
सोना किन लोगों का लाड़ला है?
Answer:
राजाओं और धनिकों का।

Question 2.
अब किन लोगों के दिन आए हैं?
Answer:
श्रमिकों के।

Question 3.
लोहा किन लोगों का प्यारा है?
Answer:
किसानों और मजदूरों का।

Question 4.
लोहा किसकी रक्षा करता है?
Answer:
सोने की।

Question 5.
सोने का रंग कैसा है?
Answer:
पीला।

निम्नलिखित वाक्य किसने, किससे कहे?

Question 1.
संसार में मैं सबसे सुंदर हूँ।
Answer:
सोने ने लोहे से कहा।

Question 2.
अच्छा, तू राजा और मैं नौकर?
Answer:
लोहे ने सोने से कहा।

Question 3.
अरे, लोहे से कैसे पेट भरता है।
Answer:
सोने ने लोहे से कहा।

Question 4.
मुझसे तो मेहनत नहीं होती।
Answer:
सोने ने लोहे से का।

Question 5.
छोड़ दूँगा भैया, मगर मेरी रक्षा करना।
Answer:
सोने ने लोहे से कहा।

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
सबको किसकी चाह होती है।
Answer:
सबको सोने की चाह होती है।

Question 2.
राजा की रक्षा कौन करते हैं?
Answer:
राजा की रक्षा उसके नौकर – चाकर करते हैं

Question 3.
रोटियाँ किस पर सेकी जाती है।
Answer:
रोटियाँ लोहे के तवे पर सेंकी जाती है।

Question 4.
जीवन की सफलता किसमें होती है?
Answer:
जीवन की सफलता श्रम करने में होती है।
Question 5.
लोहे ने सोने को कौन-सा वचन दिया?
Answer:
लोहे ने सोने को उसकी रक्षा करने का वचन दिया।

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के दो-दो पर्यायवाची शब्द लिखिए:

1. राजा
2. रात
3. श्रम
4. नौकर
5. मकान

Answer:

1. नृप, नरेश
2. रात्रि, निशा
3. कष्ट, मेहनत
4. सेवक, चाकर
5. घर, गृह

निम्नलिखित शब्दों के विरुद्धार्थी लिखिए:

1. राजा
2. दिन
3. भीतर
4. गुण
5. भला

Answer:

1. रंक
2. रात
3. बाहर
4. दोष
5. बुरा

निम्नलिखित वाक्यों में कारक को रेखांकित करके उनके भेद लिखिए:

Question 1.
मेरे एक चाँटे से तेरा रूप बदल जाएगा।
Answer:
से – करण कारक

Question 2.
राजा की रक्षा उसके नौकर – चाकर करते हैं।
Answer:
की – संबंध कारक

Question 3.
तू तिजोरी से बाहर क्यों आया?
Answer:
से – अपादान कारक

Question 4.
कोई बड़ा काम करना हो, लोहे के बिना हो ही नहीं सकता।
Answer:
के – संबंध कारक

Question 5.
श्रम में ही जीवन की सफलता है।
Answer:
Answer:
में – अधिकरण

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 2 बसंती हवा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 2 बसंती हवा

Hindi Sulabhbharti Class 6 Solutions Chapter 2 बसंती हवा Textbook Questions and Answers

लेखन विभाग

स्वयं अध्ययन:

नीचे दिए गए चित्रों की सहायता से प्राकृतिक सुंदरता दर्शाने वाला एक चित्र बनाकर उसमें रंग भरो।
अपने चित्र के बारे में बोलो।

Answer:
(१) किसान: किसान परिश्रमी होते हैं। उनके परिश्रम से ही सबको अन्न मिलता है।
(२) साँड़: साँड़ खेती के काम आते हैं
(३) वृक्ष: वृक्षों से हमें फल-फूल मिलते हैं। वृक्षों से ऑक्सीजन मिलती है। वृक्ष हमारे लिए बहुत उपयोगी हैं।
(४) पहाड़: भारत में कई ऊँचे-ऊँचे पहाड़ हैं। उत्तर में हिमालय भारत का प्रहरी है। महाराष्ट्र में भी कई पहाड़ हैं।
(५) चिड़िया: चिड़िया बहुत प्यारी लगती है। सुबह होते ही वह दाना चुगने जाती है। शाम को वापस घोंसले में लौट आती है।
(६) झरना: पहाड़ों से गिरते जल को झरना कहा जाता है। यह बहुत ही आकर्षक होता है।

भाषा की ओर

Answer:
दिए गए शब्दों के लययुक्त शब्द:

• हवा – रवा
• बावली – साँवली
• सरसों – बरसों
• अलसी – कलसी, तुलसी
• महुआ – बथुआ

खोजबीन: 

ऋतुओं के नाम बताते हुए उनके परिवर्तन की जानकारी प्राप्त करो और लिखो।
Answer:
वसंत ऋतु, ग्रीष्म ऋतु, वर्षा ऋतु, शरद ऋतु, हेमन्त ऋतु,शिशिर ऋतु। ऋतुओं में परिवर्तन का मुख्य कारण है – धरती का अपने अक्ष पर घूमते हुए सूर्य की परिक्रमा करना।

सुनो तो जराः 

त्योहार संबंधी कोई एक गीत सुनो और दोहराओ।
Answer:
होली गीत –
आज बिरज में होरी रे रसिया
आज बिरज में होरी रे रसिया
घर घर से ब्रज बनिता आई
कोई श्याम कोई गोरी रे रसिया
आज बिरज ………. में.
इत ते आए कुंवर कन्हाई,
उत ते आई राधा गोरी रे रसिया
आज बिरज ………..में
कोई लावे चोवा कोई लावे चंदन
कोई मले मुख रोरी रे रसिया
आज बिरज में …………..।

बताओ तो सही: 

‘शालेय स्वच्छता अभियान’ में तुम्हारा सहयोग बताओ।
Answer:
‘शालेय स्वच्छता अभियान के तहत मेरे विद्यालय में २ अक्टूबर को स्वच्छता अभियान रखा गया था। सबसे पहले एक प्रभात फेरी निकली, जिसमें मैंने भाग लिया। उसके बाद हमने विद्यालय एवं विद्यालय परिसर में साफसफाई की।

वाचन जगत से: 

कविवर सुमित्रानंदन पंत की कविता का मुखर वाचन करो।
Answer:
गाता खग प्रातः उठकर
सुंदर, सुखमय जग-जीवन
गाता खग संध्या-तट पर
मंगल, मधुमय जग जीवन
कहती अपलक तारावलि
अपनी आँखों का अनुभव
अवलोक आँख आँसू की
भर आती आँखें नौरव

मेरी कलम से: 

सप्ताह में एक दिन किसी कविता का सुलेखन करो।
Answer:
विद्यार्थियों द्वारा लिखा जाए।

रिक्त स्थानों की पूर्ति कीजिए:

Basanti Hawa Question Answer In Hindi Question 1.
नहीं कुछ ……………..
Answer:
फिकर

बसंती हवा कविता का प्रश्न उत्तर  Question 2.
गिरी ……………… से फिर, चढ़ी आम ऊपर।
Answer:
धम्म

Basanti Hawa Ke Question Answer  Question 3.
वहाँ ……………… में, लहर खूब मारी।
Answer:
गेहुँओं

बसंती हवा प्रश्न उत्तर  Question 4.
हिलाया-झुलाया गिरी पर न ……
Answer:
कलसी

बसंती हवा के प्रश्न उत्तर  Question 5.
हिलाई न ……………
Answer:
सरसों

बसंती हवा Question 6.
…………….. दो पहर क्या।
Answer:
पहर

Question 7.
सुनो बात मेरी ………………. हवा हूँ।
Answer:
अनोखी

सदैव ध्यान में रखो

प्लास्टिक, थर्माकोल आदि प्रदूषण बढ़ाने वाले घटकों का उपयोग हानिकारक है।
Answer:
प्लास्टिक व थर्माकोल जैसे घटक आसानी से नष्ट नहीं होते हैं। इन्हें जलाने पर भी पर्यावरण बहुत प्रदूषित होता है। यदि खुले में घूमने वाले जानवर गलती से इन्हें निगल लेते हैं तो उनकी मौत भी हो सकती है। वर्षा ऋतु में नालों व गटरों के जाम होने की घटना हमें प्राय: देखने व सुनने को मिलती है। इसका मुख्य कारण भी प्लास्टिक व थर्माकोल जैसे घटक ही हैं। हर प्रकार से इनका उपयोग पर्यावरण के लिए हानिकारक है। अत: पर्यावरण को बचाने के लिए हमारी यह जिम्मेदारी बनती है कि हम इनका उपयोग न करें और दूसरों को भी इसके दुष्पपरिणामों के प्रति जागरूक करें।

विचार मंथन: 

“हवा प्रकृति का उपहार है, यही जीवन का आधार है।
Answer:
हम सभी श्वास लेते हैं और श्वास छोड़ते हैं। हम श्वास के रूप में ऑक्सीजन ग्रहण करते हैं और श्वास कार्बन डाय आक्साइड के रूप में छोड़ते हैं। पेड़ पौधे कार्बन डाय आक्साइड को पुन: ऑक्सीजन बनाते हैं। इस प्रकार हम ऑक्सीजन के बिना जीवित नहीं रह सकते हैं।

अध्ययन कौशल: 

वायुमंडलीय स्तर दर्शानेवाली आकृति बनाओ।
Answer:
विद्यार्थी स्वंय आकृति बनाएँगे।

जरा सोचो …. बताओ: 

यदि प्रकृति में सुंदर-सुंदर रंग नहीं होते तो…..?
Answer:
यदि प्रकृति में सुंदर-सुंदर रंग नहीं होते तो प्राकृतिक सौंदर्य एक दम नीरस होता। हमारे जीवन में भी बिना रंग के सब कुछ सूना-सा लगता। कोई बाग-बगीचे में घूमने नहीं जाता। फूल भी एक ही रंग के अच्छे नहीं लगते।

Hindi Sulabhbharti Class 6 Solutions Chapter 2 बसंती हवा Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
ऋतुओं का राजा किसे कहा जाता है?
Answer:
वसंत ऋतु को ऋतुओं का राजा कहा जाता है।

Question 2.
हवा किधर घूमती है?
Answer:
हवा जिधर चाहती है, उधर घूमती है।

Question 3.
हवा ने किसे झकोरा?
Answer:
हवा ने आम पर चढ़कर उसे झकोरा।

Question 4.
आम से उतरकर बसंती हवा कहाँ पहुँची?
Answer:
आम से उतरकर बसंती हवा गेहूँ के हरे खेत में पहुंची।

Question 5.
अलसी सिर पर क्या लेकर खड़ी है?
Answer:
अलसी सिर पर कलसी लिए खड़ी है।

Question 6.
बसंती हवा सरसों को क्यों नहीं हिला-झुला पाई?
Answer:
बसंती हवा अलसी से हार जाने के कारण सरसों को नहीं हिला-झुला पाई।

Question 7.
कविता में आए हुए लयात्मक शब्दों को ढूँढकर लिखिए:
उदाहरण:
अलसी – कलसी
Answer:
सरसों – बरसों
पहर – प्रहर
हिलाया – झुलाया

Question 8.
बसंती हवा कैसी है?
Answer:
बसंती हवा अनोखी, बावली, मस्तमौला, बेफ़िक्र, निडर और अजब है।

Question 9.
बसंती हवा कहाँ-कहाँ घूमती रही?
Answer:
बसंती हवा ने महुआ के पेड़ पर चढ़कर थपाथप मचाई और धम्म से गिर पड़ी। फिर आम के पेड़ पर चढ़कर उसे झकोरा और कान में ‘कू’ करके वहाँ से उतर कर भागी। वहाँ से गेहूँ के खेत में पहुंची तथा अलसी और सरसों के खेत में घूमती रही।

उचित जोड़ियाँ मिलाइए:

Answer:
१ – ख
२ – क
३ – घ
४ – ड़
५ – ग

व्याकरण और भाषाभ्यास:

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. फ़िक्र
2. मुसाफिर
3. अजब
4. पेड़
5. निडर
6. हार

Answer:

1. चिंता
2. यात्री
3. विचित्र
4. वृक्ष
5. अभय
6. पराजय

निम्नलिखित शब्दों के लिंग बदलिए:

1. बावली
2. अनोखी
3. बड़ी
4. खड़ी

Answer:

1. बावला
2. अनोखा
3. बड़ा
4. खड़ा

निम्नलिखित शब्दों के विलोम शब्द लिखिए:

1. निडर
2. ऊपर
3. बड़ी
4. चढ़ी
5. हार

Answer:

1. भयभीत
2. नीचे
3. छोटी
4. उतरी
5. जीत

निम्नलिखित शब्दों में अनुस्वार -” या अनुनासिक लगाकर शब्द लिखिए:

1. हू
2. बसती
3. नही
4. मे
5. अनेको
6. सरसो
7. पहुची
8. वहा
9. गेहुओ

Answer:

1. हूँ
2. बसंती
3. नहीं
4. में
5. अनेकों
6. सरसों
7. पहुंची
8. वहाँ
9. गेहुँओं

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 2 माझा अनुभव Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 2 माझा अनुभव

Marathi Sulabhbharti Class 6 Solutions Chapter 2 माझा अनुभव Textbook Questions and Answers

1. का ते लिहा.

प्रश्न अ.
रिमाने आनंदाने उड्या मारल्या.
उत्तर:
आगगाडीने मामाच्या गावाला जायचे म्हणून रिमाने आनंदाने उड्या मारल्या.

प्रश्न आ.
मुलाने बाळाला मांडीवर घेतले.
उत्तर:
मावशींच्या मांडीवर बसलेले बाळ खुदकन हसले म्हणून मुलाने बाळाला मांडीवर घेतले.

प्रश्न इ.
मुलाचे मन आनंदाने थुईथुई नाचू लागले.
उत्तर:
पानांची सळसळ, नदीची खळखळ, पक्ष्यांची किलबिल, गाईंचे हंबरणे, पशु, पक्षी, शेते पाहून मुलाचे मन आनंदाने थुईथुई नाचू लागले.

प्रश्न ई.
मुलांना गहिवरून आले.
उत्तर:
आजीच्या हाताचा थरथरणारा स्पर्श खूप प्रेमळ अन् बोलका होता म्हणून मुलांना गहिवरून आले.

2. ‘सुट्टी कधी संपली, ते आम्हांला समजलेच नाही.’ असे मुलाला का वाटले? तुमच्या शब्दांत लिहा.

प्रश्न 1.
‘सुट्टी कधी संपली, ते आम्हांला समजलेच नाही.’ असे मुलाला का वाटले? तुमच्या शब्दांत लिहा.
उत्तर:
सुट्टीत विहिरीवर पोहायला जाणे, शेतात बागडणे, आंब्याच्या झाडावर चढून कैऱ्या, पाडाचा आंबा तोडून खाणे, बैलगाडीतून मामाबरोबर फेरफटका मारणे, कधी शेतावर तर कधी आमराईत मामाबरोबर फिरायला जाणे या सर्व मजेत सुट्टी कधी संपली ते मुलांना कळलेच नाही.

3. वाचा. सांगा. लिहा.
नादमय शब्द उदा., छुमछुम, झुकझुक.

प्रश्न अ.
वाचा. सांगा. लिहा.
नादमय शब्द उदा., छुमछुम, झुकझुक.
उत्तर:
फडफड, खडखड, सळसळ, खळखळ, खुळखुळ, थुईथुई

4. खालील शब्दाचे समानार्थी शब्द लिहा.
(अ) वारा, (आ) तोंड, (इ) रस्ता, (ई) आई, (उ) शेत

प्रश्न अ.
वारा
उत्तर:
वारा – पवन, वायू

प्रश्न आ.
तोंड
उत्तर:
तोंड – मुख, चेहरा

प्रश्न इ.
रस्ता
उत्तर:
रस्ता – मार्ग, सडक

प्रश्न ई.
आई
उत्तर:
आई – माता, जननी

प्रश्न उ.
शेत
उत्तर:
शेत – शिवार

5. जोड्या जुळवा.

प्रश्न अ.

उत्तर:

6. गाईचे हंबरणे’ तसे खालील पशुपक्ष्यांचे आवाजदर्शक शब्द लिहा.

प्रश्न 1.
गाईचे हंबरणे’ तसे खालील पशुपक्ष्यांचे आवाजदर्शक शब्द लिहा.
उत्तर:
(अ) बकरी – बेंऽ बेंऽ
(आ) वाघ – डरकाळी
(इ) बेडूक – डराँव डराँव
(ई) कुत्रा – भुंकणे
(उ) मांजर – म्याँव म्याँव करणे
(ऊ) मोर – माओ माओ

7. खालील वाक्प्रचाराचा वाक्यात उपयोग करा.

प्रश्न 1.
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:
(अ) खुदकन हसणे – बाळ खुदकन हसले.
(आ) गाढ झोपणे – आई गाढ झोपली होती.
(इ) कडकडून भेटणे – अमेरिकेतून आल्यावर मी भावाला कडकडून भेटलो.
(ई) टुकुटुकु पाहणे – बाळ सर्वांकडे टुकुटुकु पहात होते.
(उ) आनंदाने थुईथुई नाचणे – काळे मेघ पाहून मोर आनंदाने थुईथुई नाचतो.
(ऊ) गहिवरून येणे – निरोप देताना मला गहिवरून आले.

8. बाजारहाट’ यासारखे आणखी काही जोडशब्द लिहा.

प्रश्न 1.
बाजारहाट’ यासारखे आणखी काही जोडशब्द लिहा.
उत्तर:

1. धावपळ
2. नातीगोती
3. पाटपाणी
4. नरमगरम
5. भाजीपाला
6. धुणीभांडी
7. गणगोत

9. तुम्ही एखादे चांगले काम केले आहे त्या प्रसंगाचे अनुभवलेखन करा.

प्रश्न 1.
तुम्ही एखादे चांगले काम केले आहे त्या प्रसंगाचे अनुभवलेखन करा.
उत्तर:
आमच्याकडे घरकामासाठी येणाऱ्या बाईच्या मुलीला मी रोज खाऊ देतो. ती दुसरीत असल्याने तिचा अभ्यासही घेतो. तिची आई काम करेपर्यंत गाणी, कविता शिकवतो. कधी कधी गोष्टीची पुस्तके वाचून दाखवतो. मी तिला चार वया व काही पेन्सीलीही दिल्या आहेत. तिच्यात अभ्यासाची गोडी निर्माण करण्याचा मी प्रयत्न केला आहे. खाल्लेल्या गोळीचा कागद कचरापेटीत टाकायला शिकवले. नखे कापायला व स्वच्छ रहायला शिकवले. तिच्यात बरीच सुधारणा आहे. या चांगल्या कामाने मला समाधान मिळाले.

10. तुमच्या घरातील व्यक्तींबरोबर सुट्टीच्या दिवशी

प्रश्न 1.
तुमच्या घरातील व्यक्तींबरोबर सुट्टीच्या दिवशी
उत्तर:

11. खालील शब्दांसारखे दोन – दोन शब्द लिहा. 

प्रश्न 1.
खालील शब्दांसारखे दोन – दोन शब्द लिहा.
उत्तर:
(अ) सळसळ – (1) मळमळ (2) जळजळ
(आ) भुरभुर – (1) फुरफुर (2) गुरगुर
(इ) लुकलुक – (1) झुकझुक (2) टुकटुक
(ई) खडखड – (1) धडधड (2) बडबड

12. हे शब्द असेच लिहा.

प्रश्न 1.
हे शब्द असेच लिहा.
उत्तर:
उद्या, उन्हाने, तल्लीन, स्टेशन, स्वागत, वाऱ्यांच्या, तेवढ्यात, येणाऱ्या, रस्त्याला, कोंबड्यांचा, स्पर्श, प्रेमळ, दुसऱ्या, कैऱ्या, सुट्टी, आंब्याच्या.

13. खालील शब्द आपण कधी वापरतो?

आपण एका वस्तूबद्दल बोलू लागलो, की त्यास एकवचन म्हणतो आणि अनेकांबद्दल बोलू लागलो, की त्यास अनेकवचन म्हणतो.
उदा., एक झाड – अनेक झाडे.
खालील शब्दांच्या जोड्या वाचा व समजून घ्या.

उत्तर:

• कृपया – विनंती करताना.
  उदा. ’कृपया, मला एक पेन्सिल दे.“
• माफ करा – क्षमा मागताना.
  उदा. ’माफ करा. तुम्हांला चुकून धक्का लागला.“
• आभारी आहे – आभार मानताना.
  उदा. ’तू मला पेन्सिल दिलीस, त्याबद्दल मी आभारी आहे.“

14. खालील वाक्यातील नामांना अधोरेखित करा.

प्रश्न अ.
बाबांचा सदरा उसवला.
उत्तर:
बाबांचा सदरा उसवला.

प्रश्न आ.
सुमनने गुलाबाचे रोपटे लावले.
उत्तर:
सुमनने गुलाबाचे रोपटे लावले.

प्रश्न इ.
पाकिटात पैसे नव्हते.
उत्तर:
पाकिटात पैसे नव्हते.

प्रश्न ई.
मुले बागेत खेळत होती
उत्तर:
मुले बागेत खेळत होती.

प्रश्न उ.
समोरून बैल येत होता.
उत्तर:
समोरून बैल येत होता.

प्रश्न ऊ.
सरिता व फरिदा चांगल्या मैत्रिणी आहेत.
उत्तर:
सरिता व फरिदा चांगल्या मैत्रिणी आहेत.

प्रश्न ए.
पंकजने परीक्षेत पहिला नंबर मिळवला.
उत्तर:
पंकजने परीक्षेत पहिला नंबर मिळवला.

Marathi Sulabhbharti Class 6 Solutions Chapter 2 माझा अनुभव Important Additional Questions and Answers

खालील वाक्यात रिकाम्या जागा भरून वाक्ये पुन्हा लिहा.

प्रश्न 1.

1. पायांतले …………… छुमछुम वाजवत ती घरभर फिरली.
2. आगगाडी ………… करत चालली होती.
3. तिचा चेहरा …………. दिसत होता.
4. मी ……………. मांडीवर घेतले.
5. स्टेशनवर ………….. घेऊन मामा आला होता.
6. बैलांच्या गळ्यातील …………. खुळखुळ वाजत होत्या.
7. मन …………… थुईथुई नाचत होते.
8. आम्ही …………………. बिलगलो.
9. आमची ………….. कधी संपली ते आम्हांला समजलेच नाही.

उत्तर:

1. पैंजण
2. झुकझुक
3. प्रसन्न
4. बाळाला
5. बैलगाडी
6. घुगूरमाळा
7. आनंदाने
8. आजीला
9. सुट्टी

का ते लिहा.

माझा अनुभव प्रश्न उत्तर प्रश्न 1.
रिमाचे डोळे लुकलुकत होते.
उत्तर:
खिडकीतून येणाऱ्या उन्हामुळे रिमाचे डोळे लुकलुकत होते.

Marathi Sulabhbharti Class 6 Solutions Chapter 2 प्रश्न 2.
सुट्टी कधी संपली, ते मुलांना समजलेच नाही.
उत्तर:
पोहणे, बागडणे, आंबे खाणे, शेतात-आमराईत जाणे या सर्व मजेत सुट्टी कधी संपली ते कळलेच नाही.

खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.

माझा अनुभव प्रश्न 1.
मावशींच्या मांडीवर कोण बसले होते?
उत्तर:
मावशींच्या मांडीवर छोटेसे बाळ बसले होते.

Maza Anubhav Question Answers प्रश्न 2.
स्टेशनवर बैलगाडी घेऊन कोण आला होता?
उत्तर:
स्टेशनवर बैलगाडी घेऊन मामा आला होता.

अनुभव समानार्थी शब्द मराठी प्रश्न 3.
शेतातली पिके कशी डुलत होती?
उत्तर:
शेतातली पिके वाऱ्यावर मंद मंद डुलत होती.

Maza Anubhav In Marathi प्रश्न 3.
घरी येताच कोणी स्वागत केले?
उत्तर:
घरी येताच मामीने स्वागत केले.

आनंदी समानार्थी शब्द मराठी प्रश्न 4.
आजीने मुलांचे लाड कसे केले?
उत्तर:
आजीने मुलांच्या डोक्यावरून, तोंडावरून प्रेमाने हात फिरवून मुलांचे लाड केले.

प्रश्न 5.
मुले कोठे पोहायला जात?
उत्तर:
मुले विहिरीवर पोहायला जात.

प्रश्न 6.
सुट्टी संपल्यावर सगळे कुठे परतले?
उत्तरः
सुट्टी संपल्यावर सगळे गावी आपल्या घरी परतले.

प्रश्न 7.
मुले मामाबरोबर कुठे फिरायला जात?
उत्तर:
मुले मामाबरोबर आमराईत फिरायला जात.

प्रश्न 8.
मामाच्या मुलांची नावे लिहा.
उत्तर:
राजू आणि चिमी ही मामाच्या मुलांची नावे आहेत.

खालील प्रश्नांची दोन-तीन वाक्यात उत्तरे लिहा.

प्रश्न 1.
मामाच्या गावातील सायंकाळचे वर्णन करा.
उत्तर:
घरी जाण्यासाठी सर्व बैलगाडीत बसले. तोवर सायंकाळ झाली होती. पाने सळसळत होती. पाण्याची खळखळ, पक्ष्यांची किलबिल, शेतात चरणाऱ्या गाईंचे हंबरणे, बकऱ्यांचे बेंऽ बेंऽ ऐकू येत होते. शेतातील पिके वाऱ्यावर मंद मंद डुलत होती.

प्रश्न 2.
मामाच्या घरी सर्वांचे स्वागत कसे झाले?
उत्तर:
मामा स्वत: बैलगाडी घेऊन स्टेशनवर घ्यायला आला होता. घरी येताच मामीने तोंडभर हसून सगळ्यांचे स्वागत केले, राजू व चिमी ही मामाची मुले वाटच पहात होती. ते सगळ्यांना कडकडून भेटले. आजी हळूहळू काठी टेकवत आली व तिने मुलांच्या डोक्यावरून, तोंडावरून प्रेमाने हात फिरवला.

व्याकरण व भाषाभ्यास:

• एकवचन – जेव्हा आपण एका वस्तूबद्दल बोलतो तेव्हा ते एकवचन असते.
• अनेकवचन – जेव्हा आपण अनेक वस्तूंबद्दल बोलतो तेव्हा ते अनेकवचन असते.

खालील शब्दांचे वचन बदला.

प्रश्न 1.

1. आंबा
2. आगगाडी
3. केस
4. खिडकी
5. पीक
6. धुंगूरमाळ
7. पान
8. घर
9. पक्षी
10. चेहरा
11. नदी
12. परीक्षा
13. कैऱ्या

उत्तर:

1. आंबे
2. आगगाड्या
3. केस
4. खिडक्या
5. पिके
6. घुगूरमाळा
7. पाने
8. घरे
9. पक्षी
10. चेहरे
11. नदया
12. परीक्षा
13. कैरी

खालील वाक्यातील नामांना अधोरेखित करा.

प्रश्न 1.
मुलांनी खाऊ खाल्ला.
उत्तर:
मुलांनी खाऊ खाल्ला.

खालील शब्दांचे समानार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. धमाल
2. बिलगणे
3. झुळूक
4. छोटे
5. बागडणे

उत्तरः

1. मजा
2. प्रेमाने जवळ येणे
3. वाऱ्याची लहर
4. लहान
5. खेळणे.

प्रश्न 2.
‘गाईचे हंबरणे’ तसे खालील पशुपक्ष्यांचे आवाजदर्शक शब्द लिहा.

1. कोल्हा
2. चिमणी
3. कोकीळ
4. कावळा

उत्तर:

1. कुई कुई
2. चिव-चिव
3. कुहू कुहू
4. काव-काव

प्रश्न 3.
खालील शब्दांसारखे दोन दोन शब्द लिहा.
उत्तर:

• सरसर – (1) झरझर (2) घरघर
• झपझप – (1) धपधप (2) रपरप

प्रश्न 4.
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:
तल्लीन होणे – मालिनी सतार वाजवताना तल्लीन होते.

लेखन विभाग:

प्रश्न 1.
खालील शब्द आपण कधी वापरतो? (कृपया, माफ करा, आभारी आहे.)

उत्तर:

1. कृपया येथे माझे सामान ठेवाल कां?
2. माफ करा माझ्या हातून कप फुटला.
3. आपण मला मदत केलीत, आभारी आहे.

प्रश्न 2.
तुमच्या वर्गात तुम्ही कोणते सुविचार लिहाल?
उत्तर:

1. प्रयत्न केल्याने यश मिळते. अपयशाने खचू नका.
2. निसर्ग तुमचे भविष्य आहे. त्याची काळजी घ्या. निसर्ग जपा. झाडांशी मैत्री करा.
3. चांगला आहार मन, बुद्धी व शरीराला पोषक असतो.
4. खूप वाचा. खूप शिका. मोठ्यांचा आदर करा.
5. अंधश्रद्धेला बळी पडू नका. ज्ञानाची ज्योत पेटवा.

प्रश्न 3.
बागेत तुम्ही कोणते सुचना फलक पाहता?
उत्तर:

प्रश्न 4.
सामाजिक समस्यांवर आधारित घोषवाक्ये लिहा.
उत्तर:

1. पाणी जीवन आहे. जपून वापरा.
2. नका तोडू वृक्ष, रहा नेहमी दक्ष.
3. निसर्गाचा ठेवा मान, राखा पर्यावरणाचे भान.
4. वीज, पाणी, पेट्रोल, डिझेल ही साधनसंपत्ती; नका करू नाश, नाहीतर ओढवेल आपत्ती.
5. कापडी पिशव्यांची साथ खरी; प्लॅस्टिक नको दारोदारी.

माझा अनुभव Summary in Marathi

पाठ परिचयः

प्रस्तुत पाठात वार्षिक परीक्षा संपल्यानंतर मामाच्या गावाला जाण्याचे प्रवासवर्णन व मामाच्या गावात पोहचल्यावर केलेली मौजमजा शब्दचित्रीत केली आहे. उन्हाळ्याच्या सुट्टीचा आनंद कसा लुटला याचा अनुभव मांडला आहे.

शब्दर्थ:

1. झुळूक – वाऱ्याची लहर (breeze)
2. छोटे – लहान (small)
3. गाढ झोपणे – शांत झोपणे (deep sleep)
4. हंबरणे – गाईचा आवाज (bellow)
5. प्रेमळ – प्रेमाने भरलेला (loving)
6. धमाल – मजा (enjoyment, great fun)
7. बागडणे – खेळणे (to play)
8. कैऱ्या – कच्चे आंबे (raw mangoes)
9. पाडाचा आंबा – अर्धवट पिकलेला आंबा (half riped mango)
10. आमराई – आंब्यांची बाग (mango orchard)

वाक्प्रचार व अर्थ:

1. तल्लीन होणे- दंग होणे, गुंग होणे
2. गहिवरून येणे – मन भरून येणे
3. कडकडून भेटणे – प्रेमाने मिठी मारणे
4. गाठणे – जाऊन भेटणे
5. बिलगणे – प्रेमाने आलिंगन देणे

Balbharti Maharashtra State Board Class 6 History Solutions Chapter 6 Janapadas and Mahajanapadas Notes, Textbook Exercise Important Questions and Answers.

Maharashtra Board Class 6 History Solutions Chapter 6 Janapadas and Mahajanapadas

Class 6 History Chapter 6 Janapadas and Mahajanapadas Textbook Questions and Answers

1. Answer in one sentence:

Janapadas And Mahajanapadas Class 6 Questions And Answers Question 1.
What is meant by janapada?
Answer:
Small city states came to be known as janapadas.

Janapadas And Mahajanapadas Class 6 Answers Question 2.
What is meant by mahajanapada?
Answer:
Some janapadas gradually became stronger and expanded their geographical bounderies, such janapadas came to be known as Mahajanapadas.

Janapadas And Mahajanapadas Class 6 Question 3.
Where was the first Buddhist council held?
Answer:
The first Buddhist council or sangiti was held at Rajgriha.

Janapadas Class 6 Question 4.
Who introduced the system of standard weights and measures?
Answer:
The Nandas introduced the system of standard weights and measures.

2. Can you name the following?

Janapadas And Mahajanapadas Class 6 Pdf Question 1.
Some part of today’s Maharashtra was occupied by this janapada.
Answer:
Ashamak

Question 2.
This was an assembly of the senior citizens of a janapada
Answer:
Gana-parishad

Question 3.
This was the venue of discussion.
Answer:
Santhagar

Question 4.
Gautam Buddha belonged to this janapada.
Answer:
Shakya Republic

Question 5.
They had a four-column army.
Answer:
The Nanda Kings

3. Match the following:

Question 1.

Answer:
1 – b
2 – d
3 – a

4. Make a table showing the various kingdoms in the Indian sub-continent and their capitals.
Answer:

Activity:

• Visit a nearby fort and find out the following:

1. Type of the fort
2. In whose reign it was built
3. The Killedar………..
4. The main feature.

• Find out the different arms and services of the Indian Army.
• Complete the following table:
  

  S.no	Name of the mahajanapada	Location	Capital	Name of the most important king
  (1)		At the foot of the Himalayas.
  (2)	Vatsa
  (3)				Pradyot
  (4)		Region around the cities of Patna, Gaya.

Class 6 History Chapter 6 Janapadas and Mahajanapadas InText Questions and Answers

Activity:

Question 1.
Find out the different arms and services of the Indian Army.
Answer:
Combat Arms :

• Infantry
• Armoured Corps
• Regiment of Artillery

Supporting Arms :

• Army Aviation Corps
• Corps of Engineers
• Corps of Signals
• Mechanized Infantry
• Army Air Defence

Services :

• Army Education Corps
• Army Medical Corps
• Army Ordinance Corps
•  Army Postal Service Corps
• Army Service Corps
• Corps of Electronics and Mechanical Engineers
• Corps of Military Police
• Judge Advocate Generals Department
• Army Dental Corps
• Remount and Veterinary Corps
• Other Services

Question 2.
Complete the following table:

Answer:

Class 6 History Chapter 6 Janapadas and Mahajanapadas Additional Important Questions and Answers

Complete the sentence by choosing the correct option:

Question 1.
The period from about 1000 BCE to 600 BCE is considered to be the ______ period.
(a) medieval
(b) Vedic
(c) post-Vedic
Answer:
(c) post-Vedic

Question 2.
The ______ came into existence in the post-Vedic period.
(a) janapadas
(b) mahajanapads
(c) angas
Answer:
(a) janapadas

Question 3.
The janapada called Ashmak occupied a part of today’s _______.
(a) Karnataka
(b) Maharashtra
(c) Bihar
Answer:
(b) Maharashtra

Question 4.
Some of the janapadas were monarchies, while others were ________.
(a) republics
(b) independent
(c) dependent
Answer:
(a) republics

Question 5.
Every janapada had its own ______.
(a) library
(b) palace
(c) coinage
Answer:
(c) coinage

Question 6.
Some janapadas gradually became stronger and ______ their geographical boundaries.
(a) contracted
(b) expanded
(c) built
Answer:
(b) expanded

Question 7.
By sixth century BCE, _______ Mahajanapadas acquired special importance.
(a) fifteen
(b) sixteen
(c) seventeen
Answer:
(b) sixteen

Question 8.
Ajatshatru was the son of _______.
(a) Chandragupta
(b) Shishunag
(c) Bimbisara
Answer:
(c) Bimbisara

Question 9.
The kingdom of Magadha prospered during the reign of ______.
(a) Ajatshatru
(b) Bimbisara
(c) Chandragupta
Answer:
(a) Ajatshatru

Question 10.
Ajatashatru became the ______ of Gautam Buddha.
(a) leader
(b) follower
(c) descendant
Answer:
(b) follower

Question 11.
The first Buddhist Council or sangiti was held at ______.
(a) Rajgriha
(b) Ashmak
(c) Panchal
Answer:
(a) Rajgriha

Question 12.
The foundation for the new _______ Pataligram of Magadha was laid during Ajatshatru’s period.
(a) city
(b) palace
(c) capital
Answer:
(c) capital

Question 13.
_______ was probably in the vicinity of today’s Patna city.
(a) Pataliputra
(b) Vatra
(c) Avanti
Answer:
(a) Pataliputra

Question 14.
A noteworthy successor of Ajatshatru was the Magadha king _______.
(a) Dhananand
(b) Chandragupta
(c) Shishunag
Answer:
(c) Shishunag

Question 15.
Nearly the entire region of northern India came under the ______ of Magadha.
(a) control
(b) influence
(c) subjection
Answer:
(a) control

Question 16.
The _____ ruled the Magadha Empire between 364 BCE and 324 BCE.
(a) Guptas
(b) Nandas
(c) Mauryas
Answer:
(b) Nandas

Question 17.
The Nandas set up a good ________ system necessary to run the huge empire.
(a) political
(b) financial
(c) administrative
Answer:
(c) administrative

Question 18.
The Nandas also ________ the system of standard weights and measures.
(a) introduced
(b) exploited
(c) destroyed
Answer:
(a) introduced

Question 19.
King _______ was the last king of the Nanda dynasty.
(a) Nanda
(b) Dhanananda
(c) Bimbisara
Answer:
(b) Dhanananda

Question 20.
Chandragupta Maurya won ______ and ended the Nanda regime.
(a) Pataliputra
(b) Kashi
(c) Ashmak
Answer:
(a) Pataliputra

Answer the following in one sentence:

Question 1.
Which period is considered to be the post- Vedic period?
Answer:
The period from about 1000 BC to 600 BC is considered to be the post-Vedic period.

Question 2.
When did the janapadas come into existance?
Answer:
The janapadas came into existence during the post-Vedic period.

Question 3.
Around which region did the janapadas spread?
Answer:
The janapadas spread from today’s Afghanistan which is to the north west of the Indian subcontinent to Bengal and Odisha in the east and to Maharashtra in the south.

Question 4.
Which janapada occupied a part of today’s Maharashtra?
Answer:
The janapada called ‘Ashmak’ occupied a part of today’s Maharashtra.

Question 5.
What is the organisation of senior citizens called?
Answer:
The organization of senior citizens is called gana-parishad.

Question 6.
What was the work of the gana-parishad?
Answer:
The members of the gana-parishad came together for discussion and made decisions regarding administrative issues.

Question 7.
What was the place where the gana-parishad met called?
Answer:
The place where the gana-parishad met and took decisions was known as the ‘Santhagar’.

Question 8.
From which Republican state did Gautam Buddha hail?
Answer:
Gautam Buddha hailed from the Shakya Republic.

Question 9.
How many mahajanapadas had acquired special importance in the sixth century BCE?
Answer:
Upto the sixth century BCE, sixteen mahajanapadas had acquired special importance.

Question 10.
Name some powerful mahajanapada.
Answer:
Some of the powerful mahajanapadas were Kosala, Vatsa, Avanti and Magadha.

Question 11.
Who was Bimbisara’s son?
Answer:
Bimbisara’s son was Ajatshatru.

Question 12.
Whose ardent follower did Ajatshatru become?
Answer:
Ajatshatru became the follower of Gautam Buddha.

Question 13.
When was the foundation for the new capital Pataligram laid?
Answer:
The foundation for the new capital Pataligram of Magadha was laid during Ajatshatru’s period.

Question 14.
Which ancient city was in the vicinity of today’s city of Patna?
Answer:
The ancient city Pataliputra was in the vicinity of today’s city of Patna.

Question 15.
Who was the successor of Ajatshatru?
Answer:
A noteworthy successor of Ajatshatru was the Magadha King Shishunag.

Question 16.
Which kingdoms did King Shishunag annex?
Answer:
King Shishunag annexed the kingdoms of Avanti, Kosala, and Vatsa to Magadha.

Question 17.
State the period of Nanda rule.
Answer:
The Nandas ruled the Magadha Empire between 364 BCE and 324 BCE.

Question 18.
Describe the army of the Nanda Kings.
Answer:
The Nanda Kings had a huge four column army of infantry, cavalry, chariots and elephants.

Question 19.
Who was the last king of the Nanda dynasty?
Answer:
King Dhananand was the last king of the Nanda dynasty.

Question 20.
How did the Nanda dynasty decline?
Answer:
During Dhananand’s reign, an ambitious youth Chandragupta Maurya won Pataliputra and brought about an end to the Nanda regime.

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 13 मोठी आई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 13 मोठी आई

Marathi Sulabhbharti Class 6 Solutions Chapter 13 मोठी आई Textbook Questions and Answers

1. एका वाक्यात उत्तर लिहा.

प्रश्न अ.
घर बांधण्यासाठी कोणकोणत्या वस्तू लागतात?
उत्तर:
दगड, माती, विटा, चुना व लाकूड इत्यादी या वस्तू घर बांधण्यासाठी लागतात.

प्रश्न आ.
जमिनीच्या पोटात कोणकोणती खनिजे सापडतात?
उत्तर:
चांदी, रूपे, पितळ, तांबे, कथील, दगडी कोळसा, लोखंड इ. खनिजे जमिनीच्या पोटात सापडतात.

प्रश्न इ.
कारखान्यात धातूपासून कोणकोणत्या वस्तू तयार होतात?
उत्तर:
लोखंडी खुा, पलंग, सुया, टाचण्या, चाकू, कात्र्या, गुंड्या, काचेचे सामान, मोटारी, आगगाड्या, विमाने इत्यादी वस्तू कारखान्यात धातूपासून तयार होतात.

प्रश्न ई.
चुना कशासन तयार करतात?
उत्तर:
चुनखडीच्या खडकापासून चुना तयार करतात.

प्रश्न उ.
लेखिकेच्या मते मातृभूमीबद्दल प्रेमभाव का बाळगावा?
उत्तर:
माणसांना प्रत्येक गोष्ट या भूमीनेच दिली आहे, म्हणून लेखिकेच्या मते मातृभूमीबद्दल प्रेमभाव बाळगायला हवा.

2. तुम्ही खात असलेल्या अन्नपदार्थांतील कोणकोणत्या वस्तू जमिनीकडून आपणांस मिळतात, यांची यादी बनवा.

प्रश्न 1.
तुम्ही खात असलेल्या अन्नपदार्थांतील कोणकोणत्या वस्तू जमिनीकडून आपणांस मिळतात, यांची यादी बनवा.
उत्तर:

1. धान्य – ज्वारी, बाजरी, नाचणी, गहू, मळा, तांदूळ इ.
2. कडधान्य – मूग, मटकी, चवळी, वाटाणा, हरभरा, वाल, तूर, उडीद इ.
3. पालेभाज्या – मेथी, शेपू, तांदळी, चाकवत, पालक, माठ इ.
4. फळभाज्या – वांगी, कोबी, फ्लॉवर, दुधीभोपळा, दोडका, कारले, टोमॅटो, गवार, शेवगा, भेंडी, घेवडा, राजमा इ.
5. कंदमुळे – कांदा, गाजर, बीट, मुळा, रताळे, भुईमुगाच्या शेंगा इ.
6. फळे – केळी, चिकू, पेरू, आंबा, फणस, अननस, द्राक्षे, सफरचंद, जांभळे, कवठ, बोरे, पपई, काजू, बदाम, अक्रोड इ.

3. आपण मातृभूमीबद्दल प्रेमभाव का बाळगायला हवा ते तुमच्या शब्दांत लिहा.

प्रश्न 1.
आपण मातृभूमीबद्दल प्रेमभाव का बाळगायला हवा ते तुमच्या शब्दांत लिहा.
उत्तर:
मातृभूमी म्हणजेच जमीन, काळी आई आपणास अन्न-वस्त्र देते, दाग-दागिने देते, घरदार देते, धनधान्य देते, भांडीकुंडी देते, पाटी-पेन्सिल देते. त्या भूमीतले अन्न खाऊनच आपण मोठे झालो, शहाणे झालो. माणसांना प्रत्येक गोष्ट दिली ती या भूमीनेच. माती आहे म्हणूनच आपण जिवंत आहोत. म्हणून अशा या दातृत्वपूर्ण मातृभूमीबद्दल प्रेमभाव बाळगायला हवा.

4. ‘मोठी आई’ साठी पाठात वापरले गेलेले शब्द शोधून लिहा.

प्रश्न 1.
‘मोठी आई’ साठी पाठात वापरले गेलेले शब्द शोधून लिहा.
उत्तर:

1. भूमी
2. जमीन
3. भूमाता
4. धरणीमाता
5. मातृभूमी
6. मायभूमी

5. पाटीपेन्सिल’ सारखे जोडशब्द पाठातून शोधून लिहा.

प्रश्न 1.
पाटीपेन्सिल’ सारखे जोडशब्द पाठातून शोधून लिहा.
उत्तरः

1. सोनेरूपे
2. दागदागिने
3. दगडमाती
4. दूधदही
5. गाई-म्हशी
6. अन्न-वस्त्र
7. चहासाखर
8. धरणीमाता
9. मायभूमी
10. प्रेमभाव

6. खालील शब्दांचे समनार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे समनार्थी शब्द लिहा.
उत्तर:
(अ) मातृभूमी – धरित्री, धरती, पृथ्वी
(आ) आई – माता, माय, जननी

7. हे शब्दा असेच लिहा.

प्रश्न 1.
हे शब्दा असेच लिहा.
उत्तर:

8. खालील पदार्थ कशापासून बनतात ते लिहा.

प्रश्न 1.
खालील पदार्थ कशापासून बनतात ते लिहा.
उदा. साखर – ऊस
उत्तर:
(अ) फुटाणे – चणे
(आ) मनुके – द्राक्षे
(इ) भाकरी – ज्वारी, बाजरी, तांदूळ, नाचणी
(ई) चपाती – गहू
(उ) वेफर्स – बटाटे
(ऊ) सॉस – टोमॅटो
(ए) सरबत – कोकम, लिंबू इ.
(ऐ) चिक्की – गुळ, शेंगदाणे, तीळ.

9. खालील शब्दांचे अनेकवचन लिहा.

(अ) तुळई – तुळया
(आ) बिजागरी – बिजागऱ्या
(इ) झाड – झाडे
(ई) दागिना – दागिने
(उ) कवठ – कवठे

10. खालील तक्ता भरा.

प्रश्न 1.
खालील तक्ता भरा.

उत्तर:

11. शेतात पीक यावे म्हणून शेतकरी कोणकोणती कामे करतो ते खालील वेबमध्ये लिहा.

प्रश्न 1.
शेतात पीक यावे म्हणून शेतकरी कोणकोणती कामे करतो ते खालील वेबमध्ये लिहा.
उत्तरः

12. खालील तक्ता पूर्ण करा.

प्रश्न 1.
खालील तक्ता पूर्ण करा.

उत्तर:

13. जमिनीच्या खाली येणारी पिके व जमिनीच्या वर येणारी पिके यांची माहिती करून घ्या. त्यांची यादी तयार करा.

प्रश्न 1.
जमिनीच्या खाली येणारी पिके व जमिनीच्या वर येणारी पिके यांची माहिती करून घ्या. त्यांची यादी तयार करा.
उत्तरः

14. खालील वस्तूंपासून तुमच्या घरी कोणकोणते पदार्थ तयार केले जातात. याविषयी आपापसांत गप्पा मारा.

प्रश्न 1.
खालील वस्तूंपासून तुमच्या घरी कोणकोणते पदार्थ तयार केले जातात. याविषयी आपापसांत गप्पा मारा.

उत्तरः

15. मोठ्या आईपासून प्राप्त होणाऱ्या गोष्टी लिहून आकृती पूर्ण करा.

प्रश्न 1.
मोठ्या आईपासून प्राप्त होणाऱ्या गोष्टी लिहून आकृती पूर्ण करा.

उपक्रम: आई, मातृभूमी या विषयावरील कवितांचा संग्रह करून त्या कवितांचे वर्गात वाचन करा.
प्रकल्प: शिक्षक किंवा पालकांच्या मदतीने जवळच्या शेताला भेट दया. शेतात येणाऱ्या विविध पिकांचे निरीक्षण करून शेतातील अन्नधान्याबद्दल माहिती मिळवा.
उत्तरः

16. खालील वाक्यांत (?, !, ‘-‘, “-“, . , ,) ही विरामचिन्हे घालून वाक्ये पुन्हा लिहा.

प्रश्न अ.
आवडले का तुला पुस्तक आई म्हणाली.
उत्तर:
“आवडले का तुला पुस्तक?” आई म्हणाली.

प्रश्न आ.
तो प्रामाणिक आहे बाबांनी सांगितले.
उत्तर:
तो ‘प्रामाणिक’ आहे बाबांनी सांगितले.

प्रश्न इ.
गणू म्हणाला अगं आई उदया सुट्टी आहे असे दिनूने सांगितले म्हणून मी शाळेत गेलो नाही
उत्तरः
गणू म्हणाला, “अगं आई, उदया सुट्टी आहे, असे दिनूने सांगितले. म्हणून मी शाळेत गेलो नाही.”

प्रश्न ई.
अहाहा किती छान चित्र आहे.
उत्तर:
अहाहा! किती छान चित्र आहे!

प्रश्न उ.
तुला लाडू आवडतो भका.
उत्तर:
तुला लाडू आवडतो का?

प्रश्न ऊ.
माझे काका मुंबईला राहतात
उत्तरः
माझे काका ‘मुंबईला’ राहतात.

प्रश्न ए.
मधू राजा रझिया व मारिया गप्पा मारत बसले
उत्तर:
मधू, राजा, रझिया व मारिया गप्पा मारत बसले.

Class 6 Marathi Chapter 13 मोठी आई Additional Important Questions and Answers

रिकाम्या जागी योग्य शब्द भरून वाक्य पूर्ण करून लिहा.

प्रश्न 1.
आपली आई आपल्यावर किती …………… करते.
उत्तर:
माया

प्रश्न 2.
तिचे नाव भूमी ! ……………!
उत्तर:
जमीन

प्रश्न 3.
माती आहे म्हणूनच आपण …….. आहोत.
उत्तर:
जिवंत

प्रश्न 4.
जेवणाच्या ताटातला प्रत्येक ………….. मोठ्या आईने दिला.
उत्तर:
जिन्नस

प्रश्न 5.
दाराच्या कड्या, तुळया व बिजागऱ्या आहेत.
उत्तर:
लोखंडी

प्रश्न 6.
त्या मोठ्या आईचे केवढे …..मानले पाहिजेत!
उत्तर:
उपकार

प्रश्न 7.
त्या भूमीतले …………….. खाऊनच आपण मोठे झालो.
उत्तर:
अन्न

प्रश्न 8.
माणसांना प्रत्येक गोष्ट दिली ती या …………………
उत्तर:
भूमीनेच

प्रश्न 9.
त्या मायभूमीबद्दल आपण मनात नेहमी ………………….. बाळगावयास नको का?
उत्तर:
प्रेमभाव

प्रश्न 10.
पली मोठी ………………… म्हणजेच आपली मायभूमी!
उत्तर:
आई

खालील प्रश्नांची एक ते दोन वाक्यात उत्तर लिहा.

प्रश्न 1.
आपल्या आईहूनही एक मोठी आई आहे ती कोण?
उत्तर:
आपल्या आईहूनही एक मोठी आई आहे, तिचे नाव ‘भूमी! जमीन’!

प्रश्न 2.
जमिनीत काय आहे?
उत्तर:
जमिनीत माती आहे.

प्रश्न 3.
आपण आज जिवंत कोणामुळे आहोत?
उत्तर:
माती आहे म्हणून आज आपण जिवंत आहोत.

प्रश्न 4.
जेवणाच्या ताटातला प्रत्येक जिन्नस आपणास कोणी दिला?
उत्तर:
जेवणाच्या ताटातला प्रत्येक जिन्नस आपणास मोठ्या आईने दिला.

प्रश्न 5.
गहू, तांदूळ व जोंधळे कोठे तयार होतात?
उत्तर:
गहू, तांदूळ व जोंधळे आपणास शेतातूनच म्हणजेच मातीतून मिळतात.

प्रश्न 6.
कापूस कोठून मिळतो?
उत्तर:
कापूस कपाशीच्या झाडापासून मिळतो.

प्रश्न 7.
रेशीम कोठून मिळते?
उत्तर:
रेशीम रेशमाच्या किड्यापासून मिळते.

प्रश्न 8.
रेशमाचे किडे कोणत्या झाडावर जगतात?
उत्तर:
रेशमाचे किडे तुतीच्या झाडावर जगतात.

प्रश्न 9.
प्रत्येक गिरणी व प्रत्येक कारखाना कशामुळे चालतो?
उत्तर:
प्रत्येक गिरणी व प्रत्येक कारखाना लोखंड व कोळसा यामुळे चालतो.

प्रश्न 10.
विटा कशापासून बनवल्या जातात?
उत्तर:
विटा लाल मातीपासून बनवल्या जातात.

प्रश्न 11.
लाकूड कोठून आणतात?
उत्तर:
मोठमोठ्या रानांतील वाळलेली प्रचंड झाडे तोडून लाकूड आणतात.

प्रश्न 12.
गाई-म्हशींपासून आपण काय मिळवतो?
उत्तर:
दूध, दही, तूप आपण गाई-म्हशींपासून मिळवतो.

प्रश्न 13.
गाई-म्हशी कशावर जगतात?
उत्तर:
गवत व कडबा यांवर गाई-म्हशी जगतात.

व्याकरण व भाषाभ्यास.

प्रश्न 1.
एक- अनेक लिहा.

1. गोष्ट
2. छान
3. जिन्नस
4. घर
5. भूमी
6. फूल
7. औषध
8. झाड
9. कापूस
10. रूपे
11. दागिने
12. उत्तर
13. दार
14. प्रचंड

उत्तर:

1. कथा, कहाणी
2. सुंदर
3. नग, वस्तू
4. सदन
5. जमीन
6. पुष्प, सुमन
7. दवा
8. वृक्ष, तरू
9. कपासी
10. चांदी
11. अलंकार
12. जवाब
13. दरवाजा
14. मोठा

प्रश्न 2.
एक – अनेक लिहा.
उत्तर:

प्रश्न 3.
पाठात आलेले जोडशब्द शोधून लिहा.
उत्तरः

1. जिन्नस
2. प्रचंड
3. प्रत्येक
4. खुर्ध्या
5. काव्या
6. गुंड्या
7. तुळ्या
8. गोष्ट
9. उत्पन्न
10. वस्त्र
11. कड्या
12. म्हशी
13. अन्न
14. पेन्सिल
15. टाचण्या
16. साऱ्या
17. धनधान्य
18. पाटीपेन्सिल

प्रश्न 13.
खालील वस्तूंपासून तुमच्या घरी कोणकोणते पदार्थ करतात ते वेब मध्ये लिहा.
उत्तरः

लेखन विभाग

प्रश्न अ.
जमिनीच्या वर येणारी पिके यांची यादी खालील वेबमध्ये लिहा.
उत्तरः

मोठी आई Summary in Marathi

काव्य परिचय:

आपल्या आईपेक्षाही आपणास अजून एक मोठी आई असते. ती म्हणजे ‘भूमी ! जमीन!’ याच आईचा मोठेपणा या पाठात लेखिकेने गायला आहे. आज आपण सर्व व आपणास जन्म देणारी आई ही सुद्धा याच आईची लेकरे आहेत. तिनेच आपणास या सर्व वस्तू पुरवल्या आहेत. ती नसती तर आपले अस्तित्वच या भूतलावर नसते आणि म्हणून त्या भूमीविषयी कृतज्ञतेची भावना आपण सतत मनात जपली पाहिजे हाच संदेश या पाठातून लेखिकेने दिला आहे.

शब्दार्थ:

1. आई – माता,जननी (mother)
2. माया – प्रेम, ममता (love)
3. पोटोशी – गरोदर (pregnant)
4. गोष्ट – कथा (story)
5. स्वरूप – रूप (charm, beauty)
6. जिन्नस – वस्तू (an article)
7. भूमी – जमीन, धरित्री, धरती (Land, earth)
8. जोंधळा – ज्वारी (jowar)
9. पाटी – (slate)
10. ऊस – (sugarcane)
11. तुतीचे झाड – (murberry tree)
12. सापडणे – मिळणे (to be found)
13. लोखंड – लोह (iron)
14. गिरणी – मिल (a mill)
15. खांब – स्तंभ (a pillar)
16. दार – दरवाजा (a door)
17. खिडकी – झरोका (window)
18. तुळई – घराच्या मध्यावरील लाकूड
19. बिजागरी – सांधपट्टी (hinger)
20. कडबा – कणसे कापून घेऊन उरलेला गुरांना खाण्याचा भाग, वैरण (fodder)
21. दागिने – अलंकार (jewellery)
22. मायभूमी – पृथ्वी (motherland)
23. भांडीकुंडी – छोटी मोठी भांडी (vessles and pots)

वाक्प्रचार व अर्थ:

1. माया करणे – प्रेम करणे.
2. लक्षात येणे – कळणे, समजणे, ध्यानात येणे.
3. प्रेमभाव बाळगणे – मनात प्रेम बाळगणे.

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 7 उद्यानात भेटलेला विद्यार्थी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 7 उद्यानात भेटलेला विद्यार्थी

Marathi Sulabhbharti Class 6 Solutions Chapter 7 उद्यानात भेटलेला विद्यार्थी Textbook Questions and Answers

1. एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
चर्नी रोड उद्यानात केळूस्कर गुरुजी कशासाठी येत ?
उत्तर:
चर्नी रोड उद्यानात केळूस्कर गुरुजी बाकावर बसून पुस्तक वाचण्यासाठी येत.

प्रश्न आ.
उद्यानात गुरुजींचे कोणाकडे लक्ष गेले?
उत्तर:
उद्यानात गुरुजींचे लक्ष थोड्या अंतरावर बसून पुस्तक वाचणाऱ्या विद्यार्थ्याकडे गेले.

प्रश्न इ.
गुरुजींना उद्यानात वाचन करत बसलेल्या विदयार्थ्यांची विचारपूस करावी असे का वाटले ?
उत्तर:
गुरुजींना उद्यानात एक विद्यार्थी सलग तीन दिवस वाचन करत बसलेला दिसला. तो इतर मुलांसारखी मस्ती करताना दिसत नसे, म्हणून गुरुजींना त्याची विचारपूस करावी असे वाटले.

प्रश्न ई.
केळूस्कर गुरुजींची व डॉ. आंबेडकरांची गट्टी का जमली?
उत्तर:
केळूस्कर गुरुजी व डॉ. आंबेडकर यांची रोज उद्यानात भेट होऊ लागली. गुरुजी त्यांना चांगल्या लेखकांची पुस्तके वाचायला देऊ लागले, त्यामुळे दोघांची गट्टी जमली.

प्रश्न उ.
डॉ. आंबेडकरांनी कोणता नावलौकिक मिळवला?
उत्तर:
डॉ. आंबेडकरांनी मिळालेल्या उच्च शिक्षणाच्या संधीचे सोने करून, उच्चविद्याविभूषित होऊन, जगातील एक विद्वान म्हणून नावलौकिक मिळवला.

2. खालील वाक्ये कोण, कोणास व का म्हणाले ते लिहा.

प्रश्न अ.
“बाळ, तुझं नाव काय?”
उत्तर:
भीमराव रोज उदयानात पुस्तक वाचत असलेला पाहून गुरुजी भीमरावला म्हणाले.

प्रश्न आ.
“चांगली पुस्तके वाचली पाहिजेत.”
उत्तर:
भीमरावला अवांतर वाचनाची आवड असलेली पाहून गुरुजी भीमरावला म्हणाले.

प्रश्न इ.
“मला ती पुस्तके वाचायला आवडतील!”
उत्तर:
काही लेखकांची पुस्तके वाचायला देईन, असे गुरुजींनी सांगितल्यावर भीमराव गुरुजींना म्हणाले.

3. असे का घडले? ते लिहा.

प्रश्न अ.
केळूस्कर गुरुजींच्या मनात उदयानात वाचत बसलेल्या विदयार्थ्याबाबत कुतूहल निर्माण झाले.
उत्तर:
उदयानात वाचत बसलेला विदयार्थी इतर मुलांसारखी मस्ती करताना दिसत नव्हता तर सतत तीन दिवस गुरुजी त्याला वाचन करताना पाहत होते. म्हणूनच त्यांच्या मनात या मुलाबद्दल कुतूहल निर्माण झाले.

प्रश्न आ.
भीमराव उदयानात वाचत बसायचे.
उत्तर:
भीमरावांना शाळेतील पुस्तकांशिवाय अवांतर पुस्तके वाचण्याची आवड होती म्हणून शाळा सुटल्यानंतर उदयानात काही वेळ पुस्तक वाचत बसायचे.

प्रश्न इ.
गुरुजी व भीमराव यांच्यात गट्टी जमली.
उत्तर:
गुरुजी नेहमी भीमरावाला पुस्तके वाचायला देत. भीमरावच्या वाचनामुळे गुरुजी व भीमराव यांच्यात गट्टी जमली.

प्रश्न ई.
गुरुजींनी भीमरावच्या डोक्यावरून हात फिरवला.
उत्तर:
भीमरावला वाचन कसे करावे हे गुरुजींनी समजाविले. काही लेखकांची पुस्तके वाचायला देईन असे जेव्हा गुरुजी म्हणाले तेव्हा भीमरावने वाचनाची तयारी दर्शवली. तेव्हा मायेने गुरुजींनी भीमरावच्या डोक्यावरून हात फिरवला.

प्रश्न उ.
गुरुजींनी भीमरावच्या उच्च शिक्षणासाठी शिफारस केली.
उत्तर:
केळूस्कर गुरुजींनी भीमरावची तल्लख बुद्धिमत्ताओळखून महाविदयालयीन आणि उच्च शिक्षणासाठी अमेरिकेत पाठवण्यासाठी सयाजीराव गायकवाड महाराजांकडे शिफारस केली.

4. पाठातील खालील घटना योग्य क्रमाने लिहा. 

प्रश्न 1.
पाठातील खालील घटना योग्य क्रमाने लिहा.
(अ) गुरुजी व भीमराव यांच्यात गट्टी जमली.
(आ) गुरुजींनी विद्यार्थ्याकडे फारसे लक्ष दिले नाही.
(इ) त्या विदयार्थ्यानेदेखील गुरुजींकडे बघितले.
(ई) डॉ. आंबेडकरांनी स्वतंत्र भारताची राज्यघटना लिहिली.
(उ) गुरुजींनी भीमरावाला वाचन कसे करावे याविषयी माहिती दिली.
(ऊ) गुरुजी मुलाजवळ आले.
उत्तरः
(अ) गुरुजींनी विदयार्थ्याकडे फारसे लक्ष दिले नाही.
(आ) त्या विद्यार्थ्यानेदेखील गुरुजींकडे बघितले.
(इ) गुरुजींनी भीमरावाला वाचन कसे करावे याविषयी माहिती दिली.
(ई) गुरुजी व भीमराव यांच्यात गट्टी जमली
(उ) डॉ. आंबेडकरांनी स्वतंत्र भारताची राज्यघटना लिहिली.

5. खालील शब्दांत लपलेले शब्द शोधा व लिहा.
उदा., वाचनाला – वाचन, नाच, नाला, लावा, चना.
(अ) तुझ्याजवळ
(आ) दिवसापासून
(इ) मार्गदर्शन
(ई) आवडतील

प्रश्न 1.
खालील शब्दांत लपलेले शब्द शोधा व लिहा.
उदा., वाचनाला – वाचन, नाच, नाला, लावा, चना.
उत्तरः

1. वाचनाला – वाचला, नाच, नाला, लावा, चना
2. दिवसापासून – दिवसा, सून, पान, वसा, दिन, पाव, सासू
3. मार्गदर्शन – मार्ग, दर्श, दमा, दर्शन, मान
4. आवडतील – वड, आड, आव, आतील, लव
5. महाविदयालयीन – मन, हाल, महाल, नदया, मल, विमल

6. खालील शब्दांचे वचन बदला.

प्रश्न 1.
खालील शब्दांचे वचन बदला.
(अ) लेखक
(आ) पुस्तक
(इ) शाळा
(ई) भेट
(उ) शिफारस
(ऊ) शब्द
उत्तरः
(अ) लेखक
(आ) पुस्तके
(इ) शाळा
(ई) भेटी
(उ) शिफारसी
(ऊ) शब्द

7. आंतरजालावरून खालील मुद्द्यांच्या आधारे डॉ. आंबेडकर यांची माहिती मिळवा व लिहा.
(अ) पूर्ण नाव
(आ) जन्म स्थळ
(इ) जन्म दिनांक
(ई) आई – वडिलांचे नाव
(उ) शिक्षण
(ऊ) लिहिलेली पुस्तके
(ए) कार्य

प्रश्न 1.
आंतराजालावरून खालील मुद्द्यांच्या आधारे डॉ. आंबेडकर यांची माहिती मिळवा व लिहा.
उत्तर:
डॉ. बाबासाहेब आंबेडकर यांचे पूर्ण नाव भीमराव रामजी आंबेडकर. रत्नागिरी जिल्ह्यात आंबवडे गावात दिनांक 14 एप्रिल 1891 साली त्यांचा जन्म झाला. त्यांच्या आईचे नाव भीमाबाई व वडिलांचे नाव रामजी होते. त्यांनी एम.ए., पी.एच.डी. पर्यंत शिक्षण घेतलेच पण डी.एस.सी, एल.एल.डी., डी.लि.ट, बॅरिस्टर एंट लॉ. या पदव्याही प्राप्त केल्या. भगवान बुद्ध आणि धम्म, धर्मांतर कां? जातिप्रथेचे विध्वंसन, पुणे करार, शुद्र पूर्वी कोण होते, बुद्ध की कार्ल मार्क्स अशी अनेक पुस्तके त्यांनी लिहिली.

हिंदू स्त्रियांची उन्नती आणि अवनती हे स्त्रीविषयक माहितीपर व माझी आत्मकथा हे व्यक्तिचित्रण ही त्यांनी लिहिले आहे. त्यांनी महाडच्या तळ्यातील पाणी अस्पृश्यांना खुले करून दिले. नाशिकच्या काळाराम मंदिरात अस्पृश्यांना प्रवेश मिळवून दिला. ‘शिका, संघटीत व्हा व संघर्ष करा’ हा मुलमंत्र त्यांनी दलितांना दिला. त्यांना मरणोत्तर भारतरत्न’ हा किताब भारत सरकारने बहाल केला.

8. खालील शब्द शिक्षकांच्या मदतीने समजून घ्या.
(अ) शब्द – सुशब्द, अपशब्द.
(आ) स्पष्ट – सुस्पष्ट, अस्पष्ट.
(इ) बुद्धी – सुबुद्धी, बुद्धिमत्ता, बुद्धिमान, निर्बुद्ध, दुर्बुद्धी

9. खालील शब्द असेच लिहा.

उपक्रम: वेगवेगळ्या वृत्तपत्रांत डॉ. बाबासाहेब आंबेडकर यांच्या कार्याविषयी आलेल्या माहितीची कात्रणे गोळा करा व वहीत चिकटवा. त्याचे वाचन करा.

सांगा पाहू.

प्रश्न 1.
कधी हातावर, कधी भिंतीवर जाऊन मी बसतो, तीन हात माझे सतत फिरवत मी असतो, वेळ वाया घालव नका असा नेहमी उपदेश करतो
उत्तर:
घड्याळ

प्रश्न 2.
शिस्तीचे धडे, उत्तम गडे, कणकण शोधते, कधीच न रडे
उत्तर:
मुंगी

Marathi Sulabhbharti Class 6 Solutions Chapter 7 उद्यानात भेटलेला विद्यार्थी Important Additional Questions and Answers

चूक की बरोबर ते लिहा.

प्रश्न 1.
चूक की बरोबर ते लिहा.

1. चर्नी रोड उद्यानात सायंकाळच्या वेळी अनेक नागरिक फिरायला यायचे.
2. गुरुजी सोबत आणलेले वर्तमानपत्र वाचत.
3. भीमरावाला अवांतर पुस्तके वाचनाची आवड होती.
4. इतर मुलांसारखा भीमरावही मस्ती करीत होता.
5. गुरुजींनी भीमरावला वाचन कसे करावे याविषयी माहिती दिली.

उत्तर:

1. बरोबर
2. चूक
3. बरोबर
4. चूक
5. बरोबर

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
चर्नीरोड उद्यानात सायंकाळी कोण कोण येत?
उत्तर:
चर्नीरोड उदयानात सायंकाळी अनेक नागरिक फिरायला येत. तसेच विल्सन हायस्कूलचे मुख्याध्यापक आणि विदयाव्यासंगी लेखक केळूस्कर गुरुजी व भीमराव येत असत.

प्रश्न 2.
भीमरावांनी स्वत:बद्दलची कोणती माहिती गुरुजींना सांगितली?
उत्तर:
भीमराव एलफिन्स्टन हायस्कूल, भायखळा येथे शिकत आहेत. शाळेतील पुस्तकांशिवाय अवांतर पुस्तके वाचण्याची त्यांना आवड आहे व शाळा सुटल्यानंतर ते चर्नी रोड उदयानात काही वेळ पुस्तक वाचत बसतात ही माहिती भीमरावांनी गुरुजींना सांगितली.

प्रश्न 3.
भीमरावांनी संधीचे सोने कसे केले?
उत्तर:
आपल्या तल्लख बुद्धिमत्तेने, वाचनाने व कष्टाने ते जगातील एक विद्वान म्हणून नावलौकिक प्राप्त करणारे उच्च विदयाविभूषित डॉ. बाबासाहेब आंबेडकर झाले. त्यांनी स्वतंत्र भारताची राज्यघटना लिहिली. अशाप्रकारे भीमरावांनी संधीचे सोने केले.

व्याकरण व भाषाभ्यास

प्रश्न 1.
खालील शब्दांचे वचन बदला.

1. संधी
2. महाविदयालय
3. विद्वान
4. विदयार्थी

उत्तर:

1. संधी
2. महाविदयालये
3. विद्वान
4. विदयार्थी

खालील वाक्यांत योग्य ठिकाणी विरामचिन्हे घालून वाक्य पुन्हा लिहा.

प्रश्न 1.
बाळ तुझं नाव काय.
उत्तर:
“बाळ तुझं नाव काय?”

प्रश्न 2.
वा छान नाव आहे तुझं.
उत्तर:
“वा! छान नाव आहे तुझं!”

प्रश्न 3.
जरुर दया गुरुजी मला ती पुस्तके वाचायला आवडतील.
उत्तर:
“जरुर दया गुरुजी! मला ती पुस्तके वाचायला आवडतील!”

प्रश्न 4.
खालील शब्दांचे लिंग बदला.

1. मुख्याध्यापक
2. विदयार्थी
3. बालक
4. माता
5. महाराजा
6. विद्वान
7. शिक्षक
8. लेखक
9. मित्र

उत्तर:

1. मुख्याध्यापिका
2. विद्यार्थिनी
3. बालिका
4. पिता
5. महाराणी
6. विदूषी
7. शिक्षिका
8. लेखिका
9. मैत्रिण

खालील वाक्प्रचारांचे अर्थ सांगून वाक्यात उपयोग करा.

प्रश्न 1.
कुतूहल निर्माण होणे – जिज्ञासा निर्माण होणे.
उत्तर:
शास्त्रीय प्रयोगामुळे विदयार्थ्यांच्या मनात कुतूहल निर्माण झाले.

प्रश्न 2.
संधीचे सोने करणे – वेळेचा सदुपयोग करणे
उत्तर:
अपार कष्टाने डॉ. रघुनाथ माशेलकरांनी संधीचे सोने केले.

प्रश्न 3.
नावलौकिक मिळवणे – प्रसिद्धी मिळवणे
उत्तर:
गायनामुळे लता मंगेशकरने नावलौकिक मिळवला.

लेखन विभाग:

सांगा पाहू.

प्रश्न 1.
भिंतीवर चढतो, खाली पडतो प्रयत्नांची पराकाष्ठा करतो. जाळे विणतो, हार न मानतो.
उत्तर:
कोळी

उद्यानात भेटलेला विद्यार्थी Summary in Marathi

पाठ परिचयः

प्रस्तुत पाठात बालपणी डॉ. भीमराव आंबेडकरांना वाचनाची किती आवड होती व त्यांचा हा वाचननाद केळूस्कर गुरुजींनी कसा ओळखला याचे वर्णन केले आहे. पुढे त्यांच्या मार्गदर्शनाने व शिफारसीने भीमराव उच्च शिक्षण घेऊ शकले व उच्च विद्याविभूषित होऊन स्वतंत्र भारताची राज्यघटना लिहू शकले, ‘वाचाल तर वाचाल’ हे किती सार्थ आहे हे या पाठातून कळते.

शब्दर्थ:

1. उदयान – बाग (garden)
2. सायंकाळ – संध्याकाळ (evening)
3. नागरिक – रहिवासी (citizen)
4. विदयाव्यासंगी- अभ्यासाची आवड असणारे (studious)
5. बाक – बसण्याची जागा (bench)
6. कुतूहल – जिज्ञासा (curiosity)
7. आपुलकीने – आपलेपणाने (affectionately)
8. आदर – सन्मान (respect)
9. आतुरता – उत्सुकता (excitement, eagerness)
10. विस्तृत – अफाट, मोठे (vast)
11. अभेदय – तोडता न येणारी (imperitrable)
12. तल्लख – तीक्ष्ण (sharp)
13. गट्टी – मैत्री, दोस्ती (friendship)
14. शिफारस – नाव सुचविणे (recommendation)
15. नावलौकिक – प्रसिद्धी (fame, popularity)
16. राज्यघटना – संविधान (constitution)

वाक्प्रचार व अर्थ:

1. कुतूहल निर्माण होणे – जिज्ञासा निर्माण होणे
2. संधीचे सोने करणे – वेळेचा सदुपयोग करणे
3. नावलौकिक मिळवणे – प्रसिद्धी मिळवणे