Category: Class 6

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 4 माहिती घेऊया Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 4 माहिती घेऊया

Marathi Sulabhbharti Class 6 Solutions Chapter 4 माहिती घेऊया Textbook Questions and Answers

1. भारतीय संशोधकांची नावे व त्यांनी लावलेले शोध यांची माहिती घेऊन तक्ता तयार करा. वर्गात लावा.

प्रश्न 1.
भारतीय संशोधकांची नावे व त्यांनी लावलेले शोध यांची माहिती घेऊन तक्ता तयार करा. वर्गात लावा.
उत्तर:

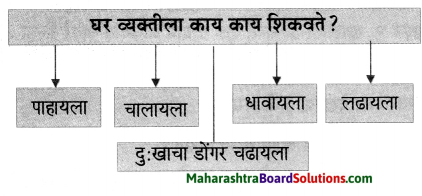
2. कोणकोणत्या गोष्टींमध्ये संशोधन व्हावे असे तुम्हांला वाटते? विचार करा व लिहा.

प्रश्न 1.
कोणकोणत्या गोष्टींमध्ये संशोधन व्हावे असे तुम्हांला वाटते? विचार करा व लिहा.
उत्तर:

1. कॅन्सरच्या सर्व पातळ्यांवर
2. अवयव प्रत्यारोपण
3. थर्माकोल विघटन
4. इलेक्ट्रॉनिक्स कचऱ्याची विल्हेवाट

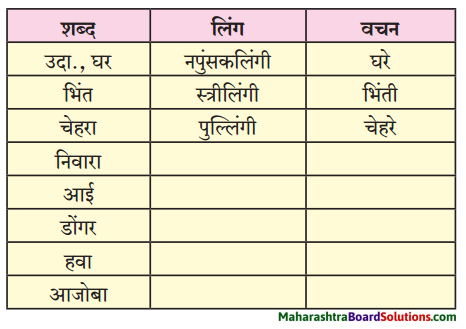
3. खालील वाक्याचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा., भिंत कोसळली – भिंती कोसळल्या.

उप्रकम: आंतरजालाचा उपयोग करून डॉ. वसंत गोवारीकर यांची माहिती मिळवा. कोलाज तयार करा.
प्रकल्प: वर्तमानपत्रात शास्त्रज्ञ, संशोधक यांच्याविषयी येणाऱ्या माहितीची कात्रणे काढून चिकटवही बनवा.

प्रश्न 1.
खालील वाक्याचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा., भिंत कोसळली – भिंती कोसळल्या.

उत्तर:

Marathi Sulabhbharti Class 6 Solutions Chapter 4 माहिती घेऊया Important Additional Questions and Answers

योग्य पर्याय निवडून उत्तरे लिहा.

1. डॉ. वसंत गोवारीकरांचा जन्म …………… (25 मार्च, 1933, 25 मार्च 1923)
2. त्यांनी पत्र पाठविले …………… (विक्रम साराभाईंना, हेन्री फोर्डला)
3. डॉ. वसंत गोवारीकरांनी नवीन पद्धत शोधून काढली. ……………(मान्सूनच्या अंदाजाची, उर्जेची)

उत्तर:

1. 25 मार्च 1933
2. हेन्री फोर्डला
3. मान्सूनच्या अंदाजाची

एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
डॉ. वसंत गोवारीकरांचे पदवीपर्यंतचे शिक्षण कुठे झाले?
उत्तर:
डॉ. वसंत गोवारीकरांचे पदवीपर्यंतचे शिक्षण कोल्हापूरला झाले.

प्रश्न 2.
डॉ. वसंत गोवारीकरांनी कोणते तंत्र विकसित केले?
उत्तर:
डॉ. वसंत गोवारीकरांनी अग्निबाणाच्या मोटारीकरिता घन इंधन बनवण्याचे तंत्र विकसित केले.

प्रश्न 3.
देशभर कोणती चिंता असते?
उत्तर:
पाऊस केव्हा पडेल? किती पडेल? याची देशभर चिंता असते.

प्रश्न 4.
पत्राचे इंग्रजी भाषांतर करण्यासाठी गोवारीकरांनी कोणाची मदत घेतली?
उत्तर:
पत्राचे इंग्रजी भाषांतर करण्यासाठी गोवारीकरांनी मित्राची मदत घेतली.

प्रश्न 5.
गोवारीकरांचा कोणत्या दोन गुणांची चुणूक लहानपणीच दिसून आली?
उत्तर:
त्यांच्या कुशाग्र बुद्धिमत्तेची आणि दृढ संकल्पाची चुणूक लहानपणीच दिसून आली.

प्रश्न 6.
पदवीपर्यंतच्या शिक्षणानंतर गोवारीकर उच्च शिक्षणासाठी कुठे गेले?
उत्तर:
पदवीपर्यंतच्या शिक्षणानंतर गोवारीकर उच्च शिक्षणासाठी इंग्लंडला गेले.

प्रश्न 7.
कोणत्या विदयापीठात त्यांनी ‘रासायनिक अभियांत्रिकी’ विषयात संशोधन केले?
उत्तर:
बर्मिंगहॅम विद्यापीठात त्यांनी ‘रासायनिक अभियांत्रिकी’ विषयात संशोधन केले.

प्रश्न 8.
संशोधक म्हणून त्यांनी कोठे काम केले?
उत्तर:
इंग्लंडच्या उर्जा संशोधन केंद्रात संशोधक म्हणून काम केले.

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
भारताच्या विज्ञान क्षेत्रातील डॉ. गोवारीकरांनी केलेली
कामगिरी लिहा.
उत्तर:
विक्रम साराभाईंच्या आग्रहामुळे 1967 साली ते भारताच्या अवकाश संशोधन केंद्रात रुजू झाले. ‘घन पदार्थातील उर्जा’ या विषयाच्या संशोधनासाठी त्यांच्या पुढाकाराने नवा प्रकल्प सुरू करण्यात आला. अग्निबाणाच्या मोटारीकरिता घन इंधन बनवण्याचे तंत्र त्यांनी विकसित केले. मान्सूनच्या अंदाजाची नवी पद्धत शोधून काढली.

प्रश्न 2.
शाळेत असताना त्यांना कोणती कल्पना सुचली? त्याची कशी दखल घेतली गेली?
उत्तर:
शाळेत असताना आपण मोटार बनवावी असे त्यांना वाटले. तेराव्या वर्षी त्यांनी अमेरिकेतील हेन्री फोर्डला पत्र लिहून आपली इच्छा कळवली. हेनरी फोर्डला मराठीतील पत्र कळणार नाही म्हणून मित्राच्या मदतीने पत्राचे इंग्रजी भाषांतर केले. हेन्री फोर्डने डॉ. गोवारीकरांच्या पत्राची दखल घेऊन उत्तरही पाठवले. सोबत काही पुस्तके पाठविली.

व्याकरण व भाषाभ्यास:

प्रश्न 1.
खालील वाक्यांचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा. भिंत कोसळली – भिंती कोसळल्या
उत्तर:

प्रश्न 2.
लिंग बदला.

1. मित्र
2. आजोबा
3. भाऊ
4. मुलगा
5. मामा
6. लेखक
7. कवी
8. समाजसेवक
9. बाई
10. नट

उत्तर:

1. मैत्रिण
2. आजी
3. बहिण
4. मुलगी
5. मामी
6. लेखिका
7. कवयित्री
8. समाजसेविका
9. माणूस
10. नटी

प्रश्न 3.
विरूद्धार्थी शब्द लिहा.

1. दूर
2. नवी
3. मित्र
4. कुशाग्र
5. दृढ
6. मोठी
7. विकसित
8. घन

उत्तर:

1. जवळ
2. जुनी
3. शत्रू
4. मंद
5. डळमळीत
6. छोटी, लहान
7. अविकसित
8. द्रव

प्रश्न 4
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:

1. विकसित करणे – शेतकऱ्यांनी संत्रांचा वापर करून शेती विकसित केली.
2. रुजू होणे – बरेच दिवसांच्या सुट्टीनंतर रमेश कामावर रुजू झाला.

लेखन विभाग:

प्रश्न 1.
आंतरजालाचा उपयोग करून डॉ. वसंत गोवारीकर यांची माहिती मिळवा.
उत्तर:
डॉ. वसंत रणछोड गोवारीकर यांचा जन्म 25 मार्च 1933 रोजी झाला. एक भारतीय शास्त्रज्ञ म्हणून त्यांचा नावलौकिक आहे. इंडियन स्पेस रिसर्च ऑर्गनायझेशन मध्ये ते मुख्य पदावर विराजमान होते. अंतराळ, हवामान, लोकसंख्या विषयांवरचे त्यांचे योगदान महत्त्वपूर्ण आहे. पद्मश्री व पद्मभूषण या पुरस्करांनी त्यांना सन्मानित केले गेले. 2 जानेवारी 2015 रोजी ते अनंतात विलीन झाले.

माहिती घेऊया Summary in Marathi

पाठ परिचयः

पद्मश्री व पद्मभूषण पुरस्कार प्राप्त असलेले श्री. वसंत गोवारीकर एक भारतीय संशोधक होते. अवकाश संशोधनाच्या मुख्य पदावर कार्यरत असलेले वसंत गोवारीकर 1991 – 1993 च्या काळात पंतप्रधानांचे सल्लागारही होते. अंतराळ संशोधन, हवामान, लोकसंख्या या विविध विषयांवरचे त्यांचे योगदान अमूल्य आहे. प्रस्तुत पाठात त्यांच्याविषयी अधिक माहिती जाणून घेता येईल.

शब्दर्थ:

1. देश – राष्ट्र (nation)
2. चिंता – काळजी (worry)
3. शोधणे – हुडकून काढणे (to invent)
4. कल्पना – युक्ती (idea)
5. भाषांतर – एका भाषेतून दुसऱ्या भाषेत लिहिणे. (translation)
6. थेट – सरळ (direct)
7. कुशाग्र – तीक्ष्ण (sharp)
8. संकल्प – figale (resolution)
9. संशोधन – नवीन शोध (invention)
10. प्रकल्प – योजना (project)
11. क्षेत्र – विभाग (field, area)
12. कामगिरी – कार्यवाही (execution of work)
13. इंधन – जळाऊ पदार्थ (fuel)
14. विकसित करणे – वाढविणे (to develop)
15. घन – कठीण (solid)
16. चुणूक – झलक (a faint indication)

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 9 वह देश कौन-सा है? Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 9 वह देश कौन-सा है?

Hindi Sulabhbharti Class 6 Solutions Chapter 9 वह देश कौन-सा है? Textbook Questions and Answers

चित्रकथाः

चित्र के आधार पर काल संबंधी वाक्य बनाओ और समझोः

Answer:
(१) रामू ने लड्डू खाया।
(२) रामू लड्डू खा रहा है।
(३) रामू लड्डू खाएगा।

जरा सोचो ….. बताओ:

‘यदि हिमालय की बर्फ पिघलना बंद हो जाए तो…’ (कहानी लेखन)
Answer:
यदि हिमालय की बर्फ पिघलना बंद हो जाए तो हमारे देश में जल-संकट उत्पन्न हो जाएगा। हिमालय पर जमी बर्फ ईश्वर द्वारा संचित जल का भंडार है, जो धीरे-धीरे पिघलती है। वहीं जल नीचे आते – आते नदियों का रूप धारण कर लेती है। इस प्रकार पूरे वर्ष जल की आपूर्ति वहाँ से होती रहती है। यदि यह बंद हो जाए तो नदियाँ सूख जाएँगी। नदियों के बिना जीना एकदम कठिन हो जाएगा।

खोजबीनः

‘परमवीर चक्र’ पुरस्कार प्राप्त सैनिकों की सूची बनाओ। (परियोजना-कार्य)
Answer:
(१) मेजर सोमनाथ शर्मा
(२) लांस नायक करम सिंह
(३) सेकेंड लेफ्टिनेंट राम राघोबा राने
(४) नायक जादुनाथ सिंह
(५) कंपनी हवलदार मेजर प्रभु सिंह
(६) कैप्टन गुरु बचन सिंह
(७) मेजर धनसिंह थापा
(८) सुबेदार जोगिन्दर सिंह
(९) मेजर शैल्तान सिंह
(१०) कंपनी हवलदार मेजर अब्दुल हमीद आदि

सुनो तो जराः

देशभक्ति पर आधारित कविता सुनो और सुनाओ। (कविता-लेखन)
Answer:
भारत कितना प्यारा है!
यहीं हिमालय – सा पहाड़ है, यहीं गंग की धारा है। यमुना लहराती है सुंदर, भारत कितना प्यारा है।
फल-फूलों से भरी भूमि है, खेतों में हरियाली है। आमों की डाली पर बैठी,
गाती कोयल काली है। बच्चों ! माँ ने पाल-पोसकर तुमको बड़ा बनाया है। लेकिन यह मत भूलो तुमने अन्न कहाँ का खाया है।
तुमने पानी पिया कहाँ का, खेले मिट्टी में किसकी। चले हवा में किसकी बोलो, बच्चे, प्यारे भारत की।

बताओ तो सही:

अपने परिवेश में शांति किस प्रकार स्थापित की जा सकती है? (अनुच्छेद लेखन)
Answer:
अपने परिवेश में जब सब लोग मिल जुलकर प्रेम से रहने लगेंगे, तो शांति स्थापित की जा सकती है। इसके लिए सभी को याद रखना होगा कि हम सब एक देश के निवासी हैं। सभी लोग आपस में भाई – बहन हैं। पूरा विश्व ही हमारा परिवार है। इस प्रकार की भावना यदि सब में जागृत हो जाए, तो पूरे विश्व में शांति स्थापित की जा सकती है।

वाचन जगत से:

वैज्ञानिक की जीवनी पढ़ो और उसके आविष्कार लिखोः
Answer:
डॉ. ए. पी. जे. अब्दुल कलाम हमारे भारत के पूर्व राष्ट्रपति डॉ. अब्दुल पकीर जैनुलाबदीन अब्दुल कलाम का जन्म १४ अक्टूबर, सन् १९३१ ई. को रामेश्वरम में हुआ था। उनके पिता का नाम पकौर जैनुलाबदीन था। बी. एससी. करने के बाद इन्होंने मद्रास इंस्टीट्यूट ऑफ टेक्नोलॉजी, चेन्नई में एरोनाटिकल इंजीनियरिंग में प्रवेश ले लिया। सन् १९६३ ई. में वे विक्रम साराभाई स्पेस सेंटर में आ गए। इनके द्वारा तैयार किए गए प्रमुख प्रक्षेपास्त्र निम्नलिखित हैं – पृथ्वी, आकाश, त्रिशूल, नाग, अग्नि आदि। २५ नवंबर, १९९७ को उन्हें देश का सर्वोच्च सम्मान भारत रत्न से सम्मानित किया गया। दिनांक २५ जुलाई, २००२ ई. को वे भारत के राष्ट्रपति बने।

कलम से:

क्रमानुसार भारत के राष्ट्रपति, प्रधानमंत्री के नाम लिखो। (परियोजन-कार्य)
Answer:
भारत के राष्ट्रपति:

(१) डॉ. राजेंद्र प्रसाद
(२) डॉ. राधाकृष्णन
(३) डॉ. ज़ाकिर हुसैन
(४) वी. वी. गिरी
(५) डॉ. फकरुद्दीन अहमद
(६) नीलम संजीवा रेड्डी
(७) ज्ञानी जैल सिंह
(८) आर वेंकटरमन
(९) डॉ. शंकर दयाल शर्मा
(१०) के. आर. नारायणन
(११) डॉ. ए.पी.जे. अब्दुल कलाम
(१२) प्रतिभा देवी सिंह पाटिल
(१३) प्रणव मुखर्जी

भारत के प्रधानमंत्री:

(१) जवाहरलाल नेहरू १९६४
(२) गुलज़ारीलाल नंदा १९६४, १९६६
(३) लालबहादुर शास्त्री १९६४ – १९६६
(४) इंदिरा गांधी १९६६-७७, १९८०-८४
(५) मोरार जी देसाई १९७७-७९
(६) चरण सिंह १९७९-८०
(७) राजीव गांधी १९८४ – ८९
(८) वी. पी. सिंह १९८९ – ९०
(९) चंद्रशेखर १९९० – ९१
(१०) पी. वी. नरसिंहाराव १९९१ – ९६
(११) अटल बिहारी बाजपेई १९९६, १९९८ – २००४
(१२) एच डी देवेगौड़ा १९९६ – ९७
(१३) इंद्रकुमार गुजराल १९९७ – ९८
(१४) मनमोहन सिंह २००४ – २०१४
(१५) नरेंद्र मोदी २०१४ से

इस कविता के आधार पर भारत की विविधता एवं विशेषताएँ सात – आठ वाक्यों में लिखो। (अनुच्छेद लेखन)
Answer:
भारत विविधताओं से भरा देश है। एक तरफ हिमालय की बफीर्ली वादियाँ हैं, तो दूसरी तरफ रेगिस्तान। एक तरफ नदियों का अमृत जल धरती को हरा-भरा बना रहा है, तो दूसरी तरफ समुद्र। कहीं पहाड़, कहीं मैदान तो कहीं घनघोर जंगल हैं। धरती के अंदर कहीं कोयला, तो कहीं हीरा पन्ना आदि बहुमूल्य रल भरे पड़े हैं। अनेक बोलियाँ एवं भाषाएँ हैं। तीज-त्योहार भी अलग-अलग हैं। खान-पान, रहन-सहन अलग होते हुए भी हम सब एक हैं। यही भारत की विशेषता हैं।

सदैव ध्यान में रखोः

ऐतिहासिक वस्तुओं का संरक्षण हम किस तरह से करते है?
Answer:
ऐतिहासिक वस्तुओं का संरक्षण करना हमारा कर्तव्य है। ऐसी वस्तुओं से हमें अतीत के बारे में जानकारी मिलती है। अतीत में पूर्वजों जो ने गल्तियाँ कौं, उनसे बचने की प्रेरणा मिलती है। साथ ही हमें हमारी गौरवशाली परंपराओं पर गर्व होता है।

विचार मंथन:

‘स्वतंत्रता मेरा जन्मसिद्ध अधिकार है।'(संस्मरण लेखन)
Answer:
आजादी सभी को प्रिय है। ईश्वर ने सभी प्राणियों को जीने का अधिकार दिया है। अत: सभी को स्वतंत्र रहने का अधिकार है। दुर्भाग्य से हमारा देश परतंत्र रहा और ऐसे गुलामी के समय लोकमान्य बाल गंगाधर तिलक ने यह नारा लोगों को दिया। लोगों ने इस बात को समझा और गुलामी की जंजीरों को तोड़ दिया। अब सब स्वतंत्र हैं और सभी को यह अधिकार जन्म से प्राप्त है।

स्वयं अध्ययनः

नीचे दिए गए राष्ट्रीय प्रतीकों के चित्र देखो और उनके नाम लिखो:

Answer:
(१) राष्ट्रीय ध्वज तिरंगा
(२) राष्ट्रीय पशु बाघ
(३) राष्ट्रीय पक्षी मोर
(४) राष्ट्रीय फल आम
(५) राष्ट्रीय फूल कमल
(६) राष्ट्रीय खेल हॉकी

स्वयं अध्ययन:

चित्रों का वाचन करके अपने शब्दों में कहानी लिखो और उचित शीर्षक बताओ? (कहानी लेखन)
Answer:
राष्ट्रीय पशु बाघ किसी गाँव में एक चित्रकार रहता था। उसका नाम कृष्ण कांत था। वह एक दिन प्राकृतिक दृश्य का चित्र बनाने के लिए नदी के किनारे पहुँचा। नदी की दूसरी ओर पहाड़ियाँ थीं। कृष्ण कांत को यह स्थान बहुत सुंदर लगा। वे उस स्थान का चित्र बनाने लगे। चित्र बनाते-बनाते वे एकदम लीन हो गए थे। तभी वहाँ एक बाघ आकर बैठ गया। चित्रकार अपनी धुन में मग्न थे। उन्होंने बाघ का भी चित्र बनाना शुरू कर दिया। थोड़ी देर बाद बाघ नदी की तरफ जाने लगा। चित्रकार कृष्ण कांत का चित्र अभी अधूरा था। वे नाव में बैठकर बाघ की ओर चल दिए। बाघ जब सामने आया, उन्होंने अपनी कलाकृति को पूरा किया और अपने गाँव की ओर चल दिए। शिक्षा – हमें अपना कार्य तन्मयता के साथ मन लगाकर करना चाहिए।

हमें जानो:

मार्ग पर चलते हुए तुमने कुछ यातायात संकेत देखे होंगे। इन सांकेतिक चिह्नों का क्या अर्थ है, लिखो:

Answer:
(१) रुको।
(२) घूमना मना है। (यू टर्न मना है)
(३) एक तरफ का मार्ग प्रतिबंधित है।
(४) एकल मार्ग।
(५) प्रवेश निषेध।
(६) हार्न बजाना मना है।
(७) भारी वाहन प्रवेश वर्जित।
(८) आगे विद्यालय है।

Hindi Sulabhbharti Class 6 Solutions Chapter 9 वह देश कौन-सा है? Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्द में लिखिए:

Question 1.
भारत किसकी गोद में बसा है?
Answer:
प्रकृति।

Question 2.
भारत का चरण कौन धो रहा है?
Answer:
रत्नेश।

Question 3.
भारत का मुकुट किसे कहा गया है?
Answer:
हिमालय।

Question 4.
भारत में सुधा की धारा कौन बहा रही हैं?
Answer:
नदियाँ।

Question 5.
मैदान, गिरि और वनों में क्या लहराती हैं?
Answer:
हरियालियाँ।

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
भारत कैसी प्रकृति की गोद में बसा है?
Answer:
भारत मनमोहिनी प्रकृति की गोद में बसा है।

Question 2.
भारत के सब अंगों में क्या सजे हैं?
Answer:
भारत के सब अंगों में रसीले फल, कंद, अनाज और मेवे सजे हैं।

Question 3.
भारत की धरती कैसी है?
Answer:
भारत की धरती अनंत धन-धान्य से भरी पड़ी है।

Question 4.
संसार का शिरोमणि किसे कहा गया है?
Answer:
संसार का शिरोमणि भारत को कहा गया है।

Question 5.
भारत के लोग कैसे हैं?
Answer:
भारतवासी नवक्रांति के पुजारी, सेवक और सपूत हैं।

रिक्त स्थानों की पूर्ति कीजिए:

Question 1.
मनमोहिनी प्रकृति की जो ……………… में बसा है।
Answer:
गोद

Question 2.
सींचा हुआ ……………… वह देश कौन-सा है?
Answer:
सलोना

Question 3.
……………… हँस रहे हैं, वह देश कौन-सा है?
Answer:
दिन-रात

Question 4.
जिसके ……………… धन से धरती भरी पड़ी है।
Answer:
अनंत

Question 5.
भारत सिवाय दूजा वह ………………?
Answer:
देश कौन-सा है

उचित जोड़ियाँ मिलाइए:

Answer:
१ – १
२ – घ
३ – क
४ – च
५ – ख
६ – ग

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. मनमोहिनी
2. प्रकृति
3. गोद
4. रत्नेश
5. सुधा
6. प्रसून
7. सलोना
8. दुलारा
9. सेवक
10. धरती

Answer:

1. मनोहारिणी
2. निसर्ग
3. अंक
4. समुद्र
5. अमृत
6. फूल
7. सुंदर
8. प्यारा
9. दास
10. वसुंधरा

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. नदी
2. धारा
3. रसीला
4. मेवा
5. हरियाली

Answer:

1. नदियाँ
2. धाराएँ
3. रसीले
4. मेवे
5. हरियालियाँ

‘खेलना’ इस क्रिया के सकर्मक, अकर्मक, संयुक्त, सहायक और प्रेरणार्थक दोनों रूपों का वाक्यों में प्रयोग करो और लिखोः
Answer:
सकर्मक . लड़की क्रिकेट खेल रही है। अकर्मक – लड़की खेलती है। संयुक्त – रमेश क्रिकेट खेलने लगा है। सहायक – रमेश ने क्रिकेट खेल लिया। प्रथम प्रेरणार्थक – शिक्षक वरुण को क्रिकेट खिलाता
द्वितीय प्रेरणार्थक- शिक्षक छात्रों को कोच से क्रिकेट खिलवाता है।

निम्नलिखित शब्द युग्मों से विशेषण शब्द छाँटिए:

1. मनमोहिनी प्रकृति
2. रसीले फल
3. सुंदर प्रसून
4. अनंत धन

Answer:

1. मनमोहिनी
2. रसीले
3. सुंदर
4. अनंत

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 1 उपयोग हमारे Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 1 उपयोग हमारे

Hindi Sulabhbharti Class 6 Solutions Chapter 1 उपयोग हमारे Textbook Questions and Answers

चित्रो का परिचय: चित्र का निरीक्षण करो और बताओ।

डाकघर:

विद्यार्थियों से चित्रों का निरीक्षण कराकर उनको प्रश्न पूछने के लिए कहें । बड़ों की सहायता से उन्हें डाकघर में जाकर टिकट खरीदने तथा बैंक में बाल-बचत खाता खुलवाने और परिचित डाकिए, बैंक कर्मचारी, नर्स, हवलदार से बातचीत करने की सूचना दें।

Answer:
प्रस्तुत चित्र डाकघर का है। डाकघर भारत-सरकार का सबसे पुराना व बड़ा उपक्रम है। चित्र में डाकघर के अलग-अलग हिस्सों में होने वाले काम के बारे में बताया गया है। लोग अपना पत्र और मनी ऑर्डर भेजने के लिए कतार में खड़े हैं। पोस्टमैन पत्रों पर कुछ लिख रहे हैं। एक व्यक्ति बचत खाता-काउन्टर पर डाक कर्मचारी से कुछ पूछताछ कर रहा है। दूसरा व्यक्ति मनी ऑर्डर-काउन्टर पर बैठी डाक-कर्मचारी से कुछ जानकारी प्राप्त कर रहा है। डाकघर में सूचना-फलक लगा हुआ है। डाकघर के अन्य कर्मचारी भी अपने काम में व्यस्त हैं। हम आपकी आवश्यकता समझते हैं।’ इस सुविचार के माध्यम से ग्राहकों में अपनेपन का भाव पैदा करने का प्रयास किया गया है। छोटे बच्चे अपने माता-पिता के साथ डाकघर में आए हैं और सभी चीज़ों का निरीक्षण कर रहे हैं। गमले के पास कूड़ेदान रखा गया है। ‘बचत आपकी, प्रगति देश की।’ इस सुंदर पंक्ति द्वारा लोगों में देश की प्रगति की भावना भी जागृत करने का प्रयत्न किया गया है। प्रगति के आज के दौर में हमारी सरकार डाकघरों का महत्त्व बरकरार रखने के लिए बैंकों की तर्ज पर उनका पुनर्गठन कर रही है।

बैंक:

उपरोक्त स्थानों की कार्य प्रक्रिया संबंधी जानकारी देकर चर्चा करें । प्रत्यक्ष जाकर विद्यार्थियों को वहाँ की सूचना पढ़ने के लिए कहें । उनसे अपने गाँव/शहर के महत्त्वपूर्ण स्थानों के दूरध्वनि क्रमांकों की सूची बनवाएँ और सहायता लेने की सूचना दें।

Answer:
प्रस्तुत चित्र बैंक का है। प्रतिदिन के कार्य का चित्रण इसमें किया गया है। छोटे बच्चे अपने माता-पिता के साथ बैंक में आए हैं। बैंक में आए कई ग्राहक अपना कार्य कर रहे हैं। एक महिला पूछताछ-काउन्टर पर बैठे बैंक कर्मचारी से कुछ बातचीत कर रही है। दूसरी महिला बचत खाता काउन्टर पर अपना कार्य करने के लिए खड़ी है। कुछ ग्राहक कैशिअर के पास से अपने रुपये लेने के लिए कतार में खड़े हैं। एक महिला कैशिअर काउन्टर पर रुपये जमा कर रही है। कुछ ग्राहक अपने कार्य की प्रतीक्षा में बैठे हैं। एक ग्राहक शाखा प्रबंधक (मैनेजर) के कक्ष में बैठकर कुछ वार्तालाप कर रहा है। बंदूकधारी सुरक्षा कर्मचारी बैंक की सुरक्षा के लिए खड़ा है। अन्य ग्राहक अपने काम में व्यस्त दिखाई दे रहे हैं। बैंक की ओर से ग्राहकों को सूचना देने के लिए सूचना फलक लगा हुआ है।

Hindi Sulabhbharti Class 6 Solutions Chapter 1 उपयोग हमारे Additional Important Questions and Answers

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(प्रगति, सूचना, टिकट, कूड़ेदान)

Question 1.
डाकघर में लोगों और कर्मचारियों को सूचित करने के लिए ………………… फलक लगाया जाता है।
Answer:
सूचना

Question 2.
हमें कचरा ……………….. में फेंकना चाहिए।
Answer:
कूड़ेदान

Question 3.
हमारे बचत करने से देश की …………………. होगी।
Answer:
प्रगति

Question 4.
पत्र पर ……………… लगाकर हम उसे डाकघर में देते है।
Answer:
टिकट प्रश्न

निम्नलिखित वाक्य सही हैं या गलत लिखिए:

Question 1.
डाकघर में हम पैसे जमा कर सकते हैं।
Answer:
सही

Question 2.
हमें कचरा गमले में फेंकना चाहिए।
Answer:
गलत

Question 3.
बच्चे डाकघर में खेल रहे हैं।
Answer:
गलत

Question 4.
मेज पर पत्र बिखरे पड़े हैं।
Answer:
सही

Question 5.
बचत खाता काउंटर पर महिला कर्मचारी बैठी है।
Answer:
गलत

निम्नलिखित चित्रों के साथ सही जोड़ियाँ मिलाइए:

Answer:
१ – घ
२ – ग
३ – ड़
४ – क
५ – ख

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
डाकघर में हम क्यों जाते हैं?
Answer:
हम डाकघर में पत्र डालने, लाने अथवा मनी ऑर्डर तथा रजिस्ट्री करने जाते हैं।

Question 2.
डाकघर के चित्र में कितने विभाग दिखाये गए हैं और कौन से?
Answer:
डाकघर के चित्र में तीन विभाग दिखाये गए है।

• बचत खाता
• मनी ऑर्डर
• रजिस्ट्री/टिकट

Question 3.
डाकघर के फलक पर कौन-सा सुंदर वाक्य लिखा है?
Answer:
डाकघर के फलक पर ‘बचत आपकी, प्रगति देश की’ यह सुंदर वाक्य लिखा है।

Question 4.
छोटे बच्चे किसके साथ डाकघर में आए है?
Answer:
छोटे बच्चे अपने माता – पिता के साथ डाकघर में आए है।

Question 5.
‘हम आपकी आवश्यकता समझते हैं।’ इस वाक्य से आप क्या समझते हैं?
Answer:
इस वाक्य से हम यह समझते है कि आपका समय और आपका कार्य हमारे लिए महत्त्वपूर्ण है।

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(ग्राहक, पूछताछ, बंदूक, बचत, छड़ी)

Question 1.
महिला . …………… कर रही है।
Answer:
पूछताछ

Question 2.
दूसरी महिला ……………… खाता काउन्टर के पास खड़ी है।
Answer:
बचत

Question 3.
सुरक्षा कर्मचारी के पास ……………… है।
Answer:
बंदूक

Question 4.
मैनेजर ……………….. से बातचीत कर रहा है।
Answer:
ग्राहक

Question 5.
बूढ़े ग्राहक के हाथ में ………………….
Answer:
छड़ी

निम्नलिखित बाक्य सही हैं या गलत लिखिए:

Question 1.
बैंक में कैशिअर पैसे का लेन-देन एवं हिसाब का काम देखता है।
Answer:
सही

Question 2.
बैंक में हमें पत्र मिलता है।
Answer:
गलत

Question 3.
मैनेजर का काम लोगों की रक्षा करना होता है।
Answer:
गलत

Question 4.
आज-कल बैंक का अधिकतर काम संगणक पर होता है।
Answer:
सही

Question 5.
बैंक से हमें कर्ज मिलता है।
Answer:
सही

निम्नलिखित बैंक व पोस्ट से संबंधित शब्दों को अलग अलग करके लिखिए:

(पूछताछ, बचत खाता, कैशिअर, डाकिया, मैनेजर, डाक अधिकारी, रजिस्ट्री, चालू खाता, पत्र, धनादेश, मनी ऑर्डर)
Answer:
पोस्ट ऑफिस:

• डाकिया
• बचत खाता
• डाक अधिकारी
• रजिस्ट्री
• पत्र
• मनी ऑर्डर

बैंक:

• बचत खाता
• कैशिअर
• चालू खाता
• धनादेश
• पूछताछ

निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए:

Question 1.
बैंक में खजांची क्या कार्य करते हैं?
Answer:
बैंक में खजांची रुपये लेन-देन का एवं उसका हिसाब रखने का कार्य करते हैं।

Question 2.
बैंक में पूछताछ-कक्ष क्यों होता है?
Answer:
बैंक में आने वाले ग्राहकों की समस्याओं का निवारण करने के लिए बैंक में पूछताछ-कक्ष होता है।

Question 3.
बैंक में सुरक्षा कर्मचारी क्यों तैनात किए जाते हैं?
Answer:
बैंक में आने-जाने वाले ग्राहकों एवं बैंक के मालमत्ते की रक्षा करने के लिए बैंक में सुरक्षा कर्मचारी तैनात किए जाते हैं।

Question 4.
बैंकों की आवश्यकता क्यों होती है?
उत्तर :
हमारी धन-संपत्ति को सुरक्षित रखने के लिए हमें बैंकों की आवश्यकता होती है।

Question 5.
बैंक के मुख्य अधिकारी को क्या कहते हैं?
Answer:
बैंक के मुख्य अधिकारी को शाखा प्रबंधक कहते हैं।

Question 6.
साधारण या आम जनता बैंक में किस प्रकार का खाता खोलती है?
Answer:
साधारण या आम जनता बैंक में बचत खाता खोलती है।

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 8 टीटू और चिंकी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 8 टीटू और चिंकी

Hindi Sulabhbharti Class 6 Solutions Chapter 8 टीटू और चिंकी Textbook Questions and Answers

मैं कौनः

चित्रों के आधार पर वाक्य बनाओ। (काल्पनिक लेखन)

Answer:
पहले चित्र – के आधार पर दो चिड़ियाँ आसमान में उड़ रही हैं। आसमान में बादल छाए हैं। नीचे सुंदर फूल खिले हैं। चित्र में एक छोटा घर भी दिखाई दे रहा है।
दूसरा चित्र – दूसरे चित्र में एक पेड़ दिखाई पड़ रहा है। पेड़ के ऊपर एक चिड़िया उड़ रही है। पीछे पहाड़ दिख रहा है। पेड़ के पास कुछ फूल खिले हैं।
तीसरा चित्र – तीसरे चित्र में पहाड़ के पीछे उगता सूर्य दिख रहा है। चित्र में एक घिसकनी (फिसलपट्टी) है। बच्चे उस पर फिसलकर खेल रहे हैं।

खोजबीनः

विलुप्त होते हुए प्राणियों तथा पक्षियों की जानकारी प्राप्त करके सूची बनाओ। (परियोजना-कार्य)
Answer:

विचार मंथन:

जीवदया ही धर्म है। (अनुच्छेद लेखन)
Answer:
दया धर्म का मूल है। जीव मात्र पर दया करना सबसे बड़ा धर्म है। गाँधी जी के प्रिय भजन में भी इसका उल्लेख है। वैष्णव जन तो तेने कहिए, जे पीर पराई जाने रे। गीता में भगवान श्री कृष्ण ने कहा है – ‘समोहम सर्व भूतेषु।’ अर्थात मैं सभी सभी प्राणियों में समत्व भाव रखता हूँ। अत: सभी जीवों पर दया करना ही सभी प्राणियों पर दया करना है।

सुनो तो जरा:

विभिन्न पशु पक्षियों की बोलियों की नकल सुनाओ:
Answer:

• गाया – मां …….मां ………
• कुत्ता – भों…… भो…….
• बिल्ली – म्याऊँ……. म्याऊँ..
• बकरी – में…… में……..
• घोड़ा – हिं… हि… हिं…
• कोयल – कू… कू… कू…
• कौआ – काँव… काँव…
• चिड़िया – चिं चि चि ….

बताओ तो सही:

अपने साथ घटित कोई मज़ेदार घटना बताओ? (कहानी लेखन)
Answer:
एक दिन मेरे विद्यालय में अन्तर विद्यालयीय क्रिकेट मैच था। मेरा विद्यालय फाइनल में पहुँच चुका था। फाइनल मैच से पहले ही मेरे एक मित्र को अभ्यास करते समय चोट लग गई और मुझे फाइनल मैच में खेलने का अवसर मिल गया। मैं ओपनिंग में गया और आखिर तक टिका रहा और मेरा विद्यालय मैच जीत गया। मुझे बहुत मज़ा आया।

वाचन जगत से:

उपन्यास सम्राट प्रेम-चंद की कोई एक कहानी पढ़ो। उसका विषय बताओ?
Answer:
मैंने प्रेमचंद की एक कहानी पढ़ी, जिसका नाम था – बड़े भाई साहब। इसमें बड़े भाई साहब और उनका छोटा भाई छात्रावास में रहते हैं। दोनों में दो साल का अंतर रहता है। बड़े भाई खूब पढ़ते हैं और छोटा भाई खूब खेलता-कूदता है। फिर भी बड़े भाई नौवी में दो बार फेल हो जाते हैं और छोटा भाई उनकी कक्षा में उनकी बराबरी पर आ जाता है।

मेरी कलम से:

‘बाघ बचाओ परियोजना’ के बारे में जानकारी प्राप्त कर लिखो। (निबंध लेखन)
Answer:
सिंह, बाघ और चीता एक ही प्रजाति के जीव माने जाते हैं। इनकी नस्ल अब समाप्ति की तरफ बढ़ रही है। वर्तमान में १४११बाघ बचे हैं. इसलिए आजकल ‘बाघ बचाओ का नारा’ अनेक बार सामने आ रहा है। बाघ संविधान द्वारा संरक्षित क्षेत्रों में ही पाए जाते हैं। समाचार माध्यमों के अनुसार अनेक शिकारी अवैध रूप से वहाँ प्रवेश कर उनका शिकार करते हैं। दरअसल यह संकट वनों के सिकुड़ते दायरे की वजह से पैदा हुआ है।

जरा सोचो…. लिखो:

‘यदि प्राणी नहीं होते तो……’ (काल्पनिक लेखन)
Answer:
यदि प्राणी नहीं होते तो प्रकृति असंतुलित हो जाती। ईश्वर ने प्रकृति को संतुलित रखने के लिए विभिन्न प्राणियों को बनाया है। उनका भोजन भी इसी को ध्यान में रखते हुए निर्धारित किया है। यह धरती घास और पेड़-पौधों से संतुलित रहे, इसके लिए कुछ प्राणियों को शाकाहारी बनाया और यह धरती प्राणियों से संतुलित रहे, इसलिए कुछ को मांसाहारी बनाया। मनुष्य सभी प्राणियों में समझदार और शक्तिशाली है। उसने अपने निहित स्वार्थ के लिए ईश्वर की इस व्यवस्था में गड़बड़ी पैदा करना शुरू कर दिया है। यह अनुचित है। यहाँ सभी प्राणियों की उपयोगिता है।

स्वबं अध्ययनः

‘डिस्कवरी चैनल’ पर दिखाए जाने वाले किसी अनोखे जीव की जानकारी प्राप्त करो।
Answer:
‘डायनासोर’ जिसका अर्थ यूनानी भाषा में बड़ी छिपकली होता है। लगभग १६ करोड़ वर्ष तक पृथ्वी के सबसे प्रमुख स्थलीय कशेरूकी जीव थे। हिंदी में डायनासोर शब्द का अनुवाद भीमसरट है, जिसका संस्कृत में अर्थ भयानक छिपकली है। इन पशुओं के विविध समूह थे। जीवाश्म विज्ञानियों ने डायनासोर के अब तक ५०० विभिन्न वंशों और १००० से अधिक प्रजातियों की पहचान की है और इनके अवशेष पृथ्वी के हर महाद्वीप पर पाए जाते हैं। कुछ डायनासोर शाकाहारी तो कुछ मांसाहारी थे। कुछ द्विपाद तो कुछ चौपाए थे। कुछ आवश्यकतानुसार द्विपाद या चतुर्पाद के रूप में अपने शरीर की मुद्रा को परिवर्तित कर लेते थे।

अध्ययन कौशल:

चित्रों को पहचानकर जलचर, नभचर, थलचर और उभयचर प्राणियों में वर्गीकरण करो।

Answer:

• जलचरः मछली, मगरमच्छ, सौंप, ऑक्टोपस
• थलचरः गिलहरी, शेर, ऊँट, चूहा
• नभचर: चिड़िया, तोता, उल्लू
• उभयचर: मेंढक, भैंस, हाथी, दरयाई घोड़ा

Hindi Sulabhbharti Class 6 Solutions Chapter 8 टीटू और चिंकी Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक-एक शब्द में लिखिए:

Question 1.
गिलहरी का नाम क्या था?
Answer:
टीटू।

Question 2.
टीटू की पड़ोसिन कौन थी?
Answer:
चिकी।

Question 3.
साँप कहाँ रहता था।
Answer:
बिल में।

Question 4.
साँप बिल से निकलकर कहाँ चढ़ने लगा?
उत्तरः
पेड़ पर।

Question 5.
टीटू और चिंकी के बच्चों ने किसकी ताकत को देख लिया था?
Answer:
एकता की।

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए:

Question 1.
चिंकी का घोंसला कहाँ था?
Answer:
चिंकी का घोंसला पेड़ की शाखाओं पर था।

Question 2.
चिंकी जब दाना चुगने जाती, तब सभी बच्चो का ध्यान कौन रखता था?
Answer:
चिंकी जब दाना चुगने जाती, तब सभी बच्चों का ध्यान टीटू रखती थी।

Question 3.
अंत में पेड़ छोड़ने का मन में विचार किसने बना लिया?
Answer:
अंत में पेड़ छोड़ने का मन में विचार टीटू और चिकी ने बना लिया।

Question 4.
टीटू के बच्चों का क्या कहना था?
Answer:
टीटू के बच्चों का कहना था कि पेड़ उनका है।

Question 5.
साँप का पेड़ पर चढ़ना मुश्किल क्यों होने लगा?
Answer:
साँप का पेड़ पर चढ़ना मुश्किल होने लगा, क्योंकि जहाँ – जहाँ चिंकी ने चोंच मारी, वहाँ-वहाँ पेड़ से गाढ़ा चिपचिपा दूध बहने लगा।

कोष्ठक से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए:

(भाड़, मिलजुलकर, खोखल, गिलहरी, बसेरा).

Question 1.
हमें …………….. रहना चाहिए।
Answer:
मिलजुलकर

Question 2.
हमारा जन्म इसी ……………… में हुआ।
Answer:
खोखल

Question 3.
इसकी टहनियों पर हमारा ……………… है।
Answer:
बसेरा

Question 4.
टीटू ……………… यह सुन बड़ी परेशान हुई।
Answer:
गिलहरी

Question 5.
अकेला चना ……………… नहीं फोड़ सकता।
Answer:
भाड़

निम्नलिखित वाक्यों के सामने सही / अथवा गलत का निशान लगाइए:

Question 1.
टीटू के बच्चे का नाम मिंटू था।
Answer:
सही

Question 2.
चिंकी खोखल में रहती थी।
Answer:
गलत

Question 3.
रिंकी की माँ चिंकी थी।
Answer:
सही

Question 4.
डर के मारे चिंकी नाचने लगी।
Answer:
गलत

Question 5.
टीटू गिलहरी बिल में छिप तमाशा देख रही थी।
Answer:
गलत

किसने, किससे कहा?

Question 1.
“तुम कैसे कह सकते हो कि यह पेड़ तुम्हारा है?”
Answer:
रिंकी ने मिंटू से कहा।

Question 2.
“शाखाएँ हमारी तो फल भी हमारे।”
Answer:
टीटू के बच्चों ने रिंकी से का।

Question 3.
“सावधान टीटू बहन, साँप ऊपर आ रहा है।”
Answer:
चिंकी ने टीटू से कहा।

Question 4.
“हम तुम्हें टहनियों तक नहीं आने देंगे और न ही इसके फल खाने देंगे।”
Answer:
चिंकी के बच्चों ने टीटू के बच्चों से कहा।

Question 5.
“चिंकी चिड़िया को यह पेड़ छोड़ना होगा।”
Answer:
टीटू के बच्चों ने चिंकी के बच्चों से कहा।

व्याकरण और भाषाभ्यास:

विरामचिह्न रहित अनुच्छेद में विरामचिह्न लगाओ

काबुलीवाले ने पूछा बिटिया अब कौन सी चूड़ियाँ चाहिए मैंने अपनी गुड़िया दिखाकर कहा मेरी गुड़िया के लिए अच्छी सी चूड़ियाँ दे दो जैसे लाल नीली पीली
Answer:
काबुलीवाले ने पूछा- बिटिया ! अब कौन-सी चूड़ियाँ चाहिए? मैंने अपनी गुड़िया दिखाकर कहा, “मेरी गुड़िया के लिए अच्छी-सी चूड़ियाँ दे दो। जैसे-लाल, नीली, पीली।”

उचित जोड़ियाँ मिलाइए:

Answer:
1. – ;
2. – “ ”
3. – –
4. – ,
5. – ।
6 – ?

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. शाखा
2. चिड़िया
3. घोंसला
4. बच्चा
5. हवा
6. अंडा
7. माता
8. साँस
9. चोंच
10. मुश्किल

Answer:

1. शाखाएँ
2. चिड़ियाँ
3. घोंसले
4. बच्चे
5. हवाएँ
6. अंडे
7. माताएँ
8. साँसें
9. चोंचें
10. मुश्किलें

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. टहनियाँ
2. नीड़
3. आसमान
4. साँप
5. बसेरा

Answer:

1. शाखाएँ
2. घोंसला
3. आकाश
4. सर्प
5. घर

निम्नलिखित शब्दों के विलोम शब्द लिखिए:

1. डर
2. सुबह
3. जन्म
4. बच्चे
5. सावधान
6. अँधेरा
7. सुरक्षित
8. मुश्किल
9. नरम
10. धर्म

Answer:

1. निडर
2. शाम
3. मृत्यु
4. बूढ़े
5. असावधान
6. उजाला
7. असुरक्षित
8. आसान
9. कठोर
10. अधर्म

निम्नलिखित शब्दों के लिंग बदलिए:

1. साँप
2. पड़ोसी
3. बहन
4. माता

Answer:

1. साँपिन
2. पड़ोसिन
3. भाई
4. पिता

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 6 स्वास्थ्य संपदा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 6 स्वास्थ्य संपदा

Hindi Sulabhbharti Class 6 Solutions Chapter 6 स्वास्थ्य संपदा Textbook Questions and Answers

कार्य हमारा

चित्र देखकर क्रियायुक्त शब्दों से वाक्य बनाओ।

Answer:

1. लता सेब खाती है।
2. बच्चे हँस रहे थे।
3. गुड़िया अलमारी से गिर गई है।
4. माँ अपने बच्चे को सुला रही है।
5. रमेश अपनी बहन को खाना खिला रहा है।
6. मैं अपने-आप खाना खा लेता हूँ।
7. माँ अपनी बिटिया को खाना खिलाती है।

जरा सोचो…..लिखो:

यदि भोजन से नमक गायब हो जाए तो….
Answer:
यदि भोजन से नमक गायब हो जाए तो भोजन स्वादिष्ट नहीं लगेगा। हर चीज फीकी लगेगी। फीका भोजन करना मुश्किल होगा और हमारा पेट नहीं भरेगा। पेटभर खाना न खाने से हमें कमजोरी आ जाएगी। हम ढंग से कोई काम नहीं कर सकेंगे। नमक के बिना हमारे शरीर को आयोडीन नहीं मिलेगा, जिससे शरीर का विकास रुक जाएगा।

मैंने समझा:

__________
___________
Answer:
इस पाठ में गांधी जी यह समझाना चाहते हैं कि हमें अपना शरीर स्वस्थ रखना चाहिए। हमें पर्याप्त मात्रा में दूध, मक्खन, फल, हरी सब्जियाँ, गेहूँ की रोटी आदि पौष्टिक पदार्थ अपने भोजन में लेने चाहिए। हमें शुद्ध हवा में रहते हुए प्राणायाम व व्यायाम भी करना चाहिए।

खोजबीन:

खादी का कपड़ा कैसे बनाया जाता है इसकी जानकारी प्राप्त करके लिखो।
Answer:
चरखे पर रूई से सूत काता जाता है। फिर उस सूत से जुलाहा हथकरघे पर कपड़ा बुनता है। इसके पश्चात इस कपड़े को रंगा जाता है। हाथ से बुना कपड़ा कुछ मोटा होता है। इसी कपड़े को खादी कहते हैं।

अध्ययन कौशल:

पढ़ाई का नियोजन करते हुए अपनी दिनचर्या लिखो।
Answer:
मेरा स्कूल सुबह साढ़े सात बजे से दोपहर दो बजे तक रहता है। मैं ढाई बजे घर आ जाता हूँ। खाना खाने और थोड़ा आराम करने के बाद मैं अपने स्कूल का गृहकार्य करने बैठ जाता हूँ। फिर गृहकार्य पूरा कर मैं खेलने चला जाता हूँ, क्योंकि मेरी उम्र के सभी बच्चे उसी समय अपनी पढ़ाई आदि खत्म करके खेलने आते हैं। दो घंटा खेलने के बाद मैं घर आता हूँ। खाना खाते समय मैं टीवी पर समाचार और डिस्कवरी जैसे ज्ञानवर्धक चैनल देखता हूँ। फिर स्कूल बैग तैयार करके दस बजे मैं सोने चला जाता हूँ। इस तरह यह मेरी दिनचर्या सुबह से रात तक की है।

बताओ तो सही।

संतुलित आहार पर पाँच वाक्य बोलो।
Answer:

1. पर्याप्त मात्रा में पौष्टिक तत्त्वों से भरे आहार को संतुलित आहार’ कहते हैं।
2. मजबूत एवं स्वस्थ शरीर के लिए संतुलित आहार लेना चाहिए।
3. संतुलित आहार हमारे कार्य करने की शक्ति एवं गति को बढ़ाता है।
4. इससे हमारे शरीर का संपूर्ण रूप से शारीरिक एवं मानसिक विकास होता है।
5. संतुलित आहार हमारे शरीर की रोग-प्रतिरोधक क्षमता बढ़ाता है।

मेरी कलम से:

अपने मित्र को शुभकामना/बधाई पत्र लिखो।
Answer:

एक वाक्य में उत्तर लिखो।

Question 1.
जैतून के तेल की जगह मक्खन क्यों लिया जाना चाहिए?
Answer:
मक्खन में जो विटामिन होते हैं वह जैतून के तेल में नहीं होते, इसलिए जैतून के तेल की जगह मक्खन लिया जाना चाहिए।

Question 2.
रक्षक का धर्म कौन-सा है?
Answer:
रक्षा करना रक्षक का धर्म है।

Question 3.
किन-किन सब्जियों की गिनती अच्छी, हरी सब्जियों में होती है?
Answer:
लौकी, फूलगोभी, पत्तागोभी, बिना बीज की सेम, बैंगन आदि की गिनती अच्छी और हरी सब्जियों में होती है।

Question 4.
फेफड़ों के लिए क्या अति आवश्यक है?
Answer:
चौबीसों घंटे शुद्ध-से-शुद्ध हवा फेफड़ों के लिए अति आवश्यक है।

सदैव ध्यान में रखो:

नवयुवकों की शक्ति देशहित में लगनी चाहिए।
Answer:
मनुष्य के अंदर उसके पूरे जीवन में सबसे अधिक ऊर्जा युवावस्था में होती है। इस उम्र में वह अधिक-से-अधिक मुश्किल कार्य कर सकता है। मनुष्य का कर्तव्य होता है कि वह अपने परिवार और समाज के साथ-साथ देश के विकास के लिए भी कार्य करे। अत: नवयुवक या युवावर्ग को अपनी शक्ति देशहित में लगानी चाहिए, जिससे देश ज्यादा-से-ज्यादा सफलता प्राप्त कर सके।

विचार मंथन:

स्वस्थ शरीर, स्वस्थ मन। योगासन है, उत्तम साधन।
Answer:
स्वास्थ्य सबसे बड़ा धन है। अच्छे स्वास्थ्य के बिना सब कुछ व्यर्थ है। कहते हैं कि स्वस्थ शरीर में स्वस्थ मन वास करता है, इसलिए हमें हमेशा अपने स्वास्थ्य पर ध्यान देना चाहिए। इसके लिए अच्छे खान-पान के साथ-साथ शारीरिक व्यायाम भी अनिवार्य है। हमें सुबह जल्दी उठना चाहिए और रात को भी समय पर सो जाना चाहिए। सुबह उठकर खुली हवा में सैर करना लाभदायक होता है। साथ ही हमें योगासन भी अवश्य करना चाहिए। योगासन में शारीरिक क्रियाओं के अलावा श्वासोच्छवास पर ध्यान केंद्रित किया जाता है। इस तरह शारीरिक और मानसिक शक्तियों का विकास होता है। अत: स्वस्थ तन-मन के लिए योगासन एक उत्तम साधन है।

भाषा की ओर:

निम्न विशेषण शब्द का अपने वाक्य में प्रयोग करके उनका प्रकार लिखो।

Answer:

1. पाँच
   प्रकार: पाँच – संख्यावाचक विशेषण
   वाक्य: मैं रोज सुबह पाँच बजे सोकर उठता हूँ।
2. यही
   प्रकार: यही – सार्वनामिक विशेषण
   वाक्य: यही लड़का कल स्कूल नहीं आया था।
3. कुछ
   प्रकार: कुछ – परिमाणवाचक विशेषण
   वाक्य: कुछ फल लेते आना।
4. मीठी
   प्रकार: मीठी – गुणवाचक विशेषण
   वाक्य: रीना मीठी दही खाती है।

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 7 नदी कंधे पर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 7 नदी कंधे पर

Hindi Sulabhbharti Class 6 Solutions Chapter 7 नदी कंधे पर Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए:

Question 1.
बालक किसको कंधे पर लाना चाहता है?
Answer:
नदी को।

Question 2.
बालक किसके साथ नहाना चाहता है?
Answer:
मित्रों के साथ।

Question 3.
वह नदी का परिचय किससे कराना चाहता है?
Answer:
भद्रजनों से।

निम्नलिखित प्रश्नों के उत्तर लिखिए:

Question 1.
बालक नदी के उस पार खड़े-खड़े क्या करना चाहता
Answer:
बालक नदी के उस पार खड़े-खड़े ‘मम्मी-मम्मी’ चिल्लाना चाहता है।

Question 2.
शाम ढलने पर बालक क्या करता?
Answer:
शाम ढलने पर बालक नदी को उठाकर अपने कंधे पर रखवाता और जहाँ से उसे लाया था, वहीं रख आता।

Question 3.
वह मित्रों के साथ किस प्रकार नहाना चाहता है?
Answer:
वह मित्रों के साथ कूद-कूदकर और उछल-उछलकर नहाना चाहता है।

Question 4.
बालक नदी को कहाँ बहाना चाहता है?
Answer:
बालक नदी को अपने घर के ठीक सामने बहाना चाहता है।

Question 5.
बालक सबको किसलिए आमंत्रित करता?
Answer:
बालक सबको नदी में नहाने के लिए आमंत्रित करता।

कविता में आए हुए लयात्मक शब्दों को ढूँढकर लिखिए:

उदाहरण: बहाते – बहाते

1. मस्ताते
2. रखवाते
3. करवाते

Answer:

1. चिल्लाते
2. रख आते
3. इतराते

रिक्त स्थानों की पूर्ति कीजिए:

Question 1.
अगर हमारे ……………… में होता।
Answer:
बस

Question 2.
……………… उठाकर घर ले आते।
Answer:
नदी

Question 3.
अपने घर के ठीक ………….
Answer:
सामने

Question 4.
उसको हम ……………… बहाते।
Answer:
हर रोज़

Question 5.
……………… उछल-उछलकर।
Answer:
कूद-कूदकर

Question 6.
अपने मित्रों के साथ ………………।
Answer:
चहाते

उचित जोड़ियाँ मिलाइए:

Answer:
१ – घ
२ – ग
३ – क
४ – ड
५ – ख

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. नदी
2. कंधा
3. बहाता

Answer:

1. नदियाँ
2. कंधे
3. बहाते

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. घर
2. नदी
3. आमंत्रित
4. शाम
5. मम्मी
6. मित्र
7. झटपट
8. इतराते

Answer:

1. गृह
2. सरिता
3. निमंत्रित
4. संध्या
5. माता
6. सखा
7. जल्दी-जल्दी
8. इठलाते

निम्नलिखित शब्दों के विपरीतार्थक शब्द लिखिए:

1. खड़े-खड़े
2. यहीं
3. उपस्थित
4. झटपट
5. सामने
6. भद्र

Answer:

1. बैठे-बैठे
2. वहीं
3. अनुपस्थित
4. धीरे-धीरे
5. पीछे
6. अभद्र

निम्नलिखित शब्दों में अनुस्वार ‘ या अनुनासिक लगाकर शब्द लिखिए:

1. मित्रो
2. कधे
3. जहा
4. आमत्रित
5. जनो

Answer:

1. मित्रों
2. कंधे
3. जहाँ
4. आमंत्रित
5. जनों

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 9 वह देश कौन-सा है? Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions स्वयं अध्ययन २

Hindi Sulabhbharti Class 6 Solutions स्वयं अध्ययन २ Textbook Questions and Answers

चित्रवाचन करके अपने शब्दों में कहानी लिखो और उचित शीर्षक बताओ:

विद्यार्थियों से ऊपर दिए गए चित्रों का क्रमानुसार निरीक्षण कराएँ । चित्र में कौन-कौन-सी घटनाएं घटी होंगी, उन्हें सोचने के लिए कहें । उन्हें अन्य चित्रों एवं घटनाओं के आधार पर कहानी लिखने के लिए प्रेरित करें और उचित शीर्षक देने के लिए कहें।
Answer:
छात्र स्वयं करें

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 17 पाणपोई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 17 पाणपोई (कविता)

Marathi Sulabhbharti Class 6 Solutions Chapter 17 पाणपोई Textbook Questions and Answers

1. एक – दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
अंगाची लाही लाही कशामुळे होते?
उत्तर:
उन्हामुळे अंगाची लाही लाही होते.

प्रश्न 2.
अवखळ वारा सुटल्यावर काय होते?
उत्तर:
अवखळ वारा सुटल्यावर पालापाचोळा धुळीबरोबर उडतो.

प्रश्न 3.
थकलेल्या वाटसरूला ग्लानी का येते?
उत्तर:
रखरखत्या उन्हामुळे थकलेल्या वाटसरूला ग्लानी येते.

प्रश्न 4.
पाणपोईवर पाणी पिण्यास कोण कोण येतात?
उत्तर:
पाणपोईवर पाणी पिण्यास गरीब श्रीमंत दोन्हीही येतात.

प्रश्न 5.
ज्यांनी पाणपोई थाटली त्याला आशीर्वाद का देतात?
उत्तर:
रखरखत्या उन्हात रांजणातले थंडगार पाणी पिऊन सर्व तृप्त होतात म्हणून त्याला आशीर्वाद देतात.

2. उष्णगरम, थंडगार, पालापाचोळा या शब्दांतील दोन्ही शब्द एकाच अर्थाचे आहेत, असे शब्द शोधा व लिहा.

प्रश्न 1.
उष्णगरम, थंडगार, पालापाचोळा या शब्दांतील दोन्ही शब्द एकाच अर्थाचे आहेत, असे शब्द शोधा व लिहा.

3. घामेजणे, लाहीलाही होणे, उष्णगरम झळाई, रखरखते ऊन, तहान लागणे या शब्दसमुहांचा वापर करून पाच-सहा वाक्ये लिहा.

प्रश्न 1.
घामेजणे, लाहीलाही होणे, उष्णगरम झळाई, रखरखते ऊन, तहान लागणे या शब्दसमुहांचा वापर करून पाच-सहा वाक्ये लिहा.
उत्तर:
उन्हाळ्याचे दिवस होते. रखरखते ऊन होते. मामाच्या शेतावर जायचे होते. अंगाची लाहीलाही होत होती. आम्ही घामेजलो होतो. उष्णगरम झळाई लागत होती. घसा कोरडा पडला होता. तहान लागली होती. जवळच्या झऱ्यातून थंडगार गोड पाणी प्यायलो. मन तृप्त झाले.

4. रखरख, गरगर यांसारखे अक्षरांची पुनरावृत्ती होणारे शब्द शोधा.

प्रश्न 1.
रखरख, गरगर यांसारखे अक्षरांची पुनरावृत्ती होणारे शब्द शोधा.
उत्तर:

1. लाहीलाही
2. सारखीसारखी
3. झरझर
4. भरभर
5. पटपट

5. पाणपोई हा पाण्याशी संबंधित शब्द आहे. तसेच खालील शब्द वाचा व समजून घ्या.

पाणबुड्या, पाणलोट, पाणवठा, पाणथळ, पाणकोंबडा, पाणघोडा, पाणवनस्पती.

6. ऊन या शब्दाला विशेषणे लावलेली आहेत. ती वाचा व समजून घ्या.

7. खालील विरूद्धार्थी शब्द लिहा.

प्रश्न 1.
खालील विरूद्धार्थी शब्द लिहा.
उत्तर:

1. गार × गरम
2. रंक × राव
3. ऊन × सावली
4. तृप्त × अतृप्त
5. दुवा × शाप
6. सज्जन × दुर्जन

8. तुम्हांला खूप तहान लागली असताना अचानक पाणपोई दिसली, तर तुमच्या मनात कोणते विचार येतील ते लिहा.

प्रश्न 1.
तुम्हांला खूप तहान लागली असताना अचानक पाणपोई दिसली, तर तुमच्या मनात कोणते विचार येतील ते लिहा.
उत्तर:
डांबरी रस्त्यावरून चालताना उष्णतेच्या झळा लागत होत्या. थंडगार पाणी प्यावेसे वाटत होते आणि अचानक एक पाणपोई दिसली. माझ्या मनात विचार येतील की ही पाणपोई कोणी ठेवली असेल? त्या सज्जन माणसास मला भेटता येईल का? हे पाणी थंडगार कसे राहते? लाल फडके कोण बांधून जाते? त्या सज्जनाचे मला आभार मानता येतील का? इत्यादी.

9. चालून चालून थकलेल्या वाटसरूला थंडगार पाणी मिळाल्यावर काय वाटत असेल, कल्पना करा व लिहा.

प्रश्न 1.
चालून चालून थकलेल्या वाटसरूला थंडगार पाणी मिळाल्यावर काय वाटत असेल, कल्पना करा व लिहा.
उत्तर:
मे महिन्याची दुपार होती. वाटसरू दुसऱ्या गावाला जायला निघाला. जवळ पाणीही नव्हते. रखरखत्या उन्हात चालवत नव्हते. ग्लानी येत होती. कडक ऊन होते. थोडे पुढे जाऊन पहातो तो काय एका मोठ्या वृक्षाखाली पाणपोई दिसली. मनाला खूप बरे वाटले. ज्यानी कोणी ती पाणपोई ठेवली होती त्याला खूप दुवा दिला. समाजसेवेची ही पद्धत किती न्यारी आहे असे वाटले. तहान शमली. तृप्तता झाली.

10. तुमच्या गावातील एखादया पाणपोईवर जा. तीकोणी काढली, ती काढण्यामागचा उद्देश, त्याची निगा कशी राखतात, पाणी कसे भरले जाते याची माहिती घ्या. ती एक मोठी समाजसेवा कशी आहे, याबद्दल सात-आठ ओळी लिहा.
उत्तर:
राजापूर आमचे गाव. उन्हाळा सुरू झाला की गावातील एक ज्येष्ठ व्यक्ती व त्यांचा तरूण मुलगा मोठ्या झाडाच्या पारावर सुंदर मोठे काळे माठ आणतात. त्यात स्वच्छ गोड पाणी भरतात. त्या माठाला ओले लाल फडके बांधतात. त्यामुळे माठातील पाणी थंडगार रहाते. वाटसरूंना, तहानलेल्यांना एवढ्या प्रचंड उष्णतेत गार पाणी मिळावे व त्यांची तहान शमावी हा त्यामागील उद्देश. वाटसरूने पाणी काढण्यासाठी ठेवलेल्या डावानेच पाणी घ्यायचे हा दंडक असतो.

त्यात उष्टे भांडे किंवा हात बुडवता येत नाही. हे रांजण नीट झाकलेले असते. केरकचरा त्यात जात नाही. गाळलेले नळाचे पाणी यात भरले जाते. ते जंतुविरहीत असते. ‘तहान शमविण्यासाठी’ स्वेच्छेने केलेली ही सेवा म्हणजे समाजसेवेचे एक उत्तम उदाहरण आहे. यातून ‘परोपकार’ हा मुख्य उद्देश दिसून येतो. आपणासही यातून शिकण्यासारखे आहे. घरातील गॅलरीत व खिडकीबाहेर पक्ष्यांनाही दाणा पाण्याची सोय करता येते. करून तर पहा!

विचार करून सांगा !

प्रश्न 1.
पाराची वाडी या गावातील मुलांनी केलेल्या उपक्रमाबद्दल तुमचे मत सांगा.

प्रश्न 2.
आपण एखादी गोष्ट किंवा उपक्रम करतो, तेव्हा घरातील मोठ्या माणसांना सांगणे आवश्यक आहे का? तुमचे मत सांगा.
उत्तरः
कोणताही उपक्रम हा समाजाच्या हितासाठी असेल तर घरातील मोठ्या माणसांना निश्चितच आनंद होतो. ते देखील तुमची योजना राबवण्यासाठी पुढाकार घेतात. कमी खर्चात योग्य काम कसे होईल हे शिकवितात. त्यासाठी लागणारी शिस्त, नियोजनाचे धडे देतात. म्हणून मोठया माणसांना सांगणे आवश्यक आहे असे मला वाटतेय.

प्रश्न 3.
अशा प्रकारचे कोणकोणते सामाजिक उपक्रम करावे असे तुम्हांला वाटते? ते उपक्रम थोडक्यात सांगा.

प्रश्न 4.
‘पाणी’ या विषयावरची घोषवाक्ये तयार करून त्याच्या पाट्या तयार करा.
उत्तर:

प्रश्न 5.
‘पाणी हेच जीवन’ यांवर आधारित दहा ओळी लिहा.

प्रश्न 6.
तुम्ही एखादा उपक्रम केला असेल, तर त्याबाबतची माहिती मित्राला पत्राने कळवा.

प्रश्न 7.
खालील उतारा वाचा. त्या उताऱ्यात पूर्णविराम (.) स्वल्पविराम (,) प्रश्नचिन्ह (?) उद्गारचिन्ह (!) आणि एकेरी अवतरणचिन्ह (‘-‘) घाला व उतारा पुन्हा लिहा.

प्रश्न 8.
इयत्ता पाचवीमध्ये तुमचा शब्दसंग्रह तुम्ही तयार केला आहे. शब्दसंग्रह किंवा शब्दकोश कसा पाहावा हे आपण पाहूया.

प्रश्न 9.
वर दिलेले ‘अ’ गटातील व ‘ब’ गटातील शब्द वाचा.
‘अ’ गटातील शब्द हे बाराखडीतील स्वरचिन्हानुसार दिलेले नाहीत.
मात्र ‘ब’ गटातील शब्द हे बाराखडीतील स्वरचिन्हानुसार दिलेले आहेत.

प्रश्न 10.
पाठ्यपुस्तकातील पाठ 2 आणि पाठ 3 मधील शब्दार्थ खालील चौकटीत दिले आहेत.

प्रश्न 11.
पाठ्यपुस्तकातील पाठ 2 आणि पाठ 3 मधील शब्दार्थ शब्दकोशाप्रमाणे खालील चौकटीत दिले आहेत.

‘अ’ गट

लुकलुकणे-चमकणे.
तल्लीन होणे-दंग होणे, गुंग होणे.
कडकडून भेटणे-प्रेमाने मिठी मारणे.
बिलगणे-प्रेमाने जवळ येणे.
गहिवरून येणे-मन भरून येणे.
धमाल-मजा.
पाडाचा आंबा-अर्धवट पिकलेला आंबा.
आमराई-आंब्याच्या झाडांची बाग.
ऐन दुपारी- भर दुपारी.
भणाण वारा – वाऱ्याचा भयभीत करणारा आवाज.
खचणे-खाली खाली जाणे, ढासळणे.
चडफड- राग,
गिल्ला करणे-गोंधळ करणे.

‘ब’ गट

आमराई-आंब्याच्या झाडांची बाग,
ऐन दुपारी- भर दुपारी.
कडकडून भेटणे-प्रेमाने मिठी मारणे.
खचणे- खाली खाली येणे, ढासळणे.
गहिवरून येणे-मन भरून येणे.
गिल्ला करणे-गोंधळ करणे.
चडफड- राग.
तल्लीन होणे-दंग होणे, गुंग होणे.
धमाल-मजा.
पाडाचा आंबा-अर्धवट पिकलेला आंबा.
बिलगणे-प्रेमाने जवळ येणे.
भणाण वारा – वाऱ्याचा भयभीत करणारा आवाज.
लुकलुकणे-चमकणे.

आले का लक्षात?

‘क, ख ….. ज्ञ’ या अक्षरांच्या क्रमानुसार व बाराखडीतील चिन्हानुसार वरील शब्द लिहिले आहेत. शब्दकोश पाहताना याच पद्धतीने पाहा. पाठ्यपुस्तकातील किंवा पाठ्येतर साहित्यातील शब्दांचे अर्थ पाहताना या पद्धतीने शब्दकोश पाहा. पाठ्यपुस्तकातील इतर पाठांमध्ये आलेले शब्दार्थ पाहा व शब्दकोशाप्रमाणे लिहून अधिकचा सराव करा.

Class 6 Marathi Chapter 17 पाणपोई Additional Important Questions and Answers

योग्य पर्याय निवडून उत्तरे लिहा.

प्रश्न 1.
उन्हाने अंगाची ……………. होते. (लाहीलाही / आग)
उत्तर:
लाहीलाही

प्रश्न 2.
…………….. सावलीत पाणपोई थाटली आहे. (आंब्याच्या / वटवृक्षाच्या)
उत्तर:
वटवृक्षाच्या

प्रश्न 3.
रखरखत्या उन्हात …………….. वारा सुटला आहे. (उष्णगरम / अवखळ)
उत्तर:
अवखळ

प्रश्न 4.
पाणी पिण्यास ……………… ठेवतात. (रांजण / माठ)
उत्तर:
रांजण

प्रश्न 5.
पाणी पिऊन ………………. दुवा देतात. (लोकांना / सज्जनास)
उत्तर:
सज्जनास

खालील प्रश्नांची एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
रांजण कसे होते?
उत्तर:
रांजण गार पाण्याने भरलेले व लाल कापडाने झाकलेले होते.

प्रश्न 2.
कवितेच्या खालील ओळी पूर्ण करा.
उत्तर:

1. ……………. होतीया लाहीलाही.
2. आठवते दग्ध ………………….
3. …………………. अवखळ वारा.
4. …………………. उंच अंबरा.
5. …………………. मोठी तहान.
6. ‘रंक असो ………………….
7. धन्य असो ………………….
8. पिऊनीया ………………….

उत्तरः

1. उन्हात घामेजुनी अंगाची होतीया लाहीलाही.
2. आठवते दग्ध उन्हातली थंडगार सराई.
3. रखरखत्या उन्हात सुटतो अवखळ वारा.
4. धुळीसंगे पालापाचोळा जाई या उंच अंबरा.
5. सारखीसारखी लागते साऱ्यांना मोठी तहान.
6. ‘रंक असो वा राव,’ हे पाणी पितात सारेजण!
7. धन्य असो ज्याने थाटिली ही पाणपोई उन्हात.
8. पिऊनीया पाणी दुवा देती सारे त्या सज्जनास.

व्याकरण व भाषाभ्यास

विशेषण:
नामाबद्दल अधिक माहिती सांगणाऱ्या शब्दास विशेषण म्हणतात.
उदा. सुंदर, कोवळे, लहान, लुसलुशीत, कडक, गोजिरवाणे इ.

प्रश्न 1.
जोड्या जुळवा.

उत्तर:

प्रश्न 2.
‘वारा’ या शब्दाला विशेषणे लावा..
उत्तर:

प्रश्न 3.
एकाच अर्थाचे शब्द शोधा. जसे की – उष्णगरम, थंडगार, पालापाचोळा.
उत्तर:

1. केरकचरा
2. गोरागोमटा
3. गरमागरम
4. घनदाट
5. काळाकभिन्न

प्रश्न 4.
संबंधित शब्द लिहा.
उत्तर:

1. पाणपोई – पाणबुड्या, पाणबोट, पाणवठा, पाणथळ, पाणकोंबडा, पाणघोडा, पाणवनस्पती
2. जलचर – जलविद्युत, जलसाठा, जलसमाधी, जलाशय, जलसंपत्ती, जलधी

प्रश्न 6.
खालील विरूद्धार्थी शब्द लिहा.
उत्तर:

1. थाटणे × मोडणे
2. आठवणे × विसरणे
3. थकलेला × ताजातवाना
4. मोठी × लहान
5. भरलेले × रिकामे
6. झाकणे × उघडणे

खालील वाक्प्रचारांचा अर्थ सांगून वाक्यात उपयोग करा.

प्रश्न 1.
अंगाची लाहीलाही होणे – उन्हामुळे अंगाची आग होणे.
उत्तर:
वैशाख महिन्यात अंगाची लाहीलाही होते.

प्रश्न 2.
तृप्त होणे – समाधानी होणे.
उत्तर:
भुकेलेला भिकारी भाजीभाकरी खाऊन तृप्त झाला.

विचार करून सांगा !

प्रश्न 1.
कोणकोणते सामाजिक उपक्रम करावेत असे तुम्हांला वाटते? ते उपक्रम थोडक्यात सांगा.
उत्तरः
1. जलसाक्षरता अभियान राबवणे – पाणी ही निसर्गाची अमूल्य देणगी आहे. पाण्याचा योग्य वापर करणे ही प्रत्येकाची जबाबदारी आहे. पाण्याचे सिंचन, नियोजन, वापर अतिशय काळजीपूर्वक करण्यासाठी खेडोपाडी, शहरातून जलसाक्षरता शिबीरे घ्यायला हवी.

2. तंत्रज्ञान साक्षरता – आजच्या तंत्रज्ञान आणि माहितीच्या युगात दररोज नवनवीन बदल घडत आहेत. त्याला सामोरे
जाण्यासाठी संगणक, टॅब, मोबाईलची ओळख व त्यात कौशल्य प्राप्त करून घेण्यासाठी वृद्धांचे व जिज्ञासूंचे तंत्रज्ञान साक्षरता वर्ग मोफत घेतले पाहिजे. त्यामुळे संभाव्य अडचणींवर ते मात करू शकतील. उदा. रांगेत उभे न राहता एखादया वृद्ध व्यक्तिला ऑनलाईन बुकींग कसे करतात ते शिकविणे.

पाणपोई Summary in Marathi

काव्यपरिचयः
‘पाणपोई’ या कवितेत उन्हात अंगाची लाहीलाही होत असताना, रखरखते ऊन असताना वाटसरूंना ग्लानी येते व पाणी हवेहवेसे वाटते. तर त्या ठिकाणी स्वच्छ, थंडगार पाणी प्यायला मिळाले तर अत्यंत तृप्तता मिळते. वाटसरूंना पाणी पिण्यासाठी केलेली सोय म्हणजेच पाणपोई. भूतदयेचे हे उत्तम उदाहरण आहे.

शब्दार्थ:

1. दग्ध ऊन – भाजणारे ऊन (burning heat)
2. वाटवृक्ष – वडाचे झाड (Banyan tree)
3. पाणपोई – उन्हाळ्यामध्ये वाटसरूंसाठी केलेली पिण्याच्या पाण्याची सोय (stand to supply water to travellers)
4. अवखळ – खोडकर (naughty, mischevous)
5. थकलेला – दमलेला (tired)
6. ग्लानी – चक्कर, सुस्ती (ennui, fatigue)
7. रांजण – मोठे माठ (big earthen pot)
8. तृप्त – संतुष्ट (satisfied)
9. रंक – गरीब (poor)
10. राव – श्रीमंत (rich)

वाक्प्रचार व अर्थ:

1. अंगाची लाही लाही होणे – उन्हामुळे अंगाची आग होणे.
2. तृप्त होणे – समाधानी होणे.

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 9 घर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 9 घर (कविता)

Marathi Sulabhbharti Class 6 Solutions Chapter 9 घर Textbook Questions and Answers

1. एक – दोन वाक्यात उत्तरे लिहा.

प्रश्न अ
माणसाची पहिली शाळा कुठे सुरू होते?
उत्तर:
माणसाची पहिली शाळा घरात सुरू होते.

प्रश्न आ
घराने कोणत्या गोष्टी जवळ कराव्यात?
उत्तर:
घराने नवी मूल्ये व नवीन ज्ञान जवळ करावे.

प्रश्न इ
आईच्या हातचे जेवण कसे असते?
उत्तर:
आईच्या हातचे जेवण चविष्ट असते.

2. कवीने घराचे वर्णन कोणत्या शब्दांत केले आहे ते लिहा. 

प्रश्न 1.
कवीने घराचे वर्णन कोणत्या शब्दांत केले आहे ते लिहा.
उत्तर:
घर म्हणजे नुसते दगड, विटा, सिमेंटपासून बनवलेल्या चार भिंतीने तयार केलेली वस्तू नसून ती एक सुंदर कलाकृती असते. ती एक आनंदी वास्तू असते. घरात फक्त वेगवेगळ्या खोल्या असून चालत नाही तर घर म्हणजे जिव्हाळा व प्रेमाने भरलेल्या ओल्या भावना असते. घरातच आपण शिक्षणाच्या पहिल्या शाळेत शिकत असतो. घर म्हणजे फक्त पसारा किंवा केवळ निवारा नसून त्याला स्वत:चा असा एक चेहरा व कहाणी असते. घराला स्वत:ची अशी एक ओळख असते.

घरापासूनच आपण पाहायला, चालायला, धावायला, लढायला व दुःखाचे डोंगर चढायला शिकतो. घराने सतत सावधान व समाधानी असावे. घराने सतत काळाचे भान ठेवावे. त्याने नवीन-नवीन मूल्य स्विकारावीत व नवीननवीन ज्ञान आत्मसात करावे. घरात आई अपार कष्ट करत असते. आजी सतत घरातल्या लहानग्या मुलांना गोष्टी सांगते तर आजोबा सतत सर्वांशी गप्पा मारत असतात. घरी आई जे सर्वांसाठी जेवण बनविते ते अतिशय चविष्ट व रूचकर असते. अशा प्रकारे कवी ‘धुंडिराज जोशी’ यांनी घराचे वर्णन केले आहे.

3. खालील आकृती पूर्ण करा.

प्रश्न 1.
खालील आकृती पूर्ण करा.

उत्तर:

3. शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधून लिहा. 

वस्तू, खोल्या, जिव्हाळा, पसारा, पाहायला, सावधान, भान, गोष्ट, चविष्ट

प्रश्न 1.
शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधून लिहा.
वस्तू, खोल्या, जिव्हाळा, पसारा, पाहायला, सावधान, भान, गोष्ट, चविष्ट
उत्तर:

1. वस्तू – वास्तू
2. खोल्या – ओल्या
3. जिव्हाळा – शाळा
4. पसारा – निवारा
5. पाहायला – चालायला
6. लढायला – चढायला
7. सावधान – समाधान
8. भान – ज्ञान
9. गोष्ट – कष्ट
10. चविष्ट – गप्पिष्ट

4. योग्य पर्याय निवडून लिहा.

प्रश्न अ.
घरात हव्या भावना ओल्या – म्हणजे
(अ) घरातील व्यक्तींनी रडावे
(आ) घरातील व्यक्तींनी परस्परांवर प्रेम करावे.
(इ) घरातील व्यक्तीत एक व्यक्ती भावना नावाची असावी.
उत्तर:
(आ) घरातील व्यक्तींनी परस्परांवर प्रेम करावे.

प्रश्न ब.
घर शिक्षणाची पहिली शाळा – म्हणजे
(अ) घरामध्ये बालमंदिर भरते.
(आ) घरापासून शिक्षणाला सुरूवात होते.
(इ) घराच्या शाळेत नाव घातले जाते.
उत्तर:
(आ) घरापासून शिक्षणाला सुरूवात होते.

प्रश्न क.
जवळ करावीत नवी मूल्ये नवीन ज्ञान – म्हणजे
(अ) नवी मूल्ये व नवीन ज्ञानाच्या जवळ राहायला जावे.
(आ) रोज नवीन मूल्यांची व ज्ञानाची पुस्तके वाचावीत.
(इ) काळानुसार मूल्य व ज्ञानातील बदल स्वीकारावे.
उत्तर:
(आ) रोज नवीन मूल्यांची व ज्ञानाची पुस्तके वाचावीत.

5. तुमच्या परिसरातील घराला दिलेली नावे पाहा. यादी करा. 

प्रश्न 1.
तुमच्या परिसरातील घराला दिलेली नावे पाहा. यादी करा.
उत्तर:

1. मातृछाया
2. गोकुळधाम
3. शांतीनिवास
4. कृष्णकुंज
5. गीताई
6. ग्रीनव्हिला
7. दिपांजली
8. शिवसदन
9. राधाकृष्णनिवास
10. मातोश्री
11. सह्याद्री व्हिला
12. मनःस्मृती
13. केशवधाम
14. शांतनुनिवास
15. वृंदावन
16. उत्कर्ष

6. खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.

प्रश्न 1.
खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.
उत्तर:

1. चविष्ट – चव असणारे
2. विशिष्ट – ठरावीक प्रकारचा
3. भ्रमिष्ट – भ्रम झालेला
4. गप्पिष्ट – गप्पा मारणारा
5. कोपिष्ट – रागावलेला
6. अनिष्ट – योग्य नसलेले

7. खालील शब्दांचे लिंग ओळखा व वचन बदला. 

प्रश्न 1.
खालील शब्दांचे लिंग ओळखा व वचन बदला.

उत्तर:

8. खालील शब्द शिक्षकांच्या मदतीने समजून घ्या.

9. खालील शब्द वाचा लिहा.

10. वस्तू आणि वास्तू या दोन शब्दांतील लेखनामध्ये फक्त ‘काना’ दिल्याने फरक पडतो; परंतु अर्थामध्ये खूप फरक आहे. खाली दिलेल्या शब्दांचे अर्थ शोधा. लिहा. उदा., वस्तू – जिन्नस, नग वास्तू – घर
कप – काप, तार – तारा, खरे – खारे, गर – गार, घर – घार, चार – चारा, पर – पार, वर – वार

प्रश्न 1.
कप – काप
उत्तर:

प्रश्न 2.
तार – तारा
उत्तर:

प्रश्न 3.
खरे – खारे
उत्तर:

प्रश्न 4.
गर – गार
उत्तर:

प्रश्न 5.
घर – घार
उत्तर:

प्रश्न 6.
चार – चारा
उत्तर:

प्रश्न 7.
पर – पार
उत्तर:

प्रश्न 8.
वर – वार
उत्तर:

11. तुमच्या घराचे चित्र काढून रंगवा व त्यांचे सहा सात वाक्यांत वर्णन करा. 

प्रश्न अ.
तुमच्या घराचे चित्र काढून रंगवा व त्यांचे सहा सात वाक्यांत वर्णन करा.
उत्तर:
माझ्या घराचे नाव ‘गोकुळधाम’ आहे. माझ्या घरात मी, माझे आई-बाबा व मोठी ताई असे चार जण राहतो. माझी आई घरातील सर्व कामे करते. माझे बाबा शेताची सर्व कामे करतात. मी व ताई आम्ही रोज शाळेत जातो व अभ्यास करतो. माझ्या घराभोवती विविध प्रकारची झाडे आहेत. माझ्या घरासमोरून एक नदी वाहते. तिचे पाणी स्वच्छ व चवदार आहे. माझे घर म्हणजे फक्त दगड व माती पासून बनवलेल्या भिंती नसून त्यात एक प्रकारचा जिव्हाळा आहे.

प्रश्न आ.
चित्राच्या जागी योग्य शब्दाचा वापर करून खालील म्हणी पूर्ण करा.

उत्तर:

प्रश्न 1.

उत्तरः
पाण्यात राहून माशाशी वैर करू नये,

प्रश्न 2.

उत्तर:
वासरात लंगडी गाय शहाणी.

प्रश्न 3.

उत्तर:
अडला हरी गाढवाचे पाय धरी.

प्रश्न इ.
खालील चित्रांच्या सहसंबंध लावून गोष्ट तयार करा.

उत्तर:
काही मुले स्वच्छंदी मनाची असतात. माझे मनही तसेच आहे. मी एके दिवशी क्रिकेटचे सामान घेऊन मोकळ्या माळरानावर खेळायला गेलो होतो. तिथे गेल्यावर मी काही फुलपाखरे पाहिली. ती त्या माळावर स्वच्छंदी उडत होती. बागडत होती. त्यांच्या पंखावरील विविध रंग पाहून मी आश्चर्यचकितच झालो. निसर्ग ही रंगांची किमया कशी साधतो ते मला कळेना. त्याच मोकळ्या माळावर काही मुले पतंग उडवताना दिसली. त्यांचे त्या पतंगांचे विविध रंग पाहून मलाही पतंग उडवण्याचा मोह झाला आणि मी क्रिकेट सोडून पतंग उडवण्यात गुंग झालो.

Marathi Sulabhbharti Class 6 Solutions Chapter 9 घर Important Additional Questions and Answers

खालील पदयपंक्तींच्या रिकाम्या जागा भरून ओळी पूर्ण करा.

प्रश्न 1.

1. घर नाही चार …………….. घर असते देखण्या ……………..
2. घर नाही एक……………… .घर म्हणजे आनंदी …………….. .
3. घर नाही नुसत्या ……………. घरात हव्या भावना …………….. .
4. घरात हवा ………………., घर शिक्षणाची पहिली …………….. .
5. घर नाही पसारा, घर नाही ………………… निवारा.
6. घराला असते …………….., घराला असतो आपला .
7. घराने असावे …………….. घराने द्यावे …………….. .
8. घराने ठेवावे …………….. भान, जवळ करावीत नवी …………….. नवीन ……………….
9. घरात आईचे अपार …………….. ,आजी सांगते ……………… गोष्ट,
10. घरात आजोबा …………….. , आईच्या हातचे जेवण …………….. .

उत्तर:

1. भिंती, कृती
2. वस्तू, वास्तू
3. खोल्या, ओल्या
4. जिव्हाळा, शाळा
5. नुसता, केवळ
6. कहाणी, चेहरा
7. सावधान, समाधान
8. काळाचे, मूल्ये, ज्ञान
9. कष्ट, सुंदर
10. गप्पिष्ट, चविष्ट

खालील प्रश्नांची एक ते दोन वाक्यात उत्तरे लिहा.

प्रश्न 1.
घर कसल्या कृती असते?
उत्तर:
घर देखण्या कृती असते.

प्रश्न 2.
घर म्हणजे कशी वास्तू असते?
उत्तर:
घर म्हणजे आनंदी वास्तू असते..

प्रश्न 3.
घरात कशा भावना हव्यात?
उत्तर:
घरात ओल्या भावना हव्यात.

प्रश्न 4.
घराला स्वत:चा असा काय असतो?
उत्तर:
घराला स्वत:चा असा आपला चेहरा असतो.

प्रश्न 5.
घर काय काय शिकवते?
उत्तर:
घर पाहायला, चालायला, धावायला, लढायला, दुःखाचा डोंगर चढायला शिकवते.

प्रश्न 7.
घराने कशाचे भान ठेवावे?
उत्तर:
घराने काळाचे भान ठेवावे.

प्रश्न 8.
घरात अपार कष्ट कोण करते?
उत्तर:
घरात अपार कष्ट आई करते.

प्रश्न 9.
घरात सुंदर गोष्ट कोण सांगते?
उत्तर:
घरात सुंदर गोष्ट आजी सांगते.

प्रश्न 10.
घरात गप्पा करणारे कोण आहेत?
उत्तर:
घरात आजोबा गप्पा करणारे आहेत.

व्याकरण व भाषाभ्यास

प्रश्न 1.
समानार्थी शब्द लिहा.

1. घर
2. जिव्हाळा
3. पहिली
4. शाळा
5. कहाणी
6. चेहरा
7. डोंगर
8. काळ
9. मूल्ये
10. कष्ट ङ्के

उत्तर:

1. सदन, पास्त, निवास
2. प्रेम
3. प्रथम
4. विद्यालय
5. गोष्ट, कथा
6. तोंड, वदन
7. पर्वत
8. वेळ
9. आदर्श
10. परिश्रम

प्रश्न 5.
विरूद्धार्थी शब्द लिहा.

1. देखणा
2. एक
3. आनंद
4. ओल्या
5. जिव्हाळा
6. पहिली
7. असते
8. ज्ञान
9. सुंदर
10. आजी
11. जवळ

उत्तर:

1. विद्रुप
2. अनेक
3. दु:ख
4. सुक्या
5. द्वेष, मत्सर
6. शेवटची
7. नसते
8. अज्ञान
9. कुरूप
10. आजोबा
11. दूर

प्रश्न 6.
खालील शब्दांचे वचन बदला,

1. घर
2. भिंत
3. खोली
4. ओली
5. शाळा
6. निवारा
7. कहाणी
8. चेहरा
9. मूल्य
10. गोष्ट

उत्तर:

1. घरे
2. भिंती
3. खोल्या
4. ओल्या
5. शाळा
6. निवारे
7. कहाण्या
8. चेहरे
9. मूल्ये
10. गोष्टी

प्रश्न 2.
खालील वेब पूर्ण करा.
उत्तर:
1.

2.

खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.

प्रश्न 1.
खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.
उत्तर:

1. नादिष्ट – छंद असणारा
2. गर्विष्ट – गर्व असणारा
3. कनिष्ट – लहान असणारा
4. वरिष्ट – मोठा असणारा
5. इष्ट – चांगले

चित्राच्या जागी योग्य शब्दाचा वापर करून खालील म्हणी पूर्ण करा.

प्रश्न 1.

उत्तरः
हातच्या कंकणाला आरसा कशाला.

प्रश्न 2.
नाकापेक्षा जड
उत्तर:
नाकापेक्षा मोती जड.

घर Summary in Marathi

काव्य परिचयः

‘घर’ या कवितेत धुंडिराज जोशी यांना घर म्हणजे केवळ चार भिंती नसून त्यापलिकडेही बरेच काही असल्याचा विचार मांडला आहे. घर एक आनंदी वास्तू असून त्या घराशी जिव्हाळा, अनके भावना निगडित असतात. हे घरच आपल्याला अनेक गोष्टी शिकवते, आपल्याला समाधान देते. याच घरात आजी, आजोबा या सगळ्यांच्या आठवणीदेखील सामावलेल्या असतात. घरासंबंधीचे फार सुंदर विचार या कवितेत मांडले आहेत.

शब्दार्थ:

1. घर – निवास, निवारा (house)
2. भिंत – तट (wall)
3. देखण्या – सुंदर (beautiful)
4. कृती – काम (work)
5. वस्तू – (things)
6. वास्तू – इमारत (building)
7. नुसत्या – फक्त, केवळ (only)
8. खोली – (room)
9. हव्या – पाहिजेत (want)
10. ओल्या भावना – प्रेमळ भावना (loving feelings)
11. जिव्हाळा – आत्मीयता (attachment)
12. पहिली – प्रथम (first)
13. शाळा – विद्यालय (school)
14. नुसता – फक्त, केवळ (only)
15. निवारा – आसरा (shelter)
16. कहाणी – गोष्ट, कथा (story)
17. चेहरा – मुखवटा, तोंड (face)
18. डोंगर – पर्वत (mountain)
19. चढायला – (toclimb)
20. सावधान – जागृत (to alert, vigilant)
21. ठेवावे – मांडणे (to keep)
22. काळ – समय (period, time)
23. भान – जाणीव (consciousnest)
24. नवी – नवीन (new)
25. मूल्ये – किंमत (value)
26. ज्ञान – माहिती (knowledge)
27. अपार – खूप, जास्त (to much)
28. कष्ट – परिश्रम (hard work)
29. आजी – (grandmother)
30. सुंदर – छान (lovely)
31. आजोबा – (grandfather)
32. सांगते – (to tell) बोलणे
33. गप्पिष्ट – गप्पा करणारे (talkative, chatter)
34. चविष्ट – रूचकर, चवदार (tasty, delicious)

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati पुनरावर्तन १ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions पुनरावर्तन १

Hindi Sulabhbharti Class 6 Solutions पुनरावर्तन १ Textbook Questions and Answers

Question 1.
वर्णमाला सुनाओ और विशेष वर्गों के उच्चारण पर ध्यान दो ।
Answer:
अ आ इ ई उ ऊ ऋ ए ऐ ओ औ अं अः अँ ऑ
क ख ग घ ङ
च छ ज झ ञ
ट ठ ड ढ ण (ड़ ढ़)
त थ द ध न
प फ ब भ म
य र ल व श ष स ह
क्ष त्र ज्ञ श्र

Question 2.
विद्यालय के स्नेह सम्मेलन का वर्णन करो।
Answer:
मेरे विद्यालय में प्रत्येक वर्ष स्नेह सम्मेलन मनाया जाता है। इस वर्ष स्नेह सम्मेलन के मुख्य अतिथि थे, पुणे विश्वविद्यालय के उपकुलपति! उनका स्वागत लेझिम नृत्य द्वारा किया गया। प्राथमिक विभाग के विद्यार्थियों ने स्वागत-नृत्य प्रस्तुत कर सभी अतिथियों का मन मोह लिया। माध्यमिक विभाग के विद्यार्थियों ने देश के विभिन्न प्रांतों का लोकनृत्य दिखा कर समा बाँध दिया। उच्च माध्यमिक विभाग के विद्यार्थियों ने हिंदी और मराठी में देशभक्ति पर नाटक प्रस्तुत किए। प्रधानाध्यापक ने विद्यार्थियों को पुरस्कार दिए। इस अवसर पर विद्यार्थियों के साथ-साथ उनके माता-पिता भी उपस्थित थे। इस तरह इस वर्ष भी बड़े धूम-धाम से स्नेह सम्मेलन मनाया गया।

Question 3.
पसंदीदा विषय पर विज्ञापन बनाकर उसको पढ़ो।
Answer:

Question 4.
फल-फूलों के दस-दस नाम लिखो।

Answer:

फलों के नाम:

१.अनार
२. आम
३. अमरूद
४. केला
५. खरबूजा
६. चीकू
७. जामुन
८. मोसंबी
९. तरबूज
१०. संतरा

फूलों के नाम:

१. कमल
२. कनेर
३. गुलाब
४. गेंदा
५. गुड़हल
६. चमेली
७. चंपा
८. जूही
९. पलाश
१०. मोगरा

Question 5.
अक्षर समूह में से खिलाड़ियों के नाम बताओ और लिखो।

Answer:

1. साइना नेहवाल
2. ध्यानचंद
3. खाशाबा जाधव
4. मिल्खा सिंह
5. मेरी कॉम
6. सानिया मिर्जा
7. सचिन तेंडुलकर