Category: Class 8

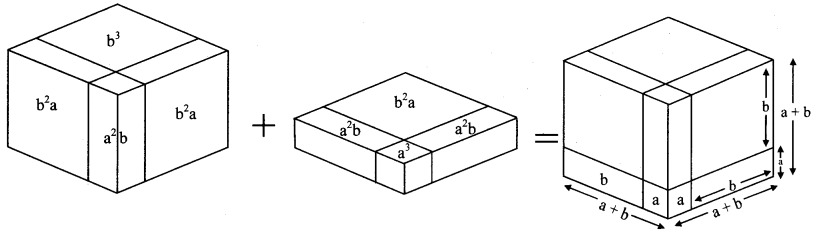
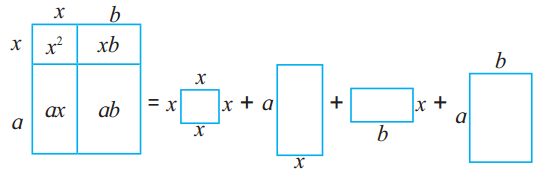Expansion Formulae Class 8 Maths Chapter 5 Practice Set 5.4 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.4 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Std 8 Maths Practice Set 5.4 Chapter 5 Solutions Answers

Question 1.
Expand:
i. (2p + q + 5)²
ii. (m + 2n + 3r)²
iii. (3x + 4y – 5p)²
iv. (7m – 3n – 4k)²
Solution:
i. (2p + q + 5)² = (2p)² + (q)² + (5)² + 2(2p) (q) + 2(q) (5) + 2(2p) (5)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 4p² + q² + 25 + 4pq + 10q + 20p

ii. (m + 2n + 3r)² = (m)² + (2n)² + (3r)² + 2(m) (2n) + 2(2n) (3r) + 2(m) (3r)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= m² + 4n² + 9r² + 4mn + 12nr + 6mr

iii. (3x + 4y – 5p)² = (3x)² + (4y)² + (- 5p)² + 2(3x) (4y) + 2(4y) (- 5p) + 2(3x) (- 5p)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 9x + 16y² + 25p² + 24xy – 40py – 30px

iv. (7m – 3n – 4k)² = (7m)² + (- 3n)² + (- 4k)² + 2(7m) (- 3n) + 2 (- 3n) (- 4k) + 2 (7m) (- 4k)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 49m² + 9n² + 16k² – 42mn + 24nk – 56km

Question 2.
Simplify:
i. (x – 2y + 3)² + (x + 2y – 3)²
ii. (3k – 4r – 2m)² – (3k + 4r – 2m)²
iii. (7a – 6b + 5c)² + (7a + 6b – 5c)²
Solution:
i. (x – 2y + 3)² + (x + 2y – 3)²
= [(x)² + (- 2y)² + (3)² + 2 (x) (- 2y) + 2 (- 2y) (3) + 2 (x) (3)] + [(x)² + (2y)² + (- 3)² + 2 (x) (2y) + 2 (2y) (- 3) + 2 (x) (- 3)]
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= x² + 4y² + 9 – 4xy – 12y + 6x + x² + 4y² + 9 + 4xy – 12y – 6x
= x + x² + 4y² + 4y² + 9 + 9 – 4xy + 4xy – 12y – 12y + 6x – 6x
= 2x² + 8y² + 18 – 24y

ii. (3k – 4r – 2m)² – (3k + 4r – 2m)²
= [(3k)² + (- 4r)² + (- 2m)² + 2 (3k) (- 4r) + 2 (- 4r) (- 2m) + 2 (3k) (- 2m)] – [(3k)² + (4r)² + (- 2m)² + 2 (3k) (4r) + 2 (4r) (- 2m) + 2 (3k) (- 2m)]
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= (9k² + 16r² + 4m² – 24kr + 16rm – 12km) – (9k² + 16r² + 4m² + 24kr – 16rm – 12km)
= 9k² + 16r² + 4m² – 24kr + 16rm – 12km – 9k² – 16r² – 4m² – 24kr + 16rm + 12km
= 9k² – 9k² + 16r² – 16r² + 4m² – 4m² – 24kr – 24kr + 16rm + 16rm – 12km + 12km
= 32rm – 48kr

iii. (7a – 6b + 5c)² + (7a + 6b – 5c)²
= [(7a)² + (- 6b)² + (5c)² + 2(7a) (-6b) + 2(-6b) (5c) + 2(7a) (5c)] + [(7a)² + (6b)² + (- 5c)² + 2 (7a) (6b) + 2 (6b) (- 5c) + 2 (7a) (- 5c)]
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 49a² + 36b² + 25c² – 84ab – 60bc + 70ac + 49a² + 36b² + 25c² + 84ab – 60bc – 70ac
= 49a² + 49a² + 36b² + 36b² + 25c² + 25c² – 84ab + 84ab – 60bc – 60bc + 70ac – 70ac
= 98a² + 72b² + 50c² – 120bc

Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 5.4 Intext Questions and Activities

Question 1.
Fill in the boxes with appropriate terms in the steps of expansion. (Textbook pg. no. 27)
(2p + 3m + 4n)²
= (2p)² + (3m)² + __ + 2 × 2p × 3m + 2 × __ × 4n + 2 × 2p × __
= __ + 9m² + __ + 12pm + __ + __
Solution:
(2p + 3m + 4n)²
= (2p)² + (3m)² + (4n)² + 2 x 2p x 3m + 2 x 3m x 4n + 2 x 2p x 4n
= 4p² + 9m² + 16n² + 12pm + 24mn + 16pn

Maharashtra Board Class 8 Maths Solutions

• Altitudes and Medians of a Triangle Practice Set 4.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.2 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.3 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.4 Class 8 Maths Solutions

Expansion Formulae Class 8 Maths Chapter 5 Practice Set 5.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.3 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Std 8 Maths Practice Set 5.3 Chapter 5 Solutions Answers

Question 1.
Expand:
i. (2m – 5)³
ii. (4 – p)³
iii. (7x – 9y)³
iv. (58)³
v. (198)³
vi. \(\left(2 p-\frac{1}{2 p}\right)^{3}\)
vii. \(\left(1-\frac{1}{a}\right)^{3}\)
viii. \(\left(\frac{x}{3}-\frac{3}{x}\right)^{3}\)
Solution:
i. Here, a = 2m and b = 5
(2m – 5)³
= (2m)³ – 3(2m)² (5) + 3(2m) (5)² – (5)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8m³ – 3(4m²)(5) + 3(2m)(25) – 125
= 8m³ – 60m² + 150m – 125

ii. Here, a = 4 and b = p
(4 – p)³ = (4)³ – 3(4)²(p) + 3(4)(p)² – (p)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 64 – 3(16)(p) + 3(4)(p²) – p³
= 64 – 48p + 12p² – p³

iii. Here, a = 7x and b = 9y
(7x – 9y)³
= (7x)³ – 3(7x)² (9y) + 3 (7x)(9y)² – (9y)³
…[(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 343x³ – 3(49x²)(9y) + 3(7x)(81y²) – 729y³
= 343x³ – 1323x²y + 1701xy² – 729y³

iv. (58)³ = (60 – 2)³
Here, a = 60 and b = 2
(58)³ = (60)³ – 3(60)²(2) + 3(60)(2)² – (2)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 216000 – 3(3600)(2) + 3(60)(4) – 8
= 216000 – 21600 + 720 – 8
=195112

v. (198)³ = (200 – 2)³
Here, a = 200 and b = 2
(198)³ = (200)³ – 3(200)²(2) + 3(200)(2)² – (2)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8000000 – 3(40000)(2) + 3(200)(4) – 8
= 8000000 – 240000 + 2400 – 8
= 7762392

vi. Here, a = 2p and b = \(\frac { 1 }{ 2p }\)

vii. Here, A = 1 and B = \(\frac { 1 }{ a }\)

viii. Here, a = \(\frac { x }{ 3 }\) and b = \(\frac { 3 }{ x }\)

Question 2.
Simplify:
i. (2a + b)³ – (2a – b)³
ii. (3r – 2k)³ + (3r + 2k)³
iii. (4a – 3)³ – (4a + 3)³
iv. (5x – 7y)³ + (5x + 7y)³
Solution:
i. (2a + b)³ – (2a – b)³
= [(2a)³ + 3(2a)²(b) + 3 (2a)(b)² + (b)³] – [(2a)³ – 3(2a)²(b) + 3 (2a)(b)² – (b)³]
… [(a + b)³ = a³ + 3a²b + 3ab² + b³, (a – b)³ = a³ – 3a²b + 3ab² – b³]
= (8a³ + 12a²b + 6ab² + b³) – (8a³ – 12a²b + 6ab² – b³)
= 8a³ + 12a²b + 6ab² + b³ – 8a³ + 12a²b – 6ab² + b³
= 8a³ – 8a³ + 12a²b + 12a²b + 6ab² – 6ab² + b³ + b³
= 24a²b + 2b³

ii. (3r – 2k)³ + (3r + 2k)³
= [(3r)³ – 3(3r)²(2k) + 3(3r)(2k)² – (2k)³] + [(3r)³ + 3(3r)²(2k) + 3(3r)(2k)² + (2k)³]
… [(a – b)³ = a³ – 3a²b + 3ab² – b³, (a + b)³ = a³ + 3a²b + 3ab² + b³]
= (27r³ – 54r²k + 36rk² – 8k³) + (27r³ + 54r²k + 36rk² + 8k³)
= 27r³ – 54r²k + 36rk² – 8k³ + 27r³ + 54r²k + 36rk² + 8k³
= 27r³ + 27r³ – 54r²k + 54r²k + 36rk² + 36rk² – 8k³ + 8k³
= 54r³ + 72rk²

iii. (4a – 3)³ – (4a + 3)³
= [(4a)³ – 3(4a)² (3) + 3(4a)(3)² – (3)³] – [(4a)³ + 3(4a)²(3) + 3(4a)(3)² + (3)³]
… [(a – b)³ = a³ – 3a²b + 3ab² – b³, (a + b)³ = a³ + 3a²b + 3ab² + b³]
= (64a³ – 144a² + 108a – 27) – (64a³ + 144a² + 108a + 27)
= 64a³ – 144a² + 108a – 27 – 64a³ -144a² – 108a – 27
= 64a³ – 64a³ – 144a² – 144a² + 108a – 108a – 27 – 27
= -288a² – 54

iv. (5x – 7y)³ + (5x + 7y)³
= [(5x)³ – 3(5x)²(7y) + 3(5x)(7y)² – (7y)³] + [(5x)³ + 3(5x)² (7y) + 3(5x) (7y)² +(7y)³]
… [(a – b)³ = a³ – 3a²b + 3ab² – b³, (a + b)³ = a³ + 3a²b + 3ab² + b³]
= (125x³ – 525x²y + 735xy² – 343y³) + (125x³ + 525x²y + 735xy² + 343y³)
= 125x³ – 525x²y + 735xy² – 343y³ + 125x³ + 525x²y + 735xy² + 343y³
= 125x³ + 125x³ – 525x²y + 525x²y + 735xy² + 735xy² – 343y³ + 343y³
= 250x³ + 1470xy²

Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 5.3 Intext Questions and Activities

Question 1.
Make two cubes of side a and of side b each. Make six parallelopipeds; three of them measuring a × a × b and the remaining three measuring b × b × a. Arrange all these solid figures properly and make a cube of side (a + b). (Textbook pg. no. 25)
Solution:
(a + b)³ = a³ + 3a²b + 3ab² + b³
= a × a × a + 3 × a × a × b + 3 × a × b × b + b × b × b

Maharashtra Board Class 8 Maths Solutions

• Altitudes and Medians of a Triangle Practice Set 4.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.2 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.3 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.4 Class 8 Maths Solutions

Discount and Commission Class 8 Maths Chapter 9 Practice Set 9.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 9.1 8th Std Maths Answers Solutions Chapter 9 Discount and Commission.

Std 8 Maths Practice Set 9.1 Chapter 9 Solutions Answers

8th Standard Maths Practice Set 9.1 Question 1. If marked price = Rs 1700, selling price = Rs 1540, then find the discount.
Solution:
Here, Marked price = Rs 1700,
selling price = Rs 1540
Selling price = Marked price – Discount
∴ 1540 = 1700 – Discount
∴ Discount = 1700 – 1540
= Rs 160
∴ The amount of discount is Rs 160.

Discount and Commission Practice Set 9.1 Question 2. If marked price Rs 990 and percentage of discount is 10, then find the selling price.
Solution:
Here, marked price = Rs 990,
discount = 10%
Let the percentage of discount be x
∴ x = 10%
i. Discount

= Rs 99

ii. Selling price = Marked price – Discount
= 990 – 99
= Rs 891
∴ The selling price is Rs 891.

Practice Set 9.1 Question 3. If selling price Rs 900, discount is 20%, then find the marked price.
Solution:
Here, selling price = Rs 900, discount = 20%
Let the marked price be Rs 100
Since, the discount given = 20%
∴ Amount of discount = Rs 20
∴ Selling price = 100 – 20 – Rs 80
Let actual marked price be Rs x
∴ For marked price of Rs x, selling price is Rs 900
\(\frac{80}{100}=\frac{900}{x}\)
∴ 80 × x = 100 × 900
∴ \(x=\frac{100 \times 900}{80}\)
∴ x = Rs 1125
∴ The marked price is Rs 1125.

Discount and Commission Std 8 Question 4. The marked price of the fan is Rs 3000. Shopkeeper gave 12% discount on it. Find the total discount and selling price of the fan.
Solution:
Here, Marked price = Rs 3000, discount = 12%
Let the percentage of discount be x.
∴ x = 12%
i. Discount

= 30 × 12
= Rs 360

ii. Selling price = Marked price – Discount
= 3000 – 360
= Rs 2640
∴ The total discount is Rs 360 and the selling price of the fan is Rs 2640.

Discount and Commission 8th Standard Question 5. The marked price of a mixer is Rs 2300. A customer purchased it for Rs 1955. Find percentage of discount offered to the customer.
Solution:
Here, marked price = Rs 2300,
selling price = Rs 1955
i. Selling price = Marked price – Discount
∴ 1955 = 2300 – Discount
∴ Discount = 2300 – 1955
= Rs 345

ii. Let the percentage of discount be x


∴ x = 15%
∴ The percentage of discount offered to the customer is 15%.

Question 6.
A shopkeeper gives 11% discount on a television set, hence the cost price of it is Rs 22,250. Then find the marked price of the television set.
Solution:
Here, selling price = Rs 22,250, discount = 11%
Let marked price be Rs 100
Since, the discount given = 11%
∴ Amount of discount = Rs 11
∴ Selling price = 100 – 11 = Rs 89
∴ Let actual marked price be Rs x
∴ For marked price of Rs x, selling price is Rs 22,250

∴ x = Rs 25,000
∴ The marked price of the television set is Rs 25,000.

8th Std Maths Discount and Commission Question 7. After offering discount of 10% on marked price, a customer gets total discount of Rs 17. To find the cost price for the customer, fill in the following boxes with appropriate numbers and complete the activity.
Solution:
Suppose, marked price of the item = 100 rupees Therefore, for customer that item costs 100 – 10 = 90 rupees.
Hence, when the discount is [10] then the selling price is [90] rupees.
Suppose when the discount is [17] rupees, the selling price is x rupees.

∴ The customer will get the item for Rs 153.

Question 8.
A shopkeeper decides to sell a certain item at a certain price. He tags the price on the item by increasing the decided price by 25%. While selling the item, he offers 20% discount. Find how many more or less percent he gets on the decided price.
Solution:
Here, price increase = 25%,
discount offered = 20%
Let the decided price be Rs 100
∴ Increase in price = Rs 25
∴ Shopkeeper marks the price = 100 + 25
= Rs 125
∴ marked price = Rs 125
Let the percentage of discount be x
∴ x = 20%

∴ Selling price = Marked price – Discount
= 125 – 25
= Rs 100
∴ If the decided price is Rs 100, then shopkeeper gets Rs 100.
∴ The shopkeeper gets neither more nor less than the decided price i.e. he gets 0% more / less.

Maharashtra Board Class 8 Maths Chapter 9 Discount and Commission Practice Set 9.1 Intext Questions and Activities

Question 1.
Write the appropriate numbers in the following boxes. (Textbook pg. no. 51)

1. \(\frac { 12 }{ 100 }=\) __ percent = __%
2. 47% = __
3. 86% = __
4. 4% of 300 = 300 × __ = __
5. 15% of 1700 = 1700 × __= __

Solution:

1. \(\frac { 12 }{ 100 }=\) 12 percent = 12%
2. 47% = \(\frac { 47 }{ 100 }\)
3. 86% = \(\frac { 86 }{ 100 }\)
4. 4% of 300 = 300 × \(\frac { 4 }{ 100 }\) = 12
5. 15% of 1700 = 1700 × \(\frac { 15 }{ 100 }\) = 255

Question 2.
You may have seen advertisements like ‘Monsoon Sale’, ‘Stock Clearance Sale’ etc offering different discount. In such a sale, a discount is offered on various goods. Generally in the month of July, sales of clothes are declared. Find and discuss the purpose of such sales. (Textbook pg. no. 51)
Solution:
(Students should attempt the above activity on their own)

Maharashtra Board Class 8 Maths Solutions

Maharashtra Board Class 8 Maths Solutions

• Discount and Commission Practice Set 9.1 Class 8 Maths Solutions
• Discount and Commission Practice Set 9.2 Class 8 Maths Solutions
• Division of Polynomials Practice Set 10.1 Class 8 Maths Solutions
• Division of Polynomials Practice Set 10.2 Class 8 Maths Solutions
• Statistics Practice Set 11.1 Class 8 Maths Solutions
• Statistics Practice Set 11.2 Class 8 Maths Solutions
• Statistics Practice Set 11.3 Class 8 Maths Solutions

Expansion Formulae Class 8 Maths Chapter 5 Practice Set 5.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.1 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Std 8 Maths Practice Set 5.1 Chapter 5 Solutions Answers

Question 1.
Expand :
i. (a + 2)(a – 1)
ii. (m – 4)(m + 6)
iii. (p + 8) (p – 3)
iv. (13 + x)(13 – x)
v. (3x + 4y) (3x + 5y)
vi. (9x – 5t) (9x + 3t)
vii. \(\left(m+\frac{2}{3}\right)\left(m-\frac{7}{3}\right)\)
viii. \(\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\)
ix. \(\left(\frac{1}{y}+4\right)\left(\frac{1}{y}-9\right)\)
Solution:
i. (a + 2)(a – 1)
= a² + (2 – 1) a + 2 × (-1)
..[∵ (x + A) (x + B) = x² + (A + B)x + AB]
= a² + a – 2

ii. (m – 4)(m + 6)
= m² + (- 4 + 6) m + (-4) × 6
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= m² + 2m – 24

iii. (p + 8) (p – 3)
= p² + (8 – 3) p + 8 x (-3)
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= p² + 5p – 24

iv. (13 + x) (13 – x)
= (13)² + (x – x) 13 + x × (-x)
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 169 + 0 × 13 – x²
= 169 – x²

v. (3x + 4y) (3x + 5y)
= (3x)² + (4y + 5y) 3x + 4y × 5y
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 9x² + 9y × 3x + 20y²
= 9x² + 27xy + 20y²

vi. (9x – 5t) (9x + 3t)
= (9x)² + [(-5t) + 3t] 9x + (-5t) × 3t
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 81x² + (-2t) × 9x – 15t²
= 81x² – 18xt – 15t²

vii. \(\left(m+\frac{2}{3}\right)\left(m-\frac{7}{3}\right)\)

viii. \(\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\)

ix. \(\left(\frac{1}{y}+4\right)\left(\frac{1}{y}-9\right)\)

Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 5.1 Intext Questions and Activities

Question 1.
Use the above formulae to fill proper terms in the following boxes. (Textbook pg. no. 23)

1. (x + 2y)² = x² + ___ + 4y²
2. (2x – 5y)² = __ – 20xy + __
3. (101)² = (100 + 1)² = ___+ ___ + 1² = ___
4. (98)² = (100 – 2)² = 10000 – ___ + ___ = ___
5. (5m + 3n) (5m – 3n) = ___ – ___ = ___ – ___

Solution:

1. (x + 2y)² = x² + 4xy + 4y²
2. (2x – 5y)² = 4x² – 20xy + 25y²
3. (101)² = (100 + 1)² = 10000 + 200 + 1² = 10201
4. (98)² = (100 – 2)² = 10000 – 400 + 4 = 9604
5. (5m + 3n) (5m – 3n) = (5m)² – (3n)² = 25m² – 9n²

Question 2.
Expand (x + a) (x + b) using formulae for areas of a square and a rectangle. (Textbook pg. no. 23)

(x + a) (x + b) = x² + ax + bx + ab
(x + a) (x + b) = x² + (a + b) x + ab
Solution:

∴ (x + a) (x + b) = x² + ax + bx + ab
∴ (x + a) (x + b) = x² + (a + b) x + ab

Maharashtra Board Class 8 Maths Solutions

• Altitudes and Medians of a Triangle Practice Set 4.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.2 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.3 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.4 Class 8 Maths Solutions

Expansion Formulae Class 8 Maths Chapter 5 Practice Set 5.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.2 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Std 8 Maths Practice Set 5.2 Chapter 5 Solutions Answers

Question 1.
Expand:
i. (k + 4)³
ii. (7x + 8y)³
iii. (7x + m)³
iv. (52)³
v. (101)³
vi. \(\left(x+\frac{1}{x}\right)^{3}\)
vii. \(\left(2 m+\frac{1}{5}\right)^{3}\)
viii. \(\left(\frac{5 x}{y}+\frac{y}{5 x}\right)^{3}\)
Solution:
i. Here, a = k and b = 4
(k + 4)³ = (k)³ + 3(k)² (4) + 3(k)(4)² + (4)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= k³ + 12k² + 3(k)(16) + 64
= k³ + 12k² + 48k + 64

ii. Here, a = 7x and b = 8y
(7x + 8y)³
= (7x)³ + 3(7x)² (8y) + 3(7x) (8y)² + (8y)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 343x³ + 3(49x²)(8y) + 3(7x)(64y²) + 512y³
= 343x³ + 1176x²y + 1344xy² + 512y³

iii. Here, a = 7 and b = m
(7 + m)³ = (7)³ + 3(7)²(m) + 3(7)(m)² + (m)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 343 + 3(49)(m) + 3(7)(m²) + m³
= 343 + 147m + 21m² + m³

iv. (52)³ = (50 + 3)³
Here, a = 50 and b = 2
(52)³ = (50)³ + 3(50)² (2) + 3(50)(2)² + (2)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 125000 + 3(2500)(2) + 3(50)(4) + 8
= 125000 + 15000 + 600 + 8
=140608

v. (101)³ = (100 + 1)³
Here, a = 100 and b = 1
(101)³
= (100)³ + 3(100)²(1) + 3(100)(1)² + (1)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 1000000 + 3(10000) + 3(100) (1) + 1
= 1000000 + 30000 + 300 + 1
= 1030301

vi. Here, a = x and b = \(\frac { 1 }{ x }\)

vii. Here, a = 2m and b = \(\frac { 1 }{ 5 }\)

viii. Here, a = \(\frac { 5x }{ y }\) and b = \(\frac { y }{ 5x }\)

Maharashtra Board Class 8 Maths Solutions

• Altitudes and Medians of a Triangle Practice Set 4.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.2 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.3 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.4 Class 8 Maths Solutions

Altitudes and Medians of a Triangle Class 8 Maths Chapter 4 Practice Set 4.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 4.1 8th Std Maths Answers Solutions Chapter 4 Altitudes and Medians of a Triangle.

Std 8 Maths Practice Set 4.1 Chapter 4 Solutions Answers

Question 1.
In ∆LMN, ___ is an altitude and __ is a median, (write the names of appropriate segments.)

Solution:
In ∆LMN, seg LX is an altitude and seg LY is a median.

Question 2.
Draw an acute angled ∆PQR. Draw all of its altitudes. Name the point of concurrence as ‘O’.
Solution:

Question 3.
Draw an obtuse angled ∆STV. Draw its medians and show the centroid.
Solution:

Question 4.
Draw an obtuse angled ∆LMN. Draw its altitudes and denote the ortho centre by ‘O’.
Solution:

Question 5.
Draw a right angled ∆XYZ. Draw its medians and show their point of concurrence by G.
Solution:

Question 6.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
Solution:

The point of concurrence of medians i.e. G and that of altitudes i.e. O lie on the same line PS which is the perpendicular bisector of seg QR.

Question 7.
Fill in the blanks.
Point G is the centroid of ∆ABC.
i. If l(RG) = 2.5, then l(GC) = ___
ii. If l(BG) = 6, then l(BQ) = ____
iii. If l(AP) = 6, then l(AG) = ___ and l(GP) = ___.

Solution:
The centroid of a triangle divides each median in the ratio 2:1.
i. Point G is the centroid and seg CR is the median.
∴ \(\frac{l(\mathrm{GC})}{l(\mathrm{RG})}=\frac{2}{1}\)
∴ \(\frac{l(\mathrm{GC})}{2.5}=\frac{2}{1}\) ……[∵ l(RG) = 2.5]
∴ l(GC) × 1 = 2 × 2.5
∴ l(GC) = 5

ii. Point G is the centroid and seg BQ is the median.
∴ \(\frac{l(\mathrm{BG})}{l(\mathrm{GQ})}=\frac{2}{1}\)
∴ \(\frac{6}{l(\mathrm{GQ})}=\frac{2}{1}\) …..[∵ l(BG) = 6]
∴ 6 × 1 = 2 × l(GQ)
∴ \(\frac { 6 }{ 2 }\) = l(GQ)
∴ 3 = l(GQ)
i.e. l(GQ) = 3
Now, l (BQ) = l(BG) + l(GQ)
∴ l(BQ) = 6 + 3
∴ l(BQ) = 9

iii. Point G is the centroid and seg AP is the median.
∴ \(\frac{l(\mathrm{AG})}{l(\mathrm{GP})}=\frac{2}{1}\)
∴ l(AG) = 2 l(GP) …..(i)
Now, l(AP) = l(AG) + l(GP) … (ii)
∴ l(AP) = 2l(GP) + l(GP) … [From (i)]
∴ l(AP) = 3l(GP)
∴ 6 = 3l(GP) ..[∵ l(AP) = 6]
∴ \(\frac { 6 }{ 3 }\) = l(GP)
∴ 2 = l(GP)
i.e. l(GP) = 2
l(AP) = l(AG) + l(GP) …[from (ii)]
∴ 6 = l(AG) + 2
∴ l(AG) = 6 – 2
∴ l(AG) = 4

Maharashtra Board Class 8 Maths Chapter 4 Altitudes and Medians of a Triangle Practice Set 4.1 Intext Questions and Activities

Question 1.
Draw a line. Take a point outside the line. Draw a perpendicular from the point to the line with the help of a set-square (Textbook pg. no, 19)
Solution:
Step 1: Draw a line l and a point P lying outside it.

Step 2: By placing a set-square on line l, draw a perpendicular to the line from point P.

Question 2.
Draw an acute angled ∆ABC and all its altitudes. Observe the location of the orthocentre. (Textbook pg. no. 20)
Solution:

Point O is the orthocentre.
Orthocentre lies in the interior of ∆ABC.

Question 3.
Draw a right angled triangle and draw all its altitudes. Write the point of concurrence. (Textbook: pg, no. 20)
Solution:

Point Q is the orthocentre.
The point of concurrence of altitudes PQ, QR and QS is Q.

Question 4.
i. Draw an obtuse angled triangle and all its altitudes.
ii. Do they intersect each other?
Draw the lines containing the altitudes. Observe that these lines are concurrent. (Textbook pg. no. 20)
Solution:
i.

Point O is the orthocentre.

ii. Yes, all the altitudes intersect at point O in the exterior of ∆PQR.

Question 5.
Draw three different triangles; a right angled triangle, an obtuse angled triangle and an acute angled triangle. Draw the medians of the triangles. Note that the centroid of each of them is in the interior of the triangle. (Textbook pg. no. 21)
Solution:
i. Right angled triangle:

ii. Obtuse angled triangle:

iii. Acute angled triangle:

Question 6.
Draw a sufficiently large ∆ABC.
Draw medians; seg AR, seg BQ and seg CP of ∆ABC.
Name the point of concurrence as G.
Measure the lengths of segments from the figure and fill in the boxes in the following table.

Observe that all of these ratios are nearly 2 : 1 (Textbook pg. no. 21)
Solution:

Question 7.
As shown in the given figure, a student drew ∆ABC using five parallel lines of a notebook. Then he found the centroid G of the triangle. How will you decide whether the location of G he found, is correct. (Textbook pg. no. 21)

Solution:
Draw seg AP ⊥ seg PE and seg EQ ⊥ seg QC.

Side AP || side EQ and AC is their transversal.
∴ ∠PAE ≅ ∠QEC …(i) [Corresponding angles]
In ∆ APE and ∆ EQC,
∠PAE ≅ ∠QEC …[From (i)]
∠APE ≅ ∠EQC
… [Each angle is of measure 90°]
side PE ≅ side QC
…. [Perpendicular distance between parallel lines]
∴ ∆ APE ≅ ∆ EQC … [By AAS test]
∴ AE = EC
… [Corresponding sides of congruent triangles]
∴ E is the midpoint of AC.
∴ seg BE is the median.
Similarly, seg CF is the median.
Since, the medians of a triangle are concurrent.
∴ G is the centroid of ∆ABC.

Question 8.
Draw an equilateral triangle. Find its circumcentre (C), incentre (I), centroid (G) and orthocentre (O). Write your observation. (Textbook pg. no. 22)
Solution:

From the figure, circumcentre (C), incentre (I), centroid (G) and orthocentre (O) of an equilateral triangle are the same.

Question 9.
Draw an isosceles triangle. Locate its centroid, orthocentre, circumcentre and incentre. Verify that they are collinear. (Textbook pg. no. 22)
Solution:

From the figure, centroid (G), orthocentre (O), circumcentre (C) and incentre (I) of an isosceles triangle lie on the same line AD.
∴ they are collinear.

Maharashtra Board Class 8 Maths Solutions

• Altitudes and Medians of a Triangle Practice Set 4.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.1 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.2 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.3 Class 8 Maths Solutions
• Expansion Formulae Practice Set 5.4 Class 8 Maths Solutions

Indices and Cube Root Class 8 Maths Chapter 3 Practice Set 3.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.3 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Std 8 Maths Practice Set 3.3 Chapter 3 Solutions Answers

Question 1.
Find the cube root of the following numbers.
i. 8000
ii. 729
iii. 343
iv. -512
v. -2744
vi. 32768
Solution:
i. 8000
= 2 × 2 × 2 × 10 × 10 × 10
= (2 × 10) × (2 × 10) × (2 × 10)
= (2 × 10)³
= 20³
∴ \(\sqrt[3]{8000}=20\)

ii. 729
= (3 × 3) × (3 × 3) × (3 × 3)
= (3 × 3)³
= 9³
∴ \(\sqrt[3]{729}=9\)

iii. 343
= 7 × 7 × 7
= 7³
∴ \(\sqrt[3]{343}=7\)

iv. -512
= 2 × 2 × 2 × 4 × 4 × 4
= (2 × 4) × (2 × 4) × (2 × 4)
= (2 × 4)³
= 8³
∴ – 512 = (- 8) × (- 8) × (- 8)
= (-8)³
∴ \(\sqrt[3]{-512}=-8\)

v. -2744
= 2 × 2 × 2 × 7 × 7 × 7
= (2 × 7) × (2 × 7) × (2 × 7)
= (2 × 7)³
= 14³
∴ -2744 = (-14) × (-14) × (-14)
= (-14)³
∴ \(\sqrt[3]{-2744}=-14\)

vi. 32768
= 2 × 2 × 2 × 4 × 4 × 4 × 4 × 4 × 4
= (2 × 4 × 4) × (2 × 4 × 4) × (2 × 4 × 4)
= (2 × 4 × 4)³
= 32³
∴ \(\sqrt[3]{32768}=32\)

Question 2.
Simplify:
i. \(\sqrt[3]{\frac{27}{125}}\)
ii. \(\sqrt[3]{\frac{16}{54}}\)
iii. If \(\sqrt[3]{729}=9\) then \(\sqrt[3]{0.000729}\) = ?
Solution:
i. \(\sqrt[3]{\frac{27}{125}}\)

ii. \(\sqrt[3]{\frac{16}{54}}\)

iii. \(\sqrt[3]{0.000729}\)


Note:
Here, number of decimal places in cube root = 6
∴ number of decimal places in cube of number = 2

Maharashtra Board Class 8 Maths Chapter 3 Indices and Cube Root Practice Set 3.3 Intext Questions and Activities

Question 1.
17 is a positive number. The cube of 17, which is 4913, is also a positive number. Cube of -6 is -216. Take some more positive and negative numbers and obtain their cubes. Find the relation between the sign of a number and the sign of its cube. (Textbook pg. no. 17)
Solution:
Consider, 6³ = 6 × 6 × 6 = 216 and (-4)³ = (- 4) × (- 4) × (- 4) = – 64
Thus, cube of a positive number is positive and cube of a negative number is negative.
∴ Sign of a number = sign of its cube.

Question 2.
In example 4 and 5 on textbook pg. no. 17, observe the number of decimal places in the number and number of decimal places in the cube of the number. Is there any relation between the two? (Textbook pg. no. 17)
Solution:
Yes, there is a relation between the number of decimal places in the number and its cube.
(1.2)³ = 1.728, (0.02)³ = 0.000008
No. of decimal places in 1.2 = 1
No. of decimal places in 1.728 = 3
No. of decimal places in 0.02 = 2
No. of decimal places in 0.000008 = 6
Thus, number of decimal places in cube of a number is three times the number of decimal places in that number.

Maharashtra Board Class 8 Maths Solutions

• Indices and Cube Root Practice Set 3.1 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.2 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.3 Class 8 Maths Solutions

Indices and Cube Root Class 8 Maths Chapter 3 Practice Set 3.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.1 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Std 8 Maths Practice Set 3.1 Chapter 3 Solutions Answers

Question 1.
Express the following numbers in index form.
i. Fifth root of 13
ii. Sixth root of 9
iii. Square root of 256
iv. Cube root of 17
v. Eighth root of 100
vi. Seventh root of 30
Solution:
i. \((13)^{\frac{1}{5}}\)
ii. \((9)^{\frac{1}{6}}\)
iii. \((256)^{\frac{1}{2}}\)
iv. \((17)^{\frac{1}{3}}\)
v. \((100)^{\frac{1}{8}}\)
vi. \((30)^{\frac{1}{7}}\)

Question 2.
Write in the form ‘nth root of a’ in each of the following numbers.
i. \((81)^{\frac{1}{4}}\)
ii. \((49)^{\frac{1}{2}}\)
iii. \((15)^{\frac{1}{5}}\)
iv. \((512)^{\frac{1}{9}}\)
v. \((100)^{\frac{1}{19}}\)
vi. \((6)^{\frac{1}{7}}\)
Solution:
i. Fourth root of 81.
ii. Square root of 49.
iii. Fifth root of 15.
iv. Ninth root of 512.
v. Nineteenth root of 100.
vi. Seventh root of 6.

Maharashtra Board Class 8 Maths Chapter 3 Indices and Cube Root Practice Set 3.1 Intext Questions and Activities

Question 1.
Using laws of indices, write proper numbers in the following boxes. (Textbook pg, no. 14)
i. \({ 3 }^{ 5 }\times { 3 }^{ 2 }={ 3 }^{ \left( \right) }\)
ii. \({ 3 }^{ 7 }\div { 3 }^{ 9 }={ 3 }^{ \left( \right) }\)
iii. \(({ 3 }^{ 4 })^{ 5 }={ 3 }^{ \left( \right) }\)
iv. \(5^{ -3 }=\frac { 1 }{ { 5 }^{ \left( \right) } }\)
v. \(5^{ 0 }=\left( \right) \)
vi. \(5^{ 1 }=\left( \right) \)
vii. \((5\times 7)^{ 2 }={ 5 }^{ \left( \right) }\times { 7 }^{ \left( \right) }\)
viii. \({ \left( \frac { 5 }{ 7 } \right) }^{ 3 }=\frac { { \left( \right) }^{ 3 } }{ { \left( \right) }^{ 3 } } \)
ix. \({ \left( \frac { 5 }{ 7 } \right) }^{ -3 }={ \left( \frac { \left( \right) }{ \left( \right) } \right) }^{ 3 }\)
Solution:
i. \({ 3 }^{ 5 }\times { 3 }^{ 2 }={ 3 }^{ 7 }\)
ii. \({ 3 }^{ 7 }\div { 3 }^{ 9 }={ 3 }^{ -2 }\)
iii. \(({ 3 }^{ 4 })^{ 5 }={ 3 }^{ 20 }\)
iv. \(5^{ -3 }=\frac { 1 }{ { 5 }^{ 3 } } \)
v. \(5^{ 0 }=1\)
vi. \(5^{ 1 }=5\)
vii. \((5\times 7)^{ 2 }={ 5 }^{ 2 }\times { 7 }^{ 2 }\)
viii. \({ \left( \frac { 5 }{ 7 } \right) }^{ 3 }=\frac { { 5 }^{ 3 } }{ { 7 }^{ 3 } } \)
ix. \({ \left( \frac { 5 }{ 7 } \right) }^{ -3 }={ \left( \frac { 7 }{ 5 } \right) }^{ 3 }\)

Maharashtra Board Class 8 Maths Solutions

• Indices and Cube Root Practice Set 3.1 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.2 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.3 Class 8 Maths Solutions

Indices and Cube Root Class 8 Maths Chapter 3 Practice Set 3.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.2 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Std 8 Maths Practice Set 3.2 Chapter 3 Solutions Answers

Question 1.
Complete the following table.

Solution:

Question 2.
Write the following numbers in the form of rational indices.
i. Square root of 5th power of 121.
ii. Cube of 4th root of 324.
iii. 5th root of square of 264.
iv. Cube of cube root of 3.
Solution:
i. \((121)^{\frac{5}{2}}\)
ii. \((324)^{\frac{3}{4}}\)
iii. \((264)^{\frac{2}{5}}\)
iv. \((3)^{\frac{3}{3}}\)

Maharashtra Board Class 8 Maths Solutions

• Indices and Cube Root Practice Set 3.1 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.2 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.3 Class 8 Maths Solutions

Parallel Lines and Transversals Class 8 Maths Chapter 2 Practice Set 2.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.2 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Std 8 Maths Practice Set 2.2 Chapter 2 Solutions Answers

Question 1.
Choose the correct alternative.
i. In the given figure, if line m || line n and line p is a transversal, then find x.

(A) 135°
(B) 90°
(C) 45°
(D) 40°
Solution:
(C) 45°

Hint:

line m || line n and line p is a transversal.
∴ m∠BFG + m∠FGD = 180°
…[Interior angles]
∴ 3x + x = 180°
∴ 4x = 180°
∴ x = \(\frac { 180 }{ 4 }\)
∴ x = 45°

ii. In the given figure, if line a || line b and line l is a transversal, then find x.

(A) 90°
(B) 60°
(C) 45°
(D) 30°
Solution:
(D) 30°

Hint:

line a || line b and line l is a transversal.
∴ m∠UVS = m∠PUV
…[Alternate angles]
= 4x
m∠UVS + m∠WVS = 180°
… [Angles in a linear pair]
∴ 4x + 2x = 180°
∴ 6x = 180°
∴ x = \(\frac { 180 }{ 6 }\)
∴ x = 30°

Question 2.
In the given figure, line p || line q. Line t and line s are transversals. Find measure of ∠x and ∠y using the measures of angles given in the figure.

Solution:

i. Consider ∠z as shown in figure.
line p || line q and line t is a transversal.
∴ m∠z = 40° …(i) [Corresponding angles]
m∠x + m∠z = 180° …[Angles in a linear pair]
∴ m∠x + 40o = 180° …[From(i)]
∴ m∠x= 180° – 40°
∴ m∠x = 140°

ii. Consider ∠w as shown in the figure.
m∠w + 70° = 180° …[Angles in a linear pair]
∴ m∠w = 180° – 70°
∴ m∠w = 110° …(ii)
line p || line q and line s is a transversal.
∴ m∠y = m∠w …[Alternate angles]
∴ m∠y =110° …[From (ii)]
∴ m∠x = 140°, m∠y = 110°

Question 3.
In the given figure, line p || line q, line l || line m. Find measures of ∠a, ∠b and ∠c, using the measures of given angles. Justify your answers.

Solution:
i. line p || line q and line l is a transversal.
∴ m∠a + 80° = 180° …[Interior angles]
∴ m∠a= 180° – 80°
∴ m∠a= 100°

ii. line l || line m and line p is a transversal.
∴ m∠c = 80° …(i) [Exterior alternate angles]

iii. line p || line q and line m is a transversal.
∴ m∠b = m∠c … [Corresponding angles]
m∠b = 80° …[From (i)]
∴ m∠a = 100°, m∠b = 80°, m∠c = 80°

Question 4.
In the given figure, line a || line b, line l is a transversal. Find the measures of ∠x, ∠y, ∠z using the given information.

Solution:
line a || line b and line l is a transversal.
∴ m∠x = 105° …(i) [Corresponding angles]

ii. m∠y = m∠x … [Vertically opposite angles]
∴ m∠y = 105° …[From (i)]

iii. m∠z + 105° = 180° …[Angles in a linear pair]
∴ m∠z = 180°- 105°
∴ m∠z = 75°
∴ m∠x = 105°, m∠y = 105°, m∠z = 75°

Question 5.
In the given figure, line p || line l || line q. Find ∠x with the help of the measures given in the figure.

Solution:

line p || line l and line IJ is a transversal.
m∠IJN = m∠JIH … [Alternate angles]
∴ m∠IJN = 40° …(i)
line l || line q and line MJ is a transversal.
m∠MJN = m∠JMK … [Alternate angles]
∴ m∠MJN = 30° …(ii)
Now, m∠x = m∠IJN + m∠MJN
…[Angle addition property]
= 40° + 30° …[From (i) and (ii)]
∴ m∠x = 70°

Maharashtra Board Class 8 Maths Chapter 2 Parallel Lines and Transversals Practice Set 2.2 Intext Questions and Activities

Question 1.
When two parallel lines are intersected by a transversal eight angles are formed. If the measure of one of these eight angles is given, can we find measures of remaining seven angles? (Textbook pg, no. 9)
Solution:
Yes, we can find the measures of the remaining angles.

In the given figure, line m || line n and line l is a transversal.
m∠a = 60°(say) …(i)
i. m∠a + m∠b = 180° …[Angles in a linear pair]
∴ 60° + m∠b =180° … [From (i)]
∴ m∠b = 180° – 60°
∴ m∠b = 120° …(ii)

ii. m∠c = m∠b …[Vertically opposite angles]
∴ m∠c = 120° .. .(iii) [From (ii)]

iii. m∠d = m∠a …[Vertically opposite angles]
∴ m∠d = 60° …(iv) [From (i)]

iv. m∠e = m∠d …[Alternate angles]
∴ m∠e = 60° … [From (iv)]

v. m∠f = m∠c …[Alternate angles]
∴ m∠f = 120° …[From (iii)]

vi. m∠g = m∠d …[Corresponding angles]
∴ m∠g = 60° … [From (iv)]

vii. m∠h = m∠c … [Corresponding angles]
∴ m∠h = 120° …[From (iii)]

Question 2.
As shown in the figure (A), draw two parallel lines and their transversal on a paper. Draw a copy of the figure on another blank sheet using a trace paper, as shown in the figure (B). Colour part Land part II with different colours. Cut out the two parts with a pair of scissors. Place, part I and part II on each angle in the figure A and answer the following questions. (Textbook pg. no. 9)

1. Which angles coincide with part I?
2. Which angles coincide with part II?

Solution:

1. ∠d, ∠f and ∠h coincide with part I.
2. ∠c, ∠e and ∠g coincide with part II.

Maharashtra Board Class 8 Maths Solutions

• Parallel Lines and Transversals Practice Set 2.1 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.2 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.3 Class 8 Maths Solutions