Category: Class 10

Class 10 English Chapter 1.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.3 On Wings of Courage Notes, Textbook Exercise Important Questions and Answers.

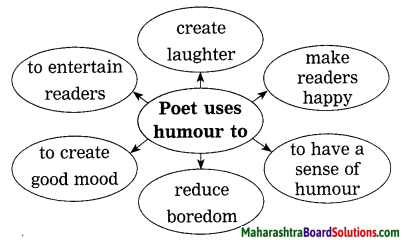
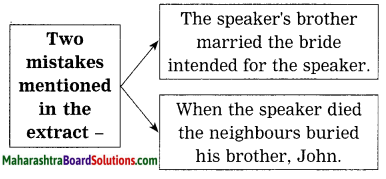
On Wings of Courage Poem 10th Std Question Answer

Maharashtra State Board Class 10 English Solutions Unit 1.3 Warming Up Questions and Answers

Question 1.
The ranks of officers in Indian Army, Navy and Air Force are jumbled up. Discuss with your group and put them in the appropriate boxes.

ARMY	NAVY	AIR FORCE

Answer:

Question 2.
Homophones/ Homographs
(A) Make sentences to bring out the difference between-
(1) (a) wear ……………………………………..
(b) ware ……………………………………..
(2) (a) here ……………………………………..
(b) hear ……………………………………..
(3) (a) there ……………………………………..
(b) their ……………………………………..
(4) (a) cell ……………………………………..
(b) sell ……………………………………..
Answer:
(1) (a) wear: The little girl wanted to wear a pink, frilly dress.
(b) ware: The silver ware laid out on the King’s table was exquisite.

(2) (a) here: “You must sit here,” said the man to his guest.
(b) hear: The children could hear the sound of the planes quite clearly.

(3) (a) there: “I had kept my bag there,” said the woman to the policeman.
(b) their: The girls picked up their bags and went home.

(4) (a) cell: The prisoner sat in the dark cell without talking.
(b) sell: The hawker wanted to sell all his wares before evening.

(B) Write what the underlined Homographs in the following sentences mean.
(1) (a) A bear is an omnivorous animal. ……………………………………..
(b) She could not bear the injustice. ……………………………………..
(2) (a) A bat is the only bird which is a mammal. ……………………………………..
(b) His bat broke as it struck the ball. ……………………………………..
(3) (a) He had to pay a fine for breaking the traffic signal. ……………………………………..
(b) Use a fine cloth for the baby’s clothes. ……………………………………..
(4) (a) We enjoyed a lot at the temple fair. ……………………………………..
(b) She has a fair complexion. ……………………………………..
Answer:
(1) (a) A bear is an omnivorous animal.
bear – a large, heavy animal
(b) She could not bear the injustice,
bear – to tolerate

(2) (a) A bat is the only bird which is a mammal.
bat – a mammal that flies
(b) His bat broke as it struck the ball.
bat – a wooden implement used for hitting the ball in many games.

(3) (a) He had to pay a fine for breaking the traffic signal.
fine – penalty
(b) Use a fine cloth for the baby’s clothes,
fine – delicate, soft

(4) (a) We enjoyed a lot at the temple fair.
fair – a gathering of stalls and amusements for public entertainment
(b) She has a fair complexion, fair – light, not dark

Maharashtra Board Class 10 English Kumarbharati Unit 1.3 Questions and Answers

Question 1.
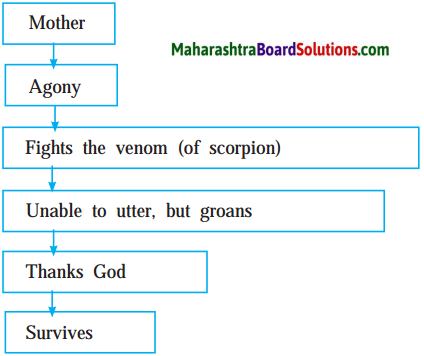
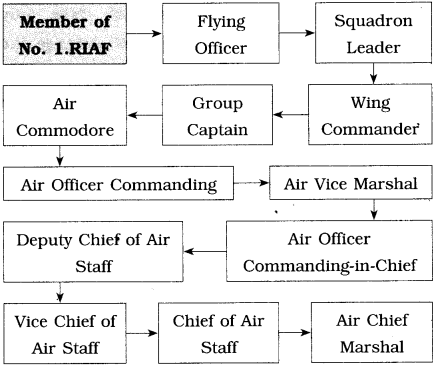
Read the text and fill in the flow chart of the promotions received by Arjan Singh.

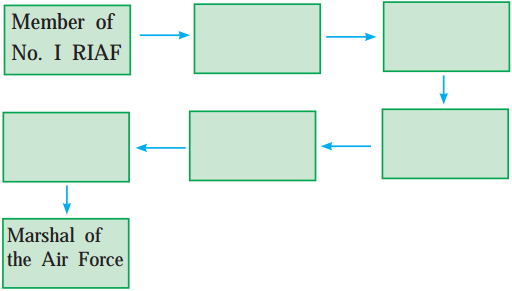
Answer:

Question 2.
With the help of facts given in the text prepare a Fact file of Air Marshal Arjan Singh.
(a) Date of Birth
(b) Place of Birth
(c) Education
(d) First Assignments
(e) Important posts held
(a) In Air Force
(b) After retirement
(f) Awards
(g) Most outstanding contribution in IAF
(h) Retirement
Answer:
(a) Date of birth: April 15, 1919
(b) Place of birth: Lyalpur
(c) Education: at Montgomery; Empire Pilot Training Course at RAF (Cranwell)
(d) First Assignment: to fly Westland Wapiti biplanes in the North-Western Frontier Province as a member of the No. 1 RIAF Squadron
(e) Important posts held:
(1) In Air Force: Member of No. 1. RIAF, Flying Officer, Squadron Leader, Wing Commander, Group Captain, Air Commodore, Air Officer Commanding, Air Vice Marshal, Air Officer Commanding-in-Chief, Deputy Chief of Air Staff, Vice Chief of Air Staff, Chief of Air Staff, Air Chief Marshal.
(2) After retirement: Ambassador to Switzerland Lieutenant Governor of Delhi
(f) Awards: Distinguished Flying Cross (1944); Padma Vibhushan
(g) Most outstanding contribution in IAF: Transforming the IAF into one of the most potent air forces globally and the fourth biggest in the world.
(h) Retirement: in August 1969.

Question 3.
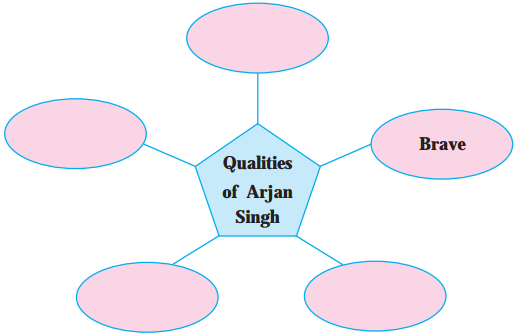
Fill in the web.

Answer:
(1) Singh had successfully led a young IAF during the 1965 Indo-Pak war.
(2) Singh played a major role in transforming the IAF into one of the most potent air forces globally and the fourth biggest in the world.
(3) Singh was honoured with the rank of Marshal on the Republic Day in 2002.
(4) Singh’s contribution was most outstanding during the 1965 Indo-Pak war.

Question 4.
Say what actions preceded the following promotions of Arjan Singh in his career in the IAF.
(a) Selected for Empire Pilot training course at RAF
(b) Promoted to Squadron Leader
(c) Leader of a flypast of over 100 aircraft at Red Fort, Delhi
(d) Awarded Padma Vibhushan
(e) First Air Chief Marshal of Indian Air Force
Answer:
(a) The authorities selected Singh for the Empire Pilot training course.
(b) He flew against the tribal forces and moved back to No. 1 Squadron as a Flying Officer to fly the Hawker Hurricane.
(c) On 15th August 1947, Arjan Singh achieved the unique honour of leading a fly-past of over a hundred IAF aircraft over the Red Fort in Delhi.
(d) He was awarded the Padma Vibhushan for his astute leadership of the Air Force and for inspiring the IAF to victory in the 1965 Indo-Pak war.
(e) He was a source of inspiration to all the personnel of the Armed Forces through the years.

Question 5.
Replace the underlined words/phrases with the appropriate ones, to retain the proper meaning.
(be the epitome of, gear up, a brief stint, play a major role, in recognition of, take over reins)
(a) He contributed notably in bringing up the school.
(b) Our school cricket team got ready for the final match against P. Q. R. High School.
(c) After a short period of working as a lecturer, Ravi took up an important post in a multi-national company.
(d) Our class monitor is a perfect symbol of duty and discipline.
(e) Accepting the great value of his research; they awarded him with a Ph.D. (degree)
(f) After the murder of King Duncan, Macbeth took over the control of Scotland.
Answer:
(a) He played a major role in bringing up the school.
(b) Our school cricket team geared up for the final match against P.Q.R.High School.
(c) After a brief stint as a lecturer, Ravi took up an important post in a multinational company.
(d) Our class monitor is the epitome of duty and discipline.
(e) In recognition of his research, they awarded him with a Ph.D. (degree)
(f) After the murder of King Duncan, Macbeth took over the reins of Scotland.

Question 6.
Build the word wall with the words related to ‘Military’.

Answer:

Question 7.
(A) State the different meanings of the following pairs of Homophones and make sentences of your own with each of them.

Answer:

(B) The following Homographs have the same spelling and pronunciation but can have different meanings. Make sentences of your own to show the difference.

Answer:
(a) firm: (i) My neighbour recently Joined an electronics firm as Sales Executive.
(ii) Many people feel that they must be firm with their children when they are growing.

(b) train: (i) The train left from platform 2 at seven p.m. sharp.
(ii) You must always train your pets to obey you.

(c) type: (i) The man asked his secretary to type the letter immediately.
(ii) Cows eat only a particular type of grass.

(d) post: (i) My aunt quit her job because she felt that the post was not suitable for her.
(ii) The little boy ran to the post office to post the letter to Santa Claus.

(e) current : (i) The minister was disturbed when he read about the current situation of unrest In the country.
(ii) It is a difficult task to row against the current in a river.

Question 8.
Glance through the text and prepare notes from the information that you get. Take only relevant points. Don’t use sentences. Arrange the points in the same order. You may use symbols or short forms. Present the points sequentially. Use highlighting techniques.
Answer:
Air Force Marshal Arjart Singh—Icon of India’s Military History

1. Date of Birth: 15 April, 1919
2. Qualifications: Empire Pilot Training Course at RAF (Cranwell)
3. Responsibilities:

• first assignment to fly Westland Wapiti biplanes in No.l RIAF Squadron
• brief stint in No.2 RIAF Squadron; moved back to No. 1 RIAF Squadron as Flying Officer
• overall commander of ‘Shiksha’
• led the IAF during the 1965 Indo-Pak war
• led a squadron against the Japanese during the Arakan Campaign; assisted the advance of Allied Forces to Yangoon
• led a fly-past on August 15, 1947
• commanded Ambala in the rank of Group Captain; took over as AOC of an operational command
• took over reins of the IAF
• ambassador to Switzerland; Lieutenant Governor of Delhi

(4) Achievements:

• selected for the Empire Pilot Training Course at RAF (Cranwell) in 1938, at age 19
• promoted to the rank of Squadron Leader in 1944
• led a fly-past over the Red Fort on August 15, 1947
• promoted to the rank of Wing Commander; promoted to the rank of Air Commodore in 1949
• longest tenure as AOC (1949-1952 and 19571961)
• appointed as Deputy Chief of Air Staff at the end of the 1962 war; appointed as Vice Chief of Air Staff in 1963
• rank of Air Marshal in August 1964; took over reins of IAF
• successfully led the IAF in 1965 Indo-Pak war
• promoted as Air Vice Marshal; appointed as AOC-in-C of an operational command
• first Air Chief to keep his flying currency till his CAS rank; has flown more than 60 different types of * aircraft
• first and only Air Chief Marshal of the IAF

(5) Awards:

– Distinguished Flying Cross (1944)
– Padma Vibhushan

(6) After retirement: Ambassador to Switzerland; Lieutenant Governor of Delhi
(Students can put these points attractively in boxes and use highlighting techniques.)

Question 9.
Develop a story suitable to the conclusion/end given below. Suggest a suitable title.
………………………………………………….. (Title)
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
………………………………………………………….. and so, with tears of joy and pride, the 10 year old Sanyogita More received the National Bravery Award from the Prime Minister.
Answer:
A WONDERFUL ACT OF BRAVERY
It was the 26th of July in Mumbai. It was raining cats and dogs. Ten-year-old Sanyogita More stood at the door of her hut. The street was flooded with water. Sanyogita was frightened. Her parents had not returned from work and she was all alone.

Suddenly, she saw two little boys, Rohan and Sohan, come out from the neighbouring hut to play in the water. As Sanyogita watched, there came a sudden gush of water and the boys were dragged towards an open manhole, which had been marked with a pole. They caught hold of the pole, but the pole began to tilt. It would soon fall—and the boys would go down the manhole!

Sanyogita ran as fast as she could towards the boys. Pulling a rope from a nearby door, she looped it around a large stone. She held onto the rope and extended her hand towards the boys. “Catch my hand, Sohan, Rohan,” she shouted. “Catch! Catch soon!”

The boys were in a panic but they did as they were told. Sohan held Rohan’s leg, Rohan held Sanyogita’s hand, and Sanyogita held onto the rope.

“Help! Help! she shouted, knowing that if the rope broke or the stone was dislodged, they would all go into the manhole.

She stood there shivering, her arms numb, for nearly 15 minutes before help arrived. Sanyogita collapsed after the incident. The news of her brave deed spread far and wide, and reached the ears of 1 the Prime Minister, who decided to honour her with an award. And so, with tears of joy and pride, the 10- I year-old Sanyogita More received the National Bravery ‘ Award from the Prime Minister.

Question 10.
You wish to join any one of the Indian Armed Forces. Fill in the following application form.
To
The Advertiser
N/AF Recruitment Service
Purangaon – 456 789

Affix recent
passport size
photograph

Application For Recruitment
Rect notice No 1234

1. Post applied for
2. Name and surname of Candidate (in Block letters)
3. Father’s Name ………………………………… Mother’s Name …………………………………
4. Date of Birth
5. Contact details :
Tel. No. (Res) ………………….. . Mobile No.
Email ID ………………….. .
6. Permanent Address :
House No./Street/Village ………………….. .
Post Office ………………….. .
District ………………….. State ………………….. .
Pincode ………………….. .
7. Educational Qualifications :

Serial Number	Qualification	Name of School/College	Name of Board/University	Percentage obtained

8. Whether registered at any employment exchange Yes/ No ………………….. (If yes, mention registration number and the name of the Employment Exchange.)

9. Outstanding achievements in extra-curricular activities/ sports/ games, etc.
………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………….

10. Why you wish to join Armed Forces. …………………………………………………………………
………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………….

English Kumarbharati 10th Digest PDF 

• Where the mind is Without fear 10th English Textbook Solutions
• The Thief’s Story 10th English Textbook Solutions
• On Wings of Courage 10th English Textbook Solutions
• All the World’s a Stage 10th English Textbook Solutions
• Joan of Arc 10th English Textbook Solutions
• The Alchemy of Nature 10th English Textbook Solutions

Class 10 English Chapter 3.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.3 Stopping by Woods on a Snowy Evening Notes, Textbook Exercise Important Questions and Answers.

Stopping by Woods on a Snowy Evening Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.3 Stopping by Woods on a Snowy Evening Textbook Questions and Answers

Warming up:
Chit-chat

Share this chat with your classmate:

Question 1.
Where did you go for a picnic recently?
Answer:
Recently I went to Mahabaleshwar.

Question 2.
Who all accompanied you?
Answer:
My family members accompanied me.

Question 3.
Why did you select that picnic spot?
Answer:
It is very close to Mumbai. We could enjoy the scenic beauty, invigorating and refreshing climate so we selected that picnic spot.

Question 4.
What games/food/sights did you enjoy there?
Answer:
We enjoyed Antakshari on the way. We also enjoyed veg, non-veg food. We visited different points, Venna lake, Panchgani and Pratapgarh.

Question 5.
What did you feel when it was time to return home?
Answer:
The memories of our pleasant picnic were unforgettable. The picnic was a nice change in our dull routine life. We returned home happily with refreshed minds.
(Note: Students may share their own experience with classmates based on the above guidelines.)

1. Look at the picture given on textbook page 101 and frame questions:

Question 1.
Look at the picture given on textbook page 101 and frame questions:

(a) Where are the trekkers trekking?
(b) …………………………………………… .
(c) …………………………………………… .
(d) …………………………………………… .
(e) …………………………………………… .
Answer:
(a) Where are the trekkers trekking?
(b) Which season is it?
(c) What equipment do you think they are carrying?
(d) In which region of India do you find such trekkers?
(e) What is the role of mountaineers in such trekking?

2. Form group of 4 to 6 students. Every student should close his/her eyes. As the group leader reads aloud the following lines, the students try to create a picture in his/her mind. Later, each one gives a heading for each description.

Question (a)
Bright blue sky – soft white clouds sweeping by tiny specks of birds flying high – sun playing hide and seek behind the clouds.
Heading: ………………………….. .
Answer:
Heading: The Enchanting Beauty of the Sky.

Question (b)
Miles of smooth barren land – sparkling sand stretched till the horizon, in wave – like forms – thorny, cacti propping here and there – an occasional cluster of palms provide a shady spot – a carvan of camels moving in a line in the distance.
Heading: ………………………….. .
Answer:
Heading: Life in the Desert

Such a figurative description that creates mental pictures, in the mind of the reader/listener is called Imagery. It is a poetic device that enhances the poem.

Compose in your group, a four to six-line poem, which contains imagery.

(1) A host of golden daffodils,
Beside the lake, beneath the trees,
Fluttering and dancing in the breeze,
Continuous as the stars that shine
And twinkle on the milky way.

(2) The night was black as ever,
but bright stars lit up the sky in beautiful and
varied constellation which were sprinkled
across the astronomical landscape.

English Workshop:

1. Put (✓) mark in front of True statement or (✗) mark in front of False statement:

Question 1.
Put (✓) mark in front of True statement or (✗) mark in front of False statement:
(Answers are directly given.)
Answer:

1. The speaker stops to watch rain falling among the trees. (✗)
2. The owner of the woods is known to the speaker. (✓)
3. The horse is worried about the cold and wants to keep going. (✗)
4. The speaker doesn’t emphasize upon the beauty of woods he is passing through. (✗)

2. Find outline/lines from the poem as a proof for the following explanation:

Question (a)
There is no one to catch the speaker trespassing.
Answer:
He will not see me stopping here
To watch his woods fill up with snow.

Question (b)
The little horse draws his master’s attention.
Answer:
He gives his harness bells a shake
To ask if there is some mistake.

Question (c)
His horse seems anxious to keep going.
Answer:
My little horse must think it queer
To stop without a farmhouse near.

Question (d)
The speaker prefers to stay but is forced to move onwards.
Answer:
But I have promises to keep And miles to go before I sleep ….

Question (e)
The poem is set in bygone era.
Answer:
He gives his harness bells a shake. Shows that the poem is set in the bygone era.

3. The poem is believed to have a reference to the poet’s life itself. What could the following signify? Choose from the brackets below:

Question 1.
The poem is believed to have a reference to the poet’s life itself. What could the following signify? Choose from the brackets below: (duties and responsibilities/old age/life/death/ everlasting peace)
Answer:

1. The speaker’s journey – life
2. Snowy Evening – old age
3. Lovely, deep, dark woods – everlasting peace
4. Promises – duties and responsibilities
5. Sleep – death

4. Tell whether the rhyming scheme of the following stanzas is right or wrong. Give the correct rhyme scheme for the wrong one:

Question 1.
Tell whether the rhyming scheme of the following stanzas is right or wrong. Give the correct rhyme scheme for the wrong one:
Answer:

1. stanza 1 – aaba : right
2. stanza 2 – bbcb : wrong – it is ‘aaba’
3. stanza 3 – ccdc : wrong – it is ‘aaba’
4. stanza 4 – dded : wrong – it is aaaa’

5. Give your own rhyming words for the following: (Answers are directly given.)

Question 1.
Give your own rhyming words for the following: (Answers are directly given.)
Answer:

1. house – spouse
2. woods – goods
3. easy – busy
4. wind – skinned
5. dark – bark
6. watch – botch

6. Match the lines of the poem with their figures of speech:

Question 1.
Match the lines of the poem with their figures of speech:

Answer:

1. Whose woods these are I think I know – Inversion
2. The woods are lovely, dark and deep – Alliteration
3. And miles to go before I sleep
   And miles to go before I sleep. – Repititon
4. My little horse must think it queer – personification

7. Match the words given in Group A with their meanings in Group B:

Question 1.
Match the words given in Group A with their meanings in Group B:

Answer:

1. mistake – error
2. downy flakes – soft snow falling
3. woods – jungle
4. queer – strange

8. Complete the following web-diagrams by adding suitable describing words in the boxes.

Question 1.
Complete the following web-diagrams by adding suitable describing words in the boxes. (Answers are directly given.)

Answer:

9. Pick out lines from the poem that contain imagery. Write them in your notebook.

Question 1.
Pick out lines from the poem that contain imagery. Write them in your notebook.

10. Prepare a set of questions to interview:

Question (a)
a person who has just returned from a trek in the woods:
Answer:

1. Welcome back, how did you feel when you visited the woods?
2. What was the purpose of your visit?
3. Did you take any precautions while roaming in the woods?
4. Which strange or rare things did you find in the woods?
5. Did you come across any wild animals ? What was your feeling then?
6. How did you manage to get your food, water and other essential things ?
7. What difference did you find in the woods and the place where you live?
8. Were you able to fulfil your expectations from this visit?
9. What should be your role to conserve the woods?
10. Would you like to suggest the youngsters to undertake such expeditions? Why?

Question (b)
a person who has recently scaled Mt. Everest:
Answer:

1. Welcome back, What preparations did you make before the climb?
2. What did you do to stay fit when you were at the base?
3. What did you do to make your climb interesting?
4. What food did you take along with you while climbing?
5. What was the purpose of your adventure?
6. How did you face difficulties on the way to the top?
7. What is the memorable moment of your ascent?
8. What was the hardest adjustment you had to make during the ascent?
9. What were your feelings when you scaled the peak?
10. What message would you give to the youngsters?

My English Coursebook 10th Digest Chapter 3.3 Stopping by Woods on a Snowy Evening Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. The speaker stops in the woods.
2. Winter season of the year is described in the poem.
3. The day described in the poem is evening.
4. The speaker is riding on his little horse.

Question 2.
Fill in the blanks:
(Answers are directly given.)
Answer:

1. The person who owns the woods lives in the village.
2. The speaker stopped his horse at a place between the frozen lake and the woods.
3. The speaker was really captivated by the lovely, dark and deep woods.
4. The little horse gives a shake to its harness bells attached to its neck.

Question 3.
List the sounds mentioned in the poem.
Answer:
harness bells, sound of wind, sound of soft feathers like snow flakes falling.

Question 4.
On what date every year is the darkest evening?
Answer:
On 21st December.

Complex Factual Activities:

Question 1.
Why does the traveller have to leave the lovely woods?
Answer:
The traveller is really captivated by the lovely woods. He is supposed to discharge his duties on time. He promises himself to keep his word. So he has to leave the lovely woods to keep his word.

Language Study:

Question 1.
Write your own lines using the words given below: (Answers are directly given.)
Answer:
(a) village: Life in my village, I long to live.
(b) wind: Wind was twisting the heads of trees.
(c) frozen: With frozen heart I stared at the remains of my dear friend.
(d) promise: Let every day of yours dawn, with the promises of new light.

Appreciation of the poem:

1. Title : The title of the poem ‘Stopping by Woods on a Snowy Evening’.
2. Poet: The poet of this poem is Robert (Lee) Frost.
3. Rhyme scheme: The rhyme scheme of the first three stanzas is ‘aaba’. The final stanza has a uniform rhyme of ‘aaaa’.
4. Figure of speech (any 1): Inversion, alliteration
5. Theme / Central Idea: The theme of the poem is that a traveller on horseback stops by a little forest on a winter evening.

The little forest in the speaker’s own words, is lovely, dark and deep. Though he is greatly fascinated by the scene, the call of duty urges him to move on. He reminds himself that he must discharge his duties before it is too late.

My English Coursebook Standard Ten Digest Answers Pdf Unit 3 

• Chapter 3.1 If … 10th English Solutions
• Chapter 3.2 A Lesson in Life from a Beggar 10th English Solutions
• Chapter 3.3 Stopping by Woods on a Snowy Evening 10th English Solutions
• Chapter 3.4 Let us March! 10th English Solutions
• Chapter 3.5 The Alchemy of Nature 10th English Solutions

Class 10 English Chapter 4.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.1 A Thing of Beauty is a Joy For Ever Notes, Textbook Exercise Important Questions and Answers.

A Thing of Beauty is a Joy For Ever Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 4.1 Warming Up Questions and Answers

A Thing Of Beauty Is A Joy Forever Question 1.
(A) Fill in the Acrostic with names of things related to Nature.
B …………………..
E …………………..
A …………………..
U …………………..
T …………………..
Y …………………..
Answer:
Birds
Earth
Animals
Uranus
Trees
Yam

(B) Make a list of 10 words related to the word ‘joy’, for example, happiness.
1. …………………..
2. …………………..
3. …………………..
4. …………………..
5. …………………..
6. …………………..
7. …………………..
8. …………………..
9. …………………..
10. ………………….
Answer:
happiness,
pleasure,
ecstasy,
delight,
rapture,
jubilation,
elation,
exultation,
glee,
euphoria.

A Thing Of Beauty Important Questions Question 2.
Recollect a picnic or a trip to a spot of natural beauty (a hill station/ a beach/forest area etc.) when you were younger.
Write four beautiful unforgettable scenes that left a deep impact on you.
(1) …………………………………………………………
(2) …………………………………………………………
(3) …………………………………………………………
(4) …………………………………………………………
Answer:
(1) The setting sun disappearing behind the hills.
(2) The river shining deep down in the valley.
(3) The early morning mist.
(4) The rain water trickling down from the leaves.

A Thing Of Beauty Is A Joy Forever Poem Question 3.
‘Meter’ in poetry is a pattern of stressed and unstressed syllables in lines of a poem. It gives rhythm to the poem.

Read the poem below aloud and with any colored pen/ pencil put stress-marks ( ‘ ) on those syllables that are stressed in the words of the poetic lines.

THE steadfast coursing of the stars,
The waves that ripple to the shore,
The vigorous trees which year by year
Spread upwards more and more ;
The jewel forming in the mine,
The snow that falls so soft and light,
The rising and the setting sun,
The growing glooms of night,
All natural things both live and move
In natural peace that is their own ;
Only in our disordered life
Almost is she unknown.

A Thing Of Beauty Extract Questions Question 4.
Consonance and Assonance
Consonance : Repetition of consonant sounds within a word, phrase or a short sentence.
For example : pitter-patter/ chuckle-fickle/ sick-duck/ Betty bought some bitter butter
Answer:
Consonance: (Repetition of consonant sounds within a word, phrase or a short sentences)
(1) The steadfast coursing of the stars
(2) The waves that ripple to the shore
(3) The snow that falls so soft and light
(4) The rising and the setting sun
(5) All natural things both live and move.

Assonance : Repetition of vowel sounds within a word/ phrase/ sentence.
For example : Jack had a bag.
Men sell metal- kettle.
Let the engineer steer without fear.
Answer:
Assonance: (Repetition of vowel sounds within a word/phrase/sentence.)
(1) The vigorous trees which year by year
(2) Spread upwards more and more
(3) Theewel forming in the mine
(4) Only in our disordered life.

Thing of Beauty is a Joy For Ever Class 10 English Workshop Questions and Answers Maharashtra Board

A Thing Of Beauty Question Answer Question 1.
Read the poem and fill in the table.

Answer:

A Thing Of Beauty Is Joy Forever Question 2.
Answer in your own words.
(a) What is the impact of a beautiful thing on us?
(b) What does a thing of beauty keep in store, for us?
(c) Who are the mighty dead? Why are they attributed with ‘grandeur’?
(d) How does the memory of a beautiful visual scene become a joy forever?
Answer:
(a) A beautiful thing gives us happiness, relaxation and peace. It inspires us and makes us love life despite troubles and sufferings.
(b) A thing of beauty provides shelter and comfort in many ways. It is like a shady place under a tree where we can rest. It helps all living creatures to sleep peacefully, have good dreams and also good health.
(c) The memory of a beautiful visual scene leaves a lasting impression on us. It is a permanent source of joy and inspiration to five our lives despite the trials and tribulations. The pleasure and happiness given by it never fades away but keeps on increasing.
(d) The mighty dead are the brave men who have sacrificed their lives for a purpose. They Eire an inspiration to all of us because of their innumerable sacrifices. They are attributed with grandeur because of their noble deeds.

A Thing Of Beauty Is A Joy Forever Question And Answer Question 3.
Pick out and rewrite 5 lines that contain Imagery.
For example :
(a) we are wreathing a flowery band…
(b) …………………………………………
(c) …………………………………………
(d) …………………………………………
(e) …………………………………………
Answer:
(a) we are wreathing a flowery band
(b) trees old and young, sprouting a shady boon
(c) and such are daffodils with the green world they live in
(d) and clear rills that for themselves a cooling covert make
(e) the mid forest brake, rich with a sprinkling of fair musk-rose blooms

Thing Of Beauty Question Answers Question 4.
Choose the correct Figure of speech that occurs in the following lines. Justify your choice.
(a) ………………….. but still we keep a bower quiet for us
(i) Simile
(ii) Irony
(iii) Metaphor
Answer:
(iii) Metaphor

(b) Some shape of beauty moves away the pall …………………..
(i) Personification
(ii) Alliteration
(iii) Hyperbole
Answer:
(ii) Alliteration

(c) A thing of beauty is a joy for ever …………………..
(i) Epigram
(ii) Antithesis
(iii) Climax
Answer:
(i) Epigram

(d) Trees old and young, sprouting a shady boon.
(i) Exclamation
(ii) Personification
(iii) Antithesis
Answer:
(iii) Antithesis

The Thing Of Beauty Is A Joy Forever Question 5.
From the poem pick out words that we do not use often in modern times. They should match the meanings given below.
(a) gift …………………..
(b) the next day …………………..
(c) a protective spot ………………….. (for animals)
(d) a cool shady spot ………………….. under tall trees.
(e) ferns …………………..
(f) edge …………………..
(g) depression …………………..
(h) cover for the dead …………………..
(i) streams …………………..
(j) poetry …………………..
Answer:
(a) gift – boon
(b) the next day – morrow
(c) a protective spot for animals – covert
(d) a cool shady spot bower under tall trees
(e) ferns – brake
(f) edge – brink
(g) depression – despondence
(h) cover for the dead – pall
(i) streams-rills
(j) poetry – poesy

A Thing Of Beauty Is A Joy For Ever Question 6.
Copy the first 8 lines and mark the stressed syllables using a coloured pen.

A Thing Of Beauty Is A Joy Question 7.
Read the poem and write-
(a) The rhyme scheme of the following lines.
Lines 1 to 8 …………………..
Last stanza …………………..
Answer:
Rhyme scheme of lines 1 – 8: aabb, ccdd
Rhyme scheme of the last stanza: aabbc.

(b) (i) The number of stressed syllables (Rhythm) in the line.
A thing of beauty is a joy forever. ………………….
Answer:
A thing of beauty is a joy forever. The title of the poem

(ii) Does the poem retain a steady rhythm throughout?
Answer:
Yes.

(c) Give four examples of each. Pick the lines from the poem.
(i) Consonance:
(1) ………………….
(2) ………………….
(3) ………………….
(4) ………………….
Answer:
(1) A flowery band to bind us to the earth
(2) For simple sheep; and such are the daffodils
(3) With the green world they live in; and clear rills.
(4) All lovely tales that we have heard or read

(ii) Assonance :
(1) ………………….
(2) ………………….
(3) ………………….
(4) ………………….
Answer:
(1) A thing of beauty is joy forever
(2) Pass into nothingness, but still will keep
(3) And such too is the grandeur of the dooms
(4) That whether there be shine or gloom o’ercast

I Think Of Beauty Is A Joy Forever Question 8.
Go through the poem again and write in your notebook an appreciation of the poem in the paragraph format. (Refer to page no. 5 )
Answer:
Point Format
(for understandig)
The title of the poem : ‘A Thing of Beauty Is a Joy Forever’
The poet : John Keats
Rhyme schenie: aabb; rhyming couplets
Figures of speech : EpIgram, Metaphor, Antithesis, etc.
Theme/Central idea: Beautiful things give unending pleasure and can change our lives.

Paragraph Format
The poem ‘A Thing of Beauty is aoy Forever’ byohn Keats is taken from a longer poem ‘Endymion’ based on Greek Mythology.

The rhyme scheme of the poem is aabb; that is, the poem is written in rhyming couplets. There Eire many figures of speech, like Metaphor, Antithesis, etc. but the one that stands out is Epigram. The line A thing of beauty is aoy forever’, is a pithy saying expressing the idea of beauty in a clever way.

The important thing that the poet tells us is that beautiful things last forever and give us immense i happiness. They give unending pleasure and can change our lives.

Question 9.
Project :
Collect from various sources proverbs or maxims related to the ‘beauty of nature.’ Make a chart/ poster with the same. Decorate it with images, drawings, pictures, and put it up by turns in your class.

Question 10.
List the things of beauty mentioned in the extract.
Answer:
The things of beauty include a quiet bower, the heavenly bodies like the sun and the moon, the old and young trees that provide cool shelter to sheep, daffodils with greenery around them, clear streams that make cool thickets for themselves and ferns with musk-roses scattered in between.

Question 11.
List the things that cause suffering and pain.
Answer:
The things that cause suffering and pain are despondence and despair, shortage of noble people, hot season, gloomy days and the unhealthy and darkened ways of life (trials and difficulties of life).

Question 12.
Choose the correct figures of speech that occur in the following lines.ustify your choice.
(1) ….but still we keep a bower quiet for us….
(a) Simile (b) Irony (c) Metaphor
Answer:
Metaphor – bower stands for rest and peace

Question 13.
Some shape of beauty moves away the pall
(a) Personification (b) Alliteration (c) Hyperbole
Answer:
Alliteration – Repetition of the sound of the letter ‘s’.
Personification – beauty is given the human quality of moving away the pall. *

Question 14.
A thing of beauty is aoy forever….
(a) Epigram (b) Antithesis (c) Climax
Answer:
Epigram – the sentence is a short, pithy statement.

Question 15.
Trees old and young, sprouting a shady boon.
(a) Exclamation (b) Personification (c) Antithesis
Answer:
Antithesis – the use of opposite words, old and young, in the same line.

Question 16.
The number of stressed syllables in the line: A thing of beauty is joy forever;
Answer:
5

Question 17.
List the things of beauty mentioned in the extract.
Answer:
The things of beauty mentioned in the extract are: lovely tales of valour, endless fountains, immortal drink, trees that whisper, passionate poetry and cheering light.

Question 18.
Fill in the web with what passion poesy can do to you:
Answer:

Question 19.
List the things which express sorrow from the extract:
Answer:
(i) dooms
(ii) glooms o’ercast/clouds of gloom
(iii) die (iv) dead.

Question 20.
Pick out and write the lines that contain imagery.
Answer:
(i) grandeur of the dooms ;
(ii) An endless fountain of immortal drink ;
(iii) Pouring onto us from the heaven’s brink
(iv) trees that whisper around a temple

English Kumarbharati 10th Digest PDF

• A Thing of Beauty is a Joy For Ever 10th English Textbook Solutions
• The Luncheon 10th English Textbook Solutions
• World Heritage 10th English Textbook Solutions
• The Height of the Ridiculous 10th English Textbook Solutions
• The Old Man and The Sea Book Review 10th English Textbook Solutions
• The Gift of the Magi 10th English Textbook Solutions

Class 10 English Chapter 1.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.1 A Teenager’s Prayer Notes, Textbook Exercise Important Questions and Answers.

A Teenager’s Prayer Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.1 A Teenager’s Prayer Textbook Questions and Answers

Warming up!
Chit-chat

1. Form Groups of 5 to 6 and discuss. Give a rating of 1 to 5 to each of the following.
When you have to make important decisions what do you generally do?
(a) Consult parents/elders [ ]
(b) Contact friends for advice [ ]
(c) Pray to God for guidance [ ]
(d) Think deeply in silence [ ]
(e) Ask your teacher for help [ ]
(f) Toss a coin to decide [ ]

Question 1.
Form Groups of 5 to 6 and discuss. Give a rating of 1 to 5 to each of the following.
When you have to make important decisions what do you generally do?
(Answer is directly given in the box.)
(a) Consult parents/elders [b]
(b) Contact friends for advice [d]
(c) Pray to God for guidance [e]
(d) Think deeply in silence [a]
(e) Ask your teacher for help [c]
(f) Toss a coin to decide [f]
Note: Students may note their own rating after discussion.

2. In poetry, very often, there are lines in which the poet seems to talk directly to an absent person, an abstract idea or thing/object.
Such a tactic/device used by the poet is the Figure of Speech ‘Apostrophe’.
For example,
Twinkle, twinkle little star …………
Death! Where is thy sting?
O Cave man! I wish I could live with you.
Now, complete the following, creating examples of Apostrophe of your own.
(a) O, Life! How ………………………………………………………………………..
(b) Dear God, Please ………………………………………………………………….
(c) Books! You are ……………………………………………………………………..
(d) Exams! I wish ………………………………………………………………………
(e) O, You beautiful sky ……………………………………………………………….

Question 1.
complete the following, creating examples of Apostrophe of your own.
(a) O, Life! How ………………………………………………………………………..
(b) Dear God, Please ………………………………………………………………….
(c) Books! You are ……………………………………………………………………..
(d) Exams! I wish ………………………………………………………………………
(e) O, You beautiful sky ……………………………………………………………….
Answer:
(a) O, Life! How Strange are your ways?
(b) Dear God, Please keep me calm in my difficult days.
(c) Books! You are my dear companions.
(d) Exams! I wish you were never there, never!
(e) O, you beautiful sky send all your beauty to the earth.

English Workshop:

1. Choose the correct alternatives and complete the sentences :

Question 1.
Choose the correct alternatives and complete the sentences :
(a) According to the poet, …………. are brought by each new day. (new beginnings/new endings)
(b) We must decide to take the road which leads to ……………. . (great distress/great success)
(c) The poet prays to the Lord to help him stand for what is ………………. . (might! right)
(d) The poet wants to see that his teenage years have been the ………… years of his life. (worst/best)
Answer:
(a) According to the poet, new beginnings are brought by each new day. (new beginnings / new endings)
(b) We must decide to take the road which leads to great success. (great distress/great success)
(c) The poet prays to the Lord to help him stand for what is right. (might/right)
(d) The poet wants to see that his teenage years have been the best years of his life, (worst/ best)

2. Find and write the pairs of rhyming words from the poem.
1. …………, 2. …………., 3. …………., 4. …………, 5. ……………

Question 1.
Find and write the pairs of rhyming words from the poem.
Answer:
1. make – take
2. success – distress
3. see – me
4. way – day

3. What is the rhyme scheme of the poem? Choose the correct one from the following options.
(i) aabb (ii) abcd (iii) abcb (iv) abba

Question 1.
What is the rhyme scheme of the poem? Choose the correct one from the following options.
(i) aabb (ii) abed (iii) abeb (iv) abba
Answer:
(iii) abeb.

4. Match the lines in Column A with the Figures of Speech in Column B.

Question 1.

Answer:

5. Elements of Planning An Interview : (Group Activity)
Form groups and discuss each element of planning an interview and prepare notes on each element.

6. Prepare a set of 10 questions to interview any successful teenager. You may use the following guidelines.

Question 1.
Prepare a set of 10 questions to interview any successful teenager. You may use the following guidelines.

Answer:
Interview questions for blind musician :

1. Could you please tell me about your family?
2. How did your blindness affect your career as a musician and composer?
3. Who supported you in your venture?
4. Who were your Gurus and what sort of training did you receive?
5. What is your speciality in singing?
6. Which was the best performance in your life according to you?
7. What are the awards you have received?
8. What are your plans for future?
9. What is your advice to young aspirants?
10. What can you do to encourage them?

7. Read the poem. Write an appreciation of the poem in about 12 to 15 sentences with the help of the following points.

Question 1.
Read the poem. Write an appreciation of the poem in about 12 to 15 sentences with the help of the following points.

Answer:

1. Title: ‘A Teenager’s Prayer’.
2. The name of the Poet: J. Morse.
3. Rhyme scheme: The rhyme scheme of the poem is ‘abeb.’
4. Figure of speech (Any 1): Apostrophe, Inversion, Metaphor.
5. Theme/Central Idea: The theme of the poem is a teenager’s dilemma about making the right decisions.

The responsibility of choice falls fully on him/her. A wrong decision may ruin the whole life. Hence the teenager in the poem prays to God for His help and guidance.

8. Compose a short prayer in English asking God to guide you in your teenage years. Later, you can even try to make the lines rhyme to give it a poetic form.

Question 1.
Compose a short prayer in English asking God to guide you in your teenage years. Later, you can even try to make the lines rhyme to give it a poetic form.
Answer:

• O God, bless me with friends
• with purest heart,
• Who’ll always stand by me in dark and dust.
• Let our friendship grow clean and right.
• My future bright will be in my sight.

9. Look around in your vicinity – your family, friends, neighbours, classmates, etc. and write about any four teenagers who have made a name for themselves by doing something extraordinary.

Question 1.
Look around in your vicinity – your family, friends, neighbours, classmates, etc. and write about any four teenagers who have made a name for themselves by doing something extraordinary.

Answer:

My English Coursebook 10th Digest Chapter 1.1 A Teenager’s Prayer Additional Important Questions and Answers

Complex Factual Activity :
Complete the webs : (Answer is directly given.)

1.

2.

Complex Factual Activities :

Question 1.
Complete the sentences with the help of the extract:
(Answers are directly given and underlined.)

1. The person should strictly say ‘no’ to any temptation that comes in his way,
2. It’ll keep a person’s body clean and fit.

Question 2.
Whose company does the poet wish for, in the walk of life? Why?
OR
What effect does the speaker wish to see in himself at the end of his teens?
Answer:
The poet wishes the company of God because, by the time his teenage years are over, he will know that the life he lived under the guidance and help of the Almighty, was the best.

Question 3.
In what condition does the poet wish to maintain his body?
Answer:
The poet wishes to maintain his body and keep it clean and fit each day, when temptation attracts him to do anything bad or wrong.

Activities based on Poetic Devices :

Question 1.
Identify the following figures of speech :
Answer:

1. Please open up my eyes, – Apostrophe dear Lord.
2. And fit for life each day. – Alliteration

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer 10th English Solutions
• An Encounter of a Special Kind 10th English Solutions
• Basketful of Moonlight 10th English Solutions
• Be SMART…! 10th English Solutions
• His First Flight 10th English Solutions

Class 10 English Chapter 4.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.2 The Luncheon Notes, Textbook Exercise Important Questions and Answers.

The Luncheon Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 4.2 Warming Up Questions and Answers

The Luncheon Questions And Answers Class 10 Question 1.
Talk with your partner and discuss the following questions:
(a) Have you ever been invited to lunch, at any hotel, by your friend?
(b) What was the occasion?
(c) Did you enjoy the lunch? Why?
Answer:
(a) Have you ever been invited for a lunch to any hotel by your friend? (You can think of the name of the hotel, what you ate there, what you saw there, etc.)
(b) What was the occasion? (Was it for a birthday, a celebration of some sort, a get-together, etc.)
(c) Did you enjoy the lunch? Why? (Was the food good/bad, was the service good/ bad, was the place clean/unclean/noisy, etc.)

The Luncheon Questions And Answers Question 2.
Discuss in pairs:
People with foibles are often not conscious of them. Do you agree or disagree? Why?
Answer:
I agree with this. My grandmother has a foible that we all know about, but she is not conscious of it. When the house is untidy, she gets irritated. She will tuck in the edge of her sari and walk about the house, muttering to herself. She is not even aware of this peculiar behavior.

The Luncheon English Workshop Question 3.
As you know, every country has its own currency. Find out the currency of at least 6 countries along with their current exchange rate in India, with the help of the internet. One is done for you.
For example, Switzerland: franc; 1 franc = 66.73 INR

Country	Currency	Exchange Rate in Indian Currency

Answer:

The Luncheon Class 10 English Workshop Questions and Answers Maharashtra Board

1. Choose the correct option from the bracket and fill in the blanks given below.
(addressed, luncheon, generously, unwise, insist)
(a) The chief guest …………………… the students.
(b) The crow was …………………… to sing.
(c) I invited my relatives to ……………………
(d) Parents always …………………… on children to be allrounders.
(e) The king decided to donate his wealth among his subjects ……………………
Answer:
(a) addressed
(b) unwise
(c) luncheon
(d) insist
(e) generously

Question 2.
Go through the story again and find out various instances which create humour in ‘The Luncheon’. Complete the table by picking up various humorous instances and the particular line from the story. One is done for you.

Answer:

Humorous instance	Line from the passage
1. The author ordered a single mutton chop.	(i) “I see you’re in the habit of eating a heavy luncheon.” (ii) “Why don’t you follow my example and eat just one thing?”
2. The woman wanted to eat asparagus.	(i) “I couldn’t possibly eat anything more unless they had some of those giant asparagus. I should be sorry to leave Paris without eating some of them.” (ii) “I’m not in the least hungry, but if you insist, I don’t mind having some asparagus.”
3. The writer was afraid that he would not have enough money to pay the bill.	I would put my hand in my pocket and with a dramatic cry. start-up and say that it had been picked.

Question 3.
Who said these words/sentences? Under what circumstances?

Answer:

Question 4.
Answer in your own words.
(a) Although the author was not a vindictive man, he was very happy to see her weigh twenty one stone and had finally had his revenge. What makes him say this? Explain.
Answer:
Twenty years earlier, the writer was earning barely enough money to make both ends meet. The lady wanted him to give her a luncheon at Foyot’s, an expensive restaurant. The writer thought that he could stand her a modest luncheon. The lady reassured him by saying that ‘she never ate anything for luncheon’. However, she ended by eating about six different items, some of which were very expensive yet she insisted till the end that she never ate more than one thing for luncheon and advised him against ‘filling his stomach with a lot of meat’ when all he had eaten was one small mutton chop – the cheapest item on the menu. The writer was finally left with a whole month before him and no money in his pocket. He could not forget this incident, and when he met her twenty years later, she had become very fat and weighed twenty-one stone. This made the writer feel that though he was not a vindictive man, he had got his revenge.

(b) There are quite a few places where the author uses the expressions ‘My heart sank, panic seized’ etc. What was the reason for this ? Explain.
Answer:
The writer was living in a tiny apartment in Paris and earning barely enough money to make both ends meet. The lady wanted him to give her a little luncheon at Foyot’s, an expensive restaurant. When they met, she ordered some of the most expensive dishes available. The writer was terribly worried about whether he had enough money to pay the bill. Hence, he has used the expressions ‘my heart sank’, ‘panic seized me’, etc.

(c) What are the instances which create humour in “The Luncheon”?
Answer:
The instances in the story that create humour are:
(i) when the writer sees the woman at Foyot’s.
(ii) when she orders dish after dish, after first saying that she eats nothing for luncheon, and then stretching the irony she insists that she ate only one thing for luncheon,
(iii) when she tells the writer, who is eating only a mutton chop – the cheapest item on the menu – that he should not overload his stomach,
(iv) when she says that the writer has insisted on her eating asparagus,
(v) when the writer imagines what he would do while paying the bill,
(vi) when the writer says that he would not eat anything for dinner that night,
(vii) when the writer tells us the woman’s weight, when he sees her aghin after twenty years.

(d) Describe the use of irony and humour in “The Luncheon”.
Answer:
In this story, the writer uses humour and irony to depict the character of the woman. The narrator takes the woman to an expensive restaurant called Foyot’s. He is startled when he sees the high prices on the menu, but relieved when his guest tells him, “I never eat anything for luncheon,” and “I never eat more than one thing.” After stating this, ironically, the woman eats some of the most expensive things available, like salmon and caviar, while the poor author only eats a mutton chop. Looking at it, she takes him to task for eating a ‘heavy’ luncheon, and tells him that he should follow her example and never eat more than one thing for luncheon. She said that she would eat the asparagus because the writer ‘insists’, when it was she who had asked for them. In the end, when she repeats once again that he should follow her example and never eat more than one thing for luncheon, the writer retorts that he would do better than that— he would not eat anything for dinner that night!

Question 5.
Pick out the words and phrases in the story that indicate that the author was not financially well off. One is done for you.

Answer:

Words	not afford	modest, cheapest, borrow, mean.
Phrases	beyond my means	earning barely enough money, manage well enough, prices were a great deal higher, horribly expensive, ten francs short, what they cost, inadequate tip, not a penny in my pocket, eat nothing for dinner.

Question 6.
After reading the story, put the following events into correct order:
(a) She gave me her last kind advice how to improve my eating habits.
(b) I met her in the theatre after many years and I could hardly recognize her.
(c) Twenty years ago, I lived in Paris and earned just enough money to get by.
(d) I was really scared what could happen when I would pay the bill.
(e) “I never eat anything for luncheon.”
(f) I ordered a mutton chop for myself.
(g) She had read a book of mine.
(h) She ordered asparagus.
(i) She suggested him to invite her to a famous and expensive restaurant.
(j) I didn’t have dinner for the rest of the month.
Answer:
(c) Twenty years ago, I lived in Paris and earned just enough money to get by.
(b) I met her in the theatre after many years and I could hardly recognize her.
(g) She had read a book of mine.
(i) I invited her to a famous and expensive restaurant.
(e) “I never eat anything for luncheon.”
(f) I ordered a mutton chop for myself.
(h) She ordered asparagus.
(d) I was really scared what could happen when I would pay the bill.
(a) She gave me her last kind advice on how to improve my eating habits.
(j) I didn’t have dinner for the rest of the month.

Question 7.
The irony is the expression of meaning through the use of language signifying the opposite. Describe the use of irony in ‘The Luncheon’. Pick the sentences from the story that are examples of irony. Fill in the table ‘A’ the general direct meaning while in table ‘B’ its hidden meaning or the opposite meaning intended by the speaker. One is done for you.

Answer:

Sentence	Direct Meaning	Irony (Hidden meaning)
(1) I never eat more than one thing.	I am careful and do not eat much; I eat only one thing.	She goes on to eat six expensive items during the luncheon.
(2) I don’t believe in overloading my stomach.	I do not eat much, but in limited quantities.	She has a hearty and expensive meal.
(3) If you insist, I don’t mind ‘ having some asparagus.	I am eating asparagus because you are forcing me to.	The writer had certainly not insisted; she had asked for it.
(4) I’m not in the least hungry.	I am not at all hungry and cannot eat anything.	She thrusts the asparagus down her throat in large mouthfuls.
(5) One thing I thoroughly believe in—one should get up from a meal feeling one could eat a little more.	One should always leave space in the stomach for more food.	She has had a hearty meal and was probably very full.
(6) I have a cup of coffee in the morning and then dinner, but I never eat more than one thing for luncheon. I’ve just had a snack.	I am a very light eater; I hardly eat anything during the day.	She has had six different items for luncheon.
(7) You’ve filled your stomach with a lot of meat.	You have eaten a lot.	The writer had just one little miserable mutton chop.
(8) I’ll eat nothing for dinner tonight.	I won’t have anything for dinner tonight.	The writer had no money left.

Question 8.
Fill in the blank a word or a phrase given in the brackets in their appropriate forms. (startle, catch sight of, overload, water, pass)
1. “I never …………………… my stomach”, she said.
2. I was …………………… when the menu was brought.
3. The author …………………… the guest at the play.
4. I had seen asparagus in the shops, my mouth often …………………… at the sight of them.
5. The author’s guest was …………………… through Paris.
Answer:
1. overload
2. startled
3. caught sight of
4. watering
5. passing

Question 9.
Use appropriate articles.
1. I have just had …………………… snack.
2. I have …………………… cup of coffee in the morning.
3. I want just …………………… ice cream and coffee.
4. Author and his guest gave …………………… order and then waited for asparagus to be cooked.
Answer:
a
a
an
The

Question 10.
Classify the following words in the given table appropriately. (modest, luncheon, generously, rank, restaurant, appearance, large, expensive, watch, coffee, brought, afford, practical, apartment, moment, brightly, started, thoroughly)

Answer:

Question 11.
Study the different uses of ‘could’. Identify what it indicates.
(a) Lack of rain could cause draught. (possibility/condition)
(b) Abhi could perform well in his school days. (suggestion/past ability)
(c) Instead of playing computer games you could play real games with friends. (past ability/suggestion)
(d) Could I use your computer for surfing net? (possibility/request)
(e) We could go on an excursion, if we didn’t have exam. (suggestion/condition)
Answer:
(1) could – possibility
(2) could – past ability
(3) could – suggestion
(4) could – request
(5) could – condition

Question 12.
Fill in the gaps with appropriate Prepositions to make the passage meaningful.
I waited …………………… the airport …………………… Atlanta. My old school-mate was going to arrive …………………… New Airlines …………………… Mumbai, …………………… 21st March …………………… the year 2018. We had not met …………………… 40 years …………………… 1978. She was going to stay …………………… a week …………………… me …………………… Atlanta …………………… 21st …………………… 27th March, 2018.

My joy knew no bounds, when I saw her …………………… 40 years. …………………… home, I introduced her …………………… my family. Then I took her …………………… a big mall …………………… shopping. It was just …………………… my house. We went …………………… the street and climbed …………………… using the elevator, …………………… the staircase.

Answer:
I waited at the airport in Atlanta. My old school-mate was going to arrive by New Airlines from Mumbai, on the 21st of March in the year 2018. We had not met for 40 years, since 1978. She was going to stay for a week with me in Atlanta, from the 21st to 27lh of March, 2018.

My joy knew no bounds when I saw her after 40 years. At home, I introduced her to my family. Then I took her to a big mall for shopping. It was just near my house. We went across the street and climbed up using the elevator near the staircase.

Question 13.
On the occasion of Diwali, write a letter to your friend to invite him/her to celebrate the festival in an innovative way. Use the following hints. time and place special dish is prepared – other friends have also invited post-lunch fun programs, innovative activity
Answer:
Manju Mhatre
8-B, Tulsi Angan
Garodia Nagar
Ghatkopar
Mumbai – 400 077
21st October, 2020

Dear Diya,
Hi there! How are you? You seem to have forgotten me completely afteroining college! Well, I haven’t, and I am writing this letter for a special reason.

This is an invitation for lunch at my place on 4 November on the occasion of Diwali. This will be a sort of house-warming too-you can see from the address above that I have shifted to a new place.

I have also called our other badminton friends—Divya, Rajni, Shubha and Kirti. My Mom has promised to I prepare traditional Diwali dishes, which I am sure ! you will enjoy. And after that—well, that’s going to be i a surprise! But I am sure all of us will enjoy this too.

So do come. Come at about 12.30. Be prepared to be here till 5. Bye.

Your friend,
Manju

Question 14.
Further reading:
(a) “The Phantom Luncheon” by Saki.
(b) “The Ant and the Grasshopper” by William Somerset Maugham.

Form 4 groups of the class. Every group will visit the school’s library or use the internet to read both the creations of Saki and W. S. Maugham. After reading them, every group will summarise both the creations and later read out in the class.

Question 15.
Choose the correct options from the bracket and fill in the blanks: (younger, eighty, twenty, interval)
(1) 1 went over during the interval and sat down beside her.
(2) None of us are getting any younger.
(3) It was twenty years ago.
(4) I had eighty francs to last me the rest of the month.
Answer:
(1) interval
(2) younger
(3) twenty
(4) eighty

Question 16.
Complete the following:
(1) The profession of the narrator: a writer.
(2) The lady was free on the following Thursday.
(3) At the time when the writer met the lady, he was living in a tiny apartment in Paris.
(4) The lady wanted to meet the narrator to have a chat with him.
Answer:
(1) a writer
(2) on the following Thursday
(3) tiny apartment in Paris
(4) have a chat with him

Question 17.
Where and when did they decide to have luncheon?
Answer:
They decided to have a little luncheon at Foyot’s restaurant on the following Thursday.

Question 18.
Choose the correct options from the brackets and fill in the blanks: (pass, caught sight of, overload, modest, addressed, luncheon, interval)
(1) The film was so boring that we went home during the interval.
(2) Though it was a modest apartment, it was extremely clean.
Answer:
(1) interval
(2) modest

Question 19.
Find out the ‘Synonyms’ from the passage for the words:
(1) A set of rooms:
(2) Acknowledged:
(3) Handle:
(4) Directed a remark:
Answer:
(1) Apartment
(2) Recognized
(3) Manage
(4) Addressed

Question 20.
Rewrite the following sentence using the antonym of the underlined word: We’re none of us getting any younger.
Answer:
We’re all of us getting older.

Question 21.
Rewrite the following sentence using ‘except’: The only free moment she had was on the following Thursday.
Answer:
She had no free moment except on the following Thursday.

Question 22.
I hardly think about it. (Begin the sentence with ‘How …!)
Answer:
How little I think about it!

Question 23.
She had read a book of mine. (Begin the sentence with ‘Hadn’t …?)
Answer:
Hadn’t she read a book of mine?

Question 24.
If you were in the place of the narrator, how would you have reacted in the given situation?
Answer:
If I were in the place of the narrator, I would have bluntly told the lady that I was a struggling writer and could not afford to give her a luncheon at Foyot’s. I would have suggested some cheaper restaurant that I could afford. I would not try to show off, or spend more than I can afford,ust to impress someone.

Question 25.
They decided to have luncheon at Foyot’s restaurant at half-past twelve on a Thursday.
Answer:
Foyot’s restaurant at half-past twelve on a Thursday.

Question 26.
The writer ‘was startled when the menu was brought because ………………
Answer:
The prices were a great deal higher than what he had thought.

Question 27.
What do you think the woman reassured the narrator about?
Answer:
The woman realized that the narrator was startled when he saw the prices on the menu. So she indirectly reassured him that he would not have to spend much, for she never ate anything for luncheon.

Question 28.
‘I never eat anything for luncheon’. Explain the irony in this line.
Answer:
The irony is that after informing the author that she never ate anything for luncheon, the lady immediately wanted salmon and caviar, some of the most expensive items available.

Question 29.
From the sentences given below pick out the sentence that indicates that the lady was doing exactly the opposite of what she was saying.
(1) ‘I think you’re unwise to eat meat.”
(2) ‘‘I don’t believe in overloading my stomach.”
Answer:
“I don’t believe in overloading my stomach.”

Question 30.
Choose the correct options from the brackets and fill in the blanks: (pass, startled, overload, imposing, afford, generously, reassured, unwise)
(1) I was …………… when I saw that I remembered all that I had revised.
(2) The monument was really very ………………… .
(3) You cannot ………… to waste time with friends during exams. (Board’s Model Activity Sheet)
Answer:
(1) reassured
(2) imposing
(3) afford

Question 31.
Change the voice of the following sentences:
(1) She reassured me.
(2) I ordered it for my guest.
Answer:
(1) I was reassured by her.
(2) It was ordered for my guest, (by me)

Question 32.
“You’re unwise to eat meat,” she said. (Rewrite in indirect speech)
Answer:
She told him that he was unwise to eat meat.

Question 33.
Are you careful in your eating habits?
Answer:
My mother sees that I eat healthily, and I like I fruits and salads. However, when I am with friends and we go out, I eatunk food. I know it is important to eat healthy food and I take good care to do so.

Question 34.
Name the food items mentioned in the passage
Answer:
The food items mentioned in the passage are:
(1) caviar,
(2) mutton chops,
(3) salmon,
(4) asparagus

Question 35.
Explain what the use of the word ‘sank’ suggests about the narrator’s feelings.:
Answer:
The use of the word ‘sank’ suggests that the narrator was getting unhappy and worried about his guest’s desire to eat expensive food.

Question 36.
From the sentences given below, pick out the sentence that indicates that the lady was doing the exact opposite of what she was saying: (Board’s Model Activity Sheet)
(1) “I see that you’re in the habit of eating a heavy luncheon.”
(2) “Why don’t you follow my example andust: eat one thing.”
Answer:
“Why don’t you follow my example andust eat one thing.”

Question 37.
Choose the correct options from the brackets and fill in the blanks: (pass, quite seriously, water, gaily, insist, mortifying, dramatic)
(1) The ……………… turn of events shocked all of us.
(2) It was ……………. to apologise to the bully.
(3) My mother waved ………………… to me as she went for the hike.
(4) The author’s guest took him ………………. to task.
Answer:
(1) dramatic
(2) mortifying
(3) gaily
(4) quite seriously

Question 38.
Fill in the blanks with the words from the brackets: (Board’s Model Activity Sheet) (task, menu, wondered)
(1) The ……………… to rescue the flood victims was very difficult.
(2) I was thinking about buying a new vehicle and …………………. if we had the money.
(3) The restaurant …………………. seemed to be tempting.
Answer:
(1) task
(2) wondered
(3) menu

Question 39.
She ate the caviar and she ate the salmon. (Begin the sentence with not only … but also and rewrite the sentence.)
Answer:
Not only did she eat the caviar but she also ate the salmon.

Question 40.
Rewrite the following sentence as an affirmative sentence: I couldn’t possibly eat anything more unless they had some of those giant asparagus.
Answer:
I could possibly eat something more only if they had some of those giant asparagus.

Question 41.
Which food do you prefer to eat-home food or restaurant food. Why?
Answer:
My mother cooks very tasty food and hence I prefer to eat home food. It is also always fresh. Restaurant food is generally oily, spicy and often prepared under unhygienic conditions. All this is unhealthy. I believe that health is wealthhence I prefer home food.

Question 42.
Complete the web: (The answers are given directly and underlined.)
Answer:

Question 43.
‘Thera a terrible thing happened.’ Describe the narrator’s emotions at this point in the story. Why does he mot express this emotion?
Answer:
At this point in the story, the writer had given up ail hopes that he could pay the bill. He was resigned to his fate. He had mentally decided on different methods to save his reputation. He does not express this emotion because the lady had already eaten a lot of expensive food: the damage was already done. Besides, he did not want to look mean in her eyes.

Question 44.
Match the columns:

Answer:

Question 45.
Complete the table:

Answer:

Question 46.
Rewrite the following in reported speech: “Are you still hungry?” I asked faintly.
Answer:
I asked her faintly whether she was still hungry.

Question 47.
Pick out the modal auxiliaries from the following sentence and write what they indicate: “One should always get up from a meal feeling one could eat a little more.”
Answer:
Should – indicates advice. Could – indicates ability.

Question 48.
‘I was past caring now’. Explain why, in your view, the narrator feels this way.
Answer:
The writer had been worried from the beginning that he would not be able to pay the bill. To add to that, his guest had ordered some of the most expensive items on the menu. He had now given up all hopes of being able to pay the bill. Hence, he says that he was past caring now.

Question 49.
Write if the following statements are True or False:
(1) The writer thought that the lady was mean.
(2) The writer’s tip was rather inadequate.
(3) The lady was now like a stone.
(4) The writer planned to have a heavy dinner.
Answer:
False
True
False
False

Question 50.
Complete the reasons:
(a) The writer planned to ‘eat nothing’ for dinner that night because….
Answer:
The writer had no money left after paying for the luncheon. He also wanted to make his luncheon guest aware of how much she had made him spend. Hence, he said that he planned to ‘eat nothing’ for dinner that night.

(b) The lady thought that the writer was mean because
Answer:
The writer had only three francs left to tip the waiter. His guest did not know this, and seeing this inadequate sum, thought he was mean.

Question 51.
Complete the table by picking the various humorous instances and the particular lines from the passage.

Humorous instance	Line from the passage

Answer:

Question 52.
Fill in the blanks with one word from the passage for the following: (The answers are given directly and underlined.)
(1) Something that is not enough: ………………….
(2) A man who is revengeful: ………………….
(3) A person who fills his or her writings with humour: ………………….
(4) A person who is stingy and does not like to spend money: ………………….
Answer:
(1) inadequate.
(2) a vindictive man.
(3) a humorist.
(4) a mean person.

Question 53.
Pick out the verbs from the following sentences and write their tense:
(1) I’ have just had a snack and I shall enjoy a peach.
(2) The bill came and when 1 paid it I found that I had only enough for a quite inadequate tip.
Answer:
(1) have had – present perfect tenseshall enjoy – simple future tense.
(2) came, paid, found, had – simple past tense.

Question 54.
Do you think that the lady never ‘ate more than one thing for luncheon’ on a regular basis?
Answer:
No, I’m sure she ate a large luncheon every day, but fooled herself into thinking that she was eating only one thing. She seems to be a foolish and thick-skinned woman who believes whatever is convenient to her.

Question 55.
(1) Pick out an infinitive from the lesson and use it in your own sentence.
(2) Punctuate: humorist she cried gailyumping into a cab youre quite a humorist
(3) Find out five hidden words from the given word: satisfaction
(4) Use the following phrase in your own sentence: the only free moment
(5) Spot the errors and rewrite the correct sentence: She have read a book of mine and have written to me about it.
(6) Identify the type of sentence: How time does fly!
(7) Write the correct verb + present/past participles from the following:
(1) attract
(2) write
(3) pass
(4) bear
(5) eat
(6) meet
(8) Arrange the following in alphabetical order: table, tumbler, tablespoon, teaspoon
Answer:
(1) to eat: I was hungry, and I knew it was time to eat.
(2) “Humorist!” she cried gaily,umping into a cab. “You’re quite a humorist!”
(3) satisfaction: fiction, fission, faint, stint, satin
(4) the only free moment: The Principal was so busy that the only free moment she had was during lunch.
(5) She had read a book of mine and had written to me about it.
(6) Exclamatory sentence
(7) (1) attract-atractting
(2) write-written
(3) pass-passing
(4) bear-bearring
(5) eat-eatten
(6) meet-meeted
(8) table, tablespoon, teaspoon, tumbler

Question 56.
Use the following word and its homograph in two separate sentences : mine
Answer:
(i) I knew that the book was mine,
(ii) Three people entered the coal mine to inspect it.

Question 57.
‘I’m not in the least hungry,” my guest sighed, “but if you insist, I don’t mind having some asparagus.” (Rewrite in reported speech.)
Answer:
My guest told me with a sigh that she was not in the least hungry, but that if I insisted, she wouldn’t mind having some asparagus.

Question 58.
Word Register: Complete the web showing the things that the woman ate or drank throughout the luncheon.

Answer:

Question 59.
Why don’t you follow my example? (Change the voice beginning Why ….)
Answer:
Why isn’t my example followed (by you)?

Question 60.
Use the following word as a verb and a noun in two separate sentences: mind
(2) I chose the cheapest dish on the menu. (Rewrite in the positive and comparative forms.)
Answer:
(1)

• “Mind your language, young man,” said the shopkeeper angrily, (verb)
• I knew that I had to keep all the instructions in my mind, (noun)

(2) I chose the dish that was cheaper than all the other dishes on the menu, (comparative)
No other dish on the menu was as cheap as the one I chose, (positive)

English Kumarbharati 10th Digest PDF

• A Thing of Beauty is a Joy For Ever 10th English Textbook Solutions
• The Luncheon 10th English Textbook Solutions
• World Heritage 10th English Textbook Solutions
• The Height of the Ridiculous 10th English Textbook Solutions
• The Old Man and The Sea Book Review 10th English Textbook Solutions
• The Gift of the Magi 10th English Textbook Solutions

Class 10 English Chapter 2.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.3 The Twins Notes, Textbook Exercise Important Questions and Answers.

The Twins Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.3 The Twins Textbook Questions and Answers

Warming up!

Chit-chat:

1. Two babies born at the same time are called twins. Guess and share who are :

• triplets
• quadraplets
• quintiplets

Question 1.
Two babies born at the same time are called twins. Guess and share who are :
Answer:

1. Three babies born at the same time to the same mother are called triplets.
2. Four babies born at the same time to the same mother are called quadruplets.
3. Five babies born at the same time to the same mother are called quintuplets.

2. Imagine you liad an identical twin (brother or sisiter). Imagine and share with your classmates what pranks you two would play on your friends, elders in the family and even in school.

Question 1.
Imagine you liad an identical twin (brother or sisiter). Imagine and share with your classmates what pranks you two would play on your friends, elders in the family and even in school.
Answer:
Points: At home : Blame your twin brother for the wrongs/breakage/damage done by you – eat his sweets/sweetmeats and demand it again as the other one – if one did some thing special good, the other pretends as it is done by him – In school: One makes mischief in the class and points his finger at the other, he is guilty of doing something wrong throws blame on the other.

1. Study the following pairs or groups of words. Cup and saucer/needle and thread/birds and beasts/take a risk/sip tea or coffee/hide and seek etc.
These are sets of words that more than often go together and occur together. We call such sets Collocation.
Insert the proper words from the bracket to form collocations.
(a) afford (b) time (c) defeat (d) clothes (e) owners (f) necessary (g) role (h) interview (i) morning (j) cold
(a) absolutely ……………
(b) cannot ………………
(c) formal ……………..
(d) job ……………….
(e) pass ………………
(f) accept …………….
(g) early ………………
(h) catch a …………….
(i) leading ……………..
(j) joint ………………..

Question 1.
Insert the proper words from the bracket to form collocations.
[(a) afford, (b) time, (c) defeat, (d) clothes, (e) owners, (f) necessary, (g) role, (h) interview, (i) morning, (j) cold.]
Answer:
(a) absolutely necessary
(b) cannot afford
(c) formal clothes
(d) job interview
(e) pass time
(f) accept defeat
(g) early morning
(h) catch a cold
(î) leading role
(j) joint owners

2. Exaggeration or overstatement often causes humour. For example, She is thin as a pin.

• He has a pea-sized brain
• My shoes are killthg me.

When such exaggerated lines occur in poetry, they are examples of the Figure of Speech: Hyperbole.
Complete the following examples of Hyperbole using words from the bracket below.
(a) She wept …………………… of tears.
(b) The hungry man ate a …………………… of food.
(c) He runs faster than a ……………………
(d) Brrrr..! I am freezing to ……………………
(e) I shall come over in just a ……………………
(horse/lion/death/an ocean/ton/second/help)

Question 1.
Complete the following examples of Hyperbole using words from the bracket below.
(a) She wept …………………… of tears.
(b) The hungry man ate a …………………… of food.
(c) He runs faster than a ……………………
(d) Brrrr..! I am freezing to ……………………
(e) I shall come over in just a ……………………
(horse/lion/death/an ocean/ton/second/help)
Answer:
(a) She wept an ocean of tears.
(b) The hungry man ate a ton of food.
(c) He runs faster than a horse.
(d) Brrrr..! I am freezing to death.
(e) I shall come over in just a second.

English Workshop:

1. Rewrite putting the mistakes in the speaker’s life, in their proper order.
(a) The speaker got beaten-up, often, at school.
(b) The speaker’s bride became his brother’s wife.
(c) The speaker desparately asked for guidance.
(d) No one in the family could distinguish between the twin – babies.
(e) At the naming ceremony wrong names were given to the two twin brothers.
(f) Even in death, the twins were not spared during burial.

Question 1.
Rewrite putting the mistakes in the speaker’s life, in their proper order.
(a) The speaker got beaten-up, often, at school.
(b) The speaker’s bride became his brother’s wife.
(c) The speaker desparately asked for guidance.
(d) No one in the family could distinguish between the twin – babies.
(e) At the naming ceremony wrong names were given to the two twin brothers.
(f) Even in death, the twins were not spared during burial.
Answer:
(a) No one in the family could distinguish between the twin-babies.
(b) At the naming ceremony wrong names were given to the twin brothers.
(c) He (the narrator) got beaten-up, often, at school.
(d) The speaker desperately asked for guidance.
(e) The speaker’s bride became his brother’s wife.
(f) Even in death, the twins were not spared during burial.

2. Pick out four situations in the lives of the twins, which are too absurd and senseless to believe.
1. ………………..
2. ………………..
3. ………………..
4. ………………..

Question 1.
Pick out four situations in the lives of the twins, which are too absurd and senseless to believe.
Answer:

1. The people began mistaking one for the other.
2. The speaker’s brother got the name John, intended for the speaker.
3. The speaker’s intended bride became his brother’s wife.
4. When the speaker died, the neighbours came and buried his brother John.

3. (A) Complete the web diagram.

(B) Write any two lines from the poem, that you find most humorous.

Question a.
Complete the web diagram.

Answer:

Question b.
Write any two lines from the poem, that you find most humorous.
Answer:
1. For somehow, my intended bride Became my brother’s wife.
2. When I died, the neighbours came And buried brother John.

4. Pick out lines that contain :
Alliteration
(a) ………………………………
(b) ………………………………
(c) ………………………………

Pun
(a) ………………………………
(b) ………………………………

Hyperbole
(a) ………………………………
(b) ………………………………

Question 1.
Pick out lines that contain
Answer:
Alliteration:
(a) In form and feature, face and limb.
(b) It puzzled all our kith and kin.
(c) One day, to make the matter worse.

Pun:
(a) I grew so like my brother.
(b) That folks got taking me for him.

Hyperbole:
(a) It reached a fearful pitch.
(b) We got completely mixed.

5. Pick out from the poem sets of words that generally go together.

Question 1.
Pick out from the poem sets of words that generally go together.
For example, kith and kin.
(a) ………………………………
(b) ……………………………….
(c) ……………………………….
(d) ……………………………….
Answer:
(a) form and feature
(b) face and limb
(c) turned the tide
(d) fearful pitch
(e) domestic life
(f) fate’s decree

6. Write in your notebook, the summary of this poem in about 15 to 20 lines in your own words. You can suggest another humourous title.

Question 1.
Write in your notebook, the summary of this poem in about 15 to 20 lines in your own words. You can suggest another humourous title.
Answer:
(Student should write the summary with the help of the paraphrase of the poem given in this book.)
Another humorous title: Twists in the lives of Twins.

7. Write an Appreciation of the poem with reference to all the points mentioned on Page 5.

Question 1.
Write an Appreciation of the poem with reference to all the points mentioned on Page 5.
Answer:
Appreciation of the Poem

1. Title: The title of the poem is ‘The Twins’.
2. Name of the poet: The name of the poet is Henry S. Leigh.
3. Rhyme scheme: The rhyme scheme of the poem is “abab”.
4. Figure of speech (Any one): Alliteration, hyperbole.
5. Theme / Central Idea: The central idea of the poem is the problems faced by one of the identical twins.
6. All the problems are so exaggerated that they create humorous effect. Still, the poet achieves a balance by making the reader believe, at least for a short time, the way of thinking of his argument.

My English Coursebook 10th Digest Chapter 2.3 The Twins Additional Important Questions and Answers

Read the extract and do the activities:

Simple Factual Activity:

Question 1.
Complete the following with the information given in the extract:
(Answers are directly given and underlined.)
Answer:

1. The twins were similar to each other in form and feature and face and limb.
2. The people mistook the twins, one for the another.
3. No one knew who was a twin.
4. Kith and Kin were puzzled by the brother’s similarity.

Question 2.
Complete the following sentences using the information from the extract:
(Answers are directly given and underlined.)
Answer:

1. The narrator should have been christened John.
2. The narrator’s brother was named as John.
3. The twins got mixed up when they were being washed by nurse.
4. The twins were mixed up before their names were fixed.

Question 3.
Complete the following sentences using the information from the extract:
(Answers are directly given and underlined.)
Answer:

1. The narrator got flogged when John turned out a fool.
2. The narrator got punishment with a flogging.
3. His likeness with his brother dogged poet’s footsteps at school.
4. The narrator asked the question fruitlessly.

Question 4.
Who became the wife of narrator’s brother ?
Answer:
The narrator’s intended wife became his brother’s wife.

Question 5.
What turned the tide of the narrator’s domestic life?
Answer:
The close resemblance between the twins turned the tide of the narrator’s domestic life.

Question 6.
What continued year after year?
Answer:
The same absurd mistakes continued year after year.

Question 7.
Who according to the poet died?
Answer:
According to the poet (narrator) he himself died.

Complex Factual Activities:

Question 1.
What was the puzzling thing about the twins?
Answer:
Both twins were so much alike in every way that no one could distinguish one from the other.

Question 2.
Pick out from the extract words/phrases that tell that the narrator was like his brother John.
Answer:
‘In form and feature, face and limb, I grew so like my brother,’ ‘That folks got taking me for him and each for one another’, and ‘not a soul knew which’

Question 3.
What is the mix-up mentioned in this extract?
Answer:
The narrator got christened his brother and the brother got christened John. The name, John, was actually intended for the narrator.

Question 4.
Write any two lines from the extract that you find humorous.
Answer:
1. As we were being washed by nurse, we got completely mixed.
2. My brother John got christened me, And I get christened him.

Question 5.
Pick out from the extract the question that narrator asks everyone. Can you answer the question?
Answer:
The narrator asked everyone what he would do if he were he (the narrator) to prove that he was actually himself. The only advice that can be given in such a case is to keep some different outward signs like mode of dress, hairstyle, mannerisms, etc. to identify oneself.

Question 6.
How did the narrator suffer at school?
OR
Who was put to disadvantage at school due to the similarity? How?
Answer:
As a result of the similarity between the narrator and his brother, he (the narrator) was always getting beaten for the mistakes committed at school by his brother.

Question 7.
Complete the web:
(Answers are directly given.)
Answer:

Activities based on Poetic Device:

Question 1.
Write the rhyming pairs from the extract:
Answer:

1. limb – him
2. brother – another
3. kin – twin
4. pitch – which.

Question 2.
Name the figures of speech:

Question a.
In form and feature, face and limb.
Answer:
Alliteration.

Question b.
For one of us was born a twin, Yet not a soul knew which.
Answer:
Hyperbole.

Question 3.
List the rhyming pairs from the extract:
Answer:

1. worse – nurse
2. fixed – mixed
3. decree – me
4. whim – him.

Question 4.
Name and explain the figure of speech:

Question a.
As we were being washed by nurse.
Answer:
Alliteration: The letter ‘w’ is pleasingly repeated.

Question b.
My brother John got christened me, And I got christened him.
Answer:
Hyperbole: The statement is exaggerated for humour.

Question 5.
Write the rhyming words for the following from the extract:

1. dogged
2. school
3. knew
4. fruitlessly

Answer:

1. dogged – flogged
2. school – fool
3. knew – you
4. fruitlessly – me.

Question 6.
Write lines from the extract that show the figure of speech:
– hyperbole
Answer:
And I was always getting flogged, For John turned out a fool.
The lines are exaggerated for creating humour.

Question 7.
Write the rhyming pairs from the extract:
Answer:

1. tide – bride
2. life – wife
3. same – came
4. on – John.

Question 8.
Write an example of the figure of speech – Hyperbole:
Answer:
And when I died, the neighbours came And buried brother John.
The statement or fact has been exaggerated to create humour.

Vocabulary Focus:

Question 1.
Find from the poem the words that generally go together:
Answer:

1. orm and features
2. face and limb
3. kith and kin
4. fearful pitch
5. fate’s decree
6. got christened
7. close resemblance
8. turn the tide
9. domestic life
10. intended bride
11. absurd mistake
12. put (this) question
13. get flogged

Question 2.
Write as many words as you can using-ful as suffix.
Answer:
basketful-bucketful-handful-spoonful- colourful-sackful-bagful-potful

My English Coursebook 10th Digest Pdf Unit 2 

• You Start Dying Slowly … 10th English Solutions
• The Boy who Broke The Bank 10th English Solutions
• The Twins 10th English Solutions
• An Epitome of Courage 10th English Solutions
• Book Review – Swami and Friends 10th English Solutions
• World Heritage 10th English Solutions

Class 10 English Chapter 3.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.2 A Lesson in Life from a Beggar Notes, Textbook Exercise Important Questions and Answers.

A Lesson in Life from a Beggar Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.2 A Lesson in Life from a Beggar Textbook Questions and Answers

Warming up:
Chit-chat

Make small groups and share:

Question 1.
A piece of advice that stopped a bad habit in you.
Answer:
“Bad habits interrupt your life and prevent you from accomplishing your goal.” The advice given by my uncle stopped a bad habit in me.

Question 2.
A quote proverb that you love to use often.
Answer:
I often love to use the quote, ‘Let’s move ahead.’

Question 3.
An experience that taught you a lifelong lesson.
Answer:
Getting up early morning is quite a difficult job for me. Once we were called at 6 o’clock in the morning to go for picnic. My mother was trying to wake me up from 5 o’clock but I got up at 5.30 and reached school by 6.30. By then our picnic bus had already left the school. I realised that I had missed the fun. It gave me a lifelong lesson to be punctual.

Question 4.
A story / news / episode / movie / play that has impressed and changed you.
Answer:
I miserably failed in Standard IX. I lost all my hopes. I had decided to discontinue my studies forever. Meanwhile I happened to read a story of King Bruce, the King of Scotland. He fought many battles to free his country from English rule. Lost many battles. Once while hiding in a cave, he saw a spider trying to make his web on the wall of the cave. He slipped and fell again and again. But perseveringly tried again and finally succeeded and made his web.

King Bruce learnt a lesson, got together his army, defeated the English and freed his country. The story impressed me. I was moved by the story and decided to study hard and make an effort to appear for the exam again. The story changed my life.

1. Many slang expressions terms are used for people having positive or negative traits.

Question 1.
Match the expressions in Column A with type of persons in Column B:

Answer:

1. Couch Potato – lazy/good for nothing
2. Worry Wart – always nervous/worried
3. Fuddy-duddy – old-fashioned / refuses change.
4. Wet blanket – spoils other people’s fun/mood
5. Whiz – brilliant / genius
6. Black sheep – shameful person
7. Live wire – very energetic/active

Question 2.
Discuss with your group and write the difference in reactions of an Optimist and a Pessimist:

Answer:

English Workshop:

1. Complete the following table:

Question 1.
Complete the following table:

Answer:

2. State whether the following statements are (✓) or (✗). Correct the wrong ones:

Question 1.
State whether the following statements are (✓) or (✗). Correct the wrong ones:
Answer:
(a) The author and Meena were Wrong great enemies.
Corrected sentence: They were good friends.
(b) Meena was a very cheerful Wrong person initially.
Corrected sentence: Meena was forever unhappy.
(c) Meena stayed alone in an Wrong apartment in Delhi.
Corrected sentence: She stayed alone in an apartment in Mumbai.
(d) Meena was the second child of Wrong her parents.
Corrected sentence: She was the only child of her parents.
(e) The author spotted Meena at Bombay’s Flora Fountain. [✓]
(f) The beggar and the young girl were playing on the road because there was a lot of traffic. [✗]
Corrected Sentence: The beggar and the young girl were playing on the road because there was no traffic.
(g) The scene of the beggar and the girl made Meena peep into her own life. [✓]
(h) The beggar became Meena’s role model. [✓]
(i) It took Meena almost two years to put the change into effect. [✓]
(j) Meena was able to give Gurudakshina directly to her Guru, the beggar. [✗]
Corrected Sentence: Meena gave Gurudakshina indirectly by sponsoring his granddaughter to a boarding school.

3. Choose the correct alternative and rewrite the sentences:
(Answers are directly given and underlined.)

Question (a)
Meena who is an LIC officer, is ………………… .

1. a pessimistic person
2. an optimistic person
3. a disabled person.

Answer:
Meena who is an LIC officer, is a pessimistic person.

1. a pessimistic person
2. an optimistic person
3. a disabled person.

Question (b)
The writer was standing near Akbarallys, a popular department store because …………………. .

1. she was waiting for her friend Meena.
2. she was waiting for the rain to stop.
3. she wanted to buy something in Akbarallys.

Answer:
The writer was standing near Akbarallys, a popular department store because she was waiting for the rain to stop.

1. she was waiting for her friend Meena.
2. she was waiting for the rain to stop.
3. she wanted to buy something in Akbarallys.

Question (c)
The only thought in the writer’s mind till they reached the Grand Hotel was ……………………. .

1. why the rain was not stopping.
2. what had brought about such a change in Meena.
3. how the beggar had changed the entire life of Meena.

Answer:
The only thought in the writer’s mind till they reached the Grand Hotel was what had brought about such a change in Meena.

1. why the rain was not stopping.
2. what had brought about such a change in Meena.
3. how the beggar had changed the entire life of Meena.

Question (d)
Meena sponsored the granddaughter of the beggar because ……………………………… .

1. she was alone in her life after his death.
2. it was a token of respect to the beggar.
3. she was rich and so she wanted to help.

Answer:
Meena sponsored the granddaughter of the beggar because it was a token of respect to the beggar.

1. she was alone in her life after his death.
2. it was a token of respect to the beggar.
3. she was rich and so she wanted to help.

4. How did the beggar change Meena’s attitude? Discuss with your partner Complete the following web.

Question 1.
How did the beggar change Meena’s attitude? Complete the following web with the help of the information from this passage:

(Answer is directly given.)
Answer:

5. Write in your own words:

Question (A)
How did Meena show her gratitude to her guru?

Question (B)
Why would Meena be sad initially? Give reasons. Pick out sentences from the passage which prove that Meena was a pessimist.

1. She was forever unhappy.
2. ………………………………………….. .
3. ………………………………………….. .
4. ………………………………………….. .
5. ………………………………………….. .
6. ………………………………………….. .

Answer:

1. She was forever unhappy.
2. Whenever author met her, she would start to feel depressed.
3. Her gloom and cynicism had a way of spreading to others.
4. She never had anything positive to say about anything.
5. She always had negative responses to everyone and everything.
6. She would be pessimist all the time.

6. Find antonyms of the following words from the story.

Question (A)
Find antonyms of the following words from the story.

1. optimistic × ………………
2. drizzle × ………………
3. lie × ………………
4. new × ………………
5. ugly × ………………
6. frowned × ………………
7. hell × ………………
8. unhappy × ………………
9. disrespect × ………………
10. unimportant × ………………

Answer:

1. optimistic × pessimistic
2. drizzle × pouring
3. lie × truth
4. new × old
5. ugly × beautiful
6. frowned × laughed
7. hell × paradise
8. unhappy × happy
9. disrespect × respect
10. unimportant × important

Question (B)
Go through the points below showing Meena’s encounter with the beggar that transformed her completely. The sequence of events are jumbled up below. Arrange the events according to the occurrence. Fill in the number as per sequence.

Answer:

7. How did the beggar change Meena’s attitude towards life? Write it down in 5 to 6 lines.

Question 1.
How did the beggar change Meena’s attitude towards life? Write it down in 5 to 6 lines.

1. The incident made Meena to look at her own life.
2. ……………………………………………………………………… .
3. ……………………………………………………………………… .
4. ……………………………………………………………………… .
5. ……………………………………………………………………… .
6. ……………………………………………………………………… .

Answer:

1. The incident made Meena to look at her own life.
2. She realized that she had many comforts of which they had none.
3. But they knew how to be happy with life as it was.
4. She found that she had more to be grateful for than most people could imagine.
5. She felt ashamed of herself.
6. She decided to change her attitude towards her life.

8. Summarise the story with the help of the points given below.

Question 1.
Summarise the story with the help of the points given below.
(a) Meena’s initial attitude
(b) Meena’s meeting with Sudha Murthy in Mumbai.
(c) Beggar’s incident
(d) Change in attitude.

Answer:
Meena and Sudha were very good friends. Meena was an LIC officer and earning a good salary. But she was always unhappy and never had anything I positive to say on any subject or about any person. So whenever Sudha met her, she would start to feel depressed. Meena stayed alone in an apartment and had the habit of complaining about anything and everything; she wasn’t a very pleasant company and nobody wanted to visit her.

After some days Meena was transferred to Bombay and soon Sudha forgot about her. Many years later, Sudha was caught in the rain at Bombay’s Flora Fountain. She didn’t have an umbrella. She was standing near Akbarallys and waiting for the rain to stop. Suddenly she saw Meena. But her first reaction was to run. She was anxious to avoid being seen by her. But she couldn’t escape.

Meena saw her and caught hold of her hands ; warmly. She was very cheerful and excited to meet Sudha. She was also ready to get wet and walk in the rain. But Sudha was so surprised that she couldn’t believe she is meeting her pessimistic friend Meena. So she enthusiastically asked her, “Was there a Prince Charming who had managed to change her so?”

Meena told her there wasn’t anybody like that but a beggar changed her life who used to stay in front of her house with his five-years-old granddaughter. She used to give her leftover to that beggar everyday. One monsoon day she was surprised to see the beggar. As it was raining heavily, she couldn’t give anything to that beggar. She didn’t want to get wet in that pouring rain she was just looking out of her bedroom window when she saw the beggar and the young girl were playing on the road because there was no traffic.

They were enjoying the rain and laughing, clapping and screaming joyously as if they were in paradise. Hunger and rain did not matter. They were totally drenched but totally happy. That scene forced Meena to look at her own life. Even though she had so many comforts, none of which they had. But they had the most important of all assets one which she lacked.

They knew how to be happy with life as it was. So she decided to change her attitude towards life using the beggar as her role model. It took her almost two years to put the change into effect but now she finds happiness in every small thing, in every situation and in every person.

Sudha was surprised to listen to the changed story of her friend and asked Meena enthusiastically, whether she had given any gurudakshina to her guru or not. But Meena told her that the beggar was dead and she had sponsored his granddaughter to a boarding school as a mark of respect to him. Sudha was stunned but happy to hear the changed story and attitude of her friend.

9. Write the above summary making Meena the narrator. Begin with I worked in Bangalore in LIC. Sudha was my school friend …………..

Question 1.
Write the above summary making Meena the narrator. Begin with I worked in Bangalore in LIC. Sudha was my school friend …………..
Answer:

Lesson in a Life from A Beggar

I worked in Bangalore in LIC. Sudha was my good friend, living in the same city. Being pessimistic and having the habit of complaining about anything and everything, nobody was friendly with me. One day I was transferred to Mumbai and no one was in contact with me.
[Note: Students should try to complete the remaining part of summary of the story as told by Meena, in their notebook.]

Project:

Question 1.
Divide the class in four groups. Collect four different stories written by Sudha Murthy. Select a story for every group and write it in the form of a play. Enact it in front of the class.

Language Study:

1. Punctuate the following sentences:

Question 1.
(a) did you give any gurudakshina to your guru i asked.
(b) no there isnt anyone like that she said.
Answer:
(a) “Did you give any gurudakshina to your guru?” I asked.

2. Add a suffix to the following words and make nouns.

Question (a)
Add a suffix to the following words and make nouns.

1. kind
2. happy
3. ignore
4. assure
5. imagine
6. depute
7. manage
8. assess

Answer:
1. Always be kind to poor, needy and disabled people in the society.
2. Why don’t you look happy today?
[Note : Students may frame sentences based on the remaining words on their own.]

Question (b)
Make four words (minimum 3 letters each). Using letters from the word ‘Pessimistic’.

1. ………………….
2. ………………….
3. ………………….
4. ………………….

Answer:

1. Pessimist,
2. mist,
3. pest,
4. pet

3. Change into indirect speech:

Question (a)
“Meena, it’s a beautiful day.” I said.
Answer:
I told Meena that it was a beautiful day.

Question (b)
“Hey! I am really excited. It’s nice to meet old friends. What are you doing here?” Meena said to the writer.
Answer:
Meena exclaimed with excitement (joy) that it was nice to meet old friends. She further asked the writer what she was doing there.

Question (c)
“We won’t get a taxi in this rain,” I grumbled,
Answer:
I grumbled that we would not get a taxi in that rain.

Question (d)
“So what? We’ll buy an umbrella and then go to the Grand Hotel,” she said.
Answer:
Meena insistently asked her (the writer) what difference could it make and further told her that they would buy an umbrella and then go to the Grand Hotel.

Question (e)
“Did you give any gurudakshina to your Guru?” I asked.
Answer:
I asked her if she had given any gurudakshina to her guru.

My English Coursebook 10th Digest Chapter 3.2 A Lesson in Life from a Beggar Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
1. Meena was a good friend of the writer.
2. The writer was caught in the rain at Bombay’s Flora Fountain.

Question 2.
What is meant by ‘She never had anything positive to say’?
Answer:
It meant that her thoughts and actions had always been negative.

Question 3.
Who said to whom?
Answer:

Question 4.
State whether the following statements are Right or Wrong. Correct the wrong ones:
Answer:

1. This wasn’t the same Meena that the writer had known. – Right
2. The writer bought an umbrella and went to the Grand Hotel with Meena.
   Corrected sentence: Instead of buying an umbrella they walked to the Hotel in rain. – Wrong
3. There was a Prince Charming in Meena’s life who managed to change her.
   Corrected sentence: A beggar had changed Meenas life. – Wrong
4. There was no change in Meena’s behaviour.
   Corrected sentence: Meena’s behaviour was completely changed. – Wrong

Question 5.
State whether the following statements are Right or Wrong. Correct the wrong ones :
Answer:

1. Rakesh’s father is a school teacher. [✓]
2. The writer was transferred to Bombay.
   Corrected sentence: The writer was in Bombay on an official work. [✗]
3. Meena is always pessimistic. [✓]
4. Meena had the habit of complaining about anything and everything. [✓]

Question 6.
Read the passage and fill in the blanks:
(Answers are directly given and underlined.)
Answer:

1. Meena was a chronic pessimist.
2. A begger changed Meena’s life.
3. The begger lived with his five-year old grand daughter.
4. The beggars were playing on the road because there was no traffic.

Complex Factual Activities:

Question 1.
What was Meena’s nature like?
Answer:
There was always something strange about Meena. She was always unhappy. Any person who came in contact with her would feel depressed. Her thoughts were negative about everything and about every person.

Question 2.
Arrange the following sentences in proper sequence according to their occurrence in the passage:

1. Many years later the writer saw Meena at Bombay’s Flora Fountain in pouring rain.
2. Unfortunately Meena saw the writer and caught hold of her hands warmly.
3. Meena was really excited to meet her old friend.
4. The writer wanted to avoid her for her never ending complaints.

Answer:

1. Many years later the writer saw Meena at Bombay’s Flora Fountain in pouring rain.
2. The writer wanted to avoid her for her never ending complaints.
3. Unfortunately Meena saw the writer and caught hold of her hands warmly.
4. Meena was really excited to meet her old friend.

Question 3.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. Old wine, old friends and memories are precious and rare.
2. A few strands of grey in her hair had reminded the writer that years had passed.
3. Meena was ready to make any number of adjustments.
4. The only thought in the writer’s mind was to find out who or what had brought about such a change in the pessimistic Meena.

Choose the correct alternative and complete the following sentences: (Answers are directly given and underlined.)

1. The only thought in the writer’s mind till they reached the Grand Hotel was what had brought about such a change in Meena.

1. why the rain was not stopping.
2. what had brought about such a change in Meena.
3. how the beggar had changed the entire life of Meena.

2. The writer wanted to attend a dinner.

1. a marriage party.
2. a dinner.
3. a birthday party.

3. When the writer met Meena in a pouring rain, she was ready to make any number of adjustments.

1. make any number of adjustments.
2. get wet in the rain.
3. buy an umbrella for them.

4. A beggar had managed to change Meena.

1. a Prince Charming,
2. The writer.
3. A beggar.

Question 4.
What surprised the writer?
Answer:
The writer was greatly surprised by the difference in Meena’s attitude of bygone days. She looked happy and was smiling. That was not the same Meena the writer had known. She seemed ready to make any number of adjustments.

Question 5.
Choose the correct alternative and rewrite the sentences:
(Answers are directly given and underlined.)
Answer:
1. The writer took almost two years to put the change into effect.

1. three years
2. two years
3. five years

2. The beggar and his granddaughter were enjoying the rain as if they were in paradise.

1. in paradise
2. in a palace
3. in front of the writer’s house

3. Attitude towards life was the most important of all assets, that the beggar and his granddaughter had but the writer was lacking.

1. Attitude towards life
2. So many comforts
3. Hunger

Question 6.
Complete the web:
(Answer is directly given.)
Answer:

Question 7.
What lesson did Meena learn from her Guru-the beggar?
Answer:
From her Guru-the beggar, Meena learnt how to be happy with life as it was. She also learnt to find happiness in every small thing, in every situation and in every person.

Question 8.
What did Meena do to show gratitude to her Guru?
Answer:
Meena changed her attitude towards life using the beggar as her role model. Unfortunately, by the time she understood things, he was dead. So she sponsored his granddaughter to a boarding school as a mark of respect to him.

Activities based on Vocabulary:

1. Find antonyms of the following words from the passage:

Question 1.

1. bad
2. never
3. negative
4. cold.

Answer:

1. bad × good
2. never × always
3. negative × positive
4. cold × hot

Question 2.
Match the following:

Answer:

1. gloom – feeling of sadness
2. cynicism – a distrustful attitude
3. subside – to abate
4. pessimistic – expecting the worst

Question 3.
Add suffix to the following words and make nouns:
(a) good
(b) happy
(c) assure
(d) feel
(e) achieve
(f) strange
(g) popular
(h) excite.
Answer:
(a) goodness
(b) happiness
(c) assurance
(d) feeling
(e) achievement
(f) stranger
(g) popularity
(h) excitement

Question 4.
Find out synonyms for the following from the passage :

1. inquisitive
2. displeased
3. attractive
4. valued.

Answer:

1. inquisitive – curious
2. displeased – disappointed
3. attractive – charming
4. valued – precious

Question 5.
Find the antonyms of the following from the passage:

1. dry
2. common
3. wrong.

Answer:

1. dry × drenched
2. common × rare
3. wrong × right

Question 6.
Write four words that have ‘ness’ as suffix :
Example – happiness
Answer:

1. kindness
2. boldness
3. greediness
4. greatness

Question 7.
Write two words that have ‘re’ as prefix :
Example – reassure
Answer:

1. rekindle
2. reappear
3. reinforce
4. repay

Question 8.
Find synonyms for the following words from the passage:
(a) heaven
(b) happily
(c) rainy
(d) very surprised
Answer:
(a) Paradise
(b) Joyously
(c) Monsoon
(d) Dumbfounded.

Activities based on Contextual Grammar:

Make the following sentences negative:

Question 1.
She was forever unhappy.
Answer:
She was never happy.

Question 2.
Meena was a pessimistic girl.
Answer:
Meena was not an optimistic girl.

Choose the correct alternative of afffirmative sentence.

Question 1.
She wasn’t a very pleasant company.
(a) She was a very unpleasant company.
(b) She wasn’t a very unpleasant company.
(c) She was a very pleasant company.
(d) She was a very beautiful company.
Answer:
She was a very unpleasant company.

Question 2.
Make it exclamatory:
She was very cheerful.
Answer:
How cheerful she was!

Question 3.
Shwetha is a very beautiful girl.
(Choose correct alternative of exclamatory sentence.)
(a) How beautiful girl Shwetha is!
(b) What a beautiful girl Shwetha is!
(c) What a beautiful girl Shwetha was!
(d) What a beautiful girl is Shwetha!
Answer:
What a beautiful girl Shwetha is!

Question 4.
Complete the following table:
(Answers are directly given and underlined.)
Answer:

Make the following sentences affirmative:

Question 1.
I couldn’t believe it.
Answer:
I was unable to believe it.
OR
I could hardly believed it.

Question 2.
I can’t stay with you tonight.
Answer:
I am unable to stay with you tonight.

Choose the correct tail tag for the following sentences from the brackets:
(wasn’t she?, will we?, were here?, weren’t there?,will you?, won’t you?)

Question 1.
We wont get a taxi in this rain;
Answer:
will we?

Question 2.
There were a few wrinkles in her face;
Answer:
weren’t there?

Question 3.
Give me your card,
Answer:
will you?

Question 4.
Meena was surprised by my question,
Answer:
wasn’t she?

Personal Response:

Question 1.
Would you avoid your friend, if you are meeting himher after a long time?
Answer:
Welcoming or avoiding our old friend totally depends upon how close you are with that person. If you are really close to some friend by heart and soul you will never avoid himher even if you are meeting himher after a long time. Whereas we always wait for such occasions to meet our old buddies.

Question 2.
What is meant by ‘ Meena never had anything positive to say ’?
Answer:
Meena was always pessimistic in her life. Whoever said or asked anything, her answer was always negative. She never thought positively. It was her habit to take everything negatively. So the writer said “Meena never had anything positive to say.”

Question 3.
What, according to you, is the difference between an optimistic person and a pessimistic person?
Answer:
According to me, an optimist enjoys every moment. Optimists are confident and hopeful in themselves and believe they can overcome whatever life throws at them and continue on their way. Pessimists always have negative thoughts. They always feel defeated. They are never hopeful and lose confidence. Pessimists are unhappy and gloomy.

Question 4.
Change is the law of life-Explain.
Answer:
Change is the law of life. And those who look only at the past or present are certain to miss the future. Change is inevitable. We can’t ignore it. Changing means doing something new and challenging. That gives you a great joy of life. If we do not change ourselves, we cannot enjoy our life to the fullest.

Question 5.
Is it possible to bring change in our life like Meena?
Answer:
Yes, it is definitely possible to bring change like Meena in our life also. We can learn a lot from the examples and attitudes of other less-gifted people. If we have clear (good) conscience and we are determined to act according to it, we can surely | change our behaviour, attitude towards our life like Meena.

Question 6.
Describe an experience, where somebody has changed your way of looking at life.
Answer:
Once while travelling by a bus, I came across one of my friends with whom I had a quarrel on a petty thing. I ignored him and asked the conductor to give a ticket by giving a 100-rupee note.

The conductor had no change so he told me to get down and come by another bus. I was about to get down when my friend came forward and paid for my ticket. I felt ashamed and asked him to pardon me. The incident changed my attitude about him and now we are friends forever.

Question 7.
According to you, how can we help beggars?
Answer:
We should convince beggars that begging is not good. We should tell them the importance of ‘Self respect.’ If possible we will provide them opportunities to earn money and insist them to give up begging.

Do as directed:

Question 1.
They were laughing and screaming.
(Choose the correct option of ‘Not only-but also’)
(a) They were not only but also laughing and screaming.
(b) They were not only laughing but also screaming.
(c) They were laughing not only but also screaming.
(d) They were not only laughing and but also screaming.
Answer:
(b) They were not only laughing but also screaming.

Question 2.
He used to stay in front of my house.
(Rewrite the sentence by using ‘would’)
Answer:
He would stay in front of my house.

Change the voice:

Question 1.
That scene forced me to look at my own life.
(Begin the sentence with “I )
Answer:
I was forced to look at my own life by that scene.

Question 2.
I find happiness in every small thing in every situation and in every person.
(Begin the sentence with “Happiness ….)
Answer:
Happiness is found in every small thing, in every situation and in every person by me.

1. Attempt anyone:

Question (a)
Make a meaningful sentence by using given phrase: ‘in the pursuit of’
Answer:
In the age of technology everyone is in the pursuit of money.

OR

Question (b)
Add a clause to expand the following sentence meaningfully.
My friend is an LIC Officer ……………
Answer:
My friend is an LIC Officer who stays at Nagpur.

2. Attempt any one:

Question (a)
Add a prefix or suffix make new words :
Note: Two words will be given in the activity sheet.
(a) kind
(b) happy
(c) ignore
(d) assure
(e) imagine
(f) depute
(g) manage
(h) assess
Answer:
(a) kindness, unkind.
(b) unhappy, happiness
(c) ignorance
(d) assurance
(e) imagine
(f) deputation
(g) management, mismanage
(h) assessment,

Activities based on Language Study:

Question 1.
Complete the words by using correct letters:
Answer:

1. g _ oo _ – gloom
2. y o_n g – young
3. p r o_f – proof
4. t o_c h – touch

Question 2.
Put the words in alphabetical order:
1. chronic, squeezing, assets, zest.
2. pleasant, parents, paradise, pause.
Answer:
1. assets, chronic, squeezing, zest.
2. paradise, parents, pause, pleasant.

Question 3.
Punctuate the following sentences:
then whats the secret of your energy i asked
Answer:
“Then, what’s the secret of your energy?” I asked.

Question 4.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 5.
Complete the word-chain of ‘nouns’. Add four words, each beginning with the last letter of the previous word:
friend, → d …………, …………., …………, ………….,
Answer:
friend → dream , minute , elephant , thief.

Projects Task:

Question 1.
Find out more about Sudha Murthy and her writing from the internet.

My English Coursebook Standard Ten Digest Answers Pdf Unit 3 

• Chapter 3.1 If … 10th English Solutions
• Chapter 3.2 A Lesson in Life from a Beggar 10th English Solutions
• Chapter 3.3 Stopping by Woods on a Snowy Evening 10th English Solutions
• Chapter 3.4 Let us March! 10th English Solutions
• Chapter 3.5 The Alchemy of Nature 10th English Solutions

Class 10 English Chapter 3.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.1 Night of the Scorpion Notes, Textbook Exercise Important Questions and Answers.

Night of the Scorpion Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 3.1 Warming Up Questions and Answers

Night Of The Scorpion Poem Questions And Answers Question 1.
Get into pairs and discuss the following with your partners and complete the table.
Many people are superstitious. This means that they have belief for which they have no logical reason.
An example of superstition is that – walking under a ladder brings bad luck.
In pairs, list any superstitions that you know of.

Superstition	What it implies
(1) Smashing a mirror (2) (3) (4) (5) (6) (7)	Brings seven years of bad luck.

Answer:

Night Of The Scorpion Questions And Answers Question 2.
Brainstorm what you know about Scorpions. Use the points given below.

Answer:

Night of the Scorpion Class 10 English Workshop Questions and Answers Maharashtra Board

Night Of The Scorpion Question 1.
After reading the poem, complete the following. What happens? There are three main parts of the poem. Do you know what they are about? The first one is done for you.

Answer:

Night Of Scorpion Question Answers Question 2.
Complete the following tables.
(A)

Answer:

Background/setting of the poem
Type	Evidence (Quote lines from the poem)
Rural	(1) ‘The peasants came like swarms of flies’. (2) ‘and buzzed,the name of God a hundred times’. (3) To paralyse the evil one’. (4) ‘With candles and with lanterns’ (5) ‘on‘the mud-baked walls’ (6) ‘His poison moved in Mother’s blood, they said.’ (7) They sat around on the floor with my mother in the centre’ (8) More candles, more lanterns’. (9) groaning on a mat (10) trying every curse and blessing, powder, mixture, herb and hybrid (11) I watched the holy man perform his rites

(B)

Answer:

(C)

Answer:

Night Of The Scorpion Question Answers Question 3.
Choose the correct alternative.

1. The child is afraid but admires …………………………
(a) the initiative of the peasants.
(b) his father trying every way to cure.
(c) the bravery of his mother.
Answer:
(c) the bravery of his mother

2. His father and the villagers panic and hastily suggest ………………………….
(a) to take her to the hospital.
(b) ayurvedic treatment.
(c) religious remedies to help.
Answer:
(c) religious remedies to help

3. The poet seems to see the villagers as impractical and almost irritating which suggests that …………………………
(a) the poet is critical of caste
(b) the poet is critical of religion
(c) the poet is critical of tradition.
Answer:
(c) the poet is critical of tradition

4. This is a ………………………… poem as it tells a story.
(a) reflective
(b) imaginative
(c) narrative
Answer:
(c) narrative

5. Using the first person gives the feeling that it is told from …………………………
(a) personal experience
(b) public experience
(c) private experience
Answer:
(a) personal experience

6. ‘The scorpion picked on me. And spared my children’ depicts …………………………
(a) mother’s bravery
(b) mother’s endurance
(c) selfless and unconditional love of mother.
Answer:
(c) selfless and unconditional love of a mother

7. The poem does not have a rhyme scheme, which means the poem is a perfect example of a …………………………
(a) Ballad
(b) Sonnet
(c) Free verse
Answer:
(c) free verse

8. The poem is titled ‘Night of the Scorpion’, for, the major part of the poem, …………………………
(a) the mother remains triumphant at the end.
(b) the scorpion is the victor.
(c) the father succeeds in curing the mother.
Answer:
(b) the scorpion is the victor

9. The peasants chant the name of God to …………………………
(a) nullify the stinging experience
(b) praise God.
(c) appease God.
Answer:
(a) nullify the stinging experience

10. The click of tongues reflects their ………………………… to the predicament.
(a) individual response
(b) collective response
(c) group response
Answer:
(b) collective response

Night Of The Scorpion Questions Question 4.
From the poem provide evidence for the following :

Stages	Evidence (lines from the poem)
(a) the attempts by the peasants to help alleviate the mother’s pain. (b) the action of these same peasants to kill the scorpion (c) the reaction of the rational father. (d) the various superstitions versus the ‘scientific’ (e) evil versus good.

Answer:

Night Of Scorpion Question Answers Question 5.
Read the poem and complete the table showing the qualities of the father and mother giving sufficient evidences from the poem.

Answer:

Qualities
Father	Mother
sceptic, rationalist,  loving, desperate	patient, long-suffering, brave, self-sacrificing, selfless
Lines as evidence: My father, sceptic, rationalist, Trying every curse and blessing, Powder, mixture, herb and hybrid. He even poured a little paraffin Upon the bitten toe and put a match to it. I watched the holy man perform his rites to tame the poison with an incantation.	Lines as evidence : My mother twisted through and through, groaning on a mat. My mother only said Thank God the scorpion picked on me and spared my children.

Night Of The Scorpion Question Answers Question 6.
(A) Match the Figures of Speech with the correct definition.

Answer:

(B) Find examples from the poem that contain :
Similie : …………………………
Metaphor : …………………………
Onomatopoeia : …………………………
Answer:
Similie: A comparison between two different things, especially a phrase, containing the words ‘like’ or ‘as’
Metaphor: An implied comparison.
Onomatopoeia: A word which resembles the sound it represents.

Question 7.
Expand the flow chart in writing a paragraph in your own words.

Answer:
The poet’s mother is bitten by a scorpion and is in great agony. She fights the venom of the scorpion with the help of her husband and the villagers. She is unable to say anything, but only groans in pain. Finally, the poison is tamed after twenty hours. In the end, the mother thanks God that she has survived the ordeal, and that the scorpion had picked on her and spared her children.

Question 8.
The poet has used various kinds of imagery to create an image which appeal to our senses. Pick out various kinds of imagery and complete the table.

Answer:

Question 9.
Write an appreciation of the poem in a paragraph format.
Answer:
Point Format
(for understanding)
The title of the poem : Night of the Scorpion’
The poet: Nissirn Ezekiel
Rhyme scheme : written In frcc verse without any rhyme scheme or mctrc
Figures of speech : Onomatopoeia, Metaphor, Alliteraüon, Sim Ile, Antithesis, etc.
Theme/Central idea : The poet depicts the selflessness and unconditional love of a mother who stung by a scorpion.

Paragraph Format
Thc poem ‘Night of the Scorpion’ is written by Nissim Ezekiel. The poem is written in free verse without any rhyme scheme or metre. There are many figures of speech e.g. Onomatopoeia like ‘and buzzed the name of God a hundred times’. Here, we feel we can actually hear the buzzing of the prayers of the many peasants. The other figures of speech are Metaphor. Alliteration. Simile. Antithesis, etc.

The theme of the poem is the sense of sacrifice shown by a devoted mother. Even as she suffers the pangs of a scorpion-bite, she thanks God for sparing her children from such an ordeal.

Question 10
Project
Prepare a Presentation (on paper or on a PC) as a piece of reference to other students. Make use of the following points.
(1) Title page
(2) Introduction of the poet
(3) The Complete poem (All 48 lines)
(4) Learning objectives

(5) Style of writing
(6) Scorpion lines (1-7)
(7) The peasants
(8) The poet’s father
(10) The poet’s mother
(11) Vocabulary
(12) Credits (positive aspects)

Question 11.
Complete the following: (The answers are given directly and underlined.)
(1) The scorpion was forced to take shelter in the poet’s house to …………………
(2) In line no. 3, the word ‘him’ refers to …………………
(3) To ‘paralyse the Evil One’ in stanza 3 means ………………….
(4) ‘They’ in stanza 4 refers to ………………….
Answer:
(1) escape the heavy rain.
(2) the scorpion.
(3) to stop the activity of the devil, the scorpion.
(4) the peasants M10 had come to help.

Question 12.
Explain why the poem begins with the poet \ remembering the night.
Answer:
The poem begins with the poet remembering | the night because the whole incident that is narrated in the poem was very memorable and took place in the night. It created a strong impression on the poet.

Question 13.
Write the reactions of the people when they knew that the mother was stung by a scorpion.
Answer:
When the people knew that the poet’s mother was stung by a scorpion:
(i) The peasants came in swarms to help.
(ii) They buzzed the name of God a hundred times.
(iii) They searched for the scorpion with candles and lanterns.
(iv) They clicked their tongues because he was not found.

Question 14.
Pick out an example of Simile from the extract.
Answer:
The peasants came like swarms of flies. The peasants are compared directly to swarms of flies, with the use of the word like’.

Question 15.
Pick out an example of Metaphor from the extract.
Answer:
to paralyse the Evil One’. The scorpion is Implicitly compared to the devil.

Question 16.
Pick out examples of Onomatopoeia from the extract.
Answer:
(1) ‘and buzzed the name of God’
The word ‘buzzed’ indicates sound.

(2) ‘They clicked their tongues.’
The word ‘clicked’ indicates sound.

Question 17.
Pick out examples of Alliteration from the extract.
Answer:
(1) Parting with his poison-flash
Repetition of the sound of the letter ‘p’.

(2) of diabolic tail in the dark room
Repetition of the sound of the letter ‘d’.

(3) throwing giant scorpion shadows.
Repetition of the sound of the letter ‘s’.

Question 18.
Pick out an example of Antithesis from the extract:
Answer:
‘they searched for him: he was not found’ Words having opposite or contradictory meanings are used in the same line.

Question 19.
Write down the rhyming words from the stanzas for the following:
(i) fight
(ii) clash
Answer:
(i) fight-night
(ii) clash-flash.

Question 20.
Complete the following: The peasants consoled the mother, saying:
(1) the poison will burn away ………………………
(2) her suffering will decrease …………………….
(3) the evil in this world will be …………………………
(4) the poison will purify her …………………………..
Answer:
(1) the sins of her previous birth
(2) the misfortunes of her next birth
(3) diminished by her pain.
(4) flesh of desire and her spirit of ambition.

Question 21.
(a) Pick out examples of Alliteration from the extract:
Answer:
(1) ‘May he sit still, they said’.
Repetition of the sound of the letter ‘s’.

(2) ‘May the poison purify your flesh’
Repetition of the sound of the letter ‘p’.

(b) Pick out an example of Antithesis from the extract:
Answer:
‘May the sum of all evil balanced in this unreal world against the sum of good’ Words having opposite meanings are placed close for contrast.

(c) Pick out an example of Repetition from the extract:
Answer:
‘More candles, more lanterns, more. neighbours’ Repetition of the word ‘more’ for emphasis.

Question 22.
Complete the following: (The answers are given directly and underlined.)
(1) The mother found relief …………………….
(2) All through the ordeal, the poet’s mother ………………..
Answer:
(1) after twenty hours.
(2) twisted and groaned in pain.

Question 23.
(1) Pick out an example of Onomatopoeia from the extract.
Answer:
‘groaning on a mat’ The word ‘groaning’ indicates sound.

Question 24.
Pick out examples of Alliteration from the extract.
Answer:
(1) ‘powder, mixture, herb and hybrid’
Repetition of the sound of the letter ‘h’.

(2) ‘He even poured a little paraffin’
Repetition of the sound of the letter ‘p’.

(3) ‘I watched the flame feeding on my mother’
Repetition of the sound of the letter ‘f.

Question 25.
Pick out an example of Antithesis from the extract:
Answer:
‘trying every curse and blessing’ Words having opposite meanings are placed close for contrast.

Question 26.
Pick out an example of Personification from the extract:
Answer:
‘I watched the flame feeding on my mother’ The flame is given the human quality of feeding.

English Kumarbharati 10th Digest PDF

• Night of the Scorpion 10th English Textbook Solutions
• The Night I Met Einstein 10th English Textbook Solutions
• Stephen Hawking 10th English Textbook Solutions
• The Will to Win 10th English Textbook Solutions
• Unbeatable Super Mom-Mary Kom 10th English Textbook Solutions
• The Concert 10th English Textbook Solutions

Class 10 English Chapter 4.6 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.6 The Gift of the Magi Notes, Textbook Exercise Important Questions and Answers.

The Gift of the Magi Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 4.6 Warming Up Questions and Answers

The Gift Of The Magi Questions And Answers Question 1.
The moment you hear the word ‘Gift’, what feelings do you experience? Complete the web with those feelings.

Answer:

Gift Of Magi Questions And Answers Question 2.
‘Gifts’ need not be material gifts. They can be abstract and yet priceless. For example, favours, kindness, help in times of need etc.
Think of and enlist such unforgettable gifts given to you by :
(1) Parents/ Grand parents : ………………………………………..
(2) Siblings/ relatives : ………………………………………..
(3) Friends : ………………………………………..
(4) Strangers : ………………………………………..
Answer:
(1) love, kindness, etc.
(2) support, empathy, etc.
(3) loyalty, sympathy, etc.
(4) courtesy, help, etc.

Gift Of The Magi Questions And Answers Question 3.
Say whether the words underlined are infinitives/ participles or gerunds.
(1) The athletes wanted to take part in the running race.
(a) ………………………………………..
(b) ………………………………………..
Answer:
(a) to take – infinitive:
(b) running – participle

(2) Would you like to eat at the dinning table?
(a) ………………………………………..
(b) ………………………………………..
Answer:
(a) to eat – infinitive;
(b) dining – participle

(3) Reading is good for the mind and soul. So take up reading books.
(a) ………………………………………..
(b) ………………………………………..
Answer:
(a) Reading – gerund;
(b) reading – gerund

(4) I like to eat fruits rather than eating sweets.
(a) ………………………………………..
(b) ………………………………………..
Answer:
(a) to eat – infinitive;
(b) eating – gerund

(5) Listening and speaking sharpen your language skills.
(a) ………………………………………..
(b) ………………………………………..
Answer:
(a) Listening – gerund;
(b) speaking-gerund

The Gift of the Magi Class 10 English Workshop Questions and Answers Maharashtra Board

The Gift Of The Magi Answers Question 1.
Complete the following.
(a) Della had saved ………………………………………..
(b) Della wanted to buy ………………………………………..
(c) Della’s beautiful hair tell about ………………………………………..
Answer:
(a) one dollar and eighty-seven cents.
(b) a Christmas present for Jim
(c) her rippling and shining like a cascade of brown waters.

The Gift Of The Magi Questions Question 2.
Answer the following questions:
(a) How much did Della save for Christmas ? What does it show ?
(b) Why did Della take pride in the beauty of her hair?
(c) Why and how did Della sell her hair? Do you think she did well ?
(d) Why did Jim sell his gold watch? Do you think he did well ?
(e) Why did Jim and Della want to present the gifts?
(f) Why did Della feel sad on losing her hair?
(g) What did Jim bring out from his coat? Describe the scene.
(h) How beautiful was the gold watch chain? Would you have liked to own it?
(i) How did the Magi want to celebrate their Christmas (OR) Who were the first people to give Christmas gifts ?
(j) What is the moral of the story?
Answer:
(a) Della saved one dollar and eighty-seven cents for Christmas. It shows that she was very poor.
(b) because Jim thought that she was pretty because of her hair.
(c) Della sold her lovely long hair to get money to buy a Christmas present for Jim.
(d) She sold it to a woman who dealt in hair goods of all kinds. Yes, she did it willingly even though it was her prized possession.
(e) it was Christmas Eve, a time for giving gifts.
(f) it was very beautiful and her prized possession.
(g) Jim brought out a package from his coat.
(h) The watch chain was very beautiful. It was made of platinum, and simple and chaste in design. No, I would not have liked to own it, because I do not carry a watch that needs a chain. It is old-fashioned.
(i) The Magi wanted to celebrate their Christmas by exchanging gifts. They werejhe first people to give Christmas gifts.
(j) The moral of the story is that unselfish love is the greatest of all gifts, and those who realize this fact are the wisest.

The Gift Of The Magi Question Answers Question 3.
Complete the following activity :
Map the problems and solutions in “The Gift of the Magi” on the diagram below. Two problems have already been filled in.

Answer:

The Gift Of Magi Solutions Question 4.
Read the following and answer.
(A) Say WHAT
(a) ……………………………….. troubled Della on Christmas Eve?
(b) ……………………………….. was the current family income?
(c) ……………………………….. could have outshone Queen of Sheba’s jewels?
(d) ……………………………….. was the cost of the fob chain?
(e) ……………………………….. sent Jim into a trance, on his return?
Answer:
(a) The next day was Christmas Day and Della had only one dollar and eighty-seven cents with which to buy Jim a present. She had spent a lot of time thinking about a good present for him. but with the money she had saved she would not get anything worthy of him. Hence, she was feeling disturbed.
(b) $20 per week.
(c) Della’s beautiful hair
(d) twenty-one dollars.
(e) Jim saw that Della had cut off her beautiful hair. It was seeing this that sent him into a trance.

(B) Say WHY
(a) ……………………………….. did Della sell her lovely long hair ?
(b) ……………………………….. was Della a bit apprehensive after she had sold her hair ?
(c) ……………………………….. did Jim avoid checking the time in his gold watch, in a public place?
(d) ……………………………….. did Della’s scream of joy change to loud wails ?
(e) ……………………………….. in the end, did Jim ask Della to put the chops on?
Answer:
(a) to get money to buy a Christmas present for Jim.
(b) she was afraid of Jim’s reaction.
(c) the leather strap he used in place of a chain was old.
(d) Jim’s gift to Della was the set of tortoise shell combs that she had adored. She had craved and yearned for them, so that they could adorn her beautiful hair. When she opened the package and saw them, she was first ecstatic with joy that she had got what she had coveted; but her scream of joy turned to wails when she remembered that the beautiful hair they would have adorned was now cut off. The gift was hence useless.
(e) Jim knew that neither of them could use their Christmas gifts for the time being. Hence, he wanted to put them away and keep them for some time. He wanted to get back to daily life. Hence, he asked Della to put the chops on.

(C) Say WHEN
(a) ……………………………….. had Jim added ‘Dillingham’ as his middle name ?
(b) ……………………………….. did a tear or two drop on the old red carpet ?
(c) ……………………………….. did Della go through goods in the stores ?
(d) ……………………………….. did Della say a silent prayer to God ?
(e) ……………………………….. did Jim try to divert their attention for ten seconds, at least?
Answer:
(a) a former period of prosperity, when he was earning $30 per week.
(b) Della made up her mind to cut off her beautiful hair.
(c) she was searching for a suitable present for Jim.
(d) she heard Jim’s step on the stairway down on the first flight.
(e) Jim realized that Della was afraid of his reaction to her short hair. In order to console her, he probably hugged her and the narrator tries to divert our attention to something else, to give them privacy. It could also mean that the narrator is asking us to think about the importance of riches-how important is it to happiness.

The Gift Of The Magi Question Answer Question 5.
Complete Use the chart below to explain situational irony in ‘The Gift of the Magi’. For each character, identify what is expected to happen and what actually happens.

Answer:

The Gift Of Magi Question Answer Question 6.
Complete the following activity.
Word List :
agile, cascade, coveted, instigate, prudence, assertion, chronicle, inconsequential, predominating, subside, gobbling.

Fill in each set of blanks with the correct word from the word list. The boxed letters will spell out something that Della receives.

Answer:

COMBS

The Gift Of The Magi Questions And Answers For Class 6 Question 7.
Complete the following basic plot diagram :

Answer:

A Gift For Christmas 10th Class Question Answer Question 8.
Pick out from the story words that mean the following.
Against each consumer write (N) if it is a Noun (V) for Verb and (Adj) for Adjective.
(1) reluctance to spend money …………………………….. (  )
(2) relating to …………………………….. (  )
(3) urge …………………………….. (  )
(4) reduce in value …………………………….. (  )
(5) wisdom …………………………….. (  )
(6) very huge …………………………….. (  )
(7) foolishness …………………………….. (  )
Answer:
(1) reluctance to spend money …………………………….. (  )
(2) relating to …………………………….. (  )
(3) urge …………………………….. (  )
(4) reduce in value – depreciate ( Verb )
(5) wisdom – prudence ( Noun )
(6) very huge – mammoth ( Adjective )
(7) foolishness – idiocy (Noun)

The Gift Of Magi Question And Answers Question 9.
Think and answer on your own in a few sentences, in your notebook.
(a) What would you do if you ran short of money, to buy a birthday gift for one of your parents/siblings?
Answer:
If I ran short of money to buy a gift for one of my parents/siblings, I would borrow from someone else close to me. For example, if I wanted to buy a bag for my sister and fell short of money, I would ask my mother to lend it to me. If I wanted to buy something for Mom and did not have the money for it, I would borrow from dad.

(b) Think of two alternatives that could have prevented Della as well as Jim from selling their most precious possessions.
Answer:
Both knew that they were poor and couldn’t afford expensive gifts. So they could have just given each other small token gifts of flowers or cards. This would have prevented them from selling their most precious possessions.

(c) Justify the title of the story, ‘The Gift of the Magi’.
Answer:
The Magi were three wise men who brought gifts for baby Jesus during Christmas. They knew how to give and gave unique gifts with special emphasis. In the same way, Della and Jim gave each other unique gifts. The author compares their giving to the gifts the Magi gave to baby Jesus, ffe calls them tire ‘Magi’ because of their wisdom in realizing that unselfish love is the greatest of all gifts.

(d) Gifts that you buy have fixed prices/ rates. How can the buyer increase the value of a gift bought for someone very dear in the family?
Answer:
The buyer can increase the value of a gift bought for someone very dear in the family by giving it with words of love and gratitude. He /She can also write something loving on a card and attach it to the gift.

(e) What situation is the climax of the story ? How does it end up as an Anticlimax?
Answer:
The climax should have been the happiness and joy on the faces of Jim and Della when they see their gifts. It ends up as an anti-climax because though they had got what they coveted, neither of them could now use the gifts.

(f) If you share this story with some friends in a junior class, how would they react in the end?
Answer:
They would probably just feel that all the sacrifice was wasted. They would not have realized the deeper meaning of the story.

(g) Who were the very first people to give Christmas gifts? What had inspired them to do so?
Answer:
The Magi visited Jesus after his birth to give gifts to honour him. The Magi wanted to celebrate their Christmas by exchanging gifts. They werejhe first people to give Christmas gifts.

(h) At the end of the story, O Henry remarks that of all who give gifts, Della and Jim were the wisest. Think and explain this paradoxial remark.
Answer:
Jim and Della were initially foolish enough to believe that they needed to give material gifts in order to show their love for one another and that they had to sacrifice their most precious possessions to do so. However, they were also wise enough to know later that unselfish love is the greatest of all gifts.

The Gift Of Magi Question And Answer Question 10.
Pick out and rewrite the exact sentence which indirectly imply the following :
(a) Della was not too happy about bargaining for grocery etc.
……………………………………………………………………………………………………
Answer:
Pennies saved one and two at a time by bulldozing the grocer and the vegetable man and the butcher until one’s cheeks burned.

(b) The flat was in a dilapidated condition.
……………………………………………………………………………………………………
Answer:
It did not actually beggar description, but certainly had that word on the look out for the mendicancy squad.

(c) King Soloman would express his jealousy of Jim.
……………………………………………………………………………………………………
Answer:
Had King Solomon been the janitor, with all his treasures piled up in the basement, Jim would have pulled out his watch every time he passed, just to see him pluck at his beard with envy.

(d) Della spent a joyful time, for two hours.
……………………………………………………………………………………………………
Answer:
The next two hours tripped by on rosy wings.

(e) Della’s elated mood underwent a change as she opened her gift.
……………………………………………………………………………………………………
Answer:
An ecstatic scream of joy; and then alas! A quick feminine change to hysterical tears and wails.

(f) The weekly income amount does not matter.
……………………………………………………………………………………………………
Answer:
Whenever Mr. James Dillingham Young came home and reached his flat above he was called ‘Jim’ and greatly hugged by Mrs. James Dillingham Young.

The Gift Of The Magi Class 10 Question 11.
Frame wh-questions to get the underlined answers.
(1) Life is made up of sobs, sniffles and smiles.
……………………………………………………………………………………………………
Answer:
What is life made up of?

(2) Many a happy hour she had spent planning for something nice for him.
……………………………………………………………………………………………………
Answer:
Who had spent many a happy hour planning something nice for him?

(3) Her hair reached below her knee.
……………………………………………………………………………………………………
Answer:
Where did her hair reach?

(4) She was ransacking the stores for Jim’s present.
……………………………………………………………………………………………………
Answer:
She has been ransacking the stores for Jim’s present.

(5) At 7 o’clock the coffee was made.
……………………………………………………………………………………………………
Answer:
When was the coffee made?

(6) The magi were wise men.
……………………………………………………………………………………………………
Answer:
Who were the magi?

The Gift Of The Magi Questions And Answers Pdf Question 12.
(A) Add appropriate question tags.
(1) Della leaped up, …………………….?
(2) You’ll have to look at the time, ………………….?
(3) They were expensive combs, ………………..?
(4) I just had to do it, ……………………..?
(5) I am still pretty, ………………………..?
(6) Give it to me quick, …………………?
(7) There was clearly nothing to do,…………..?
(8) My hair grows so fast, …………………?
(9) Let’s put our Christmas presents away, ………………….?
(10) She had a habit for saying a silent prayer, ………………….. ?
Answer:
(1) Della leaped up, didn’t she?
(2) You’ll have to look at the time, won’t you?
(3) They were expensive combs, weren’t they?
(4) I just had to do it, didn’t I?
(5) I am still pretty, aren’t I?
(6) Give it to me quick, won’t you?
(7) There was clearly nothing to do, was there?
(8) My hair grows so fast, doesn’t it?
(9) Let’s put our Christmas presents away, shall we?
(10) of saying a little silent prayer about the simplest everyday things.

(B) Supply short answers (Pronoun + Auxiliary Verb)
Questions – Answers
(1) Don’t you like me ? Yes, ………………..
(2) Have you cut off your hair ? Yes, ………………..
(3) Shall I put the chops on ? Yes, ………………..
(4) Isn’t it a dandy ? Yes, ………………..
(5) Does it make difference ? No, ………………..
(6) Will you buy my hair ? No, ………………..
(7) Can you afford it ? No, ………………..
(8) Are you fooling me ? No, ………………..
Answer:
(1) Yes, I do.
(2) Yes, I have.
(3) Yes, you shall/can.
(4) Yes, it is.
(5) No, It doesn’t.
(6) No, I won’t.
(7) No, I can’t.
(8) No, I’m not.

The Gift Of The Magi Story Questions And Answers Question 13.
Pick out the infinitives/ gerunds/ participles from the following sentences and state what each one is.
(1) I want to see how it looks.
………………………………………………………….

(2) I don’t like frightening stories.
………………………………………………………….

(3) We decided to settle in Pune.
………………………………………………………….

(4) Playing sitar is Arjun’s hobby.
………………………………………………………….

(5) It was a horrifying experience for all of us.
………………………………………………………….
Answer:
(1) to see – infinitive
(2) frightening – participle
(3) to settle – infinitive
(4) playing – gerund
(5) horrifying – participle

The Gift Of The Magi Solution Question 14.
List the signs that indicate that Della was very poor.
Answer:
The following things show us that Della was very poor:
(i) The house was a poorly furnished flat at $8 per week.
(ii) The couch was small and shabby.
(iii) In the vestibule below was a letter-box and an electric bell, both of which were not functioning.
(iv) The current family income was $20 per week.
(v) After a lot of bargaining and penny-pinching, Della had saved only one dollar and eighty-seven cents for Christmas.

The Gift Of Magi Questions And Answers Question 15.
Pick out from the passage words that mean the following, and state if it is a Noun, Verb or Adjective: (The answers are given directly and underline.)
Answer:

The Gift Of The Magi Question And Answer Question 16.
Rearrange the letters given below to form sensible words:
(i) stedoih
(ii) eilpmid
(iii) teccirle
(iv) ectubrh.
Answer:
(i) stedom – modest
(ii) teccirle – electric
(iii) eilpmid – implied
(iv) ectubrh – butcher

Question 17.
Della counted the money thrice. Explain what you think the reason for this may be.
Answer:
Della had struggled and bargained a lot to save money. She had hoped that she had saved enough money to buy Jim a proper Christmas present. She could not believe that it was only 1 dollar and 87 cents. She probably counted the money thrice in the hope that it was actually more than that.

Question 18.
Write whether the following statements are True or False:
(1) Della wanted to buy a Christmas present for Jim.
(2) There was a pier glass between the windows of the room.
(3) Jim now earned $30 per week.
(4) It was Christmas Eve.
Answer:
(1) True
(2) True
(3) False
(4) True

Question 19.
(1) Write the part of speech of each of the words given below:
(1) fairly accurate conception.
(ii) very agile person.
Answer:
(i) fairly-adverb
accurate – adj ective
conception – noun

(ii) very-adverb
agile-adjective
person-noun

Question 20.
Find from the passage the antonyms of the following words:
(1) common
(2) slow
(3) spending
(4) dully
Answer:
(1) common x rare
(2) slow x agile
(3) spending X saving
(4) dully x brilliantly

Question 21.
Rewrite the following sentence as an interrogative sentence: Twenty dollars a week doesn’t go far.
Answer:
Does twenty dollars a week go far?

Question 22.
Rewrite the following sentence beginning ‘Though ’: Her eyes were shining brilliantly, but her face had lost its colour.
Answer:
Though her eyes were shining brilliantly, her face had lost its colour.

Question 23.
Complete the following:
(1) The couple’s prized possessions were …………………………
(2) Della’s beautiful hair fell about ………………….
(3) Della felt sad on losing her hair because …………………….
Answer:
(1) Jim’s gold watch and Della’s beautiful hair.
(2) her rippling and shining like a cascade of brown waters.
(3) it was very beautiful and her prized possession.

Question 24.
Write the adjective forms of the following words and pick out those that are participles:
(1) possessions
(2) treasures
(3) envy
(4) sparkle
Answer:
(1) possessions – possessive
(2) treasures – treasured (past participle)
(3) envy – envious
(4) sparkle – sparkling (present participle)

Question 25.
Complete the following:
(a) The gift Della bought for Jim was ………………………
Answer:
(a) a platinum fob chain.

Question 26.
Explain why Della looked at her reflection critically.
Answer:
Della had cut off her beautiful hair, which Jim had loved. She was worried about his reaction to her short hair, and to make it look better she had curled her newly-cut hair. She looked at her reflection critically hoping that Jim would like it.

Question 27.
Pick out 4 adverbs of manner from the passage.
Answer:
properly, wonderfully, carefully, critically.

Question 28.
Frame a Wh-question to get the underlined part as the answer: She was ransacking the store for Jim’s present.
Answer:
Why was she ransacking the store?

Question 29.
Rewrite the following sentence using ‘No sooner., than..’: As soon as she saw it she knew that it must be Jim’s.
Answer:
No sooner did she see it, than she knew that it must be Jim’s.

Question 30.
Complete the following: (The answers are given directly and underlined.)
(a) Jim stared at Della ………………….
(b) Della took pride in the beauty of her hair ………………….
Answer:
(a) because she had cut off her hair.
(b) because Jim thought that she was pretty because of her hair.

Question 31.
Complete the web with words to describe Jim.
Answer:

Question 32.
Pick out two words from the passage formed by using prefixes:
Answer:
immovable, disapproval.

Question 33.
Match the adjectives in column ‘A’ with the nouns in column ‘B’:

Answer:

Question 34.
Give your opinion: ‘It is important to give gifts.’
Answer:
Yes, it is. When you give gifts, you show your love and affection for the person. You also show that you have remembered the occasion-maybe a birthday or an anniversary. However, the gift should be thoughtfully chosen, keeping the likes and dislikes of the receiver in mind.

Question 35.
Put the following statements in the correct order of occurrence:
(1) “If you’ll unwrap that package you may see why you had me going a while at first.”
(2) “It’s Christmas Eve, boy.”
(3) “Don’t you like me just as well, anyhow?”
(4) “It’s sold, I tell you.”
Answer:
(3) “Don’t you like me just as well, anyhow?”
(4) “It’s sold, I tell you.”
(2) “It’s Christmas Eve, boy.”
(1) “If you’ll unwrap that package you may see why you had me going a while at first.”

Question 36.
Give reason: Della asked Jim to be good to her.
Answer:
Della asked Jim to be good to her for she had cut off her hair for his sake.

Question 37.
Complete the following:
This conversation took place on ………………….
Answer:
Christmas Eve.

Question 38.
Complete the following table:
Answer:

Question 39.
(1) Jim drew a package from his overcoat pocket and threw it upon the table. (Rewrite beginning ‘Drawing….’.)
(2) The magi brought valuable gifts, but that was not among them. (Rewrite beginning ‘Though ’.)
Answer:
(1) Drawing a package from his overcoat pocket, Jim threw it upon the table.
(2) Though the magi brought valuable gifts, that was not among them.

Question 40.
(1) The gift Jim had brought for Della was ………………………
(2) The beautiful present flashed with ……………………
(3) Jim and Della wanted to present the gifts because ………………….
Answer:
(1) a set of beautiful, pure tortoise shell combs, with jewelled rims.
(2) a reflection of Della’s bright and ardent spirit.
(3) it was Christmas Eve, a time for giving gifts.

Question 41.
Jim wanted to put the Christmas presents away and get back to daily life.
Answer:
And now, suppose you put the chops on.

Question 42.
Describe the scene when Della opened the package that Jim gave her.
Answer:
Della opened the package that Jim had given her with nimble fingers. She first gave an ecstatic scream of joy, which soon changed to hysterical tears and wails. Jim had to immediately comfort and soothe her. However, she hugged the gift lovingly to her bosom.

Question 43.
why Jim sold his gold watch. Do you think he did it willingly?
Answer:
Jim sold his gold watch to buy a Christmas gift for Della. Yes, he did it willingly, even though it was his prized possession.

Question 44.
why Jim and Della are referred to as the Magi.
Answer:
Jim and Della are referred to as the Magi because first each willingly sacrificed his/her prized possession for the sake of the loved one. Then they wisely realized that unselfish love is the greatest of all gifts.

Question 45.
Pick out from the story the word that means the following, and state if it is a Noun, Verb or Adjective: sought after
Answer:
sought after – coveted (Adjective)

Question 46.
Fill in the blanks with words from the passage that are the opposites of the underlined words: (The answers are given directly and underlined.)
(1) Something that is not ……………………..
(2) Something that is not ………………
(3) Men who are not ……………….. are ………………..
(4) Something that is not ………………… is ………………
Answer:
(1) cheap is expensive.
(2) bright is dull.
(3) foolish, wise.
(4) hated, worshipped.

Question 47.
(1) Pick out two compound words from the lesson.
(2) Pick out a gerund from the lesson and use it in your own sentence.
(3) Punctuate: youve cut off your hair asked jim laboriously
(4) Find out five hidden words from the given word: ornamentation
(5) Use the following phrase in your own sentence: on the corner of the table
(6) Spot the error and rewrite the correct sentence: Jim be never late.
(7) Identify the type of sentence: Isn’t it a dandy. Jim?
(8) Arrange the following in alphabetical order: Christmas, cheeks, chaste, chain, chops, coveted
(9) Complete the word chain of animal names: duck, k……., o……., h……., e……. .
Answer:
(1) backyard, letter-box
(2) saying: He had the habit of saying cruel things with a smile on his face.
(3) “You’ve cut off your hair?” asked Jim, laboriously.
(4) ornamentation: ornament, remain, mentor, meant, rotate
(5) The little boy sat on the corner of the table.
(6) Jim was never late.
(7) Interrogative and negative.
(8) chain, chaste, cheeks, chops, Christmas, coveted
(9) duck, kangaroo, ostrich, hare, elephant.

Question 48.
“You say your hair is gone?” he said, with an air almost of idiocy. (Rewrite in reported speech.)
Answer:
He asked her, with an air of almost idiocy, whether she said that her hair was gone.

Question 49.
(1) Use the following word as a verb and a noun in two separate sentences: look
(2) Use the given two words in a single sentence of your own: reflection, terrified
Answer:
(1) (i) “Look to your left and right before crossing the road,” said the policeman, (verb)
(ii) The woman gave the shopkeeper an angry look, (noun)
(2) The lion was terrified when it saw its reflection in the water.

English Kumarbharati 10th Digest PDF

• A Thing of Beauty is a Joy For Ever 10th English Textbook Solutions
• The Luncheon 10th English Textbook Solutions
• World Heritage 10th English Textbook Solutions
• The Height of the Ridiculous 10th English Textbook Solutions
• The Old Man and The Sea Book Review 10th English Textbook Solutions
• The Gift of the Magi 10th English Textbook Solutions

Class 10 English Chapter 2.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.4 The Pulley Notes, Textbook Exercise Important Questions and Answers.

The Pulley Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 2.4 Warming Up Questions and Answers

The Pulley Poem Questions And Answers Question 1.
Go through the following images and try to link them with our lives. For example, Storm – Hardships that we face in our life.

Answer:
For example : storms – hardships that we face in our lives
Owl – Wisdom
Rose – Life
Tree – Determination
Clouds – Sorrowful moments
Bouquet of flowers – Beauty
Waterfall – Strength
Mountains – Honour
Sunrise – Hope

Pulley Or The Gift Of God Questions And Answers Question 2.
You may have often indulged in talking to yourself audibly.
For example,

• “Oh, dear! Why didn’t I get up sooner?”
• “Let me finish this quickly and then I’ll be free”.
• “How silly of me! Why didn’t I think of it before?”

Such expressions are called Dramatic Monologues.
Imagine and write Monologues suitable in the following situations.

→ It’s your birthday next week.
…………………………………………………………….
Answer:
I wonder what presents I’ll get. I hope dad gets me the bicycle he promised

→ You have been waiting long at the city of bus-stop.
…………………………………………………………….
Answer:
Oh, bother Now I shall be late for school again.

→ Your final exam results are to be declared tomorrow.
…………………………………………………………….
Answer:
I wish it were tomorrow

→ Your mother has been chatting for very long on the telephone.
…………………………………………………………….
Answer:
This conversation could go on for ages When will I get a chance to call?

Question 3.
‘The Pulley’ is a mechanical device.
Try and write down places where it can be used, and for what purpose.
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
Answer:

– To draw water out of a well
– In elevators
– In exercise machines
– In theatres to open curtains
– To lift up heavy objects at construction sites

The Pulley Class 10 English Workshop Questions and Answers Maharashtra Board

Pulley Poem Questions And Answers Question 1.
With the help of the clues, pick out words containing the letter ‘a’ from the poem and build a word-pyramid.

(a) an article
(b) a preposition
(c) past tense of ‘lie’
(d) maximum length of your open palm
(e) make much of
(f) loveliness
(g) in place of
(h) a collection of priceless valuables
(i) restlessness and discontent
Answer:

(a) an article
(b) a preposition
(c) the past tense of ‘lie’
(d) the maximum length of your open palm
(e) make much of
(f) loveliness
(g) in place of
(h) a collection of priceless articles
(i) restlessness and discontent

The Pulley Poem Question 2.
Choose the correct alternative from the following.
(a) Herbert’s poem ‘The Pulley’ displays . . . . . . . . as the two main themes.
(i) Origin of Morality/Spirituality
(ii) Origin of species
(iii) Origin of the universe/galaxy
(iv) Origin of the earth/space
Answer:
(i) Origin of Morality/Spirituality

(b) The theme of the poem ‘The Pulley’ is (Find two correct statements from the given alternatives.)
(i) to focus on the mechanical operation of a pulley.
(ii) to teach a lesson to a creation (man) by the Creator (God)
(iii) to know the different gifts bestowed on man by God.
(iv) to remind man about his creator in his exhaustion.
(v) God pulled man towards Him by making him restless and weary.
Answer:
(iv) to remind man about his Creator in his exhaustion.

(c) In the poem, ‘The Pulley’ is considered ………………….
(i) a mechanical device.
(ii) a gift to mankind
(iii) an image to lift objects.
(iv) an image by which God compels people to become devout.
Answer:
(ii) a gift to mankind.

(d) . . . . . . . . is an example of Pun from the poem.
(i) Rest in the bottom lay.
(ii) So strength first made a way.
(iii) Having a glass of blessings . . . . . .
(iv) So both should losers be
Answer:
(i) Rest in the bottom lay.

(e) . . . . . . . . is an example of Paradox from the poem.
(i) And rest in Nature, not the God of Nature.
(ii) He would adore my gifts instead of me.
(iii) Let him be rich and weary.
(iv) When God at first made man.
Answer:
(iii) Let him be rich and weary.

(f) . . . . . . is an example of Synecdoche from the poem.
(i) So both should losers be.
(ii) Then beauty flowed.
(iii) “Let us” said he “pour on him.”
(iv) May toss him to my breast.
Answer:
(iv) May toss him to my breast.

(g) . . . . . . is an example of Alliteration from the poem.
(i) made a way
(ii) bottom lay.
(iii) repining restlessness
(iv) keep the rest.
Answer:
(iii) repining restlessness

(h) . . . . . . is an example of Inversion from the poem.
(i) Contract into a span.
(ii) So both should losers be.
(iii) Bestow this jewel.
(iv) And rest in nature.
Answer:
(ii) So both should losers be.

(i) The rhyme scheme of the poem is . . . . . .
(i) a a b b c
(ii) a b c b c
(iii) a b c c b
(iv) a b a b a
Answer:
(iv) a b a b a

Pulley Poem Question 3.
Discuss and answer in your own words, and write in your notebook.
(a) The poet has used the word REST thrice in the poem. Write what the word implies in each of the three lines it occurs.
Answer:
. . . rest in nature – give importance to, enjoy the benefits of
. . . let him keep the rest – the remaining gifts (except the gift of ‘rest’)
. . . rest – contentment, satisfaction

(b) What does God want in return from man, for the gifts He has bestowed upon him?
Answer:
In return for the gifts He has bestowed on man, God wants him to lead a life of goodness and to keep on adoring the God who has been so generousto him.

(c) Why did God withhold the gift of ‘Rest’ from man?
Answer:
‘Rest’ makes us feel satisfied and contented,When we have ‘rest’, we do not desire anything more. We might even stop remembering God, our Creator, or seeking His blessings. Hence, God withheld the gift of ‘Rest’ from man.

(d) Besides those given in the poem, what other gifts has God blessed mankind with above his other creations? Enlist them.
Answer:
Besides those given in the extract, God has bestowed on mankind the ability to use language as well as other cognitive abilities like reasoning, abstract thinking, etc. Above all, He has given human beings a marvellous brain, with which man has invented millions of things, right from the wheel to the computer.

(e) When does man generally turn to God? Give one example to support your response.
Answer:
Man , generally turns to God when he is troubled or is facing some difficulty. I remember a neighbour of mine who professed to be an atheist, but when there was a stock market crash, we were all surprised to see him at our temple with hands joined and eyes closed, praying to God.

Question 4.
(A) Discuss with your group and justify the title of the poem ‘The Pulley’ in your own words.
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
Answer:
The pulley works when pressure is exerted on either side of the rope passing through it. If one side comes down, the other goes up. Here, the poet expresses the idea that when weariness weighs down man on one end his spiritual aspects on the other end gets an uplift. According to the poet, God deliberately withheld bestowing ‘rest’ to man so that the very ‘restlessness’ wojild bring him nearer to Him. Thus, the title ‘The Pulley’ is appropriate.

(B) Pick out 3 lines that contain Monologues of God.
…………………………………………………………….
…………………………………………………………….
…………………………………………………………….
Answer:
(1) For if I should bestow this jewel also on my creature.
(2) He would adore my gifts instead of me.
(3) If goodness lead him not, yet weariness may toss him to my breast.

Question 5.
(A) Pick out two lines that contain the following figures of speech.
(a) Antithesis
1. …………………………..
2. …………………………..
Answer:
1. Antithesis: Let the world’s riches which dispersed lie.
2. Contract into a span.

(b) Alliteration
1. …………………………..
2. …………………………..
Answer:
1. And rest in the Nature, not the God of the Nature.
2. Repetition of ‘n’ sound.

(c) Inversion
1. …………………………..
2. …………………………..
Answer:
1. Let us {said He)
2. Rest in the bottom lay.

(B) Explain the Figures of Speech in the following lines.
(a) Rest in the bottom lay-PUN because
……………………………………………………….
Answer:
It is a Pun because the word ‘rest’ has two meanings – ‘the last one remaining’ and ‘a quality that helps us stop doing something and relax’.

(b) Bestow this jewel also on my creature-METAPHOR because
……………………………………………………….
Answer:
Extended Metaphor: The simple meaning of the ‘pulley’ is extended to show an implicit comparison between the ‘gift’ of ‘rest’ that is not bestowed on man S by God, and by which he will be pulled towards God finally.

(c) And rest in nature, not the God of Nature-REPETITION because
……………………………………………………….
Answer:
Repetition: The word ‘Nature’ is repeated for emphasis.

Question 6.
Write Critical Appreciation of the poem in a paragraph format. (Refer to page no. 5)
Answer:
Point Format
(for understanding)

• Title of the poem: ‘The Pulley’
• The poet: George HerbertRhyme scheme: a-b-a-b-a
• Figures of speech: Metaphor, Pun, Inversion, Paradox, etc.
• The central idea theme the reason why man is continually restless

Paragraph Format
The title of the poem is ‘The Pulley’. The poet is George Herbert.

Each stanza of the poem has five lines. The rhyme scheme of the poem is a-b-a-b-a.

The chief figure of speech used in the poem is Metaphor. The ‘glass of blessings’ signifies the sum of all human qualities bestowed on man. The quality of ‘rest’ or ‘contentment’ is implicitly compared to a ‘jewel’. The other figures of speech are Pun, Inversion, Paradox, etc.

The central idea of the poem is the reason for man’s continual restlessness all his life. According to the poet, this is because God withheld the quality of ‘rest’ from man, so that man’s thoughts would ultimately turn towards God, his creator.

Question 7.
‘Pun’ can be defined as play on words based on their different meanings. Example ‘Writing with a broken pencil is pointless.’ In this poem there is an example of Pun. Find and make a sentence of your own. Share a joke with the class where the use of ‘Pun’ creates humour.
Answer:
(i) Rest in the bottom lay
(ii) So strength first made away.
(iii) Having a glass of blessings
(iv) So both should losers be.

Question 8.
Write a paragraph on the points in each block given below to get a summary on each of the four stanzas of the poem.

Answer:
(1) The poel says dial at the lime when God fir.si 1 created man. He had a glass of blessings standing by. He thought dial He would be generous and shower on man all the gifts possible. God intended lhal all the treasures of die earth which lay scallcred should be eollecled and concentrated in die small space He had created – which was man.

(2) The first gift God gave man was strength. This was followed by beauty, then wisdom, honour and pleasure. When nearly all the gifts had been bestowed on man. God slopped awhile. He noticed that of all the treasures, only one gill remained at Ihe bottom of the glass, and that was rest.

(3) God said to Himself that if He bestowed this precious and valuable gift on His creation, man would love anil worship only the gifts of Nature, and would not love the God who-had created all the things in Nature. Thus both God and man would end up as losers.

(4) So God let man retain all the other gifts, but at the same lime, He left man restless and continually anxious and dissatisfied, lie thought that in should be rich with the abundance of gifts, but he should always remain tired and restless. God reasoned that only then, at the end. if the quality of goodness did not lead man back to God. sheer fatigue (tiredness) would draw man back to God’s heart.

Question 9.
Choose the correct alternatives from the following:
(a) Herbert’s poem ‘The Pulley’ displays Origins and Morality/Spirituality as the two main themes.
(i) Origins and Morality/Spirituality
(ii) Origin of species
(iii) Origin of the universe galaxy
(iv) Origin of the earth space
Answer:
(i) Origins and Morality/Spirituality

(b) The first gift was strength.
(i) strength
(ii) beauty
(iii) wisdom
(iv) rest
Answer:
(i) strength

(c) The last gift left was rest.
(i) strength
(ii) beauty
(iii) wisdom
(iv) rest
Answer:
(iv) rest

(d) The gifts blessings lay in a glass.
(i) the world
(ii) a span
(iii) a glass
(iv) a pathway
Answer:
(iii) a glass

Question 10.
What did God’s glass of blessings contain?
Answer:
God’s glass of blessings contained gifts such as strength, beauty, wisdom, honour, pleasure, other treasures and the gift of rest.

Question 11.
Write the rhyming words from the extract:
Answer:
man – can – spanby – lieway – stay – laypleasure – treasure.

Question 12.
Explain the figures of speech in the following lines:
a glass of blessings
Answer:
It is a Metaphor because the sum of attributes or qualities given to man are implicitly compared to a ‘glass of blessings’.

Question 13.
Explanation: The words are not in the correct prose order. The correct prose orders are:
Answer:
1. Let us (He said) …
2. Rest lay in the bottom.]

Question 14.
What would human beings do if God gifted them with ‘Rest’?
Answer:
If God had gifted human beings with ‘Rest’,’ they would never have cared to remember God since they would have nothing to long for or to feel restless about. This is because self-satisfaction and contentment wduld have made human beings feel: complete and pleased with themselves. They mightthus lose their spiritual and moral values.

Question 15.
Pick out two lines from the extract that contain the figure of speech ‘Inversion’.
Answer:
(a) For if I should (said He)
(b) So both should losers be.
(c) If goodness lead him not, yet weariness May toss him to my breast.

Question 16.
Choose the correct alternative from the following: (The answers are given directly and underlined.)
(a) Let him be rich and weary’ is an example of I Paradox from the poem.
(i) And rest in Nature, not the God of Nature.
(ii) He would adore my gifts instead of me.
(iii) Let him be rich and weary.
(iv) When God first made man.
Answer:
(iii) Let him be rich and weary.

(b) ‘repining restlessness’ is an example of Alliteration from the poem.
(i) made a way
(ii) bottom lay
(iii) repining restlessness
(iv) keep the rest
Answer:
(iii) repining restlessness

Question 17.
Write the rhyming words from the lines.
Answer:
he – me – becreature – Nature; rest – breastrestlessness – weariness.

Question 18.
Bestow this jewel also on my creature.
Answer:
Metaphor: The gift of rest is implicitly compared to a ‘jewel’.

English Kumarbharati 10th Digest PDF

• Animals 10th English Textbook Solutions
• Three Questions 10th English Textbook Solutions
• Connecting the Dots 10th English Textbook Solutions
• The Pulley 10th English Textbook Solutions
• Let’s March 10th English Textbook Solutions
• Science and Spirituality 10th English Textbook Solutions