Category: Class 10

Class 10 English Chapter 4.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.5 The Old Man and The Sea Book Review Notes, Textbook Exercise Important Questions and Answers.

The Old Man and The Sea Book Review Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 4.5 Warming Up Questions and Answers

The Old Man And The Sea Book Review Class 10 Question 1.
Pair up with your partner and answer the following questions :
(a) Which animal would you relate yourself to and why?
Answer:
I would relate to a cat. This is because like a cat, I am lazy. I am also reserved and do not show my emotions easily. I choose my friends carefully and am not friendly with anybody and everybody.

(b) Do you have a hero or a role model to look up to? Who is he/she?
Answer:
Yes, my role model is my grandmother. Though she has led a very difficult life because she was poor, she is always optimistic and sees the best in people. She is always cheerful and ready to learn new things. She has learnt how to use the computer and surfs the internet regularly. She is even learning a new language with the help of the computer! She is health-conscious and does yoga regularly. I wish to be like her.

(c) Do you have a passion you would fight for? Why?
Answer:
Yes, my passion is planting trees. Afforestation is the answer to. many of the ills plaguing our country, like water shortage and soil erosion. Planting forests will stop this. When I grow up. I plan to fight for a green cover for our planet.

(d) What is meant by a review?
Answer:
A ‘review’ is a critical evaluation of something – a book, a film, a play, etc.

(e) Have you ever read any book review? If yes, which one? If no, make it a point to read one.
Answer:
Yes, I have read a book review. It was of a Harry Potter book. I read it in a newspaper and it gave me an idea of what to expect in the book, without knowing the details.

The Old Man And The Sea Section 1 Answers Question 2.
Make a list of famous novels of Ernest Hemingway. Two are given to you.
(1) A Farewell to Arms
(2) For Whom the Bell Tolls.
(3) ………………………………………
(4) ………………………………………
(5) ………………………………………
(6) ………………………………………
(7) ………………………………………
Answer:
(1) A Farewell to Arms.
(2) For Whom the Bells Toll.
(3) The Sun also Rises.
(4) The Garden of Eden.
(5) Islands in the Stream.
(6) To Have and Have Not.
(7) The Torrents of Spring.

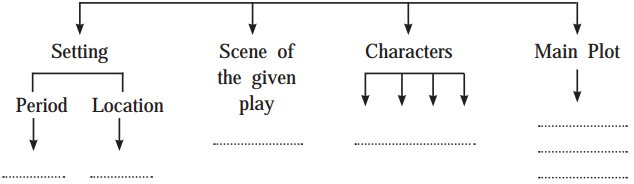
The Old Man And The Sea Question Answers Question 3.
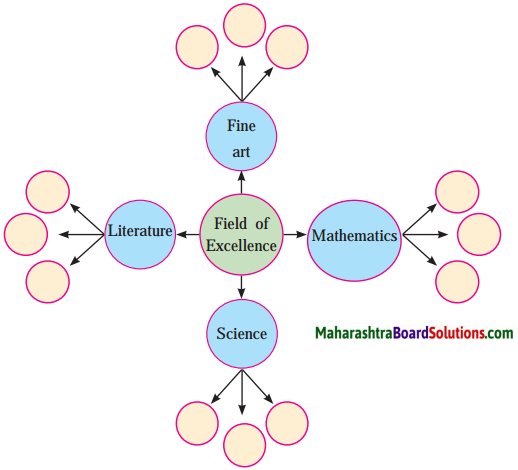
Ernest Miller Hemingway was a famous American novelist, short story writer and journalist. Make a list of other famous American novelists. Complete the web filling the boxes with the names of famous American novelists.

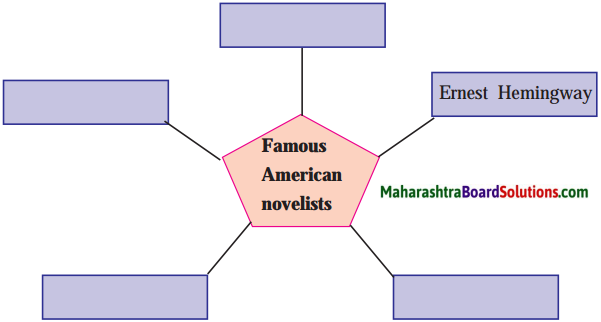
Answer:

The Old Man and The Sea Book Review Class 10 English Workshop Questions and Answers Maharashtra Board

The Old Man And The Sea Book Report Question 1.
Read the passage and name the following.
(a) Young and devoted apprentice
(b) The place where Hemingway had experience of fishing
(c) That which Hemingway was injured by, during First World War
(d) Language of the novel
(e) In his first reading, the review writer was left
Answer:
(a) Manolin
(b) Cuban waters
(c) shrapnel
(d) simple and pithy
(e) unimpressed

The Old Man And The Sea Book Review Question 2.
Correct the following sentences using facts from the review.
(a) Manolin’s parents insisted on his working with the same old fisherman.
(b) This novel is pure fiction.
(c) Hemingway’s style of writing does not unfold the hidden meaning.
(d) The relationship between the old man and Manolin is coarse.
Answer:
(a) Manolin’s parents insisted on his working with another fisherman.
(b) This novel is based on real events and draws heavily from incidents in Hemingway’s own life.
(c) Hemingway’s style of writing is such that a reader can read his work again and again and find new layers of meaning every time.
(d) The relationship between the old man and Manolin is heart-warming.

The Old Man And The Sea Questions And Answers Question 3.
Compare the points that you would use for a book review with those of the review of a play and write in your notebook.
Answer:

Book Review	Review of a play	Review of a film
(1) Story Line	(1) Story Line, Theme and Climax	(1) Story Line
(2) Social/Historical Context	(2) Actors/Actresses and their Presentations	(2) Acting
(3) Writing Style	(3) Use of lights, music and special effects	(3) Direction
(4) My Thoughts.	(4) Use of Sets, Costumes and Make-up (5) My Thoughts and rating.	(4) Editing (5) Cinematography (6) Music and sound effects (7) Special effects (8) My thoughts and rating

The Old Man And The Sea Review Question 4.
The line – ‘I first read this novel years ago, when I did not understand it at all and was left unimpressed.’ tells us about the book reviewer’s opinion about the book. Complete the following sentences using the expressions.
(1) In my opinion, every hard working person achieves success in life.
(2) I strongly feel that ……………………………………………………….
(3) I wish I could ……………………………………………………….
(4) As far as I know you ……………………………………………………….
(5) I think ……………………………………………………….
Answer:
(1) every hardworking person achieves success in life.
(2) there should be a complete ban on tobacco.
(3) go to the moon.
(4) have never taken part in a debate.
(5) they know what they are doing.

Old Man And The Sea Book Review Question 5.
The review describes the struggle between the old man with the marlin and sharks, Ernest Hemingway’s struggle against defeat or death and noble struggle against destruction. Find all the words from the text that are related to the word ‘brave’ or ‘courage’.

• strength
• ……………………………………….
• ……………………………………….
• ……………………………………….
• ……………………………………….

Answer:

• strength,
• formidable.
• strong,
• determination,
• endurance,
• triumph,
• struggle.

The Old Man And The Sea Answers Question 6.
The review mentions struggles of both the writer, Ernest Hemingway and the old man. Fill the incidents of struggle of Hemingway in table A and those of the old man in table B.

Answer:

Question 7.
Read the text again. You will find that the text contains many phrases. Match the phrases in ‘A’ and their meanings in ‘B’. After matching their meanings, make sentences of your own

Answer:

Question 8.
(A) Rewrite as directed, without change of meaning, in your notebook.
(1) Hemingway’s novel is based on real events. (Convert the underlined adjective to an Adjectival Clause)
(2) He hooks a marlin but the marlin is too strong for him. (Rewrite beginning with ‘Although’)
(3) The reader can read his work again and again and find new layers of menaing. (Begin the sentence with ‘On reading’)
(4) As the novel progresses, the old man and the marlin are inseparably linked. (Rewrite using ‘progress’ as a Noun)
(5) Being strong, the marlin starts pulling the boat. (Rewrite inserting ‘and’ as a Co-ordinator)
(6) When I first read this novel, I was unimpressed. (Rewrite using ‘but’ as a Co-ordinator)
Answer:
(1) Hemingway’s novel is based on events which are real.
(2) Although he hooks a marlin, the marlin is, too strong for him.
(3) On reading his work again and again, the reader can find new layers of meaning.
(4) In the course of the progress of the novel, the old man and the marlin are inseparably linked.
(5) The marlin is strong and starts pulling the boat.
(6) I had read this novel before but I was unimpressed at that time.

(B) Write the ‘root-word’ after dropping the prefix or suffix or both.
(1) unable ……………………………………….
(2) heavily ……………………………………….
(3) determination ……………………………………….
(4) endurance ……………………………………….
(5) unimpressed ……………………………………….
(6) relationship ……………………………………….
(7) inseparably ……………………………………….
(8) empathetic ……………………………………….
(9) beautiful ……………………………………….
(10) simplicity ……………………………………….
Answer:
(1) unable – able
(2) heavily – heavy
(3) determination – determine
(4) endurance – endure
(5) unimpressed – impress
(6) relationship – relate
(7) inseparably – separate
(8) empathetic – empathy
(9) beautiful – beauty
(10) simplicity – simple

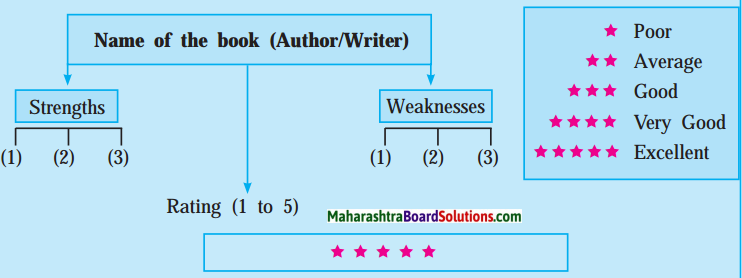
Question 9.
Write a book review on any book of your choice with the help of the following points.

• Story line
• Social/Historical content
• Writing style
• My thought

Answer:

Pride and Prejudice: Book review.

Story Line:
‘Pride and Prejudice’ is a romantic novel written by Jane Austen and first published in 1813. The book follows the life of Elizabeth Bennet, a headstrong, intelligent woman. It takes place in the early 1800s and is about the emotional development of the main character.

Elizabeth has four sisters and no brother. According to the succession rights, none of the girls can inherit the property, and Mrs. Bennet (Elizabeth’s mother) thinks that good marriages are the only way for them to lead a good life. Her main ambition in life is to see that her daughters marry wealthy men. However, the novel emphasizes that one should marry for love and not only for money. Mr. Bennet tolerates his wife’s behaviour and is dryly sarcastic when she is silly. There are villainous characters like George Wickham and comic ones like Mr. Collins.

Social/Historical Context:
In Pride and Prejudice, the Bennets are members of the educated upper middle class. At that time, a man’s income was always reported as a ‘number of pounds per year’. Mr Bingley has ‘four or five thousand a year’ while Darcy’s income is a very impressive 10,000 a yepr. Thus, Darcy is considered to possess a fortune, and hence a very eligible bachelor.

The formal manners of behaviour are obvious in the custom of paying visits and leaving calling cards, the necessity of giving formal introductions, etc. Marriage was considered to be the only acceptable role for any woman, and getting married was high on the list of priorities. The clothes and customs all reflect the time. The French revolution was in progress during the time of the writing of this novel. Though it is difficult to relate to such customs and such priorities today, the novel still holds our interest.

Writing Style:
Jane Austen has portrayed her characters well, and given good character sketches of all, whether it is the silly, materialistic Mrs. Bennet as the mother or Elizabeth as the strong-willed daughter. Jane Austen’s writing is sharp, with plenty of sarcasm and irony. Many times it is a bit too detailed; but that was the style of writing at that time. She wrote about ordinary people and their ordinary lives in an exceptional way. She recognized the flaws in society, especially as far as marriage is concerned. The opening words of her novel, ’It is a truth universally acknowledged, that a single man in possession of a good fortune, must be in want of a wife.’, are unforgettable and are still quoted.

My Thoughts:
When I first read it, it was out of compulsion; it was a part of our school activity, and I disliked it. I was too small to appreciate the undertones. I found too many unnecessary details. However, when I read it a few years later, I had already read many other books based in that time period. Hence, I could appreciate their customs, their dresses and their way of talking. I had alsu seen a film based on it. and things became clearer. I plan to read it again and see if I can find new meaning in it now.

Question 10.
You know the essential points required for a book review. Now form pairs and find essential points required for a play review and film review. You can take help of your teacher, library or the internet.

Answer:

Question 11.
Project
Classroom Library :
Ask all your classmates to donate a book each to the class. In this way everyone will have a book of his/her own to read. Read the book in a week or two. After reading it, exchange your book with your classmate. Keep exchanging and reading books for the whole year. Every fortnight give the book review of the book that you have read recently in the form of a presentation.

Question 12.
Complete the following:
(1) Hemingway had experience of …………………..
(2) He worked for ………………….. during the First World War.
(3) ‘The Old Man and The Sea’ was published in …………………….
Answer:
(1) fishing in the Cuban waters.
(2) The Red Cross
(3) 1952

Question 13.
Describe the general mood of the people when the novel was published.
Answer:
When the novel was published, people were trying to recover from the mass destruction caused by the two World Wars.

Question 14.
Sentences:
(1) The young actor had a …………………… at the beginning of his career.
(2) This painter …………………… the old masterpieces.
(3) The girl’s sad story immediately …………………… with the news reporter.
(4) Lata Mangeshkar’s songs …………………… for a long time.
Answer:
(1) run of terrible bad luck
(2) draws heavily on
(3) struck a chord
(4) will live on

Question 15.
Find the synonyms (one word) for the following from the passage:
(i) The ability to do something difficult for a long time: ……………
(ii) Formed or worked: ……………
Answer:
(i) endurance
(ii) wrought

Question 16.
The old man is, at the end of the novel, very near death, but we know that the story of his suffering and loss will live on in the memories of the people of his village. (Rewrite the sentence using ‘Though’)
Answer:
Though the old man is, at the end of the novel, very near death, we know that the story of his suffering and loss will live on in the memories of the people of his village.

Question 17.
During the First World War, Hemingway was injured by shrapnel. (Begin the sentence with ‘Shrapnel….’)
Answer:
Shrapnel injured Hemingway during the First World War.

Question 18.
Do you like to read books? If so, what type? If not, why?
Answer:
I do like to read books. I like to read mystery novels. I find them very thrilling and interesting. I am a big fan of Agatha Christie and Arthur Conan Doyle. I have read nearly the whole Sherlock Holmes series of short stories.

Question 19.
(a) After recent reading the reviewer was left: ……………………
(b) It fights for its life desperately: ……………………
Answer:
(a) moved and impressed
(b) the marlin

Question 20.
Hemingway practises an extreme economy in his use of words’. What does this mean?
Answer:
It means he uses very few words to express his thoughts and ideas.

Question 21.
What are the ideals that the old man and the marlin both stand for?
Answer:
The old man and the marlin both stand for the same ideals, that is, a noble struggle against destruction.

Question 22.
Complete the following web:
Answers:

Question 23.
Sentences:
(1) Hussain was ill; in spite of this, he stood first in the test.
(2) I could see the new rider holding on to the reins desperately.
(3) The little boy looked longingly at the puppy again and again.
(4) The symbol of a white dove stands for peace.
Answer:
(1) in spite of
(2) holding on
(3) again and again
(4) stands for

Question 24.
Find the synonyms for the following from the passage:
(i) Brief: …………………..
(ii) Likely to make someone believe something that is not true: ………………….
Answer:
(i) pithy
(ii) deceptive

Question 25.
Write four to five sentences about your favorite writer.
Answer:
My favorite writer is Arthur Conan Doyle, the creator of Sherlock Holmes. Every story written by Doyle is different and holds my interest right till the end. The stories are so gripping that one cannot put the book down easily. I borrow the books from the library to read during the vacation.

Question 26.
(1) Write down two compound words from the passage.
(2) Pick out an infinitive from the lesson and use it in your own sentence.
(3) Find out five hidden words from the given word t endurance
(4) Use the following phrase in your own sentence: even after his death
(5) Spot the error/errors and rewrite the correct sentence: The novel was publishing in 1952
(6) Identify the type of sentence: I first read this novel years ago, when I did not understand it at all.
(7) Hemingway always talks about the need to struggle. (Replace the infinitive with a gerund.)
(8) From the following verbs, pick out the verb which forms its present and past participle by doubling the last letter: run, write, swim, fan.
(9) Complete the word chain with verbs of your own. write, e………., r………., r………., t……… .
Answer:
(1) fisherman, baseball
(2) to catch: The fielder tried to catch the ball.
(3) endurance: endure, dance, under, crane, creed.
(4) even after his death: People remembered the great leader with love and respect even after his death.
(5) The novel was published in 1952
(6) Assertive (negative)
(7) Hemingway always talks about the need for struggling.
(8) fan – fanning, fanned.
(9) write, enter, remember, report, think.

Question 27.
(1) Use the following word and its homophone in two separate sentences: sail
(2) He worked for the Red Cross. (Rewrite using the past progressive tense of the verb.)
(3) A reader can read his work again and again. (Change the voice beginning ‘His work ….)
Answer:
(1) (i) The sail of the huge boat fluttered in the breeze,
(ii) The old woman loves shopping wherever there is a sale.
(2) He was working for the Red Cross.
(3) His work can be read again and again (by a reader).

Question 28.
(1) Use the given two words in one meaningful sentence: formidable, beautiful.
(2) Recently, I read this book again and was extremely moved. (Rewrite as a complex sentence.)
Answer:
(1) It was a formidable job to make the dilapidated old house beautiful again.
(2) I was extremely moved when I recently read the book again.

English Kumarbharati 10th Digest PDF

• A Thing of Beauty is a Joy For Ever 10th English Textbook Solutions
• The Luncheon 10th English Textbook Solutions
• World Heritage 10th English Textbook Solutions
• The Height of the Ridiculous 10th English Textbook Solutions
• The Old Man and The Sea Book Review 10th English Textbook Solutions
• The Gift of the Magi 10th English Textbook Solutions

Class 10 English Chapter 1.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.5 His First Flight Notes, Textbook Exercise Important Questions and Answers.

His First Flight Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.5 His First Flight Textbook Questions and Answers

Warming up!

Chit-chat:

1. Form Groups of 5. Remember your past days and share with your friends about memories of your first day at school or your first attempt at cooking. What role did your parents, siblings play to help you to overcome your fear?

1. Discuss and answer.

Question 1.
Discuss and answer.

Answer:

2. Complete the following table.

Question 1.
Complete the following table.

Answer:

Find more such idioms using the following keywords.

Question 1.
Find more such idioms using the following keywords.

Answer:

• Fly – with flying colours, fly high, fly the nest, fly the coop, fly at somebody, fly into rage/temper, get off to flying start.
• Animals – the lion’s share, let sleeping dog lie, a dog in the manger, a snake in the grass, rain cats and dogs, to lead a cat and dog life, let the cat out of the bag, to smell a rat.
• Colours – loose colours, with flying colours on black and white, catch red-handed, to become red and blue, a bolt from blue, once in a blue moon, look at the black side of things, stick to one’s colour.
  (Note: Students may collect more such idioms and their meanings from good dictionary.)

English Workshop:

1. State whether the following statements are true or false.

Question 1.
State whether the following statements are true or false.
(a) The young seagull was not confident about the ability of his wings.
(b) The young seagull’s parents guided and improved his siblings in the art of flying.
(c) When the young seagull pretended to be falling asleep, his parents noticed him.
(d) Flying across the young seagull, the mother dropped a piece of fish into his beak.
Answer:
(a) The young seagull was not confident about the ability of his wings. – True
(b) The young seagull’s parents guided and improved his siblings in the art of flying. – True
(c) When the young seagull pretended to be falling asleep, his parents took notice of him. – False
(d) Flying across the young seagull, the mother dropped into his beak a piece of fish. – False

2. Complete the following statements.

Question 1.
Complete the following statements.
(a) The seagull was afraid to fly because …………………………………………………………….
……………………………………………………………………………………………………………………………………..
(b) Young birds are afraid to make their first flight because …………………………..
………………………………………………………………………………………………………………………………………
(c) Human beings find it difficult to face great challenges because ……………….
………………………………………………………………………………………………………………………………………
Answer:
(a) the seagull is afraid to fly because he thought that his small, short wings would never support him to fly and he would fall and drown in the sea.
(b) Young birds are afraid to make their first flight because they are not confident at their first flight.
(c) Human beings find it difficult to face great challenges because I think, human being also finds it a challenge to take its first steps. It is their natural instinct. When they try to stand and then to take further steps, they are afraid of falling and getting injured, so they are cautious and alert but do not give up.

3. Read the following words carefully and make meaningful sentences of your own, and write in your notebook.

Question 1.
Read the following words carefully and make meaningful sentences of your own, and write in your notebook.

4. Read the following words carefully and fill in the blanks by choosing appropriate word given in brackets.

Question 1.
Read the following words carefully and fill in the blanks by choosing appropriate word given in brackets.
(afraid, plunged, appeared, shrilly, skimmed, devoured, cowardice)
(a) Arun is full of ……….. .
(b) The violin played very ……….. .
(c) Ravi said, “Are you really ……….. of the dark?”
(d) The whole village ……….. into darkness.
(e) The lions ……….. their prey, hungrily.
(f) He ……….. through the report.
(g) One by one, the stars ……….. in the sky.
Answer:
(a) Arun is full of cowardice.
(b) The violin played very shrilly and merrily.
(c) Ravi said, “Are you really afraid of the dark?”
(d) The whole village plunged into darkness.
(e) The lions devoured their prey, hungrily.
(f) He skimmed through the report.
(g) One by one, the stars appeared in the sky.

5. Read about the space mission of Sunita Williams. Imagine you are going to interview her. Frame 10 to 12 interview relevant questions regarding –

1. her early life, training
2. education
3. her actual flight into space
4. future plans
5. her message to viewers.

Question 1.
Read about the space mission of Sunita Williams. Imagine you are going to interview her. Frame 10 to 12 interview relevant questions regarding –
Answer:
Interview Questions to Sunita Williams :
Hello Madam! Congratulations on your great achievements in the Space Mission! May I ask you a few questions about your career and mission?

1. 1. Could you please tell me about your birthplace, family and early education?
   2. What motivated you to do M.Sc. in engineering Management? Where did you do it?
   3. What was your experience as a Naval Aviator in 1989?
   4. When and where did you begin your Astronaut Candidate Training?
   5. When were you selected by NASA for Astronaut Program?
   6. Will you please tell me about your experience at NASA?
   7. How did you feel when you were aboard the space shuttle Discovery to join the Expedition 14?
   8. How many days did you stay in the space during the Expedition 14?
   9. You have eclipsed the record in space by a woman. What was that record?
   10. What can you tell me about your second Expedition 32/33. What was your part in it?
   11. You took to the ISS a copy of Bhagavat Gita and a figurine of the God Ganesh and samosas. What was the thought behind it?
   12. How did the Government of India honour you? Why?
   13. What is your message to the young Indian generation?

6. Describe in your notebook the challenges you faced while learning to ride a bicycle, swimming or any skilL Take hints from the web to complete your write-up.

Question 1.
Describe in your notebook the challenges you faced while learning to ride a bicycle, swimming or any skilL Take hints from the web to complete your write-up.
Answer:
Riding a Bicycle:
Though some people think that riding a bicycle is a very simple easy thing, but it is not true. It is a challenging job. When you begin to learn cycle you must have to drive away and win over the fear of falling. While riding a cycle you are bound to fall once or twice or more and may get injured. So you must be bold and forget your fear of falling.

Secondly as a beginner don’t fully depend on a trainer or a supporter, otherwise you will never learn cycling. You should ride on your own with determination. You must be steady, stable and patient. You will have to look straight ahead of you and not to the handle or pedal or anywhere else. Sit properly on the seat and hold the handle firmly. Balancing is the next task/challenge. Be alert and ride the cycle carefully.

Pay attention to the vehicles coming in your way and you should be able to avoid them or there will be a possibility of an accident. Your concentration must be only on riding. Remember the traffic rules and follow them. After practising a lot you will be able to ride a bicycle confidently.

7. Project :

Question a.
Collect the career options related to flying. Find out the institutes where training of your options is given.
Find out the detailed information about the fees, duration of training and future prospects of it.
Answer:
(Students should collect the information asked for and present them in their class.)

Question b.
Collect or draw different pictures of birds from your surroundings and write about them. Make a chart with some information about each.
Answer:
(Make a chart with some information about the birds.)

Language Study:

1. There are words that have the same pronunciation but differ in spellings. They are called Homophones. For example, (a) fair – fare (b) know – no Sometimes the words have the same spellings and pronunciation but can have different meanings in different situations.
They are called Homographs.
For example:
(a) watch – observe watch – portable timepiece
(b) fair – not very good, not very bad
fair – an exhibition and sale of items
fair – of complexion, skin tone
Note: Homophones and Homographs are together known as Homonyms.
Give the Homophones of the following.
(a) blue …. (b) bear …… (c) beet……… (d) to……… (e) son …………

Question 1
Give the Homophones of the following.
Answer:
(a) blue – blew
(b) bear – bare
(c) beet – beat
(d) to – two
(e) son – sun

2. Find from the lesson the Homophones of the following.

Question a.
Pick the Homophones from the text.

1. see –
2. wood –
3. there –
4. scene –
5. won –
6. eye –
7. peace –
8. threw –
9. hence –
10. knot –

Answer:

1. see – sea
2. wood – would
3. there – their
4. scene – seen
5. won – one
6. I – eye
7. peace – piece
8. threw – through
9. hence – hens
10. knot – not

Question b.
Explain how the underlined Homographs differ in meaning.
1. (a) He saw his two brothers. ……………………….
(b) The woodcutter cut the weakened branch with his sharp saw ……………………….
2. (a) The bird injured his wings. ………………………..
(b) He lives in the ‘c’ wing of the building. ……………………….
3. (a) The aeroplane will land at 9.00 pm. sharp. ……………………….
(b) He owns 10 acres of land ………………………..
4. (a) The head of the institution was on leave. ……………………….
(b) He bent his head down with chin. ………………………….
Answer:
1. (a) He saw his two brothers.
(b) The woodcutter cut the weakened branch with his sharp saw.
Answer:
In the sentence:
(a) the Homograph ‘saw’ is the past tense of the word ‘see’.

In the sentence:
(b) the Homograph ‘saw’ means a tool of a carpenter used for cutting wood.

2. (a) The bird injured his wing.
(b) He lives in the ‘C’ wing of the building.
Answer:
In the sentence:
(a) the Homograph ‘wing’ means the part of the body of a bird used for flying.

In the sentence:
(b) the Homograph ‘wing’ is one of the parts of a large building.

3. (a) The aeroplane will land at 9.00 pm. sharp.
(b) He owns 10 acres of land.
Answer:
In the sentence
(a) the Homograph ‘land’ means to come down through the air onto the ground.

In the sentence
(b) land means an area of ground used for some purpose.

4. (a) The head of the institution was on leave.
(b) He bend his head down with respect.
Answer:
In sentence
(a) head means the person in charge of an institution/organization.

In sentence
(b) head means the part of the body on top of the neck.

3. Read the following sentences carefully, underline the verbs and find out the tenses in the sentences.

Question 1.
(a) The sun was now ascending the sky.
(b) Still they took no notice of him.
(c) She is standing on a little high hump on the plateau.
(d) He leaned out eagerly.
(e) He just felt dizzy.
Answer:
(a) The sun was now ascending the sky. – Past Continuous Tense
(b) Still they took no notice of him. – Simple Past Tense
(c) She is standing on a little high hump on the plateau. – Present Continuous Tense
(d) He leaned out eagerly. – Simple Past Tense
(e) He just felt dizzy. – Simple Past Tense

Live English :

Form Filling:

Form filling is a skill. It is a functional skill and a life skill. Today, a big amount of data is collected offline and online through forms. From a tedious task to an interesting task, the online tools have made form filling a unique experience. We will see how offline and online forms are filled and what steps are followed and what care is taken while filling the forms.

Preparing for the form filling process:

• Gather all the essential information. (personal, professional, educational etc.)
• Verify names, addresses, references, contact details to be entered.
• Know the information not to be provided.
• Get a template and create a model form.

Question 1.


Answer:

My English Coursebook 10th Digest Chapter 1.5 His First Flight Additional Important Questions and Answers

Read the following passage and do the activities :

Simple Factual Activity :

Question 1.
State whether the following statements are True or False :
Answer:

1. The wings of the young seagull were not as short as his own. – False
2. The whole family of seagulls commended him for his cowardice. – False
3. The young seagull was fed a piece of fish by his mother. – False
4. The young seagull’s father was preening the feathers on his white back. –True

Question 2.
Complete the following sentences using information in the passage:
(Answers are directly given and underlined.)
Answer:

1. The young seagull commended himself to dive and soar and curve.
2. He completely forgot that he had not always been able to fly.
3. He flapped his wings once and he soared upwards.
4. He turned his beak sideways and cawed amusedly.

Complex Factual Activities :

Question 1.
How did the seagull parents perfect the young seagull’s brothers and sister in the art Of flight?
Answer:
The parents of the seagull flew about with his brothers and sister, perfecting them in the art of flying. They trained them how to skim the waves and how to dive for fish. When they succeeded in the art, the parents circled about them raising a proud cackle to encourage them.

Question 2.
Complete the web describing the young seagull’s feelings while trying to fly:
(Answers are directly given.)
Answer:

Question 3.
What were the young seagull’s parents doing?
Answer:
The young seagull’s father was cleaning his white back feathers smooth with his beak. His mother was looking at the young seagull. She stood on a little high hump on the plateau. Her white breast was thrust forward. Now and again, she tore at a piece of fish that lay at her feet and then scrapped each side of her beak on the rock. She was trying to attract the young one’s attention towards the piece of fish.

Question 4.
Complete the web :
(Answers are directly given and underlined.)
Answer:

Question 5.
How did the young seagull learn his first flight?
Answer:
When the young seagull was calling his mother plaintively, his mother had picked up a piece of fish and was flying across to him with it. He leaned out eagerly trying to get nearer to her as she flew across. But when the piece of fish in her beak was almost within his reach, his mother halted, her wings motionless. Maddened by hunger, the young one dived at the fish.

While doing so he fell outwards and downwards into space. He was frightened but the next moment he felt his wings spread outwards. The wind rushed against his breast, then under his stomach and against his wings. His wings cut through the air. He was not falling headlong now. He was soaring gradually downwards and outwards. This is how he learnt his first lesson of flight.

Question 6.
Complete the web :
(The answers are directly given and underlined.)
Answer:

Question 7.
What did the young seagull forget? What did he do then?
Answer:
The young seagull completely forgot that he had not always been able to fly. He commended himself for his diving and soaring and curveting shrieking shrilly.

Question 8.
When did the young seagull get his prized scraps of dog-fish?
Answer:
The young seagull was completely exhausted after his first flight. He drooped his legs to stand on the green sea. His legs sank in it. He screamed with fright and tried to rise again flapping his wings. But he was tired and weak with hunger and he could not rise. His feet sank into the green sea and then his belly touched it and he could sink no farther. He was floating on it. His family admired his feat (achievement) and offered him scraps of dog-fish which he deserved.

Activities based on Vocabulary:

Question 1.
Guess the meanings of:
Answer:

1. muster up courage – to gather courage
2. cliff – a high steep face of a rock
3. upbraiding – scolding
4. brink – the edge of a steep place

Question 2.
Match the words in Column ‘A’ with their meanings in Column ‘B’ :

Answer:

Question 3.
Find the present participles from the passage :
Answer:
ascending, standing, falling, lying, dozing, preening, looking, scrapping, begging, calling, flying, tapping, trying, wondering, cutting, soaring.

Question 4.
Match adjectives given in Column ‘A’ with the nouns given in Column ‘B’ :

Answer:

Question 5.
Read the following words carefully and make meaningful sentences of your own by using them :

1. plaintively
2. monstrous
3. whet
4. soar.

Answer:

1. The young widow plaintively mourned when she saw her husband’s dead body in a coffin covered by tricolour.
2. A monstrous wave swallowed the boat with some fishermen in it.
3. He whetted his knife to cut the unwanted plants in the garden.
4. The rocket soared up into the air.

Question 6.
Read the following words and fill in the blanks by using appropriate words given in the brackets :
(Answers are directly given and underlined.)
(commended, attempted, exhausted, soared)
Answer:

1. The rocket soared up into space.
2. Our achievements in Science Exhibition was highly commended by our Principal.
3. He was totally exhausted after the day’s tedious work.
4. The thief attempted to give the slip, but was caught by the police.

Question 7.
Match the words in Column ‘A’ with their meanings in Column ‘B’ :

Answer:

Question 8.
Read the following words and make meaningful sentences of your own by using them :

1. beckon
2. curveting
3. exhausted
4. amusedly

Answer:

1. They were all beckoning him to join their team, but he did not respond.
2. The eagle was curveting to land onto the ground to catch his prey.
3. The old man was completely exhausted after the day’s long work.
4. The children played in the rain merrily and amusedly.

Activity-based on Contextual Grammar :

Question 1.
Read the following sentences carefully, underline the verbs and then find out the tenses in the sentences : (Verbs are directly underlined.)
Answer:

1. His two brothers and his sister had already flown away. – Past Perfect Tense
2. But for the life of him he could not move. – simple Past Tense
3. He became afraid. – simple Past Tense
4. Since then nobody had come near him. – Past Perfect Tense

Question 2.
Identify the tense and then change it to Present Perfect Continuous tense:
The sun is ascending the sky.
Answer:
The sun has been ascending the sky.

Personal Response:

Question 1.
Are you afraid of playing any outdoor game? Explain why?
Answer:
Yes, I am afraid of playing Kabbadi. It appears to me that it is a very rough and tough game. I am very much afraid of the injuries caused in it. I cannot endure the thought of injury. I believe that it is a game for only strong and hefty people.

Question 2.
You are a teacher directing a play for your school/Annual Gathering. A boy is not acting according to your instructions. How will you make him act well?
Answer:
At first I shall tell the boy about the scene and the emotions in dialogues by giving him demonstration. If he goes wrong, I myself will show him how to do the piece. If he repeatedly makes mistakes, I will scold him and even threaten him of the consequences. But anyhow finally I will make him act well, acting the scene myself repeatedly.

Question 3.
How does your family help you to achieve your goal?
Answer:
My family is always there to help me in my work. Each one of them, especially my parents, help me in deciding my goal. If I neglect any day, they remind me of my goal all the while. They all are ready to guide me, in their own way, to achieve whatever I desire. They always encourage, admire and praise me even for my smallest achievement.

Activity-based on Contextual Grammar:

Do as directed:

Question 1.
He was near the sea now. (Frame a Wh-question to get the underlined as an answer.)
Answer:
Where was he now?

Question 2.
He could not rise. (Add a question tag.)
Answer:
He could not rise, could he?

Question 3.
But he was tired and weak with hunger.
(Use ‘not only – but also’.)
Answer:
But he was not only tired but also weak with hunger.

Activities based on Language Study

Do as directed :

Question 1.
Complete the words by using correct

1. s t _ n d
2. y o _ n g
3. c l _ f f
4. d i z _ y

Answer:

1. s t a n d
2. y o u n g
3. c 1 i f f
4. d i z z y

Question 2.
Put the following words in alphabetical order :

1. motionless, scrapped, leaned, opposite
2. feathers, felt, flapped, father

Answer:

1. leaned, motionless, opposite, scrapped.
2. father, feathers, felt, flapped

Question 3.
Punctuate the following sentences :

1. ga ga ga he cried begging her to bring him some food
2. the young seagulls father was curveting banking and soaring

Answer:

1. “Ga, ga, ga”, he cried begging her, to bring him some food.
2. The young seagull’s father was curveting, banking and soaring.

Question 4.
Make four words each (minimum 3 letters each) using the letters in the given word brother:
Answer:
both, bother, rot, other

Question 5.
Write related words as shown in the example :
(Answer is directly given and underlined.)
Answer:

Question 6.
Complete the following word chain of nouns. Add four words each beginning with the last letter of the previous word :
ledge → ……………… → ……………… → ……………… → ………………
Answer:
ledge → egg → goal → land → doll

Do as directed :

1. Attempt anyone :

a. Make a meaningful sentence using the given phrase:
to muster up courage
Answer:
The young man could not muster up courage to pick up the mysterious box on the road.

OR

b. Add a clause to the following sentence to expand it meaningfully :
The bird dared not fly
Answer:
The bird dared not fly because he was afraid of falling in the sea.

2. Attempt anyone :

a. Add a prefix or suffix to make new words :
1. manage
2. arrange
Answer:
1. management
2. rearrange

OR

b. Make a meaningful sentence using any one of the following words :
1. manage
2. arrange
Answer:
1. He could manage to collect enough money to pay his school fees.
2. She arranged the flowers in a vase.

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer 10th English Solutions
• An Encounter of a Special Kind 10th English Solutions
• Basketful of Moonlight 10th English Solutions
• Be SMART…! 10th English Solutions
• His First Flight 10th English Solutions

Class 10 English Chapter 3.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Solutions Chapter 3.4 Let us March! Notes, Textbook Exercise Important Questions and Answers.

Let us March! Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.4 Let us March! Textbook Questions and Answers

Warming up:
Chit-chat

Discuss in your group:

Question 1.
What difference do you notice in the two images?
Answer:
The boy in the first picture is working and the boy in the second picture is going to school on his bicycle.

Question 2.
Which of the two situations should change?
Answer:
The situation in the first picture should change.

Question 3.
How and when can the situation be changed?
Answer:
The boy in the first picture should be sent to school. Somebody should convince his parents that it is not his right age to work. He should go to school at this age. Then the situation can change.

Question 4.
How can you, as a student, contribute and help make a difference to the needy children?
Answer:
As a student I will help the needy children to go to school and take education. If possible I will try to give them monetary help to take education. I will also convince their parents
to understand the importance of education.

1. A good well-organized speech contains the following characteristics and steps.

Question (A)
A good well-organized speech contains the following characteristics and steps.
Answer:

1. A speech should be well-planned.
2. The language used should be suitable to the audience.
3. It should have the right duration.
4. It should be supported with good examples, episodes or visual aids, where possible.

Question (B)
Refer to Page 26 for a reference to the steps to be followed in the speech and do the activity given below. Read the expressions given below on Coursebook and insert them in the proper boxes:
(a) Imagine what will happen after ten years.
(b) I would like to share with you an example from my own experience.
(c) Hon. chief guest, eminent dignitaries, respected management and staff, student – friends
(d) The research report says that ……………
(e) I don’t understand why we are so negative about this issue.
(f) Think again and again and then move forward.
(g) Today, I would like to put forth my views on ………………
(h) The renowned personality xyz says “……………..”
(i) Good Morning, one and all present today.
(j) I would like to express my gratitude towards the organisers of this function for giving me opportunity ……………
(k) If we think about the situation around us, we notice that ………………
(l) Let me explain this to you ……………..

Answer:

English Workshop:

1. Name the following:

Question (a)
The persons to whom Kailash Satyarthi gives the highest credit of his honour:
Answer:
Kaalu Kumar, Dhoom Das and Adarsh Kishore from India and Iqbal Masih from Pakistan.

Question (b)
The greatest personalities from the great land-India.
Answer:
Lord Buddha, Guru Nanak and Mahatma Gandhi.

Question (c)
The daughters of Kailash Satyarthi mentioned in this speech:
Answer:
Malala, Kayanat and Shazia

Question (d)
The foreign activists of equal rights mentioned in this speech:
Answer:
Nelson Mandela and Martin Luther King.

2. Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.

Question 1.
Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.
(a) Child labour
(b) …………………
(c) …………………
(d) …………………
(e) …………………

3. Complete the following diagram/chart:

Question 1.
Complete the following diagram/chart:

Answer:

4. Complete the following web-chart:

Question 1.
Complete the following web-chart:

Answer:

5. Find out the describing words used for the following nouns and make your own sentences by using any three combinations.

Question 1.
Find out the describing words used for the following nouns and make your own sentences by using any three combinations.
(a) …………… sacrifice
(b) …………… faces
(c) …………… militia
(d) …………… challenge
(e) …………… globalise
(f) …………… agencies
Answer:
(a) supreme sacrifice
(b) beautiful faces
(c) extremist-militia
(d)great challenge
(e) globalise – globe, globalization
(f) intergovernmental agencies

6. Choose the correct option and write in front of the given word:

Question (a)
divinity: ……………
Answer
divinity: godliness
1. goodness
2. godliness
3. god fearing

Question (b)
extremist: militant
1. militant
2. robber
3. spy

Question (c)
culminate: rise to a peak
1. destroy
2. succeed
3. rise to a peak

7. What will you do in the following situations?

Question (a)
If you see a child working in a restaurant.
Answer:
I will lodge a complaint against the owner under the Child Labour Act, 1986.

Question (b)
If you find a child working on a construction site.
Answer:
I will lodge a complaint in the police station nearby and convince them to send him to a nearby school.

Question (c)
If you find a child working on a brickwork site.
Answer:
I will tell his parents not to do so, instead to send him to a school nearby.

Question (d)
If you come across a beggar child.
Answer:
I will tell the child, it is not good to beg. I will also tell him the importance of schooling and help him to go to school.

(B) Write any 2 efforts that you can make to enrol deprived children/ out of school children into a school. One is given for you.
(a) I will persuade parents of such children to send them to school.
(b) …………………………………………………………………………………….. .
(c) …………………………………………………………………………………….. .
(d) …………………………………………………………………………………….. .
(e) …………………………………………………………………………………….. .

8. Today, it is time for every child to have a right to –

education, ……………….., ……………….. .
……………….., ……………….., ……………….. .
……………….., ……………….., ……………….. .

9. Make a list of Indian Nobel laureates.

Question 1.
Make a list of Indian Nobel laureates.
Answer:

10. Make a list of prestigious awards in India:

Question 1.
Make a list of prestigious awards in India:

Answer:

11. Make a meaningful sentence by using the phrases:

Question 1.
Make a meaningful sentences by using the phrases: (Note: One phrase will be asked in the activity sheet.)
(a) in the pursuit of
(b) to be afraid of
(c) to give up
Answer:
(a) Most of the people spend a lot of time in the pursuit of money.
(b) Don’t be afraid of saying what you sincerely think.
(c) His wife finally persuaded him to give up smoking.

12. Write minimum 5 hidden words of more than 4 letters from- ‘intergovernmental’.

Question 1.
Write minimum 5 hidden words of more than 4 letters from- ‘intergovernmental’
Answer:

1. internal
2. government
3. torment
4. term
5. governmental

13. Imagine your school invites Malala to preside over celebration of ‘Children’s Day’. Draft a welcome speech for this noble young girl. Gather her bio-data from the internet.

Question 1.
Imagine your school invites Malala to preside over celebration of ‘Children’s Day’. Draft a welcome speech for this noble young girl. Gather her bio-data from the internet.
Answer:
Honourable Chairperson, respected Principal, teachers, our today’s guest Malala Didi and all my dear friends.

We have gathered here to celebrate Children’s Day. On this auspicious occasion I would like to limit my few words on the Children’s Day. Children are the integral part of the society and home as well as the future of the country. We cannot ignore their involvement and contribution in the life of parents teachers and other related people all through the life.

Children are blessed by God and they conquer our hearts with their beautiful eyes, innocent activities and smiles. Life becomes very boring andupset without them. This day is celebrated every year to pay tribute to all the children all over the world. In India it is celebrated on 14th November on the birth anniversary of the legendary freedom fighter and the first Prime Minister of the independent India; Pandit Jawaharlal Nehru.

The celebration of this day reminds us to renew our commitment towards children’s welfare including their health, care and education. It is an occasion to appreciate the qualities of childhood. Children are considered as the building blocks of the strong nation. They have capabilities to change the nation positively. They are the responsible citizens of tomorrow. The development of the country lies in their hand. Children’s Day celebration also reminds us about their rights.

Children are leaders of tomorrow so they need to get respect, special care and protection from their parents, teachers and from the society. Do they really get it? They are being abused in many ways in our nation by their family members, relatives, neighbours or other people. Government should work on it to help them to live life happily. Malala Didi is a Pakistani activist who works for girls’ females’ education. She works for the human rights, especially the right to education of women and children.

We are really proud of her. On this auspicious day if we take inspiration from her, no child will be abused, no girl will be molested. She is a great source of inspiration and so she is here with us. We are eager to hear her valuable thoughts and voice, so I think I would better stop here. Wish you all happy Children’s Day and all the best for your future endeavour. Thanks a lot for listening to me patiently and attentively.

Jai Hind!

14. Use the following words as a noun and a verb and make meaningful sentences:

Question 1.
Use the following words as a noun and a verb and make meaningful sentences:

1. march
2. honour
3. credit
4. stitch

Answer:

1. march – The workers began their march to protest against their factory owners, (noun)
   The physical education teacher marched the children to the playground, (verb)
2. honour – A dinner was arranged in his honour, (noun)
   The actor was honoured with the Padmashri.(verb)
3. credit – The bank refused to extend their credit.(Noun)
   She has been wrongly credited as the author. (Verb)
4. stitch – The wound needed eight stitches, (noun)
   The tailor was asked to stitch the clothes quickly, (verb)

Language Study:

Question (a)
Match the sentences given in part ‘A’ with the sentences given in part ‘B’. Note the differences in structure.
Answer:

Question (b)
Observe the following underlined phrases. Here ‘have/has’ are followed by the past participle form of the verb. This construction indicates the perfect present tense. Find more such sentences from the speech.
Answer:

1. We have made progress in the last couple of decades.
2. We have prevented millions of child deaths.
3. It has happened.
4. We have reduced the number of out-of-school children by half.
5. We have reduced the child labourers by a third.

Question (c)
In the following sentences the underlined words are called infinitives. Find such examples from the speech and underline the infinitives.
Answer:

1. Every child is free to grow.
2. I refuse to accept that all the laws and constitutions, police and judges are unable to protect our children.
3. that all the temples and mosques and churches and prayer houses have no place for the dreams of our children.
4. just one week of global military expenditure can bring all the children to classrooms.
5. The shackles of slavery can be stronger than the quest for freedom.

Question (d)
Pick out from the lesson, the Antonyms of
Answer:

1. ignorance × knowledge
2. deny × admit
3. immortality × mortality
4. violence × non-violence
5. well-known × known
6. slavery × freedom

(e) Do as directed.

Question (i)
Make nouns of the following.

Answer:

Question (ii)
Make verbs of the following.

Answer:

1. universal – universalize
2. global – globalize

Question (f)
Complete the following sentences with the help of the sentence given below:
(Answers are directly given and underlined.)
(a) The biggest challenge knocking on the doors of human kind is fear and intolerance.

(i) No other challenge knocking …………………………………………………… .
as big as …………………………………………………………………………………… .
(ii) Fear and intolerance are bigger ……………………………………………….. .
………………………………………………………………………………………………… .

(b) The Nobel Prize is one of the greatest honours in the world.

(i) Very few honours …………………………………………………………… .
(ii) The Nobel Prize is greater than …………………………………………. .
………………………………………………………………………………………………… .
Answer:
(a) The biggest challenge knocking on the doors of humankind is fear and intolerance.
1. No other challenge knocking on the doors of humankind is as big as fear and intolerance.
2. Fear and intolerance are bigger than any other challenge knocking on the doors of humankind.

(b) The Nobel Prize is one of the greatest honour in the world.
1. Very few honours in the world are as great as the Nobel Prize.
2. The Nobel Prize is greater than most other honours in the world.

My English Coursebook 10th Digest Chapter 3.4 Let us March! Additional Important Questions and Answers

Simple Factual Activities:

1. Name the following:

Question 1.
The American politician, attorney and author mentioned in the speech –
Answer:
Tom Harkin.

Question 2.
Answer in one word:
Answer:

1. The motherland of Kailash Satyarthi – India
2. The country which Iqbal Masih represents – Pakistan
3. The place where Nobel Prize distribution programme was held – Norway
4. The ancient texts of wisdom – Vedas

Question 3.
State whether you agree or disagree with the following statements:
Answer:

1. The Holy Quran s ays the kingdom of God belongs to the children.
2. Jesus says not to kill your children because of poverty. – Disagree
3. Denying the dreams of our children is greater violence. – Agree
4. The writer has never given up against any threat or attack. – Agree

Question 4.
Match the following:
Answer:

1. A small, skinny child labourer – to care for our children
2. A Sudanese child-soldier – children’s frightened and exhausted eyes
3. Satyarthi had looked into – was forced to kill his friends and family.
4. The great religions teach us – The world forced me to take a gun or a tool

Question 5.
State whether the following statements are True or False:
Answer:

1. The biggest challenge of humankind is fear and intolerance. – True
2. Education gives the meaning and objective of life. – True
3. An unprecedented violence will not be suicidal for humankind. – False
4. Rights, security, hope can only be restored through education. – True

Question 6.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. Even though we have made progress in the last couple of decades, we are facing great challenges.
2. An education gives a sense of global citizenship among the youth.
3. Small groups, local organisations and individuals are confronting with the problem every day.

Question 7.
Answer in few words:

1. he age in which we live –
2. The serious disconnect of the world –
3. We can unite the world through –
4. Children are questioning and watching our –

Answer:

1. rapid globalization
2. lack of compassion
3. the compassion for our children
4. inactions and actions

Question 8.
Complete the sentences:
(Answers are directly given and underlined.)
Answer:

1. A tiny bird was rushing towards the fire.
2. A heavy fire had broken out in the forest.
3. The speaker is appealing to compassion.
4. The tiny bird was going to extinguish the fire.

Question 9.
Make a list of the problems that we are facing and creating violence against children –
Answer:

1. slavery
2. trafficking
3. child marriage
4. child labour
5. sexual abuse
6. illiteracy

Question 10.
Complete the following web:
(Answers are directly given and underlined.)
Answer:

Question 11.
State whether the following statements are Right or Wrong:
Answer:

1. We should have vision for today not tomorrow. – Right
2. If we close our eyes and feel the child inside us, we can listen to that child. – Right
3. Mahatma Gandhi, Nelson Mandela and Martin Luther King are calling on us. – Right
4. Mahatma Gandhi, Nelson Mandela and Martin Luther King are calling on us. – Right
5. Satyarthi’s vision of tomorrow is to see that cobbler’s boy sitting with him in his classroom. – Right

Complex Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. We can create knowledge for all that benefits all by learning from the experiences of our ancestors.
2. The mantras that carries a prayer has the potential to liberate humanity from all man-made crises.
3. The writer humbly accepts this award on behalf of all martyrs, his fellow activists across the world and his countrymen.
4. The journey of the writer, that is India to Norway is a connect between two centres of global peace and brotherhood, ancient and modern.
5. The speaker feels honoured to recite a mantra from the ancient text of wisdom.

Question 2.
Complete the following web:
Answer:

Question 3.
What are the children’s issues highlighted by Kailash Satyarthi in this passage?
Answer:
The children’s issues highlighted by Kailash Satyarthi in this passage are-

1. The burning problem in India-child labour
2. The Right of children to free and compulsory education
3. Mortality and malnutrition,
4. Child labour as a human rights issue as well as a welfare matter and charitable cause.

Question 4.
Complete the following web stating the sign of progress mentioned by Satyarthi:
Answer:

Question 5.
What social role are the ‘three daughters’ laying?
Answer:
These three daughters are rising up and choosing peace over violence, tolerance over extremism and courage over fear.

Question 6.
Complete the following web:
Answer:

Question 7.
What problems do the poor children face?
Answer:
The poor children face the following problems –

1. They harvest cocoa yet they have never tasted chocolate.
2. They are dying of Ebola.
3. They are kidnapped and held hostage.
4. They stitch football, yet they never play with it.

Question 8.
What did millions of individuals demand eighteen years ago?
Answer:
Eighteen years ago, millions of individuals demanded a new international law for the abolition of worst form of child labour.

Question 9.
Why does the eight-year-old girl’s question shake Mr Satyarthi? (r^T srrc qqMi HyfMi srt SKcfTT Wt?)
Answer:
The eight-year-old girl’s question ‘Why did you not come earlier?’ itself implies that the girl was really suffering a lot. Even though we are grown ups, we have failed to rescue number of small girls from forced labour. So her question shakes not only Satyarthi, but also the whole world.

Question 10.
What matters according to Satyarthi?
Answer:
Every single minute, every single child and every single childhood matters according to Satyarthi.

Question 11.
Complete the following web:
(Answer is directly given and underlined.)
Answer:

Question 12.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
1. Government should make child-friendly policies and invest in education and young people.
2. Faith leaders, institutions and all of us must stand with our children.

Question 13.
Complete the following web:
(Answer is directly given.)
Answer:

Question 14.
What was the response of the boy’s father? What was Satyarthi’s reaction to it?
Answer:
The response of the boy’s father was that he had never thought about it and they were born to work. His answer made Satyarthi angry and it still makes him angry.

Question 15.
Complete the following:
(Answers are directly given and underlined.)
Answer:
1. Satyarthi requests the listeners to put their hands close to their heart, close their eyes and feel the child inside them.
2. The writer calls all the listeners for a march,

1. from → exploitation to → education
2. from → exploitation to → education
3. from → poverty to → shared prosperity
4. from → slavery to → liberty
5. from → violence to → peace
6. from → ignorance to → awakening
7. from → darkness to → light
8. from → mortality to → divinity

Question 16.
Complete the following web-chart:
(Answers are directly given)
Answer:

Activities based on Vocabulary:

Question 1.
Find out the describing words used for the following nouns and make your own sentences using any two combinations:
(a) peace
(b) chair
Answer:
(a) global peace
(b) empty chair

Sentences:
1. UNO was founded (established) for global peace.
2. We should never forget the supreme sacrifice of our martyrs.

Question 2.
Match the words with their meanings:

Answer:

1. aspiration – ambition
2. potential – inherent capacity
3. dignity – self-respect
4. liberate – set free

Question 3.
1. eyes
Answer:
1. exhausted-eyes.
Sentence: Extremist militia is an active force found in Sudan.

Question 4.
Choose the correct option and write in front of the given word:
(Answers are directly given.)
Answer:
courageous: brave

1. cowards
2. brave
3. friendly

Question 5.
Make a word register related with “God” from the passage.
Answer:
Jesus, Holy Quran, temples, mosques, churches, prayer houses, religions, the kingdom of God.

Question 6.
Find out antonyms for the following from the passage:

1. reject
2. ignore
3. timid

Answer:

1. reject × accept
2. ignore × notice
3. timid × fearless

Question 7.
Choose the correct option and write infront of the given word:
(Answers are directly given and underlined.)
Answer:
crisis: unstable situation

1. unstable situation
2. problems
3. difficulty

Question 8.
Find out the describing words used forthe following nouns and make your own sentences by using any three combinations:

1. organizations
2. citizenship
3. groups

Answer:

1. local organizations
2. global citizenship
3. small groups

Sentences:

1. Global citizenship nurtures personal respect and respect for others.
2. The role of local organizations are often overlooked by the government.
3. We can understand any difficult thing very well in small groups.

Question 9.
Classify the following words in Nouns and Verbs in the form of a table:
labour, prevent, knock, start, include, peace, world, problem.
Answer:

Question 10.
Find out the describing words used for the following nouns and make your own sentence by using any one combination:
1. globalization
2. compassion
Answer:
1. rapid globalization
2. global compassion
Sentence: Due to rapid globalization we have been facing number of problems.

Question 11.
Choose the correct meaning from the option and write in front of the given word:
Answer:
1. adamant: stubborn
(a) stubborn
(b) flexible
(c) kind

2. abolition: termination
(a) fixation
(b) termination
(c) prevention

3. neutrality: indifference
(a) interesting
(b) sadness
(c) indifference

4. compassion: kindness
(a) kindness
(b) passion
(c) wish

Question 12.
Find out the describing words from the passage for the following words:
(Answers are directly given and underlined.)
Answer:

1. rapid globalization
2. tiny bird
3. high-speed internet
4. serious disconnect.

Question 13.
Write the antonyms of:
(Answers are directly given and underlined.)
Answer:
1. recognized × unrecognized
2. known × unknown

Question 14.
Write the infinitive forms of the following and use any two of them in your own sentences:
Answer:

1. dancing – to dance
2. playing – to play
3. growing – to grow
4. happening – to happen

Sentences:
1. Anish wanted to dance in the procession but his father did not allow him.
2. It is our duty to grow more and more trees to save the planet Earth.

Question 15.
Choose the correct option and write in front of the given word:
(Answers are directly given and underlined.) J
Answer:
mortality: death rate

1. birth rate
2. life rate
3. death rate

Question 16.
Find out the describing words used for the following noun and make your own sentences by using any combination:
…………………… partnership
Answer:
innovative partnership

Sentence: In a developing country like India, intergovernmental agencies play important role in / the process of development.

Question 17.
Pick out any four “infinitives” from the passage:
Answer:
to put, to innovate, to accelerate, to work

Activities based on Contextual Grammar:

Question 1.
Indirect speech:
1. I asked my teachers, “Why is he working outside? Why is he not with us in the school?”
2. The boy’s father said to the writer, “I have never thought about it. We are born to work.”
Answer:
1. I asked my teacher why he was working outside and why he was not with them in the school.
2. The boy’s father told the writer that he had ; never thought about it. He further told him that ; they were born to work.

2. Make the sentences affirmative:

Question 1.
My teacher had no answer,
Answer:
My teacher was speechless.

Question 2.
I have never thought about it.
Answer:
I have always ignored it.

Activity-based on Contextual Grammar:

Question 1.
Name the tense:

1. The Nobel committee has generously invited me to present a “Lecture.”
2. I am representing the millions of children.
3. I humbly accept this award on behalf of all my fellow activists across the world.
4. I have kept an empty chair here as a reminder.

Answer:

1. Present Perfect Tense
2. Present Continuous Tense
3. Simple Present Tense
4. Present Perfect Tense

Question 2.
Make adjectives of:

1. honour
2. create
3. silence
4. peace

Answer:

1. honour – honourable
2. create – creative
3. silence – silent
4. peace – peaceful.

1. Change the voice:

Question 1.
He was kidnapped by an extremist militia. (Begin the sentence with “An extremist militia….)
Answer:
An extremist militia kidnapped him.

Question 2.
He was forced to kill his friends and family.
(Begin the sentence with “They….”)
Answer:
They forced him to kill his friends and family.

Question 3.
All the great religions teach us to care for our children. (Begin the sentence with “We are….)
Answer:
We are taught to care for our children by all the great religions.

Question 4.
I have held their injured bodies. (Begin the sentence with “Their injured bodies…)
Answer:
Their injured bodies have been held by me.

Rewrite the following into indirect speech:

Question 1.
Rewrite the following into indirect speech:
Answer:
A skinny child labourer asked Satyarthi, “Is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool?” Ans. A skinny child labourer asked Satyarthi if the world was so poor that it could not give him a toy and a book, instead of forcing him to take a gun or a tool.

Question 1.
Change these sentences into indirect speech:

1. The lion asked the bird, “What are you doing?”
2. The bird said to the lion, “I am going to extinguish the fire.”
3. The lion said, “How can you do it keeping just one drop of water in your beak?”
4. The bird said, “I am doing my bit.”

Answer:

1. The lion asked the bird what it was doing.
2. The bird told the lion that it was going to extinguish the fire.
3. The lion asked how it could do it keeping just one drop of water in its beak.
4. The bird said that it was doing its bit.

Question 2.
Add a question tag:

1. We are connected through high-speed internet.
2. We exchange our goods and services in one single global market.
3. Let us globalize compassion.
4. All the animals were running away.

Answer:

1. We are connected through high-speed internet, aren’t we?
2. We exchange our goods and services in one single global market, don’t we?
3. Let us globalize compassion, shall we?
4. All the animals were running away, weren’t they?

Question 3.
He asked the bird “What are you doing?” (Make it indirect)
Answer:
He asked the bird what he was doing.

Question 4.
Make nouns of the following:
1. play
2. grow
Answer:
1. play – play, player
2. grow – growth

Question 5.
Make verbs of the following:
1. knowledge
2. exploitation
Answer:
1. knowledge – know
2. exploitation – exploit

Personal Response:

Question 1.
What type of text is this? How do you decide it?
Answer:
This text is a speech. I have decided it on the basis of the beginning of the text. In the beginning the speaker has addressed the dignitaries and the audience assembled in the hall /auditorium. This shows that the text is a speech/lecture.

Question 2.
What do you know about Kailash Satyarthi?
Answer:
Kailash Satyarthi is an activist who fought for the Indian children’s rights. He is a Nobel Peace Prize recipient and the Founder of Bachpan Bachao Andolan. He and his team at the Bachpan Bachao Andolan have liberated more than 86,000 children in India from child labour slavery and trafficking. He is basically from Vidisha in Madhya Pradesh.

Question 3.
What efforts will you take to enrol the out-of-school children?
Answer:
If I see any children out of school, I will tell them the importance of education in their life. I will also tell them about the Right of Children to Free and Compulsory Education. By convincing them I will help them to take admission in schools nearby so that they can stand and face the life independently and get success in their life. Also, I shall try to convince their parents to send their children to school.

Question 4.
What is the role of education in nation-building?
Answer:
Education plays a very critical and crucial role in deciding the growth of a nation. Educated citizens of the country bring fame, wealth and prosperity to the country which helps in development of a country. People who are educated think and work to achieve the dream of any country. Education helps in dream building so education is a big invaluable asset in nation-building.

Question 5.
What lesson does the story of the lion and the tiny bird teach us?
Answer:
I think the story of the lion and the tiny bird teaches us not to belittle other individuals who atleast do something and make an effort. No matter how small it is in their eyes but it might be big in result. Small things shouldn’t be valued too little sometimes. Big things always start from something small.

Question 6.
What will you do for our country?
Answer:
First I will try to take higher education. As for as possible I will try to use that knowledge for the developement of our country, I will also help the people to take education so that they will also help our country to prosper and become a developed country.

Question 7.
What is your vision of tomorrow?
Answer:
My vision for tomorrow is to empower the people with a vision to have the confidence and ability to achieve their dream. If I help them to gain their confidence, they will work hard to achieve their goal. Ultimately they will help the nation to prosper.

Question 8.
Do you think, our parents are the most beautiful gift of our life?
Answer:
Our life is a journey full of joy, sorrow fantasy, expectations, hellos, goodbyes and farewells. Our parents are always with us in all ups and downs; so we can live our life happily. They are always with us to solve our problems and to sort out any situation. So they are the most beautiful gift of our life.

Question 9.
What do you mean by “Every child has a right to life”?
Answer:
The right to life is a moral principle based on the belief that a human being has the right to live. Every child has some inherent right to life which is protected by laws. No one shall be arbitrarily deprived of his life. So it is our duty to protect every child and help him/her to live a happy and healthy life.

Question 10.
Why should the government invest in education and young people?
Answer:
Education is the systematic process of gaining knowledge and skills. It has positive impact on our life. It also promotes national interest. It is the backbone of developing countries. If the government invests in education and young people, they help the nation to develop as they are called real nation-builders and future of the country so the government should invest in education and young people.

Question 11.
Why should we stop “Child labour”?
Answer:
“Child labour” is a stigma on our society. It is sure to interfere with his/her right to education. It is also harmful to their physical, mental, spiritual, moral and social development. It is harmful to the development of any country, as “the child” is the future citizen of every country. So we should stop child labour and child exploitation.

Do as directed:

Question 1.
Complete the words/spellings by using correct letters:
Answer:

1. m a _ c h – m a r c h
2. p l _ n t – p l a n t
3. w o _ l d – w o r l d
4. N _ b e l – N o b e l

Question 2.
Put the words in alphabetical order:
1. create, activist, world, freedom
2. exhausted, experience, extinguish, equality
Answer:
1. activist, create, freedom, world.
2. equality, exhausted, experience, extinguish.

Question 3.
Punctuate the following sentences:
1. the lion laughed and said how can you do it keeping just one drop of water in your beak
2. lets walk together.
Answer:
1. The lion laughed and said, “How can you do it keeping just one drop of water, in your beak?”
2. Let’s walk together.

Question 4.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 5.
Complete the word-chain of ‘adjective’. Add four words each beginning with last letter of the previous letter :
Supreme, → e ……………, …………., …………., ……………..
Answer:
Supreme, → easy, young , grateful, less.

1. Attempt anyone:

Question (a)
Add a clause to expand the following sentence meaningfully.
The bird ………………
Answer:
The bird which was in a cage was at last freed by his owner.

2. Attempt any one:

Question (a)
Add preffix or suffix to make new words:
1. inspire
2. expend
Answer:
1. inspiration
2. expenditure

OR

Question (b)
Make a meaningful sentence by using one of the following words:
1. inspire
2. expand
Answer:
1. Our parents always inspire us to do something good.
2. Reading always expands our knowledge.

Writing Skill

Malala’S Bio-Data

Name: Malala Yousafzai
Father’s Name: Ziauddin Yousafzai
Mother’s Name: Tar Pekal Yousafzai
Date of birth: 12 July, 1997
Religion: Sunni Islam
Occupation: Activist for rights to female education.
Awards:

• Nobel Peace Prize
• Simone de Beauvour Prize
• National Youth Peace Prize
• Honorary Canadian
• Citizenship

My English Coursebook Standard Ten Digest Answers Pdf Unit 3 

• Chapter 3.1 If … 10th English Solutions
• Chapter 3.2 A Lesson in Life from a Beggar 10th English Solutions
• Chapter 3.3 Stopping by Woods on a Snowy Evening 10th English Solutions
• Chapter 3.4 Let us March! 10th English Solutions
• Chapter 3.5 The Alchemy of Nature 10th English Solutions

Class 10 English Chapter 1.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.3 Basketful of Moonlight Notes, Textbook Exercise Important Questions and Answers.

Basketful of Moonlight Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.3 Basketful of Moonlight Textbook Questions and Answers

warming up!

Chit-chat:

Question 1.
Did you like to hear bedtime stories when you were a child?
Answer:
Points: Yes, very much-crazy for hearing-got into the habit.

Question 2.
Who usually told you the stories?
Answer:
Points: Mostly grandmother or grandfather-mother, father, old servant.

Question 3.
Why did you like them?
Answer:
Points: Because of simple, interesting, amusing narration-teaching lessons of life-sometimes very funny.

Question 4.
Do you still like to hear those stories again?
Answer:
Points: Yes, sure-everlasting excitement- attraction-inspire reading more stories.

1. Discuss in groups about the procedure of planting a tree. Write the steps in bullet points and present them before the class.

Question 1.
Discuss in groups about the procedure of planting a tree. Write the steps in bullet points and present them before the class.
Answer:

• Choosing good seeds of plants.
• Digging in the ground/garden
• Putting seeds in the loose soil
• Add manure
• Fill in the pit/hole
• Water it.

2. Discuss in pairs and write what your father and mother do for your family.

Question 1.
Discuss in pairs and write what your father and mother do for your family.
Answer:

English Workshop:

1. Complete the following sentences with the help of the poem.

Question 1.
Complete the following sentences with the help of the poem.
(a) The child wants to sow small moons of light from ………….. .
(b) According to the child the route of his village is tough and full of ………….. .
(c) The child wants a basketful of moonlight on ………….. .
(d) The child wants to light the dark route so that his ………….. .
Answer:
(a) The child wants to sow moons of light from the city to his village on the sides of the path.
(b) According to the child, the route of his village is tough and full of snakes and scorpions.
(c) Thechild wants a basketful of moonlight on loan.
(d) The child wants to light the dark route so that his father returns early.

2. Write down the describing words used for the following nouns.

Question 1.
Write down the describing words used for the following nouns.

1. ………… moons
2. ………… route
3. ………… village
4. ………… morning

Answer:

1. small moons
2. tough route
3. my/whole village
4. early morning

3. The child in the poem wants to solve the problems of his vifiage. How can the child solve them with the following wishes? Answer in your notebook.

Question a.
Give me moonlight, basketful or two baskets full, with seeds of moonlight.
Answer:
He can seek help of local people and urge the government or local bodies to provide lights on the roads from the city to his village.

Question b.
I want to light the dark route so that my father returns early.
Answer:
He can, with the help of villagers/government, build good roads and make the roads safe so that his father and other villagers can return safe and early to their village.

4. Pick out and write the lines from the poem that prove the following.
(a) Father reaches home late, after dark. …………………..
(b) Eager to hear fairy tales from his father. ………………….
(c) Remove darkness and bring light among the darker paths. …………

Question a.
Father reaches home late, after dark.
Answer:
When my father returns home, I am asleep.

Question b.
Eager to hear fairy tales from his father.
Answer:
I too want to hear fairy tales and stories from him.

Question c.
Remove darkness and bring light among the darker paths.
Answer:
I want to light the dark route so that my father returns early.

5. Write as many words as you can, using – ‘ful’ as suffix.

For example basketful, ……………………… bucketful, ……………………… ……………………… ………………………
……………………… ……………………… ……………………… ………………………

Question 1.
Write as many words as you can, using – ‘ful’ as suffix.
For example basketful, ……………………… bucketful, ……………………… ……………………… ………………………
……………………… ……………………… ……………………… ………………………
Answer:
basketful – bucketful – handful – spoonful – colourful – sackful – bagful – potful

6. Pick out the examples of Alliteration and Repeiltion from the poem.

Question 1.
Pick out the examples of Alliteration and Repeiltion from the poem.
Answer:
1. Alliteration:

• O moon, give me a basketful of moonlight on loan.
• I want to sow seeds of moon on the sides of the path.

2. Repetition: No repetition in these stanzas.

7. Write an appreciation of the poem. (Refer to Page 5.)

Question 1.
Write an appreciation of the poem. (Refer to Page 5.)
Answer:

1. Title: The title of the poem is “Basketful of Moonlight.”
2. The name of the Poet: The name of the poet is Sunil Sharma.
3. Rhyme scheme: There is no rhyme scheme in this poem. This a poem is in ‘free verse.’
4. Figure of Speech: Repetition, alliteration, apostrophy.
5. Theme/Central Idea: The central idea of the poem is the loneliness of a child in a remote village untouched by modern amenities.
6. The child is too far from the modern urban life that even his remedy for the plight of his villagers seems quite innocent and plain.

8. Write an imaginary letter to the moon, to convey your feelings about it. Discuss about it with your partner and draft the letter using the poem as a basis for the letter.
Supporting points:
(a) Sign of beauty
(b) Symbol of joy
(c) Infinite pleasure
(d) Urge to compose poems/songs/music

Question 1.
Write an imaginary letter to the moon, to convey your feelings about it. Discuss about it with your partner and draft the letter using the poem as a basis for the letter.
Supporting points:
(a) Sign of beauty
(b) Symbol of joy
(c) Infinite pleasure
(d) Urge to compose poems/songs/music
Answer:

A Letter to the Moon

Atul More,
Gavali Pada,
Chandrapur,
17th August, 2020.
Dear Chandamama,
How we love you!
Dear, you are the symbol of love and beauty not only for children like us but also for the grown¬ups. You are the one who looks after all the living ‘ things on the earth and gives joy to all of them. Looking at you gives us a great heavenly joy. Your cool light gives us comfort and soothes our body and soul.

Your cool light guides the travellers at night and gives infinite pleasure of walking in the serenely: beautiful light. Mothers sing your songs to make children sleep. Your beauty inspires poets and musicians to compose songs.

Without your presence, who will write lullabies for us, your dear children? Who will write romantic poems without your presence? Chandamama, be with us all the time to fill our hearts with your beauty, love and pleasant appearance.
With Basketful of Love,
Your loving nephew,
Atul More

9. Discuss with your friend/brother/sister/your classmate and write your list of wishes to make your village town city people happy.
You can use the following words.

Question 1.
Discuss with your friend/brother/sister/your classmate and write your list of wishes to make your village town city people happy.
You can use the following words.
Answer:

1. To provide all modern facilities like electricity, good roads, water supply, etc. to villagers living in remote areas.
2. To improve the conditions of poor farmers with aids, funds and full support during drought.
3. To eradicate poverty, ignorance and illiteracy.
4. To keep their surroundings clean and healthy.
5. To fight against injustice, corruption and terrorism.
6. To maintain peace and order in the society.
7. To remove their beliefs in superstitions.
8. To make them aware of their sense of duty.

10. Let’s compose imaginary poetic lines.

Question 1.
Let’s compose imaginary poetic lines.
Answer:

My English Coursebook 10th Digest Chapter 1.3 Basketful of Moonlight Additional Important Questions and Answers

Read the extract and do the activities:

Simple Factual Activity:

Question 1.
Complete the following lines with the help of the poem:
(Answers are directly given and underlined.)
Answer:

1. The poet wants to sow many small moons of light.
2. The whole village goes to the city daily to work.
3. It becomes dark on its way back as his village is quite far.
4. When the poet’s father returns home he is asleep.

Complex Factual Activities:

Question 1.
What does the poet wish to get from the moon and why?
Answer:
The poet wishes to get basketful or two baskets of moon-light from the moon so that he can sow the seeds of moonlight to light the dark path from the city to his village.

Question 2.
Why is the road from the city to the village dangerous?
Answer:
The road from the city to the village is dangerous because it is dark, tough and full of snakes and scorpions.

Question 3.
Choose from the options, appropriate message in the poem:
(a) Bring light to the villages.
(b) Help his father to reach home early.
(c) Listen fairy tales from his father.
(d) Remove darkness and bring light along the darker paths.
Answer:
(a) Bring light to the villages.

Question 4.
Pick out and write the lines from the poem that prove the following:

b. The path from city to village is having many difficulties.
Answer:
The route is tough and full of snakes and scorpions.

Question 5.
What does deliberate repetition of lines ‘O moon, give me moonlight, basketful of moonlight’ signify?
Answer:
The repetition of lines emphasises the intense desire of the child to light the dark route from city to his village with a lot of moonlight. The lines tell us that the child is repeatedly requesting the moon to give him basketful of moonlight because he is in a state of agitation and anxiety. The lines show the child’s intensity and eagerness to free his villagers from their sufferings of dark paths.

Question 6.
Tell what is implied in the following lines:
I want to light the dark route so that my father returns early.
OR
Complete the web:
(Answer is directly given and underlined.)
Answer:

Activities based on Poetic Device:

Question 1.
Pick out the examples of alliteration and repetition:
Answer:
1. Alliteration: O moon, give me moonlight, basketful or two baskets full’,
2. Repetition: ‘I want to sow many, small small moons of light,’

Question 2.
Write rhyming words for the following from the extract:

1. Pack
2. deeds
3. any
4. pity

Answer:

1. Pack-back
2. deeds-seeds
3. any-many
4. pity-city

Question 3.
Give your own rhyming words for the following:
1. dark
2. sow
Answer:
1. dark – park
2. sow – bow.

Vocabulary Focus:

Question 1.
Write down from the extract the describing words used for the following nouns:

1. …………… baskets
2. ……………. route
3. …………….. tales

Answer:

1. two baskets
2. dark route
3. fairy tales

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer 10th English Solutions
• An Encounter of a Special Kind 10th English Solutions
• Basketful of Moonlight 10th English Solutions
• Be SMART…! 10th English Solutions
• His First Flight 10th English Solutions

Class 10 English Chapter 2.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.5 Let’s March Notes, Textbook Exercise Important Questions and Answers.

Let’s March Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 2.5 Warming Up Questions and Answers

Question 1.
Observe the pictures and answer.

(a) Main difference between the two images …………………..
……………………………………………………………………………………..
(b) Change required ………………………………………………………
……………………………………………………………………………………..
(c) Your contribution as a student to help and make a difference to needy children.
……………………………………………………………………………………..
Answer:
(1) Main difference between the two images : In the first picture, the little boy is working at a construction site or kiln. He is a child labourer. In the second, the boy is going to school.
(2) Change required : The boy in the first picture should not work but go to school.
(3) Your contribution as a student to help and make a difference to needy children : I donate my old books, school bag, etc. to needy children.

Question 2.
Put a [✓] or [✗]
A good speech delivered requires the following characteristics.
(1) Well planned and thoughts well-organized. [ ]
(2) Delivered softly and in a low voice. [ ]
(3) Speaker need not greet the dignitaries and audience. [ ]
(4) Language used should be suitable to the audience. [ ]
(5) Speech should be of a proper duration. [ ]
(6) Speaker should be passive, and have no facial expressions. [ ]
(7) Speech should be supported by good examples/episodes/ visual aids. (where possible) [ ]
(8) Speaker should switch over from one language to another [ ]
Answer:
(1) Well planned and thoughts well-organized. [✓]
(2) Delivered softly and in a low voice. [✗]
(3) Speaker need not greet the dignitaries and audience. [✗]
(4) Language used should be suitable to the audience. [✓]
(5) Speech should be of a proper duration. [✓]
(6) Speaker should be passive and have no facial expressions. [✗]
(7) Speech should be supported by good examples/episodes/visual aids, where possible. [✓]
(8) Speaker should switch over from one language to another. [✗]

Question 3.
Read the expressions and insert them in the proper columns. Put the proper expression numbers in the right column.

Expressions
(1) Imagine ! After ten years, what will happen?
(2) Let me begin, today, by sharing my own experience.
(3) Honourable Chief Guest ………………….., eminent dignitaries, ladies and gentlemen.
(4) I don’t understand why we accept this issue so passively.
(5) I am Adarsh Birajdar, (designation) standing before you …………………..
(6) A renowned personality (name) says “ ………………….. ”
(7) Good morning, to one and all present today.
(8) I express my deep gratitude to the organisers of this event/function …………………..
(9) Let me give you an example …………………..
(10) Thank you all for a patient listening and your interest in my talk.
(11) You must have noticed that …………………..
(12) Before I conclude, I would like you to think over the fact that …………………..
Answer:

Question 4.
With the help of your teacher and classmates make a list of as many Indian Nobel Laureates as you can. (You can use Internet or school library.)

Let’s March Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
Name the following.
(a) The persons to whom Kailash Satyarthi gives the highest credit of his honour –
(b) The greatest personalities from the land of Buddha –
(c) So called daughters of Kailash Satyarthi –
(d) The foreign activists of equal rights, mentioned in the speech –
Answer:
(a) Kaalu Kumar, Dhoom Das, Adarsh Kishore and Iqbal Masih.
(b) Buddha, Guru Nanak, Mahatma Gandhi
(c) Daughters of Kailash Satyarthi
(d) Iqbal Masih, Malala Yousafzai and Tom Harkin.

Question 2.
Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.
(a) Child labor
(b) …………………..
(c) …………………..
(d) …………………..
(e) …………………..
(f) …………………..
Answer:

Question 3.
Complete the following diagram/chart.

Answer:

Question 4.
Complete the following web-chart.

Answer:

Question 5.
Think and give your own response.
(a) How can education help the deprived children and child laborers?
Answer:
Education will help the deprived children and child labourers to stand on their own feet and earn a decent living. It will help them to have financial independence. Education plays a huge role in building confidence, tolerance, and making children global: citizens.

(b) Name any other social activist who has worked/is working earnestly for child-welfare. Write about his/her activities.

(c) What message does the little bird’s story of the forest fire convey to us? Explain.
Answer:
The message the little bird story of the forest fire conveys to us is that we must try to do whatever we can to improve matters. We must not think that our efforts are insignificant. We must not think ‘What can one person do?’ Every little drop counts. If each of us makes a little bit of effort, the sum total will be substantial.

(d) Besides the political freedom that our nation enjoys, what other freedom should it strive for? Say why.
Answer:
Besides the political freedom that our nation enjoys. it should strive for social freedom, where everybody is treated equally irrespective of caste, creed and gender. Our nation should also strive for economic freedom, where everyone is above the poverty line. Only then will our nation progress.

(e) What is your impression of the acceptance speech given by Kailash Satyarthi, when he received the Nobel Prize? Write in 3 to 4 sentences.
Answer:
The speech was very emotional. It could be due to the fact that the speech was an earnest appeal to the hearts of the people world over. If we wish the children of the world to be looked after well, we have to rouse the adults to act in a responsible and compassionate manner. This can be done only by trying to touch their hearts and their emotions, which the speaker has attempted to do.

Question 6.
Choose the correct option and write in front of the given word, to convey the exact meaning.
(a) divinity : ………………………..
(i) goodness
(ii) godliness
(iii) god – fearing
Answer:
(ii) godliness

(b) extremist : ………………………..
(i) militant
(ii) robber
(iii) spy
Answer:
(i) militant

(c) culminate : ………………………..
(i) destroy
(ii) succeed
(iii) rise to a peak
Answer:
(iii) rise to a peak

(d) exploitation : ………………………..
(i) explosion
(ii) misuse
(iii) employment
Answer:
(ii) misuse

(e) mortality : ………………………..
(i) death
(ii) virtues
(iii) starvation
Answer:
(i) death

(f) dignity : ………………………..
(i) self-pride
(ii) self-support
(iii) self-esteem
Answer:
(i) self-esteem

Question 7.
Pick out from the lesson the-
(A) Noun forms of the following words-
(a) dignified
(b) pacify
(c) pursue
(d) ignore
(e) poor
(f) divine
Answer:
(a) dignity
(b) pacification
(c) pursuit
(d) ignorance
(e) honor
(f) divinity

(B) Verb forms of-
(a) democracy
(b) global
(c) hindrance
(d) resolution
(e) liberty
(f) service
Answer:
(a) democret
(b) globalise
(c) hinder
(d) resolve
(e) liberate
(f) serve

Question 8.
(A) Use the following words as a noun as well as a verb and make meaningful sentences with each set, in your notebook. march, honour, credit, stitch
Answer:
March:
(a) Gandhiji led the legendary salt march against the British, (noun)
(b) The women marched to the police station angrily, (verb)

Honour:
(1) honour – (a) The poor old man had the honour of shaking hands with the King, (noun)
(b) We must honour oui’ national heroes. (verb)

Credit:
(a) The athlete said that the full credit for her success goes to hci- coach. (noun)
(b) She credits ‘her success to her farnlly’s support. (verb)

Stitch:
(a) A stitch in time saves nine, (noun)
(b) Mary always stitched her school uniform herself, (verb)

(B) Write minimum 4 hidden words of more than 4 letters from – intergovernmental
Answer:
intergovernmental:

• governmental,
• meant,
• government,
• internal,
• train

(C) Make meaningful sentences by using the following phrases, in your notebook.
(a) in the pursuit of
(b) be afraid of
(c) give up
Answer:
(a) In pursuit of a ha1thier diet, more people now turn to organic foods.
(b) One should not be afraid of facing difficult situations.
(c) We must never give up hope even when we face problems.

(D) Pick from the lesson the antonyms of
(i) ignorance x ……………………….
(ii) immortality x ……………………….
(iii) deny x ……………………….
(iv) violence x ……………………….
(v) well- known x ……………………….
(vi) slavery x ……………………….
Answer:
(i) knowledge
(ii) freedom
(iii) accept
(iv) peace
(v) unknown
(vi) mortality

Question 9.
(A) What will you do in the following situations?
(a) If you see a child working in a restaurant.
……………………………………………………..
(b) If you find a child working at a construction site.
……………………………………………………..
(c) If you find a child working at a brickwork site.
……………………………………………………..
(d) If you come across a beggar child.
……………………………………………………..
Answer:
(a) I will talk to the restaurant owner and ask him to send the child to a government school. I will offer to give the child my old books and clothes.
(b) I will talk to the child’s parents and ask them to send him to school. I will also inform my parents and ask them to help.
(c) I will find an NGO and inform them about it.
(d) I will find an orphanage or NGO in the area and ask them to help him. I will also give him some picture books so that he begins to take an interest in books.

(B) Write any 2 efforts that you can make to enroll deprived children/ out of school children into a school. One is given for you.
(a) I will persuade parents of such children to send them to school.
(b) ……………………………………………………..
(c) ……………………………………………………..

Question 10.
(A) Types of Sentence
A sentence is a group of words that expresses a complete idea. Sentences can be classified in various ways. The following is a classification of sentences.

(i) Assertive sentence (Statement) : A sentence that makes a statement or assertion is a sentence.
For example, ‘There are many villages in India.’

(ii) Interrogative sentence : It is a sentence that asks a question. It is of two sub-types.
Yes/no interrogative sentence :
It generally begins with a helping verb or an auxiliary verb and can be answered by saying ‘Yes’ or ‘No’. For example, ‘Are you coming with us?’

Wh-interrogative sentence : It begins with a wh – word, such as ‘who’ and ‘why’ and cannot be answered by saying ‘yes’ or ‘no’. For example, ‘What is the time?’

(iii) Imperative sentence : It expresses commands, requests etc. It generally begins with a verb. For example, ‘Open your books’.

(iv) Exclamatory sentence : It expresses a strong feeling.
For example, ‘How wonderful the river looks !’ ‘What a shame !’

(B) Say whether the following sentences are Assertive (Statements), Imperative (Commands, Requests, etc.), Interrogative (Questions) or Exclamatory (Exclamations).
(1) The Mantra carries a prayer. ………………………….. .
(2) Is the world so poor? ………………………….. .
(3) Kill not your children because of poverty. ………………………….. .
(4) Let’s walk together. ………………………….. .
(5) What can one person do? ………………………….. .
(6) We have made progress. ………………………….. .
(7) How utterly we have failed our children! ………………………….. .
(8) What a big challenge it is! ………………………….. .
Answer:
(1) Assertive
(2) Interrogative
(3) Imperative
(4) Imperative
(5) Interrogative
(6) Assertive
(7) Exclamatory
(8) Exclamatory

(C) Rewrite the following sentences as Assertive (statements).
(1) Why didn’t you come earlier? ………………………….. .
(2) How frightened their eyes look! ………………………….. .
(3) How angry it makes me! ………………………….. .
(4) Should I accept such shackles of slavery? ………………………….. .
(5) What can one person do? ………………………….. .
Answer:
(1) You should have come earlier.
(2) Their eyes look very frightened.
(3) It makes me very angry.
(4) I should not accept such shackles of slavery.
(5) One person cannot do much.

Question 11.
(A) Observe the following underlined phrases. Here ‘have /has’ are followed by the past participle form of the verb. This construction indicates the present perfect tense. Find more such sentences from the text.
(1) We have made progress in the last couple of decades.
(2) We have prevented millions of child deaths.
(3) It has happened.
(4) ………………………….. .
(5) ………………………….. .
Answer:
(4) Let us inculcate….
(5) Let us globalise compassion.

(B) In the following sentences the underlined words are called infinitives. Find such examples from the speech and underline the infinitives.
(1) Every child is free to grow.
(2) I refuse to accept that all the laws and constitutions, police and judges are unable to protect our children.
(3) ………………………….. .
(4) ………………………….. .
(5) ………………………….. .
Answer:
(3) To grow and develop, to eat, to laugh, to play, to go to school, to dream
(4) Kailash Satyarthi is. not ready to accept:
(5) The Nobel Committee has generously invited me to present a lecture.

(C) Complete the following sentences with the help of the sentence given below.
(a) The biggest challenge knocking on the doors of human kind is fear and intolerance.
(i) No other challenge knocking ………………………….. as big as ………………………….. .
(ii) Fear and intolerance are bigger ………………………….. .
Answer:
(i) No other challenge knocking on the doors of humankind is as big as fear and intolerance.
(ii) Fear and intolerance are bigger than any other challenge knocking on the doors of humankind.

(b) The Nobel Prize is one of the greatest honours in the world.
(i) Very few honours ………………………….. .
(ii) The Nobel Prize is greater than ………………………….. .
Answer:
(i) Very few honours in the world are as great as the Nobel Prize.
(ii) The Nobel Prize is greater than most other honours in the world.

Question 12.
(A) Match the sentences given in part ‘A’ with the sentences given in part ‘B’. Note the differences in structure.

Answer:

(B) You might have observed that The sentences in Part A are in the passive voice while the sentences in Part B are in the active voice. Now change the following sentences into the passive voice.
1. We can do it. ……………………………
2. Her angry question still shakes me. ……………………………
3. Governments must make child-friendly policies. ……………………………
4. His answer made me angry. ……………………………
Answer:
1. It can be done by us.
2. I am still shaken by her angry question.
3. Child-friendly policies must be made by governments.
4. I was made angry by his answer.

Question 13.
Imagine your school invites Malala to preside over ‘Children’s Day’ celebration programme. Draft a welcome speech for this guest of honour. Gather information about her from Internet or your school library. While drafting a speech the following points should be kept in mind.
(1) Greeting and salutation
(2) Self-introduction and introduction of the topic
(3) A catchy thought/piece of news/short episode, to start with
(4) Body of the speech supported with related examples and episodes
(5) Conclusion
Answer:
A Welcome Speech

Honorable Chief Guest, respected Principal, teachers and my dear friends,

A pleasant good morning to you all. I am Ananya Iyer, the Cultural Secretary of our school. Today, on Children’s Day, I have the pleasure and privilege of welcoming an eminent personality, Ms. Malala Yousafzai. as our Guest of Honour. Ms. Yousafzai is a Pakistani activist who took up the cause of female education and fought for it with a missionary zeal. She is the youngest Nobel Prize laureate. She is known for human rights activities, especially the education of women and ’children in her native Swat Valley in Khyber Pakhtunkhwa. northwest Pakistan.

On 9 October 2012, while on a bus in the Swat District, Ma’am Yousafzai and two other girls were shot by a Taliban gunman in an assassination attempt in retaliation for her activism. Ma’am Yousafzai was hit in the head with a bullet and remained unconscious and in a critical condition. Following her recovery, she became a prominent voice for the right to education. She founded the Malala Fund, a non-profit organisation and in 2013 co-authored I am Malala, an international best seller.

In 2012, she was the recipient of Pakistan’s first National Youth Peace Prize and the 2013 Sakharov Prize. In 2014, she was the co-recipient of the 2014 Nobel Peace Prize, along with Shri Kailash Satyarthi. Aged 17 at the time, this made her the youngest-ever Nobel Prize laureate. In 2015, Ma’am Yousafzai was a subject of the Oscar- shortlisted documentary He Named Me Malala. The 2013, 2014 and 2015 issues of Time magazine featured her as one of the most influential people

Ma’am, we are proud and privileged to have you with us today. We hope that your presence will inspire and motivate all of us here to take up issues relating to women and children’s rights in earnest. We request you to say a few words to the audience before the inauguration of the function. Thank You.

Question 14.
Select the correct alternative and complete the following: Kailash Satyarthi:
(1) Wants to do this, so that no one is left behind in any corner of the world: walk together. (walk tog ether/remember his ancestors)
(2) Wants to do this, to show respect to his late parents: bow to them, (bow to them/speak to them)
(3) Feels if we do this, our minds will come together: speak together. (smile/speak together)
(4) Feels this, each time he frees a child from slavery: liberated. (honoured/liberated)
Answer:
(1) walk together.
(2) bow to them
(3) speak together
(4) liberated

Question 15.
Match the words to their meanings: (Board’s Model Activity Sheet)

Answer:

Question 16.
This mantra carries a prayer, an aspiration and a resolve that has the potential to liberate humanity from all man-made crises.
Answer:
This mantra carries not only a prayer, but also an aspiration and a resolve that has the potential to liberate humanity from all man-made crises.

Question 17.
I bow to my late parents, to my motherland India and to the mother earth.
Answer:
I bow not only to my late parents, but also to my motherland India and to the mother earth.

Question 18.
Find sentences in the present perfect tense from the passage:
Answer:
I have freed a child from slavery.

Question 19.
Find sentences from the passage that’ contain infinitives: (Board’s Model Activity Sheet)
Answer:
(1) I am deeply honoured to recite a mantra.
(2) …the potential to liberate humanity…
(3) Let’s walk together. (The infinitives without ‘to’ before them are called ‘Bare Infinitives’.)
(4) Let’s speak together.
(5) Let our minds come together.
(6) Let us create knowledge together.

Question 20.
Let us create knowledge for all. (Begin the sentence with ‘Let knowledge …’ and rewrite) (Board’s Model Activity Sheet)
Answer:
Let knowledge be created for all.

Question 21.
Write about the various problems that children are facing today. (Board’s Model Activity Sheet)
Answer:
Children in cities face problems like severe competition, addiction to social networking and video games, etc. Children in rural areas face problems like exploitation, bonded labour, poverty, lack of: opportunities, etc.

Question 22.
Explain the reason why a chair is kept empty on the podium by Shri Satyarthi.
Answer:
The empty chair kept on the podium by Shri Satyarthi represents or symbolises the suffering and struggles of millions of children who are left behind.

Question 23.
Find the odd man out:
(a) dream, tiny, militia, expenditure
(b) compassion, liberty, children, pessimism
Answer:
(a) tiny-this is an adjective; the other words are nouns.
(b) children-this is a common noun; the other words are abstract nouns.

Question 24.
I am representing here – the sound of silence.
Answer:
(1) met – simple past tense
(2) am representing – present continuous tense

Question 25.
Find sentences in the present perfect tense from the passage:
Answer:
The Nobel Committee has generously invited me to present a lecture.

Question 26.
Make a list of the things that Kailash Satyarthi is not ready to accept:
Answer:
Kailash Satyarthi is. not ready to accept:
(1) that all the temples, churches, mosques and prayer houses have no place for the dreams of our 1 children, when all great religions and all countries ! teach us to care for our children.
(2) that the world is so poor, whenust one week of global military expenditure is sufficient to pay for the education of all the children.
(3) that all the laws and constitutions, police and judges, are unable to protect our children.
(4) that the shackles of slavery can eves be’ stronger than the quest for freedom.

Question 27.
Pick out from the passage the noun form of poor:
Answer:
poverty

Question 28.
I have the privilege of working with many courageous people who have the same aim. (Rewrite using the noun form of the underlined wofd.)
Answer:
I have the privilege of working with many people with courage who have the same aim.

Question 29.
All the great religions teach us to care for our children. (Frame a Wh-question to get the underlined words as the answer.)
Answer:
What do all the great religions teach us?

Question 30.
Find sentences in the present perfect tense from the passage:
Answer:
We have never given up against any threat.

Question 31.
Find sentences in the present perfect tense from the passage:
Answer:
(1) We have made progress.
(2) We have reduced the number……..
(3) We have prevented millions of child deaths.
(4) We have utterly failed our children…

Question 32.
Find sentences from the passage that contain infinitives.
Answer:
Let us make no mistake.

Question 33.
(1) Eighteen years ago, millions of individuals! demanded a new international law for the abolition of ’ the worst form’of child labour.
(2) Satyarthi wants to inculcate and transform individuals’ compassion into a global compassion.
Answer:
(1) A new international law for the abolition of ’ the worst form’of child labour.
(2) Individuals’ compassion into a global compassion.

Question 34.
List the examples Kailash Satyarthi gives to show how the world is interconnected.
Answer:
Kailash Satyarthi says that we live in an age of rapid globalisation. We are connected through:
(i) the high-speed internet
(ii) the exchange of goods and services in one single global market and
(iii) the thousands of flights from one corner to another corner of the globe.

Question 35.
Change the following sentence into the passive voice: We can do it.
Answer:
It can be done by us.

Question 36.
Do as directed:
We are connected through high-speed internet. (Frame a Wh-question to get the underlined part as the answer.)
Answer:
How are we connected?

Question 37.
The bird said, “I am doing my bit.” (Frame 2 questions which will give the above sentence as the answer.)
Answer:
(i) Who said, “I am doing my bit.”?
(ii) What did the bird say?

Question 38.
Find an example of present perfect tense from the passage.
Answer:
…….. and it has happened, …

Question 39.
Find sentences from the passage that contain infinitives.
Answer:
(1) Let us inculcate….
(2) Let us globalise compassion.

Question 40.
Pick out from the passage the noun forms of the following words:
(i) passive
Answer:
(i) passivity

Question 41.
Rewrite the sentences as directed:
(1) I challenge the passivity and pessimism surrounding our children. (Rewrite replacing the participle with the finite verb.)
(2) Children are questioning our inaction and watching our actions. (Rewrite as a rhetorical question.)
Answer:
(1) I challenge the passivity and pessimism that surrounds our children.
(2) Aren’t children questioning our inaction and watching our actions? ‘

Question 42.
Find an example of present perfect tense from the passage:
Answer:
….. yet have never tasted chocolate…

Question 43.
Find sentences from the passage that contain infinitives.
Answer:
(1) If we are to teach real peace…
(2) We shall have to begin …….
(3) ….let us unite the world….
(4) ….the power to shake the whole world…
(5) …will we allow to go without rescue….

Question 44.
Explain why the eight-year-old girl’s question shakes Mr. Satyarthi.
Answer:
The eight-year-old girl’s question shakes Mr. Satyarthi because he realizes that we are doing too little too late for the exploited children of this world. Our collective inaction is robbing them of their childhood and allowing them to be exploited.

Question 45.
What was the response of the boy’s father? What was Satyarthi’s reaction to it?
Answer:
The boy’s father said that he had never thought about the fact that his son was working outside the gate of the school and not studying with the others in the school. His answer made Satyarthi angry at that time and still makes him angry.

Question 46.
Choose the correct verb forms of the following from the given options:
(1) slavery: (a) sloven (b) slave (c) enslave.
(2) bold: (a) bolden (b) embolden (c) embold.
Answer:
(1) enslave
(2) embolden.

Question 47.
Pick out from the following the words formed by using a prefix:
(1) illiteracy
(2) innovative
(3) invest
(4) abuse.
Answer:
(1) illiteracy
(4) abuse.

Question 48.
Replace the modal auxiliary in the following sentences with another showing obligation:
(1) All of us must stand with our children.
(2) We must keep our promises.
Answer:
(1) All of us ought to stand with our children.
(2) We ought to keep our promises.

Question 49.
Find a sentence in the present perfect tense from the passage:
Answer:
I have never thought about it.

Question 50.
Find sentences from the passage that contain infinitives.
Answer:
(1) … to put an end to all forms….
(2) … must work together to accelerate action…
(3) I gathered the courage to ask the boy’s father.
(4) We are born to work.

Question 51.
Do you think that it is possible to stop child labour in our country?
Answer:
Yes. If the government is determined enough, it can be done. The programme to eradicate small pox was conducted on a war footing, and we have managed to eradicate small pox from our country., In the same way, if a programme to educate children is conducted on similar lines, we will be able to send all our children to school and stop child labour.

Question 52.
Complete the following: (The answers are given directly and underlined.)
(1) Mr Satyarthi’s vision as a child was a vision of the future, of the cobbler boy sitting’ with him in his classroom.
(2) The foreign activists of equal rights mentioned in the speech are Nelson ivfandela and Martin Luther King.
(3) Mr Satyarthi requests the listeners to put their hands close to their hearts, close their eyes and feel and listen to the child inside them.
(4) According to Mr. Satyarthi, thousands of Mahatma Gandhis. Nelson Mandelas and Martin Luther Kings are calling on us.
Answer:
(1) A vision of the future, of the cobbler boy sitting’ with him in his classroom.
(2) Nelson ivfandela and Martin Luther King.
(3) their hands close to their hearts, close their eyes and feel and listen to the child inside them.
(4) thousands of Mahatma Gandhis. Nelson Mandelas and Martin Luther Kings are calling on us.

Question 53.
Complete the chart with the speaker’s words:
Answer:

Question 54.
Pick out from the passage the verb form of emocracy
Answer:
democratise

Question 55.
As a child, I had a vision of tomorrow. (Rewrite as a complex sentence.)
Answer:
When I was a child. I had a vision of tomorrow.

Question 56.
Find an example of present perfect tense from the passage:
…that tomorrow has become today
Answer:
has become

Question 57.
Find sentences from the passage that contain infinitives.
Answer:
(1) …for every child to have a right to life….
(2) I want you to see and feel this…
(3) I request you to put your hand….
(4) let us democratise knowledge…universalise justice….globalise compassion…let us march….

Question 58.
What is your vision of tomorrow?
Answer:
My vision of tomorrow is of an India where there is no corruption and no poverty. In my vision of India everybody can live a life of comfort and ease.

Question 59.
(1) Write two compound words of your own.
(2) Pick out an infinitive from the lesson and use it in your own sentence.
(3) Find out five hidden wordš from the given word : intergovernmental.
(4) Use the following phrase in your own sentence: in small groups
(5) Spot the error and rewrite the correct sentence: Let us made no mistake, great challenges still remain.
(6) Identify the type of sentence: We have utterly failed our children in imparting education.
(7) Write the following words in alphabetical order: invisibility, innocence, deliberations, expenditure
(8) Write the present and past participles of a verb where the last letters are doubled:
(9) Complete the word chain using nouns from the lesson: shackles →s_ _ _e, →e_ _ _e, → e_ _ _e, → e_ _ _n
Answer:
(1) classroom, motherland.
(2) to teach: Someone needs to teach her what is right and wrong.
(3) intergovernmental: governmental, meant, government, internal, train
(4) The hikers waited in small groups at the base camp.
(5) Let us make no mistake, great challenges still remain.
(6) Assertive sentence
(7) deliberations, expenditure, innocence, invisibility.
(8) plot: plotting, plotted.
(9) shackles → sense → expense → essence → education

Question 60.
(1) Use the following word and its homophone in two separate sentences: peace
(2) Prepare a word register of 4 abstract nouns from the lesson.
(3) He asked me, “What is my fault?”(Rewrite in reported speech.)
Answer:
(1) (i) We said a prayer for world peace, (ii) We are missing one piece of their saw puzzle.
(2) Abstract nouns: knowledge,ustice, compassion, prosperity, slavery, liberty, violence, peace.
(3) He asked me what his fault was.

Question 61.
(1) Use both the given words in a single meaningful sentence: privilege, progress.
(2) Analyse the sentence: I refuse to accept that all the laws and constitutions, police andudges, are unable to protect our children.
Answer:
(1) Today, we have the privilege of witnessing the progress our country is making.
(2) Complex Sentence: I refuse to accept – Main Clause; that all the laws and constitutions, police andudges, are unable to protect our children – subordinate noun clause.

English Kumarbharati 10th Digest PDF

• Animals 10th English Textbook Solutions
• Three Questions 10th English Textbook Solutions
• Connecting the Dots 10th English Textbook Solutions
• The Pulley 10th English Textbook Solutions
• Let’s March 10th English Textbook Solutions
• Science and Spirituality 10th English Textbook Solutions

Class 10 English Chapter 1.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.1 Where the Mind is Without Fear Notes, Textbook Exercise Important Questions and Answers.

Where the Mind is Without Fear Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 1.1 Warming Up Questions and Answers

Where The Mind Is Without Fear Question Answer Class 10 Question 1.
Pair up with your partner and match the terms with their given meanings: (The answers are given directly)

Answer:

Where The Mind Is Without Fear Questions And Answers Question 2.
Taking the help of a dictionary/the internet, guess and write the type of poem against its description:
Sonnet, Epic, Limerick, Lyric, Ballad, Humorous, Elegy, Idyll, Free verse
Answer:
A long story-poem, often mythical – epic
A short story poem with a message – ballad
A poem of 14 lInes – sonnet
A song-like poem – lyric
A poem with no uniformity of rhyme. rhythm, &c. – free verse
A poem set in a picturesque. rustic background – idyll
A sad poem lamenting the death ofa loved one – elegy
A 5-line short funny poem with rhyme scheme aabba – limerIck
A poem written, just to create htniour – humorous

Where The Mind Is Without Fear Class 10 English Workshop Questions and Answers Maharashtra Board

Where The Mind Is Without Fear Question Answer Question 1.
In your notebook write down lines from the poem as a proof for the following.

(a) Tagore wishes for a nation where people are truthful.
Answer:
Line: Where words come out from the depth of truth.

(b) The poet would like everyone to work hard to reach their goal and in the long run to reach perfection.
Answer:
Line: Where tireless striving stretches its arms towards perfection.

(c) The poet wishes that everyone in his country holds his head high in dignity.
Answer:
Line: Where the mind is without fear and the head is held high.

(d) The poet dreams of a nation where knowledge should be free to all.
Answer:
Line: Where knowledge is free.

(e) The poem is a ‘prayer’.
Answer:
Lines:
(i) Where the mind is led forward by Thee.
(ii) Into that heaven of freedom, my Father, let my country awake.

Where The Mind Is Without Fear English Workshop Answers Question 2.
Read the columns carefully and match the expressions with their meanings.

Answer:

Where The Mind Is Without Fear Class 10 Question 3.
(A) Answer the following questions in your own words.

(a) How is the world broken into fragments?
Answer:
The world is broken into fragments by divisions on the basis of religion, caste, class, race and colour in societies all over the world.

(b) Explain what the ‘tireless striving’ should, be for.
Answer:
Tireless striving’ should be to attain one’s goals as well as to achieve perfection.

(c) ‘Where words come out from the depth of truth.’ Explain in your own words.
Answer:
It means when people speak truthfully and with complete’ sincerity of heart.

(d) Who is ‘Thee’ in the poem? What does the poet appeal to ‘Thee’ to do?
Answer:
‘Thee’ in this poem is God. The poet wishes God to awaken his country into a heaven of freedom, where the people are all truly free and total freedom of good thoughts, good words and good actions exists.

(e) What qualities does the poet wish to inculcate in his countrymen?
Answer:

(B) Write in your notebook your own response and justify, where needed.
(a) Is the poem a prayer for India alone?
Answer:
The poem is a prayer for India alone, but it is also relevant for countries all over the world.

(b) What should the words we speak reflect?
Answer:
The words we speak should reflect our sincerity and truthfulness.

(c) What should people keep on widening? How can it be done?
Answer:
People should keep on widening their attitude and outlook. This can be done by getting rid of prejudices, travelling to different places and through education.

(d) From what darkness of night should our nation awake?
Answer:
Our nation should awaken from the darkness of prejudices, division of society, old traditional rituals and customs that are harmful, discrimination in imparting knowledge, insincerity, untruthfulness, fear and lack of self-respect.

(e) What attributes of Rabindranath Tagore does the poem (prayer) reflect?
Answer:
The poem reflects Rabindranath Tagore’s patriotism and love for his countrymen, his clear- thinking, his broad outiook, his, scientific attitude and his emphasis on hard work.

(f) What effect does the repetition of the word ‘where’ at the begining of each line?
Answer:
The repetition of the word ‘where’ at the beginning of each line denotes the increasing intensity of hope and trust the poet puts in his vision.

Where The Mind Is Without Fear Solutions Question 4.
Read the poem carefully and complete the table after the discussion in pairs. One is done for you.
Answer:

Answer:

Where The Mind Is Without Fear Rhyme Scheme Question 5.
(A) Complete the following sentences using your own interpretation.

(a) When the mind is without fear and head unbowed, we enjoy ………………………….. freedom.
(b) When knowledge is free, every citizen enjoys the right to ………………………….. and …………………………. .
(c) We can prevent ………………………….. injustice when we pull down discriminatory walls of caste, class, religion etc.
(d) Constant effort and strife leads to …………………………. .
(e) Logical thinking and reasoning can put a stop to ………………………….. .
(f) Tagore appeals to God to make his country a …………………………. .
Answer:
(a) When the mind is without fear and the head is unbowed, we enjoy complete freedom.
(b) When knowledge is free, every citizen enjoys the right to learn and obtain knowledge.
(c) We can prevent social injustice when we pull down the discriminatory walls of caste, class, religion, etc.
(d) Constant effort and strife leads to achieving our goals and td perfection.
(e) Logical thinking and reasoning can put a stop to the following of old traditions and customs that are harmful.
(f) Tagore appeals to God to make his country a heaven where people have good thoughts, say good words and do good actions.

(B) Fill in the blanks.
(a) Students should keep themselves aloof from ………………………….. .
(b) When ………………………….. everyone will be literate.
(c) It is a social duty of every student of modern world to uproot ………………………….. from societies.
(d) Students must develop ………………………….. outlook and attitudes.
(e) In the world of sycophancy, students must ………………………….. .
Answer:
(a) Students should keep themselves aloof from old harmful traditions.
(b) When knowledge is free everyone will be literate.
(c) It is the social duty of every student of the modern world to uproot narrow-mindedness from societies.
(d) Students must develop broad outlook and attitudes.
(e) In the world of sycophancy, students must have self-respect.

Question 6.
Find out the examples of ‘Metaphor’ from the poem.
Answer:

• ‘Clear stream of reason’. Here reason has been implicitly compared to a clear stream.
• ‘Dreary desert sand of dead habit’. Here old j habits have been implicitly compared to the dreary desert! sand.

Where The Mind Is Without Fear Question Answers Question 7.
Almost every line of the poem begins with the word ‘Where’ and it expects an idealistic country and countrymen. Now work in a group of six students and compose your poem regarding ‘Ideal School’. Begin your lines with the word ‘Where’ . . . . .
Answer:
Ideal School
An ‘Ideal School’ is one…
Where fun, games and studies go hand in hand,
Where teachers come from all over the land,
Where no punishment is given to one, nor any 5 blame,
Where motivation and encouragement is the name I of the game.
(Students can write their own poems.)

Question Answer Of Where The Mind Is Without Fear Question 8.
Read the poem. Write an Appreciation of the poem in about 12 to 15 sentences with the help of the following points. Use a paragraph format.

Points

• Title
• Poet
• Rhyme scheme
• Favourite line
• Theme/Central idea
• Figures of speech
• Special features – Type of the poem, language, tone, implied meaning, etc.
• Why I like/ dislike the poem

Answer:
Note : The points format given in Appreciation of Poem is for east), understanding. IU.nvever, it is io he written in the form of a [laragraph in the examination.

Question 9.
Imagine that you have to deliver a speech on the occasion of ‘Independence Day’ or the ‘Republic Day’ in the school assembly. Prepare a speech to deliver on ‘India of my dreams’

Use the following steps :
Greeting and salutation
Self Introduction
Introduction of the topic
Elaboration of the topic with examples
Conclusion
Thanking audience
Answer:

My Dream India

Respected Principal, teachers and my dear friends. Today, 15th August. is the day India won her freedom. No a0bL, at that time the citizens of free

India had many dreams for their country, some of which would have certainly come true. I, Rohan Mehta, often think about my ‘dream’ India too, and I would like to tell you something about it.

In the India of my dreams, there would be no poverty. Every Indian would be able to live a comfortable life. Every single person would be literate and the pursuit and acquisition of knowledge would be open to all, irrespective of caste, creed or religion. Corruption eats away a country, and in my dream India there would be no corrupt people. Truth and sincerity would reign. The large population will turn out to be an advantage rather than a handicap. We will be using renewable energy sources more and more. Every man, woman and child would be able to hold up his or her head with dignity and self-respect. India will be a ‘Super power’; but unlike the current ‘Super powers’ India will always lend a helping hand to the developing nations. There would be no need to have a police force because there would be no crime and no criminals—everyone would be happy and content.

This is my dream India in brief and there are many more things I would like to add to this list. I will certainly do my bit to make my dream come j true. Thank you.

Question 10.
Read the short story written by Rabindranath Tagore ‘The Kabuliwala’ or ‘The Home Coming.’
Answer:
Visit the website and collect more information about Rabindranath Tagore’s life and work.

Question 11.
Explain the following :

(a) what the poet prays to the Almighty for :
Answer:
The poet prays to the Almighty asking Him to awaken his country into a heaven of freedom, where the people are all truly free and total freedom of good thoughts, good words and good actions exists, while respecting those of others.

(b) what ‘reason’ and ‘dead habit’ are compared to :
Answer:
‘Reason’ is compared to a clear stream, and ‘dead habit’ is compared to the dreary desert sand.

(c) what the poet wishes for :
Answer:
The poet wishes that his country awakens into a heaven of freedom, where the people are all truly free and total freedom of good thoughts, good words and good actions exists.

(d) how the world is broken into fragments :
Answer:
The world is broken into fragments by divisions on the basis of religion, caste, class, race and colour in societies all over the world.

(e) what ‘tireless striving’ should be for :
Answer:
Tireless striving’ should be to attain one’s goals as well as to achieve perfection.

(f) the meaning of ‘Where words come out from the depth of truth’ :
Answer:
It means when people speak truthfully and with complete’ sincerity of heart.

(g) who ‘Thee’ is in the poem and what the poet appeals to ‘Thee’ to do :
Answer:
‘Thee’ in this poem is God. The poet wishes God to awaken his country into a heaven of freedom, where the people are all truly free and total freedom of good thoughts, good words and good actions exists.

Question 12.
Find out lines from the poem as a proof for the following :

(a) Tagore wishes for a nation where people are truthful.
Answer:
Line : Where words come out from the depth of truth.

(b) The poet would like everyone to work hard to reach their goal and in the long run to reach perfection.
Answer:
Line : Where tireless striving stretches its arms towards perfection.

(c) The poet wishes that everyone in his country holds his head high in dignity.
Answer:
Line : Where the mind is without fear and the head is held high.

(d) The poet dreams of a nation where knowledge should be free to all.
Answer:
Line : Where knowledge is free.

(e) The poem is a ‘prayer’.
Answer:
Lines : (i) Where the mind is led forward by Thee.
(ii) Into that heaven of freedom, my Father, let my country awake.

Question 13.
Find examples of Alliteration from the poem.
Answer:

1. Where the mind is without fear and the head is held high.
   Repetition of the sound of ‘w’ and ‘h’.
2. Where the world has not been broken up into fragments.
   Repetition of the sound 4of ‘w’.
3. Where words come out from the depth of truth.
   Repetition of the sound of ‘w’.
4. Where tireless striving stretches its arms towards perfection.
   Repetition.of the sound of ‘t’ and ‘s’.
5. Into the dreary desert sand of dead habit
   Repetition of the sound of ‘d’.

Question 14.
Find examples of Personification from the poem.
Answer:

1. ‘Where tireless striving stretches its arms towards perfection.’ Here ‘tireless striving’ has been given the human quality of stretching its arms.
2. ‘Dreary desert sand of dead habit’. Here ‘habit’ has been given the quality of death.

Question 15.
Find the figures of speech in the line: ‘Into that heaven of freedom, my Father, let my country awake.’
Answer:

• Synecdoche: ‘Country’ stands for the people of the country.
• Apostrophe: The poet is addressing the Almighty.

Question 16.
Comment on the rhyme scheme of the poem.
Answer:
The poem is written in free verse without! any rhyme scheme.

English Kumarbharati 10th Digest PDF 

• Where the mind is Without fear 10th English Textbook Solutions
• The Thief’s Story 10th English Textbook Solutions
• On Wings of Courage 10th English Textbook Solutions
• All the World’s a Stage 10th English Textbook Solutions
• Joan of Arc 10th English Textbook Solutions
• The Alchemy of Nature 10th English Textbook Solutions

Class 10 English Chapter 3.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.3 Stephen Hawking Notes, Textbook Exercise Important Questions and Answers.

Stephen Hawking Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 3.3 Warming Up Questions and Answers

Question 1.
Get into pairs and match the prominent personalities with the disabilities they had :

‘A’	‘B’
(1) John Milton	(a) The great German composer and musician who became deaf at the age of 28 years.
(2) Beethoven	(b) The great English poet who became blind at the age of 43 years.
(3) Stephen Hawking	(c) An American entrepreneur, animator, voice actor, had a learning disability.
(4) Walt Disney	(d) Famous scientist of the 20th century who was paralyzed.
(5) Albert Einstein	(e) Great inventor who has over 1000 patents had a learning disability and became deaf.
(6) Thomas Edison	(f) Great 20th Century scientist and noted physicist who had a learning disability.
(7) Hellen Keller	(g) Dancer whose leg had to be amputated because of an accident.
(8) Sudha Chandran	(h) Was blind and deaf.
(9) Tanay Grey-Thompson	(i) Had polio and was elected as the President of the United States for four terms.
(10) Franklin Roosevelt	(j) Is a wheelchair racer.

Answer:

A	B
(1) John Milton	(b) The great English poet who became blind at the age of 43 years.
(2) Beethoven	(a) The great German composer and musician who became deaf at the age of 28 years.
(3) Stephen Hawking	(d) Famous scientist of the 20th century who was paralyzed.
(4) Walt Disney	(c) An American entrepreneur, animator, voice actor, had a learning disability.
(5) Albert Einstein	(f) Great 20th Century scientist and noted physicist who had a learning disability.
(6) Thomas Edison	(e) Great inventor who has over 1000 patents had a learning disability and became deaf.
(7) Hellen Keller	(h) Was blind and deaf.
(8) Sudha Chandran	(g) Dancer whose leg had to be amputated because of an accident.
(9) Tanay Grey-Thompson	(j) Is a wheelchair racer.
(10) Franklin Roosevelt	(i) Had polio and was elected as the President of the United States for four terms.

Question 2.
Word Building.
(a) Reduplication : The root/stem of a word is repeated exactly the same or with a slight change.
For example,

• tweet-tweet,
• pitter-patter,
• chit-chat,
• bang-bang,
• riff-raff.

Answer:
(a) Reduplication : bow-wow; hee-haw; cheep! cheep; chomp-chomp; ping-pong

(b) Blending : Parts of two or more words combine to form a new one.
For example,

• breakfast + lunch = brunch
• smoke + fog = smog
• motor + hotel = motel

Answer:
(b) Blending : bionic, carjack, Chunnel, cineplex, cyborg, emoticon, infotainment, internet, liger (lion + tiger), netizen, telethon, vidiot, workaholic

(c) Clipping : Reducing a word to one of its syllables or a part of it.
For example, l Mathematics – Maths

• Advertisement – Ad
• Laboratory – Lab

Answer:
(c) Clipping : exam, gym (gymnasium), ‘flu (influenza), gas (gasoline), memo (memorandum)

(d) Acronym : Words formed from the first letter of each of the words involved.
For example, l radar, scuba, Unicef, Nasa

• BBC, CID, USA, ATM, VIP
• DOB, KYC, PM, GN, TY etc.

Answer:
(d) Acronym : laser, CD-ROM, IOU, K9, PIN

In your notebook, write five examples of each of the above types of word-building devices. (You may take the help of a Dictionary/Internet)

Night of the Scorpion Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
Observe the time line and search the occurances according to it. Prepare a chart.

Answer:

Question 2.
Make a list of books written by Stephen Hawking.

Answer:

Question 3.
Make a list of Hawking’s physical inabilities after 1963.
(a) …………………………..
(b) …………………………..
(c) …………………………..
(d) …………………………..
(e) …………………………..
(f) …………………………..
Answer:
Hawking’s physical inabilities after 1963
(a) could not go anywhere except on a wheelchair
(b) an ever-worsening physical state
(c) needed someone 24/7 to manage his care and. work
(d) except for feeding himself and getting out of bed, had need of assistance for virtually everything else
(e) speech increasingly slurred, finally lost his voice for good
(f) ability to do his work in peril

Question 4.
Shape your mind. Complete the network of cluster diagram with the name of great personalities and their contribution.

Answer:

Question 5.
Complete the following web.

Answer:

Question 6.
Explain how the life of Stephen Hawking proves the proverb ‘Every cloud has a silver lining’. Write it down in your notebook.
Answer:
Every cloud has a silver lining.
This proverb ‘Every cloud has a silver lining’ means that you should never feel hopeless because difficult times always lead to better days. Difficult times are like dark clouds that pass overhead and block the sun. But at the same time, on the outer edge of the clouds you will invariably observe a silver lining that provides some measure of light and hope.

The problems and difficulties that we face in life are like those dark clouds. Stephen Hawking started experiencing problems with his health while he was barely 21, a student at Oxford. On occasion he would trip and fall, or slur his speech. Later on, he was diagnosed with ALS, Amyotrophic Lateral Sclerosis. It was a disease in which the nerves that controlled his muscles were shutting down. He was given two and a half years to live. But as we know -he went on to live more than a half century beyond.

Thanks to an early diagnosis, advanced medical treatment and complete support from family, friends and students, he lived a full life and made major contributions to existing theories in physics and cosmology. These, in fact, were the silver linings that brightened what would otherwise have been a lacklustre life.

The life of Stephen Hawking proves that even though the difficulty we face might seem enormous, there is always hope, there are always ways to circumvent them and to keep on achieving and contributing to the world.

Question 7.
Do you agree or disagree with the following statements? Justify your stand/answer by quoting a line from the text.
(a) Stephen Hawking was diagnosed with Alzheimer’s disease.
(b) Hawking believed that man cannot live on other planets in the future.
(c) Though Hawking lost control over his body, he writes with a prolific rate with the help of assistants.
(d) Hawking has written or co-written more than 25 books.
Answer:
(a) No, I do not agree.
The line from the text justifying this stand is Eventually, however, doctors did diagnose Hawking with the early stages of ALS.

(b) No, I do not agree.
The line from the text justifying this stand is He’s convinced that time travel is possible and that humans may indeed colonize other planets in the future,

(c) Yes, I do agree.
The line from the text justifying this stand is Through the program and the help of assistants, Stephen Hawking has continued to write at a prolific rate.

(d) No, I do not agree.
The line from the text justifying this stand is Over the years, Stephen Hawking has written or co-written a total of 15 books.

Question 8.
The following incidents in Stephen Hawking’s life are given in jumbled order. Arrange the incidents in proper sequence as per their order of occurrence in Hawking’s life.
(a) Hawking’s book ‘The Universe in a Nutshell’ offered an illustrated guide to cosmology’s big theories.
(b) Hawking published the book ‘A Brief History of Time’ that offered an overview of space and time.
(c) Hawking was unable to attend a conference in Arizona.
(d) Hawking was diagnosed with ALS while studying cosmology at the University of Cambridge.
(e) Hawking published ‘A Brief History of Time’ that contained the newest development.
Answer:
(c) Hawking’s book ‘The Universe in a Nutshell’ offered an illustrated guide to cosmology’s big theories,
(d) Hawking published the book ‘A Brief History of Time’ that offered an overview of space and time.
(b) Hawking was unable to attend a conference in Arizona.
(a) Hawking was diagnosed with ALS while studying cosmology at the University of Cambridge.
(e) Hawking authored ‘A Briefer History of Time’ that contained the newest developments.

Question 9.
Fill in the blanks with the proper form of the Verbs as per the Subject :
(1) Mother ………………………………… a good meal. (cook/cooks)
(2) Mother and her daughter ………………………………… a good meal. (cook/cooks)
(3) The rise and fall of the Empire ………………………………… recorded in History. (is/are)
(4) Neither Ritesh nor Alok ………………………………… well. (play/plays)
(5) Either of the two ………………………………… guilty. (is/are)
(6) Everyone ………………………………… mistakes. (make/makes)
(7) That news ………………………………… published today. (is/are)
(8) Eight lakh rupees ………………………………… a big amount. (was/were)
(9) The Committee ………………………………… approved of it. (has/have)
(10) The cost of all the goods ………………………………… risen. (has/have)
Answer:
(1) cooks
(2) cook
(3) is
(4) plays
(5) is
(6) makes
(7) is
(8) was
(9) has
(10) has

Question 10.
From the following sentences, underline the Nouns and encircle their Determiners that specify the noun in a noun phrase.
(articles/possessive pronouns/demonstratives or quantifiers)
(1) He lost his voice for good.
(2) Over the years, Hawking has written 15 books.
(3) These three books articulate his search for science’s Holy Grail.
(4) A few events prevented him from despondency.
(5) That dream made him realize it.
Answer:

Question 11.
Complete the information from following graphic organiser and prepare summary.

Summary Maker

Title of the text :
(a) Name of the personality : ………………………………………………..
(b) Age : ………………………………………………..
(c) Books (As Author) : ………………………………………………..
(d) Field of Excellence : ………………………………………………..
(e) Achievements : ………………………………………………..
Answer:

Title of the text	Stephen Hawking
Name of the personality	Stephen Hawking
Age	born 8 January 1942
Books as author	‘A Brief History of Time’ ‘The Grand Design’ ‘The Universe in a Nutshell’ ‘A Briefer History of Time’ ‘Black Holes and Baby Universes’
Film	‘The Theory of Everything’
Field of excellence	Theoretical Physics, Cosmology
Achievements	Albert Einstein Award, 1978; Co-founder of Microsoft Research

Question 12.
You have come to know from the text that ‘The Theory of Everything’ is a film describing the life and work of Stephen Hawking. Watch the film on internet and write a complete review of it. You can take help of the following points while writing the review of the film.
(1) Title
(2) Characters
(3) Story
(4) Dialogues
(5) Picturisation
(6) Music
(7) Special features (if any)
(8) Opinion / Views
(9) Message/Moral values.
Answer:
The Theory of Everything – Movie Review
The movie ‘The Theory of Everything’ is based on ! the life of Stephen Hawking. He was diagnosed with ALS at the age of 21, but because of the love of fellow Cambridge student, Jane Wilde, whom he married, he went on to secure achievement after achievement and began to be called the successor to Einstein.

He and Jane defy terrible odds and break new ground In the fields of medicine and science, achieving more than either could hope to Imagine. Hawkings physical decline weakens his already frail body. His mind, on the other hand, remains sharp, always in pursuit of that single equation that would explain the elusive ‘Theory of Everything’. Right up to his mid-seventies, Stephen Hawking has no plans to retire.

The dialogue smoothly carries the narrative forward, at times Indulging In monosyllabic repartee, which, at times, provides crisp tongue-in-cheek humour. It is a very enjoyable film. It is tasteful and engaging and beautiful visually.

The music, which is quite haunting, was nominated for the best musical score at the Oscars.

The film has been criticised for harping on the theme of ‘Time’ throughout, and for being too sentimental!

However, its message that a person can accomplish much in one’s lifetime despite being afflicted with a severe physical disability is universally relevant. Moral values of love and loyalty permeate the film and thus makes it a’treat to watch.

Question 13.
Answer in one word
(1) At what age was Stephen diagnosed with amyotrophic lateral sclerosis?
(2) Over the years, how many books has Stephen written or co-written?
(3) When did Stephen catapult to international prominence?
(4) In which year was his life story depicted?
Answer:
21
15
1988
2014

Question 14.
(a) Hawking’s book ‘A Brief History of Time’ spent more than four years atop the ‘London Sunday Times’.
Answer:
(a) Hawking’s book ‘A Brief History of Time’ spent more than four years atop the ‘London Sunday Times’.

Question 15.
Observe the timellne and search from the passage the occurrences according to It. (The answers are given directly and underlined.)
Answer:

Question 16.
Complete the table with relevant information about Hawking: (The answer is given directly.)
Answer:

Question 17.
Write from the passage words for
(a) status
(b) summary
(c) people
(d) immediate.
Answer:
(a) status – prominence
(b) summary – overview
(c) people – masses
(d) immediate – instant.

Question 18.
Find out the antonyms from the passage for the following
(i) worst
(ii) exclude
(iii) duplicate
(iv) oldest
Answer:
(i) worst x best
(ii) exclude xinclude
(iii) duplicate x original
(iv) oldest x newest

Question 19.
(1) He was diagnosed with amyotrophic lateral sclerosis. (Rewrite using the present perfect tense of the underlined part.)
Answer:
He has been diagnosed with amyotrophic lateral sclerosis.

Question 20.
It has sold millions of copies worldwide and been translated into more than 40 languages. (Change into a simple sentence)
Answer:
Having sold millions of copies worldwide, it has been translated into more than 40 languages.

Question 21.
The short informative book became an account of cosmology. (Add a question tag.)
Answer:
The short informative book became an account of cosmology, didn’t it?

Question 22.
Stephen Hawking wps a versatile personality. Justify.
Answer:
Stephen Hawking was a versatile personality. He has not only done groundbreaking work in physics and cosmology but also written or co-written 15 books. He worked as a professor of mathematics for a long time. He used to attend various conferences and could think in 11 dimensions.

Question 23.
Fill in the blanks (The answers are given directly and underlined.)
(a) Hawking claimed that he could think in …………… dimensions.
(b) ……………. is the study of the big. …………….. is the study of the small.
(c) ………………. is a single unifying theory that can combine cosmology with quantum mechanics.
Answer:
(a) 11
(b) Cosmology, Quantum Mechanics
(c) Science’s Holy Grail

Question 24.
*(1) Record the occurrence according to the time chart (The answer is given directly and underlined.)
Answer:

Question 25.
Complete the table
Answer:

Question 26.
Complete the following: What is Hawking convinced of?
Answer:

Question 27.
(1) Write words ending in ‘-ity’ using the words given
(a) unify
(b) possible
(c) compatible
(d) inevitable.
Answer:
(a) unify – unity
(b) possible – possibility
(c) compatible – compatibility
(d) inevitable – inevitability.

Question 28.
Match the words in Column A with their meanings in Column B

Answer:

Question 29.
Write sentences using the given phrases
(a) lay out
(b) be the consequence of
(c) is compatible with.
Answer:
(a) I want you to lay out your plans for the future before you graduate.
(b) Your present sad condition is the consequence of your past bad habits.
(c) “The king’s view on this topic is compatible with mine,” said the queen.

Question 30.
Hawking spoke against the idea. (Rewrite using ‘did not’.)
Answer:
Hawking did not speak in favour of the idea,

Question 31.
State the function of the underlined auxiliaries
(a) Humans may colonize other planets in the future.
(b) The universe can create itself from nothing.
(c) The universe will create itself from nothing.
Answer:
(a) may – possibility
(b) can – ability
(c) will – future action/prediction.

Question 32.
Add question tags
(a) The Big Bang was the inevitable consequence of the laws of physics.
(b) There is something rather than nothing.
Answer:
(a) The Big Bang was the inevitable consequence of the laws of physics, wasn’t it?
(b) There is something rather than nothing, isn’t there?

Question 32.
Do you believe that there is a God? Why?
Answer:
I believe that there is a God. This world had to have had a Creator. There is infinite variety of creation all around us and it is not possible that all of it came on its own.

Question 33.
The Big Bang was a natural occurrence.
Answer:
In the context of the passage, yes, I agree. The line from the text justifying this stand is The Big Bang was the inevitable consequence of the laws of physics and nothing more.

Question 34.
Arrange the following in order of occurrence
(a) Hawking is admitted into a medical clinic.
(b) Hawking notices problems with his physical health while at Oxford and later at Cambridge.
(c) Hawking undergoes a series of tests.
(d) Hawking’s father takes him to see a doctor.
(e) Hawking’s father takes notice of the condition.
Answer:
(b) Hawking notices problems with his physical health while at Oxford and later at Cambridge,
(e) Hawking’s father takes notice of the condition,
(d) Hawking’s father takes him to see a doctor.
(a) Hawking is admitted into a medical clinic.
(c) Hawking undergoes a series of tests.

Question 35.
Fill in the blanks in the boxes (The answers are given directly.)
(a) Two scientists other than Stephen Hawking mentioned in this passage are ………………….. and Lou Gehrig.
(b) Hawking was ……………… years old when he was admitted Into a medical clinic.
(c) Hawking first began to notice problems with his physical health while he was at …………………..
Answer:
(a) Sir Isaac Newton
(b) 21
(c) Oxford

Question 36.
Complete the following map:
Answer:

Question 37.
Complete the following:
(a) A decade is a period of ………………….
(b) ……………. refers to the formless matter supposed to have existed before the creation of the universe.
(c) To ……………. one’s speech is to speak (words) indistinctly so that the sounds run into one another.
Answer:
(a) 10 years.
(b) Chaos
(c) slur

Question 38.
The Grand Design was Hawking’s first major publication in almost a decade.
Answer:
The Grand Design was Hawking’s first major publications in almost a decade.

Question 39.
Hawking first began to notice problems with his physical health while he was at Oxford.
(Frame a ‘Wh-’ question to get the underlined part as answer.)
Answer:
When did Hawking first begin to notice problems with his physical health?

Question 40.
He would trip and fall or slur his speech. (Rewrite using ‘not only … but also …’.)
Answer:
He would not only trip and fall but also slur his speech.

Question 41.
He didn’t look into the problem until 1963. (Rewrite without ‘didn’t’.)
Answer:
He avoided looking into the problem until 1963.

Question 42.
(1) You must have suffered from some illness or sickness. Mention two or three symptoms.
That I was an atypical case.
Answer:
Once I suffered from a viral infection of the throat. It began with a slight irritation in the throat. Then there was pain and I found difficulty in swallowing food and even water. I developed high fever, a runny nose and even had fits of shivering. I visited a doctor’ who confirmed the illness and who prescribed tablets for the cure.

(2) Explain in your own words the following statement made by Stephen Hawking
That I was an atypical case.
Answer:
Stephen Hawking describes how after undergoing a series of tests at the hospital, it became clear that he had a physical condition called Amyotrophic Lateral Sclerosis (ALS). In fact, the doctors made it clear that his was a very unusual case, and not representative of a type, group or class.

Question 43.
(1) The following incidents in Stephen Hawking’s life are given in jumbled order. Arrange the incidents in proper sequence as per their order of occurrence in Hawking’s life
(a) At college, Hawking was bored with life.
(b) Hawking reflected on the condition of the boy suffering from leukemia.
(c) After the diagnosis, Hawking went on to became a noted scientist.
Answer:
(a) Hawking reflected on the condition of the boy suffering from leukemia.
(b) At college. Hawking was bored with life.
(c) After the diagnosis, Hawking went on to became a noted scientist.

Question 44.
In the mid-1970’s what did the Hawking’s family do?
Answer:
In the mid-1970’s, the Hawking family had taken in one of Hawking’s graduate students to help manage his care and work.

Question 45.
What effect did the incidents mentioned below have on Hawking?

(a) Hawking saw a boy in the same room he was in suffering from leukemia.
Answer:
Hawking reflected that his situation seemed more tolerable.

(b) Hawking had a dream that he was going to be executed.
Answer:
Hawking realized that there were still things to do with his life.

Question 46.
Why was Hawking forced to use a wheelchair?
Answer:
Hawking was forced to use a wheelchair because physical control over his body had diminished becoming completely despondent.

Question 47.
Only those who knew him well could understand him. (Rewrite using ‘no one’.)
Answer:
Other than (Apart from) those who knew him well, no one could understand him.

Question 48.
The resulting situation required 24-hour nursing care for the acclaimed physicist. (Underline the words used as adjectives.)
Answer:
The resulting situation .required 24-hour nursing care for the acclaimed physicist.

Question 49.
Fill in the blanks (The answers are given directly and underlined.)
(a) For 30 years, Stephen Hawking held the post of ………………….
(b) Stephen Hawking selected his words with a ………………..
(c) Stephen Hawking failed to appear at the conference because of a ………………
(d) ……………… remains a constant anxiety.
Answer:
(a) Lucasian Professor of Mathematics at Cambridge.
(b) hand-held clicker.
(c) chest infection.
(d) Hawking’s health

Question 50.
The following incidents in Stephen Hawking’s life are given in jumbled order. Arrange the incidents in proper sequence as per their order of occurrence in Hawking’s life
(a) Hawking was rushed to hospital.
(b) Hawking’s predicament caught the attention of a California computer programmer.
(c) Hawking announced that he was retiring.
Answer:
(a) Hawking’s predicament caught the attention of ; a California computer programmer.
(b) Hawking announced that he was retiring.
(c) Hawking was rushed to hospital.

Question 51.
What do Stephen Hawking’s works include?
Answer:
Stephen Hawking’s works include numerous scientific papers as well as information for the non- scientific community.

Question 52.
Complete the following.
Answer:

Question 53.
Record the occurrence according to the time chart (The answer is given directly.)
Answer:
2009 – Hawking failed to appear at a conference in Arizona because of a chest infection.

Question 54.
Find evidences of Stephen Hawking’s special life.
Answer:
(a) Hawking used a computer speaking program to select words on a screen that were then passed through a speech synthesizer.
(b) Hawking directed the program through a cheek muscle attached to a sensor.
(c) Hawking had virtually lost all control of his body.

Question 55.
Explain the life of Stephen Hawking with reference to the following statement:
Hawking’s health, of course, remains a constant concern.
Answer:
Due to his physical condition, Hawking’s health is always a source of worry. There are times when his body is not able to cope with the physical challenges of a routine day. There are times when his health deteriorates to such an extent that he has to be rushed to hospital. Despite all this, he continues to share his ideas with the world.

Question 56.
Guess the meaning of predicament.
Answer:
a difficult or unpleasant situation.

Question 57.
Write the adjective forms of:
(a) infection
(b) office.
Answer:
(a) infectious
(b) official.

Question 58.
Write from the last paragraph phrases that give an indication of Stephen Hawking’s health situation.
Answer:
a constant concern, a worry, rushed to the hospital, ‘gravely ill’, make a full recovery

Question 59.
Underline the determiners. (The answers are given directly and underlined.)
Today, with virtually …………. control of ………….. body gone, Hawking directs ……………. program through ………….. cheek muscle attached to ………… sensor.
Answer:
all
his
the
a
a

Question 60.
Pick out the verbs and state the tense.
(a) Stephen Hawking has continued to write at a prolific rate.
(b) He had already announced he was retiring.
Answer:
(a) has continued – Present perfect
(b) had – announced – Past perfect.

Question 61.
He failed to appear at a conference. (Rewrite using ‘not’.)
Answer:
He did not appear at a conference.

Question 62.
Pick out the prepositions
(a) Hawking directs the program through a cheek muscle attached to a sensor.
(b) He was rushed to the hospital for being what ! the university officials described as being ‘gravely ill’.
Answer:
(a) through, to
(b) to, for, as.

Question 63.
(1) Write two compound words of your own
(2) Pick out the present participle and use it in a sentence He has done groundbreaking work in physics and cosmology.
(3) Spot the errors in the sentence and rewrite the sentence It been translated into many than 40 languages.
(4) Frame a sentence using the given phrase to look into
(5) Identify the sentence Hawking’s health, of course, remains a constant concern.
(6) Write the present participle verb form of the given words (a) simplify, (b) argue
(7) Arrange the words in alphabetical order speech, spontaneous, space, spine
(8) Write two hidden words in the word international
Answer:
(1) noteworthy, worldwide (humankind, handheld)
(2) Present Participle groundbreaking Sentence C V Raman carried out groundbreaking work in the field of light scattering.
(3) It has been translated into more than 40 languages.
(4) The teacher said he would look into the matter of the missing chocolates.
(5) Assertive Sentence.
(6) (a) simplifying (b) arguing
(7) space, speech, spine, spontaneous
(8) inter, intern (nation, national)

Question 64.
(1) Write a word that sounds the same as the given word and make sentences with both the words allowed
(2) Complete the word chain of nouns from the lesson. cosmology y………….. …………… …………..
(3) Prepare a word register of 4 words for the given word time.
(4) Rewrite using the indirect form of narration. “Because there is a law such as gravity, the universe can and will create itself from nothing,” Hawking said.
Answer:
(1) allowed – He allowed the students to take a break. aloud – He was angry when the student spoke aloud.
(2) cosmology, years, scientist, time, existence
(3) time age, day, date, year, (month, clock, tide, moment, second, present, past, future, term, hour, era, century, interval, tempo, week)
(4) Hawking said that because there was a law such as gravity, the universe could and would create itself from nothing.

Question 65.
(1) Change to the comparative degree It is the highest civilian award in the US.
(2) Use the given word as a noun and verb in sentences focus
Answer:
(1) It is the higher than any other civilian award in the US.
(2) focus (a) After Std. X, you must focus on your career, (verb)
(b) Never lose focus of your goals in life, (noun)

English Kumarbharati 10th Digest PDF

• Night of the Scorpion 10th English Textbook Solutions
• The Night I Met Einstein 10th English Textbook Solutions
• Stephen Hawking 10th English Textbook Solutions
• The Will to Win 10th English Textbook Solutions
• Unbeatable Super Mom-Mary Kom 10th English Textbook Solutions
• The Concert 10th English Textbook Solutions

Class 10 English Chapter 3.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.2 The Night I Met Einstein Notes, Textbook Exercise Important Questions and Answers.

The Night I Met Einstein Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 3.2 Warming Up Questions and Answers

The Night I Met Einstein Questions And Answers Question 1.
With your bench-mate prepare a profile of Albert Einstein.
ALBERT EINSTEIN

• Profession : ………………………………….
• Field of Science : ………………………………….
• World-famous theory proposed : ………………………………….
• Awards : ………………………………….
• Disability in childhood : ………………………………….
• Books wrote: ………………………………….

Answer:
ALBERT EINSTEIN

• Profession : Scientist
• Field of Science : Theoretical Physics
• World famous theory proposed : Theory of Relativity
• Awards : Nobel Prize in Physics (1921), Copley j Medal by the Royal Society (1925), Gold Medal of the Royal Astronomical Society (1926), Max Planck medal of the German Physical Society (1929), Prix Jules Janssen (1931)
• Disability in childhood : Dyslexia (Asperger’s Syndrome, Autism)
• Books written :
  • The World as I see it
  • Relativity : The Special and the General Theory
  • The Evolution of Physics
  • The Meaning of Relativity
  • Einstein’s Essays in Science
  • Einstein on Peace
  • Why War?
  • Essays in Humanism

The Night I Met Einstein English Workshop Question 2.
Look at the picures of musical instruments and write their names; what the player of the instrument is called and a famous player of the instrument.

Answer:

The Night I Met Einstein Pdf Questions And Answers Question 3.
Separate the words in the columns they belong to.
(chorus, ballet, melody, swar, kathak, raga, salsa, symphony, mudra, serenade, choreography, tune, audience, tango, allegro, duet, odissi, choir, concert, performance, hip-hop)

Answer:

The Night I Met Einstein Class 10 English Workshop Questions and Answers Maharashtra Board

The Night I Met Einstein Question 1.
Complete the following sentences.
(a) The narrator was not happy about the concert because …………………………………….. .
(b) When the narrator turned to look at his neighbour, he …………………………………….. .
(c) Einstein was surprised to hear that …………………………………….. .
(d) The narrator’s memory has an image of Einstein as …………………………………….. .
(e) The greatest act towards human beings is …………………………………….. .
Answer:
(a) he did not understand classical music.
(b) he saw a very famous face with a shock of white hair and a pipe.
(c) the narrator had never heard any of Bach’s music and did not know anything about him.

Question 2.
Who said to whom?

Answer:

Statement	Who	To Whom	Effect on the listener
“We are going to listen to a very good pianist.”	The hostess	The narrator	not very happy
“You’re fond of Bach?”	A guest at the party (Albert Einstein)	The narrator	wanted to say something ordinary to get out of the situation
“You are not tone deaf.”	Albert Einstein	The narrator/writer	The listener tried to justify himself
“Just allow yourself to listen. That’s all there is to it.”	Einstein	the narrator	The listener was able to appreciate the concert and clap sincerçy.

Question 3.
List all the words from the story related to ‘Music’.
……………………………………………………………………………………………….
……………………………………………………………………………………………….
Answer:
concert, pianist. classical music, tone-deaf, piece, Bach, gramophone, song, tune, Bing Crosby, John McCormack. The Trumpeter.

Question 4.
Rewrite the following sentences inserting the appropriate phrases in their proper form.
(to get out of, to come up, to turn on, to give in, to get into, to come down, to work out, to turn off, to give off, to give out, to work in)
(a) He ………………………….. bed and ………………………….. the living room, to see if the door was closed.
(b) To enjoy the music and relax, he ………………………….. the music and ………………………….. the lights.
(c) Smita ………………………….. to her desire and ………………………….. her favourite toys to the poor.
(d) You should ………………………….. Mathematics so that you can ………………………….. problem.
Answer:
(a) got out of, came down
(b) turned on, turned off
(c) gave In, gave off
(d) get into, work out

Question 5.
(A) Give two points of difference between :

Answer:

Instrumental Music	Vocal Music
(1) Instruments are used.	The voice (vocal cords) are used.
(2) Some part of the body is used as a medium to produce the sound, but the final sound is produced by the instrument.	Some parts of the body aid the production of sound (e.g., lungs, vocal tract, etc.), but the final sound emerges through the mouth.
(3) The output of the instrument is more or less of the same type, although the way the musician plays can give it an individualistic flavour.	Individual voices vary from the very low bass to the very high tenor. Hence the output varies and is very individualistic.
(4) An instrument can hardly be expected to sound like a voice (although some musicians try).	The voice can be used to imithte the sound of an instrument.

(B)

Answer:

Question 6.
Prepare a word list of occupations in alphabetical order from the letters A upto T. (You may skip ‘K’ and ‘Q’)

Answer:
Actor – Banker – Carpenter
Driver – Engineer – Farmer
Gardener – Hairdresser – Inspector
Jockey – Keyboardist – Labourer
Musician – Neurosurgeon – Optician
Painter – Quarryworker – Radiologist
Singer – Tailor – Upholsterer
Vendor – Walter – Zoologist

Question 7.
Rewrite the following in indirect narration.
(a) ‘‘You are not tone-deaf’’, he said to me.
(b) ‘‘Could you have done it?’’, said Einstein.
(c) ‘‘Sing that back’’, he ordered me.
(d) He said, ‘‘What kind of music do you like?’’
(e) ‘‘I’m so sorry, Dr. Einstein’’, she said.
Answer:
(a) He told me that I was not tone-deaf.
(b) Einstein asked whether (if) I could have done it.
(c) He ordered me to sing that back.
(d) He asked what kind of music I (the narrator) liked.
(e) She told Dr Einstein that she was very sorry.

Question 8.
(A) Degrees of Comparison (Positive / Comparative / Superlative) Insert the appropriate expressions, choosing from those given after each sentences, for the positive degree.
(1) I am not ……………………………. my friend.
(taller than/ more taller/just as tall as)

(2) They are ……………………………. their neighbours.
(as helpful as/most helpful/more helpful)

(3) No other desert in Africa is ……………………………. the Sahara Desert.
(biggest of all/nearly so big as/bigger as)

(4) Very few animals in the wild are ……………………………. an elephant.
(exactly huger than/exactly as huge as/hugest than)

(5) Some snacks are ……………………………. a pizza.
(at least as tasty as/tastier as/most tasty as)
Answer:
(1) as tall as
(2) as helpful as
(3) nearly as big as
(4) exactly as huge as
(5) at least as tasty as

(B) Change the Degree of Comparision, as directed and rewrite without changing the meaning.
(1) No one in the class is as brilliant as Tanvi. (Superlative)
……………………………………………………………………………………………………………………….
Answer:
Tanvi is the most brilliant one in class.

(2) A diamond is one of the most precious of all stones. (Comparative)
……………………………………………………………………………………………………………………….
Answer:
A diamond is more precious than most other stones.

(3) Her handwriting is better than that of her sister. (Positive)
……………………………………………………………………………………………………………………….
Answer:
Her sister’s handwriting is not as good as hers.

(4) Jupiter is the largest of all planets. (Comparative)
……………………………………………………………………………………………………………………….
Answer:
Jupiter is larger than any other planet.

(5) He is not the greatest of all leaders. (Positive)
……………………………………………………………………………………………………………………….
Answer:
He is not as great as some of the other leaders.

(6) This painting is better than any other painting in the palace. (Superlative)
……………………………………………………………………………………………………………………….
Answer:
This is the best painting in the palace.

Question 9.
Prepare a word chain.

Answer:

Question 10.
Pick out words that refer to the following:
(1) A musical performance in public …………………………….
(2) A lady who invites and looks after guests …………………………….
(3) A device used to play recorded music …………………………….
(4) One who is poor at deciphering musical notes …………………………….
(5) Boundaries or limits of a field …………………………….
Answer:
(1) concert
(2) hostess
(3) gramophone
(4) tone-deaf
(5) frontiers

Question 11.
‘Music is the medicine of the mind’. Narrate an experience that leads to the above conclusion. Write it in your own words, in
your notebook.
Answer:
Music is the medicine of the mind Music is good therapy. It is particularly effective because it registers on multiple sites of the brain. This means that even if the brain is very badly affected by a stroke or illness, there are s^till parts of the brain that recognise music.

I remember how upset all of us were when Grandfather suffered a stroke. The left side of his body and almost all of his face were affected. The once great and active Grandpa now lay still on the bed and had to be fed through a tube going down his nostrils. Little Rani could not stop weeping.

Grandfather had once presented me with a mobile phone. He knew my love for music and had told me I could download my favourite songs and create a playlist and listen to them whenever I wanted to.

I would sit by Grandfather’s bed whenever I was at home and had finished my studies and play the songs and listen to them.

One evening, to my surprise, I saw a shadow of a smile beginning to appear on Grandpa’s face. At first I couldn’t believe it. Then it became more definite and prominent. Grandpa was actually smiling!

I called Mom and Dad and Rani and everyone to see. Yes, Grandpa was indeed smiling. The music had reached out to him and had drawn out a response from him.

That was one of the happiest moments during his illness.

Question 12.
You will come across many famous personalities in the story. Go to library or search on internet the following names and write a few lines about the personalities given below.
(a) Albert Einstein
(b) Johann S. Bach
(c) Bing Crosby
(d) John McCormack
Answer:
(a) The last line tells us that Einstein believes in making others understand the joy there is in knowing the beauty that is all around us.
(b) Einstein then made him hear a little more advanced song by John.
(c) Two singers mentioned in the passage are : Bing Crosby
(d) The singer whose song was more advanced was : John McCormack

Question 13.
Imagine you are the monitor of the class. You are asked to conduct an interview of a famous scientist who is in your city/village. Frame 8 to 10 interview questions with the help of the following points.
(1) Early life and education
(2) Interest for this particular field
(3) Any inspirational incident that occurred in his/her life
(4) Guru or mentor
(5) Inventions and awards
(6) Future plans
(7) Advice/Message to youngsters
Answer:
Interview questions to be asked to the scientist :
(1) Good morning, Sir. I ani prMleged to interview an eminent scientist like you. Sir, could you tell me about your early life and education?
(2) Apart from science were there any other subjects that Interested you in school or college?
(3) Is there any specific incident you can mention that Inspired you to go ahead and achieve greatness?
(4) Who would you say was your Guru or mentor?
(5) Sir, could you give us a brief idea about your Inventions?
(6) WhIch awards have you received?
(7) Sir, what are your future plans?
(8) What advice do you have for the youngsters of today?

Question 14.
Project :
Divide the class into four groups. Collect pictures or draw images of various musical instruments, of the following categories.
(a) Stringed Instruments (Guitar)
(b) Wind Instruments (Flute)
(c) Percussion Instruments (Tabla)
(d) Solid Metal Instruments (Cymbals)
Paste and decorate pictures on separate sheets of paper. Give proper headings and names. Compile into a file with a cover and suitable file-title.

Question 15.
Complete the following sentences :
(a) The entertainment arranged-for by the hostess was a concert where everyone ……………………..
Answer:
(a) would listen to a very good pianist.

Question 16.
What was the writer’s reaction to classical music?
Answer:
The writer did not understand classical music.

Question 17.
Rewrite the following sentences using the phrases given in the brackets : (to pay attention to, to be fond of, to get out of shock of hair)
(a) Sachin ………………….. of playing cricket.
(b) The teacher asked her students ………………….. their studies.
(c) The rabbit trapped in the snare was trying to ……………….. it.
(d) He moved and I saw a ………………….. gleaming in the sun.
Answer:
(a) was fond
(b) to pay attention to
(c) get out of
(d) shock of hair

Question 18.
Write one word for :
(a) a man who helps the poor by giving them money
(b) one who plays the piano
Answer:
(a) philanthropist
(b) pIanist

Question 19.
Chairs were being arranged. (Change to the active voice.)
Answer:
They were arranging chairs.

Question 20.
I heard a gentle, but firm, voice saying, “You’re fond of Bach?” (Rewrite using the indirect form of narration.)
Answer:
I heard a gentie, but firm voice asking if (whether) I was fond of Bach.

Question 21.
I heard everyone clapping, so I realised that the piece was over. (Rewrite using ‘when/because’.)
Answer:
I realized that the piece was over when/because I heard everyone clapping.

Question 22.
Have you ever attended a concert? Write a few lines about it.
Answer:
Yes, I have’ attended a concert of Justin Bieber. It was so exciting to see my favourite popstar live on stage and to hear him singing my favouritesongs. It was quite ecstatic to be part of a crowd that were equally enthusiastic fans.

Question 23.
Write True or False for the statements :
(a) The narrator had heard of Bach.
(b) The narrator’s answer displeased Einstein.
(c) The upper room had a gramophone.
(d) The narrator liked the kind of music where he could follow the words.
Answer:
(a) False
(b) True
(c) True
(d) False

Question 24.
Complete the following sentences : (The answers are given directly and underlined.)
(a) The narrator could not understand music because …………………..
Answer:
(a) he was tone-deaf.

Question 25.
How were Einstein and the writer different in the way they listened to music?
Answer:
Einstein was used to listening to classical music, whereas the writer preferred songs that had words and the kind of music where he could follow the tune. Einstein had a keen ear for music, but the writer was tone-deaf and so could not understand music.

Question 26.
I’m not able to. (Rewrite using a modal auxiliary.)
Answer:
I cannot.

Question 27.
State what the underlined modal auxiliaries indicate :
(a) I must tell this man the truth.
(b) You can give me an example, perhaps?
Answer:
(a) compulsion – obligation
(b) formal request.

Question 28.
What do you learn from Einstein’s treatment of the young man?
Answer:
From Einstein’s treatment of the young man, we learn that Einstein expected others to be truthful. He questioned the young man and managed to persuade him into trying to understand another point of view. This shows Einstein as a man who gave importance to the perceptions of others, but at the same time, was quite persistent about his own viewpoint. Being a man of science, he liked to use the question-answer method to put across his point of view.

Question 29.
Complete the following :
(a) The writer thought that the simplest answerwas ……………………
Answer:
(a) to sing the lines back to him.

Question 30.
How did Einstein help the narrator appreciate music?
Answer:
Einstein made the narrator first hear Bing Crosby, who sang popular songs. The narrator was able to sing the lines back to Einstein. This was because he had heard it hundreds of times before. Not stopping at this, Einstein then made him hear a little more advanced song by John McCormack. Thus they went from lower level to higher level. In this way, Einstein helped the narrator to appreciate higher forms of music.

Question 31
Rewrite the sentences inserting the appropriate phrases in their proper form : (in order to, to get into, to work out)
(a) You should ……………………. Mathematics so that you can ………………. problems.
(b) He read the passage two or three times in ……………. understand it.
Answer:
(a) get Into, work out
(b) order to

Question 32.
The simplest answer seemed to be to sing the lines. So I sang it back to him.
Answer:
The simplest answer seemed to be to sing the lines. So I sang it back to him.

Question 33.
Add question tags:
(a) It proves everything.
(b) It’s like learning maths.
(c) Sing that back.
Answer:
(a) It proves everything, doesn’t it?
(b) It’s like learning maths, isn’t it?
(c) Sing that back, will you?

Question 34.
(1) What do you learn from Einstein’s treatment of the young man?
Answer:
From Einstein’s treatment of the young man we learn how patient and polite Einstein was. We come to know that he was a very good teacher, moving step by step in attempting to teach the young man to appreciate classical music. Also by using a comparison from maths and the question and answer method, Einstein comes across as a true scientist.

Question 35.
Do you think the comparison between music and arithmetic was a good one? In what way?
Answer:
Yes, I think that the comparison between music and arithmetic was a good one because music too involves timing, rhythm and beats that require some mathematical knowledge. Also Einstein showed how when we are taught arithmetic, we begin with the simple and then move on to the complicated. It is the same thing with music. From music with words – which is within the grasp of the average listener, Einstein progressed to music without words – which is what classical music is all about.

Question 36.
Choose the correct alternatives and fill in the blanks:
(1) Whenever the narrator hears the piece of Bach, he remembers ………………… (Einstein/the hostess)
(2) The hostess was …………. with the narrator. (happy/angry)
(3) Finally, the narrator …………….. the concert. (enjoyed/did not enjoy)
(4) Einstein was …………… with the narrator. (pleased/displeased)
Answer:
(1) Einstein
(2) angry
(3) enjoyed
(4) pleased

Question 37.
Complete the following:
(a) The narrator’s memory has an image of Einstein as …………………………
(b) The greatest act towards human beings is ……………………..
Answer:
(a) a small man with a shock of untidy hair and a pipe in his mouth.
(b) opening up the frontiers of beauty.

Question 38.
What does the last line tell you about Einstein?
Answer:
The last line tells us that Einstein believes in making others understand the joy there is in knowing the beauty that is all around us.

Question 39.
(1) Choose the correct meaning in the context of the passage:

(i) down:
(a) southwards
(b) downstairs
(c) soft feathers
Answer:
(b) down – downstairs

(ii) piece:
(a) a thing
(b) an example of artistic workmanship
(c) musical composition
Answer:
(c) piece – musical composition.

Question 40.
Rewrite the sentences inserting the appropriate phrases in their proper form: (to open up, to turn on, to turn off)
(a) His new discovery is …………………. new areas of research in digital technology.
Answer:
(a) opening-up

Question 41.
Write from the passage words that sound the same as:
(a) grate
(b) knew
(c) their
(d) peace
(e) sew
(f) two.
Answer:
(a) great
(b) new
(c) there
(d) piece
(e) so
(f) to.

Question 42.
Pick out from the passage words that refer to:
(a) an unfriendly expression on the face: ………………..
Answer:
(a) a cold look

Question 43.
I was the most important person in the world. (Rewrite in the comparative and positive degree.)
Answer:
(a) I was more important than any other person in the world. (Comparative)
(b) No other person in the world was as important as I was. (Positive)

Question 44.
Why, do you think, did the lady look ‘puzzled’?
Answer:
The lady believed that listening to classical music was the highest form of human activity. Einstein did not stay to listen. Instead he took the narrator to the next room and played songs on the gramophone. Through his efforts he was able to make the narrator really appreciate classical music. For Einstein, opening the minds of others to the appreciation of beauty was the highest form of human activity. This viewpoint ‘puzzled’ the lady.

Question 45.
(1) Write two compound words from the lesson.
(2) Identify the type of sentence: Please come with me.
(3) Punctuate the sentence: can you give me an example perhaps he said
(4) Write the hidden words in the given words: understand
(5) Frame a sentence using given the phrase: in order to
(6) Pick out the gerund and use it in your own sentence: It’s like learning maths.
(7) Spot the error and correct the sentence: I was hear everyone is clapping.
(8) Write the present and past participles of the given verbs: clap, rot.
Answer:
(1) anything, everything
(2) Imperative sentence
(3) “ Can you give me an example, perhaps?” he said.
(4) under, stand, sand, rest
(5) In order to succeed, one must work hard.
(6) gerund: learning Sentence: She is interested in learning French.
(7) I heard everyone clapping.
(8) clapping, clapped; rotting, rotted.

Question 46.
(1) The word ‘kind’ has two different meanings. Write sentences to bring out the two meanings.
(2) Rewrite the following sentence using the underlined verb in the present perfect continuous tense : Can you tell me what you just heard?
(3) I must tell this man the truth. (Rewrite beginning ‘This man…’)
Answer:
(1) (a) This was a different kind of music that he had never heard before, (a group of things having the same characteristics)
(b) The old lady was kind to the little children in the neighbourhood, (generous or considerate)
(2) Can you tell me what you have just been hearing?
(3) This man must be told the truth. (by me)

Question 47.
(1) Change to the positive degree of comparison. He was one of the kindest persons I ever met.
(2) Use the word ‘face’ as a noun as well as a verb in sentences.
Answer:
(1) Not many people I had ever met were as kind as he was.
(2) (a) He has an aristocratic face. (noun)
(b) Let us face the danger together.

English Kumarbharati 10th Digest PDF

• Night of the Scorpion 10th English Textbook Solutions
• The Night I Met Einstein 10th English Textbook Solutions
• Stephen Hawking 10th English Textbook Solutions
• The Will to Win 10th English Textbook Solutions
• Unbeatable Super Mom-Mary Kom 10th English Textbook Solutions
• The Concert 10th English Textbook Solutions

Class 10 English Chapter 1.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.5 Joan of Arc Notes, Textbook Exercise Important Questions and Answers.

Joan of Arc Poem 10th Std Question Answer

Maharashtra Board Class 10 English Solutions Unit 1.5 Warming Up

Question 1.
Discuss in groups/pairs and make a list of the weapons used in the old times and in the present times.

Answer:

Question 2.
Imagine that you are the captain of your school Kabaddi team. Your final match is against a very strong team. Your team members are sure that you will lose. How will you boost their morale? Work in groups and prepare a short list of what can encourage the team.
Answer:
(Some points: pointing out your team’s strong points—the opponent’s weak points—the hard practice you have put in—the various occasions where underdogs have won unexpectedly, etc.)

Question 3.
Adding different prepositions to the same action verb changes the meaning of the phrases, thus formed.
For example,
call out – announce
call at – visit
call for – summon
call up – make a telephonic call
call off – cancel

Guess the difference in meanings of the underlined phrases.
(1) (a) He promised to look into the matter …………………….. .
(b) He asked me to look for his lost book …………………….. .
(c) I shall look forward to your arrival …………………….. .
Answer:
(a) He promised to look investigate into the matter.
(b) He asked me to look search for his lost book.
(C) I shall look forward await eagerly to your arrival

(2) (a) An epidemic of cholera broke out in the village …………………….. .
(b) The thieves broke into the locked house …………………….. .
(c) They broke up their friendship …………………….. .
Answer:
(a) An epidemic of started sudden’y cholera broke out in
(b) The thieves broke entered illegally a Into the locked house. forcibly
(c) They broke up their ended friendship.

(3) (a) You must carry out your duty faithfully …………………….. .
(b) Please carry on with your work …………………….. .
(c) They carried off the trophy in the football matches …………………….. .
(d) Carry forward the remaining balance to the next page …………………….. .
Answer:
(a) You must carry out complete: execute your duty faithfully.
(b) Please carry on with continue tork
(c) They carried off the won trophy in the football matches.
(d) You may carry forward to transfer the remaining balance to the next page.

Phrasal verbs : A phrasal verb is a verb that is made up of a main verb together with an adverb or preposition or both.

Maharashtra Board Class 10 English Kumarbharati Unit 1.5 Questions and Answers

Question 1.
Read the extract from G. B. Shaw’s play on Joan of Arc and fill in the Tree diagram.
Joan of Arc

Answer:

Question 2.
(A) Pick out from the extract of the play two lines that provide evidence for each of the following.
Joan of Arc
(a) Her confidence
(1) …………………….
(2) …………………….
Answer:
(1) The Dauphin will give me all I need to free Orleans.
(2) I will teach them all to fight for France.

(b) Her courage
(1) …………………….
(2) …………………….
Answer:
(1) She really doesn’t seem to be afraid of anything.
(2) The Squire’s glare neither frightens her nor stops her.

(c) Her optimism
(1) …………………….
(2) …………………….
Answer:
(1) If she can put some fight into him, she can put it into anybody.
(2) I don’t think it can be very difficult if God is on your side.

(d) Her determination
(1) …………………….
(2) …………………….
Answer:
(1) I have arranged it all. You have only to give the order.
(2) Yqu said that you would not see me. But here I am.

(e) Her patriotism
(1) …………………….
(2) …………………….
Answer:
(1) I will teach them all to fight for France.
(2) You and Polly will live to see the day when there will not be a single English soldier on the soil of France.

(B) Using the above points, frame a character-sketch of Joan of Arc, in your own words and write it in your notebook. Suggest an attractive title for the same.
Answer:
The Heroine of France-Joan of Arc Joan, a well-built, strong country girl of 17 to 18 years, _is brave and courageous and unafraid of anything. She is confident and asks directly for whatever she wants and is sure of getting It. She is optimistic and feels that if God is on one’s side, one can do anything. She is determined to go to Orleans and motivate the Dauphin to fight the English and save OrleAnswer: Squire Robert and the others feel that if anyone can put some fight into the Dauphin, It is Joan. She ¡s extremely patriotic and confidently says that she will motivate the French soldiers to fight, and soon there will not be a single English soldier left on the soil of France.

Question 3.
From the extract, find what the following are compared to and why:
(a) as easy as …………………………………………………………………….
………………………………………………………………………………………….
Answer:
as easy as chasing a cow out of the meadow. This comparison is made because Joan was a country girl and had probably chased many cows out of the meadows. Besides, cows are docile creatures and can be driven away very easily.

(b) as mad as …………………………………………………………………….
………………………………………………………………………………………….
Answer:
as mad as Joan, for Joan was planning to go to the Dauphin, who was frightened, and motivate him to fight for Orleans.

(c) The Dauphin in Chinon is like …………………………………………………………………….
………………………………………………………………………………………….
Answer:
The Dauphin in Chinon Is like a rat In a corner, for just like a cornered rat gives up, he too had given up and refused to fight to save Orleans.

(d) The (enemy) soldiers will be driven away like …………………………………………………………………….
………………………………………………………………………………………….
Answer:
The enemy soldiers will be driven away like sheep. This comparison is made because sheep, always move in flocks and their herd mentality forces them to free if the leading ones flee.

(e) Joan of Arc is a bit of …………………………………………………………………….
………………………………………………………………………………………….
Answer:
Joan of Arc is a bit of a miracle because she is courageous, confident and determined enough to go to the Dauphin and motivate him to fight for Orleans, when everybody else had given up.

Question 4.
Say WHY? Write it in your notebook.
(a) Joan wanted to meet Captain Squire.
(b) Joan did not ask for many soldiers from the Captain Squire.
(c) Poulengey, Jack and Dick had offered to accompany Joan.
(d) French soldiers were always beaten in war.
(e) Captain Squire Robert said, “I wash my hands off it.”
Answer:
(a) Joan wanted Captain Squire to give her a ’ horse, an armour and some soldiers and send her to meet the Dauphin. That was the reason she wanted to meet him.

(b) Joan did not ask for many soldiers from the Captain Squire because the Dauphin would give her all that she needed.

(c) Poulengey, Jack and Dick felt there was something about Joan, and that she was a bit of a miracle. Her words had put fire into them. They also felt that it was their last chance of saving OrleansHence they offered to accompany her.

(d) The French soldiers were always trying to save their lives, and would run away from the battlefield. Hence they were always beaten in war.

(e) Captain Robert Squire was uncertain about allowing Joan to go to the Dauphth. He could not believe that Joan would be successful In her mission. Even then, he could not withstand her determination and confidence; he also felt that this was the last chance of saving Orleans, and that there was something special about Joan. However, he did not want to be held responsible for anything; hence he said “I wash my hands of it.”

Question 5.
Using a dictionary, find the difference between the following pairs of phrases. Make sentences of your own with each of them.

Phrases	Meaning	Own Sentences
1. cut in cut out	………………………………………… …………………………………………	………………………………………… …………………………………………
2. be held by be held up	………………………………………… …………………………………………	………………………………………… …………………………………………
3. run away run for	………………………………………… …………………………………………	………………………………………… …………………………………………
4. be known as be known for	………………………………………… …………………………………………	………………………………………… …………………………………………
5. go with go after	………………………………………… …………………………………………	………………………………………… …………………………………………
6. put fire into put fire out	………………………………………… …………………………………………	………………………………………… …………………………………………

Answer:

Question 6.
From an Indian History Book or Internet find out information about Indian Women (queens) who led battles. (For example, Rani of Jhansi and Rani Karnawati of Mewad). Write 3 points of similarity and 3 points of contrast between any one of the above Indian Queens and Joan of Arc. Write in your own words.

Similarities Contrast
(a) …………………… (i) ……………………
(b) …………………… (ii) ……………………
(c) …………………… (iii) ……………………

Question 7.
Read the script from :
Joan (Girl) : Good morning, Captain
Squire …………………… up to
Joan : (simply) ……………………
Polly and Jack have promised to come with me.

Write a summary of that part of the script (in the indirect speech) in 15 to 20 lines. Do it in your notebook.
Answer:
Joan asked the Squire to give her a horse, an armour and some soldiers, and send her to the Dauphin. On hearing this, Robert angrily asked the steward why he had not told him that she was mad.

The steward told Robert to give Joan what she wanted. Robert then told Joan that he would send her back to her father with orders to lock her up. Joan replied that it wouldn’t happen that way; Robert had not wanted to see her, yet she had managed to see him.

Joan then asked him for a horse which would cost 16 francs. It was a big amount of money, but she would save It on the armour, as she did not need a beautiful, fitting armour. A soldier’s armour would do. She said that she would not want many soldiers, for the Dauphin would give her what she needed to free Orleans. Three men would be enough for him to send with her. She adds that Polly and Jack had promised to go with her.

Question 8.
(A) Make the following sentences Affirmative without change of meaning.
(a) Negative : I am not so sure, now.
Affirmative : …………………………………………
(b) Negative : He will not be able to stop them.
Affirmative : …………………………………………
(c) Negative : I don’t remember.
Affirmative : …………………………………………
(d) Negative : I can do no more.
Affirmative : …………………………………………
(e) Negative : Sir, do not anger her.
Affirmative : …………………………………………
(f) Negative : I shall not want many soldiers.
Affirmative : …………………………………………
Answer:
(a) I am a bit doubtful, now.
(b) He will be unable to stop them.
(c) I fail to remember.
(d) I can do only this much.
(e) Sir, please refrain from angering her.
(f) I shall want only a few soldiers.

(B) Fill in the gaps in the table.
Word-Forms

Answer:

Question 9.
Fill in the blanks with the correct alternatives: (The answers are given directly and underlined.)
Answer:
(1) The steward is called a ‘blockhead’ by the squire. (Robert/steward)
(2) The squire’s name is Robert. (Robert/Dauphin)
(3) The price of a horse is sixteen francs. (17 to 18 francs / sixteen francs)
(4) The Dauphin will give the girl whatever she needs to free Orleans: (Dauphin/Squire)

Question 10.
Complete the following: (The answers are given directly and underlined.)
Answer:
(1) The Hundred Years War was fought between 1337 and 1453.
(2) All of northern France and some parts of the south-west were under foreign control.

Question 11.
Classify the following words into adjectives and nouns and complete the table given below:
armed, courage, brave, armour, orders, well-built, squire, strong, amount, beautiful, Orleans
Answer:
Adjectives – Nouns
armed, brave, well-built, courage, armour, orders, strong, beautiful sqtiire, amount, Orleans

Question 12.
Write the verb forms of the following words:
(1) strong
(2) mad
(3) beautiful
(4) afraid
Answer:
(1) strengthen
(2) madden
(3) beautify
(4) fear

Question 13.
You have fifty armed soldiers and dozens of strong servants to carry out my orders.
Answer:
You have fifty armed soldiers as well as dozens of strong servants to carry out my orders.

Question 14.
You are to give me a horse and armour and some soldiers.
Answer:
You are to give me a horse and armour as well as some soldiers.

Question 15.
What, according to you, is the steward’s opinion about Joan?
Answer:
The steward has a high opinion of Joan. He feels that she isn’t afraid of anything, and she puts courage in others. He feels that she should not be angered and be given what she wants.

Question 16.
Write if the following statements are True or False: (The answers are given directly and underlined.)
Answer:
(1) Joan is angry when Robert tells her to get out. False
(2) Joan feels that Squire Jack is kind. True
(3) The steward’s name is Bertrand de Poulengey. False
(4) Robert thinks that the girl’s idea is crazy. True

Question 17.
Name the persons needed by Joan to free Orleans:
Answer:
Joan needed the following persons to free Orleans Bertrand de Poulengey, Squire Jack, John Godsave, Dick the Archer, and their servants John of Honecourt and Julian.

Question 18.
Complete the following: (The answers are given directly and underlined.)
Answer:
(1) The squire wants the steward to go with Joan, stay within call and keep an eye on her.
(2) Joan’s aim was to meet the Dauphin and free Orleans.

Question 19.
Pick out four adverbs of manner from the passage.
Answer:
simply, willingly, eagerly, brightly (hastily, seriously). ,

Question 20.
Pick out the antonyms of the following words from the passage:
(1) exit
(2) request
(3) advance
(4) slowly
Answer:
(1) exit x enter
(2) request x order
(3) advance x retreat
(4) slowly x hastily

Question 21.
Polly and Jack have promised to come with me. (Rewrite using ‘that’.)
Answer:
Polly and Jack have promised that they will come with me.

Question 22.
You have only to give the order. (Rewrite using ‘nothing’.)
Answer:
You have to do nothing but give the order.

Question 23.
‘I have arranged it all’. What does this statement tell you about Joan?
Answer:
It tells us that Joan had good leadership qualities. She had the ability to inspire others and make them do as she wished. She was also a good organiser.

Question 24.
What/Whom do the underlined pronouns stand for?
Answer:
(1) Her words have put fire into me. Poultney
(2) I feel sure enough to take her to Chinon. Joan
(3) He beat the English at Montargis. Dauphin
(4) ! feel like a fool. Robert

Question 25.
Complete the following: (The answers are given directly and underlined.)
Answer:
(1) The Squire’s opinion of miracles was that though they were airight, they did not happen in their time.
(2) Robert accused Poulengey of being as mad as Joan.

Question 26.
The Dauphin was not fit to be the king and heir.
Answer:
The Dauphin was not fit to be the king and heir because he was a coward and retreated to Chinon and spent time there like a rat in a corner. He was not able to motivate his men or stop the English from taking Orleans’

Question 27.
Make sentences of your own using the words/ expressions given below:
(1) cowed
(2) obstinately
(3) worth hying
(4) out of your mind
Answer:
(1) We should not be cowed when we are threatened by bullies.
(2) The little girl obstinately refused to answer the teacher.
(3) “Your idea will keep the neighbourhood clean. It is worth trying,” said the minister.
(4) “You are out of your mind,” I told my friend when she wanted to save the stray dog.

Question 28.
I tell you nothing cai save our side now but a miracle. (Rewrite using ‘only’.)
Answer:
I tell you only a rriracle can save our side now:

Question 29.
After talking to Poulengey what change do you notice In Robert?
Answer:
Robert was initially unwilling even to listen to Joan.. But after talking to Poulengey, he agreed that it was their last chance of trying to free Qrleans and there was no other hope for them. Poulengey’s certainty about Joan made him waver and change his mind and give her a chance.

Question 30.
Pick out the statements that are True:
(1) Joan was unsure about her ideas.
(2) Joan had no belief in God.
(3) The soldiers called Joan ‘the Maid’.
(4) Robert had a poor opinion of English soldiers.
Answer:
True statements:
(3) The soldiers called Joan ‘the Maid’.
(4) Robert had a poor opinion of English soldiers.

Question 31.
how one knows that Joan is a person of immense faith.
Answer:
Joan’s statement ‘I don’t think soldiering can be difficult if God Is on your side’ shows that she is a person of immense faith.

Question 32.
Pick out the words ending In -ing from the passage and classify them Into gerunds and participles.
Answer:
Gerunds – Participles
raising, chasing. soldiering, fighting, plundering, burning, – turning, fighting

Question 33.
Pick the odd man out from each group:
(1) gravely, always. heard, very
(2) they, see, you. them
Answer:
(1) heard- (this is a verb; the other words are adverbs.)
(2) see-(this is a verb; the other words are pronouns.)

Question 34.
Rewrite the following as Assertive sentences:
(1) Have you ever seen English soldiers fighting?
Answer:
You have never seen English soldiers fighting.

Question 35.
Have you ever seen them plundering, burning, turning the countryside into a desert?
Answer:
You have never seen them plundering, burning, turning the countryside into a desert.

Question 36.
Do you think that soldiers should run away to ‘save their skins’?
Answer:
No, I don’t think so. Soldiers must fight till their last breath. No soldier worth his sa1t should run away from the scene of battle to save his/her own life.

Question 37.
What dress did Joan want?
Answer:
Joan wanted a soldier’s dress.

Question 38.
Robert finally agreed to the plan.
Answer:
Robert thought that Joan might be able to motivate the Dauphin and the troops to fight. He felt that she had the courage and determination to succeed. He also felt that there was something special about her. Hence he finally agreed to the plan.

Question 39.
Pick out the modal auxiliary and state its function.
Even the Dauphin might believe it.
Answer:
might—showing possibility.

Question 40.
Do you think that Joan succeeds in her plan?
Answer:
I would not be sure only by reading the play; but history tells us that she did succeed and led the French army to victory in several battles during the Hundred Years War. Her bravery, determination and confidence won the day.

Question 41.
I can do no more.
Answer:
I can do only this much.

Question 42.
Pick out the modal auxiliary and state its function.
Even the Dauphin might believe it.
Answer:
might—showing possibility.

Question 43.
Do you think that Joan succeeds in her plan?
Answer:
I would not be sure only by reading the play; but history tells us that she did succeed and led the French army to victory In several battles during the Hundred Years War. Her bravery, determination and confidence won the day.

Question 44.
(1) WrIte two compound words from the text.
(2) Use the following word as a gerund in your own sentence : chasing
(3) Find out two hidden words from the given word : confidently
(4) Make a sentence of your own using the phrase: to save their skins.
(5) Spot the error and rewrite the correct sentence: I is taking a big chance.
(6) Identify the type of sentence: I don’t think it can be very difficult.
(7) Write the following words in alphabetical order : understand, steward, window, squire.
(8) Write the present and past participles of ‘stop’.
(9) Prepare a word chain using the following nouns: Denmark, France, Austria, England, Korea, Alaska. France →
Answer:
(1) courtyard, blockhead
(2) I would not even think of chasing a defenceless animal.
(3) confidently — confident, confide
(4) The thieves jumped into the lake to save their skins.
(5) I am taking a big chance.
(6) Assertive (negative).
(7) squire. steward, understand, window.
(8) stop: stopping, stopped.
(9) France → England → Denmark → Korea → Austria → Alaska.

Question 45.
(1) Use the following word and its homograph in two separate sentences: lock
(2) The Dauphin will give me all I need. (Rewrite using the future progressive tense of the verb.)
(3) Prepare a word register of 4 words relating to war from the lesson.
Answer:
(1) (i) There was a lock of hair on the table.
(ii) The lock and the key were both missing.
(2) The Dauphin will be giving me all I need.
(3) War : soldier, armour, fight, siege, plundering, soldiering, troops. captain. (any 4)

Question 46.
(1) I used to think so. (Pick out the modal auxiliary and state its function).
(2) Analyse the sentence: Stay within a11 and keep your cyc on her.
Answer:
(1) used to — past habit
(2) Compound Sentence.
Stay within call — coordinate (main) clause: keep your eye on h& — coordinate (main) clause.

English Kumarbharati 10th Digest PDF 

• Where the mind is Without fear 10th English Textbook Solutions
• The Thief’s Story 10th English Textbook Solutions
• On Wings of Courage 10th English Textbook Solutions
• All the World’s a Stage 10th English Textbook Solutions
• Joan of Arc 10th English Textbook Solutions
• The Alchemy of Nature 10th English Textbook Solutions

Class 10 English Chapter 2.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.5 Book Review – Swami and Friends Notes, Textbook Exercise Important Questions and Answers.

Book Review – Swami and Friends Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.5 Book Review – Swami and Friends Textbook Questions and Answers

Warming up!

Chit-chat:

1. Form groups of 3 to 4 and share the following with your groups.

• Your favourite book
• Type of book (short storieslbiography/thriller/adventure science fiction/historical) etc.
• Author/Writer
• Main character
• Background (Time and place)
• Problem/dilemma
• Any special message

2. You have recently read a short story/noveL/dramalscience fìctionlghost-story. Write in short 3 of its strong points that made you like the book and 2 or 3 drawbacks it has. Fill them up in the tree – diagram given.

Question 1.
You have recently read a short story/novel/drama/science fìctionlghost-story. Write in short 3 of its strong points that made you like the book and 2 or 3 drawbacks it has. Fill them up in the tree – diagram given.
Answer:

3. Determiners are words that modify a noun or noun phrase and occur before them in a sentence. Determiners provide a context to the noun they precede.
They may be:

• Articles – a, an, the
• Demonstratives – this, that, these, those, which etc.
• Possessives – my, your, our, their, liLs, her etc. my friend’s, her mother’s etc.
• Quantifiers – few, many, much, more, every, each, some etc.
• Numerals – one, four, hundred, first, fourth, hundredth

Question 1.
Determiners are words that modify a noun or noun phrase and occur before them in a sentence. Determiners provide a context to the noun they precede.
Answer:
They may be:

• Articles – a, an, the
• Demonstratives – this, that, these, those, which etc.
• Possessives – my, your, our, their, liLs, her etc. my friend’s, her mother’s etc.
• Quantifiers – few, many, much, more, every, each, some etc.
• Numerals – one, four, hundred, first, fourth, hundredth

4. Underline only Determiners in the following.

Question 1.
Underline only Determiners in the following.

1. My brother bought a few magazines.
2. What is your friend’s naine?
3. Which writer was also the President of our country?
4. These are some toys.
5. These toys are new.
6. That doctor is an expert dentist and he has many patients.

Answer:

1. 1. My brother bought a few magazines.
   2. What is your friend’s naine?
   3. Which writer was also the President of our country?
   4. These are some toys.
   5. These toys are new.
   6. That doctor is an expert dentist and he has many patients.

English Workshop:

1. Refer to the story ‘The Boy who Broke the Bank’ (Lesson 2.2.) by Ruskin Bond. Read it carefully and write a review of the same, referring the points given on Coursebook page 71 in mind. 
(a) Name of Story and Writer/Author
(b) Type of story
(c) Background and setting (Time and Place)
(d) Main characters
(e) Problem faced
(f) Language used
(g) What you liked about the story
(h) What you did not like about it
(i) Your general opinion of the story

Question 1.
Refer to the story ‘The Boy who Broke the Bank’ (Lesson 2.2.) by Ruskin Bond. Read it carefully and write a review of the same, referring the points given on Coursebook page 71 in mind.
Answer:
Review of the story – The Boy who Broke the Bank
The story ‘The Boy who Broke the Bank’ is a very interesting and informative story written by Ruskin Bond, an eminent Indian author of British descent. It is a realistic social story full of wit and humour.

The main characters in the story are Nathu-the sweeper, Sitaram-the washerman’s son, Mrs Srivastava, Mrs Bhushan and Mr Bhushan, Kamal Kishore, the owner of the photographic shop, Deep Chand, the barber and an elderly gentleman and Ganpat, the begger.

The story is about the Pipalnagar Bank owned by Seth Govind Ram and the people of Pipalnagar. It begins at the steps of the Pipalnagar Bank when Nathu, the sweeper boy was sweeping the steps. He was irritated and decided to leave the job because he had not received his pay for the month. He told this to Sitaram, his friend and a washerman’s son. While delivering the clothes Sitaram told Nathu’s story to Mrs Srivastava who also needed a sweeper.

She, when met her friend Mrs Bhushan in bazaar, told her that the Bank is not able to pay the poor sweeper’s salary. Then from Mrs Bhushan to her husband, then to Deep Chand, to the barber and elderly gentleman, the news took different turns and twists and reached people to tell them that the Pipalnagar Bank has gone bankrupt. The rumour created havoc in Pipalnagar.

The news went from one man to another and from one place to another and spread over the whole bazaar and among all the customers of the Bank. Crash of the Pipalnagar Bank set everyone talking and speculating and rushing about in a frenzy. Many different rumours spread, moods of people aggravated and chaos was beyond control and it led to violence. The author has described and connected every incident in simple, easy language and depicted how a news spreads like wild fire without people going to the root of the fact.

He has used satirical style for emphasising the effects of rumours. The incidents of the elderly gentleman in the barber’s shop and the fake beggar’s (Ganpat’s) running at top speed, split our sides with laughter. liked the humour in the story and the tactful narration of the incidents to raise the awareness ‘ among the public about the rumours and their effects. According to my opinion it is a good read for a common man. It gives a good message to all.

2. Look inside your thinking hat.
Read the evidence/sentences given below and offer a possible explanation of what happened in this house? Make up some questions to gather more information.
Now collect all your evidence and write a story in your notebook. Give a suitable title.

Question 1.
Look inside your thinking hat.
Read the evidence/sentences given below and offer a possible explanation of what happened in this house? Make up some questions to gather more information.
Now collect all your evidences and write a story in your notebook. Give a suitable title.

Answer:

The Tiny Gang who robbed our kitchen!
My parents and I were leaving to Panvel to see one of our near relatives who was ill. Before leaving we warned my younger brother Chintu who was ten years old. We told him to stay with our uncle who was staying in the same building of ours on the ground floor and to have food with uncle in their house. We asked Chintu to keep the key to himself carefully and not to leave uncle’s room until we returned. He happily agreed.

We returned from Panvel late in the evening. Mother took the key from Chintu, went up and opened the lock. Mother put on the light and hurriedly went to the kitchen. She shouted loudly. I ran to her. Both of us were awfully shocked to see the kitchen in a messy state. Plates, glasses, pans, bowls and other utensils were scattered everywhere. The whole kitchen was untidy and dirty. Some gram flour and peels of boiled potatoes were scattered all over. We were panic-stricken. We thought that some thief must have entered our house to try his luck.

We called Chintu but he said he was at uncle’s house all the time. First we began to clear the mess. Mother lifted some tins and jars lying there and to her surprise the laddoos and chivda kept in them had vanished, gone! Who could it be and what the thieves must have taken away. But all other cupboards were intact.

When I examined the kitchen I found some children’s footprints in the scattered flour. In a flash I got it and deduced that it was the handiwork of the children, including Chintu. I instantly remembered that when we were leaving for Panvel, Chintu and some friends of his age were sitting in a space near the staircase, whispering something as if in secret. They were planning the day’s work.

I called all those mischievous, naughty children including Chintu before father. When father gave them harsh scolding and beating, they blurted out everything. The truth was revealed. In the noon when elderly persons were taking their naps, these boys entered our house, had a lot of fun, emptied the jars of laddoos and chivda and more than that they tried their hand on preparing Potato vadas on their own and hence they used gram flour and potatoes, but did not care to clean the mess. I should have been there to taste their Potato vadas!

3. Identify the new words and phrases which seem to be important, in the review. Try to guess their meaning from the context. You can use a dictionary to confirm it. Fifi up the table.

Question 1.
Identify the new words and phrases which seem to be important, in the review. Try to guess their meaning from the context. You can use a dictionary to confirm it. Fifi up the table.

Answer:
(Note: Students should do this project on their own and present it in the class.)

4. (A) Find from the lesson the Noun forms of:

Question 1.
Find from the lesson the Noun forms of
(a) happen …………
(b) true ………….
(c) simple ……….
(d) conclude …………..
Answer:
(a) happen – happening
(b) true – truth
(c) simple – simplicity
(d) conclude – conclusion

(B) Find Verb forms of:

Question 1.
Find Verb forms of :
(a) hatred ……………..
(b) thought …………….
(c) meaning …………….
(d) improvement …………….
(e) description …………….
(f) attribution …………….
Answer:
(a) hatred – hate
(b) thought – think
(c) meaning – mean
(d) improvement – improve
(e) description – describe
(f) attribution – attribute

(C) Find Adjective forms of:

Question 1.
Find Adjective forms of:
(a) talk …………….
(b) interest …………….
(c) purity …………….
(d) technique …………….
(e) literature …………….
Answer:
(a) talk – talkative
(b) interest – interesting
(c) purity – pure
(d) technique – technical
(e) literature – literary

Tips For Reading For A Review (Guidelines)

Skimming – (While you read for a review you should know –

(a) What is the title/text/content?
(b) What exactly is to be read? (Selectivity)
(c) What support/related resources/references/help is to be generated or found?
(d) What will you search to get complete details/associated ideas?
(e) Use technology if required (web. e-books. gazettes) to correlate the content that is read.

scanning – We might use scanning to –

(a) Look up for meanings of related words/phrases/novel ideas.
(b) Find exact associations or inter – relationship of words.
(c) Check perfection in the start and finish time, while reading.
(d) identify the exact sequence of ideas and occurence of events.
(e) Use technology if required (web, e-books, gazettes) to correlate the content that is read.

Project – (A Book Review)

Write a complete review on any book that you have recently read. Use the points for your Book Review.

Question 1.
Write a complete review on any book that you have recently read. Use the points for your Book Review.
(a) Introduction
(b) Selectivity of contents
(c) Subject/Title Apporpriacy
(d) Sequence of Contents
(e) Language Appropriacy/Type
(f) Good Points/Novelty in the book.
(g) Advantages/Scope of the book. (if any)
(h) Demerits/Shortcomings (if any)
(i) Message/OpinionNiews (Personal)
(j) Conclusion (in short)
Answer:
Book: ‘Gulliver’s Travels’
Recently I read the book ‘Gulliver’s Travels’ by Jonathan Swift. It describes the strange and unique adventures, escapades and experiences of captain Lemuel Gulliver. I found it very interesting book. Out of four parts of the book first two – his voyage to Lilliput and the voyage to Brobdingnag are very amusing, funny and imaginative. But the other two parts are not that pleasant. In Lilliput, people were six inch tall and they treated Gulliver as a ‘man-mountain’.

In Brobdingnag people were sixty-feet high and Gulliver was just a pigmy before them. Many fearful as well as funny incidents hold us spell-bound. Though it has no big literary values or it does not preach you any moral values, it is a must read book for amusement. The book written in a simple, lucid and humorous style, is easy to read for entertainment. It is everlasting source of amusement and instruction, laughter and learning, wit and wisdom. It has become one of the finest of fairy tales.

My English Coursebook 10th Digest Chapter 2.5 Book Review – Swami and Friends Additional Important Questions and Answers

Read the following passage and do the activities:

Simple Factual Activity:

Question 1.
State whether you Agree or Disagree with the following statements:
Answer:

1. Swami is a close-mouthed little kid.
2. Swami hated Mathematics worse.
3. No event or parts of the story are mentioned in this book review.
4. Mischievousness was the most striking quality of 10-year-old Swami.

Answer:

1. Disagree
2. Agree
3. Agree
4. Agree

Question 2.
State whether the following statements are True or False:

1. The book is filled with heavy grammar and difficult technical words.
2. The book circles round the mischief of the kids in a view of the kid.
3. R. K. Narayan’s ‘Swami and Friends’ is a good read for the kids and teens alike.
4. Mischievous kids are not as sensitive as other people.

Answer:

1. The book is filled with heavy grammar and difficult technical words. – False
2. The book circles round the mischief of the kids in a view of the kid. – True
3. R. K. Narayan’s ‘Swami and Friends’ is a good read for the kids and teens alike. – True
4. Mischievous kids are not as sensitive as other people. – False

Question 3.
Say whether the following statements are True or False:

1. The author of ‘Swami and Friends’ is Ruskin Bond.
2. This book is a good read only for kids.
3. The author has written this book I to capture the spirit of the mind and life of a teenage kid.
4. The Mahabharata’ is a great Indian Epic.

Answer:

1. The author of ‘Swami and Friends’ is Ruskin Bond. – False
2. This book is a good read only for kids. – False
3. The author has written this book I to capture the spirit of the mind and life of a teenage kid. – True
4. The Mahabharata’ is a great Indian Epic. – True

Complex Factual Activities:

Question 1.
Describe Swami’s characteristics in 3-4 sentences.
Answer:
Swami is a mischievous and talkative little kid of about 10 years old. He cannot stay at one place. He hates going to school, hates Mathematics even worse. School is a frightening and unpleasant experience for him. He always gets into trouble and a good beating from his father. All he wants to do is play under the sun, kick something, climb a tree break or damage something and harass (trouble) somebody. This is a typical life of the kid.

Question 2.
Complete the following sentences that tell you about author Narayan’s magic:
(Answers are directly given and underlined.)
Answer:
(a) Narayan gets deeply into the working of Swami’s ten-year-old mind.
(b) Explains in pleasing manner how Swami thinks.
(c) He too explains what is his perspective of the world is.
(d) The reader feels like Swami and gets attached with the character.

Question 3.
Complete the web
Answer:

Question 4.
Why some parents may be worried about the description of a mischievous ten-year-old boy in the book? What does the reviewer say about it?
Answer:
Some parents may be worried about the description of a mischievous ten-year-old boy because they think, that might influence their already mischievous children. But the reviewer reassures them that the book describes the mischief of the kids in a view of the kid which is harmlessand pure.

Also amidst all the mischief and naughtiness, we actually find that Swami is a loving and tender kid who is really very sensitive. And it is a known fact that mischievous kids are most sensitive and loving people of all. So this is the message that the description conveys to all of us.

Question 5.
Complete the following web:
(Answer is directly given.)
Answer:

Question 6.
What information do you get from the passage about R. K. Narayan’s literary works from this passage?
Answer:
R. K. Narayan has produced many of the outstanding literary works India has ever produced. Apart from ‘Swami and Friends’ other great works by Narayan include ‘Malgudi Days’, ‘The Guide’, ‘The Painter Signs’ and many more literary works such as the shortened Modern Prose Versions of the Indian Epics ‘ The Ramayana’ and ‘The Mahabharata’.

Activities based on Vocabulary:

Question 1.
Underline the odd man:
(Answers are directly given and underlined.)
Answer:

1. mentioning, happenings, everything, facing
2. mischievous, truth, talkative, typical
3. give, mention, stay, life
4. constantly, absolutely, lovely, deeply

Question 2.
Find the following from the passage:

1. Adjective forms of: mischief
2. Noun forms of: naughty
3. Verb forms of: imagination, loving

Answer:

1. mischief – mischievous
   
2. naughty – naughtiness
3. imagination – imagine, loving – love

Question 3.
Write from the passage the words related to ‘study’:
Answer:
book, literary values, literature, grammar, read, text, subject, technical words, English, genius, sentences.

Question 4.
Find the following from the passage:

1. Noun forms of: rule
2. Verb forms of: inclusion
3. Adjective forms of: Britain

Answer:

1. rule – rule/ruling
2. inclusion – include
3. Britain – British

Question 5.
Find the adjectives for the following from the passage:

1. authors
2. works
3. rule
4. Prose
5. Epic

Answer:

1. the greatest authors
2. literary works
3. British ruling
4. modern prose
5. Indian Epic

Activities based on Contextual Grammar:

Frame Wh-questions to get the underlined parts as answers:

Question 1.
Narayan gets deeply into the working of Swami’s mind.
Answer:
How does Narayan get into working of Swami’s mind?

Question 2.
That’s the magic of Narayan.
Answer:
Whose magic is that?

Find the error and rewrite the corrected sentences:

Question 1.
Swami think that’s his way of living life.
Answer:
Swami thinks that’s his way of living life.

Question 2.
Swami is an mischievous little kid.
Answer:
Swami is a mischievous little kid.

Question 3.
Technology isn’t big in kids life.
Answer:
Technology isn’t big in a kid’s life.

Question 4.
All they wants is to play havoc!
Answer:
All they want is to play havoc!

Add question tags:

Question 1.
This does not mean that the book is filled with heavy Grammar.
Answer:
This does not mean that the book is filled with heavy grammar, does this?

Question 2.
R. K. Narayan does a great job conveying that to all of us.
Answer:
R. K. Narayan does a great job conveying that to all of us, doesn’t he?

Do as directed:

Question 1.
The use of simple and short sentences adds to the simplicity of the book
(Rewrite the sentence using ‘not only … but also’)
Answer:
The use of not only simple but also short sentences adds to the simplicity of the book.

Question 2.
It is also known fact
(Complete the sentence by adding one more clause.)
Answer:
It is also known fact that small children yield to temptations.

Complete the following sentences adding one more clause:

Question a.
It can be said
Answer:
It can be said that you will find that atmosphere very pleasant.

Question b.
Take a look at the exhibition
Answer:
Take a look at the exhibition if you are interested in watching good photographs.

Do as directed:

Question 1.
The author is one of the greatest authors of all the time.
(Change the sentence into positive degree.)
Answer:
Very few (Not many) authors of all the time are so (as) great as him. (the author).

Question 2.
R. K. Narayan is responsible for many of the outstanding literary works.
(Frame a Wh-question to get the underlined as answer.)
Answer:
What is R. K. Narayan responsible for?

Personal Response:

Question 1.
Do you think, that even today most of our kids like to live the life Swami was living?
Answer:
Yes, I definitely think so. It is the natural instinct of most of the kids to play, to make fun, to play mischiefs and enjoy the life like Swami. They try to avoid going to school under some pretext and dislike to learn some particular subjects. They are often get beaten for their naughtiness, mistakes and their mischievous deeds. They do anything that comes to their mind, unintentionally.

Question 2.
What difference do you find between the children of Swami’s days and today’s children?
Answer:
I don’t think there is any peculiar difference between the children of Swami’s days and today’s children. Children all over the world and of all the times are the same. The only difference between them, according to me, is that many of today’s children keep themselves busy in mobiles, other gadgets and mobile games instead of playing in open space.

Question 3.
Which magazine for children do you like the most?Why?
Answer:
I like the magazine ‘Tin-Tin’ the most. I ike it because it provides all kinds of literature the children like. It gives fairy tales, mythological stories, historical stories, jokes and vivid information related to every field of children’s life. It also gives cartoons for the kids in view of the kids which are harmless and pure. It is a priceless gift for me, every month.

Activities based on Language Studies:

(A) Do as directed:

Question 1.
Complete the words by using correct letters:

1. p r _ s e
2. p l a _ e
3. c l _ m b
4. m _ g i c

Answer:

1. p r o s e
2. p l a c e
3. c l i m b
4. m a g i c

Question 2.
Put the following words in alphabetical order:
1. outstanding, author, prose, modern
2. conclusion, capture, can, children
Answer:
1. author, modern, outstanding, prose
2. can, capture, children, conclusion

Question 3.
Punctuate the following sentences:
1. he said it will be a difficult task,
2. “how s that?” said nathu. “Havent you heard.
Answer:
1. He said, “It will be a difficult task.”
2. “How’s that?” said Nathu. “Haven’t you heard?”

Question 4.
Make four words each (minimum 3 letters each) using the letters in the word ‘scattering’:
Answer:
catering, sing, ring, caring

Question 5.
Write related words as shown in the example:
(Answers are directly given and underlines.)
Answer:

Question 6.
Complete the word-chain of verbs. Add four words, each beginning with the last letter of the previous word:
Lead → ___________ → ___________ → ___________ → ___________.
Answer:
Lead → deal → leave → eat → tell.

(B) Do as directed:

1. Attempt anyone:

a. Make your own meaningful sentence using the phrase ‘take a glance’.
Answer:
The officer took a glance through the report submitted by his assistant.

OR

b. Add a clause to expand the sentence meaningfully:
Swami is a kid ………………………
Answer:
Swami is a kid who cannot stay at one place.

2. Attempt anyone:

a. Add a prefix or suffix to make new words.
1. complete
2. justice
Answer:
1. completion
2. injustice

OR

b. Make a meaningful sentence using any one of the following words:
1. complete
2. justice
Answer:
1. I have to complete my work by tomorrow.
2. The employees were protesting against the owner to get justice.

My English Coursebook 10th Digest Pdf Unit 2 

• You Start Dying Slowly … 10th English Solutions
• The Boy who Broke The Bank 10th English Solutions
• The Twins 10th English Solutions
• An Epitome of Courage 10th English Solutions
• Book Review – Swami and Friends 10th English Solutions
• World Heritage 10th English Solutions