Bhagya

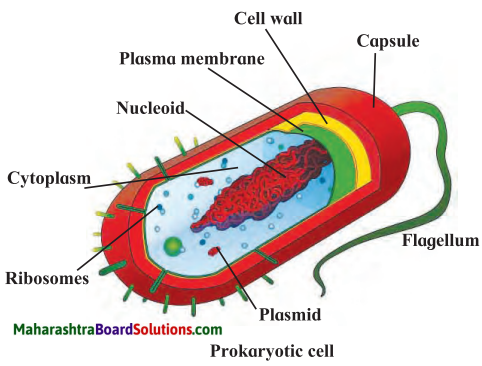
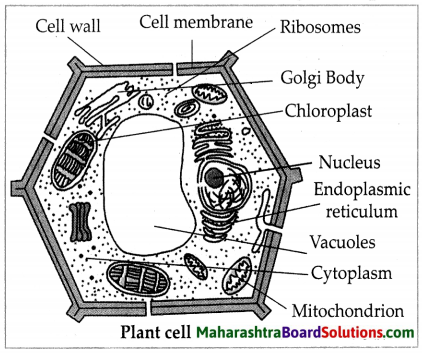
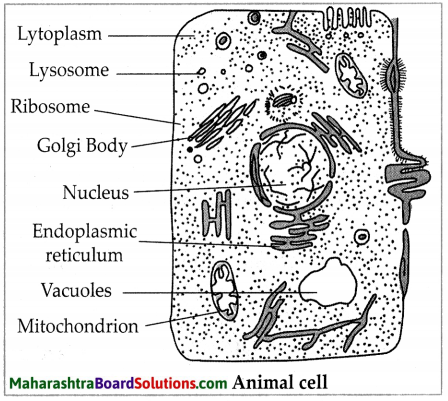
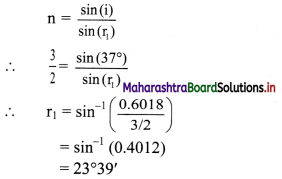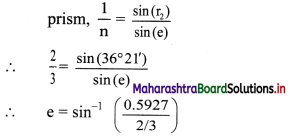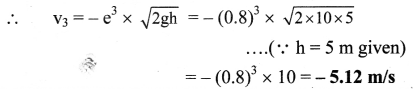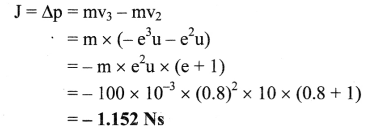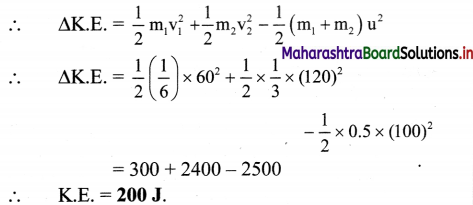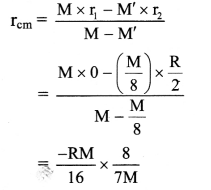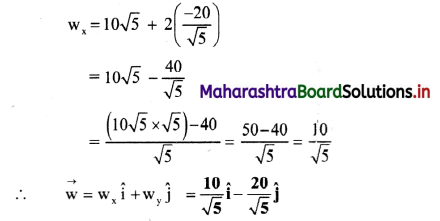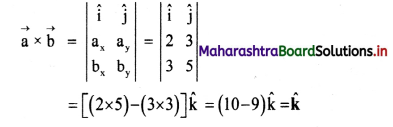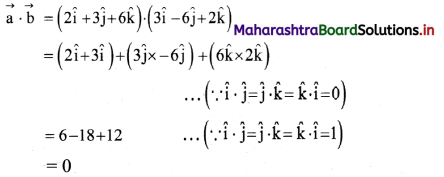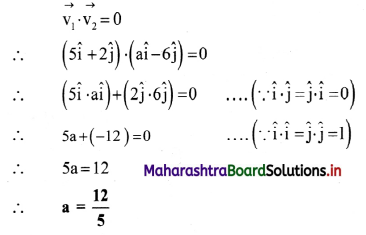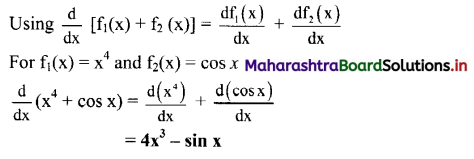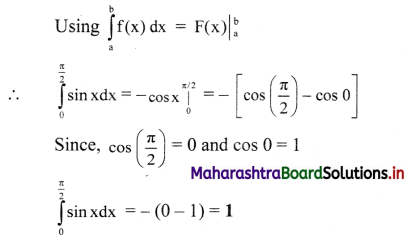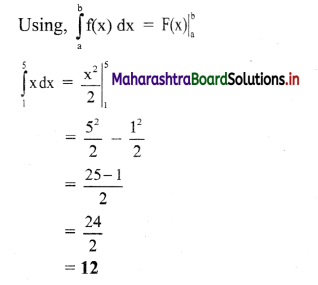Electrostatics Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 10 Electrostatics Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 10 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 10 Exercise Solutions

1. Choose the correct option.

Question 1.
A positively charged glass rod is brought close to a metallic rod isolated from the ground. The charge on the side of the metallic rod away from the glass rod will be
(A) same as that on the glass rod and equal in quantity
(B) opposite to that on the glass of and equal in quantity
(C) same as that on the glass rod but lesser in quantity
(D) same as that on the glass rod but more in quantity
Answer:
(A) same as that on the glass rod and equal in quantity

Question 2.
An electron is placed between two parallel plates connected to a battery. If the battery is switched on, the electron will
(A) be attracted to the +ve plate
(B) be attracted to the -ve plate
(C) remain stationary
(D) will move parallel to the plates
Answer:
(A) be attracted to the +ve plate

Question 3.
A charge of + 7 µC is placed at the centre of two concentric spheres with radius 2.0 cm and 4.0 cm respectively. The ratio of the flux through them will be
(A) 1 : 4
(B) 1 : 2
(C) 1 : 1
(D) 1 : 16
Answer:
(C) 1 : 1

Question 4.
Two charges of 1.0 C each are placed one meter apart in free space. The force between them will be
(A) 1.0 N
(B) 9 × 10⁹ N
(C) 9 × 10^-9 N
(D) 10 N
Answer:
(B) 9 × 10⁹ N

Question 5.
Two point charges of +5 µC are so placed that they experience a force of 80 × 10^-3 N. They are then moved apart, so that the force is now 2.0 × 10^-3 N. The distance between them is now
(A) 1/4 the previous distance
(B) double the previous distance
(C) four times the previous distance
(D) half the previous distance
Answer:
(B) double the previous distance

Question 6.
A metallic sphere A isolated from ground is charged to +50 µC. This sphere is brought in contact with other isolated metallic sphere B of half the radius of sphere A. The charge on the two sphere will be now in the ratio
(A) 1 : 2
(B) 2 : 1
(C) 4 : 1
(D) 1 : 1
Answer:
(D) 1 : 1

Question 7.
Which of the following produces uniform electric field?
(A) point charge
(B) linear charge
(C) two parallel plates
(D) charge distributed an circular any
Answer:
(C) two parallel plates

Question 8.
Two point charges of A = +5.0 µC and B = -5.0 µC are separated by 5.0 cm. A point charge C = 1.0 µC is placed at 3.0 cm away from the centre on the perpendicular bisector of the line joining the two point charges. The charge at C will experience a force directed towards
(A) point A
(B) point B
(C) a direction parallel to line AB
(D) a direction along the perpendicular bisector
Answer:
(C) a direction parallel to line AB

2. Answer the following questions.

Question 1.
What is the magnitude of charge on an electron?
Answer:
The magnitude of charge on an electron is 1.6 × 10^-19 C

Question 2.
State the law of conservation of charge.
Answer:
In any given physical process, charge may get transferred from one part of the system to another, but the total charge in the system remains constant”
OR
For an isolated system, total charge cannot be created nor destroyed.

Question 3.
Define a unit charge.
Answer:
Unit charge (one coulomb) is the amount of charge which, when placed at a distance of one metre from another charge of the same magnitude in vacuum, experiences a force of 9.0 × 10⁹ N.

Question 4.
Two parallel plates have a potential difference of 10V between them. If the plates are 0.5 mm apart, what will be the strength of electric charge.
Answer:
V=10V
d = 0.5 mm = 0.5 × 10^-3 m
To find: The strength of electric field (E)
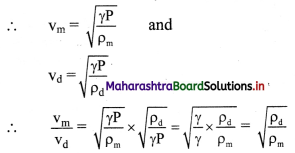
Formula: E = \(\frac {V}{d}\)
Calculation: From formula,
E = \(\frac {10}{0.5×10^{-3}}\)
20 × 10³ V/m

Question 5.
What is uniform electric field?
Answer:
A uniform electric field is a field whose magnitude and direction are same at all points. For example, field between two parallel plates as shown in the diagram.

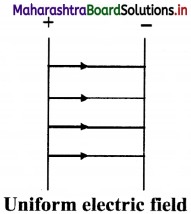
Question 6.
If two lines of force intersect of one point. What does it mean?
Answer:
If two lines of force intersect of one point, it would mean that electric field has two directions at a single point.

Question 7.
State the units of linear charge density.
Answer:
SI unit of λ is (C / m).

Question 8.
What is the unit of dipole moment?
Answer:
i. Strength of a dipole is measured in terms of a quantity called the dipole moment.

ii. Let q be the magnitude of each charge and 2\(\vec{l}\) be the distance from negative charge to positive charge. Then, the product q(2\(\vec{l}\)) is called the dipole moment \(\vec{p}\).

iii. Dipole moment is defined as \(\vec{p}\) = q(2\(\vec{l}\))

iv. A dipole moment is a vector whose magnitude is q (2\(\vec{l}\)) and the direction is from the negative to the positive charge.

v. The unit of dipole moment is coulomb-metre (C m) or debye (D).

Question 9.
What is relative permittivity?
Answer:
i. Relative permittivity or dielectric constant is the ratio of absolute permittivity of a medium to the permittivity of free space.
It is denoted as K or ε_r.
i.e., K or ε_r = \(\frac {ε}{ε_0}\)

ii. It is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.
i.e., K or ε_r = \(\frac {F_{vacuum}}{F_{medium}}\)

iii. It is also called as specific inductive capacity or dielectric constant.

3. Solve numerical examples.

Question 1.
Two small spheres 18 cm apart have equal negative charges and repel each other with the force of 6 × 10^-8 N. Find the total charge on both spheres.
Solution:
Given: F = 6 × 10^-8 N, r = 18 cm = 18 × 10^-2 m
To find: Total charge (q₁ + q₂)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,

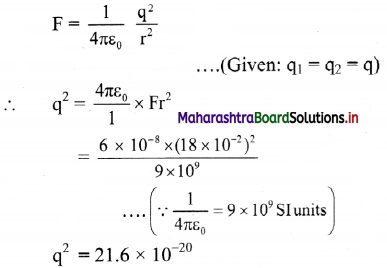
Taking square roots from log table,
∴ q = -4.648 × 10^-10 C
….(∵ the charges are negative)
Total charge = q₁ + q₂ = 2q
= 2 × (-4.648) × 10^-10
= -9.296 × 10^-10 C

Question 2.
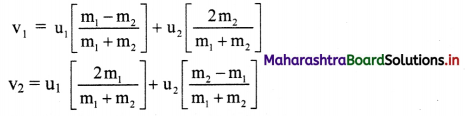
A charge + q exerts a force of magnitude – 0.2 N on another charge -2q. If they are separated by 25.0 cm, determine the value of q.
Answer:
Given: q₁ = + q, q₂ = -2q, F = -0.2 N
r = 25 cm = 25 × 10^-2 m
To find: Charge (q)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,

[Note: The answer given above is calculated in accordance with textual method considering the given data]

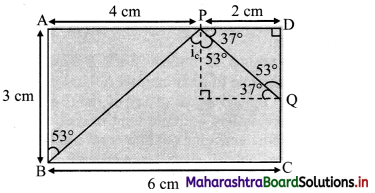
Question 3.
Four charges of +6 × 10^-8 C each are placed at the corners of a square whose sides are 3 cm each. Calculate the resultant force on each charge and show in direction on a diagram drawn to scale.
Answer:
Given: q_A = q_B = q_C = q_D = 6 × 10^-8 C, a = 3 cm

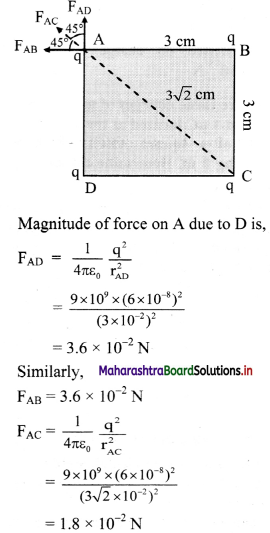
∴ Resultant force on ‘A’
= F_AD cos 45 + F_AB cos 45 + F_AC
= (3.6 × 10^-2 × \(\frac {1}{√2}\)) + (3.6 × 10^-2 × \(\frac {1}{√2}\)) + 1.8 × 10^-2
= 6.89 × 10^-2 N directed along \(\vec{F_{AC}}\)

Question 4.
The electric field in a region is given by \(\vec{E}\) = 5.0 \(\hat{k}\) N/C Calculate the electric flux through a square of side 10.0 cm in the following cases
i. The square is along the XY plane
ii. The square is along XZ plane
iii. The normal to the square makes an angle of 45° with the Z axis.
Answer:
Given: \(\vec{E}\) = 5.0 \(\hat{k}\) N/C, |E| = 5 N/C
l = 10 cm = 10 × 10^-2 m = 10^-1 m
A = l² – 10^-2m²
To find: Electric flux in three cases.
(ø₁) (ø₂) (ø₃)
Formula: (ø₁) = EA cos θ
Calculation:
Case I: When square is along the XY plane,
∴ θ = 0
ø₁ = 5 × 10^-2 cos 0
= 5 × 10^-2 V m

Case II: When square is along XZ plane,
∴ θ = 90°
ø₁ = 5 × 10^-2 cos 90° = 0 V m

Case III: When normal to the square makes an angle of 45° with the Z axis.
∴ 0 = 45°
∴ ø₃ = 5 × 10^-2 × cos 45°
= 3.5 × 10^-2 V m

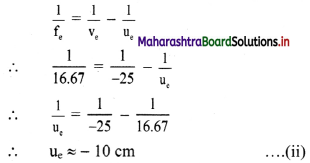
Question 5.
Three equal charges of 10 × 10^-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm and 25 cm respectively. Find the force exerted on the charge located at the 90° angle.
Answer:
Given: q_A = q_B = q_C = 10 × 10^-8

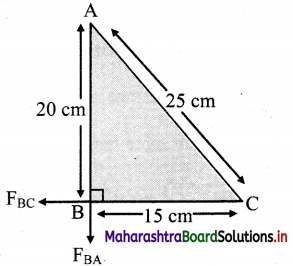
Force on B due to A,

Question 6.
A potential difference of 5000 volt is applied between two parallel plates 5 cm apart. A small oil drop having a charge of 9.6 x 10-19 C falls between the plates. Find (i) electric field intensity between the plates and (ii) the force on the oil drop.
Answer:
Given: V = 5000 volt, d = 5 cm = 5 × 10^-2 m
q = 9.6 × 10^-19 C
To find:
i. Electric field intensity (E)
ii. Force (F)
Formula:
i. E = \(\frac {V}{d}\) \(\frac {q}{r}\)
ii. E = \(\frac {F}{q}\)
Calculation: From formula (i),
E = \(\frac {F}{q}\) = 10⁵ N/C
From formula (ii)
F = E x q
= 10⁵ × 9.6 × 10^-19
= 9.6 × 10^-14 N

Question 7.
Calculate the electric field due to a charge of -8.0 × 10^-8 C at a distance of 5.0 cm from it.
Answer:
Given: q = – 8 × 10^-8 C, r = 5 cm = 5 × 10^-2 m
To Find: Electric field (E)
Formula: E = \(\frac {1}{4πε_0}\) \(\frac {q}{r^2}\)
Calculation: From formula,
E = 9 × 10⁹ × \(\frac {(-8×10^{-8})}{(5×10^{-2})^2}\)
= -2.88 × 10⁵ N/C

11th Physics Digest Chapter 10 Electrostatics Intext Questions and Answers

Can you recall? (Textbookpage no. 188)

Question 1.
Have you experienced a shock while getting up from a plastic chair and shaking hand with your friend?
Answer:
Yes, sometimes a shock while getting up from a plastic chair and shaking hand with friend is experienced.

Question 2.
Ever heard a crackling sound while taking out your sweater in winter?
Answer:
Yes, sometimes while removing our sweater in winter, some crackling sound is heard and the sweater appears to stick to body.

Question 3.
Have you seen the lightning striking during pre-monsoon weather?
Answer:
Yes, sometimes lightning striking during pre-pre-monsoon weather seen.

Can you tell? (Textbook page no. 189)

i. When a petrol or a diesel tanker is emptied in a tank, it is grounded.
ii. A thick chain hangs from a petrol or a diesel tanker and it is in contact with ground when the tanker is moving.
Answer:
i. When a petrol or a diesel tanker is emptied in a tank, it is grounded so that it has an electrically conductive connection from the petrol or diesel tank to ground (Earth) to allow leakage of static and electrical charges.

ii. Metallic bodies of cars, trucks or any other big vehicles get charged because of friction between them and the air rushing past them. Hence, a thick chain is hanged from a petrol or a diesel tanker to make a contact with ground so that charge produced can leak to the ground through chain.

Can you tell? (Textbook page no. 194)

Three charges, q each, are placed at the vertices of an equilateral triangle. What will be the resultant force on charge q placed at the centroid of the triangle?
Answer:

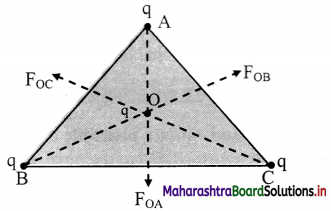
Since AD. BE and CF meets at O, as centroid of an equilateral triangle.
∴ OA = OB = OC
∴ Let, r = OA = OB = OC
Force acting on point O due to charge on point A,
\(\overrightarrow{\mathrm{F}}_{\mathrm{OA}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}_{i}^{2}} \hat{\mathrm{r}}_{\mathrm{AO}}\)
Force acting on point O due to charge on point B,
\(\overrightarrow{\mathrm{F}}_{O \mathrm{~B}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}_{\mathrm{BO}}\)
Force acting on point O due to charge on point C,
\(\overrightarrow{\mathrm{F}}_{\mathrm{OC}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}} \mathrm{co}\)
∴ Resultant force acting on point O,
F = \(\vec{F}\)_OA + \(\vec{F}\)_OB + \(\vec{F}\)_OC
On resolving \(\vec{F}\)_OB and \(\vec{F}\)_OC, we get –\(\vec{F}\)_OA
i.e., \(\vec{F}\)_OB + \(\vec{F}\)_OC = –\(\vec{F}\)_OA
∴ \(\vec{F}\) = \(\vec{F}\)_OA – \(\vec{F}\)_OA = 0
Hence, the resultant force on the charge placed at the centroid of the equilateral triangle is zero.

Can you tell? (Textbook page no. 197)

Why a small voltage can produce a reasonably large electric field?
Answer:

1. Electric field produced depends upon voltage as well as separation distance.
2. Electric field varies linearly with voltage and inversely with distance.
3. Hence, even if voltage is small, it can produce a reasonable large electric field when the gap between the electrode is reduced significantly.

Can you tell? (Textbook page no. 198)

Lines of force are imaginary; can they have any practical use?
Answer:
Yes, electric lines of force help us to visualise the nature of electric field in a region.

Can you tell? (Textbook page no. 204)

The surface charge density of Earth is σ = -1.33 nC/m². That is about 8.3 × 10⁹ electrons per square metre. If that is the case why don’t we feel it?
Answer:
The Earth along with its atmosphere acts as a neutral system. The atmosphere (ionosphere in particular) has nearly equal and opposite charge.

As a result, there exists a mechanism to replenish electric charges in the form of continual thunderstorms and lightning that occurs in different parts of the globe. This makes average charge on surface of the Earth as zero at any given time instant. Hence, we do not feel it.

Internet my friend (Textbook page no. 205)

i. https://www.physicsclassroom.com/class
ii. https://courses.lumenleaming.com/physics/
iii. https://www,khanacademy.org/science
iv. https://www.toppr.com/guides/physics/
[Students are expected to visit the above mentioned websites and collect more information about electrostatics.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Optics Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 9 Optics Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 9 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 9 Exercise Solutions

1. Multiple Choise Questions

Question 1.
As per the recent understanding, light consists of
(A) rays
(B) waves
(C) corpuscles
(D) photons obeying the rules of waves
Answer:
(D) photons obeying the rules of waves

Question 2.
Consider the optically denser lenses P, Q, R, and S drawn below. According to the Cartesian sign convention which of these have a positive focal length?

(A) Only P
(B) Only P and Q
(C) Only P and R
(D) Only Q and S
Answer:
(B) Only P and Q

Question 3.
Two plane mirrors are inclined at angle 40° between them. Number of images seen of a tiny object kept between them is
(A) Only 8
(B) Only 9
(C) 8 or 9
(D) 9 or 10
Answer:
(C) 8 or 9

Question 4.
A concave mirror of curvature 40 cm, used for shaving purpose produces image of double size as that of the object. Object distance must be
(A) 10 cm only
(B) 20 cm only
(C) 30 cm only
(D) 10 cm or 30 cm
Answer:
(D) 10 cm or 30 cm

Question 5.
Which of the following aberrations will NOT occur for spherical mirrors?
(A) Chromatic aberration
(B) Coma
(C) Distortion
(D) Spherical aberration
Answer:
(A) Chromatic aberration

Question 6.
There are different fish, monkeys and water of the habitable planet of the star Proxima b. A fish swimming underwater feels that there is a monkey at 2.5 m on the top of a tree. The same monkey feels that the fish is 1.6 m below the water surface. Interestingly, height of the tree and the depth at which the fish is swimming are exactly same. Refractive index of that water must be
(A) 6/5
(B) 5/4
(C) 4/3
(D) 7/5
Answer:
(B) 5/4

Question 7.
Consider following phenomena/applications: P) Mirage, Q) rainbow, R) Optical fibre and S) glittering of a diamond. Total internal reflection is involved in
(A) Only R and S
(B) Only R
(C) Only P, R and S
(D) all the four
Answer:
(A) Only R and S

Question 8.
A student uses spectacles of number -2 for seeing distant objects. Commonly used lenses for her/his spectacles are
(A) bi-concave
(B) piano concave
(C) concavo-convex
(D) convexo-concave
Answer:
(A) bi-concave

Question 9.
A spherical marble, of refractive index 1.5 and curvature 1.5 cm, contains a tiny air bubble at its centre. Where will it appear when seen from outside?
(A) 1 cm inside
(B) at the centre
(C) 5/3 cm inside
(D) 2 cm inside
Answer:
(B) at the centre

Question 10.
Select the WRONG statement.
(A) Smaller angle of prism is recommended for greater angular dispersion.
(B) Right angled isosceles glass prism is commonly used for total internal reflection.
(C) Angle of deviation is practically constant for thin prisms.
(D) For emergent ray to be possible from the second refracting surface, certain minimum angle of incidence is necessary from the first surface.
Answer:
(A) Smaller angle of prism is recommended for greater angular dispersion.

Question 11.
Angles of deviation for extreme colours are given for different prisms. Select the one having maximum dispersive power of its material.
(A) 7°, 10°
(B) 8°, 11°
(C) 12°, 16°
(D) 10°, 14°
Answer:
(A) 7°, 10°

Question 12.
Which of the following is not involved in formation of a rainbow?
(A) refraction
(B) angular dispersion
(C) angular deviation
(D) total internal reflection
Answer:
(D) total internal reflection

Question 13.
Consider following statements regarding a simple microscope:
(P) It allows us to keep the object within the least distance of distinct vision.
(Q) Image appears to be biggest if the object is at the focus.
(R) It is simply a convex lens.
(A) Only (P) is correct
(B) Only (P) and (Q) are correct
(C) Only (Q) and (R) are correct
(D) Only (P) and (R) are correct
Answer:
(D) Only (P) and (R) are correct

2. Answer the following questions.

Question 1.
As per recent development, what is the nature of light? Wave optics and particle nature of light are used to explain which phenomena of light respectively?
Answer:

1. As per recent development, it is now an established fact that light possesses dual nature. Light consists of energy carrier photons. These photons follow the rules of electromagnetic waves.
2. Wave optics explains the phenomena of light such as, interference, diffraction, polarisation, Doppler effect etc.
3. Particle nature of light can be used to explain phenomena like photoelectric effect, emission of spectral lines, Compton effect etc.

Question 2.
Which phenomena can be satisfactorily explained using ray optics?
Answer:
Ray optics or geometrical optics: Ray optics can be used for understanding phenomena like reflection, refraction, double refraction, total internal reflection, etc.

Question 3.
What is focal power of a spherical mirror or a lens? What may be the reason for using P = \(\frac {1}{f}\) its expression?
Answer:

1. Converging or diverging ability of a lens or of a mirror is defined as its focal power.
2. This implies, more the power of any spherical mirror or a lens, the more is its ability to converge or diverge the light that passes through it.
3. In case of convex lens or concave mirror, more the convergence, shorter is the focal length as shown in the figure.
4. Similarly, in case of concave lens or convex mirror, more the divergence, shorter is the focal length.
5. This explains that the focal power of any spherical lens or mirror is inversely proportional to the focal length.
6. Hence, the expression of focal power is given by the formula, P = \(\frac {1}{f}\).

Question 4.
At which positions of the objects do spherical mirrors produce (i) diminished image (ii) magnified image?
Answer:
i. Amongst the two types of spherical mirrors, convex mirror always produces a diminished image at all positions of the object.

ii. Concave mirror produces diminished image when object is placed:

• Beyond radius of curvature (i.e., u > 2f)
• At infinity (i.e., u = ∞)

iii. Concave mirror produces magnified image when object is placed:

• between centre of curvature and focus (i.e., 2f > u > f)
• between focus and pole of the mirror (i.e., u < f)

Question 5.
State the restrictions for having images produced by spherical mirrors to be appreciably clear.
Answer:
i. In order to obtain clear images, the formulae for image formation by mirrors or lens follow the given assumptions:

• Objects and images are situated close to the principal axis.
• Rays diverging from the objects are confined to a cone of very small angle.
• If there is a parallel beam of rays, it is paraxial, i.e., parallel and close to the principal axis.

ii. In case of spherical mirrors (excluding small aperture spherical mirrors), rays farther from the principle axis do not remain parallel to the principle axis. Thus, the third assumption is not followed and the focus gradually shifts towards the pole.

iii. The relation (f = \(\frac {R}{2}\)) giving a single point focus is not followed and the image does not get converged at a single point resulting into a distorted or defective image.

iv. This defect arises due to the spherical shape of the reflecting surface.

Question 6.
Explain spherical aberration for spherical mirrors. How can it be minimized? Can it be eliminated by some curved mirrors?
Answer:

1. In case of spherical mirrors (excluding small aperture spherical mirror), The rays coming from a distant object farther from principal axis do not remain parallel to the axis. Thus, the focus gradually shifts towards the pole.
2. The assumption for clear image formation namely, ‘If there is a parallel beam of rays, it is paraxial, i.e., parallel and close to the principal axis’, is not followed in this case.
3. The relation f (f = \(\frac {R}{2}\)) giving a single point focus is not followed and the image does not get converged at a single point resulting into a distorted or defective image.
4. This phenomenon is known as spherical aberration.
5. It occurs due to spherical shape of the reflecting surface, hence known as spherical aberration.
6. The rays near the edge of the mirror converge at focal point F_M Whereas, the rays near the principal axis converge at point F_P. The distance between F_M and F_P is measured as the longitudinal spherical aberration.
7. In spherical aberration, single point image is not possible at any point on the screen and the image formed is always a circle.
8. At a particular location of the screen (across AB in figure), the diameter of this circle is minimum. This is called the circle of least confusion. Radius of this circle is transverse spherical aberration.

Remedies for Spherical Aberration:

1. Spherical aberration can be minimized by reducing the aperture of the mirror.
2. Spherical aberration in curved mirrors can be completely eliminated by using a parabolic mirror.

Question 7.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
Answer:
i. Absolute refractive index of a medium is defined as the ratio of speed of light in vacuum to that in the given medium.

ii. A stick or pencil kept obliquely in a glass containing water appears broken as its part in water appears to be raised.

iii. As the speed of light is different in two media, the rays of light coming from water undergo refraction at the boundary separating two media.

iv. Consider speed of light to be v in water and c in air. (Speed of light in air ~ speed of light in vacuum)
∴ refractive index of water = \(\frac {n_w}{n_s}\) = \(\frac {n_w}{n_{vacuum}}\) = \(\frac {c}{v}\)

v. Relative refractive index of a medium 2 is the refractive index of medium 2 with respect to medium 1 and it is defined as the ratio of speed of light v₁ in medium 1 to its speed v₁ in medium 2.
∴ Relative refractive index of medium 2,
¹n₂ = \(\frac {v_1}{v_2}\)

vi. Consider a beaker filled with water of absolute refractive index n₁ kept on a transparent glass slab of absolute refractive index n₂.

vii. Thus, the refractive index of water with respect to that of glass will be,
ⁿw₂ = \(\frac {n_2}{n_1}\) = \(\frac {c/v_2}{c/v_1}\) = \(\frac {v_1}{v_2}\)

Question 8.
Explain ‘mirage’ as an illustration of refraction.
Answer:
i. On a hot clear Sunny day, along a level road, there appears a pond of water ahead of the road. Flowever, if we physically reach the spot, there is nothing but the dry road and water pond again appears some distance ahead. This illusion is called mirage.

ii. Mirage results from the refraction of light through a non-uniform medium.

iii. On a hot day the air in contact with the road is hottest and as we go up, it gets gradually cooler. The refractive index of air thus decreases with height. Hot air tends to be less optically dense than cooler air which results into a non-uniform medium.

iv. Light travels in a straight line through a uniform medium but refracts when traveling through a non-uniform medium.

v. Thus, the ray of light coming from the top of an object get refracted while travelling downwards into less optically dense air and become more and more horizontal as shown in Figure.

vi. As it almost touches the road, it bends (refracts) upward. Then onwards, upward bending continues due to denser air.

vii. As a result, for an observer, it appears to be coming from below thereby giving an illusion of reflection from an (imaginary) water surface.

Question 9.
Under what conditions is total internal reflection possible? Explain it with a suitable example. Define critical angle of incidence and obtain an expression for it.
Answer:
Conditions for total internal reflection:
i. The light ray must travel from denser medium to rarer medium.

ii. The angle of incidence in the denser medium must be greater than critical angle for the given pair of media.

Total internal reflection in optical fibre:
iii. Consider an optical fibre made up of core of refractive index n₁ and cladding of refractive index n₂ such that, n₁ > n₂.

iv. When a ray of light is incident from a core (denser medium), the refracted ray is bent away from the normal.

v. At a particular angle of incidence i_c in the denser medium, the corresponding angle of refraction in the rarer medium is 90°.

vi. For angles of incidence greater than ic, the angle of refraction become larger than 90° and the ray does not enter into rarer medium at all but is reflected totally into the denser medium as shown in figure.

critical angle of incidence and obtain an expression:
i. Critical angle for a pair of refracting media can be defined as that angle of incidence in the denser medium for which the angle of refraction in the rarer medium is 90°.

ii. Let n be the relative refractive index of denser medium with respect to the rarer.

iii. Then, according to Snell’s law,
n = \(\frac {n_{denser}}{n_{rarer}}\) = \(\frac {sin r}{sin i_c}\) = \(\frac {sin 90°}{sin i_c}\)
∴ sin (i_c) = \(\frac {1}{n}\)

Question 10.
Describe construction and working of an optical fibre. What are the advantages of optical fibre communication over electronic communication?
Answer:

Construction:

1. An optical fibre consists of an extremely thin, transparent and flexible core surrounded by an optically rarer flexible cover called cladding.
2. For protection, the whole system is coated by a buffer and a jacket.
3. Entire thickness of the fibre is less than half a mm.
4. Many such fibres can be packed together in an outer cover.

Working:

1. Working of optical fibre is based on the principle of total internal reflection.
2. An optical signal (a ray of light) entering the core suffers multiple total internal reflections before emerging out after a several kilometres.
3. The optical signal travels with the highest possible speed in the material.
4. The emerged optical signal has extremely low loss in signal strength.

Advantages of optical fibre communication over electronic communication:

1. Broad bandwidth (frequency range): For TV signals, a single optical fibre can carry over 90000 independent signals (channels).
2. Immune to EM interference: Optical fibre being electrically non-conductive, does not pick up nearby EM signals.
3. Low attenuation loss: loss being lower than 0.2 dB/km, a single long cable can be used for several kilometres.
4. Electrical insulator: Optical fibres being electrical insulators, ground loops of metal wires or lightning do not cause any harm.
5. Theft prevention: Optical fibres do not use copper or other expensive material which are prone to be robbed.
6. Security of information: Internal damage is most unlikely to occur, keeping the information secure.

Question 11.
Why are prism binoculars preferred over traditional binoculars? Describe its working in brief.
Answer:

1. Traditional binoculars use only two cylinders. Distance between the two cylinders can’t be greater than that between the two eyes. This creates a limitation of field of view.
2. A prism binocular has two right angled glass prisms which apply the principle of total internal reflection.
3. The incident light rays are reflected internally twice giving the viewer a wider field of view. For this reason, prism binoculars are preferred over traditional binoculars.

Working:

1. The prism binoculars consist of 4 isosceles, right angled prisms of material having critical angle less than 45°.
2. The prism binoculars have a wider input range compared to traditional binoculars.
3. The light rays incident on the prism binoculars, first get total internally reflected by the isosceles, right angled prisms 1 and 4.
4. These reflected rays undergo another total internal reflection by prisms 2 and 3 to form the final image.

Question 12.
A spherical surface separates two transparent media. Derive an expression that relates object and image distances with the radius of curvature for a point object. Clearly state the assumptions, if any.
Answer:
i. Consider a spherical surface YPY’ of radius curvature R, separating two transparent media of refractive indices n₁ and n₂ respectively with ni₁ < n₂.

ii. P is the pole and X’PX is the principal axis. A point object O is at a distance u from the pole, in the medium of refractive index n₁.

iii. In order to minimize spherical aberration, we consider two paraxial rays.

iv. The ray OP along the principal axis travels undeviated along PX. Another ray OA strikes the surface at A.

v. As n₁ < n₂, the ray deviates towards the normal (CAN), travels along AZ and real image of point object O is formed at I.

vi. Let α, β and γ be the angles subtended by incident ray, normal and refracted ray with the principal axis.
∴ i = (α + β) and r = (β – γ)

vii. As, the rays are paraxial, all the angles can be considered to be very small.
i.e., sin i ≈ i and sin r ≈ r
Angles α, β and γ can also be expressed as,

viii. According to Snell’s law,
n₁ sin (i) = n₂ sin (r)
For small angles, Snell’s law can be written
as, n₁i = n₂r
∴ n₁ (α + β) = n₂ (β – γ)
∴ (n₂ – n₁)β = n₁α + n₂γ
Substituting values of α, β and γ, we get,
(n₂ – n₁) \(\frac {arc PA}{R}\) = n₁(\(\frac {arc PA}{-u}\)) + n₂(\(\frac {arc PA}{v}\))
∴ \(\frac {(n_2-n_1)}{R}\) = \(\frac {n_2}{v}\) – \(\frac {n_1}{u}\)

Assumptions: To derive an expression that relates object and image distances with the radius of curvature for a point object, the two rays considered are assumed to be paraxial thus making the angles subtended by incident ray, normal and refracted ray with the principal axis very small.

Question 13.
Derive lens makers’ equation. Why is it called so? Under which conditions focal length f and radii of curvature R are numerically equal for a lens?
Answer:
i. Consider a lens of radii of curvature Ri and R2 kept in a medium such that refractive index of material of the lens with respect to the medium is denoted as n.

ii. Assuming the lens to be thin, P is the common pole for both the surfaces. O is a point object on the principal axis at a distance u from P.

iii. The refracting surface facing the object is considered as first refracting surface with radii R₁.

iv. In the absence of second refracting surface, the paraxial ray OA deviates towards normal and would intersect axis at I₁. PI₁ = V₁ is the image distance for intermediate image I₁.

Before reaching I₁, the incident rays (AB and OP) strike the second refracting surface. In this case, image I₁ acts as a virtual object for second surface.

vii. For second refracting surface,
n₂ = 1, n₁ = n, R = R₂, u = v₁ and PI = v
∴ \(\frac{(1-\mathrm{n})}{\mathrm{R}_{2}}=\frac{1}{\mathrm{v}}-\frac{\mathrm{n}}{\mathrm{v}_{1}}-\frac{(\mathrm{n}-1)}{\mathrm{R}_{2}}=\frac{1}{\mathrm{v}}-\frac{\mathrm{n}}{\mathrm{v}_{1}}\) ………… (2)

viii. Adding equations (1) and (2),
(n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)=\frac{1}{v}-\frac{1}{u}\)
For object at infinity, image is formed at focus, i.e., for u = ∞, v = f. Substituting this in above equation,
\(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) …………. (3)
This equation in known as the lens makers’ formula.

ix. Since the equation can be used to calculate the radii of curvature for the lens, it is called the lens makers’ equation.

x. The numeric value of focal length f and radius of curvature R is same under following two conditions:
Case I:
For a thin, symmetric and double convex lens made of glass (n = 1.5), R₁ is positive and R₂ is negative but, |R₁| = |R₂|.
In this case,
\(\frac{1}{\mathrm{f}}=(1.5-1)\left(\frac{1}{\mathrm{R}}-\frac{1}{-\mathrm{R}}\right)=0.5\left(\frac{2}{\mathrm{R}}\right)=\frac{1}{\mathrm{R}}\)
∴ f = R

Case II:
Similarly, for a thin, symmetric and double concave lens made of glass (n = 1.5), R₁ is negative and R₂ is positive but, |R₁| = |R₂|.
In this case,
\(\frac{1}{\mathrm{f}}=(1.5-1)\left(\frac{1}{-\mathrm{R}}-\frac{1}{\mathrm{R}}\right)=0.5\left(-\frac{2}{\mathrm{R}}\right)=-\frac{1}{\mathrm{R}}\)
∴ f = -R or |f| = |R|

3. Answer the following questions in detail.

Question 1.
What are different types of dispersions of light? Why do they occur?
Answer:
i. There are two types of dispersions:
a. Angular dispersion
b. Lateral dispersion

ii. The refractive index of material depends on the frequency of incident light. Hence, for different colours, refractive index of material is different.

iii. For an obliquely incident ray, the angles of refraction are different for each colour and they separate as they travel along different directions resulting into angular dispersion.

iv. When a polychromatic beam of light is obliquely incident upon a plane parallel transparent slab, emergent beam consists of all component colours separated out.

v. In this case, these colours are parallel to each other and are also parallel to their initial direction resulting into lateral dispersion

Question 2
Define angular dispersion for a prism. Obtain its expression for a thin prism. Relate it with the refractive indices of the material of the prism for corresponding colours.
Answer:
i. If a polychromatic beam is incident upon a prism, the emergent beam consists of all the individual colours angularly separated. This phenomenon is known as angular dispersion for a prism.

ii. For any two component colours, angular dispersion is given by,
δ₂₁ = δ₂ – δ₁

iii. For white light, we consider two extreme colours viz., red and violet.
∴ δ_VR = δ_V – δ_R

iv. For thin prism,
δ = A(n – 1)
δ₂₁ = δ₂ – δ₁
= A(n₂ – 1) – A(n₁ – 1) = A(n₂ – n₁)
where n₁ and n₂ are refractive indices for the two colours.

v. For white light,
δ_VR = δ_V – δ_R
= A(n_V – 1) – A(n_R – 1) = A(n_V – n_R).

Question 3.
Explain and define dispersive power of a transparent material. Obtain its expressions in terms of angles of deviation and refractive indices.
Answer:
Ability of an optical material to disperse constituent colours is its dispersive power.

It is measured for any two colours as the ratio of angular dispersion to the mean deviation for those two colours. Thus, for the extreme colours of white light, dispersive power is given by,
\(\omega=\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)} \approx \frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\delta_{\mathrm{Y}}}=\frac{\mathrm{A}\left(\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}\right)}{\mathrm{A}\left(\mathrm{n}_{\mathrm{Y}}-1\right)}=\frac{\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}}{\mathrm{n}_{\mathrm{Y}}-1}\)

Question 4.
(i) State the conditions under which a rainbow can be seen.
Answer:
A rainbow can be observed when there is a light shower with relatively large raindrop occurring during morning or evening time with enough sunlight around.

(ii) Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
Answer:
i. A ray AB incident from Sun (white light) strikes the upper portion of a water drop at an incident angle i.

ii. On entering into water, it deviates and disperses into constituent colours. The figure shows the extreme colours (violet and red).

iii. Refracted rays BV and BR strike the opposite inner surface of water drop and suffer internal reflection.

iv. These reflected rays finally emerge from V’ and R’ and can be seen by an observer on the ground.

v. For the observer they appear to be coming from opposite side of the Sun.

vi. Minimum deviation rays of red and violet colour are inclined to the ground level at θ_R = 42.8° ≈ 43° and θ_V = 40.8 ≈ 41° respectively. As a result, in the rainbow, the red is above and violet is below.

(iii) Explain the formation of a secondary rainbow. For which angular range with the horizontal is it visible?
Answer:
i. A ray AB incident from Sun (white light) strikes the lower portion of a water drop at an incident angle i.

ii. On entering into water, it deviates and disperses into constituent colours. The figure shows the extreme colours (violet and red).

iii. Refracted rays BV and BR finally emerge the drop from V’ and R’ after suffering two internal reflections and can be seen by an observer on the ground.

iv. Minimum deviation rays of red and violet colour are inclined to the ground level at θ_R ≈ 51° and θ_V ≈ 53° respectively. As a result, in the rainbow, the violet is above and red is below.

(iv) Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
Answer:
Yes, it is possible to see primary and secondary rainbows simultaneously. This can occur when the centres of both the rainbows coincide.

Question 5.
(i) Explain chromatic aberration for spherical lenses. State a method to minimize or eliminate it.
Answer:
Lenses are prepared by using a transparent material medium having different refractive index for different colours. Hence angular dispersion is present.
If the lens is thick, this will result into notably different foci corresponding to each colour for a polychromatic beam, like a white light. This defect is called chromatic aberration.
As violet light has maximum deviation, it is focussed closest to the pole.

Reducing/eliminating chromatic aberration:

1. Eliminating chromatic aberrations for all colours is impossible. Hence, it is minimised by eliminating aberrations for extreme colours.
2. This is achieved by using either a convex and a concave lens in contact or two thin convex lenses with proper separation. Such a combination is called achromatic combination.

(ii) What is achromatism? Derive a condition to achieve achromatism for a lens combination. State the conditions for it to be converging.
Answer:
i. To eliminate chromatic aberrations for extreme colours from a lens, either a convex and a concave lens in contact or two thin convex lenses with proper separation are used.

ii. This combination is called achromatic combination. The process of using this combination is termed as achromatism of a lens.

iii. Let ω₁ and ω₂ be the dispersive powers of materials of the two component lenses used in contact for an achromatic combination.

iv. Let V, R and Y denote the focal lengths for violet, red and yellow colours respectively.

v. For lens 1, let
K₁ = (\(\frac {1}{R_1}\)–\(\frac {1}{R_2}\))₁ and K₂ = (\(\frac {1}{R_1}\)–\(\frac {1}{R_2}\))₂

vi. For the combination to be achromatic, the resultant focal length of the combination must be the same for both the colours,

This is the condition for achromatism of a combination of lenses.

Condition for converging:
For this combination to be converging, fY must be positive.
Using equation (3), for f_Y to be positive, (f_Y)₁ < (f_Y)₂ ⇒ ω₁ < ω₂

Question 6.
Describe spherical aberration for spherical lenses. What are different ways to minimize or eliminate it?
Answer:
i. All the formulae used for image formation by lenses are based on some assumption. However, in reality these assumptions are not always true.

ii. A single point focus in case of lenses is possible only for small aperture spherical lenses and for paraxial rays.

iii. The rays coming from a distant object farther from principal axis no longer remain parallel to the axis. Thus, the focus gradually shifts towards pole.

iv. This defect arises due to spherical shape of the refracting surface, hence known as spherical aberration. It results into a blurred image with unclear boundaries.

v. As shown in figure, the rays near the edge of the lens converge at focal point F_M. Whereas, the rays near the principal axis converge at point F_P. The distance between F_M and F_P is measured as the longitudinal spherical aberration.

vi. In absence of this aberration, a single point image can be obtained on a screen. In the presence of spherical aberration, the image is always a circle.

vii. At a particular location of the screen (across AB in figure), the diameter of this circle is minimum. This is called the circle of least confusion. Radius of this circle is transverse spherical aberration.

Methods to eliminate/reduce spherical aberration in lenses:
i. Cheapest method to reduce the spherical aberration is to use a planoconvex or planoconcave lens with curved side facing the incident rays.

ii. Certain ratio of radii of curvature for a given refractive index almost eliminates the spherical aberration. For n = 1.5, the ratio is
\(\frac {R_1}{R_2}\) = \(\frac {1}{6}\) and for n = 2, \(\frac {R_1}{R_2}\) = \(\frac {1}{5}\)

iii. Use of two thin converging lenses separated by distance equal to difference between their focal lengths with lens of larger focal length facing the incident rays considerably reduces spherical aberration.

iv. Spherical aberration of a convex lens is positive (for real image), while that of a concave lens is negative. Thus, a suitable combination of them can completely eliminate spherical aberration.

Question 7.
Define and describe magnifying power of an optical instrument. How does it differ from linear or lateral magnification?
Answer:
i. Angular magnification or magnifying power of an optical instrument is defined as the ratio of the visual angle made by the image formed by that optical instrument (β) to the visual angle subtended by the object when kept at the least distance of distinct vision (α).

ii. The linear magnification is the ratio of the size of the image to the size of the object.

iii. When the distances of the object and image formed are very large as compared to the focal lengths of the instruments used, the magnification becomes infinite. Whereas, the magnifying power being the ratio of angle subtended by the object and image, gives the finite value.

iv. For example, in case of a compound microscope,
M_min = \(\frac {D}{f}\) = \(\frac {25}{5}\) = 5 and M_max = 1 + \(\frac {D}{f}\) = 6
Hence image appears to be only 5 to 6 times bigger for a lens of focal length 5 cm.
For M_min = \(\frac {D}{f}\) = 5, V = ∞
∴ Lateral magnification (m) = \(\frac {v}{u}\) = ∞
Thus, the image size is infinite times that of the object, but appears only 5 times bigger.

Question 8.
Derive an expression for magnifying power of a simple microscope. Obtain its minimum and maximum values in terms of its focal length.
Answer:
i. Figure (a) shows visual angle a made by an object, when kept at the least distance of distinct vision (D = 25 cm). Without an optical instrument this is the greatest possible visual angle as we cannot get the object closer than this.

ii. Figure (b) shows a convex lens forming erect, virtual and magnified image of the same object, when placed within the focus.

iii. The visual angle p of the object and the image in this case are the same. However, this time the viewer is looking at the image which is not closer than D. Hence the same object is now at a distance smaller than D.

iv. Angular magnification or magnifying power, in this case, is given by
M = \(\frac {Visual angle of theimage}{Visual angle of the object at D}\) = \(\frac {β}{α}\)
For small angles,
M = \(\frac {β}{α}\) ≈ \(\frac {tan(β)}{tan(α)}\) = \(\frac {BA/PA}{BA/D}\) = \(\frac {D}{u}\)

v. For maximum magnifying power, the image should be at D. For thin lens, considering thin lens formula.

Question 9.
Derive the expressions for the magnifying power and the length of a compound microscope using two convex lenses.
Answer:
i. The final image formed in compound microscope (A” B”) as shown in figure, makes a visual angle β at the eye.
Visual angle made by the object from distance D is α.

From figure,
tan β = \(\frac {A”B”}{v_c}\) = \(\frac {A’B’}{u_c}\)
and tan α = \(\frac {AB}{D}\)

Question 10.
What is a terrestrial telescope and an astronomical telescope?
Answer:

1. Telescopes used to see the objects on the Earth, like mountains, trees, players playing a match in a stadium, etc. are called terrestrial telescopes.
2. In such case, the final image must be erect. Eye lens used for this purpose must be concave and such a telescope is popularly called a binocular.
3. Most of the binoculars use three convex lenses with proper separation. The image formed by second lens is inverted with respect to object. The third lens again inverts this image and makes final image erect with respect to the object.
4. An astronomical telescope is the telescope used to see the objects like planets, stars, galaxies, etc. In this case there is no necessity of erect image. Such telescopes use convex lens as eye lens.

Question 11.
Obtain the expressions for magnifying power and the length of an astronomical telescope under normal adjustments.
Answer:
i. For telescopes, a is the visual angle of the object from its own position, which is practically at infinity.

ii. Visual angle of the final image is p and its position can be adjusted to be at D. However, under normal adjustments, the final image is also at infinity making a greater visual angle than that of the object.

iii. The parallax at the cross wires can be avoided by using the telescopes in normal adjustments.

iv. Objective of focal length f₀ focusses the parallel incident beam at a distance f₀ from the objective giving an inverted image AB.

v. For normal adjustment, the intermediate image AB forms at the focus of the eye lens. Rays refracted beyond the eye lens form a parallel beam inclined at an angle β with the principal axis.

vi. Angular magnification or magnifying power for telescope is given by,
M = \(\frac {β}{α}\) ≈ \(\frac {tan(β)}{tan(α)}\) = \(\frac {BA/P_cB}{BA/P_0B}\) = \(\frac {f_0}{f_e}\)

vii. Length of the telescope for normal adjustment is, L = f₀ + f_e.

Question 12.
What are the limitations in increasing the magnifying powers of (i) simple microscope (ii) compound microscope (iii) astronomical telescope?
Answer:
i. In case of simple microscope
\(\mathrm{M}_{\max }=\frac{\mathrm{D}}{\mathrm{u}}=1+\frac{\mathrm{D}}{\mathrm{f}}\)
Thus, the limitation in increasing the magnifying power is determined by the value of focal length and the closeness with which the lens can be held near the eye.

ii. In case of compound microscope,
M = \(\mathrm{m}_{0} \times \mathrm{M}_{\mathrm{e}}=\frac{\mathrm{v}_{0}}{\mathrm{u}_{\mathrm{o}}} \times \frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}\)
Thus, in order to increase m₀, we need to decrease u₀. Thereby, the object comes closer and closer to the focus of the objective. This increases v₀ and hence length of the microscope. Therefore, mQ can be increased only within the limitation of length of the microscope.

iii. In case of telescopes,
M = \(\frac {f_0}{f_e}\)
Where f₀ = focal length of the objective
f_e = focal length of the eye-piece
Length of the telescope for normal adjustment is, L = f₀ + f_e.
Thus, magnifying power of telescope can be increased only within the limitations of length of the telescope.

4. Solve the following numerical examples

Question 1.
A monochromatic ray of light strikes the water (n = 4/3) surface in a cylindrical vessel at angle of incidence 53°. Depth of water is 36 cm. After striking the water surface, how long will the light take to reach the bottom of the vessel? [Angles of the most popular Pythagorean triangle of sides in the ratio 3 : 4 : 5 are nearly 37°, 53° and 90°]
Answer:
From figure, ray PO = incident ray
ray OA = refracted ray
QOB = Normal to the water surface.
Given that,
∠POQ = angle of incidence (θ₁) = 53°
Seg OB = 36 cm and n_water = \(\frac {4}{3}\)
From Snell’s law,
n₁ sin θ₁ = n₂ sin θ₂
∴ n_water = \(\frac {sinθ_1}{sinθ_2}\)
Or sin θ₂ = \(\frac {sinθ_1}{n_{water}}\) = \(\frac {sin(53°)×3}{4}\)
∴ θ₂ ~ 37°
ΔOBA forms a Pythagorean triangle with angles 53°, 37° and 90°.
Thus, sides of ΔOBA will be in ratio 3 : 4 : 5 Such that OA forms the hypotenuse. From figure, we can infer that,
Seg OB = 4x = 36 cm
∴ x = 9
∴ seg OA = 5x = 45 cm and
seg AB = 3x = 27 cm.
This means the light has to travel 45 cm to reach the bottom of the vessel.
The speed of the light in water is given by,
v = \(\frac {c}{n}\)
∴ v = \(\frac {3×10^8}{4/3}\) = \(\frac {9}{4}\) × 10⁸ m/s
∴ Time taken by light to reach the bottom of vessel is,
t = \(\frac {s}{v}\) = \(\frac {45×10^{-2}}{\frac {9}{4} × 10^8}\) = 20 × 10^-10 = 2 ns or 0.002 µs

Question 2.
Estimate the number of images produced if a tiny object is kept in between two plane mirrors inclined at 35°, 36°, 40° and 45°.
Answer:
i. For θ₁ =35°
n₁ = \(\frac {360}{θ_1}\) = \(\frac {360}{35}\) = 10.28
As ni is non-integer, N₁ = integral part of n₁ = 10

ii. For θ₂ = 36°
n₂ = \(\frac {360}{36}\) = 10
As n₂ is even integer, N₂ = (n₂ – 1) = 9

iii. For θ₃ = 40°
n₃ = \(\frac {360}{36}\) = 9
As n₃ is odd integer.
Number of images seen (N₃) = n₃ – 1 = 8
(if the object is placed at the angle bisector) or Number of images seen (N₃) = n₃ = 9
(if the object is placed off the angle bisector)

iv. For θ₄ = 45°
n₄ = \(\frac {360}{45}\) = 8
As n₄ is even integer,
N₄ = n₄ – 1 = 7

Question 3.
A rectangular sheet of length 30 cm and breadth 3 cm is kept on the principal axis of a concave mirror of focal length 30 cm. Draw the image formed by the mirror on the same diagram, as far as possible on scale.

Answer:

[Note: The question has been modified and the ray digram is inserted in question in order to find the correct position of the image.]

Question 4.
A car uses a convex mirror of curvature 1.2 m as its rear-view mirror. A minibus of cross section 2.2 m × 2.2 m is 6.6 m away from the mirror. Estimate the image size.
Answer:
For a convex mirror,
f = +\(\frac {R}{2}\) = \(\frac {1.2}{2}\) = +0.6m
Given that, a minibus, approximately of a shape of square is at distance 6.6 m from mirror.
i.e., u = -6.6 m

∴ h₂ = 0.183 m
i.e., h₂ 0.2 m

Question 5.
A glass slab of thickness 2.5 cm having refractive index 5/3 is kept on an ink spot. A transparent beaker of very thin bottom, containing water of refractive index 4/3 up to 8 cm, is kept on the glass block. Calculate apparent depth of the ink spot when seen from the outside air.
Answer:
When observed from the outside air, the light coming from ink spot gets refracted twice; once through glass and once through water.
∴ When observed from water,

∴ Apparent depth = 2 cm
Now when observed from outside air, the total real depth of ink spot can be taken as (8 + 2) cm = 10 cm.
∴ \(\frac {n_w}{n_{air}}\) = \(\frac {Real depth}{Apparent depth}\)
∴ Apparent depth = \(\frac {10}{4/3}\)
= \(\frac {10×3}{4}\) = 7.5 cm

Question 64.
A convex lens held some distance above a 6 cm long pencil produces its image of SOME size. On shifting the lens by a distance equal to its focal length, it again produces the image of the SAME size as earlier. Determine the image size.
Answer:
For a convex lens, it is given that the image size remains unchanged after shifting the lens through distance equal to its focal length. From given conditions, it can be inferred that the object distance should be u = –\(\frac {f}{2}\)
Also, h₁ = 6 cm, v₁ = v₂
From formula for thin lenses,

Question 7.
Figure below shows the section ABCD of a transparent slab. There is a tiny green LED light source at the bottom left corner B. A certain ray of light from B suffers total internal reflection at nearest point P on the surface AD and strikes the surface CD at point Question Determine refractive index of the material of the slab and distance DQ. At Q, the ray PQ will suffer partial or total internal reflection?

Answer:

As, the light ray undergo total internal reflection at P, the ray BP may be incident at critical angle.
For a Pythagorean triangle with sides in ratio 3 : 4 : 5 the angle opposite to side 3 units is 37° and that opposite to 4 units is 53°.
Thus, from figure, we can say, in ΔBAP
∠ABP = 53°
∠BPN = i_c = 53°
∴ n_glass = \(\frac {1}{sin_c}\) = \(\frac {1}{sin(53°)}\) ≈ \(\frac {1}{0.8}\) = \(\frac {5}{4}\)
∴ Refractive index (n) of the slab is \(\frac {5}{4}\)
From symmetry, ∆PDQ is also a Pythagorean triangle with sides in ratio QD : PD : PQ = 3 : 4 : 5.
PD = 2 cm ⇒ QD = 1.5 cm.
As critical angle is i_c = 53° and angle of incidence at Q, ∠PQN = 37° is less than critical angle, there will be partial internal reflection at Question

Question 8.
A point object is kept 10 cm away from a double convex lens of refractive index 1.5 and radii of curvature 10 cm and 8 cm. Determine location of the final image considering paraxial rays only.
Answer:
Given that, R₁ = 10 cm, R₂ = -8 cm,
u = -10 cm and n = 1.5
From lens maker’s equation,

Question 9.
A monochromatic ray of light is incident at 37° on an equilateral prism of refractive index 3/2. Determine angle of emergence and angle of deviation. If angle of prism is adjustable, what should its value be for emergent ray to be just possible for the same angle of incidence.
Answer:
By Snell’s law, in case of prism,

For equilateral prism, A = 60°
Also, A= r₁ + r₂
∴ r₂ = A – r₁ = 60° – 23°39′ = 36°21′
Applying snell’s law on the second surface of

= sin^-1 (0.889)
= 62°44′
≈ 63°
For any prism,
i + e = A + δ
∴ δ = (i + e) – A
= (37 + 63) – 60
= 40°
For an emergent ray to just emerge, the angle r’₂ acts as a critical angle.
∴ r’₂ = sin^-1 (\(\frac {1}{n}\))
= sin^-1 (\(\frac {2}{3}\))
= 41°48′
As, A = r’₁ + r’₂ and i to be kept the same.
⇒ A’ = r’₁ + r’₂‘
= 23°39′ + 41°48′
= 65°27’

Question 10.
From the given data set, determine angular dispersion by the prism and dispersive power of its material for extreme colours. n_R = 1.62 nv = 1.66, δ_R = 3.1°
Answer:
Given: n_R = 1.62, n_V = 1.66, δ_R = 3.1°
To find:
i. Angular dispersion (δ_vr)
ii. Dispersive power (ω_VR)
Formula:
i. δ = A (n – 1)
ii. δ_VR = δ_V – δ_R
(iii) ω = \(\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)}\)
Calculation: From formula (i),
δ_R = A(n_R – 1)
∴ A = \(\frac{\delta_{R}}{\left(n_{R}-1\right)}=\frac{3.1}{(1.62-1)}=\frac{3.1}{0.62}\)
= 5
δV = A(n_v – 1) = 5 × (1.66 – 1) = 3.3C
From formula (ii),
δ_VR = 3.3 – 3.1 = 0.2°
From formula (iii),
ω_VR = \(\frac{3.3-3.1}{\left(\frac{3.3+3.1}{2}\right)}=\frac{0.2}{6.4} \times 2=\frac{0.2}{3.2}=\frac{1}{16}\)
= 0.0625

Question 11.
Refractive index of a flint glass varies from 1.60 to 1.66 for visible range. Radii of curvature of a thin convex lens are 10 cm and 15 cm. Calculate the chromatic aberration between extreme colours.
Answer:
Given the refractive indices for extreme colours. As, n_R < n_V
n_R = 1.60 and n_V = 1.66
For convex lens,
R₁ = 10 cm and R₁₀ = -15 cm

= 0.11
∴ f_V = 11 cm
∴ Longitudinal chromatic aberration
= f_V – f_R = 11 – 10 = 1 cm

Question 12.
A person uses spectacles of ‘number’ 2.00 for reading. Determine the range of magnifying power (angular magnification) possible. It is a concave convex lens (n = 1.5) having curvature of one of its surfaces to be 10 cm. Estimate that of the other.
Answer:
For a single concavo-convex lens, the magnifying power will be same as that for simple microscope As, the number represents the power of the lens,
P = \(\frac {1}{f}\) = 2 ⇒ f = 0.5 m.
∴ Range of magnifying power of a lens will be,
M_min = \(\frac {D}{f}\) = \(\frac {0.25}{0.5}\) = 0.5
and M_min = 1 + \(\frac {D}{f}\) = 1 + 0.5 = 1.5
Given that, n = 1.5, |R₁| = 10 cm
f = 0.5 m = 50 cm
From lens maker’s equation,

Question 13.
Focal power of the eye lens of a compound microscope is 6 dioptre. The microscope is to be used for maximum magnifying power (angular magnification) of at least 12.5. The packing instructions demand that length of the microscope should be 25 cm. Determine minimum focal power of the objective. How much will its radius of curvature be if it is a biconvex lens of n = 1.5.
Answer:
Focal power of the eye lens,
P_e = \(\frac {1}{f_e}\) = 6D
∴ f_e = \(\frac {1}{6}\) = 0.1667 m = 16.67 cm
Now, as the magnifying power is maximum,
v_e = 25 cm,
Also (M_e)_max = 1 + \(\frac {D}{f_e}\) = 1 + \(\frac {25}{16.67}\) ≈ 2.5
Given that,
M = m₀ × M_e = 12.5
∴ m₀ × 2.5 = 12.5
∴ m₀ = \(\frac {v_0}{u_0}\) = 5 ……….. (1)
From thin lens formula,

Length of a compound microscope,
L = |v₀| +|u₀|
∴ 25 = |v₀| + 10
∴ |v₀|= 15 cm
∴ |u₀| = \(\frac {v_0}{5}\) = 3 cm …………… (from 1)
From lens formula for objective,
\(\frac {1}{f_0}\) = \(\frac {1}{v_0}\) – \(\frac {1}{u_0}\)
= \(\frac {1}{15}\) – \(\frac {1}{-3}\)
= \(\frac {2}{5}\)
∴ f₀ = 2.5 cm = 0.025 m
Thus, focal power of objective,
P = \(\frac {1}{f_0(m)}\)
= \(\frac {1}{0.025}\) = 40 D
Using lens maker’s equation for a biconvex lens,
\(\frac{1}{f_{o}}=(n-1)\left(\frac{1}{R}-\frac{1}{-R}\right)\)
∴ \(\frac{1}{2.5}=(1.5-1)\left(\frac{2}{R}\right)=\frac{1}{R}\)
∴ R = 2.5 cm

11th Physics Digest Chapter 9 Optics Intext Questions and Answers

Can you recall? (Textbook rage no 159)

What are laws of reflection and refraction?
Answer:
Laws of reflection:
a. Reflected ray lies in the plane formed by incident ray and the normal drawn at the point of incidence and the two rays are on either side of the normal.
b. Angles of incidence and reflection are equal (i = r).

Laws of refraction:
a. Refracted ray lies in the plane formed by incident ray and the normal drawn at the point of incidence; and the two rays are on either side of the normal.

b. Angle of incidence (θ₁) and angle of refraction (θ₂) are related by Snell’s law, given by, n₁ sin θ₁ = n₂ sin θ₂ where, n₁, n₂ = refractive indices of medium 1 and medium 2 respectively.

Can you recall? (Textbook page no. 159)

Question 1.
What is refractive index?
Answer:
The ratio of velocity of light in vacuum to the velocity’ of light in a medium is called the refractive index of the medium.

Question 2.
What is total internal reflection?
Answer:
For angles of incidence larger than the critical angle, the angle of refraction is larger than 90°. Thus, all the incident light gets reflected back into the denser medium. This is called total internal reflection.

Question 3.
How does a rainbow form?
Answer:

1. The rainbow appears in the sky after a rainfall.
2. Water droplets present in the atmosphere act as small prism.
3. When sunlight enters these water droplets it gets refracted and dispersed.
4. This dispersed light gets totally reflected inside the droplet and again is refracted while coming out of the droplet.
5. As a combined effect of all these phenomena, the seven coloured rainbow is observed.

Question 4.
What is dispersion of light?
Answer:
Splitting of a white light into its constituent colours is known as dispersion of light.

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Sound Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 8 Sound Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 8 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 8 Exercise Solutions

1. Choose the correct alternatives

Question 1.
A sound carried by the air from a sitar to a listener is a wave of the following type.
(A) Longitudinal stationary
(B)Transverse progressive
(C) Transverse stationery
(D) Longitudinal progressive
Answer:
(D) Longitudinal progressive

Question 2.
When sound waves travel from air to water, which of these remains constant?
(A) Velocity
(B) Frequency
(C) Wavelength
(D) All of above
Answer:
(B) Frequency

Question 3.
The Laplace’s correction in the expression for velocity of sound given by Newton is needed because sound waves
(A) are longitudinal
(B) propagate isothermally
(C) propagate adiabatically
(D) are of long wavelength
Answer:
(C) propagate adiabatically

Question 4.
Speed of sound is maximum in
(A) air
(B) water
(C) vacuum
(D) solid
Answer:
(D) solid

Question 5.
The walls of the hall built for music concerns should
(A) amplify sound
(B) Reflect sound
(C) transmit sound
(D) Absorb sound
Answer:
(D) Absorb sound

2. Answer briefly.

Question 1.
Wave motion is doubly periodic. Explain.
Answer:
i. A wave particle repeats its motion after a definite interval of time at every location, making it periodic in time.
ii. Similarly, at any given instant, the form of a wave repeats itself at equal distances making it periodic in space.
iii. Thus, wave motion is a doubly periodic phenomenon, i.e., periodic in time as well as periodic in space.

Question 2.
What is Doppler effect?
Answer:
The apparent change in the frequency of sound heard by a listener, due to relative motion between the source of sound and the listener is called Doppler effect in sound.

Question 3.
Describe a transverse wave.
Answer:
Transverse wave:
A wave in which particles of the medium vibrate in a direction perpendicular to the direction of propagation of the wave is called transverse wave.
Example: Ripples on the surface of water, light waves.

Characteristics of transverse waves:

1. All the particles of medium in the path of wave vibrate in a direction perpendicular to the direction of propagation of wave with same period and amplitude.
2. When transverse wave passes through the medium, the medium is divided into alternate crests i.e., regions of positive displacements and troughs i.e., regions of negative displacement, that are periodic in time.
3. A crest and an adjacent trough form one cycle of a transverse wave. The distance between any two successive crests or troughs is called wavelength ‘λ’ of the wave.
4. Crests and troughs advance in the medium and are responsible for transfer of energy.
5. Transverse waves can travel only through solids and not through liquids and gases. Electromagnetic waves are transverse waves, but they do not require material medium for propagation.
6. When transverse waves advance through a medium, there is no change of pressure and density at any point of the medium, but the shape changes periodically.
7. Transverse wave can be polarised.
8. Medium conveying a transverse wave must possess elasticity of shape, i.e., modulus of rigidity.

Question 4.
Define a longitudinal wave.
Answer:
A wave in which particles of medium vibrate in a direction parallel to the direction of propagation of the wave is called longitudinal wave. Example: Sound waves.

Question 5.
State Newton’s formula for velocity of sound.
Answer:
Newton’s formula for velocity of sound:
i. Sound wave travels through a medium in the form of compression and rarefaction. At compression, the density of medium is greater while at rarefaction density is smaller. This is possible only in elastic medium.

ii. Thus, the velocity of sound depends upon density and elasticity of medium. It is given by
v = \(\sqrt{\frac {E}{ρ}}\) ….(1)
Where, E is the modulus of elasticity of medium and ρ is density of medium.

Assumptions:
1. Newton assumed that during propagation of sound wave in air, average temperature of the medium remains constant. Hence, propagation of sound wave in air is an isothermal process and isothermal elasticity should be considered.

2. The volume elasticity of air determined under isothermal change is called isothermal bulk modulus.

Calculations:
1. For a gas or air, the isothermal elasticity E is equal to the atmospheric pressure P.
Substituting this value in equation (1), the velocity of sound in air or a gas is given by
v = \(\sqrt{\frac {P}{ρ}}\) ….(∵ E = P)
This is the Newton’s formula for velocity of sound in air.

2. But atmospheric pressure is given by,
P = hdg
∴ v = \(\sqrt{\frac {hdg}{ρ}\) ….(2)

3. At N.T.P., h = 0.76 m of mercury, density of mercury d = 13600 kg/m³ and acceleration due to gravity, g = 9.8 m/s², density of air ρ = 1.293 kg/m³

4. From equation (2) we have velocity of sound,
v = \(\sqrt{\frac {0.76×13600×9.8}{1.293}}\) = 279.9 m/s at N.T.P

Question 6.
What is the effect of pressure on velocity of sound?
Answer:
Effect of pressure:
i. Let v be the velocity of sound in air when the pressure is P and density is ρ.

ii. Using Laplace’s formula, we can write,
v = \(\sqrt{\frac {γP}{ρ}}\) ….(1)

iii. If V be the volume of a gas having mass M then, ρ = \(\frac {M}{V}\)

iv. Substituting ρ in equation (1), we get,
v = \(\sqrt{\frac {γPV}{M}}\) ….(2)

v. But according to Boyle’s law,
PV = constant (at constant temperature)
Also, M and γ are constant.
∴ v = constant

vi. Hence, the velocity of sound does not depend upon the change in pressure, as long as the temperature remains constant.

vii. For a gaseous medium, PV= nRT.
Substituting in equation (2), we get,
v = \(\sqrt{\frac {γnRT}{M}}\)

viii. Thus, even for a gaseous medium obeying ideal gas equation, the velocity of sound does not depend upon the change in pressure, as long as the temperature remains constant.

Question 7.
What is the effect of humidity of air on velocity of sound?
Answer:
Effect of humidity:
i. Let v_m and v_d be the velocities of sound in moist air and dry air respectively.

ii. Humid air contains a large proportion of water vapour. Density of water vapour at 0 °C is 0.81 kg/m³ while that of dry air at 0°C is 1.29 kg/m³. So, the density ρ_m of moist air is less than the density ρ_d of dry air i.e., ρ_m < ρ_d.

iii. Thus \(\frac {v_m}{v_d}\) > 1
∴ v_m > v_d

iv. Hence, sound travels faster in moist air than in dry air. It means that velocity of sound increases with increase in moistness (humidity) of air.

Question 8.
What do you mean by an echo?
Answer:
An echo is the repetition of the original sound because of reflection from some rigid surface at a distance from the source of sound.

Question 9.
State any two applications of acoustics.
Answer:
Application of acoustics in nature:
i. Bats apply the principle of acoustics to locate objects. They emit short ultrasonic pulses of frequency 30 kHz to 150 kHz. The resulting echoes give them information about location of the obstacle. This helps the bats to fly in even in total darkness of caves.

ii. Dolphins navigate underwater with the help of an analogous system. They emit subsonic frequencies which can be about 100 Hz. They can sense an object about 1.4 m or larger.

Medical applications of acoustics:
i. High pressure and high amplitude shock waves are used to split kidney stones into smaller pieces without invasive surgery. A reflector or acoustic lens is used to focus a produced shock wave so that as much of its energy as possible converges on the stone. The resulting stresses in the stone causes the stone to break into small pieces which can then be removed easily.

ii. Ultrasonic imaging uses reflection of ultrasonic waves from regions in the interior of body. It is used for prenatal (before the birth) examination, detection of anomalous conditions like tumour etc. and the study of heart valve action.

iii. Ultrasound at a very high-power level, destroys selective pathological tissues which is helpful in treatment of arthritis and certain type of cancer.

Underwater applications of acoustics:
i. SONAR (Sound Navigational Ranging) is a technique for locating objects underwater by transmitting a pulse of ultrasonic sound and detecting the reflected pulse.
ii. The time delay between transmission of a pulse and the reception of reflected pulse indicates the depth of the object.
iii. Motion and position of submerged objects like submarine can be measured with the help of this system.

Applications of acoustics in environmental and geological studies:
i. Acoustic principle has important application to environmental problems like noise control. The quiet mass transit vehicle is designed by studying the generation and propagation of sound in the motor’s wheels and supporting structures.

Reflected and refracted elastic waves passing through the Earth’s interior can be measured by applying the principles of acoustics. This is useful in studying the properties of the Earth.

Principles of acoustics are applied to detect local anomalies like oil deposits etc. making it useful for geological studies.

Question 10.
Define amplitude and wavelength of a wave.
Answer:
i. Amplitude (A): The largest displacement of a particle of a medium through which the wave is propagating, from its rest position, is called amplitude of that wave.
SI unit: (m)

ii. Wavelength (λ): The distance between two successive particles which are in the same state of vibration is called wavelength of the wave.
SI unit: (m)

Question 11.
Draw a wave and indicate points which are (i) in phase (ii) out of phase (iii) have a phase difference of π/2.
Answer:

i. In phase point: A and F; B and H; C and I; D and J
ii. Out of phase points: A and B, B and D, FI and J, E and F,
iii. Point having phase difference of π/2: A and B; B and C; D; D and F; F and H; H and I; J and I

Question 12.
Define the relation between velocity, wavelength and frequency of wave.
Answer:
i. A wave covers a distance equal to the wavelength (λ) during one period (T).
Therefore, the magnitude of the velocity (v) is given by,
Magnitude of velocity = \(\frac {Distance covered}{Corresponding time}\)

ii. v = \(\frac {22}{7}\) i.e., v = λ × (\(\frac {1}{T}\)) …………….. (1)

iii. But reciprocal of the period is equal to the frequency (n) of the waves.
∴ \(\frac {1}{T}\) = n …………… (2)

iv. From equations (1) and (2), we get
v = nλ
i.e., wave velocity = frequency × wavelength.

Question 13.
State and explain principle of superposition of waves.
Answer:
Principle:
As waves don’t repulse each other, they overlap in the same region of the space without affecting each other. When two waves overlap, their displacements add vectorially.

Explanation:
i. Consider two waves travelling through a medium arriving at a point simultaneously.

ii. Let each wave produce its own displacement at that point independent of the others. This displacement can be given as,
y₁ = displacement due to first wave.
y₂ = displacement due to second wave.

iii. Then according to superposition of waves, the resultant displacement at that point is equal to the vector sum of the displacements due to all the waves.
∴\(\vec{y}\) = \(\vec{y_1}\) + \(\vec{y_2}\)

Question 14.
State the expression for apparent frequency when source of sound and listener are
i) moving towards each other
ii) moving away from each other
Answer:
i. Let,
n = actual frequency of the source.
n₀ = apparent frequency of the source,
v = velocity of sound in air.
v_s = velocity of the source.
v_l = velocity of the listener.

ii. Apparent frequency heard by the listener is given by,
n = n₀(\(\frac {v±v_L}{v±v_s}\))
Where upper signs (+ ve in numerator and -ve in denominator) indicate that source and observer move towards each other. Lower signs (-ve in numerator and +ve in denominator) indicate that source and listener move away from each other.

iii. If source and listener are moving towards each other, then apparent frequency is given by,
n = n₀(\(\frac {v+v_L}{v-v_s}\)) i.e., apparent frequency increases.

iv. If source and listener are moving away from each other, then apparent frequency is given by,
n = n₀(\(\frac {v-v_L}{v+v_s}\)) i.e., apparent frequency decreases.

Question 15.
State the expression for apparent frequency when source is stationary and listener is
1) moving towards the source
2) moving away from the source
Answer:
Let,
n = actual frequency of the source.
n₀ = apparent frequency of the source,
v = velocity of sound in air.
v_s = velocity of the source.
v_l = velocity of the listener.

i. If listener is moving towards source then apparent frequency is given by,
n = n₀(\(\frac {v+v_L}{v}\)) i.e., apparent frequency increases.

ii. If listener is receding away from source then apparent frequency is given by,
n = n₀(\(\frac {v-v_L}{v}\)) i.e., apparent frequency decreases.

Question 16.
State the expression for apparent frequency when listener is stationary and source is.

(i) moving towards the listener
(ii) moving away from the listener
Answer:
Let,
n = actual frequency of the source.
n₀ = apparent frequency of the source,
v = velocity of sound in air.
v_s = velocity of the source.
v_l = velocity of the listener.

i. If source is moving towards observer then apparent frequency is given by,
n = n₀(\(\frac {v}{v-v_s}\)) i.e., apparent frequency increases.

ii. If source is receding away from observer then apparent frequency is given by,
n = n₀(\(\frac {v}{v+v_s}\)) i.e., apparent frequency decreases.

Question 17.
Explain what is meant by phase of a wave.
Answer:

i. The state of oscillation of a particle is called the phase of the particle.

ii. The displacement, direction of velocity and oscillation number of the particle describe the phase of the particle at a place.

iii. Particles r and t (q and u or v and s) have same displacements but the directions of their velocities are opposite.

iv. Particles having same magnitude of displacements and same direction of velocity are said to be in phase during their respective oscillations. Example: particles v and p.

v. Separation between two particles which are in phase is wavelength (λ).

vi. The two successive particles differ by ‘1’ in their oscillation number i.e., if particle v is at its n^th oscillation, particle p will be at its (n + 1)^th oscillation as the wave is travelling along + X direction.

vii. In the given graph, if the disturbance (energy) has just reached the particle w, the phase angle corresponding to particle is 0°. At this instant, particle v has completed quarter oscillation and reached its positive maximum (sin θ = +1). The phase angle θ of this particle v is \(\frac {π^c}{2}\) = 90° at this instant.

viii. Phase angles of particles u and q are π^c (180°) and 2rcc (360°) respectively.

ix. Particle p has completed one oscillation and is at its positive maximum during its second oscillation.
∴ phase angle = 2π^c + \(\frac {π^c}{2}\)
= \(\frac {5π^c}{2}\)

x. v and p are the successive particles in the same state (same displacement and same direction of velocity) during their respective oscillations. Phase angle between these two differs by 2π^c.

Question 18.
Define progressive wave. State any four properties.
Answer:
i. Waves in which a disturbance created at one place travels to distant points and keeps travelling unless stopped by an external force are known as travelling or progressive waves.
Properties of progressive waves are:
Amplitude, wavelength, period, double periodicity, frequency and velocity.

Question 19.
Distinguish between traverse waves and longitudinal waves.
Answer:

Question 20.
Explain Newtons formula for velocity of sound. What is its limitation?
Answer:
Newton’s formula for velocity of sound:
i. Sound wave travels through a medium in the form of compression and rarefaction. At compression, the density of medium is greater while at rarefaction density is smaller. This is possible only in elastic medium.

ii. Thus, the velocity of sound depends upon density and elasticity of medium. It is given by
v = \(\sqrt{\frac {E}{ρ}}\) ….(1)
Where, E is the modulus of elasticity of medium and ρ is density of medium.

Assumptions:
1. Newton assumed that during propagation of sound wave in air, average temperature of the medium remains constant. Hence, propagation of sound wave in air is an isothermal process and isothermal elasticity should be considered.

2. The volume elasticity of air determined under isothermal change is called isothermal bulk modulus.

Calculations:
1. For a gas or air, the isothermal elasticity E is equal to the atmospheric pressure P.
Substituting this value in equation (1), the velocity of sound in air or a gas is given by
v = \(\sqrt{\frac {P}{ρ}}\) ….(∵ E = P)
This is the Newton’s formula for velocity of sound in air.

2. But atmospheric pressure is given by,
P = hdg
∴ v = \(\sqrt{\frac {hdg}{ρ}}\) ….(2)

3. At N.T.P., h = 0.76 m of mercury, density of mercury d = 13600 kg/m³ and acceleration due to gravity, g = 9.8 m/s², density of air ρ = 1.293 kg/m³

4. From equation (2) we have velocity of sound,
v = \(\sqrt{\frac {0.76×13600×9.8}{1.293}}\) = 279.9 m/s at N.T.P

Limitations:
1. Experimentally, it is found that the velocity of sound in air at N. T. P is 332 m/s. Thus, there is considerable difference between the value predicted by Newton’s formula and the experimental value.

2. Experimental value is 16% greater than the value given by the formula. Newton failed to provide a satisfactory explanation for the difference.

3. Solve the following problems.

Question 1.
A certain sound wave in air has a speed 340 m/s and wavelength 1.7 m for this wave, calculate
(i) the frequency
(ii) the period.
Answer:
Given: v = 340 m/s, λ = 1.7 m
To find: frequency (n), period (T)
Formulae:
i. n = \(\frac {v}{λ}\)
ii. T = \(\frac {1}{n}\)
Calculation: From formula, (i)
n = \(\frac {340}{1.7}\)
∴ n = 200 Hz
From formula, (ii)
T = \(\frac {1}{n}\) = \(\frac {1}{2×10^2}\)
= 5 × 10^-3
…….. (using reciprocal Table)
∴ T = 0.005 s

Question 2.
A tuning fork of frequency 170 Hz produces sound waves of wavelength 2m. Calculate speed of sound.
Answer:
Given: n = 170 Hz, λ = 2 m
To find: velocity of sound (v)
Formula: v = nλ
Calculation: From formula,
v = 170 × 2
∴ v = 340 m/s

Question 3.
An echo-sounder in a fishing boat receives an echo from a shoal of fish 0.45s after it was sent. If the speed of sound in water is 1500 m/s, how deep is the shoal?
Answer:
Given: t = 0.45 s, v = 1500 m/s,
To Find: depth (d)
Formula: speed (v) = \(\frac {distance}{time}\)
Calculation:
For an echo distance travelled by the sound wave = 2 × (distance between echo sounder and shoal) (d)
v = \(\frac {2 × d}{t}\)
∴ d = \(\frac {1500 × 0.45}{2}\) = 337.5 m

Question 4.
A girl stands 170 m away from a high wall and claps her hands at a steady rateso that each clap coincides with the echo of the one before.
a) If she makes 60 claps in 1 minute, what value should be the speed of sound in air?
b) Now, she moves to another location and finds that she should now make 45 claps in 1 minute to coincide with successive echoes. Calculate her distance for the new position from the wall.
Answer:
i. When the girl makes 60 claps in 1 minute, the value of speed of is 340 m/s.

ii. The girl is at a distance of 226.67 m from the wall when she produces 45 claps per minute.
[Note: The answer given above is calculated in accordance with textual method considering the given data]

Question 5.
Sound wave A has period 0.015 s, sound wave B has period 0.025. Which sound has greater frequency?
Answer:
Given: T_A = 0.015 s, T_B = 0.025 s
To find: greater frequency (n)
Formula: n = \(\frac {1}{T}\)
Calculation: From formula,
n_A = \(\frac {1}{T_A}\) = \(\frac {1}{0.025}\) = \(\frac {1}{2.5 ×10^{-2}}\)
∴ n_A = 66.67
…. (using reciprocal table)
n_B = \(\frac {1}{T_B}\) = \(\frac {1}{0.025}\) = \(\frac {1}{2.5 ×10^{-2}}\)
∴ n_B = 40 Hz
…. (using reciprocal table)
∴ n_A > n_B

Question 6.
At what temperature will the speed of sound in air be 1.75 times its speed at N.T.P?
Answer:
Given:
v_air = 1.75 V_S.T.P = \(\frac {7}{4}\) v_S.T.P
T_S.T.P = 273 K
To find: temperature T_air
Formula: v ∝ √T
Calculation: From formula,

Question 7.
A man standing between 2 parallel eliffs fires a gun. He hearns two echos one after 3 seconds and other after 5 seconds. The separation between the two cliffs is 1360 m, what is the speed of sound?
Answer:
distance (s) = 1360 m,
time for first echo = 3 s,
time for second echo = 5 s
To Find : speed of sound (v)
Formula : speed = \(\frac {distence}{time}\)
Calculation:
Time for first echo = 3 s
∴ time taken by sound to travel given distance t₁
= \(\frac {3}{2}\) = 1.5 s
Time for second echo = 5 s
∴ time taken by sound to travel given distance t₂
= \(\frac {5}{2}\) = 2.5 s
∴Total time taken by sound to travel given distance, T = 1.5 + 2.5 = 4 s
From formula,
v = \(\frac {1360}{4}\)
∴v = 340 m/s

Question 8.
If the velocity of sound in air at a given place on two different days of a given week are in the ratio of 1 : 1.1. Assuming the temperatures on the two days to be same what quantitative conclusion can your draw about the condition on the two days?
Answer:
Let v₁ and v₂ be the velocity of sound on day 1 and day 2 respectively.
\(\frac {v_1}{v_2}\) = \(\frac {1}{1.1}\)
We know, v ∝ \(\frac {1}{√ρ}\)
Let ρ₁ and ρ₂ be the density of air on day 1 and day 2 respectively.
∴ \(\sqrt{\frac {ρ_2}{ρ_1}}\) = \(\frac {1}{1.1}\)
∴ \(\frac {ρ_2}{ρ_1}\) = (\(\frac {1}{1.1}\))²
∴ ρ₁ = 1.1² ρ₂ = 1.21 ρ²
From above equation, we can conclude,
ρ₁ > ρ₂
∴ v₂ > v₁ i.e., the velocity of sound is greater on the second day than on the first day.
We know, speed of sound in moist air (v_m) is greater than speed of sound in dry air (v_d).
∴ We can conclude, air is moist on second day and dry on the first day.

Question 9.
A police car travels towards a stationary observer at a speed of 15 m/s. The siren on the car emits a sound of frequency 250 Hz. Calculate the recorded frequency. The speed of sound is 340 m/s.
Answer:
Given: v_s = 15 m/s, n0 = 250 Hz, v = 340 m/s
To find: Frequency (n)
Formula: n = n₀(\(\frac {v}{v-v_s}\))
Calculation: As the source approaches listener, apparent frequency is given by,
n = 250 (\(\frac {340}{340-15}\)) = \(\frac {3400}{13}\)
∴ n = 261.54 Hz

Question 10.
The sound emitted from the siren of an ambulance has frequency of 1500 Hz. The speed of sound is 340 m/s. Calculate the difference in frequencies heard by a stationary observer if the ambulance initially travels towards and then away from the observer at a speed of 30 m/s.
Answer:
Given: v_s = 30 m/s, n₀ = 1500 Hz, v = 340 m/s
To find: Difference in apparent frequencies (n_A – n’_A)
Formulae:
i. When the ambulance moves towards he stationary observer then n_A = n₀(\(\frac {v}{v-v_s}\))

ii. When the ambulance moves away from the stationary observer then, n’_A = n₀(\(\frac {v}{v+v_s}\))

Calculation:
From formula (i), icon’ 340
n_A = 1500(\(\frac {340}{340-30}\))
∴ n_A = 1645 Hz
From (ii)
n’_A = 1500(\(\frac {340}{340+30}\))
∴ n_A = 1378 Hz
Difference between n_A and n’_A
= n_A – n’_A = 1645 – 1378 = 267 Hz

11th Physics Digest Chapter 8 Sound Intext Questions and Answers

Can you recall? (Textbook page no. 142)

i. What type of wave is a sound wave?
ii. Can sound travel in vacuum?
iii. What are reverberation and echo?
iv. What is meant by pitch of a sound?
Answer:
i. Sound wave is a longitudinal wave.

ii. Sound cannot travel in vacuum.

iii. a. Reverberation is the phenomenon in which sound waves are reflected multiple times causing a single sound to be heard more than once.
b. An echo is the repetition of the original sound because of reflection by some surface.

iv. The characteristic of sound which is determined by the value of frequency is called as the pitch of the sound.

Activity (Textbook page no. 144)

i. Using axes of displacement and distance, sketch two waves A and B such that A has twice the wavelength and half the amplitude of B.
ii. Determine the wavelength and amplitude of each of the two waves P and Q shown in figure below.

Answer:

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

11th Physics Chapter 7 Exercise Thermal Properties of Matter Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 7 Thermal Properties of Matter Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 7 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 7 Exercise Solutions

1. Choose the correct option.

Question 1.
The range of temperature in a clinical thermometer, which measures the temperature of the human body, is
(A) 70 ºC to 100 ºC
(B) 34 ºC to 42 ºC
(C) 0 ºF to 100 ºF
(D) 34 ºF to 80 ºF
Answer:
(B) 34 ºC to 42 ºC

Question 2.
A glass bottle completely filled with water is kept in the freezer. Why does it crack?
(A) Bottle gets contracted
(B) Bottle is expanded
(C) Water expands on freezing
(D) Water contracts on freezing
Answer:
(C) Water expands on freezing

Question 3.
If two temperatures differ by 25 °C on Celsius scale, the difference in temperature on Fahrenheit scale is
(A) 65°
(B) 45°
(C) 38°
(D) 25°
Answer:
(B) 45°

Question 4.
If α, β and γ are coefficients of linear, area l and volume expansion of a solid then
(A) α: β:γ 1:3:2
(B) α:β:γ 1:2:3
(C) α:β:γ 2:3:1
(D) α:β:γ 3:1:2
Answer:
(B) α:β:γ 1:2:3

Question 5.
Consider the following statements-
(I) The coefficient of linear expansion has dimension K^-1
(II) The coefficient of volume expansion has dimension K^-1
(A) I and II are both correct
(B) I is correct but II is wrong
(C) II is correct but I is wrong
(D) I and II are both wrong
Answer:
(A) I and II are both correct

Question 6.
Water falls from a height of 200 m. What is the difference in temperature between the water at the top and bottom of a water fall given that specific heat of water is 4200 J kg^-1 °C^-1?
(A) 0.96 °C
(B) 1.02 °C
(C) 0.46 °C
(D) 1.16 °C
Answer:
(C) 0.46 °C

2. Answer the following questions.

Question 1.
Clearly state the difference between heat and temperature?
Answer:

Question 2.
How a thermometer is calibrated?
Answer:

1. For the calibration of a thermometer, a standard temperature interval is selected between two easily reproducible fixed temperatures.
2. The fact that substances change state from solid to liquid to gas at fixed temperatures is used to define reference temperature called fixed point.
3. The two fixed temperatures selected for this purpose are the melting point of ice or freezing point of water and the boiling point of water.
4. This standard temperature interval is divided into sub-intervals by utilizing some physical property that changes with temperature.
5. Each sub-interval is called as a degree of temperature. Thus, an empirical scale for temperature is set up.

Question 3.
What are different scales of temperature? What is the relation between them?
Answer:

1. Celsius scale:
   • The ice point (melting point of pure ice) is marked as O °C (lower point) and steam point (boiling point of water) is marked as 100 °C (higher point).
   • Both are taken at one atmospheric pressure.
   • The interval between these points is divided into two equal parts. Each of these parts is called as one degree celsius and it is ‘written as 1 °C.
2. Fahrenheit scale:
   • The ice point (melting point of pure ice) is marked as 32 °F and steam point (boiling point of water) is marked as 212 °F.
   • The interval between these two reference points is divided into 180 equal parts. Each part is called as degree fahrenheit and is written as 1 °F.
3. Kelvin scale:
   • The temperature scale that has its zero at -273.15 °C and temperature intervals are same as that on the Celsius scale is called as kelvin scale or absolute scale.
   • The absolute temperature, T and celsius temperature, T_C are related as, T = T_C + 273.15
     eg.: when T_C = 27 °C,
     T = 27+273.15 K = 300.15 K

Relation between different scales of temperature:
\(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}=\frac{\mathrm{T}_{\mathrm{C}}-0}{100}=\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\)
where,
T_F = temperature in fahrenheit scale,
T_C = temperature in celsius scale,
T_K = temperature in kelvin scale,
[Note: At zero of the kelvin scale, every substance in nature has the least possible activity.]

Question 4.
What is absolute zero?
Answer:

1. When the graph of pressure (P) against temperature T (°C) at constant volume for three ideal gases A, B and C is plotted, in each case, P -T graph is straight line indicating direct proportion between them. The slopes of these graphs are different.
2. The individual straight lines intersect the pressure axis at different values of pressure at O °C. but each line intersects the temperature axis at the same point, i.e., at absolute temperature (-273.15 °C).
3. Similarly graph at constant pressure for three different ideal gases A, B and C extrapolate to the same temperature intercept -273.15 °C i.e., absolute zero temperature.
4. It is seen that all the lines for different gases Cut the temperature axis at the same point at -273.15 °C.
5. This point is termed as the absolute zero of temperature.
6. It is not possible to attain a temperature lower than this value. Even to achieve absolute zero temperature is not possible in practice.
   [Note: The point of zero pressure or zero volume does not depend on am specific gas.]

Question 5.
Derive the relation between three coefficients of thermal expansion.
Answer:
Consider a square plate of side l₀ at 0 °C and h at T °C.

1. l_T = l₀ (1 + αT)
   If area of plate at 0 °C is A₀, A₀ = \(l_{0}^{2}\)
   If area of plate at T °C is A_T,
   A_T = \(l_{\mathrm{T}}^{2}=l_{0}^{2}\) (1 + αT)²
   or A_T = A₀ (1 + αT)² …………… (1)
   Also,
   A_T = A₀(1 + βT)² …………… (2)
   ……………. [∵ β = \(\frac{\mathrm{A}_{\mathrm{T}}-\mathrm{A}_{0}}{\mathrm{~A}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)]
2. Using Equations (1) and (2),
   A₀ (1 + αT)² = A₀(1 + βT)
   ∴ 1 + 2αT + α²T² = 1 + βT
3. Since the values of a are very small, the term α²T² is very small and may be neglected,
   ∴ β = 2a
4. The result is general because any solid can be regarded as a collection of small squares.

Relation between coefficient of linear expansion (α) and coefficient of cubical expansion (γ).

1. Consider a cube of side l₀ at 0 °C and l_T at T °C.
   ∴ l_T = l₀(1 + αT)
   If volume of the cube at 0 °C is V₀, V₀ = \(l_{0}^{3}\)
   If volume of the cube at T °C is
   V_T, V_T = \(l_{\mathrm{T}}^{3}=l_{0}^{3}\) (1 + αT)³
   V_T = V₀ (1 + αT)³ ………. (1)
   Also,
   V_T = V₀(1 + γT) …………. (2)
   …………. [∵ γ = \(\frac{\mathrm{V}_{\mathrm{T}}-\mathrm{V}_{0}}{\mathrm{~V}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)]
2. Using Equations (1) and (2),
   V₀(1 + αT)³ = V₀(1 + γT)
   ∴ 1 + 3αT + 3α²T² + α³T³ = 1 + γT
3. Since the values of a are very small, the terms with higher powers of a may be neglected,
   ∴ γ = 3α
4. The result is general because any solid can be regarded as a collection of small cubes.

Relation between α, β and γ is given by,
α = \(\frac{\beta}{2}=\frac{\gamma}{3}\)
where, α = coefficient of linear expansion.
β = coefficient of superficial expansion,
γ = coefficient of cubical expansion.

Question 6.
State applications of thermal expansion.
Answer:
Applications of thermal expansion:

• The steel wheel is heated to expand. This expanded wheel can easily fit over axle. The wheel is then cooled quickly. Upon cooling, wheel contracts and fits tightly upon the axle.
• An electric light bulb gets hot quickly when in use. The wire leads to the filament are sealed into the glass. 1f the glass of the bulbs has significantly different thermal expansivity from the wire leads, the glass and the wire would separate, breaking down the vacuum. To prevent this, wires are made of platinum or some suitable alloy with the same expansivity as ordinary glass.

Question 7.
Why do we generally consider two specific heats for a gas?
Answer:

• A slight change in temperature causes considerable change in pressure as well as volume of the gas.
• Therefore, two principal specific heats are defined for a gas viz., specific heat capacity at constant volume (S_V) and specific heat capacity at constant pressure (S_p).

Question 8.
Are freezing point and melting point same with respect to change of state ? Comment.
Answer:
Though freezing point and melting point mark same temperature (0°C or 32° F), state of change is different for the two points. At freezing point liquid gets converted into solid, whereas at melting point solid gets converted into its liquid state.

Question 9.
Define
(i) Sublimation
(ii) Triple point.
Answer:

1. The change from solid state to vapour stale without passing through the liquid state is called sublimation and the substance is said to sublime.
   Examples: Dry ice (solid CO₂) and iodine.
2. The triple point of water is that point where water in a solid, liquid and gas state co-exists in equilibrium and this occurs only at a unique temperature and a pressure.

Question 10.
Explain the term ‘steady state’.
Answer:

1. When one end of a metal rod is heated, the heat flows by conduction from hot end to the cold end.
   
2. As a result, the temperature of every section of the rod starts increasing.
3. Under this condition, the rod is said to be in a variable temperature state.
4. After some time, the temperature at each section of the rod becomes steady i.e., does not change.
5. Temperature of each cross-section of the rod now becomes constant though not the same. This is called steady state condition.

Question 11.
Define coefficient of thermal conductivity. Derive its expression.
Answer:
Coefficient of thermal conductivity of a material is defined as the quantity of heat that flows in one second between the opposite faces of a cube of side 1 m, the faces being kept at a temperature difference of 1°C (or 1 K).

Expression for coefficient of thermal conductivity:

1. Under steady state condition, the quantity of heat ‘Q’ that flows from the hot face at temperature T₁ to the cold face at temperature T₂ of a cube with side x and area of cross-section A is
   • directly proportional to the cross-sectional area A of the face. i.e.. Q ∝ A
   • directly proportional to the temperature difference between the two faces i.e., Q ∝ (T₁ – T₂)
   • directly proportional to time t (in seconds) for which heat flows i.e.. Q ∝ t
   • inversely proportional to the perpendicular distance x between hot and cold faces i.e., Q ∝ 1/x
2. Combining the above four factors, we have the quantity of heat
   Q ∝ \(\frac{\mathrm{A}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right) \mathrm{t}}{\mathrm{x}}\)
   ∴ Q = \(\)
   where k is a constant of proportionality and is called coefficient of thermal conductivity. Its value depends upon the nature of the material.

Question 12.
Give any four applications of thermal conductivity in every day life.
Answer:
Answer: Applications of thermal conductivity:

1. • Thick walls are used in the construction of cold storage rooms.
   • Brick being a bad conductor of heat is used to reduce the flow of heat from the surroundings to the rooms.
   • Better heat insulation is obtained by using hollow bricks.
   • Air being a poorer conductor than a brick, it further avoids the conduction of heat from outside.
2. Street vendors keep ice blocks packed in saw dust to prevent them from melting rapidly.
3. The handle of a cooking utensil is made of a bad conductor of heat, such as ebonite, to protect our hand from the hot utensil.
4. Two bedsheets used together to cover the body help retain body heat better than a single bedsheet of double the thickness. Trapped air being a bad conductor of heat, the layer of air between the two sheets reduces thermal conduction better than a sheet of double the thickness. Similarly, a blanket coupled with a bedsheet is a cheaper alternative to using two blankets.

Question 13.
Explain the term thermal resistance. State its SI unit and dimensions.
Answer:

1. Consider expression for conduction rate,
   P_cond = kA \(\frac{\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\mathrm{x}}\)
   ⇒ \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}=\frac{\mathrm{x}}{\mathrm{kA}}\) ……………. (1)
2. Ratio \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}\) is called as thermal resistance (R_T) of material.

The SI unit of thermal resistance is °C s/kcal or °C s/J and its dimensional formula is [L^-2M^-1T³K¹].

Question 14.
How heat transfer occurs through radiation in absence of a medium?
Answer:

1. All objects possess thermal energy due to their temperature T(T > 0 K).
2. The rapidly moving molecules of a hot body emit EM waves travelling with the velocity of light. These are called thermal radiations.
3. These carry energy with them and transfer it to the low-speed molecules of a cold body on which they fall.
4. This results in an increase in the molecular motion of the cold body and its temperature rises.
5. Thus transfer of heat by radiation is a two fold process-the conversion of thermal energy into waves and reconversion of waves into thermal energy by the body on which they fall.

Question 15.
State Newton’s law of cooling and explain how it can be experimentally verified.
Answer:
The rate of loss of heat dT/dt of the both’ is directly proportional to the difference of temperature (T – T₀) of the body and the surroundings provided the difference in temperatures is small.

Mathematically, Newton’s law of cooling can be expressed as:
\(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ (T – T₀)
∴ \(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ C(T – T₀)
where, C is constant of proportionality. Experimental verification of Newton’s law of cooling:

1. Fill a calorimeter upto \(\frac{2}{3}\) of its capacity with a boiling water. Cover it with lid with a hole for passing the thermometer.
2. Insert the thermometer through the hole and adjust it so that the bulb of the thermometer is fully immersed in hot water.
3. Keep calorimeter vessel in constant temperature enclosure or just in open air since room temperature will not change much during the experiment.
4. Note down the temperature (T) on the thermometer at every one minute interval until the temperature of water decreases by about 25 °C.
5. Plot a graph of temperature (T) on Y-axis against time (t) on X-axis. This graph is called cooling curve as shown in figure (a).
   
6. Draw tangents to the curve at suitable points on the curve. The slope of each tangent is \(\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathrm{T}}{\Delta \mathrm{t}}\) and gives the rate of fall of temperature at that temperature (T).
7. Now the graph of \(\left|\frac{\mathrm{dT}}{\mathrm{dt}}\right|\) on Y-axis against (T – T₀) on X-axis is plotted with (0, 0) origin. The graph is straight line and passes through origin as shown in figure (b), which verities Newton’s law of cooling.
   
   (b) Graphical verification of Newton’s law of cooling

Question 16.
What is thermal stress? Give an example of disadvantages of thermal stress in practical use?
Answer:

1. Consider a metallic rod of length l₀ fixed between two rigid supports at T °C.
   If the temperature of rod is increased by ∆T, length of rod would become,
   l = l₀(1 + α∆T)
   Where, α is the coefficient of linear expansion of material of the rod.
   But the supports prevent expansion of rod. As a result, rod exerts stress on the supports. Such stress is termed as thermal stress.
2. Disadvantage: Thermal stress can lead to fracture or deformation in substance under certain conditions.
3. Railway tracks are made up of metals which expand upon heating. If no gap is kept between tracks, in hot weather, expansion of metal tracks may exert thermal stress on track. This may lead to bending of tracks which would be dangerous. Hence, railway track is not a continuous piece but is made up of segments separated by gaps.

Question 17.
Which materials can be used as thermal insulators and why?
Answer:

1. Substances such as glass, wood, rubber, plastic, etc. can be used as thermal insulators.
2. These substances do not have free electrons to conduct heat freely throughout the body. Hence, they arc poor conductors of heat.

3. Solve the following problems.

Question 1.
A glass flask has volume 1 × 10^-4 m³. It is filled with a liquid at 30 ºC. If the temperature of the system is raised to 100 ºC, how much of the liquid will overflow. (Coefficient of volume expansion of glass is 1.2 × 10^-5 (ºC)^-1 while that of the liquid is 75 × 10^-5 ºC^-1)
Solution:
Given: V₁ = 1 × 10^-4 m³ = 10^-4 m³, T₁ = 30°C,
T₂ = 100 °C
To find: Volume of liquid that overflows
Formula: γ = \(\frac{V_{2}-V_{1}}{V_{1}\left(T_{2}-T_{1}\right)}\)
Calculation: From formula,
Increase is volume = V₂ – V₁
= γV₁(T₂ – T₁)
increase in volume of beaker
= γ_glass × V₁ (T₂ – T₁)
= 1.2 × 10^-5 × 10^-4 × (100 – 30)
= 1.2 × 70 × 10^-9
= 4 × 10^-9 m³
∴ Increase in volume of beaker
= 84 × 10^-9 m³
Increase in volume of liquid
= γ_liquid × V₁ (T₂ – T₁)
= 75 × 10^-5 × 10 × (100 – 30)
= 75 × 70 × 10
= 5250 × 10^-9 m³
∴ Increase in volume of liquid = 5250 × 10^-9 m³
∴ Volume of liquid which overflows
= (5250 – 84) × 10^-9 m³
= 5166 × 10^-9 m³
= 0.5166 × 10^-7 m³
Volume of liquid that overflows is 0.5166 × 10^-7 m³.
[Note: The answer given above is presented considering standard conventions of writing number with its correct order of magnitude.]

Question 2.
Which will require more energy, heating a 2.0 kg block of lead by 30 K or heating a 4.0 kg block of copper by 5 K? (s_lead = 128 J kg^-1 K^-1, s_copper = 387 J kg^-1 K^-1)
Solution:
Given: m_lead = 2 kg, ∆T_lead = 30 K,
s_lead = 128 J/kg K,
m_Cu =4 kg, ∆T_Cu = 5 K,
s_Cu = 387 J/kg K
To find: Substance requiring more heat energy.
Formula: Q = ms ∆T
Calculation: From formula,
For lead, Q_lead = 2 × 128 × 30 = 7680J
For Copper, Q_Cu = 4 × 387 × 5 = 7740 J
Q_Cu > Q_lead, copper will require more heat energy.
Copper will require more heat energy.

Question 3.
Specific latent heat of vaporization of water is 2.26 × 10⁶ J/kg. Calculate the energy needed to change 5.0 g of water into steam at 100 ºC.
Solution:
Given: L_vap = 2.26 × 10⁶ J/kg
m = 5g = 5 × 10^-3 kg
In this case, no temperature change takes place only change of state occurs.
To find: Heat required to convert water into steam.
Formula: Heat required = mL_vap
Calculation: From formula,
Heat required = 5 × 10^-3 × 2.26 × 10⁶
= 11300J
= 1.13 × 10⁴ J
Heat required to convert water into steam is 1.13 × 10⁴ J
[Note: The answer given above is presented considering standard conventions of writing number with its correct order of magnitude.]

Question 4.
A metal sphere cools at the rate of 0.05 ºC/s when its temperature is 70ºC and at the rate of 0.025 ºC/s when its temperature is 50 ºC. Determine the temperature of the surroundings and find the rate of cooling when the temperature of the metal sphere is 40 ºC.
Solution:

∴ 2(50 – T₀) = 70 – T₀
∴ T₀ = 30 πC
Substituting value of T₀.
0.05 = C (70 – 30)
∴ C = \(\frac{0.05}{40}\) = 0.00125/s.
For T₃ = 40 °C
\(\left(\frac{\mathrm{d} \mathrm{T}}{\mathrm{dt}}\right)_{3}\) = C(T₃ – T₀)
= 0.00125 (40 – 30)
= 0.00125 × 10
= 0.0125°C/s.
i) Temperature of surrounding is 30 °C.
ii) Rate of cooling at 40 °C is 0.0125 °C/s.

Question 5.
The volume of a gas varied linearly with absolute temperature if its pressure is held constant. Suppose the gas does not liquefy even at very low temperatures, at what temperature the volume of the gas will be ideally zero?
Answer:
At temperature of -273.15 °C, the volume of the gas will be ideally zero.

Question 6.
In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 ºC. If maximum temperature in the region is 45 ºC and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10^-5 K^-1 for the material of the rail section?
Solution:
Given. T₁ = 27 °C, T₂ = 45 °C,
L₁ = 10m.
α = 1.2 × 10^-5 K^-1
To find: Gap that should be left (L₂ – L₁)
Formula: L₂ – L₁ = L₁ α(T₂ – T₁)
Calculation: From formula,
L₂ – L₁ = 10 × 1.2 × 10^-5 × (45 – 27)
= 2.16 × 10^-3 m
= 2.16 mm
The gap that should be left between rail sections is 2.16 mm.

Question 7.
A blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the wooden rim and the iron ring are 1.5 m and 1.47 m respectively at room temperature of 27 ºC. To what temperature the iron ring should be heated so that it can fit the rim of the wheel (α_iron = 1.2 × 10^-5 K^-1).
Solution:
Given: d_w = 1.5 m, d = 1.47 m, T₁ = 27 °C.
α_i = 1.2 × 10^-5/ K
To find: Temperature (T₂)
Formula. α = \(\frac{\mathrm{d}_{\mathrm{w}}-\mathrm{d}_{\mathrm{i}}}{\mathrm{d}_{\mathrm{i}}\left(\mathrm{T}_{2}-\mathrm{T}_{1}\right)}\)
Calculation: From formula,
T₂ = \(\frac{\mathrm{d}_{\mathrm{w}}-\mathrm{d}_{\mathrm{i}}}{\mathrm{d}_{\mathrm{i}} \alpha}\) + T₁
= \(\frac{1.5-1.47}{1.47 \times 1.2 \times 10^{-5}}\) + 27
= 1700.7 + 27
= 1727.7 °C
Iron ring should be heated to temperature of 1727.7 °C.

Question 8.
In a random temperature scale X, water boils at 200 °X and freezes at 20 °X. Find the boiling point of a liquid in this scale if it boils at 62 °C.
Solution:
Here thermometric property P is temperature at some random scale X.
Using equation,
T = \(\frac{100\left(P_{T}-P_{1}\right)}{\left(P_{2}-P_{1}\right)}\)
For P₁ = 20 °X,
P₂ = 200 °X,
T = 62°C
∴ 62 = \(\frac{100\left(\mathrm{P}_{\mathrm{T}}-20\right)}{(200-20)}\)
∴ P_T = \(\frac{62 \times(200-20)}{100}\) + 20 = 111.6 + 20
= 131.6 °X
The boiling point of a liquid in this scale is 131.6 °X.

Question 9.
A gas at 900°C is cooled until both its pressure and volume are halved. Calculate its final temperature.
Solution:
Given: T₁ = 900 °C = 900 + 273.15 = 1173.15 K
V₂ = \(\frac{\mathrm{V}_{1}}{2}\), P₂ = \(\frac{\mathrm{P}_{1}}{2}\)
To find: Final temperature (T₂)
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{\mathrm{I}}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: From formula.
\(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{1173.15}=\frac{\mathrm{P}_{1} \mathrm{~V}_{\mathrm{l}}}{4 \mathrm{~T}_{2}}\)
∴ T₂ = \(\frac{1173.15}{4}\) = 293.29 K
Final temperature of gas is 293.29 K.

Question 10.
An aluminium rod and iron rod show 1.5 m difference in their lengths when heated at all temperature. What are their lengths at 0 °C if coefficient of linear expansion for aluminium is 24.5 × 10^-6 /°C and for iron is 11.9 × 10^-6 /°C
Solution:
Given: (L_T)_i – (L_T)_al = 1.5 m, T₀ = 0 °C
α_al = 24.5 × 10^-6/°C
α_i = 11.9 × 10^-6 /°C
To find: Lengths of aluminium and iron rod (L₀)_al and (L₀)_i
Formula: L_T = L₀[(1 + α(T – T₀)]
Calculation: For T₀ = 0 °C
From formula,
L_T = L₀(1 + αT)
For aluminium,
(L₀)_al = (L₀)_al(1 + α_alT) ……………. (1)
For iron,
(L_T)_i = (L₀)_i (1 + α_iT) ………….. (2)
Subtracting equation (2) by (1),
(L_T)_i – (L_T)_al = [(L₀)_i + (L₀)_i α_iT] – [(L₀)_al + (L₀)_alα_alT]
= (L₀)_i – (L₀)_al + [(L₀)_i α_i – (L₀)_al α_al]T
∴ 1.5 = 1.5 + [(L₀)_i α_i – (L₀)_al α_al)]T
⇒ [(L₀)_iα_i – (L₀)_alα_al] T = 0
∴ (L₀)_alα_al = (L₀)_iα_i

Length of aluminium rod at 0 °C is 1.417 m and that of iron rod is 2.917 m.

Question 11.
What is the specific heat of a metal if 50 cal of heat is needed to raise 6 kg of the metal from 20°C to 62 °C ?
Solution:
Given: Q = 50 cal, m =6 kg,
∆T = 62 – 20 = 42 °C
To find: Specific heat (s)
Formula: Q = ms ∆T
Calculation: From formula,
s = \(\frac{\mathrm{Q}}{\mathrm{m} \Delta \mathrm{T}}=\frac{50}{6 \times 42}\) = 0.198 cal/kg °C
Specific heat of metal is copper 0.198 cal/kg °C.

Question 12.
The rate of flow of heat through a copper rod with temperature difference 30 °C is 1500 cal/s. Find the thermal resistance of copper rod.
Solution:
Given: ∆T = 30 °C, P_cond = 1500 cal/s
To find: Thermal resistance (R_T)
Formula: R_T = \(\frac{\Delta \mathrm{T}}{\mathrm{P}_{\text {cond }}}\)
Calculation: From formula,
R_T = \(\frac{30}{1500}\)
= 0.02 °C s/cal.
Thermal resistance of copper rod is 0.02 °C s/cal.

Question 13.
An electric kettle takes 20 minutes to heat a certain quantity of water from 0°C to its boiling point. It requires 90 minutes to turn all the water at 100°C into steam. Find the latent heat of vaporisation. (Specific heat of water = 1cal/g°C)
Solution:
Let heat supplied by kettle in 20 minutes be Q₁ and that in 90 min. be Q₂.
Using heat temperature of water is raised from O °C to 100 °C.
If mass of water in the kettle is ‘m’ then.
Q₁ = ms_water∆T m × 1 × (100 – 0)
= 100 m ………….. (i)
…………. (∵ S_water = 1 cal/g °C)
Similarly using heat Q₂ water is converted from liquid to gas,
∴ Q₂ = mL_vap ……………. (ii)
Given that heat Q₁, Q₂ are supplied to water in 20 min. (t₁) and 90 min (t₂) respectively.
Kettle being same its conduction rate (P_cond) is same.
Using P_cond = \(\frac{\mathrm{Q}_{1}}{\mathrm{t}_{1}}=\frac{\mathrm{Q}_{2}}{\mathrm{t}_{2}}\) …………… (iii)
From (i), (ii) and (iii),
\(\frac{100 \mathrm{~m}}{20}=\frac{\mathrm{mL}_{\text {vap }}}{90}\),
∴ L_vap = 5 × 90 = 450 cal/g
Latent heat of vaporisation for water is 450 cal/g.

Question 14.
Find the temperature difference between two sides of a steel plate 4 cm thick, when heat is transmitted through the plate at the rate of 400 k cal per minute per square metre at steady state. Thermal conductivity of steel is 0.026 kcal/m s K.
Solution:

Temperature difference between two sides is 10.26 K.
[Note: Above answer is expressed in K (‘kelvin considering that thermal conductivity is expressed in units of kcal / ms K, and not as kcal / m s °C. As 1 °C equivalent to 1 K. conceptually temperature difference of 10.26 K will correspond to 10.26 t]

Question 15.
A metal sphere cools from 80 °C to 60 °C in 6 min. How much time with it take to cool from 60 °C to 40 °C if the room temperature is 30°C?
Solution:
Given: T₁ = 80 °C, T₂ = 60 °C, T₃ = 40 °C, T₀ = 30 °C, (dt)₁ = 6 min.
To find: Time taken in cooling (dt)₂

Time taken in cooling is 10 min.

11th Physics Digest Chapter 7 Thermal Properties of Matter Intext Questions and Answers

Can you tell? (Textbook Page No. 125)

Question 1.
i) Why the metal wires for electrical transmission lines sag?
ii) Why a railway track is not a continuous piece but is made up of segments separated by gaps?
iii) How a steel wheel is mounted on an axle to fit exactly?
Answer:

1. In hot weather, metal wires get heated due to increased temperature of surrounding. As a result, they expand increasing the slack between transmission line structure, causing them to sag.
2. Railway tracks are made up of metals which expand upon heating. If no gap is kept between tracks, in hot weather, expansion of metal tracks may exert thermal stress on track. This may lead to bending of tracks which would be dangerous. Hence, railway track is not a continuous piece but is made up of segments separated by gaps.
3. The steel wheel is heated to expand. This expanded wheel can easily fit over axle. The wheel is then cooled quickly. Upon cooling, wheel contracts and fits tightly upon the axle.

Intext question. (Textbook Page No 124)

Question 1.
Can you now tell why the balloon bursts sometimes when you try to fill air in it?
Answer:

1. When balloon is blown, air that is blown inside makes the balloon expand.
2. A given size of balloon can expand upto certain limit.
3. Once that limit is reached and air is still blown inside the balloon, balloon cannot expand further.
4. As a result, air causes additional pressure on inner surface of balloon.
5. Since, pressure inside balloon is now greater than pressure outside balloon, balloon bursts equalizing the two pressures.

Can you tell? (Textbook Page No. 125)

Question 1.
Why lakes freeze first at the surface?
Answer:

1. In cold climate, temperature of water in ponds and lakes starts falling.
2. On getting colder, water contracts. As a result, density of water increases and it goes down. To replace it, warmer water from below rises up. This process continues till temperature of water at the bottom of pond becomes 4 °C.
3. Water, due to its anomalous behaviour possesses maximum density at 4 °C.
4. If the temperature lowers further, ice is formed at the surface of pond with water below it.
5. Ice being poor conductor of heat blocks the further heat exchange between atmosphere and water in the pond and maintains water below surface in liquid state.

Activity (Textbook Page No. 129)

Question 1.
To understand the process of change of state:
Take some cubes of ice in a beaker. Note the temperature of ice (0 °C). Start heating it slowly on a constant heat source. Note the temperature after every minute. Continuously stir the mixture of water and ice. Observe the change in temperature. Continue heating even after the whole of ice gets converted into water. Observe the change in temperature as before till vapours start coming out. Plot the graph of temperature (along Y-axis) versus time (along X-axis). Obtain a graph of temperature versus time.
Answer:
[Students are expected to attempt the activity on their own.]

Can you tell? (Textbook Page No. 130)

Question 1.
What is observed after point D in graph? Can steam be hotter than 100 °C?
Answer:
Beyond point D, thermometer again shows rise in temperature. This means, steam can be hotter than 100 °C and is termed as superheated steam.

Question 2.
Why steam at 100 °C causes more harm to our skin than water at 100 °C?
Answer:

1. Though steam and boiling water have same temperature, the heat contained in steam is more than that in boiling water.
2. Steam is formed when boiling water absorbs specific latent heat of vaporisation i.e.. 22.6 × 10⁵ J/kg.
3. As a result, when steam comes in contact with the skin of a person, it gives off additional 22.6 × 10⁵ joule per kilogram causing severe (more serious) burns.
   Hence, burns caused from steam are more serious than those caused from boiling water at same temperature.

Activity (Textbook Page No. 130)

Activity to understand the dependence of boiling point on pressure:
Take a round bottom flask, more than half filled with water. Keep it over a burner and fix a thermometer and steam outlet through the cork of the flask as shown in figure. As water in the flask gets heated, note that first the air, which was dissolved in the water comes out as small bubbles. Later bubbles of steam form at the bottom but as they rise to the cooler water near the top, they condense and disappear. Finally, as the temperature of the entire mass of the water reaches 100 oc, bubbles of steam reach the surface and boiling is said to occur. The steam in the flask may not be visible hut as it comes out of the flask, It condenses as tiny droplets of water giving a foggy appearance.

If now the steam outlet is closed for a few seconds to increase the pressure in the flask, you will notice that boiling stops. More heat would be required to raise the temperature (depending on the increase in pressure) before boiling starts again. Thus, boiling point increases with increase in pressure. Let us now remove the burner. Allow water to cool to about 80°C. Remove the thermometers and steam outlet. Close the flask with a air tight cork. Keep the flask turned upside down on a stand. Pour icecold water on the flask. Water vapours in the flask condense reducing the pressure on the water surface inside the flask. Water begins to boil again, now at a lower temperature. Thus boiling point decreases with decrease in pressure and increases with increase in pressure.
Answer:
[Students are expected to attempt the activity an their own.]

Can you tell? (Textbook Page No. 131)

Question 1.
i) Why is cooking difficult at high altitude?
ii) Why is cooking faster in pressure cooker?
Answer:

1. • At high altitude density of air is low which causes reduction in atmospheric pressure.
   • As pressure is less, boiling point of water lowers.
   • Water, at high altitude, starts boiling below 100 OC.
   • As food is cooked mostly through the water boiling, cooking of food becomes difficult.
2. • Pressure cooker operates by expelling air within the cooker and trapping steam produced from the liquid. (mostly water) boiling inside.
   • Due to high internal pressure, boiling point of liquid increases and liquid boils at temperature higher than its boiling point.
   • The increased boiling point allows more absorption of heat by liquid and steam formed is superheated.
   • As a result, food gets cooked quickly.

Internet my friend (Textbook Page No. 139)

i) https ://hyperphysics. phy-astr.gsu.edul/base/hframe.html
ii) https://youtu.be/7ZKHc5J6R5Q
iii) https://physics. info/expansion
Answer:
[Students are expected to visit the above mentioned webs it es and collect more information about the thermal properties of matter.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Mechanical Properties of Solids Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 6 Mechanical Properties of Solids Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 6 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 6 Exercise Solutions

1. Choose the correct answer:

Question 1.
Change in dimensions is known as …………..
(A) deformation
(B) formation
(C) contraction
(D) strain.
Answer:
(A) deformation

Question 2.
The point on stress-strain curve at which strain begins to increase even without increase in stress is called…………
(A) elastic point
(B) yield point
(C) breaking point
(D) neck point
Answer:
(B) yield point

Question 3.
Strain energy of a stretched wire is 18 × 10^-3 J and strain energy per unit volume of the same wire and same cross section is 6 × 10^-3 J/m³. Its volume will be………….
(A) 3cm³
(B) 3 m³
(C) 6 m³
(D) 6 cm³
Answer:
(B) 3 m³

Question 4.
……………. is the property of a material which enables it to resist plastic deformation.
(A) elasticity
(B) plasticity
(C) hardness
(D) ductility
Answer:
(C) hardness

Question 5.
The ability of a material to resist fracturing when a force is applied to it, is called……………
(A) toughness
(B) hardness
(C) elasticity
(D) plasticity.
Answer:
(A) toughness

2. Answer in one sentence:

Question 1.
Define elasticity.
Answer:
If a body regains its original shape and size after removal of the deforming force, it is called an elastic body and the property is called elasticity.

Question 2.
What do you mean by deformation?
Answer:
The change in shape or size or both of u body due to an external force is called deformation.

Question 3.
State the SI unit and dimensions of stress.
Answer:

1. SI unit: N m^-2 or pascal (Pa)
2. Dimensions: [L^-1M¹T^-2]

Question 4.
Define strain.
Answer:
Strain:

1. Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
   Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\)
2. Types of strain:
   • Longitudinal strain,
   • Volume strain,
   • Shearing strain.

Question 5.
What is Young’s modulus of a rigid body?
Answer:
Young’s modulus (Y): It is the modulus of elasticity related to change in length of an object like a metal wire, rod, beam, etc., due to the applied deforming force.

Question 6.
Why bridges are unsafe after a very long use?
Answer:
A bridge during its use undergoes recurring stress depending upon the movement of vehicles on it. When bridge is used for long time, it loses its elastic strength and ultimately may collapse. Hence, the bridges are declared unsafe after long use.

Question 7.
How should be a force applied on a body to produce shearing stress?
Answer:
A tangential force which is parallel to the top and the bottom surface of the body should be applied to produce shearing stress.

Question 8.
State the conditions under which Hooke’s law holds good.
Answer:
Hooke’s Taw holds good only when a wire/body is loaded within its elastic limit.

Question 9.
Define Poisson’s ratio.
Answer:
Within elastic limit, the ratio of lateral strain to the linear strain is called the Poisson‘s ratio.

Question 10.
What is an elastomer?
Answer:
A material that can be elastically stretched to a larger value of strain is called an elastomer.

Question 11.
What do you mean by elastic hysteresis?
Answer:

1. In case of some materials like vulcanized rubber, when the stress applied on a body decreases to zero, the strain does not return to zero immediately. The strain lags behind the stress. This lagging of strain behind the stress is called elastic hysteresis.
2. Below figure shows the stress-strain curve for increasing and decreasing load. It encloses a loop. Area of loop gives the energy dissipated during deformation of a material.
   

Question 12.
State the names of the hardest material and the softest material.
Answer:
Hardest material: Diamond
Softest material: Aluminium
[Note: Material with highest strength is steel whereas material with lowest strength is plasticine clay.]

Question 13.
Define friction.
Answer:
The property which resists the relative motion between two surfaces in contact is called friction.

Question 14.
Why force of static friction is known as ‘self-adjusting force?
Answer:
The force of static friction varies in accordance with applied force. Hence, it is called as self adjusting force.

Question 15.
Name two factors on which the coefficient of friction depends.
Answer:
Coefficient of friction depends upon:

1. the materials of the surfaces in contact.
2. the nature of the surfaces.

3. Answer in short:

Question 1.
Distinguish between elasticity and plasticity.
Answer:

Question 2.
State any four methods to reduce friction.
Answer:
Friction can be reduced by using polished surfaces, using lubricants, using grease and using ball bearings.

Question 3.
What is rolling friction? How does it arise?
Answer:

1. Friction between two bodies in contact when one body is rolling over the other, is called rolling friction.
2. Rolling friction arises as the point of contact of the body with the surface keep changing continuously.

Question 4.
Explain how lubricants help in reducing friction?
Answer:

1. The friction between lubricant to surface is much less than the friction between two same surfaces. Hence using lubricants reduces the friction between the two surfaces.
2. When lubricant is applied to machine parts, it fills the depression present on the surface in contact. Thus, less friction is occurred between machine parts.
3. Application of lubricants also reduces wear and tear of machine parts which in turn reduces friction.
4. Advantage: Reduction in function reduces dissipation of energy in machines due to which efficiency of machines increases.

Question 5.
State the laws of static friction.
Answer:
Laws of static friction:

1. First law: The limiting force of static friction (F_L) is directly proportional to the normal reaction (N) between the two surfaces in contact.
   F_L ∝ N
   ∴ F_L = µ_s N
   where, µ_s = constant called coefficient of static friction.
2. Second law: The limiting force of friction is
   independent of the apparent area between the surfaces in contact, so long as the normal reaction remains the same.
3. Third law: The limiting force of friction depends upon materials in contact and the nature of their surfaces.

Question 6.
State the laws of kinetic friction.
Answer:
Laws of kinetic friction:

1. First law: The force of kinetic friction (Fk) is directly proportional to the normal reaction (N) between two surfaces in contact.
   F_k ∝ N
   ∴ F_k = µ_kN
   where, µ_k = constant called coefficient of kinetic friction.
2. Second law: Force of kinetic friction is independent of shape and apparent area of the surfaces in contact.
3. Third law: Force of kinetic friction depends upon the nature and material of the surfaces in contact.
4. Fourth law: The magnitude of the force of kinetic friction is independent of the relative velocity between the object and the surface provided that the relative velocity is neither too large nor too small.

Question 7.
State advantages of friction.
Answer:
Advantages of friction:

1. We can walk due to friction between ground and feet.
2. We can hold object in hand due to static friction.
3. Brakes of vehicles work due to friction; hence we can reduce speed or stop vehicles.
4. Climbing on a tree is possible due to friction.

Question 8.
State disadvantages of friction.
Answer:
Disadvantages of friction:

1. Friction opposes motion.
2. Friction produces heat in different parts of machines. It also produces noise.
3. Automobile engines consume more fuel due to friction.

Question 9.
What do you mean by a brittle substance? Give any two examples.
Answer:

1. Substances which breaks within the elastic limit are called brittle substances.
2. Examples: Glass, ceramics.

4. Long answer type questions:

Question 1.
Distinguish between Young’s modulus, bulk modulus and modulus of rigidity.
Answer:

Question 2.
Define stress and strain. What are their different types?
Answer:
i) Stress:

1. The internal restoring force per unit area of a both is called stress.
   Stress = \(\frac{\text { deforming force }}{\text { area }}=\frac{|\vec{F}|}{\mathrm{A}}\)
   where \(\vec{F}\) is internal restoring force or external applied deforming force.
2. Types of stress:
   • Longitudinal stress,
   • Volume stress,
   • Shearing stress.

ii. Strain:

1. Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
   Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\)
2. Types of strain:
   • Longitudinal strain,
   • Volume strain,
   • Shearing strain.

Question 3.
What is Young’s modulus? Describe an experiment to find out Young’s modulus of material in the form of a long straight wire.
Answer:
Definition: Young ‘s modulus is the ratio of longitudinal stress to longitudinal strain.
It is denoted by Y.
Unit: N/m² or Pa in SI system.
Dimensions: [L^-1M¹T^-2]

Experimental description to find Young’s modulus:

i. Consider a metal wire suspended from a rigid support. A load is attached to the free end of the wire. Due to this, deforming force gets applied to the free end of wire in downward direction and it produces a change in length.
Let,
L = original length of wire,
Mg = weight suspended to wire,
l = extension or elongation,
(L + l) = new length of wire.
r = radius of the cross section of wire

ii. In its equilibrium position,

Question 4.
Derive an expression for strain energy per unit volume of the material of a wire.
Answer:
Expression for strain energy per unit volume;

i. Consider a wire of original length L and cross sectional area A stretched by a force F acting along its length. The wire gets stretched and elongation l is produced in it

ii. If the wire is perfectly elastic then,
Longitudinal stress = \(\frac{F}{A}\)
Longitudinal strain = \(\frac{l}{L}\)

iii. The magnitude of stretching force increases from zero to F during elongation of wire.
Let ‘f’ be the restoring force and ‘x’ be its corresponding extension at certain instant during the process of extension.
∴ f = \(\frac{\text { YAx }}{\mathrm{L}}\) ……………. (2)

iv. Let ‘dW’ be the work done for the further small extension ‘dx’.
Work = force × displacement
∴ dW = fdx
∴ dW= \(\frac{\text { YAx }}{L}\) dx …………..(3) [From (2)]

v. The total amount of work done in stretching the wire from x = 0 to x = l can be found out by integrating equation (3).

∴ Work done in stretching a wire,
W = \(\frac{1}{2}\) × load × extension

vi. Work done by stretching force is equal to strain energy gained by the wire.
∴ Strain energy = \(\frac{1}{2}\) × load × extension

vii. Work done per unit volume

∴ Strain energy per unit volume = \(\frac{1}{2}\) × stress × strain

viii. Other forms:

Question 5.
What is friction? Define coefficient of static friction and coefficient of kinetic friction. Give the necessary formula for each.
Answer:

1. The property which resists the relative motion between two surfaces in contact is called friction.
2. The coefficient of static friction is defined as the ratio of limiting force of friction to the normal reaction.
   Formula: \(\mu_{\mathrm{S}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}\)
3. The coefficient of kinetic friction is defined as the ratio of force of kinetic friction to the normal reaction between the two surfaces in contact.
   Formula: \(\mu_{\mathrm{k}}=\frac{\mathrm{F}_{\mathrm{K}}}{\mathrm{N}}\)

Question 6.
State Hooke’s law. Draw a labelled graph of tensile stress against tensile strain for a metal wire up to the breaking point. In this graph show the region in which Hooke’s law is obeyed.
Answer:
i) Statement: Within elastic limit, stress is directly proportional to strain.
Explanation;

1. According to Hooke’s law,
   Stress ∝ Strain
   
   This constant of proportionality is called modulus of elasticity.
2. Modulus of elasticity of a material is the slope of stress-strain curve in elastic deformation region and depends on the nature of the material.
3. The graph of strain (on X-axis) and stress (on Y-axis) within elastic limit is shown in the figure.

ii)

iii) Hooke’s law is completely obeyed in the region OA.

5. Answer the following

Question 1.
Calculate the coefficient of static friction for an object of mass 50 kg placed on horizontal table pulled by attaching a spring balance. The force is increased gradually it is observed that the object just moves when spring balance shows 50N.
[Answer: µs = 0.102]
Solution:
Given: m = 50 kg, F_L = 50 N, g = 9.8 m/s²
To find: Coefficient of static friction (µ_s)
Formula: µ_s = \(\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{mg}}\)
µ_s = \(\frac{50}{50 \times 9.8}\) = 0.102
Answer:
The coefficient of static friction is 0.102.

Question 2.
A block of mass 37 kg rests on a rough horizontal plane having coefficient of static friction 0.3. Find out the least force required to just move the block horizontally.
[Answer: F= 108.8N]
Solution:
Given: m = 37 kg, µ_s = 0.3, g = 9.8 m /s²
To find: Limiting force (F_L)
Formula: F_L = µ_SN = µ_S mg
Calculation: From formula,
F_L = 0.3 × 37 × 9.8 = 108.8 N
Answer:
The force required to move the block is 108.8 N.

Question 3.
A body of mass 37 kg rests on a rough horizontal surface. The minimum horizontal force required to just start the motion is 68.5 N. In order to keep the body moving with constant velocity, a force of 43 N is needed. What is the value of
a) coefficient of static friction? and
b) coefficient of kinetic friction?
Asw:
a) µ_s = 0.188
b) µ_k = 0.118]
Solution:
Given:
F_L = 68.5 N, F_k = 43 N,
m = 37 kg, g = 9.8 m/s²

To find:

i. Coefficient of static friction (µ_s)
ii. Coefficient of kinetic friction (µ_k)

Formulae:

i. µ_s = \(\frac{F_{L}}{N}\) = \(\frac{F_{L}}{m g}\)
ii. µ_k = \(\frac{F_{k}}{N}\) = \(\frac{\mathrm{F}_{\mathrm{k}}}{\mathrm{mg}}\)

Calculation:
From formula (i),
∴ µ_s = \(\frac{F_{S}}{N}=\frac{68.5}{37 \times 9.8}\) = 0.1889
From formula (ii),
∴ µ_k = \(\frac{F_{k}}{N}=\frac{43}{37 \times 9.8}\) = 0.1186
Answer:

1. The coefficient of static friction is 0.1889.
2. The coefficient of kinetic friction is 0.1186.

[Note: Answers calculated above are in accordance with textual methods of calculation.]

Question 4.
A wire gets stretched by 4mm due to a certain load. If the same load is applied to a wire of same material with half the length and double the diameter of the first wire. What will be the change in its length?
Solution:
Given. l₁ = 4mm = 4 × 10^-3 m
L₂ = \(\frac{\mathrm{L}_{1}}{2}\), D₂ = 2D, r₂ = 2r₁
To find: Change in length (l₂)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,

= 0.5 × 10^-3 m
= 0.5 mm
The new change in length of the wire is 0.5 mm.

Question 5.
Calculate the work done in stretching a steel wire of length 2m and cross sectional area 0.0225mm² when a load of 100 N is slowly applied to its free end. [Young’s modulus of steel= 2 × 10¹¹ N/m²]
Solution:
Given. L = 2m, F = 100 N,
A = 0.0225 mm² = 2.25 × 10^-8 m²,
Y = 2 × 10^-11 N/m²,
To find: Work (W)
Formula: W = \(\frac{1}{2}\) × F × l
Claculation:

= antilog [log 10 – log 4.5]
= antilog [1.0000 – 0.6532 ]
= antilog [0.3468]
∴ W = 2.222 J
Answer:
The work done in stretching the steel wire is 2.222 J.

Question 6.
A solid metal sphere of volume 0.31m³ is dropped in an ocean where water pressure is 2 × 10⁷ N/m². Calculate change in volume of the sphere if bulk modulus of the metal is 6.1 × 10¹⁰ N/m²
Solution:
Given: V= 0.31 m³, dP = 2 × 10⁷ N/m²,
K = 6.1 × 10¹⁰ N/m²
To find: Change in volume (dV)
Formula: K = V × \(\frac{\mathrm{dP}}{\mathrm{dV}}\)
Calculation: From formula,
dV = \(\frac{\mathrm{V} \times \mathrm{dP}}{\mathrm{K}}\)
∴ dV = \(\frac{0.31 \times 2 \times 10^{7}}{6.1 \times 10^{10}}\) ≈ 10^-4 m³
The change in volume of the sphere is 10^-4 m³.

Question 7.
A wire of mild steel has initial length 1.5 m and diameter 0.60 mm is extended by 6.3 mm when a certain force is applied to it. If Young’s modulus of mild steel is 2.1 × 10¹¹ N/m², calculate the force applied.
Solution:
Given:
L = 1.5m, d = 0.60 mm,
r = \(\frac{d}{2}\) = 0.30 mm = 3 × 10^-4 m,
Y = 2.1 × 10¹¹ N/m²,
l = 6.3 mm = 6.3 × 10^-3 m
To find: Force (F)
Calculation:
From formula,

= 2.1 × 3.142 × 6 × 6.3
= antilog [log 2.1 + log 3.142 + log 6 + log 6.3]
= antilog [0.3222 + 0.4972 + 0.7782 + 0.7993]
= antilog [2.3969]
= 2.494 × 10²
≈ 250 N
The force applied on wire is 250 N.

Question 8.
A composite wire is prepared by joining a tungsten wire and steel wire end to end. Both the wires are of the same length and the same area of cross section. If this composite wire is suspended to a rigid support and a force is applied to its free end, it gets extended by 3.25mm. Calculate the increase in length of tungsten wire and steel wire separately.
[Given: Y_steel = 2 × 10¹¹ Pa, Y_Tungsten = 4.11 × 10¹¹ Pa]
Solution:
Given: l_s + l_T = 3.25 mm,
Y_T = 4.11 × 10¹¹ Pa
Y_s = 2 × 10¹¹ Pa
To find: Extension in tungsten wire (l_T)
Extension in steel wire (l_s)

But l_s + l_T = 3.25
l_s + 0.487 l_s = 3.25
l_s(1 + 0.487) = 3.25
l_s = 2.186 mm
∴ l_T = 3.25 – 2.186
= 1.064 mm
The extension in tungsten wire is 1.064 mm and the extension in steel wire is 2.186 mm.

[Note: Values of Young’s modulus of tungsten and steel considered above are standard values. Using them, calculation is carried out ¡n accordance with textual method.]

Question 9.
A steel wire having cross sectional area 1.2 mm² is stretched by a force of 120 N. If a lateral strain of 1.455 mm is produced in the wire, calculate the Poisson’s ratio.
Solution:
Given: A = 1.2 mm² = 1.2 × 10^-6 m²,
F = 120 N, Y_steel = 2 × 10¹¹ N/m²,
Lateral strain = 1.455 × 10^-4
To find: Poisson’s ratio (σ)

The Poisson’s ratio of steel is 0.291.
[Note: Lateral strain being ratio of two same physical quantities, is unitless. hence, value given in question ¡s modified to 1.455 × 10^-4 to reach the answer given in textbook.]

Question 10.
A telephone wire 125m long and 1mm in radius is stretched to a length 125.25m when a force of 800N is applied. What is the value of Young’s modulus for material of wire?
Solution:
Given: L = 125m,
r = 1 mm= 1 × 10^-3 m
l = 125.25 – 125 = 0.25 m,
F = 800N
To find: Young’s modulus (Y)
Formula: Y \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,
Y = \(\frac{800 \times 125}{3.142 \times 10^{-6} \times 0.25}\)
= {antilog [log 800 + log 125 – log 3.142 – log 0.25 ]} × 10⁶
= {antilog [2.9031 + 2.0969 – 0.4972 – \(\overline{1}\) .3979]} × 10⁶
= {antilog[5.1049]} × 10⁶
= 1.274 × 10⁵
= 1.274 × 10¹¹ N/m²
The Young’s modulus of telephone wire is 1.274 × 10¹¹ N/m².

Question 11.
A rubber band originally 30cm long is stretched to a length of 32cm by certain load. What is the strain produced?
Solution:
Given: L = 30 cm = 30 × 10 ^-2 m,
∆l = 32 cm – 30 cm = 2cm = 2 × 10 ^-2 m
To find. Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2 \times 10^{-2}}{30 \times 10^{-2}}\) = 6.667 × 10 ^-2
The strain produced in the wire is 6.667 × 10 ^-2.

Question 12.
What is the stress in a wire which is 50m long and 0.01cm² in cross section, if the wire bears a load of 100kg?
Solution:
Given: M = 100 kg, L 50 m, A = 0.01 × 10^-4 m
To find: Stress
Formula: Stress = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{\mathrm{Mg}}{\mathrm{A}}\)
Calculation: From formula,
Stress = \(\frac{100 \times 9.8}{0.01 \times 10^{-4}}\) = 9.8 × 10⁸ N/m²
The stress in the wire is 9.8 × 10⁸ N/m².

Question 13.
What is the strain in a cable of original length 50m whose length increases by 2.5cm when a load is lifted?
Solution:
Given: L = 50m, ∆l = 2.5cm = 2.5 × 10 ^-2 m
To find: Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2.5 \times 10^{-2}}{50}\) = 5 × 10^-4
The Strain produced in wire is 5 × 10^-4 .

11th Physics Digest Chapter 6 Mechanical Properties of Solids Intext Questions and Answers

Can you recall? (Textbook Page No. 100)

Question 1.

1. Can you name a few objects which change their shape and size on application of a force and regain their original shape and size when the force is removed?
2. Can you name objects which do not regain their original shape and size when the external force is removed?

Answer:

1. Objects such as rubber, metals, quartz, etc. change their shape and size on application of a force (within specific limit) and regain their original shape and size when the force is removed.
2. Objects such as putty, clay, thick mud. etc. do not regain their original shape and size when the external force is removed.

Can you tell? (Textbook Page No. 107)

Question 1.
Why does a rubber band become loose after repeated use?
Answer:

1. After repeated use of rubber band, its stress-strain curve does not remain linear.
2. In such case, since rubber crosses its elastic limit, there is a permanent set formed on the rubber due to which it becomes loose.

Can you tell? (Textbook Page No.111)

Question 1.
i. It is difficult to run fast on sand.
ii. It is easy to roll than pull a barrel along a road.
iii. An inflated tyre rolls easily than a flat tyre.
iv. Friction is a necessary evil.
Answer:
i.

1. The intermolecular space between crystals of sand is very large as compared to that in a rigid surface.
2. Thus, there are number of depressions at the points of contact of feet and sand surface.
3. Projections and depressions between sand and feet are not completely interlocked.
4. Thus, action and reaction force become unbalanced. The horizontal component of force helps to move forward and vertical component of the force resist to move.
   Hence, it becomes difficult to run fast on sand.

ii.

1. When a barrel is pulled along a road, the friction between the tyres and road is kinetic friction, but when its rolls along the road it undergoes rolling friction.
2. The force of kinetic friction is greater than force of rolling friction.
   Hence, it is easy to roll than pull a barrel along a road.

iii.

1. When the tyre is inflated, the pressure inside the tyre is reducing the normal force between tyre and the ground, and thus reducing the friction between the tyre and the road.
2. When the tyre gets deflated, it gets deformed during rolling, the supplied energy is used up in changing the shape and not overcoming the friction, and thus due to deformation, friction increases.
   Hence, an inflated tyre rolls easily than a flat tyre.

iv.

1. Friction helps us to walk, hold objects in hand, lift objects and without friction we cannot walk, we cannot grip or hold objects with our hands,
2. Friction is responsible for wear and tear of various part of machines, it produces heat in different parts of machine and also produces noise but it also helps in ball bearing or connecting screws.
   Hence, friction is said to be a necessary evil because it is useful as well as harmful.

Internet my friend (Textbook Page No. 111)

Question 1.
i. https ://opentextbc. ca/physicstestbook2/ chapter/friction/
ii. https://www.livescience.com/
iii. https://www.khanacademy.org/science/physics
iv. https://courses.lumenleaming.com/physics/ chapter/5-3-elasticity-stress-and-strain/
v. https://www.toppr.com/guides/physics/
Answer:
[Students are expected to visit the above mentioned websites and collect more information about mechanical properties of solid.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Std 7 Science Chapter 11 Cell Structure and Micro-organisms Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Science Solutions Chapter 11 Cell Structure and Micro-organisms Notes, Textbook Exercise Important Questions and Answers.

Class 7 Science Chapter 11 Cell Structure and Micro-organisms Question Answer Maharashtra Board

1. Answer the following questions.

Question a.
What is a cell?
Answer:
The cell is the fundamental, structural and functional unit of living organism.

Question b.
Name the different organelles in a cell.
Answer:
The nucleus, endoplasmic reticulum, Golgi bodies, lysosomes, mitochondria, vacuoles, plastids, chloroplasts are the different organelles in a cell.

Question c.
What are micro-organisms?
Answer:
The organisms which cannot be seen with our eyes but can only be observed under a microscope are called micro-organisms.

Question d.
Which are the different types of micro-organisms?
Answer:
Algae, fungi, bacteria, protozoa and viruses are various types of micro-organism. Some are unicellular and others are multicellular. Some of them are useful and some are harmful.

2. Fill in the blanks with the proper word.

Question a.
The organelle called the ……………. is present in the plant cells only.
Answer:
chloroplasts

Question b.
Garbage is converted into ……….. by microorganisms.
Answer:
fertilizer

Question c.
In the cell, photosynthesis is carried out with the help of …………… .
Answer:
chloroplast

Question d.
An electron microscope is necessary for the study of ……………… .
Answer:
micro-organism

Question e.
The process of preparing their own food in presence of sunlight and chloroplast by plants cells is known as ……….. .
Answer:
photosynthesis.

3. What is the difference between us?

Question a.
Plant cell and animal cell.
Answer:

Question b.
Prokaryotic cell and Eukaryotic cell
Answer:

4. Sketch and describe in your on words, the plant cell and animal cell.

Question a.
Sketch and describe ¡n your on words, the plant cell and animal cell.
Answer:
There are two types of cell-animal cells and plant cells. These cells contain various types of membrane beyond cell-organelles. Plant cells have a definite shape due to the presence of cell wall. Besides, unlike animal cells, plant cells contain single large vacuole. All these cells are known as eukaryotic cells. It cell has four main parts: the cell wall, cell membrane, cytoplasm and cell organelles.
1. Cell wall: The cell wall is the outermost covering of a cell. It is present only in plant cells.

2. Plasma membrane: The plasma membrane, also called the cell membrane, is a kind of thin covering, (a) It is extremely delicate and flexible, (b) It is the outermost covering of animal cells.

3. Cytoplasm: The liquid part in the cell, present around the nucleus is called cytoplasm, (a) It occupies the space between the plasma membrane and nucleus, (b) Cell organelles are scattered in the cytoplasm.

4. Cell organelles: These mainly include the nucleus, endoplasmic reticulum, Golgi bodies, lysosomes, mitochondria, vacuoles, plastids etc.

Plant cells contain chloroplasts.
(a) The nucleus is the most important organelle of the cell, (b) There is a porous double membrane around it. (c) The nucleus controls all functions of the cell, (d) The endoplasmic reticulum is a sprawling net-like organelle. Its function is to make necessary changes in the proteins produced by ribosomes and send them to the Golgi bodies, (e) Golgi bodies are made up of several flat sacs. Their function is the proper distribution of proteins.

(f) Mitochondria and plastids are organelles with double outer coverings, (g) As mitochondria produce energy, they are called the powerhouses of the cell, (h) The chloroplasts in plant cells carry out the function of photosynthesis, (i) Vacuoles help to throw out waste products of the cell, (j) Vacuoles in animal cells are small whereas there is only one large vacuole in a plant cell.

5. Explain the uses and the harmful effects of micro-organisms.

Question a.
Explain the uses and the harmful effects of, micro-organisms.
Answer:
Micro-organisms which are helpful are called useful micro-organisms.
Uses:
1. Micro-organisms present in nodules of leguminous plants, convert atmospheric nitrogen into its compounds and these compounds help to increase the soil fertility and protein content in the soil.

2. Some micro-organisms are useful in process of fermentation, making the food easily digestible and more nutritious. For producing milk products like butter, buttermilk, cheese, paneer, etc.

3. Microbes present in soil, dung etc. decompose garbage and convert into manure of best quality and surrounding is kept clean.

4. Microbes are also useful for sewage disposal. They help in decomposition of organic compounds in it.
5. Microbes are used in production of vaccines.

6. Microbes are also used in processes like tanning of skin, production of ropes and strings, from agave.
7. Some microbes use oil for their growth. Such microbes are used to clear a layer of oil floating on the surface of an ocean or lake formed due to leak or spill.

8. Farm waste, human urine and faeces, wet garbage etc. is collected and used in a biogas plant to produce biogas and fertilizer.

Harmful effects:
1. Disease producing micro-organisms are called pathogens, they are harmful micro-organisms.

2. Fungus grows on moist food, and microbes release enterotoxins into the food. Such toxins spoil the foods. Eating such spoiled food causes food poisoning i.e. loose motions and vomiting.

3. Pathogens may be present in water bodies contaminated with sewage, and dirt from surroundings, in food with flies sitting on it. If such contaminated food or water is consumed, we may fall ill with diseases like amoebiasis, typhoid, cholera, hepatitis, gastro, etc.

4. Pathogens are released in the air by a person having infection of the respiratory, sneezes or coughs. A healthy person may get infected by pathogens on breathing in the same air and contract diseases like common cold, cough, diphtheria, pneumonia, tuberculosis, etc.

5. Microbes that cause diseases like malaria, dengue, elephantiasis, yellow fever, chikunguniya, zike
fever etc. gain entry into the human body through the bite of a female mosquito.

6. Give reasons.

Question a.
Diseases spread on a large scale during periods of heavy rainfall and floods.
Answer:

1. Due to floods there is shortage of clean, safe drinking water.
2. It gets contaminated with sewage and dirt having disease causing pathogens, causing disease of alimentary canal, typhoid, cholera, dysentery.
3. Due to stagnant water, many mosquitoes breed on it and cause diseases like malaria, dengue, etc.

Question b.
There is a possibility of food poisoning if we eat stale food.
Answer:

1. Fungus grows quickly on moist and stale food. Micro-organisms grown on the food release toxic materials like enterotoxin into the food.
2. Such toxins spoil the food.
3. Eating such spoiled food may cause loose motions and vomiting. So, we should eat food which is freshly prepared.

Question c.
Soil is turned over during tilling.
Answer:

1. Tilling is done to loosen the soil in initial agricultural practice.
2. Loose soil allows the penetration of roots of the plant.
3. By turning of soil, it allows uniform mixing of manure and fertilizer.
4. It increases the fertility of soil. Seeds also germinate easily in aerated soil. Hence, soil is turned during tilling.

Question d.
Fungus grows quickly in moist or humid condition.
Answer:

1. Fungus needs water and moisture for its growth.
2. Humidity brings about spore germination and the fungus is able to grow and reproduce quickly in moist or humid condition.

Question e.
A refrigerator is used in almost every home.
Answer:

1. Refrigerator is used to keep food item in healthy condition and to keep them fresh.
2. If the food items are kept outside, they spoil very fast due to growth of micro-organisms and they make food spoiled and harmful.
3. The optimum temperature for the growth of micro-organism is 15°C to 35°C.
4. In refrigerator the temperature is kept very low. So, the food is preserved in refrigerator.

Question f.
Bread rises during baking.
Answer:

1. The process of fermentation is used in baking, for example, in making bread. Yeast is added to make the dough rise.
2. The fermentation is a chemical process of conversion of one type of carbon compound into another type of carbon compound by the action of micro-organisms.
3. Heat is generated in this process. Carbon dioxide (CO₂) and some other gases are released.
4. These gases cause an increase in volume so the bread dough rises.

Question g.
Fodder is soaked in water before offering to cattle.
Answer:

1. In dry fodder only some part of it is useful for cattle and rest is wasted.
2. When fodder is soaked in water, it sprouts.
3. So, to make the fodder more nutritious and more easy to digest it is soaked in water before offering to cattle.

7. When will you use a simple microscope and when a compound microscope?

Question a.
When will you use a simple microscope and when a compound microscope?
Answer:

1. I will use a simple microscope to magnify the objects and to see the growth of a fungi or mucor on a piece of moist bread.
2. I will use a compound microscope in Research Laboratory and high school science lab to observe micro-organisms which we are not able to see with our naked eye.

Project:

Question 1.
Visit a bakery in your area, collect information about the process of manufacture of their products and make one of them at home.

Class 7 Science Chapter 11 Cell Structure and Micro-organisms Important Questions and Answers

Fill in the blanks and rewrite the sentences:

Question 1.
………… is the fundamental, structural and functional unit of living organism.
Answer:
Cell

Question 2.
The four main parts of the plant cell are …………, …………, ………… and ………… .
Answer:
cell wall, cell membrane, cytoplasm, cell organelle

Question 3.
Plant cell contains ………… which carry out the process of photosynthesis.
Answer:
chloroplast

Question 4.
…………… are called the power houses of the cell.
Answer:
Mitochondria

Question 5.
The outermost covering of plant cell is …………. .
Answer:
cell wall

Question 6.
The outermost covering of animal cell is ………….
Answer:
plasma membrane

Question 7.
The ………… is the most important organelle of the cell.
Answer:
nucleus

Question 8.
………… is a national movement started several years ago to increase awareness about public hygiene and personal hygiene.
Answer:
Swach Bharat Abhiyan

Question 9.
The body temperature of a healthy human being is about ………… .
Answer:
37°C

Question 10.
Micro-organisms use food stuffs for their own nutrition and release toxic materials called ………. .
Answer:
enterotoxins

Name the following:

Question 1.
An instrument used to observe cells.
Answer:
Microscope

Question 2.
I control the function of a cell.
Answer:
Nucleus

Question 3.
I am like a policeman. I do not allow anything and everything to get in and out of the cell.
Answer:
Cell membrane

Question 4.
Outermost layer of the plant cell.
Answer:
Cell wall

Question 5.
Outermost layer of the animal cell.
Answer:
Cell membrane

Question 6.
I am the jelly like substance containing all the organelles.
Answer:
Cytoplasm

Question 7.
I contain thread like structures called chromosome.
Answer:
Nucleus

Question 8.
Which part of the cell contain organelles.
Answer:
Cytoplasm

Question 9.
The unit of measurement used for expressing dimension, size of the cell.
Answer:
Nanometer, micrometer

Question 10.
The power house of the cell.
Answer:
Mitochondria

Question 11.
Largest organelle in the plant cell.
Answer:
Vacuole

Question 12.
It is necessary for photosynthesis.
Answer:
Chlorophyll

Question 13.
The living substance in the cell.
Answer:
Cytoplasm

Question 14.
A group of cells.
Answer:
Tissue

Question 15.
Empty structures in cytoplasm.
Answer:
Vacuole

State whether the following statements are True or False. Correct and rewrite the false statement:

Question 1.
Cells can be easily seen with naked eyes.
Answer:
False. We can’t see cells with naked eyes, can be seen under microscope

Question 2.
A single cell can perform all the functions in a unicellular organism.
Answer:
True

Question 3.
Cell wall is present in both plant cells and animal cells.
Answer:
False. Cell wall is present only in plant cell

Question 4.
Vacuoles are not found in plant cell.
Answer:
False. Large vacuole is found in plant cell

Question 5.
Tissue is a group of dissimilar cells.
Answer:
False. Tissue is a group of similar cells.

Question 6.
Unicellular organisms have one celled body.
Answer:
True.

Question 7.
The basic living unit of an organism is an organ.
Answer:
False. The basic living unit of an organism is the cell.

Question 8.
The unit of measurement used for expressing dimension size of the cell is centimetre.
Answer:
False. It is nanometer.

Question 9.
Micro-organism cannot grow in extreme adverse conditions.
Answer:
False. Some micro-organisms can survive in extreme adverse conditions e.g. ocean floor, ice polar region, hot water spring.

Question 10.
Some micro-organisms can grow without oxygen.
Answer:
True

Question 11.
Amoeba has irregular shape.
Answer:
True

Question 12.
The process of fermentation is used for making yogurt from milk.
Answer:
True

Question 13.
Micro-organisms need an optimum temperature of 55°C to 70°C to grow.
Answer:
False. They need temperatures between 15°C to 35°C to grow well.

Question 14.
Cells with membrane bound organelles inside them are called prokaryotic cells.
Answer:
False. Cells with membrane bound organelles inside them are called eukaryotic cells.

Question 15.
Golgi bodies are the power houses of the cells.
Answer:
False. Mitochondria are the power houses of the cell.

Choose the correct word.

Question 1.
Which one of the following terms is not a part of the nucleus?
(a) ribosome
(b) DNA
(c) chromosome
(d) gene
Answer:
(a) ribosome

Question 2.
A suitable term for the various components of cell is.
(a) tissue
(b) cell organelle
(c) chromosome
(d) gene
Answer:
(b) cell organelle

Question 3.
The jelly like fluid substance present in the cells is called.
(a) protoplasm
(b) chromosome
(c) chloroplast
(d) cytoplasm
Answer:
(d) cytoplasm

Question 4.
The units of measurement used for expressing dimension size of the cell are,
(a) centimetre
(b) micrometre
(c) nanometre
(d) metre
Answer:
(c) nanometre, (b) micrometre.

Question 5.
The largest cell in the human body
(a) nerve
(b) muscle
(c) liver
(d) kidney
Answer:
(a) nerve

Question 6.
The barrier between protoplasm and other environment in animal cell
(a) plasma membrane
(b) cell wall
(c) nucleus membrane
Answer:
(a) plasma membrane

Question 7.
The term cell wall is given by
(a) Leeuwenhoek
(b) Robert Hooke
(c) Fleming
Answer:
(b) Robert Hooke

Question 8.
The cell theory was proposed by.
(a) Watsonar Cricks
(b) Schleiden
(c) Schwann
(d) Mengal Morgan
Answer:
(b) Schleiden, (c) Schwann.

Question 9.
Which of the following features will help you in distinguishing a plant cell from an animal cell.
(a) cell wall
(b) cell membrane
(c) mitochondria
(d) nucleus
Answer:
(a) cell wall

Question 10.
The gas released during the preparation of bread,
(a) O₂
(b) CO₂
(c) nitrogen
(d) sulphur oxide
Answer:
(b) CO₂

Question 11.
The structural-functional unit of life is called.
(a) cell
(b) tissue
(c) organ
(d) organism
Answer:
(a) cell

Question 12.
Which organelle is called power house of the cell?
(a) centrosome
(b) lysosome
(c) plastid
(d) mitochondria
Answer:
(d) mitochondria

Question 13.
Living substance of cell is called.
(а) cytoplasm
(b) protoplasm
(c) nucleus
(d) chromosome
Answer:
(а) cytoplasm

Give scientific reasons:

Question 1.
Mitochondria are called the power houses of the cell.
Answer:

1. Mitochondria are tiny organelles inside the cells that are involved in releasing energy from food.
2. This process is known as cellular respiration.
3. It is for this reason that mitochondria are often referred to as the power houses of the cell.

Question 2.
A compound microscope is used for observing cells.
Answer:

1. Cell are extremely minute in size.
2. We cannot see cells with naked eye.
3. An object when kept on a glass slide is magnified many times by the lenses of this microscope.
4. Hence, compound microscope is used for observing cells.

Question 3.
Cells are the basic structural units of living organism.
Answer:

1. Cells are the smallest unit from which a living organism is made.
2. A cell contains all the necessary structures which are required to carry out various biological processes.
3. A group of cells makes a tissue, which further makes an organ and many organs together make an organ system and finally organism. Thus, the cells are the basic structural units of living organism.

Answer the following in short:

Question 1.
What is a vaccine?
Answer:
Vaccine is a live micro-organism which is weak but in a very small amount, and is injected into a person so that antibodies are produced against that micro-organism.

Question 2.
What are the similarities between the Plant cell and Animal cell?
Answer:
They both have cell membrane, cytoplasm, nucleus, ribosomes, golgi bodies, mito-chondria, vacuoles and chromosomes.

Question 3.
What do micro-organisms need for growth?
Answer:
Micro-organisms need soil, water and decaying material. Temperature suitable for microbial growth is 15 to 35°C moist, humid and warm climate.

What is the difference between us:

Question 1.
Simple microscope and Compound microscope.
Answer:

Answer in details:

Question 1.
Explain the functions of organelles in a cell.
Answer:
1. Functions of cell wall: It consist of cellulose. It is present in plant cell only. It is a protective layer outside the cell membrane. It provides structural support and protection.

2. Function of cell membrane: It controls the movement of substances in and out of the cell. It protect the cell from its surrounding.

3. Function of cytoplasm: It is the jelly like liquid, it occupies space between cell membrane and nucleus. All the organelles are scattered in it.

4. Function of Nucleus: It is the brain of the cell. It directs all cell activities, and contains genetic material called chromosomes made of DNA.

5. Function of mitochondria: It is the power house of cell. It produces energy in the form of ATP from the food.

6. Vacuoles: It is the largest organelle in the plant cell surrounded by membrane. It holds material and waste. It maintains proper pressure. It helps to throw out waste products of cell.

Explain:

Question 1.
Ram ate chaat from a street hawker, when he reached home he fell ill and complained of stomach ache. What could be the reason?
Answer:

1. he chaat Ram ate from a street hawker must be contaminated with harmful micro-organism due to dirty water used in it or stale potato used in it.
2. Toxins are produced by micro-organisms in food.
3. Ram ate that and suffered from food poisoning.

Question 2.
With the help of diagram describe Prokaryotic cell.

Answer:

1. Prokaryotic cell do not have well-defined nucleus.
2. The plasma membrane, cytoplasm and nucleoid are the only components.
3. The prokaryotic cells have smaller ribosomes compared to eukaryotic cells.
4. Bacteria and blue green algae are examples of prokaryotic cell.

Question a.
Draw neat and labelled diagram of plant cell.
Answer:

Question b.
Draw neat and labelled diagram of animal cell.
Answer:

Name the types of cells shown in the diagrams.

Question 1.

Answer:

(a) A fat cell
(b) A nerve cell
(c) A sperm cell
(d) Spirogyra
(e) Red Blood cells

Try this:

Answer the following questions:

Question 1.
Keep a moistened piece of bread or bhakari in a closed box. What will you observe after 3-4 days?
Answer:

1. I will observe growth of fungus or mucor. White cotton like layer or black spots.
2. As we know fungus grows in presence of moisture.

Question 2.
Observe a drop of muddy water or water from a stagnant puddle, under the compound microscope.
Answer:

1. We will observe, living things, micro-organism, bacteria, fungi.
2. It will be swarming withbacteria,paramoecium, amoeba, ciliated bacteria and protozoa, etc.

Question 3.
Take a drop of yoghurt or buttermilk on a glass slide and observe it under a compound microscope.
Answer:

1. I will see Lactobacillus rod shapted bacteria and streptococcus spherical shape bacteria which may be in clusters.
2. Lactobacillus use lactose present in the milk and produce lactic acid which gives tangy taste to yoghurt.

Find out:

Answer the following questions:

Question 1.
Which diseases do micro-organism cause in plants and animals?
Answer:
Diseases caused by micro-organism in plants and animals are:

Question 2.
Why are infants vaccinated according to fixed time schedule?
Answer:
Vaccination is done to protect the child against diseases.
1. If a baby is vaccinated by true vaccine schedule, that baby will have immunity to over 14 diseases by the age of two. With the recommended schedule, babies visit their doctor 5 times in the first 15 months and receive protection against upto 14 diseases in as little as 18 shots.
2. We immunize children so young against these diseases because infancy is the time period that kids are most vulnerable to life threatening diseases.
3. It is not advisable to skip or delay vaccines as this will leave the child vulnerable to disease for a longer period of time.

Can you tell?

Answer the following questions:

Question 1.
Observe cells from various parts of plants like leaves, bark, root tips, etc.
Answer:
Question a.
Are the cells that you observed, all alike?
Answer:
No, all cells do not look alike, each one has different shape and size.

Question b.
What are their shapes?
Answer:

1. The cells of leaves, show a green pigment because of chloroplast.
2. The shape of the cell may be spherical or polygonal.
3. The shape of root tips are oval or polygonal and the cells of back are hexagonal in shape.

Question 2.
Observe the roots of the pea, bean and fenugreek plants. What could be the functions of the nodules on their roots.
Answer:

1. Micro-organisms are present in the root nodules.
2. They fix the atmospheric nitrogen and make it available for plants.

Question 3.
What happens if clothes remain damp in the rainy season?
Answer:

1. During rainy season the humidity in the air is quite high and also.
2. Due to presence of moisture in clothes it becomes breeding ground for fungus.
3. It is the favourable condition for growth of fungus.
4. We can see white cotton like growth of fungus on clothes.

Question 4.
What are the black or white spots sometimes seen on gunny bags?
Answer:
These spots are the growth of many microbes such as fungi, mucus, mold, etc.

Question 5.
Why are leather articles like purses, wallets, belts, footwear always polished before storing away?
Answer:
They are polished so as to protect them from the growth of fungus.

1. Polish creates a layer of wax on them so that moisture cannot enter from atmosphere.
2. It prevents the growth of fungus, which damages the leather.

Question 6.
What is the powdery material found on old currency notes or old rubber or paper?
Answer:

1. The powdery material is the spores of fungi.
2. All the materials like gunny bags, cotton clothes, paper, rubber, etc. are plant products and leather is an animal product.
3. In a humid atmosphere, fungi and some other micro-organisms grow on these articles and spoil or damage them.

Question 7.
Why children are vaccinated?
Answer:

1. A vaccine is produced in a laboratory with the help of microbes, that gives immunity against particular diseases.
2. Vaccine is actually a live micro-organism which is weak.
3. When injected into a person in small amount, antibodies are produced.
4. It increases the resistance power against the disease produced by that micro-organism. So, the possibility of contracting that disease is greatly reduced.

Question 8.
Try this and answer the following questions:

Question a.
Did the garbage in pot B remain unchanged.
Answer:

1. Yes, the garbage in pot B remained unchanged because micro-organisms need nutrients for their growth.
2. In pot B there was no medium for growth of micro-organisms.

Question b.
Where did the garbage in pot ‘A’ disappear? Why?
Answer:

1. Microbes present in soil, dung, etc. decompose the garbage to obtain food material.
2. As a result garbage is soon converted into manure of the best quality and our surroundings are kept clean.

Question 9.
What does your mother do to make yoghurt from milk?
Answer:

1. Few drops of yoghurt or buttermilk are mixed with lukewarm milk and it is kept at room temperature for 8-10 hours.
2. Microbes present in the drops of yoghurt quickly multiply and the milk gets converted into yoghurt. This is a process of fermentation.

Question 10.
Who discovered the process of fermentation?
Answer:

1. Louis Pasteur established that fermentation is initiated by living organisms.
2. It involves yeast microbes, breaking down molecules of complex carbohydrates into simple sugar, alcohol and CO₂.

Use your brain power!

Answer the following questions:

Question 1.
How will you know that a foodstuff is spoilt?
Answer:

1. When the food is kept for a long time it allows the growth of bacteria and fungi.
2. We can see the white layer of bacterial or fungal growth on it, it causes a typical odour, or smell, and also the food tastes sour due to presence of enterotoxins produced by fungi in the food.

Question 2.
What precautions will you take while purchasing food? Why?
Answer:

1. We will see the expiry date. If the food is kept for a long period of time, it may allow the growth of many microbes which can cause disease or food poisoning.
2. We will check for any fungal growth, any white or black spots on it.

Question 3.
Why do food poisoning incidents occur during marriage or other community feasts?
Answer:
1. During marriage feast, food is prepared in very large quantity and food may not be properly washed or if it is cooked with water contaminated, with sewage or dirt which has many disease causing microbes, or the people handling the food may be having dirty hands

2. Also the utensils used for cooking and storing food may be dirty, contaminated with dirt and may produce microbes. The consumption of such food is responsible for food poisoning.

Question 4.
How do the cells acquire definite shapes?
Answer:
The cells acquire definite shapes due to the presence of cell wall.

Question 5.
How are cells protected?
Answer:

1. Plant cells are protected due to presence of cell wall.
2. Animal cells are protected by the double plasma membrane.

Question 6.
What are the needs of cells?
Answer:

1. The most important things for a cell are oxygen and glucose.
2. Cell uses these during process of glycolysis and makes ATP which is energy source.

Question 7.
Can the point of a needle accommodate micro-organism?
Answer:
Yes, they are smaller than the point of a needle.

Question 8.
Why should dry and wet waste be collected separately?
Answer:

1. Dry waste consist of plastic, glass, metals, paper, etc. It is easier to segregate dry waste so that it is easier for treatment and recycling of waste.
2. Wet waste consists of organic matter. Wet garbage is converted into manure of the best quality and surroundings are kept clean.

Question 9.
Why is yoghurt mixed in the batter or dough for making rava-idli, butter naan?
Answer:

1. The microbes present in yoghurt are allowed to grow in batter or dough.
2. They break down these substances producing new compound and gases are released as they grow and multiply in them which allows the batter, dough to rise.
3. This process is called fermentation.
4. This makes the food soft and nutritious.

Question 10.
How do preparation like yoghurt, idli, dosa become easy to digest?
Answer:
Fermentation does detoxification and splits complex carbohydrates and proteins into simple ones. Thus, making it easy to digest.

Question 11.
What is the co-relation between the normal body temperature of humans which is 37°C and the optimum temperature for the growth of micro-organism, 15 °C to 35 °C?
Answer:

1. Each micro-organism needs a specific environment for growth and reproduction.
2. Optimum temperature for the growth of micro-organism is 15°C to 35°C.
3. Normal body temperature of human body is 37°C. At that temperature micro-organism can not grow and cause disease.

Question 12.
How do micro-organism survive the adverse conditions?
Answer:

1. During adverse conditions micro-organisms form a thick covering around themselves and stop their life processes.
2. On return of favourable conditions they come out of the protective covering and continue their life processes.

Maharashtra State Board Class 7 Science Textbook Solutions

• Cell Structure and Micro-organisms Class 7 Science Textbook Solutions
• The Muscular System and Digestive System in Human Beings Class 7 Science Textbook Solutions
• Changes – Physical and Chemical Class 7 Science Textbook Solutions
• Elements, Compounds and Mixtures Class 7 Science Textbook Solutions
• Materials We Use Class 7 Science Textbook Solutions
• Natural Resources Class 7 Science Textbook Solutions
• Effects of Light Class 7 Science Textbook Solutions
• Sound: Production of Sound Class 7 Science Textbook Solutions
• Properties of a Magnetic Field Class 7 Science Textbook Solutions
• In the World of Stars Class 7 Science Textbook Solutions

Gravitation Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 5 Gravitation Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 5 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 5 Exercise Solutions

1. Choose the correct option.

Question 1.
The value of acceleration due to gravity is maximum at
(A) the equator of the Earth
(B) the centre of the Earth.
(C) the pole of the Earth.
(D) slightly above the surface of the Earth.
Answer:
(C) the pole of the Earth.

Question 2.
The weight of a particle at the centre of the Earth is _________
(A) infinite.
(B) zero.
(C) same as that at other places.
(D) greater than at the poles.
Answer:
(B) zero.

Question 3.
The gravitational potential due to the Earth is minimum at
(A) the centre of the Earth.
(B) the surface of the Earth.
(C) a points inside the Earth but not at its centre.
(D) infinite distance.
Answer:
(A) the centre of the Earth.

Question 4.
The binding energy of a satellite revolving around planet in a circular orbit is 3 × 10⁹ J. Its kinetic energy is _________
(A) 6 × 10⁹ J
(B) -3 × 10⁹ J
(C) -6 × 10⁺⁹ J
(D) 3 × 10⁺⁹J
Answer:
(D) 3 × 10⁺⁹J

2. Answer the following questions.

Question 1.
State Kepler’s law equal of area.
Answer:
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.

Question 2.
State Kepler’s law of period.
Answer:
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.

Question 3.
What are the dimensions of the universal gravitational constant?
Answer:
The dimensions of universal gravitational constant are: [L³M^-1T^-2].

Question 4.
Define binding energy of a satellite.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.

Question 5.
What do you mean by geostationary satellite?
Answer:
Some satellites that revolve around the Earth in equatorial plane have same sense of rotation as that of the Earth. The also have the same period of rotation as that of the Earth i.e.. 24 hours. Due to this, these satellites appear stationary from the Earth’s surface and are known as geostationary satellites.

Question 6.
State Newton’s law of gravitation.
Answer:
Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Question 7.
Define escape velocity of a satellite.
Answer:
The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (v_e) of the body.

Question 8.
What is the variation in acceleration due to gravity with altitude?
Answer:
Variation in acceleration due to gravity due to altitude is given by, g_h = g\(\left(\frac{R}{R+h}\right)^{2}\)
where,
g_h = acceleration due to gravity of an object placed at h altitude
g = acceleration due to gravity on surface of the Earth
R = radius of the Earth
h = attitude height of the object from the surface of the Earth.
Hence, acceleration due to gravity decreases with increase in altitude.

Question 9.
On which factors does the escape speed of a body from the surface of Earth depend?
Answer:
The escape speed depends only on the mass and radius of the planet.
[Note: Escape velocity does not depend upon the mass of the body]

Question 10.
As we go from one planet to another planet, how will the mass and weight of a body change?
Answer:

1. As we go from one planet to another, mass of a body remains unaffected.
2. However, due to change in mass and radius of planet, acceleration due to gravity acting on the body changes as, g ∝ \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\).
   Hence, weight of the body also changes as, W ∝ \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\)

Question 11.
What is periodic time of a geostationary satellite?
Answer:
The periodic time of a geostationary satellite is same as that of the Earth i.e., one day or 24 hours.

Question 12.
State Newton’s law of gravitation and express it in vector form.
Answer:

1. Statement:
   Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
2. In vector form, it can be expressed as,
   \(\overrightarrow{\mathrm{F}}_{21}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\left(-\hat{\mathrm{r}}_{21}\right)\)
   where, \(\hat{\mathbf{r}}_{21}\) is the unit vector from m₁ to m₂.
   The force \(\overrightarrow{\mathrm{F}}_{21}\) is directed from m₂ to m₁.

Question 13.
What do you mean by gravitational constant? State its SI units.
Answer:

1. From Newton’s law of gravitation,
   F = G \(\frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
   where, G = constant called universal gravitational constant Its value is 667 X 10^-11 N m²/kg².
2. G = \(\frac{\mathrm{Fr}^{2}}{\mathrm{~m}_{1} \mathrm{~m}_{2}}\)
   If m₁ = m₂ = 1 kg, r = 1 m thenF = G.
   Hence, the universal gravitational constant is the force of gravitation between two particles of unit mass separated by unit distance.
3. Unit: N m²/kg² in SI system.

Question 14.
Why is a minimum two stage rocket necessary for launching of a satellite?
Answer:

1. For the projection of an artificial satellite, it is necessary for the satellite to have a certain velocity.
2. In a single stage rocket, when the fuel in first stage of rocket is ignited on the surface of the Earth, it raises the satellite vertically.
3. The velocity of projection of satellite normal to the surface of the Earth is the vertical velocity.
4. If this vertical velocity is less than the escape velocity (v_e), the satellite returns to the Earth’s surface. While, if the vertical velocity is greater than or equal to the escape velocity, the satellite will escape from Earth’s gravitational influence and go to infinity.
5. Hence, minimum two stage rocket, one to raise the satellite to desired height and another to provide required hori7ontal velocity, is necessary for launching of a satellite.

Question 15.
State the conditions for various possible orbits of a satellite depending upon the horizontal speed of projection
Answer:
The path of the satellite depends upon the value of horizontal speed of projection v_h relative to critical velocity v_c and escape velocity v_e.
Case (I) v_h < v_c:
The orbit of satellite is an ellipse with point of projection as apogee and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere. it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth.
Case (II) v_h = v_c:
The satellite moves in a stable circular orbit around the Earth.
Case (III) v_c < v_h < v_e:
The satellite moves in an elliptical orbit round the Earth with the point of projection as perigee.
Case (IV) v_h = v_e
The satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity.
Case (V) v_h > v_e:
The satellite escapes from gravitational influence of Earth traversing a hyperbolic path.

3. Answer the following questions in detail.

Question 1.
Derive an expression for critical velocity of a satellite.
Answer:
Expression for critical velocity:

1. Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius.
2. If the satellite is moving in a circular orbit of radius (R + h) = r, its speed must be equal to the magnitude of critical velocity v_c.
3. The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the satellite on the Earth.
   ∴ Centripetal force = Gravitational force
   
   This is the expression for critical speed at the orbit of radius (R + h).
4. The critical speed of a satellite is independent of the mass of the satellite. It depends upon the mass of the Earth and the height at which the satellite is revolving or gravitational acceleration at that altitude.

Question 2.
State any four applications of a communication satellite.
Answer:
Applications of communication satellite:

1. For the transmission of television and radiowave signals over large areas of Earth’s surface.
2. For broadcasting telecommunication.
3. For military purposes.
4. For navigation surveillance.

Question 3.
Show that acceleration due to gravity at height h above the Earth’s surface is g_h = g(\(\frac{R}{R+h}\))²
Answer:
Variation of g due to altitude:

1. Let,
   R = radius of the Earth,
   M = mass of the Earth.
   g = acceleration due to gravity at the surface of the Earth.
2. Consider a body of mass m on the surface of the Earth. The acceleration due to gravity on the Earth’s surface is given by,
   
3. The body is taken at height h above the surface of the Earth as shown in figure. The acceleration due to gravity now changes to,
   g_h = \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}\) …………. (2)
4. Dividing equation (2) by equation (1), we get,
   
   We can rewrite,
   
   This expression can be used to calculate the value of g at height h above the surface of the Earth as long as h<< R.

Question 4.
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Answer:

v_h = horizontal speed of projection
v _c = critical velocity
v_e = escape velocity

Question 5.
Derive an expression for binding energy of a body at rest on the Earth’s surface.
Answer:

1. Let,
   M = mass of the Earth
   m = mass of the satellite
   R = radius of the Earth.
2. Since the satellite is at rest on the Earth, v = 0
   ∴ Kinetic energy of satellite.
   K.E = \(\frac{1}{2}\) mv² = 0
3. Gravitational potential at the Earth’s surface
   = – \(\frac{\mathrm{GM}}{\mathrm{R}}\)
   ∴ Potential energy of satellite = Gravitational potential × mass of satellite
   = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
4. Total energy of sitellite = T.E = P.E + K.E
   ∴ T.E. = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\) + 0 = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
5. Negative sign in the energy indicates that the satellite is bound to the Earth, due to gravitational force of attraction.
6. For the satellite to be free form Earth’s gravitational influence, its total energy should become positive. That energy is the binding energy of the satellite at rest on the surface of the Earth.
   ∴ B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)

Question 6.
Why do astronauts in an orbiting satellite have a feeling of weightlessness?
Answer:

1. For an astronaut, in a satellite, the net force towards the centre of the Earth will always be, F = mg – N.
   where, N is the normal reaction.
2. In the case of a revolving satellite, the satellite is performing a circular motion. The acceleration for this motion is centripetal, which is provided by the gravitational acceleration g at the location of the satellite.
3. In this case, the downward acceleration, a_d = g, or the satellite (along with the astronaut) is in the state of free fall.
4. Thus, the net force acting on astronaut will be, F = mg – ma_d i.e., the apparent weight will be zero, giving the feeling of total weightlessness.

Question 7.
Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Answer:

Question 8.
At which place on the Earth’s surface is the gravitational acceleration maximum? Why?
Answer:

1. Gravitational acceleration on the surface of the Earth depends on latitude of the place as well as rotation and shape of the Earth.
2. At poles, latitude θ = 90°.
   ∴ g’ = g
   i.e., there is no reduction in acceleration due to gravity at poles.
3. Also, shape of the Earth is actually an ellipsoid, bulged at equator. The polar radius of the Earth is 6356 km which minimum. As g ∝ \(\frac{1}{\mathrm{R}^{2}}\), acceleration due to gravity is maximum at poles i.e., 9.8322 m/s².

Question 9.
At which place on the Earth surface the gravitational acceleration minimum? Why?
Answer:

1. Gravitational acceleration on the surface of the Earth depends on latitude of the place as well as rotation and shape of the Earth.
2. At equator, latitude θ = 0°.
   ∴ g’ = g – Rω²
   i.e., the acceleration due to gravity ¡s reduced by amount Rω²(≈ 0.034 m/s²) at equator.
3. Also, shape of the Earth is actually an ellipsoid, bulged at equator. The equatorial radius of the Earth is 6378 km, which is maximum. As g ∝ \(\frac{1}{\mathrm{R}^{2}}\) acceleration due to gravity is minimum on equator i.e., 9.7804 m/s².

Question 10.
Define the binding energy of a satellite. Obtain an expression for binding energy of a satellite revolving around the Earth at certain attitude.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Expression for binding energy of satellite revolving in circular orbit round the Earth:

1. Consider a satellite of mass m revolving at height h above the surface of the Earth in a circular orbit. It possesses potential energy as well as kinetic energy.
2. Let M be the mass of the Earth, R be the Radius of the Earth, v_c be critical velocity of satellite, r = (R + h) be thc radius of the orbit.
3. Kinetic energy of satellite = \(\frac{1}{2} \mathrm{mv}_{\mathrm{c}}^{2}=\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\)
4. The gravitational potential at a distance r from the centre of the Earth is –\(\frac{\mathrm{GM}}{\mathrm{r}}\)
   ∴ Potential energy of satellite = Gravitational potential × mass of satellite
   = –\(\frac{\mathrm{GMm}}{\mathrm{r}}\)
5. The total energy of satellite is given as T.E. = KF. + P.E.
   = \(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}-\frac{\mathrm{GMm}}{\mathrm{r}}=-\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\)
6. Total energy of a circularly orbiting satellite is negative. Negative sign indicates that the satellite is bound to the Earth, due to gravitational force of attraction. For the satellite to be free from the Earth’s gravitational influence its total energy should become zero or positive.
7. Hence the minimum energy to be supplied to unbind the satellite is +\(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\). This is the binding energy of a satellite.

Question 11.
Obtain the formula for acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
Answer:

1. The Earth can be considered to be a sphere made of large number of concentric uniform spherical shells.
2. When an object is on the surface of the Earth it experiences the gravitational force as if the entire mass of the Earth is concentrated at its centre.
3. The acceleration due to gravity on the surface of the Earth is, g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
4. Assuming that the density of the Earth is uniform, mass of the Earth is given by
   M = volume x density = \(\frac{4}{3}\) πR³ρ
   ∴ g = \(\frac{\mathrm{G} \times \frac{4}{3} \pi \mathrm{R}^{3} \rho}{\mathrm{R}^{2}}\) = \(\frac{4}{3}\) πRρG ………….. (1)
5. Consider a body at a point P at the depth d below the surface of the Earth as shown in figure.
   
   Here the force on a body at P due to outer spherical shell shown by shaded region, cancel out due to symmetry.
   The net force on P is only due to the inner sphere of radius OP = R – d.
6. Acceleration due to gravity because of this sphere is,
   
   This equation gives acceleration due to gravity at depth d below the Earth’s surface.

Question 12.
State Kepler’s three laws of planetary motion.
Answer:

• All planets move in elliptical orbits around the Sun with the Sun at one of the foci of the ellipse.
• The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
• The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.

Question 13.
State the formula for acceleration due to gravity at depth ‘d’ and altitude ‘h’ Hence show that their ratio is equal to \(\left(\frac{R-d}{R-2 h}\right)\) by assuming that the altitude is very small as compared to the radius of the Earth.
Answer:

1. For an object at depth d, acceleration due to gravity of the Earth is given by,
   g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) ………………. (1)
2. Also, the acceleration due to gravity at smaller altitude h is given by,
   g_h = g(1 – \(\frac{2 \mathrm{~h}}{\mathrm{R}}\)) ……………. (2)
3. Hence, dividing equation (1) by equation (2),
   we get,
   

Question 14.
What is critical velocity? Obtain an expression for critical velocity of an orbiting satellite. On what factors does it depend?
Answer:
The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbIt round the Earth is called the critical velocity or orbital velocity (v_c).
Expression for critical velocity:

1. Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius.
2. If the satellite is moving in a circular orbit of radius (R + h) = r, its speed must be equal to the magnitude of critical velocity v_c.
3. The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the satellite on the Earth.
   ∴ Centripetal force = Gravitational force
   
   This is the expression for critical speed at the orbit of radius (R + h).
4. The critical speed of a satellite is independent of the mass of the satellite. It depends upon the mass of the Earth and the height at which the satellite is revolving or gravitational acceleration at that altitude.

Question 15.
Define escape speed. Derive an expression for the escape speed of an object from the surface of the earth.
Answer:

1. The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (v_e) of the body.
2. As the gravitational force due to Earth becomes zero at infinite distance, the object has to reach infinite distance in order to escape.
3. Let us consider the kinetic and potential energies of an object thrown vertically upwards with escape velocity v_e.
4. On the surface of the Earth,
   K.E.= \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}\)
   P.E. = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
   Total energy = P.E. + K.E.
   ∴ T.E. = \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}\) ………………. (1)
5. The kinetic energy of the object will go on decreasing with time as it is pulled back by Earth’s gravitational force. It will become zero when it reaches infinity. Thus, at infinite distance from the Earth,
   K.E. = 0
   Also,
   P.E. = –\(\frac{\mathrm{GMm}}{\infty}\) = 0
   ∴ Total energy = P.E. + K.E. = 0
6. As energy is conserved
   \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}=0\) ……[From(1)]
   or, v_e = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)

Question 16.
Describe how an artificial satellite using two stage rocket is launched in an orbit around the Earth.
Answer:

1. Launching of a satellite in an orbit around the Earth cannot take place by use of single stage rocket. It requires minimum two stage rocket.
2. With the help of first stage of rocket, satellite can be taken to a desired height above the surface of the Earth.
3. Then the launcher is rotated in horizontal direction i.e.. through 900 using remote control and the first stage of the rocket is detached.
4. With the help of second stage of rocket, a specific horizontal velocity (v_h) is given to satellite so that it can revolve in a circular path around the Earth.
5. The satellite follows different paths depending upon the horizontal velocity provided to it.

4. Solve the following problems.

Question 1.
At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given radius of Earth is 6400 km.
Solution:
Given: g_d = 90% of g i.e., \(\frac{\mathrm{g}_{\mathrm{d}}}{\mathrm{g}}\) = 0.9,
R = 6400km = 6.4 × 10⁶ m
To find: Distance below the Earth’s surface (d)

At distance 640 km below the surface of the Earth, value of acceleration due to gravity decreases by 10%.

Question 2.
If the Earth were made of wood, the mass of wooden Earth would have been 10% as much as it is now (without change in its diameter). Calculate escape speed from the surface of this Earth.
Solution:

As, we know that the escape speed from surface of the Earth is 11.2 km/s, Substituting value of v_e = 11.2 km/s
V_ew = 11.2 × \(\frac{1}{\sqrt{10}}=\frac{11.2}{3.162}\)
= 11.2 × \(\frac{1}{3.162}\)
…………… [Taking square root value]
= antilog {log(1 1.2) –  Log(3.162)}
= antilog {1.0492 – 0.5000}
= antilog {0.5492} = 3.542
∴ V_ew = 3.54km/s
The escape velocity from the surface of wooden Earth is 3.54 km/s.

Question 3.
Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth.
Given:- G = 6.67 × 10^-11 Nm²/kg²
R = 6400 km
M = 6 × 10²⁴ kg
Solution:
Given:- m = 2000 kg, h = 3600 km = 3.6 × 10⁶ m,
G = 6.67 × 10^-11 Nm²/kg²
R = 6400 km
M = 6 × 10²⁴ kg

To find: i) Kninetic energy (K.E.)
ii) Potential Energy (P.E.)
iii) Total Energy (T.E.)
iv) Binding Energy (B.E.)

From formula (ii),
P.E. = -2 × 40.02 × 10⁹
= -80.04 × 10⁹ J
From formula (iii),
T.E. = (40.02 × 10⁹) + (-80.02 × 10⁹)
= -40.02 × 10⁹ J
From formula (iv),
B.E.= -(-40.02 × 10⁹)
= 40.02 × 10⁹ J
Kinetic energy of the satellite is 40.02 × 10⁹ J, potential energy is -80.04 × 10⁹ J, total energy is -40.02 × 10⁹ J and binding energy is 40.02 × 10⁹ J.
[Note: Total energy of orbiting satellite is negative.]

Question 4.
Two satellites A and B are revolving around a planet. Their periods of revolution are 1 hour and 8 hours respectively. The radius of orbit of satellite B is 4 × 10⁴ km. find radius of orbit of satellite A .
Solution:
Given: T_A = 1 hour, T_B = 8 hour,
r_B = 4 × 10⁴ km
To find: Radius of orbit of satellite A (r_A)

Radius of orbit of satellite A will be 1 × 10⁴ km.

Question 5.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 10³⁰ kg
Mass of the Earth = 5.98 × 10²⁴ kg
The average distance between the Earth and the Sun = 1.5 × 10¹¹ m.
Solution:
Given: M_S = 1.99 × 10³⁰ kg
M_E = 5.98 × 10²⁴ kg, R = 1.5 × 10¹¹ m.
To find: Gravitational force between the Sun and the Earth (F)
Formula: F = \(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
Calculation:As, we know, G = 6.67 × 10^-11 N m²/kg²
From formula,

= antilog {(log(6.67) + log( 1.99) + log(5.98) – log(2.25)} × 10²¹
= antilog {(0.8241) + (0.2989) + (0.7767) – (0.3522)} × 10²¹
= antilog {1.5475} × 10²¹
= 35.28 × 10²¹
= 3.5 × 10²² N
The gravitational force between the Sun and the Earth is 3.5 × 10²² N.

Question 6.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 10²⁴ kg, R = 6400 km).
Solution:
Given: h = 300 km = 0.3 × 10⁶ m,
M = 5.98 × 10²⁴ kg,
R = 6400km = 6.4 × 10⁶ m
G = 6.67 × 10^-11 Nm²/kg²
To find: Acceleration due to gravity at height (g_h)
Formula: g_h = \(\frac{G M}{(R+h)^{2}}\)

Calculation: From formula,
g_h = \(\frac{6.67 \times 10^{-11} \times 5.98 \times 10^{24}}{\left[\left(6.4 \times 10^{6}\right)+\left(0.3 \times 10^{6}\right)\right]^{2}}\)
= \(\frac{6.67 \times 5.98 \times 10^{13}}{(6.7)^{2} \times 10^{12}}\)
6.67 X 10” x 5.98 X iO
= antilog {log(6.67) + log(5.98) – 2log(6.7)} × 10
= antilog{0.8241 + 0.7767 – 2(0.8261)} × 10
= antilog {1.6008 – 1.6522} × 10
= antilog {\(\overline{1}\) .9486} × 10
= 0.8884 × 10 = 8.884 m/s²
Acceleration due to gravity at 300 km will be 8.884 m/s².

Question 7.
Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface. M_E = 5.98 × 10²⁴ kg, R = 6.4 × 10⁶ m.
Solution:
Given: h = 1000 km = 1 × 10⁶ m,
ME = 5.98 × 10²⁴ kg, R = 6.4 × 10⁶ m,
G = 6.67 × 10^-11 N m²/kg²
To find: Speed of satellite (v_c)

Speed of the satellite at height 1000 km is 7.34 × 10³ m/s.

Question 8.
Calculate the value of acceleration due to gravity on the surface of Mars if the radius of Mars = 3.4 × 10³ km and its mass is 6.4 × 10²³ kg.
Solution:
Given:
M = 6.4 × 10²³ kg
R = 3.4 × 10³ = 3.4 × 10⁶ m,
To find: Acceleration due to gravity on the surface of the Mars (g_M)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: As, G = 6.67 × 10^-11 N m²/kg²
From formula,
g_M = \(\frac{6.67 \times 10^{-11} \times 6.4 \times 10^{23}}{\left(3.4 \times 10^{6}\right)^{2}}=\frac{6.67 \times 6.4}{3.4 \times 3.4}\)
= antilog {log(6.67) + log(6.4) – log(3.4) – log(3.4)}
= antilog {(0.8241) + (0.8062) – (0.5315) – (0.53 15)}
= antilog {0.5673}
= 3.693 m/s²
Acceleration due to gravity on the surface of Mars is 3.693 m/s².

Question 9.
A planet has mass 6.4 × 10²⁴ kg and radius 3.4 × 10⁶ m. Calculate energy required to remove on object of mass 800 kg from the surface of the planet to infinity.
Solution:
Given: M = 6.4 × 10²⁴ kg, R = 3.4 × 10⁶ m, m = 800 kg
To find:   Energy required to remove the object from surface of planet to infinity = B.E.
Formula:    B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Calculation: We know that,
G = 6.67 × 10^-11 N m²/kg²
From formula,

= antilog{log(6.67) + log(51.2) – log(3.4)} × 10⁹
= antilog{0.8241 + 1.7093 – 0.5315} × 10⁹
= antilog {2.0019} × 10⁹
= 1.004 × 10² × 10⁹
= 1.004 × 10¹¹ J
Energy required to remove the object from the surface of the planet is 1.004 × 10¹¹ J.
[Note: Answer calculated above ¡s in accordance with retual methods of calculation.]

Question 10.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 10²⁴ kg, Radius of the Earth = 6400 km and the acceleration due to gravity on the surface = 9.8 m/s²
Solution:
Given: M = 6 × 10²⁴ kg,
R = 6400km = 6.4 × 10⁶ m,
g = 9.8 m/s²
To find: Gravitational constant (G)
Formula. g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,
G = \(\frac{\mathrm{gR}^{2}}{\mathrm{M}}\)
G = \(\frac{9.8 \times\left(6.4 \times 10^{6}\right)^{2}}{6 \times 10^{24}}=\frac{401.4 \times 10^{12}}{6 \times 10^{24}}\)
∴ G = 6.69 × 10^-11 N m²/kg²
The value of gravitational constant is 6.69 × 10^-11 N m²/kg².

Question 11.
A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 1/7 times the mass of the Earth and radius twice that of the Earth’s radius.
Solution:
Given: W_E = 5.6 kg-wt.,
\(\frac{\mathrm{M}_{\mathrm{p}}}{\mathrm{M}_{\mathrm{E}}}=\frac{1}{7}, \frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{E}}}\) = 2
To find: Weight of the body on the surface of planet (W_p)
Formula: W = mg = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\)
Calculation: From formula,

Weight of the body on the surface of a planet will be 0.2 kg-wt.
[Note: The answer given above is calculated in accordance with textual method considering the given data].

Question 12.
What is the gravitational potential due to the Earth at a point which is at a height of 2R_E above the surface of the Earth, Mass of the Earth is 6 × 10²⁴ kg, radius of the Earth = 6400 km and G = 6.67 × 10^-11 Nm² kg^-2.
Solution:
Given: M = 6 × 10²⁴ kg,
R_E = 6400km = 6.4 × 10⁶ m,
G = 6.67 × 10^-11 Nm²/kg²,
h = 2R_E
To find: Gravitational potential (V)
Formula: V = – \(\frac{\mathrm{GM}}{\mathrm{r}}\)
Calculation: From formula,

= -2.08 × 10⁷ J kg^-1
Negative sign indicates the attractive nature of gravitational potential.
Gravitational potential due to Earth will be 2.08 × 10⁷ J kg^-1 towards the centre of the Earth.
[Note: According lo definition of gravitational potential its SI unit is J/kg.]

11th Physics Digest Chapter 5 Gravitation Intext Questions and Answers

Can you recall? (Textbook Page No. 78)

Question 1.
i) What are Kepler’s laws?
ii)What is the shape of the orbits of planets?
Answer:

1. The Kepler’s laws are:
   • Kepler’s first law: The orbit of a planet is an ellipse with the Sun at one of the foci.
   • Kepler’s second law: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
   • Kepler’s third law: The square of orbital period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
2. The orbits of the planet are elliptical in shape.

Question 2.
When released from certain height why do objects tend to fall vertically downwards?
Answer:
When released from certain height, objects tend to fall vertically downwards because of the gravitational force exerted by the Earth.

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Laws of Motion Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 4 Laws of Motion Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 4 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 4 Exercise Solutions

1. Choose the correct answer.

Question 1.
Consider the following pair of forces of equal magnitude and opposite directions:
(P) Gravitational forces are exerted on each other by two-point masses separated by a distance.
(Q) Couple of forces are used to rotate a water tap.
(R) Gravitational force and normal force are experienced by an object kept on a table.
For which of these pair/pairs the two forces do NOT cancel each other’s translational
effect?
(A) Only P
(B) Only P and Q
(C) Only R
(D) Only Q and R
Answer:
(A) Only P

Question 2.
Consider the following forces: (w) Force due to tension along a string, (x) Normal force given by a surface, (y) Force due to air resistance, and (z) Buoyant force or upthrust given by a fluid.
Which of these are electromagnetic forces?
(A) Only w, y, and z
(B) Only w, x, and y
(C) Only x, y and z
(D) All four.
Answer:
(D) All four.

Question 3.
At a given instant three-point masses m, 2m, and 3m are equidistant from each other. Consider only the gravitational forces between them. Select correct statement/s for this instance only:
(A) Mass m experiences maximum force.
(B) Mass 2m experiences a maximum force.
(C) Mass 3m experiences a maximum force.
(D) All masses experience a force of the same magnitude.
Answer:
(C) Mass 3m experiences a maximum force.

Question 4.
The rough surface of a horizontal table offers a definite maximum opposing force to initiate the motion of a block along with the table, which is proportional to the resultant normal force given by the table. Forces F₁ and F₂ act at the same angle θ with the horizontal and both are just initiating the sliding motion of the block along with the table. Force F₁ is a pulling force while the force F₂ is a pushing force. F₂ > F₁, because
(A) Component of F₂ adds up to weight to increase the normal reaction.
(B) Component of F₁ adds up to weight to increase the normal reaction.
(C) Component of F₂ adds up to the opposing force.
(D) Component of F₁ adds up to the opposing force.
Answer:
(A) Component of F2 adds up to weight to increase the normal reaction.

Question 5.
A mass 2m moving with some speed is directly approaching another mass m moving with double speed. After some time, they collide with coefficient of restitution 0.5. Ratio of their respective speeds after collision is
(A) 2/3
(B) 3/2
(C) 2
(D) ½
Answer:
(B) 3/2

Question 6.
A uniform rod of mass 2m is held horizontal by two sturdy, practically inextensible vertical strings tied at its ends. A boy of mass 3m hangs himself at one third length of the rod. Ratio of the tension in the string close to the boy to that in the other string is
(A) 2
(B) 1.5
(C) 4/3
(D) 5/3
Answer:
(B) 1.5

Question 7.
Select WRONG statement about centre of mass:
(A) Centre of mass of a ‘C’ shaped uniform rod can never be a point on that rod.
(B) If the line of action of a force passes through the centre of mass, the moment of that force is zero.
(C) Centre of mass of our Earth is not at its geometrical centre.
(D) While balancing an object on a pivot, the line of action of the gravitational force of the earth passes through the centre of mass of the object.
Answer:
(D) While balancing an object on a pivot, the line of action of the gravitational force of the earth passes through the centre of mass of the object.

Question 8.
For which of the following objects will the centre of mass NOT be at their geometrical centre?
(I) An egg
(II) a cylindrical box full of rice
(III) a cubical box containing assorted sweets
(A) Only (I)
(B) Only (I) and (II)
(C) Only (III)
(D) All, (I), (II) and (III).
Answer:
(D) All, (I), (II) and (III).

2. Answer the following questions.

Question 1.
In the following table, every entry on the left column can match with any number of entries on the right side. Pick up all those and write respectively against A, B, C and D.

Answer:

1. Force due to tension in string: Electromagnetic (EM) force, reaction force, non-conservative force.
2. Normal force: Electromagnetic (EM) force, non-conservative force. Reaction force
3. Frictional force: Electromagnetic (EM) force, reaction force, non-conservative force.
4. Resistive force offered by air or water for objects moving through it: Electromagnetic (EM) force, non-conservative force.

Question 2.
In real life objects, never travel with uniform velocity, even on a horizontal surface, unless something is done? Why
is it so? What is to be done?
Answer:

1. According to Newton’s first law, for a body to achieve uniform velocity, the net force acting on it should be zero.
2. In real life, a body in motion is constantly being acted upon by resistive or opposing force like friction, in the direction opposite to that of the motion.
3. To overcome these opposing forces, an additional external force is required. Thus, the net force is not maintained at zero, making it hard to achieve uniform velocity.

Question 3.
For the study of any kind of motion, we never use Newton’s first law of motion directly. Why should it be studied?
Answer:

1. Newton’s first law shows an equivalence between the ‘state of rest’ and ‘state of uniform motion along a straight line.’
2. Newton’s first law of motion defines force as a physical quantity that brings about a change in ‘state of rest’ or ‘state of .uniform motion along a straight line’ of a body.
3. Newton’s first law of motion defines inertia as a fundamental property of every physical object by which the object resists any change in its state of rest or of uniform motion along a straight line. Due to all these reasons, Newton’s first law should be studied.

Question 4.
Are there any situations in which we cannot apply Newton’s laws of motion? Is there any alternative for it?
Answer:

1. Limitation: Newton’s laws of motion cannot be applied for objects moving in non-inertial (accelerated) frame of reference.
   Alternative solution: For non-inertial (accelerated) frame of reference, pseudo force needs to be considered along with all the other forces.
2. Limitation: Newton’s laws of motion are applicable to point objects and rigid bodies. Alternative solution: Body needs to be approximated as a particle as the laws can be applied to individual particles in a rigid body and then summed up over the body.
3. Limitation: Newton’s laws of motion cannot be applied for objects moving with speeds comparable to that of light.
   Alternative solution: Einstein’s special theory of relativity has to be used.
4. Limitation: Newton’s laws of motion cannot be applied for studying the behaviour and interactions of objects having atomic or molecular sizes.
   Alternative solution: Quantum mechanics has to be used.

Question 5.
You are inside a closed capsule from where you are not able to see anything about the outside world. Suddenly you feel that you are pushed towards your right. Can you explain the possible cause (s)? Is it a feeling or a reality? Give at least one more situation like this.
Answer:

1. In a capsule, if we suddenly feel a push towards the right it is because the capsule is in motion and taking a turn towards the left.
2. The push towards the right is a feeling. In reality, when the capsule is beginning its turning motion towards the left, we continue in a straight line.
3. This happens because we try to maintain our direction of motion while the capsule takes a turn towards the left.
4. An external force is required to change our direction of motion. In accordance with one of the inferences from Newton’s first law of motion, in the absence of any external force, we continue to move in a straight line at constant speed and feel the sudden push in the direction opposite to the motion of the capsule.
5. Example: While travelling by bus, when the bus takes a sudden turn we feel the push in the opposite direction.

Question 6.
Among the four fundamental forces, only one force governs your daily life almost entirely. Justify the statement by stating that force.
Answer:

1. Electromagnetic force is the attractive and repulsive force between electrically charged particles.
2. Since electromagnetic force is much stronger than the gravitational force, it dominates all the phenomena on atomic and molecular scales.
3. Majority of the forces experienced in our daily life like friction, normal reaction, tension in strings, elastic forces, viscosity etc. are electromagnetic in nature.
4. The structure of atoms and molecules, the dynamics of chemical reactions etc. are governed by electromagnetic forces.

Thus, out of the four fundamental forces, electromagnetic force governs our daily life almost entirely.

Question 7.
Find the odd man out:
(i) Force responsible for a string to become taut on stretching
(ii) Weight of an object
(iii) The force due to which we can hold an object in hand.
Answer:
Weight of an object.
Reason: Weight of an object (force due to gravity) is a non-contact force while force responsible for a string to become taut (tension force) and force due to which we can hold an object in hand (normal force) are contact forces.

Question 8.
You are sitting next to your friend on ground. Is there any gravitational force of attraction between you two? If so, why are you not coming together naturally? Is any force other than the gravitational force of the earth coming in picture?
Answer:

1. Yes, there exists a gravitational force between me and my friend sitting beside each other.
2. The gravitational force between any two objects is given by, \(\overrightarrow{\mathrm{F}}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\) Where,
   G = universal gravitational constant, m₁ and m₂ = mass of the two objects, r = distance between centres of the two objects
3. Thus, me and my friend attract each other. But due to our small masses, we exert a force on each other, which is too small as compared to the gravitational force of the earth. Hence, me and my friend don’t move towards each other.
4. Apart from gravitational force of the earth, there is the normal force and frictional force acting on both me and my friend.

In Chapter 5, you will study about force of gravitation in detail.

Question 9.
Distinguish between:
(A) Real and pseudo forces,
(B) Conservative and non-conservative forces,
(C) Contact and non-contact forces,
(D) Inertial and non-inertial frames of reference.
Answer:
(A) Real and pseudo forces,

(B) Conservative and non-conservative forces,

(C) Contact and non-contact forces,

(D) Inertial and non-inertial frames of reference.

Question 10.
State the formula for calculating work done by a force. Are there any conditions or limitations in using it directly? If so, state those clearly. Is there any mathematical way out for it? Explain.
Answer:

1. Suppose a constant force \(\overrightarrow{\mathrm{F}}\) acting on a body produces a displacement \(\overrightarrow{\mathrm{S}}\) in the body along the positive X-direction. Then the work done by the force is given as,
   W = F.s cos θ
   Where θ is the angle between the applied force and displacement.
2. If displacement is in the direction of the force applied, θ = 0°
   W = \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{s}}\)

Conditions/limitations for application of work formula:

1. The formula for work done is applicable only if both force \(\overrightarrow{\mathrm{F}}\) and displacement \(\overrightarrow{\mathrm{s}}\) are constant and finite i.e., it cannot be applied when the force is variable.
2. The formula is not applicable in several real- life situations like lifting an object through several thousand kilometres since the gravitational force is not constant. It is not applicable to viscous forces like fluid resistance as they depend upon speed and thus are often not constant with time.
3. The method of integration has to be applied to find the work done by a variable force.

Integral method to find work done by a variable force:

1. Let the force vary non-linearly in magnitude between the points A and B as shown in figure (a).
2. In order to calculate the total work done during the displacement from s₁ to s₂, we need to use integration. For integration, we need to divide the displacement into large numbers of infinitesimal (infinitely small) displacements.
3. Let at P₁, the magnitude of force be F = P₁P₁‘. Due to this force, the body displaces through infinitesimally small displacement ds, in the direction of force.
   It moves from P₁ to P₂.
   ∴ \(\mathrm{d} \overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}}\)
4. But direction of force and displacement are same, we have
   \(\mathrm{d} \overrightarrow{\mathrm{s}}=\mathrm{P}_{1}{ }^{\prime} \mathrm{P}_{2}^{\prime}\)
5. \(\mathrm{d} \overrightarrow{\mathrm{s}}\) is so small that the force F is practically constant for the displacement. As the force is constant, the area of the strip \(\overrightarrow{\mathrm{F}} \cdot \mathrm{d} \overrightarrow{\mathrm{s}}\) is the work done dW for this displacement.
6. Hence, small work done between P₁ to P₂ is dW and is given by
   dW = \(\overrightarrow{\mathrm{F}} \cdot \mathrm{d} \overrightarrow{\mathrm{s}}\) = \(\mathrm{P}_{1} \mathrm{P}_{1}^{\prime} \times \mathrm{P}_{1}^{\prime} \mathrm{P}_{2}^{\prime}\)
   = Area of the strip P₁P₂P₂‘P₁‘.
7. The total work done can be found out by dividing the portion AB into small strips like P₁P₂P₂‘P₁‘ and taking sum of all the areas of the strips.
   ∴ W = \int_{s_{1}}^{s 2} \vec{F} \cdot d \vec{s}=\text { Area } A B B^{\prime} A^{\prime}\(\)
8. Method of integration is applicable if the exact way of variation in \(\overrightarrow{\mathrm{F}}\) and \(\overrightarrow{\mathrm{s}}\) is known and that function is integrable.
9. The work done by the non-linear variable force is represented by the area under the portion of force-displacement graph.
10. Similarly, in case of a linear variable force, the area under the curve from s₁ to s₂ (trapezium APQB) gives total work done W [figure (b)].
    

Question 11.
Justify the statement, “Work and energy are the two sides of a coin”.
Answer:

1. Work and energy both are scalar quantities.
2. Work and energy both have the same dimensions i.e., [M¹L²T^-2].
3. Work and energy both have the same units i.e., SI unit: joule and CGS unit: erg.
4. Energy refers to the total amount of work a body can do.
5. A body capable of doing more work possesses more energy and vice versa.
6. Work done on a body by a conservative force is equal to the change in its kinetic energy.

Thus, work and energy are the two sides of the same

Question 12.
From the terrace of a building of height H, you dropped a ball of mass m. It reached the ground with speed v. Is the relation mgH = \(\frac{1}{2} m \mathrm{v}^{2}\) applicable exactly? If not, how can you account for the difference? Will the ball bounce to the same height from where it was dropped?
Answer:

1. Let the ball dropped from the terrace of a building of height h have mass m. During free fall, the ball is acted upon by gravity (accelerating conservative force).
2. While coming down, the work that is done is equal to the decrease in the potential energy.
3. This work done however is not entirely converted into kinetic energy but some part of it is used in overcoming the air resistance (retarding non-conservative force). This part of energy appears in some other forms such as heat, sound, etc.
4. Thus, in this case of an accelerating conservative force along with a retarding non-conservative force, the work-energy theorem is given as, Decrease in the gravitational
   P.E. = Increase in the kinetic energy + work done against non-conservative forces.
5. Thus, the relation mgh = \(\frac{1}{2} \mathrm{mv}^{2}[latex] is not applicable when non-conservative forces are considered. The part of the energy converted to heat, sound etc also needs to be added to the equation,
6. The ball will not bounce to the same height from where it was dropped due to the loss in kinetic energy during the collision making it an inelastic collision.

Question 13.
State the law of conservation of linear momentum. It is a consequence of which law? Given an example from our daily life for conservation of momentum. Does it hold good during burst of a cracker?
Answer:

1. Statement: The total momentum of an isolated system is conserved during any interaction.
2. The law of conservation of linear momentum is a consequence of Newton’s second law of motion, (in combination with Newton’s third law)
3. Example: When a nail is driven into a wall by striking it with a hammer, the hammer is seen to rebound after striking the nail. This is because the hammer imparts a certain amount of momentum to the nail and the nail imparts an equal and opposite amount of momentum to the hammer.
   Linear momentum conservation during the burst of a cracker:
   • The law of conservation of linear momentum holds good during bursting of a cracker.
   • When a cracker is at rest before explosion, the linear momentum of the cracker is zero.
   • When cracker explodes into number of pieces, scattered in different directions, the vector sum of linear momentum of these pieces is also zero. This is as per the law of conservation of linear momentum.

Question 14.
Define coefficient of restitution and obtain its value for an elastic collision and a perfectly inelastic collision.
Answer:

i. For two colliding bodies, the negative of ratio of relative velocity of separation to relative velocity of approach is called the coefficient of restitution.

ii. Consider an head-on collision of two bodies of masses m₁ and m₂ with respective initial velocities u₁ and u₂. As the collision is head on, the colliding masses are along the same line before and after the collision. Relative velocity of approach is given as,
u_a = u₂ – u₁
Let v₁ and v₂ be their respective velocities after the collision. The relative velocity of recede (or separation) is then v_s = v₂ – v₁

iii. For a head on elastic collision, According to the principle of conservation of linear momentum,
Total initial momentum = Total final momentum

iv. For a perfectly inelastic collision, the colliding bodies move jointly after the collision, i.e., v₁ = v₂
∴ v₁ – v₂ = 0
Substituting this in equation (1), e = 0.

Question 15.
Discuss the following as special cases of elastic collisions and obtain their exact or approximate final velocities in terms
of their initial velocities.
(i) Colliding bodies are identical.
(ii) A very heavy object collides on a lighter object, initially at rest.
(iii) A very light object collides on a comparatively much massive object, initially at rest.
Answer:
The final velocities after a head-on elastic collision is given as,

i. Colliding bodies are identical
If m₁ = m₂, then v₁ = u₂ and v₂ = u₁
Thus, objects will exchange their velocities after head on elastic collision.

ii. A very heavy object collides with a lighter object, initially at rest.
Let m₁ be the mass of the heavier body and m₂ be the mass of the lighter body i.e., m₁ >> m₂; lighter particle is at rest i.e., u₂ = 0 then,

i.e., the heavier colliding body is left unaffected and the lighter body which is struck, travels with double the speed of the massive striking body.

iii. A very light object collides on a comparatively much massive object, initially at rest.
If m₁ is mass of a light body and m₂ is mass of heavy body i.e., m₁ << m₂ and u₂ = 0. Thus, m₁ can be neglected.
Hence v₁ ≅ -u₁, and v₂ ≅ 0.
i.e., the tiny (lighter) object rebounds with same speed while the massive object is unaffected.

Question 16.
A bullet of mass m₁ travelling with a velocity u strikes a stationary wooden block of mass m₂ and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
Answer:

1. A bullet of mass m₁ travelling with a velocity u, striking a stationary wooden block of mass m₂ and getting embedded into it is a case of perfectly inelastic collision.
2. In a perfectly inelastic collision, although there is a loss in kinetic energy, the principle of conservation of energy is not violated as the total energy of the system is conserved.

Loss in the kinetic energy during a perfectly inelastic head on collision:

1. Let two bodies A and B of masses m₁ and m₂ move with initial velocity [latex]\overrightarrow{\mathrm{u}_{1}}\), and \(\overrightarrow{\mathrm{u}_{2}}\) respectively such that particle A collides head- on with particle B i.e., u₁ > u₂.
2. If the collision is perfectly inelastic, the particles stick together and move with a common velocity \(\overrightarrow{\mathbf{V}}\) after the collision along the same straight line.
   loss in kinetic energy = total initial kinetic energy – total final kinetic energy,
3. By the law of conservation of momentum, m₁u₁ + m₂u₂ = (m₁ + m₂) v
   ∴ v = \(\frac{\mathrm{m}_{1} \mathrm{u}_{1}+\mathrm{m}_{2} \mathrm{u}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\)
4. Loss of Kinetic energy,
   
5. Both the masses and the term (u₁ – u₂)² are positive. Hence, there is always a loss in a perfectly inelastic collision. For a perfectly inelastic collision, as e = 0, the loss is maximum.

Question 17.
One of the effects of a force is to change the momentum. Define the quantity related to this and explain it for a variable
force. Usually when do we define it instead of using the force?
Answer:

1. Impulse is the quantity related to change in momentum.
2. Impulse is defined as the change of momentum of an object when the object is acted upon by a force for a given time interval.

Need to define impulse:

1. In cases when time for which an appreciable force acting on an object is extremely small, it becomes difficult to measure the force and time independently.
2. In such cases, however, the effect of the force i.e, the change in momentum due to the force is noticeable and can be measured.
3. For such cases, it is convenient to define impulse itself as a physical quantity.
4. Example: Hitting a ball with a bat, giving a kick to a foot-ball, hammering a nail, bouncing a ball from a hard surface, etc.

Impulse for a variable force:

1. Consider the collision between a bat and ball. The variation of the force as a function of time is shown below. The force axis is starting from zero.
2. From the graph, it can be seen that the force is zero before the impact. It rises to a maximum during the impact and decreases to zero after the impact.
3. The shaded area or the area under the curve of the force -time graph gives the product of force against the corresponding time (∆t) which is the impulse of the force.
   Area of ABCDE = F. ∆t = impulse of force
4. For a constant force, the area under the curve is a rectangle.
5. In case of a softer tennis ball, the collision time becomes larger and the maximum force becomes less keeping the area under curve of the (F – t) graph same.
   Area of ABCDE = Area of PQRST

In chapter 3, you have studied the concept of using area under the curve.

Question 18.
While rotating an object or while opening a door or a water tap we apply a force or forces. Under which conditions is this process easy for us? Why? Define the vector quantity concerned. How does it differ for a single force and for two opposite forces with different lines of action?
Answer:

1. Opening a door can be done with ease if the force applied is:
   • proportional to the mass of the object
   • far away from the axis of rotation and the direction of force is perpendicular to the line joining the axis of rotation with the point of application of force.
2. This is because, the rotational ability of a force depends not only upon the magnitude and direction of force but also on the point where the force acts with respect to the axis of rotation.
3. Rotating an object like a water tap can be done with ease if the two forces are equal in magnitude but opposite in direction are applied along different lines of action.
4. The ability of a force to produce rotational motion is measured by its turning effect called ‘moment of force’ or ‘torque’.
5. However, a moment of couple or rotational effect of a couple is also called torque.
6. For differences in the two vector quantities.

Question 19.
Why is the moment of a couple independent of the axis of rotation even if the axis is fixed?
Answer:

1. Consider a rectangular sheet free to rotate only about a fixed axis of rotation, perpendicular to the plane.
2. A couple of forces \(\overrightarrow{\mathrm{F}}\) and –\(\overrightarrow{\mathrm{F}}\) is acting on the sheet at two different locations.
3. Consider the torque of the couple as two torques due to individual forces causing rotation about the axis of rotation.
4. Case 1: The axis of rotation is between the lines of action of the two forces constituting the couple. Let x and y be the perpendicular distances of the axis of rotation from the forces \(\overrightarrow{\mathrm{F}}\) and –\(\overrightarrow{\mathrm{F}}\) respectively.
   In this case, the pair of forces cause anticlockwise rotation. As a result, the direction of individual torques due to the two forces is the same.
   
5. Case 2: Lines of action of both the forces are on the same side of the axis of rotation. Let q and p be the perpendicular distances of the axis of rotation from the forces \(\overrightarrow{\mathrm{F}}\) and –\(\overrightarrow{\mathrm{F}}\)

Question 20.
Explain balancing or mechanical equilibrium. Linear velocity of a rotating fan as a whole is generally zero. Is it in
mechanical equilibrium? Justify your answer.
Answer:

1. The state in which the momentum of a system is constant in the absence of an external unbalanced force is called mechanical equilibrium.
2. A particle is said to be in mechanical equilibrium, if no net force is acting upon it.
3. In case of a system of bodies to be in mechanical equilibrium, the net force acting on any part of the system should be zero i.e., the velocity or linear momentum of all parts of the system must be constant or zero. There should be no acceleration in any part of the system.
4. Mathematically, for a system in mechanical equilibrium, \(\sum \vec{F}\) = 0.
5. In case of rotating fan, if linear velocity is zero, then the linear momentum is zero. That means there is no net force acting on the fan. Hence, the fan is in mechanical equilibrium.

Question 21.
Why do we need to know the centre of mass of an object? For which objects, its position may differ from that of the centre of gravity?
Use g = 10 m s^-2, unless, otherwise stated.
Answer:

1. Centre of mass of an object allows us to apply Newton’s laws of motion to finite objects (objects of measurable size) by considering these objects as point objects.
2. For objects in non-uniform gravitational field or whose size is comparable to that of the Earth (size at least few thousand km), the position of centre of mass will differ than that of centre of gravity.

3. Solve the following problems.

Question 1.
A truck of mass 5 ton is travelling on a horizontal road with 36 km hr^-1 stops on travelling 1 km after its engine fails suddenly. What fraction of its weight is the frictional force exerted by the road? If we assume that the story repeats for a car of mass 1 ton i.e., can moving with same speed stops in similar distance same how much will the fraction be?
[Ans: \(\frac{1}{200}\) in the both]
Solution:
Given: m_truck = 5 ton = 5000 kg,
m_car = 1 ton = 1000 kg,
u = 36km/hr = 10 m/s,
v = 0 m/s, s = 1 km = 1000 m
To find: Ratio of force of friction to the weight of vehicle
Formulae:
i. v² = u² + 2as
ii. F = ma
Calculation: From formula (i),
2 × a_truck × s = v² – u²
∴ 2 × a_truck × 1000 = 0² – 10²
∴ 200a_truck = -100
∴ a_truck = -0.05 m/s²
Negative sign indicates that velocity is decreasing
From formula (ii),
F_truck = m_truck × a_truck = 5000 × 0.05
= 250 N

Answer:
The frictional force acting on both the truck and the car is \(\frac{1}{200}\) of their weight.

Question 2.
A lighter object A and a heavier object B are initially at rest. Both are imparted the same linear momentum. Which will start with greater kinetic energy: A or B or both will start with the same energy?
[Ans: A]
Solution:

1. Let m₁ and m₂ be the masses of light object A and heavy object B and v₁ and v₂ be their respective velocities.
2. Since both are imparted with the same linear momentum,
   m₁ v₁ = m₂ v₂
3. Kinetic energy of the lighter object A
   
4. As m₁ < m₂, therefore K.E._A > K.E._B, i.e, the lighter body A has more kinetic energy.

Question 3.
As i was standing on a weighing machine inside a lift it recorded 50 kg wt. Suddenly for few seconds it recorded 45 kg wt. What must have happened during that time? Explain with complete numerical analysis. [Ans: Lift must be coming down with acceleration \(\frac{\mathrm{g}}{10}\) = 1 ms^-2]
Solution:
The weight recorded by weighing machine is always apparent weight and a measure of reaction force acting on the person. As the apparent weight (45 kg-wt) in this case is less than actual weight (50 kg-wt) the lift must be accelerated downwards during that time.

Numerical Analysis

1. Weight on the weighing machine inside the lift is recorded as 50 kg-wt
   ∴ mg = 50 kg-wt
   
2. This weight acts on the weighing machine which offers a reaction R given by the reading of the weighing machine
   ∴ R = 45kg-wt = \(\frac{9}{10}\)mg
3. The forces acting on person inside lift are as follows:
   • Weight mg downward (exerted by the earth)
   • Normal reaction (R) upward (exerted by the floor)
4. As, R < mg, the net force is in downward direction and given as,
   mg – R=ma
   But R = \(\frac{9}{10}\)mg.
   ∴ mg – \(\frac{9}{10}\)mg = ma
   ∴ \(\frac{mg}{10}\) = ma
   ∴ a = g/10
   ∴ a = 1 m/s² (∵ g = 1 m/s²)
5. Therefore, the elevator must be accelerated downwards with an acceleration of 1 m/s² at that time.

Question 4.
Figure below shows a block of mass 35 kg resting on a table. The table is so rough that it offers a self adjusting resistive force 10% of the weight of the block for its sliding motion along the table. A 20 kg wt load is attached to the block and is passed over a pulley to hang freely on the left side. On the right side there is a 2 kg wt pan attached to the block and hung freely. Weights of 1 kg wt each, can be added to the pan. Minimum how many and maximum how many such weights can be added into the pan so that the block does not slide along the table? [Ans: Min 15, maximum 21].

Solution:
Frictional (resistive) force f = 10% (weight)
= \(\frac{10}{100}\) × 35 × 10 = 35N 100

i. Consider FBD for 20 kg-wt load. Initially, the block kept on the table is moving towards left, because of the movement of block of mass 20 kg in downward direction.
Thus, for block of mass 20 kg,
ma = mg – T₁ …. (1)
Consider the forces acting on the block of mass 35 kg in horizontal direction only as shown in figure (b). Thus, the force equation for this block is, m₁a = T₁ – T₂ – f ….(2)
To prevent the block from sliding across the table,
m₁a = ma = 0
∴ T₁ = mg = 200 N ….[From (1)]
T₁ = T₂ + f ….[From (2)]
∴ T₂ + f = 200
∴ T₂ = 200 – 35 = 165 N
Thus, the total force acting on the block from right hand side should be 165 N.
∴ Total mass = 16.5 kg
∴ Minimum weight to be added = 16.5 – 2 = 14.5 kg
≈ 15 weights of 1 kg each

ii. Now, considering motion of the block towards right, the force equations for the masses in the pan and the block of mass 35 kg can be determined from FBD shown

From figure (c)
m₁a = T₂ – T₁ – f ….(iii)
From figure (d),
m₂a = m₂g – T₂ … .(iv)
To prevent the block of mass 35 kg from sliding across the table, m₁a = m₂a = 0
From equations (iii) and (iv),
T₂ = T₁ + f
T₂ = m₂g
∴ m₂g = 200 + 35 = 235 N
∴ The maximum mass required to stop the sliding = 23.5 – 2 = 21.5kg ≈ 21 weights of 1 kg
Answer:
The minimum 15 weights and maximum 21 weights of 1 kg each are required to stop the block from sliding.

Question 5.
Power is rate of doing work or the rate at which energy is supplied to the system. A constant force F is applied to a body
of mass m. Power delivered by the force at time t from the start is proportional to
(a) t
(b) t²
(c) \(\sqrt{t}\)
(d) t⁰
Derive the expression for power in terms of F, m and t.
[Ans: p = \(\frac{F^{2} t}{m}\), ∴ p ∝ t]
Solution:
Derivation for expression of power:

i. A constant force F is applied to a body of mass (m) initially at rest (u = 0).

ii. We have,
v = u + at
∴ v = 0 + at
∴ v = at …. (1)

iii. Now, power is the rate of doing work,
∴ P = \(\frac{\mathrm{d} \mathrm{W}}{\mathrm{d} \mathrm{t}}\)
∴ P = F. \(\frac{\mathrm{d} \mathrm{s}}{\mathrm{dt}}\) [∵ dW = F. ds]

iv. But \(\frac{\mathrm{d} \mathrm{s}}{\mathrm{dt}}\) = v, the instantaneous velocity of the particle.
∴ P = F.V … (2)

v. According to Newton’s second law,
F = ma … (3)

vi. Substituting equations (1) and (3) in equation (2)
P = (ma) (at)
∴ P = ma²t
∴ P = \(\frac{m^{2} a^{2}}{m}\) × t
∴ P = \(\frac{\mathrm{F}^{2}}{\mathrm{~m}} \mathrm{t}\)

vii. As F and m are constant, therefore, P ∝ t.

Question 6.
40000 litre of oil of density 0.9 g cc is pumped from an oil tanker ship into a storage tank at 10 m higher level than the ship in half an hour. What should be the power of the pump? [Ans: 2 kW]
Solution:
h = 10 m, ρ = 0.9 g/cc = 900 kg/m³, g = 10 m/s²,
V = 40000 litre = 40000 × 10³ × 10^-6 m³
= 40 m³
T = 30 min = 1800 s
To find: Power(P)
Formula: P = \(\frac{\mathrm{W}}{\mathrm{t}}=\frac{\mathrm{h} \rho \mathrm{gV}}{\mathrm{t}}\)
Calculation: From formula,
P = \(\frac{10 \times 900 \times 10 \times 40}{1800}\)
∴ P = 2000 W
∴ P = 2 kW
Answer:
The power of the pump is 2 kW.

Question 7.
Ten identical masses (m each) are connected one below the other with 10 strings. Holding the topmost string, the system is accelerated upwards with acceleration g/2. What is the tension in the 6th string from the top (Topmost string being the first string)? [Ans: 6 mg]
Solution
Consider the 6^th string from the top. The number of masses below the 6^th string is 5. Thus, FBD for the 6^th mass is given in figure (b).

Answer:
Tension in the 6^th string is 7.5 mg.
[Note: The answer given above is modified considering the correct textual concepts.]

Question 8.
Two galaxies of masses 9 billion solar mass and 4 billion solar mass are 5 million light-years apart. If, the Sun has to cross the line joining them, without being attracted by either of them, through what point it should pass? [Ans: 3 million light-years from the 9 billion solar mass]
Solution:
The Sun can cross the line joining the two galaxies without being attracted by either of them if it passes from a neutral point. A neutral point is a point on the line joining two objects where the effect of gravitational forces acting due to both the objects is nullified.
Given that;
m₁ = 9 × 10⁹ M_s
m₂ = 4 × 10⁹ M_s
r = 5 × 10⁶ light years
Let the neutral point be at distance x from mi. If sun is present at that point,

Answer: The Sun has to cross the line from a point at a distance 3 million light years from the galaxy of mass 9 billion solar mass.

Question 9.
While decreasing linearly from 5 N to 3 N, a force displaces an object from 3 m to 5 m. Calculate the work done by this force during this displacement. [Ans: 8 N]
Solution:
For a variable force, work done is given by area under the curve of force v/s displacement graph. From given data, graph can be plotted as follows:

= 8 J
Ans: Work done is 8 J.
[Note: According to the definition of work done, S.J. unit of wõrk done is joule (J)]

Alternate solution:
Work done, w = Area of trapezium ADCB
∴ W = \(\frac{1}{2}\)(AD + CB) × DC
∴ W = 1 (5N + 3N) × (5m – 3m)
= \(\frac{1}{2}\) × 8 × 2 = 8J

Question 10.
Variation of a force in a certain region is given by F = 6x² – 4x – 8. It displaces an object from x = 1 m to x = 2 m in this region. Calculate the amount of work
done. [Ans: Zero]
Solution:

Answer:
The work done is zero.

Question 11.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce 64% of the potential energy is converted into kinetic energy. Calculate the following:
(a) Coefficient of restitution.
(b) Speed with which the ball comes up from the ground after third bounce.
(c) Impulse given by the ball to the ground during this bounce.
(d) Average force exerted by the ground if this impact lasts for 250 ms.
(e) Average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm².
[Ans: 0.8, 5.12 m/s, 1.152N s, 4.608 N, 9.216 × 104 N/m²]
Solution:
Given that, for every bounce, 64% of the initial energy is converted to final energy.
i. Coefficient of restitution in case of inelastic collision is given by,

ii. From equation (1),
∴ v = – eu
∴ After first bounce,
v₁ = – eu
after second bounce,
v₂ = -ev₁ = -e(-eu)= e²u
and after third bounce,
v₃ = – ev₂ = – e(e²u) = – e³u
But u = \(\sqrt{2 \mathrm{gh}}\)

iii. Impulse given by the ball during third bounce, is,

iv. Average force exerted in 250 ms,

v. Average pressure for area
0.5 cm² = 0.5 × 10^-4m²
P = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{4.608}{0.5 \times 10^{-4}}\) = 9.216 × 10⁴ N/m²

Question 12.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of
mass ratio 1:2. The lighter fragment continues to travel downwards with speed of 60 m/s. Calculate the kinetic energy supplied during explosion. [Ans: 200 J]
Solution:
m₁ + m₂ = 0.5 kg, m₁ : m₂ = 1 : 2,
m₁ = \(\frac{1}{6}\) kg,
∴ m₂ = \(\frac{1}{3}\) kg
Initially, when the ball is falling freely for 10s,
v = u + at = 0 + 10(10)
∴ v = 100 m/s = u₁ = u₂
(m₁ + m₂)v = m₁v₁ + m₂v₂
∴ 0.5 × 100 = \(\frac{1}{6}\)(60) + \(\frac{1}{3}\)v₂
∴ 50 = 10 + \(\frac{1}{3}\)v₂
∴ 40 = \(\frac{1}{3}\)v₂
∴ v₂ = 120m/s

∴ K.E. = 200J.
Ans: Kinetic energy supplied is 200 J.

Question 13.
A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution. [Ans: 0.5]
Solution:
Given: m₁ = 2m, m₂ = m, u₁ = 6 cm/s,
u₂ = 2u₁ = 12 cm/s,
v₁ = \(\frac{\mathrm{u}_{1}+\mathrm{u}_{2}}{2}\) = 9cm/s
To find: Coefficient of restitution(e)
Formulae:

i. m₁u₁ +m₂u₂ = m₁v₁ + m₂v₂
ii. e = \(\frac{v_{2}-v_{1}}{u_{1}-u_{2}}\)
Calculation: From formula (i),
[(2m) × 6] + (m × 12) = (2m × 9) + mv₂
∴ v₂ = 6cm/s

From formula (ii),
e = \(\frac{6-9}{6-12}\) = \(\frac{-3}{-6}\) = 0.5

Answer: The coefficient of restitution is 0.5

Question 14.
A 2 m long wooden plank of mass 20 kg is pivoted (supported from below) at 0.5 m from either end. A person of mass 40 kg starts walking from one of these pivots to the farther end. How far can the person walk before the plank topples? [Ans: 1.25 m]
Solution:
Let the person starts walking from pivot P₂ as shown in the figure.

Assume the person can walk up to distance x from P₁ before the plank topples. The plank will topple when the moment exerted by the person about P₁ is not balanced by a moment of force due to plank about P₂.

∴ For equilibrium,
40 × x = 20 × 0.5
∴ x = \(\frac{1}{4}\) = 0.25 m
Hence, the total distance walked by the person is 1.25 m.

Question 15.
A 2 m long ladder of mass 10 kg is kept against a wall such that its base is 1.2 m away from the wall. The wall is smooth but the ground is rough. The roughness of the ground is such that it offers a maximum horizontal resistive force (for sliding motion) half that of normal reaction at the point of contact. A monkey of mass 20 kg starts climbing the ladder. How far can it climb along the ladder? How much is the horizontal reaction at the wall? [Ans: 1.5 m, 15 N]
Solution:

From the figure,
Given that, AC = length of ladder = 2 m
BC= 1.2m
From Pythagoras theorem,
AB = \(\sqrt{\mathrm{AC}^{2}-\mathrm{BC}^{2}}\) = 1.6 m … (i)
Also, ∆ABC ~ ∆DD’C
∴ \(\frac{\mathrm{AB}}{\mathrm{DD}^{\prime}}\) = \(\frac{\mathrm{BC}}{\mathrm{D}^{\prime} \mathrm{C}}\) = \(\frac{\mathrm{AC}}{\mathrm{DC}}\)
∴ \(\frac{1.2}{\mathrm{D}^{\prime} \mathrm{C}}=\frac{2}{1}\)
∴ D’C = 0.6 m … (ii)

The ladder exerts horizontal force \(\overrightarrow{\mathrm{H}}\) on the wall at A and \(\overrightarrow{\mathrm{F}}\) is the force exerted on the ground at C.
As |\(\overrightarrow{\mathrm{F}}\)| = \(|\overrightarrow{\mathrm{H}}|=|\overrightarrow{\mathrm{F}}|=\frac{\mathrm{N}}{2}\) … (iii)

Let monkey climb upto distance x along BC (Horizontal) i.e., CM’ = x .. . .(iv)
Then, the net normal reaction at point C will be, N = 100 + 200 = 300N
From equation (iii),
H = \(\frac{\mathrm{N}}{2}=\frac{300}{2}\) = 150N
By condition of equilibrium, taking moments about C,
(-H × AB) + (W₁ × CD’) + (W₂ × CM’) + (F × 0)’0
∴ (-150 × 1.6) + (100 × 0.6) + (200 × x) = 0
∴ 60 + 200x = 240
∴ 200x = 180
∴ x = 0.9

From figure, it can be shown that,
∆ABC ~ ∆MM’C
∴ \(\frac{\mathrm{BC}}{\mathrm{CM}^{\prime}}\) = \(\frac{\mathrm{AC}}{\mathrm{CM}^{\prime}}\) ∴ \(\frac{\mathrm{1.2}}{\mathrm{0.9}^{\prime}}\) = \(\frac{\mathrm{2}}{\mathrm{CM}^{\prime}}\)
∴ CM = 1.5 m

Answer:

1. The monkey can climb upto 1.5 m along the ladder.
2. The horizontal reaction at wall is 150 N.

Question 16.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system. [Ans: 65 cm, 17.7 cm]
Solution:

The given cubes are arranged as shown in figure. Let one of the comers of smallest cube lie at the origin.
As the cubes are uniform, let their centre of masses lie at their respective centres.
r_A \(\equiv\) (5, 5), r_B \(\equiv\) (20, 10), r_C \(\equiv\) = (45, 15) and r_D \(\equiv\) – (80, 20)
Also, masses of the cubes are,
m_A = \(l_{\mathrm{A}}^{3} \times \rho=10^{3} \rho\)
m_B = (20)³ρ
m_C = (30)³ρ
m_D = (40)³ρ
As the cubes are uniform, p is same for all of them.
∴ For X – co-ordinate of centre of mass of the system,

Similarly,
Y – co-ordinate of centre of mass of system is,

Answer: Centre of mass of the system is located at point (65 cm, 17.7 cm)

Question 17.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the centre of the
sphere while the other is at the boundary. Locate centre of mass of the remaining sphere. [Ans: -R/14 ]
Solution:

Let the centre of the sphere be origin O. Then, r₁ be the position vector of centre of mass of uniform solid sphere and r₂ be the position vector of centre of mass of the cut-out part of the sphere.
Now, mass of the sphere is given as,

∴ Position vector of centre of mass of remaining part,

r_CM = \(\frac{-\mathbf{R}}{14}\)
(Negative sign indicates the distance is on left side of the origin.)
Ans: Position of centre of mass of remaining sphere \(\frac{-\mathbf{R}}{14}\)

Question 18.
In the following table, every item on the left side can match with any number of items on the right hand side. Select all those.

Answer:
i. Elastic collision: (b)
ii. Inelastic collision: (a), (c), (f), (e)
iii. Perfectly inelastic collision: (d)
iv. Head-on collision: (c), (f)

11th Physics Digest Chapter 4 Laws of Motion Intext Questions and Answers

Can you recall? (Textbook Page No. 47)

Question 1.
What are different types of motions?
Answer:
The various types of motion are linear, uniform linear, non-uniform linear, oscillatory, circular, periodic, and random motion.

Question 2.
What do you mean by kinematical equations and what are they?
Answer:
A set of three equations that analyses rectilinear motion of the uniformly accelerated body and help to predict the position of body are called kinematical equations.

1. Equation for velocity-time relation: v = u + at
2. Equation for position-time relation: s = ut + \(\frac{1}{2}\)at²
3. Position-velocity relation: v² = u² + 2as

Can you tell? (Textbook Page No. 48)

Question 1.
Was Aristotle correct? If correct, explain his statement with an illustration.
Answer:
Aristotle was not correct in stating that an external force is required to keep a body in uniform motion.

Question 2.
If wrong, give the correct modified version of his statement.
Answer:
For an uninterrupted motion of a body, an additional external force is required for overcoming opposing/resistive forces.

Can you tell? (Textbook Page No. 48)

Question 1.
What is then special about Newton’s first law if it is derivable from Newton’s second law?
Answer:

1. Newton’s first law shows an equivalence between the ‘state of rest’ and ‘state of uniform motion along a straight line.’
2. Newton’s first law of motion defines force as a physical quantity that brings about a change in ‘state of rest’ or ‘state of .uniform motion along a straight line’ of a body.
3. Newton’s first law of motion defines inertia as a fundamental property of every physical object by which the object resists any change in its state of rest or of uniform motion along a straight line.
4. Due to all these reasons, Newton’s first law should be studied.

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Motion in a Plane Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 3 Motion in a Plane Textbook Exercise Questions and Answers.

Class 11 Physics Chapter 3 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 3 Exercise Solutions

1. Choose the correct option.

Question 1.
An object thrown from a moving bus is on example of __________
(A) Uniform circular motion
(B) Rectilinear motion
(C) Projectile motion
(D) Motion in one dimension
Answer:
(C) Projectile motion

Question 2.
For a particle having a uniform circular motion, which of the following is constant ____________.
(A) Speed
(B) Acceleration
(C) Velocity
(D) Displacement
Answer:
(A) Speed

Question 3.
The bob of a conical pendulum undergoes ___________
(A) Rectilinear motion in horizontal plane
(B) Uniform motion in a horizontal circle
(C) Uniform motion in a vertical circle
(D) Rectilinear motion in vertical circle
Answer:
(B) Uniform motion in a horizontal circle

Question 4.
For uniform acceleration in rectilinear motion which of the following is not correct?
(A) Velocity-time graph is linear
(B) Acceleration is the slope of velocity time graph
(C) The area under the velocity-time graph equals displacement
(D) Velocity-time graph is nonlinear
Answer:
(D) Velocity-time graph is nonlinear

Question 5.
If three particles A, B and C are having velocities \(\overrightarrow{\mathrm{v}}_{A}\), \(\overrightarrow{\mathrm{v}}_{B}\) and \(\overrightarrow{\mathrm{v}}_{C}\) which of the following formula gives the relative velocity of A with respect to B
(A) \(\overrightarrow{\mathrm{v}}_{A}\) + \(\overrightarrow{\mathrm{v}}_{B}\)
(B) \(\overrightarrow{\mathrm{v}}_{A}\) – \(\overrightarrow{\mathrm{v}}_{C}\) + \(\overrightarrow{\mathrm{v}}_{B}\)
(C) \(\overrightarrow{\mathrm{v}}_{A}\) – \(\overrightarrow{\mathrm{v}}_{B}\)
(D) \(\overrightarrow{\mathrm{v}}_{C}\) – \(\overrightarrow{\mathrm{v}}_{A}\)
Answer:
(C) \(\overrightarrow{\mathrm{v}}_{A}\) – \(\overrightarrow{\mathrm{v}}_{B}\)

2. Answer the following questions.

Question 1.
Separate the following in groups of scalar and vectors: velocity, speed, displacement, work done, force, power, energy, acceleration, electric charge, angular velocity.
Answer:
Scalars
Speed, work done, power, energy, electric charge.

Vectors
Velocity, displacement, force, acceleration, angular velocity (pseudo vector).

Question 2.
Define average velocity and instantaneous velocity. When are they same?
Answer:
Average velocity:

1. Average velocity (\(\overrightarrow{\mathrm{v}}_{\mathrm{av}}\)) of an object is the displacement (\(\Delta \overrightarrow{\mathrm{x}}\)) of the object during the time interval (∆t) over which average velocity is being calculated, divided by that time interval.
2. Average velocity = (\(\frac{\text { Displacement }}{\text { Time interval }}\))
   \(\overrightarrow{\mathrm{V}_{\mathrm{av}}}=\frac{\overrightarrow{\mathrm{x}}_{2}-\overrightarrow{\mathrm{x}}_{1}}{\mathrm{t}_{2}-\mathrm{t}_{1}}=\frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}\)
3. Average velocity is a vector quantity.
4. Its SI unit is m/s and dimensions are [M⁰L¹T^-1]
5. For example, if the positions of an object are x +4 m and x = +6 m at times t = O and t = 1 minute respectively, the magnitude of its average velocity during that time is V_av = (6 – 4)1(1 – 0) = 2 m per minute and its direction will be along the positive X-axis.
   ∴ \(\overrightarrow{\mathrm{v}}_{\mathrm{av}}\) = 2 i m/min
   Where, i = unit vector along X-axis.

Instantaneous velocity:

1. The instantaneous velocity (\(\overrightarrow{\mathrm{V}}\)) is the limiting value of ¡he average velocity of the object over a small time interval (∆t) around t when the value of lime interval goes to zero.
2. It is the velocity of an object at a given instant of time.
3. \(\overrightarrow{\mathrm{v}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\)
   where \(\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\) derivative of \(\overrightarrow{\mathrm{x}}\) with respect to t.

In case of uniform rectilinear motion, i.e., when an object is moving with constant velocity along a straight line, the average and instantaneous velocity remain same.

Question 3.
Define free fall.
Answer:
The motion of any object under the influence of gravity alone is called as free fall.

Question 4.
If the motion of an object is described by x = f(t) write formulae for instantaneous velocity and acceleration.
Answer:

1. Instantaneous velocity of an object is given as,
   \(\overrightarrow{\mathrm{v}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\)
2. Motion of the object is given as, x = f(t)
3. The derivative f ‘(f) represents the rate of change of the position f (t) at time t, which is the instantaneous velocity of the object.
   ∴ \(\vec{v}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\) = f'(t)
4. Acceleration is defined as the rate of change of velocity with respect to time.
5. The second derivative of the position function f “(t) represents the rate of change of velocity i.e., acceleration.
   ∴ \(\overrightarrow{\mathrm{a}}=\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\mathrm{d}^{2} \mathrm{x}}{\mathrm{dt}^{2}}\) = f”(t)

Question 5.
Derive equations of motion for a particle moving in a plane and show that the motion can be resolved in two independent motions in mutually perpendicular directions.
Answer:

1. Consider an object moving in an x-y plane. Let the initial velocity of the object be \(\overrightarrow{\mathrm{u}}\) at t = 0 and its velocity at time t be \(\overrightarrow{\mathrm{v}}\).
2. As the acceleration is constant, the average acceleration and the instantaneous acceleration will be equal.
   
   This is the first equation of motion in vector form.
3. Let the displacement of the object from time t
   = 0 to t be \(\overrightarrow{\mathrm{s}}\)
   For constant acceleration, \(\overrightarrow{\mathrm{v}}_{\mathrm{av}}=\frac{\overrightarrow{\mathrm{v}}+\overrightarrow{\mathrm{u}}}{2}\)
   
   This is the second equation of motion in vector form.
4. Equations (1) and (2) can be resolved into their x and y components so as to get corresponding scalar equations as follows.
   v_x = u_x + a_xt ………….. (3)
   v_y = u_y + a_y t …………… (4)
   s_x = u_xt + \(\frac{1}{2}\) a_xt² ………….. (5)
   s_y = u_yt + \(\frac{1}{2}\) a_yt² ………..(6)
5. It can be seen that equations (3) and (5) involve only the x components of displacement, velocity and acceleration while equations (4) and (6) involve only the y components of these quantities.
6. Thus, the motion along the x direction of the object is completely controlled by the x components of velocity and acceleration while that along the y direction is completely controlled by the y components of these quantities.
7. This shows that the two sets of equations are independent of each other and can be solved independently.

Question 6.
Derive equations of motion graphically for a particle having uniform acceleration, moving along a straight line.
Answer:

1. Consider an object starting from position x = 0 at time t = 0. Let the velocity at time (t = 0) and t be u and v respectively.
2. The slope of line PQ gives the acceleration. Thus
   ∴ a = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}-0}=\frac{\mathrm{v}-\mathbf{u}}{\mathrm{t}}\)
   ∴ v = u + at …………… (1)
   This is the first equation of motion.
3. The area under the curve in velocity-time graph gives the displacement of the object.
   ∴ s = area of the quadrilateral OPQS = area of rectangle OPRS + area of triangle PQR.
   = ut + \(\frac{1}{2}\) (v – u) t
   But, from equation (1)
   at = v – u
   ∴ s = ut + \(\frac{1}{2}\) at²
   This is the second equation of motion,
4. The velocity is increasing linearly with time as acceleration is constant. The displacement is given as,
   
   ∴ s = (v² – u²) / (2a)
   ∴ v² – u² = 2as
   This is the third equation of motion.

Question 7.
Derive the formula for the range and maximum height achieved by a projectile thrown from the origin with initial velocity \(\vec{u}\) at an angel θ to the horizontal.
Answer:
Expression for range:

1. Consider a body projected with velocity \(\vec{u}\), at an angle θ of projection from point O in the co-ordinate system of the XY- plane, as shown in figure.
2. The initial velocity \(\vec{u}\) can be resolved into two rectangular components:
   
   u_x = u cos θ (Horizontal component)
   u_y = u sin θ (Vertical component)
3. The horizontal component remains constant throughout the motion due to the absence of any force acting in that direction, while the vertical component changes according to
   v_y = u_y + a_yt
   with a_y = -g and u_y = u sinθ
4. Thus, the components of velocity of the projectile at time t are given by,
   v_x = u_x = u cos θ
   v_y = u_x – gt = usin θ – gt
5. Similarly, the components of displacements of the projectile in the horizontal and vertical directions at time t are given by,
   s = (u cosθ) t
   s_y = (usinθ)t – \(\frac{1}{2}\) gt²
6. At the highest point, the time of ascent of the projectile is given as,
   t_A = \(\frac{u \sin \theta}{g}\) …………..(2)
7. The total time in air i.e., time of flight is given as, T = 2t_A = \(\frac{2u \sin \theta}{g}\) …… (3)
8. The total horizontal distance travelled by the particle in this time T is given as,
   R = u_x ∙ T
   R = u cos θ ∙ (2t_A)
   R = u cos θ ∙ \(\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\) ……………[From (3)]
   R = \(\frac{u^{2}(2 \sin \theta \cdot \cos \theta)}{g}\)
   R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\) ………..[∵ sin 2θ = 2sin∙cosθ]
   This is required expression for horizontal range of the projectile.

Expression for maximum height of a projectile:
The maximum height H reached by the projectile is the distance travelled along the vertical (y) direction in time t_A.

Substituting s_y = H and t = t_a in equation (1),
we have,
H = (u sin θ)t_A – \(\frac{1}{2}\) gt_A²

This equation represents maximum height of projectile.

Question 8.
Show that the path of a projectile is a parabola.
Answer:

1. Consider a body projected with velocity initial velocity \(\vec{u}\) , at an angle θ of projection from point O in the co-ordinate system of the XY-plane. as shown in figure.
   
2. The initial velocity \(\vec{u}\) can be resolved into two rectangular components:
   u_x = u cos θ (Horizontal component)
   u_y = u sin θ (Vertical component)
3. The horizontal component remains constant throughout the motion due to the absence of any force acting in that direction, while the vertical component changes according to,
   v_y = u_y + a_y t
   with a_y, = -g and u_y = u sinθ
4. Thus, the components of velocity of the projectile at time t are given by,
   v_x = u_x = u cosθ
   v_y = u_y – gt = u sinθ – gt
5. Similarly, the components of displacements of the projectile in the horizontal and vertical directions at time t are given by,
   s_x = (u cosθ)t …………..(1)
   s_y = (u sinθ)t – \(\frac{1}{2}\) gt² ………………. (2)
6. As the projectile starts from x = O, we can use
   s_x = x and s_y = y.
   Substituting s_x = x in equation (1),
   x = (u cosθ) t
   ∴ t = \(\frac{\mathrm{X}}{(\mathrm{u} \cos \theta)}\) …………….. (3)
   Substituting, s_y in equation (2),
   y = (u sinθ)t – \(\frac{1}{2}\) gt² …………… (4)
   Substituting equation (3) in equation (4), we have,
   y = u sin θ (\(\frac{\mathrm{X}}{(\mathrm{u} \cos \theta)}\)) – \(\frac{1}{2}\) (\(\frac{\mathrm{X}}{(\mathrm{u} \cos \theta)}\))² g
   ∴ y = x (tan θ) – (\(\frac{g}{2 u^{2} \cos ^{2} \theta}\))x² ………………. (5)
   Equation (5) represents the path of the projectile.
7. If we put tan θ = A and g/2u²cos²θ = B then equation (5) can be written as y = Ax – Bx² where A and B are constants. This is equation of parabola. Hence, path of projectile is a parabola.

Question 9.
What is a conical pendulum? Show that its time period is given by 2π \(\sqrt{\frac{l \cos \theta}{g}}\), where l is the length of the string, θ is the angle that the string makes with the vertical and g is the acceleration due to gravity.
Answer:
A simple pendulum, Ch i given such a motion that the bob describes a horizontal circle and the string making a constant angle with the vertical describes a cone, is called a conical pendulum.

1. Consider a bob of mass m tied to one end of a string of length ‘P and other end is fixed to rigid support.
2. Let the bob be displaced from its mean position and whirled around a horizontal circle of radius ‘r’ with constant angular velocity ω, then the bob performs U.C.M.
3. During the motion, string is inclined to the vertical at an angle θ as shown in the figure above.
4. In the displaced position, there are two forces acting on the bob.
   • The weight mg acting vertically downwards.
   • The tension T acting upward along the string.
5. The tension (T) acting in the string can be resolved into two components:
   • T cosθ acting vertically upwards.
   • T sinθ acting horizontally towards centre of the circle.
6. Since, there is no net force, vertical component T cosθ balances the weight and horizontal component T sinθ provides the necessary centripetal force.
   ∴ T cos θ = mg ……………. (1)
   T sin θ = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = mrω² ……….. (2)
7. Dividing equation (2) by (1),
   tan θ = \(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\) ……….. (3)
   Therefore, the angle made by the string with the vertical is θ = tan^-1 (\(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\))
8. Since we know v = \(\frac{2 \pi \mathrm{r}}{\mathrm{T}}\)
   
   where l is length of the pendulum and h is the vertical distance of the horizontal circle from the fixed point O.

Question 10.
Define angular velocity. Show that the centripetal force on a particle undergoing uniform circular motion is -mω²\(\vec{r}\).
Answer:
Angular velocity of a particle is the rate of change of angular displacement.

Expression for centripetal force on a particle undergoing uniform circular motion:
i) Suppose a particle is performing U.C.M in anticlockwise direction.
The co-ordinate axes are chosen as shown in the figure.
Let,
A = initial position of the particle which lies on positive X-axis
P = instantaneous position after time t
θ = angle made by radius vector
ω = constant angular speed
\(\overrightarrow{\mathrm{r}}\) = instantaneous position vector at time t

ii) From the figure,
\(\overrightarrow{\mathrm{r}}=\hat{\mathrm{i}} \mathrm{x}+\hat{\mathrm{j}} \mathrm{y}\)
where, \(\hat{\mathrm{i}}\) and \(\hat{\mathrm{j}}\) are unit vectors along X-axis and Y-axis respectively.


Negative sign shows that direction of acceleration is opposite to the direction of position vector. Equation (3) is the centripetal acceleration.
vii) Magnitude of centripetal acceleration is given by a = ω²r

viii) The force providing this acceleration should also be along the same direction, hence centripetal.
∴ \(\overrightarrow{\mathrm{F}}\) = m\(\overrightarrow{\mathrm{a}}\) = -mω²\(\overrightarrow{\mathrm{r}}\)
This is the expression for the centripetal force on a particle undergoing uniform circular motion.

ix) Magnitude of F = mω²r = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = mωv

[Note: The definition of angular velocity is not mentioned in this chapter but is in Ch.2 Mathematical Methods.]

3. Solve the following problems.

Question 1.
An aeroplane has a run of 500 m to take off from the runway. It starts from rest and moves with constant acceleration to cover the runway in 30 sec. What is the velocity of the aeroplane at the take off ?
Answer:
Given: Length of runway (s) = 500 m, t = 30 s
To find: Velocity (y)
Formulae. i) s = ut + \(\frac{1}{2}\) at²
ii) v = u + at
Calculation: As the plane was initially at rest, u = 0
From formula (1),
500 = 0 + \(\frac{1}{2}\) × a × (30)²
∴ 500 = 450 a
∴ a = \(\frac{10}{9}\) m/s²
From formula (ii),
v = 0 + \(\frac{10}{9}\) × 30
∴ v = \(\frac{100}{3}\) m/s = (\(\frac{100}{3} \times \frac{18}{5}\)) km/hr
∴ v = 120 km/hr
The velocity of the aeroplane at the take off is 120 km/hr.

Question 2.
A car moving along a straight road with a speed of 120 km/hr, is brought to rest by applying brakes. The car covers a distance of 100 m before it stops. Calculate
(i) the average retardation of the car
(ii) time taken by the car to come to rest.
Answer:
Given: u = 120 kmh^-1 = 120 × \(\frac{5}{18}\) = \(\frac{100}{3}\) ms^-1
s = 100 m, v = 0
To find: i) Average retardation of the car (a)
ii) Time taken by car (t)

Formulae: i) v² – u² = 2as
ii) v = u + at
Calculation: From formula (i),

i) Average retardation of the car is \(\frac{50}{9}\) ms² (in magnitude).
ii) Time taken by the car to come to rest is 6 s.

Question 3.
A car travels at a speed of 50 km/hr for 30 minutes, at 30 km/hr for next 15 minutes and then 70 km/hr for next 45 minutes. What is the average speed of the car?
Answer:
Given: v₁ = 50 km/hr. t₁ = 30 minutes = 0.5 hr,
v₂ = 30 km/hr, t₂ = 15 minutes = 0.25 hr,
v₃ = 70 km/hr, t₃ = 45 minutes 0.75 hr
To find: Average speed of car (v_av)
Formula v_av = \(\frac{\text { total path length }}{\text { total time interval }}\)
Calculation:
Path length,
x₁ = v₁ × t₁ = 50 × 0.5 = 25km
x₂ = v₂ × t₂ = 30 × 0.25 = 7.5 km
x₃ = v₃ × t₃ = 70 × 0.75 = 52.5 km
From formula,
v_av = \(\frac{x_{1}+x_{2}+x_{3}}{t_{1}+t_{2}+t_{3}}\)
∴ v_av = \(\frac{25+7.5+52.5}{0.5+0.25+0.75}=\frac{85}{1.5}\)
∴ v_av = 56.66 km/hr

Question 4.
A velocity-time graph is shown in the adjoining figure.

Determine:

1. initial speed of the car
2. maximum speed attained by the car
3. part of the graph showing zero acceleration
4. part of the graph showing constant retardation
5. distance travelled by the car in first 6 sec.

Answer:

1. Initial speed is at origin i.e. 0 m/s.
2. Maximum speed attained by car, v_max = speed from A to B = 20 m/s.
3. The part of the graph which shows zero acceleration is between t = 3 s and t = 6 s i.e., AB. This is because, during AB there is no change in velocity.
4. The graph shows constant retardation from t = 6 s to t = 8 s i.e., BC.
5. Distance travelled by car in first 6 s
   = Area of OABDO
   = A(△OAE) + A(rect. ABDE)
   = \(\frac{1}{2}\) × 3 × 20 + 3 × 20
   = 30 + 60
   ∴ Distance travelled by car in first 6 s = 90 m

Question 5.
A man throws a ball to maximum horizontal distance of 80 meters. Calculate the maximum height reached.
Answer:
Given: R = 80m
To find: Maximum height reached (H_max)
Formula: R_max = 4H_max
Calculation: From formula,
∴ H_max = \(\frac{\mathrm{R}_{\max }}{4}=\frac{80}{4}\) = 20 m
The maximum height reached by the ball is 20m.

Question 6.
A particle is projected with speed v₀ at angle θ to the horizontal on an inclined surface making an angle Φ (Φ < θ) to the horizontal. Find the range of the projectile along the inclined surface.
Answer:

i) The equation of trajectory of projectile is given by,
y(tan θ)x – (\(\frac{\mathrm{g}}{2 \mathrm{u}^{2} \cos ^{2} \theta}\))x² …………..(1)

ii) In this case to find R substitute,
y = R sinΦ ………….. (2)
x = R cosΦ ………….. (3)

iii) From equations (1), (2) and (3),
we have,

Question 7.
A metro train runs from station A to B to C. It takes 4 minutes in travelling from station A to station B. The train halts at station B for 20 s. Then it starts from station B and reaches station C in the next 3 minutes. At the start, the train accelerates for 10 sec to reach the constant speed of 72 km/hr. The train moving at the constant speed is brought to rest in 10 sec. at next station.
(i) Plot the velocity-time graph for the train travelling from station A to B to C.
(ii) Calculate the distance between stations A, B, and C.
Answer:

The metro train travels from station A to station B in 4 minutes = 240 s.
The trains halts at station B for 20 s.
The train travels from station B’ to station C in 3 minutes= 180 s.
∴ Total time taken by the metro train in travelling from station A to B to C
= 240 + 20 + 180 = 440 s.
At start, the train accelerates for 10 seconds to reach a constant speed of 72 km/hr = 20 m/s.
The train moving is brought to rest in 10 s at next station.
The velocity-time graph for the train travelling from station A to B to C is as follows:
Distance travelled by the train from station A to station B
= Area of PQRS
= A ( △PQQ’) A (☐QRR’) + A(SRR’)
= (\(\frac{1}{2}\) × 10 × 20 + (220 × 20) + (\(\frac{1}{2}\) 10 × 20)
= 100 + 4400 + 100
= 4600m = 4.6km

Distance travelled by the train from station B’ to station C
= Area of EFGD
= A(△EFF’) + A(☐F’FGG’) + A(△DGG’)
= (\(\frac{1}{2}\) × 10 × 20) × (160 × 20) + (\(\frac{1}{2}\) × 10 × 20)
= 100 + 3200 + 100
= 3400m = 3.4km

Question 8.
A train is moving eastward at 10 m/sec. A waiter is walking eastward at 1.2m/sec; and a fly is flying toward the north across the waiter’s tray at 2 m/s. What is the velocity of the fly relative to Earth.
Answer:
Given

Question 9.
A car moves in a circle at the constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of the acceleration of the car.
Answer:
Given: v = 50 m/s, t = 40 s, s = 2πr
To find: acceleration (a)
Formulae: i) v = \(\frac{\mathrm{s}}{\mathrm{t}}\)
ii) a = \(\frac{\mathrm{v}^{2}}{\mathrm{r}}\)
Calculation: From formula (i),
50 = \(\frac{2 \pi \mathrm{r}}{40}\)
∴ r = \(\frac{50 \times 40}{2 \pi}\)
∴ r = \(\frac{1000}{\pi}\) cm
From formula (ii),
a = \(\frac{v^{2}}{r}=\frac{50^{2}}{1000 / \pi}\)
∴ a = \(\frac{5 \pi}{2}\) = 7.85 m/s²
The magnitude of acceleration of the car is 7.85 m/s.

Alternate method:
Given: v = 50 m/s, t = 40 s,
To find: acceleration (a)
Formula: a = rω² = vω
Calculation: From formula,
a = vω
= v(\(\frac{2 \pi}{\mathrm{t}}\))
= 50(\(\frac{2 \times 3.142}{40}\))
= \(\frac{5}{2}\) × 3.142
∴ a = 7.85m/s²

Question 10.
A particle moves in a circle with constant speed of 15 m/s. The radius of the circle is 2 m. Determine the centripetal acceleration of the particle.
Answer:
Given: v = 15 m/s, r = 2m
To find: Centripetal acceleration (a)
Formula: a = \(\frac{\mathrm{v}^{2}}{\mathrm{r}}\)
Calculation: From formula,
a = \(\frac{(15)^{2}}{2}=\frac{225}{2}\)
∴ a = 112.5m/s²
The centripetal acceleration of the particle is 112.5 m/s².

Question 11.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s^-2.
Answer:
Given: 40 ≤ R ≤ 50, θ = 300, g = 10 m/s²
To find: Range of initial velocity (u)
Formula: R = \(\frac{\mathrm{u}^{2} \sin (2 \theta)}{\mathrm{g}}\)
Calculation: From formula,
The range of initial velocity,

∴ 21.49m/s ≤ u ≤ 24.03m/s
The range of initial velocity should be between 21.49 m/s ≤ u ≤ 24.03 m/s.

11th Physics Digest Chapter 3 Motion in a Plane Intext Questions and Answers

Can you recall? (Textbook Page No. 30)

Question 1.
What ¡s meant by motion?
Answer:
The change ¡n the position of an object with respect to its surroundings is called motion.

Question 2.
What Is rectilinear motion?
Answer:
Motion in which an object travels along a straight line is called rectilinear motion.

Question 3.
What is the difference between displacement and distance travelled?
Answer:

• Displacement is the shortest distance between the initial and final points of movement.
• Distance is the actual path followed by a body between the points in which it moves.

Question 4.
What is the difference between uniform and non-uniform motion?
Answer:

• A body is said to have uniform motion if it covers equal distances in equal intervals of time.
• A body is said to have non-uniform motion if it covers unequal distances in equal intervals of time.

Internet my friend (Textbook Page No. 44)

i. hyperphysics.phy-astr.gsu.eduJhbase/mot.html#motcon
ii. www .college-physics.comlbook/mechanics
[Students are expected to visit the above mentioned webs ires and collect more information.]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions

Mathematical Methods Class 11 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 2 Mathematical Methods Textbook Exercise Questions and Answers.

Mathematical Methods Class 11 Exercise Question Answers Solutions Maharashtra Board

Physics Class 11 Chapter 2 Exercise Solutions

1. Choose the correct option.

Question 1.
The resultant of two forces 10 N and 15 N acting along + x and – x-axes respectively, is
(A) 25 N along + x-axis
(B) 25 N along – x-axis
(C) 5 N along + x-axis
(D) 5 N along – x-axis
Answer:
(D) 5 N along – x-axis

Question 2.
For two vectors to be equal, they should have the
(A) same magnitude
(B) same direction
(C) same magnitude and direction
(D) same magnitude but opposite direction
Answer:
(C) same magnitude and direction

Question 3.
The magnitude of scalar product of two unit vectors perpendicular to each other is
(A) zero
(B) 1
(C) -1
(D) 2
Answer:
(A) zero

Question 4.
The magnitude of vector product of two unit vectors making an angle of 60° with each other is
(A) 1
(B) 2
(C) \(\frac{3}{2}\)
(D) \(\frac{\sqrt{3}}{2}\)
Answer:
(D) \(\frac{\sqrt{3}}{2}\)

Question 5.
If \(\overrightarrow{\mathrm{A}}\), \(\overrightarrow{\mathrm{B}}\), and \(\overrightarrow{\mathrm{C}}\) are three vectors, then which of the following is not correct?
(A) \(\overrightarrow{\mathrm{A}}\) . (\(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{C}}\)
(B) \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) . \(\overrightarrow{\mathrm{A}}\)
(C) \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{A}}\)
(D) \(\overrightarrow{\mathrm{A}}\) × (\(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)
Answer:
(C) \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{A}}\)

2. Answer the following questions.

Question 1.
Show that \(\overrightarrow{\mathrm{A}}\) = \(\frac{\hat{i}-\hat{j}}{\sqrt{2}}\) is a unit vector.
Solution:

Question 2.
If \(\overrightarrow{\mathbf{v}_{1}}\) = 3\(\hat{i}\) + 4\(\hat{j}\) + \(\hat{k}\) and \(\overrightarrow{\mathbf{v}_{2}}\) = \(\hat{i}\) – \(\hat{j}\) – \(\hat{k}\), determine the magnitude of \(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\).
Solution:
\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\) = (3\(\hat{i}\) + 4\(\hat{j}\) + \(\hat{k}\)) + (\(\hat{i}\) – \(\hat{j}\) – \(\hat{k}\))
= 3\(\hat{i}\) + 3\(\hat{i}\) + 4\(\hat{j}\) – \(\hat{j}\) + \(\hat{k}\) – \(\hat{k}\)
= 4\(\hat{i}\) + 3\(\hat{j}\)
∴ Magnitude of (\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\)),
|\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\)| = \(\sqrt{4^{2}+3^{2}}\) = \(\sqrt{25}\) = 5 units.
Answer:
Magnitude of \(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\) = 5 units.

Question 3.
For \(\overline{\mathrm{v}_{1}}\) = 2\(\hat{i}\) – 3\(\hat{j}\) and \(\overline{\mathrm{v}_{2}}\) = -6\(\hat{i}\) + 5\(\hat{j}\), determine the magnitude and direction of \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\).
Answer:
\(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\) = (2\(\hat{i}\) – 3\(\hat{j}\)) + (-6\(\hat{i}\) + 5\(\hat{j}\))
= (2\(\hat{i}\) – 6\(\hat{i}\)) + (-3\(\hat{j}\) + 5\(\hat{j}\))
= -4\(\hat{i}\) + 2\(\hat{j}\)
∴ |\(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\)| = \(\sqrt{(-4)^{2}+2^{2}}\) = \(\sqrt{20}\) = \(\sqrt{4 \times 5}\) = 2\(\sqrt{5}\)
Comparing \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\), with \(\overrightarrow{\mathrm{R}}\) = R_x\(\hat{i}\) + R_y\(\hat{j}\)
⇒ R_x = -4 and R_y = 2
Taking θ to be angle made by \(\overrightarrow{\mathrm{R}}\) with X-axis,

Answer:
Magnitude and direction of \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\), is
respectively 2\(\sqrt{5}\) and and tan^-1\(\left(-\frac{1}{2}\right)\) with X – axis.

Question 4.
Find a vector which is parallel to \(\overrightarrow{\mathrm{v}}\) = \(\hat{i}\) – 2\(\hat{j}\) and has a magnitude 10.
Answer:

Substituting for w_x in (i) using equation (ii),

Using equation (ii),

Answer:
Required vector is \(\frac{10}{\sqrt{5}} \hat{\mathbf{i}}\) – \(\frac{20}{\sqrt{5}} \hat{\mathbf{j}}\)

Alternate method:

When two vectors are parallel, one vector is scalar multiple of another,
i.e., if \(\overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{w}}\) are parallel then, \(\overrightarrow{\mathrm{w}}\) = n\(\overrightarrow{\mathrm{v}}\) where, n is scalar.

Question 5.
Show that vectors \(\vec{a}\) = 2\(\hat{\mathbf{i}}\) + 5\(\hat{\mathbf{j}}\) – 6\(\hat{\mathbf{k}}\) and \(\vec{b}\) = \(\hat{\mathbf{i}}\) + \(\frac{5}{2}\)\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\) are parallel.
Answer:
Let angle between two vectors be θ.

⇒ Two vectors are parallel.

Alternate method:

\(\vec{a}\) = 2(\(\hat{\mathbf{i}}\) + \(\frac{5}{2}\)\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\)) = 2\(\vec{b}\)
Since \(\vec{a}\) is a scalar multiple of \(\vec{b}\), the vectors are parallel.

3. Solve the following problems.

Question 1.
Determine \(\vec{a}\) × \(\vec{b}\), given \(\vec{a}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) and \(\vec{b}\) = 3\(\hat{\mathbf{i}}\) + 5\(\hat{\mathbf{j}}\).
Answer:
Using determinant for vectors in two dimensions,

Answer:
\(\vec{a}\) × \(\vec{b}\) gives \(\hat{\mathbf{k}}\)

Question 2.
Show that vectors \(\overrightarrow{\mathbf{a}}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) + 6\(\hat{\mathbf{k}}\), \(\overrightarrow{\mathbf{b}}\) = 3\(\hat{\mathbf{i}}\) – 6\(\hat{\mathbf{j}}\) + 2\(\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{c}}\) = 6\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\) are mutually perpendicular.
Solution:
As dot product of two perpendicular vectors is zero. Taking dot product of \(\vec{a}\) and \(\vec{b}\)


Combining two results, we can say that given three vectors \(\vec{a}\), \(\vec{b}\), and \(\vec{c}\) are mutually perpendicular to each other.

Question 3.
Determine the vector product of \(\overrightarrow{\mathrm{v}_{1}}\) = 2\(\hat{i}\) + 3\(\hat{j}\) – \(\hat{k}\) and \(\overrightarrow{\mathrm{v}_{2}}\) = \(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\) are perpendicular to each other, determine the value of a.
Solution:

Answer:
Required vector product is -7\(\hat{i}\) + 5\(\hat{j}\) + \(\hat{k}\)

Question 4.
Given \(\bar{v}_{1}\) = 5\(\hat{i}\) + 2\(\hat{j}\) and \(\bar{v}_{2}\) = a\(\hat{i}\) – 6\(\hat{j}\) are perpendicular to each other, determine the value of a.
Solution:
As \(\bar{v}_{1}\) and \(\bar{v}_{2}\) are perpendicular to each other, θ = 90°

Answer:
Value of a is \(\frac{12}{5}\).

Question 5.
Obtain derivatives of the following functions:
(i) x sin x
(ii) x⁴ + cos x
(iii) x/sin x
Answer:
(i) x sin x
Solution:
\(\frac{d}{d x}\)[f₁(x) × f₂(x)] = f₁(x)\(\frac{\mathrm{df}_{2}(\mathrm{x})}{\mathrm{dx}}\) + \(\frac{\mathrm{df}_{1}(\mathrm{x})}{\mathrm{dx}}\)f₂(x)
For f₁(x) = x and f₂(x) = sin x
\(\frac{d}{d x}\)(x sin x) = x\(\frac{\mathrm{d}(\sin \mathrm{x})}{\mathrm{dx}}\) + \(\frac{d(x)}{d x}\) sin x
= x cos x + 1 × sin x
= sin x + x cos x

(ii) x⁴ + cos x
Solution:

(iii) \(\frac{\mathbf{x}}{\sin x}\)
Solution:

[Note: As derivative of (sin x) is cos x, negative sign that occurs in rule for differentiation for quotient of two functions gets retained in final answer]

Question 6.
Using the rule for differentiation for quotient of two functions, prove that \(\frac{d}{d x}\left(\frac{\sin x}{\cos x}\right)\) = sec²x
Solution:

Question 7.
Evaluate the following integral:
(i) \(\int_{0}^{\pi / 2} \sin x d x\)
(ii) \(\int_{1}^{5} x d x\)
Answer:
(i) \(\int_{0}^{\pi / 2} \sin x d x\)
Solution:

(ii) \(\int_{1}^{5} x d x\)
Solution:

11th Physics Digest Chapter 2 Mathematical Methods Intext Questions and Answers

Can you recall? (Textbook Page No. 16)

Question 1.
Define scalars and vectors.
Answer:

1. Physical quantities which can be completely described b their magnitude (a number and unit) are called scalars.
2. Physical quantities which need magnitude, as well as direction for their complete description, are called vectors.

Question 2.
Which of the following are scalars or vectors?
Displacements, distance travelled, velocity, speed, force, work done, energy
Answer:

1. Scalars: Distance travelled, speed, work done, energy.
2. Vectors: Displacement, velocity, force.

Question 3.
What is the difference between a scalar and a vector?
Answer:

Internet my friend (Textbook page no. 28)

1. 1. hyperphysics.phy-astr.gsu.edu/hbase/vect. html#veccon
   2. hyperphysics.phy-astr.gsu.edu/hbase/ hframe.html

Answer:
[Students can use links given above as a reference and collect information about mathematical methods]

Maharashtra State Board Class 11 Physics Textbook Solutions 

• Units and Measurements Class 11 Physics Textbook Solutions
• Mathematical Methods Class 11 Physics Textbook Solutions
• Motion in a Plane Class 11 Physics Textbook Solutions
• Laws of Motion Class 11 Physics Textbook Solutions
• Gravitation Class 11 Physics Textbook Solutions
• Mechanical Properties of Solids Class 11 Physics Textbook Solutions
• Thermal Properties of Matter Class 11 Physics Textbook Solutions
• Sound Class 11 Physics Textbook Solutions
• Optics Class 11 Physics Textbook Solutions
• Electrostatics Class 11 Physics Textbook Solutions
• Electric Current Through Conductors Class 11 Physics Textbook Solutions
• Magnetism Class 11 Physics Textbook Solutions
• Electromagnetic Waves and Communication System Class 11 Physics Textbook Solutions
• Semiconductors Class 11 Physics Textbook Solutions