Prasanna

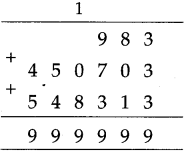
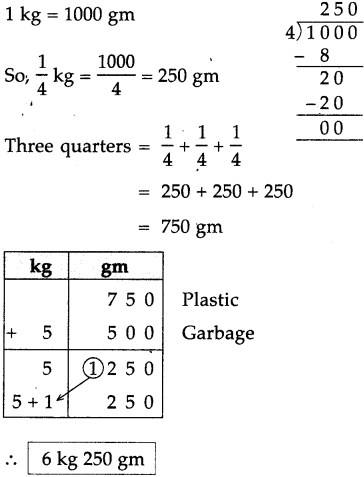
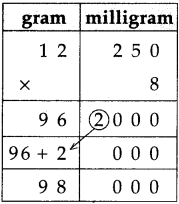
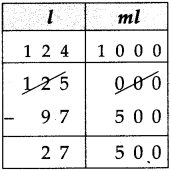
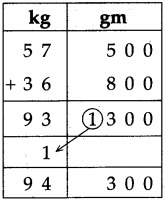
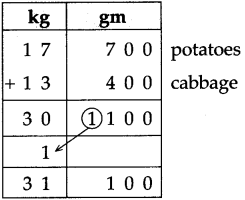
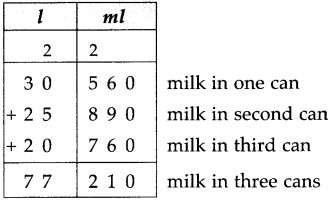
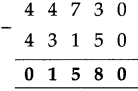
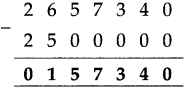
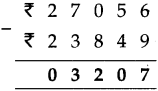
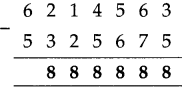
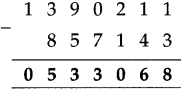
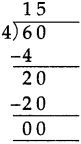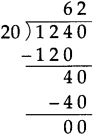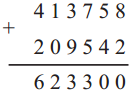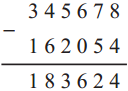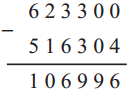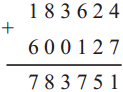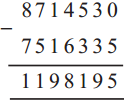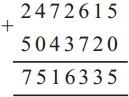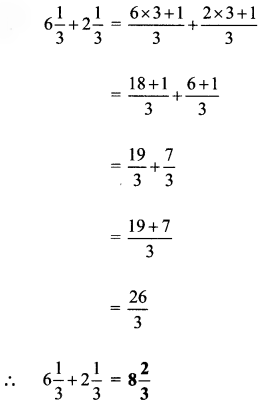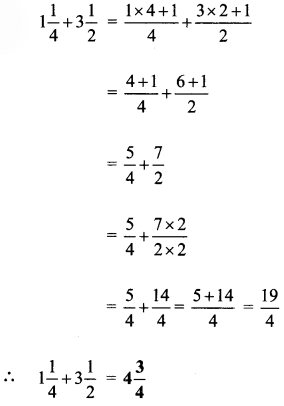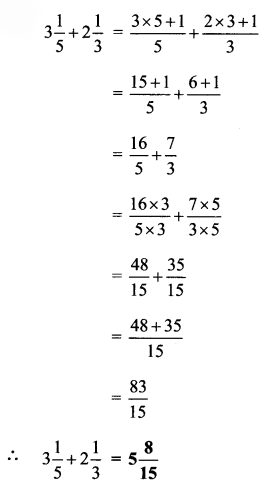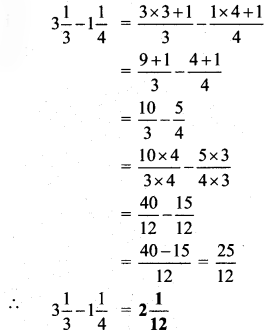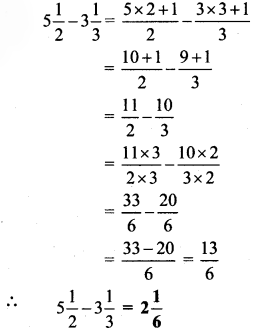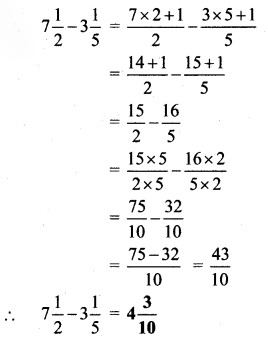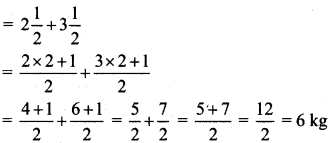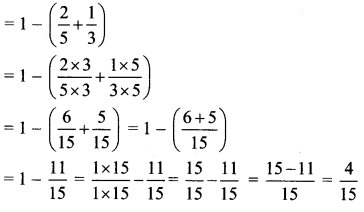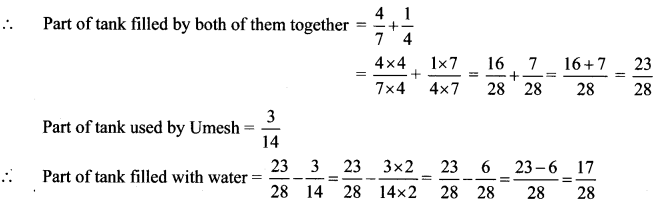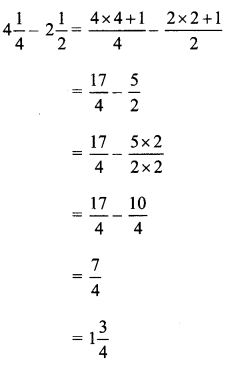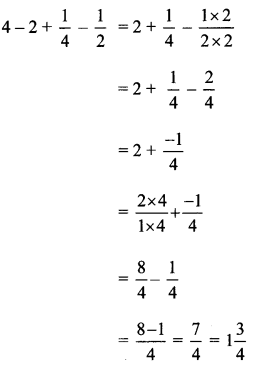Circles Class 5 Problem Set 28 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 7 Circles Problem Set 28 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 7 Circles

Question 1.
Draw circles with the radii given below.

(1) 2 cm
Answer:

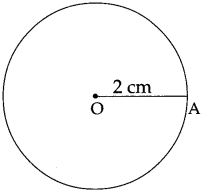
(2) 4 cm
Answer:

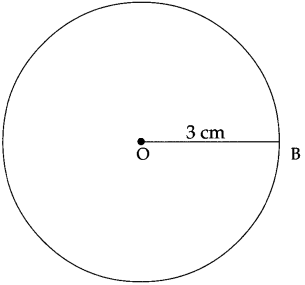
(3) 3 cm
Answer:

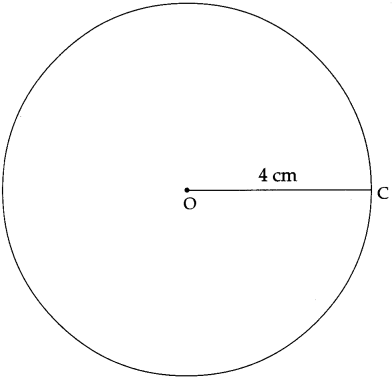
Question 2.
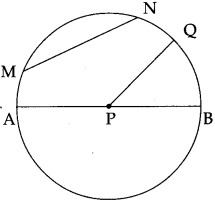
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
Answer:
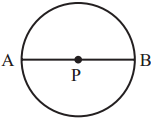
In a circle, P is the centre.
AB is a diameter.
PQ is a radius
MN is a chord

Relationship between radius and diameter
Study the circle given alongside. Think over the following questions.

• Which are the radii in the circle?
• How many radii make up diameter AB?
• If the length of one radius is 3 cm, what is the length of the diameter?
• How long is the diameter as compared to the radius?

The diameter of a circle is twice the length of its radius.

• If another diameter CD is drawn on the same circle, will its length be the same as that of AB?

All the diameters of a circle are of the same length.

Test 1 :
Measure the diameters and radii of the circles given below with a ruler and verify the relationship between their lengths.

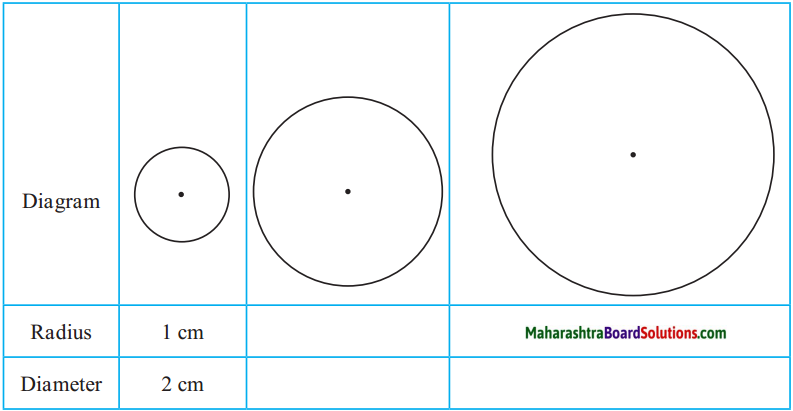
Test 2 :
1. Draw a circle on a piece of paper and cut it out.

2. Name the centre of the circle P.

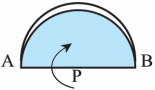
3. Draw the diameter of the circle and name it AB. Note that PA and PB are radii of the circle.

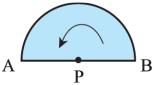
4. Fold the circular paper along AB as shown in the picture.

Fold the paper at P in such a way that point B will fall on point A. Radius PB falls exactly on radius PA. In other words, they coincide.

From this, we can see that every radius of a circle is half the length of its diameter.

Circles Problem Set 28 Additional Important Questions and Answers

Question 1.
Draw circles with the radii given below:

(1) 1.5 cm
Answer:

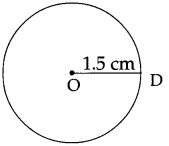
(2) 2.3 cm
Answer:

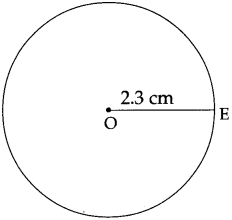
Question 2.
Which one of the following statement is true:

(1) All chords are diameters.
(2) All diameters are chords.
Answer:
Statement (2) is true.

Maharashtra Board Class 5 Maths Solutions

• Circles Problem Set 28 Class 5 Maths Solutions
• Circles Problem Set 29 Class 5 Maths Solutions
• Circles Problem Set 30 Class 5 Maths Solutions
• Circles Problem Set 31 Class 5 Maths Solutions

Decimal Fractions Class 5 Problem Set 41 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 41 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 9 Decimal Fractions

Question 1.
Convert the following into decimal fractions and add them.

(1) ‘One and a half metre’ and ‘two and a half metres’
Solution:

(2) ‘Five and three quarter rupees’ and ‘seven and a quarter rupees’
Solution:

(3) ‘Six and a half metres’ and ‘three and three quarter metres’.
Solution:

Question 2.
(1) 23.4 + 87.9

(2) 35.74 + 816.6
Solution:

(3) 6.95 + 74.88
Solution:

(4) 41.03 + 9.98
Solution:

Question 3.
(1) 51.4 cm + 68.5 cm
Solution:

(2) 94.7 m + 1738.45 m
Solution:

(3) 5158.75 + `841.25
Solution:

Subtraction of decimal fractions

Study the subtraction of decimal fractions given below.

8 hundredths cannot be subtracted from 1 hundredth, so 1 tenth (or 10 hundredths) from 4 tenths are borrowed. The borrowed 10 hundredths and the original one hundredth make 11 hundredths. 11 hundredths minus 8 hundredths are 3 hundredths. They are written in the hundredths place under the line. The rest of the subtraction is carried out using the same method.

Decimal Fractions Problem Set 41 Additional Important Questions and Answers

Convert the following into decimal fractions and add them.

(1) ‘Fourteen and a half rupees’ and ‘Fifteen and a half rupees’.
Solution:

(2) ‘Three quarters’ and ‘a half’
Solution:

Add the following:

(1) 37.84 + 12.16
Solution:

(2) 328.69 + 84.84
Solution:

Solve the following:

(1) 304.86 m + 70.94 m
Solution:

(2) 79.56 cm + 19.65 cm
Solution:

(3) ₹ 64.79 + ₹  49.5
Solution:

Maharashtra Board Class 5 Maths Solutions

• Decimal Fractions Problem Set 36 Class 5 Maths Solutions
• Decimal Fractions Problem Set 37 Class 5 Maths Solutions
• Decimal Fractions Problem Set 38 Class 5 Maths Solutions
• Decimal Fractions Problem Set 39 Class 5 Maths Solutions
• Decimal Fractions Problem Set 40 Class 5 Maths Solutions
• Decimal Fractions Problem Set 41 Class 5 Maths Solutions
• Decimal Fractions Problem Set 42 Class 5 Maths Solutions

Profit-Loss Class 6 Maths Chapter 13 Practice Set 33 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 33 Answers Solutions.

Std 6 Maths Practice Set 33 Solutions Answers

Question 1.
Maganlal bought trousers for Rs 400 and a shirt for Rs 200 and sold them for Rs 448 and Rs 250 respectively. Which of these transactions was more profitable?
Solution:
Cost price of trousers = Rs 400
Selling price of trousers = Rs 448
Profit = Selling price – Cost price
= 448 – 400 = Rs 48
Let Maganlal make x % profit on selling trousers

∴ x = 12%
Cost price of shirt = Rs 200
Selling price of shirt = Rs 250
∴ Profit = Selling price – Cost price
= 250 – 200
= Rs 50
Let Maganlal make y% profit on selling shirt.

∴ y = 25%
∴ Transaction involving selling of shirt was more profitable.

Question 2.
Ramrao bought a cupboard for Rs 4500 and sold it for Rs 4950. Shamrao bought a sewing machine for Rs 3500 and sold it for Rs 3920. Whose transaction was more profitable?
Solution:
Cost price of cupboard = Rs 4500
Selling price of cupboard = Rs 4950
∴ Profit = Selling price – Cost price
= 4950 – 4500
= Rs 450
Let Ramrao make x% profit on selling cupboard

∴ x = 10%
Cost price of sewing machine = Rs 3500
Selling price of sewing machine = Rs 3920
∴Profit = Selling price – Cost price
= 3920 – 3500
= Rs 420
Shamrao make y% profit on selling sewing machine.

∴y = 12%
∴Shamrao’s transaction was more profitable.

Question 3.
Hanif bought one box of 50 apples for Rs 400. He sold all the apples at the rate of Rs 10 each. Was there a profit or loss? What was its percentage?
Solution:
Cost price of 50 apples = Rs 400
Selling price of one apple = Rs 10
∴ Selling price of 50 apples = 10 x 50 = Rs 500
Selling price is greater than the total cost price.
∴ Hanif made a profit.
∴ Profit = Selling price – Cost price
= 500 – 400
= Rs 100
Let Hanif make of x% profit on selling apples.

∴ x = 25%
∴ Hanif made a profit of 25%.

6th Std Maths Digest Pdf Download

• Equations Practice Set 26 Class 6 Maths Solution
• Equations Practice Set 27 Class 6 Maths Solution
• Ratio-Proportion Practice Set 28 Class 6 Maths Solution
• Ratio-Proportion Practice Set 29 Class 6 Maths Solution
• Percentage Practice Set 30 Class 6 Maths Solution
• Profit-Loss Practice Set 31 Class 6 Maths Solution
• Profit-Loss Practice Set 32 Class 6 Maths Solution
• Profit-Loss Practice Set 33 Class 6 Maths Solution
• Profit-Loss Practice Set 34 Class 6 Maths Solution
• Banks and Simple Interest Practice Set 35 Class 6 Maths Solution

HCF-LCM Class 6 Maths Chapter 9 Practice Set 24 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 24 Answers Solutions.

Std 6 Maths Practice Set 24 Solutions Answers

Question 1.
Find the HCF of the following numbers.
i. 45, 30
ii. 16, 48
iii. 39, 25
iv. 49, 56
v. 120, 144
vi. 81, 99
vii. 24, 36
viii. 25, 75
ix. 48, 54
x. 150, 225
Solution:
i. Factors of 45 = 1, 3, 5, 9,15, 45
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
∴ HCF of 45 and 30 = 15

ii. Factors of 16 = 1, 2, 4, 8, 16
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
∴ HCF of 16 and 48 = 16

iii. Factors of 39 = 1, 3, 13, 39
Factors of 25 = 1, 5, 25
∴ HCF of 39 and 25 = 1

iv. Factors of 49 = 1, 7, 49
Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
∴ HCF of 49 and 56 = 7

v. Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Factors of 144 = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
∴ HCF of 120 and 144 = 24

vi. Factors of 81 = 1, 3, 9, 27, 81
Factors of 99 = 1, 3, 9, 11, 33, 99
∴ HCF of 81 and 99 = 9

vii. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
∴ HCF of 24 and 36 = 12

viii. Factors of 25 = 1, 5, 25
Factors of 75 = 1, 3, 5, 15, 25, 75
∴ HCF of 25 and 75 = 25

ix. Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 54 = 1, 2, 3, 6, 9, 18, 27, 54
∴ HCF of 48 and 54 = 6

x. Factors of 150 = 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Factors of 225 = 1, 3, 5, 9, 15, 25, 45, 75, 225
∴ HCF of 150 and 225 = 75

Question 2.
If large square beds of equal size are to be made for planting vegetables on a plot of land 18 metres long and 15 metres wide, what is the maximum possible length of each bed?
Solution:
Length of the land = 18 m
Width of the land = 15 m
The maximum length of each bed will be the greatest common factor of 18 and 15.
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 15 = 1, 3, 5, 15
∴ HCF of 18 and 15 = 3
∴ The maximum possible length of each bed is 3 metres.

Question 3.
Two ropes, one 8 metres long and the other 12 metres long are to be cut into pieces of the same length. What will the maximum possible length of each piece be?
Solution:
Length of first rope = 8 m
Length of second rope = 12 m
The maximum length of each piece will be the greatest common factor of 8 and 12.
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
∴ HCF of 8 and 12 = 4
∴ The maximum possible length of each piece is 4 metres.

Question 4.
The number of students of Std 6th and Std 7th who went to visit the Tadoba Tiger Project at Chandrapur was 140 and 196 respectively. The students of each class are to be divided into groups of the same number of students. Each group can have a paid guide. What is the maximum number of students that can be there in each group? Why do you think each group should have the maximum possible number of students?
Solution:
Number of students of Std 6th = 140
Number of students of Std 7th = 196
The maximum number of students in each group will be the greatest common factor of 140 and 196.
Factors of 140 = 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Factors of 196 = 1, 2, 4, 7, 14, 28, 49, 98, 196
∴ HCF of 140 and 196 = 28
∴ Maximum students in each group are 28.
Each group should have maximum number students so that there will be minimum number of groups and hence minimum number of paid guides.

Question 5.
At the Rice Research Centre at Tumsar there are 2610 kg of seeds of the basmati variety and 1980 kg of the indrayani variety. If the maximum possible weight of seeds has to be filled to make bags of equal weight what would be the weight of each bag? How many bags of each variety will there be?
Solution:
Weight of basmati rice = 2610 kg
Weight of indrayani rice = 1980 kg
The weight of each bag will be the greatest common factor of 2610 and 1980.
Factors of 2610 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 29, 30, 45, 58, 87, 90, 145, 174, 261, 290, 435, 522, 870, 1305, 2610
Factors of 1980 = 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 18, 20, 22, 30, 33, 36, 44, 45, 55, 60, 66, 90, 99, 110, 132, 165, 180, 198, 220, 330, 396, 495, 660, 990, 1980
∴ HCF of 2610 and 1980 = 90
Maximum weight of each bag = 90 kg
Number of bags of basmati rice = 2610 ÷ 90 = 29
Number of bags of indrayani rice = 1980 ÷ 90 = 22
Maximum weight of each bag is 90 kg.
The number of bags of basmati rice is 29, and the number of bags of indrayani rice is 22.

6th Std Maths Digest Pdf Download

• Bar Graphs Practice Set 18 Class 6 Maths Solution
• Bar Graphs Practice Set 19 Class 6 Maths Solution
• Symmetry Practice Set 20 Class 6 Maths Solution
• Symmetry Practice Set 21 Class 6 Maths Solution
• Divisibility Practice Set 22 Class 6 Maths Solution
• HCF-LCM Practice Set 23 Class 6 Maths Solution
• HCF-LCM Practice Set 24 Class 6 Maths Solution
• HCF-LCM Practice Set 25 Class 6 Maths Solution

Addition and Subtraction Class 5 Problem Set 8 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 3 Addition and Subtraction Problem Set 8 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 3 Addition and Subtraction

Question 1.
Add the following:

(1) 42,311 + 65,36,624

Answer:
65,78,635

(2) 3,17,529 + 8,04,613

Answer:
11,22,142

(3) 12,42,746 + 4,83,748

Answer:
17,26,494

(4) 24,12,636 + 23,19,058

Answer:
47,31,694

(5) 2,654 + 71,209 + 5,03,789
1 1 2
2 6 5 4
+
7 1 2 0 9
+
5 0 3 7 8 9
Answer:
5 7 7 6 5 2

(6) 29 + 726 + 51,36,274
1 1 1
_______________
2 9
+
7 2 6
+
5 1 3 6 2 7 4
Answer:
5 1 3 7 0 2 9

(7) 14,02,649 + 524 + 28,13,749
1 1 1 2
_____________
1 4 0 2 6 4 9
+
5 2 4
+
2 8 1 3 7 4 9
Answer:
4 2 1 6 9 2 2

(8) 23,45,678 + 9,87,654
1 1 1 1 1 1
_____________
2 3 4 5 6 7 8
+
9 8 7 6 5 4
Answer:
3 3 3 3 3 3 2

(9) 22 + 6,047 + 3,84,527
1 1
2 2
+
6 4 0 7
+
3 8 4 5 2 7
Answer:
3 9 0 9 5 6

(10) 2,345 + 65,432 + 76,54,369
1 1 1 1 1
_________
2 3 4 5
+
6 5 4 3 2
+
7654369
Answer:
7 7 2 2 1 4 6

Study the following word problem.

During the polio eradication campaign, 3,17,658 children were given the polio vaccine in one District and 2,04,969 children in another. Altogether, how many children got the vaccine?
3 1 7 6 5 8
+
2 0 4 9 6 9
___________
5 2 2 6 2 7
___________
Altogether, 5,22,627 children got the vaccine.

Addition and Subtraction Problem Set 8 Additional Important Questions and Answers

Question 1.
Add the following:

(1) 4,506 + 3,82,459 + 6,12,999
Solution:
1 1 2
_________
4 5 0 6
+
3 8 2 4 5 9
+
6 1 2 9 9 9
Answer:
9 9 9 9 6 4

(2) 983 + 4,50,703 + 5,48,313
Solution:
1
________
9 0 0 3
+
4 5 0 7 0 3
+
5 4 00 3 1 3
Answer:
9 9 9 9 9 9

Maharashtra Board Class 5 Maths Solutions

• Addition and Subtraction Problem Set 7 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 8 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 9 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 10 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 11 Class 5 Maths Solutions 
• Addition and Subtraction Problem Set 12 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 13 Class 5 Maths Solutions

Problems on Measurement Class 5 Problem Set 47 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 11 Problems on Measurement Problem Set 47 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 11 Problems on Measurement

Question 1.
For his birthday, Ajay gave 20 l 450 ml of milk to the children in an Ashramshala and 28 l 800 ml to the children in an orphanage. How much milk did Ajay donate?
Solution:

450 ml + 800 ml
= 1250 ml
= 11 + 250 ml

∴ Ajay donated 49 l 250 ml milk

Question 2.
Under the Rural Cleanliness Mission, college students cleaned 1 km 750m of a village road that is 2 km 575m long. How much remained to be cleaned?
Solution:

750 m cannot be subtracted from 575 m. So, convert 1 km = 1000 m.
∴ 825 m remained to be cleaned

Question 3.
Babhulgaon used 21,250 liters of treated waste water in the fields. Samvatsar used 31,350 litres of similar water. How much treated waste water was used in all?
Solution:
2 1 2 5 0 litres Babhulgaon used
+ 3 1 3 5 0 litres Samvatsar used
___________
5 2 6 0 0
___________

∴ 52,600 litres of waste water used in all

Question 4.
If half a litre of milk costs 22 rupees, how much will 7 litres cost?
Solution:
\(\begin{array}{l}\frac{1}{2}+\frac{1}{2}=\frac{1+1}{2}=\frac{2}{2}=1 \text { litre } \\ 22+22=₹ 44\end{array}\)
That is, 1 litre cost ₹ 44
∴ 7 litres costs 44 x 7 = ₹ 308
∴ 7 litres costs ₹ 308

Question 5.
If the speed of a motorcycle is 40 km per hour, how far will it travel in an hour and a quarter?
Solution:
Hour and quarter = 1 + \(\frac{1}{4}\) hours
= 40 km + \(\frac{1}{4}\) x 40 km
= 40 km + 10 km
= 50 km
∴ Motorcycle will travel in a hour and a quarter 50 km

Question 6.
If a man walks at a speed of 4 kmph, how long will it take him to walk 3 km?
Solution:
1 km = 1000 m
4 km in 1 hour, 4 km in 60 minutes
That is
2 km in 30 minutes
+ 1 km in 15 minutes
_______________________
3 km in 45 minutes

That is 1 km in 15 minutes Hence, 3
km in 15 x 3 = 45 min

∴ 3 km in 15 x 3 = 45 min

Question 7.
If a rickshaw travels at a speed of 30 kmph, how far will it travel in three quarters of an hour?
Solution:
30 kmph means
In 60 minutes 30 km and 30 minutes 15 km
and 15 minutes \(\frac{15}{2}=\frac{15 \times 5}{2 \times 5}=\frac{75}{10}\) = 7.5 km
∴ In 45 minutes 15 km + 7.5 km = 22.5 km

Question 8.
During Cleanliness Week, children cleaned the public park in their town. They collected three quarter kilograms of plastic bags and five and a half kilograms of other garbage. How much garbage did they collect in all?
Solution:

Question 9.
If one shirt needs 2 m 50cm of cloth, how much cloth do we need for 5 shirts?
Solution:

∴ 12 m 50 cm cloth needs

Question 10.
If a car travels 60 km in an hour, how far will it travel in
(1) 2 hours?
(2) 15 minutes?
(3) half an hour?
(4) three and a half hours?
Solution:
60 kmph
In 60 minutes 60 km
Hence, 1 minute 1 km
(1) 2 hours = 2 x 60 = 120 km
(2) In 15 minutes = 15 km
(3) In half an hour 60 ÷ 2 = 30 km
(4) In three and half hours
= 3 x 60 + 30
= 180 + 30
= 210 km

∴ (1) 120 km
(2) 15 km
(3) 30 km
(4) 210 km

Question 11.
If one gold bangle is made from 12 grams 250 milligrams of gold, how much gold will be needed to make 8 such bangles? (1000mg = 1 g)
Solution:

∴ 98 grams gold needed

Question 12.
How many pouches of 20g cloves each can be made from 1 kg 240g of cloves?
Solution:
1 kg 240 gm
= 1000 gm + 240 gm
= 1240 gm

∴ pouches can be made

Question 13.
Seema’s mother bought 2m 70cm of cloth for a kurta and 2 m 40cm for a shirt. How much cloth did she buy in all?
Solution:
70 cm + 40 cm
= 110 cm
= 1 m 10 cm

cloth for Kurta
cloth for Shirt

∴ 5 m 10 cm cloth in all

Question 14.
A water tank holds 125 l of water. If 97 l 500 ml of the water is used, how much water remains in the tank?
Solution:
1 litre = 1000 ml

water tank holds
water used
water remain

∴ 27 l 500 ml water remain in tank

Question 15.
Harminder bought 57 kg 500g of wheat from one shop and 36 kg 800 g of wheat from another shop. How much wheat did he buy altogether?
Solution:

bought from 1 shop
bought from another shop
500 + 800 = 1300 gm
= 1000 + 300
= 1 kg 300 gm

∴ 94 kg 300 gm bought altogether

Question 16.
Renu took part in a 100m race. She tripped and fell after running 80 m 50 cm. How much distance did she have left to run?
Solution:

Borrow l m = 100 cm
So, 100 m = 99 m + 100 cm
Total distance to run
Distance covered
Distance left to run

∴ 19 m 50 cm distance left to run

Question 17.
A sack had 40kg 300 grams of vegetables. There were 17kg 700 g potatoes, 13 kg 400g cabbage and the rest were onions. What was the weight of the onions?
Solution:

∴ Weight of onions is 9 kg 200 gm

Question 18.
One day, Gurminder Singh walked 3 km 750m and Parminder Singh walked 2km 825m. Who walked farther and by how much?
Solution:

∴ Gurminder walked more by 925 metres

Question 19.
Suresh bought 3kg 250g of tomatoes, 2 kg 500g of peas and 1kg 750g of cauliflower. How much was the total weight of the vegetables he bought?
Solution:

∴ Total weight 7 kg 500 gm

Question 20.
Jalgaon, Bhusawal, Akola, Amravati and Nagpur lie serially on a certain route. The distances between Akola and these other places are given below.

Use them to make word problems and solve the problems.
Amravati – 95 km, Bhusawal – 154 km,
Nagpur – 249 km, Jalgaon – 181 km
Solution:
(1) What is the distance between Bhusaval and Nagpur?
249 km – 154 km = 95 km

∴ The distance between Bhusaval and Nagpur is 95 km

(2) What is the distance between Amravati and Jalgaon?
181 km – 95 km = 86 km

∴ The distance between Amravati and Jalgaon is 86 km.

Question 21.
Complete the following table and prepare the total bill.

Solution:

Activity

• You have 1 kg of potatoes. Find out which other ingredients you will need to make potato vadas and approximately how much of each ingredient you will need. Also find out approximately how much each ingredient will cost and how many vadas you will be able to make.
• Fix a 1 m long stick in an open field. Measure the shadow of the stick at 9:00 in the morning, at 12:00 noon, at 3:00 in the afternoon and at 5:00 in the evening. Observe at which time of the day the shadow is shortest and at what time, it is longest.
• Measure the length of a pen refill.

Problems on Measurement Problem Set 47 Additional Important Questions and Answers

Question 1.
One can contains 30 l 560 ml of milk, while second contains 251890 ml of milk and third one contains 20 l 760 ml of milk. How much milk is there in the three cans together?
Solution:

∴ 77 l 210 ml total milk

Question 2.
Add the following:
(1) ₹ 13, 85 paise + ₹ 16, 40 paise
(2) 15 kg 280 gm + 18 kg 920 gm
(3) 24 l 690 ml + 25 l 780 ml
(4) 22 km 750 m + 27 km 500 m
(5) 17 m 40 cm + 19 m 85 cm
(6) 38 cm 8 mm + 17 cm 2 mm
(7) 10 km 950 m + 15 km 125 m
(8) 83 kg 468 gm + 109 kg 532 gm
Answer:
(1) ₹ 30, 25 paise
(2) 34 kg 200 gm
(3) 50 1 470 ml
(4) 50 km 250 m
(5) 37 m 25 cm
(6) 56 cm
(7) 26 km 75 m
(8) 193 kg

Question 3.
Subtract the following:
(1) ₹ 21, 30 paise – ₹ 13, 80 paise
(2) 16 kg 130 gm – 9 kg 250 gm
(3) 9 l 350 ml – 5 l 470 ml’
(4) 41 m 10 cm – 14 m 40 cm
(5) 38 km 175 m – 20 km 365 m
(6) 27 cm 5 mm – 11 cm 8 mm
(7) 28 km 725 m – 13 km 590 m
(8) 380 kg – 232 kg 730 gm
Answer:
(1) ₹ 7, 50 paise
(2) 6 kg 880 gm
(3) 51 880 ml
(4) 26 m 30 cm
(5) 17 km 810 m
(6) 15 cm 7 mm
(7) 15 km 135 m
(8) 147 kg 270 gm

Question 4.
Fill in the blanks:
(1) 1250 m = …………………… km …………………… m
(2) 2.5 m = …………………… m …………………… cm
(3) 3 l 50 ml = …………………… ml
(4) ₹ 2.5 = …………………… paise
Answer:
(1) 1 km 250 m
(2) 2 m 50 cm
(3) 3050 ml
(4) 250 paise

Question 5.
(A) Match the following:

Answer:
(1 – b),
(2 – d),
(3 – a),
(4 – c)

(B) Match the following:

Answer:
(1 – b),
(2 – d),
(3 – a),
(4 – e),
(5 – c)

Maharashtra Board Class 5 Maths Solutions

• Problems on Measurement Problem Set 46 Class 5 Maths Solutions
• Problems on Measurement Problem Set 47 Class 5 Maths Solutions
• Perimeter and Area Problem Set 48 Class 5 Maths Solutions
• Perimeter and Area Problem Set 49 Class 5 Maths Solutions
• Perimeter and Area Problem Set 50 Class 5 Maths Solutions

Addition and Subtraction Class 5 Problem Set 12 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 3 Addition and Subtraction Problem Set 12 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 3 Addition and Subtraction

Question 1.
Solve the following word problems:

1. Prathamesh wants to buy a laptop worth 27,450 rupees. He has 22,975 rupees. What is the amount he still needs to be able to buy the laptop?
Solution:
₹ 2 7 4 5 0 Laptop worth
–
₹ 2 2 9 7 5 Prathmesh has
0 4 4 7 5 Require more
Answer:
₹ 04,475 amount require to buy the laptop,

2. A company produced 44,730 scooters in a certain year and 43,150 in the next. How many more scooters did they produce in the previous year?
Solution:
4 4 7 3 0 In previous year
–
4 3 1 5 0 In next year
0 1 5 8 0
Answer:
1,580 scooters produced more in the previous year.

3. In a certain city, the number of men is 16,37,856 and the number of women is 16,52,978. By how many does the number of women exceed the number of men?
Solution:
1 6 5 2 9 7 8 Women
–
1 6 3 7 8 5 6 Men
0 0 1 5 1 2 2
Answer:
15,122 women more than number of men.

4. An organization decided to collect 25,00,000 rupees for a certain project. They collected 26,57,340 through donations and other kinds of aid. By how much did they exceed their target?
Solution:
2 6 5 7 3 4 0 collected
–
2 5 0 0 0 0 0 decided to collect
0 1 5 7 3 4 0 collected more
Answer:
1,57,340

5. Use the numbers 23,849 and 27,056 to make a subtraction problem. Solve the problem.
Solution:
In a certain shop the price of a computer was ₹ 23,849 and that of TV set is ₹ 27,056. Price of TV set is how much more than that of a computer.
₹ 2 7 0 5 6 Price of T.V. sets
₹ 2 3 8 4 9 Price of computer
0 3 2 0 7 Price is more
Answer:
Price of TV set is more than computer by ₹ 3,207

Mixed examples
Study the following solved examples.

Example (1)
4,13,758 + 2,09,542 – 5,16,304
4,13,758 + 2,09,542 – 5,16,304 = 1,06,996

Example (2)
345678 – 162054 + 600127
345678 – 162054 + 600127 = 7,83,751

In these examples, both operations, addition and subtraction, have to be done. They are done in the order in which they are given. In actual cases, we need to consider the specific problem to decide which operation must be done first.

Example (3)
The total amount spent on building a certain house was ₹ 87,14,530. Of this amount, ₹ 24,72,615 were spent on buying the plot of land, ₹ 50,43,720 on the construction material and the rest on labour charges. What was the amount spent on labour?

Method : 1
8 7 1 4 5 3 0 → Total amount spent
–
2 4 7 2 6 1 5 → Cost of plot
6 2 4 1 9 1 5 → Cost of material and labour

6 2 4 1 9 1 5 → Cost of material and labour
–
5 0 4 3 7 2 0 → Cost of material
1 1 9 8 1 9 5 → Amount spent on labour

Method : 2
2 4 7 2 6 1 5 Cost of plot
+
5 0 4 3 7 2 0 Cost of material
7 5 1 6 3 3 5 Cost of plot and material

8 7 1 4 5 3 0 Total amount spent
–
7 5 1 6 3 3 5 Cost of plot and material
1 1 9 8 1 9 5 Amount spent on labour

Let us verify our answer.
2 4 7 2 6 1 5 Cost of plot
+
5 0 4 3 7 2 0 Cost of material
+
1 1 9 8 1 9 5 Amount spent on labour
8 7 1 4 5 3 0 Total cost

The sum total of all the amounts spent tallies with the given total cost. It means that our answer is correct.

Addition and Subtraction Problem Set 12 Additional Important Questions and Answers

Solve the following word problems:

Question 1.
Jethalal purchased goods for ₹ 53,25,675 sold it for ₹ 62,14,563. How much he obtained more in this transaction?
Solution:
6 2 1 4 5 6 3 Sold price
5 3 2 5 6 7 5 Purchased price
8 8 8 8 8 8 Obtained more
Answer:
₹ 8,88,888

Question 2.
In an election candidate A got 13,90,211 votes and candidate B got 8,57,143 votes. By how many votes the winner A defeated the looser B?
Solution:
1 3 9 0 2 1 1 Votes obtained by A
–
8 5 7 1 4 3 Votes obtained by B
0 5 3 3 0 6 8 Votes more obtained by A
Answer:
5,33,068

Maharashtra Board Class 5 Maths Solutions

• Addition and Subtraction Problem Set 7 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 8 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 9 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 10 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 11 Class 5 Maths Solutions 
• Addition and Subtraction Problem Set 12 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 13 Class 5 Maths Solutions

Profit-Loss Class 6 Maths Chapter 13 Practice Set 32 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 32 Answers Solutions.

Std 6 Maths Practice Set 32 Solutions Answers

Question 1.
From a wholesaler, Santosh bought 400 eggs for Rs 1500 and spent Rs 300 on transport. 50 eggs fell down and broke. He sold the rest at Rs 5 each. Did he make a profit or a loss? How much?
Solution:
Cost price of 400 eggs = Rs 1500
Transportation cost = Rs 300
∴ Total cost price of 400 eggs = Cost price of 400 eggs + Transportation cost
= 1500 + 300 = Rs 1800
50 eggs fell and broke
∴ Remaining eggs = 400 – 50 = 350
Selling price of 1 egg = Rs 5
∴ Selling price of 350 eggs = 5 x 350 = Rs 1750
Total cost price is greater than the selling price.
∴ Santosh suffered a loss.
Loss = Total cost price – Selling price
= 1800 – 1750
= Rs 50
∴ Santosh incurred a loss of Rs 50.

Question 2.
Abraham bought goods worth Rs 50000 and spent Rs 7000 on transport and octroi. If he sold the goods for Rs 65000, did he make a profit or a loss? How much?
Solution:
Cost price of goods = Rs 50000
Transportation cost and octroi = Rs 7000
∴ Total cost price for buying goods = Cost price of goods + Transportation cost and octroi
= 50000 + 7000 = Rs 57000
Selling price of goods = Rs 65000
Selling price is greater than the total cost price
∴ Abraham made a profit.
Profit = Selling price – Total cost price
= 65000 – 57000
= Rs 8000
∴ Abraham made a profit of Rs 8000.

Question 3.
Ajit Kaur bought a 50 kg sack of sugar for Rs 1750, but as sugar prices fell, she had to sell it at Rs 32 per kg. How much loss did she incur?
Solution:
Cost price of 50 kg sugar = Rs 1750
Selling price of 1 kg sugar = Rs 32
∴ Selling price of 50 kg sugar = 50 x 32 = Rs 1600
Loss = Total cost price – Selling price
= 1750 – 1600 = Rs 150
∴ Ajit Kaur incurred a loss of Rs 150.

Question 4.
Kusumtai bought 80 cookers at Rs 700 each. Transport cost her Rs 1280. If she wants a profit of Rs 18000, what should be the selling price per cooker?
Solution:
Cost price of one cooker = Rs 700
∴ Cost price of 80 cookers = 700 x 80 = Rs 56000
Transportation cost = Rs 1280
∴ Total cost price = Cost price of 80 cookers + Transportation cost
= 56000 + 1280
= Rs 57280
Profit = Rs 18000
Profit = Selling Price – Total Cost Price
∴ Required selling price = Total cost price + profit
= 57280 + 18000
= Rs 75280
∴ Selling price of 80 cookers = Rs 75280
∴ Selling price of 1 cooker = \(\frac { 75280 }{ 80 }\) = Rs 941
∴ The selling price per cooker should be Rs 941.

Question 5.
Indrajit bought 10 refrigerators at Rs 12000 each and spent Rs 5000 on transport. For how much should he sell each refrigerator in order to make a profit of Rs 20000?
Solution:
Cost price of 1 refrigerator = Rs 12000
Cost price of 10 refrigerator = 10 x 12000 = Rs 120000
Transportation cost = Rs 5000
∴ Total cost price of 10 refrigerators = Cost price of 10 refrigerators + Transportation cost
= 120000 + 5000 = Rs 125000
Profit = Rs 20000
Profit = Selling Price – Total Cost Price
∴ Required selling price = Total cost price + Profit
= 125000 + 20000 = Rs 145000
∴ Selling price of 10 refrigerators = Rs 145000
∴ Selling price of 1 refrigerator = \(\frac { 145000 }{ 10 }\) = Rs 14500
∴ Indrajit must sell each refrigerator at Rs 14500 to make a profit of Rs 20000.

Question 6.
Lalitabai sowed seeds worth Rs 13700 in her field. She had to spend Rs 5300 on fertilizers and spraying pesticides and Rs 7160 on labor. If, on selling her produce, she earned Rs 35400 what was her profit or her loss?
Solution:
Cost price of seeds = Rs 13700
Cost of fertilizers and pesticides = Rs 5300
Labor cost = Rs 7160
∴ Total cost price = Cost price of seeds + Cost of fertilizers and pesticides + Labor cost
= 13700 + 5300 + 7160
= Rs 26160
Selling price = Rs 35400
Selling price is greater than the total cost price.
∴ Lalitabai made a profit.
Profit = Selling price – Cost price
= 35400 – 26160
= Rs 9240
∴ Lalitabai made a profit of Rs 9240.

Maharashtra Board Class 6 Maths Chapter 13 Profit-Loss Practice Set 32 Intext Questions and Activities

Question 1.
At Diwali, in a certain school, the students undertook a Design a Diya project. They bought 1000 diyas for Rs 1000 and some paint for Rs 200. To bring the diyas to the school, they spent Rs 100 on transport. They sold the painted lamps at Rs 2 each. Did they make a profit or incur a loss? (Textbook pg. no. 67 and 68)

i. Is Anju right?
ii. What about the money spent on paints and transport?
iii. How much money was actually spent before the diyas could be sold?
iv. How much actual profit was made in this project of colouring the diyas and selling them?

Ans:
i. No, Anju is wrong.
Cost price of diyas also includes the painting and transportation cost.
∴ Total cost price of diyas = Cost of diyas + Cost of paint + Transportation cost
= 1000 + 200+ 100
= Rs 1300
ii. The cost of paint was Rs 200 and that for transportation was Rs 100. These costs are also to be added to the cost price of diyas.
iii. Rs 1300 was actually spent before the diyas could be sold.
iv. Total Cost Price of 1000 Diyas = Rs 1300
Selling Price of 1 Diya = Rs 2
∴ Selling Price of 1000 Diyas = 2 x 1000 = Rs 2000
∴ Profit = Selling Price – Total Cost Price
= 2000 – 1300
= Rs 700
∴ The profit made by coloring the diyas and selling them was Rs 700.

Question 2.
A farmer sells what he grows in his fields. How is the total cost price calculated? What does a farmer spend on his produce before he can sell it? What are the other expenses besides seeds, fertilizers and transport? (Textbook pg. no. 68)
Solution:
The farmer, in order to calculate the total cost price of his produce, needs to consider all the expenses associated with the growing and selling of his produce.

Following are the things on which farmer spends money before he can sell it.

1. Time and energy
2. Ploughing and tilling
3. Irrigation and electricity cost
4. Harvesting and cleaning
5. Packing

As given above, there are a multiple of costs to be included besides seeds, fertilizers and transport for the farmer to price its produce appropriately.

6th Std Maths Digest Pdf Download

• Equations Practice Set 26 Class 6 Maths Solution
• Equations Practice Set 27 Class 6 Maths Solution
• Ratio-Proportion Practice Set 28 Class 6 Maths Solution
• Ratio-Proportion Practice Set 29 Class 6 Maths Solution
• Percentage Practice Set 30 Class 6 Maths Solution
• Profit-Loss Practice Set 31 Class 6 Maths Solution
• Profit-Loss Practice Set 32 Class 6 Maths Solution
• Profit-Loss Practice Set 33 Class 6 Maths Solution
• Profit-Loss Practice Set 34 Class 6 Maths Solution
• Banks and Simple Interest Practice Set 35 Class 6 Maths Solution

Operations on Fractions Class 6 Maths Chapter 4 Practice Set 10 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 10 Answers Solutions.

Std 6 Maths Practice Set 10 Solutions Answers

Question 1.
Add:
i. \(6 \frac{1}{3}+2 \frac{1}{3}\)
ii. \(1 \frac{1}{4}+3 \frac{1}{2}\)
iii. \(5 \frac{1}{5}+2 \frac{1}{7}\)
iv. \(3 \frac{1}{5}+2 \frac{1}{3}\)
Solution:
i. \(6 \frac{1}{3}+2 \frac{1}{3}\)

ii. \(1 \frac{1}{4}+3 \frac{1}{2}\)

iii. \(5 \frac{1}{5}+2 \frac{1}{7}\)

iv. \(3 \frac{1}{5}+2 \frac{1}{3}\)

Question 2.
Subtract:
i. \(3 \frac{1}{3}-1 \frac{1}{4}\)
ii. \(5 \frac{1}{2}-3 \frac{1}{3}\)
iii. \(7 \frac{1}{8}-6 \frac{1}{10}\)
iv. \(7 \frac{1}{2}-3 \frac{1}{5}\)
Solution:
i. \(3 \frac{1}{3}-1 \frac{1}{4}\)

ii. \(5 \frac{1}{2}-3 \frac{1}{3}\)

iii. \(7 \frac{1}{8}-6 \frac{1}{10}\)

iv. \(7 \frac{1}{2}-3 \frac{1}{5}\)

Question 3.
Solve:
i. Suyash bought \(2\frac { 1 }{ 2 }\) kg of sugar and Ashish bought \(3\frac { 1 }{ 2 }\) kg. How much sugar did they buy altogether? If sugar costs Rs 32 per kg, how much did they spend on the sugar they bought?

ii. Aradhana grows potatoes in \(\frac { 2 }{ 5 }\) part of her garden, greens in \(\frac { 1 }{ 3 }\) part and brinjals in the remaining part. On how much of her plot did she plant brinjals?

iii. Sandeep filled water in \(\frac { 4 }{ 7 }\) of an empty tank. After that, Ramakant filled \(\frac { 1 }{ 4 }\) part more of the same tank. Then Umesh used \(\frac { 3 }{ 14 }\) part of the tank to water the garden. If the tank has a maximum capacity of 560 litres, how many litres of water will be left in the tank?
Solution:
i. Sugar bought by Suyash = \(2\frac { 1 }{ 2 }\) kg
Sugar bought by Ashish = \(3\frac { 1 }{ 2 }\) kg
∴ Total sugar bought by both

Cost of 1 kg of sugar = Rs 32
∴ Cost of 6 kg of sugar = 32 x 6
= Rs 192
∴ They bought 6 kg sugar altogether and the total money spent on sugar is Rs 192.

ii. Part of garden occupied by potatoes = \(\frac { 2 }{ 5 }\)
Part of garden occupied by greens = \(\frac { 1 }{ 3 }\)
Since brinjals are planted in the remaining part,
∴ (Part occupied by potatoes) + (part occupied by greens) + (part occupied by brinjals) = 1 entire garden.
∴ Part of garden occupied by brinjals = 1 – (part of garden occupied by potatoes + part of garden occupied by greens)

∴ Aradhana planted brinjals on \(\frac { 4 }{ 15 }\) part of her plot.

iii. Part of tank filled by Sandeep = \(\frac { 4 }{ 7 }\)
Part of tank filled by Ramakant = \(\frac { 1 }{ 4 }\)

Since maximum capacity of tank is 560 litres
∴ Quantity of water left in tank = \(\frac { 17 }{ 28 }\times560\) = 340 litres
∴ The quantity of water left in the tank is 340 litres.

Maharashtra Board Class 6 Maths Chapter 4 Operations on Fractions Practice Set 10 Intext Questions and Activities

Question 1.
How to do this subtraction: \(4 \frac{1}{4}-2 \frac{1}{2}\) ? Is it same as \(\left[4-2+\frac{1}{4}-\frac{1}{2}\right]\) ? (Textbook pg. no. 23)
Solution:
\(4 \frac{1}{4}-2 \frac{1}{2}\)

\(\left[4-2+\frac{1}{4}-\frac{1}{2}\right]\)

The subtraction \(4 \frac{1}{4}-2 \frac{1}{2}\) is the same as \(\left[4-2+\frac{1}{4}-\frac{1}{2}\right]\).

6th Std Maths Digest Pdf Download

• Operations on Fractions Practice Set 9 Class 6 Maths Solution
• Operations on Fractions Practice Set 10 Class 6 Maths Solution
• Operations on Fractions Practice Set 11 Class 6 Maths Solution
• Operations on Fractions Practice Set 12 Class 6 Maths Solution
• Operations on Fractions Practice Set 13 Class 6 Maths Solution
• Decimal Fractions Practice Set 14 Class 6 Maths Solution
• Decimal Fractions Practice Set 15 Class 6 Maths Solution
• Decimal Fractions Practice Set 16 Class 6 Maths Solution
• Decimal Fractions Practice Set 17 Class 6 Maths Solution

Fractions Class 5 Problem Set 20 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 20 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Question 1.
Add the following
\(\text { (1) } \frac{1}{5}+\frac{3}{5}\)
Answer:
\(\frac{1}{5}+\frac{3}{5}=\frac{1+3}{5}=\frac{4}{5}\)

\(\text { (2) } \frac{2}{7}+\frac{4}{7}\)
Answer:
\(\frac{2}{7}+\frac{4}{7}=\frac{2+4}{7}=\frac{6}{7}\)

\(\text { (3) } \frac{7}{12}+\frac{2}{12}\)
Answer:
\(\frac{7}{12}+\frac{2}{12}=\frac{7+2}{12}=\frac{9}{12}\)

\(\text { (4) } \frac{2}{9}+\frac{7}{9}\)
Answer:
\(\frac{2}{9}+\frac{7}{9}=\frac{2+7}{9}=\frac{9}{9}=1\)

\(\text { (5) } \frac{3}{15}+\frac{4}{15}\)
Answer:
\(\frac{3}{15}+\frac{4}{15}=\frac{3+4}{15}=\frac{7}{15}\)

\(\text { (6) } \frac{2}{7}+\frac{1}{7}+\frac{3}{7}\)
Answer:
\(\frac{2}{7}+\frac{1}{7}+\frac{3}{7}=\frac{2+1+3}{7}=\frac{6}{7}\)

\(\text { (7) } \frac{2}{10}+\frac{4}{10}+\frac{3}{10}\)
Answer:
\(\frac{2}{10}+\frac{4}{10}+\frac{3}{10}=\frac{2+4+3}{10}=\frac{9}{10}\)

\(\text { (8) } \frac{4}{9}+\frac{1}{9}\)
Answer:
\(\frac{4}{9}+\frac{1}{9}=\frac{4+1}{9}=\frac{5}{9}\)

\(\text { (9) } \frac{5}{8}+\frac{3}{8}\)
Answer:
\(\frac{5}{8}+\frac{3}{8}=\frac{5+3}{8}=\frac{8}{8}=1\)

Question 2.
Mother gave \(\frac{3}{8}\) of one guava to Meena and \(\frac{2}{8}\) of the guava to Geeta. What part of the guava did she give them altogether?
Solution:
\(\frac{3}{8}+\frac{2}{8}=\frac{3+2}{8}=\frac{5}{8}\) given altogether
Answer:
\(\frac{5}{8}\) part of guava given altogether

Question 3.
The girls of Std V cleaned \(\frac{3}{4}\) of a field while the boys cleaned \(\frac{1}{4}\). What part of the field was cleaned altogether?
Solution:
Girls cleaned + Boys cleaned
\(\frac{3}{4}+\frac{1}{4}=\frac{3+1}{4}=\frac{4}{4}=1\)
Answer:
Full whole field cleaned altogether.

Subtraction of like fractions

A figure is divided into 5 equal parts and 4 of them are colored. That is, \(\frac{4}{5}\) part of the figure is coloured.

Now, we remove the colour from one of the coloured parts. That is, we subtract \(\frac{1}{5}\) from \(\frac{4}{5}\). The remaining coloured part is \(\frac{3}{5}\). Therefore, \(\frac{4}{5}\) – \(\frac{1}{5}\) = \(\frac{4-1}{5}\) = \(\frac{3}{5}\).

When subtracting a fraction from another like fraction, we write the difference between the numerators in the numerator and the common denominator in the denominator.

Example (1) Subtract : \(\frac{7}{13}\) – \(\frac{5}{13}\)

These two fractions have a common denominator. So, we shall subtract the second numerator from the first and write the denominator as it is.
\(\frac{7}{13}-\frac{5}{13}=\frac{7-5}{13}=\frac{2}{13}\)

Example (2) If Raju got \(\frac{5}{12}\) part of a sugarcane and Sanju got \(\frac{3}{12}\) part, how much was the extra part that Raju got?

To find out the difference, we must subtract.
\(\frac{5}{12}-\frac{3}{12}=\frac{5-3}{12}=\frac{2}{12}\). Thus, Raju got \(\frac{2}{12}\) extra.

Addition and Subtraction Problem Set 13 Additional Important Questions and Answers

\(\text { (1) } \frac{3}{6}+\frac{2}{6}+\frac{1}{6}\)
Answer:
\(\frac{3}{6}+\frac{2}{6}+\frac{1}{6}=\frac{3+2+1}{6}=\frac{6}{6}=1\)

\(\text { (2) } \frac{4}{10}+\frac{1}{10}+\frac{3}{10}+\frac{2}{10}\)
Answer:
\(\frac{4}{10}+\frac{1}{10}+\frac{3}{10}+\frac{2}{10}=\frac{4+1+3+2}{10}=\frac{10}{10}=1\)

\(\text { (3) } \frac{1}{2}+\frac{1}{2}\)
Answer:
\(\frac{1}{2}+\frac{1}{2}=\frac{1+1}{2}=\frac{2}{2}=1\)

Solve the following word problems:

Question 1.
of journey travelled by A and of journey travelled by B. What part of the journey travelled by both field was cleaned altogether?
Solution:
Travelled by A + Travelled by B
\(\frac{3}{5}+\frac{2}{5}=\frac{3+2}{5}=\frac{5}{5}=1\)
Answer:
Full (whole) journey travelled by both.

Maharashtra Board Class 5 Maths Solutions

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions