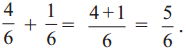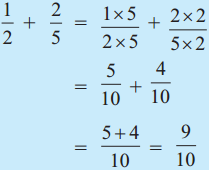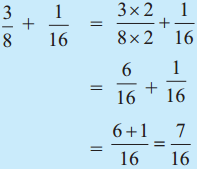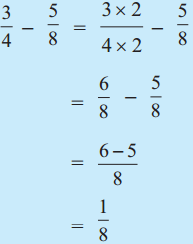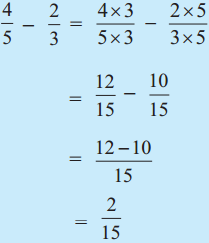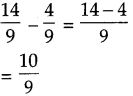Prasanna

Geometrical Constructions Class 6 Maths Chapter 17 Practice Set 40 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 17 Geometrical Constructions Class 6 Practice Set 40 Answers Solutions.

Std 6 Maths Practice Set 40 Solutions Answers

Question 1.
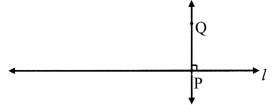
Draw line l. Take point P anywhere outside the line. Using a set square draw a line PQ perpendicular to line l.
Solution:
Step 1:

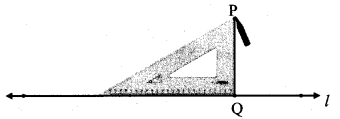
Step 2:

line PQ ⊥ line l.

Question 2.
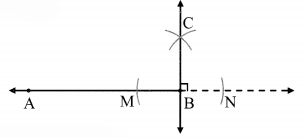
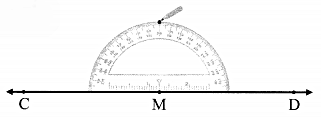
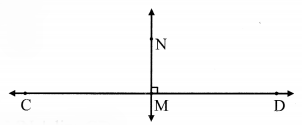
Draw line AB. Take point M anywhere outside the line. Using a compass and ruler, draw a line MN perpendicular to line AB.
Solution:
Step 1:

Step 2:

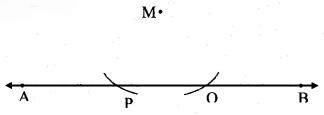
Step 3:

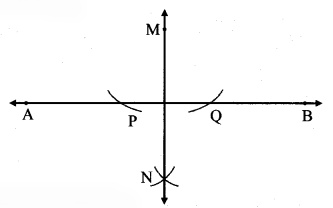
line MN ⊥ line AB.

Question 3.
Draw a line segment AB of length 5.5 cm. Bisect it using a compass and ruler.
Solution:
Step 1:

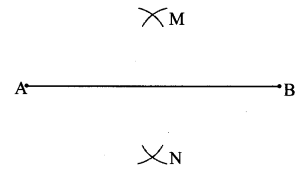
Step 2:

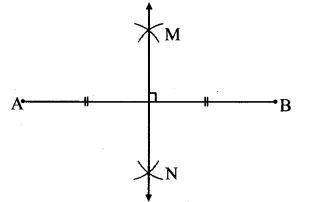
line MN is the perpendicular bisector of seg AB.

Question 4.
Take point R on line XY. Draw a perpendicular to XY at R, using a set square.
Solution:
Step 1:

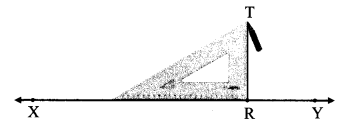
Step 2:

line TR ⊥ line XY.

Maharashtra Board Class 6 Maths Chapter 17 Geometrical Constructions Practice Set 40 Questions and Activities

Question 1.
In the above construction, why must the distance in the compass be kept constant? (Textbook pg. no. 90)
Solution:
The point N is at equal distance from points P and Q.
If we change the distance of the compass while drawing arcs from points P and Q, we will not get a point which is at equal distance from P and Q. Hence, the distance in the compass must be kept constant.

Question 2.
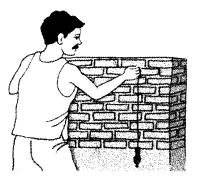
The Perpendicular Bisector. (Textbook pg. no. 90)

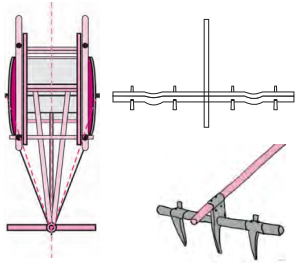
1. A wooden ‘yoke’ is used for pulling a bullock cart. How is the position of the yoke determined?
2. To do that, a rope is used to measure equal distances from the spine/midline of the bullock cart. Which geometrical property is used here?
3. Find out from the craftsmen or from other experienced persons, why this is done.

Solution:

1. For the bullock cart to be pulled in the correct direction by the yoke, its Centre O should be equidistant from the either sides of the cart.
2. The property of perpendicular bisector is used to make the point equidistant from both the ends
3. A rope is used just like a compass to get equal distances from the spine/midline of bullock cart.

Question 3.
Take a rectangular sheet of paper. Fold the paper so that the lower edge of the paper falls on its top edge, and fold it over again from right to left. Observe the two folds that have formed on the . paper. Verify that each fold is a perpendicular bisector of the other. Then measure the following distances. (Textbook pg. no. 91)
i. l(XP)
ii. l(XA)
iii. l(XB)
iv. l(YP)
v. l(YA)

You will observe that l(XP) = l(YP), l(XA) = l(YA) and l(XB) = l(YB)
Therefore we can conclude that all points on the vertical fold (perpendicular bisector) are equidistant from the endpoints of the horizontal fold.
Solution:
[Note: Students should attempt this activity on their own.]

6th Std Maths Digest Pdf Download

• Triangles and their Properties Practice Set 36 Class 6 Maths Solution
• Quadrilaterals Practice Set 37 Class 6 Maths Solution
• Quadrilaterals Practice Set 38 Class 6 Maths Solution
• Geometrical Constructions Practice Set 39 Class 6 Maths Solution
• Geometrical Constructions Practice Set 40 Class 6 Maths Solution
• Three Dimensional Shapes Practice Set 41 Class 6 Maths Solution

Multiples and Factors Class 5 Problem Set 32 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 32 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 8 Multiples and Factors

Write the factors of the following numbers.

(1) 8
Answer:
8 is exactly divisible by 1, 2, 4, 8.
So, 1, 2, 4, 8 are factors of 8.

(2) 5
Answer:
5 is exactly divisible by 1, 5.
So, 1, 5 are factors of 5.

(3) 14
Answer:
14 is exactly divisible by 1, 2, 7, 14.
So, 1, 2, 7, 14 are the factors 14.

(4) 10
Answer:
10 is exactly divisible by 1, 2, 5, 10.
So, 1, 2, 5, 10 are the factors of 10.

(5) 7
Answer:
7 is exactly divisible by 1, 7.
So, 1, 7 are factors of 7.

(6) 22
Answer:
22 is exactly divisible by 1, 2, 11, 22.
So, 1, 2, 11, 22 are the factors of 22.

(7) 25
Answer:
25 is exactly divisible by 1, 5, 25.
So, 1, 5, 25 are the factors of 25.

(8) 32
Answer:
32 is exactly divisible by 1, 2, 4, 8,16, 32.
So, 1, 2, 4, 8, 16, 32 are the factors of 32.

(9) 33
Answer:
33 is exactly divisible by 1, 3, 11, 33.
So, 1, 3, 11, 33 are the factors of 33.

Multiples

Dada : You know what a divisor and a dividend is. Do you know what a multiple is?

Anju : I don’t know what a multiple is, but I think it must be related to multiplication.

Dada : Right ! Let me give you an example. You can solve 20 ÷ 5, can’t you?

Anju : Yes. When we divide the dividend 20 by the divisor 5, the quotient is 4 and the remainder is 0.

Dada : When the division of a dividend leaves no remainder, the dividend is said to be a multiple of the divisor. In such a case, the dividend is the product of the divisor and the quotient. Here, 20 is a multiple of 5, but 21 is not.

Now tell me, can we divide 84 chalksticks into groups of six?

Suraj : Let me divide by 6. 84 can be divided exactly by 6 and the quotient is 14. Thus, we can make 14 groups of 6. So, 84 is the multiple of 6 and 6 is a factor of 84.

Dada : If the number of chalksticks is 6, 12, 18, 36 or 84, then we can make exact groups of 6 with none left over. It means that 6, 12, 18, 36 and 84 are multiples of 6, or that they are exactly divisible by 6. To see whether the number of chalksticks is a multiple of 6, divide that number by 6. If the remainder is 0, the number is a multiple of 6.

Each number in the 3 times table is exactly divisible by 3 or is a multiple of 3. Similarly, the numbers in the 7 times table are multiples of 7. Numbers in the 9 times table are multiples of 9.

We use this idea all the time. Let me ask you a few questions so as to make it clear. I have a 200 ml measure. Will I be able to measure out 1 litre of milk with it?

Suraj : I litre is 1000 ml. 1000 = 200 × 5, which means that 1000 is a multiple of 200. So we can measure out 1 litre of milk with the 200 millilitre measure. 5 measures of 200 ml make 1 litre.

Dada : Can we measure out one and a half litres of milk with the 200 ml measure?

Anju : One and a half litres is 1500 ml. 1500 is not divisible by 200. So, it is not a multiple of 200. So the 200 ml measure cannot be used to measure out one and a half litres of milk.

Dada : I have 400 grams of chana. I have to make pouches of 60 grams each. Is that possible, if I don’t want any left overs?

Anju : No. 400 is not a multiple of 60.

Dada : How much more chana will I need to make those pouches of 60 grams each?

Anju : We will have to find the multiple of 60 that comes directly after 400. 60 × 6 = 360, 60 × 7 = 420. So, we need 20 grams more of chana.

Tests for divisibility

Study the 2 times table and see which numbers appear in the units place. Similarly, divide 52, 74, 80, 96 and 98 by 2 to see if they are exactly divisible by 2. What rule do we get for determining whether a number is a multiple of 2?

Now study the 5 and 10 times tables.

See what rules you get for finding multiples of 5 and 10, that is, numbers divisible by 5 and 10.

Test for divisibility by 2 : If there is 0, 2, 4, 6 or 8 in the units place, the number is a multiple of 2, or is exactly divisible by 2.

Test for divisibility by 5 : Any number with 5 or 0 in the units place is a multiple of 5 or, is divisible by 5.

Test for divisibility by 10 : Any number that has 0 in the units place is a multiple of 10.

Multiples and Factors Problem Set 32 Additional Important Questions and Answers

Question 1.
Write the factors of the following numbers.

(1) 45
Answer:
45 is exactly divisible by 1, 3, 5, 9,15, 45.
So, 1, 3, 5, 9, 15, 45 are the factors of 45.

(2) 48
Answer:
48 is exactly divisible by 1, 2, 3, 4, 6, 8,12,16, 24, 48.
So, 1, 2, 3, 4, 6, 8,12,16, 24, 48 are the factors of 48.

(3) 60
Answer:
60 is exactly divisible by 1, 2, 3, 4, 5, 6,10,12, 15, 20, 30, 60
So, 1, 2, 3, 4, 5, 6,10, 12, 15, 20, 30, 60 are the factors of 60.

Question 2.
Is 8 a factor of 60?
Answer:
No, since 60 is not exactly divisible by 8.

Maharashtra Board Class 5 Maths Solutions

• Multiples and Factors Problem Set 32 Class 5 Maths Solutions
• Multiples and Factors Problem Set 33 Class 5 Maths Solutions
• Multiples and Factors Problem Set 34 Class 5 Maths Solutions
• Multiples and Factors Problem Set 35 Class 5 Maths Solutions

Bar Graphs Class 6 Maths Chapter 6 Practice Set 19 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 6 Bar Graphs Class 6 Practice Set 19 Answers Solutions.

Std 6 Maths Practice Set 19 Solutions Answers

Question 1.
The names of the heads of some families in a village and the quantity of drinking water their family consumes in one day are given below. Draw a bar graph for this data.
(Scale: On Y axis. 1 cm = 10 liters of water)

Solution:

Question 2.
The names and numbers of animals in a certain zoo are given below. Use the data to make a bar graph. (Scale: On Y axis, 1 cm = 4 animals).

Solution:

Question 3.
The table below gives the number of children who took part in the various items of the talent show as part of the annual school gathering. Make a bar graph to show this data.
(Scale: On Y-axis, 1 cm = 4 children)

Solution:

Question 4.
The number of customers who came to a juice centre during one week is given in the table below. Make two different bar graphs to show this data.
(On Y-axis, 1 cm = 10 customers, 1 cm = 5 customers)

Solution:

Question 5.
Students planted trees in 5 villages of Sangli district. Make a bar graph of this data. (Scale: On Y-axis, 1 cm = 100 trees).

Solution:

Question 6.
Yashwant gives different amounts of time as shown below, to different exercises he does during the week. Draw a bar graph to show the details of his schedule using an appropriate scale.

Solution:
1 hour = 60 minutes
∴ 1 hour 10 minutes = 1 hour + 10 minutes = 60 minutes +10 minutes = 70 minutes
and \(1\frac { 1 }{ 2 }\) hours = 1 hour + \(\frac { 1 }{ 2 }\) hour = 60 minutes + 30 minutes = 90 minutes
The given table can be written as follows:

Question 7.
Write the names of four of your classmates. Beside each name, write his/her weight in kilograms. Enter this data in a table like the above and make a bar graph.
Solution:

Scale: On Y-axis, 1 cm = 4 kg [Note: Students can take their own examples]

Maharashtra Board Class 6 Maths Chapter 6 Bar Graphs Practice Set 19 Intext Questions and Activities

Question 1.
Collect bar graphs from newspapers or periodicals showing a variety of data. (Textbook pg. no. 38)
Solution:
(Student should attempt the activities on their own.)

6th Std Maths Digest Pdf Download

• Bar Graphs Practice Set 18 Class 6 Maths Solution
• Bar Graphs Practice Set 19 Class 6 Maths Solution
• Symmetry Practice Set 20 Class 6 Maths Solution
• Symmetry Practice Set 21 Class 6 Maths Solution
• Divisibility Practice Set 22 Class 6 Maths Solution
• HCF-LCM Practice Set 23 Class 6 Maths Solution
• HCF-LCM Practice Set 24 Class 6 Maths Solution
• HCF-LCM Practice Set 25 Class 6 Maths Solution

Integers Class 6 Maths Chapter 3 Practice Set 7 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 7 Answers Solutions.

Std 6 Maths Practice Set 7 Solutions Answers

Question 1.
Write the proper signs >, < or = in the boxes below:

1. -4 __ 5
2. 8 __ -10
3. +9 __ +9
4. -6 __ 0
5. 7 __ 4
6. 3 __ 0
7. -7 __ 7
8. -12 __ 5
9. -2 __ -8
10. -1 __ -2
11. 6 __ -3
12. -14 __ -14

Solution:

1. -4 < 5
2. 8 > -10
3. +9 = +9
4. -6 < 0
5. 7 > 4
6. 3 > 0
7. -7 < 7
8. -12 < 5
9. -2 > -8
10. -1 > -2
11. 6 > -3
12. -14 = -14

6th Std Maths Digest Pdf Download

• Basic Concepts in Geometry Practice Set 1 Class 6 Maths Solution
• Angles Practice Set 2 Class 6 Maths Solution
• Angles Practice Set 3 Class 6 Maths Solution
• Integers Practice Set 4 Class 6 Maths Solution
• Integers Practice Set 5 Class 6 Maths Solution
• Integers Practice Set 6 Class 6 Maths Solution
• Integers Practice Set 7 Class 6 Maths Solution
• Integers Practice Set 8 Class 6 Maths Solution

Integers Class 6 Maths Chapter 3 Practice Set 6 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 6 Answers Solutions.

Std 6 Maths Practice Set 6 Solutions Answers

Question 1.
Write the opposite number of each of the numbers given below.

Solution:

6th Std Maths Digest Pdf Download

• Basic Concepts in Geometry Practice Set 1 Class 6 Maths Solution
• Angles Practice Set 2 Class 6 Maths Solution
• Angles Practice Set 3 Class 6 Maths Solution
• Integers Practice Set 4 Class 6 Maths Solution
• Integers Practice Set 5 Class 6 Maths Solution
• Integers Practice Set 6 Class 6 Maths Solution
• Integers Practice Set 7 Class 6 Maths Solution
• Integers Practice Set 8 Class 6 Maths Solution

Ratio-Proportion Class 6 Maths Chapter 11 Practice Set 28 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 11 Ratio-Proportion Class 6 Practice Set 28 Answers Solutions.

Std 6 Maths Practice Set 28 Solutions Answers

6th Standard Maths Practice Set 28 Question 1.
In each example below, find the ratio of the first number to the second:
i. 24, 56
ii. 63,49
iii. 52, 65
iv. 84, 60
v. 35, 65
vi. 121, 99
Solution:
i. 24, 56
\(\frac{24}{56}=\frac{24 \div 8}{56 \div 8}=\frac{3}{7}\)
= 3:7

ii. 63,49
\(\frac{63}{49}=\frac{63 \div 7}{49 \div 7}=\frac{9}{7}\)
= 9:7

iii. 52, 65
\(\frac{52}{65}=\frac{52 \div 13}{65 \div 13}=\frac{4}{5}\)
= 4:5

iv. 84, 60
\(\frac{84}{60}=\frac{84 \div 12}{60 \div 12}=\frac{7}{5}\)
= 7:5

v. 35, 65
\(\frac{35}{65}=\frac{35 \div 5}{65 \div 5}=\frac{7}{13}\)
= 7:13

vi. 121, 99
\(\frac{121}{99}=\frac{121 \div 11}{99 \div 11}=\frac{11}{9}\)
= 11:9

6th Maths Practice Set 28 Question 2.
Find the ratio of the first quantity to the second.
i. 25 beads, 40 beads
ii. Rs 40, Rs 120
iii. 15 minutes, 1 hour
iv. 30 litres, 24 litres
v. 99 kg, 44000 grams
vi. 1 litre, 250 ml
vii. 60 paise, 1 rupee
viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
ix. 125 cm, 1 metre
Solution:
i. Required Ratio = \(\frac{25}{40}=\frac{25 \div 5}{40 \div 5}=\frac{5}{8}\)

ii. Required Ratio = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}\)

iii. 1 hour = 60 minutes
Required Ratio = \(\frac{15}{60}=\frac{15 \div 15}{60 \div 15}=\frac{1}{4}\)

iv. Required Ratio = \(\frac{30}{24}=\frac{30 \div 6}{24 \div 6}=\frac{5}{4}\)

v. 99 kg = 99 x 1000 grams = 99000 grams
Required Ratio = \(\frac{99000}{44000}=\frac{99000 \div 1000}{44000 \div 1000}=\frac{99}{44}\)
= \(\frac{99}{44}=\frac{99 \div 11}{44 \div 11}=\frac{9}{4}\)

vi. 1 litre, 250 ml
1 litre = 1000 ml
Required Ratio = \(\frac{1000}{250}=\frac{1000 \div 10}{250 \div 10}=\frac{100}{25}\)
= \(\frac{100}{25}=\frac{100 \div 25}{25 \div 25}=\frac{4}{1}\)

viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
\(\frac { 1 }{ 2 }\) kg = \(\frac { 1000 }{ 2 }\) grams = 500 grams
Required Ratio = \(\frac{750}{500}=\frac{750 \div 10}{500 \div 10}=\frac{75}{50}\)
= \(\frac{75}{50}=\frac{75 \div 25}{50 \div 25}=\frac{3}{2}\)

ix. 125 cm, 1 metre
1 metre = 100 cm
Required Ratio = \(\frac{125}{100}=\frac{125 \div 25}{100 \div 25}=\frac{5}{4}\)

6th Std Maths Practice Set 28 Question 3.
Reema has 24 notebooks and 18 books. Find the ratio of notebooks to books.
Solution:
Ratio of notebooks to books

∴ The ratio of notebooks to books with Reema is \(\frac { 4 }{ 3 }\)

Practice Set 28 Question 4.
30 cricket players and 20 kho-kho players are training on a field. What is the ratio of cricket players to the total number of players?
Solution:
Total number of players = Cricket players + Kho-kho players
= 30 + 20 = 50
Ratio of cricket players to the total number of players

∴ The ratio of cricket players to the total number of players is \(\frac { 3 }{ 5 }\).

Question 5.
Snehal has a red ribbon that is 80 cm long and a blue ribbon 2.20 m long. What is the ratio of the length of the red ribbon to that of the blue ribbon?
Solution:
1 metre =100 cm
Length of the red ribbon = 80 cm
Length of the blue ribbon = 2.20 m = 2.20 x 100 cm
\(=\frac{220}{100} \times \frac{100}{1}=\frac{220 \times 100}{100 \times 1}\)
= 220 cm
∴ Ratio of length of the red ribbon to that of the blue ribbon

∴ The ratio of the length of the red ribbon to that of the blue ribbon is \(\frac { 4 }{ 11 }\).

11 Ratio Question 6.
Shubham’s age today is 12 years and his father’s is 42 years. Shubham’s mother is younger than his father by 6 years. Find the following ratios.
i. Ratio of Shubham’s age today to his mother’s age today.
ii. Ratio of Shubham’s mother’s age today to his father’s age today.
iii. The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old.
Solution:
Shubham’s age today = 12 years
Shubham’s father’s age = 42 years
Shubham’s mother age = Shubham’s father’s age – 6 years
= 42 years – 6 years = 36 years

i. Ratio of Shubham’s age today to his mother’s age today

∴ The ratio of Shubham’s age today to his mother’s age today is \(\frac { 1 }{ 3 }\).

ii. Ratio of Shubham’s mother age today to his father’s age today

∴ The ratio of Shubham’s mother’s age today to his father’s age today is \(\frac { 6 }{ 7 }\).

iii. Shubham’s age today is 12 years and his mothers age is 36 years.
Hence when Shubham’s age was 10 years, his mother’s age was 34 years (i.e. 36 – 2 years).
Ratio of Shubham’s age to his mother’s age when Shubham was 10 years old

∴ The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old is \(\frac { 5 }{ 17 }\)

Maharashtra Board Class 6 Maths Chapter 11 Ratio-Proportion Practice Set 28 Intext Questions and Activities

Question 1.
In the figure, colour some squares with any colour you like and leave some blank. (Textbook pg. no. 57)

i. Count all the boxes and write the number.
ii. Count the colored ones and write the number.
iii. Count the blank ones and write the number.
iv. Find the ratio of the colored boxes to the blank ones.
v. Find the ratio of the colored boxes to the total boxes.
vi. Find the ratio of the blank boxes to the total boxes.
Solution:
i. The number of all boxes is 16.
ii. The number of colored boxes is 7.
iii. The number of blank boxes is 9.
iv. Ratio of the colored boxes to the blank ones

v. Ratio of the colored boxes to the total boxes

vi. Ratio of the blank boxes to the total boxes

6th Std Maths Digest Pdf Download

• Equations Practice Set 26 Class 6 Maths Solution
• Equations Practice Set 27 Class 6 Maths Solution
• Ratio-Proportion Practice Set 28 Class 6 Maths Solution
• Ratio-Proportion Practice Set 29 Class 6 Maths Solution
• Percentage Practice Set 30 Class 6 Maths Solution
• Profit-Loss Practice Set 31 Class 6 Maths Solution
• Profit-Loss Practice Set 32 Class 6 Maths Solution
• Profit-Loss Practice Set 33 Class 6 Maths Solution
• Profit-Loss Practice Set 34 Class 6 Maths Solution
• Banks and Simple Interest Practice Set 35 Class 6 Maths Solution

Fractions Class 5 Problem Set 17 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 17 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Question 1.
Write the proper number in the box.

Answer:
Here 20 = 2 x 10

Answer:
Here 15 = 3 x 5

Answer:
Here 18 = 9 x 2
hehce,

Answer:
Here 40 + 5 = 8,
hence,

Answer:
Here 26 ÷ 2 = 13,
hence,

Answer:
Here 6 ÷ 2 = 3,
hence,

Answer:
Here 4 ÷ 4 = 1,
hence,

Answer:
Here 25 ÷ 5 = 5,
hence,

Question 2.
Find an equivalent fraction with denominator 18, for each of the following fractions.

Solution:

Question 3.
Find an equivalent fraction with denominator 5, for each of the following fractions.

Solution:

Question 4.
From the fractions given below, pair off the equivalent fractions.

Solution:

Question 5.
Find two equivalent fractions for each of the following fractions.

Solution:

Like fractions and unlike fractions

Fractions such as \(\frac{1}{7}, \frac{4}{7}, \frac{6}{7}\) whose denominators are equal, are called ‘like fractions’.
Fractions such as \(\frac{1}{3}, \frac{4}{8}, \frac{9}{11}\) which have different denominators are called unlike fractions’.

Converting unlike fractions into like fractions

Example (1) Convert 5/6 and 7/9 into like fractions.
Here, we must find a common multiple for the numbers 6 and 9.
Multiples of 6 : 6, 12, 18, 24, 30, 36, ……..
Multiples of 9 : 9, 18, 27, 36, 45 ……..
Here, the number 18 is a multiple of both 6 and 9. So, let us make 18 the denominator of both fractions.

Thus, 15/18 and 1418 are like fractions, respectively equivalent to 5/6 and 7/9.
Here, 18 is a multiple of both 6 and 9. We could also choose numbers like 36 and 54 as the common denominators.

Example (2) Convert 4/8 and 5/16 into like fractions.
As 16 is twice 8, it is easy to make 16 the common denominator.
\(\frac{4}{8}=\frac{4 \times 2}{8 \times 2}=\frac{8}{16}\) Thus, 8/16 and 5/16 are the required like fractions.

Example (3) Find a common denominator for 4/7 and 3/4.
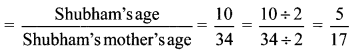
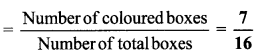
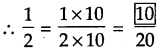
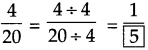
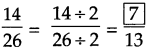
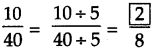
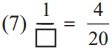
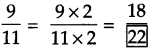
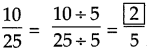
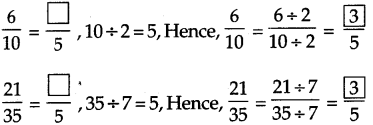
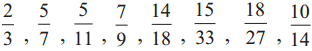
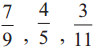
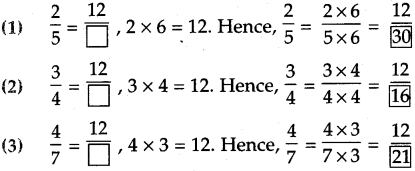
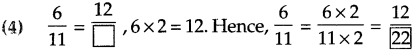
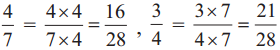The number 28 is a multiple of both 7 and 4. So, make 28 the common denominator. . Therefore, 16/28 and 21/28 are the required like fractions.

Fractions Problem Set 17 Additional Important Questions and Answers

Question 1.
Find two equivalent fractions for each of the following fraction:

Solution:

Maharashtra Board Class 5 Maths Solutions

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions

Fractions Class 5 Problem Set 21 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 21 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Question 1.
Subtract the following.

\(\text { (1) } \frac{5}{7}-\frac{1}{7}\)
Answer:

\(\text { (2) } \frac{5}{8}-\frac{3}{8}\)
Answer:

\(\text { (3) } \frac{7}{9}-\frac{2}{9}\)
Answer:

\(\text { (4) } \frac{8}{11}-\frac{5}{11}\)
Answer:

\(\text { (5) } \frac{9}{13}-\frac{4}{13}\)
Answer:

\(\text { (6) } \frac{7}{10}-\frac{3}{10}\)
Answer:

\(\text { (7) } \frac{9}{12}-\frac{2}{12}\)
Answer:

\(\text { (8) } \frac{10}{15}-\frac{3}{15}\)
Answer:

Question 2.
\(\frac{7}{10}\) of a wall is to be painted. Ramu has painted 410 of it. How much more needs to be painted?
Solution:
To be painted – painted

Answer:
\(\frac{3}{10}\) more needs to be painted.

Addition and subtraction of unlike fractions

Example (1) Add : \(\frac{2}{3}+\frac{1}{6}\)

First let us show the fraction \(\frac{2}{3}\) by coloring two of the three equal parts on a strip.

You have learnt to add and to subtract fractions with common denominators. Here, we have to add the fraction \(\frac{1}{6}\) to the fraction \(\frac{2}{3}\).

So let us divide each part on this strip into two equal parts. \(\frac{4}{6}\) is a fraction equivalent to \(\frac{2}{3}\). Now, as 16 is to be added to \(\frac{2}{3}\) i.e. to \(\frac{4}{6}\), we shall colour one more of the six parts on the strip. Now, the total coloured part is \(\frac{5}{6}\).

Therefore,
That is,

Example (2) Add : \(\frac{1}{2}+\frac{2}{5}\)
Here, the smallest common multiple of the two denominators is 10. So, we shall change the denominator of both fractions to 10.

Example (3) Add : \(\frac{3}{8}+\frac{1}{16}\)
Here, 16 is twice 8. So, we shall change the denominator of both fractions to 16.

Example (4) Subtract : \(\frac{3}{4}-\frac{5}{8}\)
Let us make 8 the common denominator of the given fractions.

Example (5) Subtract : \(\frac{4}{5}-\frac{2}{3}\)
The smallest common multiple of the denominators is 15. So, we shall change the denominator of both fractions to 15.

Addition and Subtraction Problem Set 13 Additional Important Questions and Answers

\(\text { (1) } \frac{9}{14}-\frac{3}{14}\)
Answer:

\(\text { (2) } \frac{5}{6}-\frac{3}{6}\)
Answer:

\(\text { (3) } \frac{9}{16}-\frac{5}{16}\)
Answer:

\(\text { (4) } \frac{7}{8}-\frac{3}{8}-\frac{1}{8}\)
Answer:

(5) \(\frac{7}{9}\) part of the work done by Neha and Supriya together. \(\frac{5}{9}\) part of this work was done by Neha. How much work done by Supriya?
Solution:
Total work done – work done by Neha = work done by Supriya

Answer:
\(\frac{2}{9}\) work done by Supriya

(6) Mr. Sharma is \(\frac{14}{9}\) m tall. Mrs. Sharma is \(\frac{4}{9}\) shorter than him. What is Mrs. Sharma’s height?
Solution:
Mrs. Sharma’s height

Answer:
Mrs. Sharma’s height = \(\frac{10}{9}\)

Maharashtra Board Class 5 Maths Solutions

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions

Integers Class 6 Maths Chapter 3 Practice Set 5 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 5 Answers Solutions.

Std 6 Maths Practice Set 5 Solutions Answers

Question 1.
Add:

1. 8 + 6
2. 9 + (-3)
3. 5 + (-6)
4. – 7 + 2
5. – 8 + 0
6. – 5 + (-2)

Solution:

Question 2.
Complete the table given below:

Solution:

Maharashtra Board Class 6 Maths Chapter 3 Integers Practice Set 5 Intext Questions and Activities

Question 1.
On the playground, mark a timeline showing the years from 2000 to 2024. With one child standing at the position of the 2017, ask the following questions: (Textbook pg. no. 15)

1. While playing this game, what is his/her age?
2. Five years ago, which year was it? And what was his / her age then?
3. In which year will he / she go to Std X? How old will he / she be then?

The child should find answers to such questions by walking the right number of units and in the right direction on the timeline.
[Assume child born year is 2009]
Solutions:

1. Age of child is 8 years.
2. Five years ago, year was 2012. His/her age is 3 years.
3. In 2024, he/she will go the Std X. His/her age is 15 years.

Question 2.
On a playground mark a timeline of 100 years. This will make it possible to count the years from 0 to 2100 on it. Important historical events can then be shown in proper centuries. (Textbook pg. no. 16)
Solution:
(Students should attempt this activity on their own)

Question 3.
Observe the figures and write appropriate number in the boxes given below. (Textbook pg. no. 16 and 17)
i.

a. At first the rabbit was at the number ____
b. It hopped ___ units to the right.
c. It is now at the number ___
Solution:
i.
a. +1
b. 5
c. +6

ii.

a. At first the rabbit was at the number ___
b. It hopped ____ units to the right.
c. It is now at the number ____
Solution:
ii.
a. -2
b. 5
c. +3

iii.

a. At first the rabbit was at the number ___
b. It hopped ____ units to the left.
c. It is now at the number ___
Solution:
iii.
a. -3
b. 4
c. -7

iv.

a. At first the rabbit was at the number ___
b. It hopped___units to the left.
c. It is now at the number ____
Solution:
iv.
a. +3
b. 4
c. -1

6th Std Maths Digest Pdf Download

• Basic Concepts in Geometry Practice Set 1 Class 6 Maths Solution
• Angles Practice Set 2 Class 6 Maths Solution
• Angles Practice Set 3 Class 6 Maths Solution
• Integers Practice Set 4 Class 6 Maths Solution
• Integers Practice Set 5 Class 6 Maths Solution
• Integers Practice Set 6 Class 6 Maths Solution
• Integers Practice Set 7 Class 6 Maths Solution
• Integers Practice Set 8 Class 6 Maths Solution

Geometrical Constructions Class 6 Maths Chapter 17 Practice Set 39 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 17 Geometrical Constructions Class 6 Practice Set 39 Answers Solutions.

Std 6 Maths Practice Set 39 Solutions Answers

Question 1.
Draw line l. Take any point P on the line. Using a set square, draw a line perpendicular to line l at the point P.
Solution:
Step 1:

Step 2:

line PQ ⊥ line l

Question 2.
Draw a line AB. Using a compass, draw a line perpendicular to AB at point B.
Solution:
Step 1:

Step 2:

Step 3:

line BC ⊥ line AB.

Question 3.
Draw line CD. Take any point M on the line. Using a protractor, draw a line perpendicular to line CD at the point M.
Solution:
Step 1:

Step 2:

line MN ⊥ line CD

Maharashtra Board Class 6 Maths Chapter 17 Geometrical Constructions Practice Set 39 Questions and Activities

Question 1.
When constructing a building, what is the method used to make sure that a wall is exactly upright? What does the mason in the picture have in his hand? What do you think is his purpose for using it? (Textbook pg. no. 87)

Solution:
When constructing a building, a weight (usually with a pointed tip at the bottom) suspended from a string called as plummet or plump bob is aligned from the top of the wall to make sure that the wall is built exactly upright.
The mason in the picture is holding a plumb bob.
The string of the plumb bob is suspended from the top of the wall, such that plumb bob hangs freely. By observing whether the vertical wall is parallel to the string we can check if the constructed wall is vertical.

Question 2.
Have you looked at lamp posts on the roadside? How do they stand? (Textbook pg. no. 87)
Solution:
The lamp posts on the road side are standing erect or vertical.

Question 3.
For the above explained construction, why must we take a distance greater than half of the length of AB? What will happen if we take a smaller distance? (Textbook pg. no. 88)
Solution:
For the above construction, in step-3 we take distance greater than half of the length of AB, so that the arcs drawn by keeping the compass on points A and B intersect each other at point Q.
If the distance in compass is less than half of the length of AB, then the arcs drawn by keeping the compass at A and B will not intersect each other.

6th Std Maths Digest Pdf Download

• Triangles and their Properties Practice Set 36 Class 6 Maths Solution
• Quadrilaterals Practice Set 37 Class 6 Maths Solution
• Quadrilaterals Practice Set 38 Class 6 Maths Solution
• Geometrical Constructions Practice Set 39 Class 6 Maths Solution
• Geometrical Constructions Practice Set 40 Class 6 Maths Solution
• Three Dimensional Shapes Practice Set 41 Class 6 Maths Solution