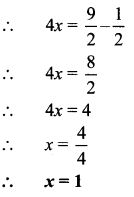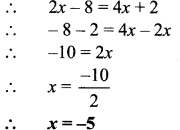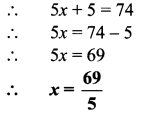Bank and Simple Interest Class 7 Maths Chapter 10 Practice Set 40 Solutions Maharashtra Board
Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 40 Answers Solutions Chapter 10 Bank and Simple Interest.
Std 7 Maths Practice Set 40 Solutions Answers
Question 1.
If Rihanna deposits Rs 1500 in the school fund at 9 p.c.p.a for 2 years, what is the total amount she will get?
Solution:
Here, P = Rs 1500, R = 9 p.c.p.a , T = 2 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{1500 \times 9 \times 2}{100}\)
= 1500 x 9 x 2
= Rs 270
∴ Total amount = Principal + Interest
= 1500 + 270
= Rs 1770
∴ Rihanna will get a total amount of Rs 1770.
Question 2.
Jethalal took a housing loan of Rs 2,50,000 from a bank at 10 p.c.p.a. for 5 years. What is the yearly interest he must pay and the total amount he returns to the bank?
Solution:
Here, P = Rs 250000, R = 10 p.c.p.a., T = 5 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{250000 \times 10 \times 5}{100}\)
= 2500 x 10 x 5
= Rs 1,25,000
∴ Yearly interest = Total interest ÷ Time = 1,25,000 ÷ 5 = Rs 25000
Total amount to be returned = Principal + Total interest
= 250000 + 125000 = Rs 375000
∴ The yearly interest is Rs 25,000 and Jethalal will have to return Rs 3,75,000 to the bank.
Question 3.
Shrikant deposited Rs 85,000 for \(2\frac { 1 }{ 2 }\) years at 7 p.c.p.a. in a savings bank account. What is the total
interest he received at the end of the period?
Solution:
Here, P = Rs 85000, R = 7 p.c.p.a., T = \(2\frac { 1 }{ 2 }\) years = 2.5 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{85000 \times 7 \times 2.5}{100}\)
= \(\frac{85000 \times 7 \times 25}{100 \times 10}\)
= 85 x 7 x 25
= Rs 14875
∴ The total interest received by Shrikant at the end of the period is Rs 14875.
Question 4.
At a certain rate of interest, the interest after 4 years on Rs 5000 principal is Rs 1200. What would be the interest on Rs 15000 at the same rate of interest for the same period?
Solution:
The interest on Rs 5000 after 4 years is Rs 1200.
Let us suppose the interest on Rs 15000 at the same rate after 4 years is Rs x.
Taking the ratio of interest and principal, we get
∴ \(\frac{x}{15000}=\frac{1200}{5000}\)
∴ \(x=\frac{1200 \times 15000}{5000}\)
= Rs 3600
∴ The interest received on Rs 15000 is Rs 3600.
Question 5.
If Pankaj deposits Rs 1,50,000 in a bank at 10 p.c.p.a. for two years, what is the total amount he will get from the bank?
Solution:
Here, P = 150000, R = 10 p.c.p.a., T = 2 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{150000 \times 10 \times 2}{100}\)
= Rs 30000
∴ Total amount = Principal + Total Interest
= 150000 + 30000
= Rs 180000
∴ Pankaj will receive Rs 180000 from the bank.
Maharashtra Board Class 7 Maths Chapter 10 Banks and Simple Interest Practice Set 40 Intext Questions and Activities
Question 1.
Observe the entries made in the page of a passbook shown below and answer the following questions. (Textbook pg. no. 70)
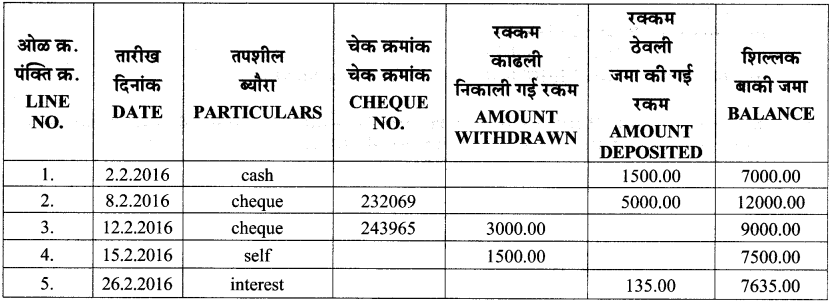
- On 2.2.16 the amount deposited was Rs__and the balance Rs__.
- On 12.2.16, Rs__were withdrawn by cheque no. 243965. The balance was Rs__
- On 26.2.2016 the bank paid an interest of Rs__
Solution:
- 1500, 7000
- 3000, 9000
- 135
Practice Set 40 Class 7 Question 2.
Suvidya borrowed a sum of Rs 30000 at 8 p.c.p.a. interest for a year from her bank to buy a computer. At the end of the period, she had to pay back an amount of Rs 2400 over and above what she had borrowed.
Based on this information fill in the blanks below. (Textbook pg. no. 70)
- Principal = Rs__
- Rate of interest =__%
- Interest = Rs__
- Time =__year.
- The total amount returned to the bank = 30,000 + 2,400 = Rs__
Solution:
- 30000
- 8
- 2400
- 1
- Rs 32400
Class 7 Maths Solution Maharashtra Board
- Direct Proportion and Inverse Proportion Practice Set 37 Class 7 Maths Solution
- Direct Proportion and Inverse Proportion Practice Set 38 Class 7 Maths Solution
- Direct Proportion and Inverse Proportion Practice Set 39 Class 7 Maths Solution
- Banks and Simple Interest Practice Set 40 Class 7 Maths Solution
- Banks and Simple Interest Practice Set 41 Class 7 Maths Solution
- Circle Practice Set 42 Class 7 Maths Solution
- Circle Practice Set 43 Class 7 Maths Solution
- Perimeter and Area Practice Set 44 Class 7 Maths Solution
- Perimeter and Area Practice Set 45 Class 7 Maths Solution
- Perimeter and Area Practice Set 46 Class 7 Maths Solution
- Perimeter and Area Practice Set 47 Class 7 Maths Solution