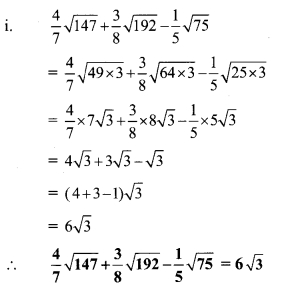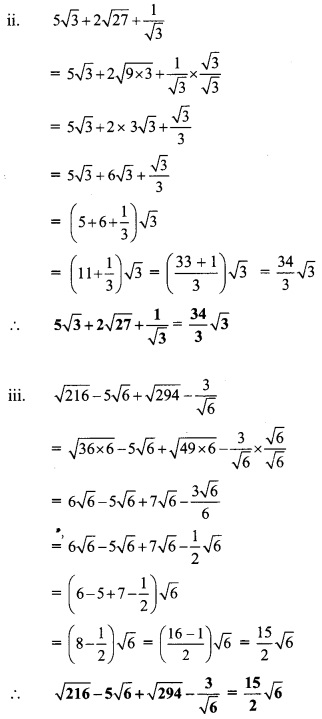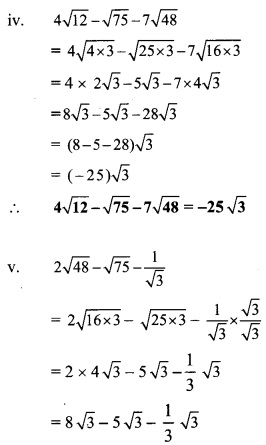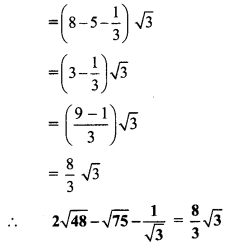Prasanna

9th Standard Maths 1 Practice Set 3.3 Chapter 3 Polynomials Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.

Class 9 Maths Part 1 Practice Set 3.3 Chapter 3 Polynomials Questions With Answers Maharashtra Board

Question 1.
Divide each of the following polynomials by synthetic division method and also by linear division method. Write the quotient and the remainder.
i. (2m² – 3m + 10) ÷ (m – 5)
ii. (x⁴ + 2x³ + 3x² + 4x + 5) ÷ (x + 2)
iii. (y³ – 216) ÷ (y – 6)
iv. (2x⁴ + 3x³ + 4x – 2x²) ÷ (x + 3)
v. (x⁴ – 3x² – 8) ÷ (x + 4)
vi. (y³ – 3y² + 5y – 1) ÷ (y – 1)
Solution:
i. Synthetic division:
(2m² – 3m + 10) ÷ (m – 5)
Dividend = 2m² – 3m + 10
∴ Coefficient form of dividend = (2, -3, 10)
Divisor = m – 5
∴ Opposite of -5 is 5.

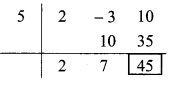
Coefficient form of quotient = (2, 7)
∴ Quotient = 2m + 7,
Remainder = 45
Linear division method:
2m² – 3m + 10
To get the term 2m², multiply (m – 5) by 2m and add 10m,
= 2m(m – 5) + 10m- 3m + 10
= 2m(m – 5) + 7m + 10
To get the term 7m, multiply (m – 5) by 7 and add 35
= 2m(m – 5) + 7(m- 5) + 35+ 10
= (m – 5) (2m + 7) + 45
∴ Quotient = 2m + 7,
Remainder = 45

ii. Synthetic division:
(x⁴ + 2x³ + 3x² + 4x + 5) ÷ (x + 2)
Dividend = x⁴ + 2x³ + 3x² + 4x + 5
∴ Coefficient form of dividend = (1, 2, 3, 4, 5)
Divisor = x + 2
∴ Opposite of + 2 is -2.

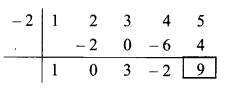
Coefficient form of quotient = (1, 0, 3, -2)
∴ Quotient = x³ + 3x – 2,
Remainder = 9

Linear division method:
x⁴ + 2x³ + 3x² + 4x + 5
To get the term x⁴, multiply (x + 2) by x³ and subtract 2x³,
= x³(x + 2) – 2x³ + 2x³ + 3x² + 4x + 5
= x³(x + 2) + 3x² + 4x + 5
To get the term 3x², multiply (x + 2) by 3x and subtract 6x,
= x³(x + 2) + 3x(x + 2) – 6x + 4x + 5
= x³(x + 2) + 3x(x + 2) – 2x + 5
To get the term -2x, multiply (x + 2) by -2 and add 4,
= x³(x + 2) + 3x(x + 2) – 2(x + 2) + 4 + 5
= (x + 2) (x3 + 3x – 2) + 9
∴ Quotient = x³ + 3x – 2,
Remainder – 9

iii. Synthetic division:
(y³ – 216) ÷ (y – 6)
Dividend = y³ – 216
∴ Index form = y³ + 0y³ + 0y – 216
∴ Coefficient form of dividend = (1, 0, 0, -216)
Divisor = y – 6
∴ Opposite of – 6 is 6.

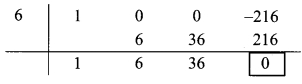
Coefficient form of quotient = (1, 6, 36)
∴ Quotient = y² + 6y + 36,
Remainder = 0

Linear division method:
y³ – 216
To get the term y³, multiply (y – 6) by y² and add 6y²,
= y²(y – 6) + 6y² – 216
= y²(y – 6) + 6ysup>2 – 216
To get the, term 6 y² multiply (y – 6) by 6y and add 36y,
= y²(y – 6) + 6y(y – 6) + 36y – 216
= y²(y – 6) + 6y(y – 6) + 36y – 216
To get the term 36y, multiply (y- 6) by 36 and add 216,
= y² (y – 6) + 6y(y – 6) + 36(y – 6) + 216 – 216
= (y – 6) (y² + 6y + 36) + 0
Quotient = y² + 6y + 36
Remainder = 0

iv. Synthetic division:
(2x⁴ + 3x³ + 4x – 2x²) ÷ (x + 3)
Dividend = 2x⁴ + 3x³ + 4x – 2x²
∴ Index form = 2x⁴ + 3x³ – 2x² + 4x + 0
∴ Coefficient form of the dividend = (2,3, -2,4,0)
Divisor = x + 3
∴ Opposite of + 3 is -3

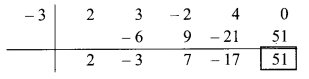
Coefficient form of quotient = (2, -3, 7, -17)
∴ Quotient = 2x³ – 3x² + 7x – 17,
Remainder = 51

Linear division method:
2x⁴ + 3x³ + 4x – 2x² = 2x² + 3x³ – 2x² + 4x
To get the term 2x⁴, multiply (x + 3) by 2x³ and subtract 6x³,
= 2x³(x + 31 – 6x³ + 3x³ – 2x² + 4x
= 2x³(x + 3) – 3x³ – 2x² + 4x

To get the term – 3x³, multiply (x + 3) by -3x² and add 9x²,
= 2x³(x + 3) – 3x²(x + 3) + 9x² – 2x² + 4x
= 2x³(x + 3) – 3x²(x + 3) + 7x² + 4x

To get the term 7x², multiply (x + 3) by 7x and subtract 21x,
= 2x³(x + 3) – 3x²(x + 3) + 7x(x + 3) – 21x + 4x
= 2x³(x + 3) – 3x²(x + 3) + 7x(x + 3) – 17x

To get the term -17x, multiply (x + 3) by -17 and add 51,
= 2x³(x + 3) – 3x²(x + 3) + 7x(x+3) – 17(x + 3) + 51
= (x + 3) (2x³ – 3x² + 7x- 17) + 51
∴ Quotient = 2x³ – 3x² + 7x – 17,
Remainder = 51

v. Synthetic division:
(x⁴ – 3x² – 8) + (x + 4)
Dividend = x⁴ – 3x² – 8
∴ Index form = x⁴ + 0x³ – 3x² + 0x – 8
∴ Coefficient form of the dividend = (1,0, -3,0, -8)
Divisor = x + 4
∴ Opposite of + 4 is -4

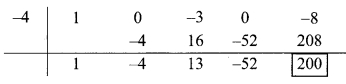
∴ Coefficient form of quotient = (1, -4, 13, -52)
∴ Quotient = x³ – 4x² + 13x – 52,
Remainder = 200

Linear division method:
x⁴ – 3x² – 8
To get the term x⁴, multiply (x + 4) by x³ and subtract 4x³,
= x³(x + 4) – 4x³ – 3x² – 8
= x³(x + 4) – 4x³ – 3x² – 8
To get the term – 4x³, multiply (x + 4) by -4x² and add 16x²,
= x³(x + 4) – 4x² (x + 4) + 16x² – 3x² – 8
= x³(x + 4) – 4x² (x + 4) + 13x² – 8
To get the term 13x², multiply (x + 4) by 13x and subtract 52x,
= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52x – 8
= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52x – 8
To get the term -52x, multiply (x + 4) by – 52 and add 208,
= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52(x + 4) + 208 – 8
= (x + 4) (x³ – 4x² + 13x – 52) + 200
∴ Quotient = x³ – 4x² + 13x – 52,
Remainder 200

vi. Synthetic division:
(y³ – 3y² + 5y – 1) ÷ (y – 1)
Dividend = y³ – 3y² + 5y – 1
Coefficient form of the dividend = (1, -3, 5, -1)
Divisor = y – 1
∴Opposite of -1 is 1.

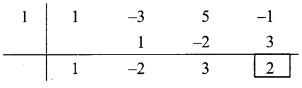
∴ Coefficient form of quotient = (1, -2, 3)
∴ Quotient = y² – 2y + 3,
Remainder = 2

Linear division method:
y³ -3y² + 5y – 1
To get the term y³ , multiply (y – 1) by y² and add y²
= y² (y – 1) + y² – 3y² + 5y – 1
= y² (y – 1) – 2y² + 5y – 1
To get the term -2y², multiply (y – 1) by -2y and subtract 2y,
= y² (y – 1) – 2y(y – 1) – 2y + 5y – 1
= y² (y – 1) – 2y(y – 1) + 3y – 1
To get the term 3y, multiply (y – 1) by 3 and add 3,
= y² (y – 1) – 2y(y – 1) + 3(y- 1) + 3 – 1
= (y – 1)(y² – 2y + 3) + 2
∴ Quotient = y² – 2y + 3,
Remainder = 2.

Maharashtra State Board 9th Maths Solution 

• Polynomials Practice Set 3.1 Class 9 Maths Solutions
• Polynomials Practice Set 3.2 Class 9 Maths Solutions
• Polynomials Practice Set 3.3 Class 9 Maths Solutions
• Polynomials Practice Set 3.4 Class 9 Maths Solutions
• Polynomials Practice Set 3.5 Class 9 Maths Solutions
• Polynomials Practice Set 3.6 Class 9 Maths Solutions
• Polynomials Problem Set 3 Class 9 Maths Solutions

9th Standard Maths 1 Practice Set 3.2 Chapter 3 Polynomials Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.

Class 9 Maths Part 1 Practice Set 3.2 Chapter 3 Polynomials Questions With Answers Maharashtra Board

Question 1.
Use the given letters to write the answer.
i. There are ‘a’ trees in the village Lat. If the number of trees increases every year by ’b‘. then how many trees will there be after ‘x’ years?
ii. For the parade there are y students in each row and x such row are formed. Then, how many students are there for the parade in all ?
iii. The tens and units place of a two digit number is m and n respectively. Write the polynomial which represents the two digit number.
Solution:
i. Number of trees in the village Lat = a
Number of trees increasing each year = b
∴ Number of trees after x years = a + bx
∴ There will be a + bx trees in the village Lat after x years.

ii. Total rows = x
Number of students in each row = y
∴ Total students = Total rows × Number of students in each row
= x × y
= xy
∴ There are in all xy students for the parade.

iii. Digit in units place = n
Digit in tens place = m
∴ The two digit number = 10 x digit in tens place + digit in units place
= 10m + n
∴ The polynomial representing the two digit number is 10m + n.

Question 2.
Add the given polynomials.
i. x³ – 2x² – 9; 5x³ + 2x + 9
ii. -7m⁴+ 5m³ + √2 ; 5m⁴ – 3m³ + 2m² + 3m – 6
iii. 2y² + 7y + 5; 3y + 9; 3y² – 4y – 3
Solution:
i. (x³ – 2x² – 9) + (5x³ + 2x + 9)
= x³ – 2x² – 9 + 5x³ + 2x + 9
= x³ + 5x³ – 2x² + 2x – 9 + 9
= 6x³ – 2x² + 2x

ii. (-7m⁴ + 5m³ + √2 ) + (5m⁴ – 3m³ + 2m² + 3m – 6)
= -7m⁴ + 5m³ + √2 + 5m⁴ – 3m³ + 2m² + 3m – 6
= -7m⁴ + 5m⁴ + 5m³ – 3m³ + 2m² + 3m +√2 – 6
= -2m⁴ + 2m³ + 2m² + 3m + √2 – 6

iii. (2y² + 7y + 5) + (3y + 9) + (3y² – 4y – 3)
= 2y² + 7y + 5 + 3y + 9 + 3y² – 4y – 3
= 2y² + 3y² + 7y + 3y – 4y + 5 + 9 – 3
= 5y² + 6y + 11

Question 3.
Subtract the second polynomial from the first.
i. x² – 9x + √3 ; – 19x + √3 + 7x²
ii. 2ab² + 3a²b – 4ab; 3ab – 8ab² + 2a²b
Solution:
i. x² – 9x + √3 -(- 19x + √3 + 7x²)
= x² – 9x + √3 + 19x – √ 3 – 7x²
= x² – 7x² – 9x + 19x + √3 – √3
= – 6x² + 10x

ii. (2ab² + 3a²b – 4ab) – (3ab – 8ab² + 2a²b)
= 2ab² + 3a²b – 4ab – 3ab + 8ab² – 2a²b
= 2ab² + 8ab² + 3a²b – 2a²b – 4ab – 3ab
= 10ab² + a²b – 7ab

Question 4.
Multiply the given polynomials.
i. 2x; x² – 2x – 1
ii. x⁵ – 1; x³ + 2x² + 2
iii. 2y +1; y² – 2y + 3y
Solution:
i. (2x) x (x² – 2x – 1) = 2x³ – 4x² – 2x

ii. (x⁵ – 1) × (x³ + 2x² + 2)
= x⁵ (x³ + 2x² + 2) -1(x³ + 2x² + 2)
= x⁸ + 2x⁷ + 2x⁵ – x³ – 2x² – 2

iii. (2y + 1) × (y² – 2y³ + 3y)
= 2y(y² – 2y³ + 3y) + 1(y² – 2y³ + 3y)
= 2y³ – 4y⁴ + 6y² + y² – 2y³ + 3y
= -4y⁴ + 2y³ – 2y³ + 6y² + y² + 3y
= -4y⁴ + 7y² + 3y

Question 5.
Divide first polynomial by second polynomial and write the answer in the form ‘Dividend = Divisor x Quotient + Remainder’.
i. x³ – 64; x – 4
ii. 5x⁵ + 4x⁴ – 3x³ + 2x² + 2 ; x² – x
Solution:
i. x³ – 64 = x3 + 0x² + 0x – 64

∴ Quotient = x² + 4x + 16, Remainder = 0
Now, Dividend = Divisor x Quotient + Remainder
∴ x³ – 64 = (x – 4)(x² + 4x + 16) + 0

ii. 5x⁵ + 4x⁴ – 3x³ + 2x² + 2 = 5x⁵ + 4x⁴ – 3x³ + 2x + 0x + 2

∴ Quotient = 5x³ + 9x² + 6x + 8,
Remainder = 8x + 2
Now, Dividend = Divisor x Quotient + Remainder
∴ 5x⁵ + 4x⁴ – 3x³ + 2x² + 2 = (x² – x)(5x³ + 9x² + 6x + 8) + (8x + 2)

Question 6.
Write down the information in the form of algebraic expression and simplify.
There is a rectangular farm with length (2a² + 3b²) metre and breadth (a² + b²) metre. The farmer used a square shaped plot of the farm to build a house. The side of the plot was (a2 – b2) metre. What is the area of the remaining part of the farm? [4 Marks]
Solution:
Length of the rectangular farm = (2a² + 3b²) m
Breadth of the rectangular farm = (a² + b²) m
Area of the farm = length x breadth = (2a² + 3b²) x (a² + b²)
= 2a²(a² + b²) + 3b²(a² + b²)
= 2a² + 2a²b² + 3a²b² + 3b⁴
= (2a⁴ + 5a²b² + 3b⁴) sq. m … (i)
The farmer used a square shaped plot of the farm to build a house.
Side of the square shaped plot = (a² – b²) m
∴ Area of the plot = (side)²
= (a² – b²)²
= (a⁴ – 2a²b² + b⁴) sq m… .(ii)

∴ Area of the remaining farm = Area of the farm – Area of the plot
= (2a⁴ + 5a²b² + 3b⁴) – (a⁴ – 2a²b² + b⁴) … [From (i) and (ii)]
= 2a⁴ + 5a²b² + 3b⁴ – a⁴ + 2a²b² – b⁴
= 2a⁴ – a⁴ + 5a²b² + 2a²b² + 3b⁴ – b⁴
= a⁴ + 7a²b² + 2b⁴
∴ The area of the remaining farm is (a⁴ + 7a²b² + 2b⁴) sq. m.

Maharashtra State Board 9th Maths Solution 

• Polynomials Practice Set 3.1 Class 9 Maths Solutions
• Polynomials Practice Set 3.2 Class 9 Maths Solutions
• Polynomials Practice Set 3.3 Class 9 Maths Solutions
• Polynomials Practice Set 3.4 Class 9 Maths Solutions
• Polynomials Practice Set 3.5 Class 9 Maths Solutions
• Polynomials Practice Set 3.6 Class 9 Maths Solutions
• Polynomials Problem Set 3 Class 9 Maths Solutions

10th Standard Maths 1 Problem Set 1 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Problem Set 1 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Choose correct alternative for each of the following questions.

Question 1.
To draw graph of 4x + 5y = 19, find y when x = 1.
(a) 4
(b) 3
(c) 2
(d) -3
Answer:
(b)

Question 2.
For simultaneous equations in variables x and y, D_x = 49, Dy = – 63, D = 7 then what is x?
(a) 7
(b) -7
(c) \(\frac { 1 }{ 7 } \)
(d) \(\frac { -1 }{ 7 } \)
Answer:
(a)

Question 3.
Find the value of

(a) -1
(b) -41
(c) 41
(d) 1
Answer:
(d)

Question 4.
To solvex + y = 3; 3x – 2y – 4 = 0 by determinant method find D.
(a) 5
(b) 1
(c) -5
(d) -1
Answer:
(c)

Question 5.
ax + by = c and mx + n y = d and an ≠ bm then these simultaneous equations have-
(a) Only one common solution
(b) No solution
(c) Infinite number of solutions
(d) Only two solutions.
Answer:
(a)

Question 2.
Complete the following table to draw the graph of 2x – 6y = 3.
Answer:

Question 3.
Solve the following simultaneous equations graphically.
i. 2x + 3y = 12 ; x – y = 1
ii. x – 3y = 1 ; 3x – 2y + 4 = 0
iii. 5x – 6y + 30 = 0; 5x + 4y – 20 = 0
iv. 3x – y – 2 = 0 ; 2x + y = 8
v. 3x + y= 10 ; x – y = 2
Answer:
i. The given simultaneous equations are

The two lines interest at point (3,2).
∴ x = 3 and y = 2 is the solution of the simultaneous equations 2x + 3y = 12 and x – y = 1.

ii. The given simultaneous equations are

The two lines intersect at point (-2, -1).
∴ x = -2 and y = -1 is the solution of the simultaneous equations x – 3y = 1 and 3x – 2p + 4 = 0.

iii. The given simultaneous equations are

The two lines intersect at point (0, 5).
∴ x = 0 and y = 5 is the solution of the simultaneous equations 5x – 6y + 30 = 0 and 5x + 4y – 20 = 0.

iv. The given simultaneous equations are


The two lines intersect at point (2, 4).
∴ x = 2 and y = 4 is the solution of the simultaneous equations 3x – y – 2 = 0 and 2x + y = 8.

v. The given simultaneous equations are

The two lines intersect at point (3, 1).
∴ x = 3 and y = 1 is the solution of the simultaneous equations 3x + y = 10 and x – y = 2.

Question 4.
Find the values of each of the following determinants.

Solution:

Question 5.
Solve the following equations by Cramer’s method.

Solution:
i. The given simultaneous equations are
6x – 3y = -10 …(i)
3x + 5y – 8 = 0
∴ 3x + 5y = 8 …(ii)
Equations (i) and (ii) are in ax + by = c form. Comparing the given equations with a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 6, b₁ = -3, c₁ = 10 and
a₂ = 3, b₂ = 5, c₂ = 8

ii. The given simultaneous equations are
4m – 2n = -4 …(i)
4m + 3n = 16 …(ii)
Equations (i) and (ii) are in am + bn = c form.
Comparing the given equations with a₁m + b₁n = c₁ and a₂m + b₂n = c₂, we get
a₁ = 4, b₁ = -2, c₁ = -4 and
a₂ = 4, b₂ = 3, c₂ = 16


∴ (m, n) = (1, 4) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are

iv. The given simultaneous equations are
7x + 3y = 15 …(i)
12y – 5x = 39
i.e. -5x + 12y = 39 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 7, b₁ = 3, c₁ = 15 and
a₂ = -5, b₂ = 12, c₂ = 39

v. The given simultaneous equations are

∴ 4(x + y – 8) = 2(3x – y)
∴ 4x + 4y – 32 = 6x – 2y
∴ 6x – 4x – 2y – 4y = -32
∴ 2x – 6y = -32
∴ x – 3y = -16 …(ii)[Dividing both sides by 2]
Equations (i) and (ii) are in ax + by = c form. Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 1, b₁ = -1, c₁ = -4 and
a₂ = 1, b₂ = -3, c₂ = -16

∴ (x, y) = (2, 6) is the solution of the given simultaneous equations.

Question 6.
Solve the following simultaneous equations:

Answer:
i. The given simultaneous equations are

Subtracting equation (iv) from (iii), we get

∴ (x, y) = (6, – 4) is the solution of the given simultaneous equations.

ii. The given simultaneous equations are

Adding equations (v) and (vi), we get

iii. The given simultaneous equations are


∴ (x, y) = (1, 2) is the solution of the given simultaneous equations.

iv. The given simultaneous equations are

∴ Equations (i) and (ii) become 7q – 2p = 5 …(iii)
8q + 7p = 15 …(iv)
Multiplying equation (iii) by 7, we get
49q – 14p = 35 …(v)
Multiplying equation (iv) by 2, we get
16q + 14p = 30 …(vi)
Adding equations (v) and (vi), we get

Substituting q = 1 in equation (iv), we get
8(1) + 7p = 15
∴ 8 + 7p = 15
∴ 7p = 15 – 8
∴ 7p = 7
∴ p = \(\frac { 7 }{ 7 } \) = 1
∴ (P, q) = (1,1)
Resubstituting the values of p and q, we get
1 = \(\frac { 1 }{ x } \) and 1 = \(\frac { 1 }{ y } \)
∴ x = 1 and y = 1
∴ (x, y) = (1, 1) is the solution of the given simultaneous equations.

v. The given simultaneous equations are

Resubstituting the values of p and q, we get

∴ 3x + 4y = 10 …(v)
and 2x – 3y = 1 …(vi)
Multiplying equation (v) by 3, we get
9x + 12y = 30 …(vii)
Multiplying equation (vi) by 4, we get
8x – 12y = 4 …(viii)
Adding equations (vii) and (viii), we get

Substituting x = 2 in equation (v), we get
3(2) + 4y = 10
⇒ 6 + 4y = 10
⇒ 4y = 10 – 6
⇒ y = 4/4 = 1
∴ y = 1
∴ (x, y) = (2, 1) is the solution of the given simultaneous equations.

Question 7.
Solve the following word problems, i. A two digit number and the number with digits interchanged add up to 143. In the given number the digit in unit’s place is 3 more than the digit in the ten’s place. Find the original number.
Solution:
Let the digit in unit’s place be x
and that in the ten’s place be y.

ii. Kantabai bought 1 \(\frac { 1 }{ 2 } \) kg tea and 5 kg sugar from a shop. She paid ₹ 50 as return fare for rickshaw. Total expense was ₹ 700. Then she realised that by ordering online the goods can be bought with free home delivery at the same price. So, next month she placed the order online for 2 kg tea and 7 kg sugar. She paid ₹ 880 for that. Find the rate of sugar and tea per kg.
Solution:
Let the rate of tea be ₹ x per kg and that of sugar be ₹ y per kg.
According to the first condition,
cost of 1 \(\frac { 1 }{ 2 } \) kg tea + cost of 5 kg sugar + fare for rickshaw = total expense

According to the second condition,
cost of 2 kg tea + cost of 7 kg sugar = total expense
2x + 7y = 880 …(ii)
Multiplying equation (i) by 2, we get
6x + 20y = 2600 …(iii)
Multiplying equation (ii) by 3, we get
6x + 21y = 2640 …(iv)
Subtracting equation (iii) from (iv), we get

∴ The rate of tea is ₹ 300 per kg and that of sugar is ₹ 40 per kg.

iii. To find number of notes that Anushka had, complete the following activity.

Solution:
Anushka had x notes of ₹ 100 and y notes of ₹ 50.
According to the first condition,
100x + 50y = 2500
∴ 2x + y = 50 …(i) [Dividing both sides by 50]
According to the second condition,
100y + 50x = 2000
∴ 2y + x = 40 … [Dividing both sides by 50]
i.e. x + 2y = 40
∴ 2x + 4y = 80 …(ii) [Multiplying both sides by 2]
Subtracting equation (i) from (ii), we get

∴ Anushka had 20 notes of ₹ 100 and 10 notes of ₹ 50.

iv. Sum of the present ages of Manish and Savita is 31, Manish’s age 3 years ago was 4 times the age of Savita. Find their present ages.
Solution:
Let the present ages of Manish and Savita be x years and y years respectively.
According to the first condition,
x + y = 31 …(i)
3 years ago,
Manish’s age = (x – 3) years
Savita’s age = (y – 3) years
According to the second condition,
(x – 3) = 4 (y – 3)
∴ x – 3 = 4y – 12
∴ x – 4y = -12 + 3
∴ x – 4y = -9 …(ii)
Subtracting equation (ii) from (i), we get

∴ x = 31 – 8
∴ x = 23
The present ages of Manish and Savita are 23 years and 8 years respectively.

v. In a factory the ratio of salary of skilled and unskilled workers is 5 : 3. Total salary of one day of both of them is ₹ 720. Find daily wages of skilled and unskilled workers.
Solution:
Let the daily wages of skilled workers be ₹ x
that of unskilled workers be ₹ y.
According to the first condition,

∴ The daily wages of skilled workers is ₹ 450 and that of unskilled workers is ₹ 270.

vi. Places A and B are 30 km apart and they are on a straight road. Hamid travels from A to B on bike. At the same time Joseph starts from B on bike, travels towards A. They meet each other after 20 minutes. If Joseph would have started from B at the same time but in the opposite direction (instead of towards A), Hamid would have caught him after 3 hours. Find the speed of Hamid and Joseph.
Solution:
Let the speeds of Hamid and Joseph be x km/hr andy km/hr respectively.
Distance travelled by Hamid in 20 minutes

According to the first condition,

∴ The speeds of Hamid and Joseph 50 km/hr and 40 km/hr respectively.

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

9th Standard Maths 1 Practice Set 3.1 Chapter 3 Polynomials Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.

Class 9 Maths Part 1 Practice Set 3.1 Chapter 3 Polynomials Questions With Answers Maharashtra Board

Question 1.
State whether the given algebraic expressions are polynomials? Justify.
i. y + \(\frac { 1 }{ y }\)
ii. 2 – 5√x
iii. x² + 7x + 9
iv. 2m^-2 + 7m – 5
v. 10
Answer:
i. No, because power of v in the term 5√x is -1 (negative number).
ii. No, because the power of x in the term 5√x is
i. e. 0.5 (decimal number).
iii. Yes. All the coefficients are real numbers. Also, the power of each term is a whole number.
iv. No, because the power of m in the term 2m^-2 is -2 (negative number).
v. Yes, because 10 is a constant polynomial.

Question 2.
Write the coefficient of m³ in each of the given polynomial.
i. m³
ii. \(\sqrt [ -3 ]{ 2 }\) + m – √3m³
iii. \(\sqrt [ -2 ]{ 3 }\)m³ + 5m² – 7m -1
Answer:
i. 1
ii. -√3
iii. – \(\frac { 2 }{ 3 }\)

Question 3.
Write the polynomial in x using the given information. [1 Mark each]
i. Monomial with degree 7
ii. Binomial with degree 35
iii. Trinomial with degree 8
Answer:
i. 5x⁷
ii. x³⁵ – 1
iii. 3x⁸ + 2x⁶ + x⁵

Question 4.
Write the degree of the given polynomials.
i. √5
ii. x°
iii. x²
iv. √2m¹⁰ – 7
v. 2p – √7
vi. 7y – y³ + y⁵
vii. xyz +xy-z
viii. m³n⁷ – 3m⁵n + mn
Answer:
i. √5 = √5 x°
∴ Degree of the polynomial = 0

ii. x°
∴Degree of the polynomial = 0

iii. x²
∴Degree of the polynomial = 2

iv. √2m¹⁰ – 7
Here, the highest power of m is 10.
∴Degree of the polynomial = 10

v. 2p – √7
Here, the highest power of p is 1.
∴ Degree of the polynomial = 1

vi. 7y – y³ + y⁵
Here, the highest power of y is 5.
∴Degree of the polynomial = 5

vii. xyz + xy – z
Here, the sum of the powers of x, y and z in the term xyz is 1 + 1 + 1= 3,
which is the highest sum of powers in the given polynomial.
∴Degree of the polynomial = 3

viii. m³n⁷ – 3m⁵n + mn
Here, the sum of the powers of m and n in the term m³n⁷ is 3 + 7 = 10,
which is the highest sum of powers in the given polynomial.
∴ Degree of the polynomial = 10

Question 5.
Classify the following polynomials as linear, quadratic and cubic polynomial. [2 Marks]
i. 2x² + 3x +1
ii. 5p
iii. √2 – \(\frac { 1 }{ 2 }\)
iv. m³ + 7m² + \(\sqrt [ 5 ]{ 2 }\)m – √7
v. a²
vi. 3r³
Answer:
Linear polynomials: ii, iii
Quadratic polynomials: i, v
Cubic polynomials: iv, vi

Question 6.
Write the following polynomials in standard form.
i. m³ + 3 + 5m
ii. – 7y + y⁵ + 3y³ – \(\frac { 1 }{ 2 }\)+ 2y⁴ – y²
Answer:
i. m³ + 5m + 3
ii. y⁵ + 2y⁴ + 3y³ – y² – 7y – \(\frac { 1 }{ 2 }\)

Question 7.
Write the following polynomials in coefficient form.
i. x³ – 2
ii. 5y
iii. 2m⁴ – 3m² + 7
iv. – \(\frac { 2 }{ 3 }\)
Answer:
i. x³ – 2 = x³ + 0x² + 0x – 2
∴ Coefficient form of the given polynomial = (1, 0, 0, -2)

ii. 5y = 5y + 0
∴Coefficient form of the given polynomial = (5,0)

iii. 2m⁴ – 3m² + 7
= 2m⁴ + Om³ – 3m² + 0m + 7
∴ Coefficient form of the given polynomial = (2, 0, -3, 0, 7)

iv. – \(\frac { 2 }{ 3 }\)
∴Coefficient form of the given polynomial = (- \(\frac { 2 }{ 3 }\))

Question 8.
Write the polynomials in index form.
i. (1, 2, 3)
ii. (5, 0, 0, 0 ,-1)
iii. (-2, 2, -2, 2)
Answer:
i. Number of coefficients = 3
∴ Degree = 3 – 1 = 2
∴ Taking x as variable, the index form is x² + 2x + 3

ii. Number of coefficients = 5
∴ Degree = 5 – 1=4
∴ Taking x as variable, the index form is 5x⁴ + 0x³ + 0x² + 0x – 1

iii. Number of coefficients = 4
∴Degree = 4 – 1 = 3
∴Taking x as variable, the index form is -2x³ + 2x² – 2x + 2

Question 9.
Write the appropriate polynomials in the boxes.

Answer:
i. Quadratic polynomial: x²; 2x² + 5x + 10; 3x² + 5x
ii. Cubic polynomial: x³ + x² + x + 5; x³ + 9
iii. Linear polynomial: x + 7
iv. Binomial: x + 7; x³ + 9; 3x² + 5x
v. Trinomial: 2x² + 5x + 10
vi. Monomial: x²

Question 1.
Write an example of a monomial, a binomial and a trinomial having variable x and degree 5. ( Textbook pg. no. 3)
Answer:
Monomial: x⁵
Binomial: x⁵ + x
Trinomial: 2x⁵ – x² + 5

Question 2.
Give example of a binomial in two variables having degree 5. (Textbook pg. no. 38)
Answer:
x³y² + xy

Maharashtra State Board 9th Maths Solution 

• Polynomials Practice Set 3.1 Class 9 Maths Solutions
• Polynomials Practice Set 3.2 Class 9 Maths Solutions
• Polynomials Practice Set 3.3 Class 9 Maths Solutions
• Polynomials Practice Set 3.4 Class 9 Maths Solutions
• Polynomials Practice Set 3.5 Class 9 Maths Solutions
• Polynomials Practice Set 3.6 Class 9 Maths Solutions
• Polynomials Problem Set 3 Class 9 Maths Solutions

10th Standard Maths 1 Practice Set 1.4 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.4 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Practice Set 1.4 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Question 1.
Solve the following simultaneous equations.

Solution:
i. The given simultaneous equations are

∴ Equations (i) and (ii) become
2p – 3q = 15 …(iii)
8p + 5q = 77 …(iv)
Multiplying equation (iii) by 4, we get
8p – 12q = 60 …(v)
Subtracting equation (v) from (iv), we get

ii. The given simultaneous equations are



Substituting x = 3 in equation (vi), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are

∴ Equations (i) and (ii) become
27p + 31q = 85 …(iii)
31p + 27q = 89 …(iv)
Adding equations (iii) and (iv), we get

iv. The given simultaneous equations are


Substituting x = 1 in equation (vi), we get
3(1) + y = 4
∴ 3 + y = 4
∴ y = 4 – 3 = 1
∴ (x, y) = (1, 1) is the solution of the given simultaneous equations.

Question 1.
Complete the following table. (Textbook pg. no. 16)
Solution:

Question 2.
In the above table the equations are not linear. Can you convert the equations into linear equations? (Textbook pg. no. 17)
Answer:
Yes, the above given simultaneous equations can be converted to a pair of linear equations by making suitable substitutions.

Steps for solving equations reducible to a pair of linear equations.

• Step 1: Select suitable variables other than those which are in the equations.
• Step 2: Replace the given variables with new variables such that the given equations become linear equations in two variables.
• Step 3: Solve the new simultaneous equations and find the values of the new variables.
• Step 4: By resubstituting the value(s) of the new variables, find the replaced variables which are to be determined.

Question 3.
To solve given equations fill the below boxes suitably. (Text book pg.no. 19)
Answer:

Question 4.
The examples on textbook pg. no. 17 and 18 obtained by transformation are solved by elimination method. If you solve these equations by graphical method and by Cramer’s rule will you get the same answers? Solve and check it. (Textbook pg. no. 18)

Solution:

The two lines intersect at point (1,-1).
∴ p = 1 and q = -1 is the solution of the simultaneous equations 4p + q = 3 and 2p – 3q = 5.
Re substituting the values of p and q, we get

The two lines intersect at point (0, -1).
∴ x = 0 and y = -1 is the solution of the simultaneous equations x – y = 1 and x + y = -1.
∴ (x, y) = (0, -1) is the solution of the given simultaneous equations.

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 1.3 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Practice Set 1.3 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Question 1.
Fill in the blanks with correct number.
Solution:

Question 2.
Find the values of following determinants.

Solution:

Question 3.
Solve the following simultaneous equations using Cramer’s rule.
i. 3x – 4y = 10 ; 4x + 3y = 5
ii. 4x + 3y – 4 = 0 ; 6x = 8 – 5y
iii. x + 2y = -1 ; 2x – 3y = 12
iv. 6x – 4y = -12 ; 8x – 3y = -2
v. 4m + 6n = 54 ; 3m + 2n = 28
vi. 2x + 3y = 2 ; x – \(\frac { y }{ 2 } \) = \(\frac { 1 }{ 2 } \)
Solution:
i. The given simultaneous equations are 3x – 4y = 10 …(i)
4x + 3y = 5 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 3, b₁ = -4, c₁ = 10 and
a₂ = 4, b₂ = 3, c₂ = 5

∴ (x, y) = (2, -1) is the solution of the given simultaneous equations.

ii. The given simultaneous equations are
4x + 3y – 4 = 0
∴ 4x + 3y = 4 …(i)
6x = 8 – 5y
∴ 6x + 5y = 8 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 4, b₁ = 3, c₁ = 4 and
a₂ = 6, b₂ = 5, c₂ = 8

∴ (x, y) = (-2, 4) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are
x + 2y = -1 …(i)
2x – 3y = 12 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = C₁ and a₂x + b₂y = c₂, we get
a₁ = 1, b₁ = 2, c₁ = -1 and
a₂ = 2, b₂ = -3, c₂ = 12

∴ (x, y) = (3, -2) is the solution of the given simultaneous equations.

iv. The given simultaneous equations are
6x – 4y = -12
∴ 3x – 2y = -6 …(i) [Dividing both sides by 2]
8x – 3y = -2 …(ii)
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 3, b₁ = -2, c₁ = -6 and
a₂ = 8, b₂ = -3, c₂ = -2

∴ (x, y) = (2, 6) is the solution of the given simultaneous equations.

v. The given simultaneous equations are
4m + 6n = 54
2m + 3n = 27 …(i) [Dividing both sides by 2]
3m + 2n = 28 …(ii)
Equations (i) and (ii) are in am + bn = c form.
Comparing the given equations with
a₁m + b₁n = c₁ and a₂m + b₂n = c₂, we get
a₁ = 2, b₁ = 3, c₁ = 27 and
a₂ = 3, b₂ = 2, c₂ = 28


∴ (m, n) = (6, 5) is the solution of the given simultaneous equations.

vi. The given simultaneous equations are
2x + 3y = 2 …(i)
x = \(\frac { y }{ 2 } \) = \(\frac { 1 }{ 2 } \)
∴ 2x – y = 1 …(ii) [Multiplying both sides by 2]
Equations (i) and (ii) are in ax + by = c form.
Comparing the given equations with
a₁x + b₁y = c₁ and a₂x + b₂y = c₂, we get
a₁ = 2, b₁ = 3, c₁ = 2 and
a₂ = 2, b₂ = -1, c₂ = 1

Question 1.
To solve the simultaneous equations by determinant method, fill in the blanks,
y + 2x – 19 = 0; 2x – 3y + 3 = 0 (Textbookpg.no. 14)
Solution:
Write the given equations in the form
ax + by = c.
2x + y = 19
2x – 3y = -3

Question 2.
Complete the following activity. (Textbook pg. no. 15)
Solution:

Question 3.
What is the nature of solution if D = 0? (Textbook pg. no. 16)
Solution:
If D = 0, i.e. a₁b₂ – b₁a₂ = 0, then the two simultaneous equations do not have a unique solution.
Examples:
i. 2x – 4y = 8 and x – 2y = 4
Here, a₁b₂ – b₁a₂ = (2)(-2) – (-4) (1)
= -4 + 4 = 0
Graphically, we can check that these two lines coincide and hence will have infinite solutions.

ii. 2x – y = -1 and 2x – y = -4
Here, a₁ b₂ – b₁ a₂ = (2)(-1) – (-1) (2)
= -2 + 2 = 0
Graphically, we can check that these two lines are parallel and hence they do not have a solution.

Question 4.
What can you say about lines if common solution is not possible? (Textbook pg. no. 16)
Answer:
If the common solution is not possible, then the lines will either coincide or will be parallel to each other.

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

10th Standard Maths 1 Practice Set 1.2 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Practice Set 1.2 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

10th Maths 2 Practice Set 1.2 Question 1.
Complete the following table to draw graph of the equations.
i. x + y = 3
ii. x – y = 4
Answer:
i. x + y = 3

ii. x – y = 4

Linear Equations In Two Variables Practice Set 1.2  Question 2.
Solve the following simultaneous equations graphically.
i. x + y = 6 ; x – y = 4
ii. x + y = 5 ; x – y = 3
iii. x + y = 0 ; 2x – y = 9
iv. 3x – y = 2 ; 2x – y = 3
v. 3x – 4y = -7 ; 5x – 2y = 0
vi. 2x – 3y = 4 ; 3y – x = 4
Solution:
i. The given simultaneous equations are
x + y = 6                                                                                                        x – y = 4
∴ y = 6 – x                                                                                                     ∴ y = x – 4
The two lines intersect at point (5, 1).
∴ x = 5 and y = 1 is the solution of the simultaneous equations x + y = 6 and x – y = 4.

ii. The given simultaneous equations are


The two lines intersect at point (4, 1).
∴ x = 4 and y = 1 is the solution of the simultaneous equations x+y = 5 and x – y = 3.

iii. The given simultaneous equations are


The two lines intersect at point (3, -3).
∴ x = 3 and y = -3 is the solution of the simultaneous equations x + y = 0 and 2x – y = 9.

iv. The given simultaneous equations are


The two lines intersect at point (-1, -5).
∴ x = -1 and y = -5 is the solution of the simultaneous equations 3x- y = 2 and 2x- y = 3.

v. The given simultaneous equations are


The two lines intersect at point (1, 2.5).
∴ x = 1 and y = 2.5 is the solution of the simultaneous equations 3x – 4y = -7 and 5x – 2y = 0.

vi. The given simultaneous equations are


The two lines intersect at point (8, 4).
∴ x = 8 and y = 4 is the solution of the simultaneous equations 2x – 3y = 4 and 3y – x = 4.

10th Math Part 2 Practice Set 1.2  Question 1.
Solve the following simultaneous equations by graphical method. Complete the following tables to get ordered pairs.

i. Plot the above ordered pairs on the same co-ordinate plane.
ii. Draw graphs of the equations.
iii. Note the co-ordinates of the point of intersection of the two graphs. Write solution of these equations. (Textbook pg. no. 8)
Solution:

The two lines intersect at point (-1, -2).
∴ (x , y) = (-1, -2) is the solution of the given simultaneous equations.

Mathematics Part 1 Standard 9 Practice Set 1.2 Answer  Question 1.
Solve the above equations by method of elimination. Check your solution with the solution obtained by graphical method. (Textbook pg. no. 8)
Solution:
The given simultaneous equations are
x – y = 1 …(i)
5x – 3y = 1 …(ii)
Multiplying equation (i) by 3, we get
3x – 3y = 3 …(iii)
Subtracting equation (iii) from (ii), we get

Substituting x = -1 in equation (i), we get
-1 -y= 1
∴ -y = 1 + 1
∴ -y = 2
∴ y = -2
∴ (x,y) = (-1, -2) is the solution of the given simultaneous equations.
∴ The solution obtained by elimination method and by graphical method is the same.

1.2 Maths Class 10 Question 2.
The following table contains the values of x and y co-ordinates for ordered pairs to draw the graph of 5x – 3y = 1.

i. Is it easy to plot these points?
ii. Which precaution is to be taken to find ordered pairs so that plotting of points becomes easy? (Textbook pg. no. 8)
Solution:
i. No

The above numbers are non-terminating and recurring decimals.
∴ It is not easy to plot the given points.

ii. While finding ordered pairs, numbers should be selected in such a way that the co-ordinates obtained will be integers.

Linear Equations ¡n Two Variables Class 10 Maths Question 3.
To solve simultaneous equations x + 2y = 4; 3x + 6y = 12 graphically, following are the ordered pairs.

Plotting the above ordered pairs, graph is drawn. Observe it and find answers of the following questions.

i. Are the graphs of both the equations different or same?
ii. What are the solutions of the two equations x + 2y = 4 and 3x + 6y = 12? How many solutions are possible?
iii. What are the relations between coefficients of x, coefficients of y and constant terms in both the equations?
iv. What conclusion can you draw when two equations are given but the graph is only one line? (Textbook pg. no. 9)
Solution:
i. The graphs of both the equations are same.
ii. The solutions of the given equations are (-2, 3), (0, 2), (1, 1.5), etc.
∴ Infinite solutions are possible.
iii. Ratio of coefficients of x = \(\frac { 1 }{ 3 } \)
Ratio of coefficients of y = \(\frac { 2 }{ 6 } \) = \(\frac { 1 }{ 3 } \)
Ratio of constant terms = \(\frac { 4 }{ 12 } \) = \(\frac { 1 }{ 3 } \)
∴ Ratios of coefficients of x = ratio of coefficients of y = ratio of the constant terms
iv. When two equations are given but the graph is only one line, the equations will have infinite solutions.

Class 10 Maths Part 1 Practice Set 1.2 Question 4.
Draw graphs of x- 2y = 4, 2x – 4y = 12 on the same co-ordinate plane. Observe it. Think of the relation between the coefficients of x, coefficients ofy and the constant terms and draw the inference. (Textbook pg. no. 10)
Solution:

ii. Ratio of coefficients of x =\(\frac { 1 }{ 2 } \)
Ratio of coefficients of y = \(\frac { -2 }{ -4 } \) = \(\frac { 1 }{ 2 } \)
Ratio of constant terms = \(\frac { 4 }{ 12 } \) = \(\frac { 1 }{ 3 } \)
∴ Ratio of coefficients of x = ratio of coefficients of y ratio of constant terms
iii. If ratio of coefficients of x = ratio of coefficients of y ≠ ratio of constant terms, then the graphs of the two equations will be parallel to each other.

Condition of consistency in Equations:

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

9th Standard Maths 1 Problem Set 2.6 Chapter 2 Real Numbers Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.

Class 9 Maths Part 1 Problem Set 2.6 Chapter 2 Real Numbers Questions With Answers Maharashtra Board

Question 1.
Choose the correct alternative answer for the questions given below. [1 Mark each]

i. Which one of the following is an irrational number?

Answer:
√5

ii. Which of the following is an irrational number?
(A) 0.17
(B) \(1.\overline { 513 }\)
(C) \(0.27\overline { 46 }\)
(D) 0.101001000……..
Answer:
(D) 0.101001000……..

iii. Decimal expansion of which of the following is non-terminating recurring?

Answer:
(C) \(\frac { 3 }{ 11 }\)

iv. Every point on the number line represents which of the following numbers?
(A) Natural numbers
(B) Irrational numbers
(C) Rational numbers
(D) Real numbers
Answer:
(D) Real numbers

v. The number [/latex]0.\dot { 4 }[/latex] in \(\frac { p }{ q }\) form is ……

Answer:
(A) \(\frac { 4 }{ 9 }\)

vi. What is √n , if n is not a perfect square number ?
(A) Natural number
(B) Rational number
(C) Irrational number
(D) Options A, B, C all are correct.
Answer:
(C) Irrational number

vii. Which of the following is not a surd ?

Answer:
(C) \(\sqrt [ 3 ]{ \sqrt { 64 } }\)

viii. What is the order of the surd \(\sqrt [ 3 ]{ \sqrt { 5 } }\) ?
(A) 3
(B) 2
(C) 6
(D) 5
Answer:
(C) 6

ix. Which one is the conjugate pair of 2√5 + √3 ?
(A) -2√5 + √3
(B) -2√5 – √3
(C) 2√3 – √5
(D) √3 + 2√5
Answer:
(A) -2√5 + √3

x. The value of |12 – (13 + 7) x 4| is ____ .
(A) – 68
(B) 68
(C) – 32
(D) 32
Answer:
(B) 68

Hints:
ii. Since the decimal expansion is neither terminating nor recurring, 0.101001000…. is an irrational number.

iii. \(\frac { 3 }{ 11 }\)
Denominator =11 = 1 x 11
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal expansion of \(\frac { 3 }{ 11 }\) will be non terminating recurring.

v. Let x = [/latex]0.\dot { 4 }[/latex]
∴10 x = [/latex]0.\dot { 4 }[/latex]
∴10 – x = [/latex]4.\dot { 4 }[/latex] – [/latex]0.\dot { 4 }[/latex]
∴9x = 4
∴ x = \(\frac { 4 }{ 9 }\)

vii. \(\sqrt[3]{61}\) = 4, which is not an irrational number.

viii. \(\sqrt[3]{\sqrt{5}}=\sqrt[3 \times 2]{5}=\sqrt[6]{5}\)
∴ Order = 6

ix. The conjugate of 2√5 + √3 is 2√5 – √3 or -2√5 + √3

x. |12 – (13+7) x 4| = |12 – 20 x 4|
= |12 – 80|
= |-68|
= 68

Question 2.
Write the following numbers in \(\frac { p }{ q }\) form.
i. 0.555
ii. \(29.\overline { 568 }\)
iii. 9.315315…..
iv. 357.417417…..
v . \(30.\overline { 219 }\)
Solution:

ii. Let x = \(29.\overline { 568 }\) …(i)
x = 29.568568…
Since, three numbers i.e. 5, 6 and 8 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 29568.568568…
1000 x= \(29568.\overline { 568 }\) …(ii)
Subtracting (i) from (ii),
1000x – x = \(29568.\overline { 568 }\) – \(29.\overline { 568 }\)
∴ 999x = 29539

iii. Let x = 9.315315 … = \(9.\overline { 315 }\) …(i)
Since, three numbers i.e. 3, 1 and 5 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 9315.315315…
∴1000x = \(9315.\overline { 315 }\) …(ii)
Subtracting (i) from (ii),
1000x – x = \(9315.\overline { 315 }\) – \(9.\overline { 315 }\)
∴ 999x = 9306

iv. Let x = 357.417417… = \(357.\overline { 417 }\) …(i)
Since, three numbers i.e. 4, 1 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 357417.417417…
∴ 1000x = 357417.417 …(ii)
Subtracting (i) from (ii),
1000x – x = \(357417.\overline { 417 }\) – \(357.\overline { 417 }\)
∴ 999x = 357060

v. Let x = \(30.\overline { 219 }\) …(i)
∴ x = 30.219219
Since, three numbers i.e. 2, 1 and 9 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x= 30219.219219…
∴ 1000x = \(30219.\overline { 219 }\) …(ii)
Subtracting (i) from (ii),
1000x – x = \(30219.\overline { 219 }\) – \(30.\overline { 219 }\)
∴ 999x = 30189

Question 3.
Write the following numbers in its decimal form.

Solution:
i. \(\frac { -5 }{ 7 }\)

ii. \(\frac { 9 }{ 11 }\)

iii. √5

iv. \(\frac { 121 }{ 13 }\)

v. \(\frac { 29 }{ 8 }\)

Question 4.
Show that 5 + √7 is an irrational number. [3 Marks]
Solution:
Let us assume that 5 + √7 is a rational number. So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that

Since, ‘a’ and ‘b’ are integers, \(\sqrt [ a ]{ b }\) – 5 is a rational number and so √7 is a rational number.
∴ But this contradicts the fact that √7 is an irrational number.
Our assumption that 5 + √7 is a rational number is wrong.
∴ 5 + √7 is an irrational number.

Question 5.
Write the following surds in simplest form.

Solution:

Question 6.
Write the simplest form of rationalising factor for the given surds.

Solution:

Now, 4√2 x √2 = 4 x 2 = 8, which is a rational number.
∴ √2 is the simplest form of the rationalising factor of √32 .

Now, 5√2 x √2 = 5 x 2 = 10, which is a rational number.
∴ √2 is the simplest form of the rationalising factor of √50 .

Now, 3√3 x √3 = 3 x 3 = 9, which is a rational number.
∴ √ 3 is the simplest form of the rationalising factor of √27 .

= 6, which is a rational number.
∴ √10 is the simplest form of the rationalising factor of \(\sqrt [ 3 ]{ 5 }\) √10 .

Now, 18√2 x √2 = 18 x 2 = 36, which is a rational number.
∴ √2 is the simplest form of the rationalising factor of 3√72.

vi. 4√11
4√11 x √11 = 4 x 11 = 44, which is a rational number.
∴ √11 is the simplest form of the rationalising factor of 4√11.

Question 7.
Simplify.

Solution:

Question 8.
Rationalize the denominator.

Solution:

Question 1.
Draw three or four circles of different radii on a card board. Cut these circles. Take a thread and measure the length of circumference and diameter of each of the circles. Note down the readings in the given table. (Textbook pg.no.23 )

Solution:
i. 14,44,3.1
ii. 16,50.3,3.1
iii. 11,34.6,3.1
From table, we observe that the ratio \(\sqrt [ c ]{ d }\) is nearly 3.1 which is constant. This ratio is denoted by π (pi).

Question 2.
To find the approximate value of π, take the wire of length 11 cm, 22 cm and 33 cm each. Make a circle from the wire. Measure the diameter and complete the following table.

Verify that the ratio of circumference to the diameter of a circle is approximately \(\sqrt [ 22 ]{ 7 }\). (Textbook pg. no. 24)
Solution:
i. 3.5, \(\sqrt [ 22 ]{ 7 }\)
ii. 7, \(\sqrt [ 22 ]{ 7 }\)
iii. 10.5, \(\sqrt [ 22 ]{ 7 }\)
∴ The ratio of circumference to the diameter of each circle is \(\sqrt [ 22 ]{ 7 }\).

Maths Solution Class 9 Maharashtra Board 

• Real Numbers Practice Set 2.1 Class 9 Maths Solutions
• Real Numbers Practice Set 2.2 Class 9 Maths Solutions
• Real Numbers Practice Set 2.3 Class 9 Maths Solutions
• Real Numbers Practice Set 2.4 Class 9 Maths Solutions
• Real Numbers Practice Set 2.5 Class 9 Maths Solutions
• Real Numbers Problem Set 2 Class 9 Maths Solutions

10th Standard Maths 1 Practice Set 1.1 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.

Class 10 Maths Part 1 Practice Set 1.1 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Question 1.
Complete the following activity to solve the simultaneous equations.
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Solution:
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Add equations (i) and (ii).

Question 2.
Solve the following simultaneous equations.
i. 3a + 5b = 26; a + 5b = 22
ii. x + 7y = 10; 3x – 2y = 7
iii. 2x – 3y = 9; 2x + y = 13
iv. 5m – 3n = 19; m – 6n = -7
v. 5x + 2y = -3;x + 5y = 4
vi. \(\frac { 1 }{ 3 } \) x+ y = \(\frac { 10 }{ 3 } \) ; 2x + \(\frac { 1 }{ 4 } \) y = \(\frac { 11 }{ 4 } \)
vii. 99x + 101y = 499 ; 101x + 99y = 501
viii. 49x – 57y = 172; 57x – 49y = 252
Solution:
i. 3a + 5b = 26 …(i)
a + 5b = 22 …(ii)
Subtracting equation (ii) from (i), we get

Substituting a = 2 in equation (ii), we get
2 + 5b = 22
∴ 5b = 22 – 2
∴ 5b = 20
∴ b = \(\frac { 20 }{ 5 } \) =4
∴ (a, b) = (2, 4) is the solution of the given simultaneous equations.

ii. x + 7y = 10
∴ x = 10 – 7y …(i)
3x – 2y = 7 …1(ii)
Substituting x = 10 – ly in equation (ii), we get
3 (10 – 7y) – 2y = 7
∴ 30 – 21y – 2y = 7
∴ -23y = 7 – 30
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \)
Substituting y = 1 in equation (i), we get
x = 10 – 7 (1)
= 10 – 7 = 3
∴ (x, y) = (3, 1) is the solution of the given simultaneous equations.

iii. 2x – 3y = 9 …(i)
2x + y = 13 …(ii)
Subtracting equation (ii) from (i), we get

∴ (x, y) = (6, 1) is the solution of the given simultaneous equations.

iv. 5m – 3n = 19 …(i)
m – 6n = -7
∴ m = 6n – 7 …(ii)
Substituting m = 6n – 7 in equation (i), we get
5(6n – 7) – 3n = 19
∴ 30n – 35 – 3n = 19
∴ 27n = 19 + 35
∴ 27n = 54
∴ n = \(\frac { 54 }{ 27 } \) = 2
Substituting n = 2 in equation (ii), we get
m = 6(2) – 7
= 12 – 7 = 5
∴ (m, n) = (5, 2) is the solution of the given simultaneous equations.

v. 5x + 2y = -3 …(i)
x + 5y = 4
∴ x = 4 – 5y …(ii)
Substituting x = 4 – 5y in equation (i), we get
5(4 – 5y) + 2y = -3
∴ 20 – 25y + 2y = -3
∴ -23y = -3 – 20
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \) = 1
Substituting y = 1 in equation (ii), we get
x = 4 – 5(1)
= 4 – 5 = -1
∴ (x, y) = (-1, 1) is the solution of the given simultaneous equations.

Substituting y = 3 in equation (i), we get
x = 10 – 3(3)
= 10 – 9 = 1
∴ (x, y) = (1, 3) is the solution of the given simultaneous equations.

vii. 99x + 101 y = 499 …(i)
101 x + 99y = 501 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 3 in equation (iii), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.

viii. 49x – 57y = 172 …(i)
57x – 49y = 252 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 7 in equation (iv), we get
7 + y = 10
∴ y = 10 – 7 = 3
∴ (x, y) = (7, 3) is the solution of the given simultaneous equations.

Complete the following table. (Textbook pg. no. 1)

Question 1.
Solve: 3x+ 2y = 29; 5x – y = 18 (Textbook pg. no. 3)
Solution:
3x + 2y = 29 …(i)
and 5x- y = 18 …(ii)
Let’s solve the equations by eliminating ‘y’.
Fill suitably the boxes below.
Multiplying equation (ii) by 2, we get

Maharashtra State Board Class 10 Maths Solutions Part 1

• Linear Equations in Two Variables Practice Set 1.1 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.2 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.3 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.4 Class 10 Maths Solutions
• Linear Equations in Two Variables Practice Set 1.5 Class 10 Maths Solutions
• Linear Equations in Two Variables Problem Set 1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.1 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.2 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.3 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.4 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.5 Class 10 Maths Solutions
• Quadratic Equations Practice Set 2.6 Class 10 Maths Solutions
• Quadratic Equations Problem Set 2 Class 10 Maths Solutions

9th Standard Maths 1 Practice Set 2.2 Chapter 2 Real Numbers Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.

Class 9 Maths Part 1 Practice Set 2.2 Chapter 2 Real Numbers Questions With Answers Maharashtra Board

Question 1.
Show that 4√2 is an irrational number.
Solution:
Let us assume that 4√2 is a rational number .
So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that
4√2 = \(\frac { a }{ b }\)
∴ √2 = \(\frac { a }{ 4b }\)
Since, a and b are integers, \(\frac { a }{ 4b }\) is a rational number and so √2 is a rational number.

Alternate Proof:
Let us assume that 4√2 is a rational number.
So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that

Since, 32 divides a², so 32 divides ‘a’ as well.
So, we write a = 32c, where c is an integer.
∴ a² = (32c)² … [Squaring both the sides]
∴ 32b² = 32 x 32c² …[From(i)]
∴ b² = 32c²
∴ c² = \(\frac { { b }^{ 2 } }{ 32 }\)
Since, 32 divides b², so 32 divides ‘b’.
∴ 32 divides both a and b.
a and b have at least 32 as a common factor.
But this contradicts the fact that a and b have no common factor other than 1.
∴ Our assumption that 4√2 is a rational number is wrong.
∴ 4√2 is an irrational number.

Question 2.
Prove that 3 + √5 is an irrational number.
Solution:
Let us assume that 3 + √5 is a rational number.
So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that

Since, a and b are integers, \(\frac { a }{ b }\) – 3 is a rational
number and so √5 is a rational number.
But this contradicts the fact that √5 is an irrational number.
∴ Our assumption that 3 – √5 is a rational number is wrong.
3 + √5 is an irrational number.

Question 3.
Represent the numbers √5 and √10 on a number line.
Solution:
i. Draw a number line and take point A at 2.
Draw AB perpendicular to the number line such that AB = 1 unit.
In ∆OAB, m∠OAB = 90°
∴ (OB)² = (OA)² + (AB)² … [Pythagoras theorem]
= (2)² + (1)²
∴ (OB)² = 5
∴ OB = √5 units. … [Taking square root of both sides]
With O as centre and radius equal to OB, draw an arc to intersect the number line at C.

The coordinate of the point C is √5 .

ii. Draw a number line and take point Pat 3.
Draw PR perpendicular to the number line such that PR = 1 unit.
In ∆OPR, m∠OPR = 90°
∴ (OR)² = (OP)² + (PR)² … [Pythagoras theorem]
= (3)² + (1)²
∴ (OR)² = 10
∴ OR= √10units. … [Taking square root of both sides]
With O as centre and radius equal to OR, draw an arc to intersect the number line at Q.

The coordinate of the point Q is √10 .

Question 4.
Write any three rational numbers between the two numbers given below.
i. 0.3 and – 0.5
ii. – 2.3 and – 2.33
iii. 5.2 and 5.3
iv. – 4.5 and – 4.6
Solution:
i. 0.3 = 0.30 and -0.5 = -0.50
We know that,
0. 30 >0.29 >….. >0.10>.. > – 0.10>…. > -0.30>…> -0.50
∴ the three rational numbers between 0.3 and -0.5 are -0.3, -0.1 and 0.1.

Alternate Method:
A rational number between two rational numbers a and b


∴ the three rational numbers between 0.3 and -0.5 are -0.3, -0.1 and 0.1.

ii. -2.3 = -2.300 and -2.33 = -2.330
We know that,
-2.300 > -2.301>… > -2.310>…> -2.320>…> -2.330
∴ the three rational numbers between -2.3 and -2.33 are -2.310, -2.320 and -2.325.

iii. 5.2 = 5.20 and 5.3 = 5.30
We know that,
5.20 < 5.21 < 5.22 < 5.23 < … < 5.30
∴ the three rational numbers between 5.2 and 5.3 are 5.21, 5.22 and 5.23.

iv. -4.5 = -4.50 and -4.6 = -4.60 We know that,
-4.50 > -4.51 > -4.52 >… > – 4.55 >…>- 4.60
∴ the three rational numbers between -4.5 and -4.6 are -4.51, -4.52 and -4.55.

Maths Solution Class 9 Maharashtra Board 

• Real Numbers Practice Set 2.1 Class 9 Maths Solutions
• Real Numbers Practice Set 2.2 Class 9 Maths Solutions
• Real Numbers Practice Set 2.3 Class 9 Maths Solutions
• Real Numbers Practice Set 2.4 Class 9 Maths Solutions
• Real Numbers Practice Set 2.5 Class 9 Maths Solutions
• Real Numbers Problem Set 2 Class 9 Maths Solutions