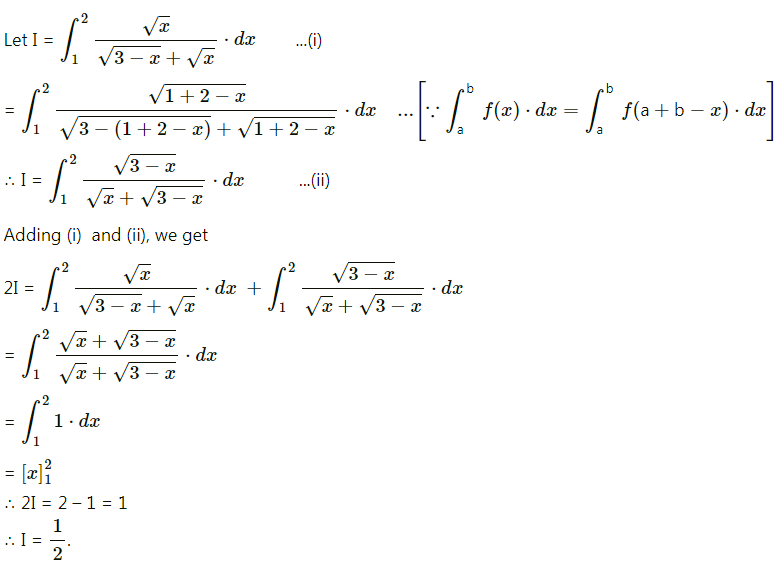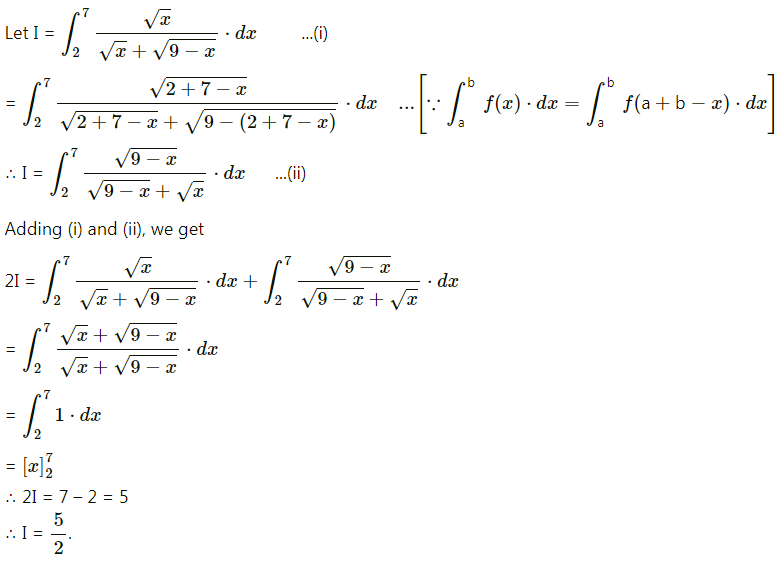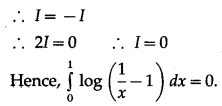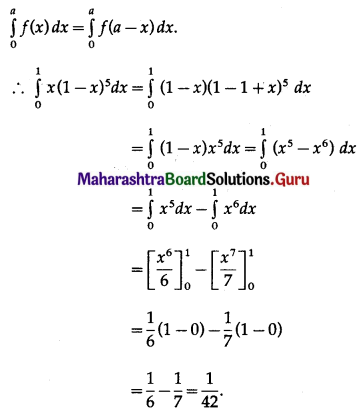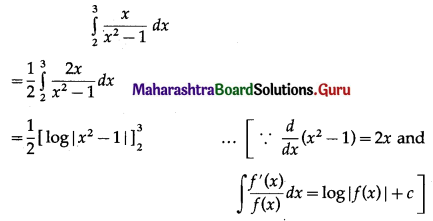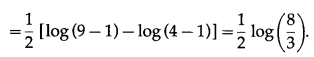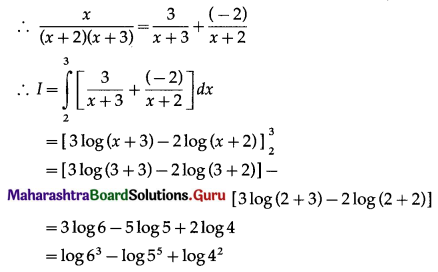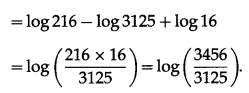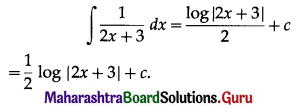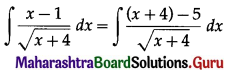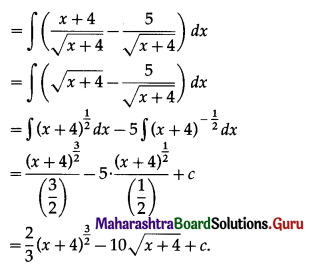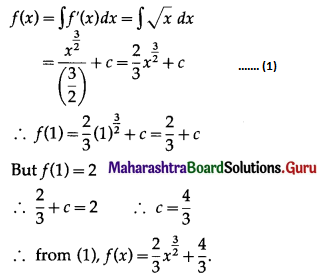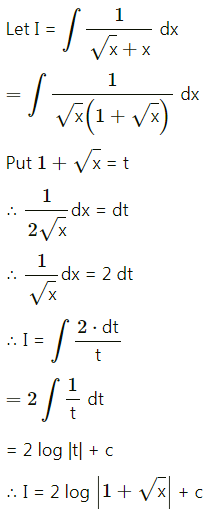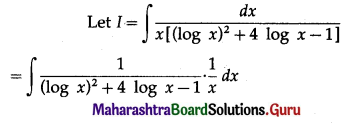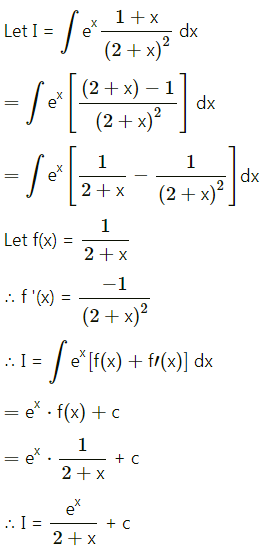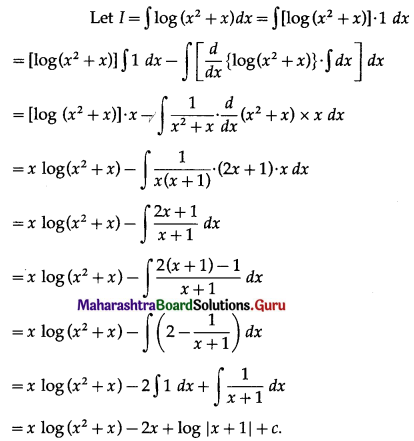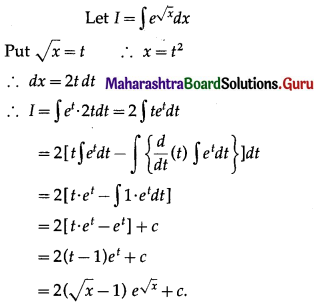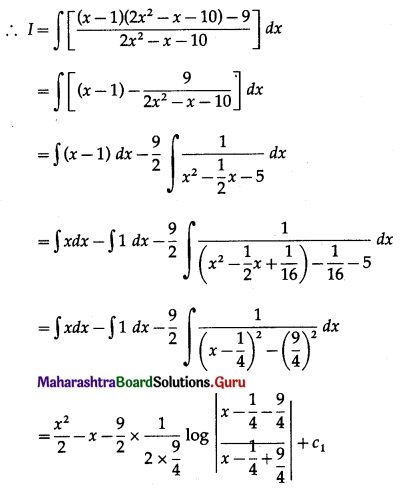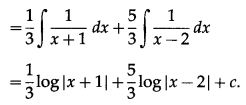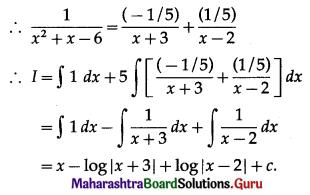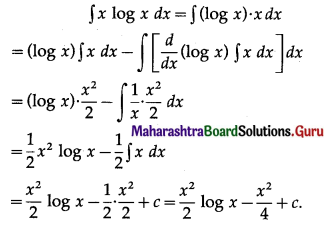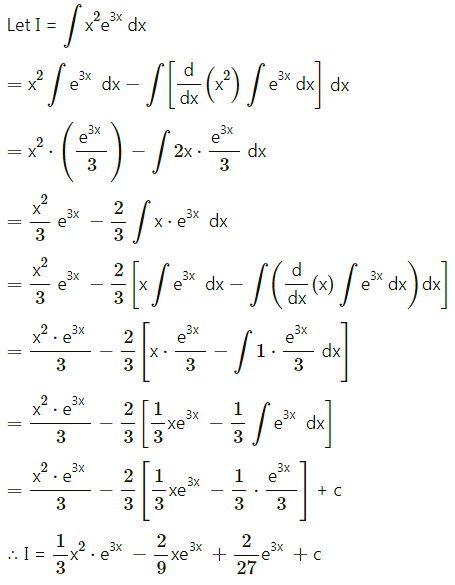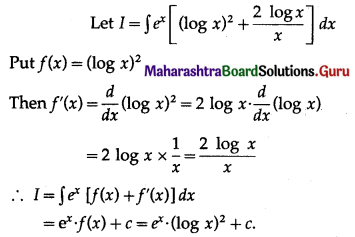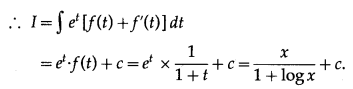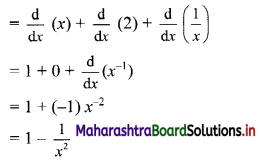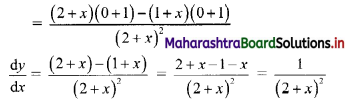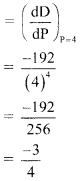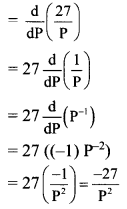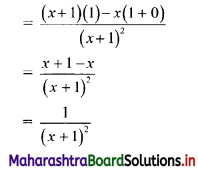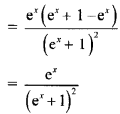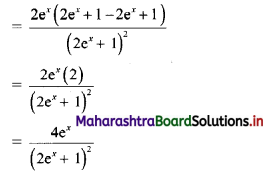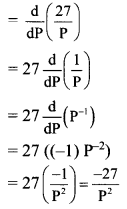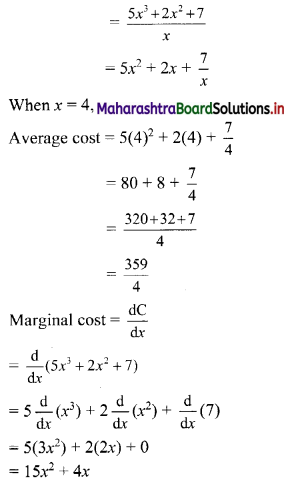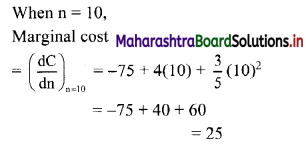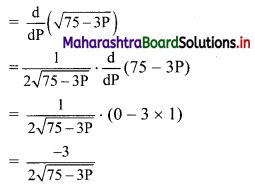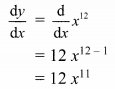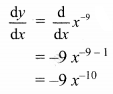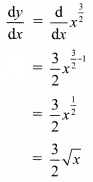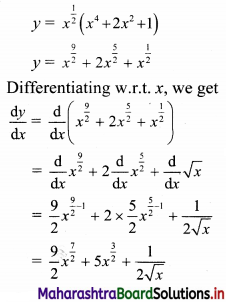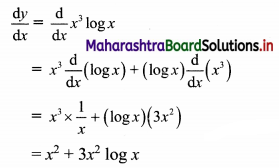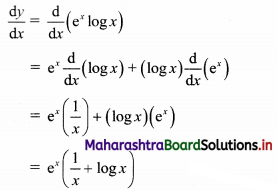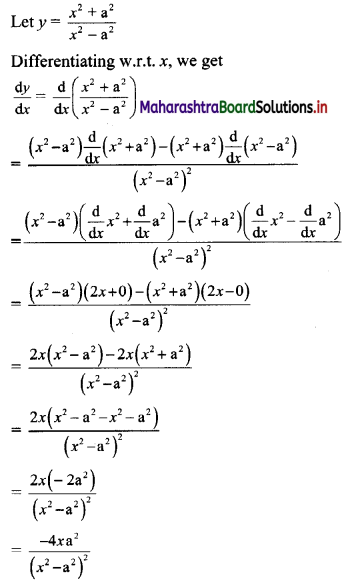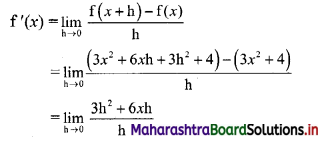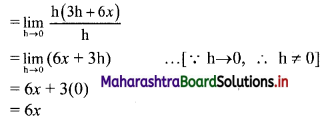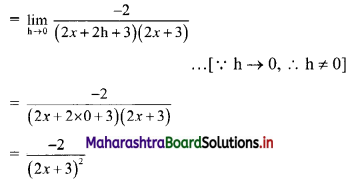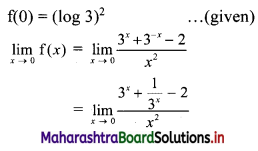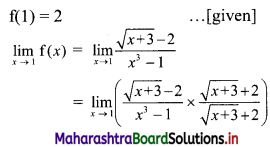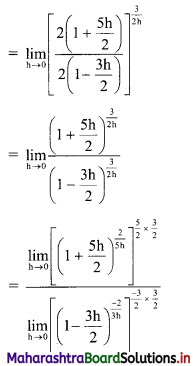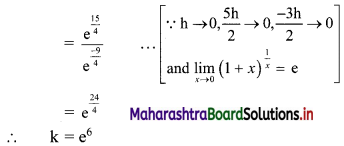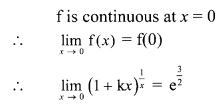Bhagya

Definite Integration Class 12 Commerce Maths 1 Chapter 6 Miscellaneous Exercise 6 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Miscellaneous Exercise 6 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 6 Solutions Commerce Maths

(I) Choose the correct alternative:

Question 1.
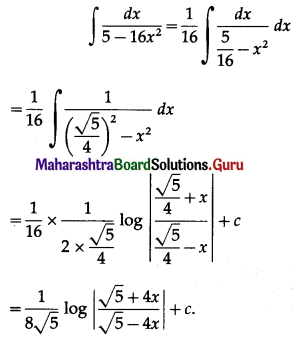
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\) = ________
(a) 0
(b) 3
(c) 9
(d) -9
Answer:
(a) 0

Question 2.
\(\int_{-2}^{3} \frac{d x}{x+5}\) = _________
(a) -log(\(\frac{8}{3}\))
(b) log(\(\frac{8}{3}\))
(c) log(\(\frac{3}{8}\))
(d) -log(\(\frac{3}{8}\))
Answer:
(b) log(\(\frac{8}{3}\))

Question 3.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\) = _________
(a) log(\(\frac{8}{3}\))
(b) -log(\(\frac{8}{3}\))
(c) \(\frac{1}{2}\) log(\(\frac{8}{3}\))
(d) \(\frac{-1}{2}\) log(\(\frac{8}{3}\))
Answer:
(c) \(\frac{1}{2}\) log(\(\frac{8}{3}\))

Question 4.
\(\int_{4}^{9} \frac{d x}{\sqrt{x}}\) = ___________
(a) 9
(b) 4
(c) 2
(d) 0
Answer:
(c) 2

Question 5.
If \(\int_{0}^{a} 3 x^{2} d x=8\), then a = __________
(a) 2
(b) 0
(c) \(\frac{8}{3}\)
(d) a
Answer:
(a) 2

Question 6.
\(\int_{2}^{3} x^{4}\) dx = ________
(a) \(\frac{1}{2}\)
(b) \(\frac{5}{2}\)
(c) \(\frac{5}{211}\)
(d) \(\frac{211}{5}\)
Answer:
(d) \(\frac{211}{5}\)

Question 7.
\(\int_{0}^{2} e^{x}\) dx = _______
(a) e – 1
(b) 1 – e
(c) 1 – e²
(d) e² – 1
Answer:
(d) e² – 1

Question 8.
\(\int_{a}^{b} f(x) d x\) = ________
(a) \(\int_{b}^{a} f(x) d x\)
(b) –\(\int_{a}^{b} f(x) d x\)
(c) –\(\int_{b}^{a} f(x) d x\)
(d) \(\int_{0}^{a} f(x) d x\)
Answer:
(c) –\(\int_{b}^{a} f(x) d x\)

Question 9.
\(\int_{-7}^{7} \frac{x^{3}}{x^{2}+7} d x\) = _________
(a) 7
(b) 49
(c) 0
(d) \(\frac{7}{2}\)
Answer:
(c) 0

Question 10.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x\) = _________
(a) \(\frac{7}{2}\)
(b) \(\frac{5}{2}\)
(c) 7
(d) 2
Answer:
(b) \(\frac{5}{2}\)

(II) Fill in the blanks:

Question 1.
\(\int_{0}^{2} e^{x} d x\) = ________
Answer:
e² – 1

Question 2.
\(\int_{2}^{3} x^{4} d x\) = __________
Answer:
\(\frac{211}{5}\)

Question 3.
\(\int_{0}^{1} \frac{d x}{2 x+5}\) = ____________
Answer:
\(\frac{1}{2} \log \left(\frac{7}{5}\right)\)

Question 4.
If \(\int_{0}^{a} 3 x^{2} d x\) = 8, then a = _________
Answer:
2

Question 5.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\) = _________
Answer:
2

Question 6.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\) = _________
Answer:
\(\frac{1}{2} \log \left(\frac{8}{3}\right)\)

Question 7.
\(\int_{-2}^{3} \frac{d x}{x+5}\) = _________
Answer:
\(\log \left(\frac{8}{3}\right)\)

Question 8.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\) = _____________
Answer:
o

(III) State whether each of the following is True or False:

Question 1.
\(\int_{a}^{b} f(x) d x=\int_{-b}^{-a} f(x) d x\)
Answer:
True

Question 2.
\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(t) d t\)
Answer:
True

Question 3.
\(\int_{0}^{a} f(x) d x=\int_{a}^{0} f(a-x) d x\)
Answer:
False

Question 4.
\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(x-a-b) d x\)
Answer:
False

Question 5.
\(\int_{-5}^{5} \frac{x^{3}}{x^{2}+7} d x=0\)
Answer:
True

Question 6.
\(\int_{1}^{2} \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}} d x=\frac{1}{2}\)
Answer:
True

Question 7.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x=\frac{9}{2}\)
Answer:
False

Question 8.
\(\int_{4}^{7} \frac{(11-x)^{2}}{(11-x)^{2}+x^{2}} d x=\frac{3}{2}\)
Answer:
True

(IV) Solve the following:

Question 1.
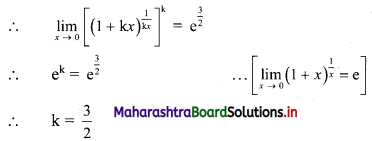
\(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Solution:

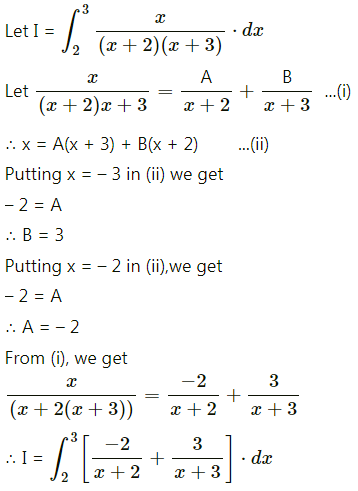
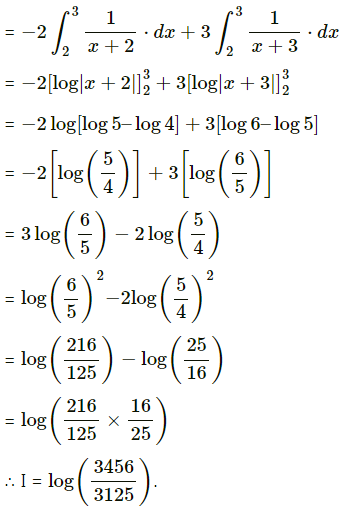
Question 2.
\(\int_{1}^{2} \frac{x+3}{x(x+2)} d x\)
Solution:
Let I = \(\int_{1}^{2} \frac{x+3}{x(x+2)} d x\)
Let \(\frac{x+3}{x(x+2)}=\frac{A}{x}+\frac{B}{x+2}\)
∴ x + 3 = A(x + 2) + Bx
Put x = 0, we get
3 = A(2) + B(0)
∴ A = \(\frac{3}{2}\)
Put x + 2 = 0, i.e. x = -2, we get
-2 + 3 = A(0) + B(-2)
∴ 1 = -2B
∴ B = \(-\frac{1}{2}\)

Question 3.
\(\int_{1}^{3} x^{2} \log x d x\)
Solution:

Question 4.
\(\int_{0}^{1} e^{x^{2}} \cdot x^{3} d x\)
Solution:

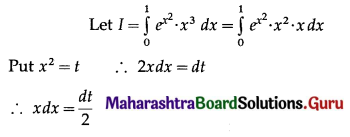
Question 5.
\(\int_{1}^{2} e^{2 x}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) d x\)
Solution:

Question 6.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\)
Solution:

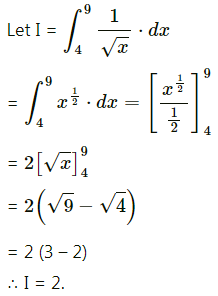
Question 7.
\(\int_{-2}^{3} \frac{1}{x+5} d x\)
Solution:

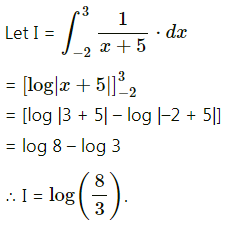
Question 8.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\)
Solution:

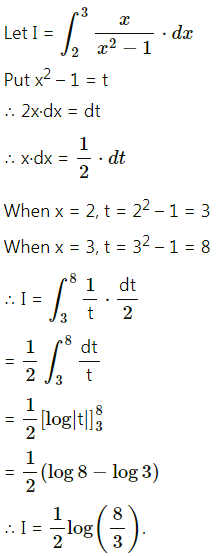
Question 9.
\(\int_{0}^{1} \frac{x^{2}+3 x+2}{\sqrt{x}} d x\)
Solution:

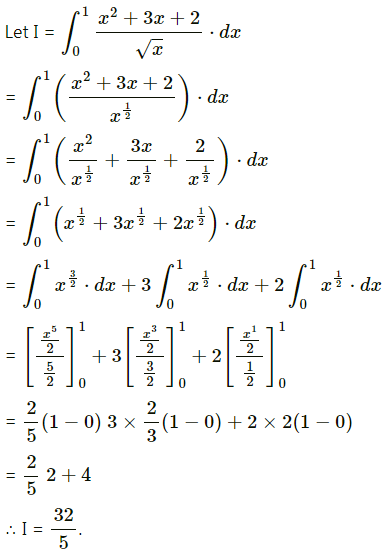
Question 10.
\(\int_{3}^{5} \frac{d x}{\sqrt{x+4}+\sqrt{x-2}}\)
Solution:

Question 11.
\(\int_{2}^{3} \frac{x}{x^{2}+1} d x\)
Solution:

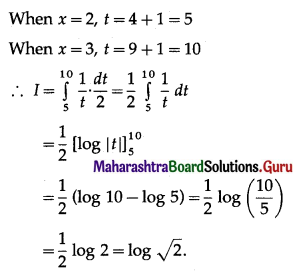
Question 12.
\(\int_{1}^{2} x^{2} d x\)
Solution:

Question 13.
\(\int_{-4}^{-1} \frac{1}{x} d x\)
Solution:

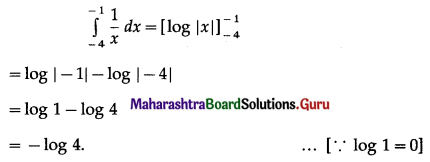
Question 14.
\(\int_{0}^{1} \frac{1}{\sqrt{1+x}+\sqrt{x}} d x\)
Solution:

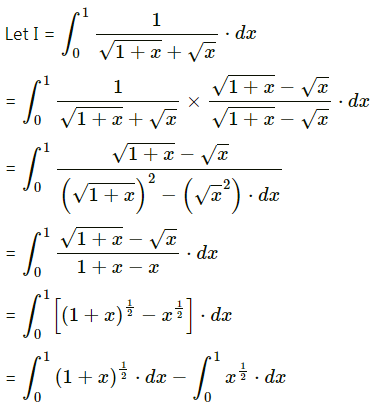
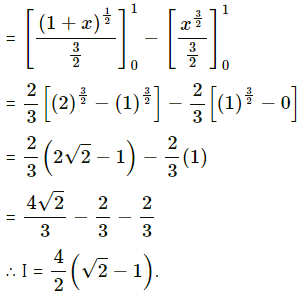
Question 15.
\(\int_{0}^{4} \frac{1}{\sqrt{x^{2}+2 x+3}} d x\)
Solution:

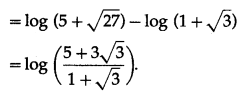
Question 16.
\(\int_{2}^{4} \frac{x}{x^{2}+1} d x\)
Solution:

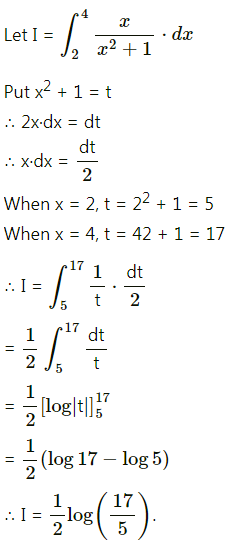
Question 17.
\(\int_{0}^{1} \frac{1}{2 x-3} d x\)
Solution:

Question 18.
\(\int_{1}^{2} \frac{5 x^{2}}{x^{2}+4 x+3} d x\)
Solution:

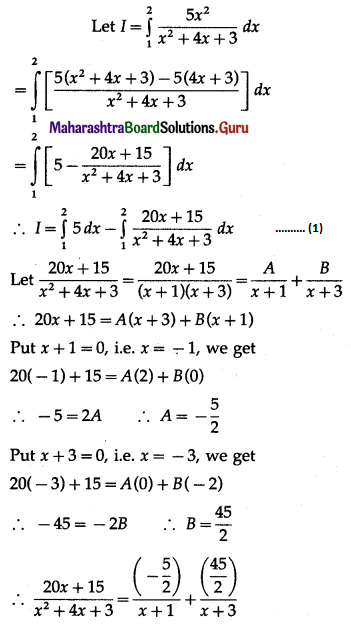
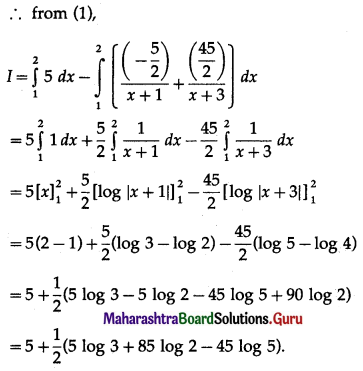
Question 19.
\(\int_{1}^{2} \frac{d x}{x(1+\log x)^{2}}\)
Solution:

Question 20.
\(\int_{0}^{9} \frac{1}{1+\sqrt{x}} d x\)
Solution:

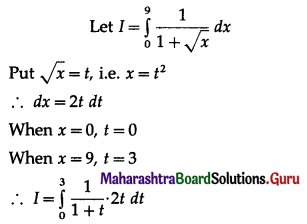
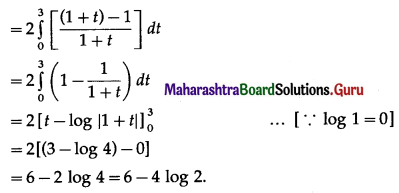
12th Commerce Maths Digest Pdf 

• Definite Integration Ex 6.1 Class 12 Commerce Maths Textbook Solutions
• Definite Integration Ex 6.2 Class 12 Commerce Maths Textbook Solutions
• Definite Integration Miscellaneous Exercise 6 Class 12 Commerce Maths Textbook Solutions

Definite Integration Class 12 Commerce Maths 1 Chapter 6 Exercise 6.2 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Ex 6.2 Questions and Answers.

Std 12 Maths 1 Exercise 6.2 Solutions Commerce Maths

Evaluate the following integrals:

Question 1.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\)
Solution:

Question 2.
\(\int_{0}^{a} x^{2}(a-x)^{3 / 2} d x\)
Solution:
We use the property

Question 3.
\(\int_{1}^{3} \frac{\sqrt[3]{x+5}}{\sqrt[3]{x+5}+\sqrt[3]{9-x}} d x\)
Solution:

Question 4.
\(\int_{2}^{5} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{7-x}} d x\)
Solution:

Question 5.
\(\int_{1}^{2} \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}} d x\)
Solution:

Question 6.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x\)
Solution:

Question 7.
\(\int_{0}^{1} \log \left(\frac{1}{x}-1\right) d x\)
Solution:

Question 8.
\(\int_{0}^{1} x(1-x)^{5} d x\)
Solution:
We use the property

12th Commerce Maths Digest Pdf 

• Definite Integration Ex 6.1 Class 12 Commerce Maths Textbook Solutions
• Definite Integration Ex 6.2 Class 12 Commerce Maths Textbook Solutions
• Definite Integration Miscellaneous Exercise 6 Class 12 Commerce Maths Textbook Solutions

Definite Integration Class 12 Commerce Maths 1 Chapter 6 Exercise 6.1 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Ex 6.1 Questions and Answers.

Std 12 Maths 1 Exercise 6.1 Solutions Commerce Maths

Evaluate the following definite integrals:

Question 1.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\)
Solution:

Question 2.
\(\int_{-2}^{3} \frac{1}{x+5} d x\)
Solution:

Question 3.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\)
Solution:

Question 4.
\(\int_{0}^{1} \frac{x^{2}+3 x+2}{\sqrt{x}} d x\)
Solution:

Question 5.
\(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Solution:
Let I = \(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Let \(\frac{x}{(x+2)(x+3)}=\frac{A}{x+3}+\frac{B}{x+2}\)
∴ x = A(x + 2) + B(x + 3)
Put x + 3 = 0, i.e. x = -3, we get
-3 = A(-1) + B(0)
∴ A = 3
Put x + 2 = 0, i.e. x = -2, we get
-2 = A(0) + B(1)
∴ B = -2

Question 6.
\(\int_{1}^{2} \frac{d x}{x^{2}+6 x+5}\)
Solution:

Question 7.
If \(\int_{0}^{a}(2 x+1) d x\) = 2, find the real values of ‘a’.
Solution:
Let I = \(\int_{0}^{a}(2 x+1) d x\)
= \(\left[2 \cdot \frac{x^{2}}{2}+x\right]_{0}^{a}\)
= a² + a – 0
= a² + a
∴ I = 2 gives a² + a = 2
∴ a² + a – 2 = 0
∴ (a + 2)(a – 1) = 0 1
∴ a + 2 = 0 or a – 1 = 0
∴ a = -2 or a = 1.

Question 8.
If \(\int_{1}^{a}\left(3 x^{2}+2 x+1\right) d x\) = 11, find ‘a’.
Solution:
Let I = \(\int_{1}^{a}\left(3 x^{2}+2 x+1\right) d x\)
= \(\left[3\left(\frac{x^{3}}{3}\right)+2\left(\frac{x^{2}}{2}\right)+x\right]_{1}^{a}\)
= \(\left[x^{3}+x^{2}+x\right]_{1}^{a}\)
= (a³ + a² + a) – (1 + 1 + 1)
= a³ + a² + a – 3
∴ I = 11 gives a³ + a² + a – 3 = 11
∴ a³ + a² + a – 14 = 0
∴ (a³ – 8) + (a² + a – 6) = 0
∴ (a – 2)(a² + 2a + 4) + (a + 3)(a – 2) = 0
∴ (a – 2)(a² + 2a + 4 + a + 3) = 0
∴ (a – 2)(a² + 3a + 7) = 0
∴ a – 2 = 0 or a² + 3a + 7 = 0
∴ a = 2 or a = \(\frac{-3 \pm \sqrt{9-28}}{2}\)
The latter two roots are not real.
∴ they are rejected.
∴ a = 2.

Question 9.
\(\int_{0}^{1} \frac{1}{\sqrt{1+x}+\sqrt{x}} d x\)
Solution:

Question 10.
\(\int_{1}^{2} \frac{3 x}{9 x^{2}-1} d x\)
Solution:
Let I = \(\int_{1}^{2} \frac{3 x}{9 x^{2}-1} d x\) = \(\int_{1}^{2} \frac{3 x}{(3 x)^{2}-1} d x\)
Put 3x = t
∴ 3 dx = dt
∴ dx = \(\frac{d t}{3}\)
When x = 1, t = 3 × 1 = 3
When x = 2, t = 3 × 2 = 6

Question 11.
\(\int_{1}^{3} \log x d x\)
Solution:

12th Commerce Maths Digest Pdf 

• Definite Integration Ex 6.1 Class 12 Commerce Maths Textbook Solutions
• Definite Integration Ex 6.2 Class 12 Commerce Maths Textbook Solutions
• Definite Integration Miscellaneous Exercise 6 Class 12 Commerce Maths Textbook Solutions

Integration Class 12 Commerce Maths 1 Chapter 5 Miscellaneous Exercise 5 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Miscellaneous Exercise 5 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 5 Solutions Commerce Maths

(I) Choose the correct alternative from the following:

Question 1.
The value of \(\int \frac{d x}{\sqrt{1-x}}\) is
(a) 20\(\sqrt{1-x}\) + c
(b) -2\(\sqrt{1-x}\) + c
(c) √x + c
(d) x + c
Answer:
(b) -2\(\sqrt{1-x}\) + c

Question 2.
\(\int \sqrt{1+x^{2}} d x\) =
(a) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left(x+\sqrt{1+x^{2}}\right)+c\)
(b) \(\frac{2}{3}\left(1+x^{2}\right)^{3 / 2}+c\)
(c) \(\frac{1}{3}\left(1+x^{2}\right)+c\)
(d) \(\frac{(x)}{\sqrt{1+x^{2}}}+c\)
Answer:
(a) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left(x+\sqrt{1+x^{2}}\right)+c\)

Question 3.
\(\int x^{2}(3)^{x^{3}} d x\) =
(a) \(\text { (3) }^{x^{3}}+c\)
(b) \(\frac{(3)^{x^{3}}}{3 \cdot \log 3}+c\)
(c) \(\log 3(3)^{x^{3}}+c\)
(d) \(x^{2}(3)^{x 3}\)
Answer:
(b) \(\frac{(3)^{x^{3}}}{3 \cdot \log 3}+c\)
Hint:
Put x³ = t

Question 4.
\(\int \frac{x+2}{2 x^{2}+6 x+5} d x=p \int \frac{4 x+6}{2 x^{2}+6 x+5} d x\) + \(\frac{1}{2} \int \frac{d x}{2 x^{2}+6 x+5}\), then p = __________
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) 2
Answer:
(c) \(\frac{1}{4}\)
Hint:
\(\int \frac{x+2}{2 x^{2}+6 x+5} d x=\int \frac{\frac{1}{4}(4 x+6)+\frac{1}{2}}{2 x^{2}+6 x+5} d x\)

Question 5.
\(\int \frac{d x}{\left(x-x^{2}\right)}\) = ________
(a) log x – log(1 – x) + c
(b) log(1 – x²) + c
(c) -log x + log(1 – x) + c
(d) log(x – x²) + c
Answer:
(a) log x – log(1 – x) + c

Question 6.
\(\int \frac{d x}{(x-8)(x+7)}\) = __________
(a) \(\frac{1}{15} \log \left|\frac{x+2}{x-1}\right|+c\)
(b) \(\frac{1}{15} \log \left|\frac{x+8}{x+7}\right|+c\)
(c) \(\frac{1}{15} \log \left|\frac{x-8}{x+7}\right|+c\)
(d) (x – 8)(x – 7) + c
Answer:
(c) \(\frac{1}{15} \log \left|\frac{x-8}{x+7}\right|+c\)

Question 7.
\(\int\left(x+\frac{1}{x}\right)^{3} d x\) = _________
(a) \(\frac{1}{4}\left(x+\frac{1}{x}\right)^{4}+c\)
(b) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x-\frac{1}{2 x^{2}}+c\)
(c) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x+\frac{1}{x^{2}}+c\)
(d) \(\left(x-x^{-1}\right)^{3}+c\)
Answer:
(b) \(\frac{x^{4}}{4}+\frac{3 x^{2}}{2}+3 \log x-\frac{1}{2 x^{2}}+c\)
Hint:
\(\left(x+\frac{1}{x}\right)^{3}=x^{3}+3 x+\frac{3}{x}+\frac{1}{x^{3}}\)

Question 8.
\(\int\left(\frac{e^{2 x}+e^{-2 x}}{e^{x}}\right) d x\)
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)
(b) \(e^{x}+\frac{1}{3 e^{3 x}}+c\)
(c) \(e^{-x}+\frac{1}{3 e^{3 x}}+c\)
(d) \(e^{-x}-\frac{1}{3 e^{3 x}}+c\)
Answer:
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)

Question 9.
∫(1 – x)^-2 dx = ___________
(a) (1 + x)^-1 + c
(b) (1 – x)^-1 + c
(c) (1 – x)^-1 – 1 + c
(d) (1 – x)^-1 + 1 + c
Answer:
(b) (1 – x)^-1 + c

Question 10.
\(\int \frac{\left(x^{3}+3 x^{2}+3 x+1\right)}{(x+1)^{5}} d x\) = _______
(a) \(\frac{-1}{x+1}+c\)
(b) \(\left(\frac{-1}{x+1}\right)^{5}+c\)
(c) log(x + 1) + c
(d) log|x + 1|⁵ + c
Answer:
(a) \(\frac{-1}{x+1}+c\)
Hint:
x³ + 3x² + 3x + 1 = (x + 1)³

(II) Fill in the blanks.

Question 1.
\(\int \frac{5\left(x^{6}+1\right)}{x^{2}+1}\)dx = x⁴ + ___x³ + 5x + c.
Answer:
\(-\frac{5}{3}\)
Hint:
x⁶ + 1 = (x² + 1)(x⁴ – x² + 1)

Question 2.
\(\int \frac{x^{2}+x-6}{(x-2)(x-1)} d x\) = x + ______ + c
Answer:
4 log|x – 1|
Hint:
x² + x – 6 = (x + 3)(x – 2)

Question 3.
If f'(x) = \(\frac{1}{x}\) + x and f(1) = \(\frac{5}{2}\) then f(x) = log x + \(\frac{x^{2}}{2}\) + _______
Answer:
2
Hint:

Question 4.
To find the value of \(\int \frac{(1+\log x) d x}{x}\) the proper substitution is __________
Answer:
1 + log x = t

Question 5.
\(\int \frac{1}{x^{3}}\left[\log x^{x}\right]^{2} d x\) = p(log x)³ + c, then p = _______
Answer:
\(\frac{1}{3}\)
Hint:
\(\frac{1}{x^{3}}\left(\log x^{x}\right)^{2}=\frac{1}{x^{3}}(x \log x)^{2}=\frac{(\log x)^{2}}{x}\)

(III) State whether each of the following is True or False:

Question 1.
The proper substitution for \(\int x\left(x^{x}\right)^{x}(2 \log x+1) d x \text { is }\left(x^{x}\right)^{x}=t\)
Answer:
True

Question 2.
If ∫x e^2x dx is equal to e^2x f(x) + c where c is constant of integration, then f(x) is \(\frac{(2 x-1)}{2}\).
Answer:
False

Question 3.
If ∫x f(x) dx = \(\frac{f(x)}{2}\), then f(x) = \(e^{x^{2}}\).
Answer:
True

Question 4.
If \(\int \frac{(x-1) d x}{(x+1)(x-2)}\) = A log|x + 1| + B log|x – 2|, then A + B = 1.
Answer:
True

Question 5.
For \(\int \frac{x-1}{(x+1)^{3}} e^{x} d x\) = e^x f(x) + c, f(x) = (x + 1)².
Answer:
False

(IV) Solve the following:

1. Evaluate:

(i) \(\int \frac{5 x^{2}-6 x+3}{2 x-3} d x\)
Solution:

(ii) \(\int(5 x+1)^{\frac{4}{9}} d x\)
Solution:

(iii) \(\int \frac{1}{2 x+3} d x\)
Solution:

(iv) \(\int \frac{x-1}{\sqrt{x+4}} d x\)
Solution:

(v) If f'(x) = √x and f(1) = 2, then find the value of f(x).
Solution:
By the definition of integral

(vi) ∫|x| dx if x < 0
Solution:
∫|x| dx = ∫-x dx …..[∵ x < 0]
= -∫x dx
= \(-\frac{x^{2}}{2}\) + c

2. Evaluate:

(i) Find the primitive of \(\frac{1}{1+e^{x}}\)
Solution:
Let I be the primitive of \(\frac{1}{1+e^{x}}\)

(ii) \(\int \frac{a e^{x}+b e^{-x}}{\left(a e^{x}-b e^{-x}\right)^{2}} d x\)
Solution:

(iii) \(\int \frac{1}{2 x+3 x \log x} d x\)
Solution:

(iv) \(\int \frac{1}{\sqrt{x}+x} d x\)
Solution:

(v) \(\int \frac{2 e^{x}-3}{4 e^{x}+1} d x\)
Solution:

3. Evaluate:

(i) \(\int \frac{d x}{\sqrt{4 x^{2}-5}} d x\)
Solution:

(ii) \(\int \frac{d x}{3-2 x-x^{2}} d x\)
Solution:

(iii) \(\int \frac{d x}{9 x^{2}-25}\)
Solution:

(iv) \(\int \frac{e^{x}}{\sqrt{e^{2 x}+4 e^{x}+13}} d x\)
Solution:

(v) \(\int \frac{d x}{x\left[(\log x)^{2}+4 \log x-1\right]}\)
Solution:

(vi) \(\int \frac{d x}{5-16 x^{2}}\)
Solution:

(vii) \(\int \frac{d x}{25 x-x(\log x)^{2}}\)
Solution:

(viii) \(\int \frac{e^{x}}{4 e^{2 x}-1} d x\)
Solution:

4. Evaluate:

(i) ∫(log x)² dx
Solution:

(ii) \(\int e^{x} \frac{1+x}{(2+x)^{2}} d x\)
Solution:

(iii) ∫x e^2x dx
Solution:

(iv) ∫log(x² + x) dx
Solution:

(v) \(\int e^{\sqrt{x}} d x\)
Solution:

(vi) \(\int \sqrt{x^{2}+2 x+5} d x\)
Solution:

(vii) \(\int \sqrt{x^{2}-8 x+7} d x\)
Solution:

5. Evaluate:

(i) \(\int \frac{3 x-1}{2 x^{2}-x-1} d x\)
Solution:

(ii) \(\int \frac{2 x^{3}-3 x^{2}-9 x+1}{2 x^{2}-x-10} d x\)
Solution:

(iii) \(\int \frac{1+\log x}{x(3+\log x)(2+3 \log x)} d x\)
Solution:

12th Commerce Maths Notes 

• Chapter 5 Integration Ex 5.1 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.2 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.3 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.4 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.5 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.6 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Miscellaneous Exercise 5 Class 12 Commerce Maths Textbook Solutions

Integration Class 12 Commerce Maths 1 Chapter 5 Exercise 5.6 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.6 Questions and Answers.

Std 12 Maths 1 Exercise 5.6 Solutions Commerce Maths

Evaluate:

Question 1.
\(\int \frac{2 x+1}{(x+1)(x-2)} d x\)
Solution:
Let I = \(\int \frac{2 x+1}{(x+1)(x-2)} d x\)
Let \(\frac{2 x+1}{(x+1)(x-2)}=\frac{A}{x+1}+\frac{B}{x-2}\)
∴ 2x + 1 = A(x – 2) + B(x + 1)
Put x + 1 = 0, i.e. x = -1, we get
2(-1) + 1 = A(-3) + B(0)
∴ A = \(\frac{1}{3}\)
Put x – 2 = 0, i.e. x = 2, we get
2(2) + 1 = A(0) + B(3)
∴ B = \(\frac{5}{3}\)

Question 2.
\(\int \frac{2 x+1}{x(x-1)(x-4)} d x\)
Solution:
Let I = \(\int \frac{2 x+1}{x(x-1)(x-4)} d x\)
Let \(\int \frac{2 x+1}{x(x-1)(x-4)}=\frac{A}{x}+\frac{B}{x-1}+\frac{C}{x-4}\)
∴ 2x + 1 = A(x – 1)(x – 4) + Bx(x – 4) + Cx(x – 1)
Put x = 0, we get
2(0) + 1 = A(-1)(-4) + B(0)(-4) + C(0)(-1)
∴ 1 = 4A
∴ A = \(\frac{1}{4}\)
Put x – 1 = 0, i.e. x = 1, we get
2(1) + 1 = A(0)(-3) + B(1)(-3) + C(1)(0)
∴ 3 = -3B
∴ B = -1
Put x – 4 = 0, i.e x = 4, we get
2(4) + 1 = A(3)(0) + B(4)(0) + C(4)(3)
∴ 9 = 12C
∴ C = \(\frac{3}{4}\)

Question 3.
\(\int \frac{x^{2}+x-1}{x^{2}+x-6} d x\)
Solution:

∴ 1 = A(x – 2) + B(x + 3)
Put x + 3 = 0, i.e. x = -3, we get
1 = A(-5) + B (0)
∴ A = \(\frac{-1}{5}\)
Put x – 2 = 0, i.e. x = 2, we get
1 = A(0) + B(5)
∴ B = \(\frac{1}{5}\)

Question 4.
\(\int \frac{x}{(x-1)^{2}(x+2)} d x\)
Solution:
Let I = \(\int \frac{x}{(x-1)^{2}(x+2)} d x\)
Let \(\frac{x}{(x-1)^{2}(x+2)}=\frac{A}{x-1}+\frac{B}{(x-1)^{2}}+\frac{C}{x+2}\)
∴ x = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)²
Put x – 1 = 0, i.e. x = 1, we get
1 = A(0)(3) + B(3) + C(0)
∴ B = \(\frac{1}{3}\)
Put x + 2 = 0, i.e. x = -2, we get
-2 = A (-3)(0) + B(0) + C(9)
∴ C = \(-\frac{2}{9}\)
Put x = -1, we get,
-1 = A(-2)(1) + B(1) + C(4)
But B = \(\frac{1}{3}\) and C = \(-\frac{2}{9}\)

Question 5.
\(\int \frac{3 x-2}{(x+1)^{2}(x+3)} d x\)
Solution:
Let I = \(\int \frac{3 x-2}{(x+1)^{2}(x+3)} d x\)
Let \(\frac{3 x-2}{(x+1)^{2}(x+3)}=\frac{A}{x+1}+\frac{B}{(x+1)^{2}}+\frac{C}{x+3}\)
∴ 3x – 2 = A(x + 1)(x + 3) + B(x + 3) + C(x + 1)²
Put x + 1 = 0, i.e. x = -1, we get
3(-1) – 2 = A(0)(2) + B(2) + C(0)
∴ -5 = 2B
∴ B = \(-\frac{5}{2}\)
Put x + 3 = 0, i.e. x = -3, we get
3(-3) – 2 = A(-2)(0) + B(0) + C(4)
∴ -11 = 4C
∴ C = \(-\frac{11}{4}\)
Put x = 0, we get
3(0) – 2 = A(1)(3) + B(3) + C(1)
∴ -2 = 3A + 3B + C
But B = \(-\frac{5}{2}\) and C = \(-\frac{11}{4}\)

Question 6.
\(\int \frac{1}{x\left(x^{5}+1\right)} d x\)
Solution:
Let I = \(\int \frac{1}{x\left(x^{5}+1\right)} d x\)
= \(\int \frac{x^{4}}{x^{5}\left(x^{5}+1\right)} d x\)

Question 7.
\(\int \frac{1}{x\left(x^{n}+1\right)} d x\)
Solution:

Question 8.
\(\int \frac{5 x^{2}+20 x+6}{x^{3}+2 x^{2}+x} d x\)
Solution:

Let \(\frac{5 x^{2}+20 x+6}{x(x+1)^{2}}=\frac{A}{x}+\frac{B}{x+1}+\frac{C}{(x+1)^{2}}\)
∴ 5x² + 20x + 6 = A(x + 1)² + Bx(x + 1) + Cx
Put x = 0, we get
0 + 0 + 6 = A(1) + B(0)(1) + C(0)
∴ A = 6
Put x + 1 = 0, i.e. x = -1, we get
5(1) + 20(-1) + 6 = A(0) + B(-1)(0) + C(-1)
∴ -9 = -C
∴ C = 9
Put x = 1, we get
5(1) + 20(1) + 6 = A(4) + B(1)(2) + C(1)
But A = 6 and C = 9
∴ 31 = 24 + 2B + 9
∴ B = -1

12th Commerce Maths Notes 

• Chapter 5 Integration Ex 5.1 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.2 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.3 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.4 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.5 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.6 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Miscellaneous Exercise 5 Class 12 Commerce Maths Textbook Solutions

Integration Class 12 Commerce Maths 1 Chapter 5 Exercise 5.5 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.5 Questions and Answers.

Std 12 Maths 1 Exercise 5.5 Solutions Commerce Maths

Evaluate the following.

Question 1.
∫x log x
Solution:

Question 2.
∫x² e^4x dx
Solution:

Question 3.
∫x² e^3x dx
Solution:

Question 4.
\(\int x^{3} e^{x^{2}} d x\)
Solution:

Question 5.
\(\int e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right) d x\)
Solution:

Question 6.
\(\int e^{x} \frac{x}{(x+1)^{2}} d x\)
Solution:

Question 7.
\(\int e^{x} \frac{x-1}{(x+1)^{3}} d x\)
Solution:

Question 8.
\(\int e^{x}\left[(\log x)^{2}+\frac{2 \log x}{x}\right] d x\)
Solution:

Question 9.
\(\int\left[\frac{1}{\log x}-\frac{1}{(\log x)^{2}}\right] d x\)
Solution:

Question 10.
\(\int \frac{\log x}{(1+\log x)^{2}} d x\)
Solution:

12th Commerce Maths Notes 

• Chapter 5 Integration Ex 5.1 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.2 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.3 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.4 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.5 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Ex 5.6 Class 12 Commerce Maths Textbook Solutions
• Chapter 5 Integration Miscellaneous Exercise 5 Class 12 Commerce Maths Textbook Solutions

Differentiation Class 11 Commerce Maths 1 Chapter 9 Miscellaneous Exercise 1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Miscellaneous Exercise 9 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 9 Solutions Commerce Maths

I. Differentiate the following functions w.r.t.x.

Question 1.
x⁵
Solution:
Let y = x⁵
Differentiating w.r.t. x, we get
\(\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d}}{\mathrm{d} x} x^{5}=5 x^{4}\)

Question 2.
x^-2
Solution:
Let y = x^-2
Differentiating w.r.t. x, we get
\(\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d}}{\mathrm{d} x}\left(x^{-2}\right)=-2 x^{-3}=\frac{-2}{x^{3}}\)

Question 3.
√x
Solution:
Let y = √x
Differentiating w.r.t. x, we get
\(\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d}}{\mathrm{d} x} \sqrt{x}=\frac{1}{2 \sqrt{x}}\)

Question 4.
x√x
Solution:
Let y = x√x
∴ y = \(x^{\frac{3}{2}}\)
Differentiating w.r.t. x, we get
\(\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d}}{\mathrm{d} x} x^{\frac{3}{2}}=\frac{3}{2} x^{\frac{1}{2}}\)

Question 5.
\(\frac{1}{\sqrt{x}}\)
Solution:
Let y = \(\frac{1}{\sqrt{x}}\)
∴ y = \(x^{\frac{-1}{2}}\)
Differentiating w.r.t. x, we get
\(\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{-1}{2} x^{\frac{-3}{2}}=\frac{-1}{2 x^{\frac{3}{2}}}\)

Question 6.
7^x
Solution:
Let y = 7^x
Differentiating w.r.t. x, we get
\(\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d}}{\mathrm{d} x} 7^{x}=7^{x} \log 7\)

II. Find \(\frac{d y}{d x}\) if

Question 1.
y = x² + \(\frac{1}{x^{2}}\)
Solution:

Question 2.
y = (√x + 1)²
Solution:

Question 3.
y = \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}\)
Solution:

Question 4.
y = x³ – 2x² + √x + 1
Solution:

Question 5.
y = x² + 2x – 1
Solution:

Question 6.
y = (1 – x)(2 – x)
Solution:

Question 7.
y = \(\frac{1+x}{2+x}\)
Solution:

Question 8.
y = \(\frac{(\log x+1)}{x}\)
Solution:

Question 9.
y = \(\frac{e^{x}}{\log x}\)
Solution:

Question 10.
y = x log x (x² + 1)
Solution:

III. Solve the following:

Question 1.
The relation between price (P) and demand (D) of a cup of Tea is given by D = \(\frac{12}{P}\). Find
the rate at which the demand changes when the price is ₹ 2/-. Interpret the result.
Solution:
Demand, D = \(\frac{12}{P}\)
Rate of change of demand

When price P = 2,
Rate of change of demand,
\(\left(\frac{\mathrm{dD}}{\mathrm{dP}}\right)_{\mathrm{P}=2}=\frac{-12}{(2)^{2}}=-3\)
∴ When the price is 2, the rate of change of demand is -3.
∴ Here, the rate of change of demand is negative demand would fall when the price becomes ₹ 2.

Question 2.
The demand (D) of biscuits at price P is given by D = \(\frac{64}{P^{3}}\), find the marginal demand
when the price is ₹ 4/-.
Solution:
Given demand D = \(\frac{64}{P^{3}}\)
Now, marginal demand

When P = 4
Marginal demand

Question 3.
The supply S of electric bulbs at price P is given by S = 2p³ + 5. Find the marginal supply when the price is ₹ 5/-. Interpret the result.
Solution:
Given, supply S = 2p³ + 5
Now, marginal supply

∴ When p = 5
Marginal supply = \(\left(\frac{\mathrm{dS}}{\mathrm{dp}}\right)_{\mathrm{p}=5}\)
= 6(5)²
= 150
Here, the rate of change of supply with respect to the price is positive which indicates that the supply increases.

Question 4.
The total cost of producing x items is given by C = x² + 4x + 4. Find the average cost and the marginal cost. What is the marginal cost when x = 7?
Solution:
Total cost C = x² + 4x + 4
Now. Average cost = \(\frac{C}{x}=\frac{x^{2}+4 x+4}{x}\)
= x + 4 + \(\frac{4}{x}\)
and Marginal cost = \(\frac{\mathrm{dC}}{\mathrm{d} x}=\frac{\mathrm{d}}{\mathrm{d} x}\)(x² + 4x + 4)
= \(\frac{\mathrm{d}}{\mathrm{d} x}\) (x²) + 4\(\frac{\mathrm{d}}{\mathrm{d} x}\) (x) + \(\frac{\mathrm{d}}{\mathrm{d} x}\) (4)
= 2x + 4(1) + 0
= 2x + 4
∴ When x = 7,
Marginal cost = \(\left(\frac{\mathrm{d} \mathrm{C}}{\mathrm{d} x}\right)_{x=7}\)
= 2(7) + 4
= 14 + 4
= 18

Question 5.
The demand D for a price P is given as D = \(\frac{27}{P}\), find the rate of change of demand when the price is ₹ 3/-.
Solution:
Demand, D = \(\frac{27}{P}\)
Rate of change of demand = \(\frac{dD}{dP}\)

When price P = 3,
Rate of change of demand,
\(\left(\frac{\mathrm{dD}}{\mathrm{dP}}\right)_{\mathrm{P}=3}=\frac{-27}{(3)^{2}}=-3\)
∴ When price is 3, Rate of change of demand is -3.

Question 6.
If for a commodity; the price demand relation is given as D = \(\left(\frac{P+5}{P-1}\right)\). Find the marginal demand when price is ₹ 2/-
Solution:

Question 7.
The price function P of a commodity is given as P = 20 + D – D² where D is demand. Find the rate at which price (P) is changing when demand D = 3.
Solution:
Given, P = 20 + D – D²
Rate of change of price = \(\frac{dP}{dD}\)
= \(\frac{d}{dD}\)(20 + D – D²)
= 0 + 1 – 2D
= 1 – 2D
Rate of change of price at D = 3 is
\(\left(\frac{\mathrm{dP}}{\mathrm{dD}}\right)_{\mathrm{D}=3}\) = 1 – 2(3) = -5
∴ Price is changing at a rate of -5, when demand is 3.

Question 8.
If the total cost function is given by C = 5x³ + 2x² + 1; find the average cost and the marginal cost when x = 4.
Solution:
Total cost function C = 5x³ + 2x² + 1
Average cost = \(\frac{C}{x}\)
= \(\frac{5 x^{3}+2 x^{2}+1}{x}\)
= 5x² + 2x + \(\frac{1}{x}\)
When x = 4,
Average cost = 5(4)² + 2(4) + \(\frac{1}{4}\)
= 80 + 8 + \(\frac{1}{4}\)
= \(\frac{320+32+1}{4}\)
= \(\frac{353}{4}\)
Marginal cost = \(\frac{\mathrm{dC}}{\mathrm{d} x}\)
= \(\frac{d}{dx}\) (5x³ + 2x² + 1)
= 5\(\frac{d}{dx}\) (x³) + 2 \(\frac{d}{dx}\) (x²) + \(\frac{d}{dx}\) (1)
= 5(3x²) + 2(2x) + 0
= 15x² + 4x
When x = 4, marginal cost = \(\left(\frac{\mathrm{dC}}{\mathrm{d} x}\right)_{x=4}\)
= 15(4)² + 4(4)
= 240 + 16
= 256
∴ The average cost and marginal cost at x = 4 are \(\frac{353}{4}\) and 256 respectively.

Question 9.
The supply S for a commodity at price P is given by S = P² + 9P – 2. Find the marginal supply when the price is 7/-.
Solution:
Given, S = P² + 9P – 2

∴ The marginal supply is 23, at P = 7.

Question 10.
The cost of producing x articles is given by C = x² + 15x + 81. Find the average cost and marginal cost functions. Find the marginal cost when x = 10. Find x for which the marginal cost equals the average cost.
Solution:
Given, cost C = x² + 15x + 81

If marginal cost = average cost, then
2x + 15 = x + 15 + \(\frac{81}{x}\)
∴ x = \(\frac{81}{x}\)
∴ x² = 81
∴ x = 9 …..[∵ x > 0]

Maharashtra State Board 11th Commerce Maths

• Limits Ex 7.1 11th Commerce Maths
• Limits Ex 7.2 11th Commerce Maths
• Limits Ex 7.3 11th Commerce Maths
• Limits Ex 7.4 11th Commerce Maths
• Limits Miscellaneous Exercise 7 11th Commerce Maths
• Continuity Ex 8.1 11th Commerce Maths
• Continuity Miscellaneous Exercise 8 11th Commerce Maths
• Differentiation Ex 9.1 11th Commerce Maths
• Differentiation Ex 9.2 11th Commerce Maths
• Differentiation Miscellaneous Exercise 9 11th Commerce Maths

Differentiation Class 11 Commerce Maths 1 Chapter 9 Exercise 9.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Ex 9.2 Questions and Answers.

Std 11 Maths 1 Exercise 9.2 Solutions Commerce Maths

I. Differentiate the following functions w.r.t. x.

Question 1.
\(\frac{x}{x+1}\)
Solution:

Question 2.
\(\frac{x^{2}+1}{x}\)
Solution:

Question 3.
\(\frac{1}{e^{x}+1}\)
Solution:

Question 4.
\(\frac{e^{x}}{e^{x}+1}\)
Solution:

Question 5.
\(\frac{x}{\log x}\)
Solution:

Question 6.
\(\frac{2^{x}}{\log x}\)
Solution:

Question 7.
\(\frac{\left(2 e^{x}-1\right)}{\left(2 e^{x}+1\right)}\)
Solution:

Question 8.
\(\frac{(x+1)(x-1)}{\left(e^{x}+1\right)}\)
Solution:

II. Solve the following examples:

Question 1.
The demand D for a price P is given as D = \(\frac{27}{P}\), find the rate of change of demand when the price is 3.
Solution:
Demand, D = \(\frac{27}{P}\)
Rate of change of demand = \(\frac{dD}{dP}\)

When price P = 3,
Rate of change of demand,
\(\left(\frac{\mathrm{dD}}{\mathrm{dP}}\right)_{\mathrm{P}=3}=\frac{-27}{(3)^{2}}=-3\)
∴ When price is 3, Rate of change of demand is -3.

Question 2.
If for a commodity; the price-demand relation is given as D = \(\frac{P+5}{P-1}\). Find the marginal demand when the price is 2.
Solution:

Question 3.
The demand function of a commodity is given as P = 20 + D – D². Find the rate at which price is changing when demand is 3.
Solution:
Given, P = 20 + D – D²
Rate of change of price = \(\frac{dP}{dD}\)
= \(\frac{d}{dD}\)(20 + D – D²)
= 0 + 1 – 2D
= 1 – 2D
Rate of change of price at D = 3 is
\(\left(\frac{\mathrm{dP}}{\mathrm{dD}}\right)_{\mathrm{D}=3}\) = 1 – 2(3) = -5
∴ Price is changing at a rate of -5, when demand is 3.

Question 4.
If the total cost function is given by; C = 5x³ + 7x² + 7; find the average cost and the marginal cost when x = 4.
Solution:
Total cost function, C = 5x³ + 7x² + 7
Average cost = \(\frac{C}{x}\)

When x = 4, Marginal cost = \(\left(\frac{\mathrm{dC}}{\mathrm{d} x}\right)_{x=4}\)
= 15(4)² + 4(4)
= 240 + 16
= 256
∴ the average cost and marginal cost at x = 4 are \(\frac{359}{4}\) and 256 respectively.

Question 5.
The total cost function of producing n notebooks is given by
C = 1500 – 75n + 2n² + \(\frac{n^{3}}{5}\)
Find the marginal cost at n = 10.
Solution:
The total cost function,


∴ Marginal cost at n = 10 is 25.

Question 6.
The total cost of ‘t’ toy cars is given by C = 5(2t) + 17. Find the marginal cost and average cost at t = 3.
Solution:
Total cost of ‘t’ toy cars, C = 5(2t) + 17

∴ at t = 3, the Marginal cost is 40 log 2 and the Average cost is 19.

Question 7.
If for a commodity; the demand function is given by, D = \(\sqrt{75-3 P}\). Find the marginal demand function when P = 5.
Solution:
Demand function, D = \(\sqrt{75-3 P}\)
Now, Marginal demand = \(\frac{dD}{dP}\)

Question 8.
The total cost of producing x units is given by C = 10e^2x, find its marginal cost and average cost when x = 2.
Solution:

Question 9.
The demand function is given as P = 175 + 9D + 25D². Find the revenue, average revenue, and marginal revenue when demand is 10.
Solution:
Given, P = 175 + 9D + 25D²
Total revenue, R = P.D
= (175 + 9D + 25D²)D
= 175D + 9D² + 25D³
Average revenue = P = 175 + 9D + 25D²
Marginal revenue = \(\frac{dR}{dD}\)
= \(\frac{d}{dD}\) (175D + 9D² + 25D³)
= 175 \(\frac{d}{dD}\) (D) + 9 \(\frac{d}{dD}\) (D²) + 25 \(\frac{d}{dD}\) (D³)
= 175(1) + 9(2D) + 25(3D²)
= 175 + 18D + 75D²
When D = 10,
Total revenue = 175(10) + 9(10)² + 25(10)³
= 1750 + 900 + 25000
= 27650
Average revenue = 175 + 9(10) + 25(10)²
= 175 + 90 + 2500
= 2765
Marginal revenue = 175 + 18(10) + 75(10)²
= 175 + 180 + 7500
= 7855
∴ When Demand = 10,
Total revenue = 27650, Average revenue = 2765, Marginal revenue = 7855.

Question 10.
The supply S for a commodity at price P is given by S = P² + 9P – 2. Find the marginal supply when the price is 7.
Solution:
Given, S = P² + 9P – 2

∴ The marginal supply is 23, at P = 7.

Question 11.
The cost of producing x articles is given by C = x² + 15x + 81. Find the average cost and marginal cost functions. Find marginal cost when x = 10. Find x for which the marginal cost equals the average cost.
Solution:
Given, cost C = x² + 15x + 81

If marginal cost = average cost, then
2x + 15 = x + 15 + \(\frac{81}{x}\)
∴ x = \(\frac{81}{x}\)
∴ x² = 81
∴ x = 9 …..[∵ x > 0]

Maharashtra State Board 11th Commerce Maths

• Limits Ex 7.1 11th Commerce Maths
• Limits Ex 7.2 11th Commerce Maths
• Limits Ex 7.3 11th Commerce Maths
• Limits Ex 7.4 11th Commerce Maths
• Limits Miscellaneous Exercise 7 11th Commerce Maths
• Continuity Ex 8.1 11th Commerce Maths
• Continuity Miscellaneous Exercise 8 11th Commerce Maths
• Differentiation Ex 9.1 11th Commerce Maths
• Differentiation Ex 9.2 11th Commerce Maths
• Differentiation Miscellaneous Exercise 9 11th Commerce Maths

Differentiation Class 11 Commerce Maths 1 Chapter 9 Exercise 9.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Ex 9.1 Questions and Answers.

Std 11 Maths 1 Exercise 9.1 Solutions Commerce Maths

I. Find the derivatives of the following functions w.r.t. x.

Question 1.
x¹²
Solution:
Let y = x¹²
Differentiating w.r.t. x, we get

Question 2.
x^-9
Solution:
Let y = x^-9
Differentiating w.r.t. x, we get

Question 3.
\(x^{\frac{3}{2}}\)
Solution:
Let y = \(x^{\frac{3}{2}}\)
Differentiating w.r.t. x, we get

Question 4.
7x√x
Solution:

Question 5.
3⁵
Solution:
Let y = 3⁵
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x} 3^{5}=0\) …..[3⁵ is a constant]

II. Differentiate the following w.r.t. x.

Question 1.
x⁵ + 3x⁴
Solution:
Let y = x⁵ + 3x⁴
Differentiating w.r.t. x, we get

Question 2.
x√x + log x – e^x
Solution:
Let y = x√x + log x – e^x
= \(x^{\frac{3}{2}}+\log x-e^{x}\)
Differentiating w.r.t. x, we get

Question 3.
\(x^{\frac{5}{2}}+5 x^{\frac{7}{5}}\)
Solution:
Let y = \(x^{\frac{5}{2}}+5 x^{\frac{7}{5}}\)
Differentiating w.r.t. x, we get

Question 4.
\(\frac{2}{7} x^{\frac{7}{2}}+\frac{5}{2} x^{\frac{2}{5}}\)
Solution:
Let y = \(\frac{2}{7} x^{\frac{7}{2}}+\frac{5}{2} x^{\frac{2}{5}}\)
Differentiating w.r.t. x, we get

Question 5.
\(\sqrt{x}\left(x^{2}+1\right)^{2}\)
Solution:
Let y = \(\sqrt{x}\left(x^{2}+1\right)^{2}\)

III. Differentiate the following w.r.t. x.

Question 1.
x³ log x
Solution:
Let y = x³ log x
Differentiating w.r.t. x, we get

Question 2.
\(x^{\frac{5}{2}} e^{x}\)
Solution:
Let y = \(x^{\frac{5}{2}} e^{x}\)
Differentiating w.r.t. x, we get

Question 3.
e^x log x
Solution:
Let y = e^x log x
Differentiating w.r.t. x, we get

Question 4.
x³ . 3^x
Solution:
Let y = x³ . 3^x
Differentiating w.r.t. x, we get

IV. Find the derivatives of the following w.r.t. x.

Question 1.
\(\frac{x^{2}+a^{2}}{x^{2}-a^{2}}\)
Solution:

Question 2.
\(\frac{3 x^{2}+5}{2 x^{2}-4}\)
Solution:

Question 3.
\(\frac{\log x}{x^{3}-5}\)
Solution:

Question 4.
\(\frac{3 e^{x}-2}{3 e^{x}+2}\)
Solution:

Question 5.
\(\frac{x \mathrm{e}^{x}}{x+\mathrm{e}^{x}}\)
Solution:

V. Find the derivatives of the following functions by the first principle:

Question 1.
3x² + 4
Solution:
Let f(x) = 3x² + 4
∴ f(x + h) = 3(x + h)² + 4
= 3(x² + 2xh + h²) + 4
= 3x² + 6xh + 3h² + 4
By first principle, we get

Question 2.
x√x
Solution:
Let f(x) = x√x
∴ f(x + h) = \((x+h)^{\frac{3}{2}}\)
By first principle, we get

Question 3.
\(\frac{1}{2 x+3}\)
Solution:
Let f(x) = \(\frac{1}{2 x+3}\)
∴ f(x + h) = \(\frac{1}{2(x+\mathrm{h})+3}=\frac{1}{2 x+2 \mathrm{~h}+3}\)
By first principle, we get

Question 4.
\(\frac{x-1}{2 x+7}\)
Solution:
Let f(x) = \(\frac{x-1}{2 x+7}\)
∴ f(x + h) = \(\frac{x+\mathrm{h}-1}{2(x+\mathrm{h})+7}=\frac{x+\mathrm{h}-1}{2 x+2 \mathrm{~h}+7}\)
By first principle, we get

Maharashtra State Board 11th Commerce Maths

• Limits Ex 7.1 11th Commerce Maths
• Limits Ex 7.2 11th Commerce Maths
• Limits Ex 7.3 11th Commerce Maths
• Limits Ex 7.4 11th Commerce Maths
• Limits Miscellaneous Exercise 7 11th Commerce Maths
• Continuity Ex 8.1 11th Commerce Maths
• Continuity Miscellaneous Exercise 8 11th Commerce Maths
• Differentiation Ex 9.1 11th Commerce Maths
• Differentiation Ex 9.2 11th Commerce Maths
• Differentiation Miscellaneous Exercise 9 11th Commerce Maths

Continuity Class 11 Commerce Maths 1 Chapter 8 Miscellaneous Exercise 8 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Continuity Miscellaneous Exercise 8 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 8 Solutions Commerce Maths

I. Discuss the continuity of the following functions at the point(s) or in the interval indicated against them.

Question 1.
If f(x) = 2x² – 2x + 5 for 0 ≤ x < 2
= \(\frac{1-3 x-x^{2}}{1-x}\) for 2 ≤ x < 4
= \(\frac{7-x^{2}}{x-5}\) for 4 ≤ x ≤ 7 on its domain.
Solution:
The domain of f is [0, 5) ∪ (5, 7]
We observe that x = 5 is not included in the domain as f is not defined at x = 5
a. For 0 ≤ x < 2
f(x) = 2x² – 2x + 5
It is a polynomial function and is continuous at all point in [0, 2)

b. For 2 < x < 4
f(x) = \(\frac{1-3 x-x^{2}}{1-x}\)
It is a rational function and is continuous everwhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 1
But x = 1 does not lie in the interval.
f(x) is continuous at all points in (2, 4)

c. For 4 < x ≤ 7, x ≠ 5
i.e. for x ∈ [4, 5) ∪ (5, 7]
∴ f(x) = \(\frac{7-x^{2}}{x-5}\)
It is a rational function and is continuous everywhere except possibly at points where its denominator becomes zero.
Denominator becomes zero at x = 5
But x = 5 ∉ [4, 5) ∪ (5, 7]
∴ f is continuous at all points in (4, 7] – {5}.

d. Since the definition of function changes around x = 2, x = 4 and x = 7
∴ there is disturbance in behaviour of the function.
So we examine continuity at x = 2, 4, 7 separately.
Continuity at x = 2:
\(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{-}}\left(2 x^{2}-2 x+5\right)\)
= 2(2)² – 2(2) + 5
= 8 – 4 + 5
= 9

∴ f is continuous at x = 2

e. Continuity at x = 4:

∴ f is continuous at x = 4

Question 2.
f(x) = \(\frac{3^{x}+3^{-x}-2}{x^{2}}\) for x ≠ 0
= (log 3)² for x = 0 at x = 0
Solution:


∴ \(\lim _{x \rightarrow 0} f(x)=f(0)\)
∴ f is continuous at x = 0

Question 3.
f(x) = \(\frac{5^{x}-e^{x}}{2 x}\) for x ≠ 0
= \(\frac{1}{2}\) (log 5 – 1) for x = 0 at x = 0
Solution:

∴ \(\lim _{x \rightarrow 0} f(x)=f(0)\)
∴ f is continuous at x = 0

Question 4.
f(x) = \(\frac{\sqrt{x+3}-2}{x^{3}-1}\) for x ≠ 1
= 2 for x = 1, at x = 1
Solution:


∴ \(\lim _{x \rightarrow 1} \mathrm{f}(x) \neq \mathrm{f}(1)\)
∴ f is discontinuous at x = 1

Question 5.
f(x) = \(\frac{\log x-\log 3}{x-3}\) for x ≠ 3
= 3 for x = 3, at x = 3
Solution:

(II) Find k if following functions are continuous at the points indicated against them.

Question 1.
f(x) = \(\left(\frac{5 x-8}{8-3 x}\right)^{\frac{3}{2 x-4}}\) for x ≠ 2
= k for x = 2 at x = 2
Solution:

Question 2.
f(x) = \(\frac{45^{x}-9^{x}-5^{x}+1}{\left(k^{x}-1\right)\left(3^{x}-1\right)}\) for x ≠ 0
= \(\frac{2}{3}\) for x = 0, at x = 0
Solution:

Question 3.
f(x) = \((1+k x)^{\frac{1}{x}}\), for x ≠ 0
= \(e^{\frac{3}{2}}\), for x = 0, at x = 0
Solution:

III. Find a and b if following functions are continuous at the point indicated against them.

Question 1.
f(x) = x² + a, for x ≥ 0
= 2\(\sqrt{x^{2}+1}\) + b, for x < 0 and
f(1) = 2, is continuous at x = 0
Solution:

Question 2.
f(x) = \(\frac{x^{2}-9}{x-3}\) + a, for x > 3
= 5, for x = 3
= 2x² + 3x + b, for x < 3
is continuous at x = 3
Solution:

Question 3.
f(x) = \(\frac{32^{x}-1}{8^{x}-1}\) + a, for x > 0
= 2, for x = 0
= x + 5 – 2b, for x < 0
is continuous at x = 0
Solution:

Maharashtra State Board 11th Commerce Maths

• Limits Ex 7.1 11th Commerce Maths
• Limits Ex 7.2 11th Commerce Maths
• Limits Ex 7.3 11th Commerce Maths
• Limits Ex 7.4 11th Commerce Maths
• Limits Miscellaneous Exercise 7 11th Commerce Maths
• Continuity Ex 8.1 11th Commerce Maths
• Continuity Miscellaneous Exercise 8 11th Commerce Maths
• Differentiation Ex 9.1 11th Commerce Maths
• Differentiation Ex 9.2 11th Commerce Maths
• Differentiation Miscellaneous Exercise 9 11th Commerce Maths