Angles Class 5 Problem Set 27 Question Answer Maharashtra Board
Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 6 Angles Problem Set 27 Textbook Exercise Important Questions and Answers.
Std 5 Maths Chapter 6 Angles
Question 1.
Give two examples of parallel lines you can see in your environment.
Answer:
(i) Bars on the window.
(ii) Horizontal lines in the notebook are the examples of parallel lines.
![]()
Question 2.
Give two examples of perpendicular lines you can see in your environment.
Answer:
(i) The angles formed by a pole and its shadow on the ground.
(ii) The adjacent sides of a notebook.
Question 3.
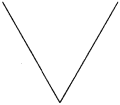
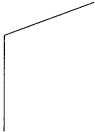
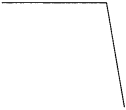
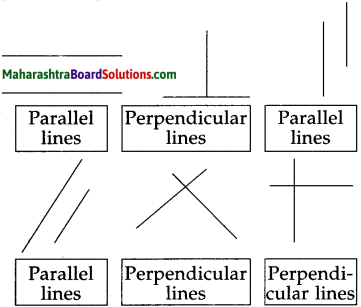
Look at the pictures given below. Decide whether the lines given in each picture are parallel or perpendicular to each other and write the answer in the box.

Answer:
Angles Problem Set 27 Additional Important Questions and Answers
Question 1.
Give some examples of perpendicular lines from capital letters of the English alphabet.
Answer:

![]()
Question 2.
Complete the following:
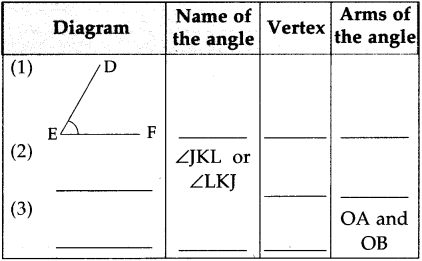
Answer:
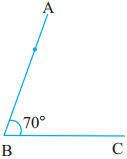
(1) ZDEF or ZFED, Vertex E, arms are ED


Question 3.
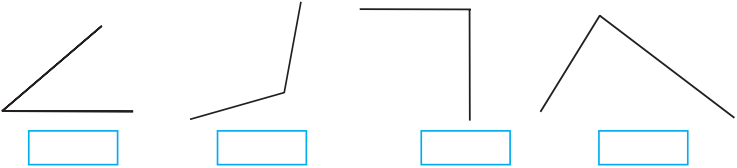
Which of the following figures show angle?
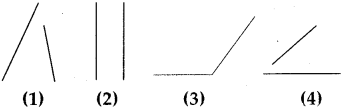
Answer:
Figure 3
![]()
Question 4.
(A) Measure the angles given below and write the measure in the given boxes:
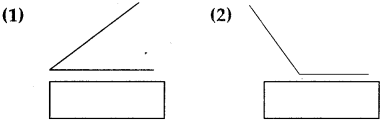
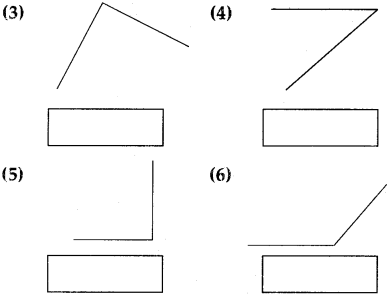
Answer:
(1) 30°
(2) 135°
(3) 90°
(4) 50°
(5) 90°
(6) 150°
![]()
B) Classify the above figures according to types of the angles.
Answer:
Acute angles: (1) and (4),
Right angles: (3) and (5),
Obtuse angles: (2) and (6)
Question 5.
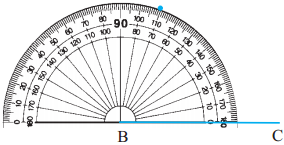
Draw and name the following angles with the help of a protractor:



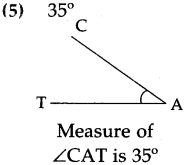
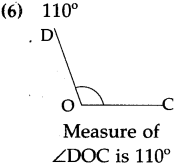
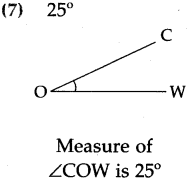
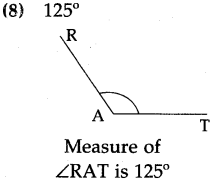
Answer:
Students to draw angles.
![]()
Question 6.
Look at the pictures given below. Decide whether the lines given in each picture are parallel or perpendicular to each other and write the answer in the box:
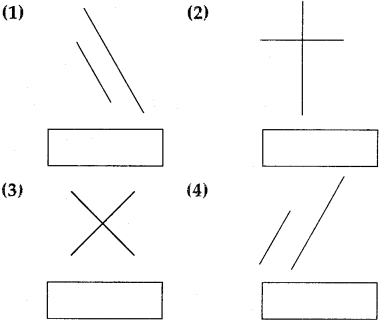
Answer:
(1) Parallel lines
(2) Perpendicular lines
(3) Perpendicular lines
(4) Parallel lines
![]()
Question 7.
Say, true or false of the following:
(1) Parallel lines do not intersect each other.
(2) Pole and its shadow on the ground makes a cute angle.
(3) Angle between two parallel lines is 90°.
(4) Angle between two intersecting lines may or may not be 90°.
Answer:
(1) True
(2) False
(3) False
(4) True
Maharashtra Board Class 5 Maths Solutions



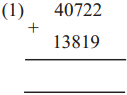
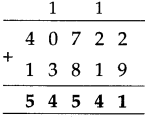
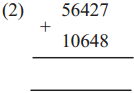
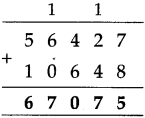
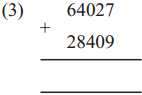
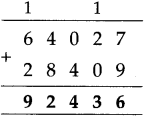
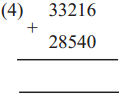
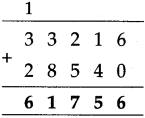
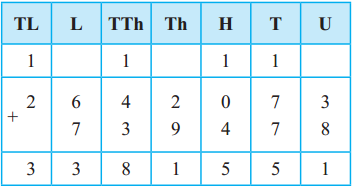
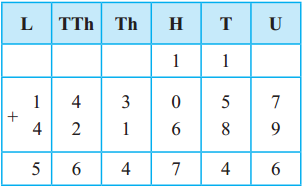
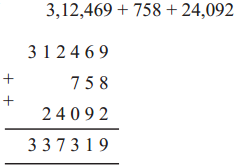
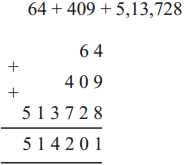
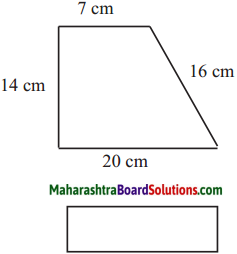
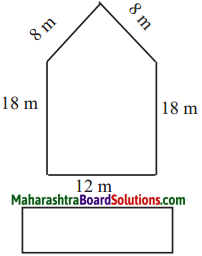
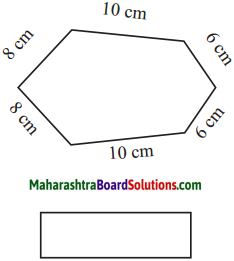

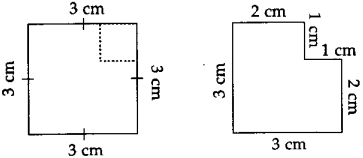
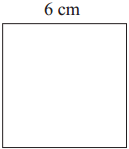
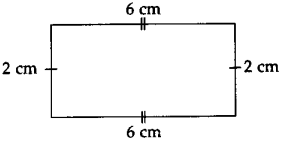
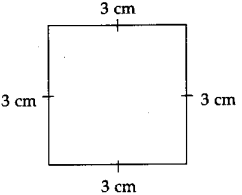
 The lengths of all the sides of a square are equal. Therefore, the perimeter of a square = four times the length of one of its sides.
The lengths of all the sides of a square are equal. Therefore, the perimeter of a square = four times the length of one of its sides.