Category: Class 5

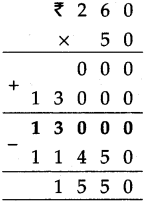
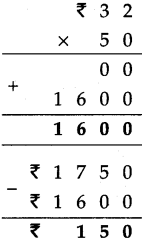
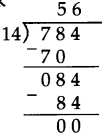
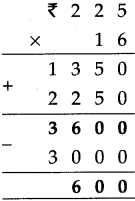
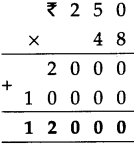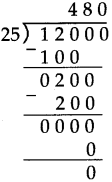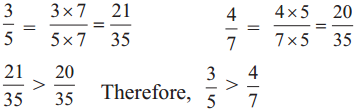Fractions Class 5 Problem Set 19 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 19 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Write the proper symbol from < , > , or = in the box.

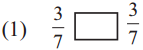
Answer:
=

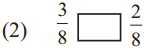
Answer:
>

Answer:
<

Answer:
=

Answer:
>

Answer:
>

Answer:
>

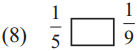
Answer:
>

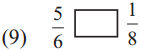
Answer:
>

Answer:
>

Answer:
=

Answer:
=

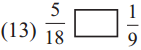
Answer:
>

Answer:
>

Answer:
<

Answer:
>

Addition of like fractions
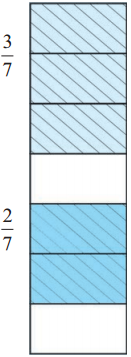
Example (1) 3/7 + 2/7 = ?
Let us divide a strip into 7 equal parts. We shall colour 3 parts with one colour and 2 parts with another.
The part with one colour is 3/7, and that with the other colour is 2/7.
The total coloured part is shown by the fraction 5/7.
It means that, \(\frac{3}{7}+\frac{2}{7}=\frac{3+2}{7}=\frac{5}{7}\)

Example (2) Add : \(\frac{3}{8}+\frac{2}{8}+\frac{1}{8}\)
The total coloured part is \(\frac{3}{8}+\frac{2}{8}+\frac{1}{8}=\frac{3+2+1}{8}=\frac{6}{8}\)

When adding like fractions, we add the numerators of the two fractions and write the denominator as it is.
Example (3) Add : 2/6 + 4/6 \(\frac{2}{6}+\frac{4}{6}=\frac{2+4}{6}=\frac{6}{6}\)
However, we know that 6/6 means that all 6 of the 6 equal parts are taken. That is, 1 whole figure is taken. Therefore, 6/6 = 1.

Note that:
If the numerator and denominator of a fraction are equal, the fraction is equal to one.
That is why, \(\frac{7}{7}=1 ; \frac{10}{10}=1 ; \frac{2}{5}+\frac{3}{5}=\frac{2+3}{5}=\frac{5}{5}=1\)
Remember that, if we do not divide a figure into parts, but keep it whole, it can also be written as 1.
This tells us that \(1=\frac{1}{1}=\frac{2}{2}=\frac{3}{3}\) and so on.
You also know that if the numerator and denominator of a fraction have a common divisor, then the fraction obtained by dividing them by that divisor is equivalent to the given fraction.
\(\frac{5}{5}=\frac{5 \div 5}{5 \div 5}=\frac{1}{1}=1\)

Fractions Problem Set 19 Additional Important Questions and Answers

Question 1.

Answer:
>

Question 2.

Answer:
=

Maharashtra Board Class 5 Maths Solutions

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions

Three Dimensional Objects and Nets Class 5 Problem Set 51 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 13 Three Dimensional Objects and Nets Problem Set 51 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 13 Three Dimensional Objects and Nets

Question 1.
The first column shows a structure made of blocks. The other columns show different views of the structure in two dimensions. Say whether each view is from the front, from a side or from above.

Answer:

Question 2.
Draw three pictures of each of these three-dimensional objects – a table, a chair and a water bottle as viewed from the front, from a side and from above.
Answer:

Nets
Last year we saw that cutting some edges of a box and laying it out flat gives us the net from which it was made.
The two dimensional shape from which a three dimensional object can be made by folding is called the ‘net’ of that object.

1. By folding the cardboard shown below, along the lines shown in it, we get a three dimensional object (box). In this shape, all surfaces are square.
   An object of this shape is called a cube.
   
2. The net of another cardboard box is shown in the figure below. By folding along the lines in this net and joining the edges to each other, we can see that a three dimensional box is formed. The surfaces of this box are rectangular in shape.
   An object of this shape is called a cuboid.
   

Activity :
Draw the nets shown below on card sheet. Cut out the shapes and find out the shapes of the boxes they form.

A five-square net (Pentomino)

In the figure alongside, five squares of the same size are placed together with their sides joined.

Such an arrangement of five squares is called a ‘five-square net’ or a ‘pentomino’.

By folding along the edges of such a five-square net, an open box is formed.

Activity :
Some five-square nets are given below. Draw these nets on a card sheet. Make open boxes from these nets.

Try to find out other five-square nets that can be used to make open boxes.

A riddle

The net of a cube-shaped dice is given alongside. If a dice is made of this net, which of the following shapes will it definitely not resemble?

Chapter 12 Perimeter and Area Problem Set 49 Additional Important Questions and Answers

Question 1.
Draw the pictures of each of these three dimensional objects – Mobile, Oil tin as viewed from the front, from a side and from above.
Answer:

Question 2.
The three dimensional figure of block formation is shown in the figure along side. Draw as view from the front, from a side and from above (fig. drawn in answer part)
Answer:

Question 3.
Draw the nets shown below on card sheet. Cut out the shapes and find out the shapes of the boxes they form.
Answer:

Maharashtra Board Class 5 Maths Solutions

• Three Dimensional Objects and Nets Problem Set 51  Class 5 Maths Solutions
• Pictographs Problem Set 52 Class 5 Maths Solutions
• Patterns Problem Set 53 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 54 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 55 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 56 Class 5 Maths Solutions

Decimal Fractions Class 5 Problem Set 38 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 38 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 9 Decimal Fractions

Read the decimal fraction and write down the place value of each digit.

(1) 6.13
Answer:
Six point one three.
Here 6 is in the units place. Hence, its place value is 6 x 1 = 6
1 is in tenths place. Hence, its place value is
\(1 \times \frac{1}{10}=0.1\)
3 is in the hundredths place. Its place value is 3 x \(\frac{1}{100}\) = 0.03 100

(2) 48.84
Answer:
Fourty eight point eight four
Place value of 4 is 4 x 10 = 40 and of 8, it is 8 x 1 = 8
Place value of 8 is 8 x \(\frac{1}{10}=\frac{8}{10}\) = 0.8 and
Place value of 4 is 4 x \(\frac{1}{100}=\frac{4}{100}\) = 0.04

(3) 72.05
Answer:
Seventy two point zero five
Place value of 7 is 7 x 10 = 70 and of 2 is, it is 2 x 1 = 2
Place value of 5 is 5 x \(\frac{1}{100}=\frac{5}{100}\) = 0.05

(4) 3.4
Answer:
Three point four.
Place value of 3 is 3 x 1 = 3
Place value of 4 is 4 x \(\frac{1}{10}\) = 0.4

(5) 0.59
Answer:
Zero point five nine.
Place value of 5 is 5 x \(\frac{1}{10}=\frac{5}{10}\) = 0.5 and
Place value of 9 is 9 x \(\frac{1}{100}=\frac{9}{100}\) = 0.09

Use of decimal fractions

Sir : Now we will see how 24.50 equals 24 rupees and 50 paise. How many rupees is one paisa?
Sumit : 100 paise make one rupee, therefore, 1 paisa is one-hundredth of a rupee or 0.01 rupee.
Sir : And 50 paise are?
Sumit : 50 hundredths of a rupee, or 0.50 rupees, so 24.50 rupees is 24 rupees and 50 paise.
Sir : When a large unit of a certain quantity is divided into 10 or 100 parts to make smaller units, it is more convenient to write them in decimal form. As we just saw, 100 paise = 1 rupee. Similarly, 100 cm = 1 metre, so 75 cm = 0.75 m. 10 mm = 1 cm, so 1 mm = 0.1cm. 3 mm are 0.3 cm. 6.3 cm are 6 cm and 3 mm.

Now study the following table.

Decimal Fractions Problem Set 38 Additional Important Questions and Answers

(1) 12.34
Answer:
Twelve point three four.
Place value of 1 is 1 x 10 = 10
Place value of 2 is 2 x 1 = 2
Place value of 3 is 3 x \(\frac{1}{10}\) = 0.3
Place value of 4 is 4 x \(\frac{1}{100}\) = 0.04

(2) 369,58
Answer:
Three hundred sixty nine point five eight. Place value of 3, which is in the hundreds place is 3 x 100 = 300
Place value of 6, which is in the tens place is 6 x 10 = 60
Place value of 9, which is in the units place is 9 x 1 = 9
Place value of 5, which is in the tenths place is 5 x \(\frac{1}{10}\) = 0.5
Place value of 8, which is in the hundredths place is 8 x \(\frac{1}{100}\) = 0.08

(3) 5.5
Answer:
Five point five.
Place value of 5, which is in the units place is 5 x 1 = 5
Place value of 5, which is in the tenths place is 5 x \(\frac{1}{10}\) = 0.5

Maharashtra Board Class 5 Maths Solutions

• Decimal Fractions Problem Set 36 Class 5 Maths Solutions
• Decimal Fractions Problem Set 37 Class 5 Maths Solutions
• Decimal Fractions Problem Set 38 Class 5 Maths Solutions
• Decimal Fractions Problem Set 39 Class 5 Maths Solutions
• Decimal Fractions Problem Set 40 Class 5 Maths Solutions
• Decimal Fractions Problem Set 41 Class 5 Maths Solutions
• Decimal Fractions Problem Set 42 Class 5 Maths Solutions

Addition and Subtraction Class 5 Problem Set 7 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 3 Addition and Subtraction Problem Set 7 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 3 Addition and Subtraction

Question 1.
Add the following

Answer:

Answer:

Answer:

Answer:

Addition of six-digit and seven-digit numbers

Last year, you have learned to add five-digit numbers. Six-and seven-digit numbers can
be added using the same method.

Study the following examples.

Add :
Example (1)
1,43,057 + 4,21,689

Example (2)
26,42,073 + 7,39,478

Example (3)
3,12,469 + 758 + 24,092
3 1 2 4 6 9
+ 7 5 8
+ 2 4 0 9 2
____________
3 3 7 3 1 9
____________

Example (4)
64 + 409 + 5,13,728
6 4
+ 4 0 9
+ 5 1 3 7 2 8
_____________
5 1 4 2 0 1
_____________

In the examples 3 and 4, the numbers are carried over mentally.

Question 2.
(1)

Answer:

(2)

Answer:

Maharashtra Board Class 5 Maths Solutions

• Addition and Subtraction Problem Set 7 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 8 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 9 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 10 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 11 Class 5 Maths Solutions 
• Addition and Subtraction Problem Set 12 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 13 Class 5 Maths Solutions

Perimeter and Area Class 5 Problem Set 48 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 12 Perimeter and Area Problem Set 48 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 12 Perimeter and Area

Question 1.
Write the perimeter of each figure in the box given below it.

(1)

Solution:
Perimeter [ ] DABCD
= 20 + 16 + 7 + 14
= 57 cm

∴ 57 cm

(2)

Solution:
Perimeter of the figure
= 12 + 18 + 8 + 8 + 18
= 64m

∴ 64m

(3)

Solution:
Perimeter of the figure
= 10 + 6 + 6 + 10 + 8 + 8
= 48 cm

∴ 48 cm

Question 2.
If a square of side 1 cm is cut out of the corner of a larger square with side 3 cm (see the figure), what will be the perimeter of the remaining shape?

Solution:

Perimeter
= 2 + 3 + 3 + 2 + 1 + 1
= 12 cm

∴ 12 cm

Formula for the perimeter of a rectangle

Perimeter = length + breadth + length + breadth Opposite sides of a rectangle are of the same length.
So, the perimeter of a rectangle
= twice the length + twice the breadth
= 2 × length + 2 × breadth

Perimeter of a rectangle = 2 × length + 2 × breadth

Example : The length of the rectangle below is 7 cm and its breadth, 3 cm. Let us find its perimeter.

Perimeter of rectangle PQRS = 2 × length + 2 × breadth
= 2 × 7 + 2 × 3
= 14 + 6
= 20
Therefore, the perimeter of the rectangle is 20 cm.

Formula for the perimeter of a square

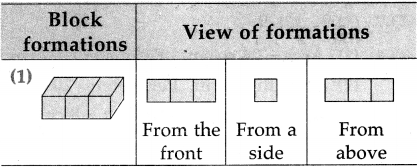
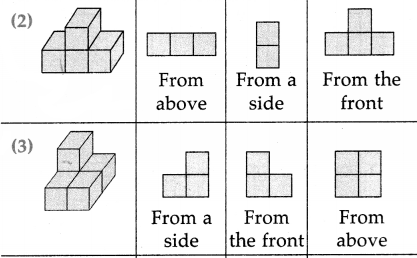
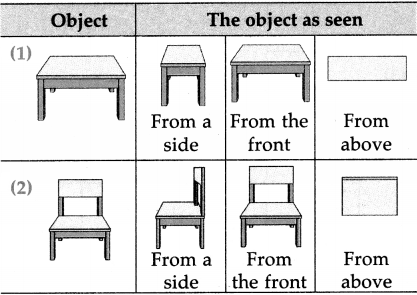
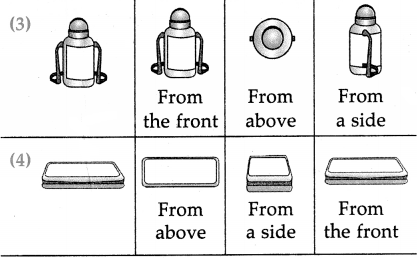
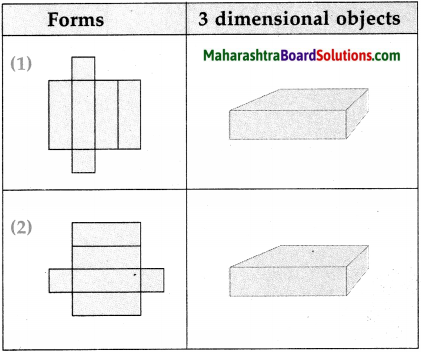
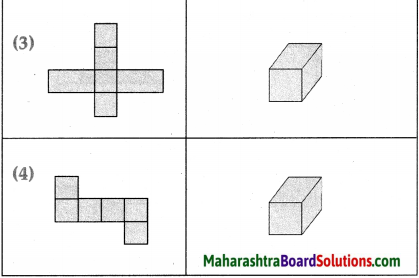
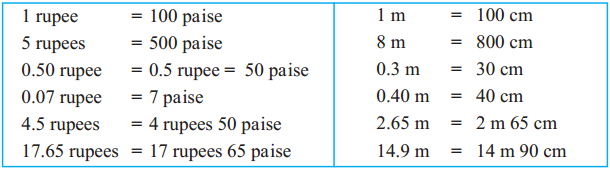
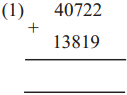
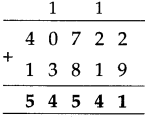
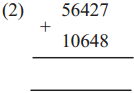
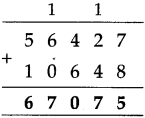
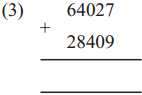
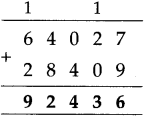
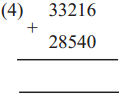
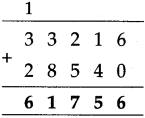
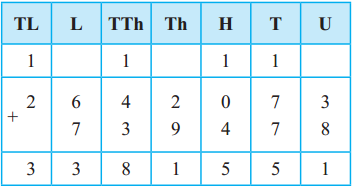
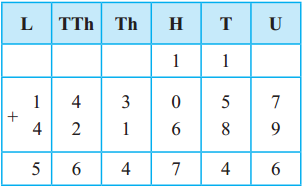
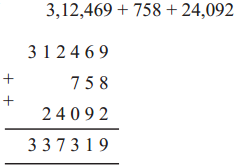
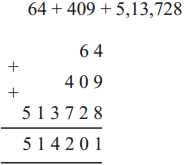
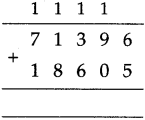
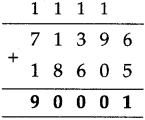
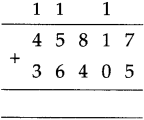
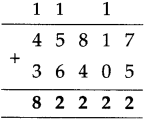
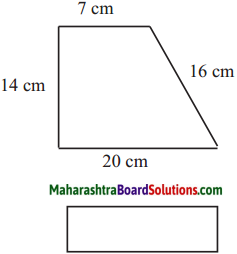
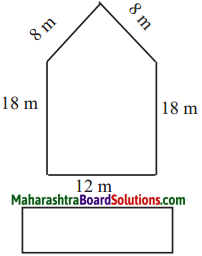
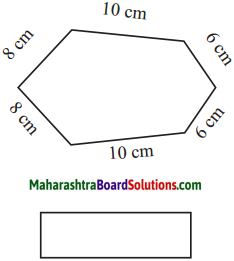
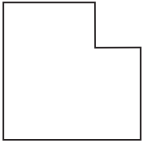
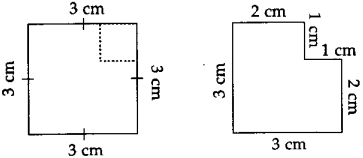
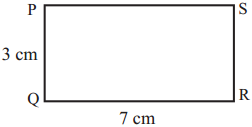
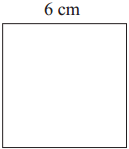
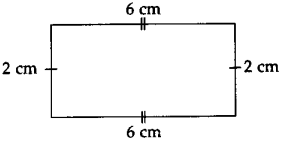
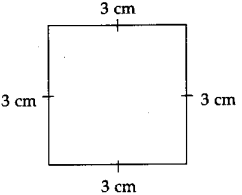
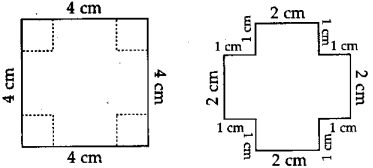
The lengths of all the sides of a square are equal. Therefore, the perimeter of a square = four times the length of one of its sides.

Perimeter of a square = 4 × the length of one side

Example : The length of one side of a square is 6 cm. Find its perimeter. The perimeter of a square is four times the length of one side.

Perimeter of a square = 4 × length of one side
= 4 × 6
= 24

Therefore, the perimeter of the square is 24 cm.

Word problems

Example (1) The length of a rectangular park is 100 m, while its width is 80 m. What is its perimeter?

Perimeter of the rectangle = 2 × length + 2 × breadth
= 2 × 100 + 2 × 80
= 200 + 160
= 360

The perimeter of the rectangular park is 360 m.

Example (2) How much wire will be needed to put a triple fence around a square plot with side 30 m? What will be the total cost of the wire at ₹ 70 per metre ?

To put a single fence around the square plot, we need to find its perimeter.

Perimeter of a square = 4 × length of one side = 4 × 30 = 120

The perimeter of the square plot is 120 metres. Since the fence is to be a triple fence, we must triple the perimeter.

120 × 3 = 360 m of wire will be needed.

Now let us find out how much the wire will cost. One metre of wire costs ₹ 70.

Therefore, the cost of 360 m of wire will be 360 × 70 = 25, 200.

The total cost of wire for putting a triple fence around the plot will be ₹ 25, 200.

Perimeter and Area Problem Set 48 Additional Important Questions and Answers

Question 1.

Solution:
Perimeter of the figure
= 2 + 6 + 2 + 6
= 16 cm

∴ 16 cm

Question 2.

Solution:
Perimeter of the figure
= 3 + 3 + 3 + 3
= 12 cm

∴ 12 cm

Question 3.

Solution:
Perimeter of the figure
= 12 + 13 + 5
= 30 cm

∴ 30 cm

Question 4.
If four squares of side 1 cm ¡s cut out of all the corners of a larger square with side 4 cm (see the figure), what will be the perimeter of the remaining shape?

Solution:
Perimeter
= 2 + 1 + 1 + 2 + 1 + 1 + 2 + 1 + 1 + 2 + 1 + 1
= 16 cm

∴ 16 cm

Maharashtra Board Class 5 Maths Solutions

• Problems on Measurement Problem Set 46 Class 5 Maths Solutions
• Problems on Measurement Problem Set 47 Class 5 Maths Solutions
• Perimeter and Area Problem Set 48 Class 5 Maths Solutions
• Perimeter and Area Problem Set 49 Class 5 Maths Solutions
• Perimeter and Area Problem Set 50 Class 5 Maths Solutions

Angles Class 5 Problem Set 25 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 6 Angles Problem Set 25 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 6 Angles

Measure the angles given below and write the measure in the given boxes.

Answer:
(1) 40°
(2) 120°
(3) 90°
(4) 85°

Drawing an angle of the given measure
Example Draw ∠ABC of measure 70°.
B is the vertex of∠ABC and BA and BC are its arms.

1. First draw arm BC with a ruler.

2. Since B is the vertex, we must draw a 70° angle at that point.

Put the centre of the protractor on B. Place the protractor so that the baseline lies on arm BC. Count the divisions starting from the 0 near point C. Mark a point with your pencil at the division that shows 70°. Lift the protractor.

Draw a line from vertex B through the point marking the 70° angle. Name the other end of the line A.

∠ABC is an angle of measure 700.
Rahul and Sayali drew ∠PQR of measure 800 as shown below.

Teacher : Have Rahul and Sayali drawn the angles correctly?
Shalaka : Sir, Rahul’s angle is wrong. Sayali’s angle is correct.
Teacher : Why is Rahul’s angle wrong?
Rahul : I counted 10, 20, 30…from the left and drew the angle at 80.
Teacher : Rahul measured the angle from the left. Under the baseline on the left of Q, there is nothing. The arm of the angle is on the right of Q. Therefore, the point should have been marked 80° counting from the right side, that is, on the side on which point R lies.

Angles Problem Set 25 Additional Important Questions and Answers

Answer:
60°

Answer:
110°

Answer:
100°

Answer:
90°

Maharashtra Board Class 5 Maths Solutions

• Angles Problem Set 24 Class 5 Maths Solutions
• Angles Problem Set 25 Class 5 Maths Solutions
• Angles Problem Set 26 Class 5 Maths Solutions
• Angles Problem Set 27 Class 5 Maths Solutions

Preparation for Algebra Class 5 Problem Set 56 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 16 Preparation for Algebra Problem Set 56 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 16 Preparation for Algebra

Question 1.
Use a letter for ‘any number’ and write the following properties in short.

(1) The sum of any number and zero is the number itself.
Answer:
a + 0 = a

(2) The product of any two numbers and the product obtained after changing the order of those numbers is the same.
Answer:
a x b = b x a

(3) The product of any number and zero is zero.
Answer:
a x 0 = 0

Question 2.
Write the following properties in words :

(1) m – 0 = m
Answer:
Subtracting zero from any number, gives the number itself.

(2) n ÷ 1 = n
Answer:
Dividing any number by 1, gives the number itself.

Preparation for Algebra Problem Set 56 Additional Important Questions and Answers

Use a letter for any number and write the following properties in short.

Question 1.
The product of any number and 1 is the number itself.
Answer:
a x 1 = a

Question 2.
The division of any two different numbers and the divisions obtained after changing the order of those numbers is not the same.
Answer:
a ÷ b ≠ b + a

Write the following properties in words:

Question 1.
p x 0 = 0
Answer:
The product of any number and zero is zero.

(4) a + b = b + a
Answer:
The sum of any two numbers and the sum obtained after changing the order of these numbers is the same.

Using brackets write three pairs of numbers whose

(1) Sum is 9
Answer:
5 + 4 = 9,
7 + 2 = 9,
8 + 1 = 9

(2) difference is 9
Answer:
12 – 3 = 9,
11 – 2 = 9,
10 – 1 = 9

(3) multiplication is 16 and
Answer:
4 x 4 = 16,
8 x 2 = 16,
16 x 1 = 16

(4) division is 16.
Answer:
32 ÷ 2 = 16,
48 ÷ 3 = 16,
64 ÷ 4 = 16,

Fill in the blanks.

(1) 4 + 2 = 7 – ……….
(2) 4 + 2 = 3 x ……….
(3) 4 + 2 = 12 ÷ ……….
Answer:
(1) 1
(2) 2
(3) 2

Match the columns:

(A)

Answer:
(1 – c),
(2 – a),
(3-d),
(4-b)

(B)

Answer:
(1-d),
(2 – c),
(3 – a),
(4 – b)

Say whether right or wrong.

(1) (6 + 5) = (5 + 6)
(2) (8 + 5) > 10
(3) (8 + 5) < 10
(4) 108 > 108
(5) 108 = 108
(6) 108 < 108
(7) (6 x 3) = (20 – 2)
(8) 40 + 8 > 5
(9) (3 x 7) = (7 x 3)
(10) (5 + 0) = (5 x 1)
(11) (6 + 5) = 10
(12) (30 + 5) < (30 – 25)
Answer:
Right : (1), (2), (5), (7), (9), (10)
Wrong : (3), (4), (6), (8), (11), (12)

Fill in the blanks with the right symbol from <, > or =

(1) (24 ÷ 5) ……… (9 – 5)
(2) (4 + 2) ……… (5 x 1)
(3) (7 x 3) ……… (20 + 2)
(4) (8 x 2) (5 x 3)
(5) (5 x 6) ……… (25 + 5)
(6) (6 x 7) (9 x 5)
Answer:
(1) =
(2) >
(3) <
(4) >
(5) =
(6) <

Fill in the blanks in the expressions with the proper numbers.

(1) (4 x 4) = (………. x 2)
(2) (2 x 7) > (4 x ……….)
(3) (30 + 5) < ( x 3)
(4) (5 + 0)> (4 x ……….)
(5) (36 +3) = ( + )
(6) (9 – ……….) < (4 + 1)
(7) (8 + 9) < (3 x ……….)
(8) (0 + 3) > (4 x ……….)
(9) (28 ÷ 2) = (7 x ……….)
Answer:
(1) 8
(2) 3
(3) 9
(4) 1
(5) 7 + 5
(6) 5,
(7) 6
(8) 0
(9) 2

Use a letter for any number and write the following properties in short:

(1) Dividing zero by any non zero number is zero.
Answer:
0 + a = 0

(2) The difference of any two different numbers and the difference obtained after changing the order of those numbers is not same.
Answer:
a – b ≠ b – a

(3) Dividing non zero number by itself gives us 1.
Answer:
a ÷ a = 1

Write the followîng properties in words:

(1) a x 1 = a
Answer:
The product of any number and 1 is the number itself.

(2) a – a = 0
Answer:
Difference of the same two numbers is zero.

Maharashtra Board Class 5 Maths Solutions

• Three Dimensional Objects and Nets Problem Set 51  Class 5 Maths Solutions
• Pictographs Problem Set 52 Class 5 Maths Solutions
• Patterns Problem Set 53 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 54 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 55 Class 5 Maths Solutions
• Preparation for Algebra Problem Set 56 Class 5 Maths Solutions

Multiplication and Division Class 5 Problem Set 16 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 4 Multiplication and Division Problem Set 16 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 4 Multiplication and Division

Question 1.
From a total of 10,000 rupees, Anna donated 7,000 rupees to a school. The remaining amount was to be divided equally among six students as the ‘all-round student’ prize. What was the amount of each prize?
Solution:
1 0 0 0 0 Total rupees
–
7 0 0 0 rupees donated
_______
3 0 0 0 remained
_______
This amount was divided among 6 students 500

Answer:
Amount of the prize is ₹ 500.

Question 2.
An amount of 260 rupees each was collected from 50 students for a picnic. If 11,450 rupees were spent for the picnic, what is the amount left over?
Solution:
₹ 2 6 0 Collected from 1 student
x
5 0 No. of students
0 0 0
+
1 3 0 0 0
1 3 0 0 0 Rupees, collected amount
–
1 1 4 5 0 Rupees spent
1 5 5 0 Rupees left over

Answer:
1,550 Rupees leftover

Question 3.
A shopkeeper bought a sack of 50kg of sugar for 1750 rupees. As the price of sugar fell, he had to sell it at the rate of 32 rupees per kilo. How much less money did he get than he had spent?
Solution:
₹ 3 2 Sale price of 1 kg
x
5 0 kg sold
0 0
+
1 6 0 0
1 6 0 0 Amount received
₹ 1 7 5 0 Purchased price
–
₹ 1 6 0 0 Obtained price
₹ 1 5 0 Lesshegot

Answer:
₹ 150 less he got than he had spent

Question 4.
A shopkeeper bought 7 pressure cookers at the rate of 1870 rupees per cooker. He sold them all for a total of 14,230 rupees. Did he get less or more money than he had spent?
Solution:
₹ 1 8 7 0 Purchase price of 1 cooker
x
7 No. of cookers
₹ 1 3 0 9 0 Purchase price
₹ 1 4 2 3 0 Sell price
–
₹ 1 3 0 9 0 Purchase price
₹ 0 1 1 4 0 he got more

Answer:
₹ 1,140 he got more

Question 5.
Fourteen families in a Society together bought 8 sacks of wheat, each weighing 98 kilos. If they shared all the wheat equally, what was the share of each family?
Solution:
9 8 Kilo weight of 1 sack
x
8 No. of sacks
7 8 4 Kilo

Answer:
Share of each family = 56 kilo

Question 6.
The capacity of an overhead water tank is 3000 litres. There are 16 families living in this building. If each family uses 225 litres every day, will the tank filled to capacity be enough for all the families? If not, what will the daily shortfall be?
Solution:
₹ 2 2 5 Litres uses 1 family
x 1 6 No. of families
1 3 5 0
+
2 2 5 0
3 6 0 0 Litres required
–
3 0 0 0 Litres capacity
6 0 0 Litres daily shortfall

Answer:
600 litres is daily shortfall

Multiplication and Division Problem Set 16 Additional Important Questions and Answers

Solve the following word problems:

(1) A farmer brought 250 trays of tomatoes seedlings. Each tray had 48 seedlings. He planted all the seedlings in his field, putting 25 in a row. How many rows of tomatoes did he plant?
Solution:
₹ 2 5 0 Tray of tomatoes seedlings
x
4 8 Seedlings in 1 tray
2 0 0 0
+
1 0 0 0 0
1 2 0 0 0 Total no. of seedlings


Answer:
The number of rows is 480.

Q.l. Solve the following :
Multiply :
(1) 438 x 76
(2) 594 x 208
(3) 3467 x 926
(4) 3581 x 87
(5) 425 x 87
(6) 579 x 49
Answer:
(1) 33,288
(2) 1,23,552
(3) 32,10,442
(4) 3,11,547
(5) 36,975
(6) 28,371

Solve the following and write the quotient and remainder:

(1) 1345 ÷ 37
(2) 9682 ÷ 83
(3) 6371 ÷ 42
(4) 72534 ÷ 23
(5) 1284 ÷ 32
(6) 63240 ÷ 37
Answer:
(1) Quotient 36, Remainder 13
(2) Quotient 116, Remainder 54
(3) Quotient 151, Remainder 29
(4) Quotient 3153, Remainder 15
(5) Quotient 40, Remainder 4
(6) Quotient 1709, Remainder 7

Fill in the blanks :

(1) 88 x 17; 17 is called …………………………. and 88 is called
(2) Product of the greatest three-digit number and smaller two-digit number is ………………………… .
(3) Multiplicand and multiplier are interchanged the product remains the ………………………… .
(4) While multiplying by tens digit, we have to put in the units place ………………………… .
Answer:
(1) multiplier, multiplicand
(2) 99,900
(3) same
(4) zero

Maharashtra Board Class 5 Maths Solutions

• Multiplication and Division Problem Set 14 Class 5 Maths Solutions
• Multiplication and Division Problem Set 15 Class 5 Maths Solutions
• Multiplication and Division Problem Set 16 Class 5 Maths Solutions

Decimal Fractions Class 5 Problem Set 37 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 37 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 9 Decimal Fractions

Write the following mixed fractions in decimal form and read them aloud.

\(\text { (1) } 9 \frac{1}{10}\)
Answer:
9.1, Nine point one.

\(\text { (2) } 9 \frac{1}{100}\)
Answer:
9.01, Nine point zero one.

\(\text { (3) } 4 \frac{53}{100}\)
Answer:
4.53, Four point five three.

\(\text { (4) } \frac{78}{100}\)
Answer:
0.78, Zero point seven eight.

\(\text { (5) } \frac{5}{100}\)
Answer:
0.05, Zero point zero five.

\(\text { (6) } \frac{5}{10}\)
Answer:
0.5, Zero point five.

\(\text { (7) } \frac{2}{10}\)
Answer:
0.2, Zero point two.

\(\text { (8) } \frac{20}{100}\)
Answer:
0.20, Zero point two zero.

Place value of the digits in decimal fractions

We can determine the place value of the digits in decimal fractions in the same way that we determine the place values of digits in whole numbers.

Example (1)
In 73.82, the place value of 7 is 7 × 10 = 70, and of 3, it is 3 × 1 = 3.
Similarly, the place value of 8 is 8 × \(\frac{1}{10}=\frac{8}{10}\) = 0.8 and the place value of 2 is 2 × \(\frac{1}{100}=\frac{2}{100}\) = 0.02

Example (2)
Place values of the digits in 210.86.

Decimal Fractions Problem Set 37 Additional Important Questions and Answers

\(\text { (1) } 3 \frac{3}{100}\)
Answer:
3.03, Three point zero three.

\(\text { (2) } 3 \frac{33}{100}\)
Answer:
3.33, Three point three three.

\(\text { (3) } 30 \frac{41}{100}\)
Answer:
30.41, Thirty point four one.

\(\text { (4) } 11 \frac{11}{100}\)
Answer:
11.11, Eleven point one one.

Q.3. Write the following numbers using the decimal point:
(1) Sixty-eight point seven six .
Answer:
68.76

(2) Nine point five zero one
Answer:
9.501

(3) Eighty-four point zero three.
Answer:
84.03

(4) Eighty-four point zero zero seven.
Answer:
84.007

(5) Two hundred ftinety-eight point zero seven.
Answer:
298.07

Maharashtra Board Class 5 Maths Solutions

• Decimal Fractions Problem Set 36 Class 5 Maths Solutions
• Decimal Fractions Problem Set 37 Class 5 Maths Solutions
• Decimal Fractions Problem Set 38 Class 5 Maths Solutions
• Decimal Fractions Problem Set 39 Class 5 Maths Solutions
• Decimal Fractions Problem Set 40 Class 5 Maths Solutions
• Decimal Fractions Problem Set 41 Class 5 Maths Solutions
• Decimal Fractions Problem Set 42 Class 5 Maths Solutions

Fractions Class 5 Problem Set 18 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 18 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Convert the given fractions into like fractions.

Solution :
8 is the multiple of 4 So, make 8, the common denominator \(\frac{3}{4}=\frac{3 \times 2}{4 \times 2}=\frac{6}{8}\).Thus 6/8 and 5/8are the required like fractions.

Solution :
The number 35 is a multiple of both 5 and 7 So, making 35 as the common denominater \(\frac{3}{5}=\frac{3 \times 7}{5 \times 7}=\frac{21}{35}, \frac{3}{7}=\frac{3 \times 5}{7 \times 5}=\frac{15}{35}\) Therefore, 21/35 and 15/35 are required like fractions.

Solution :
Here 10 is the multiples of 5. So make 10 as the common denominator \(\frac{4}{5}=\frac{4 \times 2}{5 \times 2}=\frac{8}{10}\). Thus 8/10 and 3/10 are required like fractions.

Solution :
Least common multiple of 9 and 6 is 18. So, make, 18 as the common denominator. \(\frac{2}{9}=\frac{2 \times 2}{9 \times 2}=\frac{4}{18}, \frac{1}{6}=\frac{1 \times 3}{6 \times 3}=\frac{3}{18}\). Thus, 4/18 and 3/18 are the required like fractions.

Solution :
Least common multiple of 4 and 3 is 12 So, make 12 as common denominator \(\frac{1}{4}=\frac{1 \times 3}{4 \times 3}=\frac{3}{12}, \frac{2}{3}=\frac{2 \times 4}{3 \times 4}=\frac{8}{12}\). so, \(\frac{3}{12}, \frac{8}{12}\) are required like fractions.

Solution :
Least common multiple of 6 and 5 is 30 So, make 30 as common denominator \(\frac{5}{6}=\frac{5 \times 5}{6 \times 5}=\frac{25}{30}, \frac{4}{5}=\frac{4 \times 6}{5 \times 6}=\frac{24}{30}\) So, \(\frac{25}{30}, \frac{24}{30}\) are required like fractions.

Solution :
Least common multiple of 8 and 6 is 24 So, make 24 as common denominator \(\frac{3}{8}=\frac{3 \times 3}{8 \times 3}=\frac{9}{24}, \frac{1}{6}=\frac{1 \times 4}{6 \times 4}=\frac{4}{24}\) So, \(\frac{9}{24}, \frac{4}{24}\) are required like fractions.

Solution :
Least common multiple of 6 and 9 is 18 So, make 18 as common denominator \(\frac{1}{6}=\frac{1 \times 3}{6 \times 3}=\frac{3}{18}, \frac{4}{9}=\frac{4 \times 2}{9 \times 2}=\frac{8}{18}\) So, 3/18 and 8/18 are the required like fractions.

Comparing like fractions
Example (1) A strip was divided into 5 equal parts. It means that each part is 1/5 . The coloured part is \(\frac{3}{5}=\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\).

The white part is \(\frac{2}{5}=\frac{1}{5}+\frac{1}{5}\). The coloured part is bigger than the white part. This tells us that 3/5 is greater than 2/5. This is written as 3/5 > 2/5.

Example (2) This strip is divided into 8 equal parts. 3 of the parts have one colour and 4 have another colour. Here, 3/8 < 8/4.

In like fractions, the fraction with the greater numerator is the greater fraction.

Comparing fractions with equal numerators
You have learnt that the value of fractions with numerator 1 decreases as the denominator increases.

Even if the numerator is not 1, the same rule applies so long as all the fractions have a common numerator. For example, look at the figures below. All the strips in the figure are alike.
2 of the 3 equal parts of the strip
2 of the 4 equal parts of the strip
2 of the 5 equal parts of the strip
The figure shows that 2/3 > 2/4 > 5/2.

Of two fractions with equal numerators, the fraction with the greater denominator is the smaller fraction.

Comparing unlike fractions
Teacher : Suppose we have to compare the unlike fractions 3/5 and 4/7. Let us take an example to see how this is done. These two boys are standing on two blocks. How do we decide who is taller?

Sonu : But the height of the blocks is not the same. If both blocks are of the same height, it is easy to tell who is taller.

Nandu : Now that they are on blocks of equal height, we see that the boy on the right is taller.

Teacher : The height of the boys can be compared when they stand at the same height. Similarly, if fractions have the same denominators, their numerators decide which fraction is bigger.

Nandu : Got it! Let’s obtain the same denominators for both fractions.

Sonu : 5 × 7 can be divided by both 5 and 7. So, 35 can be the common denominator.

To compare unlike fractions, we convert them into their equivalent fractions so that their denominators are the same.

Fractions Problem Set 18 Additional Important Questions and Answers

Question 1.
\(\frac{5}{9}, \frac{17}{36}\)
Solution :
36 is the multiple of 9 So, make 36 the common denominator \(\frac{5}{9}=\frac{5 \times 4}{9 \times 4}=\frac{20}{36}\), Thus 20/36 and 17/36 are the required like fractions.

Question 2.
\(\frac{5}{6}, \frac{7}{9}\)
Solution:
Least common multiple of 6 and 9 is 18 So, make 18 as the common denominator \(\frac{5}{6}=\frac{5 \times 3}{6 \times 3}=\frac{15}{18}, \quad \frac{7}{9}=\frac{7 \times 2}{9 \times 2}=\frac{14}{18}\) So, 15/18 and 14/18 are the required like fractions.

Question 3.
\(\frac{7}{11}, \frac{3}{5}\)
Solution:
Least common multiple of 11 and 5 is 55 So, make 55 as the common denominator. \(\frac{7}{11}=\frac{7 \times 5}{11 \times 5}=\frac{35}{55}, \frac{3}{5}=\frac{3 \times 11}{5 \times 11}=\frac{33}{55}\). Thus 35/55 and 33/55 are required like fractions.

Maharashtra Board Class 5 Maths Solutions

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions