Bhagya

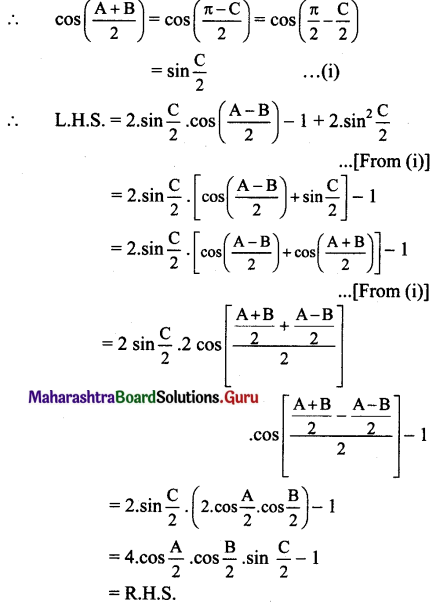
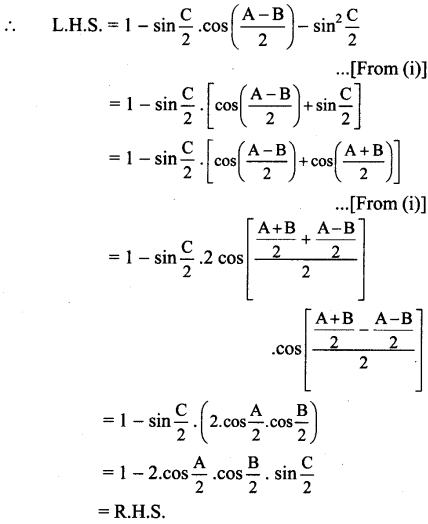
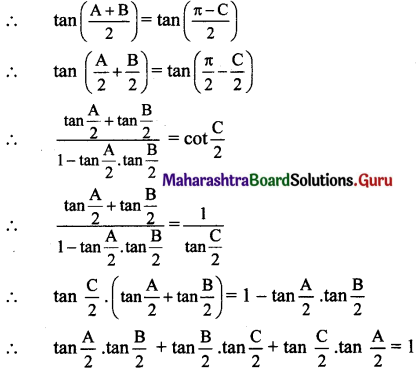
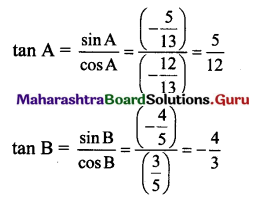
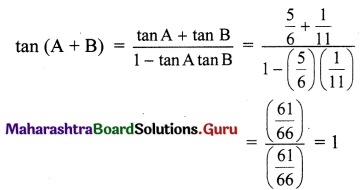
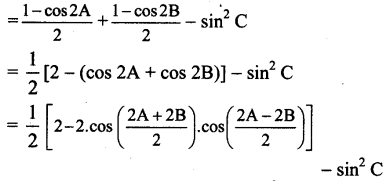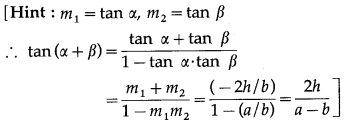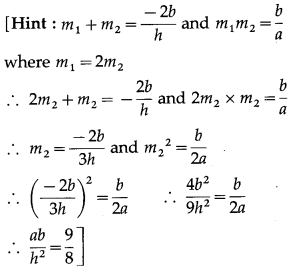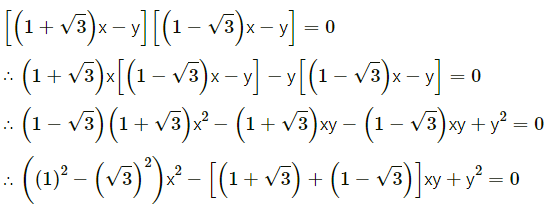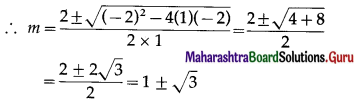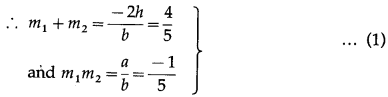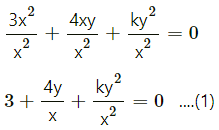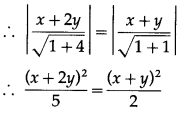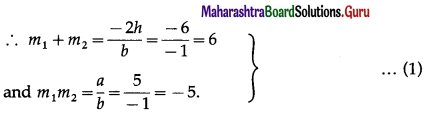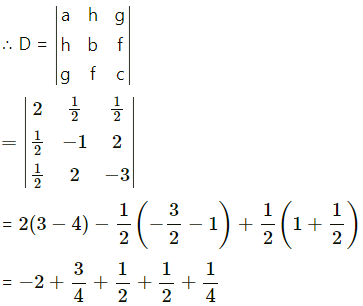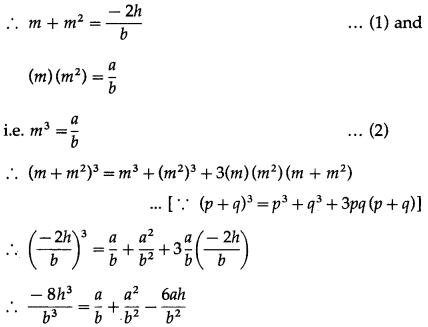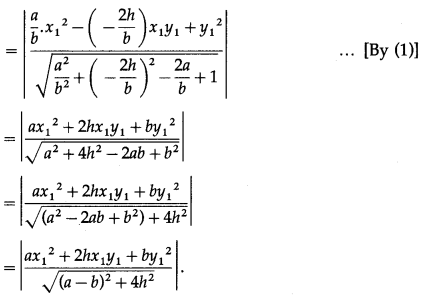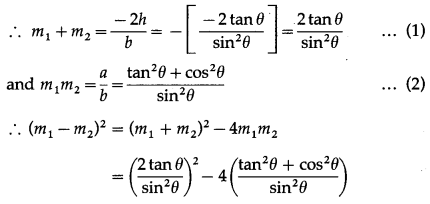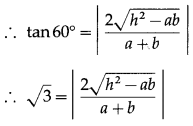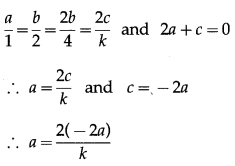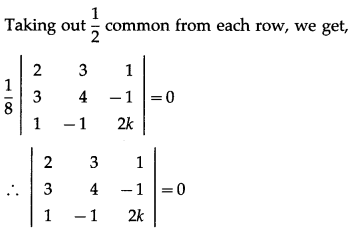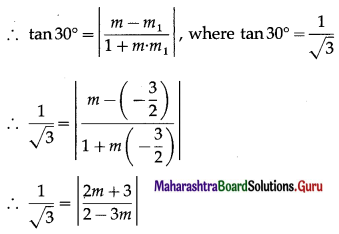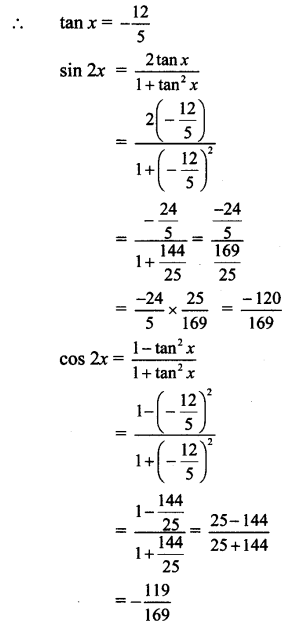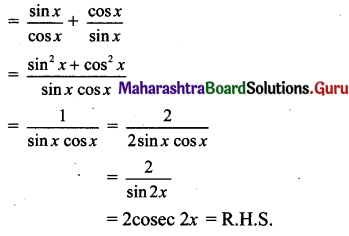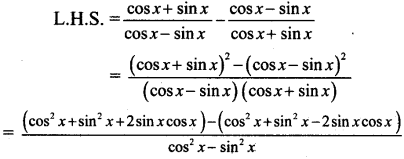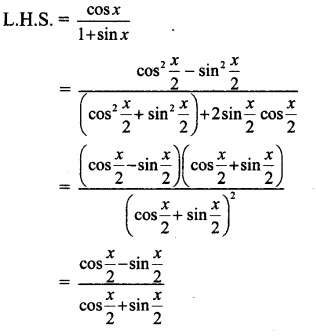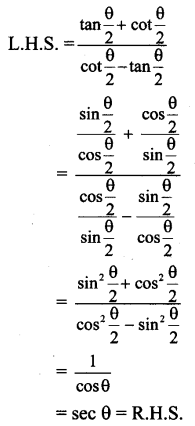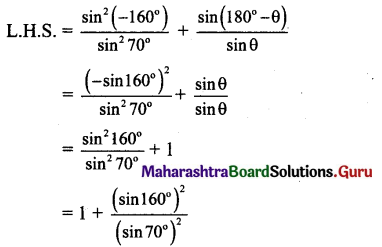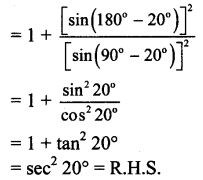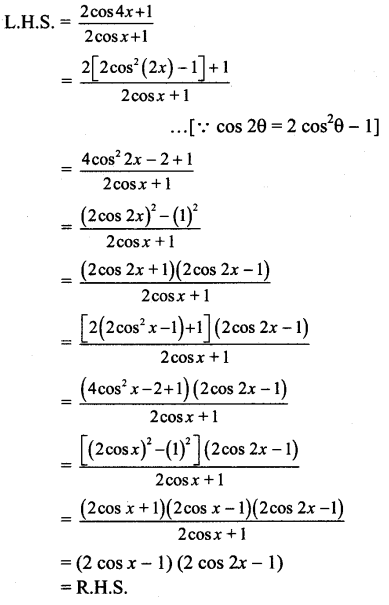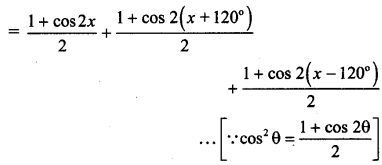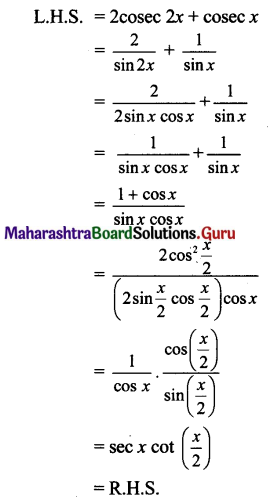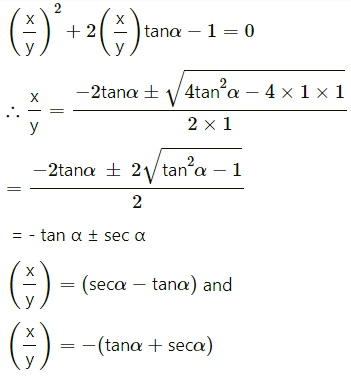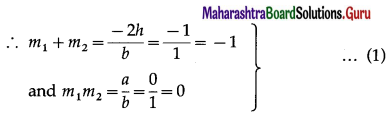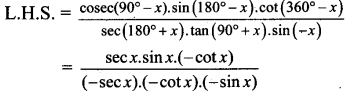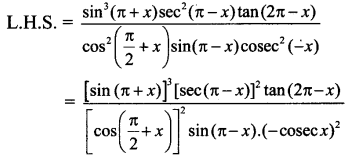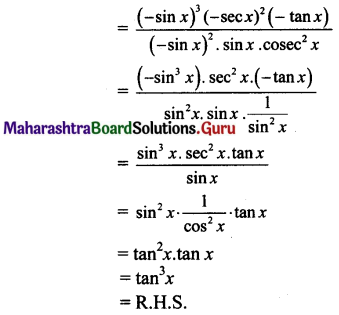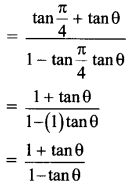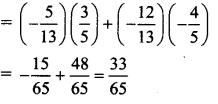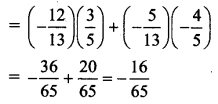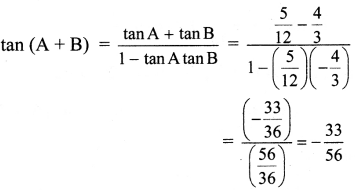Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.1 Questions and Answers.

12th Maths Part 1 Vectors Exercise 5.1 Questions And Answers Maharashtra Board

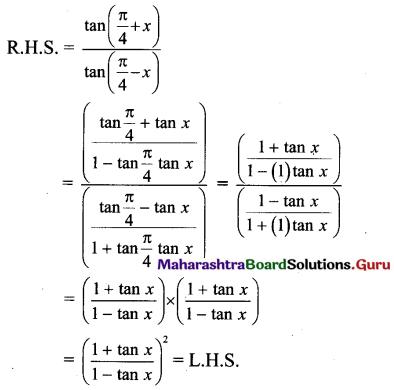
Question 1.
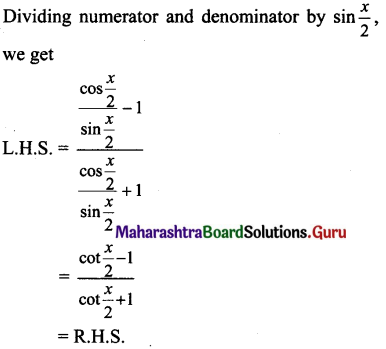
The vector \(\bar{a}\) is directed due north and \(|\bar{a}|\) = 24. The vector \(\bar{b}\) is directed due west and \(|\bar{b}|\) = 7. Find \(|\bar{a}+\bar{b}|\).
Solution:

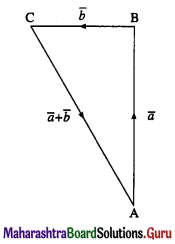
Let \(\overline{\mathrm{AB}}\) = \(\bar{a}\), \(\overline{\mathrm{BC}}\) = \(\bar{b}\)
Then \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{BC}}\) = a + b
Given : \(|\bar{a}|\) = \(|\overline{\mathrm{AB}}|\) = l(AB) = 24 and
\(|\bar{b}|\) = \(|\overline{\mathrm{BC}}|\) = l(BC) = 7
∴ ∠ABC = 90°
∴ [l(AC)]² = [l(AB)]² + [l(BC)]²
= (24)² + (7)² = 625
∴ l(AC) = 25 ∴ \(|\overline{\mathrm{AC}}|\) = 25
∴ \(|\bar{a}+\bar{b}|\) = \(|\overline{\mathrm{AC}}|\) = 25.

Question 2.
In the triangle PQR, \(\overline{\mathrm{PQ}}\) = 2\(\bar{a}\) and \(\overline{\mathrm{QR}}\) = 2\(\bar{b}\). The mid-point of PR is M. Find following vectors in terms of \(\bar{a}\) and \(\bar{b}\).
(i) \(\overline{\mathrm{PR}}\)
Solution:

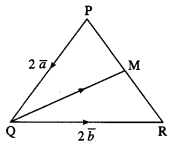
Given : \(\overline{\mathrm{PQ}}\) = 2\(\bar{a}\), \(\overline{\mathrm{QR}}\) = 2\(\bar{b}\)
(i) \(\overline{\mathrm{PR}}\) = \(\overline{\mathrm{PQ}}\) + \(\overline{\mathrm{QR}}\)
= 2\(\bar{a}\) + 2\(\bar{a}\).

(ii) \(\overline{\mathrm{PM}}\)
Solution:
∵ M is the midpoint of PR
∴ \(\overline{\mathrm{PM}}\) = \(\frac{1}{2} \overline{\mathrm{PR}}\) = \(\frac{1}{2}\)[2\(\bar{a}\) + 2\(\bar{b}\)]
= \(\bar{a}\) + \(\bar{b}\).

(iii) \(\overline{\mathrm{QM}}\)
Solution:
\(\overline{\mathrm{RM}}\) = \(\frac{1}{2}(\overline{\mathrm{RP}})\) = \(-\frac{1}{2} \overline{\mathrm{PR}}\) = \(-\frac{1}{2}\)(2\(\bar{a}\) + 2\(\bar{b}\))
= –\(\bar{a}\) – \(\bar{b}\)
∴ \(\overline{\mathrm{QM}}\) = \(\overline{\mathrm{QR}}\) + \(\overline{\mathrm{RM}}\)
= 2\(\bar{b}\) – \(\bar{a}\) – \(\bar{b}\)
= \(\bar{b}\) – \(\bar{a}\).

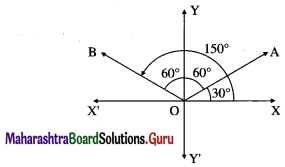
Question 3.
OABCDE is a regular hexagon. The points A and B have position vectors \(\bar{a}\) and \(\bar{b}\) respectively, referred to the origin O. Find, in terms of \(\bar{a}\) and \(\bar{b}\) the position vectors of C, D and E.
Solution:

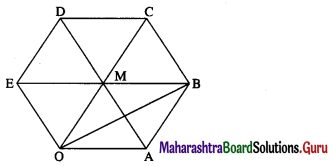
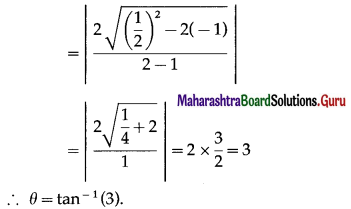
Given : \(\overline{\mathrm{OA}}\) = \(\bar{a}\), \(\overline{\mathrm{OB}}\) = \(\bar{a}\) Let AD, BE, OC meet at M.
Then M bisects AD, BE, OC.
\(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{AO}}\) + \(\overline{\mathrm{OB}}\) = –\(\overline{\mathrm{OA}}\) + \(\overline{\mathrm{OB}}\) = –\(\bar{a}\) + \(\bar{b}\) = \(\bar{b}\) – \(\bar{a}\)
∵ OABM is a parallelogram

Hence, the position vectors of C, D and E are 2\(\bar{b}\) – 2\(\bar{a}\), 2\(\bar{b}\) – 3\(\bar{a}\) and \(\bar{b}\) – 2\(\bar{a}\) respectively.

Question 4.
If ABCDEF is a regular hexagon, show that \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{AC}}\) + \(\overline{\mathrm{AD}}\) + \(\overline{\mathrm{AE}}\) + \(\overline{\mathrm{AF}}\) = 6\(\overline{\mathrm{AO}}\), where O is the center of the hexagon.
Solution:

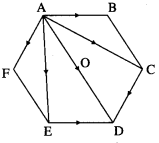
ABCDEF is a regular hexagon.
∴ \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{ED}}\) and \(\overline{\mathrm{AF}}\) = \(\overline{\mathrm{CD}}\)
∴ by the triangle law of addition of vectors,

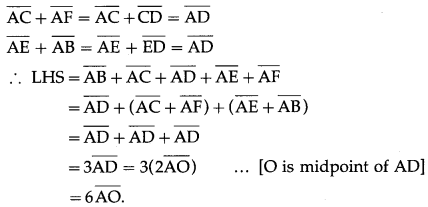
Question 5.
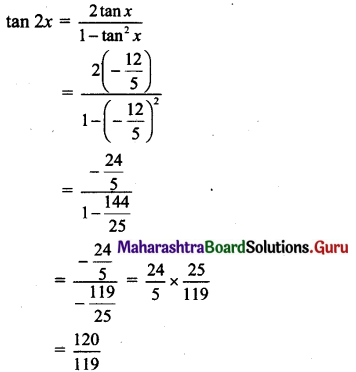
Check whether the vectors \(2 \hat{i}+2 \hat{j}+3 \hat{k}\), + \(-3 \hat{i}+3 \hat{j}+2 \hat{k}\), + \(3 \hat{i}+4 \hat{k}\) form a triangle or not.
Solution:
Let, if possible, the three vectors form a triangle ABC
with \(\overline{A B}\) = \(2 \hat{i}+2 \hat{j}+3 \hat{k}\), \(\overline{B C}\) = \(3 \hat{i}+3 \hat{j}+2 \hat{k}\), \(\overline{A C}\) = \(3 \hat{i}+4 \hat{k}\)
Now, \(\overline{A B}\) + \(\overline{B C}\)
= \((2 \hat{i}+2 \hat{j}+3 \hat{k})\) + \((-3 \hat{i}+3 \hat{j}+2 \hat{k})\)
= \(-\hat{i}+5 \hat{j}+5 \hat{k} \neq 3 \hat{i}+4 \hat{k}\) = \(\overline{\mathrm{AC}}\)
Hence, the three vectors do not form a triangle.

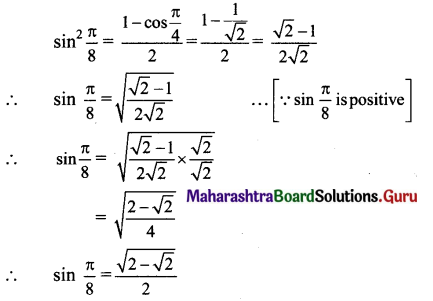
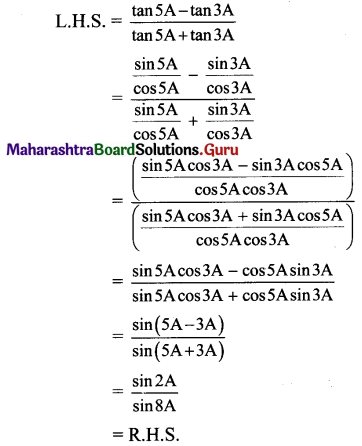
Question 6.
In the figure 5.34 express \(\bar{c}\) and \(\bar{d}\) in terms of \(\bar{a}\) and \(\bar{b}\). Find a vector in the direction of \(\bar{a}\) = \(\hat{i}-2 \hat{j}\) that has magnitude 7 units.

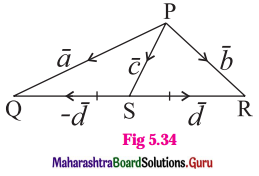
Solution:
\(\overline{\mathrm{PQ}}\) = \(\overline{\mathrm{PS}}\) + \(\overline{\mathrm{SQ}}\)
∴ \(\bar{a}\) = \(\bar{c}\) – \(\bar{d}\) … (1)
\(\overline{\mathrm{PR}}\) = \(\overline{\mathrm{PS}}\) + \(\overline{\mathrm{SR}}\)
∴ \(\bar{b}\) = \(\bar{c}\) + \(\bar{d}\) … (2)
Adding equations (1) and (2), we get
\(\bar{a}\) + \(\bar{b}\) = (\(\bar{c}\) – \(\bar{d}\)) + (\(\bar{c}\) + \(\bar{d}\)) = 2\(\bar{c}\)

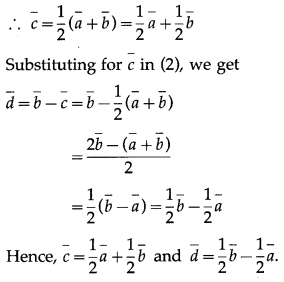
Question 7.
Find the distance from (4, -2, 6) to each of the following :
(a) The XY-plane
Solution:
Let the point A be (4, -2, 6).
Then,
The distance of A from XY-plane = |z| = 6

(b) The YZ-plane
Solution:
The distance of A from YZ-plane = |x| = 4

(c) The XZ-plane
Solution:
The distance of A from ZX-plane = |y| = 2

(d) The X-axis
Solution:
The distance of A from X-axis
= \(\sqrt{y^{2}+z^{2}}\) = \(\sqrt{(-2)^{2}+6^{2}}\) = \(\sqrt{40}\) = \(2 \sqrt{10}\)

(e) The Y-axis
Solution:
The distance of A from Y-axis
= \(\sqrt{z^{2}+x^{2}}\) = \(\sqrt{6^{2}+4^{2}}\) = \(\sqrt{52}\) = \(2 \sqrt{13}\)

(f) The Z-axis
Solution:
The distance of A from Z-axis
= \(\sqrt{x^{2}+y^{2}}\) = \(\sqrt{4^{2}+(-2)^{2}}\) = \(\sqrt{20}\) = \(2 \sqrt{5}\)

Question 8.
Find the coordinates of the point which is located :
(a) Three units behind the YZ-plane, four units to the right of the XZ-plane and five units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located 3 units behind the YZ- j plane, 4 units to the right of XZ-plane and 5 units , above the XY-plane,
x = -3, y = 4 and z = 5
Hence, coordinates of the required point are (-3, 4, 5)

(b) In the YZ-plane, one unit to the right of the XZ-plane and six units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located in the YZ plane, x = 0. Also, the point is one unit to the right of XZ-plane and six units above the XY-plane.
∴ y = 1, z = 6.
Hence, coordinates of the required point are (0, 1, 6).

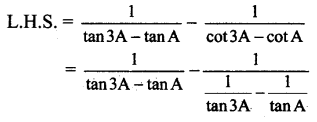
Question 9.
Find the area of the triangle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Solution:
Let A = (1, 1, 0), B = (1, 0, 1), C = (0, 1, 1)

Question 10.
If \(\overline{\mathrm{AB}}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\) and initial point A ≡ (1, 5, ,0). Find the terminal point B.
Solution:
Let \(\bar{a}\) and \(\bar{b}\) be the position vectors of A and B.
Given : A = (1, 5, 0) .’. \(\bar{a}\) = \(\hat{i}+5 \hat{j}\)
Now, \(\overline{\mathrm{AB}}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\)
∴ \(\bar{b}\) – \(\bar{a}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\)
∴ \(\bar{b}\) = \((2 \hat{i}-4 \hat{j}+7 \hat{k})\) + \(\bar{a}\)
= \((2 \hat{i}-4 \hat{j}+7 \hat{k})\) + \((\hat{i}+5 \hat{j})\)
= \(3 \hat{i}+\hat{j}+7 \hat{k}\)
Hence, the terminal point B = (3, 1, 7).

Question 11.
Show that the following points are collinear :
(i) A (3, 2, -4), B (9, 8, -10), C (-2, -3, 1).
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) be the position vectors of the points.
A = (3, 2, -4), B = (9, 8, -10) and C = (-2, -3, 1) respectively.

∴ \(\overline{\mathrm{BC}}\) is a non-zero scalar multiple of \(\overline{\mathrm{AB}}\)
∴ they are parallel to each other.
But they have the point B in common.
∴ \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AB}}\) are collinear vectors.
Hence, the points A, B and C are collinear.

(ii) P (4, 5, 2), Q (3, 2, 4), R (5, 8, 0).
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) be the position vectors of the points.
P = (4, 5, 2), Q = (3, 2, 4), R = (5, 8, 0) respectively.

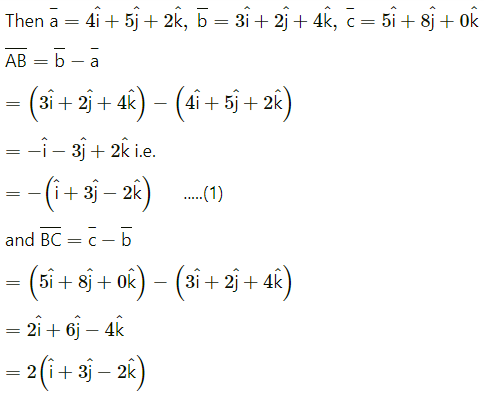
= 2.\(\overline{\mathrm{AB}}\) …[By (1)]
∴ \(\overline{\mathrm{BC}}\) is a non-zero scalar multiple of \(\overline{\mathrm{AB}}\)
∴ they are parallel to each other.
But they have the point B in common.
∴ \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AB}}\) are collinear vectors.
Hence, the points A, B and C are collinear.

Question 12.
If the vectors \(2 \hat{i}-q \hat{j}+3 \hat{k}\) and \(4 \hat{i}-5 \hat{j}+6 \hat{k}\) are collinear, then find the value of q.
Solution:
The vectors \(2 \hat{i}-q \hat{j}+3 \hat{k}\) and \(4 \hat{i}-5 \hat{j}+6 \hat{k}\) are collinear
∴ the coefficients of \(\hat{i}, \hat{j}, \hat{k}\) are proportional

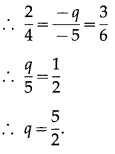
Question 13.
Are the four points A(1, -1, 1), B(-1, 1, 1), C(1, 1, 1) and D(2, -3, 4) coplanar? Justify your answer.
Solution:
The position vectors \(\bar{a}\), \(\bar{b}\), \(\bar{c}\), \(\bar{d}\) of the points A, B, C, D are

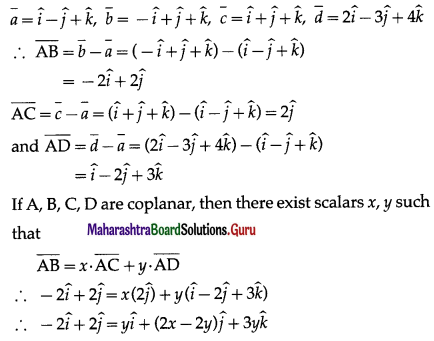
By equality of vectors,
y = -2 ….(1)
2x – 2y = 2 … (2)
3y = 0 … (3)
From (1), y = -2
From (3), y = 0 This is not possible.
Hence, the points A, B, C, D are not coplanar.

Question 14.
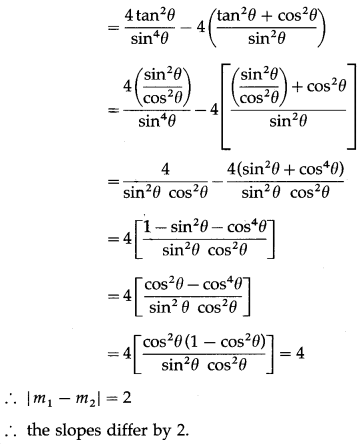
Express \(-\hat{i}-3 \hat{j}+4 \hat{k}\) as linear combination of the vectors \(2 \hat{i}+\hat{j}-4 \hat{k}\), \(2 \hat{i}-\hat{j}+3 \hat{k}\) and \(3 \hat{i}+\hat{j}-2 \hat{k}\).
Solution:

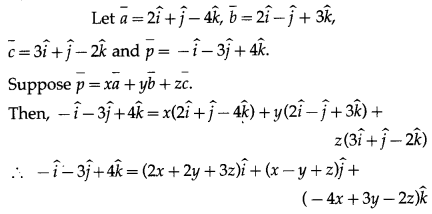
By equality of vectors,
2x + 2y + 3 = -1
x – y + z = -3
-4x + 3y – 2z = 4
We have to solve these equations by using Cramer’s Rule
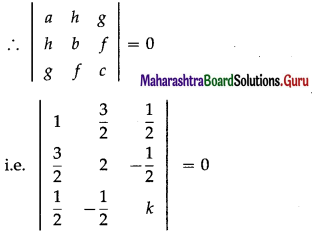
D = \(\left|\begin{array}{rrr}
2 & 2 & 3 \\
1 & -1 & 1 \\
-4 & 3 & -2
\end{array}\right|\)
= 2(2 – 3) – 2(-2 + 4) + 3(3 – 4)
= -2 – 4 – 3 = -9 ≠ 0

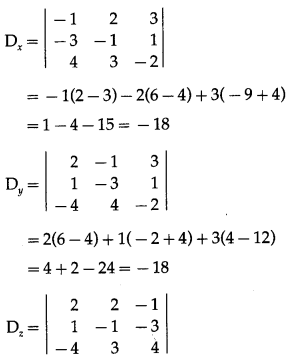
= 2(-4 + 9) – 2(4 – 12) – 1(3 – 4)
= 10 + 16 + 1 = 27

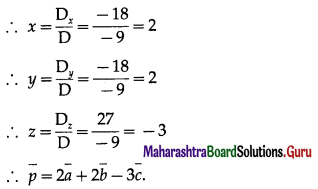
12th Maharashtra State Board Maths Solutions Pdf Part 1

• Vectors Ex 5.1 Class 12 Maths Solutions
• Vectors Ex 5.2 Class 12 Maths Solutions
• Vectors Ex 5.3 Class 12 Maths Solutions
• Vectors Ex 5.4 Class 12 Maths Solutions
• Vectors Ex 5.5 Class 12 Maths Solutions
• Vectors Miscellaneous Exercise 5 Class 12 Maths Solutions
• Line and Plane Ex 6.1 Class 12 Maths Solutions
• Line and Plane Ex 6.2 Class 12 Maths Solutions
• Line and Plane Ex 6.3 Class 12 Maths Solutions
• Line and Plane Ex 6.4 Class 12 Maths Solutions
• Line and Plane Miscellaneous Exercise 6A Class 12 Maths Solutions
• Line and Plane Miscellaneous Exercise 6B Class 12 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.5 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.5 Questions And Answers Maharashtra Board

Question 1.
In Δ ABC, A + B + C = π, show that
cos2A + cos2B + cos2C = – 1 – 4 cosA cosB cosC
Solution:
L.H.S. = cos 2A + cos 2B + cos 2C
= \(2 \cdot \cos \left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right) \cdot \cos \left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)+\cos 2 \mathrm{C}\)
= 2.cos(A + B).cos (A – B) + 2cos²C – 1
In ΔABC, A + B + C = π
∴ A + B = π – C
∴ cos(A + B) = cos(π – C)
∴ cos(A + B) = – cosC ………….(i)

∴ L.H.S. = – 2.cos C.cos (A – B) + 2.cos²C – 1 …[From(i)]
= – 1 – 2.cosC.[cos(A – B) – cosC]
= – 1 – 2.cos C.[cos(A – B) + cos(A + B)]
… [From (i)]
= – 1 – 2.cos C.(2.cos A.cos B)
= – 1 – 4.cos A.cos B.cos C = R.H.S.

Question 2.
sin A + sin B + sin C = 4 cos A/2 cos B/2 cos C/2
Solution:

Question 3.
cos A + Cos B + Cos C = 4 cos A/2 cos B/2 cos C/2
= \(2 \cdot \cos \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cdot \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)-\left(1-2 \sin ^{2} \frac{\mathrm{C}}{2}\right)\)
Solution:
L.H.S. = sin A + sin B + sin C
= \(2 \cdot \cos \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cdot \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)-\left(1-2 \sin ^{2} \frac{\mathrm{C}}{2}\right)\)
In Δ ABC, A + B + C = π ,
∴ A + B = π – C

Question 4.
sin² A + sin² B – sin² C = 2 sin A sin B cos C
Solution:
We know that, sin² = \(\frac{1-\cos 2 \theta}{2}\)
L.H.S.
= sin² + sin² B + sin² C

= 1 – cos(A + B). cos(A – B) – sin²C
= (1 – sin² C ) – cos (A + B). cos (A – B)
= cos² C – cos(A + B). cos(A – B)
∴ cos(A + B) = cos(it — C)
∴ cos(A + B) = — cos C …(i)
∴ L.H.S. = cos²C + cos C.cos(A – B)
… [From (i)]
= cos C[cos C + cos(A – B)]
= cos C[- cos(A + B) + cos(A – B)]
… [From (i)]
= cos C[cos (A-B) – cos(A + B)]
= cos C(2 sin A.sin B)
= 2 sin A.sin B. cos C
= R.H.S.
[Note: The question has been modified.]

Question 5.
\(\sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}-\sin ^{2} \frac{C}{2}\) = \(1-2 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\)
Solution:

Question 6.
tan \(\frac{\mathbf{A}}{2}\) tan \(\frac{\mathbf{B}}{2}\) tan \(\frac{\mathbf{B}}{2}\) tan \(\frac{\mathbf{C}}{2}\) tan \(\frac{\mathbf{C}}{2}\) tan \(\frac{\mathbf{A}}{2}\) = 1
Solution:
In Δ ABC,
A + B + C = π
∴ A + B = π – C

Question 7.
\(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\cot \frac{A}{2} \cot \frac{B}{2} \cot \frac{C}{2}\)
Solution:
In Δ ABC,
A + B + C = π
∴ A + B = π – C

Question 8.
tan 2A + tan 2B + tan 2C = tan 2A tan 2B + tan 2C
Solution:
In Δ ABC,
A + B + C = π
∴ 2A + 2B + 2C = 2π
∴ 2A + 2B = 2π – 2C
tan(2A + 2B) = tan(2n — 2C)
\(\frac{\tan 2 \mathrm{~A}+\tan 2 \mathrm{~B}}{1-\tan 2 \mathrm{~A} \cdot \tan 2 \mathrm{~B}}\) = -tan 2C
∴ tan2A+tan2B=—tan2C.(1-tan2A.tan2B)
∴ tan 2A + tan 2B = – tan2C+ tan2A.tan2B.tan2C
∴ tan 2A + tan 2B + tan 2C = tan2A.tan2B.tan2C

Question 9.
cos² A + cos² B – cos² C = 1 – 2 sin A sin B sin C
Solution:
we know that cos²θ = \(\frac{1+\cos 2 \theta}{2}\)
L.H.S.
= cos² A + cos² B + cos² C

= 1 + cos (A + B).cos(A — B) – cos2 C
In ΔABC,
A + B + C = π
A + B = π — C
cos(A + B) = cos(π — C)
cos(A + B) = -cosC ………….. (i)
L.H.S. = 1 — cos C.cos(A — B) — cos² C
…[From(i)]
= 1 — cos C.[cos(A — B) + cos C]
= 1 — cos C.[cos(A — B) — cos(A + B)]
.. .[From (i)]
= 1 — cos C.(2.sin A.sin B)
= 1 — 2.sinA.sin B.cos C
= R.H.S.

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4 Questions and Answers.

12th Maths Part 1 Pair of Straight Lines Miscellaneous Exercise 4 Questions And Answers Maharashtra Board

I : Choose correct alternatives.
Question 1.
If the equation 4x² + hxy + y² = 0 represents two coincident lines, then h = _________.
(A) ± 2
(B) ± 3
(C) ± 4
(D) ± 5
Solution:
(C) ± 4

Question 2.
If the lines represented by kx² – 3xy + 6y² = 0 are perpendicular to each other then _________.
(A) k = 6
(B) k = -6
(C) k = 3
(D) k = -3
Solution:
(B) k = -6

Question 3.
Auxiliary equation of 2x² + 3xy – 9y² = 0 is _________.
(A) 2m² + 3m – 9 = 0
(B) 9m² – 3m – 2 = 0
(C) 2m² – 3m + 9 = 0
(D) -9m² – 3m + 2 = 0
Solution:
(B) 9m² – 3m – 2 = 0

Question 4.
The difference between the slopes of the lines represented by 3x² – 4xy + y² = 0 is _________.
(A) 2
(B) 1
(C) 3
(D) 4
Solution:
(A) 2

Question 5.
If the two lines ax² +2hxy+ by² = 0 make angles α and β with X-axis, then tan (α + β) = _____.
(A) \(\frac{h}{a+b}\)
(B) \(\frac{h}{a-b}\)
(C) \(\frac{2 h}{a+b}\)
(D) \(\frac{2 h}{a-b}\)
Solution:
(D) \(\frac{2 h}{a-b}\)

Question 6.
If the slope of one of the two lines \(\frac{x^{2}}{a}+\frac{2 x y}{h}+\frac{y^{2}}{b}\) = 0 is twice that of the other, then ab:h² = ___.
(A) 1 : 2
(B) 2 : 1
(C) 8 : 9
(D) 9 : 8
Solution:
(D) 9 : 8

Question 7.
The joint equation of the lines through the origin and perpendicular to the pair of lines 3x² + 4xy – 5y² = 0 is _________.
(A) 5x² + 4xy – 3y² = 0
(B) 3x² + 4xy – 5y² = 0
(C) 3x² – 4xy + 5y² = 0
(D) 5x² + 4xy + 3y² = 0
Solution:
(A) 5x² + 4xy – 3y² = 0

Question 8.
If acute angle between lines ax² + 2hxy + by² = 0 is, \(\frac{\pi}{4}\) then 4h² = _________.
(A) a² + 4ab + b²
(B) a² + 6ab + b²
(C) (a + 2b)(a + 3b)
(D) (a – 2b)(2a + b)
Solution:
(B) a² + 6ab + b²

Question 9.
If the equation 3x² – 8xy + qy² + 2x + 14y + p = 1 represents a pair of perpendicular lines then
the values of p and q are respectively _________.
(A) -3 and -7
(B) -7 and -3
(C) 3 and 7
(D) -7 and 3
Solution:
(B) -7 and -3

Question 10.
The area of triangle formed by the lines x² + 4xy + y² = 0 and x – y – 4 = 0 is _________.
(A) \(\frac{4}{\sqrt{3}}\) Sq. units
(B) \(\frac{8}{\sqrt{3}}\) Sq. units
(C) \(\frac{16}{\sqrt{3}}\) Sq. units
(D)\(\frac{15}{\sqrt{3}}\) Sq. units
Solution:
(B) \(\frac{8}{\sqrt{3}}\) Sq. units
[Hint : Area = \(\frac{p^{2}}{\sqrt{3}}\), where p is the length of perpendicular from the origin to x – y – 4 = 0]

Question 11.
The combined equation of the co-ordinate axes is _________.
(A) x + y = 0
(B) x y = k
(C) xy = 0
(D) x – y = k
Solution:
(C) xy = 0

Question 12.
If h² = ab, then slope of lines ax² + 2hxy + by² = 0 are in the ratio _________.
(A) 1 : 2
(B) 2 : 1
(C) 2 : 3
(D) 1 : 1
Solution:
(D) 1 : 1
[Hint: If h² = ab, then lines are coincident. Therefore slopes of the lines are equal.]

Question 13.
If slope of one of the lines ax² + 2hxy + by² = 0 is 5 times the slope of the other, then 5h² = _________.
(A) ab
(B) 2 ab
(C) 7 ab
(D) 9 ab
Solution:
(D) 9 ab

Question 14.
If distance between lines (x – 2y)² + k(x – 2y) = 0 is 3 units, then k =
(A) ± 3
(B) ± 5\(\sqrt {5}\)
(C) 0
(D) ± 3\(\sqrt {5}\)
Solution:
(D) ± 3\(\sqrt {5}\)
[Hint: (x – 2y)² + k(x – 2y) = 0
∴ (x – 2y)(x – 2y + k) = 0
∴ equations of the lines are x – 2y = 0 and x – 2y + k = 0 which are parallel to each other.
∴ \(\left|\frac{k-0}{\sqrt{1+4}}\right|\) = 3
∴ k = ± 3\(\sqrt {5}\)

II. Solve the following.
Question 1.
Find the joint equation of lines:
(i) x – y = 0 and x + y = 0
Solution:
The joint equation of the lines x – y = 0 and
x + y = 0 is
(x – y)(x + y) = 0
∴ x² – y² = 0.

(ii) x + y – 3 = 0 and 2x + y – 1 = 0
Solution:
The joint equation of the lines x + y – 3 = 0 and 2x + y – 1 = 0 is
(x + y – 3)(2x + y – 1) = 0
∴ 2x² + xy – x + 2xy + y² – y – 6x – 3y + 3 = 0
∴ 2x² + 3xy + y² – 7x – 4y + 3 = 0.

(iii) Passing through the origin and having slopes 2 and 3.
Solution:
We know that the equation of the line passing through the origin and having slope m is y = mx. Equations of the lines passing through the origin and having slopes 2 and 3 are y = 2x and y = 3x respectively.
i.e. their equations are
2x – y = 0 and 3x – y = 0 respectively.
∴ their joint equation is (2x – y)(3x – y) = 0
∴ 6x² – 2xy – 3xy + y² = 0
∴ 6x² – 5xy + y² = 0.

(iv) Passing through the origin and having inclinations 60° and 120°.
Solution:
Slope of the line having inclination θ is tan θ .
Inclinations of the given lines are 60° and 120°
∴ their slopes are m₁ = tan60° = \(\sqrt {3}\) and
m₂ = tan 120° = tan (180° – 60°)
= -tan 60° = –\(\sqrt {3}\)
Since the lines pass through the origin, their equa-tions are
y = \(\sqrt {3}\)x and y= –\(\sqrt {3}\)x
i.e., \(\sqrt {3}\)x – y = 0 and \(\sqrt {3}\)x + y = 0
∴ the joint equation of these lines is
(\(\sqrt {3}\)x – y)(\(\sqrt {3}\)x + y) = 0
∴ 3x² – y² = 0.

(v) Passing through (1, 2) amd parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0
∴ the equations of the lines passing through (1, 2) and parallel to the coordinate axes are x = 1 and y =1
i.e. x – 1 = 0 and y – 2 0
∴ their combined equation is
(x – 1)(y – 2) = 0
∴ x(y – 2) – 1(y – 2) = 0
∴ xy – 2x – y + 2 = 0

(vi) Passing through (3, 2) and parallel to the line x = 2 and y = 3.
Solution:
Equations of the lines passing through (3, 2) and parallel to the lines x = 2 and y = 3 are x = 3 and y = 2.
i.e. x – 3 = 0 and y – 2 = 0
∴ their joint equation is
(x – 3)(y – 2) = 0
∴ xy – 2x – 3y + 6 = 0.

(vii) Passing through (-1, 2) and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0.
Solution:
Let L₁ and L₂ be the lines passing through the origin and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 respectively.
Slopes of the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 are \(-\frac{1}{2}\) and \(-\frac{3}{-4}=\frac{3}{4}\) respectively.
∴ slopes of the lines L₁and L₂ are 2 and \(\frac{-4}{3}\) respectively.
Since the lines L₁ and L₂ pass through the point (-1, 2), their equations are
∴ (y – y₁) = m(x – x₁)
∴ (y – 2) = 2(x + 1)
⇒ y – 1 = 2x + 2
⇒ 2x – y + 4 = 0 and
∴ (y – 2) = \(\left(\frac{-4}{3}\right)\)(x + 1)
⇒ 3y – 6 = (-4)(x + 1)
⇒ 3y – 6 = -4x + 4
⇒ 4x + 3y – 6 + 4 = 0
⇒ 4x + 3y – 2 = 0
their combined equation is
∴ (2x – y + 4)(4x + 3y – 2) = 0
∴ 8x² + 6xy – 4x – 4xy – 3y² + 2y + 16x + 12y – 8 = 0
∴ 8x² + 2xy + 12x – 3y² + 14y – 8 = 0

(viii) Passing through the origin and having slopes 1 + \(\sqrt {3}\) and 1 – \(\sqrt {3}\)
Solution:
Let l₁ and l₂ be the two lines. Slopes of l₁ is 1 + \(\sqrt {3}\) and that of l₂ is 1 – \(\sqrt {3}\)
Therefore the equation of a line (l₁) passing through the origin and having slope is
y = (1 + \(\sqrt {3}\))x
∴ (1 + \(\sqrt {3}\))x – y = 0 ..(1)
Similarly, the equation of the line (l₂) passing through the origin and having slope is
y = (1 – \(\sqrt {3}\))x
∴ (1 – \(\sqrt {3}\))x – y = 0 …(2)
From (1) and (2) the required combined equation is

∴ (1 – 3)x² – 2xy + y² = 0
∴ -2x² – 2xy + y² = 0
∴ 2x² + 2xy – y² = 0
This is the required combined equation.

(ix) Which are at a distance of 9 units from the Y – axis.
Solution:
Equations of the lines, which are parallel to the Y-axis and at a distance of 9 units from it, are x = 9 and x = -9
i.e. x – 9 = 0 and x + 9 = 0

∴ their combined equation is
(x – 9)(x + 9) = 0
∴ x² – 81 = 0.

(x) Passing through the point (3, 2), one of which is parallel to the line x – 2y = 2 and other is perpendicular to the line y = 3.
Solution:
Let L₁ be the line passes through (3, 2) and parallel to the line x – 2y = 2 whose slope is \(\frac{-1}{-2}=\frac{1}{2}\)
∴ slope of the line L₁ is \(\frac{1}{2}\).
∴ equation of the line L₁ is
y – 2 = \(\frac{1}{2}\)(x – 3)
∴ 2y – 4 = x – 3 ∴ x – 2y + 1 = 0
Let L₂ be the line passes through (3, 2) and perpendicular to the line y = 3.
∴ equation of the line L₂ is of the form x = a.
Since L₂ passes through (3, 2), 3 = a
∴ equation of the line L₂ is x = 3, i.e. x – 3 = 0
Hence, the equations of the required lines are
x – 2y + 1 = 0 and x – 3 = 0
∴ their joint equation is
(x – 2y + 1)(x – 3) = 0
∴ x² – 2xy + x – 3x + 6y – 3 = 0
∴ x² – 2xy – 2x + 6y – 3 = 0.

(xi) Passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18.
Solution:
Let L₁ and L₂ be the lines passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18 respectively.
Slopes of the lines x + 2y = 19 and 3x + y = 18 are \(-\frac{1}{2}\) and \(-\frac{3}{1}\) = -3 respectively.
Since the lines L₁ and L₂ pass through the origin, their equations are
y = 2x and y = \(\frac{1}{3}\)x
i.e. 2x – y = 0 and x – 3y = 0
∴ their combined equation is
(2x – y)(x – 3y) = 0
∴ 2x² – 6xy – xy + 3y² = 0
∴ 2x² – 7xy + 3y² = 0.

Question 2.
Show that each of the following equation represents a pair of lines.
(i) x² + 2xy – y² = 0
Solution:
Comparing the equation x² + 2xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 2, i.e. h = 1 and b = -1
∴ h² – ab = (1)² – 1(-1) = 1 + 1=2 > 0
Since the equation x² + 2xy – y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(ii) 4x² + 4xy + y² = 0
Solution:
Comparing the equation 4x² + 4xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 4, 2h = 4, i.e. h = 2 and b = 1
∴ h² – ab = (2)² – 4(1) = 4 – 4 = 0
Since the equation 4x² + 4xy + y² = 0 is a homogeneous equation of second degree and h² – ab = 0, the given equation represents a pair of lines which are real and coincident.

(iii) x² – y² = 0
Solution:
Comparing the equation x² – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 0, i.e. h = 0 and b = -1
∴ h² – ab = (0)² – 1(-1) = 0 + 1 = 1 > 0
Since the equation x² – y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(iv) x² + 7xy – 2y² = 0
Solution:
Comparing the equation x² + 7xy – 2y² = 0
a = 1, 2h = 7 i.e., h = \(\frac{7}{2}\) and b = -2
∴ h² – ab = \(\left(\frac{7}{2}\right)^{2}\) – 1(-2)
= \(\frac{49}{4}\) + 2
= \(\frac{57}{4}\) i.e. 14.25 = 14 > 0
Since the equation x² + 7xy – 2y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(v) x² – 2\(\sqrt {3}\) xy – y² = 0
Solution:
Comparing the equation x² – 2\(\sqrt {3}\) xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h= -2\(\sqrt {3}\), i.e. h = –\(\sqrt {3}\) and b = 1
∴ h² – ab = (-\(\sqrt {3}\))² – 1(1) = 3 – 1 = 2 > 0
Since the equation x² – 2\(\sqrt {3}\)xy – y² = 0 is a homo¬geneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

Question 3.
Find the separate equations of lines represented by the following equations:
(i) 6x² – 5xy – 6y² = 0
Solution:
6x² – 5xy – 6y² = 0
∴ 6x² – 9xy + 4xy – 6y² = 0
∴ 3x(2x – 3y) + 2y(2x – 3y) = 0
∴ (2x – 3y)(3x + 2y) = 0
∴ the separate equations of the lines are
2x – 3y = 0 and 3x + 2y = 0.

(ii) x² – 4y² = 0
Solution:
x² – 4y² = 0
∴ x² – (2y)² = 0
∴(x – 2y)(x + 2y) = 0
∴ the separate equations of the lines are
x – 2y = 0 and x + 2y = 0.

(iii) 3x² – y² = 0
Solution:
3x² – y² = 0
∴ (\(\sqrt {3}\) x)² – y² = 0
∴ (\(\sqrt {3}\)x – y)(\(\sqrt {3}\)x + y) = 0
∴ the separate equations of the lines are
\(\sqrt {3}\)x – y = 0 and \(\sqrt {3}\)x + y = 0.

(iv) 2x² + 2xy – y² = 0
Solution:
2x² + 2xy – y² = 0
∴ The auxiliary equation is -m² + 2m + 2 = 0
∴ m² – 2m – 2 = 0

m₁ = 1 + \(\sqrt {3}\) and m₂ = 1 – \(\sqrt {3}\) are the slopes of the lines.
∴ their separate equations are
y = m₁x and y = m₂x
i.e. y = (1 + \(\sqrt {3}\))x and y = (1 – \(\sqrt {3}\))x
i.e. (\(\sqrt {3}\) + 1)x – y = 0 and (\(\sqrt {3}\) – 1)x + y = 0.

Question 4.
Find the joint equation of the pair of lines through the origin and perpendicular to the lines
given by :
(i) x² + 4xy – 5y² = 0
Solution:
Comparing the equation x² + 4xy – 5y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 4, b= -5
Let m₁ and m₂ be the slopes of the lines represented by x² + 4xy – 5y² = 0.

Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² + \(\frac{4}{5}\)xy – \(\frac{1}{5}\)y² = 0 …[By (1)]
∴ 5x² + 4xy – y² = 0

(ii) 2x² – 3xy – 9y² = 0
Solution:
Comparing the equation 2x² – 3xy – 9y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 2, 2h = -3, b = -9
Let m₁ and m₂ be the slopes of the lines represented by 2x² – 3xy – 9y² = 0
∴ m₁ + m₂ =\(\frac{-2 h}{b}=-\frac{3}{9}\) and m₁m₂ = \(\frac{a}{b}=-\frac{2}{9}\) …(1)
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² + \(\left(-\frac{3}{9}\right)\)xy + \(\left(-\frac{2}{9}\right)\)y² = 0 …[By (1)]
∴ 9x² – 3xy – 2y² = 0

(iii) x² + xy – y² = 0
Solution:
Comparing the equation x²+ xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 1, b = -1
Let m₁ and m₂ be the slopes of the lines represented by x² + xy – y² = 0
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{-1}{-1}\) and m₁m₂ = \(\frac{\mathrm{a}}{\mathrm{b}}=\frac{1}{-1}\) = -1 ..(1)
Now, required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂) + m₁m₂y² = 0
∴ x² + 1xy + (-1)y² = 0 …[By (1)]
∴ x² + xy – y² = 0

Question 5.
Find k if
(i) The sum of the slopes of the lines given by 3x² + kxy – y² = 0 is zero.
Solution:
Comparing the equation 3x² + kxy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 3, 2h = k, b = -1
Let m₁ and m₂ be the slopes of the lines represented by 3x² + kxy – y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{-k}{-1}\) = k
Now, m₁ + m₂ = 0 … (Given)
∴ k = 0.

(ii) The sum of slopes of the lines given by 2x² + kxy – 3y² = 0 is equal to their product.
Question is modified.
The sum of slopes of the lines given by x² + kxy – 3y² = 0 is equal to their product.
Solution:
Comparing the equation x² + kxy – 3y² = 0, with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = k, b = -3
Let m₁ and m₂ be the slopes of the lines represented by x² + kxy – 3y² = 0.
∴ m₁ + m₂ = \(-\frac{2 h}{b}=\frac{-k}{-3}=\frac{k}{3}\)
and m₁m₂ = \(\frac{a}{b}=\frac{1}{-3}=\frac{-1}{3}\)
Now, m₁ + m₂ = m₁m₂ … (Given)
∴ \(\frac{k}{3}=\frac{-1}{3}\)
∴ k = -1.

(iii) The slope of one of the lines given by 3x² – 4xy + ky² = 0 is 1.
Solution:
The auxiliary equation of the lines given by 3x² – 4xy + ky² = 0 is km² – 4m + 3 = 0.
Given, slope of one of the lines is 1.
∴ m = 1 is the root of the auxiliary equation km² – 4m + 3 = 0.
∴ k(1)² – 4(1) + 3 = 0
∴ k – 4 + 3 = 0
∴ k = 1.

(iv) One of the lines given by 3x² – kxy + 5y² = 0 is perpendicular to the 5x + 3y = 0.
Solution:
The auxiliary equation of the lines represented by 3x² – kxy + 5y² = 0 is 5m² – km + 3 = 0.
Now, one line is perpendicular to the line 5x + 3y = 0, whose slope is \(-\frac{5}{3}\).
∴ slope of that line = m = \(\frac{3}{5}\)
∴ m = \(\frac{3}{5}\) is the root of the auxiliary equation 5
5m² – km + 3 = 0.
∴ 5\(\left(\frac{3}{5}\right)^{2}\) – k\(\left(\frac{3}{5}\right)\) + 3 = 0
∴ \(\frac{9}{5}-\frac{3 k}{5}\) + 3 = 0
∴ 9 – 3k + 15 = 0
∴ 3k = 24
∴ k = 8.

(v) The slope of one of the lines given by 3x² + 4xy + ky² = 0 is three times the other.
Solution:
3x² + 4xy + ky² = 0
∴ divide by x²

∴ y = mx
∴ \(\frac{\mathrm{y}}{\mathrm{x}}\) = m
put \(\frac{\mathrm{y}}{\mathrm{x}}\) = m in equation (1)
Comparing the equation km² + 4m + 3 = 0 with ax² + 2hxy+ by² = 0, we get,
a = k, 2h = 4, b = 3
m₁ = 3m₂ ..(given condition)
m₁ + m₂ = \(\frac{-2 h}{k}=-\frac{4}{k}\)
m₁m₂ = \(\frac{a}{b}=\frac{3}{k}\)
m₁ + m₂ = \(-\frac{4}{\mathrm{k}}\)
4m₂ = \(-\frac{4}{\mathrm{k}}\) …(m₁ = 3m₂)
m₂ = \(-\frac{1}{\mathrm{k}}\)
m₁m₂ = \(\frac{3}{k}\)
\(3 \mathrm{~m}_{2}^{2}=\frac{3}{\mathrm{k}}\) …(m₁ = 3m₂)
\(3\left(-\frac{1}{\mathrm{k}}\right)^{2}=\frac{3}{\mathrm{k}}\) …(m₂ = \(-\frac{1}{k}\))
\(\frac{1}{k^{2}}=\frac{1}{k}\)
k² = k
k = 1 or k = 0

(vi) The slopes of lines given by kx² + 5xy + y² = 0 differ by 1.
Solution:
Comparing the equation kx² + 5xy +y² = 0 with ax² + 2hxy + by²
a = k, 2h = 5 i.e. h = \(\frac{5}{2}\)
m₁ + m₂ = \(\frac{-2 h}{b}=-\frac{5}{1}\) = -5
and m₁m₂ = \(\frac{a}{b}=\frac{k}{1}\) = k
the slope of the line differ by (m₁ – m₂) = 1 …(1)
∴ (m₁ – m₂)² = (m₁ + m₂)² – 4m₁m₂
(m₁ – m₂)² = (-5)² – 4(k)
(m₁ – m₂)² = 25 – 4k
1 = 25 – 4k ..[By (1)]
4k = 24
k = 6

(vii) One of the lines given by 6x² + kxy + y² = 0 is 2x + y = 0.
Solution:
The auxiliary equation of the lines represented by 6x² + kxy + y² = 0 is
m² + km + 6 = 0.
Since one of the line is 2x + y = 0 whose slope is m = -2.
∴ m = -2 is the root of the auxiliary equation m² + km + 6 = 0.
∴ (-2)² + k(-2) + 6 = 0
∴ 4 – 2k + 6 = 0
∴ 2k = 10 ∴ k = 5

Question 6.
Find the joint equation of the pair of lines which bisect angle between the lines given by x² + 3xy + 2y² = 0
Solution:
x² + 3xy + 2y² = 0
∴ x² + 2xy + xy + 2y² = 0
∴ x(x + 2y) + y(x + 2y) = 0
∴ (x + 2y)(x + y) = 0
∴ separate equations of the lines represented by x² + 3xy + 2y² = 0 are x + 2y = 0 and x + y = 0.
Let P (x, y) be any point on one of the angle bisector. Since the points on the angle bisectors are equidistant from both the lines,

the distance of P (x, y) from the line x + 2y = 0
= the distance of P(x, y) from the line x + y = 0

∴ 2(x + 2y)² = 5(x + y)²
∴ 2(x² + 4xy + 4y²) = 5(x² + 2xy + y²)
∴ 2x² + 8xy + 8y² = 5x² + 10xy + 5y²
∴ 3x² + 2xy – 3y² = 0.
This is the required joint equation of the lines which bisect the angles between the lines represented by x² + 3xy + 2y² = 0.

Question 7.
Find the joint equation of the pair of lies through the origin and making equilateral triangle with the line x = 3.
Solution:

Let OA and OB be the lines through the origin making an angle of 60° with the line x = 3.
∴ OA and OB make an angle of 30° and 150° with the positive direction of X-axis
∴ slope of OA = tan 30° = 1/\(\sqrt {3}\)
∴ equation of the line OA is y = \(\frac{1}{\sqrt{3}}\)x
∴ \(\sqrt {3}\)y = x ∴ x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= – tan 30°= -1/\(\sqrt {3}\)
∴ equation of the line OB is y = \(\frac{-1}{\sqrt{3}}\)x
∴ \(\sqrt {3}\)y = -x ∴ x + \(\sqrt {3}\)y = 0
∴ required combined equation of the lines is
(x – \(\sqrt {3}\)y) (x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.

Question 8.
Show that the lines x² – 4xy + y² = 0 and x + y = 10 contain the sides of an equilateral triangle. Find the area of the triangle.
Solution:
We find the joint equation of the pair of lines OA and OB through origin, each making an angle of 60° with x + y = 10 whose slope is -1.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
Also, tan 60° = \(\left|\frac{m-(-1)}{1+m(-1)}\right|\)
∴ \(\sqrt {3}\) = \(\left|\frac{m+1}{1-m}\right|\)
Squaring both sides, we get,
3 = \(\frac{(m+1)^{2}}{(1-m)^{2}}\)
∴ 3(1 – 2m + m²) = m² + 2m + 1
∴ 3 – 6m + 3m² = m² + 2m + 1
∴ 2m² – 8m + 2 = 0
∴ m² – 4m + 1 = 0
∴ \(\left(\frac{y}{x}\right)^{2}\) – 4\(\left(\frac{y}{x}\right)\) + 1 = 0 …[By (1)]
∴ y² – 4xy + x² = 0
∴ x² – 4xy + y\left(\frac{y}{x}\right) = 0 is the joint equation of the two lines through the origin each making an angle of 60° with x + y = 10
∴ x² – 4xy + y² = 0 and x + y = 10 form a triangle OAB which is equilateral.
Let seg OM ⊥^r line AB whose question is x + y = 10

Question 9.
If the slope of one of the lines represented by ax² + 2hxy + by² = 0 is three times the other then prove that 3h² = 4ab.
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.
∴ m₁ + m₂ = \(-\frac{2 h}{b}\) and m₁m₂ = \(\frac{a}{b}\)
We are given that m₂ = 3m₁
∴ m₁ + 3m₁ = \(-\frac{2 h}{b}\) 4m₁ = \(-\frac{2 h}{b}\)
∴ m₁ = \(-\frac{h}{2 b}\) …(1)
Also, m₁(3m₁) = \(\frac{a}{b}\) ∴ 3m₁² = \(\frac{a}{b}\)
∴ 3\(\left(-\frac{h}{2 b}\right)^{2}\) = \(\frac{a}{b}\) ….[By (1)]
∴ \(\frac{3 h^{2}}{4 b^{2}}=\frac{a}{b}\)
∴ 3h² = 4ab, as b ≠0.

Question 10.
Find the combined equation of the bisectors of the angles between the lines represented by 5x² + 6xy – y² = 0.
Solution:
Comparing the equation 5x² + 6xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 5, 2h = 6, b = -1
Let m₁ and m₂ be the slopes of the lines represented by 5x² + 6xy – y² = 0.

The separate equations of the lines are
y = m₁x and y = m₂x, where m1 ≠ m2
i.e. m₁x – y = 0 and m₁x – y = 0.
Let P (x, y) be any point on one of the bisector of the angles between the lines.
∴ the distance of P from the line m₁x – y = 0 is equal to the distance of P from the line m₂x – y = 0.

∴ (m₂² + 1)(m₁x – y)² = (m₁² + 1)(m₂x – y)²
∴ (m₂² + 1)(m₁²x² – 2m₁xy + y²) = (m₁² + 1)(m₂²x² – 2m₂xy + y²)
∴ m₁²m₂²x² – 2m₁m₁²y²xy + m₂²y² + m₁²x² – 2m₁²xy + y²
= m₁²m₂²x² – 2m₁²m₂xy + m₁²y² + m₂²x² – 2m₂xy + y²
∴ (m₁² – m₂²)x² + 2m₁m₂(m₁ – m₂)xy – 2(m₁ – m₂)xy – (m₁² – m₂²)y² = 0
Dividing throughout by m₁ – m₂ (≠0), we get,
(m₁ + m₂)x² + 2m₁m₂xy – 2xy – (m₁ + m₂)y² = 0
∴ 6x² – 10xy – 2xy – 6y² = 0 …[By (1)]
∴ 6x² – 12xy – 6y² = 0
∴ x² – 2xy – y² = 0
This is the joint equation of the bisectors of the angles between the lines represented by 5x² + 6xy – y² = 0.

Question 11.
Find a, if the sum of the slopes of the lines represented by ax² + 8xy + 5y² = 0 is twice their product.
Solution :
Comparing the equation ax² + 8xy + 5y² = 0 with ax² + 2hxy + by² = 0,
we get, a = a, 2h = 8, b = 5
Let m₁ and m₂ be the slopes of the lines represented by ax² + 8xy + 5y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=-\frac{8}{5}\)
and m₁m₂ = \(\frac{a}{b}=\frac{a}{5}\)
Now, (m₁ + m₂) = 2(m₁m₂)
\(-\frac{8}{5}\) = \(2\left(\frac{a}{5}\right)\)
a = -4

Question 12.
If the line 4x – 5y = 0 coincides with one of the lines given by ax² + 2hxy + by² = 0, then show that 25a + 40h +16b = 0.
Solution :
The auxiliary equation of the lines represented by ax² + 2hxy + by² = 0 is bm² + 2hm + a = 0
Given that 4x – 5y = 0 is one of the lines represented by ax² + 2hxy + by² = 0.
The slope of the line 4x – 5y = 0 is \(\frac{-4}{-5}=\frac{4}{5}\)
∴ m = \(\frac{4}{5}\) is a root of the auxiliary equation bm² + 2hm + a = 0.
∴ b\(\left(\frac{4}{5}\right)^{2}\) + 2h\(\left(\frac{4}{5}\right)\) + a = 0
∴ \(\frac{16 b}{25}+\frac{8 h}{5}\) + a = 0
∴ 16b + 40h + 25a = 0 i.e.
∴ 25a + 40h + 16b = 0

Question 13.
Show that the following equations represent a pair of lines. Find the acute angle between them :
(i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
Solution:
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 9, h = -3, b = 1, g = 9, f = -3 and c = 8.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
9 & -3 & 9 \\
-3 & 1 & -3 \\
9 & -3 & 8
\end{array}\right|\)
= 9(8 – 9) + 3(-24 + 27) + 9(9 – 9)
= 9(-1) + 3(3) + 9(0)
= -9 + 9 + 0 = 0
and h² – ab = (-3)² – 9(1) = 9 – 9 = 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.

∴ tan θ = tan0°
∴ θ = 0°.

(ii) 2x² + xy – y² + x + 4y – 3 = 0
Solution:
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy+ c = 0, we get,
a = 2, h = \(\frac{1}{2}\), b = -1, g = \(\frac{1}{2}\), f = 2 and c = -3

= -2 + 1 + 1
= -2 + 2= 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.

∴ tan θ = tan 3
∴ θ = tan^-1(3)

(iii) (x – 3)² + (x – 3)(y – 4) – 2(y – 4)² = 0.
Solution :
Put x – 3 = X and y – 4 = Y in the given equation, we get,
X² + XY – 2Y² = 0
Comparing this equation with ax² + 2hxy + by² = 0, we get,
a = 1, h = \(\frac{1}{2}\), b = -2
This is the homogeneous equation of second degreeand h² – ab = \(\left(\frac{1}{2}\right)^{2}\) – 1(-2)
= \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
Hence, it represents a pair of lines passing through the new origin (3, 4).
Let θ be the acute angle between the lines.

∴ tanθ = 3 ∴ θ = tan^-1(3)

Question 14.
Find the combined equation of pair of lines through the origin each of which makes angle of 60° with the Y-axis.
Solution:

Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.
∴ slope of OA = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ equation of the line OA is
y = \(\frac{1}{\sqrt{3}}\) = x, i.e. x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= tan 30° = \(-\frac{1}{\sqrt{3}}\)
∴ equation of the line OB is
y = \(-\frac{1}{\sqrt{3}}\)x, i.e. x + \(\sqrt {3}\) y = 0
∴ required combined equation is
(x – \(\sqrt {3}\)y)(x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.

Question 15.
If lines representedby ax² + 2hxy + by² = 0 make angles of equal measures with the co-ordinate
axes then show that a = ± b.
OR
Show that, one of the lines represented by ax² + 2hxy + by² = 0 will make an angle of the same measure with the X-axis as the other makes with the Y-axis, if a = ± b.
Solution:

Let OA and OB be the two lines through the origin represented by ax² + 2hxy + by² = 0.
Since these lines make angles of equal measure with the coordinate axes, they make angles ∝ and \(\frac{\pi}{2}\) – ∝ with the positive direction of X-axis or ∝ and \(\frac{\pi}{2}\) + ∝ with thepositive direction of X-axis.
∴ slope of the line OA = m₁ = tan ∝
and slope of the line OB = m₂
= tan(\(\frac{\pi}{2}\) – ∝) or tan(\(\frac{\pi}{2}\) + ∝)
i.e. m₂ = cot ∝ or m₂ = -cot ∝
∴ m₁m₂ – tan ∝ x cot ∝ = 1
OR m₁m₂ = tan ∝ (-cot ∝) = -1
i.e. m₁m₂ = ± 1
But m₁m₂ = \(\frac{a}{b}\)
∴ \(\frac{a}{b}\)= ±1 ∴ a = ±b
This is the required condition.

Question 16.
Show that the combined equation of a pair of lines through the origin and each making an angle of ∝ with the line x + y = 0 is x² + 2(sec 2∝) xy + y² = 0.
Solution:
Let OA and OB be the required lines.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
It makes an angle ∝ with x + y = 0 whose slope is -1. m +1
∴ tan ∝ = \(\left|\frac{m+1}{1+m(-1)}\right|\)
Squaring both sides, we get,
tan²∝ = \(\frac{(m+1)^{2}}{(1-m)^{2}}\)
∴ tan²∝(1 – 2m + m²) = m² + 2m + 1
∴ tan²∝ – 2m tan²∝ + m²tan²∝ = m² + 2m + 1
∴ (tan²∝ – 1)m² – 2(1 + tan²∝)m + (tan²∝ – 1) = 0

∴ y² + 2xysec2∝ + x² = 0
∴ x² + 2(sec2∝)xy + y² = 0 is the required equation.

Question 17.
Show that the line 3x + 4y+ 5 = 0 and the lines (3x + 4y)² – 3(4x – 3y)² =0 form an equilateral triangle.
Solution:
The slope of the line 3x + 4y + 5 = 0 is \(\frac{-3}{4}\)
Let m be the slope of one of the line making an angle of 60° with the line 3x + 4y + 5 = 0. The angle between the lines having slope m and m₁ is 60°.

On squaring both sides, we get,
3 = \(\frac{(4 m+3)^{2}}{(4-3 m)^{2}}\)
∴ 3 (4 – 3m)² = (4m + 3)²
∴ 3(16 – 24m + 9m²) = 16m² + 24m + 9
∴ 48 – 72m + 27m² = 16m² + 24m + 9
∴ 11m² – 96m + 39 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = \(\frac{y}{x}\).
∴ the combined equation of the two lines is
11\(\left(\frac{y}{x}\right)^{2}\) – 96\(\left(\frac{y}{x}\right)\) + 39 = 0
∴ \(\frac{11 y^{2}}{x^{2}}-\frac{96 y}{x}\) + 39 = 0
∴ 11y² – 96xy + 39x² = 0
∴ 39x² – 96xy + 11y² = 0.
∴ 39x² – 96xy + 11y² = 0 is the joint equation of the two lines through the origin each making an angle of 60° with the line 3x + 4y + 5 = 0.
The equation 39x² – 96xy + 11y² = 0 can be written as :
-39x² + 96xy – 11y² = 0
i.e., (9x² – 48x²) + (24xy + 72xy) + (16y² – 27y²) = 0
i.e. (9x² + 24xy + 16y²) – (48x² – 72xy + 27y²) = 0
i.e. (9x² + 24xy + 16y²) – 3(16x² – 24xy + 9y²) = 0
i.e. (3x + 4y)² – 3(4x – 3y)² = 0
Hence, the line 3x + 4y + 5 = 0 and the lines
(3x + 4y)² – 3(4x – 3y)² form the sides of an equilateral triangle.

Question 18.
Show that lines x² – 4xy + y² = 0 and x + y = \(\sqrt {6}\) form an equilateral triangle. Find its area and perimeter.
Solution:
x² – 4xy + y² = 0 and x + y = \(\sqrt {6}\) form a triangle OAB which is equilateral.
Let OM be the perpendicular from the origin O to AB whose equation is x + y = \(\sqrt {6}\)

In right angled triangle OAM,
sin 60° = \(\frac{\mathrm{OM}}{\mathrm{OA}}\) ∴ \(\frac{\sqrt{3}}{2}\) = \(\frac{\sqrt{3}}{\mathrm{OA}}\)
∴ OA = 2
∴ length of the each side of the equilateral triangle OAB = 2 units.
∴ perimeter of ∆ OAB = 3 × length of each side
= 3 × 2 = 6 units.

Question 19.
If the slope of one of the lines given by ax² + 2hxy + by² = 0 is square of the other then show that a²b + ab² + 8h³ = 6abh.
Solution:
Let m be the slope of one of the lines given by ax² + 2hxy + by² = 0.
Then the other line has slope m²

Multiplying by b³, we get,
-8h³ = ab² + a²b – 6abh
∴ a²b + ab² + 8h³ = 6abh
This is the required condition.

Question 20.
Prove that the product of lengths of perpendiculars drawn from P (x₁, y₁) to the lines repersented by ax² + 2hxy + by² = 0 is \(\left|\frac{a x_{1}^{2}+2 h x_{1} y_{1}+b y_{1}^{2}}{\sqrt{(a-b)^{2}+4 h^{2}}}\right|\)
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.
∴ m¹ + m² = \(-\frac{2 h}{b}\) and m¹m² = \(\frac{a}{b}\) …(1)
The separate equations of the lines represented by
ax² + 2hxy + by² = 0 are
y = m₁x and y = m₂x
i.e. m₁x – y = 0 and m₂x – y = 0
Length of perpendicular from P(x₁, ₁) on

Question 21.
Show that the difference between the slopes of lines given by (tan²θ + cos²θ )x² – 2xytanθ + (sin²θ )y² = 0 is two.
Solution:
Comparing the equation (tan²θ + cos²θ)x² – 2xy tan θ + (sin²θ) y² = 0 with ax² + 2hxy + by² = 0, we get,
a = tan²θ + cos²θ, 2h = -2 tan θ and b = sin2θ
Let m₁ and m₂ be the slopes of the lines represented by the given equation.

Question 22.
Find the condition that the equation ay² + bxy + ex + dy = 0 may represent a pair of lines.
Solution:
Comparing the equation
ay² + bxy + ex + dy = 0 with
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0, we get,
A = 0, H = \(\frac{b}{2}\), B = a,G = \(\frac{e}{2}\), F = \(\frac{d}{2}\), C = 0
The given equation represents a pair of lines,

i.e. if bed – ae² = 0
i.e. if e(bd – ae) = 0
i.e. e = 0 or bd – ae = 0
i.e. e = 0 or bd = ae
This is the required condition.

Question 23.
If the lines given by ax² + 2hxy + by² = 0 form an equilateral triangle with the line lx + my = 1 then show that (3a + b)(a + 3b) = 4h².
Solution:
Since the lines ax² + 2hxy + by² = 0 form an equilateral triangle with the line lx + my = 1, the angle between the lines ax² + 2hxy + by² = 0 is 60°.

∴ 3(a + b)² = 4(h² – ab)
∴ 3(a² + 2ab + b²) = 4h² – 4ab
∴ 3a² + 6ab + 3b² + 4ab = 4h²
∴ 3a² + 10ab + 3b² = 4h²
∴ 3a² + 9ab + ab + 3b² = 4h²
∴ 3a(a + 3b) + b(a + 3b) = 4h²
∴ (3a + b)(a + 3b) = 4h²
This is the required condition.

Question 24.
If line x + 2 = 0 coincides with one of the lines represented by the equation x² + 2xy + 4y + k = 0 then show that k = -4.
Solution:
One of the lines represented by
x² + 2xy + 4y + k = 0 … (1)
is x + 2 = 0.
Let the other line represented by (1) be ax + by + c = 0.
∴ their combined equation is (x + 2)(ax + by + c) = 0
∴ ax² + bxy + cx + 2ax + 2by + 2c = 0
∴ ax² + bxy + (2a + c)x + 2by + 2c — 0 … (2)
As the equations (1) and (2) are the combined equations of the same two lines, they are identical.
∴ by comparing their corresponding coefficients, we get,

∴ 1 = \(\frac{-4}{k}\)
∴ k = -4.

Question 25.
Prove that the combined equation of the pair of lines passing through the origin and perpendicular to the lines represented by ax² + 2hxy + by² = 0 is bx² – 2hxy + ay² = 0
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.

Now, required lines are perpendicular to these lines.
∴ their slopes are and \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(-\frac{1}{m_{1}}\)x and y = \(-\frac{1}{m_{2}}\)x
i.e. m₁y= -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x²\(\frac{-2 h}{b}\)x + \(\frac{a}{b}\)y² = 0
∴ bx² – 2hxy + ay² = 0.

Question 26.
If equation ax² – y² + 2y + c = 1 represents a pair of perpendicular lines then find a and c.
Solution:
The given equation represents a pair of lines perpendicular to each other.
∴ coefficient of x² + coefficient of y² = 0
∴ a – 1 = 0 ∴ a = 1
With this value of a, the given equation is
x² – y² + 2y + c – 1 = 0
Comparing this equation with
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0, we get,
A = 1, H = 0, B = -1, G = 0, F = 1, C = c – 1
Since the given equation represents a pair of lines,
D = \(\left|\begin{array}{ccc}
A & H & G \\
H & B & F \\
G & F & C
\end{array}\right|\) = 0
∴ \(\left|\begin{array}{rrr}
1 & 0 & 0 \\
0 & -1 & 1 \\
0 & 1 & c-1
\end{array}\right|\) = 0
∴ 1(-c + 1 – 1) – 0 + 0 = 0
∴ -c = 0
∴ c = 0.
Hence, a = 1, c = 0.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Trigonometric Functions Ex 3.1 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.2 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.3 Class 12 Maths Solutions
• Trigonometric Functions Miscellaneous Exercise 3 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.1 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.2 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.3 Class 12 Maths Solutions
• Pair of Straight Lines Miscellaneous Exercise 4 Class 12 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.3 Questions and Answers.

12th Maths Part 1 Pair of Straight Lines Exercise 4.3 Questions And Answers Maharashtra Board

Question 1.
Find the joint equation of the pair of lines:
(i) Through the point (2, -1) and parallel to lines represented by 2x² + 3xy – 9y² = 0
Solution:
The combined equation of the given lines is
2x² + 3 xy – 9y² = 0
i.e. 2x² + 6xy – 3xy – 9y² = 0
i.e. 2x(x + 3y) – 3y(x + 3y) = 0
i.e. (x + 3y)(2x – 3y) = 0
∴ their separate equations are
x + 3y = 0 and 2x – 3y = 0
∴ their slopes are m₁ = \(\frac{-1}{3}\) and m₂ = \(\frac{-2}{-3}=\frac{2}{3}\).
The slopes of the lines parallel to these lines are m₁ and m₂, i.e. \(-\frac{1}{3}\) and \(\frac{2}{3}\).
∴ the equations of the lines with these slopes and through the point (2, -1) are
y + 1 = \(-\frac{1}{3}\) (x – 2) and y + 1 = \(\frac{2}{3}\)(x – 2)
i.e. 3y + 3= -x + 2 and 3y + 3 = 2x – 4
i.e. x + 3y + 1 = 0 and 2x – 3y – 7 = 0
∴ the joint equation of these lines is
(x + 3y + 1)(2x – 3y – 7) = 0
∴ 2x² – 3xy – 7x + 6xy – 9y² – 21y + 2x – 3y – 7 = 0
∴ 2x² + 3xy – 9y² – 5x – 24y – 7 = 0.

(ii) Through the point (2, -3) and parallel to lines represented by x² + xy – y² = 0
Solution:
Comparing the equation
x² + xy – y² = 0 … (1)
with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 1, b = -1
Let m₁ and m₂ be the slopes of the lines represented by (1).

The slopes of the lines parallel to these lines are m₁ and m₂.
∴ the equations of the lines with these slopes and through the point (2, -3) are
y + 3 = m₁(x – 2) and y + 3 = m₂(x – 2)
i.e. m₁(x – 2) – (y + 3) = 0 and m₂(x – 2) – (y + 3) = 0
∴ the joint equation of these lines is
[m₁(x – 2) – (y + 3)][m₂(x – 2) – (y + 3)] = 0
∴ m₁m₂(x – 2)² – m₁(x – 2)(y + 3) – m₂(x – 2)(y + 3) + (y + 3)² = o
∴ m₁m₂(x – 2)² – (m₁ + m₂)(x – 2)(y + 3) + (y + 3)³ = 0
∴ -(x – 2)² – (x – 2)(y + 3) + (y + 3)² = 0 …… [By (2)]
∴ (x – 2)² + (x – 2)(y + 3) – (y + 3)² = 0
∴ (x² – 4x + 4) + (xy + 3x – 2y – 6) – (y² + 6y + 9) = 0
∴ x² – 4x + 4 + xy + 3x – 2y – 6 – y² – 6y – 9 = 0
∴ x² + xy – y² – x – 8y – 11 = 0.

Question 2.
Show that equation x² + 2xy+ 2y² + 2x + 2y + 1 = 0 does not represent a pair of lines.
Solution:
Comparing the equation
x² + 2xy + 2y² + 2x + 2y + 1 = 0 with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 1, h = 1, b = 2, g = 1, f = 1, c = 1.
The given equation represents a pair of lines, if
D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|\) = 0 and h² – ab ≥ 0
Now, D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= 1 (2 – 1) – 1(1 – 1) + 1 (1 – 2)
= 1 – 0 – 1 = 0
and h² – ab = (1)² – 1(2) = -1 < 0
∴ given equation does not represent a pair of lines.

Question 3.
Show that equation 2x² – xy – 3y² – 6x + 19y – 20 = 0 represents a pair of lines.
Solution:
Comparing the equation
2x² – xy – 3y² – 6x + 19y – 20 = 0
with ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 2, h = \(-\frac{1}{2}\), b = -3, g = -3, f = \(\frac{19}{2}\), c = -20.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
2 & -\frac{1}{2} & -3 \\
-\frac{1}{2} & -3 & \frac{19}{2} \\
-3 & \frac{19}{2} & -20
\end{array}\right|\)
Taking \(\frac{1}{2}\) common from each row, we get,
D = \(\frac{1}{8}\left|\begin{array}{rrr}
4 & -1 & -6 \\
-1 & -6 & 19 \\
-6 & 19 & -40
\end{array}\right|\)
= \(\frac{1}{8}\)[4(240 – 361) + 1(40 + 114) – 6(-19 – 36)]
= \(\frac{1}{8}\)[4(-121) + 154 – 6(-55)]
= \(\frac{11}{8}\)[4(-11) + 14 – 6(-5)]
= \(\frac{1}{8}\)(-44 + 14 + 30) = 0
Also h² – ab = \(\left(-\frac{1}{2}\right)^{2}\) – 2(-3) = \(\frac{1}{4}\) + 6 = \(\frac{25}{4}\) > 0
∴ the given equation represents a pair of lines.

Question 4.
Show the equation 2x² + xy – y² + x + 4y – 3 = 0 represents a pair of lines. Also find the acute angle between them.
Solution:
Comparing the equation
2x² + xy — y² + x + 4y — 3 = 0 with
ax² + 2hxy + by² + 2gx + 2fy + c — 0, we get,
a = 2, h = \(\frac{1}{2}\), b = -1, g = \(\frac{1}{2}\), f = 2, c = – 3.
∴ D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{lrr}
2 & \frac{1}{2} & \frac{1}{2} \\
\frac{1}{2} & -1 & 2 \\
\frac{1}{2} & 2 & -3
\end{array}\right|\)
Taking \(\frac{1}{2}\) common from each row, we get,
D = \(\frac{1}{8}\left|\begin{array}{rrr}
4 & 1 & 1 \\
1 & -2 & 4 \\
1 & 4 & -6
\end{array}\right|\)
= \(\frac{1}{8}\)[4(12 —16) — 1( —6 — 4) + 1(4 + 2)]
= \(\frac{1}{8}\)[4( – 4) – 1(-10) + 1(6)]
= \(\frac{1}{8}\)(—16 + 10 + 6) = 0
Also, h² – ab = \(\left(\frac{1}{2}\right)^{2}\) – 2(-1) = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
∴ the given equation represents a pair of lines. Let θ be the acute angle between the lines
∴ tan θ = \(\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|\)

Question 5.
Find the separate equation of the lines represented by the following equations :
(i) (x – 2)² – 3(x – 2)(y + 1) + 2(y + 1)² = 0
Solution:
(x – 2)² – 3(x – 2)(y + 1) + 2(y + 1)2 = 0
∴ (x – 2)² – 2(x – 2)(y + 1) – (x – 2)(y + 1) + 2(y + 1)² = 0
∴ (x – 2) [(x – 2) – 2(y + 1)] – (y + 1)[(x – 2) – 2(y + 1)] = 0
∴ (x – 2)(x – 2 – 2y – 2) – (y + 1)(x – 2 – 2y – 2) = 0
∴ (x – 2)(x – 2y – 4) – (y + 1)(x – 2y – 4) = 0
∴ (x – 2y – 4)(x – 2 – y – 1) = 0
∴ (x – 2y – 4)(x – y – 3) = 0
∴ the separate equations of the lines are
x – 2y – 4 = 0 and x – y – 3 = 0.
Alternative Method :
(x – 2)² – 3(x – 2)(y + 1) + 2(y + 1)² = 0 … (1)
Put x – 2 = X and y + 1 = Y
∴ (1) becomes,
X² – 3XY + 2Y² = 0
∴ X² – 2XY – XY + 2Y² = 0
∴ X(X – 2Y) – Y(X – 2Y) = 0
∴ (X – 2Y)(X – Y) = 0
∴ the separate equations of the lines are
∴ X – 2Y = 0 and X – Y = 0
∴ (x – 2) – 2(y + 1) = 0 and (x – 2) – (y +1) = 0
∴ x – 2y – 4 = 0 and x – y – 3 = 0.

(ii) 10(x + 1)² + (x + 1)( y – 2) – 3(y – 2)² = 0
Solution:
10(x + 1)² + (x + 1)( y – 2) – 3(y – 2)² = 0 …(1)
Put x + 1 = X and y – 2 = Y
∴ (1) becomes
10x² + xy – 3y² = 0
10x² + 6xy – 5xy – 3y² = 0
2x(5x + 3y) – y(5x + 3y) = 0
(2x – y)(5x + 3y) = 0
5x + 3y = 0 and 2x – y = 0
5x + 3y = 0
5(x + 1) + 3(y – 2) = 0
5x + 5 + 3y – 6 = 0
∴ 5x + 3y – 1 = 0
2x – y = 0
2(x + 1) – (y – 2) = 0
2x + 2 – y + 2 = 0
∴ 2x – y + 4 = 0

Question 6.
Find the value of k if the following equations represent a pair of lines :
(i) 3x² + 10xy + 3y² + 16y + k = 0
Solution:
Comparing the given equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0,
we get, a = 3, h = 5, b = 3, g = 0, f= 8, c = k.
Now, given equation represents a pair of lines.
∴ abc + 2fgh – af² – bg² – ch² = 0
∴ (3)(3)(k) + 2(8)(0)(5) – 3(8)² – 3(0)² – k(5)² = 0
∴ 9k + 0 – 192 – 0 – 25k = 0
∴ -16k – 192 = 0
∴ – 16k = 192
∴ k= -12.

(ii) kxy + 10x + 6y + 4 = 0
Solution:
Comparing the given equation with
ax² + 2 hxy + by² + 2gx + 2fy + c = 0,
we get, a = 0, h = \(\frac{k}{2}\), b = 0, g = 5, f = 3, c = 4
Now, given equation represents a pair of lines.
∴ abc + 2fgh – af² – bg² – ch² = 0
∴ (0)(0)(4) + 2(3)(5)\(\left(\frac{k}{2}\right)\) – 0(3)² – 0(5)² – 4\(\left(\frac{k}{2}\right)^{2}\) = 0
∴ 0 + 15k – 0 – 0 – k² = 0
∴ 15k – k² = 0
∴ -k(k – 15) = 0
∴ k = 0 or k = 15.
If k = 0, then the given equation becomes
10x + 6y + 4 = 0 which does not represent a pair of lines.
∴ k ≠ o
Hence, k = 15.

(iii) x² + 3xy + 2y² + x – y + k = 0
Solution:
Comparing the given equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0,
we get, a = 1, h = \(\frac{3}{2}\), b = 2, g = \(\frac{1}{2}\), f= \(-\frac{1}{2}\), c = k.
Now, given equation represents a pair of lines.


∴ 2(8k – 1) – 3(6k + 1) + 1(-3 – 4) = 0
∴ 16k – 2 – 18k – 3 – 7 = 0
∴ -2k – 12 = 0
∴ -2k = 12 ∴ k = -6.

Question 7.
Find p and q if the equation px² – 8xy + 3y² + 14x + 2y + q = 0 represents a pair of perpendicular lines.
Solution:
The given equation represents a pair of lines perpendicular to each other
∴ (coefficient of x²) + (coefficient of y²) = 0
∴ p + 3 = 0 p = -3
With this value of p, the given equation is
– 3x² – 8xy + 3y² + 14x + 2y + q = 0.
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we have,
a = -3, h = -4, b = 3, g = 7, f = 1 and c = q.
D = \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
-3 & -4 & 7 \\
-4 & 3 & 1 \\
7 & 1 & q
\end{array}\right|\)
= -3(3q – 1) + 4(-4q – 7) + 7(-4 – 21)
= -9q + 3 – 16q – 28 – 175
= -25q – 200= -25(q + 8)
Since the given equation represents a pair of lines, D = 0
∴ -25(q + 8) = 0 ∴ q= -8.
Hence, p = -3 and q = -8.

Question 8.
Find p and q if the equation 2x² + 8xy + py² + qx + 2y – 15 = 0 represents a pair of parallel lines.
Solution:
The given equation is
2x² + 8xy + py² + qx + 2y – 15 = 0
Comparing it with ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 2, h = 4, b = p, g = \(\frac{q}{2}\), f = 1, c = – 15
Since the lines are parallel, h² = ab
∴ (4)² = 2p ∴ P = 8
Since the given equation represents a pair of lines

i.e. – 242 + 240 + 2q + 2q – 2q² = 0
i.e. -2q² + 4q – 2 = 0
i.e. q² – 2q + 1 = 0
i.e. (q – 1)² = 0 ∴ q – 1 = 0 ∴ q = 1.
Hence, p = 8 and q = 1.

Question 9.
Equations of pairs of opposite sides of a parallelogram are x² – 7x+ 6 = 0 and y² – 14y + 40 = 0. Find the joint equation of its diagonals.
Solution:
Let ABCD be the parallelogram such that the combined equation of sides AB and CD is x² – 7x + 6 = 0 and the combined equation of sides BC and AD is y² – 14y + 40 = 0.
The separate equations of the lines represented by x² – 7x + 6 = 0, i.e. (x – 1)(x – 6) = 0 are x – 1 = 0 and x – 6 = 0.
Let equation of the side AB be x – 1 = 0 and equation of side CD be x – 6 = 0.
The separate equations of the lines represented by y² – 14y + 40 = 0, i.e. (y – 4)(y – 10) = 0 are y – 4 = 0 and y – 10 = 0.
Let equation of the side BC be y – 4 = 0 and equation of side AD be y – 10 = 0.

Coordinates of the vertices of the parallelogram are A(1, 10), B(1, 4), C(6, 4) and D(6, 10).
∴ equation of the diagonal AC is
\(\frac{y-10}{x-1}\) = \(\frac{10-4}{1-6}\) = \(\frac{6}{-5}\)
∴ -5y + 50 = 6x – 6
∴ 6x + 5y – 56 = 0
and equation of the diagonal BD is
\(\frac{y-4}{x-1}\) = \(\frac{4-10}{1-6}\) = \(\frac{-6}{-5}\) = \(\frac{6}{5}\)
∴ 5y – 20 = 6x – 6
∴ 6x – 5y + 14 = 0
Hence, the equations of the diagonals are 6x + 5y – 56 = 0 and 6x – 5y + 14 = 0.
∴ the joint equation of the diagonals is (6x + 5y – 56)(6x – 5y + 14) = 0
∴ 36x² – 30xy + 84x + 30xy – 25y² + 70y – 336x + 280y – 784 = 0
∴ 36x² – 25y² – 252x + 350y – 784 = 0.

Question 10.
∆OAB is formed by lines x² – 4xy + y² = 0 and the line 2x + 3y – 1 = 0. Find the equation of the median of the triangle drawn from O.
Solution:

Let D be the midpoint of seg AB where A is (x₁, y₁) and B is (x₂, y₂).
Then D has coordinates \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\).
The joint (combined) equation of the lines OA and OB is x² – 4xy + y² = 0 and the equation of the line AB is 2x + 3y – 1 = 0.
∴ points A and B satisfy the equations 2x + 3y – 1 = 0
and x² – 4xy + y² = 0 simultaneously.
We eliminate x from the above equations, i.e.,
put x = \(\frac{1-3 y}{2}\) in the equation x² – 4xy + y² = 0, we get,
∴ \(\left(\frac{1-3 y}{2}\right)^{2}\) – 4\(\left(\frac{1-3 y}{2}\right)\)y + y² = 0
∴ (1 – 3y)² – 8(1 – 3y)y + 4y² = 0
∴1 – 6y + 9y² – 8y + 24y² + 4y² = 0
∴ 37y² – 14y + 1 = 0
The roots y₁ and y₂ of the above quadratic equation are the y-coordinates of the points A and B.
∴ y₁ + y₂ = \(\frac{-b}{a}=\frac{14}{37}\)
∴ y-coordinate of D = \(\frac{y_{1}+y_{2}}{2}=\frac{7}{37}\).
Since D lies on the line AB, we can find the x-coordinate of D as
2x + 3\(\left(\frac{7}{37}\right)\) – 1 = 0
∴ 2x = 1 – \(\frac{21}{37}=\frac{16}{37}\)
∴ x = \(\frac{8}{37}\)
∴ D is (8/37, 7/37)
∴ equation of the median OD is \(\frac{x}{8 / 37}=\frac{y}{7 / 37}\),
i.e., 7x – 8y = 0.

Question 11.
Find the co-ordinates of the points of intersection of the lines represented by x² – y² – 2x + 1 = 0.
Solution:
Consider, x² – y² – 2x + 1 = 0
∴ (x² – 2x + 1) – y² = 0
∴ (x – 1)² – y² = 0
∴ (x – 1 + y)(x – 1 – y) = 0
∴ (x + y – 1)(x – y – 1) = 0
∴ separate equations of the lines are
x + y – 1 = 0 and x – y +1 = 0.
To find the point of intersection of the lines, we have to solve
x + y – 1 = 0 … (1)
and x – y + 1 = 0 … (2)
Adding (1) and (2), we get,
2x = 0 ∴ x = 0
Substituting x = 0 in (1), we get,
0 + y – 1 = 0 ∴ y = 1
∴ coordinates of the point of intersection of the lines are (0, 1).

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Trigonometric Functions Ex 3.1 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.2 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.3 Class 12 Maths Solutions
• Trigonometric Functions Miscellaneous Exercise 3 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.1 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.2 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.3 Class 12 Maths Solutions
• Pair of Straight Lines Miscellaneous Exercise 4 Class 12 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.4 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.4 Questions And Answers Maharashtra Board

Question 1.
Express the following as a sum or difference of two trigonometric functions.
i. 2sin 4x cos 2x
ii. 2sin \(\frac{2 \pi}{3}\) cos \(\frac{\pi}{2}\)
iii. 2cos 4θ cos 2θ
iv. 2cos 35° cos 75°
Solution:
i. 2sin 4x cos 2x = sin(4x + 2x ) + sin (4x – 2x)
= sin 6x + sin 2x

ii.

[Note: Answer given in the textbook is sin \(\frac{7 \pi}{12}\) + sin \(\frac{\pi}{12}\) However, as per our calculation it is sin \(\frac{7 \pi}{6}\) + sin \(\frac{\pi}{6}\)

iii. 2cos 4θ cos 2θ = cos(4θ + 2θ)+cos (4θ – 2θ)
= cos 6θ + cos 2θ

iv. 2cos 35° cos75°
= cos(35° + 75°) + cos (35° – 75°)
= cos 110° + cos (-40)°
= cos 110° + cos 40° … [∵ cos(-θ) = cos θ]

Question 2.
Prove the following:
i. \(\frac{\sin 2 x+\sin 2 y}{\sin 2 x-\sin 2 y}=\frac{\tan (x+y)}{\tan (x-y)}\)
Solution:

ii. sin 6x + sin 4x – sin 2x = 4 cos x sin 2x cos 3x
Solution:
L.H.S. = sin 6x + sin 4x — sin 2x
= 2sin \(\left(\frac{6 x+4 x}{2}\right)\) cos \(\left(\frac{6 x-4 x}{2}\right)\) – 2 sin x cos x
= 2 sin 5x cos x — 2 sin x cos x
= 2 cos x (sin 5x — sin x)
= 2 cos \(\left[2 \cos \left(\frac{5 x+x}{2}\right) \sin \left(\frac{5 x-x}{2}\right)\right]\)
= 2 cos x (2 cos 3x sin 2x)
= 4 cos x sin 2x cos 3x
= R.H.S.
[Note: The question has been modified.]

iii. \(\frac{\sin x-\sin 3 x+\sin 5 x-\sin 7 x}{\cos x-\cos 3 x-\cos 5 x+\cos 7 x}\) = cot 2x
Solution:

iv. sin 18° cos 39° + sin 6° cos 15° = sin 24° cos 33°
Solution:
L.H.S. = sin 18°.cos 39° + sin 6°.cos 15°
= \(\frac{1}{2}\) (2 cos 39°sin 18° + 2.cos 15°.sin 6°)
= \(\frac{1}{2}\)[sin(39° + 18°) — sin(39° — 18°) + sin (15° + 6°) — sin (15° — 6°)]
= \(\frac{1}{2}\)(sin57° – sin21° + sin 21°- sin9°)
= \(\frac{1}{2}\)(sin57° – sin9°)
= \(\frac{1}{2}\) x 2. cos \(\left(\frac{57^{\circ}+9^{\circ}}{2}\right) \cdot \sin \left(\frac{57^{\circ}-9^{\circ}}{2}\right)\)
= cos 33° .sin 24°
= sin 24°. cos 33°
= R.H.S.

v. cos 20° cos 40° cos 60°cos 80° = 1/16
Solution:
L.H.S. = cos 20°.cos 40°.cos 60°.cos 80°
= cos 20°.cos 40°.\(\frac{1}{2}\) .cos 80°
= \(\frac{1}{2 \times 2}\)(2 cos 40°.cos 20°).cos 80°
= \(\frac{1}{4}\)[cos(40° + 20°) + cos(40°- 20°)].cos80°
= \(\frac{1}{4}\)(cos 60° + cos 20°) cos 80°
=\(\frac{1}{4}\)cos 60°. cos 80° + \(\frac{1}{4}\) cos 20°. cos 80°
= \(\frac{1}{4}\left(\frac{1}{2}\right) \cos 80^{\circ}+\frac{1}{2 \times 4}\left(2 \cos 80^{\circ} \cos 20^{\circ}\right)\)
= \(\frac{1}{8}\) cos 80° + \(\frac{1}{8}\)[cos (80° + 20°) + cos (80° — 20°)]
= \(\frac{1}{8}\)cos 80° + \(\frac{1}{8}\)(cos 100° + cos 60°)
= \(\frac{1}{8}\) cos 80° + \(\frac{1}{8}\)cos 100° + \(\frac{1}{8}\)cos 60°
= \(\frac{1}{8}\) cos 80° = \(\frac{1}{8}\) cos (180° – 80°) + \(\frac{1}{8} \times \frac{1}{2}\)
= \(\frac{1}{8}\) cos 80° – \(\frac{1}{8}\) cos 80° + \(\frac{1}{16}\) … [∵ cos (180 – θ) = – cos θ]
= \(\frac{1}{16}\) = R.H.S

vi. sin 20° sin 40° sin 60° sin 80° = 3/16
Solution:

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.2 Questions and Answers.

12th Maths Part 1 Pair of Straight Lines Exercise 4.2 Questions And Answers Maharashtra Board

Question 1.
Show that lines represented by 3x² – 4xy – 3y² = 0 are perpendicular to each other.
Solution:
Comparing the equation 3x² – 4 xy – 3y² = 0 with ax² + 2hxy + by² = 0, we get, a = 3, 2h = -4, b = -3 Since a + b = 3 + (-3) = 0, the lines represented by 3x² – 4xy – 3y² = 0 are perpendicular to each other.

Question 2.
Show that lines represented by x² + 6xy + gy²= 0 are coincident.
Question is modified.
Show that lines represented by x² + 6xy + 9y²= 0 are coincident.
Solution:
Comparing the equation x² + 6xy + 9y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 6, i.e. h = 3 and b = 9
Since h² – ab = (3)² – 1(9)
= 9 – 9 = 0, .
the lines represented by x² + 6xy + 9y² = 0 are coincident.

Question 3.
Find the value of k if lines represented by kx² + 4xy – 4y² = 0 are perpendicular to each other.
Solution:
Comparing the equation kx² + 4xy – 4y² = 0 with ax² + 2hxy + by² = 0, we get,
a = k, 2h = 4, b = -4
Since lines represented by kx² + 4xy – 4y² = 0 are perpendicular to each other,
a + b = 0
∴ k – 4 = 0 ∴ k = 4.

Question 4.
Find the measure of the acute angle between the lines represented by:
(i) 3x² – 4\(\sqrt {3}\)xy + 3y² = 0
Solution:
Comparing the equation 3x² – 4\(\sqrt {3}\)xy + 3y² = 0 with
ax² + 2hxy + by² = 0, we get,
a = 3, 2h = -4\(\sqrt {3}\), i.e. h = -24\(\sqrt {3}\) and b = 3
Let θ be the acute angle between the lines.

∴ θ = 30°.

(ii) 4x² + 5xy + y² = 0
Solution:
Comparing the equation 4x² + 5xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 4, 2h = 5, i.e. h = \(\frac{5}{2}\) and b = 1.
Let θ be the acute angle between the lines.

(iii) 2x² + 7xy + 3y² = 0
Solution:
Comparing the equation
2x² + 7xy + 3y² = 0 with
ax² + 2hxy + by² = 0, we get,
a = 2, 2h = 7 i.e. h = \(\frac{7}{2}\) and b = 3
Let θ be the acute angle between the lines.


tanθ = 1
∴ θ = tan 1 = 45°
∴ θ = 45°

(iv) (a² – 3b²)x² + 8abxy + (b² – 3a²)y² = 0
Solution:
Comparing the equation
(a² – 3b²)x² + 8abxy + (b² – 3a²)y² = 0, with
Ax² + 2Hxy + By² = 0, we have,
A = a² – 3b², H = 4ab, B = b² – 3a².
∴ H² – AB = 16a²b² – (a² – 3b²)(b² – 3a²)
= 16a²b² + (a² – 3b²)(3a² – b²)
= 16a²b² + 3a⁴ – 10a²b² + 3b⁴
= 3a⁴ + 6a²b² + 3b⁴
= 3(a⁴ + 2a²b² + b⁴)
= 3 (a² + b²)²
∴ \(\sqrt{H^{2}-A B}\) = \(\sqrt {3}\) (a² + b²)
Also, A + B = (a² – 3b²) + (b² – 3a²)
= -2 (a² + b²)
If θ is the acute angle between the lines, then
tan θ = \(\left|\frac{2 \sqrt{H^{2}-A B}}{A+B}\right|=\left|\frac{2 \sqrt{3}\left(a^{2}+b^{2}\right)}{-2\left(a^{2}+b^{2}\right)}\right|\)
= \(\sqrt {3}\) = tan 60°
∴ θ = 60°

Question 5.
Find the combined equation of lines passing through the origin each of which making an angle of 30° with the line 3x + 2y – 11 = 0
Solution:
The slope of the line 3x + 2y – 11 = 0 is m₁ = \(-\frac{3}{2}\) .
Let m be the slope of one of the lines making an angle of 30° with the line 3x + 2y – 11 = 0.
The angle between the lines having slopes m and m1 is 30°.

On squaring both sides, we get,
\(\frac{1}{3}=\frac{(2 m+3)^{2}}{(2-3 m)^{2}}\)
∴ (2 – 3m)² = 3 (2m + 3)²
∴ 4 – 12m + 9m² = 3(4m² + 12m + 9)
∴ 4 – 12m + 9m² = 12m² + 36m + 27
3m² + 48m + 23 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = \(\frac{y}{x}\).
∴ the combined equation of the two lines is
3\(\left(\frac{y}{x}\right)^{2}\) + 48\(\left(\frac{y}{x}\right)\) + 23 = 0
∴ \(\frac{3 y^{2}}{x^{2}}+\frac{48 y}{x}\) + 23 = 0
∴ 3y² + 48xy + 23x² = 0
∴ 23x² + 48xy + 3y² = 0.

Question 6.
If the angle between lines represented by ax² + 2hxy + by² = 0 is equal to the angle between lines represented by 2x² – 5xy + 3y² = 0 then show that 100(h² – ab) = (a + b)².
Solution:
The acute angle θ between the lines ax² + 2hxy + by² = 0 is given by
tan θ = \(\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|\) ..(1)
Comparing the equation 2x² – 5xy + 3y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 2, 2h= -5, i.e. h = \(-\frac{5}{2}\) and b = 3
Let ∝ be the acute angle between the lines 2x² – 5xy + 3y² = 0.

This is the required condition.

Question 7.
Find the combined equation of lines passing through the origin and each of which making angle 60° with the Y- axis.
Solution:

Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.
∴ slope of OA = tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ equation of the line OA is
y = \(\frac{1}{\sqrt{3}}\) = x, i.e. x – \(\sqrt {3}\)y = 0
Slope of OB = tan 150° = tan (180° – 30°)
= tan 30° = \(-\frac{1}{\sqrt{3}}\)
∴ equation of the line OB is
y = \(-\frac{1}{\sqrt{3}}\)x, i.e. x + \(\sqrt {3}\) y = 0
∴ required combined equation is
(x – \(\sqrt {3}\)y)(x + \(\sqrt {3}\)y) = 0
i.e. x² – 3y² = 0.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Trigonometric Functions Ex 3.1 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.2 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.3 Class 12 Maths Solutions
• Trigonometric Functions Miscellaneous Exercise 3 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.1 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.2 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.3 Class 12 Maths Solutions
• Pair of Straight Lines Miscellaneous Exercise 4 Class 12 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.3 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.3 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
i. sin \(\frac{\pi}{8}\)
ii. \(\frac{\pi}{8}\)
Solution:
We know that sin² θ = \(\frac{1-\cos 2 \theta}{2}[/atex]
Substituting θ = [latex]\frac{\pi}{8}\), we get

ii. We know that, cos² θ = \(\frac{1+\cos 2 \theta}{2}\)
Substituting θ = \(\frac{\pi}{8}\), we get

Question 2.
Find sin 2x, cos 2x, tan 2x if sec x = \(-\frac{13}{5}\), \(\frac{\pi}{2}\) < x < π
Solution:
sec x = \(-\frac{13}{5}\), \(\frac{\pi}{2}\) < x < π
We know that
Sect² x = 1 + tan²x
tan²x = \(\frac{169}{25}-1=\frac{144}{25}\)
tan x = \(\pm \frac{12}{5}\)
Since \(\frac{\pi}{2}\) < x < π
x lies in the 2nd quadrant.
tan x < 0

Question 3.
i. \(\) = tan² θ
Solution:
L. H. S. = \(\frac{1-\cos 2 \theta}{1+\cos 2 \theta}\)
= \(\frac{2 \sin ^{2} \theta}{2 \cos ^{2} \theta}\)
= 2tan² θ
= R.H.S.

ii. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
Solution:
L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cosx)cosx
= sin 3x sin x + sin2 x + cos 3x cos x – cos² x
= (cos 3x cos x + sin 3x sin x)
— (cos²x — sin²x)
= cos (3x – x) – cos 2x
= cos 2x – cos 2x
= 0
= R.H.S.

iii. (cos x + cos y )² + (sin x + sin y)² = 4cos² \(\left(\frac{x-y}{2}\right)\)
Solution:
L.H.S. = (cos x + cos y)² + (sin x + sin y)²
= cos²x + cos²y + 2cos x.cos y + sin² x + sin²y + 2sin x.siny
= (cos²x + sin²x) + (cos²y + sin²y) + 2(cos x.cos y + si x.sin y)
= 1 + 1 +2cos(x – y)
= 2 + 2 cos (x – y)
= 2[1 + cos(x – y)]
= 2[2cos² [(\(\left(\frac{x-y}{2}\right)\))] … [∵ 1 + cos θ = 2 cos² \(\frac{\theta}{2}\)]
= 4 cos² (\(\frac{x-y}{2}\))
= R.H.S.
[ Note: The question has been modified]

iv. (cos x – cos y)² + (sin x – sin y)² = 4sin² \(\left(\frac{x-y}{2}\right)\)
Solution:

L.H.S. = (cos x – cos y)² + (sin x – sin y)²
= cos²x + cos²y + 2cos x.cos y + sin² x + sin²y + 2sin x.siny
= (cos²x + sin²x) + (cos²y + sin²y) – 2(cos x.cos y + sin x.sin y)
= 1 + 1 – 2cos(x – y)
= 2 – 2 cos (x – y)
= 2[1 – cos(x – y)]
= 2[2sin² [(\(\left(\frac{x-y}{2}\right)\))] … [∵ 1 – cos θ = 2 sin² \(\frac{\theta}{2}\)]
= 4 sin² (\(\frac{x-y}{2}\))
= R.H.S.

v. tan x + cot x = 2 cosec 2x
Solution:
L.H.S. = tan x + cot x

vi. \(\frac{\cos x+\sin x}{\cos x-\sin x}-\frac{\cos x-\sin x}{\cos x+\sin x}\) = 2 tan 2x
Solution:

vii. \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 8 x}}}\) = 2 cos x
Solution:

= 2 cos x
= R.H.S.
[Note : The question has been modified.]

viii. 16 sin θ cos θ cos 2θ cos 4θ cos 8θ = sin 16θ
Solution:
L.H.S. = 16 sin θ cos θ cos 2θ cos 4θ cos 8θ
= 8(2sinθ cosθ) cos2θ cos 4θ cos 8θ
= 8sin 2θ cos 2θ cos 4θ cos 8θ
= 4(2sin 2θ cos 2θ) cos 4θ cos 8θ
= 4sin 4θ cos 4θ cos 8θ
= 2(2sin 4θ cos 4θ) cos 8θ
= 2sin 8θ cos 8θ
= sin 16θ
= R.H.S.

ix. \( = 2 cot 2x
Solution:

x. [latex]\frac{\cos x}{1+\sin x}=\frac{\cot \left(\frac{x}{2}\right)-1}{\cot \left(\frac{x}{2}\right)+1}\)
Solution:

xi. \(\frac{\tan \left(\frac{\theta}{2}\right)+\cot \left(\frac{\theta}{2}\right)}{\cot \left(\frac{\theta}{2}\right)-\tan \left(\frac{\theta}{2}\right)}=\sec \theta\)
Solution:

xii. \(\frac{1}{\tan 3 \mathbf{A}-\tan A}-\frac{1}{\cot 3 A-\cot A}\) = cot 2A
Solution:

xiii. cos 7° cos 14° cos 28° cos 56° \(\frac{\sin 68^{\circ}}{16 \cos 83^{\circ}}\)
Solution:
L.H.S. = cos 7° cos 14° cos 28° cos 56°
= \(\frac{1}{2 \sin 7^{\circ}}\)(2sin 7°cos 7°)cos 14°cos 28°cos 56°
= \(\frac{1}{2 \sin 7^{\circ}}\) (sin 14° cos 14° cos 28° cos 56°)
…[∵ 2sinθ cosθ = sin 2θ]
= [\frac{1}{2\left(2 \sin 7^{\circ}\right)}latex][/latex] (2sin 14° cos 14°) cos 28° cos 56°
= \(\frac{1}{4 \sin 7^{\circ}}\)(sin 28° cos 28° cos 56°)
= \(\frac{1}{2\left(4 \sin 7^{\circ}\right)}\)(2 sin 28° cos 28°) cos 56°
= \(\frac{1}{8 \sin 7^{\circ}}\) (sin 56° cos 56°)
= \(\frac{1}{8 \sin 7^{\circ}}\) (2 sin 56° cos 56°)
= \(\frac{1}{16 \sin 7^{\circ}}\)(sin 112°)
= \(\frac{\sin \left(180^{\circ}-68^{\circ}\right)}{16 \sin \left(90^{\circ}-83^{\circ}\right)}\)
= \(\frac{\sin 68^{\circ}}{16 \cos 83^{\circ}}\)
= R.H.S.

xiv. = \(\frac{\sin ^{2}\left(-160^{\circ}\right)}{\sin ^{2} 70^{\circ}}+\frac{\sin \left(180^{\circ}-\theta\right)}{\sin \theta}\) = sec² 20°
Solution:

xv. \(\frac{2 \cos 4 x+1}{2 \cos x+1}\) = (2 cos x – 1)(2 cos 2x – 1)
Solution:

xvi. = cos² x + cos² (x + 120°) + cos²(x – 120°) = \(\frac{3}{2}\)
Solution:
L.H.S = cos² x + cos² (x + 120°) + cos²(x – 120°) =

\(\frac{3}{2}+\frac{1}{2}\) [cos 2x + cos(2x + 240°) + cos(2x 240°)]
= \(\frac{3}{2}+\frac{1}{2}\)(cos 2x + cos 2x cos 240°— sin 2x sin 240° + cos 2x cos 240° + sin 2x sin 240°)
= \(\frac{3}{2}+\frac{1}{2}\)(cos 2x + 2 cos 2x cos 240°)
= \(\frac{3}{2}+\frac{1}{2}\) [cos 2x + 2 cos 2x cos( 180° + 60°)]
= \(\frac{3}{2}+\frac{1}{2}\) [cos 2x + 2cos 2x(-cos 600)]
= \(\frac{3}{2}+\frac{1}{2}\) [cos 2x —2 cos 2x(\(\frac{1}{2}\))]
= \(\frac{3}{2}+\frac{1}{2}\) ( cos 2x – cos 2x)
= \(\frac{3}{2}+\frac{1}{2}\) (0)
= \(\frac{3}{2}\) = R.H.S.

xvii. 2 cosec 2x + cosec x = sec cot \(\frac{x}{2}\)
Solution:

xviii. 4 cos x cos (\(\frac{\pi}{3}\) + x) cos (\(\frac{\pi}{3}\) – x) = cos 3x
\(\)
Solution:

= cos³x — 3cos x.sin²x
= cos³ x — 3cos x (1— cos² x)
= cos³x — 3cos x + 3 cos³x
=4 cos³x — 3cos x
= cos 3x = R.H.S.
INote: The question has been modijìed.I

xix. sin x tan \(\frac{x}{2}\) + 2cos x = \(\frac{2}{1+\tan ^{2}\left(\frac{x}{2}\right)}\)
Solution:
L.H.S. = sin x tan (x/2)+ 2cos x
= \(\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\) + 2cos x
= \(\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\) + 2 cos x
= 2sin² x/2 + 2cosx
= 1 – cosx + 2cosx
= 1 + cos x
=2cos² x/2
= \(\frac{2}{\sec ^{2} \frac{x}{2}}=\frac{2}{1+\tan ^{2} \frac{x}{2}}\) =R.H.S.

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Pair of Straight Lines Ex 4.1 Questions and Answers.

12th Maths Part 1 Pair of Straight Lines Exercise 4.1 Questions And Answers Maharashtra Board

Question 1.
Find the combined equation of the following pairs of lines:
(i) 2x + y = 0 and 3x – y = 0
Solution:
The combined equation of the lines 2x + y = 0 and 3x – y = 0 is
(2x + y)( 3x – y) = 0
∴ 6x² – 2xy + 3xy – y² = 0
∴ 6x² – xy – y² = 0.

(ii) x + 2y – 1 = 0 and x – 3y + 2 = 0
Solution:
The combined equation of the lines x + 2y – 1 = 0 and x – 3y + 2 = 0 is
(x + 2y – 1)(x – 3y + 2) = 0
∴ x² – 3xy + 2x + 2xy – 6y² + 4y – x + 3y – 2 = 0
∴ x² – xy – 6y² + x + 7y – 2 = 0.

(iii) Passing through (2, 3) and parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0.
∴ the equations of the lines passing through (2, 3) and parallel to the coordinate axes are x = 2 and
i.e. x – 2 = 0 and y – 3 = 0.
∴ their combined equation is
(x – 2)(y – 3) = 0.
∴ xy – 3x – 2y + 6 = 0.

(iv) Passing through (2, 3) and perpendicular to lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0
Solution:
Let L₁ and L₂ be the lines passing through the point (2, 3) and perpendicular to the lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0 respectively.
Slopes of the lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0 are \(\frac{-3}{2}\) and \(\frac{-1}{-3}=\frac{1}{3}\) respectively.
∴ slopes of the lines L₁ and L₂ are \(\frac{2}{3}\) and -3 respectively.
Since the lines L₁ and L₂ pass through the point (2, 3), their equations are
y – 3 = \(\frac{2}{3}\)(x – 2) and y – 3 = -3 (x – 2)
∴ 3y – 9 = 2x – 4 and y – 3= -3x + 6
∴ 2x – 3y + 5 = 0 and 3x – y – 9 = 0
∴ their combined equation is
(2x – 3y + 5)(3x + y – 9) = 0
∴ 6x² + 2xy – 18x – 9xy – 3y² + 27y + 15x + 5y – 45 = 0
∴ 6x² – 7xy – 3y² – 3x + 32y – 45 = 0.

(v) Passsing through (-1, 2),one is parallel to x + 3y – 1 = 0 and the other is perpendicular to 2x – 3y – 1 = 0.
Solution:
Let L₁ be the line passing through (-1, 2) and parallel to the line x + 3y – 1 = 0 whose slope is –\(\frac{1}{3}\).
∴ slope of the line L₁ is –\(\frac{1}{3}\)
∴ equation of the line L₁ is
y – 2 = –\(\frac{1}{3}\)(x + 1)
∴ 3y – 6 = -x – 1
∴ x + 3y – 5 = 0
Let L₂ be the line passing through (-1, 2) and perpendicular to the line 2x – 3y – 1 = 0
whose slope is \(\frac{-2}{-3}=\frac{2}{3}\).
∴ slope of the line L₂ is –\(\frac{3}{2}\)
∴ equation of the line L₂ is
y – 2= –\(\frac{3}{2}\)(x + 1)
∴ 2y – 4 = -3x – 3
∴ 3x + 2y – 1 = 0
Hence, the equations of the required lines are
x + 3y – 5 = 0 and 3x + 2y – 1 = 0
∴ their combined equation is
(x + 3y – 5)(3x + 2y – 1) = 0
∴ 3x² + 2xy – x + 9xy + 6y² – 3y – 15x – 10y + 5 = 0
∴ 3x² + 11xy + 6y² – 16x – 13y + 5 = 0

Question 2.
Find the separate equations of the lines represented by following equations:
(i) 3y² + 7xy = 0
Solution:
3y² + 7xy = 0
∴ y(3y + 7x) = 0
∴ the separate equations of the lines are y = 0 and 7x + 3y = 0.

(ii) 5x² – 9y² = 0
Solution:
5x² – 9y² = 0
∴ (\(\sqrt {5}\) x)² – (3y)² = 0
∴ (\(\sqrt {5}\)x + 3y)(\(\sqrt {5}\)x – 3y) = 0
∴ the separate equations of the lines are
\(\sqrt {5}\)x + 3y = 0 and \(\sqrt {5}\)x – 3y = 0.

(iii) x² – 4xy = 0
Solution:
x² – 4xy = 0
∴ x(x – 4y) = 0
∴ the separate equations of the lines are x = 0 and x – 4y = 0

(iv) 3x² – 10xy – 8y² = 0
Solution:
3x² – 10xy – 8y² = 0
∴ 3x² – 12xy + 2xy – 8y² = 0
∴ 3x(x – 4y) + 2y(x – 4y) = 0
∴ (x – 4y)(3x +2y) = 0
∴ the separate equations of the lines are x – 4y = 0 and 3x + 2y = 0.

(v) 3x² – \(2 \sqrt{3}\) xy – 3y² = 0
Solution:
3x² – 2\(\sqrt {3}\)xy – 3y2 = 0
∴ 3x² – 3\(\sqrt {3}\)xy + \(\sqrt {3}\)xy – 3y² = 0
∴ 3x(x – \(\sqrt {3}\)y) + \(\sqrt {3}\)y(x – \(\sqrt {3}\)y) = 0
∴ (x – \(\sqrt {3}\)y)(3x + \(\sqrt {3}\)y) = 0
∴ the separate equations of the lines are
∴ x – \(\sqrt {3}\)y = 0 and 3x + \(\sqrt {3}\)y = 0.

(vi) x² + 2(cosec ∝)xy + y² = 0
Solution:
x² + 2 (cosec ∝)xy – y² = 0
i.e. y² + 2(cosec∝)xy + x² = 0
Dividing by x², we get,

∴ the separate equations of the lines are
(cosec ∝ – cot ∝)x + y = 0 and (cosec ∝ + cot ∝)x + y = 0.

(vii) x² + 2xy tan ∝ – y² = 0
Solution:
x² + 2xy tan ∝ – y² = 0
Dividind by y²

The separate equations of the lines are
(sec∝ – tan ∝)x + y = 0 and (sec ∝ + tan ∝)x – y = 0

Question 3.
Find the combined equation of a pair of lines passing through the origin and perpendicular
to the lines represented by following equations :
(i) 5x² – 8xy + 3y² = 0
Solution:
Comparing the equation 5x² – 8xy + 3y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 5, 2h = -8, b = 3
Let m₁ and m₂ be the slopes of the lines represented by 5x² – 8xy + 3y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{8}{3}\)
amd m₁m₂ = \(\frac{a}{b}=\frac{5}{3}\) …(1)
Now required lines are perpendicular to these lines
∴ their slopes are -1 /m₁ and -1/m₂ Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y) (x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² + \(\frac{8}{3}\)xy + \(\frac{5}{3}\)y² = 0 … [By (1)]
∴ x² + 8xy + 5y\(\frac{8}{3}\) = 0

(ii) 5x² + 2xy – 3y² = 0
Solution:
Comparing the equation 5x² + 2xy – 3y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 5, 2h = 2, b = -3
Let m₁ and m₂ be the slopes of the lines represented by 5x² + 2xy – 3y² = 0
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{-2}{-3}=\frac{2}{3}\) and m₁m₂ = \(\frac{a}{b}=\frac{5}{-3}\) ..(1)
Now required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{\mathrm{~m}_{1}}\)x and y = \(\frac{-1}{\mathrm{~m}_{2}}\)x
i.e. m₁y = -x amd m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
∴ (x + m₁y)(x + m₂y) = 0
x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² + \(\frac{2}{3}\)xy – \(\frac{5}{3}\)y = 0 …[By (1)]
∴ 3x² + 2xy – 5y² = 0

(iii) xy + y² = 0
Solution:
Comparing the equation xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 0, 2h = 1, b = 1
Let m₁ and m₂ be the slopes of the lines represented by xy + y² = 0

Now required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\).
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m₁y = -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y) (x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0
∴ x² – xy = 0.y² = 0 … [By (1)]
∴ x² – xy = 0.
Alternative Method :
Consider xy + y² = 0
∴ y(x + y) = 0
∴ separate equations of the lines are y = 0 and
3x² + 8xy + 5y² = 0.
x + y = 0.
Let m₁ and m₂ be the slopes of these lines.
Then m₁ = 0 and m₂ = -1
Now, required lines are perpendicular to these lines.
∴ their slopes are \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since, m₁ = 0, \(-\frac{1}{m_{1}}\) does not exist.
Also, m₂ = -1, \(-\frac{1}{m_{2}}\) = 1
Since these lines are passing through the origin, their separate equations are x = 0 and y = x,
i.e. x – y = 0
∴ their combined equation is
x(x – y) = 0
x² – xy = 0.

(iv) 3x² – 4xy = 0
Solution:
Consider 3x² – 4xy = 0
∴ x(3x – 4y) = 0
∴ separate equations of the lines are x = 0 and 3x – 4y = 0.
Let m₁ and m₂ be the slopes of these lines.
Then m₁ does not exist and and m₁ = \(\frac{3}{4}\).
Now, required lines are perpendicular to these lines.
∴ their slopes are \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\).
Since m₁ does not exist, \(-\frac{1}{m_{1}}\) = 0
Also m₂ = \(\frac{3}{4^{\prime}}-\frac{1}{m_{2}}=-\frac{4}{3}\)
Since these lines are passing through the origin, their separate equations are y = 0 and y = \(-\frac{4}{3}\)x,
i.e.   4x + 3y = 0
∴ their combined equation is
y(4x + 3y) = 0
∴ 4xy + 3y² = 0.

Question 4.
Find k if,
(i) the sum of the slopes of the lines represented by x² + kxy – 3y² = 0 is twice their product.
Solution:
Comparing the equation x² + kxy – 3y² = 0 with ax² + 2hxy + by² = 0, we get, a = 1, 2h = k, b = -3.
Let m₁ and m₂ be the slopes of the lines represented by x² + kxy – 3y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=-\frac{k}{(-3)}=\frac{k}{3}\)
and m₁m₂ = \(\frac{a}{b}=\frac{1}{(-3)}=-\frac{1}{3}\)
Now, m₁ + m₂ = 2(m₁m₂) ..(Given)
∴ \(\frac{k}{3}=2\left(-\frac{1}{3}\right)\) ∴ k = -2

(ii) slopes of lines represent by 3x² + kxy – y² = 0 differ by 4.
Solution:
(ii) Comparing the equation 3x² + kxy – y² = 0 with ax² + 2hxy + by² = 0, we get, a = 3, 2h = k, b = -1.
Let m₁ and m₂ be the slopes of the lines represented by 3x² + kxy – y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=-\frac{k}{-1}\) = k
and m₁₂ = \(\frac{a}{b}=\frac{3}{-1}\) = -3
∴ (m₁ – m₂)² = (m₁ + m₂)² – 4m₁m₂
= k² – 4 (-3)
= k² + 12 … (1)
But |m₁ – m₂| =4
∴ (m₁ – m₂)² = 16 … (2)
∴ from (1) and (2), k² + 12 = 16
∴ k² = 4 ∴ k= ±2.

(iii) slope of one of the lines given by kx² + 4xy – y² = 0 exceeds the slope of the other by 8.
Solution:
Comparing the equation kx² + 4xy – y² = 0 with ² + 2hxy + by² = 0, we get, a = k, 2h = 4, b = -1. Let m₁ and m₂ be the slopes of the lines represented by kx² + 4xy – y² = 0.
∴ m₁ + m₂ = \(\frac{-2 h}{b}=\frac{-4}{-1}\) = 4
and m₁m₂ = \(\frac{a}{b}=\frac{k}{-1}\) = -k
We are given that m₂ = m₁ + 8
m₁ + m₁ + 8 = 4
∴ 2m₁ = -4 ∴ m₁ = -2 … (1)
Also, m₁(m₁ + 8) = -k
(-2)(-2 + 8) = -k … [By(1)]
∴ (-2)(6) = -k
∴ -12= -k ∴ k = 12.

Question 5.
Find the condition that :
(i) the line 4x + 5y = 0 coincides with one of the lines given by ax² + 2hxy + by² = 0.
Solution:
The auxiliary equation of the lines represented by ax² + 2hxy + by² = 0 is bm² + 2hm + a = 0.
Given that 4x + 5y = 0 is one of the lines represented by ax² + 2hxy + by² = 0.
The slope of the line 4x + 5y = 0 is \(-\frac{4}{5}\).
∴ m = \(-\frac{4}{5}\) is a root of the auxiliary equation bm² + 2hm + a = 0.
∴ b\(\left(-\frac{4}{5}\right)^{2}\) + 2h\(\left(-\frac{4}{5}\right)\) + a = 0
∴ \(\frac{16 b}{25}-\frac{8 h}{5}\) + a = 0
∴ 16b – 40h + 25a = 0
∴ 25a + 16b = 40k.
This is the required condition.

(ii) the line 3x + y = 0 may be perpendicular to one of the lines given by ax² + 2hxy + by² = 0.
Solution:
The auxiliary equation of the lines represented by ax² + 2hxy + by² = 0 is bm² + 2hm + a = 0.
Since one line is perpendicular to the line 3x + y = 0
whose slope is \(-\frac{3}{1}\) = -3
∴ slope of that line = m = \(\frac{1}{3}\)
∴ m = \(\frac{1}{3}\)is the root of the auxiliary equation bm² + 2hm + a = 0.
∴ b\(\left(\frac{1}{3}\right)^{2}\) + 2h\(\left(\frac{1}{3}\right)\) + a = 0
∴ \(\frac{b}{9}+\frac{2 h}{3}\) + a = 0
∴ b + 6h + 9a = 0
∴ 9a + b + 6h = 0
This is the required condition.

Question 6.
If one of the lines given by ax² + 2hxy + by² = 0 is perpendicular to px + qy = 0 then show that ap² + 2hpq + bq² = 0.
Solution:
To prove ap² + 2hpq + bq² = 0.
Let the slope of the pair of straight lines ax² + 2hxy + by² = 0 be m₁ and m₂
Then, m₁ + m₂ = \(\frac{-2 h}{b}\) and m₁m₂ = \(\frac{a}{b}\)
Slope of the line px + qy = 0 is \(\frac{-p}{q}\)
But one of the lines of ax² + 2hxy + by² = 0 is perpendicular to px + qy = 0

⇒ bq² + ap² = -2hpq
⇒ ap² + 2hpq + bq² = 0

Question 7.
Find the combined equation of the pair of lines passing through the origin and making an equilateral triangle with the line y = 3.
Solution:
Let OA and OB be the lines through the origin making.an angle of 60° with the line y = 3.
∴ OA and OB make an angle of 60° and 120° with the positive direction of X-axis.
∴ slope of OA = tan60° = \(\sqrt {3}\)
∴ equation of the line OA is
y = \(\sqrt {3}\) x, i.e. \(\sqrt {3}\) x – y = 0

Slope of OB = tan 120° = tan (180° – 60°)
= -tan 60°= –\(\sqrt {3}\)
∴ equation of the line OB is
y = –\(\sqrt {3}\) x, i.e. \(\sqrt {3}\) x + y = 0
∴ required joint equation of the lines is
(\(\sqrt {3}\) x – y)(\(\sqrt {3}\) x + y) = 0
i.e. 3x² – y² = 0.

Question 8.
If slope of one of the lines given by ax² + 2hxy + by² = 0 is four times the other then show that 16h² = 25ab.
Solution:
Let m₁ and m₂ be the slopes of the lines given by ax² + 2hxy + by² = 0.
∴ m₁ + m₂ = \(-\frac{2 h}{b}\)
and m₁m₂ = \(\frac{a}{b}\)
We are given that m₂ = 4m₁

∴ 16h² = 25ab
This is the required condition.

Question 9.
If one of the lines given by ax² + 2hxy + by² = 0 bisects an angle between co-ordinate axes then show that (a + b) ² = 4h².
Solution:
The auxiliary equation of the lines given by ax² + 2hxy + by² = 0 is bm² + 2hm + a = 0.
Since one of the line bisects an angle between the coordinate axes, that line makes an angle of 45° or 135° with the positive direction of X-axis.
∴ slope of that line = tan45° or tan 135°
∴ m = tan45° = 1
or m = tan 135° = tan (180° – 45°)
= -tan 45°= -1
∴ m = ±1 are the roots of the auxiliary equation bm² + 2hm + a = 0.
∴ b(±1)² + 2h(±1) + a = 0
∴ b ± 2h + a = 0
∴ a + b = ±2h
∴ (a + b)² = 4h²
This is the required condition.

12th Maharashtra State Board Maths Solutions Pdf Part 1

• Trigonometric Functions Ex 3.1 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.2 Class 12 Maths Solutions
• Trigonometric Functions Ex 3.3 Class 12 Maths Solutions
• Trigonometric Functions Miscellaneous Exercise 3 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.1 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.2 Class 12 Maths Solutions
• Pair of Straight Lines Ex 4.3 Class 12 Maths Solutions
• Pair of Straight Lines Miscellaneous Exercise 4 Class 12 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.2 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.2 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
i. sin 690°
ii. sin 495°
iii. cos 315°
iv. cos 600°
v. tan 225°
vi. tan (- 690°)
vii. sec 240°
viii. sec (- 855°)
ix. cosec 780°
x. cot (-1110°)
Solution:
i. sin 690° = sin (720° -30°)
Solution:
i. sin 690° = sin (720° -30°)
= sin (2 x 360° – 30°)
= – sin 30°
= \(\frac{-1}{2}\)

ii. sin 495° = sin (360° + 135°)
= sin (135°)
= sin (90° + 45°)
= cos 45°
= \(\frac{1}{\sqrt{2}}\)

iii. cos 315° = cos (270° + 45°)
sin 45° = \(\frac{1}{\sqrt{2}}\)

iv. cos 600° = cos (360° + 240°)
= cos 240°
= cos (180° + 60°)
= – cos 60°
= \(-\frac{1}{2}\)

v. tan 225° = tan (180° + 45°)
= tan 45°
= 1 .

vi. tan (- 690°) = – tan 690°
= – tan (720° – 30°)
= – tan (2 x 360° – 30°)
= – (- tan 30°)
= tan 30°
= \(\frac{1}{\sqrt{3}}\)

vii. sec 240° = sec (180° + 60°)
= – sec 60°
= – 2

viii. sec (-855°) = sec (855°)
= sec (720°+135°)
= sec (2 x360°+ 135°) = sec 135°
= sec (90° + 45°)
= – cosec 45°
= –\(\sqrt{2}\)

ix. cosec 780° = cosec (720° + 60°)
= cosec (2 x 360° + 60°)
= cosec 60°
= \(\frac{2}{\sqrt{3}}\)

x. cot (-1110°) =-cot (1110°)
= -cot (1080°+ 30°)
= – cot (3 x 360° + 30° )
= – cot 30°
= – \(\sqrt{3}\)

Question 2.
Prove the following:
i. \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}=\cot ^{2} x\)
ii. \(\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]\)
iii. sec 840° cot (- 945°) + sin 600° tan (- 690°) = 3/2
iv. \(\frac{{cosec}\left(90^{\circ}-x\right) \sin \left(180^{\circ}-x\right) \cot \left(360^{\circ}-x\right)}{\sec \left(180^{\circ}+x\right) \tan \left(90^{\circ}+x\right) \sin (-x)}=1\)
v. \(\frac{\sin ^{3}(\pi+x) \sec ^{2}(\pi-x) \tan (2 \pi-x)}{\cos ^{2}\left(\frac{\pi}{2}+x\right) \sin (\pi-x) {cosec}^{2}(-x)}=\tan ^{3} x\)
vi. cos θ + sin (270° + θ) – sin (270° – θ) + cos (180° + θ) = 0
Solution:
i.

ii. L.H.S.
= cos ( \(\frac{3 \pi}{2}\) + x) cos (2π + x) . [cot ( – x) + (2π + x)]
= (sin x)(cos x) (tan x + cot x)
= sin x cos x ( \(\left(\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right)\))
= sin x cos x \(\left(\frac{\sin ^{2} x+\cos ^{2} x}{\sin x \cos x}\right)\)
= sin x cos x \(\left(\frac{1}{\sin x \cos x}\right)\)
= 1 = R.H.S

iii. sec 840° = sec (720° + 120°)
= sec (2 x 360° + 120°)
= sec (120°)
= sec (90° + 30°)
= – cosec 30°
= -2

cot(-945°) = -cot 945°
= -cot (720° + 225°)
= -cot (2 x 360° +225°)
= -cot (225°)
= -cot (180° + 459)
= -cot 45°
= -1

sin 600° = sin (360° + 240°)
= sin (240°)
= sin (180° +60°)
= – sin 60° = –\(\frac{\sqrt{3}}{2}\)

tan (-690°) = – tan 690°
= – tan (360° +330°)
= -tan (330°)
=- tan (360° – 30°)
=-(-tan 30°)
= tan 30°0 = \(\frac{1}{\sqrt{3}}\)

L.H.S. = sec 840° cot (-945°) + sin 600° tan (-690°)
= (-2)(-1) + \(\left(-\frac{\sqrt{3}}{2}\right)\left(\frac{1}{\sqrt{3}}\right)\)
= 2 – \(\frac{1}{2}=\frac{3}{2}\)
= R. H. S.

iv.

= 1
= R.H.S

v.

vi. L.H.S. = cos θ + sin (270° + θ) – sin (270° – θ) + cos (180° + θ)
= cos θ + (- cos θ)-(- cos θ) – cos θ
= cos θ – cos θ + cos θ – cos θ
= 0
= R.H.S.

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.1 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.1 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
i. sin 150°
ü. cos 75°
iii. tan 105°
iv. cot 225°
Solution:
i. sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
\(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
[Note: Answer given in the textbook is \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\) However, as per our calculation it is \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

ii. cos 75° = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°

iii. tan 105° = tan (60° +45°)

iv. cot 225°

Question 2.
Perove the following:
i. \(\cos \left(\frac{\pi}{2}-x\right) \cos \left(\frac{\pi}{2}-y\right) -\sin \left(\frac{\pi}{2}-x\right) \sin \left(\frac{\pi}{2}-y\right)=-\cos (x+y)\)
Solution:
L.H.S

= -(cos x cos y – sin x sin y)
= – cos (x+y)
= R.H.S

ii. \(\tan \left(\frac{\pi}{4}+\theta\right)=\frac{1+\tan \theta}{1-\tan \theta}\)
L.H.S =\(\tan \left(\frac{\pi}{4}+\theta\right)\)

R.H.S.
[Note : The question has been modified.]

iii. \(\left(\frac{1+\tan x}{1-\tan x}\right)^{2}=\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}\)
Solution:

iv. sin [(n+1)A] . sin [(n+2)A] + cos [(n+1)A] . cos [(n+2)A] = cos A
Solution:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let(n+2)Aaand(n+l)Ab …(i)
∴ L.H.S. = cos a. cos b + sin a. sin b
= cos (a — b)
= cos [(n + 2)A — (n + I )A]
…[From (i)]
cos[(n+2 – n – 1)A]
= cos A
= R.H.S.

v. \(\sqrt{2} \cos \left(\frac{\pi}{4}-\mathrm{A}\right)=\cos \mathrm{A}+\sin \mathrm{A}\)
Solution:

vi. \(\frac{\cos (x-y)}{\cos (x+y)}=\frac{\cot x \cot y+1}{\cot x \cot y-1}\)
Solution:

vii. cos (x + y). cos (x – y) = cos²y – sin²x
Solution:
L.H.S. = cos(x + y). cos(x – y)
= (cos x cos y – sin x sin y). (cos x cos y + sin x sin y)
= cos² x cos²y – sin²x sin²y
…[∵ (a – b) (a + b) = a² – b²]
= (1 – sin²x) cos²y – sin²x (1 – cos²y)
…[∵ sin²e + cos²0 = 1]
= cos²y – cos²y sin²x – sin²x + sin²x cos²y
= cos²y – sin²x
=R.H.S.

viii.\(\frac{\tan 5 A-\tan 3 A}{\tan 5 A+\tan 3 A}=\frac{\sin 2 A}{\sin 8 A}\)
Solution:

ix. tan 8θ – tan 5θ – tan 3θ = tan 8θ tan 5θ tan 3θ
Solution:
Since, 8θ = 5θ + 3θ
∴ tan 8θ = tan (5θ + 3θ)
∴ tan 8θ = \(\frac{\tan 5 \theta+\tan 3 \theta}{1-\tan 5 \theta \tan 3 \theta}\)
∴ tan 8θ (1 – tan 5θ.tan 3θ) = tan 5θ + tan 3θ
∴ tan 8θ – tan8θ.tan5θ.tan3θ = tan5θ + tan 3θ
∴ tan 8θ – tan 5θ – tan 3θ = tan 8θ.tan 5θ.tan 3θ

x. tan 50° = tan 40° + 2tan 10°
Solution:
Since, 50° = 10° +40°
∴ tan 50° = tan (10° + 40°)
∴ \(\frac{\tan 10^{\circ}+\tan 40^{\circ}}{1-\tan 10^{\circ} \tan 40^{\circ}}\)
∴ tan 50° (1 – tan 10° tan 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan 50° = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan (90° – 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° cot 40°
= tan 10° + tan 40° …[∵ tan (90° – θ) = cot θ]
∴ tan 50° – tan 10° tan 40°. \(\frac{1}{\tan 40^{\circ}}\) = tan 10° + tan 40°
∴ tan 50° – tan 10°. 1 = tan 10° + tan 40°
∴ tan 50° = tan 40° + 2 tan 10°

xi. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\) = tan 72°
Solution:
\(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\)
Dividing numerator and cos 27°, we get denominator by cos 27°, we get

= tan (45° + 27°)
= tan 72° = R.H.S

xii. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}=\tan 72^{\circ}\)
Solution:
Since 45° = 10° + 35°,
tan 45° = tan (10° +35°)
∴ \(\frac{\tan 10^{\circ}+\tan 35^{\circ}}{1-\tan 10^{\circ} \tan 35^{\circ}}\)
∴ 1 – tan 10° tan 35o = tan 10° + tan 35°
∴ tan 10° + tan 35° + tan 10° tan 35° = 1

xiii. tan 10° + tan 35° + tan 10°. tan 35° = 1
Solution:

xiv. \(\frac{\cos 15^{\circ}-\sin 15^{\circ}}{\cos 15^{\circ}+\sin 15^{\circ}}=\frac{1}{\sqrt{3}}\)
Solution:
Dividing numerator and cos 15°, we get

= tan (45° + 15°)
= tan 30° = \(\frac{1}{\sqrt{3}}\) = R.H.S

Question 3.
If sin A = \(-\frac{5}{13}\),π < A < \(\frac{3 \pi}{2}\) and cos B = \(\frac{3}{5}, \frac{3 \pi}{2}\) < B < 2π, find
i. sin (A+B)
ii. cos (A-B)
iii. tan (A + B)
Solution:
Given, sin A = \(-\frac{5}{13}\)
We know that,
cos² A = 1 – sin²A = \(1-\left(-\frac{5}{13}\right)^{2}=1-\frac{25}{169}=\frac{144}{169}\)
∴ cos A = \(\pm \frac{12}{13}\)
Since, π < A < \(\frac{3 \pi}{2}\)
∴ ‘A’ lies in the 3rd quadrant.
∴ cos A<0
cos A = \(\frac{-12}{13}\)
Also,cos B = \(\frac{3}{5}\)
∴ sin²B = 1 – cos²B = \(1-\left(\frac{3}{5}\right)^{2}=1-\frac{9}{25}=\frac{16}{25}\)
∴ sin B = \(\pm \frac{4}{5}\)
Since, \(\frac{3 \pi}{2}\) < B < 2π
∴ ‘B’ lies in the 4th quadrant.
∴ sin B<0
Sin B = \(\frac{-4}{5}\)

i. sin (A + B) = sin A cos B+cos A sin B

ii. cos (A -B) = cos A cos B + sin A sin B

iii.

Question 4.
If tan A = \(\frac{5}{6}\) , tan B = \(\frac{1}{11}\) prove that A + B = \(\frac{\pi}{4}\)
Solution:
Given tan A = \(\frac{5}{6}\), tan B = \(\frac{1}{11}\)

∴ tan (A + B) = tan \(\frac{\pi}{4}\)
∴ A + B = \(\frac{\pi}{4}\) Class 11 Maths Solutions

Maharashtra State Board 11th Maths Solutions

• Trigonometry – II Ex 3.1 Class 11 Maths Solutions
• Trigonometry – II Ex 3.2 Class 11 Maths Solutions
• Trigonometry – II Ex 3.3 Class 11 Maths Solutions
• Trigonometry – II Ex 3.4 Class 11 Maths Solutions
• Trigonometry – II Ex 3.5 Class 11 Maths Solutions
• Trigonometry – II Miscellaneous Exercise 3 Class 11 Maths Solutions